Prerpints.org logo
Preprint
Article

Quantifying the Role of Model Internal Year-to-Year Variability in Estimating Anthropogenic Aerosol Radiative Effects

Altmetrics

Downloads

100

Views

18

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

07 November 2023

Posted:

08 November 2023

You are already at the latest version

Alerts
Abstract
The model internal year-to-year variability (hereafter, internal variability) is a significant source of uncertainty when estimating anthropogenic aerosol effective radiative forcing (ERF). In this study, we investigate the impact of internal variability using large ensemble simulations (600 years in total) with the same climate model under prescribed anthropogenic aerosol forcings. A comparison of the magnitudes (i.e., standard deviation, Std) of these influences confirms that internal variability has negligible impacts on the instantaneous radiative forcing (RF) diagnosed by double radiation calls but has considerable impacts on estimating ERF through rapid adjustments (ADJ). Approximately half of the model grids exhibit strong internal variability influence on ERF (Std > 5 W m−2). These strong internal variabilities lead to a 50% probability that 30-year linear change can reach 2 W m−2, and 10-year linear change can reach 4 W m−2. A 50-year simulation can provide a relatively stable annual mean map of ERF (ERF = ADJ + RF), but it fails for ADJ. The statistically significant areas in the annual mean maps of both ERF and ADJ from a 10-year simulation exhibit instability with evident chaotic features. These analyses contribute to the setup of comparative experiments and a more comprehensive understanding of the modeled anthropogenic aerosol ERF.
Keywords: 
Subject: Environmental and Earth Sciences  -   Atmospheric Science and Meteorology

1. Introduction

Compared to observation-based analyses, climate models can efficiently provide comparative experiment results and corresponding mechanisms for their differences. Thus, climate models have become important tools for examining the Earth system’s response to anthropogenic activities [1,2,3]. In addition, it is important to note that estimations based on models come with a significantly higher degree of uncertainty [4,5]. Uncertainty in model results can be attributed to two primary sources. The first is the systematic model bias when compared to the real world, which includes the discrepancies in the representation of physical mechanisms described within the model’s code and the climate forcers used as model input data [7,8]. The second source is the model year-to-year internal variability (hereafter, internal variability), which represents the natural year-to-year fluctuations that occur during model simulations without year-to-year changes in external climate forcers [9,10,11,12,13].
In spite of decades of research on the radiative forcing of anthropogenic aerosols, reducing the uncertainty in model estimates remains a formidable challenge [14,15,16,17,18,19]. Due to inadequate understanding of aerosol-related processes and imprecise numerical calculation methods, climate models vary widely in the systematic model bias [20,21]. This kind of uncertainty can be reduced by simplifying the models [8]. For example, the Coupled Model Intercomparison Project Phase 6 (CMIP6) provides a predefined distribution of anthropogenic aerosol direct radiative forcing along with an associated Twomey effect (MACv2-SP; [22]). After implementing the same MACv2-SP (i.e., top-down approach), there is a noticeable reduction in the difference among climate models [23,24]. Furthermore, the impact of internal variability induced by nonlinear climate systems on estimating aerosol radiative effects should not be underestimated. To enhance the stability of these estimates and reduce such uncertainty, the adoption of ensemble simulations is crucial. To estimate a global annual mean value with a precision of 0.1 W m−2 would require a simulation length of decades [25]. However, if the analysis is performed on a regional scale instead of the global mean, the required simulation lengths may need to increase by dozens of times (at least several hundred years). It is worth noting that large ensemble simulations are invariably computationally expensive [10]. Therefore, there are few studies specifically focused on the influence of internal variability on estimating anthropogenic aerosol radiative effects.
In this study, we investigate the influences of internal variability on annual mean maps and decadal trends using large ensemble simulations conducted with the same climate model (the simulation length of each experiment is 600 years). These influences are analyzed from three perspectives: different components of anthropogenic aerosol radiative effects, decadal trends of time series, and sensitivity to simulation lengths. The structure of this study is as follows: the calculation methods and experimental design are described in Section 2; the ensemble simulation results are presented and analyzed in Section 3; the discussion is presented in Section 4, and the conclusions are provided in Section 5.

2. Experiments and Methods

2.1. Modified CAM5 Model and Experiment Setup

The climate model used in this study is version 5.3 of the Community Atmosphere Model (CAM5; [26]) with CMIP6 anthropogenic aerosol forcing. In the default CAM5 model, a two-moment stratiform cloud microphysics scheme [27,28] is used and coupled to an aerosol module [29,30] for considering aerosol-cloud interactions. The RRTMG radiation package is used to improve the accuracy of aerosol and cloud effects calculations [31]. To estimate aerosol effects based on the CMIP6 protocol (i.e., prescribed forcing), the MACv2-SP is implemented into the CAM5 model. In the radiation scheme, total aerosol shortwave optical properties are calculated based on the anthropogenic aerosol optical properties from MACv2-SP and natural aerosol optical properties from the host model’s default mechanism. To represent the anthropogenic aerosol Twomey effect, MACv2-SP provides a normalized change in cloud droplet number (rNc). The rNc is the ratio of the increase in cloud droplet number (Nc) compared to the background Nc of the host model (i.e., only the natural aerosol contribution). The rNc is only used to calculate shortwave optical properties of warm clouds in the radiation scheme. In the cloud microphysics scheme, the Nc is not affected by the rNc (i.e., no cloud-lifetime effect). The year-parameter in MACv2-SP can be set differently from the host model time system. In the year 1850 (pre-industrial times, PI), there is no anthropogenic aerosol forcing.
Taking the advantage of the prescribed anthropogenic aerosol forcing, the instantaneous radiative forcing (RF) from direct radiative effect (RFari) and Twomey effect (RFaci) can be calculated by double radiation calls at each model time step [23,32,33]. To achieve this, the radiation subroutine needs to be called many times to provide different net radiative fluxes at the top of the atmosphere (TOA). Table 1 lists the radiative variables used in this study. Here, the RFari can be calculated by two methods, denoted as RFari (Fari,aci − Faci) and RFari (Fari − F). Both of them are diagnosed by the updated radiation package. Meanwhile, model simulations also output two RFaci (i.e., Fari,aci − Fari and Faci − F). Compared to RFari (Fari,aci − Faci), RFari (Fari − F) is calculated in a background cloud without Twomey effect. In other words, the difference between these two RFari indicates the impact of Twomey effect. Similarly, the difference between these two RFaci indicates the impact of anthropogenic aerosol direct radiative effect. These impacts will be shown through the model simulation results in Section 3.
A pair of experiments are carried out to estimate anthropogenic aerosol radiative effects, which use the pre-industrial (PI, 1850) and present-day (PD, 2005) year-parameters of MACv2-SP. Both PD and PI experiments are atmosphere-only simulations (i.e., sea surface temperature and sea ice are given) with a horizontal resolution of 1.9° latitude × 2.5° longitude and a model time step of 30 minutes. Considering the impact of internal variability, ensemble simulations are conducted. Each experiment comprised twelve simulations, each starting in a different month. The 1st ensemble member starts on January 1, the 2nd ensemble member starts on February 1, and so on. All simulations are executed for approximately 51–52 years, and analysis focus on the results from the last 50 complete calendar years (from January to December). Both the PD and PI experiments have a simulation length of 600 years used for analysis.

2.2. Estimating Methods and Significance Tests

Effective radiative forcing (ERF) is widely accepted as the useful measurement for quantifying the impact of radiative perturbations on Earth’s energy imbalance [1,14]. In this study, ERF is estimated following the approach of Hansen et al. (2005), Ghan et al. (2013), and Forster et al. (2016) [34,35,36]. ERF is defined as the difference in the Fari,aci between PD and PI experiments (i.e., Fari,aciPD−PI). For clarity of expressions, we denote the experiment name as a superscript to indicate the source of the variable. Additionally, we calculate the contribution of rapid adjustments (ADJ) to ERF by subtracting RF from ERF. Based on the equation, ERF (Fari,aciPD−PI) = RF (RFari + RFaci, Fari,aciPD − FPD) + ADJ, it is easy to derive the calculation equation for ADJ, ADJ = FPD−PI. ADJ (FPD−PI) is associated with changes in background atmosphere state (i.e., factors that affect radiation transfer, except for anthropogenic aerosol). In contrast to RF (RF = RFari + RFaci), ADJ (FPD−PI) cannot be decomposed into adjustments induced by direct radiative effect and adjustments induced by Twomey effect. This is due to the interactions among all adjustments at each model time step. It is necessary to point out that ERF (Fari,aciPD−PI) and ADJ (FPD−PI) are calculated based on a pair of corresponding simulations (e.g., the 11th ensemble member of PD experiment and the 11th ensemble member of PI experiment). In total, 600 annual estimates are included in this study. We analyze variability using standard deviations, abbreviated as Std, which are calculated from the averages of each year.
Significance tests are performed with t-test, a commonly used method for assessing the statistical significance of differences in comparative experiments [37]. To perform a t-test, a t-value is calculated first
t = n x 1 ¯ − x 2 ¯ − μ d S t d
S t d = 1 n − 1 ∑ i = 1 n x 1 − x 2 − x 1 − x 2 ¯ 2
where x 1 ¯ and x 2 ¯ are the sample means from two experiments, μd is the proposed population difference, Std is the standard deviation of these samples, and n is the sample size. A critical value corresponding to the chosen significance level and the degree of freedom (n−1) is also needed. Critical values for common significance levels can be easily obtained from given tables in textbooks. For the convenience of discussion, this study only employs a 90% significance level. If the calculated t-value exceeds the critical value, there is a 90% probability that a difference (i.e., | x 1 ¯ − x 2 ¯ |> μd) indeed exists. Based on the t-value equation and critical value lookup table, passing a significance test requires that the difference (| x 1 ¯ − x 2 ¯ |− μd) exceeds 0.59, 0.24, and 0.07 times Std for sample size of n = 10, 50, and 600, respectively. The required difference decreases as n increases. For example, Std = 0.4, a sample size of n ≥ 50 is needed for estimating the difference from paired experiments with a precision of approximately 0.1 (0.4 × 0.24 = 0.096). Typically, μd is set to zero (i.e., null hypothesis), and the assessment focuses only on determining whether there is a significant difference (i.e., | x 1 ¯ − x 2 ¯ | ≠ 0).

3. Results

In this study, we only analyze shortwave radiative variables, consistent with the anthropogenic aerosol forcings provided by MACv2-SP. Furthermore, in this section, all radiative variables are analyzed under all-sky conditions, and all radiative forcings (i.e., ERF, RF, and ADJ) are induced by anthropogenic aerosols. Unless explicitly stated otherwise, the annual means and corresponding standard deviations are calculated based on ensemble experiment results (i.e., 600 annual values), and the default assumption for statistical tests is the null hypothesis.

3.1. Impacts on different components of ERF

Based on model output results, ERF can be decomposed into three components: ERF (Fari,aciPD−PI) = RFari (Fari,aciPD − FaciPD) + RFaci (Faci PD − FPD) + ADJ (FPD−PI) or ERF (Fari,aciPD−PI) = RFari (FariPD − FPD) + RFaci (Fari,aciPD − FariPD) + ADJ (FPD−PI). Unlike ERF and ADJ, both RFari and RFaci are diagnosed during PD model simulation (i.e., derived from one experiment). The year-to-year variability of the annual time series of the four radiative fluxes (Fari,aci, Fari, Faci, and F) diagnosed in a single simulation is almost the same because they are calculated from the same background atmospheric state (natural aerosol and cloud without Twomey effect etc.). Clearly, both RFari and RFaci, representing differences among the above four radiative fluxes, are not significantly sensitive to their year-to-year variabilities (i.e., internal variability). However, a common radiative flux variable (e.g., Fari,aci and F) from two comparative experiments (i.e., PD and PI) exhibits different annual variation curves due to the chaotic year-to-year variability induced by internal variability. Accordingly, internal variability can have a significant impact on estimates of ERF and ADJ. Figure 1 illustrates the annual mean of ERF and its decomposition. As expected, all regions of RFari and RFaci are statistically significant. RFari calculated from two methods is almost the same. However, global mean values show that the RFari (FariPD − FPD, −0.31 W m−2) is a little bit stronger (more negative) than the RFari (Fari,aciPD − FaciPD, −0.30 W m−2). The reason is that the RFari (FariPD − FPD) is calculated based on the background cloud without Twomey effect. The aerosol radiative effect would be decreased under dense cloud conditions, such as the comparison between clear-sky RFari and all-sky RFari shown in previous studies. RFaci calculated from two methods is also almost the same, and the reason for the presence of small differences in global means (−0.28 W m−2 and −0.29 W m−2) is similar to that for RFari. Unlike RFari and RFaci diagnosed from radiation package, there are few statistically significant regions of ADJ. The global mean of ADJ is very small (0.02 W m−2). Generally speaking, RFari and RFaci contribute the most to ERF, especially over Europe, North America, East and South Asia, and their adjacent oceans (i.e., areas with a high anthropogenic aerosol burden). This is the main reason why ERF is statistically significant over the regions above. For other regions, ERF is statistically nonsignificant due to the uncertainty from ADJ. In summary, the magnitude of ERF mostly depends on RF, and the uncertainty in ERF mostly comes from ADJ. If feasible (e.g., MACv2-SP), it is better to decompose ERF into robust RF and uncertain ADJ.
To better understand the uncertainties induced by internal variability, the magnitudes of year-to-year variabilities (i.e., Std) are shown in Figure 2. The Std of ERF is almost the same as that of ADJ. This analysis confirms that uncertainty in ERF almost entirely comes from ADJ. The Std of ERF and ADJ exceeds 1 W m−2 in most regions and exceeds 5 W m−2 in major anthropogenic aerosol source regions. Under the conditions of Std = 5 W m−2 and 600 samples, the minimum radiative forcing (absolute value) that passes statistical testing is 0.35 (i.e., 5 × 0.07) W m−2. This is the reason why most regions on the annual mean map of ADJ are statistically nonsignificant. Regionally, the radiative forcing thresholds for ERF and ADJ are also almost the same. Therefore, ERF, which includes robust RF, shows more areas where signals (i.e., the absolute value of radiation forcing) are statistically significant (Figure 1). Unlike ERF and ADJ, the year-to-year variability of RFari depends not only on the background atmosphere state (e.g., clouds) but also on the magnitude of anthropogenic aerosol direct radiative forcing (i.e., RFari itself). This could be the main reason why the Std of RFari is obvious (>0.1 W m−2) over Europe, North America, Central Africa, East and South Asia (anthropogenic aerosol source regions). In contrast to the RFari, the Std of RFaci becomes much weaker. In summary, both RFari and RFaci exhibit much weaker Std values compared to the annual mean (Figure 1 and Figure 2). This suggests that the influence of internal variability on the diagnosis of RFari and RFaci is negligible. In the following analysis, we focus on the influence of internal variability on the estimation of ADJ, which is the source of uncertainty in ERF.

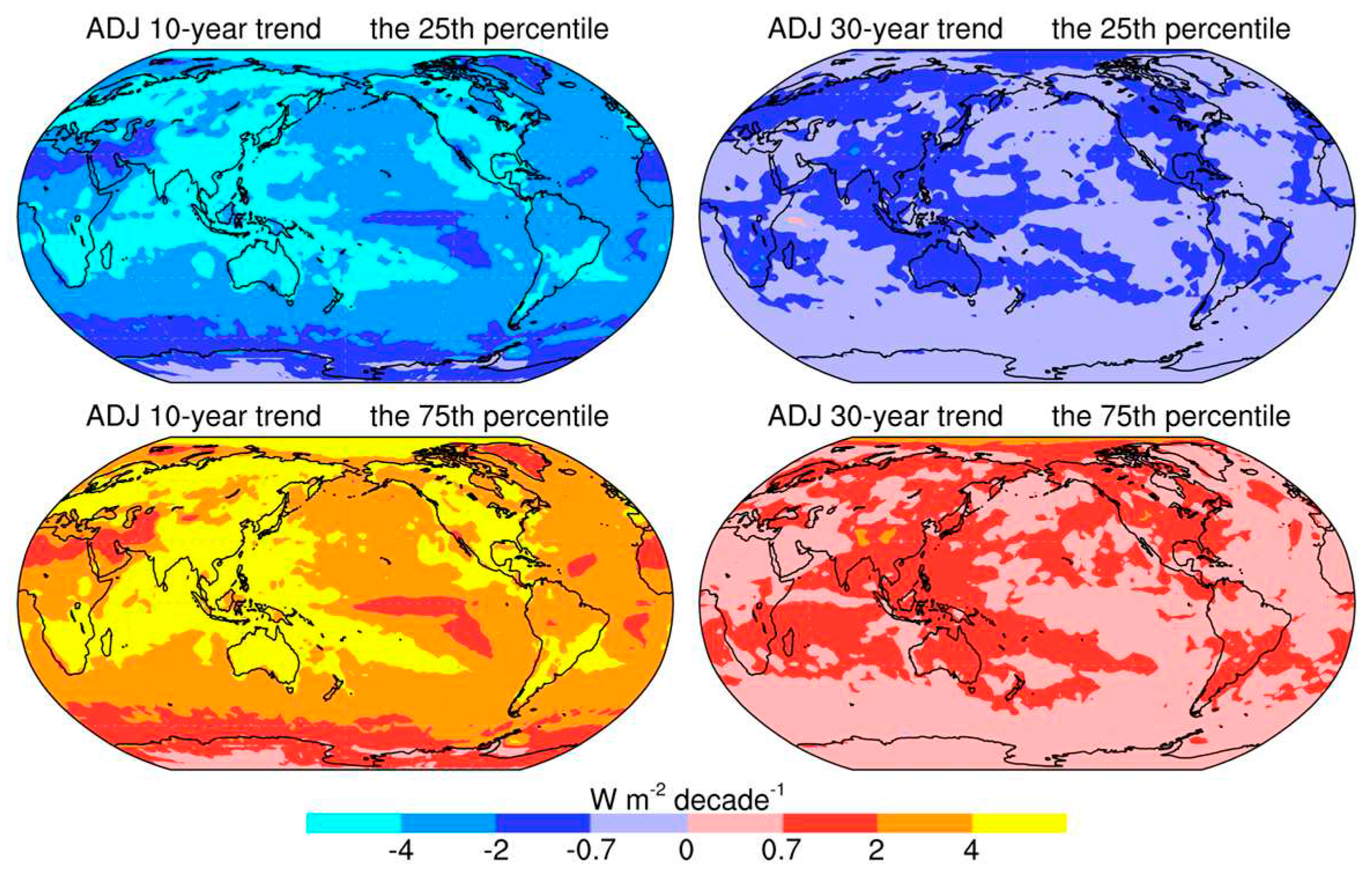
3.2. Impacts on time series trend

The time series of annual means provides an intuitive representation of internal variability. Figure 3 shows the annual ADJ time series in different spatial areas. It is necessary to point out that the annual ERF time series also shows similar year-to-year variation features (not displayed here). In all cases (i.e., global mean, region A, grid B and grid C), the F curves from PD and PI simulations show different year-to-year variations. As a result, their difference (i.e., ADJ) also shows obvious year-to-year variation. Clearly, the amplitude of the time series is related to the spatial area of the research object. The larger the area, the more mutual cancellation occurs between positive and negative variations. As expected, the amplitude of the global mean ADJ time series is much smaller than that of other time series. This is why the simulation length required for estimating a global mean is much shorter than that needed for regional values. The amplitude of the time series for an individual model grid box depends on its location. Consisting with the spatial distribution of Std shown in Figure 2, grid B shows a much larger amplitude than grid C.
Internal variability is an intrinsic year-to-year fluctuation in the climate system that occurs during model simulation in the absence of external forcing. In theory, the annual ADJ time series should not exhibit long-term trends under constant forces. However, the time series may show obvious increasing or decreasing trends on decadal scales due to the chaotic feature of internal variability. Figure 3 shows a variety of 10-year ADJ time series windows with strong increasing or decreasing trends, such as the 33rd to 42nd years in region A. There are also some 30-year ADJ time series windows with obvious trends, such as the 15th to 44th years in grid B. However, the strength of the trend over a longer period (i.e., 30 years) is hardly the same as the strength of the trend over a 10-year period. The following paragraphs will analyze the probability distributions of 10-year trends and 30-year trends.
Figure 4 shows the probability distributions of ADJ 10-year and 30-year trends. The trend is defined as the linear regressions slope for every 10-year or 30-year period in the time series of 50-year simulation. Each ensemble member can produce 41 10-year trends and 21 30-year trends. Because the year-to-year fluctuations are chaotic, these trends possess an approximately normal distribution, especially the 10-year trends. This is consistent with previous studies about internal variability on decadal time scales (e.g., [10,13]). It is also necessary to point out that the 75th percentile of the trend distribution is not completely opposite to the 25th percentile because of the limited sample size. The trend distributions of ERF are almost the same as ADJ (not shown). In order to better understand these trends, 10-year and 30-year changes are compared with annual mean ERF. The 25th and 75th percentiles of the 10-year trend distributions of global mean are −0.16 W m−2 decade−1 and 0.13 W m−2 decade−1, respectively. The 10-year changes caused by these two trends equal about a quarter of the magnitude of the global annual mean ERF (−0.57 W m−2). Based on statistical theory, 30-year trends are usually much weaker than 10-year trends. The 25th and 75th percentiles of the 30-year trend distribution of global mean are −0.03 W m−2 decade−1 and 0.02 W m−2 decade−1, respectively. In other words, there is a 50% probability that 30-year changes are outside the range of −0.09 (−0.03 × 3) to 0.06 (0.02 × 3) W m−2. In region A, half of the 30-year changes are outside the range of −0.96 (−0.32 × 3) to 1.47 (0.49 × 3) W m−2. Compared to the magnitude of spatial and temporal averaged ERF in region A (−2.44 W m−2), these 30-year changes cannot be neglected. On grid B, the annual mean ERF is −1.90 W m−2, and half of 30-year changes are outside the range of −2.94 (−0.96 × 3) to 2.58 (0.86 × 3) W m−2. On grid C, the annual mean ERF is −0.08 W m−2, and half of 30-year changes are outside the range of −1.02 (−0.34 × 3) to 0.39 (0.13 × 3) W m−2. Figure 5 shows the 25th and 75th percentiles of trend distribution at each model grids. Here, the 75th percentile of the trend distribution is generally opposite to the 25th percentile. There is a 50% probability that the 10-year trend is stronger than 4 W m−2 decade−1 (≤−4 and ≥4) over high Std areas (Std > 5 W m−2 in Figure 2). Over most high Std areas, the 25th and 75th percentiles of the 30-year trend are also relatively strong. In about half of the cases, 30-year changes can reach 2 (0.7 × 3 > 2) W m−2. In short, the influence of internal variability on 10-year and 30-year trends cannot be neglected even on global scales.

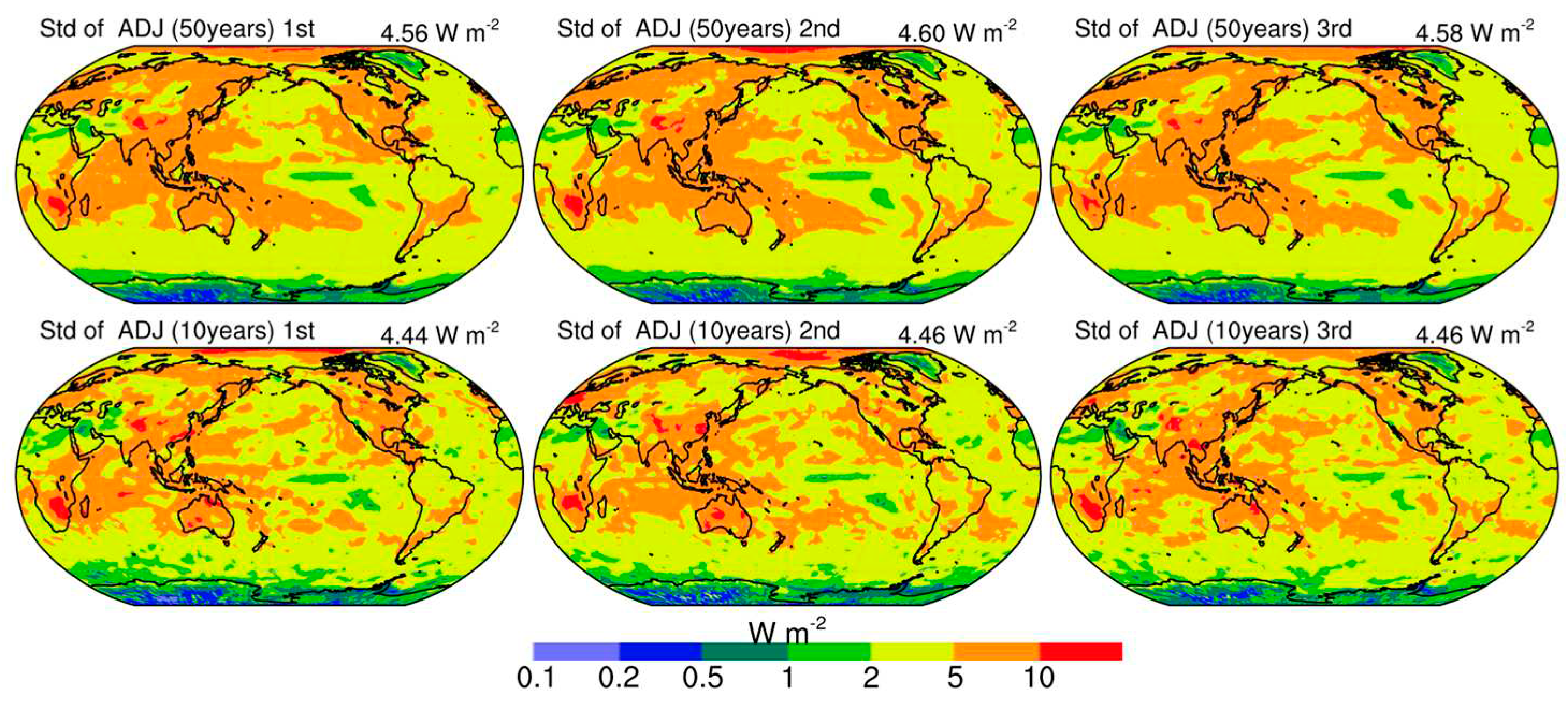
3.3. Sensitivity to simulation lengths

Considering the computational expense of simulations, anthropogenic aerosol effects are usually estimated based on a pair of experiments with simulation lengths of decades (e.g., 10 and 50 years). Here, we investigate the stability of annual mean maps over 50-year and 10-year periods. Firstly, the Std of 50-year and 10-year simulations are analyzed. Since the Std of ERF is almost the same as that of ADJ and the differences among the twelve ensemble members can be represented briefly by the difference among any three ensemble members (not shown), only the Std of ADJ calculated from the 1st, 2nd, and 3rd ensemble members are shown in Figure 6. All the three 50-year simulations show a spatial Std pattern similar to the entire experiment (i.e., 600 years, Figure 2). Meanwhile, the differences among these three maps are not obvious. Compared to 50-year simulations, the maps from 10-year simulations display more chaotic features, resulting in more noticeable differences among these three 10-year simulations. In summary, a 50-year simulation can provide a relatively reliable estimate of internal variables (i.e., Std), while it is difficult to obtain the same level of stability from a 10-year simulation. It is noteworthy that even under the condition of stable Std, the multi-year averages also have obvious fluctuations, which depend on the sample size (i.e., the number of years). This issue will be discussed in the following paragraph.
Figure 7 shows the annual mean maps of ADJ for different simulation lengths. The original (i.e., without significance tests) annual mean map from the entire experiment (i.e., 600 years) does not exhibit any obvious chaotic features. However, chaotic features become noticeable in the maps from 50-year simulations, and even worse in the maps from 10-year simulations. Meanwhile, as compared to the entire experiment, the values on model grids become strong in the 50-year simulation maps, and even stronger in the 10-year simulation maps. The distinctions among the three 50-year simulation maps are evident, and the 10-year simulation maps show almost different spatial patterns. These mentioned issues are more obvious in statistically significant areas (second and third columns in Figure 7). Two hypotheses are used for significance tests: the commonly used null hypothesis (i.e., ADJ ≠ 0) and a more rigorous hypothesis (|ADJ| > 0.5), which analyzes the existence of significant areas under a more rigorous significance test. Using the more rigorous significance test results in an expected reduction in statistically significant areas. In term of statistical probability, 10-year and 50-year simulations might produce some significant areas caused by low-probability events rather than prescribed aerosol forcing. These significant areas usually show chaotic features. This is the main reason that neither 50-year nor 10-year simulations are capable of generating large, contiguous, and reliable statistically significant areas. In contrast, statistically significant areas from the 600-year experiment are relatively large and contiguous, indicating that simulation with a length of 600 years can provide reliable maps of statistically significant areas for further analysis of ADJ. The significant areas under the commonly used null hypothesis do not display obvious common features among these 50-year simulations. This indicates that these significant areas are mostly unreliable. However, conducting a more rigorous significance test might provide significant areas with higher reliability. Using the significant areas from the entire experiment as a benchmark, under the more rigorous test, 50-year simulations could provide some useful information about significant areas, while 10-year simulations are nearly incapable of providing reliable significant areas. In summary, on regional scales, neither 50-year nor 10-year simulations can offer a stable estimate of annual mean ADJ, 50-year simulations might provide limited useful information about significant areas under more rigorous significance tests.
Most studies directly estimate ERF without decomposing it into RF and ADJ. The annual mean ERF map shows much more statistically significant areas compared to ADJ (Figure 7 and 8). This is because ERF includes robust RF and robust RF contributes most to ERF. All the three 50-year simulations can produce relatively large and contiguous statistically significant areas, and their common significant areas among these three maps are dominant. This suggests that a 50-year simulation can provide a relatively reliable estimate of ERF. The magnitudes of ADJ (the uncertain component of ERF) from 10-year simulations are generally much larger than those from 50-year simulations (as shown in Figure 7). Therefore, there are obvious differences among these three annual mean maps of ERF from 10-year simulations, especially for statistically significant areas. This indicates that a 10-year simulation cannot provide a stable estimate of ERF. The above analyses are consistent with the notion that the simulation lengths required for comparative experiments with atmosphere-only integrations are typically on the scale of decades, such as a ≥30-year simulation required in the protocol of the CMIP6 Radiative Forcing Model Intercomparison Project (RFMIP) [5].

4. Discussion

It should be noted that this study employs only one climate model, due to the considerable computational cost of large ensemble experiments. Certain features of Std (i.e., internal variability) in the figures presented above may differ from those in other model simulations. For example, this study shows that the Std exhibits a high value (>5 W m−2) in the Arctic region (Figure 2), while Fiedler et al. (2017) reported a relatively low Std (<2 W m−2) for the Arctic region based on 30-year simulations using another atmospheric model [25]. Moreover, it is worth noting that even using the same model, different experiment settings (e.g., different resolution, different cloud scheme, atmosphere-only or atmosphere-ocean coupled simulations) can lead to different results. Thus, we did not explore the mechanisms underlying the magnitude and pattern of Std in this study. However, we conducted a comparison of the Std under clear-sky and all-sky conditions and found that the year-to-year variability of simulated clouds is the main contributing factor (not shown). Unfortunately, this model-based analysis cannot be confirmed by observations because it is unfeasible to observe climate system internal variability in the real natural world. This may explain why there are few studies that discuss the mechanisms underlying internal variability.
Although this study focuses on anthropogenic aerosol radiative effects, it also offers some representative analyses for comparative experiment design. As an example, internal variability has a significant impact on estimates of ERF or ADJ derived from a pair of comparative experiments but does not have a significantly impact on the RF diagnosed during model simulation. This conclusion is also valuable for estimating the effects of other short-lived climate forcers, including transient responses and rapid adjustments. If feasible, it would be advantageous for climate models to supervise transient response processes and output diagnostic variables such as RF in radiation package. These variables, diagnosed at each model time step, are seldom influenced by internal variability. It is relatively easy to figure out the mechanisms for these robust variables (i.e., transient response), and then facilitate a better understanding of the final estimate (i.e., the difference between a pair of comparative experiments). Another representative experience is that statistically significant areas with chaotic features are probably unreliable as illustrated by the ERF from 10-year simulations in Figure 8. If the aforementioned case occurs, it is better to further check the stability of simulation results via comparison among three ensemble members.

5. Conclusions

This study explores the role of internal variability in estimating anthropogenic aerosol radiative effects. We conducted large ensemble simulations using the same climate model to quantify the impact of internal variability on regional scales (i.e., per model grid). Taking the advantage of prescribed aerosol forcing (i.e., CMIP6 protocol), ERF can be decomposed into robust RF and unstable ADJ as RF [23,25].
Here, the maps of multi-year averages and corresponding Std from the large ensemble simulation (600 years) appear to be reliable as there are no obvious chaotic features in these maps. The Std, which represents the magnitude of internal variability influences, is neglectable in the time series of RF (i.e., RFari and RFaci). This implies that RFari and RFaci diagnosed from radiation package can be considered as offline simulation results, and a one-year simulation could provide a reliable estimate. In contrast to RF, the Std of ERF and ADJ are both strong, and their values are almost identical. This comparison supports the previous studies, indicating that the uncertainty in estimating ERF induced by internal variability primarily comes from ADJ [23,24].
Internal variability can result in considerable decadal trends in ERF and ADJ time series. In theory, the probability of these trends follows a normal distribution, with the 75th percentile of the trend distribution being the negative counterpart of the 25th percentile. Here, the above features are generally reproduced by large ensemble simulations. The maps of the 25th and 75th percentiles exhibit similar spatial patterns to those of the corresponding Std. This confirms that the decadal trend distributions are primarily influenced by the magnitude of year-to-year variability. Over the model grids with high Std (Std > 5 W m−2, about half of the world), there is a 50% probability that 30-year changes can reach 2 W m−2 and 10-year changes can reach 4 W m−2. These changes occurring over 10-year and 30-year periods induced by internal variability are typically much larger than the multi-year mean ERF. Therefore, it is crucial to be aware that conspicuous decadal trends might be a consequence of internal variability rather than increasing or decreasing climate forcers.
The uncertainty from internal variability can be reduced by extending simulation lengths. However, this solution requires additional computational resources. Therefore, estimates of anthropogenic aerosol effects typically rely on paired experiments with decades-long simulation periods, such as 10, 30 and 50 years. Compared to ADJ, it is relatively easy to provide a reliable annual mean map of ERF because the dominant contributor of ERF (i.e., RF) is robust. A 50-year simulation can provide a relatively stable annual mean map of ERF, whereas it fails for ADJ. The statistically significant areas in the annual mean maps of both ERF and ADJ from a 10-year simulation display instability and may exhibit noticeable chaotic features. Finally, it is necessary to point out that differences among the twelve ensemble members can be briefly represented by differences among any three members of the ensemble. This experience may explain why ensemble simulations usually comprise three members.

Author Contributions

X.S. designed this study and carried out simulations. X.S. and Y.X. analyzed simulation results and wrote the manuscript. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China (grant nos. 41775095 and 42075145). The APC was supported by the same funders.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The modified CAM model code, the Fortran code for analyzing the model results, the NCL scripts for making plots and corresponding data have been archived in a public repository (https://doi.org/10.5281/zenodo.10056701, accessed on 6 November 2023).

Acknowledgments

The authors would like to thank Bjorn Stevens for guidance in using MACv2-SP. This study was conducted at the High-Performance Computing Center of Nanjing University of Information Science and Technology.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Boucher, O.; Randall, D.; Artaxo, P.; Bretherton, C.; Feingold, G.; Forster, P.; Kerminen, V.M.; Kondo, Y.; Liao, H.; Lohmann, U.; et al. Clouds and Aerosols. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; pp. 571–658. [Google Scholar] [CrossRef]
  2. Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef]
  3. Szopa, S.; Naik, V.; Adhikary, B.; Artaxo, P.; Berntsen, T.; Collins, W.D.; Fuzzi, S.; Gallardo, L.; Kiendler-Scharr, A.; Klimont, Z.; et al. Short-Lived Climate Forcers. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021; pp. 817–922. [Google Scholar] [CrossRef]
  4. Hawkins, E.; Sutton, R. The Potential to Narrow Uncertainty in Regional Climate Predictions. Bull. Amer. Meteor. Soc. 2009, 90, 1095–1108. [Google Scholar] [CrossRef]
  5. Pincus, R.; Forster, P.; Stevens, B. The Radiative Forcing Model Intercomparison Project (RFMIP): Experimental Protocol for CMIP6. Geosci. Model Dev. 2016, 9, 3447–3460. [Google Scholar] [CrossRef]
  6. Stouffer, R.J.; Eyring, V.; Meehl, G.; Bony, S.; Senior, C.; Stevens, B.; Taylor, K.E. CMIP5 scientific gaps and recommendations for CMIP6. Bull. Amer. Meteor. Soc. 2016, 98, 95–105. [Google Scholar] [CrossRef]
  7. O’Neill, B.C.; Tebaldi, C.; van Vuuren, D.P.; Eyring, V.; Friedlingstein, P.; Hurtt, G.; Knutti, R.; Kriegler, E.; Lamarque, J.F.; Lowe, J.; et al. The Scenario Model Intercomparison Project (ScenarioMIP) for CMIP6. Geosci. Model Dev. 2016, 9, 3461–3482. [Google Scholar] [CrossRef]
  8. Sanchez, K.J.; Roberts, G.C.; Calmer, R.; Nicoll, K.; Hashimshoni, E.; Rosenfeld, D.; Ovadnevaite, J.; Preissler, J.; Ceburnis, D.; O’Dowd, C.; et al. Top-down and bottom-up aerosol–cloud closure: Towards understanding sources of uncertainty in deriving cloud shortwave radiative flux. Atmos. Chem. Phys. 2017, 17, 9797–9814. [Google Scholar] [CrossRef]
  9. Deser, C.; Phillips, A.; Bourdette, V.; Teng, H. Uncertainty in climate change projections: The role of internal variability. Clim. Dyn. 2012, 38, 527–546. [Google Scholar] [CrossRef]
  10. Thompson, D.W.J.; Barnes, E.A.; Deser, C.; Foust, W.E.; Phillips, A.S. Quantifying the Role of Internal Climate Variability in Future Climate Trends. J. Climate 2015, 28, 6443–6456. [Google Scholar] [CrossRef]
  11. Dai, A.; Bloecker, C. Impacts of internal variability on temperature and precipitation trends in large ensemble simulations by two climate models. Clim. Dyn. 2019, 52, 289–306. [Google Scholar] [CrossRef]
  12. Ji, D.F.; Liu, L.; Li, L.J.; Sun, C.; Yu, X.Z.; Li, R.Z.; Zhang, C.; Wang, B. Uncertainties in the simulation of 1.5°C and 2°C warming threshold-crossing time arising from model internal variability based on CMIP5 models. Clim. Chang. Res. 2019, 15, 343–351. [Google Scholar] [CrossRef]
  13. Chtirkova, B.; Folini, D.; Correa, L.; Wild, M. Internal Variability of All-Sky and Clear-Sky Surface Solar Radiation on Decadal Timescales. J. Geophys. Res. Atmos. 2022, 127, e2021JD036332. [Google Scholar] [CrossRef]
  14. Myhre, G.; Samset, B.H.; Schulz, M.; Balkanski, Y.; Bauer, S.; Berntsen, T.K.; Bian, H.; Bellouin, N.; Chin, M.; Diehl, T.; et al. Radiative forcing of the direct aerosol effect from AeroCom Phase II simulations. Atmos. Chem. Phys. 2013, 13, 1853–1877. [Google Scholar] [CrossRef]
  15. Seinfeld, J.H.; Bretherton, C.; Carslaw, K.S.; Coe, H.; DeMott, P.J.; Dunlea, E.J.; Feingold, G.; Ghan, S.; Guenther, A.B.; Kahn, R.; et al. Improving our fundamental understanding of the role of aerosol−cloud interactions in the climate system. Proc. Natl. Acad. Sci. 2016, 113, 5781–5790. [Google Scholar] [CrossRef]
  16. McCoy, D.; Bender, F.; Mohrmann, J.; Hartmann, D.; Wood, R.; Grosvenor, D. The global aerosol-cloud first indirect effect estimated using MODIS, MERRA and AeroCom: MODIS-MERRA Indirect Effect. J. Geophys. Res. Atmos. 2017, 122, 1779–1796. [Google Scholar] [CrossRef]
  17. Bellouin, N.; Quaas, J.; Gryspeerdt, E.; Kinne, S.; Stier, P.; Watson-Parris, D.; Boucher, O.; Carslaw, K.; Christensen, M.; Daniau, A.L.; et al. Bounding Global Aerosol Radiative Forcing of Climate Change. Rev. Geophys. 2020, 58, e2019RG000660. [Google Scholar] [CrossRef] [PubMed]
  18. Wang, Z.; Lin, L.; Xu, Y.; Che, H.; Zhang, X.; Zhang, H.; Dong, W.; Wang, C.; Gui, K.; Xie, B. Incorrect Asian aerosols affecting the attribution and projection of regional climate change in CMIP6 models. npj Clim. Atmos. Sci. 2021, 4, 2. [Google Scholar] [CrossRef]
  19. Vogel, A.; Alessa, G.; Scheele, R.; Weber, L.; Dubovik, O.; North, P.R.J.; Fiedler, S. Uncertainty in Aerosol Optical Depth From Modern Aerosol-Climate Models, Reanalyses, and Satellite Products. J. Geophys. Res. Atmos. 2022, 127, e2021JD035483. [Google Scholar] [CrossRef]
  20. Shindell, D.T.; Lamarque, J.F.; Schulz, M.; Flanner, M.; Jiao, C.; Chin, M.; Young, P.J.; Lee, Y.H.; Rotstayn, L.; Mahowald, N.; et al. Radiative forcing in the ACCMIP historical and future climate simulations. Atmos. Chem. Phys. 2013, 13, 2939–2974. [Google Scholar] [CrossRef]
  21. Regayre, L.A.; Johnson, J.S.; Yoshioka, M.; Pringle, K.J.; Sexton, D.M.H.; Booth, B.B.B.; Lee, L.A.; Bellouin, N.; Carslaw, K.S. Aerosol and physical atmosphere model parameters are both important sources of uncertainty in aerosol ERF. Atmos. Chem. Phys. 2018, 18, 9975–10006. [Google Scholar] [CrossRef]
  22. Stevens, B.; Fiedler, S.; Kinne, S.; Peters, K.; Rast, S.; Musse, J.; Smith, S.J.; Mauritsen, T. MACv2-SP: A parameterization of anthropogenic aerosol optical properties and an associated Twomey effect for use in CMIP6. Geosci. Model Dev. 2017, 10, 433–452. [Google Scholar] [CrossRef]
  23. Fiedler, S.; Kinne, S.; Huang, W.T.K.; Räisänen, P.; O’Donnell, D.; Bellouin, N.; Stier, P.; Merikanto, J.; van Noije, T.; Makkonen, R.; et al. Anthropogenic aerosol forcing—Insights from multiple estimates from aerosol-climate models with reduced complexity. Atmos. Chem. Phys. 2019, 19, 6821–6841. [Google Scholar] [CrossRef]
  24. Shi, X.; Zhang, W.; Liu, J. Comparison of Anthropogenic Aerosol Climate Effects among Three Climate Models with Reduced Complexity. Atmosphere 2019, 10, 456. [Google Scholar] [CrossRef]
  25. Fiedler, S.; Stevens, B.; Mauritsen, T. On the sensitivity of anthropogenic aerosol forcing to model-internal variability and parameterizing a Twomey effect. J. Adv. Model. Earth Syst. 2017, 9, 1325–1341. [Google Scholar] [CrossRef]
  26. Neale, R.B.; Gettelman, A.; Park, S.; Chen, C.-C.; Lauritzen, P.H.; Williamson, D.L.; Conley, A.J.; Kinnison, D.; Marsh, D.; Smith, A.K.; et al. Description of the NCAR Community Atmosphere Model (CAM 5.0). 2012, NCAR/TN-486+STR. [Google Scholar] [CrossRef]
  27. Morrison, H.; Gettelman, A. A New Two-Moment Bulk Stratiform Cloud Microphysics Scheme in the Community Atmosphere Model, Version 3 (CAM3). Part I: Description and Numerical Tests. J. Clim. 2008, 21, 3642–3659. [Google Scholar] [CrossRef]
  28. Gettelman, A.; Morrison, H. Advanced Two-Moment Bulk Microphysics for Global Models. Part I: Off-Line Tests and Comparison with Other Schemes. J. Clim. 2015, 28, 1268–1287. [Google Scholar] [CrossRef]
  29. Ghan, S.J.; Liu, X.; Easter, R.C.; Zaveri, R.; Rasch, P.J.; Yoon, J.-H.; Eaton, B. Toward a Minimal Representation of Aerosols in Climate Models: Comparative Decomposition of Aerosol Direct, Semidirect, and Indirect Radiative Forcing. J. Clim. 2012, 25, 6461–6476. [Google Scholar] [CrossRef]
  30. Liu, X.; Easter, R.C.; Ghan, S.J.; Zaveri, R.; Rasch, P.; Shi, X.; Lamarque, J.F.; Gettelman, A.; Morrison, H.; Vitt, F.; et al. Toward a minimal representation of aerosols in climate models: Description and evaluation in the Community Atmosphere Model CAM5. Geosci. Model Dev. 2012, 5, 709–739. [Google Scholar] [CrossRef]
  31. Iacono, M.; Delamere, J.; Mlawer, E.; Shephard, M.; Clough, S.; Collins, W. Radiative Forcing by Long-Lived Greenhouse Gases: Calculations with the AER Radiative Transfer Models. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
  32. Boucher, O.; Lohmann, U. The sulfate–CCN–cloud albedo effect: A sensitivity study with two general circulation models. Tellus 1995, 47, 281–300. [Google Scholar] [CrossRef]
  33. Kinne, S. Aerosol radiative effects with MACv2. Atmos. Chem. Phys. 2019, 19, 10919–10959. [Google Scholar] [CrossRef]
  34. Hansen, J.; Sato, M.; Ruedy, R.; Nazarenko, L.; Lacis, A.; Schmidt, G.A.; Russell, G.; Aleinov, I.; Bauer, M.; Bauer, S.; et al. Efficacy of climate forcings. J. Geophys. Res. Atmos. 2005, 110, D18104. [Google Scholar] [CrossRef]
  35. Ghan, S. Technical Note: Estimating aerosol effects on cloud radiative forcing. Atmos. Chem. Phys. Discuss. 2013, 13, 9971–9974. [Google Scholar] [CrossRef]
  36. Forster, P.; Richardson, T.; Maycock, A.; Smith, C.; Samset, B.H.; Myhre, G.; Andrews, T.; Pincus, R.; Schulz, M. Recommendations for diagnosing effective radiative forcing from climate models for CMIP6: Recommended Effective Radiative Forcing. J. Geophys. Res. Atmos. 2016, 121, 12460–12475. [Google Scholar] [CrossRef]
  37. Mishra, P.; Singh, U.; Pandey, C.; Mishra, P.; Pandey, G. Application of student’s t-test, analysis of variance, and covariance. Ann. Card. Anaesth. 2019, 22, 407–411. [Google Scholar] [CrossRef] [PubMed]
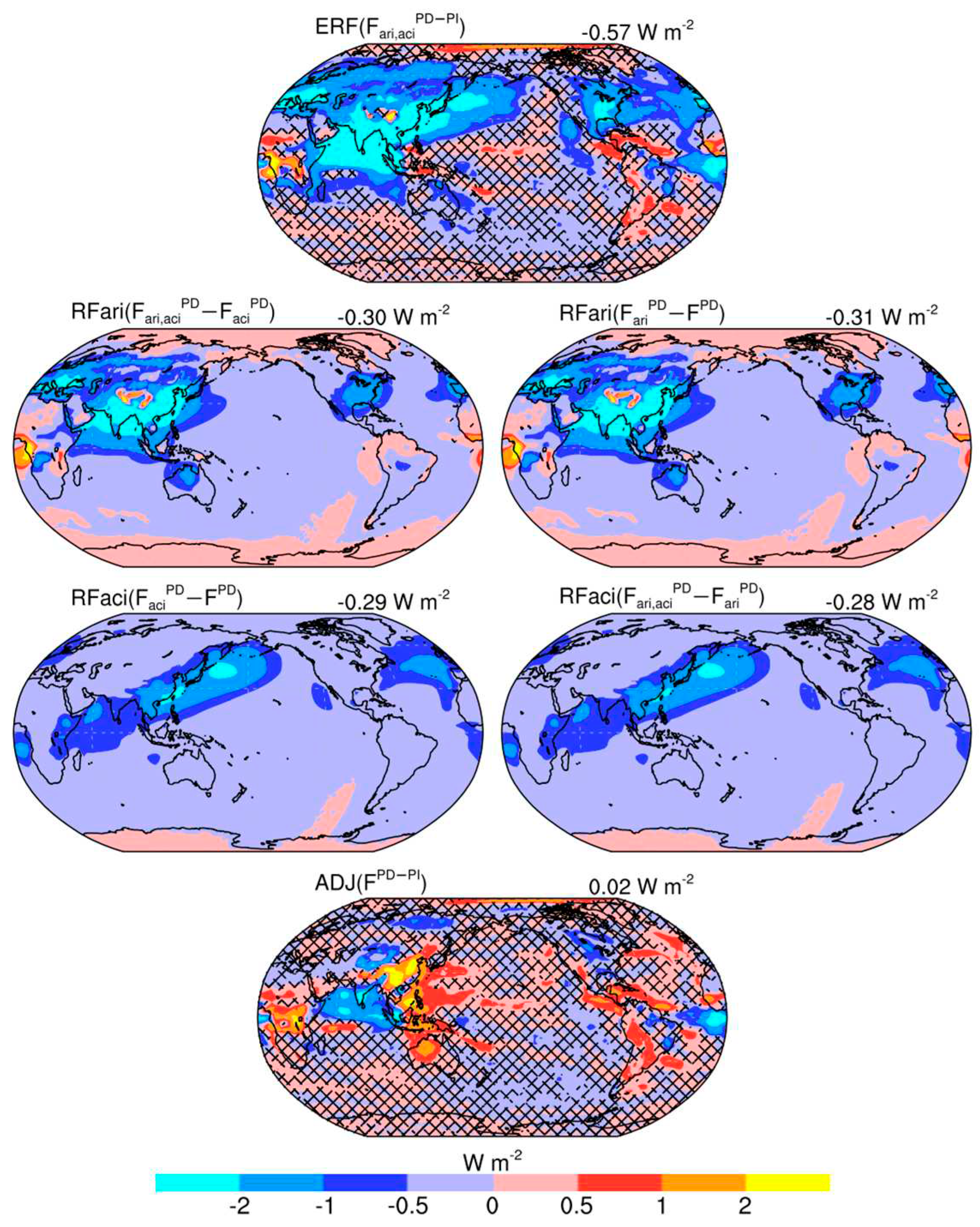
Preprints 89910 g001
Figure 1. Annual mean maps of annual anthropogenic aerosol effective radiative forcing (ERF, first row), instantaneous radiative forcing from direct radiative effect (RFari, second row) and Twomey effect (RFaci, third row), and rapid adjustments (ADJ, fourth row). The global average is provided in the upper-right corner. Hatching represents the nonsignificant area at the 90% confidence level.
Figure 1. Annual mean maps of annual anthropogenic aerosol effective radiative forcing (ERF, first row), instantaneous radiative forcing from direct radiative effect (RFari, second row) and Twomey effect (RFaci, third row), and rapid adjustments (ADJ, fourth row). The global average is provided in the upper-right corner. Hatching represents the nonsignificant area at the 90% confidence level.
Preprints 89910 g001
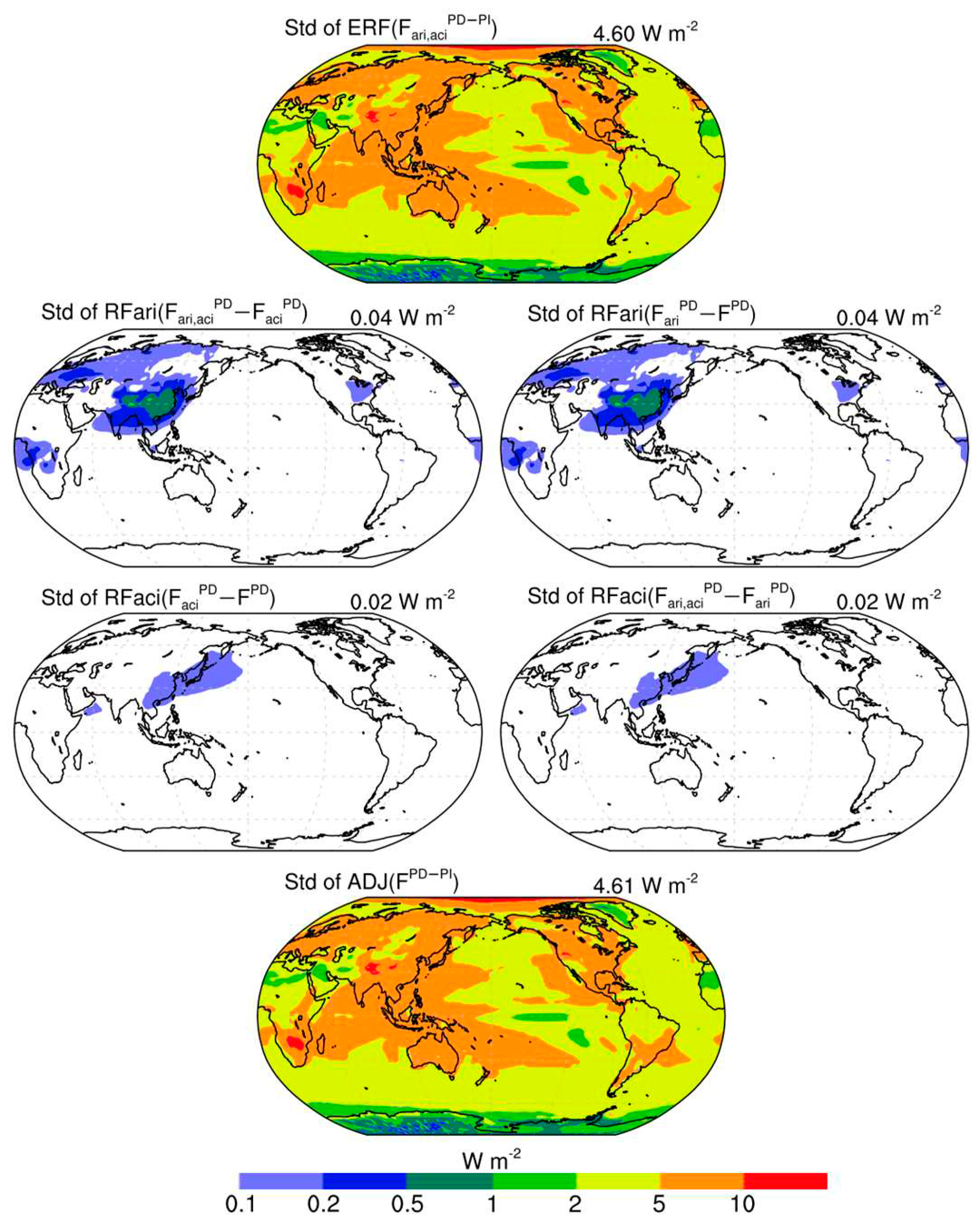
Preprints 89910 g002
Figure 2. Similar to Figure 1, but for the corresponding standard deviations (Std) calculated from the averages of each year (600 values).
Figure 2. Similar to Figure 1, but for the corresponding standard deviations (Std) calculated from the averages of each year (600 values).
Preprints 89910 g002
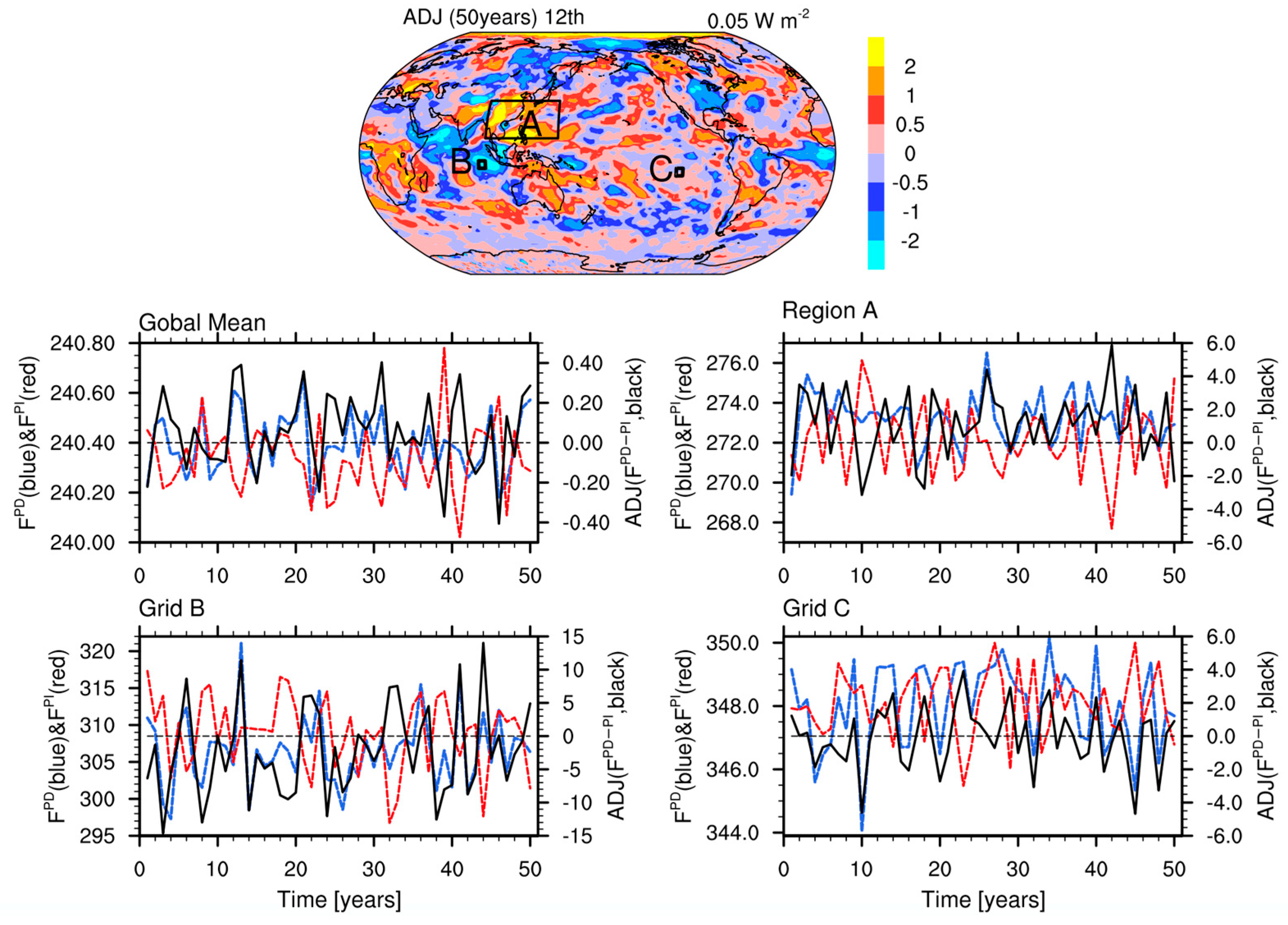
Preprints 89910 g003
Figure 3. Annual mean anthropogenic aerosol ADJ from the 12th ensemble member (1st row), and the annual ADJ time series (2nd and 3rd rows) calculated by global mean, region A, model grids B and C (marked in the annual mean map).
Figure 3. Annual mean anthropogenic aerosol ADJ from the 12th ensemble member (1st row), and the annual ADJ time series (2nd and 3rd rows) calculated by global mean, region A, model grids B and C (marked in the annual mean map).
Preprints 89910 g003
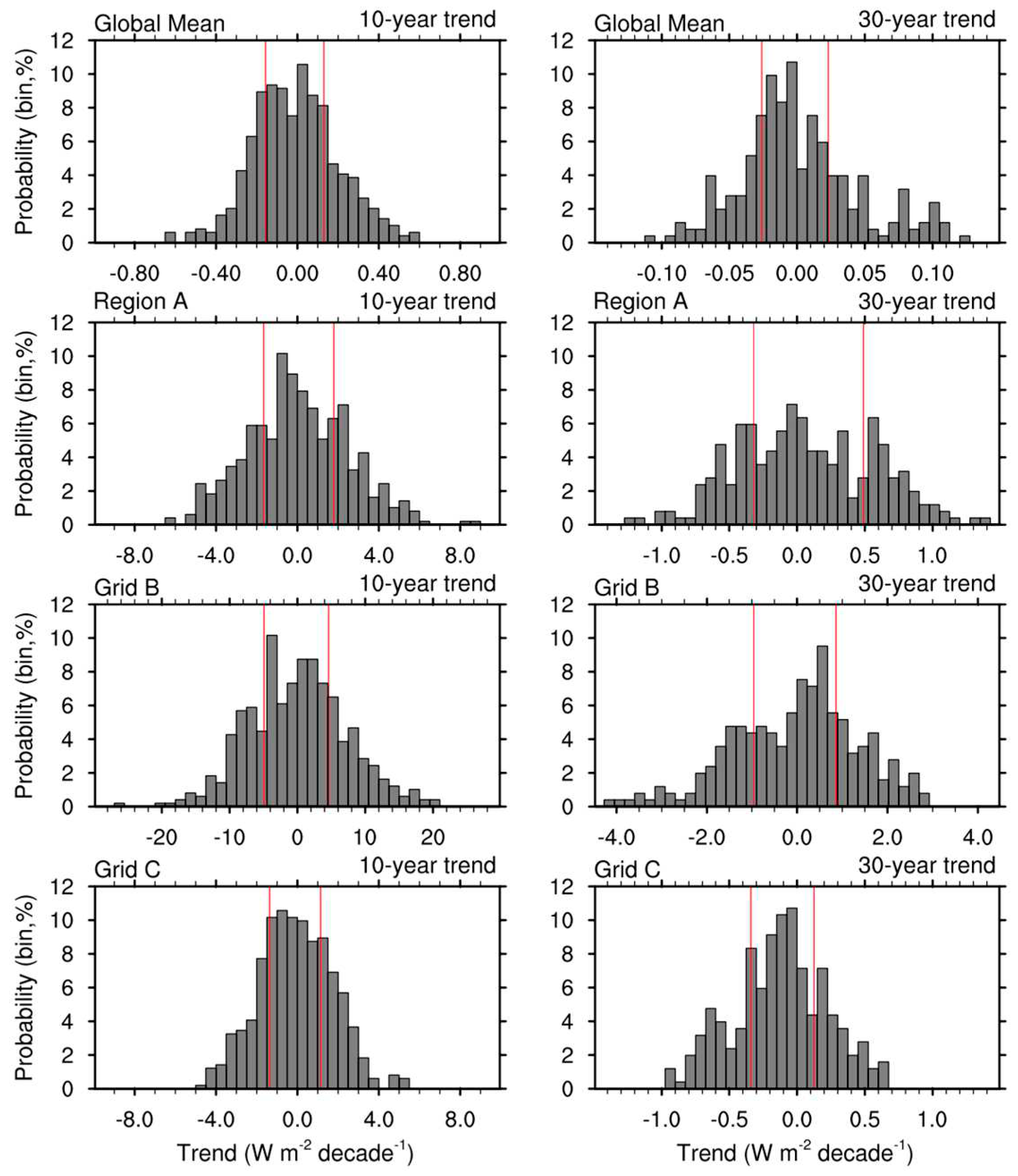
Preprints 89910 g004
Figure 4. The probability distributions of the ADJ 10-year (left column) and 30-year (right column) trend from global mean, region A, model grids B and C. A total of 40 bins were used here. The vertical red lines indicate the 25th and 75th percentiles. Unlike Figure 3, all ensemble members were used for statistical analysis.
Figure 4. The probability distributions of the ADJ 10-year (left column) and 30-year (right column) trend from global mean, region A, model grids B and C. A total of 40 bins were used here. The vertical red lines indicate the 25th and 75th percentiles. Unlike Figure 3, all ensemble members were used for statistical analysis.
Preprints 89910 g004
Preprints 89910 g005
Figure 5. Maps showing the 25th and 75th percentiles of ADJ 10-year (left column) and 30-year (right column) trend distributions.
Figure 5. Maps showing the 25th and 75th percentiles of ADJ 10-year (left column) and 30-year (right column) trend distributions.
Preprints 89910 g005
Preprints 89910 g006
Figure 6. Maps for Std of ADJ calculated from the 1st, 2nd, and 3rd ensemble members using the entire simulation lengths (50 years, first rows) and only the first 10 years (second rows). The global average is shown in the upper-right corner.
Figure 6. Maps for Std of ADJ calculated from the 1st, 2nd, and 3rd ensemble members using the entire simulation lengths (50 years, first rows) and only the first 10 years (second rows). The global average is shown in the upper-right corner.
Preprints 89910 g006
Preprints 89910 g007
Figure 7. Annual mean maps for the ADJ calculated from all ensemble experiment members (600 years, first row), the 1st, 2nd, and 3rd ensemble members with entire simulation lengths (50 years, second, third, and fourth rows) and only the first 10 years (fifth, sixth, and seventh rows). This first column shows the original multi-year averages without significance tests. The global average is given in the upper-right corner. The nonsignificant areas under ADJ ≠ 0 hypothesis (second column) and |ADJ| > 0.5 hypothesis (third column) are denoted by white color. Note that, the colorbar is different from Figure 1.
Figure 7. Annual mean maps for the ADJ calculated from all ensemble experiment members (600 years, first row), the 1st, 2nd, and 3rd ensemble members with entire simulation lengths (50 years, second, third, and fourth rows) and only the first 10 years (fifth, sixth, and seventh rows). This first column shows the original multi-year averages without significance tests. The global average is given in the upper-right corner. The nonsignificant areas under ADJ ≠ 0 hypothesis (second column) and |ADJ| > 0.5 hypothesis (third column) are denoted by white color. Note that, the colorbar is different from Figure 1.
Preprints 89910 g007
Preprints 89910 g008
Figure 8. Similar to Figure 7, but for ERF.
Figure 8. Similar to Figure 7, but for ERF.
Preprints 89910 g008
Table 1. List of model output radiative variables used in this study.
Table 1. List of model output radiative variables used in this study.
Names Description
Fari,aci The default shortwave net radiative fluxes, considering anthropogenic aerosol direct radiative effect and Twomey effect
Faci Similar to Fari,aci, but excluding anthropogenic aerosol direct radiative effect
Fari Similar to Fari,aci, but excluding anthropogenic aerosol Twomey effect
F Similar to Fari,aci, but excluding anthropogenic aerosol effects
RFari Anthropogenic aerosol instantaneous radiative forcing from direct radiative effect, RFari = Fari,aci − Faci, RFari = Fari − F
RFaci Anthropogenic aerosol instantaneous radiative forcing from Twomey effect, RFaci = Fari,aci − Fari, RFaci = Faci− F
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated