Efficiency and Vulnerability in Networks. A Game Theoretical Approach

Preprint

Article

Efficiency and Vulnerability in Networks. A Game Theoretical Approach

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

08 November 2023

Posted:

09 November 2023

You are already at the latest version

Alerts

Abstract

Defining measures of network efficiency and vulnerability for networks is a pivotal aspect in modern networking paradigms. We approach this problem from a game-theoretical perspective. We will consider networks in which actors have social or economic interests modeled by means of a cooperative game. This allows to define, for each network, a family of efficiency measures and another of vulnerability measures, parameterized by the game. The proposed measures use the within groups and the between groups Myerson values. These two values respectively measure which part of the classical allocation of Myerson corresponds to the productivity of players and which part to the intermediation costs. Also, which part of total centrality in social networks is due to communication or to beteewnness. In our proposal, the efficiency of a network is the proportion of the total productivity (or centrality) that players can retain using the network topology. The intermediation costs (and the betweenness centrality) can be viewed as a weakness with a negative impact. Then, we propose to calculate vulnerability as the proportion expent by players in intermediation payments. We explore the properties of these measures and we particularize them to several structures and particular games, also analyzing their asymptotic behaviour.

Keywords:

Subject: Computer Science and Mathematics - Applied Mathematics

1. Introduction

Networks are the backbone of our interconnected world. They are therefore ubiquitous today. Internet, power grids, infrastructure, transportation, neural, computer and social networks play a crucial role in our daily lives.

Then, understanding the structural properties of the networks is of paramount importance to provide a comprehensive perspective on network dynamics that can help decision-makers and stakeholders across different domains.

In this paper we will focus on the study of two highly relevant properties of social or economic networks, namely, efficiency and vulnerability.

Efficiency in social networks refers to the network ability to connect individuals, facilitate communication, optimize interactions and the flow of information in order to enhance social cohesion. For economic networks informs on the network capacity to allocate resources, maximizing productivity, reducing transactions costs an minimizing waste.

On the other side, vulnerability in a social network denotes the exposure of the network or its members to external or internal risks as miss information, lost of information and harmful interactions. In the case of economic networks refers to the possibility that the network has weakness that can disrupt economic activities generating a negative impact in the productivity.

Game theory is devoted to analyze the strategic interactions and decision-making processes and thus it can be effectively used to analyze dynamics within networks. As mentioned, our goal in this paper is to analyze efficiency and vulnerability in a network, and we will do so from a game theoretical perspective. The analysis of efficiency networks from a game theoretical point of view is not new. Wireline and wireless networks have been widely studied but from a non-cooperative game perspective. Ozdaglar and Menache (2022) is a remarkable survey of this type of contribution. In our framework, we will assume that the nodes of the network are simultaneously players in a TU-game (a cooperative game with transferable utility) that represents their social or economic interests. In this way we will propose a family of game-theoretical measures of efficiency and vulnerability for a network that has as a parameter the game. That is to say, we will assume that efficiency and vulnerability depend on the purpose for which individuals use the network, where this purpose, whether it is information dissemination, economic productivity or communication, is modeled by a TU-game.

As mentioned, the analysis of networks from a game theoretical point of view has a long tradition. Myerson (1977) is the seminal work in which he proposed to analyze the impact of restrictions in the communication of players in a TU-game by means of a network (graph). Then, he defined a new TU-game, the graph-restricted game. Given the prominence of the Shapley value (Shapley, 1953), Myerson proposed as solution for graph-restricted games, the Shapley value. From this original work, there exists an extensive literature in games with cooperation restricted by a graph. Gómez et al. (2003) and González-Arangüena et al. (2017), used the Myerson value as a centrality measure for actors in a symmetrical TU-game with communication restricted by a graph. Trying to capture both the communication and the betweens centrality, they decompose the Myerson value in the within groups Myerson value (WG-Myerson value, for short)and the between groups Myerson value (BG-Myerson value, for short). These values, when calculated for a general game, respectively measure the productivity of the player in the game and his intermediation opportunities among the others.

The proposed measures of efficiency and vulnerability introduced in this paper use this decomposition of the Myerson value. In our proposal, the efficiency of a network, parameterized by a game, is the proportion of the value of the grand coalition that players can retain (the sum of the within groups Myerson values of all the players) as a consequence of the network topology. And thus more efficient economic networks allow players a greater proportion of productivity, reducing intermediates cost. These intermediation cost can be viewed precisely as a weakness with a negative impact in the productivity. Then, our proposal for the family of vulnerability measures (also parameterized by the game) is to calculate the proportion of the value of the grand coalition that players must expend in intermediation payments (the sum of the between groups Myerson values of players). These payments reduce productivity and expose the players to the disruption of economic activities generated by the lack of communication between different groups of players (coalitions). For social networks, roughly speaking, the efficiency is viewed as the proportion of the total centrality in the network due to communication among players. The vulnerability is the proportion of the total centrality due to betweeness. In this way, efficiency is measured in terms of the relational abilities of players whereas vulnerability increases when third-party control of communication between pairs of players increases. After defining the measures we explore the more relevant properties including their asymptotic behavior for particular games.

The remainder of the paper is organized as follows. After some preliminaries on games, graphs and communication situations (graph-games), in Section 3 we introduce the family of efficiency measures, analyzing its properties. In Section 4 we particularize the values of this family for several games and several structures including the asymptotic behaviour. In Section 5 we propose the family of vulnerability measures. The paper ends with a section of conclusions and final remarks and the references.

2. Preliminaries

2.1. Games

A cooperative n-person game of transferable utility ( TU-game for short) is a pair

(N, v)

where

N = {1, \dots, n}

is the set of players an

v : 2^{N} \to R

, satisfying

v (\emptyset) = 0

, is the characteristic function that assigns to each coalition

S \subseteq N

the payoff

v (S)

that its

s = | S |

members can obtain by cooperating.

We will denote by

G^{N}

the vector space of all TU-games with players set N. A very useful basis of

G^{N}

is the unanimity games basis

{(N, u_{S})}_{\emptyset \neq S \subseteq N}

, with characteristic functions given by

u_{S} (T) = \{\begin{matrix} 1, & if S \subseteq T, \\ 0, & otherwise . \end{matrix}

Consequently, for each

(N, v) \in G^{N}

we can write v as the following linear combination,

v = \sum_{\emptyset \neq S \subseteq N} Δ_{v} (S) u_{S},

in which the coefficients,

Δ_{v} (S)

, known as Harsanyi dividends (Harsanyi, 1959), can be calculated as:

Δ_{v} (S) = \sum_{T \subseteq S} {(- 1)}^{s - t} v (T) .

We will say that

(N, v) \in G^{N}

is zero-normalized if

v ({i}) = 0

for all

i \in N

, is superadditive if

v (S \cup T) \geq v (S) + v (T)

for all

S, T \subseteq N, S \cap T = \emptyset,

is convex if

v (S \cup T) + (v (S \cap T) \geq v (S) + v (T)

for all

S, T \subseteq N

, and is almost-positive if

Δ_{v} (S) \geq 0

for all

S \subseteq N

. Almost-positive games are superaditive and convex.

Given

(N, v) \in G^{N}

, a player

i \in N

is a null player in

(N, v)

v (S \cup {i}) - v (S) = 0

for all

S \subseteq N ∖ {i}

and is a necessary player (van den Brink and Gilles, 1996) if

v (S) = 0

for all

S \subseteq N ∖ {i}

An allocation rule or point solution

ψ

G^{N}

assigns to every

(N, v) \in G^{N}

a vector

ψ (N, v) \in R^{n}

ψ_{i} (N, v)

representing the outcome of the player i in the game. A very relevant point solution was introduced in Shapley (1953). It assigns to every player i in the game

(N, v)

the following expected value of his marginal contributions:

S h_{i} (N, v) = \sum_{S \subseteq N ∖ {i}} \frac{(n - s - 1)! s!}{n!} (v (S \cup {i}) - v (S)), i \in N .

2.2. Graphs

A graph or a (network) is a pair

(N, γ)

, where

N = {1, 2, \dots, n}

is the set of nodes and

γ

is a set of links included in the complete graph

γ_{N} = {{i, j} | i, j \in N, i \neq j}

. If the link

{i, j} \in γ

we will say that i and j are directly connected. In other case, i and j could be connected if there exist a path, i.e., a sequence of nodes (intermediaries)

i_{1}, i_{2}, \dots i_{k}, k > 2

, with

i_{1} = i

i_{k} = j

, such that

{i_{l}, i_{l + 1}} \in γ

, for

l = 1, \dots, k - 1

A set

S \subseteq N

S \neq \emptyset

, is connected (internally connected) in

(N, γ)

if every pair of nodes in S are directly connected or they can be connected with intermediaries in S. Singletons will be considered connected. A connected component, C, of the graph

(N, γ)

is a maximal connected subset, that is, C is connected and, for all

C^{'} \subseteq N

, if

C C^{'}

then,

C^{'}

is not connected. A graph

(N, γ)

induces a partition

N / γ

of the set N into connected components.

A connected set in

(N, γ)

S^{*}

, is a minimal connection set of

S \subseteq S^{*}

if there is no

S^{'} ⊊ S^{*}

with

S \subseteq S^{'}

and

S^{'}

connected.

M C S (S, N, γ)

will denote the family (occasionally empty) of all minimal connection sets of S in

(N, γ)

Given

(N, γ)

and

S \subseteq N

S / γ

will denote de set of all connected components in the restriction of

(N, γ)

to S, i.e., in

(S, γ_{|_{S}})

, where

γ_{|_{S}} = {{i, j} \in γ | i, j \in S}

A subgraph of a graph

(N, γ)

(N, γ^{'})

with

γ^{'} \subseteq γ

. Given

(N, γ)

and

l \in γ

(N, γ ∖ {l})

is the subgraph obtained when the link l is removed;

(N, γ_{i})

is the subgraph of

(N, γ)

of the links incident on i, i.e.:

γ_{i} = {l \in γ | i \in l}

, and

(N, γ_{- i}) = (N, γ ∖ γ_{i})

(N, γ)

is a tree if it is connected and it has no cycles. We will denote

(N, γ_{i}^{S})

the star with center in the node i and thus

γ_{i}^{S} = {{i, j}, j \in N, j \neq i}

(N, γ^{C})

will denote the chain ordered in the natural way (from 1 to n).

(N, γ^{W})

is the wheel with

γ^{W} = {{1, 2}, {2, 3}, \dots, {n, 1}}

2.3. Communications situations

Myerson (1977,1980) introduced the games with cooperation restricted by a graph (also graph-games or communications situations),

(N, v, γ)

, in which the players in the game

(N, v)

are restricted to communicate using only the links in the graph

(N, γ)

C S^{N}

will denote the set of all communication situations with player-nodes set N and

C S_{0}^{N}

will denote the set of all communication situations with player-nodes set N and game v zero-normalized. Finally

C S_{*}^{N}

will be the subset of

C S_{0}^{N}

with

(N, v)

a non null and superadditive game.

An allocation rule

ψ

C S^{N}

is a map

ψ : C S^{N} \to R^{n}

ψ_{i} (N, v, γ)

representing the outcome for player i in the communication situation

(N, v, γ)

. An allocation rule

ψ

defined on

C S^{N}

satisfies component efficiency if for all

(N, v, γ) \in C S^{N}

and all

C \in N / γ, \sum_{i \in C} ψ_{i} (N, v, γ) = v (C)

Following Myerson(1977), for

(N, v^{γ}) \in C S^{N}

a new game

(N, v^{γ})

captures the impact of the restrictions in the communication imposed by

(N, γ)

in the formation of coalitions (an thus in their value). The characteristic function is given by

v^{γ} (S) = \sum_{C \in S / γ} v (C), for all S \subseteq N .

Given the relevance of the Shapley value, Myerson defined

μ

, the allocation rule in

C S^{N}

(nowadays known as the Myerson value) given by

μ (N, v, γ) = S h (N, v^{γ})

. Exploring the possibilities of the Myerson value as a centrality measure Gómez et al. (2003) and González-Arangüena et al. (2017) highlight the vector character of the Myerson value decomposing it into two new allocation rules: the within groups Myerson value,

μ^{W}

, (the WG-Myerson value for short) and the between groups Myerson value,

μ^{B}

, (the BG-Myerson value for short). For each

(N, v, γ) \in C S^{N}

and each

i \in N

they are defined as

μ_{i}^{W} (N, v, γ) = μ_{i} (N, v_{i}, γ)

and

μ_{i}^{B} (N, v, γ) = μ_{i} (N, v_{- i}, γ)

, where

v_{i} = \sum_{S \subseteq N : i \in S} Δ_{v} (S) u_{S}

and

v_{- i} = v - v_{i} .

3. A family of efficiency measures

In the following definition we introduce a family of game-theoretical measures for the efficiency of a network. We will assume that nodes in the network are players in a TU-game, this game representing the economic or social interests that motivate the interaction of players. The network represents the feasible communications between players (and, as a consequence, also the existing restrictions that motivate the need for intermediaries when players have not direct communication). The proposed family of efficiency measures, assigns to each network and each TU-game a value representing which part of the total productivity of the game,

v (N)

, players can maintain given the geometry of the network.

We will use super-additive games in which cooperation between individuals is not detrimental to them. We will also assume that the games are zero-normalized so that the total absence of communication between players - the impossibility to cooperate, empty graph-, corresponds to the minimum (and null) efficiency.

Definition 3.1.

We define a measure of efficiency,

E

, for each communication situation

(N, v, γ) \in C S_{*}^{N}

as:

E (N, v, γ) = \frac{\sum_{i \in N} μ_{i}^{W} (N, v, γ)}{v (N)} .

Remark 3.1.

In the special case in which

(N, v)

is a symmetric game and

(N, γ)

is a connected graph, the defined measure represents the proportion of

v (N)

corresponding to the total communication centrality of players introduced in Gómez et al. (2003).

To motivate our definition let us consider the following example also included in Gómez et al. (2003).

Example 3.1.

Let as denote with

(N, v_{1})

(N, v_{2})

and

(N, v_{3})

, respectively, the messages game, the zero-normalized overhead game and the conference game with characteristic functions given by:

i): $v_{1} (S) = s (s - 1)$ ,
ii): $v_{2} (S) = s - 1$ ,
iii): $v_{3} (S) = 2^{s} - s - 1,$

for

S \subseteq N = {1, 2, 3, 4}

. Suppose

(N, γ)

is one of the four-node connected graphs. Then, the efficiency (calculated with the proposed measure) of the (eighteen) different communication situations is given in the Table 1. For the within groups Myerson values of the nodes-players (communication centrality of the nodes), see Table 2 in Gómez et al. (2003).

Table 1.

E (N, v_{i}, γ)

for

N = {1, 2, 3, 4}

i = {1, 2, 3}

and

(N, γ)

a four-node graph.

Table 1.

E (N, v_{i}, γ)

for

N = {1, 2, 3, 4}

i = {1, 2, 3}

and

(N, γ)

a four-node graph.

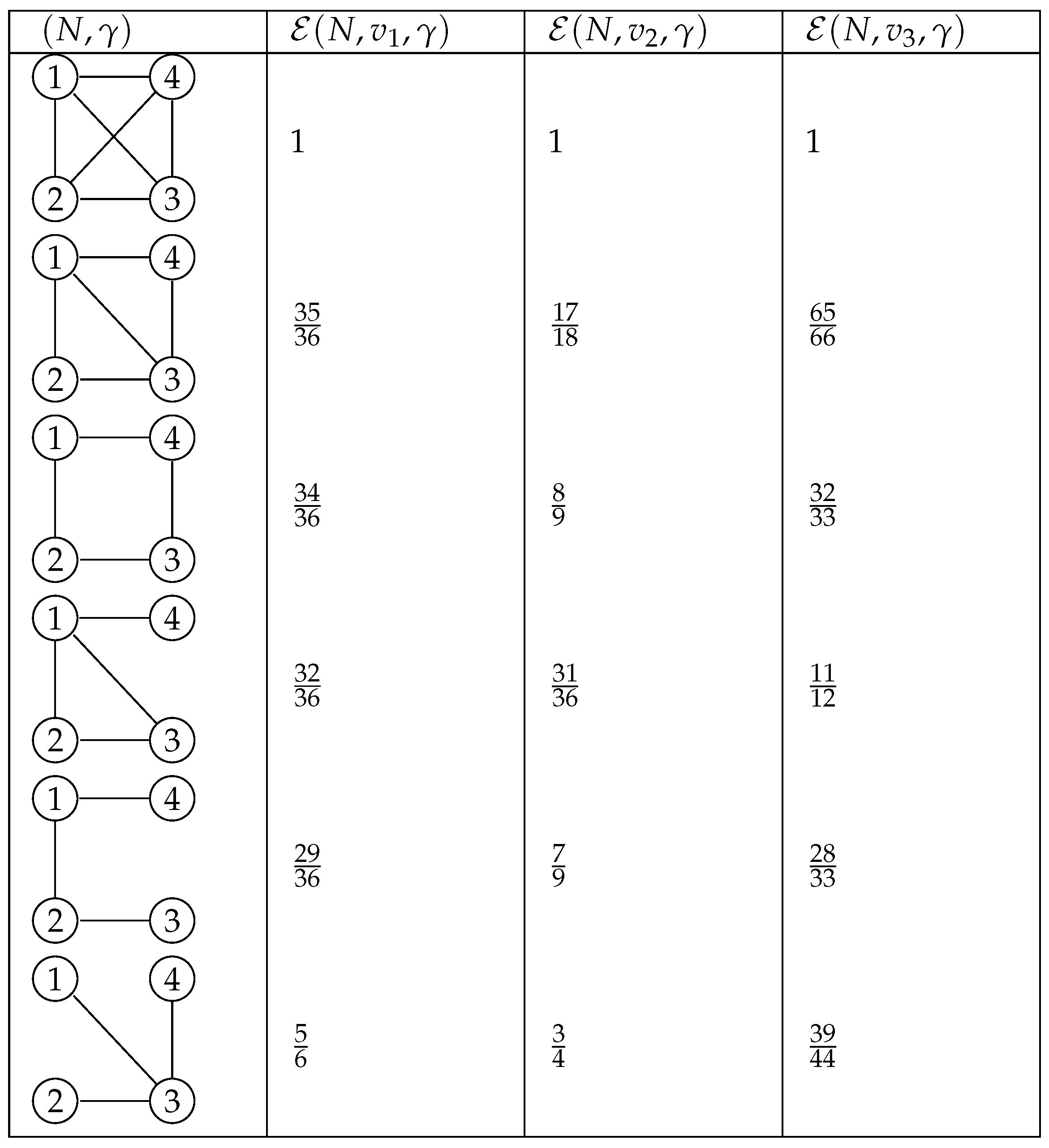Table 2. Asymptotic behavior of the efficiency of chains, stars and wheels

$n ⟼ \infty$	$E (N, v_{1})$	$E (N, v_{2})$	$E (N, v_{3})$
$(N, γ^{C})$	0	$\frac{2}{3}$	$\frac{1}{2}$
$(N, γ_{1}^{S})$	$\frac{2}{3}$	$\frac{1}{2}$	1
$(N, γ^{W})$	0	$\frac{2}{3}$	$\frac{3}{4}$

We can observe some properties of the obtained figures that correspond to general properties of the introduced measures that will be proved throughout this paper. In particular, efficiency always remains between 0 and 1. It increases when adding edges if the game is convex, it equals 1 if the graph is complete, and among all trees, it is maximum in the star and minimum in the chain, provided that the game is almost-positive as in cases

v_{1}

and

v_{3}

The following proposition includes some properties related to the the range of values of the defined measures. The corresponding proofs can be found in Appendix I.

Proposition 3.1.

Given

(N, v, γ) \in C S_{*}^{N}

, we have:

i): $0 \leq E (N, v, γ) \leq \frac{v^{γ} (N)}{v (N)} .$

Moreover, if $(N, γ)$ is also a connected graph then $0 \leq E (N, v, γ) \leq 1 .$
ii): The lower and upper bounds of $E$ are reached, respectively, for the empty and the complete network. If $(N, γ_{N})$ is the complete graph and $(N, γ_{\emptyset})$ is the empty graph, then

$E (N, v, γ_{N}) = 1 a n d E (N, v, γ_{\emptyset}) = 0,$

and if the game is not zero-normalized, then $E (N, v, γ) \geq \frac{\sum_{i \in N} v ({i})}{v (N)} .$

The following proposition lists some properties regarding the behavior of these measures in the face of changes in the network, ceteris paribus. Again, the corresponding proofs can be found in Appendix I.

Proposition 3.2.

Given

(N, v, γ) \in C S_{*}^{N}

i): The disconnection of a player who is simultaneously null in the game and terminal in the graph does not affect the efficiency of the network. Then the network can be lightened by eliminating both null and terminal players, i.e., if $i \in N$ is a null player in $(N, v)$ such that $| γ_{i} | = 1$ , we have that $E (N, v, γ) = E (N, v, γ ∖ γ_{i})$ .
ii): If we isolate an essential player in the game the efficiency of the network, whatever it is, becomes zero. This property can be seen as a possibility to override the efficiency of potentially dangerous networks (e.g. terrorist networks). Formally, if $i \in N$ is an essential player in $(N, v)$ and isolated in the graph $(N, γ)$ , then $E (N, v, γ) = 0$ .
iii): The star whose center is an essential player has maximum efficiency. This justifies that, in the construction of certain networks, a key player controls the entire communication flow. Formally, if $i \in N$ is an essential player in $(N, v)$ which is also the hub of the star $(N, γ_{i}^{S})$ , then $E (N, v, γ_{i}^{S}) = 1$ .
iv): If the game is convex, the efficiency of a network does not decrease when adding a new link, i.e. if $(N, v)$ a convex game, then

$E (N, v, γ) \leq E (N, v, γ \cup {l}), f o r a l l l \notin γ .$

In iv) of Proposition 3.2, the convexity condition cannot be weakened as it is seen in the following example.

Example 3.2.

Consider

(N, v)

with

N = {1, 2, 3}

and

v = u_{{1, 2}} + u_{{1, 3}} + u_{{2, 3}} - 2 u_{{1, 2, 3}}

which is a superadditive but not convex game. Let

γ_{1} = {{1, 2}}

and

γ_{2} = γ_{1} \cup {{2, 3}}

, then

E (N, v, γ_{1}) = \frac{1}{1} = 1 a n d E (N, v, γ_{2}) = \frac{2}{3} .

As this example shows, in the case of a non-convex game, it may happen that a non-connected network is more efficient than a connected one.

The following proposition groups some more properties relating the measurements corresponding to different games. The proofs can be found in Appendix I.

Proposition 3.3.

E

satisfied the following properties:

1.: It is invariant by strategic equivalence of the game. That is to say, efficiency is not changed if we transform the economic units in which the outcome of coalitions are measured, i.e., given $(N, v, γ)$ and $(N, w, γ) \in C S_{*}^{N}$ with $(N, v)$ and $(N, w)$ strategically equivalent, we have $E (N, v, γ) = E (N, w, γ)$ .
2.: When the measures are calculated for communication situations in which the network is not connected, it can be obtained as a linear combination of the efficiencies in the respective (component) communication situations, i.e., given $(N, v, γ) \in C S_{*}^{N}$ , if $N / γ = {C_{1}, . . ., C_{r}}$ , then,

$E (N, v, γ) = \sum_{k = 1}^{r} \frac{v (C_{i})}{v (N)} E (C_{k}, v_{|_{C_{k}}}, γ_{|_{C_{k}}}) .$
3.: It is not linear in the game, ceteris paribus. Nevertheless the efficiency of a communication situation in which the game is the sum of other games, can be calculated as a convex linear combination of the efficiencies in the corresponding to these games communication situations, i.e., if $(N, v_{1}, γ), \dots, (N, v_{r}, γ), (N, \sum_{k = 1}^{r} v_{k}, γ) \in C S_{*}^{N}$ , then it holds that,

$E (N, \sum_{k = 1}^{r} v_{k}, γ) = \sum_{k = 1}^{r} \frac{v_{k} (N)}{(\sum_{k = 1}^{r} v_{k}) (N)} E (N, v_{k}, γ) .$
4.: Fixed the network, we can obtain the efficiency in a communication situation in terms of efficiencies in communication situations with unanimity games, i.e., if $(N, v, γ) \in C S_{*}^{N}$ , then,

$E (N, v, γ) = \frac{1}{v (N)} \sum_{\emptyset \neq S \subseteq N} Δ_{v} (S) E (N, u_{S}, γ) .$
v): The efficiency of a connected network to communicate the coalition S is s times the probability of that coalition is connected in the graph, i.e., if $(N, u_{S}, γ) \in C S_{*}^{N}$ , then

$E (N, u_{S}, γ) = \{\begin{matrix} s α_{γ} (S), & i f M C S (S, N, γ) = {S_{1}, . . ., S_{r}} \neq \emptyset \\ 0, & o t h e r w i s e, \end{matrix}$

where

$α_{γ} (S) = \sum_{i = 1}^{r} \frac{1}{| S_{i} |} - \sum_{i < j} \frac{1}{| S_{i} \cup S_{j} |} + . . . {(- 1)}^{r + 1} \frac{1}{| \cup_{i = 1}^{r} S_{i} |} .$

As a consequence of iv) and v) of previous proposition, we can easily obtain the expression of

E (N, v, γ)

in terms of the Harsanyi dividends for some particular structures as trees, stars and chains.

Example 3.3.

For

(N, v)

superaditive and zero-normalized game,

1.: If $(N, γ^{T})$ is a tree then,

$E (N, v, γ^{T}) = \frac{1}{v (N)} \sum_{\emptyset \neq S \subseteq N} Δ_{v} (S) \frac{s}{| H (S) |},$

where $H (S)$ is the connected hull of S in $(N, γ^{T})$ , i.e. the unique minimal connection set of S in $(N, γ^{T})$ .
2.: If $(N, γ^{C})$ is a chain ordered in the natural way then,

$E (N, v, γ^{C}) = \frac{1}{v (N)} \sum_{\emptyset \neq S \subseteq N} Δ_{v} (S) \frac{s}{max_{j} {S} - min_{j} {S} + 1} .$
3.: If $(N, γ_{1}^{S})$ is a star with center at node 1 then,

$E (N, v, γ_{1}^{S}) = \frac{1}{v (N)} [\sum_{\emptyset \neq S \subseteq N, 1 \in S} Δ_{v} (S) + \sum_{\emptyset \neq S \subseteq N, 1 \notin S} Δ_{v} (S) \frac{s}{s + 1}] .$

In the following proposition we prove that, if the game is zero-normalized, symmetric and almost positive, then the maximum efficiency of the trees is attained in the star.

Proposition 3.4.

Let

(N, v, γ_{1}^{S})

and

(N, v, γ^{T})

two communication situations in which

(N, v)

is a zero-normalized, symmetric and almost positive game,

(N, γ_{1}^{S})

is the star with

1 \in N

as its hub and

(N, γ^{T})

is a tree. Then,

E (N, v, γ_{1}^{S}) \geq E (N, v, γ^{T}) .

Proof.

We have:

E (N, v, γ_{1}^{S}) = \frac{1}{v (N)} [\sum_{S \subseteq N, 1 \in S} Δ_{v} (S) + \sum_{S \subseteq N, 1 \notin S} Δ_{v} (S) \frac{s}{s + 1}],

and

E (N, v, γ^{T}) = \frac{1}{v (N)} \sum_{S \subseteq N} Δ_{v} (S) \frac{s}{| H (S) |}

= \frac{1}{v (N)} [\sum_{\begin{matrix} S \subseteq N \\ \begin{matrix} S connected \end{matrix} \end{matrix}} Δ_{v} (S) + \sum_{\begin{matrix} S \subseteq N \\ \begin{matrix} S not connected \end{matrix} \end{matrix}} Δ_{v} (S) \frac{s}{| H (S) |}] .

As for

S \subseteq N

, S not connected in

(N, γ_{T})

| H (S) | \geq s + 1

, to obtain the result it is sufficient to prove that, for

s = 2, . . ., n

, the number of connected sets in

(N, γ_{S})

with s elements is greater or equal that the number of connected set in

(N, γ_{T})

Effectively, for

s = 2, . . ., n

, the number of connected sets in

(N, γ_{1}^{S})

of size s is

(\binom{n - 1}{s - 1})

, the total number of choosing

s - 1

links from the

n - 1

total links of the star. Clearly, the number of connected sets of size

s = 2, . . ., n

in a tree is bounded by

(\binom{n - 1}{s - 1})

as a connected set needs

s - 1

links and, in a tree, it is obvious that not all

s - 1

links generate a connected set of s elements.

□

In the following proposition we prove that, if the game is zero-normalized, symmetric and almost positive, among all the trees the minimum efficiency is reached in the chain.

Proposition 3.5.

Let

(N, v, γ^{T})

and

(N, v, γ^{C})

two communication situations in which

(N, v)

is a zero-normalized, symmetric and almost positive game,

(N, γ^{C})

is a chain and

(N, γ^{T})

is a tree. Then,

E (N, v, γ^{T}) \geq E (N, v, γ^{C}) .

Proof. Let us consider in

(N, γ^{T})

the longest path (chain) and, without loss of generality, let us suppose that

γ^{T}

is labeled so that path is

{1, 2}, {2, 3}, . . ., {r - 1, r}

r = n

, then

(N, γ^{T}) = (N, γ^{C})

and the result is proved.

Otherwise, we will transform

(N, γ^{T})

in other

(N, γ^{T^{'}})

in which the longest path has length strictly greater that r and such that

E (N, v, γ^{T}) \geq E (N, v, γ^{T^{'}})

. It is clear that repeating this process a finite number of times we prove the result.

Let us denote

h = min_{j \in {1, . . . r}} {j | \deg (j) > 2}

, the first node from 1 to r having degree greater that 2. As the longest path of

(N, γ^{T})

differs from

(N, γ^{T})

this node must exists.

Let k a node directly connected with h,

k \neq h - 1

and

k \neq h + 1

and let us define

A = {i \in N | the path joining i with h contains k}

Consider the new tree

(N, γ^{T^{'}})

defined as

γ^{T^{'}} = (γ^{T} ∖ {{h, k}}) \cup {{1, k}}

To prove that

E (N, v, γ^{T}) \geq E (N, v, γ^{T^{'}})

, let

\emptyset \neq S \subseteq N

. Then we can distinguish three different situations:

1.: $h \notin H_{γ^{T}} (S)$ .

Then $H_{γ^{T}} (S) = H_{γ^{T^{'}}} (S)$ and for these sets,

$\frac{s}{| H_{γ^{T}} (S) |} = \frac{s}{| H_{γ^{T^{'}}} (S) |} .$
2.: $h \in H_{γ^{T}} (S) \cap H_{γ^{T^{'}}} (S)$ .

Then clearly $H_{γ^{T}} (S) \subseteq H_{γ^{T^{'}}} (S)$ and thus,

$\frac{s}{| H_{γ^{T}} (S) |} \geq \frac{s}{| H_{γ^{T^{'}}} (S) |} .$
3.: $h \in H_{γ^{T}} (S)$ and $h \notin H_{γ^{T^{'}}} (S)$ .

In this case, $h \notin S$ . Let us denote $B_{S} = S \cap {1, . . ., h}$ . Then,

$| H_{γ^{T}} (S) | - | H_{γ^{T^{'}}} (S) | = h - min_{i \in B_{S}} {i} + 1 - max_{i \in B_{S}} {i} .$

If $h - min_{i \in B_{S}} {i} + 1 - max_{i \in B_{S}} {i} \leq 0$ then the result is proved.

Otherwise, there is exactly one coalition $S^{'} \subseteq N$ such that,

$| S | = | S^{'} |$ and,

$| H_{γ^{T}} (S^{'}) | - | H_{γ^{T^{'}}} (S^{'}) | = | H_{γ^{T^{'}}} (S) | - | H_{γ^{T}} (S) |$

$S^{'}$ is defined as $S^{'} = (S ∖ B_{S}) \cup {h - j + 1, j \in B_{S}}$ . If $B_{S}^{'} = S^{'} \cap {1, . . ., h}$ then,

$| H_{γ^{T}} (S^{'}) | - | H_{γ^{T^{'}}} (S^{'}) | = h - min_{i \in B_{S}^{'}} {i} + 1 - max_{i \in B_{S}^{'}} {i}$

$= h - (h - max_{i \in B_{S}} {i} + 1) + 1 - (h - min_{i \in B_{S}} {i} + 1)$

$= min_{i \in B_{S}} {i} - 1 + max_{i \in B_{S}} {i} - h = | H_{γ^{T^{'}}} (S) | - | H_{γ^{T}} (S) |,$

which concludes the proof.

□

Remark 3.2.

The results of the last two propositions are not satisfied if the game

(N, v)

is only superadditive or even convex. We have a counterexample in Example 3.1 where if the game is

(N, v_{2})

(overhead game), the chain efficiency is strictly higher than the star efficiency.

4. Efficiency and its asymptotic behavior in some particular cases

In this section we calculate the efficiency of the star, the chain and the wheel for a general superaditive symmetric an zero-normalized game. We particularize the obtained result for the three games considered in Example 3.1. Moreover, we analyze the asymptotic behavior of these efficiencies as the number of players/nodes increases.

4.1. The star

Consider the communication situation

(N, v, γ_{1}^{S})

in which

(N, v)

is a superaditive, symmetric and zero-normalized game and

(N, γ_{1}^{S})

is a star with node 1 as the hub.

In this case,

μ_{1}^{W} (N, v, γ_{1}^{S}) = \sum_{S \subseteq N ∖ {1}} \frac{(n - s - 1)! s!}{n!} [v (C_{1}^{S \cup {1}, γ_{1}^{S}}) - v (C_{1}^{S \cup {1}, γ_{1}^{S}} ∖ {1})]

= \sum_{S \subseteq N ∖ {1}} \frac{(n - s - 1)! s!}{n!} [v (S \cup {1}) - v (S)]

= \sum_{s = 0}^{n - 1} \frac{(n - s - 1)! s!}{n!} (\binom{n - 1}{s}) [v (s + 1) - v (s)] = \sum_{s = 0}^{n - 1} \frac{1}{n} [v (s + 1) - v (s)],

where the symmetry of the game is used in the third equality.

The within groups Myerson value for the node 2 (and thus for any other node different from the node 1) is:

μ_{2}^{W} (N, v, γ_{1}^{S}) = \sum_{S \subseteq N ∖ {2}} \frac{(n - s - 1)! s!}{n!} [v (C_{2}^{S \cup {2}, γ_{1}^{S}}) - v (C_{2}^{S \cup {2}, γ_{1}^{S}} ∖ {2})]

= \sum_{S \subseteq N ∖ {2}, 1 \in S} \frac{(n - s - 1)! s!}{n!} [v (S \cup {2}) - v (S)]

= \sum_{s = 1}^{n - 1} \frac{(n - s - 1)! s!}{n!} (\binom{n - 2}{s - 1}) [v (s + 1) - v (s)] = \sum_{s = 1}^{n - 1} \frac{s}{n (n - 1)} [v (s + 1) - v (s)],

the second equality holding as if the hub does not belong to a coalition, the connected components are singletons worthless (the game is zero-normalized) and the third equality holding as the game is symmetric.

Then,

E (N, v, γ_{1}^{S}) = \frac{1}{v (n)} \sum_{i = 1}^{n} μ_{i}^{W} (N, v, γ_{1}^{S})

= \frac{1}{v (n)} [\sum_{s = 0}^{n - 1} \frac{1}{n} [v (s + 1) - v (s)] + (n - 1) \sum_{s = 1}^{n - 1} \frac{s}{n (n - 1)} [v (s + 1) - v (s)]]

= \frac{1}{n v (n)} \sum_{s = 1}^{n - 1} (s + 1) [v (s + 1) - v (s)] = 1 - \sum_{s = 2}^{n - 1} \frac{v (s)}{n v (n)} .

Particularizing for the game

(N, v_{1})

, with characteristic function

v_{1} (S) = s (s - 1)

for all

s \geq 1

, we have:

E (N, v_{1}, γ_{1}^{S}) = 1 - \frac{1}{n^{2} (n - 1)} \sum_{s = 2}^{n - 1} (s^{2} - s) = \frac{2 (n + 1)}{3 n},

and thus

lim_{n \to \infty} E (N, v_{1}, γ_{1}^{S}) = \frac{2}{3} .

This means that, when the number of players increases the proportion of messages that can be sent without intermediation approaches to

\frac{2}{3}

If the game is

(N, v_{2})

, which has characteristic function equal to

v_{2} (S) = s - 1

, for all

s \geq 1

, we have:

E (N, v_{2}, γ_{1}^{S}) = 1 - \frac{1 + 2 + 3 + . . . + (n - 2)}{n (n - 1)} = \frac{n + 2}{2 n},

which converges to

\frac{1}{2}

and thus, only half of the total value can be retained by the grand coalition in the limit.

Finally, for the game

(N, v_{3})

, with

v_{3} (S) = 2^{s} - s - 1

for all

s \geq 1

we have,

E (N, v_{3}, γ_{1}^{S}) = 1 - \sum_{2}^{n - 1} \frac{(2^{s} - s - 1)}{n (2^{n} - n - 1)},

and after some manipulations,

E (N, v_{3}, γ_{1}^{S}) = \frac{(n - 1) 2^{n + 1} - n^{2} - n + 2}{2 n (s^{n} - n - 1)},

which converges to 1 when n tends to infinity.

In this case the star is "efficient" in the sense that the total worth of the grand coalition can be retained by players as their number increases.

As it can be seen, the asymptotic behavior of the efficiency also depends on the game considered.

4.2. The chain

Consider the communication situation

(N, v, γ^{C})

in which

(N, v)

is a superaditive, symmetric and zero-normalized game and

(N, γ^{C})

is a chain of n nodes that we assume to be numbered consecutively starting with 1 at one end.

In this case we have that,

E (N, v, γ^{C}) = \frac{1}{v (n)} [\sum_{s = 2}^{n - 1} \frac{2 (n + 1)}{(s + 2) (s + 1)} [v (s) - v (s - 1)] + [v (n) - v (n - 1)]] .

The proof of this result is in the Appendix II.

In the following, we particularize the previous expression of the efficiency in the chain for the three games considered above. Also we analyze their asymptotic behavior.

For the game

(N, v_{1})

, with characteristic function

v_{1} (S) = s (s - 1)

for all

s \geq 1

, we have:

E (N, v_{1}, γ^{C}) = \frac{1}{n (n - 1)} [\sum_{s = 2}^{n - 1} \frac{2 (n + 1)}{(s + 2) (s + 1)} 2 (s - 1) + 2 (n - 1)]

= \frac{1}{n (n - 1)} [4 (n + 1) \sum_{s = 2}^{n - 1} \frac{s - 1}{(s + 2) (s + 1)} + 2 (n - 1)]

= \frac{4 (n + 1)}{n (n - 1)} \sum_{s = 2}^{n - 1} \frac{1}{(s + 1)} + \frac{6 - 2 n}{n (n - 1)} .

H_{n} = \sum_{i = 1}^{n} \frac{1}{i},

we have

H_{n} = \int_{0}^{1} \frac{1 - x^{n}}{1 - x} d x \approx l n (n) + K

, with K a constant between 0 and 1, and thus,

lim_{n \to \infty} E (N, v_{1}, γ^{C})

= lim_{n \to \infty} \frac{4 (n + 1)}{n (n - 1)} [l n (n) - \frac{3}{2} + K] + lim_{n \to \infty} \frac{6 - 2 n}{n (n - 1)} = 0 .

For the game

(N, v_{2})

, with characteristic function

v_{2} (S) = s - 1

for all

s \geq 1

, we have:

E (N, v_{2}, γ^{C}) = \frac{1}{n - 1} [\sum_{s = 2}^{n - 1} \frac{2 (n + 1)}{(s + 2) (s + 1)} + 1]]

= \frac{2 (n + 1)}{n - 1} \sum_{s = 2}^{n - 1} \frac{1}{(s + 2) (s + 1)} + \frac{1}{n - 1}

= \frac{2 (n + 1)}{(n - 1)} (\frac{1}{3} - \frac{1}{(n + 1)}) + \frac{1}{(n - 1)} = \frac{2 n - 1}{3 (n - 1)},

and thus,

lim_{n \to \infty} E (N, v_{2}, γ^{C}) = \frac{2}{3} .

For the game

(N, v_{3})

, with characteristic function

v_{3} (S) = 2^{s} - s - 1

for all

s \geq 1

, we have:

E (N, v_{3}, γ^{C}) = \frac{2 (n + 1)}{2^{n} - n - 1} \sum_{s = 2}^{n - 1} \frac{2^{s - 1} - 1}{(s + 2) (s + 1)} + \frac{1}{2^{n} - n - 1} (2^{n - 1} - 1),

and thus

lim_{n \to \infty} E (N, v_{3}, γ^{C}) = \frac{1}{2} .

4.3. The wheel

Consider the communication situation

(N, v, γ^{W})

in which

(N, v)

is a superaditive, symmetric and zero-normalized game and

(N, γ^{W})

is a wheel of n nodes that we assume to be numbered consecutively.

E (N, v, γ^{W}) = \frac{1}{v (n)} \sum_{i = 1}^{n} μ_{i}^{W} (N, v, γ^{W}) .

We have,

\sum_{i = 1}^{n} μ_{i}^{W} (N, v, γ^{W})

= \sum_{s = 1}^{n - 2} n s \sum_{k = 0}^{n - s - 2} (\binom{n - s - 2}{k}) \frac{(n - s - k)! (s + k - 1)!}{n!} [v (s) - v (s - 1)]

+ \frac{n (n - 1) 1! (n - 2)!}{n!} [v (n - 1) - v (n - 2)] + \frac{n 0! (n - 1)!}{n!} [v (n) - v (n - 1)]

= \sum_{s = 1}^{n - 2} 2 n \frac{s!}{(s + 2)!} \sum_{k = 0}^{n - s - 2} \frac{(\binom{n - s - k}{n - s - k - 2}) (\binom{s + k - 1}{k})}{(\binom{n}{n - s - 2})} [v (s) - v (s - 1)]

+ [v (n - 1) - v (n - 2)] + [v (n) - v (n - 1)]

= \sum_{s = 1}^{n - 2} \frac{2 n}{(s + 1) (s + 2)} [v (s) - v (s - 1)] + [v (n) - v (n - 2)],

and thus,

E (N, v, γ^{W}) = \frac{1}{v (n)} [\sum_{s = 2}^{n - 2} \frac{2 n}{(s + 1) (s + 2)} [v (s) - v (s - 1)] + [v (n) - v (n - 2)]] .

In the following we calculate expressions for the efficiency of the wheel in three games considered, and its asymptotic behavior as the number of players increases.

For the game

(N, v_{1})

, with characteristic function

v_{1} (S) = s (s - 1)

for all

s \geq 1

, we have,

E (N, v_{1}, γ^{W}) = \frac{1}{v (n)} [\sum_{s = 2}^{n - 2} \frac{2 n}{(s + 1) (s + 2)} [v (s) - v (s - 1)] + [v (n) - v (n - 2)]]

= \frac{2 n}{n (n - 1)} [\sum_{s = 2}^{n - 2} \frac{s (s - 1) - (s - 1) (s - 2)}{(s + 1) (s + 2)}] + \frac{1}{n (n - 1)} [n (n - 1) - (n - 2) (n - 3)]

= \frac{4}{(n - 1)} [\sum_{s = 2}^{n - 2} \frac{s - 1}{(s + 1) (s + 2)}] + [1 - \frac{(n - 2) (n - 3)}{n (n - 1)}]

= \frac{4}{(n - 1)} [\sum_{s = 2}^{n - 2} \frac{- 2}{s + 1} + \frac{3}{s + 2}] + [1 - \frac{(n - 2) (n - 3)}{n (n - 1)}]

= \frac{4}{(n - 1)} [\sum_{s = 4}^{n - 1} \frac{1}{s} + \frac{3}{n} - \frac{2}{3}] + [1 - \frac{(n - 2) (n - 3)}{n (n - 1)}],

an thus,

lim_{n \to \infty} E (N, v_{1}, γ^{W}) = 0 .

For the game

(N, v_{2})

, with characteristic function

v_{2} (S) = s - 1

for all

s \geq 1

, we have:

E (N, v_{2}, γ^{W}) = \frac{1}{v (n)} [\sum_{s = 2}^{n - 2} \frac{2 n}{(s + 1) (s + 2)} [v (s) - v (s - 1)] + [v (n) - v (n - 2)]]

= \frac{2 n}{(n - 1)} [\sum_{s = 2}^{n - 2} \frac{1}{(s + 1) (s + 2)}] + \frac{2}{(n - 1)} = \frac{2 n}{(n - 1)} [\sum_{s = 2}^{n - 2} \frac{1}{s + 1} - \frac{1}{s + 2}] + \frac{2}{(n - 1)}

= \frac{2 n}{(n - 1)} (\frac{1}{3} - \frac{1}{n}) + \frac{2}{(n - 1)} = \frac{2 n (n - 3)}{3 n (n - 1)} + \frac{2}{(n - 1)},

and thus,

lim_{n \to \infty} E (N, v_{2}, γ^{W}) = \frac{2}{3} .

For the game

(N, v_{3})

, with characteristic function

v_{3} (S) = 2^{s} - s - 1

for all

s \geq 1

, we have,

E (N, v_{3}, γ^{W}) \frac{1}{v (n)} [\sum_{s = 2}^{n - 2} \frac{2 n}{(s + 1) (s + 2)} [v (s) - v (s - 1)] + [v (n) - v (n - 2)]]

= \frac{2 n}{(2^{n} - n - 1)} [\sum_{s = 2}^{n - 2} \frac{1}{(s + 1) (s + 2)} (2^{(s - 1)} + 1)] + \frac{3 . 2^{(n - 2)} - 2}{(2^{n} - n - 1)},

and,

lim_{n \to \infty} E (N, v_{3}, γ_{W}) = \frac{3}{4}

In the following table we summarize the asymptotic behavior of the efficiency of chains, stars and wheels for the tree games considered. It can be seen that the introduced measure is sensible to the geometry of the network and the considered game.

5. A family of vulnerability measures

In this section we introduce a game theoretic family of measures for vulnerability of a network. We will continue with the same setting of communication situations used for efficiency measures. In our approach the vulnerability in

(N, v, γ)

can have two different origins.

On one hand it can be due to lack of connection between components of the graph. This causes that part of the value of the gran coalition

v (N)

is lost and players can obtain only

v^{γ} (N) = \sum_{C \in N / γ} v (C)

. Then, we define the vulnerability due to disconnection in

(N, v, γ)

as,

V_{d} (N, v, γ) = \frac{v (N) - v^{γ} (N)}{v (N)},

i.e., as the proportion of the total productivity in the game lost for lack of connection in the graph.

On the other side, by looking inside the components, lack of links generates costs of intermediation. The proportion of the productivity lost because of these intermediation costs can be seen as other type of vulnerability of the network, the betweenness vulnerability

V_{b}

. In our definition it is given by,

V_{b} (N, v, γ) = \frac{\sum_{i \in N} μ_{i}^{B} (N, v, γ)}{v (N)} .

We will assume that these two types of vulnerability are additive and thus we propose the following definition.

Definition 5.1.

Given a communication situation

(N, v, γ) \in C S_{*}^{N}

, we define a measure of vulnerability of the network

(N, γ)

for the game

(N, v)

as,

V (N, v, γ) = \frac{v (N) - v^{γ} (N)}{v (N)} + \frac{\sum_{i \in N} μ_{i}^{B} (N, v, γ)}{v (N)} = V_{d} (N, v, γ) + V_{b} (N, v, γ) .

The following proposition includes some properties related to the the range of values of the defined measures. The corresponding proofs can be found in Appendix III.

Proposition 5.1.

Given

(N, v, γ) \in {CS}_{*}^{N}

1.: We have that, $0 \leq V (N, v, γ) \leq 1 .$
2.: $V (N, v, γ) + E (N, v, γ) = 1 .$
3.: For connected graphs (ceteris paribus), the disconnection vulnerability vanishes, i.e, if $(N, γ)$ is a connected graph, then,

$V (N, v, γ) = V_{b} (N, v, γ) .$
4.: In any communication situation in which the network is complete, vulnerabilities due to lack of connection and intermediation are both null, i.e., for all $(N, v, γ_{N}) \in {CS}_{*}^{N}$ , where $(N, γ_{N})$ is the complete graph, we have

$V_{d} (N, v, γ_{N}) = V_{b} (N, v, γ_{N}) = 0 .$
5.: In the case of the empty graph all vulnerability is due to disconnection, i.e., for all $(N, v, γ_{\emptyset}) \in {CS}_{*}^{N}$ , where $(N, γ_{\emptyset})$ is the empty graph, we have

$V (N, v, γ_{\emptyset}) = V_{d} (N, v, γ_{\emptyset}) = 1 .$

Proposition 5.2.

Given

(N, v, γ) \in {CS}_{*}^{N}

1.: If $i_{0} \in N$ is a terminal node in the graph and additionally, he is a null player in the game, the disconnection of $i_{0}$ neither $V_{b} (N, v, γ)$ nor $V_{d} (N, v, γ)$ changes, i.e., if $i_{0} \in N$ such that $| γ_{i_{0}} | = 1$ , and $i_{0}$ is a null player in $(N, v)$ it holds that $V_{b} (N, v, γ) = V_{b} (N, v, γ ∖ γ_{i_{0}})$ and $V_{d} (N, v, γ) = V_{d} (N, v, γ ∖ γ_{i_{0}}) .$
2.: If all the links incident in the node of an essential player in the game are broken, the disconnection vulnerability becomes 1 and the betweenness vulnerability vanishes, i.e., if $i_{0} \in N$ is an essential player in $(N, v)$ we have that, $V_{b} (N, v, γ ∖ γ_{i_{0}}) = 0$ and $V_{d} (N, v, γ ∖ γ_{i_{0}}) = 1$ .
3.: $V_{d} (N, v, γ)$ reduces when adding links to a graph, ceteris paribus, i.e., given $(N, v, γ)$ and $(N, v, γ^{'}) \in {CS}_{*}^{N}$ with $γ \subseteq γ^{'}$ , we have $V_{d} (N, v, γ) \geq V_{d} (N, v, γ^{'}) .$ This property is not satisfied for the other component of the vulnerability, the betweenness vulnerability, as the intermediation can increase. This is shown in the example following this proposition.

Example 5.1.

Consider

(N, v, γ)

and

(N, v, γ^{'}) \in {CS}_{*}^{N}

with

v = u_{{1, 2}} + u_{{1, 3}} - u_{{1, 2, 3}}

γ = {{1, 2}}

and

γ^{'} = {{1, 2}, {2, 3}}

. Then, it is easy to verify that

V_{d} (N, v, γ) = 0

and

V_{d} (N, v, γ^{'}) = \frac{1}{3}

The following proposition groups some more properties relating the measurements corresponding to different games. The proofs can be found in Appendix III.

Proposition 5.3.

V

satisfied the following properties:

1.: The strategic equivalence between games preserves the vulnerability. And thus vulnerability does not depend on linear transformations, i.e., given $(N, v, γ)$ and $(N, w, γ) \in {CS}_{*}^{N}$ , $(N, v)$ and $(N, w)$ strategically equivalent, we have that $V_{d} (N, v, γ) = V_{d} (N, w, γ)$ and $V_{b} (N, v, γ) = V_{b} (N, w, γ)$ .
2.: The betweenness vulnerability of a not connected graph can be written in terms of the betweenness vulnerability in the graph restricted to different components, as it is proved in the next proposition, i.e.,suppose $(N, v, γ) \in {CS}_{*}^{N}$ and $N / γ = {C_{1}, C_{2}, \dots, C_{r}} .$ Then,

$V_{b} (N, v, γ) = \sum_{j = 1}^{r} \frac{v (C_{j})}{v (N)} V_{b} (N, v_{| C_{j}}, γ_{| C_{j}}) .$
3.: The betweenness vulnerability can be written as a linear combination of betweenness vulnerabilities in communication situations corresponding to unanimity games (fixed the graph), i.e., given $(N, v, γ) \in {CS}_{*}^{N}$ we have,

$V_{b} (N, v, γ) = \sum_{\emptyset \neq S \subseteq N} \frac{Δ_{v} (S)}{v (N)} V_{b} (N, u_{S}, γ) .$

6. Conclusions and final remarks

In this paper we have introduced a family of efficiency measures and a family of vulnerability measures for a network, from a game theoretical perspective. We have assumed that actors can use the network for different purposes or with different social or economic interests modeled by means of a cooperative game or transferable utility. In this way both families are parameterized by the game. The proposed measures satisfy properties that can be considered as appealing when measuring efficiency or vulnerability in a network.

Given the extensión of the paper, we have excluded additional analyses that we consider relevant and that deserve to be studied. Some examples are the possible relation between these measures and others existing (not necessarily game-theoretic) in the literature, the asymptotic behaviour of the measures in other different structures and games than the studied here, and the problem of determining algorithms to calculate the measurements.

Funding

This research has been partially supported by the “Plan Nacional de I+D+i” of the Spanish Government under the project PID2020-116884GB-I00.

Appendix I

Proof of Proposition 3.1:

1.

Given that

(N, v)

is a non null, superadditive and zero-normalized game we have:

(a): $v (N) > 0$ .
(b): $\sum_{i \in N} μ_{i}^{W} (N, v, γ)$

$= \sum_{i \in N} \sum_{S \subseteq N ∖ {i}} \frac{(n - s - 1)! s!}{n!} [v (C_{i}^{S \cup {i}, γ}) - v (C_{i}^{S \cup {i}, γ} ∖ {i})] \geq 0$

.
(c): $\sum_{i \in N} μ_{i}^{B} (N, v, γ)$

$= \sum_{i \in N} \sum_{S \subseteq N ∖ {i}} \frac{(n - s - 1)! s!}{n!} [v (C_{i}^{S \cup {i}, γ} ∖ {i}) - \sum_{C \in {(C_{i}^{S \cup {i}, γ} ∖ {i})}_{| γ}} v (C)] \geq 0,$

and thus, using

a)

and

b)

, we obtain that

E (N, v, γ) \geq 0

. On the other hand, as

\sum_{i \in N} μ_{i}^{W} (N, v, γ) + \sum_{i \in N} μ_{i}^{B} (N, v, γ) = \sum_{i \in N} μ_{i} (N, v, γ) = v^{γ} (N),

we have that

E (N, v, γ) \leq \frac{v^{γ} (N)}{v (N)}

The second part is straightforward because if a graph is connected then,

v^{γ} (N) = v (N)

2.

To prove that

E (N, v, γ_{N}) = 1

we have that,

\sum_{i \in N} μ_{i}^{W} (N, v, γ)

= \sum_{i \in N} \sum_{S \subseteq N ∖ {i}} \frac{(n - s - 1)! s!}{n!} [v (C_{i}^{S \cup {i}, γ_{N}}) - v (C_{i}^{S \cup {i}, γ_{N}} ∖ {i})]

= \sum_{i \in N} \sum_{S \subseteq N ∖ {i}} \frac{(n - s - 1)! s!}{n!} [v (S \cup {i}) - v (S)]

= \sum_{i \in N} S h_{i} (N, v) = v (N),

the first equality holding by the definition of the within groups Myerson value, the second one because of the connected component of

S \cup {i}

(N, γ_{N})

, for all

S \subseteq N ∖ {i}

i \in N

, is

S \cup {i}

, the third one because of the definition of the Shapley value and the last one using the efficiency of the Shapley value.

To prove that

E (N, v, γ_{\emptyset}) = 0

, we have

\sum_{i \in N} μ_{i}^{W} (N, v, γ)

= \sum_{i \in N} \sum_{S \subseteq N ∖ {i}} \frac{(n - s - 1)! s!}{n!} [v (C_{i}^{S \cup {i}, γ_{\emptyset}}) - v (C_{i}^{S \cup {i}, γ_{\emptyset}} ∖ {i})]

= \sum_{i \in N} \sum_{S \subseteq N ∖ {i}} \frac{(n - s - 1)! s!}{n!} [v ({i}) - v (\emptyset)] = \sum_{i \in N} v ({i}) = 0,

as in this case the connected component of

S \cup {i}

(N, γ_{\emptyset})

for all

S \subseteq N ∖ {i}

i \in N

, is

{i}

, the sum of the marginal contributions weighs in the Shapley formula is equal to one, and the game is zero-normalized.

□

Proof of Proposition 3.2:

1.: If i is a null player in $(N, v)$ then,

$μ_{i}^{W} (N, v, γ) = μ_{i}^{W} (N, v, γ ∖ γ_{i}) = 0 .$

On the other hand, for all $j \in N, j \neq i$ ,

$μ_{j}^{W} (N, v, γ) = \sum_{S \subseteq N ∖ {j}} \frac{(n - s - 1)! s!}{n!} [v (C_{j}^{S \cup {j}, γ}) - v (C_{j}^{S \cup {j}, γ} ∖ {j})] .$

If $i \notin S$ then, $C_{j}^{S \cup {j}, γ} = C_{j}^{S \cup {j}, γ ∖ {l}}$ , and if $i \in S$ then, either $C_{j}^{S \cup {j}, γ} = C_{j}^{S \cup {j}, γ ∖ {l}}$ or $C_{j}^{S \cup {j}, γ} = C_{j}^{S \cup {j}, γ ∖ {l}} \cup {i}$ . As i is a null player in $(N, v)$ , in any case,

$v (C_{j}^{S \cup {j}, γ}) = v (C_{j}^{S \cup {j}, γ ∖ {l}})$

and,

$v (C_{j}^{S \cup {j}, γ} ∖ {j}) = v (C_{j}^{S \cup {j}, γ ∖ {l}} ∖ {j}) .$

Then for all $k \in N$ , $μ_{k}^{W} (N, v, γ) = μ_{k}^{W} (N, v, γ ∖ {l})$ and the result is proved.
2.: For all $j \in N, j \neq i$ ,

$μ_{j}^{W} (N, v, γ) = \sum_{S \subseteq N ∖ {j}} \frac{(n - s - 1)! s!}{n!} [v (C_{j}^{S \cup {j}, γ}) - v (C_{j}^{S \cup {j}, γ} ∖ {j})] = 0,$

as i does not belong to the connected component of j (and thus $i \notin C_{j}^{S \cup {j}, γ} ∖ {j}$ ), because he is isolated.

On the other hand,

$μ_{i}^{W} (N, v, γ) = \sum_{S \subseteq N ∖ {i}} \frac{(n - s - 1)! s!}{n!} [v (C_{i}^{S \cup {i}, γ}) - v (C_{i}^{S \cup {i}, γ} ∖ {i})]$

$= \sum_{S \subseteq N ∖ {i}} \frac{(n - s - 1)! s!}{n!} [v ({i}) - v (\emptyset)] = v ({i}) = 0,$

as for all $S \subseteq N ∖ {i}$ , $C_{i}^{S \cup {i}, γ} = {i}$ and $(N, v)$ is zero-normalized.
3.: Under the hypothesis,

$μ_{i}^{B} (N, v, γ_{i}^{S}) = \sum_{S \subseteq N ∖ {i}} \frac{(n - s - 1)! s!}{n!} [v (C_{i}^{S \cup {i}, γ_{i}^{S}} ∖ {i}) - \sum_{C \in (C_{i}^{S \cup {i}, γ_{i}^{S}} ∖ {i}) / γ_{i}^{S}} v (C)],$

which is equal to zero because i is an essential player and therefore the value of any coalition to which he does not belong is null.

On the other hand, for $j \neq i$ ,

$μ_{j}^{B} (N, v, γ) = \sum_{S \subseteq N ∖ {j}} \frac{(n - s - 1)! s!}{n!} [v (C_{j}^{S \cup {j}, γ_{i}^{S}} ∖ {j}) - \sum_{C \in (C_{j}^{S \cup {j}, γ_{i}^{S}} ∖ {j}) / γ_{i}^{S}} v (C)] .$

If $i \notin S \subseteq N ∖ {j}$ , then $C_{j}^{S \cup {j}, γ_{i}^{S}} = {j}$ and thus $C_{j}^{S \cup {j}, γ_{i}^{S}} ∖ {j} = \emptyset$ . Then in such case,

$v (C_{j}^{S \cup {j}, γ_{i}^{S}} ∖ {j}) - \sum_{C \in (C_{j}^{S \cup {j}, γ_{i}^{S}} ∖ {j}) / γ_{i}^{S}} v (C)] = v (\emptyset) - v (\emptyset) = 0 .$

If, on the other hand, $i \in S \subseteq N ∖ {j}$ , then $C_{j}^{S \cup {j}, γ_{i}^{S}}$ is a connected set and thus,

$v (C_{j}^{S \cup {j}, γ_{i}^{S}} ∖ {j}) - \sum_{C \in (C_{j}^{S \cup {j}, γ_{i}^{S}} ∖ {j}) / γ_{i}^{S}} v (C)]$

$= v (C_{j}^{S \cup {j}, γ_{i}^{S}} ∖ {j}) - v (C_{j}^{S \cup {j}, γ_{i}^{S}} ∖ {j}) = 0 .$

Finally, for all $j \in N$ ,

$μ_{j} (N, v, γ_{i}^{S}) = μ_{j}^{W} (N, v, γ_{i}^{S}) + μ_{j}^{B} (N, v, γ_{i}^{S}) = μ_{j}^{W} (N, v, γ_{i}^{S}) + 0$ , and then,

$E (N, v, γ_{i}^{S}) = \frac{\sum_{j \in N} μ_{j}^{W} (N, v, γ_{i}^{S})}{v (N)} = \frac{\sum_{j \in N} μ_{j} (N, v, γ_{i}^{S})}{v (N)} = \frac{v (N)}{v (N)} = 1,$

given that, as it is known, the Myerson value satisfies component efficiency and the star is a connected graph.
4.: As it is proved in González Arangüena et al. (2017) (Prop 3.3. pag. 590), under convexity of the game

$μ_{i}^{W} (N, v, γ) \leq μ_{i}^{W} (N, v, γ \cup {l}), f o r a l l i \in N,$

and thus the result.

□

Proof of Proposition 3.3:

1.: If $(N, v)$ and $(N, w)$ are strategically equivalent and zero-normalized then, for all $S \subseteq N$ , $w (S) = α v (S), α \in R^{+}$ . As $μ^{W}$ is clearly linear in the game, we have,

$E (N, w, γ) = \frac{\sum_{i \in N} μ_{i}^{W} (N, w, γ)}{w (N)} = \frac{\sum_{i \in N} μ_{i}^{W} (N, α v, γ)}{α v (N)}$

$= \frac{α \sum_{i \in N} μ_{i}^{W} (N, v, γ)}{α v (N)} = E (N, v, γ) .$
2.: We have,

$E (N, v, γ) = \frac{1}{v (N)} \sum_{i \in N} μ_{i}^{W} (N, v, γ) = \frac{1}{v (N)} \sum_{k = 1}^{r} \sum_{i \in C_{k}} μ_{i}^{W} (N, v, γ)$

$μ_{i}^{W} (N, v_{|_{C_{k}}}, γ_{|_{C_{k}}}) = \frac{1}{v (N)} \sum_{k = 1}^{r} v (C_{k}) \sum_{i \in C_{k}} \frac{μ_{i}^{W} (C_{k}, v_{|_{C_{k}}}, γ_{|_{C_{k}}})}{v (C_{k})}$

$= \sum_{k = 1}^{r} \frac{v (C_{i})}{v (N)} E (C_{k}, v_{|_{C_{k}}}, γ_{|_{C_{k}}}),$

where the third equality holds as the within groups Myerson value of a player only depends on the component to which he belong. The other equalities are straightforward.
3.: $E (N, \sum_{k = 1}^{r} v_{k}, γ) = \frac{1}{(\sum_{k = 1}^{r} v_{k}) (N)} \sum_{i \in N} μ_{i}^{W} (N, \sum_{k = 1}^{r} v_{k}, γ)$

$= \frac{1}{(\sum_{k = 1}^{r} v_{k}) (N)} \sum_{i \in N} \sum_{k = 1}^{r} μ_{i}^{W} (N, v_{k}, γ) = \frac{1}{(\sum_{k = 1}^{r} v_{k}) (N)} \sum_{k = 1}^{r} \sum_{i \in N} μ_{i}^{W} (N, v_{k}, γ)$

$= \sum_{k = 1}^{r} \frac{v_{k} (N)}{(\sum_{k = 1}^{r} v_{k}) (N)} E (N, v_{k}, γ) .$

The first and third equalities are by the definition of the measure and the second one by the additivity of $μ^{W}$ .
4.: The result is straightforward particularizing the previous paragraph to communication situations ${(N, Δ_{v} (S) u_{S}, γ)}_{\emptyset \neq S \subseteq N}$ and $(N, v, γ)$ .
5.: We have,

$E (N, u_{S}, γ) = 0, i f MCS (S, N, γ) = \emptyset$

and,

$E (N, u_{S}, γ) = \sum_{i \in N} μ_{i}^{W} (N, u_{S}, γ)$

$= s [\sum_{i = 1}^{r} \frac{1}{| S_{i} |} - \sum_{i < j} \frac{1}{| S_{i} \cup S_{j} |} + . . . {(- 1)}^{r + 1} \frac{1}{| \cup_{i = 1}^{r} S_{i} |}] = s α_{γ} (S),$

$if M C S (S, N, γ) = {S_{1}, . . ., S_{r}},$ where the second equality is obtained in González Arangüena et al. (2017).

□

Appendix II

Consider the communication situation

(N, v, γ^{C})

in which

(N, v)

is a superaditive, symmetric and zero-normalized game and

(N, γ^{C})

is a chain of n nodes that we assume to be numbered consecutively starting with 1 at one end.

In this case we have that,

\sum_{i = 1}^{n} μ_{i}^{W} (N, v, γ^{C}) =

\sum_{s = 1}^{n - 2} \sum_{r = 1}^{n - s - 1} \sum_{l = 0}^{r - 1} \sum_{k = 0}^{n - r - s - 1} s (\binom{r - 1}{l}) (\binom{n - r - s - 1}{k}) \frac{(n - s - l - k)! (s + l + k - 1)!}{n!}

\times [v (s) - v (s - 1)]

+ 2 \sum_{s = 1}^{n - 2} \sum_{k = 0}^{n - s - 1} s (\binom{n - s - 1}{k}) \frac{(n - s - k)! (s + k - 1)!}{n!} [v (s) - v (s - 1)]

+ 2 (n - 1) \frac{1! (n - 2)!}{n!} [v (n - 1) - v (n - 2)] + 2 n \frac{0! (n - 1)!}{n!} [v (n) - v (n - 1)] .

The first summand corresponds to the efficiency generated by the n players from coalitions that have a component of size s,

s = 1, . . ., n - 2

, having these coalitions other components of variable size. Moreover, the component of size s possibly has other component "before" and "after" in the chain labeled from 1 to n. The second summand corresponds to coalitions in which the component of size s is on the left or on the right of the chain. The last two summands are for the case in which the component has size

n - 1

or n.

We have,

\sum_{l = 0}^{r - 1} \sum_{k = 0}^{n - r - s - 1} s (\binom{r - 1}{l}) (\binom{n - r - s - 1}{k}) \frac{(n - s - l - k)! (s + l + k - 1)!}{n!}

\times [v (s) - v (s - 1)]

= s \sum_{l = 0}^{r - 1} \frac{(r + l - 1)! (s + l - 1)!}{(r + s + 1)!} \frac{(r - 1)!}{l! (r - l - 1)!}

\times \sum_{k = 0}^{n - r - s - 1} \frac{(\binom{n - s - l - k}{n - r - s - k - 1}) (\binom{s + l + k - 1}{k})}{(\binom{n}{n - r - s - 1})} [v (s) - v (s - 1)]

= s [v (s) - v (s - 1)] \sum_{l = 0}^{r - 1} \frac{(r + l - 1)! (s + l - 1)!}{(r + s + 1)!} \frac{(r - 1)!}{l! (r - l - 1)!}

= 2 \frac{s!}{(s + 2)!} [v (s) - v (s - 1)] \sum_{l = 0}^{r - 1} \frac{(\binom{s + l - 1}{l}) (\binom{r - l + 1}{r - l - 1})}{(\binom{r + s + 1}{r - 1})}

= 2 \frac{s!}{(s + 2)!} [v (s) - v (s - 1)] .

An thus,

\sum_{s = 1}^{n - 2} \sum_{r = 1}^{n - s - 1} \sum_{l = 0}^{r - 1} \sum_{k = 0}^{n - r - s - 1} s (\binom{r - 1}{l}) (\binom{n - r - s - 1}{k}) \frac{(n - s - l - k)! (s + l + k - 1)!}{n!}

\times [v (s) - v (s - 1)]

= \sum_{s = 1}^{n - 2} \sum_{r = 1}^{n - s - 1} 2 \frac{s!}{(s + 2)!} [v (s) - v (s - 1)] = \sum_{s = 1}^{n - 2} \frac{2 (n - s - 1)}{(s + 2) (s + 1)} [v (s) - v (s - 1)] .

On the other hand, for the second summand,

2 \sum_{s = 1}^{n - 2} \sum_{k = 0}^{n - s - 1} s (\binom{n - s - 1}{k}) \frac{(n - s - k)! (s + k - 1)!}{n!} [v (s) - v (s - 1)]

= 2 \sum_{s = 1}^{n - 2} \frac{s!}{(s + 1)!} \sum_{k = 0}^{n - s - 1} \frac{(\binom{n - s - k}{n - s - k - 1}) (\binom{s + k - 1}{k})}{(\binom{n}{n - s - 1})} [v (s) - v (s - 1)]

= 2 \sum_{s = 1}^{n - 2} \frac{1}{s + 1} [v (s) - v (s - 1)] .

Finally,

\sum_{i = 1}^{n} μ_{i}^{W} (N, v, γ_{C})

= \sum_{s = 1}^{n - 2} \frac{2 (n - s - 1)}{(s + 2) (s + 1)} [v (s) - v (s - 1)] + \sum_{s = 1}^{n - 2} \frac{2}{(s + 1)} [v (s) - v (s - 1)]

+ \frac{2}{n} [v (n - 1) - v (n - 2)] + [v (n) - v (n - 1)]

= \sum_{s = 1}^{n - 1} \frac{2 (n + 1)}{(s + 2) (s + 1)} [v (s) - v (s - 1)] + [v (n) - v (n - 1)]

= \sum_{s = 2}^{n - 1} \frac{2 (n + 1)}{(s + 2) (s + 1)} [v (s) - v (s - 1)] + [v (n) - v (n - 1)],

the last equality holding as for

s = 1

, if

(N, v)

is a zero-normalized game we have that

v (s) - v (s - 1) = v (1) - v (0) = 0

And thus,

E (N, v, γ^{C}) = \frac{1}{v (n)} [\sum_{s = 2}^{n - 1} \frac{2 (n + 1)}{(s + 2) (s + 1)} [v (s) - v (s - 1)] + [v (n) - v (n - 1)]] .

□

Appendix III

Proof of Proposition 5.1:

1.: As $v^{γ} (N) = \sum_{i \in N} μ_{i}^{W} (N, v, γ) + \sum_{i \in N} μ_{i}^{B} (N, v, γ),$ substituting in the definition of $V (N, v, γ)$ ,

$V (N, v, γ) = \frac{v (N) - v^{γ} (N)}{v (N)} + \frac{\sum_{i \in N} μ_{i}^{B} (N, v, γ)}{v (N)}$

$= \frac{v (N) - \sum_{i \in N} μ_{i}^{W} (N, v, γ)}{v (N)} = 1 - E (N, v, γ),$

and given that $0 \leq E (N, v, γ) \leq 1$ , the result is proved.
2.: If $(N, v, γ) \in {CS}_{*}^{N}$ and $(N, γ)$ is a connected graph, we have that $v^{γ} (N) = v (N)$ and thus $V_{d} (N, v, γ) = 0$ .
3.: For all $(N, v, γ_{N}) \in {CS}_{*}^{N}$ we have that $v^{γ_{N}} (N) = v (N)$ and thus $V_{d} (N, v, γ_{N}) = 0$ . Then

$V (N, v, γ_{N}) = V_{d} (N, v, γ_{N}) + V_{b} (N, v, γ_{N}) = V_{b} (N, v, γ_{N}) .$

On the other hand, using i) and that the efficiency in the complete graph is 1,

$V (N, v, γ_{N}) = V_{b} (N, v, γ_{N}) = 1 - E (N, v, γ_{N}) = 1 - 1 = 0 .$
4.: For all $(N, v, γ_{\emptyset}) \in {CS}_{*}^{N}$ we have that $v^{γ_{\emptyset}} (N) = \sum_{i \in N} v ({i} = 0$ (since the game is zero-normalized) and $μ^{B} (N, v, γ_{\emptyset})$ is the null vector, and thus $V (N, v, γ_{\emptyset}) = V_{d} (N, v, γ_{\emptyset}) = 1 .$

□

Proof of Proposition 5.2:

1.: If $i_{0} \in N$ is such that $| γ_{i_{0}} | = 1$ and also he is a null player, we will prove that $μ^{B} (N, v, γ) = μ^{B} (N, v, γ ∖ γ_{i_{0}})$ which implies that $V_{b} (N, v, γ) = V_{b} (N, v, γ ∖ γ_{i_{0}})$ .

For $i_{0}$ ,

$μ_{i_{0}}^{B} (N, v, γ) = \sum_{S \subseteq N ∖ {i_{0}}} \frac{(n - s - 1)! s!}{n!} [v (C_{i_{0}}^{S \cup {i_{0}}, γ} ∖ {i_{0}}) - \sum_{C \in {(C_{i_{0}}^{S \cup {i_{0}}, γ} ∖ {i_{0}})}_{| γ}} v (C)]$

$= \sum_{S \subseteq N ∖ {i_{0}}} \frac{(n - s - 1)! s!}{n!} [v (C_{i_{0}}^{S \cup {i_{0}}, γ} ∖ {i_{0}}) - v (C_{i_{0}}^{S \cup {i_{0}}, γ} ∖ {i_{0}})] = 0 .$

On the other hand,

$μ_{i_{0}}^{B} (N, v, γ ∖ γ_{i_{0}}) = \sum_{S \subseteq N ∖ {i_{0}}} \frac{(n - s - 1)! s!}{n!} [v (C_{i_{0}}^{S \cup {i_{0}}, γ ∖ γ_{i_{0}}} ∖ {i_{0}})$

$- \sum_{C \in {(C_{i_{0}}^{S \cup {i_{0}}, γ ∖ γ_{i_{0}}} ∖ {i_{0}})}_{| γ ∖ γ_{i_{0}}}} v (C)]$

$= \sum_{S \subseteq N ∖ {i_{0}}} \frac{(n - s - 1)! s!}{n!} [v (\emptyset) - v (\emptyset)] = 0 .$

For $i \neq i_{0}$ ,

$μ_{i}^{B} (N, v, γ) = \sum_{S \subseteq N ∖ {i}} \frac{(n - s - 1)! s!}{n!} [v (C_{i}^{S \cup {i}, γ} ∖ {i}) - \sum_{C \in {(C_{i}^{S \cup {i}, γ} ∖ {i})}_{| γ}} v (C)]$

$= \sum_{S \subseteq N ∖ {i}} \frac{(n - s - 1)! s!}{n!} [v (C_{i}^{S \cup {i}, γ ∖ γ_{i_{0}}} ∖ {i}) - \sum_{C \in {(C_{i}^{S \cup {i}, γ ∖ γ_{i_{0}}} ∖ {i})}_{| γ ∖ γ_{i_{0}}}} v (C)],$

the equality holding as for all $S \subseteq N ∖ {i}$ we have that,

$C_{i}^{S \cup {i}, γ} = C_{i}^{S \cup {i}, γ ∖ γ_{i_{0}}}$

or

$C_{i}^{S \cup {i}, γ} = C_{i}^{S \cup {i}, γ ∖ γ_{i_{0}}} \cup {i_{0}},$

and thus,

$v (C_{i}^{S \cup {i}, γ}) = v (C_{i}^{S \cup {i}, γ ∖ γ_{i_{0}}}),$

because $i_{0}$ is a null player. Similarly for each $C \in {(C_{i}^{S \cup {i}, γ} ∖ {i})}_{| γ}$ .

Then

$\sum_{i \in N} μ_{i}^{B} (N, v, γ) = \sum_{i \in N} μ_{i}^{B} (N, v, γ ∖ γ_{i_{0}}),$

and thus,

$V_{b} (N, v, γ) = V_{b} (N, v, γ ∖ γ_{i_{0}}) .$

On the other hand,

$v^{γ} (N) - v^{γ ∖ γ_{i_{0}}} (N) = v (C_{i_{0}}^{N, γ}) - v (C_{i_{0}}^{N, γ} ∖ {i_{0}}) ∖ v ({i_{0}}) = 0,$

the first equality holding as the unique connected component that changes is the one to which $i_{0}$ belongs, and the second because $i_{0}$ is a null player in the zero-normalized game $(N, v)$ , and then $V_{d} (N, v, γ) = V_{d} (N, v, γ ∖ γ_{i_{0}})$ .
2.: If $i_{0} \in N$ is an essential player in $(N, v)$ , as he is isolated in $(N, γ ∖ γ_{i_{0}})$ we have that,

$v^{γ ∖ γ_{i_{0}}} (N) = \sum_{C \in N / (γ ∖ γ_{i_{0}})} v (C) = 0,$

the second equality holding as all the components to which $i_{0}$ does not belong have null value and the game is zero-normalized.
3.: Suppose $(N, v, γ)$ and $(N, v, γ^{'}) \in {CS}_{*}^{N}$ with $γ \subseteq γ^{'}$ then,

$v^{γ^{'}} (N) = \sum_{C^{'} \in N / γ^{'}} v (C^{'}) \geq \sum_{C \in N / γ} v (C) = v^{γ} (N),$

the inequality holding as possibly several (disjoint) connected components in $(N, γ)$ become a unique connected component in $(N, γ^{'})$ , and the game is superadditive. As a consequence,

$V_{d} (N, v, γ) = 1 - \frac{v^{γ} (N)}{v (N)} \geq 1 - \frac{v^{γ^{'}} (N)}{v (N)} = V_{d} (N, v, γ^{'}),$

and the result is proved.

□

Proof of Proposition 5.3:

1.: If $(N, v)$ and $(N, w)$ are strategically equivalents, its exists $α \in R^{+}$ such that $w = α v$ and thus $w (N) = α v (N)$ , $w^{γ} (N) = α v^{γ} (N)$ , and $μ^{B} (N, w, γ) = α μ^{B} ((N, v, γ)$ because the between groups Myerson value is linear in the game (ceteris paribus). Then, we have the result.
2.: Under the given hypothesis,

$V_{b} (N, v, γ) = \frac{\sum_{i = 1}^{n} μ_{i}^{B} (N, v, γ)}{v (N)} = \frac{\sum_{j = 1}^{r} \sum_{i \in C_{j}} μ_{i}^{B} (N, v, γ_{| C_{j}})}{v (N)}$

$= \frac{\sum_{j = 1}^{r} \sum_{i \in C_{j}} μ_{i}^{B} (N, v_{| C_{j}}, γ_{| C_{j}})}{v (N)} = \sum_{j = 1}^{r} \frac{v (C_{j})}{v (N)} \frac{\sum_{i \in C_{j}} μ_{i}^{B} (N, v_{| C_{j}}, γ_{| C_{j}})}{v (C_{j})}$

$= \sum_{j = 1}^{r} \frac{v (C_{j})}{v (N)} \frac{\sum_{i \in C_{j}} μ_{i}^{B} (N, v_{| C_{j}}, γ_{| C_{j}})}{v_{| C_{j}} (C_{j})} = \sum_{j = 1}^{r} \frac{v (C_{j})}{v (N)} V_{b} (N, v_{| C_{j}}, γ_{| C_{j}}),$

where the third equality holds as the between groups Myerson value of a player only depends on the component to which he belong. The other equalities are straightforward.
3.: Using the linearity of the between groups Myerson value we have,

$V_{b} (N, v, γ) = \frac{\sum_{i = 1}^{n} μ_{i}^{B} (N, v, γ)}{v (N)} = \frac{\sum_{i \in N} \sum_{\emptyset \neq S \subseteq N} Δ_{v} (S) μ_{i}^{B} (N, u_{S}, γ)}{v (N)}$

$= \sum_{\emptyset \neq S \subseteq N} \frac{Δ_{v} (S)}{v (N)} \sum_{i \in N} μ_{i}^{B} (N, u_{S}, γ) = \sum_{\emptyset \neq S \subseteq N} \frac{Δ_{v} (S)}{v (N)} V_{b} (N, u_{S}, γ) .$

□

References

Gómez, D., González-Arangüena, E., Manuel, C., Owen, G., del Pozo, M., Tejada, J. (2003). Centrality and power in social networks: a game theoretic approach. Mathematical Social Sciences 46, 27-54. [CrossRef]
González-Arangüena, E., Manuel, C., Owen, G., del Pozo, M. (2017). The within groups and the between groups Myerson values, European Journal of Operational Research, 257, 586-600. [CrossRef]
Harsanyi, J.C. (1959). A bargaining model for cooperative n-person games. In: Tucker, A.W., Luce, R.D. (Eds) Contributions to the Theory of Games IV, Princeton University Press, Princeton, pp. 325-355.
Myerson, R.B., (1977). Graphs and cooperation in games, Mathematics of Operations Research, 2, 225-229. [CrossRef]
Myerson R.B., (1980). Conference structures and fair allocation rules. International Journal of Game Theory 9: 169-182. [CrossRef]
Ozdaglar, A., Menache, I. (2022). Network Games. Springer Nature.
Shapley L.S. (1953). A value for n-person games. In: Kuhn, H.W., Tucker, A.W. (Eds), Annals of Mathematics Studies, 28, Princeton University Press, Princeton, NJ, pp. 307-317. [CrossRef]
van den Brink, R., Gilles, R. P. (1996). Axiomatizations of the conjunctive permission value for games with permission structures. Games and Economic Behaviour, 12, 113-126. [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Efficiency and Vulnerability in Networks. A Game Theoretical Approach

Abstract

1. Introduction

2. Preliminaries

2.1. Games

2.2. Graphs

2.3. Communications situations

3. A family of efficiency measures

4. Efficiency and its asymptotic behavior in some particular cases

4.1. The star

4.2. The chain

4.3. The wheel

5. A family of vulnerability measures

6. Conclusions and final remarks

Funding

Appendix I

Appendix II

Appendix III

References

MDPI Initiatives

Important Links

Subscribe