Prerpints.org logo
Preprint
Article

In situ SAXS-WAXS Temperature Evolution Study of the Nanostructure of Self-Reinforced Ultra High Molecular Weight Polyethylene (UHMWPE)

Altmetrics

Downloads

154

Views

97

Comments

0

Submitted:

08 November 2023

Posted:

09 November 2023

You are already at the latest version

Alerts
Abstract
Ultra high molecular weight polyethylene (UHMWPE) is a thermoplastic high-performance polymer in high demand for biomedicine, ship and machine building, anthropomorphic robots and smart prostheses. Highly oriented UHMWPE fibers possess record specific strength and may also be used for the fabrication of self-reinforced PE-PE composites (SRPEC). The temperature evolution study of the small-angle X-ray scattering (SAXS) signature of the supramolecular structure of UHMWPE can help reveal their important role in the mechanism of the shape memory effect in SRPEC. The laboratory SAXS–WAXS beamline XEUSS 3.0 was used for in situ studies of the nanostructure parameters in unidirectional SRPEC. Namely, the radius of gyration and the dimensionality factor were extracted from 2D SAXS patterns using several fitting algorithms. Significant changes of these parameters occurred in temperature ranges that correspond to the initiation of the shape memory effect and melting. The relationship between the material anisotropy and 2D SAXS patterns are discussed in the context of the supramolecular structure evolution.
Keywords: 
Subject: Chemistry and Materials Science  -   Materials Science and Technology

INTRODUCTION

The typical molecular backbone of ultra high molecular weight polyethylene (UHMWPE) contains from a few to tens hundred thousand –[CH2]– units. Free molecule ends occur very rarely, and this peculiarity of the molecular structure predetermines the most known meritorious properties of UHMWPE – the chemical (and hence biological) inertness, very low friction coefficient (and hence high wear resistance), high fracture toughness [1] and the ability to recover the original shape upon heating, i.e. the temperature shape memory effect (SME). The supramolecular structure, i.e. the manner of molecule spatial organization, is the next up hierarchical dimensional level that includes the crystalline and non-crystalline domains of nanometer to micrometer size. Supramolecular structure is formed during synthesis and processing and may vary significantly. In UHMWPE, it causes the variation of the elastic moduli and strength over a few orders of magnitude [2]. The supramolecular structure of UHMWPE is diverse and can be described as lamellar, spherulitic, shish-kebab, etc. [3]. In the case of shape memory effect, the supramolecular structure of UHMWPE manifests itself in different values of recovery stresses and strains, and the variation of the activation temperature when the shape memory effect is triggered.
The characterization of the supramolecular structure is a challenging task since X-ray diffraction, SEM, TEM, AFM techniques often fail to provide unambiguous information due to the difficulties in sample preparation, while the theoretical approaches – density functional theory (DFT), molecular dynamics (MD) [4,5] – leave wide gaps for validation and interpretation. Nevertheless, the tuning of the shape memory effect through the modification and control of the supramolecular structure is of particular practical interest in connection with SME-driven artificial muscles for smart prostheses, anthropomorphic robots and energy harvesting that promise many successful applications.
A successful example of the great potential of supramolecular structure engineering in UHMWPE are the highly oriented UHMWPE fibers that possess world record specific strength and are used in high performance ropes. Moreover, highly oriented UHMWPE fibers provide an ideal reinforcement of polyethylene matrix giving birth to the so-called self-reinforced PE-PE composites (SRPEC) [6]. We recently proposed a technique for the fabrication of “matrix-free” SRPEC where matrix is obtained via the local partial melting of unidirectionally laid-out oriented fibers [7] and shows the best matrix-fiber adhesion. The interweaving of molecules at the boundary of fibers during melting and the formation of the new supramolecular structure at the boundary after melting and cooling determine the fiber-matrix adhesion and thus the overall composite strength.
We report the results of in situ SAXS studies of SRPEC that was heated up to premelting temperature (140° C) inside the Linkam HFSX350+RH compact heating chamber mounted in the X-ray beam path of the laboratory SAXS-WAXS beamline XEUSS 3.0. A series of 2D SAXS patterns was acquired which showed strong anisotropy. These 2D patterns were segmented into pie sectors (‘caked’), and after radial integration the 1D spectra were analyzed extract the nanostructure parameters – the radius of gyration and the dimensionality factor – using a number of fitting algorithms. These parameters were further used as initial inputs for secondary fitting of 2D patterns. Significant changes of these parameters take place in the temperature ranges that correspond to the shape memory effect triggering and melting. These new insights provide additional arguments for conceptual modelling of the supramolecular structure.

MATERIALS AND METHODS

The UHMWPE fibers Dyneema® SGX (DSM Dyneema, Heerlen, Netherlands) were cut and aligned together to form a layer in a stainless-steel mold base with the dimensions of 10.5×80 mm. The fibers have an average diameter of 15 μm and a linear density of 220 Dtex. The self-reinforced composite was produced through hot compaction at 170 °C temperature and 25 MPa pressure for 10 min. A more comprehensive description of the procedure is available in an prior publication [8].
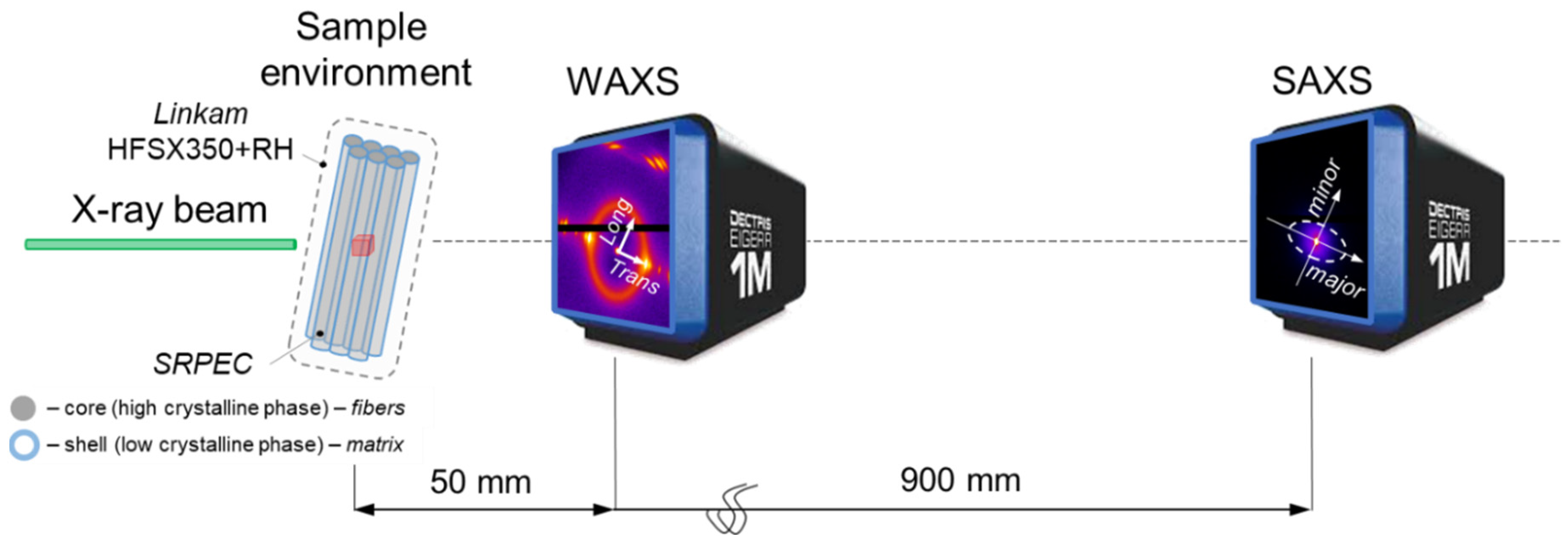
The thermal evolution of the nanostructure of the self-reinforced UHMWPE composite was studied using a laboratory X-ray beamline Xeuss 3.0 (Xenocs Inc, Grenoble, France) equipped with a dedicated temperature control stage Linkam HFSX350+RH (Linkam Scientific, Salford, United Kingdom). The in situ study included both wide-angle x-ray scattering (WAXS) and small-angle x-ray scattering (SAXS) measurements captured at 50 mm and 900 mm sample to detector distances, respectively. Each 2D pattern was collected over a 10 min duration. The dataset was acquired across a temperature range from 23 °C (room temperature) to 140 °C (0.95 T m of this polymer) with 20 °C intervals. The sketch of the experimental setup is shown in Figure 1. The major axis of the elliptical SAXS scattering pattern or the longitudinal direction in real space corresponds to the fiber axis of SRPEC, while the scattering minor axis corresponds to the transverse direction in real space (across the fiber axis).
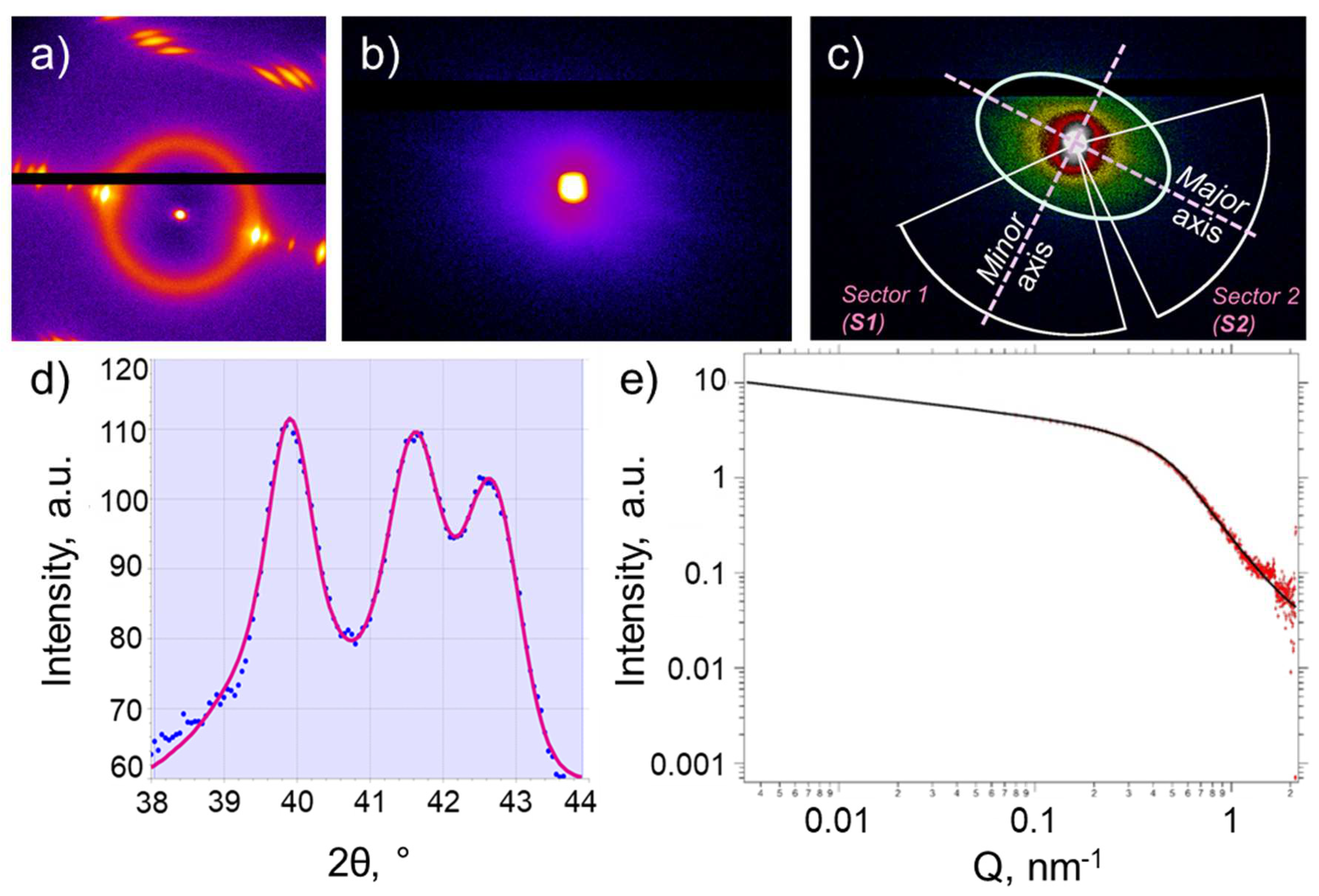
The anisotropic scattering of the self-reinforced composite was analyzed using the 2D WAXS and SAXS patterns collected at room temperature, as illustrated in Figure 2a) and Figure 2b). The subsequent data analysis was carried out separately for the longitudinal (minor axis) and transverse (major axis) directions by dividing each pattern into two sectors, as shown in Figure 2c). Every sector spanning the angle of 60° was azimuthally integrated. Next, we applied a Gauss function to fit every peak of the 1D WAXS profile and extract the peak position and full width at half maximum (FWHM). These estimates were used to determine the thermal expansion coefficient of both the amorphous and crystalline phases as well as the crystallite size. The example of multipeak fitting is illustrated in Figure 2d). The thermal expansion coefficient was calculated according to the formula
α = 1 d ⋅ Δ d Δ T ,
where α is a thermal expansion coefficient K − 1 ;
Δ d is a change in interplanar distance nm ;
d is a particular interplanar distance n m ;
Δ T is a change in temperature [ K ] .
The crystallite size was estimated according to the Scherrer equation [9]
D = K λ B ( 2 θ ) cos ⁡ θ
where D is the average size of the ordered (crystalline) domains n m ;
K = 0.9 is a dimensionless shape factor, which actually varies from 0.62 to 2.08;
λ is the X-ray wavelength [ n m ] ;
B 2 θ is line broadening at FWHM of a peak r a d ;
θ is the Bragg angle [ r a d ] .
On the other hand, a generalized Guinier-Porod model [10]
I Q = G Q s exp ⁡ − Q 2 R g 2 3 − s   f o r   Q ≤ Q 1 , I Q = D Q d   f o r   Q ≥ Q 1 ,
where I Q is the scattered intensity [a.u.];
Q is the scattering variable [nm-1];
Q 1 = 1 R g 3 d 2 1 / 2 is a value, where the values of the Guinier and Porod terms and their slopes (derivatives) must be continuous [nm-1];
R g is the radius of gyration [nm];
d is the Porod exponent;
s is the parameter, which helps model nonspherical objects;
G and D are the Guinier and Porod scale factors.
was used to fit each 1D SAXS profile as depicted in Figure 1e). This enabled the radius of gyration ( R g ) and dimensionality factor (3- s ) of the scattering particles to be extracted. In this case, the radius of gyration means the root mean square distance of electron density increment from the center of mass of a scattering object. The ‘dimensionality’ parameter was introduced to describe non-spherical scattering objects, such as rods or lamellae. This empirical model has been validated, showing that s = 0 corresponds to three-dimensional near equiaxed globular objects such as spheroids, s = 1 is relevant for rods, and s = 2 for lamellae (or platelets), respectively.
Furthermore, a 1D correlation function analysis was utilized to find the ideal lamellar structural parameters like long period ( L ), local crystallinity value and average hard block thickness ( L c ). The mathematical description for this analysis is documented in reference [11].

RESULTS AND DISCUSSION

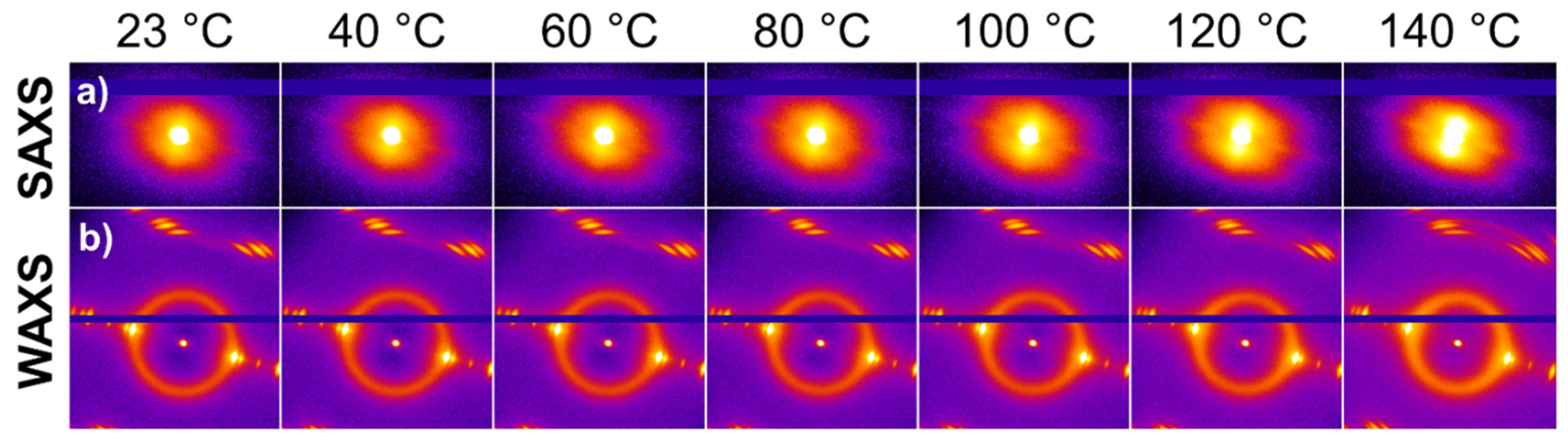
The combination of 2D SAXS and WAXS analyses reveals information regarding the crystalline structure, phase behavior, molecular packing, and orientation of the material at the nanoscale level. Additionally, it provides information about the size, shape, and distribution of nanoparticles or other nanostructures within the material. The evolution of the composite structure is reflected in the 2D SAXS and WAXS patterns shown in Figure 3a) and Figure 3b), respectively. The elongation of the pattern along the ‘major’ axis is apparent, indicating molecular rearrangement and crystallite re-alignment during the heating process.
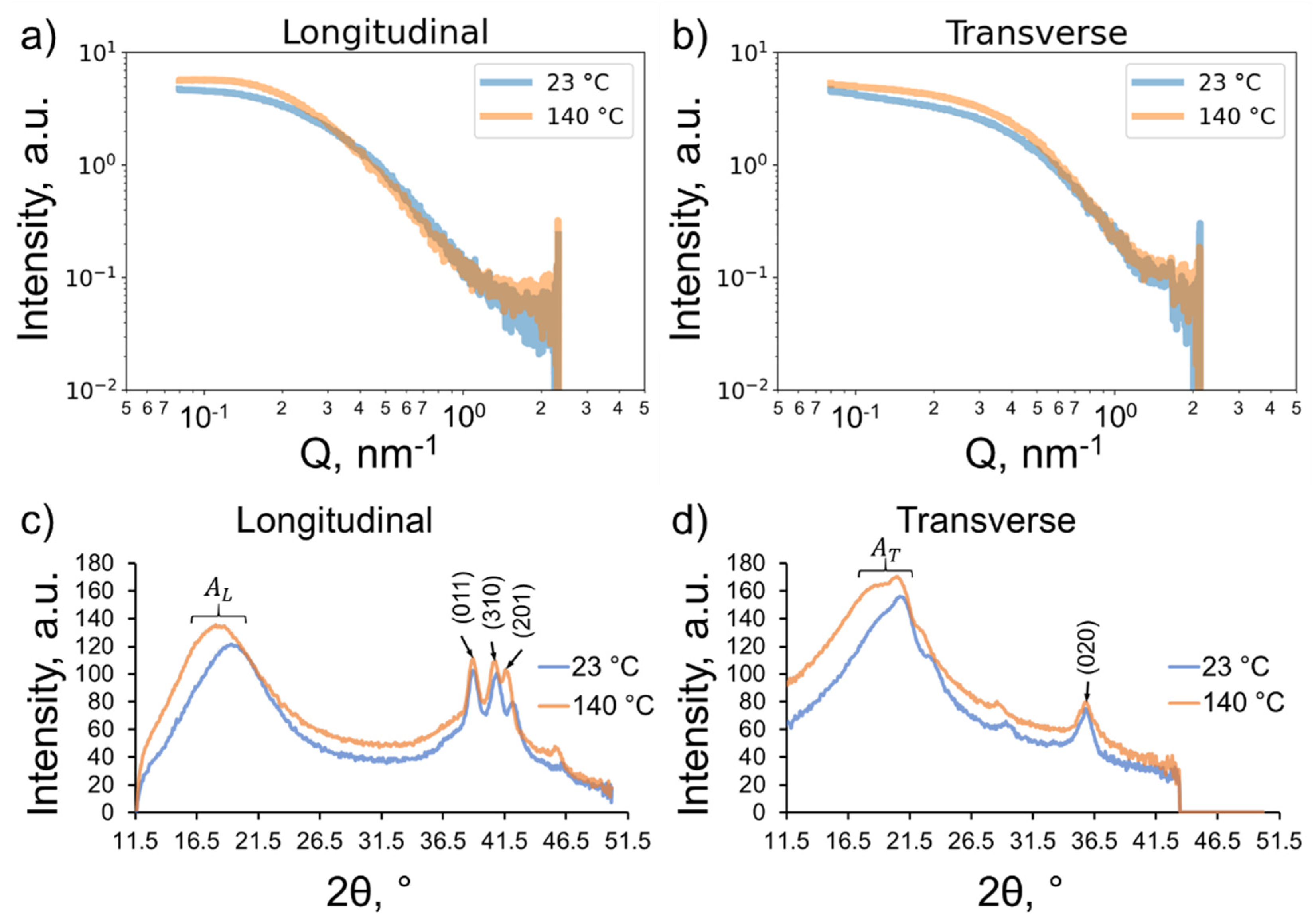
The azimuthally integrated profiles for the SAXS and WAXS patterns taken at temperatures of 23 °C and 140 °C are established in Figure 4, highlighting the temperature effects on the amorphous and crystalline regions in SRPEC. Notably, the amorphous halo shift is significantly greater than crystalline one as observed in Figure 4c) and Figure 4d). Moreover, different orientations of crystallites were detected in both the longitudinal and transverse directions of SRPEC.
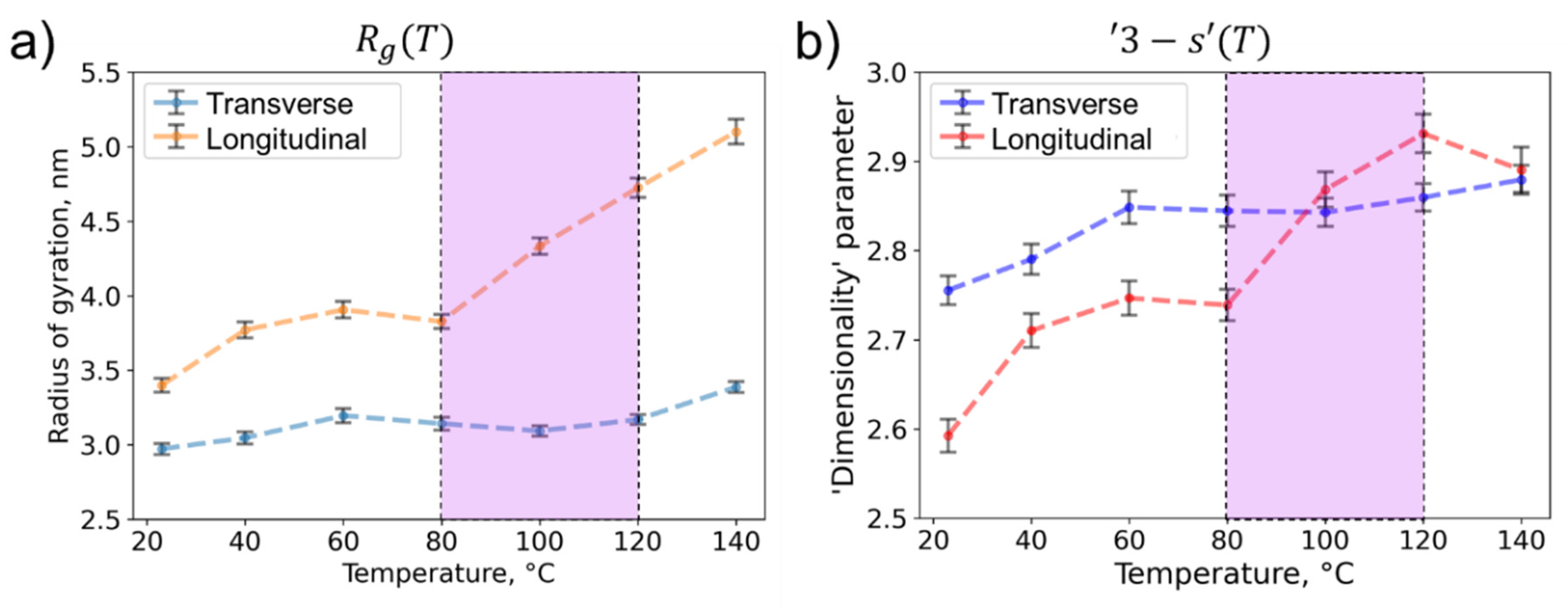
The temperature-dependent variations of the radius of gyration and the ‘dimensionality’ parameter are illustrated in Figure 5. The results obtained for the ‘major’ (transverse) axis exhibit insignificant changes with increasing temperature for both parameters. The radius of gyration slightly increases from about 3.0 to 3.4 nm over the entire temperature range, whereas the ‘dimensionality’ parameter steadily increases from 2.8 to 2.9. Interestingly, both parameters have an anomaly point at 60 °C where the growth decelerates.
On the other hand, the data determined for the ‘minor’ (longitudinal) axis demonstrate faster growth with local minima at 80 °C. As the result, the characteristic size of the nanostructure (radius of gyration) increases by ~1.5 times, from approximately 3.4 to 5.1 nm, while the ‘dimensionality’ parameter changes by 10 % from about 2.6 to 2.9. It is worth noting a transition in the nanostructure evolution that is observed at the temperature of ~80 °C, as the gradient of the parameters increases twofold. Additionally, the ‘dimensionality’ parameter exhibits a slight drop after reaching the temperature of 120 °C.
The detected change in the slope of nanostructure evolution observed at 80 °C can be linked to the recognized onset of the SME that has been thoroughly studied for different types of UHMWPE [12]. The SME in UHMWPE, as well as in other semi-crystalline polymers, arises as the result of the interaction between its crystalline domains and amorphous phase.
The crystalline regions in UHMWPE are distinguished by the regular chain folding into a lattice containing physical crosslinks and can be thought to act as “stiff blocks”, that may be thought of as somewhat analogous with the structure of other thermoplastic polymers [13]. These domains provide a reference structure and remain relatively stable during the SME process. The “programming” phase of the SME involves setting a temporary shape, whilst the crystalline regions act as ‘anchors’ to preserve the deformed shape during sample cooling.
In contrast, the amorphous regions in UHMWPE are more mobile flexible/compliant and can be deformed relatively easily. When the polymer is heated to set a temporary shape and then cooled, the strained and aligned amorphous regions are “frozen” in the deformed state due to the anchoring effect of the crystalline domains. Upon reheating during the shape recovery phase, the increased mobility of the polymer chains in the amorphous regions allows the polymer to revert to its original configuration. The tendency of the amorphous chains to return to their lowest free energy state (i.e., their initial, undeformed state of higher entropy) provides the driving force for shape recovery.
From a molecular perspective, the driving force behind the SME is the polymer chains propensity to return to their most favorable relaxed state. Deforming (ordering, texturing, alignment) the polymer decreases the entropy of the amorphous regions. When the stimulus (usually heat) is applied, the chains tend to revert to their original state, boosting the entropy and manifesting macroscopically as the SME [14].
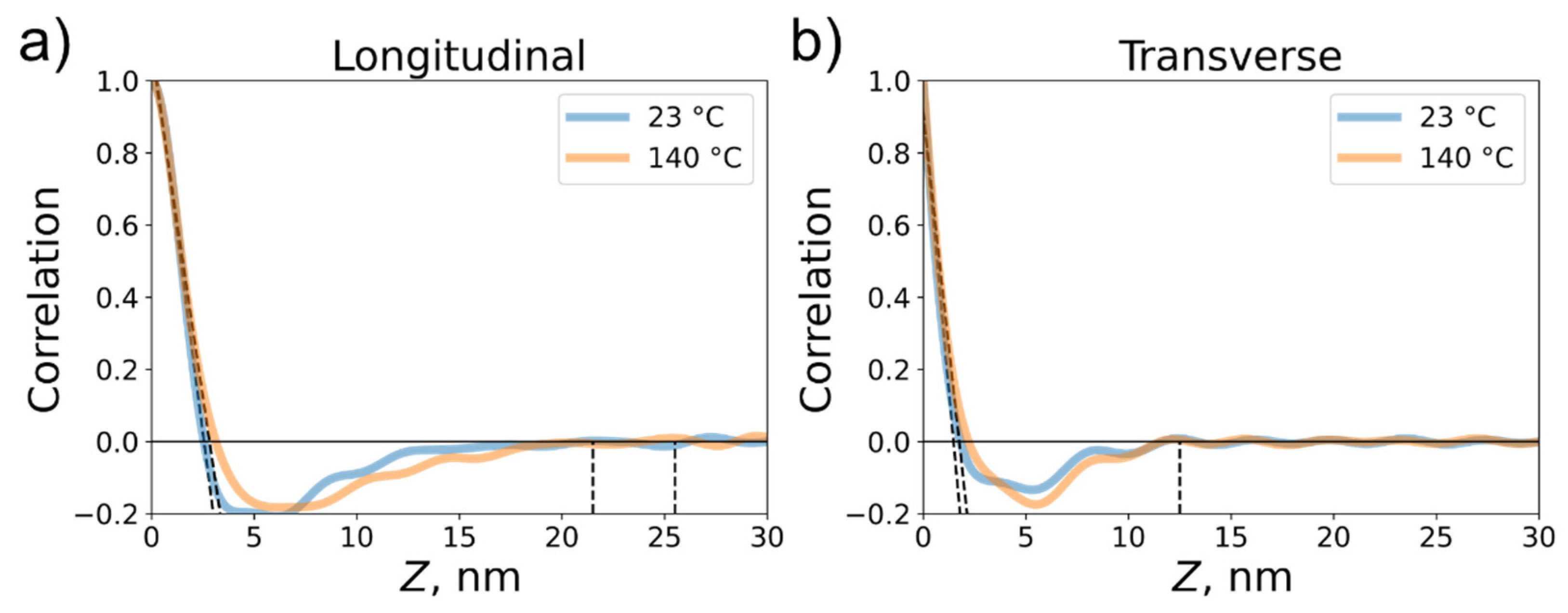
The analysis of 1D correlation function is shown in Figure 6. It confirmed changes in dimensions that were identified in relation to the dependence on radius of gyration. Specifically, the long period of the lamellar structure increases from 21.5 to 25.5 nm in longitudinal direction and it remains permanent at 12.5 nm for transverse direction during temperature rise. Since the change of the average hard block thickness is small and relatively constant, we assume greater contribution of amorphous (soft) phase mobility because L a = L p − L c .
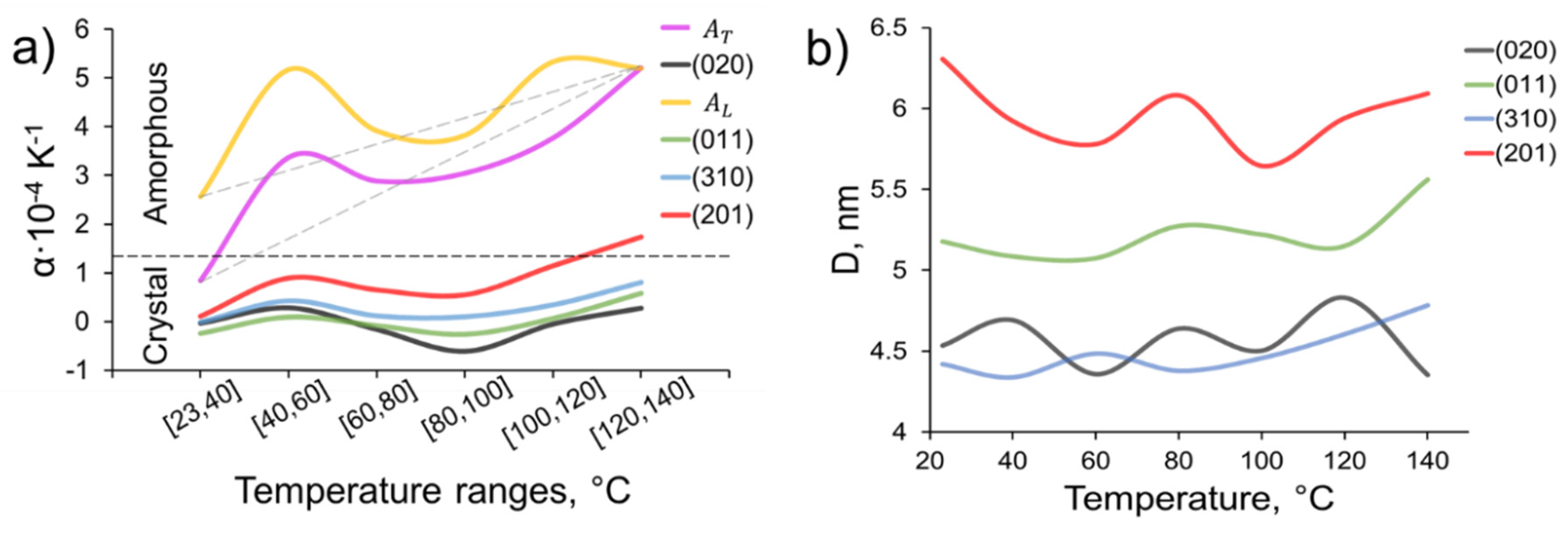
As shown previously, WAXS analysis can provide complementary insights into the internal ultrastructure of polymer fibers [15]. In particular, the results of thermal expansion coefficient (TEC) as well as crystallite size for different crystal planes over temperature are shown in Figure 7. The thermal expansion coefficient of the amorphous phase is over ten times larger than that of the crystalline phase. This confirms a significant tendency for large changes of amorphous phase caused by temperature increase. Additionally, the TEC of the crystalline phase remains almost constant and independent of direction and temperature while amorphous TEC is consistently greater in the longitudinal direction than in the transverse direction up to 140 °C. Crystallite sizes also remain constant regardless of the direction and temperature.
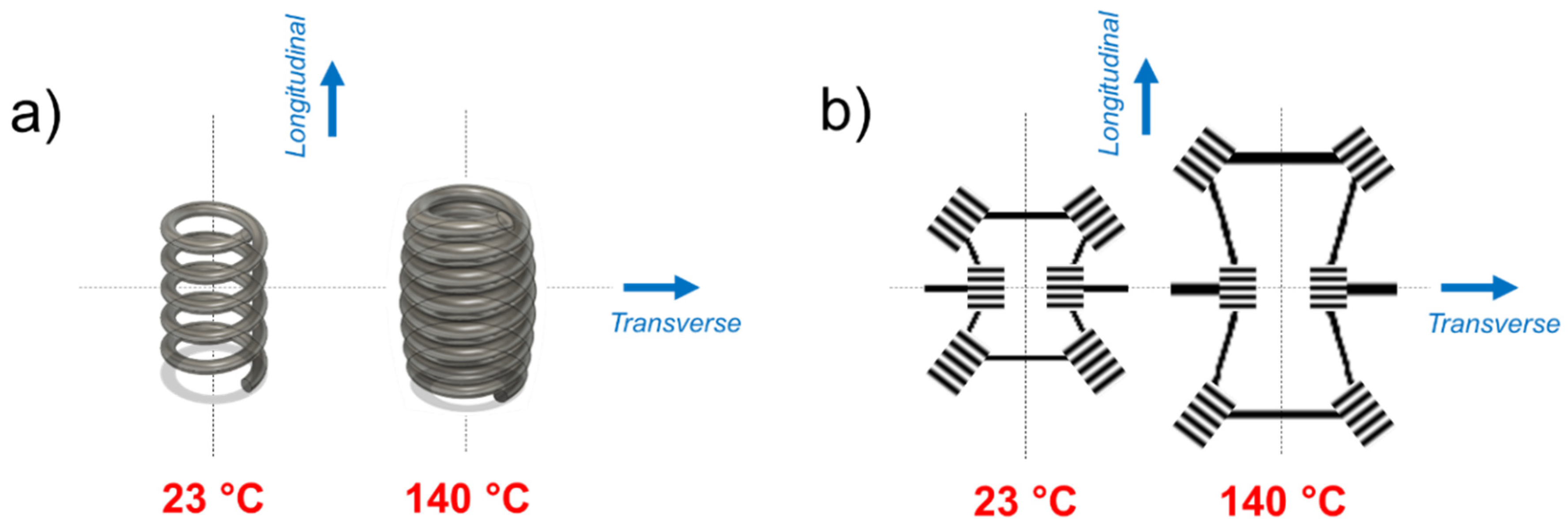
Summarizing experimental data on the described above parameters, we put forward a conceptual model of geometry and topology changes of the amorphous domain entrapped between hard crystalline domains that may be thought to resemble spiral springs (with decreasing density of coils when SME unfolds) or as auxetic twisted structures [16], or a combination of both, as shown in Figure 8.
This conceptual model needs to be explored further by attracting the full power of computational science to simulate 2D SAXS patterns, and also to estimate the entropic contribution to SME recovery.
Overall, it became apparent from combined SAXS-WAXS analysis that in the case of highly aligned fibrillar structure of self-reinforced UHMWPE most significant changes occurred in the longitudinal direction. The observed increase in the radius of gyration can be associated with the expansion of amorphous regions that results in their considerably higher apparent thermal expansion coefficient. This effect alone can account for the shape recovery mechanism in these systems.

CONCLUSIONS

The present article investigated the thermal nanostructure evolution in self-reinforced UHMWPE composites. To accomplish this goal, a series of in situ SAXS-WAXS experiments was conducted.
It was determined that the size of nanostructure as well as the ‘dimensionality’ parameter did not reveal significant changes along the ‘major’ axis during the heating process, in contrast with the results obtained for the ‘minor’ axis (longitudinal fiber direction). The observed temperature-dependent relationships for this direction demonstrated more significant growth, with an apparent slope discontinuity corresponding to a mechanism change in the nanostructure evolution at 80 °C. Specifically, the radius of gyration increased 1.5 times while the ‘dimensionality’ parameter changed by 10 %. The detected anomalous behavior at 80 °C was attributed to the well-known shape memory effect. It has been established that the temperature range for this effect was from 80 °C to 120 °C.
Understanding the phenomena of SME in UHMWPE is vital for optimizing and tailoring the shape memory behavior for specific applications. Adjusting the processing conditions or the structure of the UHMWPE, e.g., through blending or copolymerization, has the potential to allow fine-tuning of these phenomena to achieve the desired performance characteristics.

Funding

This research was supported by the Russian Science Foundation in the frame of the 21-73-20205 project “Operando study of evolution of structural elements in composite and hybrid polymer-matrix materials during the development of the shape memory effect”, https://rscf.ru/en/project/21-73-20205/.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Acknowledgments

E.S. Statnik and A.I. Salimon thank the Russian Science Foundation for providing support in the frame of the 21-73-20205 project, https://rscf.ru/en/project/21-73-20205/.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Kurtz SM. A primer on UHMWPE. In Kurtz SM. The UHMWPE Handbook http://ci.nii.ac.jp/ncid/BA79230584; 2009:1-6. doi:10.1016/b978-0-12-374721-1.00001-8.
  2. Spiegelberg SH. Characterization of physical, chemical, and mechanical properties of UHMWPE. In Kurtz SM. The UHMWPE Handbook http://ci.nii.ac.jp/ncid/BA79230584; 2009:355-368. doi:10.1016/b978-0-12-374721-1.00024-9.
  3. Michler GH, Baltá-Calleja FJ. Nano- and Micromechanics of Polymers.; 2012. [CrossRef]
  4. Petrov A, Rudyak VYu, Chertovich AV. Optimal entanglement of polymers promotes the formation of highly oriented fibers. Macromolecules. 2022;55(15):6493-6504. [CrossRef]
  5. Petrov A, Rudyak VYu, Kos P, Chertovich AV. Polymerization of Low-Entangled Ultrahigh Molecular Weight Polyethylene: analytical model and computer simulations. Macromolecules. 2020;53(16):6796-6808. [CrossRef]
  6. Capiati NJ, Porter RS. The concept of one polymer composites modelled with high density polyethylene. Journal of Materials Science. 1975;10(10):1671-1677. [CrossRef]
  7. Zherebtsov DD, Chukov DI, Royaud I, et al. On the Structural Peculiarities of Self-Reinforced Composite Materials Based on UHMWPE Fibers. Polymers. 2021;13(9):1408. [CrossRef]
  8. Zherebtsov DD, Chukov DI, Torokhov V, Statnik ES. Manufacturing of Single-Polymer composite materials based on Ultra-High Molecular weight polyethylene fibers by hot compaction. Journal of Materials Engineering and Performance. 2020;29(3):1522-1527. [CrossRef]
  9. Patterson AL. The Scherrer formula for X-Ray particle size determination. Physical Review. 1939;56(10):978-982. doi:10.1103/physrev.56.978.
  10. Hammouda B. A new Guinier–Porod model. Journal of Applied Crystallography. 2010;43(4):716-719. doi:10.1107/s0021889810015773.
  11. SASview software. Correlation Function Analysis. URL: https://www.sasview.org/docs/user/qtgui/Perspectives/Corfunc/corfunc_help.html (accessed on 07.11.2023).
  12. Zhang R, Yang Q, Liu M, Chen X, Xue P. Thermal actuation shape memory of ultra-high-molecular-weight polyethylene (UHMWPE) with molecular orientation. Materials Letters. 2022;325:132813. [CrossRef]
  13. Sui T, Baimpas N, Dolbnya IP, Prisăcariu C, Korsunsky AM. Multiple-length-scale deformation analysis in a thermoplastic polyurethane. Nature Communications. 2015;6(1). [CrossRef]
  14. Maksimkin AV, Kaloshkin SD, Zadorozhnyy MYu, Tcherdyntsev VV. Comparison of shape memory effect in UHMWPE for bulk and fiber state. Journal of Alloys and Compounds. 2014;586:S214-S217. [CrossRef]
  15. Gazzano M, Gualandi C, Zucchelli A, et al. Structure-morphology correlation in electrospun fibers of semicrystalline polymers by simultaneous synchrotron SAXS-WAXD. Polymer. 2015;63:154-163. [CrossRef]
  16. Salimon AI, Senatov FS, Kalyaev V, Korsunsky AM. Shape memory polymer blends and composites for 3D and 4D printing applications. Editor(s): Kishor Kumar Sadasivuni, Kalim Deshmukh, Mariam Alali Almaadeed, 3D and 4D Printing of Polymer Nanocomposite Materials, Elsevier, 2020, p. 161-189. ISBN 9780128168059. [CrossRef]
Preprints 90049 g001
Figure 1. The schematic diagram of the experimental setup.
Figure 1. The schematic diagram of the experimental setup.
Preprints 90049 g001
Preprints 90049 g002
Figure 2. The example of obtained 2D patterns acquired for self-reinforced UHMWPE: a) WAXS and b) SAXS. c) The schematic indication of the two sectors separated by the angle of 90° along the longitudinal (‘minor’ axis) and transverse (‘major’ axis) directions. The dimensionality data reduction by azimuthal integration: d) 1D WAXS profile (blue points) and fitted Gauss function to multiple peaks (pink line), e) 1D SAXS profile (red points) and fitted generalized Guinier-Porod model (black line).
Figure 2. The example of obtained 2D patterns acquired for self-reinforced UHMWPE: a) WAXS and b) SAXS. c) The schematic indication of the two sectors separated by the angle of 90° along the longitudinal (‘minor’ axis) and transverse (‘major’ axis) directions. The dimensionality data reduction by azimuthal integration: d) 1D WAXS profile (blue points) and fitted Gauss function to multiple peaks (pink line), e) 1D SAXS profile (red points) and fitted generalized Guinier-Porod model (black line).
Preprints 90049 g002
Preprints 90049 g003
Figure 3. The evolution of 2D a) SAXS and b) WAXS patterns during heating of the self-reinforced UHMWPE composite.
Figure 3. The evolution of 2D a) SAXS and b) WAXS patterns during heating of the self-reinforced UHMWPE composite.
Preprints 90049 g003
Preprints 90049 g004
Figure 4. The average 1D profiles of SAXS and WAXS patterns taken at two temperatures: a) SAXS, longitudinal direction, b) SAXS, transverse direction, c) WAXS, longitudinal direction, d) WAXS, transverse direction.
Figure 4. The average 1D profiles of SAXS and WAXS patterns taken at two temperatures: a) SAXS, longitudinal direction, b) SAXS, transverse direction, c) WAXS, longitudinal direction, d) WAXS, transverse direction.
Preprints 90049 g004
Preprints 90049 g005
Figure 5. The temperature variation of (a) the radius of gyration and (b) the ‘dimensionality’ parameter for self-reinforced UHMWPE composite.
Figure 5. The temperature variation of (a) the radius of gyration and (b) the ‘dimensionality’ parameter for self-reinforced UHMWPE composite.
Preprints 90049 g005
Preprints 90049 g006
Figure 6. The 1D correlation function analysis done for SAXS profiles obtained for a) longitudinal and b) transverse directions at 23 °C and 140 °C.
Figure 6. The 1D correlation function analysis done for SAXS profiles obtained for a) longitudinal and b) transverse directions at 23 °C and 140 °C.
Preprints 90049 g006
Preprints 90049 g007
Figure 7. a) The temperature-dependent thermal expansion coefficient and b) crystallite size obtained for different planes in SRPEC.
Figure 7. a) The temperature-dependent thermal expansion coefficient and b) crystallite size obtained for different planes in SRPEC.
Preprints 90049 g007
Preprints 90049 g008
Figure 8. The schematic illustration of a conceptual model of geometry and topology changes in SRPEC during heating: a) spiral spring structure, b) auxetic structure.
Figure 8. The schematic illustration of a conceptual model of geometry and topology changes in SRPEC during heating: a) spiral spring structure, b) auxetic structure.
Preprints 90049 g008
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated