Identification of Myofascial Trigger Point Using the Combination of Texture Analysis in B-mode Ultrasound with Machine Learning Classifiers

Myofascial Pain Syndrome (MPS) is a prevalent chronic pain disorder characterized by myofascial trigger points (MTrPs). Current diagnosis relies on manual detection of MTrPs, which has low inter-rater reliability. This study aims to enhance diagnosis through machine learning (ML) and a combination of texture-features extracted from B-mode ultrasound (B-mode-US) images. Four texture-features were investigated: statistical-features, and their combination with Gabor, local binary (LBP), and SEGL, LBP + gray-level-co-occurrence-matrices + Edge for the classification of MTrPs on the B-mode-US images. B-mode-US images of trapezius muscles (n=90) were examined for MTrPs and healthy muscle. Three methods of LBP, SEGL, and Gabor were separately calculated for each B-mode-US image. Then, the statistical-features (e.g., entropy) were calculated over the B-mode-US images and those three methods. Seven Machine learning (ML) classifiers (e.g., neural network) with the calculated statistical-features were applied to discriminate MTrPs from healthy muscle. Additionally, traditional statistical analysis (i.e., ANOVA) was calculated between statistical-features within each method. The results indicated that the combination of statistical-features effectively discriminated between MTrPs and healthy muscles, based on traditional statistical analysis. However, ML classifiers struggled due to high variation and similar mean values among them. This discrepancy between them prompts further exploration of US texture-based automated ML for MTrPs diagnosis.

Keywords:

Subject: Physical Sciences - Acoustics

1. Introduction

Nearly one-hundred million adults in the United States are affected by chronic pain (e.g., myofascial pain syndrome (MPS)), with an annual cost between $560 to $635 billion USD¹. MPS is one of the most prevalent musculoskeletal (MSK) pain disorders that occur in every age group and has been associated with primary pain conditions including osteoarthritis, disc syndrome, tendinitis, migraines, spinal dysfunction². MPS is characterized by myofascial trigger points (MTrPs)³. Active MTrPs (A-MTrPs) are spontaneously painful nodules while latent MTrPs (L-MTrPs) are palpable nodules that are painful when palpated.

MTrPs are classically defined as a ‘hyperirritable spot’ in skeletal muscle that is associated with a hypersensitive palpable nodule in a taut band⁴. The diagnostic criteria for MPS involves physical screening but studies have shown that manual detection of MTrPs is unreliable⁵. Techniques that are more quantitative in nature can help improve detection of MTrPs. Ultrasound is an attractive modality for this problem as it has been used to identify MTrPs^5–7, and are relatively cost-effective, non-invasive way to assess muscles, tendons and ligaments^8–10. It has been shown that MTrPs can be visualized and distinguished within a taut band on an affected muscle from normal tissue using US imaging techniques such as Doppler US and elastography US^8,11–14. Unfortunately, not all clinical US machines are equipped with elastography capability and both Doppler and elastography US techniques require comprehensive training sessions. Brightness mode (B-mode) US is readily available and is thus the preferred option for diagnosing and screening musculoskeletal disorders.

Since B-mode US imaging has high variability in echo intensity, texture features have been widely used to discriminate variables on B-mode US images. Texture features plays a vital role in computer vision and radiomics cases providing information such as muscle fiber orientation in the region of the MTrPs, and normal anatomy as well as the extent of adipose, fibrous, and other connective tissues within muscle¹⁵. Previous studies have shown that the muscle fibers within the MTrPs in the affected zone and the muscle fibers in the surrounding regions have different orientation in comparison with normal skeletal muscle.

Although, texture feature analysis of US images has been explored to distinguish MTrPs in affected muscle from normal tissue^9,16,17, there is currently no “gold standard” for the presence of MTrPs in US images. Previous research has used various methods of analyzing texture to tackle this problem such as using entropy characteristics¹⁶, gray level co-occurrence matrices (GLCM), blob analysis, local binary pattern (LBP), and statistical analysis¹⁷. A comprehensive overview of techniques employed for texture analysis or classification, categorize these techniques into four main categories:

Transform-Based: Transform-based techniques employ a set of predefined filters or kernels to extract texture information from an image. Common filters include Gabor filters, and LBP^18,19. These filters highlight certain frequency components or local variations in pixel values, making them suitable for tasks where texture patterns are characterized by specific spatial frequencies or orientations.
Structural: Structural techniques focus on describing the spatial arrangement and relationships between different elements in an image. They often involve identifying and characterizing specific patterns or structures within the texture (e.g., GLCM). These methods are valuable for capturing details related to texture regularity, directionality, or organization.
Statistical: Statistical methods involve the analysis of various statistical properties of pixel intensities within an image or a region of interest (ROI). Common statistical features include entropy, contrast, correlation, homogeneity, energy, mean, and variance. These metrics quantify the distribution and variation of pixel values, providing insights into the texture’s overall properties, such as roughness, homogeneity, or randomness.
Model-Based: Model-based methods involve fitting mathematical or statistical models to texture patterns in an image. These models can be simple, such as parametric distributions like Gaussian or Markov Random Fields, or more complex, such as deep learning models like convolutional neural networks. Model-based approaches are versatile and can capture intricate texture patterns, making them increasingly popular for texture analysis.

For many clinicians and investigators, the finding of one or more MTrPs is required to assure the diagnosis of MPS. A wide variety of studies describe the MTrPs as a hyperechoic band, hypoechoic elliptical region, or simply a different echo-architecture than the surrounding muscle tissue in clinical examination (e.g., US screening) ^14,20. In addition, MTrPs are typically known to be “knots” in the muscle. However, there remains a gap in knowledge regarding the optimal methods for characterizing these muscle structures (e.g., the associated texture pattern and edge). It was suggested that achieving an objective characterization and quantitative assessment of MTrPs properties has the potential to enhance their localization and diagnosis, while also facilitating the development of clinical outcome measures¹⁶.

Previously, Gabor filters were used to enhance the fiber orientation patterns and detect edges in the US images of the muscle^21,22. Also, LBP feature was used to characterize skeletal muscle (e.g., trapezius) composition in patients with MPS compared with normal healthy participants^9,23. Another proposed technique in which the statistical features were computed over the combination of Edge, GLCM, and LBP features, known as a “SEGL” method, to discriminate stone textures²⁴. It demonstrated the highest performance compared to LBP and GLCM features alone and may be a beneficial way for classifying MTrPs. As an extension of these image processing techniques, machine learning (ML) methods represent a powerful approach for automating the classification of muscle characteristics (e.g., muscle with MTrPs from healthy muscle).

ML techniques offer highly effective means of classification due to their ability to autonomously learn patterns and relationships from data^25–27. Futurists have anticipated that novel autonomous technologies, embedded with ML, will substantially influence healthcare. ML is focused on making predictions as accurate as possible, while traditional statistical models are aimed at inferring relationships between variables²⁷. ML offers advantages in terms of flexibility and scalability when contrasted with conventional statistical methods, allowing its utilization across various tasks like diagnosing, classifying, and predicting survival. Nevertheless, it is crucial to assess and compare the accuracy of muscle characterization through traditional statistical methods and ML within the context of clinical screening²⁸. Supervised ML algorithms (e.g., neural networks, decision trees, etc.) can generalize from training data to make accurate predictions or classifications on new, unseen data. Their adaptability allows them to handle diverse domains and tasks, making them invaluable tools for tasks ranging from image recognition to medical diagnosis, enhancing efficiency and precision in decision-making processes²⁶.

Building upon the advantages of ML and recognizing its potential in healthcare, this study delves into the utilization of various texture feature approaches and ML techniques to classify and characterize MTrPs in US images. We investigate different texture feature approaches (i.e., LBP, Gabor, SEGL method and their combination with texture features) extracted from US images to classify MTrPs. We further employ various ML techniques as well as traditional statistical analysis to explore the effectiveness of the extracted features from the US images to characterize and classify the muscle between A-MTrPs, L-MTrPs and healthy control.

2. Materials and Methods

2.1. Participants

Participants (n = 90) were recruited from the musculoskeletal/pain specialty outpatient clinic at the Toronto Rehabilitation Institute. The upper trapezius muscle of all participants was examined. All participants underwent a physical examination by a trained clinician on our team (BD), who determined the presence or absence of MTrPs (i.e., as A-MTrPs, L-MTrPs) in the upper trapezius muscle according to the standard clinical criteria defined by Travell and Simons⁴, and through visual confirmation on B-mode US. Participants who demonstrated no symptoms or history related to neuromuscular disease, based on diagnostic criteria, were included in this study. Each participant’s muscle was labeled as A-MTrPs, L-MTrPs or healthy control (Table 1).

Informed consent was obtained from all participants involved in the study prior to participating and their upper trapezius muscles were included in our study. This individual protocol was approved by the Institutional Review Board of the University Heath Network (UHN) (protocol code 15-9488). The procedures adhered to the guidelines set out in the Declaration of the World Medical Association of Helsinki.

2.2. Ultrasound Acquisition Protocol & Pre-processing

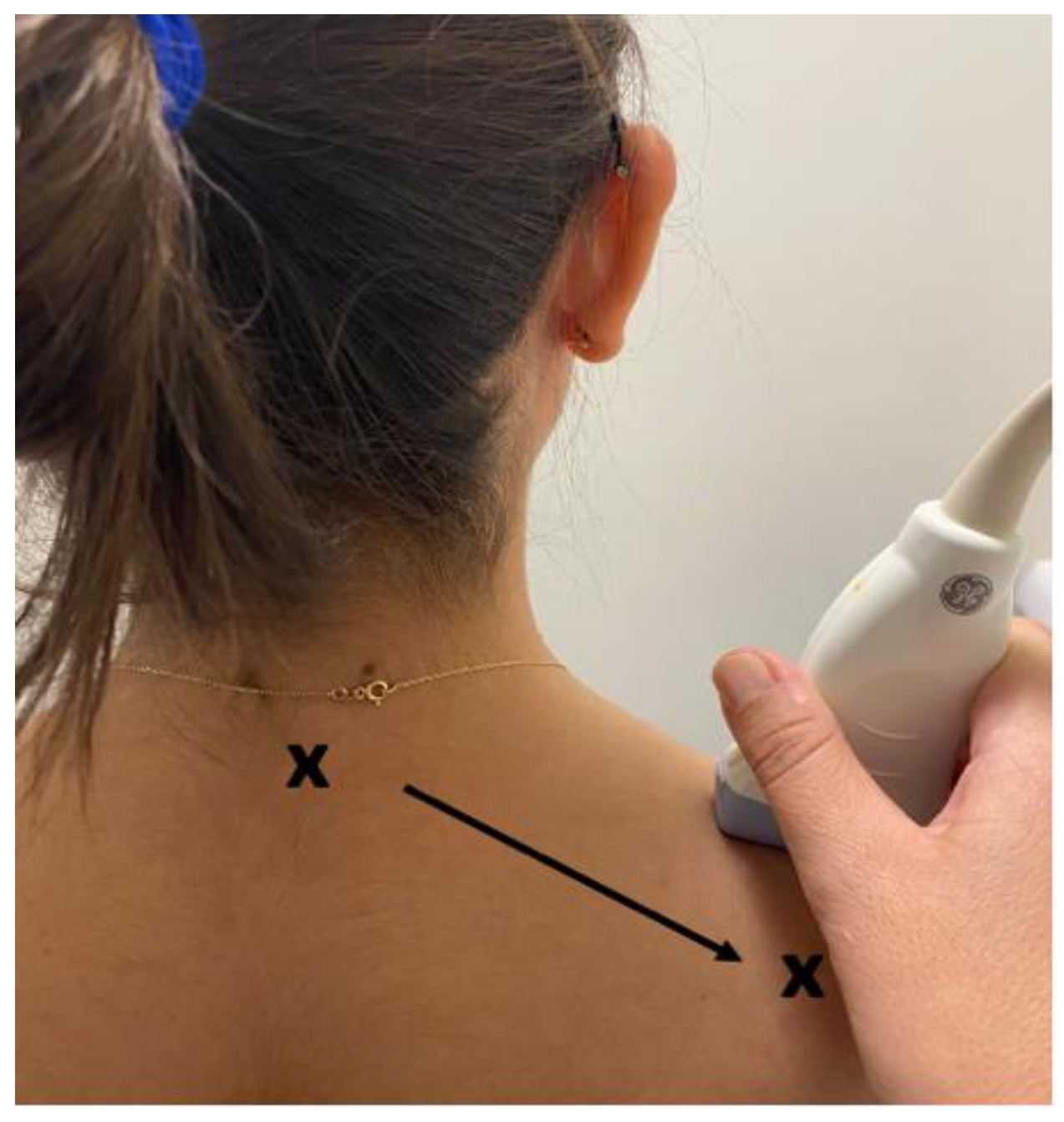
US videos were acquired using an US system (SonixTouch Q+, Ultrasonix Medical Corporation, British Columbia, Canada) with a linear ultrasonic transducer of 6-15MHz and a depth set to 2.5 cm. The acquisition settings including time gain compensation, depth and sector size were held constant across all participants. Acquisition was performed by the experienced sonographer with the participant sitting upright in a chair with their arms relaxed on their sides, and forearms resting on their thighs. The transducer was placed on the skin in the center of the trapezius muscle (i.e., the midpoint of the muscle belly between the C7 spinous process and the acromioclavicular joint) with enough gel to cover the entire surface (Figure 1). A ten second video (sampling frequency: 30 frames / second) of the trapezius muscle from each side per participant was recorded by moving the transducer towards the acromioclavicular joint (parallel to the orientation of the muscle fibers) at approximately 1 cm/s, generating 300 images per participant for analysis (Figure 1). While recording the video, the researcher manipulated the transducer’s position to reduce artifacts and mitigate muscle distortion caused by the transducer, such as applying downward pressure. From each video, 4 unique frames/images were manually selected out of 300 B-mode images. These selected images captured various section of the muscle (i.e., lateral to medial), and were used to validate the presence or absence of MTrPs evident in the video (Figure 2A). Images from each side of a participant (e.g., left, or right trapezius) were treated as independent sites.

A region of interest (ROI) of the muscle (i.e., the region between the upper trapezius muscle’s superior and inferior fascia) were manually extracted from the acquired images by visual localization. Theses muscle ROIs were further analyzed using the following texture features: LBP, Gabor, SEGL method and combination of them with statistical features.

2.3. Texture Feature Analyses

I. Local Binary Patterns. One of the most popular texture feature analysis operators is LBP, a rotationally invariant texture feature²⁹. It can evaluate the local spatial patterns and contrast of grayscale images. This technique provides eigenvalues for the different patterns in an image, such as edges, and corners within the ROI. LBP was calculated for every B-mode image using the following equation below (Eq. 1).

L B P_{P, R} = \sum_{p = 0}^{P - 1} s (g_{p} - g_{c}) 2^{p}, s (x) = \{\begin{matrix} 1, x \geq 0 \\ 0, x < 0, \end{matrix}

(1)

Where P is the number of pixels within the neighborhood,

g_{p}

represents the p^th neighboring pixel, and c represents the center pixel. In our study, a 3 by 3 neighborhood was used, and its central pixel intensity was compared with its surrounding eight neighbor pixels³⁰. The eight neighbors are labeled using a binary code {0, 1} obtained by comparing their values to the central pixel value. If the tested gray value is below the gray value of the central pixel, then it is labeled 0, otherwise it is assigned the value 1.

s (x)

is the obtained binary code,

s (x)

is the original pixel value at position x and

s (0)

is the central pixel value. With this technique there is 256 (2⁸) possible patterns (or texture units). The obtained value is then multiplied by weights given to the corresponding pixels. Summing the obtained values gives the measure of the LBP (Eq. 1). The central pixel is replaced by the obtained value (LBP measure). A new LBP image is constructed by processing each pixel and its 3x3 neighbors in the original image.

The LBP is calculated across the entire image and the outer layer of the image (i.e., the border), which does not have eight neighbors, was replaced with the next closest layer’s values (Figure 2C,D).

II. Gabor Feature. Gabor filtering or Gabor filter bank for image textural analysis was introduced by Daugman and used in pattern analysis applications^31–33. Gabor features are obtained by subjecting each filtered image to a nonlinear transformation and computing a measure of “energy” in a window around each pixel in each response image. The Gabor filter is characterized by preferred orientation spatial frequency. The Gabor filter-based features are directly extracted from the gray-level images (i.e., B-mode images). In the spatial domain, a two-dimensional Gabor filter is a Gaussian kernel function modulated by a complex sinusoidal plane wave, defined as (Eq. 2)³⁴:

G (x, y) = e x p \{\frac{- 1}{2} (\frac{x^{' 2}}{σ_{1}^{2}} + \frac{{y^{'}}^{2}}{σ_{2}^{2}})\} c o s (2 π ƒ x^{'} + φ),

(2)

x^{'} = x s i n θ + y c o s θ, y^{'} = - x c o s θ + y s i n θ,

where ƒ is the spatial frequency of the wave at an angle θ with the x axis,

σ_{1}

and

σ_{2}

are the standard deviations of the 2-D Gaussian envelope, and

φ

is the phase.

Gabor features were calculated using the Gabor Feature Extraction function in MATLAB (The MathWorks, Natick, USA) created by Haghighat et al.³⁵; the outputs of this function were used for the Gabor feature. In summary, in their study, forty Gabor filters were calculated in five scales (frequencies) and eight orientations in steps of 45 degrees (i.e., θ: 0°, 45°, 90°, 135°, 180°, 225°, 270°, 315°) for each image (5 x 8). The bank of Gabor filters (40 Gabor filters) extracted the variations in different frequencies and orientations from each image and generated forty ‘Gabor feature image’ corresponding to each B-mode US image (Figure 2B). All the Gabor feature images were normalized to 0 to 255.

III. SEGL Method. This method was proposed by Fekri Ershad S. and used a combinational feature extraction method for textual analysis²⁴. The term SEGL stand for (Statistical, Edge, GLCM, and LBP). This method first uses the LBP image as an input image, described in section I. The GLCM is then calculated on the LBP images, and the edge feature is then calculated from the resulting image.

GLCM was proposed by Haralick and Shanmugam³⁶. GLCM depicts how often different combinations of gray levels co-occur in an image. The GLCM is created by calculating how often a pixel with the intensity value i occurs in a specific spatial relationship to a pixel with the value j. In this study, GLCM were calculated along 8 directions (θ: 0°, 45°, 90°, 135°, 180°, 225°, 270°, 315°) with an empirically determined distance (offset = one pixel).

Edge detection is the process of localizing pixel intensity transitions that has been used to extract information in the image by object recognition, target tracking, segmentation, and etc. It is defined by a discontinuity in gray-level values or a boundary between two regions with relatively distinct gray level values³⁷. Canny Edge detection method was used, as previous literature has shown that Sobel Edge detection method cannot produce smooth and thin edge compared to Canny method³⁸, and this may reduce structural information (e.g., edge) of MTrPs within the muscle.

Finally, the seven statistical features, described below (Section, IV), were calculated over the edge detected images. As described above, the GLCM was calculated in 8 directions; as a result, the total number of extracted attributes is 56 statistical values (8 x 7).

IV. Statistical Feature. Statistical features were used to measure the image variation. In our study, 7 statistical features: entropy, energy, mean, contrast, homogeneity, correlation, and variance were computed over each calculated image from the texture features described above (sections I, II, III) in addition to the B-mode US images using the following equations in Table 2 (Eq. 3 - 9). Therefore, for each US image: 7 (B-mode), 7 (LBP), 280 (Gabor, i.e., 40 Gabor features x 7), and 56 (SEGL: i.e., 8 directions x 7) statistical values were calculated for each approach. 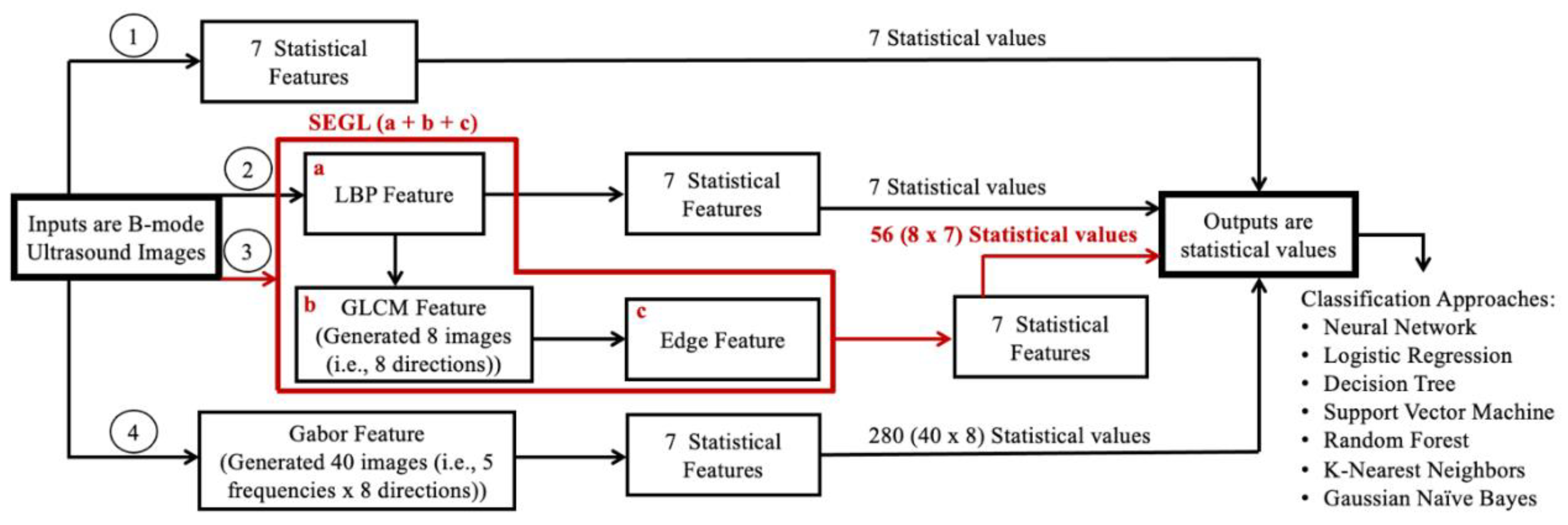Figure 3 shows the summary of the methods that were used for feature extraction of each image in this study.

2.4. Classification Approaches, Evaluation

The statistical features (values) from each image within each method were classified using a variety of supervised ML approaches to discriminate muscle with MTrPs (A-MTrPs and L-MTrPs) from healthy muscle. Classification accuracy was evaluated using following approaches outlined in Table 3. These algorithms were implemented in python using the Scikit Learn library using their common hyperparameters and their associated default values as outlined below in the Table 3.

The NN was a 3-layer network (256 x 512 x 128) with dropout layers between each (70% of nodes dropped). All activation functions were Rectified Linear Units (ReLU). The output layer was a 3-node output with an activation function of SoftMax. The NN was trained for 250 epochs with early stopping criterion of 7 epochs of no improvement in the validation loss. The learning rate was the default set by Keras and was decreased by a factor of 0.1 after 3 epochs of no improvement to a minimum of learning rate = 0.00001.

The inputs to the ML approaches were the 7 statistical features calculated on the B-mode image, the LBP images, the Gabor filtered images or the SEGL output images.

Due to the low number of images a leave-one-out site was used to better evaluate the performance. After the leave-one-out procedure the remaining examples were either used as is for training (i.e., LR, DT, RF, k-NN, NB, SVM) or split into 75% training and 25% validation sets (i.e., NN).

For all approaches, the classification accuracy, F1-score, sensitivity, specificity, positive predictive value (PPV), and negative predictive value (NPV) was used to evaluate the performance of the methods.

2.5. Ensemble Approaches & feature importance and Statistical Analysis

All the ML approaches with their associated parameters (shown above in Table 3) were used to further investigate the combination of statistical features (e.g., entropy, mean etc.) extracted from the 4 texture features (B-mode LBP, Gabor, SEGL) within each ML algorithm. This was performed to see the effects that statistical feature had on the different classification algorithms. This was done using:

(1): A single statistical feature from all texture feature approaches on all ML approaches
(2): A leave-one-feature out approach from all texture feature approaches on all ML approaches

Of the ML approaches investigated, the parameters that provided the best results for each technique were used to investigate ensemble approaches as well as feature importance. These best results associated with selected parameters were shown with asterisks (*) for each ML approach in the Table 3. These techniques were used in a simple majority vote to determine if an ensemble approach could provide improved results on the 4 different images (B-mode, LBP, Gabor, SEGL).

In addition, the mean and standard-deviation (SD) of each statistical feature within each group (A-MTrPs, L-MTrPs, healthy control) and each texture feature (B-mode LBP, Gabor, SEGL) were computed for further traditional statistical analysis (i.e., one-way analysis of variance (ANOVA)). In each texture feature, the ANOVA was computed between each statistical feature (mean values) to compare all 3 groups: A-MTrPs, L-MTrPs, healthy control. For example, ANOVA was performed between the calculated entropy of Gabor filtered image for A-MTrPs, L-MTrPs, and healthy control.

3. Results

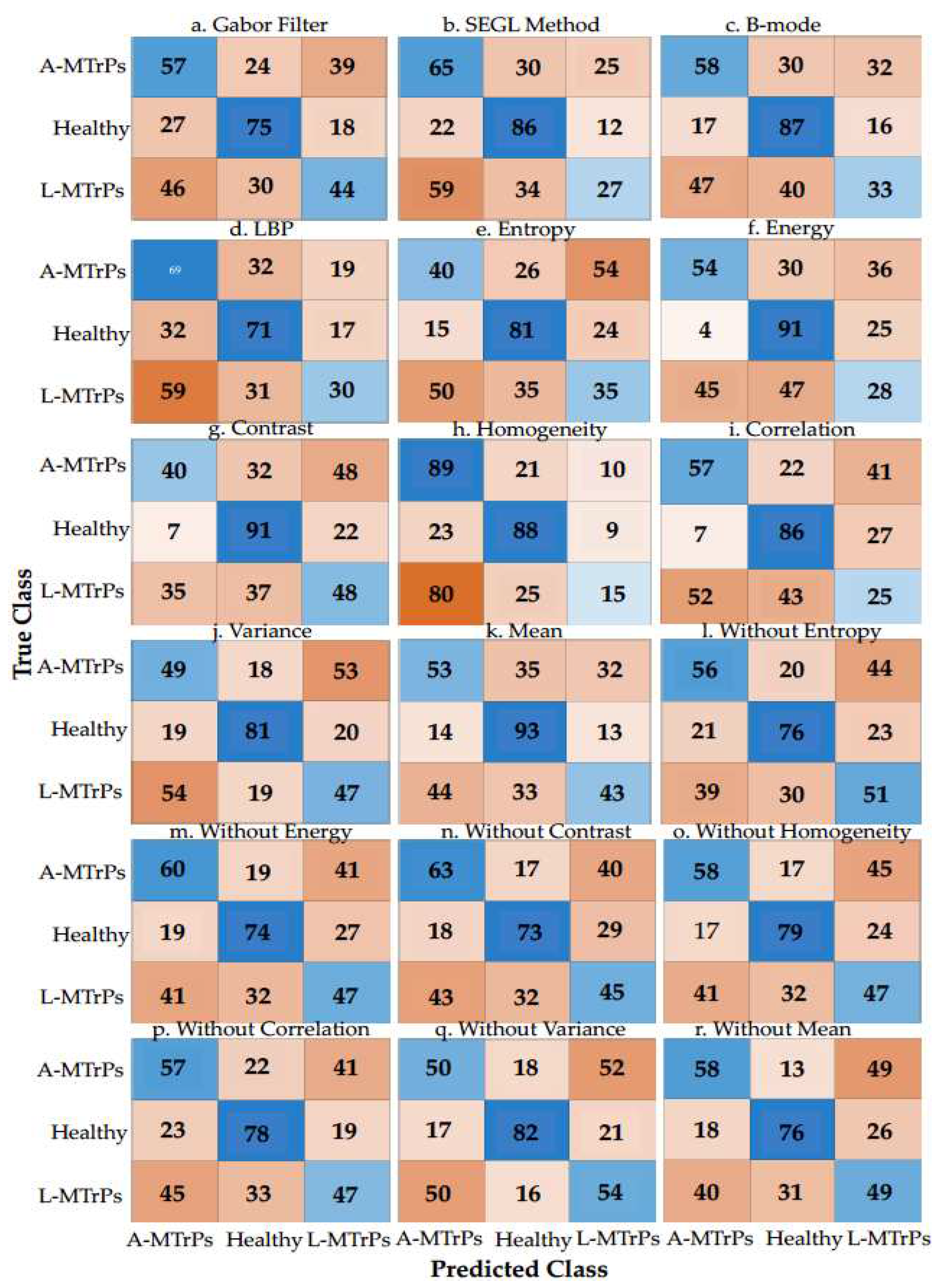
Table 4 shows the highest classification accuracy (%), F1-score, sensitivity, specificity, PPV, and NPV for the ML algorithms: between the 7 statistical features for each method: B-mode, LBP, Gabor feature, and SEGL for the majority voting; between each statistical feature of four methods, separately; and between each six-statistical features of four methods, separately, to classify the muscle with MTrPs from healthy muscle.

As shown in Table 4, the ML algorithms for ‘without variance’ with accuracy = 51.67% and F1-score = 0.518, and ‘correlation’ with accuracy = 53.33% and F1-score = 0.4861 showed highest performance. In addition, the ML algorithms for the majority voting approximately performed better than NN between the statistical features for all four methods (B-mode: 49.44% vs. 42.5%, LBP: 47.22% vs. 47.22 %, Gabor: 48.86% vs. 47.78%, and SEGL: 49.44% vs. 43.89).

In addition, the classification accuracies vary between 42.5% (min) and 53.33% (max); there was a low difference (10.83%) between the performance of all approaches between the statistical features and methods (Table 4).

Table 5 shows the traditional statistical analysis (i.e., one-way ANOVA) results between each statistical feature within each method (i.e., B-mode, LBP, Gabor filter, and SEGL) when comparing all 3 groups: A-MTrPs, L-MTrPs, and healthy controls. Statistically significant differences were seen for all statistical features within each method except: the ‘entropy’, ‘contrast’, and ‘energy’ of B-mode, ‘mean’ and ‘correlation’ of Gabor feature (p < 0.05) (Table 5). Nevertheless, Table 5 demonstrated the similar mean and low standard deviation (SD) statistical values between the groups and the four approaches (i.e., Gabor feature, SEGL method, B-mode, LBP).

Figure 3 shows the confusion matrixes of the ML algorithms with the best performance between the 7 statistical features for four methods: B-mode, LBP, Gabor filter, and SEGL for the majority voting; between four methods for each statistical feature, separately; and between four methods for six statistical features, separately. According to the true and predicted classes/labels (e.g., true negative, true positive, false negative, and false positive) for each group, ‘without variance’ approach presents better performance than other approaches for classifying all 3 groups: A-MTrPs, L-MTrPs, and healthy controls.

In addition, as shown in Figure 3, ‘Gabor filter’ approach show better performance than the other three methods between the 7 statistical features for classifying all 3 groups: A-MTrPs, L-MTrPs, and healthy controls.

Figure 3. Confusion matrixes of the learning algorithms with the best performance between the 7 statistical features for four methods: B-mode itself, LBP, Gabor filter, and SEGL for the majority voting and NN, between four methods for each statistical feature, separately, and between four methods for six statistical features, separately, for discriminating the A-MTrPs, L-MTrPs, and healthy controls. This figure shows how many predictions are correct and incorrect per class.

4. Discussion

Our study investigated the effectiveness of combining statistical features (specifically focused on edges and spots) derived from US images, utilizing B-mode, LBP, Gabor feature, and SEGL method for the purpose of accurately discriminating muscle with A-MTrPs, L-MTrPs, from healthy muscle (control). Our findings indicate that this combination approach (i.e., statistical-features, + B-mode, LBP, Gabor, and SEGL) did not achieve a high level of accuracy in distinguishing between A-MTrPs, L-MTrPs and healthy. Although, this combination approach showed approximately higher accuracies for B-mode and SEGL method, compared to the LBP and Gabor feature (49.44% and 49.44% vs 47.22% and 48.89%, respectively). We hypothesized that structural, statistical, and combination of them could better classify muscle with MTrPs from healthy muscle. However, the overall accuracies obtained from these combination approaches exhibited a similar range, ranging from 47.22% to 49.40%.

Through the utilization of traditional statistical analysis (i.e., ANOVA) and automated techniques (i.e., seven ML classifier approaches), this study reveals the significant statistical differences among the three groups within the most of statistical features extracted from the four methods (B-mode, LBP, Gabor feature, and SEGL method) (p < 0.05) (Table 5). However, these observed differences do not exhibit sufficient ability to enable high classification accuracy of these three groups, primarily due to the low degree of variation (i.e., SD) and overlapping observed in statistical values between the groups and the four approaches (i.e., Gabor feature, SEGL method, B-mode, LBP), as seen in Table 5.

Notably, the results demonstrated that the ‘correlation’ and ‘mean’ statistical features compared to other statistical features exhibited better discriminatory ability in distinguishing between muscle with MTrPs and healthy muscle (Table 4). These ML algorithms yielded the highest accuracies of 53.33% and 52.5% when utilizing the approaches involving ‘correlation’ and ‘mean’, respectively. Surprisingly, these accuracies decreased to the lowest values of 49.17% and 50.83% when the approaches ‘without correlation’ and ‘without mean’ were employed. It is important to note that despite an increase in the number of training features, which sometimes enhances classification performance, the aforementioned approaches experienced a decline in accuracy. Conversely, other statistical features (i.e., entropy, energy, contrast, variance, homogeneity) exhibited an improvement in performance with an increase in the number of training features. This discrepancy suggests the presence of distinct characteristics among the US images characterizing these three groups (i.e., A-MTrPs, L-MTrPs, and healthy controls) that may be better captured and evaluated by the ‘correlation’ and ‘mean’ statistical features. This suggests differences (different gray-scale values (i.e., echo-intensities)) between the structural patterns of muscle with MTrPs (A- MTrPs and L- MTrPs) and healthy muscle. This is in the agreement with the previous findings that showed the MTrPs as hypoechoic (dark grey) nodules in B-mode US images^39,40.

However, traditional statistical values showed that no statistically significant differences were observed for the ‘correlation’ and ‘mean’ statistical features of the Gabor feature approach (p = 0.0857 and p = 0.2338). This can be attributed to the fact that the Gabor feature measures the gray level of US images⁴¹, and there are similar mean and low standard deviations between and within the correlation and mean values of A-MTrPs and L-MTrPs, as indicated in Table 5. These findings align with previous studies that have reported muscle with MTrPs to exhibit anisotropy⁴².

Overall, MTrPs have been identified and labeled as hypoechoic (dark grey) nodules in previous US studies^39,40. However, recent research has proposed the identification of MTrPs as large hypoechoic contracture knots, which also exhibit smaller hyperechoic “speckles” within the hypoechoic contracture knot⁴³. The presence of these “speckles” can affect the structural information of MTrPs within the muscle ROI and interfere with the characterization of muscle with MTrPs using texture feature analysis. For instance, entropy is capable of describing homogeneity and randomness in the observed patterns in US images, while LBP depict the structural elements (spots, edges, etc.) of US backscatter. Consequently, the presence of different patterns within muscles affected by MTrPs may lead to variations in the values of calculated texture features within each group, thereby reducing the predictive accuracy of the ML techniques. The results seen in this study are in the agreement with the performance found in a recent study using convolutional neural network for discriminating MTrPs from healthy muscle (F1-score = 0.4697 Vs. F1-score = ranging from 0.4582 to 0.4855 in our study)⁴⁴.

Another critical consideration is the relationship between the US image and the clinical scenario. Existing literature has proposed certain clinical criteria for MTrPs; however, these criteria have not been clearly associated with specific US abnormalities. Currently, most researchers in this field concur that MTrPs are a physical entity that exhibits a spherical or elliptical shape, although this assumption is temporary and subject to further investigation. Therefore, it becomes crucial to identify the characteristics of the “center” of this entity, which may appear as hypoechoic and exhibit either homogeneous or heterogeneous features on the US image. Additionally, defining the “border zone” that separates this region from the surrounding normal area is necessary, as preliminary methods suggest that this border or transition zone may provide more valuable information than the lesion (i.e., hypoechoic contracture knot) itself ⁴⁵. Moreover, in cases where a patient experiences pain but does not present a formed MTrPs, it is uncertain if there is an ‘at-risk’ area that later transforms into a visually defined spherical/elliptical MTrPs, and the US characteristics of this at-risk area require further clarification. In our study, the entire muscle region, including the border zone, MTrPs, and normal areas, was considered, which may impact the calculated statistical values. Therefore, this study suggests additional research utilizing quantitative techniques such as texture analysis to analyze the effects of border zones and central regions of visually evident MTrPs within US images.

Here, to the best of our knowledge, this study represents the first attempt to investigate the potential of combining texture features mainly focused on structural information (e.g., spots, edges) within the muscle for discriminating muscle with MTrPs from healthy muscle. Moreover, previous studies have primarily relied on traditional statistical analysis methods, such as ANOVA, as opposed to automated analysis techniques, such as ML classifiers, for distinguishing between these three groups^17,46. Although our study demonstrated significant results using ANOVA in differentiating the groups, the classifier approaches did not show as robust outcomes. Therefore, we propose further exploration and utilization of automated classifier approaches (e.g., ML techniques) with the incorporation of texture features derived from US images, to achieve improved discrimination between MTrPs and healthy controls. Because the key characteristic that sets ML methods apart is their reliance on data-driven processes rather than user-selected approaches, with the aim of achieving precise predictions. This approach helps avoid the mistake of using an inappropriate traditional statistical model on the dataset, which could limit accuracy²⁷. We believe that these imaging techniques have the potential to aid clinicians in confirming the presence of MTrPs and enhancing diagnostic capabilities in the future.

4.1. Limitations

One limitation of this study lies in the proper definition and localization of the region of MTrPs within the US images from the muscle for the analysis. The MTrPs appeared to be 0.05 to 0.5 cm² nodules of varying hypo-echogenicity. However, the consensus was not absolute as there are notable deviations in described presentation, specifically: clusters of hypoechoic structures, and curved muscle form with MTrPs, as well as the hyperechoic presentation. Therefore, in this study, the entire region of muscle was cropped and considered for analysis, limiting the assessment to the textural information of the entire muscle region (ROI) rather than focusing solely on MTrPs themselves. By not confining the ROI to just the MTrPs, which requires more expertise, solving it with just the extraction of muscle would lower the barrier to use the developed technique. However, this approach may reduce the ability to detect required differences between the statistical features (values) within each group.

Furthermore, while hypoechoic images are generally associated with hyperperfused areas and hyperechoic images with hypo perfused areas⁴⁷, it is important to acknowledge the possibility of image artifacts, such as anisotropy, in our patient population. Hypoechoic areas may also arise from acoustic shadowing behind calcifications, lymph nodes, and certain pathological conditions. However, in this study, the manual selection of images aimed to alleviate the presence of any artifacts, and to maintain consistency across all participants, the entire muscle region (ROI) was evaluated.

5. Conclusions

In conclusion, this paper sheds light on the utilization of texture features and their combination (i.e., statistical features with B-mode, Gabor, LBP, and SEGL method) for the classification of A-MTrPs, L-MTrPs, and healthy muscle. The focus was to capture structural information such as edges, spots, and other relevant features. In comparison to traditional statistical analysis methods (e.g., ANOVA), the employed classification approaches did not achieve high classification results, likely due to the significant overlapping observed among the statistical values between the groups (maximum reported accuracy of 53.33%) but were still much higher than chance suggesting the feasibility of discriminating between the three groups; however, some improvements may be required.

Therefore, this study highlights the need for further investigations to explore the potential of extracting advanced texture features in combination with non-traditional statistical analysis, for effectively identifying MTrPs in contrast to healthy muscle. Such endeavors can contribute to the development of more robust diagnostic criteria based on US image characteristics. The findings from these future studies hold promise for the development of improved mechanisms to aid in the accurate identification and diagnosis of MTrPs.

Author Contributions

Conceptualization: F. Sh., R. G.L. K., K. M., and D. K.; Data curation: D. K.; Formal analysis: F. Sh. and R. G.L. K.; Funding acquisition: D. K.; Investigation: B. D. and D. K.; Methodology: F. Sh. and R. G.L; Project administration: F. Sh., R. G.L. K., K. M., and D. K.; Resources: B. D. and D. K.; Software: F. Sh. and R. G.L. K; Supervision: K. M., and D. K; Validation: F. Sh., R. G.L. K., K. M., and D. K; Writing – original draft: F. Sh; Writing – review & editing: F. Sh,, R. G.L. K., K. M., and D. K.

Funding

Banu Dilek was supported by the Tubitak 2219 grant program (Grant number: 1059B192100800).

Institutional Review Board Statement

This individual protocol was approved by the Institutional Review Board of the University Heath Network (UHN) (protocol code 15-9488).

Institutional Review Board Statements

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

The data collected and analyzed in this study are available from the corresponding authors on reasonable request.

Acknowledgments

None.

Conflicts of Interest

The authors declare no conflict of interest.

References

Gaskin, D.J.; Richard, P. The Economic Costs of Pain in the United States. Journal of Pain 2012, 13, 715–724. [Google Scholar] [CrossRef]
Suputtitada, A. Myofascial Pain Syndrome and Sensitization. Phys Med Rehabil Res 2016, 1. [Google Scholar] [CrossRef]
Gerwin, R.D. Classification, Epidemiology, and Natural History of Myofascial Pain Syndrome. Current pain and headache reports 2001, 412–420. [Google Scholar] [CrossRef] [PubMed]
Simons, D.; Travell, JG.; Simons, L. Travell & Simons’ Myofascial Pain and Dysfunction: The Trigger Point Manual, 2nd ed.; Williams & Wilkins: Baltimore, 1999; Vol. 1. [Google Scholar]
Hsieh, C.-Y. J.; Hong, C.-Z.; Adams, A.H.; Platt, K.J.; Danielson, C.D.; Hoehler, F.K.; Tobis, J.S. Interexaminer Reliability of the Palpation of Trigger Points in the Trunk and Lower Limb Muscles. Arch Phys Med Rehabil 2000, 81, 258–264. [Google Scholar] [CrossRef] [PubMed]
Gerwin, R.D.; Shannon, S.; Hong, C.Z.; Hubbard, D.; Gevirtz, R. Interrater Reliability in Myofascial Trigger Point Examination. Pain 1997, 69, (1–2). [Google Scholar] [CrossRef]
Rathbone, A.T.L.; Grosman-Rimon, L.; Kumbhare, D.A. Interrater Agreement of Manual Palpation for Identification of Myofascial Trigger Points: A Systematic Review and Meta-Analysis. Clin J Pain 2017, 33, 715–729. [Google Scholar] [CrossRef] [PubMed]
Kumbhare, D.; Shaw, S.; Grosman-Rimon, L.; Noseworthy, M.D. Quantitative Ultrasound Assessment of Myofascial Pain Syndrome Affecting the Trapezius: A Reliability Study: A. Journal of Ultrasound in Medicine 2017, 36, 2559–2568. [Google Scholar] [CrossRef]
Kumbhare, D.; Shaw, S.; Ahmed, S.; Noseworthy, M.D. Quantitative Ultrasound of Trapezius Muscle Involvement in Myofascial Pain: Comparison of Clinical and Healthy Population Using Texture Analysis. J Ultrasound 2020, 23, 23–30. [Google Scholar] [CrossRef]
Mourtzakis, M.; Wischmeyer, P. Bedside Ultrasound Measurement of Skeletal Muscle. Curr Opin Clin Nutr Metab Care 2014, 17, 389–395. [Google Scholar] [CrossRef]
Ballyns, J.J.; Shah, J.P.; Hammond, J.; Gebreab, T.; Gerber, L.H.; Sikdar, S. Objective Sonographic Measures for Characterizing Myofascial Trigger Points Associated with Cervical Pain. J Ultrasound Med 2011, 30, 1331–1340. [Google Scholar] [CrossRef]
Lewis, J.; Tehan, P. A Blinded Pilot Study Investigating the Use of Diagnostic Ultrasound for Detecting Active Myofascial Trigger Points. Pain 1999, 79, 39–44. [Google Scholar] [CrossRef] [PubMed]
Niraj, G.; Collett, B.J.; Bone, M. Ultrasound-Guided Trigger Point Injection: First Description of Changes Visible on Ultrasound Scanning in the Muscle Containing the Trigger Point. Br J Anaesth 2011, 107, 474–475. [Google Scholar] [CrossRef] [PubMed]
Thomas, K.; Shankar, H. Targeting Myofascial Taut Bands by Ultrasound. Curr Pain Headache Rep 2013, 17. [Google Scholar] [CrossRef] [PubMed]
Bird, M.; Le, D.; Shah, J.; Gerber, L.; Tandon, H.; Destefano, S.; Sikdar, S. Characterization of Local Muscle Fiber Anisotropy Using Shear Wave Elastography in Patients with Chronic Myofascial Pain. In IEEE International Ultrasonics Symposium, IUS; IEEE Computer Society, 2017. [CrossRef]
Turo, D.; Otto, P.; Shah, J.P.; Heimur, J.; Gebreab, T.; Zaazhoa, M.; Armstrong, K.; Gerber, L.H.; Sikdar, S. Ultrasonic Characterization of the Upper Trapezius Muscle in Patients with Chronic Neck Pain. Ultrason Imaging 2013, 35, 173–187. [Google Scholar] [CrossRef] [PubMed]
Kumbhare, D.A.; Ahmed, S.; Behr, M.G.; Noseworthy, M.D. Quantitative Ultrasound Using Texture Analysis of Myofascial Pain Syndrome in the Trapezius. Crit Rev Biomed Eng 2018, 46, 1–30. [Google Scholar] [CrossRef] [PubMed]
Ojala, T.; Pietikäinen, M.; Harwood, D. A Comparative Study of Texture Measures with Classification Based on Featured Distributions. Pattern Recognit 1996, 29, 51–59. [Google Scholar] [CrossRef]
Jain, A.K. Unsupervised Texture Segmentation Using Gabor Filters1.
Kumbhare, D.A.; Elzibak, A.H.; Noseworthy, M.D. Assessment of Myofascial Trigger Points Using Ultrasound. Am J Phys Med Rehabil 2016, 95, 72–80. [Google Scholar] [CrossRef] [PubMed]
Udomhunsakul, S. Edge Detection in Ultrasonic Images Using Gabor Filters. 2004 IEEE Region 10 Conference TENCON 2004. 2004, A. [Google Scholar] [CrossRef]
Zhou, Y.; Zheng, Y.P. Longitudinal Enhancement of the Hyperechoic Regions in Ultrasonography of Muscles Using a Gabor Filter Bank Approach: A Preparation for Semi-Automatic Muscle Fiber Orientation Estimation. Ultrasound Med Biol 2011, 37, 665–673. [Google Scholar] [CrossRef]
Paris, M.T.; Mourtzakis, M. Muscle Composition Analysis of Ultrasound Images: A Narrative Review of Texture Analysis. Ultrasound Med Biol 2021, 47, 880–895. [Google Scholar] [CrossRef]
Ershad, S.F. Texture Classification Approach Based on Combination of Edge & Co-Occurrence and Local Binary Pattern. 2012.
Gobeyn, S.; Mouton, A.M.; Cord, A.F.; Kaim, A.; Volk, M.; Goethals, P.L.M. Evolutionary Algorithms for Species Distribution Modelling: A Review in the Context of Machine Learning. Ecol Modell 2019, 392, 179–195. [Google Scholar] [CrossRef]
Sarker, I.H. Machine Learning: Algorithms, Real-World Applications and Research Directions. SN Comput Sci 2021, 2, 1–21. [Google Scholar] [CrossRef]
Ley, C.; Martin, R.K.; Pareek, A.; Groll, A.; Seil, R.; Tischer, T. Machine Learning and Conventional Statistics: Making Sense of the Differences. Knee Surgery, Sports Traumatology, Arthroscopy 2022, 30, 753–757. [Google Scholar] [CrossRef] [PubMed]
Rajula, H.S.R.; Verlato, G.; Manchia, M.; Antonucci, N.; Fanos, V. Comparison of Conventional Statistical Methods with Machine Learning in Medicine: Diagnosis, Drug Development, and Treatment. Medicina (B Aires) 2020, 56, 1–10. [Google Scholar] [CrossRef] [PubMed]
(12) (PDF) Texture Classification Based on Random Threshold Vector Technique. Available online: https://www.researchgate.net/publication/242611926_Texture_Classification_Based_on_Random_Threshold_Vector_Technique (accessed on 20 August 2023).
Ojala, T.; Pietikäinen, M.; Mäenpää, T. Multiresolution Gray-Scale and Rotation Invariant Texture Classification with Local Binary Patterns. IEEE Trans Pattern Anal Mach Intell 2002, 24, 971–987. [Google Scholar] [CrossRef]
Haghighat, M.; Zonouz, S.; Abdel-Mottaleb, M. Identification Using Encrypted Biometrics. Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) 2013, 8048 LNCS (PART 2), 440–448. [CrossRef]
Gdyczynski, C.M.; Manbachi, A.; Hashemi, S.M.; Lashkari, B.; Cobbold, R.S.C. On Estimating the Directionality Distribution in Pedicle Trabecular Bone from Micro-CT Images. Physiol Meas 2014, 35, 2415–2428. [Google Scholar] [CrossRef] [PubMed]
Daugman, J.G. Uncertainty Relation for Resolution in Space, Spatial Frequency, and Orientation Optimized by Two-Dimensional Visual Cortical Filters. J Opt Soc Am A 1985, 2, 1160. [Google Scholar] [CrossRef] [PubMed]
Vazquez-Fernandez, E.; Dacal-Nieto, A.; Martin, F.; Torres-Guijarro, S. Entropy of Gabor Filtering for Image Quality Assessment. Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) 2010, 6111 LNCS((PART 1)), 52–61. [Google Scholar] [CrossRef]
(13) CloudID: Trustworthy cloud-based and cross-enterprise biometric identification | Request PDF. Available online: https://www.researchgate.net/publication/279886437_CloudID_Trustworthy_cloud-based_and_cross-enterprise_biometric_identification (accessed on 16 August 2023).
Haralick, R.M.; Dinstein, I.; Shanmugam, K. Textural Features for Image Classification. IEEE Trans Syst Man Cybern 1973, SMC-3, 610–621. [Google Scholar] [CrossRef]
Kumar, R.; Arthanari, M.; Sivakumar, M. Image Segmentation Using Discontinuity-Based Approach. 2011.
Othman, Z.; Haron, H.; Kadir, M.A. Comprison of Canny and Sobel Edge Detection in MRI Images. 2009.
Mazza, D.F.; Boutin, R.D.; Chaudhari, A.J. Assessment of Myofascial Trigger Points via Imaging: A Systematic Review. Am J Phys Med Rehabil 2021, 100, 1003–1014. [Google Scholar] [CrossRef]
Duarte, F.C.K.; West, D.W.D.; Linde, L.D.; Hassan, S.; Kumbhare, D.A. Re-Examining Myofascial Pain Syndrome: Toward Biomarker Development and Mechanism-Based Diagnostic Criteria. Curr Rheumatol Rep 2021, 23. [Google Scholar] [CrossRef] [PubMed]
Gao, X.; Sattar, F.; Venkateswarlu, R. Corner Detection of Gray Level Images Using Gabor Wavelets. Proceedings - International Conference on Image Processing, ICIP 2004, 4, 2669–2672. [Google Scholar] [CrossRef]
Bird, M.; Shah, J.; Gerber, L.; Tandon, H.; DeStefano, S.; Srbely, J.; Kumbhare, D.; Sikdar, S. Characterization of Local Muscle Fiber Anisotropy Using Shear Wave Elastography in Patients with Chronic Myofascial Pain. Ann Phys Rehabil Med 2018, 61, e13. [Google Scholar] [CrossRef]
Dommerholt, J.; Gerwin, R.D. Contracture Knots vs. Trigger Points. Comment on Ball et al. Ultrasound Confirmation of the Multiple Loci Hypothesis of the Myofascial Trigger Point and the Diagnostic Importance of Specificity in the Elicitation of the Local Twitch Response. Diagnostics 2022, 12, 321. Diagnostics 2022, 12. [Google Scholar] [CrossRef]
Koh, R.G.L.; Dilek, B.; Ye, G.; Selver, A.; Kumbhare, D. Myofascial Trigger Point Identification in B-Mode Ultrasound: Texture Analysis Versus a Convolutional Neural Network Approach. Ultrasound Med Biol 2023, 000. [Google Scholar] [CrossRef] [PubMed]
Lefebvre, F.; Meunier, M.; Thibault, F.; Laugier, P.; Berger, G. Computerized Ultrasound B-Scan Characterization of Breast Nodules. Ultrasound Med Biol 2000, 26, 1421–1428. [Google Scholar] [CrossRef] [PubMed]
Zçakar, L.O.; Merve Ata, A.; Kaymak, B.; Kara, M.; Kumbhare, D. Ultrasound Imaging for Sarcopenia, Spasticity and Painful Muscle Syndromes. Curr Opin Support Palliat Care 2018, 12, 373–381. [Google Scholar] [CrossRef]
Ihnatsenka, B.; Boezaart, A.P. Ultrasound: Basic Understanding and Learning the Language. Int J Shoulder Surg 2010, 4, 55–62. [Google Scholar] [CrossRef]

Figure 1. US transducer location from upper trapezius muscle (x = acromion, x = C7).

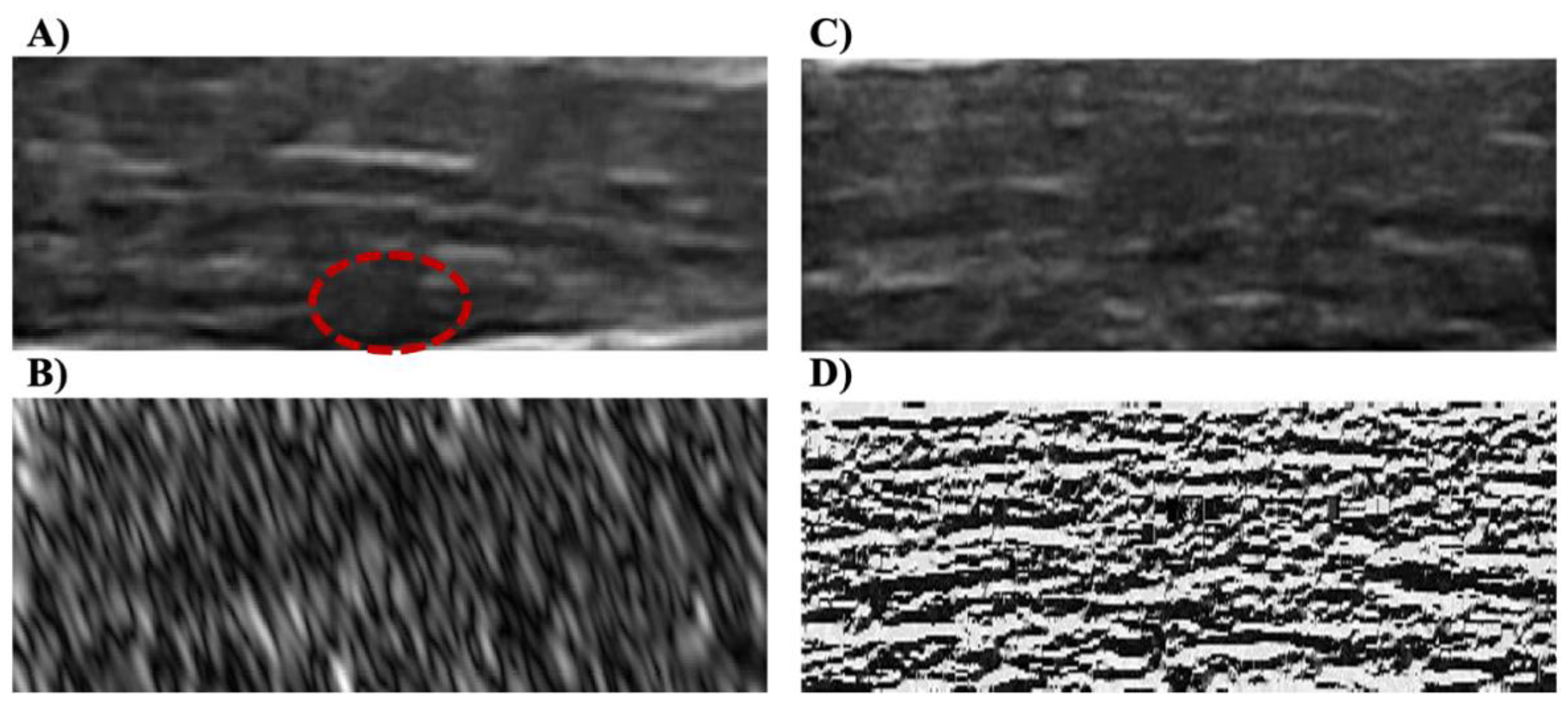
Figure 2. (A) An example of the B-mode US image from the participant with A-MTrPs. The red circle shows the MTrPs, a hypoechoic region. (B) An example of Gabor feature corresponding to one filtered image (at θ = 45 degree and Frequency = 5.657) from the participant with A-MTrPs. (C) Example of the B-mode US image from the healthy control participant, and (D) its corresponding LBP image.

Figure 3. This chart shows the summary of the methods that were used for feature extraction in this study. Note: The numbers in circles represent each method.

Table 1. Number of participants in each Group.

Group	Participants
A-MTrPs	30
L-MTrPs	30
Healthy Control	30

Table 2. The equations of used seven statistical features.

a1) Entropy: The degree of randomness of pixel intensities within an image^8,19,32.	$a_{1} = - \sum_{i, j = 0}^{N - 1} Ln (p_{i, j}) p_{i, j}$	(Eq. 3)
a2) Contrast: Measures the local contrast of an image.	$a_{2} = \sum_{i, j = 0}^{N - 1} P_{i, j} ({i - j)}^{2}$	(Eq. 4)
a3) Correlation: A correlation between the two pixels in the pixel pair.	$a_{3} = \sum_{i, j = 0}^{N - 1} P_{i, j} (({i - μ) (j - μ) / σ}^{2})$	(Eq. 5)
a4) Homogeneity: Measures local homogeneity of a pixel pair.	$a_{4} = \sum_{i, j = 0}^{N - 1} \frac{P_{i, j}}{{1 + (i - j)}^{2}}$	(Eq. 6)
a5) Energy: Measures the number of repeated pairs.	$a_{5} = \sum_{i, j = 0}^{N - 1} {{(P}_{i, j})}^{2}$	(Eq. 7)
a6) Mean	$a_{6} = \sum_{i, j = 0}^{N - 1} {i (P}_{i, j})$	(Eq. 8)
a7) Variance	$a_{7} = \sum_{i, j = 0}^{N - 1} {P_{i, j} (i - μ)}^{2}$	(Eq. 9)

Note: Pi, j is the pixel value in position (i, j) in the output image and N is the number of gray levels in the output image.

Table 3. The following ML classifier approaches with their associated parameters are used. * Shows the best accuracy performance for each classifier approach.

Classifier Approaches	Hyperparameters
k-nearest neighbors (kNN)	n_neighbors = 3, 5*, 7
Decision tree (DT)	Criterion = ‘gini’*, ‘entropy’, ‘log_loss’
Random forest (RF)	Criterion = ‘gini’*, ‘entropy’, ‘log_loss’
Logistic regression (LR)	C = 0.1, 1, 10*
Naives bayes (NB)	Gaussian (var_smoothing = 1.0, 1e-5, 1e-9*)
Support vector machine (SVM)	C = 0.1, 1, 10*
Vanilla neural network (NN)

Table 4. The highest classification accuracy (%), F1-score, sensitivity, specificity, PPV, and NPV for the ML algorithms: between the 7 statistical features for each method: B-mode, LBP, Gabor feature, and SEGL for the majority voting (highlighted with the orange color); between each statistical feature of four methods, separately (highlighted with the green color); and between each six-statistical features of four methods, separately (highlighted with the blue color). (SVM: support vector machine, LR: logistic regression, KNN: K-nearest neighbors, DT: decision tree).

Approach	Accuracy (%)	F1-score	Sensitivity	Specificity	PPV
SEGL Method (Majority Vote)	49.44	0.4731	0.4944	0.7472	0.5034	0.7384
LBP (Majority Vote)	47.22	0.4582	0.4722	0.7361	0.4703	0.7311
B-Mode (Majority Vote)	49.44	0.4786	0.4944	0.7472	0.5078	0.7397
Gabor Filter (Majority Vote)	48.89	0.4855	0.4889	0.7444	0.4922	0.7429
Entropy (SVM, C = 10)	43.33	0.4248	0.4333	0.7167	0.4472	0.7125
Energy (LR, C = 0.1)	48.06	0.4614	0.4806	0.7403	0.4993	0.7309
Contrast (SVM, C = 1)	49.72	0.4831	0.4972	0.7486	0.5082	0.7415
Correlation (SVM, C = 1)	53.33	0.4861	0.5333	0.7667	0.525	0.7485
Variance (KNN, K = 3)	49.17	0.405	0.4917	0.7458	0.4901	0.7462
Homogeneity (LR, C = 0.1)	46.67	0.4508	0.4667	0.7333	0.4882	0.7258
Mean (SVM, C = 10)	52.5	0.51	0.525	0.7625	0.5359	0.7551
Without-Entropy (SVM, C = 10)	50.83	0.507	0.5083	0.7542	0.5107	0.7535
Without-Energy (SVM, C = 10)	50.28	0.5014	0.5028	0.7514	0.5053	0.7507
Without-Contrast (SVM, C = 10)	50.28	0.5014	0.5028	0.7514	0.5051	0.7507
Without-Correlation (DT, Criterion = gini)	49.17	0.4868	0.4917	0.7458	0.4983	0.7435
Without-Variance (LR, C = 10)	51.67	0.518	0.5167	0.7583	0.5135	0.759
Without-Homogeneity (SVM, C = 10)	51.11	0.509	0.5111	0.7556	0.5149	0.7545
Without-Mean (SVM, C = 10)	50.83	0.5088	0.5083	0.7542	0.5071	0.7544

Note: The bolded numbers represent the highest classification accuracy (%) for the ML algorithms in each category.

Table 5. The traditional statistical analysis (i.e., one-way ANOVA) results between each statistical feature within each method (i.e., B-mode, LBP, Gabor feature, and SEGL) between all 3 groups: A-MTrPs, L-MTrPs, and healthy controls. The mean and standard deviation (SD) of each statistical feature within each method for each group.

	Approach	P-value	Mean (A-MTrPs)	SD (A-MTrPs)	Mean (Healthy)	SD (Healthy)	Mean (L-MTrPs)	SD (A-MTrPs)
Entropy	Gabor	2.32E-02	7.30E-04	1.58E-04	6.23E-04	2.00E-04	7.40E-04	1.77E-04
	SEGL	1.70E-02	7.67E-02	2.96E-02	5.34E-02	3.04E-02	7.19E-02	3.72E-02
	B-mode	6.88E-01	6.19E+00	4.17E-1	5.72E+00	4.12E-01	6.10E+00	4.58E-01
	LBP	1.00E-03	5.37E+00	1.75E-01	5.36E+00	2.47E-01	5.36E+00	1.81E-01
Energy	Gabor	1.00E-03	9.36E+08	1.83E+08	1.13E+09	2.87E+08	9.31E+08	2.05E+08
	SEGL	1.38E-02	-2.27E+08	9.94E+07	-1.86E+08	4.25E+07	-2.17E+08	6.56E+07
	B-mode	6.38E-02	1.73E+08	9.50E+07	9.28E+07	5.42E+07	1.47E+08	9.62E+07
	LBP	1.40E-03	1.40E+09	2.57E+08	1.56E+09	4.37E+08	1.37E+08	2.68E+08
Mean	Gabor	2.34E-01	1.23E+02	1.58E+0	1.24E+02	1.26E+00	1.23E+02	1.64E+04
	SEGL	1.38E-02	9.74E-03	4.13E-03	6.47E-03	4.10E-07	9.17E-03	5.20E-03
	B-mode	4.20E-03	4.72E+01	1.73E+01	3.08E+01	1.03E+01	4.31E+01	1.80E+01
	LBP	1.40E-03	1.17E+02	7.90E+00	1.09E+02	1.00E+01	1.16E+02	9.89E+00
Contrast	Gabor	3.8-E-03	4.13E+11	5.36E+10	4.62E+11	7.85E+10	4.11E+11	5.95E+10
	SEGL	2.04E-02	7.65E+06	3.53E+06	4.95E+06	3.57E+06	7.09E+06	4.42E+06
	B-mode	1.9E-01	1.59E+11	5.37E+10	1.23E+11	4.220E+10	1.41E+11	5.05E+10
	LBP	2.01E-02	3.98E+11	4.96E+10	4.20E+11	7.70E+10	3.93E+11	4.90E+10
Homogeneity	Gabor	1.7E-03	4.58E+04	9.30E+03	5.54E+04	1.44E+04	4.57E+04	1.05E+04
	SEGL	1.02E-02	39.76E+00	1.18E+01	2.9W+01	1.20E+01	3.8E+01	1.52E+01
	B-mode	3.24E-02	1.74E+04	6.61E+03	1.30E+04	5.60E+3	1.54E+04	6.69E+03
	LBP	3.14E-02	4.30E+04	8.12E+03	4.82E+04	1.40E+04	4.11E+04	8.63E+03
Correlation	Gabor	8.56E-02	-2.27E+08	9.94E+07	-1.86E+08	4.26E+07	-2.17E+08	6.56E+07
	SEGL	3.10E-02	1.39E+09	1.89E+08	1.51E+09	2.56E+08	1.39E+09	1.43E+08
	B-mode	3.00E-04	1.05E+07	2.71E+07	7.01E+07	5.83E+07	1.90E+07	3.14E+07
	LBP	2.00E-05	-5.08E+06	7.12E+05	-3.88E+06	1.33E+06	-4.86E+06	9.44E+05
Variance	Gabor	6.00E-04	2.71E+07	5.72E+06	3.18E+07	6.45E+06	2.63E+07	4.96E+06
	SEGL	1.40E-02	6.30E+02	2.66E+02	4.19E+02	2.64E+02	5.93E+02	3.35E+02
	B-mode	4.70E-03	3.06E+07	1.40E+07	1.97E+07	1.01E+07	2.80+07	1.13E+07
	LBP	1.70E-03	5.94E+08	1.12E+08	7.04E+08	1.83E+08	5.93E+08	1.36E+08

Note: The bolded numbers represent significant differences between the statistical feature of these three groups within each method (p < 0.05).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer