Prerpints.org logo
Preprint
Review

The Neutron Skin of 48Ca and 208Pb: A Critical Analysis

Altmetrics

Downloads

65

Views

24

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

09 November 2023

Posted:

10 November 2023

You are already at the latest version

Alerts
Abstract
We discuss the neutron skins of 48Ca and 208Pb. We review and critically examine modern predictions and empirical constraints, with special attention to the di erent interpretations of the ndings from the PREX-II experiment and the recently reported value of the neutron skin in 48Ca extracted from the CREX experiment. We argue that, in the spirit of the ab initio philosophy, the path to understanding the behavior of dense neutron-rich matter must not circumvent fundamental nuclear forces. Based only on that argument, a thick neutron skin in 208Pb is highly unlikely.
Keywords: 
Subject: Physical Sciences  -   Nuclear and High Energy Physics

I. Introduction

The existence of the neutron skin is a remarkable feature of neutron-rich nuclei. Because neutrons don’t bind, neutron excess, typically measured by the isospin asymmetry α = ( N − Z ) / A , is a destabilizing effect in a nucleus. As a consequence, some of the excess neutrons are “pushed out" from the (neutron-enriched) core and form the skin. The same physics plays an important role in neutron stars, which are supported against gravitational collapse by the outward pressure existing in dense systems with high neutron concentration. Studies of nuclear interactions in systems with high or extreme neutron to proton ratio are crucial for understanding the neutron driplines, the location of which is not well known. The new Facility for Rare Isotope Beams (FRIB), operational since May 2022, is expected to increase the number of known rare isotopes from 3000 to about 6000 [1].
The role of microscopic nuclear physics is to predict observables based on fundamental nuclear forces derived from first principles. Comparison with measurements is then a true test of the predictive power of the theory. The neutron skin is not a “conventional" observable, in that it’s not measured directly. Instead, it is extracted from measurements of observables that are sensitive to the neutron density distribution in nuclei. Naturally, the neutron density cannot be probed with electron scattering the way it’s done for proton densities, and so different methods must be employed, such as experiments with hadronic probes or measurements which exploit the neutron weak charge. Those will be reviewed in Section II.
We recall that the neutron skin is defined as
S = < r 2 > n 1 / 2 − < r 2 > p 1 / 2 ,
that is, the difference between the root mean square radii of the neutron and the proton distributions.
The common goal of experimentalists and theorists is to shed light on fundamental questions. In the case of neutron skins, the physics one wants to pin down concerns the aforementioned pressure that determines the spatial extension of the neutron skin, an information contained in the equation of state (EoS) of neutron-rich matter. The importance of this quantity cannot be overstated, given that its relevance extends from nuclei to compact astrophysical systems. These connections will be elucidated in Section III.
The purpose of this article is to review and critically examine modern predictions and empirical constraints as well as the different points of view currently being debated. A special focus is placed on the recently reported value of the neutron skin in 48Ca extracted from the CREX experiment [3], relative to the findings from the PREX-II [2] experiment. We end with thoughts and suggestions on the best way forward to strengthen the link between experiment and ab initio theory.

II. Extracting neutron skins from experiments

A. Brief review of useful facts

We will go through the main steps leading to the energy per nucleon in neutron-rich matter and related expressions, because they will be useful for the present discussion. We introduce the energy per nucleon, e ( ρ , α ) , in an infinite system of nucleons at density ρ and isospin asymmetry α = ρ n − ρ p ρ – namely, the EoS of neutron-rich matter – and expand this quantity with respect to the isospin asymmetry parameter, α :
e ( ρ , α ) = e ( ρ , 0 ) + 1 2 ∂ 2 e ( ρ , α ) ∂ α 2 ( α = 0 ) α 2 + O ( α 4 ) .
Neglecting terms of order O ( α 4 ) , Equation (2) takes the well-known form:
e ( ρ , α ) ≈ e 0 ( ρ ) + e s y m ( ρ ) α 2 .
Note that e s y m ( ρ ) = 1 2 ∂ 2 e ( ρ , α ) ∂ α 2 α = 0 and e 0 ( ρ ) = e ( ρ , 0 ) , the EoS of isospin-symmetric nuclear matter. Within the quadratic approximation applied in Equation (3), the symmetry energy becomes the difference between the energy per neutron in neutron matter (NM) and the energy per nucleon in symmetric nuclear matter (SNM):
e s y m ( ρ ) = e n ( ρ ) − e 0 ( ρ ) ,
where e n ( ρ ) = e ( ρ , 1 ) , the energy per neutron in pure NM.
We recall that e 0 ( ρ ) exhibits a minimum at a density approximately equal to the average central density of nuclei, ρ 0 , a reflection of the saturating nature of the nuclear force. Next, we expand the symmetry energy about the saturation point:
e s y m ( ρ ) ≈ e s y m ( ρ 0 ) + L ρ − ρ 0 3 ρ 0 + K 2 ( ρ − ρ 0 ) 2 ( 3 ρ 0 ) 2 ,
where the expansion parameters are obviously related to the first and higher-order derivatives of e s y m ( ρ ) . L is a measure of the slope of the symmetry energy at saturation:
L = 3 ρ 0 ∂ e s y m ( ρ ) ∂ ρ ρ 0 .
Furthermore, from Equations (4) and (6), we see that L is a measure of the slope of the NM EoS at saturation density, since the SNM EoS has a vanishing slope at that point.
Using the relation between pressure and energy density, we define the symmetry pressure:
P s y m ( ρ ) = ρ 2 ∂ e s y m ∂ ρ = P N M ( ρ ) − P S N M ( ρ ) .
If the derivative is evaluated at or very near ρ 0 , the symmetry pressure is essentially the pressure in NM because the pressure in SNM vanishes at saturation. Then:
P N M ( ρ 0 ) = ρ 2 ∂ e n ( ρ ) ∂ ρ ρ 0 .
From Equation (6) and Equation (8), it is clear that the slope parameter L is a measure of the pressure in NM around saturation density:
P N M ( ρ 0 ) = ρ 0 L 3 .
It is then easy to understand how the symmetry energy slope, essentially a pressure gradient acting on excess neutrons, determines the formation and size of the neutron skin. Therefore, constraints on L have the ability to provide constraints on the skin, and vice versa.

B. Experiments and phenomenological analyses

Indirect measurements of the neutron skin in 208Pb and 48Ca have been performed using a variety of techniques, such as those listed below. Parity-violating electron scattering will be addressed separately. Some representative measurements are:
  • Proton-nucleus elastic scattering [4,5,6,7];
  • Polarized proton-nucleus elastic scattering [8,9];
  • Pionic probes [10,11];
  • Coherent pion photoproduction [12,13];
  • Antiprotonic atom data [14,15,16];
  • Electric dipole polarizability [17,18,19,20];
  • Pygmy dipole resonsnces [21];
  • Interaction cross sections with microscopic optical potentials [22];
  • ( α , α ′ ) giant dipole resonance (GDR) [23];
  • α -particle scattering [24];
Constraints directly on the symmetry energy and its density dependence have also been sought through a variety of techniques, such as: data on nuclear masses across the periodic table [25], giant dipole resonance energies [26], electric dipole polarizability [27], measurements of directed and elliptic flows in HI collisions [28], isobaric analog states [29], isospin diffusion in HI collisions [30], neutron and proton transverse emission ratio measurements [31], HI collisions at intermediate energies [32].
In Table 1, we summarize values for 208Pb and 48Ca neutron skins deduced from the indicated experiments. There is a considerable spread, as the result of a multitude of methods and theoretical input over decades. Analyses of hadronic scattering experiments, in particular, require modeling of the nuclear potential. Based on previous measurements of the skin in 48Ca, we see no strong reasons to deem the CREX result surprising or unexpected, whereas the opposite is true for 208Pb. These observations are well captured in Figure 1, the content of which we have extracted from Figure 8 of Ref. [33]. On the Calcium side, from left to right, the data points are from Refs. [4,7,8,9,10,11,24]. On the Lead side, in the same order, the first two points correspond to Refs. [12] and [10]. The third point is at 0.18 ± 0.06 fm, as in Ref. [33], whereas, from the same references, [14,15], we read the values reported in Table 1. The remaining points are from Refs. [4,5,6,8,10]. A comment is in place with regard to the values from Ref. [4], 3rd and 6th data points, at 0.098 ± 0.043 fm and 0.119 ± 0.045 fm, for 48Ca and 208Pb, respectively. From Ref. [4], we read the smaller values shown in Table 1.
For 48Ca (208Pb), the last point on the right is the result of CREX [3] (PREX-II [2]).
We end this section with Figure 2, showing our predictions of the neutron skin for selected nuclei as a function of the isospin asymmetry [34], confirming a nearly linear relation between these two quantities and, thus, motivating the expectation that the skins of 48Ca and 208Pb should be close. The boundaries of the grey area are linear fits to the data from Ref. [35].

C. Parity-violating electron scattering

The parity-violating electron scattering asymmetry, A P V , is defined for a spin-zero nucleus as
A P V = σ R − σ L σ R + σ L ,
where σ R ( L ) is the elastic cross section for right (left) handed electrons [36]. A P V is proportional to the ratio of weak ( F W ( q ) ) to charge ( F c h ( q ) ) form factors, whith q the four-momentum transfer. F c h ( q ) is taken from existing measurements and F W ( q ) is extracted from the measured A P V . We recall that the weak and charge form factors are the Fourier transforms of the weak charge density and the charge density, respectively:
F W ( q ) = 1 Q W ∫ d 3 r j 0 ( q r ) ρ W ( r ) ,
where Q W is the weak charge of the nucleus, and
F c h ( q ) = 1 Z ∫ d 3 r j 0 ( q r ) ρ c h ( r ) .
In Equation (11), a form is assumed for ρ W ( r ) and the radius parameter of the density function is adjusted to reproduce the experimental A P V . The CREX result is found insensitive to the assumed form for the weak charge density [3].

III. The status of ab initio theory

A. Development of microscopic nuclear forces

Our still incomplete knowledge of nuclear forces is the result of decades of struggle. Currently, the optimal approach to the construction of nuclear forces is based on the understanding that the energy scale determines the appropriate degrees of freedom of the theory – the central concept to the development of chiral effective field theory (EFT) [41,42]. Here, we provide only a brief summary of the strongest features of chiral EFT.
Chiral EFT allows the development of nuclear interactions as an expansion where theoretical uncertainties can be assessed at each order. The organizational scheme that controls the expansion is known as “power counting." The crucial point is that chiral EFT maintains consistency with the underlying fundamental theory of strong interactions, quantum chromodynamics (QCD), through the symmetries and symmetry breaking mechanisms of the low-energy QCD Lagrangian. The first step towards the development of an EFT is the identification of a “soft scale” and a “hard scale," which is suggested by the hadron spectrum, observing the large separation between the mass of the pion and the mass of the vector meson ρ . It is therefore natural to identify the pion mass and the ρ mass (approximately 1 GeV) with the soft and the hard scale, respectively. Moreover, since quarks and gluons are ineffective degrees of freedom in the low-energy regime, pions and nucleons can be taken as the appropriate degrees of freedom of the EFT. Having identified pions and nucleons as the appropriate degrees of freedom of the EFT, one can proceed to construct the Lagrangian of the effective theory:
L e f f = L π π + L π N + L N N + . . . ,
which is then expanded in terms of a natural parameter, identified with the ratio of the “soft scale” over the “hard scale,” Q Λ χ . Q is of the order of the pion mass, whereas Λ χ is the energy scale of chiral symmetry breaking, approximately 1 GeV. The contributions to the effective Lagrangian are arranged according to the power counting scheme, with increasing order resulting in smaller terms. While the expansion itself is, of course, infinite, at each order we are assured that the number of terms is finite and the contributions well defined. The combination of meson-theoretic NN potentials augmented with selected 3NF is an outdated paradigm, from which it’s essentially impossible to estimate the theoretical uncertainty of a prediction.
With chiral EFT, there has been enormous progress in the understanding and development of few-nucleon forces. We are on the right path, but there is still much to accomplish. Convergence at N3LO needs to be on more robust grounds. Furthermore, there are indications that specific components of the 3NF at N4LO have the potential to solve some outstanding problems in microscopic nuclear structure [43].

B. Neutron skin predictions

We show in Table 2 recent predictions for the skins in 48Ca and in 208Pb. Some comments are in place. In both Ref. [37] and Ref. [38], the nature of the NN chiral potentials, N2LOsat and Δ N2LOGO, is such that the results are not truly ab initio. Note, also, that the value for 208Pb from Ref. [38] is not a prediction, but was obtained using the linear regression the authors constructed from the skins of lighter nuclei.
Figure 3 shows the neutron skin in 48Ca vs. the one in 208Pb. All values, except for the green bars, have been extracted from Figure 5 of Ref. [3]. The PREX-II and PREX-I combined experimental result is shown by the blue bar, while the red vertical bar is the CREX result. The gray circles (pink diamonds) show results from a variety of relativistic (non-relativistic) density functionals, which give values of the L parameter ranging from small and negative to large and positive. Coupled cluster (CC) [37,38] and dispersive optical model (DOM) predictions [39] are also displayed. Our predictions are shown by the green bars [40]. There exist, of course, relativistic mean-field (RMF) models that agree with the PREX result, and, correspondingly, generate values for 48Ca that are also on the larger side.
We conclude that a value between 0.212 fm and 0.354 fm (0.283 ± 0.071) for the skin of 208Pb is outside the boundaries set by microscopic theory. Simultaneous consistency with both CREX and PREX seems to be a challenge even for phenomenology. On the other hand, PREX aside, a small skin for 48Ca does not appear to be peculiar based on the facts we reviewed above, see also Figure 1.

IV. Further Discussion

Irrespective of the inconsistency between PREX and CREX, there are far-reaching questions one must consider with regard to a thick skin in 208Pb and its ramifications.

A. Direct Urca processes

We define the total energy per baryon in β -equilibrated matter (in absence of muons) as
e T ( ρ , Y p ) = e 0 ( ρ ) + e s y m ( 1 − 2 Y p ) 2 + e e + ∑ i = n , p Y i · m i ,
where Y p is the proton fractions. The last term accounts for the baryon rest masses (in units of energy), while e e is the electron energy. The particle fractions are
Y i = ρ i ρ ,
and the chemical potentials are given by:
μ i = ∂ ϵ i ∂ ρ i = ∂ e i ∂ Y i .
Naturally, we impose the constraints of fixed baryon density, Equation (17), and global charge neutrality, Equation (18):
ρ p + ρ n = ρ ⇒ Y p + Y n = 1 ,
ρ p = ρ e ⇒ Y p = Y e .
The electron energy is easily written as
e e = ℏ c 4 π 2 ρ 1 3 ( 3 π 2 Y p ) 4 3 ,
and thus
∂ e e ∂ Y p = ℏ c 3 π 2 ( 3 π 2 ) 4 3 ( ρ Y p ) 1 3 .
Noting that
∂ e p ∂ Y p = ∂ e n ∂ Y n − ∂ e e ∂ Y e ,
and using Equations (14) and (21), we obtain:
4 e s y m ( ρ ) ( 1 − 2 · Y p ) = ℏ c ( 3 π 2 ) 1 3 ( ρ Y p ) 1 3 ,
where we have neglected the mass difference between the proton and the neutron.
If ρ D U is the density at which Y p is equal to the value needed for direct Urca processes (DU), about 1 / 9 , the following relation holds:
e s y m ( ρ D U ) = ℏ c 9 28 ( π 2 / 3 ) 1 3 ( ρ D U ) 1 / 3 .
This simple relation can be quite insightful. If, for example, ρ D U is close to saturation density, the symmetry energy would be over 50 MeV at that point. If ρ D U = 2 3 ρ 0 , the symmetry energy at that density would be over 40 MeV. In microscopic predictions, DU processes are more likely to open at a few to several times normal density (based on projections, since chiral EFT predictions cannot be extended to such high densities). Using PREX II constraints, the Urca threshold is found to be approximately 1.5 ρ 0 or just above 0.2 f m − 3 [45]. From Equation (23), the value of the symmetry energy at 1.5 ρ 0 is then about 58 MeV, clearly indicationg an unusually steep density dependence, taking the PREX II value of 38.1 ± 4.7 MeV at saturation.
In Ref. [45], the authors develop different parametrizations of RMF models constrained by CREX results, PREX II results, or a combination of both, and report that the direct Urca threshold density decreases from 0.71 fm−3 to 0.21 fm−3 as the skin of 208Pb increases from 0.13 fm to 0.28 fm, with expected implication for cooling processes. To the best of our knowledge, there is no evidence for rapid neutrino cooling via direct Urca for low-mass (low central density) neutron stars. In fact, from analyses including luminosities and ages determined from observations of isolated neutron stars [46], one may conclude that the direct Urca process, although possible at the central densities of neutron stars with masses between 1.7 and 2.0 solar masses, is unlikely around M = 1.7 M ⊙ , and is likely, but not the principal cooling mechanism, for the M = 2.0 M ⊙ stars.

B. Impact of the isovector component of the free-space nuclear force

The importance of a realistic isovector component of the nuclear force (that is, carefully calibrated through free-space NN data), on the density dependence of the symmetry energy has been demonstrated [44,47]. Relaxing the constraint of accurate phase shifts for the isospin-1 S and P waves leads to drastic variations of the pressure in NM [47] and, consequently, the neutron skin.
For the purpose of the present discussion, it’s useful to recall that, typically, the isovector sector of RMF functionals includes coupling of the nucleon to the isovector ρ -meson and a nonlinear ω − ρ isoscalar-isovector cross-coupling term. In the models of Ref. [48], designed to reconcile the PREX and CREX results, the novel feature is the inclusion of the scalar isovector δ -meson (better known as the a 0 -meson). The isospin splitting resulting from the isovector nature of the new contribution opens an additional fitting degree of freedom [48].
As mesons heavier than the pion do not enter the development of the nucleon-nucleon (NN) force in chiral EFT, we will discuss this important point from the perspective of quantitative one-boson-exchange potentials (OBEP), as we already did over 10 years ago [49]. Studies of the ρ and δ contributions to the potential part of the symmetry energy in quantum hydrodynamics (QHD) models can be found in Refs. [30-35] of Ref. [48], where those contributions are shown to be opposite in sign and very large in magnitude around normal density. Thus, in QHD-inspired models, the interplay between ρ and δ is treated as the equivalent, in the isovector channel, of the interplay between σ and ω in the isoscalar channel. In contrast, the role of the δ -meson in meson theory is subtle (although important) and it’s seen in the difference of its contributions to isospin-1 or isospin-0 partial waves, particularly 1S0 and 3S1. The dramatic difference between the description of the isovector channel in QHD-based models or realistic meson models on originate from several sources, including the absence of the pion in QHD, and the fact that meson contributions in a microscopic approach are iterated, and thus reduced by Pauli blocking.
In Ref. [49], we have shown the difference between the potential energy contributions to NM and SNM from the isovector mesons, to estimate the effect of each meson on the potential energy part of the symmetry energy. The impact of the pion on the symmetry energy is by far the largest. On the other hand, mean-field theories are generally pionless, because the bulk of the attraction-repulsion balance needed for a realistic description of nuclear matter can be technically obtained from σ and ω only, an observation that is at the very foundation of the Walecka model [50]. On the other hand, in any theory of nuclear forces, the pion is the most important ingredient. Chiral symmetry is spontaneously broken in low-energy QCD and the pion emerges as the Goldstone boson of this symmetry breaking. Moreover, NN scattering data, and most definitely the deuteron, cannot be described without the pion.
In conclusion, developing additional density functionals with unrealistic isovector contributions for the purpose of reconciling the parity-violating experiments does not provide more clarity. The road to understanding the behavior of dense neutron-rich matter must go through ab initio nuclear forces.

V. Conclusions

The above has been a critical analysis of the available facts on the neutron skins in 208Pb and 48Ca, from both the experimental and the theoretical side.
We have pointed out and discussed problematic aspects that arise in conjunction with a stiff EoS and the corresponding thick skin in 208Pb. We emphasized that such thick skin is outside the boundaries of ab initio nuclear theory.
On the other hand, in the context of existing measurements and microscopic predictions, the CREX result for the skin of 48Ca does not appear to be an outlier.
We wait with excitement for the MREX experiment at the MESA accelerator, which promises to measure the neutron skin of 208Pb with ultimate precision [51].
Laboratory neutron skin measurements have important implications for neutron star properties, such as radius, tidal deformability, and cooling processes, and are complementary to astronomical observations. In the “multi-messanger" era, it is especially important to keep a broad view and, at the same time, stay in close touch with first principles, as we study the remarkable connection between microscopic physics and “telescope physics" enabled by the equation of state.

Acknowledgments

This work was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Award Number DE-FG02-03ER41270.

References

  1. https://frib.msu.edu.
  2. Reed, B.T.; Fattoyev, F.J.; Horowitz, C.J.; Piekarewicz, J. Implications of PREX-II on the equation of state of neutron-rich matter. Phys. Rev. Lett. 2021, 126, 172503. [Google Scholar] [CrossRef] [PubMed]
  3. Adhikari, D.; et al. (CREX Collaboration). Precision Determination of the Neutral Weak Form Factor of 48Ca. Phys. Rev. Lett. 2022, 129, 042501. [Google Scholar] [CrossRef]
  4. Clark, B.C.; Kerr, L.J.; Hama, S. Neutron densities from a global analysis of medium-energy proton-nucleus elastic scattering. Phys. Rev. C 2003, 67, 054605. [Google Scholar] [CrossRef]
  5. Zenhiro, J.; Sakaguchi, H.; Murakami, T.; Yosoi, M.; Yasuda, Y.; Terashima, S.; Iwao, Y.; Takeda, H.; Itoh, M.; Yoshida, H.P.; et al. Neutron density distributions of 204,206,208Pb deduced via proton elastic scattering at Ep=295 MeV Phys. Rev. C 2010, 82, 044611. [Google Scholar]
  6. Starodubnsky, V.E.; Hintz, N.M. Extraction of neutron densities from elastic proton scattering by 206,207,208Pb at 650 MeV. Phys. Rev. C 1994, 49, 2118. [Google Scholar] [CrossRef] [PubMed]
  7. Shlomo, S.; Schaeffer, R. The difference between neutron and proton radii in the Ca isotopes. Phys. Lett. B 1979, 83, 5. [Google Scholar] [CrossRef]
  8. Ray, L. Neutron isotopic density differences deduced from 0.8 GeV polarized proton elastic scattering. Phys. Rev. C 1979, 19, 1855. [Google Scholar] [CrossRef]
  9. Zenhiro, J.; Sakaguchi, H.; Terashima, S.; Uesaka, T.; Hagen, G.; Itoh, M.; Murakami, T.; Nakatsugawa, Y.; Ohnishi, T.; Sagawa, H.; et al. Direct determination of the neutron skin thicknesses in 40,48Ca from proton elastic scattering at Ep=295 MeV. arXiv 2018, arXiv:1810.11796. [Google Scholar]
  10. Friedman, E. Neutron skins of 208Pb and 48Ca from pionic probes. Nucl. Phys. A 2012, 896, 46. [Google Scholar] [CrossRef]
  11. Gibbs, W.R.; Dedonder, J.-P. Neutron radii of the calcium isotopes. Phys. Rev. C 1992, 46, 1825. [Google Scholar] [CrossRef]
  12. Tarbert, C.M.; Watts, D.P.; Glazier, D.I.; Aguar, P.; Ahrens, J.; Annand, J.R.M.; Arends, H.J.; Beck, R.; Bekrenev, V.; Boillat, B.; et al. Neutron Skin of 208Pb from Coherent Pion Photoproduction. Phys. Rev. Lett. 2014, 112, 242502. [Google Scholar] [CrossRef] [PubMed]
  13. Zana, L.; for the A2 Collaboration at MAMI. Neutron skins from Coherent Pion Photoproduction. EPJ Web of Conferences 2015, 96, 01036. [Google Scholar] [CrossRef]
  14. Brown, B.A.; Shen, G.; Hillhouse, G.C.; Meng, J.; Trzcinska, A. Neutron skin deduced from antiprotonic atom data. Phys. Rev. C 2007, 76, 034305. [Google Scholar] [CrossRef]
  15. Klos, B.; et al. Neutron density distributions from antiprotonic 208Pb and 209Bi atoms. Phys. Rev. C 2007, 76, 014311. [Google Scholar] [CrossRef]
  16. Trzcinska, A.; Jastrzebski, J.; Lubinski, P.; Hartmann, F.J.; Schmidt, R.; von Egidy, T.; Kłos, B. Neutron Density Distributions Deduced from Antiprotonic Atoms. Phys. Rev. Lett. 2001, 87, 082501. [Google Scholar] [CrossRef] [PubMed]
  17. Roca-Maza, X.; Viñas, X.; Centelles, M.; Agrawal, B.K.; Colò, G.; Paar, N.; Piekarewicz, J.; Vretenar, D. Neutron skin thickness from the measured electric dipole polarizability in 68Ni, 120Sn, and 208Pb. Phys. Rev. C 2015, 92, 064304. [Google Scholar] [CrossRef]
  18. Roca-Maza, X.; Brenna, M.; Colò, G.; Centelles, M.; Viñas, X.; Agrawal, B.K.; Paa, N.; Vretenar, D.; Piekarewicz, J. Electric dipole polarizability in 208Pb: Insights from the droplet model. Phys. Rev. C 2013, 88, 024316. [Google Scholar] [CrossRef]
  19. Tamii, A. ; Complete Electric Dipole Response and the Neutron Skin in 208Pb. Phys. Rev. Lett. 2011, 107, 062502. [Google Scholar] [CrossRef] [PubMed]
  20. Birkham, J.; et al. Electric Dipole Polarizability of 48Ca and Implications for the Neutron Skin. Phys. Rev. Lett. 2017, 118, 252501. [Google Scholar] [CrossRef]
  21. Klimkiewicz, A.; Paar, N.; Adrich, P.; Fallot, M.; Boretzky, K.; Aumann, T.; Cortina-Gil, D.; Pramanik, U.D.; Elze, T.W. , Emling, H.; et al. Nuclear symmetry energy and neutron skins derived from pygmy dipole resonances. Phys. Rev. C 2007, 76, 051603. [Google Scholar] [CrossRef]
  22. Matsuzaki, M.; Yahiro, M. Neutron skin of 48Ca deduced from interaction cross section. Mod. Phys. Lett. A 2022, 37, 2250123. [Google Scholar] [CrossRef]
  23. Krasznahorkay, A.; et al. Excitation of the isovector GDR by inelastic α scattering as a measure of the neutron skin of nuclei. Nucl. Phys. A 1994, 567, 521. [Google Scholar] [CrossRef]
  24. Gils, H.J.; Rebel, H.; Friedman, E. Isotopic and isotonic differences between a particle optical potentials and nuclear densities of 1f7/2 nuclei. Phys. Rev. C 1984, 29, 1295. [Google Scholar] [CrossRef]
  25. Mondal, C.; Agrawal, B.K.; De, J.N. Constraining the symmetry energy content of nuclear matter from nuclear masses: a covariance analysis. Phys. Rev. C 2015, 92, 024302. [Google Scholar] [CrossRef]
  26. Trippa, L.; Colo`, G.; Vigezzi, E. Giant dipole resonance as a quantitative constraint on the symmetry energy. Phys. Rev. C 2008, 77, 061304. [Google Scholar] [CrossRef]
  27. Zhang, Z.; Chen, L.-W. Electric dipole polarizability in 208Pb as a probe of the symmetry energy and neutron matter around ρ0/3. Phys. Rev. C 2015, 92, 031301. [Google Scholar] [CrossRef]
  28. Russotto, P.; et al. Results of the ASY-EOS experiment at GSI: The symmetry energy at suprasaturation density. Phys. Rev. C 2016, 94, 034608. [Google Scholar] [CrossRef]
  29. Danielewicz, P.; Lee, J. Symmetry energy II: Isobaric analog states. Nucl. Phys. A 2014, 922, 1. [Google Scholar] [CrossRef]
  30. Tsang, M.B.; Liu, T.X.; Shi, L.; Danielewicz, P.; Gelbke, C.K.; Liu, X.D.; Lynch,W. G.; Tan,W.P.; Verde, G.;Wagner, A.; et al. Isospin Diffusion and the Nuclear Symmetry Energy in Heavy Ion Reactions. Phys. Rev. Lett. 2004, 92, 062701. [Google Scholar] [CrossRef]
  31. Famiano, M.A.; Liu, T.; Lynch, W.G.; Mocko, M.; Rogers, A.M.; Tsang, M.B.; Wallace, M.S.; Charity, R.J.; Komarov, S.; Sarantites, D.G.; et al. Neutron and proton transverse emission ratio measurements and the density dependence of the asymmetry term of the nuclear equation of state. Phys. Rev. Lett. 2006, 97, 052701. [Google Scholar] [CrossRef]
  32. Yong, G.-C.; Guo, Y.-F. Probing High-density Symmetry Energy Using Heavy-ion Collisions at Intermediate Energies. Nucl. Phys. Rev. 2020, 37, 136. [Google Scholar]
  33. Lattimer, J.M. Constraints on Nuclear Symmetry Energy Parameters. arXiv 2023, arXiv:2301.03666. [Google Scholar] [CrossRef]
  34. Sammarruca, F. Neutron skin systematics from microscopic equations of state. Phys. Rev. C 2022, 105, 064303. [Google Scholar] [CrossRef]
  35. Swiatecki, W.J.; Trzcinska, A.; Jastrzebski, J. Difference of the root-mean-square sizes of neutron and proton distributions in nuclei: Comparison of theory with data. Phys. Rev. C 2005, 71, 047301. [Google Scholar] [CrossRef]
  36. Donnelly, T.W.; Dubach, J.; Sick, I. Isospin dependences in parity-violating electron scattering. Nucl. Phys. A 1989, 503, 589. [Google Scholar] [CrossRef]
  37. Hagen, G. et al. Neutron and weak-charge distributions of the 48Ca nucleus. Nat. Phys. 2016, 12, 186. [Google Scholar] [CrossRef]
  38. Novario, S.J.; et al. Trends of Neutron Skins and Radii of Mirror Nuclei from First Principles. Phys. Rev. Lett. 2023, 130, 032501. [Google Scholar] [CrossRef] [PubMed]
  39. Atkinson, M.C.; et al. Dispersive optical model analysis of 208Pb generating a neutron-skin prediction beyond the mean field. Phys. Rev. C 2020, 101, 044303. [Google Scholar] [CrossRef]
  40. Sammarruca, F. Neutron skin systematics from microscopic equations of state. Phys. Rev. C 2022, 105, 064303. [Google Scholar] [CrossRef]
  41. Weinberg, S. Nuclear forces from chiral lagrangians. Phys. Lett. B 1990, 251, 288. [Google Scholar] [CrossRef]
  42. Weinberg, S. Three-body interactions among nucleons and pions. Phys. Lett. B bf 1992, 295, 114. [Google Scholar] [CrossRef]
  43. Machleidt, R. What is ab initio? arXiv 2023, arXiv:2307.06416. [Google Scholar] [CrossRef]
  44. Hu, B.; Jiang, W.; Miyagi, T.; Sun, Z.; Ekström, A.; Forssen, C.; Hagen, G.; Holt, J.D.; Papenbrock, T.; Stroberg, S.R.; Vernon, I. Ab initio predictions link the neutron skin of 208Pb to nuclear forces. Nat. Phys. 2022, 18, 1196. [Google Scholar] [CrossRef] [PubMed]
  45. Kumar, M.; Kumar, S.; Thakur, V.; Kumar, R.; Agrawal, B.K.; Dhiman, S.K. CREX- and PREX-II-motivated relativistic interactions and their implications for the bulk properties of nuclear matter and neutron stars. Phys. Rev. C 2023, 107, 055801. [Google Scholar] [CrossRef]
  46. Beloin, S.; Han, S.; Steiner, A. W.; Odbadrakh, K. Simultaneous fitting of neutron star structure and cooling data. Phys. Rev. C bf 2019, 100, 055801. [Google Scholar] [CrossRef]
  47. Sammarruca, F. The Symmetry Energy: Current Status of Ab Initio Predictions vs. Empirical Constraints. Symmetry 2023, 15(2), 450. [Google Scholar] [CrossRef]
  48. Reed, B.T.; Fattoyev, F.J.; Horowitz, C.J.; Piekarewicz, J. Density Dependence of the Symmetry Energy in the Post PREX-CREX Era. arXiv 2023, arXiv:2305.19376. [Google Scholar] [CrossRef]
  49. Sammarruca, F. Contribution of isovector mesons to the symmetry energy in a microscopic model. Phys. Rev. C 2011, 84, 044307. [Google Scholar] [CrossRef]
  50. Serot, B.D.; Walecka, J.D. Recent Progress in Quantum Hadrodynamics. Int. J. Mod. Phys. 1997, E6, 515. [Google Scholar] [CrossRef]
  51. Becker, D.; et al. The P2 Experiment - A future high-precision measurement of the electroweak mixing angle at low momentum transfer. EPJ A 2018, 54, 208. [Google Scholar] [CrossRef]
Preprints 90143 g001
Figure 1. (Color online) An overview of experimental constraints, taken from Ref. [33] (see text for explanation). On the 48Ca (208Pb) side, the last point on right is the result of CREX [3] (PREX-II [2]). The horizontal lines mark the weighted means of the experiments ± one standard deviation, not including parity-violating electron scattering.
Figure 1. (Color online) An overview of experimental constraints, taken from Ref. [33] (see text for explanation). On the 48Ca (208Pb) side, the last point on right is the result of CREX [3] (PREX-II [2]). The horizontal lines mark the weighted means of the experiments ± one standard deviation, not including parity-violating electron scattering.
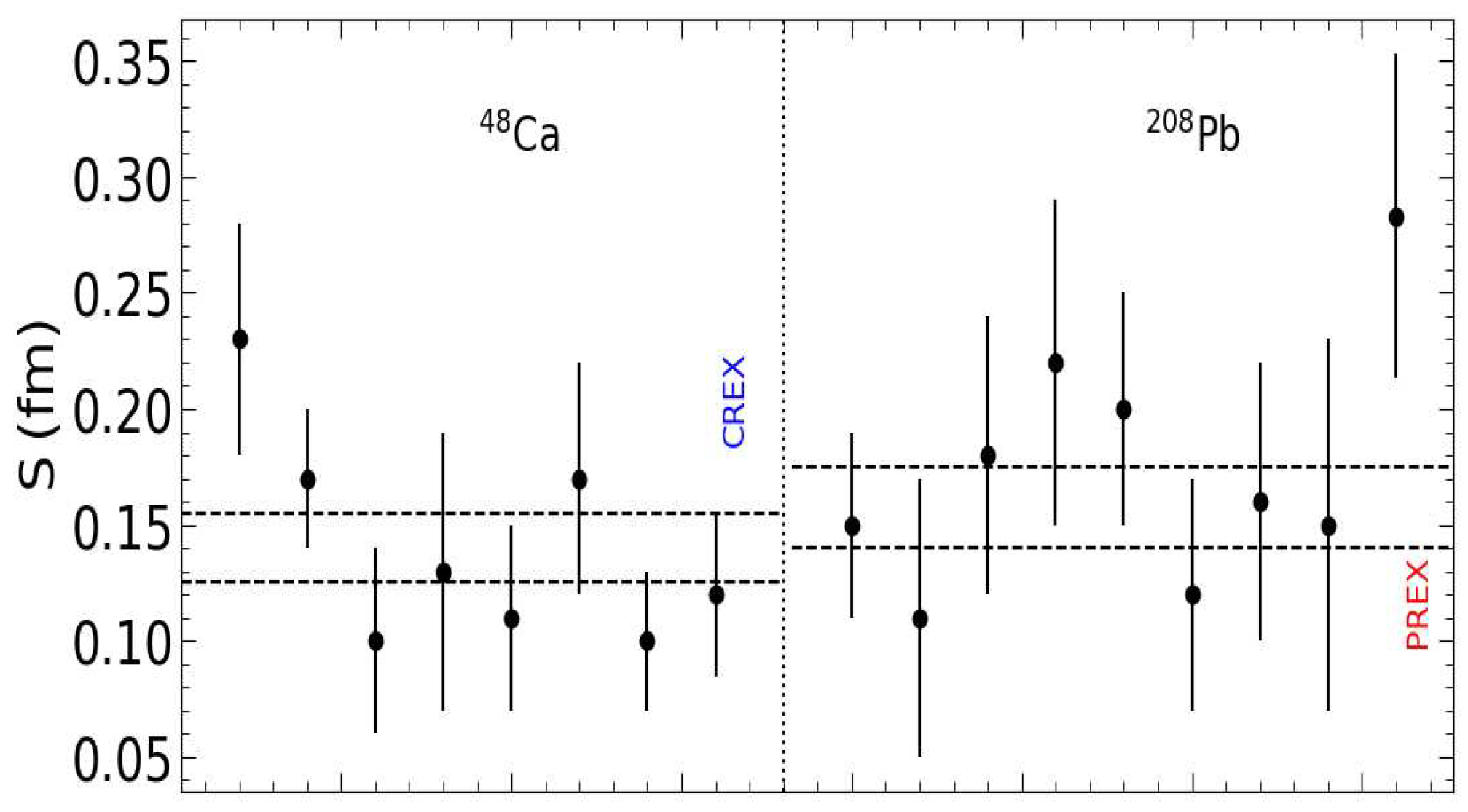
Preprints 90143 g001
Preprints 90143 g002
Figure 2. (Color online) Red bars: Neutron skin of 58Ni, 27Al, 59Co, 90Zr, 48Ca, and 208Pb, in order of increasing isospin asymmetry, from Ref. [34]. The shaded area is bounded by linear fits to the data [35].
Figure 2. (Color online) Red bars: Neutron skin of 58Ni, 27Al, 59Co, 90Zr, 48Ca, and 208Pb, in order of increasing isospin asymmetry, from Ref. [34]. The shaded area is bounded by linear fits to the data [35].
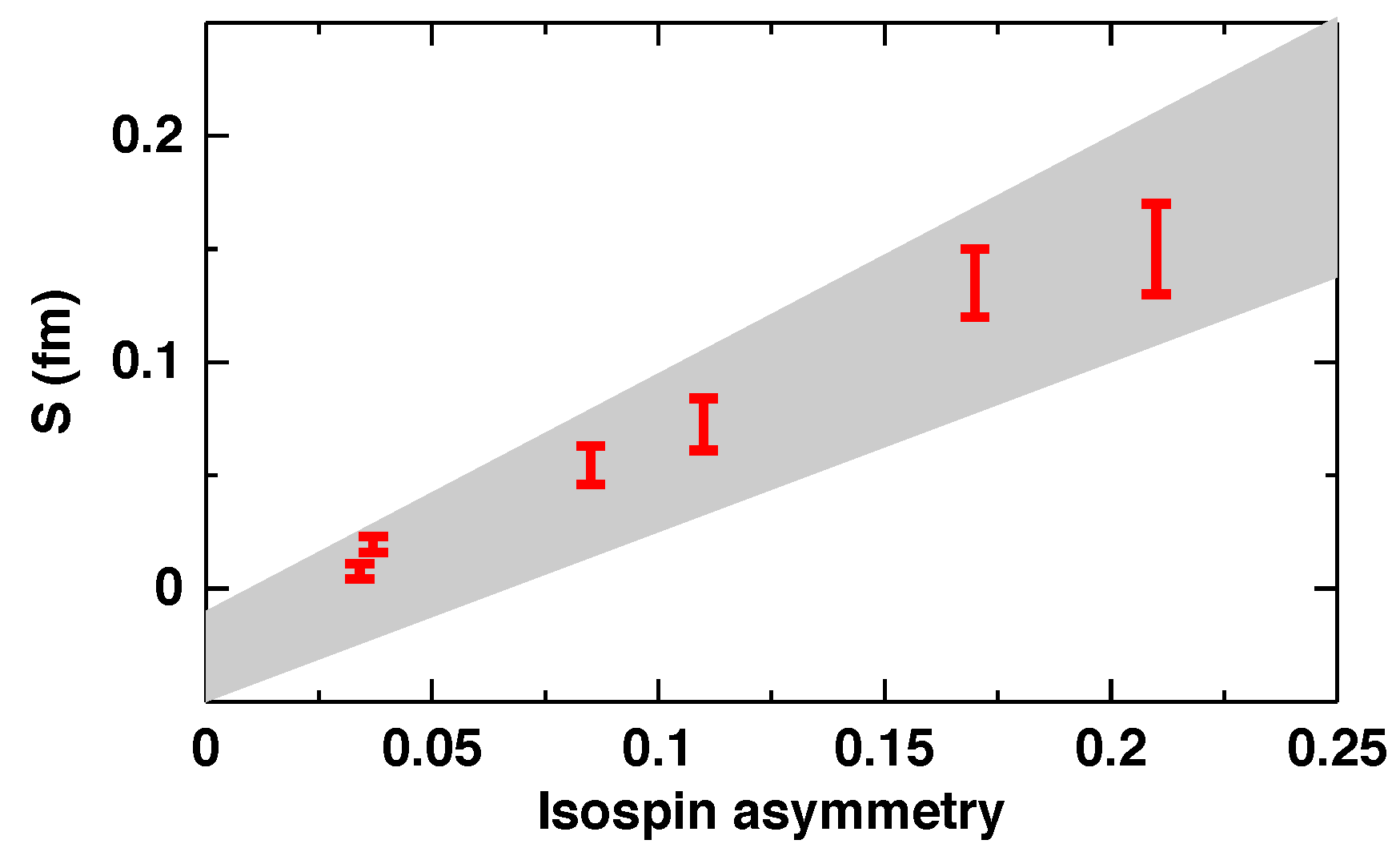
Preprints 90143 g002
Preprints 90143 g003
Figure 3. (Color online) The neutron skin of 48Ca vs. the one of 208Pb. The red and blue bars are the results from CREX and combined PREX-I and PREX-II, respectively. The gray circles and pink diamonds are the result of relativistic and non-relativistic mean-field models, respectively. Coupled cluster and dispersive optical model predictions are indicated as CC and DOM, respectively.
Figure 3. (Color online) The neutron skin of 48Ca vs. the one of 208Pb. The red and blue bars are the results from CREX and combined PREX-I and PREX-II, respectively. The gray circles and pink diamonds are the result of relativistic and non-relativistic mean-field models, respectively. Coupled cluster and dispersive optical model predictions are indicated as CC and DOM, respectively.
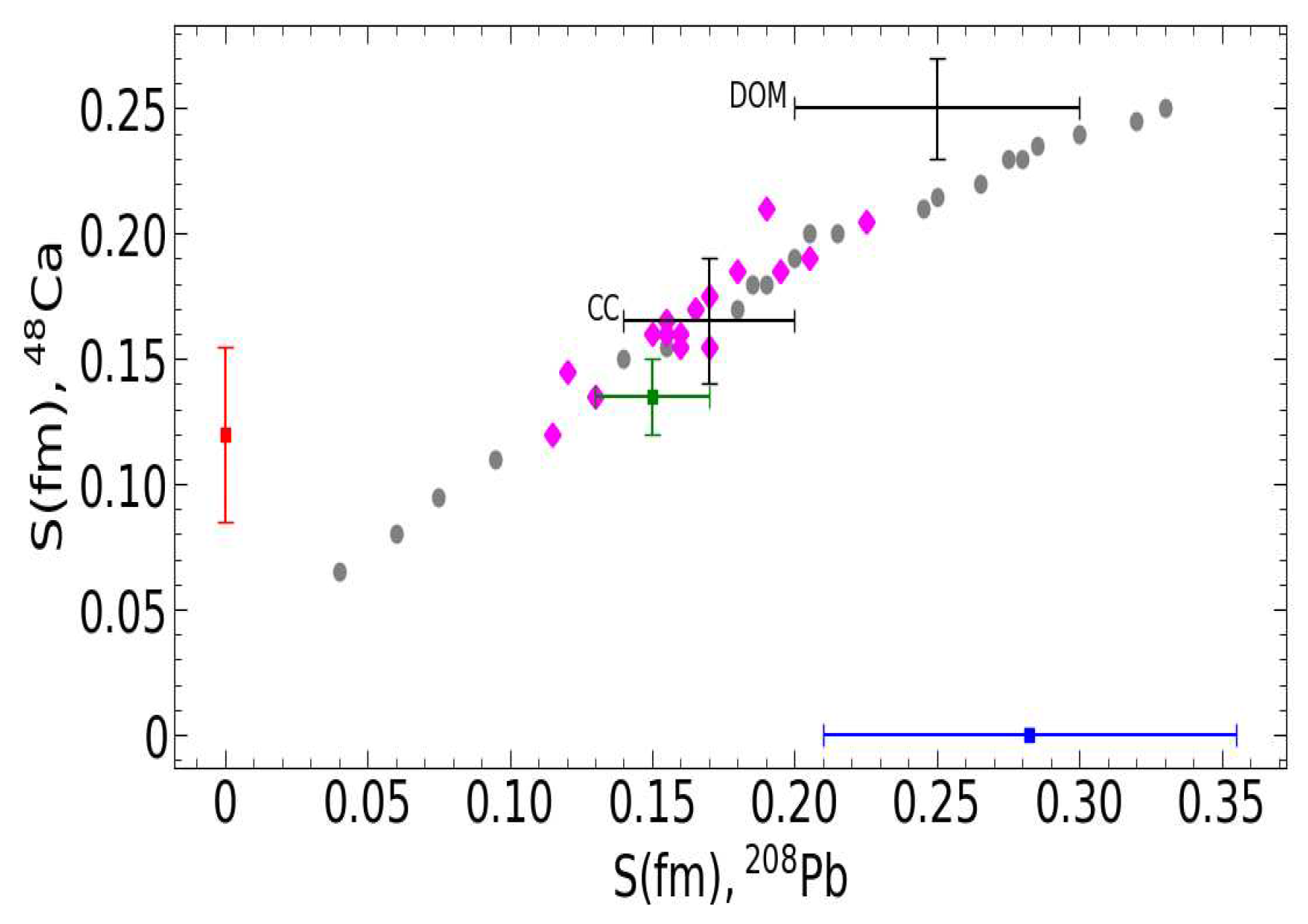
Preprints 90143 g003
Table 1. Values of the neutron skins in 48Ca and in 208Pb from a variety of experimental methods.
Table 1. Values of the neutron skins in 48Ca and in 208Pb from a variety of experimental methods.
Type of measurement Extracted neutron skin in 48Ca Extracted neutron skin in 208Pb
Proton-nucleus scattering [4] 0.056 - 0.102 0.083 - 0.111
Proton-nucleus scattering [5] 0.211 − 0.063 + 0.054
Proton-nucleus scattering [6] 0.20 ± 0.04
Proton-nucleus scattering [7] 0.10 ± 0.03
Polarized proton-nucleus scattering [8] 0.23 ± 0.05 0.16 ± 0.05
Polarized proton-nucleus scattering [9] 0.168 − 0.028 + 0.025
Polarized proton-nucleus scattering [5] 0.211 − 0.063 + 0.054
Pionic probes [10] 0.13 ± 0.06 0.11 ± 0.06
Pionic probes [11] 0.11 ± 0.04
Coherent π photoproduction [12] 0.15 ± 0.03 − 0.03 + 0.01
Coherent π photoproduction [13] 0.20 − 0.03 + 0.01
Antiprotonic atoms [14] 0.20 (± 0.04) (± 0.05)
Antiprotonic atoms [15] 0.16 (± 0.02) (± 0.04)
Antiprotonic atoms [16] 0.15 ± 0.02
Electric dipole polarizability [17] 0.13 - 0.19
Electric dipole polarizability [18] 0.165 (±0.09)(± 0.013) (±0.021)
Electric dipole polarizability
via polarized scattering at forward angle [19] 0.156 − 0.021 + 0.025
Electric dipole polarizability [20] 0.14 - 0.20
Pygmy dipole resonances [21] 0.18 ± 0.035
Interaction cross sections [22] 0.105 ± 0.06
( α , α ′ ) GDR 120 MeV [23] 0.19 ±0.09
α -particle scattering [24] 0.171 ± 0.05
Table 2. Status of ab initio predictions for the skins (in fm) in 48Ca and in 208Pb. The two results from Ref. [44] for both 48Ca and in 208Pb show acceptable ranges within 68% and 90% of the credibility region (CR).
Table 2. Status of ab initio predictions for the skins (in fm) in 48Ca and in 208Pb. The two results from Ref. [44] for both 48Ca and in 208Pb show acceptable ranges within 68% and 90% of the credibility region (CR).
Nucleus Predicted skin Source
48Ca 0.120 - 0.150 Ref. [37]
48Ca 0.141 - 0.187 Ref. [44] 68% CR
48Ca 0.123 - 0.199 Ref. [44] 90% CR
208Pb 0.139 - 0.200 Ref. [44] 68% CR
208Pb 0.120 - 0.221 Ref. [44] 90% CR
48Ca 0.114 - 0.186 Ref. [38]
208Pb 0.184 - 0.236 Ref. [38]
48Ca 0.12 - 0.15 Ref. [40]
208Pb 0.13 - 0.17 Ref. [40]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated