Prerpints.org logo
Preprint
Article

Ultrasound Experimental Approach for Knee Intra-articular Femur-Tibia Movements at Different Loads

Altmetrics

Downloads

124

Views

110

Comments

1

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

10 December 2023

Posted:

12 December 2023

You are already at the latest version

Alerts
Abstract
The purpose of the present study was to develop an experimental model for studying of the intra-articular knee movements depending on the work of the knee joint and applied muscle groups in isometric stretching conditions with different tens. The experimental procedure includes ultrasound examination of a knee joint after isometric stretching of healthy men (n=32). The changes in millimeters of the distances between the femur and tibia were measured with ultrasound sonographer at three stages. The first stage was performed on ten (n=10) healthy men at five different sitting and upright positions. In the second and third experimental model stages the lower limbs loading was on 22 participants. Our hypothesis which was confirmed, was that as a result of increasing extraloads on the participants back (2, 5, 10, 15, 17, 20 kg), a intra-articular decrease in the femur-tibia cartilage surface distance wiil be observed. The accuracy of the created experimental model was improved over its three stages from 30% to 9%. Quantitative model data can help to create a mathematical model for the mechanical effects during deformation of the knee joint bone cartilage, as well as to outlines the some future tasks: increasing loading weights; enlarge participant groups; comparison men and women; healthy and pathology comparison.
Keywords: 
Subject: Biology and Life Sciences  -   Anatomy and Physiology

Introduction

The specific anatomy of each human joint determines the limits in which the quantitative parameters of the performed movements, their variety and characteristics change [1,2,3]. Here it is necessary to list the main factors affecting the mobility of the joints, such as: the difference in the sizes of the contact cartilage surfaces; the volume and shape of the intra-articular cartilages; the peculiarities in the construction of the joint capsule; the amount and location of the ligaments strengthening the joints; the muscle groups involved (agonists, antagonists, fixators and neutralizers) in the joint moving; the presence of intra-articular bone synovial fluid and formations, etc.
Over 70% of the traumas that occur in the human musculoskeletal system are of joint origin, like in some specific categories of work, including sports, it is significantly higher [4,5,6]. From this point of view, the joint study of intra-articular bone movements in norm and pathology as a result of different loads, from inner and outer forces, can give some benefits as:
-
finding optimal physical exercises related to individual sportsman fitness status;
-
joint rehabilitation;
-
modelling and design of artificial joints, supporting human movements;
-
creation of general purpose technical devices (robots, mobile lever systems in lifting equipment, etc.);
-
intra-articular biomechanical processes mathematical modeling;
-
information for intra-articular cartilage deformation at different loads.

1. Mechanical response to physical loads

1.1. Composition and structure of cartilage

Bone cartilage contains a layer of soft tissue, providing low friction and surface load, that covers the articulating bone surface in the synovial joint. It allows to establish basic biomechanical functions, such as resistance to wear, resistance to load and shock absorption. From a biomechanical point of view, these important functional characteristics are related to the multiphasic nature of the state [7]. From an engineering point of view, porous tissue is a porous, viscoelastic material, consisting of three main phases: 1) a rigid phase, which is composed primarily of a densely woven, tough collagenous (mainly type II) fibrous network (15–22 % of wet weight). , covered with proteoglycan macromolecules (4–7% of wet weight). The mesh of collagen and proteoglycans represents the pores, reinforced with fibers forming a rigid matrix. The interstices on this porous rigid matrix are filled with water and dissolved ions. The “average” size on the pores is approximately 60 angstroms; 2) wet phase, which is water (usually 80% of wet weight); and 3) ionic phase, which has many types of ions – dissolved electrolytes with positive and negative charges [7,8]. These three phases react together to strengthen the tissue, which is remarkable in its ability to withstand enormous load pressure (several times that of body weight), and the high shear stresses associated with them. It is reported that the stress pressure reaches up to 20 MPa in the overburdened structure [7]. The bone cartilage ability to withstand such high compressive loads without being torn is due to the multiphasic nature of the cartilage tissue and the unique combination of related properties of the cartilage material [9].

1.1. Mechanical cartilage response under physical loading with different profiles

Several authors considered cartilage as a viscoelastic material [8,10,11]. Hayes and Mockros [10] on the basis of generalized Kelvin solid evaluated shear and bulk creep compliances of human articular cartilage from independent creep tests in torsion and uniaxial strain. Linearity of the compliance coefficients in the loading range tested indicated that the results are applicable to visco- elastic analyses of synovial joint mechanics. The measured compliances for normal and degenerative tissue are compared and found to differ significantly. Preliminary investigations also suggest that flow processes are not important in the initial stages of the deformation of normal tissue. Some authors considered cartilage to be porousviscoelastic material. For instance, Wouters et al., 2015 [11] applied Burger’s model and reported that the data revealed nonlinear relations between the applied force and the resulting deformation, with time and frequency dependence.
The cartilage, like many fine connective tissues, functions mechanically across a wide range of daily frequency loads, from <1 Hz for slow activities such as walking, to 1000 Hz for high-speed activities such as jumping and impact sports [12]. Poroelasticity is known to be the basic mechanism underlying the mechanical cartilage functions. Poroelasticity is manifested by friction between the synovial fluid and the hardened matrix of the cartilage and when the synovial fluid is injected under pressure into the cartilage tissue. These two elements of poroelasticity are at the basis of important mechanical cartilage functions, such as self-reinforcement, energy dissipation and hydraulic permeability [12].
Nia et al., 2013 estimated the high frequency cartilage nanomechanics on normal cartilage and a cartilage with denatured glycosaminoglycans (GAG) [12]. The last is due to the degradation of the cartilage matrix, which occurs in the earliest stages of osteoarthritis. In this research, high-frequency measurements that simulate velocity under load during activities such as running and jumping are made possible by developing a combined high-frequency nanorheological system coupled to an atomic-force microscope. Through this system the authors investigate the interaction between synovial fluid and the stiffness of the cartilage matrix at the molecular level, which occurs mainly at high frequency loads. The authors get some important results. The first is that GAG chains play a major role in the permeability of the synovial fluid, which is known to protect the tissue from wear and tear during activities with high load. Secondly, GAG depletion occurs in the early stages is more vulnerable to high-frequency and rapid loading than to high-force loading. These derivatives have a direct relationship with the influence of the frequency and speed of loading on the endurance of the muscles in certain sports disciplines [12].

1. Methods for joint biomechanical characterization

The wide penetration of the test of nuclear-magnetic resonance (NMR) in scientific research made it possible to evaluate some processes in the joint capsule in vivo under fixed loads. For example, Cotofana et al., found that cartilage thickness decreased to 5.2% when loading the knee with a force equal to 50% of body weight [13]. Herberthold et al. with in situ measurement of articular cartilaged compression in intact femoro-patellar joints loading observed a mean in situ deformation of 44% in patellar cartilage after 3.5 h of loading (mean contact pressure 3,6 MPa) [14]. As well as they make the conclusion that the femoral cartilage showing a smaller amount of deformation than the patella. They determine for the first time and the amount of fluid flow from the crust into the capsular cavity. In the last research, however, the load is on the foot and does not involve the participation of muscle groups.
In another review [15] it was found that physical activity (sliding on stairs, running and climbing) leads to mild deformation of the articular cartilage, which recovers after 90 minutes. In another research type Kubo’s group studies [16,17] show that isometric exercises increase up to 7% of muscle group volume as well as their elasticity and Young’s modulus.
Recent research [18] has been reported on changes in the volume of the knee joint capsule with isometric stretching. These data convincingly show that during active isometric exercise there is a change in the distance between the articular surface of the large bone in the femur, which is associated with a change in the size of the muscle-tendon system of the adjacent muscle group as a result of its contraction. Additionally, Ranchev et al. [6] performed preliminary studies on the change in length of the kinematic chain of the upper extremity during isometric stretching on a group of 10 men and 10 women. The results show that the increase in chain length reaches up to 40 mm in some individuals.
So it can be established what processes take place inside the joint capsule – the size change of the contact surface of the participating bone, a movement of the synovial fluid, bone cartilage deformation etc. [19].
It is also necessary to know the specific force (in newton), which acts in the joint. These are muscular forces and joint reactions. The magnitude and direction of the erect response depend greatly on the position of the extremity and on the acting muscle force. They cannot be calculated directly, because the numbers on the unknown muscle force and reaction at the joint are much larger than the equations for equilibrium that can be written down. Therefore, in most cases modeling and optimization methods are used, choosing the optimization function according to the preferences of the researcher or from some physiological considerations [20]. For example, different mathematical and biomechanical models for knee joint muscle joint inclusion were obtained [21,22,23,24,25,26]. For verification of modeled results in the some of enumerated papers surface electromyographic signals (EMGs) are often used [27]. The direct relationship between these signals and the developing force is very complex and varies with different motor tasks. Nevertheless, some authors use processed EMGs as the input excitation signal [28,29] to the so-called Hill-type model of the muscle. Also unclear and discussed is the question how to process EMG signals - they are low-amplitude, noise-like, depending on many individual characteristics of the person being examined - gender, age, training, skin resistance, electrode placement, and others [30].
From what has been said so far, some effects of isometric muscle work and stretching on the muscle-tendon complex can be seen. However, the influence of isometric muscle work and stretching on the functions and biomechanics of joints and the processes within them is very poorly studied. In other words, what happens inside the joint during the intra-joint bone movements in norm and pathology, as well as the effects of different loads (from inner and outer forces) on the joint elements kinematics and why, as far as we know, has not been investigated and clarified.
Ultrasound Echography (ultrasonography, sonorography) is an aproach often applied for diagnostic of different muscle, tendon and joint injures [31,32,33]. Ultrasound method for the lower limbs joint visualization is important in medicine, kinesitherapy and biomechanics from diagnostic, therapeutic and prophylactic standpoint [34,35,36,37,38,39]. The easy work with ultrasound and lack of ionizing radiation are benefits in comparison with a computer tomography (CT) and fluoroscopy [40].
The knee joint is complex joint and is the commonly injured joint now a day because of increased vehicular trauma and sports related injuries [41]. Complex kinematics of knee weight bearing position and complex ligamentous stability and articular congruency are the main reason why these traumas are of concern to surgeon and cause disability to the patients [41].
The aim of the present study was to create an experimental in vivo ultrasonographycal model for evaluation the change in the distance between the bony cartilaginous surfaces of the tibia and femur inside the knee capsule under different vertical external loads with isometric muscle work of applied muscle groups.

Materials and Methods

The presented experimental model includes an ultrasound examination on the change in the distance between the bony surfaces of the tibia and femur inside the knee capsule under different inner and vertical external loads with isometric muscle work of applied muscle groups of healthy men (n=32). Whole group age was between 19 and 24 years (Table 1). The subjects were athletic students from the National Sports Academy “Vassil Levski”, Sofia, Bulgaria. They did not report any health problems. They completed an injury record and were informed in detail about the aim of the experiments and the procedure. All participants gave informed consent. The experimental procedure was approved by the Scientific Council of the Institute of Biophysics and Biomedical Engineering, Sofia, Bulgaria. For some of the participants, the ultrasound scans were with low quality because of knee movement and/or ultrasound transducer position changes around the knee joint center. Therefore, these data were excluded from Table 1 (empty cells) and from further statistical analyses of bone-to-bone distance.
The changes in millimeters of the distances between the femur and tibia were measured with portable ultrasound system Vinno 6, China, 8 - 10 MHz transducer frequency, musculo-sceletal and thyroid test mode (good intraarticular knee visualization). The RadiAnt DICOM Viewer 2022.1.1 was used in obtaining the distances in millimeters. The statistical analysis was conduct with Sigma Plot All ultrasound scanning was made from the same medical physicist.
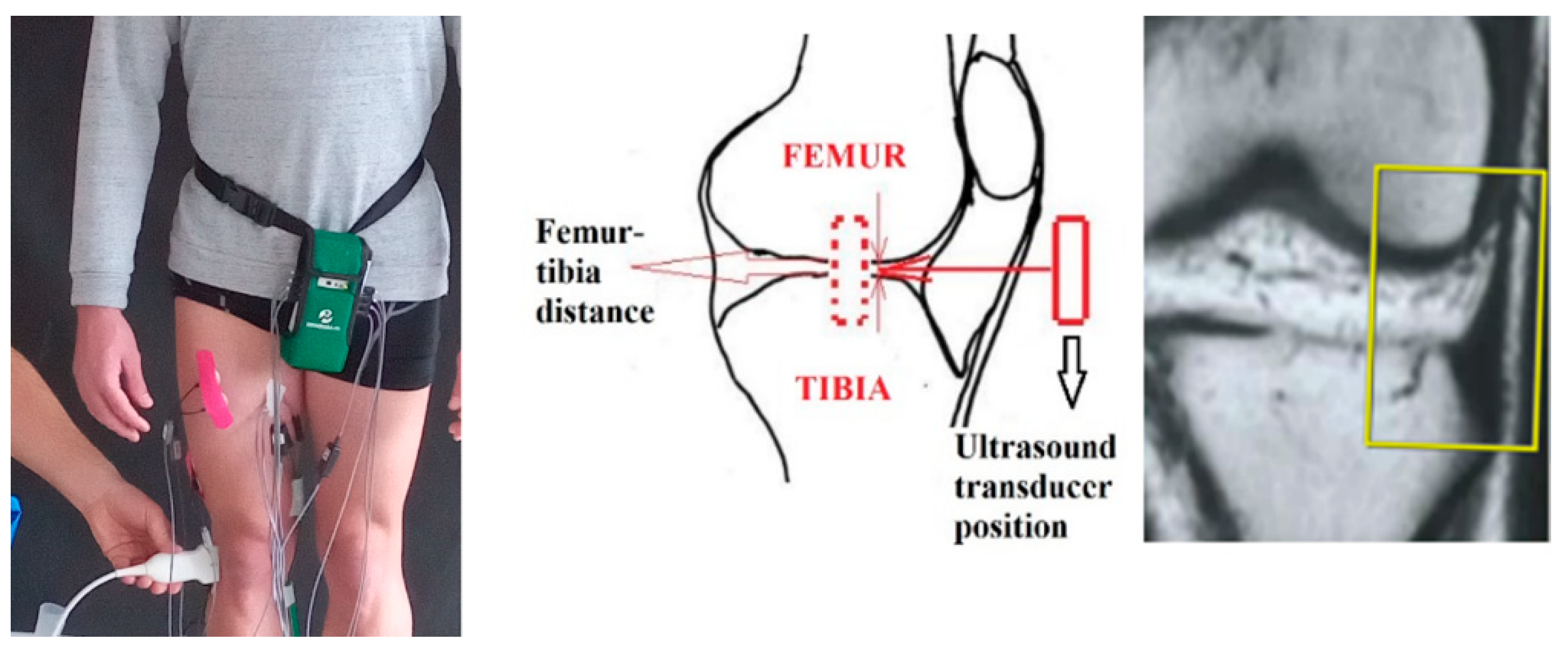
For all experiments the ultrasound transducer was laterally placed outside the right knee joint with long axis coaxially oriented with femur-tibia line (Figure 1). The transducer vision field was focused between iliotibial band and long head biceps femoral tendon on tibia (Figure 1, Figure 2, Figure 3, Figure 4).
Preprints 92858 g001
Figure Ultrasound tranducer position to the knee joint.
Figure Ultrasound tranducer position to the knee joint.
Preprints 92858 g001
The model development was carried out through three stages. The first stage was performed on ten (n=10) healthy men at two different sitting positions and at three different upright positions – all with a knee angle between femur and tibia of 140 degrees (Figure 2) for better femur-tibia distance visualization. In two of the three upright positions, extra loads of 4 and 8 kg were applied vertically down to the lower right limb to induce isometric stretching, by foot pack (Figure 2). The first stage of ultrasound testing was performed on 5 different lower limb pose to achieve different knee joint response:
at rest, femur-tibia angle 140˚, leg on the floor;
own weight stretched, femur-tibia angle 140˚, leg in the air;
straight, femur-tibia angle 140˚, leg without extraload;
straight, femur-tibia angle 140˚, leg with 4 kg extraload;
straight, femur-tibia angle 140˚, leg with 8 kg extraload.
Preprints 92858 g002
Figure Stage 1 experimental setup with used lower limb poses with loads.
Figure Stage 1 experimental setup with used lower limb poses with loads.
Preprints 92858 g002
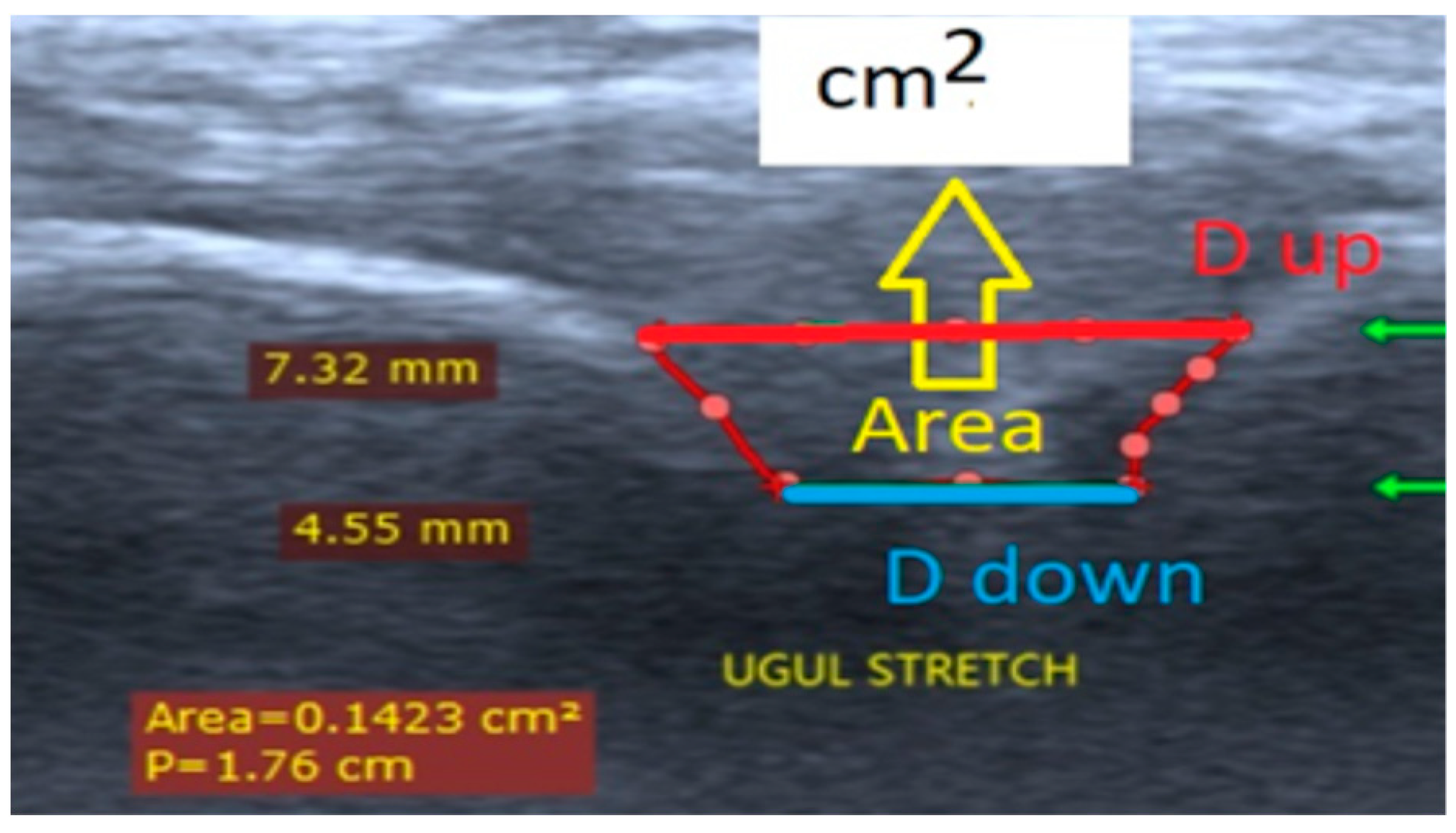
Three quantitative parameters - distance up (Dup, femur-tibia distance nearest to measurement transduser surface), distance down (Ddown, femur-tibia distance in depth to measurement transducer surface), and an area (A) from ultrasound pictures were introduced (Figure 5). The defined two displacements Dup and Ddown were separated with 2,5 mm (Figure 5). The parameter Dup was measured for every participant in depth of knee joint space interval (D, mm) shown in column 7 at Table 1.
The second (on fifteen healthy men, n=15) (Figure 3) and the third stage (on seven healthy men, n=7) (Figure 4) was performed at straight upright body position with increasing of loads on the back – 0, 2, 5, 10, 15, 17 and 20 kg.
Preprints 92858 g003
Figure Experimental setup in stage 2 [37].
Figure Experimental setup in stage 2 [37].
Preprints 92858 g003
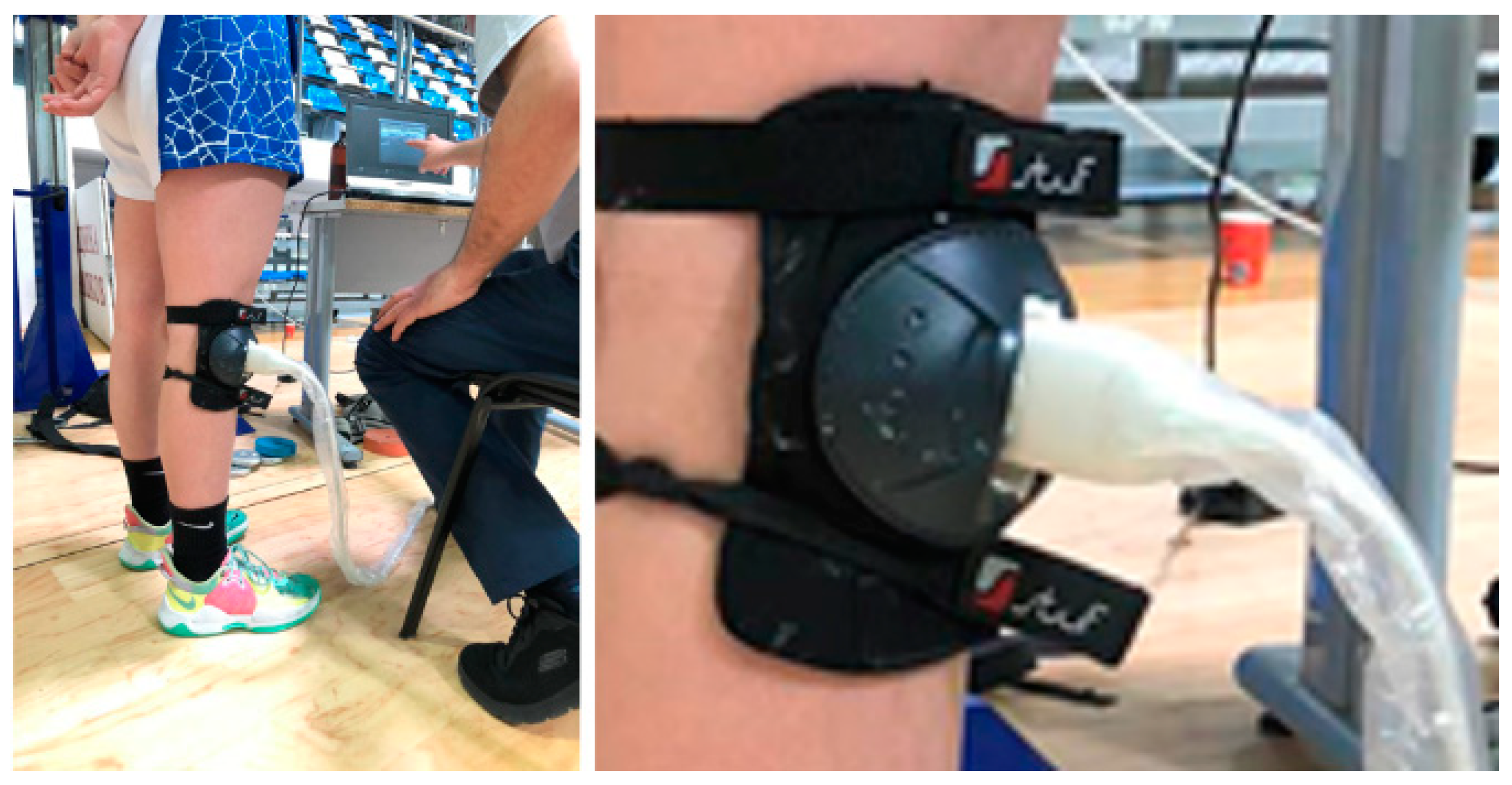
Preprints 92858 g004
Figure Experimental setup in stage 3 with ultrasound transducer muff for immobility of the transducer regarding the knee joint.
Figure Experimental setup in stage 3 with ultrasound transducer muff for immobility of the transducer regarding the knee joint.
Preprints 92858 g004
Preprints 92858 g005
Figure The screen view of the echograph VINNO 6 with measured distances between the femur and tibia bones in the knee joint for one participant [42].
Figure The screen view of the echograph VINNO 6 with measured distances between the femur and tibia bones in the knee joint for one participant [42].
Preprints 92858 g005

Results and discussion

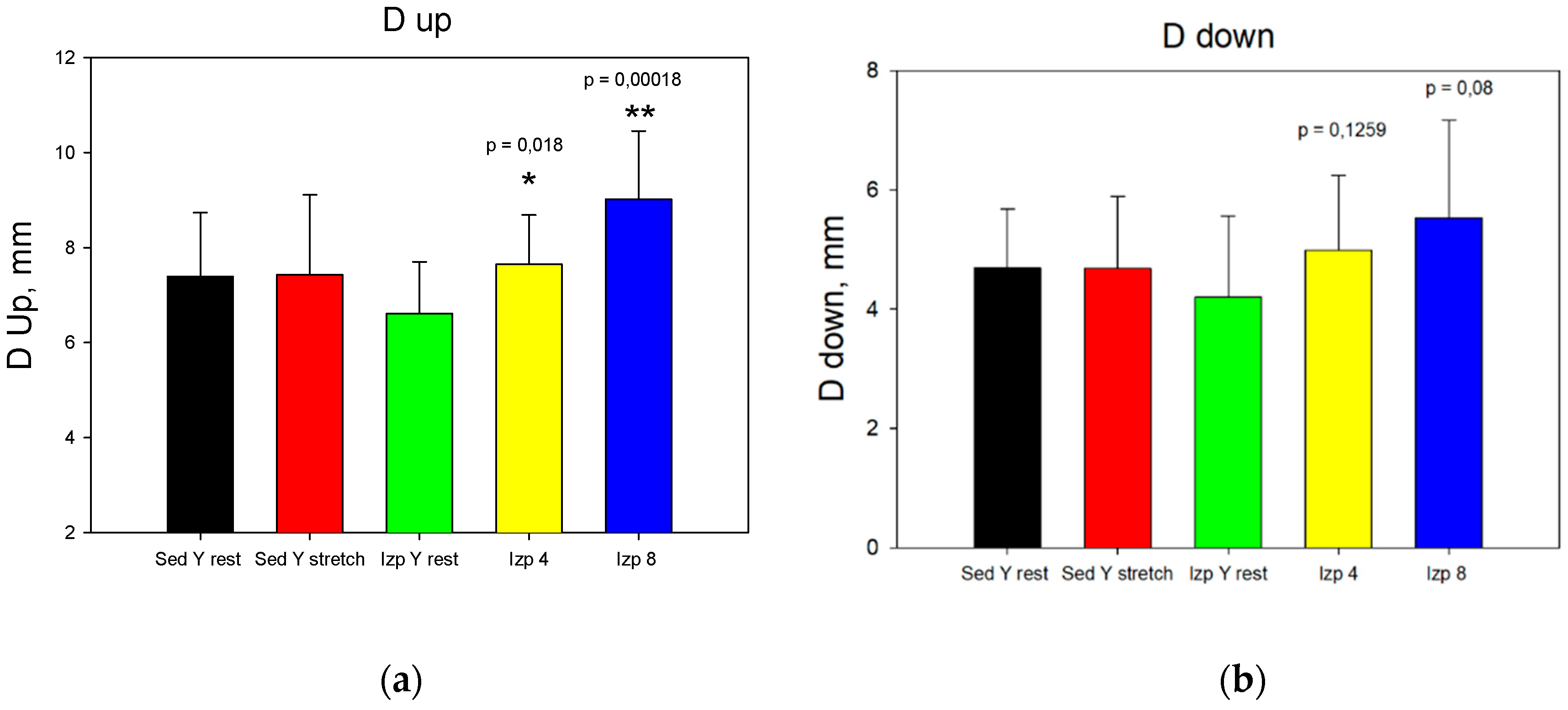
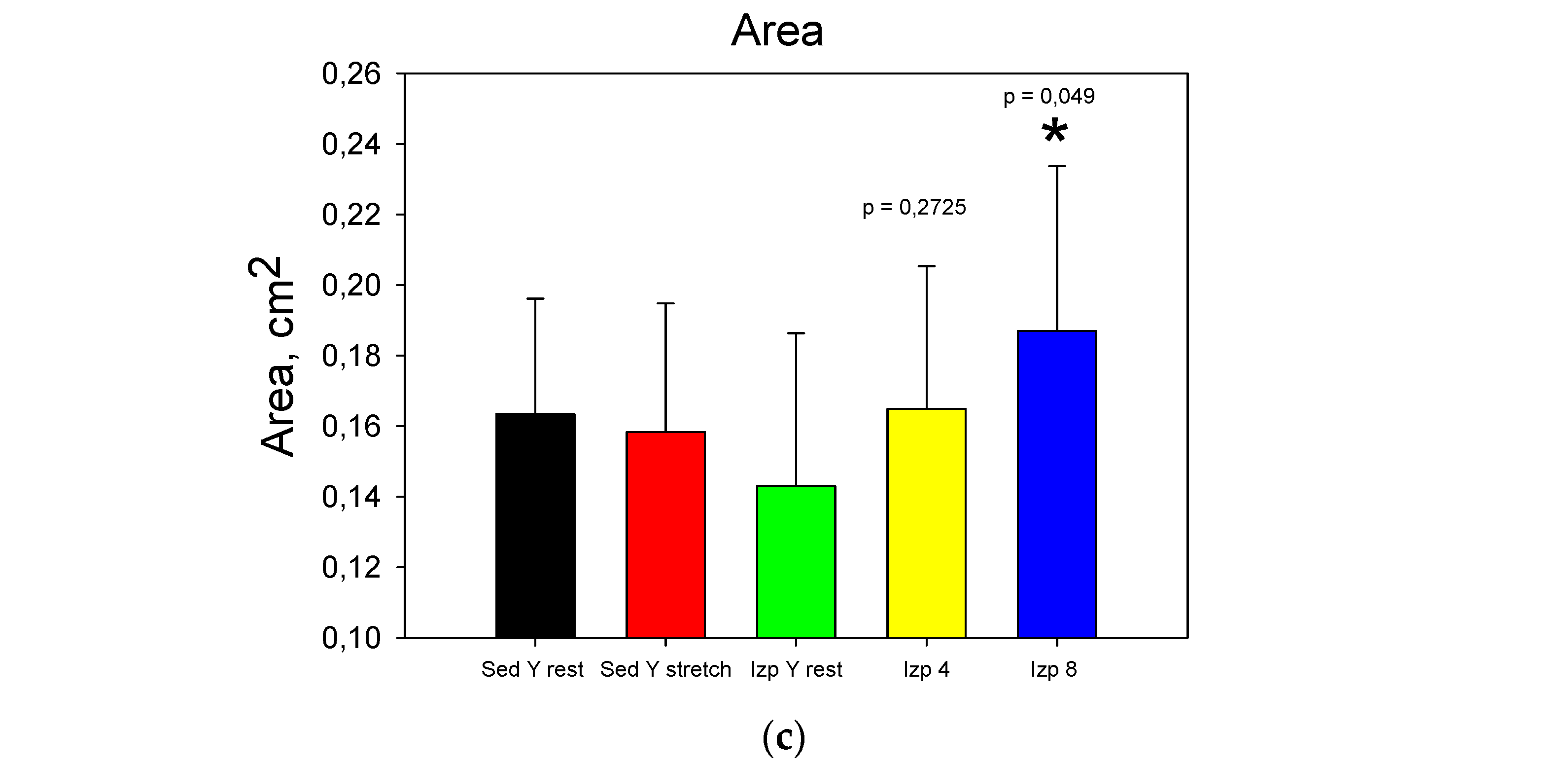
The results from stage 1 (Figure 6) show that applying extra loads statistical significantly increase Dup at 4 and 8 kg, Ddown only at 8 kg and A only at 8 kg. The obtained results for the change of the intra-articular geometry under loads can serve as a quantitative assessment of the internal joint kinematics and determination of the individual joint mobility of the participants in the experiment [6,42,43].
The results obtained in stage one showed that the undetermination (accuracy or error in %) in obtaining the distances in millimeters between the femur and the tibia in the knee joint is high. The reason for this was mainly the unaccuracy at ultrasound transducer positioning about the knee joint for the same participant, despite of the used marker outline for ultrasound transducer on the knee joint skin. The authors concluded that the reproducibility of the obtained ultrasound pictures was poor. For this reason, it was decided to minimize the undetermination (inaccuracy) by testing the same distance in the knee joint, but in a straight posture with increasing loads on the back (Figure 3) to induce a lower limb shortening. Some of the results of this second stage have been published yet [42,43,44,45].
Preprints 92858 g006aPreprints 92858 g006b
Figure Data comparison for the first stage: a). Dup; b). Ddown; c). Area.
Figure Data comparison for the first stage: a). Dup; b). Ddown; c). Area.
Preprints 92858 g006aPreprints 92858 g006b
Тhe second stage was performed on fifteen (n=15) healthy men at stright upright body position with increasing of loads on the back – 0, 2, 5, 10, 15, 17 and 20 kg [42] (Figure 3).
Our hypothesis which was confirmed, was that as a result of increasing extraloads on the participants back (2, 5, 10, 15, 17, 20 kg), an intra-articular decrease in the femur-tibia cartilage surface distance will be observed during static straight participant pose. This change in the distance between the bones indicates the presence of intra-articular processes, which in turn depends on the factors as:
-
the extraload levels;
-
the biomechanical properties of the knee joint components – femur, tibia, fibula and patella cartilage deformability, knee joint ligaments and tendons viscoelasticity, knowing that they are individual for each person and depend on many other factors (age, gender, height, level of training, etc.);
-
amount and viscosity of synovial fluid;
-
the lower limb pose when is extraloading;
-
age, sex, weight.
Regression values for femur-tibia distances D for the twenty two tested participants in stages two and three were determined from the individual linear regression equations for all subjects. All collected data fell within the 95% confidence interval around the regression line. The relative reduction in femur-tibia distances in percentage was calculated based on the obtained regression model with individual angle coefficients (Figure 7, Table 1).
The third stage was carried out to further model optimization by increasing its accuracy. For this purpose, it was made ultrasound transducer muff for immobility of the transducer regarding the knee joint (Figure 4). The results obtained in the third stage were shown in Table 1 (N26-N32). The mean percent decrease for this seven participants (column % decrease in Table 1) is smaller than the others N11-NThis is indirect measure for the aimed model optimization.
Table Results.
Table Results.
Participants D,
mm		 0 kg 2 kg 5 kg 10 kg 15 kg 17 kg 20 kg Angle coeficient %, decrease Stage
Number Age Height,
cm		 Weight,
kg		 BMI
(kg/m2)		 BSA
(m2)
N11 20 175 70 22,86 1,85 1 1,5 1,58 1,3 1,39 1,26 1,23 1,36 -0,0117 15,74 II
N12 22 171 70 23,94 1,82 1 1,65 1,57 1,6 1,55 1,46 1,7 1,37 -0,0072 8,81
N13 21 176 77 24,86 1,93 1 1,28 1,24 1,14 1,13 1,09 1,06 1,02 -0,0116 18,55
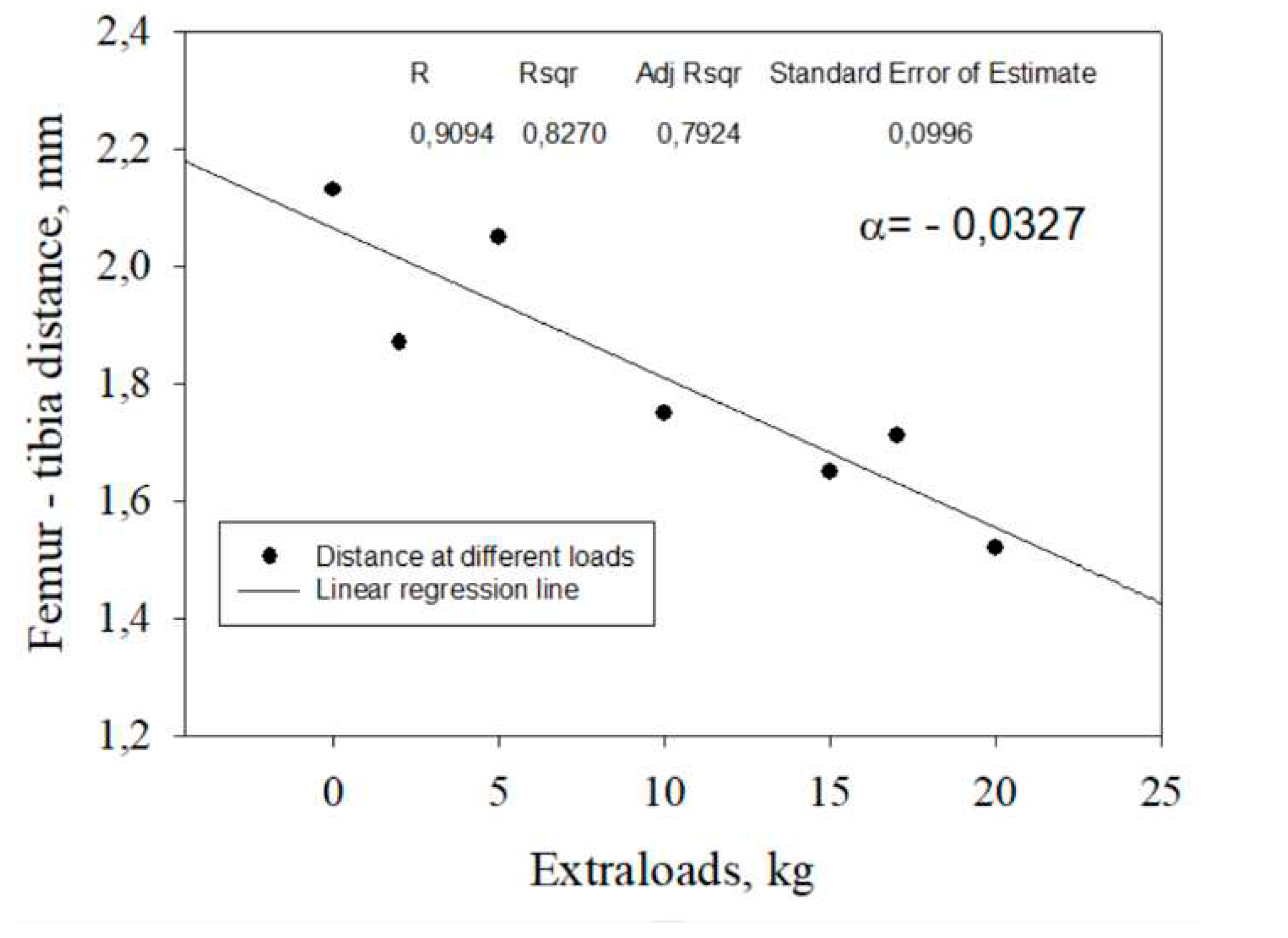
N14 22 188 103 29,14 2,29 1,5 2,21 1,9 2,05 2,06 1,53 1,46 1,6 -0,0327 30,35
N15 20 183 76 22,69 1,98 1 1,45 1,02 1,09 1,16 0,996 1,03 1,05 -0,0119 19,18
N16 20 181 86 26,25 2,07 2,05 2 1,85 1,8 1,78 1,71 -0,0147 14,61
N17 20 183 90 26,87 2,12 1 1,78 1,54 1,52 1,47 1,62 1,71 1,49 -0,0032 3,94
N18 19 1 0,895 0,651 0,673 0,456 0,439 -0,022 53,92
N19 19 170 78 26,99 1,89 1 1,41 1,36 1,4 1,32 1,25 1,19 1,17 -0,0121 17,08
N20 20 177 96 30,64 2,13 1,25 1,66 1,58 1,51 1,47 1,57 1,38 1,37 -0,0112 13,89
N21 22 175 64 20,90 1,78 0,75 1,62 1,44 1,51 1,52 1,44 -0,0094 11,76
N22 20 190 80 22,16 2,08 0,9 1,80 1,71 1,57 1,55 1,56 1,54 -0,0132 14,9
N23 20 185 90 26,30 2,14 1 2,13 1,87 2,05 1,75 1,65 1,71 1,52 -0,0256 24,78
N24 191 85 23,30 2,14 1 1,84 1,39 -0,0225 24,46
N25 21 167 70 25,10 1,79 1,25 1,93 1,82 1,76 1,54 1,41 -0,0233 24,27
N26 22 184 73 21,56 1,95 0,875 1,09 1,08 1,07 1,03 0,979 0,99 -0,0059 10,737 III
N27 20 184 69 20,38 1,90 1,5 0,595 0,489 -0,0053 17,81
N28 21 183 86 1 1,25 1,22 1,2 1,25 1,21 1,18 -0,0022 3,54
N29 24 185 79 23,08 2,03 1 1,86 1,8 1,77 1,75 1,77 -0,0052 5,7
N30 20 193 79 21,21 2,09 1,125 1,84 1,8 1,89 1,66 1,61 1,61 -0,0139 15
N31 24 178 80 25,25 1,98 1 1,19 1,18 1,14 1,05 1,07 1,08 -0,0064 10,92
N32 19 187 74 21,16 1,99 1,5 0,648 0,656 0,629 0,619 -0,0684 6,87
The obtained results through the three stages for the change of the intra-articular geometry under load and stretching serve as a quantitative assessment of the internal joint kinematics and determination of the individual joint mobility of the participants in the experiment [6,42,43].
Preprints 92858 g007
Figure Femur – tibia distance versus extraloads for the participant N14 with the highest femur – tibia distance decreasing – 30,35% and the highest weight 103 kg.
Figure Femur – tibia distance versus extraloads for the participant N14 with the highest femur – tibia distance decreasing – 30,35% and the highest weight 103 kg.
Preprints 92858 g007
The accuracy of our measurements in the proposed experimental model by used device VINNO 6 is limited by three components. The first is related with the used transducer accuracy characteristics. The second is dependent by the accuracy in identity of the transducer-knee joint image position reproduction. The third is determined by the researcher skill at pictures scan, treatment and obtaining the distances in millimeters.
The first accuracy component is lower than 5 % and is defined and described in Vinno 6 user manual for our concrete transducer type (F4-12L) and used experimental mode. This accuracy level is the same for all three stages (Table 2).
The second component accuracy was different for the model stages. For the first stage this second component reaches to 20 %. In the second stage this component decreased to 7 %, because the identity of the transducer-knee joint image position reproduction is strictly observing and the ultrasound transducer position in relation to the knee joint at each participant is maximal stationary.
In the third stage the model accuracy decreased to 2%. The third accuracy component is minimized to 2% by the fact that all ultrasound pictures scan was made by ultrasound transducer muff for immobility of the transducer regarding the knee joint.
At the moment the present experimental model accuracy is defined as a sum of three described components and is lower than 9 % (Table 2).
Table Experimental model acuracy.
Table Experimental model acuracy.
Stage \ Component 1 2 3 Total
Stage 1 ≤ 5% ≤ 20% ≤ 5% ≤ 30%
Stage 2 ≤ 5% ≤ 7% ≤ 5% ≤ 17%
Stage 3 ≤ 5% ≤ 2% ≤ 2% ≤ 9%

Limitations of the study

There are several limitations of the present study. Firstly, we have a methodological limitation related to ultrasound transducer positioning about the knee joint for the same participant, despite of the used marker outline for ultrasound transducer on the knee joint skin. Although we have made several eforts to minimize this methodological limitations, the final approach accuracy stay high – 9%. [46]. Secondly, the tested group of participants were only males with different movement habits and fitness status. As a result, they showed femur-tibia displacements which were appropriate only for model verification. In future investigations it was needed to include females and regular sportsman. Third, the maximal used extraloads were 20 kg on compression. The reasons were related to save participants joint and body protection. This extraloading levels will be increased in the future as percent of body weight in order to be emphasized the observed processes. Fourtly, the tested group were with only 32 males divided to the three experimental model stages (n1=10; n2=15; n3=7). This relatively small participant number decrease the model findings depth and the obtained scientific conclusion importance. Тhe analyzed limitations of the study show the directions for future tasks related to improving the model accuracy and increasing its scientific value [47,48,49,50,51,52,53].

Conclusion

To the best of our knowledge, our experimental model is the first for investigation the reduction of the distance between the femur and the tibia in the knee joint at 0° flexion with increased load. In this paper the authors summarize and clearly described all stages for experimental model development with obtained quantitative results. Presented ultrasound model findings will be the basis for the future investigations: (1) determination of the change in the contact area between the femur and the tibia under different axial loads; (2) evaluation of the deformation of the cartilage tissue from the contact area between the femur and the tibia under different axial loads; (3) modelling the interaction between cartilage deformation and interstitial fluid flow from the cartilage into the joint cavity under loading conditions. The difficulties of the method for accurate measurement of the femur-tibia distance are related to ensuring the immobility of the ultrasound transducer regarding the knee joint and second, minimizing small movements in the knee of the tested participants
In the world literature there are an information that the contact surface between the femur and the tibia varies between 2 cm2 and 6 cm2 and it was influenced by the menisci [54,55]. Some authors concluded that the menisci may occupied 70 per cent of the total femur-tibia contact area [56].
The obtained quantitative data for femur-tibia distances combined with the femur-tibia contact surface area, will help to create in a future a mathematical model for the mechanical effects during deformation of the knee joint femur and tibia cartilages, as well as to attempt to prepare quantitative method with software program for automatic calculation of femur-tibia kinematics from ultrasound images.
On the basis of our experimental model one can outline some future tasks:
-
increasing loading weight;
-
enlarge participant groups;
-
comparison men and women; study of cartilage deformation at stretching loading;
-
looking for isometric stretching influence on knee hemorheology [57];
-
development/design of exercises in order to divide and estimate the contribution to the load of the joint cavity separately from stretching only and in combination with other loads;
-
development of practically applicable mechanical trainer for joint fitness.

Author Contributions

"Conceptualization, I.I.; Methodology, I.I.; Software, I.I.; Validation, I.I.; Formal Analysis, I.I.; Investigation, I.I.; Resources, I.I. and S.R.; Data Curation, I.I.; Writing – Original Draft Preparation, I.I.; Writing – Review & Editing, I.I.; Visualization, I.I.; Supervision, I.I.; Project Administration, I.I.; Funding Acquisition, I.I. and S.R.”.

Funding

This work was supported by the Bulgarian National Science Fund - grant КП-06-Н57/18 from 16.11.2021.

References

  1. Hamill, J.; Knutzen, K. M. Biomechanical basis of human movement. Lippincott Williams & Wilkins,.
  2. He, Y.; Li, Z.; Alexander, P. G.; Ocasio-Nieves, B. D.; Yocum, L.; Lin, H.; Tuan, R. S. Pathogenesis of osteoarthritis: risk factors, regulatory pathways in chondrocytes, and experimental models. Biology, 2020, 9(8), 194. [CrossRef]
  3. Eschweiler, J.; Li, J.; Quack, V.; Rath, B.; Baroncini, A.; Hildebrand, F.; Migliorini, F. Anatomy, biomechanics, and loads of the wrist joint. Life, 2022, 12(2), 188. [CrossRef]
  4. 4, Orejel Bustos, A.; Belluscio, V.; Camomilla, V.; Lucangeli, L.; Rizzo, F.; Sciarra, T.; ... & Giacomozzi, C. Overuse-related injuries of the musculoskeletal system: systematic review and quantitative synthesis of injuries, locations, risk factors and assessment techniques. Sensors, 2021, 21(7), 2438. [CrossRef]
  5. Wan, M.; Gray-Gaillard, E. F.; Elisseeff, J. H. Cellular senescence in mus-culoskeletal homeostasis, diseases, and regeneration. Bone Research, 2021, 9(1), 41. [CrossRef]
  6. Ranchev, S.; Ivanov, I. M;, Yotov, I.; Stoytchev, S. STUDIES ON A PARADOX IN THE WORK OF THE MUSCULOSKELETAL SYSTEM IN ISOMETRIC TRETCHING. Journal of Applied Sports Sciences, 2020, (2), 80-90. [CrossRef]
  7. Lu, X. L.; Mow, V. C. Biomechanics of Articular Cartilage and Determination of Material Properties. Med. Sci. Sports Exerc., 2008, Vol. 40, No. 2, 193–199. [CrossRef]
  8. Stoytchev, S.; Ivanov, I.; Ranchev, S.; Iotov, I. A review of the biomechanics of synovial joints with emphasize to static stretching exercise. Series on Biomechanics, 2021, Vol.35 No.2, 3-20.
  9. Edwards, J. Physical characteristics of articular cartilage, In: Proc. Inst. Mech. Engrs., 1967, 181, 16-24. [CrossRef]
  10. Hayes, W. C.; Mockros, L. F. Viscoelastic properties of human articular cartilage. J. Appl. Physiol., 1971, 31 (4), 562-568. [CrossRef]
  11. Wouters, K.; Puers, R.; Gasik, M. Modelling of poro-visco-elastic biological systems. Journal of.
  12. Physics: Conference Series, 2015, Vol. 633, p.
  13. Nia, H. T.; Bozchalooi, I. S.; Li, Y., Han; L., Hung, H. H.; Frank, E., ... & Grodzinsky, A. High-bandwidth AFM-based rheology reveals that cartilage is most sensitive to high loading rates at early stages of impairment. Biophysical Journal, 2013, 104(7), 1529-1537. [CrossRef]
  14. Cotofana, S.; Eckstein, F.; Wirth, W.; Souza, R. B.; Li, X., Wyman; B., Majumdar, S. In vivo measures of cartilage deformation: patterns in healthy and osteoarthritic female knees using 3T MR imaging. European radiology, 2011, 21(6), 1127-1135. [CrossRef]
  15. Herberhold, C.; Faber, S.; Stammberger, T.; Steinlechner, M.; Putz, R.; Englmeier, K. H.; Eckstein, F. In situ measurement of articular cartilage deformation in intact femoropatellar joints under static loading. Journal of biomechanics, 1999, 32(12), 1287-1295. [CrossRef]
  16. Eckstein , F.; Hudelmaier, M.; Putz, R. The effects of exercise on human articular cartilage. J. Anat. 2006, 206, pp.491–512. [CrossRef]
  17. Kubo, K.; Kanehisa, H.; Fukunaga, T. Is passive stiffness in human muscles related to the elasticity of tendon structures? Eur J Appl Physiol, 2001; 85:226-. [CrossRef]
  18. Kubo, K.; Kanehisa, H.; Fukunaga, T. Effects of resistance and stretching training programmes on the viscoelastic properties of human tendon structures in vivo. J Physiol, 2002; 538:219-226. [CrossRef]
  19. Ranchev, S.; Ivanov, I.; Iotov, I.; Stoytchev, S. On the biomechanical processes in human knee joint during active isometric stretching. Series on Biomechanics, 2019, Vol. 33, No. 3, 56-61.
  20. Scott, C. E. Brandon, Colin R. Smith, and Darryl G. Thelen. Simulation of Soft Tissue Loading from Observed Movement Dynamics. In: Springer International Publishing AG 2017 B. Müller, S.I. Wolf (eds.), Handbook of Human Motion.
  21. Raikova, R.; Prilutsky, B. Sensitivity of predicted muscle forces to parameters of optimization-based human leg model revealed by analytical and numerical analyses. Journal of Biomechanics, 2001, 34(10):1243-55. [CrossRef]
  22. Lloyd, D. G.; Besier, T. F. An EMG-driven musculoskeletal model to estimate muscle forces and knee joint moments in vivo. Journal of biomechanics, 2003, 36(6), 765-. [CrossRef]
  23. Kim, H. J.; Fernandez, J. W.; Akbarshahi, M.; Walter, J. P.; Fregly, B. J.; Pandy, M. G. Evaluation of predicted knee-joint muscle forces during gait using an instrumented knee implant. Journal of orthopaedic research 2009, 27, 1326. [Google Scholar] [CrossRef] [PubMed]
  24. Shelburne, K. B.; Torry, M. R.; Pandy, M. G. Muscle, ligament, and joint-contact forces at the knee during walking. Medicine & Science in Sports & Exercise 2005, 37, 1948. [Google Scholar]
  25. Shelburne, K. B.; Pandy, M. G. A musculoskeletal model of the knee for evaluating ligament forces during isometric contractions. Journal of biomechanics 1997, 30, 163–176. [Google Scholar] [CrossRef] [PubMed]
  26. Sasaki, K.; Richard, R. N. Individual Muscle Contributions to the Axial Knee Joint Contact Force during Normal Walking. J Biomech., 2010, 43(14): 2780–2784. [CrossRef]
  27. Shelburne, K. B.; Torry, M. R.; Pandy, M. G. Muscle, ligament, and joint-contact forces at the knee during walking. Med Sci Sports Exerc., 2005, 37(11):1948-56. [CrossRef]
  28. Kumar, D.; Manal, K.T.; Rudolph, K.S. Knee joint loading during gait in healthy controls and individuals with knee osteoarthritis. Osteoarthritis and Cartilage, 2012, 21(2):298-305. [CrossRef]
  29. Koehle, M.; Hull, M. The Effect of Knee Model on Estimates of Muscle and Joint Forces in Recumbent Pedaling. Journal of Biomechanical Engineering, 2010, 132(1):011007. [CrossRef]
  30. Dumas, R.; Moissenet, F.; Gasparutto, X.; Cheze, L. Influence of joint models on lower-limb musculo-tendon forces and three-dimensional joint reaction forces during gait. Proc Inst Mech Eng H., 2012, 226(2):146-60. [CrossRef]
  31. Raikova, R. A general approach for modelling and mathematical investigation of the human upper limb. Journal of Biomechanics, 1992, Volume 25, Issue 8, August 1992, Pages 857-867. [CrossRef]
  32. Zhu, J.; Li, B.; Qiu, L.; Liu, H.; Zhang, M.; Wang, Y.; Du, G. A measurement method of knee joint space width by ultrasound: a large multicenter study. Quantitative Imaging in Medicine and Surgery, 2020, 10(5), doi: 10.21037/qims-20-373. [CrossRef]
  33. Razek, A.A.K.A.; Fouda, N.S.; Elmetwaley, N.; Elbogdady, E. Sonography of the knee joint. J Ultrasound., 2009,12(2): 53. [CrossRef]
  34. Okano, T.; Filippucci, E.; Di Carlo, M.; Draghessi, A.; Carotti, M.; Salaffi, F.; Wright, G.; Grassi, W. Ultrasonographic evaluation of joint damage in knee osteoarthritis: feature-specific comparisons with conventional radiography, Rheumatology, 2016, Volume 55, Issue 11, Pages 2040–2049. [CrossRef]
  35. Riecke, B. F.; Christensen, R.; Torp-Pedersen, S.; Boesen, M.; Gudbergsen, H.; Bliddal, H. An ultrasound score for knee osteoarthritis: a cross-sectional validation study. Osteoarthritis and Cartilage, 2014, 22(10), 1675-1691; [CrossRef]
  36. Bevers, K.; Zweers, M. C.; van den Ende, C. H.; Martens, H. A.; Mahler, E.; Bijlsma, J. W. J.; den Broeder, A. A. Ultrasonographic analysis in knee osteoarthritis: evaluation of inter-observer reliability. Clinical and Experimental Rheumatology-Incl Supplements, 2012, 30(5), 673;
  37. Bevers, K.; Bijlsma, J. W.; Vriezekolk, J. E.; van den Ende, C. H.; den Broeder, A. A. Ultrasonographic features in symptomatic osteoarthritis of the knee and relation with pain. Rheumatology 2014, 53, 1625–1629; [Google Scholar] [CrossRef] [PubMed]
  38. Giokits-Kakavouli, G.; Karokis, D.; Raftakis, I.; Siagkri, C. Ultrasound of the knee in Rheumatology: Pitfalls, what is new? Use of US in Rheumatology. Mediterranean Journal of Rheumatology, 2016, 27(4), 151-160; [CrossRef]
  39. Shimozaki, K.; Nakase, J.; Asai, K.; Yoshimizu, R.; Kimura, M.; Kanayama, T.; ... Tsuchiya, H. Usefulness of ultrasonography for dynamic evaluation of medial meniscus hoop function in early knee osteoarthritis. Scientific Reports, 2021, 11(1), 20091; [CrossRef]
  40. Otsuka, S.; Shan, X.; Yoshida, K.; Yakura, T.; Naito, M.; Kawakami, Y. Site dependent elastic property of human iliotibial band and the effect of hip and knee joint angle configuration. Journal of Biomechanics 2020, 109, 109919. [Google Scholar] [CrossRef] [PubMed]
  41. Patel, A.; Chadwick, N.; von Beck, K.; Goswami, P.; Soliman, S. B.; Patel, A.; McGill, K. C. Ultrasound-guided joint interventions of the lower extremity. Skeletal radiology, 2022, 1-11. [CrossRef]
  42. Patel, Yogesh C.; Ahir, B. K. Study of intraarticular proximal tibia fractures treated with plating. Int J Orthop Sci, 2020; 6(1):216. [CrossRef]
  43. Raikova, R.; Ivanov, I.; Hristov, O.; Markova, N.; Trenev, l.; Angelova, S. Detailed Investigation of Knee Biomechanics during Posture Maintenance while Applying Different Static Loadings on the Spine, Int J Bioautomation, 2023, 27 (2), 83-98. [CrossRef]
  44. Zvetkova, E.; Koytchev, E.; Ivanov, I.; Ranchev, S.; Antonov, A. Biomechanical, Healing and Therapeutic Effects of Stretching: A Comprehensive Review. Applied Sciences, 2023; 13(15). [CrossRef]
  45. Zvetkova, E.; Koytchev, E.; Ivanov, I.; Ranchev, S.; Antonov, A. Biomechanical, Healing and Therapeutic Effects of Stretching. A Review. Preprints.org, 2023; 13(15). https://www.preprints.org/manuscript/202306.1884/v1. [CrossRef]
  46. Zvetkova, E.; Koytchev, E.; Ivanov, I.; Ranchev, S.; Antonov, A. Biomechanical, Healing and Therapeutic Effects of Stretching. Encyclopedia, Available online: https://encyclopedia.pub/entry/47615. [CrossRef]
  47. Shimozaki, K.; Nakase, J.; Asai, K.; Yoshimizu, R.; Kimura, M.; Kanayama, T.; ... & Tsuchiya, H. Usefulness of ultrasonography for dynamic evaluation of medial meniscus hoop function in early knee osteoarthritis. Scientific Reports, 2021, 11(1), 20091. [CrossRef]
  48. Otsuka, S.; Shan, X.; Yoshida, K.; Yakura, T.; Naito, M.; Kawakami, Y. Site dependent elastic property of human iliotibial band and the effect of hip and knee joint angle configuration. Journal of Biomechanics, 2020, 109, 109919. [CrossRef]
  49. Riecke, B. F.; Christensen, R.; Torp-Pedersen, S.; Boesen, M.; Gudbergsen, H.; Bliddal, H. An ultrasound score for knee osteoarthritis: a cross-sectional validation study. Osteoarthritis and Cartilage, 2014, 22(10), 1675-1691. [CrossRef]
  50. Alshami, A.; Elsayed, M.; Ali, E.; Eltoukhy, A. E.; Zayed, T. Harnessing the Power of ChatGPT for Automating Systematic Review Process: Methodology, Case Study, Limitations, and Future Directions. Systems, 2023, 11(7), 351. [CrossRef]
  51. Romano, A.; Staber, D.; Grimm, A.; Kronlage, C.; Marquetand, J. Limitations of muscle ultrasound shear wave elastography for clinical routine—Positioning and muscle selection. Sensors, 2021, 21(24), 8490. [CrossRef]
  52. Leitner, C.; Hager, P. A.; Penasso, H.; Tilp, M.; Benini, L.; Peham, C.; Baumgartner, C. Ultrasound as a tool to study muscle–tendon functions during locomotion: A systematic review of applications. Sensors, 2019, 19(19), 4316. [CrossRef]
  53. Kronlage, C.; Grimm, A.; Romano, A.; Stahl, J. H.; Martin, P.; Winter, N.; Marquetand, J. Muscle ultrasound shear wave elastography as a non-invasive biomarker in myotonia. Diagnostics, 2021, 11(2), 163. [CrossRef]
  54. Buda, N.; Cylwik, J.; Mróz, K.; Rudzińska, R.; Dubik, P.; Malczewska, A.; ... & Wełnicki, M. Lung Ultrasound examination in patients with SARS-CoV-2 Infection: Multicenter study. Journal of Clinical Medicine, 2021, 10(15), 3255. [CrossRef]
  55. Kettelkamp, D. B.; Jacobs, A. W. Tibiofemoral Contact Area – Determination and Implications. J Bone Joint Surg Am, 1972, 54(2), 349-356; [CrossRef]
  56. Shiramizu, K.; Vizesi, F.; Bruce, W.; Herrmann, S.; Walsh, WR. Tibiofemoral contact areas and pressures in six high flexion knees. Int Orthop., 2009 Apr;33(2):403. [CrossRef] [PubMed]
  57. Fukubayashi, Т.; Kurosawa, H. The Contact Area and Pressure Distribution Pattern of the Knee: A Study of Normal and Osteoarthrotic Knee Joints, Acta Orthopaedica Scandinavica, 1980, 51:1-6, 871-879. [CrossRef]
  58. Ivanov, I. Hemorheological Alterations and Physical Activity. Appl. Sci., 2022, 12. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated