Prerpints.org logo
Preprint
Article

Connecting Global Modes of Variability to Climate in High Mountain Asia

Altmetrics

Downloads

105

Views

33

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

10 November 2023

Posted:

13 November 2023

You are already at the latest version

Alerts
Abstract
Oscillations in global modes of variability (MoV) form global teleconnections that affect regional climate variability and modify the potential for severe and damaging weather conditions. Understanding the link between certain MoVs and regional climate can improve the ability to more accurately predict environmental conditions that impact human life and health. In this study, we explore the connection between different MoVs, including the Arctic Oscillation (AO), Eurasian teleconnection, Indian Ocean Dipole (IOD), North Atlantic Oscillation (NAO), and El Niño Southern Oscillation (Nino34), with winter and summer climate in the High Mountain Asia (HMA) region, including geopotential height at 250 hPa (z250), 2-m air temperature (T2M), total precipitation (PRECTOT), and fractional snow cover area (fSCA). Relationships are explored for the same monthly period between the MoVs and the climate variables, but also using a lagged correlation analysis to investigate whether any relationship exists at different time lags. We find that T2M has a negative correlation with the Eurasian teleconnection in the Inner Tibetan Plateau and Central China in both winter and summer and a positive correlation in Western China in summer. PRECTOT has a positive correlation with all MoV in most regions in winter, especially with the IOD, and a negative correlation in summer, especially with the Eurasian teleconnection. Snow cover in winter is positively correlated with most indices throughout many regions in HMA, likely due to wintertime precipitation also being positively correlated with most indices. Generally, the AO and NAO show similar correlation patterns with all climate variables, especially in the winter, possibly due to their oscillations being so similar. Furthermore, the AO and NAO are shown to be less significant in explaining the variation in HMA climate compared to other MoVs such as the Eurasian teleconnection. Overall, our results pinpoint different time-windows and specific regions within HMA that exhibit high correlation between climate and MoVs, which might offer additional predictability of the MoVs as well as of climate and weather patterns in HMA and throughout the globe.
Keywords: 
Subject: Environmental and Earth Sciences  -   Atmospheric Science and Meteorology

1. Introduction

High Mountain Asia (HMA) is considered to be Earth’s third pole and one of its main ‘water towers’ [1]. HMA has been hypothesized to influence global weather patterns through its impact on teleconnections [2]. Global modes of variability (MoV) have shown to influence weather and climate for HMA and the surrounding region. For instance, [3,4] demonstrated the importance of the Eurasian teleconnection in driving the planetary-scale Rossby-wave propagation that causes the intraseasonal variability over central Asia and the northern part of India. Other studies investigated climate variations over HMA by the impact of the Indian Ocean Dipole (IOD) and El Niño Southern Oscillation (Nino34) [5,6,7,8], the North Atlantic Oscillation (NAO) [9,10], the Central Indian Ocean mode [11], and the boreal summer intraseasonal oscillation [12,13]. The influence of global MoV on weather patterns within the HMA region has not been thoroughly investigated historically, but such studies are becoming more common [2,12,13,14,15,16].
Studies that investigated relationships between MoV and climate patterns in HMA include Jiang et al., (2014) [12] and Hatsuzuka et al., (2017) [13], who looked at the northward propagation of the boreal summer intraseasonal oscillation which originates in the northern Indian Ocean and tends to dissipate near the foot of Himalayas, and brings high humidity along the southern slope of the Himalayas and Tibetan Plateau, leading to enhanced precipitation events. Yu and Zhou (2004) [14] examined the impacts of winter-NAO on cooling trends over subtropical Eurasia and found a high correlation in March between positive NAO values and lower temperatures within HMA. Lü et al., (2008) [15] investigated the Arctic Oscillation (AO) and the autumn/winter snow depth over the Tibetan Plateau and found there is high positive correlation in winter and a high negative correlation in autumn months. Jiang et al., (2019) [16] explored the impacts of the IOD and Nino34 on snow depth over the Tibetan Plateau, and found there is high positive correlations in December, especially during certain years. Specifically, this study found that in winter of 1997-1998 there was a simultaneous increase in the IOD and the Nino34 indices as well as a corresponding increase in snow depth, indicating that the IOD and the Nino34 may have more impact on snow depth over the Tibetan Plateau when they are both anomalously positive. Wu and Qian (2003) [17] investigated the relation between the Tibetan winter snow and the Asian summer monsoon and rainfall and found that in low snow years there is high rainfall over south and southeast Asia, and in heavy snow years the opposite occurs. These are just some examples of studies that try to explore relationships between MoV and climate or weather in HMA, but studies that thoroughly investigate relationships between different MoV with different climate variables in HMA simultaneously are rare.
In this study we aim to explore five MoV that have been hypothesized to influence weather and climate regimes over HMA, and their relationships with four climate variables in the region. These MoV include the AO, the Eurasian teleconnection, the IOD, the NAO, and the Nino34. The hydrometeorologically important climate variables to be explored in this study include geopotential height at 250 hPa (z250), 2-m air temperature (T2M), total precipitation (PRECTOT), and fractional snow cover area (fSCA). We calculate first-order correlations between each of the MoV and each of the climate variables, to identify regional relationships (e.g., [16]) and potential predictability of weather and climate patterns of the variables of interest (e.g., [18]).
The questions addressed in this study are: 1) what regions have a statistically significant relationship between climate variables and MoVs? 2) What are the implications of any relationships found for both scientific understanding as well as for predictability on a weather, seasonal, or climate timescale? The investigation is completed for winter (December, January, February, or DJF) and summer seasons (June, July, August, or JJA) since these seasons are important for snow cover extent in HMA and the Indian Summer Monsoon. To address these questions, it is important to investigate how the large-scale atmospheric patterns, as expressed through the geopotential height anomalies at 250 hPa, or z250, affect the impact of MoV on weather and climate in HMA. Therefore, the z250 data is obtained for a much larger domain than the HMA region (covering most of the globe), because it is hypothesized that any apparent large-scale patterns that can impact the HMA region can be much farther away (potentially 1,000’s of km away).
The paper is set up as follows: Section 2 will discuss the HMA region and the materials and the methods used to conduct this analysis, Section 3 will present an overview of the correlation results, Section 4 will provide a discussion on the main findings and their implications for the broader community, and Section 5 will summarize our conclusions.

2. Materials and Methods

The data in this study describing the MoV are obtained from the National Oceanic and Atmospheric Administration (NOAA) Earth System Research Laboratory (ESRL) Physical Sciences Laboratory, and the data for the climate variables are obtained from the Modern-Era Retrospective analysis for Research and Applications, version 2 (MERRA-2; [19]). The next sections explain these data sets in more detail. The abbreviations used in this study are explained in Table 1.

2.1. Modes of Variability

MoV can affect global and regional climates on different spatial and temporal scales, have important impacts on human activities and ecosystems, and are a useful tool for simplifying the understanding of the climate system [20]. This section briefly describes each of the five MoV investigated here. 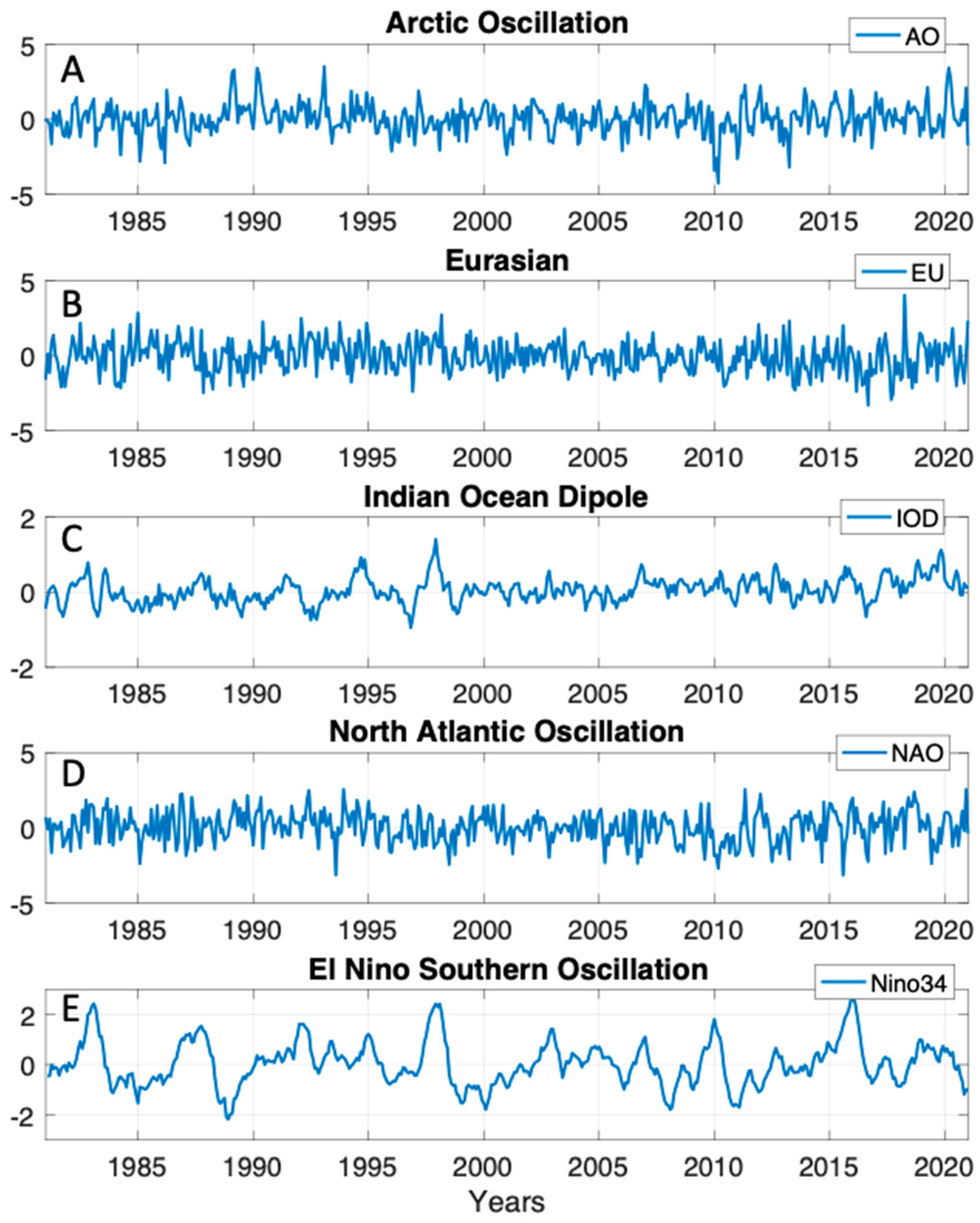The monthly data used to represent the AO, Eurasian teleconnection, IOD, NAO, and Nino34 are obtained directly from the NOAA ESRL database (http://psl.noaa.gov/) for the period January 1981-December 2020. The five timelines are shown in Figure 1.
The AO is an oscillation of atmospheric pressure between the Arctic and the mid-latitudes of the North Pacific and North Atlantic. The AO is an important mode of climate variability for the Northern Hemisphere [21], because when the AO is strongly positive, a strong mid-latitude jet stream steers storms northward, reducing cold air outbreaks in the mid-latitudes, which can include the HMA region. The Eurasian teleconnection is one of the major MoV in the Northern Hemisphere winter and features a mid-tropospheric, west–east-oriented wave train over Eurasia [22]. This pattern may be the most important mid-tropospheric teleconnection pattern to the interannual variations of the East Asian winter monsoon [23]. The IOD, also known as the Indian Niño, is an irregular oscillation of sea surface temperatures in which the western Indian Ocean becomes alternately warmer (positive phase) and then colder (negative phase) than the eastern part of the ocean. The IOD affects the strength of monsoons over the Indian subcontinent [24]. The NAO is a close relative of the AO [21] and is commonly defined as a weather phenomenon over the North Atlantic Ocean of fluctuations in the difference of atmospheric pressure at sea level between the Icelandic Low and the Azores High. It has been suggested that the NAO influences the strength and direction of westerly winds and location of storm tracks across the North Atlantic [25]. The Nino34 (also commonly known as ENSO) is an episodic departure from expected sea surface temperatures in the equatorial Pacific Ocean [20]. These warmer or cooler than normal ocean temperatures can affect weather patterns around the world by influencing high- and low-pressure systems, winds, and precipitation. Nino34 is the largest source of interannual climate variability on a global scale and arises from interactions between the ocean and atmosphere in the tropical pacific [20] and may bring much needed moisture to a region while causing extremes of too much or too little water in others.

2.2. Region of focus

There are two regions of analysis in this study, a larger domain that covers 60W-120E and 5S-90N (Figure 2 and Figure 3), and a smaller domain that covers 65E-105E and 20N-45N (Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9). The larger domain is used to examine spatial correlations between MoV and the z250 data, to investigate how the large-scale atmospheric patterns affect the MoV’s impact on weather and climate in HMA, because these large-scale patterns impact the HMA region from potentially 1,000’s of km away. The smaller domain is used to examine spatial correlations between MoV and HMA climate variables, such as temperature, precipitation, and snow cover. We refer to HMA as the region that includes parts of China, Afghanistan, Pakistan, Nepal, India, Bangladesh, Myanmar, Kazakhstan, and Tajikistan and stretches across several mountain ranges, including the Himalayas, Hindu Kush, Karakoram, and Inner Tibetan Plateau.

2.3. MERRA-2

MERRA-2 is the dataset used for investigating the climate variables in this study. MERRA-2 is the NASA’s most recent global atmospheric reanalysis product [19,26]. We obtain information from MERRA-2 on four variables for the period January 1981-December 2020 (see Table 1). The first variable we obtain from MERRA-2 is the geopotential height at 250 hPa (H250 from the “Single-Level Diagnostics” collection; GMAO 2015a), referred to as z250 for the remainder of this paper. The second variable from MERRA-2 is 2-m air temperature (T2M from the “Single-Level Diagnostics” collection [27]). The third variable from MERRA-2 is total precipitation (PRECTOT from the “Surface Flux Diagnostics” collection; [28]), however MERRA-2 uses observation-based precipitation data as forcing for the land surface parameterization [29], and the precipitation forcing data derived from this approach is archived as the output variable called PRECTOTCORR, which is available as part of the “Surface Flux Diagnostics”’ collection [28]). For our analysis, we use the PRECTOTCORR variable, and refer to it as PRECTOT for the remainder of the paper. The final variable from MERRA-2 is snow cover area fraction (FRSNO from the “Land Surface Diagnostics” collection and called fSCA for the remainder of this paper; [30]). It is important to note that the spatial resolution of the MERRA-2 data (~0.5 degrees) can be sufficient to capture medium-to-large scale features but is not adequate to resolve fine-scale features that can be present in the complex topography of the HMA region. Yet, we choose MERRA-2 as the data set to investigate the climate variables because it provides spatially and temporally consistent information that other forms of data may not provide (e.g., see Massoud et al., 2023 [18] on data coverage for the HMA region).

2.4. Correlation tests

The relationship between the MoV and the climate data examined in this study are first calculated as the correlation of the long-term vector of each mode of climate variability (monthly data from January 1981-December 2020, as shown in Figure 1) with the time vector in each grid cell of the climate variables of interest. Correlations are estimated using the ‘corr’ function in MATLAB (www.mathworks.com/help/stats/corr.html [31]). In Figure 2 and Figure 3, the anomalies of the z250 data are estimated to calculate this correlation, where the anomalies are estimated by removing the monthly climatology (i.e., the long-term mean value for each calendar month throughout the length of the available data record). For the remainder of the results, grids with less than 90% confidence (estimated through the ‘corr’ function p-value output) are masked out in these figures, so that the shown colors in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 only display regions that are significantly correlated. In these figures, red indicates a positive correlation and blue depicts negative correlation.
To investigate if there are any time lags that show a higher level of correlation between the MoV and the climate data, we also apply a time-shift on the data and test for lagged cross-correlations between the MoV at time t and the climate variables at time t+lag (and t-lag), where lag is the number of months that are shifted for the correlation analysis. For example, this can explain how well the IOD value in December can help predict T2M in June, how well the Nino34 value in July can predict PRECTOT one year later, or how well the fSCA in December can help predict the Eurasian teleconnection in March. To do this, we use the ‘xcorr’ function in MATLAB (https://www.mathworks.com/help/matlab/ref/xcorr.html), which is similar to the ‘corr’ function but applies a moving window for the time lag and computes a lagged cross-correlation for each time window. We set a maximum time lag of 6 months to check for any lagged relationships that may be present in the data. To generate a timeline for each climate variable that can be used in the time-lagged cross-correlation test with the MoV data, a spatial average of the whole domain is used for each climate variable at each time step.

3. Results

3.1. Correlating modes of climate variability with geopotential height (z250)

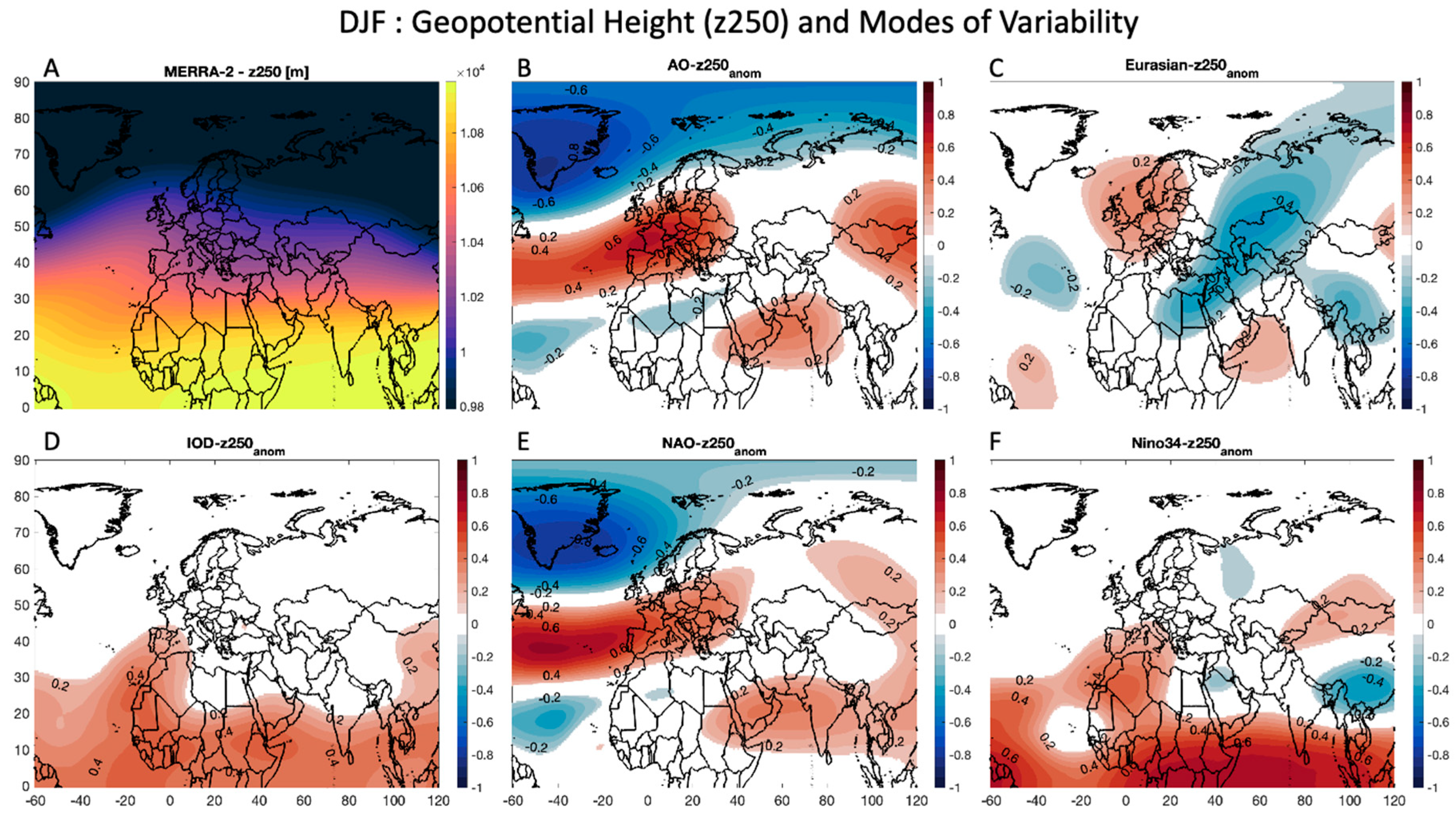
The results in this paper are split up by season, and we separate the correlation analysis for the winter (DJF) and summer (JJA) seasons. Figure 2 and Figure 3 display the results for the z250 data. In Figure 2A, information on mean wintertime z250 is shown, with high latitudes (e.g., 40° N and higher) showing lower geopotential height values of less than 10,000 m (or 10 km), and tropical latitudes showing values close to 11,000 m (or 11 km). When estimating the correlation in each grid cell to the MoV data from Figure 1, different regions emerge as potentially having a significant relationship. Figure 2B shows the correlation between the AO and z250 anomalies, and the region spanning the Arctic Ocean and Greenland show a significant negative correlation (lower than -0.2 in most regions and lower than -0.6 over Greenland). There is also a region that spans from the North Atlantic through most of Europe (greater than 0.6 in some regions) and a region in Eastern Asia (greater than 0.4) that show a pattern of positive correlation between the AO and z250 anomalies in the winter. Figure 2C shows the correlation between the Eurasian teleconnection and z250 anomalies in the winter, and again the region over Europe has a positive correlation (greater than 0.2). There is also a broad region spanning Russia, the Middle East, and parts of North Africa that have a negative correlation (less than -0.4) between the Eurasian teleconnection and the z250 anomalies. Figure 2D shows the correlation between the IOD and z250 anomalies in the winter, with all regions in the tropics having a positive correlation (greater than 0.4). The relationship of wintertime NAO to z250 (Figure 2E) shows a very similar pattern to that of the AO (Figure 2A), and the relationship of wintertime Nino34 to z250 (Figure 2F) shows a very similar pattern to that of the IOD (Figure 2D), with the only exception being in the southeast Asia region where a negative correlation is found (as low as -0.4).
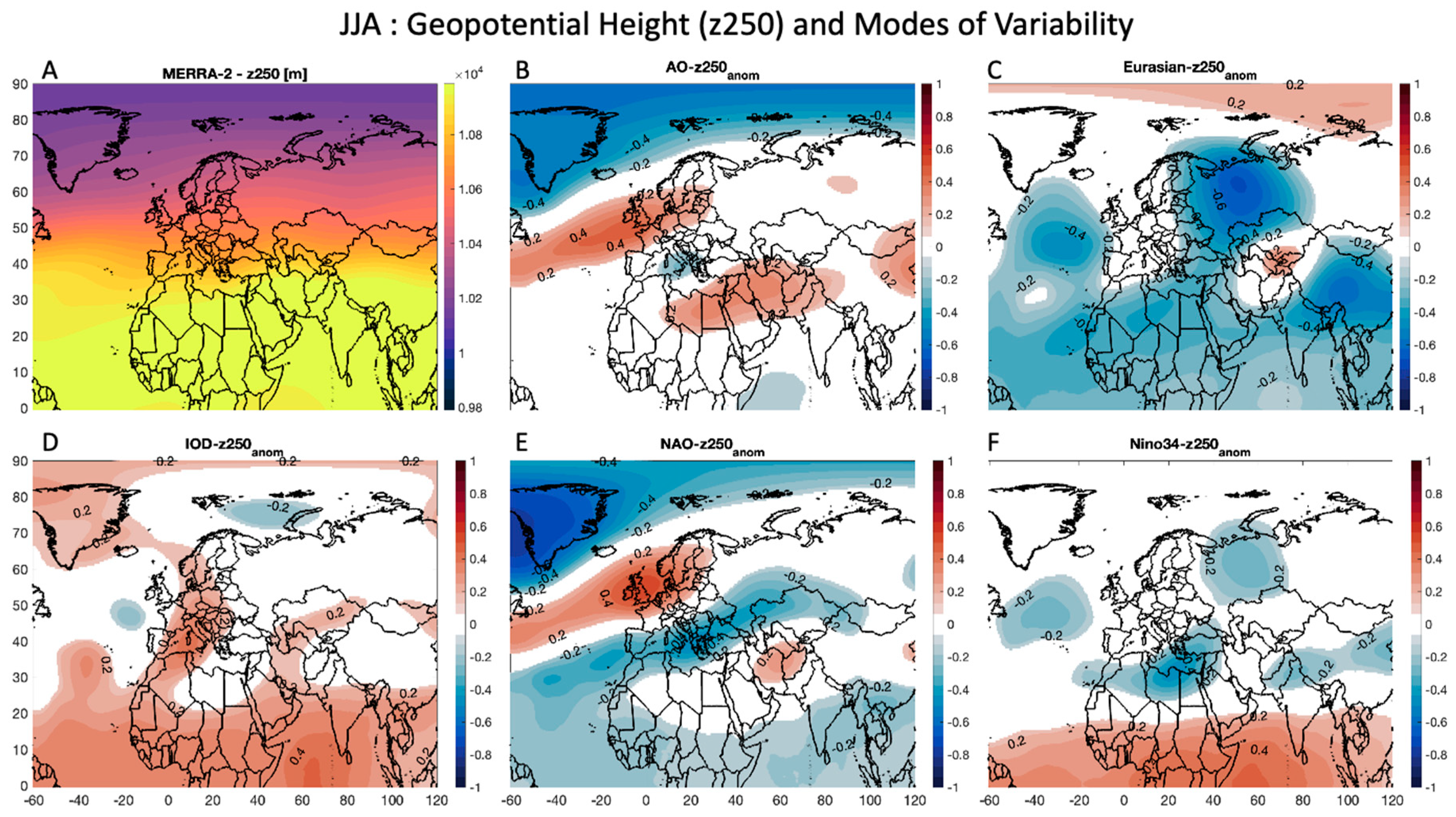
Figure 3A shows information on mean summertime z250, with high latitudes (e.g., 40° N and higher) again showing lower geopotential height values of just slightly over 1e4 m (or 10 km), and tropical latitudes shown values higher than 1.1e4 m (or 11 km). Summertime z250 values are consistently higher than those in the winter. When looking at the correlation of summertime z250 anomalies with the MoV (Figure 3B,F), many of the relationships are very similar to those shown for the wintertime in Figure 2. For example, the AO (Figure 3B) and NAO (Figure 3E) show roughly an identical pattern to their counterparts in Figure 2B,E, except for a northward shift in the positive correlation seen over Europe and a band of negative correlation between the NAO and z250 anomalies stretching from the Atlantic through southern Europe and into central Asia (Figure 3E). The relationship for the IOD (Figure 3D) is also very similar to its counterpart in Figure 2, with positive values seen throughout the globe and with the extension of positive relationships throughout Europe and over Greenland (greater than 0.2). The relationship with the Eurasian teleconnection (Figure 3C) is mostly negative throughout the domain with a peak over western Russia (less than -0.6). For Nino34 (Figure 3F), the tropical latitudes have a positive correlation (greater than 0.4) with various regions having negative correlations (e.g., North Atlantic, Mediterranean Sea, Western Russia, and East Asia).

3.2. Correlating modes of climate variability with temperature (T2M)

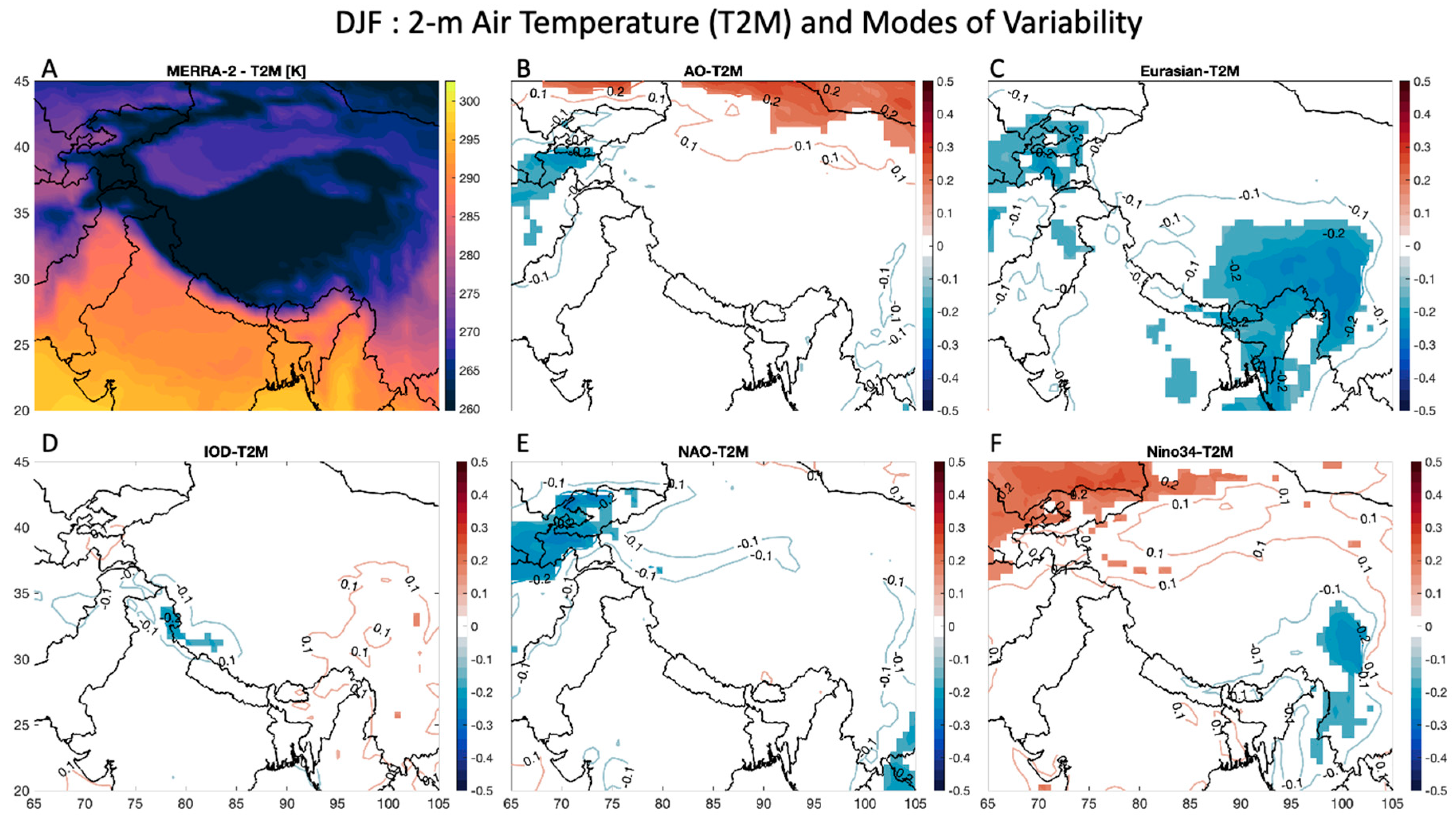
Figure 4 and Figure 5 display the results for the T2M over the HMA region. In Figure 4A, information on mean wintertime T2M data is shown, with high altitudes (e.g., mountain ranges and Inner Tibetan Plateau) exhibiting temperatures that are below freezing and regions with low elevation (e.g., Indian Subcontinent) having higher temperatures of up to 295 K. When determining the correlation in each grid cell to each MoV, no noticeable regions emerge as potentially having a significant relationship with the IOD (Figure 4D). For the AO (Figure 4B), the Eurasian teleconnection (Figure 4C), and the NAO (Figure 4E), there is a negative correlation with wintertime T2M (less than -0.2) in the Hindu Kush, the mountainous regions near Afghanistan. For the Eurasian teleconnection (Figure 4C), there is also a region of negative correlation in the Inner Tibetan Plateau and Eastern India (less than -0.2). For Nino34 (Figure 4F), there a region of positive correlation in the northwest portion of the domain (higher than 0.2), and a small region of negative correlation in Central China (less than -0.2).
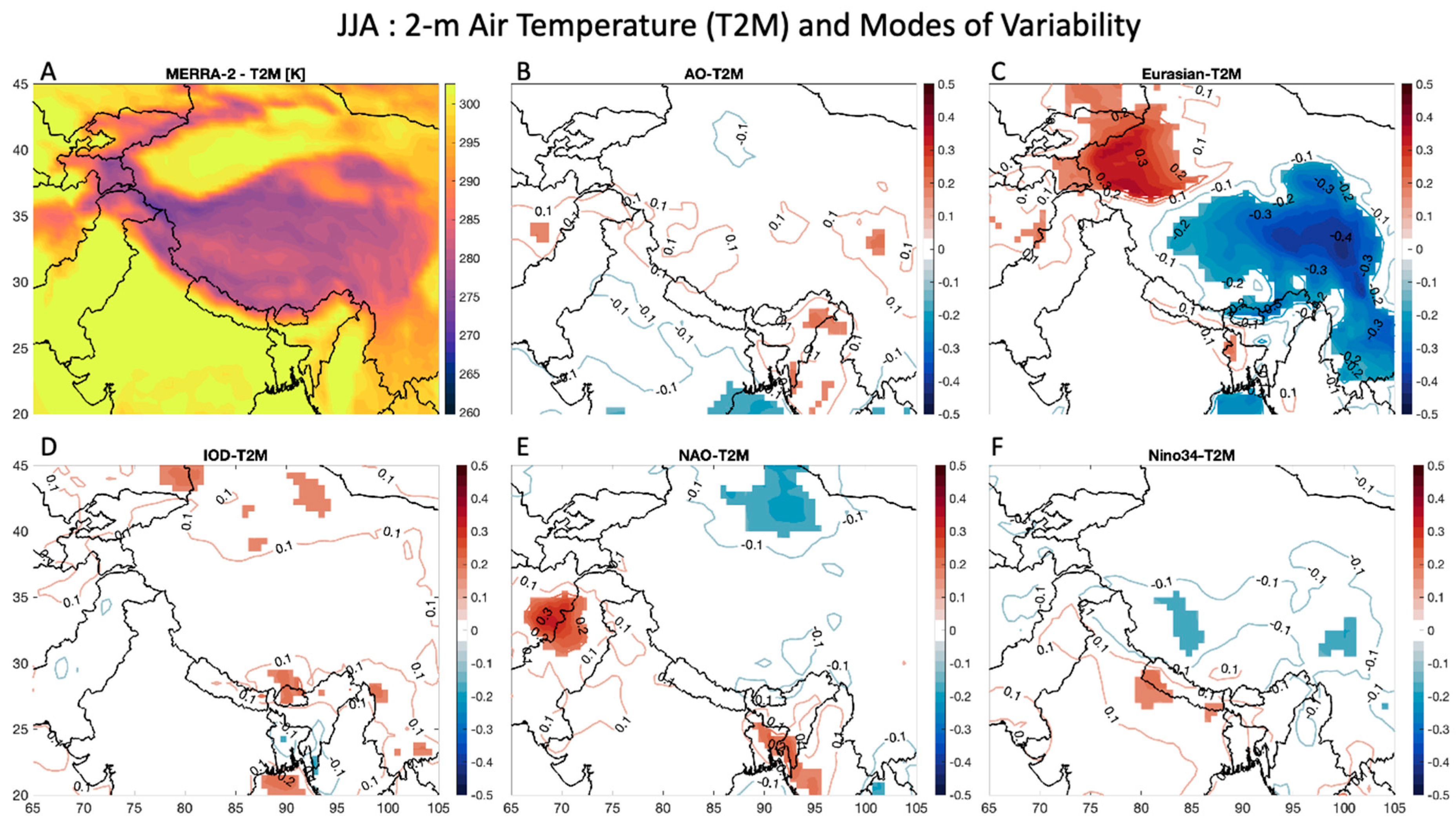
Figure 5A shows information on mean summertime T2M in HMA, again with high altitudes exhibiting temperatures that are close to freezing and regions with low elevation having temperatures higher than 300 K. The AO (Figure 5B), the IOD (Figure 5D), and Nino34 (Figure 5F) show no significant relationship with summertime T2M in HMA. However, the Eurasian Teleconnection (Figure 5C) shows a strong dipole, with regions near western China having a positive correlation (greater than 0.3) and a large portion of the Inner Tibetan Plateau and South China having a negative correlation (less than -0.4). The NAO (Figure 5E) plot shows small regions between Afghanistan and Pakistan and in Bangladesh that have positive correlations (greater than 0.3).

3.3. Correlating modes of climate variability with precipitation (PRECTOT)

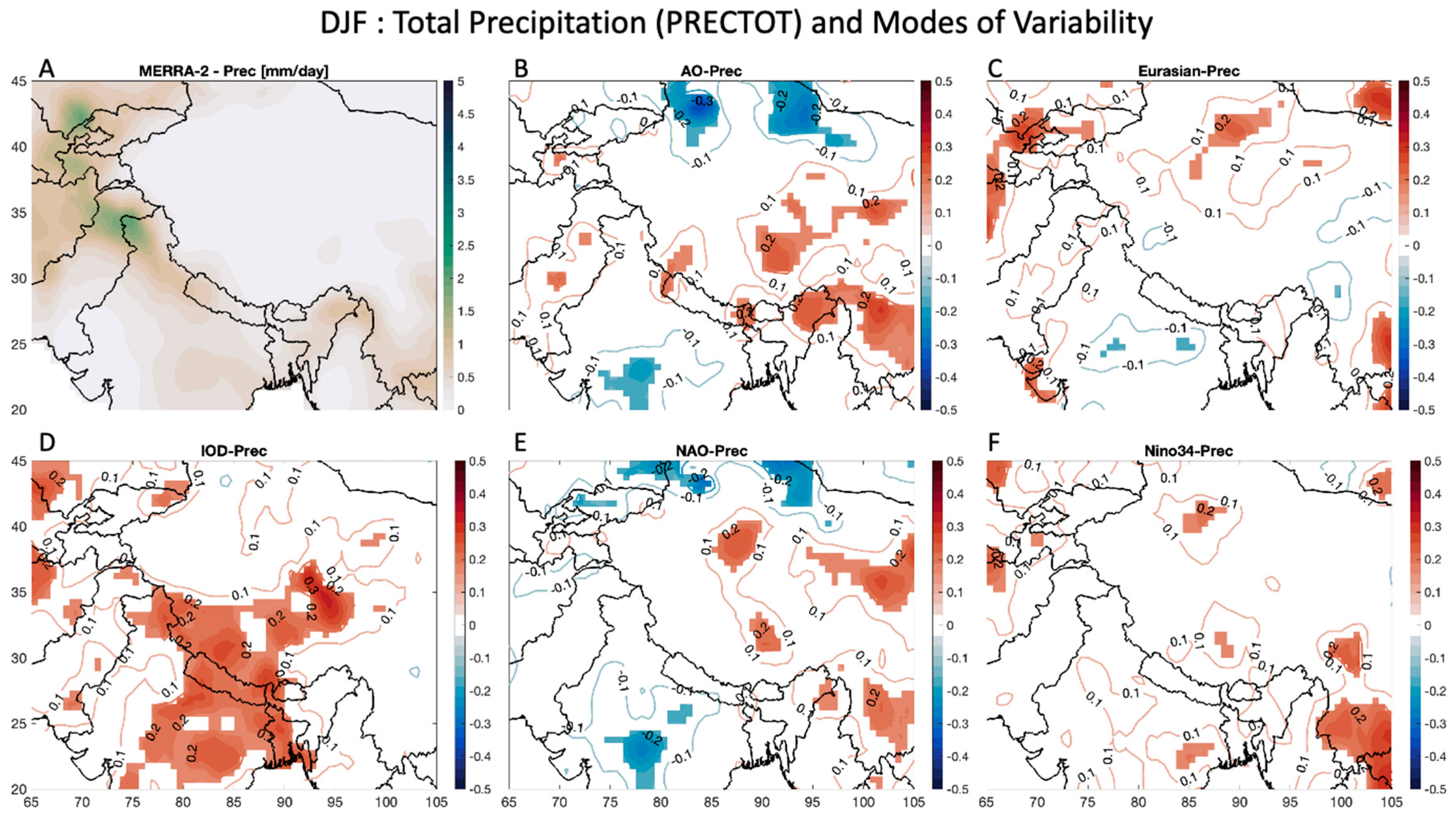
Figure 6 and Figure 7 display the results for the PRECTOT over the HMA region. In Figure 6A, information on mean wintertime PRECTOT data is shown, and regions with high topographic variability (e.g., Hindu Kush and Karakoram) exhibiting slightly higher precipitation rates of up to 5 mm/day and the remainder of the domain showing values of less than 1 mm/day. When determining the correlation in each grid cell to each MoV, no noticeable regions emerge as potentially having a significant relationship with the Eurasian teleconnection (Figure 6C) and Nino34 (Figure 6F), except for a few regions throughout the domain that show a positive correlation (e.g., South China for Nino34). For the AO (Figure 6B) and the NAO (Figure 6E), the patterns are very similar, with some regions in China having positive correlations (greater than 0.2) and some regions in North China and in India having negative correlations (as low as -0.3). For the IOD (Figure 6D), there is broad region through India and western China (and through the Himalayan Mountain range) that has a positive correlation (up to 0.3).
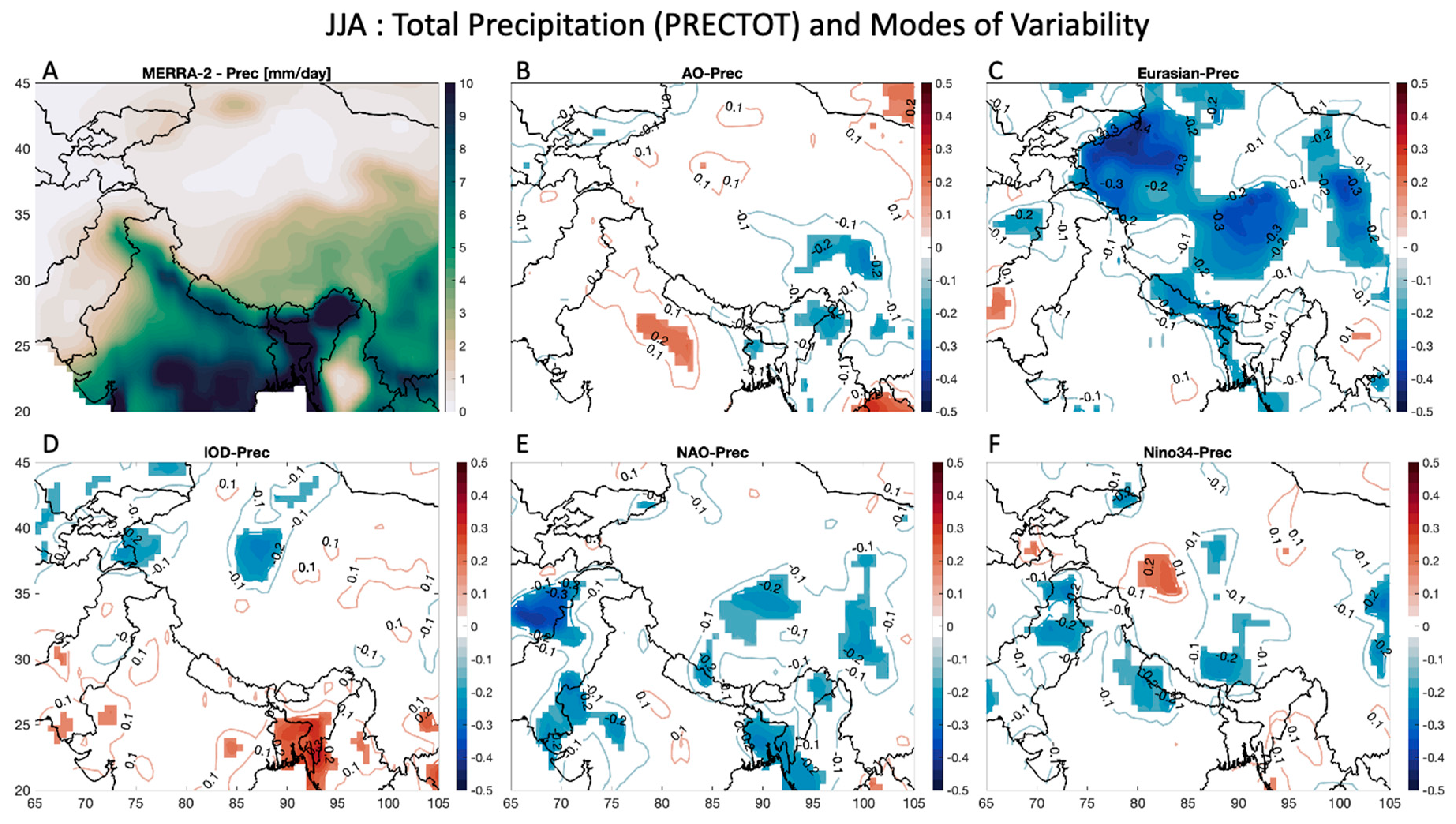
Figure 7A shows information on mean summertime PRECTOT in HMA, with much higher precipitation rates shown in the domain compared to the wintertime, mostly due to the impacts of the Indian Summer Monsoon. Some regions in the Indian Subcontinent experience precipitation rates higher than 10 mm/day in the summer (Figure 7A), with many other parts of the domain seeing rates as high as 5 mm/day. When estimating the relationship of summertime PRECTOT with the MoV, most relationships are significantly negative, such as that with the Eurasian teleconnection (Figure 7C) which has a negative correlation pattern in most of western China and in the Himalayas (as low as -0.4). The other indices have many smaller regions with negative correlation patterns, such as the NAO (Figure 7E) and Nino34 (Figure 7F). There are also small positive correlation patterns seen for the AO (Figure 7B) in India (higher than 0.2) and for the IOD (Figure 7D) in Bangladesh (higher than 0.3).

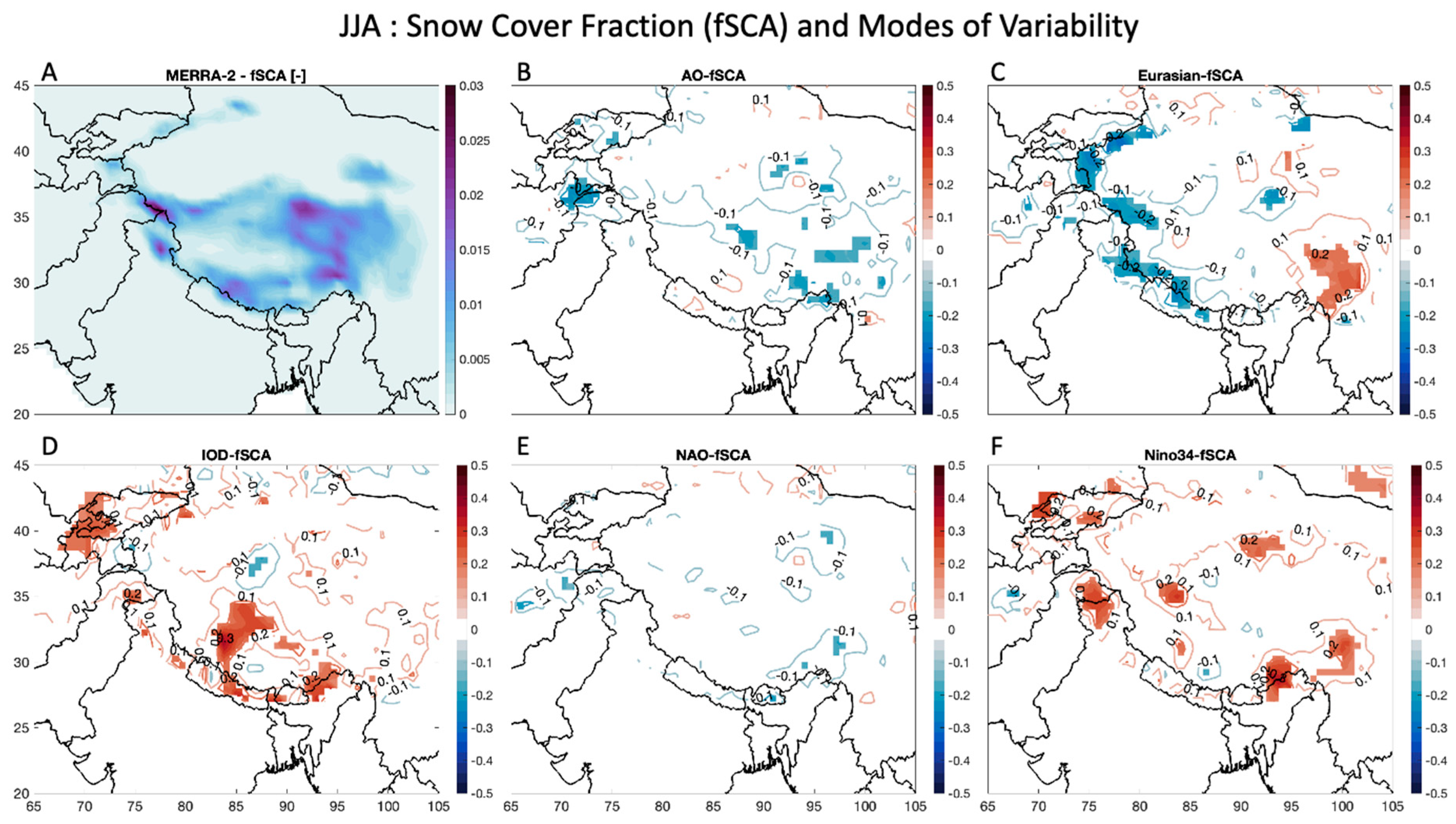
3.4. Correlating modes of climate variability with fractional snow cover area (fSCA)

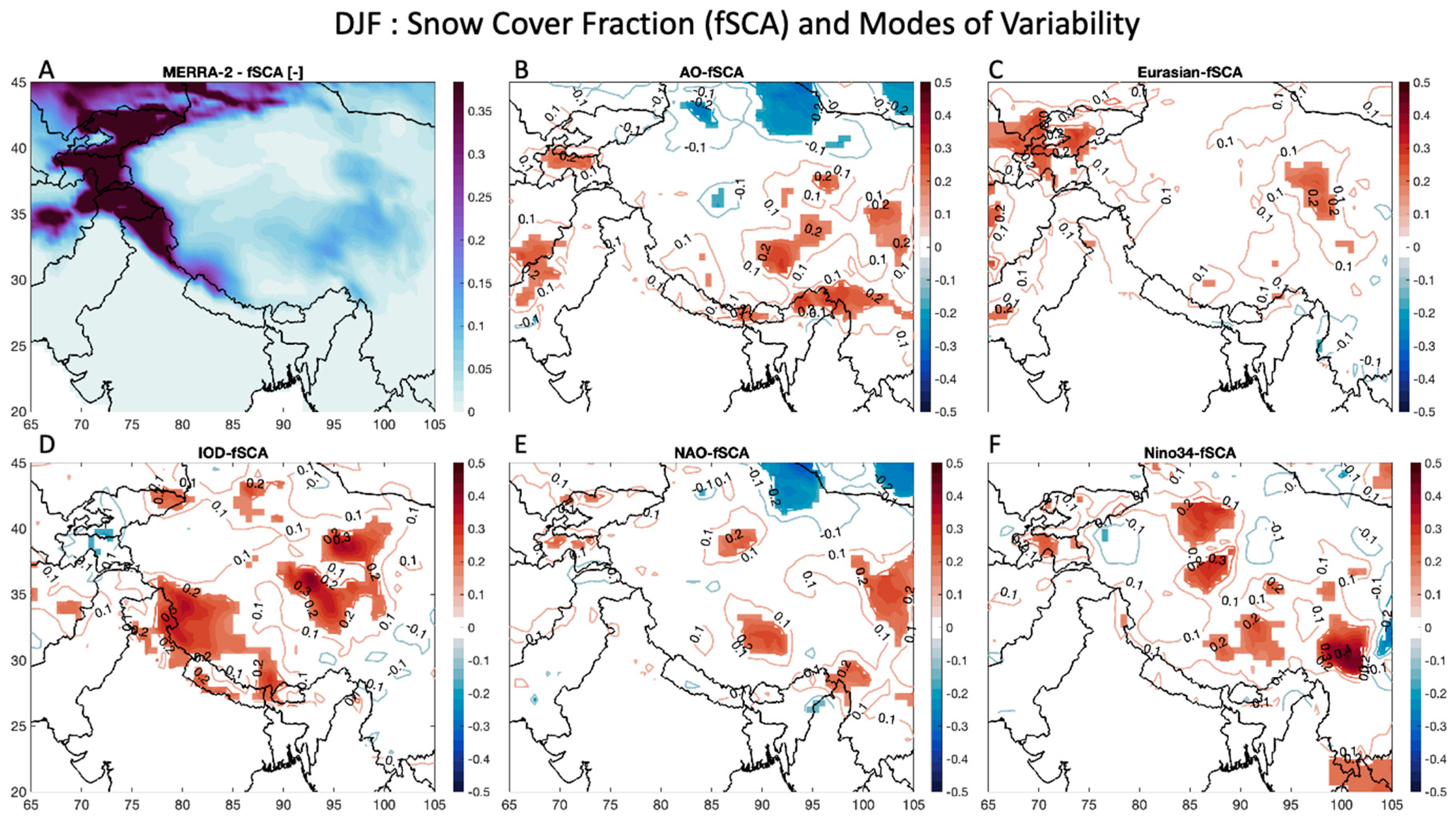
Figure 8 and Figure 9 display the results for the fSCA over the HMA region. In Figure 8A, information on mean wintertime fSCA data is shown, and regions with high elevation are shown to have noticeable fSCA values, with regions of high topographic variability (e.g., Hindu Kush and Karakoram) exhibiting the highest fSCA values (e.g., greater than 0.35 and in some locations up to 1). When determining the correlation in each grid cell to each MoV, no noticeable regions emerge as potentially having a significant relationship with the Eurasian teleconnection (Figure 8C), except for small regions of positive correlation, e.g., northwest part of the domain (higher than 0.2). For the other indices, many regions of positive correlations are shown, such as for the IOD (Figure 8D) in the Himalayas and Central China (higher than 0.3) and other various regions for the AO (Figure 8B), NAO (Figure 8E), and Nino34 (Figure 8F), such as in China (higher than 0.4).
Figure 9A shows information on mean summertime fSCA in HMA, with much lower snow cover shown in the domain compared to the wintertime, mostly due to higher temperatures experienced in the summer. Some regions in the Himalayas and Inner Tibetan Plateau experience fSCA higher than 0.02 in the summer (Figure 9A), with the remainder of the domain seeing close to 0 snow cover area. When estimating the relationship of summertime fSCA with the MoV, no noticeable regions emerge as potentially having a significant relationship with the AO (Figure 9B) or the NAO (Figure 9E), except for the AO which has a small region of negative correlation in the Hindu Kush region (lower than -0.2). The Eurasian teleconnection (Figure 9C) has different regions of negative correlation (as low as -0.2), such as in the Himalayas and the Karakoram, and a region of positive correlation (higher than 0.2) near Central China. For the IOD (Figure 9D) and Nino34 (Figure 9F), there are some regions with positive correlation (as high as 0.3) throughout HMA, such as the Himalayas for the IOD and the Karakoram for Nino34.

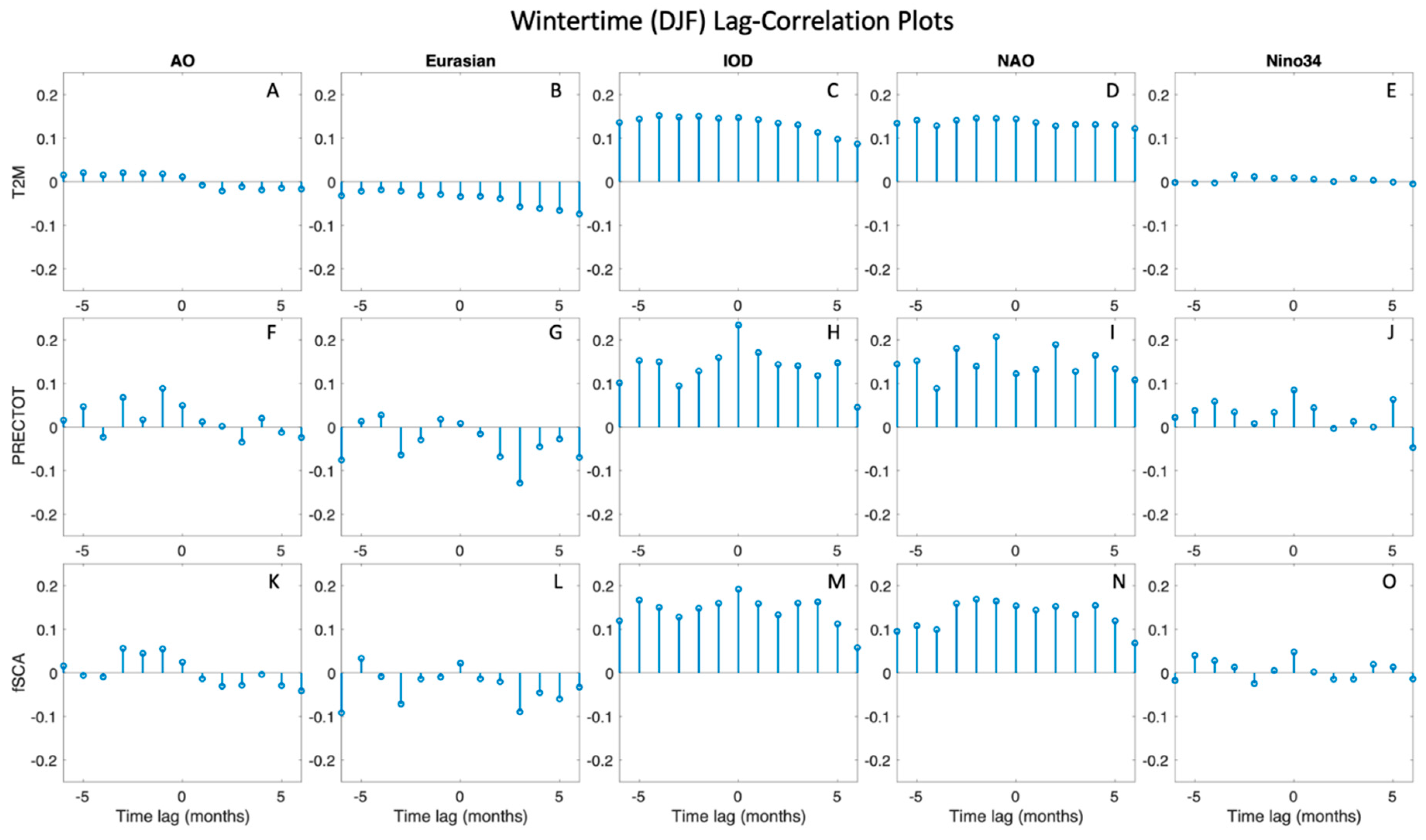
3.5. Time-lagged cross-correlation of MoVs with climate variables

Figure 10 shows the results from the time-lagged cross-correlation analysis of the MoVs with the spatially averaged climate variable timelines during the winter (DJF) months. These figures show the strength of the signal at each time-window. A peak in the negative time-lag can indicate that knowing the MoV can help predict the climate variable, whereas a peak in the positive time-lag can indicate that knowing the climate variable can help predict the MoV. For T2M during the winter (Figure 10 A-E), the lagged cross-correlation with the AO, Eurasian, and Nino34 data did not show any strong correlations, whereas for the IOD and the NAO there is a low-to-moderate correlation, with a peak of ~0.15 at the 0-month mark. Similar patterns can be seen for the relationships of the MoV with wintertime precipitation (Figure 10 F-J) and snow cover (Figure 10 K-O), with peak correlations of ~0.2 at the 0-month mark. This positive lagged cross-correlation between the IOD and NAO and the climate variables can indicate that higher T2M, PRECTOT, and fSCA can be expected on average in the HMA region whenever the IOD and the NAO are in the positive phases in the winter. These results reinforce those shown in Figure 6 and Figure 8.
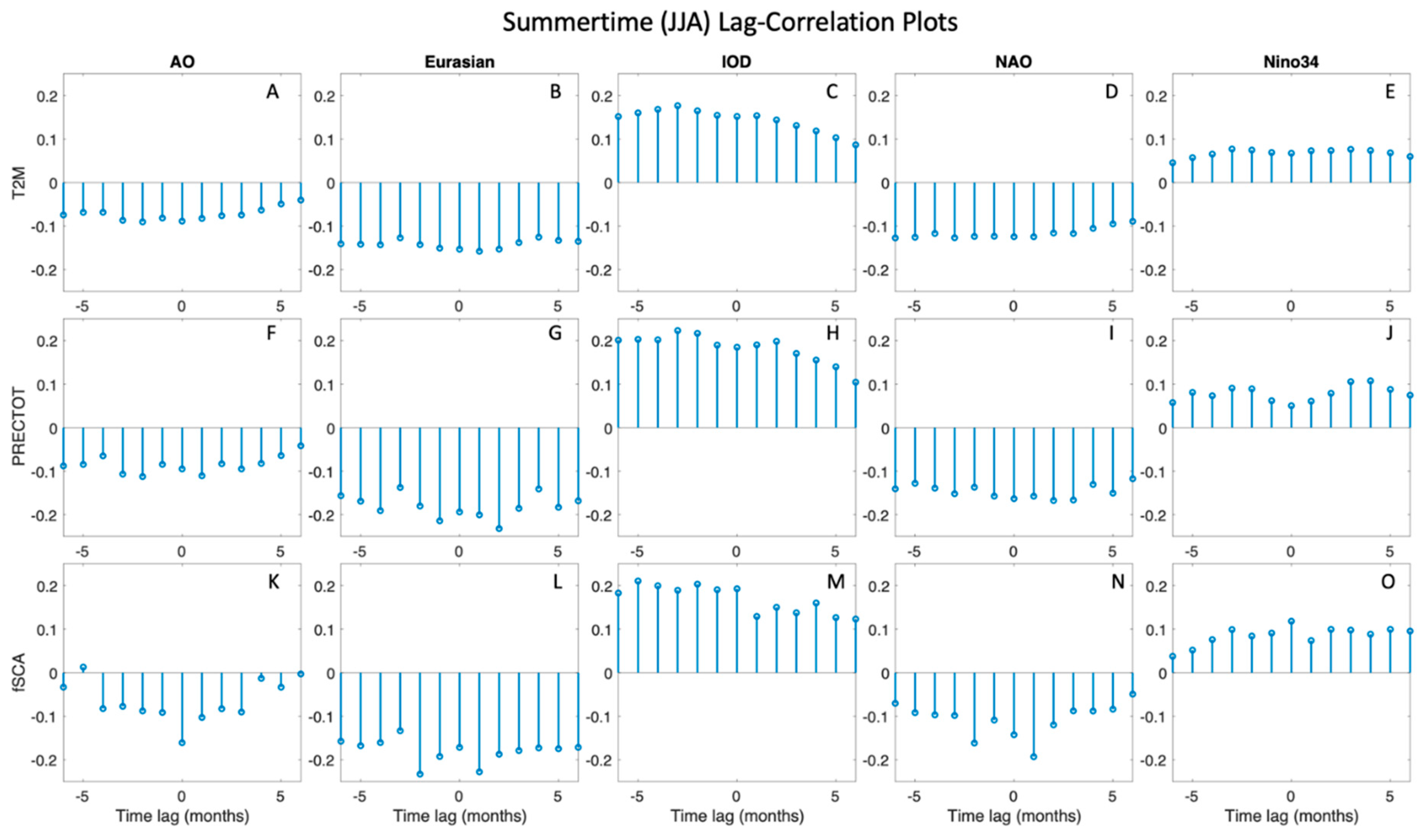
Figure 11 shows the results from the time-lagged cross-correlation analysis of the MoVs with the spatially averaged climate variable timelines during the summer (JJA) months. In the summertime (Figure 11) there seems to be more predictability than for the winter (Figure 10). For T2M during the summer (Figure 11A-E), the lagged cross-correlation with the AO, Eurasian teleconnection, and the NAO had negative relationships, whereas the correlations with the IOD and the Nino34 had positive relationships, with peaks at the 0-month mark of nearly -0.2 and +0.2 respectively. Very similar results can be seen for summertime precipitation (Figure 11F-J) and snow cover (Figure 11K-O). This positive lagged cross-correlation between the IOD and Nino34 and the climate variables can indicate that higher T2M, PRECTOT, and fSCA can be expected on average in the HMA region whenever the IOD and the Nino34 are in the positive phases in the summer. The opposite can be expected for the AO, Eurasian teleconnection, and the NAO, where lower T2M, PRECTOT, and fSCA can be expected on average in the HMA region whenever these MoVs are positive in the summer. These results reinforce those shown in Figure 5, Figure 7, and Figure 9.

4. Discussion

4.1. Implications of evident correlations between MoVs and climate in HMA

In this section, we aim to answer some of the questions regarding the search for evidence that shows relationships between the considered MoVs and climate variables in HMA. If any relationships exist, this work also searches for specific regions that exhibit significant correlations. If this is found, we aim to explore the implications of these relationships for both scientific understanding as well as for predictability.
To this end, there are some obvious patterns and relationships that emerge. For example, Figure 4 shows the relationship between wintertime T2M and the MoV explored in this study, and the mountain ranges just north of Afghanistan, also known as the Karakoram and Hindu Kush regions, show a significant negative correlation for the AO (Figure 4B), the Eurasian teleconnection (Figure 4C), and the NAO (Figure 4E). This is also shown for a large region in Central China and Eastern India for the Eurasian teleconnection. This implies that when either the AO, the Eurasian teleconnection, or the NAO are in the positive phase of their oscillation, that colder temperatures can be expected in these regions of HMA in the winter. As for summertime T2M, a similar finding can be seen in Figure 5C, which shows a significant negative correlation with the Eurasian teleconnection in the Inner Tibetan Plateau and Central and Southern China, but a significant positive correlation in Northwest China. This finding suggests that when the Eurasian teleconnection is in the positive (negative) phase of its oscillation, that colder temperatures can be expected in the Inner Tibetan Plateau and Central China (Northwestern China) in the summer.
For exploring relationships between MoV and wintertime precipitation in HMA, Figure 6 shows that there are some regions that have a significant positive correlation with the IOD (Figure 6D), such as in India, the Himalayas, and the Inner Tibet Plateau. Furthermore, the remaining MoV also have a positive correlation with wintertime precipitation in various regions, especially some regions within China for the AO (Figure 6B) and the NAO (Figure 6E). In India, however, there is a region that shows a negative correlation with the AO and the NAO. These results imply that when any of the MoV are in the positive phase of their oscillation, especially the IOD, that wetter conditions can be expected in most of the HMA region in the winter. For summertime precipitation (Figure 7), there are mostly negative correlations with the MoV, especially the Eurasian teleconnection (Figure 7C). This indicates that when the MoV are in their positive phase in the summer, drier conditions can be expected in different parts of HMA. The exception here is shown in the Indian subcontinent, where summertime PRECTOT has a significant positive correlation with the AO (Figure 7B) and the IOD (Figure 7D).
As for the relationships between MoV and wintertime fSCA in HMA, Figure 8 shows evidence of similar relationships as those shown for wintertime precipitation from Figure 6. That is, some regions have a significant positive correlation with the IOD (Figure 8D), such as in the Himalayas and the Inner Tibet Plateau, and the remaining MoV also have a positive correlation with wintertime fSCA in various regions, especially some regions in the Karakoram and within China for the AO (Figure 8B), Eurasian teleconnection (Figure 8C), the NAO (Figure 8E), and Nino34 (Figure 8F). These results highlight similar patterns as wintertime precipitation, which imply that when any of the MoV are in the positive phase of their oscillation, especially the IOD, that more snow cover can be expected in most of the HMA region in the winter. For the summertime fSCA (Figure 9) in HMA, there are rare clear relationships that emerge in our study that exhibit any patterns or significant correlations, except for the Eurasian teleconnection (Figure 9C) which shows a negative correlation in the Himalayas, and the IOD (Figure 9D) and Nino34 (Figure 9F) which show a positive correlation in some parts of HMA, indicating there could be some predictability of summertime snow cover in these regions when information on the Eurasian teleconnection, the IOD, or Nino34 becomes available.

4.2. Connecting results to previous findings and underlying physcial mechanisms

When the AO is strongly positive, a strong mid-latitude jet stream steers storms northward, reducing cold air outbreaks in the mid-latitudes [21]. This is confirmed with our results in Figure 2B and Figure 3B, which show a northward shift of a positive correlation pattern between the AO and z250 between winter and summer over Europe. Figure 4B and Figure 6B also confirm this, with regions in the northern most part of the domain showing a positive correlation between the AO and wintertime temperature and negative correlation with precipitation. This could be explained because the AO is characterized by non-seasonal sea-level pressure anomalies of one sign in the Arctic, balanced by anomalies of opposite sign centered at about 37–45° N [21]. When the AO index is positive, surface pressure is high in the polar region. This helps the middle latitude jet stream to blow strongly and consistently from west to east, thus keeping cold Arctic air locked in the polar region. When the AO index is negative, there tends to be low pressure in the polar region, weaker zonal winds, and greater movement of frigid polar air into middle latitudes [21].
For the Eurasian teleconnection, results in Figure 5C, Figure 7C, and Figure 9C show a positive correlation with temperatures and a negative correlation with precipitation and snow cover in the summer in Western China, near the Hindu Kush and Karakoram. Therefore, in this region, we find that the positive phase of the Eurasian teleconnection may cause higher temperatures as well as less rainfall which results in less overall snow cover in the summer. These results reinforce previous findings that state the Eurasian teleconnection explains up to 20% of the interannual variance of surface temperature over East Asia, and the positive phase of the Eurasian teleconnection produces less precipitation over East and Central Asia [22].
When the IOD is in the positive phase, sea-surface temperatures and precipitation in the western Indian Ocean region are higher than normal, with a corresponding cooling of waters in the eastern Indian Ocean [24]. When the IOD is in the negative phase the opposite conditions occur, with warmer water and greater precipitation in the eastern Indian Ocean, and cooler and drier conditions in the west. Our results extend on this understanding of the IOD’s impact on weather and climate in HMA, and Figure 4D, Figure 6D, and Figure 8D indicate that when the IOD is in the positive phase there are lower temperatures as well as higher precipitation rates which result in higher snow cover area in HMA in the winter.
For the NAO, like the AO, a positive phase can cause mid-latitude jet streams to shift northward, reducing precipitation rates and decreasing cold air outbreaks which in turn causes higher temperatures. Our results show that a positive NAO phase in the winter can result in lower temperatures over some parts of HMA, such as the Hindu Kush region (Figure 4E), and a positive phase in the summer can result in higher temperatures and lower precipitation rates in this region (Figure 5E and Figure 7E), which can lead to lower snow cover (Figure 9E) in this region. This can be explained by the fact that Westerly winds blowing across the Atlantic bring moist air into Europe, and in the years when westerlies are strong the summers are cooler, winters are mild, and rain is frequent [32]. If westerlies are suppressed, the temperature is more extreme in summer and winter leading to heat waves, deep freezes, and reduced rainfall. However, these correlations for the NAO are generally higher for regions in Europe [32] compared to the results reported here for the HMA region.
A positive Nino34, or the El Niño phase, coincides with colder temperatures in the southeast and warmer temperatures in the northwest parts of the domain in the winter (Figure 4F), and can be related to warmer conditions over India and cooler conditions in the Karakoram and Inner Tibetan Plateau in the summer (Figure 5F). Our results show evidence that during the El Niño phase wetter conditions can be expected in the winter (Figure 6F) which can result in more snow cover (Figure 8F), and drier conditions are expected in the summer (Figure 7F), yet with higher amounts of snow cover (Figure 9F), which could be due to the cooler temperatures (Figure 5F). Our results match those reported in [2], who showed that the positive phases of Nino34 have been shown to increase precipitation in western Himalaya during the winter, attributed to increased convergence over Southeastern Asia due to increased subsidence over the maritime continent [33,34]. Furthermore, [35] explains that increased precipitation in Central Southwest Asia during winter season El Niño years is mainly attributed to a deepened trough over Central Southwest Asia with cyclonic circulation that enhances southwesterly flow and moist air advection from the Indian Ocean basin into Central Southwest Asia.
In a broader context, [33] found that the interannual variability of precipitation in Northwest India is influenced by the AO, the NAO, and the Nino34 modes, and reported that wetter conditions are associated with the positive phase of AO/NAO and the warm phase of Nino34, which match the findings in our study shown for the winter (e.g., Figure 6B, Figure 6E, and Figure 6F). Their study also reported a physical mechanism for such effect, by which western disturbances are intensified over northwest India by the intensification of the Asian westerly jet stream over the Middle East during the positive phase of AO/NAO and shift and intensification of the Asian jet to the lower latitudes during the warm phase of Nino34. Furthermore, [16] reported high correlations in December between the IOD and Nino34 and snow depth, which match the results we find here for snow cover (Figure 8D and Figure 8F).

4.3. Potential sources of predictability

The results shown here do hint at relationships in the Earth’s climate system that can offer some sources of predictability, and a deeper look into the results may provide additional details. For example, the impact of the Eurasian teleconnection is emphasized in Figure 2C and Figure 3C, which seem to provide some clue to explain the correlations of HMA temperature and precipitation for both seasons. When the Eurasian teleconnection is in positive phase, southwesterlies over the western side of HMA and northwesterlies over the eastern side of HMA can be expected in winter (Figure 2C) and anticyclonic circulation is feasible in summer (Figure 3C). This pattern can lead to warmer conditions over the western side and cooler condition over the eastern side of HMA in both seasons, consistent with Figure 4C and Figure 5C. This pattern (i.e., Figure 2C and Figure 3C) may not have a clear effect on precipitation in winter, but the negative effect on precipitation is possible in summer due to the anticyclonic circulation cell, matching well with Figure 6C and Figure 7C.
Another method that is implemented in this study to gain insight on predictability is the lag of the period in which the lagged cross-correlations were made (Figure 10 and Figure 11). In the results shown in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9, correlations were estimated from the same months the data were obtained in (e.g., DJF AO correlated with DJF T2M, or JJA IOD with JJA fSCA). These results represented spatial variability of the correlation maps, but the temporal relationships were constrained to those in the same months. However, modes of climate variability can impact weather patterns after many months or years later, or the alternative can happen where the state of the climate system may impact modes of climate variability many months later. Hence, the time-lagged cross-correlation analysis shown in Figure 10 and Figure 11 can provide some details regarding predictability on different time scales. Although these time-lagged cross-correlations considered different temporal windows of correlation, the spatial characteristics of that analysis was restricted to cover the spatially averaged dynamics of the climate variables seen for the whole HMA domain. So future studies can utilize time lags in the investigation of the lagged cross-correlations between different MoV and climate in HMA for specific regions of HMA. This more defined spatiotemporal analysis may shed some light on predictability of climate variables many months ahead of time and for specific regions within HMA and can potentially offer some clues on the different sources of predictability that exist in Earth’s climate system, especially pertaining to the HMA region.

4.4. Caveats of current study

The dynamics investigated in the data here can allow us to understand how teleconnections in the Earth system affect climate variables throughout the globe on the monthly time scale, which allows us to probe the limits of predictability that can be relevant for S2S forecasting. Future studies can look at how teleconnections in the Earth system affect climate variables throughout the globe on different time scales, such days or years, which can be beneficial as for weather forecasting or climate studies, respectively.
Spatially, the results presented here cover the broad HMA region. Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 show correlation results spatially, which allows one to understand the relationship between MoV and climate variables for each grid cell. However, Figure 10 and Figure 11 shows lagged cross-correlation results for spatially averaged climate variable dynamics. It is assumed that considering more local regions for the lagged cross-correlation analysis in Figure 10 and Figure 11 may generate stronger signals that show more robust relationships between the MoV and climate variables in specific domains within HMA.
An important factor in our study is the use of MERRA-2 data, which has been shown to have potential biases in temperature, precipitation, and snow cover for HMA [18,36,37]. We hypothesize that using other reanalysis data in this investigation, such as ERA5, would result in similar findings [38]. However, other data sources, such as model data or information from remote sensing can still present their own issues like resolution and data consistency and completeness. The benefit of using MERRA-2 is that it offers a systematic and consistent source of information for the climate variables investigated in this study. Future work on this topic can incorporate different streams of data to have a more thorough investigation into each climate variable and its relationship with the different MoV in this study.
Another caveat in this study relates to the regions within HMA that have persistent as well as ephemeral snow cover. Variability in fSCA will only be in the ephemeral regions, which for the most part won’t have snow in JJA. Therefore, much of the results in Figure 8 and Figure 9 are subject to this caveat, and any relationships of fSCA with MoV may be diminished because of this lack of variability in fSCA. However, the first-order correlations of fSCA with the MoV considered here are still presented and discussed in this paper for completeness.
Lastly, an important caveat in this study is the assumption that there has not been any temporal changes or trends in the strength of the MoV or in the dynamics of the climate data. In other words, this study assumes that the long-term MoV dynamics and their impact on subsequent climate variables are stationary. There might not be enough years in the data to thoroughly test for this assumption. Therefore, the results presented in this paper implicitly assume stationarity in time for the MoV and the climate data.

5. Conclusions

This study explored the relationships between various modes of climate variability and climate variables in the HMA region for the winter and summer seasons. We considered modes such as the Arctic Oscillation (AO), Eurasian teleconnection, Indian Ocean Dipole (IOD), North Atlantic Oscillation (NAO), and El Niño southern oscillation (Nino34), and looked for relationships with climate variables such as geopotential height (z250), 2-m air temperature (T2M), total precipitation (PRECTOT), and fractional snow cover area (fSCA). We searched for evidence of significant correlation between the different modes and climate variables in HMA and looked for specific regions that exhibit significantly higher correlations. We explored the implications of these relationships for both scientific understanding as well as for predictability.
We found that the correlation patterns between the MoV and z250 remain mostly unchanged between winter and summer for most climate variables considered, with minor exceptions such as a northward shift of the positive correlation with the AO and NAO in Europe in the summer. Between the MoV and T2M, we found that when either the AO, the Eurasian teleconnection, or the NAO are in the positive phase of their oscillation, that colder temperatures can be expected in the Karakoram and Hindu Kush regions in the winter. Furthermore, when the Eurasian teleconnection is in the positive (negative) phase of its oscillation, that colder temperatures can be expected in the Inner Tibetan Plateau and Central China (Northwestern China) in the summer. Between the MoV and PRECTOT, we found that when any of the MoV are in the positive phase of their oscillation, especially the IOD, that wetter conditions can be expected in most of the HMA region (except for the Indian subcontinent) in the winter. For summertime precipitation, we found that when the MoV are in their positive phase in the summer, drier conditions can be expected in different parts of HMA (again except for the Indian subcontinent). Between the MoV and fSCA, like precipitation, we found that when any of the MoV are in the positive phase of their oscillation, especially the IOD, that more snow cover can be expected in most of the HMA region in the winter, likely as a result of wintertime precipitation also being positively correlated with most indices. As for summertime fSCA, no clear relationships emerge in our study that exhibit any patterns or significant correlations, except for some predictability of summertime snow cover in the Himalayas and Karakoram when information on the Eurasian teleconnection, the IOD, or Nino34 becomes available.
We also showed that the AO and NAO generally show very similar correlation patterns for all climate variables, especially in the winter, possibly due to their oscillations being so similar. More specifically, we found that when the AO is strongly positive, there is a northward shift of a positive correlation pattern between the AO and z250 between winter and summer over Europe, and a positive correlation between the AO and wintertime temperature and negative correlation with precipitation. As for the NAO, a positive NAO phase in the winter can result in lower temperatures over some parts of HMA, such as the Hindu Kush region, and a positive phase in the summer can result in higher temperatures and lower precipitation rates, which can lead to lower snow cover in this region. Furthermore, we found that the positive phase of the Eurasian teleconnection may cause higher temperatures as well as less rainfall which results in less overall snow cover in the summer. For the IOD, we found that when the IOD is in the positive phase there are lower temperatures as well as higher precipitation rates which result in higher snow cover area in HMA in the winter. Lastly, we found that a positive Nino34, or the El Niño phase, coincides with colder temperatures in the southeast and warmer temperatures in the northwest parts of the domain, and can be related to warmer conditions over India and cooler conditions in the Karakoram and Inner Tibetan Plateau in the summer. During the El Niño phase, wetter conditions can be expected in the winter which can result in more snow cover, and drier conditions are expected in the summer, yet with higher amounts of snow cover, which could be due to the cooler temperatures.
We also investigated the effect of time-lag on the cross-correlation, since MoVs can impact weather patterns after many months later, or alternatively, the state of the climate system may impact MoVs many months later. Our discussion aimed to explore some of the physical mechanisms that explain the results reported here and tried to connect our findings to the broader literature. Our results helped highlight specific regions within HMA or specific time-windows that experience a correlation between climate and different modes of variability and shed light on future areas of research that can uncover fundamental scientific understanding of these phenomena with the aim of potentially finding different sources of predictability in the Earth system.

Author Contributions

Conceptualization, E.M. Y.L. L.A. and M.G.; methodology, E.M. and Y.L.; validation, E.M. Y.L. L.A. and M.G.; formal analysis, E.M. Y.L.; investigation, E.M. Y.L. L.A. and M.G.; resources, E.M. Y.L.; data curation, E.M. Y.L.; writing—original draft preparation, E.M. writing—review and editing, E.M. Y.L. L.A. and M.G.; visualization, E.M.; funding acquisition, E.M. L.A. and M.G.; All authors have read and agreed to the published version of the manuscript.

Funding

The authors acknowledge the NASA HiMAT team for funding this work (GRANT # 80NSSC20K1301). The APC was generally funded by the journal (Atmosphere – MDPI).

Data Availability Statement

The data used to represent the AO, Eurasian teleconnection, IOD, NAO, and Nino34 are obtained from the NOAA ESRL database (http://psl.noaa.gov/). MERRA-2 data can be downloaded at no cost from (https://disc.gsfc.nasa.gov/datasets?project=MERRA-2).

Acknowledgments

The authors thank Andrea Molod and Rolf Reichle for comments that helped shape the manuscript. The authors acknowledge the NASA HiMAT team for funding this work as well as for generous data sharing and broader discussions that helped shape the paper. This manuscript has been authored by UT-Battelle, LLC, under contract DE-AC05-00OR22725 with the US Department of Energy (DOE). The US government retains and the publisher, by accepting the article for publication, acknowledges that the US government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this manuscript, or allow others to do so, for US government purposes. DOE will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan (http://energy.gov/downloads/doe-public-access-plan).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Immerzeel, W.W., Lutz, A.F., Andrade, M. et al. Importance and vulnerability of the world’s water towers. Nature 577, 364–369. 2020. [CrossRef]
  2. Nash, D., Carvalho, L., Jones, C. and Ding, Q., 2022. Winter and spring atmospheric rivers in High Mountain Asia: climatology, dynamics, and variability. Climate dynamics, 58(9), pp.2309-2331. [CrossRef]
  3. Ding, Qinghua, and Bin Wang. "Intraseasonal teleconnection between the summer Eurasian wave train and the Indian monsoon." Journal of Climate 20, no. 15: 3751-3767. 2007. [CrossRef]
  4. Lim, Young-Kwon. "The East Atlantic/West Russia (EA/WR) teleconnection in the North Atlantic: climate impact and relation to Rossby wave propagation." Climate dynamics 44, no. 11: 3211-3222. 2015. [CrossRef]
  5. Stuecker, Malte F., Axel Timmermann, Fei-Fei Jin, Yoshimitsu Chikamoto, Wenjun Zhang, Andrew T. Wittenberg, Esther Widiasih, and Sen Zhao. "Revisiting ENSO/Indian Ocean dipole phase relationships." Geophysical Research Letters 44, no. 5: 2481-2492. 2017. [CrossRef]
  6. Sang, Yan-Fang, Vijay P. Singh, and Kang Xu. "Evolution of IOD-ENSO relationship at multiple time scales." Theoretical and Applied Climatology 136, no. 3: 1303-1309. 2019. [CrossRef]
  7. Power, Katherine, Josefine Axelsson, Norbu Wangdi, and Qiong Zhang. "Regional and Local Impacts of the ENSO and IOD Events of 2015 and 2016 on the Indian Summer Monsoon—A Bhutan Case Study." Atmosphere 12, no. 8: 954. 2021. [CrossRef]
  8. Meena, Narendra Kumar, Pranaya Diwate, and Sundeep Pandita. "Evidence of ENSO and IOD Interplay in Continental Climatic Records from Southern Himalaya (Renuka Lake), India." (2022).
  9. Li, Jian, Rucong Yu, Tianjun Zhou, and Bin Wang. "Why is there an early spring cooling shift downstream of the Tibetan Plateau?." Journal of Climate 18, no. 22: 4660-4668. 2005. [CrossRef]
  10. Li, Jian, Rucong Yu, and Tianjun Zhou. "Teleconnection between NAO and climate downstream of the Tibetan Plateau." Journal of Climate 21, no. 18: 4680-4690. 2008. [CrossRef]
  11. Zhou, Lei, Raghu Murtugudde, Dake Chen, and Youmin Tang. "A Central Indian Ocean mode and heavy precipitation during the Indian summer monsoon." Journal of Climate 30, no. 6: 2055-2067. 2017. [CrossRef]
  12. Jiang, X., Li, T. and Wang, B., 2004. Structures and mechanisms of the northward propagating boreal summer intraseasonal oscillation. Journal of Climate, 17(5), pp.1022-1039. [CrossRef]
  13. Hatsuzuka, Daisuke, and Hatsuki Fujinami. "Effects of the South Asian monsoon intraseasonal modes on genesis of low pressure systems over Bangladesh." Journal of Climate 30, no. 7: 2481-2499. 2017. [CrossRef]
  14. Yu, R. and Zhou, T., 2004. Impacts of winter-NAO on March cooling trends over subtropical Eurasia continent in the recent half century. Geophysical Research Letters, 31(12). [CrossRef]
  15. Lü, J.M., Ju, J.H., Kim, S.J., Ren, J.Z. and Zhu, Y.X., 2008. Arctic Oscillation and the autumn/winter snow depth over the Tibetan Plateau. Journal of Geophysical Research: Atmospheres, 113(D14). [CrossRef]
  16. Jiang, X., Zhang, T., Tam, C.Y., Chen, J., Lau, N.C., Yang, S. and Wang, Z., 2019. Impacts of ENSO and IOD on snow depth over the Tibetan Plateau: Roles of convections over the western North Pacific and Indian Ocean. Journal of Geophysical Research: Atmospheres, 124(22), pp.11961-11975. [CrossRef]
  17. Wu, T.W. and Qian, Z.A., 2003. The relation between the Tibetan winter snow and the Asian summer monsoon and rainfall: An observational investigation. Journal of Climate, 16(12), pp.2038-2051. [CrossRef]
  18. Massoud, E. C., Andrews, L., Reichle, R., Molod, A., Park, J., Ruehr, S., and Girotto, M.: Seasonal forecasting skill for the High Mountain Asia region in the Goddard Earth Observing System, Earth Syst. Dynam., 14, 147–171. 2023. [CrossRef]
  19. Gelaro, Ronald, Will McCarty, Max J. Suárez, Ricardo Todling, Andrea Molod, Lawrence Takacs, Cynthia A. Randles et al. "The modern-era retrospective analysis for research and applications, version 2 (MERRA-2)." Journal of climate 30, no. 14: 5419-5454. 2017. [CrossRef]
  20. Hernández, A., Martin-Puertas, C., Moffa-Sánchez, P., Moreno-Chamarro, E., Ortega, P., Blockley, S., Cobb, K.M., Comas-Bru, L., Giralt, S., Goosse, H. and Luterbacher, J., 2020. Modes of climate variability: Synthesis and review of proxy-based reconstructions through the Holocene. Earth-Science Reviews, 209, p.103286. [CrossRef]
  21. Ambaum, M.H., Hoskins, B.J. and Stephenson, D.B., 2001. Arctic oscillation or North Atlantic oscillation?. Journal of Climate, 14(16), pp.3495-3507. [CrossRef]
  22. Liu, Y., Wang, L., Zhou, W. and Chen, W., 2014. Three Eurasian teleconnection patterns: Spatial structures, temporal variability, and associated winter climate anomalies. Climate dynamics, 42(11), pp.2817-2839. [CrossRef]
  23. Wang, L. and Chen, W., 2014. An intensity index for the East Asian winter monsoon. Journal of Climate, 27(6), pp.2361-2374. [CrossRef]
  24. Saji, N. H., and T. J. C. R. Yamagata. "Possible impacts of Indian Ocean dipole mode events on global climate." Climate Research 25, no. 2 (2003): 151-169. [CrossRef]
  25. Visbeck, M., Chassignet, E.P., Curry, R.G., Delworth, T.L., Dickson, R.R., Krahmann, G., Hurrell, J.W., Kushnir, Y. and Ottersen, G., 2003. The North Atlantic Oscillation: climatic significance and environmental impact. Geophys. Monogr, 134.
  26. Bosilovich, M. G., R. Lucchesi, and M. Suarez: MERRA-2: File Specification. GMAO Office Note No. 9 (Version 1.1), 73 pp. 2016. Available online: http://gmao.gsfc.nasa.gov/pubs/office_notes.
  27. Global Modeling and Assimilation Office (GMAO), MERRA-2 tavgM_2d_slv_Nx: 2d, Monthly mean, Time-Averaged, Single-Level, Assimilation, Single-Level Diagnostics V5.12.4, Greenbelt, MD, USA, Goddard Earth Sciences Data and Information Services Center (GES DISC), Accessed: [August 2021]. 2015a. [CrossRef]
  28. Global Modeling and Assimilation Office (GMAO), MERRA-2 tavgM_2d_flx_Nx: 2d, Monthly mean, Time-Averaged, Single-Level,Assimilation, Surface Flux Diagnostics V5.12.4, Greenbelt, MD, USA, Goddard Earth Sciences Data and Information Services Center (GES DISC), Accessed: [August 2021]. 2015b. [CrossRef]
  29. Reichle, Rolf H., Q. Liu, Randal D. Koster, Clara S. Draper, Sarith PP Mahanama, and Gary S. Partyka. "Land surface precipitation in MERRA-2." Journal of Climate 30, no. 5: 1643-1664. 2017. [CrossRef]
  30. Global Modeling and Assimilation Office (GMAO), MERRA-2 tavgM_2d_lnd_Nx: 2d, Monthly mean, Time-Averaged, Single-Level, Assimilation, Land Surface Diagnostics V5.12.4, Greenbelt, MD, USA, Goddard Earth Sciences Data and Information Services Center (GES DISC), Accessed: [August 2021]. 2015c. [CrossRef]
  31. Press, W.H., Teukolsky, S.A., Vetterling, W.T., and Flannery, B.P. Numerical Recipes in C, 2nd Ed., Cambridge University Press, 1992.
  32. Hurrell, J.W., 1995. Decadal trends in the North Atlantic Oscillation: Regional temperatures and precipitation. Science, 269(5224), pp.676-679. [CrossRef]
  33. Yadav, R.K., Rupa Kumar, K. and Rajeevan, M., 2009. Increasing influence of ENSO and decreasing influence of AO/NAO in the recent decades over northwest India winter precipitation. Journal of Geophysical Research: Atmospheres, 114(D12). [CrossRef]
  34. Cannon, F., Carvalho, L., Jones, C. and Bookhagen, B., 2015. Multi-annual variations in winter westerly disturbance activity affecting the Himalaya. Climate dynamics, 44(1), pp.441-455. [CrossRef]
  35. Rana, S., McGregor, J. and Renwick, J., 2019. Dominant modes of winter precipitation variability over Central Southwest Asia and inter-decadal change in the ENSO teleconnection. Climate Dynamics, 53(9), pp.5689-5707. [CrossRef]
  36. Yoon Y, Kumar SV, Forman BA, Zaitchik BF, Kwon Y, Qian Y, Rupper S, Maggioni V, Houser P, Kirschbaum D, Richey A, Arendt A, Mocko D, Jacob J, Bhanja S and Mukherjee A (2019) Evaluating the Uncertainty of Terrestrial Water Budget Components Over High Mountain Asia. Front. Earth Sci. 7:120. [CrossRef]
  37. Liu Y and Margulis SA (2019) Deriving Bias and Uncertainty in MERRA-2 Snowfall Precipitation Over High Mountain Asia. Front. Earth Sci. 7:280. [CrossRef]
  38. Mehmood, S., Ashfaq, M., Kapnick, S. et al. Dominant controls of cold-season precipitation variability over the high mountains of Asia. npj Clim Atmos Sci 5, 65 (2022). [CrossRef]
Preprints 90234 g001
Figure 1. Global Modes of Variability (MoV) investigated in this study, shown on a monthly timescale. The years explored for each index spans from January 1981-December 2020.
Figure 1. Global Modes of Variability (MoV) investigated in this study, shown on a monthly timescale. The years explored for each index spans from January 1981-December 2020.
Preprints 90234 g001
Preprints 90234 g002
Figure 2. Wintertime (DJF) relationship between the various MoV explored in this study and geopotential height. (a) DJF Geopotential height at 250 hPa (z250) from MERRA-2, with units [m]. Correlation of DJF z250 with (b) the AO, (c) the Eurasian teleconnection, (d) the IOD, (e) the NAO, and (f) Nino34 at each grid cell. Grids with less than 90% confidence are masked out in these figures. Red indicates a positive correlation and blue depicts negative correlation.
Figure 2. Wintertime (DJF) relationship between the various MoV explored in this study and geopotential height. (a) DJF Geopotential height at 250 hPa (z250) from MERRA-2, with units [m]. Correlation of DJF z250 with (b) the AO, (c) the Eurasian teleconnection, (d) the IOD, (e) the NAO, and (f) Nino34 at each grid cell. Grids with less than 90% confidence are masked out in these figures. Red indicates a positive correlation and blue depicts negative correlation.
Preprints 90234 g002
Preprints 90234 g003
Figure 3. Like Figure 2, but for the summertime (JJA) geopotential height at 250 hPa (z250).
Figure 3. Like Figure 2, but for the summertime (JJA) geopotential height at 250 hPa (z250).
Preprints 90234 g003
Preprints 90234 g004
Figure 4. Wintertime (DJF) relationship between the various MoV explored in this study and 2-m air temperature (T2M). (a) DJF T2M from MERRA-2, with units [K]. Correlation of DJF T2M with (b) the AO, (c) the Eurasian teleconnection, (d) the IOD, (e) the NAO, and (f) Nino34 at each grid cell. Grids with less than 90% confidence are masked out in these figures. Red indicates a positive correlation and blue depicts negative correlation.
Figure 4. Wintertime (DJF) relationship between the various MoV explored in this study and 2-m air temperature (T2M). (a) DJF T2M from MERRA-2, with units [K]. Correlation of DJF T2M with (b) the AO, (c) the Eurasian teleconnection, (d) the IOD, (e) the NAO, and (f) Nino34 at each grid cell. Grids with less than 90% confidence are masked out in these figures. Red indicates a positive correlation and blue depicts negative correlation.
Preprints 90234 g004
Preprints 90234 g005
Figure 5. Like Figure 4, but for summertime (JJA) 2-m air temperature (T2M).
Figure 5. Like Figure 4, but for summertime (JJA) 2-m air temperature (T2M).
Preprints 90234 g005
Preprints 90234 g006
Figure 6. Wintertime (DJF) relationship between the various MoV explored in this study and total precipitation (PRECTOT). (a) DJF PRECTOT from MERRA-2, with units [mm/day]. Correlation of DJF PRECTOT with (b) the AO, (c) the Eurasian teleconnection, (d) the IOD, (e) the NAO, and (f) Nino34 at each grid cell. Grids with less than 90% confidence are masked out in these figures. Red indicates a positive correlation and blue depicts negative correlation.
Figure 6. Wintertime (DJF) relationship between the various MoV explored in this study and total precipitation (PRECTOT). (a) DJF PRECTOT from MERRA-2, with units [mm/day]. Correlation of DJF PRECTOT with (b) the AO, (c) the Eurasian teleconnection, (d) the IOD, (e) the NAO, and (f) Nino34 at each grid cell. Grids with less than 90% confidence are masked out in these figures. Red indicates a positive correlation and blue depicts negative correlation.
Preprints 90234 g006
Preprints 90234 g007
Figure 7. Like Figure 6, but for summertime (JJA) total precipitation (PRECTOT). Note: The maximum value of PRECTOT in Figure 7A is just over 10 mm/day.
Figure 7. Like Figure 6, but for summertime (JJA) total precipitation (PRECTOT). Note: The maximum value of PRECTOT in Figure 7A is just over 10 mm/day.
Preprints 90234 g007
Preprints 90234 g008
Figure 8. Wintertime (DJF) relationship between the various MoV explored in this study and fractional snow cover area (fSCA). (a) DJF fSCA from MERRA-2, with no units [-]. Correlation of DJF fSCA with (b) the AO, (c) the Eurasian teleconnection, (d) the IOD, (e) the NAO, and (f) Nino34 at each grid cell. Grids with less than 90% confidence are masked out in these figures. Red indicates a positive correlation and blue depicts negative correlation.
Figure 8. Wintertime (DJF) relationship between the various MoV explored in this study and fractional snow cover area (fSCA). (a) DJF fSCA from MERRA-2, with no units [-]. Correlation of DJF fSCA with (b) the AO, (c) the Eurasian teleconnection, (d) the IOD, (e) the NAO, and (f) Nino34 at each grid cell. Grids with less than 90% confidence are masked out in these figures. Red indicates a positive correlation and blue depicts negative correlation.
Preprints 90234 g008
Preprints 90234 g009
Figure 9. Like Figure 8, but for summertime (JJA) fractional snow cover area (fSCA).
Figure 9. Like Figure 8, but for summertime (JJA) fractional snow cover area (fSCA).
Preprints 90234 g009
Preprints 90234 g010
Figure 10. Winter (DJF) time-lag cross-correlation plots for each MoV and climate variable pair. The spatial means of the climate variables were taken at each time step and used for this analysis. At a time lag of 0, the value shows the lagged cross-correlation between the MoV and the climate variable at the same time steps (0 lag). For negative time lags, the value shows the lagged cross-correlation between the MoV prior to the timestep of the climate variable (e.g. lagged cross-correlation between AO at time t and T2M at time t+lag). For positive time lags, the value shows the lagged cross-correlation between the MoV after the timestep of the climate variable (e.g. lagged cross-correlation between AO at time t+lag and T2M at time t). The maximum time lag analyzed in this plot is 6 months.
Figure 10. Winter (DJF) time-lag cross-correlation plots for each MoV and climate variable pair. The spatial means of the climate variables were taken at each time step and used for this analysis. At a time lag of 0, the value shows the lagged cross-correlation between the MoV and the climate variable at the same time steps (0 lag). For negative time lags, the value shows the lagged cross-correlation between the MoV prior to the timestep of the climate variable (e.g. lagged cross-correlation between AO at time t and T2M at time t+lag). For positive time lags, the value shows the lagged cross-correlation between the MoV after the timestep of the climate variable (e.g. lagged cross-correlation between AO at time t+lag and T2M at time t). The maximum time lag analyzed in this plot is 6 months.
Preprints 90234 g010
Preprints 90234 g011
Figure 11. Same as in Figure 10, but for summer (JJA) time-lag cross-correlation results.
Figure 11. Same as in Figure 10, but for summer (JJA) time-lag cross-correlation results.
Preprints 90234 g011
Table 1. Abbreviations used in this study. Note: The total precipitation variable listed here is ‘PRECTOT’, but as indicated in the text, the variable from MERRA-2 that is used to represent total precipitation is the corrected version, or ‘PRECTOTCORR’.
Table 1. Abbreviations used in this study. Note: The total precipitation variable listed here is ‘PRECTOT’, but as indicated in the text, the variable from MERRA-2 that is used to represent total precipitation is the corrected version, or ‘PRECTOTCORR’.
Abbreviation Name
MoV Mode of Variability
HMA High Mountain Asia
AO Arctic Oscillation
Eurasian Eurasian Teleconnection
IOD Indian Ocean Dipole
NAO North Atlantic Oscillation
Nino34 El Niño Southern Oscillation
z250 Geopotential Height at 250 hPa
T2M 2-m Air Temperature
PRECTOT Total Precipitation
fSCA Fractional Snow Cover Area
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated