Prerpints.org logo
Preprint
Article

An Improved 3D OPC Method for the Fabrication of High-Fidelity Micro Fresnel Lenses

Altmetrics

Downloads

85

Views

30

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

10 November 2023

Posted:

13 November 2023

You are already at the latest version

Alerts
Abstract
Based on three-dimensional optical proximity correction (3D OPC), recent advancements in 3D lithography have enabled the high-fidelity customization of 3D micro-optical elements. However, micron-to-millimeter scale structures represented by Fresnel lens design bring more stringent requirements for 3D OPC, which poses significant challenges to the accuracy of models and the efficiency of algorithms. Thus, a lithographic model based on optical imaging and photo-chemical reaction curve is developed in this paper, and a sub-domain division method with a statistics principle is proposed to improve the efficiency and accuracy of 3D OPC. Both the simulation and the experimental results showed the superiority of the proposed 3D OPC method in the fabrication of the Fresnel lenses. The computation memory requirements of the 3D OPC are reduced to below 1 %, and the profile error of the fabricated Fresnel lens reduced 79.98%. Applying the Fresnel lenses to an imaging system, the average peak signal to noise ratio (PSNR) of the image increased by 18.92 %, and the average contrast of the image enhanced by 36 %. We believe the proposed 3D OPC method can be extended to the fabrication of vision-correcting ophthalmological lenses.
Keywords: 
Subject: Engineering  -   Control and Systems Engineering

1. Introduction

Three-dimensional lithography based on laser direct writing, or mask-less lithography, refers to the process of selective exposure of thick photoresist from the features of the computer-aided design (CAD) model. This technique can effectively modulate the light intensity on the surface and inside of the photoresist, so as to obtain a three-dimensional photoresist pattern after development. The characteristics of smaller volume, lower manufacturing costs, and fast manufacturing efficiency make it widely used in two-dimensional (2D) micro-manufacturing applications, such as microfluidics [1], meta-materials [2], and reticles for X-ray lithography [3,4]. Recently, the flexibility of LDW based free form grayscale mask design has attracted widespread attention and rapid development in the potential of three-dimensional (3D) microfabrication. Examples include customized micro-lens arrays (MLA) for wave-front sensing [5,6], virtual reality/augmented reality display [7,8], super hydrophobic lenses for the humid outdoor environment [9], bionic compound eye lens [10,11] for zoom imaging, Fresnel zone plate [12,13] for lens-less imaging, Fresnel lens for vision-correcting [14,15], and achromatic lens based on Fresnel design [16,17,18,19]. All integrated optical devices above require collaborative optimization in design and manufacturing. Therefore, the 3D optical proximity correction (OPC) method has been introduced to ensure the fidelity of customized optical device morphology and its optical performance. The 3D OPC method is particularly useful in the fabrication of Fresnel lenses with complex geometries. However, when simulating the millimeter scale Fresnel lenses, the existing 3D OPC method requires a huge amount of computing power and terabyte memory storage. Thus, it is necessary to develop a 3D OPC method that requires fewer computational resources, while retaining the high geometric fidelity of micro-Fresnel lenses.
Figure 1 (a) illustrates the schematic diagram of the 3D lithography system with 405nm illumination. First, the CAD mask carrying the micro-structure layout is uniformly sampled, and the exposure scheme is generated. Second, the optical signal is transferred to the photo-resist-covered substrate through an electrical modulation system, and the platform scans and steps at a constant speed. Finally, the photo-resist patterns are formed after a series of developing processes. Taking the red dotted line of the CAD mask as an example, the grayscale 3D lithography mechanism based on LDW is shown in Figure 1 (b). The selective exposure on the surface of the photo-resist causes the change of the light intensity in z-direction I(z), and the photochemical reaction results in the response of the photo-active compound concentration (PAC) in z-direction M(z). As a result, 3D photo-resist image Ip(z) is obtained after development process. However, the photo-resist image is distorted due to the optical proximity effect (OPE) [20,21] and the photo-chemical effect. Figure 1(c) shows the compensation effect of 3D OPC, which improves the fidelity of the photo-resist pattern by pre-distorting the CAD mask pattern and inserting assistant features around the structure. Along the way, the model-based OPC is proposed to improve the lithographic fidelity [22,23], the regularization term with exposed dosage [24] and the interior-point optimization with a barrier function [25] is developed to accelerate optimization, and the neural network-based compensation method [26] is researched for predicting CAD masks. All these methods provide superior theories for later generations and become essential to compensate for the undesired distortions of lithography, but the computational and storage efficiency is still unacceptable, such as, for an  N × N  OPC problem, the derivative calculation requires  N 2 × N 2  matrix storage. The OPC of projection lithography also has computational efficiency problems, and a series of algorithms have been developed. The development of these algorithms can serve as guidelines for investigating 3D OPC. Examples of such algorithms are: the conjugate gradient methods [27,28], the augmented Lagrangian methods [29], the compressive sensing methods [30,31], the semi-implicit methods [32,33], and the model-driven neural network methods [34,35]. Inspired by these algorithms, Peng et al simplify the derivatives as a matrix form and proposed the 3D OPC method based on 3D lithography [36], Jidling et al focus on the memory efficiency and a constrained gradient search method (L-BFGS-B) with pattern segmentation is proposed [37]. However, these algorithms still require a significant amount of memory and computing resources. This is even more the case when optimizing the Fresnel designs at the micron-to-millimeter scale. In addition, the existing 3D OPC models didn’t consider the interplay between optical and photochemical reaction processes, leading to inaccurate model results. Therefore, it is necessary to develop an algorithm that accurately model and optimize such complex designs, and realize effectively utilize computing and memory resources.
This paper focuses on the establishment of numerical models for 3D OPC, and the optimization of central symmetric structures based on the Fresnel design. In particular, the imaging model can be described as the convolution operation of the point spread function (PSF) and CAD mask [38,39,40]. The photo-chemical reaction of thick resist can be described by the Dill model [41,42,43], which considers the change of refractive index of the photo-resist during exposure, energy absorption in the photo-resist, and concentration distribution of photosensitive. Thus, the nonlinear relationship between aerial images and printed photo-resist images can be calibrated. To deal with the memory requirements, a sub-domain division method with statistics is proposed, which combines the principle of statistics and perceives the global region through sub-domains. Subsequently, total variation (TV) is used during optimization to ensure the continuity of the subdomains. After optimization, the sub-domain-based CAD mask is searched, and the optimal global CAD mask is perceived. Finally, the Fresnel lenses are transferred into PDMS, and the transferred concave Fresnel lenses are applied in a vision correction system. The fabrication of Fresnel lenses and the experimental results of visual correction systems show the superiority of the proposed 3D OPC method.

2. Computational lithography model with subdomain division

In the numerical model of 3D lithography, the intensity of the laser beam on the focal plane (surface of photo-resist) is analytically expressed as an ideal Gaussian distribution; the thickness of the photo-resist is assumed to be uniform; the reflection from the substrate is ignored in the thick film; and a series of optical effects, such as scattering and cavity formation, is also neglected; Thus, the lithographic process from CAD mask patterns to photo-resist can be simplified into two numerical models: the optical scanning (aerial image  I a  formation) based on programmable logic controller, and the resist effect (photo-resist image  I p  formation) described by the Dill exposure model.
As illustrated in Figure 2, the 3D OPC framework with a central symmetric centimeter target can be divided into three steps. Figure 2 (a) depicts the parameter calibration of lithography, which mainly includes the light spot distribution and the static nonlinear response (Depth curve) of photo-resist approximated by the Dill exposure model. In Figure 2 (b), a 3D OPC model with total variation (TV) is established, which penalizes discontinuities in all directions; through this TV term, the centrally symmetric exposure dose distribution is optimized. Subsequently, the target structure is segmented as  M s u b t a r g e t  to ensure the efficiency of optimization, and the optimal distribution of the sub-CAD mask is synthesized through 3D OPC. The scheme of sub-domain segmentation and global recovery of the mask is shown in Figure 2 (c).

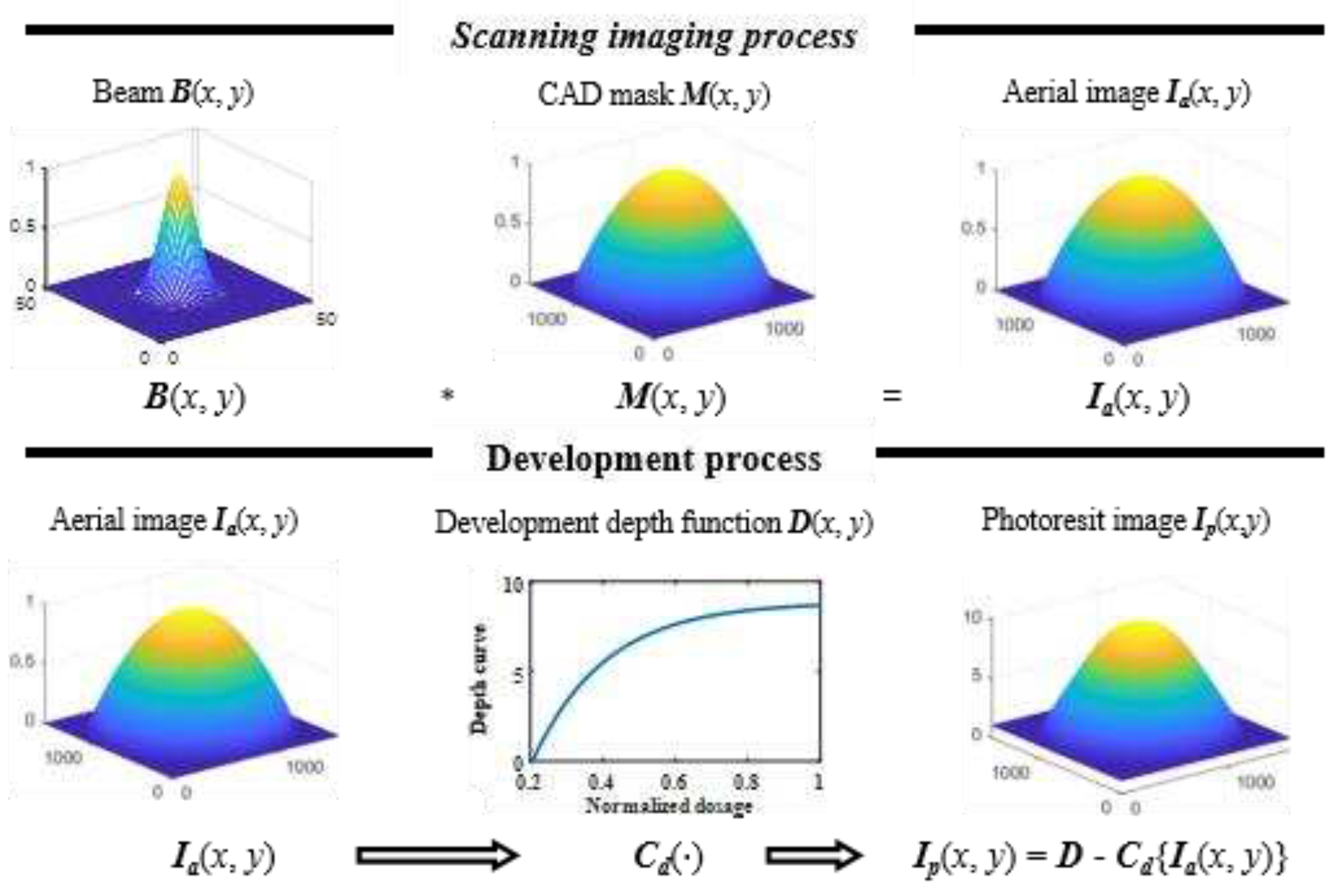
2.1. Forward imaging model

Under the assumption of linear time-invariant system, the scanning imaging process of LDW is assumed to be incoherent imaging. As Figure 3 shows, given an input CAD mask M, the laser power is regulated according to the mask gray level, and the focused spot of different power is obtained through electrical modulation. After selective exposure by focusing spots of different power, the approximate aerial image of the photo-resist surface can be calculated as:
Preprints 90235 g003
Figure 3. Numerical model of 3D lithography system, with the features on the CAD mask are transferred to the photo-resist by a direct exposure and development process.
Figure 3. Numerical model of 3D lithography system, with the features on the CAD mask are transferred to the photo-resist by a direct exposure and development process.
Preprints 90235 g003
I a = M ( x , y ) ⊗ B ( x , y )
in which,  ⊗  is the convolution operation, and B is the Gaussian spot, which can be calculated by:
B ( x , y ) = 2 P π ω 0 2 e − 2 ( x 2 + y 2 ) ω 0 2
where P and  ω 0 = FWHM / 2 l n 2  are the total power and the waist of the beam.
As a semi-empirical model to describe the exposure process, the Dill exposure model leverages the photochemical reaction through the transport equation and non-linear kinetic model. Therefore, the Dill model can accurately predict the formation of photo-resist patterns and the generation of defects [41,42,43]. Such predictions can guide the optimization of exposure parameters and process flow, hence improving print fidelity. The numerical model of the Dill expose model can be described as:
∂ I ( z , t ) ∂ z = − I ( z , t ) [ A M P A C ( z , t ) + B ]
∂ M P A C ( z , t ) ∂ t = − C I ( z , t ) M P A C ( z , t )
in which,  I ( z , t )  and  M P A C ( z , t )  are intensity and photo-active compound concentration (PAC) at the depth z in the resist. A, B and C are Dill parameters, which can be calculated by the transmittance of exposed and unexposed photo-resists [41]. Although 3D lithography is discontinuous in the exposure time of the resist surface, the quasi-static approximation method based on the surface exposure is also useful [44]. Such prediction allows optimization of exposure parameters and process flow, thereby improving print fidelity. To this end, it is possible to set the boundary condition of  I ( 0 ,   0 ) = I a  and  M P A C ( 0 , ​ ​   ​ ​ 0 ) = 1 . Assuming the development time is sufficient, and the properties of photo-resist are not damaged, an accurate development result can be obtained by setting the PAC concentration threshold  M t r . Figure 4 depicts the simulation results and experiment results of the Dill model. Figure 4 (a) and (c) give the normalized PAC computed by different incident intensities  I a , with the resist curves computed by the Dill model and experiment results are given in Figure 4 (b) and (d). However, the iteration of partial differential equations based on Equation (3) and Equation (4) is impractical in 3D OPC, because it brings huge computational resource requirements in derivation. Therefore, it is necessary to convert the 3D model into a 2D model.
Fortunately, Equation (3) and Equation (4) were solved analytically by Herrick, and B can often be safely neglected while A >> B [45]. Thus, the relationship between intensity and PAC can be approximated as:
I ( z ) = I ( 0 ) ⋅ 1 − M ( z ) 1 − M ( 0 ) = I ( 0 ) ⋅ M ( z ) M ( 0 ) e − A z
Using the threshold method, assume  I ( z ) = I t r  and  M ( z ) = M t r  are the development thresholds at depth z. The PAC at the top of photo-resist  M ( 0 ) = M M I n  below the photochemical reaction threshold. The Equation (5) is converted to Equation (6) by setting boundary condition  I ( 0 ) = I a :
z = 1 A ln [ ( M t r M min I t r ) ⋅ I a ]
Considering that the derivation of the photochemical reaction curve uses a series of approximate conditions, we have adopted a more general form in calibration:
C d ( I a ) = z = a 1 ⋅ ln ( I a + a 2 ) + a 3
And the Quasi-static approximation result can be calibrated as Figure 4 (e) shows. To this end, the photo-resist image after development  C d  can be uniformly computed as:
I p = T { M ( x , y ) } = D − C d ( I a )
in which,  T {   ⋅   }  presents the mapping relationship from CAD mask and photo-resist image, and D is the thickness of photo-resist.

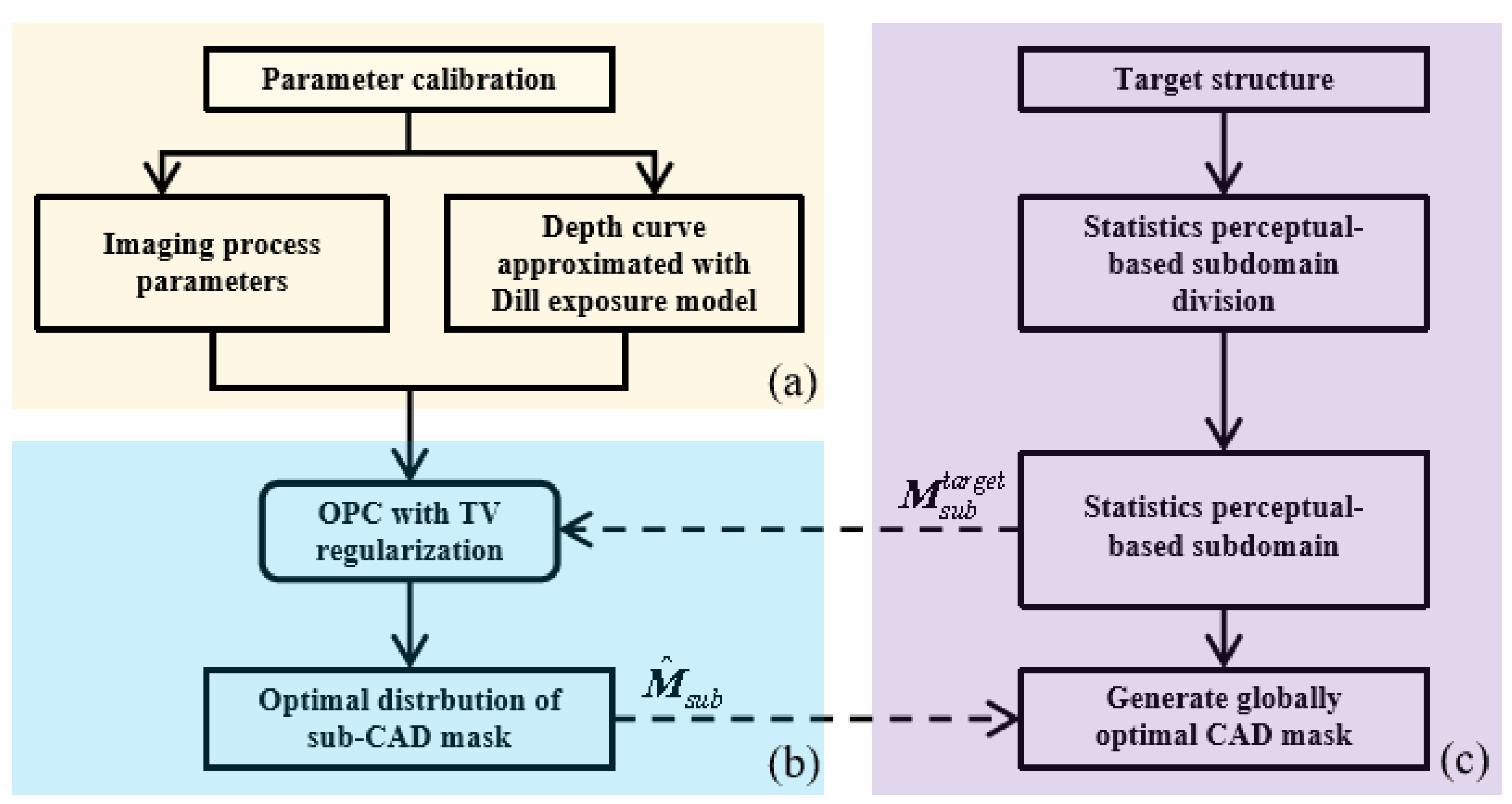
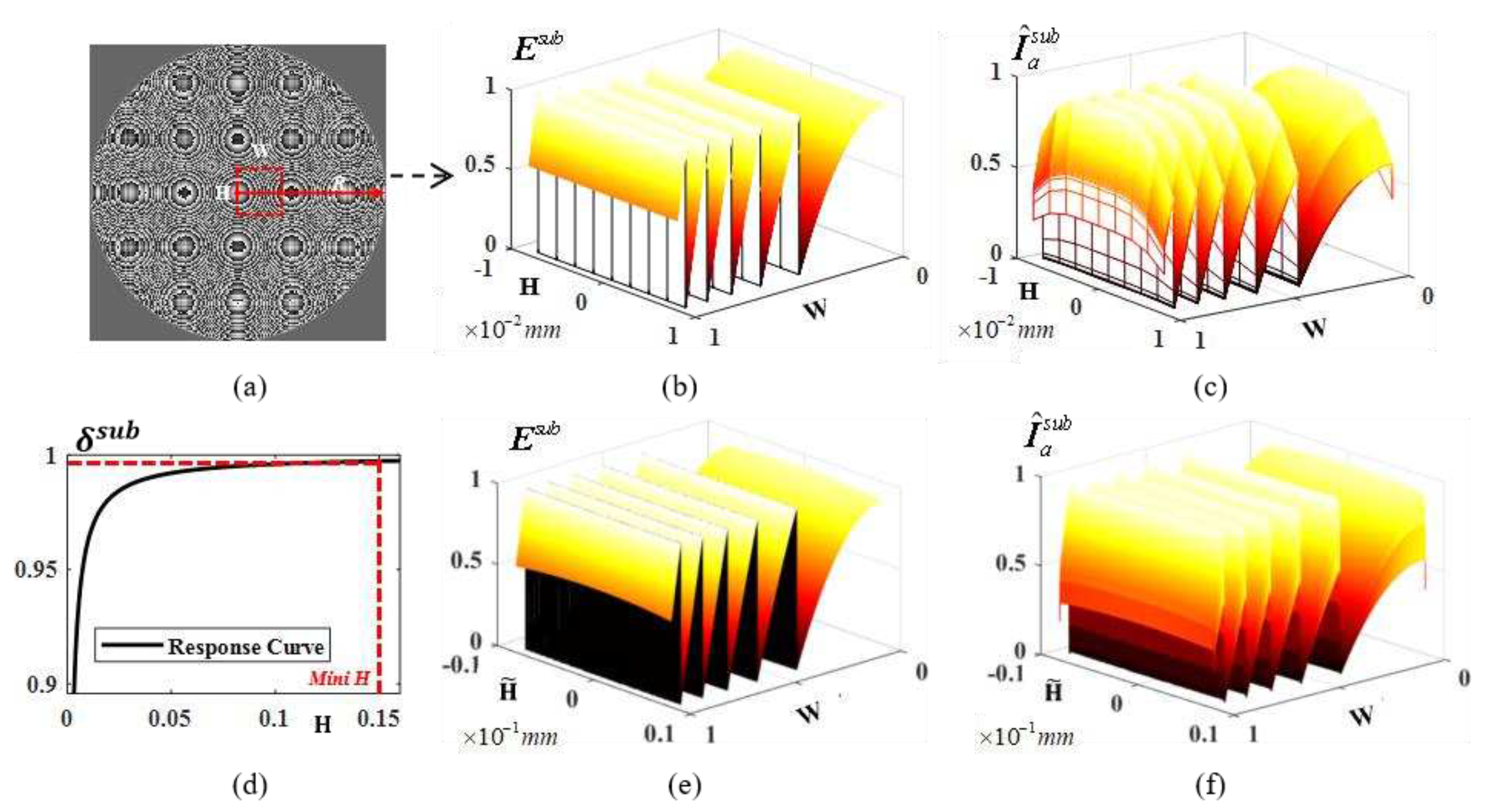
2.2. Inverse optimization method with statistics subdomain division

The goal of 3D OPC is to inversion the optimal CAD mask  M ˜ , and minimizes the dissimilarity between desired target pattern  I 0  and photo-resist image  I p  over all pixels. The score function  S p e  employee in convex optimization can be computed by:
S p e ( M ) =   1 2 ‖ I p -   I 0 ‖ 2 2
However, the optimization is impracticable while the pixel number N reaches millions. An effective way to solve this problem is to divide the optimization into sub-domains, then sub-domains are optimized respectively, and the global solution can be obtained by combing these sub-domains solutions finally. Considering the uniqueness of Fresnel design, the symmetrical structure is characterized through a limited area. Therefore, the inverted solutions in a limited sub domains  M s u b  can perceive global solutions  M ˜ . According Equation (1), the optical proximity effect (OPE) always exists, the distortion degree of aerial image in the subdomain  I a s u b  is increased as sub-domain  M s u b  decreases. As Figure 5 (a) shows, the sub-domain mask with width W and height H is denoted as  M s u b , the mask intensity in polar coordinates is determined by the radius and independent of the angle. The 3D profile of subdomain is given in Figure 5 (b), and the aerial image in the subdomain  I a s u b  has an obvious distortion at the edges while H < 0.002 m m . Figure 5 (c) gives the normalized aerial image  I ^ a s u b computed by:
I ^ a s u b ( x , y ) = M s u b ( x , y ) ⊗ B s u M − 1 ( x , y )
where  B s u M − 1 ( x , y ) = B ( x , y ) / ∑ ( x , y ) B ( x , y )
According the linear characteristic of convolution operation,  I ^ a s u b ( x , y ) ≈ M s u b ( x , y ) in the convolution fully region, and  I ^ a s u b ( x , y ) ≪ M s u b ( x , y )  in the convolution incompletely region. Thus, the responses of convolution on subdomain  M s u b  can be computed to describe the overall response relationship. To quantify the extent of distortion, we utilized the linear characteristic of convolution operation. With the response relationship between  I ^ a s u b  and  M s u b  is defined as:
δ s u b = 1 k h ⋅ k w ∑ x = 1 k h ∑ y = 1 k w I ^ a s u b ( x , y ) ⋅ [ M s u b ( x , y ) + ε δ ] − 1
in which, kh and kw present the pixel number in x/y-direction of sub-domain  M s u b , and Figure 5 (d) shows the relationship between respond  δ s u b  and height H. Thus, the optimal height  H ˜ = 0.16 m m  is determined by  δ s u b = 0.997  according to the 3 δ  statistic principle. The subdomain and corresponding aerial image of subdomain  I ^ a s u b  are shown in Figure 5 (e) and (f). Similarly, the optimal width  W ˜ = R + H ˜  can be obtained from the circular symmetry property, and the area to be optimized is compressed to  W ˜ ⋅ H ˜ ⋅ ( 2 ⋅ R ) − 2 . Thus, the memory requirement is reduced to 0.83 % when R = 10mm. Without loss of generality, the optimization scheme is carried out in Cartesian coordinate system, the discontinuity of optimal  M ^ s u b  should be punished by total variation (TV) in each radial directions, and it is worth noting that we used the square of TV to avoid arithmetic errors. Thus, the optimization problem can be formulated as:
minimize       S = λ 1 S p e ( M s u b )     + λ 2 S T V 2 ( M s u b ) subject   to       M s u b = ( 1 + cos ω s u b ) / 2            
where  λ 1 = S p e / | S p e |  and  λ 2 = S T V 2 / | S T V 2 |  represent the weights of  S p e  and  S T V 2 , and  S T V 2 ( M s u b )  is given by:
S T V 2 ( M s u b ) = ‖ ∇ x M s u b ( x , y ) ‖ 2 2 + ‖ ∇ y M s u b ( x , y ) ‖ 2 2
in which,  ∇ x M s u b ( x , y )  and  ∇ y M s u b ( x , y )  denote the gradients of  M s u b ( x , y )  in x and y directions:
{ ∇ x M s u b ( x , y ) = M s u b ( x + 1 , y ) − M s u b ( x − 1 , y ) 2 ∇ y M s u b ( x , y ) = M s u b ( x , y + 1 ) − M s u b ( x , y − 1 ) 2
Therefore, the optimal sub-domain  M ^ s u b  with respect to  ω  can be solved numerically by steepest gradient descent (SGD) method, with the update rules given by:
ω t + 1 s u b = ω t s u b − η ⋅ ∂ S t / ∂ ω t s u b
with  η  is set to a reasonable value,  ω  will converge under the impetus of  ∂ S / ∂ ω , the calculation detail of  ∂ S / ∂ ω  is shown in Appendix A. It is worth noting that Equation (14) is converted to matrix multiplication to realize the solution of partial differential.

2.3. Accelerated algorithms

Although Equation (13) gives a stable and reliable optimization scheme, the convergence speed suffers the challenge of the multi-task optimization (optimization with constraints), which brings inconsistency in time steps  η  as we studied before [20,21]. Thus, 3D OPC with Adam optimizer [44] is employed in this paper, with the finite-difference schemes at time-step t+1 is:
ω t + 1 s u b = ω t + 1 s u b − η ⋅ m ^ t / ( v ^ t + ε )
in which,  η   =   0.01  is global learning rate.  m ^ t = m t / ( 1 − β 1 t )  is the first bias-corrected moment estimate of first bias moment  m t = β 1 ⋅ m t - 1   +   ( 1   -   β 1 ) ⋅ g t .  ν t = β 2 ⋅ ν t - 1   +   ( 1   -   β 2 ) ⋅ g t 2 is the second bias-corrected moment estimate of second bias moment  ν t = β 2 ⋅ ν t - 1   +   ( 1   -   β 2 ) ⋅ g t 2 , the gradient is set as  g t = ∂ S / ∂ ω , with the global decay rates  β 1 = 0.99  and  β 2 = 0.999 .The additional term  ε = 10 - 8  is embed to ensure denominator is not zero.
On the other hand, the Fourier transform operations is applied to accelerate the convolution operation:
M s u b ( x , y ) ⊗ B ( x , y ) = ℱ - 1 { ℱ { M s u b ( x , y ) } ⊙ ℱ { B ( x , y ) } }
in which,  ℱ {   ⋅   }  and  ℱ - 1 {   ⋅   }  represent the forward and inverse Fourier transform operations, respectively. And  ⊙  denotes the entry-by-entry multiplication operation.

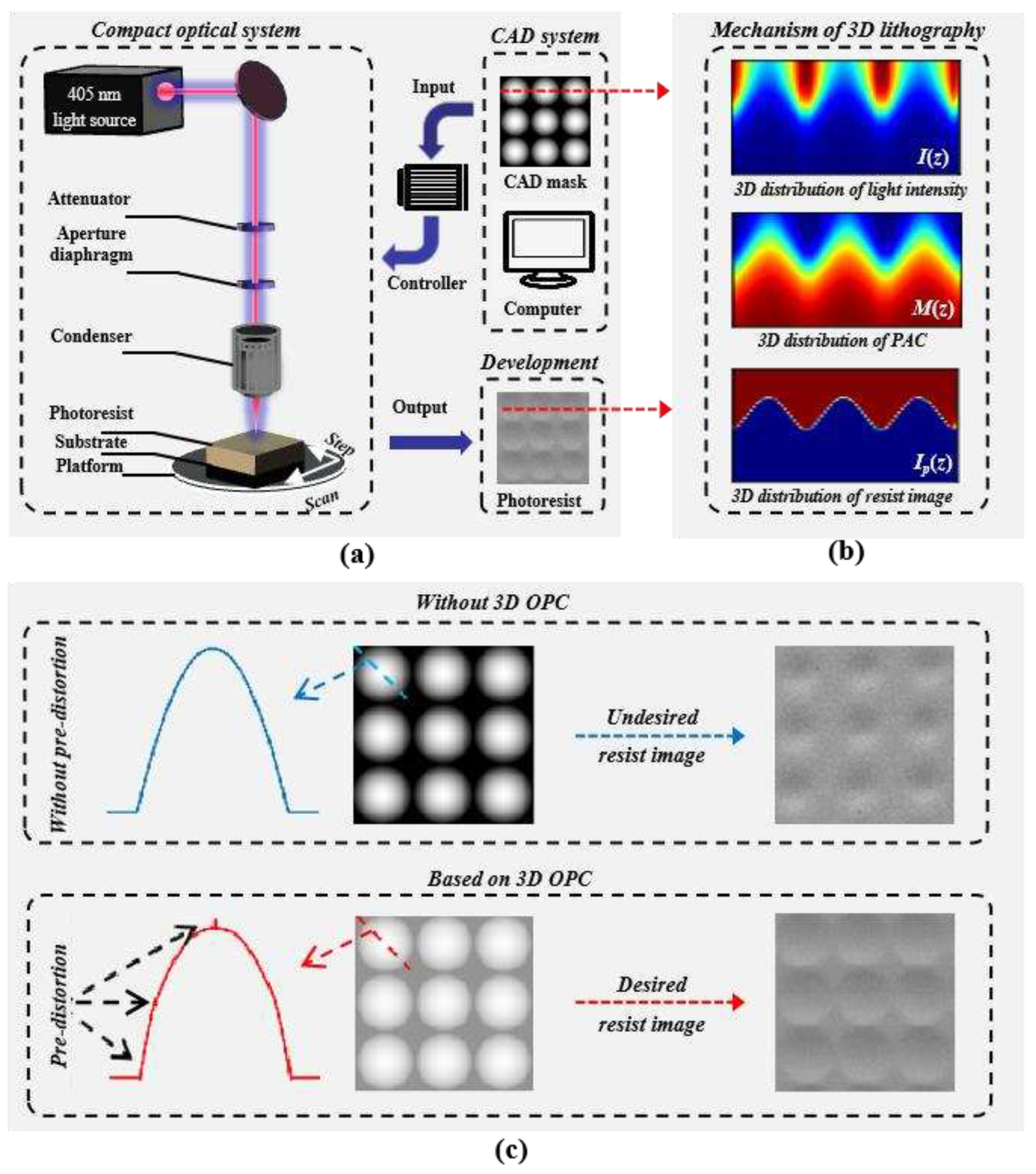
3. Fabrication of the Fresnel lens

3.1. Design of the Fresnel lens

Similar to our previous work, a hyperbolic lens is designed in advance [15,16]:
( z − a ) 2 a 2 − r 2 b 2 = 1
in which, a = -7.475 mm and b = 8.356 mm are the semi-perimeters of the real and imaginary axes of the hyperbola, respectively. The conical coefficient and radius of curvature being  k = − 2.5  and  R = 9.34   m m , the focal length and f-number of lens are  f = 23.35   m m and  f / # = 2.335 .Thus, the depth of the Fresnel lens grooves with a constant height, can be simplified as [35,36]:
z I + 1 = R − R 2 − ( I p ) 2
where i and p are the point coordinate and pitch size of the groove.

3.2. Equipment and process parameters

As illustrated in Figure 1 (a), the lithography device based on the 4096-order electrical modulation we used is PicoMaster-100 (4PICO Litho). The full width at half maximum (FWHM) of the Gaussian beam profile is 850nm, the scan speed and step size are  v = 100 ​ m m / s  and  s = 200 n M , the minimum and maximum exposure dose are 50 mj/cm2 and 1000 mj/cm2, respectively. The customized 10-inch glass substrate is covered by the AZ4562 photo-resist with thickness of 10um. The development process uses 25% KOH solvent for 120 seconds at room temperature of 22 °C

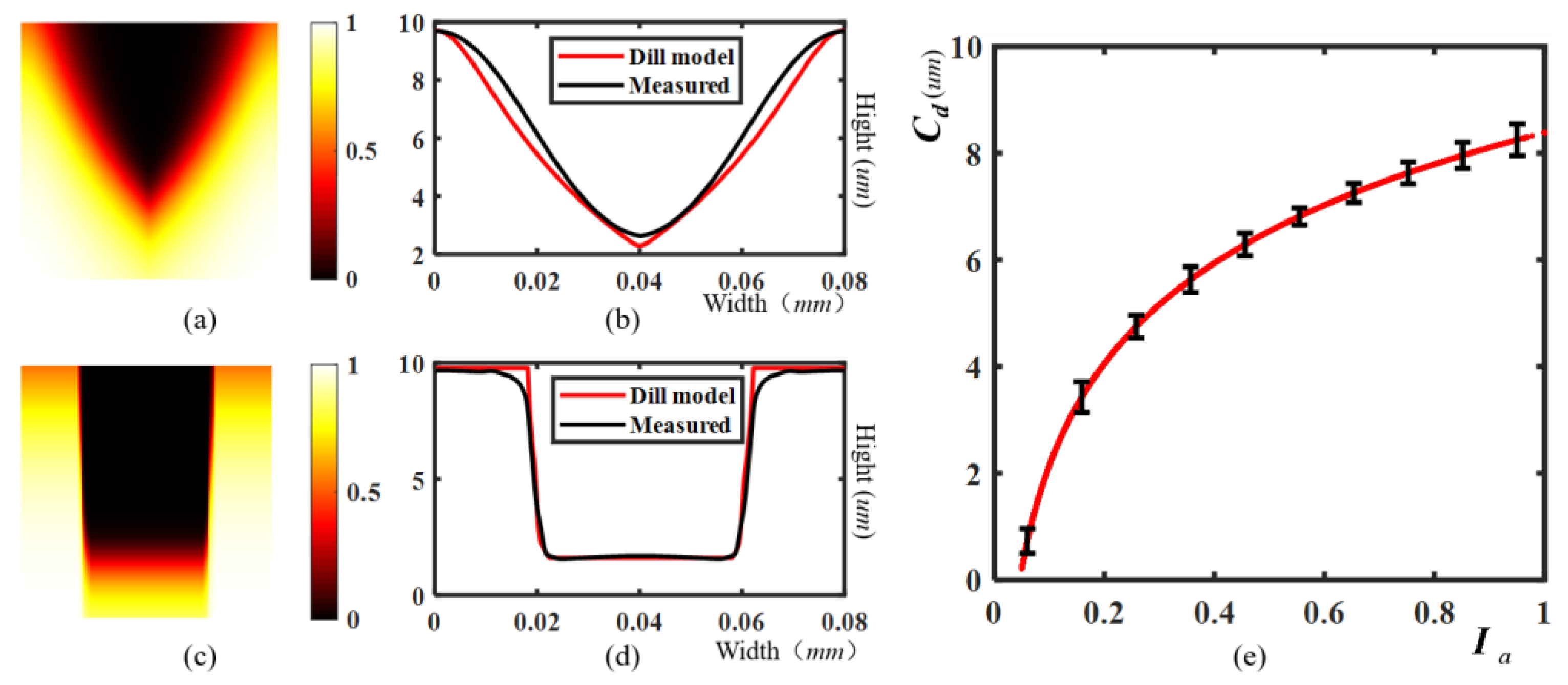
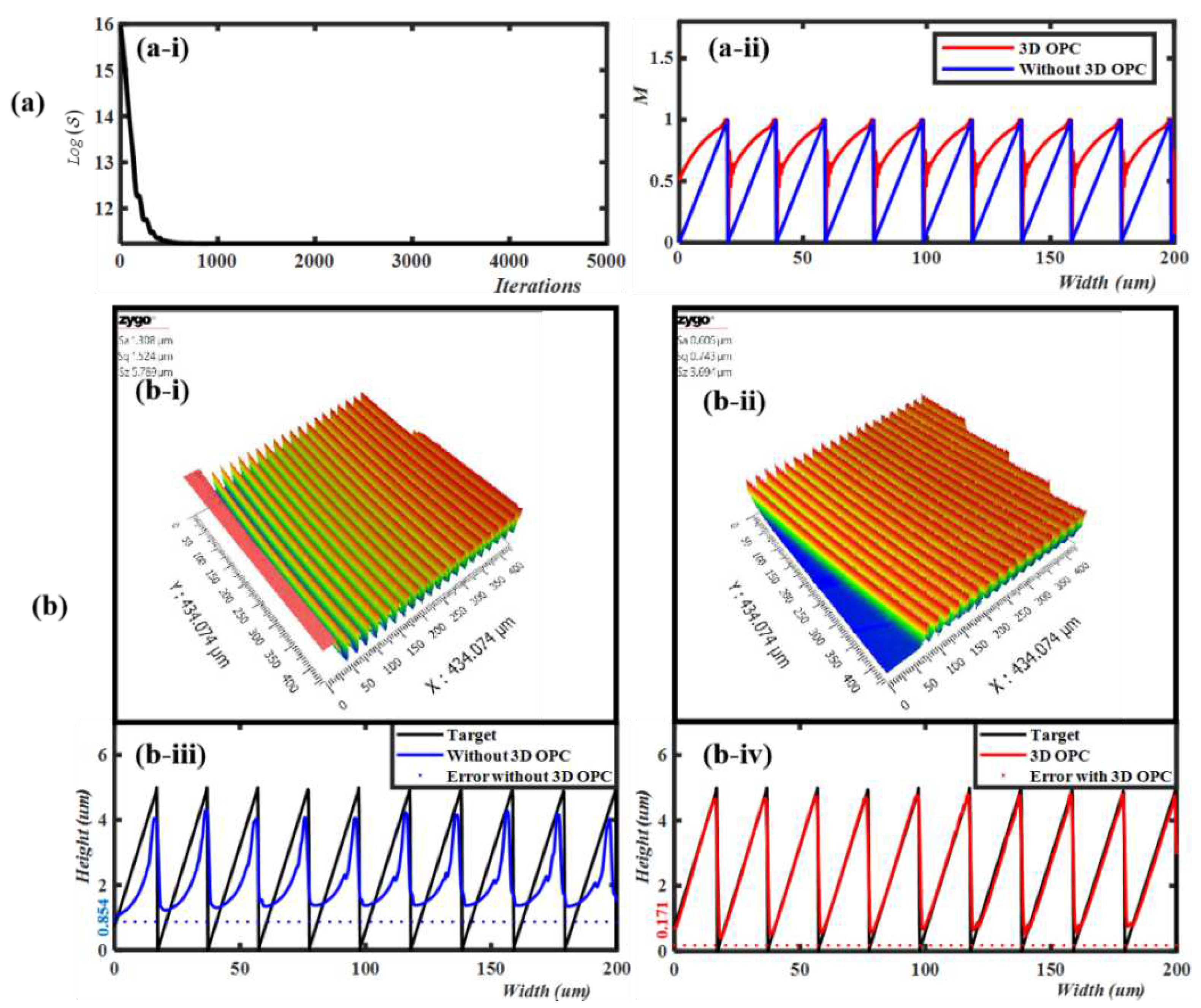
3.3. Simulation parameters of 3D OPC

The parameters used for numerical simulations are: full width at half maxima FWHM = 850nm, spatial resolution  Δ x = Δ y = 200 nm / pixel , Dill parameters A = 0.45, B = 0.022, C = 0.017 and  M t r =   0 . 6 , quasi-static approximation coefficient a1 = 3.38, a2 = 47.76, and a3 = -17.6, the height of sub-domain is  H ˜ = 0.16 m m . All computations are performed on the RTX 3090 GPU with 24GB memory.

3.4. Results and Discussion

Optimization and experimental results are given in Figure 7. In which, Figure 7 (a) and Figure 7 (b) depicts the simulation results, the lithography results before and after 3D OPC. Figure 7 (a-i) gives convergence performance of 3D OPC method, the score function  S  reduced from 8.5 million to 76 thousand; Figure 7 (a-ii) shows the cross section of CAD mask of last 10-grooves, where the blue and red lines represent the CAD mask before and after 3D OPC. Where the CAD mask values based on 3D OPC are increased due to the resist effect, and the discontinues of edges is searched to deal with optical proximity effect (OPE); Figure 7 (b) gives the lithography result before (Figure 7 (b-i)) and after (Figure 7 (b-ii)) 3D OPC, which were measured by an optical profiler (ZYGO Co., Ltd, Nexview NX2); Figure 7 (b-iii) illustrates the target structure (black line), the lithographic structures before (blue line) 3D OPC, with the absolute error (blue horizontal dotted line) between target one (black line) and lithographic one before (read line) is 0.854 um. Figure 7 (b-iv) illustrates the target structure (black line), the lithographic structures after (red line) 3D OPC, with the absolute error (red horizontal dotted line) between target one (black line) and lithographic one before (read line) is 0.171 um. According to the experiments, the absolute error of optimized profile is reduced 79.98% compared with the profile fidelity without 3D OPC.
Figure 8 shows a comparison of the focusing spot of Fresnel lenses (before and after 3D OPC). With the focal length is  f = 32.55   m m before 3D OPC, the multiple undesired peaks with considerable intensity in the image, the focal spot image of Fresnel lens without 3D OPC is give in Figure 8 (a), corresponding f-number are and   f / # = 3.255 . Figure 8 (b) depicts the focusing spot of Fresnel lens based on 3D OPC, with a clear peak optimized by 3D OPC, and the improved performance of focus and f-number are  f = 24.25   m m  and  f / # = 2.425 . The comparison of spot profile given in Figure 8 (c), where the simulated profile, the profile before and after 3D OPC optimization are represented by red solid lines, green dashed lines, and blue dashed lines.

4. Application of the Fresnel lens

4.1. Fabrication of the transferred Fresnel lens

We convert convex Fresnel lenses into concave Fresnel lenses for myopia correction. The transferred process from photoresist to PDMS is divided into 3 steps. The first step is to mix PDMS (Sylgard 184, Dow Corning) with a curing agent at a weight ratio of 1:10, and remove bubbles through a vacuum environment. The second step is to cover PDMS on a Fresnel lens, and use the spin coating method to prepare mixture film. The spin coating process includes two stages: the film is spun with the speed of 400 rpm for 20 seconds in the first stage; then spun with the speed of 700 rpm for 40 seconds in second stage. In the third step, the PDMS mixture coating on the zoom MLA is fed into an oven at 60 for 7 hours. After baking process, the PDMS mixture is peeled off from the Fresnel lens.

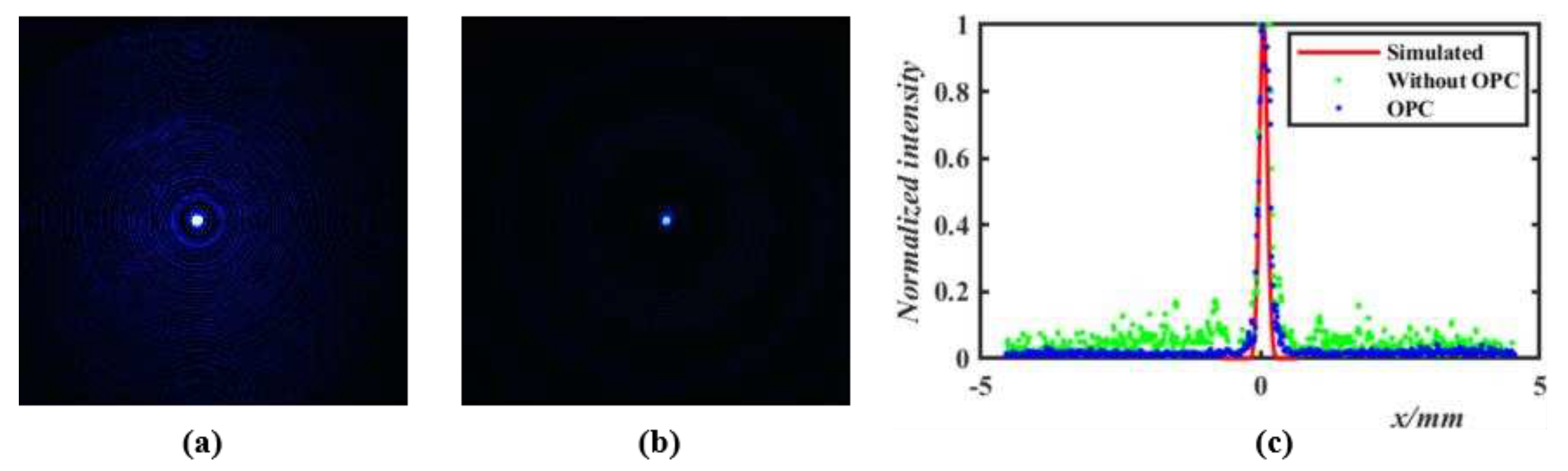
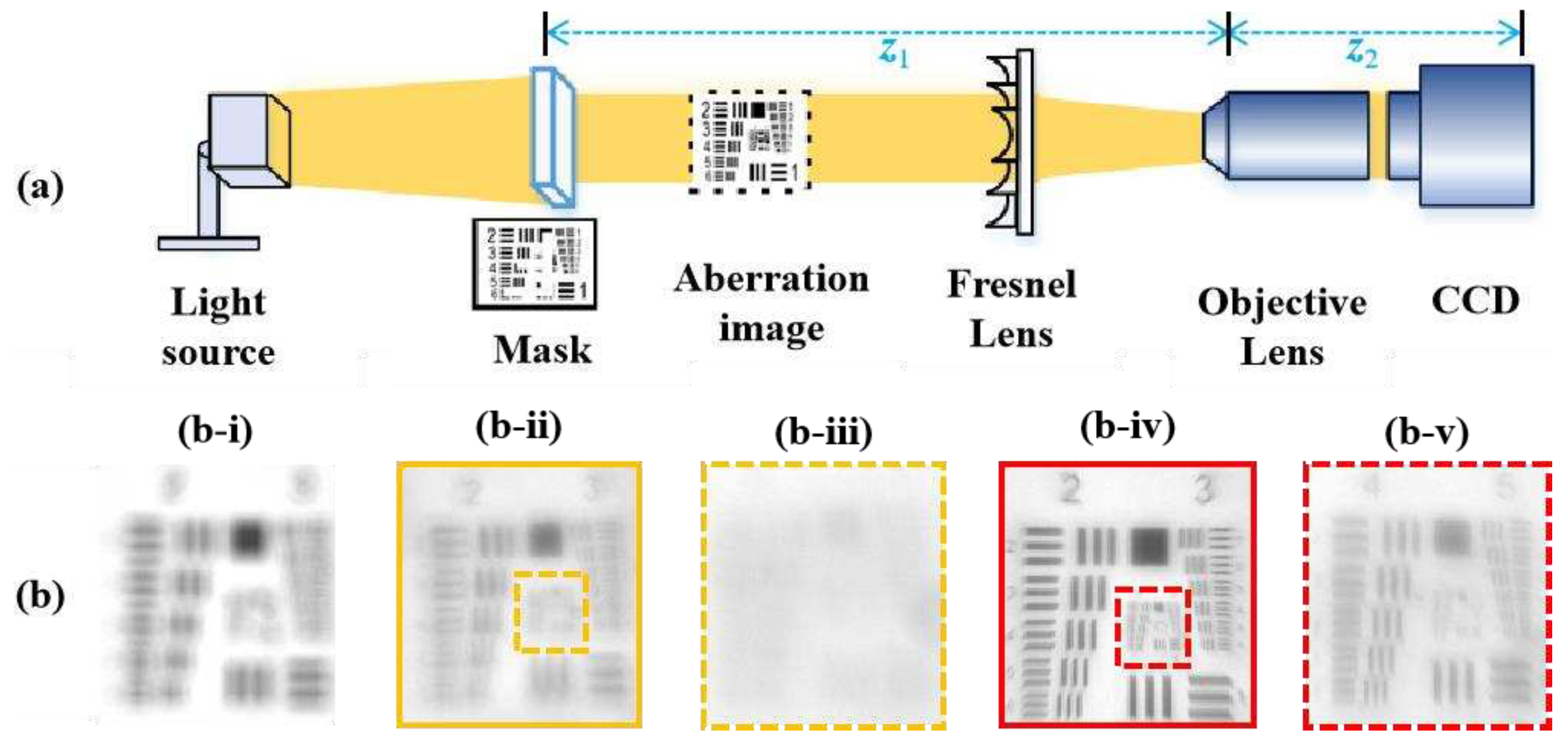
4.2. Vision-correcting System

In the experiments of vision-correcting system, a 4× objective lens (Daheng, GCO- 2121) is used to represent the human crystalline lens; a CCD (Daheng, MER-2000-19U3C-L, acquisition frame rate 25 Hz, exposure time 50000 us) is used to observe the images, which is simply approximated as an image on the retina; a white light source was selected to imitate natural light imaging, and used for testing on the 1951 USAF resolution test card; the color image target is displayed on the OLED screen; adjustment of the object (mask) and the image distances is realized by two three-dimensional motion platforms (Daheng, GCM-901602 M).

4.3. Results and Discussion

In this paper, we consider the correction of myopia, where the retina receives blurred images in the distance. Therefore, a concave lens needs to be placed in front of the human eye to extend the focal length. With the transferred process provided by Section 3.4, the vision correction lens (transferred Fresnel lens) is used to extend the focal length. Figure 9 (a) shows the optical system for vision correction, the distance between mask and objective lens is defined as z1, the distance between objective lens and CCD is defined as z2. In practice, the vision correction approximation experiment can be divided into three steps: normal vision imaging, myopia vision imaging and vision correction imaging.
The first step is to obtain normal vision imaging without using vision correction lens: the positions of mask and objective lens are continuously adjusted to enable the CCD to capture a clear image. During this process, white light illumination was used, and a 1951 USAF resolution test card was used as the mask, resulting in z1 = 40 mm, z2 = 90 mm. The second step is to obtain myopia vision imaging without using vision correction lens: stabilize the position of the objective lens and CCD, and move the mask away from the objective lens to allow CCD to receive aberration images. Figure 9 (b-i) given the aberration images received by CCD, with the distance between mask and objective lens is z1 = 80 mm. The third step is to obtain vision correction imaging by using a vision correction lens: place a transferred Fresnel lens in front of the objective lens to extend the focal length of the optical path. Continuously adjust the position of the vision correction lens to achieve the best image quality received by the CCD. Based on a visual correction lens without 3D OPC, the corrected image in Figure 9 (b-ii) is blurry, and the zoom-in images of group 5 is given in Figure 9 (b-iii). It can be observed that only the features in element 2 of group 3 can be distinguished. Figure 9 (b-iv) shows the imaging correction result of the vision correction lens optimized by 3D OPC, with the zoom-in images of group 5 elements are placed in Figure 8 (b-v), and the equivalent corrected resolutions are 14.25 lp/mm (Group 3, Element 6) and 32 lp/mm (Group 5, Element 6). Although the blurred grayscale images of Group 5 can’t represent absolute resolution of corrected vision, all of the resolution features are captured.
Through the above operations, the optimal placement of vision correction lenses can be fixed. Thus, color image masks can be employed in the imaging system to quantify the imaging performance. The portrait and blocks shown in Figure 10 (a) and 10 (b) are displayed on the OLED screen. The contrast is calculated as shown in Figure 10 (c), that is, the contrast -H and -V of the whole image are averaged horizontally and vertically.
Figure 11 depicts the imaging correction results based on vision correction lenses. The columns from left to right lie the imaging results at z1 = 80, 85, 90, and 95 mm. With the portrait mask employed in Rows (a) and (b), the imaging results based on the vision correction lens (before and after 3D OPC) are compared. In row (a) of Figure 11, the imaging results are corrected by the Fresnel lens without 3D OPC, where PSNR = 13.4, 13.2, 13.2, 12.4 dB and Contrast = 0.24, 0.24, 0.24, 0.23 at z1 = 80, 85, 90 and 95 mm, respectively. Row (b) gives the imaging correct results by the Fresnel lens based on 3D OPC, with the improved PSNR = 16.6, 16.5, 16.2, 15.0 dB and Contrast = 0.37, 0.34, 0.32, 0.27. Similarly, the imaging correct results with blocks target are depicts in Rows (c) and (d). In which, the PSNR = 18.2, 18.3, 18.1, 17.9 dB and Contrast = 0.18, 0.18, 0.18, 0.17 based on Fresnel lens without 3D OPC are given in row (c). The improved performance of corrected imaging is shown in row (d), with the PSNR = 21.8, 21.6, 21.4, 21.2 dB and Contrast = 0.26, 0.25, 0.23, 0.22. Although the PSNR and contrast calculated based on different complexity masks are different, the Fresnel lens based on 3D OPC greatly improves the imaging performance of vision correction systems. The average PSNR and the average contrast (computed based on different positions z1) before and after 3D OPC are summarized in Table 1. Conservatively quantified, we only take smaller values. Compared with the imaging results formed by a vision correction lens without 3D OPC, the average PSNR and average contrast with a 3D OPC-based vision correction lens are improved by 18.92 % and 36 %, respectively. Without loss of generality, we take the minimum improvement ratio as quantification.

5. Conclusions

In this paper, an improved 3D OPC based on statistical principle is proposed, which reduces the memory requirement to less than 1% and realizes the 3D OPC in the micron to millimeter scale. With the quasi-static approximated Dill exposure model embedded in 3D OPC, the 3D model is approximated as a 2D model and transformed into a differentiable scheme. Benefit from the proposed methods, the CAD mask of Fresnel lens is inversed within 10 minutes, and experimental results shows that the reduction in geometric profile error after optimization is 79.98%. With a vision-correcting lens transferred from a 3D OPC-based Fresnel lens by PDMS, the resolution of the vision-correcting system reaches 32 lp/mm. Compared with the transferred vision correction lens without 3D OPC, the PSNR and average image contrast of the vision correction system are improved by 18.92 % and 36 %, respectively. In addition, the shadow effect of the captured image is aroused by the multi-imaging, which is obvious in the Fresnel structure. In our future work, the achromatic Fresnel structure design based on computational imaging will be considered to solve the problem.

Author Contributions

Conceptualization, F.P. and C.G.; writing—original draft preparation, F.P.; data measurement C.S.; writing—review H.W. and C.G. All authors have read and agreed to the published version of the manuscript.

Funding

This work was funded by the National Natural Science Foundation of China (NO. U20A6004)

Data Availability Statement

The data presented in this study are available from the corresponding author on request.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. T. Trantidou, M. S. Friddin, K. B. Gan, L. Han, G. Bolognesi, N. J. Brooks, and O. Ces. Mask-free laser lithography for rapid and low-cost microfluidic device fabrication. Analytical Chemistry 2018, 90, 13915-13921. [CrossRef]
  2. Melnikov, S. Köble, S. Schweiger, Y. K. Chiang, S. Marburg, and D. A. Powell. Microacoustic metagratings at ultra-high frequencies fabricated by two-photon lithography. Advanced Science 2022, 9, 2198-3844. [CrossRef]
  3. M. Guizar-Sicairos, I. Johnson, A. Diaz, M. Holler, P. Karvinen, H.-C. Stadler, R. Dinapoli, O. Bunk, and A. Menzel. High-throughput ptychography using Eiger: scanning X-ray nano-imaging of extended regions. Opt. Express 2014, 22, 14859–14870. [CrossRef]
  4. S. Achenbach, S. Hengsbach, J. Schulz, and J. Mohr. Optimization of laser writer-based UV lithography with high magnification optics to pattern X-ray lithography mask templates. Microsyst. Technol. 2019, 25, 2975–2983. [CrossRef]
  5. Lin, V., Liu, X., Huo, T., and Zheng, G. Design and fabrication of long-focal-length microlens arrays for Shack–Hartmann wavefront sensors. Micro & Nano Letters 2011, 6 (7), 523-526. [CrossRef]
  6. L. Zhang, W. Zhou, Neil J. Naples, and Allen Y. Yi. Fabrication of an infrared Shack–Hartmann sensor by combining high-speed single-point diamond milling and precision compression molding processes. Appl. Opt. 2018, 57, 3598-3605. [CrossRef]
  7. Zhou, X. T. et al. Fabrication of large-Scale microlens arrays based on screen printing for integral imaging 3D display. ACS Applied Materials & Interfaces 2016, 8, 24248-24255. [CrossRef]
  8. J. Hong, Y. Kim, S. Park, J. Hong, S. Min, S. Lee, and B. Lee, 3D/2D convertible projection-type integral imaging using concave half mirror array. Opt. Express 2010, 18, 20628-20637. [CrossRef]
  9. S. Luan, P. Xu, Y. Zhang, L. Xue, Y. Song, and C. Gui. Flexible Superhydrophobic Microlens Arrays for Humid Outdoor Environment Applications. ACS Applied Materials & Interfaces 2022, 14, 53433-53441. [CrossRef]
  10. S. Luan, H. Cao, H. Deng, G. Zheng, Y. Song, and C. Gui. Artificial Hyper Compound Eyes Enable Variable-Focus Imaging on both Curved and Flat Surfaces. ACS Applied Materials & Interfaces 2022, 14, 46112-46121. [CrossRef]
  11. S. Su, J. Liang, X. Li, W. Xin, X. Ye, J. Xiao, J. Xu, L. Chen, and P. Yin. Hierarchical Artificial Compound Eyes with Wide Field-of-View and Antireflection Properties Prepared by Nanotip-Focused Electrohydrodynamic Jet Printing. ACS Applied Materials & Interfaces 2021, 13, 60625-60635. [CrossRef]
  12. Wu, J., Zhang, H., Zhang, W. et al. Single-shot lensless imaging with fresnel zone aperture and incoherent illumination. Light: Science and Applications 2020, 9, 53. [CrossRef]
  13. Y. Ma, J. Wu, S. Chen, and L. Cao. Explicit-restriction convolutional framework for lensless imaging. Opt. Express 2022, 30, 15266-15278. [CrossRef]
  14. V. Vu, S. Hasan, H. Youn, Y. Park, and H. Lee. Imaging performance of an ultra-precision machining-based Fresnel lens in ophthalmic devices. Opt. Express 2021, 29, 32068-32080. [CrossRef]
  15. V. Vu, H. Yeon, H. Youn, J. Lee, and H. Lee. High diopter spectacle using a flexible Fresnel lens with a combination of grooves. Opt. Express 2022, 30, 38371-38382. [CrossRef]
  16. X. Dun, H. Ikoma, G. Wetzstein, Z. Wang, X. Cheng, and Y. Peng. Learned rotationally symmetric diffractive achromat for full-spectrum computational imaging. Optica 2020, 7, 913-922. [CrossRef]
  17. Xiao, X., Zhao, Y., Ye, X. et al. Large-scale achromatic flat lens by light frequency-domain coherence optimization. Light: Science and Applications 2022, 11, 323. [CrossRef]
  18. H. Arguello, S. Pinilla, Y. Peng, H. Ikoma, J. Bacca, and G.Wetzstein. Shift-variant color-coded diffractive spectral imaging system. Optica 2021, 8, 1424-1434. [CrossRef]
  19. V. Sitzmann, S. Diamond, Y. Peng, X. Dun, S. Boyd, W. Heidrich, F. Heide, and G. Wetzstein. End-to-end optimization of optics and image processing for achromatic extended depth of field and super-resolution imaging. ACM Transactions on Graphics, 2018, 37, pp. 1-13. [CrossRef]
  20. S. Luan, F. Peng, G. Zheng, C. Gui, Y. Song, S. Liu. High-speed, large-area and high-precision fabrication of aspheric micro-lens array based on 12-bit direct laser writing lithography. Light: Advanced Manufacturing 2022, 3, 47. [CrossRef]
  21. Z. Yang, F. Peng, S. Luan, H. Wan, Y. Song, and C. Gui. 3D OPC method for controlling the morphology of micro structures in laser direct writing. Opt. Express 2023, 31, 3212-3226. [CrossRef]
  22. A. J. Fleming, A. G. Wills, and B. S. Routley. Exposure optimization in scanning laser lithography. IEEE Potentials 2016, 35, pp. 33–39. [CrossRef]
  23. O. T. Ghalehbeygi, J. O'Connor, B. S. Routley and A. J. Fleming. Iterative Deconvolution for Exposure Planning in Scanning Laser Lithography. In Proceedings of 2018 Annual American Control Conference (ACC), Milwaukee, WI, 27-29 June, 2018 pp. 6684-6689.
  24. O. T. Ghalehbeygi, A. G. Wills, B. S. Routley, and A. J. Fleming. Gradient-based optimization for efficient exposure planning in maskless lithography. J. Micro/Nanolithogr., MEMS, MOEMS 2017, 16. [CrossRef]
  25. A. J. Fleming, O. T. Ghalehbeygi, B. S. Routley, and A. G. Wills. Scanning laser lithography with constrainedquadratic exposure optimization. IEEE Trans. Contr. Syst. Technol. 2019, 27, 2221–2228. [CrossRef]
  26. X. Sun, S. Yin, H. Jiang, W. Zhang, M. Gao, J. Du, and C. Du. U-Net convolutional neural network-based modification method for precise fabrication of three-dimensional microstructures using laser direct writing lithography. Opt. Express 2021, 29, 6236. [CrossRef]
  27. W. Lv, S. Liu, Q. Xia, X. Wu, Y. Shen and E. Y. Lam. Level-set-based inverse lithography for mask synthesis using the conjugate gradient and an optimal time step. J. Vac. Sci. Technol. B. 2013, 31, 041605–041605–13. [CrossRef]
  28. J. Li and E. Y. Lam. Robust source and mask optimization compensating for mask topography effects in computational lithography. Opt. Express 2014, 22, 9471-9485. [CrossRef]
  29. J. Li, S. Liu and E. Y. Lam. Efficient source and mask optimization with augmented lagrangian methods in optical lithography. Opt. Express 2013, 21, 8076–8090. [CrossRef]
  30. X. Ma, D. Shi, Z. Wang, Y. Li, and G. R. Arce. Lithographic source optimization based on adaptive projection compressive sensing. Opt. Express 2017, 25, 7131–7149. [CrossRef]
  31. X. Ma, Z. Wang, Y. Li, G. R. Arce, L. Dong, and J. Garcia-Frias. Fast optical proximity correction method based on nonlinear compressive sensing. Opt. Express 2018, 26, 14479–14498. [CrossRef]
  32. Y. Shen, F. Peng, and Z. Zhang. Efficient optical proximity correction based on semi-implicit additive operator splitting. Opt. Express 2019, 27, 1520-1528. [CrossRef]
  33. Y. Shen, F. Peng, and Z. Zhang. Semi-implicit level set formulation for lithographic source and mask optimization. Opt. Express 2019, 27, 29659-29668. [CrossRef]
  34. Xu Ma, Qile Zhao, Hao Zhang, Zhiqiang Wang, and Gonzalo R. Arce. Model-driven convolution neural network for inverse lithography. Opt. Express 2018, 26, 32565-32584. [CrossRef]
  35. Xu Ma, Xianqiang Zheng, and Gonzalo R. Arce. Fast inverse lithography based on dual-channel model-driven deep learning. Opt. Express 2020, 28, 20404-20421. [CrossRef]
  36. F. Peng, Z. Yang, and Y. Song. 3D grayscale lithography based on exposure optimization. In International Workshop on Advanced Patterning Solutions (IWAPS), (IEEE, 2021), pp. 1-3. [CrossRef]
  37. C. Jidling, A. J. Fleming, A. G. Wills, and T. B. Schön. Memory efficient constrained optimization of scanning-beam lithography. Opt. Express 2022, 30, 20564-20579. [CrossRef]
  38. K. Yuan, B. Yu, and D. Z. Pan. E-beam lithography stencil planning and optimization with overlapped characters. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2012, 31, 167–179. [CrossRef]
  39. F. Yesilkoy, K. Choi, M. Dagenais, and M. Peckerar. Implementation of e-beam proximity effect correction using linear programming techniques for the fabrication of asymmetric bow-tie antennas. Solid-State Electron. 2010, 54, 1211–1215. [CrossRef]
  40. J. Bolten, T. Wahlbrink, M. Schmidt, H. D. Gottlob, and H. Kurz. Implementation of electron beam grey scale lithography and proximity effect correction for silicon nanowire device fabrication. Microelectron. Eng. 2011, 88, 1910–1912. [CrossRef]
  41. F. H. Dill, W. P. Hornberger, P. S. Hauge, J. M. Shaw. Characterization of positive photoresist. IEEE Trans. On Electron Devices 1975, 22, 445-452. [CrossRef]
  42. F. L, Y. Xie, Q. Sun. Analyzing of line profile for laser direct writing lithograph. ACTA PHOTONICA SINICA 2004, 33, 136-139.
  43. C. Du, X. Dong, C. Qiu, Q. Deng, C. Zhou. Profile control technology for high-performance microlens array. Opt. Eng. 2004, 43, 2595-2602. [CrossRef]
  44. C. A. Mack, Fundamental Principles of Optical Lithography: The Science of Microfabrication (John Wiley & Sons,Ltd., 2007). [CrossRef]
Preprints 90235 g001
Figure 1. (a) Schematic of 3D lithography system, in which a 405nm light source is used, and the layout on the CAD mask is transferred to the photo-resist by a scanning exposure and development process. (b) The 3D distribution of light intensity and photo-active compound concentration (PAC) in the photo-resist is changed by selective exposure, and the 3D photo-resist pattern is formed after development. (c) The CAD mask compensate method is based on three-dimensional optical proximity correction (3D OPC), where the pixelated mask is numerically solved by a convex optimization to improve the print fidelity.
Figure 1. (a) Schematic of 3D lithography system, in which a 405nm light source is used, and the layout on the CAD mask is transferred to the photo-resist by a scanning exposure and development process. (b) The 3D distribution of light intensity and photo-active compound concentration (PAC) in the photo-resist is changed by selective exposure, and the 3D photo-resist pattern is formed after development. (c) The CAD mask compensate method is based on three-dimensional optical proximity correction (3D OPC), where the pixelated mask is numerically solved by a convex optimization to improve the print fidelity.
Preprints 90235 g001
Preprints 90235 g002
Figure 2. (a) Parameter calibration based on imaging model and dill exposure approximation model. (b) The 3D OPC model with total variation (TV). (c) Subdomain segmentation and global recovery of mask.
Figure 2. (a) Parameter calibration based on imaging model and dill exposure approximation model. (b) The 3D OPC model with total variation (TV). (c) Subdomain segmentation and global recovery of mask.
Preprints 90235 g002
Preprints 90235 g004
Figure 4. Comparison of Dill model and experiment. Where (a) and (c) are normalized PAC concentration of resist with two different incident intensities  I a , and the corresponding resist curves computed by Dill model and experiment given in (b) and (d), respectively. (e) depicts the nonlinear relationship between normalized aerial image  I a  and photo-resist depth  C d ( I a ) .
Figure 4. Comparison of Dill model and experiment. Where (a) and (c) are normalized PAC concentration of resist with two different incident intensities  I a , and the corresponding resist curves computed by Dill model and experiment given in (b) and (d), respectively. (e) depicts the nonlinear relationship between normalized aerial image  I a  and photo-resist depth  C d ( I a ) .
Preprints 90235 g004
Preprints 90235 g005
Figure 5. Subdomain division based on statistics perceptual. (a) Fresnel lens with radius R = 1cm, (b) is the initial subdomain with the corresponding aerial image in (c). (d) gives the convolution response between the mask and aerial image, (e) shows the global performance of the convolution response, (f) is the optimal width and height of subdomain.
Figure 5. Subdomain division based on statistics perceptual. (a) Fresnel lens with radius R = 1cm, (b) is the initial subdomain with the corresponding aerial image in (c). (d) gives the convolution response between the mask and aerial image, (e) shows the global performance of the convolution response, (f) is the optimal width and height of subdomain.
Preprints 90235 g005
Preprints 90235 g006
Figure 7. Simulation and experimental results with last 10-grooves. Rows (a) and (b): the simulation results, the lithography results before and after 3D OPC, respectively. (a-i) Convergence performance of score function . (a-ii) The cross section profile of CAD mask before (blue line) and after (red line) 3D OPC. (b-i) and (b-ii) shows the lithography result before and after 3D OPC, with the 3D profile measured by optical profiler. (b-iii) Schematic illustration for target profile (black line), the profiles before (blue line) 3D OPC, with the absolutely error between target profile and lithographic profiles (blue horizontal dotted line) is 0.854 um. (b-iv) Schematic illustration for target profile (black line), the profiles after (red line) 3D OPC, with the absolutely error between target profile and lithographic profiles (read horizontal dotted line) is 0.171 um.
Figure 7. Simulation and experimental results with last 10-grooves. Rows (a) and (b): the simulation results, the lithography results before and after 3D OPC, respectively. (a-i) Convergence performance of score function . (a-ii) The cross section profile of CAD mask before (blue line) and after (red line) 3D OPC. (b-i) and (b-ii) shows the lithography result before and after 3D OPC, with the 3D profile measured by optical profiler. (b-iii) Schematic illustration for target profile (black line), the profiles before (blue line) 3D OPC, with the absolutely error between target profile and lithographic profiles (blue horizontal dotted line) is 0.854 um. (b-iv) Schematic illustration for target profile (black line), the profiles after (red line) 3D OPC, with the absolutely error between target profile and lithographic profiles (read horizontal dotted line) is 0.171 um.
Preprints 90235 g006
Preprints 90235 g007
Figure 8. Schematic illustration of focusing spot, with the wavelength 450 nm . (a) Focal spot of Fresnel lens without 3D OPC. (b) Focusing spot of Fresnel lens based on 3D OPC. (c) Intensity profile of focal spot image and simulated intensity profile.
Figure 8. Schematic illustration of focusing spot, with the wavelength 450 nm . (a) Focal spot of Fresnel lens without 3D OPC. (b) Focusing spot of Fresnel lens based on 3D OPC. (c) Intensity profile of focal spot image and simulated intensity profile.
Preprints 90235 g007
Preprints 90235 g008
Figure 9. (a) Schematic illustration of an experimental for vision-correcting. (b) Comparisons of best imaging performance with 1951 USAF resolution test chart. (b-i) is optical images without lens, (b-ii) is the optical images corrected by transferred lens (without 3D OPC), (b-iii) is the zoom-in images of group 5 element of (b-ii), (b-iv) is the optical images corrected by transferred lens (3D OPC), (b-v) is the zoom-in images of group 5 element of (b-iv).
Figure 9. (a) Schematic illustration of an experimental for vision-correcting. (b) Comparisons of best imaging performance with 1951 USAF resolution test chart. (b-i) is optical images without lens, (b-ii) is the optical images corrected by transferred lens (without 3D OPC), (b-iii) is the zoom-in images of group 5 element of (b-ii), (b-iv) is the optical images corrected by transferred lens (3D OPC), (b-v) is the zoom-in images of group 5 element of (b-iv).
Preprints 90235 g008
Preprints 90235 g009
Figure 10. (a) The portrait target. (b) The color blocks target. (c) Schematic diagram of contrast calculation
Figure 10. (a) The portrait target. (b) The color blocks target. (c) Schematic diagram of contrast calculation
Preprints 90235 g009
Preprints 90235 g010
Figure 11. Experimental results of imaging correction for vision correction lenses. Columns from left to right: the imaging results at z1 = 80, 85, 90 and 95 mm, respectively. Rows (a-b) give the imaging correction results using portrait mask, Rows (c-d) show the imaging correction results using color blocks mask.
Figure 11. Experimental results of imaging correction for vision correction lenses. Columns from left to right: the imaging results at z1 = 80, 85, 90 and 95 mm, respectively. Rows (a-b) give the imaging correction results using portrait mask, Rows (c-d) show the imaging correction results using color blocks mask.
Preprints 90235 g010
Table 1. Performance of mask imaging based on vision correction lens before and after 3D OPC.
Table 1. Performance of mask imaging based on vision correction lens before and after 3D OPC.
Mask Vision correction lens without 3D OPC Vision correction lens with 3D OPC Improvement
PSNR (dB) Contrast PSNR (dB) Contrast PSNR Contrast
Portrait 13.0 0.24 16.1 0.32 23.3 % 37.29 %
Color Blocks 18.1 0.18 21.5 0.24 18.92 % 36 %
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated