Prerpints.org logo
Preprint
Brief Report

Parameterization of Quantum Interactions

Altmetrics

Downloads

137

Views

43

Comments

0

This version is not peer-reviewed

Analytical and Numerical Methods for Stochastic Biological Systems

Submitted:

11 November 2023

Posted:

13 November 2023

Read the latest preprint version here

Alerts
Abstract
Background: Previous papers have developed a statistical mechanics of neocortical interactions (SMNI) fit to short-term memory and EEG data (Ingber, 2018). Adaptive Simulated Annealing (ASA) was used for all fits to data. A numerical path-integral for quantum systems, qPATHINT, was used. Objective: The quantum path-integral for Calcium ions was used to derive a closed-form analytic solution at arbitrary time. The quantum effects is parameterized here, whereas the previous 2018 paper applied a nominal ratio of 1/2 to these effects. Method: Methods of mathematical-physics for optimization and for path integrals in classical and quantum spaces are used. The quantum path-integral is used to derive a closed-form analytic solution at arbitrary time, and is used to calculate interactions with classical-physics SMNI interactions among scales. Results: The mathematical-physics and computer parts of the study are successful, in that three cases with Subjects (blind to this author) after 1,000,000 visits to the cost function gave: Subject-07 = 0.04, Subject-08 = 0.55, and Subject-09 = 1.00. All other 9 Subjects gave 0.
Keywords: 
Subject: Biology and Life Sciences  -   Neuroscience and Neurology

1. Introduction

This project calculates quantum Ca2+ using EEG for data. Only specific calcium ions Ca2+ are considered, those arising from regenerative calcium waves generated at tripartite neuron-astrocyte-neuron synapses.
This project is speculative, but it is testable, e.g., by fitting EEG.
SMNI has been developed since 1981. This evolving model including ionic scales have been published since 2012. Quantum physics calculations also support these extended SMNI models.

2. Statistical Mechanics of Neocortical Interactions (SMNI)

SMNI has been developed since 1981, scaling aggregate synaptic interactions to neuronal firings, up to minicolumnar-macrocolumnar columns of neurons to mesocolumnar dynamics, up to columns of neuronal firings, up to regional macroscopic sites (Ingber, 1981; Ingber, 1982; Ingber, 1983; Ingber, 1984; Ingber, 1985; Ingber, 1994).
SMNI has calculated agreement/fits with experimental data from various aspects of neocortical interactions, e.g., properties of short-term memory (STM) (Ingber, 2012a), including its capacity (auditory 7 ± 2 and visual 4 ± 2) (Ericsson & Chase, 1982; Zhang & Simon, 1985), duration, stability, primacy versus recency rule, Hick’s law (Hick, 1952; Jensen, 1987; Ingber, 1999), and interactions within macrocolumns calculating mental rotation of images (Ingber, 1982; Ingber, 1983; Ingber, 1984; Ingber, 1985; Ingber, 1994). SMNI has scaled mesocolumns across neocortical regions to fit EEG data (Ingber, 1997b; Ingber, 1997a; Ingber, 2012a).
Recent work in SMNI includes explicitly showing how neural-networks can be improved by adding SMNI nonlinearities (Ingber, 2022).

2.1. Synaptic Interactions

The short-time conditional probability distribution of firing of a given neuron firing given just-previous firings of other neurons is calculated from chemical and electrical intra-neuronal interactions (Ingber, 1982; Ingber, 1983). With previous interactions with k neurons within τj of 5−10 msec, the conditional probability that neuron j fires (σj= +1) or does not fire (σ j= −1) is
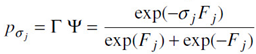
Preprints 90272 i001
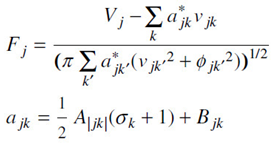
Preprints 90272 i002
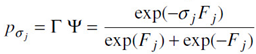
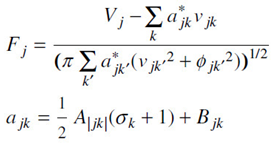
V j is the depolarization threshold in the somatic-axonal region. v jk is the induced synaptic polarization of E or I type at the axon, and ϕ jk is its variance. The efficacy a jk is a sum of A jk from the connectivity between neurons, activated if the impinging k-neuron fires, and B jk from spontaneous background noise.

2.2. Neuronal Interactions

Aggregation up to the mesoscopic scale from the microscopic synaptic scale uses mesoscopic probability
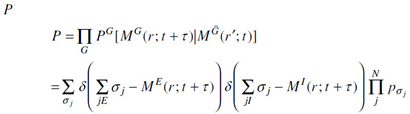
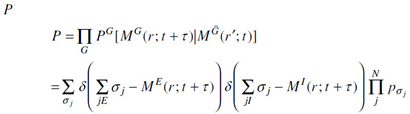
Preprints 90272 i003
M represents a mesoscopic scale of columns of N neurons, with subsets E and I , represented by pqi . The “delta”-functions δ -constraint represents an aggregate of many neurons in a column. G is used to represent excitatory (E) and inhibitory (I ) contributions. G designates contributions from both E and I .
The path integral is derived in terms of mesoscopic Lagrangian L. The short-time distribution of firings in a minicolumn, given its just previous interactions with all other neurons in its macrocolumn is thereby defined.

2.3. Columnar Interactions

In the prepoint (Ito) representation the SMNI Lagrangian L is
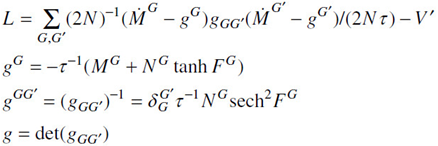
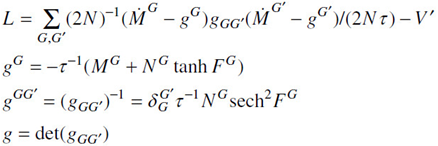
Preprints 90272 i004

2.4. SMNI Parameters From Experiments

Values of parameters and their bounds are taken from experimental data, not fit to specific phenomena.
NG = {N E = 160, N I = 60} was set for for visual neocortex, {N E = 80, N I = 30} was set for all other neocortical regions, MG′ and NG′ in FG are afferent macrocolumnar firings scaled to efferent minicolumnar firings by N /N * ≈ 10−3. N * is the number of neurons in a macrocolumn, about 105. V ′ includes nearest-neighbor mesocolumnar interactions. τ is usually considered to be on the order of 5−10 ms. VG = 10 mV, vG = 0. 1 mV, ϕ G= 0. 031/2 mV.
Nearest-neighbor interactions among columns give dispersion relations consistent with speeds of mental visual rotation (Ingber, 1982; Ingber, 1983).
The wave equation cited by EEG theorists, permitting fits of SMNI to EEG data (Ingber, 1995), is derived using the variational principle applied to the SMNI Lagrangian. This creates an audit trail from synaptic parameters to the averaged regional Lagrangian.

2.4.1. Basic SMNI Model

Consistent with experimental evidence of shifts in background synaptic activity under conditions of selective attention (Mountcastle et al, 1981; Briggs et al, 2013), a Centering Mechanism (CM) on case BC, giving BC′, where the numerator of FG only has terms proportional to ME′, MI′ and M ‡E′, i.e., zeroing other constant terms by resetting the background parameters BG , still within experimental ranges. This brings in a maximum number of minima into the physical firing MG-space, due to the minima of the new numerator in being in a parabolic trough defined by
Preprints 90272 i005
about which nonlinearities develop multiple minima identified with STM phenomena.
A Dynamic CM (DCM) model is used, resetting BG every few epochs of τ . Such changes in background synaptic activity on such time scales are seen during attentional tasks (Briggs et al, 2013).

2.5. Comparing EEG Testing Data with Training Data

EEG data was used from http://physionet.nlm.nih.gov/pn4/erpbci (Goldberger et al, 2000; Citi et al, 2010), SMNI was again fit to highly synchronous waves (P300) during attentional tasks, for each of 12 subjects (Ingber, 2016b). The electric potential Φ is experimentally measured by EEG, but both are due to the same currents I. A is linearly proportional to Φ with a scaling factor included as a parameter in fits to data. Additional parameterization of background synaptic parameters, BG and B‡E , modify previous work.

2.5.1. Canonical Momentum Π = p + qA

In the Feynman (midpoint) representation of the path integral, the canonical momentum, Π, defines the dynamics of a moving particle with momentum p in an electromagnetic field. In SI units,
Π = p + qA
where q = −2e for Ca2+, e is the magnitude of the charge of an electron = 1. 6 × 10−19 C (Coulomb), and A is the electromagnetic vector potential. A represents three components of a 4-vector.

2.5.2. Vector Potential of Wire

A columnar firing state is modeled as a wire/neuron with current I measured in A = Amperes = C/s,
Preprints 90272 i006
along a length z observed from a perpendicular distance r from a line of thickness r0. If far-field retardation effects are neglected, this yields
Preprints 90272 i007
where µ is the magnetic permeability in vacuum = 4π 10−7 H/m (Henry/meter).
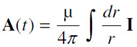
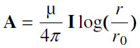
A includes minicolumnar lines of current from hundreds to thousands of macrocolumns, within a region not so large to include many convolutions, but still contributing to large synchronous bursts of EEG.
Electric E and magnetic B fields, derivatives of A with respect to r, do not possess this logarithmic insensitivity to distance, and they do not linearly accumulate strength within and across macrocolumns.
Estimates of contributions from synchronous firings to P300 measured on the scalp are tens of thousands of macrocolumns spanning 100 to 100’s of cm2. Electric fields generated from a minicolumn may fall by half within 5−10 mm, the range of several macrocolumns.

2.5.3. Reasonable Estimates

Classical physics calculates qA from macroscopic EEG to be on the order of 10−28 kg-m/s, while the momentum p of a Ca2+ ion is on the order of 10−30 kg-m/s. This numerical comparison includes the influence of A on p at classical scales.
Direct calculations in both classical and quantum physics show ionic calcium momentum-wave effects neuron-astrocyte-neuron tripartite synapses modify background SMNI parameters and create feedback between ionic/quantum and macroscopic scales (Ingber, 2012a; Ingber, 2012b; Nunez et al, 2013; Ingber et al, 2014; Ingber, 2015; Ingber, 2016b; Ingber, 2017a).

2.6. PATHINT/qPATHINT Code

qPATHINT is an N-dimensional code which calculates the propagation of quantum variables in the presence of shocks. Applications have been made to SMNI and Statistical Mechanics of Financal Markets (SMFM) (Ingber, 2017a; Ingber, 2017b; Ingber, 2017c).
The PATHINT C code of 7500 lines of code using the GCC C-compiler was rewritten to use double complex variables instead of double variables, developed for arbitrary N dimensions, creating qPATHINT (Ingber, 2016a; Ingber, 2017a; Ingber, 2017b).

3. Results Including Quantum Scales

The wave function ψ e describing the interaction of A with p of Ca2+ wave packets was derived in closed form from the Feynman representation of the path integral using path-integral techniques (Schulten, 1999), modified to include A.
p of the Ca2+ wave packet and qA of the EEG field make about equal contributions to Π (Ingber, 2015).

3.1. SMNI + Ca2+ wave-packet

Tripartite influences on synaptic BG , is measured by the ratio of packet’s < p(t) >ψ *ψ to < p0(t0) >ψ *ψ , at the onset of each attentional task. Here <>ψ *ψ is taken over ψ * ψ e. A changes slower than p, and the static approximation of A used to derive ψ e and < p >ψ *ψ is use within P300 EEG epochs, resetting t = 0 at the onset of each classical EEG measurement (1.953 ms apart), using the current A.

3.2. Supercomputer Resources

1000 hours of supercomputer CPUs are required for an ASA fit of SMNI to the same EEG data used previously, i.e., from http://physionet.nlm.nih.gov/pn4/erpbci (Goldberger et al, 2000; Citi et al, 2010), using mostly the same codes used previously (Ingber, 2016b).

3.3. Results Using < p >ψ *ψ

< p >ψ *ψ was used in classical-physics SMNI fits to EEG data using ASA. Runs using 1M or 100K generated states gave results not much different. The current calculations use one additional parameter across all EEG regions to weight the contribution to synaptic background BG . A is taken to be proportional to the currents measured by EEG, i.e., firings MG. Otherwise, the “zero-fit-parameter” SMNI philosophy was enforced, wherein parameters are picked from experimentally determined values or within experimentally determined ranges (Ingber, 1984).
As with previous studies using this data, results sometimes give Testing cost functions less than the Training cost functions. This is due to differences in data, likely from differences in subjects’ contexts, e.g., possibly due to subjects’ STM strategies. Further tests of these multiple-scale models with more EEG data are required, and with the PATHINT-qPATHINT coupled algorithm described previously.

4. Results

The mathematical-physics and computer parts of the study are successful, in that three cases with Subjects (blind to this author) after 1,000,000 visits to the cost function gave: Subject-07 = 0.04, Subject-08 = 0.55, and Subject-09 = 1.00. All other 9 Subjects gave 0.

5. Conclusions

The SMNI model demonstrates can be very well fit to experimental data, e.g., EEG recordings under STM experimental paradigms. qPATHINT permits an inclusion of quantum scales in the multiple-scale SMNI model, by evolving Ca2+ wave-packets with momentum p, including serial shocks, interacting with the magnetic vector potential A derived from EEG data, marching forward in time with experimental EEG data.

Acknowledgement

The author thanks Stony Brook Research Computing and Cyberinfrastructure, and the Institute for Advanced Computational Science at Stony Brook University for access to the innovative high- performance Ookami computing system, which was made possible by a $5M National Science Foundation grant (#1927880)

References

  1. F. Briggs, G.R. Mangun & W.M. Usrey (2013). Attention enhances synaptic efficacy and the signal-to- noise ratio in neural circuits. Nature. 499(7459), 476-480. [CrossRef]
  2. L. Citi, R. Poli & C. Cinel (2010). Documenting, modelling and exploiting P300 amplitude changes due to variable target delays in Donchin’s speller. Journal of Neural Engineering. 7(056006), 1-21. [CrossRef]
  3. K.A. Ericsson & W.G. Chase (1982). Exceptional memory. American Scientist. 70, 607-615.
  4. A.L. Goldberger, L.A.N. Amaral, L. Glass, J.M. Hausdorff, P.Ch. Ivanov, R.G. Mark, J.E. Mietus, G.B. Moody, C.-K. Peng & H.E. Stanley (2000). PhysioBank, PhysioToolkit, and PhysioNet: Components of a New Research Resource for Complex Physiologic Signals. Circulation. 101(23), e215-e220. [URL http://circ.ahajournals.org/cgi/content/full/101/23/e215 ]. [CrossRef]
  5. W. Hick (1952). On the rate of gains of information. Quarterly Journal Experimental Psychology. 34(4), 1-33. [CrossRef]
  6. L. Ingber (1981). Towards a unified brain theory. Journal Social Biological Structures. 4, 211-224. [URL https://www.ingber.com/smni81_unified.pdf ]. [CrossRef]
  7. L. Ingber (1982). Statistical mechanics of neocortical interactions. I. Basic formulation. Physica D. 5, 83-107. [URL https://www.ingber.com/smni82_basic.pdf ]. [CrossRef]
  8. L. Ingber (1983). Statistical mechanics of neocortical interactions. Dynamics of synaptic modification. Physical Review A. 28, 395-416. [URL https://www.ingber.com/smni83_dynamics.pdf ]. [CrossRef]
  9. L. Ingber (1984). Statistical mechanics of neocortical interactions. Derivation of short-term-memory capacity. Physical Review A. 29, 3346-3358. [URL https://www.ingber.com/smni84_stm.pdf ]. [CrossRef]
  10. L. Ingber (1985). Statistical mechanics of neocortical interactions: Stability and duration of the 7+-2 rule of short-term-memory capacity. Physical Review A. 31, 1183-1186. [URL https://www.ingber.com/smni85_stm.pdf ]. [CrossRef]
  11. L. Ingber (1994). Statistical mechanics of neocortical interactions: Path-integral evolution of short-term memory. Physical Review E. 49(5B), 4652-4664. [URL https://www.ingber.com/smni94_stm.pdf]. [CrossRef]
  12. L. Ingber (1995). Statistical mechanics of multiple scales of neocortical interactions, In: Neocortical Dynamics and Human EEG Rhythms, ed. P.L. Nunez. Oxford University Press, 628-681. [ISBN 0-19-505728-7. URL https://www.ingber.com/smni95_scales.pdf ].
  13. L. Ingber (1997a). EEG Database. UCI Machine Learning Repository, Irvine, CA. [URL http://archive.ics.uci.edu/ml/datasets/EEG+Database ].
  14. L. Ingber (1997b). Statistical mechanics of neocortical interactions: Applications of canonical momenta indicators to electroencephalography. Physical Review E. 55(4), 4578-4593. [URL https://www.ingber.com/smni97_cmi.pdf ]. [CrossRef]
  15. L. Ingber (1999). Statistical mechanics of neocortical interactions: Reaction time correlates of the g factor. Psycholoquy. 10(068). [Invited commentary on The g Factor: The Science of Mental Ability by Arthur Jensen. URL https://www.ingber.com/smni99_g_factor.pdf and http://www.cogsci.ecs.soton.ac.uk/cgi/psyc/newpsy?10.068 ].
  16. L. Ingber (2012a). Columnar EEG magnetic influences on molecular development of short-term memory, In: Short-Term Memory: New Research, ed. G. Kalivas & S.F. Petralia. Nova, 37-72. [Invited Paper. URL https://www.ingber.com/smni11_stm_scales.pdf ].
  17. L. Ingber (2012b). Influence of macrocolumnar EEG on Ca waves. Current Progress Journal. 1(1), 4-8. [URL https://www.ingber.com/smni12_vectpot.pdf ].
  18. L. Ingber (2015). Calculating consciousness correlates at multiple scales of neocortical interactions, In: Horizons in Neuroscience Research, ed. A. Costa & E. Villalba. Nova, 153-186. [ISBN 978-1-63482-632-7. Invited paper. URL https://www.ingber.com/smni15_calc_conscious.pdf ].
  19. L. Ingber (2016a). Path-integral quantum PATHTREE and PATHINT algorithms. International Journal of Innovative Research in Information Security. 3(5), 1-15. [URL https://www.ingber.com/path16_quantum_path.pdf ].
  20. . [CrossRef]
  21. L. Ingber (2017a). Evolution of regenerative Ca-ion wave-packet in neuronal-firing fields: Quantum path- integral with serial shocks. International Journal of Innovative Research in Information Security. 4(2), 14-22. [URL https://www.ingber.com/path17_quantum_pathint_shocks.pdf ].
  22. L. Ingber (2017b). Options on quantum money: Quantum path-integral with serial shocks. International Journal of Innovative Research in Information Security. 4(2), 7-13. [URL https://www.ingber.com/path17_quantum_options_shocks.pdf ].
  23. L. Ingber (2017c). Quantum Path-Integral qPATHINT Algorithm. The Open Cybernetics Systemics Journal. 11, 119-133. [URL https://www.ingber.com/path17_qpathint.pdf. [CrossRef]
  24. L. Ingber (2018). Quantum calcium-ion interactions with EEG. Sci. 1(7), 1-21. [URL https://www.ingber.com/smni18_quantumCaEEG.pdf]. [CrossRef]
  25. L. Ingber (2022). Realistic Neural Networks. American Journal of Engineering Research. 11(11), 8-10. [URL https://www.ingber.com/smni22_realistic_neural_nets.pdf ].
  26. L. Ingber, M. Pappalepore & R.R. Stesiak (2014). Electroencephalographic field influence on calcium momentum waves. Journal of Theoretical Biology. 343, 138-153. [URL https://www.ingber.com/smni14_eeg_ca.pdf]. [CrossRef]
  27. A. Jensen (1987). Individual differences in the Hick paradigm, In: Speed of Information-Processing and Intelligence, ed. P.A. Vernon. Ablex, 101-175.
  28. V.B. Mountcastle, R.A. Andersen & B.C. Motter (1981). The influence of attentive fixation upon the excitability of the light-sensitive neurons of the posterior parietal cortex. Journal of Neuroscience. 1, 1218-1235.
  29. P.L. Nunez, R. Srinivasan & L. Ingber (2013). Theoretical and experimental electrophysiology in human neocortex: Multiscale correlates of conscious experience, In: Multiscale Analysis and Nonlinear Dynamics: From genes to the brain, ed. M.M. Pesenson. Wiley, 149-178.
  30. K. Schulten (1999). Quantum Mechanics. Lecture Notes. U. Illinois. [URL http://www.ks.uiuc.edu/Services/Class/PHYS480/ ].
  31. G. Zhang & H.A. Simon (1985). STM capacity for Chinese words and idioms: Chunking and acoustical loop hypotheses. Memory & Cognition. 13, 193-201.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated