Prerpints.org logo
Preprint
Article

Contact Analysis for Cycloid Pinwheel Mechanism by Isogeometric Finite Element

Altmetrics

Downloads

87

Views

25

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

13 November 2023

Posted:

14 November 2023

You are already at the latest version

Alerts
Abstract
Cycloid drives are generally used in precision machinery requiring high reduction ratios, such as robot joint (RV) reducers, in which the contact load and stress property of the internal meshing pairs greatly affect the dynamic transmission performance of the reducers. Therefore, in this study, Isogeometric Analysis (IGA) was employed to explore the multi-tooth contact problem of the cycloid pinwheel drive. Based on the NURBS curved surface generation method, the NURBS tooth profile of the cycloid gear was reconstructed. In addition, the NURBS surface of the cycloid gear - pin tooth - output pin was generated via the element splicing method. A geometrical analysis model of cycloid pinwheel drive was established to solve the contact force of the meshing pair under different input angles, and compared with the finite element method in terms of convergence, resultant accuracy, and solving timeliness. The results show that the Isogeometric analysis has higher accuracy and efficiency than the finite element method in calculating the contact stress and contact force. This method can improve the contact simulation accuracy of the cycloid drive and provides a reference for the design evaluation of RV reducer.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

Cycloidal drive has various advantages, including high reduction ratio, high transmission efficiency, high load carrying capacity and low noise. So it is widely applied in robotic joints and other transmission fields with high precision transmission [1,2,3,4]. Due to the repeated loading and contact between the gear teeth in the transmission process, it is easy to cause the wear of cycloidal gear profiles in the mechanism, thus affecting the load carrying capacity and transmission efficiency of the mechanism. Hence, it is essential to investigate the contact load and stress characteristics of the cycloid drive.
Currently, most contact analyses for cycloid pinwheel were well done by finite element methods(FEM) for life prediction. SV Thube [5] performed static force analysis for a simple structure of a cycloid pinwheel reducer and summarized the variation of cycloid pinwheel contact stress and strain for a given drive cycle based FEM. Blagojevic [6] conducted a finite element analysis of a new two stages cycloid reducer to investigate the contact stress under static conditions and verified whether the meshing strength meets the design requirements. Hsieh [7,8] analyzed the dynamic stress of each component of the cycloidal reducer based on the FEM, and concluded that the increase of the number of output pins resulted in weakening of the vibration of the mechanism and reduction of the power loss. He Weidong [9] calculated the contact stress and deduced the meshing stiffness with gear tooth clearance and elastic deformation by FEM. Ahn H [10] established a FE model for a two-disk RV reducer and the eccentric shaft, and investigated the effects of tolerance and friction on multi-contact and the output torque of the RV reducer. Zhang Yueming [11] used the Ansys Workbench software to simulate and analyze the maximum contact stress of cycloidal pinwheel under different eccentric distances, and deviation of each tooth stress within the allowable range, which verified the accuracy of the theoretical model of load carrying capacity.
The contact analysis model designed based on the traditional FEM is formed on the original geometric model using Lagrangian basis functions to generate the mesh, which makes the geometric boundary low order continuity and ignores some detailed features. So it cannot accurately describe the curvature of complex surfaces, and does not reflect the small tooth profile changes of cycloidal gear with manufacturing errors, which leads to the low calculation accuracy of the contact force. Moreover, in common FEM, the mesh division often cost much time and reduce the analysis efficiency. In contrast, Hughs [12] et al. proposed a numerical analysis method based on nonuniform rational B spline (NURBS) isogeometric analysis, which directly transforms the model into a body parametric model with NURBS surfaces and uses the higher-order continuity of basis functions to achieve an accurate description of the model boundary. It is called “Isogeometric Analysis” because the geometric model representation used in CAD and CAE is identical, and this feature makes IGA a great advantage in contact analysis. Subsequently, Bazilevs [13] verified the stability of the isogeometric analysis method through formula derivation and numerical analysis. Agarawal [14] modified the original finite element analysis code to complete the implementation of the code structure of the IGA hydrostatic analysis and verified it through the experiments of the stress manifestation of a flat plate with holes in tension. LU [15] sub-proposed the framework of the IGA contact algorithm and utilized it into the classical Hertzian contact arithmetic case to verify the effectiveness of the contact algorithm in comparison with the theoretical solution. Huan Xu [16] used the isogeometric contact algorithm for frictionless contact analysis of planar gears, and the contact stresses calculated by the isogeometric method are more accurate compared with the finite element method, which provides an effective method for gear contact analysis. Chen Long [17] performed isogeometric contact analysis using the surface splicing method for a pair of complete gears with single tooth contact, and the analysis results were compared with the finite element solution to verify the effectiveness of the method in the application of nonlinear contact. The isogeometric analysis method was applied to the bending strength analysis of planar gears by Yutong Xue [18] et al. The maximum stress and elastic deformation of the tooth face of a straight gear were solved for a given input torque, and the tooth root stress and solution time were compared with the simulation results of finite element commercial software to verify the efficiency of the isogeometric analysis. Greco [19] used the isogeometric analysis framework for complex contact model boundaries in the contact region interior using a meshless formulation to calculate the contact force. This method maintains the advantages of IGA in complex surface contact analysis and provides more flexibility in geometric design.
In this paper, the isogeometric analysis method was introduced to analyze the meshing contact between the teeth of a cycloid pinwheel transmission, and The NURBS surface was used to construct the model of the cycloid gear and other components, which was substituted into the IGA contact analysis process to analyze the contact force performance of the gear teeth under a given load. The accuracy of the isogeometric analysis results was verified by the cycloid pinwheel transmission theory. Besides, it was compared with the finite element method, highlighting the advantages of IGA in contact analysis.

2. Geometry Model of Cycloidal Gear for Isogeometric Contact Analysis

2.1. NURBS Theory of Surface Model

The basic idea of the isogeometric analysis method is to use the same geometric model representation in both modeling and analysis, which provides higher accuracy of geometric boundaries compared to the traditional finite element secondary modeling models. The analysis method is based on non-uniform rational B spline (NURBS) modeling [20]. NURBS can describe the geometric model more flexibly and accurately, and NURBS surfaces are designed and analyzed mainly using basis functions containing geometric information such as node vectors, control points, and weights. Given the node vectors Ξ={ξ1, ξ2, ξ3, ……ξn+p+1} and δ={η1, η2, η3, ……ηn+p+1} in both directions of the NURBS surface, where λi denotes the ith node (knot), i= 1,2......n+p+1, and the nodes divide the vector into nodal intervals [λi, λi+1], each of which contains a nonzero basis function of ξ+1. The B spline basis function is denoted as Eq. 1.
R i , j p , q ( ξ , η ) = N i , p ( ξ ) M j , q ( η ) W i , j ∑ k = 1 n ∑ l = 1 m N k , p ( ξ ) M l , q ( η ) W k , l
where p and q are the orders of the spline basis functions, i and j are the number of basis functions for constructing B-sample curves, Pi,j are defined as the surface control points, ωi are the control point weights, each control point is mapped to a lower one-dimensional space in a certain way to obtain a NURBS surface. The NURBS surface of order p in the ξ direction and order q in the η direction is expressed in Eq. 2.
S ( ξ , η ) = ∑ i = 1 n ∑ j = 1 m R i , j p , q ( ξ , η ) P i , j

2.2. NURBS Model of Cycloidal Gear

The use of NURBS to construct the cycloid gear surface can improve the smooth continuity of the tooth boundary, which can build the cycloid pinwheel transmission model more accurately and provide accurate model support for the subsequent IGA. In this paper, we take a cycloid gear with given parameters and a simplified planar model as an example to construct a parametric model. The design parameters of the cycloid gear are shown in Table 1, and the order of the NURBS surface basis function is set to second order, and the number of nodes in each direction is set to five. Since the NURBS surface is a quadrilateral surface, to express a single tooth and the whole cycloid gear, the model must be divided into several sub-pieces and then stitched together, and the control points between the sub-piece boundaries are overlapped. The initial cycloid single tooth NURBS surface is constructed by dividing the single tooth into 4 NURBS patches, as shown in Figure 1, and the sub-pieces are shown in Figure 1(a). Then, the IGA specific step-up plus node insertion, i.e., the k-refinement method, is used to refine the isogeometric NURBS element [21], which raises the order of the basis functions to the third-order while inserting new values in the node vectors to increase the number of control points. The number of control points in each direction of the surface after refinement is thirteen, making the number of each patch mapping element 10×10. The single tooth of the cycloid is shown in Figure 1(b), and according to the cycloid gear design parameters, the entire cycloid gear model is obtained by arraying the single tooth by the center point for one full cycle, as shown in Figure 2.
The cycloid boundary described by the NURBS surface has higher order continuity compared with the Lagrangian boundary of the traditional finite element method. For a NURBS curve of order p, its basis function has Cp-k continuity at node ui, and k is the repetition degree of node ui in the node vector. Since the basis function is third order after refinement in this paper, the repetition degree of the node vector k =2, the cycloid boundary that has C2 continuity, while the boundary of the traditional finite element method is always for C0 continuity. Figure 3 shows the local boundary comparison between NURBS and finite element method gear. The higher order continuous NURBS boundary is smoother, which also affects the accuracy of contact stress calculation.

2.3. Deviation between NURBS and Actual Profile of Cycloidal Gear

In order to ensure that the fitted cycloid gear profile can be used for tooth contact analysis, the reconstructed cycloid gear profile needs to be verified for reconstruction accuracy. Taking the design parameters in Table 1 as an example, the actual tooth profile and the NURBS tooth profile are discretized into 101 tooth surface points, and the coordinates of the theoretical tooth profile and the NURBS tooth profile after discretization are Qi(xi, yi) and Qi′(xi′ yi′), respectively, when xi is taken as xi’, the absolute error is defined as Δy= yi′-yi and the relative error is fy=Δy/ yi′. Four tooth surface points in a segment of the cycloid gear profile are selected for key comparison, as shown in Table 2. The comparison of the profile curves of the two tooth profile segments is shown in Figure 4. The amount of deviation of the NURBS reconstructed tooth profile from the standard tooth profile data points in the common normal direction is shown in Figure 5.
The deviation table shows that the absolute error between the standard tooth profile and the NURBS tooth profile data points is about 10-4 mm, and the deviation in the common normal of the two tooth profiles is about 10-7 mm. The error values are minimal, so the NURBS tooth profile constructed by this method can meet the accuracy of equal geometric contact analysis.

3. Procedure of Isogeometric Contact Analysis for Cycloid Pinwheel

3.1. Applied Force Analysis of Cycloid Pinwheel Mechanism

Based on the principle and geometric characteristics of the cycloid drive, and according to the design parameters in Table 1, a theoretical static force analysis model of the cycloid pinwheel is established as shown in Figure 6, in which point O is the center of rotation of the input crank shaft and the center of the pin teeth distribution, Oc is the center of the cycloid gear, point P is the tangent point between the base circle of the cycloid gear and the base circle of the pinwheel, Φin is the input crank angle. From the X-axis to the counterclockwise direction, the first pin tooth is located in the plus X-axis and the others are in order from No. 1 to No. 11. Similarly, the numbering of the pin is also from the counterclockwise direction, in order from No. 1 to No. 6 of the output pin.
In the theoretical force model proposed in this paper, the cycloid gear is regarded as a plane motion, so the influence of axial thickness on tooth contact is not considered. At the same time, the effect of elastic deformation is not taken into account, and all the components are set as rigid bodies. Figure 7 shows the schematic diagram of the force analysis of the cycloid gear, and Figure 8 shows the force analysis of the crank. At this time, the crank shaft input angle Φin is 45 degrees. FC is the crank input shaft force on the cycloid gear, the force extension line through the eccentric point Oc, and with the input crank shaft eccentric direction angle of ε. FN is the pin tooth force on the cycloid gear, FK is the output pin force on the cycloid gear. lN is the force arm of the pin tooth force; lK is the force arm of the output pin force. αi is the pin tooth force and X-axis line angle. Tin is the input torque and FC′ is the force of the cycloid gear on the input crank shaft, which is equal in magnitude and opposite in direction to the FC value.
Taking the input angle in the figure as an example, the ideal cycloid pinwheel drive is a full tooth contact, and the contact force exists only between the pin tooth and the output pin within 180 degrees from the direction of the input crank eccentricity. The direction of the force FN on all the pin teeth in contact passes through point P, while the direction of the force FK on the output pin in contact is parallel and opposite to the direction of the input crank eccentricity.
According to the force analysis diagram of each component, the equilibrium equation between the component’s contact force and its own moment can be listed. With the center of the cycloid gear Oc as the center point, the balance equation of the force on the cycloid gear is:
F C cos Φ i n + ε + ∑ F N i cos α − ∑ F K j cos Φ i n = 0 F C sin Φ i n + ε + ∑ F N i sin α − ∑ F K j sin Φ i n = 0 ∑ F K j ⋅ l K j − ∑ F N i ⋅ l N i = 0 T i n − e ⋅ F C ⋅ sin ε = 0
where i is the serial number of the pin tooth and j is the serial number of the output pin. By the geometric characteristics of the cycloid pinwheel drive mechanism, the pin tooth force and its force arm, the output pin force and its force arm are proportional, and the proportionality constant is kN, kK. According to the cycloid pinwheel transmission dynamics, the input torque is related to the output torque by the following equation:
F N i = k N ⋅ l N i
F K i = k K ⋅ l K i
T i n ⋅ m − T o u t = 0
T o u t = ∑ F K j ⋅ l K j
where, m is the mechanism transmission ratio, solving the combined force balance equation under the conditions of given mechanism design parameters and input torque, the meshing contact force of the pin tooth, output pin and cycloid gear can be obtained at any crank angle. The contact force distribution of the transmission components is calculated by taking 1000 N·mm as an example of the applied load torque. Figure 9 and Figure 10 show the distribution of the pin tooth contact force FNi and the output pin contact force FKi in each tooth at different input angles. It shows that the contact areas of the pin tooth and the output pin change with the position of the input angle, and the magnitude of the value is proportional to the length of the force arm. Figure 11 and Figure 12 show the changes of input crank contact force FC under different input angles. Different input angle position has little effect on the crank contact force, the value of which fluctuates up and down around 960N, and the values of the input crank contact force components FCX and FCY are presented as sinusoidal function curves with different phases.
According to the solution, the engagement force between the cycloid gear, the pin tooth and the output pin can be obtained, as well as the regional distribution of the engagement force on the tooth profile of the cycloid gear. Then the distribution of the contact stress σH on the cycloid gear tooth profile can be solved according to the Hertz contact equation. The contact stress between the cycloid gear and the pinwheel is calculated as Equation 8.
σ H = 0.418 E s F i b ρ s i
where, ρ si = ρ i r r p ρ i − r r p , E s = 1 1 − ν 1 E 1 + 1 − ν 2 E 2 , ρsi is the integrated radius of curvature, ρi is the actual tooth profile radius of curvature, E1, ν1 and E2, ν2 are the modulus of elasticity and poisson’s ratio for the cycloid gear and pin teeth materials, and b is the cycloid gear width.

3.2. Isogeometric Contact Analysis of Cycloidal Pinwheel Mechanism

The isogeometric analysis uses an accurate geometric model based on NURBS, and its own control mesh can be refined and analyzed without changing the geometry, which avoids the problem of model reconstruction and dividing a distorted mesh affecting the model profile and analysis accuracy as in the finite element method. And the IGA uses the higher-order NURBS basis function, which has better characteristics than the Lagrangian basis function, and has the properties of non-interpolation and differentiability [22]. The basic flowchart of isogeometric contact analysis is shown in Figure 13.
The first step of isogeometric analysis is to input the geometric model. For the cycloid drive mechanism analyzed in this paper, it is more difficult to express the cycloid gear with holes directly by NURBS modeling, so it is still necessary to carry out structured element division based on the cycloid gear NURBS surface established in the previous paper, and divide the output pin hole part of the cycloid gear into different NURBS slices before stitching. The quarter of the cycloid gear NURBS surface shown in Figure 14 is re-divided, with the order of the basis function in each NURBS slice set as second order and the surface containing four control points in each direction. According to the symmetry, the surfaces are arrayed and the coordinates of the overlapping boundary control points are changed to construct the initial NURBS tooth surface of the complete cycloid gear as shown in Figure 15(a). The refined model is shown in Figure 15(b), and the number of elements per surface sheet is 100. The pin tooth and output pin surfaces are constructed in the same way, while the cross section is divided into five NURBS slices for the subsequent application of boundary conditions, and their initial cross sections are shown in Figure 16. The same k-refinement is used, and each surface slice contains 100 elements after refinement, as shown in Figure 17.
The created NURBS geometry model is saved in IGES format for data storage and exchange, and then entered into the IGA contact analysis process. Define the material density of the cycloid gear, pin tooth and output pin as 7800 kg/m3, the modulus of elasticity as E=210 GPA and Poisson’s ratio as ν = 0.3. Fix the control points of the pin tooth and output pin in the central NURBS slice and constrain all their degrees of freedom. For the cycloid gear, the axial motion is constrained and the circumferential and tangential degrees of freedom are released. The control point around the cycloid gear center hole is coupled as a rigid node to which a clockwise torque of 100 N·mm is applied according to the mechanism transmission ratio calculation formula. For the meshing pair in which the contact element is handled in a face-to-face contact mode, the master-slave contact search algorithm is used, and the contact pair is set with the cycloid gear tooth face as the master contact face and the pin tooth and the output pin face as the slave contact surface. Traverse all NURBS elements with the set constraint conditions and contact settings and assemble the overall stiffness matrix, the solver uses LS-DYNA R13.0 to compute the contact stress nephogram of the cycloid pinwheel mechanism for three different input angles as shown in Figure 18.
According to the stress nephogram, the maximum stress occurs in tooth No.3. The maximum stress contact tooth number is consistent with the theoretical contact analysis. From the color change of the contact surface, the stress trend is all from yellow-green to light blue. Observing the NURBS element on the contact pair with stress distribution, it is concluded that the number of contact stresses generated by the pin tooth, output pin and cycloid gear under this input angle is consistent with the theoretical analysis, and the stress area from the equal geometric analysis is consistent with the theoretical cycloid drive stress characteristics, and the IGA model is reasonably constructed, and the maximum contact stress is 390.1 MPA.

4. Results and Discussion

4.1. Contact Analysis of Cycloidal Gear and Pins by FEA

Using the commercial FEM software Ansys workbench 2020, the contact stresses of the cycloid pinwheel drive are solved to facilitate comparison with subsequent geometric results. According to the characteristics of the mechanism, the 2D plane stress static analysis module is used to extract the cycloid gear - pin tooth - output pin plane. Using the same material parameters, boundary conditions, and contact pair settings as the isogeometric method, the crank input angle is solved at 0 degrees, and the solution time and load step are defined and solved using the direct solver, resulting in the contact stress nephogram of the component as shown in Figure 19.
It can be observed that the contact pin teeth are No. 2-6 and the contact output pins are No. 1-3. The number of stressed pin teeth and output pins is also in accordance with the theory of stress area within 0 to 180 degrees in the crank input direction under the ideal tooth profile. The maximum contact stress of the pin is 362.89 MPA.

4.2. Comparison of Contact Force from IGA and FEA

Since the contact stress distribution of the pin tooth and output pin derived from the two methods are the same as the theoretical stress areas, they are consistent with the force characteristics of the cycloid pinwheel and prove that the analytical model design is reasonable. The results of isogeometric analysis, finite element results and theoretical solution results are compared, and the values of maximum contact stress are listed in Table 3.
From the table, it can be obtained that the maximum stress error out of the isogeometric analysis of the cycloid drive is smaller than ones from the finite element method, and the error of the isogeometric method compared to the theoretical solution is all between 1% and 2%. The contact force of the pin, output pin and cycloid gear in the stressed area is extracted and compared with the theoretical values, as shown in Figure 20. The error comparisons are shown in Table 4 and Table 5.
From the graph, the pin tooth contact force FN and the output pin contact force FK solved by isogeometric analysis are smaller than the finite element, and the error of the isogeometric contact force solved value is about 3% compared with the theoretical value. In the isogeometric contact analysis, the mesh deformation due to the lack of accuracy of the geometric model contour surface can be improved to some extent because of the high-order continuity property of the NURBS basis function. Thus, it avoids the jump of the contact force value of the finite element method, which differs too much from the theoretical value due to the occurrence of slippage or separation phenomenon when analyzing the contact pair. By comparing the analysis results of the two methods, the principle that the contact force calculation of isogeometric analysis is more accurate due to the higher accuracy of the NURBS surface boundary is verified.
The results of iso-geometry and finite element were compared under the same number of elements divided by the model surface to verify the accuracy of the iso-geometry analysis method in the cycloid gear tooth surface with fewer elements, and the contact stress of the most stressed gear tooth was selected to compare the results.
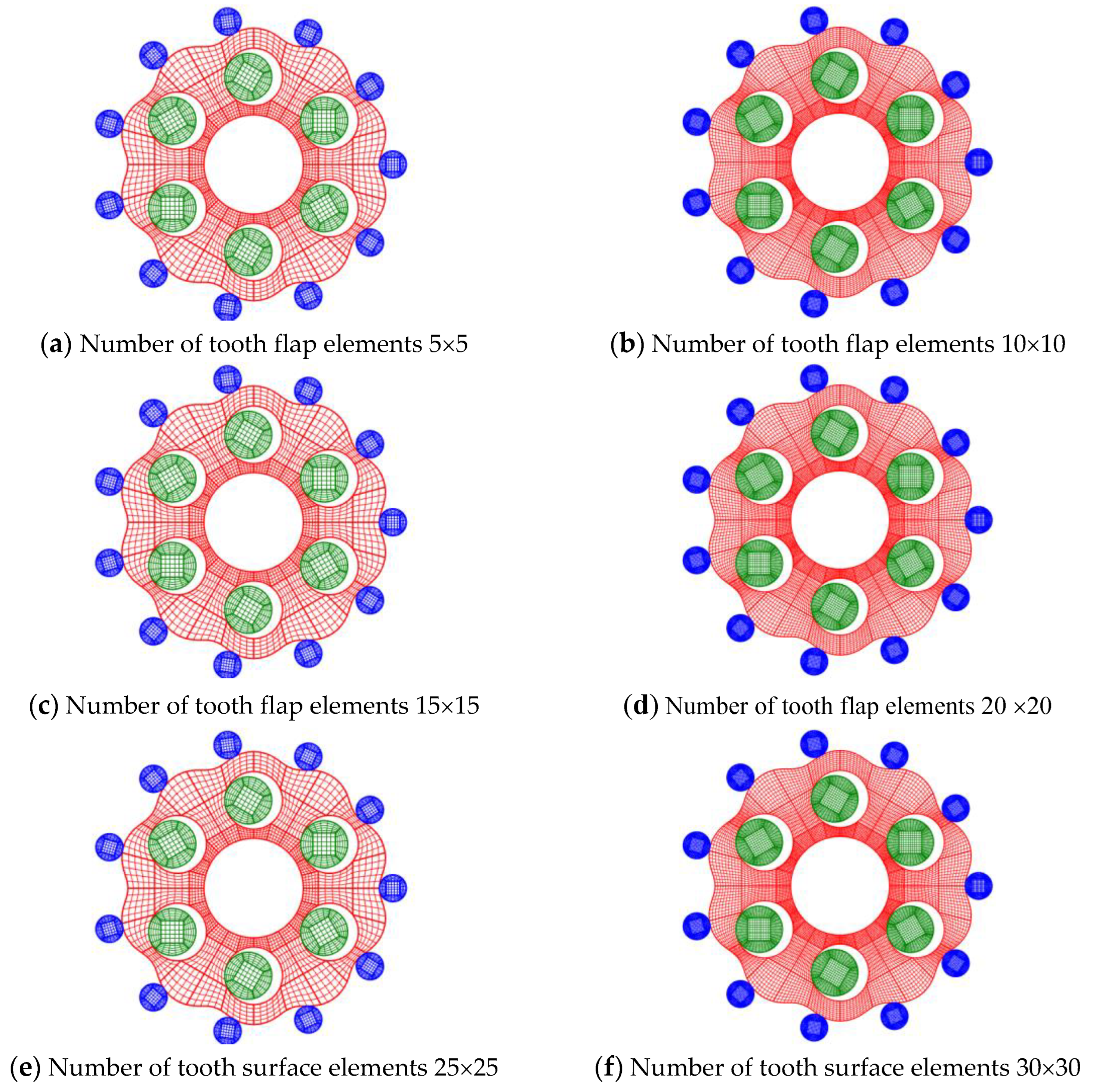
Preprints 90335 g021
Figure 21. IGA model with different NURBS elements for tooth face.
Figure 21. IGA model with different NURBS elements for tooth face.
Preprints 90335 g021
In the FEA model with the same number of elements as the control group, the comparison of the IGA method and the finite element method for the change of the maximum contact stress regularity with different numbers of element on the contact tooth surface of the cycloid gear is shown in Figure 22, and the comparison of the maximum stress with the theoretical value of the calculation error is shown in Table 6.
Figure 22 shows that the calculated values of both the isogeometric method and the finite element method can converge to the accurate value when the number of elements is increasing, but the isogeometric method can achieve a relatively high accuracy when the number of elements is small. From the specific error comparison in Table 6, it can be seen that the error of the finite element method is larger when the distribution of elements on the tooth surface is small. The error of the isogeometric method is only 8.8% when only 10×10 elements are arranged on the surface piece in contact, while the error of the finite element method reaches about 40%. Moreover, when the number of surface elements at the contact position is increased to 25×25, the finite element result error is still 10%, while the isogeometric result has already converged to a slight error of 2.5%. It is because the mesh divided by the finite element method consists of interpolation for the Lagrangian function, which makes the model boundary continuity low. When the cycloid gear tooth contact area is larger, it will cause the two element boundaries to enter the contact calculation simultaneously, equivalent to the increase of contact area, resulting in the increase of contact force error. However, the isogeometric method still has high accuracy when the number of meshes is small, and the errors are all within 10% because the stresses between adjacent NURBS patches are continuous based on the higher-order continuous nature of the basis function. As a result, the isogeometric analysis method is able to produce contact analysis results with high accuracy with a small number of surface elements. It avoids the complex meshing process while ensuring accuracy, resulting in a significant reduction in the computational degrees of freedom and a significant advantage over the traditional finite element method in terms of result accuracy.
The traditional finite element method is required to refine a high-density mesh for contact analysis to obtain an approximate theoretical solution. However, as the mesh increases, the meshing time increases and consumes considerable solving time and computer resources. In contrast, isogeometric analysis can get more accurate solutions with fewer NURBS elements, and the essence of isogeometric analysis is to analyze NURBS model elements directly, without the requirement for finite element method of mesh reconstruction to approximate the model boundary, avoiding the complex mesh division and approximation process in finite element, so it will greatly reduce the analysis time and save computational costs. A comparison of the analysis time of the cycloid drive mechanism converging to the exact solution under the same computer hardware conditions is shown in Table 7.
The comparison of the solution time shows that the iso-geometry is faster than the finite element method under the same conditions, thereby verifying the high efficiency of iso-geometry in contact analysis. Therefore, the isogeometric analysis method is more suitable than the finite element method for the analysis of the contact problems of cycloid pinwheel transmission. It can significantly improve the computational efficiency and provide guidance for the high performance design and manufacturing of cycloid pinwheel transmission.

5. Conclusions

In this paper, the isogeometric analysis method was applied to the contact analysis of the cycloid drive meshing pair, and the static force analysis model of the cycloid drive was established. The results of the isogeometric analysis were compared with the theoretical values and calculated ones from finite element software. The main conclusion is as follows:
The isogeometric analysis uses NURBS basis functions to construct the cycloid pinwheel transmission model. Its higher order continuity can accurately describe the contact boundary of the cycloid gear, which gives more accurate results of the contact force of the meshing pair compared to the finite element method. The isogeometric analysis avoids the re-meshing of the model in the finite element analysis, and instead uses a parametric unified NURBS model at all stages of the calculation, which gives the method high accuracy even with a small number of elements in the model. The isogeometric analysis substantially saves the solution time and cost, and significantly improves the efficiency of cycloid pinwheel contact analysis.
In the future, the 3D NURBS model of the cycloid drive mechanism can be further constructed and isogeometric contact analysis will be applied to simulate the dynamic contact force performance of each component in actual operations.

Author Contributions

Conceptualization, C.-X.G.; Methodology, & Software, Y.-W.S.; Validation, P.-H.G.; Writing—review & editing, K.ZHANG. All authors have read and agreed to the published version of the manuscript.

Funding

This work was funded by the Youth Innovation Team of Shaanxi Universities: Metal Corrosion Protection and Surface Engineering Technology, Research and application of key component materials for engines, Shaanxi Provincial Natural Science Foundation (2023-JC-YB-380), Shaanxi Provincial Key Research and Development Project (2019ZDLGY05-09), Local Serving Special Scientific Research Pro-jects of Shaanxi Provincial Department of Education (19JC022).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Qiao XT, Zhang LB, Yan CF et al. Analysis on Development Status of RV Reducer Used in Industrial Robot in China. Journal of Mechanical Strength 2019, 41, 1486–1492.
  2. Song, S. Industrial robot RV reducer key components manufacturing and thinking about the development of China’s precision machine tools. Metal Working(Metal Cutting) 2015, 08, 34–36. [Google Scholar]
  3. Li, X. Benchmarking Research on Patent Technology of RV Reducer of Robot in China and Japan from the Perspective of Chinese Patent Intelligence. Journal of Library and Information Science in Agriculture 2021, 33, 5–11. [Google Scholar] [CrossRef]
  4. Duc A P ,Joon H A . Rigid Precision Reducers for Machining Industrial Robots. International Journal of Precision Engineering and Manufacturing 2021, 22, 1469–1486. [CrossRef]
  5. Thube S V, Bobak T R. Dynamic analysis of a cycloidal gearbox using finite element method. AGMA Technical Paper, 2012: 1-13.
  6. Blagojevic M, Marjanovic N, Djordjevic Z, et al. A new design of a two-stage cycloidal speed reducer. Journal of Mechanical Design 2011, 133, 085001-1. [CrossRef]
  7. Hsieh C, F. Traditional versus improved designs for cycloidal speed reducers with a small tooth difference: The effect on dynamics. Mechanism and Machine Theory 2015, 86, 15–35. [Google Scholar] [CrossRef]
  8. Hsieh C F, Fuentes-Aznar A. Performance prediction method of cycloidal speed reducers. Journal of the Brazilian Society of Mechanical Sciences and Engineering 2019, 41, 1–15. [CrossRef]
  9. He WD, Zhang ZY, Wu XH. Study of Time Varying Meshing Stiffness of RV Drive based on ANSYS. Journal of Dalian Jiaotong University, 2017, 38, 55-57, 66.
  10. Ahn H ,Choi M B ,Lee H Y , et al. Impact Analysis of Tolerance and Contact Friction on a RV Reducer using FE Method. International Journal of Precision Engineering and Manufacturing 2021, 22, 1285–1292. [CrossRef]
  11. Zhang YM, Li LS, Ji ST. Influence of the eccentricity of cycloid-pin transmission mechanism on bearing capacity. Journal of Harbin Engineering University 2022, 43, 873–881.
  12. Hughs T J R, Cottrell J A, Bazilevs Y. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Computer Methods in Applied Mechanics and Engineering, 2005, 194, 4135-4195. [CrossRef]
  13. Bazilevs Y, Beirao da Veiga L, Cottrell J A, et al. Isogeometric analysis: approximation, stability and error estimates for h-refined meshes. Mathematical Models and Methods in Applied Sciences 2006, 16, 1031–1090. [CrossRef]
  14. Agrawal V, Gautam S S. IGA: A simplified introduction and implementation details for finite element users. Journal of The Institution of Engineers (India): Series C 2019, 100, 561–585. [CrossRef]
  15. Lu, J. Isogeometric contact analysis: geometric basis and formulation for frictionless contact. Computer Methods in Applied Mechanics and Engineering 2011, 200, 726–741. [Google Scholar] [CrossRef]
  16. Xu H, Yang GL, Zheng JG et al. Research of the Isogeometric Analysis of Gear Frictionless Contact. Journal of Mechanical Transmission 2015, 39, 30–32.
  17. Chen L, Hao CJ, Wang CH, et al. Isogeometric analysis of gear contact for single tooth meshing. Journal of Mechanical Engineering 2021, 57, 107–115. [CrossRef]
  18. Xue YT, Zhao G, Wang AZ, et al. Isogeometric analysis of bending strength of spur gear. Journal of Graphics 2022, 43, 79–84. [CrossRef]
  19. Greco F, Rosolen A, Coox L, et al. Contact mechanics with maximum-entropy meshfree approximants blended with Isogeometric analysis on the boundary. Computers & Structures 2017, 182, 165–175. [CrossRef]
  20. Wu ZJ, Huang ZD, Zuo BQ, et al. Perspectives on Isogeometric Analysis. Journal of Mechanical Engineering 2015, 51, 114–129. [CrossRef]
  21. Zhao YY. Isogeometric Method for Static and Dynamic Analysis of Shell Structure. Doctral thesis, Jilin University, Changchun, 2022.
  22. Xu H. Research on the theory and algorithm of Isogeometric analysis of contact problems. Master thesis, Nanjing University of Science and Technology, Nanjing, 2015.
Preprints 90335 g001
Figure 1. Model of single tooth surface of cycloidal gear: (a) Initial surface; (b) Refined surface.
Figure 1. Model of single tooth surface of cycloidal gear: (a) Initial surface; (b) Refined surface.
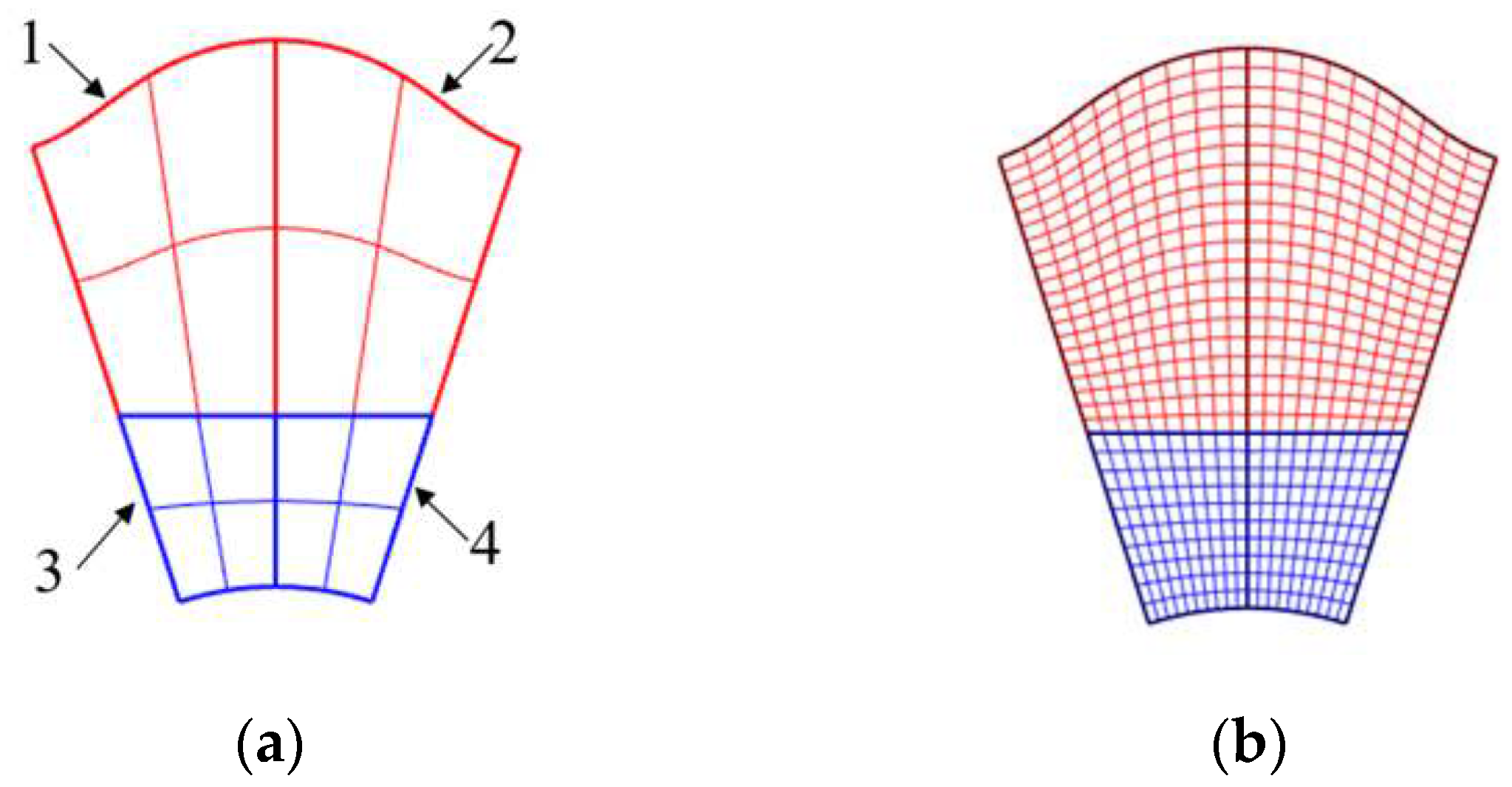
Preprints 90335 g001
Preprints 90335 g002
Figure 2. Complete cycloid gear model.
Figure 2. Complete cycloid gear model.
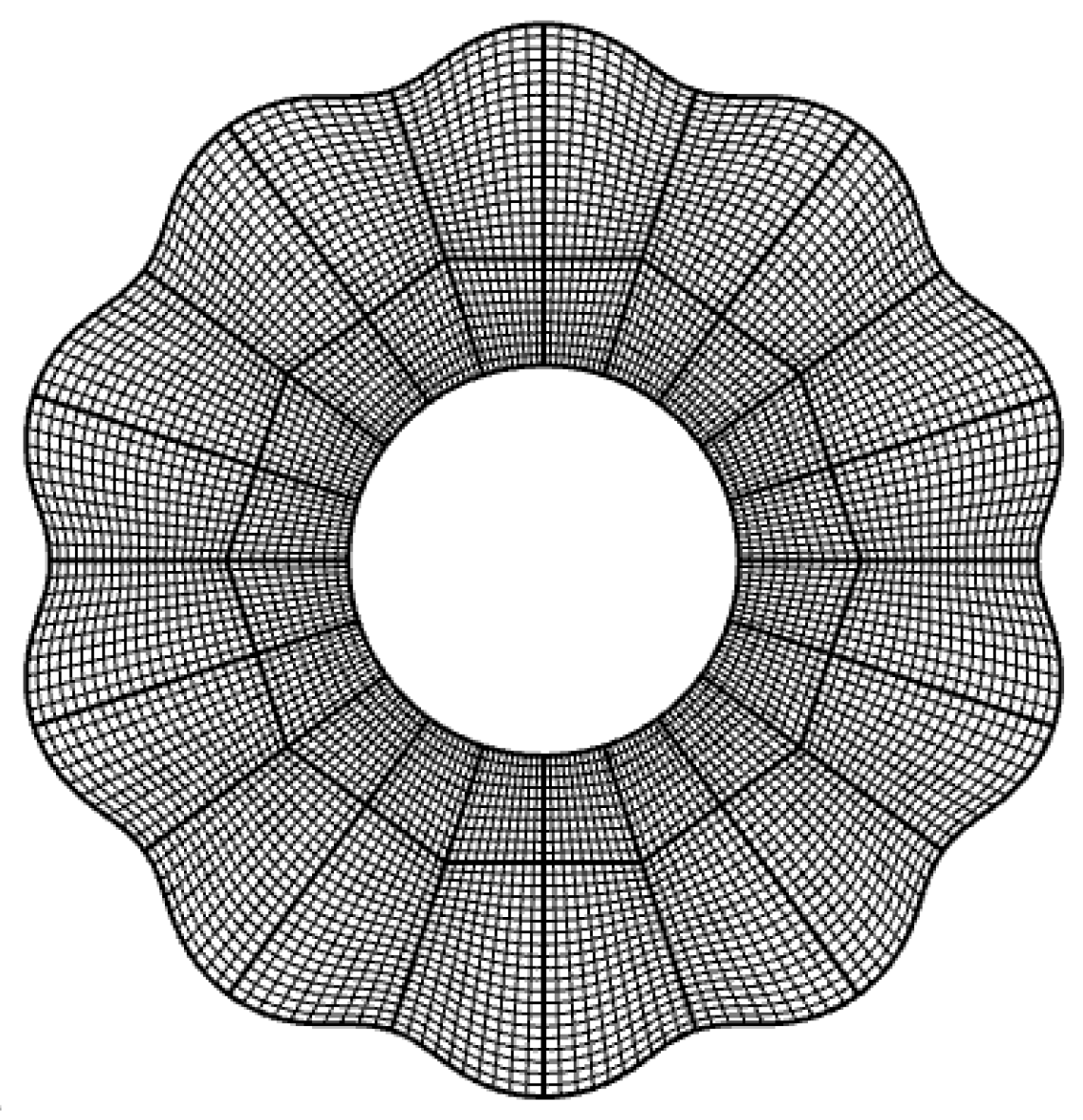
Preprints 90335 g002
Preprints 90335 g003
Figure 3. Boundary comparison: (a) NURBS surface boundary; (b) Lagrange mesh of FEM.
Figure 3. Boundary comparison: (a) NURBS surface boundary; (b) Lagrange mesh of FEM.
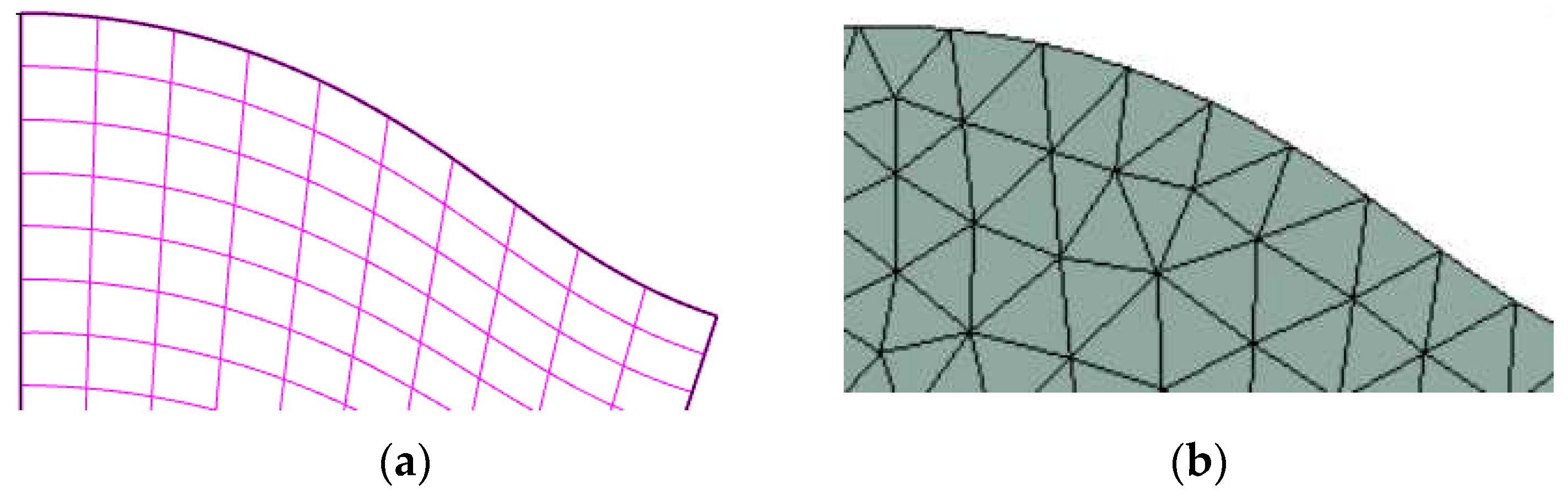
Preprints 90335 g003
Preprints 90335 g004
Figure 4. Comparison of tooth profile.
Figure 4. Comparison of tooth profile.
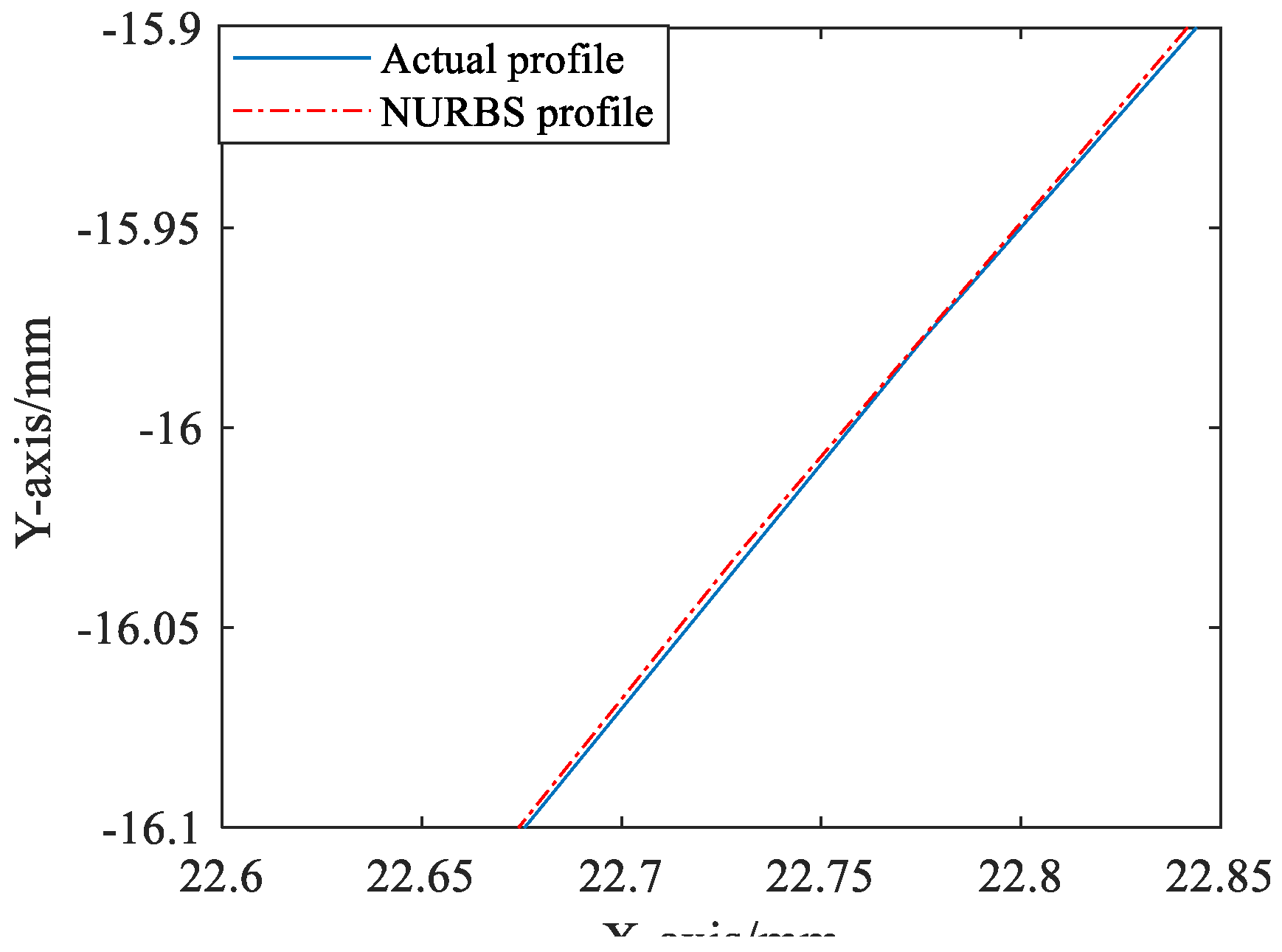
Preprints 90335 g004
Preprints 90335 g005
Figure 5. Tooth profile deviation amount.
Figure 5. Tooth profile deviation amount.
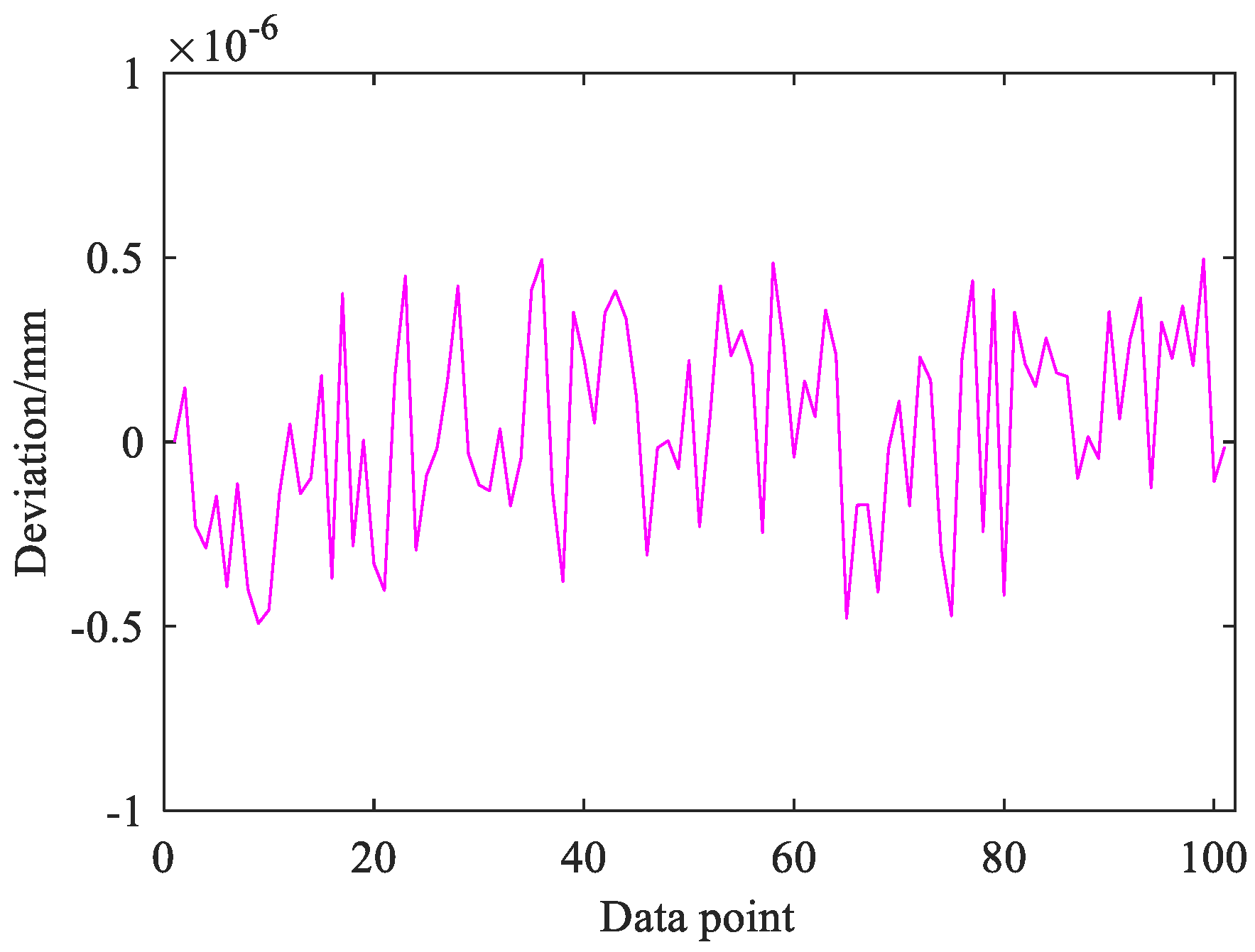
Preprints 90335 g005
Preprints 90335 g006
Figure 6. Schematic diagram of the model of cycloid pinwheel transmission.
Figure 6. Schematic diagram of the model of cycloid pinwheel transmission.
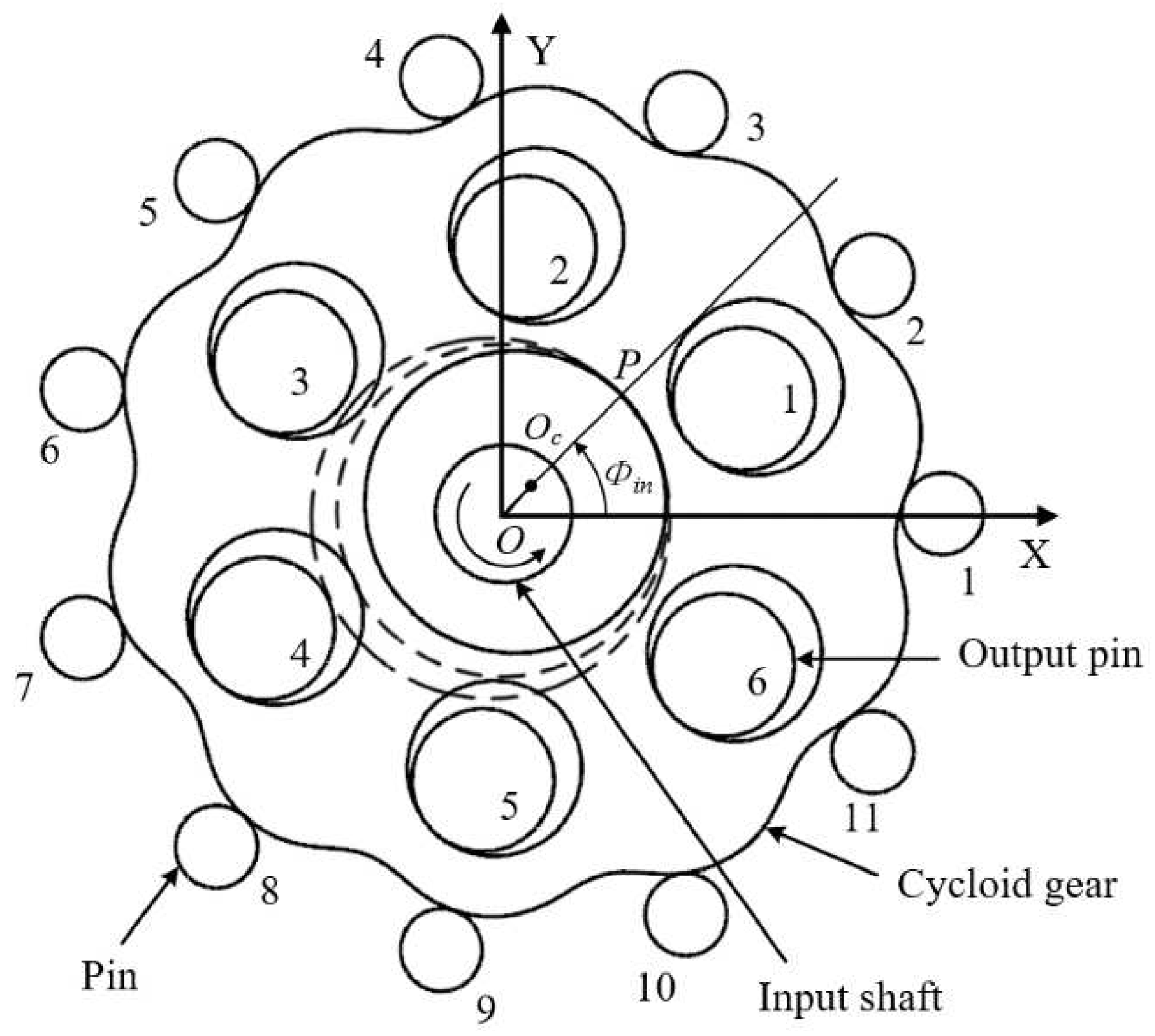
Preprints 90335 g006
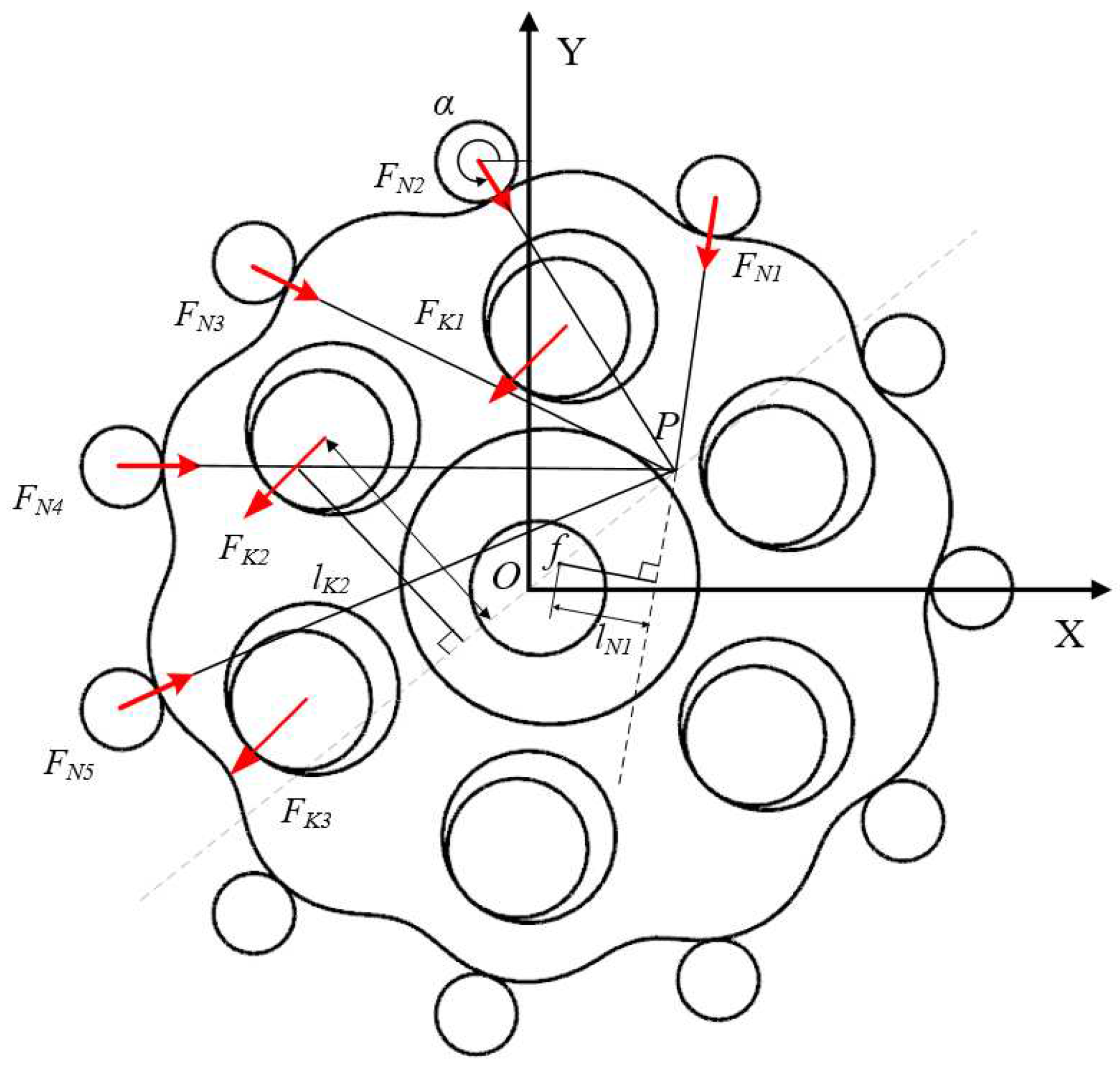
Preprints 90335 g007
Figure 7. Analysis of the applied force on the cycloid gear at 45 degrees of input angles.
Figure 7. Analysis of the applied force on the cycloid gear at 45 degrees of input angles.
Preprints 90335 g007
Preprints 90335 g008
Figure 8. Force diagram of input crank at 45 degrees of input angles.
Figure 8. Force diagram of input crank at 45 degrees of input angles.
Preprints 90335 g008
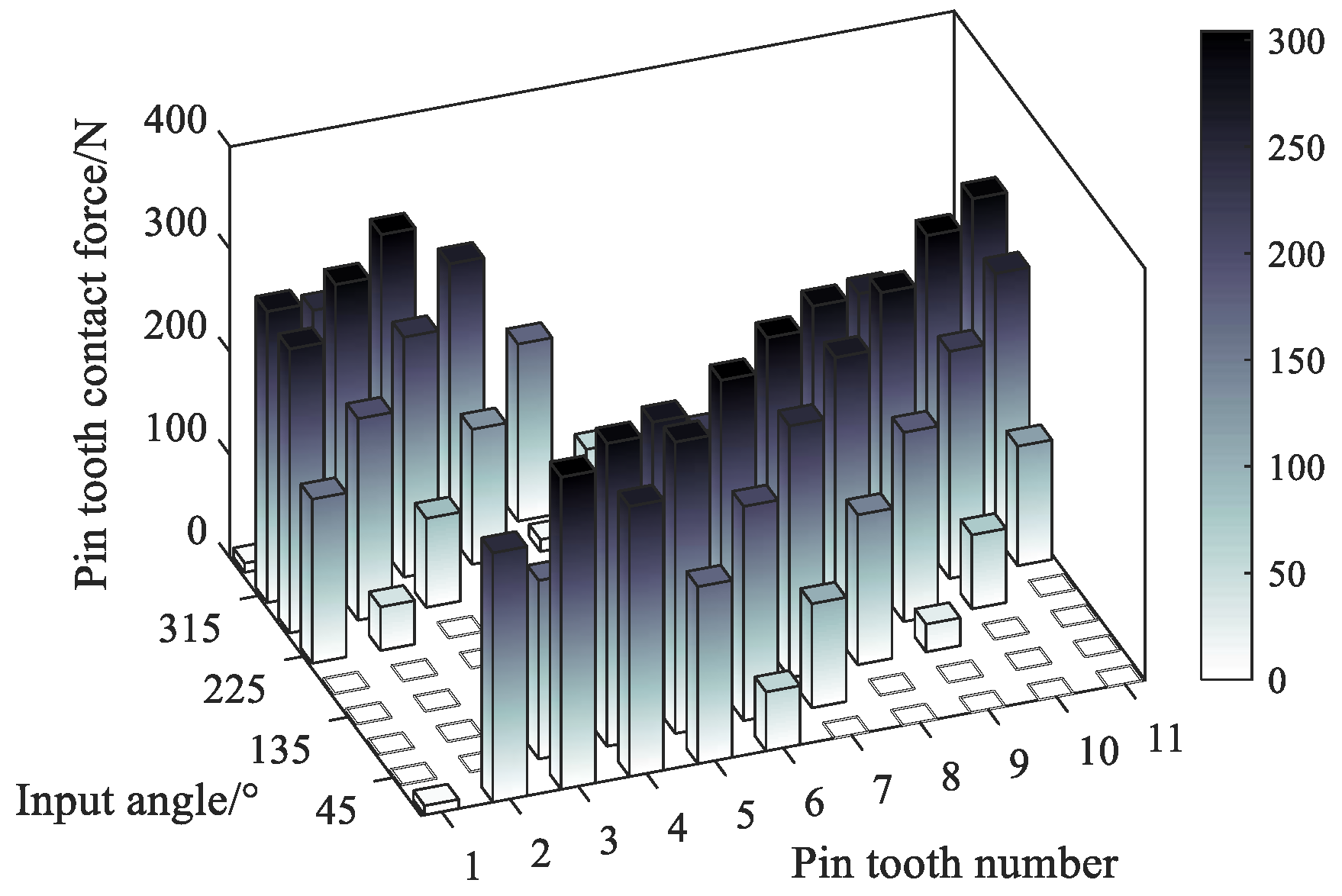
Preprints 90335 g009
Figure 9. Pin tooth contact force distribution.
Figure 9. Pin tooth contact force distribution.
Preprints 90335 g009
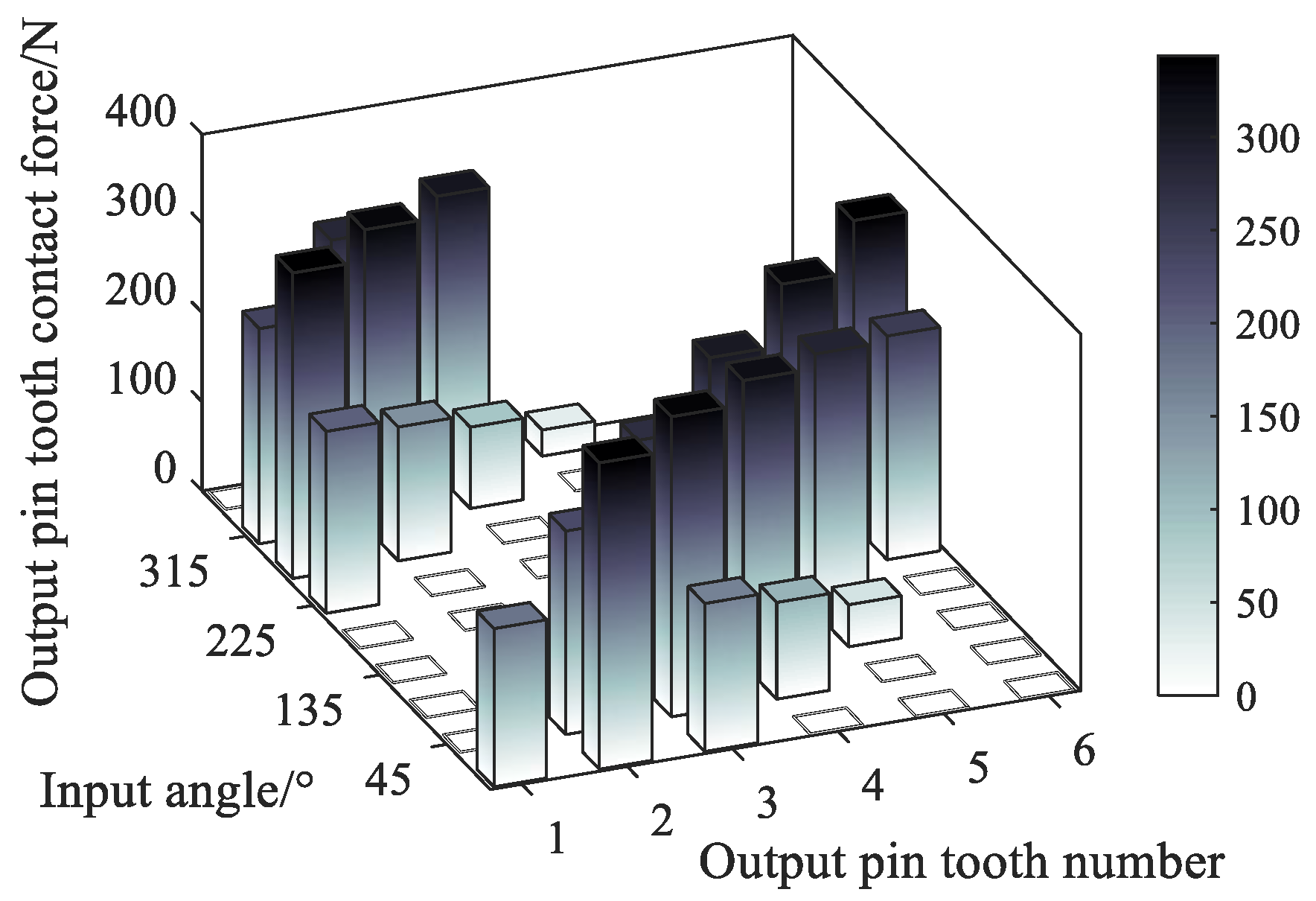
Preprints 90335 g010
Figure 10. Output pin contact force distribution.
Figure 10. Output pin contact force distribution.
Preprints 90335 g010
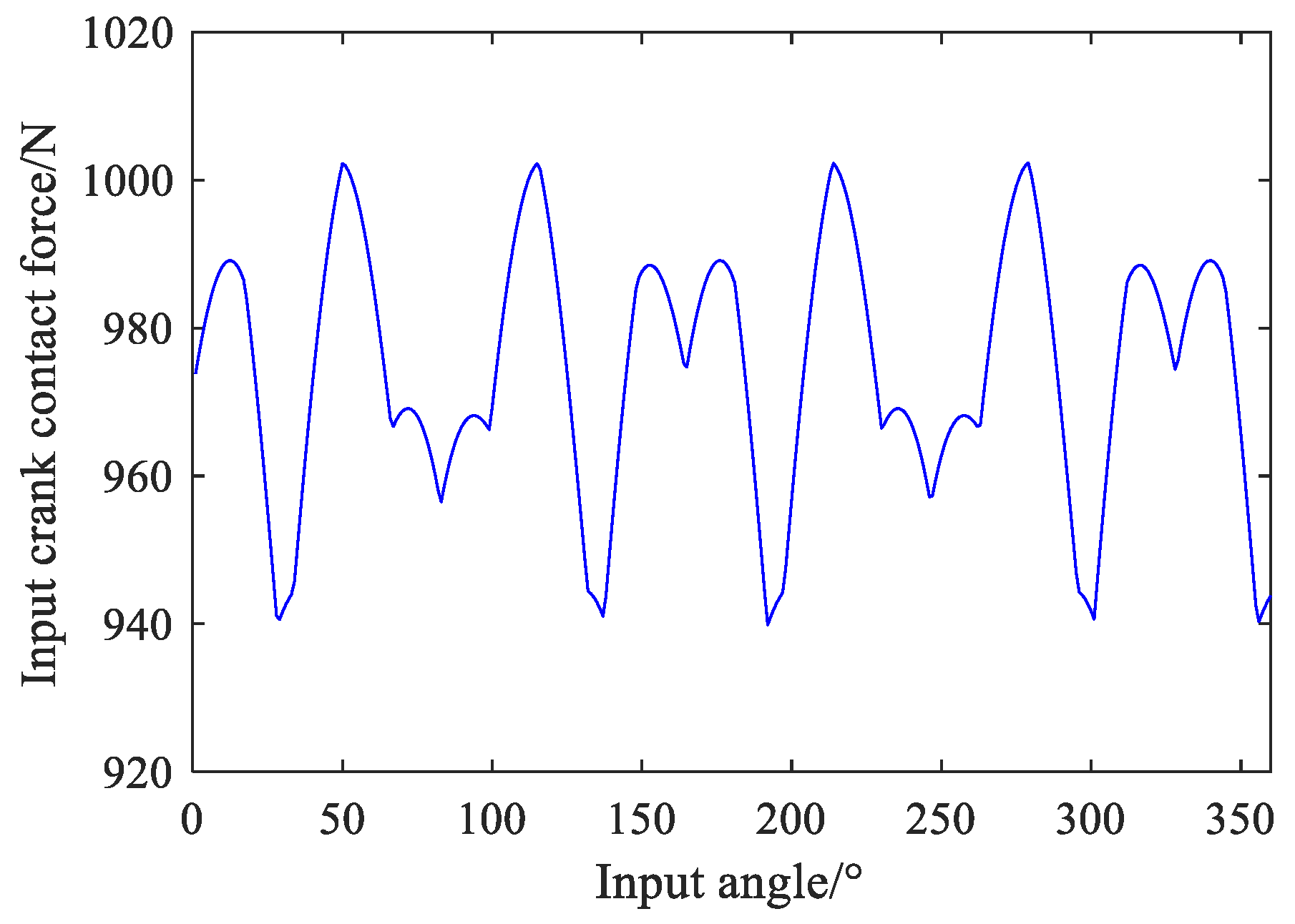
Preprints 90335 g011
Figure 11. Amplitude of crank contact force at different input angles.
Figure 11. Amplitude of crank contact force at different input angles.
Preprints 90335 g011
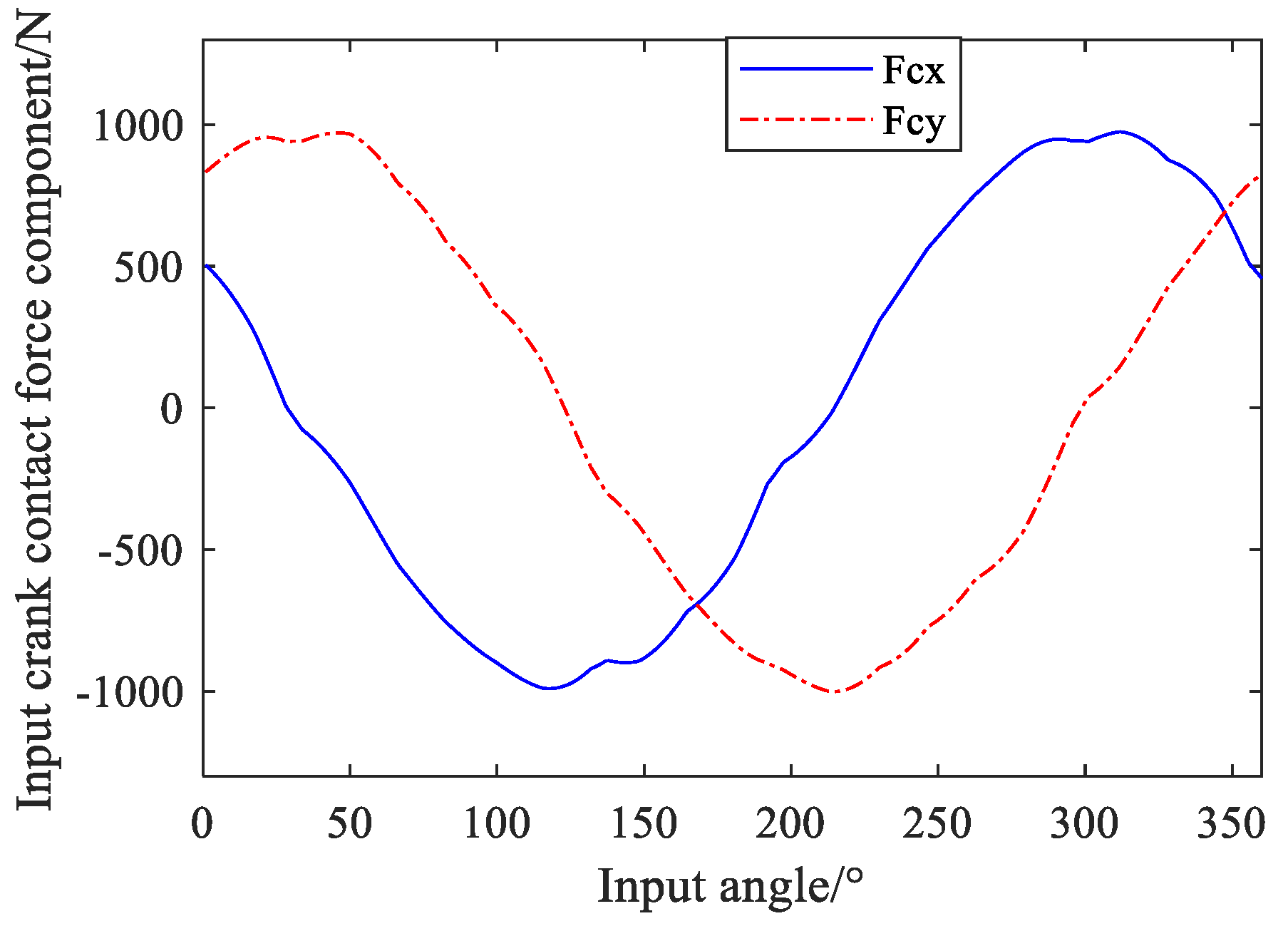
Preprints 90335 g012
Figure 12. Crank contact force components at different input angles.
Figure 12. Crank contact force components at different input angles.
Preprints 90335 g012
Preprints 90335 g013
Figure 13. Isogeometric contact analysis flow.
Figure 13. Isogeometric contact analysis flow.
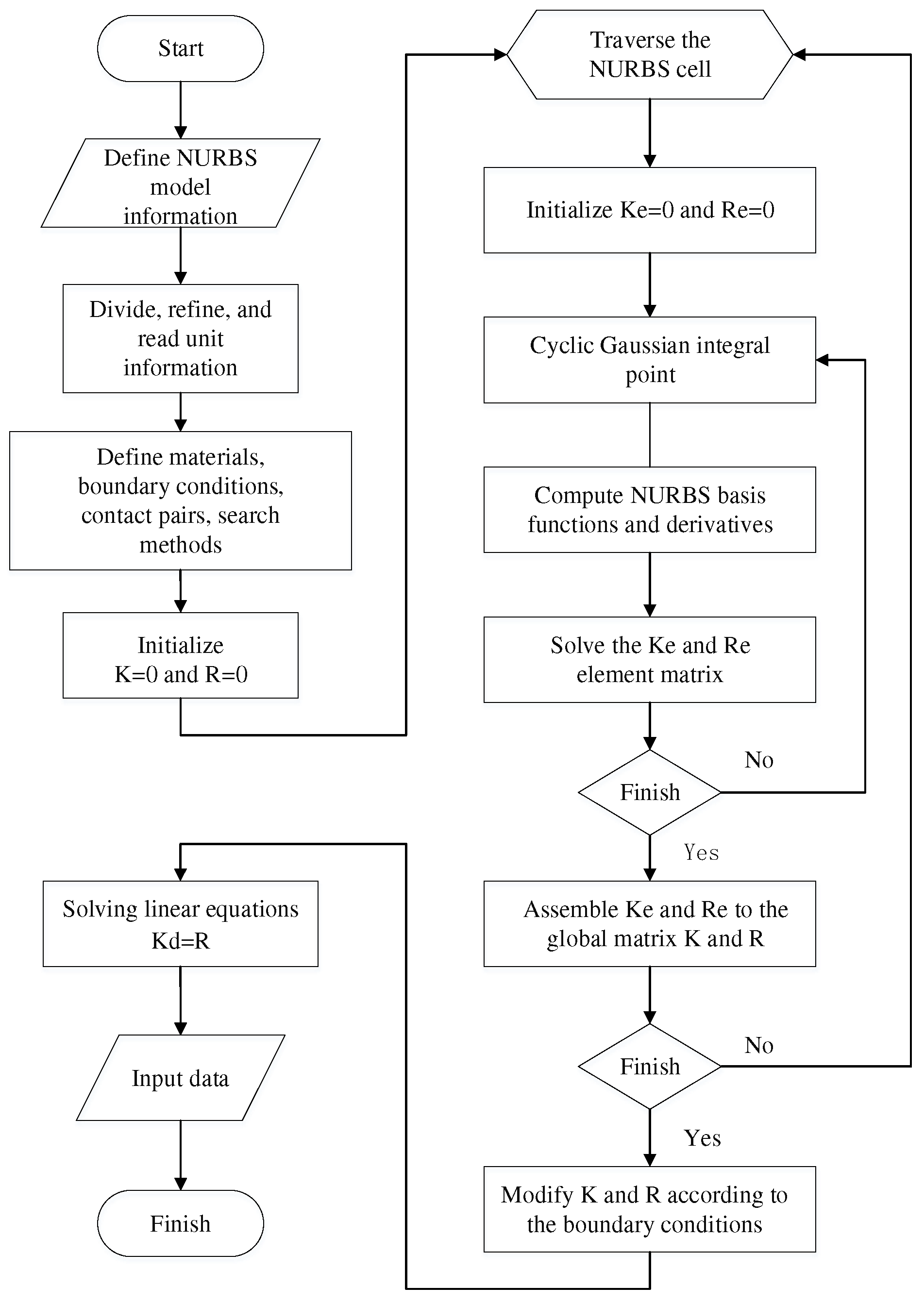
Preprints 90335 g013
Preprints 90335 g014
Figure 14. Quarter of the cycloid gear.
Figure 14. Quarter of the cycloid gear.
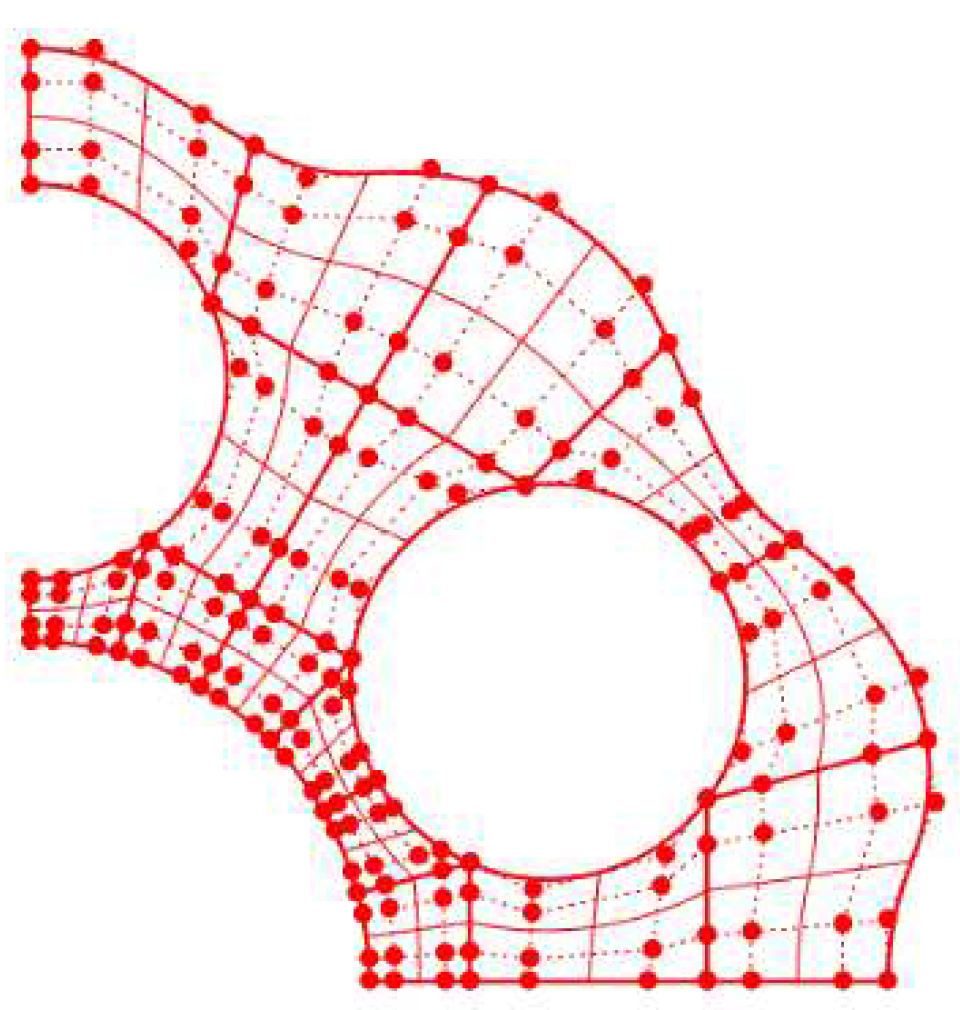
Preprints 90335 g014
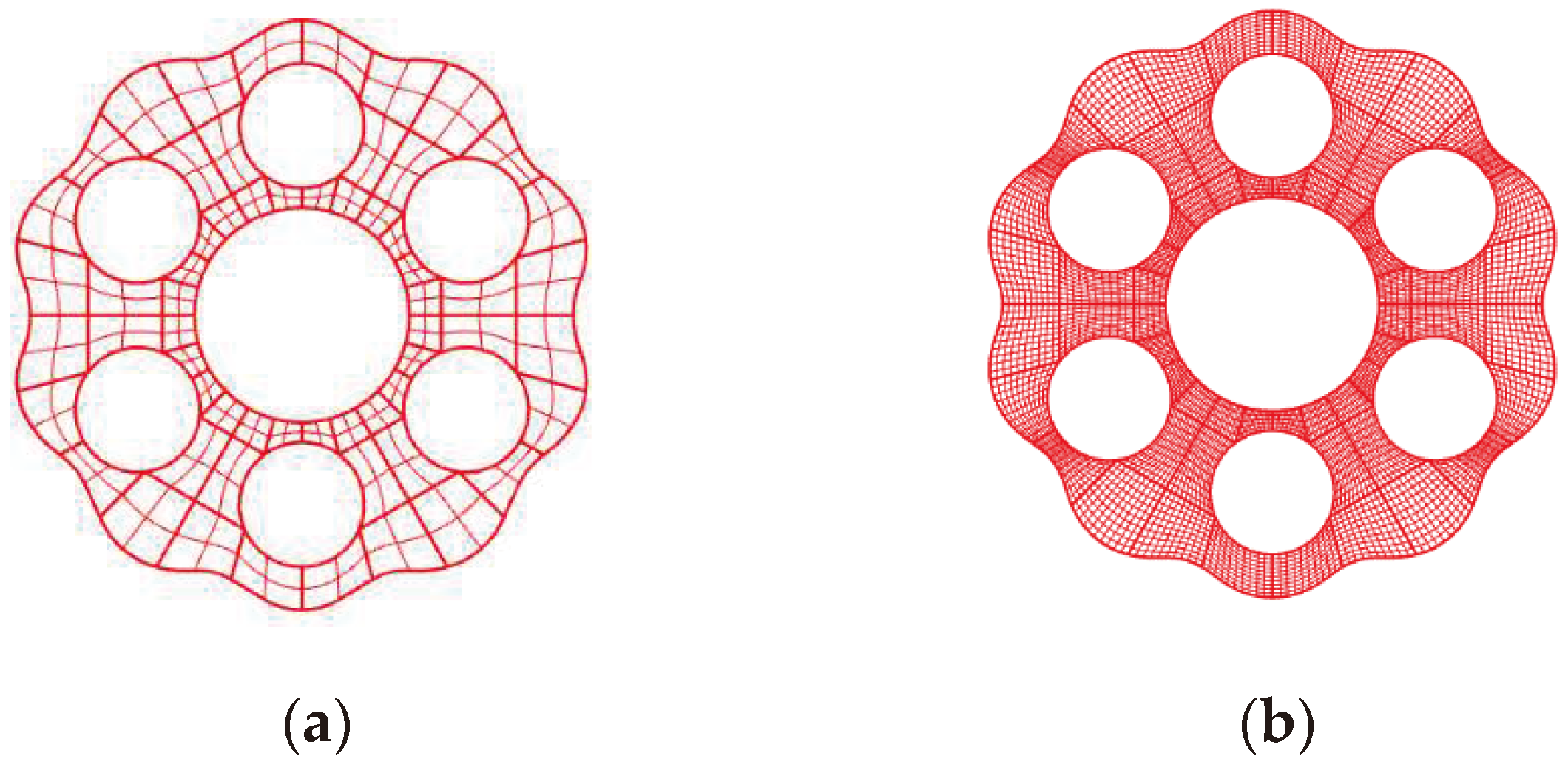
Preprints 90335 g015
Figure 15. Complete tooth surface of the cycloidal gear: (a) Before refinement; (b) After refinement.
Figure 15. Complete tooth surface of the cycloidal gear: (a) Before refinement; (b) After refinement.
Preprints 90335 g015
Preprints 90335 g016
Figure 16. Output pin and pin tooth NURBS section: (a) Output pin; (b) Pin tooth.
Figure 16. Output pin and pin tooth NURBS section: (a) Output pin; (b) Pin tooth.
Preprints 90335 g016
Preprints 90335 g017
Figure 17. NURBS section after refinement: (a) Output pin (b) Pin tooth.
Figure 17. NURBS section after refinement: (a) Output pin (b) Pin tooth.
Preprints 90335 g017
Preprints 90335 g018
Figure 18. IGA contact stress nephogram.
Figure 18. IGA contact stress nephogram.
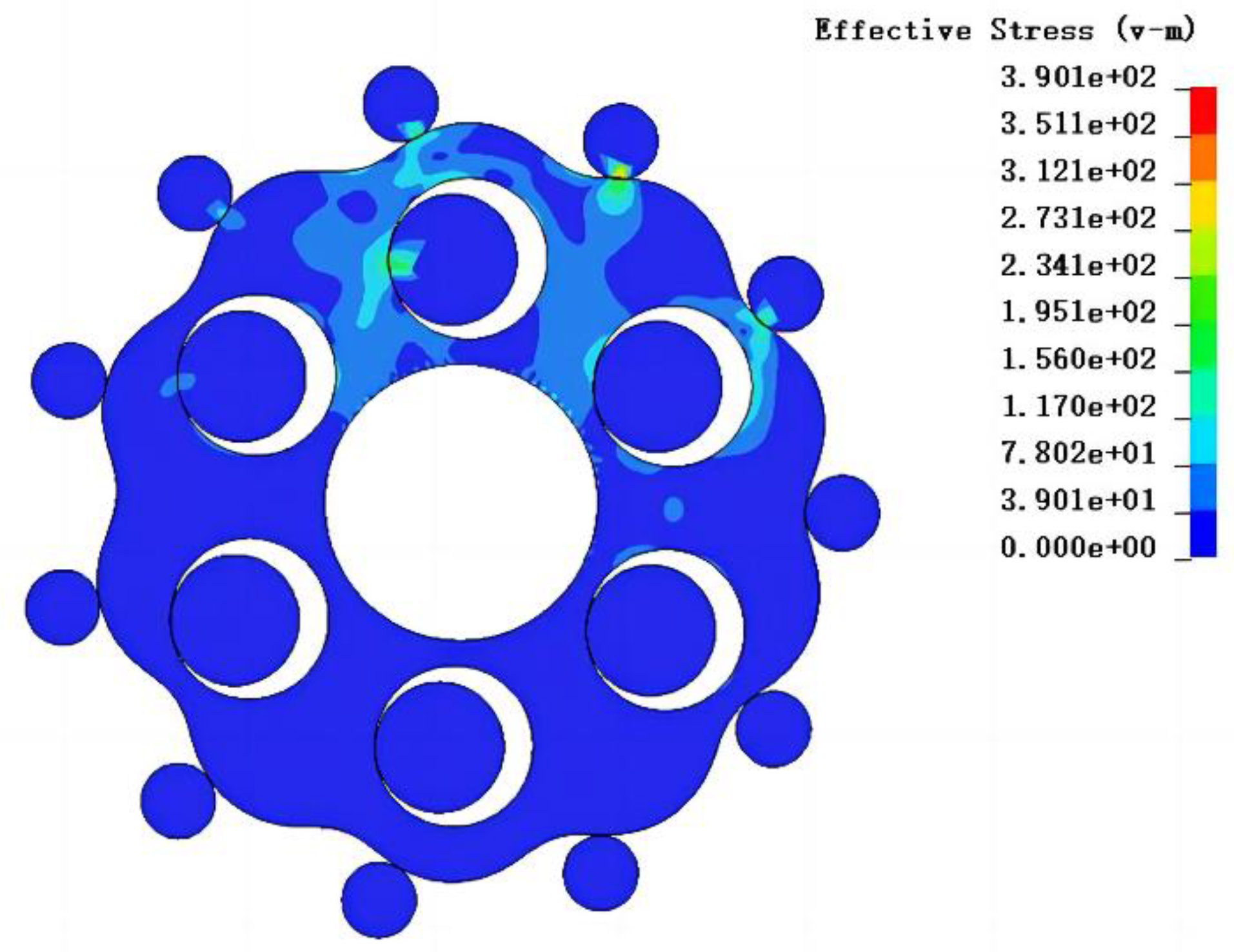
Preprints 90335 g018
Preprints 90335 g019
Figure 19. Finite element pin tooth contact stress diagram.
Figure 19. Finite element pin tooth contact stress diagram.
Preprints 90335 g019
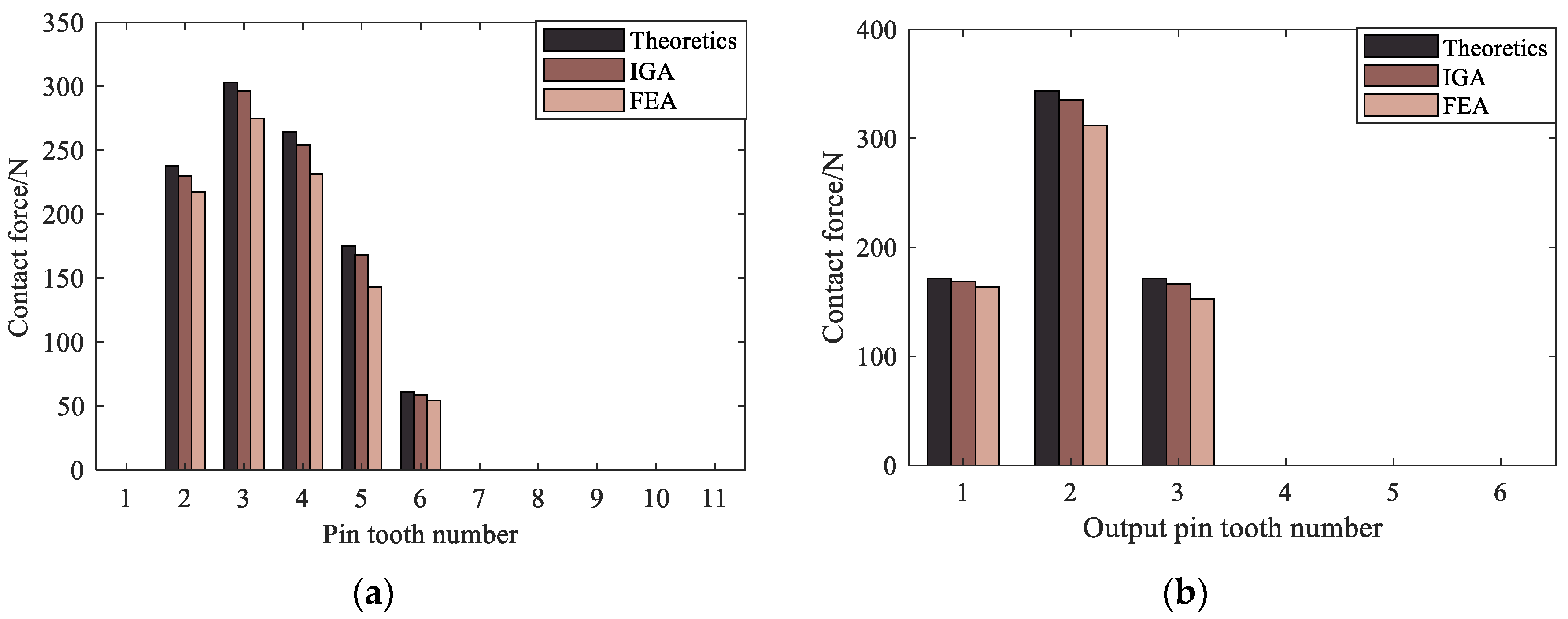
Preprints 90335 g020
Figure 20. Comparison of IGA and FEM contact force (a) Comparison of pin tooth contact force; (b) Comparison of output pin contact force.
Figure 20. Comparison of IGA and FEM contact force (a) Comparison of pin tooth contact force; (b) Comparison of output pin contact force.
Preprints 90335 g020
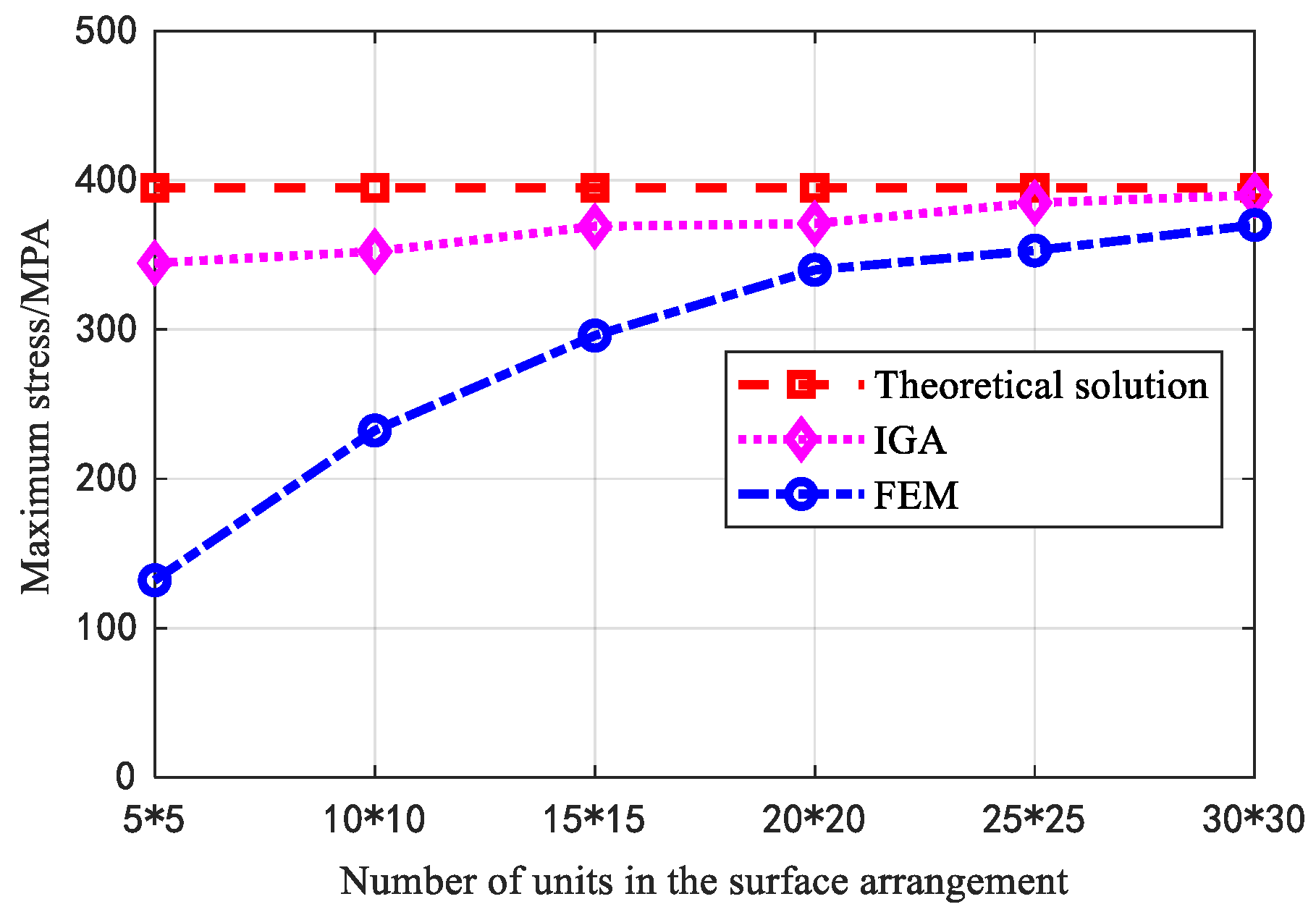
Preprints 90335 g022
Figure 22. Maximum contact stress versus element density.
Figure 22. Maximum contact stress versus element density.
Preprints 90335 g022
Table 1. Design parameters of cycloid drive.
Table 1. Design parameters of cycloid drive.
Design parameters value
Number of cycloid teeth 10
Number of pin teeth 11
Pin tooth radius 3mm
Pin tooth distribution radius 32mm
Output pin radius 6.4mm
Radius of output pin distribution 19.4mm
Eccentric distance 1.2mm
Table 2. Comparison of tooth profile points.
Table 2. Comparison of tooth profile points.
Number xi yi yi′ Fy
1 22.49 -16.3403 -16.3501 5.99×10-4
2 22.63 -16.1524 -16.1529 3.2×10-5
3 22.77 -15.9712 -15.9718 3.7×10-5
4 22.82 -15.8054 -15.8032 2.02×10-4
Table 3. Comparison of contact stress results for the pin teeth of the cycloid gear.
Table 3. Comparison of contact stress results for the pin teeth of the cycloid gear.
Method Maximum stress value /MPA Error/%
Theoretics 395.80 /
IGA 390.10 1.26
FEM 362.89 8.11
Table 4. Comparison of contact force error of pin tooth.
Table 4. Comparison of contact force error of pin tooth.
Contact tooth number FEM/% IGA/%
2 8.4 3.1
3 9.3 2.3
4 12.5 3.7
5 18.2 4.2
6 10.8 3.2
Table 5. Comparison of contact force error of output pin.
Table 5. Comparison of contact force error of output pin.
Contact tooth number FEM/% IGA/%
1 4.6 1.7
2 9.3 2.3
3 11.2 2.9
Table 6. Comparison of errors between IGA and finite element results at different element numbers.
Table 6. Comparison of errors between IGA and finite element results at different element numbers.
Element number IGA/% FEM/%
5×5 61.5 11.6
10×10 41.1 8.8
15×15 25.1 6.3
20×20 13.9 4.5
25×25 10.1 2.5
30×30 8.7 1.2
Table 7. Comparison of total time spent on analysis and calculation.
Table 7. Comparison of total time spent on analysis and calculation.
Method Mesh division time/min Mesh division time/min Total time/min
FEM 12 47 59
IGA / 6 6
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated