Hubble Diagram Test of SN1a Supernovae and High Redshift Gamma Ray Bursts: Data Analysis of the Log(z)/µ, ln(z+1)/T(d) and Linear Photon Flight Time T/(z+1) Scales. – Comparison of Observational Data with Model Calculations.

Preprint

Article

Hubble Diagram Test of SN1a Supernovae and High Redshift Gamma Ray Bursts: Data Analysis of the Log(z)/µ, ln(z+1)/T(d) and Linear Photon Flight Time T/(z+1) Scales. – Comparison of Observational Data with Model Calculations.

This version is not peer-reviewed.

Laszlo Marosi^*

This version is not peer-reviewed.

Altmetrics

Downloads

145

Views

309

Comments

Submitted:

10 May 2024

Posted:

13 May 2024

You are already at the latest version

Abstract

Hubble diagrams are examined for SN1a supernovae in the redshift range z = 0.01–1.3 and for gamma ray bursts in the range z = 0.034–8.1. It is shown that in the low redshift range, the Hubble diagram shows an innate equivocality between the ΛCDM and the tired light model. This means that the strong agreement between the z/µ data, calculated with the parameters of the ΛCDM model, and the experimentally measured z/µ values cannot be considered as definite evidence for the expansion hypothesis. The exponential function , which is characteristic of the tired light redshift mechanism, fits the data with similarly high accuracy. Hence, on the premise of low redshift data, a decision for or against either model is completely arbitrary. The Hubble diagram for high redshift gamma ray bursts shows poor agreement with the ΛCDM model, but concurs with the exponential energy decay following from the tired light redshift hypothesis.

Keywords:

Subject:

Physical Sciences - Astronomy and Astrophysics

1. Introduction

The essential premise of Big Bang (BB) cosmology is that the universe is expanding, and Hubble's law [1] is viewed as the most persuasive proof for cosmic expansion. In present-day cosmology, the velocity interpretation of the redshift (RS) of spectral lines has achieved a dogmatic status, and objections against it have gone unobserved.

Regardless of whether this interpretation is correct or not, Hubble’s law is a RS/distance (d) relation, and an interpretation of this as a velocity is only a hypothesis. Supporting the velocity interpretation is the good agreement between the observed z/µ data for SN1a supernovae in the RS range z < ~ 1.3 with data determined based on the parameters Ώ_M, Ώ_λ, w and H₀ of the ΛCDM model, which is viewed as proof for general expansion. Despite its widespread acceptance, however, this conclusion is equivocal, and the current circumstance is fairly confounding. Based on a semiquantitative examination of SN1a data, Sorrell [2] reported that in the low-RS range, the Hubble diagram (HD) for a tired light (TL) cosmology gives good agreement with the Type Ia supernova data. A comparable outcome was described by Traunmüller [3], whose examination of 892 SN1a supernovae z/µ data also indicated that these were well-matched with the TL model.

The interpretation of the RS of atomic spectral lines suffers from the fact that none of the proposed systems (the expanding space paradigm or the TL mechanism) can be confirmed experimentally, meaning that confidence in each hypothesis should be estimated based on its ability to explain the observational data. One important issue in cosmology is therefore to explain which of the two models fits the observed data better, i.e., whether the HD follows the linear (expanding universe) or the exponential TL relation. In the high RS range, it should be more feasible to check more precisely whether the HD follows a linear or exponential slope.

Very exact z/μ data for SN1a supernovae, however, are accessible only for a limited range of distances. At RS > ~ 1.3, the optical light emitted by a s, upernova gradually diminishes with distance, making definite estimations difficult. Many attempts have been made to utilize GRB data for computing HDs in the high RS range. The difficulty in building HDs from experimentally measured LGBR z/µ raw data lies in standardising GRB luminosity as a reliable distance indicator in a cosmologically independent way. Additional problems arise from observational biases - like selection and evolution effects - and gravitational lensing biases. To overcome these problems, various calibration methods were proposed, such as those by Liu and Wei [4], Amati et al. [5] and calibration through the Dainotti relationship [6], for example. HDs were created based on the calibrated data [5,7,8,9,10] and compared with the CDM model. It was asserted that the data has a good fit to the ΛCDM model. However, a comparison with the competing TL model was not considered. A detailed profile analysis of mixed SN1a, GRB and exclusively GRB data Marosi [11,12,13,14] has shown that in the RS range 0.031–8.1, the slope of the HD is (or is extremely close to) exponential, which is characteristic of the TL model [15]. In contrast, the ΛCDM model shows poor agreement with the observation. In contrast, ongoing investigations by Gupta [16] and Shirokov et al. [17,18] have found that although none of the existing studies has given probative affirmation for the ΛCDM model, the conclusion can be drawn that based on the HD test, the TL model can be precluded. This cosmologically significant inconsistency between these two contradictory conclusions requires an amendment.

2. Aims

The HD test represents possibly the most significant proof for identifying the underlying physical nature of the Hubble constant (abbreviated as h^CDM = (km s^-1 Mpc^-1)/100 for ΛCDM and h^TL = (Hz s^-1 Hz^-1)/100 for the TL model), and could provide solid support for the expansion hypothesis, or, in the contrary case, for the legitimacy of the TL model (although this would require modification to the ΛCDM itself).

The aim of the present study was to perform a comparative HD test using cosmology-independent SN1a data and high RS LGRB RS/μ data. Since both the ΛCDM and the TL model make precise forecasts about the shape of the HD, it ought to be possible to confirm whether the HD shows a linear

z = h_{0} \times t (d)

(1)

or exponential relationship

z + 1 = e^{h^{T L} \times t (d)}

(2)

(where t represents the flight time of the photons from the co-moving radial distance d to the observer; for simplicity, we will use t instead of d in the following discussion). This could set significant constraints on these contrasting cosmological models.

We do not plan to examine existing issues related to the ΛCDM and TL cosmology, or to accept or reject either model on the basis of hypothetical contentions or hypotheses. The present study is completely cosmology-independent; it is a mathematically based statistical investigation based on cosmology-independent data without the need to turn to cosmological suspicions, meaning that it is unbiased.

3. Datasets and Methods

3.1. SN1a Supernovae

For the model calculations, the cosmological parameters Ώ_M = 0.295, Ώ_λ = 0.705, w = −1.018 and h₀ = 0.7 were used, based on 374 spectroscopically affirmed, upgraded SN1a supernovae from the most recent joint light-curve analysis (JLA) data index, Betoule et al. [19].

3.2. Choice of GRB Data

60 low RS and 78 high RS GRB data samples from the Union1 compilation, collected by Liu and Wei [4](2015). One outlier at ln(z+1) = 1.2095 with t = 17491×10^-14 was excluded from the calculation.

193 GRB data samples collected by Amati et al. (2018).

69 LGBR samples calibrated with the Dainotti relationship [10]. One extreme outlier at z = 2.03 was excluded from thecalculation.

99 calibrated data consisting of the 69 bursts supplemented with 30 further data points collected by Wang et al. [20].

A comparison of the goodness of fit indicators for data sets b), c), d) and e) is shown in Table 1. The default parameter for GRBs h = 0.70, Ώ = 0.287 were used for calculation.

Based on the above quality criteria, we selected 138 calibrated, cosmology-independent GRB data points in the RS range z = 0.0331–8.1 b) and d) and e) for a detailed analysis.

4. Data Processing

Data were introduced on the usual, strongly attenuated logarithmic z/μ scale, and since the contrast between the measured and the modelled data turned out to be clearer on the linear scale, we also considered the less commonly used but more sensitive linear photon flight time t/(z+1) scale. A conspicuous benefit of the t/(z +1) representation is the direct illustration of the shape of the HD, which can be definitively contrasted with the expectations following from equations (1) and (2).

4.1. Data Conversion from µ to t(d) and Vice Versa

For data conversion from µ to t we used equation (3), and for conversion from t to µ we used equations (4) and (5), as follows:

t = \frac{D}{c} = \frac{10^{(μ + 5) / 5}}{(z + 1) \times 3 * 10^{10}} \times 3, 0857 \times 10^{18}

(3)

x = \frac{t}{3, 0857 \times 10^{18}} \times (z + 1) \times 3 \times 10^{10}

(4)

μ = (\log (x) \times 5) - 5

(5)

Conversion of the SN1a µ data to a linear scale was straightforward, as the data were of high precision and equation (3) could directly be applied for conversion without producing disruptive amplification of measurement errors.

Due to experimental difficulties in determining z/μ data at high RS, these data were overwhelmed by substantial scatter, meaning that they could not be converted to the linear t/(z +1) scale without amplifying the scatter and making the converted data unmanageable. Hence, before data conversion, there was a need to either smooth the data scatter by calculating the line of best fit using a suitable arithmetical function or to multiply the t values by an appropriate damping factor, which in this case was selected as 10^-14. For data fitting, a third-order polynomial regression was used.

4.2. Goodness of Fit

The goodness of fit was calculated using the likelihood estimator

χ^{2} = \sum_{i = 1}^{N} \frac{{(μ o b s . - μ c a l c .)}^{2}}{μ c a l c .}

(6)

4.3. Calculations of RS/µ Data

For the ΔCDM model, the ICRAR cosmology calculator was used to calculate the theoretical z/µ data. For the TL models, the z/µ data were calculated as follows:

μ = 25 + 5 \times \log (c / H^{T L}) + 5 \times \log (1 + z) + 5 \times \log \ln (1 + z)

(7)

(see: Sorrell 2009[2]; Traunmüller 2014[3]; Vigoureux, Vigoureux & Langlois 2014 [21]).

4.4. Data Presentation

Excel was used for data fitting, refinement, and presentation.

5. Results

5.1. Equivocality of the SN1a Supernovae Hubble Diagram

Since for ΛCDM models the distances in equation (1) are nonlinear in z (the distances are limited by the maximum value for d, i.e., the radius of the universe), it is usual to express d as

d \approx 10^{(μ + 5) / 5}

. This leads to a linear relationship for the variables

\log (z) \approx μ

(8)

which are the usual coordinates for the graphical presentation of the HD.

For TL models, it follows from equation (2) that

\ln (z + 1) = h^{T L} \times t

(9)

which is linear with distance, with an intercept on zero.

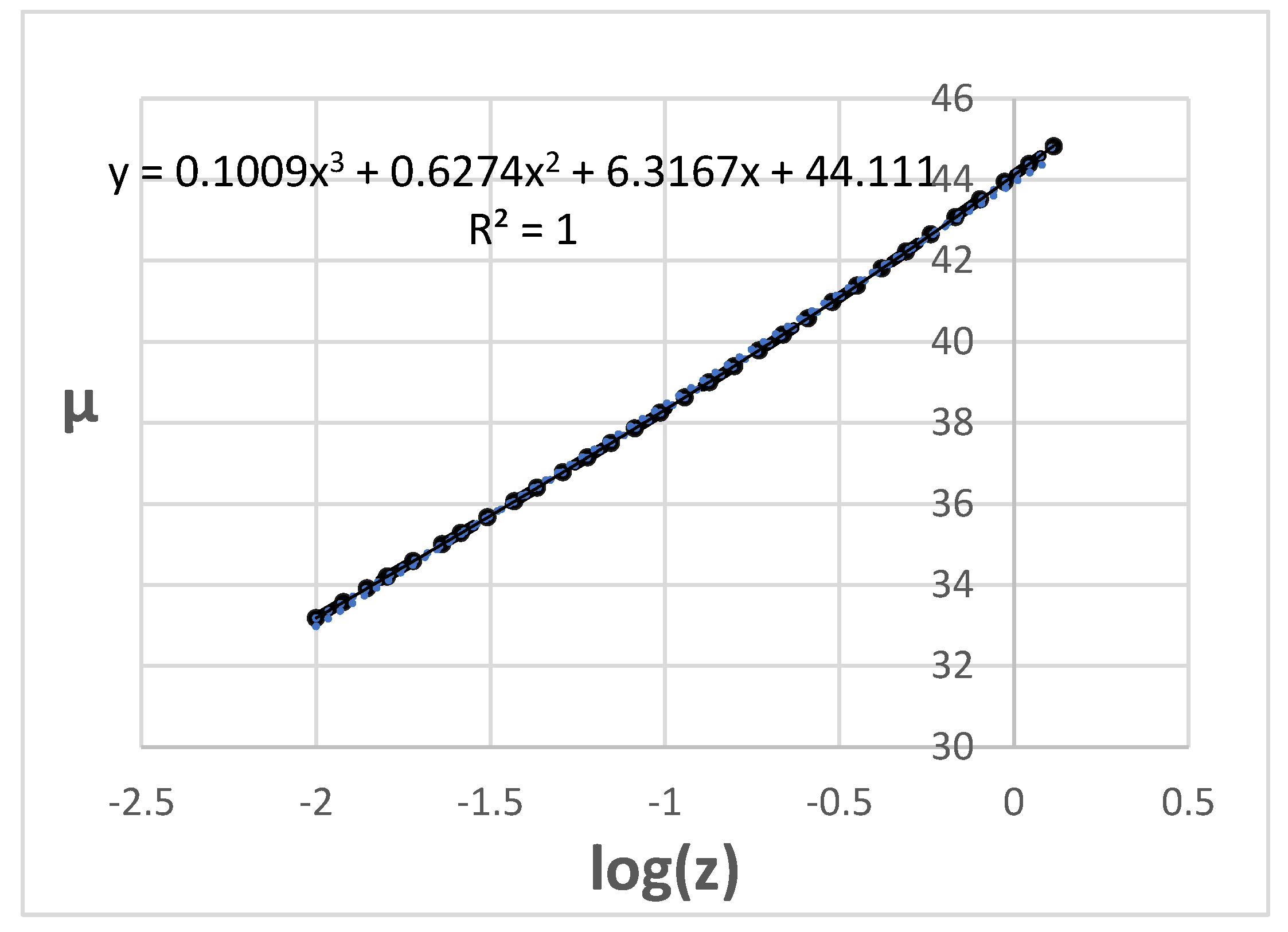
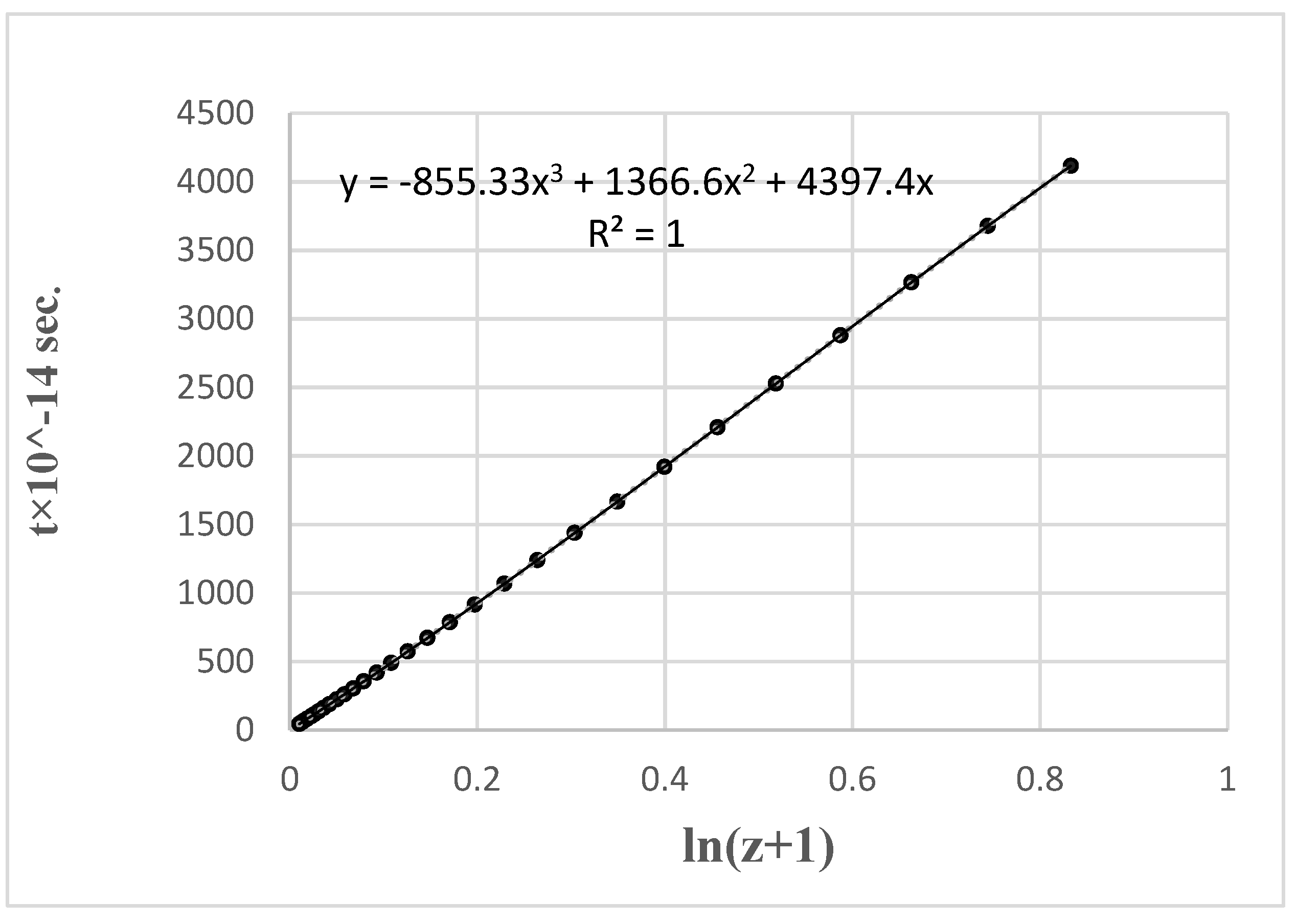
Figure 1 shows the HD calculated with the parameters of the ΛCDM model, as set down by Betoule et al. (2014), in the RS range z = 0.01–1.35 for the log(z)/µ presentation. Figure 2 shows the same data plotted on the ln(z+1)/t scale.

The fit parameters and goodness of fit indicators are presented in Table 2 and Table 3.

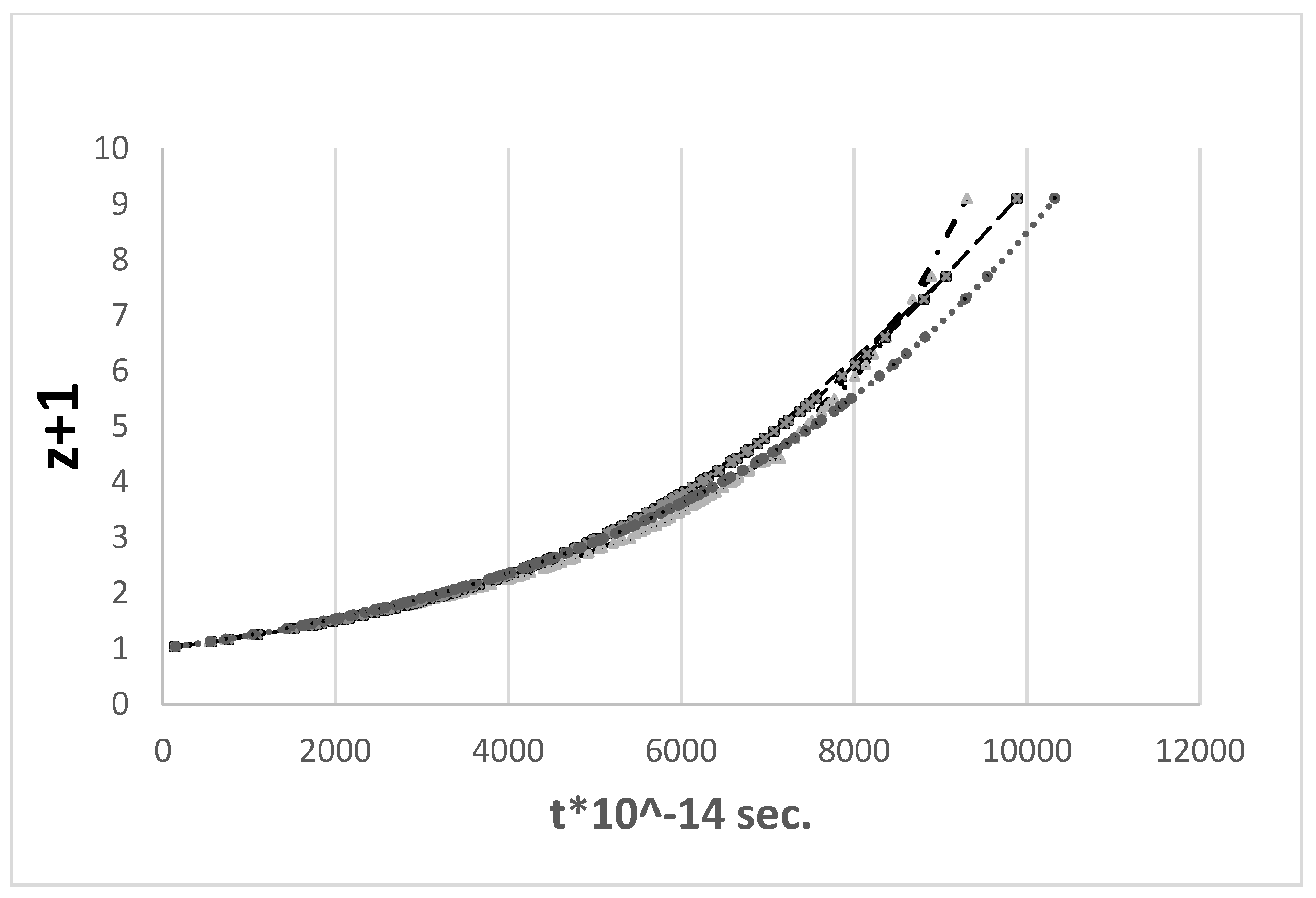
As illustrated by Figs. 1 and 2, both equation (8) (the expanding universe model) and equation (9) (the TL model) match the calculated data with very high accuracy. The exceptionally small ∑χ² values on the order of 10^-5–10^-6 offer convincing evidence of the equivocality of the ΛCDM and TL model in the low RS range.

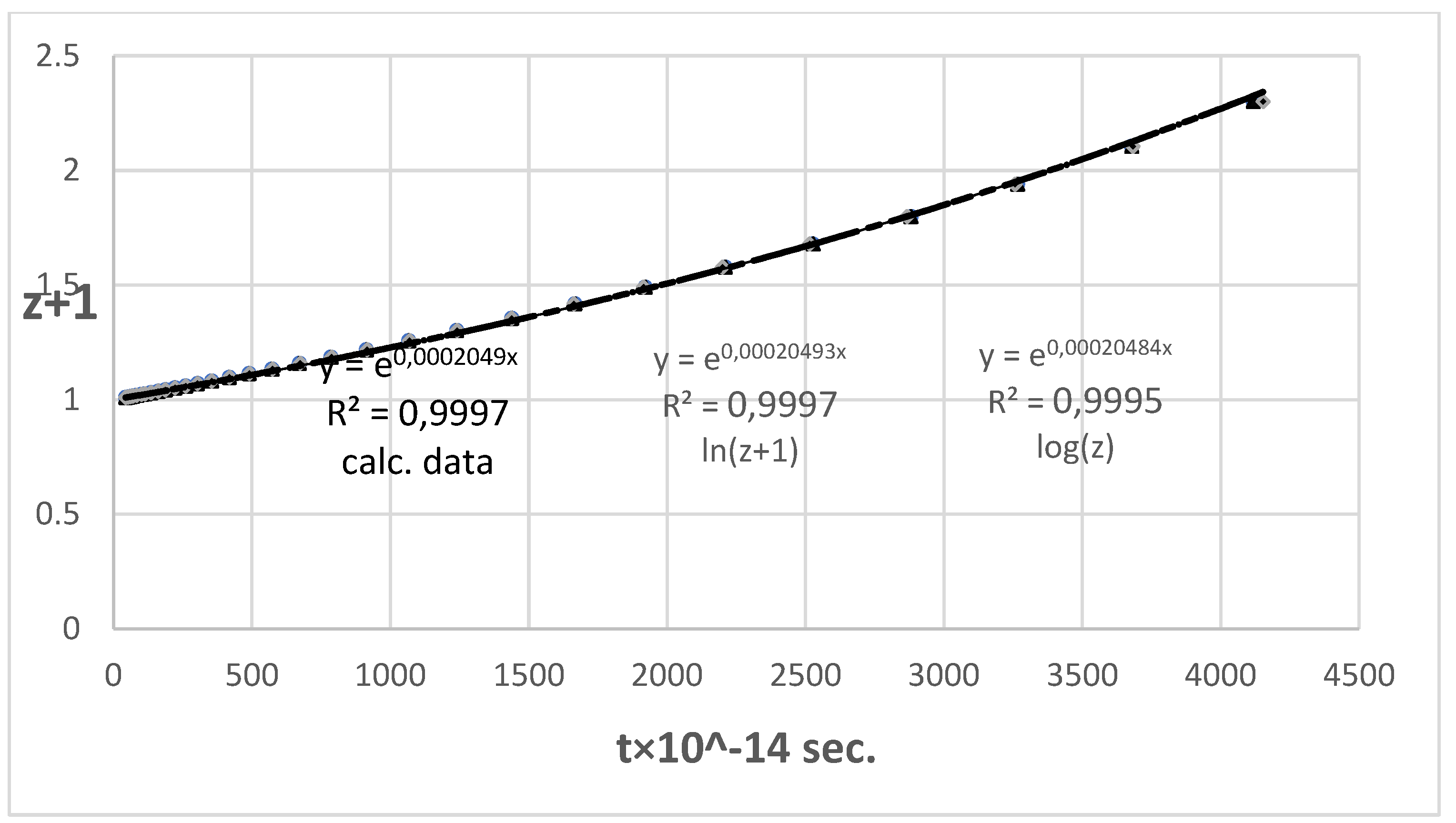
The corresponding linear t/(z+1) HDs were derived by converting µ to t using equations (3-5) based on the fit coefficients from equations (8) and (9). The linear HDs for both the log(z) and the ln(z+1) representations and the linear HD for the calculated data are shown in Figure 3.

The three curves (i.e., the one calculated based on the parameters of the ΛCDM model, and the log(z)/µ and d/ln(z+1) lines) have an exponential slope, are closely congruent, and cannot be told apart by visual examination. The corresponding Hubble constants and variances are shown in Table 4.

The Hubble constants are similar to within 0.5%, with values of h^TL = 0.6319 for the logarithmic log(z)/µ fit and 0.6322 for the ln(z+1) fit and calculated data.

Based on model calculations using 35 equidistant data points in the RS range z = 0.03–1.02, the h^TL equivalents for h^CDM = 0.68, 0.70 and 0.73 were determined in a similar way. The results are summarised in Table 5.

An obvious but frequently overlooked outcome is that, as shown in Table 5, the equivalent Hubble constants h^CDM and h^TL are different, and this has a significant effect on the comparative evaluation of the ΛCDM and TL models in the high RS range. It can be seen from Table 6 that the comparison of the observed high RS GRB data with the competing ΛCDM and TL models using h^CDM = h^TL is imprecise.

The ∑χ² differences between h^CDM = 0.70 and h^TL = 0.70 for the observed data show that h^TL = 0.70 gives the poorest fit, whereas a comparison of h^CDM = 0.70 with h^TL = 0.66 shows the opposite: the h^TL = 0.66 model gives the best fit to the observed data. The use of h^TL = h^CDM instead of the best fit h^TL for comparison inevitably leads to the wrong conclusion, that the TL model does not fit the data and can therefore be rejected. The results presented here show that for a proper comparison of ∑χ² for TL models, the correct approach is a Hubble constant close to the expectation value of h^TL, as shown in Table 5, or, depending on data quality (influence of scatter and/or outliers on χ²), the best-fit value of h^TL.

6. Hubble Diagram for High RS GRBs, Data Set b

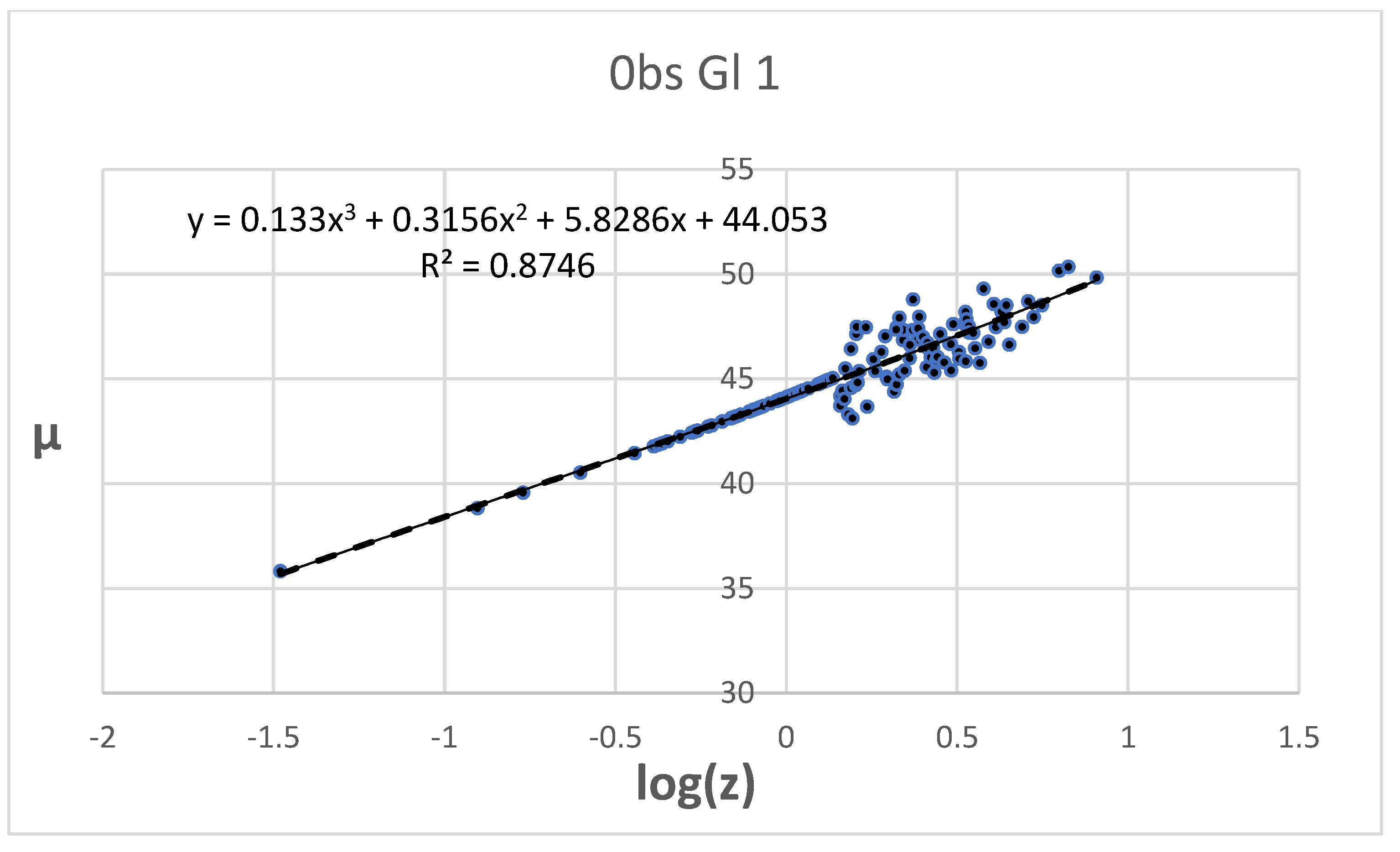
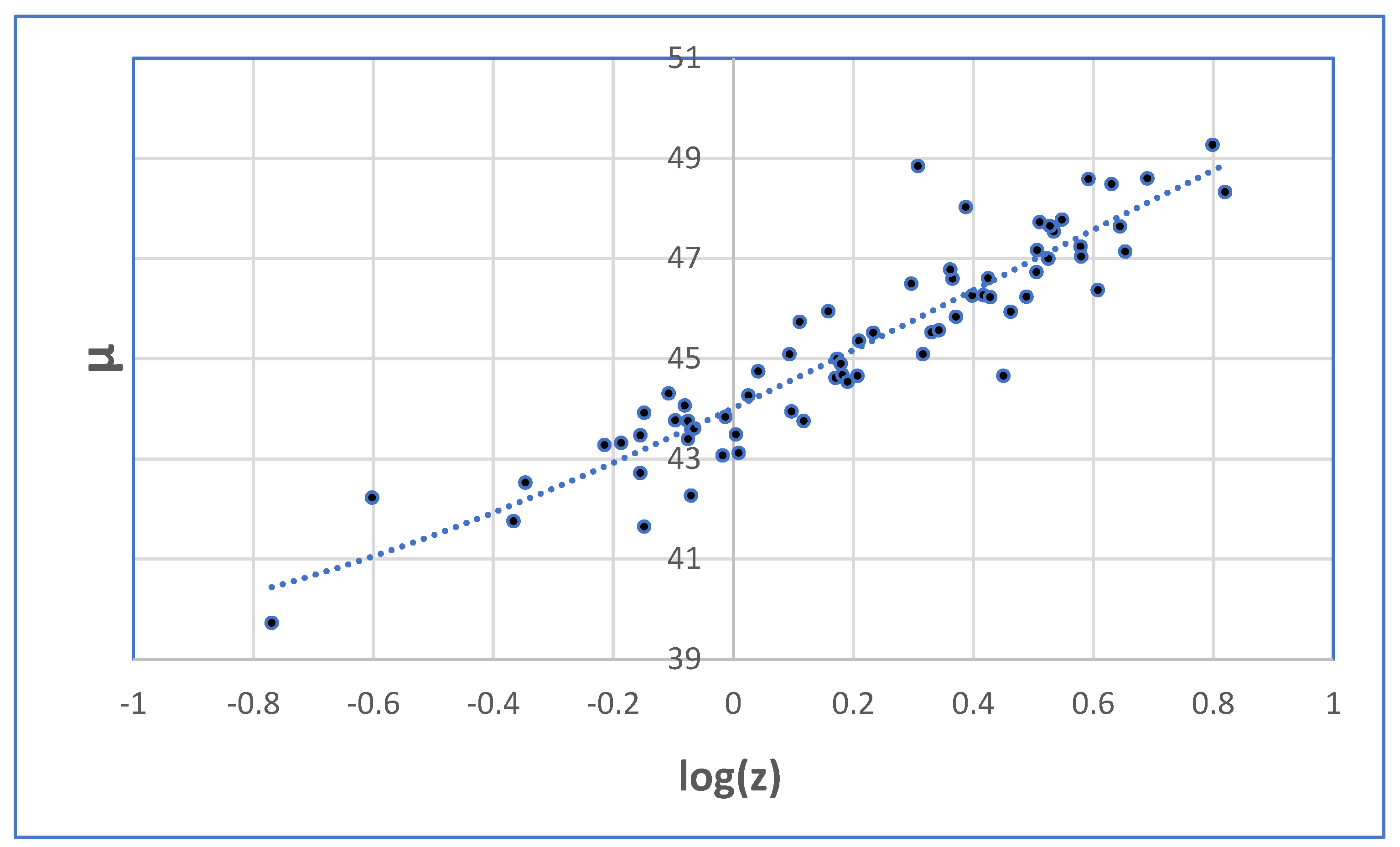
6.1. log(z)/µ Hubble Diagram

The log(z)/µ Hubble diagram is depicted in Figure 4.

As the data points for high RS show pronounced scatter, the variance of the fit reaches only R² = 0.8746, and cannot be improved by any other reasonable mathematical function. The fit coefficients are shown in Table 7.

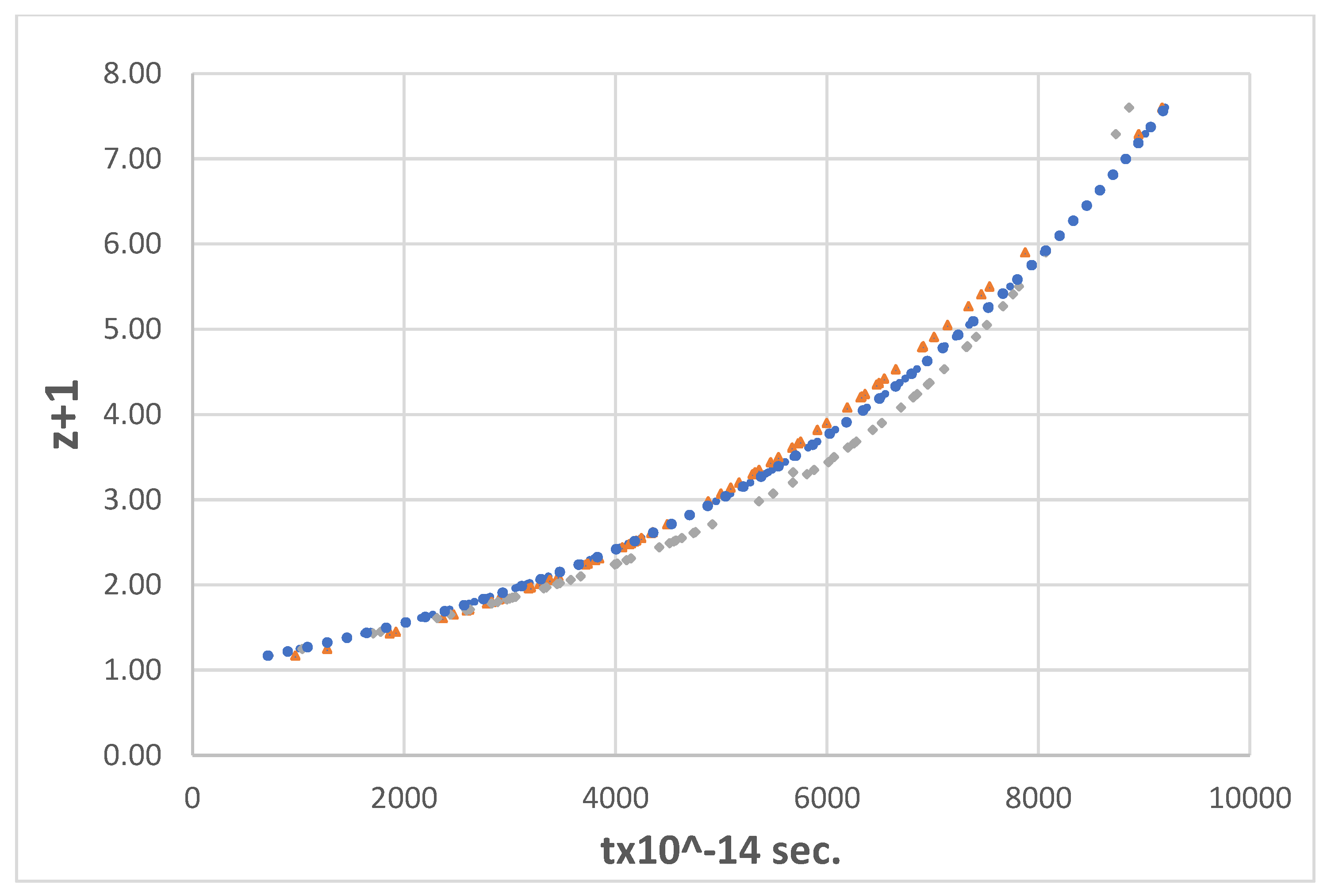
Figure 5 shows the linear t/(z+1) HDs inferred from the best fit coefficients of the observed data (squares) together with the corresponding exponential h^TL = 0.66 (dots) and the HD for h^CDM = 0.70 (triangles).

The GRB HD exhibits some irregular shape between h^TL = 0.66 and h^CDM = 0.7 with

χ^{2} = \sum_{i = 1}^{N} \frac{{(μ f i i, o b s . - μ T L, c a l c .)}^{2}}{μ T L, c a l c .} = 0.0196

and

χ^{2} = \sum_{i = 1}^{N} \frac{{(μ f i t, o b s . - μ C D M, c a l c .)}^{2}}{μ C D M, c a l c .} = 0.03028

(µfit,obs stands for calculated magnitudes inferred from the polynomial best-fit function, µTl calc. and µCDM calc. were calculated from h^TL = 0.66 for the TL and from Ώ_M = 0.287, w = -1 and h^CDM = 0.7 for the ΔCDM model, respectively.)

The result favours the TL model, but as can be seen from Figure 5, the deviation from the ideal exponential shape is too large to draw safe conclusions. A profile examination shows systematic deviations, especially at RS ≥ ~ 3–4, where data points are visible above the exponential line.

In summary, the ΔCDM model shows a poorer fit to the HD calculated on the basis of observed data, which suggests a somewhat better but still not correct portrayal of the TL model. No safe conclusion in favour of or against either of the competing models can be drawn from this result.

6.2. ln(z+1)/t Hubble Diagram

The linear ln(z+1)/t Hubble diagram is shown in Figure 6.

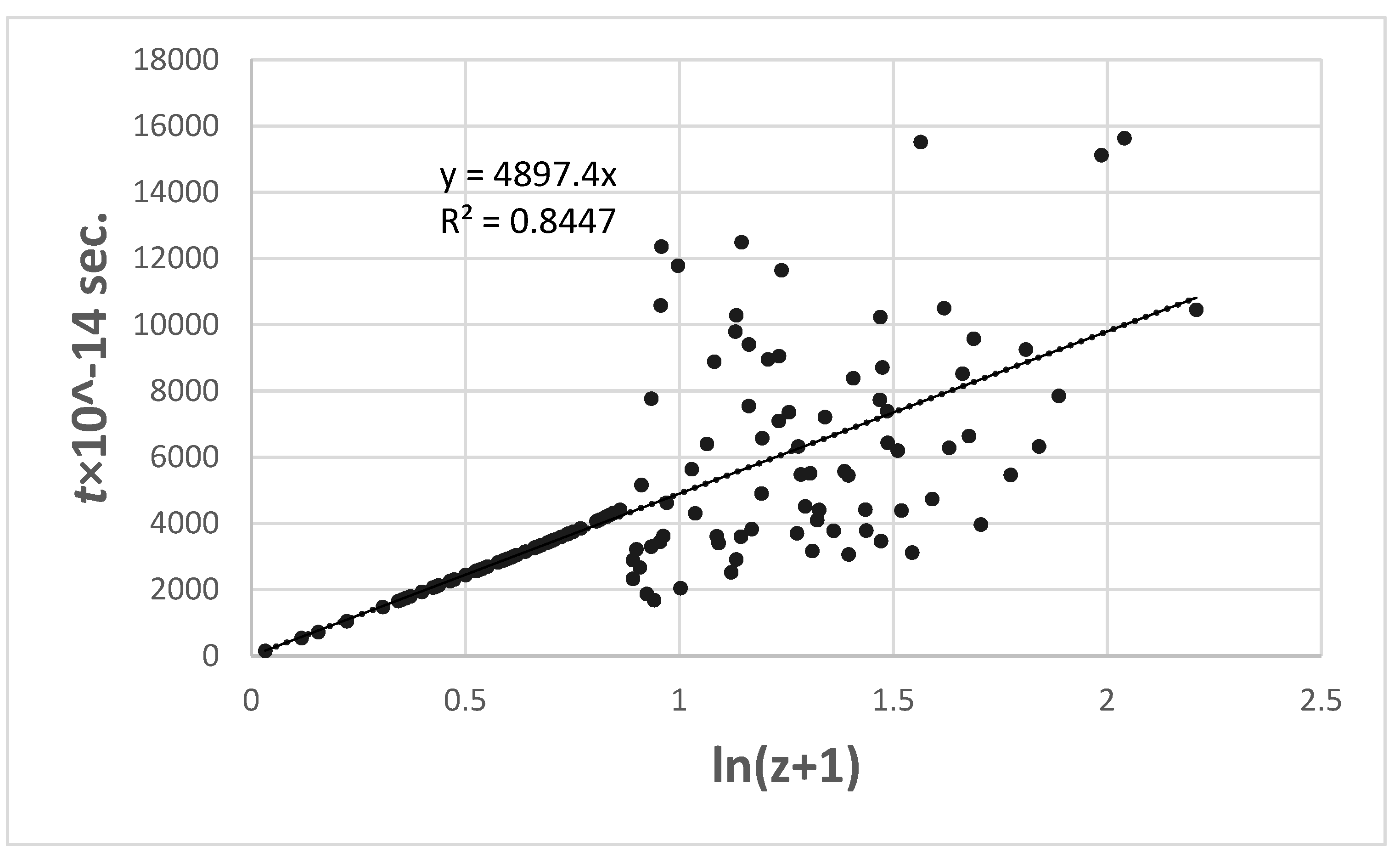
Despite the extensive scatter in the observed photon flight times even at values of z ≥ ~ 1.4, the ln(z+1)/t diagram is linear. Considering the quality of the data, it shows an astonishingly good variance of R² = 0.8447 that could only be worsened by fitting the observed data with higher-order polynomials. From Figure 6, the equation that describes the photon flight time/z relationship on the t×10^-14 scale that goes into the linear t/(z+1) diagram is

t = 4897 \times \ln (z + 1)

(10)

Figure 7 shows the corresponding t/ln(z+1) HD.

The linear HD has a perfect exponential slope, with h^TL = 0.63. This is in exceptionally good agreement with the expected value of h^TL = 0.632 obtained from model calculations, although it is in clear conflict with the presently accepted point of view that the TL model does not fit the observed RS/µ data. The conclusion from the outcome of the ln(z+1) t-test is that both the low RS SN1a data and the high RS GRB HDs for a TL cosmology give an adequately good fit to the observed data. From an unbiased examination of the data, we see that the TL model cannot be dismissed from further consideration.

7. Hubble Diagram for High RS GRBs, Data Sets d and e

7.1. log(z)/µ Hubble Diagram

The log(z)/µ Hubble diagram for data set d) is depicted in Figure 8. The fit variance reaches R² = 0.8553, an acceptable value given the considerable scatter. The fit coefficients are shown in Table 9.

Figure 9 shows the linear t/(z+1) HD inferred from the best fit coefficients of the observed data (squares), alongside the corresponding exponential h^TL = 0.68 (dots) and the HD for h^CDM = 0.70 (triangles). In the RS range of (z + 1) = 2 - 6 particularly, the disparities between the observed and reference HDs are evident even upon visual examination: the GRB HD shows poor agreement with the ΛCDM model, and the conformity with the TL model is also unconvincing.

χ^{2} = \sum_{i = 1}^{N} \frac{{(μ f i t, o b s . - μ C D M, c a l c .)}^{2}}{μ C D M, c a l c .} = 0.0469

χ^{2} = \sum_{i = 1}^{N} \frac{{(μ f i i, o b s . - μ T L, c a l c .)}^{2}}{μ T L, c a l c .} = 0.02891

(µfit,obs stands for calculated magnitudes inferred from the polynomial best-fit function, µTl calc. and µΛCDM calc. were calculated from h^TL = 0.68 for the TL and from Ώ_M = 0.287, w = -1 and h^CDM = 0.7 for the ΔCDM model, respectively.)

The result is clear: the ΛCDM model can be ruled out, while the deviation from the exponential line is smaller but still too large to draw safe conclusions.

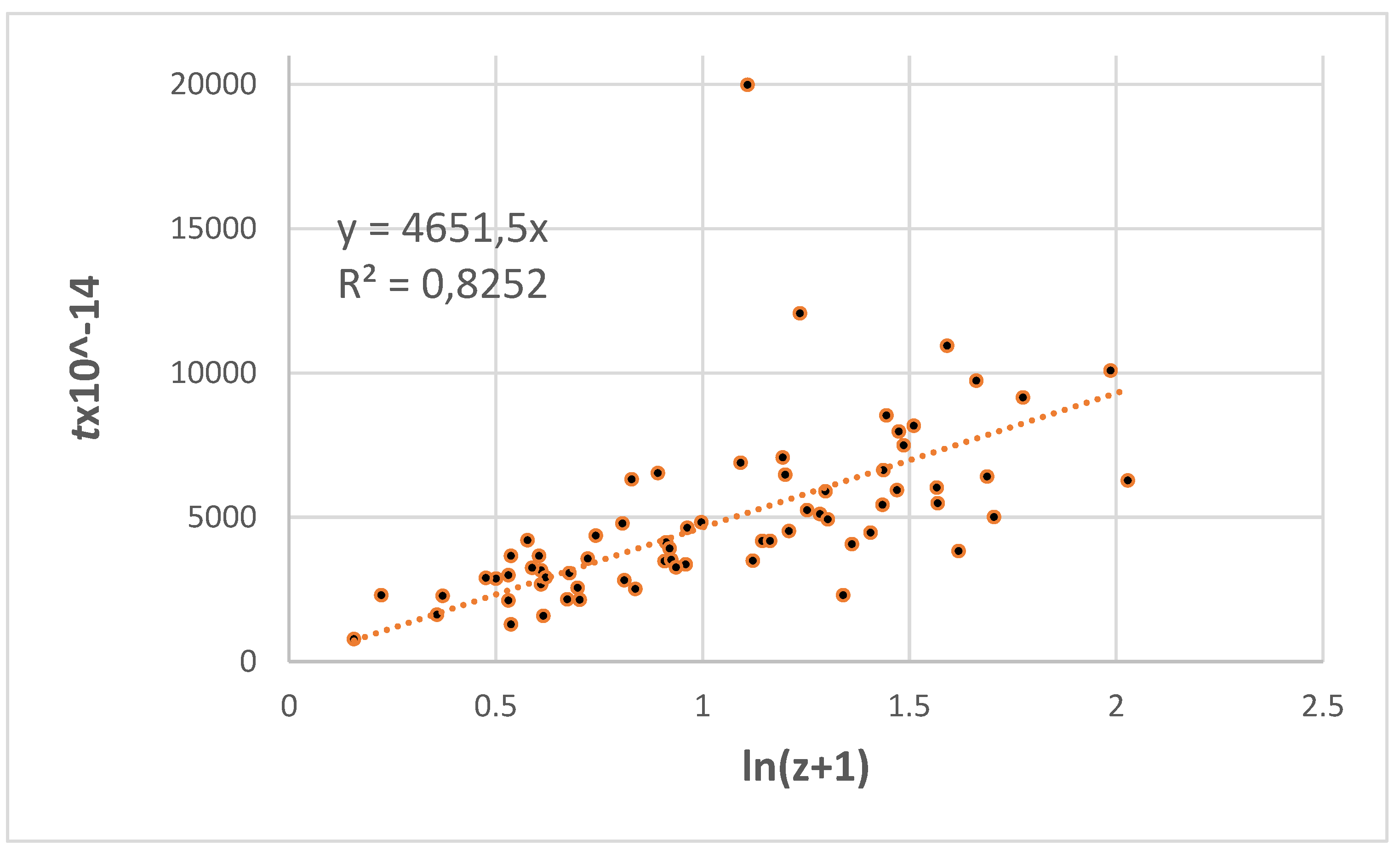
7.2. ln(z+1)/t Hubble Diagram

The linear ln(z+1)/t Hubble diagram is depicted in Figure 10. Despite the extensive scatter of the photon flight times, the ln(z+1)/t diagram is linear. Considering the quality of the data, the fit exhibits a remarkable variance of R² = 0.8252, which would only deteriorate if the observed data is fitted with higher-order polynomials. From Figure 10, the equation that describes the photon flight time/z relationship on the t×10^-14 scale, which goes into the linear t/(z+1) diagram, is t = 4651.5xln(z+1). Figure 11 depicts the corresponding t/(z+1) HD, illustrating its perfect exponential slope, with h^TL = 0.663, in clear conflict with the prevailing view that the TL model does not align with the observed RS/µ data.

8. Possible Source and Magnitude of Error

As can be seen in Figure 10 the burst at ln(z+1) = 1.1085 with tx10^14 = 19984 is obviously an outlier. The usual way to test the influence of an outlier on the shape of the HD is to compute the HD with and without the outlier. Results are summarized in Table 10 and shw that the burst at z = 2.03 with µ = 48.85 is an influential outlier. By removing this burst the slope of the HDs changes greatly from h^TL = 0.6634 to 0.6918 for data set d) and from 0.6677 to 0.6779 for data set e). As the number of data points increases, the outlier's influence becomes more moderate (data set e). Rather than removing this extreme outlier, substituting the uncalibrated Fid data point for the obviously problematic calibrated one yields more reliable results. The Fid data point, with µ = 47.93, is close to the bottom of the error limit for the calibrated data with 48.85±1.02. Thus, using the Fid data point is not arbitrary. Furthermore, a comparison of the Hubble constants calculated using the outlier (rows 1 and 2 in Table 10) and the Fid data point (rows 5 and 6 in Table 10) shows minimal differences, indicating that the magnitude of the Fid data point has only little impact on the overall result, which remains within an acceptable level of plausibility.

9. Discussion

The most noticeable result from the HD tests is that the prediction of the ΛCDM model with reference to the shape of the HD cannot be verified based on known high RS LGRB data. The linear log(z)/µ HD does not align with the data within acceptable error limits and can therefore be ruled out with a high degree of certainty. This finding is consistent with recent findings from Schokolov et al. (2022). Their analysis of data set (c) reveals that the standard CDM model does not match the observed z/µ data.

The cosmologically important result is that the shape of the HD exhibits an exponential slope, aligning well with data (b), (d) and (e), obtained using different calibration methods, such as Liu and Wang 2015, as well as the Dainotti relationship (Dainotti 2008). The numerical results are summarised in Table 10

The results from data sets (b), (d) and (e) are individually consistent in their statements regarding the e ponential slope of the HD. However, as shown in Paragraph 6.2 and Table 10, the derived Hubble constants are numerically different, ranging from h^TL = 0.64 for data set (b) to h^TL = 0.667 for data sets (c) and (d). (The corresponding expectation values for the equivocal CDM and TL models in the low RS range z < 1, as shown in Table 5, range from h^CDM = 0.70 for h^TL = 0.64 to h^CDM = 0.735 for h^TL = 0.667, and reflect the discrepancy between the default value of h = 0.70 and the considerably larger value of h = 0.735 advocated by Riess et al. It is speculated that this discrepancy stems from the variations in data calibration methods and is therefore not a contradiction.)

10. Conclusions

The most remarkable outcome of the HD test introduced in this analysis is that in the low RS range of z = 0.01–1.3, the HD is equivocal and permits no distinction, based on the data, between the ΛCDM and TL models. The HD can be equally well described with the parameter of the ΛCDM model as with the exponential function

z + 1 = e^{h^{T L} \times t (d)}

In the high RS ranges up to z = 8.1, regardless of the calibration method, the observed z/µ data conflict with the ΛCDM and favour the TL model for data sets (b), (d) and (e). The key question regarding the actual shape of the HD, as predicted by the ΛCDM or the exponential TL model, seems to lean in favour of the TL model, and the presented results show that excluding the TL model from further consideration is not justified.

Data availability

The author confirms that the data supporting the findings of this study are available within the article and the reference list.

References

Hubble E., 1929, Proc. Natl. Acad. Sci. U. S. A., 15, 168.
Sorrell W.H., 2009, Ap&SS, 323, 205.
Traunmüller H., 2014, Ap&SS, 350, 755.
Liu J., Wei H., 2015, Gen. Relativ. Gravit., 47,.
Amati L., D’Agostino R., Luongo O., Muccino M. & Tantalo M., 2018, MNRAS Lett., 486, L46.
Dainotti M., Cardone M.G. & Capociello V.F. 2008, MNRAS Lett., 391, L 79-L83.
Schaefer B.E., 2003, ApJ, 583, L67.
Schaefer B.E., 2003, ApJ, 583, L67.
Wei H., 2010, J. Cosmol. Astropart. Phys., 2010, 20.
Cardone M. G., Capociello V.F. & Dainotti M., 2009, Mon. Not. R. Astron. Soc. 400, 775-790 (2009).
Marosi L.A., 2013, Adv. Astron., 2013, 917104.
Marosi L.A., 2014, J. Mod. Phys., 5, 29.
Marosi L.A., 2016, Int. J. Astron. Astrophys., 6, 272.
Marosi L.A., 2019, Int. J. Astron. Astrophys., 9, 1.
Zwicky F., 1932, Proc. Natl. Acad. Sci. U. S. A., 15, 773.
Gupta R.P., 2019, Universe, 5, 102.
Shirokov S., Sokolov I., Lovyagin N.Y., Amati L. Baryshev Y.V., Sokolov V., Gorokhov V., 2020a, MNRAS, 496, 1530.
Shirokov S., Sokolov I.V., Vlasyuk V., Amati L., Sokolov V. & Baryshev Y.V. & 2020b, Astrophys. Bull., 75, 207.
Betoule M. et al., 2014, A&A, 568, A22.
Wang F.Y., Hu J.P., Zhang G.Q. & Dai Z.G., 2022 The Astrophysical Journal, 924,9 7 (11pp), 2022 January 10.
Vigoureux J.M., Vigoureux B. & Langlois M., 2014, arXiv:preprint arXiv:1411.3648.

Figure 1. log(z)/µ Hubble diagram for the 31 calculated z/µ data points.

Figure 2. ln(z+1)/t Hubble diagram for the 31 calculated z/d data points.

Figure 3. Linear HDs for the calculated data (dots) and for the log(z)/µ (triangles) and d/ln(z+1) (squares) models.

Figure 4. Log(z)/µ Hubble diagram of the observed GRB data.

Figure 5. h^CDM = 0.7 (triangles), best fit of the observed data (squares).

Figure 6. Linear HD on the t/(z+1) scale of the observed GRB data.

Figure 7. t/ln(z+1) HD for the observed GRB data.

Figure 8. Linear log(z)/µ HD.

Figure 9. triangles: observed line, squares: CDM with h = 0.7, dots: TL with h = 68.

Figure 10. linear ln(z+1)/tx10^-14 HD.

Figure 11. HD in the t/(z+1) presentation. h^TL = 0.6634.

Table 1. Descritive statistics from the considered DRB data sets.

Data set	(b)	(c)	(d)	(e)
No. of data points	138	193	69	69 +30
Data calibration method	Liu, Wei	Amati	Dainotti	Dainotti. Wang et al.
z range	0.031–8.1	0.03354–8.1	0.17-6.6	0.17-6.6
Data points z ⸖ 5	6	5	2	2
R²	0.8746	0.7848	0.8789	0.842
∑χ²(best fit:obs)	1.9193	5.1282	0.9225	1.2405
∑χ²/data point	0.0139	0.02657	0.01337	0.01257
Standard deviation	2.196	2.2256	1.9604	1.8314

Table 2. Fit parameters on the linear log(z)µ and ln(z+1)/t scales.

	Parameter 1	Parameter2	Parameter3	Parameter 0
log fit	0.1009	0.6274	6.3167	44.111
ln fit	−855.33	1366.6	4397.4	0

Table 3. Goodness of fit indicators the linear log(z)µ and ln(z+1)/t scales.

Fit coordinates	∑χ²µcalc: µ fit	R²	P test	Chiqu-test	F test
log(z)/µ	2.673×10^-5	1	0.9999985	1	0.9987774
ln(z+1)/t	1.810×10^-6	1	1	1	0.9987774

Table 4. Hubble constants and variances for the linear t/(z+1) HD.

Model	Calculated data	ln fit	log fit
h	0.6322	0.6322	0.6319
R²	0.99967	0.99967	0.99948

Table 5. Equivalent values for h^CDM and h^TL.

h^CDM	h^TL	h^TL/h^CDM
73	65.92	0.9031
70	63.22	0.9031
68	61.41	0.9031

Table 6. Comparison of ∑ χ2 values for h^CDM = 0.70, h^TL = 0.70 and the Best fit h^TL = 0 66 with the observed data in the RS range 0.031–8.1.

Model, calc. µ	h^CDM = 0.70	h^TL = 0.66	h^TL = 0.70
∑ χ² µ_obs/µ_calc	1.9415	1.9397	1.9923

Table 7. Fit coefficients for the log(z)/µ Hubble diagram.

Parameter 1	Parameter 2	Parameter 3	Parameter 0	R²
0.133	0.3156	5.8286	44.0533	0.8746

Table 9. Fit parameters on the linear log(z)/µ scale.

Parameter	1	2	3	0	R²
Data set d)	-0.5384	0.849	5.6176	44.011	0.8553

Table 10. comparison of data sets d) and e).

Data set	h^TL from ln(z+1)/t fit	∑χ² TL from µobs:µTL	∑χ² CDM 70 µobs:µCDM
(d) all data	0.6634	0.9692	0.9844
(e) all data	0.6677	1.3041	1.3271
(d) without outlier	0.6918	0.7752	0.8018
(e) without outlier	0.6779	1.1108	1.3271
(d) fid for z = 2.03	0.6602	0.8539	0.8721
(e) fid for z = 2.03	0.6619	1.1968	1.4065

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Alerts

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Hubble Diagram Test of SN1a Supernovae and High Redshift Gamma Ray Bursts: Data Analysis of the Log(z)/µ, ln(z+1)/T(d) and Linear Photon Flight Time T/(z+1) Scales. – Comparison of Observational Data with Model Calculations.

Abstract

Keywords:

Subject:

1. Introduction

2. Aims

3. Datasets and Methods

3.1. SN1a Supernovae

3.2. Choice of GRB Data

4. Data Processing

4.1. Data Conversion from µ to t(d) and Vice Versa

4.2. Goodness of Fit

4.3. Calculations of RS/µ Data

4.4. Data Presentation

5. Results

5.1. Equivocality of the SN1a Supernovae Hubble Diagram

6. Hubble Diagram for High RS GRBs, Data Set b

6.1. log(z)/µ Hubble Diagram

6.2. ln(z+1)/t Hubble Diagram

7. Hubble Diagram for High RS GRBs, Data Sets d and e

7.1. log(z)/µ Hubble Diagram

7.2. ln(z+1)/t Hubble Diagram

8. Possible Source and Magnitude of Error

9. Discussion

10. Conclusions

Data availability

References

MDPI Initiatives

Important Links

Subscribe