Optimized Dispatch of Regional Integrated Energy System Considering Wind Power Consumption in Low-temperature Environment

1. Introduction

With the intensification of the energy crisis, increasing the utilization rate of renewable energy and reducing fossil energy dependence has become an important research direction. Integrated regional energy systems have rapidly developed as an effective way to increase the utilization of renewable energy and reduce pollutant emissions [1]. Cogeneration units centered on Combined, Heating and Power (CHP) technology are capable of generating both electricity and heat and are used in a wide range of applications. As CHP units are often in heat-determined power operation in winter, the heat load is at its peak during the nighttime when the electric load is in the trough, and the system peaking capacity is smaller than that of conventional units, making it more prone to the phenomenon of wind abandonment [2].

In an integrated energy system, energy storage devices change load distribution in the space-time dimension and improve system stability and economy. Reference [3] based on the RIES optimal dispatch model including ground source heat pumps and energy storage, verified the effect of ground source heat pumps and energy storage devices on system economy. Reference [4] proposed a day-ahead optimization scheduling method based on park RIES based on the multi-energy coupling and energy conversion characteristics of cold, heat, electricity and gas, combined with the energy storage characteristics of the system. Reference [5] analyzes the energy storage capacity and economics of RIES from the perspective of integrated demand response and uncertainty. References [6,7] proposed the possibility of using shared energy storage instead of traditional energy storage to realize low-cost wind power consumption. However, none of the above literature takes into account the differences in the characteristics of the energy storage devices in RIES, such as the effect of charging and discharging power of the battery at low temperatures and the effect of the heat loss of the thermal storage tanks by the ambient temperature. Therefore, it is particularly important to consider the characteristics of energy storage devices under low temperature and other conditions for accurate scheduling of integrated energy systems. The RIES addresses the phenomena of wind power and photovoltaic uncertainty and large load peak-to-valley differences on the source and load side, which leads to the problems of impeded wind power and photovoltaic consumption and high integrated cost of dispatch. On the energy supply side, the current mainstream methods for dealing with the wind power and photovoltaic uncertainty problem include stochastic optimization and robust optimization. Reference [8] coordinates the robustness and economy of the system by flexibly adjusting the robust parameters to improve the system's consumption of wind power. Reference [9,10] established a stochastic optimization model of an integrated energy system containing electric vehicles, and simulated wind power output based on the scenario reduction technique with improved probabilistic distance, which improved the accuracy of the scheduling results. References [11,12] address the feature that robust optimization is only affected by the worst-case scenarios of uncertain input parameters, and the final results obtained are too conservative, and propose to deal with the uncertainty set with conditional value at risk (CVaR) theory to obtain a more economically efficient optimization scheme. On the energy demand side, reference [13] developed a tariff-based demand response optimization model based on RIES demand side characteristics. Reference [14] established an integrated energy system containing electricity-to-gas and energy storage devices based on gas-electricity joint demand response, and established a demand response optimization model based on electricity tariffs based on the characteristics of the energy demand side of RIES. Reference [15] developed an integrated energy system economic dispatch model for thermoelectricity integrated demand response (IDR) with the objective of minimizing the wind abandonment rate. However, these literatures are single consideration of the influence of source-side or load-side characteristics on the system operation, and do not consider the source and load sides comprehensively, so there is still room for further research in source-load coordinated optimal scheduling.

Aiming at the above problems, this paper proposes a coordinated optimization model of RIES based on fine energy storage and wind power consumption. Firstly, a fine energy storage model more in line with the low-temperature environment is established, and consideration is given to increasing the thermal load to safeguard the available capacity of the storage battery and the charge/discharge speed, and to improve the utilization rate of the energy storage system. Secondly, to address the uncertainty of wind power output on the energy supply side, the Latin hypercube-synchronous back generation elimination method is used to obtain more accurate wind power output based on the historical data of wind power output, and the CVaR theory is used to quantify the risk of revenue and enhance the system's ability to consume wind power. At the same time, the introduction of heat and power demand response mechanism on the load side cuts down the peak-to-valley difference of the system load and further improves the system's level of wind power consumption. After comprehensively considering the energy conversion characteristics of the source and load sides and the operation characteristics of the energy storage device, the model is solved using MATLAB to obtain the wind abandonment rate and operation scheme under the lowest operation cost. The example results show that compared with the traditional model, the RIES model based on fine energy storage and wind power consumption can effectively improve the level of wind power consumption and reduce the operating cost of the system.

2. Integrated Energy System Architecture

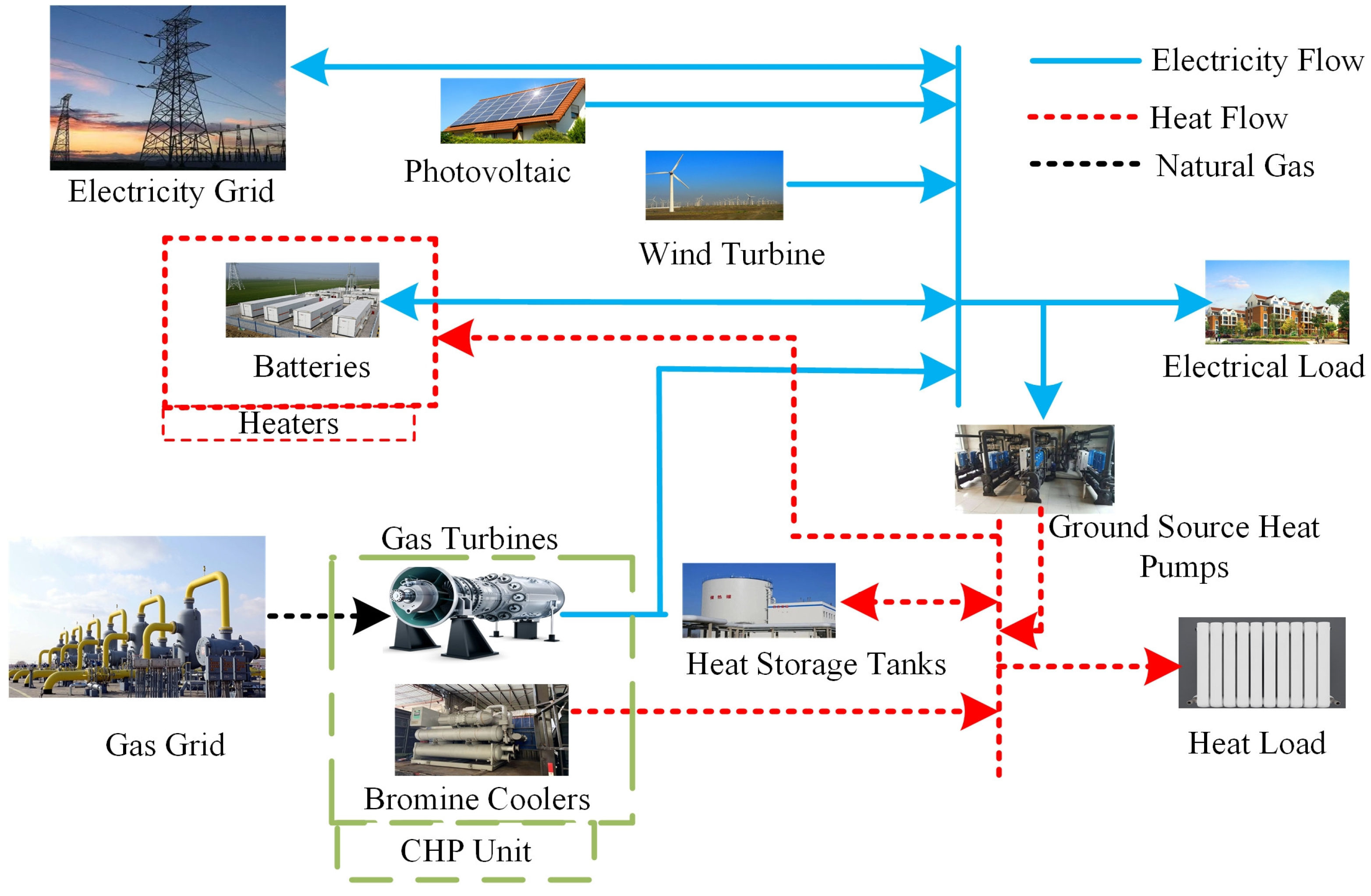
Due to the cold winter climate in the north, there is a high demand for heating. At the same time, the region is rich in geothermal energy, wind energy, solar energy ,and other renewable energy sources, which provides a good foundation for the application of ground source heat pumps and CHP in the region [16,17]. Compared with the traditional RIES which is limited to the independent operation of a single form of energy, this paper establishes a RIES containing integrated energy storage (IES) equipment, wind turbines (WT), photovoltaic (PV), ground source heat pumps (GSHP) and CHP units, with the structure shown in Figure 1, which is able to utilize and synergize the outputs of different forms of energy in a more effective way. The power load demand is met by the superior grid, wind turbines, photovoltaic power plants and cogeneration units; the heat load demand is met by the cogeneration units and ground-source heat pumps, and the energy storage equipment includes heat storage tank (HST) and IES to provide support for the heat and power loads. Considering that the actual available capacity of the IES is greatly affected by the temperature in winter, the working efficiency of the IES is guaranteed by increasing part of the thermal load.

2.1. CHP System

CHP systems are capable of delivering both heat and power at the same time. It converts high-quality heat from the combustion of natural gas into electricity and absorbs the waste heat to meet the heat load by using a bromine chiller, which usually consists of a bromine chiller(BC) and a gas turbine(GT)[18], and is mathematically modeled as follows:

$$P_{\mathrm{B},\mathrm{h}}(t)=Q_{\mathrm{G}}(t){\delta }_{\mathrm{B}}{\lambda }_{\mathrm{B},\mathrm{h}}$$

(1)

$$Q_{\mathrm{G}}(t)=P_{\mathrm{G}}{ }_{\mathrm{T}}(t)(1-{\beta }_{\mathrm{G}}-{\beta }_{\mathrm{l}})/{\beta }_{\mathrm{G}}$$

(2)

Where: $P_{\mathrm{B},\mathrm{h}}(t)$, $P_{GT}(t)$, $Q_{\mathrm{G}}(t)$ represent the heating power of BC and the electric power output and waste heat generated by GT at the moment t, respectively; ${\delta }_{\mathrm{B}}$, ${\lambda }_{\mathrm{B},\mathrm{h}}$, β_G, β_l are, in order, the recovery rate of the flue gas of BC, the heat production coefficient of the flue gas of BC, the power generation efficiency of GT, and the heat loss coefficient of GT.

2.2. Ground Source Heat Pump

Compared with traditional heating equipment such as electric boilers, ground source heat pumps convert a large number of low-temperature heat sources in the shallow ground into high-quality energy to meet heating and cooling needs with a small electrical energy input. The mathematical model for its heat supply is as follows:

$$P_{\mathrm{lh},\mathrm{l}}\left(t\right)={\lambda }_{\mathrm{l}}{P}_{\mathrm{lh}}\left(t\right)$$

(3)

Where: P_lh,l(t) and P_lh(t) are the heating power and power consumption of GSHP at the moment t, respectively; λ_l is its heating efficiency.

2.3. Fine Energy Storage Equipment

As an important component of RIES, energy storage equipment mainly includes thermal storage tanks and batteries. These devices absorb and release energy, thus reducing system fluctuations, especially suppressing fluctuations due to the uncertainty of new energy output. The charging and discharging mathematical model of the energy storage system is as follows:

$$S_{\mathrm{IES}}(t)=(1-{\eta }_{\mathrm{IES}})S_{\mathrm{IES}}(t-1)+(M{P}_{\mathrm{in}}(t){\lambda }_{\mathrm{in}}\mathsf{\Delta }t-N{P}_{\mathrm{out}}(t){\lambda }_{\mathrm{out}}\mathsf{\Delta }t)$$

(4)

$$M+N\le 1,M\subseteq \{0,1\},N\subseteq \{0,1\}$$

(5)

Where: SIES (t) is the remaining energy of the energy storage device at time t; $P_{\mathrm{in}}(t)$, $P_{\mathrm{out}}(t)$ represent the energy input and output power of the energy storage device at time t, respectively; ${\lambda }_{\mathrm{in}}$, ${\lambda }_{\mathrm{out}}$ represent the conversion efficiencies of the energy input and output of the energy storage device, respectively; M, N are Boolean variables that represent the state of the energy storage device, which is in a state of charging at M=1 and in a state of energy release at N=1; and ${\eta }_{\mathrm{IES}}$ is the energy loss coefficient of the energy storage device.

2.3.1. Battery Storage Model

The traditional energy storage model does not consider the effect of ambient temperature on the battery, but the actual usable capacity is related to the surface temperature of the battery [19,20], which is mathematically expressed as follows:

$$S_{\mathrm{IESN}}(t)=S_{\mathrm{EIESN}}[1+{\xi }_{\mathrm{a}}(T_{\mathrm{a}}(t)-T_{\mathrm{N}})]$$

(6)

Where: for the standard state of the rated capacity of the battery; for the battery surface temperature at the moment of t; for the standard state of the temperature, taking the value of 25 ℃.

The surface temperature of the battery is determined by its heat generation and heat dissipation during the working period, and its mathematical expression is as follows

$$\left\{\begin{array}{l}{T}_{\mathrm{a}}(t)=T_{\mathrm{a}}(t-1)+\frac{{\mathsf{\Phi }}_{\mathrm{in}}(t)-{\mathsf{\Phi }}_{\mathrm{out}}(t)}{K_{\mathrm{tep}}{S}_{\mathrm{ele}}}\\ {\mathsf{\Phi }}_{\mathrm{in},\mathrm{e}}(t)={\lambda }_{\mathrm{IES}}[M_{\mathrm{ele}}·P_{\mathrm{IES},\mathrm{in}}(t)+N_{\mathrm{ele}}·P_{\mathrm{IES},\mathrm{out}}(t)]\mathsf{\Delta }t\\ \\ {\mathsf{\Phi }}_{\mathrm{out},\mathrm{e}}(t)=K_{\mathrm{tep}}{S}_{\mathrm{ele}}(T_{\mathrm{a}}(t-1)-T_{\mathrm{evr}}(t))\end{array}\right.$$

(7)

Where: ${\mathsf{\Phi }}_{\mathrm{in},\mathrm{e}}(t)$, ${\mathsf{\Phi }}_{\mathrm{out},\mathrm{e}}(t)$ are the heat generation and dissipation of the battery at the moment of t; $P_{\mathrm{IES},\mathrm{in}}(t)$, $P_{\mathrm{IES},\mathrm{out}}(t)$ are the charging and discharging power of the battery at the moment of t; $M_{\mathrm{ele}}$, $N_{\mathrm{ele}}$ indicates the working state of the battery, $M_{\mathrm{ele}}$=1 when the battery is in the charging state, $N_{\mathrm{ele}}$=1 when the battery is in the discharging state; $T_{\mathrm{evr}}(t)$ for the ambient temperature at the moment of t; ${\xi }_{\mathrm{a}}$ for the capacity temperature coefficient; $S_{\mathrm{ele}}$ for the surface area of the battery; $K_{\mathrm{tep}}$ for the heat convection coefficient; ${\lambda }_{\mathrm{IES}}$ for the battery heat generation coefficient.

In addition, the service life of the battery is also affected by its charging and discharging rate. If the charge/discharge rate is too high, the service life will be seriously damaged. Therefore, the maximum charging and discharging power per hour should be limited to not more than 20% of the actual usable capacity [21], and its mathematical model is as follows:

$$\left\{\begin{array}{l}{P}_{\mathrm{IES},\mathrm{in}}(t)\le 0.2S_{\mathrm{IESN}}(t)/\mathsf{\Delta }t\\ P_{\mathrm{IES},\mathrm{out}}(t)\le 0.2S_{\mathrm{IESN}}(t)/\mathsf{\Delta }t\end{array}\right.$$

(8)

In order to improve the utilization of the battery in practical applications, this paper optimizes the problems that may occur in the energy storage process. Specific measures include the rational design of battery charging and discharging programs and artificially increasing the ambient temperature to increase the actual available capacity.

2.3.2. Model of Heat Storage Tank

The heat storage tank model consists of an atmospheric pressure hot water storage tank, a circulating pump and additional equipment such as a heat exchanger. In practice, due to the influence of the ambient temperature, there is a certain amount of heat loss in the heat storage tank, mainly the inner wall of the tank to transfer heat and the outer surface of the tank to the surrounding air to emit heat [22,23]. The mathematical model of heat storage tank storage and heat release is as follows:

$$\left\{\begin{array}{l}{S}_{\mathrm{LES}}(t)={\eta }_{\mathrm{wat}}m{T}_{\mathrm{LES}}(t)\\ T_{\mathrm{LES}}(t)=T_{\mathrm{LES}}(t-1)+\frac{{\mathsf{\Phi }}_{\mathrm{in},\mathrm{w}}(t)-{\mathsf{\Phi }}_{\mathrm{out},\mathrm{w}}(t)}{K_{\mathrm{wat}}{S}_{\mathrm{wat}}}\\ {\mathsf{\Phi }}_{\mathrm{in},\mathrm{w}}(t)=\left(H_{\mathrm{dis}}(t){\omega }_{\mathrm{dis}}-\frac{H_{\mathrm{ch}}(t)}{{\omega }_{\mathrm{ch}}}\right)\mathsf{\Delta }t\\ {\mathsf{\Phi }}_{\mathrm{out},\mathrm{w}}(t)=K_{\mathrm{wat}}{S}_{\mathrm{wat}}(T_{\mathrm{LES}}(t-1)-T_{\mathrm{evr}}(t))\end{array}\right.$$

(9)

Where: $S_{\mathrm{LES}}(t)$ is the heat storage capacity of the heat storage tank at time t; ${\eta }_{\mathrm{wat}}$ is the specific heat capacity of water; m is the mass of hot water in the heat storage tank; $K_{\mathrm{wat}}$ and $S_{\mathrm{wat}}$ are the integrated thermal convection coefficient and surface area of the heat storage tank, respectively; ${\mathsf{\Phi }}_{\mathrm{in},\mathrm{w}}(t)$ and ${\mathsf{\Phi }}_{\mathrm{out},\mathrm{w}}(t)$ are the heat input and heat loss from the heat storage tank, respectively; $H_{\mathrm{ch}}(t)$ and $H_{\mathrm{dis}}(t)$ are the storage and discharge thermal power of the heat storage tank, respectively; ${\omega }_{\mathrm{ch}}$ and${\omega }_{\mathrm{dis}}$ are the storage and discharge efficiencies of the heat storage tank, respectively.

3. Combined Heat and Power Demand Response Mechanism

3.1. Electric Load Demand Response

A price-based DR (PBDR) model is established based on the price-based demand response mechanism. Through PBDR, the demand side electricity consumption is regulated so as to effectively realize peak shifting and valley filling, and to reduce the peak pressure of the system [24,25]. The demand elasticity of consumer load is as follows:

$$M_{t_1,t_2}=\frac{\mathsf{\Delta }{K}^{{\mathrm{t}}_1}}{K_0^{{\mathrm{t}}_1}}·\frac{C_0^{{\mathrm{t}}_2}}{\mathsf{\Delta }{C}^{{\mathrm{t}}_2}}\left\{\begin{array}{l}{M}_{{\mathrm{t}}_1{,\mathrm{t}}_2}\ge 0,t_1\ne t_2\\ M_{{\mathrm{t}}_1}{ }_{{,\mathrm{t}}_2}\le 0,t_1=t_2\end{array}\right.$$

(10)

Where: is the amount of electric load at t1 before taking demand response; is the change of electric load at t1 after taking demand response; is the electric price at t2 before taking demand response; is the change of electric price at t2 after taking demand response; is the cross-elasticity coefficient when t1 ≠ t2; and is the self-elasticity coefficient when t1=t2. After the introduction of the PBDR model, the change amount of electric load is as follows:

$$\left[\begin{array}{l}\mathsf{\Delta }{K}^1/K_0^1\\ \mathsf{\Delta }{K}^2/K_0^2\\ ⋮\\ \mathsf{\Delta }{K}^{24}/K_0^{24}\end{array}\right]=\left[\begin{array}{l}{M}_{11}\cdots {\mathrm{M}}_{124}\\ M_{21}\cdots {\mathrm{M}}_{224}\\ ⋮\cdots ⋮\\ M_{241}\cdots {\mathrm{M}}_{2424}\end{array}\right]\left[\begin{array}{l}\mathsf{\Delta }{C}^1/C_0^1\\ \mathsf{\Delta }{C}^2/C_0^2\\ ⋮\\ \mathsf{\Delta }{C}^{24}/C_0^{24}\end{array}\right]$$

(11)

With the introduction of the PBDR model, the magnitude of the electrical load at time t is as follows:

$$K_{\mathrm{load},\mathrm{e}}^t=K_0^t(1+\mathsf{\Delta }{K}^t/K_0^t)$$

(12)

3.2. Heat Load Demand Response

The heat load of a residential area consists of two parts: domestic hot water and heating heat load. The heating heat load is more elastic and accounts for a higher proportion in the total heat load, while domestic hot water is a rigid load with little change and accounts for a smaller proportion in the total heat load. In order to accurately assess the impact of heat load on wind power consumption in RIES, only analyzes and calculates the heating heat load [26]. The current outdoor temperature and the expression for the relationship between the required thermal power and the amount of change in the indoor temperature of the house are as follows:

$$\left\{\begin{array}{l}{P}_{\mathrm{l},\mathrm{h}}(t)=\frac{N_0}{R}(\frac{T_{\mathrm{i}}(t+1)-e^{-\mathsf{\Delta }t/\tau }{T}_{\mathrm{i}}(t)}{1-e^{-\mathsf{\Delta }t/\eta }}-T_{\mathrm{o}}(t))\\ \eta =R{C}_0\end{array}\right.$$

(13)

Where: $P_{\mathrm{l},\mathrm{h}}(t)$ represents the thermal power required in the room at the moment t; $N_0$ is the number of heating households in the residential area; $C_0$ is the air heat capacity in the room; R is the equivalent thermal impedance of the house; $T_{\mathrm{i}}(t)$, $T_{\mathrm{o}}(t)$ are the indoor and outdoor temperatures of the house at the moment t.

Due to the human body's ambiguity in perceiving temperature changes in the surrounding environment, when the indoor temperature changes in a slow and small range, it does not cause discomfort. In order to assess the degree of living comfort, reference [27] used the Predicted Mean Vote (PMV) as a quantitative indicator. This literature states that when ${\gamma }_{\mathrm{PMV}}$ is between -0.5 and 0.5, the comfort level of the inhabitants is not affected. Based on the above, the constraints on indoor temperature are as follows:

$$T_{\mathrm{i},\min }\le T_{\mathrm{i}}(t)\le T_{\mathrm{i},\max }$$

(14)

Where: $T_{\mathrm{i},\max }$ and $T_{\mathrm{i},\min }$ are the maximum and minimum indoor temperatures, respectively.

4. RIES Coordinated Optimization Model Considering CVaR

4.1. Uncertain Scene Selection

In this paper, using historical wind power output data, the kernel density estimation method is used to establish the actual probability density distribution function of the prediction error of wind power output at each scheduling moment, and Latin hypercubic sampling is applied to obtain the set of prediction error samples at each scheduling time point of the system [28]. In order to improve the computational efficiency, this paper adopts the synchronized back generation elimination method to cut down the scenes and get the corresponding probability values. Let the set of scenes be $W_s=\left\{W_{s,0},W_{s,1},W_{s,t},W_{s,T}\right\}$, where $W_{\mathrm{s},t}$ is the outgoing value of scene s at time t, and the sum of the probability of occurrence of each scene is 1. The expressions for the distances between the different scenarios are as follows:

$$D(W_{\mathrm{s}},W_{\mathrm{j}})={[{\displaystyle \sum _{t=1}^T(W_{\mathrm{s}}(t)}-W_{\mathrm{j}}(t))}^2{]}^{\frac{1}{2}}$$

(15)

In order to make the sample set better approximate the original scene set, the paper adopts the scene cutting technique to obtain multiple scene sets with corresponding probabilities by clustering similar scenes. At the same time, it is also necessary to satisfy the minimization of the probability distance between the cut scene sets. The mathematical expression is as follows:

$$\min {\displaystyle \sum _{\mathrm{s}\in \mathrm{J},\mathrm{j}\in \mathrm{J}}^{T}D(W_{\mathrm{s}},W_{\mathrm{j}}})$$

(16)

4.2. CVaR Overview

CVaR is developed from Value at Risk (VaR), which represents the worst possible loss that a portfolio can suffer at a certain confidence level [29]. Specifically, assuming that the decision variable is u, the uncertainty variable is v and its probability density function is R(v), the loss function of u is S(u, v); then when u is fixed, the loss function S(u, v) caused by the loss function S(u, v) does not exceed the threshold θ of the cumulative distribution function is as follows:

$$\pi (u,\theta )={\displaystyle {\int }_{S(u,v)\le \theta }^{ }R(v)dv}$$

(17)

At a specific confidence level α, VaR represents the maximum loss of revenue that RIES may face in a future dispatch cycle, which is mathematically modeled as follows:

$$f_{\mathrm{VaR}}(u)=\min \{\theta :\pi (u,v)\ge \alpha \}$$

(18)

CVaR is a measure of the average return loss of RIES in the event that a given VaR value is exceeded in the system return. Its mathematical model can be expressed as follows:

$$f_{\mathrm{CVaR}}(u)=\frac{1}{1-\alpha }{\displaystyle {\int }_{S\left(u,v\right)\ge f_{\mathrm{VAR}(u)}}^{ }S(u,v)R(v)dv}$$

(19)

Considering that Equation (18) is more difficult to calculate CVaR directly, a simple calculation method is proposed as follows:

$$f_{\mathrm{CVaR}}(u)=\min \left\{\theta +\frac{1}{1-\alpha }\left.{\displaystyle \sum _{S=1}^S\max \{S\left(u,v\right)-\theta },0\right\}\right.$$

(20)

4.3. Objective Function

Due to the uncertainty of wind turbine output, there is a potential risk in the economic dispatch scheme. In order to comprehensively consider the performance of the model in different operating environments, this paper adopts the conditional value at risk (CVaR) to quantify the risk of returns in various situations [30,31]. The RIES coordination optimization model is established with the objective function of minimizing the total cost of RIES operation, which is shown as follows:

$$\left\{\begin{array}{l}\min f=\beta f_{\mathrm{EX}}+(1-\beta )f_{\mathrm{CVaR}}\\ f_{\mathrm{EX}}={\displaystyle \sum _{S=1}^S{P}_S·f_S}\\ f_{\mathrm{CVaR}}(x)=\theta +\frac{1}{1-\alpha }{\displaystyle \sum _{S=1}^S{P}_{\mathrm{S}}·\max \{f_{\mathrm{S}}-\theta },0\}\\ f_{\mathrm{S}}={\displaystyle \sum _{t=1}^T{C}_{\mathrm{w}}^S(t)+C_{\mathrm{grid}}^S(t)+C_{\mathrm{e}}^S(t)+C_{\mathrm{fu}}^S(t)+C_{\mathrm{wt}}^S(t)}\end{array}\right.$$

(21)

Where: f is the total economic cost of system operation; f_CVaR is the CVaR cost; f_EX is the expected cost; θ is the auxiliary variable; α is the confidence level; β is the weighting coefficient; P_S is the corresponding probability of scenario S; S is the number of scenarios; T is the period of scheduling; and $C_{\mathrm{w}}^S\left(t\right)$,$C_{\mathrm{grid}}^S\left(t\right)$,$C_{\mathrm{e}}^S\left(t\right)$,$C_{\mathrm{fu}}^S\left(t\right)$,$C_{\mathrm{wt}}^S\left(t\right)$ are the Operation and maintenance (O&M) cost, the cost of power interaction with the superior grid, the cost of environmental cost with the superior grid, the cost of gas purchased with the superior grid, and the cost of wind abandonment with the superior grid, at the time t under scenario S, respectively.

• O&M costs;

• The O&M costs consist of the operation and maintenance costs of controllable units, new energy units and energy storage equipment, which are expressed as follows:

  $$C_{\mathrm{w}}^S(t)={\displaystyle \sum _{i=1}^K{P}_{\mathrm{a}}^{{ }_S}(t)W_{\mathrm{a}}}+{\displaystyle \sum _{j=1}^{N_1}{P}_{\mathrm{b}}^{{ }_S}(t)W_{\mathrm{b}}}+{\displaystyle \sum _{n=1}^{N_2}\left|P_{\mathrm{ES},\mathrm{n}}^{{ }_S}(t)\right|}{W}_{\mathrm{n}}$$

  (22)
• Where: $P_{\mathrm{a}}^{{ }_S}(t)$, $P_{\mathrm{b}}^{{ }_S}(t)$, $P_{\mathrm{ES},\mathrm{n}}^{{ }_S}(t)$ are the output power per unit O&M cost of controllable unit a, renewable energy machine b and energy storage device n at moment t under scenario S, and $W_{\mathrm{a}}$ , $W_{\mathrm{b}}$ , $W_{\mathrm{n}}$ are the unit O&M cost per unit of controllable unit a, renewable energy machine b and energy storage device n at moment t under scenario S, respectively.

• Electricity Interaction Costs;

3.

The cost of electricity interaction represents the sum of the cost of electricity purchased by the RIES from the main grid and the benefit of electricity sold to the main grid, expressed as follows:

4.

$$C_{\mathrm{grid}}^S(t)=L_{{ }_{\mathrm{g}}}^{ }(t)·\max \{P_{{ }_{\mathrm{d}}}^S(t),0\}-L_{\mathrm{s}}^{ }(t)·\max \{-P_{\mathrm{d}}^S(t),0\}$$

(23)

5.

Where: $L_{{ }_{\mathrm{g}}}^{ }(t)$ and $L_{\mathrm{s}}^{ }(t)$ represent the prices at which the grid makes power purchases and sells power at moment t, respectively; $P_{{ }_{\mathrm{d}}}^S(t)$ denotes the power on the contact line of the grid at moment t under scenario S, which is greater than 0 for power purchases and less than 0 for power sales.

• Environmental costs;

6.

The environmental costs represent the GHG emissions emitted during the operation of the controllable units and the GHG treatment costs caused by purchasing electricity from the main grid, which are specified as follows:

$$C_{\mathrm{e}}^S(t)={\displaystyle \sum _{m=1}^{\mathrm{M}}{\lambda }_m[E_m{P}_{\mathrm{a}}^S(t)+E_m{P}_{\mathrm{d},\mathrm{b}}^S(t)]}$$

(24)

7.

Where: $P_{\mathrm{d},\mathrm{b}}^S(t)$ is the power purchased by the system at moment t under scenario S; Em and λm are the share coefficient of the mth greenhouse gas and the treatment cost, respectively; and M is the type of greenhouse gas.

• Wind abandonment costs;

8.

The cost of maintaining the wind turbine system during the period of wind abandonment is the cost of wind abandonment, which is expressed as follows:

$$C_{\mathrm{wt}}^S(t)=P_{\mathrm{wt}}^S(t)D_{\mathrm{wt}}$$

(25)

9.

Where: $P_{\mathrm{wt}}^S(t)$and $D_{\mathrm{wt}}$ are the abandoned wind power and unit abandoned wind cost at moment t under scenario S, respectively.

• Cost of gas purchases;

10.

The cost of purchasing gas for the CHP system is the cost of purchasing gas, which is specifically expressed as:

11.

$$C_{\mathrm{fu}}^S(t)=\frac{P_{\mathrm{a}}^S(t)}{{\beta }_{\mathrm{G}}}·\frac{\mathsf{\Delta }t}{L_{{\mathrm{CH}}_4}}{D}_{{\mathrm{CH}}_4}$$

(26)

12.

Where: $L_{{\mathrm{CH}}_4}$ and $D_{{\mathrm{CH}}_4}$ are the average calorific value and gas price of the gas, respectively.

4.4. Restrictive Condition

Considering the operating parameters of the various devices, the RIES needs to satisfy the following constraints.

• Electrical and thermal power balance constraints;

  $$\left\{\begin{array}{r}{K}_{{ }_{\mathrm{load},\mathrm{e}}}^{ }(t)+P_{{ }_{\mathrm{lh}}}^S(t)=P_{{ }_{\mathrm{GT}}}^S(t)+P_{\mathrm{WT}}^S(t)+\\ P_{{ }_{\mathrm{d}}}^S(t)+P_{{ }_{\mathrm{PV}}}^S(t)+P_{{ }_{\mathrm{IES}}}^S(t)\\ P_{{ }_{\mathrm{l},\mathrm{h}}}^S(t)=P_{\mathrm{BC},\mathrm{h}}^S(t)+P_{{ }_{\mathrm{lp},\mathrm{h}}}^S(t)+H_{\mathrm{in}}^S(t)\end{array}\right.$$

  (27)

Where: $K_{{ }_{\mathrm{load},\mathrm{e}}}^{ }(t)$ and $P_{{ }_{\mathrm{l},\mathrm{h}}}^S(t)$ are the power of the system electrical and thermal loads, respectively.

• Controllable unit operating constraints;

  $$\left\{\begin{array}{l}{P}_{\mathrm{a},\min }\le P_{{ }_{\mathrm{a}}}^S(t)\le P_{\mathrm{a},\max }\\ -{\lambda }_{i,\min }\mathsf{\Delta }t\le P_{{ }_{\mathrm{a}}}^S(t)-P_{{ }_{\mathrm{a}}}^S(t-1)\le {\lambda }_{\mathrm{i},\max }\mathsf{\Delta }t\end{array}\right.$$

  (28)

Where: ${\lambda }_{\mathrm{i},\max }$, ${\lambda }_{i,\min }$ are the upper and lower limits of the climbing rate of controllable unit i, respectively; $P_{\mathrm{a},\max }$, $P_{\mathrm{a},\min }$ are the upper and lower limits of the output force of controllable unit a, respectively.

• Interactive power constraints with the higher grid;

  $$P_{\mathrm{d},\min }\le P_{{ }_{\mathrm{d}}}^S(t)\le P_{\mathrm{d},\max }$$

  (29)

Where: $P_{\mathrm{d},\max }$, $P_{\mathrm{d},\min }$are the maximum and minimum values of grid interaction power.

• Wind power output constraints

  $$\left\{\begin{array}{l}0\le P_{\mathrm{WT}}^S(t)\le P_{\mathrm{ut}}^S(t)\\ \frac{P_{\mathrm{WT}}^S(t)}{P_{\mathrm{ut}}^S(t)}\le h_{\mathrm{ut}}\end{array}\right.$$

  (30)

Where: $P_{\mathrm{WT}}^S(t)$ and $P_{\mathrm{ut}}^S(t)$ denote the actual and predicted power of wind power at moment t under scenario S, respectively, and $h_{\mathrm{ut}}$ is the minimum rate of wind power consumption.

• Energy storage device constraints

  $$\left\{\begin{array}{l}{P}_{{ }_{\min }}^S(t)\le P_{{ }_{\mathrm{IES}}}^S(t)\le P_{{ }_{{ }_{\max }}}^S(t)\\ E_{{ }_{\min }}^S(t)\le E_{{ }_{\mathrm{IES}}}^S(t)\le E_{\max }^S(t)\\ E_{{ }_{\mathrm{IES}}}^S(0)=E_{{ }_{\mathrm{IES}}}^S(24)\end{array}\right.$$

  (31)

Where: $P_{{ }_{{ }_{\max }}}^S(t)$and $P_{{ }_{\min }}^S(t)$ are the maximum and minimum values of the transmission power of the energy storage device at moment t under scenario S within the constraints; $E_{\max }^S(t)$and $E_{{ }_{\min }}^S(t)$ are the maximum and minimum available energy storage capacity of the energy storage device at moment t under scenario S.

• Electric load demand response constraints

  $$\left\{\begin{array}{l}{\displaystyle \sum _{t=1}^{24}{K}_{\mathrm{up}}^S(t)}={\displaystyle \sum _{t=1}^{24}{K}_{\mathrm{down}}^S(t)}\\ 0\le K_{\mathrm{up}}^S(t)\le {\delta }_{\mathrm{up}}·K_{{ }_{\mathrm{load},\mathrm{e}}}^{ }(t)\\ 0\le K_{\mathrm{up}}^S(t)\le {\delta }_{\mathrm{down}}·K_{{ }_{\mathrm{load},\mathrm{e}}}^{ }(t)\end{array}\right.$$

  (32)

Where: $K_{\mathrm{up}}^S(t)$ and $K_{\mathrm{down}}^S(t)$ denote the amount of load transfer in and out at moment t under scenario S, respectively; ${\delta }_{\mathrm{up}}$ and ${\delta }_{\mathrm{down}}$ are the proportions of the maximum upward and maximum downward load transfers, respectively.

5. Calculus Analysis

5.1. Parameterization

In order to verify the RIES model in the paper in terms of the economy of system operation and scheduling and the timeliness of wind power consumption, the paper sets up the simulation of the RIES coordinated optimization model in the following four scenarios for verification. Scenario 1 is the traditional RIES model without considering demand response and battery heating; Scenario 2 is the RIES model with fine energy storage, without considering demand response and battery heating; Scenario 3 is the RIES model with fine energy storage, considering demand response and battery heating; Scenario 4 is the RIES model with fine energy storage, considering demand response and battery heating; Scenario 4 is the RIES model with fine energy storage, considering demand response and battery heating; Scenario 4 is the RIES model with fine energy storage, considering demand response and battery heating; Scenario 4 is the RIES model with fine energy storage, considering demand response and battery heating; where scenario 4 is the model proposed in the paper. The model parameters are taken as confidence level α=0.85 and weighting factor β=0.9. 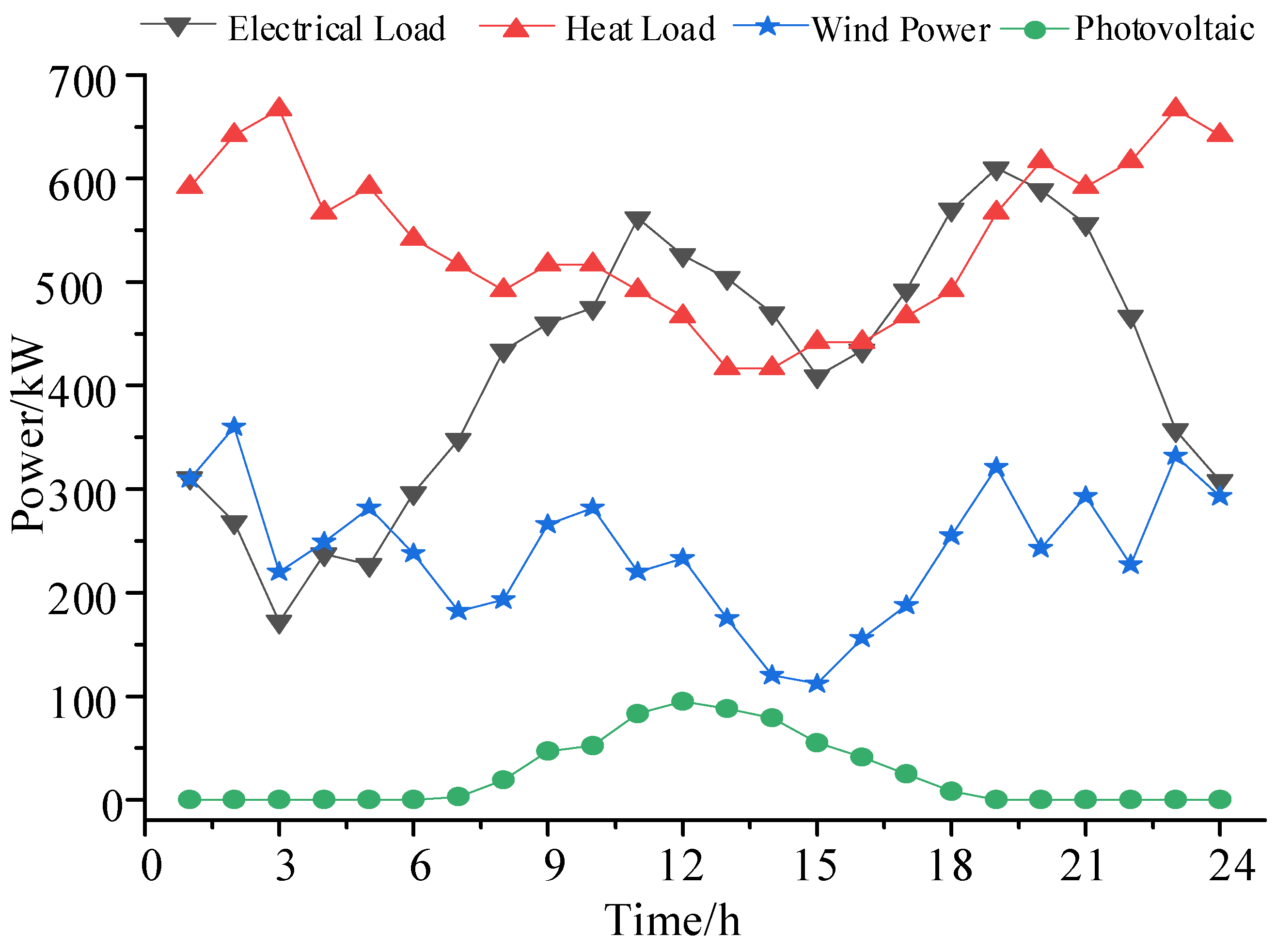The parameters of the energy storage system are shown in Table 1, and the pollutant treatment cost and unit operation parameters are shown in Table 2 and Table 3. 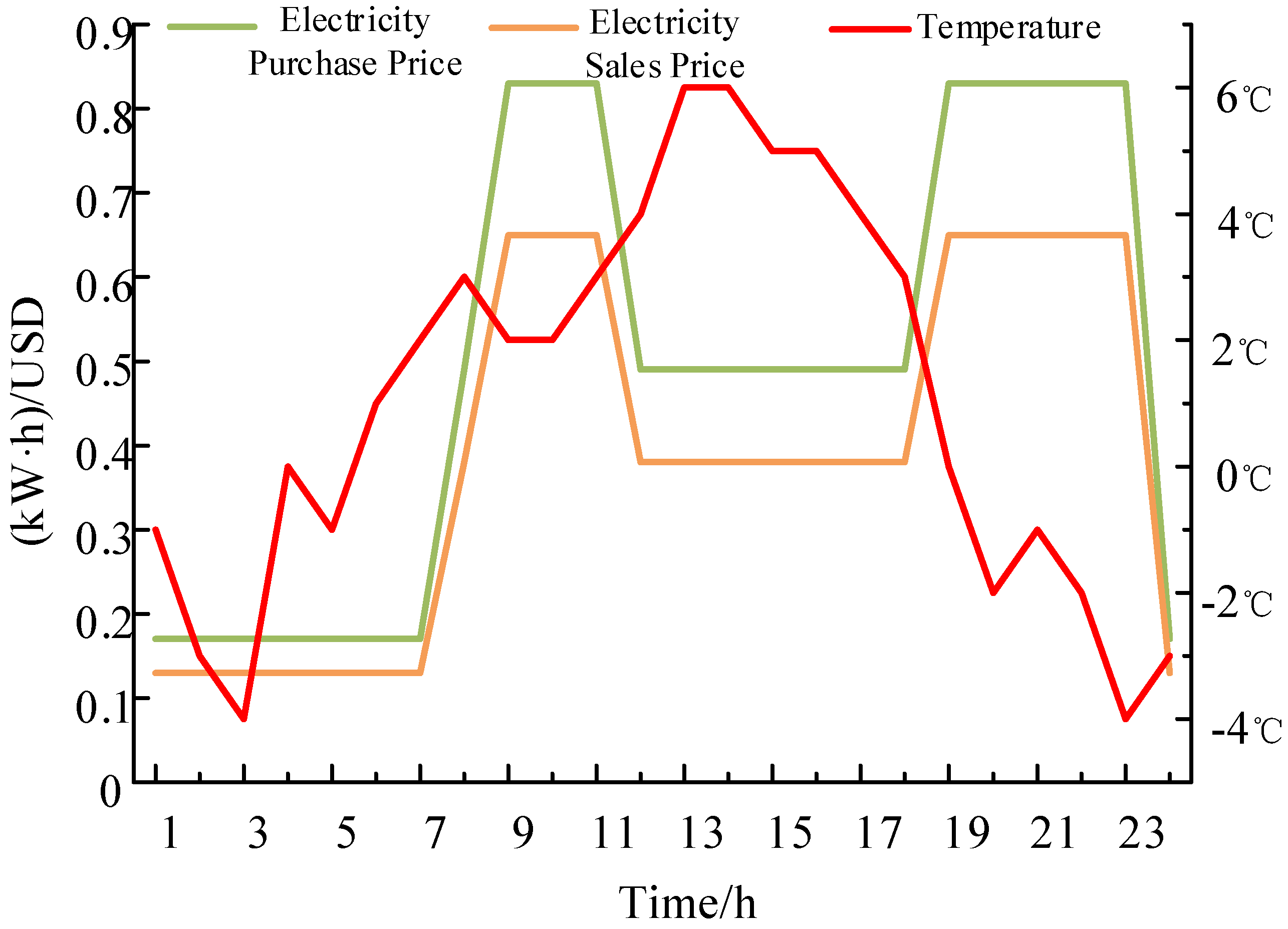The forecast data of PV, wind power and electric heat loads are shown in Figure 2, and the temperature and the purchase and sale price of electricity are shown in Figure 3. Taking the economy of system optimization operation and the timeliness of wind power consumption as the goal, the MATLAB platform is used to build the RIES coordinated optimization operation model and call the CPLEX solver to solve the model.

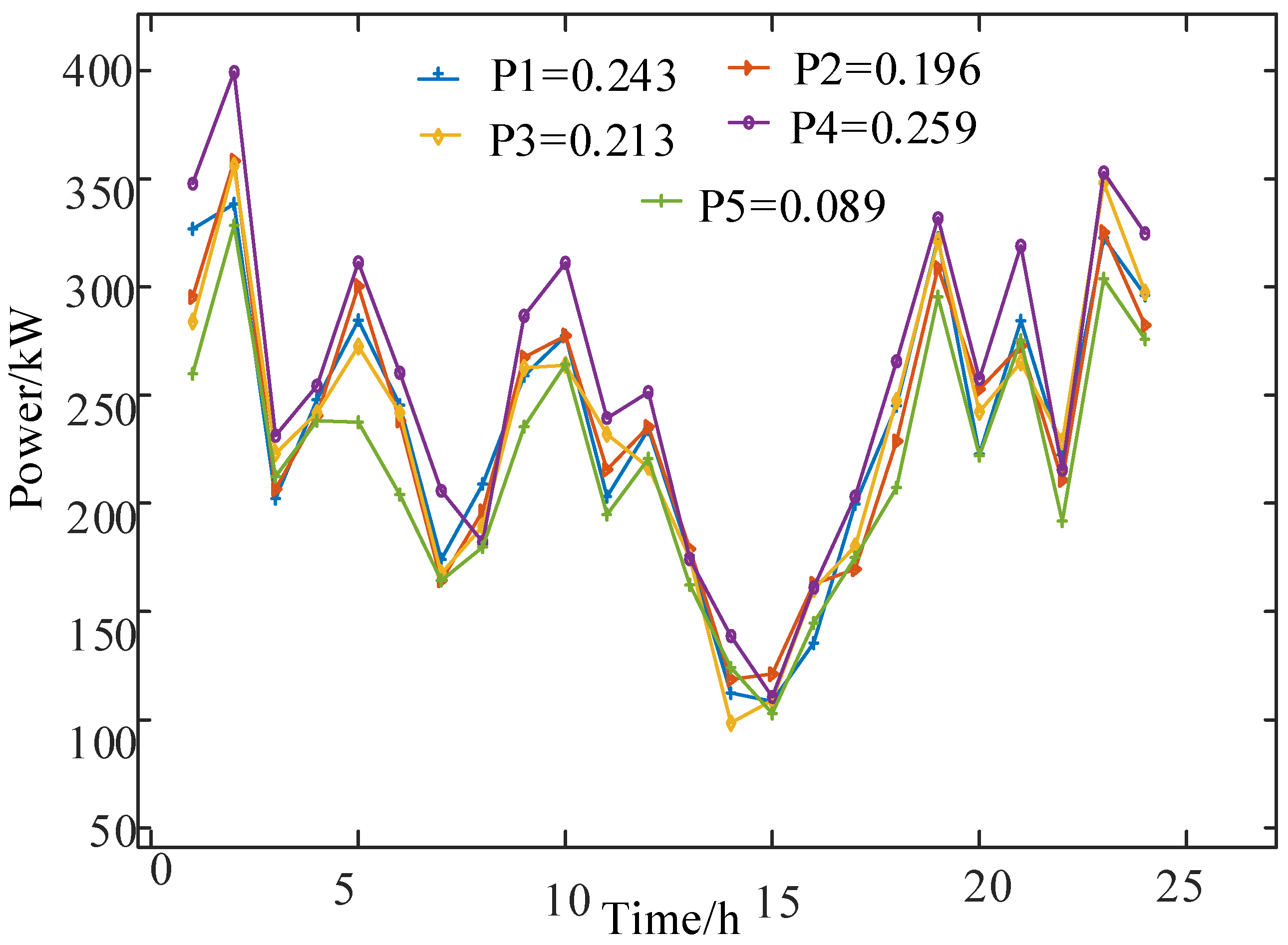
We introduce the Latin Hypercubic Sampling method to deal with the uncertainty introduced by wind power output. The method can quickly generate 1000 typical wind power scenarios and reduce them to 5 typical scenarios by synchronized back generation elimination. Its sample space and reduced scenarios are shown in Figure 4 and Figure 5, and the probability sum after the reduced scenarios is 1. It is assumed that the wind turbine output day-ahead prediction error is within 20%.

5.2. Optimized Operation Results and Analysis

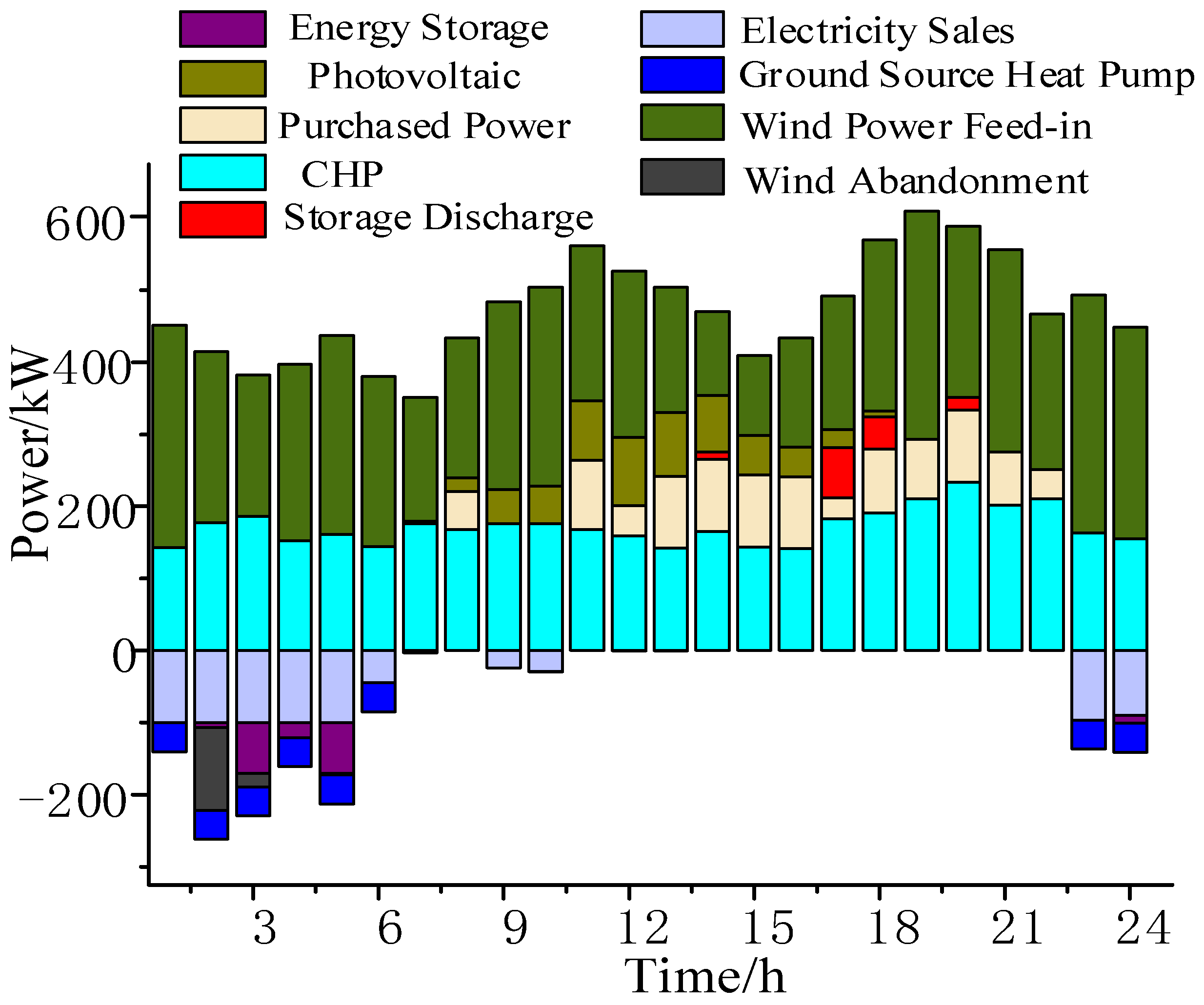
The optimal scheduling results of RIES are shown in Figure 6, Figure 7, Figure 8 and Figure 9: The scheduling results of Scenario 1 are shown in Figure 6, at this time, the electric load of RIES mainly consists of electricity purchased and sold between CHP, wind power, PV, storage battery and the main grid. During the hours of 1:00-7:00 and 23:00-24:00, the electricity price is in the trough, so the CHP units and the ground source heat pumps are operating in the heat-determined electricity operation mode. However, limited by the transmission power of the contact line, there is wind abandonment in the system, resulting in energy waste.

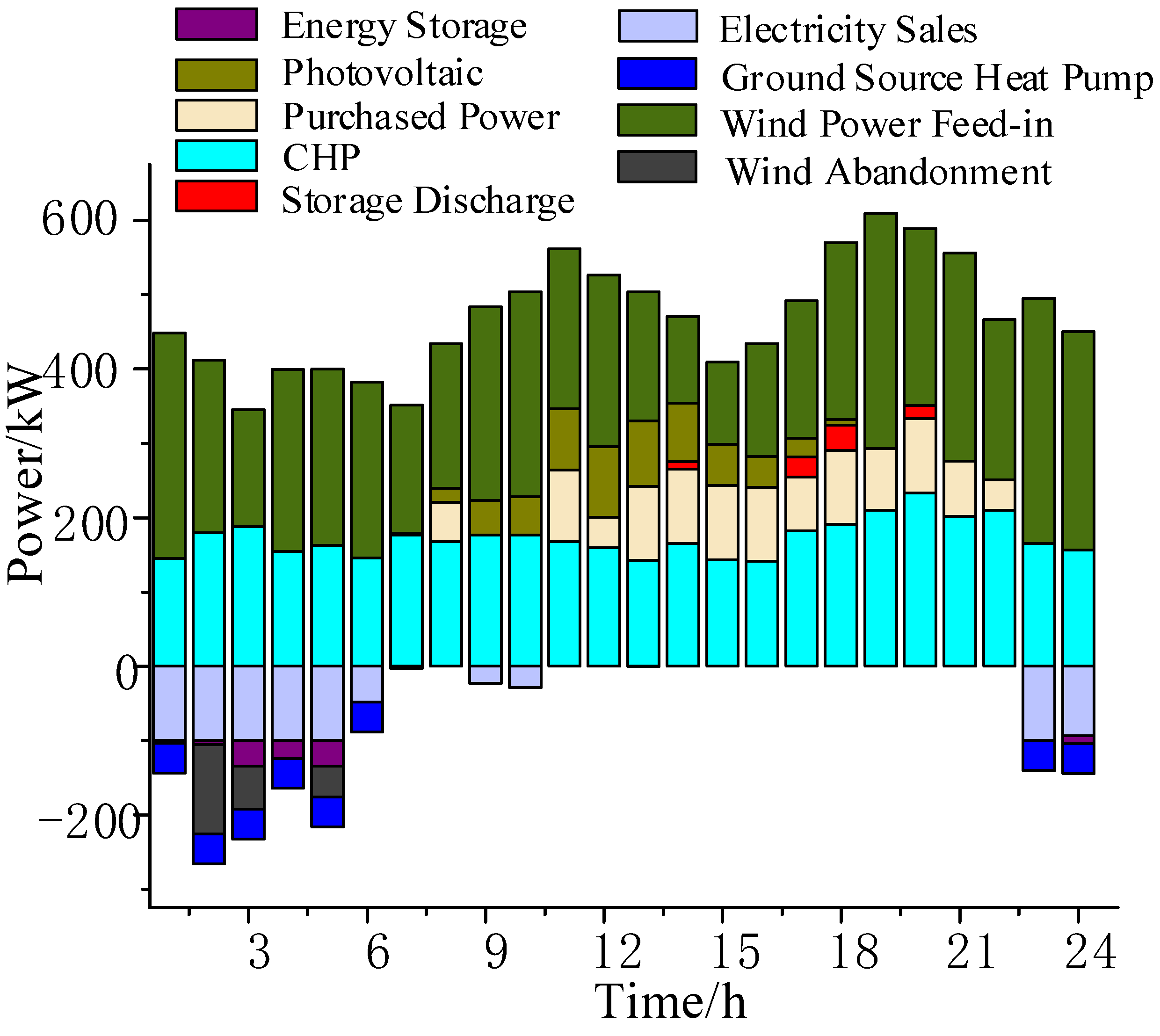
Scenario 2 considers the influence of low temperature environment on the available capacity and energy transfer rate of the energy storage system on the basis of Scenario 1, and its scheduling results are shown in Figure 7. As the available capacity and charging/discharging rate of the storage battery are affected, the actual available capacity of the storage system is limited to be insufficient in the 1:00-7:00 time period, and it is difficult to consume the wind power in this time period, which leads to a significant increase in wind abandonment phenomenon, the peak-to-valley difference of the system increases by 2.33% compared with Scenario 1, and the wind abandonment rate increases by 4.12%.

Scenario 3 introduces a combined heat and power demand response mechanism on the basis of Scenario 2. The use of electric load demand response mechanism regulates the user's power consumption habits, optimizes the distribution of power consumption, makes the power consumption increase in the price of electricity in the trough time, and reduces the power consumption in the price of electricity in the peak time; effectively reduces the peak-valley difference of the electric load; the scheduling results of the system are shown in 8, in the time period of 1:00-7:00, the wind power consumption rate of the system increases by 5.95% compared to Scenario 2, and the peak-valley difference decreases by 5.04%.

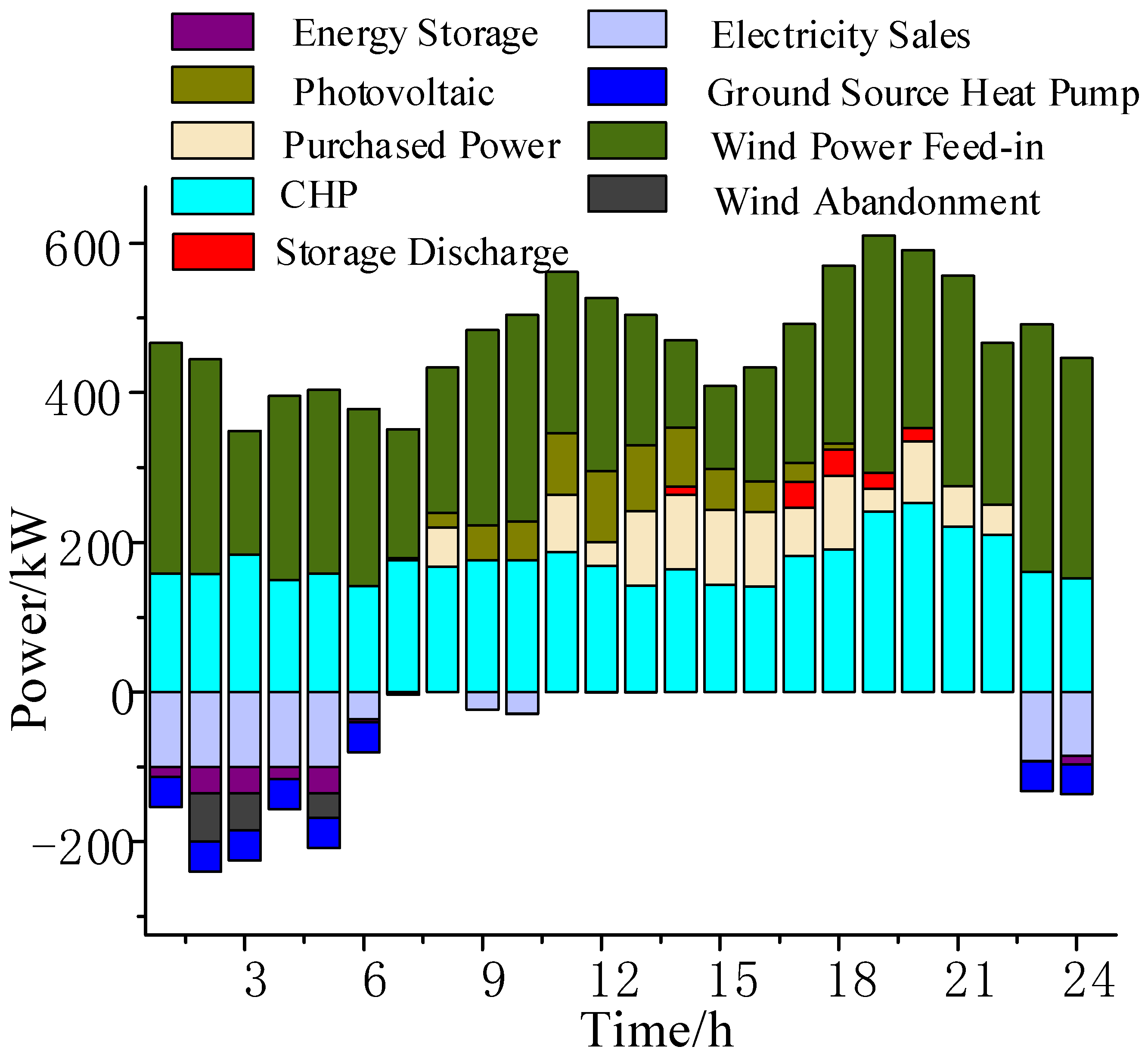
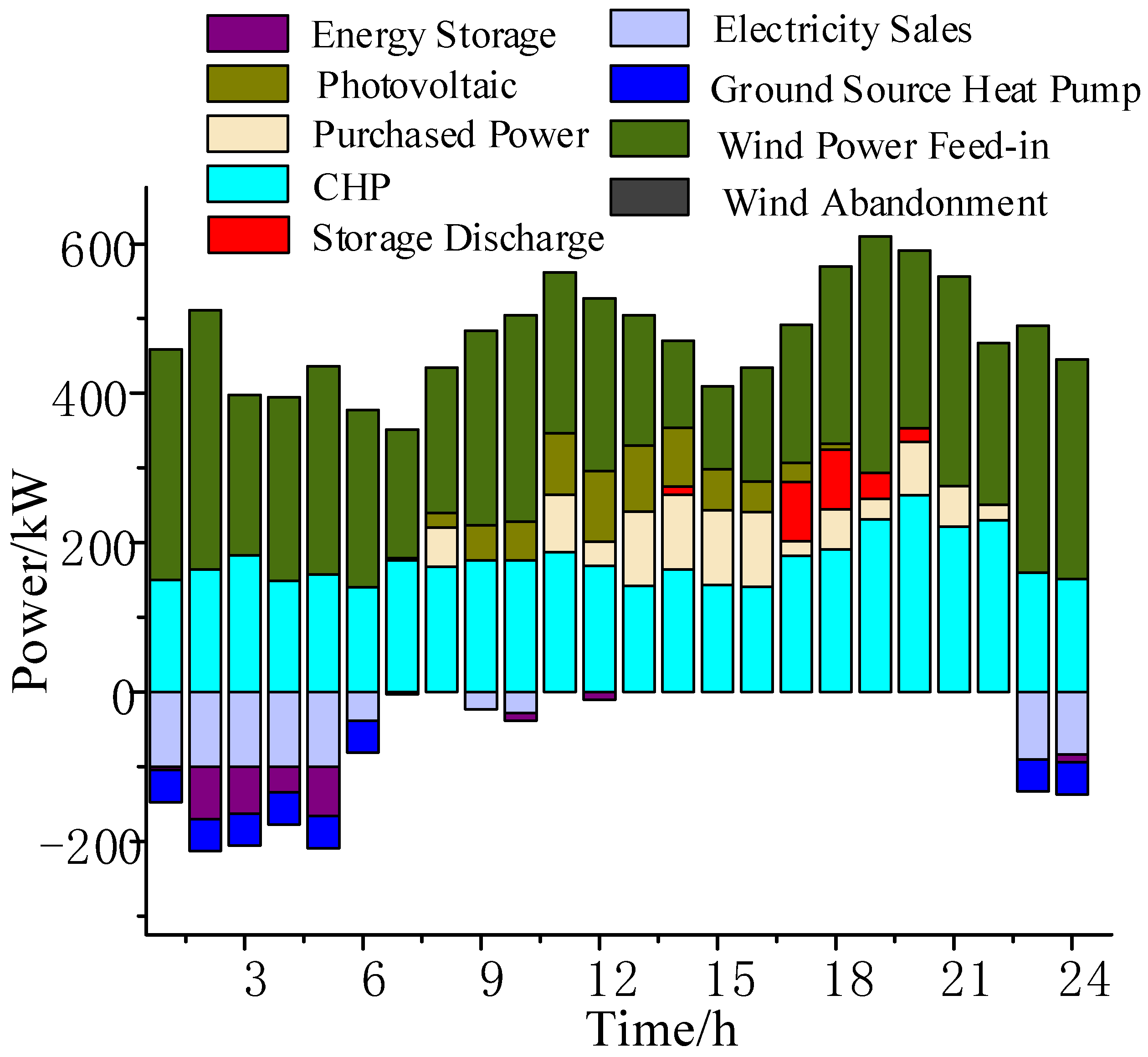
Scenario 4 adds a battery insulation device on the basis of Scenario 3. The battery is always in the best working condition by adding part of the thermal load. The scheduling results are shown in Figure 9, the system achieves complete consumption of wind power from 1:00 to 7:00, and the peak-to-valley difference of the system is reduced by 10.03% compared with Scenario 3.

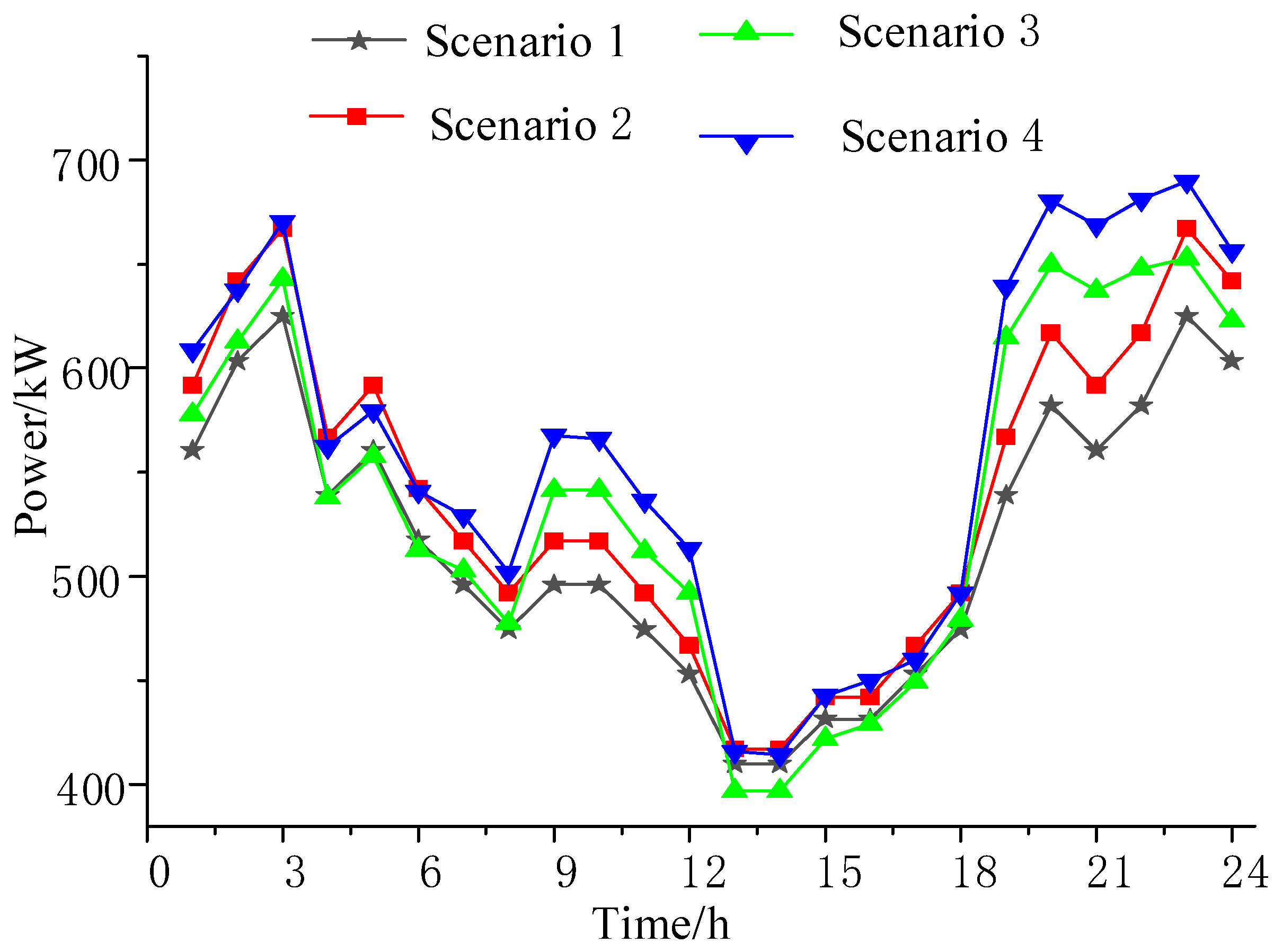
The results of the optimized scheduling of heat load and the comprehensive cost of each scenario in this process are shown in Figure 10 and Table 4. Scenario 2 takes into account that the heat dissipation of the heat storage tank in the low-temperature environment increases significantly, and compared with Scenario 1 Scenario 2 the heat load increases by 4.71% due to heat loss, and the total cost increases by 1.53%.

Scenario 3 introduces a heat load response mechanism to regulate the indoor temperature on the basis of scenario 2, which reduces the demand for heat load without affecting the comfort of the residents. Its total cost is reduced by 1.74% compared to Scenario 2, but the heat load is only reduced by 0.54%, which is due to the fact that the power purchase price is higher than the generation cost of the CHP unit from 7:00-11:00 and 19:00-22:00, and the room temperature is increased in order to reduce the amount of purchased power from the grid and increase the generation of the CHP unit, which leads to an insignificant effect of the optimization of the heat load in this scenario.

Scenario 4 increases the thermal load of the system compared to Scenario 3 due to the additional consumption of part of the thermal load by the storage heater, but the total cost is reduced by 2.58% compared to Scenario 2 by realizing the complete consumption of wind power, which effectively improves the comprehensive benefit of the system.

5.3. Analysis of the Effect of Weighting Coefficients on the Results of RIES Scheduling

The weighting coefficient can reflect the degree of risk preference of the decision maker, in order to explore the influence of the weighting coefficient β on the scheduling results of RIES, the paper derives the scheduling results under different weighting coefficients under scenario 4 according to the change of weighting coefficients from 0.1 to 0.9 as shown in Figure 11. The results show that in the process of gradually increasing weight coefficients, the total system cost gradually increases, the expected cost share gradually increases, and the CVaR share gradually decreases. This indicates that the greater the degree of risk preference of the decision maker, the smaller the CVaR percentage, the more it can improve the operational safety of the system, but at the same time, it will reduce the unity economy. In actual scheduling, operators should choose appropriate weighting coefficients to balance the benefits and risks of the system according to specific needs.

6. Conclusions

By establishing a coordinated and optimized operation model of RIES considering wind power consumption in low-temperature environment, the following conclusions can be drawn based on the comparative analysis of the four scenarios:

(1)

The fine energy storage model takes into account the influence of ambient temperature, capacity and other constraints, and the way of equipment output is more in line with the actual situation than the traditional energy storage model, and the reliability of system optimization and scheduling is higher.

(2)

Comprehensive consideration of electricity and heat flexible load demand response, can effectively reduce the peak and valley difference of the user load, while taking into account the wind power consumption capacity and economic benefits.

(3)

Compared to traditional deterministic models, it is more reasonable to utilize CVaR theory to describe the risk of returns from wind power uncertainty.

(4)

The adjustment of the weight coefficients in the CVaR theory according to the historical operation information and the actual situation during the actual scheduling process can further improve the comprehensive efficiency of the system.