Prerpints.org logo
Preprint
Article

The Component Connectivity of Leaf-Sort Graphs

Altmetrics

Downloads

75

Views

31

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

12 November 2023

Posted:

14 November 2023

You are already at the latest version

Alerts
Abstract
In large-scale parallel computing and communication systems, an interconnect network structure is usually modeled as a graph, in which vertices and edges correspond to processors and communication links, respectively. In a graph, the vertices and edges are likely to fail, so we must think about the fault tolerance of a graph. Connectivity is an important parameter in the study of faulty tolerance for a graph. In this paper, we study a special class of connectivity: $m$-component connectivity, this is a natural generalization of the classical connectivity of graphs defined in terms of the minimum vertex-cut. Let $F$ is a vertex set of $G$ $(i.e, F\subseteq V(G))$, if the following conditions are satisfied, we say $F$ is a $m$-component cut: $(1)$ $G-F$ is disconnected; $(2)$ the number of components in $G-F$ is greater than or equal to $m$. In another word, the $m$-component connectivity $c\kappa_{m}(G)$ is defined as $min\{|F|~|~F\subseteq V(G)$ and $F$ is a $m$-component cut$\}$. Determining $m$-component connectivity is still unsolved in most interconnection networks even for small $m'$s. Leaf-sort graph is a special Cayley graph, it has many special properties that are different from other Cayley graphs. So we need to pay attention to some of it's special properties when we study it. In this paper, we can get the values: $c\kappa_{3}(CF_{n})=3n-6$ $(n$ is odd$)$ and $c\kappa_{3}(CF_{n})=3n-7$ $(n$ is even$)$ for $n\geq3$; $c\kappa_{4}(CF_{n})=\frac{9n-21}{2}$ $(n$ is odd$)$ and $c\kappa_{4}(CF_{n})=\frac{9n-24}{2}$ $(n$ is even$)$ for $n\geq4$; $c\kappa_{5}(CF_{n})=6n-16$ $(n$ is odd$)$ and $c\kappa_{5}(CF_{n})=6n-18$ $(n$ is even$)$ for $n\geq5$.
Keywords: 
Subject: Computer Science and Mathematics  -   Discrete Mathematics and Combinatorics

1. Introduction

With the rapid development of technologies, interconnection networks play an important role in large multiprocessor system. An interconnection network is usually modeled as an undirected graph G = ( V ( G ) , E ( G ) ) , where V ( G ) is the vertex set and E ( G ) is the edge set. In this graph, the vertices and edges correspond to the process and communication links respectively. In the large-scale interconnected network, the failure of vertices or edges is inevitable. Therefore, in order to have an unimpeded interconnection network, we must think about the fault tolerance of a graph. Connectivity is an important parameter to measure the fault tolerance of an interconnection network, so the research of connectivity is very important. Connectivity can be divided into many kinds: maximal connectivity, local connectivity, maximal local connectivity, generalized connectivity and so on. In this paper, we study a special class of connectivity: m-component connectivity. Next, we firstly introduce the traditional connectivity of a graph G.
Let G = ( V ( G ) , E ( G ) ) be a simple connected graph, where V ( G ) is the vertex set and E ( G ) is the edge set. Let F ⊆ V ( G ) , we use G − F to denote the subgraph of G with vertex set V ( G ) − F and edge set E ( G ) − { ( u , v ) ∈ E ( G ) | { u , v } ∩ F ≠ ∅ } . Let x and y be any two distinct vertices, a path P between them is a sequence of adjacent vertices < x , w 1 , w 2 , ⋯ , w k , y > , where w 1 , w 2 , ⋯ , w k are distinct ones. The vertices w i , i = 1 , 2 , ⋯ , k are called internal vertices of the path P. For any two vertices { u , v } ⊆ V ( G ) , if there exists a u v -path, we say G is connected. Furthermore, if G − F is disconnected or has only one vertex, we called F is a vertex cut. Meanwhile, we call the biggest component in G − F a big component. It’s well know that, when G is not a complete graph, the traditional connectivity κ ( G ) is defined as m i n { | F | | F ⊆ V ( G ) and F is a vertex cut }. Otherwise, we say κ ( G ) = n − 1 , where n is the number of vertices in G. A graph G is k-connected if κ ( G ) ≥ k .
As an extension of traditional connectivity, let’s look at the m-component connectivity of a graph G. By referring to the relevant literature, we can find that the notion concerning the number of components in G − F was first introduced by Chartrand et al. [1] and Sampathkumar [2]. Furthermore, the definition of c κ m ( G ) was first proposed by Hsu et al. [3]. Let F is a vertex set of G ( i . e , F ⊆ V ( G ) ) , if the following conditions are satisfied, we say F is a m-component cut: ( 1 ) G − F is disconnected; ( 2 ) the number of components in G − F is greater than or equal to m. The m-component connectivity c κ m ( G ) is defined as m i n { | F | | F ⊆ V ( G ) and F ia a m-component cut}. By the above definition, we can easily get that c κ 2 ( G ) = κ ( G ) and c κ m + 1 ( G ) ≥ c κ m ( G ) . By referring to the relevant literature, we can also get there exists a certain relationship between m-component connectivity c κ m ( G ) and m-extra connectivity. The m-extra connectivity, denoted by κ m ( G ) , is defined as the minimum number of vertices whose removal from G results in every component in G − F has at least ( m + 1 ) vertices [4]. Li et al. [5], Hao et al. [6] and Guo et al. [7] have studied the relationship between extra (edge) connectivity and component (edge) connectivity in networks. So far, the m-component (edge) connectivity of many graphs has been studied [8,9,10,11,12,13,14,15,16,17]. However, these results most are about small m. If we want to get a result about a bigger m, we must expend greater effort. Next, we give some definitions that will be used in the following sections.
For a vertex v ∈ V ( G ) , N G ( v ) = { u | ( u , v ) ∈ E ( G ) } is the set of neighbors of v. We let d e g G ( v ) = | N G ( v ) | be the degree of v and δ ( G ) = min { d e g G ( v ) | v ∈ V ( G ) } be the minimum degree of G. If d e g G ( v ) = k for every v ∈ V ( G ) , then G is k-regular. A singleton of G is a vertex v with d e g G ( v ) = 0 . For a vertex set X, N G ( X ) = { ∪ x ∈ X N G ( x ) } − X is the neighbor of X. The distance between any two vertices u and v, denoted by d G ( u , v ) , is the length of the shortest path from u to v. G is bipartite if there exist two vertex subsets V 1 , V 2 with V 1 ∩ V 2 = ∅ such that V ( G ) = V 1 ∪ V 2 and for each edge ( u , v ) ∈ E ( G ) , | { u , v } ∩ V 1 | = | { u , v } ∩ V 2 | = 1 . It is well known that bipartite graphs contain no odd cycles. We use Bondy and Murty [18] for terminology and notation not defined here.
In this paper, we study the m-component connectivity of C F n , prove that c κ 3 ( C F n ) = 3 n − 6 ( n is odd) and c κ 3 ( C F n ) = 3 n − 7 ( n is even) for n ≥ 3 ; c κ 4 ( C F n ) = 9 n − 21 2 ( n is odd) and c κ 4 ( C F n ) = 9 n − 24 2 ( n is even) for n ≥ 4 ; c κ 5 ( C F n ) = 6 n − 16 ( n is odd) and c κ 5 ( C F n ) = 6 n − 18 ( n is even) for n ≥ 5 .
The detailed arrangement of the paper ia as follows: Section 2 introduces the definition of C F n and gives some properties of C F n . In Section 3, we discuss c κ 3 ( C F n ) . In Section 4, we prove the value of c κ 4 ( C F n ) . In Section 5, we prove some useful lemmas firstly, and then calculate the value of c κ 5 ( C F n ) . Section 6 concludes this paper. Next, let’s first introduce the Leaf-sort graph.

2. Preliminaries

Let l 1 , l 2 be two integers with 1 ≤ l 1 ≤ l 2 . Set [ l 1 , l 2 ] = { l | l is an integer with l 1 ≤ l ≤ l 2 } . In the permutation 1 2 ⋯ n p 1 p 2 ⋯ p n , i → p i . For the convenience, we denote the permutation 1 2 ⋯ n p 1 p 2 ⋯ p n by p 1 p 2 ⋯ p n . In [19], every permutation can be denoted by a product of disjoint cycles. For example, 1 2 3 2 3 1 = ( 123 ) . Specially, 1 2 ⋯ n 1 2 ⋯ n = ( 1 ) . The product σ τ of two permutations is the composition function τ followed by σ , e.g., ( 12 ) ( 13 ) = ( 132 ) . For terminology and notation not defined here, we follow [19]. Now we give the definition of n-dimensional leaf-sort graphs C F n .
Let [ 1 , n ] = { 1 , 2 , ⋯ , n } , and let S n be the symmetric group on [ 1 , n ] containing all permutations p = p 1 p 2 ⋯ p n of [ 1 , n ] . It is well known that { ( 1 i ) : i = 2 , 3 , ⋯ , n } is a generating set for S n . So { ( 1 , i ) : i = 2 , 3 , ⋯ , n } ∪ { ( j , j + 1 ) : j = 2 , 4 , ⋯ , n − 1 } (n is odd.) is also a generating set for S n and { ( 1 , i ) : i = 2 , 3 , ⋯ , n } ∪ { ( j , j + 1 ) : j = 2 , 4 , ⋯ , n − 2 } (n is even.) is also a generating set for S n . The n-dimensional leaf-sort graph C F n is the graph with vertex set V ( C F n ) = S n in which two vertices u , v are adjacent if and only if u = v ( 1 , i ) , 2 ≤ i ≤ n , or u = v ( j , j + 1 ) , 2 ≤ j ≤ n − 1 when j is even and n is odd, or u = v ( j , j + 1 ) , 2 ≤ j ≤ n − 2 when j and n are even. By the definition, we can get C F n is a 3 n − 3 2 -regular graph on n ! vertices for odd n, and 3 n − 4 2 -regular graph on n ! vertices for even n. The graphs C F 2 , C F 3 and C F 4 are depicted in Figure 1.
We can partition C F n into n subgraphs C F n 1 , C F n 2 , ⋯ , C F n n where every vertex u = x 1 x 2 ⋯ x n   ∈ C F n i has a fixed integer i in the last position x n for i ∈ [ 1 , n ] . It is obvious that C F n i is isomorphic to C F n − 1 for i ∈ [ 1 , n ] [20]. The edges whose end vertices in different C F n i are called cross-edges. Two edges are said to be independent if they are not adjacent. For any u ∈ C F n i , we denote u + = u ( 1 , n ) , u − = u ( n − 1 , n ) , and N u + = { u + , u − } , which are called outgoing neighbors of u. Denote E i , j ( C F n ) = E C F n ( V ( C F n i ) , V ( C F n j ) ) for i , j ∈ [ 1 , n ] .
Proposition 2.1.([20]) Let C F n i ( 1 ≤ i ≤ n ) be defined as above. Then there are 2 ( n − 2 ) ! independent cross-edges between two different C F n i when n is odd; there are ( n − 2 ) ! independent cross-edges between two different C F n i when n is even.
Proposition 2.2. ([20]) Let v ∈ V ( C F n i ) ( 1 ≤ i ≤ n ) which be defined as above. Then v ( 1 , n ) and v ( n − 1 , n ) belong to two different C F n j ’s ( j ≠ i ) when n is odd; v ( 1 , n ) belong to C F n j ( j ≠ i ) when n is even.
Proposition 2.3. For any u , v ∈ V ( C F n i ) , N u + ∩ N v + = ∅ when n is odd; u + ≠ v + when n is even.
Proof. Let u = u 1 u 2 ⋯ u n − 1 i and v = v 1 v 2 ⋯ v n − 1 i , where u j ≠ v j for some j ∈ [ 1 , n − 1 ] . Then u + = i u 2 ⋯ u n − 1 u 1 ≠ i v 2 ⋯ v n − 1 v 1 = v + , u − = u 1 u 2 ⋯ i u n − 1 ≠ v 1 v 2 ⋯ i v n − 1 = v − . Moreover, u + ≠ v − and v + ≠ u − . Hence when n is odd, N u + ∩ N v + = ∅ ; when n is even, u + ≠ v + .
Proposition 2.4.([20]) For any integer n ≥ 2 , C F n is bipartite.
Proposition 2.5. For any two vertices x , y ∈ V ( C F n ) ( n ≥ 3 ) , | N C F n ( x ) ∩ N C F n ( y ) | ≤ 3 .
Proof. If d C F n ( x , y ) = 1 or d C F n ( x , y ) ≥ 3 , then | N C F n ( x ) ∩ N C F n ( y ) | = 0 ; Otherwise ( i . e . , | N C F n ( x ) ∩ N C F n ( y ) | ≥ 1 ), there will be a 3-circle or d C F n ( x , y ) = 2 , a contradiction. So we consider d C F n ( x , y ) = 2 . Next, we proof this result by induction on n.
For n = 3 , | N C F 3 ( x ) ∩ N C F 3 ( y ) | = 3 as C F 3 ≅ K 3 , 3 and d C F 3 ( x , y ) = 2 .
For n = 4 , if x , y ∈ V ( C F 4 i ) , | N C F 4 ( x ) ∩ N C F 4 ( y ) | = 3 as C F 4 i ≅ C F 3 and x + ≠ y + . If x ∈ V ( C F 4 i ) , y ∈ V ( C F 4 j ) ( i ≠ j ) , let x = x 1 x 2 x 3 i and y = y 1 y 2 y 3 j , we know x + ≠ y + . If y + ∈ C F 4 i or x + ∈ C F 4 j , then N C F 4 ( x ) ∩ N C F 4 ( y ) ⊆ { x + , y + } . Thus | N C F 4 ( x ) ∩ N C F 4 ( y ) | ≤ 2 .
Now we assume n ≥ 5 and the result holds for C F n − 1 . If x , y ∈ V ( C F n i ) for i ∈ [ 1 , n ] , then by Proposition 2.3 and the inductive hypothesis, the result holds. So we let x ∈ V ( C F n i ) , y ∈ V ( C F n j ) ( i ≠ j ) , x = x 1 x 2 ⋯ x n − 1 i , y = y 1 y 2 ⋯ y n − 1 j . Then x + = i x 2 ⋯ x n − 1 x 1 , x − = x 1 x 2 ⋯ i x n − 1 , y + = j y 2 ⋯ y n − 1 y 1 , y − = y 1 y 2 ⋯ j y n − 1 . We know x + ≠ x − and y + ≠ y − . Since i ≠ j , x + ≠ y + and x − ≠ y − . As d C F n ( x , y ) = 2 and N C F n ( x ) ∩ N C F n ( y ) ⊆ { x + , x − , y + , y − } , we can assume y + ∈ N C F n ( x ) ∩ N C F n ( y ) .
When n is odd. If y + = x − , then j y 2 y 3 ⋯ y n − 1 y 1 = x 1 x 2 ⋯ i x n − 1 , x 1 = j , y 2 = x 2 , y 3 = x 3 , ⋯ , y n − 2 = x n − 2 , y n − 1 = i , y 1 = x n − 1 . Thus x + = y n − 1 y 2 y 3 ⋯ y n − 2 y 1 j ∈ C F n j and y − = x n − 1 x 2 x 3 ⋯ x n − 2 x 1 i ∈ C F n i , y x + ∈ E ( C F n j ) , x y − ∈ E ( C F n i ) . So | N C F n ( x ) ∩ N C F n ( y ) | = 3 . If y + ∈ C F n i and adjacent to x, then y + = j y 2 ⋯ y n − 1 i , N C F n ( x ) ∩ N C F n ( y ) ⊆ { x + , y + , x − } . Thus | N C F n ( x ) ∩ N C F n ( y ) | ≤ 3 . Furthermore, if and only if y − = x + , there will be | N C F n ( x ) ∩ N C F n ( y ) | = 3 , this is similar to the situation y + = x − . When y − ≠ x + , | N C F n ( x ) ∩ N C F n ( y ) | ≤ 2 . So when n is odd, this result holds.
When n is even. Note that x + ≠ y + . If y + ∈ C F n i or x + ∈ C F n j , then N C F n ( x ) ∩ N C F n ( y ) ⊆ { x + , y + } . Thus | N C F n ( x ) ∩ N C F n ( y ) | ≤ 2 .
In summary, this proposition is proven.
Corollary 2.6. When n ≥ 4 is even, if x and y belong to two different subgraphs in C F n , then | N C F n ( x ) ∩ N C F n ( y ) | ≤ 2 .
Corollary 2.7. When n ≥ 3 is odd, for any two vertices x , y ∈ V ( C F n ) , where x ∈ V ( C F n i ) , y ∈ V ( C F n j ) ( i ≠ j ) . Then | N C F n ( x ) ∩ N C F n ( y ) | = 3 if and only if y + = x − or y − = x + .
Proposition 2.8.([20]) Let C F n be the leaf-sort graph. Then the connectivity κ ( C F n ) = 3 n − 3 2 when n is odd and κ ( C F n ) = 3 n − 4 2 when n is even.
Lemma 1. ([21]) Let F ⊆ V ( C F n ) with | F | ≤ 3 n − 6 when n is odd ( n ≥ 5 ) and | F | ≤ 3 n − 7 when n is even ( n ≥ 4 ) . If C F n − F is disconnected, then C F n − F satisfies one of the following conditions:
( 1 )   C F n − F has two components, one of which is a singleton;
( 2 )   C F n − F has three components, two of which are singletons.
The conclusion of Lemma 1 is closely linked to the proof of m-component connectivity of C F n , that is why we listed it first. Next, we will discuss the component connectivity of C F n .

3. The 3-component connectivity of C F n

In this section, we will discuss the 3-component connectivity of C F n , and will prove that: when n is odd, c κ 3 ( C F n ) = 3 n − 6 for n ≥ 3 ; When n is even, c κ 3 ( C F n ) = 3 n − 7 for n ≥ 3 . Before proving our main results, we prove some useful lemmas firstly. Let S is a subset of V ( G ) ( i . e . , S ⊆ V ( G ) ) , if any two vertices x 1 and x 2 in S are nonadjacent, we call S an independent set. For convenience, we can simply write the independent set as I n d -set.
Lemma 3.1. When n is odd, if x 1 ∈ V ( C F n i ) , then there exists only ( n − 3 ) vertices in C F n i , which can satisfy that | N C F n i ( x 1 ) ∩ N C F n i ( x 2 ) | = 3 ; When n is even, if x 1 ∈ V ( C F n i ) , then there exists only ( n − 2 ) vertices in C F n i such that | N C F n i ( x 1 ) ∩ N C F n i ( x 2 ) | = 3 . In addition, these vertices are all regular.
Proof. Note that C F n i ≅ C F n − 1 . When n is odd, n − 1 is even, { x 1 , x 2 } ⊆ V ( C F n i ) . Since | N C F n i ( x 1 ) ∩ N C F n i ( x 2 ) | = 3 , by Corollary 2.6, we know that x 1 , x 2 must belong to a common subgraph in C F n i ; Otherwise, if x 1 , x 2 are in different subgraphs in C F n i , then | N C F n i ( x 1 ) ∩ N C F n i ( x 2 ) | ≤ 2 . So we can assume x 1 = i 1 i 2 i 3 ⋯ i n − 2 j i , x 2 = j 1 j 2 j 3 ⋯ j n − 2 j i . Now we let x 1 ′ = i 1 i 2 i 3 ⋯ i n − 2 , x 2 ′ = j 1 j 2 j 3 ⋯ j n − 2 , then { x 1 ′ , x 2 ′ } ⊆ V ( G 1 ) , G 1 ≅ C F n − 2 , n − 2 is odd. Since | N G 1 ( x 1 ′ ) ∩ N G 1 ( x 2 ′ ) | = 3 , by the proof process of Proposition 2.5, we know x 1 ′ , x 2 ′ have two different situations:
Case 1.  x 1 ′ , x 2 ′ belong to two different subgraphs in G 1 , and ( x 1 ′ ) + = ( x 2 ′ ) − or ( x 1 ′ ) − = ( x 2 ′ ) + .
In this case, we have i n − 2 ≠ j n − 2 . If ( x 1 ′ ) + = i n − 2 i 2 i 3 ⋯ i n − 3 i 1 = ( x 2 ′ ) − = j 1 j 2 j 3 ⋯ j n − 2 j n − 3 , then j 1 = i n − 2 , j 2 = i 2 , … , j n − 4 = i n − 4 , j n − 3 = i 1 , j n − 2 = i n − 3 . Thus x 2 = i n − 2 i 2 i 3 ⋯ i n − 4 i 1 i n − 3   j i . If ( x 1 ′ ) − = i 1 i 2 i 3 ⋯ i n − 2 i n − 3 = ( x 2 ′ ) + = j n − 2 j 2 j 3 ⋯ j n − 3 j 1 , then j n − 2 = i 1 , j 2 = i 2 , … , j n − 4 = i n − 4 , j n − 3 = i n − 2 , j 1 = i n − 3 . Thus x 2 = i n − 3 i 2 i 3 ⋯ i n − 4 i n − 2 i 1 j i .
Case 2.  x 1 ′ , x 2 ′ belong to the same subgraph in G 1 .
In this case, we have i n − 2 = j n − 2 , x 1 ′ = i 1 i 2 i 3 ⋯ i n − 2 , x 2 ′ = j 1 j 2 j 3 ⋯ i n − 2 . As G 1 i n − 2 ≅ C F n − 3 , n − 3 is even, | N G 1 i n − 2 ( x 1 ′ ) ∩ N G 1 i n − 2 ( x 2 ′ ) | = 3 , we can get x 1 ′ , x 2 ′ belong to a common subgraph in G 1 i n − 2 . Then i n − 3 = j n − 3 . Let x 1 ′ ′ = i 1 i 2 i 3 ⋯ i n − 4 , x 2 ′ ′ = j 1 j 2 j 3 ⋯ j n − 4 , then { x 1 ′ ′ , x 2 ′ ′ } ⊆ V ( G 2 ) , G 2 ≅ C F n − 4 and | N G 2 ( x 1 ′ ′ ) ∩ N G 2 ( x 2 ′ ′ ) | = 3 . As n − 4 is odd, there are two different situations:
Subcase 2.1.  x 1 ′ ′ , x 2 ′ ′ belong to two different subgraphs in G 2 , and ( x 1 ′ ′ ) + = ( x 2 ′ ′ ) − or ( x 1 ′ ′ ) − = ( x 2 ′ ′ ) + .
If ( x 1 ′ ′ ) + = ( x 2 ′ ′ ) − , we can get j 1 = i n − 4 , j 2 = i 2 , … , j n − 6 = i n − 6 , j n − 4 = i n − 5 , j n − 5 = i 1 . Thus x 2 = i n − 4 i 2 i 3 ⋯ i n − 6 i 1 i n − 5 i n − 3 i n − 2 j i . If ( x 1 ′ ′ ) − = ( x 2 ′ ′ ) + , then j 1 = i n − 5 , j 2 = i 2 , … , j n − 4 = i 1 , j n − 5 = i n − 4 . Thus x 2 = i n − 5 i 2 i 3 ⋯ i n − 6 i n − 4 i 1 i n − 3 i n − 2 j i .
Subcase 2.2.  x 1 ′ ′ , x 2 ′ ′ belong to a same subgraph in G 2 .
This case is similar to case 2, this is a finite cycle process.
Finally, when n is odd, we can get ( n − 3 ) vertices such that | N C F n i ( x 1 ) ∩ N C F n i ( x 2 ) | = 3 , they are i n − 2 i 2 i 3 ⋯ i n − 4 i 1 i n − 3 j i , i n − 3 i 2 i 3 ⋯ i n − 4 i n − 2 i 1 j i , i n − 4 i 2 i 3 ⋯ i n − 6 i 1 i n − 5 i n − 3 i n − 2 j i , i n − 5 i 2 i 3 ⋯ i n − 4 i 1 i n − 3 i n − 2 j i ,…, i 3 i 1 i 2 i 4 ⋯ i n − 2 j i , i 2 i 3 i 1 i 4 ⋯ i n − 2 j i .
When n is even, n − 1 is odd, C F n i ≅ C F n − 1 . Let x 1 = i 1 i 2 i 3 ⋯ i n − 1 i , x 2 = j 1 j 2 j 3 ⋯ j n − 1 i , | N C F n i ( x 1 ) ∩ N C F n i ( x 2 ) | = 3 . Assume x 1 ′ = i 1 i 2 i 3 ⋯ i n − 1 , x 2 ′ = j 1 j 2 j 3 ⋯ j n − 1 , then { x 1 ′ , x 2 ′ } ⊆ V ( G 1 ) , G 1 ≅ C F n − 1 , similarly, we can also divide it into two different situations:
Case 1.  x 1 ′ , x 2 ′ belong to two different subgraphs in G 1 , and ( x 1 ′ ) + = ( x 2 ′ ) − or ( x 1 ′ ) − = ( x 2 ′ ) + .
In this case, we have i n − 1 ≠ j n − 1 . If ( x 1 ′ ) + = ( x 2 ′ ) − , then j 1 = i n − 1 , j 2 = i 2 , … , j n − 1 = i n − 2 , j n − 2 = i 1 . Thus x 2 = i n − 1 i 2 i 3 ⋯ i n − 3 i 1 i n − 2 i . If ( x 1 ′ ) − = ( x 2 ′ ) + , then j 1 = i n − 2 , j 2 = i 2 , … , j n − 2 = i n − 1 , j n − 1 = i 1 . Thus x 2 = i n − 2 i 2 i 3 ⋯ i n − 3 i n − 1 i 1 i .
Case 2.  x 1 ′ , x 2 ′ belong to a same subgraph in G 1 .
In this case, i n − 1 = j n − 1 . Since G 1 i n − 1 ≅ C F n − 2 and | N G 1 i n − 1 ( x 1 ′ ) ∩ N G 1 i n − 1 ( x 2 ′ ) | = 3 , x 1 ′ and x 2 ′ are in a same subgraph in G 1 i n − 1 . So i n − 2 = j n − 2 . Let x 1 ′ ′ = i 1 i 2 i 3 ⋯ i n − 3 , x 2 ′ ′ = j 1 j 2 j 3 ⋯ j n − 3 , then { x 1 ′ ′ , x 2 ′ ′ } ⊆ V ( G 2 ) , G 2 ≅ C F n − 3 , n − 3 is odd. As | N G 2 ( x 1 ′ ′ ) ∩ N G 2 ( x 2 ′ ′ ) | = 3 , we can also consider the following two situations:
Subcase 2.1.  x 1 ′ ′ and x 2 ′ ′ belong to two different subgraphs in G 2 , and ( x 1 ′ ′ ) + = ( x 2 ′ ′ ) − or ( x 1 ′ ′ ) − = ( x 2 ′ ′ ) + .
If ( x 1 ′ ′ ) + = ( x 2 ′ ′ ) − , then j 1 = i n − 3 , j 2 = i 2 , … , j n − 3 = i n − 4 , j n − 4 = i 1 . Thus x 2 = i n − 3 i 2 i 3 ⋯ i n − 5
i 1 i n − 4 i n − 2 i n − 1 i . If ( x 1 ′ ′ ) − = ( x 2 ′ ′ ) + , then j 1 = i n − 4 , j 2 = i 2 , … , j n − 3 = i 1 , j n − 4 = i n − 3 . Thus x 2 = i n − 4 i 2 i 3 ⋯ i n − 5 i n − 3 i 1 i n − 2 i n − 1 i .
Subcase 2.2.  x 1 ′ ′ and x 2 ′ ′ belong to a same subgraph in G 2 .
This case is similar to case 2, this is also a finite cycle process.
Finally, when n is even, we can get ( n − 2 ) vertices such that | N C F n i ( x 1 ) ∩ N C F n i ( x 2 ) | = 3 , they are i n − 1 i 2 i 3 ⋯ i n − 3 i 1 i n − 2 i , i n − 2 i 2 i 3 ⋯ i n − 3 i n − 1 i 1 i , i n − 3 i 2 i 3 ⋯ i n − 5 i 1 i n − 4 i n − 2 i n − 1 i , i n − 4 i 2 i 3 ⋯
i n − 5 i n − 3 i 1 i n − 2 i n − 1 i , …, i 3 i 1 i 2 i 4 ⋯ i n − 2 i n − 1 i , i 2 i 3 i 1 i 4 ⋯ i n − 2 i n − 1 i .
Corollary 3.2. Let C F n is an n-dimension leaf-sort graph, { x 1 , x 2 } ⊆ V ( C F n i ) . If x 1 = i 1 i 2 i 3 ⋯ i n − 1 i , x 2 = j 1 j 2 j 3 ⋯ j n − 1 i and | N C F n i ( x 1 ) ∩ N C F n i ( x 2 ) | = 3 , then j 1 ≠ i 1 .
Lemma 3.3. For n ≥ 3 , let S is an I n d -set and | S | = 2 , then when n is odd, | N C F n ( S ) | ≥ 3 n − 6 ; when n is even, | N C F n ( S ) | ≥ 3 n − 7 .
Proof. Let S = { x 1 , x 2 } , as S is an I n d -set, so x 1 and x 2 are nonadjacent. By Proposition 2.5 and the definition of C F n , we know that | N C F n ( x 1 ) ∩ N C F n ( x 2 ) | ≤ 3 and C F n is a 3 n − 3 2 -regular graph ( n is odd) or 3 n − 4 2 -regular graph ( n is even). So when n is odd, | N C F n ( S ) | = | N C F n ( x 1 ) | + | N C F n ( x 2 ) | − | N C F n ( x 1 ) ∩ N C F n ( x 2 ) | ≥ 2 × 3 n − 3 2 − 3 = 3 n − 6 . When n is even, | N C F n ( S ) | = | N C F n ( x 1 ) | + | N C F n ( x 2 ) | − | N C F n ( x 1 ) ∩ N C F n ( x 2 ) | ≥ 2 × 3 n − 4 2 − 3 = 3 n − 7 .
Corollary 3.4. For n ≥ 4 , let F is a subset of V ( C F n ) ( i . e . , F ⊆ V ( C F n ) ) and when n is odd, | F | ≤ 3 n − 7 ; when n is even, | F | ≤ 3 n − 8 , then C F n − F contains a big component C, which satisfies | V ( C ) | ≥ n ! − | F | − 1 .
Theorem 1. For n ≥ 3 , when n is odd, c κ 3 ( C F n ) = 3 n − 6 ; when n is even, c κ 3 ( C F n ) = 3 n − 7 .
Proof. For n = 3 , since c κ l + 1 ( C F n ) ≥ c κ l ( C F n ) , we can get c κ 3 ( C F 3 ) ≥ 3 n − 3 2 = 3 = 3 n − 6 by Proposition 2.8. For n ≥ 4 , by Corollary 3.4, we can also get c κ 3 ( C F n ) ≥ 3 n − 6 when n is odd and c κ 3 ( C F n ) ≥ 3 n − 7 when n is even. Next, we will prove that: when n is odd, c κ 3 ( C F n ) ≤ 3 n − 6 and when n is even, c κ 3 ( C F n ) ≤ 3 n − 7 . Since | N C F n ( x 1 ) ∩ N C F n ( x 2 ) | ≤ 3 , we can choose two different vertices x 1 , x 2 ∈ V ( C F n ) , which can satisfy the condition | N C F n ( x 1 ) ∩ N C F n ( x 2 ) | = 3 . From the definition of C F n , we know that C F n is a 3 n − 3 2 -regular ( n is odd) and 3 n − 4 2 -regular graph ( n is even), so when n is odd, | N C F n ( { x 1 , x 2 } ) | = 2 × 3 n − 3 2 − 3 = 3 n − 6 ; when n is even, | N C F n ( { x 1 , x 2 } ) | = 2 × 3 n − 4 2 − 3 = 3 n − 7 . Thus let F = N C F n ( { x 1 , x 2 } ) , we know C F n − F contains three components and two of them only has a singleton. So we can get c κ 3 ( C F n ) ≤ 3 n − 6 ( n is odd) and c κ 3 ( C F n ) ≤ 3 n − 7 ( n is even).

4. The 4-component connectivity of C F n

Lemma 4.1. When n = 4 , let S is an I n d -set and | S | = 3 , | N C F 4 ( S ) | ≥ 6 .
Proof. Let S = { x 1 , x 2 , x 3 } , since S is an I n d -set, x 1 , x 2 , x 3 are nonadjacent with each other. Note that C F 4 i ≅ C F 3 , C F 3 ≅ K 3 , 3 . Next, we will think about the following three cases.
Case 1.  x 1 , x 2 , x 3 belong to the same subgraph C F 4 i .
In this case, since C F 4 i ≅ K 3 , 3 and S is an I n d -set, | N C F 4 i ( S ) | = 3 . By Proposition 2.3, we know the outgoing neighbors of { x 1 , x 2 , x 3 } are different. Thus, | N C F 4 ( S ) | = 3 + 3 = 6 .
Case 2.  x 1 , x 2 , x 3 belong to two different subgraphs C F 4 i , C F 4 j ( i ≠ j ) .
In this case, we can let { x 1 , x 2 } ⊆ V ( C F 4 1 ) , x 3 ∈ V ( C F 4 2 ) . Since x 1 and x 2 are nonadjacent, we can get | N C F 4 1 ( { x 1 , x 2 } ) | = 3 , | N C F 4 2 ( x 3 ) | = 3 . By the definition of C F n , we know x i ( i ∈ { 1 , 2 , 3 } ) only has one outgoing neighbor. If the structure shown in Figure 2 (a) exists, | N C F 4 ( S ) | ≥ | N C F 4 1 ( { x 1 , x 2 } ) | + | N C F 4 2 ( x 3 ) | = 6 . Now we can show that this structure does not exist. As | N C F 4 1 ( { x 1 , x 2 } ) | = 3 and { x 1 , x 2 } ⊆ V ( C F 4 1 ) , we assume x 1 = 2341 , then x 2 = 4231 or x 2 = 3421 . Thus x 1 + ∈ V ( C F 4 2 ) , x 2 + ∉ V ( C F 4 2 ) , the structure shown in Figure 2 (a) does not exist. Thus | N C F 4 ( S ) | ≥ 7 .
Case 3.  x 1 , x 2 , x 3 belong to three different subgraphs C F 4 i , C F 4 j , C F 4 k ( i , j , k are different from each other).
In this case, we can let x i ∈ V ( C F 4 i ) . By the definition of C F n , we know | N C F 4 i ( x i ) | = 3 , thus | N C F 4 ( S ) | ≥ 3 × 3 = 9 .
Combining the above three situations, we can get | N C F 4 ( S ) | ≥ 6 .
Lemma 4.2. When n = 5 , let S is an I n d -set and | S | = 3 , | N C F 5 ( S ) | ≥ 12 .
Proof. Let S = { x 1 , x 2 , x 3 } , since S is an I n d -set, x 1 , x 2 , x 3 are nonadjacent with each other. Note that C F 5 i ≅ C F 4 ( 1 ≤ i ≤ 5 ) . We think about the following three cases.
Case 1.  x 1 , x 2 , x 3 belong to the same subgraph C F 5 i .
Since C F 5 i ≅ C F 4 , by Lemma 4.1, we can get | N C F 5 i ( S ) | ≥ 6 . By the definition of C F n and Proposition 2.3, we know the outgoing neighbors of { x 1 , x 2 , x 3 } are different and every vertex has two different outgoing neighbors. Thus | N C F 5 ( S ) | = | N C F 5 i ( S ) | + 6 ≥ 6 + 6 = 12 .
Case 2.  x 1 , x 2 , x 3 belong to two different subgraphs C F 5 i , C F 5 j ( i ≠ j ) .
In this case, we can let { x 1 , x 2 } ⊆ V ( C F 5 1 ) , x 3 ∈ V ( C F 5 2 ) . Since C F 5 1 ≅ C F 4 , by Lemma 3.3, we know that | N C F 5 1 ( { x 1 , x 2 } ) | ≥ 3 ( n − 1 ) − 7 = 3 × 5 − 10 = 5 . By Proposition 2.8, we can get | N C F 5 2 ( x 3 ) | = 3 ( n − 1 ) − 4 2 = 4 . By Proposition 2.2, we can get x 1 and x 2 have at most two neighbors which belong to C F 5 2 . In other words, there are at least two neighbors of x 1 and x 2 belong to C F 5 − C F 5 1 − C F 5 2 . If the structure shown in Figure 2 (b) exists, then | N C F 5 ( S ) | ≥ | N C F 5 1 ( { x 1 , x 2 } ) | + | N C F 5 2 ( x 3 ) | + 2 = 5 + 4 + 2 = 11 . Furthermore, | N C F 5 ( S ) | = 11 if and only if this structure exists. Now, we can prove this structure does not exist.
Since { x 1 , x 2 } ⊆ V ( C F 5 1 ) , C F 5 1 ≅ C F 4 and | N C F 5 1 ( x 1 ) ∩ N C F 5 1 ( x 2 ) | = 3 , by Corollary 2.6, we can know that x 1 , x 2 must belong to a common subgraph in C F 5 1 . So we can assume x 1 = i 1 i 2 i 3 i 4 1 , x 2 = j 1 j 2 j 3 i 4 1 . As the subgraph of C F 5 1 is isomorphic to C F 3 , thus x 2 = i 3 i 1 i 2 i 4 1 or x 2 = i 2 i 3 i 1 i 4 1 ( i 1 , i 2 , i 3 , i 4 are different from each other).
If x 2 = i 3 i 1 i 2 i 4 1 , then x 2 + = 1 i 1 i 2 i 4 i 3 , x 2 − = i 3 i 1 i 2 1 i 4 . Since x 1 + = 1 i 2 i 3 i 4 i 1 , x 1 − = i 1 i 2 i 3 1 i 4 and one of the two outgoing neighbors of x 1 , x 2 belong to C F 5 2 , we can get i 4 = 2 . Thus { x 1 − , x 2 − } ⊆ V ( C F 5 2 ) . As x 1 − , x 2 − are adjacent to x 3 , so x 3 = i 2 i 1 i 3 12 or x 3 = i 3 i 2 i 1 12 or x 3 = i 1 i 3 i 2 12 . When x 3 = i 2 i 1 i 3 12 , x 3 + = 2 i 1 i 3 1 i 2 ∈ V ( C F 5 i 2 ) , x 3 − = i 2 i 1 i 3 21 ∈ V ( C F 5 1 ) , and x 3 − is adjacent to x 2 . Since x 1 + = 1 i 2 i 3 2 i 1 ∈ V ( C F 5 i 1 ) , x 2 + = 1 i 1 i 2 2 i 3 ∈ V ( C F 5 i 3 ) , x 3 + ≠ x 1 + , x 3 + ≠ x 2 + . When x 3 = i 3 i 2 i 1 12 , x 3 + = 2 i 2 i 1 1 i 3 ∈ V ( C F 5 i 3 ) , x 3 − = i 3 i 2 i 1 21 ∈ V ( C F 5 1 ) , and x 3 − is adjacent to x 1 . Since x 1 + = 1 i 2 i 3 2 i 1 , x 2 + = 1 i 1 i 2 2 i 3 and 1 ≠ 2 , x 3 + ≠ x 1 + , x 3 + ≠ x 2 + . When x 3 = i 1 i 3 i 2 12 , x 3 + = 2 i 3 i 2 1 i 1 ∈ V ( C F 5 i 1 ) , x 3 − = i 1 i 3 i 2 21 ∈ V ( C F 5 1 ) , and x 3 − is adjacent to x 2 . Since x 1 + = 1 i 2 i 3 2 i 1 , x 2 + = 1 i 1 i 2 2 i 3 and 1 ≠ 2 , x 3 + ≠ x 1 + , x 3 + ≠ x 2 + . So this structure does not exist.
If x 2 = i 2 i 3 i 1 i 4 1 , then x 2 + = 1 i 3 i 1 i 4 i 2 , x 2 − = i 2 i 3 i 1 1 i 4 . Since x 1 + = 1 i 2 i 3 i 4 i 1 , x 1 − = i 1 i 2 i 3 1 i 4 and one of the two outgoing neighbors of x 1 , x 2 belong to C F 5 2 , we can get i 4 = 2 . Thus { x 1 − , x 2 − } ⊆ V ( C F 5 2 ) . As x 1 − , x 2 − are adjacent to x 3 , so x 3 = i 3 i 2 i 1 12 or x 3 = i 1 i 3 i 2 12 or x 3 = i 2 i 1 i 3 12 . When x 3 = i 3 i 2 i 1 12 , x 3 + = 2 i 2 i 1 1 i 3 ∈ V ( C F 5 i 3 ) , x 3 − = i 3 i 2 i 1 21 ∈ V ( C F 5 1 ) , and x 3 − is adjacent to x 2 . Since x 1 + = 1 i 2 i 3 2 i 1 ∈ V ( C F 5 i 1 ) , x 2 + = 1 i 3 i 1 2 i 2 ∈ V ( C F 5 i 2 ) , x 3 + ≠ x 1 + , x 3 + ≠ x 2 + . When x 3 = i 1 i 3 i 2 12 , x 3 + = 2 i 3 i 2 1 i 1 ∈ V ( C F 5 i 1 ) , x 3 − = i 1 i 3 i 2 21 ∈ V ( C F 5 1 ) , and x 3 − is adjacent to x 1 . Since x 1 + = 1 i 2 i 3 2 i 1 , x 2 + = 1 i 3 i 1 2 i 2 and 1 ≠ 2 , x 3 + ≠ x 1 + , x 3 + ≠ x 2 + . When x 3 = i 2 i 1 i 3 12 , x 3 + = 2 i 1 i 3 1 i 2 ∈ V ( C F 5 i 2 ) , x 3 − = i 2 i 1 i 3 21 ∈ V ( C F 5 1 ) , and x 3 − is adjacent to x 2 . Since x 1 + = 1 i 2 i 3 2 i 1 , x 2 + = 1 i 3 i 1 2 i 2 and 1 ≠ 2 , x 3 + ≠ x 1 + , x 3 + ≠ x 2 + .
Thus the structure shown in Figure 2 (b) does not exist, | N C F 5 ( S ) | ≥ 12 .
Case 3.  x 1 , x 2 , x 3 belong to three different subgraphs C F 5 i , C F 5 j , C F 5 k ( i , j , k are different from each other).
Without loss of generality, we can let x 1 ∈ V ( C F 5 1 ) , x 2 ∈ V ( C F 5 2 ) , x 3 ∈ V ( C F 5 3 ) . By the definition of C F n , we can get | N C F 5 i ( x i ) | = 3 ( n − 1 ) − 4 2 = 4 ( i ∈ { 1 , 2 , 3 } ) , thus | N C F 5 ( S ) | ≥ | N C F 5 1 ( x 1 ) | + | N C F 5 2 ( x 2 ) | + | N C F 5 3 ( x 3 ) | = 12 .
Combining the above three situations, we can get | N C F 5 ( S ) | ≥ 12 .
Lemma 4.3. When n is odd, let S = { x 1 , x 2 , x 3 } is an I n d -set, where { x 1 , x 2 } ⊆ V ( C F n i ) , x 3 ∈ V ( C F n j ) ( i ≠ j ) and | N C F n i ( { x 1 , x 2 } ) | = 3 n − 10 . Then | N C F n ( S ) | ≠ 9 n − 23 2 .
Proof. When n is odd, | N C F n ( S ) | = 9 n − 23 2 occurs if and only if the structure in Figure 3 appears. Next, we will prove that these structures can not appear.
Firstly, we prove that the structure shown in Figure 3 (a) does not exist. Suppose on the contrary, we assume this structure exists and { x 1 , x 2 } ⊆ V ( C F n 1 ) , then x 1 = i 1 i 2 i 3 ⋯ i n − 2 i n − 1 1 , x 2 = j 1 j 2 j 3 ⋯ j n − 2 j n − 1 1 . As | N C F n i ( { x 1 , x 2 } ) | = 3 n − 10 , by the proof process of Lemma 3.3, we can know that x 1 , x 2 must have three common neighbors in C F n 1 . Note that n is odd, then n − 1 is even, and C F n i ≅ C F n − 1 . By Corollary 2.6, we can get x 1 , x 2 must belong to a common subgraph in C F n 1 ; Otherwise, if x 1 , x 2 belong to two different subgraphs in C F n 1 , then | N C F n 1 ( { x 1 , x 2 } ) | ≤ 2 , a contradiction. So j n − 1 = i n − 1 , x 1 + = 1 i 2 i 3 ⋯ i n − 2 i n − 1 i 1 , x 1 − = i 1 i 2 i 3 ⋯ i n − 2 1 i n − 1 , x 2 + = 1 j 2 j 3 ⋯ j n − 2 i n − 1 j 1 , x 2 − = j 1 j 2 j 3 ⋯ j n − 2 1 i n − 1 . By Corollary 3.2, we know j 1 ≠ i 1 . As one of the two outgoing neighbors of x 1 and x 2 belong to a common subgraph with x 3 , so { x 1 − , x 2 − } ⊆ V ( C F n i n − 1 ) and x 3 ∈ V ( C F n i n − 1 ) . Now we assume x 3 = k 1 k 2 k 3 ⋯ k n − 2 k n − 1 i n − 1 . As one of the two outgoing neighbors of x 3 belongs to C F n 1 , so x 3 = k 1 k 2 k 3 ⋯ k n − 2 1 i n − 1 or x 3 = 1 k 2 k 3 ⋯ k n − 2 k n − 1 i n − 1 . When x 3 = k 1 k 2 k 3 ⋯ k n − 2 1 i n − 1 , x 3 + = i n − 1 k 2 k 3 ⋯ k n − 2 1 k 1 , x 3 − = k 1 k 2 k 3 ⋯ k n − 2 i n − 1 1 . In this situation, x 3 − ∈ V ( C F n 1 ) , x 3 + ∈ V ( C F n k 1 ) , since i n − 1 ≠ 1 , we have x 3 + ≠ x 1 + , x 3 + ≠ x 2 + . Thus this structure does not exist. When x 3 = 1 k 2 k 3 ⋯ k n − 2 k n − 1 i n − 1 , as x 1 − , x 2 − are adjacent to x 3 , we can get x 1 − = x 3 ( 1 , n − 1 ) , x 2 − = x 3 ( 1 , n − 1 ) , this contradicts to the fact x 1 − ≠ x 2 − , thus this structure does not exist.
Next we will prove that the structure in Figure 3 (b) does not exist. Similarly, we know that j 1 ≠ i 1 , j n − 1 = i n − 1 , { x 1 − , x 2 − } ⊆ V ( C F n i n − 1 ) and x 3 ∈ V ( C F n i n − 1 ) . We let x 3 = k 1 k 2 k 3 ⋯ k n − 2 k n − 1 i n − 1 , then x 3 + = i n − 1 k 2 k 3 ⋯ k n − 2 k n − 1 k 1 , x 3 − = k 1 k 2 k 3 ⋯ k n − 2 i n − 1 k n − 1 . Thus x 3 − ≠ x 1 + and x 3 − ≠ x 2 + , the structure in Figure 3 (b) does not exist.
Lemma 4.4. When n is even, let S = { x 1 , x 2 , x 3 } is an I n d -set, where { x 1 , x 2 } ⊆ V ( C F n i ) , x 3 ∈ V ( C F n j ) ( i ≠ j ) and | N C F n i ( { x 1 , x 2 } ) | = 3 n − 9 . Then | N C F n ( S ) | ≠ 9 n − 24 2 .
Proof. When n is even, | N C F n ( S ) | = 9 n − 24 2 occurs if and only if the structure in Figure 4 appears. Next, we will prove that this structure does not exist. Note that C F n i ≅ C F n − 1 , n − 1 is odd.
Suppose on the contrary, we assume this structure exists, as | N C F n i ( { x 1 , x 2 } ) | = 3 n − 9 , we know x 1 , x 2 must have three common neighbors in C F n i by Lemma 3.3. Now, we let x 1 = i 1 i 2 i 3 ⋯ i n − 2 i n − 1 i , x 2 = j 1 j 2 j 3 ⋯ j n − 2 j n − 1 i . By Corollary 3.2, we know j i ∈ [ i 1 , i n − 1 ] and j 1 ≠ i 1 . Thus x 1 + ∈ V ( C F n i 1 ) , x 2 + ∈ V ( C F n j 1 ) , x 1 + and x 2 + can not belong to a common subgraph in C F n , this contradicts to this structure. Thus | N C F n ( S ) | ≠ 9 n − 24 2 .
Lemma 4.5. When n ≥ 4 , let S is an I n d -set and | S | = 3 , then when n is odd, | N C F n ( S ) | ≥ 9 n − 21 2 ; when n is even, | N C F n ( S ) | ≥ 9 n − 24 2 .
Proof. Let S = { x 1 , x 2 , x 3 } , since S is an I n d -set, x 1 , x 2 , x 3 are nonadjacent with each other. We proof this result by induction on n. By Lemma 4.1 and Lemma 4.2 , we know when n = 4 , 5 , this result holds. Now we assume that n ≥ 6 and the result holds for C F n − 1 . Note that C F n i ≅ C F n − 1 . Next, we think about the following three cases:
Case 1.  x 1 , x 2 , x 3 belong to a same subgraph C F n i .
When n is odd, by induction hypothesis, we have | N C F n i ( S ) | ≥ 9 ( n − 1 ) − 24 2 = 9 n − 33 2 . By Proposition 2.3 and the definition of C F n , we know the neighbors of x 1 , x 2 , x 3 in C F n − C F n i are different and every vertex has two outgoing neighbors. Thus | N C F n ( S ) | = | N C F n i ( S ) | + | N C F n − C F n i ( S ) | ≥ 9 n − 33 2 + 6 = 9 n − 21 2 .
When n is even, by induction hypothesis, we have | N C F n i ( S ) | ≥ 9 ( n − 1 ) − 21 2 = 9 n − 30 2 . By Proposition 2.3 and the definition of C F n , we know the neighbors of x 1 , x 2 , x 3 in C F n − C F n i are different and every vertex has only one outgoing neighbor. Thus | N C F n ( S ) | = | N C F n i ( S ) | + | N C F n − C F n i ( S ) | ≥ 9 n − 30 2 + 3 = 9 n − 24 2 .
Case 2.  x 1 , x 2 , x 3 belong to two different subgraphs C F n i , C F n j ( i ≠ j ) .
In this case, we can let { x 1 , x 2 } ⊆ V ( C F n i ) , x 3 ∈ V ( C F n j ) . By Lemma 3.3 , we can get: when n is odd, | N C F n i ( { x 1 , x 2 } ) | ≥ 3 ( n − 1 ) − 7 = 3 n − 10 ; when n is even, | N C F n i ( { x 1 , x 2 } ) | ≥ 3 ( n − 1 ) − 6 = 3 n − 9 . By Proposition 2.8, we know when n is odd, | N C F n j ( x 3 ) | = 3 ( n − 1 ) − 4 2 = 3 n − 7 2 ; when n is even, | N C F n j ( x 3 ) | = 3 ( n − 1 ) − 3 2 = 3 n − 6 2 . When n is odd, by Proposition 2.2, we know x 1 , x 2 have at most two outgoing neighbors can belong to C F n j , in another word, there are at least two outgoing neighbors of { x 1 , x 2 } can belong to C F n − C F n i − C F n j . So | N C F n ( S ) | ≥ | N C F n i ( { x 1 , x 2 } ) | + | N C F n j ( x 3 ) | + 2 = 9 n − 23 2 . By Lemma 4.3, we know | N C F n ( S ) | ≠ 9 n − 23 2 , thus | N C F n ( S ) | ≥ 9 n − 23 2 + 1 = 9 n − 21 2 . When n is even, if the structure of Figure 4 exist, then | N C F n ( S ) | ≥ | N C F n i ( { x 1 , x 2 } ) | + | N C F n j ( x 3 ) | = 3 n − 9 + 3 n − 6 2 = 9 n − 24 2 . By Lemma 4.4, we know this structure does not exist, so | N C F n ( S ) | ≥ 9 n − 24 2 + 1 = 9 n − 22 2 .
Case 3.  x 1 , x 2 , x 3 belong to three different subgraphs C F n i , C F n j , C F n k ( i , j , k are different from each other).
Without loss of generality, we can let x 1 ∈ V ( C F n 1 ) , x 2 ∈ V ( C F n 2 ) , x 3 ∈ V ( C F n 3 ) . By Proposition 2.8, we have when n is odd, | N C F n i ( x i ) | = 3 n − 7 2 ( i ∈ { 1 , 2 , 3 } ) ; when n is even, | N C F n i ( x i ) | = 3 n − 6 2 ( i ∈ { 1 , 2 , 3 } ) . Thus when n is odd, | N C F n ( S ) | ≥ 3 × 3 n − 7 2 = 9 n − 21 2 ; when n is even, | N C F n ( S ) | ≥ 3 × 3 n − 6 2 = 9 n − 18 2 .
Thus the result holds.
Corollary 4.6. When n is even, let S = { x 1 , x 2 , x 3 } is an I n d -set, if | N C F n ( S ) | = 9 n − 24 2 , then x 1 , x 2 , x 3 belong to a same subgraph in C F n .
Lemma 4.7. For n = 5 , if | F | ≤ 11 , then C F 5 − F contains a big component C, which satisfies the result | V ( C ) | ≥ n ! − | F | − 2 .
Proof. We are not going to think about C F 5 − F is connected for the moment, so we assume that C F 5 − F is disconnected. Let F i = F ∩ V ( C F 5 i ) for i = 1 , 2 , 3 , 4 , 5 with | F i 1 | ≥ | F i 2 | ≥ | F i 3 | ≥ | F i 4 | ≥ | F i 5 | , where i j ∈ { 1 , 2 , 3 , 4 , 5 } . If | F i 3 | = 0 , then | F i 4 | = | F i 5 | = 0 and C F 5 [ i 3 , i 5 ] − F [ i 3 , i 5 ] is connected. By Proposition 2.2 , we know there exists a vertex in C F 5 i 1 − F i 1 ( r e s p . , C F 5 i 2 − F i 2 ) , which has neighbor in C F 5 [ i 3 , i 5 ] − F [ i 3 , i 5 ] . So C F 5 − F is connected, a contradiction. Hence we consider | F i 3 | ≥ 1 . Since | F | ≤ 11 , we have | F i 5 | ≤ 2 , | F i 4 | ≤ 2 , 1 ≤ | F i 3 | ≤ 3 , 1 ≤ | F i 2 | ≤ 5 , 1 ≤ | F i 1 | ≤ 9 . Firstly, we proof the following Claim is correct.
Claim 1. If | F i j | ≤ 3 for some i j ∈ [ i 1 , i 4 ] , then C F 5 [ i j , i 5 ] − F [ i j , i 5 ] is connected.
Proof of Claim 1. By Proposition 2.8 , we can get C F 5 j − F j is connected for each j ∈ [ i j , i 5 ] . On the other hand, as | F i 5 | ≤ 2 , we can get | E p , i 5 ( C F 5 ) | = 12 > 5 ≥ | F p | + | F i 5 | , which implies E p , i 5 ( C F 5 − F ) ≠ ∅ for p ∈ [ i j , i 4 ] . Hence C F 5 [ i j , i 5 ] − F [ i j , i 5 ] is connected.
Since | F i 5 | ≤ | F i 4 | ≤ | F i 3 | ≤ 3 , by Claim 1, we can get C F 5 [ i 3 , i 5 ] − F [ i 3 , i 5 ] is connected. If C F 5 i 1 − F i 1 and C F 5 i 2 − F i 2 are all connected, we know C F 5 − F is connected. As | E i 2 , i 3 ( C F 5 ) | = 12 > 8 ≥ | F i 2 ∪ F i 3 | , C F [ i 2 , i 5 ] − F [ i 2 , i 5 ] is connected. As | E i 1 , i 5 ( C F 5 ) | = 12 > 9 + 2 = 11 ≥ | F i 1 ∪ F i 5 | , we have C F 5 − F is connected. Since C F 5 − F is disconnected, at least one of C F 5 i − F i , i ∈ { i 1 , i 2 } is disconnected, which leads to the following two cases.
Note that if | F i 3 ∪ F i 4 ∪ F i 5 | ≤ 1 , by Proposition 2.3 , we can get C F 5 i − F i ( i ∈ { i 1 , i 2 } ) has a big component C i and at most two vertices, which has a neighbor in F i 3 ∪ F i 4 ∪ F i 5 . Thus, if C F 5 i 1 − F i 1 or C F 5 i 2 − F i 2 is connected, then C F 5 − F satisfies the condition ( 1 ) . If C F 5 i 1 − F i 1 and C F 5 i 2 − F i 2 are all disconnected, then C F 5 − F satisfies the condition ( 2 ) . Hence we only think about this situation: | F i 3 ∪ F i 4 ∪ F i 5 | ≥ 2 .
Case 1. Both C F 5 i 1 − F i 1 and C F 5 i 2 − F i 2 are disconnected.
In this case, we know | F i 1 | ≥ | F i 2 | ≥ 4 . Since | F i 3 ∪ F i 4 ∪ F i 5 | ≥ 2 , | F i 1 ∪ F i 2 | ≤ | F | − | F i 3 ∪ F i 4 ∪ F i 5 | ≤ 11 − 2 = 9 . Hence | F i 2 | = 4 , 4 ≤ | F i 1 | ≤ 5 . By Corollary 3.4, we know C F 5 i 2 − F i 2 has a big component C 2 and a singleton x 2 . By Lemma 1, C F 5 i 1 − F i 1 should consider the following two situations: ( 1 )   C F 5 i 1 − F i 1 has two components, one of which is a singleton. ( 2 )   C F 5 i 1 − F i 1 has three components, two of which are singletons. For ( 1 ) , let C 1 is the big component and x 1 is the singleton of C F 5 i 1 − F i 1 , since | V ( C 1 ) | = | V ( C 2 ) | = | V ( C F 5 i ) − F i − { x i } | ≥ 4 ! − 5 − 1 = 18   ( i ∈ { i 1 , i 2 } ) and | F i 3 ∪ F i 4 ∪ F i 5 | ≤ 3 , by Proposition 2.3 , we can get C F 5 [ V ( C F 5 [ i 3 , i 5 ] − F [ i 3 , i 5 ] ) ∪ V ( C 1 ) ] is connected. Similarly, we can also get C F 5 [ V ( C F 5 [ i 3 , i 5 ] − F [ i 3 , i 5 ] ) ∪ V ( C 2 ) ] is connected. Thus the result holds. For ( 2 ) , let C 1 is the big component and x 1 , x 3 are singletons of C F 5 i 1 − F i 1 . If x 2 is nonadjacent to { x 1 , x 3 } , then { x 1 , x 2 , x 3 } are three singletons in C F 5 − F . By Lemma 4.2 , we can get | F | ≥ 12 , this contradicts to the fact | F | ≤ 11 . If x 2 is adjacent to { x 1 , x 3 } , say ( x 1 , x 2 ) ∈ E ( C F 5 − F ) , then C F 5 − F only has two components; Otherwise, we let C F 5 − F has three components, then x 3 is a singleton in C F 5 − F . By Proposition 2.5, we have | F | ≥ | N C F 5 ( { x 1 , x 2 } ) ∪ N C F 5 ( x 3 ) | ≥ 5 × 2 + 6 − 3 = 13 > 11 , a contradiction. Thus the result holds.
Case 2. Only C F 5 i 2 − F i 2 is disconnected.
Since | F i 3 ∪ F i 4 ∪ F i 5 | ≥ 2 , | F i 1 ∪ F i 2 | ≤ 9 . As C F 5 i 2 − F i 2 is disconnected, we have | F i 2 | ≥ 4 and then | F i 1 | ≤ 5 . If | F i 2 | = 5 , then | F i 1 | ≥ 5 , | F | ≥ | F i 1 | + | F i 2 | + | F i 3 ∪ F i 4 ∪ F i 5 | ≥ 5 + 5 + 2 = 12 , a contradiction. Thus | F i 2 | = 4 . Since | E i 1 , i 3 ( C F 5 ) | = 12 > 8 ≥ | F i 1 ∪ F i 3 | , C F 5 [ V ( C F 5 [ i 3 , i 5 ] − F [ i 3 , i 5 ] ) ∪ V ( C F 5 i 1 − F i 1 ) ] is connected. As | F i 2 | = 4 , by Corollary 3.4 , we know C F 5 i 2 − F i 2 has a big component S and at most one singleton. By the same argument as that of Case 1, we can get C F 5 [ V ( C F 5 [ i 3 , i 5 ] − F [ i 3 , i 5 ] ) ∪ V ( C F 5 i 1 − F i 1 ) ∪ V ( S ) ] is connected. Then C F 5 − F must satisfies condition ( 1 ) .
Case 3. Only C F 5 i 1 − F i 1 is disconnected.
In this case, we have | F i 1 | ≥ 4 by Proposition 2.8 and | F i 2 | ≤ 4 since | F | ≤ 11 and | F i 3 ∪ F i 4 ∪ F i 5 | ≥ 2 . As | E i 2 , i 3 ( C F 5 ) | = 12 > 7 ≥ | F i 2 ∪ F i 3 | , we have C F 5 [ i 2 , i 5 ] − F [ i 2 , i 5 ] is connected.
If | F i 1 | ≤ 5 , by Lemma 1, C F 5 i 1 − F i 1 has a big component S and one single and two singletons. By the same argument as that of Case 1, we can get C F 5 [ V ( C F 5 [ i 2 , i 5 ] − F [ i 2 , i 5 ] ) ∪ V ( S ) ] is connected. Then C F 5 − F must be one of conditions ( 1 ) and ( 2 ) .
Now, we suppose | F i 1 | ≥ 6 . Then | F i 2 ∪ F i 3 ∪ F i 4 ∪ F i 5 | ≤ 5 . Let W be the union of components of C F 5 − F , whose vertices, which are totally contained in C F 5 i 1 − F i 1 , are not connected with C F 5 [ i 2 , i 5 ] − F [ i 2 , i 5 ] . By Proposition 2.2 and Proposition 2.3 , we know 2 | W | ≤ | F − F i 1 | ≤ 5 , which implies | W | ≤ 2 . Thus C F 5 − F satisfies ( 1 ) or ( 2 ) .
Combing the above three cases, we know this result holds.
Lemma 4.8. For n = 6 , if | F | ≤ 14 , then C F 6 − F contains a big component C, which satisfies the result | V ( C ) | ≥ n ! − | F | − 2 .
Proof. Similarly, we do not think about the situation C F 6 − F is connected, so we let C F 6 − F is disconnected. Let F i = F ∩ V ( C F 6 i ) for i ∈ [ 1 , 6 ] with | F i 1 | ≥ | F i 2 | ≥ | F i 3 | ≥ | F i 4 | ≥ | F i 5 | ≥ | F i 6 | , where i j ∈ { 1 , 2 , 3 , 4 , 5 , 6 } . If | F i 2 | = 0 , then | F i 3 | = | F i 4 | = ⋯ = | F i 6 | = 0 and C F [ i 2 , i 6 ] − F [ i 2 , i 6 ] is connected. By Proposition 2.2 , we can get C F 6 − F is connected. So we assume | F i 2 | ≥ 1 . Since | F | ≤ 14 , we have | F i 6 | ≤ 2 , | F i 5 | ≤ 2 , | F i 4 | ≤ 3 , | F i 3 | ≤ 4 , 1 ≤ | F i 2 | ≤ 7 , 1 ≤ | F i 1 | ≤ 13 . Firstly, we proof the following Claim is correct.
Claim 2. If | F i j | ≤ 5 , then C F 6 [ i j , i 6 ] − F [ i j , i 6 ] is connected.
Proof of Claim 2. By Proposition 2.8 , we know C F 6 j − F j is connected for each j ∈ [ i j , i 6 ] . On the other hand, since | E p , i 6 ( C F 6 ) | = ( 6 − 2 ) ! = 24 > 7 ≥ | F p ∪ F i 6 | for p ∈ [ i j , i 5 ] , we can get E p , i 6 ( C F 6 − F ) ≠ ∅ . Thus C F 6 [ i j , i 6 ] − F [ i j , i 6 ] is connected.
By Claim 2, we know C F 6 [ i 3 , i 6 ] − F [ i 3 , i 6 ] is connected. If both C F 6 i 1 − F i 1 and C F 6 i 2 − F i 2 are connected, we can get C F 6 − F is connected. As | E i 2 , i 3 ( C F 6 ) | = ( 6 − 2 ) ! = 24 > 11 ≥ | F i 2 ∪ F i 3 | , | E i 1 , i 3 ( C F 6 ) | = ( 6 − 2 ) ! = 24 > 17 ≥ | F i 1 ∪ F i 3 | and C F 6 [ i 3 , i 6 ] − F [ i 3 , i 6 ] is connected, thus C F 6 − F is connected. Since C F 6 − F is disconnected, at least one of C F 6 i − F i ( i ∈ { i 1 , i 2 } ) is disconnected, which leads to the following cases.
Case 1. Both C F 6 i 1 − F i 1 and C F 6 i 2 − F i 2 are disconnected.
In this case, we know 6 ≤ | F i 2 | ≤ | F i 1 | ≤ | F | − | F i 2 | ≤ 8 < 9 . By Corollary 3.4, we know that C F 6 i 1 − F i 1 ( r e s p . , C F 6 i 2 − F i 2 ) has a big component C 1 ( r e s p . , C 2 ) and one singleton x 1 ( r e s p . , x 2 ) . As | E C F 6 − F ( V ( C 1 ) , V ( C F 6 i 3 − F i 3 ) ) | ≥ 24 − 2 − 8 − 1 = 13 > 1 . Thus C F 6 − F [ V ( C F 6 [ i 3 , i 6 ] − F [ i 3 , i 6 ] ) ∪ V ( C 1 ) ] is connected. Similarly, we can get C F 6 − F [ V ( C F 6 [ i 3 , i 6 ] − F [ i 3 , i 6 ] ) ∪ V ( C 2 ) ] is also connected. Thus the result holds.
Case 2. Only C F 6 i 2 − F i 2 is disconnected.
As C F 6 i 2 − F i 2 is disconnected, we have | F i 2 | ≥ 6 and then | F i 1 | ≤ 8 . Since | E i 1 , i 3 ( C F 6 ) | = 24 > 10 ≥ | F i 1 ∪ F i 3 | , C F 6 [ V ( C F 6 [ i 3 , i 6 ] − F [ i 3 , i 6 ] ) ∪ V ( C F 6 i 1 − F i 1 ) ] is connected. Since | F i 2 | ≤ | F i 1 | ≤ 8 , by Corollary 3.4, C F 6 i 2 − F i 2 has a big component C and one singleton. Since | E i 2 , i 3 ( C F 6 ) | = 24 > 11 ≥ | F i 2 ∪ F i 3 | + 1 , we can get C F 6 [ V ( C F 6 [ i 3 , i 6 ] − F [ i 3 , i 6 ] ) ∪ V ( C F 6 i 1 − F i 1 ) ∪ V ( C ) ] is connected. Then C F 6 − F must be one of conditions ( 1 ) .
Case 3. Only C F 6 i 1 − F i 1 is disconnected.
In this case, 6 ≤ | F i 1 | ≤ 13 , | F i 2 | ≤ 8 . As | E i 2 , i 3 ( C F 6 ) | = 24 > 11 > | F i 2 ∪ F i 3 | , we have C F 6 [ i 2 , i 6 ] − F [ i 2 , i 6 ] is connected.
If | F i 1 | ≤ 11 , by Lemma 4.8 , C F 6 i 1 − F i 1 has a big component C with | V ( C ) | ≥ 5 ! − | F i 1 | − 2 . By the same argument as that of Case 2, we can get C F 6 [ V ( C F 6 [ i 2 , i 6 ] − F [ i 2 , i 6 ] ) ∪ V ( C ) ] is connected. Thus the result holds.
If | F i 1 | ≥ 12 , then | F i 2 ∪ F i 3 ∪ F i 4 ∪ F i 5 ∪ F i 6 | ≤ 2 . Let W be the union of components of C F 6 − F , whose vertices, which are totally contained in C F 6 i 1 − F i 1 , and are not connected with C F 6 [ i 2 , i 6 ] − F [ i 2 , i 6 ] . By Proposition 2.2 and Proposition 2.3 , we have | W | ≤ | F − F i 1 | ≤ 2 . Thus the result holds.
Lemma 4.9. Let | F | ≤ 9 n − 23 2 for odd n ( n ≥ 5 ) and | F | ≤ 9 n − 26 2 for even n ( n ≥ 6 ) , then C F n − F contains a big component C, which satisfies that | V ( C ) | ≥ n ! − | F | − 2 .
Proof. By Lemma 4.7 and Lemma 4.8 , the result holds for n = 5 , 6 . We proof this result by induction on n. Assume n ≥ 7 and the result holds for C F n − 1 . Now we suppose C F n − F is disconnected for any F ⊆ V ( C F n ) with | F | ≤ 9 n − 23 2 or | F | ≤ 9 n − 26 2 . Let F i = F ∩ V ( C F n i ) for i ∈ [ 1 , n ] with | F i 1 | ≥ | F i 2 | ≥ ⋯ ≥ | F i n | , where i j ∈ [ 1 , n ] .
When n is odd, if | F i 3 | = 0 , then | F i 4 | = | F i 5 | = ⋯ = | F i n | = 0 and C F [ i 3 , i n ] − F [ i 3 , i n ] is connected, and thus, by Proposition 2.2 , we can get C F n − F is connected. Now we assume | F i 3 | ≥ 1 ; When n is even, if | F i 2 | = 0 , then | F i 3 | = | F i 4 | = ⋯ = | F i n | = 0 and C F [ i 2 , i n ] − F [ i 2 , i n ] is connected, and thus, by Proposition 2.2 , we can get C F n − F is connected. Now we assume | F i 2 | ≥ 1 .
Claim 3. When n is even, if | F i j | ≤ 3 n − 8 2 ( i j ∈ [ i 1 , i n − 1 ] ) , then C F n [ i j , i n ] − F [ i j , i n ] is connected; When n is odd, if | F i j | ≤ 3 n − 9 2 ( i j ∈ [ i 1 , i n − 1 ] ) , then C F n [ i j , i n ] − F [ i j , i n ] is connected;
Proof of Claim 3. By Proposition 2.8 , we know C F n j − F j is connected for each j ∈ [ i j , i n ] . On the other hand, since | E p , i n ( C F n ) | = ( n − 2 ) ! > 3 n − 8 > | F p ∪ F i n | for p ∈ [ i j , i n − 1 ] ( n is even) and | E p , i n ( C F n ) | = 2 ( n − 2 ) ! > 3 n − 9 > | F p ∪ F i n | for p ∈ [ i j , i n − 1 ] ( n is odd), we can get E p , i n ( C F n − F ) ≠ ∅ . Thus C F n [ i j , i n ] − F [ i j , i n ] is connected.
Since | F | ≤ 9 n − 26 2 ( n is even) and | F | ≤ 9 n − 23 2 ( n is odd), we have 3 n − 8 2 > | F i 3 | ≥ | F i 4 | ≥ ⋯ ≥ | F i n | for even n and 3 n − 9 2 ≥ | F i 3 | ≥ | F i 4 | ≥ ⋯ ≥ | F i n | for odd n. By Claim 3, we can get C F n [ i 3 , i n ] − F [ i 3 , i n ] is connected. If C F n i 1 − F i 1 and C F n i 2 − F i 2 are all connected, as | E i 2 , i 3 ( C F n ) | = ( n − 2 ) ! > 9 n − 26 2 > | F i 2 ∪ F i 3 | ( n is even) and | E i 2 , i 3 ( C F n ) | = 2 ( n − 2 ) ! > 9 n − 23 2 > | F i 2 ∪ F i 3 | ( n is odd), then C F n [ i 2 , i n ] − F [ i 2 , i n ] is connected. Similarly, we can also get C F n − F is connected. So at least one of C F n i − F i ( i ∈ { i 1 , i 2 } ) is disconnected, which leads to the following cases.
Note that, when n is odd, if | F i 3 ∪ F i 4 ∪ F i 5 ∪ ⋯ ∪ F i n | ≤ 1 , by the same argument of Lemma 4.7, we know C F n − F satisfies condition ( 1 ) or ( 2 ) . Hence we assume that | F i 3 ∪ F i 4 ∪ F i 5 ∪ ⋯ ∪ F i n | ≥ 2 .
Case 1. Both C F n i 1 − F i 1 and C F n i 2 − F i 2 are disconnected.
When n is even, we have 3 n − 6 2 ≤ | F i 2 | ≤ | F i 1 | ≤ | F | − | F i 2 | ≤ 9 n − 26 2 − 3 n − 6 2 = 3 n − 10 . By Corollary 3.4, we know C F n i 1 − F i 1 and C F n i 2 − F i 2 all have a big component C 1 , C 2 and one singleton. As | E C F n − F ( V ( C 1 ) , V ( C F n i 3 − F i 3 ) ) | ≥ ( n − 2 ) ! − 1 − 9 n − 26 2 > 1 , | E C F n − F ( V ( C 2 ) , V ( C F n i 3 − F i 3 ) ) | ≥ ( n − 2 ) ! − 1 − 9 n − 26 2 > 1 , Thus C F n − F [ V ( C F n [ i 3 , i n ] − F [ i 3 , i n ] ) ∪ V ( C 1 ) ∪ V ( C 2 ) ] is connected, the result holds.
When n is odd, we have 3 n − 7 2 ≤ | F i 2 | ≤ | F i 1 | ≤ | F | − | F i 2 | − | F i 3 ∪ F i 4 ∪ ⋯ ∪ F i n | ≤ 9 n − 23 2 − 3 n − 7 2 − 2 = 3 n − 10 .So by Lemma 1, we would consider the following three subcases: ( 1 ) Both C F n i 1 − F i 1 and C F n i 2 − F i 2 have three components, two of which are singletons; ( 2 ) Only one of C F n i 1 − F i 1 and C F n i 2 − F i 2 has three components, two of which are singletons; ( 3 ) Both C F n i 1 − F i 1 and C F n i 2 − F i 2 have two components, one of which is singleton. Now, we just proof the first subcase and the other two subcases could be proved by the same argument. Let x 1 , y 1 , C 1 (resp., x 2 , y 2 , C 2 ) be the two singletons and the other big component of C F n i 1 − F i 1 (resp., C F n i 2 − F i 2 ). Since | V ( C 1 ) | = | V ( C F n i 1 ) − F i 1 − { x 1 , y 1 } | ≥ ( n − 1 ) ! − ( 3 n − 10 ) − 2 and | F i 3 ∪ F i 4 ∪ ⋯ ∪ F i n | ≤ 3 n − 9 2 , by Proposition 2.3 , we know C F n [ V ( C F n [ i 3 , i n ] − F [ i 3 , i n ] ) ∪ V ( C 1 ) ] is connected. Similarly, we can get C F n [ V ( C F n [ i 3 , i n ] − F [ i 3 , i n ] ) ∪ V ( C 2 ) ] is connected.
If x 1 , x 2 , y 1 , y 2 are four singletons in C F n − F , then by Proposition 2.5 , we know | F | ≥ | N C F n i 1 ( { x 1 , y 1 } ) ∪ N C F n i 2 ( { x 2 , y 2 } ) ∪ ( F i 3 ∪ F i 4 ∪ ⋯ ∪ F i n ) | ≥ [ 3 ( n − 1 ) − 4 2 × 2 − 3 ] × 2 + 2 = 6 n − 18 > 9 n − 23 2 , a contradiction.
If C F n − F has three singletons, then by Lemma 4.5 , we can get | F | ≥ 9 n − 21 2 , this contradicts to the fact | F | ≤ 9 n − 23 2 . So C F n − F has two singletons or only one singleton.
Claim 4. If ( C F n − F ) [ { x 1 , y 1 , x 2 , y 2 } ] has at least one edge, say ( x 1 , x 2 ) ∈ E ( C F n − F ) , then C F n − F only has two components.
Proof of Claim 4. Suppose C F n − F has at least three components. Then y 1 is a singleton or ( y 1 , y 2 ) ∈ E ( C F n − F ) . If y 1 is a singleton, then | F | ≥ | N C F n ( { x 1 , x 2 } ) ∪ N C F n ( y 1 ) | ≥ ( 3 n − 3 2 − 1 ) × 2 + 3 n − 3 2 − 3 = 9 n − 19 2 > 9 n − 23 2 , a contradiction. If ( y 1 , y 2 ) ∈ E ( C F n − F ) , then | F | ≥ | N C F n ( { x 1 , x 2 } ) ∪ N C F n ( { y 1 , y 2 } ) | ≥ ( 3 n − 3 2 − 1 ) × 4 − 3 × 2 = 6 n − 16 > 9 n − 23 2 , a contradiction.
Thus, by Claim 4, the result holds.
Case 2. Only C F n i 2 − F i 2 is disconnected.
As C F n i 2 − F i 2 is disconnected, we have | F i 2 | ≥ 3 n − 6 2 for even n and | F i 2 | ≥ 3 n − 7 2 for odd n, then | F i 1 | ≤ 3 n − 10 < 3 n − 9 ( n is even) and | F i 1 | ≤ 3 n − 10 ( n is odd). Since | E i 1 , i 3 ( C F n ) | = ( n − 2 ) ! > 9 n − 26 2 ≥ | F i 1 ∪ F i 3 | ( n is even) and | E i 1 , i 3 ( C F n ) | = 2 ( n − 2 ) ! > 9 n − 23 2 ≥ | F i 1 ∪ F i 3 | ( n is odd), C F n [ V ( C F n [ i 3 , i n ] − F [ i 3 , i n ] ) ∪ V ( C F n i 1 − F i 1 ) ] is connected. Since | F i 2 | ≤ | F i 1 | ≤ 3 n − 10 , when n is even, by Corollary 3.4, we know C F n i 2 − F i 2 has a big component C and one singleton; When n is odd, by Lemma 1, we know C F n i 2 − F i 2 has a big component C and at most two singletons. By the same argument as that of Case 1, we can get C F n [ V ( C F n [ i 3 , i n ] − F [ i 3 , i n ] ) ∪ V ( C F n i 1 − F i 1 ) ∪ V ( C ) ] is connected. Then C F n − F must be one of conditions ( 1 ) and ( 2 ) .
Case 3. Only C F n i 1 − F i 1 is disconnected.
In this case, 3 n − 6 2 ≤ | F i 1 | ≤ 9 n − 28 2 for even n and 3 n − 7 2 ≤ | F i 1 | ≤ 9 n − 29 2 for odd n. As | E i 2 , i 3 ( C F n ) | = ( n − 2 ) ! > 9 n − 26 2 ≥ | F i 2 ∪ F i 3 | ( n is even) and | E i 2 , i 3 ( C F n ) | = 2 ( n − 2 ) ! > 9 n − 23 2 ≥ | F i 2 ∪ F i 3 | ( n is odd), we have C F n [ i 2 , i n ] − F [ i 2 , i n ] is connected.
When n is even, if | F i 1 | ≤ 9 n − 32 2 , by introduction, we know C F n i 1 − F i 1 has a big component C with | V ( C ) | ≥ ( n − 1 ) ! − | F i 1 | − 2 . By the same argument as that of Case 1, we can get C F n [ V ( C F n [ i 2 , i n ] − F [ i 2 , i n ] ) ∪ V ( C ) ] is connected. Thus the result holds. If | F i 1 | ≥ 9 n − 30 2 , then | F i 2 ∪ F i 3 ∪ ⋯ ∪ F i n | ≤ 2 . Let W be the union of components of C F n − F , whose vertices, which are totally contained in C F n i 1 − F i 1 , and are not connected with C F n [ i 2 , i n ] − F [ i 2 , i n ] . By Proposition 2.2 and Proposition 2.3 , we have | W | ≤ | F − F i 1 | ≤ 2 . Thus the result holds.
When n is odd, if | F i 1 | ≤ 9 n − 35 2 , by introduction, C F n i 1 − F i 1 has a big component C with | V ( C ) | ≥ ( n − 1 ) ! − | F i 1 | − 2 . By the same argument as that of Case 1, we can get C F n [ V ( C F n [ i 2 , i n ] − F [ i 2 , i n ] ) ∪ V ( C ) ] is connected. Thus the result holds. If | F i 1 | ≥ 9 n − 33 2 , then | F i 2 ∪ F i 3 ∪ ⋯ ∪ F i n | ≤ 5 . Let W be the union of components of C F n − F , whose vertices, which are totally contained in C F n i 1 − F i 1 , and are not connected with C F n [ i 2 , i n ] − F [ i 2 , i n ] . By Proposition 2.3 , 2 | W | ≤ | F − F i 1 | ≤ 5 . Then we have | W | ≤ 2 . Thus the result holds.
Theorem 2. For n ≥ 4 , when n is odd, c κ 4 ( C F n ) = 9 n − 21 2 ; when n is even, c κ 4 ( C F n ) = 9 n − 24 2 .
Proof. By Lemma 1, we have c κ 4 ( C F 4 ) ≥ 6 = 9 × 4 − 24 2 . For n ≥ 5 , by Lemma 4.9 , we can get when n is odd, c κ 4 ( C F n ) ≥ 9 n − 21 2 ; when n is even, c κ 4 ( C F n ) ≥ 9 n − 24 2 . Next, we will prove that c κ 4 ( C F n ) ≤ 9 n − 21 2 and c κ 4 ( C F n ) ≤ 9 n − 24 2 . For n = 4 , if we let F = { 2314 , 3124 , 1234 , 4213 , 4132 , 4321 } , then C F n − F has three singletons: x 1 = 3214 , x 2 = 2134 , x 3 = 1324 . Thus c κ 4 ( C F 4 ) ≤ 6 = 9 × 4 − 24 2 . For n ≥ 5 , when n is odd, let S = { x 1 , x 2 , x 3 } , where x 1 = i 1 i 2 i 3 ⋯ i n − 4 3214 , x 2 = 2 i 2 i 3 ⋯ i n − 4 i 1 314 , x 3 = 2 i 2 i 3 ⋯ i n − 4 3 i 1 41 , then | N C F n ( S ) | = 3 n − 10 + 3 n − 7 2 + 3 = 9 n − 21 2 and there are three singletons { x 1 , x 2 , x 3 } in C F n − N C F n ( S ) . Thus when n is odd, c κ 4 ( C F n ) ≤ 9 n − 21 2 . When n is even, let S = { x 1 , x 2 , x 3 } , where x 1 = i 1 i 2 i 3 ⋯ i n − 4 3214 j , x 2 = 2 i 2 i 3 ⋯ i n − 4 i 1 314 j , x 3 = 2 i 2 i 3 ⋯ i n − 4 3 i 1 41 j , then { x 1 , x 2 , x 3 } ⊆ V ( C F n j ) and | N C F n j ( S ) | = 9 ( n − 1 ) − 21 2 = 9 n − 30 2 . As x 1 , x 2 , x 3 belong to a common subgraph, by Proposition 2.3, we know x 1 , x 2 , x 3 have different outgoing neighbors. So | N C F n ( S ) | = 9 n − 30 2 + 3 = 9 n − 24 2 and x 1 , x 2 , x 3 are three singletons in C F n − N C F n ( S ) . Thus when n is even, c κ 4 ( C F n ) ≤ 9 n − 24 2 .

5. The 5-component connectivity of C F n

Lemma 5.1. For n = 4 , let S is an I n d -set and | S | = 4 , then | N C F 4 ( S ) | ≥ 8 .
Proof. Let S = { x 1 , x 2 , x 3 , x 4 } , since S is an I n d -set, x 1 , x 2 , x 3 , x 4 are nonadjacent to each other. As C F 4 i ≅ C F 3 ( i ∈ { 1 , 2 , 3 , 4 } ) , we know x 1 , x 2 , x 3 , x 4 can not belong to a same subgraph of C F 4 . So we need think about the following cases:
Case 1: x 1 , x 2 , x 3 , x 4 belong to two different subgraphs of C F 4 .
In this case, we can divide it into two subcases:
Subcase 1.1: There are two subgraphs of C F 4 which contain only two vertices of S. Without loss of generality, we can let { x 1 , x 2 } ⊆ V ( C F 4 1 ) , { x 3 , x 4 } ⊆ V ( C F 4 2 ) . By the definition of C F n , | N C F 4 1 ( { x 1 , x 2 } ) | = | N C F 4 2 ( { x 3 , x 4 } ) | = 3 . Now we let x 1 = 2341 , then x 2 = 4231 or x 2 = 3421 . Thus x 1 + ∈ V ( C F 4 2 ) , x 2 + = 1234 ∈ V ( C F 4 4 ) or x 2 + = 1423 ∈ V ( C F 4 3 ) . Hence x 1 + and x 2 + can not belong to a common subgraph of C F 4 . Similarly, we know x 3 + and x 4 + can not belong to a common subgraph of C F 4 . If x 1 + or x 2 + belong to C F 4 2 and adjacent to { x 3 , x 4 } , meanwhile x 3 + or x 4 + belong to C F 4 1 and adjacent to { x 1 , x 2 } , then | N C F 4 ( S ) | = 3 + 3 + 2 = 8 . Now, we illustrate this structure exists. Let x 3 = 3142 , x 4 = 1432 , then x 1 + is adjacent to x 3 , x 4 + is adjacent to x 1 . Thus | N C F 4 ( S ) | ≥ 8 .
Subcase 1.2: There is a subgraph of C F 4 which contains three vertices of S. In this subcase, we can let { x 1 , x 2 , x 3 } ⊆ V ( C F 4 1 ) , x 4 ∈ V ( C F 4 2 ) . We let x 1 = 2341 , x 2 = 4231 , x 3 = 3421 , then x 1 + = 1342 ∈ V ( C F 4 2 ) , x 2 + = 1234 ∈ V ( C F 4 4 ) , x 3 + = 1423 ∈ V ( C F 4 3 ) . Clearly, | N C F 4 1 ( { x 1 , x 2 , x 3 } ) | = 3 , | N C F 4 2 ( x 4 ) | = 3 . If x 4 + ∈ V ( C F 4 1 ) and is adjacent to { x 1 , x 2 , x 3 } , meanwhile x 1 + is adjacent to x 4 , then | N C F 4 ( S ) | = 3 + 3 + 2 = 8 . Let x 4 = 1432 , then x 4 + = 2431 . Thus x 1 + is adjacent to x 4 and x 4 + is adjacent to x 1 . Thus | N C F 4 ( S ) | ≥ 8 .
Case 2: x 1 , x 2 , x 3 , x 4 belong to three different subgraphs of C F 4 .
In this case, there exists a subgraph C F 4 i which must contains two vertices of S. Now we can let { x 1 , x 2 } ⊆ V ( C F 4 i ) , x 3 ∈ V ( C F 4 j ) , x 4 ∈ V ( C F 4 k ) . Then | N C F 4 i ( { x 1 , x 2 } ) | = 3 , | N C F 4 j ( x 3 ) | = | N C F 4 k ( x 4 ) | = 3 , | N C F 4 ( S ) | ≥ | N C F 4 i ( { x 1 , x 2 } ) | + | N C F 4 j ( x 3 ) | + | N C F 4 k ( x 4 ) | = 9 .
Case 3: x 1 , x 2 , x 3 , x 4 belong to four different subgraphs of C F 4 .
In this case, we can let x k ∈ V ( C F n k ) , then | N C F n k ( x k ) | = 3 . Thus | N C F 4 ( S ) | ≥ 4 × | N C F n k ( x k ) | = 4 × 3 = 12 .
Combing the above three cases, we have | N C F 4 ( S ) | ≥ 8 .
Lemma 5.2. When n is odd, let S = { x 1 , x 2 , x 3 , x 4 } is an I n d -set and { x 1 , x 2 } ⊆ V ( C F n i ) , { x 3 , x 4 } ⊆ V ( C F n j ) ( i ≠ j ) . If | N C F n i ( { x 1 , x 2 } ) | = | N C F n j ( { x 3 , x 4 } ) | = 3 n − 10 , then | N C F n − C F n i − C F n j   ( S ) | ≥ 4 .
Proof. Since | N C F n i ( { x 1 , x 2 } ) | = | N C F n j ( { x 3 , x 4 } ) | = 3 n − 10 , by the proof process of Lemma 3.3, we know x 1 , x 2 ( r e s p . , x 3 , x 4 ) have three common neighbors in C F n i ( r e s p . , C F n j ) . So by Lemma 3.1, we can let x 1 = i 1 i 2 ⋯ i n − 2 i n − 1 i , x 2 = k 1 k 2 ⋯ k n − 2 i n − 1 i , where k i ∈ [ i 1 , i n − 2 ] and k 1 ≠ i 1 . Then x 1 + = i i 2 i 3 ⋯ i n − 2 i n − 1 i 1 , x 1 − = i 1 i 2 i 3 ⋯ i n − 2 i i n − 1 , x 2 − = k 1 k 2 ⋯ k n − 2 i i n − 1 , x 2 + = i k 2 k 3 ⋯ k n − 2 i n − 1 k 1 . By Proposition 2.3 and Proposition 2.2, we have 2 ≤ | N C F n − C F n i − C F n j ( { x 1 ,   x 2 } ) | ≤ 4 , 2 ≤ | N C F n − C F n i − C F n j ( { x 3 , x 4 } ) | ≤ 4 . Then we think about the following three cases:
Case 1: | N C F n − C F n i − C F n j ( { x 1 , x 2 } ) | = 4 .
In this case, we can easily get | N C F n − C F n i − C F n j ( S ) | ≥ 4 .
Case 2: | N C F n − C F n i − C F n j ( { x 1 , x 2 } ) | = 3 .
In this case, only one of the outgoing neighbors of { x 1 , x 2 } belong to C F n j . So i 1 = j or k 1 = j . We assume i 1 = j , then x 1 + ∈ V ( C F n j ) . If | N C F n − C F n i − C F n j ( { x 3 , x 4 } ) | = 4 , then | N C F n − C F n i − C F n j ( S ) | ≥ 4 . If | N C F n − C F n i − C F n j ( { x 3 , x 4 } ) | ≤ 3 , one of the outgoing neighbors of { x 3 , x 4 } must belong to C F n i , we assume x 3 + or x 3 − belong to C F n i , then x 3 = i j 2 j 3 ⋯ j n − 2 j n − 1 j or x 3 = j 1 j 2 j 3 ⋯ j n − 2 i j . When x 3 = i j 2 j 3 ⋯ j n − 2 j n − 1 j , then by the proof process of Lemma 3.1, we can let x 4 = l 1 l 2 l 3 ⋯ l n − 2 j n − 1 j , where l i ∈ ( [ j 2 , j n − 2 ] ∪ { i } ) and l 1 ≠ i . Thus x 3 + = j j 2 j 3 ⋯ j n − 2 j n − 1 i , x 3 − = i j 2 j 3 ⋯ j n − 2 j j n − 1 , x 4 + = j l 2 l 3 ⋯ l n − 2 j n − 1 l 1 , x 4 − = l 1 l 2 l 3 ⋯ l n − 2 j j n − 1 . Then x 3 + ∈ V ( C F n i ) . Since j n − 1 ≠ i , x 4 − ∉ V ( C F n i ) . Thus | N C F n − C F n i − C F n j ( S ) | ≥ 4 as x 4 − ≠ x 1 − , x 4 − ≠ x 2 − , x 4 − ≠ x 2 + . When x 3 = j 1 j 2 j 3 ⋯ j n − 2 i j , then by the proof process of Lemma 3.1, we can let x 4 = l 1 l 2 l 3 ⋯ l n − 2 i j , where l i ∈ [ j 1 , j n − 2 ] and l 1 ≠ j 1 . Then x 3 + = j j 2 j 3 ⋯ j n − 2 i j 1 , x 3 − = j 1 j 2 j 3 ⋯ j n − 2 j i , x 4 + = j l 2 l 3 ⋯ l n − 2 i l 1 , x 4 − = l 1 l 2 l 3 ⋯ l n − 2 j i , { x 3 − , x 4 − } ⊆ V ( C F n i ) . Since j 1 ≠ i , l 1 ≠ i , we know { x 3 + , x 4 + } ⊆ V ( C F n − C F n i − C F n j ) . As i ≠ j and k 1 ≠ j , then x 1 − ≠ x 3 + , x 3 + ≠ x 2 + , x 3 + ≠ x 2 − . Thus | N C F n − C F n i − C F n j ( S ) | ≥ 4 .
Case 3: | N C F n − C F n i − C F n j ( { x 1 , x 2 } ) | = 2 .
In this case, two outgoing neighbors of { x 1 , x 2 } belong to C F n j . Thus { x 1 − , x 2 − } ⊆ V ( C F n j ) and { x 3 , x 4 } ⊆ V ( C F n j ) . Now we let x 3 = j 1 j 2 j 3 ⋯ j n − 2 j n − 1 j , then x 4 = u 1 u 2 u 3 ⋯ u n − 2 j n − 1 j , where u i ∈ [ j 1 , j n − 2 ] and u 1 ≠ j 1 . If | N C F n − C F n i − C F n j ( { x 3 , x 4 } ) | = 4 , clearly | N C F n − C F n i − C F n j ( S ) | ≥ 4 . If | N C F n − C F n i − C F n j ( { x 3 , x 4 } ) | = 3 , the proof process is similar to Case 2, we can get | N C F n − C F n i − C F n j ( S ) | ≥ 4 . So we let | N C F n − C F n i − C F n j ( { x 3 , x 4 } ) | = 2 , then one of the outgoing neighbors of x 3 and x 4 belong to C F n i , we assume x 3 = i j 2 j 3 ⋯ j n − 2 j n − 1 j or x 3 = j 1 j 2 j 3 ⋯ j n − 2 i j . When x 3 = i j 2 j 3 ⋯ j n − 2 j n − 1 j , we can get j n − 1 ≠ i , so x 4 = i u 2 u 3 ⋯ u n − 2 j n − 1 j . By Corollary 3.2, we know x 3 and x 4 can not have three common neighbors in C F n j , so x 3 = j 1 j 2 j 3 ⋯ j n − 2 i j , x 4 = u 1 u 2 u 3 ⋯ u n − 2 i j . Since x 4 + = j u 2 u 3 ⋯ u n − 2 i u 1 , x 3 + = j j 2 j 3 ⋯ j n − 2 i j 1 and i ≠ j , we have x 3 + ≠ x 1 + , x 3 + ≠ x 2 + , x 4 + ≠ x 1 + , x 4 + ≠ x 2 + . Thus | N C F n − C F n i − C F n j ( S ) | ≥ 4 .
Lemma 5.3. When n is odd, let S = { x 1 , x 2 , x 3 , x 4 } is an I n d -set and { x 1 , x 2 , x 3 } ⊆ V ( C F n i ) , x 4 ∈ V ( C F n j ) ( i ≠ j ) . If | N C F n i ( S ) | = 9 ( n − 1 ) − 24 2 = 9 n − 33 2 , | N C F n j ( S ) | = 3 n − 7 2 , then | N C F n − C F n i − C F n j ( S ) | ≥ 4 .
Proof. Since { x 1 , x 2 , x 3 } ⊆ V ( C F n i ) , C F n i ≅ C F n − 1 , n − 1 is even and | N C F n i ( S ) | = 9 n − 33 2 , by Corollary 4.6, we know x 1 , x 2 , x 3 must belong to a common subgraph in C F n i . So we let x 1 = i 1 i 2 i 3 ⋯ i n − 2 i n − 1 i , x 2 = j 1 j 2 j 3 ⋯ j n − 2 i n − 1 i , x 3 = k 1 k 2 k 3 ⋯ k n − 2 i n − 1 i . Then x 1 + = i i 2 i 3 ⋯ i n − 2 i n − 1 i 1 , x 1 − = i 1 i 2 i 3 ⋯ i n − 2 i i n − 1 , x 2 + = i j 2 j 3 ⋯ j n − 2 i n − 1 j 1 , x 2 − = j 1 j 2 j 3 ⋯ j n − 2 i i n − 1 , x 3 + = i k 2 k 3 ⋯ k n − 2 i n − 1 k 1 , x 3 − = k 1 k 2 k 3 ⋯ k n − 2 i i n − 1 . If | N C F n − C F n i − C F n j ( { x 1 , x 2 , x 3 } ) | ≥ 4 , then | N C F n − C F n i − C F n j ( S ) | ≥ 4 . Thus we assume | N C F n − C F n i − C F n j ( { x 1 , x 2 , x 3 } ) | = 3 , then one of the two outgoing neighbors of x 1 , x 2 , x 3 must belong to a common subgraph of C F n , we need to think about the following two situations:
Case 1: { x 1 − , x 2 − , x 3 − } ⊆ V ( C F n i n − 1 ) and x 4 ∈ V ( C F n i n − 1 ) .
In this case, we let x 4 = l 1 l 2 l 3 ⋯ l n − 2 l n − 1 i n − 1 , then x 4 + = i n − 1 l 2 l 3 ⋯ l n − 2 l n − 1 l 1 , x 4 − = l 1 l 2 l 3 ⋯ l n − 2 i n − 1 l n − 1 . If x 4 + ∉ V ( C F n i ) and x 4 − ∉ V ( C F n i ) , then | N C F n − C F n i − C F n j ( S ) | ≥ 4 as i n − 1 ≠ i and x 4 + ≠ x 1 + , x 4 + ≠ x 2 + , x 4 + ≠ x 3 + . If one of the two outgoing neighbors of x 4 belong to C F n i , we can assume x 4 = l 1 l 2 l 3 ⋯ l n − 2 i i n − 1 or x 4 = i l 2 l 3 ⋯ l n − 2 l n − 1 i n − 1 . If x 4 = i l 2 l 3 ⋯ l n − 2 l n − 1 i n − 1 , since | N C F n j ( S ) | = 3 n − 7 2 , we know x 1 − , x 2 − , x 3 − are adjacent to x 4 , so x 1 − = x 4 ( 1 , n − 1 ) , x 2 − = x 4 ( 1 , n − 1 ) , x 3 − = x 4 ( 1 , n − 1 ) , this contradicts to the fact that x 1 − , x 2 − , x 3 − are different from each other. So x 4 = l 1 l 2 l 3 ⋯ l n − 2 i i n − 1 , then x 4 + = i n − 1 l 2 l 3 ⋯ l n − 2 i l 1 , x 4 − = l 1 l 2 l 3 ⋯ l n − 2 i n − 1 i . Hence x 4 − ∈ V ( C F n i ) , x 4 + ≠ x 1 + , x 4 + ≠ x 2 + , x 4 + ≠ x 3 + . Thus | N C F n − C F n i − C F n j ( S ) | ≥ 4 .
Case 2: Let i 1 = j 1 = k 1 , { x 1 + , x 2 + , x 3 + } ⊆ V ( C F n i 1 ) and x 4 ∈ V ( C F n i 1 ) .
In this case, x 1 = i 1 i 2 i 3 ⋯ i n − 2 i n − 1 i , x 2 = i 1 j 2 j 3 ⋯ j n − 2 i n − 1 i , x 3 = i 1 k 2 k 3 ⋯ k n − 2 i n − 1 i . Then x 1 + = i i 2 i 3 ⋯ i n − 2 i n − 1 i 1 , x 2 + = i j 2 j 3 ⋯ j n − 2 i n − 1 i 1 , x 3 + = i k 2 k 3 ⋯ k n − 2 i n − 1 i 1 , x 1 − = i 1 i 2 i 3 ⋯ i n − 2 i i n − 1 , x 2 − = i 1 j 2 j 3 ⋯ j n − 2 i i n − 1 , x 3 − = i 1 k 2 k 3 ⋯ k n − 2 i i n − 1 . We let x 4 = l 1 l 2 l 3 ⋯ l n − 2   l n − 1 i 1 , then x 4 + = i 1 l 2 l 3 ⋯ l n − 2 l n − 1 l 1 , x 4 − = l 1 l 2 l 3 ⋯ l n − 2 i 1 l n − 1 . If x 4 + ∉ V ( C F n i ) and x 4 − ∉ V ( C F n i ) , then | N C F n − C F n i − C F n j ( S ) | ≥ 4 as x 4 − ≠ x 1 − , x 4 − ≠ x 2 − , x 4 − ≠ x 3 − . If one of the two outgoing neighbors of x 4 belong to C F n i , we can assume x 4 = l 1 l 2 l 3 ⋯ i i 1 or x 4 = i l 2 l 3 ⋯ l n − 1 i 1 . When x 4 = l 1 l 2 l 3 ⋯ i i 1 , as x 1 + , x 2 + , x 3 + are adjacent to x 4 , so x 1 + = x 4 ( 1 , n − 1 ) , x 2 + = x 4 ( 1 , n − 1 ) , x 3 + = x 4 ( 1 , n − 1 ) , this contracts to the fact x 1 + , x 2 + , x 3 + are different from each other. So x 4 = i l 2 l 3 ⋯ l n − 1 i 1 , x 4 + = i 1 l 2 l 3 ⋯ l n − 1 i , x 4 − = i l 2 l 3 ⋯ i 1 l n − 1 . Then x 4 + ∈ V ( C F n i ) , x 4 − ≠ x 1 − , x 4 − ≠ x 2 − , x 4 − ≠ x 3 − . Thus | N C F n − C F n i − C F n j ( S ) | ≥ 4 .
Lemma 5.4. When n is odd, let S = { x 1 , x 2 , x 3 , x 4 } is an I n d -set and { x 1 , x 2 } ⊆ V ( C F n i ) , { x 3 } ⊆ V ( C F n j ) , { x 3 } ⊆ V ( C F n k ) ( i , j , k are different from each other). If | N C F n i ( { x 1 , x 2 }   ) | = 3 n − 10 , then | N C F n − C F n i − C F n j − C F n k ( S ) | ≥ 1 .
Proof. If | N C F n − C F n i − C F n j − C F n k ( S ) | = 0 , the structure in Figure 5 must exists. Now we can proof this structure does not exist. As | N C F n i ( { x 1 , x 2 } ) | = 3 n − 10 , we can get x 1 , x 2 must have three common neighbors in C F n i . So we can assume x 1 = i 1 i 2 i 3 ⋯ i n − 2 j i , then by Lemma 3.1, we can let x 2 = j 1 j 2 j 3 ⋯ j n − 2 j i , where j i ∈ [ i 1 , i n − 2 ] and j 1 ≠ i 1 . Then x 1 + = i i 2 i 3 ⋯ i n − 2 j i 1 , x 2 + = i j 2 j 3 ⋯ j n − 2 j j 1 , x 1 − = i 1 i 2 i 3 ⋯ i n − 2 i j , x 2 − = j 1 j 2 j 3 ⋯ j n − 2 i j . Since i 1 ≠ j and i 1 ≠ j 1 , x 1 + can not belong to a common subgraph with x 2 + or x 2 − . Thus the structure in Figure 5 does not exist, | N C F n − C F n i − C F n j − C F n k ( S ) | ≥ 1 .
Lemma 5.5. For n = 5 , let S is an I n d -set and | S | = 4 , then | N C F 5 ( S ) | ≥ 14 .
Proof. Let S = { x 1 , x 2 , x 3 , x 4 } , since S is an I n d -set, x 1 , x 2 , x 3 , x 4 are nonadjacent to each other. Note that C F 5 i ≅ C F 4 . Now we think about the following four cases:
Case 1: S = { x 1 , x 2 , x 3 , x 4 } belong to a same subgraph C F 5 i .
By Lemma 5.1, we have | N C F 5 i ( S ) | ≥ 8 . By Proposition 2.3, we know | N C F 5 − C F 5 i ( S ) | = 8 . Thus | N C F 5 ( S ) | = | N C F 5 i ( S ) | + | N C F 5 − C F 5 i ( S ) | ≥ 8 + 8 = 16 .
Case 2: S = { x 1 , x 2 , x 3 , x 4 } belong to two different subgraphs C F 5 i , C F 5 j ( i ≠ j ) .
In this case, we need to think about the following two situations:
Subcase 2.1: { x 1 , x 2 } ⊆ V ( C F 5 i ) , { x 3 , x 4 } ⊆ V ( C F 5 j ) .
By Lemma 3.3, we can get | N C F 5 i ( { x 1 , x 2 } ) | ≥ 3 n − 10 = 5 , | N C F 5 j ( { x 3 , x 4 } ) | ≥ 3 n − 10 = 5 . By Lemma 5.2, we have | N C F 5 ( S ) | = | N C F 5 i ( { x 1 , x 2 } ) | + | N C F 5 j ( { x 3 , x 4 } ) | + | N C F 5 − C F 5 i − C F 5 j ( S ) | ≥ 2 × 5 + 4 = 14 .
Subcase 2.2: { x 1 , x 2 , x 3 } ⊆ V ( C F 5 i ) , x 4 ∈ V ( C F 5 j ) .
By Lemma 4.1, we have | N C F 5 i ( { x 1 , x 2 , x 3 } ) | ≥ 6 , | N C F 5 j ( x 4 ) | = 3 × 4 − 4 2 = 4 . By Lemma 5.3, we know | N C F n − C F n i − C F n j ( S ) | ≥ 4 . Thus | N C F n ( S ) | = | N C F 5 i ( { x 1 , x 2 , x 3 } ) | + | N C F 5 j ( x 4 ) | + | N C F n − C F n i − C F n j ( S ) | ≥ 6 + 4 + 4 = 14 .
Case 3: S = { x 1 , x 2 , x 3 , x 4 } belong to three different subgraphs C F 5 i , C F 5 j , C F 5 k ( i , j , k are different from each other).
In this case, there exists a subgraph C F 5 i , which contains two vertices of S, we let { x 1 , x 2 } ⊆ V ( C F 5 i ) . Clearly, | N C F 5 i ( { x 1 , x 2 } ) | ≥ 3 n − 10 = 5 , | N C F 5 j ( x 3 ) | = | N C F 5 k ( x 4 ) | = 4 . Thus, by Lemma 5.4, we have | N C F 5 ( S ) | = | N C F 5 i ( { x 1 , x 2 } ) | + | N C F 5 j ( x 3 ) | + | N C F 5 k ( x 4 ) | + | N C F 5 − C F 5 i − C F 5 j − C F 5 k   ( S ) | ≥ 5 + 4 + 4 + 1 = 14 .
Case 4: S = { x 1 , x 2 , x 3 , x 4 } belong to four different subgraphs.
In this case, we can let x k ∈ V ( C F 5 k ) . Clearly, | N C F 5 k ( x k ) | = 4 , thus | N C F 5 ( S ) | ≥ 4 × | N C F 5 k ( x k ) | = 4 × 4 = 16 > 14 .
Combing the above four cases, we can get | N C F 5 ( S ) | ≥ 14 .
Lemma 5.6. For n = 6 , let S is an I n d -set and | S | = 4 , then | N C F 6 ( S ) | ≥ 18 .
Proof. Let S = { x 1 , x 2 , x 3 , x 4 } , since S is an I n d -set, x 1 , x 2 , x 3 , x 4 are nonadjacent to each other. Note that C F 6 i ≅ C F 5 . Now we think about the following four cases:
Case 1: S = { x 1 , x 2 , x 3 , x 4 } belong to a same subgraph C F 6 i .
By Lemma 5.5 , we can get | N C F 6 i ( S ) | ≥ 14 . By the definition of C F n , we know every vertex in C F 6 has only one outgoing neighbor. Thus | N C F 6 ( S ) | = | N C F 6 i ( S ) | + 4 ≥ 18 .
Case 2: S = { x 1 , x 2 , x 3 , x 4 } belong to two different subgraphs C F 6 i , C F 6 j ( i ≠ j ) .
In this case, we also need to think about the following two situations:
Subcase 2.1: { x 1 , x 2 } ⊆ V ( C F 6 i ) , { x 3 , x 4 } ⊆ V ( C F 6 j ) .
By Lemma 3.3, we can get | N C F 6 i ( { x 1 , x 2 } ) | ≥ 3 n − 9 = 9 , | N C F 6 j ( { x 3 , x 4 } ) | ≥ 3 n − 9 = 9 . Thus | N C F 6 ( S ) | ≥ | N C F 6 i ( { x 1 , x 2 } ) | + | N C F 6 j ( { x 3 , x 4 } ) | = 9 + 9 = 18 .
Subcase 2.2: { x 1 , x 2 , x 3 } ⊆ V ( C F 6 i ) , x 4 ∈ V ( C F 6 j ) .
By Lemma 4.2, we have | N C F 6 i ( { x 1 , x 2 , x 3 } ) | ≥ 12 , | N C F 6 j ( x 4 ) | = 3 × 5 − 3 2 = 6 . Thus | N C F 6 ( S ) | ≥ | N C F 6 i ( { x 1 , x 2 , x 3 } ) | + | N C F 6 j ( x 4 ) | = 12 + 6 = 18 .
Case 3: S = { x 1 , x 2 , x 3 , x 4 } belong to three different subgraphs C F 6 i , C F 6 j , C F 6 k ( i , j , k are different from each other).
In this case, there exists a subgraph C F 6 i , which contains two vertices of S, we let { x 1 , x 2 } ⊆ V ( C F 6 i ) . Clearly, | N C F 6 i ( { x 1 , x 2 } ) | ≥ 3 n − 9 = 9 , | N C F 6 j ( x 3 ) | = | N C F 6 k ( x 4 ) | = 6 . Thus, | N C F 6 ( S ) | ≥ | N C F 6 i ( { x 1 , x 2 } ) | + | N C F 6 j ( x 3 ) | + | N C F 6 k ( x 4 ) | = 9 + 6 + 6 = 21 > 18 .
Case 4: S = { x 1 , x 2 , x 3 , x 4 } belong to four different subgraphs.
In this case, we can let x k ∈ V ( C F 6 k ) . Clearly, | N C F 6 k ( x k ) | = 6 , thus | N C F 6 ( S ) | ≥ 4 × | N C F 6 k ( x k ) | = 4 × 6 = 24 > 18 .
Combing the above four cases, we can get | N C F 6 ( S ) | ≥ 18 .
Lemma 5.7. For n ≥ 5 , let S is an I n d -set and | S | = 4 , then when n is odd, | N C F n ( S ) | ≥ 6 n − 16 ; when n is even, | N C F n ( S ) | ≥ 6 n − 18 .
Proof. We proof this result by induction on n. By Lemma 5.5 and Lemma 5.6, we know when n = 5 , 6 , this result holds. Now we assume n ≥ 7 and the result holds for C F n − 1 . Let S = { x 1 , x 2 , x 3 , x 4 } , since S is an I n d -set, x 1 , x 2 , x 3 , x 4 are nonadjacent to each other. Note that C F n i ≅ C F n − 1 . Now we think about the following four cases:
Case 1: S = { x 1 , x 2 , x 3 , x 4 } belong to a same subgraph C F n i .
By induction hypothesis, we know when n is odd, | N C F n i ( S ) | ≥ 6 ( n − 1 ) − 18 = 6 n − 24 ; when n is even, | N C F n i ( S ) | ≥ 6 ( n − 1 ) − 16 = 6 n − 22 . By Proposition 2.3, we know when n is odd, | N C F n − C F n i ( S ) | = 8 ; when n is even, | N C F n − C F n i ( S ) | = 4 . Thus | N C F n ( S ) | = | N C F n i ( S ) | + | N C F n − C F n i ( S ) | ≥ 6 n − 24 + 8 = 6 n − 16 (n is odd) and | N C F n ( S ) | ≥ 6 n − 22 + 4 = 6 n − 18 (n is even).
Case 2: S = { x 1 , x 2 , x 3 , x 4 } belong to two different subgraphs C F n i , C F n j ( i ≠ j ) .
In this case, we need to think about two situations:
Subcase 2.1: { x 1 , x 2 } ⊆ V ( C F n i ) , { x 3 , x 4 } ⊆ V ( C F n j ) .
By Lemma 3.3, we can get when n is odd, | N C F n i ( { x 1 , x 2 } ) | ≥ 3 n − 10 , | N C F n j ( { x 3 , x 4 } ) | ≥ 3 n − 10 ; when n is even, | N C F n i ( { x 1 , x 2 } ) | ≥ 3 n − 9 , | N C F n j ( { x 3 , x 4 } ) | ≥ 3 n − 9 . When n is odd, by Lemma 5.2, we have | N C F n ( S ) | = | N C F n i ( { x 1 , x 2 } ) | + | N C F n j ( { x 3 , x 4 } ) | + | N C F n − C F n i − C F n j ( S ) | ≥ 2 × ( 3 n − 10 ) + 4 = 6 n − 16 . When n is even, | N C F n ( S ) | ≥ | N C F n i ( { x 1 , x 2 } ) | + | N C F n j ( { x 3 , x 4 } ) | = 2 × ( 3 n − 9 ) = 6 n − 18 .
Subcase 2.2: { x 1 , x 2 , x 3 } ⊆ V ( C F n i ) , x 4 ∈ V ( C F n j ) .
When n is odd, by Lemma 4.5, we have | N C F n i ( { x 1 , x 2 , x 3 } ) | ≥ 9 ( n − 1 ) − 24 2 = 9 n − 33 2 . By Lemma 5.3, we know | N C F n − C F n i − C F n j ( S ) | ≥ 4 . As | N C F n j ( x 4 ) | = 3 × ( n − 1 ) − 4 2 = 3 n − 7 2 , so | N C F n ( S ) | = | N C F n i ( { x 1 , x 2 , x 3 } ) | + | N C F n j ( x 4 ) | + | N C F n − C F n i − C F n j ( S ) | ≥ 9 n − 33 2 + 3 n − 7 2 + 4 = 6 n − 16 . When n is even, by Lemma 4.5, we have | N C F n i ( { x 1 , x 2 , x 3 } ) | ≥ 9 ( n − 1 ) − 21 2 = 9 n − 30 2 . As | N C F n j ( x 4 ) | = 3 × ( n − 1 ) − 3 2 = 3 n − 6 2 , so | N C F n ( S ) | ≥ | N C F n i ( { x 1 , x 2 , x 3 } ) | + | N C F n j ( x 4 ) | = 9 n − 30 2 + 3 n − 6 2 = 6 n − 18 .
Case 3: S = { x 1 , x 2 , x 3 , x 4 } belong to three different subgraphs C F n i , C F n j , C F n k ( i , j , k are different from each other).
In this case, there exists a subgraph C F n i , which contains two vertices of S, we let { x 1 , x 2 } ⊆ V ( C F n i ) . When n is odd, by Lemma 3.3, we have | N C F n i ( { x 1 , x 2 } ) | ≥ 3 n − 10 . Clearly, | N C F n j ( x 3 ) | = | N C F n k ( x 4 ) | = 3 n − 7 2 . Thus, by Lemma 5.4, we have | N C F n ( S ) | = | N C F n i ( { x 1 , x 2 } ) | + | N C F n j ( x 3 ) | + | N C F n k ( x 4 ) | + | N C F n − C F n i − C F n j − C F n k ( S ) | ≥ 3 n − 10 + 2 × 3 n − 7 2 + 1 = 6 n − 16 . When n is even, by Lemma 3.3, we have | N C F n i ( { x 1 , x 2 } ) | ≥ 3 n − 9 . Clearly, | N C F n j ( x 3 ) | = | N C F n k ( x 4 ) | = 3 n − 6 2 . Thus, | N C F n ( S ) | ≥ | N C F n i ( { x 1 , x 2 } ) | + | N C F n j ( x 3 ) | + | N C F n k ( x 4 ) | = 3 n − 9 + 2 × 3 n − 6 2 = 6 n − 15 > 6 n − 18 .
Case 4: S = { x 1 , x 2 , x 3 , x 4 } belong to four different subgraphs.
In this case, we can let x i ∈ V ( C F n i ) . Clearly, when n is odd, | N C F n i ( x i ) | = 3 n − 7 2 ; when n is even, | N C F n i ( x i ) | = 3 n − 6 2 . Thus when n is odd, | N C F n ( S ) | ≥ 4 × | N C F n i ( x i ) | = 4 × 3 n − 7 2 = 6 n − 14 > 6 n − 16 ; when n is even, | N C F n ( S ) | ≥ 4 × | N C F n i ( x i ) | = 4 × 3 n − 6 2 = 6 n − 12 > 6 n − 18 .
Combing the above four cases, we know the result holds.
Lemma 5.8. For n = 5 , if F satisfies the condition | F | ≤ 13 , then C F 5 − F contains a big component C with | V ( C ) | ≥ 5 ! − | F | − 3 .
Proof. In this Lemma, we do not think about the situation C F 5 − F is connected, so we let C F 5 − F is disconnected. Let F i = F ∩ C F n i ( i ∈ [ 1 , 5 ] ) . By Proposition 2.8, we know κ ( C F 5 i ) = 3 ( n − 1 ) − 4 2 = 3 × 4 − 4 2 = 4 . Since | F | ≤ 14 , we can get there exists at most three vertex set F i , which can satisfies the condition | F i | ≥ 4 . Now we think about the following situations:
Case 1: | F i | ≤ 3 for every i ∈ [ 1 , 5 ] .
By Proposition 2.8, we know C F 5 i − F i is connected for i ∈ [ 1 , 5 ] . Since E i , j ( C F 5 ) = 2 ( n − 2 ) ! = 12 > 6 ≥ | F i | + | F j | , C F 5 i and C F 5 j are connected. Thus we can get C F 5 − F is connected, this contradicts to the assumption C F 5 − F is disconnected.
Case 2: There exists only one F i , which can satisfies that | F i | ≥ 4 .
In this case, we can let | F 1 | ≥ 4 , then | F i | ≤ 3 for i ∈ [ 2 , 5 ] . Hence by Proposition 2.8, we can get C F 5 i − F i is connected ( i ∈ [ 2 , 5 ] ) . Let M = C F 5 − F − C F 5 1 , similarly to the discussion of Case 1, we know M is connected. Now we think about the following two situations:
Subcase 2.1: | F − F 1 | ≤ 7 .
By the definition of C F n and Proposition 2.3, we know every vertex has two outgoing neighbors, and these outgoing neighbors are different from each other. Thus, if C F 5 1 − F 1 is connected and | C F 5 1 − F 1 | ≥ 4 , there must exists a vertex x 1 in C F 5 1 − F 1 such that it has a good neighbor in M. Thus C F 5 − F is connected, this contradicts to the assumption C F 5 − F is disconnected. If C F 5 1 − F 1 is connected and | C F 5 1 − F 1 | ≤ 3 , the result is certainly true. If C F 5 1 − F 1 is disconnected, we can assume C 1 is the vertex set in C F 5 1 − F 1 , which has no good neighbors in M. As | F − F 1 | ≤ 7 , we can get | V ( C 1 ) | ≤ 3 , so the result holds.
Subcase 2.2: | F − F 1 | ≥ 8 .
In this case, if C F 5 1 − F 1 is connected, similar to the case 1, we can get C F 5 − F is connected. Now we assume C F 5 1 − F 1 is disconnected. Since | F − F 1 | ≥ 8 , we have | F 1 | ≤ | F | − 8 ≤ 13 − 8 = 5 , by Lemma 1, we know C F 5 1 − F 1 has a big component C 1 and one singleton or two singletons. Since | V ( C 1 ) | ≥ | V ( C F 5 1 − F 1 ) | − 2 ≥ 4 ! − 5 − 2 = 17 > 13 > | F 2 ∪ F 3 ∪ F 4 ∪ F 5 | , C 1 is connected to M. Thus C F 5 − F has a big component C with | V ( C ) | ≥ n ! − | F | − 2 .
Case 3: There exists two vertex set F i , F j , which satisfy that | F i | ≥ 4 , | F j | ≥ 4 .
In this case, we can let | F 1 | ≥ | F 2 | ≥ 4 . Then | F i | ≤ 3 ( i ∈ [ 3 , 5 ] ) , | F 1 | ≤ | F | − | F 2 | ≤ 13 − 4 = 9 . Let M = C F 5 − F − C F 5 1 − C F 5 2 , similarly, we can get M is connected. If C F 5 i − F i ( i ∈ { 1 , 2 } ) is connected, by the same argument with Subcase 2.2, we know it connected to M. Thus, if C F 5 1 − F 1 and C F 5 2 − F 2 are all connected, then C F 5 − F is connected, this contradicts to the assumption that C F 5 − F is disconnected. Hence at least one of C F 5 i − F i ( i ∈ { 1 , 2 } ) is disconnected. Now we think about the following three cases:
Subcase 3.1: | F 2 | = | F 1 | = 4 .
By Corollary 3.4, we know if C F 5 i − F i ( i ∈ { 1 , 2 } ) is disconnected, then it has a big component C i and one singleton. Similarly, we can get C i is connected to M. Thus C F 5 − F has a component C with | V ( C ) | ≥ 5 ! − | F | − 2 .
Subcase 3.2: | F 1 | = 5 .
In this case, we know 4 ≤ | F 2 | ≤ | F 1 | = 5 . By Lemma 1, we can get if C F 5 1 − F 1 is disconnected, then it has a big component C 1 and one singleton or two singletons. If | F 2 | = 4 , by Corollary 3.4, we can get C F 5 2 − F 2 has a big component C 2 and at most one singleton. Similarly, we can also get C i is connected to M. Thus C F 5 − F has a big component C with | V ( C ) | ≥ n ! − | F | − 3 , the result holds. If | F 2 | = 5 , then | F − F 1 − F 2 | ≤ 13 − 5 − 5 = 3 . By Lemma 1, we know, if C F 5 i − F i ( i ∈ { 1 , 2 } ) is disconnected, it has a big component C i and one singleton or two singletons. If one of C F 5 i − F i is connected or has only one singleton, then the result holds. Now we consider C F 5 1 − F 1 and C F 5 2 − F 2 are all disconnected and they all have two singletons, we let { x 1 , x 2 } ⊆ V ( C F 5 1 − F 1 ) , { y 1 , y 2 } ⊆ V ( C F 5 2 − F 2 ) . Similarly, we can know that C i must connected to M, then C F 5 − F has a big component C with | V ( C ) | ≥ 5 ! − | F | − 4 . Since | F 1 | = | F 2 | = 5 and x 1 , x 2 (resp., y 1 , y 2 ) are two singletons, x 1 , x 2 must have three common neighbors in C F 5 1 (resp., y 1 , y 2 must have three common neighbors in C F 5 2 ) . If x 1 , x 2 , y 1 , y 2 are singletons in C F 5 − F , then by Lemma 5.2, we can get | N C F 5 − C F 5 1 − C F 5 2 ( { x 1 , x 2 , y 1 , y 2 } ) | ≥ 4 . Since | F − F 1 − F 2 | ≤ 3 , we know at least one vertex in { x 1 , x 2 , y 1 , y 2 } must connected to M. Thus C F 5 − F has a big component C with | V ( C ) | ≥ 5 ! − | F | − 3 . If ( C F 5 − F ) [ { x 1 , x 2 , y 1 , y 2 } ] has at least one edge, we assume ( x 2 , y 1 ) ∈ E ( C F 5 − F ) , then C F 5 − F has a big component C with | V ( C ) | ≥ 5 ! − | F | − 3 . Suppose | V ( C ) | = 5 ! − | F | − 4 , then x 1 , y 2 are singletons in C F 5 − F or ( x 1 , y 2 ) ∈ E ( C F 5 − F ) . If x 1 , y 2 are singletons in C F 5 − F , then | F | ≥ | N C F 5 ( { x 2 , y 1 } ) ∪ N C F 5 ( x 1 ) ∪ N C F 5 ( y 2 ) | ≥ 5 × 2 + 6 × 2 − 3 × 2 = 16 > 13 , a contradiction. If ( x 1 , y 2 ) ∈ E ( C F 5 − F ) , then | F | ≥ | N C F 5 ( { x 2 , y 1 } ) ∪ N C F 5 ( { x 1 , y 2 } ) ≥ 5 × 4 − 3 × 2 = 14 > 13 , a contradiction. Thus C F 5 − F has a big component C with | V ( C ) | ≥ n ! − | F | − 3 .
Subcase 3.3: 6 ≤ | F 1 | ≤ 9 .
In this case, we can get 4 ≤ | F 2 | ≤ | F | − | F 1 | ≤ 13 − 6 = 7 . If | F 2 | = 7 , then | F 1 | ≥ 7 , | F | ≥ | F 1 | + | F 2 | ≥ 14 , a contradiction. Thus 4 ≤ | F 2 | ≤ 6 .
If | F 2 | = 4 and C F 5 2 − F 2 is disconnected, then C F 5 2 − F 2 has a big component C 2 and one singleton x 4 . Furthermore, we have | F | − | F 1 | − | F 2 | ≤ 13 − 6 − 4 = 3 . When | F | − | F 1 | − | F 2 | ≤ 2 , since every vertex in C F 5 has two outgoing neighbors, there are at most two vertices in C F 5 1 − F 1 , which can satisfy that one of the two outgoing neighbors belong to F 2 and the other belongs to F − F 1 − F 2 . Thus the result holds. When | F | − | F 1 | − | F 2 | = 3 , C F 5 1 − F 1 has at most three vertices, which can satisfy that one of their outgoing neighbors belongs to F 2 and the other belongs to F − F 1 − F 2 . We let they are x 1 , x 2 , x 3 . If C F 5 1 − F 1 is connected or has at most two vertices, then the result holds. Now we consider there are three vertices in C F 5 1 − F 1 , we can get C F 5 − F has a big component C with | V ( C ) | ≥ 5 ! − | F | − 4 . If | V ( C ) | = 5 ! − | F | − 4 , the structure in Figure 6 must exists. If there exists one edge between { x 1 , x 2 , x 3 } , then there will be a 5-circle in C F 5 , a contradiction. So x 1 , x 2 , x 3 are three singletons in C F 5 1 − F 1 . If x 4 is adjacent to x 1 , x 2 , x 3 , then there exists a 3-circle in C F 5 . Thus x 1 , x 2 , x 3 , x 4 are four singletons in C F 5 − F . By Lemma 5.3, we know | N C F 5 − C F 5 1 − C F 5 2 ( S ) | ≥ 4 , this contradicts to the fact | F | − | F 1 | − | F 2 | = 3 , thus | V ( C ) | ≥ n ! − | F | − 3 .
If 5 ≤ | F 2 | ≤ 6 , then | F | − | F 1 | − | F 2 | ≤ 13 − 5 − 6 ≤ 2 . When | F | − | F 1 | − | F 2 | ≤ 1 , C F 5 − F has a big component and at most two vertices x 1 , x 2 , where x i ∈ V ( C F 5 i − F i ) and they have common outgoing neighbor vertex in F ∖ ( F 1 ∪ F 2 ) and the other outgoing neighbor vertex belong to C F 5 2 or C F 5 1 , so the result holds. When | F | − | F 1 | − | F 2 | = 2 , we can get | F 1 | = 6 , | F 2 | = 5 , and if C F 5 i − F i ( i ∈ { 1 , 2 } ) is disconnected, then it has at most two vertices which has neighbors in F − F 1 − F 2 . Thus C F 5 − F has a big component C with | V ( C ) | ≥ 5 ! − | F | − 4 . Now, we proof | V ( C ) | = 5 ! − | F | − 4 can not exist. Suppose on the contrary, the structure in Figure 7 exists. Since | F 2 | = 5 , we can get x 1 , x 2 are two singletons and have three common neighbors in C F 5 2 ; Otherwise, if x 1 is adjacent to x 2 , then | F 2 | = 6 , a contradiction. So by Lemma 3.1, we let x 1 = i 1 i 2 i 3 i 4 2 and x 2 = j 1 j 2 j 3 i 4 2 , where j i ∈ [ i 1 , i 3 ] and j 1 ≠ i 1 . Then x 1 + = 2 i 2 i 3 i 4 i 1 , x 1 − = i 1 i 2 i 3 2 i 4 , x 2 + = 2 j 2 j 3 i 4 j 1 , x 2 − = j 1 j 2 j 3 2 i 4 . Since one of the out neighbor vertices of x 1 , x 2 belong to C F 5 1 and j 1 ≠ i 1 , i 1 ≠ i 4 , j 1 ≠ i 4 , we have i 4 = 1 . Thus x 1 + = 2 i 2 i 3 1 i 1 , x 2 + = 2 j 2 j 3 1 j 1 . From the structure of Figure 7, we have ( x 1 + ) − = 2 i 2 i 3 i 1 1 = x 3 , ( x 2 + ) − = 2 j 2 j 3 j 1 1 = x 4 . Let x 3 ′ = 2 i 2 i 3 i 1 , x 4 ′ = 2 j 2 j 3 j 1 , then { x 3 ′ , x 4 ′ } ⊆ V ( G 1 ) , G 1 ≅ C F 4 . Since j 1 ≠ i 1 , x 4 ′ and x 3 ′ belong to different subgraph in G 1 . As ( x 3 ′ ) + = i 1 i 2 i 3 2 , ( x 4 ′ ) + = j 1 j 2 j 3 2 , we know ( x 3 ′ ) + ≠ ( x 4 ′ ) + . Thus x 3 and x 4 have no common neighbors in C F 5 1 . Clearly, we have x 3 is nonadjacent to x 4 ; Otherwise, there is a 7-circle in C F 5 (as shown in Figure 7 by read line). Thus, | F 1 | ≥ 8 , this contradicts to the fact | F 1 | = 6 , this structure does not exist. So C F 5 − F has a large component C with | V ( C ) | ≥ n ! − | F | − 3 .
Case 4: There exists three vertex set F i , F j , F k , which can satisfy that | F i | ≥ 4 , | F j | ≥ 4 and | F k | ≥ 4 ( i , j , k are different from each other).
In this case, we have | F i | ≤ | F | − | F j | − | F k | ≤ 13 − 4 − 4 = 5 . Similarly, we can get | F j | ≤ 5 , | F k | ≤ 5 . Let M = C F 5 − C F 5 i − C F 5 j − C F 5 k , we can get M is connected. If | F i | ≤ 4 , | F j | ≤ 4 and | F k | ≤ 4 , by Corollary 3.4, we know this result holds. If | F i | = 5 , | F j | ≤ 4 and | F k | ≤ 4 , then by Lemma 1, there are at most two singletons in C F 5 i − F i . Thus C F 5 − F has a big component C with | V ( C ) | ≥ 5 ! − | F | − 4 . If | V ( C ) | = n ! − | F | − 4 , then C F 5 i − F i has two singletons { x 1 , x 2 } and C F 5 j − F j , C F 5 k − F k only has one singleton. Since | F i | = 5 , x 1 and x 2 have three common neighbors in C F 5 i . Since | F | − | F i | − | F j | − | F k | ≤ 13 − 5 − 4 − 4 = 0 , we know x 1 + belong to a common subgraph with x 2 + or x 2 − . By the proof process of Lemma 5.4, we know this situation will not exist. So | V ( C ) | ≠ n ! − | F | − 4 , C F 5 − F has a big component C with | V ( C ) | ≥ n ! − | F | − 3 . If | F i | = 5 , | F j | = 5 , | F k | ≤ 4 , then | F | ≥ | F i | − | F j | − | F k | ≥ 5 + 5 + 4 = 14 , a contradiction. If there are three F i , F j , F k , such that | F i | = 5 , | F j | = 5 , | F k | = 5 , then | F | ≥ | F i | − | F j | − | F k | ≥ 5 + 5 + 5 = 15 , a contradiction.
Lemma 5.9. For n = 6 , if F satisfies the condition | F | ≤ 17 , then C F 6 − F contains a big component C with | V ( C ) | ≥ 6 ! − | F | − 3 .
Proof. In this Lemma, we do not think about C F 6 − F is connected, so we assume that C F 6 − F is disconnected. Let F i = F ∩ C F 6 i , note that C F 6 i ≅ C F 5 . By Proposition 2.8, we have κ ( C F 6 i ) = 3 n − 6 2 = 6 . Since | F | ≤ 17 , we can get there exists at most two vertex set F i , which can satisfy | F i | ≥ 6 . Next we think about the following three cases:
Case 1: | F i | ≤ 5 for every i ∈ [ 1 , 6 ] .
In this case, we know C F 6 i − F i is connected. Since there are ( n − 2 ) ! = 4 ! = 24 cross-edges in different C F 6 i and 24 > 5 + 5 = 10 , C F 6 − F is connected, a contradiction.
Case 2: There exists only one vertex set F i , which can satisfies the condition | F i | ≥ 6 .
In this case, we know | F j | ≤ 5 ( j ∈ [ 6 ] ∖ { i } ) . So C F 6 j − F j is connected. Let M = C F 6 − F − C F 6 i , similarly, we can get M is connected. When C F 6 i − F i is connected, since 24 > 17 , C F 6 − F is connected, this contradicts to the assumption C F 6 − F is disconnected. When C F 6 i − F i is disconnected, let S be the set of vertices in C F 6 i − F i , which have no good neighbors in M. If | F | − | F i | ≤ 3 , at most three vertices in C F 6 i − F i such that their out neighbor vertex belong to F − F i . Thus | V ( S ) | ≤ 3 . If | F | − | F i | ≥ 4 , then | F i | ≤ | F | − 4 = 17 − 4 = 13 . By Lemma 5.8, we know the result holds.
Case 3: There exists two vertex set F i , F j , which can satisfy that | F i | ≥ 6 and | F j | ≥ 6 .
In this case, we have | F i | ≤ | F | − | F j | ≤ 17 − 6 = 11 . Similarly, we can get | F j | ≤ 11 . By Lemma 4.7, we know C F 6 i − F i and C F 6 j − F j contain a big component C k ( k ∈ { i , j } ) with | V ( C k ) | ≥ 5 ! − | F k | − 2 . If 6 ≤ | F i | ≤ 8 , by Corollary 3.4, we have C F 6 i − F i has a big component C i with | V ( C i ) | ≥ 5 ! − | F i | − 1 . Thus C F 6 − F has a big component C with | V ( C ) | ≥ 6 ! − | F | − 3 . If 9 ≤ | F i | ≤ 11 , then | F j | ≤ | F | − | F i | ≤ 17 − 9 = 8 . By Corollary 3.4, we can also get C F 6 j − F j has a big component C j with | V ( C j ) | ≥ 5 ! − | F j | − 1 . Thus C F 6 − F has a big component C with | V ( C ) | ≥ 6 ! − | F | − 3 .
Lemma 5.10. For n ≥ 5 , if F satisfies that | F | ≤ 6 n − 17 ( n is odd) and | F | ≤ 6 n − 19 ( n is even), then C F n − F has a big component C with | V ( C ) | ≥ n ! − | F | − 3 .
Proof. In this Lemma, we only think about the case C F n − F is disconnected. Let F i = F ∩ C F n i , we proof this result by induction on n. By Lemma 5.8 and Lemma 5.9, we know this result holds for n = 5 , 6 . Now we assume n ≥ 7 and the result holds for C F n − 1 . Note that C F n i ≅ C F n − 1 . By Proposition 2.8, we know when n is odd, κ ( C F n i ) = 3 n − 7 2 ; when n is even, κ ( C F n i ) = 3 n − 6 2 . Since | F | ≤ 6 n − 17 (n is odd) and | F | ≤ 6 n − 19 (n is even), we can get there exists at most three vertex set F i , which can satisfy that | F i | ≥ 3 n − 7 2 (n is odd) and | F i | ≥ 3 n − 6 2 (n is even); Otherwise, for n ≥ 7 , when n is odd, | F | ≥ 4 × 3 n − 7 2 = 6 n − 14 > 6 n − 17 ; when n is even, | F | ≥ 4 × 3 n − 6 2 = 6 n − 12 > 6 n − 19 . Next, we will think about the following situations:
Case 1. When n is odd, | F i | ≤ 3 n − 7 2 − 1 = 3 n − 9 2 for every i ∈ [ 1 , n ] ; when n is even, | F i | ≤ 3 n − 6 2 − 1 = 3 n − 8 2 for every i ∈ [ 1 , n ] .
By Proposition 2.8, we can get C F n i − F i is connected for i ∈ [ 1 , n ] . By Proposition 2.1, we know when n is odd, there are 2 ( n − 2 ) ! cross-edges between C F n i and C F n j ( i ≠ j ) ; when n is even, there are ( n − 2 ) ! cross-edges between C F n i and C F n j ( i ≠ j ) . Since n ≥ 7 , 2 ( n − 2 ) ! ≥ 6 n − 17 and ( n − 2 ) ! ≥ 6 n − 19 , there are at least one cross-edge between C F n i − F i and C F n j − F j . Thus C F n − F is connected, a contradiction.
Case 2. When n is odd, there exists only one vertex set F i , which satisfies that | F i | ≥ 3 n − 7 2 ; when n is even, there exists only one vertex set F i , which satisfies that | F i | ≥ 3 n − 6 2 ( i ∈ [ 1 , n ] ) .
In this case, we can assume | F 1 | ≥ 3 n − 7 2 (n is odd) and | F 1 | ≥ 3 n − 6 2 (n is even). Then we can get | F j | ≤ 3 n − 9 2 (n is odd) and | F j | ≤ 3 n − 8 2 (n is even) for every j ∈ [ n ] ∖ { 1 } . By Proposition 2.8, we know C F n j − F j is connected. Let M = C F n − ( F ∪ C F n 1 ) , by the same argument with Case 1, we know M is connected. Now we think about the following two subcases:
Subcase 2.1: When n is odd, | F − F 1 | ≤ 7 ; when n is even, | F − F 1 | ≤ 3 .
By the definition of C F n , we know when n is odd, every vertex in C F n has two outgoing neighbors; when n is even, every vertex in C F n has only one outgoing neighbor. If C F n 1 − F 1 is connected with | C F n 1 − F 1 | ≥ 4 , since | F − F 1 | ≤ 7 (n is odd) and | F − F 1 | ≤ 3 (n is even), we can get C F n 1 − F 1 is connected to M. Thus we can get C F n − F is connected, this contradicts to the assumption C F n − F is disconnected. If C F n 1 − F 1 is connected with | C F n 1 − F 1 | ≤ 3 , the conclusion is certainly true. If C F n 1 − F 1 is disconnected, we can let S is the set of vertices in C F n 1 − F 1 which has no good neighbors in M. Since | F − F 1 | ≤ 7 (n is odd) and | F − F 1 | ≤ 3 (n is even), we can get | V ( S ) | ≤ 3 , the result holds.
Subcase 2.2: When n is odd, | F − F 1 | ≥ 8 ; when n is even, | F − F 1 | ≥ 4 .
In this case, since | V ( C F n 1 ) − F 1 | − | F − F 1 | ≥ ( n − 1 ) ! − ( 6 n − 17 ) > 1 (n is odd) and | V ( C F n 1 ) − F 1 | − | F − F 1 | ≥ ( n − 1 ) ! − ( 6 n − 19 ) > 1 (n is even) for n ≥ 7 , we know if C F n 1 − F 1 is connected, then C F n − F is also connected, this contradicts to the assumption C F n − F is disconnected. Now we assume C F n 1 − F 1 is disconnected. Since | F − F 1 | ≥ 8 (n is odd) and | F − F 1 | ≥ 4 (n is even), we can get when n is odd, | F 1 | ≤ | F | − 8 ≤ 6 n − 17 − 8 = 6 n − 25 = 6 ( n − 1 ) − 19 ; when n is even, | F 1 | ≤ | F | − 4 ≤ 6 n − 19 − 4 = 6 n − 23 = 6 ( n − 1 ) − 17 . Thus by inductive hypothesis, we know C F n 1 − F 1 has a big component C 1 with | V ( C 1 ) | ≥ ( n − 1 ) ! − | F 1 | − 3 . Next, we will prove that C 1 is connected to M. Clearly, we can get | F − F 1 | ≤ 6 n − 17 − 8 = 6 n − 25 (n is odd) and | F − F 1 | ≤ 6 n − 19 − 4 = 6 n − 23 (n is even). As 2 | V ( C 1 ) | − ( 6 n − 25 ) ≥ 2 [ ( n − 1 ) ! − | F 1 | − 3 ] − ( 6 n − 25 ) ≥ 1 (n is odd) and | V ( C 1 ) | − ( 6 n − 13 ) ≥ ( n − 1 ) ! − | F 1 | − 3 − ( 6 n − 23 ) ≥ 1 (n is even) for n ≥ 7 , we know C 1 must has one vertex which must has a good neighbor in M. So the result holds.
Case 3. When n is odd, there exists two vertex set F i , F j , which can satisfies that | F i | ≥ 3 n − 7 2 and | F j | ≥ 3 n − 7 2 ; when n is even, there exists two vertex set F i , F j , which can satisfies that | F i | ≥ 3 n − 6 2 and | F j | ≥ 3 n − 6 2 ( i ≠ j ) .
In this case, we know | F k | ≤ 3 n − 9 2 ( n is odd) and | F k | ≤ 3 n − 8 2 ( n is even), where k ∈ [ n ] ∖ { i , j } . By Proposition 2.8, we know C F n k − F k is connected. Let M = C F n − ( F ∪ V ( C F n i ) ∪ V ( C F n j ) ) , by the same argument with Case 1, we know M is connected.
Firstly, we think about n is odd. Now we can let | F 1 | ≥ | F 2 | ≥ 3 n − 7 2 , then as | F | ≥ | F 1 | + | F 2 | , we can get | F 1 | ≤ | F | − | F 2 | ≤ 6 n − 17 − 3 n − 7 2 = 9 n − 27 2 . Now, we think about the following three cases:
Case 3.1: 3 n − 7 2 ≤ | F 2 | ≤ | F 1 | ≤ 3 n − 11 .
In this case, since | F | − | F 1 | − | F 2 | ≤ 6 n − 17 − ( 3 n − 7 ) = 3 n − 10 , | V ( C F n 1 ) − F 1 | ≥ ( n − 1 ) ! − ( 3 n − 11 ) , | V ( C F n 2 ) − F 2 | ≥ ( n − 1 ) ! − ( 3 n − 11 ) and ( n − 1 ) ! − ( 3 n − 11 ) − ( 3 n − 10 ) > 1 , we can get if C F n 1 − F 1 or C F n 2 − F 2 is connected, then they are connected to M. Hence, if C F n 1 − F 1 and C F n 2 − F 2 are all connected, then C F n − F is connected, this contradicts to the assumption C F n − F is disconnected. Now we assume C F n i − F i ( i ∈ { 1 , 2 } ) is disconnected. Since C F n i ≅ C F n − 1 and 3 n − 7 2 ≤ | F 2 | ≤ | F 1 | ≤ 3 n − 11 = 3 ( n − 1 ) − 8 , by Corollary 3.4, we know C F n i − F i has a big component C i with | V ( C i ) | ≥ ( n − 1 ) ! − | F i | − 1 . Since ( n − 1 ) ! − ( 3 n − 11 ) − 1 − ( 3 n − 10 ) > 1 for n ≥ 7 , we know C i must connected to M. Thus C F n − F contains a big component C with | V ( C ) | ≥ n ! − | F | − 2 .
Case 3.2: 3 n − 10 ≤ | F 1 | ≤ 9 n − 35 2 .
In this case, we can get 3 n − 7 2 ≤ | F 2 | ≤ | F − F 1 | ≤ 6 n − 17 − ( 3 n − 10 ) = 3 n − 7 . If C F n 1 − F 1 and C F n 2 − F 2 are all connected, by the similarly discussion with Case 3.1, we can get C F n − F is connected, this contradicts to the assumption C F n − F is disconnected. Thus at least one of C F n 1 − F 1 and C F n 2 − F 2 is disconnected. Without loss of generality, we let C F n 1 − F 1 is disconnected. Since | F 1 | ≤ 9 n − 35 2 = 9 ( n − 1 ) − 26 2 , by Lemma 4.9, we can get C F n 1 − F 1 has a big component C 1 with | V ( C 1 ) | ≥ ( n − 1 ) ! − | F 1 | − 2 . Similarly, we can get C 1 is connected to M. If C F n 2 − F 2 is connected, we know C F n 2 − F 2 is connected to M, thus C F n − F has a big component C with | V ( C ) | ≥ n ! − | F | − 2 , the result holds. Now we consider C F n 2 − F 2 is disconnected. If | F 2 | ≤ 3 n − 11 = 3 ( n − 1 ) − 8 , by Corollary 3.4, we know C F n 2 − F 2 has a big component and a singleton, the conclusion is certainly true. Now we think about 3 n − 10 ≤ | F 2 | ≤ 3 n − 7 , then | F − F 1 − F 2 | ≤ 6 n − 17 − 2 ( 3 n − 10 ) = 3 . If | F − F 1 − F 2 | = 0 , we know the vertices in C F n 1 − F 1 and C F n 2 − F 2 are all connected to M, thus C F n − F is connected, a contradiction. If | F − F 1 − F 2 | = 1 , then C F n − F has a big component and at most two vertices u , v , where u ∈ V ( C F n 1 ) , v ∈ V ( C F n 2 ) and they have a common outgoing neighbor in F ∖ ( F 1 ∪ F 2 ) and the other outgoing neighbor of u (resp., v) belong to F 2 ( r e s p . , F 1 ) .
If | F − F 1 − F 2 | = 3 , then | F 1 | = | F 2 | = 3 n − 10 . Since | F 2 | ≤ | F 1 | ≤ 9 n − 35 2 = 9 ( n − 1 ) − 26 2 , by Lemma 4.9, we can get C F n 1 − F 1 and C F n 2 − F 2 have a big component C i with | V ( C i ) | ≥ ( n − 1 ) ! − | F i | − 2 ( i ∈ { 1 , 2 } ) . If one of C i satisfies | V ( C i ) | ≥ ( n − 1 ) ! − | F i | − 1 , the conclusion is certainly true. Now we consider | V ( C i ) | = ( n − 1 ) ! − | F i | − 2 for all i ∈ { 1 , 2 } , in another word, C F n i − F i has a big component and two vertices. Similarly, we can get C i is connected to M. Since | F 1 | = | F 2 | = 3 n − 10 , we know C F n i − F i contains two singletons u i , v i and these two singletons have three common neighbors in C F n i ; Otherwise, if u i is adjacent to v i , then | F i | ≥ ( 3 n − 7 2 − 1 ) × 2 = 3 n − 9 > 3 n − 10 , a contradiction. Thus C F n − F has a big component C with | V ( C ) | ≥ n ! − | F | − 4 . Let S = { u 1 , u 2 , v 1 , v 2 } . If S is an I n d -set, by Lemma 5.2, we have | N C F n − C F n 1 − C F n 2 ( S ) | ≥ 4 . Since | F − F 1 − F 2 | = 3 , C F n − F can not has a big component and four vertices. Thus C F n − F has a big component C with | V ( C ) | ≥ n ! − | F | − 3 . If there exists at least one edge in S, say ( v 1 , u 2 ) ∈ E ( C F n − F ) , then | V ( C ) | ≥ n ! − | F | − 3 . Suppose on the contrary, we let | V ( C ) | = n ! − | F | − 4 . If there exists only one edge between S and u 1 , v 2 are singletons in C F n − F , then | F | ≥ | N C F n ( { v 1 , u 2 } ) | + | N C F n ( u 1 ) | + | N C F n ( v 2 ) | − 3 × 2 = ( 3 n − 3 2 − 1 ) × 2 + 3 n − 3 2 × 2 − 3 × 2 = 6 n − 14 > 6 n − 17 , a contradiction. If there exists two edges between S in C F n − F , then ( v 1 , u 2 ) ∈ E ( C F n − F ) , ( v 2 , u 1 ) ∈ E ( C F n − F ) . Thus | F | ≥ | N C F n ( { v 1 , u 2 } ) | + | N C F n ( { v 2 , u 1 } ) | − 3 × 2 = ( 3 n − 3 2 − 1 ) × 4 − 3 × 2 = 6 n − 16 > 6 n − 17 , a contradiction.
If | F − F 1 − F 2 | = 2 , then | F 1 | = 3 n − 10 or | F 2 | = 3 n − 10 . We assume | F 1 | = 3 n − 10 , then | F 2 | = 3 n − 9 . By the same argument with the above discussion, we know if one of C i satisfies | V ( C i ) | ≥ ( n − 1 ) ! − | F i | − 1 , the result holds, so we consider | V ( C i ) | = ( n − 1 ) ! − | F i | − 2 for all i ∈ { 1 , 2 } . Hence C F n − F has a big component C with | V ( C ) | ≥ n ! − | F | − 4 . If we want | V ( C ) | = n ! − | F | − 4 , the structure in Figure 8 must exists. Now we proof this structure can not exist. Since | F 1 | = 3 n − 10 , C F n 1 − F 1 contains two singletons u 1 , v 1 and this two singletons have three common neighbors in C F n 1 . Let C F n 2 − F 2 has a big component and two vertices u 2 , v 2 , then u 2 , v 2 are nonadjacent; Otherwise, there exists a 7-circle (as shown by the red line in Figure 8). By Lemma 3.1, we can let u 1 = i 1 i 2 i 3 ⋯ i n − 2 i n − 1 1 , then v 1 = j 1 j 2 j 3 ⋯ j n − 2 i n − 1 1 , where j i ∈ [ i 1 , i n − 2 ] and j 1 ≠ i 1 . So u 1 + = 1 i 2 i 3 ⋯ i n − 2 i n − 1 i 1 , u 1 − = i 1 i 2 i 3 ⋯ i n − 2 1 i n − 1 , v 1 + = 1 j 2 j 3 ⋯ j n − 2 i n − 1 j 1 , v 1 − = j 1 j 2 j 3 ⋯ j n − 2 1 i n − 1 . Since j 1 ≠ i 1 , i 1 ≠ i n − 1 and i n − 1 ≠ j 1 , we can get i n − 1 = 2 , then u 1 − , v 1 − ∈ V ( C F n 2 ) and u 2 , v 2 ∈ V ( C F n 2 ) . By the structure in Figure 8, we know u 2 = 1 i 2 i 3 ⋯ i n − 2 i 1 2 , v 2 = 1 j 2 j 3 ⋯ j n − 2 j 1 2 . Let u 2 ′ = 1 i 2 i 3 ⋯ i n − 2 i 1 , v 2 ′ = 1 j 2 j 3 ⋯ j n − 2 j 1 , then { u 2 ′ , v 2 ′ } ⊆ V ( G 1 ) , G 1 ≅ C F n − 1 and u 2 ′ , v 2 ′ belong to different subgraphs in G 1 . Since n − 1 is even and ( u 2 ′ ) + = i 1 i 2 i 3 ⋯ i n − 2 1 , ( v 2 ′ ) + = j 1 j 2 j 3 ⋯ j n − 2 1 , we know ( u 2 ′ ) + ≠ ( v 2 ′ ) + . Thus u 2 ′ and v 2 ′ have no common neighbors in G 1 . In other words, u 2 and v 2 have no common neighbors in C F n 2 . So | F 2 | ≥ 3 n − 7 , this contradicts to the fact that | F 2 | = 3 n − 9 . Thus this structure does not exist, C F n − F has a big component C with | V ( C ) | ≥ n ! − | F | − 3 .
Case 3.3: 9 n − 33 2 ≤ | F 1 | ≤ 9 n − 27 2 .
By the same argument with Case 3.2, we know if C F n 1 − F 1 and C F n 2 − F 2 are all connected, then C F n − F is connected, this contradicts to the assumption C F n − F is disconnected. Thus we assume C F n 2 − F 2 is disconnected. In this case, we can get | F − F 1 − F 2 | ≤ 6 n − 17 − 9 n − 33 2 − 3 n − 7 2 = 3 , 3 n − 7 2 ≤ | F 2 | ≤ | F | − | F 1 | ≤ 6 n − 17 − 9 n − 33 2 = 3 n − 1 2 . Thus if C F n 2 − F 2 is disconnected, then it has a big component and only one singleton; Otherwise, we assume C F n 2 − F 2 has two vertices u 2 , v 2 . If u 2 is adjacent to v 2 , then | F 2 | = 3 n − 9 > 3 n − 1 2 , a contradiction. If u 2 is nonadjacent to v 2 , then | F 2 | ≥ 3 n − 10 > 3 n − 1 2 , a contradiction. If C F n 1 − F 1 is connected, the result is certainly true. Now, we assume C F n 1 − F 1 is disconnected. If | F − F 1 − F 2 | ≤ 1 , be the similarly discussion with Case 3.2, the conclusion is certainly true. If | F − F 1 − F 2 | = 2 , then C F n 1 − F 1 contains a big component C 1 and at most two vertices, which have no neighbors in F − F 1 − F 2 , the result holds.
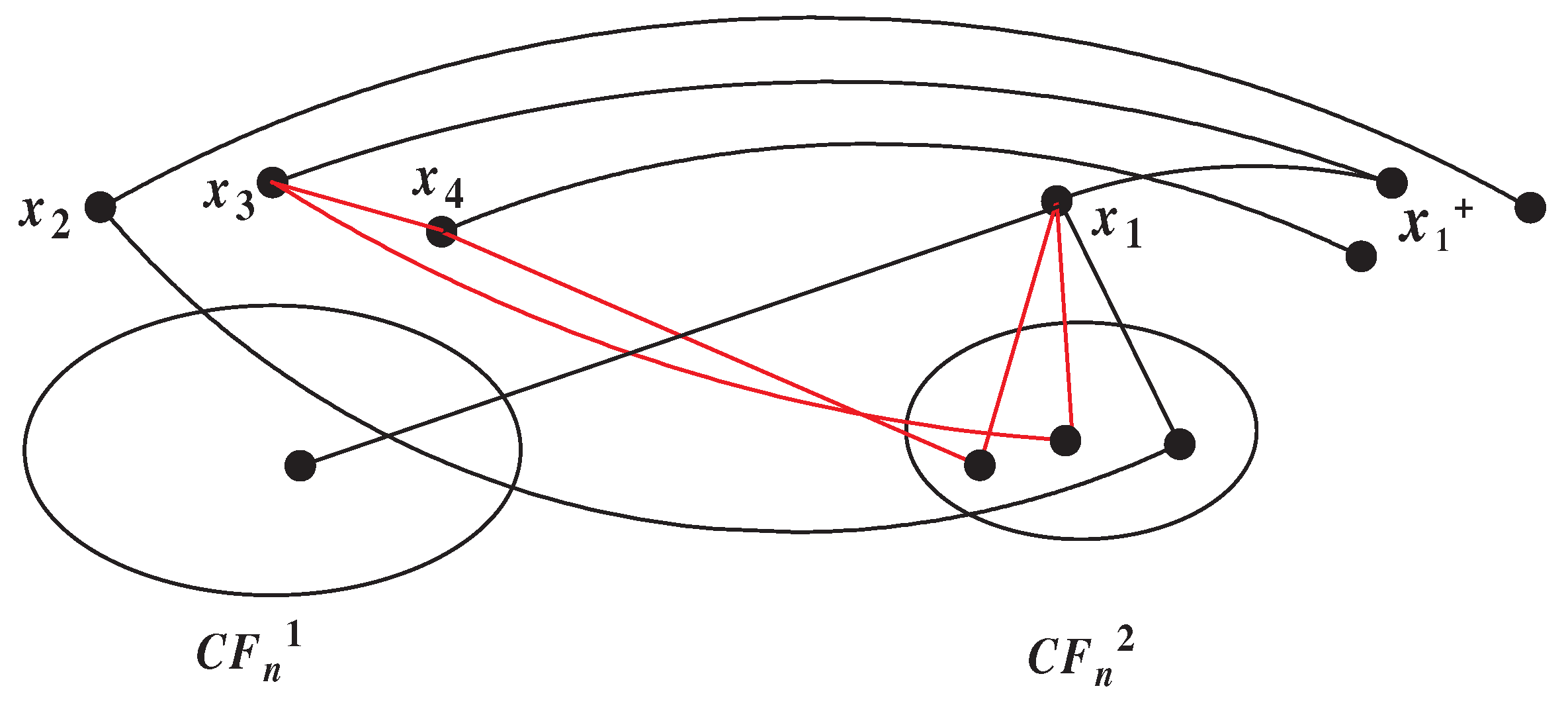
When | F − F 1 − F 2 | = 3 , we have | F 1 | = 9 n − 33 2 and | F 2 | = 3 n − 7 2 . Thus we can let H is the vertex set in C F n 1 − F 1 , which are not adjacent to M, as | F − F 1 − F 2 | = 3 , we can get | V ( H ) | ≤ 3 . Hence C F n − F contains a big component C with | V ( C ) | ≥ n ! − | F | − 4 . Furthermore, | V ( C ) | = n ! − | F | − 4 if and only if the structure in Figure 9 exists. Now we can proof this structure does not exist. Let C F n 1 − F 1 has a big component and three vertices x 2 , x 3 , x 4 and C F n 2 − F 2 has a big component and one singleton x 1 . Firstly, we can get x 2 , x 3 , x 4 are three singletons in C F n 1 − F 1 ; Otherwise, there exist a 5-circle in C F n (as shown by the red line in Figure 9). Furthermore, we can get x 1 is nonadjacent to { x 2 , x 3 , x 4 } ; Otherwise, there exists a 3-circle in C F n . Thus { x 1 , x 2 , x 3 , x 4 } is an I n d -set in C F n − F . We let x 1 = i 1 i 2 i 3 ⋯ i n − 2 i n − 1 2 , then x 1 + ∈ V ( C F n i 1 ) , x 1 − ∈ V ( C F n i n − 1 ) . Since | F − F 1 − F 2 | = 3 , x 1 + or x 1 − must equal to one of the outgoing neighbors of { x 2 , x 3 , x 4 } in F ∖ ( F 1 ∪ F 2 ) . We assume x 1 + = x 3 − , then x 3 = 2 i 2 i 3 ⋯ i n − 2 i 1 i n − 1 . Thus i n − 1 = 1 , x 1 − ∈ V ( C F n 1 ) . The neighbors of x 1 in C F n 2 are follows: a 1 = i 2 i 1 i 3 ⋯ i n − 2 12 , …, a n − 2 = 1 i 2 i 3 i 4 ⋯ i n − 2 i 1 2 , b n − 1 = i 1 i 3 i 3 ⋯ i n − 2 12 , …, b 3 n − 7 2 = i 1 i 2 i 3 ⋯ i n − 2 i n − 3 12 . In these vertices, we need to choose three vertices such that one of their outgoing neighbor belong to C F n 1 . Then x 2 , x 3 , x 4 must belong to A, where A = { a 1 − , … , a n − 3 − , a n − 2 + , b n − 1 − , … , b 3 n − 7 2 − } . Now, we choose a vertex in A such that one of it’s outgoing neighbors equal to x 1 + , we assume this vertex is x 3 , x 3 = 2 i 2 i 3 i 4 ⋯ i n − 2 i 1 1 . As C F n 1 ≅ C F n − 1 , x 2 , x 3 , x 4 are three singletons, and | F 1 | = 9 n − 33 2 = 9 ( n − 1 ) − 24 2 , by Corollary 4.6, we can get x 2 , x 3 , x 4 must belong to a common subgraph of C F n 1 . From the choose of x 2 , x 3 , x 4 , we know there have not one vertex which belongs to a common subgraph with x 3 in C F n 1 . Thus this structure does not exist, C F n − F has a big component C with | V ( C ) | ≥ n ! − | F | − 3 .
When n is even, we can assume | F 1 | ≥ | F 2 | ≥ 3 n − 6 2 . Then | F 1 | ≤ | F | − | F 2 | ≤ 6 n − 19 − 3 n − 6 2 = 9 n − 32 2 , we think about the following cases:
Case 3.1: 3 n − 6 2 ≤ | F 2 | ≤ | F 1 | ≤ 3 n − 10 .
In this case, since | F | − | F 1 | − | F 2 | ≤ 6 n − 17 − ( 3 n − 6 ) = 3 n − 11 , | V ( C F n 1 ) − F 1 | ≥ ( n − 1 ) ! − ( 3 n − 10 ) , | V ( C F n 2 ) − F 2 | ≥ ( n − 1 ) ! − ( 3 n − 10 ) and ( n − 1 ) ! − ( 3 n − 10 ) − ( 3 n − 11 ) > 1 , we can get if C F n 1 − F 1 or C F n 2 − F 2 is connected, then it is connected to M. If C F n 1 − F 1 and C F n 2 − F 2 are all connected, then C F n − F is connected, this contradicts to the assumption C F n − F is disconnected. Thus we assume C F n i − F i ( i ∈ { 1 , 2 } ) is disconnected. Since C F n i ≅ C F n − 1 and 3 n − 6 2 ≤ | F 2 | ≤ | F 1 | ≤ 3 n − 10 = 3 ( n − 1 ) − 7 , by Corollary 3.4, we know C F n i − F i ( i ∈ { 1 , 2 } ) contains a big component C i , which satisfies that | V ( C i ) | ≥ ( n − 1 ) ! − | F i | − 1 . Similarly to the above discussion, we know the big component of C F n i − F i is connected to M. Thus C F n − F contains a big component C, which can satisfies that | V ( C ) | ≥ n ! − | F | − 2 .
Case 3.2: 3 n − 9 ≤ | F 1 | ≤ 9 n − 32 2 .
In this case, we know | F 2 | ≤ | F | − | F 1 | ≤ 6 n − 19 − ( 3 n − 9 ) = 3 n − 10 = 3 ( n − 1 ) − 7 . By the same argument with Case 3.1, we know if C F n 1 − F 1 and C F n 2 − F 2 are all connected, then C F n − F is connected, a contradiction. Thus we assume C F n 2 − F 2 is disconnected. By Corollary 3.4, we know C F n 2 − F 2 contains a big component C 2 , which can satisfies that | V ( C 2 ) | ≥ ( n − 1 ) ! − | F 2 | − 1 . If C F n 1 − F 1 is connected, the conclusion is certainly true. Now we think about C F n 1 − F 1 is disconnected. Since ≤ | F 1 | ≤ 9 n − 32 2 = 9 ( n − 1 ) − 23 2 , C F n 1 − F 1 has a big component C 1 with | V ( C 1 ) | ≥ ( n − 1 ) ! − | F 1 | − 2 . Thus the result holds.
Case 4. When n is odd, there exists three vertex set F i , F j , F k , which can satisfy that | F i | ≥ 3 n − 7 2 , | F j | ≥ 3 n − 7 2 , | F k | ≥ 3 n − 7 2 ; when n is even, there exists three vertex set F i , F j , F k , which can satisfy that | F i | ≥ 3 n − 6 2 , | F j | ≥ 3 n − 6 2 , | F k | ≥ 3 n − 6 2 ( i , j , k are different from each other).
In this case, we let M = C F n − ( F ∪ C F n i ∪ C F n j ∪ C F n k ) .
When n is even, we have | F i | ≤ | F | − | F j | − | F k | ≤ 6 n − 19 − 2 × 3 n − 6 2 = 3 n − 13 < 3 n − 10 , by Corollary 3.4, we know this result holds.
When n is odd, we have | F i | ≤ | F | − | F j | − | F k | ≤ 6 n − 17 − 2 × 3 n − 7 2 = 3 n − 10 . If | F i | ≤ 3 n − 11 , | F j | ≤ 3 n − 11 , | F k | ≤ 3 n − 11 , by Corollary 3.4, we know the result holds. If | F i | = 3 n − 10 , | F j | ≤ 3 n − 11 and | F k | ≤ 3 n − 11 . By Lemma 1, we know there exists one singleton or two singletons in C F n i − F i . Thus C F n − F contains a big component C with | V ( C ) | ≥ n ! − | F | − 4 . If | V ( C ) | = n ! − | F | − 4 , then C F n i − F i has two singletons x 1 , x 2 and C F n j − F j , C F n k − F 5 only has one singleton, meanwhile, these singletons are not connected to M, then | F | − | F i | − | F j | − | F k | ≤ 6 n − 17 − ( 3 n − 10 ) − 2 × 3 n − 7 2 = 0 . Since | F i | = 3 n − 10 , by the proof process of Lemma 5.4, we know x 1 + can not belong to a common subgraph with x 2 + and x 2 − . Thus | F | − | F i | − | F j | − | F k | ≥ 1 , this contradicts to the fact | F | − | F i | − | F j | − | F k | ≤ 0 . Thus | V ( C ) | ≠ n ! − | F | − 4 , C F n − F has a big component C with | V ( C ) | ≥ n ! − | F | − 3 . If | F i | = | F j | = 3 n − 10 , then | F | ≥ | F i | + | F j | + | F k | = 2 × ( 3 n − 10 ) + 3 n − 7 2 = 15 n − 47 2 > 6 n − 17 , a contradiction. If | F i | = | F j | = | F k | = 3 n − 10 , then | F | ≥ | F i | + | F j | + | F k | = 3 × ( 3 n − 10 ) = 9 n − 30 > 6 n − 17 , a contradiction.
Thus, for n ≥ 5 , if F satisfies the condition | F | ≤ 6 n − 17 ( n is odd) and | F | ≤ 6 n − 19 ( n is even), then C F n − F has a big component C with | V ( C ) | ≥ n ! − | F | − 3 .
Theorem 3. For n ≥ 5 , when n is odd, c κ 5 ( C F n ) = 6 n − 16 ; when n is even, c κ 5 ( C F n ) = 6 n − 18 .
Proof. By Lemma 5.10, we can get when n is odd, c κ 5 ( C F n ) ≥ 6 n − 16 ; when n is even, c κ 5 ( C F n ) ≥ 6 n − 18 . Next, we will proof c κ 5 ( C F n ) ≤ 6 n − 16 (n is odd) and c κ 5 ( C F n ) ≤ 6 n − 18 (n is even). When n is odd, let x 1 = i 1 i 2 i 3 ⋯ i n − 2 j i , x 2 = i n − 2 i 2 i 3 ⋯ i 1 i n − 3 j i , x 3 = i 3 i 2 i 1 i 4 ⋯ i n − 2 i j , x 4 = i n − 2 i 2 i 1 i 4 ⋯ i 3 i n − 3 i j . Then | N C F n ( { x 1 , x 2 , x 3 , x 4 } ) | = 6 n − 16 . Let F = N C F n ( { x 1 , x 2 , x 3 , x 4 } ) , then C F n − F has a big component and four singletons x 1 , x 2 , x 3 , x 4 . Thus c κ 5 ( C F n ) ≤ 6 n − 16 . When n is even, we let x 1 = i 1 i 2 i 3 ⋯ i n − 2 j i k , x 2 = i n − 2 i 2 i 3 ⋯ i 1 i n − 3 j i k , x 3 = i 3 i 2 i 1 i 4 ⋯ i n − 2 i j k , x 4 = i n − 2 i 2 i 1 i 4 ⋯ i 3 i n − 3 i j k . Then { x 1 , x 2 , x 3 , x 4 }   ⊆ V ( C F n k ) and | N C F n k ( { x 1 , x 2 , x 3 , x 4 } ) | = 6 ( n − 1 ) − 16 = 6 n − 22 . In C F n k , if we remove N C F n k ( { x 1 , x 2 , x 3 , x 4 } ) , we can get four singletons. From the definition of C F n , we know any two vertices in C F n k have different outgoing neighbors. So, if we remove N C F n k ( { x 1 , x 2 , x 3 , x 4 } ) ∪ { x 1 + , x 2 + , x 3 + , x 4 + } in C F n , we can get a big component and four singletons x 1 , x 2 , x 3 , x 4 . Thus c κ 5 ( C F n ) ≤ 6 n − 22 + 4 = 6 n − 18 .

6. Conclusions

It is very useful to study the connectivity of a graph. In this paper, we study the m-component connectivity of C F n . The Leaf-sort graph is a special Cayley graph, it has many special properties. We have shown that for n ≥ 3 , c κ 3 ( C F n ) = 3 n − 6 ( n is odd) and c κ 3 ( C F n ) = 3 n − 7 ( n is even); for n ≥ 4 , c κ 4 ( C F n ) = 9 n − 21 2 ( n is odd) and c κ 4 ( C F n ) = 9 n − 24 2 ( n is even); for n ≥ 5 , c κ 5 ( C F n ) = 6 n − 16 ( n is odd) and c κ 5 ( C F n ) = 6 n − 18 ( n is even). So far, we only get the value of c κ 3 ( C F n ) , c κ 4 ( C F n ) and c κ 5 ( C F n ) , for m ≥ 6 , this problem is still unsolved. So in the future, this problem is well worth studying. Furthermore, by referring to the references, we can find that: there is a regularity between c κ m ( B S n ) and κ ( m ) ( B S n ) . Similarly, c κ m ( B P n ) and κ ( m ) ( B P n ) also have regularity. So we can think about, is there some sort of relationship between c κ m ( C F n ) and κ ( m ) ( C F n ) ?

Funding

This work is supported by the National Natural Science Foundation of China (61772010), Shanxi Provincial Fundamental Research Program of China (202203021221128) and Shanxi Province Graduate Research Innovation Project (2023KY429).

Conflicts of Interest

The authors declare no conflict of interes.

References

  1. G. Chartrand, S.F. Kapoor, Linda Lesniak, D.R. Lick, Generalized connectivity in graphs, Bull. Bombay Math. Colloq. 2 (1984) 1-6.
  2. E. Sampathkumar, Connectivity of a graph-a generalization, Journal of Combinatorics Information System Sciences 9 (1984) 71-78.
  3. Lih-Hsing Hsu, Eddie Cheng, László Liptók, Jimmy J.M. Tan, Cheng-Kuan Lin, Tung-Yang Ho, Component connectivity of the hypercubes, International Journal of Computer Mathematics 89 (2012) 137-145.
  4. J. Fóbrega, M.A. Fiol, On the extraconnectivity of graphs, Discrete Mathematics 155 (1996) 49-57.
  5. Xiaoyan Li, Chengkuan Lin, Jianxi Fan, Xiaohua Jia, Baolei Cheng, Jingya Zhou, Relationship between extra connectivity and component connectivity in networks, The Computer Journal 64 (2021) 38-53.
  6. Rongxia Hao, Meimei Gu, Jouming Chang, Relationship between extra edge connectivity and component edge connectivity for regular graphs, Theoretical Computer Science 833 (2020) 41-55.
  7. Litao Guo, Mingzu Zhang, Shaohui Zhai, Liqiong Xu, Relation of Extra Edge Connectivity and Component Edge Connectivity for Regular Networks, International Journal of Foundations of Computer Science 32 (2021) 137-149.
  8. Shuli Zhao, Weihua Yang, Shurong Zhang, Liqiong Xu, Component Edge Connectivity of Hypercubes, International Journal of Foundations of Computer Science 29 (2018) 995-1001.
  9. Yunxia Zhang, Shuli Zhao, Weihua Yang, Component edge connectivity of BC networks, Ars Combinatoria: An Australian-Canadian Journal of Combinatorics 142 (2019) 369-380.
  10. Dong Liu, Pingshan Li, Bicheng Zhang, Component edge connectivity of hypercube-like networks, Theoretical Computer Science 911 (2022) 19-25.
  11. Shuli Zhao, Rongxia Hao, Eddie Cheng, Two kinds of generalized connectivity of dual cubes, Discrete Applied Mathematics 257 (2019) 306-316.
  12. Shuli Zhao, Weihua Yang, Conditional connectivity of folded hypercubes, Discrete Applied Mathematics 257 (2019) 388-392.
  13. Shuli Zhao, Weihua Yang, Shurong Zhang, Component connectivity of hypercubes, Theoretical Computer Science 640 (2016) 115-118.
  14. Jouming Chang, Kungjui Pai, Royu Wu, Jinnshyong Yang, The 4-component connectivity of alternating group networks, Theoretical Computer Science 766 (2019) 38-45.
  15. Jouming Chang, Kungjui Pai, Jinnshyong Yang, Royu Wu, Two kinds of generalized 3-connectivities of alternating group networks, in: Proc. 12th International Frontiers of Algorithmics Workshop (FAW 2018), in: Lecture Notes in Computer Science, vol. 10823, 2018, pp. 12-C23, Guangzhou, China.
  16. Eddie Cheng, Ke Qiu, Zhizhang Shen, Connectivity results of complete cubic networks as associated with linearly many faults, Journal of Interconnection Networks 15 (2015) 155007.
  17. Litao Guo, Reliability analysis of twisted cubes, Theoretical Computer Science 707 (2018) 96-101.
  18. J.A. Bondy, U.S.R. Murty, Graph Theory, in: GTM, 244 (2008).
  19. Thomas W. Hungerford, Algebra, Springer-Verlag, New York, 1974.
  20. Shiying Wang, Yanling Wang, Mujiangshan Wang, Connectivity and matching preclusion for leaf-sort graphs, Journal of Interconnection Networks 19 (3) (2019) 1940007.
  21. Jutao Zhao, Shiying Wang, Connectivity and Nature Diagnosability of Leaf-sort graphs, Journal of Interconnection Networks 20 (3) (2020).
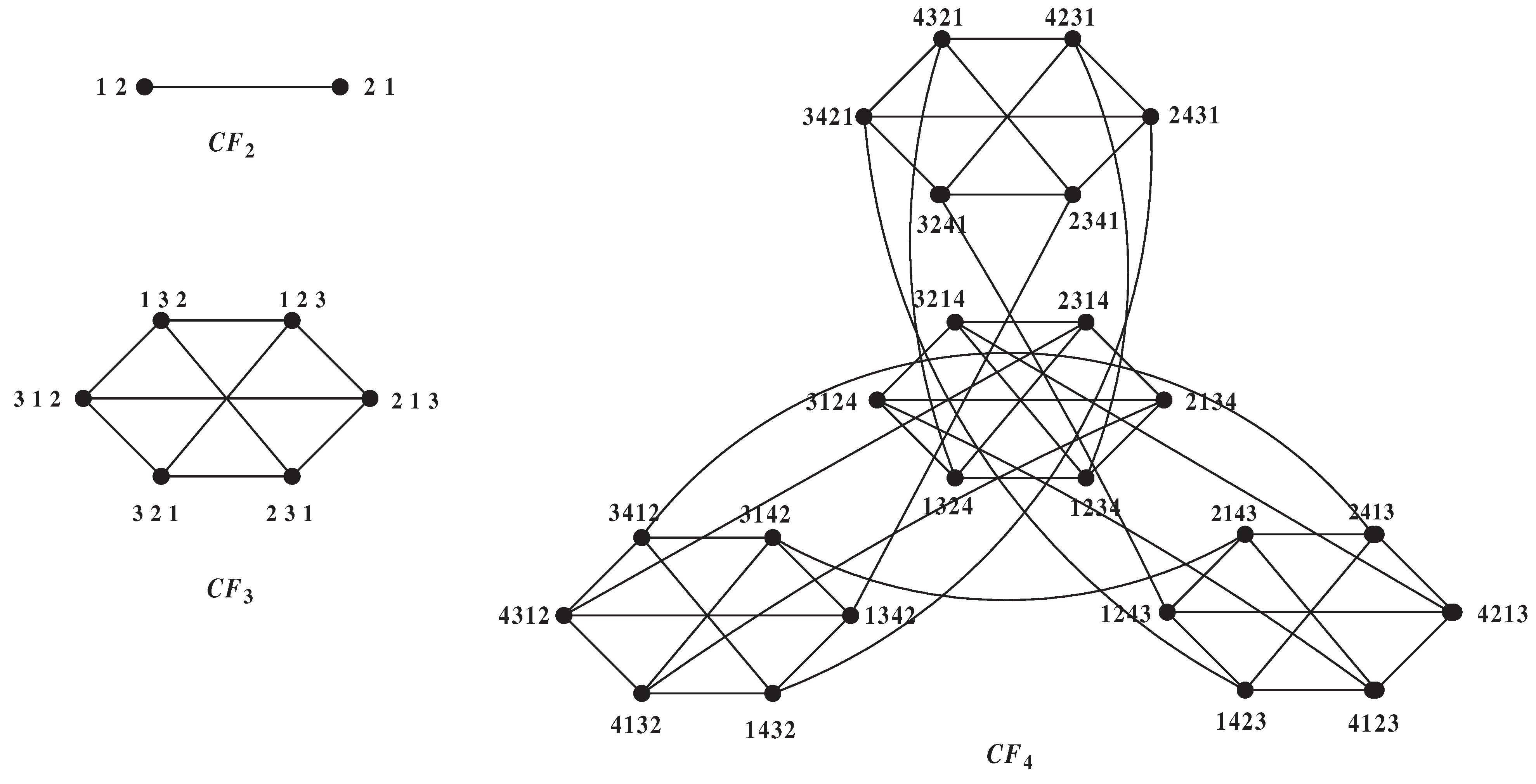
Preprints 90294 g001
Figure 1. The leaf-sort graphs C F 2 , C F 3 and C F 4 .
Figure 1. The leaf-sort graphs C F 2 , C F 3 and C F 4 .
Preprints 90294 g001
Preprints 90294 g002
Figure 2. The illustration of Case 2.
Figure 2. The illustration of Case 2.
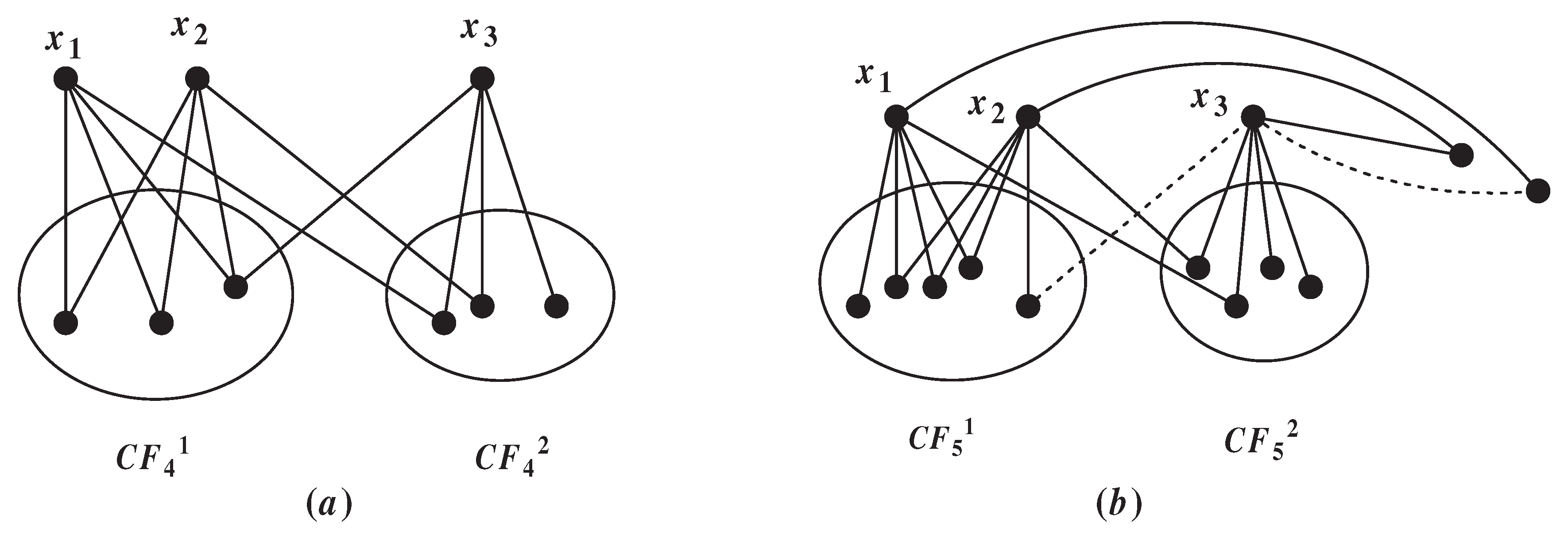
Preprints 90294 g002
Preprints 90294 g003
Figure 3. The case of | N C F n ( S ) | = 9 n − 23 2 .
Figure 3. The case of | N C F n ( S ) | = 9 n − 23 2 .
Preprints 90294 g003
Preprints 90294 g004
Figure 4. The case of | N C F n ( S ) | = 9 n − 24 2 .
Figure 4. The case of | N C F n ( S ) | = 9 n − 24 2 .
Preprints 90294 g004
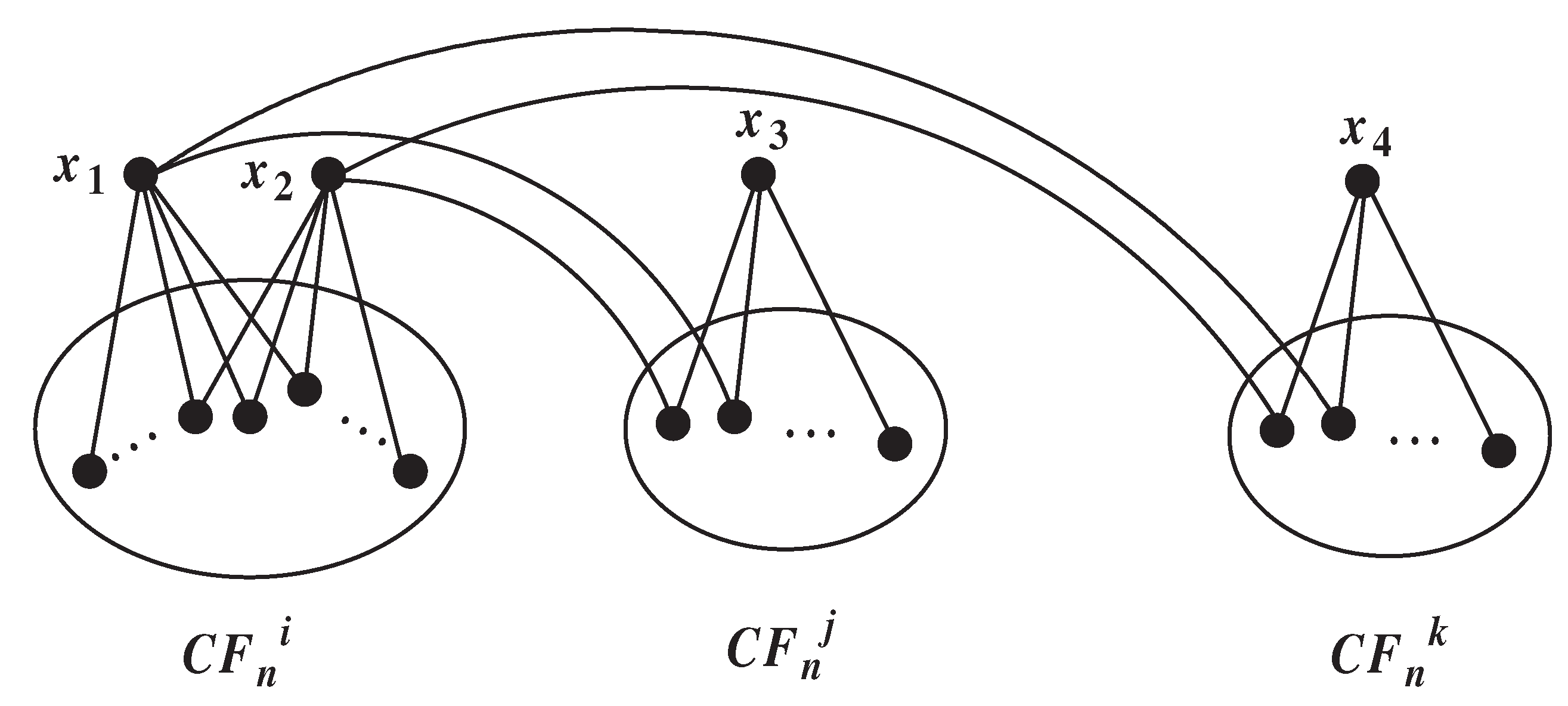
Preprints 90294 g005
Figure 5. The case of | N C F n − C F n i − C F n j − C F n k ( S ) | = 0 .
Figure 5. The case of | N C F n − C F n i − C F n j − C F n k ( S ) | = 0 .
Preprints 90294 g005
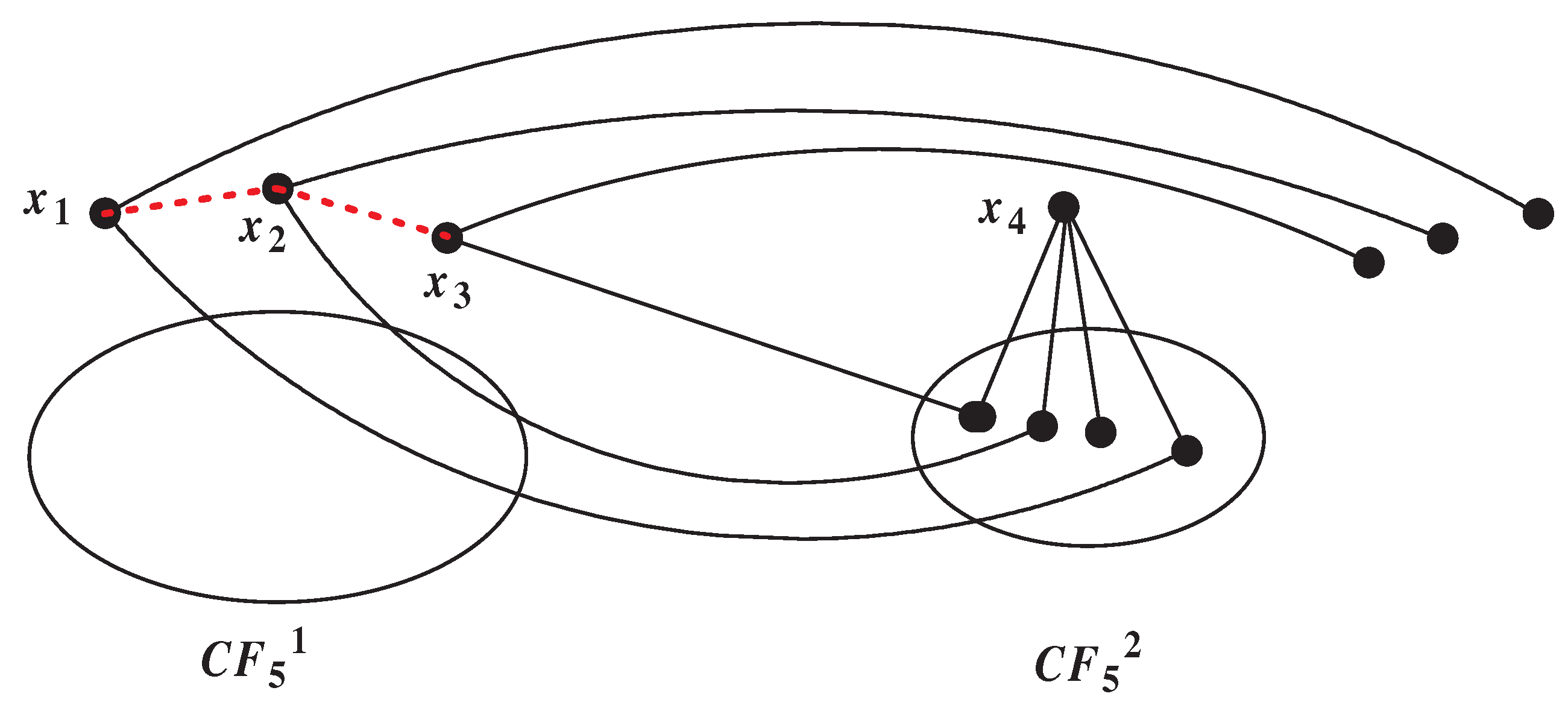
Preprints 90294 g006
Figure 6. The illustration of Subcase 3.3 ( | F 2 | = 4 ) .
Figure 6. The illustration of Subcase 3.3 ( | F 2 | = 4 ) .
Preprints 90294 g006
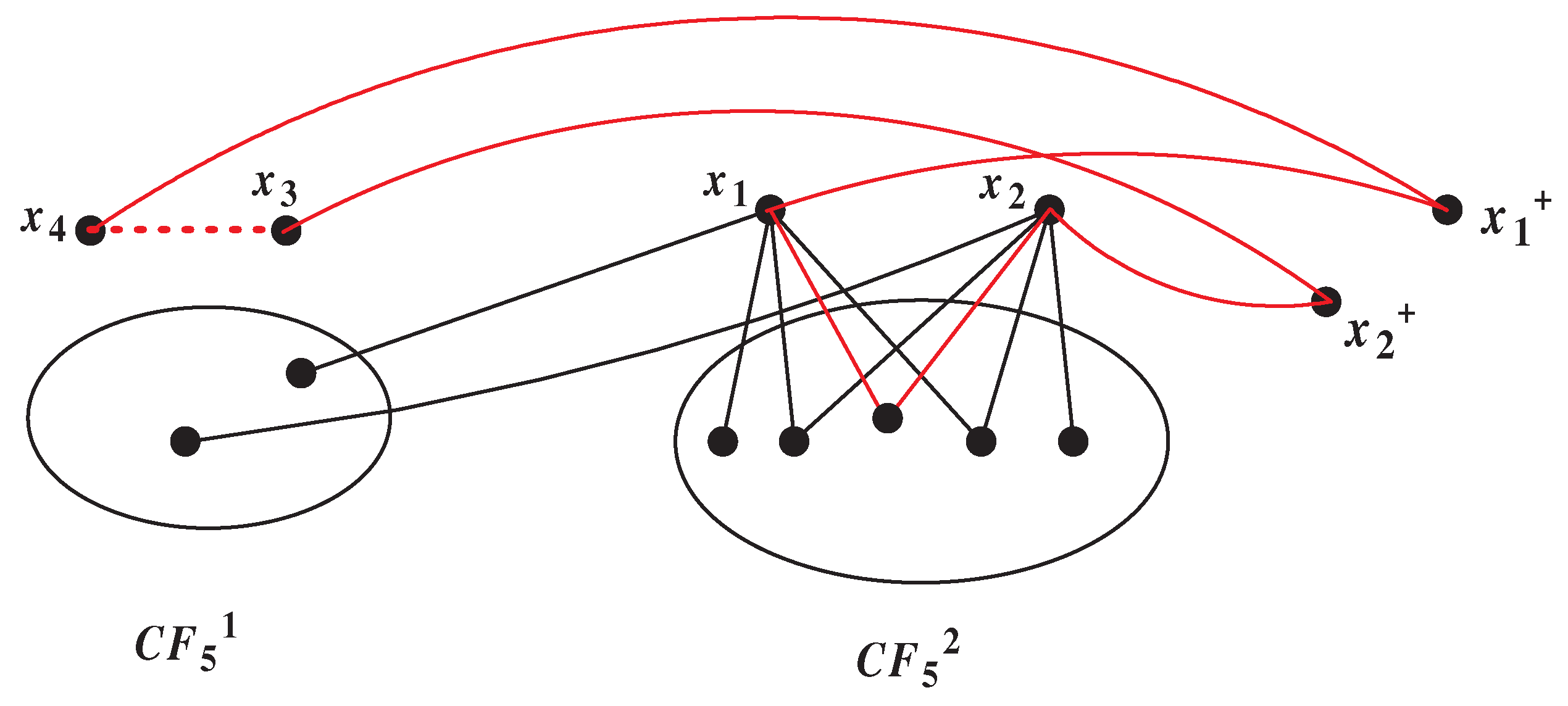
Preprints 90294 g007
Figure 7. The illustration of Subcase 3.3 ( 5 ≤ | F 2 | ≤ 6 ) .
Figure 7. The illustration of Subcase 3.3 ( 5 ≤ | F 2 | ≤ 6 ) .
Preprints 90294 g007
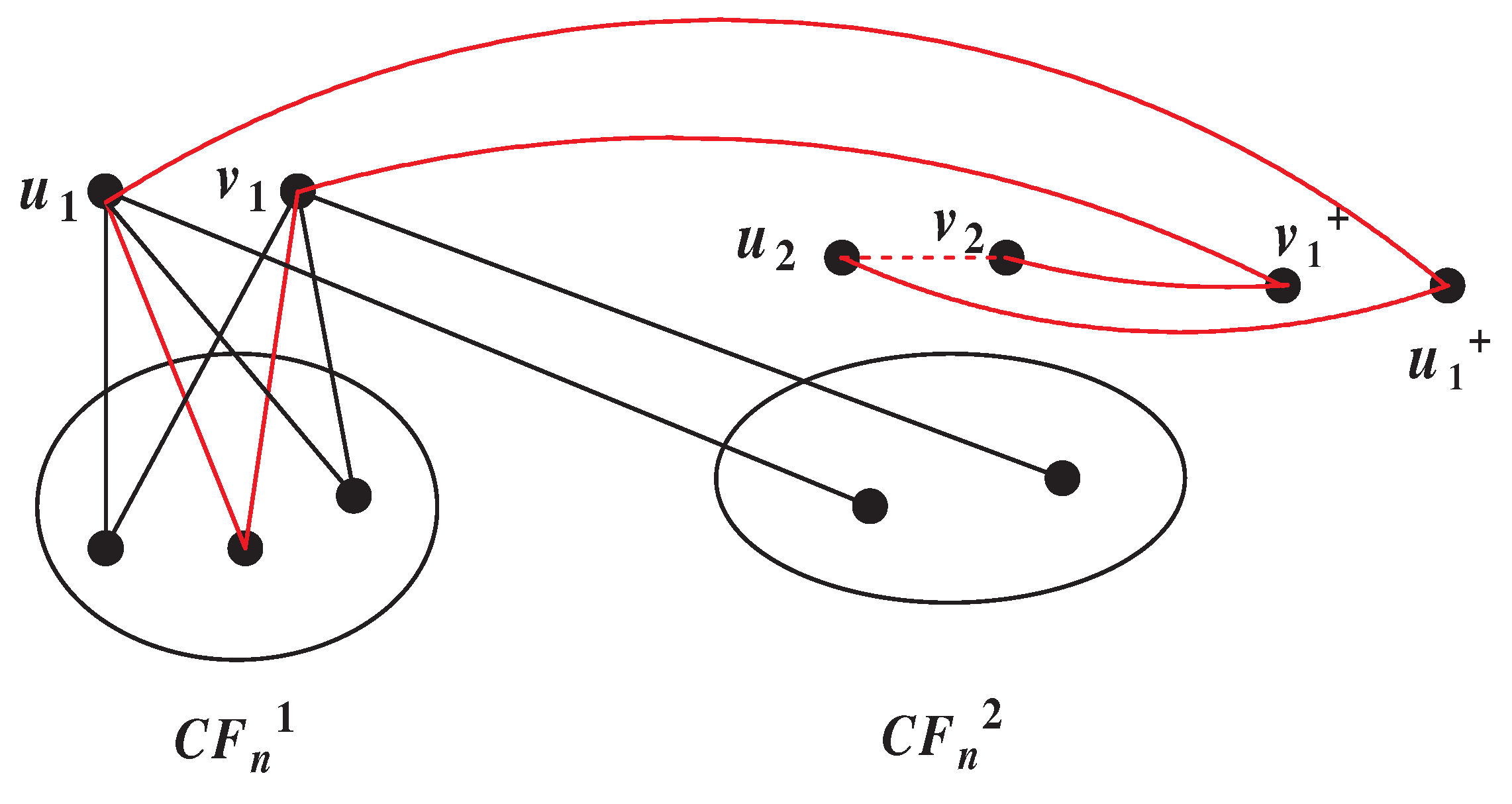
Preprints 90294 g008
Figure 8. The case of | V ( M ) | = n ! − | F | − 4 in Case 3.2 .
Figure 8. The case of | V ( M ) | = n ! − | F | − 4 in Case 3.2 .
Preprints 90294 g008
Preprints 90294 g009
Figure 9. The case of | V ( M ) | = n ! − | F | − 4 in Case 3.3 .
Figure 9. The case of | V ( M ) | = n ! − | F | − 4 in Case 3.3 .
Preprints 90294 g009
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated