Prerpints.org logo
Preprint
Article

Modelling Initial Imperfections using Scaled Buckling Modes: A Strain Energy and Entropy Approach

Altmetrics

Downloads

171

Views

73

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

13 November 2023

Posted:

14 November 2023

You are already at the latest version

Alerts
Abstract
A new utilization of entropy in the context of buckling is presented. The novel concept connecting strain energy and entropy for a pin-ended strut is derived. This concept rationalizes the ranking of buckling modes based on strain energy under the assumption of given entropy. By assigning identical entropy to all buckling modes, they can be ranked according to their deformation energy. Conversely, with identical strain energy assigned to all modes, ranking according to entropy is possible. Decreasing entropy was found to represent the scaling factors of buckling modes that coincide with the measurement of initial out-of-straightness imperfections in IPE160 beams. Applied to steel plane frames, scaled buckling modes can be used to model initial imperfections. It is demonstrated that the entropy (scale factor) for given energy roughly decreases with the inverse square of the mode index. For practical engineering, the study presents the possibility of using scaled buckling modes of steel plane frames to model initial geometric imperfections. Entropy proves to be a valuable complement to strain energy in structural mechanics.
Keywords: 
Subject: Engineering  -   Civil Engineering

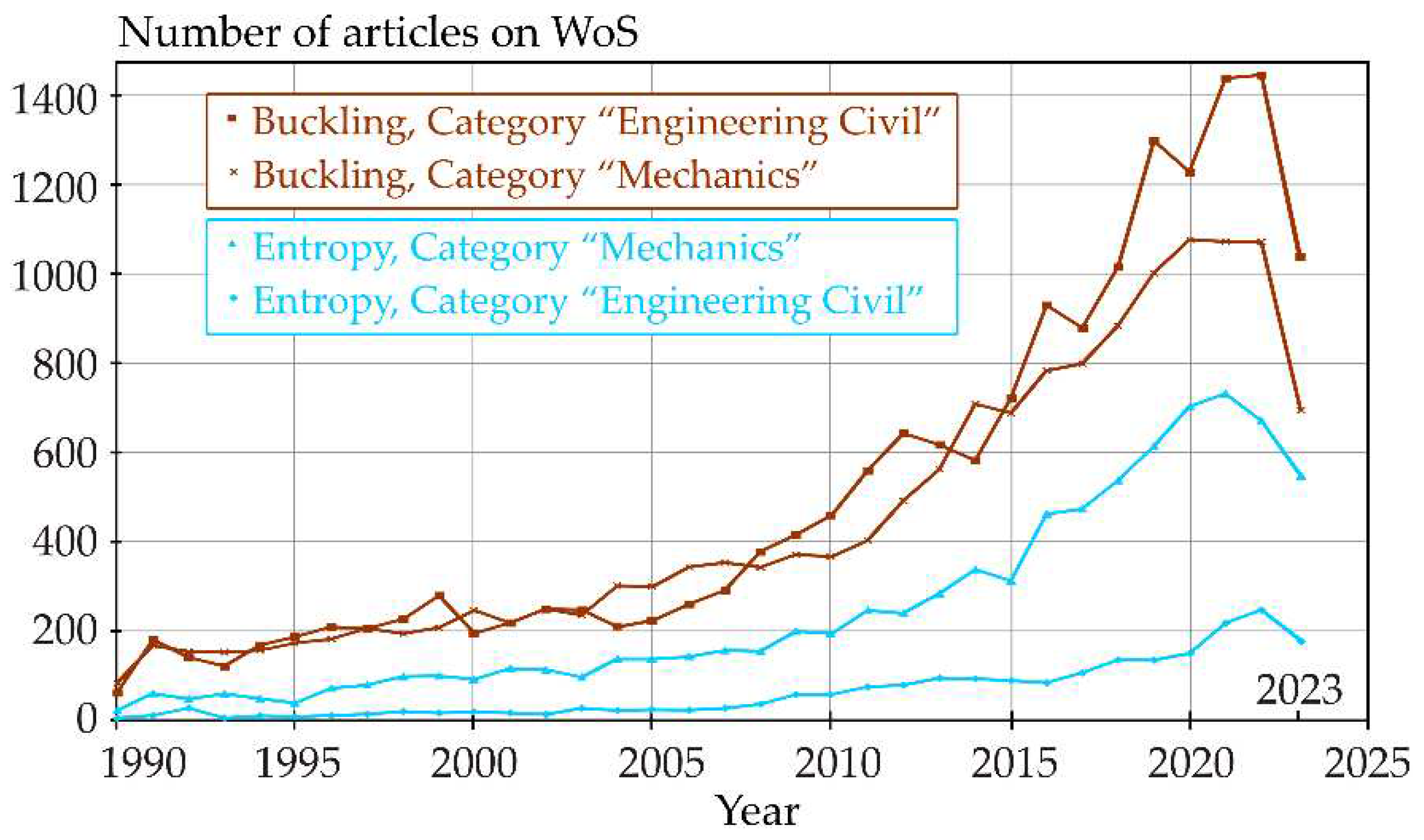
1. Introduction

The investigation of buckling modes is of great importance in the field of structural engineering and structural mechanics. Understanding the stability behaviour of structures under various loads and conditions is essential to ensuring their safety and reliability [1,2].
Throughout history, the study of structural stability has been intertwined with the evolution of engineering and mathematics [3]. The concept of buckling, where slender columns or beams, which are subjected to axial loads, deform and potentially fail under compression, has captured the attention of engineers and mathematicians for centuries [4]. The history of buckling analysis can be traced back to the 18th century in the works of Euler, who has made significant contributions to the understanding of the stability of columns [5].
As theory advances, so does the capability to investigate the structural behaviour of frame structures [6,7]. The emergence of computer-based analysis and numerical methods have enabled engineers to explore the intricacies of buckling modes in various configurations. A significant advancement has been the introduction of finite element methods and geometrically and materially non-linear solutions [8], capable of analysing the load-bearing capacity of structures with initial imperfections; see, e.g., [9,10,11].
Currently, the design of structural steel employs a systematic design approach known as the Direct Design Method [12], which explicitly accounts for material and geometric nonlinearities, residual stresses, and the presence of initial imperfections. The shape of these initial imperfections should be defined to take into account their influence on the load-carrying capacity while respecting real-world measures from experiments; see, e.g., [13,14,15]. Typically, the first buckling mode shape is used to represent these initial imperfections, assuming it to be the most critical [16,17]. However, in cases where the critical buckling loads of two distinct buckling modes coincide, the sensitivity to imperfections increases significantly [18,19]. In these cases, the buckling mode shapes may be more important than the magnitude of the critical force when modelling initial imperfections.
This article is based on the heuristic argument that if two distinct buckling modes coincide, the system tends to follow the buckling mode with lower energy and higher entropy. Since the entropy of the buckling mode has not yet been studied, a concept of a surrogate model is proposed based on thermodynamics, where entropy naturally occurs.
Thus, a new concept of entropy and virtual temperature based on the equivalence of strain and heat energy in the surrogate model is introduced. The surrogate model is based on an unconventional connection of classical theories: entropy [20], heat energy [20], strain energy [21], and buckling [1]. The entropy is presented as a new indicator of stability and resistance to buckling. The research progresses from a simple beam to more complex structures, such as steel plane frames.

2. State of the Art

The principle of minimum total energy is a fundamental concept in structural mechanics, which is used to determine equilibrium conditions and the behaviour of structural systems [22,23,24,25,26]. In statics of structures, the total energy is composed of the strain energy and the potential energy of the applied static loads. The basic idea is that the structure tends to find a deformation that minimizes the total energy.
Strain energy has been used to calculate the elastic lateral stiffness in frame members [27], to investigate the low yield strain steel energy dissipater [28], to optimize the seismic performance of modular prefabricated four-side connected composite shear walls [29], to model the damage and failure of quasibrittle structures [30], to analyse the effects of aftershocks on structural stability [31], to calculate the elastic global buckling stress of box-shape cold-formed steel built-up columns [32], to achieve an optimized unstiffened steel plate shear wall configuration [33], to study rock deformation [34,35], to evaluate the structural damage of reinforced concrete members [36], to analyse the lateral torsional buckling of corrugated steel web girders [37], to analyse the lateral-torsional buckling of I-beams [38], to analyse the extreme properties of the structural strain energy using eigenvalues problem [39], to analyse the plastic buckling of stainless steel circular cylindrical shells [40], to study the mechanical properties of fiber-reinforced lime-cement concrete [41], to predict the cumulative strain energy of isolators and dampers for seismic design [42], to study the buckling problems of structures with single delamination [43], to analyse the buckling behaviour of carbon nanotubes [44], to study the cyclic hardening-softening characteristics of duplex stainless steel [45], to analyse the shear stress distribution in corrugated steel web bridges [46], to perform elasto-plastic analysis of prestressed reinforced concrete beams [47], to examine the nonlinear buckling behaviour of porous linings reinforced with graphene platelets [48], to investigate the cyclic behaviour of titanium-clad bimetallic steel under large-magnitude cyclic strains [49], to study of limit states of bar structures [50], to analyse the bifurcations points of von Mises trusses [51], to compare the pre-failure and post-failure structural strain energy in order to reflect the structural robustness [52], to study steel columns in fire using a concept based on voxels [53], to derive the stiffness matrix of tapered members with warping and Wagner effects [54], to investigate the elastic buckling behaviour of oblate hemi-ellipsoidal shells under the influence of hydrostatic pressure [55], to study the wind flow loading scenarios of modular steel constructions [56], to develop an accurate model for lateral-torsional buckling analysis and the prediction of inelastic behaviour [57], to study the mechanical properties of rocks under different moisture content [58], to analyze the strain in the concrete and reinforcement within the context of the bending performance [59], to study the plastic buckling of cylindrical oil storage tanks [60], to introduce a novel approach to derive the total potential energy equations of steel members [61], to assess the safety and predict the stability of fractured rocks [62], to study the behaviour of reinforced concrete beams strengthened with externally bonded fiber reinforced polymer materials [63].
Entropy is a term that originated from thermodynamics [64] and informatics [20], but has many applications in other scientific fields, including civil engineering and structural mechanics. Examples of the application of entropy in these fields include: the assessment of the evolution and abrupt changes in water use structure in China [65], structural engineering, water management and urban modelling [66], structural uncertainties in global response prediction in seismic hazard mitigation [67], decision-making models for selecting subcontractors of large construction companies [68], investigation of mechanical properties of polyurethane porous mixtures [69], seismic performance of underground large-scale frame structures [70], toolbox design for calculating geological entropy in heterogeneous systems [71], signal analysis for assessing wind speed in wind tunnel testing of long span bridges [72], optimization of the performance of tuned mass dampers in reducing seismic responses in tall buildings [73], characterization of the degree of disorder and accumulation of rock microcracks [74], durability of concrete structures affected by environmental conditions [75], development of a dynamic risk control system for sleeve grouting in prefabricated constructions [76], identification of unbalanced bidding using a multi-criteria decision-making approach [77], investigation of the presence of undeclared leader-follower structures in pedestrian evacuation scenarios [78], reliability analysis of a Tibetan timber frame using entropy-based sensitivity analysis [79], construction safety risks in prefabricated subway stations in China [80], assessment of the reliability of steel civil engineering structures exposed to fire temperatures [81], reliability assessment of structural systems [82], damage assessment of civil structures and infrastructures based on entropy measurements [83], modelling of hot flow behaviour and grain evolution of alloys [84], assessment of asphalt mixture uniformity with consideration to the characteristics of particles [85], establishment of attribute weights in multi-criteria decision-making [86], global sensitivity analysis of reliability [87], categorization of buckling modes in steel plane frames [88]. Shannon's entropy was used as a measure of the uniformity or orderliness of examined data spectrum in articles [66,71,74,83,85,88].
In civil engineering, the topic of buckling is much more attractive than the topic of entropy, see Figure 1. On the topic of buckling 17898 articles have been published in the category of Civil Engineering, 16167 articles in the category of Mechanics and 7783 articles in the category of Construction Building Technology. On the topic of entropy 2199 articles have been published in the category of Civil Engineering, 8459 articles in the category of Mechanics and 662 articles in the category of Construction Building Technology. Entropy is most attractive in the Materials Science Multidisciplinary category, where a total of 28710 articles have been published. In total, 277728 articles were published on entropy, while only 64808 were published on buckling. The data was obtained from the Web of Science database on November 12th, 2023.

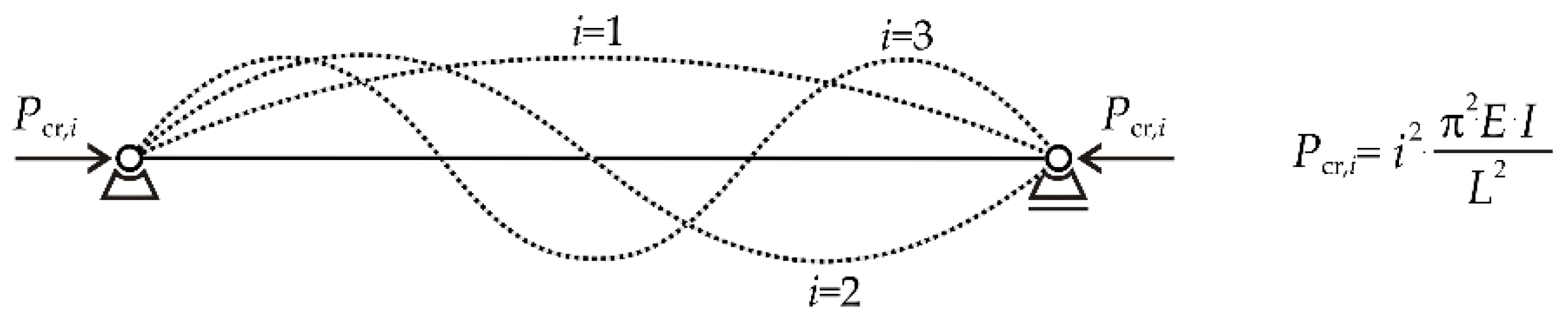
3. Buckling of a Pin-ended Strut

Consider a slender strut with pin-ended supports subjected to an axial compressive load P. The strut remains ideally straight until the load reaches its critical value Pcr and buckling occurs [1,2]. The critical load places the strut in a state of unstable equilibrium, where, in addition to equilibrium on the straight beam, there also exists equilibrium on the deflected beam, see Figure 2.
For a strut under critical load, bending deformation can be described according to the Euler–Bernoulli beam theory using the differential equation:
d y 2 ( x ) d x 2 + P E ⋅ I y = 0 ,
where y(x) is the lateral deflection, E is Young's modulus, and I is the second moment of area. This equation is a linear, nonhomogeneous differential equation of the second order with constant coefficients. Upon substituting α² = P/(E·I), the particular solution of the differential equation can be expressed in the form:
y ( x ) = c 1 ⋅ sin ( α ⋅ x ) + c 2 ⋅ cos ( α ⋅ x ) ,   for   x ∈ [ 0 ,   L ] .
From the boundary conditions, it can be calculated that c2=0 for y(0)=0 and c1·sin(α·L)=0 for y(L)=0, where L is the strut length and c1 is indeterminate amplitude. By using c1>0, it can be obtained that sin(α·L)=0, and thus α =i*π/L, where i represents a natural number of the buckling mode. The corresponding buckling modes can be derived from Equation (2) as eigenmodes, resulting in deformation patterns that are characterized by sine functions.
y ( x ) = c 1 ⋅ sin ( i π ⋅ x L ) ,   for   x ∈ [ 0 ,   L ] ,   i =   1 ,   2 ,   . . ,
where i is the number of half-sine curvatures that occur lengthwise. Buckling modes can be described as the shapes the strut assumes during buckling, with the sine function playing a crucial role in their formulation, see Figure 3.
Using the previously defined equation α² = P/(E·I), the critical loads are:
P c r , i = i 2 ⋅ π 2 E ⋅ I L 2 ,   for   i =   1 ,   2 ,   . . ,
Equation (4) provides the standard critical load at which buckling occurs in a pin-ended strut. This provides insight into the behaviour of slender struts under axial compression, and valuable understanding of the design and analysis of structural systems.

3.1. Strain Energy

The discretization of y(x) is performed at the centroids of finite elements. By introducing (j-0.5)/N instead of x/L, Equation (3) can be rewritten in the discrete form:
f i j = c 1 ⋅ sin ( i π ⋅ ( j − 0.5 ) N ) ,   for   j =   0 ,   1 ,   … N ,
where j = 1, 2, .. N and N is the number of beam elements. The elements are considered to have the same length. In differential form, the total internal potential energy (strain energy) of the i-th buckling mode can be obtained as:
Δ Π i = 1 2 ∫ 0 L E ⋅ I ( d y 2 ( x ) d x 2 ) 2 d x = 1 2 ∫ 0 L E ⋅ I ( c 1 ⋅ ( i π L ) 2 ⋅ sin ( i π ⋅ x L ) ) 2 d x = i 4 ⋅ E ⋅ I ⋅ c 1 2 ⋅ π 4 4 ⋅ L 3 .
The value of ΔΠi represents the difference between the zero-strain energy of the unloaded beam and the strain energy of the buckled beam.
It can be noted that the square of the second derivative can be replaced by the product of the function value and the fourth derivative, E·I·(y’’)2 = y·E·I·y’’’’. In this expression, the term involving the fourth derivative, E·I·y’’’’, represents a fictitious transverse load action.
According to the principle of conservation of mechanical energy, strain energy from internal forces ΔΠi (from bending moment) is equal to the potential energy of external forces ΔΠe (from load action Pcr,i).
Δ Π e = 1 2 ⋅ P c r , i ⋅ ∫ 0 L ( d y ( x ) d x ) 2 d x = 1 2 ⋅ i 2 ⋅ π 2 E ⋅ I L 2 ⋅ ∫ 0 L ( c 1 ⋅ i π L ⋅ cos ( i π ⋅ x L ) ) 2 d x = i 4 ⋅ E ⋅ I ⋅ c 1 2 ⋅ π 4 4 ⋅ L 3 .
The discrete form of Equation (6) is used to introduce discrete entropy. By introducing L/N instead of dx and j/N instead of x/L, Equation (6) can be rewritten in the discrete form as:
Δ Π i = ∑ j = 1 N Δ Π i j = 1 2 ∑ j = 1 N E ⋅ I ⋅ ( c 1 ⋅ ( i π L ) 2 ⋅ sin ( i π ⋅ ( j − 0.5 ) N ) ) 2 L N ,   for   N > i .
when N > i and i is the index of buckling mode. The discrete form is suitable both for use in the finite element method and in connection with entropy. One member of the series ΔΠij is the strain energy of a single element of the strut. The square of the sine function in Equation (8) converges to the value of N/2.
∑ j = 1 N ( sin ( i π ⋅ ( j − 0.5 ) N ) ) 2 = N 2 ,   for   N > i .
Let each buckling mode have its own scale factor using amplitude ci. By substituting Equation (9) into Equation (8), the sum of discrete strain energy is equal to the value calculated from Equation (6).
Δ Π i = i 4 ⋅ E ⋅ I ⋅ c i 2 ⋅ π 4 4 ⋅ L 3 ,
where i is the buckling mode number, E is the elastic Young's modulus, I is the second moment of area, L is the length of the specimen and ci is the amplitude of the half-sine curvature that occurs lengthwise.

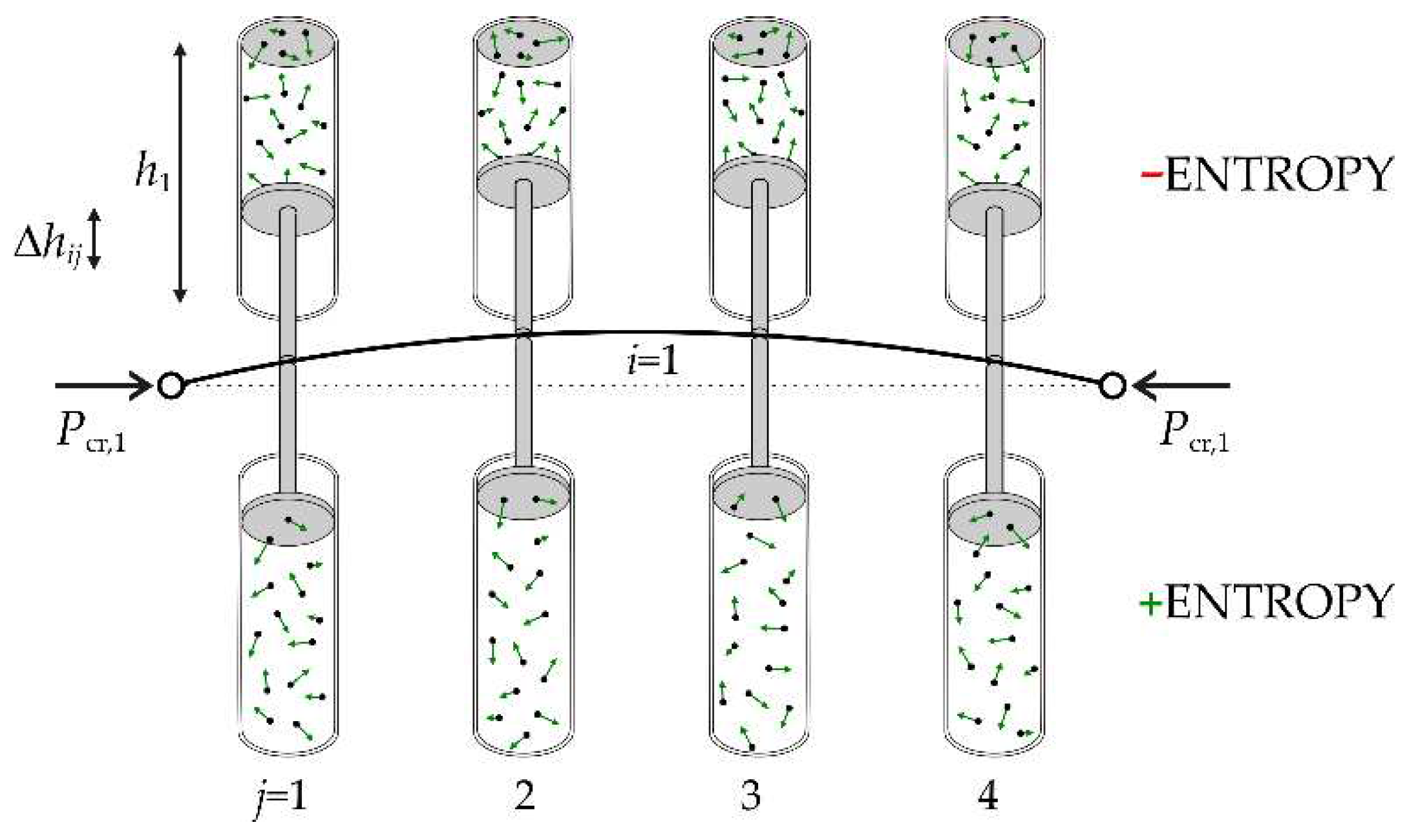
3.2. Why Entropy?

In thermodynamics, any equilibrium state can be characterized either as a state of maximum entropy for a given energy or as a state of minimum energy for a given entropy [89]. In structural mechanics, the principle of minimum total potential energy exists [90], but the principle of maximum entropy is not commonly considered.
In structural mechanics, the total potential energy is the sum of the strain energy stored in a deformed structure and the potential energy associated with load action. Structural mechanics uses the fundamental principles of Lagrangian mechanics. In the case of static loading, the structure is in equilibrium when its total potential energy is minimized.
In Euler buckling, the rank of buckling modes is determined by the ranking from the smallest critical force to the largest. This is the most common approach for ranking buckling modes, with the first one considered the most dangerous [91]. Ranking based on the total potential energy is not possible without solving the indeterminate deformation because the total energy is a function of the indeterminate amplitude ci, as seen, for example, in Equation (10). However, if it is possible to link energy with entropy, ranking based on the total potential energy is justified. It is sufficient to perform the analysis solely based on strain energy since the potential energy of the load action has the same value.
If it is possible to decompose strain energy using entropy, then ranking of buckling modes based on energy will be possible. By assigning the same entropy to all buckling modes, buckling modes can be ranked by strain energy (from the smallest to the largest). Analogously, when the same strain energy is assigned to all buckling modes, buckling modes can be ranked by entropy from the largest to the smallest. It can be expected that the first in the ranking will be the buckling mode with the lowest critical force, and that ranking by critical forces will be the same or very similar to the ascending ranking by strain energy or the descending ranking by entropy. A new perspective is introduced by considering entropy, justifying the ranking of buckling modes based on strain energy.
Structural mechanics uses the energies in the system following the fundamental principles of Lagrangian mechanics but does not consider entropy. The question is how to calculate entropy for a deformed structure. One of the approaches may involve a surrogate model based on thermodynamics and an isothermal process in gases.
Entropy can be viewed as a characteristic closely related to energy [64,92]. In thermodynamics, the heat energy is generated as a result of changes in the entropy of the system [20]. In modern theories, the entropy can be described using the relationship based on the energy balance [93].
F ⋅ Δ x = T ⋅ Δ S .
Equation (11) relates mechanical work to the thermodynamic work. The left-hand side of the equation is the mechanical work performed by force F on path Δx as the body moves. The right-hand side of Equation (11) is the heat energy produced by the system at temperature T due to changes in the entropy of the system ΔS; see, e.g., [20]. Temperature can be understood as the statistical weight by which energy is assessed in terms of entropy [92].

3.3. Entropy in the Surrogate model

Let us consider a surrogate model where the strain energy of the deformed structure can be decomposed into temperature and entropy. For this purpose, the strain energy is transformed into gas energy. Since we are investigating the characteristics of a surrogate model, the terms entropy ΔSi and virtual temperature Ti are used. Following Equation (11), we can write:
Δ Π i = T i ⋅ Δ S i ,
where ΔΠi is the strain energy of the buckled strut from the previous chapter, and the right-hand side is heat energy associated with a gas surrogate model from the following chapter.
When virtual temperature Ti is constant, the change in entropy ΔS can be expressed as the work of an ideal gas with constant mass m during an isothermal process. Under constant Ti, the internal energy of the gas remains unchanged. Thus, the heat absorbed during pressure change equals the work done by the gas; see, e.g., [94]. The entire system is isolated, meaning there is no exchange of particles or energy with the surrounding environment, i.e., the number of particles and energy remain constant.
The change in entropy of an isothermal process for gases, where pressure varies as a function of volume, can be expressed as:
Δ S = m ⋅ R M m ln ρ 1 ρ 2 = m ⋅ R M m ln V 2 V 1 ,
where ρ1 is the initial pressure, ρ2 is the final pressure, V1 is the initial volume, V2 is the final volume, Mm is the molar mass of the gas and R = 8.314 Jmol−1K−1 is the molar gas constant; see, e.g., [95].
The change in entropy will be described using volume change. Let us assume that buckling causes gas compression (volume reduction) on the deflection side and expansion (volume increase) on the opposite side of the beam; see Figure 4. The pistons are located at the centroids of the finite elements in the direction of deformation, and the mesh of the finite elements is uniform.
The change in entropy ΔSij can be written on the basis of Equation (13). The gas loading the j-th element (compression and expansion) has a mass of m/N, where N is the number of beam elements. The mass of gas in one piston is 0.5·m/N. For the j-th element, the equation for the change in entropy on one side of the beam (compression or expansion) can be obtained as:
Δ S ¯ i j = m ⋅ R 2 ⋅ N ⋅ M m ln V i j V 1 = m ⋅ R 2 ⋅ N ⋅ M m ln A ⋅ h i j A ⋅ h 1 = m ⋅ R 2 ⋅ N ⋅ M m ln h i j h 1 ,
where Vij is the final gas volume and hij je final piston height. The volume V is expressed as the product of the area A and the height h. The change in volume can be expressed as the change in the height h1 of the piston in the gas vessel, where h1 is a constant.
Although the link is not direct, the surrogate model converts element deformation into entropy. The change in entropy of the gas on both sides of the beam element can be expressed as the difference between two entropies caused by expansion (h1 + Δhij)/h1 and compression (h1 - Δhij)/h1.
Δ S i j = Δ S i j E − Δ S i j C = m ⋅ R 2 ⋅ N ⋅ M m ( ln h 1 + Δ h i j h 1 − ln h 1 − Δ h i j h 1 ) ≈ m ⋅ R N ⋅ M m ⋅ Δ h i j h 1 ,
where displacement Δhij represents a small change in the piston height. It can be noted that the same formula can be derived by Shannon's entropy, which measures the information content in a given system [20]. The characteristic Δhij/h1 can be interpreted as an analogy to strain ε in Hooke's laws. The small displacements are a standard condition in Euler–Bernoulli beam theory in structural mechanics. The magnitude of ΔSij can be expressed as:
Δ S i j ≈ m ⋅ R h 1 ⋅ M m ⋅ 1 N ⋅ | Δ h i j | = k 1 ⋅ 1 N ⋅ | Δ h i j | ,   where   Δ h i j < < h 1 .
This equation expresses that there is an entropy change in the direction of deformation proportional to a constant and the displacement Δhij. The change in entropy is linearly dependent on displacement, similar to [93]. By substituting Δhij = fij in Equation (5) into Equation (16), Equation (12) can be followed. In the following text, the change in entropy will be briefly referred to as entropy.

3.4. Entropy and Virtual temperature

In Equation (12), entropy and strain energy are additive quantities, so their values can be obtained by the summation of all elements. After introducing Δhij = fij, the summation of all j-th elements leads to:
i 4 ⋅ E ⋅ I ⋅ c i 2 ⋅ π 4 2 ⋅ L 3 ⋅ 1 N ∑ j = 1 N [ sin ( i π ⋅ ( j − 0.5 ) N ) ] 2 ︸ Δ Π i = T i ⋅ k 1 ⋅ 1 N ⋅ ∑ j = 1 N | c i ⋅ sin ( i π ⋅ ( j − 0.5 ) N ) | ︸ Δ S i ,
where ci>0 is a scale factor of the i-th buckling mode. Equation (17) creates a connection between the products of the second derivative (bending moment) on the left-hand side and the product of deformation on the right-hand side. The sum of the absolute value of the sine function in Equation (17) converges to the value of 2·N/π.
lim N → ∞ ∑ j = 1 N | c i ⋅ sin ( i π ⋅ ( j − 0.5 ) N ) | = 2 ⋅ N ⋅ c i π .
For N > i, Equation (18) takes the form of an approximate relationship. By substituting Equation (18) and Equation (9) into Equation (17), Equation (17) can be simplified to the form of Equation (19).
i 4 ⋅ E ⋅ I ⋅ c i 2 ⋅ π 4 4 ⋅ L 3 ︸ Δ Π i = T i ⋅ 2 ⋅ k 1 ⋅ c i π ︸ Δ S i ,
where the left-hand side is the change in strain energy ΔΠi and the right-hand side Ti·ΔSi takes into account the change in entropy. Due to the specific shape of the sine functions of the buckling modes, the entropy of the gas is a function of only the amplitude ci and constant k1.
Δ S i = 2 ⋅ k 1 ⋅ c i π ,
where m is the mass of gas in all pistons and m, R, Mm, h1 are constants. Equation (20) expresses the entropy of the gas in the surrogate model. The virtual temperature Ti of the gas calculated from the surrogate model of the pin-ended strut can be written using Equation (19) as:
T i = i 4 ⋅ c i ⋅ E ⋅ I ⋅ π 5 8 ⋅ k 1 ⋅ L 3 .
The decomposition of ΔΠi into Ti and ΔSi introduced both Ti and ΔSi as dependent on ci, but only the virtual temperature Ti is a fourth power function of index i.
Equation (19) can be written using Pcr,i
π 2 E ⋅ I L 2 ︷ P c r , 1 ⋅ i 4 ⋅ c i 2 ⋅ π 2 4 ⋅ L ︸ Δ Π i = π 2 E ⋅ I L 2 ︷ P c r , 1 ⋅ i 4 ⋅ c i ⋅ π 3 8 ⋅ k 1 ⋅ L ︸ T i ⋅ 2 ⋅ k 1 ⋅ c i π ︸ Δ S i .
Equation (22) introduced the decomposition of strain energy ΔΠi into terms of virtual temperature Ti and entropy ΔSi. Changes in entropy exhibit linear dependence on displacement, analogous to [93]. The utilization of Equation (22) can be presented in two fundamental cases.
The case of constant entropy ΔSi = constant: If we introduce ci = c1 as a constant for all buckling modes, then the strain energy increases with the fourth power of the index i, and entropy remains constant across all buckling modes. The first buckling mode, which has the lowest strain energy at constant entropy, is realized first.
The case of constant energy ΔΠi = constant. If we introduce ci = c1/i2, then the strain energy remains constant across all buckling modes, and entropy decreases with the square of index i. The first buckling mode, which has the highest entropy at constant energy, is realized first.

3.5. The Case study

Let us consider a pin-ended IPE240 steel beam with the length of L = 3m. The member has Young's modulus of E=210 GPa, and its second moment of area is I = 2.83·10-6 m4. Euler’s critical load is Pcr,1 = 651.7 kN. The results in Table 1 are obtained with the assumption of ci = 1 m and k1 = 1000 Jm−1K−1. Table 1 presents a scenario of constant entropy, as entropy does not depend on the buckling mode index.
In Equation (22), considering the decomposition of strain energy into entropy, virtual temperature is the measure by which energy is evaluated in terms of entropy.
The criterion that the equilibrium state can be characterized as a state of minimum energy for given entropy can be applied. The minimal strain energy occurs for the first buckling mode, which occurs first, see Table 1. Subsequent buckling modes are ranked in ascending order, just like according to critical forces. It holds that ΔΠi = i4·ΔΠ1.
The same conclusion can be obtained using the criterion that the equilibrium state can be characterized as a state of maximum entropy for a given energy. By using Equation (22), the amplitude (scale factor) needs to be set as decreasing across buckling modes ci = c1/i2 in order to keep the strain energy constant across all modes. Using this new scale, the entropy of the buckling modes is computed, see the last column in the Table 2.
In Table 2, the criterion of maximum entropy for a given energy is applied. The first buckling mode, which occurs first, corresponds to the maximum entropy. Subsequent buckling modes are ranked in descending order, inversely to the ranking by critical forces.
The scale factor ci in Table 2 decreases approximately as intensively as the mean values of the scale factors of the first three buckling modes for I-sections in [96]. The article [96] presents data in Table 1 from measurements of initial out-of-straightness from nine IPE 160 columns performed at the Polytechnic University of Milan and published by the ECCS 8.1 committee [97]. In addition, the article [96] uses the results from the measurements of 428 samples [98]. The scale factors ci in Table 2 obtained from the analysis of strain energy and entropy are practically the same (differences are minimal) compared to the scale factors from experiments [96,97]. It is apparent that the scale factors ci in Table 2 represent the measure of real initial imperfection. Thus, the initial imperfection can be introduced as a linear combination of the scaled buckling modes using their amplitudes ci = c1/i2, where i is the index of the buckling mode and c1 is the amplitude of the first buckling mode. The amplitudes ci also express the (virtual) entropy for a given strain energy.
The ranking of buckling modes by strain energy in Table 1 and by entropy in Table 2 is the same. In the case study, both the criteria of minimum energy and maximum entropy lead to the same ranking of buckling modes.

4. Buckling of Cantilever

Let us assume that the entropy in Equation (16) can be applied to other patterns of buckling modes of other compression columns with different boundary conditions. The entropy of the i-th buckling mode can be obtained by summing the terms from Equation (16).
Δ S i = k 1 ⋅ 1 N ⋅ ∑ j = 1 N | Δ h i j | ,
where k1 is constant and hij is a deflection from the eigenvalue vector of the i-th buckling mode. Each eigenvector is dimensionless, with an indeterminate scale factor ci. For example, the deformation of the i-th buckling mode of a cantilever can be expressed by the function:
y c ( x ) = c i ⋅ ( 1 − cos ( ( 2 i − 1 ) π ⋅ x 2 ⋅ L ) ) ,   for   x ∈ [ 0 ,   L ] ,   i =   1 ,   2 ,   . . ,
where ci>0. By substituting j/N for x/L, the continuous function can be written in the discrete form as:
f i j c = c i ⋅ ( 1 − cos ( ( 2 i − 1 ) π ⋅ ( j − 0.5 ) 2 ⋅ N ) ) ,   for   j =   0 ,   1 ,   … N .
For Δhij = cfij, the entropy of the i-th buckling mode of the cantilever can be written as:
Δ c S i = k 1 ⋅ 1 N ⋅ ∑ j = 1 N | c i ⋅ ( 1 − cos ( ( 2 i − 1 ) π ⋅ ( j − 0.5 ) 2 ⋅ N ) ) | .
In contrast to a pin-ended strut, the entropy of cantilever buckling modes is not constant but slightly dependent on the i-th index, especially for the first buckling modes.
Δ c S i = k 1 ⋅ c i ⋅ [ 1 + cos ( π ⋅ i ) π ⋅ ( i − 0.5 ) ] ,
where [·] is not constant across buckling modes. However, the change in entropy is small compared to the change in strain energy. The change in strain energy ΔΠi of the i-th buckling mode of the cantilever can be derived analogously to the solution in Chapter 2.
Δ c Π i = 1 2 ⋅ ∫ 0 L E ⋅ I ( d y 2 ( x ) d x 2 ) 2 d x = E ⋅ I ⋅ π 4 ⋅ c i 2 64 ⋅ L 3 ⋅ ( 2 ⋅ i − 1 ) 4 .
By substituting Equation (27) and Equation (28) into Equation (12), the virtual temperature cTi can be written as:
T i c = Δ c Π i Δ c S i = ( 2 ⋅ i − 1 ) 4 ⋅ c i ⋅ E ⋅ I ⋅ π 4 64 ⋅ k 1 ⋅ L 3 ⋅ [ π ⋅ ( i − 0.5 ) π ⋅ ( i − 0.5 ) + cos ( π ⋅ i ) ] .
If we introduce ci = c2 as a constant for all buckling modes, the strain energy greatly increases with the fourth power of index i. However, the entropy computed from the surrogate model changes slightly across the buckling modes.

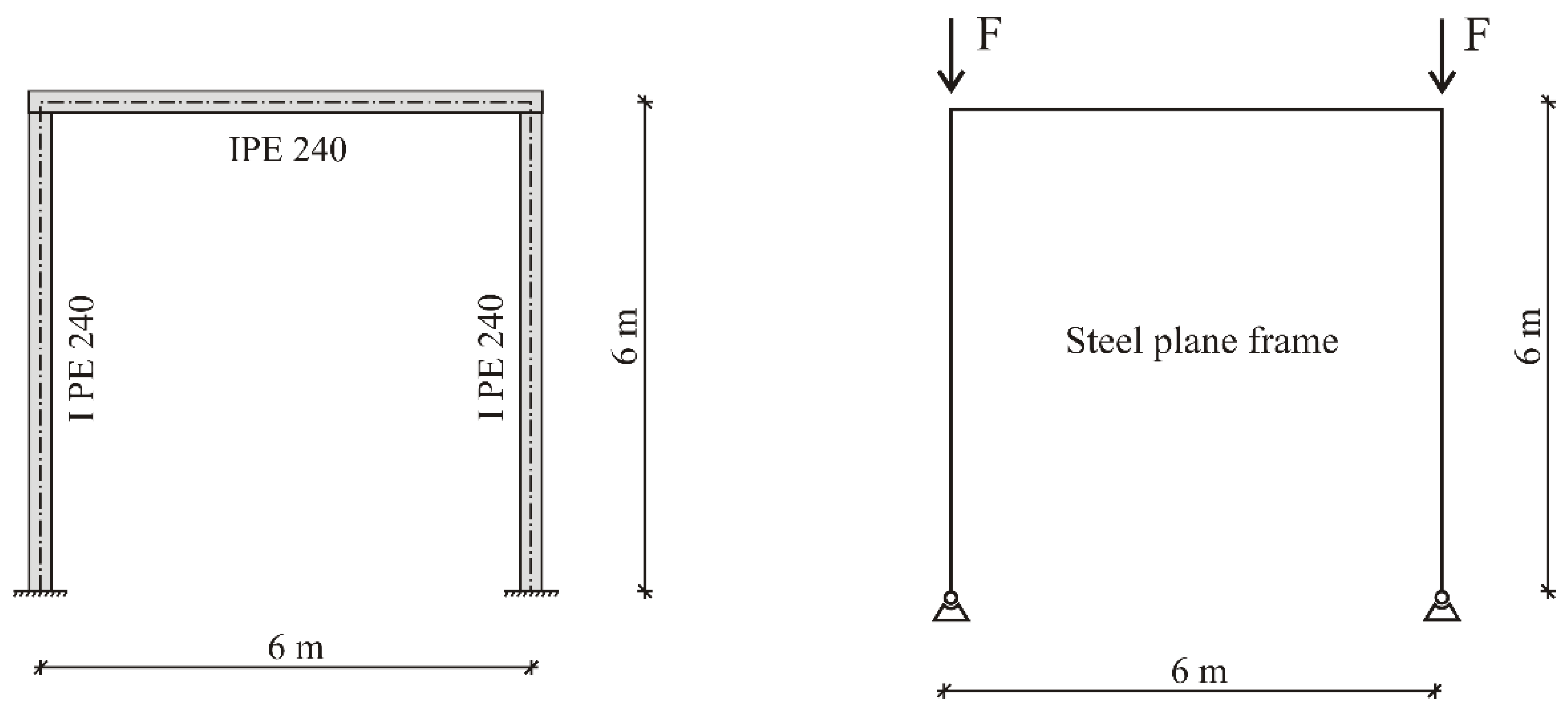
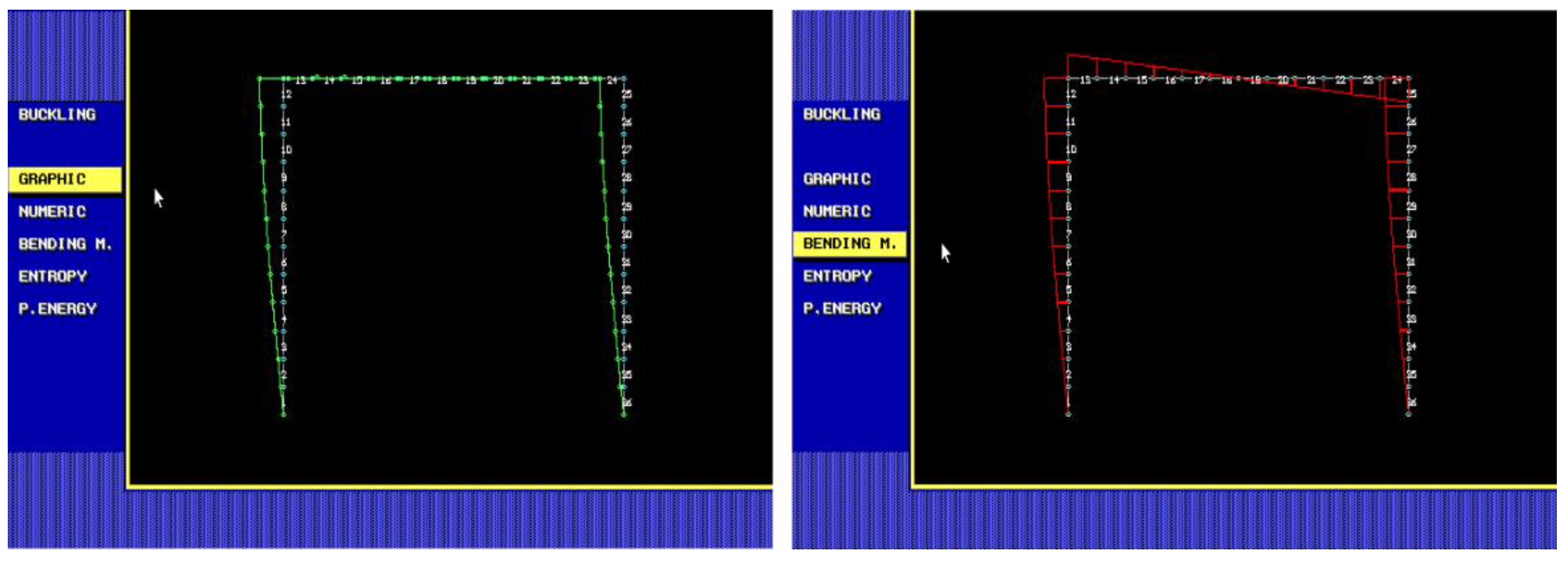
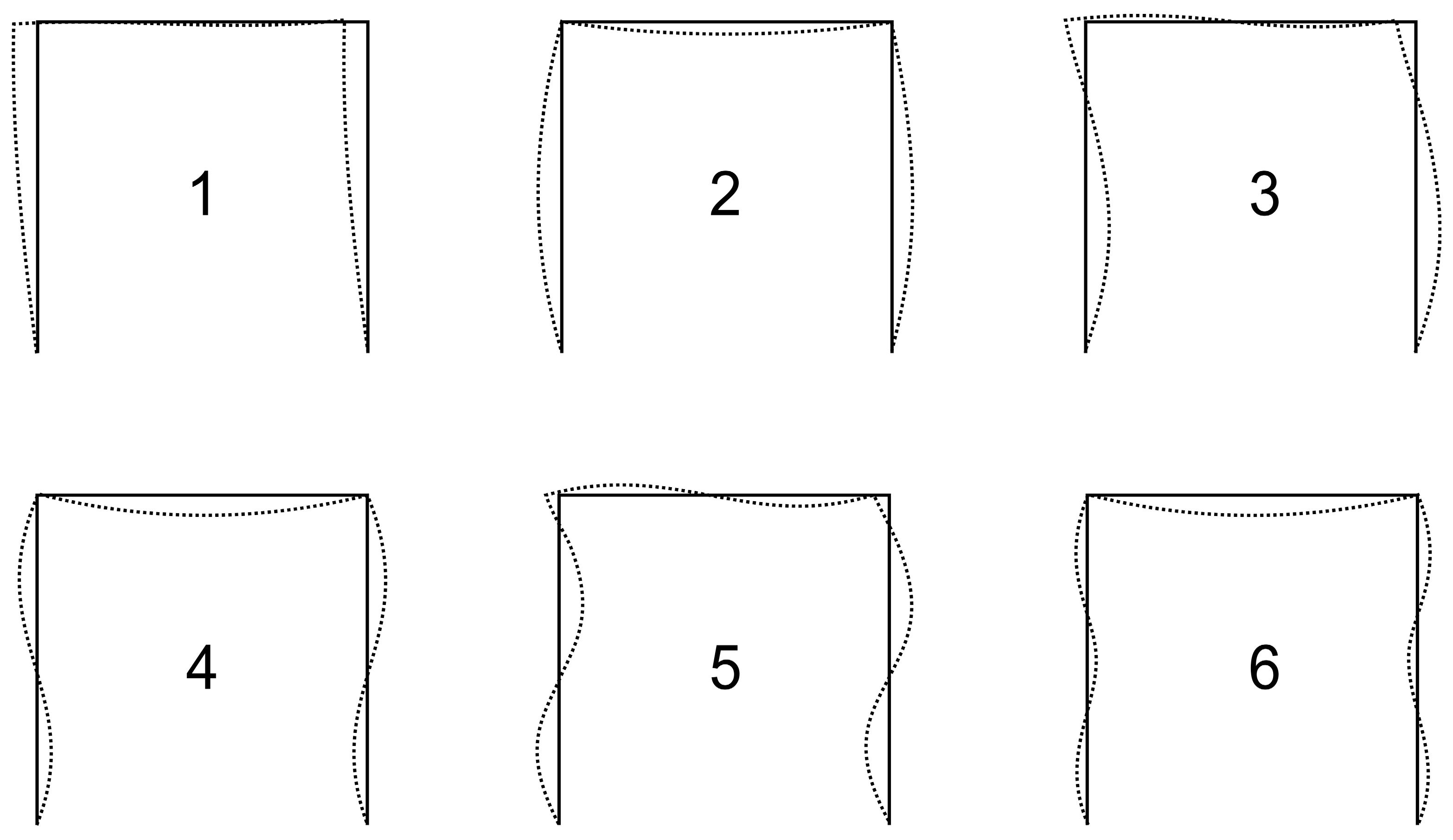
5. Buckling of Steel Plane Frames

The design criteria for steel structures are built on the principles of natural sciences and empirical experience [2]. Engineers combine theoretical knowledge with practical expertise and innovations to design safe and reliable structures.
In the case of steel plane frames, it is typically assumed that the most critical mode is the first buckling mode with the lowest critical buckling load. This analysis suffices when the second critical load significantly exceeds the first critical load. However, if the first and second critical buckling loads coincide, it may be useful to explore alternative approaches for the ranking of buckling modes [18].
The change in strain energy for the i-th elastic buckling mode of the steel plane frame can be calculated using a second-order theory based finite element model (FEM); see, e.g., [19].
Δ Π i = ∑ k = 1 K [ 1 2 ⋅ ∫ 0 L k E ⋅ I k ( κ i ⋅ d y k 2 ( x ) d x 2 ) 2 d x ] ,
where Lk is the length of the k-th member, Ik is the second moment of area of the k-th member, and yk(x) represents the deformation of the i-th elastic buckling mode of the k-th member. The input condition for addressing Equation (30) involves incorporating eigenmodes normalized to the sum of deformations equal to one.
A significant gap exists regarding the calculation of entropy change in buckled frames. Without consideration of entropy, strain energy is analysed with an undetermined scale, denoted as κi in Equation (30). It can be assumed that, for a given strain energy, the entropy will decrease analogously to the results in Table 2. The scale factor κi can be calibrated in such a way that the strain energy of each buckling mode is equal to the strain energy of the first mode. The most critical mode should have the highest entropy corresponding to the lowest critical force.

5.1. Steel Plane Frame: Case Study

The methodology for ranking buckling modes of steel plane frames can be illustrated in a case study. The columns and cross-beam of the frame are made of hot-rolled IPE240 members. The structural material is steel grade S235, with Young's modulus of elasticity E = 210 GPa, and the second moment of area for the IPE profile is Iy = 3890 cm^4. The geometry of the frame is shown in Figure 5
The frame is modelled using the finite element method, with stiffness matrices and geometric matrix of the beam finite element published in [19]. The frame is meshed using 37 nodes and 36 beam finite elements. Each element has 9 internal points where deformations are utilized. In total, there are 37 + 36*9 = 361 deformation points, where each point has one horizontal and one vertical deformation. The total deformation in each point, which has a general direction, is calculated using the Pythagorean theorem. Rotations are not considered. The vector of all 361 total deformations is normalized so that the sum of all total deformations equals one. The critical forces and corresponding buckling modes are computed using a second-order theory-based FEM [19], see Figure 6.
The first six eigenvalues (critical forces) and eigenvector deformations (buckling modes) are computed using the step-by-step loading method, see Figure 7.
The procedure was practically carried out as follows: The critical forces Fcr,i and the corresponding buckling modes (eigenvectors) were computed. Using κi =1 and the normalized scale of total deformations, the strain energies of the buckling modes were computed, see third column in Table 3. The strain energy from the third column approximately correlates with the strain energy calculated using the approximation formula i4 ΔΠ1, where formula i4 ΔΠ1 was explicitly derived for pin-ended struts.
Equation (30) uses the scale factor κi, which influences ΔΠi. If the value κi =1, then ΔΠi is solely computed from the normalized total deformations. The last column in Table 4 provides the approximation of entropy ~ κi, which sets the strain energy of the i-th buckling mode equal to the strain energy of the first buckling mode. The value of κi is calculated according to Equation (31).
κ i = Δ Π 1 Δ Π i ,
where strain energies under the square root are calculated solely from the normalized total deformations.
The strain energy can be roughly approximated as ΔΠi ≈ i4 ΔΠ1. Similarly, to the strain energy relationship between the frame and the pin-ended strut, a similar relationship for entropy can be assumed. Although the link is not direct, it can be expected that the change in entropy can be found to be linear in κi, albeit with the potential influence of additional factors. Although the equation for computing the frame's entropy has not been derived, a strong correlation between entropy (for a given energy) and results in the last column of Table 4 can be expected. The scale factor κi in the penultimate column can be heuristically considered as the entropy estimate, see Table 4.
If there is an estimate of entropy, the criterion that the equilibrium state can be characterized as a state of maximum entropy for a given energy can be applied. The maximum entropy occurs for the first buckling mode, which occurs first, see last column in Table 4. The same conclusion can be obtained using the criterion of minimum energy for the given entropy, see third column of Table 3.

6. Initial Geometrical Imperfections

The scaling of buckling modes can be used to create an initial imperfection to account for second-order geometrical nonlinearity. The classical method uses scaling the lowest eigenmode, see, e.g. [99,100]. The concept behind this theory is that the most critical imperfect geometry is the closest to the final collapse configuration since it requires the least deformation energy to go from the unloaded state to the final collapse situation [101].
Initial imperfections of frame structures can be based on scaled buckling modes. Such fitting of randomly generated shapes of imperfection have been introduced, e.g., in [102]. The method is based on the scale factors of cold-formed steel members calculated on the basis of experimental measurements [103]. Using the energy measure of eigenmodes to introduce initial imperfections has been presented for cold-formed steel columns [104] and axially compressed cylindrical shells [105]. In the case of shells, the energy measure of geometric imperfections was defined by the square root of the strain energy [104].
The introduction of initial frame imperfections using entropy as a supporting energy factor has not yet been presented. Entropy, as a complement to strain energy, plays an important role in structural stability analysis by justifying the scaling of buckling modes based on strain energy. The case study demonstrated rational scales of buckling modes with the dominant position of the first buckling mode. The ranking by strain energy is possible when the entropy remains constant across all buckling modes, and analogously, ranking by entropy is achievable only under constant strain energy.
The scales of buckling modes exhibit a decreasing trend if the same strain energy is considered in each buckling mode, see Table 3. Such scaled buckling modes can be applied in the modelling of initial geometric imperfections. Examples of initial geometric imperfection shapes using combinations of scaled buckling modes are shown in Figure 8.
The signs of the scale factors of buckling modes create 26 = 64 combinations. The first buckling mode is dominant and the other modes only slightly change its shape, see Figure 8. The basic assumption is that enough modes must be applied to ensure that deformations of critical elements are induced by imperfections [96]. However, the scale factors of higher-order modes decrease rapidly and their contribution can be neglected from a certain order. It can be noted that common engineering practice often uses only the first buckling mode [96]. To estimate the limit state, the initial imperfection should be close to the critical mode, which replaces the shape of the frame in the limit state with failure due to buckling. This approach is consistent with the EUROCODE 3 design standard [91].
In the stochastic approach, the initial imperfection can be thought of as an approximation of the real imperfection from measurements on a large number of frames. Scaled buckling modes can be used for the random simulation of the shapes of initial imperfections. One possibility is to consider the contributions of buckling modes with a mean value of zero (perfect strain frame) and random variability based on the scale factor. A similar approach has been applied in probabilistic reliability analyses [17,106].

7. Conclusions

The article investigated the duality of minimum energy and maximum entropy in the context of buckling. Entropy analysis of structures supports energy-based computational results and provides a rationale for ranking buckling modes based on strain energy. An explicit solution was derived for the relationship between strain energy and change in entropy within the context of the pin-ended strut. The change in entropy was found to be linear in displacement.
Entropy extends the applicability of the criterion of minimum energy in structural mechanics. Buckling modes can be ranked according to strain energy for the given entropy. Alternatively, buckling modes can be ranked according to entropy for the given strain energy. In both cases, the ranking aligns with the traditional method based on critical forces. For a given energy, scaled buckling modes coincide with experimentally determined initial imperfections of steel beams IPE160 [96,97].
In the case of frame structures, the scale factors of buckling modes demonstrate a decreasing trend when strain energy is constant in each mode. These scale factors can heuristically be interpreted as an estimate of entropy. Scaled buckling modes are valuable when dealing with initial geometric imperfections formed as their linear combination. Each buckling mode is assigned the same strain energy through a change in scale. The initial imperfection can be considered as a linear combination of these scaled buckling modes.
The case study illustrated rational scales with a dominant first buckling mode. The contribution of other modes diminishes as scale and entropy decrease. In future research, the initial imperfections can be further studied, opening up new possibilities for structural stability analysis.

Author Contributions

All aspects of this work, including software development, writing, and more, were solely undertaken by the single author.

Funding

The work has been supported and prepared within the project “Importance of Stochastic Interactions in Computational Models of Structural Mechanics” of The Czech Science Foundation (GACR, https://gacr.cz/) no. 23-04712S, Czechia.

Institutional Review Board Statement

Not applicable

Informed Consent Statement

Not applicable

Data Availability Statement

Not applicable

Conflicts of Interest

The author declares no conflict of interest

References

  1. Bažant, Z.P.; Cedolin, L. Stability of Structures: Elastic, Inelastic, Fracture and Damage Theories; Oxford University Press: New York, 1991. [Google Scholar]
  2. Galambos, T.V. Guide to Stability Design Criteria for Metal Structures, 5th ed.; Wiley: Hoboken, NJ, USA, 1998; 911p. [Google Scholar]
  3. Godoy, L.A. Historical sense in the historians of the theory of elasticity. Meccanica 2006, 41, 529–538. [Google Scholar] [CrossRef]
  4. Van Den Broek, J.A. Euler's classic paper “On the strength of columns”. Journal of Physics 1947, 12, 309–318. [Google Scholar] [CrossRef]
  5. Euler, L. Methodus Inveniendi Lineas Curvas Maximi Minimive Proprietate Gaudentes, Sive Solutio Problematis Isoperimetrici Lattissimo Sensu Accepti; Marcum Michaelem Bosquet: Lausanne, 1744. [Google Scholar]
  6. Von Mises, R.; Ratzersdorfer, J. Die Knicksicherheit von Rahmentragwerken. Zeitschrift für Angewandte Mathematik und Mechanik (ZAMM) 1926, 6, 181–199. [Google Scholar] [CrossRef]
  7. Chwalla, E. Die Stabilität zentrisch und exzentrisch gedrückter Stäbe aus Baustahl. Sitzungsberichte der Akademie der Wissenschaften mathematisch-naturwissenschaftliche Klasse 1928, 137, 469–512. [Google Scholar]
  8. Belytschko, T.; Liu, W.K.; Moran, B.; Elkhodary, K. Nonlinear Finite Elements for Continua and Structures. John Wiley & Sons, 2014. [Google Scholar]
  9. Chan, S.L.; Huang, H.Y.; Fang, L.X. Advanced analysis of imperfect portal frames with semirigid base connections. Journal of Engineering Mechanics 2005, 131, 633–640. [Google Scholar] [CrossRef]
  10. Mageirou, G.E.; Lemonis, M.E. Influence of imperfections on the progressive collapse of steel moment resisting frames. Journal of Constructional Steel Research 2021, 183, 106744. [Google Scholar] [CrossRef]
  11. Kala, Z.; Valeš, J. Sensitivity assessment and lateral-torsional buckling design of I-beams using solid finite elements. Journal of Constructional Steel Research 2017, 139, 110–122. [Google Scholar] [CrossRef]
  12. Zhang, H.; Shayan, S.; Rasmussen, K.J.R.; Ellingwood, B.R. System-based design of planar steel frames, I: Reliability framework. Journal of Constructional Steel Research 2016, 123, 135–143. [Google Scholar] [CrossRef]
  13. Kala, Z.; Valeš, J.; Jönsson, J. Random fields of initial out of straightness leading to column buckling. Journal of Civil Engineering and Management 2017, 23, 902–913. [Google Scholar] [CrossRef]
  14. Jindra, D.; Kala, Z.; Kala, J. Buckling curves of stainless steel CHS members: Current state and proposed provisions. Journal of Constructional Steel Research 2022, 198, 107521. [Google Scholar] [CrossRef]
  15. Jindra, D.; Kala, Z.; Kala, J. Flexural buckling of stainless steel CHS columns: Reliability analysis utilizing FEM simulations. Journal of Constructional Steel Research 2022, 188, 107002. [Google Scholar] [CrossRef]
  16. Gu, J.X.; Chan, S.L. Second-order analysis and design of steel structures allowing for member and frame imperfections. International Journal for Numerical Methods in Engineering 2005, 62, 601–615. [Google Scholar] [CrossRef]
  17. Kala, Z. Global sensitivity analysis in stability problems of steel frame structures. Journal of Civil Engineering and Management 2016, 22, 417–424. [Google Scholar] [CrossRef]
  18. Bažant, Z.; Xiang, Y. Postcritical imperfection-sensitive buckling and optimal bracing of large regular frames. Journal of Structural Engineering 1997, 123, 513–522. [Google Scholar] [CrossRef]
  19. Kala, Z. Geometrically non-linear finite element reliability analysis of steel plane frames with initial imperfections. Journal of Civil Engineering and Management 2012, 18, 81–90. [Google Scholar] [CrossRef]
  20. Ben–Naim, A. A Farewell to Entropy: Statistical Thermodynamics Based on Information; World Scientific: Singapore, 2008. [Google Scholar]
  21. Charlton, T.M. Energy Principles in Theory of Structures; Oxford University Press, 1973. [Google Scholar]
  22. Arthurs, A.M.; Jones, M.E. On variational principles for linear initial value problems. Journal of Mathematical Analysis and Applications 1976, 54, 840–845. [Google Scholar] [CrossRef]
  23. Van Groesen, E.W.C. Variational Methods in Mathematical Physics; Technische Hogeschool Eindhoven, 1978; p. 216. [Google Scholar] [CrossRef]
  24. Washizu, K. Variational Methods in Elasticity and Plasticity; Pergamon Press: Oxford, UK, 1982; p. 630. [Google Scholar]
  25. Auchmuty, G. Duality for non-convex variational principles. Journal of Differential Equations 1983, 50, 80–145. [Google Scholar] [CrossRef]
  26. Berdichevsky, V.L. Variational Principles of Continuum Mechanics; Springer: Berlin/Heidelberg, Germany, 2009; p. 1011. [Google Scholar]
  27. Fanaie, N.; Shirpour, A. Analytical and numerical evaluation of quarter-elliptic-braced steel moment frames (QEB-MFs). Structures 2023, 49, 426–442. [Google Scholar] [CrossRef]
  28. Zheng, A.; Shi, H.-R.; Gong, Z.; Wang, C.-L.; Meng, S. Experimental study on bamboo-shaped buckling-retrained energy dissipater with different grades of steel. Journal of Constructional Steel Research 2023, 211, 108164. [Google Scholar] [CrossRef]
  29. Ou, T.; Mei, C.; Mao, J.; Wang, D. Seismic analysis and connection optimization of the side column on modular prefabricated four-sided connected composite shear wall. The Structural Design of Tall and Special Buildings 2022, 32, 426–442. [Google Scholar] [CrossRef]
  30. Gorgogianni, A.; Eliáš, J.; Le, J.-L. Mesh objective stochastic simulations of quasibrittle fracture. Journal of the Mechanics and Physics of Solids 2022, 159, 104745. [Google Scholar] [CrossRef]
  31. Zheng, X.; Shen, Y.; Zong, X.; Su, H.; Zhao, X. Vulnerability analysis of main aftershock sequence of aqueduct based on incremental dynamic analysis method. Buildings 2023, 13, 1490. [Google Scholar] [CrossRef]
  32. Yang, J.; Wang, W.; Xu, L.; Shi, Y. Global buckling analysis on cold-formed steel built-up box-shape columns at ambient and elevated temperatures. Structures 2023, 57, 105301. [Google Scholar] [CrossRef]
  33. Hamed, A.A.; Samadi, A.; Charkhtab Basim, M. Topology and shape optimization of steel plate shear walls for enhancing the seismic energy dissipation capacity. Journal of Building Engineering 2022, 57, 104828. [Google Scholar] [CrossRef]
  34. Zheng, Z.-Q.; Liu, H.-Z.; Zhuo, L.; Xiao, M.-L.; Xie, H.-Q.; He, J.-D.; Peng, M.-L. Experimental study on the dilatancy and energy evolution behaviors of red-bed rocks under unloading conditions. Materials 2023, 16, 5759. [Google Scholar] [CrossRef] [PubMed]
  35. Lu, H.; Pan, Y.; He, K.; Wang, F.; Gao, L.; Pu, S.; Li, E. Dynamic Mechanical Properties and Damage Evolution Characteristics of Beishan Deep Granite under Medium and High Strain Rates. Materials 2023, 16, 5235. [Google Scholar] [CrossRef]
  36. Fujii, K. Peak and Cumulative Response of Reinforced Concrete Frames with Steel Damper Columns under Seismic Sequences. Buildings 2022, 12, 275. [Google Scholar] [CrossRef]
  37. Pandit, U.K.; Mondal, G.; Punera, D. Lateral torsional buckling analysis of corrugated steel web girders using homogenization approach. Journal of Constructional Steel Research 2023, 210, 108099. [Google Scholar] [CrossRef]
  38. Rezaiee-Pajand, M.; Masoodi, A.R.; Alepaighambar, A. Critical buckling moment of functionally graded tapered mono-symmetric I-beam. Steel and Composite Structures 2021, 39, 599–614. [Google Scholar] [CrossRef]
  39. Stupishin, L.; Mondrus, V. Implementation of the weak link problem for trusses. Buildings 2023, 13, 1230. [Google Scholar] [CrossRef]
  40. Dehwah, O.H.A.; Al-Gahtani, H.J. Energy-based solution for the plastic buckling of stainless steel circular cylindrical shells. Structures 2023, 48, 2024–2036. [Google Scholar] [CrossRef]
  41. Jafari, M.M.; Jahandari, S.; Ozbakkaloglu, T.; Rasekh, H.; Jahed Armaghani, D.; Rahmani, A. Mechanical properties of polyamide fiber-reinforced lime–cement concrete. Sustainability 2023, 15, 11484. [Google Scholar] [CrossRef]
  42. Fujii, K.; Mogi, Y.; Noguchi, T. Predicting maximum and cumulative response of a base-isolated building using pushover analysis. Buildings 2020, 10, 91. [Google Scholar] [CrossRef]
  43. Muc, A. Buckling of composite structures with delaminations—laminates and functionally graded materials. Appl. Sci. 2022, 12, 11408. [Google Scholar] [CrossRef]
  44. Shima, H. Buckling of carbon nanotubes: A state of the art review. Materials 2012, 5, 47–84. [Google Scholar] [CrossRef] [PubMed]
  45. Chen, L.; Yao, X.; Sun, Z. Wang, D. Study seismic performance of duplex stainless steel under large strain amplitude by cyclic loading test. Journal of Constructional Steel Research 2022, 194, 107332. [Google Scholar] [CrossRef]
  46. Liu, C.; Sun, Z. Calculation theory of shear stress distribution in box girder with corrugated steel webs based on the energy method. Buildings 2023, 13, 2547. [Google Scholar] [CrossRef]
  47. Khaleel Ibrahim, S.; Movahedi Rad, M. Optimal elasto-plastic analysis of prestressed concrete beams by applying residual plastic deformation limitations. Sustainability 2023, 15, 5742. [Google Scholar] [CrossRef]
  48. Xiao, X.; Zhang, Q.; Zheng, J.; Li, Z. Analytical model for the nonlinear buckling responses of the confined polyhedral FGP-GPLs lining subjected to crown point loading. Engineering Structures 2023, 282, 115780. [Google Scholar] [CrossRef]
  49. Hai, L.; Ban, H.; Yang, X.; Huang, C.; Shi, Y. Cyclic behavior of hot-rolled titanium-clad bimetallic steel under large plastic strain reversals. Journal of Constructional Steel Research 2023, 210, 108112. [Google Scholar] [CrossRef]
  50. Stupishin, L.; Mondrus, V. Critical Energy Properties Study for Unsymmetrical Deformable Structures. Buildings 2022, 12, 779. [Google Scholar] [CrossRef]
  51. Kala, Z.; Kalina, M. Static equilibrium states of von Mises trusses. International Journal of Mechanics 2016, 10, s. 294–298. [Google Scholar]
  52. Chen, L.-M.; Li, Z.-B.; Zhang, H.; Liu, Y.-J.; Zeng, Y.-H.; Zhou, Y.-Y.; Dong, S.-L. Design optimisation of a cable–strut tensile structure according to the importance of elements. Buildings 2022, 12, 1528. [Google Scholar] [CrossRef]
  53. Simão, P.D.; Rodrigues, J.P.C.; Fernandes, H.D. A voxels-based Rayleigh-Ritz method for the post-buckling elasto-plastic analysis of restrained steel columns in fire. Journal of Constructional Steel Research 2023, 210, 107736. [Google Scholar] [CrossRef]
  54. Abdelrahman, A.H.A.; Lotfy, S.; Liu, S.-W. Generalized line-element formulations for geometrically nonlinear analysis of nonsymmetric tapered steel members with warping and Wagner effects. Engineering Structures 2022, 273, 115052. [Google Scholar] [CrossRef]
  55. Kerdsuk, P.; Pulngern, T.; Tangbanjongkij, C.; Chucheepsakul, S.; Jiammeepreecha, W. Elastic buckling of oblate hemi-ellipsoidal shells subjected to hydrostatic pressure. International Journal of Structural Stability and Dynamics, 2023, 2023, 2450028. [Google Scholar] [CrossRef]
  56. Elsayed, M.; A. Mutalib, A.; Elsayed, K. Numerical study of structural performance and wind flow dynamic behavior for PPVC steel modular construction (MSC) under various extreme wind loads. Buildings 2022, 12, 1347. [Google Scholar] [CrossRef]
  57. Hajdú, G.; Pasternak, H.; Papp, F. Lateral-torsional buckling assessment of I-beams with sinusoidally corrugated web. Journal of Constructional Steel Research 2023, 207, 107916. [Google Scholar] [CrossRef]
  58. Li, C.; Liu, N.; Liu, W.; Feng, R. Study on characteristics of energy storage and acoustic emission of rock under different moisture content. Sustainability 2021, 13, 1041. [Google Scholar] [CrossRef]
  59. Zhang, X.; Sun, Y.; Yang, X.; Sun, L.; Wang, P. Study on the bending performance of high-strength and high-ductility CRE-reinforced concrete beams. Buildings 2023, 13, 2746. [Google Scholar] [CrossRef]
  60. Godoy, L.A.; Ameijeiras, M.P. Plastic buckling of oil storage tanks under blast loads. Structures 2023, 53, 361–372. [Google Scholar] [CrossRef]
  61. Luo, L.; Zhang, Y. A new method for establishing the total potential energy equations of steel members based on the principle of virtual work. Structures 2023, 52, 904–920. [Google Scholar] [CrossRef]
  62. Zhang, Y.; Zhong, L.; Pang, F.; Li, P.; Liu, F. Characteristics of energy dissipation in T-Shaped fractured rocks under different loading rates. Sustainability 2023, 15, 13695. [Google Scholar] [CrossRef]
  63. Sun, G.; Lai, J.; Zheng, Y.; Zheng, K.; Shi, J. Investigation of the performance of RC beams reinforced with FRP and ECC materials. Journal of Civil Engineering and Management 2022, 28, 523–535. [Google Scholar] [CrossRef]
  64. Clausius, R. Ueber verschiedene für die Anwendung bequeme Formen der Hauptgleichungen der mechanischen Wärmetheorie. Annalen der Physik 1865, 201, 353–400. (In German) [Google Scholar] [CrossRef]
  65. Wang, X.; Qian, L.; Hong, M.; Zhang, J. Evolution and abrupt change for water use structure through matrix-based Renyi's alpha order entropy functional. Stochastic Environmental Research and Risk Assessment 2022, 36, 1413–1428. [Google Scholar] [CrossRef]
  66. Jessop, A. Some reflections on maxEnt. Civil Engineering and Environmental Systems 2023, 40, 60–71. [Google Scholar] [CrossRef]
  67. Chen, C.; Yang, Y.; Hou, H.; Peng, C.; Xu, W. Real-time hybrid simulation with multi-fidelity Co-Kriging for global response prediction under structural uncertainties. Earthquake Engineering and Structural Dynamics 2022, 51, 2591–2609. [Google Scholar] [CrossRef]
  68. Gao, C.; Elzarka, H.; Yan, H.; Chakraborty, D.; Zhou, C. A hybrid TOPSIS-structure entropy weight group subcontractor selection model for large construction companies. Buildings 2023, 13, 1535. [Google Scholar] [CrossRef]
  69. Wang, Y.; Sun, Q.; Leng, S.; Cui, H.; Xu, B. Effect of dry-wet cycles on mechanical properties of polyurethane porous mixture. International Journal of Pavement Engineering 2023, 24, 2212315. [Google Scholar] [CrossRef]
  70. Qiu, D.; Chen, J.; Fu, H. Research on the comprehensive evaluating index of seismic performance of underground large-scale frame structures. Structures 2022, 37, 645–660. [Google Scholar] [CrossRef]
  71. Pedretti, D.; Bianchi, M. GEOENT: A toolbox for calculating directional geological entropy. Geosciences 2022, 12, 206. [Google Scholar] [CrossRef]
  72. Keerthana, M.; Harikrishna, P. Signal complexity approach based investigation of flutter instability in sectional models of bridges in wind tunnel. Advances in Structural Engineering 2023, 26, 2520–2542. [Google Scholar] [CrossRef]
  73. Wang, Y.; Qu, Z. TMD Design by an Entropy Index for Seismic Control of Tall Shear-Bending Buildings. Entropy 2023, 25, 1110. [Google Scholar] [CrossRef] [PubMed]
  74. Abi, E.; Yuan, H.; Cong, Y.; Wang, Z.; Jiang, M. Experimental study on the entropy change failure precursors of marble under different stress paths. KSCE Journal of Civil Engineering 2023, 27, 356–370. [Google Scholar] [CrossRef]
  75. Luo, D.; Dong, H.; Niu, D. Geographic division of exposure environment for concrete structure based on fuzzy clustering-rough set information entropy. Structural Concrete 2023, 24, 485–503. [Google Scholar] [CrossRef]
  76. Wang, C.; Zou, F.; Yap, J.B.H.; Wood, L.C.; Li, H.; Ding, L. System dynamics tool for entropy-based risk control on sleeve grouting in prefabricated buildings. Engineering, Construction and Architectural Management 2023, 30, 538–567. [Google Scholar] [CrossRef]
  77. Su, L.; Wang, T.; Li, H.; Chao, Y.; Wang, L. Multi-criteria decision making for identification of unbalanced bidding. Journal of Civil Engineering and Management 2020, 26, 43–52. [Google Scholar] [CrossRef]
  78. Xie, W.; Gao, D.; Lee, E.W. Detecting undeclared-leader-follower structure in pedestrian evacuation using transfer entropy. IEEE Transactions on Intelligent Transportation Systems 2022, 23, 17644–17653. [Google Scholar] [CrossRef]
  79. Yang, N.; Jia, Y.T.; Bai, F.; Qin, S.J. Reliability estimation of a Tibetan heritage timber structure with inclination in its Que-Ti joints. Structures 2022, 43, 257–270. [Google Scholar] [CrossRef]
  80. Luo, Z.; Guo, J.; Han, J.; Wang, Y. Reliability estimation of a Tibetan heritage timber structure with inclination in its Que-Ti joints. Engineering, Construction and Architectural Management 2022. [Google Scholar]
  81. Kamiński, M.; Strąkowski, M. An application of relative entropy in structural safety analysis of elastoplastic beam under fire conditions. Energies 2023, 16, 207. [Google Scholar] [CrossRef]
  82. Wang, T.; Li, Z.; Fan, W.; Ang, A.H.-S. Structural system reliability assessment using generalized factorized dimensional reduction method and iterative maximum entropy method. Structure and Infrastructure Engineering 2022. [Google Scholar] [CrossRef]
  83. Civera, M.; Surace, C. Instantaneous spectral entropy: An application for the online monitoring of multi-storey frame structures. Buildings 2022, 12, 310. [Google Scholar] [CrossRef]
  84. Qu, S.; Fang, Y.; Liang, J.; Zheng, J.-H.; Zheng, K. A Physical mechanism-based model of CoCrFeMnNi high entropy alloy considering adiabatic heat effect for hot bulk forming processes. Metals 2022, 12, 1011. [Google Scholar] [CrossRef]
  85. Shi, J.; Gong, H.; Yang, F.; Liang, H.; Cong, L. Image processing of aggregate skeleton structure of asphalt mixture for aggregate uniformity quantification. Journal of Materials in Civil Engineering 2023, 35, 04022388. [Google Scholar] [CrossRef]
  86. Krylovas, A.; Kosareva, N.; Zavadskas, E.K. WEBIRA-Comparative analysis of weight balancing method. International Journal of Computers, Communications and Control 2017, 12, 238–253. [Google Scholar] [CrossRef]
  87. Kala, Z. New importance measures based on failure probability in global sensitivity analysis of reliability. Mathematics 2021, 9, 2425. [Google Scholar] [CrossRef]
  88. Kala, Z. Modelling initial geometric imperfections of steel plane frames using entropy and eigenmodes. International Journal of Mechanics 2023, 17, 64–73. [Google Scholar] [CrossRef]
  89. Callen, H.B. Thermodynamics and an Introduction to Thermostatistics; John Wiley & Sons, 1985. [Google Scholar]
  90. Yang, B. Stress, Strain, and Structural Dynamics; Elsevier Inc., 2005. [Google Scholar]
  91. European Committee for Standardization (CEN). EN 1993-1-9. Eurocode3: Design of Steel Structures, Part 1–1: General Rules and Rules for Buildings; European Standards: Brussels, Belgium, 2005. [Google Scholar]
  92. Feistel, R.; Ebeling, W. Entropy and the self-organization of information and value. Entropy 2016, 18, 193. [Google Scholar] [CrossRef]
  93. Verlinde, E. On the origin of gravity and the laws of Newton. Journal of High Energy Physics 2011, 2011, 29. [Google Scholar] [CrossRef]
  94. Klotz, I.M.; Rosenberg, R.M. Chemical Thermodynamics: Basic Concepts and Methods; John Wiley & Sons, 2008. [Google Scholar]
  95. Atkins, P.W. Physical Chemistry; Freeman: New York, 1998. [Google Scholar]
  96. Liu, W.; Rasmussen, K.J.R.; Zhang, H.; Xie, Y.; Liu, Q. , Dai, L. Probabilistic study and numerical modelling of initial geometric imperfections for 3D steel frames in advanced structural analysis. Structures 2023, 57, 105190. [Google Scholar] [CrossRef]
  97. Sfintesco, D. Fondement expérimental des courbes européennes de flambement. Construction Métallique 1970, 3, 5–12. [Google Scholar]
  98. Fukumoto, Y.; Itoh, Y. Evaluation of multiple column curves using the experimental data-base approach. Journal of Constructional Steel Research 1983, 3, 2–19. [Google Scholar] [CrossRef]
  99. Gu, J.X.; Chan, S.L. Second-order analysis and design of steel structures allowing for member and frame imperfections. International Journal for Numerical Methods in Engineering 2005, 62, 601–615. [Google Scholar] [CrossRef]
  100. Kim, S.-E.; Lee, D.-H. Second-order distributed plasticity analysis of space steel frames. Engineering Structures 2002, 24, 735–744. [Google Scholar] [CrossRef]
  101. Alvarenga, A.R.; Silveira, R.A.M. Second-order plastic-zone analysis of steel frames - Part II: Effects of initial geometric imperfection and residual stress. Latin American Journal of Solids and Structures 2009, 6, 323–342. [Google Scholar]
  102. Shayan, S.; Rasmussen, K.J.R.; Zhang, H. On the modelling of initial geometric imperfections of steel frames in advanced analysis. Journal of Constructional Steel Research 2014, 98, 167–177. [Google Scholar] [CrossRef]
  103. Zeinoddini, V.M.; Schafer, B.W. Simulation of geometric imperfections in cold-formed steel members using spectral representation approach. Thin-Walled Structures 2012, 60, 105–117. [Google Scholar] [CrossRef]
  104. Sadovský, Z.; Kriváček, J.; Ivančo, V.; Ďuricová, A. Computational modelling of geometric imperfections and buckling strength of cold-formed steel. Journal of Constructional Steel Research 2012, 78, 1–7. [Google Scholar] [CrossRef]
  105. Sadovský, Z.; Kriváček, J. Influential geometric imperfections in buckling of axially compressed cylindrical shells – A novel approach. Engineering Structures 2020, 223, 111170. [Google Scholar] [CrossRef]
  106. Kala, Z. Sensitivity analysis of steel plane frames with initial imperfections. Engineering Structures 2011, 33, 2342–2349. [Google Scholar] [CrossRef]
Preprints 90354 g001
Figure 1. Number of publications in “Civil engineering” and “Mechanics” Web of Science categories (Web of Science core collection database, 12 November 2023), topic “buckling” and “entropy”.
Figure 1. Number of publications in “Civil engineering” and “Mechanics” Web of Science categories (Web of Science core collection database, 12 November 2023), topic “buckling” and “entropy”.
Preprints 90354 g001
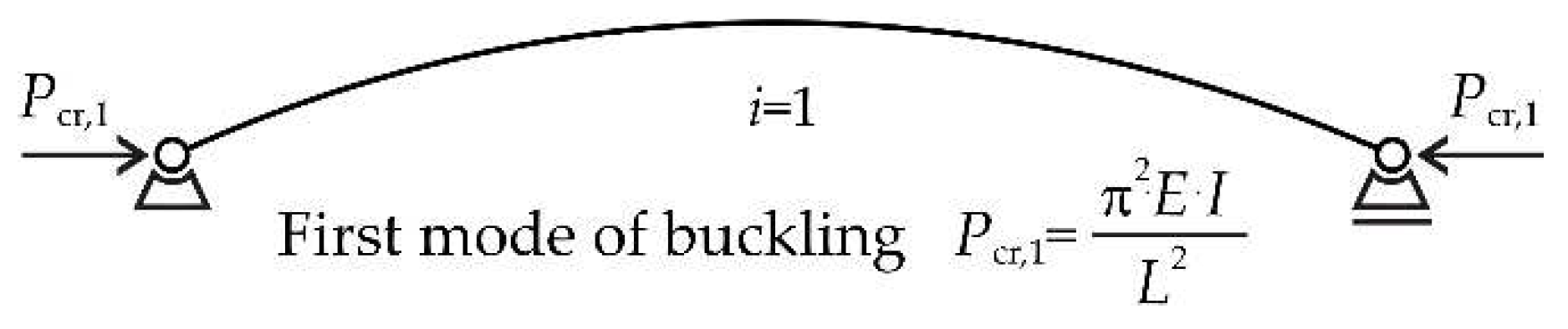
Preprints 90354 g002
Figure 2. The flexural buckling of the pin-ended strut.
Figure 2. The flexural buckling of the pin-ended strut.
Preprints 90354 g002
Preprints 90354 g003
Figure 3. The buckling modes of the pin-ended strut.
Figure 3. The buckling modes of the pin-ended strut.
Preprints 90354 g003
Preprints 90354 g004
Figure 4. Surrogate model for the transformation buckling mode into entropy.
Figure 4. Surrogate model for the transformation buckling mode into entropy.
Preprints 90354 g004
Preprints 90354 g005
Figure 5. The geometry of the steel plane frame.
Figure 5. The geometry of the steel plane frame.
Preprints 90354 g005
Preprints 90354 g006
Figure 6. Second-order theory-based FEM: first buckling mode and bending moment.
Figure 6. Second-order theory-based FEM: first buckling mode and bending moment.
Preprints 90354 g006
Preprints 90354 g007
Figure 7. First six buckling modes of steel plane frame.
Figure 7. First six buckling modes of steel plane frame.
Preprints 90354 g007
Preprints 90354 g008
Figure 8. Initial imperfections from scaled buckling modes, first six combinations.
Figure 8. Initial imperfections from scaled buckling modes, first six combinations.
Preprints 90354 g008
Table 1. Ranking of buckling modes according to strain energy, assuming constant entropy.
Table 1. Ranking of buckling modes according to strain energy, assuming constant entropy.
Buckling mode index Critical force
Frc,i [kN]		 ci Strain energy
ΔΠi [MJ]		 Virtual
temperature
Ti [K]		 Entropy
ΔSi[J·K-1]
1 651.7 1 0.536 842.0 636.62
2 2606.9 1 8.576 13472.7 636.62
3 5865.5 1 43.418 68200.3 636.62
4 10427.6 1 137.221 215546.7 636.62
5 16293.1 1 335.013 526237.0 636.62
6 23462.0 1 694.683 1091205.0 636.62
Table 2. Ranking of buckling modes according to entropy, assuming constant strain energy.
Table 2. Ranking of buckling modes according to entropy, assuming constant strain energy.
Buckling mode index Critical force
Frc,i [kN]		 ci Strain energy
ΔΠi [MJ]		 Virtual
temperature
Ti [K]		 Entropy
ΔSi[J·K-1]
1 651.7 1 0.536 1.0000 636.62
2 2606.9 0.25 0.536 15.3229 159.15
3 5865.5 0.111 0.536 25.0961 70.74
4 10427.6 0.063 0.536 58.2375 39.79
5 16293.1 0.04 0.536 72.6713 25.46
6 23462.0 0.028 0.536 130.7333 17.68
Table 3. Ranking of the buckling modes according to the strain energy for given entropy.
Table 3. Ranking of the buckling modes according to the strain energy for given entropy.
Buckling mode index Critical force
Frc,i [kN]		 Strain energy ΔΠi [J] (from normalized eigenmodes) Scale factor κi (~ entropy) Approximation of strain energy
≈ i4 ΔΠ1 [J]
1 412.5 1.1056 1.0000 1.1056
2 2925.8 61.3416 1.0000 17.6905
3 3830.9 101.8158 1.0000 89.5581
4 9784.0 451.7487 1.0000 283.0477
5 11085.0 880.4734 1.0000 691.0345
6 21023.4 1406.9822 1.0000 1432.9292
Table 4. Ranking of the buckling modes according to the entropy for given strain energy.
Table 4. Ranking of the buckling modes according to the entropy for given strain energy.
Buckling mode index Critical force
Frc,i [kN]		 Given strain energy
ΔΠi [J]
(by scaled eigenmodes)		 Scale factor κi
(for ΔΠi = ΔΠ1)		 Entropy ~ κi
1 412.5 1.1056 1.0000 1.0000
2 2925.8 1.1056 0.1343 0.1343
3 3830.9 1.1056 0.1042 0.1042
4 9784.0 1.1056 0.0495 0.0495
5 11085.0 1.1056 0.0354 0.0354
6 21023.4 1.1056 0.0180 0.0180
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated