Prerpints.org logo
Preprint
Review

Physical and Technological Aspects of Laser Induced Damage of ZGP Single Crystals under Periodically-Pulsed Laser Irradiation at 2.1 μm

Altmetrics

Downloads

134

Views

50

Comments

1

A peer-reviewed article of this preprint also exists.

Submitted:

22 November 2023

Posted:

23 November 2023

You are already at the latest version

Alerts
Abstract
Nonlinear properties of zinc germanium diphosphide (ZGP) crystals enable their ap-plications in powerful mid-IR optical parametric oscillators and second-harmonic generators. This paper summarizes mechanisms of the laser induced damage (LID) in high-purity ZGP crystals under periodically pulsed nanosecond irradiation by a Ho3+:YAG laser at 2.1 μm. The ZGP samples were manufactured by “LOC” Ent., Tomsk, Russia, or Harbin Institute of Technology, China. The impact of processing techniques and the post-growing methods for polishing and anti-reflection coating on the LID threshold are discussed. The importance of the defect structure of the crystal lattice and the parameters of transparent coatings for increasing the LID threshold is discussed. The impact of the test laser parameters on the LID threshold is analyzed. The transient area near the LID threshold obtained using digital holography is ana-lyzed. Influence of the pre-damage processes on the optical parametric oscillations is reported. Prospects for improving ZGP crystals to further increase the LID threshold are discussed.
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics

1. Introduction

Periodically pulsed sources of powerful coherent mid-infrared (mid-IR) radiation have a wide range of applications in many areas of science and technology. In particular, frequency converters operating in the 3.5-5 μm and 8-12 μm wavelength ranges are promising for optical communications in the atmosphere within the framework of global 6G-generation information transmission systems [1]. Sources of coherent mid-IR radiation are also used for processing materials (glasses, ceramics, or semiconductors) by scribing and thermal splitting [2,3], in medicine, including disease diagnosis using gas analysis and resonant ablation of biological tissues due to the strong water and collagen absorptions [4-9]. Sources of coherent radiation capable of generating powerful pulsed radiation in the 3.5-5 μm wavelength range are relevant for the creation of lidar systems based on the method of differential absorption for greenhouse gas emission control (since the most intense absorption lines of most greenhouse gases lie in this spectral range) [10-13]. One of the most efficient solid-state sources of coherent radiation in the mid-IR range are optical parametric oscillators (OPOs) and optical parametric generators and amplifiers (OPGs and OPAs).
The most powerful OPOs in the practically important mid-IR windows are currently based on nonlinear-optical ZnGeP2 (ZGP) crystals [14-16]. These OPOs are pumped by the well-established Q-switched Ho3+:YAG lasers at 2.1 µm and are capable of high-efficiently generating at 3.5-5 µm with an average power of up to 160 W or pulse energy of up to 200 mJ at the pulse width of 10-60 ns and the repetition rate from a few Hz to 100 kHz [17-22]. Moreover, the Ho3+:YAG–laser pumped OPOs based on ZnGeP2 crystals operate efficiently at wavelengths 6-7 µm, 8.1-8.3 µm and 9-10 µm [23-26]. The ZGP crystals were also used for mid-IR OPGs and OPAs in broadband laser systems that were able to generate ultra-short picosecond and femtosecond pulses [15, 27-30]. However, the prolonged operation of powerful OPOs and OPGs/OPAs based on ZGP is limited by the laser-induced damage (LID) of this material. In accordance with the results of numerous studies [31-48], the ZGP LID always occurred at the sample surface or in the sub-surface layer rather than in the bulk in samples subjected to the repetitively-pulsed nanosecond-pulse-width infrared radiation. A combination of factors associated with defects in the crystal structure in the sub-surface layer and the quality of polishing of the surface itself affects the LID. In this regard, the potential for practical use of the optical parametric devices in the mid-IR range is associated, in particular, with the need to improve the methods of synthesis, growth, and processing of the working surfaces of the ZGP crystals in order to increase the LID threshold (LIDT).
There has been a number of publications on the problem of the ZGP LID induced by lasers operating at wavelengths from 1.064 μm to 10 μm [31-48]. These studies have revealed a significant difference in the LIDT of the ZGP crystal at wavelengths of 1.064 μm and 2.1 μm [31]. Dynamic visualization of the breakdown process initiated by the laser radiation at 2.1 μm in the ZGP volume showed that the optical damage of the ZGP single crystal under nanosecond repetitively-pulsed radiation is mainly initiated by thermal effects [32]. The increase in the ZGP LIDT with a decrease in the pulse width of the pump radiation reported in [33] also “supports the thermal nature of the breakdown for nanosecond pulses due to anomalous infrared absorption.” In [35], it was reported that the ZGP LIDT at 9.55 μm was determined by the intensity of the incident beam of 142 MW/cm2 at a pulse duration of 85 ns and a repetition rate of 1 Hz, which is ~ 9.5 J/cm2 in terms of the pulse energy density. A direct dependence of the LIDT on the growth technology and optical quality of crystals was demonstrated in [34].
In [40], it was shown that the LIDTs measured on the ZGP samples with an anti-reflection (AR) coating are much lower compared to samples without a coating. In [37], it was shown that the application of the AR interference coatings leads to a twofold increase in the LIDT. In [41], the authors concluded that in order to increase the output power and efficiency of parametric frequency conversion in the ZGP crystal in the spectral range of 3-5 μm further research should be focused on improving the quality of the AR coating using a high-quality ZGP crystal.
The conflicting information about the effect of interference coatings on the ZGP LIDT presented in [37,40] suggests that the different design of coatings and methods of their application on a nonlinear crystal significantly affects the efficiency of its use in OPOs. In [42-45], comprehensive studies were conducted on the influence of the parameters of application of AR coatings and film-forming materials on the ZGP LIDT under the mid-IR laser irradiation with femtosecond, picosecond, and nanosecond pulse durations.
In [34,37,38] it was shown that improving the polishing of ZGP working surfaces and either reducing or completely removing the near-surface crack layer leads to an increase in the LIDT. In [37,38] when the near-surface crack layer was reduced, Rq was reduced by half and the PV parameter changed by more than 5 times, while the optical breakdown threshold by energy density increased 2 times. LIDT at a wavelength of 2.05 μm and a pulse repetition frequency (PRR) of 10 kHz for ZGP samples with a deposited antireflection coating was improved from 1 J/cm2 to 2 J/cm2. The increase in LIDT was achieved by improving the polishing of the surface of ZGP samples. At the same time, the research results presented in [34] show that no changes in LIDT when the polishing parameter Rz was almost the same but the Rq parameter was changed by over four times and the Ra parameter by more than 5 times. It was suggested that it is the roughness of the polished surface (peaks and valleys), described by the Rz parameter, that contributes to the mechanism of optical breakdown and can be “seeding” inhomogeneities for the initiation of optical breakdown due to field effects at a wavelength of 2091 nm.
One of the promising methods for improving surface quality is magnetorheological polishing [46], which is increasingly being used in the processing of laser crystals to improve the threshold of radiation resistance and reduce the level of roughness. In [47], magnetorheological processing was first used for polishing the working surfaces of a ZGP single crystal. A non-aqueous liquid with magnetic particles of carbonyl iron with the addition of nanodiamonds was used in the process. This enabled samples of a ZGP single crystal with a surface roughness level measured in angstroms. The use of magnetorheological polishing made it possible to more accurately characterize possible structural defects with the size of ~0.5–1.5 μm that appeared on the surface of a single crystal. The value of the LIDT caused by the laser at the specified surface roughness parameters was determined not by the quality of polishing, but by the number of point recesses caused by physical limitations of the structural configuration of the crystal volume. These results are in good agreement with the assumption about the significant influence of the dislocation concentration in the ZGP crystal on LIDT put forward in [48]. Despite the fact that the sample subjected to MRP showed a significant improvement in the surface roughness parameters compared to the sample polished using traditional technology, LIDT practically did not change. The absence of a difference in the LIDT for the two samples was due to the physical limitations of the structural configuration of the crystal.
Based on the data provided in Table 1 the LIDT of our tested ZGP samples can be affected by the structural imperfection and impurity composition of the crystal, the quality of the crystal's working surfaces, as well as the external factors that include the parameters of the testing laser radiation and crystal temperature.
Note that the discrepancies between different interpretations of experimental ZGP LID data indicate several possible scenarios of the damage spot formation even at the same wavelength and pulse width. This fact is an indication of several complex mechanisms that include the combination of thermal damage and field-induced optical breakdown, physical effects (such as photoionization to or from impurity levels, multi-stage excitation, generation of free carriers with subsequent avalanche ionization, formation of electron-hole solid-state plasma with optical absorption increasing, nonlinear dependence of the thermo-optical parameters, etc.) and dynamic peculiarities (such as accumulation effects and multiple-pulse material degradation) associated with the LID of the high-transmitting dielectric crystals irradiated with nanosecond laser pulses at high PRR [49,50]. In contrast, a more defined dominant LID mechanism for the longer pulses (with microsecond’s or more pulse width) is the thermal effect related to the melting and/or vaporization of the material. The field-induced breakdowns of the crystal surfaces, multiphoton absorption and avalanche ionization under super-high intensity irradiation can be the main LID-initiation effects for the ultra-short picosecond or sub-picosecond pulses without the accumulation effects that occur at high PRR [49,51].
This paper will give an overview of the research conducted to determine the contribution of each of the factors listed above to the value of LIDT. The tested ZGP samples were manufactured by “LOC” Ent., Tomsk, Russia, or Harbin Institute of Technology (HIT), Harbin, China. The single-crystalline ZGP samples had the high purity and structural perfection [34,48]. The repetitively-pulsed Ho3+:YAG lasers at 2097 nm pumped by a Tm fiber laser at 1908 nm were used for the LID tests [52]. The tests were done at the wavelength of 2097 nm due to the common use of the high-power repetitively pulsed Ho3+:YAG lasers as the pumping source of the ZGP-based mid-IR OPOs. The "R-on-1" method was applied for all ZGP LIDT tests [53].

2. The effect of the defect structure of the ZGP crystal lattice on the LIDT value

The effect of the ZGP structure on the LIDT was tested in the first series for the samples manufactured by Harbin Institute of Technology. The first tested element with dimensions of 6×6×20 mm3 was cut from a ZGP crystal grown in the year 2012 (samples N1). The axis of the samples N1 element was oriented at angles of Ө = 57.20 and ϕ = 00 with respect to crystal optical axis.
The second tested elements with dimensions of 6×6×3 mm3 (2 plates) were cut from a novel ZGP crystal grown in 2020 year (samples N2). The samples N2 elements was cut at angles Ө = 57.20 and ϕ = 00 with respect to the crystal optical axis.
The ZGP crystals, samples N1 and samples N2, were grown under different technological conditions: the growth rate was 0.8 mm/h and 0.3 mm/h, the temperature gradient was 9.0 K/cm and 5.0 K/cm for samples N1 and samples N2 ZGP crystals, respectively. The different growth parameters resulted in a difference of LIDT of the ZGP crystals. In our previous reports, the main types of defects detected by X-ray topography in ZGP were macroscopic stress fields, dislocations, growth striate, and microdefects [54,55]. The different growth parameters resulted in the difference of quality of the ZGP crystals. The high quality of the crystal would be attributed to the high LIDT. Recently, the samples N2 was grown under improved growth conditions attributing to a higher structural perfection, smaller density of inclusions, free from twins and stacking faults. Instead, the samples 1 had macroscopical bends, tilt of blocks, twins, high density of dislocations. 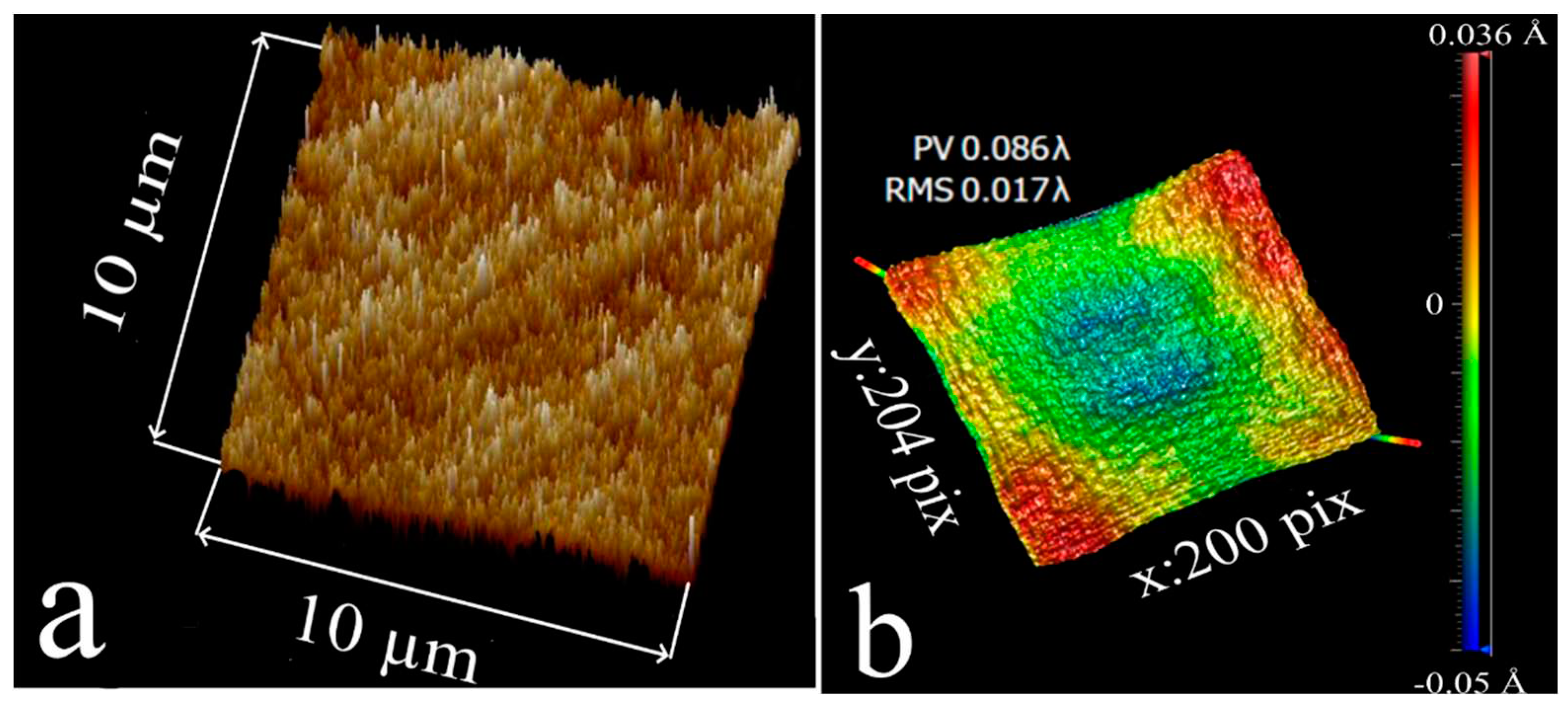The average dislocation density in the samples studied decreased from Ndis ≈ 6×104 cm-2 to Ndis ≈ 6×103 cm-2. As shown in Fig. 1, the ZGP samples (both the samples N1 and samples N2 elements) were polished to fit laser optic quality requirements (PV ≈ 55 nm, RMS ≈ 10 nm). For artificial polished samples, the roughness and the flatness were less than 0.233 nm and 0.683λ (at wavelength λ = 632.8 nm), respectively.
Preprints 91194 g001
Figure 1. Patterns of roughness and flatness of the ZGP elements, registered by ZYGO interferometer (adapted from [48]).
Figure 1. Patterns of roughness and flatness of the ZGP elements, registered by ZYGO interferometer (adapted from [48]).
Preprints 91194 g001
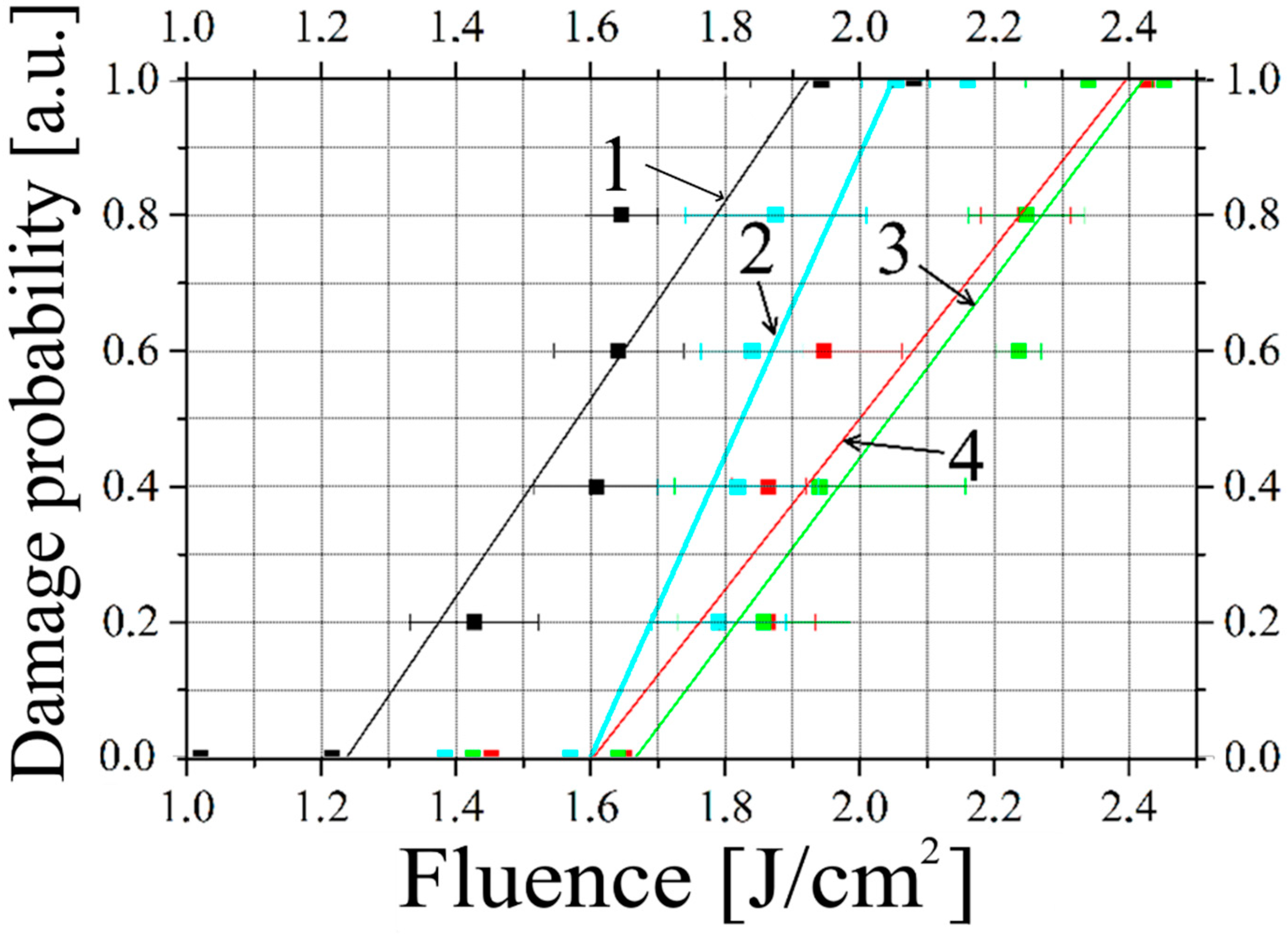
The probability of the optical damages of the samples N1 and samples N2 elements were compared at the same parameters of the experiments (PRR, the pulse width, the exposure duration) (Figure 2).
The comparison of the experimental results and the calculated statistical parameters demonstrated 4-times higher LIDT (both the average fluence and the 0-probability LIDT fluence) for samples N2 in comparison with samples N1 (Figure 2).
The critical values of the pulse fluence, peak and average power were measured to be much higher for the samples N2 elements compared to the samples N1 elements. It is well known that the ZGP LIDT depends on surface polishing [31,34,37,38].
The LIDs of the ZGP samples (manufactured in HIT or in LOC) were comparatively examined by the same R-on-1 test method and at the same test conditions: the testing laser wavelength was ~2.1 μm, the PRR was 10-12 kHz. The pulse width and the beam diameter of the Ho3+:YAG laser were 18 ns or 35 ns, 180 μm or 350 μm (at the e-2 level of the maximum intensity) for the HIT’s or LOC’s samples, respectively [44,48]. The measured ZGP LIDT for the pulse fluence was 3.45 J/cm2 or 3.9 J/cm2 for the LOC’s or HIT’s samples.
It was experimentally found that the change in the crystal growth technology resulted in the biggest increase in the LIDT. The growth conditions resulted in high lattice quality with a low occurrence of impurities. The improved growth technology leads also to a reduced number of microdefects and a more uniform distribution of dislocations. This, in turn, resulted in higher optical homogeneity and higher LIDT of the material.
Various crystal impurities can affect the surface LIDT, both decreasing and increasing it. Recently it was reported, for example, the effect of the annealing atmosphere of chalcogenide crystals with the presence of Ar, Se and Zn on the mid-IR LIDT [56]. For our presented studies influence impurity composition of LIDT, a ZGP single crystal (manufactured by LOC) was used, from which 8 samples were cut with (100) orientation and dimensions 5 × 5 × 2.45 mm3. Mg, Se, Ca was thermally sputtered onto the pre-polished faces of the samples (the thickness of the sprayed film was 1 μm). After that, the ZGP samples with deposited films and two control samples without deposition were annealed in a sealed evacuated ampoule, into which a weighed amount of ZGP powder was added, at temperatures of 650°C for one set of samples and at 750°C for another similar set for 180 hours. After diffusion doping, the working surfaces of the test samples were re-polished. The LID of the obtained ZGP samples was tested by the following parameters of the Ho3+:YAG laser: the pulse width was 35 ns, the PRR was 10 kHz, the laser beam diameter at the input surface of the studied samples was 350 ± 10 μm, similar as in the above-described experiments.
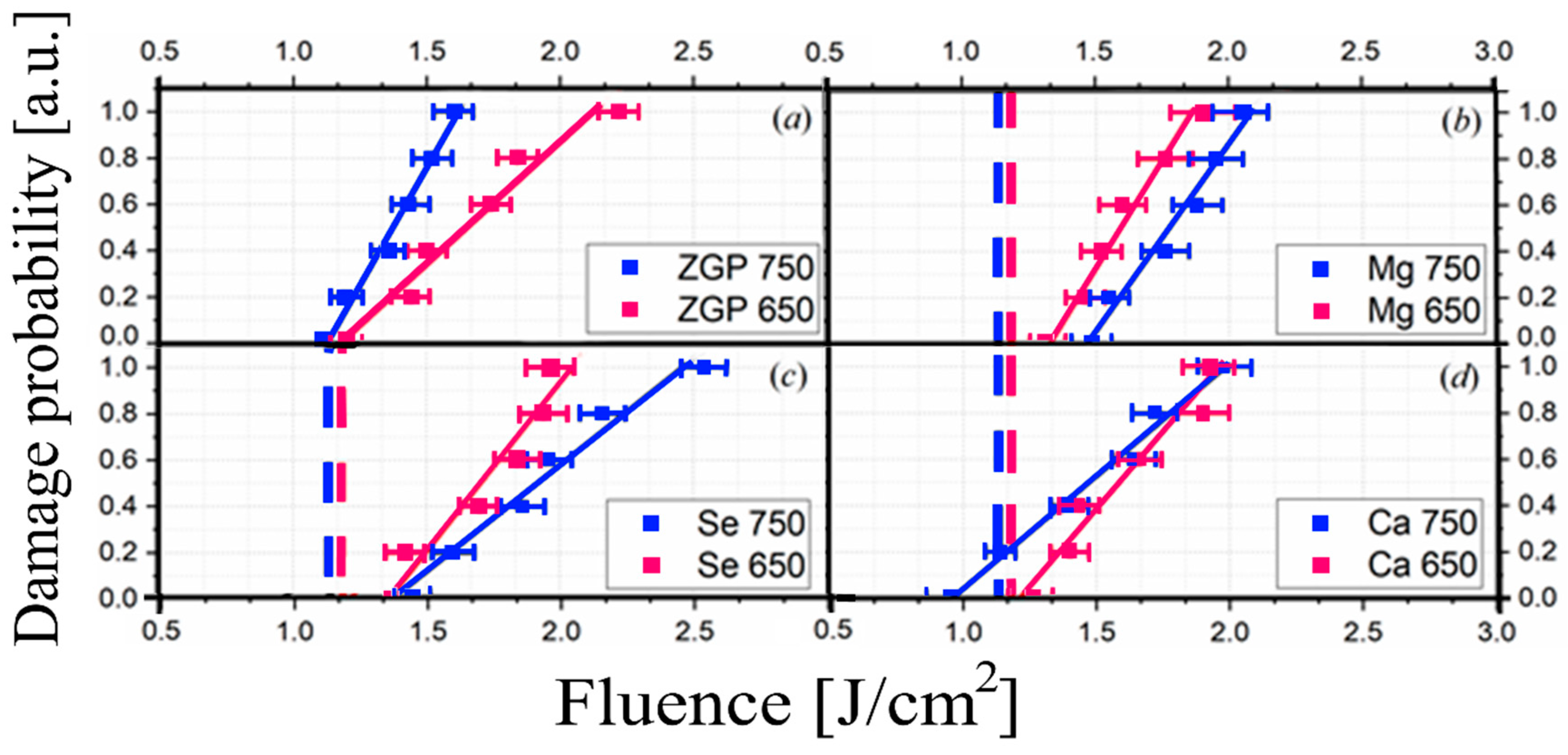
The results of measuring the LIDT of ZGP samples annealed at temperatures of 650 ⁰C and 750 ⁰C without doping and with doping Mg, Se and Ca using the R-on-1 method are shown in Figure 3.
In the undoped samples (Figure 3 a), there are no significant changes in the LIDT (the detected changes were within the measurement error) depending on the annealing temperature, which is in good agreement with the results of [34]. At the same time, in samples doped with Mg or Se by diffusion, after annealing at a temperature of 650°C, the LIDT increases by 15% and 17%, respectively. When annealing at a temperature of 750°C, the LIDT of samples doped with Mg and Se increased by 31% and 21%, respectively. An inverse dependence was observed for the sample doped with Ca. When annealing at a temperature of 650°C, the LIDT changes weren’t found, and when annealing at a temperature of 750°C, the damage threshold decreased by 14%. The presented results indicate a qualitative tendency for the LIDT to decrease or increase depending on the concentration of the doped material. It should be noted that for doped samples with Mg and Se, there was a tendency for LIDT to increase with increasing dopant concentration (since samples annealed at 750°C have a higher optical damage threshold than samples annealed at 650°C). An inverse dependence was observed for the samples doped with Ca by diffusion. The best results were the results of the single crystal ZGP doped with Mg at a temperature of 750°C.
From the results of measuring LIDT and electrical conductivity (Table 2), a qualitative dependence can be seen. Doping with chemical elements causing a decrease in the electrical conductivity of the samples (σ) leads to an increase in LIDT, and vice versa, doping with chemical elements causing an increase in the electrical conductivity of the samples leads to a decrease in LIDT. For example, when ZGP is doped with calcium, σ increases by about an order of magnitude, while when ZGP is doped with Mg and Se, on the contrary, σ decreases by about an order of magnitude.
From the presented data in Table 2, the diffusion doping with various chemical elements leads to increase or decrease in the LIDT.
LID in semiconductor materials at nanosecond pulse width can be a consequence of direct thermal effects or the electric-field-induced processes associated with the generation of electron-hole plasma [49,50]. A local increase in temperature near small crystalline defects and inclusions under the pulsed radiation can initiate the LID. Indeed, point defects in a crystal lattice can enhance, for example, additional electronic sublevels, which facilitate multiphoton absorption at 2.09 μm and a sharp increase in temperature. The dislocation regions located inside the ZGP, especially near the surface of the sample, accumulate a number of point defects and inclusions, which provide an increase in temperature to a critical value. On the other hand, the local electric field at the dislocation point is stronger than in a homogeneous lattice, which leads to lower LIDT enhanced by the electric field [34,48]. Thus, it becomes obvious that the decrease in the conductivity of ZGP doped with Mg and Se should contribute to an increase of the LIDT.

3. The effect of ZGP antireflection coatings on LIDT

Comprehensive studies of the influence of the deposition parameters of AR interference coatings and film-forming materials on the LIDT of the ZGP samples (manufactured by LOC) under the Ho3+:YAG laser irradiation were made [42-45]. The coatings were performed on the Aspira-200 vacuum deposition machine by ion beam sputtering (IBS). The maximum diameter of the targets is 101.6 mm, the thickness of each is up to 10 mm. The gas supply system had electronic flowmeters and valves. The system was supplied with gases - ultra-pure argon (Ar 99.999%) and technical pure oxygen (O2 99.7%). The ion source was an accelerator with an anodic layer. Control of the gas parameters and control of the ion source parameters was carried out from the control computer of the vacuum installation. Compensation of the positive charge formed on the target surface during sputtering was performed using thermos-emission of electrons from a heated tungsten cathode. Before loading into the deposition chamber, the substrates were cleaned using ultra-pure acetone and then washed with distilled water. Immediately before applying the coating in the vacuum chamber, the substrates were additionally cleaned with an auxiliary ion source at a source power of ~ 40 W and ion energy of ~ 150 eV for 10 minutes. The substrate temperature was maintained at 100 ⁰C throughout the entire deposition process.
Using the specified technology, AR coatings for various pairs of film-forming materials were developed. Information on the coating materials and their parameters is given in Table 3. For clarity, a histogram of the LIDT of ZGP depending on the type of AR coating is shown in Figure 4.
Table 3. Pairs of film-forming materials and AR coating parameters and the LIDT fluence.
Table 3. Pairs of film-forming materials and AR coating parameters and the LIDT fluence.
Sample LIDT fluence, J/cm2 Coating thickness, nm Number of layers
Nb2O5/SiO2_1 1.8 2900 5
Nb2O5/Al2O3 2.35 2133 3
ZnS/Al2O3 3.45 825 3
Nb2O5/SiO2_2 1.86 700 4
YbF3/ZnS 2.9 1305 7
ZnSe/Al2O3 3.51 721 3
From the results presented in Figure 4 and Table 3, which are the result of summarizing the information obtained in [42 - 45], the following patterns can be observed:
  • The smaller the thickness of the AR coating, the higher the LIDT under otherwise equal conditions (deposition regimes and film-forming materials);
  • The magnitude of the radiation resistance of ZGP with a deposited AR coating is significantly affected by the optimal selection of a pair of film-forming materials (it is necessary that the mechanical properties of the coating layers be close to the properties of the ZGP substrate).
  • Optimal deposition conditions for AR coatings allow to reduce the number of film defects and the LIDT increase.
As can be seen from the results presented in Table 3 and Figure 4, it is possible to increase the LIDT of ZGP by 50% compared to uncoated samples by optimizing the parameters for the AR coatings, when applying interference coatings based on pairs of ZnS/Al2O3 and ZnSe/Al2O3 materials.

4. Effect of external factors on LIDT ZGP

The effects of laser exposure duration and laser beam diameter on the LIDT of a ZGP crystal at room temperature as well as the effect of crystal temperature on LIDT were studied [34]. The Ho3+:YAG laser radiation at 2091 nm with 12 kHz PRR, 18 ns pulse width were used.
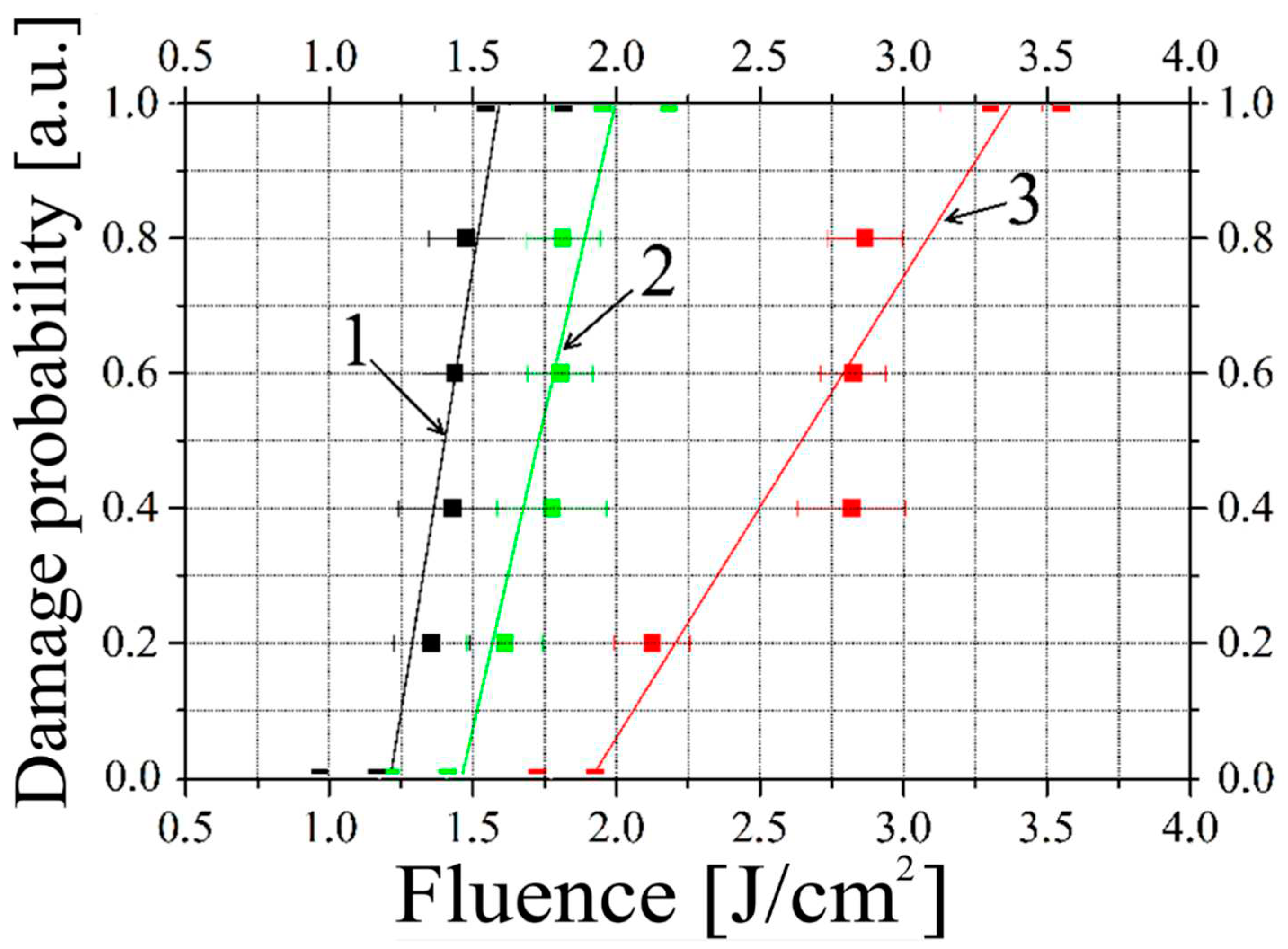
It was shown that with an increase in exposure duration from 2 to 30 s, the LIDT decreases by 1.2 times: from 1.57 to 1.28 J/cm2 (Figure 5).
Measurements at room temperature showed that when the diameter of the test laser beam gets smaller the LIDT increases: when the diameter of the beam was reduced by 2.9 times from 580 to 200 μm (at the level of e-2) W0d increased 1.4 times from 1.32 to 1.91 J/cm2 (Figure 6).
The increase in LIDT with a decrease in the diameter of the laser beam and the decrease in LIDT with an increase in exposure time can be explained by the thermal effects when the crystal is exposed to radiation at 2091 nm.
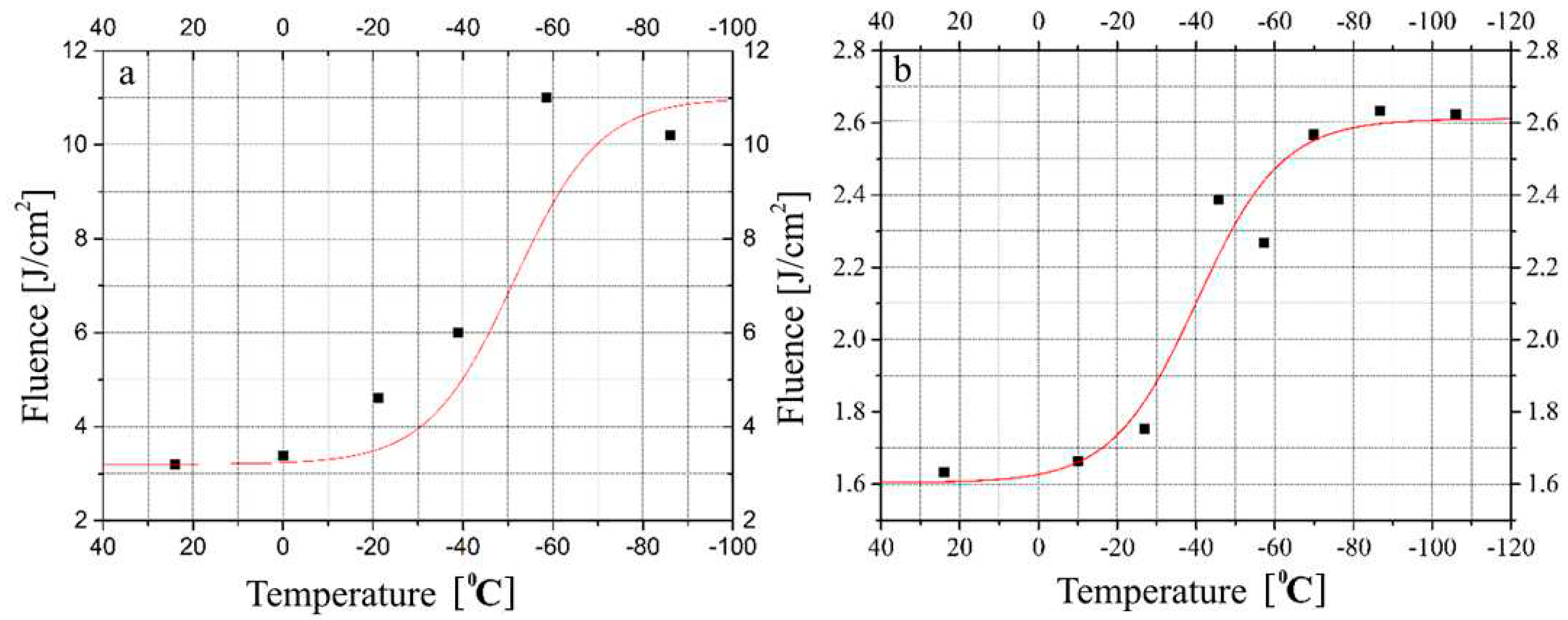
To study the temperature dependence of LIDT, in [34] ZGP samples were placed in a sealed cuvette filled with dry nitrogen at normal pressure. Using a calorimetric cup filled with liquid nitrogen and having thermal contact with the cuvette, the sample was cooled to a temperature of -106 °C (the sample temperature was controlled by an electronic thermometer). The windows of the cuvette were made of crystalline sapphire without AR coatings with a transmission coefficient (at 2091 nm) ≈ 85 %. The incident laser beam was focused onto the front face of the ZGP into a spot with a diameter of d ≈ 100 μm and into a spot with a diameter of d ≈ 270 μm.
At room temperature and a laser beam diameter of 270 μm, the threshold breakdown values for the ZGP sample were W0d = 2.3 J/cm2 and WD = (3.4 ± 0.4) J/cm2. The measurement results demonstrated a significant increase in LIDT, especially noticeable when the temperature was reduced from 20 °C to -60 °C (Figure 7a). In the temperature range from +24 to -86 °C, an increase in the LIDT value with a laser beam diameter of 100 μm was observed by more than 3 times (from 3.2 to 10.2 J/cm2), however, at temperatures below -60 °C, the increase in LIDT stopped.
Measurements of the dependence of LIDT on the crystal temperature were also performed with a laser beam diameter of 270 μm. The measurement results demonstrated a similar dependence of LIDT on the crystal temperature (Figure 7b). In the temperature range from +24 to -106 °C, an increase in the LIDT value of more than 1.5 times (from 1.6 to 2.6 J/cm2) was observed, and the increase in LIDT also stopped at temperatures below -60 °C.
It is known that ZGP is a high-ohm semiconductor with stable hole conductivity, the magnitude of which is difficult to change [57]. The typical temperature dependence of the concentration of free charge carriers in ZGP is described by an exponential curve with an activation energy of deep impurity centers of 0.3÷0.6 eV. However, the obtained temperature dependence of LIDT has a sigmoidal character and therefore cannot be explained by absorption on free carriers (holes), arising by ionization of individual point defects, as well as defects associated with edge dislocations.
Preprints 91194 g007
Figure 7. Dependence of the LIDT fluence W0d on the temperature of the ZGP crystal when exposed to Ho3+:YAG laser radiation at a wavelength of 2091 nm with a laser beam diameter of 100 μm (a) and with a laser beam diameter of 270 μm (b) (adapted from [34]).
Figure 7. Dependence of the LIDT fluence W0d on the temperature of the ZGP crystal when exposed to Ho3+:YAG laser radiation at a wavelength of 2091 nm with a laser beam diameter of 100 μm (a) and with a laser beam diameter of 270 μm (b) (adapted from [34]).
Preprints 91194 g007
The obtained temperature dependence of LIDT was explained by the temperature dependence of the phonon occupation numbers, which participate together with optical quanta in indirect transitions of nonlinear absorption: valence band - impurity level [58]. In support of this assumption, it can be noted that with a decrease in the temperature of the crystal, the phonon occupation numbers increase, leading to a decrease in the probability of their participation in indirect transitions of electrons from the valence band to impurity levels [58,59].

5. Dynamic Processes in the ZGP Pre-Damage Region

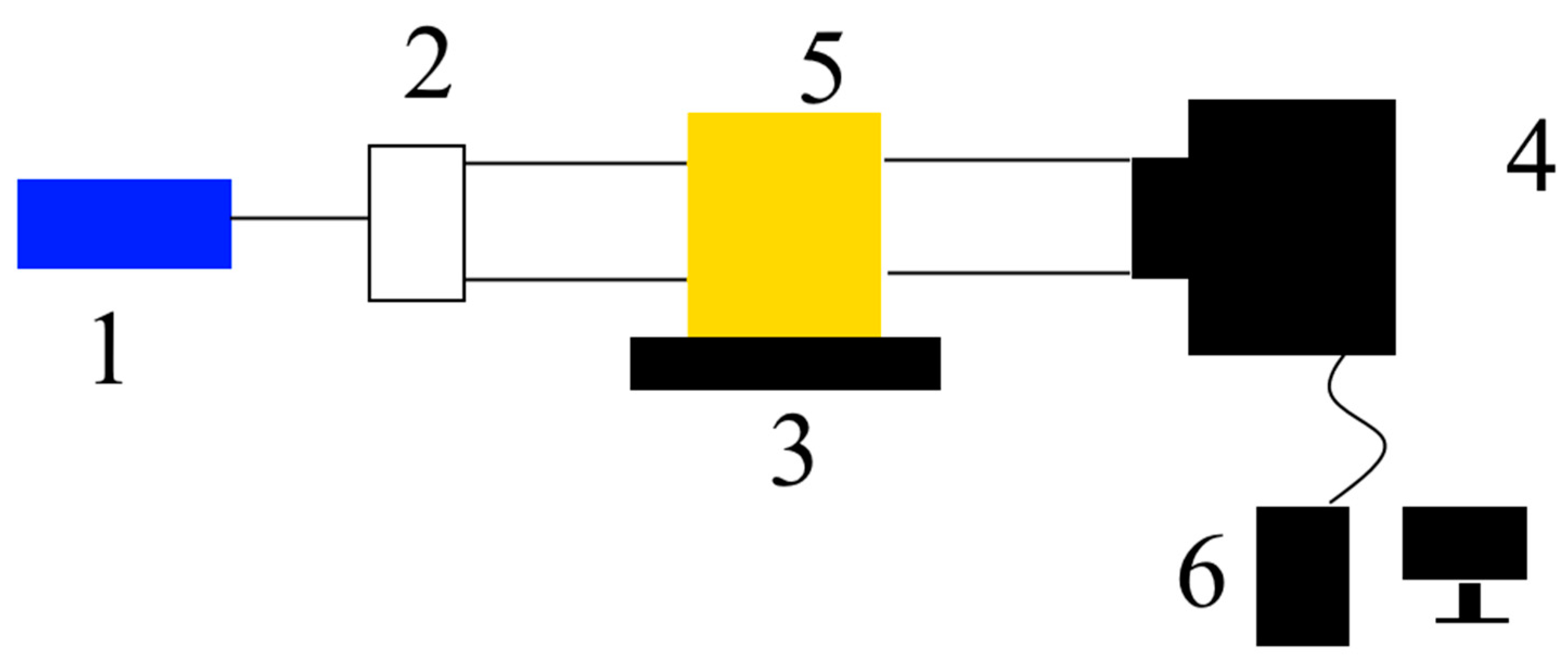
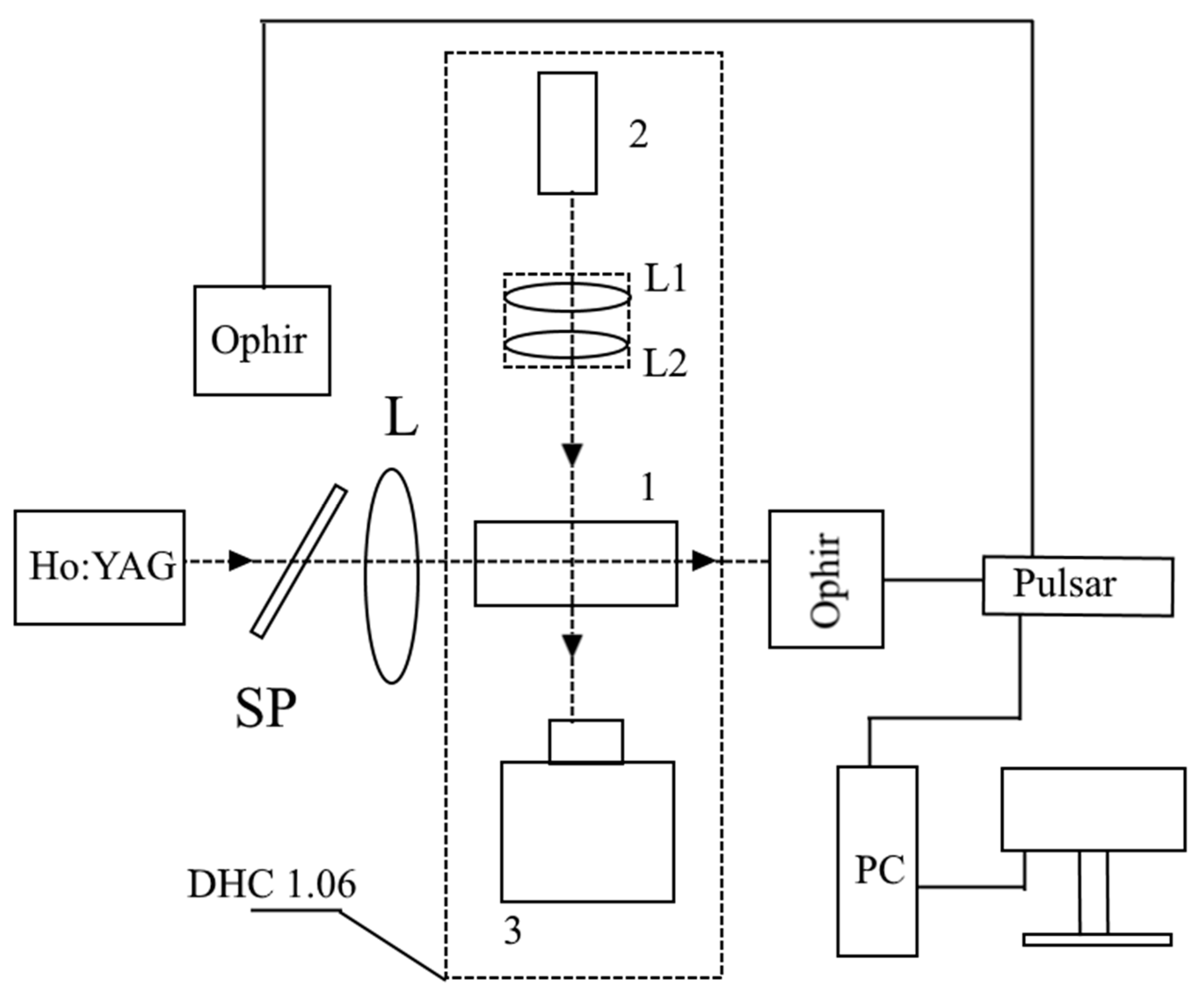
Modern technologies allow using a CCD camera to register the interference pattern of the reference and object waves. This process of recording holograms on a CCD camera and subsequent numerical recovery of an image from them is called digital holography. Figure 7 shows the axial scheme of recording Gabor digital holograms. Light from a laser source (1) passes through a collimator (2), forming a beam of the required cross section, then passes through the sample under study.
As a result, an interference pattern of the reference (part of the radiation that passed by the inclusions) and object (part of the radiation scattered by the inclusions) waves is formed. The camera registers this interference pattern and transfers it to the computer memory. Subsequent mathematical processing by special computational algorithms [60] allows to restore the spatial distribution in the investigated volume, namely three-dimensional coordinates, sizes, shapes, and location of each area of interest. Image restoration is numerical, with the image of the investigated volume being formed during processing layer by layer.
Since the Gabor scheme allows for reduced requirements for the spatial and temporal coherence of the light source [61], a semiconductor laser diode with a wavelength of 1.064 μm (position 1 in Figure 8) with an output power of 100 mW was used. A CCD camera with a matrix of 1600 × 1200 pixels, a pixel size of 7.4 μm × 7.4 μm, and physical dimensions of the matrix of 2/3” was used as the recording camera (position 4 in Figure 8). The long-wavelength boundary of the CCD camera's photosensitivity is limited to a wavelength of 1.1 μm. The spectral transparency ranges of the ZnGeP2 compound, calculated for short wavelengths based on the bandgap width and for the long-wavelength edge based on the maximum three-phonon absorption, include the region of 0.64 – 9.0 μm, but the actual working spectral range at a coefficient of absorption not exceeding a value of 1 cm-1 is determined by wavelengths of 0.9 ÷ 8.3 μm. Thus, for studies of ZnGeP2 using digital holography on "transparency", sources that generate radiation in the spectral region near 1.06 μm and CCD matrices of the visible range can be used. These issues are discussed in detail in [62].
It is clear that the investigated area is limited by the camera aperture of ~ 11 mm. The holographic camera was used to study the ZGP optical damage, designed for the creation of parametric converters of radiation tunable in the range of 3-8 μm, pumped by lasers emitting in the wavelength range of about 2 μm. The study of LID was carried out using a scheme of the digital hologram recording (Figure 8). Pulsed radiation from a Ho3+:YAG laser with a PRR of ~ 10 kHz, pulse width of ~ 25 ns, and average power, varied from 500 mW to 9 W, was focused by a short-focus lens L, onto the input face of a ZGP single crystal (manufactured by LOC). The use of a short-focus lens excluded self-focusing of radiation in the volume of the investigated crystal. The exposure duration was ~30 s. Further, if optical damage wasn’t observed, the laser radiation power was increased, and the irradiation process was repeated. The beam diameter at the front face of the single crystal was ~ 200 μm at the 1/e2 level. The side faces of the crystal were polished. The crystal was placed in a digital holographic camera DGK 1.06, using which holograms of the internal volume of the single crystal (in the direction perpendicular to the direction of the incident radiation) were recorded with a frame rate of ~ 7 Hz.
Figure 10 shows the reconstructed images obtained in the study of optical damage on the setup shown in Figure 9. Figure 10a shows the reconstructed image of the plane of the best installation of the area of the single crystal where the breakdown develops, before the formation of the damage track and the formation of the glowing area, the red arrow shows the direction of the radiation incidence. Figure 10b is a splicing of frames of the reconstructed image of the plane of the best installation, on which the process of development of optical damage and the spread of the glowing area in the single crystal is recorded with reference to the length of the crystal and time, the red arrow shows the direction of the radiation incidence, the yellow arrow shows the direction of movement of the area in which the optical damage is formed. Figure 10c is the reconstructed image of the plane of the best installation of the area of the single crystal with a characteristic damage track above LIDT.
The impact of the Ho3+:YAG laser pulses on the ZGP crystal caused the appearance of a luminous spot with a diameter of 0.7-1 mm on the output optical surface, and its subsequent movement in the crystal towards the input optical surface, i.e. in the direction opposite to the propagation of the Ho3+:YAG laser radiation (Figure 10b). The resulting luminous spot can be associated with luminescence arising from the recombination of non-equilibrium carriers through the levels of point defects [32]. The movement of the luminescent "cloud" is accompanied by the formation of an optical damage channel (track) with a diameter of 70-75 µm. The dynamics of the development of optical damage at an average laser fluence of 0.3 J/cm2 is shown in Figure 10b, which was obtained by splicing frames reconstructed from a series of holograms obtained with an interval of ~143 ms. The frames are separated from each other by black lines, each frame corresponds to the path traveled by the luminous spot that is fixed when the damage track is formed inside the crystal.
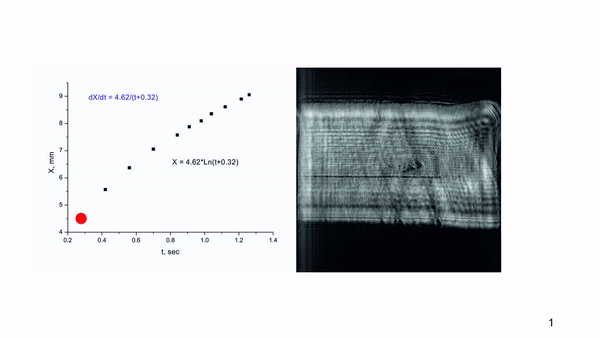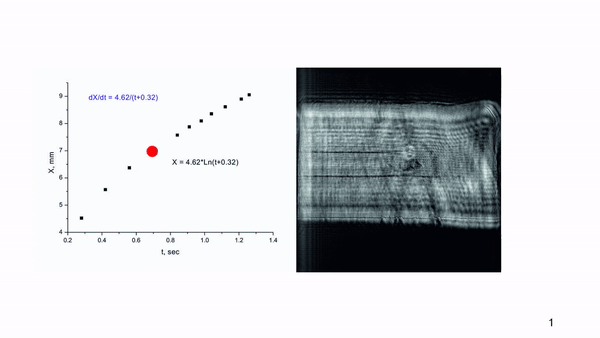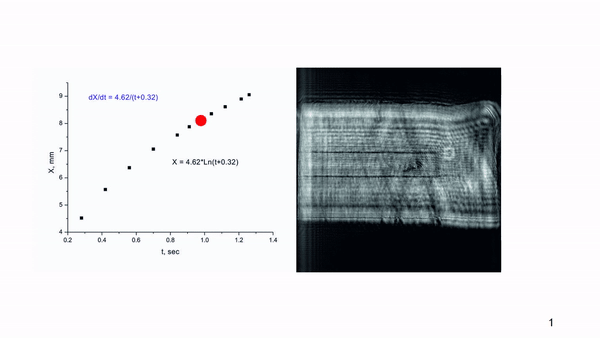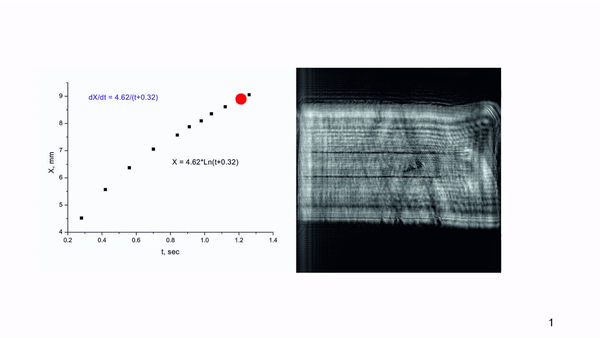
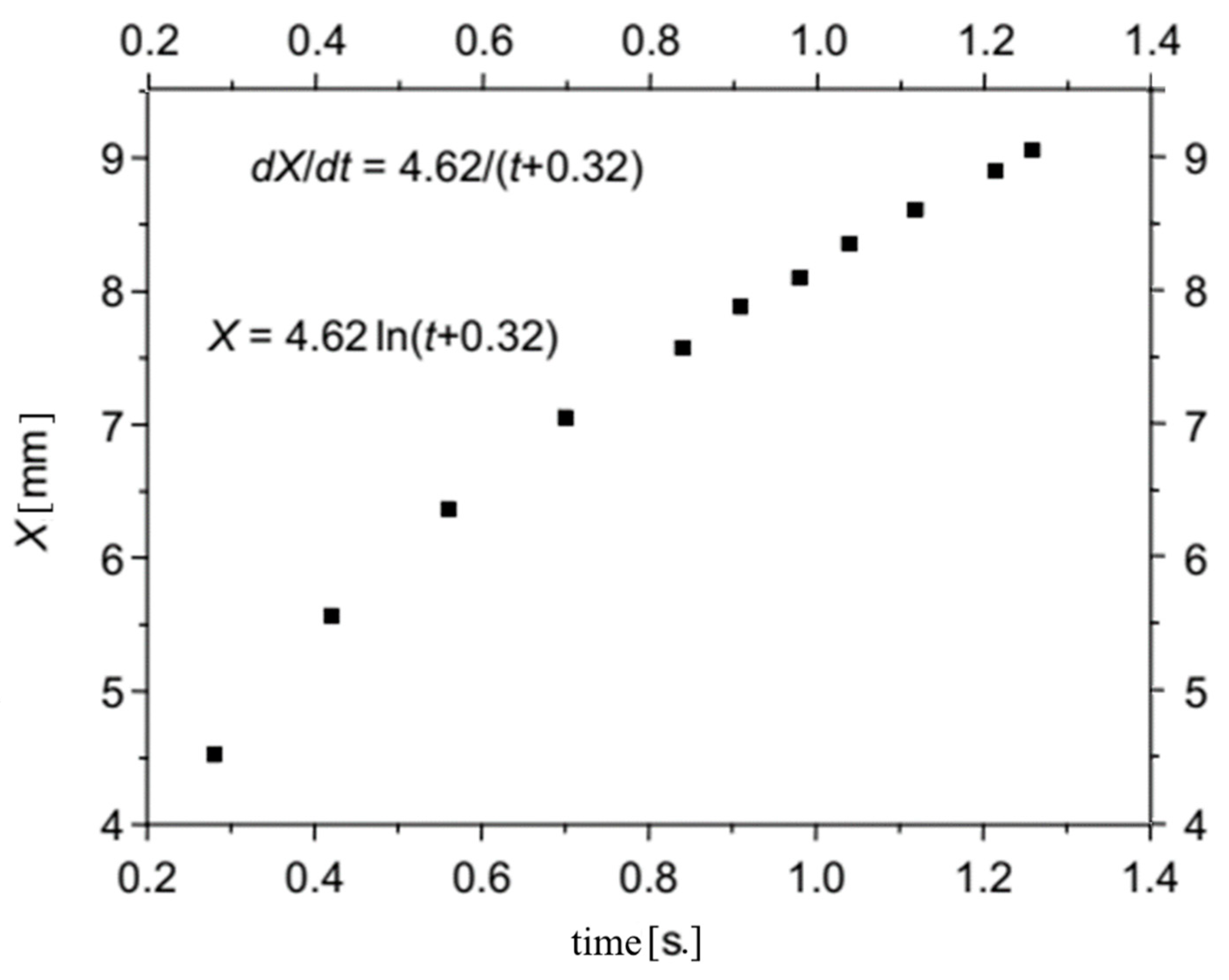
The position of the luminous spot relative to the exit crystal face, X, was determined at the time, t, relative to the LID start (Figure 11).
The full duration of the optical damage formation in a 10 mm ZGP crystal was determined as ~1.3 seconds. The instantaneous speed of movement of the luminous spot - V (mm/s) =dX/dt - in the initial period, as it turned out, was significantly higher than the speed of its advancement in the second half of the crystal. So, if the first 4.5 mm were damaged with a speed of Vin= 4.52/0.28 ≈ 16 mm/s, then at the final stage of the damage, the speed of track formation was Vfin= (9.055-8.095)/0.14 ≈ 3 mm/s. The damage stops at the destruction of the entrance face of the crystal with a conical damaged track formation.
Using the available experimental data and the ORIGIN LAB mathematical software, a logarithmic dependence of the track length on the time of exposure was obtained (see Figure 11). The dependence of the speed of propagation of the luminous spot in a ZGP crystal at the beam fluence of 0.3 J/cm2 obtained by the least squares method is a smooth monotonic function of the current time:
V(mm/s)=dx/dt=4,62/(t+0,32),
where t is the time in seconds relative to the LID initial moment (when the glowing spot appeared).
According to the given approximation, the speeds of the spot propagation (the damage track formation) were determined as Vin = 14.4 mm/s at the initial stage, and Vfin = 3.5 mm/s at the final stage of the LID. The slowing down of the track formation process isn’t consistent with the impact ionization model with a power law dependence of the avalanche generation of electron-hole plasma. At the same time, positive feedback between the temperature increase and the ZGP absorption coefficient increase can be an alternative to impact ionization and can provide a high concentration of non-equilibrium carriers due to a sharp temperature jump during the absorption of pumping radiation in the crystal volume. Then, the time delay of the beginning of track formation can be attributed to the time spent on heating the crystal volume to high temperatures by laser radiation.
The generation of carriers by increasing temperature does not create non-equilibrium carriers capable of recombination accompanied by luminescence. Therefore, in order to explain the appearance of a luminous area in the crystal excited by an intense laser beam, it was necessary to take into account dimensional factors, namely: the ratio of the diameters of the laser beam (200 μm) and the luminescent "cloud", the brightest glow of which is recorded at a distance of 250-400 μm (Figure 10b) from the forming "dark" LID track.
The change in the crystal structure under the laser irradiation indicates an increase in the instantaneous effective temperature to values that exceed the melting point of the ZGP compound - 1025⁰ C [32,63]. A lower-temperature phase transition ZnGeP2(sph)→ZnGeP2 (halc) near 950⁰ C can be excluded from consideration, since it is observed only at low temperatures and is associated with the ordering of atoms in the caution sub lattice.
A sharp increase in the temperature of the crystal and its local melting led to subsequent solidification of the melt, forming a LID track along the laser beam, and diffusion of free carriers from the heated area of the crystal in the direction perpendicular to the laser beam. The transverse temperature gradient perpendicular to the direction of propagation of laser radiation causes free carriers to diffuse from the high-temperature generation zone (in which they are in equilibrium and cannot be manifested in luminescence) to the unheated regions of the crystal, in which they become non-equilibrium and recombine, at least partially, at the luminescence transitions (levels of point defects), creating a toroidal distribution of the intensity of luminescence.
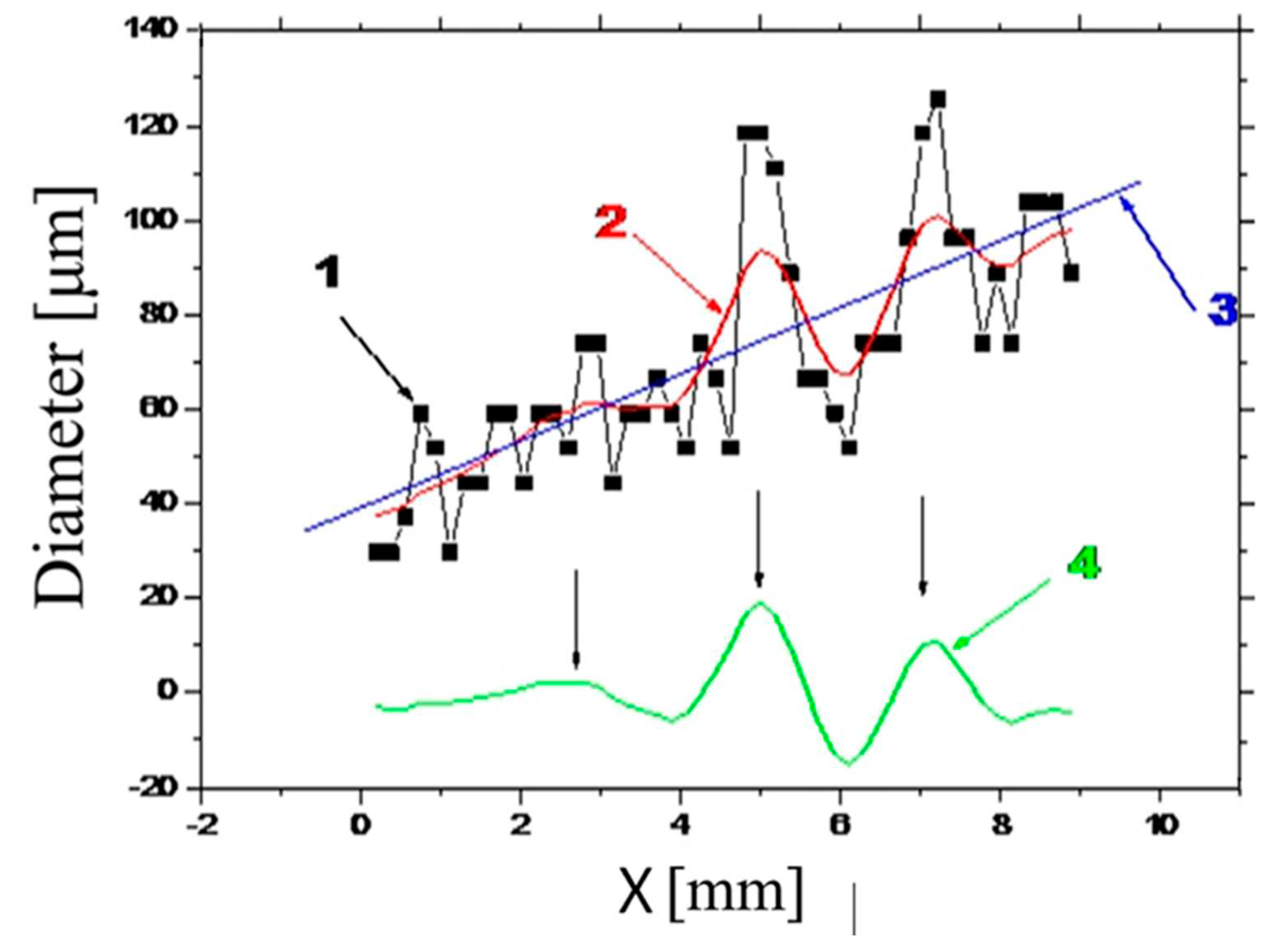
In order to explain the decrease in the speed of formation of the damage tracks from the coordinate (from the time), in [32] it was assumed that it is related to the conical form of the track, i.e. with the volume of the material heated by the laser beam. As it turned out, (see Figure 12), indeed, the diameter of the conical track increases from ≈40 μm at the initial section of the track (at the crystal exit) to ≈100 μm at the entrance aperture of the crystal. Accordingly, the cross-section changes by approximately 3-4 times, which is close to the ratio of the track formation speeds on the input and output surfaces of the crystal. But in addition to the pronounced tendency for the track diameter to increase with the coordinate, there were quasi-periodic variations in the diameter of the LID tracks with maxima at ≈3 mm, 5 mm, and 7 mm, which were compared with areas near the intersection points of the optical damage track with "dark" growth bands, i.e. in places with an increased absorption coefficient, relative to the average value.
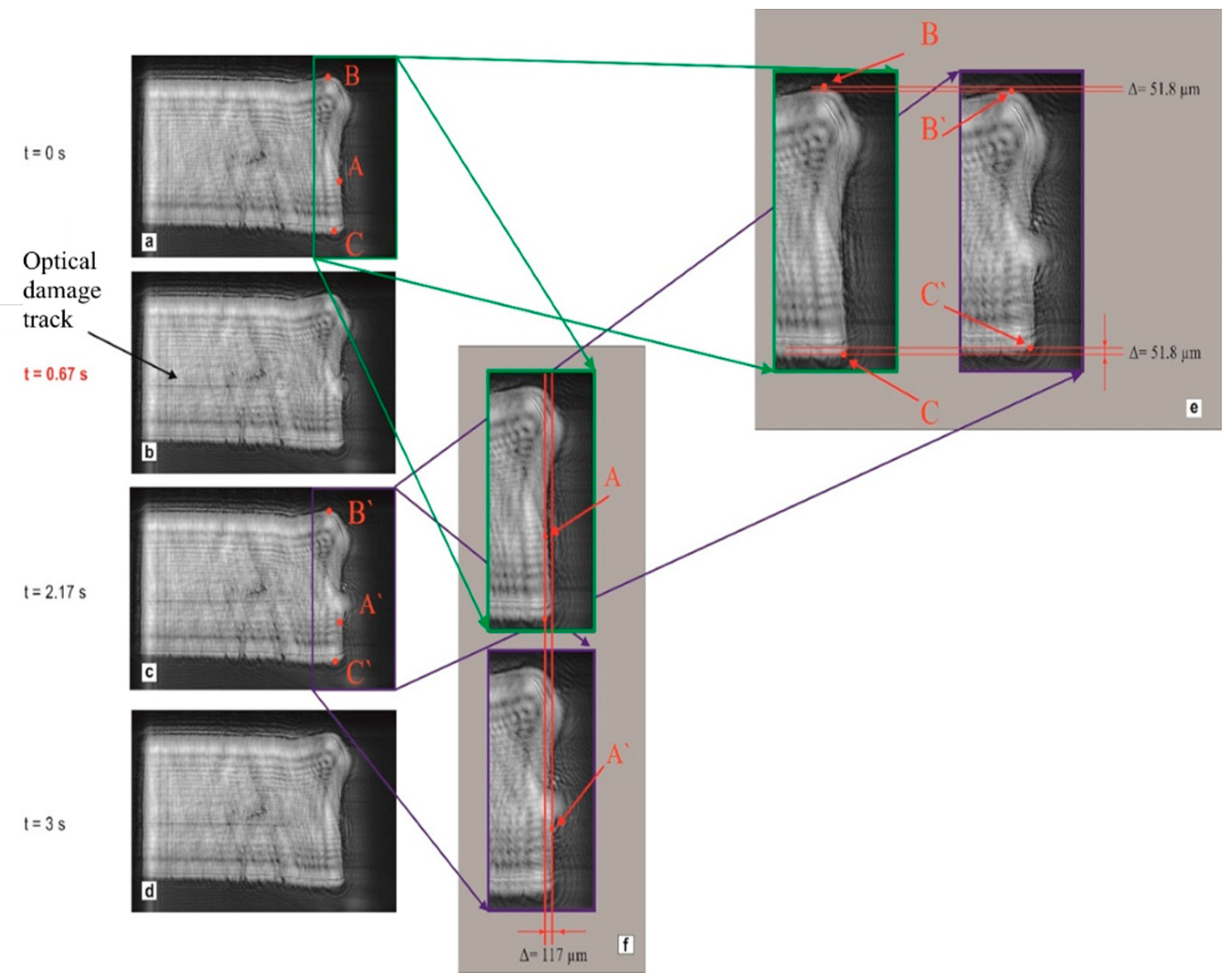
Figure 13 shows a LID in another point of the same crystal under the more powerful laser irradiation – with the fluence of 0.6 J/cm2. In this case, the optical damage also occurred near the exit surface, but the track formation process proceeds significantly 2 times faster, which, in principle, agrees with the twofold increase in the beam fluence and the thermal origin of the LID. Processing of holographic data shows that the duration of the damage-track formation was ~0.67 s.
On the photographs in Figure 13f and Figure 13e, the reconstructed images of the crystal before laser exposure and at the moment when the glowing (luminescent) spot reaches the front surface of the crystal are shown. By comparing the geometric (dimensional) parameters of the images, it was found that at the final stage of optical damage, when the formation of the track is completed, the length of the crystal in the longitudinal direction at the point of exit of the track to the surface increases by ~ dL=117 μm (Figure 13f), and in the transverse direction it decreases by ~ 103 μm (Figure 13e).
A rough estimate of the temperature developing in the central part of the damage track can be made based on the relative longitudinal deformation of the crystal dL/L ≈ 0.0117 and coefficients of thermal expansion (βav) of ZGP [32,63]. At temperature of > 573 K the coefficient of thermal expansion has the value β a v ( > 573 K ) = 8 , 59 ⋅ 10 − 6 K − 1 . The temperature required for an elongation of the crystal by 117 μm can be estimated by T = ( d L L ) β a v = 1362 0   K . Therefore, according to the estimation, to change the length of the crystal by 117 μm, it will be necessary to increase its temperature to T T P = 1362 0   K . The obtained value of the temperature in the damage track is higher than the melting point of the compound by approximately ≈ 60 K and, in principle, agrees with the conclusion about the thermal origin of the LID track.
At the used levels of laser beam intensity, in contrast to the degradation of optical properties in the damaged region, the mechanical deformation of the crystal was elastic, and after the completion of the damage track formation process, a rapid lattice relaxation occurs along the entire length of the crystal.
As a result of comparative studies of the crystal before, during, and after LID, it was established that the propagation channel of laser radiation darkens in the pre-damage region of the laser parameters. Visually, this effect manifested itself in the reconstructed images of the plane of the best setup in the form of darkening of the area of the crystal in which laser radiation was propagated (Figure 14). This process is clearly demonstrated in Figure 14(b): a dark track is formed in the channel of propagation of an intense laser beam (for test radiation at a wavelength of 1064 nm). The darkening was reversible: when the density of the incident radiation decreased below a certain level or when laser exposure to the crystal was completely stopped, the area of darkening disappeared - Figure 14(c). The relaxation time of the area of darkening of the laser channel was less than 5 ms.
The darkening of the channel of propagation of a powerful laser beam in the pre-damage region can be explained by a local decrease in the band gap width of ZGP upon heating. Indeed, it is known that the band gap width of semiconductors decreases with increasing temperature [34]. This leads to an increase of the absorption of the testing beam at 1064 nm.
Importantly, in most of the tests performed with ZGP elements of different lengths and manufactured with different technological growing and post-growing procedures (in more than 90 % of the total number of measurements), the LID began at the exit surface of the sample. The LIDT difference on the exit and entrance surfaces can be explained by the different intensity (and the fluence) of the laser beam at the surfaces. The last difference could be caused by two effects: thermal self-focusing (the thermal lens formation) in the ZGP crystal [64], and a difference in the maximum electric field amplitude of the optical waves at the surfaces due to a phase difference of the waves reflected from the boundaries [65]. The thermal self-focusing may be the impotent effect for the long samples or the ZGP-tandem OPOs [66], when the focal length is comparable with the element length. The second effect of the interference between incident and reflected waves at the surfaces of a sample (depended on the boundary phase changes) appears to be more reasonable for the thin element with low absorption [67]. Indeed, the basic fact that the field of the Fresnel reflected wave at the entrance surface is 180° out of phase with the incident wave field, whereas at the exit surface, the reflected wave field is in phase with the incident wave field. Thus, the net electric field is higher at the exit surface than at the entrance surface for a given input irradiance. The ratio of the exit to entrance wave intensities Iex and Ient, respectively, can be estimated (on the crystal boundaries without any AR coating and higher order reflections) by the following expression [65]:
Iex / Ient ≈ 4n2/(n+1)2 × exp(-αL),
where n is the refractive index, α is the absorption coefficient, L is the sample length. The estimation of the intensity ratio by Expression (2) for the ZGP crystal with the refractive index of ~ 3.15 (at 2.1 µm [68]) gives 2.3×exp (-αL). This value is more than 1 for αL < 0.83. Therefore, the scenario with the LID initiation near the exit surface due to the higher intensity of the exit beam appears to be quite natural even for a long ZPG sample with the length L = 3 cm and the absorption coefficient α < 0.28 cm-1 (the used ZGP samples had the much lower absorption coefficient).

6. Effect of Pre-Damage Phenomena on ZGP OPO Operation

A transparent nonlinear ZGP crystal (produced by LOC) with linear dimensions of 20x6x6 mm3 cuted at angles θ ≈ 54.5° and φ ≈ 0° was used to examine an effect of the pre-damage phenomena on ZGP OPO operation [69]. The absorption of radiation at a wavelength of 2.097 μm of the sample was 0.029 cm-1.
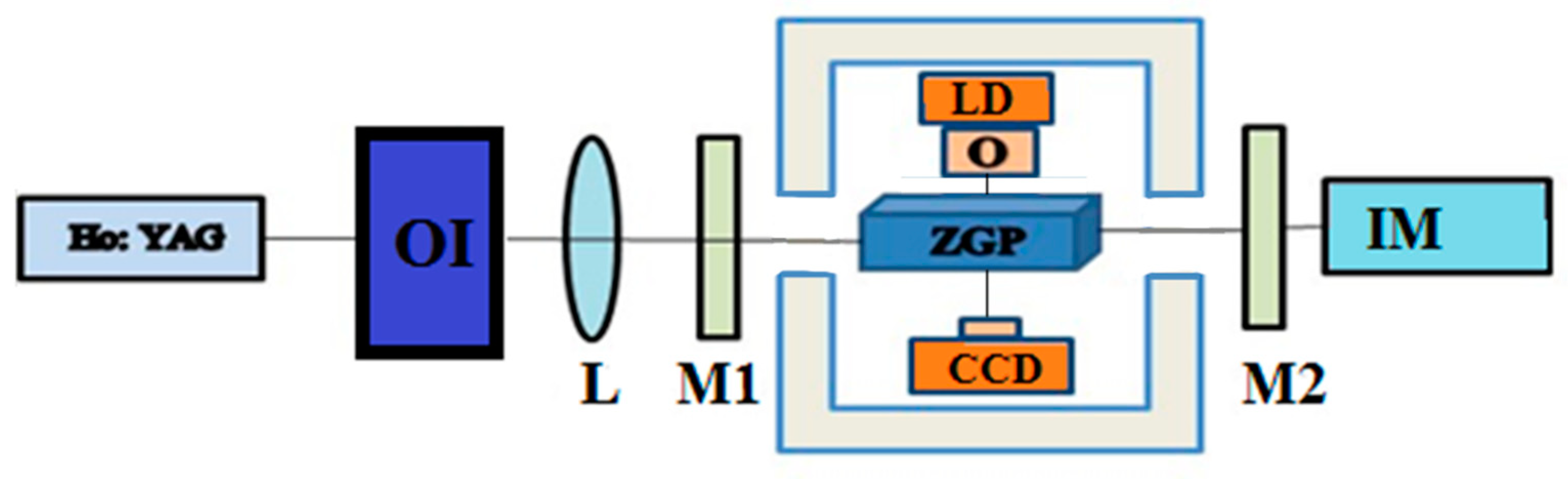
The scheme of the experimental setup is shown in Figure 15. A periodically pulsed Ho3+:YAG laser was used as a pump source for the OPO. Optical isolation between the OPO cavity and the Ho3+:YAG laser cavity is provided by an optical isolator (OI).
The Ho3+:YAG laser used for the experiments had the following energy characteristics: maximum average power of radiation in pulsed mode was 15 W, PRR was 10 kHz, pulse width at half-height was 26 ns. The OPO cavity was formed by a plane mirror M1 with transmission of ~99% at the pump wavelength and reflection of ~99% at the generated wavelength. The plane mirror M2 had a transparent coating with transmission of ~99% at the pump wavelength with a beam-splitter coating with 50% reflection at the generation wavelength, which made it possible to implement single-pass pumping. The ZGP crystal with AR coatings applied to the working surfaces at wavelengths of λ = 2.097 μm and λ = 3.5 -5 μm was placed in the cavity formed by mirrors M1 and M2. The side faces of the ZGP element were also polished. Through the side polished surfaces of the ZGP element, a hologram of the internal volume of the crystal (in the direction perpendicular to the direction of the incident radiation) was recorded using a digital holographic camera.
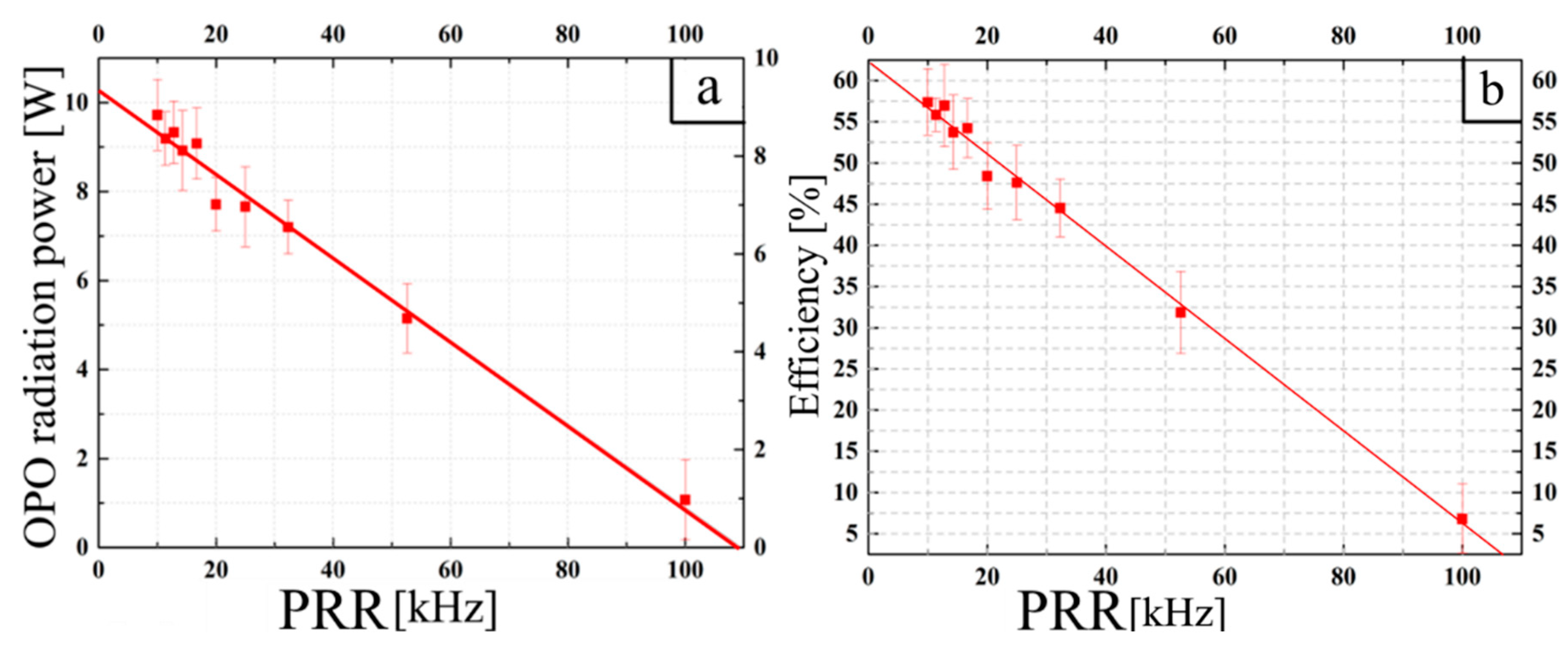
The results obtained from measuring the energy characteristics of the ZGP OPO with Ho3+:YAG laser pumping are presented in Figure 16, Figure 17 and Figure 18. Figure 16 shows the dependence of the average power of radiation generated in the OPO and the generation efficiency on the PRR pumping.
During the measurements, the average pump power at 2.097 μm remained constant at 16.3 W, while the PRR was varied from 10 to 100 kHz. It is worth noting that stable generation in the Ho3+:YAG laser was observed up to 50 kHz PRR, at a PRR of 100 kHz, the laser operation was unstable. The maximum value of the OPO efficiency achieved in the experiment was 57.35% (Figure 16b). The maximum value of the OPO average power was 9.72 W at the PRR of 10 kHz (Figure 16a).
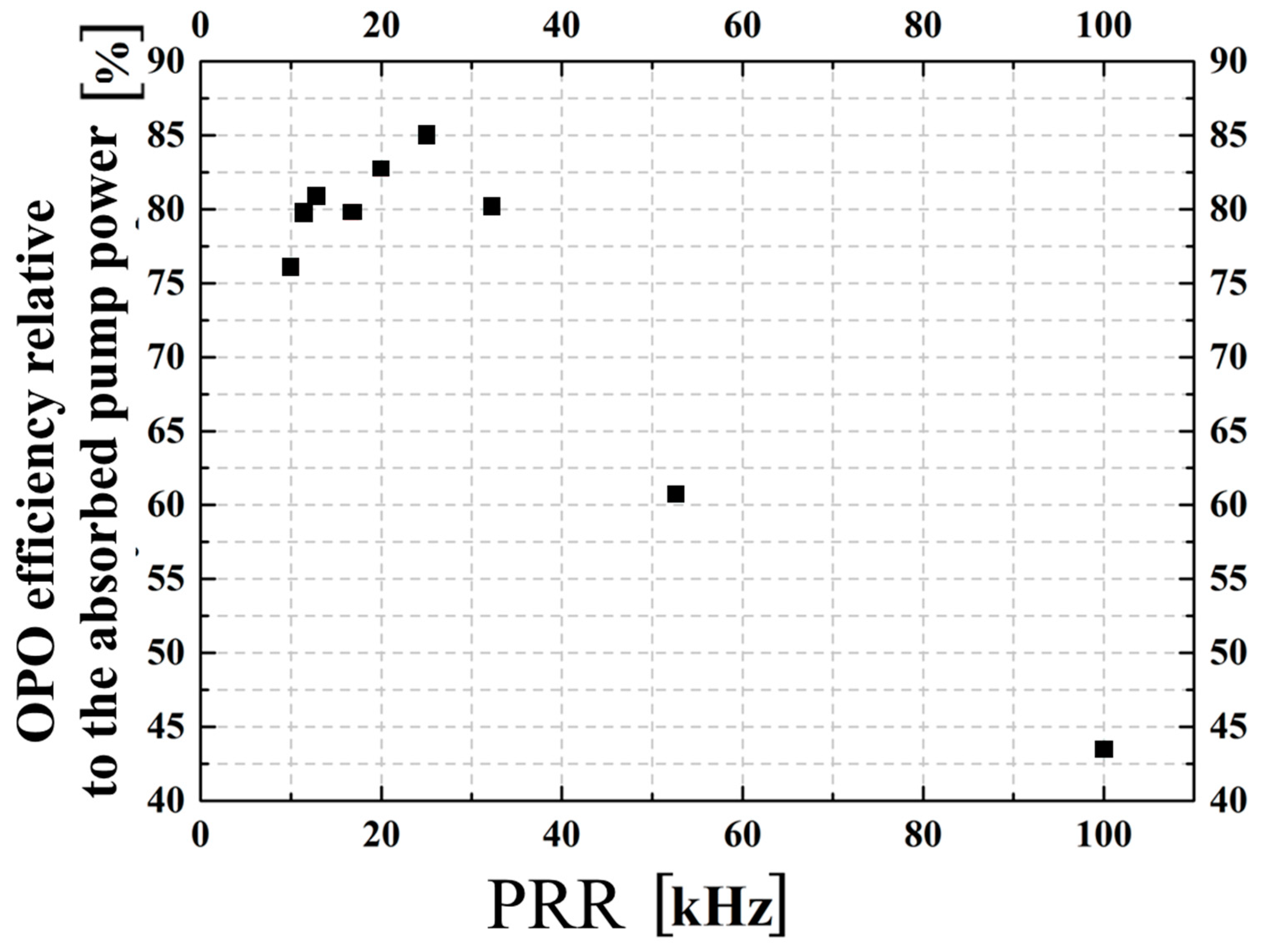
Using the available experimental data and the ORIGIN LAB mathematical software, the dependence of the efficiency of the pump power absorbed in the crystal (without taking into account the part of the pump power that escaped from the cavity) on the pumping PRR was obtained. The maximum value of the efficiency of the absorbed power was ~ 85% (Figure 17).
Preprints 91194 g017
Figure 17. Dependence of the OPO efficiency relative to the absorbed pump power on the pumping PRR( adapted from [69]).
Figure 17. Dependence of the OPO efficiency relative to the absorbed pump power on the pumping PRR( adapted from [69]).
Preprints 91194 g017
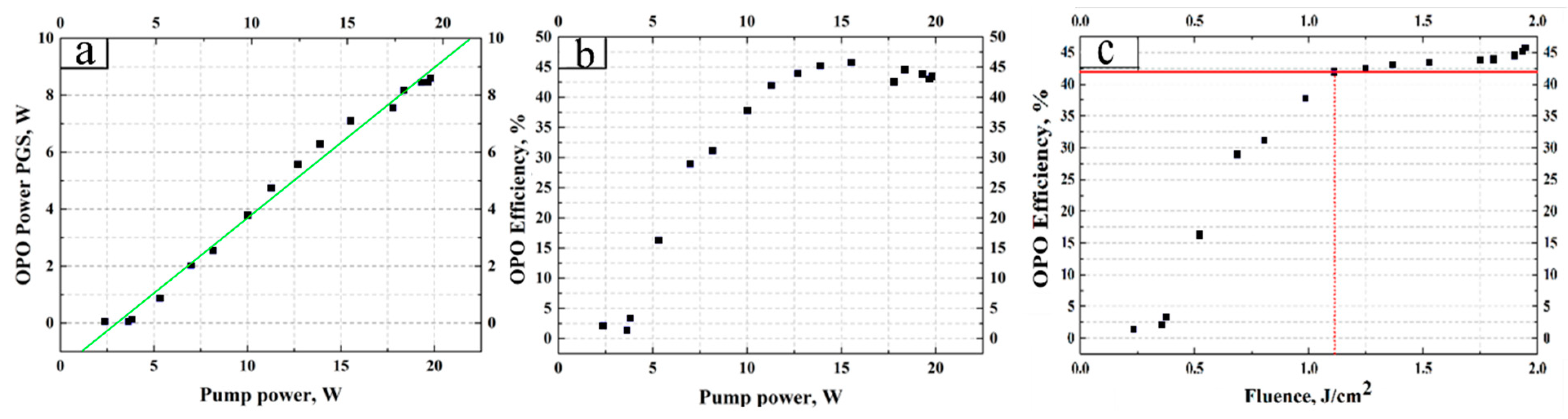
Further studies were conducted of the energy characteristics depending on the pump power at a PRR of 10 kHz. The maximum value of the OPO output power obtained in the experiment was 8.46 W (Figure 18).
Preprints 91194 g018
Figure 18. The output OPO power and efficiency vs the incident pump power (a); the OPO efficiency vs the incident pump power (Po) (a and b, respectively); the OPO efficiency on the pump fluence (c) (adapted from [69]).
Figure 18. The output OPO power and efficiency vs the incident pump power (a); the OPO efficiency vs the incident pump power (Po) (a and b, respectively); the OPO efficiency on the pump fluence (c) (adapted from [69]).
Preprints 91194 g018
The maximum efficiency is ~45.74%. From Figure 18 c, it is clear that when the pump power reaches ~11 W and the energy density reaches ~1.2 J/cm2, the efficiency stops growing and reaches a saturation point.
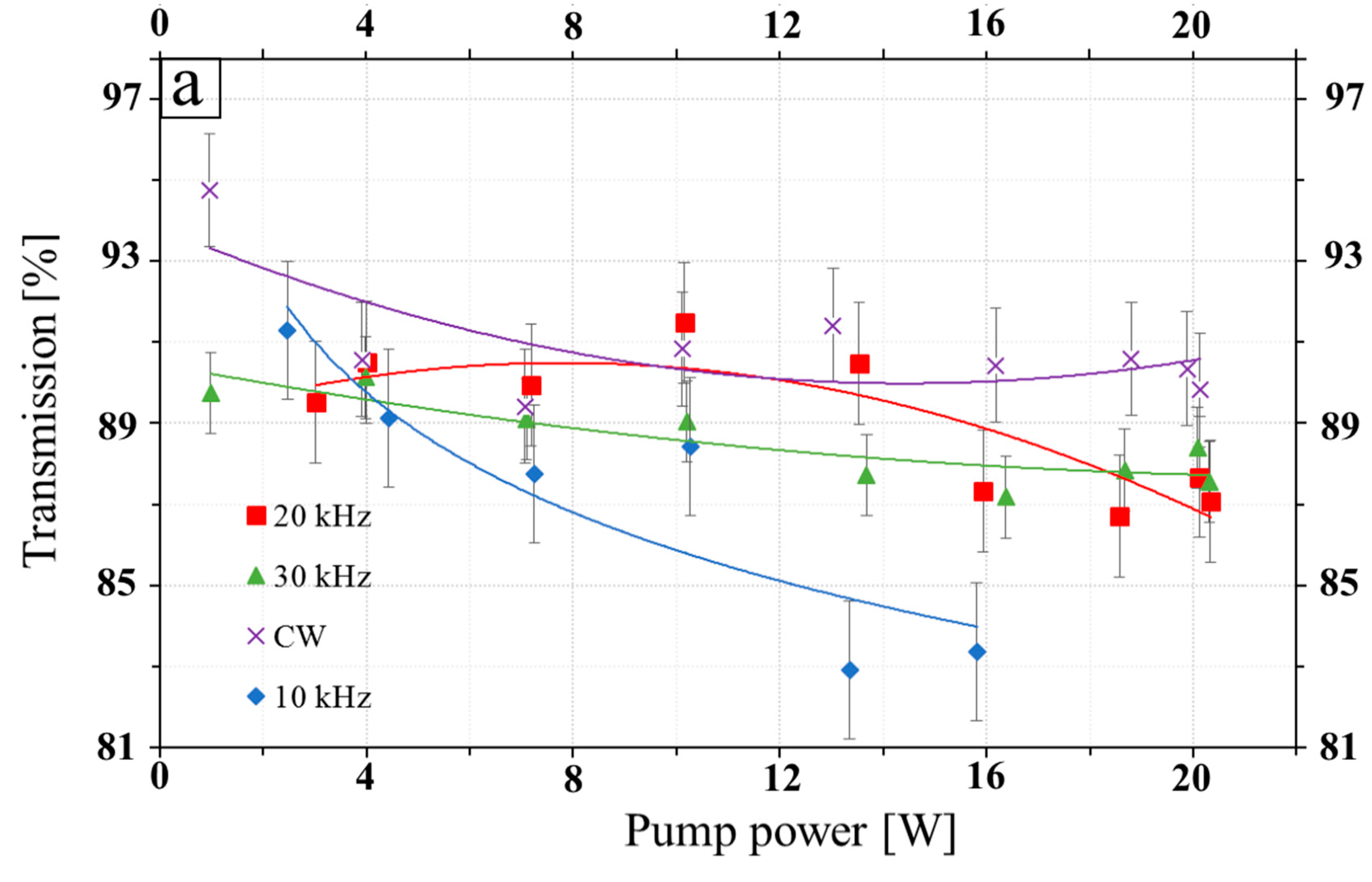
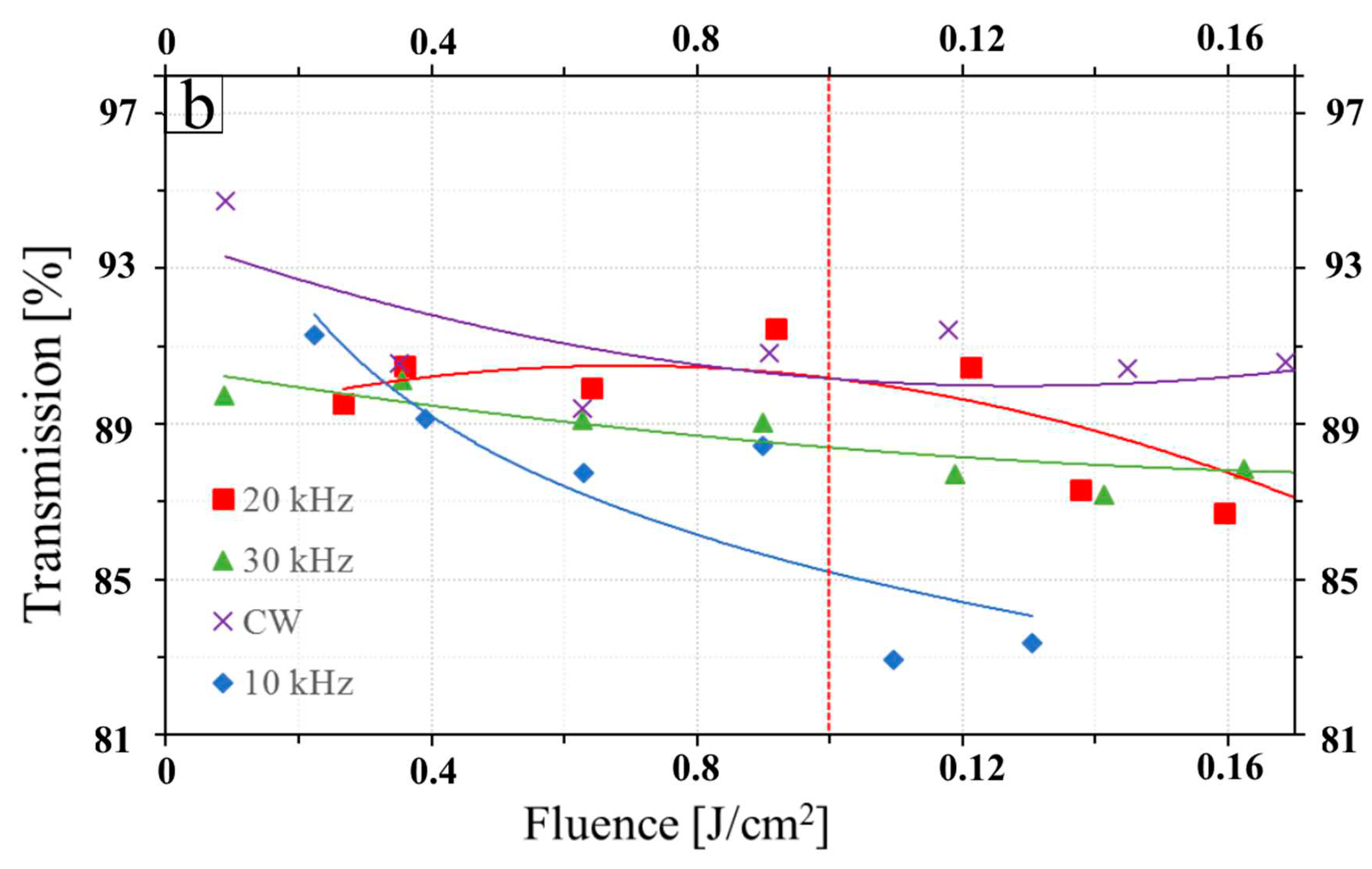
Studies were conducted on the dependence of the transmission of the nonlinear crystal on the power of the test radiation and on the energy density of the radiation falling on the crystal. The results obtained (Figure 19) were presented in the form of dependencies of the transmission on the pump power and the transmission on the energy density of the radiation falling on the crystal, the PRR was varied from 10 kHz to 30 kHz with a step of 10 kHz.
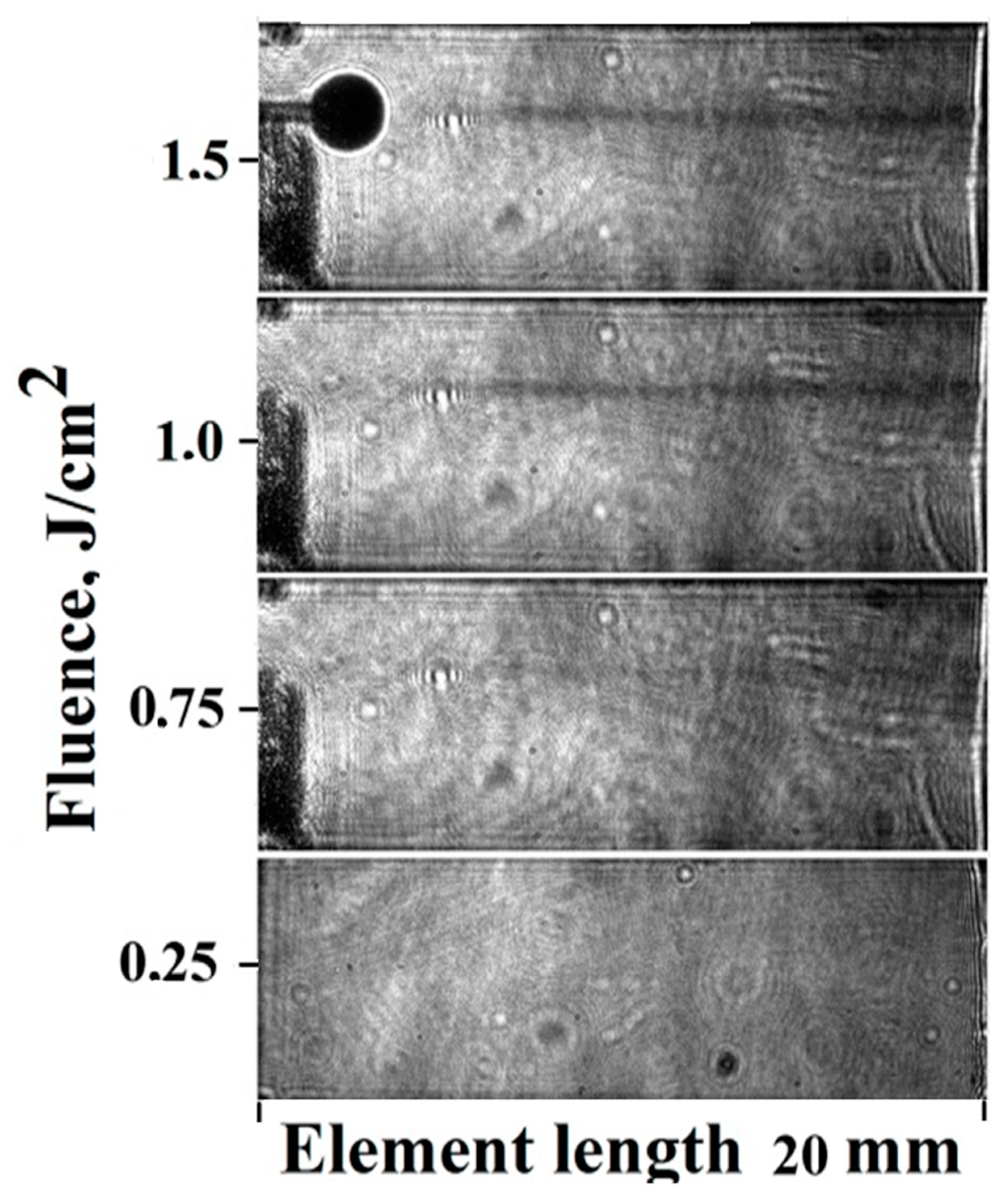
Figure 20 shows the restored holograms. At a power of up to 0.7 J/cm2, the holographic camera didn’t detect any changes. With an increase of the pump fluence from 0.7 to 0.9 J/cm2, the formation of a dark area along the entire length of the crystal was observed. With an increase of the fluence to 1.2 J/cm2, this area became darker. At a power more than 1.2 J/cm2 a damage track inside the ZGP element was registered.
Analysis of the dependencies presented in Figure 16, Figure 17, Figure 18 and Figure 19 and the dark tract images on the Figure 20 allows us to conclude that the ZGP transmission decreases near the LIDT (above the pump fluence of 1 J/cm2). With a decrease in PRR at the same average power (and an increase of the pumping pulse fluence), this dependence becomes more pronounced. These dependencies can be explained an induced nonlinear absorption near the LIDT (below the LIDT), which increased with the growth of the pumping pulse fluence. The nonlinear absorption can give an additional contribution to the ZDP optical damage.
Further studies, which were carried out with the pumping fluence of 0.9 J/cm2 (which was two times less than the ZGP LIDT), the stable OPO operation was registered during more 6 minutes (this operation time was limited only by a thermal management of the system). If the pump fluence was more than 1.3 J/cm2, when the darkening was observed, the OPO operation time was limited by the LID that occurred after 30 seconds.

7. Conclusion

The paper presented up-to-date information on the initiation of LID inside ZGP single crystals under 2-μm Ho3+:YAG nanosecond laser irradiation and methodology for increasing the ZGP LIDT. The main findings are as follows:
1) It has been shown that an order of magnitude reduction in the number of bulk defects and dislocation concentration inside ZGP crystal increased the LIDT by more than three times.
2) It has been shown that the diffusion doping of ZGP single crystals with Mg and Se leads to higher LIDT. After annealing at 750 °C, the destruction threshold of samples doped with Mg and Se increased by 31% and 21% from 2.2 ± 0.1 J/cm2 to 2.9 ± 0.1 and 2.7 ± 0.1 J/cm2, respectively. The opposite trend was observed when ZGP was doped with Ca. A correlation was observed between the optical breakdown threshold and the electro-physical parameters of crystals after doping, in particular, when it comes to the conductivity of samples. A decrease in conductivity was observed when ZGP samples were doped with Mg and Se, while the conductivity of ZGP increased after doping with Ca compared to an undoped annealed sample. Studies have shown that there is a technological possibility to increase the LIDT of ZGP crystals by reducing the conductivity of samples using controlled doping.
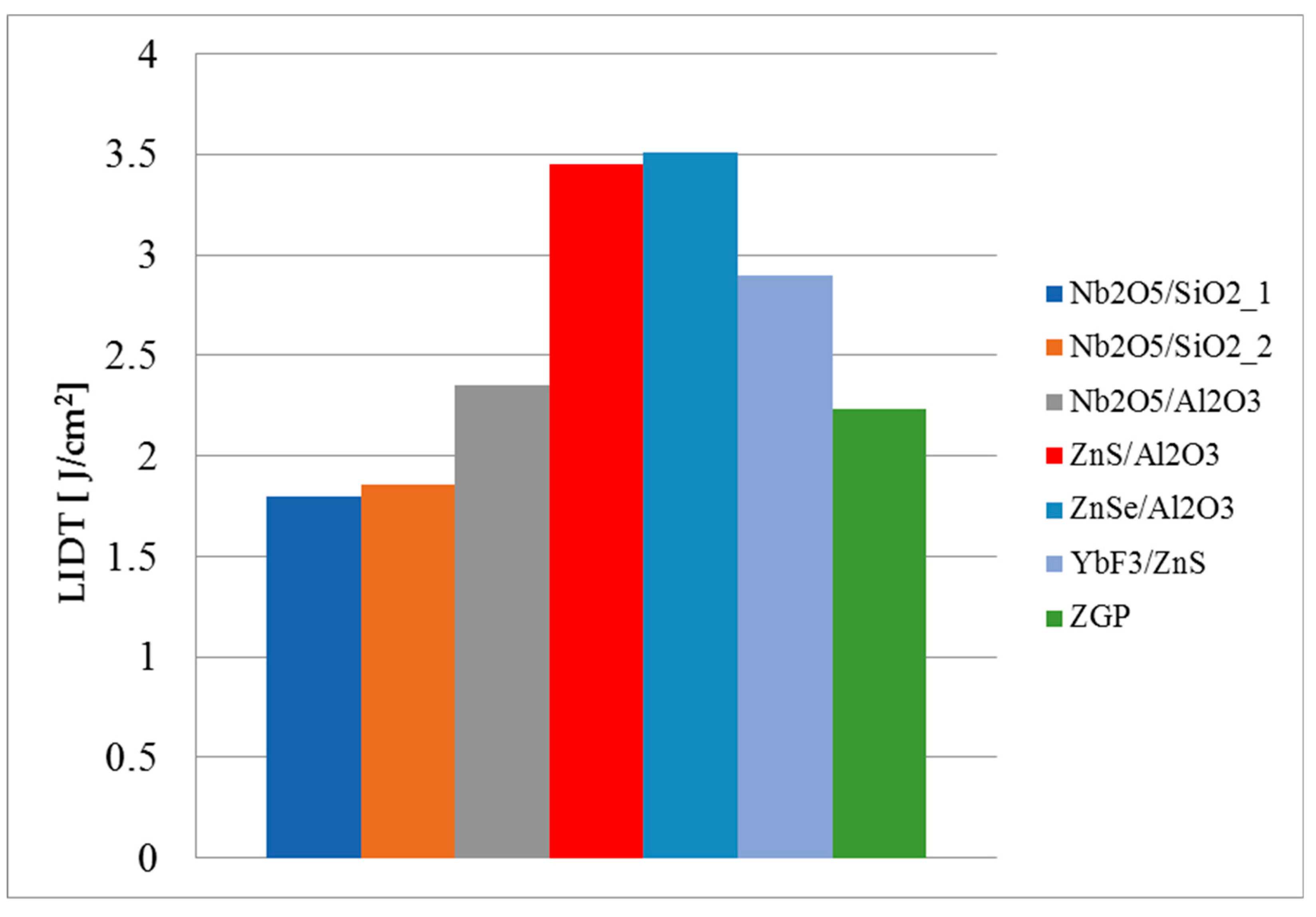
3) An increase in the LIDT has been found after applying an AR coating. In the case of a coating based on ZnS and Al2O3 materials, the LIDT increased by 55% compared to an uncoated sample. It was assumed that there are no local composition fluctuations and mechanical stress in the layers of the transparent coating, which in turn leads to good adhesion of the multilayer coating to the polished surface of the crystal and increases the LIDT compared to the uncoated sample by closing the broken chemical bonds and bulk defects that have come out on the polished surface.
4) Data has been obtained on the dependence of the LIDT fluence on the laser beam diameter and intensity, the PRR, and the exposure.
5) A strong dependence of LIDT at 2.1 μm on the crystal temperature has been found. The observed sharp increase in the threshold energy density (up to 3 times the initial value) when the ZGP temperature was reduced from 0 °C to - 60 °C can be explained by the temperature dependence of the filling number of phonons. The increase in the filling number of phonons with a decrease in the temperature of the crystal leads to a decrease in the probability of their participation in indirect electron transitions from the valence band to impurity levels, and, accordingly, to a decrease in the nonlinear absorption of the crystal.
6) Visualization of the optical damage dynamics using digital holography showed the formation of an optical pre-damage track along the laser beam. The process of solidification of the molten material leads to the diffusion of free charge carriers from the heated region of the crystal in the direction perpendicular to the laser beam. The effect above the LIDT is accompanied by the appearance of a luminous spot near the exit optical surface inside the crystal and the subsequent movement of this luminous spot towards the input optical surface, i.e. in the direction opposite to the propagation of laser radiation. This luminous spot can be explained by the recombination of the formed non-equilibrium charge carriers.
7) Using a digital holographic camera, it was found that the pulsed beam intensity greater than or equal to the LIDT of the crystal leads to elastic deformations of the crystal in the longitudinal direction at the moment of formation of the damage track. These deformations were attributed to the thermal expansion of material in the damage track area, caused by a sharp increase in the local temperature along the laser beam to values exceeding the melting temperature of the crystal.
8) The presence of the reversible "photo darkening" area along the propagation path of a powerful laser beam at 2.1 μm in ZGP below the LIDT has been established. Such reversible photo darkening of the propagation channel can be explained by the local decrease in the band gap width of ZGP due to heating.
9) Over the course of studying the energy characteristics of the OPO based on a ZGP crystal and using the results of visualization of the processes taking place inside the crystal, we established that when the pump intensity reaches half the LIDT threshold the OPO efficiency stops growing and the darkening of the beam path inside the crystal starts forming. These effects were accompanied by the decrease in transmission when the crystal was irradiated outside the resonator, which may indicate significant nonlinear absorption. The results indicate that these processes are interrelated. The nonlinear absorption may be the cause of the decrease in the efficiency of parametric conversion and can be a factor that initiates the optical damage.
10) This review shows the significant potential for increasing LIDT ZGP by improving the structural perfection of the crystal and improving the quality of crystal surfaces by improving the technology of crystal growth, post-growth processing, polishing and AR of working surfaces.

Author Contributions

Conceptualization, N.Y. and O.A.; methodology, N.Y., V.D., A.G.; software, M.Z., S.P.,V.K..; validation, E.S., I.K. and A.K.; formal analysis, V.K.; investigation, A.L.,A.K., I.E.; resources, O.A.; data curation, H.B.; writing—original draft preparation, H.B.; writing—review and editing, N.Y.; visualization, E.S.; supervision, V.D.; project administration, O.A.; funding acquisition, O.A. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the Russian Science Foundation (project No. 22-12-20035, https://rscf.ru/en/project/22-12-20035, accessed on 25 March 2022) and the Ministry of Education, Science and Youth Policy of the Nizhny Novgorod Region (agreement No. 316-06-16-17/22 accessed on 31 March 2022).

References

  1. Yulong, S.; Meng, J.; Wei, T.; Xie, Z.; Jia, S.; Tian, W.; Zhu, J.; Wang, W. 150 Gbps multi-wavelength FSO transmission with 25-GHz ITU-T grid in the mid-infrared region. Optics Express 2023, 31, 15156–15169. [Google Scholar] [CrossRef]
  2. Yevtushenko, A.; Rozniakowska-Klosinska, М. Encyclopedia of Thermal Stresses, Laser-Induced Thermal Splitting in Homogeneous Body with Coating; Springer: Berlin, Germany, 2014. [Google Scholar]
  3. Parfenov, V.A. Laser Materials Microprocessing; Saint-Petersburg, Russia, 2011; p. 5-11.
  4. Edwards, G.; Logan, R.; Copeland, M. et al. Tissue ablation by a free-electron laser tuned to the amide II band. Nature 1994, 371, 416–419. [Google Scholar] [CrossRef]
  5. Mackanos, M.A. et al. Mid infrared optical parametric oscillator (OPO) as a viable alternative to tissue ablation with the free electron laser (FEL). Lasers Surg. Med. 2007, 39, 230–236. [Google Scholar] [CrossRef] [PubMed]
  6. Soldatov, A.N.; Vasilyeva, A.V.; Polunin, Yu.P.; Kuksgauzen, D.A.; Kostyrya, I.D. Strontium vapor generator-amplifier system for bone ablation. Bio-technosphere 2012, 3–4, 47. [Google Scholar]
  7. Kozub, J.; Ivanov, B.; Jayasinghe, A.; Prasad, R.; Shen, J.; Klosner, M.; Heller, D.; Mendenhall, M.; Piston, D.W.; Joos, K.; et al. Raman-shifted alexandrite laser for soft tissue ablation in the 6- to 7-µm wavelength range. Biomed. Opt. Express 2011, 2, 1275–1281. [Google Scholar] [CrossRef] [PubMed]
  8. Serebryakov, V.S.; Boĭko, E.V.; Kalintsev, A.G.; Kornev, A.F.; Narivonchik, A.S.; Pavlova, A.L. Mid-IR laser for high-precision surgery. J. Opt. Technol. 2015, 82, 781–788. [Google Scholar] [CrossRef]
  9. Ze, L.; Shen, Y.; Zong, N.; Bian, Q.; Wang, E.; Chang, J.; Bo, Y.; Cui, D.; Peng, Q. 1.53 W all-solid-state nanosecond pulsed mid-infrared laser at 6.45 µm. Optics Letters 2022, 47, 1359–1362. [Google Scholar] [CrossRef]
  10. Todd, M.W.; Provencal, R.A.; Owano, T.G.; Paldus, B.A.; Kachanov, A. et al. Application of mid-infrared cavity-ringdown spectroscopy to trace explosives vapor detection using a broadly tunable (6–8 μm) optical parametric oscillator. Applied Phys. B 2002, 75, 367–376. [Google Scholar] [CrossRef]
  11. Bobrovnikov, S.M.; Matvienko, G.G.; Romanovsky, O.A.; Serikov, I.B.; Sukhanov, A.Y. Lidar Spectroscopic Gas Analysis of the Atmosphere; IOA SB RAS: Tomsk, Russia, 2014; p. 510. [Google Scholar]
  12. Romanovskii, O.A.; Sadovnikov, S.A.; Kharchenko, O.V.; Yakovlev, S.V. Development of Near/Mid IR differential absorption OPO lidar system for sensing of atmospheric gases. Opt. Laser Technol 2019, 116, 43–47. [Google Scholar] [CrossRef]
  13. Bochkovskii, D. A.; Vasil’eva, A. V.; Matvienko, G.; Yakovlev, S. V. Application of a strontium vapor laser to laser remote sounding of atmospheric composition. Atmospheric and Oceanic Optics 2012, 25, 166–170. [Google Scholar] [CrossRef]
  14. Schunemann, P.G.; Zawilski, K.T.; Pomeranz, L.A.; Creeden, D.J.; Budni, P.A. Advances in nonlinear optical crystals for mid- infrared coherent sources. J. Opt. Soc. Am. B 2016, 33, D36–D43. [Google Scholar] [CrossRef]
  15. Vodopyanov, K.L. Laseryanov, K.L.Infrared Sources and Applications. John Wiley & Sons Inc.: Hoboken, USA, 2020.
  16. Das, S. Optical parametric oscillator: status of tunable radiation in mid-IR to IR spectral range based on ZnGeP2 crystal pumped by solid state lasers. Opt. and Quantum Electron. 2019, 51, 70. [Google Scholar] [CrossRef]
  17. Hemming, A.; Richards, J.; Davidson, A.A.; Carmody, N.; Bennetts, S.; Simakov, N.; Haub, J. 99 W mid-IR operation of a ZGP OPO at 25% duty cycle. Opt. Express 2013, 21, 10062–10069. [Google Scholar] [CrossRef] [PubMed]
  18. Haakestad, M.W.; Fonnum, H.; Lippert, E. Mid-infrared source with 0.2 J pulse energy based on nonlinear conversion of Q-switched pulses in ZnGeP2. Opt. Express 2014, 22, 8556–8564. [Google Scholar] [CrossRef]
  19. Liu, G.; Yang, K.; Chen, Y.; Yao, B.; Wang, R.; Mi, Sh.; Yang, Ch.; Dai, T.; Duan, X. 11.6 W middle infrared ZnGeP2 optical parametric amplifier system with a 1 kHz repetition rate. Opt Lett. 2014, 39, 6589–6592. [Google Scholar] [CrossRef]
  20. Qian, C.; Fan, Y.; Sun, J.; Liu, J.; Yu, T.; Shi, X.; Ye, X. High-repetition-rate 52-mJ mid-infrared laser source based on ZnGeP2 MOPA system. J. of Lightwave Technology 2023, 3329743. [Google Scholar] [CrossRef]
  21. Qian, C.; Yao, B.; Zhao, B.; Liu, G.; Duan, X.; Ju, Y.; Wang, Y. High repetition rate 102 W middle infrared ZnGeP2 master oscillator power amplifier system with thermal lens compensation. Opt. Lett. 2019, 44, 715–718. [Google Scholar] [CrossRef] [PubMed]
  22. Liu, G.; Mi, Sh.; Yang, K.; Wei, D.; Li, J.; Yao, B.; Yang, Ch.; Dai, T.; Duan, X.; Tian, L.; Ju, Y. 161 W middle infrared ZnGeP2 MOPA system pumped by 300 W-class Ho:YAG MOPA system. Opt. Lett. 2021, 46, 82–85. [Google Scholar] [CrossRef]
  23. Lv, Ze; Shen, Yu; Wen, Ya; Wang, Er-P. ; Wang, Zhi-M.; Li, Wen-L.; Bo, Y.; Peng, Qin-J. High power widely tunable mid-IR (5–7.2 μm) ZnGeP2 optical parametric oscillator pumped by a 2.09 μm laser. Infrared Phys. & Technology 2023, 134, 104879. [Google Scholar] [CrossRef]
  24. Qian, C.-P.; Yu, T.; Liu, J.; Jiang, Yu-Yao; Wang, Si-Jie; Shi, X. -Ch.; Ye1, Xi-Sh., Chenal, W.-B. 5.4 W, 9.4 ns Pulse Width, Long-Wave Infrared ZGP OPO Pumped by Ho:YAG MOPA System. IEEE Photonics Journal 2021, 13, 1–8. [Google Scholar]
  25. Qian, Ch.; Duan, X.; Yao, B.; Shen, Y.; Zhang, Y.; Zhao, B.; Yuan, J.; Dai, T.; Ju, Y.; Wang, Y. 11.4 W long-wave infrared source based on ZnGeP2 optical parametric amplifier. Opt. Express 2018, 26, 30195–30201. [Google Scholar] [CrossRef]
  26. Liu, G.Y.; Chen, Y.; Yao, B.Q.; Wang, R.X.; Yang, K.; Yang, C.; Mi, S.Y.; Dai, T.Y.; Duan, X.M. 3.5  W long-wave infrared ZnGeP2 optical parametric oscillator at 9.8  µm. Opt Lett. 2020, 45, 2347–2350. [Google Scholar] [CrossRef]
  27. Petrov, V.; Rotermund, F.; Noack, F.; Schunemann, P. Femtosecond parametric generation in ZnGeP2. Opt. Lett. 1999, 24, 414–416. [Google Scholar] [CrossRef] [PubMed]
  28. Wandel, S.; Lin, M.-W.; Yin, Y.; Xu, G.; Jovanovic, I. Parametric generation and characterization of femtosecond mid-infrared pulses in ZnGeP2. Optics Express 2016, 24, 5287–5299. [Google Scholar] [CrossRef] [PubMed]
  29. Hinkelmann, M.; Baudisch, M.; Wandt, D.; Morgner, U.; Zawilski, K.; Schunemann, P.; Neumann, J.; Rimke, I.; Kracht, D. High-repetition rate, mid-infrared, picosecond pulse generation with µJ-energies based on OPG/OPA schemes in 2-µm-pumped ZnGeP2. Optics Express 2020, 28, 21499–21508. [Google Scholar] [CrossRef] [PubMed]
  30. Grafenstein, L.; Bock, M.; Ueberschaer, D.; Escoto, E.; Koç, A.; Zawilski, K.; Schunemann, P.; Griebner, U.; Elsaesser, T. Multi-millijoule, few-cycle 5 µm OPCPA at 1 kHz repetition rate. Opt. Lett. 2020, 45, 5998–6001. [Google Scholar] [CrossRef] [PubMed]
  31. Hildenbrand, A.; Kieleck, C.; Tyazhev, A.; Marchev, G.; Stöppler, G.; Eichhorn, M.; Schunemann, P.G.; Panyutin, V.L.; Petrov, V. Laser damage of the nonlinear crystals CdSiP2 and ZnGeP2 studied with nanosecond pulses at 1064 and 2090 nm. Opt. Eng. 2014, 53, 122511. [Google Scholar] [CrossRef]
  32. Gribenyukov, A.I.; Dyomin, V.V.; Olshukov, A.S.; Podzyvalov, S.N.; Polovcev, I.G.; Yudin, N.N. Investigation of the process of laser induced damage of ZnGeP2 crystals using digital holography. Rus.Phys. J. 2018, 61, 2042–2052. [Google Scholar] [CrossRef]
  33. Chumside, J.H.; Wilson, J.J.; Gribenyukov, A.I.; Shubin, S.F.; Dolgii, S.I.; Andreev, Yu.M.; Zuev, V.V.; Boulder, V. in Co:NOAA Technical Memorandum ERLWPL-224 WPL-224WPL 1992; p.18.
  34. Yudin, N.N.; Antipov, O.L.; Gribenyukov, A.I.; Eranov, I.D.; Podzyvalov, S.N.; Zinoviev, M.M.; Voronin, L.A.; Zhuravleva, E.V.; Zykova, M.P. Effect of postgrowth processing technology and laser radiation parameters at wavelengths of 2091 and 1064 nm on the laser-induced damage threshold in ZnGeP2 single crystal. Quantum Electronics 2021, 51, 306–316. [Google Scholar] [CrossRef]
  35. Andreev, Yu.M.; Badikov, V.V.; Voevodin, V.G.; Geiko, L.G.; Geiko, P.P.; Ivashchenko, M.V.; Karapuzikov, A.I.; Sherstov, I.V. Radiation resistance of nonlinear crystals at a wavelength of 9.55 μm. Quantum Electronics 2001, 31, 1075–1078. [Google Scholar] [CrossRef]
  36. Peterson, R.D.; Schepler, K.L.; Brown, J.L. Damage properties of ZnGeP2 at 2 mm. J. Opt. Soc. Am. B 1995, 12, 2142–2146. [Google Scholar] [CrossRef]
  37. Zawilski, K.T.; Setzler, S.D.; Schunemann, P.G.; Pollak, T.M. Increasing the laser-induced damage threshold of single-crystal ZnGeP2. JOSA B 2006, 23, 2310–2316. [Google Scholar] [CrossRef]
  38. K. T. Zawilski, P. G. Schunemann, S. D. Setzler, and T. M. Pollak. Large aperture single crystal ZnGeP2 for high-energy applications. Journal of Crystal Growth 2008, 310, 1891–1896. [Google Scholar] [CrossRef]
  39. Yudin, N.; Zinoviev, M.; Kuznetsov, V.; Slyunko, E.; Podzvalov, S.; Voevodin, V.; Lysenko, A.; Kalsin, A.; Shaimerdenova, L.; Baalbaki, H. Effect of Dopants on Laser-Induced Damage Threshold of ZnGeP2. Crystals 2023, 13, 440. [Google Scholar] [CrossRef]
  40. Guha, S.; Bartsch, M.; Hopkins, F.K.; Eaton, M.P.; Setzler, S.D.; Schunemann, P.G.; Pollak, T.M. Nonlinear absorption and laser damage threshold measurements of doped ZnGeP2. International Society for Optics and Photonics 1999, 3793, 9–12. [Google Scholar]
  41. Peng, Y.; Wei, X.; Wang, W. Mid-infrared optical parametric oscillator based on ZnGeP2 pumped by 2-um laser. Chin. Opt. Lett. 2011, 9, 061403. [Google Scholar] [CrossRef]
  42. Zinovev, M.; Yudin, N.N.; Kuznetsov, V.; Podzyvalov, S.; Kalsin, A.; Slyunko, E.; Lysenko, A.; Vlasov, D.; Baalbaki, H. High-Strength Optical Coatings for Single-Crystal ZnGeP2 by the IBS Method Using Selenide and Oxide Materials. Ceramics 2023, 6, 514–524. [Google Scholar] [CrossRef]
  43. Zinovev, M.; Yudin, N.N.; Kinyaevskiy, I.; Podzyvalov, S.; Kuznetsov, V.; Slyunko, E.; Baalbaki, H.; Vlasov, D. Multispectral Anti-Reflection Coatings Based on YbF3/ZnS Materials on ZnGeP2 Substrate by the IBS Method for Mid-IR Laser Applications. Crystals 2022, 12, 1408. [Google Scholar] [CrossRef]
  44. Zinoviev, M.; Yudin, N.N.; Podzvalov, S.; Slyunko, E.; Yudin, N.A.; Kulesh, M.; Dorofeev, I.; Baalbaki, H. Optical AR Coatings of the Mid-IR Band for ZnGeP2 Single Crystals Based on ZnS and Oxide Aluminum. Crystals 2022, 12, 1169. [Google Scholar] [CrossRef]
  45. Kinyaevskiy, I. O.; Danilov, P.A.; Kudryashov, S.I.; Pakholchuk, P.P.; Ostrikov, S.A.; Yudin, N.N.; Zinovev, M.M.; Podzyvalov, S.N.; Andreev, Yu.M. Laser-induced damage threshold of ZnGeP2 crystal for (sub) picosecond 1-µm laser pulse. Applied Optics 2023, 62, 16–20. [Google Scholar] [CrossRef]
  46. Sutowska, M.; Sutowski, P. Contemporary applications of magnetoreological fluids for finishing process. Journal of Mechanical and Energy Engineering 2017, 1, 141–152. [Google Scholar]
  47. Yudin, N.; Khudoley, A.; Zinoviev, M.; Podzvalov, S.; Slyunko, E.; Zhuravleva, E.; Kulesh, M.; Gorodkin, G.; Kumeysha, P.; Antipov, O. The Influence of Angstrom-Scale Roughness on the Laser-Induced Damage Threshold of Single-Crystal ZnGeP2. Crystals 2022, 12, 83. [Google Scholar] [CrossRef]
  48. Yudin, N.; Antipov, O.; Eranov, I.; Gribenyukov. A.; Verozubova, G.; Lei, Z.; Zinoviev, M.; Podzvalov, S.; Slyunko, E.; Voevodin, V., Yang, Ch. Laser-Induced Damage Threshold of Single Crystal ZnGeP2 at 2.1 µm: The Effect of Crystal Lattice Quality at Various Pulse Widths and Repetition Rates. Crystals 2022, 12, 652. [Google Scholar] [CrossRef]
  49. Ristau, D. (Ed.) Laser-Induced Damage in Optical Materials; CRC Press Taylor & Francis Group: Boca Raton, FL, USA, 2015. [Google Scholar]
  50. Manenkov, A.A.; Prokhorov, A.M. Laser-induced damage in solids. Sov. Phys. Uspekhi 1986, 29, 104–122. [Google Scholar] [CrossRef]
  51. Kawamori, T.; Schunemann, P.G.; Gruzdev, V.; Vodopyanov, K.L. High-order (N = 4–6) multiphoton absorption and mid-infrared Kerr nonlinearity in GaP, ZnSe, GaSe, and ZGP crystals. APL Photon. 2022, 7, 086101. [Google Scholar] [CrossRef]
  52. Antipov, O.L.; Kositsyn, R.I.; Eranov, I.D. 36W Q-switched Ho3+: YAG laser at 2097 nm pumped by a Tm fiber laser: Evaluation of different Ho3+ doping concentrations. Laser Phys. Lett. 2017, 14, 015002. [Google Scholar] [CrossRef]
  53. “The R-on-1 Test”, Lidaris LIDT Service. 2019. Available online: http://lidaris.com/laserdamage-testing/ (accessed on 16 November 2020).
  54. Lei, Z.; Okunev, A.O.; Zhu, C.; Verozubova, G.A.; Yang, C. Imaging of microdefects in ZnGeP2 single crystals by X-ray topography. J. Cryst. Growth 2020, 534, 125487–125492. [Google Scholar] [CrossRef]
  55. Lei, Z.; Okunev, A.O.; Zhu, C.; Verozubova, G.A.; Ma, T.; Yang, C. Photoelasticity method for study of structural imperfection of ZnGeP2 crystals. J. Cryst. Growth 2016, 450, 34–38. [Google Scholar] [CrossRef]
  56. Yudin, N; Antipov, O.; Balabanov, S.; Eranov, I.; Getmanovskiy, Yu.; Slyunko, E. Effects of the Processing Technology of CVD-ZnSe, Cr2+:ZnSe, and Fe2+:ZnSe Polycrystalline Optical Elements on the Damage Threshold Induced by a Repetitively Pulsed Laser at 2.1 µm. Ceramics 2022, 5, 459–471. [Google Scholar] [CrossRef]
  57. Gribenykov,A. I. ; Verozubova, G.A.; Trofimov, A.; Yunda, N.T.; Vere,A.W.; Flyun C.J. Proceedings international conference on modification of materials with particle beams and plasma flows. Materials Research Society 2002, 744, 315. [Google Scholar]
  58. Grigorieva, V.S.; Prochukhan, V.D.; Rud, Yu.V.; Yakovenko, A.A. About doping of the semiconductor compound ZnGeP2. Doped Semiconductors M.: “Science”,1975; pp. 8–11.
  59. Voevodin, V.G. Optical electronics elements based on A2B4C2 compounds: preparation, properties and application. Dissertation of Doctor of Physics and Mathematics. Sciences, SFTI, Tomsk, 2003. p.395.
  60. Schnars, U.; Juptner, W. Digital Hologram Recording, Numerical Reconstruction, and Related Techniques; Springer: Berlin, Germany, 2005; p. 164. [Google Scholar]
  61. Collier, R.; Burkhart, K.; Lin, L. Optical holography1979, 13, 686.
  62. Dyomin, V.V.; Polovcev, I.G.; Kamenev, D.V. The internal defects detection in crystals by digital holographic methods. Conference Series. Journal of Physics 2016, 737, 012072. [Google Scholar] [CrossRef]
  63. Buehler, E.; Wernick, J.H. Concerning growth of single crystals of the II-IV-V diamond-like compounds ZnSiP2, CdSiP2, ZnGeP2, and CdSnP2 and standard enthalpies of formation for ZnSiP2 and CdSiP2. Jour. of Crystal Growth. 1971, 8, 324–332. [Google Scholar] [CrossRef]
  64. Piotrowski, M. ; M. A. Medina, M.A.; Schellhorn, M.;, C. Mueller, C.; Spindler, G.; Hildenbrand- Dhollande, A. Experimental and numerical studies of thermal lensing and gain guiding effects in a high-power ZGP OPO. In Technical Digest of CLEO Europe - EQEC 2021, paper ca_8_6.
  65. Crisp, M.D. Laser-Induced Surface Damage of Transparent Dielectrics. IEEE J. Quantum Electron. 1974, QE-10, 57–62. [Google Scholar] [CrossRef]
  66. Antipov, O.L.; Eranov, I.D.; Kositsyn, R.I. 10-W mid-IR optical parametric oscillators based on ZnGeP2 elements pumped by a fibre-laser-pumped Ho: YAG Laser. Experimental and numerical study. Quantum Electronics 2017, 47, 601. [Google Scholar] [CrossRef]
  67. Antipov, O.; Dobrynin, A.; Getmanovskiy, Yu.; Karaksina, E.; Shiryaev, V.; Sukhanov, M.; Kotereva, T. Thermal Lensing and Laser-Induced Damage in Special Pure Chalcogenide Ge35As10S55 and Ge20As22Se58 Glasses under Quasi-CW Fiber Laser Irradiation at 1908 nm. Photonics 2023, 10, 252–13. [Google Scholar] [CrossRef]
  68. http://refractiveindex.info.
  69. Yudin, N.N.; Vlasov, D.V.; Antipov, O.L.; Gribenyukov, A.I.; Zinoviev, M.M.; Podzyvalov, S.N.; Slyunko, E.S.; Yudin, N.A.; Kulesh, M.M.; Kuznetsov, V.S.; Dyomin, V.V. Visualization and Characterization of Pre-breakdown Processes in the Volume of a ZnGeP2 Single Crystal During Parametric Generation of Radiation in the Wavelength Range of 3.5–5 μm when Pumped by Ho:YAG Laser Radiation. Russian Physics Journal 2023, 65, 2130–2136. [Google Scholar] [CrossRef]
Preprints 91194 g002
Figure 2. Comparison of the probability of the optical damage of the samples N1 element (red squares) and the samples N2 element (black squares) at 12-kHz PRR, 1-s exposure duration, pulse width of 18-ns and the beam diameter of 360 μm (adapted from [48]).
Figure 2. Comparison of the probability of the optical damage of the samples N1 element (red squares) and the samples N2 element (black squares) at 12-kHz PRR, 1-s exposure duration, pulse width of 18-ns and the beam diameter of 360 μm (adapted from [48]).
Preprints 91194 g002
Preprints 91194 g003
Figure 3. Dependence of the probability of optical damage on the energy density of the incident laser radiation with a wavelength of 2.1 μm in undoped samples (a), and in doped samples with Mg (b), Se (c), Ca (d). Approximate plots in black and red correspond to ZGP samples annealed at 750°C and 650°C, respectively (adapted from [39]).
Figure 3. Dependence of the probability of optical damage on the energy density of the incident laser radiation with a wavelength of 2.1 μm in undoped samples (a), and in doped samples with Mg (b), Se (c), Ca (d). Approximate plots in black and red correspond to ZGP samples annealed at 750°C and 650°C, respectively (adapted from [39]).
Preprints 91194 g003
Preprints 91194 g004
Figure 4. Histogram of the LIDT value depending on the type of AR coating.
Figure 4. Histogram of the LIDT value depending on the type of AR coating.
Preprints 91194 g004
Preprints 91194 g005
Figure 5. Dependence of the probability of optical damage on the fluence of laser radiation at 2091 nm for various exposure times τex: 30 s (black dots), 10 s (blue dots), 5 s (green dots), 2 s (red dots) (adapted from [34]).
Figure 5. Dependence of the probability of optical damage on the fluence of laser radiation at 2091 nm for various exposure times τex: 30 s (black dots), 10 s (blue dots), 5 s (green dots), 2 s (red dots) (adapted from [34]).
Preprints 91194 g005
Preprints 91194 g006
Figure 6. Dependence of the LID probability on the laser fluence at 2091 nm for various beam diameters: 580 µm (black dots of family 1), 300 µm green dots 2); 200 µm (red dots 3) (adapted from [34]).
Figure 6. Dependence of the LID probability on the laser fluence at 2091 nm for various beam diameters: 580 µm (black dots of family 1), 300 µm green dots 2); 200 µm (red dots 3) (adapted from [34]).
Preprints 91194 g006
Preprints 91194 g008
Figure 8. Axial scheme for recording digital holograms: 1 – laser emitter, 2 – collimator, 3 – two-coordinate positioner, 4 – CCD camera, 5 – studied sample, 6 – computer.
Figure 8. Axial scheme for recording digital holograms: 1 – laser emitter, 2 – collimator, 3 – two-coordinate positioner, 4 – CCD camera, 5 – studied sample, 6 – computer.
Preprints 91194 g008
Preprints 91194 g009
Figure 9. Diagram of the beam loading stand for studying the radiation resistance of the ZnGeP2 single crystal: Ho3+:YAG laser, DP is a dividing plate, Ophir is the power meter from Ophir company, synchronization is a device synchronization unit, DHC 1.06 is the digital holographic camera, PC is a personal computer. 1 is the ZGP single crystal, 2 is the laser module ML 150-1053-100-TTL, L is the short-focus lens, 3 is the matrix photo detector (adapted from [62]).
Figure 9. Diagram of the beam loading stand for studying the radiation resistance of the ZnGeP2 single crystal: Ho3+:YAG laser, DP is a dividing plate, Ophir is the power meter from Ophir company, synchronization is a device synchronization unit, DHC 1.06 is the digital holographic camera, PC is a personal computer. 1 is the ZGP single crystal, 2 is the laser module ML 150-1053-100-TTL, L is the short-focus lens, 3 is the matrix photo detector (adapted from [62]).
Preprints 91194 g009
Preprints 91194 g010
Figure 10. Results of digital hologram processing during optical damage of a ZGP single crystal by laser irradiation: before LID (a), during LID (b), after LID (c) (adapted from [32]).
Figure 10. Results of digital hologram processing during optical damage of a ZGP single crystal by laser irradiation: before LID (a), during LID (b), after LID (c) (adapted from [32]).
Preprints 91194 g010
Preprints 91194 g011
Figure 11. Dependence of the optical damage track lings X (the luminous spot position) on time t at the laser pulse fluence of 0.3 J/cm2, the diameter of the Ho3+:YAG laser beam on the entrance face of the single crystal ~ 200 μm (at the 1/e2 level), the PRR of ~ 10 kHz and the pulse width of ~ 25 ns (adapted from [32]).
Figure 11. Dependence of the optical damage track lings X (the luminous spot position) on time t at the laser pulse fluence of 0.3 J/cm2, the diameter of the Ho3+:YAG laser beam on the entrance face of the single crystal ~ 200 μm (at the 1/e2 level), the PRR of ~ 10 kHz and the pulse width of ~ 25 ns (adapted from [32]).
Preprints 91194 g011
Preprints 91194 g012
Figure 12. Dependence of the diameter D, μm, of the LID track on the distance X, mm, measured from the exit surface towards the incident laser beam. The curve 1 is the data obtained from measurements; the curve 2 is the data after double smoothing by 5 points; the line 3 is the linear regression; the curve 4 is the deviation of smoothed values from the regression line (adapted from [32]).
Figure 12. Dependence of the diameter D, μm, of the LID track on the distance X, mm, measured from the exit surface towards the incident laser beam. The curve 1 is the data obtained from measurements; the curve 2 is the data after double smoothing by 5 points; the line 3 is the linear regression; the curve 4 is the deviation of smoothed values from the regression line (adapted from [32]).
Preprints 91194 g012
Preprints 91194 g013
Figure 13. Results of the processing of digital holograms during the optical damage of a ZGP single crystal by laser radiation with a fluence of 0.6 J/cm2: single crystal before exposure to radiation (a); material breakdown (b); thermal expansion of the crystal near the location of the optical damage track (c); relaxation of the dimensions of the single crystal after exposure to radiation (d); the transverse deformation of the surface at the moment of optical damage relative to the element surface in the absence of laser radiation (e); the longitudinal deformation in the reconstructed image of the element at the LID moment relative to the element in the absence of laser radiation (f) (adapted from [32]).
Figure 13. Results of the processing of digital holograms during the optical damage of a ZGP single crystal by laser radiation with a fluence of 0.6 J/cm2: single crystal before exposure to radiation (a); material breakdown (b); thermal expansion of the crystal near the location of the optical damage track (c); relaxation of the dimensions of the single crystal after exposure to radiation (d); the transverse deformation of the surface at the moment of optical damage relative to the element surface in the absence of laser radiation (e); the longitudinal deformation in the reconstructed image of the element at the LID moment relative to the element in the absence of laser radiation (f) (adapted from [32]).
Preprints 91194 g013
Preprints 91194 g014
Figure 14. Reconstructed image of the hologram of the volume of the ZGP single crystal before the test (a), under the influence of pulsed radiation of the Ho3+:YAG laser at LIDT fluence (b), 10 ms after the cessation of the action of the Ho3+:YAG laser radiation (c) (adapted from [34]).
Figure 14. Reconstructed image of the hologram of the volume of the ZGP single crystal before the test (a), under the influence of pulsed radiation of the Ho3+:YAG laser at LIDT fluence (b), 10 ms after the cessation of the action of the Ho3+:YAG laser radiation (c) (adapted from [34]).
Preprints 91194 g014
Preprints 91194 g015
Figure 15. Scheme of the ZGP OPO setup with Ho3+:YAG laser pumping: Ho3+:YAG laser, OI is the optical isolator, L is the lens, M1 is the input mirror of the OPO cavity, M2 is the output mirror of the OPO cavity, ZGP is the single crystal, LD is the laser diode, O is an objective, IM is a power meter (adapted from [69]).
Figure 15. Scheme of the ZGP OPO setup with Ho3+:YAG laser pumping: Ho3+:YAG laser, OI is the optical isolator, L is the lens, M1 is the input mirror of the OPO cavity, M2 is the output mirror of the OPO cavity, ZGP is the single crystal, LD is the laser diode, O is an objective, IM is a power meter (adapted from [69]).
Preprints 91194 g015
Preprints 91194 g016
Figure 16. Dependence of the average power of the generated radiation on the PRR pumping at an average power of 16.3 W (a). Dependence of the efficiency of parametric generation on the PRR pumping at an average power of 16.3 W (b) (adapted from [69]).
Figure 16. Dependence of the average power of the generated radiation on the PRR pumping at an average power of 16.3 W (a). Dependence of the efficiency of parametric generation on the PRR pumping at an average power of 16.3 W (b) (adapted from [69]).
Preprints 91194 g016
Preprints 91194 g019aPreprints 91194 g019b
Figure 19. Dependence of the transmission on the incident pump power (a); dependence of the transmission on the pump fluence (b) (adapted from [69]).
Figure 19. Dependence of the transmission on the incident pump power (a); dependence of the transmission on the pump fluence (b) (adapted from [69]).
Preprints 91194 g019aPreprints 91194 g019b
Preprints 91194 g020
Figure 20. Restored image of the ZGP crystal taken with a holographic camera when laser radiation of different powers is applied to the nonlinear optical crystal ZGP (adapted from [69]).
Figure 20. Restored image of the ZGP crystal taken with a holographic camera when laser radiation of different powers is applied to the nonlinear optical crystal ZGP (adapted from [69]).
Preprints 91194 g020
Table 1. Summarizes data on the ZGP crystals and the laser parameters in the LID tests.
Table 1. Summarizes data on the ZGP crystals and the laser parameters in the LID tests.
Absorption at the exposure wavelength, cm-1 Dopant Crystal length, mm Coating Wavelength, µm Pulse repetition rate, Hz Pulse width, ns Test time, s Beam diameter, µm Temperature , 0 С
- 2,2 No 2,09 1000 21 30 200 room
1,8 - 2,2 No 1,064 100 8 30 280 room
0.03 - 20 SiO2/Nb2O5 2.091 12000 18 1 270 room
0.03 - 20 SiO2/Nb2O5 2,091 12000 18 1 100 -60
7,5 - 2,45 No 1,064 3000 10 1 - room
0.26 - - No 9,55 1 85 - - room
- - - No 2,08 1 70-75 - 750 room
- - - With coating 2,05 10000 15 30 130 room
Se 2,45 No 2,097 10000 35 10 360 room
Mg 2,45 No 2,097 10000 35 10 360 room
Ca 2,45 No 2,097 10000 35 10 360 room
- - 20 ZnSe/Al2O3 2,097 10000 35 10 350 room
0,03 - 20 YbF3/ZnS 2,097 10000 35 10 350 room
0,03 - 20 ZnS/Al2O3 2,097 10000 35 10 350 room
- - 2,45 - 1,03 Single pulse mode 0,0003-0,003 - - room
0,03 - 20 No 2,097 10000 35 10 350 room
- - 3 No 2,091 40000 45 1 270 room
Table 2. Conductivity and LIDT of the studied ZGP samples.
Table 2. Conductivity and LIDT of the studied ZGP samples.
Dopant Conductivity, (ohm×cm)-1 LIDT of the samples annealed at 650°C,
J/cm2 		LIDT of the samples annealed at 750°C, J/cm2
Mg (5.42±0.01)*10-6 2.6±0.1 2.9±0.1
Se (4.16±0.01)*10-7 2.64±0.1 2.7±0.1
Ca (1.25±0.01)*10-5 2.28±0.1 1.9±0.1
ZGP (1.24±0.01)*10-6 2.26±0.1 2.2±0.1
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated