Preprint
Article
A Substitutable Method for Hydrodynamic Calculation of Anastomosing Rivers: Expression of Channel Morphological Parameters (ECMP)
Altmetrics
Downloads
77
Views
22
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
13 November 2023
Posted:
14 November 2023
You are already at the latest version
Alerts
Abstract
Anastomosing rivers are wetland systems with multiple channels, and there are many constraints limiting in-situ observations of their hydrodynamics. Therefore, there are few reports on the hydrodynamic data of such rivers. In order to obtain the hydrodynamic parameters of the river channels without hydrological observations in the anastomosing rivers, this study proposes an expression method namely expression of channel morphological parameters (ECMP) for hydrodynamic calculations. The calculation formula of the ECMP method based on the shape factor, scale factor, and gradient factor of the flow cross-section as independent variables. This method can be used to calculate the average velocity, discharge, specific stream power, gross stream power and other hydrodynamic parameters of the flow cross-section at different water levels, only requiring the measurement of morphological parameters such as the average depth, width-depth ratio, and gradient of the flow (channel) cross-section. The applicability of the ECMP method was verified using measured hydrological data. The results show that the ECMP method is a practical calculation method with high computational accuracy and convenient application for calculating river hydrodynamic parameters. It has great application value in study on fluvial geomorphology and hydrodynamics, as well as in the reconstruction of ancient river hydrology and hydrodynamics.
Keywords:
Subject: Environmental and Earth Sciences - Geography
1. Introduction
An anastomosing river is a multiple-channel system characterized by stable morphology and separated by inter-channel wetlands [1,2]. It is an important river pattern, except for meandering, braided, straight, and anabranched rivers [3]. The developing geomorphic areas are mainly alluvial plains, river deltas, and intermountain basins, and the suitable climate environment is mainly humid and semi-humid climate zone, which can also be seen in arid and semi-arid regions [2,4,5]. The study of anastomosing rivers began in the 1970s, which is the shortest-lived and least studied river pattern among all known river patterns.
A series of in-depth studies have been conducted on the channel morphology, formation and evolution, and sedimentary characteristics of anastomosing rivers (e.g., [6,7,8,9,10,11,12,13,14,15,16,17,18,19]) The evolution rule of anastomosing rivers in different climatic zones and the distribution and transformation of anastomosing river patterns with other river patterns under different geomorphic backgrounds have also been explored (e.g., [20,21,22,23,24,25]). The majority of the riverbed materials in these anastomosing rivers are sandy sediments, while a smaller amount are silty or muddy sediments, mainly referring to abandoned or swampy anastomosing channels with very slow flow velocities. Recently, some researchers have begun preliminary research on gravel-bed anastomosing rivers with riverbed materials consisting of gravel sediments [27,28]. In contrast, there are few studies on the hydrodynamics of anastomosing rivers [14,15,16], due to the difficulty in obtaining hydrological data for such rivers.
Hydrodynamic research on alluvial rivers often involves parameters such as velocity, discharge, stream power, etc., which are primarily obtained based on long-term hydrological data observation at fixed cross-sections of the rivers. For alluvial river patterns with a single channel, the observation of hydrological data is relatively convenient. Conversely, it is extremely inconvenient to establish fixed hydrological stations for long-term hydrological observation in anastomosing rivers due to the presence of multiple channels (2–5 or more) and extensive inter-channel wetlands at a cross-section (Figure 1). As a result, many anastomosing rivers worldwide are unable to establish hydrological stations that can be used for long-term hydrological observation. This impedes further research on the hydrodynamic characteristics and mechanisms in the formation and evolution of anastomosing rivers.
Field investigation for real-time observation of hydrological data of anastomosing rivers has some limitations and difficulties. Firstly, bankfull discharge occurs only once in several years, so it is unnecessary to measure the bankfull flow velocity at any time. Secondly, it is very inconvenient to observe the velocities at different water levels for each channel of the anastomosing rivers in real-time observation, so it is difficult to obtain the curve between water level and velocity, which can be used to calculate the velocity of bankfull flow. Thirdly, to obtain the mean flow velocity under a certain water level for a river channel, several vertical surveying lines need to be set up, and each vertical line needs to observe more than 5 points of data, and then calculate the cross-section mean velocity value under the water level. When the water level changes, the cross-section mean velocity needs to be re-observed according to the above steps. For the multiple channels of the anastomosing rivers, the workload is huge and the efficiency is low. In view of this, many anastomosing rivers worldwide lack the observed values of hydrodynamic parameters.
In order to study the evolution characteristics of anastomosing rivers and their differences with other river patterns, it is necessary to understand the hydrodynamic characteristics of anastomosing rivers in different areas under different water levels including bankfull stage. However, due to the difficulties and limitations of field investigation and observation, how to obtain the hydrodynamic parameters of anastomosing rivers without hydrological observation data is one of the important scientific potential problems. Therefore, the objective of this work is to construct alternative formulas for estimating the typical hydrodynamic parameters of anastomosing rivers by using the morphological parameters of the river channels or the channels below the assumed water level, such as the channel depth (scale factor), channel width/depth ratio (morphological factor), and channel gradient (gradient factor). The novel method is called Expression of Channel Morphological Parameters (ECMP), and it is verified by the measured data of the anastomosing channels in the upper Columbia River, Canada.
2. Basic parameters and calculation formulas of river hydrodynamics
There are numerous parameters that characterize river hydrodynamics, many of which are commonly employed in the research practices of river geomorphology. The following are some of these commonly used parameters: 1) Water surface gradient, also known as energy slope, which reflects the slope of the river’s surface; 2) The average velocity of a cross-sectional area, which characterizes the flow characteristics of the water; 3) Discharge, which indicates the flow flux in a unit time; 4) Stream power, both in total and specific forms, which reflects the energy consumption parameters of the river flow in relation to promoting the movement of sediment within the riverbed; and 5) Sediment transport rate, which indicates the ability of the current to transport sediment. Additionally, three well-known equations in river hydrodynamics, that is the flow continuity equation (Formula 1), flow motion equation (Formula 2), and specific sediment discharge of water flow (Formula 3, applicable to the calculation of river sediment dominated by suspended load movement), provide means to solve for some of the aforementioned parameters.
In formulas (1–3), Q represents water discharge (m3/s), U represents the average velocity in a flow cross-section (m/s), W signifies the width of the water surface (m), D denotes the water depth (m), n represents Manning's roughness coefficient (dimensionless), r stands for the hydraulic radius (m), S denotes the gradient of the water surface (dimensionless or m/m), SS represents the bedload content in suspended sediment (dimensionless), g represents the gravity acceleration (9.8 m/s2), and 𝜈 represents the settlement velocity of bedload in suspended sediment (m/s). Finally, k and m represent coefficients and exponents, respectively.
Formula (3) can be used to calculate the specific sediment discharge of river flow. However, the parameters involved are relatively complex and some of them, such as settlement velocity, are difficult to observe accurately. Furthermore, the use of empirical parameters may be limited in different river environments, and the coefficient k and exponent m need to be determined accurately. All these practical problems make the application of the equation very inconvenient. If the calculation of sediment discharge is not involved but only the sediment transport capacity is compared, it is more convenient to use the energy consumption rate index. There are two forms of energy consumption rate to reflect the sediment transport capacity of a river. One is the gross stream power (Ω), which represents the power loss per unit length on a riverbed (Formula 4), and another is the specific stream power, which represents the power loss per unit area on a riverbed (Formula 5).
In formulas (4) and (5), Ω represents the gross stream power (W/m), ω represents the specific stream power (W/m2), γ denotes the specific gravity of water (1000kg/m3), g denotes the gravity acceleration (9.8 m/s2), Q denotes the water discharge(m3/s), S denotes the channel gradient (dimensionless or m/m), W denotes water surface width (m).
The preceding formulas all contain, either directly or indirectly, the kinetic parameter of average velocity U. Therefore, the average velocity serves as the foundation for these formulas, whether it is derived through field observation or indirect computation. Additionally, the hydraulic radius is a highly significant parameter that is inextricably linked to river channel morphology. A detailed analysis of their potential quantitative relationship will be presented below.
When the river flow reaches bankfull condition, the parameters on the left side of the preceding equations can be respectively referred to as the bankfull discharge, bankfull velocity, bankfull sediment transport rate, bankfull gross stream power, and bankfull specific stream power. In this scenario, the average depth and width of the flow cross-section can be deemed as the average depth and width of the channel cross-section, respectively, and the water surface gradient is approximately equal to the channel gradient.
The equations and related variables presented above are analytical formulas established for single-channel rivers. When it comes to anastomosing rivers with multiple channels, the velocity observation and corresponding hydrological calculations can be particularly complex and time-consuming. To avoid the huge workload of fluid characteristics observation and obtain these hydrodynamic parameters conveniently, some independent variables in the above formulas may be replaced by more intuitive and easily measurable river channel morphological parameters.
From the perspective of logical reasoning and river evolution trends, the channel morphology or flow cross-section shape in a river system is the long-term response to the hydrodynamic force under the corresponding water level. Conversely, the value of the hydrodynamic parameters under the corresponding water level can be inferred by using the relevant morphological parameters of these sections. If the above hypothesis is true, it would be a highly necessary and significant attempt to establish more convenient expression formulas with channel morphological parameters as independent variables for the hydrodynamic calculations of anastomosing rivers.
3. Establishment of ECMP method
3.1. Relationship between hydraulic radius and water depth, width-depth ratio
River flow velocity is one of the key indicators for assessing the magnitude of fluid dynamics. According to the flow motion equation (Formula 2), it is evident that the average velocity of water flow is primarily influenced by the hydraulic radius and water surface gradient. Additionally, it is also influenced by boundary material conditions, which can be characterized by the Manning roughness coefficient n. Given a specific cross-section of a river course, the boundary material composition and shoreline vegetation status are determined, allowing for a precise determination of the n value.
Usually, the average velocity of river flow changes with the change of water level. Therefore, the change of water level brings obvious uncertainty to the comparison between different river flows. For a given cross-section of a particular river course, the average velocity at bankfull discharge remains relatively stable in a short period of time, making it suitable for comparing the hydrodynamic forces of different river courses under bankfull discharge conditions. Therefore, the average velocity at bankfull discharge is typically used as a significant indicator of river dynamics in fluvial geomorphology.
Assuming that the cross-section of a river channel is rectangular (Figure 2a), the width of the channel Wbf is equal to the width of the water surface W. If the depth of the channel and the water flow are Dc and D, respectively, the width-depth ratio of the water flow is R = W/D, and the width of the water flow W can be expressed as RD. In the case of an irregular channel cross-section (Figure 2b), the average depths D and Dc are adopted for the water flow and channel cross-sections, respectively. For the water flow, when it does not reach the bankfull stage, its wetted perimeter (the boundary line between the flow and the channel in a cross-section) x (unit: m) can be expressed by formula (6).
Then, its hydraulic radius r (unit: m) can be expressed by the following formula.
Figure 2.
Schematic diagram of morphological parameters at (a) rectangular and (b) irregular cross-sections of single channel of anastomongsing river.
Figure 2.
Schematic diagram of morphological parameters at (a) rectangular and (b) irregular cross-sections of single channel of anastomongsing river.
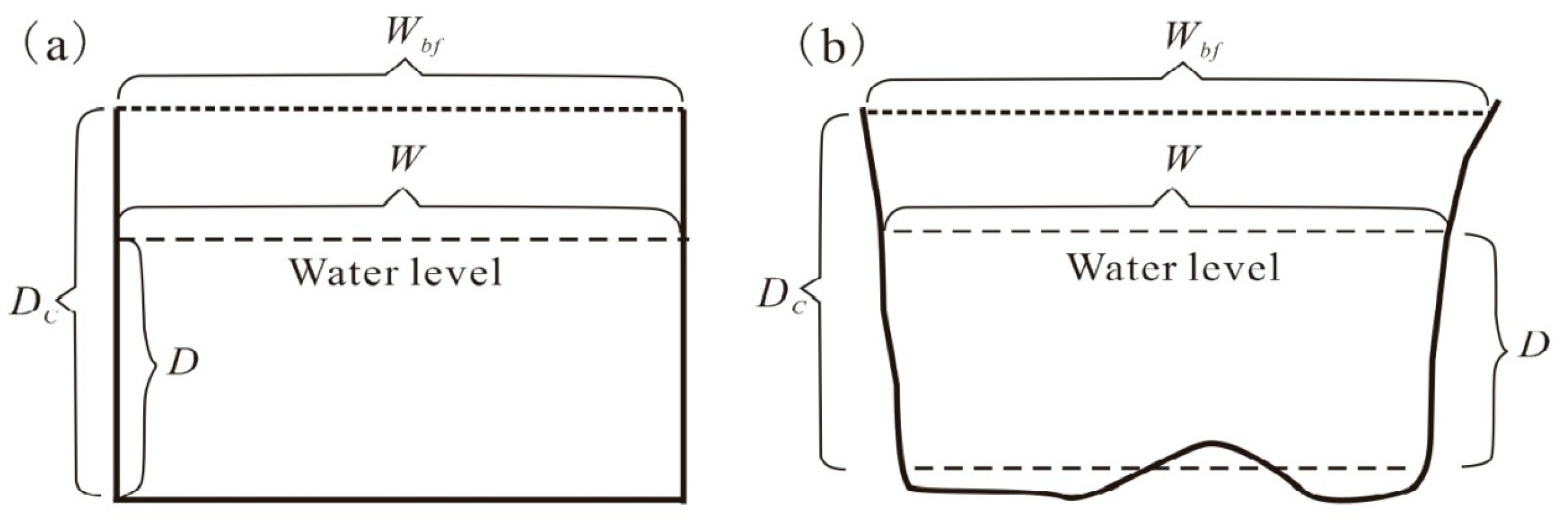
It is evident from formula (7) that the hydraulic radius is determined by the channel shape factor (width-depth ratio) and the scale factor (water depth). As the width-depth ratio of the water flow increases, the impact of the water depth factor on the hydraulic radius gradually assumes a more dominant role.
3.2. Relationship between hydraulic radius and channel width-depth ratio
At bankfull discharge, the water flow cross-section is equal to the channel cross-section. At this point, the water depth D matches the channel depth Dc, the water flow cross-section area A corresponds to the channel cross-section area Ac, and the water flow width-depth ratio R matches the channel width-depth ratio Rc (=Wbf/Dc). Hence, the calculation formula for the hydraulic radius (Rc) at bankfull discharge can be phrased as:
Formula (8) comprises two types of independent variables: channel depth Dc and channel width-depth ratio Rc. Among them, the channel width-depth ratio Rc reflects the morphological factor of a channel cross-section, which serves as a significant measurement index for assessing the river's cross-channel morphological characteristics and diagnosing the channel pattern [1,3,29].
The channel depth Dc serves as a scaling factor that indicates the size (scale) of a river channel while maintaining a constant width-depth ratio. This formula can be interpreted as follows: The hydraulic radius of any river that can be approximated as having a rectangular cross-section is equal to the ratio of water depth times the ratio of width to depth of the water flow cross-section divided by the sum of that ratio and an additional value of 2. However, for U–shaped river channels, the formula for calculating the hydraulic radius remains the same, except that the average water depth is used instead.
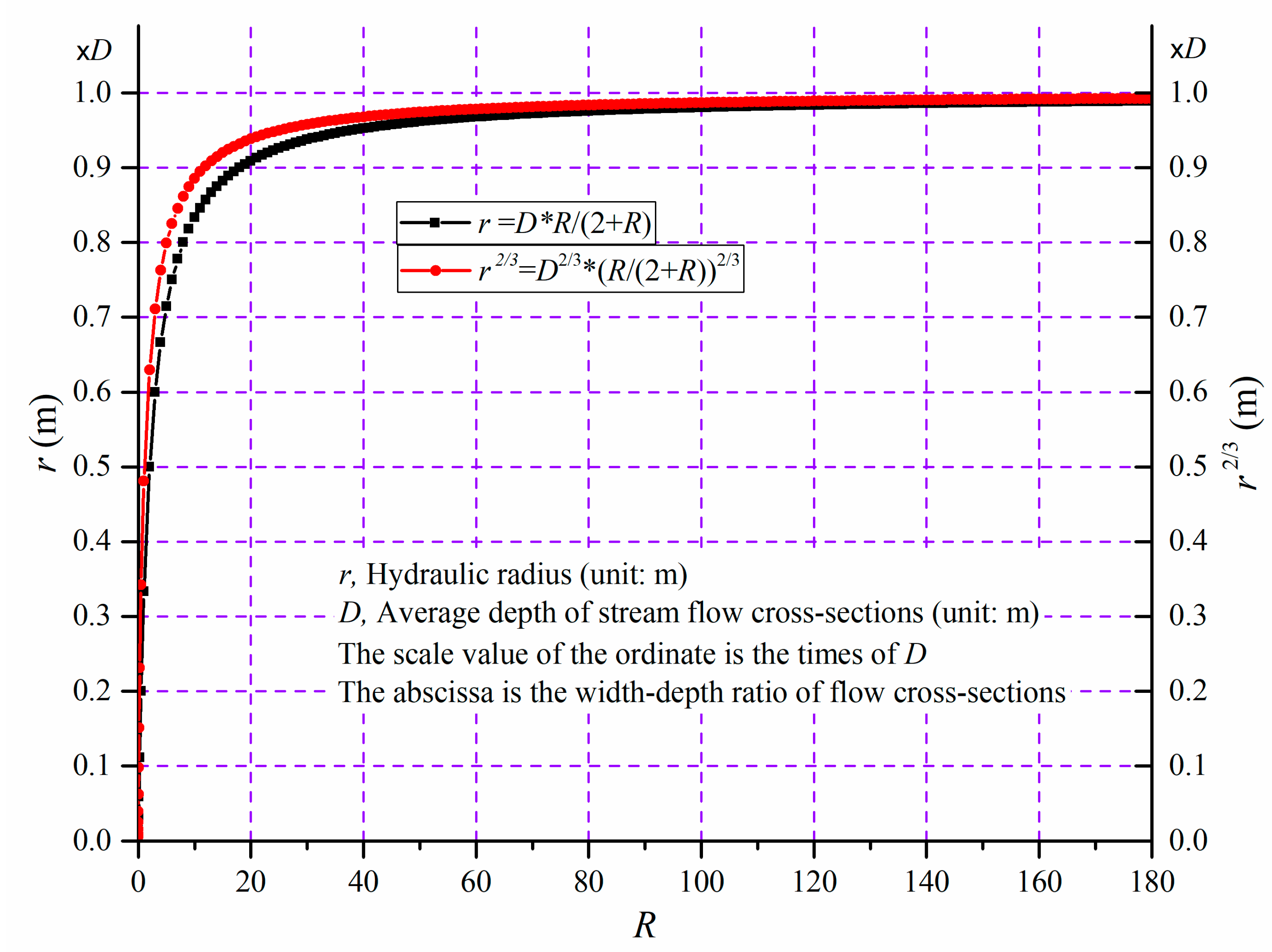
As a variable in a mathematical expression, Rc can have any value. However, as a channel morphological parameter, its variation has an upper limit. By analyzing and summarizing the data of the channel width-depth ratio of various alluvial rivers around the world, it can be seen that the width-depth ratio of the alluvial channels can reach hundreds, while those with more than a thousand are very rare. As shown in Figure 3, when the channel width-depth ratio is less than 60, the hydraulic radius of the channel significantly increases with the increase of the channel width-depth ratio. When the channel width to depth ratio is greater than 60, the hydraulic radius of the river slowly increases with the increase of the channel width to depth ratio. When the ratio of the width to depth is very large (>120), the ratio (R/(2+R)) in equation (8) tends to 1 in the process of gradual increase, then the maximum hydraulic radius is infinitely close to the asymptote limited by water depth D, that is, the hydraulic radius can be approximately regarded as equal to the depth.
As mentioned earlier, the hydraulic radius of a river is a function of the water depth and the width-depth ratio of the river's cross-section. However, each independent variable has its respective dominant advantage intervals (as shown in Figure 3). For instance, when the channel width-to-depth ratio is 100, 140, and 180, the hydraulic radius of depth D calculated using formula (8) is respectively 0.980 times, 0.986 times, and 0.989 times the actual depth. It is evident from these calculations. When the channel width-to-depth ratio exceeds 100, the hydraulic radius can be approximated as the water depth. On the other hand, when this ratio falls below 40, the hydraulic radius is significantly less than the water depth, making it impossible to replace one with the other (as shown in Figure 3). Finally, when this ratio dips below 10, the hydraulic radius becomes highly dependent on any changes in this ratio and its value increases rapidly with any increase in the ratio.
The width-depth ratio of the channel cross-sections in anastomosing rivers is less than 40, which serves as a necessary condition for identifying the anastomosing river pattern [1,3,11]. As shown in Figure 3, the hydraulic radius of a channel with a width-depth ratio less than 40, particularly one with a width-depth ratio less than 25, is not solely dependent on the water depth but also significantly affected by the width-depth ratio of the channel cross-section. For example, when the width-depth ratio (R) of the channel is 7.3, the hydraulic radius r is 0.78 times the water depth. When R is 25.2, r is 0.93 times the water depth. When R is 40, r is 0.95 times the water depth. Qian et al. [30] used water depth instead of hydraulic radius in their work, which is applicable to braided rivers with a large width to depth ratio. However, replacing the hydraulic radius with the depth of water for all anastomosing channels and for straight channels with similar gradients and channel boundary material to anastomosing channels is inaccurate due to their small width-depth ratio (<40).
Figure 3.
Relationship between hydraulic radius and water depth and width-depth ratio of flow cross-sections (D represents the average depth and R represents the width-depth ratio of cross-sections of stream flows).
Figure 3.
Relationship between hydraulic radius and water depth and width-depth ratio of flow cross-sections (D represents the average depth and R represents the width-depth ratio of cross-sections of stream flows).
3.3. Average velocity of water flow cross-section
The flow motion equation (Formula 2) can be used to solve the average flow velocity of the flow cross-section under different water levels. In a given channel cross-section, both the water depth and the water surface width vary with changes in water level. The gradient of the water surface may vary, but this change is typically ignored. Since the hydraulic radius is constantly changing with the variations in water level, the average velocity U of the cross-section will also change with the changes in water depth (and water level). If the channel morphological parameters (Dm and R) are taken as independent variables to replace the hydraulic radius in equation (2), then the calculation formula for the average flow velocity at different water depths in a channel can be obtained:
The independent variables in Equation (9) are three factors related to the channel below the water surface and its morphology, namely, the average depth Dm of the water flow cross-section (a scale factor related to the channel below the water surface), the width-depth ratio R of the flow section (a shape factor related to the channel below the water surface), and the water surface gradient S (approximately equal to the channel gradient Sc, a gradient factor related to the channel).
When the flow reaches the bankfull stage, the morphological parameters of the flow cross-section are equal to those of the corresponding channel cross-section. That is, the average depth and width-depth ratio of the water flow at the bankfull level are equal to the average depth Dcm and the width-depth ratio of the channel Rc, respectively, and the water surface gradient is equal to the channel gradient Sc. In this case, formula (9) can have the following special cases:
Clearly, the three independent variables in formula (10)—Dcm, Rc, and Sc—represent the scale factor, shape factor, and gradient factor of the channel, respectively. In other words, the average flow velocity of the water flow in the bankfull state is entirely dependent on the shape, scale, and gradient of the channel. In anastomosing river systems, the average velocity of water flow among different channels will vary due to differences in at least one of the three morphological parameters of the channels: their shape, scale, and gradient.
3.4. Discharge of water flow cross-section
The flow discharge refers to the total volume of water flowing through a cross-section per unit time. According to the flow continuity equation (Formula 1), it is the product of the average velocity and the area of the cross-section. By substituting equation (9) into equation (1), the following relationship can be derived:
Equation (11) indicates that river discharge can be expressed as a function of three factors—the shape, scale, and water surface gradient of the flow cross-section. When the river flow reaches the bankfull stage, formula (11) can be transformed into a function relationship between bankfull discharge and the channel-related parameters (which as the independent variables).
Bankfull discharge is a crucial parameter in river flow dynamics, which is influenced by the channel's scale factor, shape factor, and gradient factor. Therefore, for the channels of ephemeral or abandoned anastomosing rivers, regardless of whether there is water flow passing through or reaching the bankfull level, the bankfull discharge can be calculated using formula (12), avoiding the need to wait for years until a bankfull flow occurs for measurement.
In an anastomosing river system, the discharge of each individual channel can be calculated using Formula (11), while sometimes it is necessary to know the total discharge (Qt) of the entire cross-section of the anastomosing river system. To achieve this, the discharges of all active channels in the section can be summed up using Formula (13).
In Equation (13), P represents the sequential number of the channel through which water is flowing on a given cross-section of the anastomosing river system (excluding any abandoned river courses).
Similarly, formula (14) can be used to calculate the total bankfull discharge (Qct) when all the active channels in a cross-section of the anastomosing river system reach the bankfull state.
3.5. Stream power of anastomosing channel
The formulas for gross stream power and specific stream power (formulas 4, 5) are the most commonly used formulas to calculate stream power. The core independent variables of formula (4) are water discharge and channel gradient, while for formula (5) they are water discharge, channel gradient, and channel width under bankfull state. The discharge is the value to be observed or calculated indirectly based on relevant empirical relations. However, it is difficult to apply these formulas in anastomosing rivers where hydrological data are not available. By correlating equation (12) and (4), a calculation formula of total (bankfull) stream power (Ωbf) can be obtained, expressed solely by channel morphological parameters.
Clearly, the three independent variables, Dcm, Rc, and Sc, in Equation (15) represent the channel average depth, channel width-depth ratio, and channel gradient, respectively. These are all channel morphological parameters, and their calculation is not restricted by whether there is water flow in the channel or whether the water flow reaches the bankfull stage, etc. Additionally, there is no need to observe the discharge value in detail.
By solving Equations (6) and (15), the expression formula for specific stream power (ωbf) in the bankfull stage, expressed solely by channel morphological parameters, can be obtained as follows:
The independent variable in Equation (16) is the same as that in Equation (15). Once the necessary channel morphological parameters are obtained through on-site measurement, this equation can be used to numerically calculate specific stream power in anastomosing channels without measured hydrological data. However, specific stream power needs to be calculated for each channel in an anastomosing river system separately, due to the significant differences in specific stream power among different river channels with varying scales or shapes. In fact, the width-to-depth ratio and channel gradient are the main parameters distinguishing different river patterns, while the channel depth serves only as a scale factor for a river and alone cannot determine the characteristics of diverse river patterns. Evidently, the specific stream power of anastomosing channels can also be expressed as a function of channel shape factor, scale factor, and gradient factor.
If it is necessary to calculate stream power when the water level is below the bankfull level, the average water depth (Dm), width-depth ratio (R), and water surface slope (S) of the water flow can be used in place of the channel depth (Dcm), width-depth ratio (Rc), and channel gradient (Sc) in Formulas (15) and (16), respectively. This leads to Formulas (17) and (18), which can be used to calculate the gross stream power (Ω) and specific stream power (ω) of the water flow at the unreached bankfull stage.
4. Validation of the ECMP method
The anastomosing river in the upper reach of the Columbia River in Canada is one of the most representative rivers in the world in terms of studies on sedimentology and geomorphology. The observation of dynamic parameters for the river is relatively complete, which is rare in this river pattern. In order to verify the applicability of the ECMP method and its expression formulas under bankfull discharge conditions, the measured hydrodynamics parameters of the five active channels in the anastomosing river reach (Table 1) are selected as the comparison object to verify the calculated values of corresponding parameters calculated according to the ECMP method. The measured data used for comparison are shown in Table 1, collected from the literature [16], and the corresponding hydrodynamic parameters calculated according to the ECMP method are shown in Table 2.
According to Makaske et al. [16], detailed observations were made on the stream flow velocity of the 5 channel cross-sections in the anastomosing river reach (Figure 4a) during the bankfull stage. Other hydrodynamic parameters, such as discharge and stream power, were calculated using traditional calculation formulas and the observed velocity and other relative values (Table 1).
Table 1.
The measured values of the morphological and dynamic parameters at near banfull stage of the anastomosing channels in the upper Columbia River, Canada (collected from the literature [16]).
Table 1.
The measured values of the morphological and dynamic parameters at near banfull stage of the anastomosing channels in the upper Columbia River, Canada (collected from the literature [16]).
| № | W | Dmax | Rmin | D | S | r | Ubf | Qbf | ω | Ω |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 19.3 | 2.12 | 9.1 | 1.54 | 0.000078 | 1.40 | 0.32 | 9.5 | 0.38 | 7.3 |
| 2 | 24.8 | 1.08 | 23 | 0.65 | 0.000074 | 0.60 | 0.15 | 2.4 | 0.07 | 1.7 |
| 3 | 56.03 | 5.85 | 9.6 | 4.37 | 0.000068 | 4.10 | 0.79 | 193.5 | 2.3 | 128.9 |
| 4 | 20.7 | 1.04 | 19.9 | 0.75 | 0.000076 | 0.80 | 0.35 | 5.4 | 0.19 | 3.9 |
| 5 | 18.63 | 3.17 | 5.9 | 1.99 | 0.000074 | 1.80 | 0.40 | 14.8 | 0.58 | 10.8 |
Note: № means the number of the anastomosing channels; W represents the channel width (m); Dmax represents the maximum channel depth (m); Rmin represents the ratio of channel width to maximum depth (minimum width/depth ratio, m/m); D represents the average channel depth (m); S represents channel gradient (dimensionless); r is the hydraulic radius; Ubf represents the average velocity (m/s) of bankfull discharge. Qbf is the discharge of bankfull stage (m3/s); ω represents specific stream power (W/m2); Ω represents the gross stream power (W/m, the value calculated by present author according to the measured data).
Based on the measured hydrological data [16], the author of this article supplements the calculation of the total energy consumption rate for these 5 channels. Additionally, the traditional calculation method for river width-depth ratio, which is calculated by dividing the river width by the average river depth, was corrected for its unreasonable calculation of the width-depth ratio by dividing the river width by the maximum river depth to obtain the minimum width-depth ratio. To verify the effectiveness of the ECMP method, it is necessary to know the Manning roughness coefficient n value for each channel. Here, the measured flow velocity, hydraulic radius, and river gradient values reported in the literature were used to calculate n values (Table 2) to meet the roughness constant term in the ECMP calculation formula. Then, the ECMP formula was used to calculate the average flow velocity, discharge, specific stream power, and gross stream power for these 5 channels in the near bankfull state (Table 2), and scatter plots were created with the corresponding measured hydrodynamic parameters (Figure 4). As shown in Figure 4, the calculated hydrodynamic parameter values using the ECMP method are very close to their corresponding measured values, with most of the scatter points distributed along the diagonal y = x. Although only a few scatter points deviate slightly from this line, the deviation is very small. This indicates that the calculated and measured hydrodynamic parameter values are very close and that the ECMP method performs well in calculations.
Table 2.
The calculated hydrodynamic parameters by ECMP method under banfull stage of the anastomosing channels in the upper Columbia River, Canada.
Table 2.
The calculated hydrodynamic parameters by ECMP method under banfull stage of the anastomosing channels in the upper Columbia River, Canada.
| № | n | R | r | Ubf | Qbf | ω | Ω |
|---|---|---|---|---|---|---|---|
| 1 | 0.035 | 12.5 | 1.33 | 0.305 | 9.1 | 0.36 | 6.9 |
| 2 | 0.041 | 38.2 | 0.62 | 0.152 | 2.5 | 0.07 | 1.8 |
| 3 | 0.027 | 12.8 | 3.78 | 0.741 | 181.5 | 2.16 | 120.9 |
| 4 | 0.021 | 27.6 | 0.70 | 0.327 | 5.1 | 0.18 | 3.8 |
| 5 | 0.032 | 9.4 | 1.64 | 0.374 | 13.9 | 0.54 | 10.1 |
Note: The Manning roughness coefficient n for each river channel is calculated from the flow motion equation based on measured flow velocity and gradient values; R represents the ratio of river width to average depth (average width-depth ratio, m/m); the meaning of other symbols is the same as in Table 1.
Figure 4.
Comparison of measured values of hydrodynamic parameters (makaske et al., 2009) and calculated values by ECMP method under banfull stage of the 5 anastomosing channels in the upper Columbia River, Canada.
Figure 4.
Comparison of measured values of hydrodynamic parameters (makaske et al., 2009) and calculated values by ECMP method under banfull stage of the 5 anastomosing channels in the upper Columbia River, Canada.

To further verify the effectiveness of the ECMP method, a difference evaluation was conducted between the calculated and measured values of hydrodynamic parameters, where the measured values of hydrodynamic parameters were used as the comparison object to determine the relative error of their corresponding calculated values. The relative error values of the discharge, average velocity, specific stream power, and gross stream power are shown in Table 3, with the relative error ranges of −6.6% to 1.3%, −6.2% to 4.2%, −10.0% to 0%, and −6.5% to 0%, respectively. This also indicates that, except for the absolute value of the relative error of the ECMP method calculation for individual parameters in individual river channels, which is slightly higher than 10%, most of the relative errors are less than 6.6%. This fully demonstrates the high accuracy and effectiveness of the ECMP method for calculating the hydrodynamic parameters of anastomosing rivers.
5. Conclusions
Through the construction of the ECMP method and derivation of its core formula, as well as verification of its feasibility, the following main conclusions can be drawn:
- 1)
- The ECMP method is a method for obtaining hydrodynamic parameters of rivers without hydrological observations, especially for anastomosing rivers. It is based on the idea that a certain hydrodynamic parameter is a function of three independent variables: the shape factor, scale factor, and gradient factor of the flow cross-section or channel cross-section below corresponding water level.
- 2)
-
The hydrodynamic parameters of rivers that can be calculated using the ECMP method mainly include the following categories, but are not limited to:
- (1)
- The hydraulic radius parameter of a river can be expressed as a function of the scale factor (average depth) and shape factor (width-depth ratio) of the flow cross-section. The hydraulic radius at low water can be expressed as a function of the scale factor and shape factor of the river channel.
- (2)
- When the water flow has not reached the low water level, its hydrodynamic parameters (average velocity, discharge, total discharge, total energy consumption rate, specific energy consumption rate, etc.) can be expressed as a function of the scale factor (average depth), shape factor (width-depth ratio of the flow cross-section) and gradient factor (water surface gradient, which can be replaced by the river gradient) of the flow cross-section.
- (3)
- When the river flow rises to the bankfull stage, its river dynamics parameters (average velocity, bankfull discharge, total bankfull discharge, total bankfull stream power, and bankfull specific stream power) can be expressed as a function of the scale factor (average channel depth), shape factor (width-depth ratio of channel cross-section), and gradient factor (channel slope) as independent variables.
- 3)
- The validation results of the ECMP method indicate that this method has high computational accuracy and small relative error, making it an efficient and convenient method for calculating river hydrodynamic parameters. It has great application value in study on fluvial geomorphology and river hydrodynamics, and even in the reconstruction of ancient fluvial hydrology and hydrodynamics.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No. 42371010, 41971004) and the National Key Research and Development Program of China (Grant No. 2022YFC3203903).
Conflicts of Interest
The author declares no conflicts of interest.
References
- Rust, B.R. A classification of alluvial channel systems. in Fluvial sedimentology; Miall, A.D. ed.; Can. Soc. Petrol. Geol. Mem. 1978, 5, 187–198. [Google Scholar]
- Smith, D.G. Anastomosed fluvial deposits: modern examples from western Canada. In Modern and Ancient Fluvial Systems; Collinson, J.D., Lewin, J. eds.; Special Publication of the International Association of Sedimentologists. Blackwell: London, 1983, 155–168. London.
- Wang, S. , Ren, M., A new classification of fluvial rivers according to channel planform and sediment characteristics. Acta Geoscientia Sinica 1999, 17, 240–246. (In Chinese) [Google Scholar]
- Nanson, G.G. , Rust, B.R., Taylor, G. Coexistent mud braids and anastomosing channel in an arid-zone river: Cooper Creek, central Australia. Geology, 1986, 14, 175–178. [Google Scholar] [CrossRef]
- Wang, S. , Xie, X., Cheng, D. The progress in the research of anastomosing river. Progress in Geography, 2002, 21, 12–21. (In Chinese) [Google Scholar]
- Smith, D.G. , Smith, N.D. Sedimentation in anastomosed river systems: examples from alluvial valleys near Banff, Alberta. Journal of Sedimentary Petrology, 1980, 50, 157–164. [Google Scholar] [CrossRef]
- Rust, B.R. Sedimentation in an arid-zone anastomosing fluvial system: Cooper's Creek, central Australia. Journal of Sedimentary Petrology, 1981, 51, 745–755. [Google Scholar]
- Smith, D.G. Anastomosing river deposits, sedimentation rates and basin subsidence, Magdalena River, northwest-ern Columbia, South America. Sediment. Geol., 1986, 46, 177–196. [Google Scholar] [CrossRef]
- Knighton, A.D. , Nanson, G.C. Anastomosis and the continuum of channel pattern. Earth Surf. Procs. Land., 1993, 18, 613–625. [Google Scholar] [CrossRef]
- Nanson, G.G. , Knighton, A.D. Anabranching rivers: their cause, character and classification. Earth Surf. Procs Land., 1996, 21, 217–239. [Google Scholar] [CrossRef]
- Makaske, B. Anastomosing rivers: a review of their classification, origin and sedimentary products. Earth-Science Reviews, 2001, 53, 149–196. [Google Scholar] [CrossRef]
- Makaske, B. , Smith, D.G., Berendsen, H.J.A. Avulsions, channel evolution and floodplain sedimentation rates of the anastomosing upper Columbia River, British Columbia, Canada. Sedimentology, 2002, 49, 1049–1071. [Google Scholar] [CrossRef]
- Wang, S. Architectures, relationships between discharges and width/depth ratios of stream cross profiles, and stream powers of anastomosing rivers. Acta Sedimentologica Sinica, 2003, 21, 565–570. (In Chinese) [Google Scholar]
- Wang, S. , Ni, J., Wang, G., Cheng, D., Zhang, O. Hydrological processes of an anastomosing river system on the Zhujiang River delta, China. Journal of Coastal Research 2004, 2004, 124–133. [Google Scholar]
- Wang, S. , Chen, Z., Smith, D.G. Anastomosing river system along the middle Yangtze River Basin, Southern China. Catena 2005, 60, 147–163. [Google Scholar] [CrossRef]
- Makaske, B. , Smith, D.G., Berendsen, H.J.A., de Boer, A.G., van Nielen-Kiezebrink, M.F., Locking, T. Hydraulic and sedimentary processes causing anastomosing morphology of the upper Columbia River, British Columbia, Canada. Geomorphology, 2009, 111, 194–205. [Google Scholar] [CrossRef]
- Kleinhans, M.G. , De Haas, T., Lavooi, E. Makaske B. Evaluating competing hypotheses for the origin anddynamics of river anastomosis. Earth Surf. Proc. Land., 2012, 37, 1337–1351. [Google Scholar] [CrossRef]
- Rozo, M,G. , Nogueira, A.C.R., Truckenbrodt, W. The anastomosing pattern and the extensively distributed scroll bars in the middle Amazon River. Earth Surface Processes and Landforms, 2012, 37, 1471–1488. [Google Scholar] [CrossRef]
- Makaske, B. , Lavooi, E., Haas, T.D., Kleinhans, M.G., Smith, D.G. Upstream control of river anastomosis by sediment overloading, upper Columbia River, British Columbia, Canada. Sedimentology 2017. [Google Scholar] [CrossRef]
- Torngvist, T.E. Holocene alternation of meandering and anastomosing fluvial systems in the Rhine-Meuse delta (central Netherlands) controlled by sea-level rise and subsoil erodibility. J. Sedimemt. Petrol., 1993, 63, 683–693. [Google Scholar]
- Ni, J. , Wang, S., Wang, G. River patterns and spatial and temporal transformation modes. International Journal of Sediment Research, 2000, 15, 357–370. [Google Scholar]
- Wang, S. Analysis of river pattern transformations in the Yellow River basin. Progress in Geography, 2008, 27, 10–17. (In Chinese) [Google Scholar]
- Li, Z. , Wang, Z., Yu, G. River pattern transition and its causes along Maqu reach of Yellow River source region. Journal of Sediment Research 2013, 1–15. (In Chinese) [Google Scholar]
- Li, Z. , Wang, Z., Pan, B., Du, J., Brierley, G. Analysis of controls upon channel planform at the First Great Bend of the Upper Yellow River, Qinghai-Tibet Plateau. Journal of Geographical Sciences 2013, 23, 833–848. [Google Scholar] [CrossRef]
- Yu, G.A. , Liu, L., Li, Z.W., Li, Y.F., Huang, H.Q., Brierley, G., Blue, B., Wang, Z.Y., Pan, B.Z. Fluvial diversity in relation to valley setting in the source region of the Yangtze and Yellow Rivers. Journal of Geographical Sciences, 2013, 23, 817–832. [Google Scholar] [CrossRef]
- Liu, B. , Wang, S. Planform characteristics and developing of interchannel wetlands in a gravel-bed anastomosing river, Maqu Reach of the Upper Yellow River. Journal of Geographical Sciences 2017, 27, 1376–1388. [Google Scholar] [CrossRef]
- Gao, C. , Wang, S. Distribution rule of active channels under different discharge of anastomosing reaches in the Tibetan Plateau of the Yellow River. Scientia Geographica Sinica 2018, 38, 618–627. (In Chinese) [Google Scholar]
- Gao, C. , Wang, S. Evolution characteristics of the gravel-bedded anastomosing river at the Qihama reach in the First Great Bend of the Yellow River since 1990. Journal of Geographical Sciences, 2019, 29, 306–320. [Google Scholar] [CrossRef]
- Huang, H.Q. , Deng, C., Nanson, G.C., Fan, B., Liu, X.F., Liu, T.H., Ma, Y.X. A test of equilibrium theory and a demonstration of its practical application for predicting the morphodynamics of the Yangtze River. Earth Surface Processes and Landforms, 2014, 39, 669–675. [Google Scholar] [CrossRef]
- Qian, N. Zhang, R., Zhou, Z. In Fluvial Process; Science Press: Beijing, China, 1987. (In Chinese) [Google Scholar]
Figure 1.
Anastomosing multiple-channel system in Qihama reach of the upper Yellow River (Flowing eastward and more than 5 channels in the cross section).
Figure 1.
Anastomosing multiple-channel system in Qihama reach of the upper Yellow River (Flowing eastward and more than 5 channels in the cross section).

Table 3.
Relative errors between the calculated and measured hydrodynamic parameter values of the anastomosing channels in the upper Columbia River, Canada (unit: %).
Table 3.
Relative errors between the calculated and measured hydrodynamic parameter values of the anastomosing channels in the upper Columbia River, Canada (unit: %).
| № | Ubf | Qbf | ω | Ω |
|---|---|---|---|---|
| 1 | −4.7 | −4.2 | −5.3 | −5.5 |
| 2 | 1.3 | 4.2 | 0.0 | 0.0 |
| 3 | −6.2 | −6.2 | −6.1 | −6.2 |
| 4 | −6.6 | −5.6 | −10.0 | −5.0 |
| 5 | −6.5 | −6.1 | −6.9 | −6.5 |
Note: The meaning of the symbols is the same as in Table 1.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






