Prerpints.org logo
Preprint
Article

Stereo Matching Method for Remote Sensing Images Based on Attention and Scale Fusion

Altmetrics

Downloads

88

Views

26

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

14 November 2023

Posted:

15 November 2023

You are already at the latest version

Alerts
Abstract
With the development of remote sensing satellite technology for Earth observation, remote sensing stereo images have been used for three-dimensional reconstruction in various fields, such as urban planning and construction. However, remote sensing images often include noise, occluded regions, weakly textured areas and repeated textures, which can lead to reduced accuracy in stereo matching and affect the quality of the 3D reconstruction results. To reduce the impact of complex scenes in remote sensing images on stereo matching and to ensure both speed and accuracy, we propose a new end-to-end stereo matching network based on convolutional neural networks (CNNs). The proposed stereo matching network can learn features at different scales from the original images and construct cost volumes with varying scales to obtain richer scale information. Additionally, when constructing the cost volume, we introduce negative disparity to adapt to the common occurrence of both negative and nonnegative disparities in remote sensing stereo image pairs. For cost aggregation, we employ a 3D convolution-based encoder-decoder structure that allows the network to adaptively aggregate information. Before feature aggregation, we also introduce an attention module to retain more valuable feature information, enhance feature representation, and obtain a higher-quality disparity map. By training on the publicly available US3D dataset, we obtain the accuracy that 1.115 pixel in end-point error (EPE) and 5.32% in the error pixel ratio (D1) on the test dataset, and the inference speed is 92 ms. Comparing our model with existing state-of-the-art models, we achieve higher accuracy, and the network is beneficial for the three-dimensional reconstruction of remote sensing images.
Keywords: 
Subject: Environmental and Earth Sciences  -   Remote Sensing

1. Introduction

Stereo matching, also known as disparity estimation, is a crucial step in 3D reconstruction. Stereo matching extracts disparity information from rectified stereo image pairs and then estimates depth information, which is the critical information in 3D reconstruction [1,2]. For stereo image pairs, there are corresponding matching points in both images. After performing epipolar rectification on the image pair, which aligns matching points on the same horizontal line, these matching points have different horizontal coordinates in the image pair, and the difference in coordinates is called "disparity"[3]. By using rectified stereo image pairs, disparity maps are generated by calculating the corresponding point in the right image for each pixel in the left image. These disparity maps can then be used in conjunction with camera parameters to obtain three-dimensional information. With the advancement of satellite sensor technology, stereo matching based on satellite imagery has become a popular research topic, and the accuracy of stereo matching has become increasingly important.
Stereo matching algorithms can be categorized into traditional methods and deep learning-based methods. Traditional stereo matching methods measure the similarity between pixels in images by defining a matching cost and identifying corresponding points. The traditional stereo matching pipeline consists of four main steps: cost computation, cost aggregation, disparity computation and refinement [4]. Traditional methods can be divided into local, global, and semiglobal approaches. Local methods are fast but have limited accuracy [5,6], and global methods have high computational complexity and are not suitable for large-scale remote sensing images [7,8,9]. Semiglobal matching (SGM) methods, proposed by Hirschmüller [10] in 2005, use global frameworks and reduce computational costs by using one-dimensional optimal approaches in multiple directions, making it a popular traditional stereo matching method.
However, traditional methods have limitations, particularly when dealing with textureless regions or areas with repeated textures in remote sensing images. Moreover, their accuracy and speed may not be suitable for practical applications. In recent years, with improvements in computational power, deep learning algorithms have led to significant advances in various fields, and the integration of computer vision and deep learning has become a popular research topic [11,12]. Early researchers leveraged the strong feature extraction capabilities of convolutional neural networks (CNNs) to replace certain steps in traditional stereo matching approaches, leading to significant improvements in accuracy. The MC-CNN, proposed by Zbontar and LeCun [13], was the first deep learning model introduced in the field of stereo matching. It replaces the feature extraction and cost calculation components in the stereo matching pipeline with a convolutional neural network, demonstrating good results. However, it is still constrained by traditional methods in the pipeline and requires the manual tuning of multiple parameters based on experience. Chen [14] et al. proposed Deep Embedding, which directly calculates feature similarity using dot products, which has reduced accuracy but faster inference speed than MC-CNN. Batsos and Mordohai [15] introduced a recurrent neural network with residual connections that optimized disparities using disparity maps and reference images as inputs. While these algorithms had better accuracy than traditional methods, they still had high time complexity due to certain traditional components, such as cost volumes, limiting their practical utility.
As research progressed, many researchers proposed end-to-end networks, such as DispNet[16] and GC-Net[17], which simulate each step of the stereo matching process and directly predict disparity maps for stereo image pairs, achieving significant advancements. StereoNet[18] is a real-time stereo matching network that extracts low-resolution features to construct a cost space, obtains an initial coarse disparity map, and then progressively refines it by using edge-aware techniques to obtain the final disparity map. While it offers fast inference speeds, the disparity map's fine-grained details are lacking. Chang's PsmNet [19] employed spatial pyramid pooling (SPP) [20] for feature extraction, generating rich feature representations. This model also incorporated multiple hourglass 3D convolution modules with intermediate supervision, showing good performance in textureless regions and areas with repeated textures. However, PsmNet has a relatively large number of parameters, which places high demands on devices. GwcNet [21] introduced the concept of group correlation to construct the cost volume and achieved higher accuracy than PsmNet, but the model size remains relatively large. HsmNet [22] used a multiscale strategy to regress disparities from coarse to fine using multiscale features, enabling the network to handle high-resolution images. However, the time needed for information integration across four different scales is excessively long.
Thanks to the success of end-to-end stereo matching networks, applying them to remote sensing images becomes possible. However, compared with natural images, remote sensing images contain more complex multiscale features and nontextured, weakly textured and repetitive texture regions. Additionally, remote sensing images have low resolution, and the object boundaries are often ambiguous. Moreover, occlusions caused by tall buildings and large trees can lead to discontinuities in disparities [23,24]. The existing methods fall short in terms of both accuracy and speed and are unable to meet the requirements.
To overcome these obstacles, we propose a network for stereo matching in remote sensing images in this paper, and the key points are as follows:
The proposed network learns features at different scales and constructs cost volumes at various scales. After cost aggregation, the network integrates cost feature information across scales. This will be beneficial for matching textureless and low-texture areas.
We employ attention modules based on pixel importance to optimize feature information and enhance feature representation, which plays a significant role in optimizing the inspection of fine details.
The proposed network demonstrates good performance. We evaluated it on a challenging large-scale remote sensing stereo matching dataset. The experiments show that our model achieves competitive accuracy while maintaining fast inference speeds. Furthermore, we validated the effectiveness of the proposed approach through ablation experiments.

2. Materials and Methods

2.1. The Architecture of the Proposed Network

The network model developed in this paper is based on PsmNet and has been modified. For rectified remote sensing stereo image pairs, we utilize a feature pyramid network with feature sharing to obtain two feature maps with different scales through downsampling. Then, we apply group correlation principles to construct multiscale cost volumes for the two feature maps to capture spatial relationships. After feature fusion based on the cost volume, we perform cost aggregation and finally regress the disparities using the soft-argmin algorithm. The overall structure consists of four modules: a feature extraction module, a matching cost construction module, a cost aggregation module, and a disparity regression module (Figure 1). The modules are detailed in Section 2.2.

2.2. Component modules

2.2.1. Feature extraction

Due to the presence of a significant number of nontextured, weakly textured, repetitive texture and discontinuous disparity regions in remote sensing images, stereo matching algorithms are prone to matching errors. Therefore, accurately predicting disparities by extracting image features with rich local and global information is crucial. To accommodate this, we employ a dilated convolution [25] method to continuously expand the receptive field, aggregating extensive feature information. Furthermore, features with different scales are common in remote sensing images. Lower-scale features have lower resolution, making them less sensitive to details but richer in semantic information. In contrast, higher-scale features have higher resolution and thus include more location and detail information but have less semantic information and more noise. Therefore, fusing features of different scales is important in image processing.
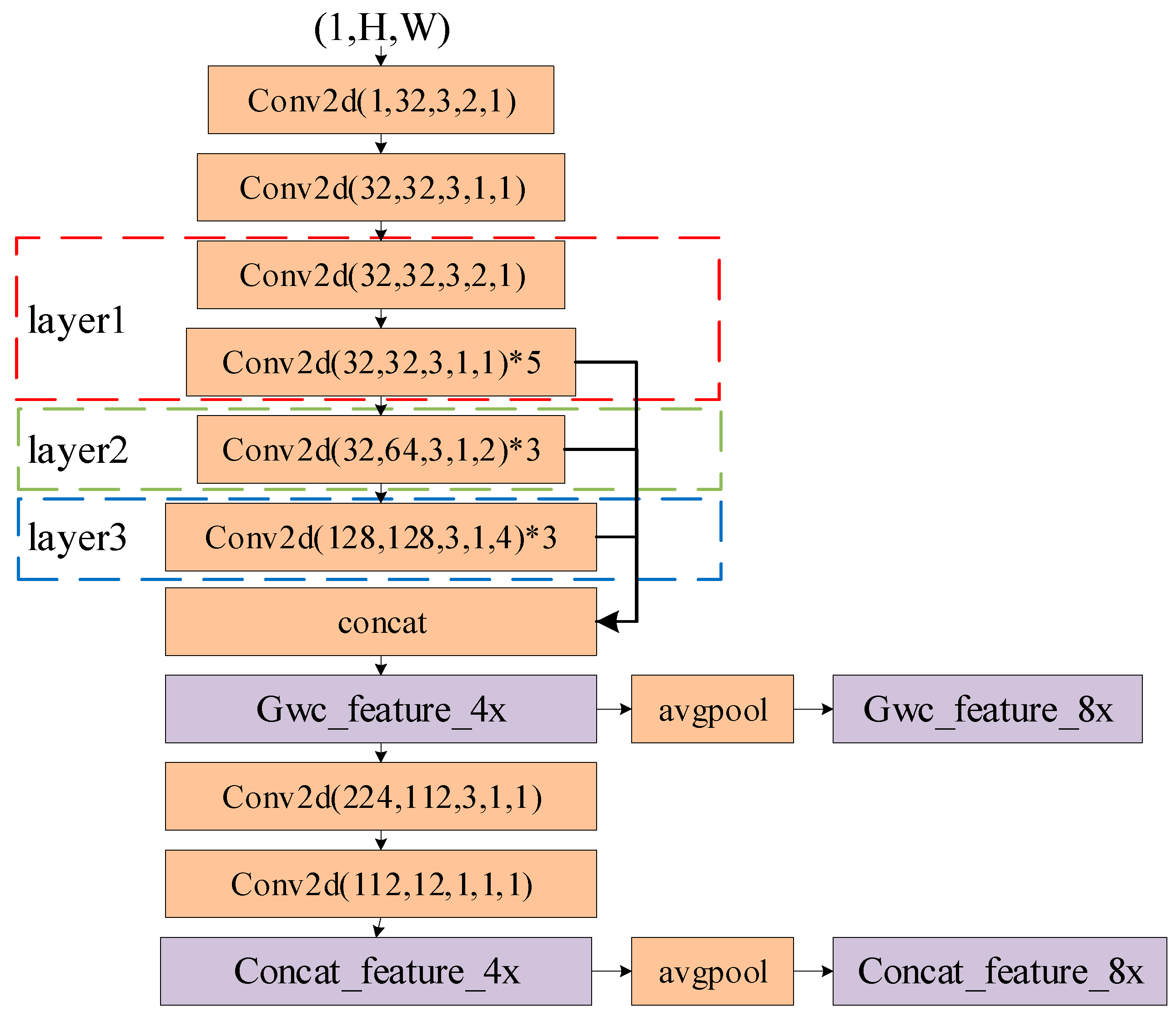
First, we employ a pyramid network method to fuse features of different scales, followed by downsampling to obtain information at even lower scales. Subsequently, we use these two feature matrices to predict the final result (Figure 2). This approach accounts for the complexity of different scale features in remote sensing images, thereby improving the performance and robustness of stereo matching algorithms for remote sensing imagery.
The input image is first downsampled and halved with a convolution. Then, the image is passed through three convolutional groups in layer 1, layer 2, and layer 3, which have dilation rates of 1, 2, and 4, respectively, to obtain feature information at different scales. The size of the image is reduced to 1/4 of the original image size, and the outputs of each convolutional group are stacked in the channel dimension to obtain the feature Gwc_Feature, which is used for constructing group correlation cost volumes. Subsequently, two additional convolutional layers are applied to reduce the number of channels to 12. Then, Concat_Feature is used to build the 3D cascaded cost volume. Finally, an average pooling layer is used to downsample the features used to construct the cost volume to 1/8 of the original image size.

2.2.2. Cost Volume Fusion

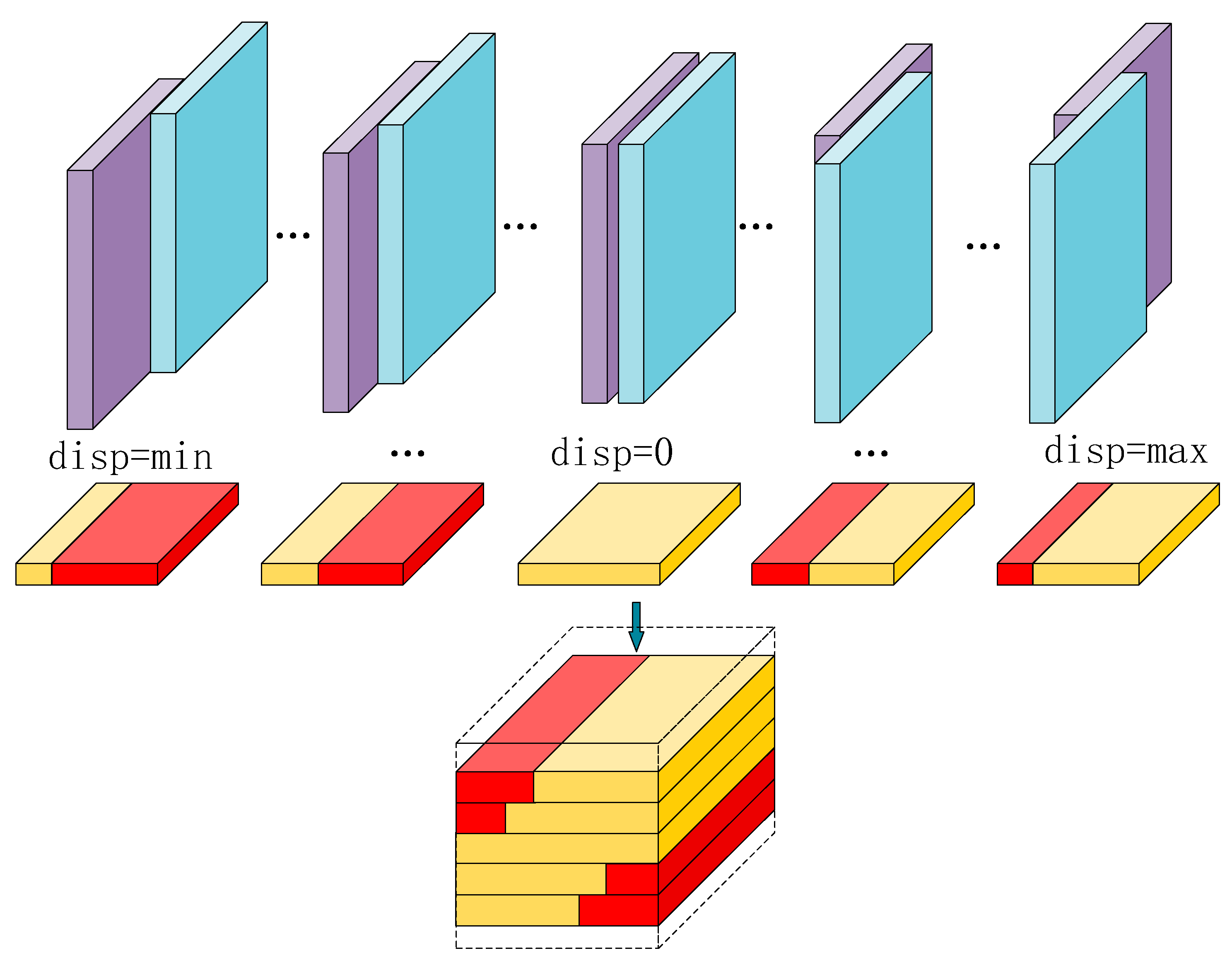
In this section, we construct a cost volume based on the features extracted from the left and right views by the feature extraction module. First, we utilize the Concat_Feature obtained with the feature extraction process to build the concatenated cost volume, as shown in Equation (1). We calculate the differences at overlapping positions after the concatenation and pad the regions outside the overlap with zeros based on the size of the left image, and the results for various disparities are stacked to form a 4D cost volume with dimensions C ,   D ,   H ,   W , where C represents the number of channels, D represents the disparity value, H represents the height, and W represents the width. A schematic diagram of this process is illustrated in Figure 3.
C c o n c a t x , y = C o n c a t d = min _ D max _ D f l x , y − f r x − d , y
In the equation, the variables are defined as follows: C represents the cost, f represents the feature matrix, x and y represent the positions within the feature matrix, and d represents the candidate disparity value.
Next, the Gwc cost volume is constructed using Gwc_Feature, as shown in Equation (2). When constructing the cost volume for each candidate disparity, Gwc_Feature is divided into G groups based on the number of channels, with each group having a size of C / G ,   H ,   W . For each group, the feature's correlations with other groups are calculated using dot products, resulting in a cost value for each candidate disparity. The cost for each candidate disparity is then stacked to create a cost volume with dimensions G ,   D ,   H ,   W , where G represents the number of groups, D represents the disparity value,   H represents the height, and W represents the width.
C G W C x , y , d = C o n c a t g = 1 G m e a n i n n e r f l g x , y , f r g x − d , y , d i m = 0
C G W C x , y = C o n c a t d = min _ D max _ D C G W C x , y , d
In the equation, the variables are defined as follows: C represents the cost, and f represents the feature matrix. x and y represent the positions within the feature matrix. d represents the candidate disparity value. g represents the number of groups. i n n e r represents the dot product operation. m e a n represents the mean (average) operation. d i m = 0 indicates that the mean operation is performed along the 0-th dimension.

2.2.3. Cost Aggregation

After obtaining the initial cost volume, we perform cost aggregation based on this volume. Attention modules are commonly incorporated into networks to optimize the outputs of previous layers [26,27]. Channel attention [28,29,30] and spatial attention [31,32] mechanisms have both been shown to be highly effective in network optimization. They are often used in conjunction or sequentially, with separate weights assigned to the channel and spatial dimensions. However, importantly, both types of attention mechanisms can be applied and should simultaneously assist in feature selection. Additionally, commonly used attention modules introduce convolution and pooling operations, which can significantly impact model efficiency when used in cost aggregation modules based on 3DCNNs. Therefore, we introduce a parameter-free attention module called simAM [33] and apply it in cost aggregation operations (Figure 4). In simAM, an energy function is defined for each feature pixel, and a unique weight is assigned to each feature pixel by minimizing the energy function. The minimization of the energy function is shown in Equation (4):
E t = σ ^ 2 + λ t − u ^ 2 + 2 σ ^ 2 + 2 λ
u ^ = 1 M − 1 ∑ i = 1 M − 1 x i
σ ^ 2 = 1 M − 1 ∑ i = 1 M − 1 x i − u ^ 2
In the equation, the variable t represents a specific feature pixel. The cost volume has dimensions B ,   C ,   D ,   H ,   W , where B is the batch size, C is the number of channels, D is the disparity value, and H and W are the height and width, respectively. Then, M , which represents the total number of feature pixels in the cost volume, is equal to D × H × W . The energy function aims to quantify the importance of each feature pixel, and lower energy values correspond to higher importance. Therefore, the term 1/E is used to represent the importance or significance of a given feature pixel. This formulation indicates that the energy function is inversely related to the importance of each feature pixel, and 1/E serves as a measure of the pixel's significance in the cost aggregation process. First, we use a 3D convolutional group to aggregate the initial features of the cost volume. Then, we calculate the importance of each feature pixel based on the energy function and constrain the values to vary between 0 and 1 using the sigmoid function. We then multiply the importance values with the original feature matrix.
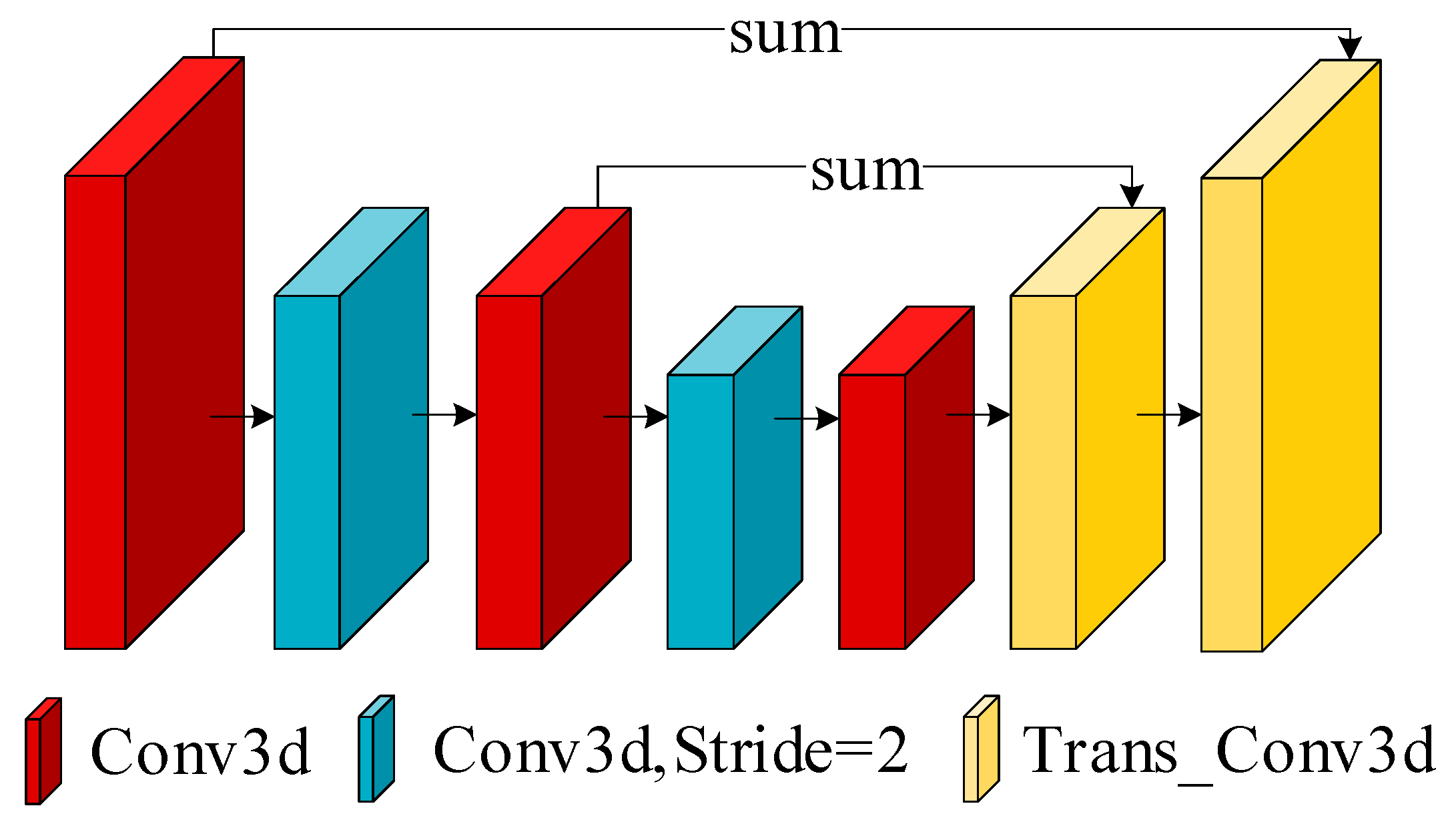
After the data are passed through the attention fusion module, we use an hourglass structure to aggregate information along both the channel and disparity dimensions, as depicted in Figure 5. We adopted an hourglass structure inspired by PsmNet, which includes convolutions, deconvolutions (transposed convolutions) and skip connections. The primary modification made to this hourglass structure is in the number of output channels, which was adjusted according to the specific requirements of our model.

2.2.4. Disparity Regression

After cost aggregation, it is necessary to convert the results into a 2D disparity map to compute the loss. We use the soft-argmin method proposed in Gc-Net to transform the cost volume into a continuous disparity map. This process is differentiable, allowing for backpropagation.
In the soft-argmin method, the softmax operation is applied along the disparity dimension of the 4D cost volume to obtain disparity probability values for each pixel. Then, the final disparity value is calculated by taking a weighted sum based on these probability values. This process is expressed mathematically in Equation (7):
d ^ = ∑ d = D m i n D m a x d × σ − c d
In the equation, d ^ represents the predicted (regressed) disparity value. d represents the candidate disparity values within the disparity range. σ represents the softmax function. c d represents the matching cost when the disparity is d .

3. Results

In this section, we assess the performance of the model. We first introduce the dataset used for evaluating the model's performance. Then, we describe the specific implementation details of the model. Finally, we present the model's disparity estimation results and compare the results with other state-of-the-art models.

3.1. Dataset

We evaluated the model's performance using the US3D track-2 dataset from the 2019 Data Fusion Contest [34,35]. This dataset is a large-scale public dataset that includes data for two cities, Jacksonville and Omaha. The data include various types of urban features, such as buildings, roads, rivers, and vegetation, with rich background information. The dataset includes rectified stereo image pairs and disparity maps. The stereo image pairs were acquired from WorldView-3 with a size of 1024×1024 pixels and no geographic overlap. The disparity maps were generated based on airborne LiDAR data. The dataset includes 2139 image pairs for Jacksonville and 2153 image pairs for Omaha. All the data from Jacksonville and 1069 image pairs from Omaha were used as the training set, and the remaining Omaha data were randomly split into 575 pairs for the validation set and 511 pairs for the test set. Additionally, due to GPU memory limitations, the data were center-cropped to a size of 768×768 for further processing.

3.2. Evaluation Metrics

We evaluated the model using two metrics as described in the reference paper from the 2019 Data Fusion Contest: (1) the average pixel error (end-point error, EPE), which measures the average disparity error between the predicted and ground truth disparity maps; and (2) the error pixel ratio (D1), which is the proportion of erroneous pixels in the predicted disparity map compared to the ground truth disparity map. The smaller the EPE and D1 are, the better the model's performance. These metrics are defined as shown in Equations (8) and (9).
E P E = 1 N ∑ p x , y − g x , y
D 1 = 1 N ∑ ( p x , y − g x , y > t )
In the equations, p and g represent the predicted disparity map and the ground truth disparity map, respectively. N represents the total number of pixels in the predicted disparity map, while x , y denotes the corresponding positions in the predicted and ground truth disparity maps. The variable t is the threshold used to determine erroneous pixels, and in this paper, this threshold was set to 3. Additionally, we employ the trained model to predict disparity maps for all image pairs in the test dataset. We calculate the average time spent to obtain these predictions and use this time as an evaluation metric for the model's efficiency.

3.3. Implementation Details

Due to the constraint that many satellite multiview images are in grayscale format, we read the images in grayscale. The original 1024 × 1024 images were center-cropped to 768 × 768 , and their data types were converted to float32. The images were directly input into the network without applying other data preprocessing steps. The total number of epochs was set to 100, with an initial learning rate of 0.001. We used the CosineAnnealingWarmRestarts (T_0=2, T_mult=2, eta_min=0.000001) method to dynamically adjust the learning rate. The loss weights λ_0, λ_1, and λ_2 were set to 0.5, 0.7, and 1.0, respectively. The model was optimized using the Adam optimizer (β=(0.9, 0.999), weight decay=0.0001) for end-to-end training. The network was trained in a PyTorch environment on the Windows 10 operating system, with a batch size of 2, and acceleration was performed using an NVIDIA GeForce RTX 3090 GPU. The loss function used in this paper is the smooth L1 loss, which is formulated as follows:
L = 1 N ∑ x , y S m o o t h L 1 ( d x , y − d x , y * )
In which:
S m o o t h L x =   0.5 x 2 ,             x < 1 x − 0.5 ,       o t h e r w i s e
where N represents the number of pixels, d x , y represents the predicted value at position (x, y), and d x , y * represents the true (ground truth) value at position (x, y). The overall loss is obtained by summing the weighted losses from each disparity prediction branch as follows:
L t o t a l = ∑ i = 0 n λ i N ∑ x , y S m o o t h L 1 ( d x , y − d x , y * )
where N represents the total number of disparity prediction branches and λ i represents the loss weight for each branch.
We perform comparative analyses with several state-of-the-art models, including the end-to-end StereoNet, PsmNet, GwcNet, and HmsmNet [36]. StereoNet is a lightweight network for real-time stereo matching that obtained good accuracy with the KITTI stereo matching dataset. PsmNet and GwcNet incorporate complex 3D convolutional hourglass modules and achieve better accuracy than StereoNet with the KITTI dataset. HmsmNet is a recent stereo matching network designed for high-resolution satellite imagery, offering fast inference speeds and good accuracy. We trained these models based on open-source code. To accommodate negative disparities in the dataset, we modified the cost volume construction methods for StereoNet, PsmNet, and GwcNet to enable regression of negative disparities. To ensure a fair performance comparison, we excluded the pixel gradient information used in HmsmNet. The same hyperparameters and loss functions were used for all models, and all models were trained in the same environment.

3.4. Comparisons with Other Stereo Methods

We conducted quantitative analyses of various models based on the test set, and the results are shown in Table 1. Our proposed model achieves the best accuracy, as our model obtains better EPE and D1 scores than the other models. StereoNet exhibits the fastest inference speed but obtains the poorest accuracy. PsmNet obtains improved accuracy by stacking computations but has an excessively long inference time. GwcNet optimizes PsmNet by accelerating the inference speed and enhancing accuracy. HmsmNet has comparable accuracy to GwcNet but faster inference speed. Our model outperforms HmsmNet, with a decrease of 0.078 in the average pixel error and a 1.043% reduction in the error pixel ratio. Moreover, our model only needed an additional 11 ms for inference. Thus, the results indicate that our model has the best overall performance.
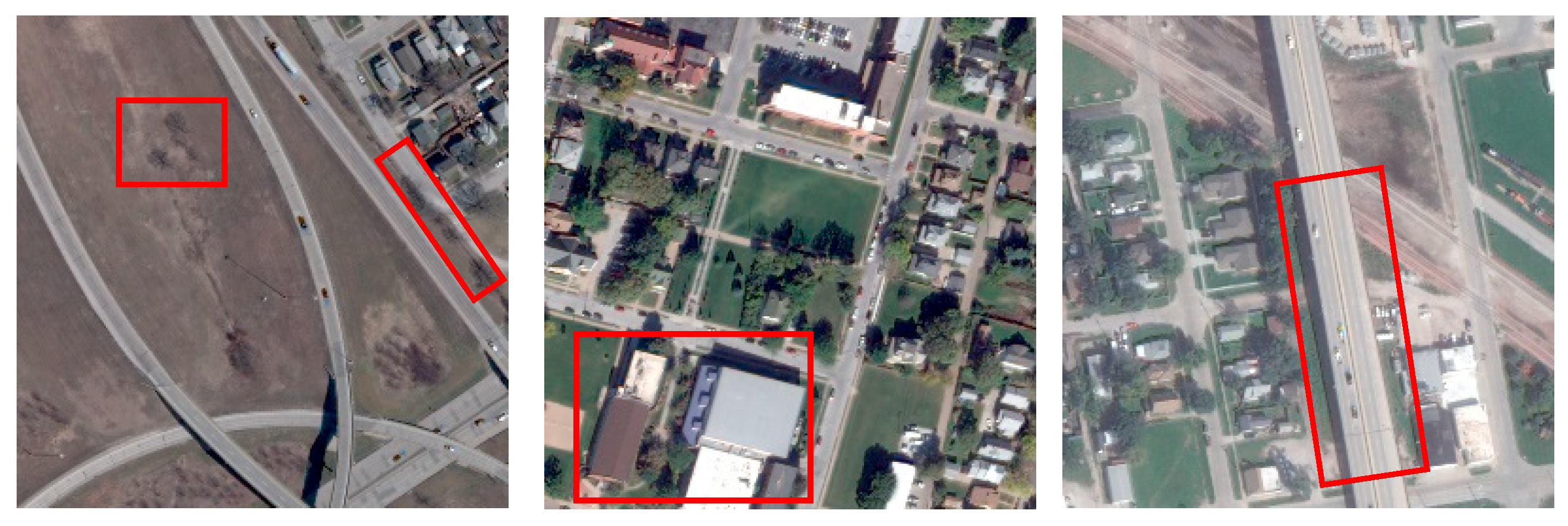
To qualitatively observe differences in results, we randomly selected some stereo pairs from the test set and predicted their disparity maps with the different networks (Figure 6). Except for StereoNet, which generated somewhat blurry results, the other models produce high-quality disparity maps. Our proposed model produces the highest-quality disparity maps, effectively capturing details for various terrain types. For instance, by examining the information within the red boxes, we find that our model obtains the best results when outputting trees and buildings with different scales.
In addition, the presence of nontextured and weakly textured regions, areas with repetitive textures, and discontinuous disparities in remote sensing images can pose challenges for stereo matching. To demonstrate the improvement of our model in these regions, we selected several representative scenes for a comparative analysis and thoroughly evaluated the performance of different models. In each scenario, we selected three classic scenes, output the disparity maps predicted by each model, and presented the accuracy results in a table.
  • Nontextured and weakly textured regions
For nontextured and weakly textured regions, where pixel variations are not pronounced, models often struggle to distinguish among features, leading to difficulties in matching. In this section, we consider three representative scenes, flat bare land, a road, and smooth houses, and provide both qualitative results (Figure 7) and quantitative results (Table 2). Our proposed model shows the best performance in recognizing sparsely textured trees in bare land areas and produces the smoothest building and road boundaries. Quantitatively, our proposed model shows a considerable improvement in nonetextured and weakly textured regions, especially over a large extent.
2.
Repetitive texture regions
In the case of repetitive texture regions where objects have similar shapes and pixel information, models are prone to making erroneous matches. We selected scenes with houses, trees, and blocky lawns with similar textures (Figure 8). Images with repetitive textures often contain connected boundaries. Our model excels in distinguishing object boundaries in most scenarios and experiences fewer mismatching issues. In contrast, StereoNet, PsmNet, and GwcNet all exhibit some degree of boundary merging. For example, when encountering trees in tile OMA391_023_022 and lawns in tile OMA389_038_040, only our model obtains accurate matching results. In addition, our proposed model performs the best quantitatively, as shown in Table 3. When facing images with a significant number of man-made objects in tile OMA278_026_021, it exhibits an excellent improvement in EPE and D1 compared to the best-performing alternative models.
3.
Discontinuous disparities
In remote sensing images, there are often tall objects with abrupt changes in height, which can lead to discontinuities in the disparity, resulting in blurry edges and inaccurate matching. In the images, we showcase predicted disparity maps for several scenes with tall buildings (Figure 9). As seen in tile OMA281_003_002, our model is the least affected by interference from the tower. When dealing with tall buildings, our proposed model also exhibits relatively minor instances of edge blurriness. From the quantitative results (Table 4), it can be summarized that faced with challenging discontinuous disparities, our model achieves considerable accuracy improvements, especially in D1.
From the comparison results in the challenging scenarios mentioned above, it is evident that our model performs well in high-resolution remote sensing image stereo matching tasks.

3.5. Ablation Experiments

In this section, we conduct ablation experiments to validate the effectiveness of various modules in the model. Our model primarily employs two strategies to improve disparity estimation performance:
1. Multiscale features and fused scale-based cost volumes.
2. Attention modules.
To verify the effectiveness of the scale fusion approach, we modified the model's structure. Net_v1 uses neither feature fusion nor cost-volume fusion. Net_v2 only uses feature fusion. Net_v3 only uses cost-volume fusion. Net_v4 utilizes both feature and cost volume fusion. For Net_v1 and Net_v2, due to the removal of the multiscale cost volume branch, to approximately maintain the number of model parameters, we stack three hour-glass modules for cost aggregation. Additionally, to evaluate the functionality of the attention modules used in the paper, no attention modules are used in Net_v1, Net_v2, Net_v3, or Net_v4. We compare the results with these ablation models to those of the baseline Net model to perform a comparative analysis. The results are presented in Table 5, and visu-alization examples are shown in Figure 10.
Comparing Net_v1, Net_v2, and Net_v3, we observe that using either multiscale features or scale fusion alone has minimal impact on improving accuracy. When comparing Net_v1, Net_v2, Net_v3, and Net_v4, it is evident that simultaneously utilizing multiscale features and cross-scale cost fusion considerably improves accuracy. This approach effectively identifies the details of various objects and mitigates the edge blurriness in discontinuous areas. The attention module effectively assigns importance scores to each pixel, leading to substantial improvements in matching accuracy in stereo matching for various types of objects, as seen from the comparison of Net_v4 and Net. Although an attention module was used, the nonparametric attention module does not have an impact on the inference speed. In summary, using multiscale features, cross-scale cost fusion and attention modules can considerably improve the model's performance while maintaining inference speed.

4. Discussion

This paper introduces a network for stereo matching in remote sensing images. It performs well in addressing practical challenges, such as nontextured and weakly textured regions with indistinct pixel changes, repetitive texture regions with similar pixel values and shapes, and discontinuous disparities caused by tall objects and occlusions. The core idea of the network involves the use of feature pyramids and cross-scale fusion to extract rich image features, resulting in an improvement in stereo matching accuracy. Additionally, we employ an attention module during cost aggregation to further enhance feature representation, leading to increased accuracy. Experimental results show that the proposed method not only enhances stereo matching accuracy but also maintains fast inference speed. This research provides a rapid and effective stereo matching solution for 3D reconstruction in remote sensing images.
However, our model has certain limitations. For instance, due to differences in the resolutions of remote sensing images, it is necessary to prespecify the disparity range. During inference, corresponding pixels falling outside the specified disparity range may not be recognized. Additionally, when regressing disparities using the soft-argmin method, we assume that the disparity probability distribution is unimodal. However, in practice, the probability distribution may be multimodal [37,38], which has an impact on the final disparity prediction.
In the future, we will investigate new network architectures that do not require prespecification of the disparity range, enabling them to adaptively determine the disparity range. We will continue to investigate the extraction of richer feature information and the improvement of loss functions to suppress multimodal distribution phenomena.

5. Conclusions

In this paper, we designed a novel end-to-end network for stereo matching with high-resolution remote sensing stereo image pairs. By utilizing a feature pyramid network to extract features at multiple scales, constructing multiscale cost volumes, and applying attention-based cost aggregation modules, our proposed model performs cross-scale fusion of cost volumes and regresses the disparity maps. The stereo matching network presented in this paper demonstrates outstanding performance, as evidenced by evaluations based on the US3D dataset. Compared to several state-of-the-art methods, our model achieved the best performance and significant accuracy improvements in challenging regions. Furthermore, we conducted ablation experiments to assess the rationality of our model design, finding that the incorporation of multiscale features and cross-scale cost fusion effectively enhances the disparity estimation capability of the model, while attention modules significantly reduce prediction errors. The proposed method can rapidly and accurately predict the disparity map and is effective in providing depth information for 3D reconstruction.

Author Contributions

Conceptualization, H.L., X.H. ; methodology, H.L., K.W. ; validation, K.W. ; writing original draft preparation, K.W., H.L., X.H. ; writing—review and editing, X.H. ; visualization, K.W. ; project administration, H.L., X. H. ; and funding acquisition, H.L., X.H.; All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China (Grant No. 41971363) and the National Key Research and Development Program of China (Grant No. 2022YFB3903705).

Data Availability Statement

The US3D track-2 dataset can be found at https://ieee-dataport.org/open-access/data-fusion-contest-2019-dfc2019. The codes and trained models are available from the authors upon reasonable request.

Acknowledgments

The authors would like to thank the Johns Hopkins University Applied Physics Laboratory and the IARPA for providing the data used in this study and the IEEE GRSS Image Analysis and Data Fusion Technical Committee for organizing the Data Fusion Contest.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Niu, J.; Song, R.; Li, Y. A Stereo Matching Method Based on Kernel Density Estimation. In Proceedings of the 2006 IEEE International Conference on Information Acquisition; 2006; pp. 321–325. [Google Scholar] [CrossRef]
  2. Sonka, M.; Hlavac, V.; Boyle, R. Image processing, analysis and machine vision; Springer: 2013.
  3. Suliman, A.; Zhang, Y.; Al-Tahir, R. Enhanced disparity maps from multi-view satellite images. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS); 2016; pp. 2356–2359. [Google Scholar] [CrossRef]
  4. Scharstein, D. A taxonomy and evaluation of dense two-frame stereo correspondence. In Proceedings of the Proceedings of the IEEE Workshop on Stereo and Multi-Baseline Vision, Kauai, HI, Dec, 2001, 2001.
  5. Zabih, R.; Woodfill, J. Non-parametric local transforms for computing visual correspondence. In Proceedings of the Computer Vision—ECCV'94: Third European Conference on Computer Vision Stockholm, Sweden, May 2–6 1994 Proceedings, Volume II 3, 1994; pp. 151-158. [CrossRef]
  6. Min, D.; Sohn, K. Cost aggregation and occlusion handling with WLS in stereo matching. IEEE Transactions on Image Processing 2008, 17, 1431–1442. [Google Scholar] [CrossRef] [PubMed]
  7. Ohta, Y.; Kanade, T. Stereo by intra-and inter-scanline search using dynamic programming. IEEE Transactions on pattern analysis and machine intelligence 1985, 139–154. [Google Scholar] [CrossRef] [PubMed]
  8. Hong, L.; Chen, G. Segment-based stereo matching using graph cuts. In Proceedings of the Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2004. CVPR 2004., 2004; pp. I-I. [CrossRef]
  9. Sun, J.; Zheng, N.-N.; Shum, H.-Y. Stereo matching using belief propagation. IEEE Transactions on pattern analysis and machine intelligence 2003, 25, 787–800. [Google Scholar] [CrossRef]
  10. Hirschmuller, H. Accurate and efficient stereo processing by semi-global matching and mutual information. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR'05); 2005; pp. 807–814. [Google Scholar] [CrossRef]
  11. Girshick, R. Fast r-cnn. In Proceedings of the Proceedings of the IEEE international conference on computer vision; 2015; pp. 1440–1448. [Google Scholar] [CrossRef]
  12. Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. Advances in neural information processing systems 2015, 28. [Google Scholar] [CrossRef] [PubMed]
  13. Zbontar, J.; LeCun, Y. Computing the stereo matching cost with a convolutional neural network. In Proceedings of the Proceedings of the IEEE conference on computer vision and pattern recognition; 2015; pp. 1592–1599. [Google Scholar]
  14. Chen, Z.; Sun, X.; Wang, L.; Yu, Y.; Huang, C. A deep visual correspondence embedding model for stereo matching costs. In Proceedings of the Proceedings of the IEEE International Conference on Computer Vision; 2015; pp. 972–980. [Google Scholar]
  15. Batsos, K.; Mordohai, P. Recresnet: A recurrent residual cnn architecture for disparity map enhancement. In Proceedings of the 2018 International Conference on 3D Vision (3DV); 2018; pp. 238–247. [Google Scholar] [CrossRef]
  16. Mayer, N.; Ilg, E.; Hausser, P.; Fischer, P.; Cremers, D.; Dosovitskiy, A.; Brox, T. A large dataset to train convolutional networks for disparity, optical flow, and scene flow estimation. In Proceedings of the Proceedings of the IEEE conference on computer vision and pattern recognition; 2016; pp. 4040–4048. [Google Scholar]
  17. Kendall, A.; Martirosyan, H.; Dasgupta, S.; Henry, P.; Kennedy, R.; Bachrach, A.; Bry, A. End-to-end learning of geometry and context for deep stereo regression. In Proceedings of the Proceedings of the IEEE international conference on computer vision; 2017; pp. 66–75. [Google Scholar]
  18. Khamis, S.; Fanello, S.; Rhemann, C.; Kowdle, A.; Valentin, J.; Izadi, S. Stereonet: Guided hierarchical refinement for real-time edge-aware depth prediction. In Proceedings of the Proceedings of the European Conference on Computer Vision (ECCV); 2018; pp. 573–590. [Google Scholar]
  19. Chang, J.-R.; Chen, Y.-S. Pyramid stereo matching network. In Proceedings of the Proceedings of the IEEE conference on computer vision and pattern recognition; 2018; pp. 5410–5418. [Google Scholar]
  20. He, K.; Zhang, X.; Ren, S.; Sun, J. Spatial pyramid pooling in deep convolutional networks for visual recognition. IEEE transactions on pattern analysis and machine intelligence 2015, 37, 1904–1916. [Google Scholar] [CrossRef] [PubMed]
  21. Guo, X.; Yang, K.; Yang, W.; Wang, X.; Li, H. Group-wise correlation stereo network. In Proceedings of the Proceedings of the IEEE/CVF conference on computer vision and pattern recognition; 2019; pp. 3273–3282. [Google Scholar]
  22. Yang, G.; Manela, J.; Happold, M.; Ramanan, D. Hierarchical deep stereo matching on high-resolution images. In Proceedings of the Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2019; pp. 5515–5524. [Google Scholar]
  23. Tao, R.; Xiang, Y.; You, H. An edge-sense bidirectional pyramid network for stereo matching of vhr remote sensing images. Remote Sensing 2020, 12, 4025. [Google Scholar] [CrossRef]
  24. Osco, L.P.; Junior, J.M.; Ramos, A.P.M.; de Castro Jorge, L.A.; Fatholahi, S.N.; de Andrade Silva, J.; Matsubara, E.T.; Pistori, H.; Gonçalves, W.N.; Li, J. A review on deep learning in UAV remote sensing. International Journal of Applied Earth Observation and Geoinformation 2021, 102, 102456. [Google Scholar] [CrossRef]
  25. Yu, F.; Koltun, V. Multi-scale context aggregation by dilated convolutions. arXiv preprint arXiv:1511.07122 2015. [CrossRef]
  26. Ying, X.; Wang, Y.; Wang, L.; Sheng, W.; An, W.; Guo, Y. A stereo attention module for stereo image super-resolution. IEEE Signal Processing Letters 2020, 27, 496–500. [Google Scholar] [CrossRef]
  27. Chen, C.; Qing, C.; Xu, X.; Dickinson, P. Cross parallax attention network for stereo image super-resolution. IEEE Transactions on Multimedia 2021, 24, 202–216. [Google Scholar] [CrossRef]
  28. Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the Proceedings of the IEEE conference on computer vision and pattern recognition; 2018; pp. 7132–7141. [Google Scholar]
  29. Wang, Q.; Wu, B.; Zhu, P.; Li, P.; Zuo, W.; Hu, Q. ECA-Net: Efficient channel attention for deep convolutional neural networks. In Proceedings of the Proceedings of the IEEE/CVF conference on computer vision and pattern recognition; 2020; pp. 11534–11542. [Google Scholar]
  30. Qin, Z.; Zhang, P.; Wu, F.; Li, X. Fcanet: Frequency channel attention networks. In Proceedings of the Proceedings of the IEEE/CVF international conference on computer vision; 2021; pp. 783–792. [Google Scholar]
  31. Jaderberg, M.; Simonyan, K.; Zisserman, A. Spatial transformer networks. Advances in neural information processing systems 2015, 28. [Google Scholar]
  32. Almahairi, A.; Ballas, N.; Cooijmans, T.; Zheng, Y.; Larochelle, H.; Courville, A. Dynamic capacity networks. In Proceedings of the International Conference on Machine Learning; 2016; pp. 2549–2558. [Google Scholar]
  33. Yang, L.; Zhang, R.-Y.; Li, L.; Xie, X. Simam: A simple, parameter-free attention module for convolutional neural networks. In Proceedings of the International conference on machine learning; 2021; pp. 11863–11874. [Google Scholar]
  34. Le Saux, B.; Yokoya, N.; Hansch, R.; Brown, M.; Hager, G. 2019 data fusion contest [technical committees]. IEEE Geoscience and Remote Sensing Magazine 2019, 7, 103–105. [Google Scholar] [CrossRef]
  35. Bosch, M.; Foster, K.; Christie, G.; Wang, S.; Hager, G.D.; Brown, M. Semantic stereo for incidental satellite images. In Proceedings of the 2019 IEEE Winter Conference on Applications of Computer Vision (WACV); 2019; pp. 1524–1532. [Google Scholar] [CrossRef]
  36. He, S.; Li, S.; Jiang, S.; Jiang, W. HMSM-Net: Hierarchical multi-scale matching network for disparity estimation of high-resolution satellite stereo images. ISPRS Journal of Photogrammetry and Remote Sensing 2022, 188, 314–330. [Google Scholar] [CrossRef]
  37. Tulyakov, S.; Ivanov, A.; Fleuret, F. Practical deep stereo (pds): Toward applications-friendly deep stereo matching. Advances in neural information processing systems 2018, 31. [Google Scholar]
  38. Chen, C.; Chen, X.; Cheng, H. On the over-smoothing problem of cnn based disparity estimation. In Proceedings of the Proceedings of the IEEE/CVF International Conference on Computer Vision, 2019; pp.8997-9005.
Preprints 90484 g001
Figure 1. Overview of our network, which consists of four main components, including feature extraction, cost volume creation, cost aggregation and disparity regression.
Figure 1. Overview of our network, which consists of four main components, including feature extraction, cost volume creation, cost aggregation and disparity regression.
Preprints 90484 g001
Preprints 90484 g002
Figure 2. The architecture of the feature extraction module. “Conv2d” represents 2D convolution, and the numbers in square brackets represent the input channels, output channels, kernel size, stride, and dilation. “avgpool” represents average pooling.
Figure 2. The architecture of the feature extraction module. “Conv2d” represents 2D convolution, and the numbers in square brackets represent the input channels, output channels, kernel size, stride, and dilation. “avgpool” represents average pooling.
Preprints 90484 g002
Preprints 90484 g003
Figure 3. The cost volume creation process. The purple and blue parts represent the right and left feature maps, respectively. The yellow part represents the differences between the left and right feature maps, while the red part represents the difference maps padded with zeros to match the size of the left feature map.
Figure 3. The cost volume creation process. The purple and blue parts represent the right and left feature maps, respectively. The yellow part represents the differences between the left and right feature maps, while the red part represents the difference maps padded with zeros to match the size of the left feature map.
Preprints 90484 g003
Preprints 90484 g004
Figure 4. The architecture of the attention fusion module.
Figure 4. The architecture of the attention fusion module.
Preprints 90484 g004
Preprints 90484 g005
Figure 5. The architecture of the hourglass module.
Figure 5. The architecture of the hourglass module.
Preprints 90484 g005
Preprints 90484 g006aPreprints 90484 g006b
Figure 6. Visualized disparity maps of different models. From left to right, the figure shows the results for OMA331_006_003, OMA355_004_003, and OMA364_004_003. From top to bottom, the images represent the left view, ground truth map, and predictions of StereoNet, PsmNet, GwcNet, HmsmNet and our proposed model.
Figure 6. Visualized disparity maps of different models. From left to right, the figure shows the results for OMA331_006_003, OMA355_004_003, and OMA364_004_003. From top to bottom, the images represent the left view, ground truth map, and predictions of StereoNet, PsmNet, GwcNet, HmsmNet and our proposed model.
Preprints 90484 g006aPreprints 90484 g006b
Preprints 90484 g007aPreprints 90484 g007b
Figure 7. Visualized disparity maps of different models for nontextured or weakly textured regions. From left to right, the figure shows the results for OMA258_025_026, OMA331_039_038 and OMA353_003_001. From top to bottom, the images represent the left view, ground truth map, and predictions of StereoNet, PsmNet, GwcNet, HmsmNet and our proposed model.
Figure 7. Visualized disparity maps of different models for nontextured or weakly textured regions. From left to right, the figure shows the results for OMA258_025_026, OMA331_039_038 and OMA353_003_001. From top to bottom, the images represent the left view, ground truth map, and predictions of StereoNet, PsmNet, GwcNet, HmsmNet and our proposed model.
Preprints 90484 g007aPreprints 90484 g007b
Preprints 90484 g008aPreprints 90484 g008b
Figure 8. Visualized disparity maps of different models for areas with repeative texture regions. From left to right, the figure shows the results for OMA278_026_021, OMA389_038_040 and OMA391_023_022. From top to bottom, the images represent the left view, ground truth map, and predictions of StereoNet, PsmNet, GwcNet, HmsmNet and our proposed model.
Figure 8. Visualized disparity maps of different models for areas with repeative texture regions. From left to right, the figure shows the results for OMA278_026_021, OMA389_038_040 and OMA391_023_022. From top to bottom, the images represent the left view, ground truth map, and predictions of StereoNet, PsmNet, GwcNet, HmsmNet and our proposed model.
Preprints 90484 g008aPreprints 90484 g008b
Preprints 90484 g009aPreprints 90484 g009b
Figure 9. Visualized disparity maps of different models for discontinuous disparities. From left to right, the figure shows the results for OMA251_006_001, OMA281_003_002 and OMA287_033_030. From top to bottom, the images represent the left view, ground truth map, and predictions of StereoNet, PsmNet, GwcNet, HmsmNet and our proposed model.
Figure 9. Visualized disparity maps of different models for discontinuous disparities. From left to right, the figure shows the results for OMA251_006_001, OMA281_003_002 and OMA287_033_030. From top to bottom, the images represent the left view, ground truth map, and predictions of StereoNet, PsmNet, GwcNet, HmsmNet and our proposed model.
Preprints 90484 g009aPreprints 90484 g009b
Preprints 90484 g010aPreprints 90484 g010b
Figure 10. Visualized disparity maps of various variants of our Net model. From left to right, the figure shows the results for OMA287_033_030, OMA288_028_026 and OMA355_025_028. From top to bottom, the images represent the left view and the predictions of Net_v1, Net_v2, Net_v3, Net_v4 and the base Net model.
Figure 10. Visualized disparity maps of various variants of our Net model. From left to right, the figure shows the results for OMA287_033_030, OMA288_028_026 and OMA355_025_028. From top to bottom, the images represent the left view and the predictions of Net_v1, Net_v2, Net_v3, Net_v4 and the base Net model.
Preprints 90484 g010aPreprints 90484 g010b
Table 1. Results of different models on the US3D dataset.
Table 1. Results of different models on the US3D dataset.
Models EPE/pixel D1/% TIME/ms
StereoNet 1.488 9.954 80
PsmNet 1.321 7.008 436
GwcNet 1.292 6.338 136
HmsmNet 1.193 6.343 82
Proposed model 1.115 5.320 92
Table 2. Results of different models with nontextured or weakly textured regions.
Table 2. Results of different models with nontextured or weakly textured regions.
Tile OMA258_025_026 OMA331_039_038 OMA353_003_001
EPE/pixel StereoNet 2.388 1.206 1.897
PsmNet 2.192 1.196 1.895
GwcNet 1.930 1.217 1.751
HmsmNet 1.819 1.121 1.871
Proposed model 1.481 0.970 1.708
D1/% StereoNet 30.426 8.414 18.939
PsmNet 22.155 6.337 16.474
GwcNet 13.943 4.761 13.368
HmsmNet 11.076 5.440 13.882
Proposed model 6.671 4.516 12.552
Table 3. Results of different models in areas with repeative texture regions.
Table 3. Results of different models in areas with repeative texture regions.
Tile OMA278_026_021 OMA389_038_040 OMA391_023_022
EPE/pixel StereoNet 2.259 1.476 1.248
PsmNet 1.638 1.909 1.375
GwcNet 1.517 2.137 1.174
HmsmNet 1.750 1.427 1.045
Proposed model 1.238 1.111 0.961
D1/% StereoNet 17.258 11.152 8.728
PsmNet 13.601 13.913 8.896
GwcNet 15.020 19.399 5.577
HmsmNet 17.018 9.463 5.761
Proposed model 7.656 5.939 4.291
Table 4. Results of different models for discontinuous disparities.
Table 4. Results of different models for discontinuous disparities.
Tile OMA281_003_002 OMA287_033_030 OMA251_006_001
EPE/pixel StereoNet 3.049 2.791 2.283
PsmNet 3.716 2.536 2.282
GwcNet 3.496 2.463 2.413
HmsmNet 3.264 2.432 2.175
Proposed model 2.698 1.668 1.463
D1/% StereoNet 37.720 21.194 17.258
PsmNet 66.067 19.493 13.601
GwcNet 60.245 15.331 15.020
HmsmNet 45.656 15. 149 17.018
Proposed model 27.188 11.651 7.656
Table 5. Results of various variants of our Net model.
Table 5. Results of various variants of our Net model.
Model EPE/pixel D1/% TIME/ms
Net-v1 1.309 6.913 82
Net-v2 1.301 6.619 82
Net-v3 1.296 6.781 86
Net-v4 1.272 6.388 91
Net 1.115 5.320 93
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated