Prioritization of Scheduled Surgeries Using Fuzzy Decision Support and Risk Assessment Methods

Preprint

Article

Prioritization of Scheduled Surgeries Using Fuzzy Decision Support and Risk Assessment Methods

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Luiza Fabisiak^*

This version is not peer-reviewed

Submitted:

14 November 2023

Posted:

16 November 2023

You are already at the latest version

Alerts

Abstract

This paper proposes a model that combines multi-criteria and multi-faceted risk assessment. Using two data sources, a fuzzy Technique for Order of Preference by Similarity to Ideal Solution FTOPSIS method combined with FMEA assessment. The FMEA method presented in this paper combines the technique of prioritising preferences according to FTOPSIS similarity to the ideal solution and conviction structure to overcome the defects of traditional FMEA indicators. The paper describes the exact process and tool selection, and the results obtained in the study verified accurate data. Finally, a numerical case study was presented on hospital reorganization services and case adaptation to prioritize surgical abandonment in Poland. The problem considered in the publication is the priority of patients’ operations in hospitals. The selection of relevant criteria, their importance and patient preferences are presented. The results obtained from the method provide a viable action plan for the proposed research problem. The proposed method is multi-faceted and can be part of an information system supporting reorganization, restructuring, and modification of the operational process.

Keywords:

Subject: Computer Science and Mathematics - Information Systems

1. Introduction

The cancellation of surgery has several consequences for employees, employers, patients, the hospital, and people surrounding the local community. An ageing population, urbanization, and the prevalence of anti-health lifestyles worldwide increasingly shape the sustainability of healthcare systems. As a result of significant demographic and disease state changes, healthcare is becoming increasingly complex and costly. Surgery accounts for 40% of hospital expenses and generates about two-thirds of hospital revenues [1]. It requires about 40% of hospital resource costs, including personnel (surgeons, anesthesiologists, nurses, etc.) and equipment (operating rooms, intensive care beds, etc.) [2].

Surgery is being performed in a challenging environment, such as high healthcare expenditures [3], rising healthcare cost ratios [4], and increasing demand for surgical procedures due to ageing populations and growing patient populations. In addition, technological advances have expanded the scope of surgical interventions [5]. Against this backdrop, hospital management is under increasing pressure to control the costs of surgical procedures while providing quality health care to surgical patients. An effective cost containment strategy must integrate decision-making at all levels: strategic, tactical, and operational. One of the main issues at the operational level is surgical case scheduling (SCS) [5]. Continued and disproportionate emphasis on specialized and specific healthcare models undermines the ability of these systems to provide equitable and economically sustainable healthcare.

2. Related works

Over the past two decades, multi-criteria decision-making (MCDM) methods have increased the effectiveness of risk assessment of failure modes [6]. Risk assessment is applied using appropriate techniques to prevent unexpected failure scenarios. Several publications have already appeared in the literature solving the problem of hospital reorganization, cost reduction or hospital care of patients. [7] considered current capacity issues in health care and the development of quantitative techniques to facilitate the strategic assessment of high hospital activity levels in a region. Another objective of one of the papers was to conduct a systemic analysis of the resources and performance of public hospitals. A multi-objective optimization (MOO) approach was proposed by [8]. This approach identifies the theoretical capacity of the entire hospital and facilitates sensitivity analysis, such as patient case mix (PCM). Combining aspects of uncertain scheduling parameters and multi-stakeholder interests and scheduling performance for operating rooms using multi-criteria optimization was described in [9].

To develop a method, precisely in the era of supporting competition in the market, scientific methods determine the risk and failure of actions [10]. One of the most well-known risk assessment methods is the FMEA (Failure Mode and Effects Analysis) method [11]. FMEA is a method known in the healthcare sector since the 1990s to determine the risk of drug production and control errors in hospitals [12]. Since the application of FMEA in healthcare has been very successful, it has been called failure modes and effects analysis (H-FMEA) [13]. Recently, several studies had published in which FMEA is used together with fuzzy sets to overcome the weaknesses of the traditional RPN (Risk Priority Number) ranking system [14]. A general FMEA method based on fuzzy logic has been proposed that simulates the traditional FMEA methodology by reducing the number of rules in the fuzzy RPN modelling process [15].

Numerous studies [6,16,17] show that the challenges of inappropriate financial allocation, healthcare efficiency, and patient safety make a compelling case for the need for changes in medical systems. New and innovative approaches to care are needed in financing, delivering, and managing health services. At the same time, these approaches should improve the quality of care, ensure financial sustainability and meet the needs and demands of individuals and communities. Patient-centred approaches that engage people and enable self-care are gaining popularity in response to these challenges. Healthcare delivery is a unique process involving real-time decision-making and complex human activity. An integrated care delivery model would effectively coordinate services based on patient and hospital needs.

2.1. Contribution

The study aimed to develop a risk-based approach considering factors contributing to surgery cancellation in classified hip osteoarthritis patients. By accurately identifying the hospital’s risks (e.g., surgery cancellation), one can select an appropriate control solution to eliminate or reduce surgery-related expenses and increase quality, efficiency, and patient safety. The study combines the multi-criteria method and FMEA to introduce a belief structure and describe expert knowledge by integrating the FMEA with FTOPSIS while calculating the criterion weights from the expert questionnaires. FTOPSIS calculate the level of performance, and FMEA calculates the risks of hospital operations in a comprehensive and ranked manner based on potential criteria through their integration. The paper also presents a detailed scheme for combining FMEA and FTOPSIS methods.

3. General Scheme of The Method

A risk-based approach and decision-support methods were used to develop the model. The method considered factors affecting hospital quality and appropriate care for a patient scheduled for surgery for hip osteoarthritis (Figure 1). The TOPSIS fuzzy method is selected because:

The group evaluation method (fuzzy TOPSIS method) with belief structure includes fuzzy evaluations and degrees of belief. In the fuzzy approach, degrees of belief allow the expert to assign a more significant value to the factors under consideration.
The FTOPSIS method is used to find high-risk options (determines the preference of the group belief structure problem of experts).
The relevant calculation procedures can be carried out using fuzzy values.
The ability to quickly identify the best alternative.
The relative weight between S - effect, O - probability, and D - detectability (FMEA method) of an undesirable scenario can "diverge" from each other. The assigning of weight to each of the mentioned factors is flexible, which gives greater consistency with the actual decision-making situation.
Input factors (S – effect, O – probability, D – detectability (FMEA method) are combined according to their weights so that they match the research problem (cancellation of planned operations) [3,18,19].

Figure 1 shows the successive stages of the work methodology. The following section describes the exact calculations according to the steps in the figure below.

The following sections present the different steps of the risk assessment method in determining the discontinuation rate in Figure 1. Stage 1 presents data processing from the acquired database and the procedure for data reduction based on the questionnaire. Stage 2 presents a mathematical model combining the risk assessment methods and the MCDA fuzzy decision-making method. Based on Figure 1. The proposed method’s calculation process had presented in the case study in Chapter Empirical Verification of The Proposed Method and Result of The Study.

4. Risk assessment based on FTOPSIS and FMEA

Based on Figure 1, which shows the risk assessment scheme, the next section of the paper presents solutions for all stages.

Based on Stage 1 in the proposed method risk assessment methodology in determining the abandonment rate is to pre-process the data obtained from the experts based on the questionnaire. This step mainly includes:

Removing rows and columns from a matrix (database) that contain incomplete data.
Calculation the criteria values from the $Δ$ set based on the data in the matrix (database).
Data normalization (replacing the values in the matrix (database) with values belonging to the same reference space).

Pre-process the data from the set

Δ

, where the elements of the set

Δ

are the expert measures

P_{1}, P_{2}, \dots, P_{n}

(where:

i \in {1, 2, ., p}

denotes the element number in the set

Δ

; d - the number of elements in the set

Δ

;

k_{i}

- the i-th element of the set

Δ

)

Δ = {k_{1}, k_{2}, . . ., k_{d}}

(1)

In further considerations, it assumed that matrix

Ω

is a matrix of dimension

N x p

where N is the number of rows in the

Ω

matrix and p is the number of its columns (the number of attributes from the

Δ

set). Some of the attributes (measures) and opinions of the evaluators (elements of the set

Δ

) may be relatively interdependent, relevant, or not for determining the availability of surgical rooms. They may also require calculations (e.g., insufficient medication or tools and materials required). They can also contain the so-called information noise, which results from various errors that may appear in the data derived from the information obtained. Having a matrix

Ω

, one should use an appropriate method of cleaning, ordering, and validating the data contained in

Ω

, which will reduce the amount of information noise are called data pre-processing. Regardless of the data pre-treatment, to ensure the credibility of the risk assessment, it is necessary to determine from among the

Δ

criteria. Those criteria are important for determining the dropout rate. This method is called, in work, the reduction of criteria. Step 1 identifies the language variables used to evaluate alternatives and to calculate the weighting of criteria importance. A formalized multi-criteria information table, will help combine the selected FTOPSIS method with the risk assessment method.

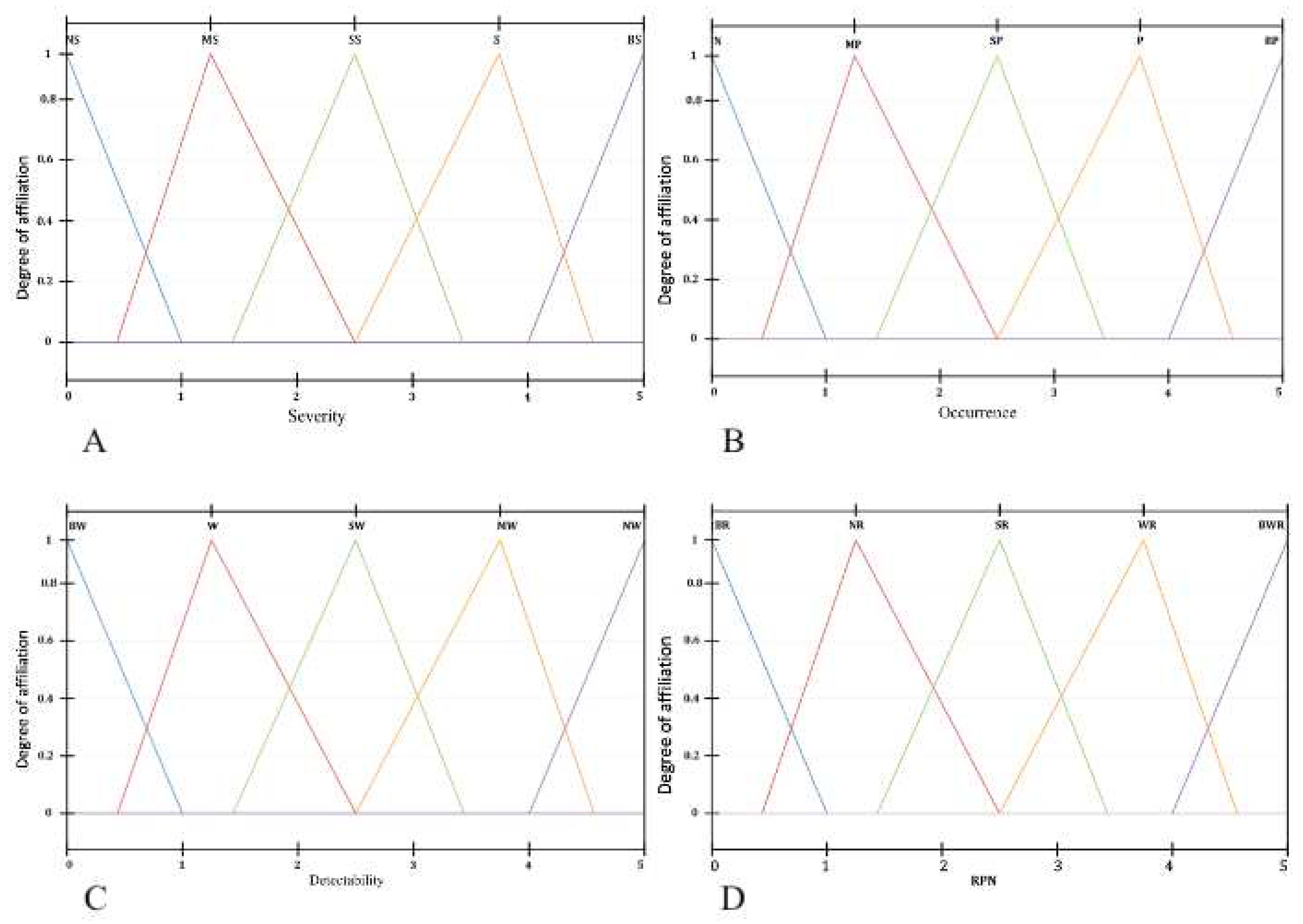
The next stage of the method (Figure 1) is the risk assessment based on FTOPSIS and FMEA. In traditional FMEA, an indicator called risk priority number (RPN) had used in qualifying failure method by multiplying three parameters, occurrence (O), detectability (D), and severity (S). In FMEA, a value within

{0, 1, . . ., 10}

had assigned to each parameter O, D, S. After calculating the RPN for the article, the higher the value assigned for a parameter, the more undesirable the effect of that parameter will be on the evaluation. Figure 2 shows the linguistic terms and triangular values for evaluating the alternatives, where the linguistic variables had transformed into fuzzy numbers. Linguistic variables were used in assigning expert importance weights and evaluating alternatives. It contains both fuzzy ratings and degrees of belief. Using linguistic terms allows the decision maker (expert) to assign a more meaningful value to the factors under consideration.

In Step 2 the linguistic variables had transformed into fuzzy numbers, which are used in expert importance weights to evaluate alternatives. Each parameter’s fuzzy function can puts into Triangle Fuzzy Number as a graphical representation of the fuzzy set. To consider the inaccurate data determining the values of alternatives, based on the data contained in the determined information matrix with criteria from the set (Equation (2)), using the FTOPSIS method, so that its corresponding calculation procedures can have carried out using fuzzy values.

Aggregate the quality values of alternatives A with weights defined for each criterion after reduction (Step 1) C from the information matrix

Ω

. It had assumed that

A_{1}, A_{2}, . . ., A_{n}

denote the alternatives among which the experts will choose the winning solution.

C_{1}, C_{2}, . . ., C_{r}

are the criteria against which the performance of each alternative had calculated. The value

a_{i j}

is a triangular fuzzy number and denotes the performance of alternatives

A_{i}

against the criterion

C_{j}

. Analytically,

w_{j}

denotes the weight of criterion

C_{j}

and is a normalized triangular fuzzy number.

A = [\begin{matrix} {\tilde{a}}_{1, 1} & {\tilde{a}}_{1, 2} & \dots & {\tilde{a}}_{1, n} \\ {\tilde{a}}_{2, 1} & {\tilde{a}}_{2, 2} & \dots & {\tilde{a}}_{2, n} \\ \dots & \dots & \dots & \dots \\ {\tilde{a}}_{m, 1} & {\tilde{a}}_{m, 2} & \dots & {\tilde{a}}_{m, n} \end{matrix}]

(2)

As well as the fuzzy weight vector W of the form:

W = [{\tilde{w}}_{1}, {\tilde{w}}_{2} . \dots, {\tilde{w}}_{n}]

(3)

Next, Step 3 is computing the fuzzy decision matrix and the normalized fuzzy decision matrix. For each triangular fuzzy value,

{\tilde{a}}_{i} = (L_{i j}, M_{i j,} U_{i j})

the set of

α

- sections of the form calculate:

{(a_{i j})}_{α} = [{(a_{i j})}_{α}^{L}, {(a_{i j})}_{α}^{U}], f o r 0 \leq α \leq 1

(4)

Thus, it can transform each fuzzy value into an interval value. Then, the following procedures had used to perform the normalization of the interval values (Step 4):

{(n_{i j})}_{α}^{L} \frac{{(a_{i j})}_{α}^{L}}{\sqrt{\sum_{i = 1}^{m} {({(a_{i j})}_{α}^{L})}^{2} + {({(a_{i j})}_{α}^{U})}^{2}}}, f o r i = 1, \dots, m a n d j = 1, \dots, m

(5)

{(n_{i j})}_{α}^{U} \frac{{(a_{i j})}_{α}^{U}}{\sqrt{\sum_{i = 1}^{m} {({(a_{i j})}_{α}^{L})}^{2} + {({(a_{i j})}_{α}^{U})}^{2}}}, f o r i = 1, \dots, m a n d j = 1, \dots, m

(6)

As a result, the interval

[{(n_{i j})}_{α}^{L}, {(n_{i j})}_{α}^{U}]

is the normalized equivalent of the interval

[{(a_{i j})}_{α}^{L}, {(a_{i j})}_{α}^{U}]

. It is then possible to transform the normalized interval back to a triangular fuzzy number of the form

\tilde{N_{i j}} = (n_{i j}, x_{i j}, y_{i j})

in such a way that the value of

n_{i j}

α = 1

will be:

n_{i j} = {(a_{i j})}_{α = 1}^{L} = {(a_{i j})}_{α = 1}^{U}

(7)

Similarly, establishing the coefficient

α = 0

, we obtain the remaining values of a triangular fuzzy number:

{(n_{i j})}_{α = 0}^{L} = n_{i j} - x_{i j} a n d {(n_{i j})}_{α = 0}^{U} = n_{i j} + y_{i j}

(8)

then

x_{i j} = n_{i j} - {(n_{i j})}_{α = 0}^{L} a n d y_{i j} = {(n_{i j})}_{α = 0}^{U} - n_{i j}

(9)

The value

\tilde{N_{i j}}

is the normalized equivalent of the triangular fuzzy number

\tilde{a_{i j}}

Next, Step 5 creates a fuzzy decision matrix considering the weights of each criterion. Step 6 creates a normalized fuzzy decision matrix considering the weights of each criterion:

{\tilde{v}}_{j} = {\tilde{w}}_{j} + {\tilde{N}}_{i j}

(10)

These normalized yield values, each of which is in the interval

[0, 1]

Step 7 determines of the ideal with fuzzy nature, both positive and negative. Determining the ideal solution and the inverse of the ideal solution (anti-ideal solution):

{\tilde{A}}^{*} = \{{\tilde{v}}_{1}^{*}, \dots, {\tilde{v}}_{n}^{*}\} w h e r e {\tilde{v}}_{j}^{*} = (1, 0, 0) a n d j = 1, \dots, n

(11)

{\tilde{A}}^{-} = \{{\tilde{v}}_{1}^{-}, \dots, {\tilde{v}}_{n}^{-}\} w h e r e {\tilde{v}}_{j}^{-} = (1, 0, 0) a n d j = 1, \dots, n

(12)

Step 8 distances of each alternative for fuzzy positive and anti-positive ideal negative solutions are calculated.

Calculating the distance of each alternative under consideration from the ideal solution and the inverse of the ideal solution (called anti-ideal solution). Calculating the distance of each considered alternative from the ideal solution and the inverse of the ideal solution between two fuzzy numbers of form

\tilde{A} = (a, m, n)

and

\tilde{B} = (b, s, r)

can have calculated as follows:

\begin{matrix} z (\tilde{A,} \tilde{B)} = \sqrt{\frac{1}{3} [{(a - b)}^{2} + {(a - b - m + s)}^{2} + {(a - b + n - r)}^{2}]} \end{matrix}

(13)

The distance of the alternatives from the ideal solution can have calculated as follows:

\tilde{Z_{i}^{*}} = \sum_{j = 1}^{n} z (\tilde{v_{i j,}} {\tilde{v}}_{i j}^{*}), f o r i = 1, \dots, m

(14)

Similarly, the distance from the inverse of the ideal solution (anti-ideal solution) is calculated:

\tilde{Z_{i}^{-}} = \sum_{j = 1}^{n} z (\tilde{v_{i j,}} {\tilde{v}}_{i j}^{-}), f o r i = 1, \dots, m

(15)

Step 9 obtains proximity coefficients for each alternative.

Calculating the relative proximity of each alternative to the ideal solution. The relative closeness of alternative

A_{i}

to the ideal solution

\tilde{A *}

defined as:

\tilde{R_{i}^{*}} = \frac{Z_{i}^{-}}{Z_{i}^{-} + Z_{i}^{*}}, f o r i = 1, \dots, m

(16)

In Step 10, depending on the result of the proximity coefficients, ranking these coefficients can determine the alternatives in the risk assessment. The result is to rank the alternatives in order from the largest to the smallest relative closeness value to the ideal solution

\tilde{R_{i}^{*}}

Figure 3 shows the graphical solution of the combination of the two methods, TOPSIS and FMEA. Conclusions of the analysis:

The proposed risk assessment approach incorporates fuzzy judgments and belief degrees (expert preferences).
The flexibility of assigning weight to each factor in the proposed approach is consistent with the actual decision situation.
The input factors (S, O, D) are combined according to their weights, enabling a more comprehensive application approach.

5. Results

Surgical scheduling involves allocating hospital resources to individual cases and deciding when to perform surgeries. This task is critical in efficiently using hospital resources while providing quality patient care. The following are the study results in the treatment process based on actual data. Research in the [Name of Institute] usually consists of three stages: patient classification, reference to treatment (therapeutic care), and elective surgery.

Patients entering the orthopedics department are first classified according to their level of urgency, using appropriate indicators.
If the patient is qualified for elective surgery, he/she is given a date for hip replacement surgery (endoprosthesis).
A patient referred to the surgery department undergoes a medical consultation by: nurses, residents, doctors performing the surgery, orthopedic doctors, and anesthesiologists.
After a screening - essential examination. The patient has surgery the next day.

To confirm the validity of the risk assessment model, three experts (a nurse, an anesthesiologist, and a physician, the so-called "operator" - who performs surgery) participated in the research. The assessment was made the day before the elective surgery [20]. The study looked at indicators affecting the cancellation of hip replacement surgery (6 variants of the cancellation process). Finally, compare the obtained grades with those of experts in the [Name of Institute].

General hospital characteristics:

3 operating rooms
Inpatient surgery room,
Operating room for patients with infections,
Operating room for trauma patients,
1 post-operative room,
42 patient bed.

Additional factors:

Hip replacement surgery is performed on Mondays, Wednesdays, or Fridays (optional).
There are 3 or 4 scheduled surgeries per day.

The questionnaire, evaluated by experts, obtained six alternatives based on 30 criteria. Figure 4 shows the obtained alternatives from the decision matrix for risk assessment based on the questionnaire.

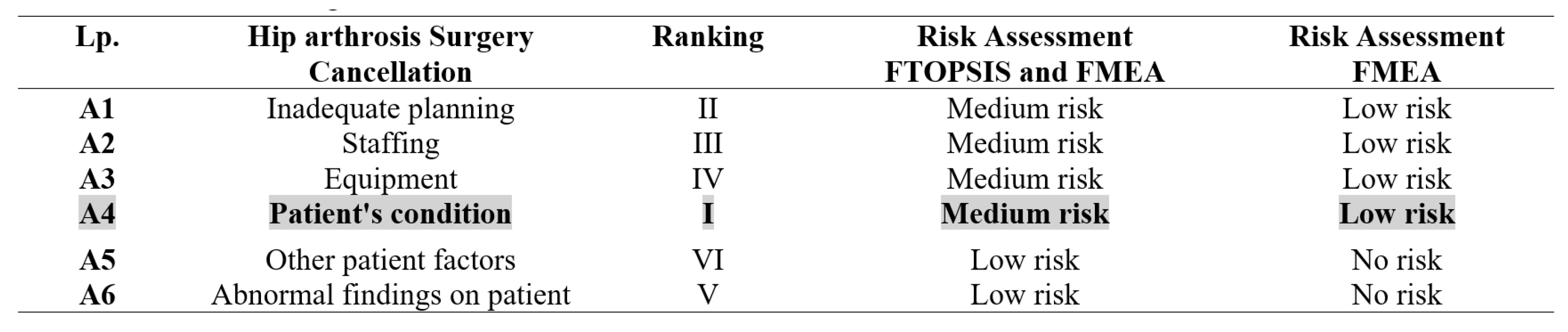
The following research presents the results from the steps based on the previous methodology. To fit the data from the questionnaires into the information matrix, determined the following factors to give us the evaluation attributes with the determination of alternatives from the decision matrix for risk assessment. These are: A1-Inadequate planning; A2 – Staffing; A3 - Equipment; A4 - Patient’s condition; A5 - Other patient factors; A6 - Abnormal findings on a patient. After obtaining the results from Stage 1 and Stage 2 obtained the belief distance measurement along (Figure 5) with a graphical representation of the fuzzy function of each parameter (Figure 6).

The results from the presented method from the measurement of belief distance are presented below, along with a graphical representation of the fuzzy function of each parameter.

Based on the proposed method, the results show that the expert’s opinion compared with the results of FMEA and FTOPSIS showed the potential of the framework in the correct prioritization of abandonment rates. Figure 8 shows the ideal solution for the designated alternatives in the risk assessment. Figure 7 shows the distance of each alternative to the ideal solution in the risk assessment

Figure 7. Designated alternatives from the decision matrix for risk assessment.

From among the six factors, tree of them: patient condition, inadequate scheduling, and personnel were identified as having the most significant impact on the surgical cancellation of elective surgery, as shown in Figure 7 and Figure 9.

Figure 8. A: The ideal solution for the alternatives in the risk assessment; B:Distance of each of the considered alternatives to the ideal solution in the risk assessment.

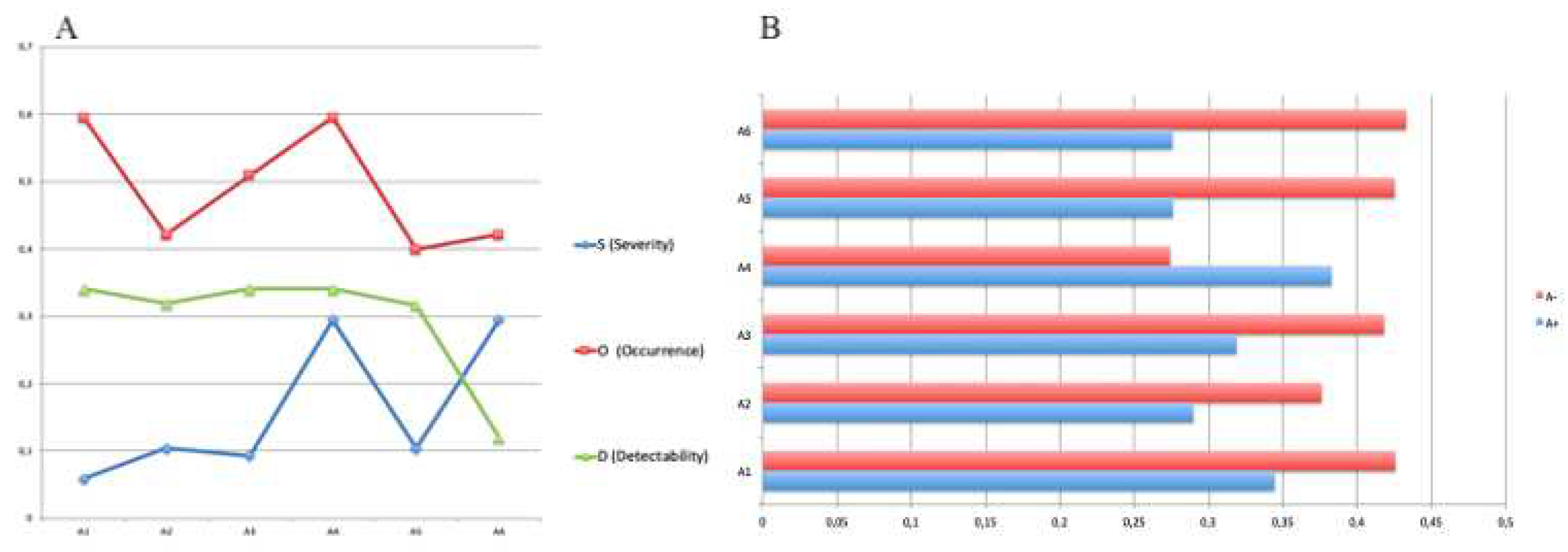
Figure 9. Relative proximity for each Alternative in the risk assessment.

The results show that the patient’s condition is the main risk of canceling surgery. Of course, it can reduce the financial risk by examining the patient before admission to the ward, but only if schedule surgery. The patient can then perform the necessary tests with health funds. During urgent operations, the risk increases, as do the hospital’s finances. What is needed is a strategy that will ultimately reduce the additional cost to the hospital. The research presented in the case study combined two methods and showed the problem in Polish hospitals. The decision to operate on patients is a daily one. The method demonstrated the validity of the procedure carried out and its importance for the future of the hospital.

6. Conclusions

The main properties of the risk assessment method in determining the surgical dropout rates are:

the method is procedural in nature, a planned and reusable activity.
considered in the method, the broad aspect of the variability of experts’ preferences is adaptive rather than rigid (once implemented). Adaptation here is the possibility of adjusting changes in the factors in which the criteria defined by the expert express the appropriate accession to the abandonment of surgery in the patient.
the method can be used in any operation performed and any hospital.
the use of fuzziness through the application of the decision support method FTOPSIS allows for better (more accurate) risk assessment.
confirmation of the method’s applicability to risk analysis by decision support method.

The novelty of the publication is the multi-criteria and multi-faceted risk assessment. This method combines two data sources, the FTOPSIS fuzzy method with the FMEA risk assessment. With this solution, it will be possible to automate the process of reorganization and redevelopment of the system in hospitals and other organizations and enterprises. The multi-faceted method makes it better and can apply to various problems. We can achieve such automation by implementing the method presented in the paper, as shown in Figure 1.

The method developed in the paper can be a part of an information system supporting reorganization, restructuring, and modification of the operational process in a hospital. The process of renewal, modernization, and reconstruction of a given system is understood as such reconstruction to make it more useful. The presented methodology belongs to the CASE systems class. It enables automation in the so-called software system reengineering. The methodology also enables external benchmarking of the organization that provides various services. It is also a tool for improving the organization’s activities in the so-called outsourcing aimed at increasing the effectiveness and efficiency of the organization in providing services related to health, industry, or learning.

References

Wong, J.; Khu, K.J.; Kaderali, Z.; Bernstein, M. Delays in the operating room: signs of an imperfect system. Canadian Journal of surgery 2010, 53, 189. [Google Scholar]
Bennell, K.L.; Hinman, R.S. A review of the clinical evidence for exercise in osteoarthritis of the hip and knee. Journal of Science and Medicine in Sport 2011, 14, 4–9. [Google Scholar] [CrossRef] [PubMed]
Liu, H.C.; You, J.X.; Chen, S.; Chen, Y.Z. An integrated failure mode and effect analysis approach for accurate risk assessment under uncertainty. Iie Transactions 2016, 48, 1027–1042. [Google Scholar] [CrossRef]
Xu, K.; Tang, L.C.; Xie, M.; Ho, S.L.; Zhu, M. Fuzzy assessment of FMEA for engine systems. Reliability Engineering and System Safety 2002, 75, 17–29. [Google Scholar] [CrossRef]
Cihoda, J.H.; Alves, J.R.; Fernandes, L.A.; de Souza Neto, E.P. The analysis for the causes of surgical cancellations in a Brazilian university hospital. Care Management Journals 2015, 16, 41–47. [Google Scholar] [CrossRef] [PubMed]
Liu, H.C.; Chen, X.Q.; Duan, C.Y.; Wang, Y.M. Failure mode and effect analysis using multi-criteria decision making methods: A systematic literature review. Computers & Industrial Engineering 2019, 135, 881–897. [Google Scholar]
Burdett, R.L.; Corry, P.; Yarlagadda, P.; Cook, D.; Birgan, S.; McPhail, S.M. A mathematical framework for regional hospital case mix planning and capacity appraisal. Operations Research Perspectives 2023, 10, 100261. [Google Scholar] [CrossRef]
Burdett, R.; Kozan, E. A multi-criteria approach for hospital capacity analysis. European Journal of Operational Research 2016, 255, 505–521. [Google Scholar] [CrossRef]
Rachuba, S.; Werners, B. A fuzzy multi-criteria approach for robust operating room schedules. Annals of Operations Research 2017, 251, 325–350. [Google Scholar] [CrossRef]
Carbone, T.A.; Tippett, D.D. Project risk management using the project risk FMEA. Engineering management journal 2004, 16, 28–35. [Google Scholar] [CrossRef]
Mahdi Bahrami, D.; Sajjadi, S.M. Innovation and Improvements In Project Implementation and Management; Using FMEA Technique. Procedia-Social and Behavioral Sciences 2012, 41, 418–425. [Google Scholar] [CrossRef]
Duwe, B.; Fuchs, B.D.; Hansen-Flaschen, J. Failure mode and effects analysis application to critical care medicine. Critical care clinics 2005, 21, 21–30. [Google Scholar] [CrossRef] [PubMed]
DeRosier, J.; Stalhandske, E.; Bagian, J.P.; Nudell, T. Using health care failure mode and effect analysis™: the VA National Center for Patient Safety’s prospective risk analysis system. The Joint Commission journal on quality improvement 2002, 28, 248–267. [Google Scholar] [CrossRef] [PubMed]
Zhang, Z.; Chu, X. Risk prioritization in failure mode and effects analysis under uncertainty. Expert Systems with applications 2011, 38, 206–214. [Google Scholar] [CrossRef]
Tay, K.M.; Lim, C.P. A guided rule reduction system for prioritization of failures in fuzzy FMEA. Applications of Soft Computing: Recent Trends. Springer, 2006, pp. 301–310.
Valentijn, P.P.; Schepman, S.M.; Opheij, W.; Bruijnzeels, M.A. Understanding integrated care: a comprehensive conceptual framework based on the integrative functions of primary care. International journal of integrated care 2013, 13. [Google Scholar] [CrossRef] [PubMed]
Goodwin, N.; Stein, V.; Amelung, V. What is integrated care? Handbook integrated care 2021, pp. 3–25.
Guerrero, H.H.; Bradley, J.R. Failure Modes and Effects Analysis: An Evaluation of Group versus Individual Performance. Production and Operations Management 2013, 22, 1524–1539. [Google Scholar] [CrossRef]
Huang, J.; Li, Z.; Liu, H.C. New approach for failure mode and effect analysis using linguistic distribution assessments and TODIM method. Reliability Engineering & System Safety 2017, 167, 302–309. [Google Scholar] [CrossRef]
Walash, N.; Mitchell, H.; Reeves, B.; Hurley, M. Integrated exercise, and self-management programmers in steoarthritis of the hip and knee A systematic review of effectiveness. Rehabil Med. 2006, 10, 57–65. [Google Scholar]

Figure 1. Scheme of a risk assessment method in determining the coefficient of resignation from surgery.

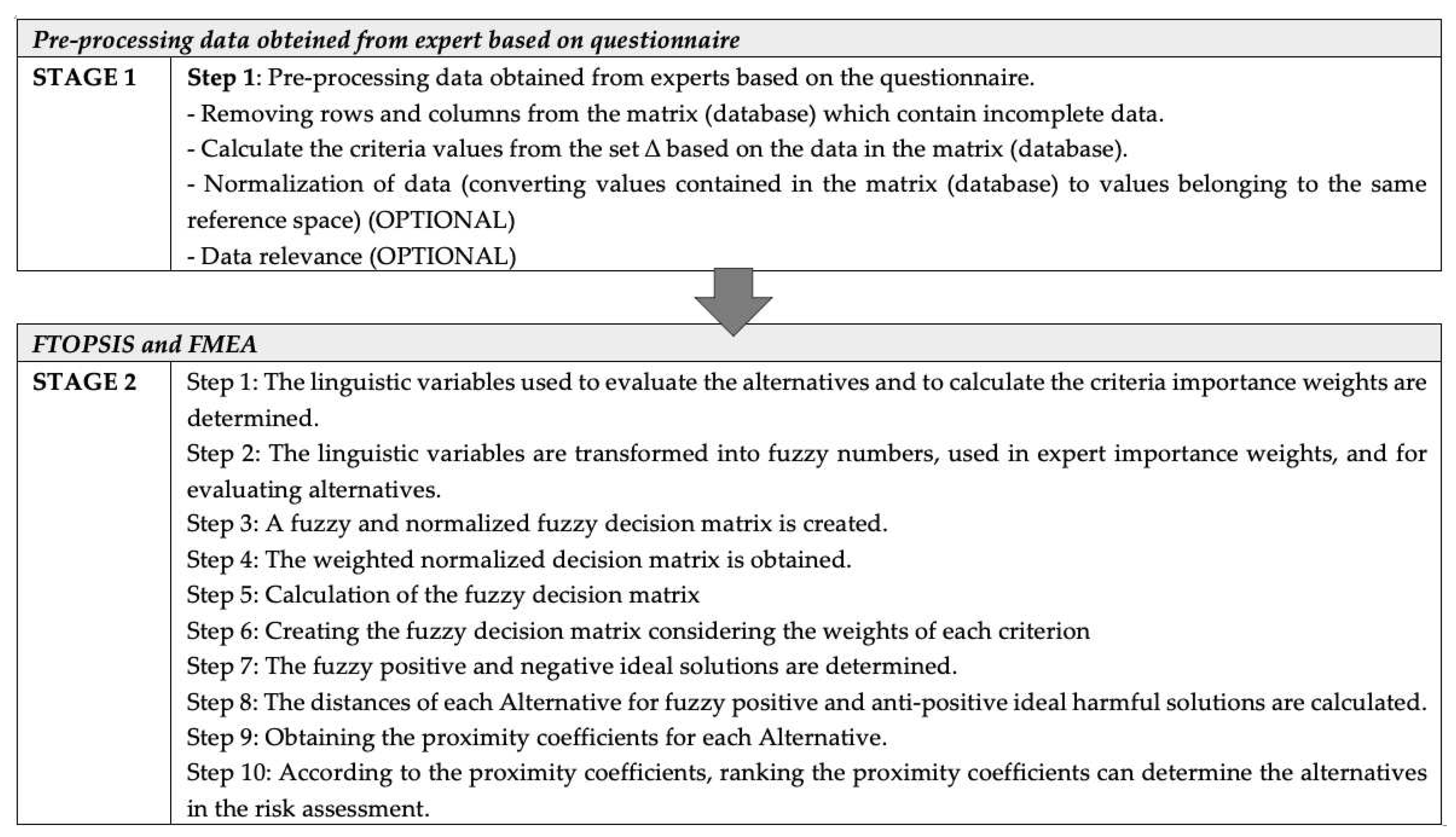
Figure 2. Language terms and triangular values to alternative assessments.

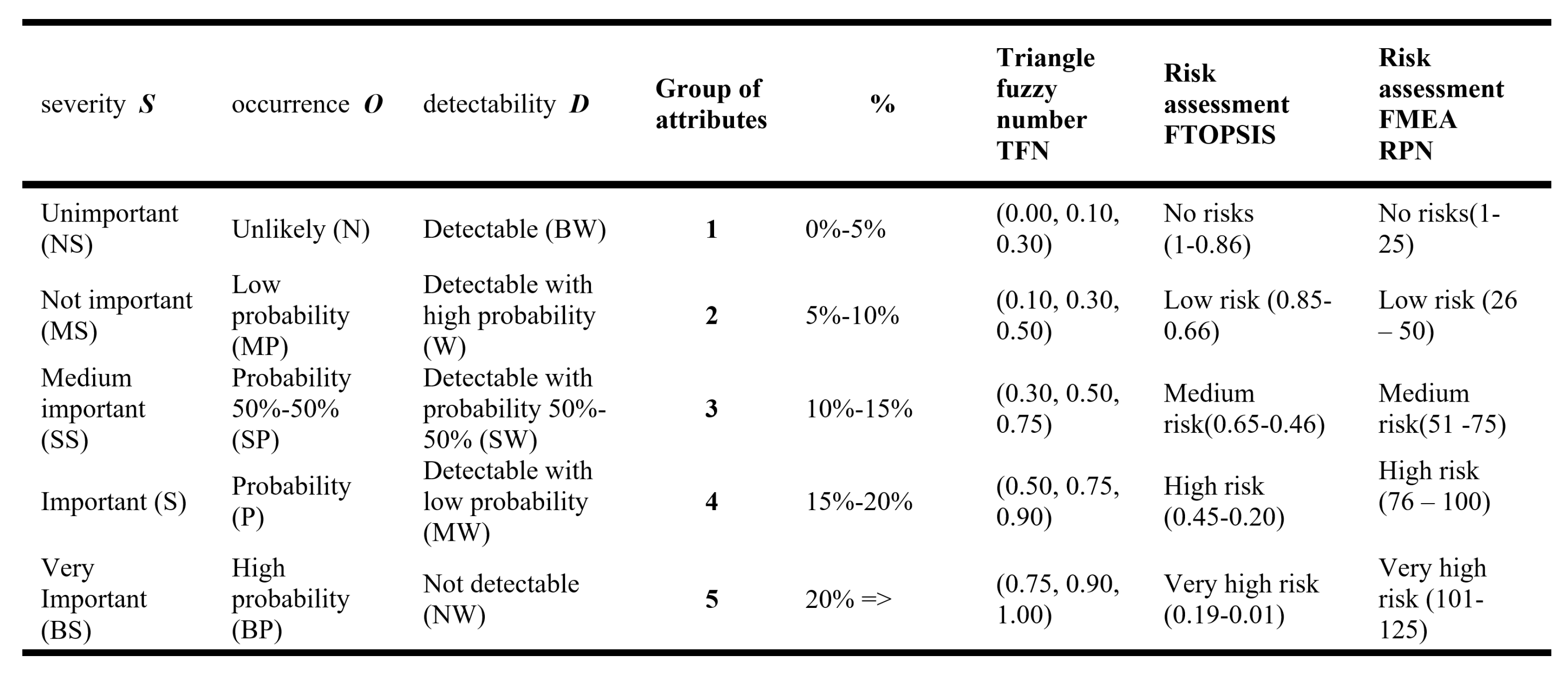
Figure 3. Combining the fuzzy method with FMEA.

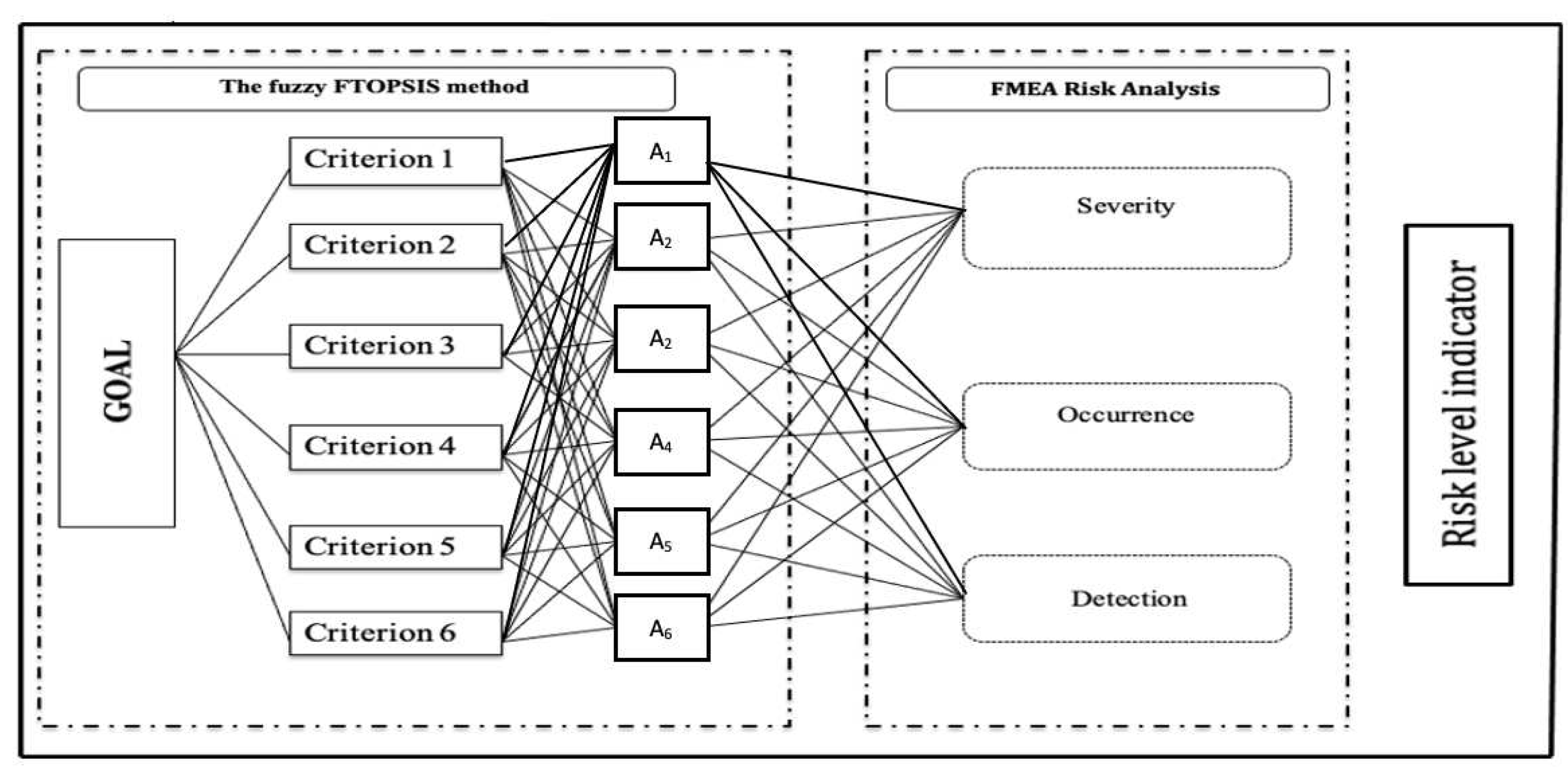
Figure 4. Designated alternatives from the decision matrix for risk assessment

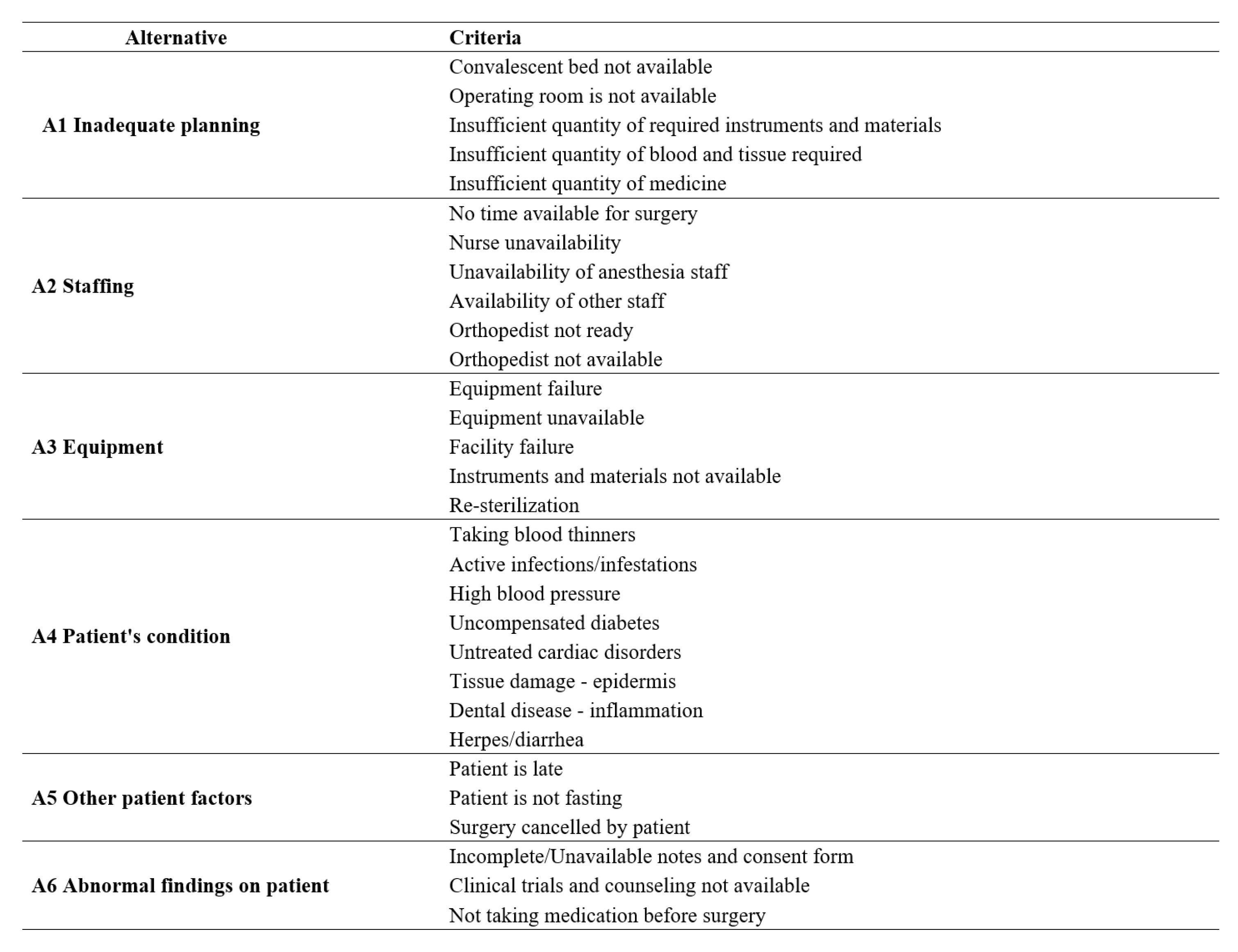
Figure 5. Belief distance measurement.

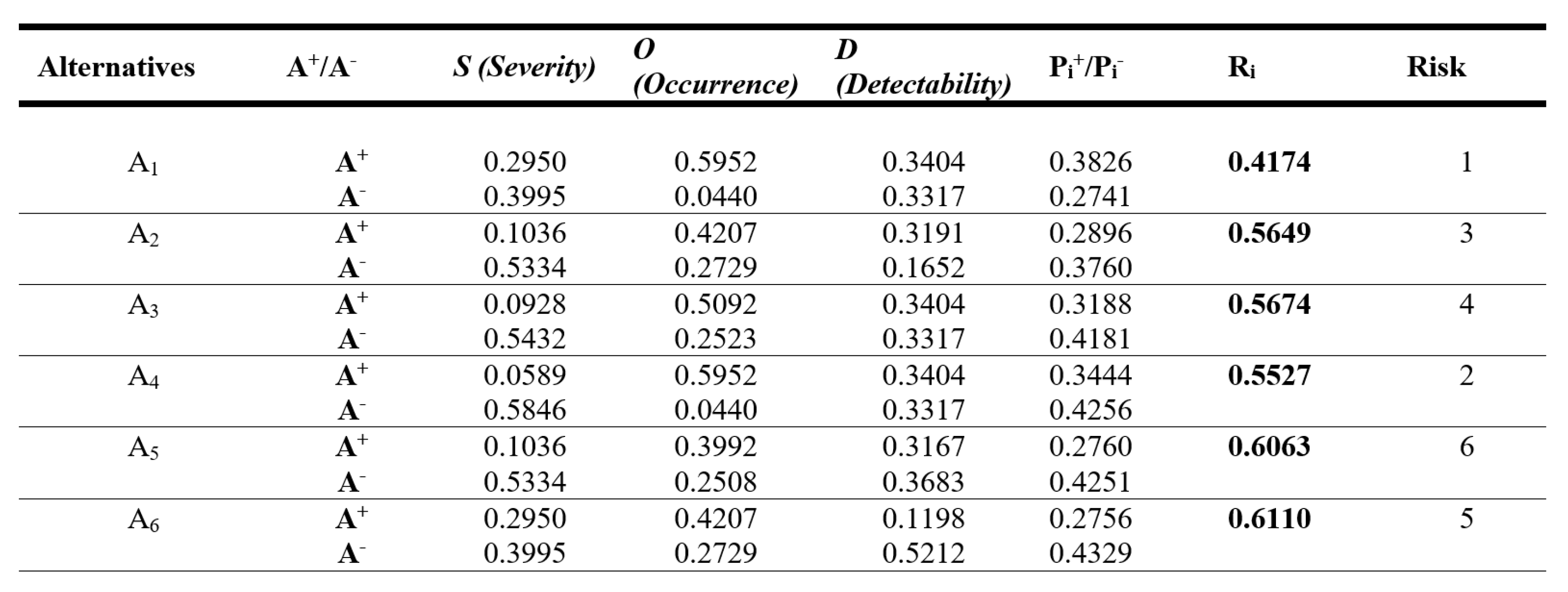
Figure 6. Fuzzy functions of each parameter. A: Fuzzy function of parameter S.; B: Fuzzy function of parameter O.; C: Fuzzy function of parameter D.; D: Fuzzy function in risk assessment (RFN).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Prioritization of Scheduled Surgeries Using Fuzzy Decision Support and Risk Assessment Methods

Abstract

1. Introduction

2. Related works

2.1. Contribution

3. General Scheme of The Method

4. Risk assessment based on FTOPSIS and FMEA

5. Results

6. Conclusions

References

MDPI Initiatives

Important Links

Subscribe