Prerpints.org logo
Preprint
Article

FL* Approach to the Coexistence of Fermi Arcs with Metal-Insulator Crossover in Strongly Underdoped Cuprates

Altmetrics

Downloads

73

Views

15

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

13 November 2023

Posted:

15 November 2023

You are already at the latest version

Alerts
Abstract
We propose that the coexistence of gapless Fermi arcs with the metal-insulator crossover of in-plane resistivity in strongly underdoped cuprates can be explained by the FL* fractionalized Fermi liquid nature of these systems and it is not due simply to disorder effects. The particle excitations of this FL* system derived from variants of the t-J model are: the gapless holon carrying charge with small Fermi momentum proportional to the doping, the gapful spinon carrying spin 1/2, gauge fluctuations coupling them and the hole as a spinon-holon bound state or resonance due to gauge binding with a Fermi surface respecting the topological Luttinger theorem. In our proposal Fermi arcs are determined by the hole resonance, whereas the metal-insulator crossover is dominated by spinon-spinon (with subleading holon-holon) gauge interactions and this dichotomy is able to explain their coexistence.
Keywords: 
Subject: Physical Sciences  -   Condensed Matter Physics

1. Introduction

In the strong underdoping low-temperature region of the phase diagram of the cuprates, ARPES experiments prove the existence of gapless Fermi arcs (see e.g., [1] and references therein). The Fermi liquid paradigm then would suggest a metallic resistivity with a temperature dependence T α , with α at least greater than 1. In the same region of the phase diagram, however, the experiments show that the in-plane resistivity has a minimum at finite temperature, i.e., a metal-insulator crossover (see e.g., [2]). Furthermore if the resistivity is suitably normalized it exhibits a universal behaviour [3] which appears hardly compatible with an explanation of that crossover in terms of disorder localization.
We propose that the coexistence of the two phenomena can be explained in term of the FL* fractionalized Fermi liquid concept, introduced in [4,5], within an approach to the low-energy physics of the cuprates in terms of the t- t ′ -J model.
There have been several proposals of a FL* nature of the above quoted region of the phase diagram of the cuprates, named “pseudogap phase” [6,7] (and references therein), but to our knowledge not a careful discussion of the consistency between Fermi arcs and metal-insulator crossover (MIC).
An FL* is an exotic fractionalized Fermi liquid which has hole-like (in the case relevant for the cuprates) excitations near a Fermi surface satisfying a generalization of Luttinger theorem, together with fractionalized excitations emerging from a topological order, in particular holons ( h ) charged spinless and spinons ( s ) neutral of spin 1 / 2 , interacting via a so-called slave-particle gauge field ( a ) . The hole is a bound state or a resonance arising from holon-spinon binding generated by the gauge attraction.
The present paper is part of a project aimed at analyzing the consequences of the proposed FL* nature of the cuprates. The general idea underlying this project is that one can explain the Fermi liquid (FL) versus non-Fermi liquid (NFL) dichotomies encountered in the cuprates, in the present case the FL nature of Fermi arcs and the NFL nature of the MIC, in the following way: If some physical response is dominated by the hole excitations (spinon-holon interaction), then its behaviour is close to that of a Fermi liquid, if instead it is dominated by spinon-spinon (and possibly also holon-holon) interaction then it has a clear Non-Fermi liquid character.
Of course it is known that the t- t ′ -J model is insufficient to explain some phenomena appearing in the cuprates such as charge density waves (see e.g., [8]), but apparently at least these phenomena are qualitatively irrelevant for the issue of the present paper at strong underdoping [9]. More generally, although clearly such a simple model cannot reproduce real experimental data, we show that even with an approximate treatment many of their doping and temperature dependencies can be indeed qualitatively understood. Furthermore with the introduction of experimentally derived but doping and temperature independent scales also a semi-quantitative agreement is obtained in many cases.

2. General Outline of the Approach

In the description of the low-energy physics of the cuprates in terms of a two-dimensional (2D) t- t ′ -J model the sites correspond to the Cu sites of a CuO plane in the cuprates and the Zhang-Rice singlets to the empty sites. The Hamiltonian is given by:
H = P G [ ∑ < i , j > n . n . − t c i α * c j α + h . c . + J S → i · S → j + ∑ < i , j > n . n . n . t ′ c i α * c j α ] P G ,
where < i , j > denotes a link between lattice sites i andj, ( n ) n . n . denotes (next-)nearest neighbor sites and α the spin index which is assumed summed up also in the following if repeated. P G denotes the Gutzwiller projection implementing the no-double occupation and describing the Mott physics of the system. It can be tackled with a spin-charge decomposition [10,11] of the hole field: c α = h s α * where the holon h is a spinless fermion, so that by Pauli principle the no double occupation is implemented, and the spinon s is a boson, satisfying in each site the constraint s α * s α = 1 [12]. This decomposition involves an unphysical degree of freedom, because one can multiply at each site s and h by arbitrary opposite phase factors leaving c unchanged. The corresponding local U ( 1 ) gauge invariance is implemented by introducing a slave-particle gauge field a μ which in turn produces an attraction between holon and spinon. To show this effect of gauge fluctuations beyond perturbation theory, as a rough approximation, we apply in [13] a kind of eikonal resummation.
However, a comparison with the corresponding one-dimensional (1D) model [14,15] suggests to modify the statistics of spinons and holons at lattice level, turning them into semions, i.e., their fields under equal time oriented exchange acquire a phase ± π / 2 (see e.g., [16]). These phase factors are opposite for spinons and holons, so that c retains its fermionic nature. This modified statistics is crucial for our discussion (as it was in 1 dimension), so let’s give some details.
The change of statistics is implemented in the Lagrangian formalism by coupling the holon to a U(1) gauge field B μ , related to the charge, with a Chern-Simons action with coefficient -1/2 and coupling the spinon to an SU(2) gauge field V μ , related to the spin, with Chern-Simons action with coefficient 1/2 [12,17]. This procedure corresponds to dressing the holon with a -1/2 charge flux and the spinon with a 1/2 spin flux. Due to the topological properties of Chern-Simons theory, if no approximations are made the result is an exact rewriting of the original model. However, if suitable approximations are introduced this rewriting provides a treatment of the model that with dimensional reduction was successful in deriving the correct large-scale behaviour of the model in 1D [14]. Therefore we suggested that this provides a good approach also for the 2D model, relevant for the low-energy physics of the cuprates. The parameter region corresponding to what we call in this paper the pseudogap (PG) “phase” of the cuprates has an upper boundary in the (in-plane) doping ( δ )-temperature (T) phase diagram identified with the inflection point of in-plane resistivity [2]. Therefore the PG “phase” appears at low δ and T.
In PG the holon dressing by the charge gauge field B μ induces a uniform charge-flux π per plaquette [12] and via Hofstadter mechanism [18] it converts the spinless femionic holons h into lattice Dirac fermions with dispersion defined in the Magnetic Brillouin Zone (MBZ). More precisely, the results of [19] prove that in the t- t ′ model for elementary circuits, triangles and squares, the optimal flux at half-filling is π / 2 for triangles and π for squares. Therefore we assume that the “uniform” component of B, denoted as in [20] by B μ m , μ = 1 , 2 at sufficiently small doping and temperature is given as follows: let i be a site in the even Néel sublattice and i ± α ^ , α = 1 , 2 be its nearest-neighbour sites in the 1 and 2 directions respectively and i + β ^ , β = ± 1 ± 2 its next-nearest-neighbour sites. Then
∫ < i , i ± α ^ > B m = ( − 1 ) α ( ± 1 ) π 4 , ∫ < i , i ± β ^ > B m = π
The fluctuations of B μ around its “uniform” component turn the holons into semions. Since semionic spinless excitations have the same Fermi surface (FS) of spin 1/2 fermions [21,22] the above π flux converts the fermionic holon with tight-binding dispersion
ω h ∼ 2 t [ ( cos k x + cos k y ) − δ ] + 4 t ′ cos k x cos k y
into a pair of lattice “Dirac fields”, ψ a , with pseudospin index a related to the two Néel sublattices and with dispersion: ω h ∼ 2 t [ cos 2 k x + cos 2 k y − δ ] − 4 t ′ cos k x cos k y restricted to the magnetic Brillouin zone. This produces small holon Fermi surfaces near ( ± π / 2 , ± π / 2 ) with Fermi momenta O ( δ ) in the MBZ, if identified with the union of two square regions, denoted as R(ight) and L(eft) centered at Q R = ( π / 2 , π / 2 ) and Q L = ( − π / 2 , π / 2 ) , respectively. In the hole spinon-holon resonance the Dirac structure of such holons induces [13] a momentum-dependent factor in the wave-function renormalization constant,
Z ( k → ) = 1 2 [ 1 − cos k x + cos k y 2 cos k x 2 + cos k y 2 ]
which reduces the spectral weight in the outer boundary of the MBZ, one key ingredient for a phenomenology of Fermi arcs at strong underdoping.
Let us turn to the gauge field associated to spin. The leading S U ( 2 ) component of the V μ field is along the magnetization axis of the undoped model and it introduces an interaction with the spinons, whose dynamics at large scales without V μ is described by a CP1 model, leading to an additional term
J ′ ( V μ ) 2 s α * s α ,
where, as result of a mean-field approximation, J ′ ≈ J ( 1 − 2 δ ) . Neglecting a staggered term with mean zero, the field V μ describes quantum vortices centered on the positions of lattice holons, with opposite chirality for the two Néel sublattices, so that we call them “antiferromagnetic (AF) spin” vortices. In a quenched treatment of such vortices we derive the mean-field expectation value < ( V μ ) 2 > = m s 2 , with m s 2 ≈ 0.5 δ | log δ | , which opens a mass gap for the spinon, consistent with th AF correlation length at small δ extracted from the neutron experiments [23]. Thus, propagating in the gas of slowly moving AF spin vortices, the AF spinons, originally gapless in the undoped Heisenberg model, acquire a finite gap, leading to a short range AF order.
This spinon gap is crucial because the spinon contribution to the slave-particle gauge action is then of Maxwell type, hence subleading with respect to the contribution of gapless holons. The holon contribution is characterized by the Reizer singularity in the dominant transverse component, killing the logarithmic confinement induced by the spinon contribution. Without the spinon gap the CP1 model would be in the broken symmetry “Higgs” phase and the spinon contribution to the gauge action would be gapped by the Anderson-Higgs mechanism, thus becoming the dominant one. As shown below the Reizer singularity of the slave-particle gauge field is a key factor for the discussion of resistivity and Fermi arcs. In particular the gauge interaction turns the spinon mass m s into a “complex temperature and frequency dependent mass” M s ( T , ω ) = m s 2 + i c ( π T ) 2 + ω 2 χ where c is a constant of O ( 1 ) and χ the holon diamagnetic susceptibility proportional to 1 / δ . Furthermore the spinon gap modifies the chemical potential of the holes with respect to that of the holons so that the Fermi momentum is of O ( δ 1 / 2 ) and the binding with the spinons produces a hole FS given by 4 small components centered at ( ± π / 2 , ± π / 2 ) . The π -flux introduces a topological order and the relevant version of the topological Luttinger theorem with the relation “fraction of the area of the BZ enclosed by the hole FS” = δ / 2 is satisfied. This is possible due to the modification of the holon chemical potential and actually, somewhat surprisingly, even a simple doping independent combination of the holon Fermi momenta and the spinon momenta corresponding to the spinon gap produces an area of the hole FS quite well compatible with that of the Luttinger theorem, for all the dopings in the physical range.
The above results show that the system behaves like a FL* liquid. Furthermore with the choice of B m made above the FS of the hole near the diagonals of the BZ, where most of the spectral weight is concentrated, almost overlaps with the large tight-binding FS, see Figure 1, as necessary for a consistency with ARPES data, although, admittedly, the overlap is not enough.
The last ingredient crucial in our discussion is a long-range attraction between the AF spin vortices centered on holons in two different Néel sublattices. If we treat in mean-field the spinons ( < s α * s α > ) in Equation (4) we see that the interaction mediated by AF spin vortices on holons is of 2D Coulomb type. From the study of planar Coulomb systems we know that below a crossover temperature T p h ∼ J ′ / 2 π , a finite density of incoherent holon pairs appears. We already remarked that the low-energy holon modes in PG have two small FS in the MBZ; the 2D Coulomb interaction acts on these modes coupling opposites sites of each FS with an attractive potential with a range given by the screening length of the Coulomb gas. A BCS treatment provides p-wave pairings on the two FS, that glued in the entire BZ for the hole resonance produce a d-wave order parameter, as first suggested in a different setting in [24]. However, we do not have condensation of holon pairs because the fluctuations of the phase of the pairing field are too strong [25], restoring the slave-particle gauge symmetry broken by the BCS approximation.

3. FL* Approach to Fermi Arcs

Let us summarize in precise terms the output of the above considerations on the self-energy of the hole resonance. The binding induced by the gauge fluctuations dominated by the Reizer singularity computed with the above cited eikonal approximation produces an imaginary part of the self-energy of the form:
Γ ( ω , T ) = I m Σ g ( ω , T ) = − I m [ J ( 1 − 2 δ ) m 2 + i c ( π T ) 2 + ω 2 χ ] ,
Notice that I m Σ ( ω , 0 ) is linear in | ω | for sufficiently small frequencies, therefore the hole-resonances in PG behave like a Marginal Fermi liquid [26]. Indeed, such behaviour has been found first in optimally [27] and then also in underdoped [28] cuprates.
The contribution to the real part of the self-energy, R e Σ g ( ω , T ) corresponding to Equation (5) is estimated by a Kramers-Kroenig procedure, with an UV cutoff at the charge-transfer gap ≈ 4 J , as suggested by experimental data.
An additional T 2 term can arise due to standard Landau hole-hole interaction.
Let us turn to the effect of the attraction induced by the AF spin vortices.
In our approximation we keep constant (up to its d-structure) the modulus of the holon-pairing parameter Δ h ( k → ) , obtained as solution of a BCS-like equation [25], near the Fermi surface. However, since the charge pairs are not condensed its phase is strongly fluctuating. Therefore, the field describing these phase fluctuations has a doping and temperature dependent gap, denoted by m ϕ , decreasing with T, that modifies the standard BCS form of self-energy near the hole Fermi surface. For m ϕ ( T , δ ) we adopt a form suggested in [29]:
m ϕ ( T , δ ) ≈ T p h ( δ ) e − T p h ( δ ) − T T − T p c ( δ ) ,
where T p c ( δ ) is (an estimate of) the temperature of condensation of holon pairs, which however never occur in the parameter range considered (in [30] it was set to 0). A reasonable approximation for the contribution to the self-energy turns out to be [31]:
Σ v ( ω , k → ) ≈ | Δ h ( k → , T ) | 2 ω − ω h ( k → , ω , T ) + i Γ ( ω , T ) [ 1 − m ϕ ( T ) − ( ω + i Γ ( ω , T ) ) 2 + ω h ( k → , ω , T ) 2 + m ϕ ( T ) 2 ]
where ω h is the hole dispersion modified by R e Σ g ( ω , T ) (sub-leading modification not taken into account in [31]) and Γ the scattering rate of the hole without charge pairing. To understand its implications, let us consider its behaviour in two regions of energy: For ω < < m ϕ expanding the self-energy up to the second order in terms of ω / m ϕ we get
Σ v ( ω , k → ) ≈ | Δ h ( k → , T ) | 2 2 m ϕ ( T ) ( ω − ω h ( k → ) + i Γ ( ω , T ) ) )
Thus for low frequencies the effect of holon pairing appears through a contribution to the wavefunction renormalization constant not modifying the Marginal FL nature, but with a strong dependence on the direction of k → that, together with the Dirac structure, heavily suppresses the spectral weight along the hole FS as we move towards the MBZ boundary from point in the diagonal inside the MBZ, see Figure 1. The “shadow band” outside of the MBZ perhaps can then be invisible because it disappears in the background incoherent continuum.
For ω > > m ϕ we expand the self-energy in powers of m ϕ / ω and we get
Σ ( ω , k → ) ≈ | Δ h ( k → , T ) | 2 ω − ω h ( k → ) + i Γ ( ω , T )
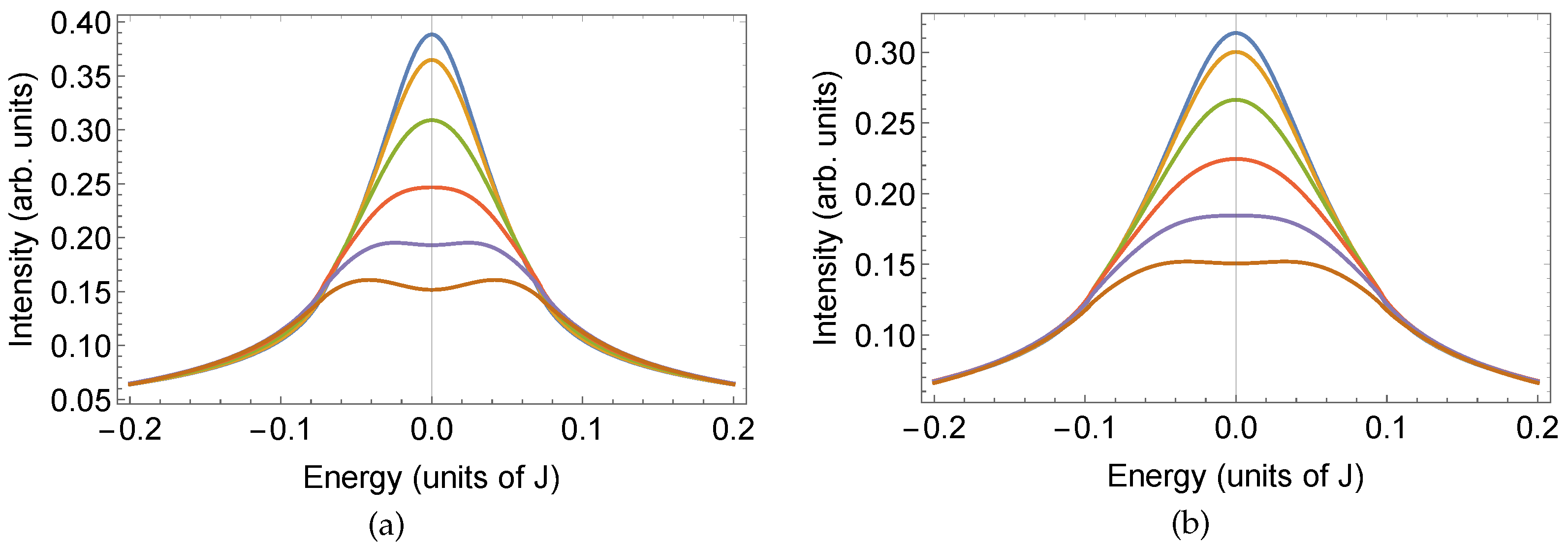
which is the self-energy of a d-wave superconductor. The spectral weight is symmetric in frequencies and non-vanishing on the FS, but it exhibits two symmetric SC-like peaks roughly at ± | Δ h ( k → , T ) | 2 + m ϕ ( T ) 2 . It turns out that approximately for | Δ h ( k → , T ) | > m ϕ ( T ) 2 / Γ ( ω , T ) such SC-like peaks cover the FL one in the spectral weight. Due to the k-dependence of Δ h ( k → , T ) near the nodal region the behaviour is always FL-like, with an effective FS, while as we move towards the antinodal directions most of the spectral weight is concentrated on the SC-like modes, and even if there is a FS, it has negligible effects. We identify the Fermi arcs as the region of the FS where the FL peak is the dominant one, see Figure 2. As a consequence of the temperature dependence of m ϕ the Fermi arcs shrink as we lower T, see Figure 3, in agreement with experiments [32,33].
The above computations clearly show that in PG on the hole resonance the effect of the gauge fluctuations is to produce an isotropic Marginal FL behaviour at small energy. Instead, the effect of the vortex attraction is an anisotropic d-wave like contribution on the Fermi arcs and an effective gap outside of them. This suppression of the spectral weight away from the diagonals of the BZ induced by AF vortices, combined with the suppression of the wave-function renormalization constant due to the Dirac structure (see Equation (3)) produces a strong suppression of the spectral weight outside of the MBZ. Perhaps in this region the corresponding ARPES signal disappears in the thermal continuum background so that the Fermi arc might appear as consistent with the tight-binding Fermi surface. Small deviations near the boundary of the MBZ are however expected, as in [34].
Actually [31], above the continuum background, besides the coherent hole peak there is an additional contribution to the hole spectral weight of the incoherent part describing the high energy—momentum contribution of the unbinded spinon—holon system, see Figure 2. Its leading contribution on the hole FS at energy ω can be approximately estimated as D O S h ( ω − m s ) / ( 2 m s ) if ω > m s , where D O S h is the density of states of the holon. Due to the linear dispersion of the holon in the PG, D O S h is approximately linear in its argument and the incoherent component of the hole gives a contribution to the spectral weight at positive ω growing approximately linearly in ω starting from m s . This additional linear contribution agrees with ARPES data in strongly underdoped cuprates (see e.g., [35]).

4. FL* Approach to Metal-Insulator Crossover

In strongly underdoped cuprates, or more precisely in PG, the in-plane resistivity ρ exhibits a quite peculiar behaviour: it increases more than linearly at intermediate temperatures, with a T 2 behaviour in the same range, but at lower temperatures, unless it drops going to zero at the critical temperature, it acquires a insulating behaviour. For sufficiently underdoped samples, therefore, one can identify a minimum in resistivity at a temperature, denoted by T M I C marking a metal—insulator crossover. As previously mentioned, at higher temperatures, above the T 2 behaviour, an inflection point in the resistivity as a function of temperature is frequently used in defining the lower pseudogap temperature T * .
Often the MIC is attributed to disorder-induced localization. However, this interpretation is at odds at least with the following facts: (i) The role of true disorder has been analyzed carefully in [36] and although it can induce a MIC, the slope of the metallic behaviour in this case is independent of the degree of disorder, whereas such slope in the standard situation depends on the doping concentration. Perhaps instead the disorder is responsible for the logarithmic behaviour found below the MIC. (ii) If the resistivity is suitably normalized it exhibits a universal behaviour [3], being both doping and even material essentially independent, in terms of T / T * . Due to this universality one can see a relation between T M I C and T * ; the last one has been shown to be independent of disorder [36], reinforcing the idea that the MIC is not caused by disorder.
If the MIC is intrinsic it would be incompatible with the FL nature of Fermi arcs. In fact, following the analysis of the previous section, on the basis of the existence of gapless Fermi arcs with marginal FL behaviour, using Drude formula one would expect the in-plane resistivity to exhibit a metallic, linear in T behaviour in PG. However, in a FL* theory since spinons and holons interact via the slave-particle gauge field, one should see if it is predominant the contribution of the hole-hole interaction, due to spinon-holon coupling, or the contribution due to spinon-spinon and holon-holon interactions. It turns out that the second alternative gives the leading effect for in-plane resistivity. To estimate the spinon-spinon interaction we employ the Kubo formula for the spinon current and adopt the eikonal approximation discussed above. For the holons, since the minimal coupling to Chern-Simons gauge fields doesn’t change local gauge-invariant quantities, we can use the Drude formula. Then the spinon and holon contributions are summed up following the Ioffe-Larkin rule [37] i.e., the resistivity of the two subsystems are added: ρ = ρ s + ρ h . Due to the slave-particle gauge interaction the holon contribution is given by the standard expression [38] ρ h ∼ ( T / ϵ h ) 4 / 3 , where ϵ h = t δ is the holon Fermi energy. As discussed in detail in [13] the Reizer singularity of the slave-particle gauge field modify the spinon current correlator giving rise to a contribution to the in-plane resistivity given by
ρ s ≈ m s δ 1 + 1 m s λ T 4 1 8 sin 1 4 arctan 1 m s λ T
with λ T = ( χ / π T c ) 1 2 ∼ ( δ T ) − 1 2 is a kind of “thermal de Broglie wavelength”. Notice that the constant c here is the same used in the discussion of Fermi arc and T * ≈ 2 χ m s 2 . For T T ≳ 100K up to almost T * one finds a metallic behaviour, ∼ T 2 , but in the limit λ T ≥ m s − 1 the ρ s exhibits an insulating behaviour, ∼ 1 T for low T. Such spinon contribution is dominating w.r.t. the metallic holon contribution, so that the resistivity emerging from the Ioffe-Larkin rule at low T is still insulating and the overall behavior is semi quantitatively consistent with the experimental data (except at lower T where, as remarked above, perhaps standard localization occurs). This metal-insulator crossover is determined by the interplay between the AF correlation length m s − 1 and the thermal de Broglie wave length λ T . Hence in the limit λ T ≥ m s − 1 we find a “peculiar” localization due to short-range AF order, producing an insulating behaviour due to the gauge interaction in the same range of parameters where Fermi arcs exist. Since the current considered in this computation is the same considered in the computation made with the hole resonances, the spinon behaviour of the resistivity is the dominating one thus providing a solution to the puzzle of the FL arcs vs NFL resistivity dichotomy. Furthermore the spinon dominance explain the universality noticed in [3]. In fact [39], let’s normalize the resistivity as follows:
ρ n ( T / T * ) = ρ ( T / T * ) − ρ ( T M I C / T * ) ρ ( 1 ) − ρ ( T M I C / T * ) .
Then, as follows from Equation (10), neglecting the holon contribution ρ n would be a universal function of the normalized temperature T / T * and the characteristic temperature T * itself is essentially determined by spinons. In the Ioffe-Larkin rule used a relative coefficient between the holon and the spinon contribution appears as a free parameter, independent of both T and δ , due to the use of a scale renormalization in the continuum limit in the computation of the spinon contribution. An optimized coefficient, while adding a slight degree of non-universality, allows for a reasonably correct fit of experimental data, over a wide range of temperatures and dopings from T M I C to T * . Let us notice as a marginal note [40] that the peculiar dependence on T of the “complex mass” M s = m s 2 + i c ( π T ) 2 χ produces for many decades of K the linear in T 2 behavior found in [41,42], without attributing it to the quasi-particle structure there advocated. A final remark: the inflection point point in temperature of the in-plane resistivity identifying T * in our formalism depends on a delicate cancellation between the doping dependence of the spinon gap m s and the Fermi momenta of the holons, k F h : T * ∼ m s 2 / k F h ∼ δ | log δ | / δ and the result well compares with the experimental data. For this cancellation to occur it is crucial that k F h ∼ δ , it would not occur for the hole Fermi momenta k F ∼ δ .

5. Discussion

In this paper, we have presented evidence that the peculiar coexistence of Fermi arcs and metal-insulator crossover of in-plane resistivity in strongly underdoped cuprates can be attributed to an FL* nature of hole-doped cuprates. A qualitative agreement with experimental data is also exhibited for the hole-spectral weight and for the in-plane resistivity, including its universal property when suitably normalized. Following the strategy advocated here a solution of the dichotomy of the spin susceptibility in the FL* approach is presented in [30]. Another phenomenon exhibiting coexistence of FL and non-FL features appears in the superconducting state of underdoped cuprates, where the superfluid density exhibit a non-BCS critical exponent and universality, whereas ARPES shows a standard BCS behavior near the nodes of the SC order parameter. Computations about this issue within the FL* framework are in progress, with positive preliminary results [43].

Funding

This research received no external funding.

Acknowledgments

I gratefully acknowledge Jürg Fröhlich, Su Zhao-Bin, Yu Lu and Ye Fei for the pleasure of a long collaboration, Dai Jian-Hui, Lorenzo De Leo, Giuliano Orso, Michele Gambaccini, Alberto Ambrosetti, Giacomo Bighin for their contributions and S. Caprara for useful discussions.

Conflicts of Interest

The author declares no conflict of interest.

References

  1. Sobota, J.A.; He, Y.; Shen, Z.-X.T. Angle-resolved photoemission studies of quantum materials. Rev. Mod. Phys. 2021, 93, 025006. [Google Scholar] [CrossRef]
  2. Ando, Y.; Komiya, S.; Segawa, K.; Ono, S.; Kurita, Y. Electronic Phase Diagram of High-Tc Cuprate Superconductors from a Mapping of the In-Plane Resistivity Curvature. Phys. Rev. Lett. 2004, 93, 267001. [Google Scholar] [CrossRef] [PubMed]
  3. Wuyts, B.; Moshchalkov, V.V.; Bruynseraede, Y. Resistivity and Hall effect of metallic oxygen-deficient YBa2Cu3Ox films in the normal state. Phys. Rev. B 1996, 53, 9418–9432. [Google Scholar] [CrossRef]
  4. Senthil, T.; Sachdev, S.; Vojta, M. Fractionalized Fermi Liquids. Phys. Rev. Lett. 2003, 90, 216403. [Google Scholar] [CrossRef] [PubMed]
  5. Paramekanti, A.; Vishwanath, A. Extending Luttinger’s theorem to Z2 fractionalized phases of matter. Phys. Rev. B 1994, 70, 245118. [Google Scholar] [CrossRef]
  6. Mei, J.-W.; Kawasaki, S.; Zheng, G.-Q.; Weng, Z.-Y.; Wen, X.G. Luttinger-volume violating Fermi liquid in the pseudogap phase of the cuprate superconductors. Phys. Rev. B 2012, 85, 134519. [Google Scholar] [CrossRef]
  7. Sachdev, S. Emergent gauge fields and the high-temperature superconductors. Phyl. Trans. R. Soc. A 2016, 374, 20150248. [Google Scholar] [CrossRef] [PubMed]
  8. Seibold, G.; Arpaia, R.; Peng, Y.Y.; Fumagalli, R.; Braicovich, L.; Di Castro, C.; Grilli, M.; Ghiringhelli, G.C.; Caprara, S. Strange metal behaviour from charge density fluctuations in cuprates. Commun. Phys. 2021, 4, 7. [Google Scholar] [CrossRef]
  9. Badoux, S.; Tabis, W.; Laliberte, F.; Grissonnanche, G.; Vignolle, B.; Vignolles, D.; Beard, J.; Bonn, D.A.; Hardy, W.N.; Liang, R.; Doiron-Leyraud, S.N.; Taillefer, L.; Proust, C. Change of carrier density at the pseudogap critical point of a cuprate superconductor. Nature 2016, 351, 210–214. [Google Scholar] [CrossRef]
  10. Baskaran, G.; Zou, Z.; Anderson, P.W. The resonating valence bond state and high-Tc superconductivity—A mean field theory. Solid State Commun. 1987, 63, 973–976. [Google Scholar] [CrossRef]
  11. Kivelson, S.A.; Rokhsar, D.S.; Sethna, J.P. Topology of the resonating valence-bond state: Solitons and high-Tc superconductivity. Phys. Rev. B 1987, 35, 8865–8868. [Google Scholar] [CrossRef] [PubMed]
  12. Marchetti, P.A.; Su, Z.-B.; Yu, L. U(1)XSU(2) Chern-Simons gauge theory of underdoped cuprate superconductors. Phys. Rev. B 1998, 58, 5808–5824. [Google Scholar] [CrossRef]
  13. Marchetti, P.A.; De Leo, L.; Orso, G.; Su, Z.-B.; Yu, L. Spin-charge gauge approach to the pseudogap phase of high-Tc cuprates: Theory versus experiments. Phys. Rev. B 2004, 69, 024527. [Google Scholar] [CrossRef]
  14. Marchetti, P.A.; Su, Z.-B.; Yu, L. Dimensional reduction of U(1) x SU(2) Chern-Simons bosonization: Application to the t-J model. Nucl. Phys. B 1996, 482, 731–757. [Google Scholar] [CrossRef]
  15. Weng, Z.Y.; Sheng, D.N.; Chen, Y.-C.; Ting, C.S. Phase string effect in the t-J model: General theory. Phys. Rev. B 1997, 55, 3894–3906. [Google Scholar] [CrossRef]
  16. Wilczek, F. Fractional Statistics and Anyon Superconductivity; World Scientific: Singapore, 1990. [Google Scholar]
  17. Fröhlich, J.; Marchetti, P.A. Slave fermions, slave bosons, and semions from bosonization of the two-dimensional t-J model. Phys. Rev. B 1992, 46, 6535–6552. [Google Scholar] [CrossRef]
  18. Hofstadter, D.R. Energy levels and wave functions of Bloch electrons in rational and irrational magnetic fields. Phys. Rev. B 1976, 14, 2239–2249. [Google Scholar] [CrossRef]
  19. Rokhsar, D.S. Solitons in chiral-spin liquids Phys. Rev. Lett. 1990, 65, 1506–1509. [Google Scholar] [CrossRef]
  20. Marchetti, P.A. Fractional Statistics of Charge Carriers in the One- and Two-Dimensional t-J Model: A Hint for the Cuprates? Condens. Matter 2020, 5, 12. [Google Scholar] [CrossRef]
  21. Ye, F.; Marchetti, P.A.; Su, Z.-B.; Yu, L. Hall effect, edge states, and Haldane exclusion statistics in two-dimensional space. Phys. Rev. B 2015, 92, 235151. [Google Scholar] [CrossRef]
  22. Marchetti, P.A.; Ye, F.; Su, Z.-B.; Yu, L. Charge carriers with fractional exclusion statistics in cuprates. Phys. Rev. B 2019, 100, 035103. [Google Scholar] [CrossRef]
  23. Birgeneau, R.J. Antiferromagnetic spin correlations in insulating, metallic, and superconducting La2-xSrxCu04. Phys. Rev. B 1988, 38, 6614–6623. [Google Scholar] [CrossRef]
  24. Belinicher, V.I.; Chernyshev, A.L.; Dotsenko, A.V.; Sushkov, O.P. Hole-hole superconducting pairing in the t-J model induced by spin-wave exchange. Phys. Rev. B 1995, 51, 6076–6084. [Google Scholar] [CrossRef] [PubMed]
  25. Marchetti, P.A.; Ye, F.; Su, Z.-B.; Yu, L. Hole pairing from attraction of opposite-chirality spin vortices: Non-BCS superconductivity in underdoped cuprates. Phys. Rev. B 2011, 84, 214525. [Google Scholar] [CrossRef]
  26. Varma, C.M.; Littlewood, P.B.; Schmitt-Rink, S.; Abrahams, E.; Ruckenstein, A.E. Phenomenology of the Normal State of Cu-0 High-Temperature Superconductors Phys. Rev. Lett. 1989, 63, 1996–1999. [Google Scholar] [CrossRef] [PubMed]
  27. Valla, T.; Fedorov, A. V.; Johnson, P. D.; Wells, B. O.; Hulbert, S.L.; Li, Q.; Gu, G.D.; Koshizuka, N. Evidence for Quantum Critical Behavior in the Optimally Doped Cuprate Bi2Sr2CaCu2O8+d. Science 1999, 285, 2110–2113. [Google Scholar] [CrossRef] [PubMed]
  28. Bok, J.M.; Yun, J.H.; Choi, H.-Y.; Zhang, W.; Zhou, X.; Varma, C.M. Momentum dependence of the single-particle self-energy and fluctuation spectrum of slightly underdoped Bi2Sr2CaCu2O8+d from high-resolution laser angle-resolved photoemission. Phys. Rev. B 2010, 81, 174516. [Google Scholar] [CrossRef]
  29. Loktev, V.M.; Quick, R.M.; Sharapov, S.G. Phase fluctuations and pseudogap phenomena. Physics Reports 2001, 349, 1–123. [Google Scholar] [CrossRef]
  30. Marchetti, P.A. FL* Interpretation of a Dichotomy in the Spin Susceptibility of the Cuprates Condens. Matter 2023, 8, 30. [Google Scholar]
  31. Marchetti, P.A.; Gambaccini, M. Gauge approach to the pseudogap phenomenology of the spectral weight in high Tc cuprates. J. Phys.: Condens. Matter 2012, 24, 475601. [Google Scholar]
  32. Kanigel, A.; Norman, M.R.; Randeria, M.; Chatterjee, U.; Souma, S.; Kaminski, A.; Fretwell, H. M.; Rosenkranz, S.; Shi, M.; Sato, T.; et al. Evolution of the pseudogap fromFermi arcs to the nodal liquid. Nat. Phys. 2006, 2, 447–451. [Google Scholar] [CrossRef]
  33. Kondo, T.; Malaeb, W.; Ishida, Y.; Sasagawa, T.; Sakamoto, H.; Takeuchi, T.; Tohyama, T.; Shin, S. Point nodes persisting far beyond Tc in Bi2212. Nat. Comm. 2015, 6, 7699. [Google Scholar] [CrossRef] [PubMed]
  34. Yang, K.-Y.; Rice, T.M.; Zhang, F.-C. Phenomenological theory of the pseudogap state. Phys. Rev. B 2006, 73, 174501. [Google Scholar] [CrossRef]
  35. Yoshida, T.; Zhou, X.J.; Lu, D.H.; Komiya, S.; Ando, Y.; Eisaki, H.; Kakeshita, T.; Uchida, S.; Hussain, Z.; Shen, Z.-X.; Fujimori, A. Low-energy electronic structure of the high-Tc cuprates La2-xSrxCu04 studied by angle-resolved photoemission spectroscopy. J. Phys. Condens. Matter 2007, 19, 125209. [Google Scholar] [CrossRef]
  36. Rullier-Albenque, F. , Alloul, H.; Balakirev, F.; Proust, C. Disorder, metal-insulator crossover and phase diagram in high-Tc cuprates. Euro Phys. Lett. 2008, 81, 37008. [Google Scholar] [CrossRef]
  37. Ioffe, L.B.; Larkin, A. Gapless fermions and gauge fields in dielectrics. Phys. Rev. B 1989, 39, 8988–8999. [Google Scholar] [CrossRef] [PubMed]
  38. Lee, P.A.; Nagaosa, N. Gauge theory of the normal state of high-Tc, superconductors Phys. Rev. B 1992, 46, 5621–5639 ; Ioffe, L. B. and Wiegmann, P. B. Linear Temperature Dependence of Resistivity as Evidence of Gauge Interaction. Phys. Rev. Lett. 1990, 65, 653–656. [Google Scholar]
  39. Marchetti, P.A.; Bighin, G. Universality in Cuprates: A Gauge Approach. J Low Temp Phys 2016, 185, 87–101. [Google Scholar] [CrossRef]
  40. Marchetti, P.A.; Su, Z.-B.; Yu, L. Transport properties of HTS cuprates via spin—Charge gauge approach. Physica C 2007, 460-62, 1081–1083. [Google Scholar] [CrossRef]
  41. Ando, Y.; Kurita, Y.; Komiya, S.; Ono, S.; Segawa, K. Evolution of the Hall Coefficient and the Peculiar Electronic Structure of the Cuprate Superconductors. Phys. Rev. Lett. 2004, 92, 197001. [Google Scholar] [CrossRef]
  42. Barisic, N.; Chan, M.K.; Li, Y.; Yu, G.; Zhao, X.; Dressel, M.; Smontara, A.; Greven, M. Universal sheet resistance and revised phase diagram of the cuprate high-temperature superconductors PNAS 2123, 110, 12235–12240.
  43. Marchetti, P.A. paper in preparation.
Preprints 90420 g001
Figure 1. (a) Exterior of the MBZ (green), interior of the tight-binding FS for the hole (blue) and interior of the small FS in PG derived as discussed in the text (orange) in the first quadrant of the BZ for t ′ / t = 0.25 and δ = 0.07 . The angle along the small FS in PG is denoted by α as in the text. (b) Intensity of the symmetrized Spectral weight of the hole along the small FS in PG shown in (a) at T = 20 K . The intensity inside the MBZ is in blue, that outside in yellow. α is measured in units of π and the origin is shifted by − 1 outside of the MBZ.
Figure 1. (a) Exterior of the MBZ (green), interior of the tight-binding FS for the hole (blue) and interior of the small FS in PG derived as discussed in the text (orange) in the first quadrant of the BZ for t ′ / t = 0.25 and δ = 0.07 . The angle along the small FS in PG is denoted by α as in the text. (b) Intensity of the symmetrized Spectral weight of the hole along the small FS in PG shown in (a) at T = 20 K . The intensity inside the MBZ is in blue, that outside in yellow. α is measured in units of π and the origin is shifted by − 1 outside of the MBZ.
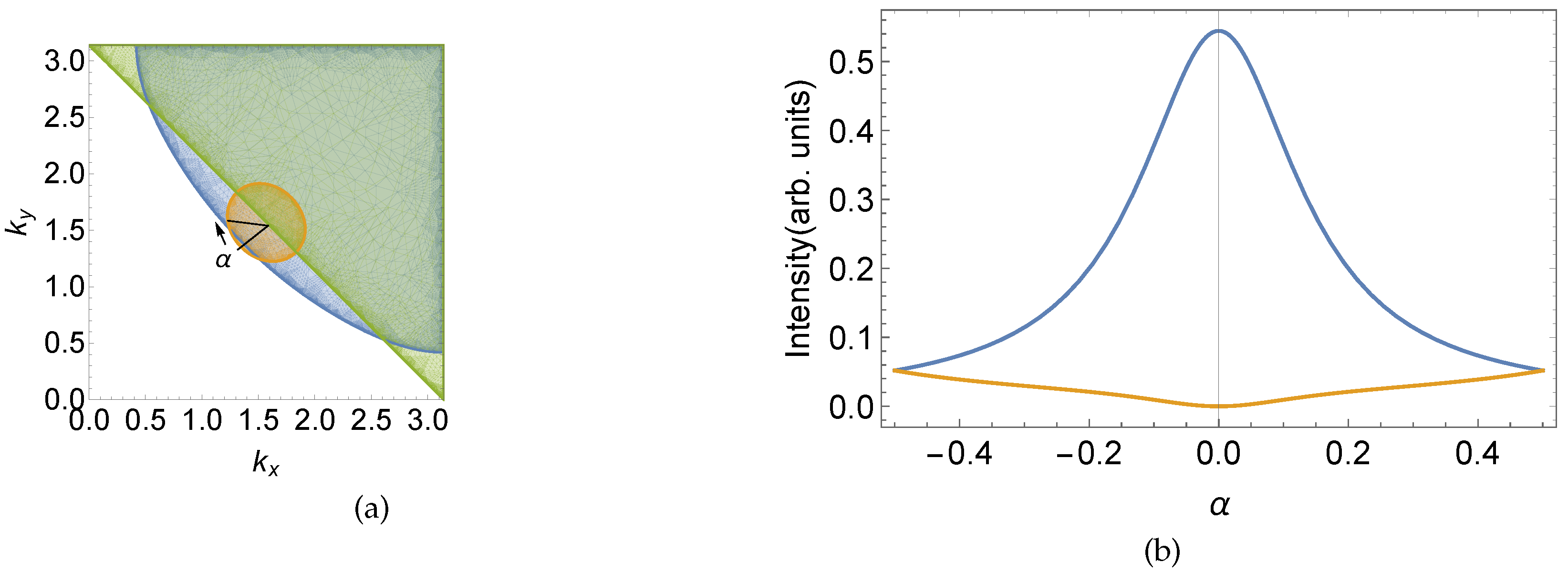
Preprints 90420 g001
Preprints 90420 g002
Figure 2. The symmetrized Spectral weight of the hole along the small FS in Figure 1 at T = 20 K for α = n 0.05 π , n = 0 (top line, blue), 2, ..., 5 (bottom line , brown). The increase at high energy is due to an approximate estimate of the incoherent holon-spinon contribution discussed in the text.
Figure 2. The symmetrized Spectral weight of the hole along the small FS in Figure 1 at T = 20 K for α = n 0.05 π , n = 0 (top line, blue), 2, ..., 5 (bottom line , brown). The increase at high energy is due to an approximate estimate of the incoherent holon-spinon contribution discussed in the text.
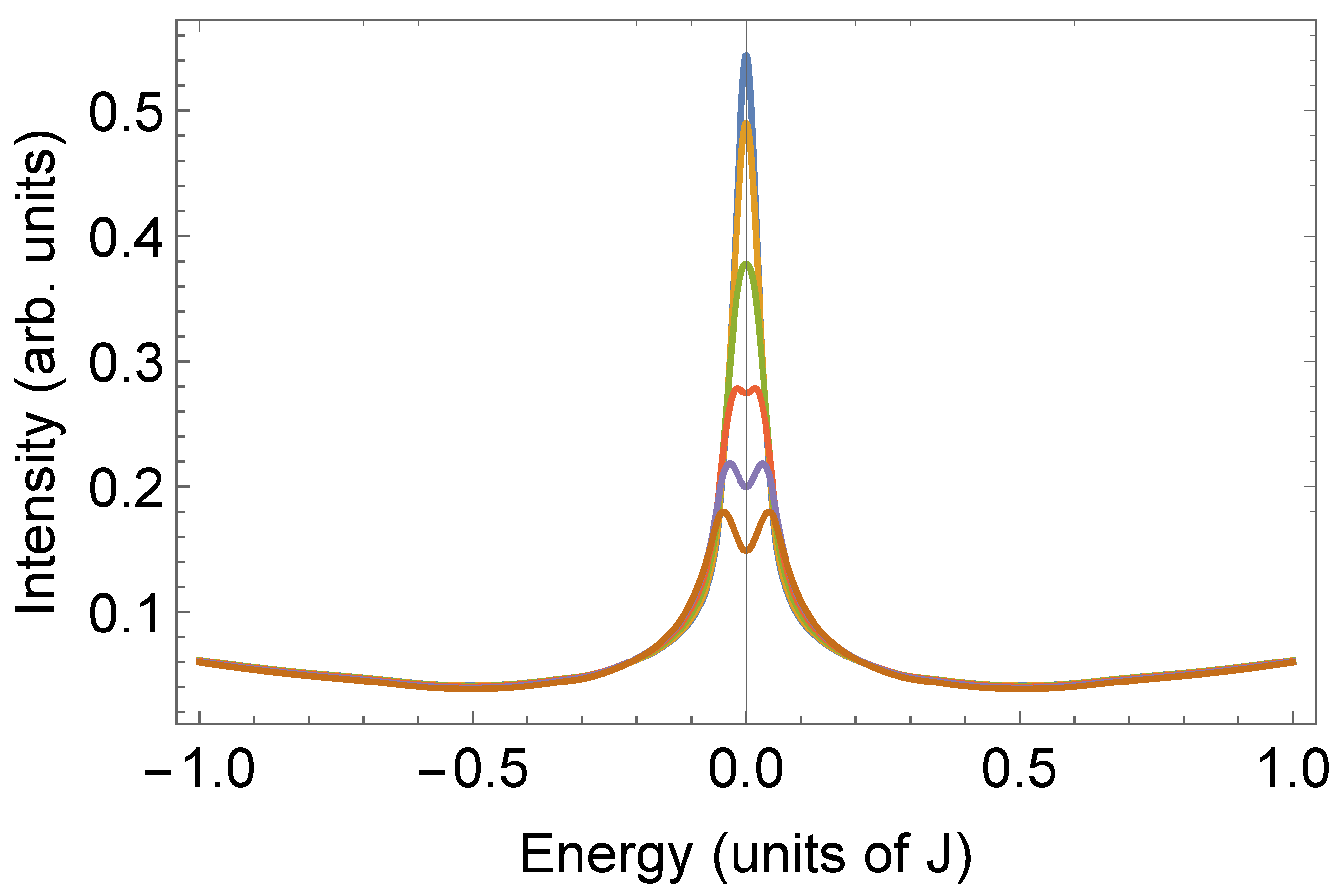
Preprints 90420 g002
Preprints 90420 g003
Figure 3. (a) Detail of the low-energy symmetrized Spectral weight of the hole along the small FS as Figure 2 at T = 30 K and (b) at T = 40 K .
Figure 3. (a) Detail of the low-energy symmetrized Spectral weight of the hole along the small FS as Figure 2 at T = 30 K and (b) at T = 40 K .
Preprints 90420 g003
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated