Prerpints.org logo
Preprint
Review

New Die-Compaction Equations for Powders as a Result of Known Equations’ Correction. Part 1. Review and Analysis of Various Die-Compaction Equations

Altmetrics

Downloads

85

Views

24

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

15 November 2023

Posted:

16 November 2023

You are already at the latest version

Alerts
Abstract
The well-known equations for the process of powder compaction (PCP) in a rigid die published over the period from the beginning of the last century to the present are considered. Most of the considered equations are converted into the dependence of the densification pressure on the relative density. The equations were analyzed and their ability to describe PCP was assessed by determining the coefficient of determination when approximating experimental data on the compaction of various powders. It is shown that most of the equations contain two constants, the values of which are determined by fitting the mathematical dependence to the experimental curve. Such equations are able to describe PCP with high accuracy in the case of compaction of powders up to a relative density of 0.9-0.95. It is also shown that different equations can describe PCP in the range of density change from the initial to 0.9 with the same and sufficiently high accuracy, but when the process of compaction is extrapolated to higher values of density, the curves diverge. This indicates the importance of equations that can unambiguously describe PCP to a relative density equal to or close to 1.0. For an adequate description of PCP to a relative density greater than 0.95, equations containing three or four constants have proven themselves well.
Keywords: 
Subject: Chemistry and Materials Science  -   Materials Science and Technology

1. Introduction

The powder compaction process (PCP) in a rigid die is one of the main processes in final products fabrication from various powders. Due to this a comprehensive study and description of PCP have attracted the attention of many specialists in the field of powder metallurgy. There are many equations that describe PCP, and various approaches have been used to derive them. Initially, to describe PCP, simple mathematical functions were used, e.g., exponential [1–3], power [4–6], and logarithmic [7–11] ones. Later proposed equations took into account various physical phenomena occurring  in PCP such as contact interaction of particles, local and general deformation, hardening, shear between particles and within particles, friction, etc. [12–17]. To derive the equations with physical constants, some researchers considered a powder body as a combination of a large number of individual particles contacting with each other [14,18,19]. An approach based on the evolution of the contact interaction between individual particles under the pressure can be designated in the theory of PCP as a discrete one. There is also an approach that considers a powder sample as a quasi-continuous two-phase body that can decrease in volume under the pressure. In this case, the compaction of a quasi-continuous body in a rigid die makes it possible to obtain the corresponding equations for describing PCP [20–25]. This approach can be named as a continuous one.
Alongside with it, equations for PCP obtained by utilizing above mentioned approaches are not able to describe the entire compaction process with high accuracy, since the process itself is complex and multi-stage. The known equations are able to adequately describe one or two of three available stages [18]. In addition, there are fundamental discrepancies between the equations associated with the description of PCP in approaching a pore-free state, where some equations give a finite value of the compaction pressure while other ones give an infinite pressure. It is therefore difficult to choose an equation that allows one to determine the compaction pressure accurately enough to achieve a relative density close to 1.0.
Certain difficulties are associated with the determination of the true plastic deformation of particles during PCP because of particle rearrangement that can take place and depends on the shape of particles and their yield strength. Many equations for PCP do not explicitly reflect the effect of particle rearrangement on the increase in sample density. Some authors [17,26] have made an attempt to take into account the degree of density change due to particle rearrangement. The authors believe that the rearrangement takes place throughout almost the entire compaction process. However, according to other researchers [27], rearrangement ends at the initial stage of the compaction process. It implies existence a porosity threshold beyond which no rearrangement occurs. The presence of a threshold or critical phenomena during PCP can be described on the base of percolation theory [28–30], but the modification of the powder compaction equations using this theory has not yet led to adequate equations.
Another issue occurs in describing compaction of “high” samples, i.e. samples with a height-to-diameter ratio exceeding 1.0. It refers to the nonuniform distribution of density both along the height and the diameter of the sample. To solve the problem of determining the density of a sample at its different points the finite element method known for metal forming is used. This method allows you to determine the density at any point of the sample with known parameters of the strength of powder particles and the hardening law, as well as the friction forces between the particles and the die wall [31–33]. However, the task of determining the true strength of particles and the law of hardening during their deformation is not easy.
To determine the properties of specific powder, the experiments on the triaxial powder compression are required and on determination of the yield surface depending on the sample density. Such experiments are relatively complex and can be carried out in special laboratories [34–36] that makes it difficult to get quick results for different powders. Alongside with it, information about the properties of the powder can also be obtained from experiments on compaction in a rigid die of "low" samples, that is, samples in which, after compaction, the height becomes half the diameter. In these samples the effect of friction forces can be neglected. It should be noted that most of the experiments are performed on low samples, and the compaction equations are tested mainly on low samples. Therefore, before solving the problems of determining the density distribution on high samples (height/diameter ≥ 1) and samples of complex shape (stepped), it is necessary to have an equation that allows one to describe the compaction process of low samples with the highest accuracy and with a change in density from initial to density close to 1.0.
The adequacy of an equation for PCP is determined by assessing the accuracy of fitting the equation to the experimental data, that is, by finding the determination coefficient R2. However, in many cases, the adequacy of the equations is unknown. Therefore, in the first part of this article, it seems appropriate to give examples of assessing the accuracy of describing PCP by various equations. It seems also appropriate to convert the known equations that show the dependence of relative or absolute density on the compacting pressure into the dependence of pressure on relative density since such a dependence can have a simpler form, and thus makes it easy to determine the specific compaction energy of the powder using the formula:
w ( ρ ) = ∫ ρ 0 ρ p ρ ρ 2 d ρ
where w is the specific energy in J/m3 or in MPa, p(ρ) is the experimental or theoretical external pressure (on the punch) dependence on the relative density, and ρ0 and ρ are the initial and current relative densities of the sample. The assessment of PCP description accuracy by various equations was performed. It was carried out by computer approximation of experimental data on the compaction of different powders. For approximation, the Russified program “Wolfram Mathematica 10.4” was used.

2. Accuracy Assessment of PCP Description Using Equations Obtained by Selecting Mathematical Functions

Equations in the form of simple mathematical functions were among the first ones, and they appeared at the beginning of the 20th century. Most researchers point out that the first to propose a powder compaction equation was E. Walker (1923) [1]. Then, almost the same equation was proposed by M. Balshin (1948) [2] and H. Lipson (1950) [3]. If we take compaction pressure as a function and relative density as an argument, then the compaction equation for the powders, by these authors, will be an exponential function:
p = E x p k 1 − k 2 β = a 1 ∙ e x p [ − ( k 2 / ρ ) ]
where p is the pressing pressure, β = 1/ρ is the relative volume of the powder sample, ρ is the relative density, k1and k2 are constants, and a1=exp(k1).
Other researchers, e.g., W. Rutkowski and H. Rutkowska (1949) [4], C. Agte and M. Petrdlik (1951) [5], and G. Meyerson (1962) [6] used a power function to describe PCP in the form of the following relationship between compaction pressure and relative density
p = a 2 ∙ ρ b
where a 2 and b are constant parameters determined by approximating experimental data on powder compaction.
The presented mathematical functions (exponential (2) and power (3)) are quite simple, but there is no clear understanding what range of density change can be accurately described by them. It is only clear that the smaller this range, the more accurately it will be described by these equations. The accuracy of approximation of real experimental data on various PCP by these exponential and power dependences is shown by approximation of experimental data on the compaction of iron, copper, and nickel powders taken from publications [37], [38], and [39], respectively. The experimental data on the compaction of these powders are given in Table 1 that makes it possible to use them for checkup the approximation carried out and to approximate with other equations by other researchers.
Table 1. Experimental data on the compaction of iron, copper, and nickel powders in a rigid die taken from [37], [38], and [39], respectively.
Table 1. Experimental data on the compaction of iron, copper, and nickel powders in a rigid die taken from [37], [38], and [39], respectively.
Mate-rial Relative density and corresponding densification pressure
Fe
[37]		 ρ 0.268 0.576 0.627 0.659 0.702 0.734 0.764 0.786 0.815 0.829 0.842
p, MPa 0 148.83 205.65 259.78 316.66 375.23 434.7 476.26 549.32 608.86 666.55
ρ 0.857 0.876 0.884
p, MPa 734.91 780.48 935.45
Cu
[38]		 ρ 0.3 0.363 0.377 0.42 0.476 0.545 0.647 0.756 0.88 0.92 0.949
p, MPa 0 4.9 9.8 19.6 39.2 78.4 157.0 294.0 588.0 784.0 980
Ni
[39]		 ρ 0.36 0.423 0.479 0.507 0.537 0.584 0.674 0.749 0.797 0.869 0.903
p, MPa 0 28.03 53.7 64.39 89.08 130.44 240.79 372.4 490.0 745.39 971.57
The results of the approximation of experimental data by exponential (2) and power (3) equations are shown in Figure 1, and the values of the constants of these equations and the coefficient of determination R2 are presented in Table 2. As seen, the exponential (2) and power (3) dependences describe PCP quite accurately from the initial relative density to a density of 0.95, and power dependence (3) describes PCP with a higher accuracy that was also noted in other research [6].
Preprints 90637 g001
Figure 1. Approximation dependences of experimental data on PCP for (a) iron, (b) copper, and (c) nickel using exponential equation (2) (dashed line) and power equation (3) (solid line). Here and below, light circles are experimental data.
Figure 1. Approximation dependences of experimental data on PCP for (a) iron, (b) copper, and (c) nickel using exponential equation (2) (dashed line) and power equation (3) (solid line). Here and below, light circles are experimental data.
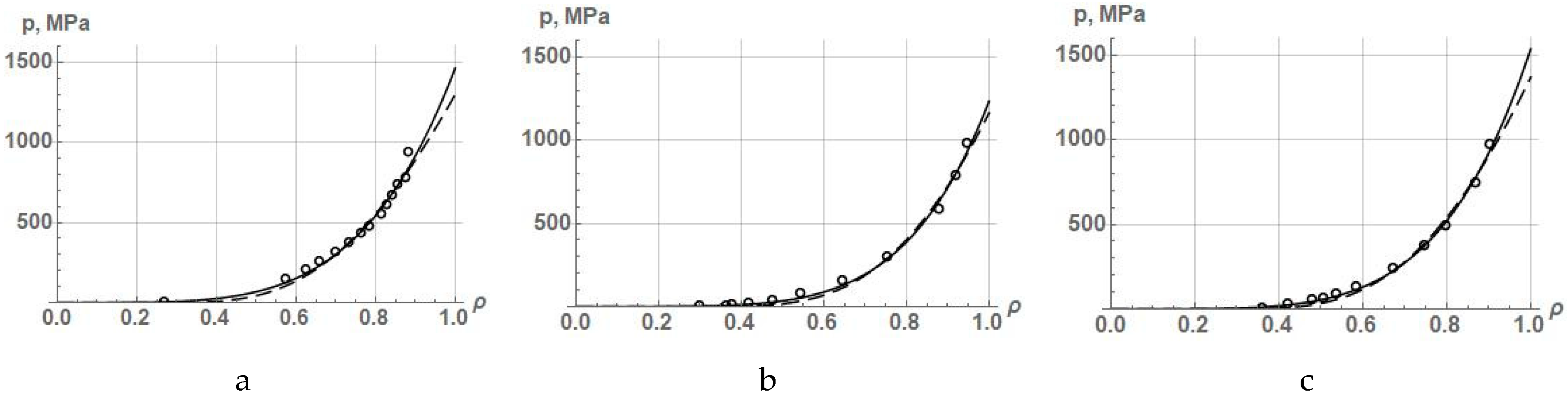
Preprints 90637 g001
Table 2. Constants and coefficient of determination R2 obtained via approximation of experimental data on PCP for iron, copper, and nickel using exponential (2) and power (3) equations.
Table 2. Constants and coefficient of determination R2 obtained via approximation of experimental data on PCP for iron, copper, and nickel using exponential (2) and power (3) equations.
Parameters Powders
Iron Copper Nickel
Equation type
(2) (3) (2) (3) (2) (3)
ρ0 0.268 0.3 0.36
а1, а2 39313 1462.8 81834 1233.5 56561 1537.6
k2, b, 3.410 4.442 4.253 5.182 3.720 4.849
pmax, MPa 1298.9 1462.8 1163.2 1233.5 1370.1 1537.6
R2 0.9763 0.9843 0.9901 0.9954 0.9897 0.9964
In the above equations, PCP is conceded to be a monotonous process without any indication that, in reality, it proceeds in several stages with their own mechanisms of powder densification. Most experts agree on the existence of three stages of PCP, although according to some authors, there are 4 stages [40,41]. The three stages are characterized as follows. The first stage is the rearrangement of particles that allows elastic and slight plastic deformation, the second stage is compaction due to the local plastic deformation of the particles during their contact, and the third stage is interpreted ambiguously: it is either the localization of plastic deformation near the pore or the general plastic deformation of particles. These stages are clearly manifested in the case of constructing a graphical dependence of the experimental relative density on the densification pressure in logarithmic coordinates [42]. Moreover, each stage can be described, as the authors [42] suggested, by a power equation with its own constants:
p = p * ρ ρ * m
where m is a constant different for each stage, ρ* and p * are the minimum relative density and pressure, respectively, for a particular compaction stage.
We note that the PCP staging was also established when considering one of the most common equations for PCP. This equation was proposed at different times by different authors, e.g., by L.F. Athy (1930) [7], I. Shapiro and I. M. Kolthoff (1947) [8], K. Konopicky (1948) [9], T. N. Znatokova and V. I. Likhtman (1954) [10], and R.W. Heckel (1961) [11], and in the original record, it had the form:
l n 1 1 − ρ = k p + a
where k and a are constants.
This equation is often referred to as the Konopicky equation or as the Heckel equation. If the experimental data on the compaction of powders are presented in the coordinates "ln(1/1-ρ)" and "p", then a broken line is obtained, indicating the presence of different stages of compaction with their own values k and a. Equation (5) often met in literature [43,44], after transformation, where pressure is a function and relative density is an argument, takes the following form:
p = k ′ ∙ l n 1 1 − ρ − a
where k ′=1/k is a new constant.
It is important to note that equation (6) allows one to describe only the intermediate or second stage of powder compaction. Therefore, in most cases, when experimental data on powder compaction are limited by low density (ρ≤ 0.9), equation (6) describes the compaction process without an initial stage. It should also be noted that equation (6) can be written otherwise if the value of the constant a is determined by substituting pressure equal to zero (p=0) into this equation. In this case, equation (6) will look like:
p = k ′ ∙ l n 1 − ρ 0 ' 1 − ρ
Here, the parameter ρ0′ means the conditional initial density that is greater than the actual initial density of the powder ρ0 that indicates that equations (6) and (7) cannot take into account the initial process of powder compaction.
Furthermore, equation (5) has been modernized several times. In one case, modernization was proposed by M. Kuntz and H. Leuenberger [30], in which the Heckel equation, i.e., equation (6), was transformed to the form:
p = 1 C ρ c − ρ − 1 − ρ c l n ⁡ 1 − ρ 1 − ρ c
where C is a constant, ρc is the conditional initial density of the powder or the second constant.
The use of equation (8) in the approximation of the experimental process of various powders compaction showed that it was more adequate than equation (6). In particular, the same experimental data on the compaction of iron, copper, and nickel powders presented in Table 1 were used for approximation by equations (6) and (8). The results of the approximation are shown in Figure 2, and the values of the constants of the equations and the coefficient of determination R2 are presented in Table 3. In addition, Table 3 shows the value of the conditional initial density ρ0', which is used in equation (7) and which is also determined by fitting the curve to the experimental data.
Figure 2 and Table 3 show that the new equation (8) describes PCP with higher accuracy than the original Heckel equation (6). In this case, the value of the conditional initial density ρc in equation (8), obtained as a result of the approximation, turns out to be lower than the actual initial density ρ0 that makes it possible to accurately describe the initial stage of the compaction process.
A higher accuracy of approximation of experimental data on PCP compared to the equation of K. Konopicky or R. W. Heckel can be reached by another modernization of the equation that leads to the appearance of the so-called double logarithmic form of the equation. Three different teams of authors proposed such an equation independently. First, the work of Ge Rong-de (1991) [45] should be noted, in which he proposed a new differential equation for PCP:
d ρ d p = K ( 1 − ρ ) ρ n p m
where K, n, and m are constants.
At the same time, Ge Rong-de claimed that at n=0, the integration of equation (9) leads to an equation that describes PCP at low and high pressures with high accuracy. This equation in the original record was as follows:
l o g l n ( 1 − ρ 0 ) ( 1 − ρ ) = A l o g p + B
where A and B are constants.
In another case, the same equation was proposed by other authors - A. B. Yu and Z. H. Gu (1993) [46], who used a differential form:
− d ( 1 − ρ ) d p = k ∙ 1 − ρ a ∙ p b
where k, a, b are constants.
Upon integrating equation (11), these authors [46] obtained an equation for PCP in the form:
l n l n ( 1 − ρ 0 ) ( 1 − ρ ) = l n K + n l n p
where K=k/(1+b) and n=1+b are new constants.
In the third case, L. Parilak and E. Dudrova (1994) [47] proposed an equation that in its original form was written as
θ = θ 0 e x p ⁡ ( − K ∙ p n )
where θ andθ0 are the current porosity and the initial porosity of the powder in the die, p is the compaction pressure, K and n are constants.
Equation (13), after making double logarithm and replacement of porosity by relative density, takes the form of equation (12), into which equation (10) can also be easily converted. Consequently, the analysis of PCP by at least three groups of authors led to the derivation of the same equation, which contains the initial density of the powder ρ0, i.e., the density of the powder after filling the die, and two constants that can be determined by fitting the curve of equation (12) to experimental data on PCP. If in equation (12) we interchange the function and the argument, i.e., we take the pressure as a function and the relative density as an argument, then we obtain a simpler equation:
p = B ln ⁡ 1 − ρ 0 1 − ρ m
where m=1/n and B=(1/K)m are new constants.
It is of interest to check the accuracy of the description of PCP by equation (12), or rather by equation (14). Prior to this, we need to remember one more equation that also contains the initial density of the powder and two constants, and which was proposed much earlier than equation (12). We are talking about the equation of K. Kawakita and K.H. Ludde (1970) [48]:
C = V 0 − V V 0 = a b P 1 + b P
where C is the degree of volume reduction, V0 is the initial volume of the powder, V is the volume of the powder under pressure P, a and b are constants characterizing the powder.
References to this equation are relatively common in the literature. If we transform it in such a way that the pressing pressure p will be a function, and the relative density ρ- an argument, then it takes the form:
p = 1 b   ∙ ( ρ − ρ 0 ) ρ a − 1 + ρ 0 = b ' ∙ ρ − ρ 0 a ρ − ρ − ρ 0
where ρ0 is the initial relative density of the powder filled into the die, a and b′=1/b are constants.
To check the approximation accuracy of the experimental data on PCP by the equation of K. Kawakita and K.H. Lüdde (16) and the equation of Ge Rong-de ¬ A. B. Yu and Z. H. Gu ¬ L. Parilak and E. Dudrova (14), we take the experimental data on the compaction of powders of iron, copper and nickel presented in Table 1. The results of the approximation are presented in the form of graphs in Figure 3, and the values of the constants of equations (16) and (14) and the coefficient of determination R2 are shown in Table 4.
Accuracy assessment of the experimental data approximation on the compaction of iron, copper and nickel powders by equations (16) and (14) show that these equations describe PCP very accurately and practically in the same way, since the coefficient of determination differs slightly. In this case, the coefficient of determination by equation (14) for copper and nickel is slightly higher than that by equation (16), and for iron it is slightly lower (Table 3).
In addition, these equations take into account the initial density of the powder and accurately describe the initial stage of powder compaction. But the fundamental difference between them consists in the fact that at a relative density ρ=1, the compaction pressure by equation (16) has a finite value, while by equation (14), it is equal to infinity. It is still difficult to say, which equation is more adequate, but the higher accuracy of equation (14) in two cases out of three may indicate that the equation in which the pressure tends to infinity as the relative density increases up to 1.0 seems to be more valid.
The above comparison of two equations shows how important it is to accurately describe the entire PCP, including the process of compaction to a relative density close to 1.0. Alongside with this, it should be noted that there are very few experimental data in the literature on the compaction of metal powders with a final density that exceeds 0.95. Such experimental data, in particular, on the compaction of various iron powders, are available in the book by R. Kieffer and W. Hotop (1948) [49]. They also show that it is difficult to achieve a relative density ρ= 1.0, even at a pressure of 3000 MPa. In this regard, of great interest are the equations able to describe PCP with high accuracy when the pressure tends to infinity at a relative density ρ<1.0. In practice, it occurs when metal powders with low plasticity or very hard powders, such as ceramics, are compacted. To describe such a case, the J. Secondi equation (2002) [50] that contains the relative density parameter at infinite pressure is used. This parameter is denoted as ρ∞, and it means that infinite pressure can occur at a relative density ρ< 1.0. In the original record, the J. Secondi equation [50] had the form:
l n ρ ∞ − ρ 0 ρ ∞ − ρ = K ∙ p n
where ρ∞ is the relative density at which the compaction pressure tends to infinity, ρ0 is the initial relative density of the powder, p is the compaction pressure, K and n are constant parameters that control the hardening and plasticity of the powder material.
With taking the pressing pressure p as a function and the relative density ρ as an argument, the J. Secondi equation (17) is converted to the form:
p = K ' ln ⁡ ρ ∞ − ρ 0 ρ ∞ − ρ m
where K′=1/Km and m=1/n are new constants.
One should pay attention to the fact that equation (17) turns into equation (14), if the limiting relative density ρ∞, will be substituted by the limiting density ρ∞= 1.0. Therefore, the Secondi equation can describe a wider class of powder materials including both hard or brittle and plastic powders. For an example of the approximation by this equation of experimental data on compaction of hard-to-deform plastic and almost non-deformable brittle powders, we take the experimental data on compaction of titanium carbide powder [51] and three iron powders [49] that were compacted to an extremely high density. The values of relative density at different compaction pressures for titanium carbide and three iron powders are given in Table 5.
The results of approximation by the Secondi equation (18) of these powders are shown in Figure 4, and the values of the constant parameters and the coefficient of determination are listed in Table 6. In addition, Figure 4 and Table 6 also show for comparison the results of the approximation of these powders by equation (14). As seen, the Secondi equation (18) describes PCP for brittle and ductile powders with higher accuracy than equation (14) does.
One of the factors for the increased accuracy of the Secondi equation (18) to an extremely high density is probably the presence of three constants. Another important advantage of the Secondi equation is that it provides for a real powder compaction process, where the compaction pressure tends to infinity at a relative density of significantly below 1.0. The equation of the authors Ge Rong-de ¬ A. B. Yu and Z. H. Gu ¬ L. Parilak and E. Dudrova (14) does not provide for such a possibility. It follows that the equations for PCP with two empirical constants cannot adequately describe this process to the relative density level of 0.96-0.99.
It was important to analyze another modified Konopicky-Heckel equation describing PCP to a high density. We mean the equation of R. Panelli and F. Ambrosio Filho (1998) [52] that in the original record had the form:
ln ⁡ 1 1 − ρ = A   p + B
where A and B are constants, and which can also be written in a shorter form:
ln ⁡ 1 − ρ 0 ' 1 − ρ = A   p
where ρ0'=1-exp(-B) is also a constant.
If pressure is taken as a function, then the equation (19) takes the form:
p = A ' ln ⁡ 1 1 − ρ − B 2
where А′ = 1/А2 is a new constant.
To evaluate the accuracy of the PCP description by this equation, we have approximated the experimental data on the compaction of two groups of powders. In one group the experimental data had a final relative density less than 0.95, and in the other group - more than 0.95. That is, we took for the previous data on iron, copper, and nickel powders from Table 1, and for the latter ones - iron powders from Table 5. The results of the approximation of PCP of these powders by equation (21) are shown in Figure 5, and the values of the constant parameters and the coefficient of determination R2 - in Table 7.
As seen from the results of this approximation, equation (21) describes PCP quite accurately when the powders are compacted to a density of less than 0.95. If the powders are compacted to a density close to 1.0, then equation (21) reflects the PCP with low accuracy, at which the beginning and middle of PCP are distorted. In this case, it is impossible to correctly assess the features of the powder and its mechanical and deformation properties. It follows that in order to determine the real properties of a powder during its compaction in a die, it is necessary to have, firstly, experimental data on the compaction of a particular powder to a density close to 1.0 and, secondly, an equation that allows to describe such a process with high precision. In this regard, of interest are the equations for PCP that contain some physical characteristics of the materials used for powder production.

3. Equations Using the Physical Characteristics of Compact Materials

The above equations for PCP description have basically two constants. In some cases, attempts were made to establish the physical meaning of these constants. E.g., two constants, K and n, in equations (13) and (17) characterize, according to the authors, the plasticity of the powder material and the hardening work during its deformation. These constants are similar to the coefficients characterizing the plasticity and strain hardening of compact materials. In this regard, some researchers have tried to obtain an equation for PCP taking the strength and plasticity characteristics of the material used for powder production, from reference books.
An attempt to relate one of the equation constants to the yield strength of the powder material was made by S. Torre (1948) [12] and A. N. Nikolaev (1962) [13]. They proposed the following equations:
p = 2 σ S l n θ 0 θ = 2 σ S   l n 1 − ρ 0 1 − ρ
and
p = С × σ S × ρ × l n ρ 1 − ρ
where σS is the yield strength of the powder material and С = 2.5-3 is a constant.
Then equation (23) was modified by G. M. Zhdanovich (1999) [14] as follows:
p = С × σ S × ρ × l n 1 − ρ 0 1 − ρ
Equation (24) does not have the disadvantage inherent in equation (23), where the pressure becomes negative when the relative density is less than 0.5, but the parameter C is not known in advance and must be determined, as G. M. Zhdanovich points out, from the experiment. The above equations are difficult to use for description of PCP, since the yield strength of particles can differ significantly from the yield strength of an absolutely dense material.
Of interest is an equation that takes into account the features of both ductile and brittle powders, as well as the effect of friction of the powder against the die wall during PCP. Such an equation was proposed in the work of Li S., Khosrovabadi P.B., Kolster B.H. (1994) [16]. Moreover, the authors presented experimental data on the compaction of not only plastic Ni powder but also a mixture of plastic (Ni) and ceramic (Al2O3) powders, as well as nickel-coated ceramic (Al2O3, SiC) powders. They took into account the forces of powder friction against the walls of the die and, as a result, proposed the following equation (original form):
l n P = m l n l n D D 0 − n 1 − D D m + l n M 0 K
where P is the external pressure, D is the absolute density of the powder blank at pressure P, D0 is the initial density of the powder, Dm is the theoretical density of the powder material, M0 is the compaction modulus for a dense sample, K is a dimensionless parameter associated with the friction coefficient of the powder (against the die wall) and workpiece geometry, and m and n are empirical constants. In this case, the parameters M0 and K are also constant.
If the above equation is potentiated and the absolute density is converted into relative density, then the following equation is obtained that associates pressure with the relative density:
p = A l n ρ ρ 0 m e x p − n ( 1 − ρ )
where the three constants A=M/K, m, and n can be determined by fitting the equation to the experimental curve.
The authors of this equation checked its adequacy when compacting nickel powder, an equivolume mixture of nickel and aluminum oxide powders, as well as aluminum oxide and silicon carbide powder coated with aluminum. They showed that equation (26) allowed the PCP description for different powders with high accuracy [16]. However, it should be kept in mind that the experimental data obtained by author had a final relative density less than 0.8. Thus, the shortened PCP can be described with high accuracy and simple equations. Of interest for approximation by equation (26) were experimental data with a higher final density, e.g., the data on the compaction of iron and copper powders from Table 1, as well as unusual data on the compaction of coarse and fine iron and copper powders from the book by F. V. Lenel [53], p. 96. The values of the experimental data on compaction of coarse and fine Fe and Cu powders, presented in the book [53], were obtained by digitizing the experimental points on the corresponding curves, and these data are given in Table 8.
The results of approximation by equation (26) of experimental data on the compaction of various iron and copper powders are shown in Figure 6, and the values of the constant parameters of equation (26) and the coefficient of determination R2 are listed in Table 9.
The presented results of approximation of experimental data on the compaction of various iron and copper powders by equation (26) show that the equation proposed by previously mentioned author [16] makes it possible to describe PCP quite accurately in individual cases associated with compaction of powders to a low density. It is possible despite the fact that the proposed equation has three constants that implicitly take into account the resistance of the powder material to deformation, the friction of the powder against the die walls, and the geometry of the compacted powders. In addition, a characteristic feature of equation (26) is the fact that it provides for obtaining a final pressure when the relative density of the powder reaches 1.0. Moreover, the value of this pressure (see pmax in Table 9) is unexpectedly low that confirms the impossibility of this equation to accurately describe PCP at the final stage.
Noteworthy is another equation for PCP presented in one of the works by G. Aryanpour and M. Farzaneh (2015) [17]. When deriving the equation, the authors resorted to the analysis of various mechanisms of PCP and, in particular two mechanisms - particle rearrangement and plastic deformation of particles. With that, they made the assumption that these two mechanisms work together up to a sufficiently high relative density of 0.95, at which, as they believe, there are no more open pores, and the particle rearrangement mechanism disappears. To describe compaction due to the particle rearrangement mechanism, the authors suggested applying the following equation:
p = b * ρ − ρ 0 1 − ρ a
where b and a are constants determined from the experiment, ρ0 is the initial density of the powder in the die.
After a simple transformation and logarithm equation (27) takes a different form:
l n 1 − ρ 0 1 − ρ = l n p c b c + 1
where c=1/a is a constant.
To describe the powder compaction due to plastic deformation, the researchers [17] used the Heckel equation [11] written in the form:
l n 1 − ρ 0 ' 1 − ρ = k p
where k is a constant, but ρ0' is the conditional initial density of the powder.
According to G. Aryanpour and M. Farzaneh, these two mechanisms are summed up during compaction of the powder, and as a result, the following equation was proposed (in this case, the conditional initial density ρ0′ in equation (29) is replaced by the actual initial density ρ0):
l n 1 − ρ 0 1 − ρ = l n p с b с + 1 + k p
The equation (30), as noted by its authors, can be used to describe PCP in the density range from ρ0 to ρ=0.95. It takes into account the action of two mechanisms - particle rearrangement and particle deformation. In this case, at the beginning of the compaction process, the rearrangement mechanism prevails, and at the end of the compaction, the deformation mechanism does. Unfortunately, this equation cannot be transformed in such a way that it could be solved with regard to the pressure p and an appropriate approximation can be made. However, to estimate the accuracy of approximation of various experimental data by equation (30), it is necessary to transform it so that the function is the relative density ρ in its pure. In this case, it will acquire the following form:
ρ = 1 − 1 − ρ 0 b c b c + p c E x p [ k p ]
But the equation (31) hides compaction mechanisms, making it less useful. At the same time, this equation makes it possible to approximate experimental data on powder compaction and determine the values of three constants – b, c, and k. Taking into consideration that this equation has three constants, its adequacy in describing PCP not only up to a relative density of 0.95 but also up to a higher density is of interest. Therefore, to approximate the experimental data on PCP by this equation, we chose the experimental results previously used by us on the compaction of powders of iron, copper, and nickel, presented in Table 1, as well as on iron powders compacted to high density presented in Table 5. The results of the approximation of experimental data on the compaction of these powders are shown in Figure 7. The values of the constants of equation (31) and the coefficient of determination R2 are given in Table 10.
As seen from presented results, the accuracy of the approximation of experimental data on the compaction of various powders by equation (31) is high for cases of powder compaction up to a density of 0.95. This may indicate the adequacy of the hypothesis that allows the simultaneous existence of the mechanisms of rearrangement and deformation of particles during the compaction process up to a relative density of 0.95. Alongside with this, the equation (31) can, in some cases, describe with high accuracy PCP up to a relative density exceeding 0.95 (Table 10, FeKH9 powder). It is also important that this equation allows one to estimate the degree of density change during powder compaction due to both particle rearrangement (Δρr) and plastic deformation (Δρd) of particles.
In order to evaluate the change in density by two mechanisms, it was suggested to determine the derivatives of the relative density with regard to pressure separately for the rearrangement and plastic deformation mechanisms [17]. If we fully expand these derivatives, then they will look like:
d ρ d p = 1 − ρ 0 c b c b c + p c 2 p ( 1 − c ) E x p [ k p ] – for particle rearrangement
d ρ d p = 1 − ρ 0 b c k b c + p c E x p [ k p ] – for plastic deformation
The areas under the curves (32) and (33) within the change in pressure from zero to a value corresponding to a given density will show the degree of change in density for the corresponding compaction mechanism. Numerical integration of dependences (32) and (33) for the examples shown in Figure 7, within the pressure range from zero to the pressure corresponding to a density of 0.95, led to the results presented in Table 11. In addition, this table presents the true value of plastic deformation of particles calculated taking into account changes in density up to 0.95 using the formula:
δ p l = l n ⁡ ( 1 1 − Δ ρ d / 0,95 )
By the data in Table 11, the degree of change in the powder density during its compaction in a rigid die due to rearrangement can exceed the degree of change in density through plastic deformation of the particles. In relatively hard powders, such as FeKH3, FeKH6, and FeKH9, densification occurs practically due to rearrangement. There cannot be excluded the case when the Eq. (27) description of solid powders particles rearrangement is very approximate. In this regard, I would also like to draw attention to the fact that equation (27) exactly corresponds to the equation of M. Yu. Balshin (1972) [18] (p. 163, equation V.47) that he proposed to describe the third stage of the densification process, i.e., the stage where practically there is no rearrangement of the particles.
It should also be noted that the process of particle rearrangement during compaction of powders in a rigid die is explicitly reflected in the equation proposed as far back as in the middle of the last century (1962) by A. R. Cooper and L. E. Eaton [26]. In the original record this equation was as follows:
V * = V 0 − V V 0 − V ∞ = a 1 ∙ e x p − k 1 P + a 2 ∙ e x p − k 2 P
where V*is the degree of powder sample volume change under pressure, V0, V,and V∞ are initial volume at zero pressure, current volume at pressure Р, and volume at infinite pressure, respectively, P is the compaction pressure, a1 and k1, are constants characterizing the rearrangement process, and a2 and k2 are constants characterizing the process of plastic deformation.
When compacting the powder, it is advisable to operate with the relative density ρ = Vcom/V (Vcom is the volume of a pore-free sample), then equation (35) can be converted into the dependence of relative density (ρ) on pressure (p):
ρ = ρ 0 1 − 1 − ρ 0 ρ ∞ ∙ a 1 e x p − k 1 p + a 2 e x p − k 2 p
where ρ0 is the initial density of the powder, ρ∞≤ 1 is the density at infinite pressure.
This equation was proposed in order to describe the compaction process of ceramic powders. Therefore, it can be used to approximate the compaction process of any hard powders. In this regard, the applicability of equation (36) was tested for describing the process of compaction of titanium carbide powders and iron powders presented in Table 5. The results are shown in Figure 8, and the values of the constant parameters of equation (36) and the coefficient of determination R2 are listed in Table 12. The approximation was performed at a given value of the parameter ρ∞ for each powder.
It follows from the presented approximation results that equation (36) that contains four constant parameters (the fifth parameter ρ∞ is predetermined) is capable of describing the compaction process of hard metal and ceramic powders with high accuracy. The most important result of approximating the process of compaction of hard powders by this equation is the fact that the process of particle rearrangement affects the change in porosity to a much greater extent than the process of powder deformation. It is evidenced by the value of the constant a1 in Table 12, which reaches 80% of the entire compaction process. A similar result takes place when describing the process of compaction of hard iron powders by equation (31), Table 11.

4. Modern Works Describing the Process of Powder Compaction in a Rigid Die

Recently published papers with new equations for PCP are of increased interest. First of all, a new article by L. Parilak, E. Dudrova et al. (2017) [54] is worth of attention. As said above, these authors previously proposed an equation with two constants that in many cases allows one to describe PCP quite accurately. In the new article, they proposed a novel equation, based on their former ones (13) and transformed into an equation with one constant due to the ratio established by them between the constants K and n in the form ln(K)=1.2952–7.3349 n. With this, equation (13) after taking a double logarithm acquires the form:
l n l n P 0 P = 1.2952 − 7.3349 ∙ n + n ∙ l n ⁡ ( p )
where P0 and P are the initial and current porosities of the powder sample.
After potentiation, equation (37) is transformed into the following expression:
l n P 0 P = 3.6517 ∙ p 1532.9 n
from which one can get an equation where the compaction pressure will be a function, and porosity or relative density (ρ = 1-P) will be an argument:
p = 1532.87 ∙ 0.2738 ∙ l n 1 − ρ 0 1 − ρ m
where m=1/n is a new constant.
There is an ambiguous attitude to this new equation for PCP. On one hand, an equation with one constant parameter is easier to describe the compaction of different powders, but, on the other hand, such an equation is not capable of taking into account the great diversity in the morphology and properties of powders. All differences in the behavior of powders during compaction are averaged in one parameter. This may reduce the accuracy of the description of the densification process of certain powders. Indeed, the approximation by equation (39) of experimental data on the compaction of powders of iron, copper and nickel (Table 1) showed a lower accuracy in two cases out of three (Table 13) than the approximation by the two-parameter equation (14) (Table 4).
With a reduced accuracy in describing PCP, we will get to know with reduced accuracy the degree of plastic deformation of particles, the work of plastic deformation, the magnitude of the resistance of particles to deformation, as well as other characteristics of the powder. Therefore, a one-parameter equation can be used to approximate assessment of the compaction process and powder properties.
Another recent work on the description and evaluation of the compressibility of powders during their compaction in a die deserves an attention, namely, the article of J.M. Montes, F.G. Cuevas, J. Cintas et al. (2018) [55]. When developing their equation, the authors aimed at minimizing the number of experimental constants in the equation and using physical parameters that are characteristic of the powder material and known in advance from reference books. Unfortunately, in many cases, such a desire cannot lead to obtaining an adequate compaction equation due to significant differences in the strength and plastic properties of powders and pore-free material they are made of. The researches [59] proposed the following equation to describe PCP:
P N = 3 2 ∙ ξ ∙ k l n 1 − Θ 1 − Θ M n ∙ 1 − Θ / Θ M Θ / Θ M
where PN is the external pressure during compaction of the powder, Θ and ΘM are the current and initial porosity of the powder sample, ξ is the coefficient that takes into account the friction of the powder against the die wall, k and n are the Hollomon equation parameters, which characterize the law of hardening during deformation of a dense sample obtained from compacted powder.
According to the authors, the parameters k and n are very close to the reference values for the powder material [55]. Therefore, in equation (40), the parameters k and n are known in advance, and the parameters ΘM and ξ are determined by fitting the curve according to equation (40) to the experimental compaction curve of a particular powder. In the authors’ opinion, the advantage of equation (40) is the use of previously known parameters k and n with a clear physical meaning. Alongside with it, the proposed equation does not take into account the phenomenon of particle rearrangement during powder compaction, as well as the possible discrepancy between the strain hardening of particles and the strain hardening of a compact sample from these particles.
In reality, such factors as the rearrangement of particles and the specific nature of the particle strain hardening especially in the compaction of fine-grained particles, are of fundamental importance in describing the compaction process and for the adequacy of the corresponding equation. Therefore, the free status of the parameters k and n in Eq. (40) can take into account both the particle rearrangement factor and the specific nature of the strain hardening of these particles. In this regard, an attempt was made to use equation (40) to approximate the experimental curves for the compaction of various powders, provided that the parameters k and n are free, and the initial porosity is known. To perform the approximation, we transformed equation (40) into the dependence of the compaction pressure p on the relative density ρ:
p = K ∙ l n ρ ρ 0 n ∙ ρ − ρ 0 1 − ρ 0 ∙ 1 − ρ
where K≈k (since ( 3 /2)×ξ ≈ 1) and n are constant parameters obtained from the experiment, ρ0 is the initial relative density of the powder in the die.
To carry out the approximation, iron, copper and nickel powders from Table 1 as well as hard-to-compact iron powders from Table 5 were used. The results of the approximation are shown in Figure 9, and the values of the constants are listed in Table 14.
The results of the approximation of various powders by equation (41) show that in some cases, this equation allows one to describe very accurately, despite the change in some principles underlying the derivation of equation (40). However, hard powders compacted to a density greater than 0.95 cannot be adequately described by this equation.
A. Molinari et al. [27] also proposed a new equation for powder compaction in a rigid die. The authors studied the compaction of low-alloyed iron powders (alloyed with CuMo, Mo, CrMo,or CuMoNi) in a mixture with graphite and lubricant and suggested describing PCP by the absolute density dependence on the average compaction pressure in the form of a power law:
1 − ρ ¯ 0 ρ ¯ = A ∙ P m B
where ρ ̅0 and ρ ̅ are the absolute initial and current density of the powder in the die (the dash above the symbol distinguishes the absolute density from the relative density, which we denote as ρ), Pm is the average compaction pressure, A and B are constant parameters obtained from the experiment.
It should be noted that a feature of the experimental PCP in the previous report [27] is a relatively narrow range of compaction pressure up to 540 MPa, as well as the use of the absolute density of the material instead of the relative density. If we transform equation (42) into the dependence of pressure on relative density, then it will also be expressed as power dependence:
p m = A – ∙ 1 − ρ 0 ρ B
where ρ0 and ρ are relative initial and current densities, А′=1/А(1/В) and В′=1/В are constant parameters obtained from the experiment.
Note that the use of the power law to describe PCP is not a new solution (see equation (3)), but equation (42) takes into account the real fact that at a density equal to the initial density ρ0, the compaction pressure is zero. However, in the long-known equation (3), it is easy to take into account this fact if instead of the current relative density ρ, we substitute the expression (ρ-ρ0)/(1-ρ0), that allows taking into account not only the initial density but also the entire range of density changes from ρ0 to ρ=1.Then equation (3) will acquire the form:
p = c ∙ ρ − ρ 0 1 − ρ 0 d
where c and d are constant parameters obtained from the experiment.
Comparison of the adequacy of equations (43) and (44) showed that in describing the compaction of the powders of iron, copper, and nickel that we used equation (44) was more accurate. This follows from the approximation results presented in Figure 10 and in Table 15.
As seen from Fig 10 and table 15, the power-law dependence of pressure on relative density does not provide a high accuracy of the PCP description, especially in the initial stage of compaction. In this case, the stage is described by Eq. (43) less accurately. Therefore, the authors [27] divided PCP into two stages, in one of which particles are rearranging, and in the other, plastic deformation occurs. In this case, each stage of compaction was approximated by a power equation with its own constant parameters. However, such a method for PCP description was proposed by researches [42] as early as in 1975.
The ability to describe almost the entire compaction process with a single equation raises the question of how one equation can describe the different stages of PCP. The answer to this question may be an assumption about the existence or the possibility of implementation one mechanism for the compaction of powders in a rigid die. An attempt to propose a unified mechanism for compacting powders from the initial density to the maximum possible will be made in the next article, devoted to obtaining new equations for PCP by correcting and generalizing various equations derived by M. Balshin in the framework of the "discrete" theory for describing PCP.
According to the results of analysis concerning the equations presented in the form of simple mathematical functions or in the form of semi-empirical equations that take into account some physical constants of the powder material, the following conclusion can be made.

5. Conclusions

1. The considered equations for the compaction of powders in a rigid die in most cases have two constants, which depend on the powder material and the type of equation and are determined from the experiment. Some of them lead to a finite value of the compaction pressure upon reaching the pore-free state of the sample, while the others lead to an infinite pressure.
2. The physical meaning of the constants in various equations is not always established, but in certain cases, they reflect the resistance to deformation of particles or their strength and the hardening degree during deformation. There are equations with three constants, e.g., the equations of S. Li, P.B. Khosrovabadi and B.H. Kolster (1994), J. Secondi (2002), G. Aryanpour and M. Farzaneh (2015), where the third constant takes into account various features in the behavior of powders during compaction, such as particle rearrangement, the influence of friction forces, and the impossibility of achieving the pore-free state of the sample even at infinite pressure.
3. The accuracy of the PCP description by the considered equations is different and depends on the type of equation, as well as on the range of changes in density during compaction. Equations with three constants describe PCP more accurately, especially in cases of compaction to a high relative density, more than 0.95. A high accuracy in describing PCP by different equations is observed in the case of using a shortened range of density changes, i.e., up to 0.8-0.9, but such a description is not complete, since fundamental differences in the behavior of powders are observed when a relative density close to 1.0. is reached.
4. In a number of proposed equations, there was an attempt to take into account both the strength and plasticity characteristics of a compact material for powder and the shape and size of particles, as well as internal friction forces between particles and external friction forces between particles and the die wall. But this came down to setting the appropriate coefficients, which are constant throughout the entire compaction process. Moreover, in most cases, the value of these coefficients must be determined in the experiment that eliminates the desire of researchers to work with the use of empirical constants.
5. The authors' opinions regarding the equations on compaction mechanisms associated with the rearrangement of particles and their plastic deformation are ambiguous.
Many researchers believe that the particle rearrangement mechanism manifests itself at the initial stage of powder compaction, whereas the plastic deformation mechanism works at the intermediate and final stages. But there is an opinion, e.g., of A. R. Cooper and L. E. Eaton or G. Aryanpour and M. Farzaneh, according to which the mechanisms of rearrangement and plastic deformation work in parallel during compaction of powders to a relative density of 0.95.
6. Some researchers tried to apply the physical characteristics or mechanical properties of dense materials used for powders production as parameters in equations for powder compaction. However, in most cases the implementation of this approach was difficult. The reason for this lies in essential differences in the mechanical behavior of the particles and the monolithic material. In many cases, the particle sizes are smaller than the grain sizes in compact material, and such properties of materials as the yield strength and the law of work hardening significantly depend on the size of grains or particles.

References

  1. Walker, E.E. The properties of powders. Part IV. The compressibility of powders. Trans. Farad. Soc. 1923, 19, 73–82. [Google Scholar] [CrossRef]
  2. Bal'shin, M.Y. Poroshkovaya metallurgiya. Мoskow: Mashgiz, 1948 (in Russian).
  3. Lipson, H. Powder metallurgy Bull. 1950; 5, 52–57. [Google Scholar]
  4. Rutkowski, W.; Rutkowska, H. Prace Glow . J. Met. 1949, 111–125. [Google Scholar]
  5. Agte, C.; Petrdlik, M. Kurs praskove metallurgia, Praha. 1951; 113 s. [Google Scholar]
  6. Meerson, G.A. Some problems of powder compacting. Powder Metall. Met. Ceram. 1964, 1, 315–324. [Google Scholar] [CrossRef]
  7. Athy, L.F. Density, porosity and compaction of sedimentary rocks. Bull. Amer. Assoc. Petrol. Geologists, 1930; 14, 1–24. [Google Scholar]
  8. Shapiro, I.; Kolthoff, I. M. The compressibility of silver bromide powders. J. Phys. and Colloid Chem. 1947, 51, 483–493. [Google Scholar] [CrossRef] [PubMed]
  9. Konopicky, K. Parallelitat der GesetzmaSigkeiten in Keramik und Pulvermetallurgie Radex- Rundschau, 1948, 7/8, 141-148.
  10. Znatokova, T.N.; Likhtman, V.I. On the regularities of pressing the metal-ceramic composition copper-graphite. DAN SSSR, 1954, 96, No 3, 577-580. (in Russian).
  11. Heckel, R.W. An analysis of powder compaction phenomena. Trans. Metall. Soc. AIME, 1961, 221, 1001–1008. [Google Scholar]
  12. Torre, C. Theory and behavior of pressed powders. Berg und Hüttenmännische Monatshefte, Montan. Hochschule Leoben, 1948, 93, No 4/5, 62-67.
  13. Nikolaev, A.N. Relationship between pressure and density of compacts from metal powders. Powder Metall. Met. Ceram., 1963, 1, 147–151. [Google Scholar] [CrossRef]
  14. Zhdanovich, G.M. Resistance of powder materials.– Minsk: PК ООО «Bestprint», 1999. (in Russian).
  15. Al-Qureshi, H.A.; Soares, M.R.F.; Hotza, D.; Alves, M.C.; Klein, A.N. Analyses of the fundamental parameters of cold die compaction of powder metallurgy. Journal of Materials Processing Technology, 2008, 199, 417–424. [Google Scholar] [CrossRef]
  16. Li, S.; Khosrovabadi, P.B.; Kolster, B.H. A new compaction equation for powder materials. Int. J. Powder Metallurgy, 1994; 30, 47–57. [Google Scholar]
  17. Aryanpour, G.; Farzaneh, M. Application of a piston equation to describe die compaction of powders. Powder Technology, 2015, 277, 120–125. [Google Scholar] [CrossRef]
  18. Bal'shin, M.Y. Scientific foundations of powder metallurgy and fiber metallurgy. Мoskow: Metallurgy, 1972. (in Russian).
  19. Zhdanovich, G.M. Theory of pressing metal powders. – M.: Metallurgy, 1969. (in Russian).
  20. Green, R.J. A plasticity theory for porous solids. Int. J. Mech. Sci. 1972, 14, 215–224. [Google Scholar] [CrossRef]
  21. Laptev, A.M. Plasticity criteria for porous metals. Powder Metall. Met. Ceram. 1982, 21, 522–526. [Google Scholar] [CrossRef]
  22. Kuhn, H.; Downey, C.L. Deformation characteristics and plasticity theory of sintered powder materials. Int. J. Powder Met. 1971, 7, 15–25. [Google Scholar]
  23. Progressive technological processes for stamping parts from powders and equipment. Ed. A.M. Dmitriev and A.G. Ovchinnikov. – Moskow: Mashinostroenie, 1991. (in Russian).
  24. Smyslov, A.Yu. On the theory of plasticity of porous media. Izv. Vuzov. Mashinostroenie, 1980. – No. 4. – p. 107-110. (in Russian).
  25. Shtern, M.B.; Serdyuk, G.G.; Maksimenko, L.A. et al. Phenomenological theories of powder pressing. Kyiv: Naukova Dumka, 1982. (in Russian).
  26. Cooper, A.R.; Eaton, L.E. Compaction Behavior of Several Ceramic Powders. Journal of the American Ceramic Society, 1962; 45, 97–101. [Google Scholar] [CrossRef]
  27. Molinari, A.; Cristofolini, I.; Pederzini, G.; Rambelli, A. A densification equation derived from the stress-deformation analysis of uniaxial cold compaction of metal powder mixes. Powder Metallurgy, 2018. [Google Scholar] [CrossRef]
  28. Beigel'zimer, Y.E.; Getmanskii, A.P. A model of the development of plastic deformation of porous solids in the percolation theory approximation. Powder Metall. Met. Ceram. 1988, 27, 773–776. [Google Scholar] [CrossRef]
  29. Leuenberger, H. The application of percolation theory in powder technology (Invited review). Adv. Powder Technol. 1999, 10, 323–353. [Google Scholar] [CrossRef]
  30. Kuntz, M.; Leuenberger, H. Pressure susceptibility of polymer tablets as a critical property: a modified Heckel equation. J Pharm. Sci. 1999, 88(2), 174–179. [Google Scholar] [CrossRef]
  31. Stuart, B. Braun, Guillermo G. A. Weber. A constitutive model for the compaction of metal powders. Modern developments in powder metallurgy, 1988, 18, 465–476. [Google Scholar]
  32. Riera, M.D.; Prado, J.M. Modeling of cold compaction process of metal powders. Proc. PM’94 Powder Metallurgy World Congress, Paris, 6-9 june, 1994, 1, 685–688. [Google Scholar]
  33. Shtern, M.B.; Mikhailov, O.V. Numerical Modelling of the Compaction of Powder Articles of Complex Shape in Rigid Dies: Effect of Compaction Scheme on Density Distribution. Part 2. Modelling Procedure and Analysis of Forming Schemes. Powder Metall. Met.Ceram. 2003, 42, 114–121. [Google Scholar] [CrossRef]
  34. Tyutenko, V.S.; Borzenko, A.P.; Beigel'zimer, Y.E. Analysis of the process of hydromechanical compression of a porous blank. Powder Metall. Met. Ceram. 1990, 29, 259–262. [Google Scholar] [CrossRef]
  35. Panfilov, Y.A.; Rud', V.D.; Shtern, M.B. Effects from loading-system rigidity on the flow of a porous material under biaxial strain. Powder Metall. Met. Ceram. 1992, 31, 562–565. [Google Scholar] [CrossRef]
  36. Pavier, E.; Doremus, P. Triaxial characterization of iron powder behaviour. Powder metallurgy, 1999; 42, 345–352. [Google Scholar]
  37. Radomysel'skii, I.D.; Serdyuk, G.G.; Kovalev, Y.V. Determination of the lateral pressure coefficient in the compaction of iron powders. Powder Metall. Met. Ceram. 1966, 5, 686–689. [Google Scholar] [CrossRef]
  38. Bal'shin, M.Y. Novel principles of calculation and analysis of powder compression. Powder Metall. Met. Ceram. 1965, 4, 975–983. [Google Scholar] [CrossRef]
  39. Martynova, I.F.; Skorokhod, V.V.; Solonin, S.M. Plastic deformation in the pressing of powders of ductile metals. Powder Metall. Met. Ceram. 1974, 13, 205–209. [Google Scholar] [CrossRef]
  40. Radomysel'skii, I.D.; Shcherban', N.I. Some features of powder densification in various stages of pressing. Powder Metall. Met. Ceram. 1980, 19, 741–748. [Google Scholar] [CrossRef]
  41. Koval’chenko, M.S. Strain hardening of a powder body in pressing. Powder Metall. Met. Ceram. 2009, 48, 133–144. [Google Scholar] [CrossRef]
  42. Andreeva, N.V.; Radomysel'skii, I.D.; Shcherban', N.I. Compressibility of powders. Powder Metall. Met. Ceram. 1975, 14, 457–464. [Google Scholar] [CrossRef]
  43. Hewitt, R.L.; Wallace, W.; deMalherbe, M. C. Plastic deformation in metal powder compaction. Powder metallurgy, 1974; 17, 1–12. [Google Scholar]
  44. James, P. J. Particle deformation during cold isostatic pressing of metal powders. Powder metallurgy, 1977; 20, 199–204. [Google Scholar]
  45. 45. Ge Rong-de. A new powder compaction equation. Int. J. Powder Metall. 1991; 27, 211–216.
  46. Yu, A.B.; Gu, Z.H. Characterization of the porosity-pressure relation of cohesionless powders. Advanced Powder Technology, 1993; 4, 199–216. [Google Scholar]
  47. Parilak, L.; Dudrova, E. New pressing equation. Proc. PM’94, Powder Metallurgy World Congress, Paris, 6-9 june, 1994, 1, 737–740. [Google Scholar]
  48. Kawakita, K.; Lüdde, K.H. Some consideration on powder compression equations. Powder Technology, 1970/1971; 61–68. [Google Scholar]
  49. Kieffer, R.; Hotop, W. Sintereisen und Sinterstahl, Wien, Springer, 1948.
  50. Secondi, J. Modelling powder compaction. From a pressure-density law to continuum mechanics. Powder metallurgy, 2002; 45, 213–217. [Google Scholar]
  51. Bal'shin, M.Yu. Some questions of formation and properties of powder materials. Proc. "Powder metallurgy and metal-working", Yerevan, 1965; 50–67. (in Russian) [Google Scholar]
  52. Panelli, R.; Filho, F. Ambrozio. A study of a new phenomenological compacting equation. Powder Technology, 2001, 114, 255–261. [Google Scholar] [CrossRef]
  53. Lenel, F.V. Powder metallurgy, Principles and Applications, Metal Powder Industries Federation, Princeton, NJ, 1980.
  54. Parilak, L.; Dudrova, E.; Bidulsky, R.; Kabatova, M. Derivation, testing and application of a practical compaction equation for cold die-compacted metal powders. Powder Technology, 2017, 322, 447–460. [Google Scholar] [CrossRef]
  55. Montes, J.M.; Cuevas, F.G.; Cintas, J.; Ternero, F.; Caballero, E.S. On the compressibility of metal powders. Powder Metallurgy, 2018. [Google Scholar] [CrossRef]
Preprints 90637 g002
Figure 2. Approximation dependences of experimental data on PCP for (a) iron, (b) copper, and (c) nickel by equations (6) (dotted line) and (8) (solid line).
Figure 2. Approximation dependences of experimental data on PCP for (a) iron, (b) copper, and (c) nickel by equations (6) (dotted line) and (8) (solid line).
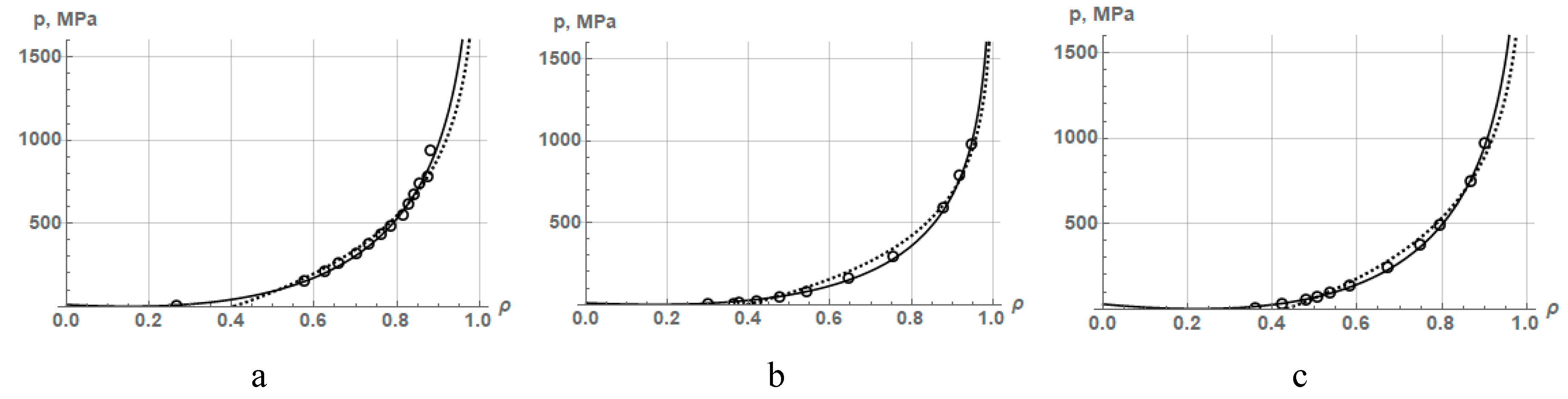
Preprints 90637 g002
Preprints 90637 g003
Figure 3. Approximation dependences of experimental data on compaction of powders of (a) iron, (b) copper, and (c) nickel by equations (16) (dashed line) and (14) (dotted line).
Figure 3. Approximation dependences of experimental data on compaction of powders of (a) iron, (b) copper, and (c) nickel by equations (16) (dashed line) and (14) (dotted line).
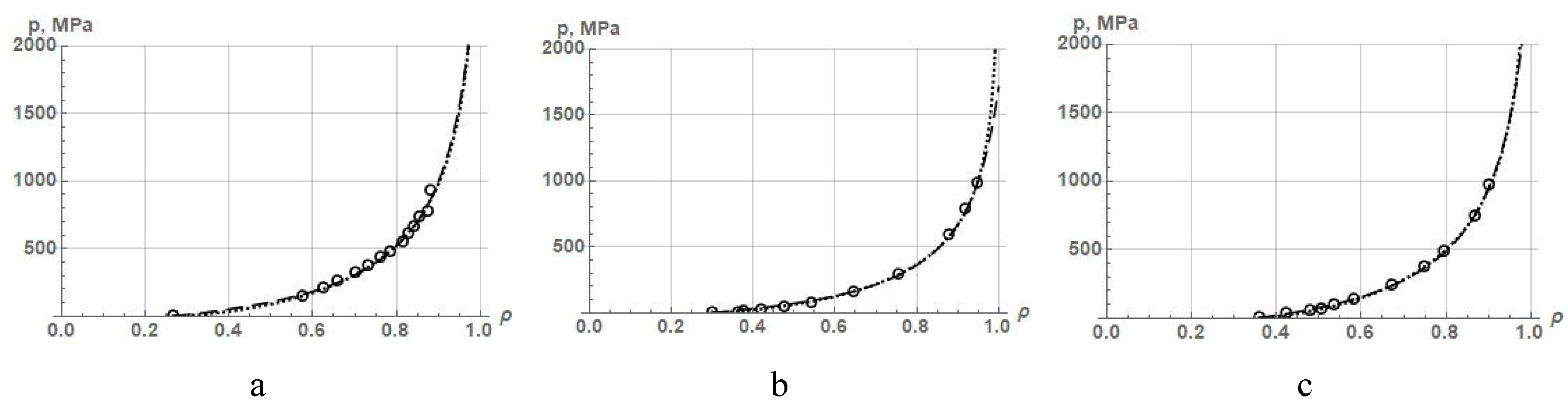
Preprints 90637 g003
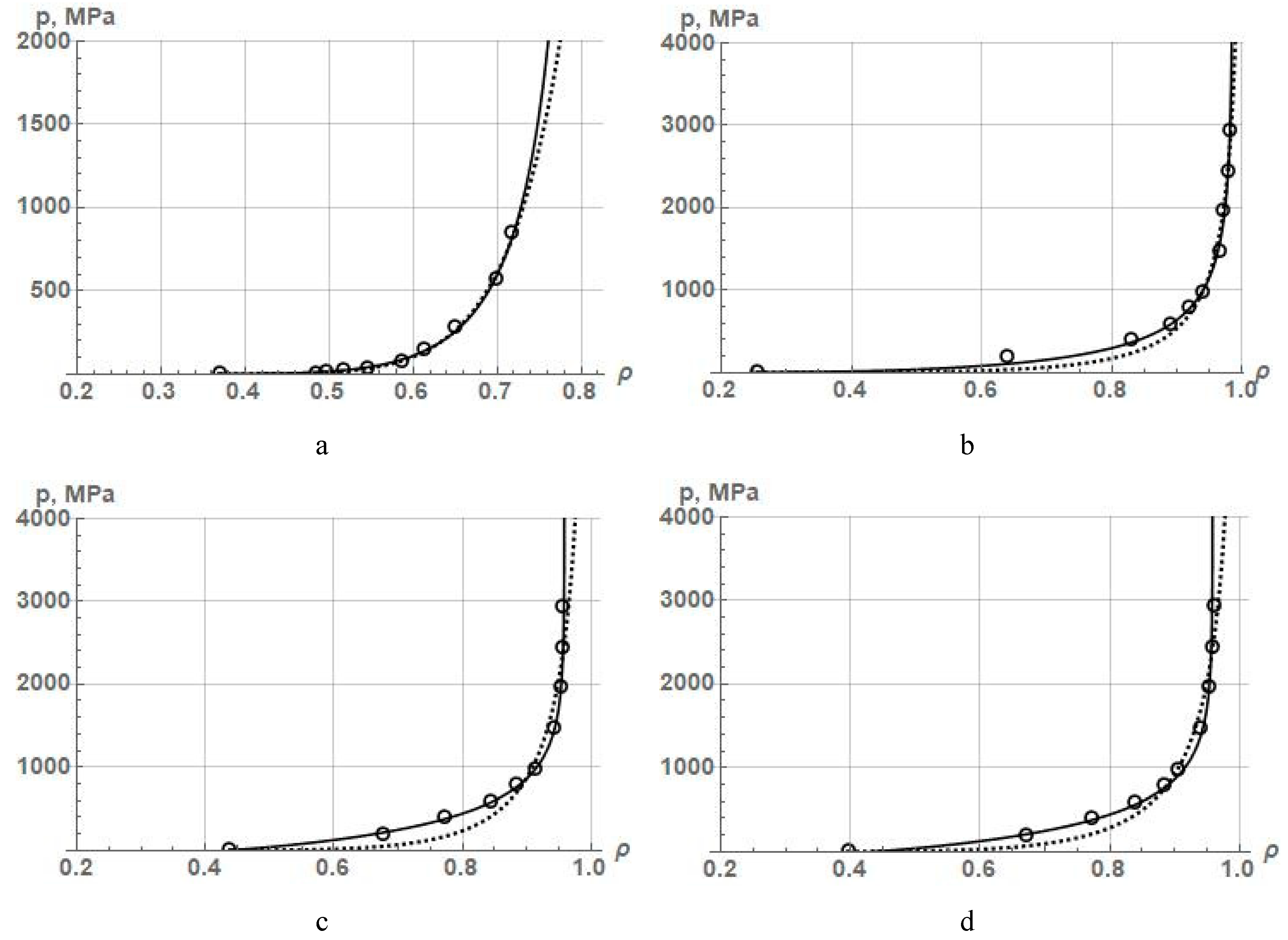
Preprints 90637 g004
Figure 4. Approximation dependences of experimental data on the compaction of (a) titanium carbide and three iron powders (b) FeKH3, (c) FeKH6, (d) FeKH9 using equations (18) (solid line) and (14) (dotted line).
Figure 4. Approximation dependences of experimental data on the compaction of (a) titanium carbide and three iron powders (b) FeKH3, (c) FeKH6, (d) FeKH9 using equations (18) (solid line) and (14) (dotted line).
Preprints 90637 g004
Preprints 90637 g005
Figure 5. Approximation dependences of experimental data on the compaction of powders of (a) iron, (b) copper, (c) nickel, and iron powders (d) FeKH3, (e) FeKH6, (f) FeKH9 using equation (21) of Panelli and Filho.
Figure 5. Approximation dependences of experimental data on the compaction of powders of (a) iron, (b) copper, (c) nickel, and iron powders (d) FeKH3, (e) FeKH6, (f) FeKH9 using equation (21) of Panelli and Filho.
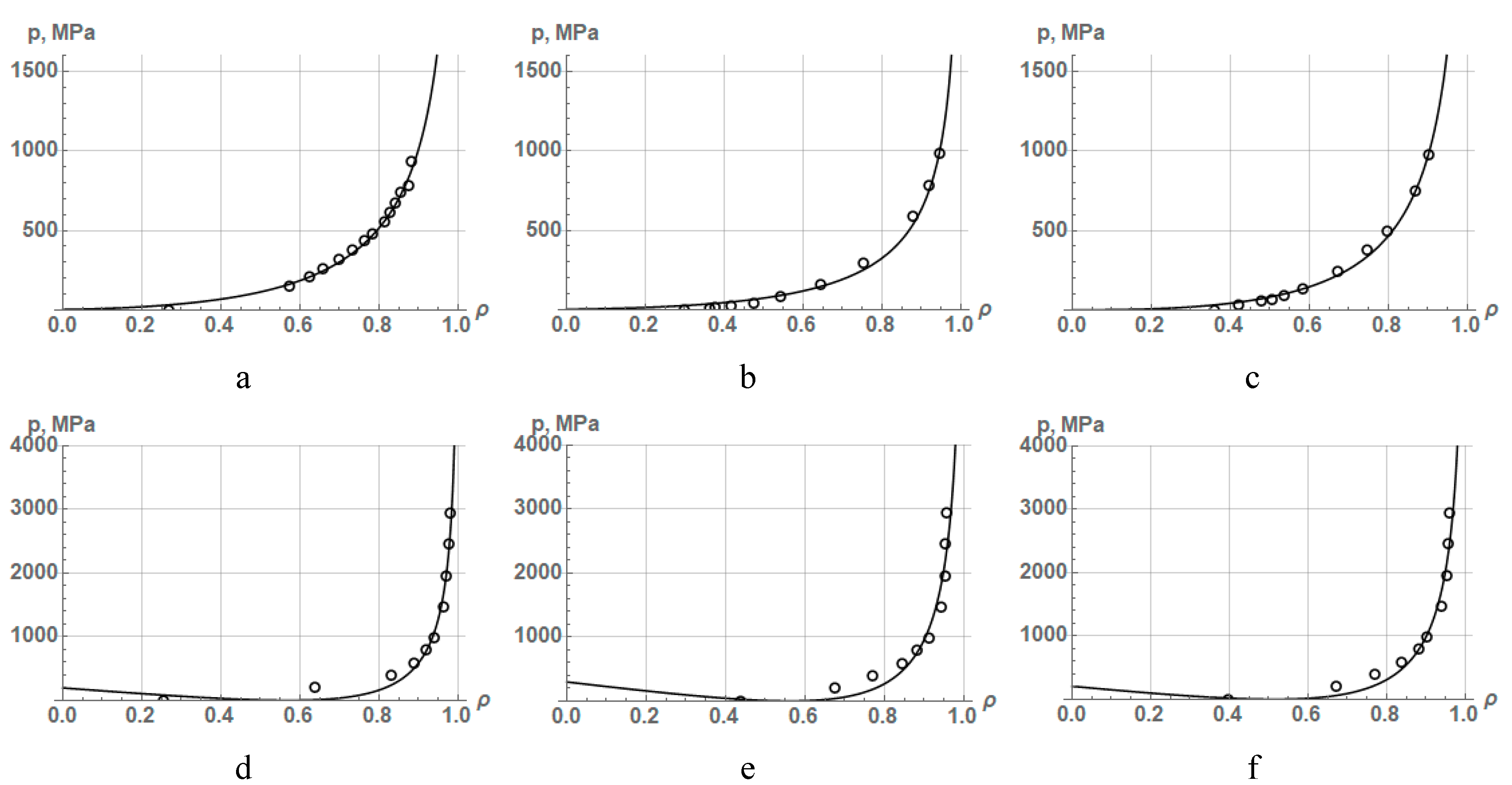
Preprints 90637 g005
Preprints 90637 g006aPreprints 90637 g006b
Figure 6. Approximation dependences according to equation (26) as a result of processing experimental data on the compaction of iron powders: (a) Fe, (b) Fe (coarse), (c) Fe (fine) as well as copper powders: (d) Cu, (e) Cu (coarse), (f) Cu (fine).
Figure 6. Approximation dependences according to equation (26) as a result of processing experimental data on the compaction of iron powders: (a) Fe, (b) Fe (coarse), (c) Fe (fine) as well as copper powders: (d) Cu, (e) Cu (coarse), (f) Cu (fine).
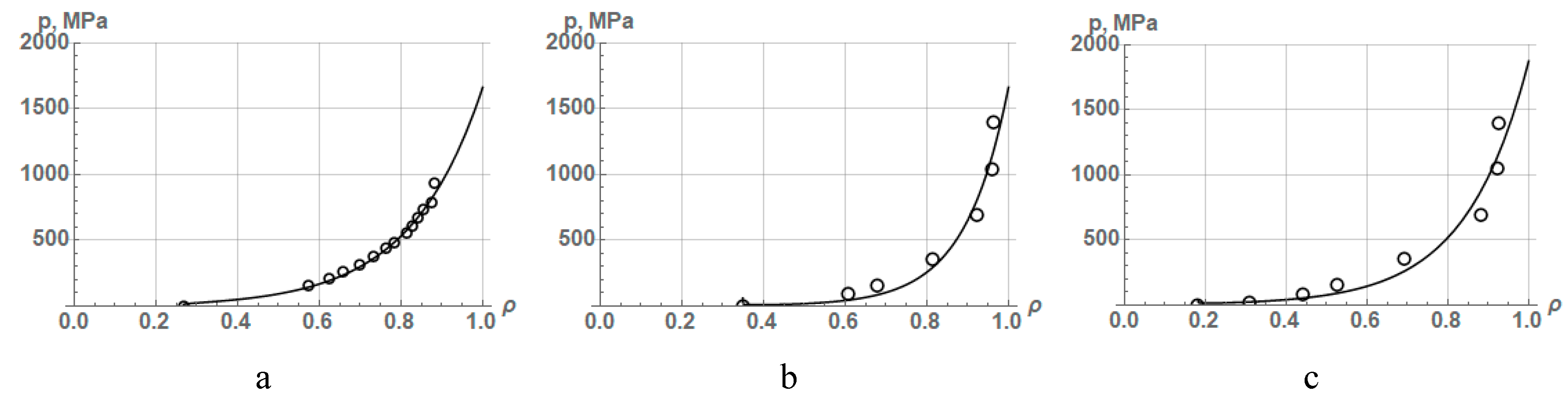
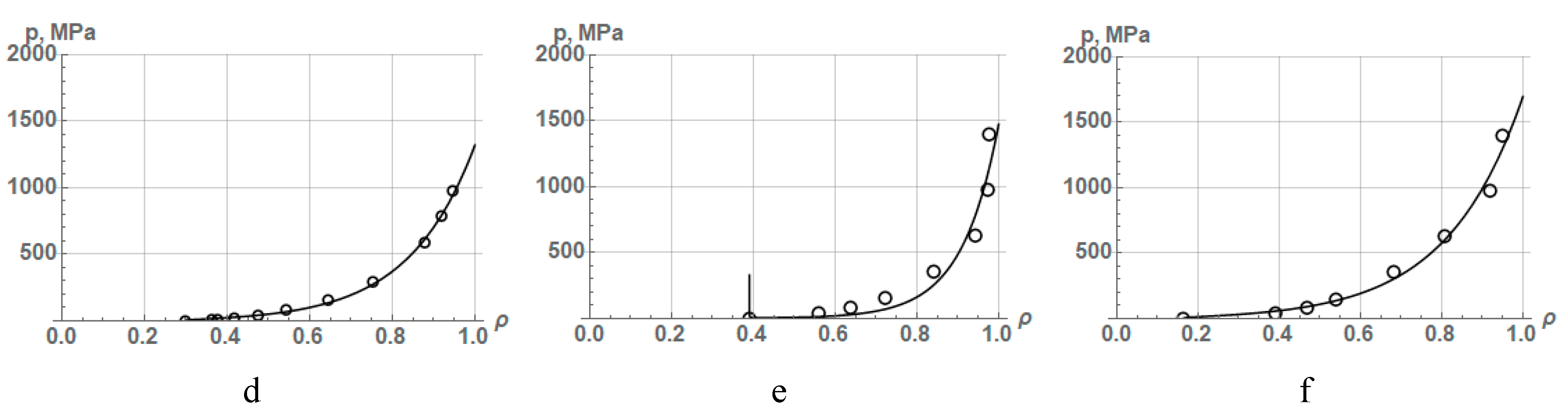
Preprints 90637 g006aPreprints 90637 g006b
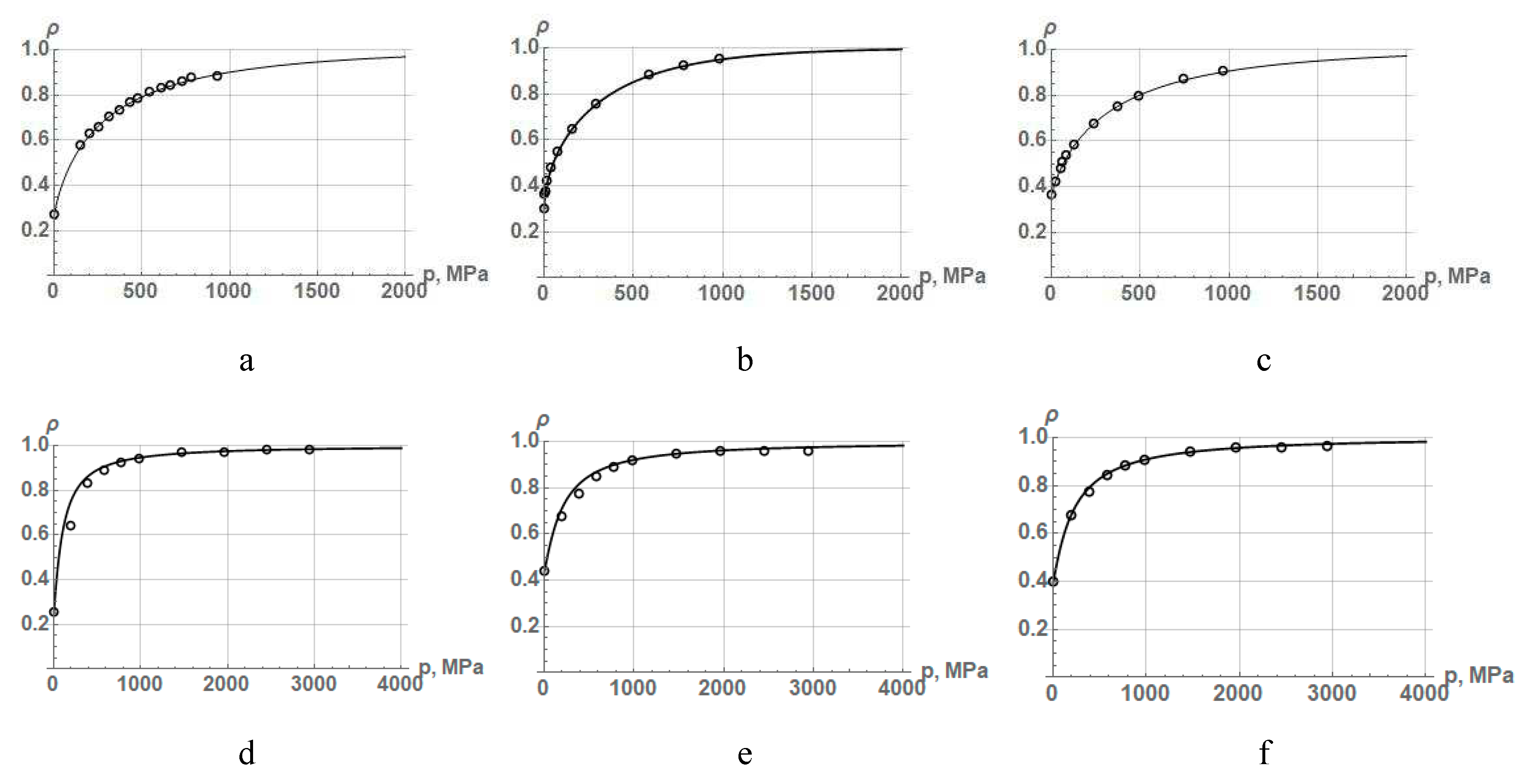
Preprints 90637 g007
Figure 7. Approximation dependences according to equation (31) obtained via processing experimental data on the compaction of (a) iron, (b) copper, and (c) nickel powders from Table 1, as well as iron powders (d)FeKH3, (e) FeKH6, and (f) FeKH9 from Table 5.
Figure 7. Approximation dependences according to equation (31) obtained via processing experimental data on the compaction of (a) iron, (b) copper, and (c) nickel powders from Table 1, as well as iron powders (d)FeKH3, (e) FeKH6, and (f) FeKH9 from Table 5.
Preprints 90637 g007
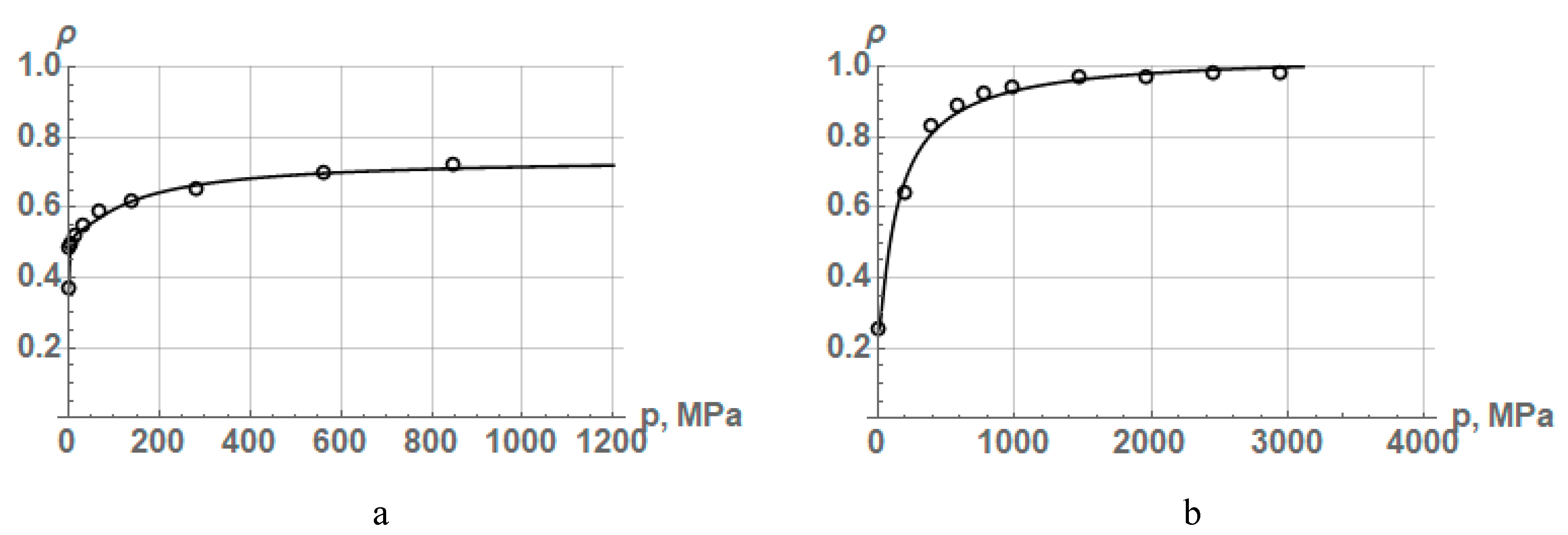
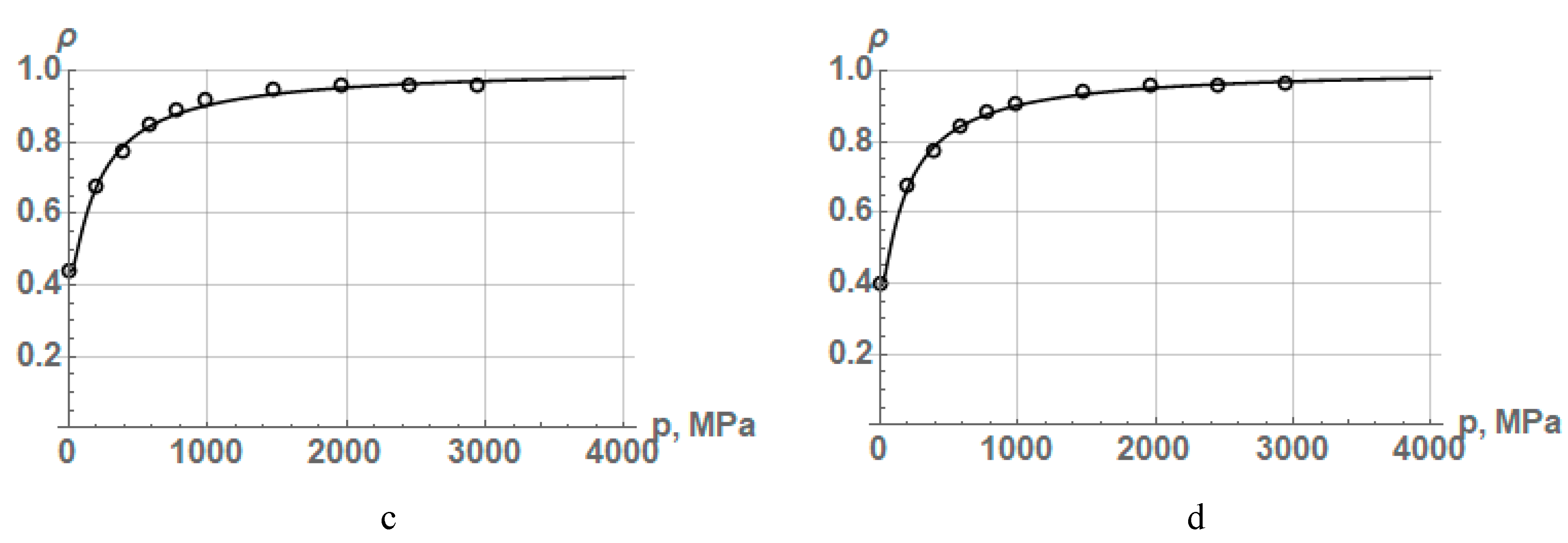
Preprints 90637 g008aPreprints 90637 g008b
Figure 8. Approximation dependences according to equation (31) obtained via processing experimental data on the compaction of (a) titanium carbide andiron powders (b)FeKH3, (c) FeKH6, and (d) FeKH9 from Table 5.
Figure 8. Approximation dependences according to equation (31) obtained via processing experimental data on the compaction of (a) titanium carbide andiron powders (b)FeKH3, (c) FeKH6, and (d) FeKH9 from Table 5.
Preprints 90637 g008aPreprints 90637 g008b
Preprints 90637 g009
Figure 9. Approximation dependences according to equation (41) as a result of processing experimental data on the compaction of (a) iron, (b) copper, and (c) nickel, as well as hard-to-compress iron powders (d) FeKH3, (e) FeKH6, and (f) FeKH9.
Figure 9. Approximation dependences according to equation (41) as a result of processing experimental data on the compaction of (a) iron, (b) copper, and (c) nickel, as well as hard-to-compress iron powders (d) FeKH3, (e) FeKH6, and (f) FeKH9.
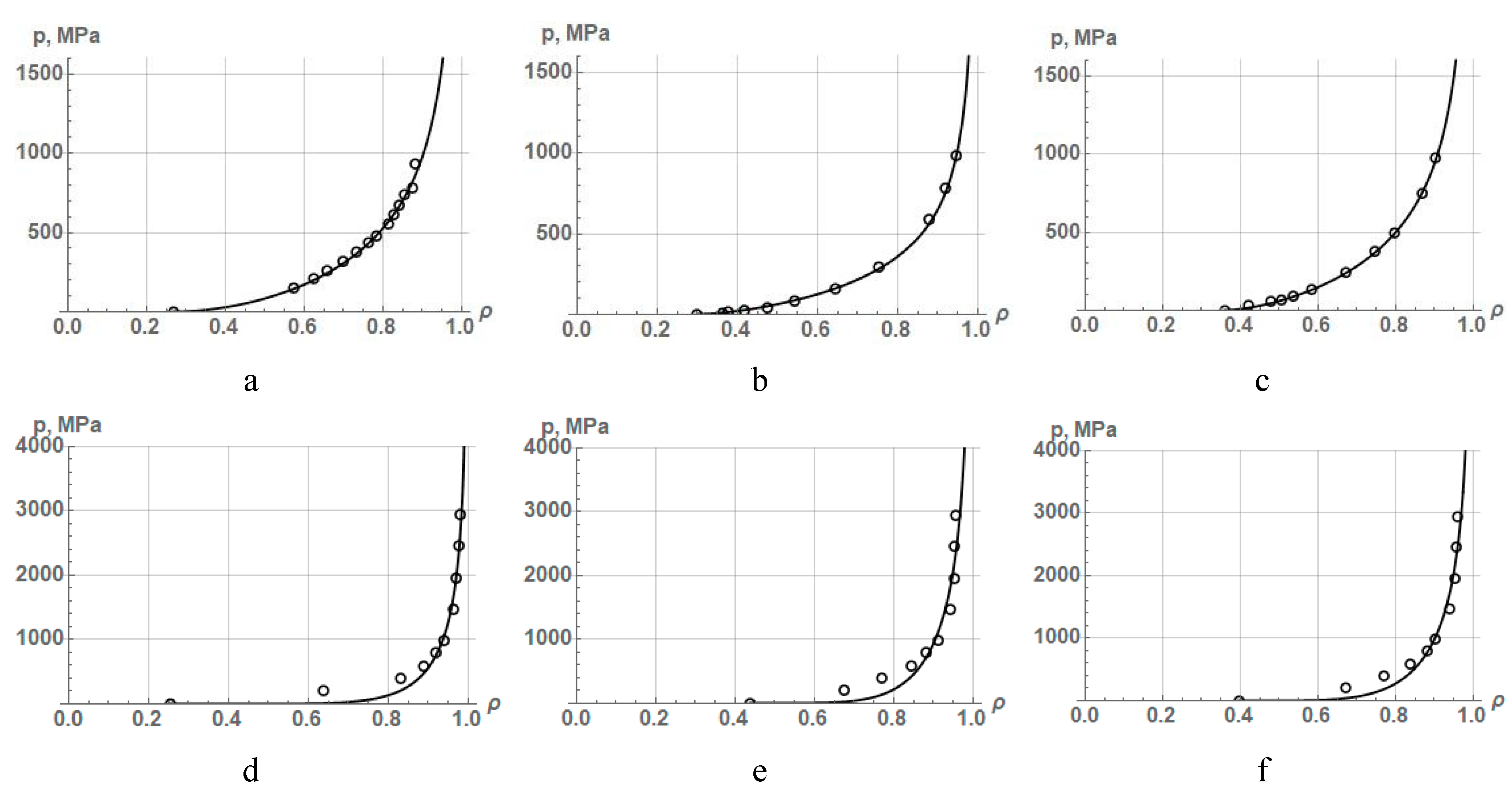
Preprints 90637 g009
Preprints 90637 g010
Figure 10. Approximation curves according to equations (43)(dotted line) and (44) (solid line)as a result of processing experimental data on the compaction of (a) iron, (b) copper, and (c) nickel powders.
Figure 10. Approximation curves according to equations (43)(dotted line) and (44) (solid line)as a result of processing experimental data on the compaction of (a) iron, (b) copper, and (c) nickel powders.
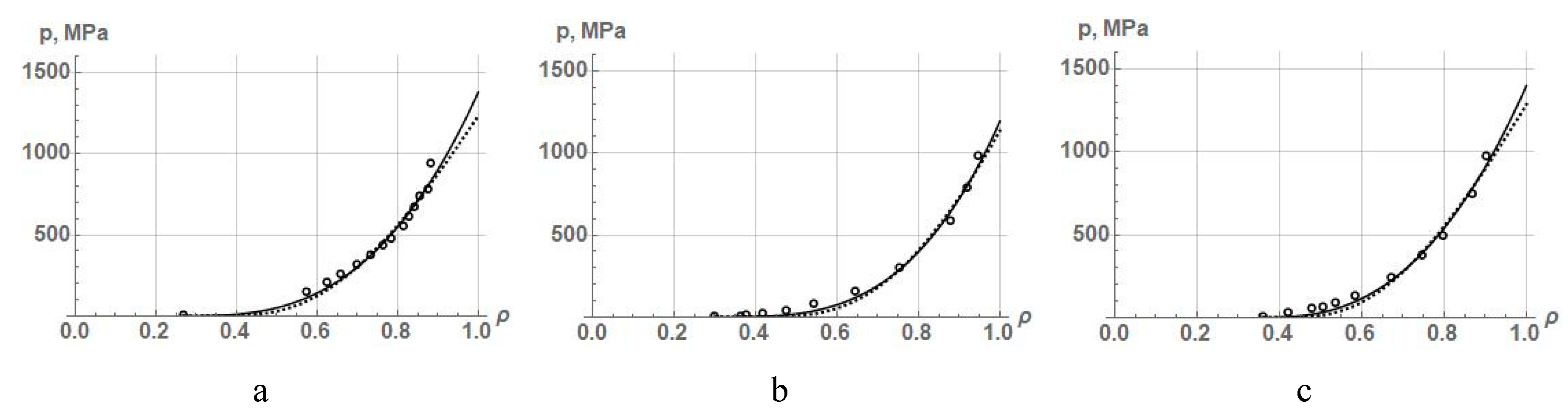
Preprints 90637 g010
Table 3. Constants and coefficient of determination R2 obtained via approximation of experimental data on PCP for iron, copper, and nickel using equations (6) and (8).
Table 3. Constants and coefficient of determination R2 obtained via approximation of experimental data on PCP for iron, copper, and nickel using equations (6) and (8).
Parameters Powders
Iron Copper Nickel
Equation type
(6) (8) (6) (8) (6) (8)
ρ0 0.268 0.3 0.36
k, C,×10–3 1.9981 1.0996 2.6300 1.5437 1.9570 0.9692
1/k, 1/C, MPa 500.5 909.4 380.2 647.8 511.0 1031.8
а 0.51893 - 0.50561 - 0.56648 -
ρ 0 ' ,ρC 0.4048 0.1504 0.3969 0.1694 0.4325 0.2228
R2 0.96549 0.99163 0.98983 0.99899 0.98464 0.99927
Table 4. Constants obtained via approximation of experimental data on the compaction of powders of iron, copper, and nickel using equations (16) and (14).
Table 4. Constants obtained via approximation of experimental data on the compaction of powders of iron, copper, and nickel using equations (16) and (14).
Parameters Powders
Iron Copper Nickel
Equation type
(16) (14) (16) (14) (16) (14)
ρ0 0.268 0.3 0.36
b′, B, MPa 64.1376 56.7495 56.7136 62.2247 101.354 83.2898
a, m, 0.7474 1.4566 0.7231 1.3547 0.6642 1.3579
pmax, MPa 3055.1 ∞ 1713.2 ∞ 2675.4 ∞
R2 0.99283 0.99212 0.99879 0.99935 0.99928 0.99958
Table 5. Experimental data on compaction of titanium carbide powders [51] and some iron powders [49].
Table 5. Experimental data on compaction of titanium carbide powders [51] and some iron powders [49].
Mate-rials* Relative density ρ and corresponding densification pressure p(MPa)
TiC
[51]		 ρ 0.37 0.485 0.498 0.518 0.547 0.587 0.614 0.65 0.699 0.719
p 0 4.41 8.82 17.64 35.28 70.56 141.12 282.24 564.48 846.72
FeKH3
[49]		 ρ 0.253 0.640 0.831 0.890 0.920 0.941 0.966 0.971 0.978 0.981
p 0 196 392 588 784 980 1470 1960 2450 2940
FeKH6
[49]		 ρ 0.439 0.677 0.772 0.846 0.885 0.914 0.944 0.955 0.956 0.958
p 0 196 392 588 784 980 1470 1960 2450 2940
FeKH9
[49]		 ρ 0.397 0.673 0.773 0.841 0.884 0.905 0.942 0.955 0.959 0.961
p 0 196 392 588 784 980 1470 1960 2450 2940
* Iron powders correspond to the following methods of their preparation: FeKH3 – vibration grinding, FeKH6 – carbonyl, and FeKH9 is steel.
Table 6. Constants and coefficient of determination R2 obtained via approximation of experimental data on the compaction of titanium carbide powder [51] and three iron powders from [49] using equations (18) and (14).
Table 6. Constants and coefficient of determination R2 obtained via approximation of experimental data on the compaction of titanium carbide powder [51] and three iron powders from [49] using equations (18) and (14).
Parameters Powders
TiC[51] FeKH3 [49] FeKH6 [49] FeKH9 [49]
Equation type
(17) (13) (17) (13) (17) (13) (17) (13)
ρ0 0.37 0.256 0.439 0.397
ρ∞ 0.8146 1.0 0.985 1.0 0.9587 1.0 0.9623 1.0
K ' , В, МPа 257.4 1793.1 171.4 81.19 364.5 214.9 355.9 221.3
m 2.739 3.642 1.725 2.715 1.102 2.561 1.175 2.428
R2 0.99787 0.99719 0.99519 0.98109 0.99344 0.93326 0.99952 0.95782
Table 7. Constants and coefficient of determination R2 obtained via approximation of experimental data on the compaction of powders of iron, copper, nickel, and FeKH3, FeKH6 and FeKH9 using equation (21).
Table 7. Constants and coefficient of determination R2 obtained via approximation of experimental data on the compaction of powders of iron, copper, nickel, and FeKH3, FeKH6 and FeKH9 using equation (21).
Parameters Powders
Iron Copper Nickel FeKH3 FeKH6 FeKH9
ρ0 0.268 0.3 0.36 0.256 0.439 0.397
А′, МРа 172.4 106.6 188.1 276.2 439.2 394.8
А -0.0761 -0.0969 0.0729 0.0602 0.0477 0.0503
В -0.1179 -0.1340 0.0362 0.8435 0.8248 0.7225
ρ0′ -0.1252 -0.1434 0.0355 0.5698 0.5617 0.5288
R2 0.99161 0.99076 0.99496 0.97272 0.92665 0.95315
Table 8. Experimental data on the compaction of coarse and fine powders of iron and copper presented in the book [53].
Table 8. Experimental data on the compaction of coarse and fine powders of iron and copper presented in the book [53].
Powders Relative density values (ρ ) and corresponding densification pressure (p)
Fe (сoarse) ρ 0.35 0.609 0.68 0.814 0.925 0.963 0.965
p, MPa 0 88.3 148.7 351.5 692.3 1042 1400
Cu (сoarse) ρ 0.391 0.561 0.64 0.725 0.844 0.945 0.976 0.978
p, MPa 0 38.7 77.4 148.7 348.5 628.8 972.6 1400
Fe (fine) ρ 0.183 0.312 0.442 0.527 0.694 0.882 0.925 0.927
p, MPa 0 17 79 148.7 348.5 692 1044 1400
Cu (fine) ρ 0.165 0.392 0.471 0.541 0.685 0.808 0.922 0.95
p,MPa 0 35.6 74.3 144 351.5 627.5 975.7 1400
Table 9. Constant parameters of equation (26) obtained via approximation of experimental data on the compaction of iron and copper powders from Table 1 and iron and copper powders from Table 8.
Table 9. Constant parameters of equation (26) obtained via approximation of experimental data on the compaction of iron and copper powders from Table 1 and iron and copper powders from Table 8.
Parameters Powders
Fe Fe(coarse) Fe(fine) Cu Cu(coarse) Cu(fine)
ρ0 0.268 0.35 0.183 0.3 0.391 0.165
A, MPa 1596.6 1689.5 2006.5 1245.7 1436.0 1380.7
m 0.1505 -0.2869 -0.1256 0.3088 -0.4430 0.3484
n 5.5610 9.6759 6.5183 6.0371 11.623 5.1606
pmax, MPa 1664.8 1664.7 1876.6 1320.4 1474.8 1697.1
R2 0.98895 0.94972 0.94289 0.99791 0.92831 0.98167
Table 10. Constant parameters in equation (31) resulted from the approximation of experimental data on the compaction of iron, copper, and nickel powders from Table 1 and iron powders FeKH3, FeKH6, and FeKH9 from Table 5.
Table 10. Constant parameters in equation (31) resulted from the approximation of experimental data on the compaction of iron, copper, and nickel powders from Table 1 and iron powders FeKH3, FeKH6, and FeKH9 from Table 5.
Parameters Powders
Fe Cu Ni FeKH3 FeKH6 FeKH9
ρ0 0.268 0.3 0.36 0.256 0.439 0.397
ρlim 0.884 0.949 0.903 0.981 0.958 0.961
c 0.70715 0.51827 0.84085 1.14893 1.14893 1.10063
a=1/c 1.4141 1.9295 1.1893 0.8704 0.8704 0.9086
b 437.1 637.8 406.3 108.21 208.21 227.31
k 0.00102 0.00184 0.00078 0.00001 0.0001 0.00009
R2 0.99883 0.99985 0.99927 0.97092 0.98165 0.99710
Table 11. Degree of change in density due to rearrangement and plastic deformation of particles during compaction of the powder from the initial density to a density of 0.95, as well as the true degree of plastic deformation of the particles and the degree of change in relative density from the initial to 0.95.
Table 11. Degree of change in density due to rearrangement and plastic deformation of particles during compaction of the powder from the initial density to a density of 0.95, as well as the true degree of plastic deformation of the particles and the degree of change in relative density from the initial to 0.95.
Density change mechanism Powders
Fe [37] Cu [38] Ni [39] FeKH3 FeKH6 FeKH9
Rearrangement, Δρr 0.3937 0.2890 0.3805 0.7053 0.5037 0.5335
Plastic deformation, Δρd 0.3141 0.3787 0.2245 0.0019 0.0234 0.0247
True plastic deformation of particles, δpl 0.40135 0.50861 0.26958 0.00198 0.02494 0.02638
Degree of change in density, Δρ =0.95–ρ0 0.682 0.65 0.59 0.694 0.511 0.553
Table 12. Constant parameters in equation (36) resulted from the approximation of experimental data on the compaction of titanium carbide andiron powders FeKH3, FeKH6, and FeKH9 from Table 5.
Table 12. Constant parameters in equation (36) resulted from the approximation of experimental data on the compaction of titanium carbide andiron powders FeKH3, FeKH6, and FeKH9 from Table 5.
Parameters Powders
TiC FeKH3 FeKH6 FeKH9
ρ0 0.37 0.256 0.439 0.397
ρ∞ 0.8 0.985 0.97 0.965
a1 0.5999 0.8089 0.8159 0.8144
k1 1.5592 37.908 100.57 87.620
a2 0.3338 0.2086 0.2173 0.2165
k2 108.40 37.945 76.678 51.647
R2 0.99324 0.99386 0.99687 0.99844
Table 13. The value of the constant m in equation (39) and the coefficient of determination R2 obtained after the approximation of experimental data on compaction of iron, copper, and nickel powders from Table 1.
Table 13. The value of the constant m in equation (39) and the coefficient of determination R2 obtained after the approximation of experimental data on compaction of iron, copper, and nickel powders from Table 1.
Parameters Powders
Fe Cu Ni
ρ0 0.268 0.3 0.36
m 1.0219 1.3317 0.9755
n=1/m 0.9786 0.7509 1.0251
R2 0.93988 0.99925 0.95445
Table 14. Constant parameters in equation (41) obtained via approximation of experimental data on the compaction of iron [37], copper [38], and nickel [39] powders, as well as FeKH3, FeKH6, and FeKH9 iron powders from the book [50].
Table 14. Constant parameters in equation (41) obtained via approximation of experimental data on the compaction of iron [37], copper [38], and nickel [39] powders, as well as FeKH3, FeKH6, and FeKH9 iron powders from the book [50].
Parameters Powders
Fe Cu Ni FeKH3 FeKH6 FeKH9
ρ0 0.268 0.3 0.36 0.256 0.439 0.397
K 345.01 270.37 462.51 26.4885 2343.95 1184.07
n 0.9927 0.5818 0.5946 9.45042 4.83775 4.58858
R2 0.99216 0.99803 0.99960 0.97298 0.92296 0.94935
Table 15. Constants in equations (43) and (44) after approximation of experimental data on the compaction of iron, copper, and nickel powders from Table 1.
Table 15. Constants in equations (43) and (44) after approximation of experimental data on the compaction of iron, copper, and nickel powders from Table 1.
Parameters Powders
Iron Copper Nickel
Equation type
(43) (44) (43) (44) (43) (44)
ρ0 0.268 0.3 0.36
A′, c 16141.4 1377.9 28987.9 1192.8 15597.6 1398.8
B′, d 8.2798 2.8891 9.1188 3.2732 5.6115 2.5511
pmax, MPa 1233.2 1377.9 1135.9 1192.8 1286.0 1398.8
R2 0.97066 0.98030 0.98623 0.99207 0.97954 0.98932
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated