Preprint
Article
Predicting Students' Progress in Intelligent Tutoring Systems
Altmetrics
Downloads
151
Views
71
Comments
1
This version is not peer-reviewed
Submitted:
20 December 2023
Posted:
20 December 2023
You are already at the latest version
Alerts
Abstract
Intelligent Tutoring Systems (ITS) are increasingly popular for online learning. These systems use adaptive algorithms to recommend relevant content based on students' profiles. However, instructors need to periodically assess students' performance to ensure learning outcomes and adjust strategies accordingly. Our objective is to predict students' progress in advance, enabling teachers to make quicker decisions and facilitating the iterative process of adaptive algorithms. For this study, we collected a dataset from ALIN, an online learning platform, consisting of over 5,000 students' learning records and test results. Using this dataset, we conducted experiments employing various machine learning algorithms. The results indicate that learning behavior contributes to improving forecast performance, while students' progress strongly correlates with their previous test results. Additionally, we discovered that students' progress can be indirectly predicted by forecasting their scores. Furthermore, by breaking down overall scores into several distinct components and predicting individual scores for each component, the accuracy of the forecasts can be improved.
Keywords:
Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning
CCS CONCEPTS
• Applied computing → Education → E-learning
1. Introduction
With the rise of online educational platforms, more students are turning to the internet for learning. Intelligent Tutoring Systems (ITS) have gained popularity as learner-centric platforms that adapt instruction to individual student needs. A typical ITS consists of four components: domain model, tutoring model, student model, and interface [1,7]. ALIN (Assistive Learning Intelligence Navigator) is an example of an online ITS developed by EdTech. 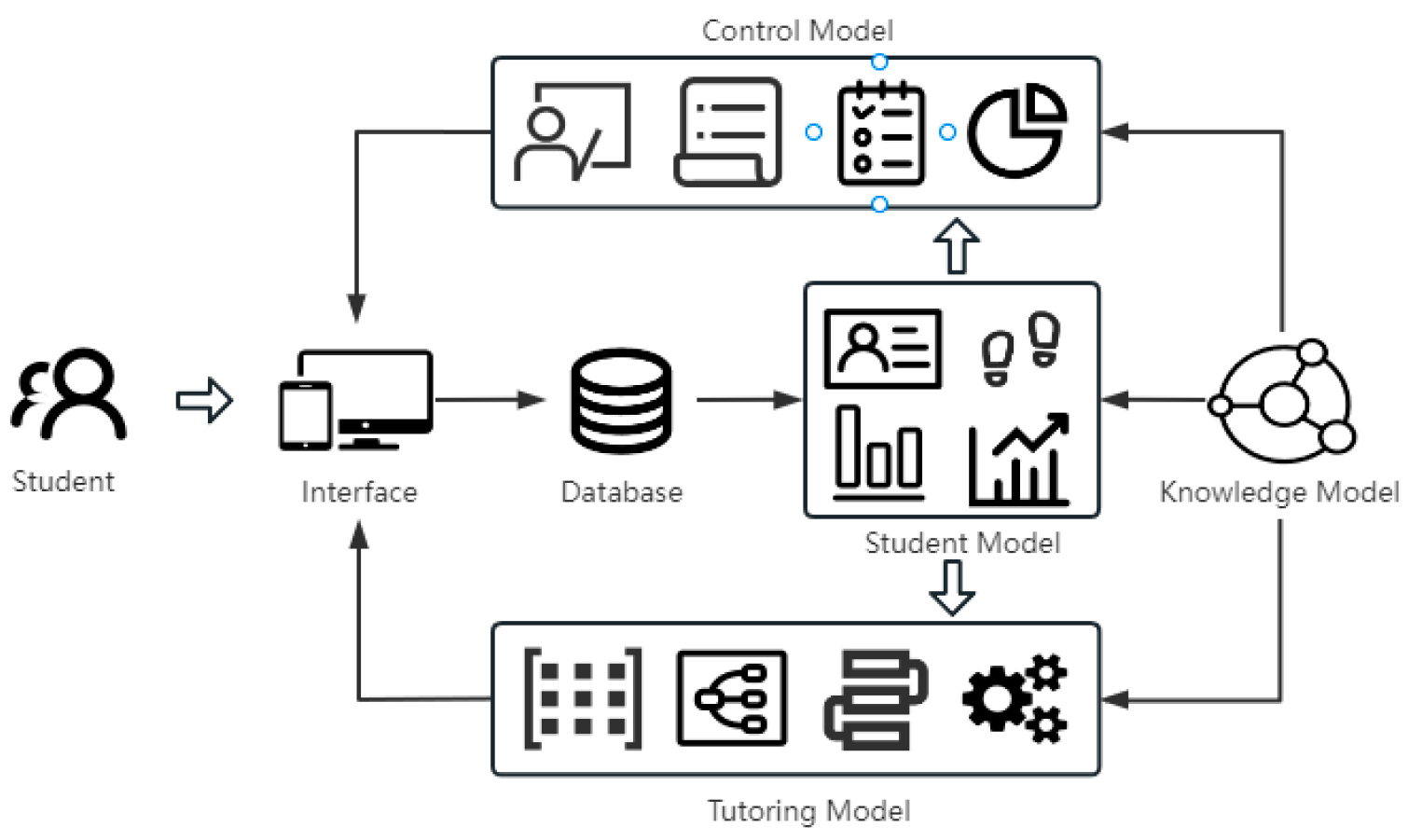Figure 1 illustrates the learning process of ALIN.
ALIN focuses on enhancing math learning outcomes by using innovative technologies and instructional strategies. The math curriculum is divided into specific topics, which are further organized into sequences. Each topic is supported by a variety of interactive worksheets designed to enhance students' understanding and proficiency. These worksheets consist of timed drill problem sets that aim to improve both accuracy and speed. As students interact with the interface, their learning behavior and results are recorded in a database. The student model analyzes these learning profiles and traces to assess topic mastery. Leveraging student features, the tutoring model generates personalized worksheets and provides adaptive decision-making, such as personalized learning paths. Additionally, the control model enables teachers to regularly evaluate students' learning outcomes and adjust their instructional strategies accordingly. In this study, we consider students' progress as an indicator of learning outcomes. Progress is defined as the improvement in scores between the first and last tests, unless the score has reached the upper limit. By forecasting students' progress early on, instructors can provide timely personalized advice, while the adaptive tutoring model can offer more tailored learning recommendations. Thus, our objective is to forecast and estimate students' progress based on their past test and learning data.
2. Related Work
In this paper, our focus is on predicting students' academic progress based on their historical data. This task shares similarities with performance prediction, as discussed by Romero and Ventura [8]. We surveyed the studies published in the past ten years, and we describe relevant and informative works below.
Saa [9] explored various factors and compared multiple classifiers for performance prediction. Ha et al. [4] found a correlation between students' performance and factors like academic progress and learning behaviors. Amrieh et al. [2] discovered a strong link between learners' behaviors and achievement. Xu et al. [11] revealed that assignment-related features could serve as potential predictors. Shahiri et al. [10] highlighted the frequent utilization of attributes such as cumulative grade point average (CGPA) and internal assessment in prediction models. Hamsa et al. [5] attempted to identify students' performance using features extracted from two exams and academic records. You [12] identified significant behavioral indicators for predicting final course scores, with mid-term exam scores proving helpful in predicting the final exam scores.
Despite these efforts, several challenges still need to be addressed for effective prediction. Ang et al. [3] highlighted technological challenges in deploying predictive systems, data collection, and data preprocessing. Many studies have used datasets with fewer than 600 students, such as Kaur's dataset [6] with only 152 high school students, Amrieh's [2] records from 500 students, and You's [12] data from 530 college students. Additionally, several questions remain unanswered, including the choice of prediction model (classification or regression) and the appropriate target for accurate prediction (overall performance or individual performance). To address these questions, we will conduct a series of experiments in the following sections.
3. Data Description
This section provides an overview of the dataset used in this study, including the data collection process and feature extraction methods.
3.1. Data Collection
The data used in this study is obtained from ALIN, an online learning platform. ALIN has been operating successfully in the Philippines for over ten years, serving more than 18,000 students. The platform allows teachers to assign math knowledge units to students and evaluate their mastery through tests. Student activities and results are recorded in the platform's database.
To investigate progress prediction, we collected test data and learning data from students who had completed exactly two tests. The time interval between the two tests had to be at least one week to provide sufficient learning and practice time. A total of 5,196 students met these criteria, and their test data and learning data were collected. It is important to note that we only gathered learning data during the two test periods. We then matched the test and learning data for each student. 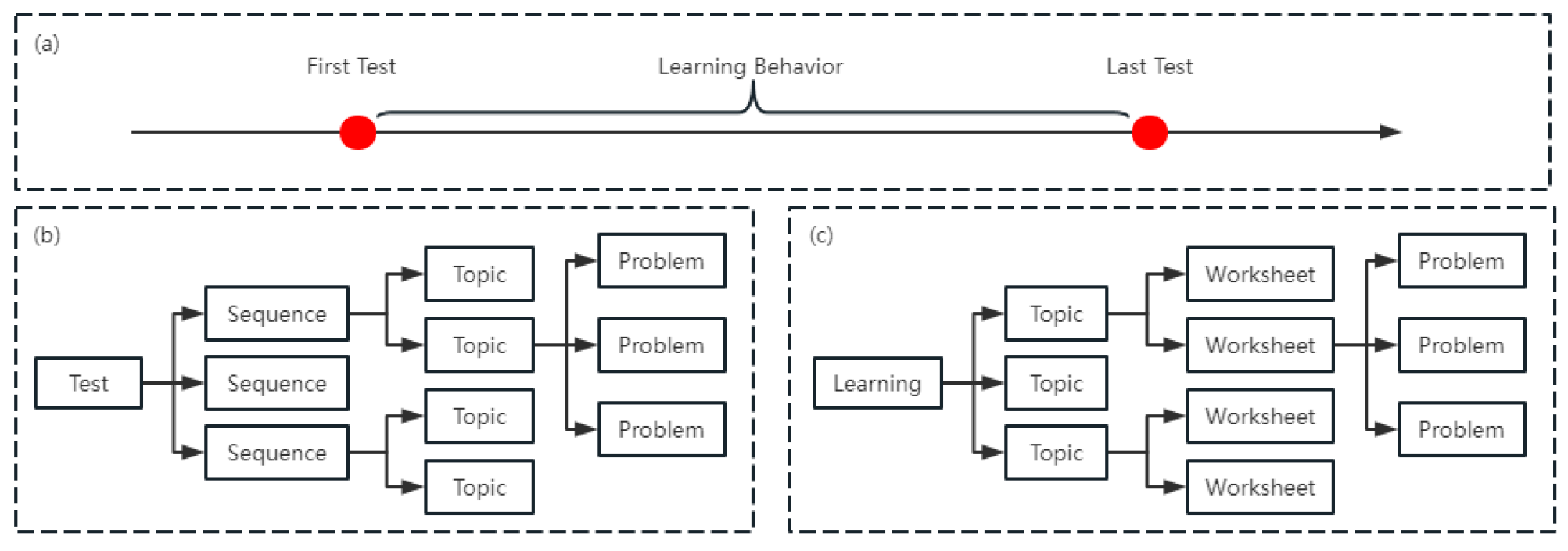Figure 2 illustrates the data structure and its temporal sequence.
A test usually consists of multiple sequences, each covering different topics. Each topic represents a series of problems that need to be solved. The overall test score is calculated by summing the scores of all the sequences, while the sequence score is determined based on the results of the topics covered. The fundamental unit of learning is a worksheet, which contains a series of problems with specific difficulty levels and time frames. During tests and learning activities, we recorded various indicators such as the total number of problems, percentage of correct answers, and time spent. These indicators are presented in Table 1. Indicators with a "test" prefix are extracted from the first test data, while those with a "beh" prefix come from the learning data. Students are expected to engage in learning activities between the two tests on the website, but it is optional. If a student chooses to practice, the system records various statistical learning indicators, such as the number of right/wrong/skipped problems. Skipped problems refer to unanswered problems, which can occur if a problem is too challenging or if the student runs out of time (timeout) to answer it.
3.2. Feature Extraction
In addition to the original indicators, we derived new features for analysis. These features, extracted from the test data and the learning data, are presented in Table 2. Worksheet-related features are specifically derived from the learning data, whereas topic-related and problem-related features can be derived from both the test and learning data. To ensure consistency, the feature values are normalized to a range of 0 to 1. Furthermore, we calculate the differences in certain features between the learning and test data to assess changes that occur. Empty values are populated with zeros. It is worth noting that the values of the features are determined by the granularity of each feature. During the experimental phase, we will train different forecast models based on various levels of granularity, such as test-grained and sequence-grained models.
4. Experiments
To predict progress, we trained various models using the Sci-kit learn library, a Python machine learning library. The models we used include Decision Tree (DT), Random Forest (RF), Artificial Neural Networking (ANN), and Gradient Boosting Decision Tree (GBDT). We kept the default parameters for each model, except for the random state. We employed K-10 cross-validation and aggregated the results for each round. We conducted ten rounds, varying the random state values. Precision, recall, and F1-measure were used to evaluate the models, with weighting based on the number of positive and negative samples. Our experiments aimed to answer the following research questions.
4.1. Does learning data contribute to prediction?
To assess the impact of learning data, we compared two groups of models. The first group uses only the students' first test data for training and prediction, while the second group incorporates both the test and learning data. The average evaluation results from ten rounds are presented in Table 3 and Table 4 respectively.
From Table 3, we observed that ensemble models like RF and GBDT performed significantly better than single models like DT. Although ANN achieved the highest precision and recall values, its F1-measure was not the best due to a higher number of false positive instances. Comparatively, RF and GBDT outperformed ANN in terms of F1-measure due to the weighted mechanism of the evaluation function. Table 4 presents the results obtained when using both test and learning data. For each model, incorporating learning data leads to improved predictive performance. Compared to the average performance in Table 3, the improvements are 0.017 for precision, 0.011 for recall, and 0.018 for F1-measure.
Furthermore, two-tailed paired T-tests confirmed that these improvements were statistically significant. While the first test data provided acceptable predictions to some extent, the learning data significantly enhanced the forecasting of students' progress on the last test. This suggests that a student's performance on a test is strongly influenced by their performance on the previous test, indicating a certain degree of inertia. Learning behaviors based on previous test scores either contribute to improvement or decline in subsequent test scores. Therefore, the learning data helps explain the deviations between the results of the two tests. Overall, the learning data plays a crucial role in predicting performance, and thus, we incorporated both test and learning data in subsequent experiments. The models achieved an average performance of precision - 0.609, recall - 0.629, and F1-measure - 0.596, which served as the baseline for comparing with the performance of subsequent models.
4.2. Can progress be predicted through score forecasting?
Since progress is defined by comparing the last test score with the first test score, we explored whether we could forecast the last test score and use it to predict progress. In this experiment, we treated the prediction as a regression problem and trained the models using the last test scores as the target variable. These models were then used to predict the score values for each student. It's important to note that the forecasted scores were constrained within the upper limit scores of the tests. The accuracy of progress prediction was determined by comparing the forecasted scores with the first test scores. The prediction results are presented in Table 5. Compared to the baseline in Table 4, the models showed an average improvement of 0.009 for precision, 0.009 for recall, and -0.004 for F1-measure. Overall, the performance of the score forecasting models was comparable to that of the classification models, with a slight decrease in F1-measure. These results demonstrate that forecasting test scores is a viable method for progress prediction.
4.3. Which performance is more appropriate to be predicted, test or sequence?
Students' overall performance often consists of multiple fine-grained components, similar to how GPA is calculated based on grades in various subjects. In our dataset, a test is composed of several sequences, and the test score is determined by summing the sequence scores. Building upon our previous finding that students' progress can be predicted by forecasting their test scores, we extended our approach to predict the test scores by predicting and summing the scores of each individual sequence. The forecasted scores were bounded by the upper limit scores of the sequences. Subsequently, the sum of the forecasted sequence scores was compared to the first test scores to determine the progress outcomes. The results are presented in Table 6.
Compared to the baseline, there were significant improvements for almost every model and evaluation indicator. The average improvements were 0.012 for precision, 0.016 for recall, and 0.022 for F1-measure, respectively. Interestingly, the DT model exhibited greater improvement compared to other ensemble models such as RF and GBDT, suggesting that predicting fine-grained targets is more suitable and achievable for weaker models. Additionally, these models outperformed those aimed at predicting the overall test scores in Table 5. The experimental results also demonstrated that we can indirectly predict a given target (test score) by dividing it into several fine-grained sub-targets (sequence scores) and forecasting them individually. This divide-and-conquer strategy proves meaningful and helpful in solving real-world problems.
5. Conclusion and Future Work
In this study, we conducted research on predicting students' progress in an intelligent tutoring system using a dataset of 5,196 students' test and learning records from the real world. Through a series of experiments, we obtained valuable insights and proposed effective solutions.
Our experimental results yielded the following findings: 1) Students' progress strongly correlates with their previous test results, and learning behavior can explain changes in performance. 2) Indirectly predicting students' progress by forecasting their test scores is a viable and accurate approach. 3) Partitioning the overall test score into distinct sequences and predicting individual scores for each sequence can enhance the accuracy of forecasts.
The contributions of this work include: 1) Introducing an alternative solution to progress prediction by employing indirect test score forecasting. 2) Demonstrating the effectiveness of the divide-and-conquer strategy in solving this problem.
For future work, we have identified two directions for further investigation. Firstly, we plan to delve deeper into the division of sequences into topics based on knowledge graphs and employ knowledge tracing techniques to estimate mastery levels for each topic. This approach will enhance the granularity of our predictions. Secondly, we aim to validate the effectiveness of the progress prediction model and iterate on the adaptive and recommendation algorithms to improve their performance. By exploring these avenues, we hope to advance the field of progress prediction in intelligent tutoring systems and contribute to the development of more personalized and effective educational interventions.
References
- Ali Alkhatlan and Jugal Kalita. 2018. Intelligent Tutoring Systems: A Comprehensive Historical Survey with Recent Developments. arXiv:1812.09628. [CrossRef]
- Elaf Abu Amrieh, Thair Hamtini, and Ibrahim Aljarah. 2016. Mining Educational Data to Predict Student’s academic Performance using Ensemble Methods. International Journal of Database Theory and Application, 9(8), 119-136. [CrossRef]
- Kenneth Li-Minn Ang, Fenglu Ge, and Kah Phooi Seng. 2020. Big Educational Data & Analytics: Survey, Architecture and Challenges. IEEE Access 8 (2020), 116392– 116414. [CrossRef]
- Dinh Thi Ha, Cu Nguyen Giap, Pham Thi To Loan, and Nguyen Thi Lien Huong. 2020. An Empirical Study for Student Academic Performance Prediction Using Machine Learning Techniques. International Journal of Computer Science and Information Security (IJCSIS), 18(3).
- Hashmia Hamsa, Simi Indiradevi, and Jubilant J. KizhaNNethottam. 2016. Student Academic Performance Prediction Model Using Decision Tree and Fuzzy Genetic Algorithm. Procedia Technology, 25, 326-332. [CrossRef]
- Parneet Kaur, Manpreet Singh, and Gurpreet Singh Josan. 2015. Classification and prediction based data mining algorithms to predict slow learners in education sector, Procedia Computer Science, vol. 57, pp. 500–508. [CrossRef]
- Kai-Chih Pai,Bor-Chen Kuo, Chen-Huei Liao, and Yin-Mei Liu. 2021. An application of Chinese dialogue-based intelligent tutoring system in remedial instruction for mathematics learning. Educational Psychology, 137-152. [CrossRef]
- Cristóbal Romero and Sebastián Ventura. 2010. Educational data mining: a review of the state of the art. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews) 40, 6 (2010), 601–618. [CrossRef]
- Amjad Abu Saa. 2016. Educational data mining & students’ performance prediction. International Journal of Advanced Computer Science and Applications 7, 5, 212–220. [CrossRef]
- Amirah Mohamed Shahiri, Wahidah Husain, and Nur’aini Abdul Rashid. 2015. A review on predicting student’s performance using data mining techniques. Procedia Computer Science 72 (2015), 414–422. [CrossRef]
- Zhuojia Xu, Hua Yuan, and Qishan Liu. 2020. Student performance prediction based on blended learning. IEEE Transactions on Education, 64(1), 66–73. [CrossRef]
- Ji Won You. 2016. Identifying significant indicators using LMS data to predict course achievement in online learning. Internet and Higher Education, 29, 23-30. [CrossRef]
Figure 1.
Learning process at ALIN.
Figure 2.
Data structure and temporal sequence.
Table 1.
Summary of test and learning data indicators.
| Source | Indicator | Description |
|---|---|---|
| Test and Learning | studentID | ID of the student |
| sequenceID | ID of the sequence | |
| topicID | ID of the topic | |
| numTopic | Number of topics in a sequence | |
| Test | testNumProblems | Number of problems in the test |
| testPercentCorrect | Percentage of correct answers in the test | |
| testTimespent | Time spent on the test | |
| firstscore | Score achieved in the first test | |
| lastscore | Score achieved in the last test | |
| scoreLimit | Maximum possible score for a sequence | |
| Learning | behNumProblems | Number of problems in the learning process |
| behNumRight | Number of right problems in the learning process | |
| behNumMissed | Number of missed problems in the learning process | |
| behNumSkipped | Number of skipped problems in the learning process | |
| behTimeSpent | Time spent on the learning process |
Table 2.
Features extracted from test and learning data.
| Source | Feature | Description |
|---|---|---|
| Test | scoreRatio | firstScore/scoreLimit |
| Learning | sheetCnt | Count of worksheets |
| topicAvgSheet | Average worksheets per topic | |
| sheetAvgTime | Average spent time per worksheet | |
| Test and Learning | topicCnt | Count of topics |
| topicRatio | topicCnt/numTopic | |
| topicAvgTime | Average spent time per topic | |
| accuracy | Average correct rate of problems | |
| probAvgTime | Average spent time of problems | |
| topicDiff | Difference of topicCnt between learning and test | |
| accuracyDiff | Difference of accuracy between learning and test | |
| topicAvgTimeDiff | Difference of topicAvgTime between learning and test | |
| probAvgTimeDiff | Difference of probAvgTime between learning and test |
Table 3.
Results of the models using the test data.
| Model | Precision | Recall | F1-measure |
|---|---|---|---|
| DT | 0.570 | 0.568 | 0.569 |
| RF | 0.586 | 0.614 | 0.591 |
| ANN | 0.607 | 0.645 | 0.573 |
| GBDT | 0.604 | 0.644 | 0.580 |
| avg. | 0.592 | 0.618 | 0.578 |
Table 4.
Results of the models using the test and learning data.
| Model | Precision | Recall | F1-measure |
|---|---|---|---|
| DT | 0.575 | 0.571 | 0.573 |
| RF | 0.616 | 0.639 | 0.619 |
| ANN | 0.625 | 0.654 | 0.598 |
| GBDT | 0.620 | 0.652 | 0.596 |
| avg. (baseline) | 0.609 | 0.629 | 0.596 |
| improvement | 0.017** | 0.011** | 0.018** |
* p < 0.05, ** p < 0.01.
Table 5.
Prediction results by forecasting test scores.
| Model | Precision | Recall | F1-measure |
|---|---|---|---|
| DT | 0.581 | 0.580 | 0.581 |
| RF | 0.624 | 0.654 | 0.602 |
| ANN | 0.630 | 0.657 | 0.588 |
| GBDT | 0.638 | 0.661 | 0.597 |
| avg. | 0.618 | 0.638 | 0.592 |
| improvement | 0.009** | 0.009** | -0.004* |
* p < 0.05, ** p < 0.01.
Table 6.
Prediction Results by forecasting sequence scores.
| Model | Precision | Recall | F1-measure |
|---|---|---|---|
| DT | 0.612 | 0.630 | 0.616 |
| RF | 0.621 | 0.646 | 0.620 |
| ANN | 0.626 | 0.652 | 0.621 |
| GBDT | 0.624 | 0.652 | 0.616 |
| avg. | 0.621 | 0.645 | 0.618 |
| improvement | 0.012** | 0.016** | 0.022** |
* p < 0.05, ** p < 0.01.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated