Evolution and Equilibrium of a Low Carbon E-commerce Closed-Loop Supply Chain Recycling System: An Evolutionary Game Approach

Preprint

Article

Evolution and Equilibrium of a Low Carbon E-commerce Closed-Loop Supply Chain Recycling System: An Evolutionary Game Approach

Altmetrics

Downloads

122

Views

Comments

This version is not peer-reviewed

Submitted:

16 November 2023

Posted:

17 November 2023

You are already at the latest version

Alerts

Abstract

The rapid advancement of technology has led to increased electronic consumption and a corresponding rise in e-waste generation. To address this issue, this study develops a low-carbon e-commerce closed-loop supply chain (LCE-CLSC) system with remanufacturer, platform, and the government as key stakeholders. An evolutionary game approach is employed to investigate the system's dynamics, analyzing the impact of stakeholder strategies on system equilibrium. Numerical simulations reveal important findings: Firstly, government initiatives promoting recycling, carbon taxes on traditional products, can incentivize remanufacturers to produce low-carbon items and encourage platform investment in recycling services. Secondly, higher sales revenues motivate remanufacturers to produce low-carbon products. Thirdly, consumer sensitivity to recycling services strengthens waste recovery when platforms increase investments in these services, leading to remanufacturers choosing low-carbon production. Lastly, government subsidies may become ineffective if the cost of remanufacturers' carbon reduction and platforms' recycling services exceeds their affordability. These findings offer insights for the sustainable development of obsolete electronic product recycling systems.

Keywords:

Subject: Business, Economics and Management - Business and Management

1. Introduction

The rapid advancement of technology in recent years has brought about a significant increase in electronic consumption, leading to a mounting problem of e-waste generation [1,2]. The disposal of waste electronic and electrical equipment (WEEE) poses serious environmental concerns due to the hazardous components they contain [3,4]. In response to these challenges, the development of a low-carbon e-commerce closed-loop supply chain (LCE-CLSC) for the remanufacturing of WEEEs has emerged as an essential solution [5].

E-commerce has become an integral part of our daily lives, offering convenience and accessibility to consumers worldwide [6,7]. However, the growing demand for electronic devices has also contributed to the staggering amount of e-waste generated. To address this issue, a closed-loop supply chain system has gained prominence, with a focus on recovering, recycling, and remanufacturing WEEEs.

The e-commerce closed-loop supply chain for remanufacturing WEEEs follows a systematic approach. It begins with the collection of discarded WEEEs from various sources, including consumers, E-commerce platforms, remanufacturer, and government [8]. E-commerce platforms can play a crucial role in facilitating this process by implementing efficient collection mechanisms, such as take-back programs, partnering with recycling organizations, and raising awareness about e-waste recycling.

Once collected, the WEEEs are transported to specialized recycling centers or remanufacturing facilities. These facilities employ advanced technologies and processes to disassemble, repair, and refurbish the components of the electronic products [9]. The goal is to extend the life cycle of these products and reintroduce them into the market, reducing the need for new manufacturing and conserving valuable resources [10].

By embracing the principles of remanufacturing, the low-carbon e-commerce closed-loop supply chain minimizes waste and environmental pollution [11]. It aims to transform WEEEs into functional, high-quality refurbished products that meet consumer demands [12]. This approach not only reduces the environmental impact associated with e-waste disposal but also contributes to carbon emissions reduction by decreasing the energy and resource consumption attributed to new manufacturing [13].

The successful implementation of a LCE-CLSC requires the collaboration of various stakeholders. E-commerce companies, electronics remanufacturers, government agencies, and consumers must actively participate in this endeavor. E-commerce platforms can promote the return and recycling of electronic products through high quality service. Remanufacturers can design low carbon products that can ensure a more circular approach. Government support in terms of policies, regulations, and financial incentives can encourage sustainable practices, while consumers can contribute by responsibly disposing of their electronic waste.

For example, The Waste Electrical and Electronic Equipment (WEEE) Directive of the European Union [14], Regulations on the Administration of the Recycling and Disposal of Waste Electrical Appliances and Electronic Products, and the Law of the People’s Republic of China on the Prevention and Control of Solid Waste Pollution [8]. Apple has launched the “Apple Reuse and Recycling Program” [15]. Alibaba has launched the "credit recovery" program that encourages consumers to recycle their used products by providing credits redeemable for new products.

In a word, the development of a LCE-CLSC for the remanufacturing of WEEEs is essential for addressing the environmental challenges posed by e-waste. By integrating recovery, recycling, and remanufacturing processes, this system aims to minimize waste generation, conserve resources, and reduce carbon emissions associated with electronic waste. Collaboration among stakeholders and the adoption of sustainable practices are key to creating a truly sustainable LCE-CLSC system.

In this paper, we aim to develop a model that captures the dynamic interactions among remanufacturer, platform, and the government in the context of a LCE-CLSC system. The evolutionary game model will consider various factors that can influence the evolution of the system and explore strategies to enhance its stability. We calculate the payoff matrix of remanufacturer, platform and government. Then, by solving and analyzing the model, we obtain replicator dynamic equations of each stakeholder. Furthermore, we get the ESS and its formation conditions by solving the Jacobian matrix. Finally, a numerical study is used to verify the feasibility and rationality of the evolutionary game model. Further, we will also examine how model parameters affect the decision-making process of remanufacturer in terms of low-carbon product choices, the investment behavior of e-commerce platforms in recycling service levels, as well as regulatory actions of government.

The rest is organized as follows. Section 2 presents the literature review. Model assumptions and construction are detailed in Section 3. Following the development of the model, the analytical results for ESSs in the evolutionary game model are presented in Section 4. Section 5 conduct numerical analysis. Finally, Section 6 is the conclusion.

2. Literature Review

2.1. Recycling in E-CLSC

With the continuous improvement of public environmental awareness, the recycling industry has been developing steadily. The innovative application of internet information technology in the recycling industry has led to the emergence of a new business model known as e-commerce platform recycling [16]. The advent of internet recycling platforms has brought innovative development opportunities to traditional recycling practices and has become a hot topic of research in the academic world [17,18]. Currently, there have been some studies conducted on the closed-loop supply chain recycling in e-commerce, primarily focusing on recycling channels and recycling pricing.

Jin et al. (2021) [19] developed three different power structures for pricing and coordination mechanisms in a reverse supply chain with competitive online and offline recycling channels, thereby providing guidance for strategic decision-making of manufacturers and recyclers in the dual recycling channel reverse supply chain. In both scenarios, with or without government subsidy, Bai et al. (2021) [20] investigated the optimal pricing and service-quality strategies in various online recycling channel structures. Wang et al. (2022) [21] proposed a game theory analysis model that considers consumer channel preferences and incorporates price prediction behavior in online recycling to determine the optimal pricing for waste products in an "Internet+" recycling platform. Through employing this model, the study identifies the optimal pricing strategy for the platform, accounting for the presence or absence of physical recycling competition. Matsui (2023) [22] employed a game theory model to conduct a comparative analysis of three distinct power structures in a dual-recycling channel reverse supply chain. Their study centered around examining the impact of competitive pricing in acquisition.

Feng et al.(2017) [23]identified four recycling modes and concluded that the dual-channel approach, integrating both online and offline channels, outperforms single-channel approaches. In a comparative analysis, Li et al. (2019) [24]examined online recycling, offline recycling, and mixed recycling models, highlighting the advantages for remanufacturers in online recycling but potential drawbacks for recyclers. Wang et al. (2022) [25] compared various decisions in both the forward and reverse channels, such as wholesale versus direct sales and entrusted recycling versus direct recycling. Wang et al. (2023) [26] developed a game model to investigate the interplay between trading patterns and recycling channel decisions of manufacturers and platforms within a supply chain. The objective was to identify the optimal trading patterns and recycling channels that suit both the platform and manufacturers.

The research mentioned above has paid limited attention to the influence of platform service level on the entire supply chain. This paper aims to incorporate the decision-making regarding service input from platforms and explore its impact on the members of the supply chain. Moreover, despite extensive research has been conducted in the field of E-CLSC, there has been limited focus on the dynamic evolution of strategy selection between remanufacturer and platforms in WEEE recycling. Furthermore, previous studies have predominantly concentrated on market-driven recycling channel selection and pricing, overlooking the influence of government regulations in shaping the E-CLSC formation process. To address these gaps, this study assumes rationality among all participants, including remanufacturer, platforms, and the government. By constructing a three-party evolutionary game model, we aim to explore how decision-making dynamically evolves for each participant in response to various factors within the system.

2.2. LC-CLSC with Government Participation

The concept of a low carbon supply chain, also referred to as a green supply chain in certain studies, involves the integration of green, low-carbon, and environmental protection principles and technologies into the overall supply chain framework. This integration enables the establishment of a supply chain that is focused on minimizing carbon emissions and promoting environmental sustainability. Numerous scholars have investigated the determinants of incorporating carbon reduction or green technologies in traditional supply chains. The role of the government in carbon reduction primarily manifests through three mechanisms: environmental taxes, government subsidies, and promoting consumer awareness.

In a study by Fukui and Miyoshi (2017) [27], they examined how various carbon tax policies influenced the establishment of carbon emission reduction targets by corporations. Yi and Li (2018) [28] investigated the effects of carbon taxes and energy-saving subsidies on enterprise decisions. Findings suggested that subsidies for energy-saving products effectively reduce carbon emissions and energy consumption, whereas the imposition of carbon taxes should be determined by manufacturers’ pollution levels. Li et al.(2022) [8] conducted an analysis of the evolutionary decision-making process of stakeholders within a traditional closed-loop supply chain, considering the influence of environmental taxes, rewards, and penalties. Zhang and Yu (2022) [29] conducted research on the government emission reduction subsidy rate and recycling subsidy rate from the perspective of altruistic behavior of different members in a low-carbon closed-loop supply chain. He et al.(2023) [30] developed a decentralized decision-making model, considering the presence or absence of subsidies, to examine the impact of subsidies and corporate social responsibility on carbon emissions within an omnichannel supply chain system. Zhang et al. (2023) [31] proposed a game model incorporating a government, low carbon manufacturer, and retailer to examine the interplay between government subsidies and supply chain collaboration. They suggested conducting surveys on the current status of low carbon technology innovation to determine an appropriate subsidy model for carbon reduction before selecting the subsidy mode.

Building upon previous research, this study comprehensively considers the impact of government carbon tax, low-carbon technology subsidies, and service technology subsidies. In addition to these measures, this paper also examines the influence of government’s use of green advertising on the quantity of waste collected from consumers. By exploring the impact of these various measures, the study aims to provide valuable insights into the effectiveness of comprehensive government interventions in fostering a more environmentally friendly and sustainable closed-loop supply chain.

3. Model Assumptions and Construction

This study focuses on a government-involved, remanufacturer-led, low-carbon closed-loop e-commerce recycling supply chain (LC-ECLSC). The remanufacturer collaborates with an e-commerce recycling platform to collect discarded products, while consumers provide relevant information about their discarded products on the platform after browsing the recycling information. The platform evaluates the value of the discarded products and provides feedback to consumers. Consumers can choose to ship the products or opt for doorstep pickup services. The platform delivers the quality-checked waste to the remanufacturer, who engage in remanufacturing and sales activities. In order to minimize environmental pollution, remanufacturer consider introducing low-carbon technologies. To ensure the sustainability of the entire supply chain, the platform also considers service input, and the government participates as a member of the supply chain. The LC-ECLSC model constructed in this study is shown in Figure 1.

3.1. Model Assumptions

Assumption 1: the remanufacturer, the e-commerce platform, and the government are key participants in LC-ECLSC system. These participants exhibit bounded rationality and gradually evolve and stabilize their strategy selection over time, aiming to reach the optimal strategies for their respective roles within the supply chain.

Assumption 2: The remanufacturer’s strategy space is (low-carbon products, traditional products), abbreviated as (LCP, TP), the remanufacturer chooses LCP with a probability of x and TP with a probability of 1-x. The platform’s strategy space is (Service Investing, Not Service Investing), abbreviated as SI, NSI), The platform chooses SI with a probability of y and NSI with a probability of 1-y. The government’s strategy space is (Strict regulation, Loose regulation), abbreviated as (SR, LR), The government chooses SR with a probability of z and LR with a probability of 1-z.

Assumption 3: The sales price of low-carbon remanufactured products increases as the level of carbon emission reduction increases [32,33]. Let p denote the price of traditional products, e represents the carbon emission reduction level, and r be the elasticity coefficient measuring the relationship between product price and emission reduction level. Accordingly, the selling price of low-carbon products can be expressed as p+re. In the context of the low-carbon remanufactured product model, higher carbon emission reduction levels correspond to increased costs. Research conducted by Nair and Narasimhan (2006) [34] reveals that remanufacturer incurs a cost of

1 / 2 m e^{2}

in order to achieve the desired carbon emission reduction level e.

Assumption 4: Assuming the recycling price of low-carbon and traditional products remains unchanged. Studies conducted by Giovanni and Zaccour [35] and Wang et al. [36] indicate that the volume of waste products recycled is directly proportional to the service level when the recycling price is constant. If the platform invests in recycling services and increases the service level to s, the quantity of discarded products collected through the platform will increase by hs, where h represents the elasticity coefficient of the recycling service level. At the same time, the platform incurs a cost of

1 / 2 n s^{2}

[37,38].

Assumption 5: According to the research conducted by Li et al. [39], Fukui and Miyoshi [27], and Wang et al. [40], government regulatory measures in the market primarily focus on three aspects: providing technical subsidies for low-carbon products, imposing carbon emission taxes, and promoting consumer awareness of green practices. Therefore, in this study, we make the following assumptions: (1) The government provides technical subsidies to remanufacturing enterprises for their investment in low-carbon products, with the subsidy amount being proportional to the investment level. Let the proportion of this subsidy to the investment be denoted as a. Similarly, subsidies are also provided to the platform for its investment in recycling services, with the subsidy proportion b. (2) Under government strict regulations, a carbon emission tax T will be imposed on traditional products, while the carbon emission tax on low-carbon products will be θT. For ease of calculation, we assume θ=0. (3) The government enhances consumer environmental awareness through green advertising, activities, etc. As highlighted in the research by Giovanni and Zaccour [35] and Wang et al. [36], increased consumer environmental awareness also leads to an increase in the quantity of discarded products collected. Let C_w represent the government’s investment in green environmental promotion, and Q_g represent the additional collection quantity by the platform under government influence.

Table 1. Summary of parameters.

Symbol	Description
p	The selling price of the remanufactured product.
r	The marginal effect of emission reduction levels on remanufactured product prices.
e	Emission reduction levels of the remanufacturer.
m	Cost sensitivity of emission reduction levels.
h	Sensitivity of consumer recycling service levels.
s	The level of recycling service.
μ	The unit commission charged by platform to remanufacturer.
n	Cost sensitivity of service level.
Q	The additional recycling quantity attributed to government environmental promotion.
a	Government subsidy proportion for remanufacturer’ low-carbon investments.
b	Government subsidy proportion for platform service investments.
T	The unit carbon emission tax levied by the government on traditional products.
C_g	The investment required by the government for regulatory implementation.
C_w	Government investment in environmental awareness promotion.
π_i^j	Profits of stakeholders under different strategy combinations. i={M, P, G}, j={1,2,…,8}.

3.2. Model Construction

Based on the aforementioned assumptions, the mixed strategy game matrix for remanufacturer, platform, and the government is shown in Table 2 and Table 3.

4. Model Analysis

4.1. Analysis of Remanufacturer’ Strategy Stability

Let the expected revenue for remanufacturer when he/she chooses between LCP or TP be represented by E₁₁, E₁₂, and the average expected revenue as

\bar{E_{1}}

\{\begin{array}{l} E_{11} = y z π_{M}^{1} + (1 - y) z π_{M}^{2} + y (1 - z) π_{M}^{5} + (1 - y) (1 - z) π_{M}^{6} \\ E_{12} = y z π_{M}^{3} + (1 - y) z π_{M}^{4} + y (1 - z) π_{M}^{7} + (1 - y) (1 - z) π_{M}^{8} \\ \bar{E_{1}} = x E_{11} + (1 - x) E_{12} \end{array}

(1)

The replicator dynamics equation for the strategy selection of remanufacturer is:

F (x) = d x / d t = x (E_{11} - \bar{E_{1}}) = x (1 - x) [T h s y z + r e h s y + (T Q + 1 / 2 a m e^{2} + r e Q) z - 1 / 2 m e^{2}]

(2)

Let the derivative of x and the designated G(y) be:

d F (x) / d x = (1 - 2 x) [T h s y z + r e h s y + (T Q + 1 / 2 a m e^{2} + r e Q) z - 1 / 2 m e^{2}]

(3)

G (z) = T h s y z + r e h s y + (T Q + 1 / 2 a m e^{2} + r e Q) z - 1 / 2 m e^{2}

(4)

According to the stability theorem of differential equations, the probability of remanufacturer choosing LCP must satisfy the following condition to be in a stable state:

F (x) = 0

and

d F (x) / d x < 0

. Due to

\partial G (z) / \partial z > 0

, Therefore,

G (z)

is an increasing function with respect to z. Therefore, when

z = z_{1} = (1 / 2 m e^{2} - r e h s y) / (T h s y + T Q + 1 / 2 a m e^{2} + r e Q)

G (z) = 0

d F (x) / d x \equiv 0

, the remanufacturer cannot determine a stable strategy. When

z > z_{1}

G (z) > 0

, in this case,

d F (x) / d x |_{x = 1} < 0

, x=1 is the Evolutionarily Stable Strategy (ESS) of the remanufacturer. Otherwise, x=0 is the ESS.

Let the stable probability of remanufacturer chooses TP be represented by volume V₁, and the stable probability of choosing LCP be represented by volume V₂. The tangent plane passing through point

(0, m e / 2 r h s, 0)

V_{1} = \int_{0}^{1} \int_{0}^{\frac{m e}{2 r h s}} \frac{0.5 m e^{2} - r e h s y}{T h s y + T Q + 0.5 a m e^{2} + r e Q} d y d x = - \frac{0.5 m e^{2}}{h s T} + \frac{e A}{h s T^{2}} (r + 0.5 m e T) \ln [1 + \frac{0.5 m e T}{r A}]

Wherein

A = 0.5 a m e^{2} + r e Q + T Q

V_{2} = 1 - V_{1}

Lemma 1: The probability of remanufacturer choosing to produce low-carbon products increases with h, s, T, Q, but decreases with m. When

m e T < 2 r A

is satisfied, the probability of remanufacturer chooses LCP varies directly with a and r, but inversely with e.

Proof: Because

1 - \frac{r A}{r A + 0.5 m e T} < \ln (1 + \frac{0.5 m e T}{r A}) < \frac{0.5 m e T}{r A}

Let’s calculate the first-order partial derivatives of each element with respect to V₂.We can obtain

\partial V_{2} / \partial h > 0

\partial V_{2} / \partial s > 0

\partial V_{2} / \partial T > 0

\partial V_{2} / \partial m < 0

\partial V_{2} / \partial Q > 0

, and when

m e T < 2 r A

\partial V_{2} / \partial a > 0

\partial V_{2} / \partial r > 0

\partial V_{2} / \partial e < 0

Lemma 1 indicates that when consumers are more sensitive to the platform’s recycling service level and the platform achieves higher levels of recycling with greater quantities collected, the cost required to achieve the desired carbon emission reduction level decreases. As a result, remanufacturer in the system tend to choose LCP more stably. Government-imposed carbon emission taxes on traditional products can further incentivize remanufacturer to choose LCP. However, the effectiveness of government subsidies for remanufacturer’ production of low-carbon products depends on certain conditions. If the ratio between investment costs and unit benefits of low-carbon products is too high, the government’s subsidies may not be effective. This phenomenon is observed in real-life low-carbon supply chain systems, where, in the early stages when low-carbon technologies are not yet mature, even with strong government subsidy policies, production enterprises may not choose to produce low-carbon products. However, as the industry reaches a relatively mature stage and the ratio between investment costs and unit benefits of low-carbon products decreases, the higher returns associated with achieving a unit carbon emission reduction incentive will motivate remanufacturer to stably choose LCP.

Lemma 2: There exists a positive correlation between the probability of remanufacturer adopting the strategy of LCP and the increase in the probability of government adopting the strategy of SR.

Proof: According to the analysis of remanufacturer’s strategy stability, when

z < z_{1}

G (z) < 0

d F (x) / d x |_{x = 0} < 0

, x=0 is the ESS. Thus, as z gradually increases, the remanufacturer’s stable strategy transitions from x=0 (TP) to x=1 (LCP).

Lemma 2 indicates that an increase in the probability of government adopting the strategy of SR is favorable for remanufacturer to choose LCP as a stable strategy. In the early stages of the system, government regulatory implementation can effectively prompt remanufacturer to adopt low-carbon technologies.

4.2. Analysis of Platform’ Strategy Stability

Let the expected revenue for the platform choosing the strategy of SI or NSI be represented by E₂₁ and E₂₂, respectively. And the average expected revenue denotes as

\bar{E_{2}}

\{\begin{array}{l} E_{21} = x z π_{P}^{1} + (1 - x) z π_{P}^{3} + x (1 - z) π_{P}^{5} + (1 - x) (1 - z) π_{P}^{7} \\ E_{22} = x z π_{P}^{2} + (1 - x) z π_{P}^{4} + x (1 - z) π_{P}^{6} + (1 - x) (1 - z) π_{P}^{8} \\ \bar{E_{2}} = y E_{21} + (1 - y) E_{22} \end{array}

(5)

The replicator dynamics equation for the strategy selection of platform is:

F (y) = d y / d t = y (E_{21} - \bar{E_{2}}) = y (1 - y) (1 / 2 n s^{2} b z + u h s - 1 / 2 n s^{2})

(6)

Let the derivative of y and the designated L(z) be:

d F (y) / d y = (1 - 2 y) (1 / 2 n s^{2} b z + u h s - 1 / 2 n s^{2})

(7)

L (z) = 1 / 2 n s^{2} b z + u h s - 1 / 2 n s^{2}

(8)

According to the stability theorem of differential equations, the probability of platform choosing strategy SI must satisfy the following condition to be in a stable state:

F (y) = 0

and

d F (y) / d y < 0

. Due to

\partial L (z) / \partial z > 0

, Therefore,

L (z)

is an increasing function with respect to z. Therefore, when

z = z_{2} = (n s - 2 u h) / b n s

L (z) = 0

d F (y) / d y \equiv 0

, the platform cannot determine a stable strategy. When

z > z_{2}

L (z) > 0

, in this case,

d F (y) / d y |_{y = 1} < 0

, y=1 is the Evolutionarily Stable Strategy (ESS) of the platform. Otherwise, y=0 is the ESS.

Let the stable probability of platform choosing NSI be represented by area S₁, and the stable probability of SI be represented by area S₂. Then,

S_{1} = \int_{0}^{1} (n s - 2 u h) / b n s d y = (n s - 2 u h) / b n s, S_{2} = 1 - S_{1} = 1 - (n s - 2 u h) / b n s

Lemma 3: When

2 u h = n s

, S₂ achieves its maximum value, indicating that the probability of the platform adopting SI strategy is 1. However, when

2 u h < n s

, the probability of the platform adopting SI strategy varies directly with u, h, and b, but varies inversely with n and s.

Proof: Let’s calculate the first-order partial derivatives of each element with respect to S₂.We can obtain

\partial S_{2} / \partial u > 0

\partial S_{2} / \partial h > 0

\partial S_{2} / \partial b = (n s - 2 h u) / b^{2} n s > 0

\partial S_{2} / \partial n = (n s - 2 h u) / b^{2} n s < 0

\partial S_{2} / \partial s = - 2 h u / b n s^{2} < 0

Lemma 3 indicates that when

2 u h = n s

in the overall game system, the platform can only adopt the recycling service investment strategy. However, when

2 u h < n s

, if the platform’s commission for recycling is higher, consumers are more sensitive to the level of recycling service, and there is a higher cost elasticity of recycling service investment for the level of recycling service or the government enhances subsidies for recycling service investment, all these factors can promote the platform’s evolution towards the stable strategy of investing in recycling services.

Lemma 4: There exists a positive correlation between the probability of the platform adopting the SI strategy and the increase in the probability of government adopting the strategy of SR.

Proof: According to the analysis of platform’s strategy stability, when

z < z_{2}

, then

L (z) < 0

d F (y) / d y |_{y = 0} < 0

, at this case, y=0 is the ESS. Thus, as z gradually increases, the platform’s stable strategy transitions from y=0 (NSI) to x=1 (SI).

Lemma 4 indicates that in the early stages of evolution, the regulatory role of the government has a significant impact. Therefore, increasing the probability of the government adopting SR strategy is advantageous for platforms to choose waste recycling services as a stable strategy. When platforms choose SI, they can attract consumers to actively participate in the recycling process with better services, thereby increasing the quantity of waste collected by the platform.

4.3. Analysis of Government’ Strategy Stability

Let the expected revenue for the government choosing SR strategy or LR strategy be represented by E₃₁ and E₃₂, respectively. And the average expected revenue denotes as

\bar{E_{3}}

\{\begin{array}{l} E_{31} = x y π_{G}^{1} + x (1 - y) π_{G}^{2} + (1 - x) y π_{G}^{3} + (1 - x) (1 - y) π_{G}^{4} \\ E_{32} = x y π_{G}^{5} + x (1 - y) π_{G}^{6} + (1 - x) y π_{G}^{7} + (1 - x) (1 - y) π_{G}^{8} \\ \bar{E_{3}} = z E_{31} + (1 - z) E_{32} \end{array}

(9)

The replicator dynamics equation for the strategy selection of government is:

\begin{array}{l} F (z) = = d z / d t = z (E_{31} - \bar{E_{3}}) \\ = z (1 - z) (- T h s x y - T Q x - 1 / 2 a m e^{2} x - 1 / 2 b n s^{2} y - C_{g} - C_{w} + T Q) \end{array}

(10)

Let the derivative of z and the designated H(x) be:

d F (z) / d z = (1 - 2 z) (- T h s x y - T Q x - 1 / 2 a m e^{2} x - 1 / 2 b n s^{2} y - C_{g} - C_{w} + T Q)

(11)

H (x) = - T h s x y - T Q x - 1 / 2 a m e^{2} x - 1 / 2 b n s^{2} y - C_{g} - C_{w} + T Q

(12)

According to the stability theorem of differential equations, the probability of government choosing SR strategy must satisfy the following condition to be in a stable state:

F (z) = 0

and

d F (z) / d z < 0

. Due to

\partial H (x) / \partial x < 0

, Therefore, H(x) is a decreasing function with respect to x. Therefore, when

x = (T Q - C_{g} - C_{w} - 1 / 2 b n s^{2} y) / (T h s y + T Q + 1 / 2 a m e^{2}) = x_{1}

H (x) = 0

d F (z) / d z \equiv 0

, the government cannot determine a stable strategy. When

x < x_{1}

H (x) > 0

, in this case,

d F (z) / d z |_{z = 1} < 0

, z=1 is the Evolutionarily Stable Strategy (ESS) of the government. Otherwise, z=0 is the ESS.

Let the stable probability of government adopting SR be represented by volume V₃, and the stable probability of adopting LR be represented by volume V₄. The tangent plane passing through point

(0, 2 (T Q - C_{g} - C_{w}) / b n s^{2}, 0)

. We can obtain,

V_{3} = \int_{0}^{1} \int_{0}^{\frac{2 (T Q - C_{g} - C_{w})}{b n s^{2}}} \frac{(T Q - C_{g} - C_{w} - 1 / 2 b n s^{2} y)}{(T h s y + T Q + 1 / 2 a m e^{2})} d y d z = - \frac{1}{h s T} D + \frac{1}{h^{2} s T^{2}} (h T D - B) \ln (1 + \frac{4 h T D}{B})

V_{4} = 1 - V_{3}

, wherein

B = a b e^{2} m n s + 2 b n s Q T

D = Q T - C_{g} - C_{w}

Lemma 5: When the system satisfies

B - 2 h T D > 0

, the probability of government adopting SR strategies is positively related to h, a, b, and Q, while it is negatively related to T, s, C_g, and C_w.

Proof: Let’s calculate the first-order partial derivatives of each element with respect to V₄.We can obtain

\partial V_{4} / \partial h > 0

\partial V_{4} / \partial a > 0

\partial V_{4} / \partial b > 0

\partial V_{4} / \partial Q > 0

\partial V_{4} / \partial s < 0

\partial V_{4} / \partial C_{g} < 0

\partial V_{4} / \partial C_{w} < 0

\partial V_{4} / \partial T < 0

Lemma 5 suggests that when the condition

B - 2 h T D > 0

is met, a higher sensitivity of consumers towards the level of recycling services and a larger subsidy ratio from remanufacturer and platform lead to a greater quantity of waste being recycled. This can result in higher profits through carbon emission taxes, which inclines the government towards a stable choice of SR strategies. Additionally, the more recycling volume that government promotion efforts can bring, the more likely the government is to choose stable implementation of SR strategies. On the other hand, higher regulatory costs, carbon emission taxes, and levels of recycling services tend to make the government choose LR strategies. A higher carbon emission tax would prompt remanufacturer to autonomously choose LCP strategy, while under a higher level of recycling services, the recycling system can operate well even without government involvement.

Lemma 6: There exists the probability of government implementing SS strategies decreases as the probability of remanufacturer adopting LCP strategies and platform choosing SI strategies increases.

Proof: According to the analysis of government’s strategy stability, when

x < x_{1}

, then

H (x) < 0

d F (z) / d z |_{z = 1} < 0

, at this case, z=1 is the ESS. Thus, as z gradually decreases, the government’s stable strategy transitions from z=1 (SR) to z=0 (LR).

Lemma 6 suggests that in the early stage of evolution, the regulatory role of the government is more pronounced. The government can influence by increasing subsidies for remanufacturers and platforms, imposing carbon emission taxes on traditional products, promoting the adoption of LCP strategies by remanufacturers, and encouraging platform to choose strategies. This will stimulate consumer participation in waste product recycling and increase the amount of waste product collected in the recycling system.

4.4. Stability Analysis of Equilibria in Three-Player Evolutionary Game Systems

Based on the analysis of pure strategies for remanufacturers, platforms, and the government in sections 4.1-4.3, we will now solve for the mixed strategies of each participant in the system. Let

F (x) = 0

F (y) = 0

F (z) = 0

, then 13 equilibrium points can be derived, E₁(0,0,0), E₂ (1,0,0), E₃ (0,1,0), E₄ (0,0,1), E₅ (1,1,0), E₆ (1,0,1), E₇ (0,1,1), E₈ (1,1,1), E₉ (

x_{1}

,1,

z_{1}

), E₁₀(

x_{1}

,0,

z_{1}

), E₁₁(1,

y_{1}

z_{1}

), E₁₂ (

x_{1}

y_{1}

z_{2}

), E₁₃ (0,

y_{1}

z_{2}

). To facilitate calculations, let us assume the following in this section: K=1/2me², L=1/2ns². Thus,

z_{1} = (K - r e h s y) / (T h s y + T Q + a K + r e Q) ， z_{2} = (L - u h s) / b L, x_{1} = (T Q - C_{g} - C_{w} - b L y) / (T h s y + T Q + a K), y_{1} = (- T Q x - a K x - C_{g} - C_{w} + T Q) / (T h s x + b L) .

In actual situations, when the government does not implement regulation, platforms prioritize their own interests. This means that the increment in revenue for the platform after engaging in recycling service investment will be greater than zero. In other words,

u h s - L > 0

, therefore, The existence of points E₁₁ (1,

y_{1}

z_{1}

) and E₁₂ (

x_{1}

y_{1}

z_{2}

) is meaningless. Furthermore, since

x, y, z \in [0, 1]

, The existence of point E₁₃ (0,

y_{1}

z_{2}

) also is meaningless. The existence of E₉(

x_{1}

,1,

z_{1}

) and E₁₀ (

x_{1}

,0,

z_{1}

), under certain conditions, it can have significance. The Jacobian matrix of the three-player evolutionary game system is as follows:

\begin{array}{l} J = [\begin{matrix} j_{11} & j_{12} & j_{13} \\ j_{21} & j_{22} & j_{23} \\ j_{31} & j_{32} & j_{33} \end{matrix}] = [\begin{matrix} \partial F (x) / \partial x & \partial F (x) / \partial y & \partial F (x) / \partial z \\ \partial F (y) / \partial x & \partial F (y) / \partial y & \partial F (y) / \partial z \\ \partial F (z) / \partial x & \partial F (z) / \partial y & \partial F (z) / \partial z \end{matrix}] \\ = [\begin{matrix} (1 - 2 x) (\begin{array}{l} T h s y z + r e h s y + (T Q \\ + a K + r e Q) z - K \end{array}) & h s x (1 - x) (e r + T z) & x (1 - x) (T h s y + T Q + a K + r e Q) \\ 0 & (1 - 2 y) (b L z + u h s - L) & b L y (1 - y) \\ z (z - 1) (T h s y + T Q + a K) & z (z - 1) (T h s x + b L) & (2 z - 1) (\begin{array}{l} T h s x y + T Q x + a K x + \\ b L y + C_{g} + C_{w} - T Q \end{array}) \end{matrix}] \end{array}

Using the first Lyapunov method: If all eigenvalues of the Jacobian matrix have negative real parts, then the equilibrium point is asymptotically stable. If at least one eigenvalue of the Jacobian matrix has a positive real part, then the equilibrium point is unstable. If the Jacobian matrix has eigenvalues with zero real parts and the rest of the eigenvalues have negative real parts, then the equilibrium point is in a critical state, and stability cannot be determined by the sign of the eigenvalues. The stability analysis of each equilibrium point is shown in Table 4.

k_{1} = \frac{\sqrt{((K - r e h s) (C g + C w + b L - T Q) (C g + C w + a K + b L + T h s) (a K + T Q + T h s) (a K + r e Q + T Q + T h s) (- K + a K + (Q + h s) (e r + T))}}{(a K + T Q + T h s) (a K + r e Q + T Q + T h s)} k_{2} = \frac{\sqrt{K (C g + C w + a K) (C g + C w - T Q) (a K + T Q) (a K + r e Q + T Q) (- K + a K + r e Q + T Q)}}{a^{2} K^{2} + a K r e Q + 2 a K T Q + r e T Q^{2} + T^{2} Q^{2}}

Lemma 7: When K-rehs<0, the replicator dynamic system only has one stable point E₅ (1,1,0).

Proof: According to Table 4, this condition satisfies Condition ②, so E₅(1,1,0) is an asymptotically stable point of the system. Conditions ①, ③, and ④ are not satisfied, so equilibrium points E₃(0,1,0) and E₇(0,1,1) are unstable. Equilibrium point E₉ (x₁, 1, z₁) does not exist, and although Condition ⑤ may be satisfied, E₁₀ (x₁, 0, z₁) is an unstable point.

Lemma 7 indicates that when the profit increase from producing low-carbon products is relatively high and the recycling quantity generated by platform investment in recycling services is high, depending on the initial strategy selection of the three parties, the evolutionary stable strategy combination converges to the stable point (LCP, SI, SR).

Lemma 8: When TQ-Cg-C_w-bL<0 and K>rehs, the replicator dynamic system has a stable point E₃ (0,1,0).

Lemma 9: When TQ-Cg-C_w-bL>0 and K>(T+re)(Q+hs)/(1-a), the replicator dynamic system has a stable point E₇ (0,1,1).

Proof: According to Table 4, when TQ-Cg-C_w-bL<0 and (T+re)(Q+hs)-(1-a)K<0, conditions ②, ④, and ⑤ are not satisfied. Therefore, equilibrium point E₅(1,1,0) becomes unstable, and equilibrium points E₉(x₁, 1, z₁) and E₁₀ (x₁, 0, z₁) do not exist. In this case, there are two stable points: E₃(0,1,0) and E₇(0,1,1). When the constraint on K is further narrowed down to rehs<K<(T+re)(Q+hs)/(1-a), condition ③ is no longer satisfied. In this case, the system only has one stable point, which is E₃ (0,1,0).

Lemma 8-9 indicate that in the early stage of product carbon reduction technology development, when the cost for remanufacturers to produce low-carbon products is very high, government regulations may not be effective. Industrial technological development generally goes through three stages: initial, intermediate, and mature. In the initial stage, the research and development costs are usually very high. Despite government subsidies, carbon emission tax exemptions, and other policies, remanufacturers still face difficulty in obtaining profits during this stage. Hence, there can be stable points in the system with the combinations of (TP, SI, SR) and (TP, SI, LR). During this stage, the government can increase subsidy levels, enhance recycling promotion efforts, provide exemptions from low-carbon product carbon emission taxes, and increase traditional product carbon emission taxes. Additionally, the country can allocate more research funding for technological innovation and encourage research institutions to conduct research and development on relevant carbon reduction technologies, allowing carbon reduction technologies to move more swiftly from the initial stage to the mature stage.

5. Result and Discussion

To validate the effectiveness of the above analysis and provide a more intuitive reflection of the impact of various parameters on the stability of the low-carbon e-commerce supply chain recycling evolutionary system, this section will assign numerical values to the model and use Matlab 2021 for simulation. The parameters for the first set are as follows: r=4, u=1, T=2, e=0.5, s=0.5, a=0.5, b=0.5, C_g=5, C_w=5, Q=40, h=100, m=400, n=200, which satisfy the conditions in Lemma 7.

Firstly, let’s assign r = 2, 4, 8, and the simulation results are shown in Figure 2.

From Figure 2, we can see that during the evolution of the system towards the stable point, an increase in the price marginal parameter of carbon emission reduction can accelerate the evolutionary speed of remanufacturers choosing to produce low-carbon products. As r increases, the probability of remanufacturers adopting the low-carbon product strategy increases, which aligns with the conclusion in Lemma 1.

Next, assign m to m = 400, 800, 1200, and the simulation results are shown in Figure 3. Similarly, assign n to n = 200, 400, 600, and the simulation results are shown in Figure 4.

From Figure 3, we can observe that in the relatively mature stage of carbon emission reduction technology, reducing the cost sensitivity coefficient of carbon emission reduction can accelerate the evolutionary speed of remanufacturers choosing to produce low-carbon products. As m decreases, the probability of remanufacturers adopting the low-carbon product strategy increases, which aligns with the conclusion in Lemma 1.

From Figure 4, it can be observed that reducing the cost sensitivity coefficient of service level can accelerate the evolutionary speed of the platform choosing to invest in recycling services. As n decreases, the probability of the platform adopting the recycling service investment strategy increases, which aligns with the conclusion in Lemma 3.

Once again, assign T = 2, 4, 8, and the simulation results are shown in Figure 5. Similarly, assign Q = 40, 80, 120, and the simulation results are shown in Figure 6.

From Figure 5, we can observe that as T increases, the probability of remanufacturers adopting the low-carbon product strategy rises, which aligns with the conclusion in Lemma 1. Therefore, the government can consider increasing the carbon emission tax on traditional products, reducing the sales profits of traditional products, thereby incentivizing remanufacturers to choose low-carbon product production.

From Figure 6, we can see that as Q increases, the probability of remanufacturers choosing the low-carbon product strategy also increases, which aligns with the conclusion in Lemma 1. Therefore, the government can implement measures such as recycling awareness campaigns and educational programs to strengthen consumers’ awareness of recycling. This can increase the amount of waste products (Q) in the system, subsequently increasing the probability of remanufacturers opting for low-carbon product production strategy.

Next, assign h = 100, 200, 400, and the simulation results are shown in Figure 7. Similarly, assign s to s = 0.2, 0.5, 0.8, and the simulation results are shown in Figure 8.

From Figure 7, we can observe that increasing the elasticity coefficient of platform’s recycling quantity with respect to service level (h) can accelerate the evolutionary speed of the platform choosing to invest in recycling services. As h increases, the probability of the platform adopting the recycling service investment strategy also increases.

From Figure 8, we can see that as the platform’s service level becomes higher, the platform’s rate of choosing to invest in recycling services decreases. This is in line with the conclusion in Lemma 3. As s increases, the probability of the platform adopting the recycling service investment strategy decreases.

Overall, the simulation results align with the conclusions in Lemma 3, indicating that an increase in the elasticity coefficient of the platform’s recycling quantity and a higher service level can accelerate or slow down the evolutionary speed of the platform’s investment in recycling services.

Array 1 satisfies the conditions in Lemma 7. Assign values to Array 2 and Array 3 to satisfy the conditions in Lemma 8 and Lemma 9, respectively. Array 2：r=1, u=1, T=0.5, e=0.5, s=0.2, a=0.5, b=0.5, C_g=10, C_w=10, Q=30, h=100, m=600, n=600. Array 3：r=1, u=1, T=0.5, e=0.5, s=0.2, a=0.5, b=0.5, C_g=5, C_w=5, Q=30, h=100, m=1000, n=200. Simulate the evolution of the system starting from different initial strategy combinations for 50 iterations. The results are shown in Figure 9-11.

Based on the given information, it appears that in the simulation results:

Figure 9 shows that when satisfying Condition ②, the system only exhibits one strategy combination (LCP, SI, LR). This aligns with the conclusion in Lemma 7, indicating that the system is in a mature stage where the government does not need to implement incentive measures. Figure 10 indicates that when satisfying Condition ①, the system has a stable point with the strategy combination of (TP, SI, LR). This aligns with the conclusion in Lemma 8, suggesting that the system is in an early stage where the investment required for carbon emission reduction technology is high and consumers have weak awareness of recycling. The government incurs low costs for regulation and promotion, resulting in low levels of recycling volume. Figure 11 illustrates that E₉ (x₁,1, z₁) and E₁₀ (x₁,0, z₁) are unstable equilibrium points. In this scenario, the system exhibits only one stable evolutionary strategy combination (TP, SI, SR). This suggests that the system is in an early stage where the investment required for carbon emission reduction technology is high. Remanufacturers do not choose the low-carbon product strategy, but the government promotes consumers’ recycling behavior by allocating a higher proportion of resources between recycling volume and investment. These observations align with the conclusions derived from the data analysis.

6. Conclusions

The role of Internet + recycling in the context of platform economy has been increasing in the field of waste recycling. Taking into account the behavior of remanufacturers in producing low-carbon products and the investment decisions of platforms in recycling services, as well as the regulatory actions of the government, this study constructed an evolutionary game model involving remanufacturer, platform, and the government. The stability of strategy choices and combinations among these participants and the relationships between different factors were analyzed. Finally, simulations were conducted to derive several conclusions.

The main findings are as follows: First, increasing government promotion of recycling and implementing carbon taxes on traditional products can encourage remanufacturers to produce low-carbon products and motivate platforms to invest in recycling services. Second, remanufacturers are incentivized to produce low-carbon products when they can enjoy higher sales revenues for such products. Third, when consumers are sensitive to the level of recycling services, platforms’ increased investment in recycling services can enhance waste recycling and prompt remanufacturers to choose low-carbon production. Forth, when the cost of improving carbon emission reduction levels for remanufacturers and the cost of enhancing recycling services for platforms are too high, the inherent subsidies provided by the government may not be effective. In such cases, external forces are needed to lower the costs associated with carbon emission reduction and service enhancement. This could be achieved through support from the national level, encouraging relevant industries and research institutions to accelerate the development of related technologies, thus advancing them to a more mature stage more quickly.

In summary, these findings demonstrate the increasing significance of Internet + recycling in waste management within the platform economy. They also shed light on the strategic choices and dynamics among remanufacturers, platforms, and the government, providing insights for policymakers and stakeholders involved in promoting sustainable practices and low-carbon production.

References

Jian L, Zhen W, Bao J and Taebok K (2017) Coordination strategies in a three-echelon reverse supply chain for economic and social benefit. Applied Mathematical Modelling, 49: 599-611.
Zhang XM, Li QW, Liu Z and Chang CT (2021) Optimal pricing and remanufacturing mode in a closed-loop supply chain of WEEE under government fund policy. Computers & Industrial Engineering, 151: 106951.
Owusu-Sekyere K, Batteiger A, Afoblikame R, Hafner G and Kranert M (2022) Assessing data in the informal e-waste sector: The Agbogbloshie Scrapyard. Waste Management, 139: 158-167.
Ling M, Xu L and Chu X (2023) Heterogeneous effects of other-regarding interventions on household recycling: A field experimental study. Journal of Environmental Management, 329: 117102.
Tian L, Vakharia AJ, Tan Y and Xu Y (2018) Marketplace, Reseller, or Hybrid: Strategic Analysis of an Emerging E-Commerce Model. Production and Operations Management, 27(8): 1595-1610.
Rao P, Balasubramanian S, Nitin Vihari SJ, Shukla V and Chanchaichujit J (2021) The e-commerce supply chain and environmental sustainability: An empirical investigation on the online retail sector. Cogent Business & Management, 8(1): 1938377.
Guo X, Li X, Bian J and Yang C (2023) Deposit or reward: Express packaging recycling for online retailing platforms. Omega, 117: 102828.
Li B, Wang Q, Chen B, Sun T, Wang Z and Cheng Y (2022) Tripartite evolutionary game analysis of governance mechanism in Chinese WEEE recycling industry. Computers & Industrial Engineering, 167:108045.
Zlamparet GI, Tan Q, Stevels AB and Li J (2017) Resource conservation approached with an appropriate collection and upgrade-remanufacturing for used electronic products. Waste Management, 73: 78-86.
Yang R, Tang W and Zhang J (2020) Technology improvement strategy for green products under competition: The role of government subsidy. European Journal of Operational Research, 289(2): 553-568.
Sarkar B, Ullah M and Sarkar M (2022) Environmental and economic sustainability through innovative green products by remanufacturing. Journal of Cleaner Production, 332: 129813.
Mejía-Moncayo C, Kenné JP and Hof LA (2023) On the development of a smart architecture for a sustainable manufacturing-remanufacturing system: A literature review approach. Computers & Industrial Engineering, 180: 109282.
Wang Q, Li B, Chen B, Cheng Y and Wang Z (2021) Implication of take-back and carbon emission capacity regulations on remanufacturing in a competitive market. Journal of Cleaner Production, 325: 129231.
Salhofer S, Steuer B, Ramusch R and Beigl P (2016) WEEE management in Europe and China - A comparison. Waste Management, 57: 27-35.
Liu J, Zhai X and Chen L (2019) Optimal pricing strategy under trade-in program in the presence of strategic consumers. Omega, 84: 1-17.
Jian H, Xu M and Zhou L (2019) Collaborative collection effort strategies based on the “Internet + recycling” business model. Journal of Cleaner Production, 241: 118120.
Li J, Jia A, Hou X, Wang X, Mao Y and Wang W (2023) Thermal co-treatment of aluminum dross and municipal solid waste incineration fly ash: Mineral transformation, crusting prevention, detoxification, and low-carbon cementitious material preparation. Journal of Environmental Management, 329: 117090.
Kurniawan TA, Dzarfan Othman MH, Hwang GH and Gikas P (2022) Unlocking digital technologies for waste recycling in Industry 4.0 era: A transformation towards a digitalization-based circular economy in Indonesia. Journal of Cleaner Production, 357: 131911.
Jin L, Zheng B and Huang S (2021) Pricing and coordination in a reverse supply chain with online and offline recycling channels: A power perspective. Journal of Cleaner Production, 298: 126786.
Bai S, Ge L and Zhang X (2022) Platform or direct channel: Government-subsidized recycling strategies for WEEE. Information Systems and e-Business Management, 20(2): 347-369.
Wang J, Xu M and Zou L (2022) Pricing decisions of the “Internet +” recycling platform considering consumer behaviour. Computers & Industrial Engineering, 174: 108831.
Matsui K (2023) Dual-recycling channel reverse supply chain design of recycling platforms under acquisition price competition. International Journal of Production Economics, 259: 108769.
Feng L, Govindan K and Li C (2017) Strategic planning: Design and coordination for dual-recycling channel reverse supply chain considering consumer behavior. European Journal of Operational Research, 260(2): 601-612.
Li C, Feng L and Luo S (2019) Strategic introduction of an online recycling channel in the reverse supply chain with a random demand. Journal of Cleaner Production, 236: 117683.
Wang Y, Yu Z, Shen L and Jin M (2022) Operational modes of E-closed loop supply chain considering platforms’ services. International Journal of Production Economics, 251: 108551.
Wang YY, Chen YL, Cheng W, Wang JC and Tao F (2023) Equilibrium analysis of transaction modes and recycling channels in a closed-loop supply chain with an online platform. Computers & Industrial Engineering, 177: 109090.
Fukui H and Miyoshi C (2017) The impact of aviation fuel tax on fuel consumption and carbon emissions: The case of the US airline industry. Transportation Research Part D: Transport and Environment, 50: 234-253.
Yuyin Y and Jinxi L (2018) The effect of governmental policies of carbon taxes and energy-saving subsidies on enterprise decisions in a two-echelon supply chain. Journal of Cleaner Production, 181: 675-691.
Zhang Z and Yu L (2022) Altruistic mode selection and coordination in a low-carbon closed-loop supply chain under the government’s compound subsidy: A differential game analysis. Journal of Cleaner Production, 366: 132863.
He X, Jiang J and Hu W (2023) Cross effects of government subsidies and corporate social responsibility on carbon emissions reductions in an omnichannel supply chain system. Computers & Industrial Engineering, 175: 108872.
Zhang P, Jin L and Wang Y (2023) Optimizing mechanisms for promoting low-carbon manufacturing industries towards carbon neutrality. Renewable and Sustainable Energy Reviews, 183: 113516.
Wang Y, Fan R, Shen L and Miller W.(2020) Recycling Decisions of Low-Carbon E-commerce Closed-Loop Supply Chain under Government Subsidy Mechanism and Altruistic Preference. Journal of Cleaner Production, 259: 120883.
Xie J, Zhang W, Liang L, Xia Y, Yin J and Yang G (2018) The revenue and cost sharing contract of pricing and servicing policies in a dual-channel closed-loop supply chain. Journal of Cleaner Production, 191: 361-383.
Nair A and Narasimhan R (2006) Dynamics of competing with quality- and advertising-based goodwill. European Journal of Operational Research, 175(1): 462-474.
Giovanni PD and Zaccour G (2019) Optimal quality improvements and pricing strategies with active and passive product returns. Omega, 88: 248-262.
Wang Y, Yu Z, Shen L and Dong W (2021) Impacts of altruistic preference and reward-penalty mechanism on decisions of E-commerce closed-loop supply chain. Journal of Cleaner Production, 315: 128132.
Wu CH (2012) Price and service competition between new and remanufactured products in a two-echelon supply chain. International Journal of Production Economics, 140(1): 496-507.
Wang Y, Yu Z and Shen L (2018) Study on the decision-making and coordination of an e-commerce supply chain with manufacturer fairness concerns. International Journal of Production Research, 57(9): 1-21.
Li Q, Xiao T and Qiu Y (2018) Price and carbon emission reduction decisions and revenue-sharing contract considering fairness concerns. Journal of Cleaner Production, 190: 303-314.
Wang M, Li Y, Cheng Z, Zhong C and Ma W (2021) Evolution and equilibrium of a green technological innovation system: Simulation of a tripartite game model. Journal of Cleaner Production, 278: 123944.

Figure 1. The structure of LC-ECLSC model.

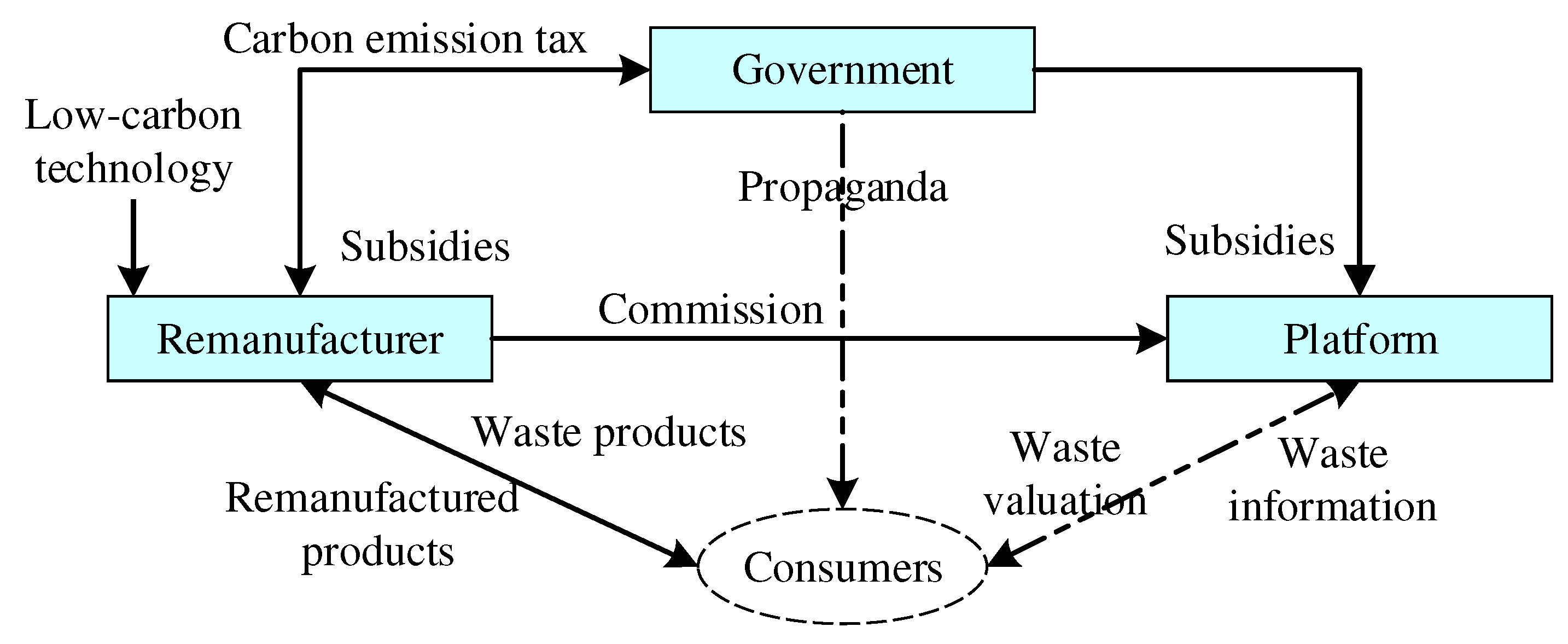
Figure 2. The impact of the carbon emission reduction sensitivity coefficient on the sales price.

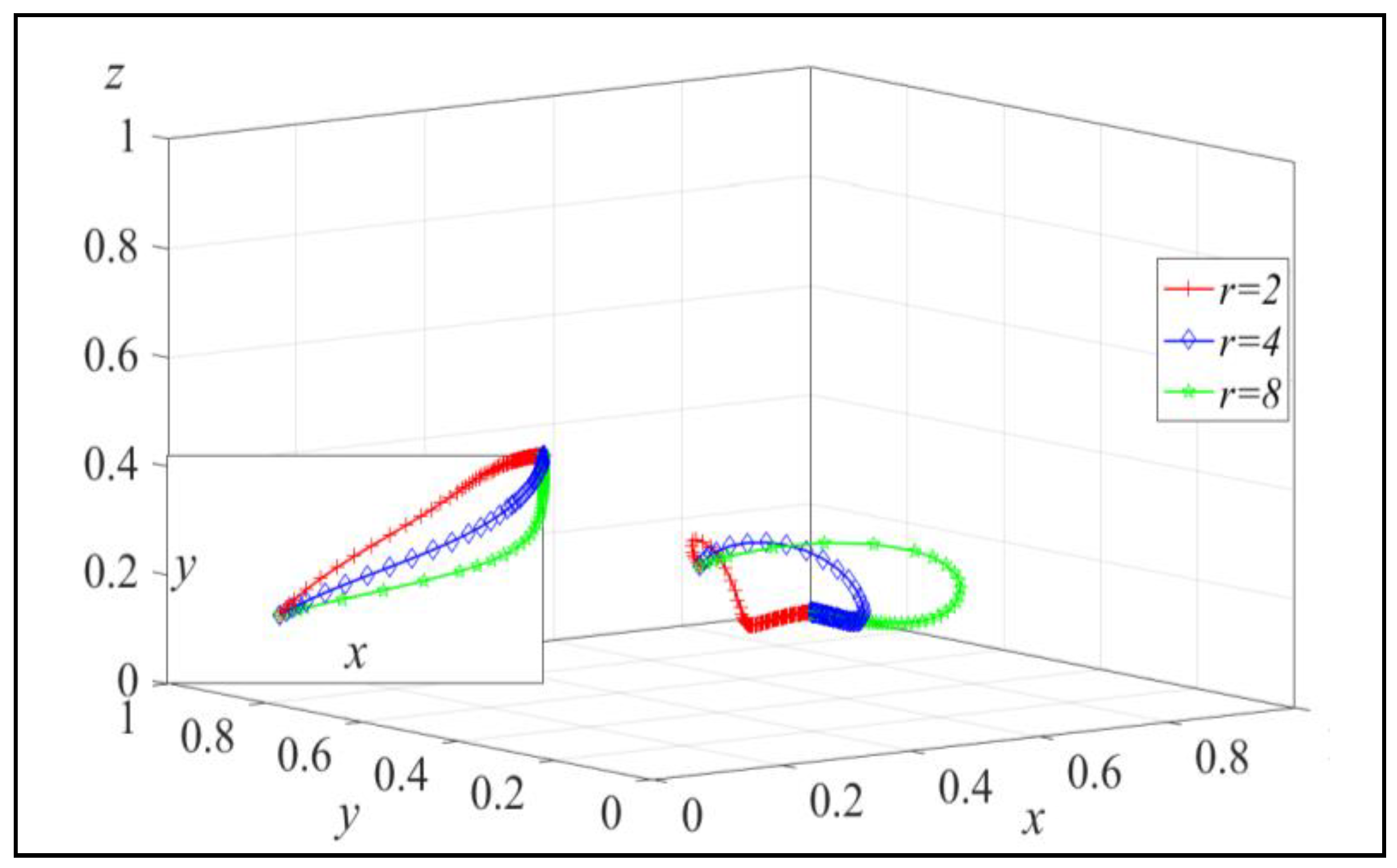
Figure 3. The influence of the carbon emission reduction cost sensitivity coefficient.Figure 4. The influence of the service level cost sensitivity coefficient.

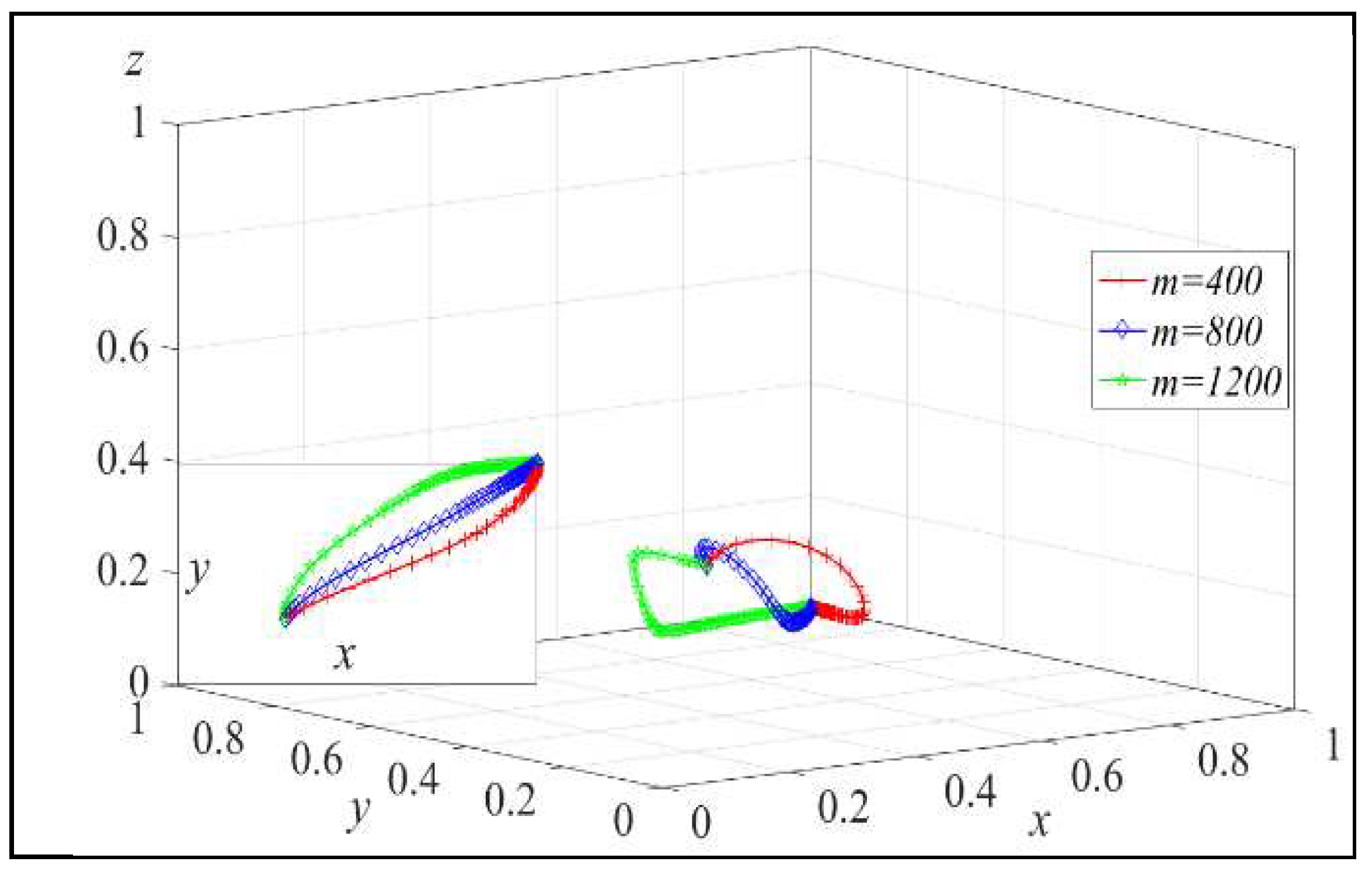
Figure 4. The influence of the service level cost sensitivity coefficient.

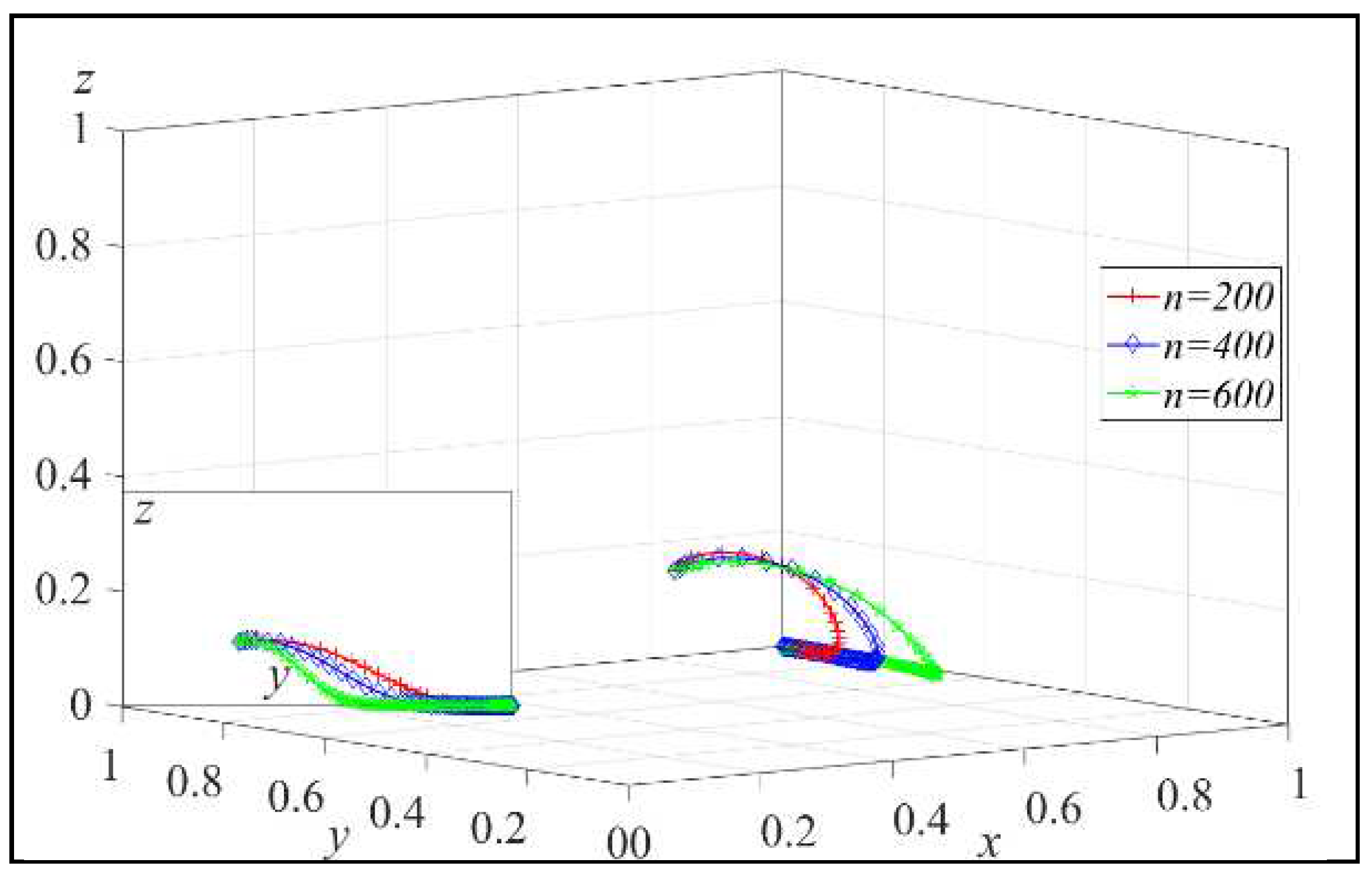
Figure 5. Carbon emission tax.

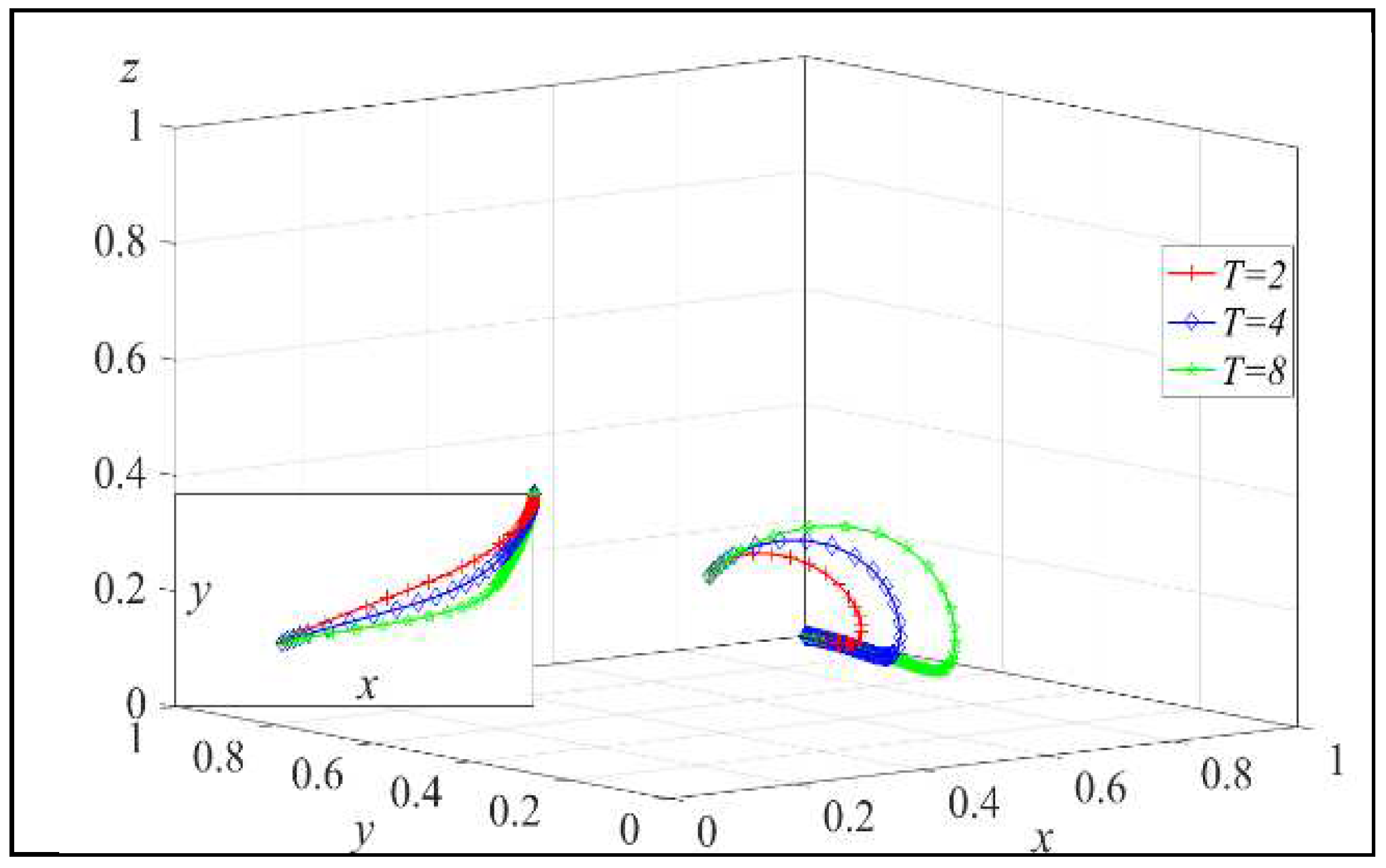
Figure 6. Increased recycling volume due to government promotion.

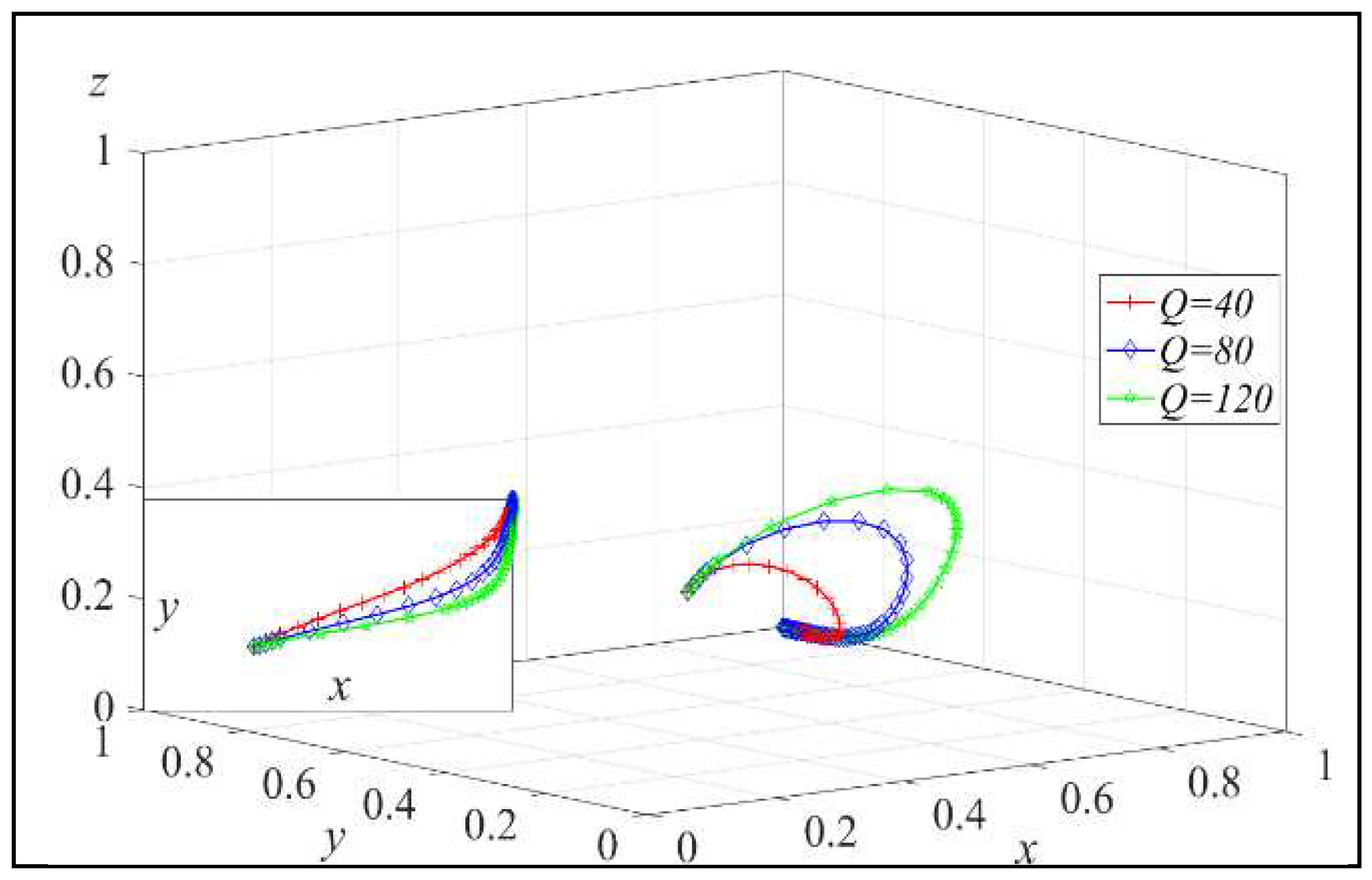
Figure 7. The elasticity coefficient of recycling quantity with respect to service level.

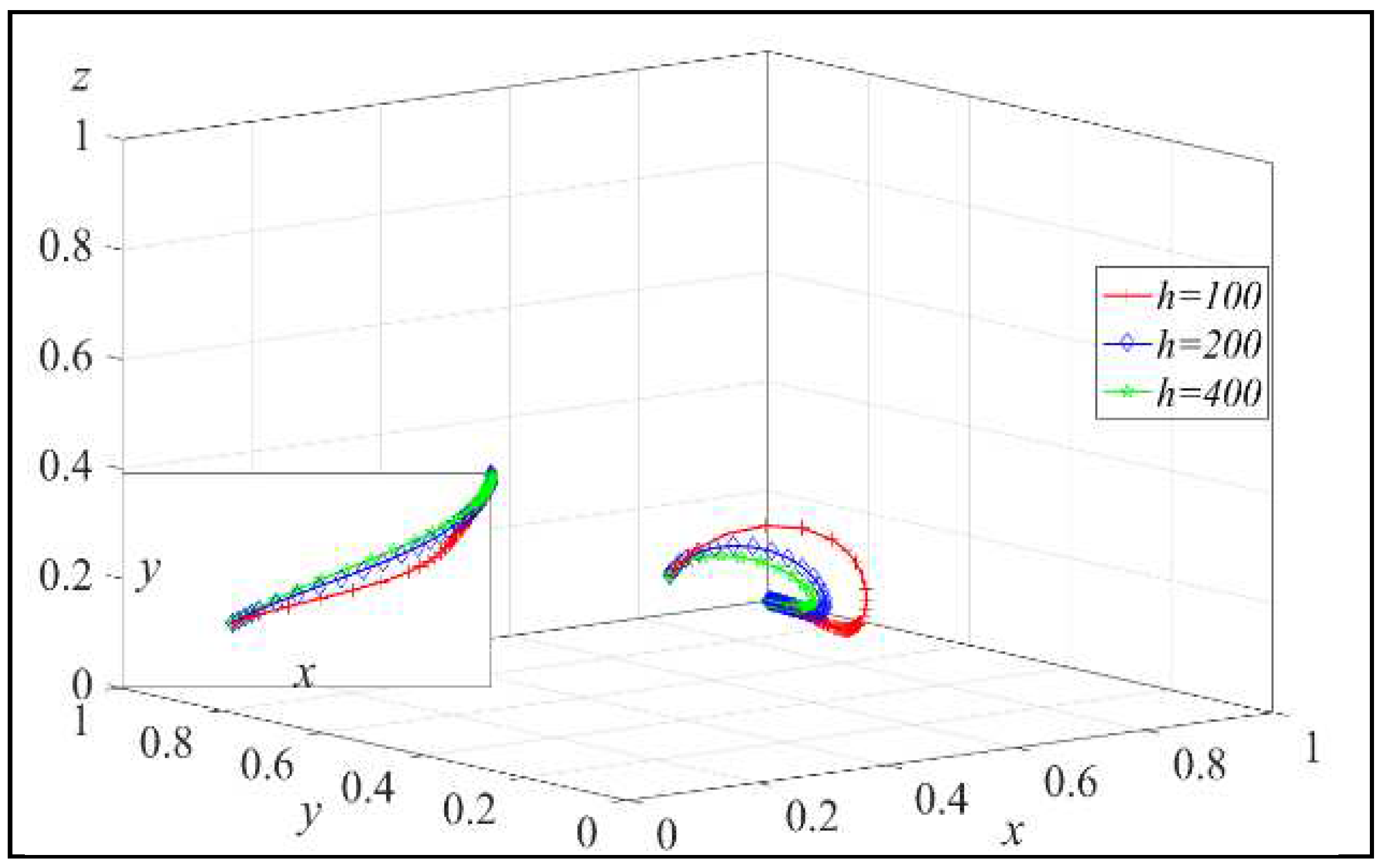
Figure 8. The impact of service level.

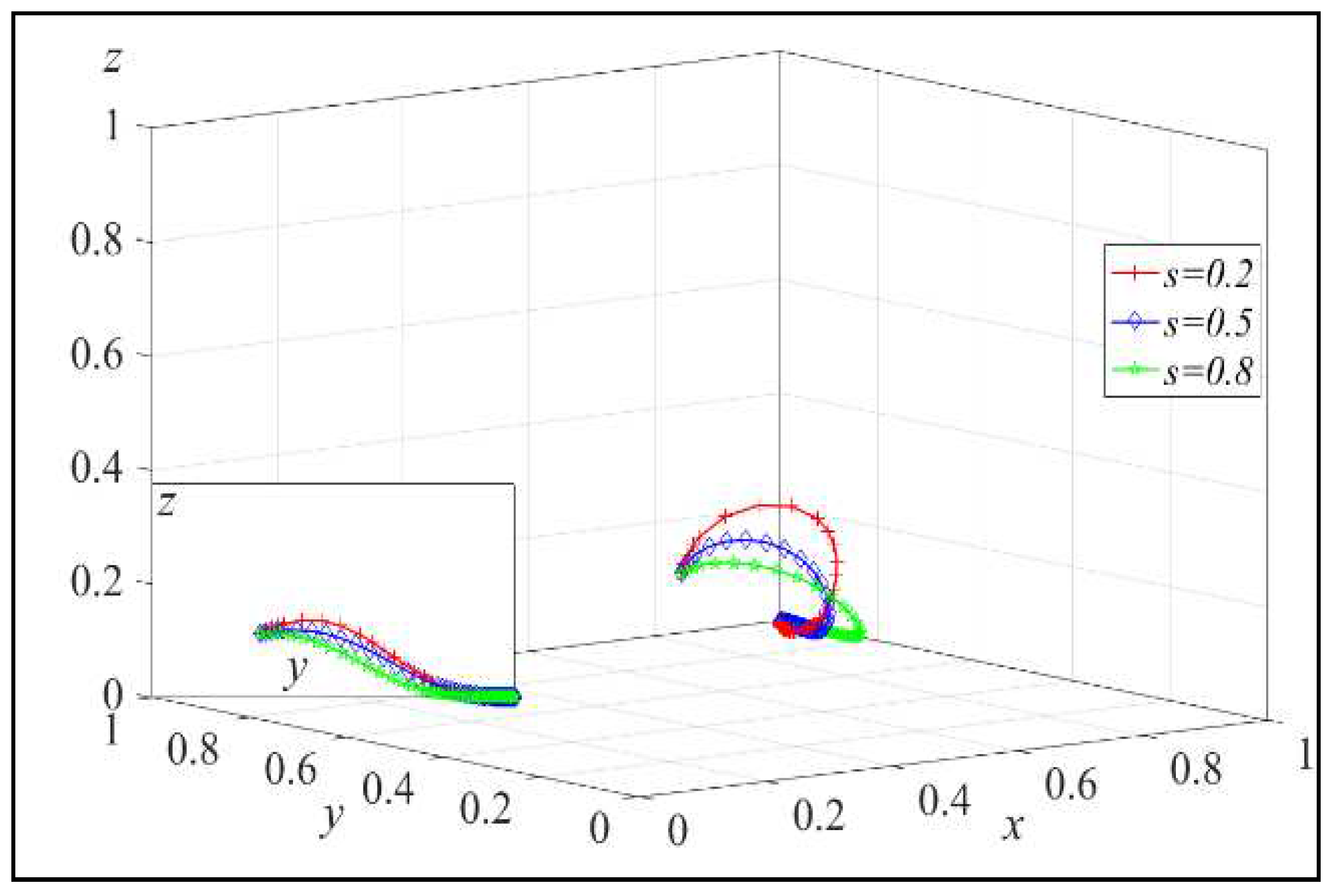
Figure 9. The result of array 1 evolving 50 times.

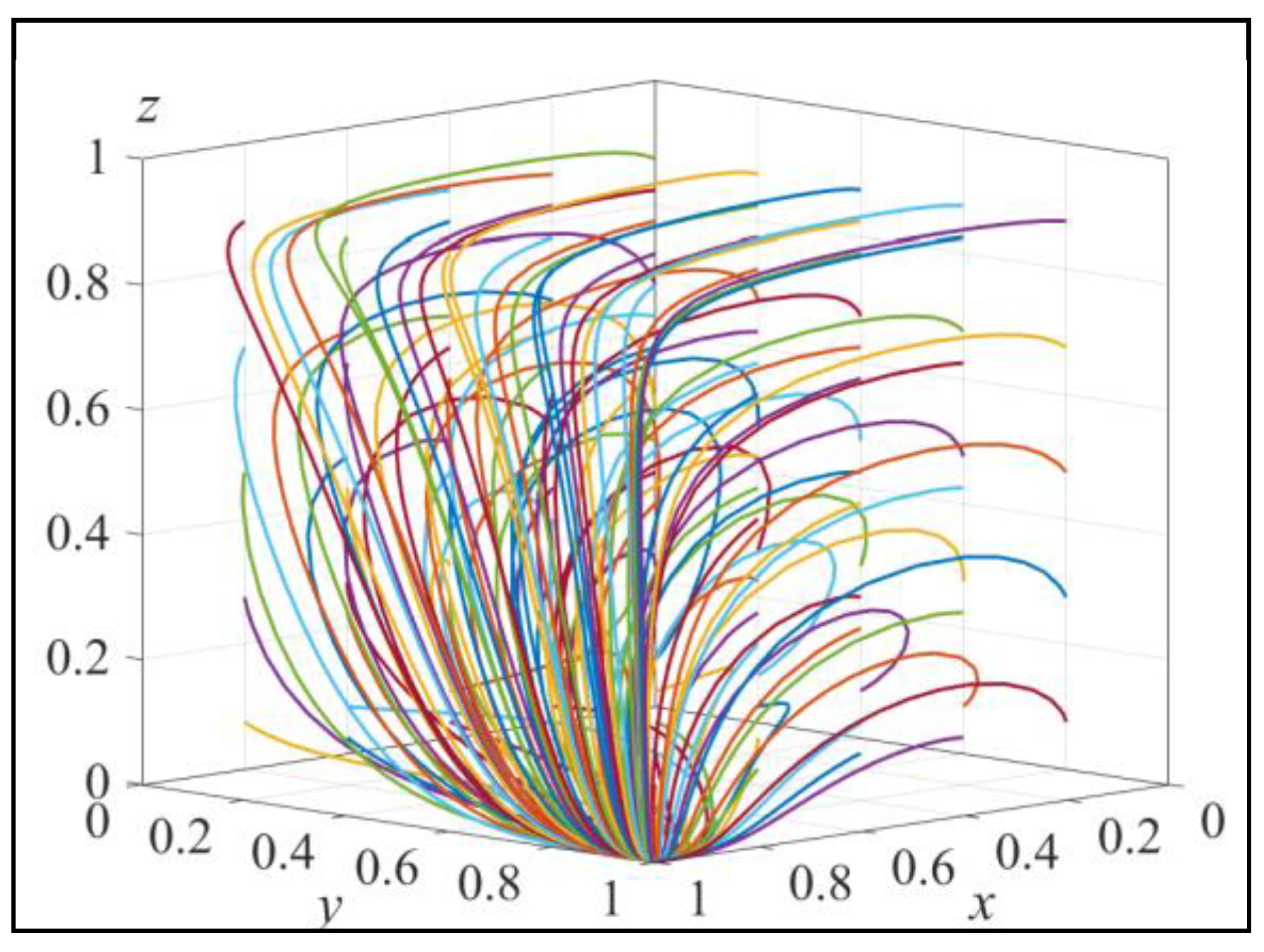
Figure 10. The result of array 2 evolving 50 times.

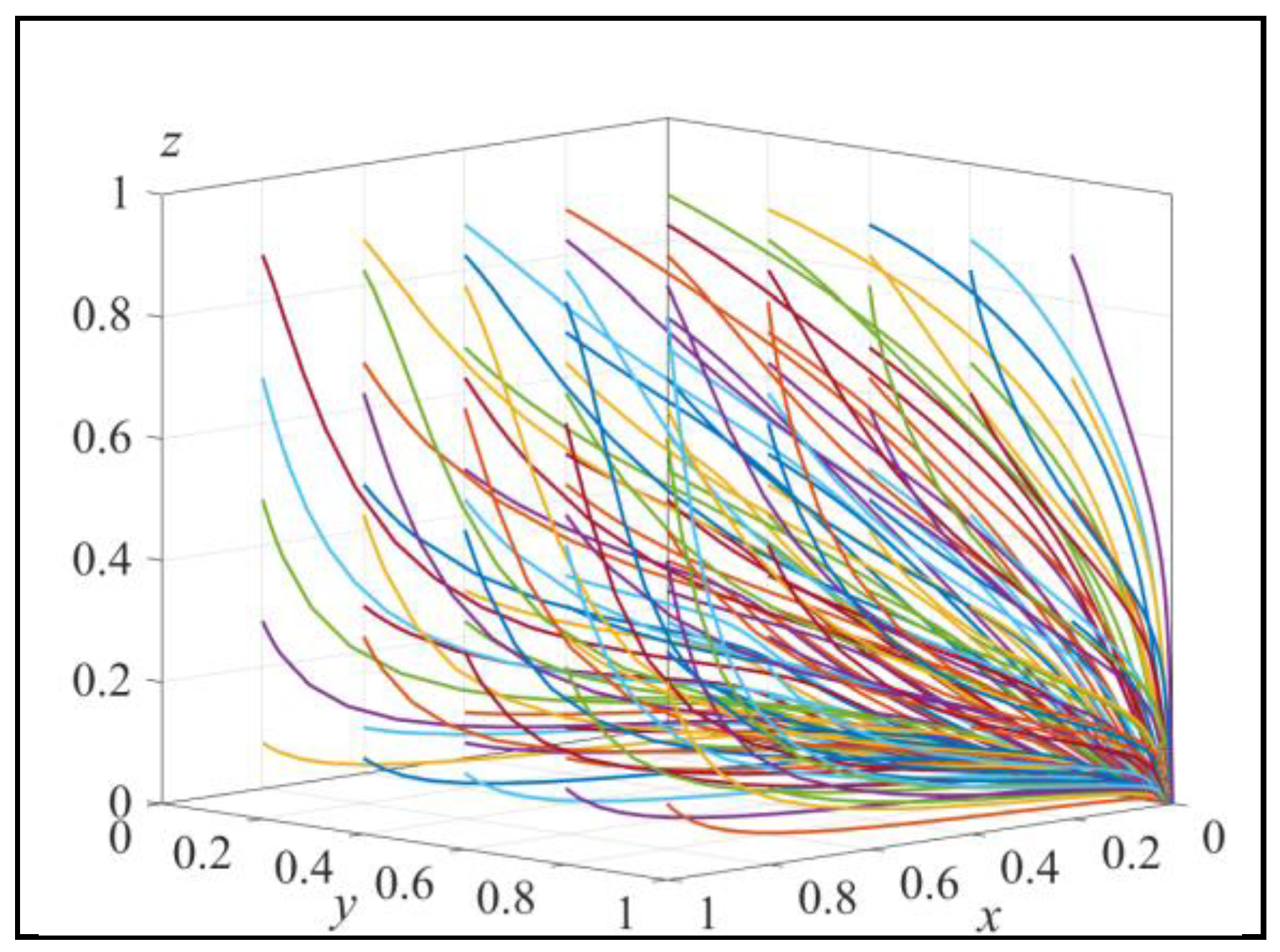
Figure 11. The result of array 3 evolving 50 times.

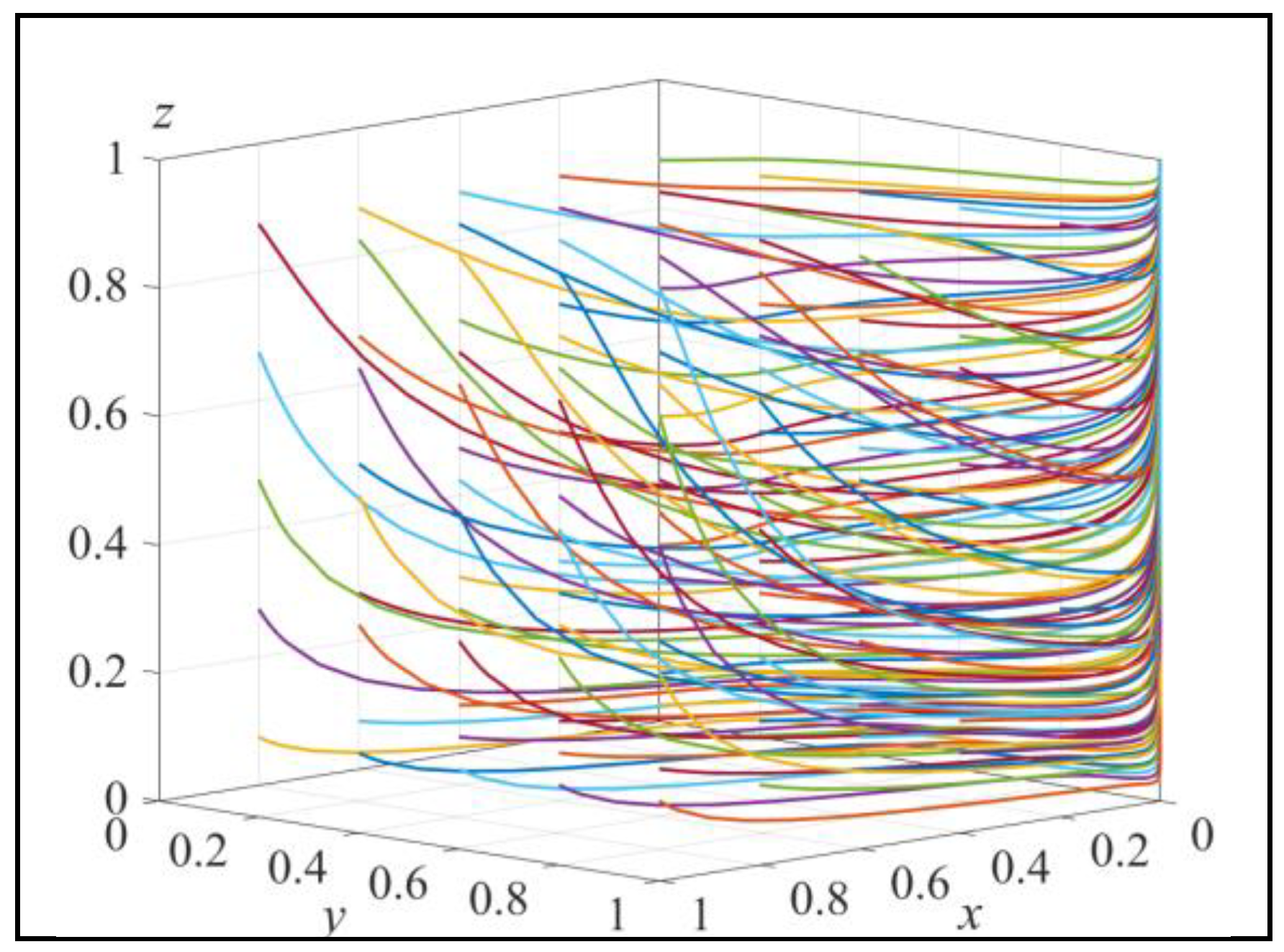
Table 2. The payoff matrix under the government’s SS strategy (z).

Remanufacturer	Platform
Remanufacturer	Service Investing (y)	Not Service Investing (1-y)
Low-carbon products (x)	$π_{M}^{1} = (p + r e - u) (h s + Q) - 1 / 2 (1 - a) m e^{2}$ $π_{P}^{1} = u (h s + Q) - 1 / 2 (1 - b) n s^{2}$ $π_{G}^{1} = - 1 / 2 a m e^{2} - 1 / 2 b n s^{2} - C_{g} - C_{w}$	$π_{M}^{2} = (p + r e - u) Q - 1 / 2 (1 - a) m e^{2}$ $π_{P}^{2} = u Q$ $π_{G}^{2} = - 1 / 2 a m e^{2} - C_{g} - C_{w}$
Traditional products (1-x)	$π_{M}^{3} = (p - u - T) (h s + Q)$ $π_{P}^{3} = u (h s + Q) - 1 / 2 (1 - b) n s^{2}$ $π_{G}^{3} = T (h s + Q) - 1 / 2 b n s^{2} - C_{g} - C_{w} - C_{k}$	$π_{M}^{4} = (p - u - T) Q$ $π_{P}^{4} = u Q$ $π_{G}^{4} = T Q - C_{g} - C_{w} - C_{k}$

Table 3. The payoff matrix under the government’s LS strategy (1-z).

Remanufacturer	Platform
Remanufacturer	Investing (y)	Not Investing (1-y)
Low-carbon products (x)	$π_{M}^{5} = (p + r e - u - T) h s - 1 / 2 m e^{2}$ $π_{P}^{5} = u h s - 1 / 2 n s^{2}$ $π_{G}^{5} = T h s$	$π_{M}^{6} = - 1 / 2 m e^{2}$ $π_{P}^{6} = 0$ $π_{G}^{6} = 0$
Traditional products (1-x)	$π_{M}^{7} = (p - u - T) h s$ $π_{P}^{7} = u h s - 1 / 2 n s^{2}$ , $π_{G}^{7} = T h s - C_{k}$	$π_{M}^{8} = 0$ $π_{P}^{8} = 0$ $π_{G}^{8} = - C_{k}$

Table 4. Stability analysis of equilibrium points.

Points	The Eigenvalues of the Jacobian Matrix		Stability	Conditions
Points	$Eigenvalues λ_{1}, λ_{2}, λ_{3}$	Sign	Stability	Conditions
E₁ (0,0,0)	$u h s - L$ , $- K$ , $T Q - C_{w} - C_{g}$	+, -, -	Unstable	\
E₂ (1,0,0)	$K$ , $u h s - L$ , $- a K - C_{w} - C_{g}$	+,+, -	Unstable	\
E₃ (0,1,0)	$r e h s - K$ , $L - u h s$ , $T Q - C_{w} - C_{g} - b L$	-, -, -	ESS	①
E₄ (0,0,1)	$u h s - (1 - b) L$ , $C_{g} + C_{w} - T Q$ , $T Q - (1 - a) K + r e Q$	+, -, -	Unstable	\
E₅ (1,1,0)	$K - r e h s$ , $L - u h s$ , $- a K - C_{w} - C_{g} - T h s - b L$	-, -, -	ESS	②
E₆ (1,0,1)	$u h s - (1 - b) L$ , $a K + C_{w} + C_{g}$ , $(1 - a) K - r e Q - T Q$	+, +, ×	Unstable	\
E₇ (0,1,1)	$(1 - b) L - u h s$ , $C_{w} + C_{g} + b L - T Q$ , $(T + r e) (Q + h s) - (1 - a) K$	-, -, -	ESS	③
E₈ (1,1,1)	$(1 - b) L - u h s$ , $a K + C_{w} + C_{g} + T h s + b L$ , $(1 - a) K - (T + r e) (Q + h s)$	-, +, ×	Unstable	\
E₉ (x₁,1, z₁)	$λ_{1} = \frac{b L (r e h s - K)}{(a K + r e Q + T Q + T h s)} + (L - u h s)$ , $λ_{2} = - λ_{3} = k_{1}$	×, +, -	Unstable	④
E₁₀ (x₁,0, z₁)	$λ_{1} = \frac{b L K}{(a K + r e Q + T Q)} - (L - u h s)$ , $λ_{2} = - λ_{3} = k_{2}$	+, +, -	Unstable	⑤

Note: "×" indicates uncertainty, and x₁, y₁, z₁ represent the coordinates of the equilibrium point. If the conditions corresponding to the equilibrium point are not satisfied, it is considered unstable or meaningless. ①rehs-K<0, TQ-C_g-C_w-bL<0; ②K-rehs<0; ③TQ-C_g-C_w-bL>0, (T+re)(Q+hs)-(1-a)K<0; ④TQ-C_g-C_w-bL>0, rehs-K<0, (T+re)(Q+hs)-(1-a)K>0; ⑤TQ-C_g-C_w >0, TQ+reQ-(1-a)K>0.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Evolution and Equilibrium of a Low Carbon E-commerce Closed-Loop Supply Chain Recycling System: An Evolutionary Game Approach

Abstract

1. Introduction

2. Literature Review

2.1. Recycling in E-CLSC

2.2. LC-CLSC with Government Participation

3. Model Assumptions and Construction

3.1. Model Assumptions

3.2. Model Construction

4. Model Analysis

4.1. Analysis of Remanufacturer’ Strategy Stability

4.2. Analysis of Platform’ Strategy Stability

4.3. Analysis of Government’ Strategy Stability

4.4. Stability Analysis of Equilibria in Three-Player Evolutionary Game Systems

5. Result and Discussion

6. Conclusions

References

MDPI Initiatives

Important Links

Subscribe