Prerpints.org logo
Preprint
Article

Strontium Ferromolybdate/Strontium Molybdate Core-Shell Ceramics—A Nanogranular Magnetic Material Possessing a Natural Core-Shell Structure

Altmetrics

Downloads

106

Views

30

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

15 November 2023

Posted:

16 November 2023

You are already at the latest version

Alerts
Abstract
In this work, we demonstrate the preparation of easy-to-fabricate nanogranular, strontium ferromolybdate/strontium molybdate core-shell ceramics and examine their properties including tunnel magnetoresistance, magnetic field sensitivity and temperature coefficient of the tunnel magnetoresistance. The tunnel magnetoresistance of nanogranular, strontium ferromolybdate/strontium molybdate core-shell ceramics was modeled yielding values suitable for magnetoresistive sensor application. Such structures possess a narrow peak of magnetic flux sensibility located at about 125 mT. For magnetic flux measurement, single domain granules with superparamagnetic behavior should be applied. The predicted TMR magnetic flux sensitivities for granules with superparamagnetic behavior amount to about 7.7 % per T and 1.5 % per T for granules sizes of 6.8 nm and 4 nm, respectively. A drawback of the tunnel magnetoresistance of such nanogranular core-shell ceramics is the unacceptable large value of the temperature coefficient. Acceptable values, lower than 2 % per K, are obtained only at low temperatures (less than 100 K) or large magnetic flux densities (exceeding 6 T). Therefore, a Wheatstone bridge configuration should be adopted for magnetoresistive sensors design to compensate the effect of temperature.
Keywords: 
Subject: Physical Sciences  -   Condensed Matter Physics

1. Introduction

In 1994, a large tunnel magnetoresistance (TMR) of 8 % at 1.2 T and room temperature was obtained in Co-Al-O nanogranular films with a resistivity of about 100 m×cm [1]. These films consist of two phases, that is superparamagnetic, metallic Co granular grains and Al2O3 narrow intergrains. In such structures, the electrical conductance is governed by tunneling between Co grains through Al2O3 intergrains. Later in 2001, TMR values up to about 14 % at room temperature and 1 T were obtained in nanogranular 32 vol%(Fe0.51Co0.49)–(Mg–F) thin films [2]. Here, the (Mg-F) intergrains were in the crystalline MgF2 state enabling a higher TMR compared to Co-Al-O film with an amorphous structure of the Al-oxide intergrain.
Similar mechanisms occur in Sr2FeMoO6- (SFMO) ceramics where the transport properties are dominated by spin-polarized intergrain tunneling through insulating grain boundaries [3]. Under specific synthesis conditions, SFMO ceramics consist of SrMoO4 (SMO) intergrain energy barriers between conductive bulks of SFMO grains induced by a small oxygen excess during material fabrication [4]. The ease of forming SMO shells around SFMO grains simply by excess oxygen during synthesis makes SFMO an easy-to-fabricate, natural core-shell material.
A consequence of intergranular tunneling in such SFMO/SMO core-shell structures is the large low-field magnetoresistance obtained in SFMO ceramics [5,6,7]. Here, the magnetoresistance is governed by the samples microstructure (especially the grain size and the thickness of the dielectric intergrain layers) [8]. Samples with smaller grain size are preferable as they demonstrate larger magnetoresistance [9].
In a recent study, the intergranular resistivity, tunnel magnetoresistance and magnetic field sensibility of superparamagnetic (SPM) and ferro(ferri)magnetic (FM) granular materials were examined theoretically [10]. Starting with the tunnel resistance of a granular metal network in which the grains are interconnected by insulating barriers, the tunnel magnetoresistance was calculated considering the temperatures dependencies of magnetization, spin polarization, and both the temperature and magnetic flux dependencies of magnetization as well as the tunneling barrier height. However, nanogranular SFMO/SMO core-shell ceramics have not been adequately addressed in [10]. This gap is now closed in this work.

2. Materials and Methods

The citrate-gel technique was used for synthesis of nanogranular SFMO ceramics using ultra-high purity Sr(NO3)2, Fe(NO3)3•9H2O, (NH4)6Mo7O24 and citric acid monohydrate C6H8O7H2O as initial reagents. To obtain a colloidal sol, aqueous solutions of Sr(NO3)2 and Fe(NO3)3•9H2O were mixed in a molar ratio of Sr/Fe = 2:1. Citric acid was added to the solution in a molar ratio of citric acid/Fe = 6.5:1. After that, an aqueous solution of (NH4)6Mo7O24 was added to the solution of strontium and iron nitrates in a molar ratio Mo/Fe = 1:1. Then, ethylenediamine was added upon constant stirring by means of an IKA C-MAG HS7 magnetic stirrer, until the pH of the solution reached 4. Thereafter, the substance was dried at a temperature of 80 °C. The resulting precipitate was placed in a furnace at a temperature of 100 °C, followed by heating at a rate of 0.4 °C min-1 up to 200 °C, a dwell time of 18 h, and a cooling-down with the time constant of the furnace. The resulting solid foam which was crushed and then subjected to heat treatment at 500 °C in an oxygen atmosphere under the pressure p(O2) = 0.21•105 Pa for 10 h. The final SFMO synthesis was carried out in a reducing ambient of a 5%H2/Ar gas mixture at 900 °C for 4 h in several stages. Single-phase SFMO powders were pressed into tablets with a diameter of 10 mm and a thickness of 3 mm under a pressure of 4 GPa at 530 °C for 1 min. Dielectric SMO shells were formed in these samples on the surface of the SFMO grains by annealing at 530 °C in an Ar flow with a rate of 11 sccm for 5 h. Details of sample fabrication were already described elsewhere [7,11,12].
In the dielectric regime, electrical conduction of granular materials results from transport of electrons and holes by tunneling from one isolated metallic grain to the next. A charge carrier in a granular material contributes to electrical conductivity when an electron is removed from a neutral grain and placed on a neighboring neutral grain. Such a process requires charging energy Ec per grain of [13]:
E c = e 2 d F ( w , d ) ,
where e is the electronic charge, d the granular or grain size, w the separation between the grains (e.g. the tunneling barrier width), and F(w,d) a function whose form depends on shape and arrangement of the grains. Assuming the grain size d to be much larger than the barrier width w, Ec is approximately given by [14]:
E c ≈ 4 e 2 w ε ε 0 d 2 ,
with ε and ε0 the dielectric and vacuum permittivities, respectively. Since the charging energy is reciprocal to the grain diameter, charging effects become significant at small grain sizes. In the case of nanogranular SFMO/SMO core-shell ceramics fabricated by the citrate-gel method with d = 75 nm and w = 1.24 nm [7], and assuming εSrMoO3 ≈ 10 [15], Ec amounts to a value of Ec ≈ 1.6 meV. This should be compared with a value of Ec ≈ 1 meV obtained after saturation of the insulating SMO phase at grain boundaries in mechanically ball-milled polycrystalline SFMO pellets [16]. Such ball-milled powders possess a grain size of about 100 nm after 6 h of grinding [17], i.e. approximately the same grain size as the considered nanogranular SFMO/SMO core-shell ceramics.
A lnσ versus T-1/2 plot with σ the electrical conductivity, yields the constant [14,18]
C = w χ E c ,
where in our case wχ is a value in the order of about 2 [19,20]. Using the lnσ versus T-1/2 plot, we find C ≈ 4.7 meV for zero magnetic field conductivities of nanosgranular SFMO/SMO core-shell ceramics fabricated by the citrate-gel method in the temperature range of 10-50 K [11]. C values of Co-Al-O insulating granular films were 9.48 meV for Co36Al22O42, 2.15 meV for Co46Al19O35, 1.55 meV for Co52Al20O28, and 0.78 meV for Co54Al21O25 [19]. In other insulating granular metal films, the lnσ versus T-1/2 plot results in much higher C values decreasing with increasing metal fraction from 1.1 eV (0.08%) to 0.13 eV (0.44%) in Ni-SiO2 composites, from 1.1 eV (0.04%) to 0.20 eV (0.18%) in Pt-SiO2 composites, and from 120 meV (0.18%) to 4 meV (0.38%) in Au-Al3O4 composites [14].
In the next step, we consider a metal network in which the metal grains are interconnected by insulating barriers. The positive-negative pairs of charged grains induced by electron tunneling through the barriers are assumed to be roughly of the same size. In this case, each grain contributes about half of the charging energy Ec resulting in density of charge carriers proportional to exp(-Ec/2kT). Thus, the resistivity caused by tunneling is given by [14,18]:
ρ T = ρ 0 exp f χ w + E c 2 k T ,
where f is a barrier shape factor with f = 2 for rectangular barriers and f = π/2 for parabolic barriers, χ is the reciprocal localization length of the wave function:
χ = 2 m * V 0 ℏ 2 ,
with m* is the effective electron mass, V0 the barrier height, ħ is the reduced Planck constant, w the barrier width, k the Boltzmann constant, T the absolute temperature and ρ0 the bulk resistivity. Note that we are considering sufficiently thin barriers in the order of 1-3 nm where direct tunneling occurs which is not disturbed by localized states in the thin barrier film [21].
Considering a constant parameter C [14,18] and assuming a rectangular barrier (f = 2) the argument of the exponent in Equation (4) becomes
f ( w ) = 2 χ w + C 2 χ w k T ,
which possesses a minimum at [14]:
w min = 1 2 χ C k T .
Then the corresponding resistivity minimum between two nearest neighbor grains which are equal or nearly equal in size yields [14]:
ρ min ( T ) ∝ exp 2 C k T ,
The value ρmin(T) governs the temperature dependence of the network resistivity ρ(T) since tunneling occurs via paths which makes the exponential factor of resistivity lowest.
The spin-dependent tunneling through a barrier between two ferromagnetic grains is a function of the angle θ between the grain magnetizations. Neglecting the correlations between magnetic moments of neighboring grains, the average 〈cos θ〉 over all pairs of grains for angles between 0 and π represents the square of the relative magnetization m2 = (M/Ms)2, i.e. the ratio of magnetization M to the saturation one Ms. Finally, we arrive at an intergrain resistivity amounting to [22]:
ρ = ρ 0 1 + m 2 P 2 exp 2 C k T ,
with P the spin polarization. Similarly, the intergrain tunnel magnetoresistance of a network of tunnel junctions whose electrodes are double-perovskite grains with an insulating oxide layer in between is given by [23]:
T M R = ρ ( B ) ρ ( 0 ) − 1 ≈ 1 1 + m ( B , T ) 2 P 2 − 1 = − m ( B , T ) 2 P 2 1 + m ( B , T ) 2 P 2 ,
where ρ(B) is the resistivity for a given magnetic flux density B, m(B,T) the relative magnetization for given values of magnetic flux B and temperature T.
In granular systems with a broad distribution in granule size, it is highly probable that large granules are well separated from each other due to their low density. This is given by the fact that granules are more separated the larger the granule size is. As a result, a number of smaller granules exist separating the large ones. Here, the ordinary tunnelling of an electron from a large granule to a small one increases the charging energy Ec, Equation (2), and suppresses tunnelling by the Coulomb blockade at low temperatures. In this case, higher-order tunnelling comes into play, i.e., the dominant contribution to the tunnelling current now comes from higher-order processes of spin-dependent tunnelling where the carrier is transferred from a charged large granule to the neighbouring neutral large granule through an array of small granules, using co-tunnelling of (n+1) electrons. The TMR is then given by [19]:
T M R = 1 ( 1 + m 2 P 2 ) 1 + n * − 1 ,
with
n * = E c 8 χ * w k T = D T ,
with χ∗ = pχ where p is a constant defined in [19], and n* is a fitting parameter of the higher-order tunneling processes. Note that we have rewritten equation (11) according to the definition of the magnetoresistance in this work given in equation (10). In a granular Co-Al-O system, n*(T→0) takes a value of 1.6, so that one or two small granules intervene between larger ones in the higher-order processes. Higher-order tunneling increases the TMR at low temperatures. On the other hand, higher-order tunneling is negligible at room temperature since here n* tends to zero [10].
For m2P2 << 1 equation (10) simplifies to:
T M R ≈ − 1 + D T ⋅ m 2 P 2 ,
Both the temperature dependence and the field dependence of the relative magnetization m of FM SFMO were calculated following [24]. For the temperature dependence this yields:
m 2 ( T , B = 0 ) = ∑ i a i T C − T T C i ,
Using m(T) values from [23,25], we obtained a1 = 1.89, a2 = -1.97, a3 = 2.2 and a4 = -1.14 for the coefficients of Equation (14) [24].
At sufficiently high magnetic fluxes when magnetic interactions may be still neglected, the magnetic flux density dependence of m may be modeled by means of a traditional analysis of the approach of magnetization to saturation [26,27]. As a result, the magnetic flux dependence of the relative magnetization is given by:
m ( B ) = 1 − ∑ i b i / 2 B i / 2 + κ B ,
with i = 1,2,3, 4 for point, line, and plane forces as well as uniform forces throughout an extended volume forces, respectively.
The κB term is often referred to as the so-called paramagnetism-like term [28]. It represents the high field magnetization resulting from an increase in spontaneous magnetization by the application of a field [29]. This term is usually small at temperatures well below the Curie point and may often be neglected [30] (p.325).
Point defects in ceramics and granular materials are concentrated at grain boundaries representing only a small part of the total sample volume. Consequently, the b1/2/B1/2 term will be small or even negligible at higher magnetic fluxes. The value of b1/2 = 0.00085 T1/2 derived based on data in [31,32], will play a role only at small magnetic fluxes B < 85 mT.
The b1/B term in equation (15) is referred to as the magnetic hardness [28]. It has been observed to be constant at high magnetic fluxes [33] and was attributed to internal stresses produced by dislocations [26], especially by pairs of dislocations of opposite sign separated by a short distance smaller than the magnetic decay distance [34]. Another theory originates b1 from the leakage field in ferromagnetic materials [35]. In general, this constant is attributed to inclusions or microstress [30] (p.325). For example, it represents the demagnetizing effects of inhomogeneities such as grain boundaries, dislocations and nonmagnetic inclusions [33].
The b2/B2 term in equation (15) is attributed to crystal anisotropy. Furthermore, it was shown that dislocation pairs of different sign separated by a long distance and surplus dislocations of one sign contribute to this term [34]. The b2/B2 term is dominant for extremely high magnetic fluxes, while the b1/B term is dominant at intermediate magnetic fluxes [36]. Thus, the b1/B term is effective only in a limited field range. If one only considers the term b1/B, for nanogranular SFMO/SMO core-shell ceramics made by means of the citrate gel method [37], the m(B) characteristics is well approximated by b1 = 0.05 T below 0.1 T, b1 = 0.085 T in the region 0.3-1 T and b1 = 0.02 T in the region 1.5 -4 T. On the other hand, the m(B) curve of a similar sample measured in a different setup [38] in this approach yields b1 ≈ 0.3 T for magnetic fluxes in the range 2-10 T. The values given by the authors of [38] are b1 = 0.968 T and b2 = 0.00292 T2.
Neglecting the influence of internal strain, a theoretical value of the coefficient of the b2/B2 term, which is attributed to magnetocrystalline anisotropy (MA) is given by [39]:
m ( B ) = 1 − ∑ i b i / 2 B i / 2 + κ B ,
with K1 the uniaxial anisotropy constant, and n the volumetric density of the formula units (f.u.), that is the inverse of the formula unit volume. Here, the numerical coefficient 8/105 applies to cubic anisotropy of randomly oriented polycrystalline samples. Table 1 compiles the values of b2MA calculated using Equation (16) for a saturated magnetization of Ms = 4 µB f.u.-1 and n = 8.086×1027 f.u. m-3 using different values of the uniaxial anisotropy constant K1. Note that a wide range of values K1 lead to a large uncertainly of the coefficient b2MA.
The contribution of internal strain (IS) to b2 is given by [42]:
b 2 I S = 3 5 ⋅ λ s σ i M s n 2 ,
where λs is the coefficient of magnetostriction and σi the internal strain. Taking λs = 10-4 [30] (chapter 8), [43] and 〈σi〉 = 150 MPa-600 MPa [44], we arrive at b2IS = 0.0015-0.0240 T2.
The coefficient b3/B3 of Equation (15) which is determined also by magnetocrystalline anisotropy may be written for cubic anisotropy of randomly oriented polycrystalline samples as [45,46]:
b 3 M A ≈ 8 105 ⋅ 72 11 ⋅ 13 ⋅ K 1 M s n 3 ≈ 0.03836 ⋅ K 1 M s n 3 ,
However, this term is negligible compared to the b2/B2 term at magnetic fluxes B > K1/Msn (0.1…0.5 T in our case). Since the coefficients bi are sensitive to point defects (vacancies, antisite positions, impurity ions), line defects (dislocations) and area defects (stacking faults, grain, twin and antiphase boundaries), they are highly dependent on the synthesis conditions of the SFMO ceramics.
For comparison, we consider Fe and Co applying a phenomenological model of the temperature dependence of the relative magnetization given by [47],
m ( T ) = 1 − T T C p β ,
The corresponding fitting parameters p and β are compiled in Table 2.
In sufficiently small granules, i.e. below a critical size of [10]:
d c r s p m = π ⋅ ln ( τ m / τ 0 ) ⋅ k T 6 ⋅ K ( T ) 1 / 3 ,
the magnetization can randomly flip direction under the influence of temperature. This applies to Fe, Co and SFMO with sizes of ca. 1 nm and 1.7 nm at 4 K as well as sizes of 5-6 nm and 12 nm at 300 K, respectively, In the absence of an external magnetic field, when the time used to measure the magnetization of the nanosized granules is much longer than the typical time between two flips (called Néel relaxation time), the granule magnetization appears to be in average zero. The magnetic behavior resembles a paramagnetic exhibiting an unusual high magnetic susceptibility attributed to a large number of formula units oriented in the same direction within a single magnetic domain. Such a magnetic behavior is known as superparamagnetism. Granular networks of noninteracting superparamagnetic (SPM) granules were modeled already in [10]. The reduced magnetization of SPM granules is determined by the Langevin function L [48]:
m = L ( ζ B ) = coth ( ζ B ) − 1 / ( ζ B ) ,
where µ is the total magnetic moment of the granule depending on its size and ζ = µ/kT.
Tunneling spin polarization and the interface magnetization follow the same temperature dependence [49,50]. As a result, based on the theory of spin waves [51], the spin polarization resembles the spontaneous magnetization behavior at low temperatures known as Bloch´s T3/2 law of variation of saturation moment with temperature near the absolute zero:
P ( T ) = P 0 ( 1 − g ⋅ T 3 / 2 ) ,
Here, P0 is the spin polarization of ordered SFMO at zero temperature and g is a fitting parameter which in the case of magnetization is generally larger for the surface than for the bulk [49]. It is very sensitive to surface contaminants [52]. For the sake of simplicity, the Bloch´s T3/2 coefficients g were estimated by means of the Curie temperature TC:
g = T C − 3 / 2 .
They are in satisfactory accordance with previous experimental data of 0.1–0.6×10-5 for Co/Al2O3 [53], 1.9×10-4 for La2/3Sr1/3MnO3/SrTiO3, 5.1x10-5 for La2/3Sr1/3MnO3/LaAlO3, 1.58x10-4 for La2/3Sr1/3MnO3/TiO2 [54], and 1.31x10-4 derived from the intergranular TMR in Ba0.8Sr0.2FeMoO6 [23].
Now, we take into account that the spin polarization has a similar dependence on the antisite disorder (ASD), that is the fraction of B-site ions, Fe or Mo, on wrong sublattice sites which varies from 0 (corresponding to a complete order) up to 0.5 (describing a completely random Fe-Mo site occupancy) as the magnetization [55]. As a result, the spin polarization P was calculated following [56] by:
P ( T ) = P 0 ⋅ ( 1 − 2 A S D ) ⋅ ( 1 − g ⋅ T 3 / 2 ) .
With regard to Equation (10), the magnetic field sensitivity of granular FM materials amounts to:
d T M R d B = − 2 m ( B , T ) P 2 ⋅ ∂ m / ∂ B ( 1 + m ( B , T ) 2 P 2 ) 2 ,
with
∂ m ∂ B = m ( T , 0 ) ⋅ 1 2 a 1 / 2 B − 3 / 2 + a 1 B − 2 + 2 a 2 B − 3 + ... ,
For SPM granules the magnetic field sensitivity yields [10}:
d ( T M R ) d B = − 2 P 2 d L ( ζ B ) / d B 1 + P 2 L ( ζ B ) 2 = − 2 P 2 ζ ⋅ ( ζ B ) − 2 − sinh − 2 ( ζ B ) 1 + P 2 ⋅ coth ( ζ B ) − 1 / ζ B 2 2 .
Temperature affects the measuring accuracy of any sensor. Thus, there always remains a small temperature inaccuracy in the considered temperature range despite a number of compensation measures. This inaccuracy is often expressed as temperature coefficient TC. It expresses the relation between a change in the sensing physical property and the change in temperature that causes it. Consequently, it represents the relative change of the sensing physical property with a given change in temperature. Correspondingly, the TC of the TMR is given by:
T C T M R = 1 T M R ⋅ d ( T M R ) d T .
The particular case of Equation (13) yields a temperature coefficient of the TMR amounting to:
T C T M R = 1 T M R d ( T M R ) d T = D 1 / 2 2 T 3 / 2 ( 1 + D / T )
In the calculations of this work, numerical derivatives of experimental data were evaluated by approximation of experimental curves by quartic polynomials.

3. Results and discussion

Table 3 compiles the parameters used for the calculations in this work.
Figure 1 illustrates a comparison of the TMR values, calculated by means of Equation (10), with experimental data of nanogranular SFMO/SMO core-shell ceramics from [11]. While the temperature dependence is well reproduced, the magnetic flux dependence is satisfactorily described only in the middle region of B where the values of the coefficient bi are most valid. Note that the calculated field dependence of the magnetoresistance strongly depends on the coefficients of Equation (15) which are subject to large uncertainties. As a result, the achieved TMR values are suitable for practical applications.
Figure 2 represents the experimental magnetic field sensitivity of FM, nanogranular SFMO/SMO core-shell ceramics. The shown curve is in good qualitative agreement with experimental data of ceramic SFMO annealed in reducing atmosphere at 10 K [60] and with calculations from [10] for nanosized SFMO ceramics using Equation (25).
The sharp sensitivity peak illustrates that nanosized SFMO/SMO core-shell granules are not suitable as a magnetic field sensor. For this purpose, superparamagnetic granules should be used. This is illustrated in figure 3 depicting the magnetic field sensitivity of superparamagnetic noninteracting SFMO granules calculated by means of equation (27). Assuming SFMO = 5.68 kg m-3 and µ = 4 µB f.u.-1, a total magnetic moment µ = 2000 µB corresponds to a granule size of 4 nm while µ = 10000 µB corresponds to a granule size of 6.8 nm Since the spin polarization of SFMO is significantly higher than that of Co and Fe, the magnetic field sensitivity of SFMO will be correspondingly larger. Contrarily to ferromagnetic SFMO granules, superparamagnetic ones provide a nearly constant magnetic field sensitivity at low magnetic fields up to 400 mT what is beneficial for low field magnetic sensor application (Figure 3). The predicted TMR magnetic flux sensitivities for granules with superparamagnetic behavior amount to about 7.7 % T-1 and 1.5 % T-1 at room temperature for granules sizes of 6.8 nm and 4 nm, respectively.
Figure 4 shows the temperature coefficients of nanogranular SFMO/SMO core-shell ceramics deduced from the numerical derivatives of the experimental data in figure 1 in comparison with data of Fe und Co low field values deduced from the numerical derivative of the TMR calculated by means of Equation (10) using Equations (19), (22) and (23) as well as data of superparamagnetic SFMO at 100 mT deduced from the numerical derivative of the TMR calculated by means of equation (10) using Equations (21), (23) and (24). The relative small TC of ferromagnetic Co and Fe is a consequence of their much weaker temperature dependence of the spin polarization attributed to higher Curie temperatures. Since the TC value of SPM SFMO reduces with increasing magnetic flux, superparamagnetic SFMO is superior to ferrimagnetic SFMO/SMO core-shell structures with the exception of very low temperatures. Note that Equation (29) which is valid for small m2P2 << 1 yields a positive, decreasing with magnetic flux TCs. In the case of of strongly disordered SFMO, the TC is in the order of 0.1 % K-1. According to Equation (11), co-tunneling of (n+1) electrons by carrier transfer from a charged large granule to the neighbouring neutral large granule through an array of small granules increases the TC. Considering an acceptable TC in the order of 2 % K-1, nanogranular SFMO/SMO core shell ceramics are suitable for application only at low temperatures (less than 100 K) or high magnetic flux densities (exceeding 6 T).

4. Conclusions

SFMO nanopowders were synthesized by means of the citrate-gel technique. The presynthesized SFMO nanopowders were first saturated with oxygen at elevated temperatures and subsequently subjected to a higher temperature thermal treatment in a reducing ambient. SFMO/SMO core shell structures were formed in hot-pressed single phase SFMO nanopowders by a third thermal treatment at elevated temperature in a nearly inert atmosphere in the presence of low but sufficient oxygen partial pressure.
The tunnel magnetoresistance of nanogranular, SFMO/SMO core-shell ceramics was modeled yielding values suitable for magnetoresistive sensor application. However, such structures possess a narrow peak of magnetic flux sensibility at about 125 mT hindering practical applications.
For magnetic flux measurement, single domain granules with superparamagnetic behavior should be applied. This provides a nearly constant magnetic field sensitivity at low magnetic flux densities (up to about 50 mT). The predicted TMR magnetic flux sensitivities for granules with superparamagnetic behavior amount to about 7.7 % T-1 and 1.5 % T-1 for granules sizes of 6.8 nm and 4 nm, respectively.
A drawback of the TMR in nanogranular, SFMO/SMO core-shell ceramics is the unacceptable large value of the temperature coefficient. Acceptable values of about 2 % K-1 are obtained only at low temperatures (less than 100 K) or large magnetic flux densities (exceeding 6 T). Therefore, a Wheatstone bridge configuration should be adopted for magnetoresistive sensors to compensate the effect of temperature.

Author Contributions

Conceptualization, G.S.; methodology, N.K.; software, E.A.; validation, G.S., N.K., and M.Y., formal analysis, E.A., investigation, G.S., N.K. and M.Y., resources, N.K. and G.G., writing—original draft preparation, G.S.; writing—review and editing, N.K. and G.G.; visualization, E.A.; supervision, N.K. and G.G.; project administration, N.K. and G.G.; funding acquisition, G.S., N.K. and G.G. All authors have read and agreed to the published version of the manuscript.

Funding

This work was funded by the EU project H2020-MSCA-RISE-2017-778308- SPINMULTIFILM.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Acknowledgments

The authors thank Nikolai A. Sobolev (University of Aveiro) for helpful discussions and suggestions. They are also grateful to Maxim Bushinsky (SSPA “Scientific-Practical Materials Research Centre of the NAS of Belarus) for the measurements of electro-physical and galvanomagnetic characteristics of the experimental samples.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Fujimori, H; Mitani, S.; Ohnuma, S. Tunnel-type GMR in metal-nonmetal granular alloy thin films. Mater. Sci. Eng. B 1995, 31(1-2), 219-223. [CrossRef]
  2. Kobayashi, N.; Ohnuma, S.; Masumoto T.; H. Fujimori, H. (Fe–Co)–(Mg-fluoride) insulating nanogranular system with enhanced tunnel-type giant magnetoresistance. J. Appl. Phys. 2001, 90(8), 4159-4162. [CrossRef]
  3. Kim, T.H.; Uehara, M.; Cheong, S.-W.; Lee, S. Large room-temperature intergrain magnetoresistance in double perovskite SrFe1-x(Mo or Re)xO3. Appl. Phys. Lett. 1999, 74(12), 1737-1739. [CrossRef]
  4. Niebieskikwiat, D.; Caneiro, A.; S!anchez, R.D.; Fontcuberta, J. Oxygen-induced grain boundary effects on magnetotransport properties of Sr2FeMoO6+Phys. Rev. B - Condens. Matter Mater. Phys. 2001, 64, 180406 (4pp), DOI: PhysRevB.64.180406.
  5. Sharma, A.; Berenov, A.; Rager, J.; Branford, W.; Bugoslavsky, Y.; Cohen, L.F.; MacManus-Driscoll, J.L. Enhanced intergrain magnetoresistance in bulk Sr2FeMoO6 through controlled processing. Appl Phys Lett. 2003, 83(12), 2384–2386. [CrossRef]
  6. Gaur, A.; Varma, G.D. (2007) Enhanced magnetoresistance in double perovskite Sr2FeMoO6- through SrMoO4 tunneling barriers. Mater. Sci. Eng. B 2007, 143(1–3). 64–69. [CrossRef]
  7. Suchaneck G.; Kalanda N.; Artiukh E.; Yarmolich M.; Sobolev N.A. Tunneling conduction mechanisms in strontium ferromolybdate ceramics with strontium molybdate dielectric intergrain barriers. J. Alloys Comp. 2020, 860, 158526 (6pp.), DOI: j.jallcom.2020.158526.
  8. Serrate D.; De Teresa J.M.; Ibarra M.R. Double perovskites with ferromagnetism above room temperature. J. Phys: Condens. Matter. 2006, 19(2), 023201. [CrossRef]
  9. Yuan C.L.; Zhu Y.; Ong P.P.; Ong C.K.; Yu T.; Shen Z.X. Grain boundary effects on the magneto-transport properties of Sr2FeMoO6 induced by variation of the ambient H2-Ar mixture ratio during annealing. Physica 2003, B 334(3–4), 408–412. [CrossRef]
  10. Suchaneck, G. Tunnel magnetoresistance of granular superparamagnetic and ferrimagnetic structures. Nanomater. Sci. Eng. 2022, 4(1), 10-20. [CrossRef]
  11. Demyanov, S.; Kalanda, N.; Yarmolich, M.; Petrov, A.; Lee, S.H.; Yu, S.C.; Oh, S.K.; Kim, D.H. Characteristic features of the magnetoresistance in the ferrimagnetic (Sr2FeMoO6-δ) - dielectric (SrMoO4) nanocomposite. AIP Adv. 2018, 8, 055919. [CrossRef]
  12. Kalanda, N.; Yarmolich, M.; Teichert, S.; Bohmann, A.; Petrov, A.; Moog, D.; Mathur, S. Charge transfer mechanisms in strontium ferromolybdate with tunneling barriers. J. Mater. Sci. 2018, 53, 8347–8354. [CrossRef]
  13. Sheng, P.; B. Abeles B.; Arie, Y. Hopping conductivity in granular metals, Phys. Rev. Lett. 1973, 31(1), 44-47. [CrossRef]
  14. Abeles, B.; Sheng P.; Coutts M.D.; Arie Y. Structural and electrical properties of granular metal films, Adv. Phys., 1975, 24(3), 407-461. [CrossRef]
  15. Vidya, S.; John, A.; Solomon S.; Thomas J.K., Optical and dielectric properties of SrMoO4 powders prepared by the combustion synthesis method, Adv. Mater. Res. 2012, 1(3), 191-204. [CrossRef]
  16. Wang, K.; Sui, Y. Influence of the modulating interfacial state on Sr2FeMoO6 powder magnetoresistance properties. Solid State Commun. 2004, 129, 135-138. [CrossRef]
  17. Alvarado-Flores, J.J.; Mondragón-Sánchez, R.; Ávalos-Rodríguez, M.L.; Alcaraz-Vera, J.V.; Rutiaga-Quiñones, J.G.; Guevara-Martínez, S. J. Synthesis, characterization and kinetic study of the Sr2FeMoO6- double perovskite: New findings on the calcination of one of its precursors. Int. J. Hydrogen Energy 2021, 46(51), 26185-26196. [CrossRef]
  18. Helman, J. S.; Abeles B. Tunneling of spin-polarized electrons and magnetoresistance in granular Ni films. Phys. Rev. Lett. 1976, 37(21), 1429-1432. [CrossRef]
  19. Mitani, S.; Takahashi, S.; Takanashi, K.; Yakushiji, K.; Maekawa, S.; Fujimori, H. Enhanced magnetoresistance in insulating granular systems: Evidence for higher-order tunneling, Phys. Rev. Lett. 1998, 81(13), 2799-2802. [CrossRef]
  20. Fisher, B.; Genossar, J.; Chashka, K.B.; Patlagan L.; Reisner, G.M. Intergrain tunnelling in the half-metallic double-perovskites Sr2BB'O6 (BB'= FeMo, FeRe, CrMo, CrW, CrRe). EPJ Web of Conferences, 2014, 75, 01001. [CrossRef]
  21. Xu, Y.; Ephron, D.; Beasley, M.R. Directed inelastic hopping of electrons through metal-insulator-metal tunnel junctions. Phys. Rev. B - Condens. Matter Mater. 1995, 52(4), 2843-2859. [CrossRef]
  22. Inoue J.; Maekawa, S. Theory of tunneling magnetoresistance in granular magnetic films, Phys. Rev. B - Condens. Matter Mater. 1996, 53(18), R11927-R11929. [CrossRef]
  23. Serrate, D.; De Teresa, J.M.; Algarabel, P.A.; Ibarra, M.R.; Galibert, J. Intergrain magnetoresistance up to 50 T in the half-metallic (Ba0.8Sr0.2)2FeMoO6 double perovskite: Spin-glass behavior of the grain boundary, Phys. Rev. B - Condens. Matter Mater. 2005, 71, 104409. [CrossRef]
  24. Artiukh E.; Suchaneck, G. Intergranular magnetoresistance of strontium ferromolybdate ceramics caused by spin-polarized tunneling. Open Ceram. 2021, 7, 100171 (5pp). [CrossRef]
  25. Kobayashi, K.I.; Kimura, T.; Sawada, H.; Terakura, K.; Tokura, Y. Room-temperature magnetoresistance in an oxide material with an ordered double-perovskite structure, Nature 1998, 395 (1998), 677–680. [CrossRef]
  26. Brown, W.F Theory of the approach to magnetic saturation, Phys. Rev. 1940, 58(8), 736–743. [CrossRef]
  27. Brown, W.F., Micromagnetics, 1st ed.; Interscience Publ., New York, USA, 1963;.
  28. Zhang, H., Zeng, D., Liu, Z. The law of approach to saturation in ferromagnets originating from the magnetocrystalline anisotropy. J. Magn. Magn. Mater. 2010, 322, 2375–2380. [CrossRef]
  29. Yoon, D.H., Muksin, Raju, K. Controlling the magnetic properties of nickel ferrites by doping with different divalent transition metal (Co, Cu, and Zn) cations. J. Supercond. Nov. Magn. 2016, 29, 439–445. [CrossRef]
  30. Cullity, B.D.; Graham, C.D. Introduction to magnetic materials, 2nd ed.; Wiley: Hoboken (NJ), USA, 2009.
  31. Navarro, J.; Nogués, J.; Muñoz, J.S.; Fontcuberta, J. Antisites and electron-doping effects on the magnetic transition of Sr2FeMoO6, Phys. Rev. B - Condens. Matter Mater. 2003, 67, 174416 (6pp). [CrossRef]
  32. Navarro, J.; Balcells, Ll.; Sandiumenge, F,; Bibes, M,; Roig, A,; Martínez, B,; Fontcuberta, J Antisite defects and magnetoresistance in Sr2FeMoO6 double perovskite, J. Phys.: Condens. Matter 2001, 13(37), 8481-8488. [CrossRef]
  33. Matin M.A.; Hossain, M.N.; Hakim M.A.; Islam M.F. Effects of Gd and Cr co-doping on structural and magnetic properties of BiFeO3 nanoparticles. Mater. Res. Express 2019, 6, 055038 (10 pp). [CrossRef]
  34. Brown, W.F. The effect of dislocations on magnetization near saturation. Phys. Rev. 1941, 60, 139-147. [CrossRef]
  35. Neél, L. La loi d'approche en a: H et une nouvelle théorie de la dureté magnétique. J. Phys. Radium 1948, 9(5), 184-192 DOI: ff10.1051/jphysrad:0194800905018400.
  36. Grady, D.E. Origin of the linear term in the expression for the approach to saturation in ferromagnetic materials. Phys. Rev. B - Condens. Matter Mater. 1971, 4(11), 3982-3989. [CrossRef]
  37. Suchaneck, G.; Kalanda, N.; Yarmolich, M.; Artiukh, E.; Gerlach, G., Sobolev, N.A. Magnetization of magnetically inhomogeneous Sr2FeMoO6-δ nanoparticles. Electron. Mater. 2022, 3(1), 82-92. [CrossRef]
  38. Kalanda, N.; Yarmolich, M.; Burko, A.; Temirov, A.; Kislyuk, A.; Demyanov, S.; Lenz, K.; Lindner, J.; Kim, D.-H. Superparamagnetism and ferrimagnetism in the Sr2FeMoO6–δ nanoscale powder, Ceram. Int., 2022, 48(16), 23931-23937. [CrossRef]
  39. Akulov, N.S. Über den Verlauf der Magnetisierungskurve in starken Feldern. Z. Physik 1931, 69, 822–831. [CrossRef]
  40. Nosach, T.; Mullady, G.; Leifer, N.; Adyam, V.; Li, Q.; Greenbaum, S.; Ren, Y. Angular dependence of spin-wave resonance and relaxation in half-metallic Sr2FeMoO6 films. J. Appl. Phys. 2008, 103, 07E311. [CrossRef]
  41. Suchaneck, G.; Artiukh, E. Magnetoresistance of Antiphase Boundaries in Sr2FeMoO6-δ, Phys. Status Solidi B 2022, 259(8), 2100353. [CrossRef]
  42. Becker, R.; Polley, H. Der Einfluß innerer Spannungen auf das Einmüdungsgesetz bei Nickel. Ann. Physik 1940, 429(7), 534-540. [CrossRef]
  43. Bozorth, R.M.; Tilden, E.F.; Williams, A.J. Anisotropy and magnetostriction of some ferrites, Phys. Rev. 1955, 99(6), 1788-1798. [CrossRef]
  44. Alam M., Kalyan M., Khan G.G., Origin and tuning of room temperature ferromagnetism and ferroelectricity in double perovskite Y2NiMnO6 nanostructured thin films, J. Alloys Comp. 2020, 822, 153540. [CrossRef]
  45. Vergne, R. L'approche à la saturation de l'aimantation des corps ferromagnétiques polycristallins de structure cubique, Phys. Status Solidi 1966, 14(1), 143-147. [CrossRef]
  46. Grössinger, R. A Critical Examination of the Law of Approach to Saturation, I. Fit Procedure, Physica Status Solidi (a) 1981, 66(2), 665-674. [CrossRef]
  47. Evans, R.F.L.; Atxitia, U.; Chantrell, R.W. Quantitative simulation of temperature-dependent magnetization dynamics and equilibrium properties of elemental ferromagnets. Phys. Rev. B - Condens. Matter Mater. 2015, 91, 144425 (7pp). [CrossRef]
  48. Bean C.P.; Livingston, J.D., Superparamagnetism. J. Appl. Phys. 1959, 30(4), 120S-129S. [CrossRef]
  49. Pierce, D.T.; Celotta, R.J.; Unguris, J.; Siegmann, H. C. Spin-dependent elastic scattering of electrons from a ferromagnetic glass, Ni40Fe40B20, Phys. Rev. B - Condens. Matter Mater. 1982, 26(5), 2566-2574. [CrossRef]
  50. MacDonald, A.H.; Jungwirth, T.; Kasner, M. Temperature dependence of itinerant electron junction magnetoresistance, Phys. Rev. Lett. 1998, 81(3), 705-708. [CrossRef]
  51. Bloch F. Zur Theorie des Ferromagnetismus. Z. Physik 1930; 61, 206–219. [CrossRef]
  52. Mauri, D.; Scholl, D.; Siegmann, H.C.; Kay, E. Observation of the exchange interaction at the surface of a ferromagnet. Phys. Rev. Lett. 1988, 61(6), 758-761, DOI: PhysRevLett.61.758.
  53. Shang, C.H.; Nowak, J.; Jansen, R.; Moodera, J.S. Temperature dependence of magnetoresistance and surface magnetization in ferromagnetic tunnel junctions. Phys. Rev. B - Condens. Matter Mater. 1998, 58, R2917–R2920. [CrossRef]
  54. Garcia, V.; Bibes, M.; Barthélémy, A.; Bowen, M.; Jacquet, E.; Contour, J.-P.; Fert, A. Temperature dependence of the interfacial spin polarization of La2/3Sr1/3MnO3. Phys. Rev. B - Condens. Matter Mater. 2004, 69, 052403 (4pp). [CrossRef]
  55. Balcells, LI.; Navarro, J.; Bibes, M.; Roig, A.; Martínez, B.; Fontcuberta, J. Cationic ordering control of magnetization in Sr2FeMoO6 double perovskite, Appl. Phys. Lett. 2001, 78(6), 781-783. [CrossRef]
  56. Suchaneck, G. Tunnel Spin-Polarization of ferromagnetic metals and ferrimagnetic oxides and its effect on tunnel magnetoresistance. Electron. Mater. 2022, 3(3), 227-234. [CrossRef]
  57. Tedrow, P.M.; Meservey, R. Spin polarization of electrons tunneling from films of Fe, Co, Ni, and Gd. Phys. Rev. B - Condens. Matter Mater 1973, 7(1), 318–326. [CrossRef]
  58. Ferromagnetic Curie Temperatures. URL: http://hyperphysics.phy-astr.gsu.edu/hbase/Tables/Curie.html (accessed November12, 2023).
  59. Paul A.A. Estimation of Magnetic Anisotropy in Ferromagnetic Elements and Their Alloy Powders by the Law of Approach to Saturation (LAS), Msc thesis, Department of Mechanical Engineering in the University of Michigan-Dearborn, 2020, p.26. [CrossRef]
  60. Wang, J.-F.; Li, Z.; Xu, X.-J.; Gu, Z.-B.; Yuan, G.-L.; Zhang, S.-T. The competitive and combining effects of grain boundary and Fe/Mo antisite defects on the low-field magnetoresistance in Sr2FeMoO6. J. Am. Ceram. Soc., 2014, 97(4), 1137-1142. [CrossRef]
Preprints 90632 g001
Figure 1. Comparison of the TMR values calculated by means of equation (10) with experimental data of nanogranular SFMO/SMO core-shell ceramics from [11].
Figure 1. Comparison of the TMR values calculated by means of equation (10) with experimental data of nanogranular SFMO/SMO core-shell ceramics from [11].
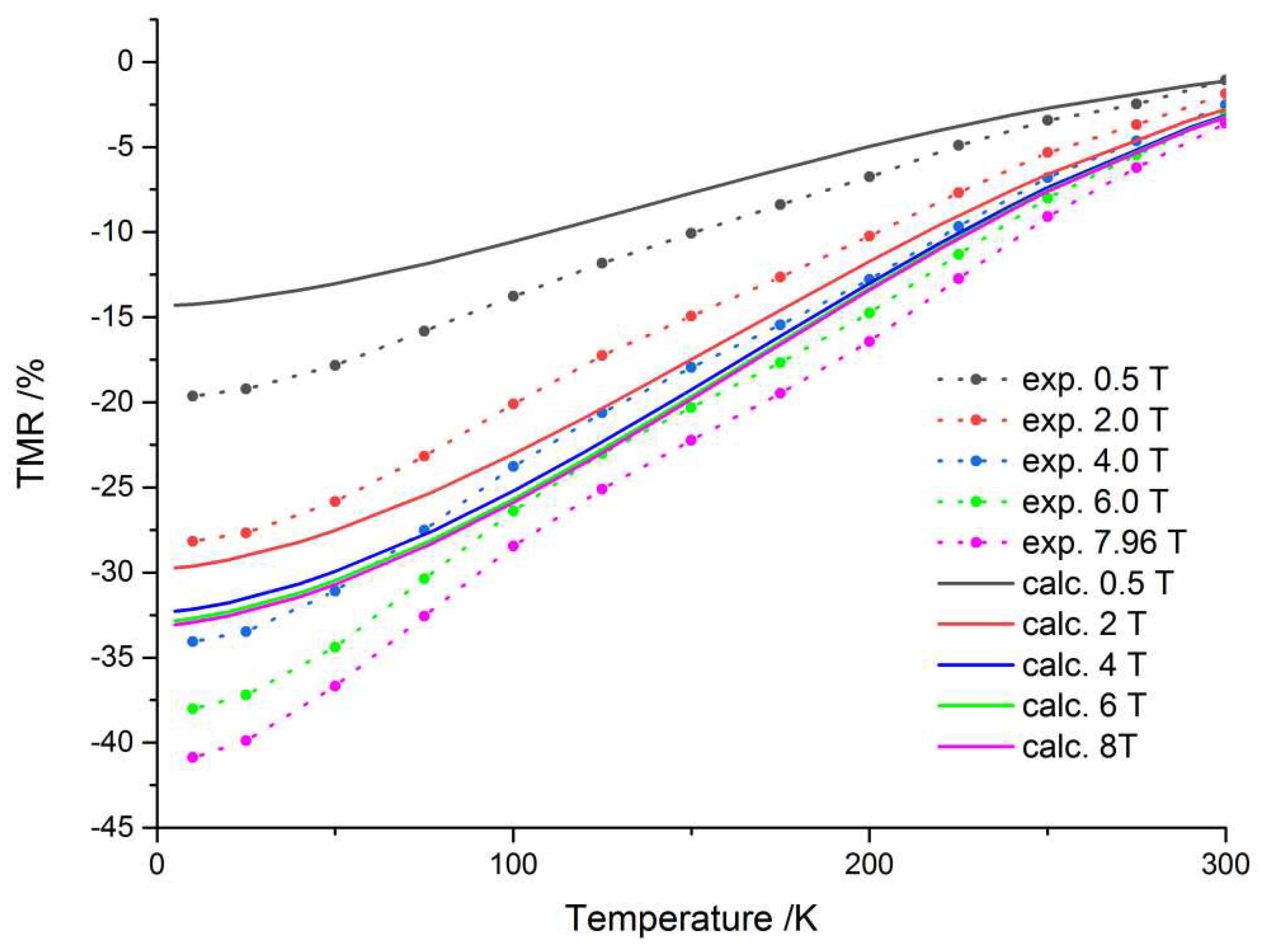
Preprints 90632 g001
Preprints 90632 g002
Figure 2. Magnetic field sensitivity of nanogranular SFMO/SMO core-shell ceramics fabricated by the citrate gel method in comparison with experimental data of ceramic SFMO annealed in reducing atmosphere at 10 K [60] and with calculations from [10] for nanosized SFMO ceramics using Equation (25).
Figure 2. Magnetic field sensitivity of nanogranular SFMO/SMO core-shell ceramics fabricated by the citrate gel method in comparison with experimental data of ceramic SFMO annealed in reducing atmosphere at 10 K [60] and with calculations from [10] for nanosized SFMO ceramics using Equation (25).
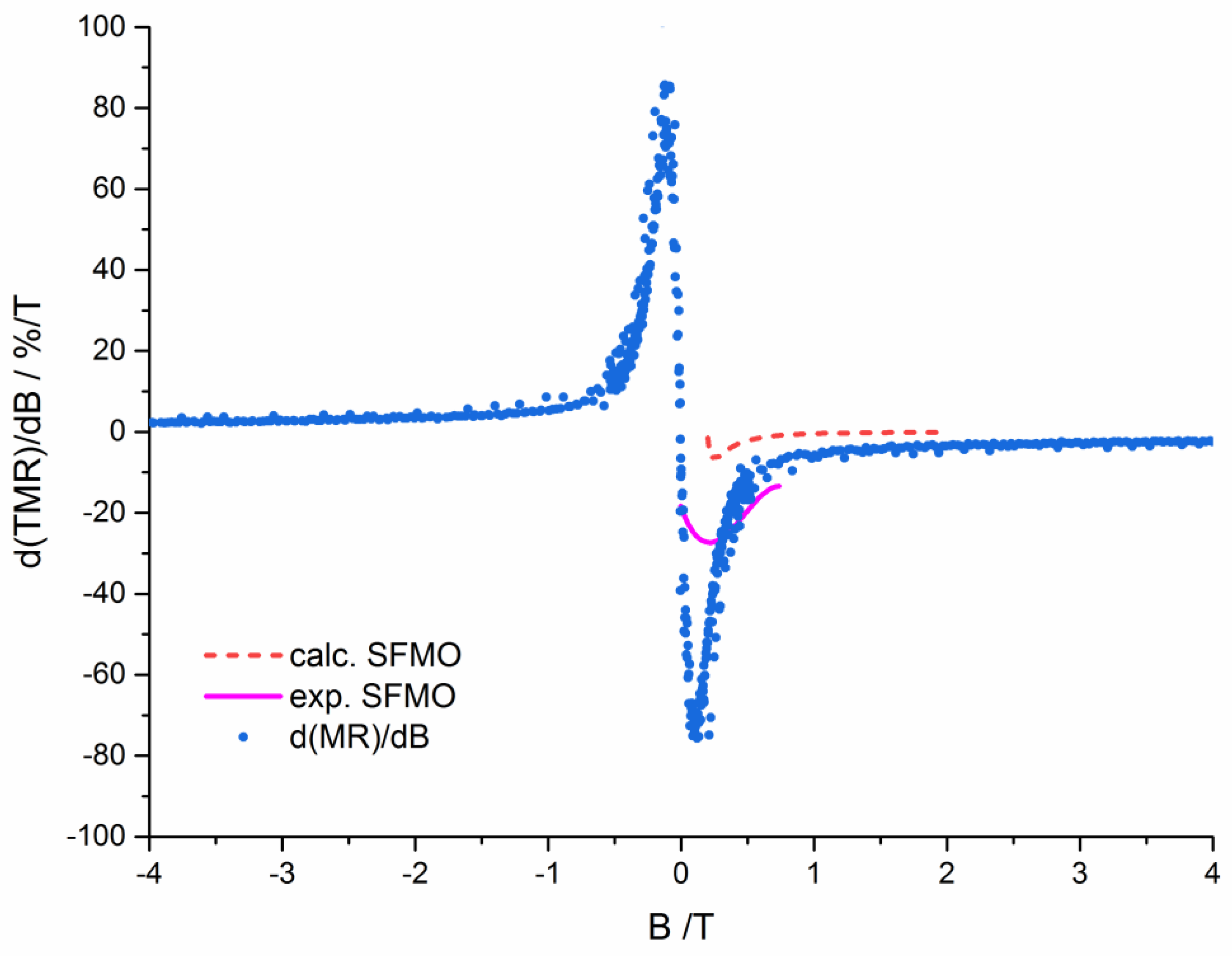
Preprints 90632 g002
Preprints 90632 g003
Figure 3. Magnetic field sensitivity of superparamagnetic noninteracting SFMO granules possessing a total magnetic moment of 2000 µB and 10000 µB respectively.
Figure 3. Magnetic field sensitivity of superparamagnetic noninteracting SFMO granules possessing a total magnetic moment of 2000 µB and 10000 µB respectively.
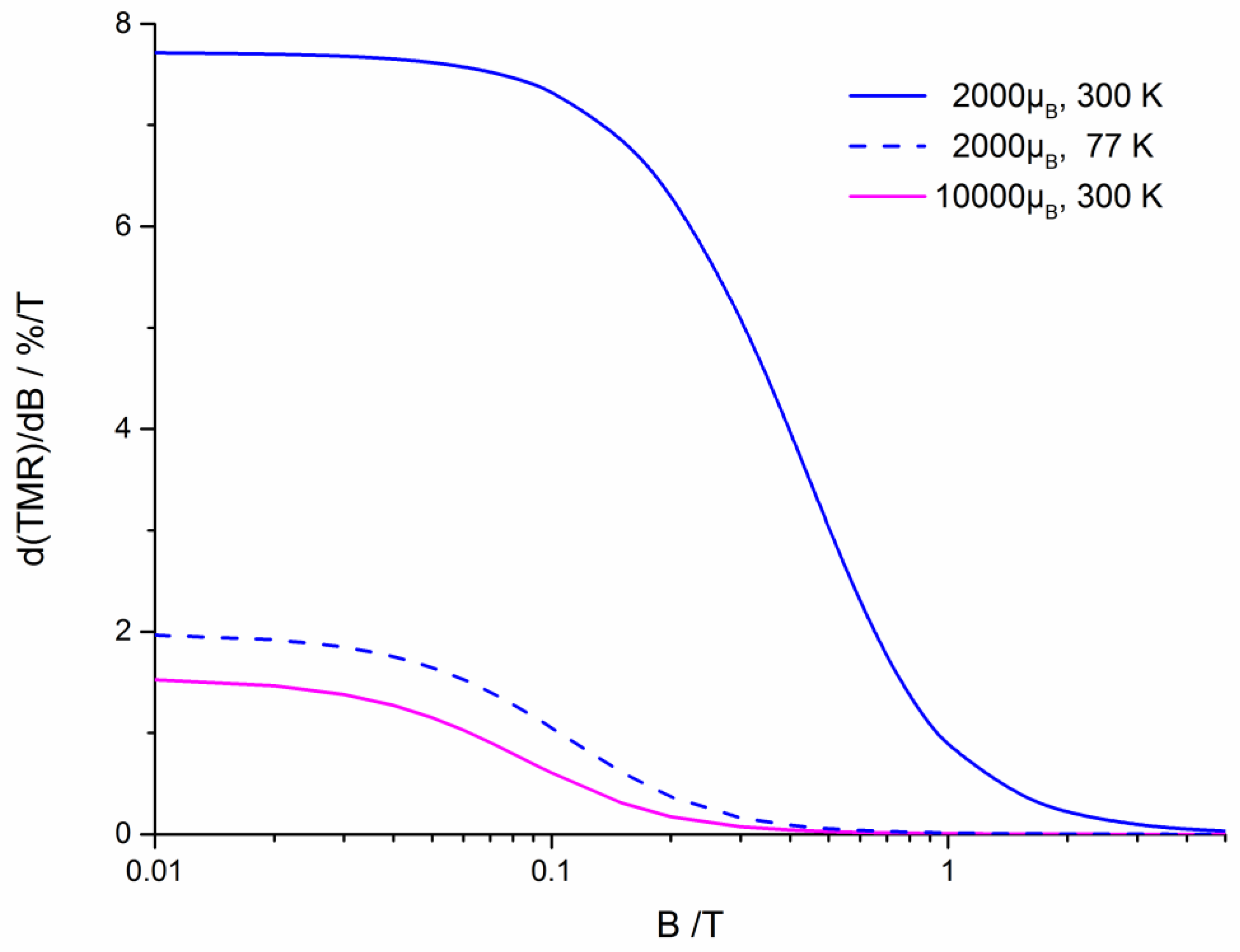
Preprints 90632 g003
Preprints 90632 g004
Figure 4. Temperature coefficients of the TMR of nanogranular SFMO/SOMO core-shell ceramics deduced from the numerical derivatives of the experimental data in figure 1 in comparison with calculated data of Fe und Co as well as calculated data of superparamagnetic SFMO.
Figure 4. Temperature coefficients of the TMR of nanogranular SFMO/SOMO core-shell ceramics deduced from the numerical derivatives of the experimental data in figure 1 in comparison with calculated data of Fe und Co as well as calculated data of superparamagnetic SFMO.
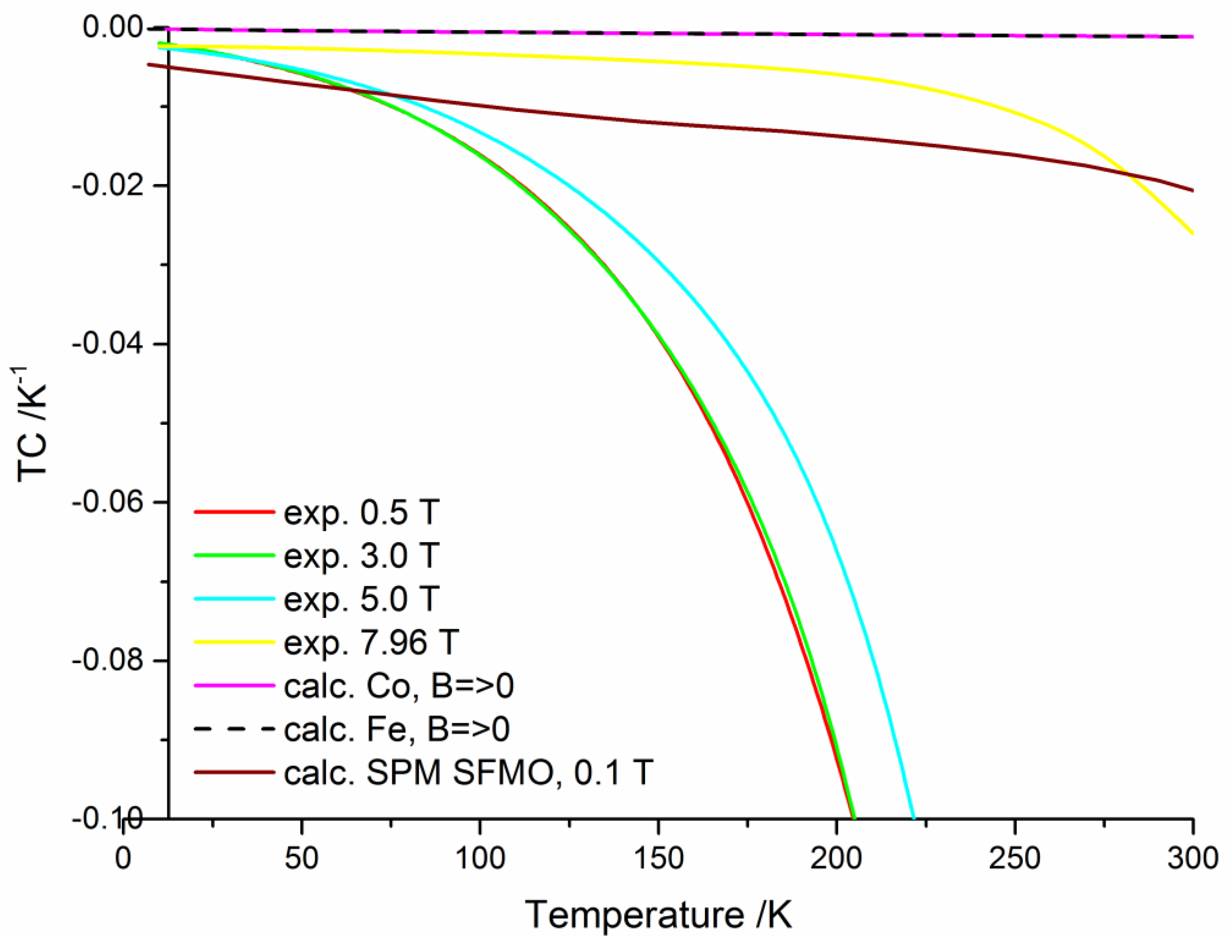
Preprints 90632 g004
Table 1. Parameter b2MA calculated for different values of the uniaxial anisotropy constant K1.
Table 1. Parameter b2MA calculated for different values of the uniaxial anisotropy constant K1.
K1, J m-3 Ref. b2MA, T2
5×103 [37] 8.468×10-5
1.99×104 [38] 1.341×10-3
1.99×104 [38] 2.921×10-3 1)
2.74×104 [40] 2.543×10-3
1.7×105 [41] 9.789×10-2
Ms = 2.5354 µB f.u.-1
Table 2. Fitting parameters of Equation (19) [47].
Table 2. Fitting parameters of Equation (19) [47].
Compound p β
Fe 2.876 0.339
Co 2.369 0.34
Table 3. Parameters used for calculations in this work.
Table 3. Parameters used for calculations in this work.
Compound P0 Ref. TC, K Ref ai Ref. bi/2, Ti/2 Ref.
SFMO 0.721) [24] 420 [25] a1 = 1.89
a2 = -1.97
a3 = 2.2
a4 = -1.14		 [24] b1/2 = 0
b1 = 0.085
b2 = 0.115
b3 = 0.118		 [24]
Co 0.34 [57] 1388 [58] eq. (19) [47] b2 = 0.042 [46]
Fe 0.44 [57] 1043 [58] eq. (19) [47] b2 = 0.050 [59]
1) ASD = 0.1.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated