Prerpints.org logo
Preprint
Article

New Potentials for Subatomic Particles to Simulate Stable Atom and Particle-Wave Nature Attosecond Simulations

Altmetrics

Downloads

186

Views

1210

Comments

1

supplementary.zip (34.35MB )

This version is not peer-reviewed

Submitted:

15 February 2024

Posted:

19 February 2024

You are already at the latest version

Alerts
Abstract
A new approach was presented in this study to simulate a stable atom along with subatomic particles in it. Subatomic particles in an atom are treated as conventional particles, exhibiting attraction and repulsion between them, giving a stable atom simulation. This new approach leads to developing new potentials for subatomic particles to simulate a stable atom. Subatomic particle dynamics (SPD) simulations were developed for within-atom simulations that give a stable atom structure for infinite time and provide many insights into electron trajectories and atom properties like energies and radius of the atom. The effect of protons and neutrons movement in the nucleus on electron trajectories was captured in SPD. Hydrogen and Carbon atom SPD were reported in this study. The Pilot-wave theory was implemented in this study to simulate the wave nature of subatomic particles in an atom. Electrons motion was guided by the interference pattern produced by the electron’s aether medium waves in SPD. SPD was implemented on molecules, resulting in a stable molecular structure giving insights into electron trajectories shared by multiple atoms.
Keywords: 
Subject: Physical Sciences  -   Atomic and Molecular Physics

1. Introduction

Coloumb’s law plays an important role in modelling electrostatic interactions and forces acting on subatomic particles [1]. Coloumb interactions have been applied in many areas in the fields of Physics, Chemistry and Biology. This law was introduced in the 18th century and plays a pivotal role in understanding and modelling electrostatics in molecular simulations of atoms and molecules. They play a crucial role in modelling chemical reactions, formation of chemical bonds, material properties like electrical conductivity and magnetism, biomolecules like protein folding and DNA double-helix formation. Many studies presented the importance of coulomb interactions in modern applications in Carbon nanotubes [2] and Bilayer Graphene [3] systems. The standard perspective on protons and electrons is that protons bear a positive charge while electrons carry a negative charge and opposite charges attract while the same charges repel each other. In this study, I provide a new perspective on looking into subatomic particles. Protons, electrons, and neutrons are treated as conventional particles in an atom, exhibiting attraction and repulsion between them, akin to the way atoms attract and repel each other in atomic simulations. This new approach leads to developing new potentials for subatomic particles to model the subatomic particle interactions.
Molecular Dynamics (MD) provides a fundamental approach to the dynamics of atoms and molecules at the atomic scale. This method was first introduced by Alder and Wainwright in 1959 [4] and evolved into an important tool in understanding the dynamics of atoms and molecules in complex systems. Its applications have diversified, ranging from biomolecular simulations [5] to materials science [6]. The introduction of enhanced sampling techniques by A. Laio and M. Parrinello [7] gives better insights into complex energy systems. In this study, I developed a simulation code similar to molecular dynamics to model the subatomic particles interaction in within-atom called subatomic particle dynamics (SPD). Results of SPD for the Hydrogen atom, Carbon atom, Hydrogen molecule and oxygen molecule were reported in this study for particle and wave nature. The time step for these simulations was calculated from dimensionless variables and found to be at attoseconds. Many attosecond studies [8,9,10,11,12] have been carried out that provide insights into electron dynamics, ionization, and quantum mechanical phenomena occurring within atoms and molecules.
The Pilot-Wave theory, also known as de Broglie-Bohm theory [13,14] is an interpretation of quantum mechanics with a deterministic framework where particles are guided by guiding waves with hidden variables. Louis de Broglie [13] and David Bohm [14] developed this theory, giving insights into wave-particle duality. Recent studies [15,16] explore the theory of light of contemporary quantum research. In this study, Pilot-Wave theory was implemented in SPD, where subatomic particles movement was affected by the presence of three-dimensional waves that were generated by the particles in an aether medium. Einstein’s theory of relativity [17] redefined the nature of space-time which led to obsolete Aether concept. In recent times, interest in aether medium was renewed by the works of Joao Magueijo [18] and others. Many studies [19,20,21,22,23] were carried out for Pilot Wave walkers where an oil droplet is allowed to bounce on the liquid surface and its motion is guided by the surface wave patterns like diffraction and interference.
In the remainder of this paper, simulation details were presented followed by results and discussion section. In the results and discussion section, SPD of particle nature for Hydrogen and Carbon atom was presented followed by wave nature simulations. Finally, subatomic particle dynamics of the Oxygen molecule was shown followed by the conclusions.

2. Simulation Details

All simulations were carried out using the code developed in Fortran. Simulation code was developed for subatomic particles in an atom like molecular dynamics (MD) using Velocity Verlet integrator [24]. A dimensionless time step of 0.02 was used in all simulations and the time step was calculated to be 1.67 attoseconds. The initial configuration was created by placing protons and neutrons in the centre of the atom (nucleus) and the electrons placed randomly around the nucleus. New potentials were introduced in this study and are used to calculate force and potential acting on the subatomic particles at each time step. All simulations were run for 16.7 picoseconds and results were collected for the last 0.2 picoseconds. All simulation videos were captured using the VMD package [25].
New potentials were developed for subatomic particles on the principle of exhibiting repulsion (at smaller distances) and attraction (at larger distances) between them and between themselves. Considering this behaviour for subatomic particles in MD code gives stable atom simulations. Simulation for a stable atom was developed using these Potentials called subatomic particle dynamics (SPD). These potentials emerge by running SPD by first considering the dimensionless variables for equations of force acting on subatomic particles. Two terms were considered for the force equation, like Leonard-Jones potential for molecular simulations. By trial-and-error method, these two terms were parameterised with the objective of keeping a stable atom in SPD and observing electron trajectories around the nucleus. Later, these force functions are integrated back to get the new potentials for electrons and protons in an atom.
Following are the dimensionless force equations parameterised by using the trial-and-error method.
For electron to proton interaction,
f * = 4 1 r * 2.5 − 8
for proton to proton, proton to neutron, neutron to neutron,
f * = 4 1.65 r * 0.4 − 5
for electron to electron,
f * = 4 1 r * 0.2 − 1.5
where f* and r* are dimensionless force and distance, respectively. More terms can be considered in these equations for complex trajectories of electrons around the nucleus. Integrating the above equations gives new potentials for subatomic particles as follows:
for electron to proton:
V r = 4 ε σ 1.5 1.5 r 1.5 + 8 r σ
for proton to proton, proton to neutron, neutron to neutron,
V r = 4 ε 5 r σ − 2.75 r 0.6 σ 0.6
for electron to electron,
V r = 4 ε 1.5 r σ − r 0.8 0.8 σ 0.8
where V(r) is the potential acting on particles, r is the distance between particles, ϵ and σ are new potential parameters. ϵ and σ are parameterised using Carbon atom simulations, by its radius and Ionisation Energy as shown in the following table (Table 1).

3. Results and Discussion

3.1. Subatomic Particle Dynamics Simulations for Particle Nature

3.1.1. Hydrogen Atom Simulation

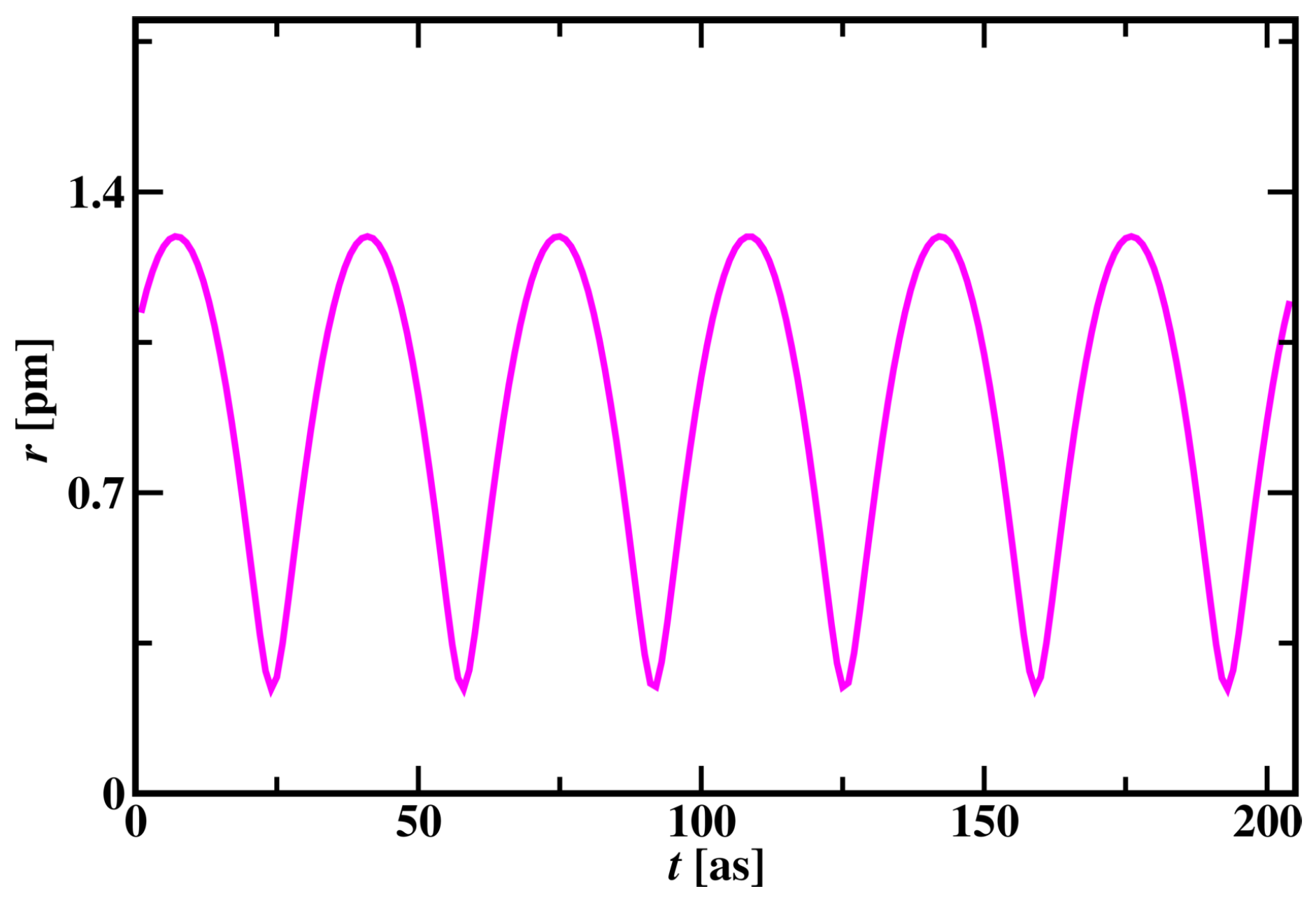
Subatomic particle dynamics simulation was carried out for the Hydrogen atom by placing the proton at the centre and placing an electron around the proton. By the trial-and-error method, new potentials were developed until the atom got stabilized and the electron rotates around the proton for an infinite time without losing its energy as shown in the supplementary material video 1. Electron revolves around the proton in three-dimensional elliptical and spherical orbits by changing its radius in cycles. The change in the radius of the Hydrogen atom is shown in Figure 1. In one cycle, the radius of the Hydrogen atom changes from 0.22 pm to 1.33 pm. For every 34 time steps, this cycle repeats with the same pattern in a three-dimensional space.
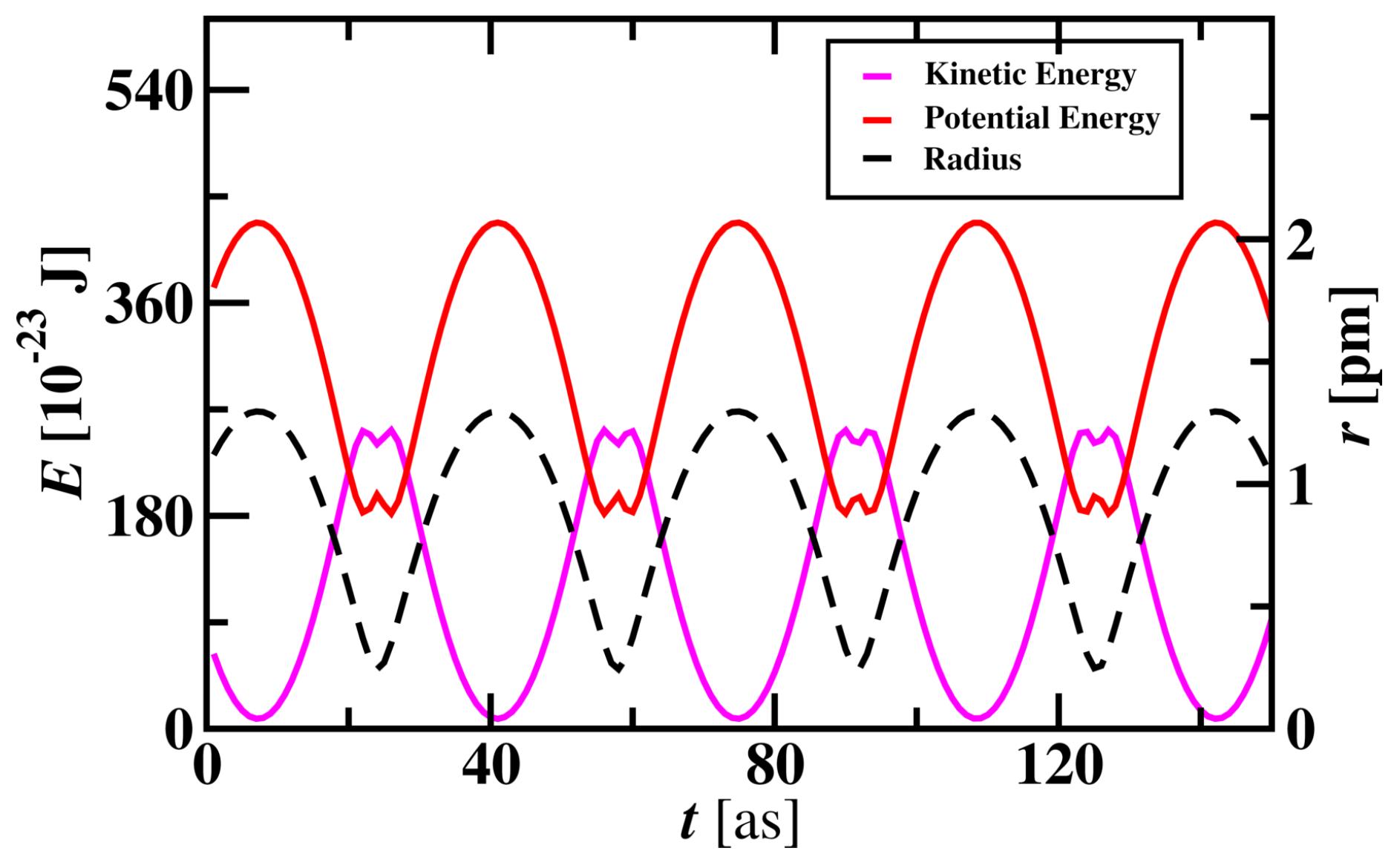
The energy variation of electron while revolving around the nucleus was studied and shown in Figure 2. When the electron travels close to the nucleus, changes in potential and kinetic energy are observed. Potential energy curves vary with the radius of the atom and are directly proportional to the radius of the Hydrogen atom. Kinetic energy is inversely proportional to the radius of the atom. These profiles show that an electron near to proton has lower potential energy and higher kinetic energy and vice versa. Due to the attraction and repulsion behaviour of proton and electron interactions, the electron approaches the proton due to attraction and Potential energy decreases. Electron gets repelled when it goes very near to the proton and moves away with higher Kinetic energy. Potential energy decreases when the electron approaches the proton with an increase in Kinetic energy.
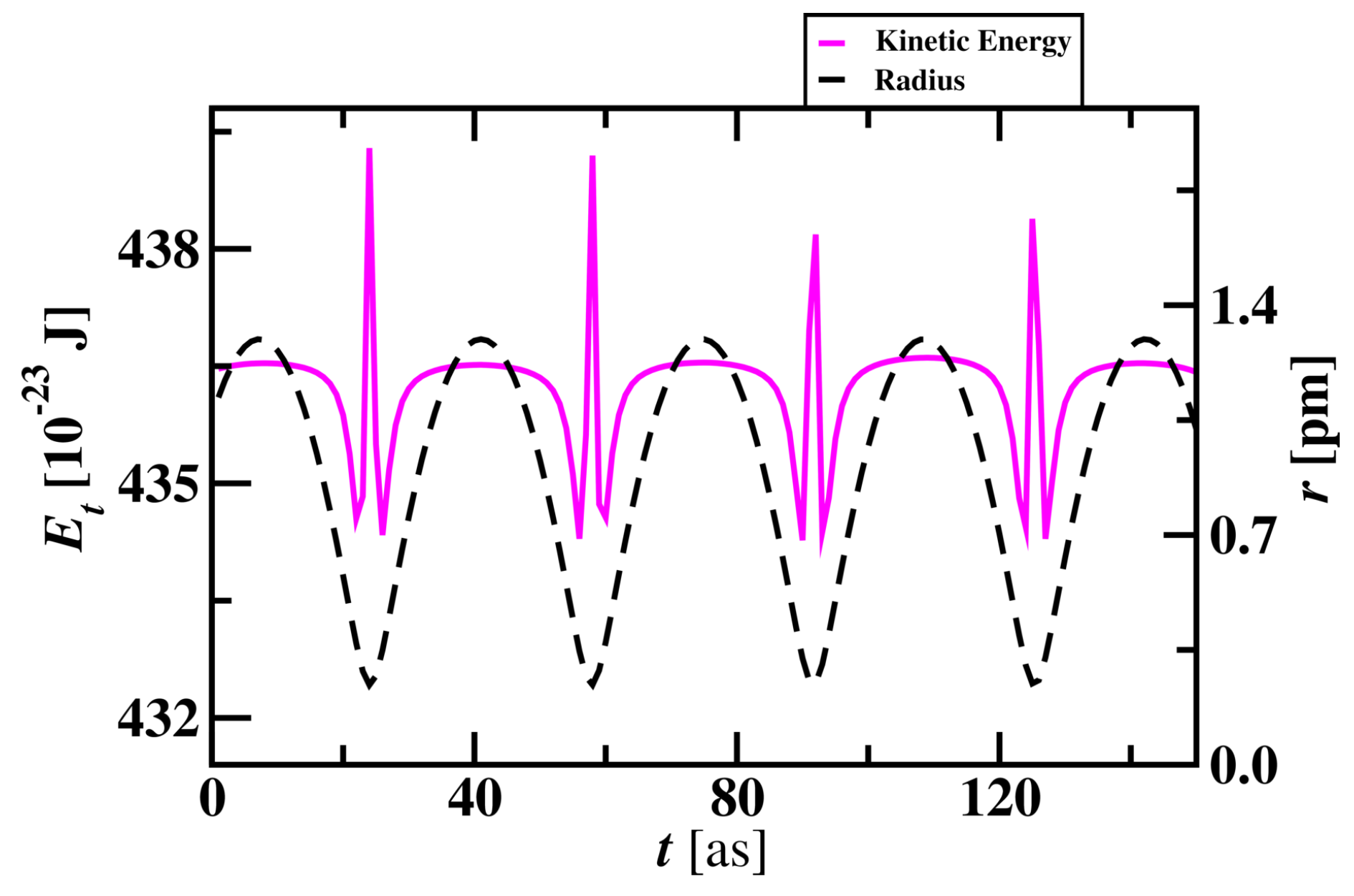
The average total energy of the electron in a Hydrogen atom is 436.05 x 10 − 23 J and is shown in Figure 3. Total energy decreases by 2.5 x 10 − 23 J when the electron approaches close to the nucleus. Total energy maintains constant through the revolution of an electron around the proton and a sharp increase in energy occurs when the radius is at minimum in each cycle. Electron’s total energy reaches minima when it approaches the proton. There is a sharp increase in total energy of 4 x 10 − 23 J when the electron approaches r m i n i m u m . After this sharp increase in energy, the electron starts to move away from the proton with the increase in total energy.
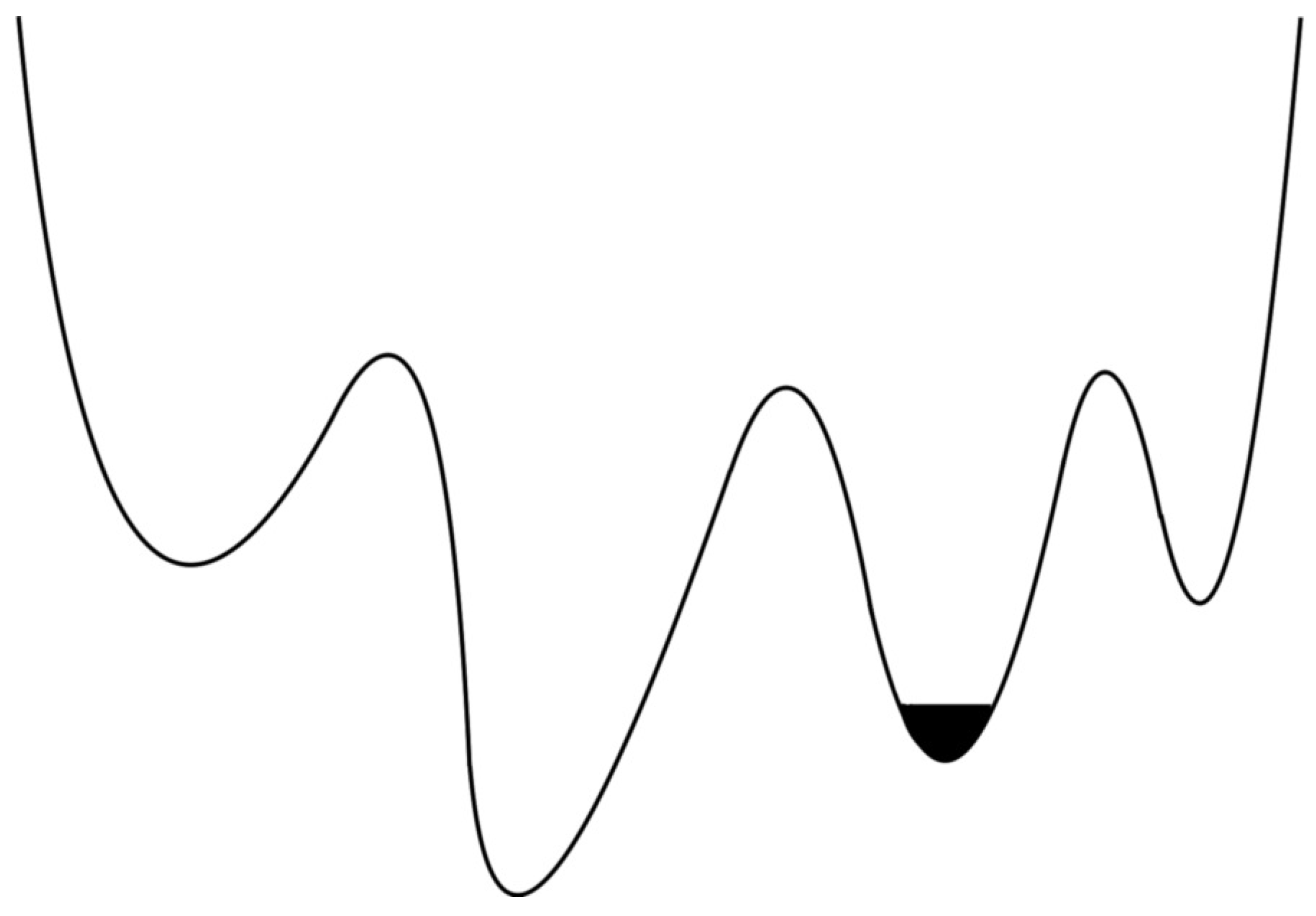
The simulation of an electron orbiting around the nucleus was oscillating in one region of Phase Space configuration as shown in the supplementary material video 2. Figure 4 shows an example of an electron phase space oscillating (represented by a black region) at the local region (local minima). To explore all the possible phase space configurations, the electron orbit has to be changed and has to be placed in other regions randomly around the nucleus. Properties of electron, proton and atom will be calculated when all the phase space configurations are captured in a simulation.

3.1.2. Randomness in Hydrogen Atom Simulation

To simulate all the possible phase space configurations for an electron revolving around the nucleus, the electron is placed randomly around the nucleus, with the probability, at each time step. x, y, and z coordinates of the electron changed with the probability, individually. An electron is placed randomly around the nucleus within the radius of 1.01 pm in x, y, and z coordinates. Changing the velocity of an electron randomly, by a very small value, shoots the electron as those random velocity values are not reasonable. Only random positions were given to the electron keeping its velocity the same. Increasing the probability of placing an electron randomly around the nucleus and keeping the velocities the same, results in the higher radius of the Hydrogen atom.
The simulation video of Hydrogen atom and electrons placed randomly in SPD is shown in the supplementary material video 3. Randomness in the Hydrogen atom gives electron revolutions around the proton in all directions, unlike in normal Hydrogen atom simulation (supplementary material video 1) where the electron revolves only in one direction. This property of electron’s revolutions in all directions explores maximum phase space configurations. The average radius of the atom, total energy, potential energy and kinetic energy of the electron and the probability of randomly changing electron position are shown in Table 2. An increase in the probability of placing an electron in random positions increases its radius and energies up to a probability of 0.00001. Further increase in probability decreases its values. The analysis shows the maximum radius and electron energies at the probability of 0.00001. The experimental value of the Hydrogen atom radius (53 pm) is reflected in the probability of 0.00001 and 0.0001. The ionization energy of the Hydrogen atom is calculated by the total energy of the electron and is 31323 x 10 − 23 J for the probability of 0.00001. This property is less than the observed value of 217896 x 10 − 23 J. This difference in ionization energy is due to new potentials being parametrized by Carbon atom properties (discussed later in this section).

3.1.3. Particle Nature of Carbon Atom Simulation

SPD for Carbon atom simulation was developed by placing six electrons around the nucleus of six protons and six neutrons in the atom. The effect of proton and neutron motion in the nucleus towards electron trajectories was seen clearly as shown in the supplementary material video 4. The trajectory of electrons revolving around the nucleus for 5,000 time steps is shown in Figure 5.
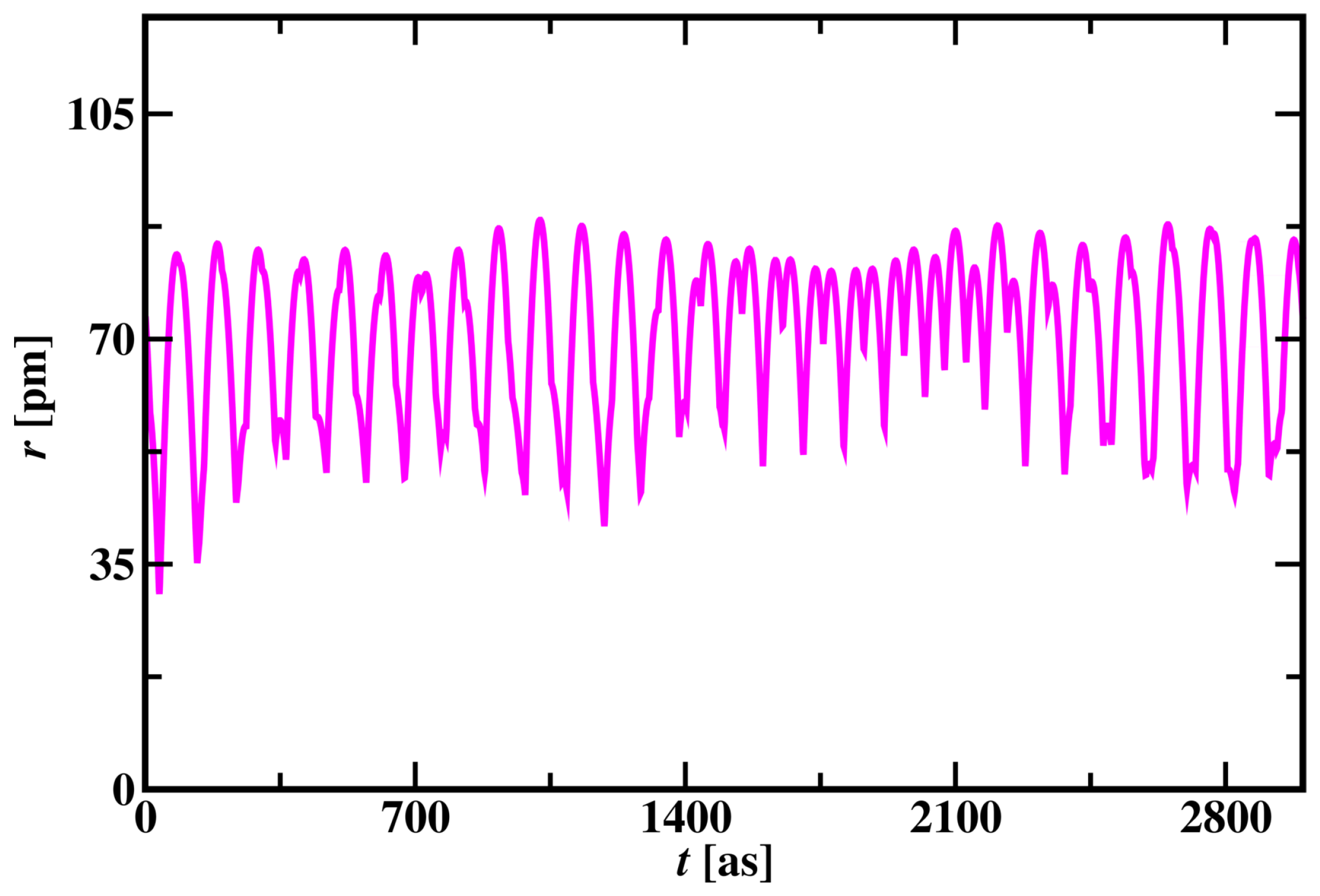
Unlike the hydrogen atom, the radius of the Carbon atom changes in an irregular pattern as shown in Figure 6. All the electrons orbit around the nucleus in cycles like the Hydrogen atom’s electron as shown in Figure S1 in the supplementary material. The valence electron is not constant and changes its position with core electrons and the core electron becomes a valence electron for a short period of time in a cycle. The rapid change in the radius of the Carbon atom is shown in Figure 6. Randomly placing electrons in carbon atom simulation gives all possible phase configurations for electron trajectories.
The range of average velocity of electrons is found to be 835,747 m/s to 1,213,998 m/s in carbon atom, as shown in Table 3. The ratio of the velocity of electrons to the velocity of light is ranging from 0.0028 to 0.0040. The carbon atom’s average radius (r*) is found to be 91.9 and σ in new potentials is found to be 0.7777 pm. The ionization energy of the valence electron was calculated from the dimensionless total energy variable (23021.3) and ϵ in new potentials were found to be 7.837 x 10 − 23 Joules. The dimensionless time step is taken as 0.02 in the simulation and the unit of time step was calculated to be 1.67 attosecond.
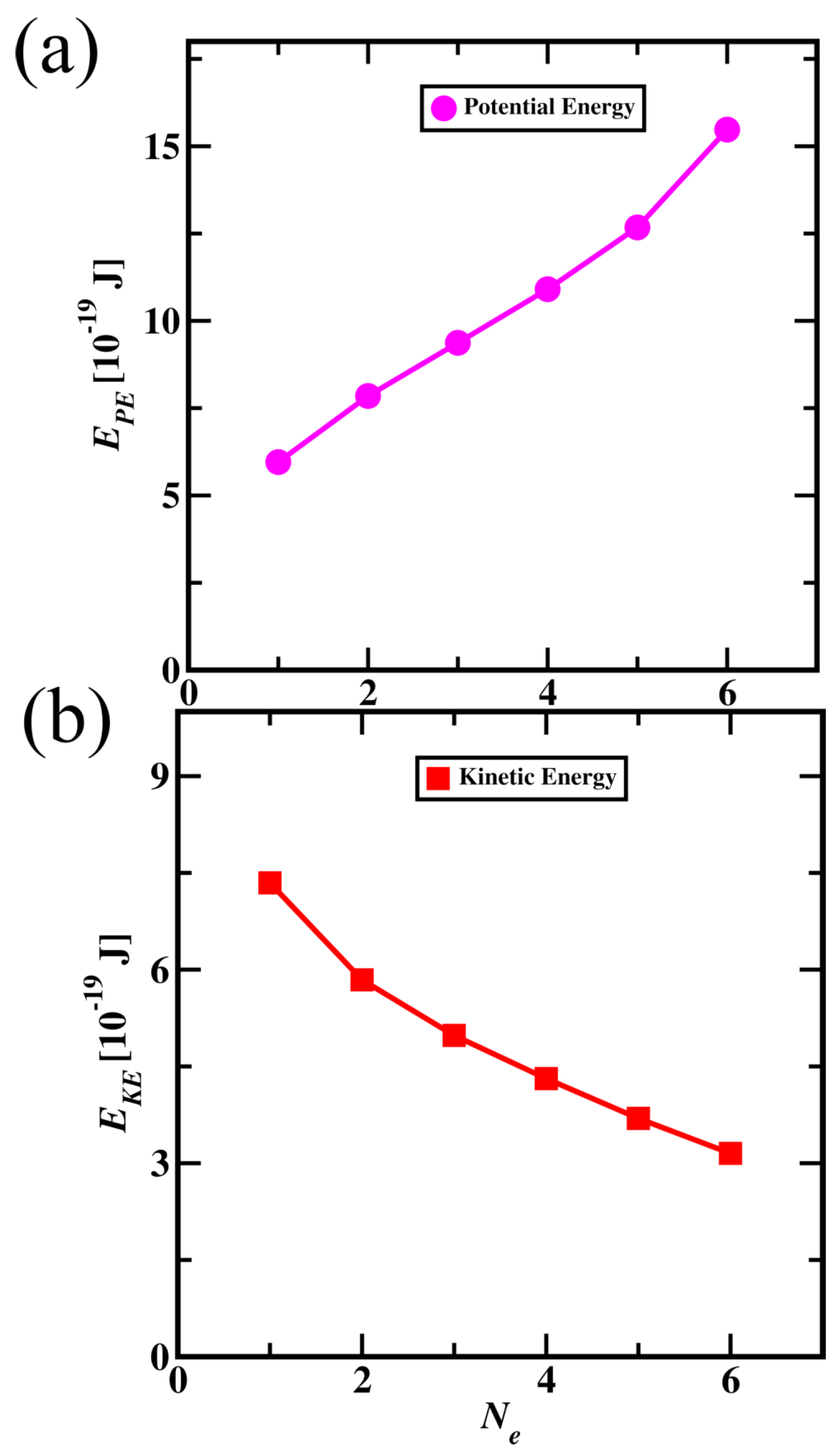
The average potential and kinetic energies of electrons (from core to valence) are shown in Figure 7. Core electron potential energies are lower when compared to valence electron, explaining core electrons are more stable than valence electron. Kinetic energy for core electrons is higher than valence electrons showing that core electrons orbit the nucleus with higher velocities than valence electrons. The total energy of electrons for core electrons is lower than for the valence electrons. The contribution of potential energy is higher than kinetic energy in total energy resulting in lower total energy for core electrons.

3.2. Wave Nature Subatomic Particle Dynamics Simulations

3.2.1. Wave Nature Simulation in Hydrogen Atom

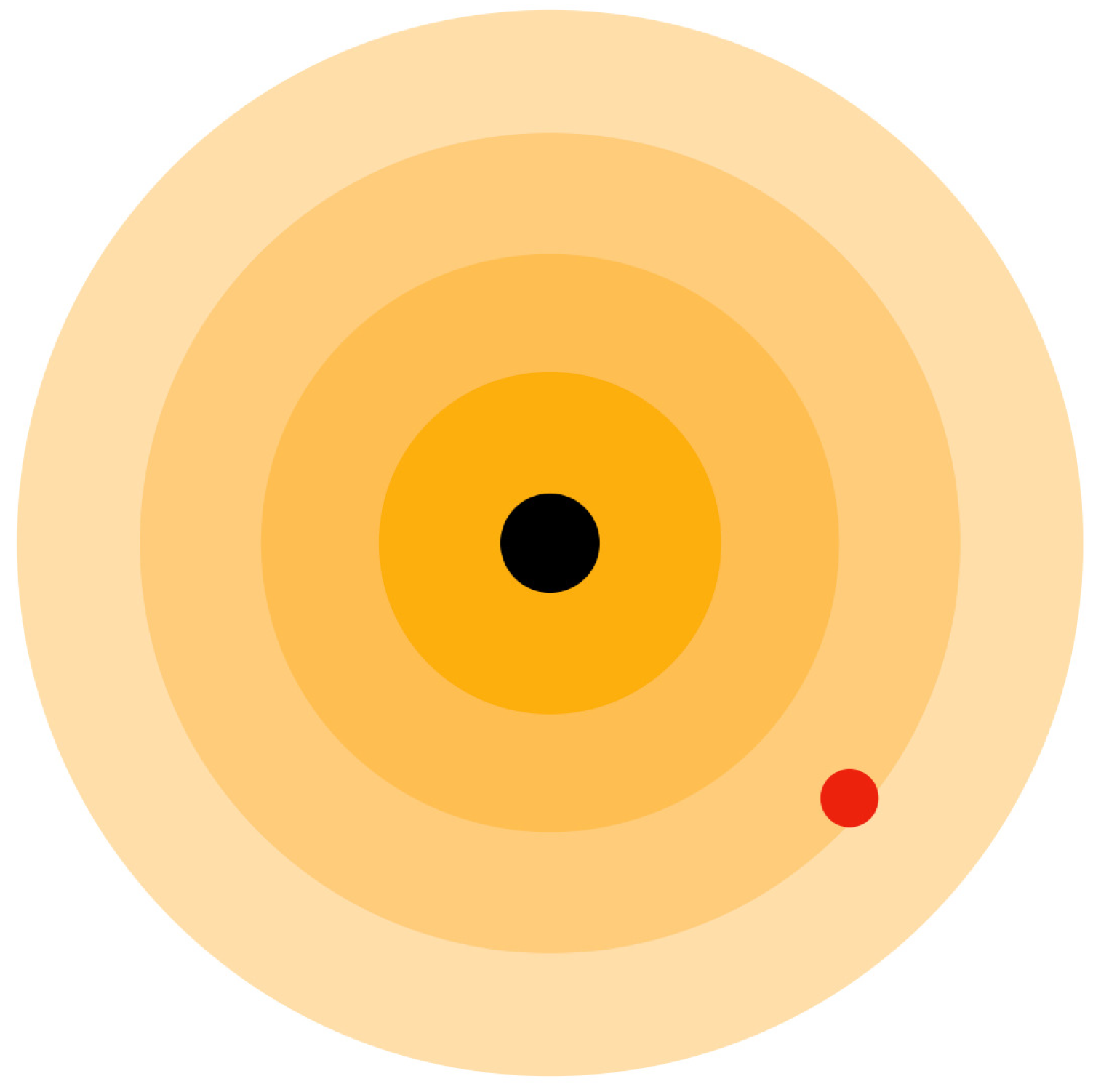
In this study, I develop a Pilot-Wave theory to mimic the particle’s wave nature in an atom simulation. This approach is similar to walkers [19,20,21,22,23] in the two-dimensional surface wave where a silicon oil drop moves along the interference pattern of the wave produced by the medium. Here, particles produce three-dimensional waves in an aether medium called aether medium waves. 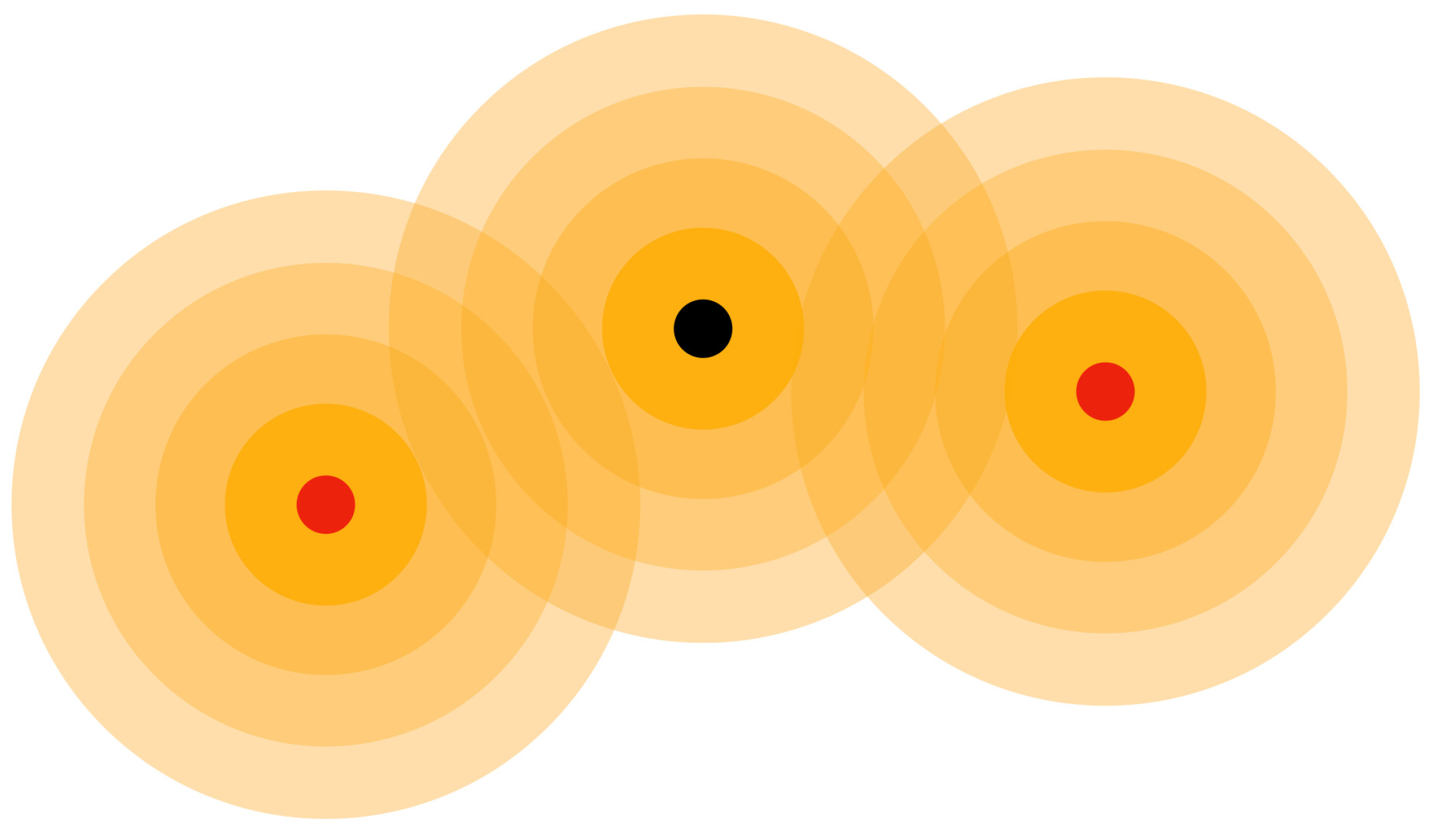Electrons are guided by the resulting interference pattern of aether medium waves produced by the presence of subatomic particles, as shown in Figure 8. Subatomic particles are assumed to produce three-dimensional waves on an aether medium, and their motion is guided by the resulting wave patterns.
In this study, these three-dimensional aether medium waves are considered as three-dimensional cos waves as a function of distance (r). The time-dependent cos wave function is not considered in this study and will be considered in future studies. This study assumes, the amplitude of the wave does not diminish over distance and propagates with constant wave amplitude, making the system nonlocal. The amplitude of aether medium cos waves is parameterised and reported here. Electron displacement was calculated as a result of the collision with aether medium waves. Proton movements are considered particle nature and the presence of proton’s aether medium waves are considered. The collisions between aether medium waves and subatomic particles were considered as perfectly elastic where momentum and kinetic energy are conserved.
The velocity of an electron as guided by aether medium waves was derived as follows: The equation for the velocity of aether medium waves as a function of radius (r):
u A e t h e r = A · c o s ( r w l )
where u A e t h e r is the velocity of aether medium waves, A is amplitude and wl is the wavelength of the waves.
For the resulting velocity of electron colliding with 3D aether medium waves, conservation of momentum and kinetic energies were applied as follows:
m e · u e + m A e t h e r · u A e t h e r = m e · v e + m A e t h e r · v A e t h e r
1 2 m e u e 2 + 1 2 m A e t h e r u A e t h e r 2 = 1 2 m e v e 2 + 1 2 m A e t h e r v A e t h e r 2
where m e is the mass of an electron,
u e is the velocity of the electron before collision
v e is the velocity of the electron after collision
m A e t h e r is the mass of aether medium wave particles
u A e t h e r is the velocity of aether medium wave particles before collision
v A e t h e r is the velocity of aether medium wave particles after collision
The resulting equation for the velocity of electron after collision with aether waves is as follows:
v e = u e ( 1 − m A e t h e r m e ) + 2 m A e t h e r m e u A e t h e r ( 1 − m A e t h e r m e )
a e = v e − u e Δ t = 2 m A e t h e r m e u A e t h e r ( 1 − m A e t h e r m e ) Δ t
where a e is the acceleration of electron due to collision.
This acceleration of the electron due to the collision was calculated and added with acceleration acting due to electron-nucleus interactions (calculated using new potentials developed in this study). In this study, the mass of aether medium wave particles ( m A e t h e r ) is taken as 30% of electron mass ( m A e t h e r / m e = 0.3). The variable wl (wavelength) is taken as 0.04777 which gives the wavelength of aether medium waves as 0.3 pm. Implementing wave interference interactions in the Hydrogen atom shows similar behaviour (supplementary material video 5) to the particle nature of the Hydrogen atom. 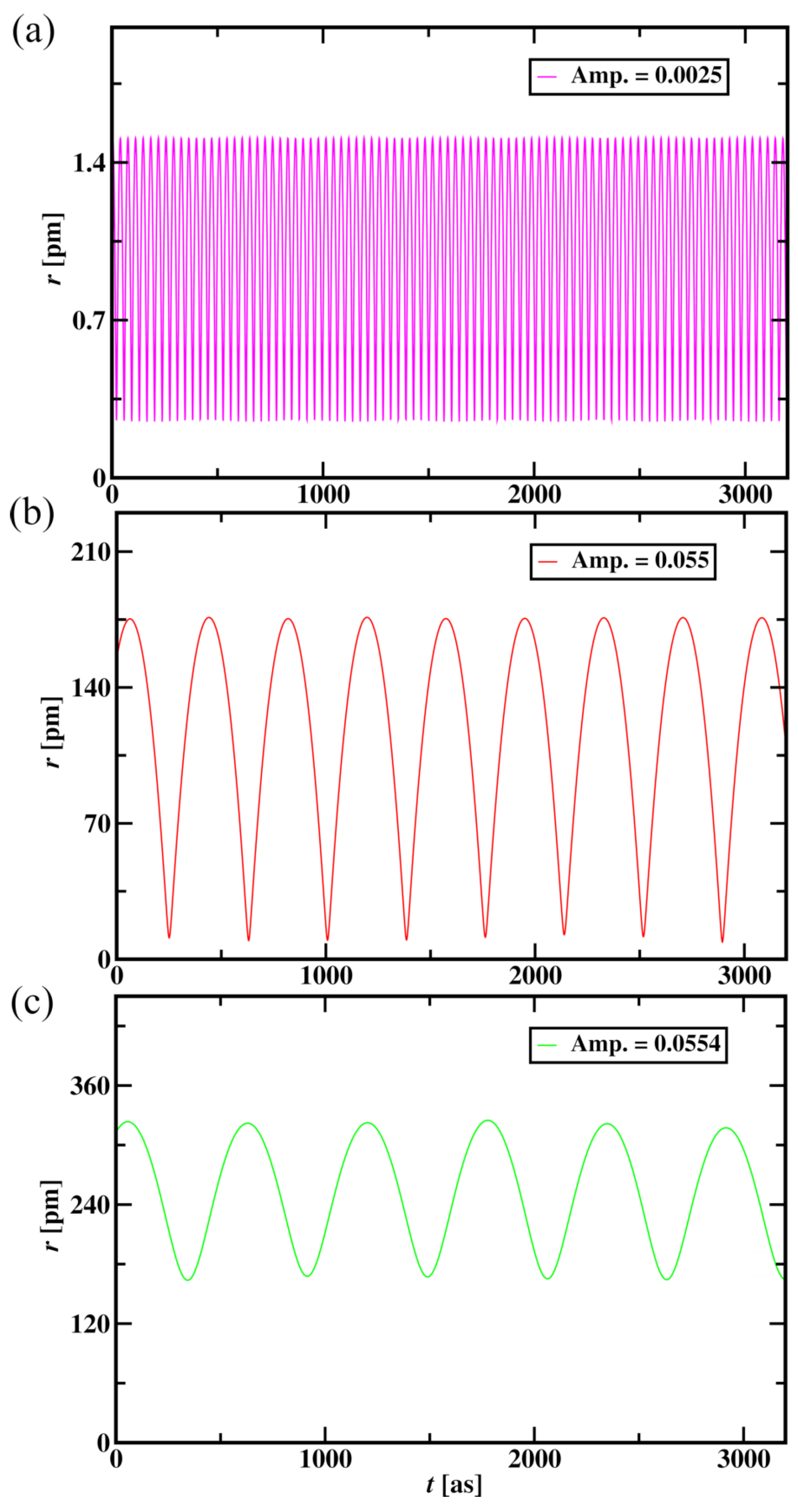As shown in Figure 9, the change in the radius of the atom shows a similar trend to the particle nature of electrons, as shown in the previous section.
The presence of crest and trough of aether medium waves on the electron’s path was not reflected immediately but showed long-term effects on trajectories of the electron that further affect the radius of the Hydrogen atom as shown in Table 4. These wave collisions with electron show an effect in increasing its potential and kinetic energies. An increase in the amplitude of aether medium waves increases the radius of the Hydrogen atom. Also, an increase in the amplitude of aether medium waves increases the wavelength of the plot shown in Figure 9. An increase in amplitude increases the potential and kinetic energy of the electron (Table 4). A small increase in the amplitude of 0.0004 shows a rapid increase in the radius of the Hydrogen atom and a rapid increase in the electron’s energy. Aether medium wave amplitude of 0.0025 for proton is considered further in this study as the radius of the atom is 1.03 pm, which is close to the particle nature of the Hydrogen atom of radius 0.89 pm. By changing the wavelength, and amplitude of Aether medium waves, one can alter the electron trajectories around the nucleus. Future studies will include an investigation of these wave properties that lead electron trajectories to follow atomic orbitals around the nucleus.

3.2.2. Wave Nature of Carbon Atom Simulation

The electron’s movement was considered by the potential acting on it and the presence of three-dimensional aether medium waves of protons, neutrons and electrons as shown in Figure 10. At each time step, past memory of the presence of aether medium waves was not considered and new aether medium waves and its interference pattern were considered. Acceleration acting on an electron is affected by the presence of protons, neutrons and other electrons which is given by summing up of equation 11 for all particles as follows:
a j = ∑ i ≠ j , i = 1 18 2 m A e t h e r m e u i , A e t h e r ( 1 − m A e t h e r m e ) Δ t = ∑ i ≠ j , i = 1 18 2 m A e t h e r m e A i c o s ( r i w l ) ( 1 − m A e t h e r m e ) Δ t
The simulation of a carbon atom with a wave nature of electrons revolving around the nucleus is shown in the supplementary material video 6. The variables m A e t h e r / m e (0.3) and wl (0.04777) are taken the same as the Hydrogen atom simulation. Parameterization of aether medium waves amplitude ( A i ) for protons, neutrons and electrons for carbon atom was taken in two stages. The first stage is considering aether medium waves only for protons and neutrons and parameterizing wave amplitude ( A i ) for them. In the second stage, aether medium waves for electrons were added and its wave amplitude ( A i ) was studied. 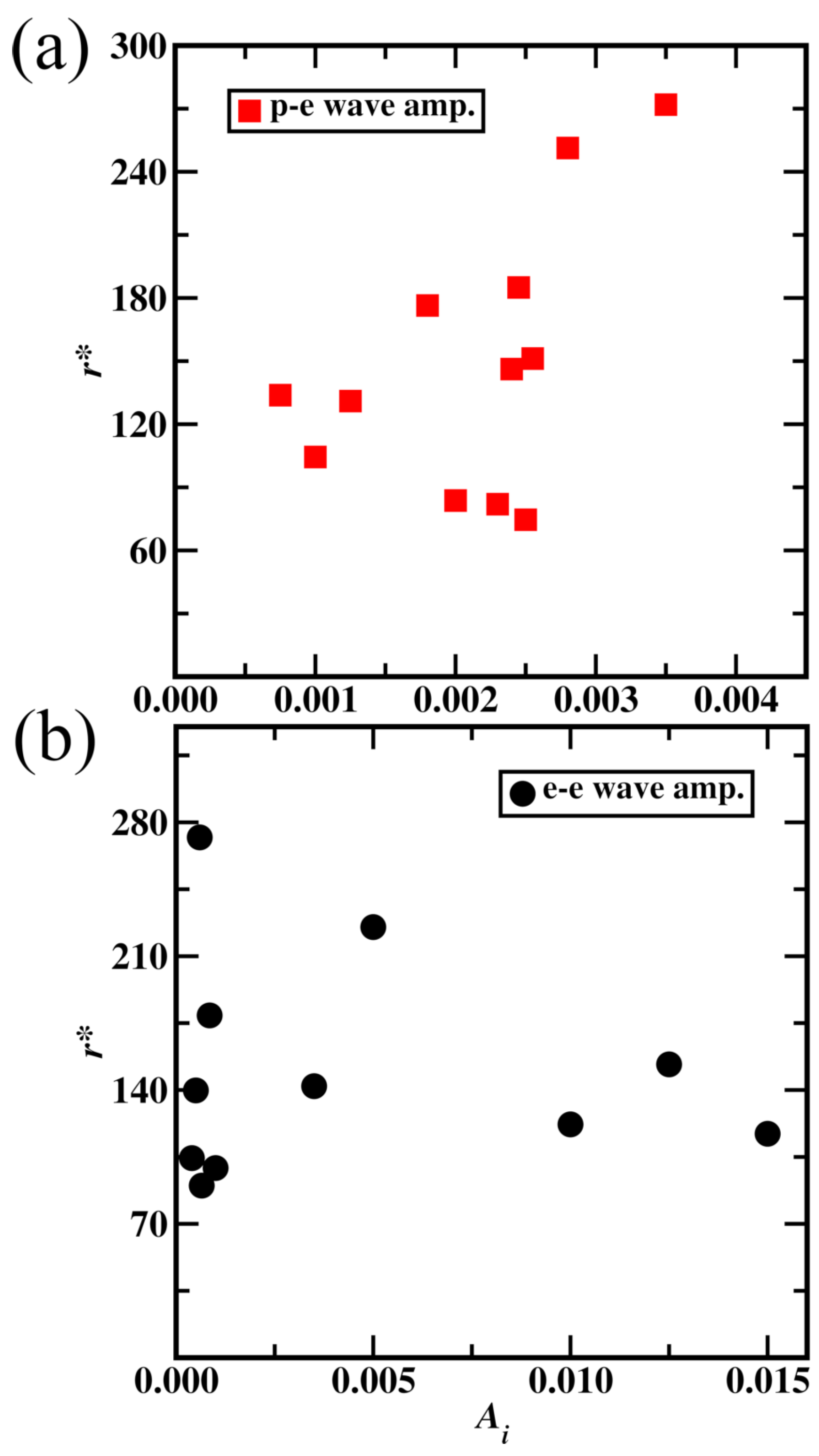The first stage of parameterization of A i was shown in Figure 11a and it shows a non-linear trend. Amplitude ( A i ) for proton and neutron aether medium waves were taken as 0.0025, resulting in a minimum carbon atom radius. For the second stage parameterization, of A i for electron aether medium waves, the carbon atom radius trend is complex as shown in Figure 11b. Lower values of A i showed a lower atom radius and a value of 0.00065 is taken resulting in an atom radius of 70 pm.
After parameterising A i based on the radius of the carbon atom for proton, neutron and electron, the radius of the carbon atom for particle nature and wave nature was shown in Table 5. Differences in particle and wave nature of Carbon atom for electron’s Potential, Kinetic and Total energies are shown in Table 6 (shown in Figures S2, S3, and S4 in the supplementary material). In both particle nature and wave nature, core electron energies are lower than valence electron energies. Electron energies (kinetic and potential energies) for particle nature carbon atom are higher than the wave nature of the Carbon atom. The differences in electron energies for particle and wave nature become less for valence electrons than for the core electrons.

3.3. Subatomic Particle Dynamics Simulations for Molecules

A simulation of an oxygen molecule with two oxygen atoms along with a nucleus was developed and shown in the video (supplementary material video 7). It was observed that the valence electrons of two atoms were shared between the two oxygen atoms. Analysis of this simulation and parameterizing new potentials, developed in this study, for molecules will be considered as future studies.

3.4. Uranium Atom Simulation

Uranium atom simulation was considered to see the advantages and limitations of this approach, as shown in the supplementary material video 8. The nucleus of a uranium atom is found to be stable and property analysis will be considered in future studies.

4. Conclusion

New potentials were introduced in this study to model subatomic particles interactions in stable atom simulations. The fundamental principle behind developing these potentials is that subatomic particles in an atom repel at small distances and attract each other at large distances. New potentials parameters were parameterized using carbon atom simulations and their properties. The time step for subatomic particle dynamics was calculated to be 1.67 attoseconds which gives good agreement with electron dynamics in attosecond science studies. Randomness in the Hydrogen atom for placing electron positions results in radius from 3 pm to 65.3 pm which gives good agreement with the experimental value. The Pilot-Wave theory was implemented in SPD where electrons motion was guided by three-dimensional aether medium waves interference patterns. SPD was carried out for Oxygen molecule that give stable molecular structure and trajectories have emerged for the electrons shared by multiple atoms. Future directions in subatomic particle dynamics are as follows:
1. To parameterize three-dimensional aether medium waves (hidden variables) to alter electron trajectories similar to atomic orbitals.
2. To model Monte Carlo simulations for within-atom simulations by placing electrons randomly around the nucleus and calculating the most favourable positions using new potentials developed in this study.
3. Electrons rotate themselves and revolve around the nucleus. Incorporating rotation of electrons in new potentials and investigating the change in rotational speed of electrons that affect the interactions between particles.
4. Replacing protons and neutrons with fundamental particles in the nucleus in subatomic particle dynamics (SPD) which represents a better atom model.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org.

Acknowledgments

I thank Gomathi, Punya Koti and Dr Delli Ganesh for their guidance in this project. I thank Dr Subhash Patri for his guidance in this project.

References

  1. Coulomb, C.A. Premier mémoire sur l’électricité et le magnétisme. Histoire de l’Academie royale des sciences 1785, 569. [Google Scholar]
  2. Kane, C.; Balents, L.; Fisher, M.P. Coulomb interactions and mesoscopic effects in carbon nanotubes. Physical review letters 1997, 79, 5086. [Google Scholar] [CrossRef]
  3. Cea, T.; Guinea, F. Coulomb interaction, phonons, and superconductivity in twisted bilayer graphene. Proceedings of the National Academy of Sciences 2021, 118, e2107874118. [Google Scholar] [CrossRef] [PubMed]
  4. Alder, B.J.; Wainwright, T.E. Studies in Molecular Dynamics. I. General Method. The Journal of Chemical Physics 1959, 31, 459–466. [Google Scholar] [CrossRef]
  5. Karplus, M.; Petsko, G.A. Molecular dynamics simulations in biology. Nature 1990, 347, 631–639. [Google Scholar] [CrossRef] [PubMed]
  6. Rapaport, D.C. The art of molecular dynamics simulation; Cambridge university press, 2004. [Google Scholar]
  7. Laio, A.; Parrinello, M. Escaping free-energy minima. Proceedings of the National Academy of Sciences 2002, 99, 12562–12566. [Google Scholar] [CrossRef] [PubMed]
  8. Corkum, P.B.; Krausz, F. Attosecond science. Nature Physics 2007, 3, 381–387. [Google Scholar] [CrossRef]
  9. Krausz, F.; Ivanov, M. Attosecond physics. Reviews of Modern Physics 2009, 81, 163–234. [Google Scholar] [CrossRef]
  10. Calegari, F.; Ayuso, D.; Trabattoni, A.; Belshaw, L.; De Camillis, S.; Anumula, S.; Frassetto, F.; Poletto, L.; Palacios, A.; Decleva, P.; others. Ultrafast electron dynamics in phenylalanine initiated by attosecond pulses. Science 2014, 346, 336–339. [CrossRef]
  11. Ciappina, M.F.; Pérez-Hernández, J.A.; Landsman, A.S.; Okell, W.A.; Zherebtsov, S.; Förg, B.; Schötz, J.; Seiffert, L.; Fennel, T.; Shaaran, T.; others. Attosecond physics at the nanoscale. Reports on Progress in Physics 2017, 80, 054401. [CrossRef]
  12. Smirnova, O.; Mairesse, Y.; Patchkovskii, S.; Dudovich, N.; Villeneuve, D.; Corkum, P.; Ivanov, M.Y. High harmonic interferometry of multi-electron dynamics in molecules. Nature 2009, 460, 972–977. [Google Scholar] [CrossRef] [PubMed]
  13. de Broglie, L. Recherches sur la théorie des quanta [Researches on the quantum theory]. Annales de Physique 1927, 3, 22–128. [Google Scholar]
  14. Bohm, D. A suggested interpretation of the quantum theory in terms of "hidden" variables. I and II. Physical Review 1952, 85, 166–179. [Google Scholar] [CrossRef]
  15. Valentini, A. Signal-locality, uncertainty, and the subquantum H-theorem. I. Physical Review A 2001, 63, 033605. [Google Scholar] [CrossRef]
  16. Norsen, T. The pilot-wave perspective on spin. American Journal of Physics 2014, 82, 337–348. [Google Scholar] [CrossRef]
  17. Einstein, A. Die Feldgleichungen der Gravitation. Sitzungsberichte der Preussischen Akademie der Wissenschaften zu Berlin 1915, pp. 844–847.
  18. Magueijo, J. Faster than the Speed of Light; Harvard University Press, 2003. [Google Scholar]
  19. Couder, Y.; Fort, E. Single-particle diffraction and interference at a macroscopic scale. Physical review letters 2006, 97, 154101. [Google Scholar] [CrossRef] [PubMed]
  20. Harris, D.M.; Moukhtar, J.; Fort, E.; Couder, Y.; Bush, J.W. Wavelike statistics from pilot-wave dynamics in a circular corral. Physical Review E 2013, 88, 011001. [Google Scholar] [CrossRef] [PubMed]
  21. Couder, Y.; Fort, E. Probabilities and trajectories in a classical wave-particle duality. Journal of Physics: Conference Series. IOP Publishing, 2012, Vol. 361, p. 012001. [CrossRef]
  22. Fort, E.; Eddi, A.; Boudaoud, A.; Moukhtar, J.; Couder, Y. Path-memory induced quantization of classical orbits. Proceedings of the National Academy of Sciences 2010, 107, 17515–17520. [Google Scholar] [CrossRef]
  23. Pucci, G.; Harris, D.M.; Faria, L.M.; Bush, J.W. Walking droplets interacting with single and double slits. Journal of Fluid Mechanics 2018, 835, 1136–1156. [Google Scholar] [CrossRef]
  24. Swope, W.C.; Andersen, H.C.; Berens, P.H.; Wilson, K.R. A computer simulation method for the calculation of equilibrium constants for the formation of physical clusters of molecules: Application to small water clusters. The Journal of chemical physics 1982, 76, 637–649. [Google Scholar] [CrossRef]
  25. Humphrey, W.; Dalke, A.; Schulten, K. VMD – Visual Molecular Dynamics. Journal of Molecular Graphics 1996, 14, 33–38. [Google Scholar] [CrossRef] [PubMed]
Preprints 98986 g001
Figure 1. Radius of Hydrogen atom versus time in a subatomic particle dynamics simulation.
Figure 1. Radius of Hydrogen atom versus time in a subatomic particle dynamics simulation.
Preprints 98986 g001
Preprints 98986 g002
Figure 2. Energies of the electron and its radius variation with time in a Hydrogen atom. The radius of a Hydrogen atom is presented on the y-axis on the right.
Figure 2. Energies of the electron and its radius variation with time in a Hydrogen atom. The radius of a Hydrogen atom is presented on the y-axis on the right.
Preprints 98986 g002
Preprints 98986 g003
Figure 3. Total energy of the electron and its radius variation with time in a Hydrogen atom. The radius of a Hydrogen atom is presented on the y-axis on the right.
Figure 3. Total energy of the electron and its radius variation with time in a Hydrogen atom. The radius of a Hydrogen atom is presented on the y-axis on the right.
Preprints 98986 g003
Preprints 98986 g004
Figure 4. Electron’s phase space configuration with local minima. The electron trajectory oscillates in one of the local minima (black region).
Figure 4. Electron’s phase space configuration with local minima. The electron trajectory oscillates in one of the local minima (black region).
Preprints 98986 g004
Preprints 98986 g005
Figure 5. Electron trajectories around the nucleus of Carbon atom for 5000 time steps.
Figure 5. Electron trajectories around the nucleus of Carbon atom for 5000 time steps.
Preprints 98986 g005
Preprints 98986 g006
Figure 6. Change in Radius of the Carbon atom with time.
Figure 6. Change in Radius of the Carbon atom with time.
Preprints 98986 g006
Preprints 98986 g007
Figure 7. Potential (a) and Kinetic (b) energies of electrons in particle nature of Carbon atom. (On the x-axis, variable ( N e ), the core electron numbered 1 and the valence electron numbered 6).
Figure 7. Potential (a) and Kinetic (b) energies of electrons in particle nature of Carbon atom. (On the x-axis, variable ( N e ), the core electron numbered 1 and the valence electron numbered 6).
Preprints 98986 g007
Preprints 98986 g008
Figure 8. Proton (black circle) having Aether medium waves and electron (red circle) revolving around the proton.
Figure 8. Proton (black circle) having Aether medium waves and electron (red circle) revolving around the proton.
Preprints 98986 g008
Preprints 98986 g009
Figure 9. Radius of the Hydrogen atom versus time for the aether medium wave amplitude of 0.0025 (a), 0.055 (b), and 0.0554 (c) for 3200 time steps.
Figure 9. Radius of the Hydrogen atom versus time for the aether medium wave amplitude of 0.0025 (a), 0.055 (b), and 0.0554 (c) for 3200 time steps.
Preprints 98986 g009
Preprints 98986 g010
Figure 10. Proton (black circle) and electrons (red circles) have aether medium waves and communicate with interference patterns.
Figure 10. Proton (black circle) and electrons (red circles) have aether medium waves and communicate with interference patterns.
Preprints 98986 g010
Preprints 98986 g011
Figure 11. Radius of carbon atom variation with aether medium wave amplitude ( A i ). (a) Proton and neutron aether medium wave amplitude, (b) electron aether medium wave amplitude.
Figure 11. Radius of carbon atom variation with aether medium wave amplitude ( A i ). (a) Proton and neutron aether medium wave amplitude, (b) electron aether medium wave amplitude.
Preprints 98986 g011
Table 1. New potentials parameters, parameterized based on Carbon Atom Simulation.
Table 1. New potentials parameters, parameterized based on Carbon Atom Simulation.
ϵ (Joules) σ (picometers)
Parameterised based on Carbon atom 7.837 * 10 − 23 0.7777
Table 2. Average Radius, Total Energy, Potential Energy and Kinetic Energy for Normal simulation and Randomness simulation in a Hydrogen Atom.
Table 2. Average Radius, Total Energy, Potential Energy and Kinetic Energy for Normal simulation and Randomness simulation in a Hydrogen Atom.
Probability of Randomly Placing Electron Average Radius (pm) Average Total Energy, 10 − 23 J Average Potential Energy, 10 − 23 J Average Kinetic Energy, 10 − 23 J
0 (Normal Hydrogen Atom) 0.8875 436.97 314.58 121.4
0.000001 3.00 1453.32 974.18 479.14
0.00001 65.32 31323.31 21066.33 10256.99
0.0001 41.77 20374.48 13472.27 6902.20
0.001 14.00 6997.81 4520.54 2477.34
0.01 6.34 4418.42 2051.65 2366.77
Table 3. The average velocity of electrons in carbon atom and compared with the velocity of light.
Table 3. The average velocity of electrons in carbon atom and compared with the velocity of light.
Average Velocity (m/s) Average Velocity/Light Velocity
Electron 1 835747.25 0.0028
Electron 2 989235.65 0.0033
Electron 3 977732.33 0.0033
Electron 4 1213998.64 0.0040
Electron 5 1058082.83 0.0035
Electron 6 980335.11 0.0033
Table 4. Properties of the Hydrogen atom for change in Aether medium wave amplitude.
Table 4. Properties of the Hydrogen atom for change in Aether medium wave amplitude.
Aether Wave Amplitude Average Radius (pm) Average Potential Energy ( 10 − 23 J) Average Kinetic Energy ( 10 − 23 J)
0 (Particle Nature) 0.8875 314.58 121.4
0.0025 1.03 355.33 152.27
0.055 41.18 13288.73 8556.51
0.0554 239.94 77371.72 38671.99
Table 5. Difference in the radius of carbon atom in particle nature and wave nature.
Table 5. Difference in the radius of carbon atom in particle nature and wave nature.
Carbon Atom Particle Nature Carbon Atom Wave Nature
Average Radius (pm) 71.48 70.00
Table 6. Difference in energies of carbon atom in particle nature and wave nature.
Table 6. Difference in energies of carbon atom in particle nature and wave nature.
Potential Energy Kinetic Energy Total Energy
( 10 − 23 J) ( 10 − 23 J) ( 10 − 23 J)
Particle Nature Wave Nature Particle Nature Wave Nature Particle Nature Wave Nature
Core Electron 1 59548.52 38095.44 73459.19 49875.38 133007.71 87970.82
Core Electron 2 78471.76 52407.55 58419.72 43061.08 136891.49 95468.63
Core Electron 3 93705.87 66293.05 49802.98 39838.54 143508.85 106131.59
Core Electron 4 109062.78 83036.78 43116.09 36906.08 152178.86 119942.86
Core Electron 5 126742.76 105527.48 36944.32 34075.01 163687.09 139602.49
Valence Electron 154750.70 150474.13 31521.12 29943.54 186271.82 180417.67
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated