1. Introduction
In multistory RC buildings in Saudi Arabia, RC wall-like columns are primarily used to maximize space efficiency. These columns are frequently in need to retrofitting for several reasons, such as addition of more stories or an increase in live load due to changes in building use. Traditional methods for upgrading RC columns involved wrapping them with RC jackets [1, 2] or steel jackets [e.g., 3-7], but these approaches are labor-intensive and complex to execute. Consequently, there has been a recent shift towards using FRP composites for upgrading RC wall-like columns, as they offer benefits such as rapid and straightforward installation with minimal alteration to the column's dimensions.
The majority of research in the field of FRP-strengthened RC rectangular columns subjected to concentric loading has focused on sections with depth-to-width ratios of up to 2. There have been only a limited number of studies [8-19] that specifically addressed the retrofitting of wall-like columns with the help of FRP composites. Tan [
8] conducted experiments to investigate FRP-enhanced columns of aspect ratio of 3.65. The study compared the peak axial load of the columns with previously proposed prediction models [20, 21]. In another study by Hosny et al. [
9], the behavior of FRP-enhanced columns with sections aspect ratio of 3 was examined. The experimental FRP strains at peak load were significantly less than the failure strains. Tanwongsval et al. [
10] conducted experimental research on wall-like columns subjected to concentric loading, both without strengthening and with strengthening, with sections of the same aspect ratio as mentioned in Ref. [
8]. Two methods were employed for column strengthening, one using conventional externally bonded GFRP sheets, and the other using GFRP wrapping after modifying the section. Columns upgraded with the second technique exhibited superior performance due to enhanced confinement of concrete. Maalej et al. [
11] conducted experiments to investigate the influence of FRP schemes on enhancing the peak load of wall-like columns with sections featuring aspect ratio of 3.65. In addition to the laboratory tests, they utilized an analytical model previously proposed in Refs. [22, 23] to calculate the columns’ peak load.
Prota et al. [
12] undertook an experimental campaign to study the effects of applying GFRP sheets for enhancing the axial resistance of wall-like columns characterized by substantial depth-to-width ratios. Their research findings indicated that the GFRP wrapping resulted in enhancements in both the ductility and strength of these columns. Notably, the failure of GFRP-retrofitted specimens was found to be contingent on the shape of the column section, occurring at considerably lower horizontal GFRP strains. De Luca et al. [
13] examined wall-like columns strengthened with GFRP sheets by testing three specimens, including one control and two that were retrofitted. These upgraded specimens utilized two different GFRP confinement ratios. The study's results demonstrated that, although GFRP confinement did not necessarily enhance the maximum load, it significantly improved the concrete crushing strain.
In their research, Alsayed et al. [
14] investigated the retrofitting of RC wall-like columns with FRP composites under concentric compression. The original rectangular section underwent a transformation into an elliptical shape using cementitious mortar, which was subsequently retrofitted with CFRP sheets. Nonlinear finite element analysis was employed to evaluate the load-displacement characteristics of these columns. The use of CFRP wrapping resulted in an enhancement of both the ductility and strength of the columns.
Triantafillou et al. [
15] examined experimentally the behavior of FRP-strengthened wall-like columns. They conducted tests on a total of forty-five columns, having section aspect ratios of either 3 or 4, subjecting them to axial compression. The study explored different strengthening methods, encompassing anchored and unanchored CFRP wrapping, both without and with the modification of section. Their findings led to the conclusion that the efficiency of CFRP confinement was nearly doubled when anchors were appropriately distributed
Elsanadedy et al. [
18] conducted a study to come up with an efficient scheme - without section modification, for strengthening existing RC wall-like columns employing a hybrid of NSM and CFRP wrapping system. Six half-scale specimens were subjected to concentric compression testing. Two of these columns remained unretrofitted, serving as reference, while the remaining four were upgraded using different schemes. Among the four schemes explored, the most efficient approach involved the use of continuous NSM rebars in combination with CFRP wrapping, resulting in an impressive 80% increase in the ultimate load. Additionally, nonlinear FE analysis was employed to assess the response of the tested columns. The test results closely aligned with the FE analysis, confirming the accuracy of the constitutive models employed for different materials. In another companion study, Elsanadedy et al. [
19] studied axial strengthening of wall-like RC columns using another four different configurations. These schemes were also without shape modification, and they incorporated the use of GFRP wrapping alone, GFRP wrapping combined with bolted steel plates, or GFRP wrapping combined with connected (or disconnected) NSM bars. Nonlinear FEA was also performed for predicting the response of columns.
Even though past research was conducted concerning the behavior of control and retrofitted RC wall-like columns, the specimens in these studies were not preloaded prior to their strengthening. This did not reflect the real practice in which unstrengthened columns carry their service load, and if strengthening is required, the load is partially or totally released. The objective of this investigation is to explore the response of concentrically preloaded wall-like RC columns after being strengthened using different configurations. In the experimental campaign, four half-scale specimens were tested in the event of concentric compressive load. The first two columns were unstrengthened, and they were loaded to 80% of their axial capacity, and the load was then totally released. After that, these specimens were retrofitted using two different schemes, and hence they were concentrically loaded till failure. Besides the testing campaign, nonlinear FE analysis was performed to examine the response of tested specimens. The validated models were then employed for conducting parametric studies of practical interest.
2. Experimental Campaign
This study comprised a testing campaign carried out on half-scale RC wall-like columns tested concentrically till failure. The studied parameter in the testing campaign was the strengthening configuration. Two strengthening techniques were applied on preloaded RC specimens.
2.1. Experimental matrix
It should be noted that the experimental campaign in this study is an extension of the previous authors’ research covered in Refs. [18, 19]. The test matrix used in this study is shown in
Table 1.
Figures 1 to 3 show details of the test specimens. The design of control and strengthened specimens are detailed in Refs. [18, 19]. As clarified from
Table 1, the test matrix included 6 casted columns having 8 concentric compression tests. Out of the six casted columns, two specimens (having four tests) were casted in this study, whereas the other four specimens were casted and tested by the authors in previous studies [18, 19]. In the designation of columns, the symbols “CON” and “ST” refer to control and strengthened specimens, respectively. For control specimens, the symbol “0.8P-TLR” means that the column was loaded axially to 80% of its ultimate failure load, and the load was then totally released. However, for strengthened specimens, the symbol “0.8P-TLR” means that the column was subjected to the following scenario: 1) the unstrengthened specimen was preloaded to a maximum of 80% of its failure load, 2) the load was totally released, 3) the column was strengthened, and finally 4) the column was loaded till failure. In the current study, two control specimens CON1-0.8P-TLR and CON2-0.8P-TLR were loaded to 80% of their failure load and then the load was totally released. Thereafter, the first control specimen CON1-0.8P-TLR was upgraded using the first scheme, which is composed of three layers of CFRP together with continuous NSM steel bars (see
Figure 2). This upgraded specimen was then denoted as ST1-0.8P-TLR. However, the second control specimen CON2-0.8P-TLR was strengthened using the second scheme, which consists of five GFRP layers combined with bolted steel plates and continuous NSM steel rebars (see
Figure 3). This strengthened column was designated as ST2-0.8P-TLR. The other previously tested four specimens in the test matrix (CON1, CON2, ST1, and ST2) were used as baseline to compare with the test specimens of this study.
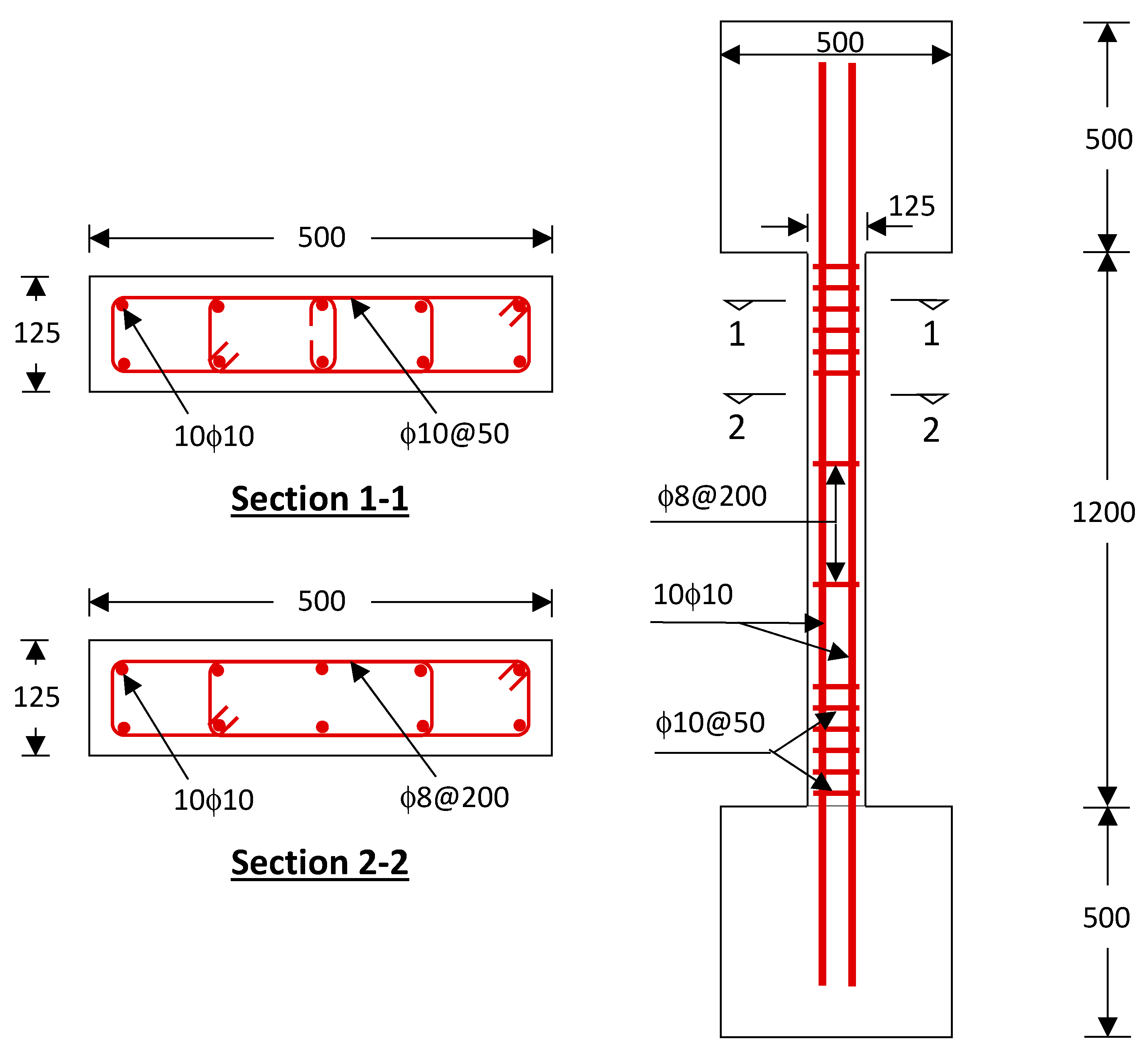
Figure 1.
Details of unstrengthened specimens (Measurements are in mm).
Figure 1.
Details of unstrengthened specimens (Measurements are in mm).
2.2. Material properties
Listed in
Table 2 are the properties of different materials used in the casting of columns. Ready-mix concrete was utilized in the fabrication of specimens, and the concrete strength at different dates was assessed via testing standard cylinders (150 mm × 300 mm) in accordance with Ref. [
24]. For steel rebars and rods, standard tension coupons were tested in accordance with Ref. [
25], and the average properties are listed in
Table 2. Standard test coupons of FRP sheets were tested in tension in accordance with Ref. [
26], and the average properties are also summarized in this table. The tensile strength in the fiber direction reported in
Table 2 for FRP material was computed as 55% of the mean strength of test coupons in tension [
27]. For plates of steel used in specimen ST2-0.8P-TLR, standard tension coupons were tested in accordance with Ref. [
28], and the mean values of properties are displayed in the table. For the adhesive mortar used in the NSM grooves, the properties depicted in the table are given as per the datasheet supplied by the manufacturer.
2.3. Preparation and testing setup of columns
Figure 4 presents the preparation steps for fabrication of columns. More details about preparation steps can be found in Refs. [18, 19].
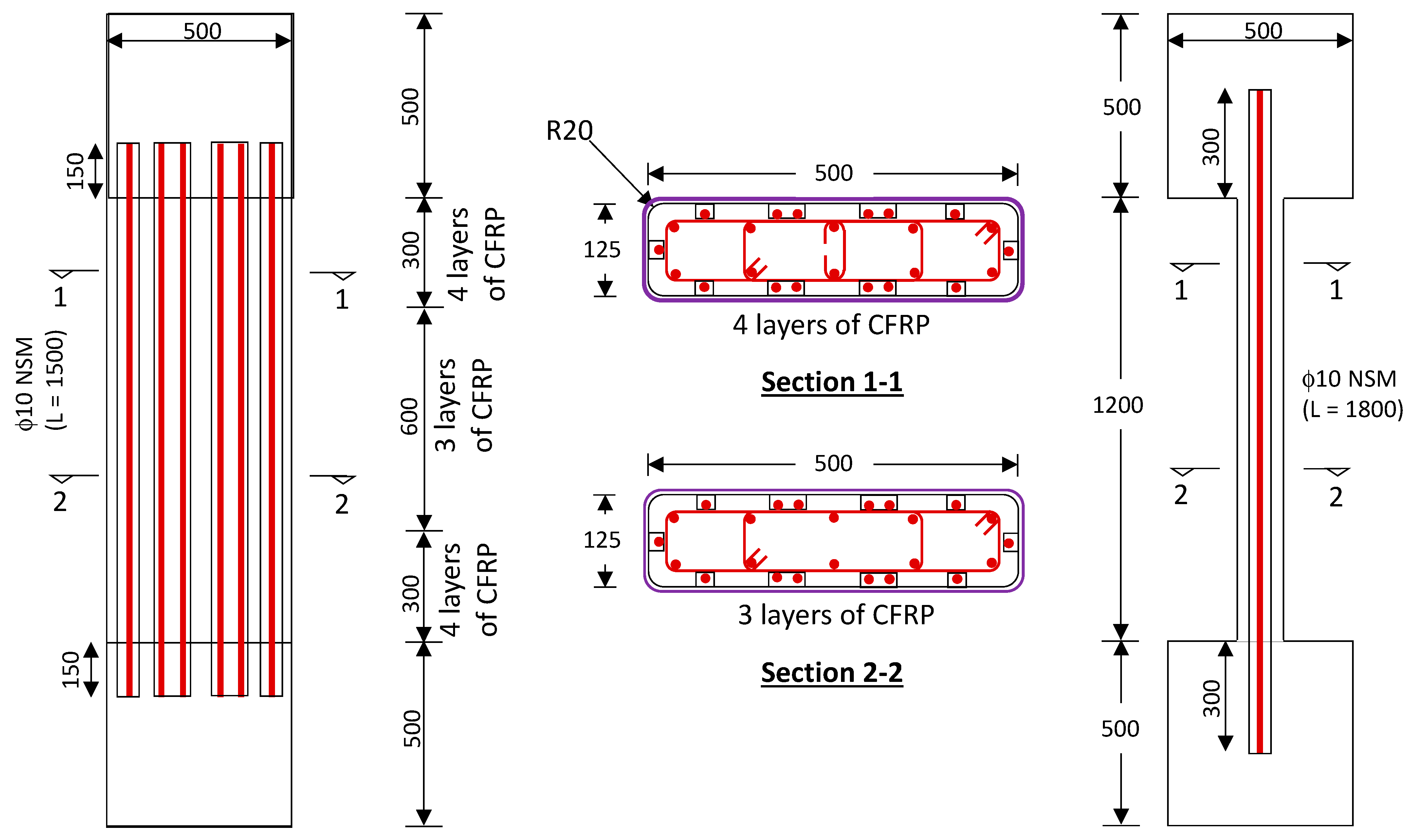
Figures 4(a) and 4(b), respectively, present the pictures of formwork having reinforcement cages before casting of concrete and the columns after concreting. As identified in
Figure 2 and
Figure 3, for the upgraded columns, the corners were filleted for 20 mm radius for minimizing the rupture of the FRP sheets at corners.
In the preparation of strengthened column ST1-0.8P-TLR, the surface of control specimen CON1-0.8P-TLR was prepared after testing via grinding, sandblasting, and cleaning. Then, grooves were cut in the concrete cover at the location of NSM bars, which were fixed in place by bonding into the top and bottom bulbs as seen in
Figure 4(c). Epoxy adhesive mortar was then applied into the NSM grooves. After mortar curing, its surface was sandblasted and cleaned. Subsequently, CFRP laminates were wrapped around column section employing the standard wet layup process (see
Figure 4(d)).
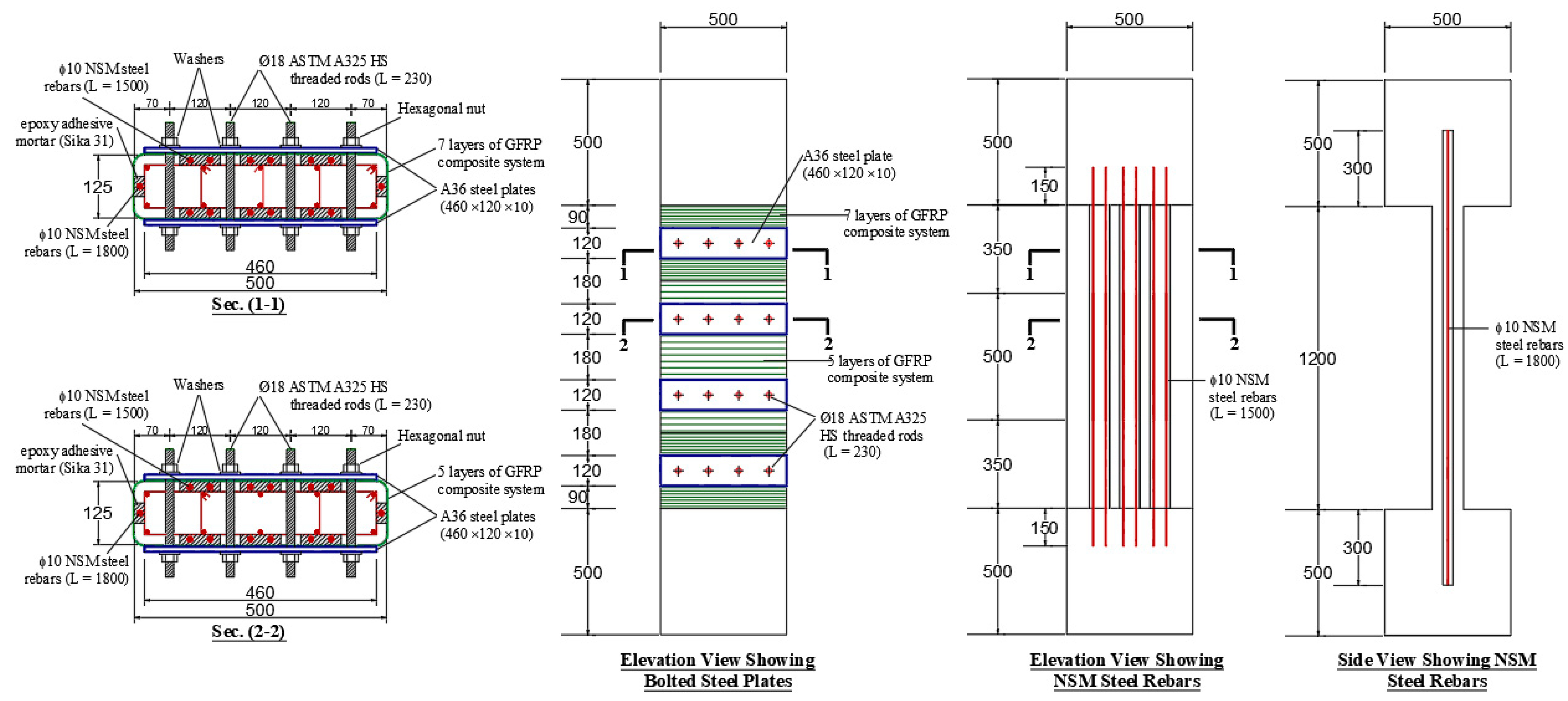
Similarly, in the preparation of upgraded specimen ST2-0.8P-TLR, the surface of the control column CON2-0.8P-TLR was grinded, sandblasted, and cleaned after testing. Then, grooves were cut in the cover concrete at the location of NSM bars. Also, holes were drilled in the longer column side at the position of threaded rods, as seen in
Figure 4(e). Thereafter, the NSM bars were fixed in the grooves by bonding into the top and bottom bulbs, and an epoxy adhesive mortar was added to the grooves for bonding of bars. Once the adhesive mortar got cured, its surface was sandblasted and cleaned. Then, the GFRP layers were wrapped around the column section following the wet layup process.
Following the curing of GFRP laminates, perforations were created in the sheets at corresponding locations of holes on the concrete surface. Subsequently, threaded rods were introduced into these holes and affixed to the concrete using an epoxy-based mortar. After the mortar had completed its curing process, steel plates were then attached to the lengthier side of the column with the help of epoxy-based mortar (see
Figure 4(f)).
Figures 4(g) and 4(h) show, respectively, the test setup and instrumentation details for control and retrofitted columns. Concentric compression was applied on the columns via a 10 mega-newton test machine. For recording the axial displacement of columns, four LVDTs were fixed around the column section at a 400 mm gage length. Also, strain gages were fixed onto the concrete surface, steel plates, FRP sheets, and steel rebars for measuring their strain. A data acquisition system was utilized for recording the test results. The control columns CON1-0.8P-TLR and CON2-0.8P-TLR were monotonically loaded to 80% of the average peak load of specimens CON1 and CON2 (tested previously in Refs. [18, 19]), and the load was then totally released. However, the strengthened specimens ST1-0.8P-TLR and ST2-0.8P-TLR were monotonically loaded till failure via a displacement-controlled strategy.
3. Discussion of Experimental Findings
Table 3 and
Table 4 list, respectively, the key experimental findings of the 8 specimens of the test matrix with regard to load-displacement and stress-strain responses.
It should be stated that even though specimens CON1, CON2, ST1, and ST2 were not tested in this study, their results are shown in
Table 3 and
Table 4 for the sake of comparison with specimens of this study. The test findings in
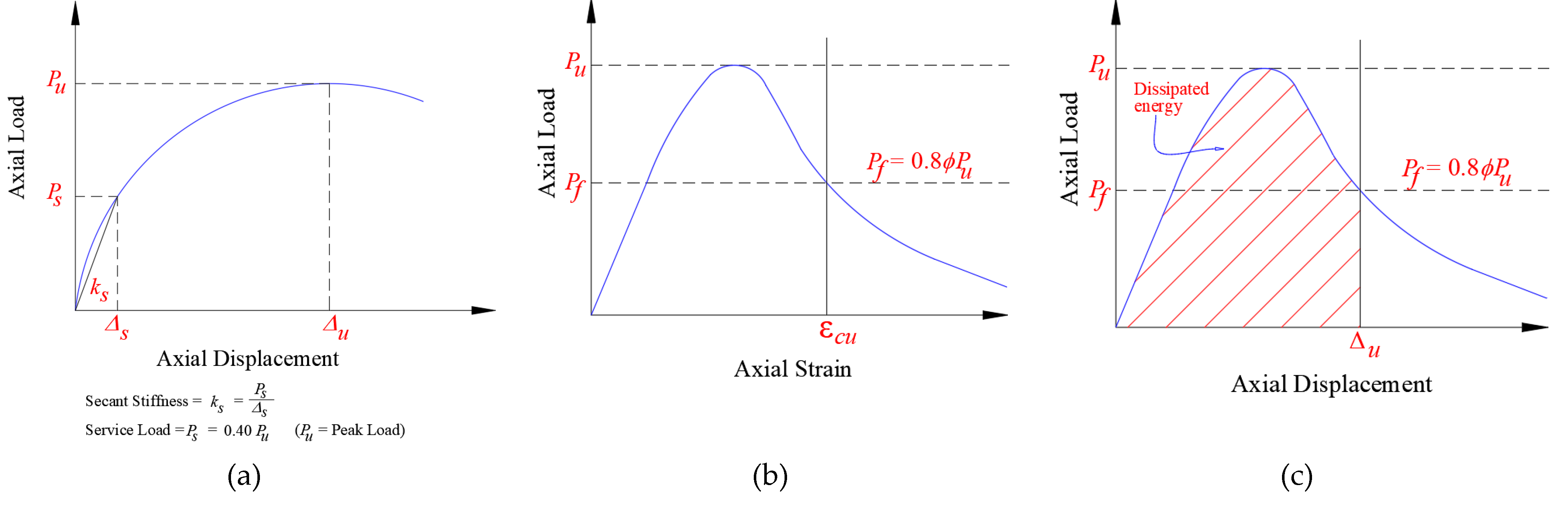
Table 3 include: service, yield, and peak loads along with their respective displacements, ultimate displacement, energy dissipated (computed at ultimate state), and stiffness at service load. As depicted in
Figure 5(a), the service load was assessed as 40% of the peak load [7, 18, 19, 29, 30]. The ultimate displacement (Δu) shown in
Figure 5(a) is estimated at the ultimate state, which is defined in
Figure 5(b) as that corresponded with concrete crushing as per the ACI 318-19 code [
31]. As displayed in
Figure 5(c), the energy dissipated was computed as the work done by the applied load (area under load-displacement plot till ultimate displacement).
The stress-strain data provided in
Table 4 encompasses several parameters, including actual and maximum average concrete strengths, concrete axial strain at the point of maximum stress, ultimate concrete axial strain, axial strain in both original and NSM bars at peak load, maximum horizontal strain in FRP layers, and maximum horizontal strain in steel plates (for specimens ST2 and ST2-0.8P-TLR). To determine the maximum load, the following equations were employed:
where
Pu is the ultimate load;
Ag,
Ast, and
ANSM are, in turn, the areas of column cross-section, main rebars, and NSM rebars. Also, the notations
fy-st and
fy-NSM stand for the yield strengths of main and NSM rebars, in turn.
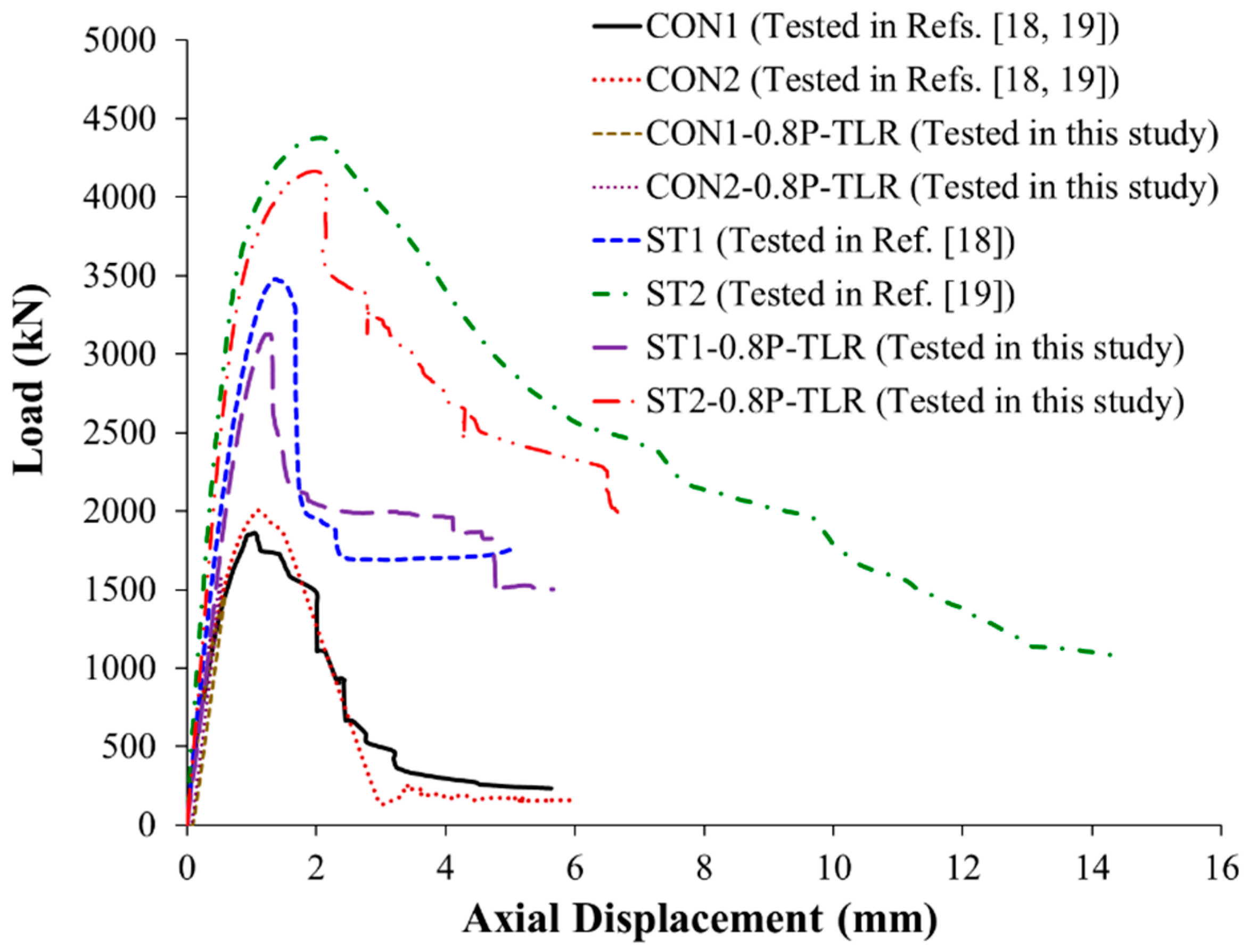
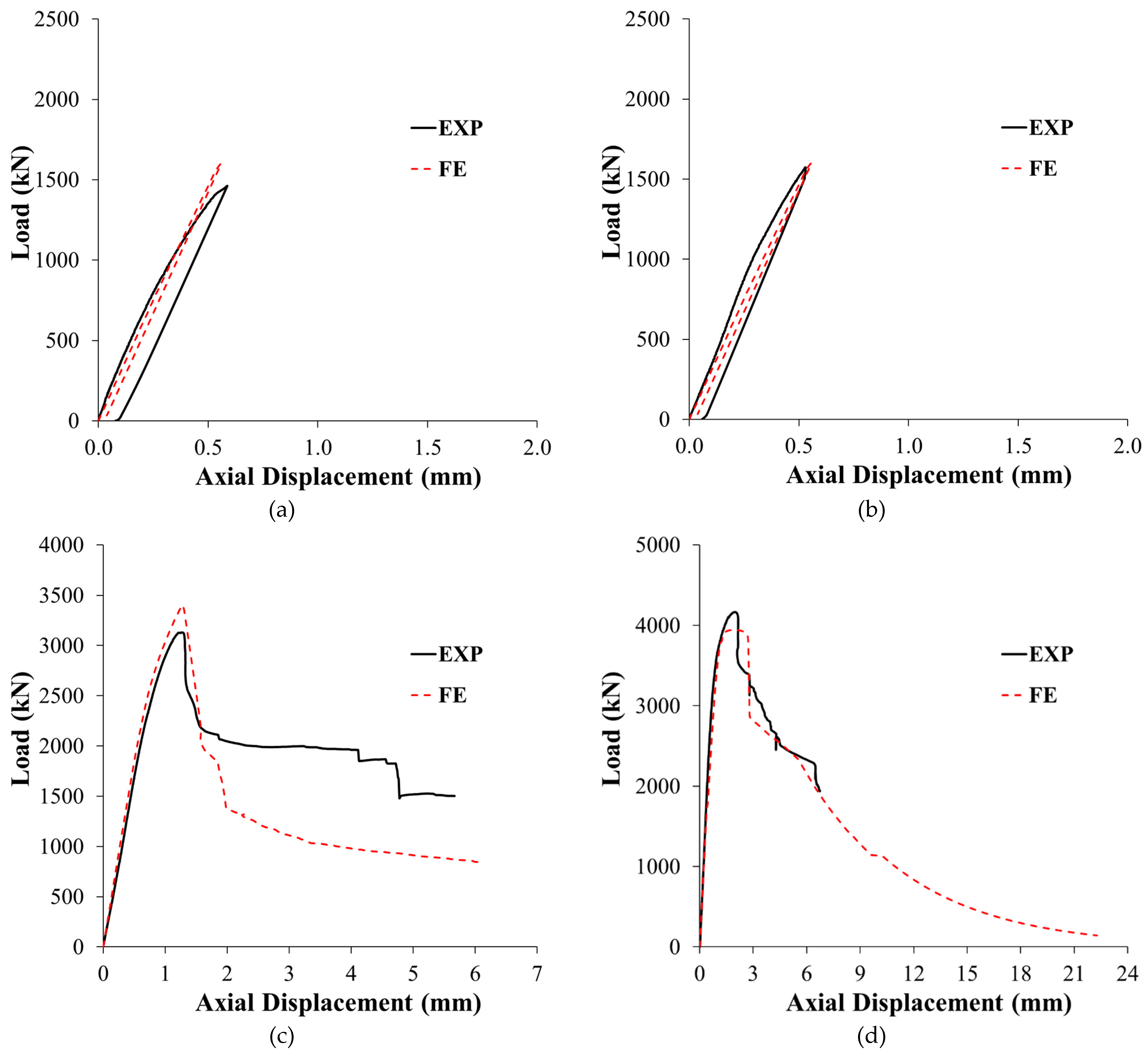
Figure 6 depicts the load versus axial compression plots of 8 specimens of the test matrix. The experimental failure patterns of tested columns are depicted in
Figure 7. Discussed below are the experimental findings of the 4 specimens of this study. Discussions of test results of other specimens are given in Refs. [18, 19].
3.1. Control specimens
As mentioned previously, the control specimens CON1-0.8P-TLR and CON2-0.8P-TLR were concentrically loaded to 80% of the average peak loads of specimens CON1 and CON2, and the load was then totally released. As clarified from
Table 3, the average ultimate load of columns CON1 and CON2 is 1934 kN. The maximum recorded loads for specimens CON1-0.8P-TLR and CON2-0.8P-TLR are 1463 kN and 1573 kN, which, respectively, represent about 76% and 81% of the average ultimate load of CON1 and CON2. As the peak loads of the two control columns CON1-0.8P-TLR and CON2-0.8P-TLR were considerably lower than their crushing load (= 1934 kN), no signs of failure were observed at the peak load of the two specimens as identified in
Figure 7(a).
3.2. Upgraded specimen ST1-0.8P-TLR
As mentioned before, this specimen was upgraded with the first scheme, which comprised of CFRP layers combined with continuous NSM rebars. As depicted in
Table 3 and
Figure 6, the improvement in peak load for this strengthening configuration is 62% with regard to the average ultimate load of reference columns CON1 and CON2. Moreover, the ultimate load for specimen ST1-0.8P-TLR (= 3129 kN) is about 90% of its counterpart column ST1 (with the same strengthening scheme yet without preloading). Therefore, it can be concluded that in practical scenarios where the unstrengthened wall-like RC column is preloaded to 80% of its peak load and then fully unloaded, this retrofitting scheme is effective enough at significantly improving the axial capacity.
The failure pattern of columns ST1-0.8P-TLR is displayed in
Figure 7(b). The concrete expands laterally with the increase of axial compression because of Poisson’s ratio. At the ultimate load of 3129 kN, large dilation of concrete was noted and the strengthening system was not able to restrain the dilation because of the large depth-to-width ratio of the cross-section of column. Consequently, NSM bars’ buckling and CFRP layers’ bulging were observed in the lower part of the central 600 mm length of the specimen. Due to NSM rebars’ buckling, there was sudden drop in the axial load to 2100 kN (a little larger than the mean peak load of reference test specimens CON1 and CON2) but became nearly flat at 1990 kN and continued until displacement of about 4.1 mm, as illustrated in
Figure 6. Further increase in the axial displacement resulted in damage of concrete and buckling of original column bars that caused the fracture of CFRP sheets in the lower part of the central 600 mm length of the column, as shown in
Figure 7(b).
3.3. Upgraded specimen ST2-0.8P-TLR
As this specimen was retrofitted with the second scheme, which was a combination of GFRP sheets, continuous NSM steel rebars, and bolted steel plates. As noted in
Table 4 and
Figure 6, the peak load of this specimen was 4166 kN, which is greater than the mean ultimate load of control columns CON1 and CON2 by about 115%. It is also found that this strengthening configuration is better than the first scheme, as the response parameters of column ST2-0.8P-TLR with regard to peak load, ultimate displacement, secant stiffness, and dissipated energy were significantly more than specimen ST1-0.8P-TLR by about 33%, 213%, 47%, and 358%, respectively. The enhancement in the load-displacement characteristics over the first scheme was because of the extra confinement due to the bolted steel plates. However, the ultimate load, stiffness, and dissipated energy of column ST2-0.8P-TLR were about 95%, 86%, and 92%, respectively, of its counterpart ST2 (with the same strengthening scheme yet without preloading). Conclusively, the second strengthening scheme is a lot better than the first one in practical scenarios where the unstrengthened column is preloaded to 80% of its peak load and then fully unloaded. It is considered as a super scheme at significantly improving the load-compression response of concentrically loaded columns.
The observed failure pattern of specimen ST2-0.8P-TLR is depicted in
Figure 7(c). The failure was initiated by the GFRP laminates’ bulging between the steel plates near the middle portion of the column length, which resulted in a decrease in the load. The ultimate failure was because of fracture of the GFRP sheets close to the corner due to the buckling of both NSM and main rebars on the shorter side of the specimen, as demonstrated in
Figure 7(c).
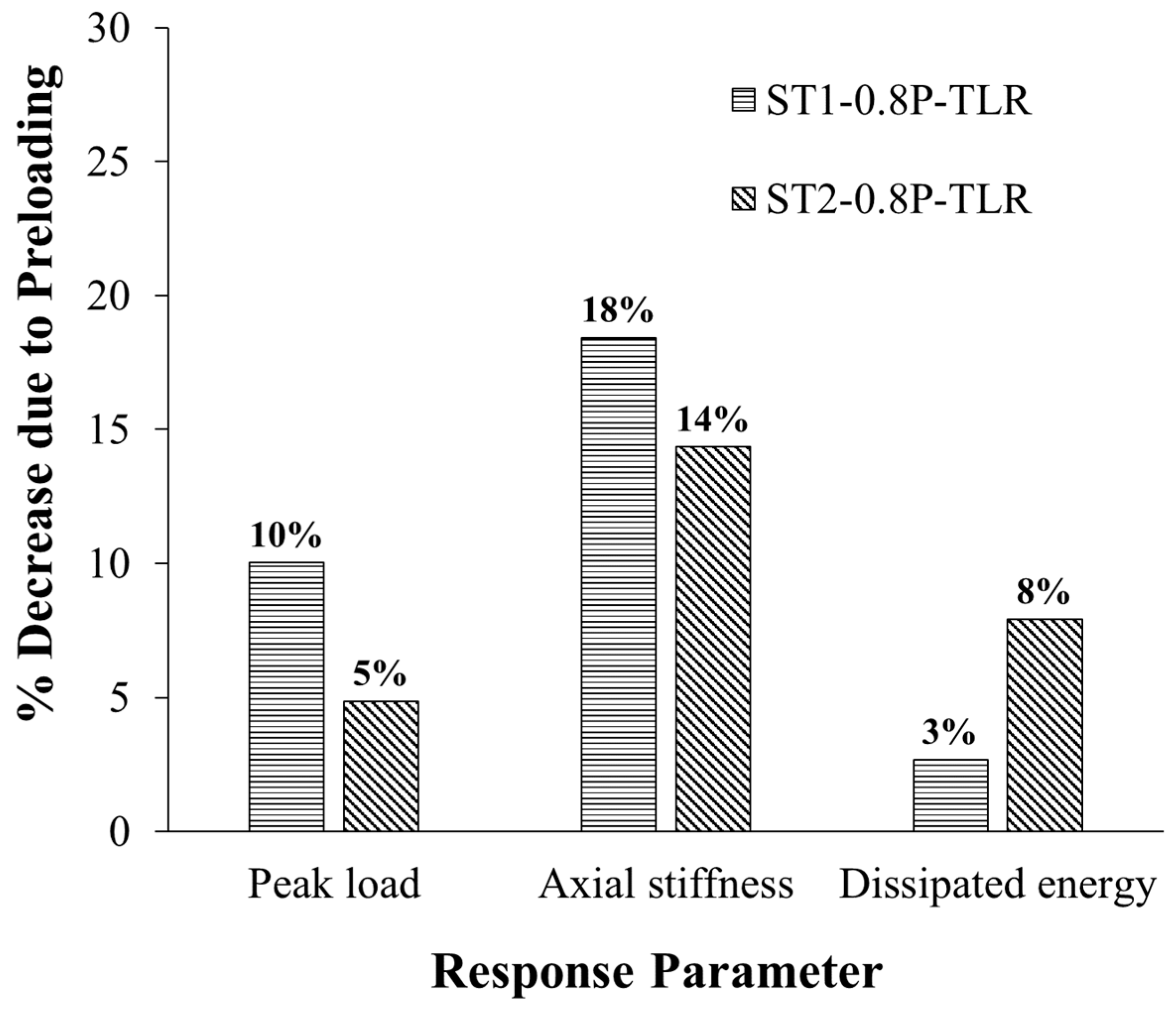
3.4. Effect of preloading
Figure 8 shows the impact of preloading in control specimens CON1-0.8P-TLR and CON2-0.8P-TLR on the percent reduction in the response parameters of strengthened specimens ST1-0.8P-TLR and ST2-0.8P-TLR with regard to upgraded specimens ST1 and ST2. It is identified that preloading the unstrengthened specimens with 80% of their axial load-bearing resistance followed by total load release marginally reduced the peak load in specimens ST1-0.8P-TLR and ST2-0.8P-TLR with respect to their counterparts ST1 and ST2 by 10% and 5%, respectively. Also, compared with columns ST1 and ST2, the dissipated energy of specimens ST1-0.8P-TLR and ST2-0.8P-TLR, in turn, was marginally reduced by 3% and 8% (see
Figure 8). However, the 80% preloading with total load release in the control specimens caused a fairly considerable reduction in the secant stiffness of upgraded specimens ST1-0.8P-TLR and ST2-0.8P-TLR by 18% and 14%, respectively, when compared with their counterparts ST1 and ST2.
4. Finite Element Analysis
Besides the experimental campaign, three-dimensional (3D) nonlinear FE modeling was carried out to explore the load-displacement response and failure pattern of test specimens. The analysis was undertaken utilizing LS-DYNA [
32]. Details of the FE modeling of the wall-like columns are given in the following subsections. However, for the other specimens of the test matrix, the FE analysis is detailed in Refs. [18, 19].
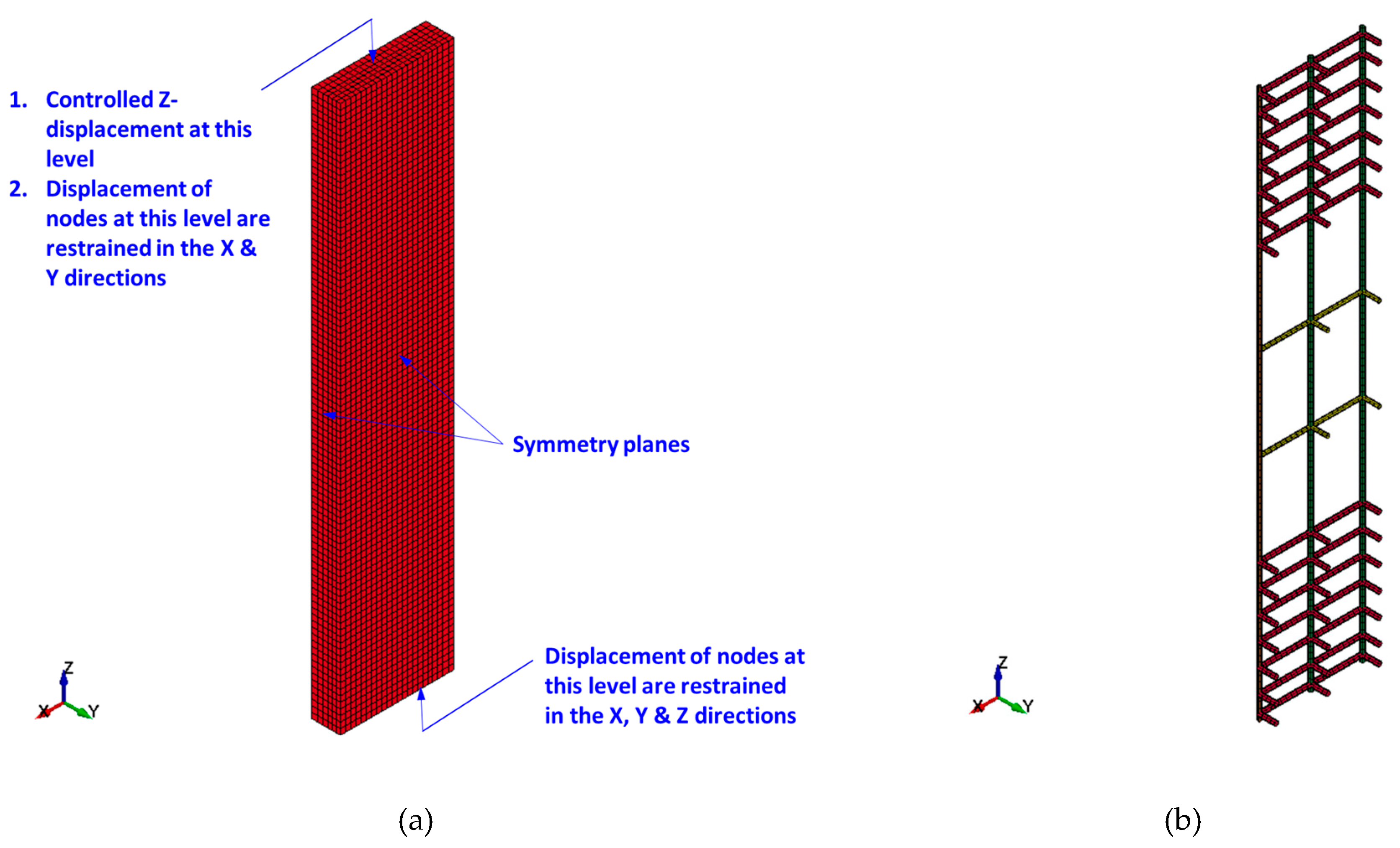
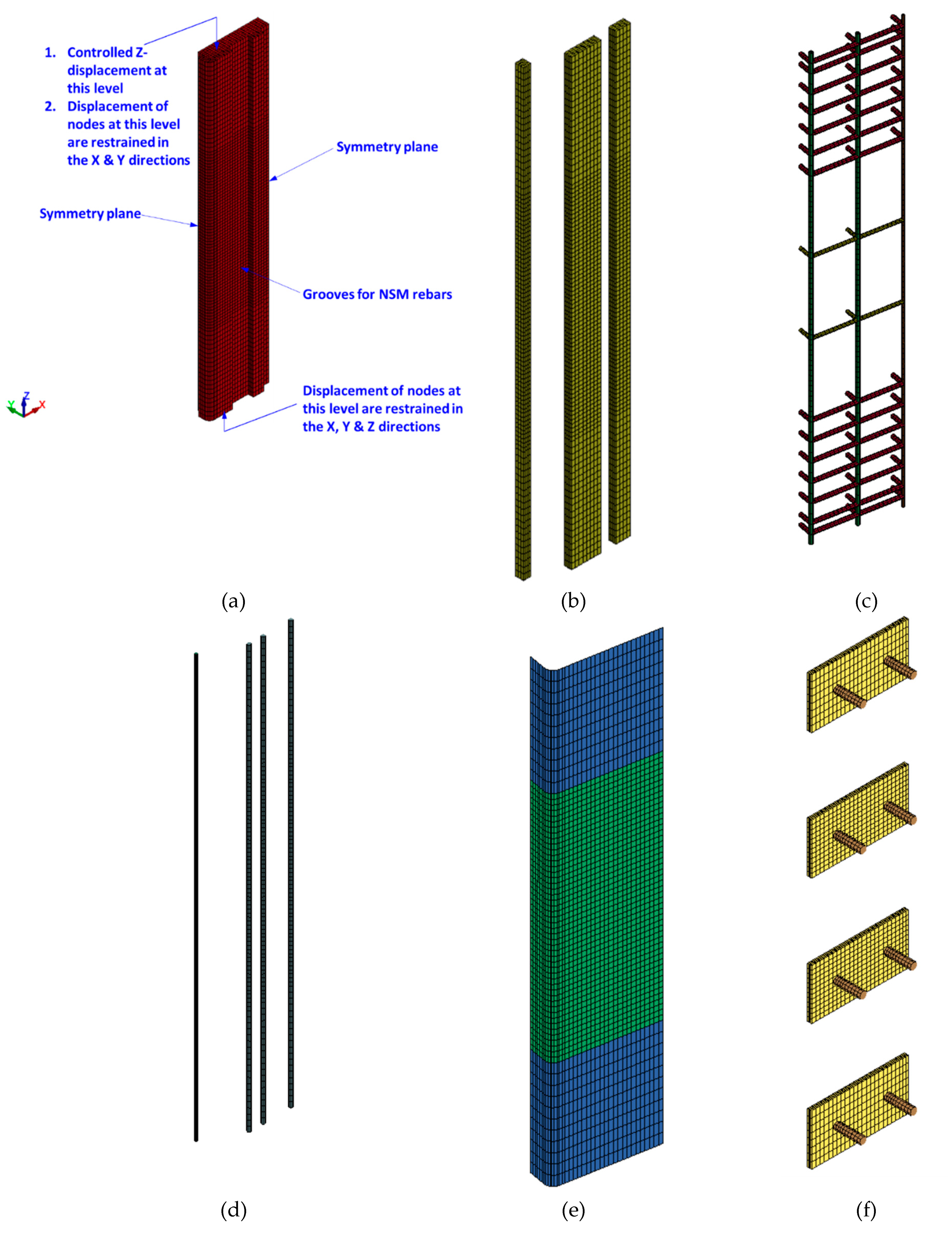
4.1. Mesh and geometry
Figure 9,
Figure 10 and
Figure 11 display the FE mesh for the test specimens. Because of the symmetrical nature of the specimens with respect to two planes, only a quarter of the column was simulated in order to conserve computational resources and memory. The end bulbs of the specimens were not included in the model since they were not damaged throughout the experiments. For modeling concrete in all specimens, mortar in strengthened specimens, and steel plates in specimen ST2-0.8P-TLR, 8-node brick elements of reduced integration were employed. However, for modeling vertical and transverse steel rebars (in all specimens) as well as threaded rods in specimen ST2-0.8P-TLR, 2-node Hughes-Liu beam elements were employed. For FRP sheets in strengthened specimens, 4-node Belytschko-Tsay shell elements [
33] were used. In the analysis, perfect bond was assumed for the interface between steel bars and concrete and also between FRP sheets and concrete surface. Mesh sensitivity study was performed and FE analysis with maximum mesh size of 25 mm was employed.
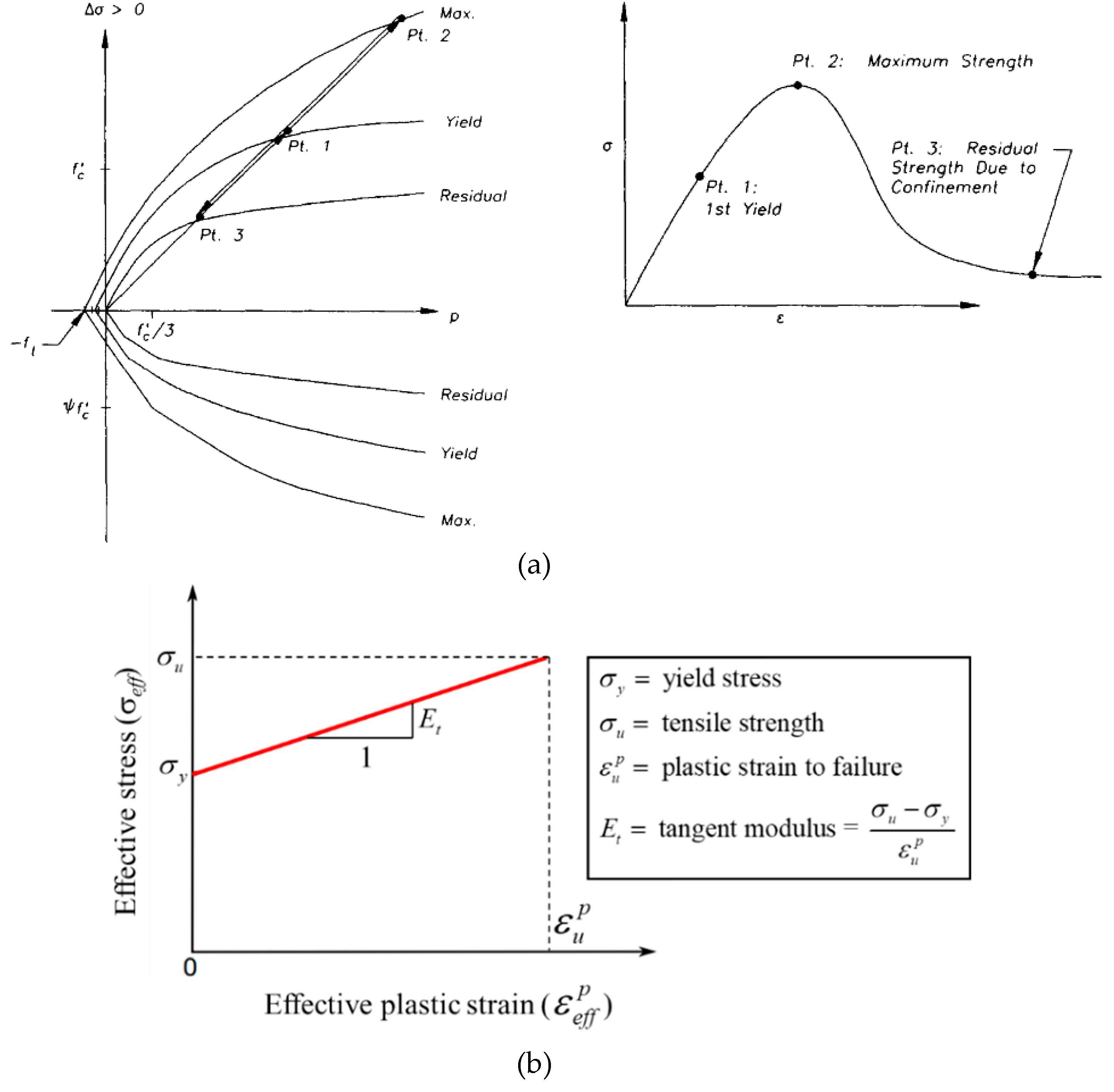
4.2. Material modeling
Table 2 reports the vital input values of the constitutive models used in the FE analysis. The damage concrete model type 72R3 [32, 34-36] was used to model both concrete and mortar.
Figure 12(a) illustrates this model, in which three individual surfaces (yield, maximum, and residual) are used to define the deviatoric strength. The modeling of steel bars, rods, and plates involved the utilization of the piecewise linear plasticity model type 24 [
32], which is characterized by a bilinear stress-strain curve illustrated in
Figure 12(b). For the modeling of FRP sheets, the enhanced composite damage model type 54-55 [
32] and the application of Chang and Chang failure criteria [
37] were employed.
4.3. Boundary conditions and analysis strategy
In setting up the boundary conditions for the column model, the lower nodes were immobilized against displacement in all the three global Cartesian directions, as depicted in
Figure 9,
Figure 10 and
Figure 11 . However, the top nodes were fixed to prevent translation in the global X and Y directions while retaining freedom of movement along the Z direction, as displayed in
Figure 9,
Figure 10 and
Figure 11 . As previously noted, only a quarter of the column was modeled due to its symmetry about two planes, and the corresponding symmetry boundary conditions were applied as depicted in
Figure 9,
Figure 10 and
Figure 11 .
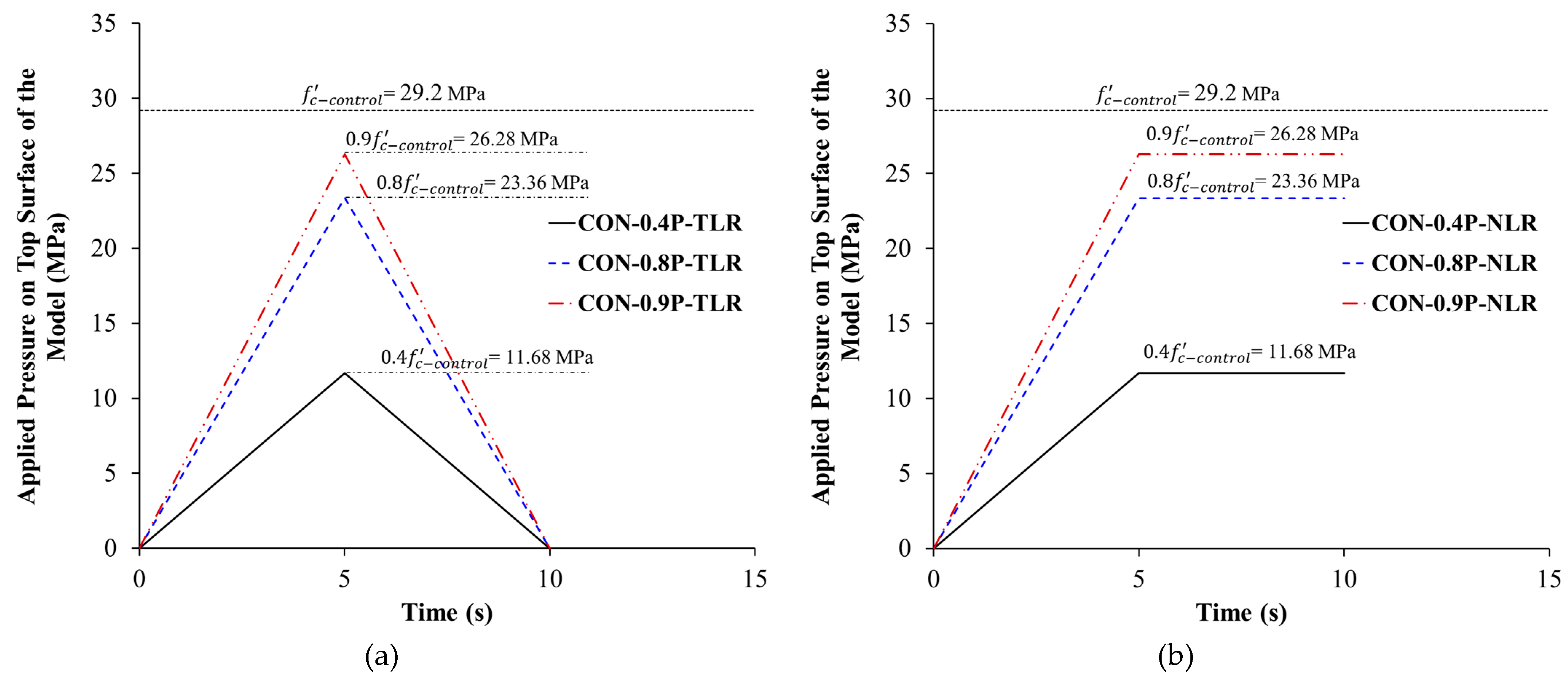
For control specimen CON-0.8P-TLR, a surface pressure was exerted on the top nodes as per the pressure-time curve (
Figure 13(a)). The pressure was linearly increased with time until its peak value of
where
is the specified concrete strength of the control specimen (= 29.2 MPa, as in
Table 2). Then, the pressure was totally released at the end of the analysis (see
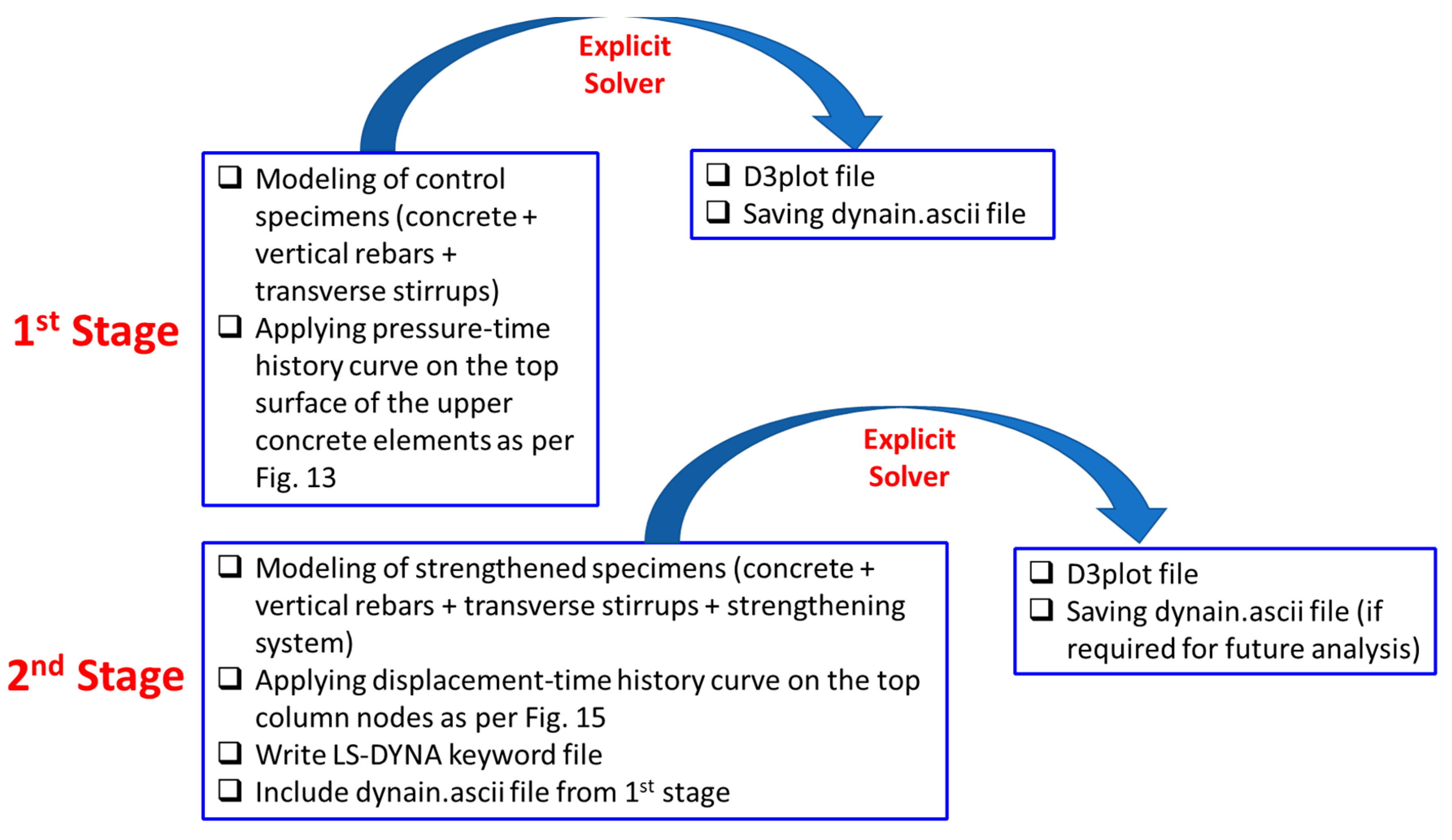
Figure 13(a)). However, for strengthened specimens ST1-0.8P-TLR and ST2-0.8P-TLR, the analysis was conducted in two stages as identified in
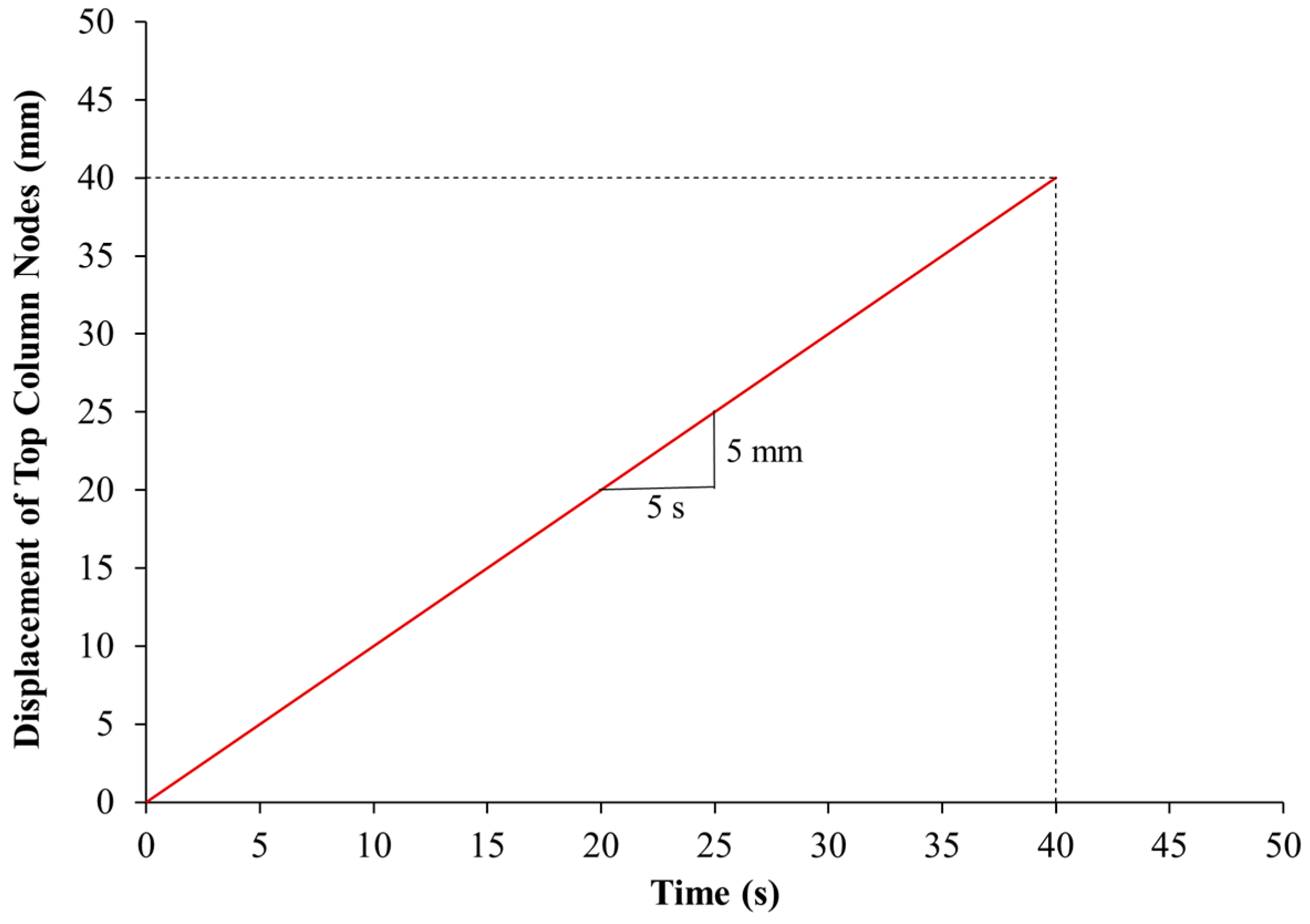
Figure 14. In the first stage, the last state in the analysis of the control specimen CON-0.8P-TLR was selected for output. The stresses in solid and beam elements were saved as ascii format (dynain.ascii file). In the second stage of analysis, the strengthened column was modeled (concrete, reinforcement cage, and strengthening system), and the displacement-time history curve shown in
Figure 15 was applied on the top nodes. After that, the LS-DYNA keyword file was generated and the ascii file from the first analysis stage (dynain.ascii file) was thus included in the keyword file. The explicit solver of the software was then used to run the analysis in the time domain, and the results were then generated (see
Figure 14).
5. Discussion of FE Findings
Table 3 and
Table 4 list, respectively, the comparison between the FE and experimental findings of the 8 specimens of the test matrix with regard to load-displacement and stress-strain responses. It should be stated that even though specimens CON1, CON2, ST1, and ST2 were analyzed in previous studies [18, 19], their FE results are shown in
Table 3 and
Table 4 for the sake of comparison with specimens of this study. In
Table 3, the comparative outputs are service, yield, and peak loads along with their respective displacements; ultimate displacement; stiffness at service load; and dissipated energy. Given in
Table 3 are also the tested-to-numerical ratios of load-displacement parameters. For the FE estimation of service, yield, and peak loads, the errors ranged from 6% to 8%, 3% to 9%, and 6% to 9%, respectively. However, the prediction errors of displacement at service, yield, and peak loads varied from 10% to 14%, 9% to 18%, and 5% to 6%, respectively. For ultimate displacement, the prediction errors were 10% to 18%. The errors in predicting the secant stiffness and dissipated energy were 11% to 16% and 9% to 11%, respectively. The comparative outputs in
Table 4 are maximum average concrete strength (prediction errors varied from 6% to 9%), maximum actual concrete strength (errors were 8% to 12%), strain in concrete at maximum stress (errors varied from 2% to 6%), ultimate strain in concrete (errors ranged from 10% to 18%), strain in original bars at maximum load (errors were 10% to 19%), strain in NSM rebars at maximum load (errors were 9% to 10%), maximum horizontal strain in FRP sheets (errors were 14% to 19%), and maximum horizontal strain in steel plates of specimen ST2-0.8P-TLR (error was 11%). The FE results of the specimens analyzed in this study (CON-0.8P-TLR, ST1-0.8P-TLR, and ST2-0.8P-TLR) are discussed below. However, discussion of FE results of other specimens listed in
Table 3 and
Table 4 are given elsewhere [18, 19].
5.1. Failure pattern
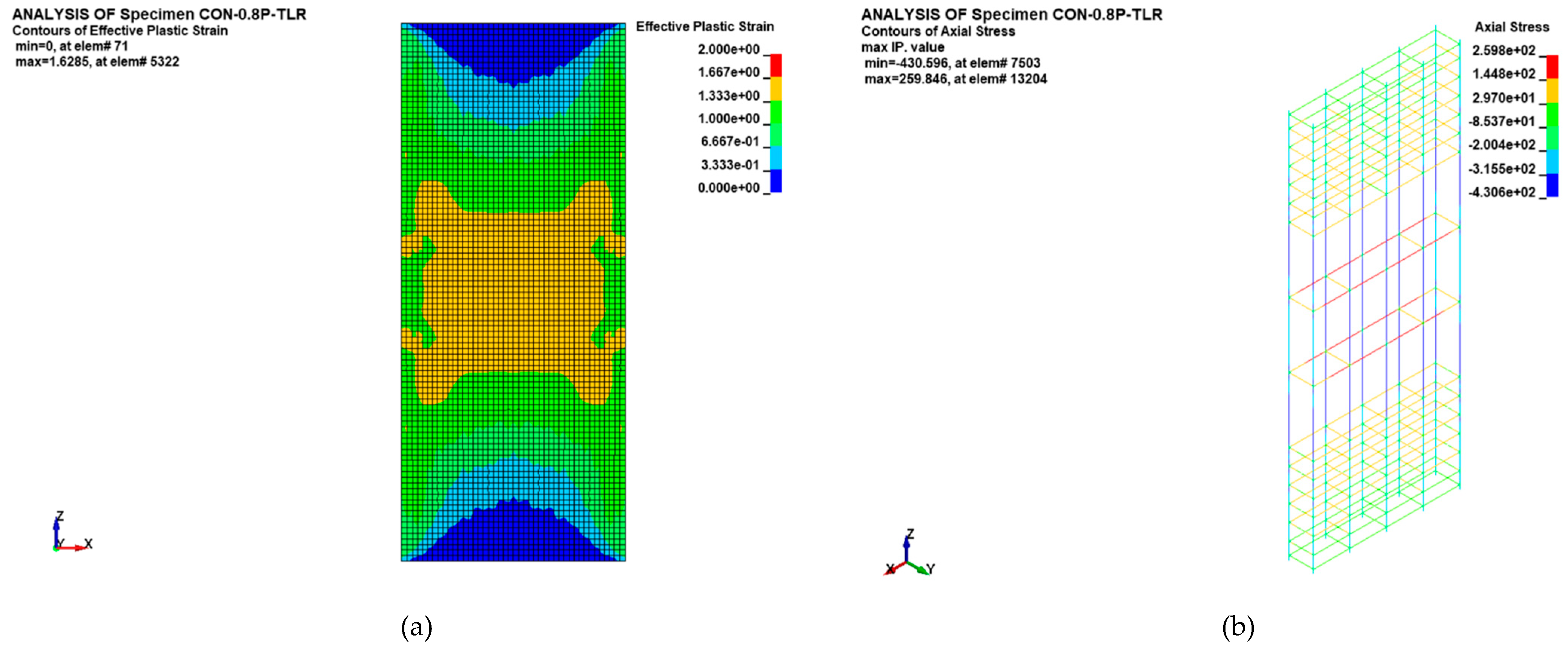
Figure 16(a) displays the failure pattern at peak load level for control specimen CON-0.8P-TLR with respect to effective plastic strain contours for concrete elements (representing the damage level), and it varied from zero (no damage) to 2 (full damage). As identified from the figure, no damage was predicted in any of the concrete elements at peak load level, which comes in reasonably close agreement with the test results shown previously in
Figure 7(a). Displayed in
Figure 16(b) are the axial stress contours for reinforcement cage of control specimen CON-0.8P-TLR at peak load level. The peak predicted compressive stress in the vertical rebars was about 431 MPa, which indicates no yielding occurred. This confirms the predicted compressive strain in vertical steel rebars at maximum load (= 0.0022) reported in
Table 4.
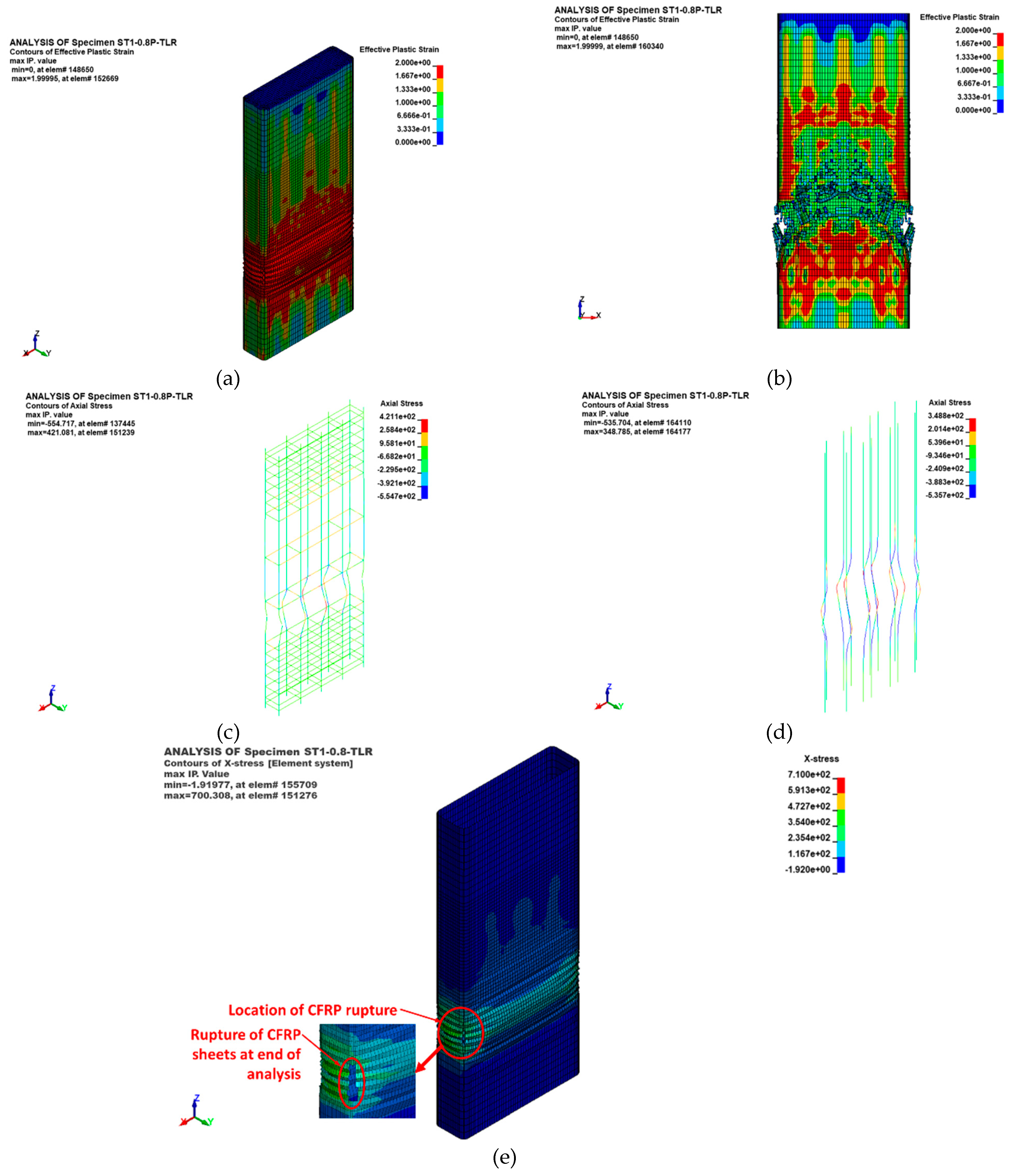
The initial failure of the column was characterized by the bulging of the CFRP sheets in the lower section of the central 600 mm length of the specimen, resulting in a sudden drop in the specimen's load-bearing capacity. The ultimate failure occurred in the lower part of the 600 mm length of the column and was attributed to concrete damage, followed by the buckling of both the original and NSM bars. As the column's displacement increased, the CFRP layers ruptured at the column corner (see
Figure 17(e)). This rupture was further confirmed by the finite element analysis, which indicated that the maximum horizontal strain in the CFRP layers, as reported in
Table 4, closely matched the fracture strain of the CFRP sheets.
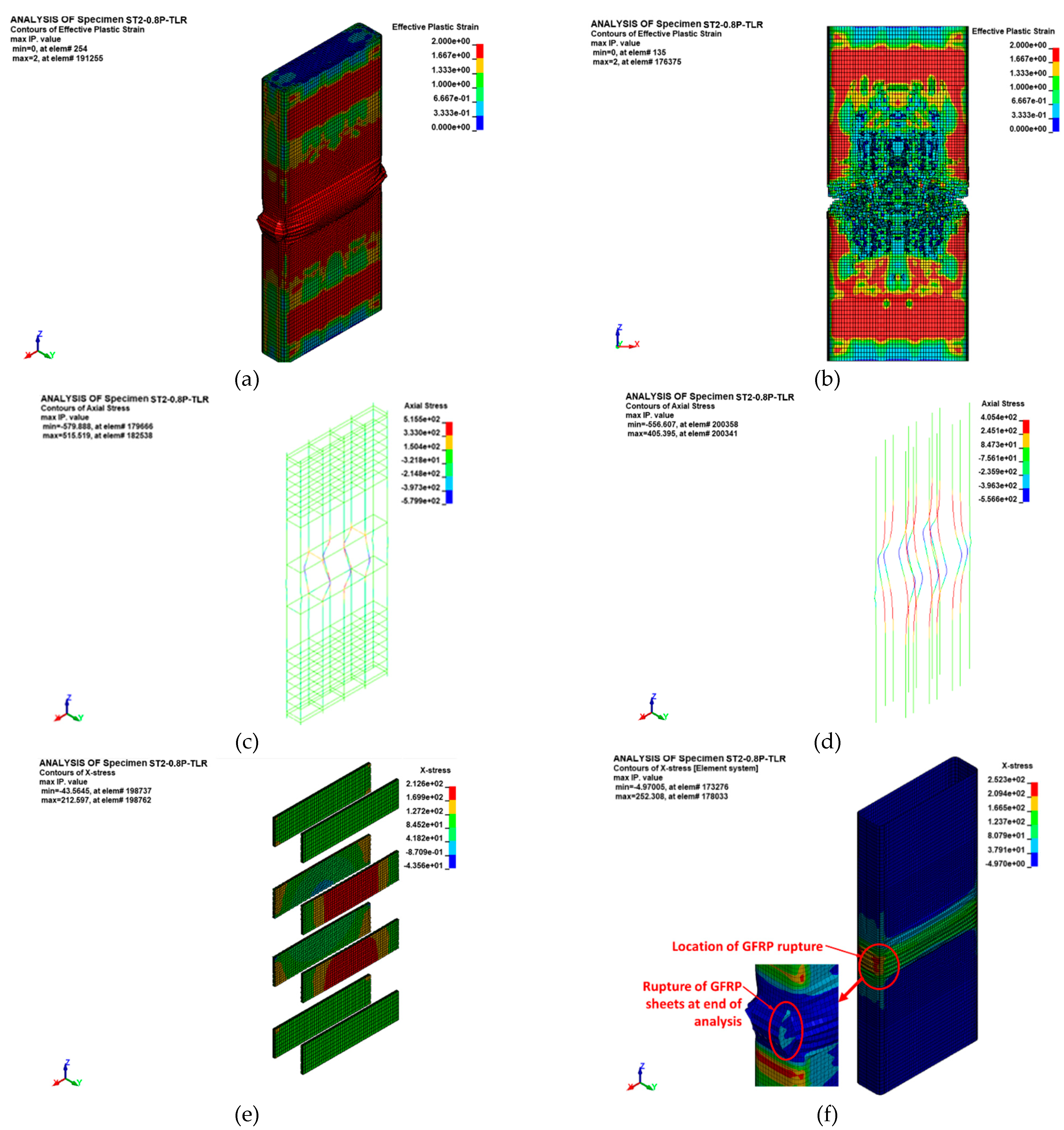
The finite element (FE) failure pattern for specimen ST2-0.8P-TLR is depicted in
Figure 18. As observed, the failure initiation occurred with the bulging of the GFRP jacket in the mid-height zone of the column, situated between the bolted steel plates. Ultimately, the failure was because of buckling of both column bars and NSM rebars, and it was succeeded by fracture of the GFRP sheets at the section corner (see
Figure 18(f)). It was also affirmed by the estimated peak strain of the GFRP sheets reported in
Table 4 (which was close to the fracture limit).
5.2. Load-displacement plots
Figure 19 illustrates the difference between the load-displacement plots obtained from the experimental data and the finite element (FE) simulations for the four tested columns. A good match was found between the two curves for both control and strengthened columns. Precisely predicted was also the post-peak portion of the load-displacement plot of the upgraded specimens. This calibrates the models used for different materials.
As depicted in
Table 3 and
Figure 19(c), strengthened specimen ST1-0.8P-TLR was assessed to have enhancement in peak load by about 72% with regard to the control columns CON1 and CON2. Moreover, the FE ultimate load for specimen ST1-0.8P-TLR (= 3400 kN) is about 92% of its counterpart column ST1 (with the same strengthening scheme yet without preloading).
Figure 19(d) and
Table 3 clarifies that the peak predicted load of strengthened specimen ST2-0.8P-TLR was 3943 kN, which is higher than the predicted peak load of reference columns CON1 and CON2 by about 100%. It is also predicted that this strengthening configuration is better than the first scheme, as the FE response parameters of column ST2-0.8P-TLR with regard to peak load, ultimate displacement, secant stiffness, and dissipated energy were significantly more than specimen ST1-0.8P-TLR by about 16%, 231%, 18%, and 332%, respectively. However, the FE peak load, stiffness, and dissipated energy of specimen ST2-0.8P-TLR were about 94%, 88%, and 84%, respectively, of its counterpart ST2 (with the same strengthening scheme yet without preloading). The FE analysis concluded that the second retrofitting scheme is considerably superior to the first scheme in practical scenarios where the unstrengthened wall-like RC column is preloaded to 80% of its peak load and then fully unloaded.
In summary, the conducted FE analysis predicted well the load-displacement behavior of preloaded RC wall-like columns after being retrofitted with different techniques. These numerical models are now validated and can be further used to study more parameters of practical interest, as will be detailed in the following section.
6. Parametric Study
The numerical models were then utilized to explore the impact of key parameters such as percent of preloading and amount of load release on the axial behavior of strengthened columns. The FE analysis matrix used for the parametric study is shown in
Table 5. Since the second strengthening scheme had superior performance to the first one, it was employed in this study. As depicted in
Table 5, the analysis matrix included three different percentages of preloading (40%, 80%, and 90% of the peak load of unstrengthened column). The 40% preloading was selected to represent the service load, and the 90% preloading was nominated to simulate preloading close to the axial load capacity of the unstrengthened specimen. In half of the preloaded specimens, the load was totally released; and in the other half, the load was sustained without releasing. The former case was selected to represent the case of full shoring of the column before strengthening; however, the latter case stands for the worst-case scenario of no shoring prior to column strengthening. In the designation of column specimens listed in
Table 5, the same symbols used previously in
Table 3 were utilized as detailed in Sec. 2.1. Also, the symbol “NLR” used in
Table 5 stands for preloaded columns with no load release. It should be reported that specimens CON and ST2 that were previously modeled in Ref. [
19] were included in the analysis matrix (
Table 2). Altogether, the FE matrix used in the parametric study incorporated 7 control specimens and 7 strengthened columns. In the preloaded control specimens CON-0.4P-TLR, CON-0.8P-TLR, and CON-0.9P-TLR, the load was totally released after reaching its peak value, and the pressure-time history curves used in the analysis are shown in
Figure 13(a). Nevertheless, in the preloaded control columns CON-0.4P-NLR, CON-0.8P-NLR, and CON-0.9P-NLR, the load was sustained without release after reaching its peak value, and the pressure-time history plot used in the models are illustrated in
Figure 13(b). As identified previously, the FE analysis of the preloaded strengthened specimens was conducted in two stages as explained earlier in
Figure 14, and the specimens were analyzed under the displacement-time history plot shown in
Figure 15.
A summary of the key FE results for the specimens of the parametric study is reported in
Table 6. These results incorporated the main load-displacement parameters such as yield and maximum loads and their corresponding displacement; ultimate displacement; secant stiffness; and dissipated energy. Included also in
Table 6 are the ultimate concrete strain and strain in main vertical steel rebars at peak load.
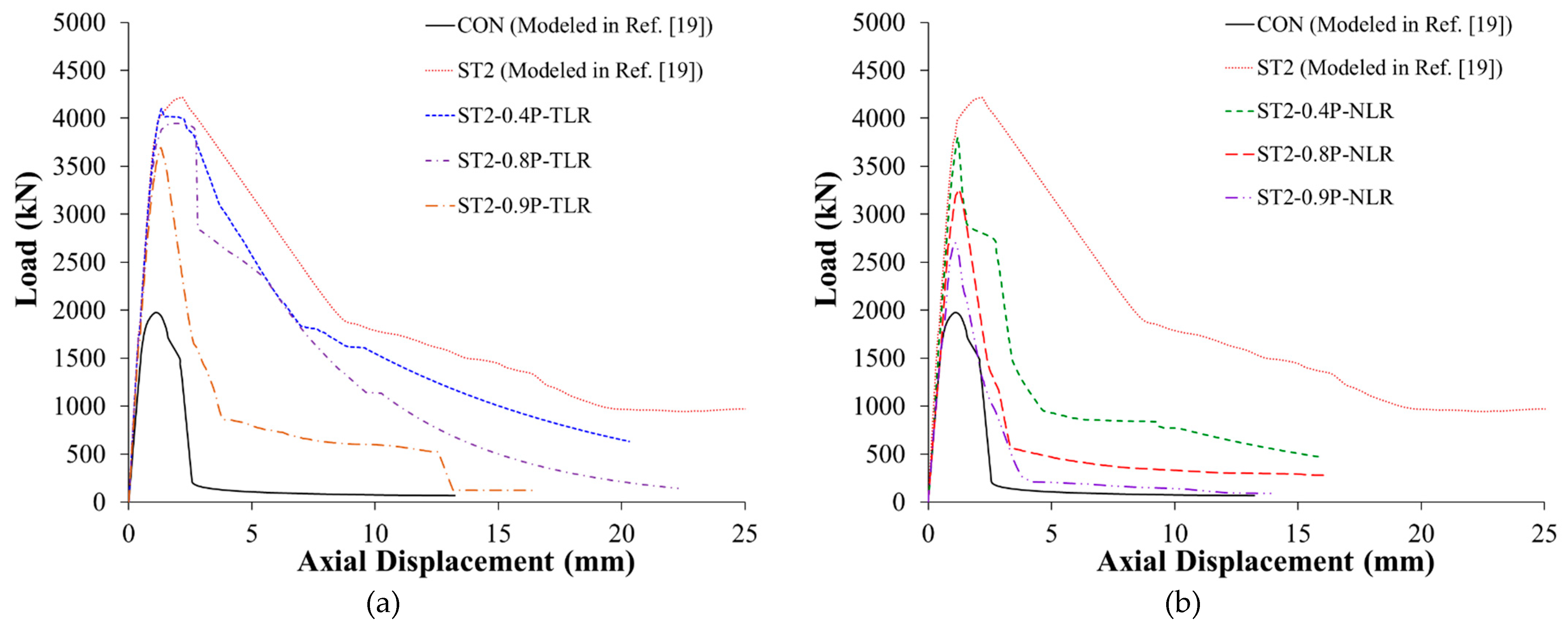
Figure 20(a) and (b) present comparisons between the FE load against displacement plots for columns with total load release and columns with no load release, respectively. It is clarified from
Figure 20 and
Table 6 that for the same amount of load release, the parameters of the load-displacement response of the strengthened specimens without preloading (ST1 and ST2) are higher than all their preloaded counterparts. Also, for the preloaded strengthened specimens, the load-displacement response got improved with the reduction of percent of preloading.
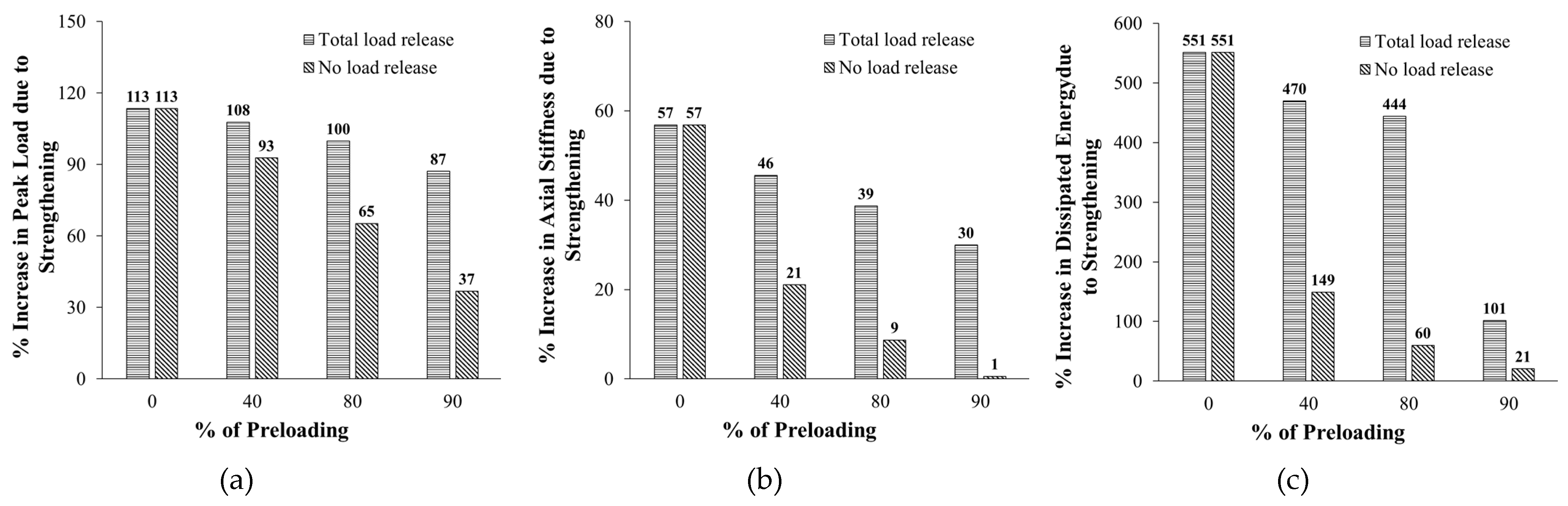
Figure 21 shows the effect of percent of preloading on the percent increase in the response parameters due to strengthening (compared with the unstrengthened specimen CON). These response parameters included peak load, secant stiffness, and dissipated energy. It is noted that for all response parameters, as the percent of preloading increased the percent increase due to strengthening decreased, and the decrease in the case of no-load release is more than the case of total-load release.
As seen in
Figure 21(a), as the percent of preloading increased from zero (specimen ST2) to 90%, the percent increase in peak load due to strengthening got significantly reduced from 113% to 87% and 37% for the cases of total-load and no-load releases, respectively. Also,
Figure 21(b) illustrates that as the percent of preloading increased from zero to 90%, the percent increase in secant stiffness decreased considerably from 57% to 30% and 1% for the cases of total-load and no-load releases, respectively. Moreover, the increase in the dissipated energy due to strengthening decreased significantly from 551% to 101% and 21% (for total-load and no-load releases, respectively) as the percent of preloading increased from zero to 90%, as presented in
Figure 21(c).
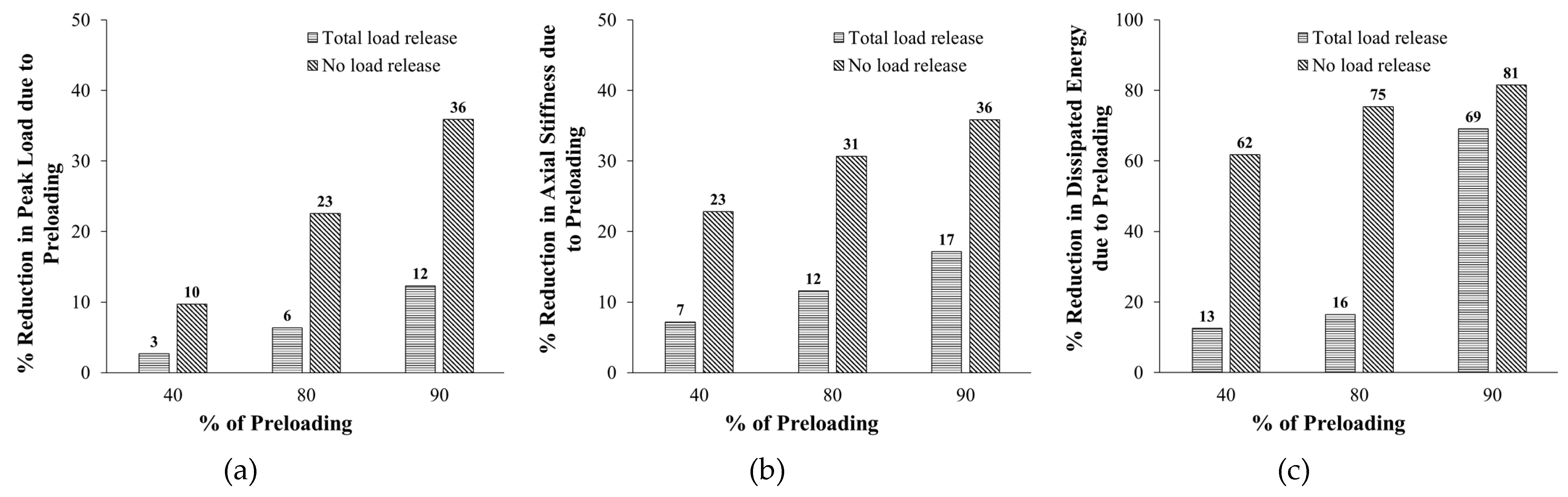
Figure 22 illustrates the impact of preloading on the reduction in peak load, stiffness, and dissipated energy for strengthened specimens. Compared with the strengthened specimen without preloading (ST2), as the percent of preloading increased, the reduction in the response parameters of the retrofitted specimens increased. For the case of total-load release, as the percent of preloading increased from 40% to 90%, the reduction in peak load, secant stiffness, and dissipated energy enhanced from 3% to 12%, 7% to 17%, and 13% to 69%, respectively. However, for the case of no-load release, the loss in maximum load, stiffness, and energy dissipated increased from 10% to 36%, 23% to 36%, and 62% to 81%, in turn.
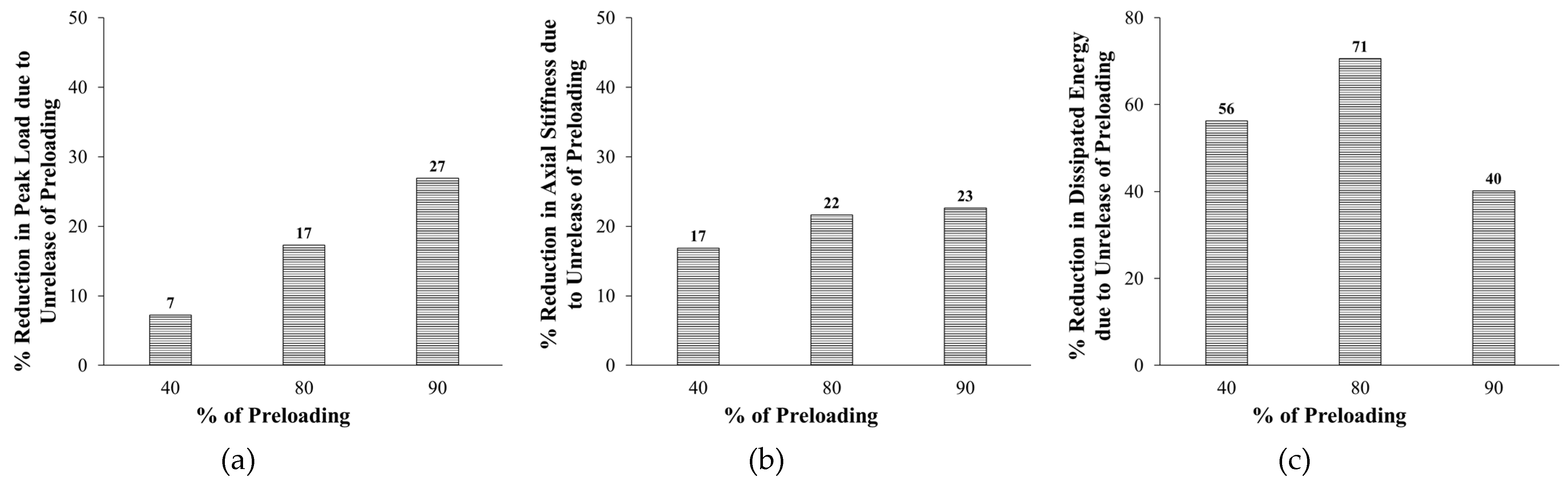
Figure 23 presents the influence of unrelease of preloading on percent reduction in response parameters for strengthened specimens. Compared with preloaded strengthened columns with total-load release, the unrelease of preloading increased the reduction in peak load from 7% to 17% and 27% as the preloading increased from 40% to 80% and 90%, respectively, as presented in
Figure 23(a). Similarly, the unrelease of preloading increased the loss in stiffness from 17% to 22% and 23% when the preloading increased from 40% to 80% and 90%, respectively (see
Figure 23(b)). The same trend was not found in the dissipated energy since the unrelease of preloading increased its reduction from 56% to 71% as the preloading increased from 40% to 80%. However, as the preloading increased further to 90%, the loss in dissipated energy due to unrelease of preloading decreased to 40%, as depicted in
Figure 23(c).
From the parametric study conducted in this research, it is ultimately concluded that even with the worst-case scenario of unstrengthened RC wall-like columns preloaded with 90% of their axial resistance without releasing the load, their strengthening using the second scheme is efficient at enhancing the load-displacement characteristics. Compared with the unstrengthened column, the upgrading scheme in such a case improved the peak load and dissipated energy by 37% and 21%; yet, it almost retained the axial secant stiffness of the column.
7. Conclusions
This research was carried out to explore experimentally and numerically the response of concentrically preloaded RC wall-like columns after being strengthened using different configurations. In the testing campaign, four half-scale specimens were tested in the event of concentric compression. The first two specimens were unstrengthened, and they were loaded to 80% of their axial capacity and the load was then totally released. After that, these specimens were strengthened with two different schemes, and hence they were concentrically loaded till failure. Moreover, FE analysis was undertaken to examine the response of tested specimens. The numerical models were then employed to carry out parametric study for investigating the impact of percent of preloading and amount of load release on the response of wall-like columns strengthened with the second scheme. The main conclusions of this study are:
The failure of the upgraded columns in the two studied retrofitting configurations began with the FRP sheets’ bulging, caused by the expansion of the column cross-section, as well as the NSM and main rebars’ buckling. Ultimately, the upgraded columns failed due to the fracture of the FRP sheets.
In practical scenarios where the unstrengthened column is preloaded to 80% of its peak load and then fully unloaded, the testing campaign proved the efficiency of the two studied schemes at improving the axial load-displacement characteristics of the columns. However, the second scheme was considerably superior to the first one due to the extra confinement provided by the bolted steel plates. This scheme improved the peak load, stiffness, and dissipated energy by 115%, 75%, and 524%, respectively.
The performed FE analysis accurately assessed the load versus axial displacement behavior of the examined wall-like columns. This affirms the appropriateness of the utilized constitutive models for steel, concrete, and FRP materials. These verified models can be applied in future studies to explore RC wall-like columns with different aspect ratios and under conditions of eccentric loading.
The conducted parametric study proved that for all response parameters of wall-like columns, as the percent of preloading increased the percent increase due to strengthening decreased, and the decrease in the case of no-load release is significantly more than the case of total-load release. For the worst-case scenario of unrelease of the preloading, as the percent of preloading increased from zero to 90%, the percent increase in peak load, stiffness, and dissipated energy due to strengthening got significantly reduced from 113% to 37%, 57% to 1%, and 551% to 21%, respectively.
From the parametric study carried out in this research, it was found that even with the worst-case scenario of unstrengthened RC wall-like columns preloaded with 90% of their axial resistance without releasing the load, their strengthening using the second scheme was efficient at enhancing the load-displacement response. Compared with the unstrengthened column, the upgrading scheme in such a case improved the peak load and dissipated energy, respectively, by 37% and 21%; yet, it almost retained the axial secant stiffness of the column.
Author Contributions
Conceptualization, Methodology, Validation, Writing—original draft, H.E.; Investigation, Writing—review and editing, H.A.; Writing—review and editing, T.A.; Writing—review and editing, Funding acquisition, Supervision, Y.A. All authors have read and agreed to the published version of the manuscript.
Funding
The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research (IFKSURC-1-2207).
Data Availability Statement
Not applicable.
Acknowledgments
The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research (IFKSURC-1-2207).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bett, B.J.; Klingner, R.E.; Jisra, J.O. Lateral load response of strengthened and repaired reinforced concrete columns. ACI Structural Journal 1988, 85, 499–508. [Google Scholar]
- Rodriguey, M. and Park, R. Seismic load tests on reinforced concrete columns strengthened by jacketing. ACI Structural Journal 1994, 91, 150–159.
- Campione, G. Load carrying capacity of RC compressed columns strengthened with steel angles and strips. Engineering Structures 2012, 40, 457–465. [Google Scholar] [CrossRef]
- Khalifa, E.S.; Al-Tersawy, S.H. Experimental and analytical behavior of strengthened reinforced concrete columns with steel angles and strips. International Journal of Advanced Structural Engineering 2014, 6. [Google Scholar] [CrossRef]
- Tarabia, A.M.; Albakry, H.F. Strengthening of RC columns by steel angles and strips. Alexandria Engineering Journal 2014, 53, 615–626. [Google Scholar] [CrossRef]
- Abdel-Hay, A.S.; Fawzy, Y.A.G. Behavior of partially defected R. C columns strengthened using steel jackets. HBRC Journal 2015, 11, 194–200. [Google Scholar]
- Salah, A.; Elsanadedy, H.; Abbas, H.; Almusallam, T.; Al-Salloum, Y. Behavior of axially loaded L-shaped RC columns strengthened using steel jacketing. Journal of Building Engineering 2022, 47, 103870. [Google Scholar] [CrossRef]
- Tan KH Strength enhancement of rectangular RC columns using, F. R.P. Journal of Composites for Construction. ASCE 2002, 6, 175–83. [CrossRef]
- Hosny, A.; Shaheen, H.; Abdelrahman, A.; Elafandy, T. Uniaxial tests on rectangular columns strengthened with, C.F.R.P. Proceedings of the third Middle East symposium on structural composites for infrastructure applications, Aswan, Egypt; December 2002.
- Tanwongsval, S.; Maalej, M.; Paramasivam, P. Strengthening of RC wall-like columns with FRP under sustained loading. RILEM Mater Struct 2003, 36, 282–90. [Google Scholar] [CrossRef]
- Maalej, M.; Tanwongsval, S.; Paramasivam, P. Modelling of rectangular RC columns strengthened with, F.R.P. Cement and Concrete Composites 2003, 25, 263–276. [Google Scholar] [CrossRef]
- Prota, A.; Manfredi, G.; Cosenza, E. Ultimate behavior of axially loaded RC wall-like columns confined with, G.F.R.P. Composites: Part B 2006, 37, 670–678. [Google Scholar] [CrossRef]
- De Luca, A.; Nardone, F.; Lignola, G.P.; Prota, A.; Nanni, A. Wall-like reinforced concrete columns externally confined by means of glass FRP laminates. Advances in Structural Engineering 2013, 16, 593–603. [Google Scholar] [CrossRef]
- Alsayed, S.H.; Almusallam, T.H.; Ibrahim, S.M.; Al-Hazmi, N.M.; Al-Salloum, Y.A.; Abbas, H. Experimental and numerical investigation for compression response of CFRP strengthened shape modified wall-like RC column. Construction and Building Materials 2014, 63, 72–80. [Google Scholar] [CrossRef]
- Triantafillou, T.C.; Choutopoulou, E.; Fotaki, E.; Skorda, M.; Stathopoulou, M.; Karlos, K. FRP confinement of wall-like reinforced concrete columns. Materials and Structures/Materiaux et Constructions 2016, 49, 651–664. [Google Scholar] [CrossRef]
- Abbas, H.; Ibrahim, S.M.; Al-Hazmi, N.; Elsanadedy, H.; Almusallam, T.; Al-Salloum, Y. Axial Compression Behavior of Wall-like Reinforced Concrete Columns Retrofitted Using Different FRP Schemes/ Buildings 2022, 13, 26. 13.
- Al-Salloum, Y.; Abbas, H.; Elsanadedy, H.; Siddiqui, N.; Almusallam, T. November. Compression behavior of RC wall-like columns strengthened using NSM/CFRP system without shape modification. In Structures; Elsevier: Amsterdam, The Netherlands, 2023; Volume 57, p. 105158. [Google Scholar]
- Elsanadedy, H.; Abbas, H.; Almusallam, T.; Al-Salloum, Y. Performance of Concentrically Loaded RC Wall-like Columns Upgraded with Innovative Hybrid NSM/CFRP System. Polymers 2023, 15, 378. [Google Scholar] [CrossRef] [PubMed]
- Elsanadedy, H.; Abbas, H.; Siddiqui, N.; Almusallam, T.; Al-Salloum, Y. Hybrid Steel/NSM/GFRP System versus GFRP Wrapping for Upgrading RC Wall-like Columns. Polymers 2023, 15, 1886. [Google Scholar] [CrossRef] [PubMed]
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical stress-strain model for confined concrete. Journal of Structural Engineering, ASCE 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- Wang, Y.C.; Resrepo, J.I. Investigations of concentrically loaded reinforced concrete columns confined with glass fiber-reinforced polymer jackets. ACI Struct J 2001, 98, 377–385. [Google Scholar]
- Saatcioglu, M.; Razvi, S.R. Strength and ductility of confined concrete. J Struct Eng 1992, 118, 590–607. [Google Scholar] [CrossRef]
- Yalcim, C.; Saatcioglu, M. Inelastic analysis of reinforced concrete columns. Comput Struct 2000, 77, 539–55. [Google Scholar] [CrossRef]
- American Society for Testing and Materials (ASTM). Standard test method for compressive strength of cylindrical concrete specimens. ASTM C39/C39M, West Conshohocken, PA, USA, 2018.
- American Society for Testing and Materials (ASTM). Standard test methods for tension testing of metallic materials. ASTM E8/E8M, West Conshohocken, PA, USA, 2016.
- American Society for Testing and Materials (ASTM). Standard test method for tensile properties of polymer matrix composite materials. ASTM D3039 / D3039M, West Conshohocken, PA, USA, 2014.
- ACI Committee 440. Guide for the design and construction of externally bonded FRP systems for strengthening concrete structures. ACI 440.2R-17, American Concrete Institute, Detroit, MI, USA, 2017.
- ASTM Standard test methods and definitions for mechanical testing of steel products. ASTM A370–16, American Society for Testing and Materials, West Conshohocken, PA, USA; 2016.
- Al-Salloum, Y.A.; Almusallam, T.H.; Elsanadedy, H.M.; Iqbal, R.A. Effect of elevated temperature environments on the residual axial capacity of RC columns strengthened with different techniques. Construction and Building Materials 2016, 115, 345–361. [Google Scholar] [CrossRef]
- Elsanadedy, H.; Almusallam, T.; Al-Salloum, Y.; Iqbal, R. Effect of high temperature on structural response of reinforced concrete circular columns strengthened with fiber reinforced polymer composites. Journal of Composite Materials 2017, 51, 333–355. [Google Scholar] [CrossRef]
- ACI Committee 318; American Concrete Institute. (2019). Building code requirements for structural concrete (ACI 318-19): an ACI standard: commentary on building code requirements for structural concrete (ACI 318R-19), an ACI report.
- Livermore Software Technology Corporation (LSTC), LS-DYNA keyword user’s manual – Vol. 1-3, Version R11, LSTC, Livermore, CA, 2018.
- Belytschko, T.B.; Tsay, C.S. Explicit algorithms for non-linear dynamics of shells. J Appl Mech 1981, 48, 209–231. [Google Scholar]
- Malvar, L.J.; Crawford, J.E.; Wesevich, J.W.; Simons, D. A plasticity concrete material model for DYNA 3D. Int Journal of Impact Eng 1997, 19, 847–873. [Google Scholar] [CrossRef]
- Malvar, L.J.; Crawford, J.E.; Morrill, K.B. K&C concrete material model Release III – Automated generation of material input. K&C Technical report TR-99-24-B1. 2000.
- Magallanes, J.M.; Wu, Y.; Malvar, L.J.; Crawford, J.E. Recent improvements to release III of the K&C concrete model, in: The 11th International LS-DYNA Users Conference, 2010.
- Chang, F.K.; Chang, K.Y. A progressive damage model for laminated composites containing stress concentration. J Compos Mater 1987, 21, 834–55. [Google Scholar] [CrossRef]
Figure 2.
Details of specimen ST1-0.8P-TLR (Measurements are in mm).
Figure 2.
Details of specimen ST1-0.8P-TLR (Measurements are in mm).
Figure 3.
Details of specimen ST2-0.8P-TLR (Measurements are in mm).
Figure 3.
Details of specimen ST2-0.8P-TLR (Measurements are in mm).
Figure 4.
Preparation and testing of column specimens: (a) Reinforcement cages; (b) Columns after casting of concrete; (c) Installation of NSM rebars for specimens ST1 & ST1-0.8P-TLR; (d) CFRP wrapping for specimens ST1 & ST1-0.8P-TLR; (e) Installation of NSM rebars for specimens ST2 & ST2-0.8P-TLR; (f) Specimens ST2 & ST2-0.8P-TLR after strengthening; (g) Test setup for control specimens; (h) Test setup for strengthened specimens ST1 & ST1-0.8P-TLR.
Figure 4.
Preparation and testing of column specimens: (a) Reinforcement cages; (b) Columns after casting of concrete; (c) Installation of NSM rebars for specimens ST1 & ST1-0.8P-TLR; (d) CFRP wrapping for specimens ST1 & ST1-0.8P-TLR; (e) Installation of NSM rebars for specimens ST2 & ST2-0.8P-TLR; (f) Specimens ST2 & ST2-0.8P-TLR after strengthening; (g) Test setup for control specimens; (h) Test setup for strengthened specimens ST1 & ST1-0.8P-TLR.
Figure 5.
Characterization of response parameters for column specimens: (a) Secant stiffness; (b) Ultimate axial concrete strain; (c) Energy dissipated at ultimate state.
Figure 5.
Characterization of response parameters for column specimens: (a) Secant stiffness; (b) Ultimate axial concrete strain; (c) Energy dissipated at ultimate state.
Figure 6.
Experimental load versus axial displacement plots for columns of the test matrix.
Figure 6.
Experimental load versus axial displacement plots for columns of the test matrix.
Figure 7.
Failure pattern of columns tested in this study: (a) CON1-0.8P-TLR; (b) ST1-0.8P-TLR; (c) ST2-0.8P-TLR.
Figure 7.
Failure pattern of columns tested in this study: (a) CON1-0.8P-TLR; (b) ST1-0.8P-TLR; (c) ST2-0.8P-TLR.
Figure 8.
Effect of preloading on percent decrease in response parameters of strengthened specimens (based on experimental results).
Figure 8.
Effect of preloading on percent decrease in response parameters of strengthened specimens (based on experimental results).
Figure 9.
FE model of control columns: (a) Solid elements for concrete; (b) Beam elements for steel rebars.
Figure 9.
FE model of control columns: (a) Solid elements for concrete; (b) Beam elements for steel rebars.
Figure 10.
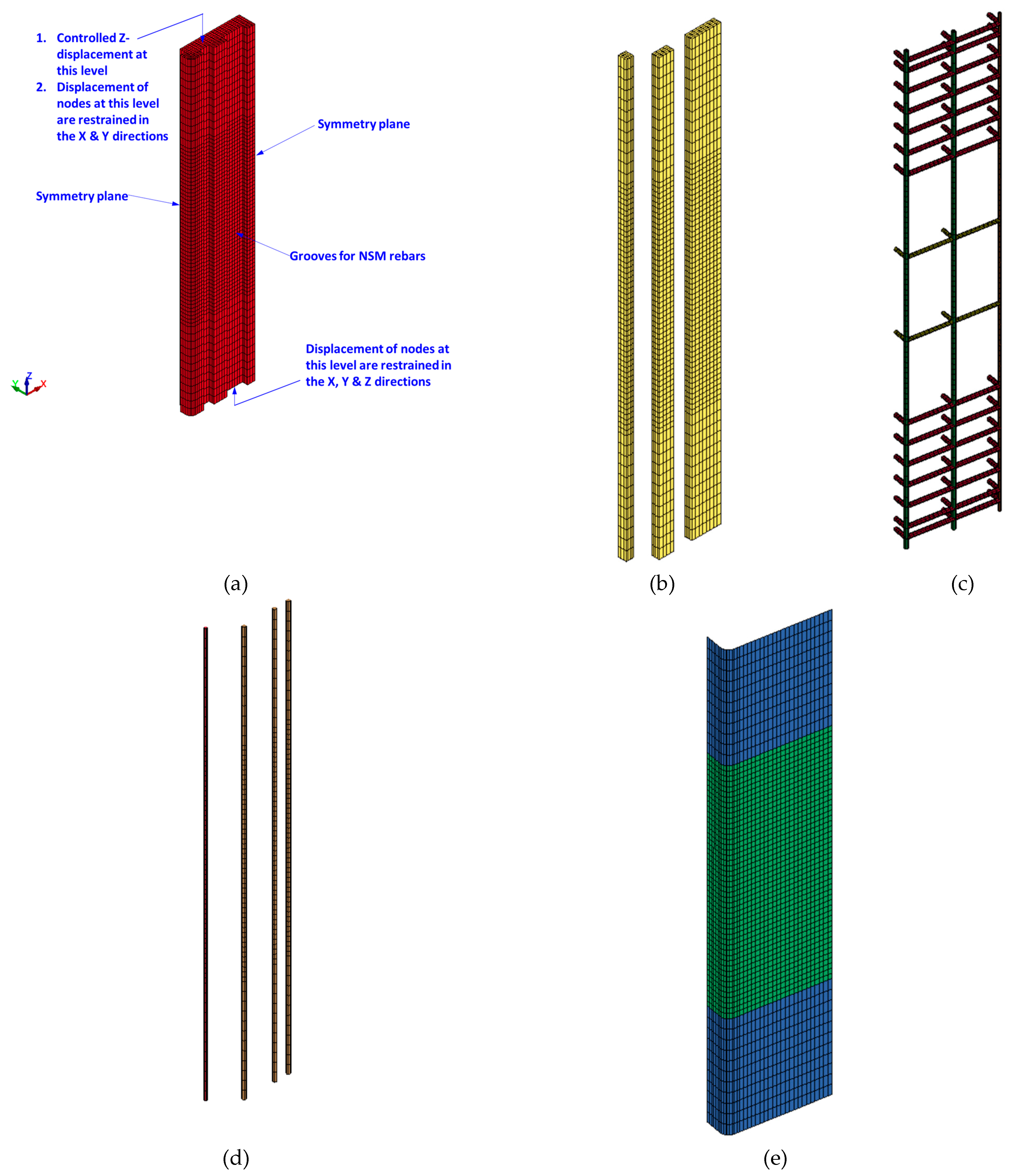
FE model of strengthened column ST1-0.8P-TLR: (a) Solid elements for concrete; (b) Solid elements for adhesive mortar; (c) Beam elements for steel rebars; (d) Beam elements for NSM rebars; (e) Shell elements for CFRP sheets.
Figure 10.
FE model of strengthened column ST1-0.8P-TLR: (a) Solid elements for concrete; (b) Solid elements for adhesive mortar; (c) Beam elements for steel rebars; (d) Beam elements for NSM rebars; (e) Shell elements for CFRP sheets.
Figure 11.
FE model of strengthened column ST2-0.8P-TLR: (a) Solid elements for concrete; (b) Solid elements for adhesive mortar; (c) Beam elements for steel rebars; (d) Beam elements for NSM rebars; (e) Shell elements for CFRP sheets; (f) Solid and beam elements for steel plates and threaded rods, respectively.
Figure 11.
FE model of strengthened column ST2-0.8P-TLR: (a) Solid elements for concrete; (b) Solid elements for adhesive mortar; (c) Beam elements for steel rebars; (d) Beam elements for NSM rebars; (e) Shell elements for CFRP sheets; (f) Solid and beam elements for steel plates and threaded rods, respectively.
Figure 12.
Material models employed in the FE analysis: (a) Damage model for concrete; (b) Piecewise linear plasticity model for steel.
Figure 12.
Material models employed in the FE analysis: (a) Damage model for concrete; (b) Piecewise linear plasticity model for steel.
Figure 13.
Pressure-time history curve used in the FE analysis of preloaded control specimens: (a) Columns with total load release; (b) Columns with no load release.
Figure 13.
Pressure-time history curve used in the FE analysis of preloaded control specimens: (a) Columns with total load release; (b) Columns with no load release.
Figure 14.
Steps used in the FE analysis of preloaded strengthened specimens.
Figure 14.
Steps used in the FE analysis of preloaded strengthened specimens.
Figure 15.
Displacement-time history curve used in the FE analysis of specimens loaded till failure.
Figure 15.
Displacement-time history curve used in the FE analysis of specimens loaded till failure.
Figure 16.
FE failure pattern at peak load of control specimens CON1-0.8P-TLR and CON2-0.8P-TLR: (a) Concrete damage contours; (b) Axial stress contours for steel rebars. The FE failure patterns of strengthened column ST1-0.8P-TLR are shown in
Figure 17. These patterns are illustrated in terms of contours depicting effective plastic strain (or damage) for concrete elements, axial stress for the reinforcement cage and NSM bars, and circumferential stress for CFRP sheets. The FE failure patterns shown in
Figure 17 match well with the test observations shown previously in
Figure 7(b).
Figure 16.
FE failure pattern at peak load of control specimens CON1-0.8P-TLR and CON2-0.8P-TLR: (a) Concrete damage contours; (b) Axial stress contours for steel rebars. The FE failure patterns of strengthened column ST1-0.8P-TLR are shown in
Figure 17. These patterns are illustrated in terms of contours depicting effective plastic strain (or damage) for concrete elements, axial stress for the reinforcement cage and NSM bars, and circumferential stress for CFRP sheets. The FE failure patterns shown in
Figure 17 match well with the test observations shown previously in
Figure 7(b).
Figure 17.
FE failure pattern of preloaded strengthened specimen ST1-0.8P-TLR: (a) Damage contours showing bulging of CFRP sheets at peak load; (b) Damage contours showing concrete crushing at end of analysis; (c) Axial stress contours showing buckling of longitudinal rebars at end of analysis; (d) Axial stress contours showing buckling of NSM rebars at end of analysis; (e) X-stress contours showing rupture of CFRP sheets at end of analysis.
Figure 17.
FE failure pattern of preloaded strengthened specimen ST1-0.8P-TLR: (a) Damage contours showing bulging of CFRP sheets at peak load; (b) Damage contours showing concrete crushing at end of analysis; (c) Axial stress contours showing buckling of longitudinal rebars at end of analysis; (d) Axial stress contours showing buckling of NSM rebars at end of analysis; (e) X-stress contours showing rupture of CFRP sheets at end of analysis.
Figure 18.
FE Failure pattern of preloaded strengthened specimen ST2-0.8P-TLR: (a) Damage contours showing bulging of GFRP sheets at peak load; (b) Damage contours showing concrete crushing at end of analysis; (c) Axial stress contours showing buckling of longitudinal rebars at end of analysis; (d) Axial stress contours showing buckling of NSM rebars at end of analysis; (e) X-stress contours in steel plates at end of analysis; (f) X-stress contours showing rupture of GFRP sheets at end of analysis.
Figure 18.
FE Failure pattern of preloaded strengthened specimen ST2-0.8P-TLR: (a) Damage contours showing bulging of GFRP sheets at peak load; (b) Damage contours showing concrete crushing at end of analysis; (c) Axial stress contours showing buckling of longitudinal rebars at end of analysis; (d) Axial stress contours showing buckling of NSM rebars at end of analysis; (e) X-stress contours in steel plates at end of analysis; (f) X-stress contours showing rupture of GFRP sheets at end of analysis.
Figure 19.
Tested versus predicted load-displacement curves for: (a) CON1-0.8P-TLR, (b) CON2-0.8P-TLR; (c) ST1-0.8P-TLR; (d) ST2-0.8P-TLR.
Figure 19.
Tested versus predicted load-displacement curves for: (a) CON1-0.8P-TLR, (b) CON2-0.8P-TLR; (c) ST1-0.8P-TLR; (d) ST2-0.8P-TLR.
Figure 20.
FE load-displacement curves for columns employed in parametric study: (a) Columns with total load release; (b) Columns with no load release.
Figure 20.
FE load-displacement curves for columns employed in parametric study: (a) Columns with total load release; (b) Columns with no load release.
Figure 21.
Effect of preloading on percent increase in response parameters due to strengthening for columns employed in parametric study: (a) Peak load; (a) Axial stiffness; (c) Dissipated energy.
Figure 21.
Effect of preloading on percent increase in response parameters due to strengthening for columns employed in parametric study: (a) Peak load; (a) Axial stiffness; (c) Dissipated energy.
Figure 22.
Effect of preloading on percent reduction in response parameters for columns employed in parametric study: (a) Peak load; (a) Axial stiffness; (c) Dissipated energy.
Figure 22.
Effect of preloading on percent reduction in response parameters for columns employed in parametric study: (a) Peak load; (a) Axial stiffness; (c) Dissipated energy.
Figure 23.
Effect of unrelease of preloading on percent reduction in response parameters for columns employed in parametric study: (a) Peak load; (a) Axial stiffness; (c) Dissipated energy.
Figure 23.
Effect of unrelease of preloading on percent reduction in response parameters for columns employed in parametric study: (a) Peak load; (a) Axial stiffness; (c) Dissipated energy.
Table 1.
Matrix of testing campaign.
Table 1.
Matrix of testing campaign.
| Specimen ID |
Strengthening scheme |
Loading condition |
No. of casted specimens |
No. of tested specimens |
Notes |
| CON1 & CON2 |
Unstrengthened to be used as control specimen |
Loaded up to failure |
2 |
2 |
Tested in Refs. [18,19] |
| ST1 |
Strengthened using 1st scheme (externally bonded CFRP layers combined with connected NSM steel rebars) |
Loaded up to failure |
1 |
1 |
Tested in Ref. [18] |
| CON1-0.8P-TLR |
Unstrengthened |
Loaded up to 80% of the average peak load of specimens CON1 and CON2, and the load was then totally released |
1 |
1 |
Tested in this study |
| ST1-0.8P-TLR |
It is the same as specimen CON1-0.8P-TLR and it was strengthened after preloading using 1st scheme |
Loaded up to failure |
- |
1 |
Tested in this study |
| ST2 |
Strengthened using 2nd scheme (externally bonded GFRP layers + bolted steel plates + connected NSM steel rebars) |
Loaded up to failure |
1 |
1 |
Tested in Ref. [19] |
| CON2-0.8P-TLR |
Unstrengthened |
Loaded up to 80% of the average peak load of specimens CON1 and CON2, and the load was then totally released |
1 |
1 |
Tested in this study |
| ST2-0.8P-TLR |
It is the same as specimen CON2-0.8P-TLR, and it was strengthened after preloading using 2nd scheme |
Loaded up to failure |
- |
1 |
Tested in this study |
| Total No. of columns |
6 |
8 |
|
Table 2.
Properties of materials utilized in the FE analysis.
Table 2.
Properties of materials utilized in the FE analysis.
| Concrete |
|
| Model No. |
72R3 |
| Model type |
Concrete damage |
| Compressive strength |
29.2 MPa |
| Poisson's ratio |
0.2 |
| Maximum size of aggregate |
10 mm |
| Epoxy mortar |
|
| Model No. |
72R3 |
| Model type |
Concrete damage |
| Compressive strength |
65 MPa |
| Poisson's ratio |
0.2 |
| Maximum size of aggregate |
5 mm |
| Steel rebars, threaded rods & plates |
ф8 rebars |
ф10 rebars |
ф18 threaded rods |
Plates |
| Model No. |
24 |
| Model type |
Piecewise linear plasticity |
| Yield strength |
548 MPa |
531 MPa |
711 MPa |
230 MPa |
| Poisson's ratio |
0.3 |
0.3 |
0.3 |
0.3 |
| Elastic modulus |
200 GPa |
200 GPa |
200 GPa |
200 GPa |
| Tangent modulus |
86.37 MPa |
133.75 MPa |
0 |
0 |
| Plastic strain at failure |
9.72% |
9.73% |
6.64% |
19.89% |
| FRP material |
CFRP sheets |
GFRP sheets |
|
|
| Model No. |
54-55 |
| Model type |
Enhanced composite damage |
| Layer thickness |
1.3 mm |
1.3 mm |
|
| Tensile modulus in fiber direction |
71.46 GPa |
20.9 GPa |
|
| Tensile modulus in transverse direction |
3.59 GPa |
1.05 GPa |
|
| Tensile strength in fiber direction |
710 MPa |
253 MPa |
|
| Tensile strength in transverse direction |
71 MPa |
25.3 MPa |
|
Table 3.
Experimental and FE outputs for load versus axial deformation behavior of tested specimens.
Table 3.
Experimental and FE outputs for load versus axial deformation behavior of tested specimens.
| Specimen ID |
Outputs |
Service load (kN) |
Displacement at service load (mm) |
Yield load (kN) |
Displacement at yield load (mm) |
Max. load (kN) |
Displacement at max. load (mm) |
Ultimate displacement (mm) |
Axial stiffness at service load (kN/mm) |
Dissipated energy at ultimate state (kN.mm) |
| CON1 |
EXP |
745 |
0.27 |
1846 |
0.93 |
1862 |
1.05 |
2.01 |
2810 |
2866 |
| |
FE |
790 |
0.25 |
1969 |
1.04 |
1974 |
1.09 |
2.15 |
3158 |
3220 |
| |
EXP/FE |
0.94 |
1.06 |
0.94 |
0.89 |
0.94 |
0.96 |
0.93 |
0.89 |
0.89 |
| CON2 |
EXP |
802 |
0.29 |
1919 |
0.93 |
2006 |
1.11 |
1.97 |
2815 |
3157 |
| |
FE |
790 |
0.25 |
1969 |
1.04 |
1974 |
1.09 |
2.15 |
3158 |
3220 |
| |
EXP/FE |
1.02 |
1.14 |
0.97 |
0.89 |
1.02 |
1.02 |
0.92 |
0.89 |
0.98 |
| ST1 |
EXP |
1391 |
0.34 |
3223 |
1.06 |
3478 |
1.37 |
1.72 |
4092 |
4212 |
| |
FE |
1475 |
0.37 |
3491 |
1.18 |
3686 |
1.40 |
1.75 |
4020 |
4343 |
| |
EXP/FE |
0.94 |
0.93 |
0.92 |
0.89 |
0.94 |
0.98 |
0.98 |
1.02 |
0.97 |
| CON1-0.8P-TLR |
EXP |
774 |
0.27 |
NY |
NY |
1463 |
0.59 |
0.59 |
2865 |
503 |
| |
FE |
790 |
0.25 |
NY |
NY |
1600 |
0.56 |
0.56 |
3158 |
461 |
| |
EXP/FE |
0.98 |
1.08 |
- |
- |
0.91 |
1.05 |
1.05 |
0.91 |
1.09 |
| ST1-0.8P-TLR |
EXP |
1252 |
0.38 |
2975 |
1.06 |
3129 |
1.27 |
2.08 |
3338 |
4099 |
| |
FE |
1360 |
0.37 |
3281 |
1.17 |
3400 |
1.28 |
1.88 |
3698 |
4052 |
| |
EXP/FE |
0.92 |
1.02 |
0.91 |
0.91 |
0.92 |
0.99 |
1.10 |
0.90 |
1.01 |
| ST2 |
EXP |
1751.5 |
0.31 |
3647 |
0.84 |
4379 |
2.06 |
5.11 |
5743 |
20396 |
| |
FE |
1684.8 |
0.34 |
3753 |
1.03 |
4212 |
2.20 |
6.25 |
4954 |
20967 |
| |
EXP/FE |
1.04 |
0.90 |
0.97 |
0.82 |
1.04 |
0.94 |
0.82 |
1.16 |
0.97 |
| CON2-0.8P-TLR |
EXP |
774 |
0.27 |
NY |
NY |
1573 |
0.53 |
0.53 |
2919 |
460 |
| |
FE |
790 |
0.25 |
NY |
NY |
1600 |
0.56 |
0.56 |
3158 |
461 |
| |
EXP/FE |
0.98 |
1.06 |
- |
- |
0.98 |
0.95 |
0.95 |
0.92 |
1.00 |
| ST2-0.8P-TLR |
EXP |
1666 |
0.34 |
3527 |
0.89 |
4166 |
1.98 |
6.50 |
4919 |
18781 |
| |
FE |
1577 |
0.36 |
3665 |
1.08 |
3943 |
2.00 |
6.24 |
4380 |
17516 |
| |
EXP/FE |
1.06 |
0.94 |
0.96 |
0.82 |
1.06 |
0.99 |
1.04 |
1.12 |
1.07 |
Table 4.
Experimental and FE outputs for stress versus strain behavior of tested specimens.
Table 4.
Experimental and FE outputs for stress versus strain behavior of tested specimens.
| Specimen ID |
Outputs |
Max. average concrete compressive strength (MPa) |
Max. actual concrete compressive strength (MPa) |
Axial strain in concrete at max. stress |
Ultimate axial strain in concrete |
Axial strain in vertical steel bars at max. load |
Axial strain in NSM bars at max. load |
Max. horizontal strain in FRP sheets |
Max. horizontal strain in steel plates |
| CON1 |
EXP |
29.8 |
23.4 |
0.0026 |
0.0050 |
0.0034 |
- |
- |
- |
| |
FE |
31.6 |
25.2 |
0.0027 |
0.0054 |
0.0033 |
- |
- |
- |
| |
EXP/FE |
0.94 |
0.93 |
0.96 |
0.93 |
1.04 |
- |
- |
- |
| CON2 |
EXP |
32.1 |
25.74 |
0.0028 |
0.0049 |
0.0031 |
- |
- |
- |
| |
FE |
31.6 |
25.23 |
0.0027 |
0.0054 |
0.0033 |
- |
- |
- |
| |
EXP/FE |
1.02 |
1.02 |
1.02 |
0.92 |
0.95 |
- |
- |
- |
| ST1 |
EXP |
56.0 |
41.1 |
0.0034 |
0.0043 |
0.0038 |
NA |
NA |
- |
| |
FE |
59.0 |
44.6 |
0.0035 |
0.0044 |
0.0038 |
0.0033 |
-0.0099 |
- |
| |
EXP/FE |
0.95 |
0.92 |
0.98 |
0.98 |
1.00 |
- |
- |
- |
| CON1-0.8P-TLR |
EXP |
23.4 |
17.0 |
0.0015 |
0.0015 |
0.0022 |
- |
- |
- |
| |
FE |
25.6 |
19.2 |
0.0014 |
0.0014 |
0.0022 |
- |
- |
- |
| |
EXP/FE |
0.91 |
0.88 |
- |
- |
0.97 |
- |
- |
- |
| ST1-0.8P-TLR |
EXP |
50.3 |
35.3 |
0.0032 |
0.0052 |
0.0038 |
0.0030 |
0.0085 |
- |
| |
FE |
54.4 |
39.8 |
0.0032 |
0.0047 |
0.0035 |
0.0027 |
0.0098 |
- |
| |
EXP/FE |
0.93 |
0.89 |
0.99 |
1.10 |
1.10 |
1.10 |
0.86 |
- |
| ST2 |
EXP |
70.45 |
56.05 |
0.0051 |
0.0128 |
0.0114 |
0.0124 |
0.0144 |
0.0034 |
| |
FE |
67.39 |
53.29 |
0.0055 |
0.0156 |
0.0123 |
0.0137 |
0.0121 |
0.0038 |
| |
EXP/FE |
1.05 |
1.05 |
0.94 |
0.82 |
0.93 |
0.91 |
1.19 |
0.89 |
| CON2-0.8P-TLR |
EXP |
25.2 |
18.7 |
0.0013 |
0.0013 |
0.0018 |
- |
- |
- |
| |
FE |
25.6 |
19.2 |
0.0014 |
0.0014 |
0.0022 |
- |
- |
- |
| |
EXP/FE |
0.98 |
0.98 |
0.95 |
0.95 |
0.81 |
- |
- |
- |
| ST2-0.8P-TLR |
EXP |
67.02 |
52.52 |
0.0049 |
0.0163 |
0.0107 |
0.0078 |
0.0123 |
NA |
| |
FE |
63.09 |
48.83 |
0.0050 |
0.0156 |
0.0098 |
0.0074 |
0.0121 |
0.0036 |
| |
EXP/FE |
1.06 |
1.08 |
0.99 |
1.04 |
1.09 |
1.06 |
1.02 |
- |
Table 5.
FE analysis matrix used in the parametric study.
Table 5.
FE analysis matrix used in the parametric study.
| Specimen ID |
Strengthening scheme |
Loading condition |
Notes |
| CON |
Unstrengthened to be used as control specimen |
Loaded up to failure |
Modeled in Refs. [19] |
| CON-0.4P-TLR |
Unstrengthened |
Loaded up to 40% of the peak load of specimen CON, and the load was then totally released |
Modeled in this study |
| CON-0.4P-NLR |
Unstrengthened |
Loaded up to 40% of the peak load of specimen CON, and the load was not released |
S/A |
| CON-0.8P-TLR |
Unstrengthened |
Loaded up to 80% of the peak load of specimen CON, and the load was then totally released |
S/A |
| CON-0.8P-NLR |
Unstrengthened |
Loaded up to 80% of the peak load of specimen CON, and the load was not released |
S/A |
| CON-0.9P-TLR |
Unstrengthened |
Loaded up to 90% of the peak load of specimen CON, and the load was then totally released |
S/A |
| CON-0.9P-NLR |
Unstrengthened |
Loaded up to 90% of the peak load of specimen CON, and the load was not released |
S/A |
| ST2 |
Strengthened using 2nd scheme (externally bonded GFRP layers + bolted steel plates + connected NSM steel rebars) |
Loaded up to failure |
Modeled in Ref. [19] |
| ST2-0.4P-TLR |
It is the same as specimen CON-0.4P-TLR, and it will be strengthened after preloading using 2nd scheme |
S/A |
Modeled in this study |
| ST2-0.4P-NLR |
It is the same as specimen CON-0.4P-NLR, and it will be strengthened after preloading using 2nd scheme |
S/A |
S/A |
| ST2-0.8P-TLR |
It is the same as specimen CON-0.8P-TLR, and it will be strengthened after preloading using 2nd scheme |
S/A |
S/A |
| ST2-0.8P-NLR |
It is the same as specimen CON-0.8P-NLR, and it will be strengthened after preloading using 2nd scheme |
S/A |
S/A |
| ST2-0.9P-TLR |
It is the same as specimen CON-0.9P-TLR, and it will be strengthened after preloading using 2nd scheme |
S/A |
S/A |
| ST2-0.9P-NLR |
It is the same as specimen CON-0.9P-NLR, and it will be strengthened after preloading using 2nd scheme |
S/A |
S/A |
Table 6.
Key FE outputs for specimens of the parametric study.
Table 6.
Key FE outputs for specimens of the parametric study.
| Specimen ID |
Yield load (kN) |
Displacement at yield load (mm) |
Max. load (kN) |
Displacement at max. load (mm) |
Ultimate displacement (mm) |
Axial stiffness at service load (kN/mm) |
Dissipated energy at ultimate state (kN.mm) |
Ultimate axial strain in concrete () |
Axial strain in vertical steel bars at max. load () |
| CON |
1969 |
1.04 |
1974 |
1.09 |
2.15 |
3158 |
3220 |
5378 |
3276 |
| CON-0.4P-TLR |
NY |
NY |
800 |
0.25 |
0.25 |
3158 |
100 |
627 |
527 |
| CON-0.4P-NLR |
NY |
NY |
800 |
0.25 |
0.25 |
3158 |
100 |
627 |
527 |
| CON-0.8P-TLR |
NY |
NY |
1600 |
0.56 |
0.56 |
3158 |
461 |
1395 |
2227 |
| CON-0.8P-NLR |
NY |
NY |
1600 |
0.56 |
0.56 |
3158 |
461 |
1395 |
2227 |
| CON-0.9P-TLR |
NY |
NY |
1800 |
0.67 |
0.67 |
3158 |
685 |
1681 |
2534 |
| CON-0.9P-NLR |
NY |
NY |
1800 |
0.67 |
0.67 |
3158 |
685 |
1681 |
2534 |
| ST2 |
3753 |
1.03 |
4212 |
2.20 |
6.25 |
4954 |
20967 |
15622 |
12269 |
| ST2-0.4P-TLR |
3847 |
1.11 |
4100 |
1.34 |
6.07 |
4598 |
18344 |
15170 |
94980 |
| ST2-0.4P-NLR |
3375 |
0.96 |
3803 |
1.22 |
3.13 |
3823 |
8018 |
7826 |
7785 |
| ST2-0.8P-TLR |
3665 |
1.08 |
3943 |
2.00 |
6.24 |
4380 |
17516 |
15593 |
9795 |
| ST2-0.8P-NLR |
2922 |
0.97 |
3262 |
1.25 |
2.40 |
3433 |
5157 |
6001 |
3998 |
| ST2-0.9P-TLR |
3350 |
1.01 |
3693 |
1.31 |
2.62 |
4105 |
6486 |
6546 |
7476 |
| ST2-0.9P-NLR |
2570 |
0.93 |
2700 |
1.09 |
2.10 |
3177 |
3881 |
5249 |
5697 |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).