Preprint
Article
Wildfire-Induced Risk Assessment to Enable Resilient and Sustainable Electric Power Grid
Altmetrics
Downloads
107
Views
73
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
16 November 2023
Posted:
17 November 2023
You are already at the latest version
Alerts
Abstract
To ensure sustainability of the future power grid, the rate of expansion of distributed renewable energy resources (DRER) has introduced operational challenges. These includes managing transmission constraints with DRER power injection, dispatching DRER efficiently, managing system frequency and ensuring sufficient reactive power for voltage support. Coupled with the intensification of wildfires, power infrastructure across the United States faces challenges to minimize the impact to maintain system reliability and resiliency. This research embarks on a comprehensive evaluation, beginning with an in-depth historical analysis to delineate regions most susceptible to wildfires. Utilizing a multidimensional approach, the study assesses wildfire-induced risks to power grids, by integrating historical wildfire occurrences, real-time wildfire proximities, Moderate Resolution Imaging Spectroradiometer (MODIS) derived vegetation metrics, and system parameters, by employing Principal Component Analysis (PCA) based optimal weights, leading to the formulation of a novel risk factor model. This risk factor has the potential to be the key to ensuring the resilience of a renewable-rich smart grid when faced with a severe weather event. Our model’s applicability was further verified through an empirical assessment, selecting representative networks from diverse regions, providing insights into the geographical variability of risk factors. Ultimately, this study offers stakeholders and policymakers a comprehensive tool-set, empowering decisions regarding infrastructure investments, grid reinforcements, and strategic power rerouting to ensure consistent energy delivery using risk assessment against wildfire.
Keywords:
Subject: Engineering - Electrical and Electronic Engineering
1. Introduction
The rapidly changing climate presents an intricate mosaic of challenges, with the relentless surge of wildfires carving an especially perilous niche. These wildfires, fed and intensified by climate anomalies are detrimental to the electric power systems. Wildfires are no longer just natural calamities; they’ve transformed into multifaceted disasters impinging upon both the natural environment and man-made infrastructures. The alarming consequences of wildfires on power systems cannot be understated. Components of the power infrastructure, when exposed to such extreme events, can suffer irreparable damage, culminating in extensive power outages. These blackouts, in turn, cause monumental economic losses and paradoxically, can even become the birthplaces for more fires, perpetuating a vicious cycle [1]. In the United States, losses from the fires of 2018 in California are estimated at a record US$19 billion [2]. The significant economic costs associated with these events are not just from direct damages but also from the subsequent ramifications on critical systems like the electric grid [3].
High-velocity winds, which often accompany wildfires, can cause power conductors to sway violently, leading to contact with nearby trees or other flammable entities. Such contacts have the potential to be the genesis of newer, often more devastating fires, further aggravating the situation [4]. In daily operations, electric utilities have fewer and more disruptive actions to reduce impacts of wildfire on the power grid, the most commonly used method being public safety power shut-offs (PSPS) [5,6,7], where certain sections of the grid is de-energized causing intentional blackouts and significantly impact customers and also impacts the ability of the power system to provide reliable electricity. In October 2019, the intentional blackouts due to PSPS turned off power to almost a million customers [8].
Confronted with such grim scenarios, the logical recourse might seem to be in reinforcing the entire grid system, rendering it impervious to the threats posed by wildfires. However, this approach is fraught with complications. Primarily, the financial implications are astronomical. A testament to this is PG&E’s estimation, which suggests a budget exceeding 100 billion dollars would be necessary to subterraneously route its high-voltage lines across two-thirds of California [9]. Moreover, this herculean task is not without its environmental quandaries. Undertaking such massive underground operations in ecologically rich zones can lead to unforeseen environmental consequences. Recent history also provides testimony to the vulnerability of the power infrastructure. The 2017 Thomas Fire serves as a stark reminder, having disrupted power transmission in the Santa Barbara region and leaving a staggering 85,000 customers in darkness. Fast forward a year, and the narrative remained equally bleak, with the Mendocino Complex Fire depriving approximately 50,000 residents of power. Northern California wasn’t spared either. The mere threat of wildfires coerced utility companies into cutting off power for nearly 800,000 customers, underscoring the gravity of the situation [10]. Statistical trends only add to the concerns. On an average, wildfires have impacted over 933,547 customers. A comprehensive study spanning 16 years reveals that damages to power transmission and distribution networks exceeded 700 million dollars, a figure that’s only expected to rise considering the escalating frequency and severity of wildfires, especially in regions like California [11].
With the resilience and reliability of the electrical infrastructure being put to the test, particularly by challenges emanating from natural disasters like wildfires, researchers have been tirelessly working to develop sustainable models for wildfire disruption mitigation. Authors in [12] propose a new optimization model to minimize wildfire risk due to electric power system components, while maintaining electricity supply to as many customers as possible, by considering how preventive wildfire risk measures impact both wildfire risk and power systems reliability at a short-term, operational time-frame. In [13], the authors propose an optimization approach for the expansion planning of a power system considering the presence of High Fire-Threat District (HFTD) Zones, while ensuring operational feasibility of the network. An optimal scheduling framework for managing power system-induced wildfire risk was proposed in [14], and demonstrated over multiple time steps so that the risk of wildfire and load delivery fluctuation with changes in temperature and power demand throughout the day could be accounted for. [15] underscores the heightened risk wildfires pose to the electric power grids, both in terms of damage to electrical equipment and the safety of personnel.
Recognizing that fortifying the entire grid is neither financially nor environmentally viable, and PSPS is not a viable option for grid reliability, we endeavor to provide a nuanced solution. By meticulously analyzing vulnerabilities, this study aims to equip policymakers with the intelligence to prioritize regions that are most at risk, thereby ensuring that reinforcement efforts are both strategic and effective.
Objective of this work is develop a proactive risk assessment of power grid to wildfire susceptibility. Key contributions include
- Developed architecture and algorithms for predictive analysis to identify power grid nodes at heightened risk even before wildfire events unfold. Developed algorithm utilizes environmental parameters, historical wildfire occurrences, vegetation types, and voltage data for predictive analysis.
- Developed solution approach and regional-specific risk analysis to wildfires using the Principal Component Analysis (PCA), isolating the most influential determinants of node vulnerability. Also, develop algorithm utilizes Moderate Resolution Imaging Spectroradiometer (MODIS) derived vegetation metrics, Hierarchical Density-Based Spatial Clustering of Applications with Noise (HDBSCAN), Voronoi-HDBSCAN and enhanced proximity analysis using overlay of electric grid and wildfire coordinates. Furthermore, by undertaking a comparative analysis across five distinct regions, our research elucidates region-specific risk profiles, paving the way for tailored future mitigation strategies.
In our work, node represents large scale geographical region overlayed with electric nodes within a regional area. This work provides a predictive analysis to help with post-detection mitigation framework with final goal to enhance grid resilience through anticipatory intelligence.
2. Historical Inference from Wildfire Data
With increased penetration of renewable generation across the grid, system operators have the onerous task of maintaining the fragile balance of power consumption and generation, while ensuring system stability. Along with reducing system inertia, renewable generation brings a certain level of uncertainty into the equation. As a result, during severe weather events such as wildfires, when several components of the grid get impacted simultaneously, it becomes a challenge to maintain stability in the rest of the network. To ensure resilience of the power network, we need to understand the behavior of wildfires. To that end, we used available historical data of various wildfires across the nation as a starting point.
Understanding the likelihood of forest fires occurring in a region should be the first step to develop a reliable risk assessment model. Using the wildfire events as data points, the construction and interpretation of a Density-based Spanning Tree (DBST) offers a robust framework for understanding and identifying clusters in a hierarchical, density-based manner. Through mutual reachability distances and persistence measures, Hierarchical Density-Based Spatial Clustering of Applications with Noise (HDBSCAN) provides a nuanced yet computationally efficient approach to clustering large datasets.
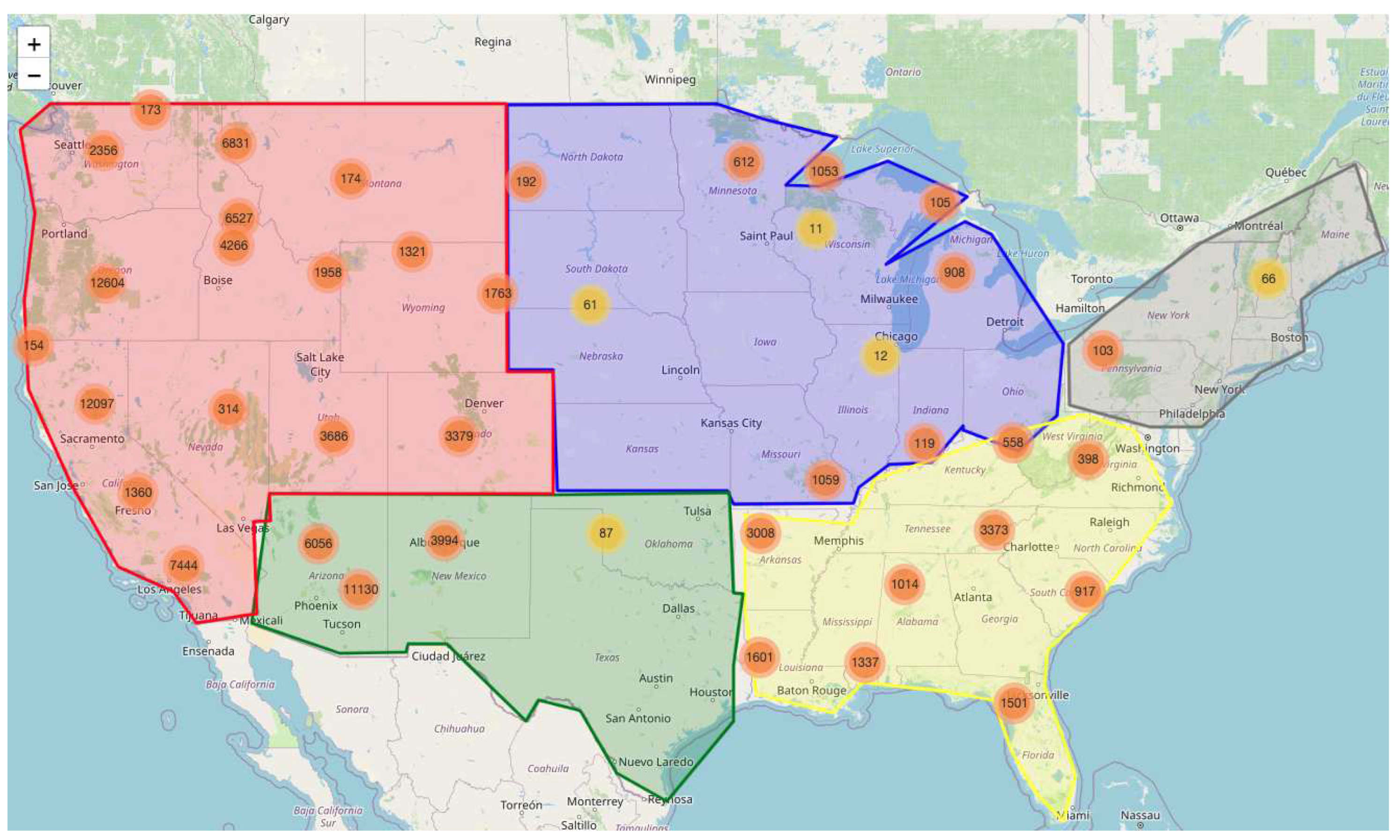
Figure 1.
Classification of various US Regions using Voronoi diagrams and HDBSCAN.
2.1. Density-Based Spatial Clustering: HDBSCAN
Hierarchical Density-Based Spatial Clustering of Applications with Noise (HDBSCAN) is an offshoot of the DBSCAN algorithm. Unlike K-means which requires the pre-specification of clusters, HDBSCAN, with its foundation in density, provides a more fluid understanding of clusters. Given a set , the algorithm calculates the core distance and the mutual reachability distance. For any point x, its core distance, , is the smallest radius such that there exists at least in its neighborhood:
Where denotes the number of points within that radius.
To formalize, let’s assume we have a dataset D with n data points. For any two points in D, the mutual reachability distance is defined as:
Here:
- is the usual distance metric, e.g., Euclidean distance.
- is the distance from point p to the nearest point in D.
This mutual reachability distance ensures that distant points in dense regions are not over-penalized. Using these distances, a Minimum Spanning Tree (MST) is created where nodes represent data points, and edges represent the mutual reachability distances between them.
The MST is then found using Kruskal’s algorithm[16], which operates efficiently with a time complexity of . Within MST, the order in which edges are considered gives insight into the hierarchical structure of the data:
- Edges with the smallest mutual reachability distance (indicating high density) are considered first.
- As we traverse edges with increasing distances, we transition from denser to sparser regions, hierarchically branching the data.
This hierarchy represents the density-based structure of the data, where each level corresponds to a varying density threshold.
The final step, pruning, is done based on a persistence measure. The persistence of a cluster is the difference between its birth (when it first appears) and death (when it merges into another cluster) in terms of mutual reachability distance. A higher persistence indicates a more stable and distinct cluster. By setting a threshold for persistence, branches (clusters) with low persistence (unstable over the range) are pruned, and the remaining ones are identified as the final clusters.
2.2. Regional Analysis with Voronoi-HDBSCAN
Introducing polygons, especially when analyzing regions, can provide contextual understanding. We used Voronoi polygons to visually represent the influence zone of each data point (wildfire event).
Given a set of points P in the plane, a Voronoi diagram divides the plane such that every point within a particular region is closer to the seed point of that region than any other. Mathematically, for a seed point in P, its Voronoi region is:
Where d is the distance measure, typically Euclidean.
Combining Voronoi diagrams with HDBSCAN clusters allows us to visualize not just where clusters are but also the influence area of each cluster’s members. For each of the five main regions of the U.S., Voronoi diagrams were superimposed on the HDBSCAN clusters. The susceptibility for each region was adjusted:
Where V represents the union of Voronoi regions associated with wildfire events, and represents the total area of region r.
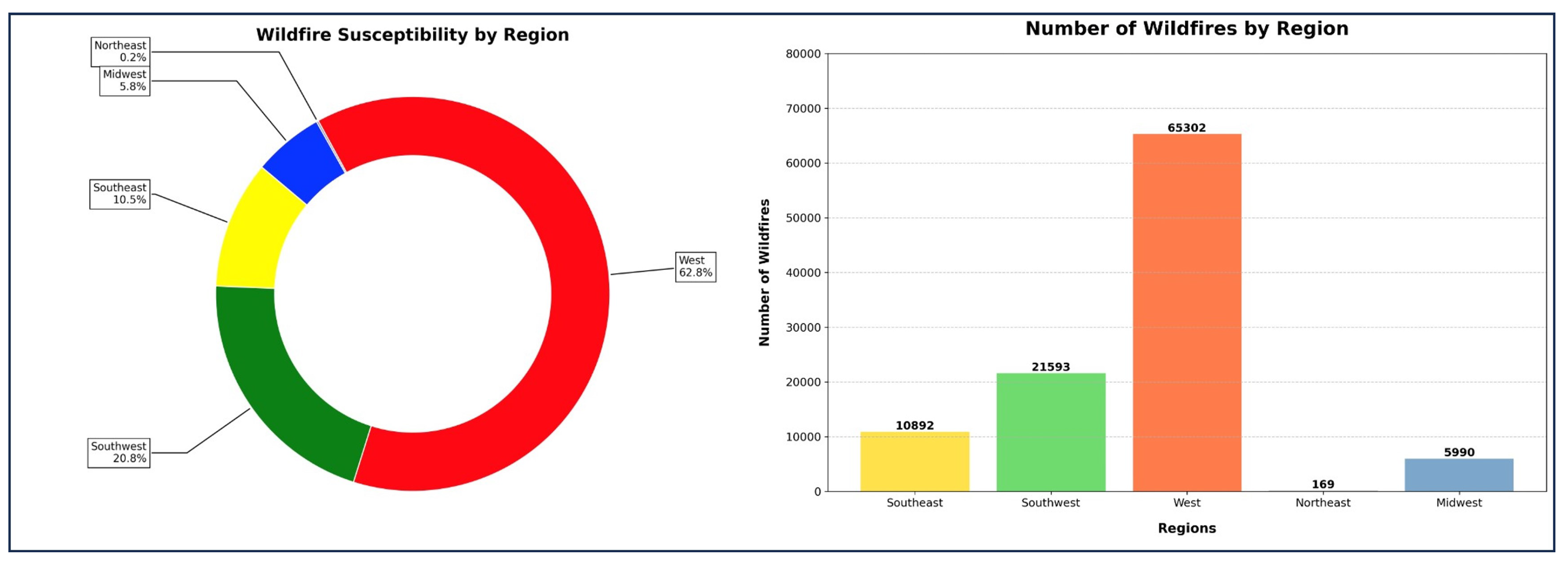
It is evident from Figure 2 that the West and Southwest regions of US showed heightened susceptibility values. The Voronoi-HDBSCAN method revealed critical insights into how wildfires are spread and their regional influence, a novel approach beneficial for strategic planning.
3. Wildfire Risk Factors
Contemporary electrical grids, with their sprawling network of transmission lines and buses, encounter multifaceted environmental challenges that necessitate sophisticated analytical approaches. One of the emergent challenges is the proximity of wildfires to critical grid infrastructures. The dynamics of these wildfires, which are both temporal and spatial, require a seamless integration of real-time monitoring and robust mathematical models to ascertain potential risks to the grid.
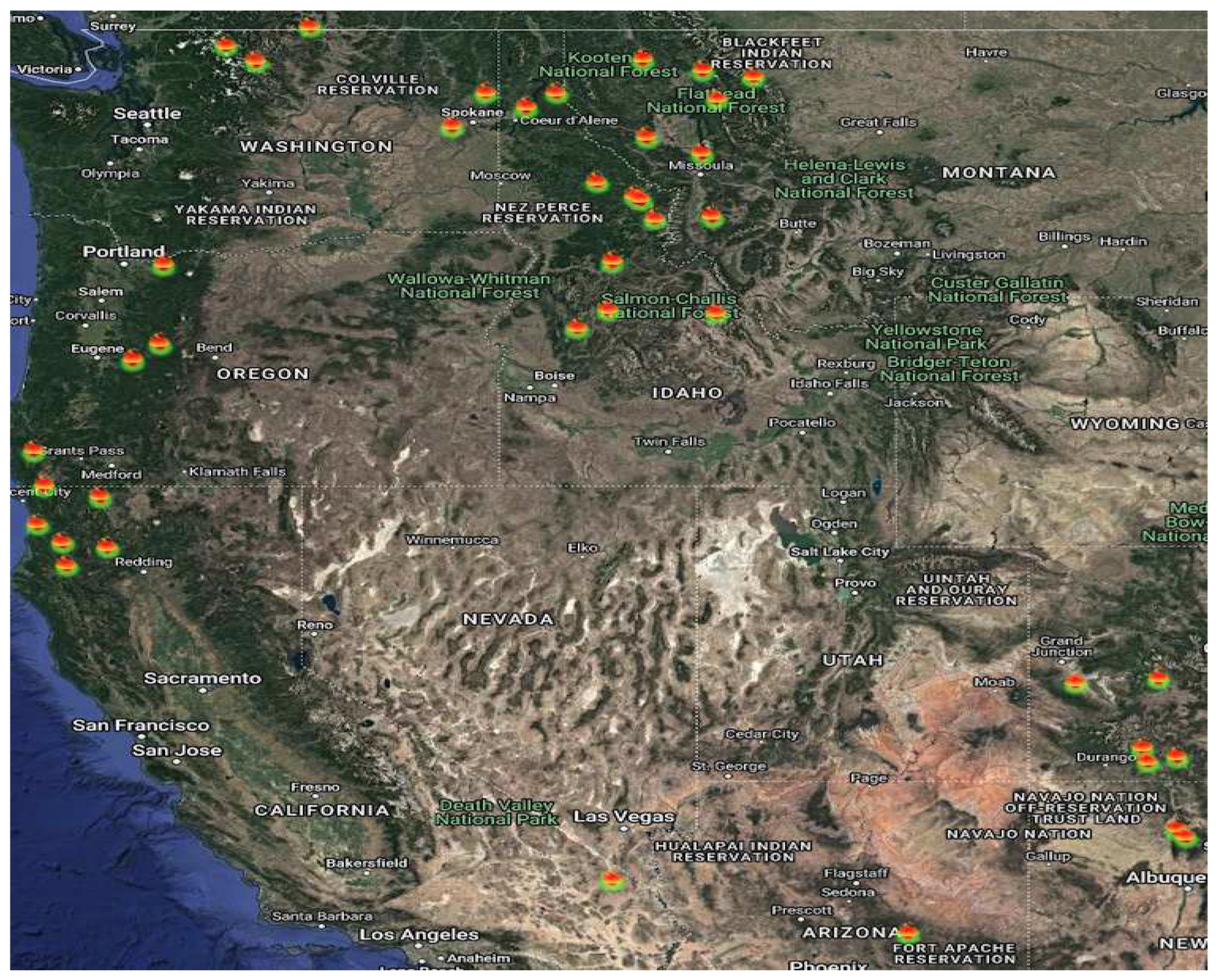
Figure 3.
Real-time wildfires being displayed in a geographical mapping format.
3.1. Enhanced Proximity Analysis between Wildfire Incidents and Electrical Grid
While there are multiple methods to determine the distance between two geographical points, the Haversine formula stands out for its accuracy, especially for significant spans on a spherical body like Earth. This formula, rooted in trigonometric principles, precisely calculates the great-circle distance, which is the shortest distance between any two points on the surface of a sphere.
For two geocoordinates and :
where R is Earth’s radius, and d is the computed distance.
Figure 4.
Combined overlay of both electric power grid, renewable generation and real-time wildfires.
Figure 4.
Combined overlay of both electric power grid, renewable generation and real-time wildfires.
In the project’s schema, the electrical grid is represented by a graph , with V and E being sets of nodes (buses) and edges (transmission lines), respectively. The vulnerability or risk factor of a node, , is influenced by various parameters, with the proximity to active wildfire regions, calculated using the Haversine formula, being a principal factor. This is denoted as for a node v and wildfire location W. Specifically:
Here, f is a risk determination function, and represents other parameters influencing risk, such as meteorological conditions, grid load, and infrastructure age.
The application protocol can be articulated as follows:
- Extract real-time geocoordinates of active wildfire incidents.
- For each node , utilize the Haversine formula to compute .
- Integrate into the risk function f to update the risk factor for each node.
- Prioritize nodes based on increasing risk values, thereby aiding in real-time grid management decisions.
A critical aspect of risk evaluation in the context of proximity analysis is the normalization of derived distances. While the Haversine formula provides an accurate measure of the great-circle distance between two geographical points, these absolute values may span a vast range. For the purpose of a uniform and comparative risk assessment, it is essential to map these distances to a normalized scale, typically between 0 and 1.
One of the most common methods for normalization is the Min-Max scaling. Given a distance and assuming and are the maximum and minimum distances observed across all nodes, the normalized distance, , can be computed as:
However, considering the context of risk, proximity to a wildfire poses a higher threat. Thus, it might be more intuitive to invert this normalized value, where a value closer to 1 indicates closer proximity and, therefore, higher risk:
Incorporating this normalized distance measure into the risk determination function ensures that the proximity influence is consistent across all nodes, regardless of their absolute geographical separations. Moreover, this allows for a clear comparison among nodes, where nodes with values closer to 1 are in more immediate danger and might require urgent interventions.
The Haversine formula provides a rigorous mathematical foundation to the proximity-based risk analysis of the electrical grid relative to wildfire threats. This, when combined with other risk parameters, offers a holistic and highly accurate risk assessment model essential for the safeguarding and efficient management of contemporary electrical grids.
3.2. Historical Wildfire Frequency as a Risk Factor
The spatial distribution of wildfires across different regions bears testament to not only environmental conditions but also human activities, forest management practices, and various socio-economic factors. However, for the sake of electrical grid robustness, it’s paramount to convert these spatial patterns into quantifiable metrics that can be used as risk indicators. Historical wildfire frequency emerges as a pivotal metric in this scenario.
From the HDBSCAN clustering methodology, clusters of historical wildfires are identified across the regions. Each cluster’s density provides an immediate measure of wildfire frequency for that specific region. Let’s denote the number of wildfires in a given cluster as .
To determine the historical wildfire frequency for a region r, the following equation can be employed:
Where are the identified clusters in the region r and is the total area of region r.
To incorporate the influence zones identified through Voronoi polygons, a weighted frequency can be used. This takes into account not just the number of wildfire events but also their spatial influence:
Where represents the union of Voronoi regions associated with wildfire events in the region r.
Figure 5.
Flowchart describing the process used to integrate the historical wildfire factor into the risk model.
Figure 5.
Flowchart describing the process used to integrate the historical wildfire factor into the risk model.
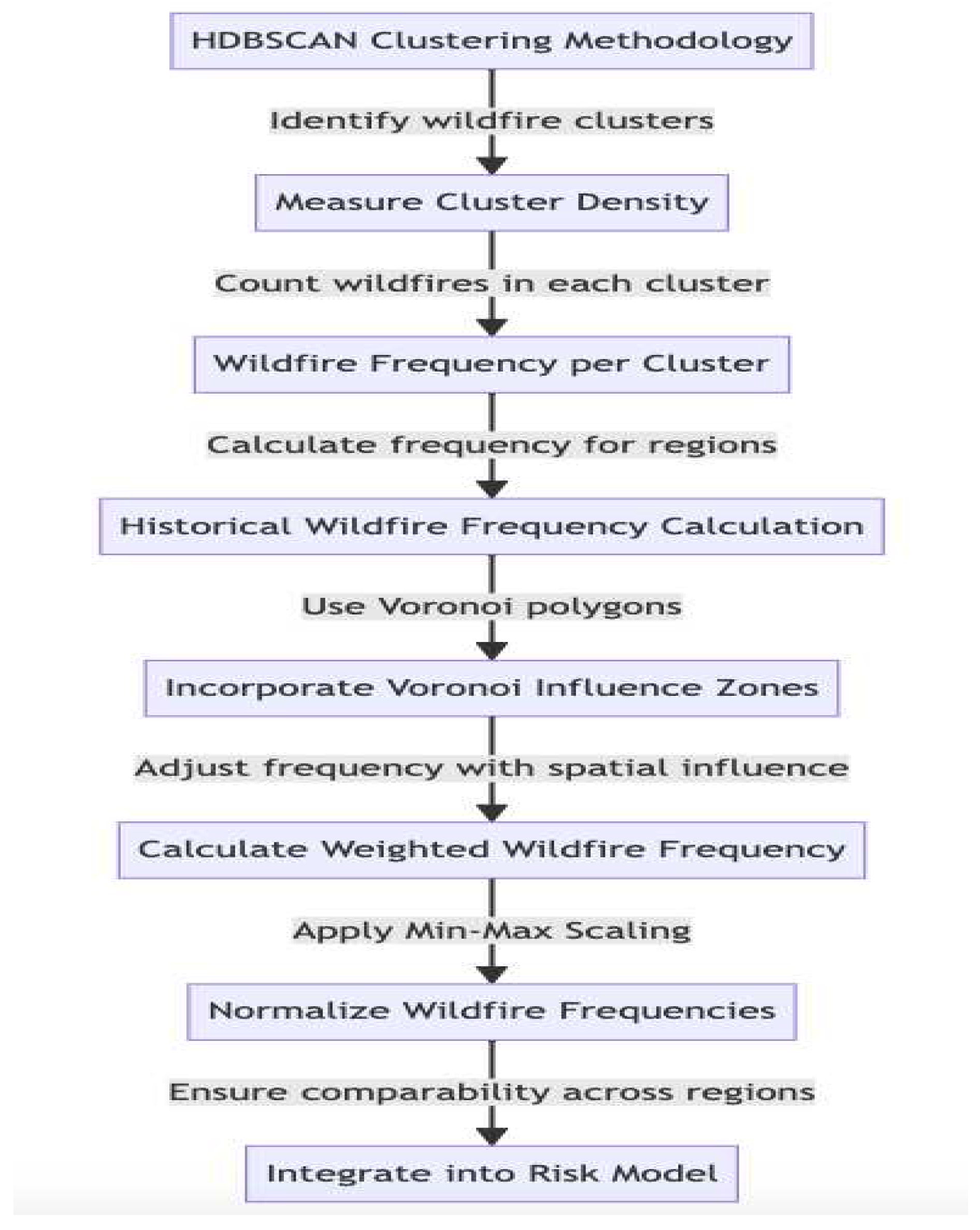
This weighted wildfire frequency, , provides a more nuanced understanding of the historical wildfire frequency by integrating spatial influence areas.
Given the vast differences in regional sizes and historical data availability, it’s essential to normalize these frequency values. Again Min-Max scaling is used where the minimum is 0 and the maximum is 1:
Where is the normalized frequency for region r, and and are the minimum and maximum weighted frequencies among all regions respectively. This normalized metric ensures comparability across regions irrespective of their size and can be directly integrated as a factor in the risk model.
The historical wildfire frequency, especially when weighted by spatial influence, provides an invaluable insight into the regions more likely to experience future events. It is grounded on the notion that past events indicate areas of inherent vulnerability, whether due to local environmental conditions or human factors. By incorporating this frequency into the risk model, the electrical grid’s representation and analysis become more in line with real-world challenges, making it a vital component in assessing potential future vulnerabilities.
3.3. Voltage Analysis in Electrical Grid Nodes and Transmission Lines
Voltage, in power systems, is not merely an electrical parameter but a crucial indicator of the system’s health, stability, and operational efficiency. The magnitude and phase of voltage across nodes (buses) and transmission lines can shed light on a plethora of system attributes, from load dynamics to reactive power compensation.
Figure 6.
Buses and transmission lines represented as nodes and edges of a graph.
The granular voltage information for each node and transmission line within our framework is acquired from a comprehensive dataset, meticulously curated from multiple sensors and telemetry equipment distributed across the grid. These sensors, often connected to sophisticated Supervisory Control and Data Acquisition (SCADA) systems, provide near-real-time measurements.
Let’s first denote the voltage at any node i as , which can be expressed in polar form as:
In power systems, the power flow equation that relates voltage and power is:
For transmission lines, the voltage drop can be represented using the line impedance :
Voltage data for each node and transmission line is dynamically linked within our advanced grid management framework.
For any node i, the voltage profile over time t can be formulated as:
The operational state of a node or transmission line is influenced by its voltage magnitude. The evaluation of the eigenvalues of the system’s Jacobian matrix is the following:
Voltage deviations, both sag (when demand is higher than generation) and swell (when generation is higher than demand) [17], and can indicate potential grid vulnerabilities. The normalization of voltage magnitudes ensures that the operational state of each node can be compared, offering a unified measure of vulnerability.
Given a node’s voltage magnitude and taking into account the permissible voltage range specified by grid standards, the normalized voltage magnitude can be computed using the Min-Max normalization.
However, from a risk perspective, significant deviations from the nominal voltage value (either too high or too low) are more concerning. Thus, it might be valuable to use a modified normalization scheme that accentuates deviations:
Here, inverts the normalized voltage such that values approaching 0 indicate nominal operation, and as the voltage deviates from nominal (either due to sag or swell), increases, approaching 1. This renders nodes with a value closer to 1 as more vulnerable, warranting monitoring or corrective action.
This normalization approach ensures that voltage magnitudes, irrespective of their absolute value, contribute consistently to the risk assessment metric. By centering the scale on nominal operational values, and expanding outward to encompass extreme vulnerabilities, grid operators and analysts can prioritize nodes based on their deviation from desired operational standards.
It’s worth noting that while this normalization provides a framework for assessing vulnerability, a comprehensive risk assessment might necessitate further refinements considering other voltage-related parameters like voltage stability margins, phase imbalances, and harmonic distortions. By integrating real-time voltage data and coupling it with mathematical models, our framework offers insights into the operational health of the grid.
3.4. Vegetation-Based Wildfire Risk Assessment using MODIS Data
The first step in the process involves retrieving vegetation data from the MODIS API provided by NASA. The primary metric to be extracted is the NDVI (Normalized Difference Vegetation Index), which provides insight into the density and health of vegetation in a given area. This is given by:
Here, NIR stands for the near-infrared reflectance, and Red stands for the red light reflectance.
Using the NDVI values, areas can be classified into different types of vegetation. The classification process would be based on established NDVI ranges that correspond to the given vegetation categories. For instance, specific NDVI value ranges can indicate grassland, while others can signify dense forests.
After classifying vegetation, it’s essential to understand the characteristics of each vegetation type. For each category, parameters such as fuel loading, fuel bed depth, surface area to volume ratio, packing ratio, etc., will be analyzed [18]. This detailed data, often will serve as one of the factors for wildfire risk assessment, giving insight into how easily a fire can ignite, spread, and how intense it might become.
Once we have detailed vegetation parameters, we can quantify the wildfire risk for each individual node. The wildfire risk for each node in relation to vegetation type is then quantified using the derived function:
This function encapsulates the cumulative risk based on vegetation characteristics.
To assimilate the vegetation-based wildfire risk into the overarching risk assessment framework, normalization is crucial. Normalizing these values ensures comparability with other risk metrics and facilitates a consolidated risk analysis.
Given the wildfire risk of a specific node, and understanding the potential risk bounds as (minimum risk) and (maximum risk), the normalized risk can be computed using the Min-Max normalization technique:
This normalization results in a value between 0 (indicating the least risk) and 1 (indicating the highest risk). By transforming the vegetation-based wildfire risk into a standardized scale, this value can then be directly incorporated into the final risk factor calculation, either as a standalone metric or in conjunction with other normalized risk factors.
It’s essential to periodically reassess and recalibrate and especially in the face of changing vegetation dynamics, climate change implications, or improved modeling techniques to maintain the relevancy and accuracy of the risk assessment.
4. Modeling Risk of Wildfires to Power Grids
4.1. Data Representation and Principal Component Analysis (PCA)
Given a dataset X with n power grid nodes (rows) and 4 risk factors (columns): distance from the nearest real-time wildfire, vegetation, voltage, and historical wildfire frequency, we aim to understand the significance of each factor in the context of wildfire risk. The matrix representation of the dataset is:
where:
- d represents the distance from the nearest real-time wildfire.
- v represents vegetation.
- represents voltage.
- h represents historical wildfire frequency.
Each column (risk factor) of X is mean-centered:
The covariance matrix is a crucial component in PCA as it captures the pairwise covariances between the different features in the dataset. The covariance between two features indicates how much the features vary together. A positive covariance indicates that as one feature increases, the other also tends to increase, while a negative covariance indicates that as one feature increases, the other tends to decrease.
Given our centered data matrix X of size (where n is the number of data points and m is the number of features), the covariance matrix C of size is computed as:
Each element of the covariance matrix represents the covariance between the feature and the feature and is given by:
where is the value of the feature for the data point, and is the mean of the feature.
The diagonal elements of the covariance matrix, , represent the variance of the feature. The variance measures the spread or dispersion of a feature around its mean. The covariance matrix provides insights into the relationships between features. Eigen decomposition of the covariance matrix is used in PCA to determine the principal components, which are the directions of maximum variance in the data.
Eigen decomposition is a fundamental operation in linear algebra that involves decomposing a matrix into its constituent eigenvalues and eigenvectors. In the context of PCA, Eigen decomposition of the covariance matrix C reveals the principal components of the data. Given the covariance matrix C, the eigenvalues and the corresponding eigenvectors v satisfy the equation:
The Eigenvector v represents a direction in the feature space, while the corresponding Eigenvalue indicates the variance of the data along that direction. In other words, the magnitude of the Eigenvalue signifies the importance or the amount of variance captured by its corresponding Eigenvector.
The steps involved in the Eigen decomposition process are as follows:
- The first step is to compute the eigenvalues. The eigenvalues of C are the solutions to the characteristic equation:where I is the identity matrix of the same size as C.
- Next, we have to compute the eigenvectors. For each eigenvalue , the corresponding eigenvector v is found by solving the linear system:
- Once all eigenvalues and eigenvectors are computed, they are ordered in decreasing order of the eigenvalues. The eigenvector corresponding to the largest eigenvalue represents the direction of maximum variance in the data, known as the first principal component. Subsequent eigenvectors represent orthogonal directions of decreasing variance.
- In PCA, it’s common to select the top k eigenvectors (principal components) that capture the most variance in the data. This allows for a reduction in dimensionality while retaining most of the data’s original variance.
The Eigen decomposition of the covariance matrix C provides a basis transformation where the new axes (principal components) are the directions of maximum variance in the data. This transformation is crucial for dimensionality reduction and feature extraction in PCA.
Given the eigenvalues and their corresponding eigenvectors , we first sort the eigenvalues in descending order:
The sorted eigenvalues have corresponding eigenvectors, which we denote as:
To reduce the dimensionality from m dimensions to k dimensions (where ), we select the first k eigenvectors:
This matrix F is our feature vector, and it will be used to transform the original data matrix X into a reduced dimensionality matrix Y
Given our original data matrix X of size (where n is the number of data points and m is the number of features) and our feature vector F of size (where k is the number of selected principal components), we can project the data onto the lower-dimensional space by multiplying X with F.
The transformed data Y is obtained by:
Each row of Y represents a data point in the original dataset but now transformed into the new lower-dimensional space spanned by the principal components. The columns of Y represent the coordinates of the data points in this new space.
Mathematically, the row of Y, denoted as , is given by:
where is the row of X.
This projection essentially captures the most significant patterns in the data while discarding the less important variations. The principal components in F act as the new axes, and the data is represented concerning these axes, ensuring that the variance (or information) is maximized in this reduced space.
Eigenvalues in PCA represent the variance captured by each principal component. Their magnitude provides insights into the significance of each component.
- Eigenvalue Interpretation: Each eigenvalue indicates the variance explained by its corresponding eigenvector. A larger denotes greater significance.
- Total Variance: Given by:where m is the number of eigenvalues.
- Proportion of Variance: For the component:
- Weight Derivation: The proportion of variance explained by a component represents the weight of the corresponding risk factor. For instance, if a component explains 50% variance, its weight is 0.5.
- Ranking Risk Factors: Risk factors can be ranked by ordering the eigenvalues in descending order.
In the context of wildfire risk, these weights help prioritize interventions based on the significance of each risk factor.
For each risk factor j:
For risk factors j and k:
Each eigenvector v is normalized:
The proportion of variance p captured by the principal component is:
The cumulative variance captured by the first k principal components is:
Table 1.
Risk Factors and their Computed Weights.
| Risk Factor | Weight |
| Distance from nearest real-time wildfire | 0.4497 |
| Historical wildfire frequency | 0.2986 |
| Vegetation Information | 0.1984 |
| Voltage | 0.0533 |
4.2. Wildfire Risk Assessment Based on PCA-Derived Weights
The objective is to model the risk to the electrical grid from wildfires based on a set of critical factors. These factors, which encompass historical data, vegetation information, voltage dynamics, and proximity to real-time wildfires, are combined in a weighted linear fashion. The weights are derived using Principal Component Analysis (PCA) to ensure that the model captures the most significant variations in the dataset.
Let the four factors be denoted by:
- : Historical wildfire factor
- : Vegetation info
- : Voltage
- : Distance of nearest real-time wildfire
Principal Component Analysis (PCA) is often favored over other weight calculation methods due to its unique advantages. While methods like Entropy Weighting, Analytic Hierarchy Process (AHP), Gini Coefficient, Variance-Based Weighting, and Inverse Variance Weighting have their specific applications, PCA stands out in several key areas.
Entropy Weighting determines weights based on the entropy or variability of each variable, which is useful for assessing the importance of variables. However, it doesn’t reduce the dimensionality of the data, which can be crucial in complex datasets. AHP, on the other hand, involves subjective pairwise comparisons and expert judgments, making it less objective and more time-consuming than PCA. While AHP is beneficial for qualitative data, PCA provides a more systematic and quantitative approach.
The Gini Coefficient, commonly used in economics to measure inequality, and Variance-Based Weighting, which assigns weights based on the variance of each variable, are both limited in their ability to transform and simplify data. PCA, in contrast, not only considers the variance but also transforms the data into principal components, reducing dimensionality and highlighting the most significant features.
Inverse Variance Weighting, often used in meta-analysis, gives more weight to less variable or more precise variables. However, it doesn’t address the issue of multicollinearity or correlation between variables, which PCA effectively handles by transforming the data into a set of linearly uncorrelated variables.
The primary advantage of PCA lies in its dimensionality reduction capability, making it exceptionally useful for high-dimensional data. It simplifies the complexity of data by transforming it into principal components, which are linearly uncorrelated and ordered so that the first few retain most of the variation present in the original variables. This not only aids in better interpretation and analysis but also enhances the efficiency of subsequent statistical modeling. Additionally, PCA’s versatility makes it applicable across various types of datasets, providing a more generalizable and robust approach compared to other methods. Therefore, for tasks involving large datasets where dimensionality reduction and feature extraction are crucial, PCA often emerges as the superior choice. Therefore, given PCA-derived weights and for these factors respectively, the risk factor R is defined as:
The formulated risk metric offers a comprehensive representation of potential threats to the grid due to wildfires:
- The historical wildfire factor, , provides insights into a region’s susceptibility to wildfires based on past occurrences. The associated weight, , underscores its importance in the overall assessment.
- The vegetation information, , is an indicator of the available fuel for potential wildfires, with its weight determining its relative contribution.
- Voltage, , serves as an indicator of the grid’s health, with its weight reflecting its significance.
- The factor offers a real-time assessment based on the proximity to an active wildfire. Its weight, , defines its influence in the risk prediction.
This risk assessment formula provides a holistic, data-driven, and adaptable approach to quantify the risks posed by wildfires to electrical grids. By leveraging both historical and real-time data, the model offers a nuanced understanding of the multifaceted threats.
5. Results: Computation of Risk Factor Analysis & Discussion
In this section, we delve into the comprehensive evaluation of risk across distinct nodes. Given the risk factor formula
Where the weights and are 0.4497, 0.2986, 0.1984, and 0.0533 respectively.
5.1. Node 1 (Western Region - Californian coast)
Risk Factor:
Elaboration: Given the Californian coast’s vulnerability to wildfires, especially in the recent decade, the distance from real-time wildfires plays a significant role in this node’s elevated risk. The extensive dry and dense vegetation, combined with a rich history of wildfires, also substantially influences the risk. The high voltage value indicates considerable stress on the grid, possibly due to a combination of renewable integration, rapid urbanization, and increased demand.
5.2. Node 2 (Midwestern Region - Plains of Kansas))
Risk Factor:
Elaboration: The plains of Kansas, characterized by grasslands, represent moderate risk due to periodic dry spells leading to flammable vegetation. While historically the area hasn’t witnessed intense wildfires, changing climate patterns necessitate monitoring. The voltage value suggests decent grid stability, although occasional fluctuations might occur due to demand shifts in agricultural activities.
5.3. Node 3 (Northeastern Region - Forests of Vermont)
Risk Factor:
Elaboration: The lush forests of Vermont, with their dense tree cover, present a potential risk, especially during dry seasons. While the historical data does not indicate frequent wildfires, the dense vegetation index suggests a latent risk. The voltage stability, slightly higher than Node 2, might arise from the colder climate affecting equipment performance or sporadic spikes in demand during the winter.
5.4. Node 4 (Southeastern Region - Florida’s wetlands)
Risk Factor:
Elaboration: The inherently moist environment of Florida’s wetlands provides a natural dampening against wildfires. However, prolonged dry spells or human activities could disrupt this balance. Voltage performance is similar to the other nodes, suggesting standard operational challenges and potential seasonal variations, especially during hurricane seasons.
5.5. Node 5 (Southwestern Region - Arizona’s desert)
Risk Factor:
Elaboration: The arid conditions of Arizona contribute significantly to the risk of wildfires. The sparse vegetation, when dry, can facilitate the rapid spread of fires. Historical incidents in neighboring regions, such as California, further influence this value. Voltage readings, the highest among the nodes, indicate stresses possibly due to high temperatures affecting grid performance and elevated cooling demands.
5.6. Node Ranking
The nodes ranked from lowest to highest risk are:
- Node 1 (Western Region - Californian coast): 0.7919
- Node 5 (Southwestern Region - Arizona’s desert): 0.6409
- Node 3 (Northeastern Region - Forests of Vermont): 0.4907
- Node 4 (Southeastern Region - Florida’s wetlands): 0.4462
- Node 2 (Midwestern Region - Plains of Kansas): 0.3259
Table 2.
Risk values associated with nodes from various U.S. regions.
| Node | Distance from Wildfire | Historical Wildfire Frequency | Vegetation Info | Voltage |
|---|---|---|---|---|
| Node 1(California) | 0.823764 | 0.783512 | 0.764915 | 0.671243 |
| Node 2(Kansas) | 0.250358 | 0.330914 | 0.418276 | 0.592117 |
| Node 3(Vermont) | 0.394821 | 0.452317 | 0.730256 | 0.623489 |
| Node 4(Florida) | 0.352715 | 0.418944 | 0.654727 | 0.610596 |
| Node 5(Arizona) | 0.724938 | 0.691423 | 0.374526 | 0.641278 |
6. Conclusions
Analyzing the risk assessment across these nodes emphasizes the importance of understanding regional variations and the unique challenges they present. From the Mediterranean climates of California to the wetlands of Florida, the nodes’ risk profiles are shaped by a combination of environmental factors, human activity, and infrastructure resilience. Building robust, adaptable, and resilient grid infrastructure requires such granular, data-driven analyses to prioritize resources effectively, optimize grid operations, and ensure public safety.
In the intricate and interconnected landscape of today’s power systems, the susceptibility of our grid infrastructure to external environmental risks has emerged as a significant concern. Among these, wildfires, amplified by climatic shifts, have demonstrated their potential to severely disrupt electrical networks, leading to widespread power outages and substantial economic ramifications. Against this backdrop, our study sought to carve out a comprehensive and nuanced understanding of the potential risks associated with wildfires, emphasizing their interplay with diverse factors and their overarching impact on the grid’s operational efficiency.
This revolved around the development and validation of a robust risk assessment model. Instead of a monolithic approach that oversimplified risk elements, we prioritized granularity. Four salient metrics became the cornerstone of our model: historical wildfire frequency, real-time proximity to active wildfires, in-depth vegetation data derived from MODIS, and voltage dynamics indicative of a node’s health and operational status. By intertwining these metrics, we aimed to capture not just the isolated risks they presented but also their symbiotic relationships.
Historical Analysis
One cannot underestimate the value of precedent. By incorporating historical wildfire data, we acknowledged the recurrent patterns and vulnerabilities of specific regions. This retroactive analysis furnished insights that laid down the foundational understanding of inherent risk across various nodes.
Real-Time Data Integration
In the rapidly evolving scenario of a wildfire, static models are inadequate. Our emphasis on real-time wildfire proximity data underscored the necessity of dynamism in risk modeling. The everchanging trajectories of wildfires necessitate a model that is not just responsive but predictive, allowing grid operators to make informed decisions promptly.
Vegetation Analysis
Utilizing MODIS data to extract vegetation parameters introduced an environmental dimension to our model. This metric not only accounted for fuel sources for potential wildfires but also provided insights into the environmental health of a region, subtly correlating with potential ignition sources and fire spread rates.
Voltage Dynamics
The inclusion of voltage parameters, although seemingly tangential, played a pivotal role. Voltage irregularities can often be indicative of equipment malfunctions, which, in turn, can serve as ignition sources. Furthermore, the stability of a grid node’s voltage profile can be emblematic of its resilience to external perturbations, including wildfires.
While these metrics were pivotal, their individual weightages in the risk assessment model were not merely heuristic determinations. Through the utilization of Principal Component Analysis (PCA), we tapped into a data-driven methodology, ensuring that the weightages were reflective of the actual variance and significance of each metric.
Key Findings:
- Geographical Vulnerabilities: Our case study brought to the fore pronounced regional disparities. Nodes in regions historically frequented by wildfires, like California, undeniably bore heightened risks. Such insights stress the imperativeness of geographically tailored mitigation strategies.
- Symbiotic Metrics: Our risk model’s potency lay not just in its individual components but in their synergistic relationships. Areas with relatively benign historical wildfire data, when juxtaposed with dense vegetation and voltage irregularities, suddenly presented amplified risk profiles.
- Model Versatility: Beyond its immediate application, our model’s adaptability emerged as a standout feature. It holds promise for potential extrapolations beyond the power grid, possibly serving as a foundational framework for assessing environmental risks to varied infrastructural domains.
- Operational Implications: Our model transcends mere academic exercise, offering tangible operational insights. Grid operators can leverage this model to delineate vulnerable nodes, optimizing resource allocation during critical wildfire scenarios.
In summation, this research enables understanding, and quantifying wildfire-induced risks to our power grid for large scale regional areas. Developed architecture can be easily extended for small regions such as power grid control areas by specific grid operators. By amalgamating diverse data sources into a cohesive risk assessment framework, we’ve provided stakeholders with a tool that is both diagnostic and predictive. As we move forward, amid the challenges of a changing climate and an ever-evolving power infrastructure, it is our hope that this research aids in fortifying our grid, ensuring its resilience and reliability.
Funding
This work was supported partly by the U.S. NSF FW-HTF award 1840192.
References
- Sathaye, J.; Dale, L.; Larsen, P.; Fitts, G.; Koy, K.; Lewis, S.; others. Estimating risk to California energy infrastructure from projected climate change. Technical report, 2011.
- Sathaye, J.A.; Dale, L.L.; Larsen, P.H.; Fitts, G.A.; Koy, K.; Lewis, S.M.; de Lucena, A.F.P. Rising Temps, Tides, and Wildfires: Assessing the Risk to California’s Energy Infrastructure from Projected Climate Change. IEEE Power and Energy Magazine 2013, 11, 32–45. [Google Scholar] [CrossRef]
- Frame, D.; Rosier, S.; Noy, I.; Harrington, L.; Carey-Smith, T.; Sparrow, S.; others. Climate change attribution and the economic costs of extreme weather events: a study on damages from extreme rainfall and drought. Climatic Change 2020, 162, 781–97. [Google Scholar] [CrossRef]
- Wang, X.; Bocchini, P. Predicting wildfire ignition induced by dynamic conductor swaying under strong winds. Sci Rep 2023, 13, 3998. [Google Scholar] [CrossRef] [PubMed]
- Pacific Gas and Electric Company. 2020 Wildfire Mitigation Plan Report 2020.
- San Diego Gas & Electric Company. Wildfire Mitigation Plan 2020.
- Southern California Edison Company. Wildfire Mitigation Plan Update 2022.
- California Public Utilities Commission. Deenergization (PSPS) 2020.
- Baker, D. Underground power lines don’t cause wildfires. But they’re really expensive. San Francisco Chronicle, 2017.
- Nazaripouya, H. Power Grid Resilience under Wildfire: A Review on Challenges and Solutions. 2020 IEEE Power & Energy Society General Meeting (PESGM); , 2020; pp. 1–5. [CrossRef]
- Dale, L.; Carnall, M.; Wei, M.; Fitts, G.; McDonald, S. Assessing the Impact of Wildfires on the California Electricity Grid. Technical Report CCCA4-CEC-2018-002, California Energy Commission, 2018.
- Rhodes, N.; Ntaimo, L.; Roald, L. Balancing Wildfire Risk and Power Outages Through Optimized Power Shut-Offs. IEEE Transactions on Power Systems 2021, 36, 3118–3128. [Google Scholar] [CrossRef]
- Zanin Bertoletti, A.; Campos do Prado, J. Transmission System Expansion Planning under Wildfire Risk. 2022 North American Power Symposium (NAPS), 2022, pp. 1–6. [CrossRef]
- Astudillo, A.; Cui, B.; Zamzam, A.S. Managing Power Systems-Induced Wildfire Risks Using Optimal Scheduled Shutoffs. 2022 IEEE Power & Energy Society General Meeting (PESGM), 2022, pp. 1–5. [CrossRef]
- Nazemi, M.; Dehghanian, P. Powering Through Wildfires: An Integrated Solution for Enhanced Safety and Resilience in Power Grids. IEEE Transactions on Industry Applications 2022, 58, 4192–4202. [Google Scholar] [CrossRef]
- Paryati.; Salahddine, K.; Salah-ddine, K. THE IMPLEMENTATION OF KRUSKAL’S ALGORITHM FOR MINIMUM SPANNING TREE IN A GRAPH. 2021.
- Agüera-Pérez, A.; Palomares-Salas, J.C.; González de la Rosa, J.J.; Sierra-Fernández, J.M.; Ayora-Sedeño, D.; Moreno-Muñoz, A. Characterization of electrical sags and swells using higher-order statistical estimators. Measurement 2011, 44, 1453–1460. [Google Scholar] [CrossRef]
- Andrews, P.L. BEHAVE: Fire Behavior Prediction and Fuel Modeling System - BURN Subsystem, Part 1. Technical Report INT-194, United States Department of Agriculture - Forest Service, Intermountain Research Station, Ogden, UT, 1986.
Figure 2.
Analysis of wildfire susceptibility of various US regions.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






