Prerpints.org logo
Preprint
Article

Frequent Errors in Modeling by Machine Learning: A Prototype Case of Predicting the Timely Evolution of COVID-19 Pandemic

Altmetrics

Downloads

112

Views

156

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Preprints on COVID-19 and SARS-CoV-2

Submitted:

16 November 2023

Posted:

17 November 2023

You are already at the latest version

Alerts
Abstract
Background: The development and application of machine learning (ML) methods became so fast that almost nobody can follow their developments in every detail. There is no wonder that numerous errors and inconsistencies in their usage have also spread with a similar speed independently from the tasks: regression and classification.. This work summarizes frequent errors committed by certain authors with the aims of helping scientists to avoid them. Methods: The principle of parsimony governs the train of thought. Fair method comparison methods can be completed with multicriteria decision making techniques, preferably sum of ranking differences (SRD). Its coupling with analysis of variance (ANOVA) decomposes the effect of several factors. Earlier findings are summarized in a review-like manner: the abuse of the correlation coefficient and proper practices for model discrimination are also outlined. Results: Using an illustrative example, the correct practice and the methodology is summarized as guidelines for model discrimination, and for minimizing the prediction errors. The following factors are all prerequisites for successful modeling: proper data preprocessing, statistical tests, suitable performance parameters, appropriate degrees of freedom, fair comparison of models, outlier detection, just to name a few. A checklist is provided on how to present ML modeling properly. The advocated practices are reviewed in the discussion. Conclusions: Many of the errors can easily be filtered out with careful reviewing. The authors’ responsibility is to adhere to the rules of modeling and validation.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

János Máttyus Nepomuk published a book entitled Horse Science in 1845 [1]. One of its figures includes a sick horse, on which all the external and internal horse diseases are indicated that can affect the animal during its life (Figure 1). Naturally, such an animal cannot exist, still it is used figuratively in the Hungarian language (állatorvosi ló, i.e., “veterinary horse”). One cannot find a scientific article, which commits all possible (known) errors, but a recent, highly cited paper [2] can be used as a prototype for illustrative purposes. In this paper, I will summarize the correct practice and the methodology to be followed for model discrimination.
The existence of any “scientific method” is seriously questioned by the appearance of Kuhn’s book, The Structure of Scientific Revolutions [3]. However, there are many rules, standards which govern scientific investigation, e.g., The principle of parsimony (Occam’s razor) [4] declares: “Entities should not be multiplied beyond necessity”. Consequently, if we have different explanations of the observed data, the simplest one should be preferred. In other words: if two models provide the same description (prediction) in the statistical sense, the simpler one should be accepted. Occam’s razor is a sort of universal feature pervading nearly all fields of science. Machine learning, deep learning, etc. might violate the principle of parsimony on a large scale while they usually provide state-of-the-art predictive performance on large datasets. Over- and underdetermined models are routinely used for prediction. Breiman called attention to the two cultures in statistics (and generally in data science) [5]: one is based on a stochastic data model, whereas the other is based on algorithmic models and assumes that the data mechanism is unknown. Ardabilli et al.’s paper [2] belongs to the latter culture definitely. Hence, rigid adherence to Occam’s razor cannot be expected. However, algorithmic modeling should only be used on large, complex datasets, but not for “small” datasets.
Let’s return to Earth from the philosophical heights. Consistent notation is a prerequisite in scientific communication, as described in detail in ref. [6].
The proper method comparison has been pioneered by Frank and Friedman [7] using simulated data sets (five algorithms, 36 situations, the performance was measured by the distance to the true model and by the average squared prediction error).
A recent review (personal reminiscences) [8] summarizes the modeling procedure according to the OECD principles, regulations, with detailed discussion on steps of modeling procedure, genetic algorithm, rigorous validation, external test sets, performance parameters, variable selection, avoiding chance correlations, giving the applicability domain, consensus modeling and alike. Quantitative Structure–Activity Relationship modeling is analogous to ML modeling completely in this sense.
After the above short summary on how to perform statistical modeling, it is high time to define the aims of the present work: i) collecting the frequent errors committed by certain authors with the intention of helping scientists to avoid them and by no means humiliate people, who are not aware of present status of knowledge; ii) Specifically, the following goals can be formulated for forecasting the epidemic: Can the progress of the COVID-19 epidemic be modeled with machine learning (ML) algorithms? Can useful predictions be made? Which algorithm is the best? Of course, the answer is yes to all questions, it is possible, it can be. The best model can be selected, and even the models can be ranked in a rigorous manner. The question remains how, and how to do it properly in a scientifically sound manner.
The gathered errors and recommendations have far-reaching consequences: The publisher MDPI should revise its editorial policy, rejection should be default if the results/discussion and conclusions contradict each other or a certain level (number) of errors found The above and similar crucial errors indicate that the reviewers have NOT read the manuscripts entirely. Sloppy reviewers should be banned from further reviewing at least for a certain period (five or ten years long). Reviewers and authors alike should go through the checklist (part 3.9) to help optimal progress in science.

2. Materials and Methods

2.1. Data

The cumulative number of cases [number of infected persons] for five countries over 30 days served as the basis of investigation (Figure 2). The starting date and evolution are different. There is no reason given why the time period is limited, when wider ranges are readily available. The outcome of the investigations does not justify urgency: several months waiting were warranted.

2.2. Models to be compared

Eight models have been compared, see Figure 3, including logistic (Lgs), linear (Lin), logarithmic (Lgt), quadratic (Qad), cubic (Cub), compound (Cop), power (Pow), and exponential (Exp) equations, respectively, where A, B, C, µ, and L are parameters (constants) to be fitted.
It should be noted that the exponential equation has been proven inappropriate in a previous part of ref. [2]: Eq. (4) of ref. [2] has been derived from differential equations and contains a misprint; the time (t) is missing from the right-hand side.

2.3. Algorithms for searching global minimum

Genetic algorithm (GA) [9], particle swarm optimization (PSO) [10], and grey wolf optimizer (GWO) [11] are search algorithms aimed at finding the proximity of global minimum. All have some “tricks” to escape local minima. They do not give one single best solution, but a population of solutions. They tend to be hybridized, i.e., coupled with other techniques to find the exact global minimum. All have regularization (meta) parameters, their initial choice greatly determines their performance. It is worth to run the computer codes multiple times with random initialization.

2.4. Fair method (model) comparison

A proven algorithm for fair model comparison is called sum of ranking differences (SRDs) as described in ref. [12]; its extension to input matrices containing equal numbers (ties) has been published in 2013 [13]. A link to a downloadable program can be found here [14]. Two validation options are available: (randomization test) [15] and cross-validation [15] with application of Wilcoxon test [16]. Although SRD was primarily developed to solve model comparison problems, it realizes a multicriteria optimization [17], as long as the input matrix is arranged as such: alternatives in the columns and features (criteria) in the rows.

3. Results

3.1. Contradictions in abstract, discussion and conclusion

Let us start with the abstract of ref. [2] (Figure 4).
The guidelines of MDPI journals suggest the partitioning of the abstract into four parts (background, methods, results, and conclusions). Figure 4 shows unbalanced partitioning to say the least. There is little or no results written in the middle gray part (starting at sentence five): SIR and SEIR do not embody the results of the authors’ work, and only two machine learning algorithms, MLP and ANFIS were examined there; it is simply impossible to generalize these findings to the “wide range of machine learning models”. The models provided in Figure 3 are not ML, but causal ones or their approximations. Algorithms for finding the global minimum (Section 2.3) are not machine learning algorithms, either. It should be noted that physicists tend to confuse ML and deep learning, although ML is not a method of artificial intelligence (AI).
The authors are probably not aware of the English understatement. Science is international and binds different cultures together. It is not appropriate to hurt anybody, and cautious formulation is mandatory. As a consequence, “promising results” and great “potential” mean just the opposite, c.f., ref. [18]. The advocated policy is to express the results explicitly, preferably with numbers and without quality terms. E.g., “successful” modeling means nothing. The reader should decide whether the modeling is successful or rudimentary. Dubious formulations should be avoided.
It is difficult to decide the truthfulness of the statements marked by yellow. I am deeply convinced that properly applied machine learning algorithms can effectively model the outbreak of the epidemic. However, the results of these investigations [2] indicate the opposite as it was stated in the discussion part “Extrapolation of the prediction beyond the original observation range of 30 days should not be expected to be realistic considering the new statistics” [2] and “The fitted models generally showed low accuracy and also weak generalization ability for the five countries” [2].
Another point is whether to publish negative results. Many scientists advocate against it, while others find them useful for the scientific community: we can avoid reproducing experiments with hopeless outcomes, thereby saving money and energy for new experiments and calculations. Therefore, it is a matter of opinion whether to report negative results. I am inclined to say yes, but in the context of a failure only: in that case the conclusions should have been red: “… advancement of global models with generalization ability would not be feasible” and “… it is not possible to select the most suitable scenario.” [2]. The authors honestly admit the fallacious modeling in the Discussion part, but then they conclude that “machine learning [is] an effective tool to model the outbreak.” Why? Why did the editor and the reviewers not notice this? Even less understandable is the next statement that occurs twice in the paper: “a genuine novelty in outbreak prediction can be realized by integrating machine learning and SEIR models.”, especially if we see that no such integration was involved in the study.
The only plausible explanation for such contradictions can be that neither the editor, nor the reviewers read the manuscript fully, if the authors. The authorship is to be determined by the Vancouver criteria [19] (see Appendix A) as prescribed by the ethical guide of MDPI ( https://www.mdpi.com/ethics#_bookmark2).

3.2. Model comparison

Ref. [2] clearly defines the aim: “This paper aims to investigate the generalization ability of the proposed ML models and the accuracy of the proposed models for different lead times”. Figure 3 collects the models to be compared: all models (with one exception) are linear or linear in parameters (curvilinear), or easily linearizable by logarithmic transformation. That is, the normal equations can be solved easily in closed form. For example, the estimated parameters of Eq. (7) in Figure 3 ( A ^ and B ^ ) can be calculated without any minimum search (using the notations of Eq. (7) in Figure 3):
A ^ = n ∑ i n x i R i − ∑ i n x i ∑ i n R i n ∑ i n x i 2 − ∑ i n x i 2
And
B ^ = b x ¯ − R ¯
What is the need to apply search algorithms when solutions are readily available? Why is it necessary to fit the models by global optimization algorithms (which are developed for complicated problems, implicit dependent variables, many hundreds or even thousands of parameters and variables)? Similarly, all parameters of other models (except the logistic one) can be derived easily by solving the normal equations (eventually after logarithmic transformation). The logistic regression can also be solved by iteration easily without the usage of global optimization algorithms. In other words, the principle of parsimony was neglected or overlooked without any justification.
Let’s be good-natured (benevolent) and assume that estimating the course of the epidemic in five countries, starting at different times is a reasonable goal. (I personally disagree, but we can assume it.) Eight models (summarized in Figure 3) were compared by using three minimum search algorithms (GA, PSO, and GWO), altogether 24 combinations. Fortunately, the authors provided detailed tables (Tables 3-10) with two evaluation (performance) criteria: correlation coefficient (r), and root mean square error (RMSE).
A data table can be constructed from r and RMSE in the rows: and algorithm combinations to be compared in the columns. Row maxima for r and row minima for RMSE served as the benchmark reference. Such a benchmark realizes the hypothetical best combination: the largest correlation coefficients and the smallest residual errors. The proximity of the different alternatives to the hypothetical best combination is measured by SRD.
Figure 5 shows the SRD values and the cumulated relative frequencies of random ranking.
Even a superficial evaluation suggests that something is not in order. No clear winner can be established: neither from the models, nor from the minimum search algorithms, though some tendencies are observed. Why could not all minimum search algorithms find the global minimum? They should! The possible reasons might be too early stopping, wrong starting values, running into local minima, presence of outliers, or a combination of these reasons.

3.3. Visual inspection

Let us see Figure 10 (ref. (2)), where the performance of all models (in Figure 3) was compared for the description of the epidemic data of Germany by GWO.
Preprints 90718 g006
Figure 6. i.e., figure 10 from ref. (2): Performance of all models of figure 3 was compared for description of epidemic data of Germany by using GWO for minimum search.
Figure 6. i.e., figure 10 from ref. (2): Performance of all models of figure 3 was compared for description of epidemic data of Germany by using GWO for minimum search.
Preprints 90718 g006
Although a residual picture would be better, even a layman can judge that all models are inadequate except the logistic one. Why are they aiming to test them? Some of the models are completely worthless (linear, quadratic, cubic, and logarithmic ones), where negative numbers of infected persons are predicted. The authors should have paid attention to the positivity constraint. Similarly disappointing is the description of a monotone increasing (concave) curve with a convex one or one that exhibits a minimum. The same statements are valid for all the countries examined. The exponential and logistic functions run together; they are indistinguishable from each other from a visual evaluation. Both models have similar theoretical backgrounds; they can be derived from differential equations. Which one is better and/or adequate? The adequacy can be determined by visual assessment, too. If both models seem to be adequate; then a decision can be made by penalization of models using more fitting parameters: the logistic function uses four, while the exponential only two parameters. Whether their difference is significant can, and should, be tested by setting null and alternative hypotheses, H0 and Ha, respectively. How to do it will be discussed in the next section.

3.4. Performance parameters (merits) and model discrimination

Two performance parameters (r and RMSE) are not sufficient. Eight to twelve parameters are commonly used in recent literature [20,21,22]. The usage of performance parameters differently for training and test sets has not been mentioned, either. Training and testing were used in the context of artificial neural networks (ANN), which are superfluous there, as parameter estimation can be completed without them. The description of MLP and ANFIS is not less than breaking a butterfly in a wheel. Similarly, over- and underfitting has not even been mentioned, along with bias-variance trade off, although online course(s) are also available [23]. It should be mentioned that many performance parameters would provide a more sophisticated evaluation; they are recommended below:
Mean absolute error (MAE) is a straightforward metric because it is simple and easily interpretable to estimate the accuracy of predictive models.
The Bayesian Information Criterion (BIC) is applied for model selection from among several rival models. It takes into account the degrees of freedom and penalizes more complex models with the number of parameters to avoid overfitting [24].
Akaike’s Information Criterion (AIC) is also a measure of the goodness of fit. AIC (similarly to BIC) is widely used for model selection from among numerous models [25]. BIC penalizes complex models more heavily than AIC does.
Instead of the number of point pairs (N) used in the denominator of the RMSE formula in ref. [2], the degrees of freedom would have been the proper choice: (N–p), where p is the number of parameters in the models. As the number of parameters in all models is known (Figure 3), one can only wonder why the degrees of freedom were not considered at all.
There are some unorthodox behaviors of the simple correlation coefficient as is defined between independent (input) variables and dependent (output) variables. It can measure linear relations only, but some of the models—Eqs. (11-13) in ref [2]—are highly nonlinear. On the other hand, a simple quadratic relation (parabola y=x2) would provide exactly r=0 (if all plus minus pairs are involved). Naturally, a multiple correlation coefficient (index) can be defined, although differently, between the input y and output y ^ variables ( y ¯ is the mean of all y i -s):
R 1 2 = ∑ i N y ^ i − y ¯ 2 ∑ i N y i − y ¯ 2
Eq. (3) was suggested by Draper and Smith [26] and it can have values larger than 1 for nonlinear equations (but not necessarily).
R 2 2 = 1 − ∑ i N y i − y ^ i 2 ∑ i N y i − y ¯ 2
Eq. (4) is often called determination coefficient in analytical chemistry textbooks. I found the first occurrence in ref. [27]. It cannot be larger than 1, but it can have negative values, if the model is worse than a simple constant, the average of all y i -s.
R 3 2 = ∑ i N y ^ i − y ¯ 2 2 ∑ i N y i − y ¯ 2 ∑ i N y ^ i − y ^ ¯ 2
Eq. (5) [28] also might suffer from being greater than 1 in the case of nonlinear models.
R 4 2 = ∑ i N y i − y ¯ ∑ i N y ^ i − y ^ ¯ 2 ∑ i N y i − y ¯ 2 ∑ i N y ^ i − y ^ ¯ 2
Eq. (6) eliminates the inconsistent behavior detailed above for ( R 1 2 , R 2 2 , R 3 2 ). To my knowledge Prof. Rolf Manne (University of Bergen) derived Eq. (6) but never published it, and his equation is not used widely, if at all.
None of the above four equations has been applied in ref. [2] for model discrimination. The comparison of correlation indices, their features and idiosyncrasies were first summarized in ref. [29].
What remains is the residual error. Its examination reveals whether the modeling is adequate or not. It is suitable for comparing linear and nonlinear methods; even statistical testing is possible (F test can be applied as a variance ratio test). Three variants of F-tests might be feasible (practicable) [30] i) ratio of residual variances (sum of squares, if the degree of freedom is equal, or known):
F c = s 1 2 s 2 2
Where s 1 2 , s 2 2 are the residual variances for model 1 and model 2 to be compared, respectively. The residual variance is to be calculated using the degree of freedom (υ = N − p ), where p is the number of parameters (two-to five, c.f., Figure 3):
s 2 = R S S υ = ∑ i N y i − y ^ i 2 N − p
F c should be compared to the tabulated F value: F t a b υ 1 , υ 2 , 0.95 , if the F c is larger than the tabulated F value, then the null hypotheses should be rejected (H0, i.e., no significant differences are in the variances of the models). The power of F c is “small”, i.e., only large differences are detected so (also called conservative estimation). A better option might be the
ii) partial F test:
F p = R S S e x t e n d e d − R S S s i m p l e r s 2 s i m p l e r
Where RSS is the residual sum of squares (nominator of Eq. (8)). Strictly speaking, the partial F test has been developed to add in and remove variables from a linear model. Formally, linear, and nonlinear models can also be compared (if the numbers of parameters are the same) as if “curvature” was introduced in the model. F p should be compared to the tabulated F value: Ftab(1,v2, 0.95) , where υ 2 is the degree of freedom of the simpler model.
iii) The termination criteria were suggested for models having nonlinearity [31]. Two models termed 2 and 1 can be compared using the sequential probability ratio:
S P R = s 2 s 1 N
The SPR value must be compared with the numbers A and B from critical tables. If SPR≥A; then, model 1 is to be accepted. If SPR≤B; then, model 2 is to be accepted. If B<SPR<A; then, no decision can be made (more information is needed, i.e., more data, more measurements). For a double 95% significance level, an approximation is highly useful: A≈19 and B≈0.0526 [31].

3.5. Variance analysis of RMSEs

A prerequisite of any data analysis is to survey the data. No data preprocessing was done in ref. [2]. Calculation of means, median, skewness and kurtosis could help to judge the residua normal behavior. A simple matrix plot suggests serious outliers in the data:
Preprints 90718 g007
Figure 7. Matrix plot for global minimum search algorithms (RMSE values from data of tables 3-10 in ref. [2]). Histograms are seen in the diagonal plots, whereas GA vs. PSO is plotted in top middle subfigure, etc. The presence of outliers is obvious.
Figure 7. Matrix plot for global minimum search algorithms (RMSE values from data of tables 3-10 in ref. [2]). Histograms are seen in the diagonal plots, whereas GA vs. PSO is plotted in top middle subfigure, etc. The presence of outliers is obvious.
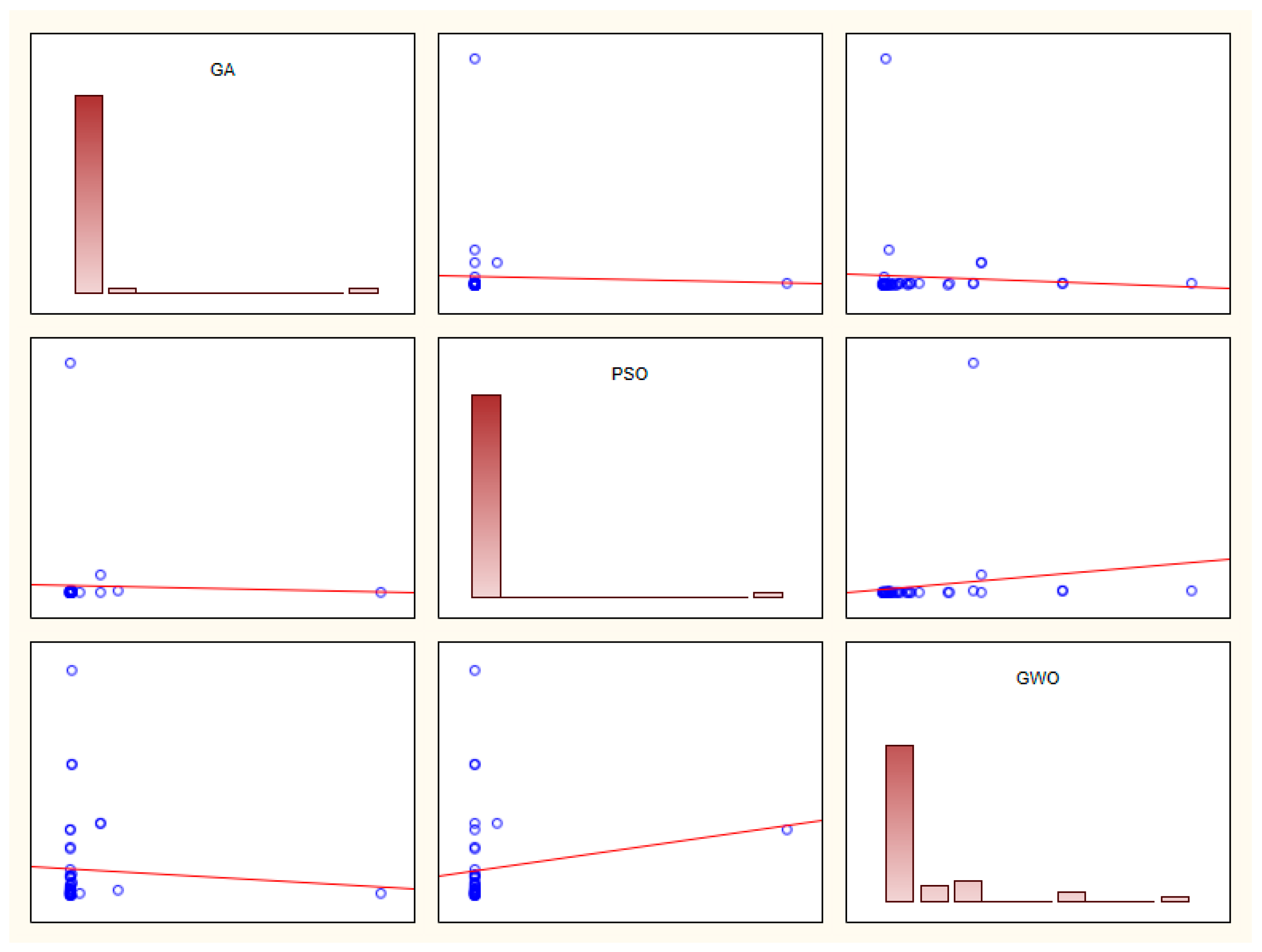
Preprints 90718 g007
At least two outliers can be observed: 1.534 × 10+07 (Germany, compound model and genetic algorithm) and 5.208 × 10+07 (Italy, exponential model and particle swarm optimization). After filtering the two outliers, a formal variance analysis (factorial ANOVA) can be completed for the RMSE data of Tables 3-10 of ref. [2]. Three factors can be decomposed: F1, countries {five levels: Italy (I), China (C), Iran (P), USA (U), Germany (G)}; F2, models (eight levels, abbreviations see at the note of Table 1)) and F3, techniques of global optimum search algorithms (three levels: GA, PSO, and GWO). One factor should be hidden as no repeated measurements are possible. The best candidate is F1 (countries), because the assumption is reasonable that the pandemic has similar trajectories in all the five countries.
Neither F2 nor F3 (nor their coupling F2*F3) are significant but the intercept only. The interaction of F2 and F3 can be seen in Figure 8.
The nonlinear models exhibit four more outliers at least. The post hoc tests (Bonferroni, Scheffé, and Tukey’s honest significant difference) show no significant differences between models and optimization algorithms either, because of the heavy outliers present. This calls for a careful data preprocessing.
However, it is interesting to know whether useful information can be obtained with wrong inputs or from inappropriate starting data. The quote "garbage in, garbage out” is a commonplace in modeling: if the input data used to build a model is biased (blemish), the predictions are likely to be unreliable and deceptive. On the other hand, the history of science is full of brilliant discoveries from mistaken standpoints (Columbus miscalculated the distance, Bohr’s atomic model with unrealistic postulates, Transition State Theory (TST) assumes that reactions occur at equilibrium, but frequency of collisions is set to one, Gregor Mendel’s laws of inheritance were formulated whereas he neglected observations deliberately not to cover expectations, Einstein’s theory of special relativity assumes the luminiferous ether, an invisible substance, etc.). Let us see whether wrong standpoints can lead to straightforward results:

3.6. ANOVA of SRD for algorithm combinations

Uncertainties can be rendered to the algorithm combinations of (Figure 5 and Table 1) if the ranking is repeated ten times leaving one row from the input matrix out at a time (each row once and only once). One new factor is introduced to factorial ANOVA: the leave-one-out (LOO) cross-validation (ten levels), whereas the countries (F1, five levels) disappear from the factors. LOO is a random factor and is, in fact, a repetition of ranking. Only robust methods are suitable, as the input data (r and RMSE of Tables 3-10) are contaminated by heavy outliers, and they are on vastly different scales. As the key step of SRD is a rank transformation, all (scaled) SRD values are on the same scale; namely, they are measured in %. All factors are significant (F2, models to be compared, F3, global optimization algorithms, and their couplings F2*F3). In Figure 9, F3 is shown only.
It should be noted that the SRD results are in accordance with the original authors’ findings: “GWO provided the highest accuracy (smallest RMSE and largest correlation coefficient) and smallest processing time compared to PSO and GA for fitting the logistic, linear, logarithmic, quadratic, cubic, power, compound, and exponential equations for all five countries. It can be suggested that GWO is a sustainable optimizer …” [2].

3.6. Reproducibility and precision

A typical error is to confuse the decimal digits and value digits. Figure 10 (derived from ref [2], Table 12 there):
Preprints 90718 g010
Figure 10. Table 12 in ref [2]: yellow markings show the different number of value precisions. Meaning of superscripts: A—2 value-, 3 decimal digits; B—3 value-, 2 decimal digits; C—3 value-, 3 decimal digits; D—4 value-, 2 decimal digits; E—5 value-, 2 decimal digits; F—6 value-, 2 decimal digits; G—7 value-, 2 decimal digits; H—7 value-, 3 decimal digits.
Figure 10. Table 12 in ref [2]: yellow markings show the different number of value precisions. Meaning of superscripts: A—2 value-, 3 decimal digits; B—3 value-, 2 decimal digits; C—3 value-, 3 decimal digits; D—4 value-, 2 decimal digits; E—5 value-, 2 decimal digits; F—6 value-, 2 decimal digits; G—7 value-, 2 decimal digits; H—7 value-, 3 decimal digits.
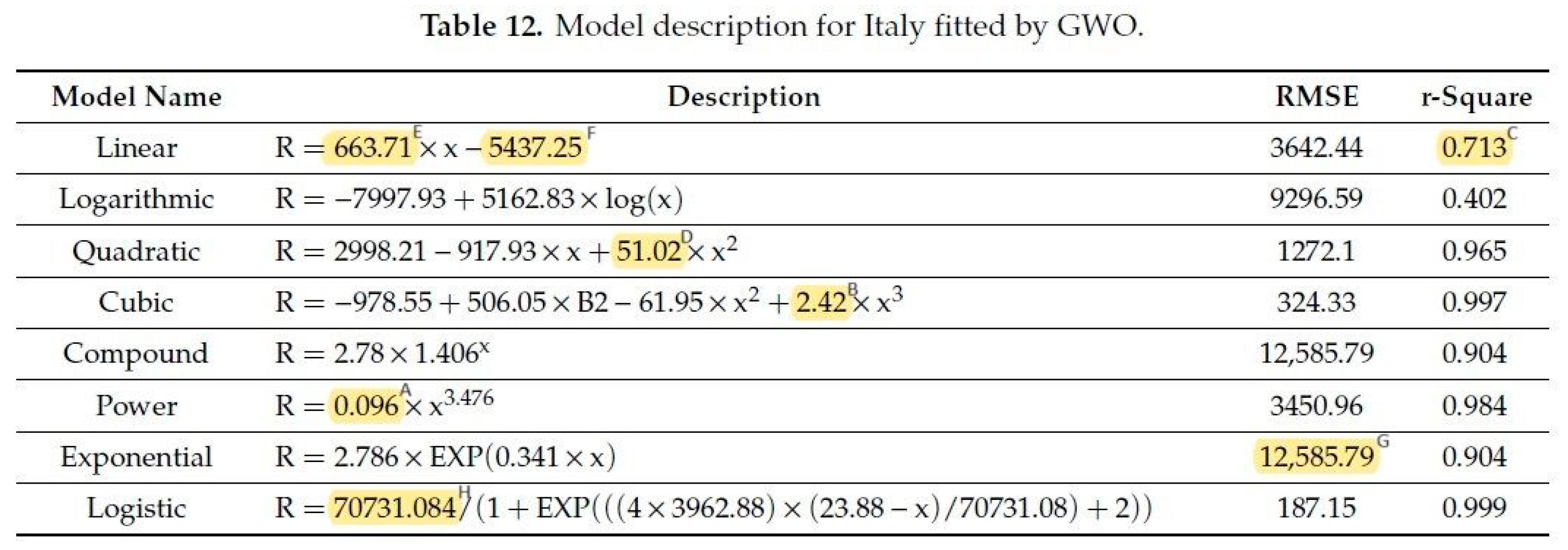
Preprints 90718 g010
Contrary to the general belief, not the decimal digits but the value digits determine the precision. The bottleneck is the minimum value digits: the end results cannot be more precise than the minimum value digits. Giving more decimal and value digits gives the false impression to obtain and handle more precise data. Fair comparison of models is simply impossible if the fitted equations are given in different precision.

3.7. Consistent notations, physical dimensions and units

Consistent notations are required for two purposes: i) within the manuscript (MS) they suggest that the concept was well thought-out, and the readers’ interest has also been taken into account and ii) outside the MS those notations are to be used, which are common in the given (sub)field of science. Common notations enhance the understanding and citation rate. Different notations for the same variable or quantity points to sloppy work and leads to rejection eventually. Furthermore, it reveals that the authorship was not set according to the Vancouver criteria (see Appendix A).
The SI standard physical dimensions are as follows (corresponding symbols are in brackets): time (T), length (L), mass (M), etc. The time is widely and unambiguously denoted by “t”, or “T”; the authors of ref. [2] use x, without any reason.
“Scalars are denoted by lower case letters x, and vectors … as bold lower-case letters: x = [x1, x2, … xn]. Matrices are denoted by bold capital letters M, …” [32].
Contrary to the common notations the authors use capital letters with arrows on the top for vectors ( X → ) and indexed scalars for the same x (time) variable, units are not given.
Even worse, the match of x were y, but authors of ref. [2] used either R or Es and T as estimated and target values in their Eqs (6-13) and Eq. (14), respectively. Moreover, Eq. (14) and (23) should be identical according to the explanation, yet the left-hand sides of the equations are different (MSE and RMSE, respectively). A summa is missing from Eq. (14) and an index (i) is missing from both.
Consistency within a document or a specific context is crucial. If you’re writing or editing a document, it’s advisable to pick one form and stick with it throughout the MS to maintain consistency.
The correlation coefficient is a dimensionless quantity, hence its popularity: it is suitable for comparing quantities measured on different scales. In contrast, mean squared error, residual error and alike have physical dimensions and consequently, units. Ref. [2] never mentions physical dimension and [units], e.g., course of infection [number of infected], time [days].

3.8. Data preprocessing

It is also called data curation, descriptor thinning, etc. Data reduction is unsupervised, it involves elimination of constant and near constant variables [33]. Similarly, highly correlated variables carry the same or highly similar information. One of them should be discarded from the input variables [33]. Even a threshold can be found by optimization [34]. Practical advice can be found in ref. [35]. No such activity has been reported in ref. [2]. Outliers can deteriorate the original distribution; their removal is also essential. Alternatively, robust methods diminish their effects, see part 3.5.
A superficial glance on Figure 2 suggests an orange banana comparison. The epidemy starts at different initial times. Many zeros could deteriorate models especially the nonlinear ones. A proper shift, data processing could eliminate this error source.
The series can be continued endlessly. As our aim was to help scientists not to commit such mistakes, a table was collected in binary form and color coding in the next section.

3.8. Orientation table

Frequent errors committed during modeling, apropos of ref. [2], but with general relevance, are collected in Figure 11.
The columns yes (exists) and no (Don’t exist) correspond to ref. [2]. The green symbol ☑ means required activity in general in any modeling paper and the red symbol ⊠ means a forbidden one. Any activity in column 2 can be formulated as a question in abbreviated form, e.g., line No 32 can be asked fully: Have the authors defined the applicability domain for which a prediction is feasible? Red color in bold indicates that the activity is required (essential), red field in the no (don’t) column indicates that this issue is missing from ref. [2], though it should be present. Similarly, a black text in column 2 indicates a mistaken standpoint: e.g., line No 12 can be formulated as such: Was the accuracy and precision insufficient to a given problem? The red field shows in the yes (exists) column that ref. [2] failed in this respect. The symbol in the fifth and the last columns advise against such usage. A question of line 3 can be written in general form: Does the start of any time evolution (decay) set properly? Can an inhibition period be assumed?
All issues can be transferred to a question similarly. I admit the enumeration of errors are not complete and the issues have some redundancies. Wordings of lines 15 and 16 are similar; line 15 objects to equal usage of correlation coefficient for linear and nonlinear models whereas line 16 concentrates on the abuse of correlation coefficient for non -linear ones.
Orange and gray marking indicates the advantageous and disadvantageous character of the same issue according to the intention of the speaker. Mitigation or even falsifying the facts are far away from science, whereas diplomatic formulation is warranted. Further on I concentrate fairly on the recommended practices.

4. Discussion and Recommendations

There are epistemological reasons for there being no flawless scientific article or manuscript. Even the most brilliant mind has limited rationality! Therefore, a 100% error-free manuscript cannot be expected. One crucial error in Figure 11 can lead to the rejection right away. However, 5% error is tolerable in most cases, i.e., the MS can be accepted with minor revision. If the errors achieve a critical level, say 50%, the MS cannot be accepted in its present form. Major revision is suggested above the 25% (but below 50%) error level. A revision is not adequate above the 75% level.
In any case, one should strive to produce a manuscript with minimal number of errors. After having produced more than 1500 detailed and competent reviews and handled many hundreds of papers as editor, the following experiences, errors, and guidelines on how to avoid misleading practices are gathered below concentrating on instances not to cover the guides of authors.
Reproducibility. A scientific paper should be fully reproducible with detailed description of the applied methods and all data sets should be provided, or eventually, should be retrievable.
Precision. The manuscript should be carefully written to convey confidence and care. Consistent notations and correct usage of terms can help a lot. The numerical precision is determined by value digits and not by decimal digits.
Validation. The findings should always be validated. Many options are available in the modeling field: i) The randomization test (y-scrambling or permutation test) is described in ref. [36]. ii) There are many variants of cross-validation: row-wise, pattern-wise [37], Venetian blinds, contiguous block, etc., [38]. The variants should also be disclosed to obtain reproducible results [39], including proper usage of the various terms: leave-one-out, leave-many-out, k-fold-, jackknife, and bootstrap with and/or without return in resampling. iii) Double cross-validation [40] and even repeated double cross-validation [41]. Some investigations clearly favor cross-validation over a single external one [42,43].
Training-test set splits. A single split external test can by no means be considered ground truth. On the contrary, single split and external validation are different [44]. Multiple external testing is advised [21]. The advocated practice by statisticians is to divide the data set into three parts: part I is to be used for model building (variable selection); part II is for the calibration of parameters of the built model and part III is reserved for testing the goodness of predictions [45]. Many authors combine Parts I and II and carry out cross-validation. Cross-validation is perhaps the most widely used method for estimating prediction error: “Overall, five- or tenfold cross-validation are recommended as a good compromise” [46].
The Kennard-Stone algorithm [47] is frequently applied to split training and test sets based on the Euclidean distance between data points. The test set is approximately uniformly spaced i.e., mirrors the training set. However, it provides overoptimistic prediction error as compared to random selection.
There are some “beatific” ratios of training and test sets, e.g., 80%, see figure 10 in ref. [48] or 50% (half sample cross validation has advantageous features [49]).
The optimum depends on the objective; Kalivas et al. have recommended the selection of harmonious (and parsimonious) models [50] and suggest better models for ridge regression over principal component regression (PCR) and partial least squares regression (PLSR) contrary to the extended simulation results of ref. [7] and to the general belief. In any case, PCR and PLSR has the smallest gap in performance parameters of calibration and prediction, see Figure 2 in ref. [51].
Allocation
The fact that the allocation problem cannot be separated from performance parameters has only now become the focus of interest [52,53]. Again, different optima can be found by changing the performance parameters and the way to place the points to be measured within the data sets.
The only reasonable conclusion is that the best model(s) differs from dataset to dataset [43,54] and the optimization should be completed several times. There must not be a problem with today’s computer facilities in most cases. Therefore, muticriteria decision making (Pareto optimization) is a feasible choice considering the number of factors (algorithms, performance parameters, allocation, validation variant, etc.). Todeschini et al. have already defined a multicriteria fitness function to eliminate bad regression models [55]. The number of performance criteria is steadily increasing [12,55]. While it was not its original purpose, it turned out that sum of ranking differences (SRD) realizes a multiciteria optimization [17,43]. Hence, SRD is recommended as the ultimate tool for model comparison, ranking and grouping models, performance parameters and other factors. SRD is also suitable to be coupled with ANOVA, hence decomposing the effects of factors [39].
Terminology. The applied terms and expressions should be explained, all abbreviations should be resolved at the first mentioning, one should not use the terms in wrong context.
Title should be brief and concise (without not resolved abbreviations); definite articles are not to be used.
Abbreviations should not be used in titles (of figures, tables, as well), in highlights, in abstract, summary and conclusions. Numerous abbreviations make the MS unreadable, though a list of terms, notations and abbreviations might be of help.
References As a rule of thumb, never cite a paper (book chapter, etc.) if you have not read it to the full. The references should always be retrievable, preferably in English. Personal communication can only be accepted if the cited person provides written consent; even then, the year should be indicated. Avoid the usage of “manuscript in preparation”, or “submitted”. “Accepted” or “in press” is OK, if the source title, link and the DOI are also given.
Language. The English usage should be understandable far all. The English uses the word order strictly: Object-predicate(verb)-subject–adverb of manner-locative-adverb of time. An adverb of time might be placed in very long sentences at the beginning and comma should be used after that.
Out of scope. The audience is not selected properly in most cases. One can imagine that in another scientific field the results are useful and welcomed. Chasing citations and impact factors is not advisable. A proper journal leads to more understanding if the aimed audience is adequate.
Novelty. It is also connected to experimental design, but the latter is rarely considered as novel in modeling journals. Nowadays, non-novelty is not a legitim reason for rejection, if we exclude plagiarism and self-plagiarism, as well.
Back to the philosophy: Michael Crichton, the most effective promoter of science of our time wrote [56]: “Most kinds of power require a substantial sacrifice by whoever wants the power. … You must give up a lot to get it … It is literally the result of your discipline … by the time someone has acquired the ability to kill with his bare hands, he has also matured to the point where he won’t use it unwisely. So that kind of power has a built-in control. The discipline of getting the power changes you so that you won’t abuse it. But scientific power is like inherited power: attained without discipline. You read what others have done and you take the next step. You can do it very young. You can make progress very fast. There is no discipline lasting many decades. There is no mastery: old scientists are ignored. There is no humility before nature. There is only …make-a-name-for-yourself-fast philosophy… No one will criticize you. No one has any standards. They are all trying to do the same thing: to do something big, and do it fast. And because you can stand on the shoulders of giants, you can accomplish something quickly. You don’t even know exactly what you have done, but already you have reported it, …”.
The words set in Italics above refer to the Ortega hypothesis which says that average or mediocre experimental scientists contribute substantially to the advancement of science [57]. Unfortunately, the false Ortega hypothesis spread and proliferated based on citation count [58] and I fully agree with the final conclusion of ref. [58]: “… the importance of correction work in science cannot be overestimated: after all, the validity of the information disseminated must be regarded as more important than the speed of the dissemination.”

5. Conclusions

One should keep the standards of scientific investigations (e.g., Figure 11). The ethical command prescribes that erroneous practice should be revealed, corrected and its propagation banned.
Manuscript rejection should be the default if the results, discussion, and conclusions contradict each other or if a certain level (number) of errors found.
Reviewers should be selected carefully from the expert pool; short reports or any sign of not reading the full manuscript should lead to be banned from the decision process and from further reviewing.
Science embodies the universal essence of humanity; let us not diminish its value by chasing after articles and citations. Our pursuit should be deeper and more meaningful.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org. Figure 11 is available as an excel sheet, as well.

Funding

This work was supported by the Ministry of Innovation and Technology of Hungary from the National Research, Development and Innovation Fund, financed under the K type funding scheme [OTKA K 134260].

Data Availability Statement

See supplementary material.

Acknowledgments

The author thanks the editor(s) for invitation.

Conflicts of Interest

The author declares no conflict of interest.

Appendix A

According to the Vancouver criteria the authorship should be based on all of the following four criteria:
  • Substantial contributions to the conception or design of the work; or the acquisition, analysis, or interpretation of data for the work;
AND
  • Drafting the work or revising it critically for important intellectual content; AND
  • Final approval of the version to be published;
AND
  • Agreement to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Further details including the usage of artificial intelligence (AI) can be found in ref. [19].

References

  1. Máttyus Nepomuk, J. Lótudomány [in Hungarian], Bands I and II. Pytheas Könyvmanufaktúra, Hungary, 2008, reprint of 1845 edition.
  2. Ardabili, S.-F.; Mosavi, A.; Ghamisi, P.; Ferdinand, F.; Varkonyi-Koczy, A.R.; Reuter, U.; Rabczuk, T.; Atkinson, P.M. COVID-19 Outbreak Prediction with Machine Learning. Algorithms 2020, 13, 249. [Google Scholar] [CrossRef]
  3. Kuhn, T.S. The Structure of Scientific Revolutions, 50th Anniversary Edition ed; University of Chicago Press: USA, 2012; pp. 1–264. [Google Scholar]
  4. https://en.wikipedia.org/wiki/Occam%27s_razo (accessed on 29 September 2023).
  5. Breiman, L. Statistical Modeling: The Two Cultures. Statistical Science 2001, 16, 199–231. [Google Scholar] [CrossRef]
  6. Teter, M.D.; Newman, A.M.; Weiss, M. Consistent notation for presenting complex optimization models in technical writing. Surveys Oper. Res. Manag. Sci. 2016, 21, 1–17. [Google Scholar] [CrossRef]
  7. Frank, I.E.; Friedman, J.H. A Statistical View of Some Chemometrics Regression Tools. Technometrics 1993, 35, 109–135. [Google Scholar] [CrossRef]
  8. Gramatica, P. Principles of QSAR Modeling: Comments and Suggestions from Personal Experience. Int. J. Quant. Struct.-Property Relat. 2020, 5, 1–37. [Google Scholar] [CrossRef]
  9. Holland, J.H. Genetic Algorithms. Sci. Amer. 1992, 267, 66–72. [Google Scholar] [CrossRef]
  10. Kennedy, J.; Eberhart, R. Particle swarm optimization. IEEE International Conference on Neural Networks—Conference Proceedings 1995, 4, 1942–1948. [Google Scholar]
  11. Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Engin. Software 2014, 69, 46–61. [Google Scholar] [CrossRef]
  12. Héberger, K. Sum of ranking differences compares methods or models fairly. TRAC—Trends in Analytical Chemistry 2010, 29, 101–109. [Google Scholar] [CrossRef]
  13. Kollár-Hunek, K.; Héberger, K. Method and model comparison by sum of ranking differences in cases of repeated observations (ties). Chemometr. Intell. Lab. Syst. 2013, 127, 139–146. [Google Scholar] [CrossRef]
  14. http://aki.ttk.mta.hu/srd (accessed on 5 October 2023).
  15. Héberger, K.; and Kollár-Hunek, K. Sum of ranking differences for method discrimination and its validation: comparison of ranks with random numbers. J. Chemometr. 2011, 25, 151–158. [Google Scholar] [CrossRef]
  16. Sziklai, B.R.; Héberger, K. Apportionment and districting by Sum of Ranking Differences. Plos ONE 2020, 15, e0229209. [Google Scholar] [CrossRef]
  17. Lourenço, J.M.; Lebensztajn, L. Post-Pareto Optimality Analysis with Sum of Ranking Differences. IEEE Transactions on Magnetics 2018, 54, 8202810. [Google Scholar] [CrossRef]
  18. https://en.wikipedia.org/wiki/English_understatement or even https://www.orchidenglish.com/british-understatement/ (accessed on 5 October 2023).
  19. http://www.icmje.org/recommendations/browse/roles-and-responsibilities/defining-the-role-of-authors-and-contributors.html (accessed on 10 October 2023).
  20. Ojha, P.K.; Roy, K. Comparative QSARs for antimalarial endochins: Importance of descriptor-thinning and noise reduction prior to feature selection . Chemometr. Intell. Lab. Syst. 2011, 109, 146–161. [Google Scholar] [CrossRef]
  21. Gramatica, P. External Evaluation of QSAR Models, in Addition to Cross-Validation: Verification of Predictive Capability on Totally New Chemicals. Mol. Inf. 2014, 33, 311. [Google Scholar] [CrossRef] [PubMed]
  22. Vincze, A.; Dargó, G.; Rácz, A.; Balogh, G.T. A corneal-PAMPA-based in silico model for predicting corneal permeability. J. Pharm. Biomed. Anal. 2021, 203, 114218. [Google Scholar] [CrossRef] [PubMed]
  23. Brownlee, J. Overfitting and Underfitting with Machine Learning Algorithms Machine Learning Mastery. https://machinelearningmastery.com/overfitting-and-underfitting-with-machine-learning-algorithms/ (accessed on 10 October 2023).
  24. Schwarz, G.E. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
  25. Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
  26. Draper, N.R.; Smith, I.L. Applied Regression Analysis, 2nd ed.; John Wiley & Sons: New York, USA, 1981; ISBN 0471170828. [Google Scholar]
  27. Rider, P.R. Introduction to Modern Statistical Methods, ASIN: B001UIDASK; John Wiley & Sons: New York, USA, 1939; p. 58. [Google Scholar]
  28. Bevington, R. Data Reduction and Error Analysis for the Physical Sciences; McGraw-Hill Book Company: New York, USA, 1969. [Google Scholar]
  29. Héberger, K. Discrimination between Linear and Non-Linear Models Describing Retention Data of Alkylbenzenes in Gas-Chromatography. Chromatographia 1990, 29, 375–384. [Google Scholar] [CrossRef]
  30. Héberger, K. Empirical Correlations Between Gas-Chromatographic Retention Data and Physical or Topological Properties of Solute Molecules. Anal. Chim. Acta 1989, 223, 161–174. [Google Scholar] [CrossRef]
  31. Bard, Y. Nonlinear Parameter Estimation; Academic press: New York, USA, 1974; pp. 269–271. [Google Scholar]
  32. Erichson, N.B.; Zheng, P.; Manohar, K.; Brunton, S.L.; Kutz, J.N.; Aravkin, A.Y. Sparse Principal Component Analysis via Variable Projection. SIAM J. Appl. Math. 2020, 80, 977–1002. [Google Scholar] [CrossRef]
  33. Todeschini, R.; Consonni, V. Molecular Descriptors for Chemoinformatics; WILEY-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2010; Volume 2, pp. 1–252. [Google Scholar] [CrossRef]
  34. Rácz, A.; Bajusz, D.; Héberger, K. Intercorrelation limits in molecular descriptor preselection for QSAR/QSPR. Mol. Inform. 2019, 38, 1800154. [Google Scholar] [CrossRef]
  35. García, S.; Luengo, J.; Herrera, F. Tutorial on practical tips of the most influential data preprocessing algorithms in data mining. Knowledge-Based Systems 2016, 98, 1–29. [Google Scholar] [CrossRef]
  36. Rücker, C.; Rücker, G.; Meringer, M. y-Randomization and Its Variants in QSPR/QSAR. J. Chem. Inf. Model. 2007, 47, 2345–2357. [Google Scholar] [CrossRef] [PubMed]
  37. Bro, R.; Kjeldahl, K.; Smilde, A.K.; Kiers, H.A.L. Cross-validation of component models: A critical look at current methods. Anal. Bioanal. Chem. 2008, 390, 1241–1251. [Google Scholar] [CrossRef] [PubMed]
  38. http://wiki.eigenvector.com/index.php?title=Using_Cross-Validation (accessed on 11 November 2023).
  39. Heberger, K.; Kollar-Hunek, K. Comparison of validation variants by sum of ranking differences and ANOVA. J. Chemometr. 2019, 33, e3104. [Google Scholar] [CrossRef]
  40. Baumann, D.; Baumann, K. Reliable estimation of prediction errors for QSAR models under model uncertainty using double cross-validation. J. Cheminform. 2014, 6, 47. [Google Scholar] [CrossRef] [PubMed]
  41. Filzmoser, P.; Liebmann, B.; Varmuza, K. Repeated double cross validation. J. Chemometrics 2009, 23, 160–171. [Google Scholar] [CrossRef]
  42. Gütlein, M.; Helma, C.; Karwath, A.; Kramer, S. A Large-Scale Empirical Evaluation of Cross-Validation and External Test Set Validation in (Q)SAR. Mol. Inf. 2013, 32, 516–528. [Google Scholar] [CrossRef] [PubMed]
  43. Rácz, A.; Bajusz, D.; Héberger, K. Consistency of QSAR models: Correct split of training and test sets, ranking of models and performance parameters. SAR QSAR in Environ. Res. 2015, 26, 683–700. [Google Scholar] [CrossRef]
  44. Esbensen, K.H.; Geladi, P. Principles of proper validation: Use and abuse of re-sampling for validation. J. Chemom. 2010, 24, 168–187. [Google Scholar] [CrossRef]
  45. Miller, A. Part 1.4 ‘Black box’ use of best-subsets techniques. In Subset selection in regression; Chapman and Hall: London, Great Britain, 1990; p. 13. [Google Scholar]
  46. Hastie, T.; Tibshirani, R.; Friedman, J.H. Chapter 7.10 Cross-validation. In The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: New York, USA, 2009; pp. 241–249. [Google Scholar]
  47. Kennard, R.W.; Stone, L.A. Computer aided design of experiments. Technometrics 1969, 11, 137–148. [Google Scholar] [CrossRef]
  48. Rácz, A.; Bajusz, D.; Héberger, K. Effect of Dataset Size and Train/Test Split Ratios in QSAR/QSPR Multiclass Classification. Molecules 2021, 26, 1111. [Google Scholar] [CrossRef] [PubMed]
  49. Efron, B. Estimating the error rate of a prediction rule: Improvement of cross-validation. J. Amer Stat. Assoc. 1983, 78, 3163–31. [Google Scholar] [CrossRef]
  50. Kalivas, J.H.; Forrester, J.B.; Seipel, H.A. QSAR modeling based on the bias/variance compromise: A harmonious and parsimonious approach. J. Comput-Aided Mol. Des. 2004, 18, 537–547. [Google Scholar] [CrossRef] [PubMed]
  51. Rácz, A.; Bajusz, D.; Héberger, K. Modelling methods and cross-validation variants in QSAR: a multi-level analysis. SAR QSAR Environ. Res. 2018, 29, 661–674. [Google Scholar] [CrossRef] [PubMed]
  52. Consonni, V.; Ballabio, D.; Todeschini, R. Evaluation of model predictive ability by external validation techniques. J. Chemometr. 2010, 24, 194–201. [Google Scholar] [CrossRef]
  53. Tóth, G.; Király, P.; Kovács, D. Effect of variable allocation on validation and optimality parameters and on cross-optimization perspectives. Chemometr. Intell. Lab. Syst. 2020, 204, 104106. [Google Scholar] [CrossRef]
  54. Roy, P.P.; Leonard, J.T.; Roy, K. Exploring the impact of size of training sets for the development of predictive QSAR models. Chemometr. Intell. Lab. Syst. 2008, 90, 31–42. [Google Scholar] [CrossRef]
  55. Todeschini, R.; Consonni, V.; Mauri, A.; Pavan, M. Detecting "bad" regression models: Multicriteria fitness functions in regression analysis. Anal. Chim. Acta 2004, 515, 199–208. [Google Scholar] [CrossRef]
  56. Crichton, M. Jurassic Park; Ballantine books: New York, 1990; p. 306. [Google Scholar]
  57. https://en.wikipedia.org/wiki/Ortega_hypothesis (accessed on 14 November 2023).
  58. Száva-Kováts, E. The false ‘Ortega Hypothesis’: a literature science case study. J. Inform. Sci. 2004, 30, 496–508. [Google Scholar] [CrossRef]
Preprints 90718 g001
Figure 1. The so-called “veterinary horse”, with all the diseases that, in practice, cannot occur in a single horse at the same time. Figure 1 derived from ref. [1].
Figure 1. The so-called “veterinary horse”, with all the diseases that, in practice, cannot occur in a single horse at the same time. Figure 1 derived from ref. [1].
Preprints 90718 g001
Preprints 90718 g002
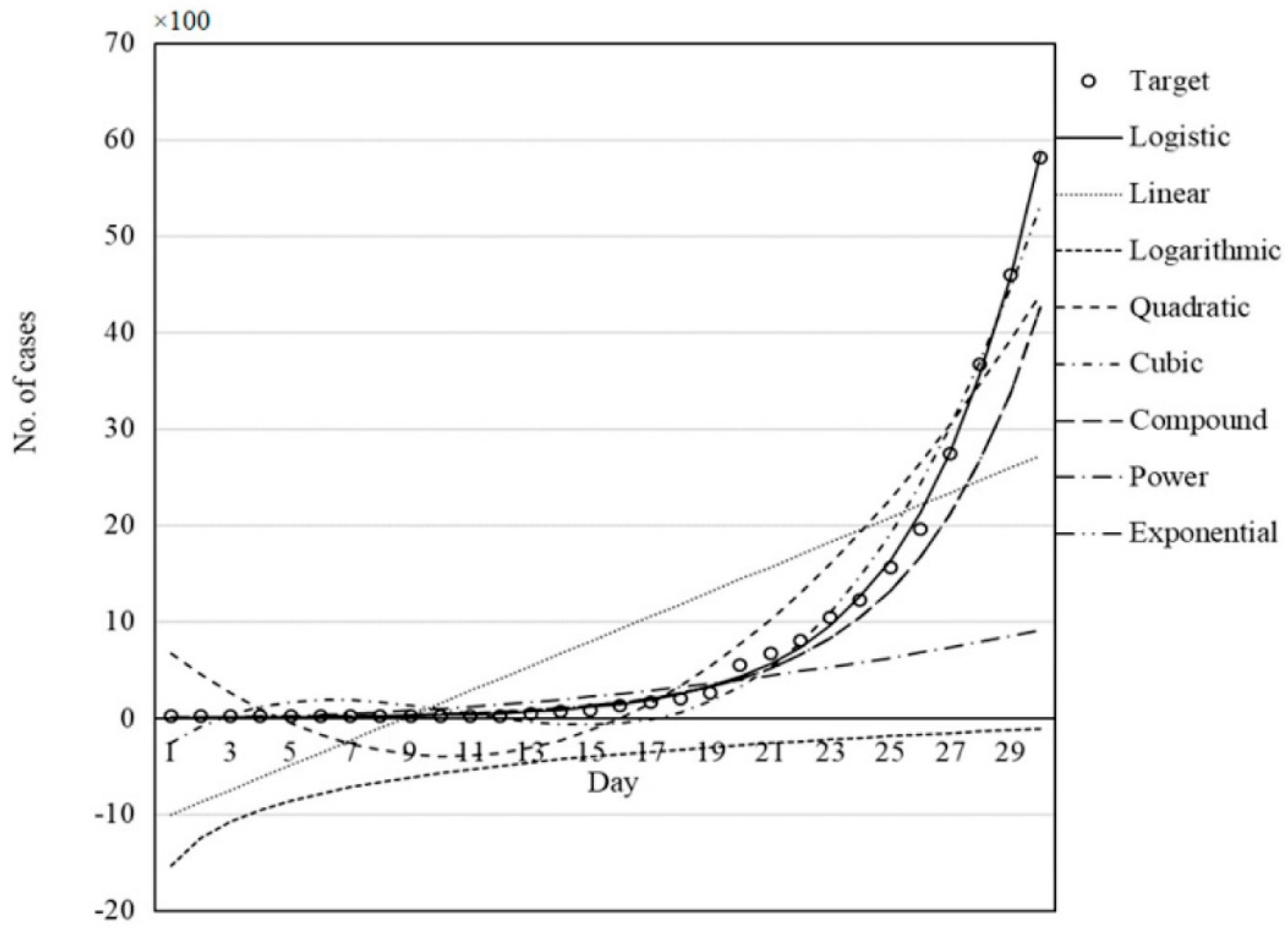
Figure 2. Cumulative number of COVID-19 cases [number of infected persons] for five countries over 30 days from ref. [2]. The starting times and the duration of the observation period are different. Something happened around 12-February (China), which cannot be explained by the epidemic, but political/regulatory reasons.
Figure 2. Cumulative number of COVID-19 cases [number of infected persons] for five countries over 30 days from ref. [2]. The starting times and the duration of the observation period are different. Something happened around 12-February (China), which cannot be explained by the epidemic, but political/regulatory reasons.
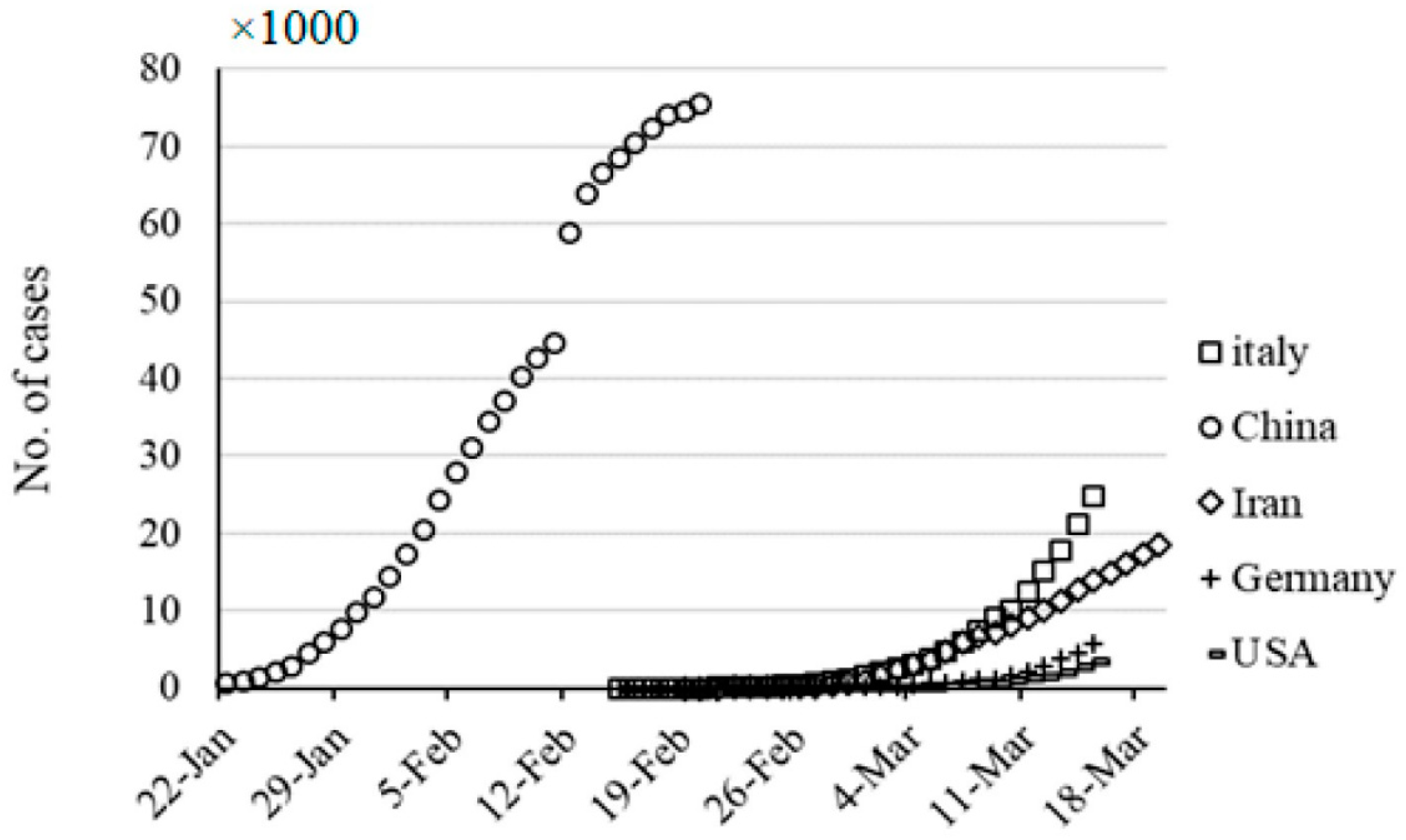
Preprints 90718 g002
Preprints 90718 g003
Figure 3. The eight models compared in ref. [2] aimed to find their optimal performance (prediction). The number of constants to be fitted varies between two to four and the equations covers linear and nonlinear (convex and concave) ones. The notation of R is not explained there.
Figure 3. The eight models compared in ref. [2] aimed to find their optimal performance (prediction). The number of constants to be fitted varies between two to four and the equations covers linear and nonlinear (convex and concave) ones. The notation of R is not explained there.
Preprints 90718 g003
Preprints 90718 g004
Figure 4. The abstract of ref. [2]. Color coding: grey: preliminaries, background, results of earlier investigations; white: filler text, without information content; turquoise: dubious meaning because of the English understatement [18]; yellow: untrue statements, not the results of present investigations or in contradiction with the discussion part.
Figure 4. The abstract of ref. [2]. Color coding: grey: preliminaries, background, results of earlier investigations; white: filler text, without information content; turquoise: dubious meaning because of the English understatement [18]; yellow: untrue statements, not the results of present investigations or in contradiction with the discussion part.
Preprints 90718 g004
Preprints 90718 g005
Figure 5. Sum of ranking differences (SRD) groups the algorithm combinations. (SRD values are scaled between 0 and 100, the smaller the better.) Scaled SRD values are plotted on the x and left y axes, the right y axis shows the cumulated relative frequencies of random ranking: black curve). The probability ranges are also given 5% (XX1), Median (Med), and 95% (XX19).
Figure 5. Sum of ranking differences (SRD) groups the algorithm combinations. (SRD values are scaled between 0 and 100, the smaller the better.) Scaled SRD values are plotted on the x and left y axes, the right y axis shows the cumulated relative frequencies of random ranking: black curve). The probability ranges are also given 5% (XX1), Median (Med), and 95% (XX19).
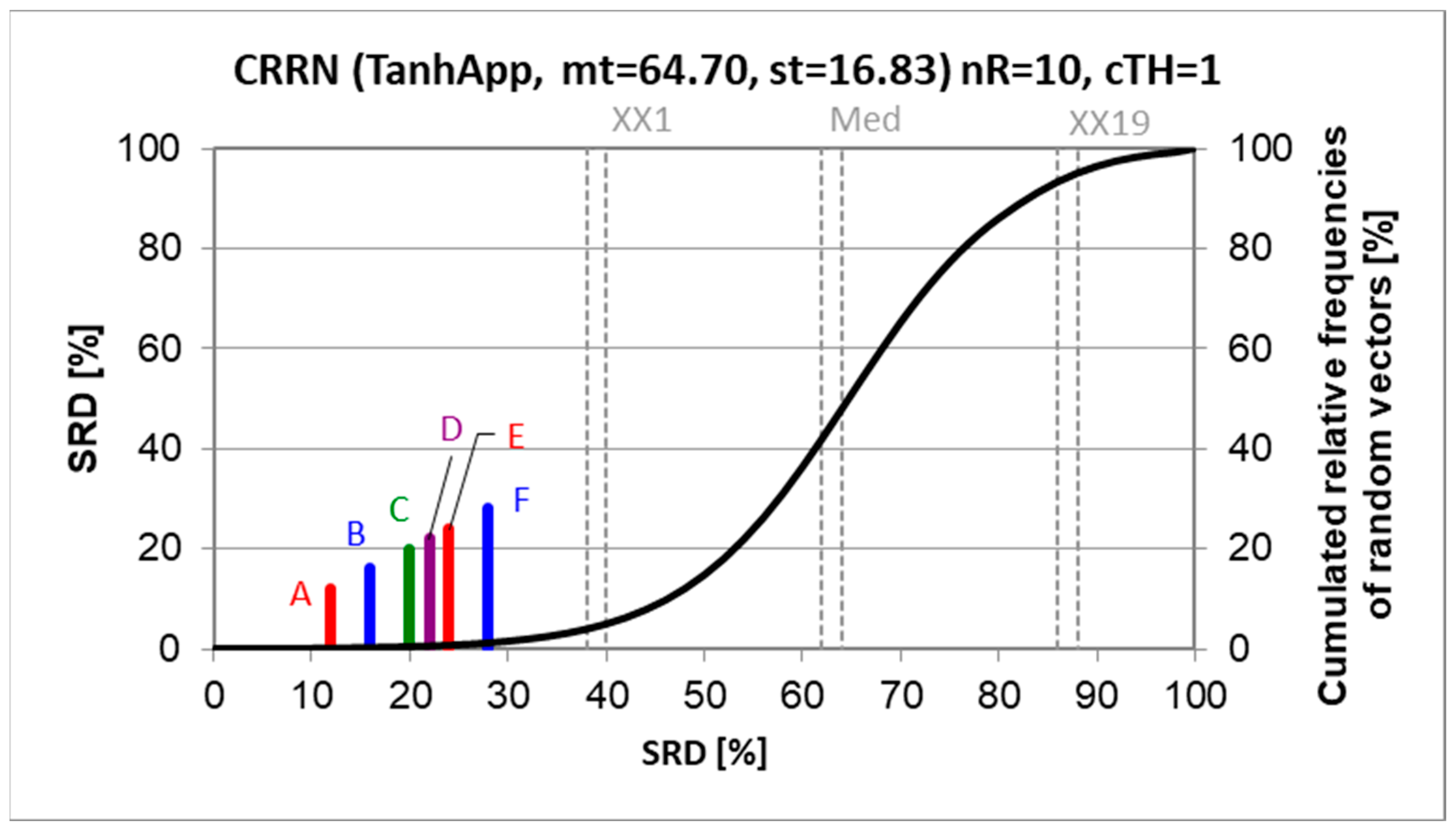
Preprints 90718 g005
Preprints 90718 g008
Figure 8. Decomposition of models (in Figure 3) and global optimization methods. For notations in x axis see at Table 1.
Figure 8. Decomposition of models (in Figure 3) and global optimization methods. For notations in x axis see at Table 1.
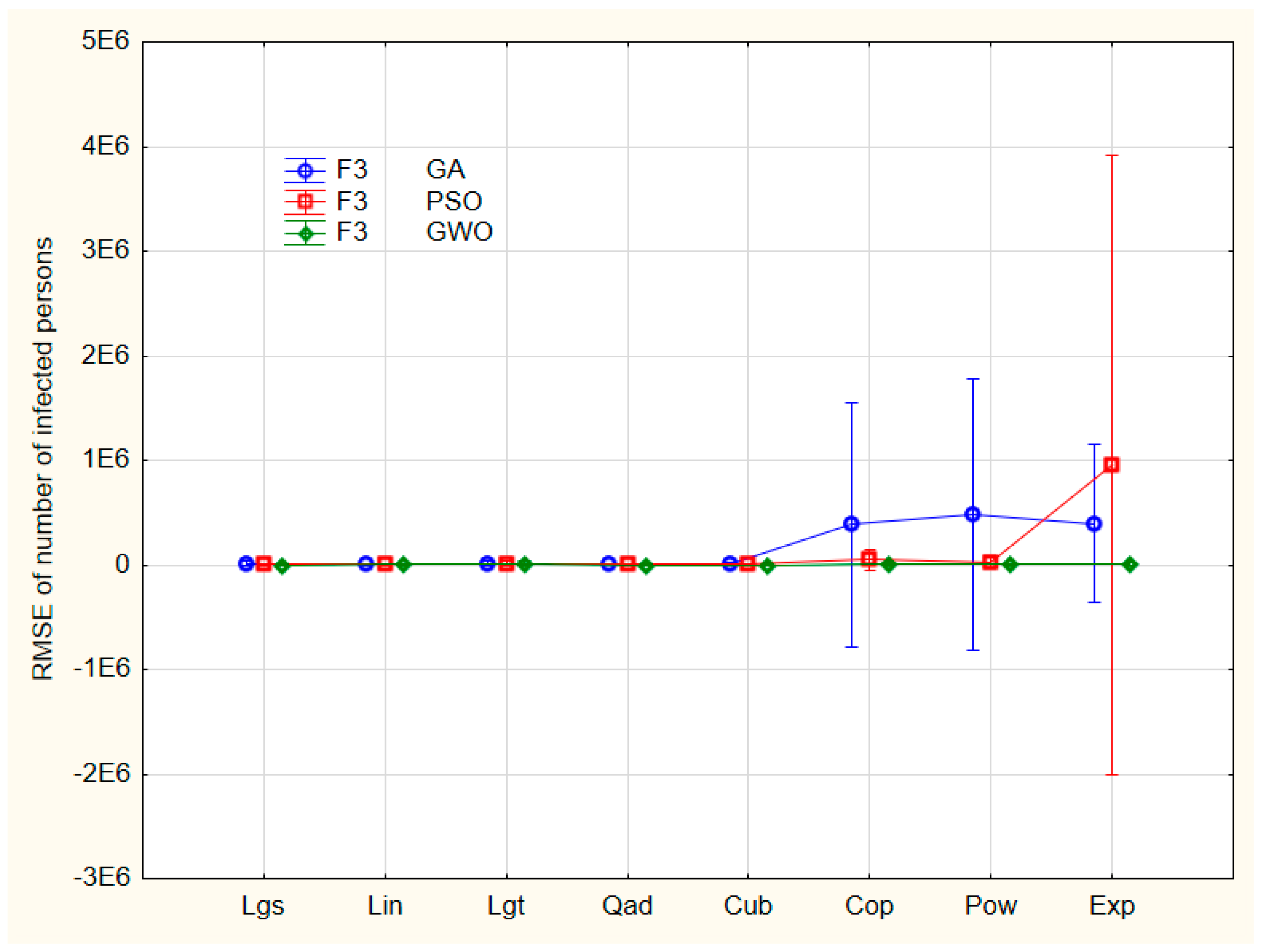
Preprints 90718 g008
Preprints 90718 g009
Figure 9. Significant differences between global optimization algorithms: Genetic algorithm is the worst; particle swarm optimization is somewhat better and grey wolf optimization is the best option as follows from SRD analysis of r and RMSE data of tables 3-10 in ref. [2].
Figure 9. Significant differences between global optimization algorithms: Genetic algorithm is the worst; particle swarm optimization is somewhat better and grey wolf optimization is the best option as follows from SRD analysis of r and RMSE data of tables 3-10 in ref. [2].
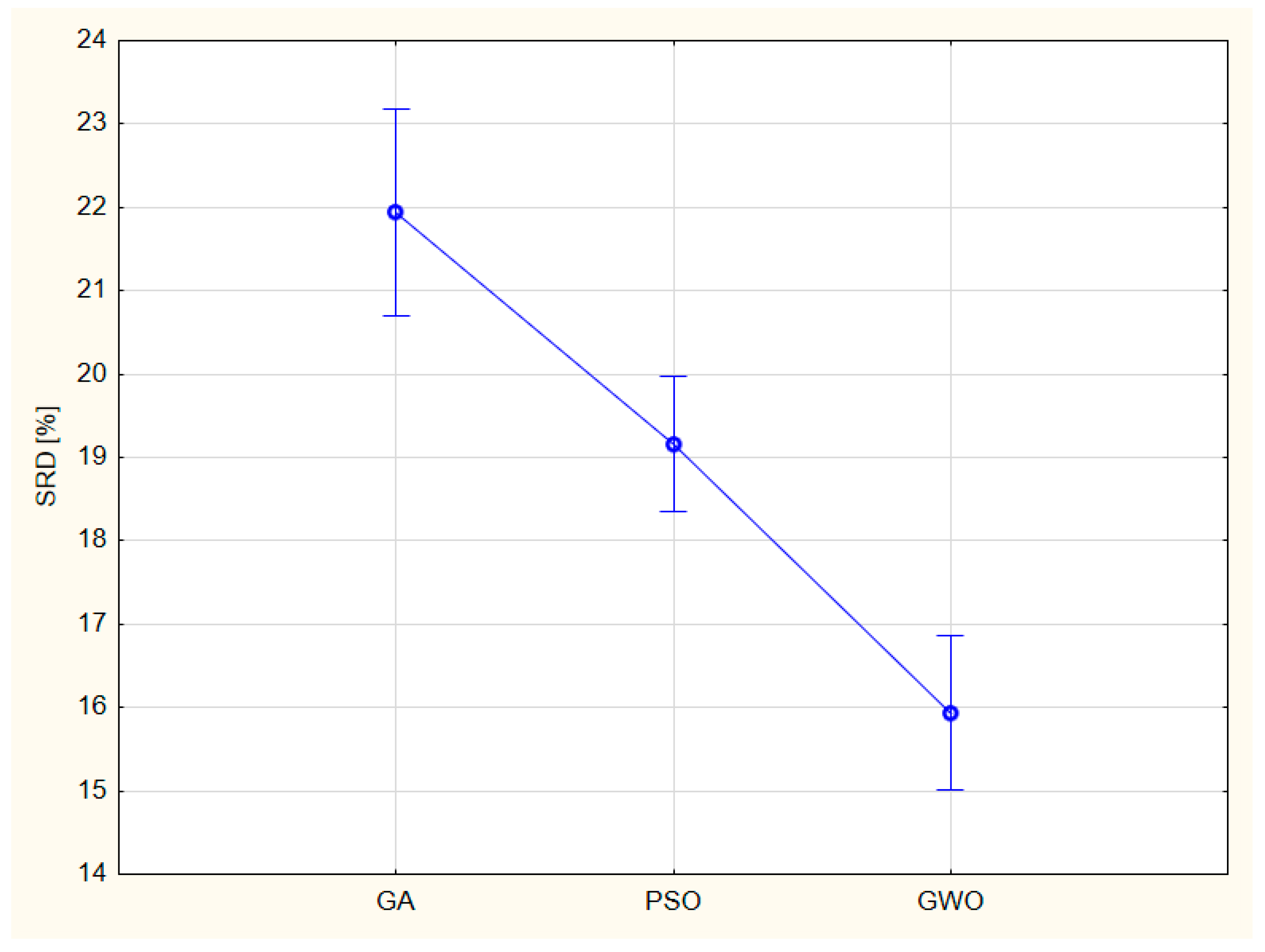
Preprints 90718 g009
Preprints 90718 g011
Figure 11. Important issues while writing a manuscript simplified to binary “yes” and “no” answers. Black text in column 2 means a negative contribution, whereas red (bold) means a positive one (orange-grey fields indicate not unambiguous meaning, non-binary answers).
Figure 11. Important issues while writing a manuscript simplified to binary “yes” and “no” answers. Black text in column 2 means a negative contribution, whereas red (bold) means a positive one (orange-grey fields indicate not unambiguous meaning, non-binary answers).
Preprints 90718 g011
Table 1. contains the grouping pattern of algorithm combinations (color coding corresponds to that of the Figure 5).
Table 1. contains the grouping pattern of algorithm combinations (color coding corresponds to that of the Figure 5).
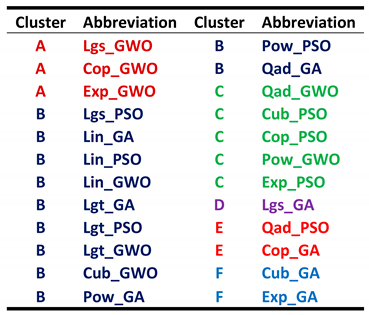Preprints 90718 i001
Notations: Lgs–logistic, Lin–linear, Lgt–logarithmic, Qad–quadratic, Cub–cubic, Cop–compound, Pow–power, and Exp–exponential equations; after underscore: GA–genetic algorithm, PSO–particle swarm optimization, GWO–grey wolf optimizer.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated