Prerpints.org logo
Preprint
Article

Tunable Switching between Slow and Fast Light in the Double Metal Nanoparticles (MNPs)-Quantum Dot (QD) Plasmonic Hybrid Systems

Altmetrics

Downloads

108

Views

50

Comments

0

This version is not peer-reviewed

Submitted:

18 November 2023

Posted:

20 November 2023

You are already at the latest version

Alerts
Abstract
Plasmonic nanocomposites have the ability to enhance light-matter interaction due to the plasmonic effects leading to promising potential applications. In this paper, we theoretically study the group index of the silver nanoparticle-gold nanoparticle-quantum dot plasmonic hybrid system in the optical region of the electromagnetic spectrum using the density matrix approach. The quantum dot is considered to be a three-level atomic system of a lambda configuration, interacting with strong control and weak probe fields. We find that the plasmonic hybrid system exhibits at near resonance a strong switching between slow and fast light, which can be controlled by the inclination angle of the gold nanoparticle and the size of the metals nanoparticles, in addition to the strength and detuning of the control field. Thus, the silver nanoparticle-gold nanoparticle-quantum dot could potentially be used in optoelectronic devices.
Keywords: 
Subject: Physical Sciences  -   Quantum Science and Technology

1. Introduction

Nanoplasmonics is a hot topic in research due to its applications in sensors [1,2,3], optical communication systems [4,5], and solar cell applications [6]. An interesting property of such systems is their ability to confine the optical energy in sub-wavelength dimensions [7]. Specifically, metal nanoparticles made of conducting metals, such as noble metals, that are subjected to an external optical wave, and will produce a Localized Surface Plasmon Resonance (LSPRs) of metal nanoparticles (MNPs) leading to focusing optical fields [8,9].
The frequency of the LSPR is controlled not only by the composition of the metal, but also by its shape and size, as well as the dielectric properties of the surrounding medium [10,11]. Metals such as silver and gold, which have high conductivity, exhibit excessive losses at optical frequencies [12,13]. Therefore, a gain medium is required to make a plasmonic system effective in various applications.
Interestingly, Quantum dots (QDs) represent a novel gain medium in nanoplasmonic systems. Quantum dots are semiconductor nanocrystals where excitons are confined in all three spatial directions in the size range of 1 ∼ 10 n m [14,15], exhibiting confinement effects in their optical and electronic properties [16].
Currently, a promising nanoscale scheme based on an MNP-QD coupling system has attracted significant interest [17,18,19], which modifies light-matter interactions with possible tunability and control. The QD in the proximity of plasmonic nanostructure will induce significant alteration of the electromagnetic field that is felt by the QD due to the interaction between the excitons of the QD and the surface plasmon of the MNP [20]. Because of the exciton-plasmon interaction, several interesting phenomena such as Rayleigh scattering spectra [21], the energy absorption and the gain without inversion [22], Fano-type resonance fluorescence [23], Absorption and Emission [24], Electromagnetically-Induced Transparency (EIT) [25], have been explored in the MNP-QD hybrid system. Also, the MNP-QD hybrid system provides a potential application in optical switching and optical storage [26], and bioelectrochemical sensing applications [27].
Since we are interested in the visible regime of the electromagnetic spectrum, systems composed of QDs and MNPs are considered to be suitable candidates for constructing nanodevices in the visible region such as solar energy conversion [28], sensing [29,30], detection [31], photonic, and optoelectronic devices [30].
In addition, the optical properties of complex nanomaterials that combine metal and graphene have attracted significant interest in developing nanoscale optoelectronic devices, which enhance light-matter interaction. The linear optical properties in metal nanoparticle-graphene nanodisk-quantum dot hybrid systems have been examined [32,33]. It has been found that these linear properties can be controlled by the geometrical features of the system and the interacting fields. Moreover, the optical response of the Double MNPs-QD hybrid system has been studied [34]. It has been found that the Fano resonance could undergo an ultrafast reversal, when the system is excited by femtosecond laser pulses. The sub-Poissonian photon statistics in the gain-assisted QD-double gold semi-ellipsoids hybrid system have been examined [35]. It has been found that the numerical results show coupling between QD and MNPs, and falls in a strong coupling regime and zero delay second-order autocorrelation function g 2 ( 0 ) = 0.356 can be achieved with a proper choice of gain coefficient. Interestingly, silver and gold are perhaps the most widely used plasmonic materials due to their high plasmonic energy in the visible regime. Therefore, we investigate in this paper, the linear optical properties of a hybrid plasmonic system nanoparticle composed of a silver nanoparticle, and a gold nanoparticle near a quantum dot with a setup similar to that introduced by M.Tohari et al. [32].
In particular, we study the linear properties in a silver nanoparticle-gold nanoparticle-quantum dot hybrid system in the visible region of the electromagnetic spectrum. We consider the self-assembled quantum dot modelled as three level atomic systems of a Λ configuration interacting with weak probe and strong control fields under the rotating wave approximation. These external fields create dipole moments in the double metal nanoparticle and quantum dot, which interact with one another via the dipole-dipole interaction (DDI). The plasmons of silver nanoparticles are adjusted to be resonant with excitons in the QD. We numerically solve the time evolution of the density matrix elements at a steady state, to investigate the group index of the system under various conditions related to the setup and interacting fields.

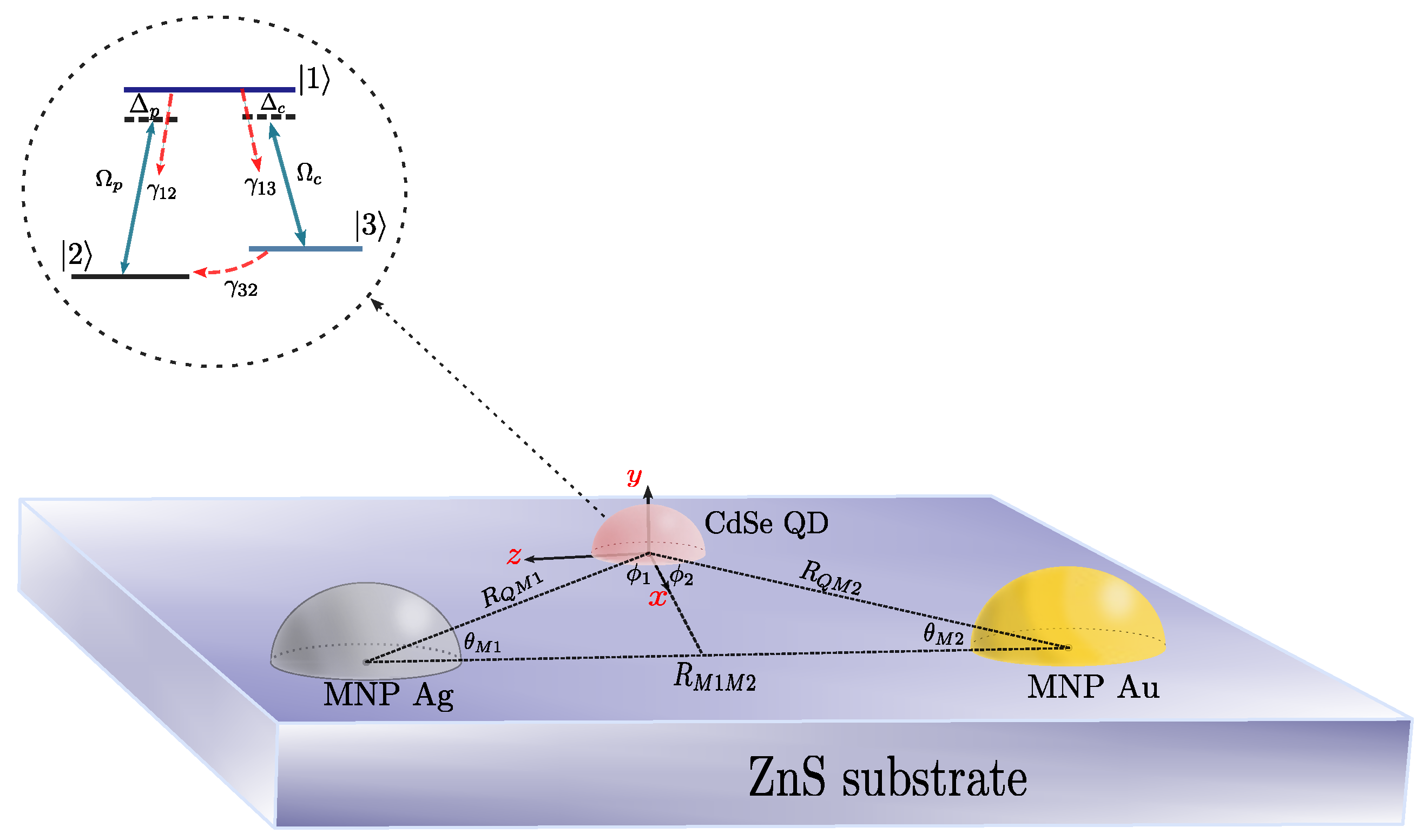
2. Theoretical Formalism

To investigate the group index of the proposed double MNP-QD hybrid system, we consider the hybrid plasmonic system depicted in Figure 1, where the QD is considered a three-level atomic system of the Λ configuration. The excitons of the CdSe QD are created by the transitions 1 ↔ 2 with a transition frequency ω 12 , dipole moment μ 12 and decay rate γ 12 due to the interaction with the probe field E p of frequency ω p and Rabi frequency Ω p = μ 12 E p ℏ , whereas the transition 1 ↔ 3 with transition frequency ω 13 , dipole moment μ 13 and decay rate γ 13 is caused by interaction with the control field E c of frequency ω c and Rabi frequency Ω c = μ 13 E c ℏ .
Note that the dipole moment μ 12 ( μ 13 ) lies along x-axis (z-axis). Therefore, the probe (control) field is applied along the x-axis (z-axis) [17]. In addition, the probe and control fields interact with the double MNP creating a localized surface plasmon in both double MNP, which produce dipole electric fields interacting with the CdSe QD. Similarly, the excitons in the CdSe QD produce electric dipole fields interacting with the double MNP. Therefore, the DDI between the components of the hybrid system can be used for studying the coupling between their optical excitions [17,36]. When the optical excitions’ frequencies of the excitons the CdSe QD is resonant with that of the surface plasmon ( ω 1 i ≈ ω s p ), the DDI will become very strong, due to the enhancement of the local dipole field in the double MNP, resulting in excitation and energy transfer between the CdSe QD and the double MNP [37].
The DDI felt by the CdSe QD induced by the external fields in our system is represented by the total field and given as:
E D D I i = ∑ i , j ℏ μ 1 i 1 ϵ * + Π x , z + Φ x , z Ω j + Λ x , z ρ 1 i
where the endex j and i indicate the enteraction fields, j=p(c) for the probe (control) field, whereas the index i=2,3 refers to the atomic levels in the CdSe QD, which are coupled to excited state 1 through ρ 1 i . ϵ * = ( 2 ϵ b + ϵ q ) is the effective dielectric constant, where ϵ b is the dielectric constant of the background medium and ϵ q is the dielectric constant of the CdSe QD.
The parameters Π x , z , Φ x , z and Λ x , z are written as:
Π x = 1 4 π ϵ * α M 1 ( 3 c o s ϕ 1 − 1 ) R Q M 1 3 + α M 2 ( 3 c o s ϕ 2 − 1 ) R Q M 2 3
Φ x = − α M 1 α M 2 ( 4 π ϵ * ) 2 R M 1 M 2 3 3 c o s ϕ 1 − 1 R Q M 1 3 + 3 c o s ϕ 2 − 1 R Q M 2 3
Λ x = μ 12 2 ( 4 π ϵ * ) 2 ℏ ϵ 0 ϵ b α M 1 ( 3 c o s ϕ 1 − 1 ) 2 R Q M 1 6 + α M 2 ( 3 c o s ϕ 2 − 1 ) 2 R Q M 2 6
Π z = 1 4 π ϵ * α M 1 ( 3 c o s θ M 1 − 1 ) R Q M 1 3 + α M 2 ( 3 c o s θ M 2 − 1 ) R Q M 2 3
Φ z = 2 α M 1 α M 2 ( 4 π ϵ * ) 2 R M 1 M 2 3 3 c o s θ M 1 − 1 R Q M 1 3 + 3 c o s θ M 2 − 1 R Q M 2 3
Λ z = μ 13 2 ( 4 π ϵ * ) 2 ℏ ϵ 0 ϵ b α M 1 ( 3 c o s θ M 1 − 1 ) 2 R Q M 1 6 + α M 2 ( 3 c o s θ M 2 − 1 ) 2 R Q M 2 6
where μ 1 i represents the dipole moment of the QD corresponding to the excitonic transition 1 ↔ i . As shown in Figure 1, R M 1 M 2 is the centre-to-centre distance between the double MNP. The parameters R Q M 1 and R Q M 2 are calculated using R M 1 M 2 and θ Q = ϕ 1 + ϕ 2 as follows:
R Q M 1 = s i n θ M 2 s i n θ Q R M 1 M 2
R Q M 2 = s i n θ M 1 s i n θ Q R M 1 M 2
The shape-dependent polarizability of the double MNP can be written as:
α M i = 4 π R M i 3 ϵ M i ( ω ) − ϵ b ϵ M i + 2 ϵ b
where i=1,2 indicates the silver MNP and the gold MNP, respectively. The parameter ϵ M ( ω ) = ϵ ∞ − ω p ω 2 + i ω γ M is the dielectric function of metals with a plasma frequency ω p and damping γ M [11].
The DDI Hamiltonian that corresponds to E D D I i is written in the following form:
H D D I = − ∑ i , j ℏ 1 ϵ * + Π x , z + Φ x , z Ω j + Λ x , z ρ 1 i σ 1 i + H . C
The total Hamiltonian of three-level atom of the Λ configuration interacting with two classical fields [38] under the rotating wave approximation (RWA) in terms of one and two photon detuning is given as:
H R W A = − ℏ Δ p σ 11 + Δ R σ 33            − ℏ Ω p 1 ϵ * + Π x + Φ x + Λ x ρ 12 σ 12                      − ℏ Ω c 1 ϵ * + Π z + Φ z + Λ z ρ 13 σ 13 + H . C .
where Δ p = ω p − ω 12 is the probe field’s detuning from 1 ↔ 2 , and Δ R = Δ p − Δ c is the two photon detuning, with Δ c = ω c − ω 13 is the detuning of the control field from 1 ↔ 3 . σ 11 and σ 33 , are the projection operators onto the upper and lower levels. However, σ 1 i gives the flip operators related to optical transitions [32,38]. The terms Π x , z , Φ x , z and Λ x , z represent the field incident of the QD, due to the DDI between the QD and the double MNP. The term Π x , z is due to the interaction of the QD with dipole electric fields from the double MNP induced by the external fields, whereas the term Φ x , z is the dipole electric field produced by the silver MNP which induces dipole electric fields in the gold MNP which in turn induces electric fields at the QD. The term Λ x , z is due to the QD’s interaction with dipole electric fields from the double MNP which arises when the external fields polarize the QD, which in turn polarize the double MNP. The density matrix method can now be used with the following Liouvillian which describes the system’s decay channels [32]:
L Λ ρ = γ 13 2 ρ σ 11 + σ 11 ρ − 2 σ 31 ρ σ 13 +            γ 12 2 ρ σ 11 + σ 11 ρ − 2 σ 21 ρ σ 12 + γ 32 2 ρ σ 33 + σ 33 ρ − 2 σ 23 ρ σ 32
Here, γ 32 is the lower state dephasing. By using the linblad master equation ( ∂ ρ ∂ t = i ℏ [ H , ρ ] + L Λ ρ ) , we can obtain the time evolution of the density matrix as:
∂ ∂ t ρ 11 = − ( γ 12 + γ 13 ) ρ 11 + i [ Ω p ( 1 ϵ * + Π x + Φ x ) + Λ x ρ 12 ] ρ 21                      + i [ Ω c ( 1 ϵ * + Π z + Φ z ) + Λ z ρ 13 ] ρ 31 + c . c ,
∂ ∂ t ρ 22 = γ 12 ρ 11 + γ 32 ρ 33 − i [ Ω p ( 1 ϵ * + Π x + Φ x ) + Λ x ρ 12 ] ρ 21 + c . c ,
∂ ∂ t ρ 33 = − γ 32 ρ 33 + γ 13 ρ 11 − i [ Ω c ( 1 ϵ * + Π z + Φ z ) + Λ z ρ 13 ] ρ 31 + c . c ,
∂ ∂ t ρ 13 = i Δ c ρ 13 − ( γ 13 2 + γ 12 2 + γ 32 2 ) ρ 13            + i [ Ω c ( 1 ϵ * + Π z + Φ z ) + Λ z ρ 13 ] ( ρ 33 − ρ 11 )                      + i [ Ω p ( 1 ϵ * + Π x + Φ x ) + Λ x ρ 12 ] ρ 23 ,
∂ ∂ t ρ 12 = − ( γ 13 2 + γ 12 2 − i Δ p ) ρ 12            + i [ Ω p ( 1 ϵ * + Π x + Φ x ) + Λ x ρ 12 ] ( ρ 22 − ρ 11 )                      + i [ Ω c ( 1 ϵ * + Π z + Φ z ) + Λ z ρ 13 ] ρ 32 ,
∂ ∂ t ρ 32 = ( − γ 32 2 + i Δ R ) ρ 32 + i [ Ω c * ( 1 ϵ * + Π z * + Φ z * ) + Λ z * ρ 31 ] ρ 12                      − i [ Ω p ( 1 ϵ * + Π x + Φ x ) + Λ x ρ 12 ] ρ 31
where the Re [ Λ x , z ( ρ i i − ρ 11 ) ] gives the non-radiative energy shift due to the DDI term Λ x , z , whereas the Im [ Λ x , z ( ρ i i − ρ 11 ) ] represents the decay rate due to the DDI term. This indicates that the plasmonic cavity enhances the spontaneous emission of the QD by Λ x , z . As a result, we can control the spontaneous emission using the system’s geometrical and structural parameters. In addition, the Rabi frequency that describes the strength of the interaction between the excitons of the QD and surface plasmons of the double MNP, is enhanced by a factor 1 ϵ * + Π x , z + Φ x , z due to the DDI, resulting in a strong coupling between the excitons and plasmons for 1 ϵ * + Π x , z + Φ x , z > 1 .
The linear optical response of the double MNP-QD hybrid system to the probe field is given as [38]:
χ ( ω p ) = N μ 12 ϵ 0 E p ρ 12
where the real and imaginary parts of the susceptibility correspond to the dispersion and the absorption properties of the QD respectively.
In a dispersive medium with frequency-dependent dispersion, the susceptibility can be represented as a frequency-dependent dispersion. Moreover, it is known that the medium’s refractive index can be related to the real part of the susceptibility ( n = 1 + R e χ / 2 ) . Therefore, the peak of the pulse travel with group velocity can be obtained as:
v g = c 1 + R e [ χ ] + ω 2 d R e [ χ ] d ω = c n g
where n g represents the group index. Remarkably, the probe field can experience subluminal light resulting in slow light for the case of n g > 1 , while for the case of n g < 1 corresponds to fast light due to superluminal light propagation.

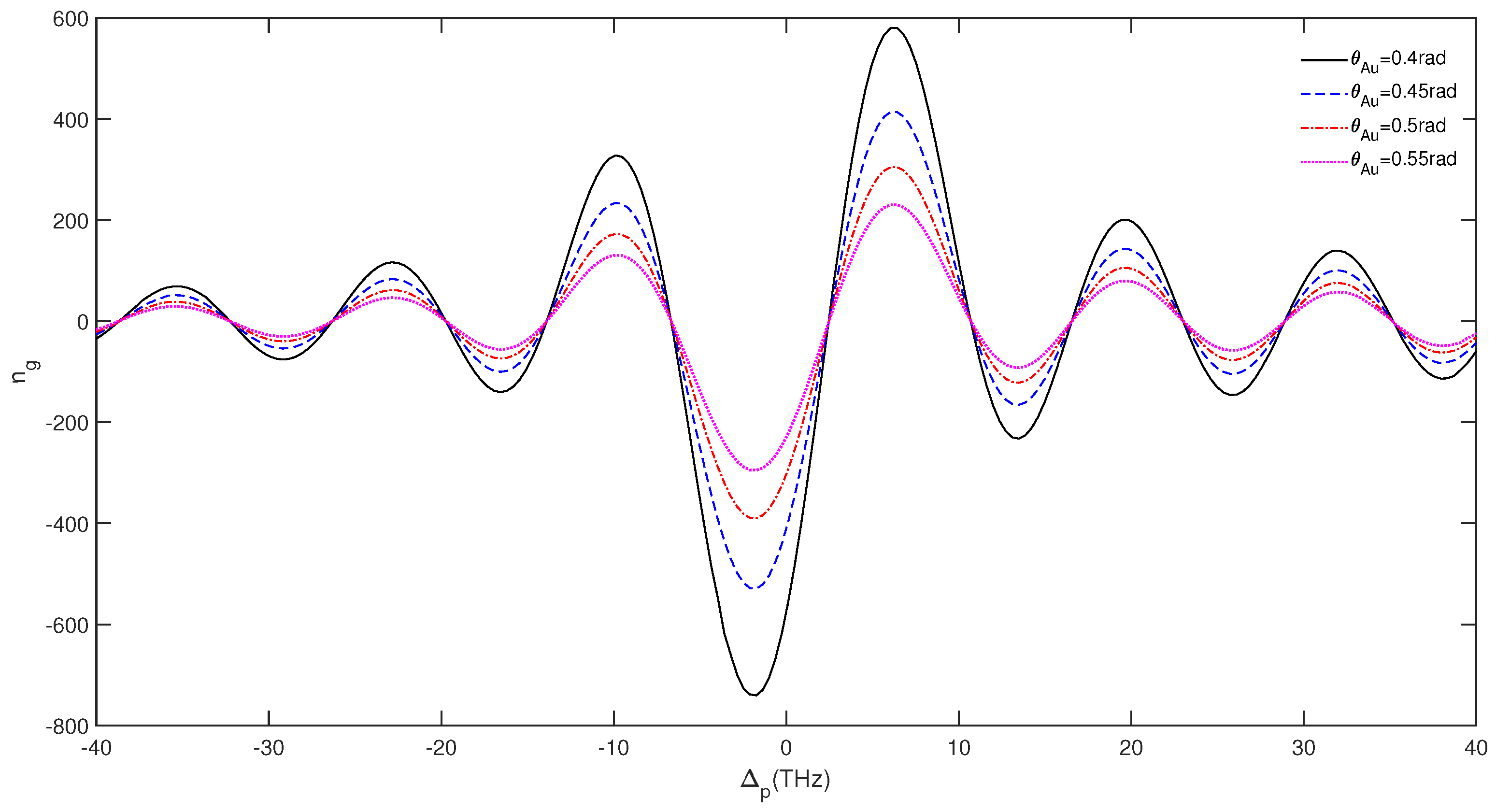
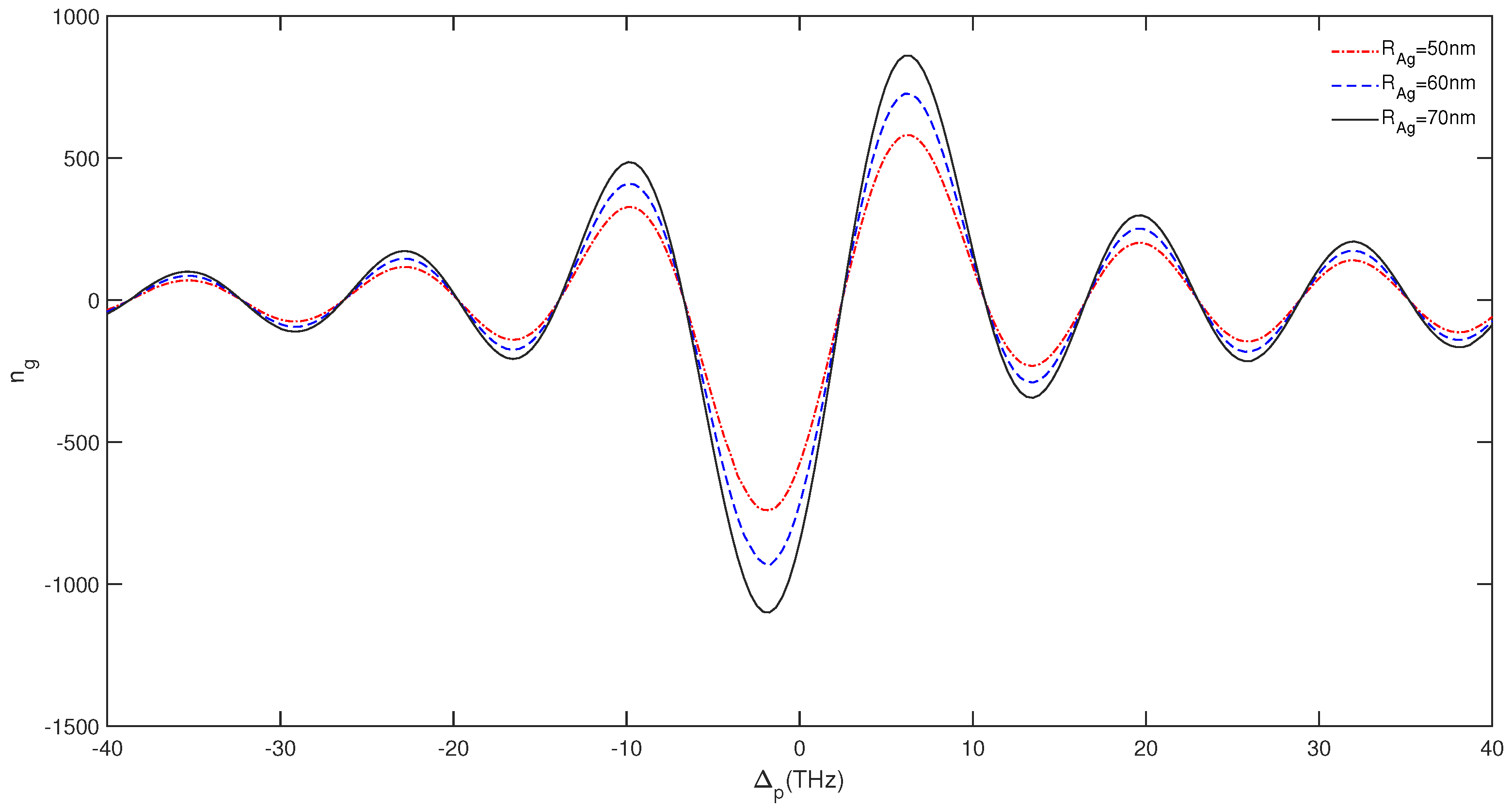
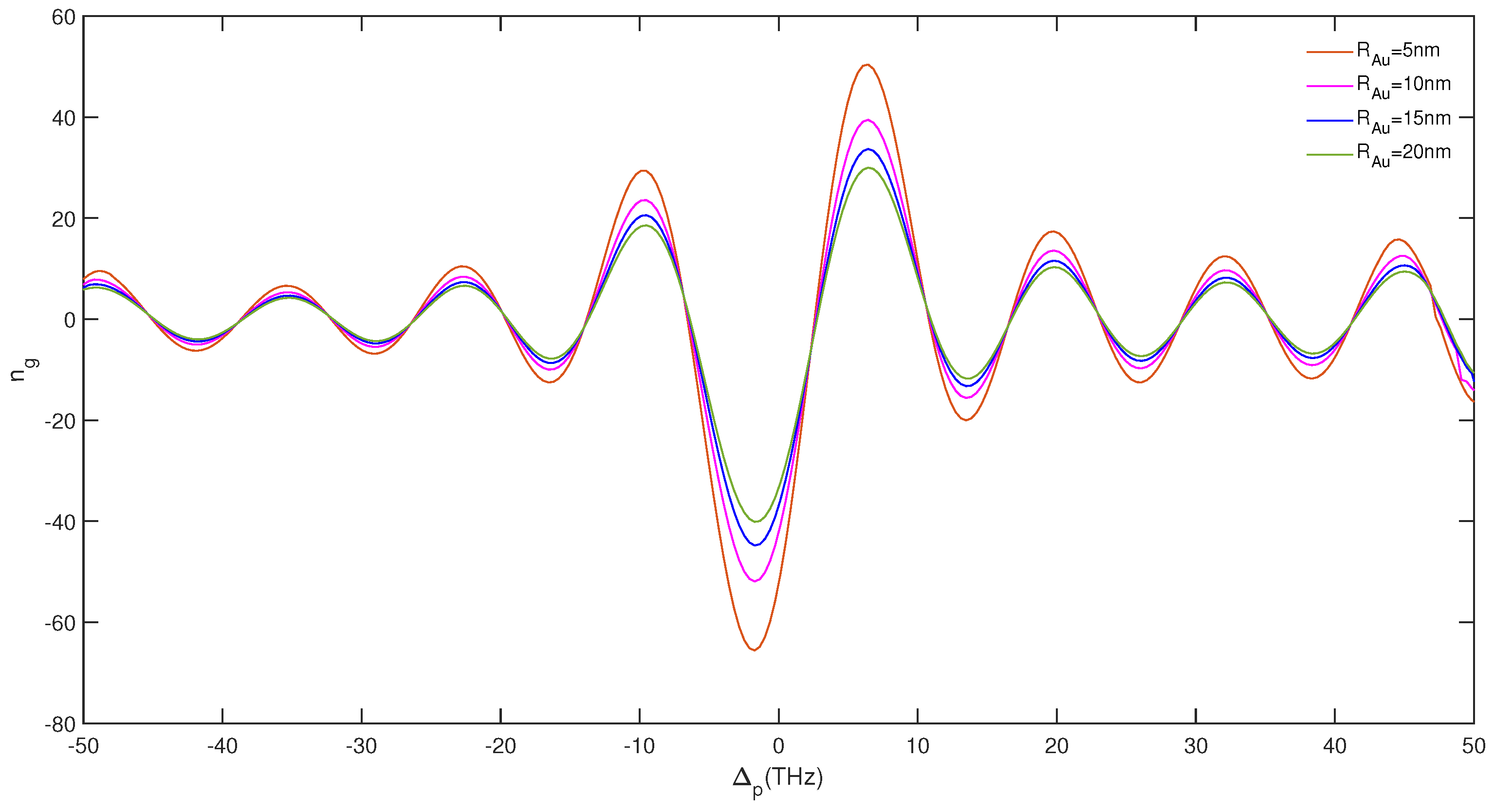
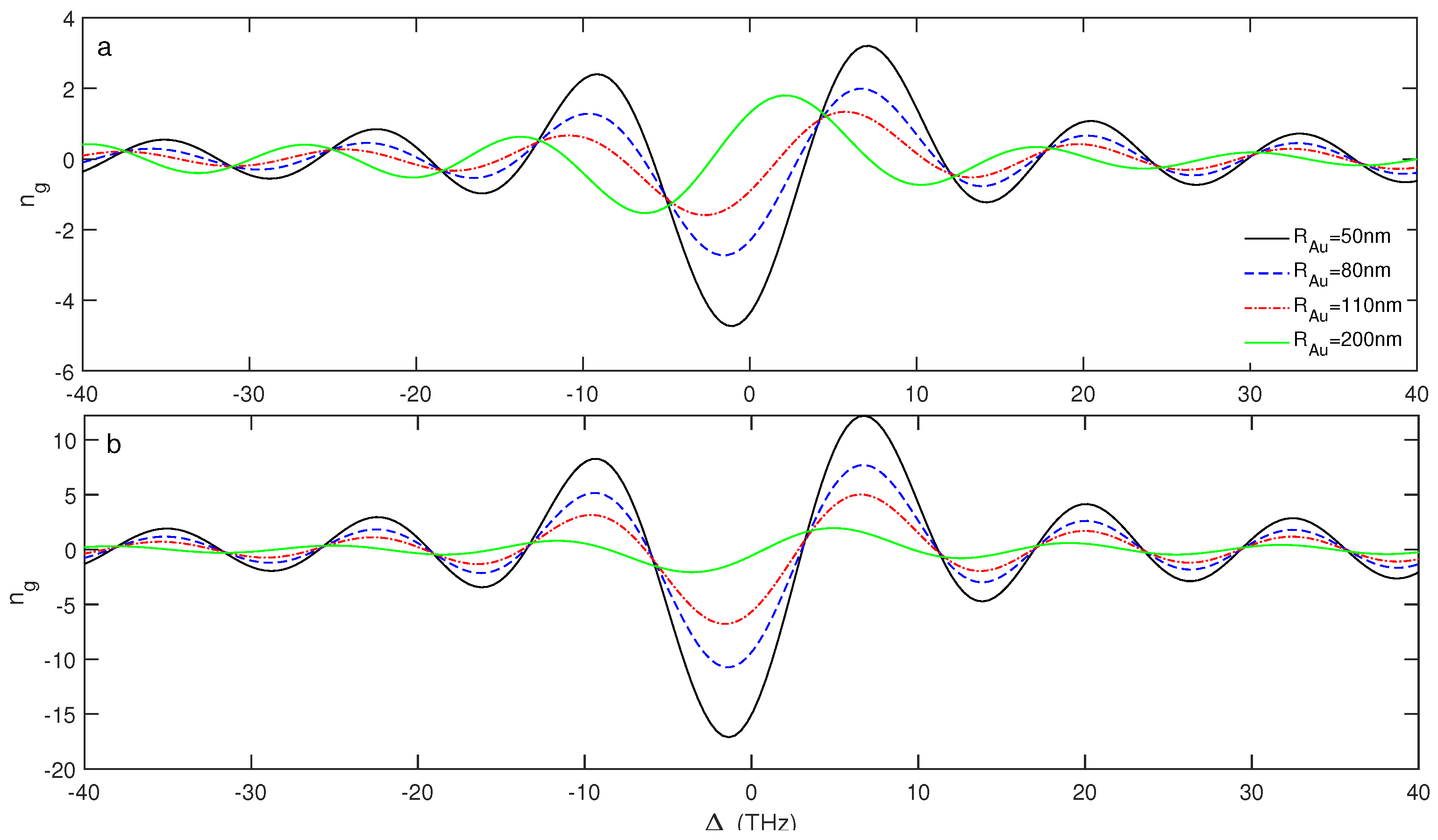
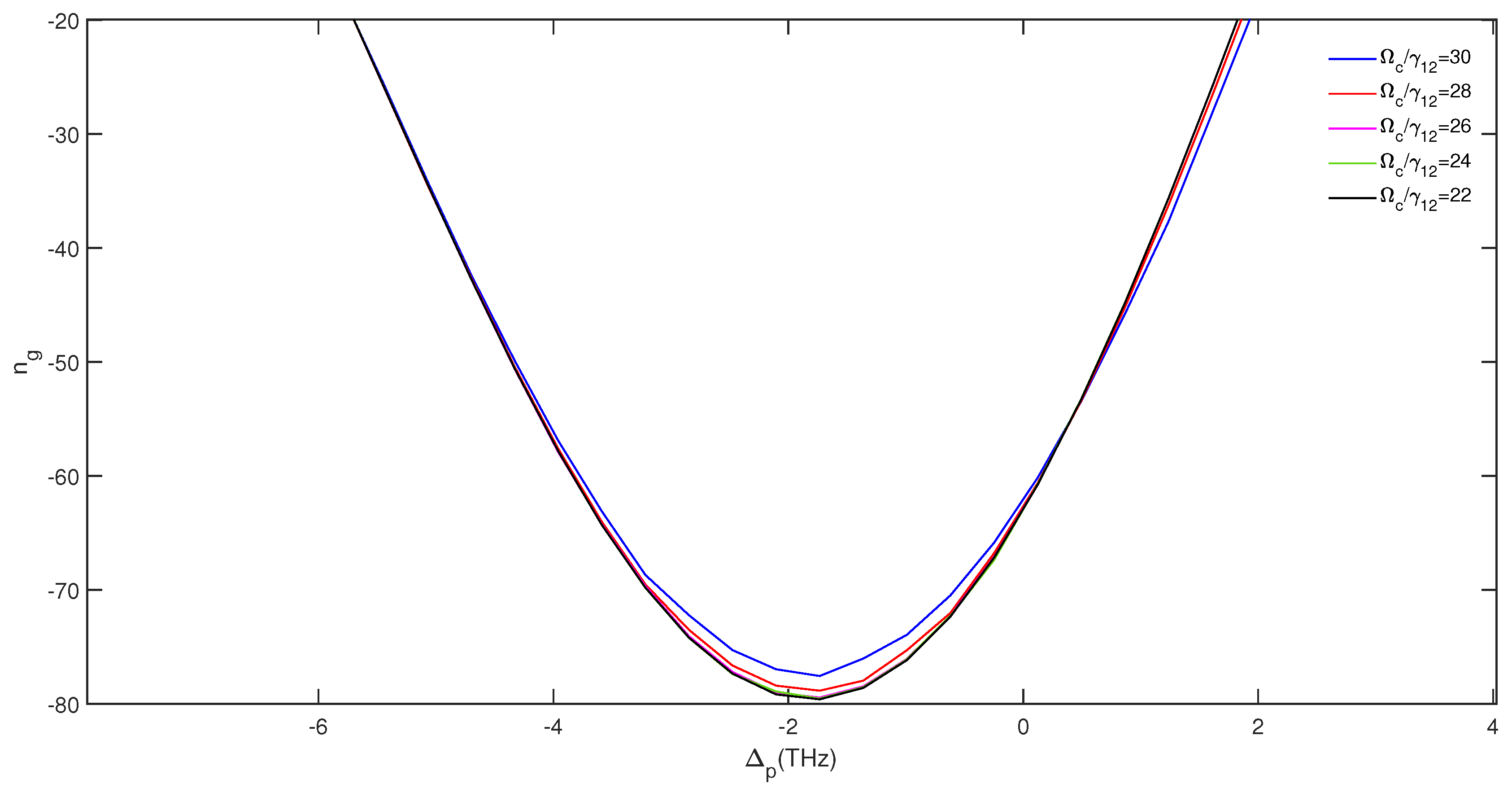
3. Results and Discussion

To investigate the group index of the QD situated at the centre-to-centre distances R Q M 1 , R Q M 2 from the silver MNP and gold MNP as illustrated in Figure 1, we consider a spherical silver of radius R A g = 50 n m , the high-frequency dielectric constant of ϵ ∞ = 1.74 [39], plasmon frequency of ω p = 1.36 × 10 16 s − 1 , damping rate of γ M = 10 14 s − 1 [11] embedded in a substrate of ZnS whose ϵ b = 5.6 . For these parameters, the extinction cross-section spectrum of the silver MNP exhibits plasmonic resonance at ℏ ω s p = 2.449 e V . To support the plasmons of the silver MNP, we also use a spherical gold MNP of ϵ ∞ = 2.2715 [39], ω p = 1.2955 × 10 16 s − 1 [11], and γ M = 10 14 s − 1 . The QD is chosen to be a self-assembled (CdSe/ZnS) of radius 1.5 n m that has energy transition 2.449 e V [40]. This transition energy is resonant with the energy of silver MNP plasmons. The QD’s atomic density is set as N = 7 × 10 20 m − 3 [41], the dielectric constant ϵ q = 6.9 , dipole moments of μ 12 = μ 13 = 1 e n m [19,41], and the decay rates are set as γ 12 = γ 13 = 1 G H z [41] and γ 32 = 0.3 γ 12 [42]. The strength of the probe field is Ω p = 0.01 Ω c [33].
In the following, we discuss controlling the switching between slow and fast light in the double MNP-QD hybrid system via the geometrical features of the system, including the inclination angle of the gold MNP, and the size of the metals, in addition to the detuning and the strength of the control field.
First, we examine the group index n g in the double MNP-QD hybrid system versus the detuning of the probe field. Figure 2 shows the group index of the probe field propagation around the resonance of the QD under the impact of the plasmonic effect caused by double MNP placed near the QD at different inclination angles of the gold MNP ( θ M 2 = θ A u ) with respect to the QD at constant ( θ M 1 = θ A g ). We observe a switching between n g > 0 , in which the probe field experiences subluminal light propagation resulting in slow light, and n g < 0 , which corresponds to the fast light due to superluminal propagation. Moreover, we observe that decreasing θ A u leads to a strong switching between slow and fast light. It is evident that the group index of the double MNP-QD hybrid system exhibits high sensitivity to θ A u . This is because decreasing θ A u leads to decreasing R Q M 1 as noted in Equation 8a. This result is reasonable since silver MNP is chosen to be resonant with QD and it is desirable to decrease its separation distance from QD to enhance DDI.
Since a plasmonic particle’s polarizability depends on its size, and in such systems like semiconductor quantum dots(QD)-graphene nanodisk(GND)-metal nanoparticle(MNP) hybrid systems, it has been shown that the switching between slow and fast light can be adjusted by changing the size of the MNP [33], Figure 3 shows how the silver MNP can be used to adjust the switching between slow and fast light of the probe field. We notice that the group index is significantly influenced by the radius of the silver MNP ( R A g ). Clearly, the switching of the group index between slow and fast light is enhanced by the large size of the silver MNP. This is a significant result due to the polarizability which increases as a result of increasing the size of the silver nanoparticle, with the energy of the excitons being resonant with that of the surface plasmons, Therefore, the strong coupling between excitons and plasmons can be affected by the size of the silver MNP.
Moreover, the effect of the size of the gold NP on the group index is explored in Figure 4. It is evident that switching of the group index between slow and fast light is also significantly affected by the size of the gold NP. Obviously, because of the small size of the gold NP, switching between slow and fast light near the resonance can be enhanced. Since the gold NP is not resonant with the QD and Ag NP, this result is due to the absorption and scattering properties of the gold NP that can be tuned by adjusting the size of the particle. The absorption spectra of the gold NP results in a blue shift due to decreasing in size [43,44].
On the other hand, Figure 5 shows to what extent the group index can be controlled by the size of the gold nanoparticle at two values of Ag nanoparticle. It is observed that the size of the gold nanoparticle increasing leads a decrease in the group index. Moreover, when the size of the gold is larger than 100nm, the peak of the group index starts to shift to the negative values in the detuning of the probe field. However, the effect of the size of the gold nanoparticle on the group index is examined when the size of the silver nanoparticle is R A g = 5 n m , as seen in Figure 5 (a). Moreover, the effect of the size of the gold nanoparticle on the group index with a large silver nanoparticle R A g = 10 n m is examined in Figure 5 (b). It is clear in Figure 5 (a), that the sensitivity of the group index behaviour of the hybrid system for the small size of silver MNP to negatively detune the probe field is larger than that in Figure 5 (b).
Finally, the effect of the Rabi frequency the strength of the control field on the group index of our proposed system is examined in Figure 6. It can be seen that the switching between slow and fast light is sensitive to the Rabi frequency of the control field. Specifically, large Rabi frequencies of the control field Ω c , strong switching of the group index between positive and negative values.
Comparison with the similar work done by M.Tohari et al.[45], it was found that the surface plasmons of GND and MNP can influence the group index in the optical region of the electromagnetic spectrum of the propagating weak probe field through a graphene nanodisk (GND)-metal nanoparticle (MNP)-quantum dot (QD) hybrid system. It is obvious that combining a silver nanoparticle-gold nanoparticle-quantum dot hybrid system, such as the proposed system, with the same setup as the GND-MNP-QD in [45] leads to a controllable stronger switching of the group index between slow and fast light via the system’s geometrical features. This can be seen in the inclination angle of the gold nanoparticle, and the size of the silver and gold nanoparticles, in addition to the strength of the control field leading to promising applications, such as tunable group velocity devices.

4. Conclusions

We have studied the group index behavior in the double MNP-QD plasmonic hybrid system in the optical region of the electromagnetic spectrum, where the self-assembled CdSe is modelled as a three-level atomic system of lambda configuration interacting with weak and strong external fields. We have found that the group index of our proposed system exhibits a switch between slow and fast light which can be controlled by the system’s geometrical features in addition to the strength of the control field. This switching shift in the negative values of the detuning of the probe field for a size of the gold nanoparticle larger than 100nm. Therefore, we think that our results can be employed in optoelectronics and photonic devices.

Author Contributions

M.A.A performed the theoretical formalism, the numerical investigations, and the manuscript writing and revised by M.M.T. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Acknowledgments

The authors are thankful to King Khalid University in Saudi Arabia for providing administrative and technical assistance.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Mauriz, E.; Dey, P.; Lechuga, L.M. Advances in nanoplasmonic biosensors for clinical applications. Analyst 2019, 144, 7105–7129. [Google Scholar] [CrossRef] [PubMed]
  2. Kurt, H.; Pishva, P.; Pehlivan, Z.S.; Arsoy, E.G.; Saleem, Q.; Bayazıt, M.K.; Yüce, M. Nanoplasmonic biosensors: Theory, structure, design, and review of recent applications. Analytica Chimica Acta 2021, 1185, 338842. [Google Scholar] [CrossRef] [PubMed]
  3. Cennamo, N.; Bossi, A.M.; Arcadio, F.; Maniglio, D.; Zeni, L. On the Effect of Soft Molecularly Imprinted Nanoparticles Receptors Combined to Nanoplasmonic Probes for Biomedical Applications. Frontiers in Bioengineering and Biotechnology 2021, 9, 801489. [Google Scholar] [CrossRef] [PubMed]
  4. Ebadi, S.M.; Örtegren, J.; Bayati, M.S.; Ram, S.B. A multipurpose and highly-compact plasmonic filter based on metal-insulator-metal waveguides. IEEE Photonics Journal 2020, 12. [Google Scholar] [CrossRef]
  5. Chauhan, D.; Kumar, A.; Adhikari, R.; Saini, R.K.; Chang, S.H.; Dwivedi, R.P. High performance vanadium dioxide based active nano plasmonic filter and switch. Optik 2021, 225, 165672. [Google Scholar] [CrossRef]
  6. Shaat, S.K.; Musleh, H.; Asad, J.; Shurrab, N.; Issa, A.; AlKahlout, A.; Al Dahoudi, N. Nanoplasmonic for Solar Energy Conversion Devices. In Solar Cells; IntechOpen, 2019.
  7. Wang, M.; Ye, M.; Iocozzia, J.; Lin, C.; Lin, Z. Plasmon-mediated solar energy conversion via photocatalysis in noble metal/semiconductor composites. Advanced Science 2016, 3, 1600024. [Google Scholar] [CrossRef] [PubMed]
  8. Mayer, K.M.; Hafner, J.H. Localized surface plasmon resonance sensors. Chemical reviews 2011, 111, 3828–3857. [Google Scholar] [CrossRef] [PubMed]
  9. Singh, J.; Williams, R.T. Excitonic and photonic processes in materials; Springer, 2015.
  10. Yu, H.; Peng, Y.; Yang, Y.; Li, Z.Y. Plasmon-enhanced light–matter interactions and applications. npj Computational Materials 2019, 5, 45. [Google Scholar] [CrossRef]
  11. Gaponenko, S.V. Introduction to nanophotonics; Cambridge University Press, 2010.
  12. Remesh, V. Spectral phase control of nanoscale nonlinear optical responses 2020.
  13. Khurgin, J.B.; Boltasseva, A. Reflecting upon the losses in plasmonics and metamaterials. MRS bulletin 2012, 37, 768–779. [Google Scholar] [CrossRef]
  14. Mansur, H.S. Quantum dots and nanocomposites. Wiley Interdisciplinary Reviews: Nanomedicine and Nanobiotechnology 2010, 2, 113–129. [Google Scholar] [CrossRef]
  15. Riel, B. An introduction to self-assembled quantum dots. American Journal of Physics 2008, 76, 750–757. [Google Scholar] [CrossRef]
  16. Koole, R.; Groeneveld, E.; Vanmaekelbergh, D.; Meijerink, A.; de Mello Donegá, C. Size effects on semiconductor nanoparticles. Nanoparticles: Workhorses of Nanoscience 2014, pp. 13–51.
  17. Singh, M.R.; Schindel, D.G.; Hatef, A. Dipole-dipole interaction in a quantum dot and metallic nanorod hybrid system. Applied Physics Letters 2011, 99, 181106. [Google Scholar] [CrossRef]
  18. Naseri, T. Electromagnetically induced grating in semiconductor quantum dot and metal nanoparticle hybrid system by considering nonlocality effects. Journal of Theoretical and Applied Physics 2020, 14, 129–135. [Google Scholar] [CrossRef]
  19. Chen, H.J. Fano resonance induced fast to slow light in a hybrid semiconductor quantum dot and metal nanoparticle system. Laser Physics Letters 2020, 17, 025201. [Google Scholar] [CrossRef]
  20. Vasa, P. Exciton-surface plasmon polariton interactions. Advances in Physics: X 2020, 5, 1749884. [Google Scholar] [CrossRef]
  21. Hapuarachchi, H.; Premaratne, M.; Bao, Q.; Cheng, W.; Gunapala, S.D.; Agrawal, G.P. Cavity QED analysis of an exciton-plasmon hybrid molecule via the generalized nonlocal optical response method. Physical Review B 2017, 95, 245419. [Google Scholar] [CrossRef]
  22. Ko, M.C.; Kim, N.C.; Choe, S.I.; So, G.H.; Jang, P.R.; Kim, Y.J.; Kim, I.G.; Li, J.B. Plasmonic effect on the optical properties in a hybrid V-Type three-level quantum dot-metallic nanoparticle nanosystem. Plasmonics 2018, 13, 39–46. [Google Scholar] [CrossRef]
  23. Shen, S.; Wu, Z.; Li, J.; Wu, Y. Insights into Fano-type resonance fluorescence from quantum-dot–metal-nanoparticle molecules with a squeezed vacuum. Physical Review A 2021, 104, 013717. [Google Scholar] [CrossRef]
  24. Kumar, V.; Nisika, N.; Kumar, M. Modified absorption and emission properties leading to intriguing applications in plasmonic–excitonic nanostructures. Advanced Optical Materials 2021, 9, 2001150. [Google Scholar] [CrossRef]
  25. Zahir, A.; Bashir, A.I.; Khan, N.; Hayat, S.S. Quantum coherence-enhanced optical properties and drag of photons and SPPs in semiconducting quantum dots and resonantly-coupled dot–nanoparticle plasmonic interfaces. Journal of Physics and Chemistry of Solids 2023, 172, 111088. [Google Scholar] [CrossRef]
  26. Bao, C.; Qi, Y.; Niu, Y.; Gong, S. Surface plasmon-assisted optical bistability in the quantum dot-metal nanoparticle hybrid system. Journal of Modern Optics 2016, 63, 1280–1285. [Google Scholar] [CrossRef]
  27. Buk, V.; Pemble, M.E.; Twomey, K. Fabrication and evaluation of a carbon quantum dot/gold nanoparticle nanohybrid material integrated onto planar micro gold electrodes for potential bioelectrochemical sensing applications. Electrochimica Acta 2019, 293, 307–317. [Google Scholar] [CrossRef]
  28. Rajender, G.; Choudhury, B.; Giri, P. In situ decoration of plasmonic Au nanoparticles on graphene quantum dots-graphitic carbon nitride hybrid and evaluation of its visible light photocatalytic performance. Nanotechnology 2017, 28, 395703. [Google Scholar] [CrossRef] [PubMed]
  29. Hapuarachchi, H.; Mallawaarachchi, S.; Hattori, H.T.; Zhu, W.; Premaratne, M. Optoelectronic figure of merit of a metal nanoparticle—quantum dot (mnp-qd) hybrid molecule for assessing its suitability for sensing applications. Journal of Physics: Condensed Matter 2018, 30, 054006. [Google Scholar] [CrossRef] [PubMed]
  30. Pandey, A.; Yadav, R.; Verma, S.; Kaur, M.; Singh, B.P.; Husale, S. Au-Nanoislands and Quantum Dots growth on Flexible Light weight MWCNTs paper exhibiting SEM resolution and NIR photodetecting capabilities. Carbon Trends 2023, 10, 100241. [Google Scholar] [CrossRef]
  31. Farzin, M.A.; Abdoos, H. A critical review on quantum dots: From synthesis toward applications in electrochemical biosensors for determination of disease-related biomolecules. Talanta 2021, 224, 121828. [Google Scholar] [CrossRef] [PubMed]
  32. Tohari, M.M.; Lyras, A.; AlSalhi, M.S. Giant Self-Kerr Nonlinearity in the Metal Nanoparticles-Graphene Nanodisks-Quantum Dots Hybrid Systems Under Low-Intensity Light Irradiance. Nanomaterials 2018, 8, 521. [Google Scholar] [CrossRef]
  33. Tohari, M.M. Near-infrared switching between slow and fast light in the metal nanoparticles-graphene nanodisks-quantum dots hybrid systems. Physica Scripta 2022, 97, 045808. [Google Scholar] [CrossRef]
  34. Shah, R.A.; Scherer, N.F.; Pelton, M.; Gray, S.K. Ultrafast reversal of a Fano resonance in a plasmon-exciton system. Physical Review B 2013, 88, 075411. [Google Scholar] [CrossRef]
  35. Wang, Y.; Ye, H.; Yu, Z.; Liu, Y.; Xu, W. Sub-Poissonian photon statistics in quantum dot-metal nanoparticles hybrid system with gain media. Scientific Reports 2019, 9, 10088. [Google Scholar] [CrossRef]
  36. Brzozowski, M.J. The Study of Nano-Optics in Hybrid Systems. PhD thesis, The University of Western Ontario (Canada), 2016.
  37. Bitton, O.; Gupta, S.N.; Haran, G. Quantum dot plasmonics: from weak to strong coupling. Nanophotonics 2019, 8, 559–575. [Google Scholar] [CrossRef]
  38. Lambropoulos, P. Fundamentals of quantum optics and quantum information; Springer, 2007.
  39. Rioux, D.; Vallières, S.; Besner, S.; Muñoz, P.; Mazur, E.; Meunier, M. An analytic model for the dielectric function of Au, Ag, and their alloys. Advanced Optical Materials 2014, 2, 176–182. [Google Scholar] [CrossRef]
  40. Sapsford, K.E.; Pons, T.; Medintz, I.L.; Mattoussi, H. Biosensing with luminescent semiconductor quantum dots. Sensors 2006, 6, 925–953. [Google Scholar] [CrossRef]
  41. Nielsen, P.K.; Thyrrestrup, H.; Mørk, J.; Tromborg, B. Numerical investigation of electromagnetically induced transparency in a quantum dot structure. Optics express 2007, 15, 6396–6408. [Google Scholar] [CrossRef] [PubMed]
  42. Wang, J.S.; Chiu, K.P.; Lin, C.Y.; Tsai, Y.H.; Yuan, C.T. Modification of spontaneous emission rates of self-assembled CdSe quantum dots by coupling to hybrid optical nanoantennas. Plasmonics 2017, 12, 433–438. [Google Scholar] [CrossRef]
  43. Huang, X.C.; Luo, Y.L.; Hsu, H.Y. 7 Redox-Triggered, Biocompatible, Inorganic Nanoplatforms for Cancer Theranostics. Biological and Pharmaceutical Applications of Nanomaterials 2015, p. 171.
  44. Kim, H.S.; Lee, D.Y. Near-infrared-responsive cancer photothermal and photodynamic therapy using gold nanoparticles. Polymers 2018, 10, 961. [Google Scholar] [CrossRef]
  45. Tohari, M.M.; Alqahtani, M.M. Gain without population inversion and superluminal propagation in the metal nanoparticles-graphene nanodisks-quantum dots hybrid systems. Journal of Physics: Condensed Matter 2021, 33, 325302. [Google Scholar] [CrossRef]
Preprints 90853 g001
Figure 1. A schematic of the QD and two MNPs hybrid system. QD has three-levels of the Λ configuration coupling with two fields.
Figure 1. A schematic of the QD and two MNPs hybrid system. QD has three-levels of the Λ configuration coupling with two fields.
Preprints 90853 g001
Preprints 90853 g002
Figure 2. Group index versus probe field detuning for different values of the inclination angle of gold MNP with respect to QD, where R A g = 50 n m , R A u = 5 n m , θ A g = 1.2 and edge-to-edge distance D=33nm. The hybrid system interacts with the resonant control field Ω c = 1 G H z .
Figure 2. Group index versus probe field detuning for different values of the inclination angle of gold MNP with respect to QD, where R A g = 50 n m , R A u = 5 n m , θ A g = 1.2 and edge-to-edge distance D=33nm. The hybrid system interacts with the resonant control field Ω c = 1 G H z .
Preprints 90853 g002
Preprints 90853 g003
Figure 3. Group index versus probe field detuning for different values of the silver MNP size, where R A g = 50 n m , R A u = 5 n m , θ A g = 1.2 , θ A u = 0.4 and edge-to-edge distance D=33nm. The hybrid system interacts with the resonant control field Ω c = 1 G H z .
Figure 3. Group index versus probe field detuning for different values of the silver MNP size, where R A g = 50 n m , R A u = 5 n m , θ A g = 1.2 , θ A u = 0.4 and edge-to-edge distance D=33nm. The hybrid system interacts with the resonant control field Ω c = 1 G H z .
Preprints 90853 g003
Preprints 90853 g004
Figure 4. Group index versus probe field detuning of the double MNP-QD hybrid system of geometry R A g = 20 n m , θ A g = 1.2 r a d , θ A u = 0.8 r a d , D = 15 n m , for different values of the size of the gold MNP. The system interacting with the resonant control field of Ω c = 1 G H z .
Figure 4. Group index versus probe field detuning of the double MNP-QD hybrid system of geometry R A g = 20 n m , θ A g = 1.2 r a d , θ A u = 0.8 r a d , D = 15 n m , for different values of the size of the gold MNP. The system interacting with the resonant control field of Ω c = 1 G H z .
Preprints 90853 g004
Preprints 90853 g005
Figure 5. Group index versus probe field detuning for different values of the radius of the R A u nanoparticle. (a) the radius of the silver nanoparticle R A g = 5 n m . (b) the radius of the silver nanoparticle R A g = 10 n m where θ A g = 1.2 r a d , θ A u = 0.4 r a d , Δ c = 0 and edge-to-edge distance D = 31 n m . The hybrid system interacts with the resonant control field Ω c = 1 G H z .
Figure 5. Group index versus probe field detuning for different values of the radius of the R A u nanoparticle. (a) the radius of the silver nanoparticle R A g = 5 n m . (b) the radius of the silver nanoparticle R A g = 10 n m where θ A g = 1.2 r a d , θ A u = 0.4 r a d , Δ c = 0 and edge-to-edge distance D = 31 n m . The hybrid system interacts with the resonant control field Ω c = 1 G H z .
Preprints 90853 g005
Preprints 90853 g006
Figure 6. Group index versus probe field detuning at different values of Ω c , where the geometry of the system R A g = 50 n m , R A u = 5 n m and D = 50 n m , θ A g = 1.3 r a d , θ A u = 0.7 r a d .
Figure 6. Group index versus probe field detuning at different values of Ω c , where the geometry of the system R A g = 50 n m , R A u = 5 n m and D = 50 n m , θ A g = 1.3 r a d , θ A u = 0.7 r a d .
Preprints 90853 g006
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated