Prerpints.org logo
Preprint
Article

Independent Control of Active and Reactive Power Flow for a Single-Phase, Unidirectional On-Board Power Converter Connecting the DC Power Bus to the AC Bus

Altmetrics

Downloads

143

Views

28

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

20 November 2023

Posted:

21 November 2023

You are already at the latest version

Alerts
Abstract
This article presents a proposed system that enables energy transfer from the dc grid to a single-phase onboard grid, operating at an hi frequency. In addition to the energy transfer function, it additionally enables compensation of reactive power in the ac grid when the converter operates at less than rated power. To operate in compensator mode, it is necessary to decouple the current from the grid into active and reactive components and control them independently. To achieve good dynamics, synchronizers that operate in the dq system are used. In the case of a single-phase grid, it requires such a synchronizer to generate virtual quadrature signals. The used systems based on second-order generalized integrator are good, but to improve dynamics in the work a quadrature generator based on trigonometric calculations was proposed. The developed system was implemented in a proportional resonant current control system. Tests performed in steady state and in dynamic states related to typical grid disturbances showed better dynamic properties than the standard integrator-based system.Keywords: power transfer; compensator; P+R controller
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

With the development of power electronic converters, electronic devices and apparatus are replacing traditional mechanical and pneumatic systems. Ease of power control, elimination of mechanical couplings are advantages that characterize more electric applications used in industry, households, as well as in ships, aircraft and space vehicles [1]. Particularly important is the use of electric devices onboard vehicles, where the weight and size of the devices are critical. With the use of electrical devices, it is possible to reduce the size of the device operating at the same power by increasing the frequency of supply voltages. This requires the use of appropriate energy converters that precisely control the power of electrical machines.
The on-board energy management system integrates a number of power buses that have different parameters. Among the typical buses used in on-board electrical systems are DC buses and AC buses. In order to effectively manage energy on an onboard mobile platform, it is often necessary to transfer power to various loads on a continuous or temporary basis. This is particularly important when there are high-power loads on board that are characterized by pulsating operation. Power transmission is carried out with the help of grid converters, which are being studied by many researchers [2,3]. The use of a grid converter connecting a dc bus to a single-phase ac grid causes a number of problems, the main one being the occurrence of power ripples with double grid frequency. The problem of their elimination has been studied in many research centers and presented in many articles [4,5,6,7,8].
The main tasks of the power flow control system of the grid inverter include control of active power and synchronization with grid voltages. If the inverter is not loaded with rated power, its reserve can be used in addition to compensate for reactive power, resulting in a decrease in the rms value of the current, thereby reducing energy losses on the ac buses. With decoupled power control, it is possible to achieve a relatively stable output voltage on the DC bus during disturbances. The most commonly used power control decoupling techniques can be divided into passive decoupling [9,10] and active decoupling [11,12,13]. Although the former is simple to implement, its applications in the aerospace industry are not desirable due to the requirement for large capacitors. Active power decoupling control, on the other hand, is more promising. In the case of DC/DC converters between energy storage and the DC bus, the voltage swing range of the decoupling capacitor can be increased. In the end, the capacitor used for power decoupling can be very small, and the power on the DC bus can be significantly increased. There are two commonly used control strategies for active decoupling, namely series decoupling [14] and parallel decoupling [15,16]. Although series decoupling has higher conversion efficiency, it requires two DC/DC conversion stages, which increases cost and reduces reliability. Meanwhile, the parallel decoupling strategy is widely used in real-world applications because only a bidirectional DC/DC converter is needed, making the system economical and helping to increase the specific power of the system. For three-phase ac systems, a phase-locked loop (PLL) system based on a dq frame is best for controlling active and reactive power [17,18]. In an unbalanced three-phase grid system, the negative sequence of the dual fundamental frequency can affect the accuracy of the PLL. In such a situation, the negative sequence of the AC component can be low-pass filtered out, and the DC component of the positive sequence can be saved for grid phase locking. The authors of [19] and [20] constructed a new array to generate the positive AC component. They used this component for phase locking, thus improving the speed and accuracy of the phase synchronization loop. The performance is affected by power quality parameters such as frequency jumps, amplitude, and phase angle fluctuations, as well as occurring harmonic distortion, so the PLL should operate effectively in a disturbed grid state [21].
For synchronization with a single-phase grid, many synchronization techniques known from three-phase systems with good performance cannot be used. In single-phase grids, Enhanced PLL (EPLL) [22] and Second-Order Generalized Integrator (SOGI-PLL)[23] based techniques are mainly applied. To improve the dynamics and accuracy of the PLL and to reduce the computational burden, the paper proposes a quadrature generator to replace the SOGI system in a PLL operating in a dq frame. The use of a quadrature signal generator, which is simple in digital implementation, eliminates the second-order integral system, replacing it with trigonometric equations. The equations are converted to a form in which only the cosine function needs to be stored in memory. In addition, the look-up table-based structure has a very short access time, which further improves the dynamics of the whole system. The proposed system based on trigonometric formulas (TFB-PLL) was used in a single-phase system for current decoupling. As a result, it is possible to independently set the reference current values corresponding to the active power and reactive power generated in the inverter. Having the ability to set the reactive component of the current has unlocked the possibility of operating the inverter in the reactive power compensator mode, while transferring energy to the on-board ac grid. This mode is limited by the current load of the inverter.
The rest of the article is organized as follows. In Section 2, a system is presented using the proposed TFB-PLL synchronization technique. The block structure of the buses is shown, along with the location of the inverter. The concept of the quadrature generator is described in detail, and the mathematical equations describing the quadrature signals are derived. Based on these equations, the generator is constructed and the general form of the PLL system that uses it is shown. The concept of controlling decoupled current components based on proportional-resonant control is also presented. In Section 3, the tuning procedure of the proposed PLL system is presented and the results of the steady-state and dynamic states of the phase synchronization loop are presented, as well as selected waveforms of the modified on-board system. Section 4 presents the final conclusions.

2. Materials and Methods

The study deals with the control system of energy flow in an on-board power system containing a dc bus and an ac bus. This paper focuses primarily on the control of a power electronic converter, with a role of unidirectional energy transfer from the dc bus to the ac bus in a way that allows simultaneous and independent control of the active and reactive components of the current, enabling simultaneous control of the active power transferred to the ac bus and the reactive power. Controlling the active power allows supply of the required power to the loads connected to the ac bus, while reducing the load of the ac generators. This situation is particularly important when the pulsed equipment on board is powered by the ac bus. Reactive power control allows the use of DC power sources to compensate for reactive power on the ac bus. The volume of transferred active power is determined by its availability on the dc bus and limited by the rating parameters of the power electronic converter. The value of the reactive components of the current is limited not only by the ratings of the converter currents, but also by the value of the active component of the current fed into the ac bus.
Research on the control system was carried out on an existing onboard system, which includes a grid converter with an H-bridge structure as the inverter. This inverter connects the dc bus to the onboard ac system at 400 Hz. An overview system showing the studied structure consisting of ac and dc buses, a grid converter, and a control system is shown in Figure 1. The tasks of the grid converter control system include managing active power and reactive power, which is achieved by controlling the active and reactive components of the current feeding the on-board ac grid. The implementation of this control task requires the use of a modulator circuit that outputs a set current from the grid. This current must have the parameters required to achieve the set values of active and reactive power. These parameters are controlled in a controller system with proportional resonant characteristics. The structure of such a controller, which has better implementation characteristics due to limited gain, is described in detail in [24].
Control of active and reactive components of the power, supplied the ac grid requires a specific system of synchronisation with the its voltage. Determining the reference value of active and reactive power requires the operation of multiplying the reference value of the active and reactive components of the grid converter current by a sine and cosine signal corresponding to the fundamental component of the voltage, respectively. The signals must hold their shape independently of measurement noise and distortion components in the grid voltage. In three-phase systems, synchronisation with the grid voltage is achieved by controlling the xy frame, using the Clark and Park transforms. The system under consideration is a single-phase system, so the Clark transformation cannot be applied. For synchronisation, rather than the SOGI system, the paper proposes a system that was developed based on trigonometric formulas. Assuming that the single-phase on-board grid is sinusoidal, the voltage is described by the formula:
vg = Vg cosωt,
where vg is the voltage waveform of the on-board ac grid, Vg is the voltage amplitude, ω is the angular frequency of the grid. The transition to orthogonal components requires synchronization of the angle θ of xy frame with the voltage vector of the grid defined by the components vα and vβ. The relations between the angles are shown in Figure 2.
Figure 2 shows that the virtual grid voltage vector V g → with orthogonal components vα and vβ can be expressed as:
V g → = v α + j v β = V g   cosω t + j V g   sinω t .
In the fully synchronized state of the system, in the steady-state, the virtual voltage vector of the grid has the same angular angle as the xy frame, which causes the condition to be satisfied:
θ = ωt.
Then the grid voltage vector in xy frame V → = V g → , that can be written as:
V   c o s = V g   c o s ω t V   s i n = V g   c o s ω t .
Applying the well-known trigonometric formulas, we can obtain:
2 s i n x c o s x = s i n 2 x ,
2   c o s 2 x − 1 = c o s 2 x ,
and assuming x = θ/2:
v α = V g c o s θ = 2 V g   c o s 2 θ 2 − V g v β = V g s i n θ = 2   V g   s i n θ 2   c o s θ 2 .
As mentioned, the system of equations (7) follows the trigonometric equations under the assumption of a steady-state. In the transient state, when the system is unsynchronised, these equations should be written as follows:
v α = 2 V g   c o s 2 θ 2 − V g v β = 2   V g   s i n ω t   c o s θ 2 .
Since the on-board system is single-phase, it is possible to use only the cosine component to synchronize the xy frame with the voltage vector. As a result, a computationally simplified system is obtained that replaces the SOGI structure. The proposed system formulates a quadrature signals system (QSS) in block form, as shown in Figure 3.
Based on the proposed equations of establishing the orthogonal components, it is possible to use the conventional PLL structure operating in the dq rotating system. The proposed PLL structure based on a trigonometric formulas (TFB-PLL) is shown in Figure 4.
The orthogonal components calculated from the trigonometric formulas are transformed into the dq system excluding the zero component, according to the relation:
V d V q = cos ⁡ θ sin ⁡ θ − sin ⁡ θ cos ⁡ θ V g cos ⁡ θ V g sin ⁡ θ = V g cos ⁡ ω t − θ sin ⁡ ω t − θ .
When the PI control system reaches steady state, the components of dq can be expressed as (10).
V d V q = V g 1 0 .
Based on the proposed synchronisation rules, when equation (10) is satisfied, control of the active and reactive components of the bus current can be carried out based on the components vα and vβ. The components vα and vβ calculated in the proposed PLL system are used to determine the deviation of the ac bus current eg relative to the reference current iref according to the expression:
e g = i r e f − i g = i a r e f c o s ω t + i r r e f s i n ω t − i g ,
where ig is the measured current of the ac bus, iaref and irref are the active and reactive reference components of the grid current, respectively. The determined value of the deviation eg is the input signal of the proportional-resonant control system with limited gain, described by transmittance shown as (12).
H ( s ) = k s 2 + 1 T k + k R T s + 1 T 2 s 2 + k R T s + 1 T 2 ,
where T is the internal integration constant of the resonant part, k and kR are the gains of the proportional and resonant part, respectively. The proposed control system is shown schematically in Figure 5.

3. Results

The system proposed in the paper for controlling the active and reactive components of the converter's current was tested in an on-board power system that used a single-phase grid inverter. This inverter transferred energy from the DC bus to the 400 Hz AC bus. The main and primary task of the inverter is to supply energy to the on-board ac system from DC power sources. As an improvement on standard control structures, a system is proposed that has the functionality of a reactive power compensator in addition to energy transfer. The system described in Section 2 was implemented in digital form in an Altera FPGA reconfigurable device of the EP2C20 type.
The parameters of the TFB-PLL system shown in Figure 4 were tuned according to the standard procedure. Information about the rated magnitude of A0 was used only to avoid a possible division by zero in the division block. This block was added to make the parameter settings depend on the amplitude of the input signal. The γ constant was assumed to be 0.001. The natural frequency ωn = 0.25ω0 = 628 rad/sec. and a reasonable value of the damping ratio ξ = 0.7 were adopted for a good trade-off between transient time and filtering strength. Based on the assumed coefficients, the TFB-PLL gains were calculated as follows:
k P = 2 ξ ω n = 879
k i = ω n 2 = 394384
By analyzing the transient time of TFB-PLL, it can be shown that the time constant of the system response is around one full cycle of 400 Hz:
τ = 1 ξ ω n ≈ 2.3   m s < 1 f .
In order to limit the range of frequency oscillations caused by a phase angle jump or during the start-up process, an adaptive integral gain ki was added, which can be calculated based on equation (16).
k i = ω n 2 1 1 + ρ v d v q + γ A 0
In the tests carried out, the adaptive function was disabled by taking λ=0. Assuming a nonzero value would reduce false fluctuations in frequency estimation caused by phase jumps at the cost of reducing the actual speed of frequency estimation, and this would limit the formulation of comparative conclusions.
The system was conducted in two directions. In the first path, tests were performed on the TFB-PLL system implemented in an FPGA as a hardware-in-the-loop (HIL) system. The PLL system was run as a system running in parallel with systems that emulate input signals. The second path involved testing using a hardware setup. The investigation conducted in both paths refers to testing in the steady-state and to transient.

3.1. HIL tests

To evaluate the proposed quadrature generator, tests were performed on the HIL system. A digital PLL system was first started and tested by observing the steady-state PLL response. The result of the recorded waveform of the input signal vg and the orthogonal components vα and vβ are shown in Figure 6a. The registration results obtained confirm the assumptions regarding the generation of orthogonal signals, where the correct phase shift and overlap of the vα component signal with the input signal are shown. In the next stage of the study, dynamic tests were performed, in which the PLL system's responses to step changes in input signal parameters were recorded. To estimate the PLL response time tr, the value of the root square error (17) was used from the difference in the instantaneous value of the signal at the PLL's input and output.
e ( t ) = ( v g ( t ) − v α ( t ) ) 2
The system was tested by recording the PLL response to a frequency jump from 400 to 401 Hz, a phase angle jump of pi/4 and a 40% amplitude jump. The results obtained for PLL input and output are shown in Figure 6b–d, respectively.
In the experiment, it was assumed for comparison that the criterion determining the response time of the PLL tr is measured until the signal e reaches a value of 0.01. Using such a criterion, response time measurements were made for step changes in the phase shift angle theta and for step jumps in the frequency Δf. The results obtained are shown in Figure 7, from which it can be concluded that for a step change in the phase shift angle less than 30 degrees and for frequency jumps less than 30 hertz, TFB-PLL establishes steady-state in less than two milliseconds. This is in accordance with the design assumptions implied by formula (15).
In addition to observing the behavior of the input and output of the PLL in steady state and with jumps in the input parameters, the waveforms of the d and q components inside the PLL system and the waveform of the squared error, calculated according to formula (17), were recorded in analogous cases. A summary of the obtained results is shown in Figure 8.
PLL system tests were also performed for an input signal that contains the third harmonic of the fundamental component Ao with an amplitude of 20%. For the cases involving the testing of step changes in the parameters of the input signal, recording of the input and output waveforms was performed along with the waveform of the e signal. The results are shown in Figure 9a. Oscillograms of the dq components along with the waveform of the input signal and the signal e are shown in Figure 9b.
From the analysis of the waveforms obtained, it can be clearly seen that the proposed concept of a quadrature generator in a PLL system based on the dq transformation meets the basic requirements and is a good alternative to other well-known quadrature systems. However, to expose the advantages of the proposed system, a comparative analysis was carried out. In this analysis, analogous tests of a quadrature system with a SOGI structure were performed and the quadrature signals for the two systems under comparison were recorded in a parallel manner. Figure 10a shows the waveforms of the orthogonal components vα and vβ during the start of the PLL loop for the variant with the proposed generator and for the SOGI generator. Since the proposed system is based on trigonometric formulas, it does not show the existence of significant transient components in this case. For the SOGI system, the transient is clearly shown and is about five periods of the input signal. In the case of a step change in frequency from 400 to 401 Hz, the obtained waveforms are shown in Figure 10b. In this case, the influence of the SOGI integrator system is also clearly shown in the form of significant values of the transient component appearing. Against the signals of the SOGI system, the transient in the proposed system is not noticeable. The same conclusions can be reached by observing the output signals of the proposed system and the SOGI-based system for a step change in phase angle by π/4 and for a step change in amplitude to 60%, as shown in Figure 10c,d, respectively.
The performed tests of the PLL system implemented in the FPGA, which included tests in steady-state and transients caused by step changes in the parameters of the input signal, allow us to conclude that the TFB system proposed in the paper can be used as a good equivalent to standard quadrature generators. This is further confirmed by a comparative analysis of the results obtained for the SOGI system.

3.2. Hardware setup tests

Successful testing of the TMB-PLL in the HIL system allowed a further experiment to be carried out. This experiment referred to the testing of the on-board system, the schematic of which is shown in Figure 1. In the same FPGA structure, the current proportional-resonant control processes and the inverter modulator were implemented. Since the control system allows independent control of the active and reactive components of the current, it was run with the TMB-PLL system proposed in the paper. The experiment was planned in such a way that the current and voltage waveforms of the grid were recorded for a dynamic state consisting of a step change in the reference value of the active component of the current with zero reactive component, a static state for the same values of the active and reactive reference components, for a dynamic state corresponding to a constant active component of the current and the appearance of an inductive reactive component, and for a dynamic state corresponding to the task of a step change in the reactive component of the current with a constant reference value of the active component. The case when the active component changes from 4 to 8 A in the absence of the reactive component is shown in Figure 11a. The recorded current is in phase with the voltage, indicating that the inverter is in the mode of injecting energy from the dc source into the 400Hz onboard grid. Figure 11b shows the current and voltage of the grid in the static state when the inverter is set in the additive reactive power compensation mode of the grid. The set values for the reference active component and the reference inductive reactive component are 4 A. In this case, the current waveform should be 45 electrical degrees ahead of the voltage waveform, which is confirmed by the oscillogram shown. The case of operation with a step forcing of the reference inductive and capacitive reactive component of 4 A with a reference active component of 4A is shown in Figure 11c and Figure 11d, respectively. The appearance of an inductive and capacitive angle shift of 45 degrees is shown in the included oscillograms. Figure 11 also confirms the rule of graphical orthogonal vector folding, where for nonzero active and reactive components, the amplitude of the grid current rises.
After experimentally verifying the current and voltage waveforms relating to the reconstruction of the reference values of the active and reactive components of the current, steps in the grid voltage parameters. The case of a drop in the grid voltage to 80% of the nominal value of the amplitude and a step change in the phase angle in the grid voltage by an angle of π/4 was recorded. In the case shown in Figure 12a, as a result of the drop in grid voltage, a step change in the active component of the voltage with zero reactive component. This is due to the fact that the analyzed case referred to a compensated grid. From the lack of change in the amplitude of the grid current, it can be deduced that the control system is feeding energy into the grid at a preset level, undisturbed by the voltage drop. A step change in the phase angle of the grid voltage results in the appearance of disturbances in the recorded vd and vq signals in TFB-PLL. These disturbances are reduced as the control system becomes synchronous with the grid voltage. The current at such a disturbance does not show changes that would allow us to conclude that the basic function of the converter, i.e. feeding energy into the grid at a set level, has been disturbed. This case is illustrated in Figure 12b.
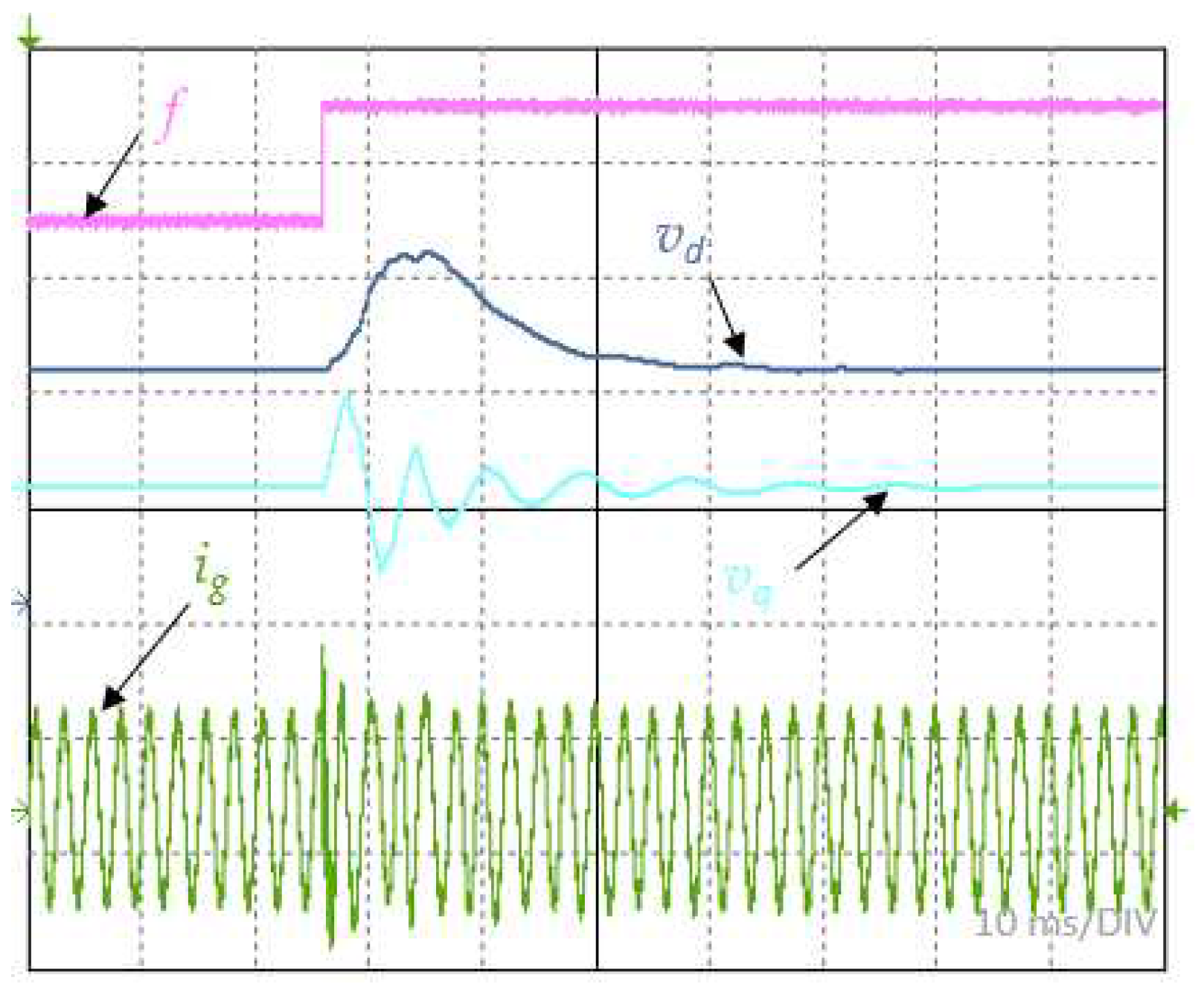
The disturbance in the flow of energy to the grid is most affected by the change in frequency of the grid voltage. This disturbance is affected not only by the dynamics of the PLL system, but also by the dynamics of the control system and delays in the measurement tract. Figure 13 shows the response observed in the amplitude of the grid current, which resulted from a 1% step change in frequency. A clear reduction in the current amplitude is shown after the disturbance occurred, which was suppressed after about 50 ms. Considering the results presented in Section 3.1, it can be concluded that this is the effect of the control system going out from its resonant frequency. Taking into account the fact that this type of disturbance generally does not occur in on-board grids, and if it does occur, it is in a transient manner, where the frequency returns to its rated value after a short time, this problem was considered to be of little importance.

4. Conclusions

The method proposed in this paper for generating quadrature signals necessary for synchronization with the grid of the proportional-resonant control system is characterized by short response times with respect to other methods used in PLL systems. Due to the fact that calculations are performed based on trigonometric formulas, the dynamics of TFB-PLL is better than that of the most commonly used SOGI-PLL system. Allowing synchronization with a single-phase dq on-board grid makes the grid current decouple into active and reactive components. Due to such decoupling of current components, the underloaded to rated values inverter can be used as a compensator for reactive power appearing in the on-board grid. Experiments show that a system with very good dynamics has been obtained, meeting the requirements formulated at the beginning. In further work on the system, studies are planned to adapt the system's parameters to improve dynamics even more.

Funding

This research was funded by the Minister of Education and Science of the Republic of Poland within the “Regional Initiative of Excellence” program for years 2019–2023. Project number 027/RID/2018/19. The APC was funded by private funds.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The author declares no conflict of interest.

References

  1. Parripati, M.; Devi, V. A Single Phase DC-AC Inverter for Aircraft Application. In Proceedings of the Fourth International Conference on Inventive Systems and Control (ICISC), Coimbatore, India, 8–10 January 2020; pp. 250–255. [Google Scholar]
  2. Kjær, S.; Pedersen, J.; Blaabjerg, F. A Review of Single-Phase Grid-Connected Inverters for Photovoltaic Modules. IEEE Trans. Ind. Appl. 2005, 41, 1292–1306. [Google Scholar] [CrossRef]
  3. Tang, Y.; Blaabjerg, F. Power decoupling techniques for single-phase power electronics systems—An overview. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 2541–2548. [Google Scholar]
  4. Vitorino, M.; Alves, L.; Wang, R.; Correa, M. Low-Frequency Power Decoupling in Single-Phase Applications: A Comprehensive Overview. IEEE Trans. Power Electron. 2017, 32, 4. [Google Scholar] [CrossRef]
  5. Zhang, L.; Ruan, X. Control Schemes for Reducing the Second Harmonic Current in Two-Stage Single-Phase Converter: An Overview from DC-Bus Port-Impedance Characteristic. IEEE Trans. Power Electron. 2019, 34, 10341–10358. [Google Scholar] [CrossRef]
  6. Zhang, L.; Ruan, X.; Ren, X. Second Harmonic Current Reduction for Two-Stage Inverter with Boost-Derived Front-End Converter: Control Schemes and Design Considerations. IEEE Trans. Power Electron. 2017, 33, 6361–6378. [Google Scholar] [CrossRef]
  7. Shi, Y.; Liu, B.; Duan, S. Low-Frequency Input Current Ripple Reduction Based on Load Current Feed-Forward in Two-Stage Single-Phase Inverter. IEEE Trans. Power Electron. 2015, 31, 7972–7985. [Google Scholar] [CrossRef]
  8. Binkowski, T. A Conductance-Based MPPT Method with Reduced Impact of the Voltage Ripple for One-Phase Solar Powered Vehicle or Aircraft Systems. Energies 2020, 13, 1496. [Google Scholar] [CrossRef]
  9. Crider, J.M.; Sudhoff, S.D. Reducing impact of pulsed power loads on microgrid power systems. IEEE Transactions on Smart Grid 2010, Volume 1, pp. 270-277. [CrossRef]
  10. Gu, Y.; Zhang, D.; Fang, M.; Zhang, X.; Qi, P. Research on low input current ripple two-stage converter for low frequency pulsed-power applications. IET Power Electronics 2020, Volume 13, pp. 340-345. [CrossRef]
  11. Huang, X.; Ruan, X.; Du, F.; Fei, L.; Li, Z. A pulsed power supply adopting active capacitor converter for low-voltage and low-frequency pulsed loads. IEEE Transactions on Power Electronics 2018, Volume 33, pp. 9219- 9230. [CrossRef]
  12. Yang, P.; Shang, Z.; Liu, C.; Peng, Y.; Zhu, Z. A three-state dual inductance bi-directional converter and its control in pulse-loaded three-port converters, CSEE Journal of Power and Energy Systems 2020, Volume 6, pp. 291-297. [CrossRef]
  13. Huang, X.; Ruan, X.; Du, F.; Fei, L.; Li, Z. High power and low voltage power supply for low frequency pulsed load. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition, Tampa, USA; 2017. [Google Scholar]
  14. Yang, X.; Chen, P.; Chen, R.; Peng, Y.; Xu, J. Stability Improvement of Pulse Power Supply With Dual-Inductance Active Storage Unit Using Hysteresis Current Control. IEEE Journal on Emerging and Selected Topics in Circuits and Systems 2021, Volume 11, pp. 111-120. [CrossRef]
  15. Crider, J.M.; Sudhoff, S.D. Reducing impact of pulsed power loads on microgrid power systems. IEEE Transactions on Smart Grid 2010, Volume 1, pp. 270-277. [CrossRef]
  16. W. Xiao, M. S. El Moursi, O. Khan, and D. Infield, Review of grid-tied converter topologies used in photovoltaic systems, IET Renew. Power Gener., vol. 10, no. 10, pp. 1543–1551, 2016. [CrossRef]
  17. C. Subramanian, and R. Kanagaraj, Single-phase grid voltage attributes tracking for the control of grid power converters, IEEE J. Emerg. Sel. Topics Power Electron., vol. 2, no. 4, pp. 1041-1048, Dec. 2014. [CrossRef]
  18. Z. Yan, H. He, J. Li, M. Su and C. Zhang, Double fundamental frequency PLL with second order generalized integrator under unbalanced grid voltages, 2014 International Power Electronics and Application Conference and Exposition, 2014, pp. 108-113.
  19. Z. Guo, Q. Zhang, C. Zhang, J. Pang and Z. Yan, A new method of double fundamental frequency phase-locked loop based on two integrators, 2016 Sixth International Conference on Instrumentation & Measurement, Computer, Communication and Control (IMCCC), 2016, pp. 659-664.
  20. L. Zheng, H. Geng and G. Yang, Fast and robust phase estimation algorithm for heavily distorted grid conditions, IEEE Trans. Ind. Electron., vol. 63, no. 11, pp. 6845-6855, Nov. 2016. [CrossRef]
  21. S. Golestan, J. M. Guerrero, and J. C. Vasquez, Single-phase PLLs: a review of recent advances, IEEE Trans. Power Electron., vol. 32, no. 12, pp. 9013–9030, Dec. 2017. [CrossRef]
  22. R. Zhang, M. Cardinal, P. Szczesny, and M. Dame, A grid simulator with control of single-phase power converters in D-Q rotating frame, in Proc. IEEE Power Electron. Spec. Conf., Jun. 2002, pp. 1431–1436. [CrossRef]
  23. M. Karimi-Ghartemani, H. Karimi, S. A. Khajehoddin and S. M. Hoseinizadeh, Efficient modeling and systematic design of enhanced phase-locked loop structures, IEEE Trans. Power Electron., vol. 37, no. 8, pp. 9061-9072, Aug. 2022. [CrossRef]
  24. Nowak, M.; Binkowski, T.; Piróg, S. Proportional-Resonant Controller Structure with Finite Gain for Three-Phase Grid-Tied Converters. Energies 2021, 14, 6726. [Google Scholar] [CrossRef]
Preprints 90949 g001
Figure 1. Diagram of the on-board power distribution system.
Figure 1. Diagram of the on-board power distribution system.
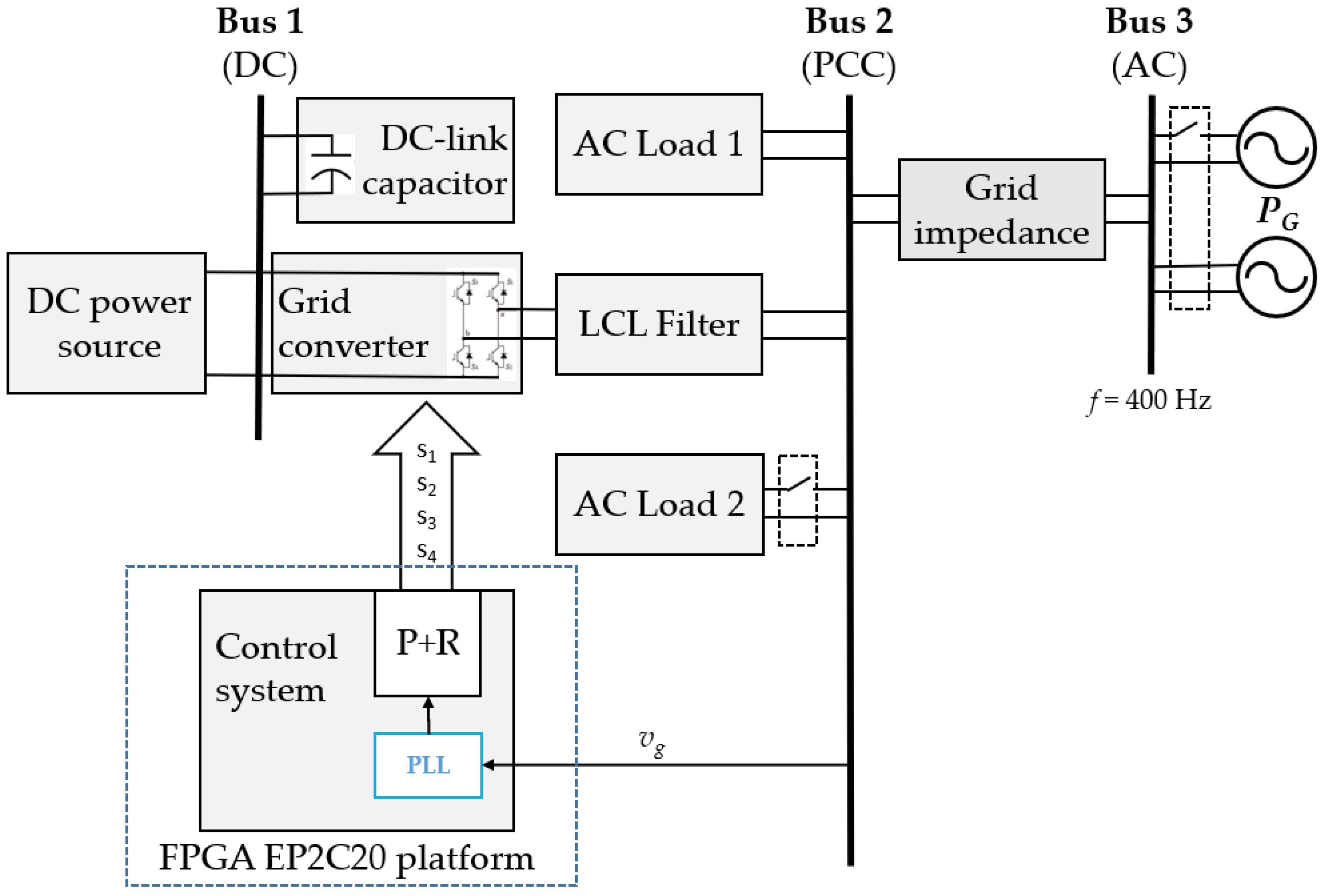
Preprints 90949 g001
Preprints 90949 g002
Figure 2. Graphical interpretation of orthogonal signal generation.
Figure 2. Graphical interpretation of orthogonal signal generation.
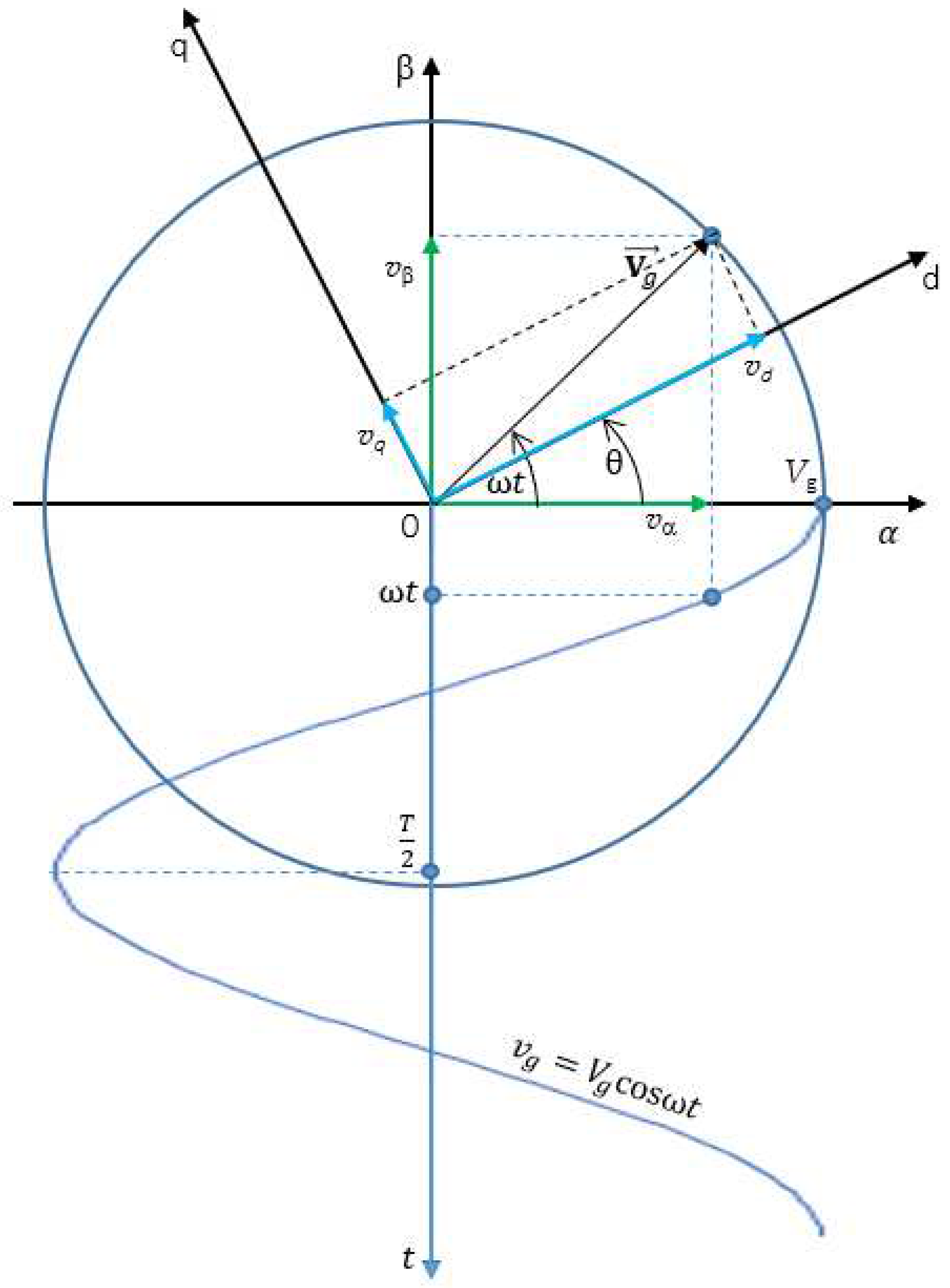
Preprints 90949 g002
Preprints 90949 g003
Figure 3. Block structure of the quadrature signal generator.
Figure 3. Block structure of the quadrature signal generator.
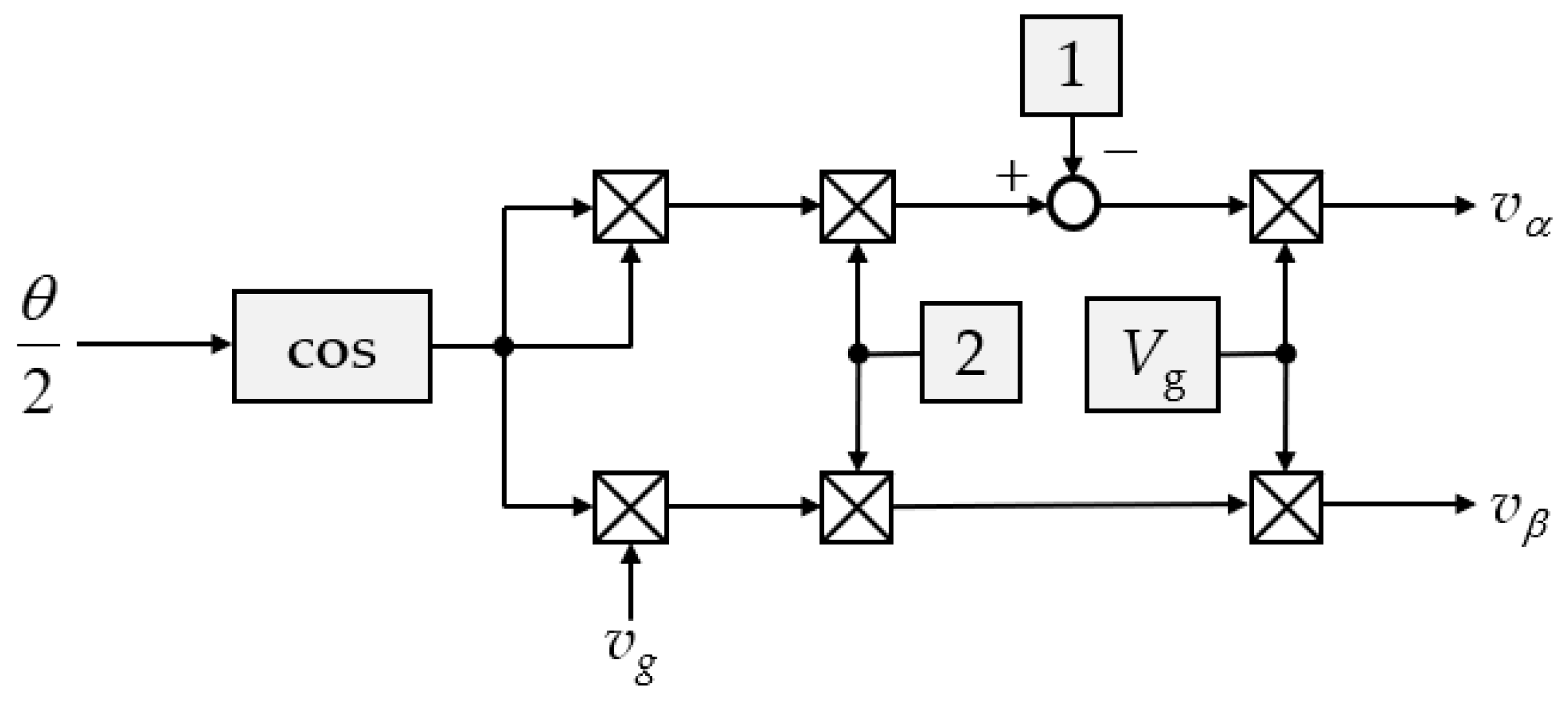
Preprints 90949 g003
Preprints 90949 g004
Figure 4. Block diagram of the single-phase PLL with proposed QSS, where: input signal (vg), orthogonal components (vα and vβ), dq0-axis components of the input (vd, vq and v0), rated frequency of the input (ω0), unitary output signal synchronous with the input (x), delayed unitary output signal (y), estimated angle (θ), estimated frequency (ω), proportional gain (kP) and integrating gain (ki).
Figure 4. Block diagram of the single-phase PLL with proposed QSS, where: input signal (vg), orthogonal components (vα and vβ), dq0-axis components of the input (vd, vq and v0), rated frequency of the input (ω0), unitary output signal synchronous with the input (x), delayed unitary output signal (y), estimated angle (θ), estimated frequency (ω), proportional gain (kP) and integrating gain (ki).
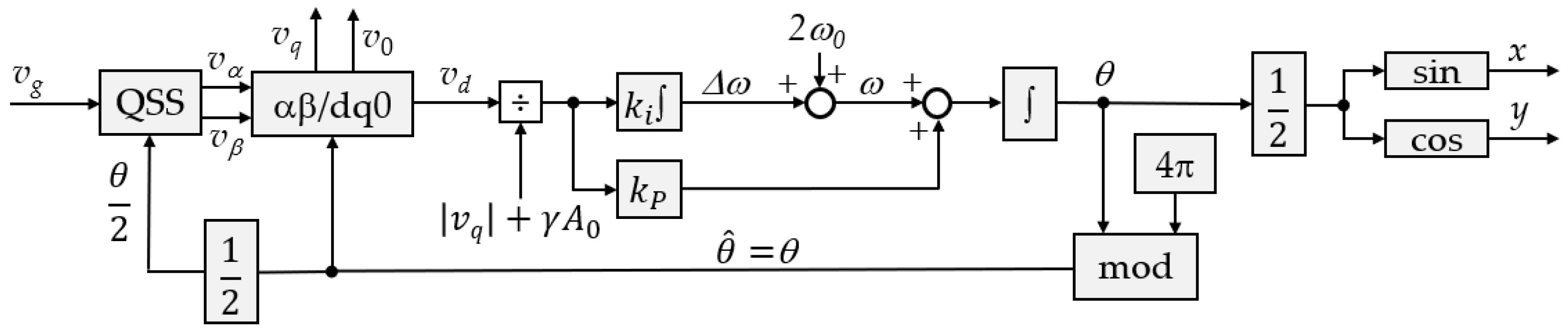
Preprints 90949 g004
Preprints 90949 g005
Figure 5. Block diagram of the proposed control system with the TFB-PLL.
Figure 5. Block diagram of the proposed control system with the TFB-PLL.
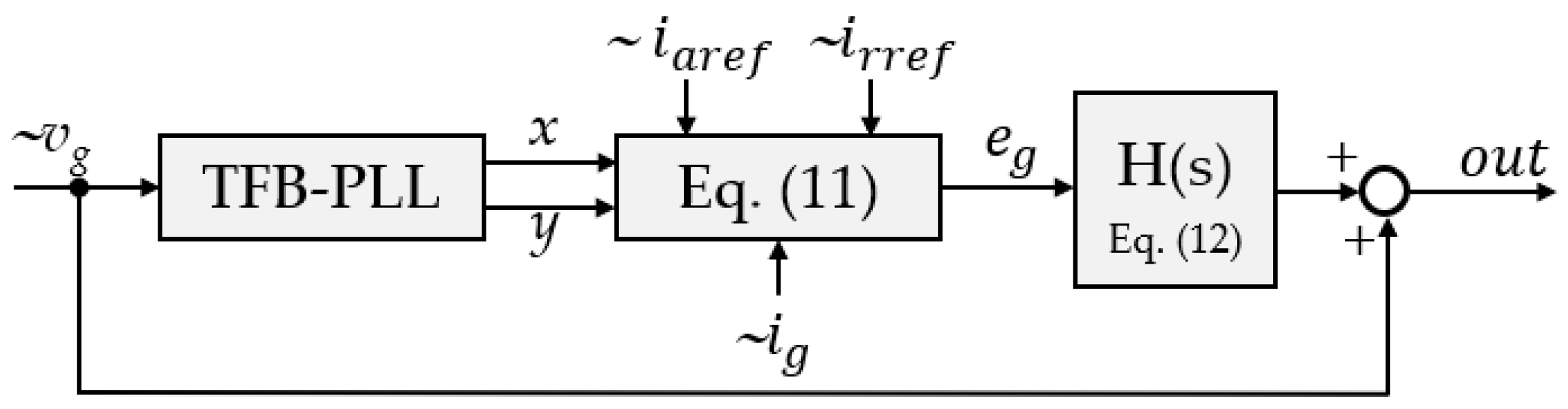
Preprints 90949 g005
Preprints 90949 g006
Figure 6. Signals of the proposed TFB-PLL: (a) waveforms of the input signal vg and orthogonal response signals vα and vβin steady-state; (b) waveforms of the input signal vg, orthogonal response signals vα and vβand frequency f during the frequency jump; (c) waveforms of the input signal vg, response signal vα , phase angle θ and error e during the phase angle jump; (d) waveforms of the input signal vg, response signal vα , amplitude A and error e during the amplitude jump.
Figure 6. Signals of the proposed TFB-PLL: (a) waveforms of the input signal vg and orthogonal response signals vα and vβin steady-state; (b) waveforms of the input signal vg, orthogonal response signals vα and vβand frequency f during the frequency jump; (c) waveforms of the input signal vg, response signal vα , phase angle θ and error e during the phase angle jump; (d) waveforms of the input signal vg, response signal vα , amplitude A and error e during the amplitude jump.
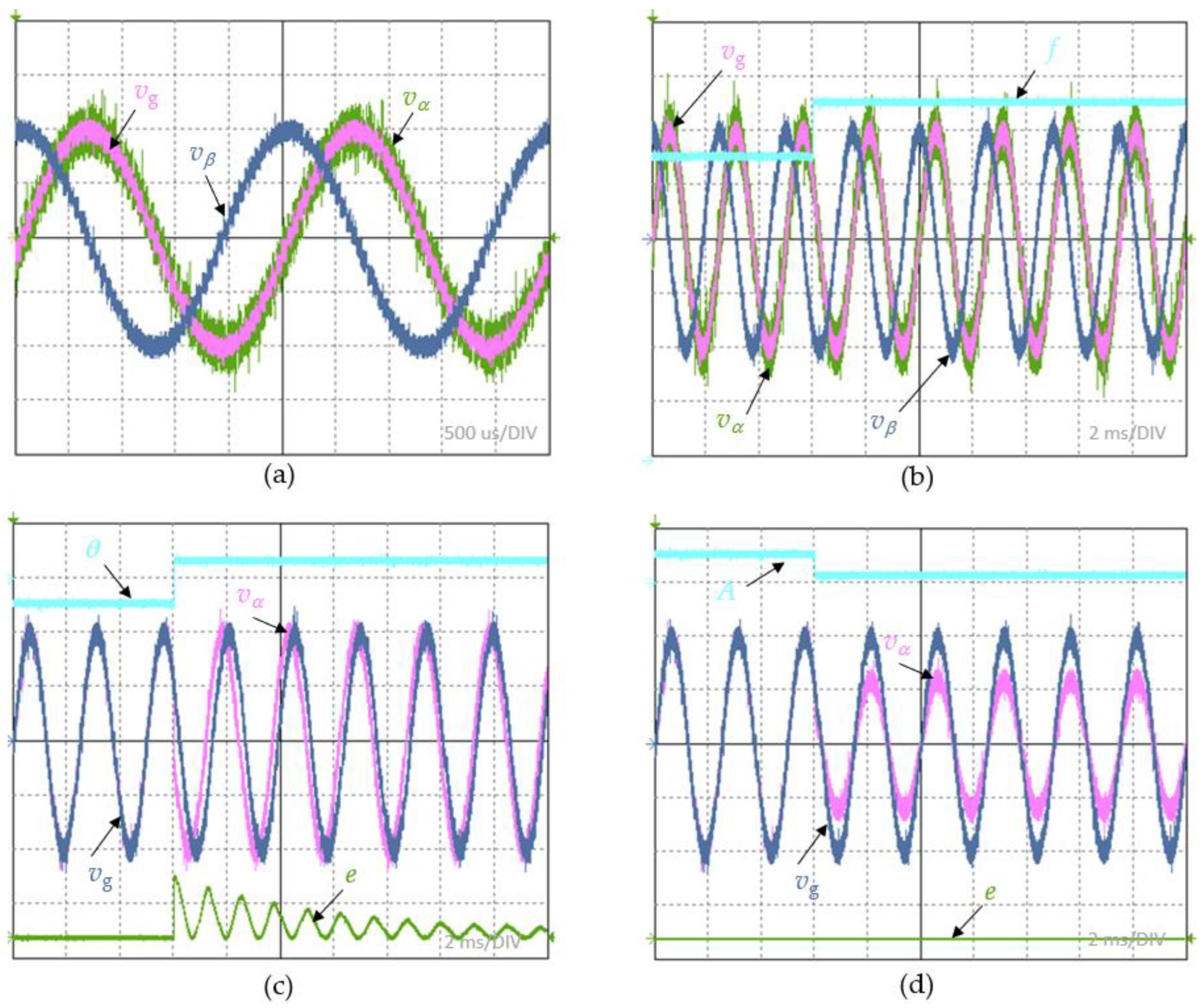
Preprints 90949 g006
Preprints 90949 g007
Figure 7. TFB-PLL response times as a function of phase angle jump and frequency jump values.
Figure 7. TFB-PLL response times as a function of phase angle jump and frequency jump values.
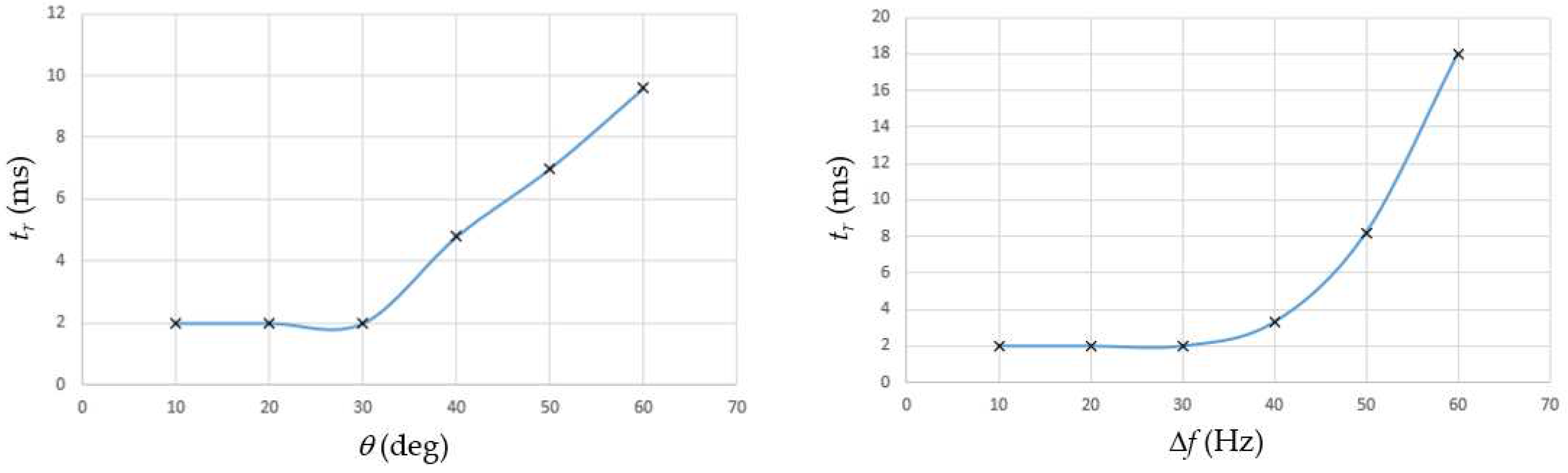
Preprints 90949 g007
Preprints 90949 g008
Figure 8. Signals of the proposed TFB-PLL: (a) waveforms of the input signal vg , response dq signals vd , vqand error signal e in steady-state; (b) waveforms of the input signal vg , response dq signals vd, vqand error signal e during the frequency jump; (c) waveforms of the input signal vg , response dq signals vd , vqand error signal e during the phase angle jump; (d) waveforms of the input signal vg , response dq signals vd , vqand error signal e during the amplitude jump.
Figure 8. Signals of the proposed TFB-PLL: (a) waveforms of the input signal vg , response dq signals vd , vqand error signal e in steady-state; (b) waveforms of the input signal vg , response dq signals vd, vqand error signal e during the frequency jump; (c) waveforms of the input signal vg , response dq signals vd , vqand error signal e during the phase angle jump; (d) waveforms of the input signal vg , response dq signals vd , vqand error signal e during the amplitude jump.
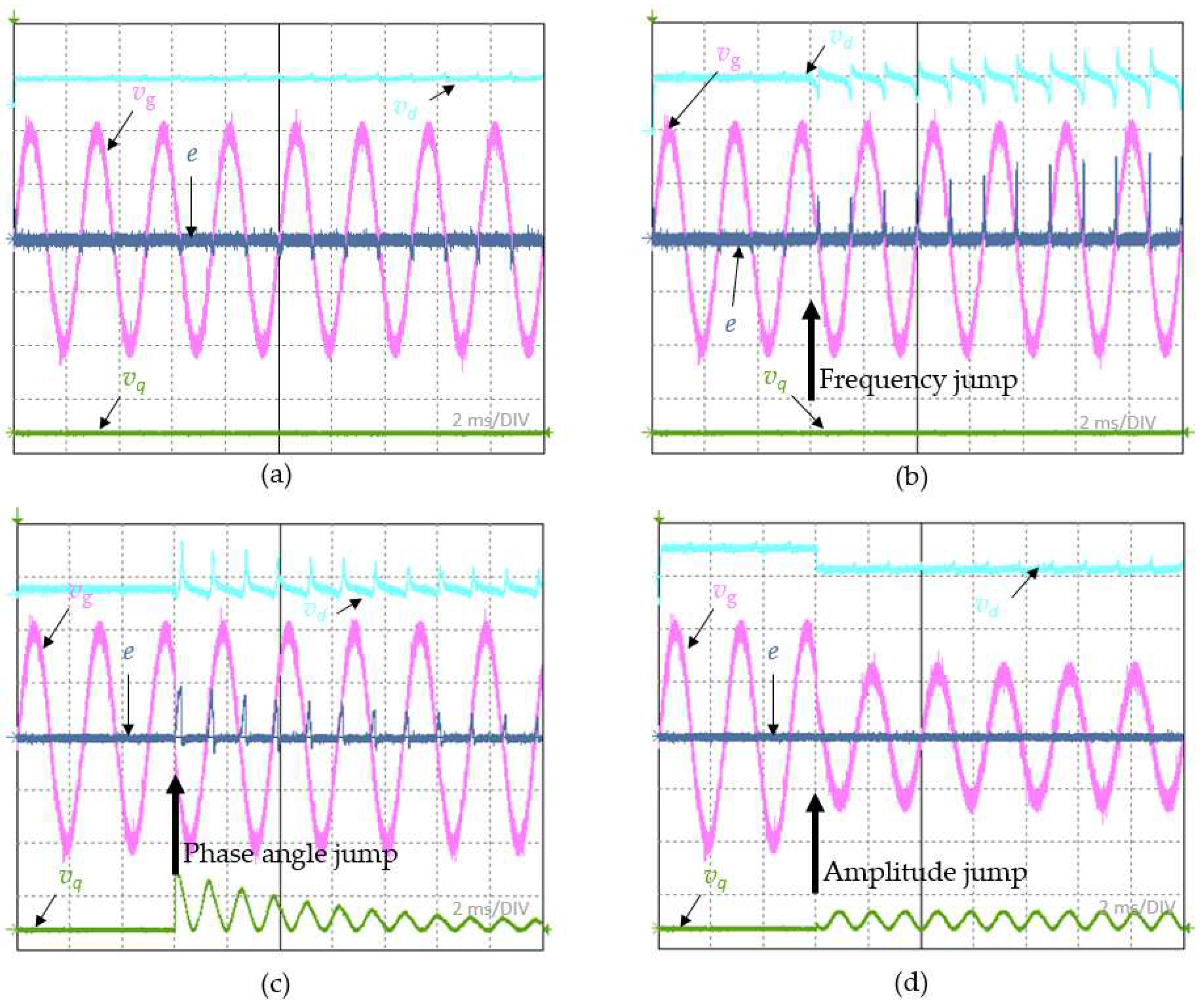
Preprints 90949 g008
Preprints 90949 g009
Figure 9. Signals of the proposed TFB-PLL for distortion of the third harmonic: (a) waveforms of the input signal vg, orthogonal response signals vα and vβand error signal e (b) waveforms of the input signal vg , response dq signals vd, vq, and error signal e.
Figure 9. Signals of the proposed TFB-PLL for distortion of the third harmonic: (a) waveforms of the input signal vg, orthogonal response signals vα and vβand error signal e (b) waveforms of the input signal vg , response dq signals vd, vq, and error signal e.
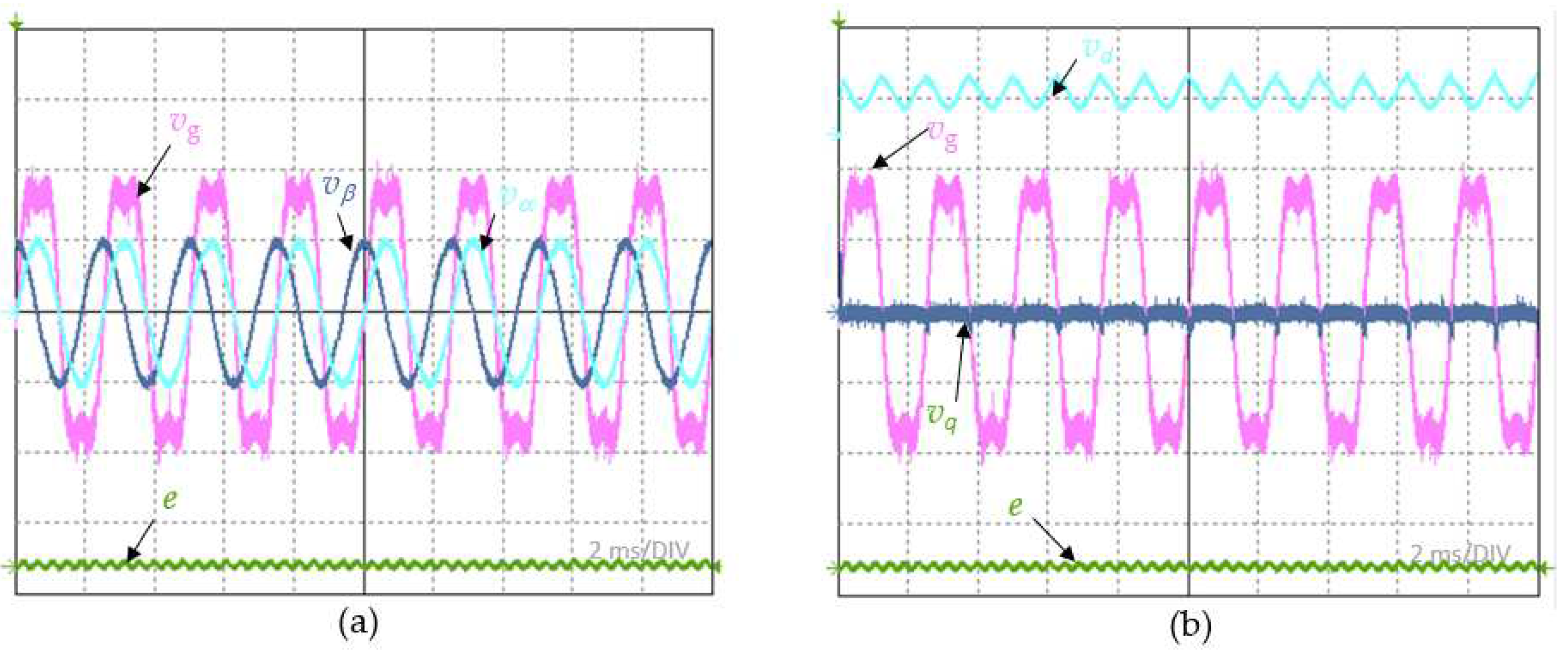
Preprints 90949 g009
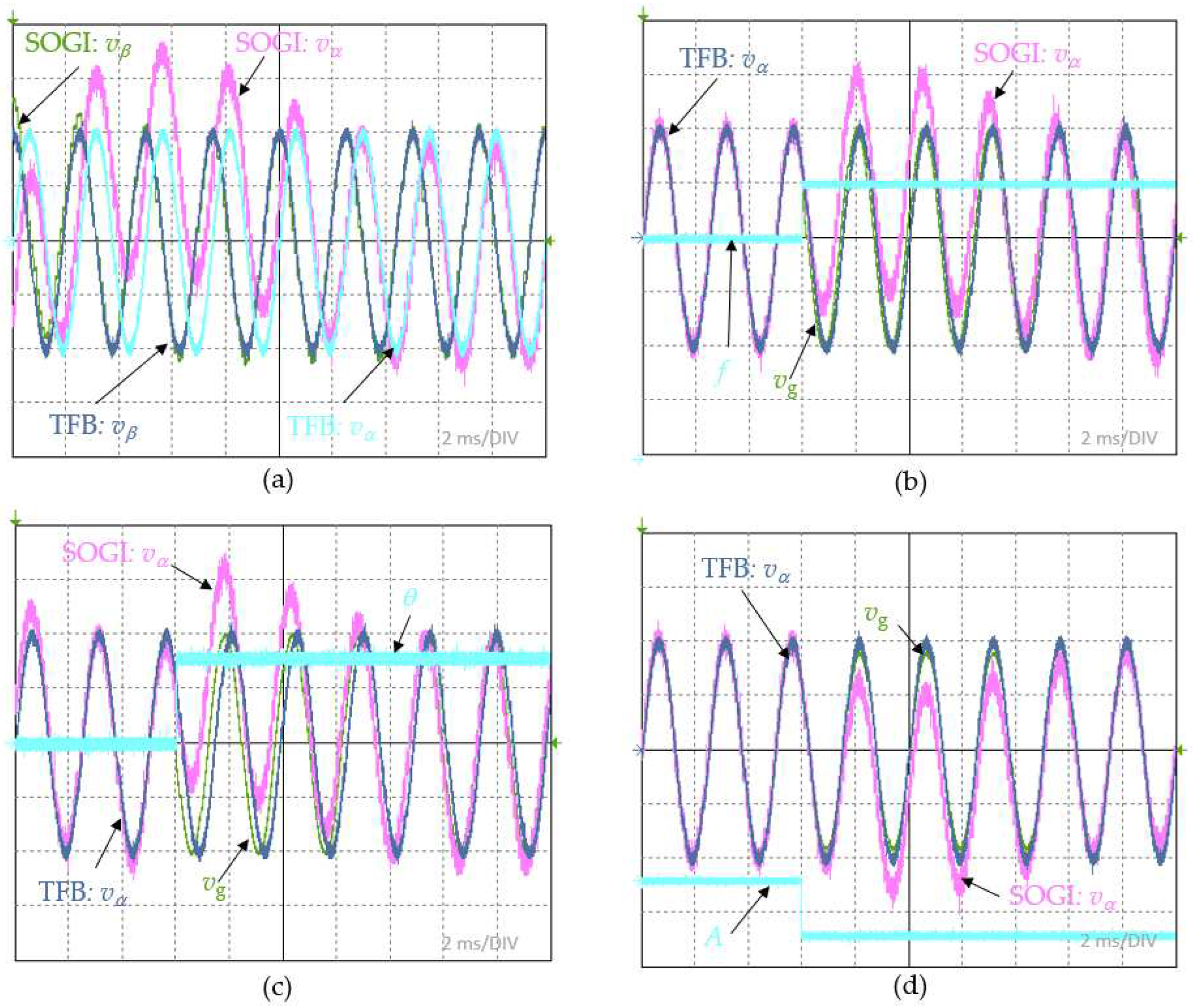
Preprints 90949 g010
Figure 10. Comparison of orthogonal waveforms for: (a) SOGI system and proposed TFB system in steady state; (b) SOGI system and proposed TFB system for the frequency jump; (c) SOGI system and proposed TFB system for the phase angle jump; (d) SOGI system and proposed TFB system for the amplitude jump;.
Figure 10. Comparison of orthogonal waveforms for: (a) SOGI system and proposed TFB system in steady state; (b) SOGI system and proposed TFB system for the frequency jump; (c) SOGI system and proposed TFB system for the phase angle jump; (d) SOGI system and proposed TFB system for the amplitude jump;.
Preprints 90949 g010
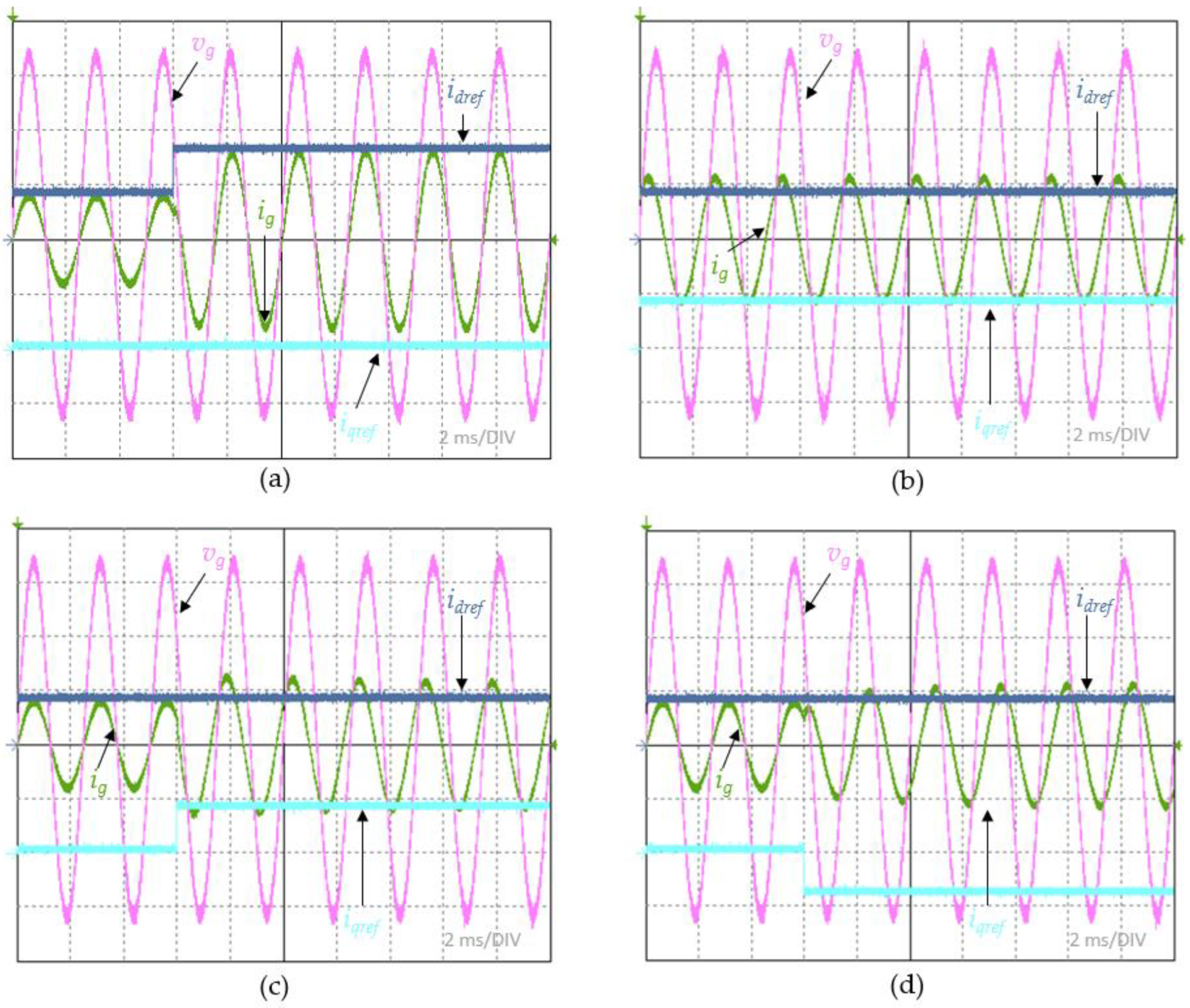
Preprints 90949 g011
Figure 11. Waveforms of the grid voltage vg, grid current ig, referenced active component idref, referenced reactive component iqref of the on-board system for: (a) zero reactive component and active component jump from 4 to 8 A; (b) 4A reactive and active component; (c) jump from 0 to 4A inductive reactive component and 4A active component; (d) jump from 0 to 4A capacitive reactive component and 4A active component.
Figure 11. Waveforms of the grid voltage vg, grid current ig, referenced active component idref, referenced reactive component iqref of the on-board system for: (a) zero reactive component and active component jump from 4 to 8 A; (b) 4A reactive and active component; (c) jump from 0 to 4A inductive reactive component and 4A active component; (d) jump from 0 to 4A capacitive reactive component and 4A active component.
Preprints 90949 g011
Preprints 90949 g012
Figure 12. Waveforms of the grid voltage vg, grid current ig, and dq components id, iq of the on-board system for: (a) 10% voltage drop; (b) phase angle jump.
Figure 12. Waveforms of the grid voltage vg, grid current ig, and dq components id, iq of the on-board system for: (a) 10% voltage drop; (b) phase angle jump.
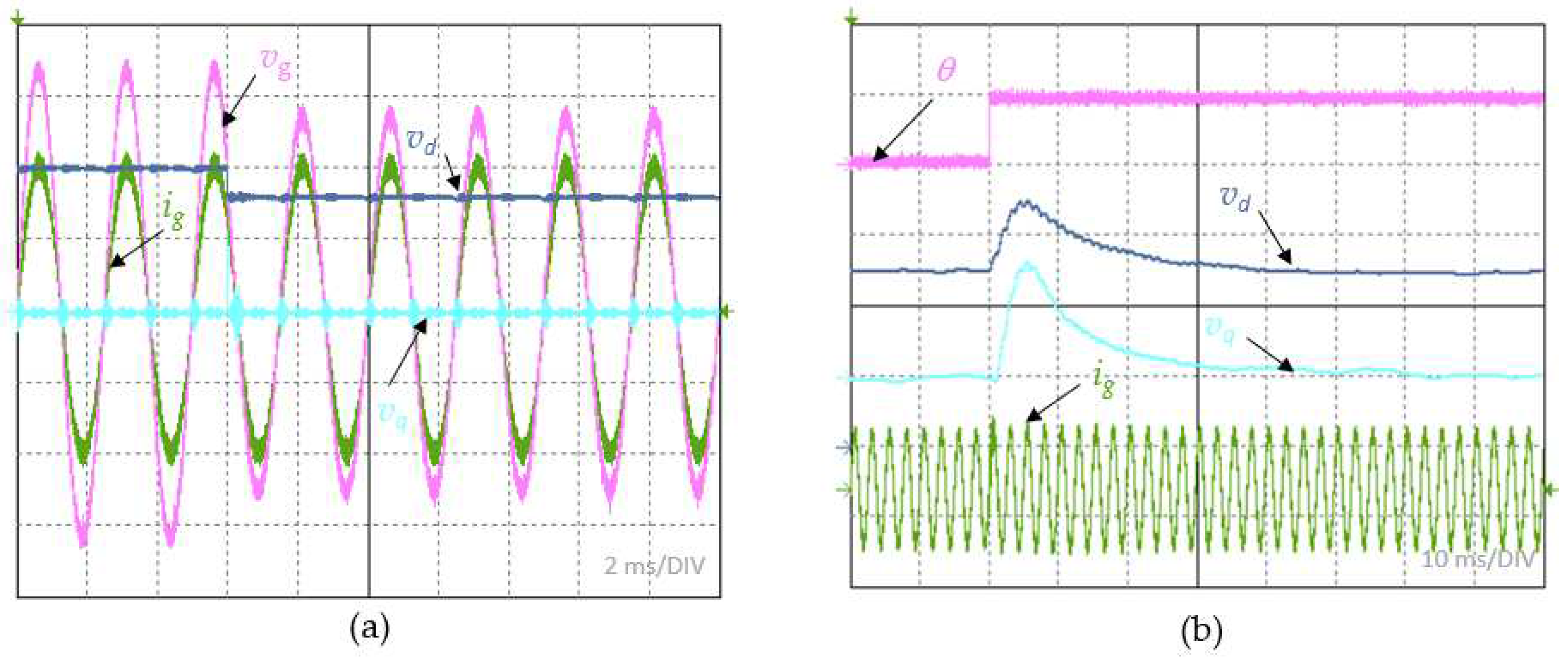
Preprints 90949 g012
Preprints 90949 g013
Figure 13. Waveforms of the grid current ig and dq components id, iq of the on-board system for the frequency jump.
Figure 13. Waveforms of the grid current ig and dq components id, iq of the on-board system for the frequency jump.
Preprints 90949 g013
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated