Prerpints.org logo
Preprint
Article

Fraxicon for Optical Applications with Aperture ∼1 mm

Altmetrics

Downloads

207

Views

77

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

19 November 2023

Posted:

21 November 2023

You are already at the latest version

Alerts
Abstract
Emerging applications of optical technologies are driving the development of miniaturised light sources, which in turn require the fabrication of matching micro-optical elements with sub-1 mm cross sections and high optical quality. This is particularly challenging for spatially-constrained biomedical applications where reduced dimensionality is required, such as endoscopy, optogenetics, or optical implants. Planarisation of a lens by the Fresnel lens approach was adapted for a conical lens (axicon) and was made by direct femtosecond 780 nm/100 fs laser writing in SZ2080™polymer with photo-initiator. Optical characterisation of the positive and negative fraxicons is presented. Numerical modeling of fraxicon optical performance under illumination by incoherent and spatially extended light sources is compared with the ideal case of plane wave illumination. Considering the potential for rapid replication in soft polymers and resists, this approach holds great promise for the most demanding technological applications.
Keywords: 
Subject: Biology and Life Sciences  -   Biophysics

1. Introduction

High resolution 3D printing over large areas remains a formidable challenge, especially for optical applications at shorter wavelengths. Maintaining low surface roughness of one-tenth of the wavelength λ / 10 or less adds to the challenge. Making flat micro-optical elements for further miniaturisation and compaction of micro-optical solutions is currently trending, but this is even more challenging for fabrication of optical micro-lenses and functional structures. For controlled phase patterns in diffractive optical elements this is of particular importance and a phase step should be defined over the most narrow lateral width (a step-like height change).
Control of focusing from tight ( < 10 λ ) to loose ( > 10 λ ) is dependent on the curvature and diameter of the lens D and its focal length f, which defines the f-number F # = f / D , i.e. the numerical aperture N A ≈ 1 / 2 F # , and the imaging resolution of the lens. More demanding precision is required for larger micro-optics with a large N A . For flat optical elements, e.g., Fresnel lenses, the 2 π phase height (along the light propagation direction) is defined over the height of wavelength ∼ λ , which approaches a comparable lateral width for the most off-center phase rings. This is a challenging 3D laser polymerisation task demanding the most high resolution laser printing.
High resolution structures can be made via photo-initiator-free laser writing at high pulse intensity I p ∼ ( 1 − 10 ) × 10 12 W/cm2 or (1-10) TW/cm2 [1]. At such high intensities, the photon energy h ν ≈ 1.24 / ( λ [ μ m ] ) [eV] approaches the ponderomotive energy (potential) of an electron, i.e. the cycle-averaged quiver energy of a free electron in an electromagnetic field of light: U p [eV] = 9.33 × ( λ [ μ m ] ) 2 × I p [ 10 14 W / cm 2 ]. For λ ∼ 1 μ m and I p ≈ 10 TW/cm2, the electron quiver energy during one optical cycle reaches U p ≈ 0.93 eV, which is comparable to the photon energy h ν ≈ 1.24 eV. Hence, photo-ionisation of the polymer matrix ( ∼ 99 wt.%) can take place without a photo-initiator, which is usually doped at below 1 wt% for the wavelength-specific two-photon absorption. Nonlinear or defect-based absorption provides free electrons which promote further ionisation and chemical bond breaking via the ponderomotive channel and avalanche ionisation.
Another effective polymerisation pathway is via high-MHz repetition rate exposure of photo-resist, which facilitates thermal accumulation and cross-linking even with a very small initial temperature augmentation due to low sub-1 nJ pulse energy. Low thermal diffusivity of the glass substrate and resist D T = χ / ( c p ρ ) ≈ 7 × 10 − 7 [m2/s] [2] enhance the local temperature rise (here χ ≈ 1 [W·m−1·K−1] is the thermal conductivity, ρ ≈ 2.2 [g/cm−3] is the mass density, and c p ≈ 700 [J/(kg·K)] is heat capacity at constant pressure). High repetition rate laser writing was therefore used in this study. Ionisation of the photo-resist modifies the real and imaginary parts of the refractive index n ˜ = n + i κ , i.e. permittivity ε ≡ n ˜ 2 , which defines energy deposition. When the real part of the permittivity ϵ r e ≡ ( n 2 − κ 2 ) → 0 (epsilon-near-zero ENZ) enters 0 < ϵ r e < 1 , the most efficient energy deposition into resist takes place [3]. It is noteworthy that the condition of ε r e = 0 (or n = κ ) defines a runaway process of dielectric breakdown at the focus, which should be avoided for high precision and resolution of 3D polymerised structures.
Designing and manufacturing 3D polymerized structures for beam modulation is more challenging in an integrated optics framework. In most research reports, including distributed Bragg reflector (DBR) laser-based optics where the periodicity of grating elements is parallel to the beam propagation [4], and cases where the periodicity is perpendicular to the beam propagation [5], binary elements are manufactured. This is because the short integration distance often demands short period grating elements, and achieving multiple levels within that short period is challenging.
Here, we demonstrate 3D laser printing of a 0.2-mm-diameter fraxicon (flat conical lens) with a triangular phase profile ( 2 π over ∼ 1 μ m height) at 5 μ m width in SZ2080 resist for integration with a micro light-emitting diode (micro-LED). The lateral step-width was defined within ∼ 1 μ m. Characterisation of the fraxicon performance was carried out with optical microscopy and several optical numerical modeling methods: ray-tracing, analytical solution for Gaussian input, Rayleigh–Sommerfeld (RS) diffraction integral, and holographic simulation.

2. Materials and Methods

2.1. Laser printing and resist

3D laser printing of fraxicons was made by 780 nm/100 fs (C-Fiber 780 Erbium Laser, MenloSystems) tightly focused conditions using an objective lens of numerical aperture N A = 1.4 with a beam diameter saturating the input aperture for optimal resolution. The radius at focus is r = 0.61 λ / N A ≈ 340 nm. The pulse repetition rate was 100 MHz. A combination of fast galvanometric scanners and synchronized precision positioning stages were used, similar to the system described in [6]. The scan velocity varied along the structure and depended on the distance to the geometric center. The writing strategy was to scan the structure concentrically in closed loops and iterate each next loop by a displacement of relative radius and height of Δ r = 50 nm (see discussion below on thermal accumulation) and Δ z = 300 nm. In the center, the beam’s travel speed was v s c = 10 2 μ m/s and increased linearly to the edge, reaching 10 3 μ m/s. Also, kinematic commands known as rapid jumps (G0), were not used to perform all movements at the same accelerations. This strategy minimizes the kinematic fabrication error, where smaller radius loops result in greater excentrical acceleration and scan deviations. For simplicity, we did not account for the cumulative dose variation; therefore, the structure features a slight spherical ramp along the radial direction. Each loop had a ramp-up and ramp-down segment of 30 degrees. A previous study showed that the difference in exposure dose affects the final refractive index and optical performance of a micro-lens, which is better described by wave optics [7], however, such intricate control of the index by polymerisation was not investigated for the fraxicon fabricated in this current study.
Commercial SZ2080™resist was used for 3D printing with 2-benzyl-2-dimethylamino-1-(4-morpholinophenyl)- butanone-1 (IRG369, Sigma Aldrich) as the photoinitiator dissolved in the initial pre-polymer at 1% wt. The peak of IRG369 absorbance (in SZ2080™) was at 390 nm with emission at 400 nm as determined by photoluminescence excitation spectrosopy [1]; for pure SZ2080™absorption/emission was at 350 nm/400 nm. To improve the resolution, pure SZ2080™is preferable; however, resist with a photoinitiator is used for a larger laser processing window. The energy of a single pulse, with transmission losses accounted for at the focal point, was E p ≈ 96 pJ, corresponding to fluence per pulse F p = 0.0275 J/cm2 and intensity I p = 0.275 TW/cm2 (average). Consequently, the pulses generated a negligible ponderomotive potential. The dwell time required for the beam to cross the focal diameter 2 r is t d w = 2 r v s c = 6.8 ms and, at the repetition rate R, defines the number of accumulated pulses over the focal spot is large N = t d w R = 680 × 10 3 . Thermal spread (cooling) of the laser-heated focal volume is defined by the time t t h = ( 2 r ) 2 / D T = 660 ns, while a time separation between pulses is only 1 / R = 10 ns. Hence, a very strong thermal accumulation takes place at the used direct laser writing. An average temperature drop at the arrival of the next pulse occurs due to heat transfer to surrounding cold material. The temperature accumulation T N can be explicitly calculated for the N pulses, when single pulse temperature jump is T 1 [8]:
T N = T 1 ( 1 + β + β 2 + . . . + β N ) ≡ T 1 1 − β N 1 − β ,
where β = t t h t t h + 1 / R is the constant which defines heat accumulation; β → 1 at high repetition rate R → ∞ . For the used experimental conditions, β ≈ 0.9925 . The first N = 10 pulses cause significant temperature jump T N = 9.67 T 1 ( N = 10 ). Considering the exothermic character of polymerization, a minute temperature rise at the focal region causes a guided thermal polymerisation [9].
The samples were prepared by drop-casting the liquid resin on a standard microscope cover slip and pre-condensating at 50∘C for 24 hours. After exposure, the samples were developed in methyl-isobutyl-ketone for 30 min, then rinsed with pure-developer and air dried under normal room conditions. The refractive index of the resist at visible wavelengths is approximately n S Z ≈ 1.5 . While the exact definition of the 2 π phase height was experimentally challenging for smaller period fraxicons, the height of polymerised phase ramps normalised by the wavelength (or 2 π in phase) is h × n S Z / λ ∼ 2 , which corresponds to the second-order ( 2 × 2 π ) phase steps. This strategy was used for fabrication because of the more straightforward definition of the exact required geometry with a focused laser pulse, which occupies a defined volume.
For more widespread practical implementation of the proposed 3D laser printing of micro-optical elements, the fabrication conditions were optimized to complete the entire laser writing step within 100 min for all 200 μ m-diameter fraxicons in this study.

2.2. Characterisation

Micro-LEDs (CREE C460TR2227, CREE, Durham, USA) were used for the design and prototyping of a low-profile implantable device. The footprint of the μ LED was 0.27 × 0.22 mm2, with an emitter area comparable to the D = 0.2 mm diameter fraxicon. The micro-LEDs were assembled on a 10 μ m thick polyimide substrate [10,11], which was formed by spin-coating first a 5- μ m-thin polyimide layer on a silicon wafer (diameter 100 mm), followed by the sputter deposition of a metallic thin film. Interconnecting tracks were then patterned using lift-off technology and the track thickness was increased by electroplating 1 μ m of gold to reduce the electrical line resistance. A second polyimide layer was subsequently deposited to insulate the metal tracks.
To access the metal tracks, small openings were formed in the top polyimide layer by reactive ion etching (RIE) with oxygen plasma. A second metallisation and electroplating step was used to define "bonding pads" for the micro-LED chips and zero-insertion force (ZIF) connector pads for wire bonding the test structure to a printed circuit board. Finally, the shape of the polyimide substrate was defined by trenching the stack of polyimide layers down to the silicon substrate with a second RIE process step. The substrates could then be peeled from the silicon wafer using tweezers and the micro-LED chips were assembled on the pads of the polyimide substrate by flip-chip bonding [10,11]. They were subsequently underfilled with a biocompatible adhesive (EPO-TEK 301-2, Epoxy Technology, Inc., Billerica, USA) to electrically insulate the pads located at the interface between micro-LED chips and polyimide substrate. Structural characterisation of fraxicon was carried out by optical microscopy, scanning electron microscopy (SEM) and atomic force microscopy (AFM). Typical results are shown in Figure 1.
Preprints 90889 g001
Figure 1. (a) Blue micro-LED assembled on a polyimide substrate chip with 460 nm emission and concept design of a flat-fraxicon for endoscopy applications made out of silicone (polydimethylsiloxane - PDMS). (b) Optical microscope image of a fraxicon made by direct laser writing at 780 nm/100 fs/100 MHz (C-Fiber 780 Erbium Laser, MenloSystems) in SZ2080™resist. Fraxicon has Λ = 1 μ m period. (c) Structural characterisation of fraxicon by SEM and AFM, showing blazed 2 π steps with period Λ = 5 μ m.
Figure 1. (a) Blue micro-LED assembled on a polyimide substrate chip with 460 nm emission and concept design of a flat-fraxicon for endoscopy applications made out of silicone (polydimethylsiloxane - PDMS). (b) Optical microscope image of a fraxicon made by direct laser writing at 780 nm/100 fs/100 MHz (C-Fiber 780 Erbium Laser, MenloSystems) in SZ2080™resist. Fraxicon has Λ = 1 μ m period. (c) Structural characterisation of fraxicon by SEM and AFM, showing blazed 2 π steps with period Λ = 5 μ m.
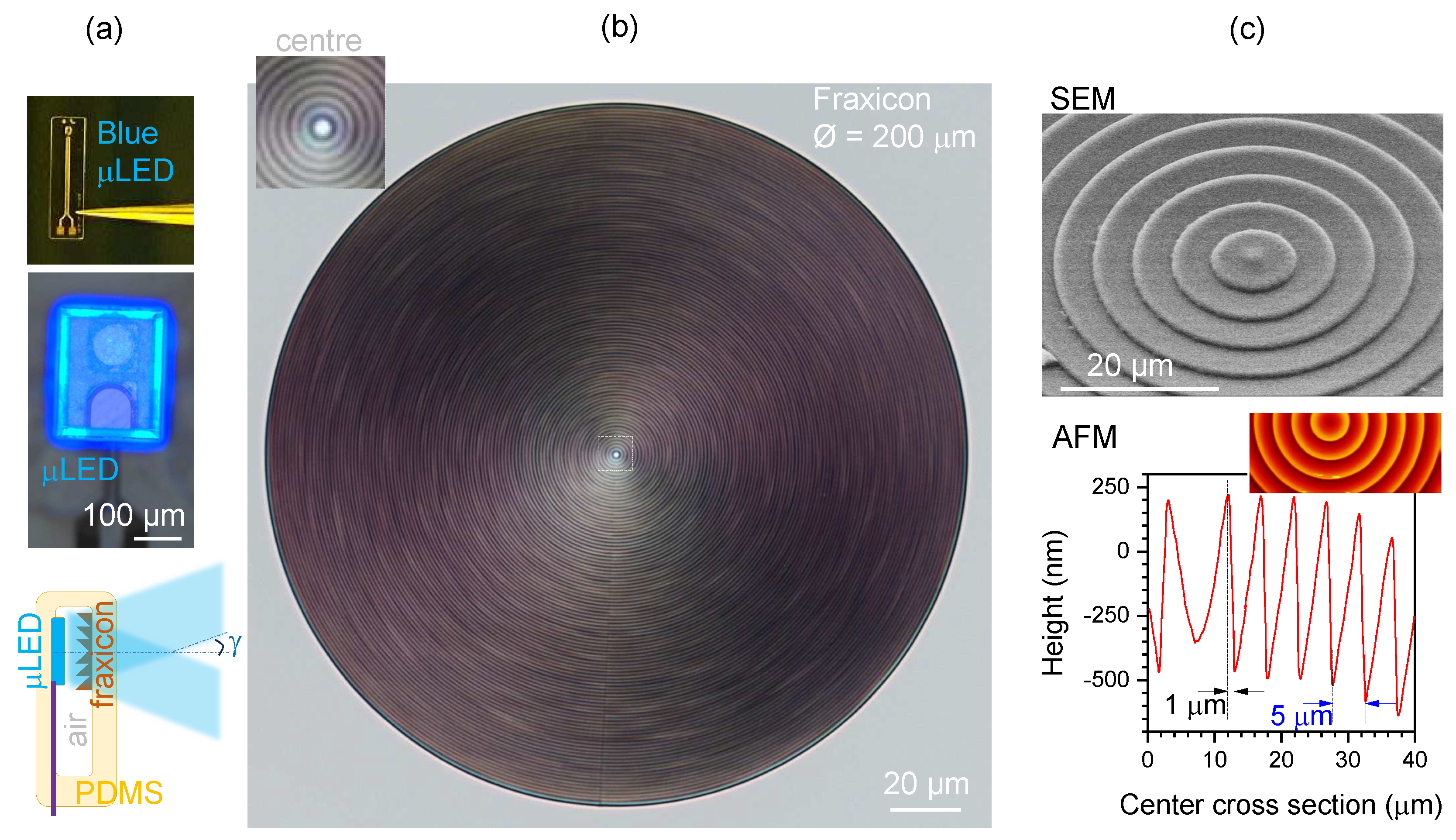
Preprints 90889 g001
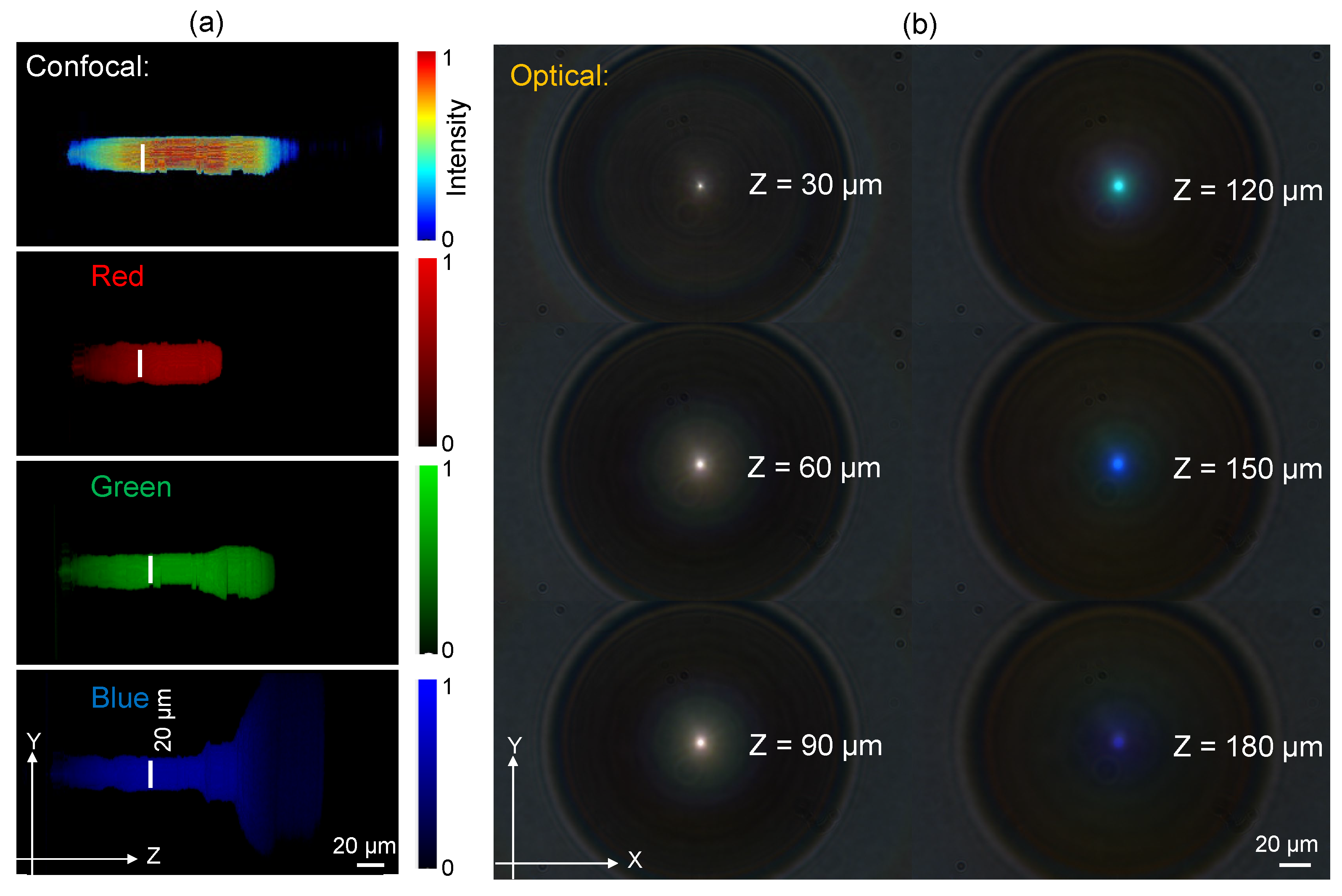
Preprints 90889 g002
Figure 2. Optical characterisation of fraxicon shown in Figure 1(b) by optical microscope with white condenser illumination. (a) Confocal intensity distribution and its RGB color content along the focus (a “ non-diffracting” part of the axial intensity). (b) Optical images at different axial positions along white light propagation (along z-axis.)
Figure 2. Optical characterisation of fraxicon shown in Figure 1(b) by optical microscope with white condenser illumination. (a) Confocal intensity distribution and its RGB color content along the focus (a “ non-diffracting” part of the axial intensity). (b) Optical images at different axial positions along white light propagation (along z-axis.)
Preprints 90889 g002

2.3. Fraxicon: basic properties and design

The positive fraxicon was designed with a diameter D = 0.2 mm and featured 20 blazed rings. The thickness profile ( t f r a ) of the fraxicon as a function of the radial coordinate ( r = x 2 + y 2 ) is given as Eqn. 2
t f r a = h − m o d r × h Λ , h
where h is the height of the fraxicon corresponding to 2 π phase retardation ( h = λ ( n S Z − 1 ) = 1 μ m, λ is the incident wavelength, and n S Z ≈ 1.5 is the refractive index of SZ2080™), Λ = 5 μ m is the period of gratings (rings), and m o d is a function of remainder after division (modulo operation).
The axial intensity A I ( z ) distribution (along the z-axis) of an axicon/fraxicon depends on the radial intensity at the input and can be found from a relation based on Snell’s law r = z ( n − 1 ) α , here n is the refractive index of axicon and α is the base angle of axicon (also, the angle required to the full π angle at the tip of the axicon). For the Gaussian beam I i n = I 0 exp − 2 r 2 w o 2 , where w o is the beam waist:
A I ( z ) = I 0 exp − 2 z 2 ( n − 1 ) 2 α 2 w o 2 × [ 2 π z ( n − 1 ) 2 α 2 ] .
This equation can be generalized and the input intensity profile I i n ( r ) can be expressed in terms of r-to-z mapping A I ( z ) as I i n ( r ) = M × A I [ z = r / ( n − 1 ) α ] / r , where M = 1 2 π ( n − 1 ) α is the axicon geometry defined constant. This is valid for the on-axis intensity in 0 < z < D O F region with depth-of-focus D O F = w / [ ( n − 1 ) α ] defined by the radius of beam w.

3. Results

3.1. Theory: fraxicon illuminated by an incoherent and extended source

The Gauss-Bessel beam generation by fraxicon is mostly discussed using spatially coherent illumination such as laser beams. The timing of photon emission from the LED is however disorganized. To describe beam generation by fraxicon for a spatially incoherent illumination, such as light from an LED, an incoherent imaging framework is needed. The LED needs to be considered as a collection of points and the generated beam is formed by the summation of intensities of the beam generated for every point. While it is difficult to discriminate beams generated for coherent and incoherent illuminations, the generation approach is quite different from one another. We consider a point in the LED as a Delta function emitting a spherical wavefront with intensity I s given as S ( 1 / z s ) = e x p [ j ( 2 π / λ ) x 2 + y 2 + z s 2 ] . The phase of the fraxicon is given as ϕ = e x p [ j ( 2 π / λ ) t f r a ] . The complex amplitude after the fraxicon is, therefore, ψ = I s C 1 L ( r s / z s ) S ( 1 / z s ) ϕ , where L is a linear phase and C 1 is a complex constant. The intensity distribution at a distance z r for a Delta-function is given as I D e l t a ≈ | ψ ⨂ Q ( 1 / z r ) | 2 , where Q ( 1 / z r ) = e x p [ j ( π / λ z r ) ( x 2 + y 2 ) ] and ’⨂’ is a 2D convolutional operator. The intensity distribution obtained for the entire LED active area can be given as I L E D ≈ | I D e l t a ⨂ O | 2 , where O is the LED active area in a square shape filled with ones and zeros around it. It must be noted that the above summation is not a complex summation but an addition of intensities as the phase information is not present. The above expression is an approximate one as Fresnel approximation was used for propagation between fraxicon and camera. To understand the beam generation deeper, let us consider the Delta function with no linear phase attached to it, i.e., the one at the center of the LED active area. This Delta function generates a spherical wave that interacts with the fraxicon. We already established that fraxicon and axicon consist of lens functions with different focal lengths multiplexed in the transverse direction [12]. At the camera plane, one of the lens functions satisfies the imaging condition generating a sharp Delta-like function. The other lens functions cause ring patterns around this sharp Delta-like function typical of a squared Bessel function. The other points in the LED active area with linear phases attached to them create off-axis squared Bessel functions on the camera. The recorded intensity distribution is the sum of all the contributions from the points of the LED active area. This is different from coherent illumination as it would depict the behaviour of light emission from a single point. Simulation results for intensity obtained for a point in an LED, intensity obtained for a circular region in the LED by incoherent superposition due to spatial incoherence and intensity obtained for the same circular region but with coherent superposition are shown in Figure 4(a), (b) and (c), respectively. The incoherent superposition do not generate distinct rings around the central maxima as expected of a Bessel distribution due to the lack of phase relations for light emitted from every point. The temporal coherence length for a Gaussian fit of LED emission spectra is given by L t c = 4 ln 2 π λ 0 2 Δ λ , where λ 0 is the central emission wavelength and Δ λ is its width or Full-Width-at-Half-Maximum (FWHM), and it coincides well with experimentally measured values L t c ≈ 2 μ m using Mach-Zehnder interferometry [13].
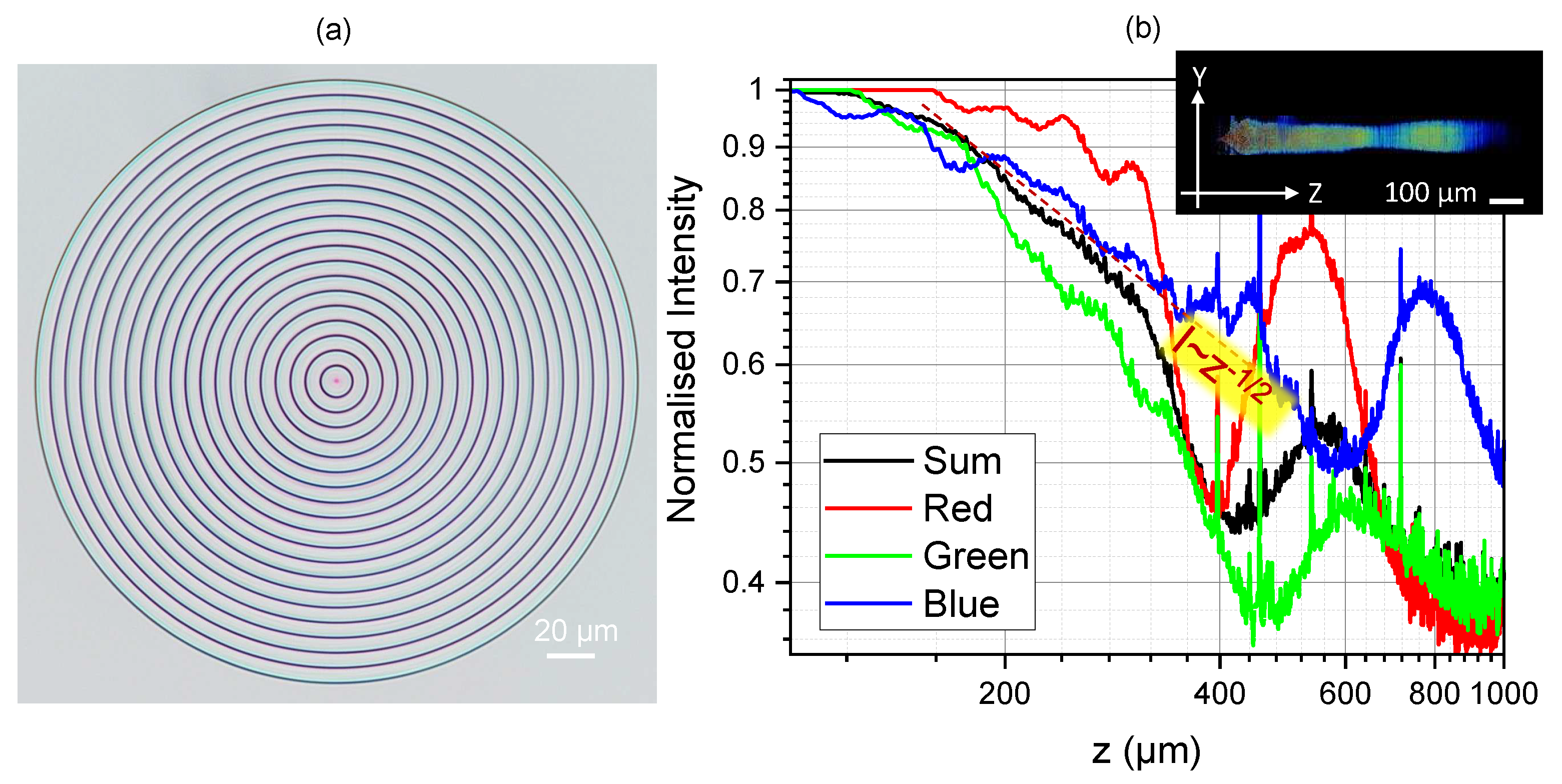
Preprints 90889 g003
Figure 3. (a) Optical image of fraxicon with 1.5 times larger width of the 2 π -steps. Image taken under white light condenser illumination. (b) Axial intensity profile calculated from the lateral image stacks (same as in Figure 2). The inset shows the confocal profile of intensity.
Figure 3. (a) Optical image of fraxicon with 1.5 times larger width of the 2 π -steps. Image taken under white light condenser illumination. (b) Axial intensity profile calculated from the lateral image stacks (same as in Figure 2). The inset shows the confocal profile of intensity.
Preprints 90889 g003

3.2. Experimental characterisation of light intensity

An axicon or a conical lens is a very useful optical element that forms an elongated axial intensity distribution when illuminated by a Gaussian beam. The formed Bessel-Gaussian beam has a diameter defined by the first minimum of the Bessel function J 0 ( k ⊥ r ) , where r is the radial coordinate in the lateral plane, and the perpendicular component of the propagation wavevector k ⊥ is defined by k ⊥ ≡ k sin γ with γ being the half-cone angle of the beam with an optical axis, wavevector k = ω / c ≡ 2 π / λ and k ⊥ 2 + k ‖ 2 = ( ω / c ) 2 ; ω , c are the cyclic frequency and speed of light, respectively. The diameter of the axially extended focus is d B = 4.816 / k ⊥ and the length depends on the diameter of the incident beam D (lens diameter) as Z m a x = D / ( 2 sin γ ) . Large D and small γ facilitates to have a long, so-called, non-diffracting region of intensity on the optical axis. Axicon can be made flat in the same way as a Fresnel lens is made from concentric segments.
A fraxicon lens of D = 300 μ m, consisting of 30 circular rings of ∼ 5 μ m width and 0.7 μ m height were polymerised in SZ2080™using fs-laser direct write (Figure 1). The step between adjacent phase-ramps was within ∼ 1 μ m. Fraxicons are especially promising for optical devices which have strong requirements for spatial constraints. If fraxicons are used for optical focusing of micro-light sources, e.g., LED, it is usual that illumination of the aperture of the fraxicon will take place from an extended, non-collimated light source with possible intensity inhomogeneities of tens-of-micrometer scale (see powered μ LED image in Figure 1(a)). Such a situation can be modeled using an optical microscope under condenser illumination of a fraxicon on a sample plane discussed next.

3.2.1. Confocal intensity mapping

Figure 2(a) shows axial intensity distribution calculated from the axial stacks as shown in (b) using a standard microscope (Nikon, Optiphot) under white-light condenser illumination in transmission mode. Images at every Δ z = 1 μ m step were recorded and 3D intensity distribution was calculated using own Matlab code. The resulting confocal axial intensity distribution was separated into basic red, green, blue (RGB) color channels. The width of the focal region has d B ≈ 20 μ m, hence, k sin γ = 4.816 / d B , or γ ≈ 1 . 1 ∘ for λ ≈ 0.5 μ m. As expected, the width for R-red axial distribution d B ( R ) was larger than for B-blue, d B ( B ) . Strong widening of the intensity profile for the blue channel is most probably defined by the comparatively high-NA of 0.9 of the imaging microcope lens, since the conical angle γ ≈ 1 . 1 ∘ is small.
The length of the most uniform intensity region is wavelength dependent since the height of the phase ramps is fixed. The longest non-diffrating region was for the blue wavelength. This is also clearly seen in the lateral cross sections at z > 150 μ m (Figure 2(b)).
Figure 3 shows fraxicon and its axial intensity cross sections under condenser illumination in the microscope. The period of concentric phase ramps was 1.5 times larger, hence ∼ 7.5 μ m while the diameter and the height of the phase ramps were the same as for fraxicon in Figure 1(b) and Figure 2. This results in a longer non-diffracting region. The intensity decreased along propagation as z and RGB colors had an effective different length. The exact axial intensity profile depends on the wavevector spread for different colors in illumination light. The ideal performance of fraxicons was modeled numerically and discussed next.

3.3. Numerical predictions by ray and wave simulations

For numerical simulations we used the ideal case of triangular phase steps as 20 rings with each of them having 5 μ m width and 1 μ m height. Material of the phase steps has a refractive index of 1.5 (dispersion-free). This makes a D = 0.2 mm diameter fraxicon, which was illuminated with a plane wave (a singe wavenumber) at different RGB colors.

3.3.1. Wave optics

The Rayleigh–Sommerfeld (RS) diffraction integral can be used for exact prediction on axial intensity profile, which is consistent with the wave-optical approach. The electric field distributions U 2 ( r 2 , z ) in the axial plane at different axial z positions were calculated using MATLAB program based on the RS diffraction integral as expressed in Eqn. 4 [14,15]:
U 2 ( r 2 , θ 2 , z ) = − i λ ∫ ∫ U 1 ′ ( r 1 , θ 1 ) · e − i k r r · cos ( n , r ) d r 1 d θ 1 ,
where λ is the incident light wavelength (R=700 nm, G=546.1 nm and B=435.8 nm), k = 2 π λ is the wave vector, ( r 1 , θ 1 ) and ( r 2 , θ 2 ) are the polar coordinates in the diffraction plane (the plane immediately behind the fraxicon) and observation plane (the focal plane), respectively; r = ( z 2 + ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 = ( z 2 + r 1 2 + r 2 2 − 2 r 1 r 2 c o s ( θ 1 − θ 2 ) , cos ( n , r ) is defined as the cosine of the angle between the unit normal vector n of the diffraction plane and the position vector r from point ( r 1 , θ 1 ) to point ( r 2 , θ 2 ) , and U 1 ′ ( r 1 , θ 1 ) is the E-field immediately behind the fraxicon. The incident wave U 1 ( r 1 , θ 1 ) is diffracted by the fraxicon through amplitude and phase modulations, and the electric field modified by the fraxicon U 1 ′ ( r 1 , θ 1 ) can be expressed by Eqn. 5 [14]:
U 1 ′ ( r 1 ) = U 1 ( r 1 ) · T ( r 1 ) · e − i k · Φ ( r 1 ) ,
where T ( r 1 ) is the transmission distribution (amplitude modulation) of the fraxicon, and Φ ( r 1 ) = n S Z · t f r a ( n S Z is the refractive index of SZ2080™, and t f r a is the thickness profile of the fraxicon) is the phase modulation provided by the fraxicon. Consequently, the light intensity distributions in the axial plane can be calculated by squaring the electric field: I ( r 2 , z ) = | U 2 ( r 2 , z ) | 2 (Figure 5).
Apparent differences between modeling of ideal plane wave illumination of a fraxicon (Figure 5) and experimental imaging using condenser illumination of the microscope (Figure 3) is due to presennce of different k components at the same wavelength. Such situation is expected in real applications where the fraxicon is placed in front of a μ LED (Figure 1(a)). However, the basic features of oscillatory nature of intensity along the propagation axis, its decay as ∝ z and sub-1 mm long extent of high intensity section are consistent. Exact intensity distributions can be well controlled using tailored illumination of an axicon [16], hence, fraxicon as well.

3.3.2. Ray optics

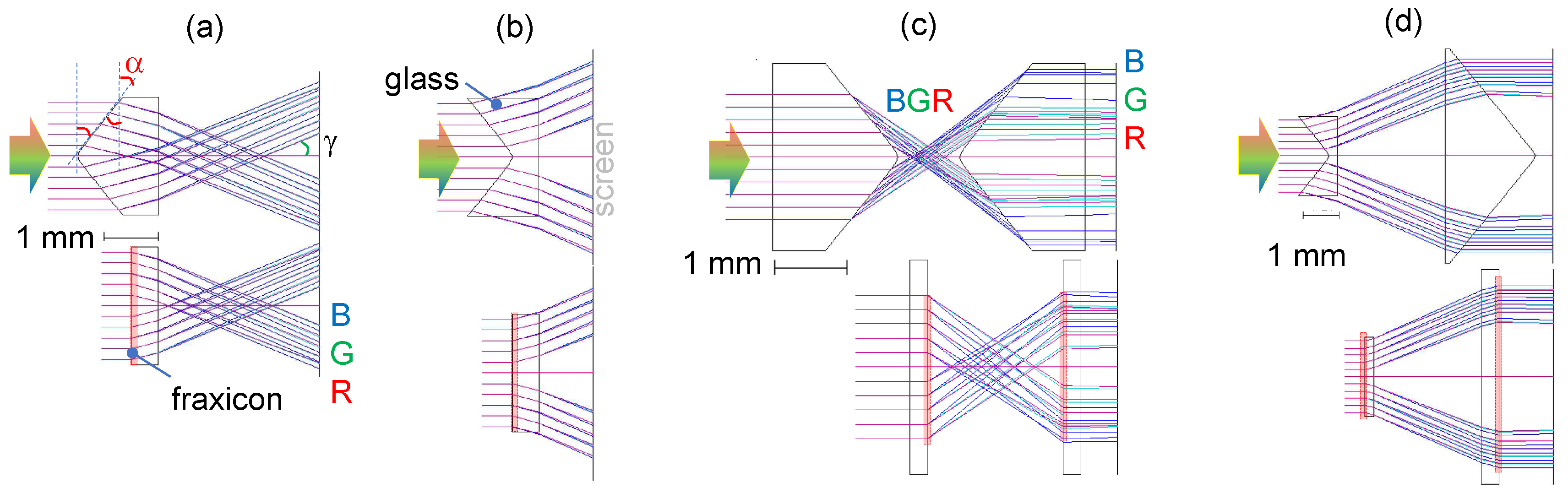
The Optical Software for Layout and Optimisation (OSLO, Lambda Research Co.) is a ray tracing tool used to model light propagation through (fr)axicons. Figure 6 shows RGB beam propagation through positive and negative (fr)axicons and their pairs, which collimates the beam. Change from an axicon to fraxicon is conveniently made by tab-selection in the OSLO input; the fraxicon surface appears flat in the viewer, however, it encodes fraxicon layout of 2 π phase ramps. As expected by the shape of axicon, a conical prism, light dispersion is evident in RGB ray tracing (Figure 6). It manifests as color aberration along the focal region. A slight color appearance of fraxicon when imaged with a microscope is evident in Figure 3(a) with red-center and blue outside edges of the phase ramps. Figure 6 clearly shows the compactness of micro-optical constructions using fraxicons and less dispersion in a pair of the flat optical elements (c,d) for the same diameter of the input beam; alignment in Figure 6 is at the plane of screen.
Such compact fraxicons have the potential for application in space telescope technologies. Recently, multiple-order diffractive engineered surface (MODE) lenses, which comprise a front-surface multiple-order diffractive lens (MOD) and a rear-surface diffractive Fresnel lens (DFL), are planned to aid in the search for Earth-like planets and exo-planets in the universe as part of the upcoming telescope array known as the Nautilus Observatory [17,18,19].

4. Discussion

The circular grating pattern makes an efficient collection of illumination at different wavelengths onto the optical axis and is useful for light delivery and collection to spot sizes of tens-of- μ m. The long focal extension is helpful for light coupling into optical fibers and laser machining using increasingly miniaturised laser sources. Photonic crystal (PhC) lasers now deliver tens of Watts output powers at near-IR wavelengths from sub-1 mm apertures at very low divergence angle [20]. Micro-optics based on a high damage threshold SZ2080™photo-resist is a promising solution [21,22].
Gauss-Bessel beams formed by phase profiles closely matching those of a fraxicon were made with a spatial light modulator for record high ∼ 10 4 aspect ratio modification of dielectrics and semiconductors for scribing and dicing with nanoscale resolution of tens-of-nm [23]. For such material modification multiple ionisation locations along the non-diffracting intensity distribution are essential and their connection occurs via back-scattering under multi-pulse irradiation. Hence oscillatory nature of Bessel beam intensity on the axis (Figure 5) is beneficial for such material modification.
Replication of polymerised fraxicons can be made using Ni-shim (plasma coating with subsequent electrochemical deposition of Ni), which replicates structures with 10 nm feature sizes, e.g., nano-needles of black-Si [24].
The emergence of a new generation of optical cochlear implants has highlighted the need for better miniaturisation and integration of optical elements. It has been shown that optical neuromodulation with visible light, facilitated by optogenetics, can confer higher spatial precision of neural activation compared to traditional electrical stimulation methods [25]. For cochlear implants, broad current spread from electrical devices reduces the number of independent stimulating channels [26,27]. Higher spatial precision of activation could greatly increase the number of independent stimulating channels and enable simultaneous channel stimulation which would greatly enrich the sound quality experienced by cochlear implant recipients [28,29]. Strategies to deliver focussed electrical stimulation, including tripolar and focussed multipolar stimulation strategies, have failed to deliver significant clinical benefit [30,31]. The emerging development of optical arrays could provide an alternative solution.
In rodents, such as mice, rats, and gerbils, auditory neurons were modified to express photosensitive ion channels. The spread of activation during optical stimulation was significantly lower compared to electrical stimulation, resulting in near-physiological spectral resolution when using light emitters that are in close proximity to the neural tissue [11,32,33]. Furthermore, during two-channel simultaneous optical stimulation in the mouse cochlea using micro-LEDs with a pitch of just 0.52 mm, channel interaction was 13-15-fold lower than simultaneous electrical channel stimulation [34]. In the human cochlea, where there is a greater distance between the emitter and the neural tissue, optical arrays of micro-LEDs are still predicted to significantly reduce the spread of activation in the cochlea to 0.4-1.0 octaves, up to 4-fold lower than electrical stimulation [35,36]. While modelling data suggests waveguides could provide even greater spectral selectivity [37], the fraxicon technology presented here could potentially be used to focus the emission cone and improve the spectral resolution provided by LEDs in the human cochlea.
Antireflection coating could be used to increase transmittance of fraxicon by coating a film with thickness λ / 4 of a refractive index n o u t n f r a x ≈ 1.25 , where n o u t = 1 (air) is the refractive index at the focal region and n f r a x = 1.5 . MgF2 is a good candidate for the antireflection coating over visible spectral range. The atomic layer deposition (ALD) is a candidate for conformal coating of 3D surfaces as well as magnetron sputtering.
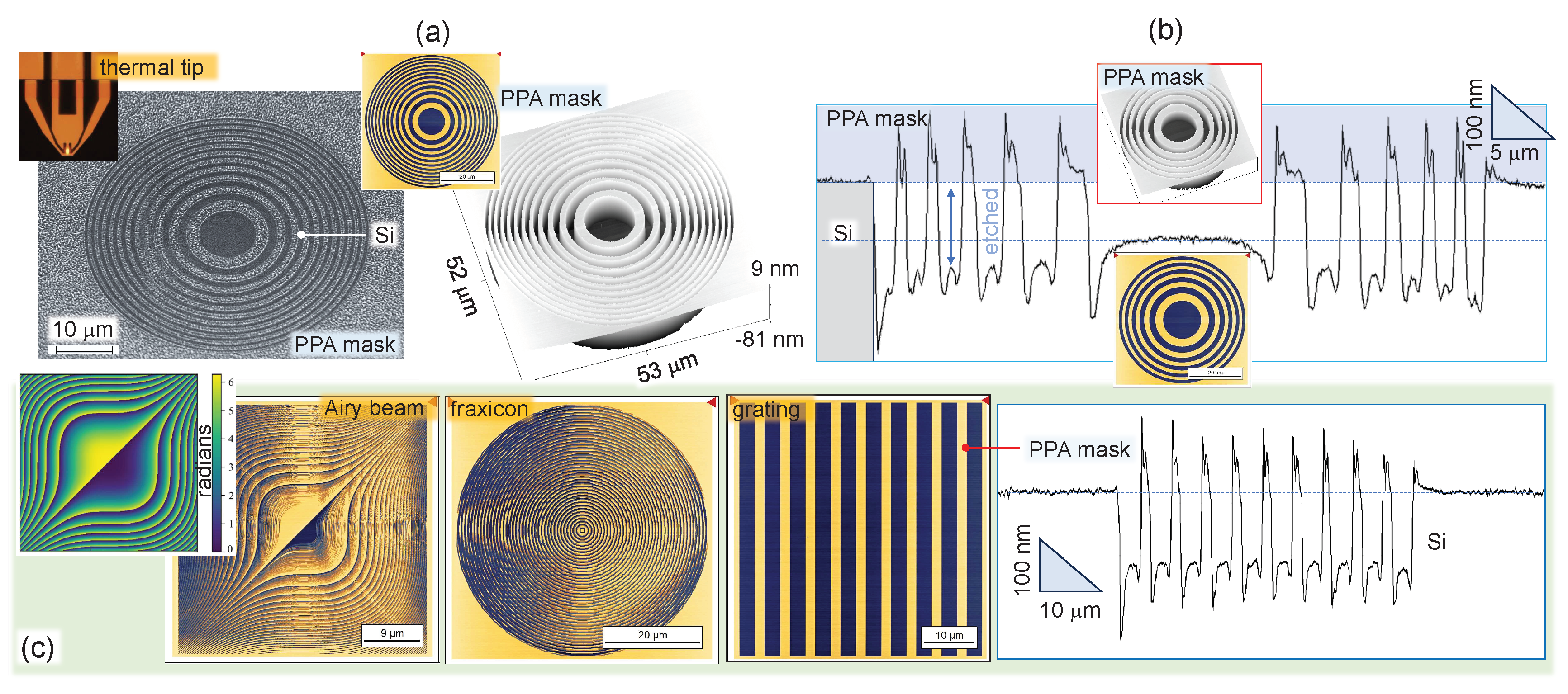
Fraxicons with ∼ 1 − μ m-tall phase ramps can be made using a scanning thermal tip (nano-cantilever) method based on the AFM principle (NanoFrazor; Appendix A). By using Polyphthalaldehyde (PPA) 4% resist for a gray scale mask, e.g., 3000 rpm spin coating for a 100 nm film, a sacrificial PPA mask can be made with high nanoscale control and resolution down to 10 nm. Such mask then is used for transfer of the 3D pattern onto a substrate by reactive ion etching (RIE). For Si etch (Figure A1), etching contrast was ∼ 2.6 and translates to 260 nm deep structures when PPA resist is ∼ 100 nm. Different patterns and metasurface structures can be easily designed for patterning into resist using open source toolbox [38]. It is based on the industry standart GDSII, a binary database file format for Electronic Design Automation data exchange of integrated circuit layout.

5. Conclusions and outlook

3D printing of 0.2-mm-diameter flat fraxicon lenses with 2 π phase step defined over 1 and 5 μ m lateral widths and ∼ 0.7 μ m height (axial length) was made in SZ2080™(with 1%wt. IRG) resist. 3D polymerisation was carried out by tightly focused 780 nm/100 fs/100 MHz laser irradiation. Entire fraxicon was printed within 1.5 hours. It was tested for illumination by an extended light source (condenser of a microscope) to simulate its performance for μ LED illumination in endoscopy and opto-probes.

Author Contributions

Conceptualization, PRS, RTR, PR, SJ; methodology, VA, SHN, TK,; validation, HM, DS, NHAL, RD, ZK, GS; investigation, HG, TB, DG; data curation, VA, HM, DS, NHAL, RD, ZK, GS; writing—original draft preparation, HM, VA, DS, PRS, DG, SJ; writing—review and editing, all the authors; visualization, VA, HM, DS, SJ; supervision, VA SHN, PRS, SJ; funding acquisition, SHN, SJ. All authors have read and agreed to the published version of the manuscript.

Funding

The project was funded by ARC LP190100505 grant, European Union’s Horizon 2020 research and innovation programme grant agreement No. 857627 (CIPHR) and ARC LP190100505 and NHMRC 2002523 grants. The thermal scanning probe lithography tool NanoFrazor was acquired via ARC LE160100124 grant.

Data Availability Statement

Data can be made available upon a reasonable request.

Acknowledgments

We are grateful for process development of fraxicons at Femtika. We acknowledge a material transfer agreement with Kyoto University for testing micro-optical elements using PhC laser. This work was performed in part at the Melbourne Centre for Nanofabrication (MCN) in the Victorian Node of the Australian National Fabrication Facility (ANFF).

Conflicts of Interest

The authors declare no conflict of interest

Appendix A. Thermal Scanning Probe Lithography (tSPL)

Scanning thermal tip nanolithography (NanoFrazor, SwissLitho) has 10 nm resolution (defined by the tip) and possibility to sublimate/evaporate solid linear Polyphthalaldehyde (PPA; anionic from Sigma-Aldrich) resist upon fast and localised heating. The height control of resist removal is adjustable; hence, 3D surface can be defined for a sacrificial mask in RIE-ICP plasma etch.
Etch depths were measured using optical profiler to estimate the etch depth into Si and etch contrast with PPA. Figure A1 shows several examples of a grating, Fresnel lens, and 3D phase patterns of cubic phase (Airy beam generator) and 4-level fraxicon. The etch depth was approximately around 160-180 nm for 65-nm-deep pattern defined in PPA; PPA thickness was 100 nm for 5% solution of PPA spin coated at 2000 rpm. This translated to an etch selectivity (Si vs. PPA) of 2.6, which is less compared to best-performing examples with NanoFrazor reaching 4-10 depending on pattern and etch conditions. The most probable reason for the lower selectivity is introduction of O2 into the process, which might have suppressed the selectivity of SF6 for Si. The RIE conditions were (Oxford, Plasmalab 100 ICP380): SF6 40 sccm, C4F8 60 sccm, O2 10 sccm, at RF of 40 W, ICP at 1500 W, etch time of 50 s and pressure of 10 mTorr. A RF strike power was increased to 50 W for the 5 s plasma ignition step only. For binary patterns, a metal hard mask (e.g., Cr) can be used for Si etching via Bosch process up to a large 150 μ m depth as shown for THz optical vortex generator elements based on a metasurface design [39].
Preprints 90889 g0a1
Figure A1. Sacrificial mask etch of micro-optical elements into Si. (a) A tilted-view SEM image of a binary Fresnel lens ( f = 50 μ m) after RIE plasma etching, optical image (yellow middle-inset) and AFM image of the pattern defined in PPA resist by thermal tip nanolithography (NanoFrazor; top-left inset shows the writing tip). (b) Optical profilometer cross section of a f = 100 μ m lens; insets show optical and AFM images. (c) Microscope images of PPA masks of the cubic phase structure (Airy beam generator; a phase 0-2 π phase map in the inset), 4-level fraxicon, binary grating with period of 5 μ m. Optical profilometer cross section of the grating after RIE.
Figure A1. Sacrificial mask etch of micro-optical elements into Si. (a) A tilted-view SEM image of a binary Fresnel lens ( f = 50 μ m) after RIE plasma etching, optical image (yellow middle-inset) and AFM image of the pattern defined in PPA resist by thermal tip nanolithography (NanoFrazor; top-left inset shows the writing tip). (b) Optical profilometer cross section of a f = 100 μ m lens; insets show optical and AFM images. (c) Microscope images of PPA masks of the cubic phase structure (Airy beam generator; a phase 0-2 π phase map in the inset), 4-level fraxicon, binary grating with period of 5 μ m. Optical profilometer cross section of the grating after RIE.
Preprints 90889 g0a1
Typical pattern writing time for 60 nm structures of Fresnel lens in PPA (Figure A1(a)) was 5 min for 50 × 50 μ m2 area of f = 50 μ m lens and 4-level fraxicon. The residuals of PPA are removed before with a gentle barrel ashing ∼5 s, 200 W, 400 sccm O2. Also, a developer Tetramethylammonium hydroxide (TMAH) can be used.

References

  1. Malinauskas, M.; Žukauskas, A.; Bičkauskaitė, G.; Gadonas, R.; Juodkazis, S. Mechanisms of three-dimensional structuring of photo-polymers by tightly focussed femtosecond laser pulses. Opt. Express 2010, 18, 10209–10221. [Google Scholar] [CrossRef] [PubMed]
  2. Katsura, T. Thermal diffusivity of silica glass at pressures up to 9 GPa. Physics and Chemistry of Minerals 1993, 20, 201–208. [Google Scholar] [CrossRef]
  3. Wang, H.; Zhang, W.; Ladika, D.; Yu, H.; Gailevičius, D.; Wang, H.; Pan, C.F.; Suseela Nair, P.; Ke, Y.; Mori, T.; En Chan, J.; Ruan, Q.; Farsari, M.; Malinauskas, M.; Juodkazis, S.; Gu, M.; Yang, J. Two-Photon Polymerization Lithography for Optics and Photonics: Fundamentals, Materials, Technologies, and Applications. Adv. Func. Mat. 2023, 33, 2214211. [Google Scholar] [CrossRef]
  4. Uemukai, M.; Matsumoto, N.; Suhara, T.; Nishihara, H.; Eriksson, N.; Larsson, A. Monolithically integrated InGaAs-AlGaAs master oscillator power amplifier with grating outcoupler. IEEE Photonics Technology Letters 1998, 10, 1097–1099. [Google Scholar] [CrossRef]
  5. Uenishi, K.; Uemukai, M.; Suhara, T. Rotation-Symmetric Multispot Focusing Phase-Shifted Grating Coupler for Integrated Semiconductor Laser. Japanese Journal of Applied Physics 2012, 51, 058001. [Google Scholar] [CrossRef]
  6. Sänger, J.C.; Pauw, B.R.; Sturm, H.; Günster, J. First time additively manufactured advanced ceramics by using two-photon polymerization for powder processing. Open Ceramics 2020, 4, 100040. [Google Scholar] [CrossRef]
  7. Gonzalez-Hernandez, D.; Sanchez-Padilla, B.; Gailevičius, D.; Thodika, S.C.; Juodkazis, S.; Brasselet, E.; Malinauskas, M. Single-Step 3D Printing of Micro-Optics with Adjustable Refractive Index by Ultrafast Laser Nanolithography. Advanced Optical Materials 2023, 11, 2300258. [Google Scholar] [CrossRef]
  8. Luther-Davies, B.; Rode, A.; Madsen, N.; Gamaly, E. Picosecond high-repetition-rate pulsed laser ablation of dielectrics: The effect of energy accumulation between pulses. Opt. Eng. 2005, 44, 051102. [Google Scholar] [CrossRef]
  9. Rekštytė, S.; Jonavicius, T.; Gailevičius, D.; Malinauskas, M.; Mizeikis, V.; Gamaly, E.G.; Juodkazis, S. Nanoscale precision of 3D polymerisation via polarisation control. Adv. Opt. Mat. 2016, 4, 1209–1214. [Google Scholar] [CrossRef]
  10. Ayub, S.; Gentet, L.; Fiáth, R.; Schwaerzle, M.; Borel, M.; David, F.; Barthó, P.; Ulbert, I.; Paul, O.; Ruther, P. Hybrid intracerebral probe with integrated bare LED chips for optogenetic studies. Biomed. Microdev. 2017, 19, 1–12. [Google Scholar] [CrossRef]
  11. Keppeler, D.; Schwaerzle, M.; Harczos, T.; Jablonski, L.; Dieter, A.; Wolf, B.; Ayub, S.; Vogl, C.; Wrobel, C.; Hoch, G.; Abdellatif, K.; Jeschke, M.; Rankovic, V.; Paul, O.; Ruther, P.; Moser, T. Multichannel optogenetic stimulation of the auditory pathway using microfabricated LED cochlear implants in rodents. Sci. Transl. Med. 2020, 12, eabb8086. [Google Scholar] [CrossRef] [PubMed]
  12. Anand, V.; Maksimovic, J.; Katkus, T.; Ng, S.H.; Ulčinas, O.; Mikutis, M.; Baltrukonis, J.; Urbas, A.; Šlekys, G.; Ogura, H.; Sagae, D.; Pikuz, T.; Somekawa, T.; Ozaki, N.; Vailionis, A.; Seniutinas, G.; Mizeikis, V.; Glazebrook, K.; Brodie, J.P.; Stoddart, P.R.; Rapp, L.; Rode, A.V.; Gamaly, E.G.; Juodkazis, S. All femtosecond optical pump and x-ray probe: holey-axicon for free electron lasers. Journal of Physics: Photonics 2021, 3, 024002. [Google Scholar] [CrossRef]
  13. Torcal-Milla, F.; Lobera, J.; Lopez, A.; Palero, V.; Andres, N.; Arroyo, M. Mach-Zehnder-based measurement of light emitting diodes temporal coherence. Optik 2022, 267, 169722. [Google Scholar] [CrossRef]
  14. Mu, H.; Smith, D.; Katkus, T.; Gailevičius, D.; Malinauskas, M.; Nishijima, Y.; Stoddart, P.R.; Ruan, D.; Ryu, M.; Morikawa, J.; others. Polarisation control in arrays of Microlenses and gratings: Performance in visible–IR spectral ranges. Micromachines 2023, 14, 798. [Google Scholar] [CrossRef] [PubMed]
  15. Wei, S.; Cao, G.; Lin, H.; Mu, H.; Liu, W.; Yuan, X.; Somekh, M.; Jia, B. High tolerance detour-phase graphene-oxide flat lens. Photonics Research 2021, 9, 2454–2463. [Google Scholar] [CrossRef]
  16. Dharmavarapu, R.; Bhattacharya, S.; Juodkazis, S. Diffractive optics for axial intensity shaping of Bessel beams. Journal of Optics 2018, 20, 085606. [Google Scholar] [CrossRef]
  17. Milster, T.D.; Kim, Y.S.; Wang, Z.; Purvin, K. Multiple-order diffractive engineered surface lenses. Appl. Opt. 2020, 59, 7900–7906. [Google Scholar] [CrossRef] [PubMed]
  18. Apai, D.; Milster, T.D.; Kim, D.W.; Bixel, A.; Schneider, G.; Liang, R.; Arenberg, J. A Thousand Earths: A Very Large Aperture, Ultralight Space Telescope Array for Atmospheric Biosignature Surveys. The Astronomical Journal 2019, 158, 83. [Google Scholar] [CrossRef]
  19. Milster, T.D.; Wang, Z.; Kim, Y.S. Design aspects of large-aperture MODE lenses. OSA Continuum 2021, 4, 171–181. [Google Scholar] [CrossRef]
  20. Yoshida, M.; Katsuno, S.; Inoue, T.; Gelleta, J.; Izumi, K.; De Zoysa, M.; Ishizaki, K.; Noda, S. High-brightness scalable continuous-wave single-mode photonic-crystal laser. Nature 2023, 618, 727–732. [Google Scholar] [CrossRef]
  21. Gailevicius, D.; Zvirblis, R.; Galvanauskas, K.; Bataviciute, G.; Malinauskas, M. Calcination-Enhanced Laser-Induced Damage Threshold of 3D Micro-Optics Made with Laser Multi-Photon Lithography. Photonics 2023, 10, 597. [Google Scholar] [CrossRef]
  22. Samsonas, D.; Skliutas, E.; Ciburys, A.; Kontenis, L.; Gailevičius, D.; Berzinš, J.; Narbutis, D.; Jukna, V.; Vengris, M.; Juodkazis, S.; Malinauskas, M. 3D nanopolymerization and damage threshold dependence on laser wavelength and pulse duration. Nanophotonics 2023. [Google Scholar] [CrossRef]
  23. Li, Z.Z.; Fan, H.; Wang, L.; Zhang, X.; Zhao, X.J.; Yu, Y.H.; Xu, Y.S.; Wang, Y.; Wang, X.J.; Juodkazis, S.; Chen, Q.D.; Sun, H.B. Super stealth dicing of transparent solids with nanometric precision. arxiv 2023, arXiv:2308.02352v2. [Google Scholar] [CrossRef]
  24. Gailevičius, D.; Ryu, M.; Honda, R.; Lundgaard, S.; Suzuki, T.; Maksimovic, J.; Hu, J.; Linklater, D.P.; Ivanova, E.P.; Katkus, T.; Anand, V.; Malinauskas, M.; Nishijima, Y.; Ng, S.H.; Staliūnas, K.; Morikawa, J.; Juodkazis, S. Tilted black-Si: ∼0.45 form-birefringence from sub-wavelength needles. Opt. Express 2020, 28, 16012–16026. [Google Scholar] [CrossRef] [PubMed]
  25. Richardson, R.; Ibbotson, M.; Thompson, A.; Wise, A.; Fallon, J. Optical stimulation of neural tissue. Healthc. Technol. Lett. 2020, 7, 58–65. [Google Scholar] [CrossRef] [PubMed]
  26. Shannon, R. Multichannel electrical stimulation of the auditory nerve in man. II. Channel interaction. Hear. Res. 1983, 12, 1–16. [Google Scholar] [CrossRef]
  27. White MW, Merzenich MM, G.J. Multichannel cochlear implants. Channel interactions and processor design. Arch. Otolaryngol. 1984, 110, 493–501. [CrossRef]
  28. Friesen, L.; Shannon, R.; Baskent, D.; Wang, X. Speech recognition in noise as a function of the number of spectral channels: comparison of acoustic hearing and cochlear implants. J. Acoust. Soc. Am. 2001, 110, 1150–63. [Google Scholar] [CrossRef] [PubMed]
  29. Wilson, B.; Finley, C.; Lawson, D.; Wolford, R.; Eddington, D.; Rabinowitz, W. Better speech recognition with cochlear implants. Nature 1991, 352, 236–8. [Google Scholar] [CrossRef]
  30. Berenstein, C.; Mens, L.; Mulder, J.; Vanpoucke, F. Current steering and current focusing in cochlear implants: comparison of monopolar, tripolar, and virtual channel electrode configurations. Ear Hear. 2008, 29, 250–60. [Google Scholar] [CrossRef]
  31. Bierer, J.; Litvak, L. Reducing channel interaction through cochlear implant programming may improve speech perception: Current focusing and channel deactivation. Trends Hear. 2016, 20. [Google Scholar] [CrossRef] [PubMed]
  32. Dieter, A.; Duque-Afonso, C.; Rankovic, V.; Jeschke, M.; Moser, T. Near physiological spectral selectivity of cochlear optogenetics. Nature Comm. 2019, 10, 1962. [Google Scholar] [CrossRef] [PubMed]
  33. Dieter, A.; Klein, E.; Keppeler, D.; Jablonski, L.; Harczos, T.; Hoch, G.; Rankovic, V.; Paul, O.; Jeschke, M.; Ruther, P.; Moser, T. μ-LED-based optical cochlear implants for spectrally selective activation of the auditory nerve. EMBO Mol. Med. 2020, e12387. [Google Scholar] [CrossRef] [PubMed]
  34. Azees, A.; Thompson, A.; Thomas, R.; Zhou, J.; Ruther, P.; Wise, A.; Ajay, E.; Garrett, D.; Quigley, A.; Fallon, J.; Richardson, R. Spread of activation and interaction between channels with multichannel optogenetic stimulation in the mouse cochlea. Hear. Res. 2023, 58–65. [Google Scholar]
  35. Keppeler, D.; Kampshoff, C.; Thirumalai, A.; Duque-Afonso, C.; Schaeper, J.; Quilitz, T.; Topperwien, M.; Vogl, C.; Hessler, R.; Meyer, A.; Salditt, T.; Moser, T. Multiscale photonic imaging of the native and implanted cochlea. Proc. Natl. Acad. Sci. USA 2021, 118. [Google Scholar] [CrossRef] [PubMed]
  36. Jurgens, T.; Hohmann, V.; Buchner, A.; Nogueira, W. The effects of electrical field spatial spread and some cognitive factors on speech-in-noise performance of individual cochlear implant users-A computer model study. PLoS One 2018, 13, e0193842. [Google Scholar] [CrossRef] [PubMed]
  37. Khurana, L.; Jablonski, D.K.L.; Moser, T. Model-based prediction of optogenetic sound encoding in the human cochlea by future optical cochlear implants. Comput. Struct. Biotechnol. J. 2022, 20, 3621–9. [Google Scholar] [CrossRef] [PubMed]
  38. Dharmavarapu, R.; Ng, S.H.; Eftekhari, F.; Juodkazis, S.; Bhattacharya, S. MetaOptics: opensource software for designing metasurface optical element GDSII layouts. Opt. Express 2020, 28, 3505–3516. [Google Scholar] [CrossRef]
  39. Dharmavarapu, R.; Izumi, K.; Katayama, I.; Ng, S.H.; Vongsvivut, J.; Tobin, M.J.; Kuchmizhak, A.; Nishijima, Y.; Bhattacharya, S.; Juodkazis, S. Dielectric cross-shaped-resonator-based metasurface for vortex beam generation at mid-IR and THz wavelengths. Nanophotonics 2019, 8, 1263–1270. [Google Scholar] [CrossRef]
Preprints 90889 g004
Figure 4. (a) Intensity distribution obtained for a single point of the LED. (b) Intensity distribution obtained for a circular region of the LED by incoherent superposition. (c) Intensity distribution obtained for the same circular region as (b) but with coherent superposition.
Figure 4. (a) Intensity distribution obtained for a single point of the LED. (b) Intensity distribution obtained for a circular region of the LED by incoherent superposition. (c) Intensity distribution obtained for the same circular region as (b) but with coherent superposition.
Preprints 90889 g004
Preprints 90889 g005
Figure 5. (a) Simulation by the Rayleigh–Sommerfeld (RS) diffraction integral for non-polarised plane wave with RGB wavelengths: R=700 nm, G=546.1 nm and B=435.8 nm (top-down). The calculated intensity cross section is given along propagation. (b) Central intensity cross section for the RGB colors; inset shows geometry of simulated positive fraxicon with Λ = 5 μ m period.
Figure 5. (a) Simulation by the Rayleigh–Sommerfeld (RS) diffraction integral for non-polarised plane wave with RGB wavelengths: R=700 nm, G=546.1 nm and B=435.8 nm (top-down). The calculated intensity cross section is given along propagation. (b) Central intensity cross section for the RGB colors; inset shows geometry of simulated positive fraxicon with Λ = 5 μ m period.
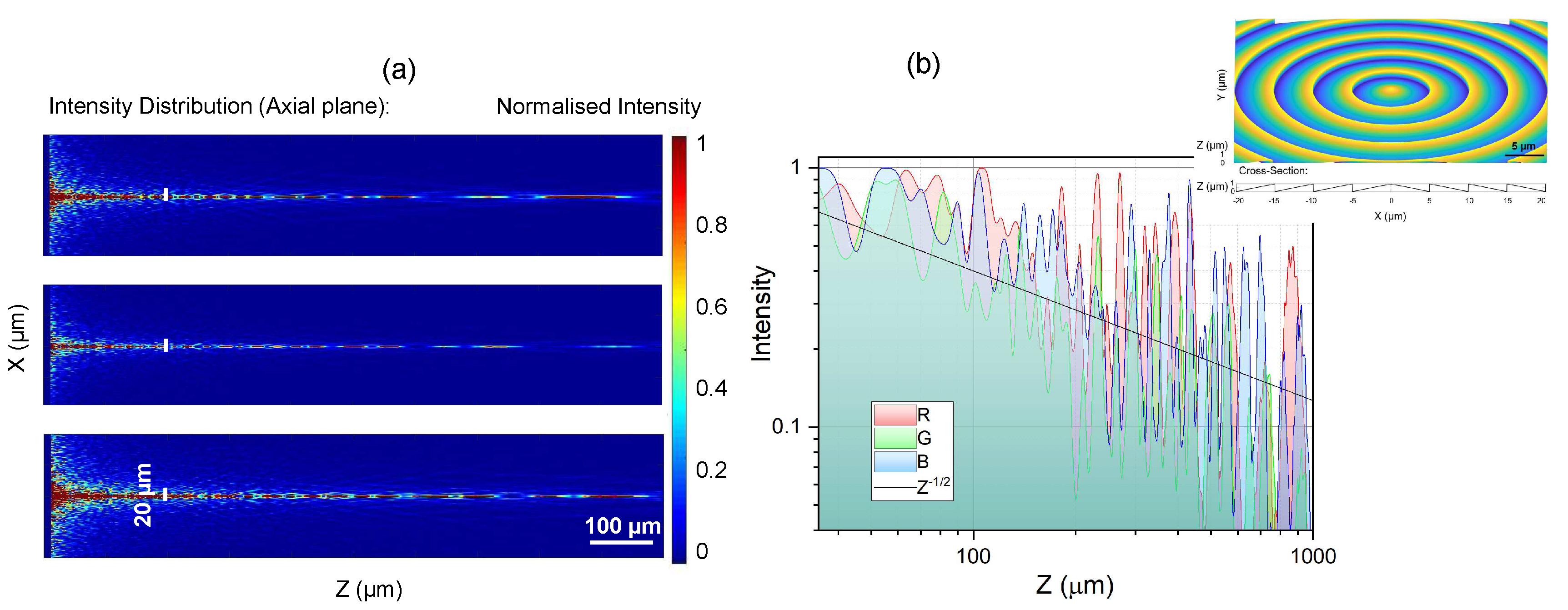
Preprints 90889 g005
Preprints 90889 g006
Figure 6. Ray tracing through (fr)axicons and their pairs (OSLO, Lambda Research Co.). Positive (a) and negative (b) fraxicon and axicon. Pairs of (fr)axicons (i.e. collimating telescopes): two positive (c) and a negative-positive pair (d) for the bulk and flat-optics realisations. Illumination with RGB color light shown by arrow. Location of the planarised (fraxicon) region is shown by shaded markers. The base angle of axicon α and γ is the half-cone angle of the Bessel beam. The refractive index of glass was n = 1.52 and the base angle α = ± 40 ∘ , where the positive sign is for real focus (a) and negative for virtual focus (b); a large angle was chosen for visualisation and a strong angular dispersion of RGB rays.
Figure 6. Ray tracing through (fr)axicons and their pairs (OSLO, Lambda Research Co.). Positive (a) and negative (b) fraxicon and axicon. Pairs of (fr)axicons (i.e. collimating telescopes): two positive (c) and a negative-positive pair (d) for the bulk and flat-optics realisations. Illumination with RGB color light shown by arrow. Location of the planarised (fraxicon) region is shown by shaded markers. The base angle of axicon α and γ is the half-cone angle of the Bessel beam. The refractive index of glass was n = 1.52 and the base angle α = ± 40 ∘ , where the positive sign is for real focus (a) and negative for virtual focus (b); a large angle was chosen for visualisation and a strong angular dispersion of RGB rays.
Preprints 90889 g006
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated