Prerpints.org logo
Preprint
Article

Supporting the Transition Towards Zero-Emission Recyclables Collection Using MARKAL-based Approach

Altmetrics

Downloads

85

Views

28

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

17 November 2023

Posted:

22 November 2023

You are already at the latest version

Alerts
Abstract
Municipal Solid Waste Management (MSWM) struggles with significant policy and operational challenges, particularly concerning recyclables collection routes and fleet composition. Within the European Union, phasing out traditional fuel-based vocational vehicles, like garbage trucks, in favor of zero-emission alternatives is mandatory to achieve sustainable development objectives. Integrating electric solid waste collection vehicles into municipal fleets presents challenges due to differences in range, capacity, and noise levels. The emission is even more crucial in the systems where recyclables are collected separately, which requires a greater number of trips to be performed. This study addresses MSWM’s strategic aspect by minimizing the total cost of replacing waste collection vehicles while meeting emission constraints. The Fleet Transition Problem (FTP) was formulated and solved using a MARKAL-based approach. The objective of the FTP and a mixed integer linear program used to solve it is minimizing the overall cost of fleet modernization throughout a multi-phase planning horizon so that the sustainable transition of the fleet can be assured. Computational experiments affirmed the model’s effectiveness in strategizing fleet transition. This research outlines a multi-period model for transitioning to a zero-emission fleet and demonstrates the FTP’s potential for strategic decision-making. Notably, the study observes a consistent reduction in permissible emissions across the planning horizon.
Keywords: 
Subject: Business, Economics and Management  -   Other

1. Introduction

The nexus between systemic circular economy principles and the efficient collection of solid waste is profoundly intricate. The realization of a systemic circular economy is contingent upon the existence of a robust and efficient solid waste collection system. Efficient and intelligent Municipal Solid Waste Management (MSWM) is indispensable for environmental cleanup, particularly when executed with technical precision and in alignment with local market dynamics and sustainability. Technological advances within the MSWM sector play a critical role in enhancing service efficiency and promoting environmental sustainability, ultimately benefiting local municipalities, solid waste collection companies, stakeholders, and citizens in their pursuit of an improved quality of life [1]. Nevertheless, the multifaceted nature of solid waste collection continues to pose a formidable challenge for decision-makers at both local and national levels. These difficulties cover various aspects, starting with educational initiatives focused on encouraging public adoption of the circular economy concept. Simultaneously, they extend to develop decision support systems customized to enhance both strategic and operational aspects of Municipal Solid Waste Management, including managing the solid waste collection fleet and routing solid waste collection vehicles.
Municipal Solid Waste Management is intrinsically linked with navigating a series of policy and governance challenges. At present, two pivotal concerns surface prominently: (1) separate recyclables collection routing, and (2) vocational fleet composition. The adoption of a separate recyclables collection approach streamlines the recycling process by providing recycling centers with pre-sorted recyclable materials. However, it necessitates repeated visits to the solid waste pickup points. These points are visited initially for collecting mixed household waste, and subsequently for retrieving segregated recyclables. The allocation of distinct garbage trucks dedicated to specific recyclable types amplifies the frequency of visits to each pickup point. The operational problem of the MSWM is intricately intertwined with routing problems, owing to the salient influence of solid waste collection vehicles’ characteristics, such as size, range, and emitted noise, on this intricate process [2,3,4]. Consequently, an imperative arises to strategically optimize the fleet used for solid waste collection service, so that multiple visits at the pickup points may not result in the increased emission produced by the vehicles used [5,6,7].
In this paper, the main research question is how useful is MARKAL-based approach for planning a gradual fleet transition toward zero-emission and sustainability minimizing the total cost for the transition in a multi-period planning horizon. The main contribution of the paper is the newly developed MARKAL-based MILP model for the Fleet Transition Problem, which aims at finding optimal schedules for modernization and substitution vehicles used for solid waste collection service. Obtained schedules are optimal which means that the total cost of modernization and substitution is minimal. This paper is structured as follows: In Section 1.1, we briefly present the importance of the fleet transition problem in Solid Waste Management from the perspective of obligations mandated by the European Green Deal. In Section 2, we present the MARKAL framework and its applications as well as the newly developed Fleet Transition Problem together with an associated mixed integer linear program. Next, in Section 3, we report computational experiments. In Section 4, we delineate potential avenues for future research.

1.1. Fleet transition in solid waste management

The European Green Deal obliges EU Member Countries to attain climate neutrality by 2050 [8]. The realization of a resource-efficient Europe hinges on the comprehensive and large-scale development and implementation of a systemic circular economy. To accomplish this, the adoption of urban and regional circular design solutions is imperative. Effective implementation requires a nuanced policy mix that maximizes synergies and addresses the inherent trade-offs across diverse domains and policy areas. As a result, it is essential to provide local authorities, citizens, and other stakeholders with a collaborative, science-informed decision-making environment conducive to exploring various waste and resource management alternatives. Such an environment should also enable the assessment of these alternatives’ impacts on environmental resilience, spatial quality, and overall quality of life.
A profound comprehension of the circular economy concept mandates a comprehensive understanding of the intricate interplay between socioeconomic and environmental dynamics, as well as the physical built environment. This expanded comprehension renders the circular economy concept more practicable and pragmatic. Consequently, there exists a pressing need for innovation in several key areas, including the integration of dynamic resource flow modeling, resource allocation in conjunction with urban and regional planning and design, and the consideration of human behavioral factors. In the EU There is a strong recommendation, even a requirement, to withdraw ON-powered vocational vehicles and compose the fleet using zero-emission alternatives, e.g. hybrid, hydrogen, or electric cars [9,10]. In Poland, where electromobility still has a small share of the market [11], the Act on Electromobility and Alternative Fuels required organizations responsible for delivering services within a municipality to undertake actions towards transforming their fleet compositions, so that by 2028 30% of their vehicle can be considered as zero-emission vehicles (ZEV). by 2028. To achieve this goal, specific interim targets have been established: 5% by 2021, 10% by 2022, and 20% by 2025 [12]. While emerging propulsion technologies and electromobility enhance the environmental efficiency of the transportation sector, the prevalence of older, less eco-friendly vehicles in car fleets undermines these advancements due to increased resource consumption and environmental degradation caused by extensive servicing and parts replacement [13].
However, the integration of electric vehicles, particularly electric solid waste collection vehicles, into municipal fleets presents significant challenges due to disparities in key characteristics compared to their conventional counterparts. Differences in range, capacity, and noise level necessitate adaptations in fleet management strategies [14,15,16]. Notably, the limited range of electric trucks may necessitate rerouting efforts. In contrast, the reduced noise level allows for nocturnal solid waste collection. As the proportion of electric garbage trucks in municipal fleets continues to grow, the demand for effective tools to manage a heterogeneous fleet becomes increasingly pressing. Amidst evolving waste management laws, there’s a pressing need for effective decision support systems. These systems are imperative for ensuring seamless integration of electric vehicles, optimizing routes, and enhancing the overall efficiency of municipal solid waste collection operations. It should not be overlooked that strategic decisions to replace the fleet with differently powered vehicles can significantly affect the operational management of transport tasks, which is very visible and acute in the case of urban public transport [17].
Managers of diverse companies and service-providing agencies reliant on transportation confront the intricate challenge of fleet replacement to meet environmental mandates. This predicament is compounded by the need to balance service quality, which can generate emissions, with the economic optimization of in-service vehicles to align with the company’s operational efficiency and long-term strategy of fleet transition towards its greener composition. Striking a harmonious balance to establish an optimal scenario for the gradual, multi-period fleet replacement with more environmentally friendly options is a complex undertaking [18]. Making informed, if not ideal, decisions in this context is a formidable task, as decision-makers must rely on economic and ecological analyses as well as their expertise. Given the intricacy and multi-period nature of this issue, the utilization of decision-support tools becomes indispensable.
Such a problem is faced in maritime transportation - where before creating an optimization model, informed market analysis was conducted, to identify the minimal number of electric vessels needed to fully replace the current diesel fleet, while considering multiple factors, including transport demand, vessel quantity, and environmental sustainability [19]. The study by Ahani et al. [20] presents an innovative framework designed to support urban freight transportation operators in optimizing their fleet configuration to minimize overall costs while adhering to regulations related to vehicle size and type and complying with specific city zones defined by local authorities. The framework takes into account various cost factors, including vehicle acquisition, energy consumption, emissions, maintenance, salvage, and labor across different vehicle types. The outcome of the model provides insights into the optimal fleet composition, specifying the necessary quantity, size, and types of vehicles required for operation in different city areas throughout the planning period.
Maritime transportation faces a similar challenge. In a recent study by Prina et al., [19], market analysis preceded the development of an optimization model. This aimed to determine the minimum number of electric vessels necessary to replace the current ON-powered fleet, considering factors like transport demand and environmental sustainability. Another study by Ahani et al. [20] introduced a novel framework for urban freight transportation operators. This framework optimizes a fleet composed of various types of vehicles, considering the demand for services, geographical and demographical characteristics of the city, and legal obligations along with costs of purchase, refueling, maintenance, and operations as well as emission. The model provides insights into the ideal fleet composition, specifying vehicle quantity, size, and types required for serving various cities in a planning horizon.

2. Matherials and Methods

In this paper, we considered the strategic problem of municipal solid waste management concerning the gradual modernization and replacement of the fleet as an optimization problem where the total cost of replacing and modernizing the fleet of waste collection vehicles is minimized. at the same time, the constraints must be satisfied, i.e. the gradual increase in the limitation on the total available emissions limit over a planning horizon. We formulated the Fleet Transition Problem (FTP) and propounded to solve it using a MARKAL-based mixed integer linear program.

2.1. MARKAL – an overwiev

The MARKAL (MARKal ALlocation) model was initially formulated as a linear program to select emerging energy technologies to fulfill best the needs of a national energy system in a chosen set of regions. It evolved towards a technology-rich framework capable of predicting energy trends over multiple periods. The model facilitates decisions regarding equipment investments, operations, and regional primary energy supply. In scenario analysis including alterations in demand for an energy service, MARKAL determines whether to optimize existing infrastructure or invest in new technologies. The assessment of technologies under consideration takes into account the economic aspects of primary energy supply. In essence, MARKAL helps to establish energy equilibrium across technologies of different technological levels to minimize overall global energy expenses [21,22].
MARKAL stands as an all-encompassing framework delving into the entirety of the energy system, calculating an inter-temporal partial equilibrium within energy markets. Essentially, MARKAL-based models aim at balancing quantities and prices of fuels, i.e. determining optimal prices for energy aligned with the demanded quantities sought by consumers which can be fulfilled by suppliers. Moreover, all the investments needed to reach that balance by the end of the planning horizon are optimally distributed across the planning period, so that the total surplus is maximized. MARKAL-based framework was widely utilized to assess developmental directions and the velocity of technological transition mainly for the energy sector, also towards its decarbonization, in Canada[23], Quebec [24], Switzerland [25], Malaysia [26], Russia [27], the UK [28,29,30,31] and the US [32,33], Austria [34], China [35,36], Portugal [37,38,39], China [40,41], Italy [42], Iran [43], Turkey [44], Kazakhstan [45], Ireland [46], Poland [47], Greece [48] nad Bulgaria [34].
In addition, Salvia et al. [49,50,51], using the MARKAL framework, developed a detailed model to analyze the human-system interactions in the Basilicata region, Italy, focusing on solid waste management. This aimed to conform to Italian regulations, ensuring an efficient regional solid waste management plan. They conducted a sensitivity analysis, particularly examining the influence of landfill fees on solid waste processing decisions. The study aimed to create a sustainable, cost-effective, and efficient waste management strategy, expanding the MARKAL model’s applications beyond energy sectors. Key factors affecting the integrated system include landfill volume restrictions, greenhouse gas emissions, and solid waste disposal charges. However, the success of such a plan depends significantly on human factors, emphasizing the importance of training, organizational strategies, and public engagement for effective implementation.

2.2. Fleet Transition Problem

Let set T denote the planning horizon which consists of t planning periods, while set R denote the types of fueling available for the solid waste collection vehicles. At each planning horizon t, the demand for the total number of vehicles to fulfill the solid waste collection service is known. We also know in advance two types of costs: (1) costs c r , l for modernizing a vehicle, so that it is shifted from operating on fuel r to fuel l, and (2) costs C r that must be incurred to purchase a new vehicle operating on the fuel r. Let b t denote the total allowable emissions that moving solid waste collection vehicles can generate in each period t. For each vehicle fuelled with fuel r, the amount of emissions generated ( e r ) is known. We also know in advance I r the initial number of vehicles fueled with fuel r in the possession of a solid waste collection company.
The decision criterion is the minimum total cost of fleet modernization and replacement discounted over time according to an assumed discount rate of q. The costs incurred are related to the decisions made about (1) the number of vehicles shifted from fuel r to fuel l (denoted with decision variable ( f r , l , t ) and (2) the number of purchased new vehicles fuelled with greener fuel r (denoted with decision variable ( u r , t ). The decision variable x r , t stands for the number of vehicles fuelled with fuel r in the possession of the company in planning period t. The notation used in the formulas of the MILP model for FTP is presented in Table 1.
A mixed integer linear program was formulated to address the Fleet Transition Problem employing formulas (1a)–(1g).
min : ∑ t ∈ T ( ∑ r ∈ R ∑ l ∈ R c r , l * f r , k , t + ∑ r ∈ R C r · u r , t ) · q t ;
∑ k ∈ R f r , k , 0 = I r , r ∈ R ;
∑ r ∈ R x r , t = d t , t ∈ T ;
∑ r ∈ R e r · x r , t ≤ b t , t ∈ T ;
x r , t = ∑ k ∈ R f k , r , t + u r , t , r ∈ R , t ∈ T : t > 0 ;
f r , r , t ≤ u r , t , r ∈ R , t ∈ T ;
∑ k ∈ R f r , k , t = ∑ k ∈ R f k , r , t − 1 + u r , t − 1 , r ∈ R , t ∈ T : t > 0 ;
∑ r ∈ R u r , t = d t − d t − 1 , t ∈ T : t > 0 ;
f r , l , t ≥ 0 , f r , l , t ∈ C , r ∈ R , l ∈ R , t ∈ T ;
x r , t ≥ 0 , x r , t ∈ C , r ∈ R , t ∈ T ;
u r , t ≥ 0 , u r , t ∈ C , r ∈ R , t ∈ T ;
The objective function (1a) aims at minimizing the total cost associated with modernizing existing vehicles (i.e. shifting them from fuel r to l) and purchasing new ones. Constraint (1b) forces the search for a solution for the initial composition of the fleet possessed by the solid waste collection company. The required number of vehicles d t in each planning period t is ensured by constraint (1c). Constraint (1d) ensures that the allowable emission limit b t is maintained for each period t. Accordingly, constraints (1e)–(1g) and constraint (1h), respectively, allow the modernization of a given number of vehicles and (or) the purchase of new ones, by maintaining the correct balance for the fleet composition in subsequent planning periods during the planning horizon.

3. Computattional Experiments

As a validation test, the following optimization problem has been formulated: Municipal Solid Waste Management (MSWM) needs to plan and manage the modernization of their vehicle and purchase of new solid waste collection vehicles so that in the next years the requirements for reducing the permissible emission standards for used vehicles can be met. To keep the example simple, let’s assume that the solid waste collection vehicles under consideration can run on four types of fuel: ON - diesel fuel, CNG - natural gas, HY - hybrid system, H2 - hydrogen.
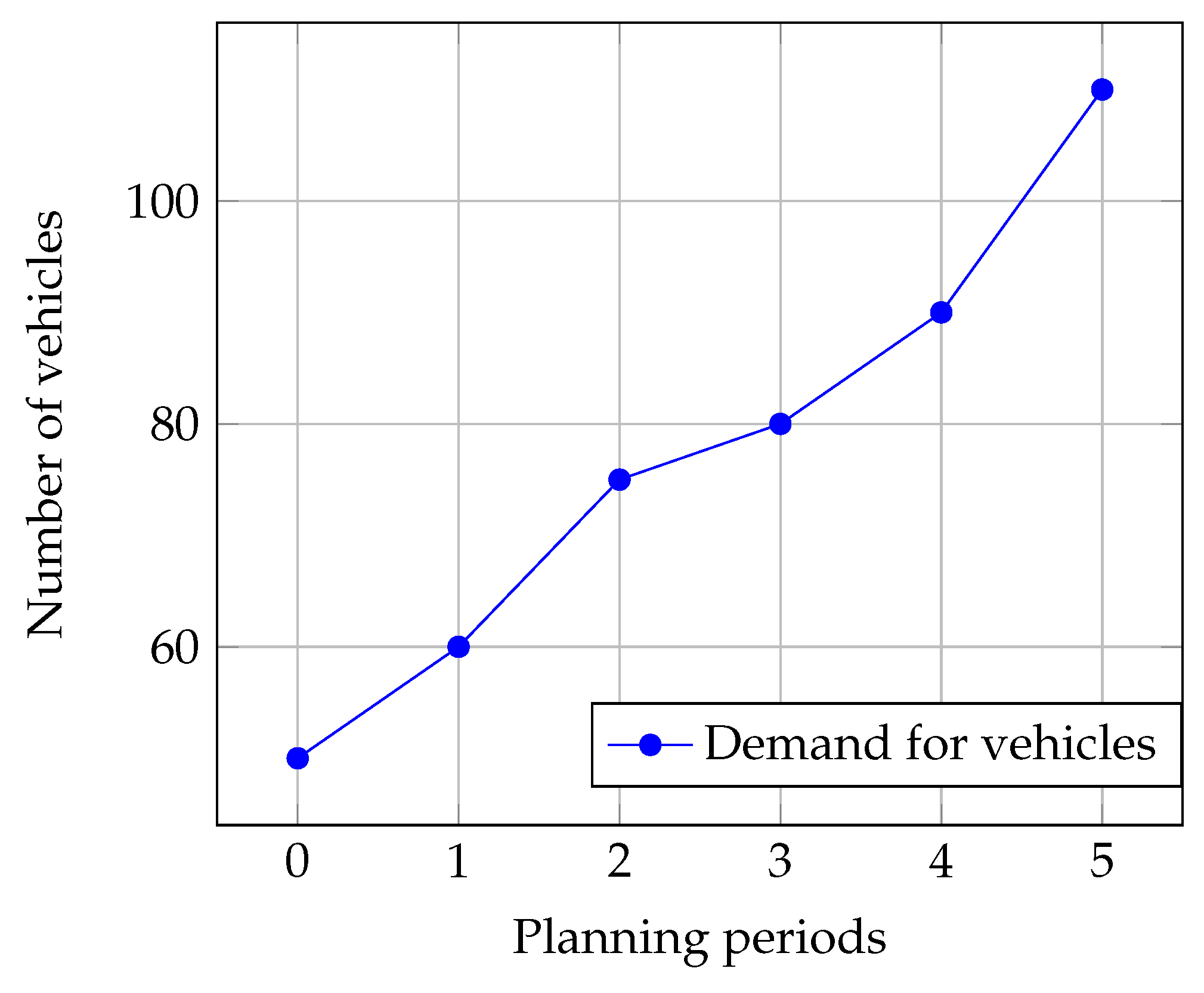
As the MSWM continues to grow we know the projected demand for the number of vehicles which from the current 50 units in the 5th year of planning should be as high as 110 units. The projected demand for vehicles is shown in Figure 1. The MSWM knows the number of vehicles currently owned, the cost of purchasing a vehicle powered by each fuel type, and the total annual emissions of each type of vehicle. The data is presented in the Table 2.
In addition, the MSWM knows the cost of modernization of a vehicle from one fuel to another which results in reduced emissions. The modernization costs are shown in Table 3.
Computational experiments were undertaken to find the solution to the exemplary FTP instance presented above. The provided MIP model could effectively solve using a standard computing setup, in line with typical computational resources available for use within the company. The solver employed for this analysis was GUROBI 9.0.1, run on a computer equipped with a dual-core Intel Core i7-4710HQ CPU operating at 2.50 GHz and 16 GB of RAM.
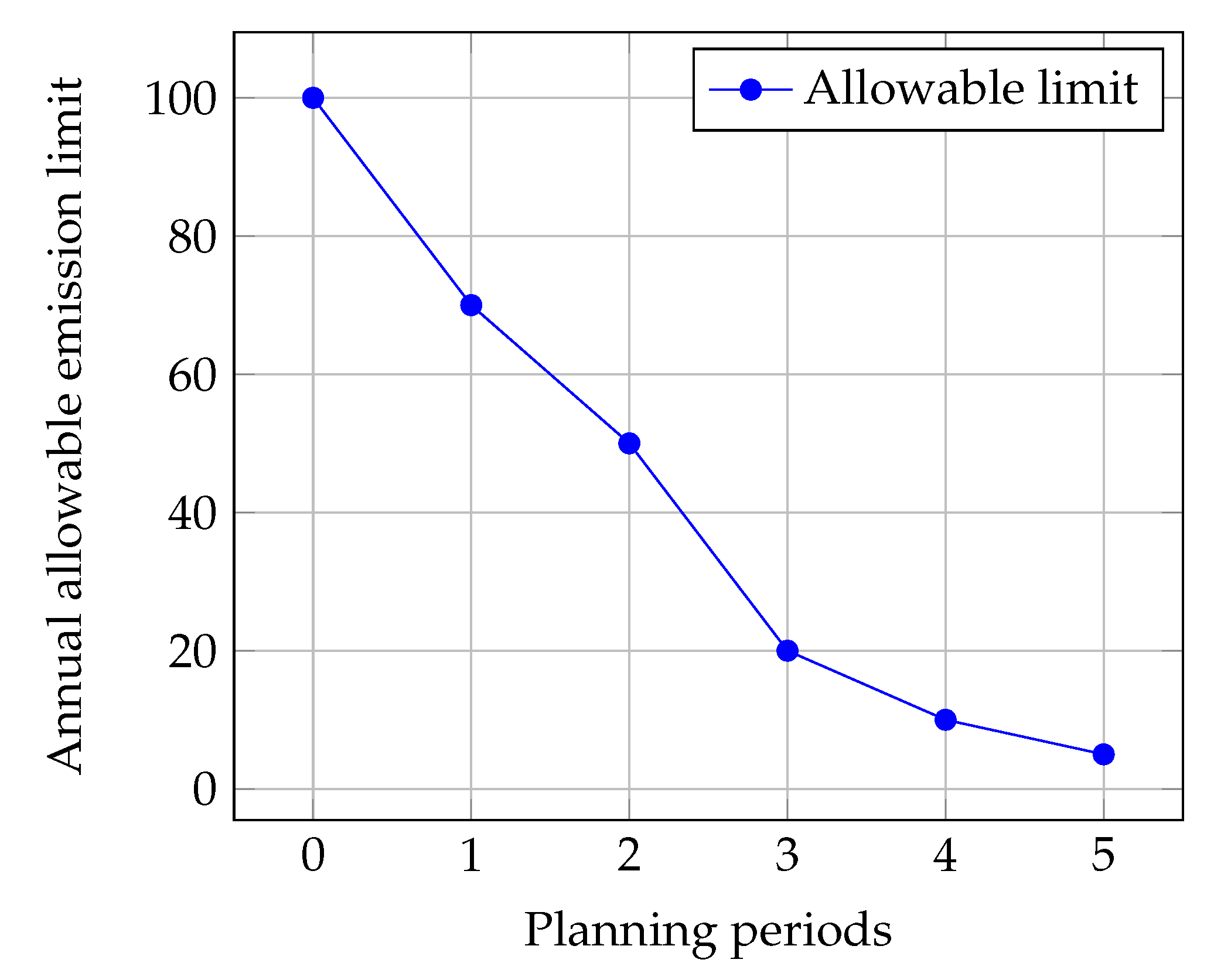
Throughout the planning horizon, there is a notable decline observed in the maximum permissible emissions. Commencing from the current emission levels (i.e 100 units per year), there is a discernible reduction over successive planning periods, reaching the minimum allowable annual emissions of 5 units per year in the latest planning period. The diminishing trend of the annual emission is graphically depicted in Figure 2.
In the instance under examination, the optimal solution was found, which minimizes the total cost for modernization and replacement of the fleet during the predefined planning horizon, considering an annual discount rate of 7%. The computed optimal total cost was 163.67 units. The MWSM under examination possessed in the initial planning period 50 vehicles. Conversely, in the ultimate planning period, as dictated by the vehicle demand data, a total of 110 vehicles are necessary. Consequently, within this planning horizon, there was a necessity to procure 60 new vehicles, including both purchasing 60 units and modernizing 50 of them. It should be highlighted that the FTP model newly developed in this paper doesn’t account for the selling or disposal of any spare parts of the existing vehicle fleet. Table 4 meticulously outlines the comprehensive schedule detailing the planned acquisitions for each vehicle category during each planning period. In total the stipulated acquisitions amounted to 60 vehicles, the predominant count among them being 47 hydrogen-powered vehicles.
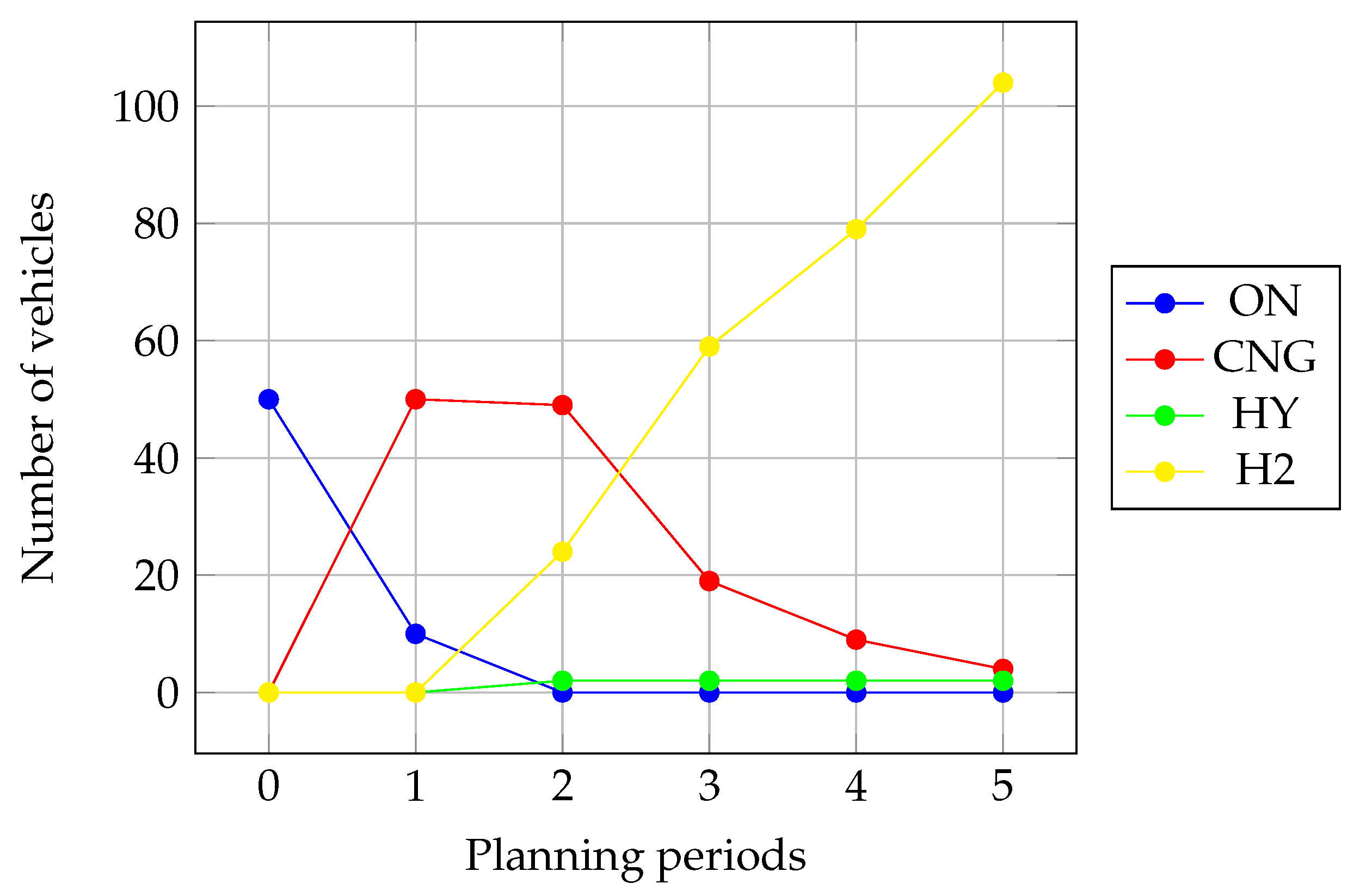
Figure 3 shows the number of available vehicles fueled by each type of fuel over each planning horizon. Due to the decreasing emission limit over the planning horizon, emission-fueled vehicles are gradually being replaced by emission-free vehicles. In the last planning horizon, the vehicle fleet consists of four CNG-fueled vehicles, two hybrid vehicles, and 104 hydrogen-fueled vehicles.
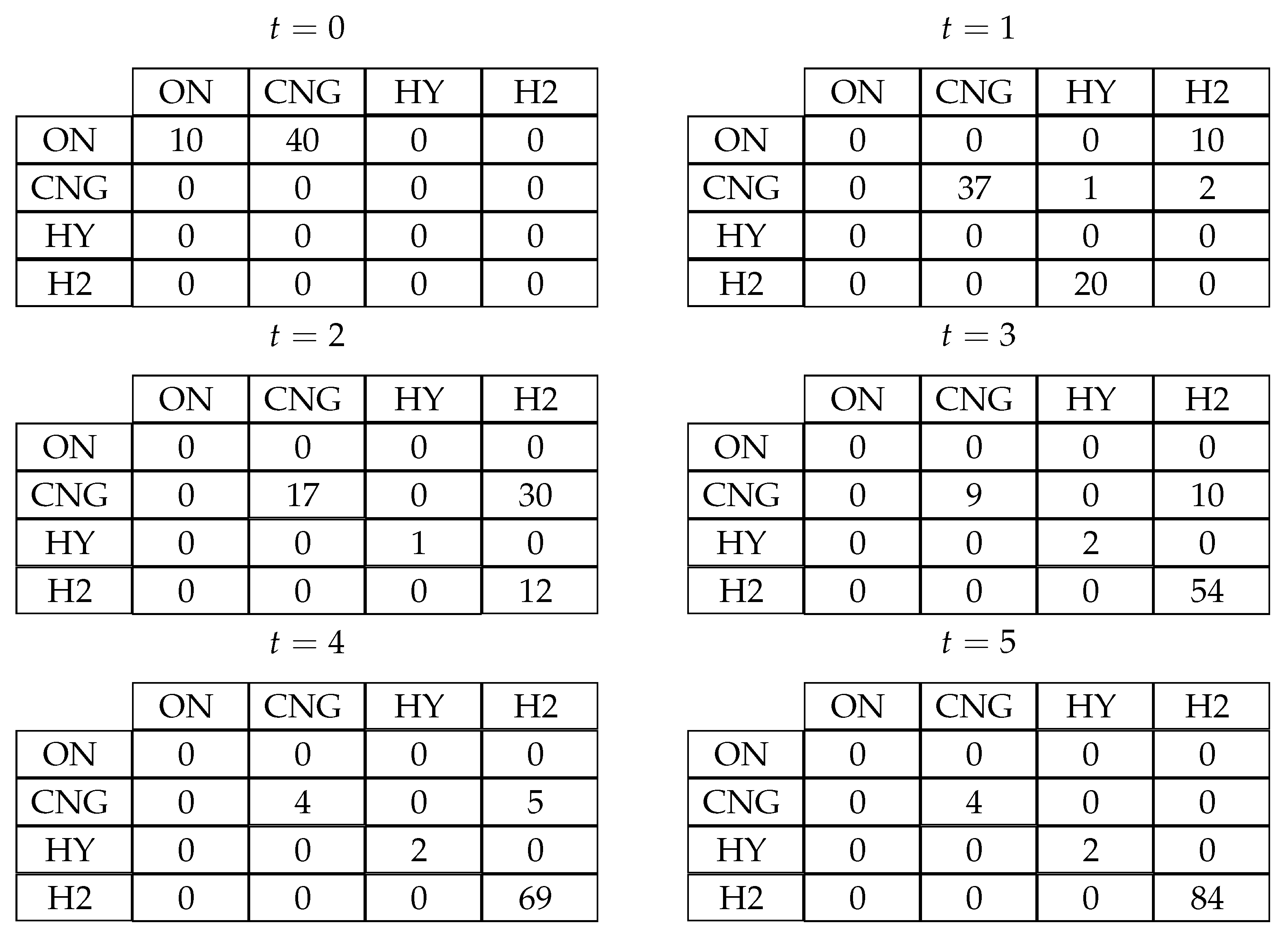
Figure 4 shows the computed values obtained of flow variable f r , k , t , denoting the count of vehicles transitioning from fuel type r to fuel k in each period. In the initial planning period t = 0 , 40 vehicles running on ON were modernized to run on CNG, while 10 vehicles remained unchanged. However, in the subsequent period t = 1 , all vehicles powered by ON were upgraded to hydrogen fuel, 37 remained unaltered, while 3 vehicles underwent modifications: one transformed into a hybrid vehicle, and two were modified into hydrogen-fuel type vehicles. Modernization of the vehicle fleet has always been carried out in the direction of lowering emissions. In the final planning phase, no further alterations occurred, with only 20 hydrogen-fueled vehicles procured,

4. Conclusions

In summary, it’s imperative to emphasize that this paper represents preliminary investigations into the potential applicability of the MARKAL model in strategizing the transition of fleets within a solid waste collection enterprise. We have presented a MARKAL-inspired MILP model for a multi-period project of modernization and replacement vehicles toward having a zero-emission fleet. The example of the Fleet Transition Problem for which computational experiments were conducted illustrates a potential application of the developed FTP model for strategic decision-making.
It is worth noting that the Fleet Transition Problem introduced in this study has been effectively validated through the resolution of illustrative cases. However, future research endeavors should aim to assess the FTP’s performance using historical data derived from an actual solid waste collection company. Given the prevailing recommendation for the incremental modernization of solid waste collection fleets in this domain, this investigation has demonstrated that the MARKAL-based model, originally designed for the energy sector, serves as a pertinent and valuable tool for the transportation sector, particularly in the context of strategic decisions concerning substantial fleet investments. Subsequently, forthcoming research endeavors should incorporate similar studies, employing the FTP on datasets derived from actual operations, and delve into more comprehensive analyses of the determinants influencing fleet replacement and modernization decisions.
In future research, the emphasis should be placed on incorporating the financial aspect into the decision-making process regarding the transition of the solid waste collection fleet through modification and gradual replacement of the vehicles. Two directions of research can be distinguished in this context. Firstly, a scenario where a fixed budget is allocated for each planning period. In this case, the model will need to optimize the mix of modernization and replacement costs, determining how to allocate the budget to vehicle modernization and replacement while adhering to the specified constraints. This approach will provide valuable insights into the optimal allocation of financial resources, balancing the integration of modernized and newly bought vehicles. Secondly, an approach involving an ideal situation with an unlimited budget. This entails a comprehensive examination of the cost implications associated with technology changes, specifically fuel-type modifications. This budget-independent analysis aims to uncover the economic considerations intrinsic to technology transitions. It will result in getting the benchmark solution where the emission is undoubtedly minimized.
By integrating the budget issue into the MARKAL-based model for the fleet transition problem, a more comprehensive and nuanced decision support tool will be developed. This will empower stakeholders and decision-makers with the tools necessary to navigate the complex landscape of fleet optimization, considering both economic constraints and environmental imperatives. Furthermore, the MARKAL-based approach seems to be potentially useful for optimizing the proportion of modified and purchased low-emission vehicles within the overall fleet over a planning horizon obtained in the available budget. This can be achieved by imposing a predetermined percentage for specific periods, aligning with demand for solid waste collection service, budget limitation for fleet transition, and environmental targets. This addition to the model will allow for a more nuanced exploration of scenarios that actively contribute to meeting regulatory conditions while balancing economic considerations.

Author Contributions

Conceptualization, A.K. and R.K.; methodology, K.G.; software, R.K.; validation, R.K., A.K, and K.G.; formal analysis, B.B.; investigation, R.K.; resources, A.K.; data curation, R.K.; writing—original draft preparation, K.G., and R.K.; writing—review and editing, A.K., B.B., R.K., and K.G.; visualization, R.K., and K.G.; supervision, B.B, and A.K.; project administration, K.G.; funding acquisition, A.K. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Acknowledgments

This work was supported by the Program "Excellence Initiative—Research University" with the AGH University of Krakow, Poland.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
CNG natural gas
FTP Fleet Transition Problem
H2 hydrogen
HY hybrid system
MILP Mixed Integer Linear Programming
MSWM Municipal Solid Waste Management
ON diesel fuel
OR Operations Research
SWM Solid Waste Management
ZEV zero-emission vehicle

References

  1. Iqbal, A.; Yasar, A.; Nizami, A.S.; Haider, R.; Sharif, F.; Sultan, I.A.; Tabinda, A.B.; Kedwaii, A.A.; Chaudhary, M.M. Municipal Solid Waste Collection and Haulage Modeling Design for Lahore, Pakistan: Transition toward Sustainability and Circular Economy. Sustainability (Switzerland) 2022, 14. [CrossRef]
  2. Korcyl, A.; Ksia̧żek, R.; Gdowska, K. A MILP model for the municipal solid waste selective collection routing problem. Decision Making in Manufacturing and Services 2019, 13, 17–35.
  3. Korcyl, A.; Ksia̧żek, R.; Gdowska, K. Modele optymalizacyjne dla problemu planowania tras odbioru odpadów. In Selected Big Data-Based Tools for Supporting Decision Making and Risk Management, 1 ed.; Iwaszczuk, N., Ed.; Wydawnictwa AGH: Kraków, 2020; pp. 215–230.
  4. Lozano, Á.; Caridad, J.; De Paz, J.F.; González, G.V.; Bajo, J. Smart waste collection system with low consumption LoRaWAN nodes and route optimization. Sensors (Switzerland) 2018, 18. [CrossRef]
  5. Ksia̧żek, R.; Gdowska, K.; Korcyl, A. Recyclables collection route balancing problem with heterogeneous fleet. Energies 2021, 14, 7406. [CrossRef]
  6. Korcyl, A.; Gdowska, K.; Ksia̧żek, R. Optymalizacja tras odbioru odpadów komunalnych z wykorzystaniem różnych typów pojazdów i ograniczeniami czasowymi w obsłudze klienta. Logistyka 2015, pp. 9202–9211.
  7. Gdowska, K.; Ksia̧żek, R.; Korcyl, A. Fleet Optimization for a Selective Solid Waste Collection System. In Challanges and modern solution in transportation; Maciej Stajniak Magdalena Kopeć Adrianna Toboła, M.S., Ed.; Instytut Naukowo-Wydawniczy Spatium: Radom, 2019; pp. 121–134.
  8. European Commission. A Clean Planet for All, A European Strategic Long Term Vision for a Prosperous, Modern, Competitive and Climate Neutral Economy by 2050 r., 2018.
  9. Koiwanit, J.; Hamontree, C. Greenhouse gas emissions comparison of solid waste transportation system: a case study in Thailand. IOP Conference Series: Earth and Environmental Science 2020, 424. [CrossRef]
  10. Schmid, F.; Taube, L.; Rieck, J.; Behrendt, F. Electrification of Waste Collection Vehicles: Technoeconomic Analysis Based on an Energy Demand Simulation Using Real-Life Operational Data. IEEE Transactions on Transportation Electrification 2021, 7, 604–615. [CrossRef]
  11. Skowrońska-Szmer, A.; Kowalska-Pyzalska, A. Key Factors of Development of Electromobility AMONG Microentrepreneurs: A Case Study from Poland. Energies 2021, 14. [CrossRef]
  12. Polish Parliament. Ustawa z dnia 11 stycznia 2018 r. o elektromobilności i paliwach alternatywnych.
  13. Danilecki, K.; Smurawski, P.; Urbanowicz, K. Optimization of Car Use Time for Different Maintenance and Repair Scenarios Based on Life Cycle Assessment. Applied Sciences 2023, 13, 9843. [CrossRef]
  14. Elangovan, R.; Kanwhen, O.; Dong, Z.; Mohamed, A.; Rojas-Cessa, R. Comparative Analysis of Energy Use and Greenhouse Gas Emission of Diesel and Electric Trucks for Food Distribution in Gowanus District of New York City. Frontiers in Big Data 2021, 4. [CrossRef]
  15. California Air Resources Board. Battery Electric Truck and Bus Energy Efficiency Compared to Conventional Diesel Vehicles.
  16. W, M.S. Preparing for the Future of Electric Garbage Trucks, 2021.
  17. Rogge, M.; van der Hurk, E.; Larsen, A.; Sauer, D.U. Electric bus fleet size and mix problem with optimization of charging infrastructure. Applied Energy 2018, 211, 282–295. [CrossRef]
  18. Plachinda, P.; Morgan, J.; Coelho, M. Towards Net Zero: Modeling Approach to the Right-Sized Facilities. Sustainability (Switzerland) 2023, 15. [CrossRef]
  19. Prina, M.G.; Zubaryeva, A.; Rotondo, G.; Grotto, A.; Sparber, W. Optimal Fleet Transition Modeling for Sustainable Inland Waterways Transport. Applied Sciences (Switzerland) 2023, 13. [CrossRef]
  20. Ahani, P.; Arantes, A.; Garmanjani, R.; Melo, S. Optimizing Vehicle Replacement in Sustainable Urban Freight Transportation Subject to Presence of Regulatory Measures. Sustainability (Switzerland) 2023, 15. [CrossRef]
  21. Fishbone, L.G.; Abilock, H. Markal, a linear-programming model for energy systems analysis: Technical description of the bnl version. International Journal of Energy Research 1981, 5. [CrossRef]
  22. Loulou, R.; Goldstein, G.; Noble, K. Documentation for the MARKAL Family of Models. International Energy Agency 2004.
  23. Berger, C.; Dubois, R.; Haurie, A.; Lessard, E.; Loulou, R.; Waaub, J.P. Canadian Markal: An Advanced Linear Programming System For Energy And Environmental Modelling. INFOR: Information Systems and Operational Research 1992, 30. [CrossRef]
  24. Kanudia, A.; Loulou, R. Robust responses to climate change via stochastic MARKAL: The case of Québec. European Journal of Operational Research 1998, 106. [CrossRef]
  25. Fragniere, E.; Haurie, A. MARKAL-Geneva: A model to assess energy-environment choices for a Swiss canton. In Operations Research and Environmental Management; Springer Netherlands: Dordrecht, 1996. [CrossRef]
  26. Zonooz, M.R.F.; Nopiah, Z.M.; Mohd.Yusof, A.; Sopian, K. A review of MARKAL energy modeling, 2009.
  27. Gryzunova, N.; Vedenyev, K.; Manuylenko, V.; Keri, I.; Bilczak, M. Distributed Energy as a Megatrend of Audit of Investment Processes of the Energy Complex. Energies 2022, 15. [CrossRef]
  28. McDowall, W.; Anandarajah, G.; Dodds, P.E.; Tomei, J. Implications of sustainability constraints on UK bioenergy development: Assessing optimistic and precautionary approaches with UK MARKAL. Energy Policy 2012, 47. [CrossRef]
  29. Strachan, N.; Kannan, R.; Pye, S. Scenarios and Sensitivities on Long-term UK Carbon Reductions using the UK MARKAL and MARKAL-Macro Energy System Models. UK Energy Research Centre 2008.
  30. Taylor, P.G.; Upham, P.; McDowall, W.; Christopherson, D. Energy model, boundary object and societal lens: 35 years of the MARKAL model in the UK. Energy Research and Social Science 2014, 4. [CrossRef]
  31. 1604Yuan, X.; Zhu, M.; Liang, Y.; Shahrestani, M.; Kosonen, R. Comparison of Short and Long-Term Energy Performance and Decarbonization Potentials between Cogeneration and GSHP Systems under MARKAL Scenarios. Sustainability 2023, 15, 1604. [CrossRef]
  32. Sarica, K.; Tyner, W.E. Analysis of US renewable fuels policies using a modified MARKAL model. Renewable Energy 2013, 50. [CrossRef]
  33. Victor, N.; Nichols, C.; Zelek, C. The U.S. power sector decarbonization: Investigating technology options with MARKAL nine-region model. Energy Economics 2018, 73. [CrossRef]
  34. Perissi, I.; Martelloni, G.; Bardi, U.; Natalini, D.; Jones, A.; Nikolaev, A.; Eggler, L.; Baumann, M.; Samsó, R.; Solé, J. Cross-validation of the MEDEAS energy-economy- environment model with the integrated MARKAL-EFOM system (TIMES) and the long-range energy alternatives planning system (LEAP). Sustainability (Switzerland) 2021, 13, 1–27. [CrossRef]
  35. Ma, X.; Chai, M.; Luo, L.; Luo, Y.; He, W.; Li, G. An assessment on Shanghai’s energy and environment impacts of using MARKAL model. Journal of Renewable and Sustainable Energy 2015, 7. [CrossRef]
  36. Li, S.; Qiao, J.; Cui, H.; Wang, S. Realizing the environmental benefits of proactive environmental strategy: The roles of green supply chain integration and relational capability. Sustainability (Switzerland) 2020, 12. [CrossRef]
  37. Amorim, F.; Pina, A.; Gerbelová, H.; Pereira da Silva, P.; Vasconcelos, J.; Martins, V. Electricity decarbonisation pathways for 2050 in Portugal: A TIMES (The Integrated MARKAL-EFOM System) based approach in closed versus open systems modelling. Energy 2014, 69. [CrossRef]
  38. Monjardino, J.; Dias, L.; Fortes, P.; Tente, H.; Ferreira, F.; Seixas, J. Carbon neutrality pathways effects on air pollutant emissions: The Portuguese case. Atmosphere 2021, 12. [CrossRef]
  39. Ioakimidis, C.S.; Genikomsakis, K.N. Integration of seawater pumped-storage in the energy system of the Island of São Miguel (Azores). Sustainability (Switzerland) 2018, 10. [CrossRef]
  40. Chen, W.; Wu, Z.; He, J.; Gao, P.; Xu, S. Carbon emission control strategies for China: A comparative study with partial and general equilibrium versions of the China MARKAL model. Energy 2007, 32. [CrossRef]
  41. Chen, W. The costs of mitigating carbon emissions in China: Findings from China MARKAL-MACRO modelling. Energy Policy 2005, 33. [CrossRef]
  42. Contaldi, M.; Gracceva, F.; Tosato, G. Evaluation of green-certificates policies using the MARKAL-MACRO-Italy model. Energy Policy 2007, 35. [CrossRef]
  43. Behzadi Forough, A.; Norouzi, N.; Fani, M. More Secure Iranian Energy System: A Markal Based Energy Security Model for Iranian Energy Demand-side. Iranian Journal of Energy and Environment 2021, 12. [CrossRef]
  44. Sulukan, E.; Sağlam, M.; Uyar, T.S.; Kirlidoğ, M. Determining Optimum Energy Strategies for Turkey by MARKAL Model. Journal of Naval Science and Engineering 2010, 6, 27–38.
  45. Zhakiyev, N.; Khamzina, A.; Zhakiyeva, S.; De Miglio, R.; Bakdolotov, A.; Cosmi, C. Optimization Modelling of the Decarbonization Scenario of the Total Energy System of Kazakhstan until 2060. Energies 2023, 16. [CrossRef]
  46. Madden, S.M.; Ryan, A.; Walsh, P. Exploratory Study on Modelling Agricultural Carbon Emissions in Ireland, 2022. [CrossRef]
  47. Jaskólski, M.; Bućko, P. Modelling long-term transition from coal-reliant to low-emission power grid and district heating systems in Poland. Energies 2021, 14. [CrossRef]
  48. Ioakimidis, C.S.; Gerbelova, H.; Bagheri, A.; Koutra, S.; Koukouzas, N. Strategic planning for carbon capture and storage implementation in the electricity sector of greece: a times based analysis. Processes 2021, 9. [CrossRef]
  49. Salvia, M.; Cosmi, C.; Macchiato, M.; Mangiamele, L. Waste management system optimisation for Southern Italy with MARKAL model. Resources, Conservation and Recycling 2002, 34, 91–106. [CrossRef]
  50. Cosmi, C.; Cuomo, V.; Macchiato, M.; Mangiamele, L.; Masi, S.; Salvia, M. Waste management modeling by MARKAL model: A case study for Basilicata Region. Technical report, 2000.
  51. Salvia, M.; Pietrapertosa, F.; Cosmi, C.; Cuomo, V.; Macchiato, M. Approaching the Kyoto targets: A case study for Basilicata region (Italy), 2004. [CrossRef]
Preprints 90795 g001
Figure 1. Forecasted demand for vehicles.
Figure 1. Forecasted demand for vehicles.
Preprints 90795 g001
Preprints 90795 g002
Figure 2. Total allowable emission limits for the assumed planning horizon.
Figure 2. Total allowable emission limits for the assumed planning horizon.
Preprints 90795 g002
Preprints 90795 g003
Figure 3. Solution, i.e. values of decision variable x r , t – the number of vehicles operating on fuel r possessed by the company in planning period t
Figure 3. Solution, i.e. values of decision variable x r , t – the number of vehicles operating on fuel r possessed by the company in planning period t
Preprints 90795 g003
Preprints 90795 g004
Figure 4. Solution, i.e. the values of decision variable f r , l , t – the number of vehicles operating on fuel r shifted to fuel l in planning period t
Figure 4. Solution, i.e. the values of decision variable f r , l , t – the number of vehicles operating on fuel r shifted to fuel l in planning period t
Preprints 90795 g004

CNG natural gas
FTP Fleet Transition Problem
H2 hydrogen
HY hybrid system
MILP Mixed Integer Linear Programming
MSWM Municipal Solid Waste Management
ON diesel fuel
OR Operations Research
SWM Solid Waste Management
ZEV zero-emission vehicle
Table 1. Notation used in the MILP model for FTP.
Table 1. Notation used in the MILP model for FTP.
Sets
T – planning horizon, i.e. the set of planning periods
R – the set of the types of fueling available for the solid waste collection vehicles
Parameters
d t – the number of solid waste collection vehicle needed in period t to perform
   solid waste collection service
c r , l – the cost of shifting a vehicle from fuel r to fuel l
C r – the cost of purchasing a vehicle fuelled with fuel r
b t – maximum allowable emission in period t
e r – emission produced by a vehicle operating on fuel r per its capacity unit
q – discount rate
q – the initial number of vahicles operating on fuel r possessed by the company
Decision variables
f r , l , t – the number of vehicles operating on fuel r shifted to fuel l in planning
   period t
x r , t – the number of vehicles operating on fuel r possessed by the company
   in planning period t
u r , t – the number of vehicles operating on fuel r purchased by the company
   in planning period t
Table 2. Values of the parameters characterizing the chosen method of vehicle power supply adopted in the computational example.
Table 2. Values of the parameters characterizing the chosen method of vehicle power supply adopted in the computational example.
Fuel The number The cost of Annual
Fuel vehicles possessed purchasing a new vehicle emission
ON 50 30 2.0
CNG 0 35 1.0
HY 0 45 0.5
H2 0 50 0.0
Table 3. The cost of modernization of a vehicle from one fuel to another.
Table 3. The cost of modernization of a vehicle from one fuel to another.
ON CNG HY H2
ON – 3 10 15
CNG – – 10 15
HY – – – 20
H2 – – 15 –
Table 4. Solution, i.e. values of decision variable u r , t – the number of vehicles operating on fuel r purchased by the company in planning period t.
Table 4. Solution, i.e. values of decision variable u r , t – the number of vehicles operating on fuel r purchased by the company in planning period t.
t 0 1 2 3 4 5
ON – – – – – –
CNG – 10 2 – – –
HY – – 1 – – –
H2 – – 12 5 10 20
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated