Prerpints.org logo
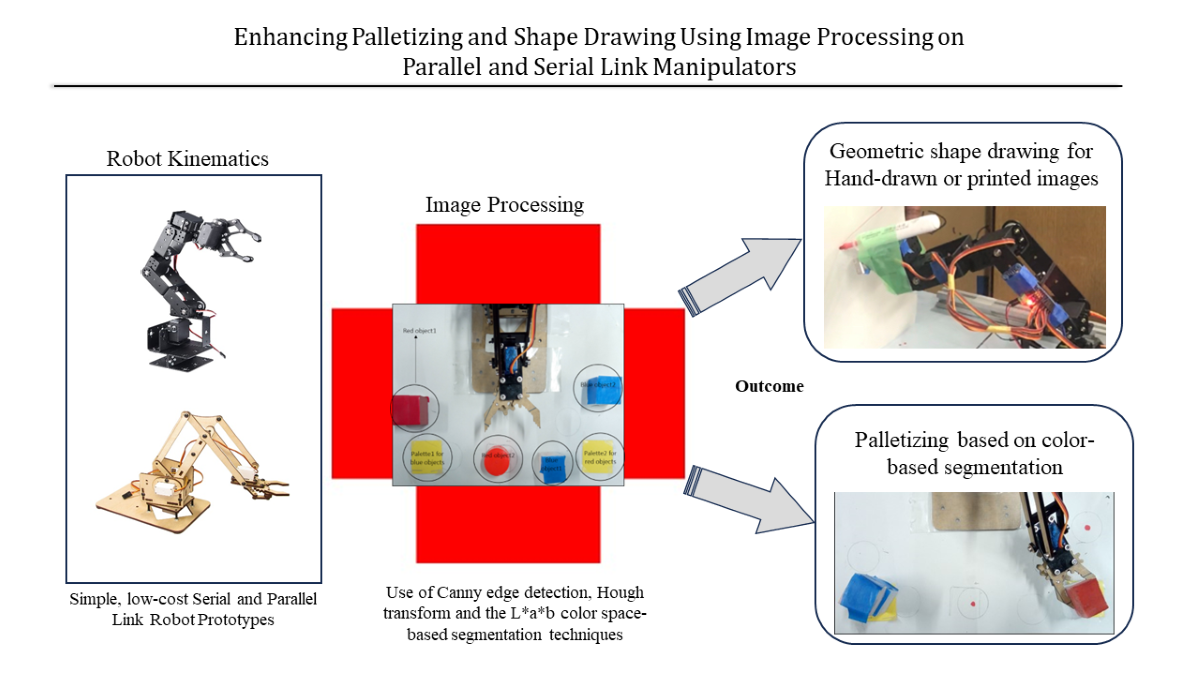
Preprint
Article

Enhancing Palletizing and Shape Drawing Using Image Processing on Parallel and Serial Link Manipulators

Altmetrics

Downloads

117

Views

71

Comments

0

Submitted:

14 November 2023

Posted:

22 November 2023

You are already at the latest version

Alerts
Abstract
The integration of robotics and image processing has led to the realization of robot autonomy in dynamic environments through the provision of visual feedback. This paper presents the application of parallel and open-link robots in palletizing and shape drawing tasks as enhanced by visual feedback from image processing. In determining the set of joint angles that could be used to reach the desired position and orientation of the end effector, the geometric approach in which the spatial geometry of the robotic arms was decomposed into several plane geometry problems was employed. Image processing techniques were used to enhance the performance of the robotic manipulators. In one approach, Color-based segmentation was used to distinguish between different objects in the workspace by using predefined color markers as references in the L*a*b color space. Classification of each pixel in the workspace image was then done by calculating the Euclidean distance between that pixel and a predefined color marker. A second approach employed Edge detection to identify the boundaries of objects within the workspace image by employing the Hough Transform mathematical model to detect the abrupt changes in the image brightness pixel-wise. The pixel locations from Hough were then sorted sequentially to outline the detected object. The integration of image processing with the robotic tasks was expected to improve the precise detection of the position of objects as well as the outline of geometric shapes. The incorporation of visual feedback allowed for dynamic robot manipulation in which prior knowledge of the workspace was not requisite. This led to improved pick and place as well as shape detection as applied in palletizing and shape drawing tasks actuated by the parallel and serial link manipulators, respectively.
Keywords: 
Subject: Engineering  -   Control and Systems Engineering

1. Introduction

The field of robotics has continued to grow tremendously in the last decade as a new research frontier and has demonstrated its relevance and impact in modern applications of industrial automation. These robots are especially useful in conducting repetitive chores, in hazardous work environment and in numerous industrial operations to mention just but a few [1,2,3,4].
Concurrently, there has been tremendous growth in the need to automate atypical tasks that are unknown or undeveloped, making them difficult to perform with conventional robotic technology. The emphasis therefore shifts from the ability to repeat simple tasks at high speed and with high precision to the ability to perform tasks reliably in unexpected situations [5]. One of the operations necessary for such a task is the ability to recognize the robot workspace, the position, shape and posture of parts or tools. The recent advances in image acquisition capabilities and processing power provides for excellent tools in designing more complex image processing and pattern recognition tasks [6]. It is the integration of image processing with robotics, referred to as Robot Vision, which has led to the evolution of perceptive robots.
Robotic manipulators belong to either open chain or closed chain configurations [7]. Serial link industrial robots are the best examples of open chain configuration. They are characterized by smaller footprints, lower specific payload capacities, large workspace and better reach. The closed chain manipulators categorized as planar manipulators and parallel robots, offers better stiffness and higher pay load capacity and faster actuation over a confined workspace [8]. Various approaches have been proposed in [9] to analyze the two groups of robot manipulators and characterize their kinematics. Some of the methods used include the special construction geometry, inverse-kinematic-residual minimization, algebraic solutions, and polynomial methods [10,11,12].
The acceptability of a manipulator is based on the comparative performance evaluation which makes estimation of the performance of manipulators a key factor in deciding its application and design. In recent years, there has also been an increasing demand for weight reduction of robot arms to realize high speed operation and energy saving [13].
The major performance characteristics considered in this paper were the manipulators’ workspace, dexterity and positional accuracy. Dexterity index is a measure of the possibility of a manipulator to achieve different orientations for each point within the workspace[8]. The ability of a serial manipulator to reach multiple orientations for a set of points results in serial manipulators being more dexterous than parallel manipulators. The workspace of parallel manipulators is smaller compared to that of serial link manipulators. This is due to the multiple independent kinematic chains connecting the end effector in parallel to the base. Conventionally, parallel manipulators are presumed to be more accurate than serial link robotic manipulators[14]. This is owing to the parallel links sharing payloads, making the structure more rigid compared to serial link configurations.
In [15], Pandilov et al. presents the performance parameters based on accuracy and repeatability. Accuracy defines a measure of how close the manipulator can come to a given point within its workspace and repeatability is a measure of how close a manipulator can return to a previously taught point. The parallel robots realize a higher repeatability performance than the serial robots [16].
From the performance features discussed above, the parallel link manipulator is most suited for a wide range of assembly, pick and place, and material handling applications with limited workspace which made the palletizing task a great fit for this study [17]. Conversely, the serial link manipulator dominates in most industrial applications [15] especially in manufacturing tasks that require high dexterity and speed such as welding, painting and parts-cutting and for this study the focus area was the geometric shape drawing.
Palletizing tasks typically involve detecting objects, sorting and stacking them based on desired features. On the other hand, shape drawing involves detecting the boundaries of objects and extracting out the shape outline. These tasks present the need for Robot Vision which as described above is the ability to recognize the robot workspace. Detection of an object by using a computer’s camera is an important aspect of Image Processing [18]. Information obtained from image processing techniques based on the captured images can then modify the motion of the robot accordingly. The application of image processing techniques to industrial automation and robotics is gaining popularity and becoming a necessity given its advantages. [19] shows ways in which image processing can be used to solve actual problems in robotics and instrumentation.
Owing to the nature of the research tasks and the above considerations, the image processing techniques used in this research were color-based segmentation for the palletizing task, and Canny edge detection coupled with Hough transform for the shape drawing task.
Another crucial part of the iterative design process used in realizing and exploring research ideas is prototyping. By practicing rapid prototyping, the advantages that can be realized are shorter development and research conceptualization time, increased quality, reduction in the initial development cost among others[20]. Cost is a crucial factor in the widespread adoption of any new concept or product and in this case, robotic applications in both academic and industrial applications [21]. This concept, which was making headlines as early as in the 1990s [22,23] is now a reality. While multiple platforms that offer the capability to perform simulations and even integrate virtual reality are available to evaluate on various research constraints, current research still holds that a physical product still supersedes both [24] The complexity in the design of a comprehensive simulation environment is also a main challenge and current research problem in fully realizing the best experience and software development complexities [25,26].
In this paper we present the application of parallel and open-link robots in palletizing and shape drawing tasks respectively based on image processing. While neither the application of image processing in robotics nor robotics control is new, one of the main factors limiting the research in robotics is the two resources of cost and time. This is especially true for small to medium scale industries as well as in the developing countries where very few research institutes or academic institutions have highly equipped robotics centers. This research therefore presents a low-cost method of rapid robotic development. By using low-cost manipulators, less than 100dollars each and utilizing easily available Arduino microcontrollers the cost decreased significantly. The choice of open-source microcontrollers also made it possible to quickly prototype the desired applications. This research paper aims to serve as an easy-to-use guide in learning on the rapid design and development of robotic applications. By presenting both the serial link and parallel link manipulators, each with a different application field based on the structural advantages presented in past research, it can serve as an excellent reference point in the practical application of foundational knowledge in robotics and a testbed for more advanced applications such as the force control [27] and more precise control operations. This would in turn lead to widespread adoption of robotics and further research knowledge in the field.

2. Manipulator Kinematics

Kinematics is the science of motion that treats the subject without regard to the forces that cause it [28]. The study of the position, velocity, acceleration, and all higher order derivatives of the position variables (with respect to time or any other variable(s)) is within the science of kinematics. In this regard, manipulator kinematics could either be static, or time-based where the velocities and acceleration are involved. In this research, we considered the position and orientation of the manipulator linkages (forward and inverse kinematics) in static situations [29].
The low-cost robot manipulators used for this research are as shown in Figure 1. Figure 1a shows a 3-DoF open-source robot arm that uses four SG90 servomotors including the gripper while Figure 1b is a 6-DoF aluminum robot arm DIY kit that uses six MG996R servomotors including the gripper. For the shape-drawing application, only 4-DoF were considered as the gripper was not part of the setup.

2.1. Forward Kinematics

Forward kinematics addresses the problem of computing the position and orientation of the end effector relative to the user’s workstation given the joint angles of the manipulator. According to the DH convention, any robot can be described kinematically by giving the values of four quantities, typically known as the DH parameters, for each link. The link length (a) and the link twist (α) describe the link itself and the remaining two, link offset (d) and the joint angle (θ), describe the link’s connection to a neighboring link. By considering the DH parameter representation in addition to the Euler angle representation, the closed chain manipulator could be expressed as an open-chain equivalent and thus simplifying the derivation of the forward kinematics. Through the considerations above, the robots were decomposed into stationary and moving frames as in Figure 2a,b.
The DH parameters for the parallel link manipulator (meArm) and the open link manipulator (ROT3U) were obtained as in Table 1 and Table 2, respectively.
Consequently, the total homogeneous transformation that specifies how to compute the position and orientation of the end effector frame with respect to the base frame for both manipulators was obtained as follows.
  • For the Parallel link manipulator
Total   transformation   Matrix :   T 0 3 = T 0 1 × T 1 2 × T 2 3
Where the homogeneous transformations of each link were obtained as:
T 0 1 = cos ( θ 1 ) 0 sin ( θ 1 ) 0 sin ( θ 1 ) 0 − cos ( θ 1 ) 0 0 1 0 − 11 2 0 0 0 1
T 1 2 = cos ( θ 2 ) − sin ( θ 2 ) 0 8 cos ( θ 2 ) sin ( θ 2 ) cos ( θ 2 ) 0 8 sin ( θ 2 ) 0 0 1 0 0 0 0 1
T 2 3 = cos ( θ 3 ) − sin ( θ 3 ) 0 12 cos ( θ 3 ) sin ( θ 3 ) cos ( θ 3 ) 0 12 sin ( θ 3 ) 0 0 1 0 0 0 0 1
Considering the three links of the meArm, the total homogeneous transformation was obtained as the product of the transformations of each individual link and was evaluated as:
  0 3 T = cos ( θ 2 + θ 3 ) cos ( θ 1 ) − sin ( θ 2 + θ 3 ) cos ( θ 1 ) sin ( θ 1 ) 4 σ 1 cos ( θ 1 ) cos ( θ 2 + θ 3 ) sin ( θ 1 ) − sin ( θ 2 + θ 3 ) sin ( θ 1 ) − cos ( θ 1 ) 4 σ 1 sin ( θ 1 ) sin ( θ 2 + θ 3 ) cos ( θ 2 + θ 3 ) 0 − 11 2 + 12 sin ( θ 2 + θ 3 ) + 8 sin ( θ 2 ) 0 0 0 1
Where the variable
σ 1 = 3 cos ( θ 2 + θ 3 ) + 2 cos ( θ 2 )
The coordinates (XYZ) of the end effector position are the top right 3x1 matrix of the total homogeneous transformation matrix:
X Y Z = 4 cos ( θ 1 ) [ 3 cos ( θ 2 + θ 3 ) + 2 cos ( θ 2 ) ] 4 sin ( θ 1 ) [ 3 cos ( θ 2 + θ 3 ) + 2 cos ( θ 2 ) ] − 11 2 + 12 sin ( θ 2 + θ 3 ) + 8 sin ( θ 2 )
b.
For the Open link manipulator
The total homogeneous transformation that specifies how to compute the position and orientation of the end effector frame with respect to the base frame was obtained as:
T 0 4 = T 0 1 × T 1 2 × T 2 3 × T 3 4
Where the homogeneous transformations of each link were obtained as:
T 0 1 = cos ( θ 1 ) − sin ( θ 1 ) cos ( α ) sin ( θ 1 ) sin ( α ) a 1 cos ( θ 1 ) sin ( θ 1 ) cos ( θ 1 ) cos ( α ) − cos ( θ 1 ) sin ( α ) a 1 sin ( θ 1 ) 0 sin ( α ) cos ( α ) d 1 0 0 0 1
T 1 2 = cos ( θ 2 ) − sin ( θ 2 ) 0 a 2 cos ( θ 2 ) sin ( θ 2 ) cos ( θ 2 ) 0 a 2 sin ( θ 2 ) 0 0 1 0 0 0 0 1
T 2 3 = cos ( θ 3 ) − sin ( θ 3 ) 0 a 3 cos ( θ 3 ) sin ( θ 3 ) cos ( θ 3 ) 0 a 3 sin ( θ 3 ) 0 0 1 0 0 0 0 1
T 3 4 = cos ( θ 4 ) − sin ( θ 4 ) 0 a 4 cos ( θ 4 ) sin ( θ 4 ) cos ( θ 4 ) 0 a 4 sin ( θ 4 ) 0 0 1 d 4 0 0 0 1
In an equivalent manner to the parallel link manipulator above, the coordinates (XYZ) of the final end-effector position were the top right 3x1 matrix of the total homogeneous transformation   0 4 A determined as:
X = a 4 c 4 c 3 c 12 − c α s 12 − s 3 ( c 1 s 2 + c 2 α s 1 ) − a 4 s 4 c 3 c 1 s 2 + c 2 α s 1 + s 3 c 12 − c α s 12 + a 3 c 3 c 12 − c α s 12 − a 3 s 3 c 1 s 2 + c 2 α s 1 + a 2 c 12 − a 2 c α s 12 Y = a 4 c 4 c 3 c 2 s 1 + c 1 α s 2 − s 3 ( s 12 − c 12 α ) − a 4 s 4 c 3 s 12 − c 12 α + s 3 c 2 s 1 − c 1 α s 2 + a 3 c 3 c 2 s 1 + c 1 α s 2 − a 3 s 3 s 12 − c 12 α + a 2 c 2 s 1 + a 2 c 1 α s 2 Z = a 4 c 2 + 3 s 4 α + s 2 + 3 s α c 4 + a 3 c 2 s 3 α + c 3 s 2 α + a 2 s 2 α + d 1
Where considering a , b = 1 , 2 , 3
c α = cos θ α , s α = sin θ α c b = cos θ b , s b = sin θ b c a + b = cos θ a + θ b , s a + b = sin θ a + θ b c a b c = cos θ a × cos θ b × cos θ c , s a b c = sin θ a × sin θ b × sin θ c

2.2. Inverse Kinematics

Inverse kinematics addresses the more difficult converse problem of computing the set of joint angles that will place the end effector at a desired position and orientation. It is the computation of the manipulator joint angles given the position and orientation of the end effector [29]. It involved extracting the Cartesian coordinates of a given position based on the image processing, translating those positions into joint angles and rotating the manipulator servo motor angles to that desired position.
In solving the inverse kinematics problem, the Geometric approach was used to decompose the spatial geometry into several plane-geometry problems based on the sine and the cosine rules.
The determination of the joint angles for both the parallel and open link manipulators was given as:
  • For the parallel link manipulator
The calculation of the joint angles ( θ 1 , θ 2 , θ 3 ) for a known position and orientation of the meArm’s end effector was done by considering the trigonometric decomposition of various planes of the manipulator as graphically illustrated below.
The angle θ1 was determined by considering Figure 3 and calculated as:
θ 1 = tan − 1 y x
With the hypotenuse r, connecting x and y obtained using the Pythagoras theorem as:
r = x 2 + y 2
The angles θ 2   a n d   θ 3 were obtained by considering the plane formed by the second and third links as illustrated in Figure 4.
θ 2 = tan − 1 s r + tan − 1 l 3 sin ( θ 3 ) l 2 + l 3 cos ( θ 3 )
where   θ 2 = α + β
θ 3 = cos − 1 x 2 + y 2 + s 2 − l 2 2 − l 3 2 2 l 2 l 3
Where s is the difference between the distance of the end effector from the base and the offset:
s = z − d
b.
For the open link manipulator
The calculation of the joint angles ( θ 1 , θ 2 , θ 3 , θ 4 ) for a known position and orientation of the ROT3U’s end effector was done by considering the trigonometric decomposition of various planes of the manipulator as graphically illustrated below.
The angle θ1 was determined by considering Figure 5 and calculated as:
θ 1 = tan − 1 ( y x )
The angles θ 2 ,   θ 3   a n d   θ 4 were obtained by considering the plane formed by the second, third and fourth links as illustrated in Figure 6.
By considering the sine and cosine rules:
θ 2 = cos − 1 ( ( a 2 ) 2 + ( H y p _ θ 4 ) 2 − ( a 3 ) 2 2 × a 2 × H y p _ θ 4 ) + sin − 1 ( z − d 1 H y p _ θ 4 )
θ 3 = − ( 180 − cos − 1 ( ( a 2 ) 2 + ( a 3 ) 2 − ( H y p _ θ 4 ) 2 2 × a 2 × a 3 ) )
θ 4 = cos − 1 ( ( H y p _ θ 4 ) 2 + ( a 3 ) 2 − ( a 2 ) 2 2 × H y p _ θ 4 × a 3 ) − sin − 1 ( z − d 1 H y p _ θ 4 )
Where H y p _ θ 4 is the length directly connecting joint 2 to joint 4 forming the triangle joining link lengths a2 and a3 and was determined as follows:
H y p _ θ 4 = ( r − a 4 ) 2 + ( Z − d 1 ) 2
With   r = X 2 + Y 2

3. Image Processing

Computer vision deals with numerous problems and object recognition is considered one of the highest priorities and has received widespread attention [30,31]. In most applications the research conducted is on the sorting of objects based on color, size or shape. In this research, image processing was employed in both the palletizing and shape drawing tasks to address the problems of detecting an object and determining its location in the workspace. Sample input images to the palletizing and shape drawing algorithms were as shown in Figure 7.
Image pre-processing techniques were used to improve the image data by suppressing unintended distortions and enhancing the features that were important in the subsequent applications of color-based segmentation in palletizing and edge detection in shape drawing. The following pre-processing techniques sufficed for image enrichment improvement for both robotic tasks:
  • RGB to Grayscale conversion - This step involved converting a colored image containing the distinct color shades (R, G, B) into a grayscale image which only carries intensity information ranging from black (0) at the weakest intensity to white (255) at the strongest.
  • Binarizing the image - This process involved converting a grayscale image into a binary image based on a luminance threshold such that all pixels with luminance greater than the threshold were classified as white while those below were black.
  • Filling the holes in the image - This process helped in accounting for and minimizing noise in the image.
Specific detection algorithms
The result of the pre-processing steps was a binary image in which the regions of interest, that is, the shape to be drawn or the objects to be detected, were clearly defined. As such, further processing techniques for the image segmentation and edge detection were applied to perform palletizing and shape drawing tasks.
  • Color-based segmentation for palletizing
The palletizing task involved sorting and stacking objects using color-based segmentation. Color-based segmentation is the process of dividing an image into regions of interest based on their color. A simple, memory efficient yet effective L*a*b* color-based segmentation was used to locate objects with similar color. L*a*b* color space is a color-opponent space with dimension L* for perceptual lightness and a* and b* for the four color-opponent dimensions of human vision: red, green, blue, and yellow [32], [33]. The L*a*b* as presented in [34] can optimize the clustering for image segmentation both in aspects of precision and computation time.
The output of the pre-processing steps was used to identify the objects where logic 1 represented the presence of an object. This information on the location of the objects allowed for subsequent application of color-based segmentation to identify the objects by color on the original RGB image. The L*a*b* color space is designed to approximate human vision and enables one to quantify the visual differences in color [35]. In this task, it was used to account for variation in color value of the RGB image across a detected object caused by problems such as camera noise. For each detected object, an average color in a*b* space was calculated, such that each detected object had a single value of ‘a*’ and ‘b*’ for all its pixels.
Since each detected object now had an 'a*' and 'b*' value, it could be classified by calculating the Euclidean distance between its pixels and a predefined color marker. The predefined color markers were a set of 'a*' and 'b*' values for standard Red, Blue, Green and Yellow colors. These were the reference colors against which an object’s color value was compared. As such the Euclidean distance d between each pixel and a corresponding marker was computed as:
d = [ a p i x e l − a c o l o r _ m a r ker 2 + b p i x e l − b c o l o r _ m a r ker 2 ] 1 2
The smallest distance indicated that a pixel most closely matched a corresponding color marker. Subsequently, by the nearest neighbor rule, if for instance the distance between a pixel and the red color marker is the smallest, then the pixel would be labelled as a red pixel and its corresponding object would be classified as red.
The last step of this algorithm involved determining the centroid locations of the segmented objects in pixels and then mapping them to the real-world manipulator’s workspace using a suitable mapping function.
Figure 8a shows two objects detected as ‘red’ since their average a*b* values closely matched those of a predefined red color marker. Figure 8b shows the result of detecting the red and blue objects, obtaining their real-world coordinates in the workspace and finally applying inverse kinematics to sort and stack them on their respective pallets.
ii.
Canny edge and Hough transform for shape drawing.
In the implementation of the geometric shape drawing, the input image which was either taken using a camera for a hand-drawn image or digitally drawn by the user was supplied to the robot. The image was in the form of an array of pixels, while the drawing manipulator required a set of points in the Cartesian space, convertible into a joint space [36]. In this study, the edge detection method was employed in the determination of the shape outline based on the input image. Following the shape outline, the pixel locations could be obtained on the image, mapped on to the corresponding workspace coordinates and the robotic manipulator could then draw the determined shape.
Edge detection is an image processing technique used to identify the boundaries of objects within images. This is by detecting discontinuities in color and brightness. Considering an image, an edge is a curve that follows a path of rapid change in image intensity and is often associated with the boundaries of objects in a scene. The Canny edge method which is a powerful edge detection method that is relatively simple and more likely to detect true weak edges was used in determining these boundaries[37], [38]. This detection of the boundaries of the input shape was achieved by selecting a suitable threshold based on the color intensity of the preprocessed input image.
On detecting the shape boundaries, the Standard Hough Transform, which is a feature extraction technique was used to identify the Hough peaks which are the potential lines in the image. The Hough lines function then finds the endpoints of the line segments corresponding to peaks in the Hough transform and fills in small gaps in the line segments [39]. The identified endpoints give the start and end points of line and thus a full identification of the shape based on the detected boundaries [40]. The identification of the shapes based on the detected boundaries was the same for both the hand-drawn and digital image. One of the main considerations in the detection based on the Hough peaks was the thickness of the line where adjusting the threshold varied the sensitivity to line thickness [41].
Once the lines on the shape had been identified, the reconstruction of the geometric shape was done by sorting the obtained endpoints for a particular line and its connected neighboring line. As a last step to the image processing, the sorted endpoints pixel locations on the image were then mapped on to the manipulator workspace. Using these points, the shape could then be drawn out by the robotic manipulator.
For the input image shown in Figure 7b, the application of Canny edge detection technique using Hough transform in the determination of the endpoints in the detected lines resulted in the image shown in Figure 9a. From this, all the lines constituting the shape were identified and an outline of the shape obtained. As the final step of the geometric shape algorithm, the image in Figure 9b was outlined by the open link manipulator (ROT3U) after the mapping and inverse kinematics of the identified endpoints.

4. Gyroscope for Path Tracking

The use of inertial measurement units, IMUs in estimation of the motion of the end effector ensures sufficient tracking of the robotic motion. The IMUs are small and lightweight and ensure an almost zero influence on the motion performance [42]. The MPU 6050 Six Axis Sensor gyroscope raw data was used to get the Cartesian coordinates of the end effector for motion characterization. The gyroscope was mounted at the tip of the end effector as an external motion sensor for trajectory tracking. The raw data obtained from the gyroscope motion was processed for the axes along which the robot moved such that reconstruction gave the path traced by the manipulator or the shape drawn.
Figure 10 shows the path moved by the meArm in in picking “Blue Object 1” and placing it on “Palette1”. This trajectory made from the gyroscope data closely approximated the trajectory traced by the meArm in performing the given palletizing task.
For the geometric shape drawing task, the rectangular input image A2-B2-C2-D2 in Figure 11 below was used as the manipulator input shape with the start point for the robot motion being at A2 and moving counterclockwise. The reconstructed shape obtained by considering the gyroscope data then resulted in the figure A1-B1-C1-D1. This was an approximate outline of the shape drawn by the manipulator which showed a decent resemblance of the input image.

5. Summary

This research presented the application of parallel and open-link robots in palletizing and shape drawing tasks based on image processing techniques, respectively. For the parallel manipulator, the meArm, a 3-DoF robotic arm was considered while a 4-DoF serial link manipulator (ROT3U) was used for the open-link manipulator task. Earlier research on the performance features such as workspace, dexterity and positional accuracy for the two manipulators was also presented. In realizing the palletizing and shape drawing tasks, the forward and inverse kinematics models of the two manipulators were developed and implemented. In both manipulators, the DH-convention was used to solve for the forward kinematics while the Geometric approach was used to solve for the inverse kinematics. Based on the chosen field of application, color-based segmentation was used to distinguish objects in the workspace for the palletizing task while edge detection was used to identify the boundaries of objects within the workspace image for the shape drawing task. This work presented the possibility of using easily accessible and inexpensive manipulators in prototyping standard industrial robots and testing new control algorithms before they are used in real life applications. This can serve as a testbed for how these robots can be used to perform and automate some of the routine, repetitive industrial and art drawing works. The inclusion of feedback control, trajectory generation and speed control in future works can significantly reduce the errors and improve performance in both manipulators.

6. Acknowledgement

The authors would like to thank Prof. Minoru Sasaki, the late Dr. Harrison Ngetha among others for their invaluable assistance during the research and Japanese Student Services Organization (JASSO) for the financial assistance during the entire research period.

References

  1. Njeri, W.; Sasaki, M.; Matsushita, K. Two degree-of-freedom vibration control of a 3D, 2 link flexible manipulator. Adv. Sci. Technol. Eng. Syst. 2018. [CrossRef]
  2. Hsu, M.H.; Nguyen, P.T.T.; Nguyen, D.D.; Kuo, C.H. Image Servo Tracking of a Flexible Manipulator Prototype with Connected Continuum Kinematic Modules. Actuators 2022. [CrossRef]
  3. Angrisani, L.; Grazioso, S.; Gironimo, G.D.; Panariello, D.; Tedesco, A. On the use of soft continuum robots for remote measurement tasks in constrained environments: A brief overview of applications. 2019. [Google Scholar] [CrossRef]
  4. Boonchai, P.; Tuchinda, K. Design and Control of Continuum Robot for Using with Solar Cell System. 2019. [Google Scholar] [CrossRef]
  5. Ito, H.; Nakamura, S. Rapid prototyping for series of tasks in atypical environment: robotic system with reliable program-based and flexible learning-based approaches. ROBOMECH J. 2022. [CrossRef]
  6. RADU, A.; MIHAELA, S. INDUSTRIAL APPLICATIONS OF IMAGE PROCESSING. ACTA UIVERSITATIS CIBINIENSIS - Tech. Ser. 2014. [Google Scholar]
  7. Saheb, S.H.; Babu, G.S.; Raju, N.V.S. Relative Kinematic Analysis of Serial and Parallel Manipulators. 2018. [Google Scholar] [CrossRef]
  8. Jawale, H.P.; Thorat, H.T. Comparison of open chain and closed chain planar two degree of freedom manipulator for positional error. J. Mech. Robot. 2014. [CrossRef]
  9. Moser, B.L.; Gordon, J.A.; Petruska, A.J. Unified parameterization and calibration of serial, parallel, and hybrid manipulators. Robotics 2021. [CrossRef]
  10. Merlet, J.P. Direct Kinematics of Parallel Manipulators. IEEE Trans. Robot. Autom. 1993. [CrossRef]
  11. McAree, P.R.; Daniel, R.W. A fast, robust solution to the Stewart platform forward kinematics. J. Robot. Syst. 1996. [CrossRef]
  12. Datta, S.; Das, A.; Gayen, R.K. Kinematic Analysis of Stewart Platform using MATLAB. 2021. [CrossRef]
  13. Sasaki, M.; Honda, N.; Njeri, W.; Matsushita, K.; Ngetha, H. Gain Tuning using Neural Network for contact force control of flexible arm. J. Sustain. Res. Eng. Vol 5 No 3 J. Sustain. Res. Eng. 2020. Available online: http://sri.jkuat.ac.ke/ojs/index.php/sri/article/view?path=.
  14. Briot, S.; Bonev, I.A. Are parallel robots more accurate than serial robots? 2007. [CrossRef]
  15. Pandilov, Z.; Dukovski, V. Comparison of the Characteristics Between Serial and Parallel Robots. Fascicule 2014.
  16. Nzue, R.M.A.; Brethé, J.F.; Vasselin, E.; Lefebvre, D. Comparison of serial and parallel robot repeatability based on different performance criteria. Mech. Mach. Theory 2013. [CrossRef]
  17. Zhao, Y.G.; Xiao, Y.F.; Chen, T. Kinematics analysis for a 4-DOF palletizing robot manipulator. 2013. [Google Scholar] [CrossRef]
  18. Murshed, S.Z.; et al. Controlling an embedded robot through image processing based object tracking using MATLAB. 2016. [CrossRef]
  19. Kurka, P.R.G.; Salazar, A.A.D. Applications of image processing in robotics and instrumentation. Mech. Syst. Signal Process. 2019, 124, 142–169. [Google Scholar] [CrossRef]
  20. Won, J.; DeLaurentis, K.; Mavroidis, C. Rapid prototyping of robotic systems. 2000. [CrossRef]
  21. Ahn, M.; Zhu, H.; Hartikainen, K.; Ponte, H.; Gupta, A.; Levine, S.; Kumar, V. ROBEL: Robotics Benchmarks for Learning with Low-Cost Robots. 2019.
  22. Ashley, S. Rapid prototyping is coming of age. Mech. Eng. 1995.
  23. Ashley, S. RP industry’s growing pains. Mech. Eng. 1998. [CrossRef]
  24. Chu, C.H.; Kao, E.T. A comparative study of design evaluation with virtual prototypes versus a physical product. Appl. Sci. 2020. [CrossRef]
  25. Choi, H.S.; et al. On the use of simulation in robotics: Opportunities, challenges, and suggestions formoving forward. Proceedings of the National Academy of Sciences of the United States of America. 2021. [CrossRef]
  26. Funk, M.G.; Cascalho, J.M.; Santos, A.I.; Mendes, A.B. Educational Robotics and Tangible Devices for Promoting Computational Thinking. Frontiers in Robotics and AI. 2021. [CrossRef] [PubMed]
  27. Maebashi, W.; Ito, K.; Matsuo, K.; Iwasaki, M. High-precision sensorless force control by mode switching controller for positioning devices with contact operation. IEEJ Trans. Ind. Appl. 2014. [CrossRef]
  28. Craig, J.J. Introduction to Robotics: Mechanics and Control, 3rd Edition. 2004.
  29. Müller, P.C. Robot dynamics and control. Mark W. Spong and M. Vidyasagar. Automatica 1992. [CrossRef]
  30. Ali, M.H.; Aizat, K.; Yerkhan, K.; Zhandos, T.; Anuar, O. Vision-based Robot Manipulator for Industrial Applications. 2018. [CrossRef]
  31. Djajadi, A.; Laoda, F.; Rusyadi, R.; Prajogo, T.; Sinaga, M. A MODEL VISION OF SORTING SYSTEM APPLICATION USING ROBOTIC MANIPULATOR. TELKOMNIKA (Telecommunication Comput. Electron. Control. 2010. [Google Scholar] [CrossRef]
  32. Hassan, B.M.R.; Ema, R.R.; Islam, T.; Hassan, M.R.; Ema, R.R.; Islam, T. Color Image Segmentation using Automated K-Means clustering with RGB and HSV Color Spaces. Glob. J. Comput. Sci. Technol. 2017, 17, 33–41. Available online: https://computerresearch.org/index.php/computer/article/view/102161%0Ahttps://computerresearch.org/index.php/computer/article/view/1587.
  33. Rathore, V.S.; Kumar, M.S.; Verma, A. Colour Based Image Segmentation Using L * A * B * Colour Space Based On Genetic Algorithm. Int. J. Emerg. Technol. Adv. Eng. 2012.
  34. Niranjana, K.K.; Professor, A.; Devi, M.K. RGB to Lab Transformation Using Image Segmentation. Int. J. Adv. Res. 2015.
  35. Mokrzycki, W.S.; Tatol, M. Perceptual difference in L * a * b * color space as the base for object colour identfication. Int. Conf. Image Process. Commun. 2009, 1–8. [Google Scholar] [CrossRef]
  36. Kumar, A.; Kala, R. Geometric shape drawing using a 3 link planar manipulator. 2015. [CrossRef]
  37. Crnokić, B.; Rezić, S. Edge Detection for Mobile Robot using Canny method. 2016.
  38. Canny, J. A Computational Approach to Edge Detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986. [CrossRef]
  39. Damaryam, G. A Method to Determine End-Points of Straight Lines Detected Using the Hough Transform. Int. J. Eng. Res. Appl. 2016, 6, 67–75. [Google Scholar]
  40. Ballard, D.H. Generalizing the Hough transform to detect arbitrary shapes. Pattern Recognit. 1981. [CrossRef]
  41. Von Gioi, R.G.; Jakubowicz, J.; Morel, J.M.; Randall, G. On straight line segment detection. J. Math. Imaging Vis. 2008. [CrossRef]
  42. Passon, A.; Schauer, T.; Seel, T. Inertial-Robotic Motion Tracking in End-Effector-Based Rehabilitation Robots. Front. Robot. AI 2020. [CrossRef]
Preprints 90441 g001
Figure 1. The robot arms utilized in the research.
Figure 1. The robot arms utilized in the research.
Preprints 90441 g001
Preprints 90441 g002
Figure 2. DH convention frames for the robot arms
Figure 2. DH convention frames for the robot arms
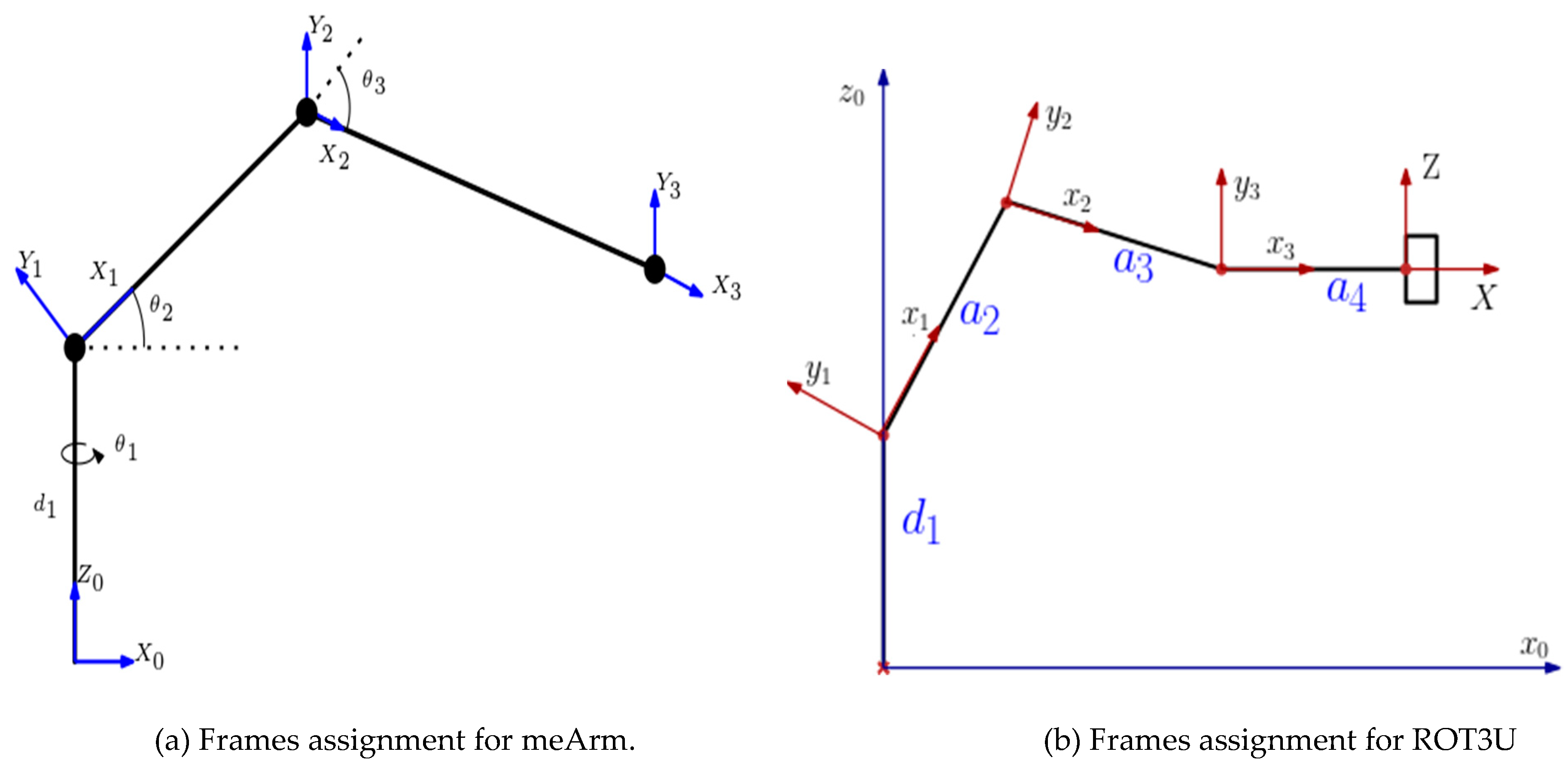
Preprints 90441 g002
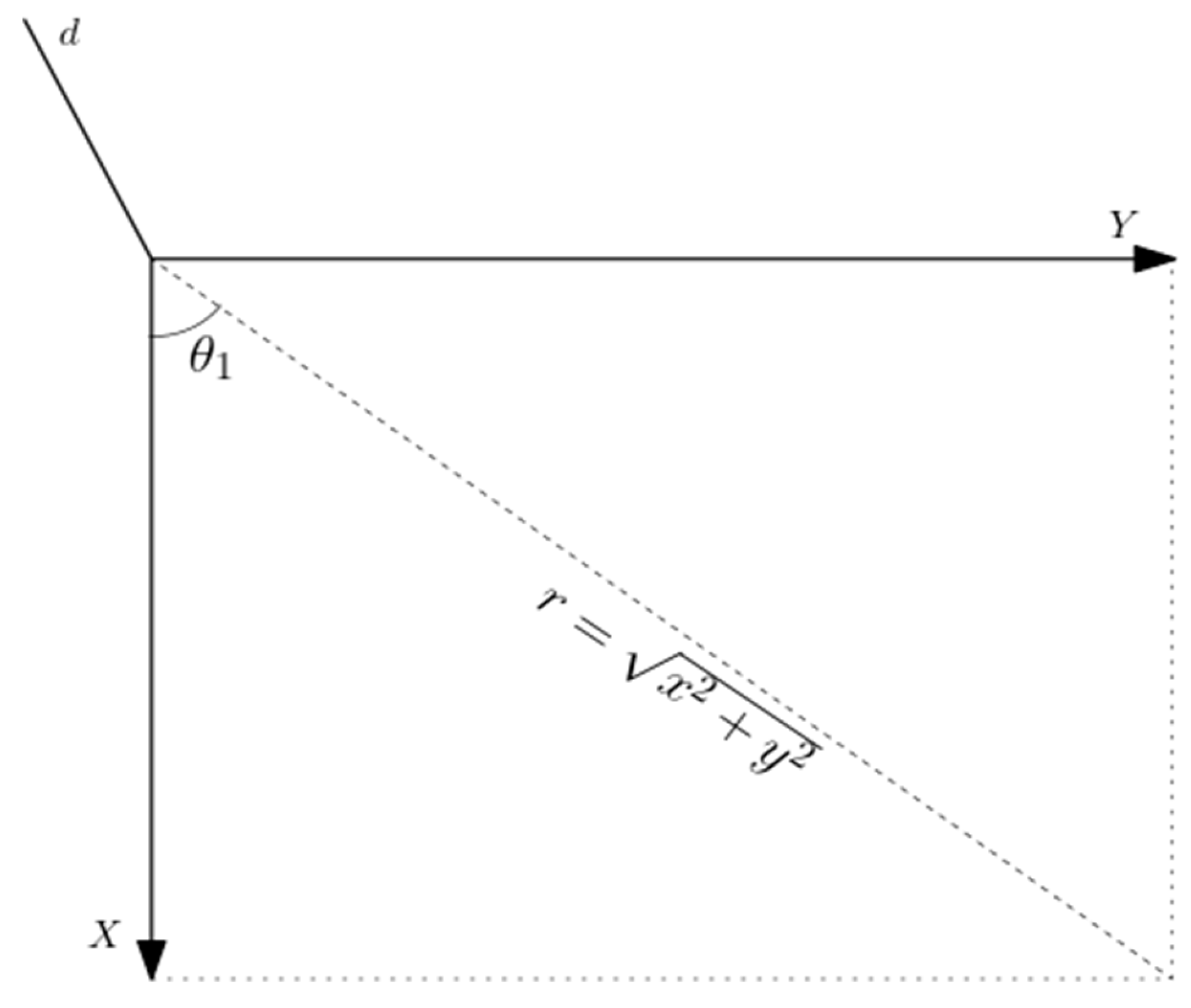
Preprints 90441 g003
Figure 3. Representation of θ1
Figure 3. Representation of θ1
Preprints 90441 g003
Preprints 90441 g004
Figure 4. Representation of θ2 and θ3
Figure 4. Representation of θ2 and θ3
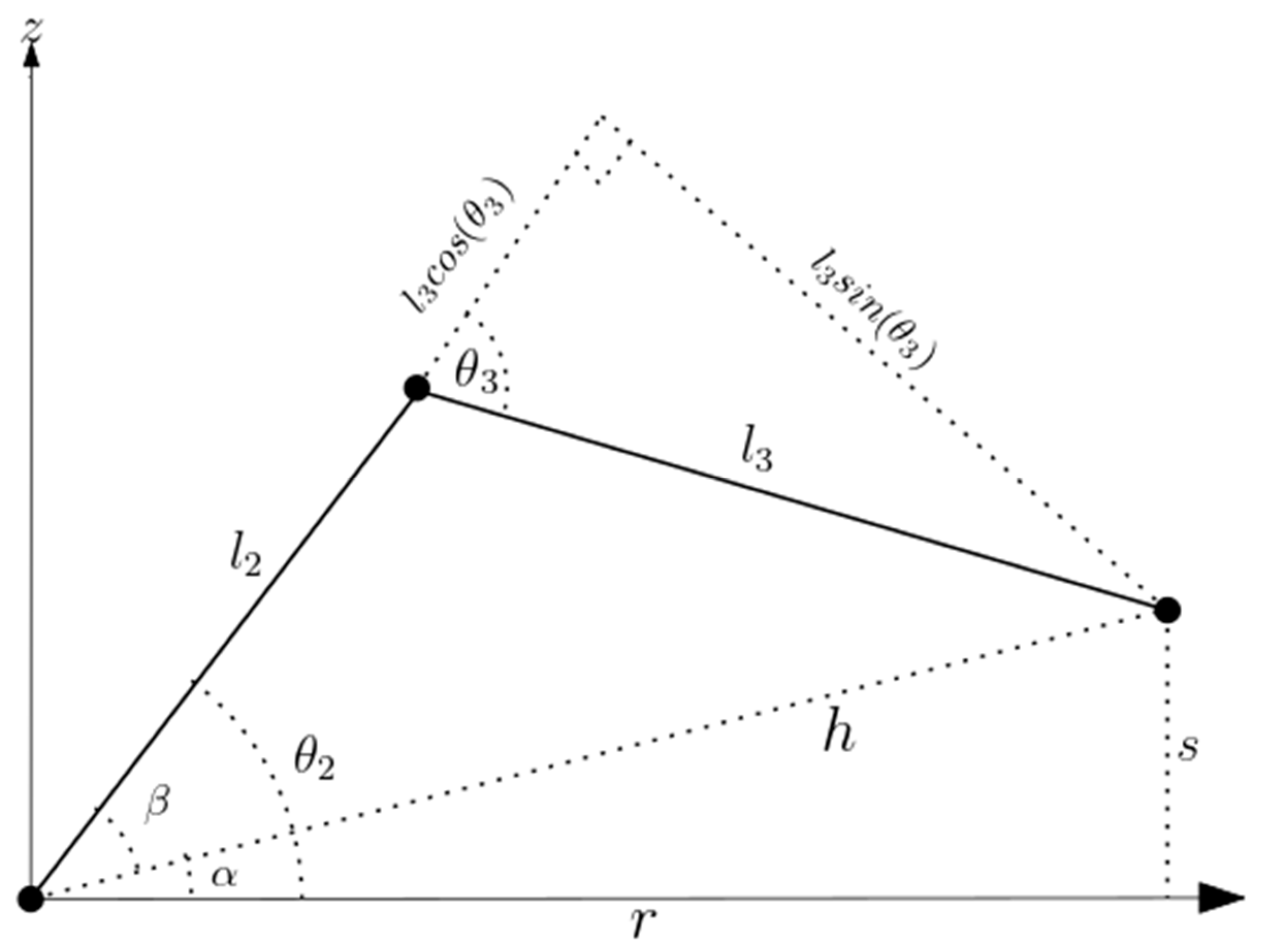
Preprints 90441 g004
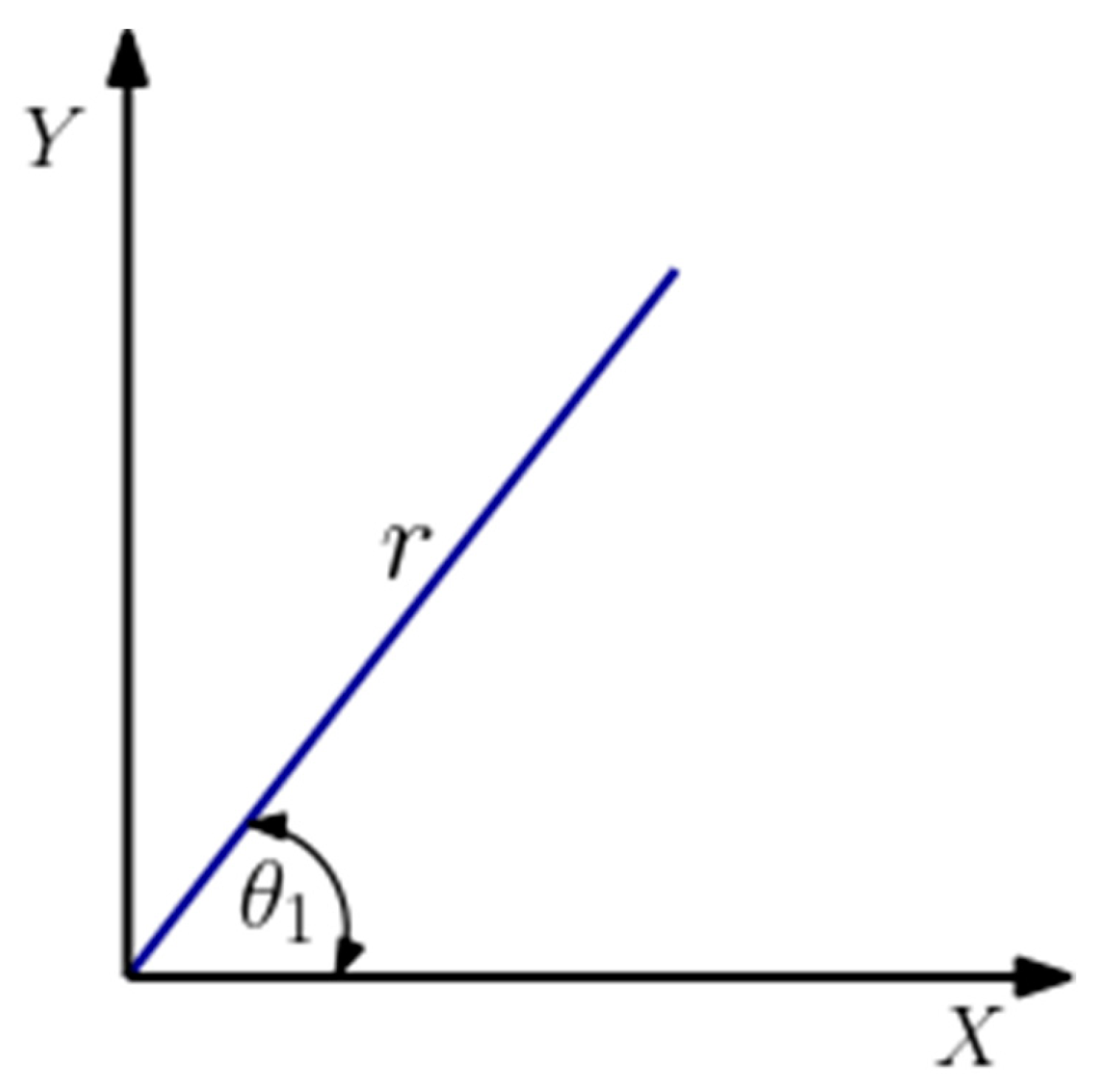
Preprints 90441 g005
Figure 5. Representation of θ1
Figure 5. Representation of θ1
Preprints 90441 g005
Preprints 90441 g006
Figure 6. Representation of θ2, θ3 and θ4
Figure 6. Representation of θ2, θ3 and θ4
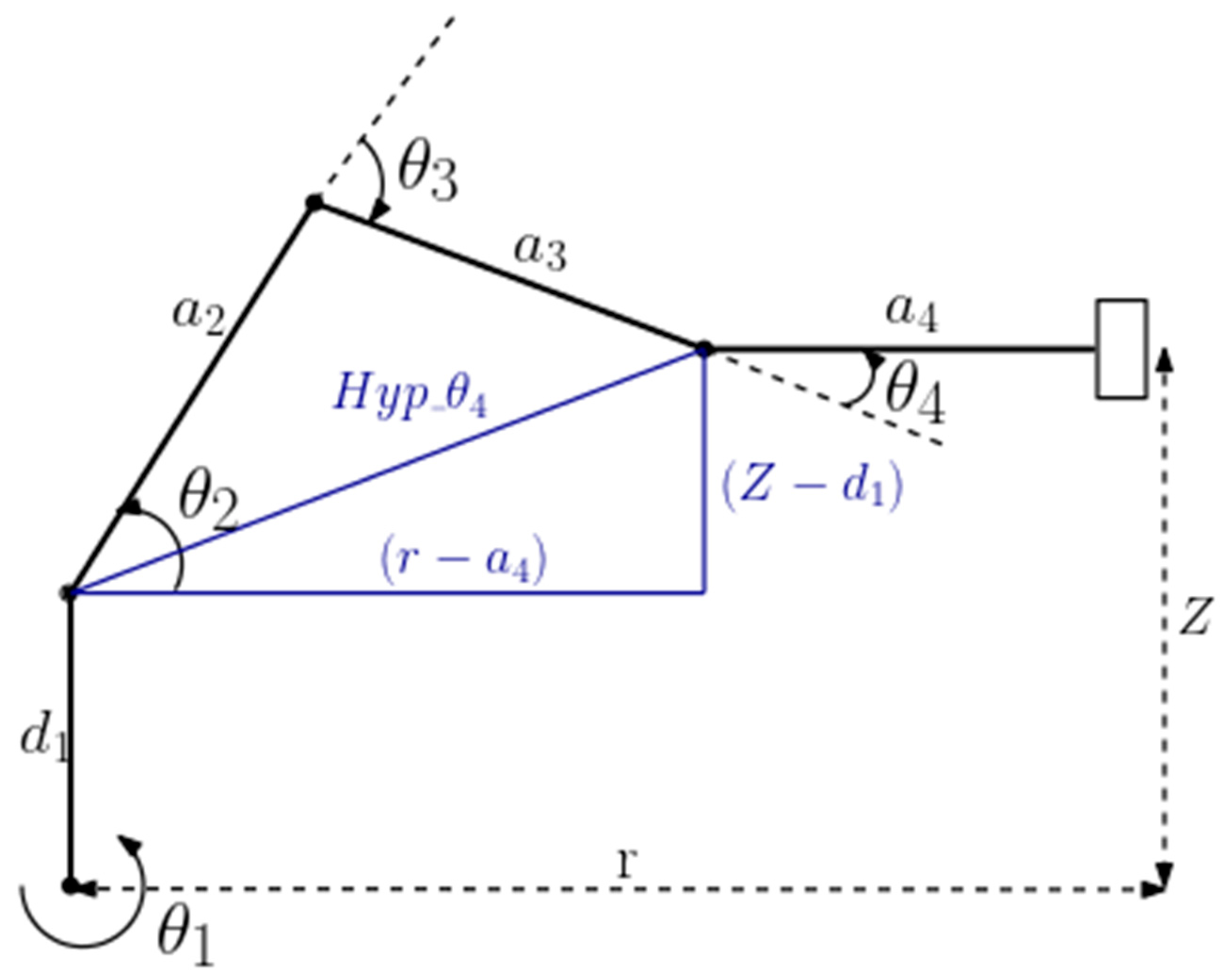
Preprints 90441 g006
Preprints 90441 g007
Figure 7. Sample input images
Figure 7. Sample input images
Preprints 90441 g007
Preprints 90441 g008
Figure 8. Demonstration of accurate detection and palletizing operation
Figure 8. Demonstration of accurate detection and palletizing operation
Preprints 90441 g008
Preprints 90441 g009
Figure 9. Sample outputs from robot operations
Figure 9. Sample outputs from robot operations
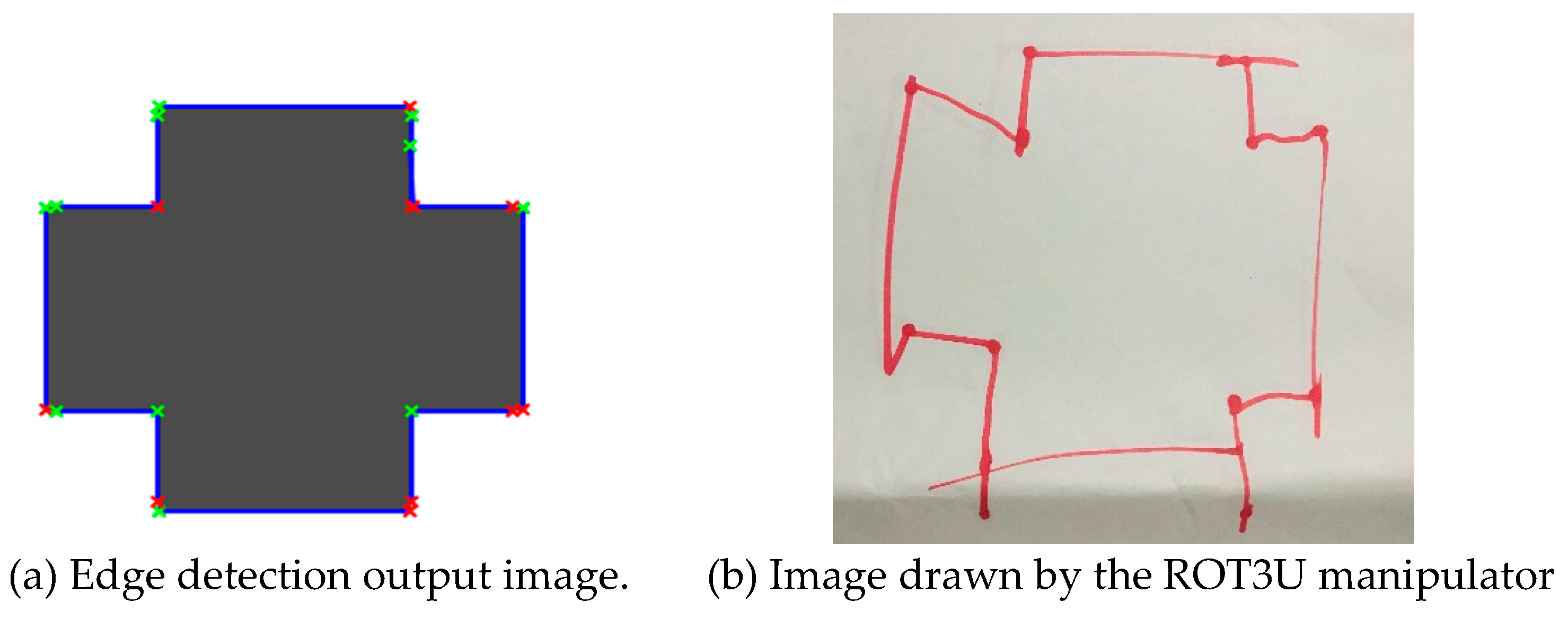
Preprints 90441 g009
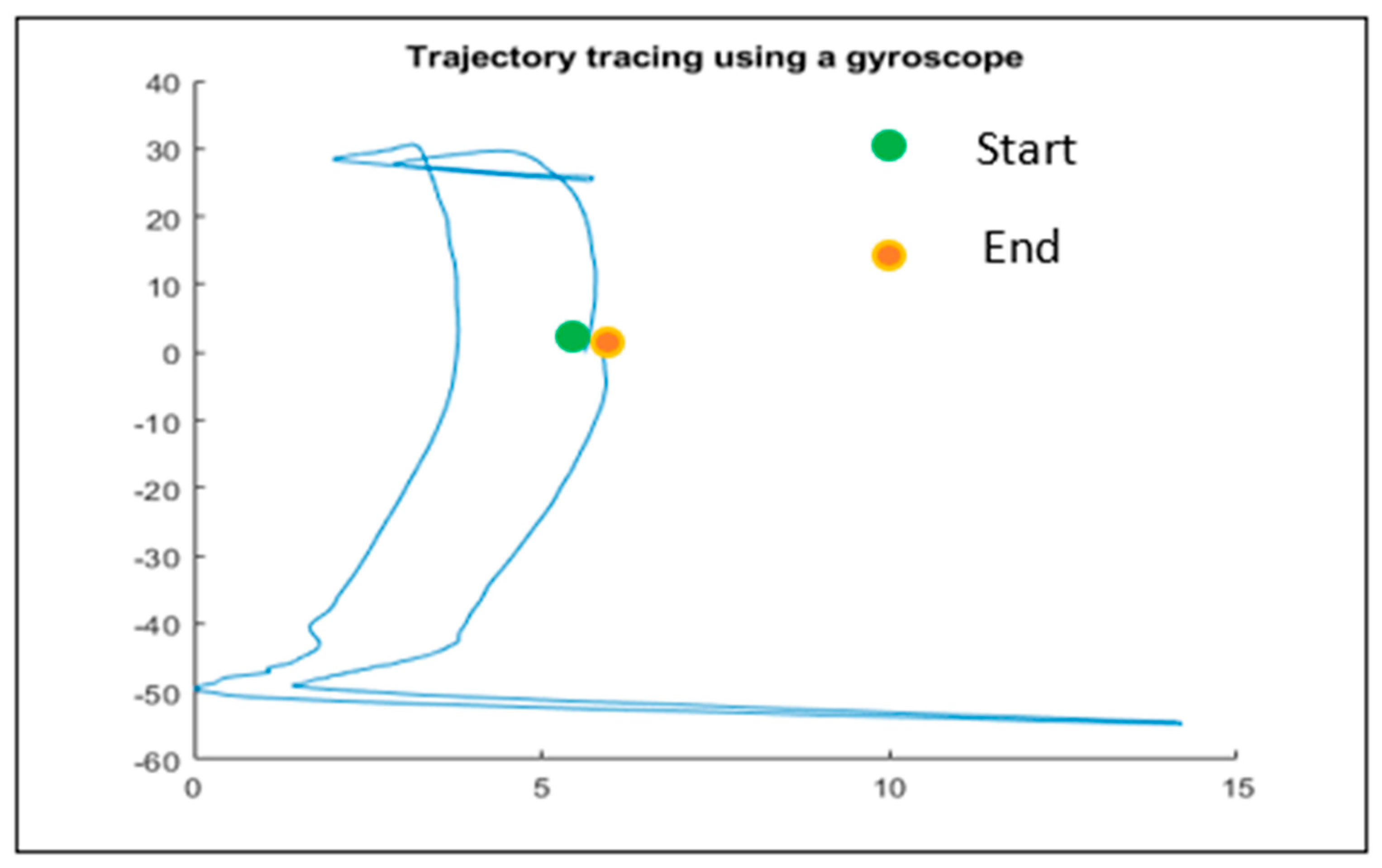
Preprints 90441 g010
Figure 10. Trajectory tracking using gyroscope for a sample palletizing task.
Figure 10. Trajectory tracking using gyroscope for a sample palletizing task.
Preprints 90441 g010
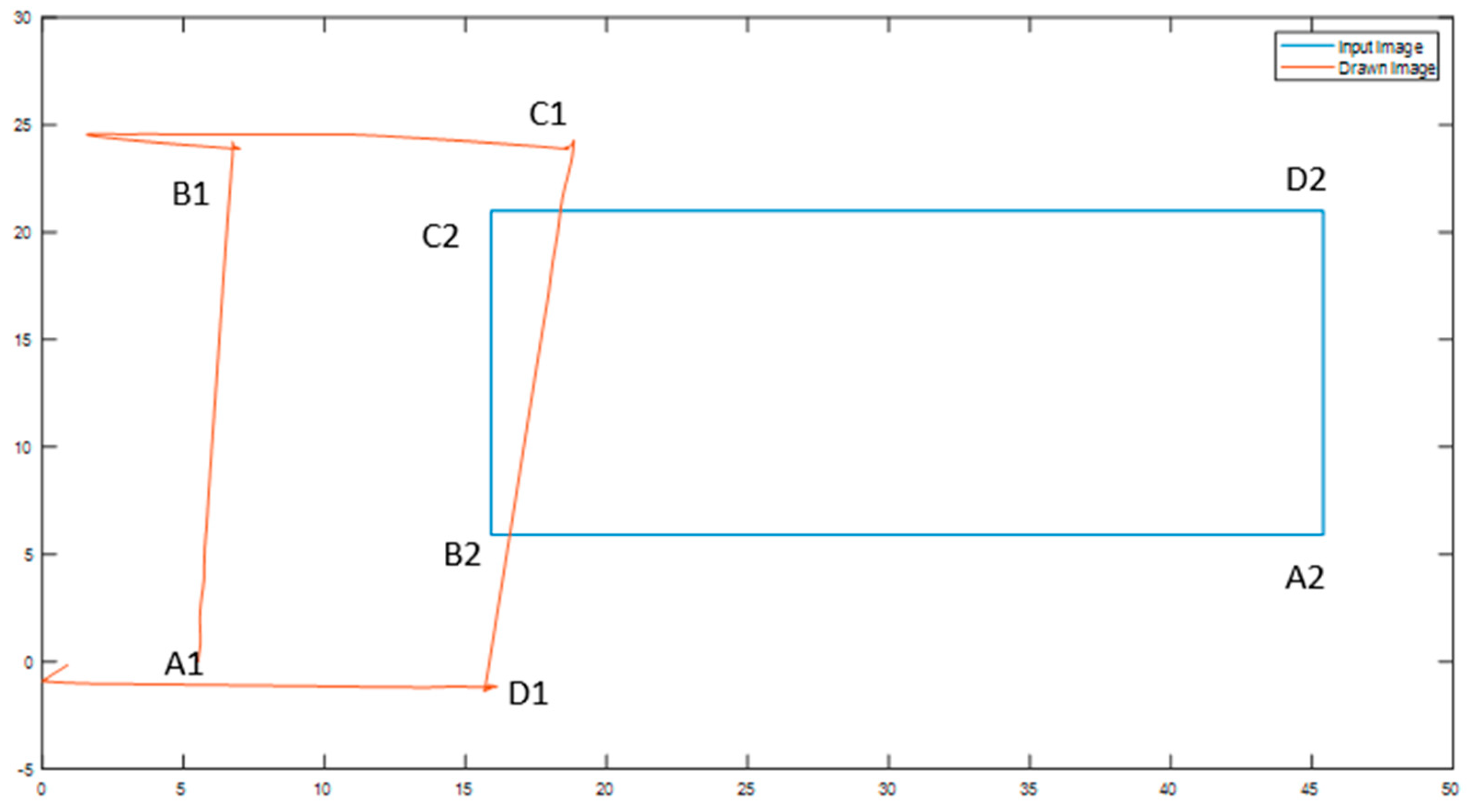
Preprints 90441 g011
Figure 11. Trajectory tracking using gyroscope for a sample shape drawing task.
Figure 11. Trajectory tracking using gyroscope for a sample shape drawing task.
Preprints 90441 g011
Table 1. DH parameters for the meArm
Table 1. DH parameters for the meArm
Link θ a(mm) α d(mm)
1 θ1 0 90˚ 55
2 θ2 80 0 0
3 θ3 120 0 0
Table 2. DH parameters for the ROT3U manipulator
Table 2. DH parameters for the ROT3U manipulator
Link θ a(mm) α d(mm)
1 θ1 0 90˚ 110
2 θ2 105 0 0
3 θ3 100 0 0
4 θ4 70 0 0
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated