Preprint
Article
Clustering of Floating Tracer in the Random Velocity Field Modulated by an Ellipsoidal Vortex Flow
Altmetrics
Downloads
76
Views
26
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Advanced Heat and Mass Transfer Technologies
Submitted:
23 November 2023
Posted:
24 November 2023
You are already at the latest version
Alerts
Abstract
The influence of a background vortex flow on clustering of floating tracer is addressed. The vortex flow considered is induced by an ellipsoidal vortex evolving in a deformation. The system exhibits various vortex motion regimes: (i) steady state, (ii) oscillation and (iii) rotation of the ellipsoidal vortex core. The latter two induce unsteady velocity field for the tracer thus leading to irregular (chaotic) tracer motion. Superimposing a stochastic divergent velocity field onto the deterministic vortex flow allows us to observe significantly different tracer evolution. We use the method of characteristics to integrate the floating tracer density evolution equation and the Euler-Ito scheme for obtaining the floating tracer trajectories with the random velocity field. The cluster area and cluster mass from the statistical topography were used as the quantitative diagnostics of floating-tracer’s clustering. For the case of the steady ellipsoidal vortex embedded into the deformation flow with a random velocity field component we found that clustering characteristics are weakened by the steady vortex. For the cases of an unsteady ellipsoidal vortex, we observed clustering in the floating-tracer density field if the contribution of the divergent component is higher or equal to that of the rotational (nondivergent) component. Even when the initial floating tracer patch was set on the boundary of oscillating ellipsoidal vortex, we observed formation of clusters. In the case of a rotating ellipsoidal vortex, we also observed pronounced clustering. Thus, we argue that unsteady ellipsoidal vortex regimes (oscillation and rotation), which induce chaotic motion of the nearby passive tracer’s trajectories, are still conducive to clustering of floating tracer observed in the density field despite the intense deformation introduced by strain and shear.
Keywords:
Subject: Physical Sciences - Fluids and Plasmas Physics
1. Introduction
Tracer evolution in various media often manifests significant heterogeneity of the tracer density and/or concentration fields even outside tracer sources and sinks. In turbulent oceanic and atmospheric flows [1,2,3], this tracer aggregation is usually attributed to clustering (and its asymptotic version - exponential clustering). Under favourable conditions tracers can be aggregating into coherent zones [4,5,6]. The area of these zones exponentially tends to zero and the dimensionless mass of tracer tends to unity. Many studies have established that ultimately the velocity divergence is responsible for the tracers clustering [3,7,8,9]. In addition, it has been pointed out the importance of the horizontal shear of the velocity field, which can mediate the intensity of the tracer clustering. However, these works addressed simplified stochastic models with limited applicability to more comprehensive models and natural experiments.
When looking at tracer aggregating induced by the compressible velocity fields including oceanic flows, Jacobs et al. [3], Huntley et al. [8], Schumacher and Eckhardt [9] have pointed out that mesoscale eddies trap tracer particles and significantly affect the tracer aggregation. These studies used gridded velocity fields, which were the output from high-resolution ocean models. The gridded velocity fields were deterministic with non-vanishing divergence. However, the spatial resolution of the ocean models is limited by the grid scale, which means that all the sub-grid scales remained unresolved. One way to model these unresolved scales would be relying on superimposing random velocity components to the large-scale deterministic velocity field. The random component thus plays the role of the small scale dynamics.
Using this framework, where the velocity field consists of deterministic and random components, Stepanov et al. [10,11] have studied the floating-tracer aggregating/clustering embedded into the velocity field with a deterministic component from high-resolution model outputs. These studies have confirmed that the shear flows associated with coherent vortex flows can significantly modulated the floating-tracer clustering. However, the deterministic component resulted from the interaction of many processes and was extremely complex to untangle all the involved processes and study them in detail. It did not allow to determine the leading physical mechanisms driving the floating-trace clustering.
The present study investigates the role of a background vortex flow in floating-tracer clustering. The vortex flow is induced by an ellipsoidal vortex embedded into a deformation flow [12,13,14]. Using the model, where the velocity field consists of deterministic and random components, we focus on the influence of the ellipsoidal vortex motion on the floating-tracer clustering. Based on the diagnostics from the stochastic topography, we qualitatively estimate the clustering rate and clustering mass to confirm the importance of the vortex motion inducing chaotic behavior of tracer trajectories for tracer clustering.
The paper is organized as follows: in Section 2, we formulate the general problem, the model of the random component and the deterministic component model. Scaling of equations and their integrating are presented in Section 3. Section 4 considers qualitative diagnostics for the floating-tracer clustering. The main results are in Section 5 followed by discussions in Section 6 and conclusions in Section 7.
2. Problem Formulation
The evolution of the passive tracer density under the rotational (nondivergent) velocity field , where and w are the horizontal and vertical velocity components, respectively is governed by equations [15,16,17,18]
where is the initial density of passive tracers, is the spatial coordinates, is the dynamic diffusivity and Q is the source term. When , and there is no tracer exchange across the region boundaries, then random velocity field with specified characteristics govern stochastic features of the equation (1).
Let us consider the evolution of the floating-tracer density . Then (1) becomes
Here, the 2D velocity field is potential (divergent) [4,15,19] and its divergence governed by changes in w
where is the horizontal divergence at the surface (). When the , then the is rotational (nondivergent).
We are interested in studying the influence of the deterministic nondivergent velocity field () on the floating-tracer clustering. Also, we assume that does not interact with the random velocity field (). So, the velocity field consists of two components:
2.1. Statistical Characteristics of the Random Velocity Field
As for our random velocity field, we consider a 2D velocity field with Gaussian, spatially homogeneous, isotropic, and stationary statistics [5]. This random velocity field consists of nondivergent and divergent components
where is a contribution of the divergent component to the random velocity field. The associated spatio-temporal velocity correlation tensors are
We suppose that the spatio-temporal velocity correlation tensors satisfy the relations
where for nondivergent and divergent components of the random velocity field. The effective diffusivities corresponding to divergent () and nondivergent () components of the random velocity field, respectively are [4,5,6,20],
where is the velocity curl and is the divergence of the random velocity field, respectively.
2.2. Velocity Field Induced by the Ellipsoidal Eddy
As for a deterministic velocity component, we consider a nondivergent 2D velocity field induced by an ellipsoidal vortex embedded in a deformation flow [12,14,21,22,23]. The detailed description of the ellipsoidal vortex model is presented in Appendix A. According to relations from the ellipsoidal vortex model (see Equation (A1) for details), the velocity field components are determined by solutions of the system of equations:
Then, the velocity components satisfy next relations
where is the stream function associated with the ellipsoidal vortex (see Appendix A. for details). Since the equations for center of the ellipsoidal vortex are split, we can null them and suppose that , then from the first two equations (10) we can obtain the relation . Denote , which features the relation between the semi-axes of the ellipsoidal vortex.
The system of equations (10)–(11) for trajectories of passive tracer is a two-and-a-half-degree-of-freedom system and thus, passive-tracer trajectories can manifest chaotic behavior.
Koshel et al. [14] have considered specific regimes of the ellipsoidal vortex motion and velocity field induced by these vortex motion regimes. This study considers these specific motions of the ellipsoidal vortex when has a separatrix (the self-intersecting stream-line), hyperbolic points and the recirculation regions outside the ellipsoidal vortex [14]. Figure 1 shows a phase portrait of the ellipsoidal vortex motion regimes depending on and the angle .
Our deterministic velocity component is considered for the three vortex motion regimes: (i) when the center of this vortex is fixed, (ii) the core of the ellipsoidal vortex oscillates or (iii) rotates. In the first case, passive tracer trajectories coincide with the closed lines both within the vortex and outside it in the recirculation zones. In the second and third cases (see Figure 1c,d), passive tracer trajectories can manifest chaotic behavior in the recirculation zones and therefore influence the floating-tracer clustering.
3. Scaling of Floating Tracer Equations and Their Integration
We suppose that the variables of (2) are dimensionless with spatial (L) and time (T) scales, and a density scale (P). Since the random velocity field is -correlated in time, than the scale T is equal to the time step. Taking the spatial step equal to the time step, we can get the velocity scale . Typical spatial scale of the ellipsoidal vortex , the typical rotation time of the vortex , and the oscillation time of the vortex , and the typical time of scattering .
For all the following numerical experiments, we consider a squared patch as initial conditions. The patch is uniformly filled by floating markers. The initial patch is placed either within the vortex or on the boundary of the adjacent recirculation zone. The initial density of the floating tracer is always equal to unity.
To integrate the equations (2) given the equations (4) we use the method of characteristics [4,5,18]:
where are coordinates of the initial patch. In order to obtain the Eulerian density the solution (12) needs to transform as follows
and then to exclude we can obtain the density field
The system equations (12) of float-tracer trajectories are integrated in time using the Euler-Ito scheme [10,11,20]. The method of the generation of the random velocity field is presented in [18,24]. We choose the integration domain very large to avoid the influence of the domain boundaries on the behavior of floating-tracer trajectories.
4. Qualitative Diagnostics of Floating-Tracer Clustering
In order to qualitatively assess the impact of the deterministic component of the velocity field induced by the ellipsoidal vortex on the clustering, we use qualitative metrics or diagnostics from the statistical topography. The area occupied by the clustered tracer or the clustering area () and another one, the clustering mass (). Let us consider the indicator Liouville’s function
then a variable ()
characterises the total area of the regions, where the floating-tracer density exceeds a predefined threshold , and variable ()
is referred to as the cluster mass characterising the mass of floating tracers in these regions. Ensemble averaging of gives the single-point in space and time probability density function [5,25], then the averaging of equations (14) and (15) on ensemble realisations of the random velocity field yields
With space and time homogeneous density field , the single-point probability density function is independent from , then equations (16) are simplified as
Here and are the specific cluster area and specific cluster mass, respectively [20].
For the random positive density field, conditions for density clustering with the unity probability, that is any realisation of the random velocity field yields the corresponding limits:
According to these relations, the area of the regions, where the density exceeds the specified threshold , tends to zero and the mass concentrated into these regions (clusters) tends to unity. When the evolution time is longer than the diffusion timescale, then we can use these estimates [5]
Here , where D is the corresponding effective diffusivity, which is related to and as follows
Regardless and relations are valid only for the divergent component, they can be useful diagnostics to quantitatively estimate the degree of the floating-tracer clustering.
According to [5], the effective diffusivity associated with the nondivergent component is modified, when the random velocity field is modulated by the shear flow (A1). In this case, the clustering process is absent. However, there is a filamentation, which is associated with the diffusion scattering of the initial tracer patch [5] and the modified effective diffusivity () becomes
which shows that both under weak shear () and under strong shear () the random component dominates over the scattering.
5. Results
In this Section we present results of numerical experiments, where the clustering of floating-tracers is simulated given the various states of the ellipsoidal vortex and contributions of divergent and nondivergent components (4).
First, let us consider the base-line experiment with no deterministic component (5). Figure 2 shows spatial distributions of the floating-tracer density (13) given various contributions of the divergent and nondivergent components. With only the divergent component the tracer clusters into coherent regions (see Figure 2a). The floating-tracer density reaches values. When the contribution of the divergent component decreases and the contribution of the nondivergent component increases, we observe increasing patches with low values of the floating-tracer density (see Figure 2b,c). In addition, due to the nondivergent component, the patches of the floating tracer with the highest density are scattered. With no divergent component, theoretical tracer clustering is prohibited (see Figure 2d), however some regions still demonstrate higher density values up to .
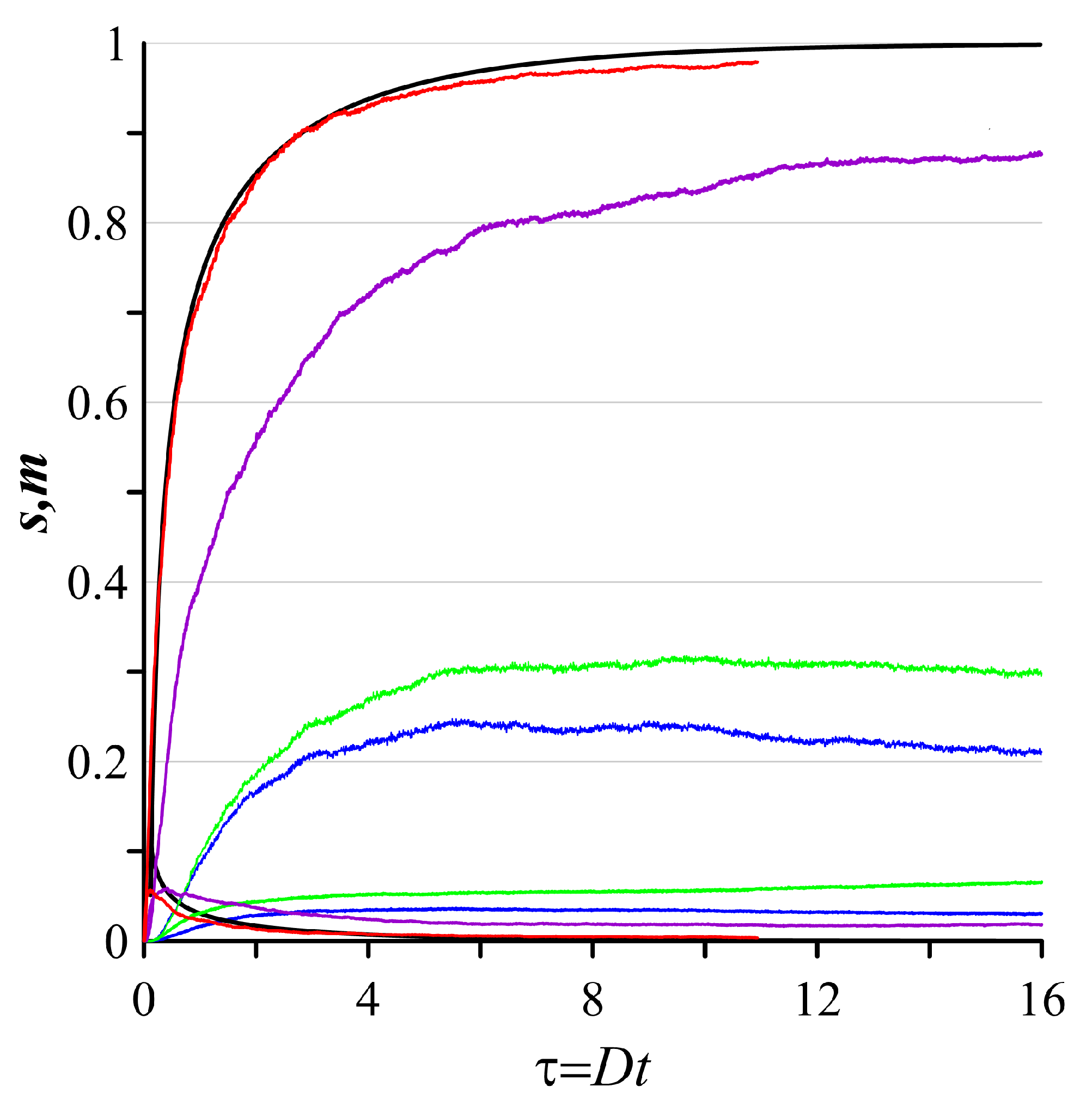
These clustering features are confirmed by quantitative diagnostics of the clustering (see Figure 2). The rate and degree of the floating-tracer clustering are dependent on the contribution of the divergent component. The higher the contribution of the divergent component, the higher the rate of and the lower the rate of , respectively. When the contribution of the divergent component is small or absent (), the dependence of differs from that of a high contribution of the divergent component. Given , , when the contribution of the divergent component is not small (), the clustering metrics continue to increase with a very low rate. When , in contrast, decreases at a more faster rate. It quantitatively reflects the decaying of the floating-tracer clustering when the contribution of the nondivergent component increases up until complete absence of clusters when the nondivergent component dominates.
Figure 2.
Base-line experiments, where the floating-tracer clustering is induced by the random velocity
field only (5). Instances of spatial distributions of the floating-tracer density (13) when: (a) there is a
divergent component only (γr = 1.0, τ = 10.94), b) contributions of the divergent and nondivergent
components are equal (γr = 0.5, τ = 34.48), c) the contribution of the divergent component is small
(γr = 0.1, τ = 34.48), d) there is a nondivergent component only (γr = 0.0, τ = 34.48).
Figure 2.
Base-line experiments, where the floating-tracer clustering is induced by the random velocity
field only (5). Instances of spatial distributions of the floating-tracer density (13) when: (a) there is a
divergent component only (γr = 1.0, τ = 10.94), b) contributions of the divergent and nondivergent
components are equal (γr = 0.5, τ = 34.48), c) the contribution of the divergent component is small
(γr = 0.1, τ = 34.48), d) there is a nondivergent component only (γr = 0.0, τ = 34.48).
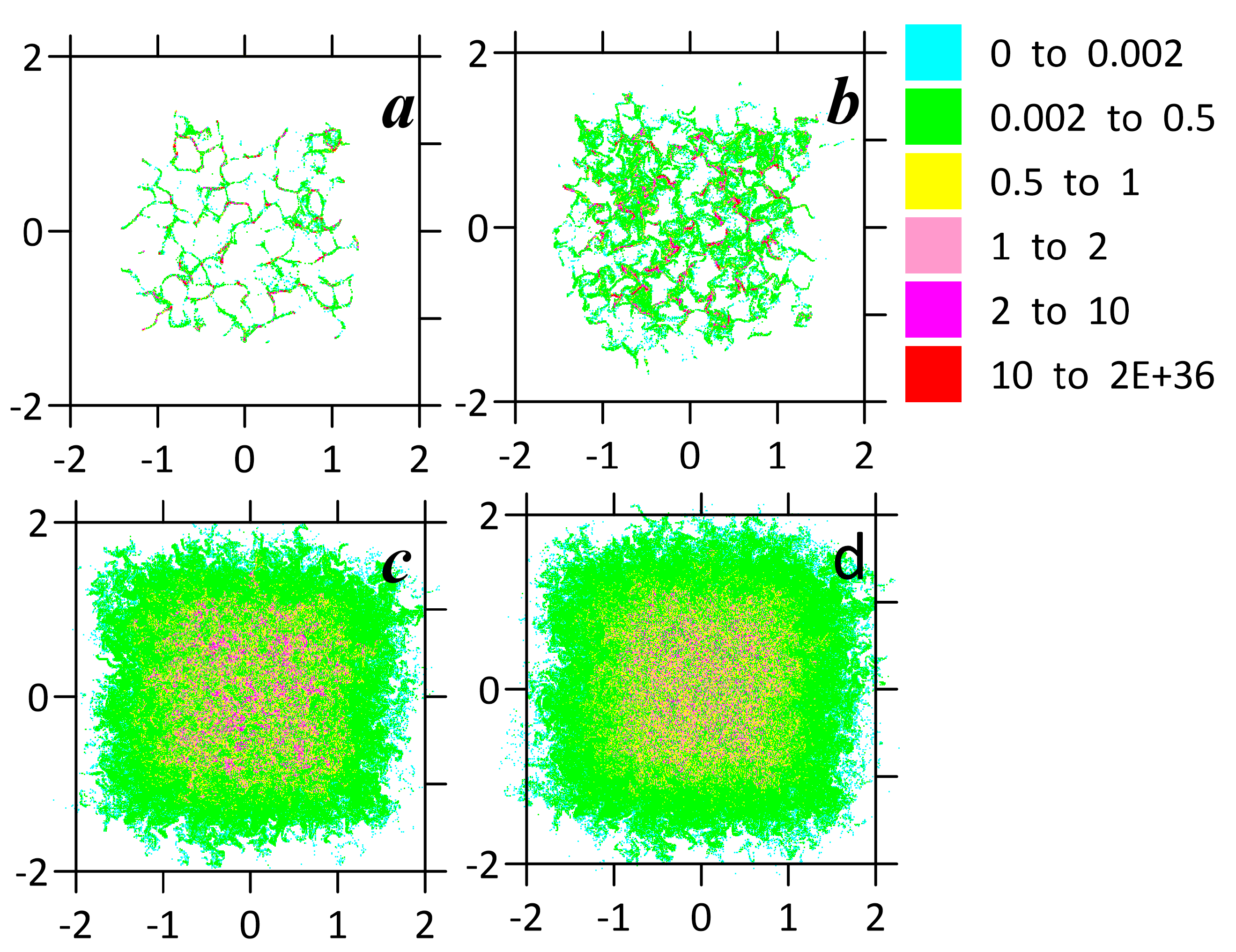
Figure 2 (Continued).
Base-line experiments, where the floating-tracer clustering is induced by the random velocity field only (5). Color lines denote the evolution of the clustering areas (lower curves) and the clustering mass (upper curves) depending on various contributions of the divergent and nondivergent components. Red lines denote and curves, corresponding to the spatial distribution of the floating-tracer density (see Figure 2(a)). Purple lines denote and curves, corresponding to the spatial distribution of the floating-tracer density (see Figure 2(b)). Green lines denote and curves, corresponding to the spatial distribution of the floating-tracer density (see Figure 2(c)). Finally, blue lines denote and curves, corresponding to the spatial distribution of the floating-tracer density (see Figure 2(d)). Black lines denote and curves, corresponding to their analytical estimates (18), when there is a divergent component only (, ). [19].
Figure 2 (Continued).
Base-line experiments, where the floating-tracer clustering is induced by the random velocity field only (5). Color lines denote the evolution of the clustering areas (lower curves) and the clustering mass (upper curves) depending on various contributions of the divergent and nondivergent components. Red lines denote and curves, corresponding to the spatial distribution of the floating-tracer density (see Figure 2(a)). Purple lines denote and curves, corresponding to the spatial distribution of the floating-tracer density (see Figure 2(b)). Green lines denote and curves, corresponding to the spatial distribution of the floating-tracer density (see Figure 2(c)). Finally, blue lines denote and curves, corresponding to the spatial distribution of the floating-tracer density (see Figure 2(d)). Black lines denote and curves, corresponding to their analytical estimates (18), when there is a divergent component only (, ). [19].
Let us consider now the cases when the velocity field consists both of a random component and deterministic component. The latter component is induced by the ellipsoidal vortex (4). To start with, we consider the case of the steady ellipsoidal vortex. In this case, the deterministic component does nor result in chaotic behavior of tracer’s trajectories (see Figure 2b)). Figure 3 shows spatial distributions of the floating-tracer density depending on contributions of the divergent component and the initial patch of floating tracer is placed within the steady ellipsoidal vortex (see Figure 3a)). When the divergent component (4) dominates, we observe regions with the highest values of the floating-tracer density up to . This confirms the theoretical exponential clustering of floating tracers. When the contribution of the divergent component decreases, the number of regions with the highest floating-tracer density decreases as well, while the number of the regions with low floating-tracer density increases. When the contribution of the nondivergent component increases, we observe diffusive scattering of the initial floating-tracer patch and markers can leave the ellipsoidal vortex due to filamenting of the boundary of the floating-tracer patch [5,18,26]. To illustrate these features of tracer-trajectory behavior, the evolution of the floating-tracer density was simulated during the for the case () (see Figure 3e)-f)). Initial floating-tracer patch is scattering and floating tracer can leave the ellipsoidal vortex and then it can be advected by the background flow.
Qualitative diagnostics of the floating-tracer clustering both for and confirm the results (see Figure 3). The rate and degree of the clustering are higher when the contribution of the divergent component is high. We observe increasing of the clustering mass and decreasing of the clustering area. On the other hand, increasing of the contribution of the nondivergent component up to leads to decreasing of the floating-tracer density within the ellipsoidal vortex. With time, we observe pronounced decreasing of the floating-tracer density in the ellipsoidal vortex and the decreases.
Figure 3.
The same as in Figure 2, but with the deterministic velocity component (4) induced by a
steady ellipsoidal vortex. For cases c) and d) see the insets e) and f), respectively at the time τ = 94.44.
Figure 3.
The same as in Figure 2, but with the deterministic velocity component (4) induced by a
steady ellipsoidal vortex. For cases c) and d) see the insets e) and f), respectively at the time τ = 94.44.
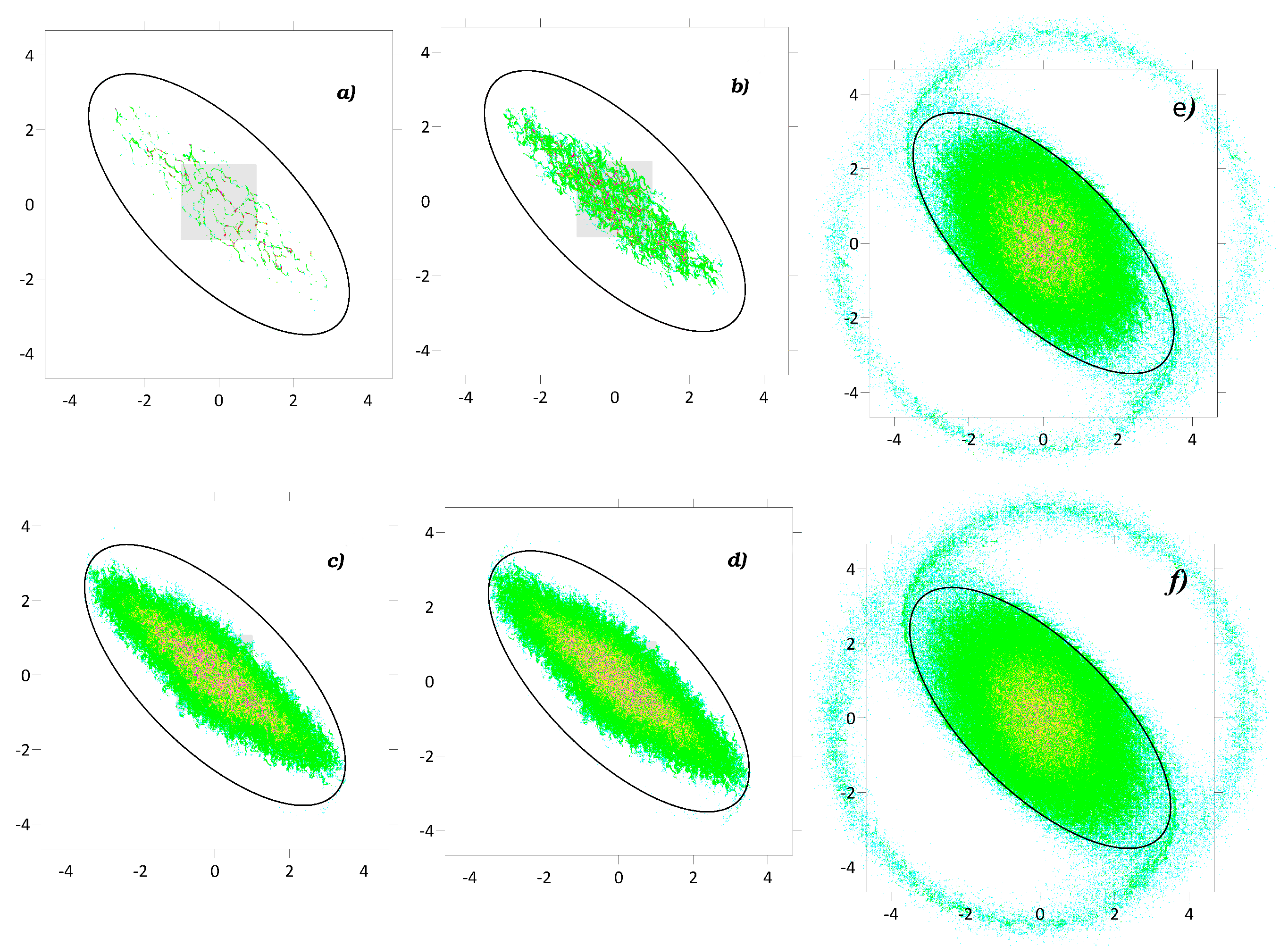
Figure 3 (Continued).
The same as in Figure 2, but the clustering of floating tracer in the velocity field (4), where the deterministic component is induced by a steady ellipsoidal vortex. Color lines denote the clustering area (lower curves) and the clustering mass (upper curves) given various contributions of the divergent and nondivergent components. Curves of for the random velocity field (5) are denoted by the colored asterisks.
Figure 3 (Continued).
The same as in Figure 2, but the clustering of floating tracer in the velocity field (4), where the deterministic component is induced by a steady ellipsoidal vortex. Color lines denote the clustering area (lower curves) and the clustering mass (upper curves) given various contributions of the divergent and nondivergent components. Curves of for the random velocity field (5) are denoted by the colored asterisks.
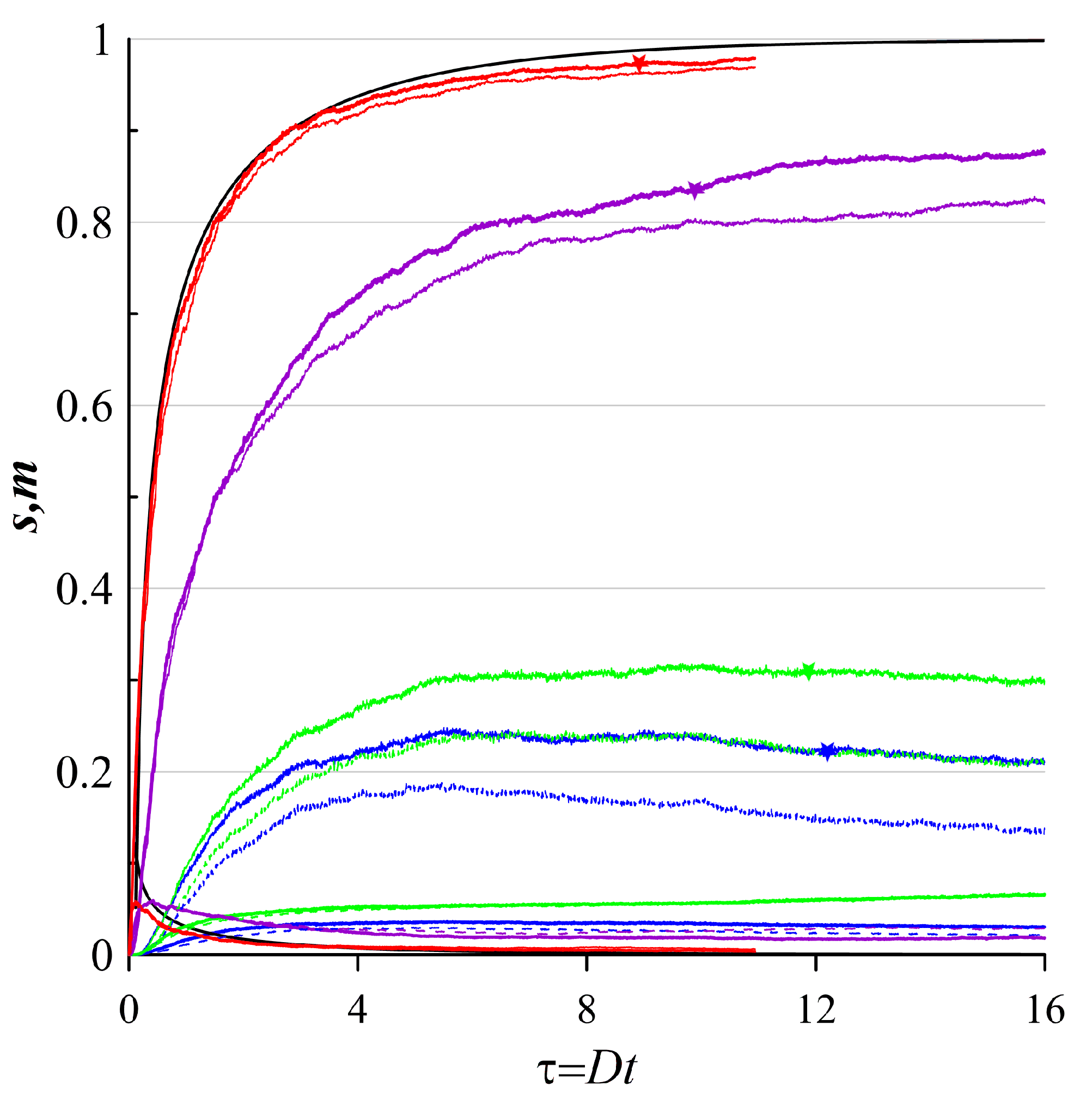
Figure 4 shows the spatial distribution of the floating-tracer density for the case, when the floating-tracer patch was initially located near the boundary of the steady ellipsoidal vortex (see Figure 4a)). In this case, the floating-tracer clustering is observed because of the contribution of the divergent component. Note that, the floating tracers are clustering both near the boundary of the ellipsoidal vortex and the boundary of the recirculation regions. When the nondivergent component increases, we observe strong diffusive scattering of the tracer (see Figure 4c)-e)). At the same time, anisotropy of the spatial distribution of the floating tracer is manifested. High density values are observed mainly near the boundary of the vortex and recirculation zones, while markers do not penetrate deep into the vortex and centers of the recirculation zones.
Quantitative diagnostics point out that floating tracer clusters exponentially when there is no nondivergent component (see Figure 4). At earlier times, sharp increase of the clustering mass is observed and the metric is non-decreasing. For the non-asymptotic cases, when the contribution of the nondivergent component is neither zero nor unity, and at longer characteristic time , we observe significant decrease of , so the clusters do not fully form. Note that the decaying rate depends on the contribution of the nondivergent component.
Let us to consider the clustering of the floating-tracer, when the deterministic component induced by the oscillating and rotating ellipsoidal vortex regimes (see Figure 2c,d). Koshel et al. [14] have established that for both cases, tracer trajectories can manifest chaotic behavior. To start with we consider the case of the oscillating vortex regime and place an initial tracer patch within the vortex or within the recirculation zone’s boundary.
Figure 5 shows spatial distributions of the tracer density when the initial patch was placed within the vortex. According to these distributions, the higher contribution of the divergent component, the more tracer is clustered. Note that the initial tracer patch is scattered along the semi-axes of the ellipsoidal vortex.
Quantitative diagnostics of the tracer clustering confirm that the highest values of the cumulative clustered mass w along with very small values of the cumulative clustered area are observed when the contribution of the divergent component is very high (see Figure 5). At the same time, when the contribution of the divergent component is minimal with time we observe little clustering. This process of no clustering also can be seen in the curve .
Figure 6 shows the spatial distributions of the tracer density, when the initial tracer patch is placed near the oscillating ellipsoidal vortex’s boundary. With a dominant divergent component, the tracer clustering manifests itself prominently. The clusters are generated mainly near the boundaries of the vortex and recirculation zones. The clusters are however not generated deeper within the vortex core and the centres of the recirculation zones. Increasing the contribution of the nondivergent component results in diffusive scattering of the tracer and weakened clustering with spatial heterogeneity.
Quantitative diagnostics of the clustering show that again when the divergent component dominates, the clustering happens at higher rates (see Figure 6). As time moves on the , curve continues its non-decreasing behavior. When the contribution of the divergent component decreases, the clustering again is not able to be sustainable. It is confirmed by the curve for larger times (see Figure 6).
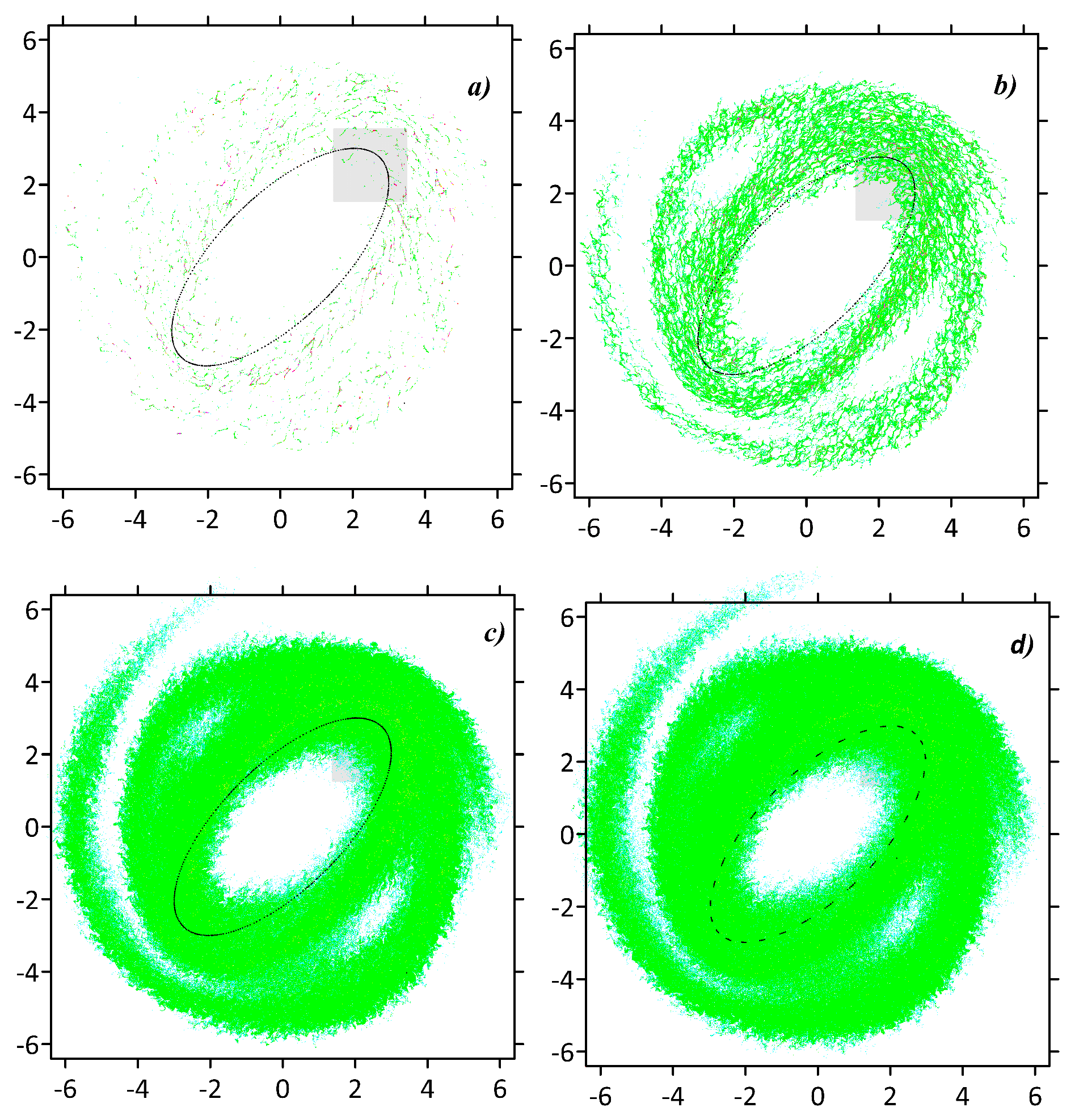
To finalize the Section, we consider clustering of the tracer in the rotating ellipsoidal vortex regime. Figure 7 shows spatial distributions of the tracer density when the initial tracer patch is placed within the ellipsoidal vortex core. Clustering of the tracer is similarly governed by the contribution of the divergent component. Reducing this contribution leads to smaller probability of the clustering. At the same time, increasing the contribution of the nondivergent component facilitates diffusive scattering of the tracer. However, even when the nondivergent component is dominant, there are still many zones of non-zero values of the tracer density within the ellipsoidal vortex.
According to diagnostics of the clustering, we observe a high clustering rate and then non-decreasing behavior of the clustering mass for the case when the contributions of the random velocity component is equal to the determiistic one () (see Figure 7). Note that if the divergent component is small, and at longer times the curve still shows no decreasing behavior, but it oscillates with the period of dimensionless unit time. When the contribution of the divergent component is equal to zero, the sharp clustering rate during initial period changes to a slow decrease of the clustering degree at similar to the previously described case with the period of dimensionless unit time.
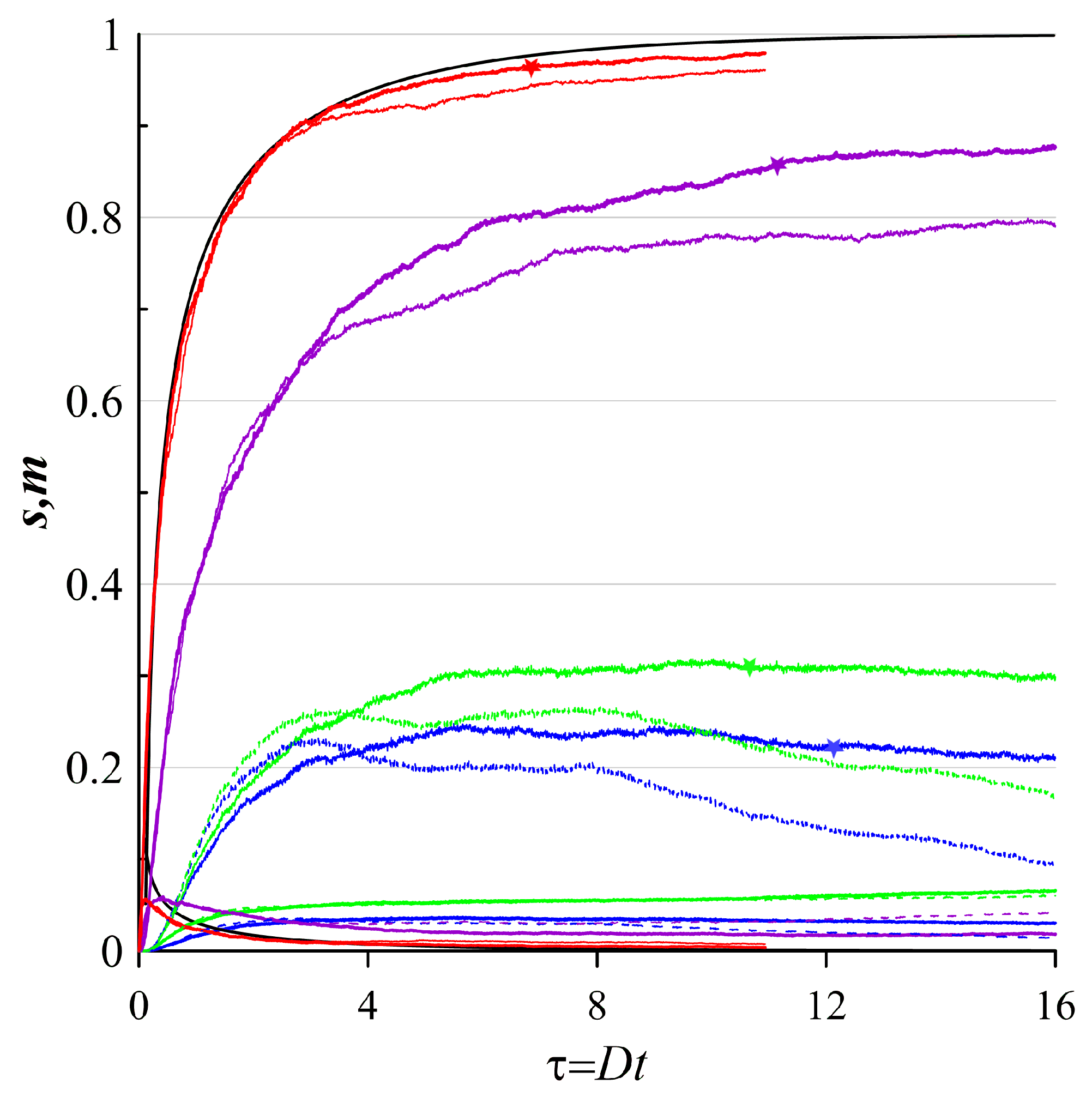
Finally, let us consider the case, when the initial tracer patch is placed near the boundary of the rotating ellipsoidal vortex (see Figure 8). Spatial distributions of the tracer density show that clustering occurs near the boundaries of the vortex and recirculation zones similarly because of the large divergent component. When the contribution of the divergent component decreases, the zones with the highest density values become less pronounced. On the other hand, with increasing the nondivergent component, we observe more pronounced diffusive scattering (see Figure 8c)-d)). When there is only the nondivergent component, there are still multiple tracer aggregations in the recirculation zones and partially the vortex itself, however the density is rather small (see Figure 8d)).
Quantitative diagnostics of the clustering confirm clustering with a dominant divergent velocity component (see Figure 8). When or cases, clustering becomes weaker. However, the curve does not manifest decreasing behavior with longer times . On the other hand, increasing the contribution of the nondivergent component results in slow increasing of the tracer mass and consequently in decreasing of the curve with longer times . Similarly, the larger contribution of the nondivergent component, the higher the cluster mass decreasing.
6. Discussion
One of the aims of the investigation is to consider results from studies [10,11,20] in more detail by employing a simpler dynamical model of the background shearing flow. The authors have studied the floating-tracer clustering in a compound velocity field, where the random velocity component consisted of divergent and nondivergent parts and the deterministic velocity component was taken from a gridded velocity field from eddy-resolving numerical simulations of the Sea of Japan circulation [27]. Various regimes of tracer aggregation were reported and analysed. However due to the complexity of the comprehensive ocean velocity field, a detailed analysis of the leading processes responsible for the observed dynamical patters were not fully addressed. The authors suggested that the observed features associated with the qualitative diagnostics of the tracer clustering were mostly affected by multiple eddies populating the deterministic velocity field. In the present study, we considered a simpler model of a vortex, namely, the velocity field induced by an ellipsoidal vortex embedded into a deformation flow. In particular, we focused on the influence the ellipsoidal vortex motion regimes (oscillating and rotating) on the tracer clustering.
Comparing the clustering metrics depending on the balance parameter for the steady ellipsoidal vortex case shows that the clustering occurs only with a dominant divergent velocity component. When is equal to 0.5, the floating tracer clusters within the vortex. In other cases, clustering does not occur. Even though the clustering mass increases initially (up to ), then it starts decreasing () as evidenced by the curve. Comparing to the base-line purely stochastic model suggests that the presence of a steady ellipsoidal vortex is not conducive to tracer clustering. It is most noticeable when the ratio is very small.
In addition, tracer clustering is sensitive to the tracer’s initial conditions. When the initial tracer patch is placed near the ellipsoidal vortex periphery, clustering is weakened, as opposed to the case when the initial tracer patch is placed within the vortex. This is because the recirculation zones near the separatrix experience the most intense shearing flows. At early times (), the clustering rate in the steady-state vortex case is similar to the base-line purely stochastic case. At later times (), the difference between these two cases increases; the clustered mass in the steady-state vortex case is less than in the base-line case.
Considering the case of an oscillating ellipsoidal vortex, we observed significant changes. For two different sets of tracer initial conditions, the tracer clustering occurs for both a dominant divergent velocity component () and for equal contributions of () the divergent and nondivergent components. It is confirmed by the non-decreasing curves for these two sets of initial conditions. Increasing the influence of the nondivergent component (), the tracer clustering never happens (the curves attenuate in both cases of initial conditions).
A noticeably different case is the rotating ellipsoidal vortex. With a dominant divergent velocity component or equal contributions of the both velocity components, the clustering rate is higher as compared to the all previous cases. Also, the clustering process differs for the two sets of the tracer initial conditions. When the initial tracer patch is placed within the rotating vortex, the clustering is stronger as compared to the case when the initial tracer patch is placed near the periphery of the recirculation zones. We also observe a high clustering rate with dominating nondivergent component ().
We thus demonstrated pronounced differences between tracer clustering occurring in the steady ellipsoidal vortex regime and in the oscillating or rotating ellipsoidal vortex regimes. When the ellipsoidal vortex is unsteady, tracer trajectories manifest chaotic behavior, which partly accounts for the differences. When the initial tracer patch is placed within the ellipsoidal vortex, the clustering mass for the case of an unsteady vortex is higher than that for the case of a steady ellipsoidal vortex.
Thus, we confirm the hypothesis from [10] that clusters can not survive strong advection near eddies for long. When an ellipsoidal vortex is steady, the tracer is advected from the vortex very slowly. However, the tracer is also trapped in the neighbourhood of the separatrix for a long time. This region has strong shearing flows that prevent clustering.
When the ellipsoidal vortex is unsteady, the tracer is advected from the neighbourhood of the separatrix (where the strongest shearing flows are observed, which are detrimental for clustering), which allows a larger part of the mass to remain clustered. This is observed for the case of the initial tracer patch placed near the periphery of the ellipsoidal vortex. In this case, due to the unsteady ellipsoidal vortex and tracer advection, the tracer leaves the neighbourhood of the separatrix away from strong shears. This prevents decreasing of the clustering rate in contrast to the steady ellipsoidal vortex case.
7. Conclusions
This study investigated the influence of a background vortex flow on clustering of floating tracers. The vortex flow was induced by the interaction of an ellipsoidal vortex with a deformation flow, which produces various vortex motion regimes: (i) steady state, (ii) oscillating and (iii) rotating of the ellipsoidal vortex. The unsteady ellipsoidal vortex induces chaotic tracer trajectories. The regions where the chaotic behavior largely manifests itself are hyperbolic points and separatrix. We focused on tracer clustering in velocity fields where the deterministic velocity component permitted chaotic tracer trajectories.
The tracer clustering was governed by a random velocity field consisting of nondivergent and divergent components. With a dominant divergent component, we observed tracer clustering. On the other hand, with a dominant nondivergent component, the clustering never occurs.
The spatial and time scales of the vortex motion exceeded these of the random velocity field by an order of magnitude. The deterministic velocity component induced by the ellipsoidal vortex the random velocity component therefore are mostly independent. We used the method of characteristics to integrate the tracer density equation and the Euler-Ito scheme for tracer trajectories evolving in the random velocity field. The clustering area and clustering mass from the statistical topography were used as the quantitative diagnostics of the tracer clustering.
In the base-line case of a random velocity field only, we confirmed that when the divergent component dominated, there were zones with a very small total area and very high mass in the tracer density field. According to the quantitative metrics, the cumulative mass of these zones is non-decreasing with time. When the contribution of the divergent component relative to the nondivergent component was less than 0.5, we registered no tracer clustering.
For the steady ellipsoidal vortex regime we observed weaker tracer clustering. Even with a higher contribution from the divergent component, the clustering rate and the clustering degree were less strong as compared to the base-line case. The most striking differences between were observed for the initial tracer patch placed near the boundary of the ellipsoidal vortex. We also observed complete floating tracer clustering when the random velocity field consisted of the divergent component only.
Fort the unsteady ellipsoidal vortex regimes, we observed tracer clustering when the contribution of the divergent component was higher or equal to that of the nondivergent component. Even when the initial tracer patch was placed near the boundary of the recirculation zones, clustering still persisted. With a rotating ellipsoidal vortex, we observed pronounced clustering as well. When the initial tracer patch was placed within the rotating vortex, the clustering rate was higher than that for the base-line case during earlier times. Thus, we suggested that the unsteady ellipsoidal vortex regimes promoted (at least not prohibited) clustering due advecting the nascent clusters away from the separatrix region, where the strongest shears existed.
Author Contributions
Conceptualization, K. Koshel; methodology, K. Koshel; software, K. Koshel and N. Kuznetsova; validation, K. Koshel., E. Ryzhov and D. Stepanov; formal analysis, K. Koshel; investigation, K. Koshel; resources, K. Koshel; data curation, K. Koshel; writing—original draft preparation, K. Koshel and D. Stepanov; writing—review and editing, D. Stepanov and E. Ryzhov; visualization, K. Koshel and N. Kuznetsova; supervision, K. Koshel; project administration, K. Koshel; funding acquisition, K. Koshel All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the Russian Science Foundation, grant no. 23-27-00188 https://rscf.ru/en/project/23-27-00188/.
Data Availability Statement
For more specific information about the simulated data e-mail to Konstantin Koshel at kvkoshel@poi.dvo.ru.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Appendix A. Ellipsoidal Vortex into the Deformation Flow
According to [12,14,21,22,23], let us consider the deformation flow in the dimensionless coordinates:
where e and are dimensionless variables controlling the time scale and is a dimensionless variable controlling the velocity scale.
We consider a vortex structure embedded in a deformation flow (A1) and the vortex is an ellipsoidal region V with the boundary:
where
and is the vortex’s center and , where is the semi-axes. The vorticity is considered piece-wise constant. There is a difference between the vorticity inside the vortex and adjacent flow
According to [14], the stream function is , where . Thus, and satisfy the relations
Here, , . The lower limit of the integration is defined as the root of the cubic equation
We take inside the ellipsoidal vortex and outside the vortex. The fluid particle advection equations are
According to [12,21,22,23], from the kinematic conditions we take relations for parameters and positions of the ellipsoid
where
Spatial derivatives of the stream-function can be obtained by introducing new coordinates as follows
which are the velocity projections onto the main semi-axes of the ellipsoid. Taking into account (A3) we obtain
References
- Okubo, A. Diffusion and Ecological Problems: Mathematical Models; Vol. 10, Biomathematics, Berlin: Springer-Verlag, 1980.
- McComb, W.D. The Physics of Fluid Turbulence; Vol. 25, Oxford Engineering Sci. Ser., Oxford: Clarendon Press, 1990.
- Jacobs, J.A.; Huntley, H.S.; Kirwan, A.D.; Lipphardt, B.L.; Campbell, T.; Smith, T.; Edwards, K.; Bartes, B. Ocean processes underlying surface clustering. Journal of Geophysical Research, Oceans 2016, 121, 180–197. [Google Scholar] [CrossRef]
- Klyatskin, V.I. The imbedding method in statistical boundary-value wave problems; Vol. 33, Book Series: Progress in Optics, Elsevier B. V., 1994; pp. 1–133. [CrossRef]
- Klyatskin, V.I. Stochastic Equations: Theory and Applications in Acoustics, Hydrodynamics, Magnetohydrodynamics, and Radiophysics; Vol. 1,2, Springer, 2015.
- Klyatskin, V.I. Stochastic structure formation in random media. Phys. Usp. 2016, 59, 67–95. [Google Scholar] [CrossRef]
- Klyatskin, V.I.; Koshel, K.V. The simplest example of the development of a cluster-structured passive tracer field in random flows. Physics-Uspekhi 2000, 170, 771–778. [Google Scholar]
- Huntley, H.S.; Lipphardt, B.L.; Jacobs, G.; Kirwan, A.D. Clusters, deformation, and dilation: Diagnostics for material accumulation regions. Journal of Geophysical Research: Oceans 2015, 120, 6622–6636. [Google Scholar] [CrossRef]
- Schumacher, J.; Eckhardt, B. Clustering dynamics of Lagrangian tracers in free-surface flows. Physcal review E 2002, 66, 017303. [Google Scholar] [CrossRef]
- Stepanov, D.V.; Ryzhov, E.A.; Zagumennov, A.A.; Berloff, P.; Koshel, K.V. Clustering of Floating Tracer Due to Mesoscale Vortex and Submesoscale Fields. Geophysical Research Letters 2020, 47. [Google Scholar] [CrossRef]
- Stepanov, D.V.; Ryzhov, E.A.; Berloff, P.; Koshel, K.V. Floating tracer clustering in divergent random flows modulated by an unsteady mesoscale ocean field. Geophysical & Astrophysical Fluid Dynamics 2020, 114, 690–714. [Google Scholar] [CrossRef]
- Zhmur, V.V. Localized eddy formation in a shear-flow. Oceanology 1988, 28, 536–538. [Google Scholar]
- Meacham, S.P.; Pankratov, K.K.; Shchepetkin, A.F.; Zhmur, V.V. The interaction of ellipsoidal vortices with background shear flows in a stratified fluid. Dyn. Atmos. Oceans 1994, 21, 167–212. [Google Scholar] [CrossRef]
- Koshel, K.V.; Ryzhov, E.A.; Carton, X.J. Vortex Interactions Subjected to Deformation Flows: A Review. Fluids 2019, 4. [Google Scholar] [CrossRef]
- Klyatskin, V.I. Clustering and diffusion of particles and passive tracer density in random hydrodynamic flows. Phys. Usp. 46, 667 2003, 46, 667–688. [Google Scholar] [CrossRef]
- Klyatskin, V.I. Diffusion and clustering of sedimenting tracers in random hydrodynamic flows. JETP 2004, 99, 1005–1017. [Google Scholar] [CrossRef]
- Cressman, J.R.; Goldburg, W.I. Compressible Flow: Turbulence at the Surface. J. Stat. Phys. 2003, 113, 875. [Google Scholar] [CrossRef]
- Klyatskin, V.; Koshel, K. Impact of diffusion on surface clustering in random hydrodynamic flows. Physical Review E 2017, 95, 013109. [Google Scholar] [CrossRef] [PubMed]
- Klyatskin, V.I.; Saichev, A.I. Statistical theory of the diffusion of a passive tracer in a random velocity field. JETP 1997, 84, 716–724. [Google Scholar] [CrossRef]
- Koshel, K.V.; Stepanov, D.V.; Ryzhov, E.A.; Berloff, P.; Klyatskin, V.I. Clustering of floating tracers in weakly divergent velocity fields. Physical Review E 2019, 100, 063108. [Google Scholar] [CrossRef]
- Zhmur, V.V. Subsurface mesoscale eddy structures in a stratificated ocean. Oceanology 1989, 29, 28–32. [Google Scholar]
- Zhmur, V.V.; Pankratov, K.K. The dynamics of the semi-ellipsoid subsurface vortex in the non-uniform flow. Oceanology 1989, 29, 205–211. [Google Scholar]
- Zhmur, V.V.; Pankratov, K.K. Dynamics of mesoscale eddy formation in the field currents of large intensive vortex. Okeanologia 1990, 30, 124–129. [Google Scholar]
- Koshel, K.V.; Alexandrova, O.V. Some results of a numerical modeling of the diffusion of passive tracers in a random field of velocities. Izv. Atmos. Ocean. Phys. 1999, 35, 578–588. [Google Scholar]
- Isichenko, M. Percolation, statistical topography, and transport in random media. Reviews of Modern Physics 1992, 64, 961. [Google Scholar] [CrossRef]
- Klyatskin, V.I. Statistical description of the diffusion of a passive tracer in a random velocity field. Physics-Uspekhi 1994, 37, 501–513. [Google Scholar] [CrossRef]
- Stepanov, D.; Fomin, V.; Gusev, A.; Diansky, N. Mesoscale Dynamics and Eddy Heat Transport in the Japan/East Sea from 1990 to 2010: A Model-Based Analysis. Journal of Marine Science and Engineering 2022, 10, 33. [Google Scholar] [CrossRef]
Figure 1.
Motion regimes of the ellipsoidal vortex embedded in a deformation flow. (a) Phase portrait of the ellipsoidal vortex motion regimes (). Various color points denote the initial states of the ellipsoidal vortex for three cases: the blue point () denotes a steady state, when the vortex is stationary, the green point () denotes an oscillation state and the blue point () denotes a case of the vortex’s rotating. (b) Passive tracer trajectories inside the vortex (blue closed lines) and outside the vortex (green closed line) in the steady state. The red line denotes a separatrix and the hyperbolic points are denoted by red points. (c) Positions of the vortex core boundary, under oscillating of the ellipsoidal vortex. Blue points denote the initial state of the ellipsoidal vortex and black points denote the positions of the vortex core boundary after 1/4, 1/2 and 3/4 of a period. Green points denote the position of the re-circulation zone boundaries at the initial time moment. (d) Positions of the vortex core boundary for a rotating ellipsoidal vortex. Blue and green points denote the initial state of the ellipsoidal vortex and its re-circulation zones, respectively. Red points denote the vortex core boundary after 1/4 and 3/4 of a period. Black points denote the vortex core boundary after 1/2 of a period.
Figure 1.
Motion regimes of the ellipsoidal vortex embedded in a deformation flow. (a) Phase portrait of the ellipsoidal vortex motion regimes (). Various color points denote the initial states of the ellipsoidal vortex for three cases: the blue point () denotes a steady state, when the vortex is stationary, the green point () denotes an oscillation state and the blue point () denotes a case of the vortex’s rotating. (b) Passive tracer trajectories inside the vortex (blue closed lines) and outside the vortex (green closed line) in the steady state. The red line denotes a separatrix and the hyperbolic points are denoted by red points. (c) Positions of the vortex core boundary, under oscillating of the ellipsoidal vortex. Blue points denote the initial state of the ellipsoidal vortex and black points denote the positions of the vortex core boundary after 1/4, 1/2 and 3/4 of a period. Green points denote the position of the re-circulation zone boundaries at the initial time moment. (d) Positions of the vortex core boundary for a rotating ellipsoidal vortex. Blue and green points denote the initial state of the ellipsoidal vortex and its re-circulation zones, respectively. Red points denote the vortex core boundary after 1/4 and 3/4 of a period. Black points denote the vortex core boundary after 1/2 of a period.
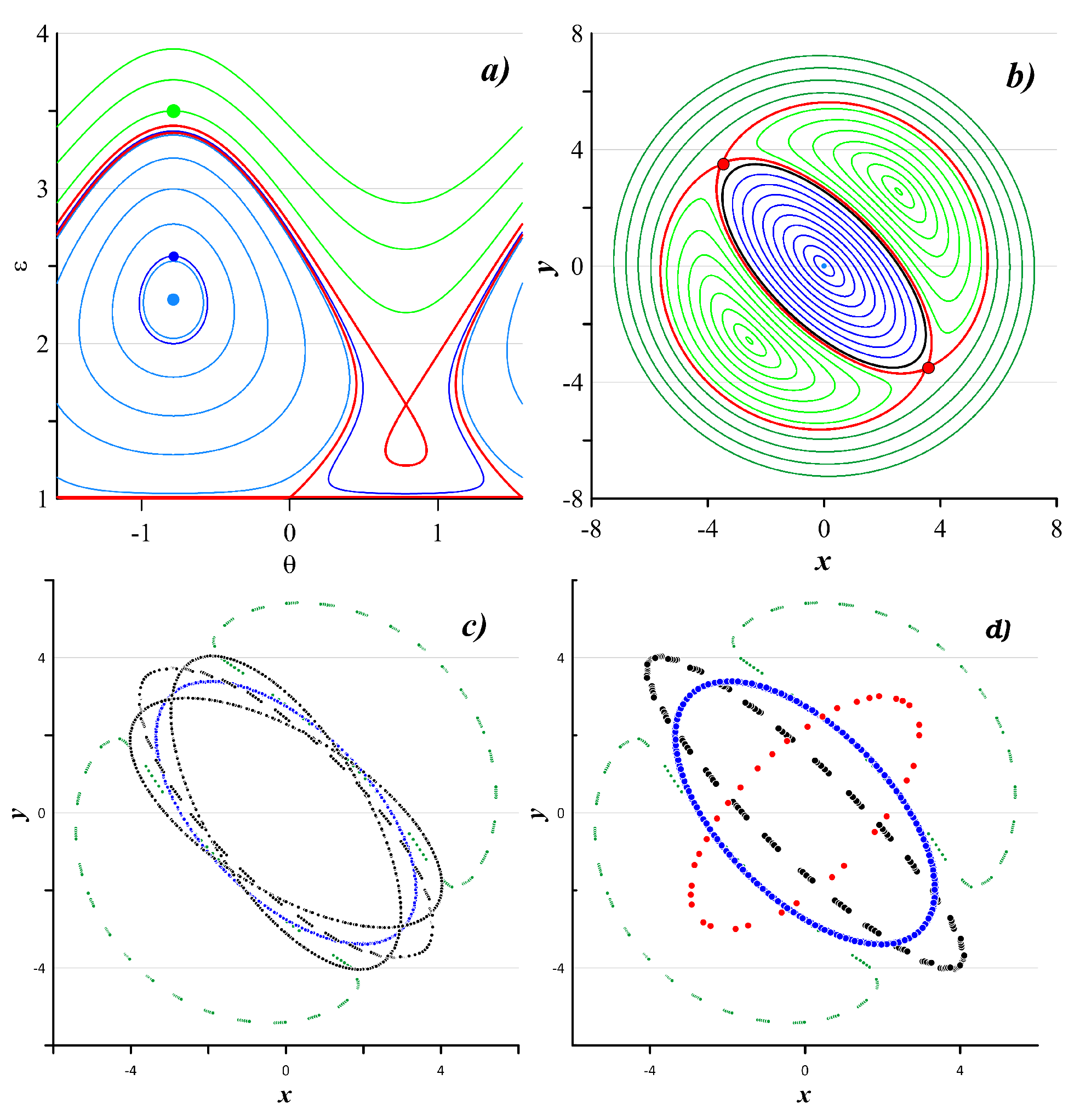
Figure 4.
The same as in Figure 3, but the initial tracer patch is placed near the boundary of the steady ellipsoidal vortex.
Figure 4.
The same as in Figure 3, but the initial tracer patch is placed near the boundary of the steady ellipsoidal vortex.
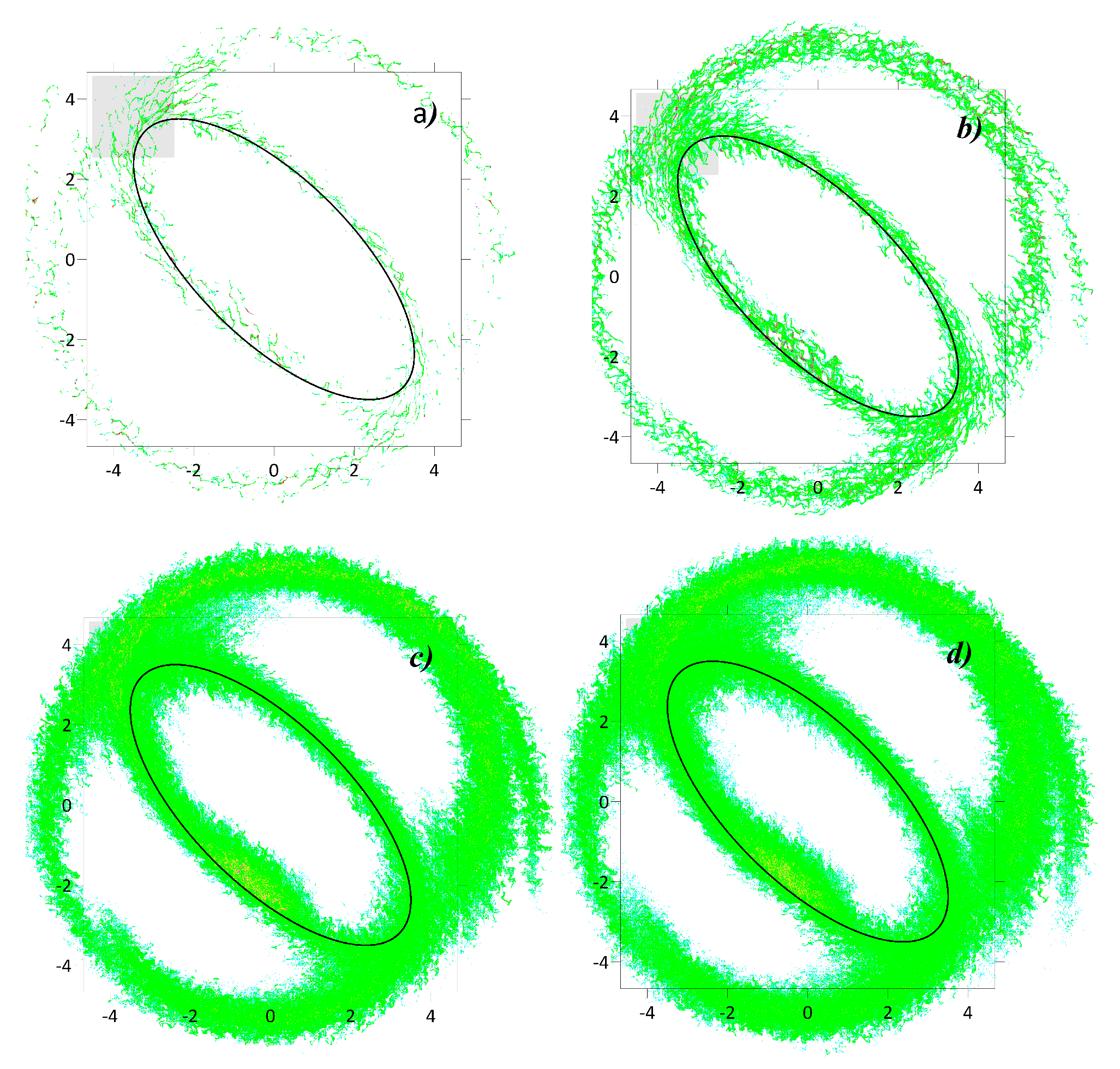
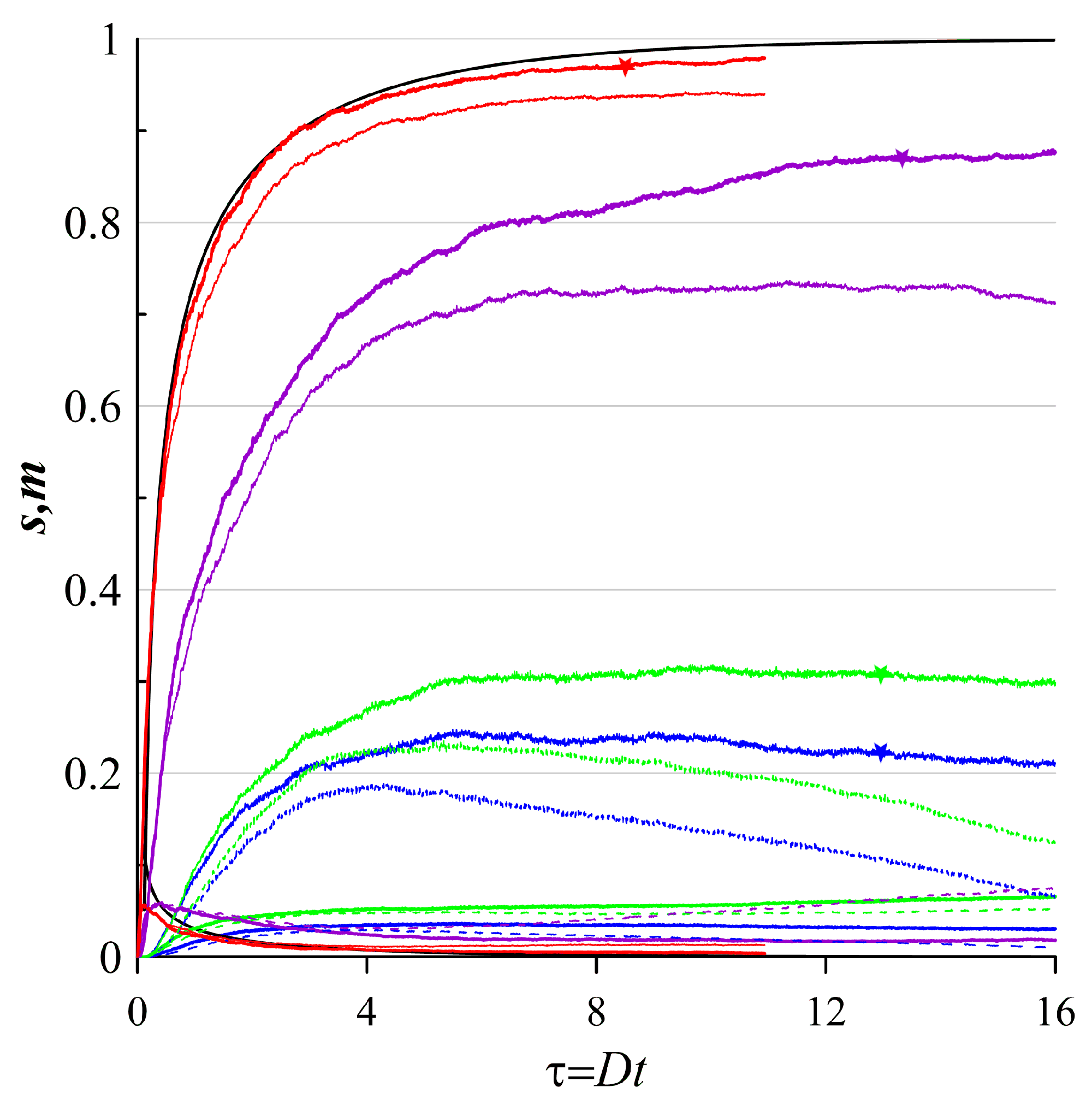
Figure 5.
The same as in Figure 3 but for the oscillating ellipsoidal vortex regime.
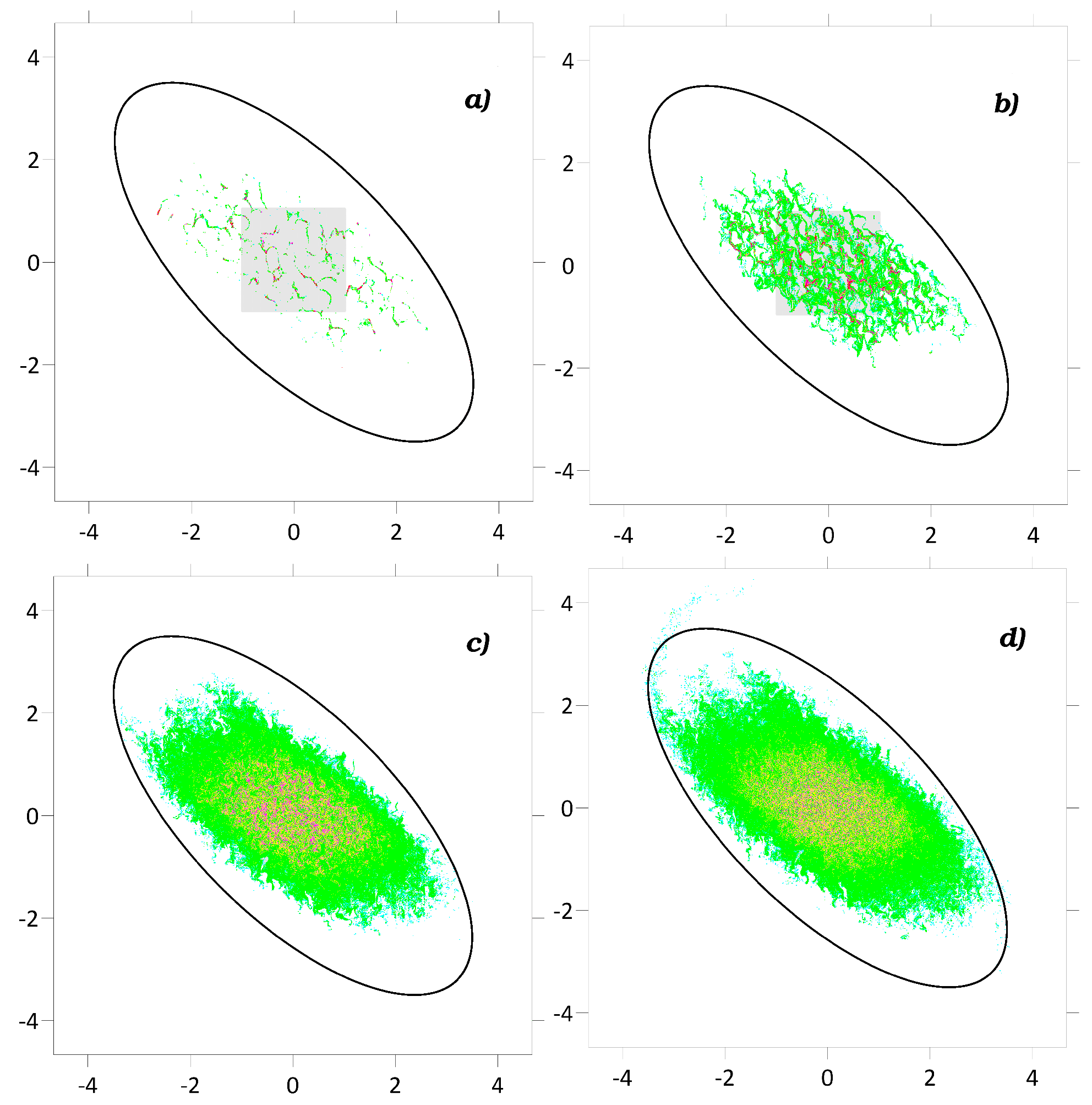
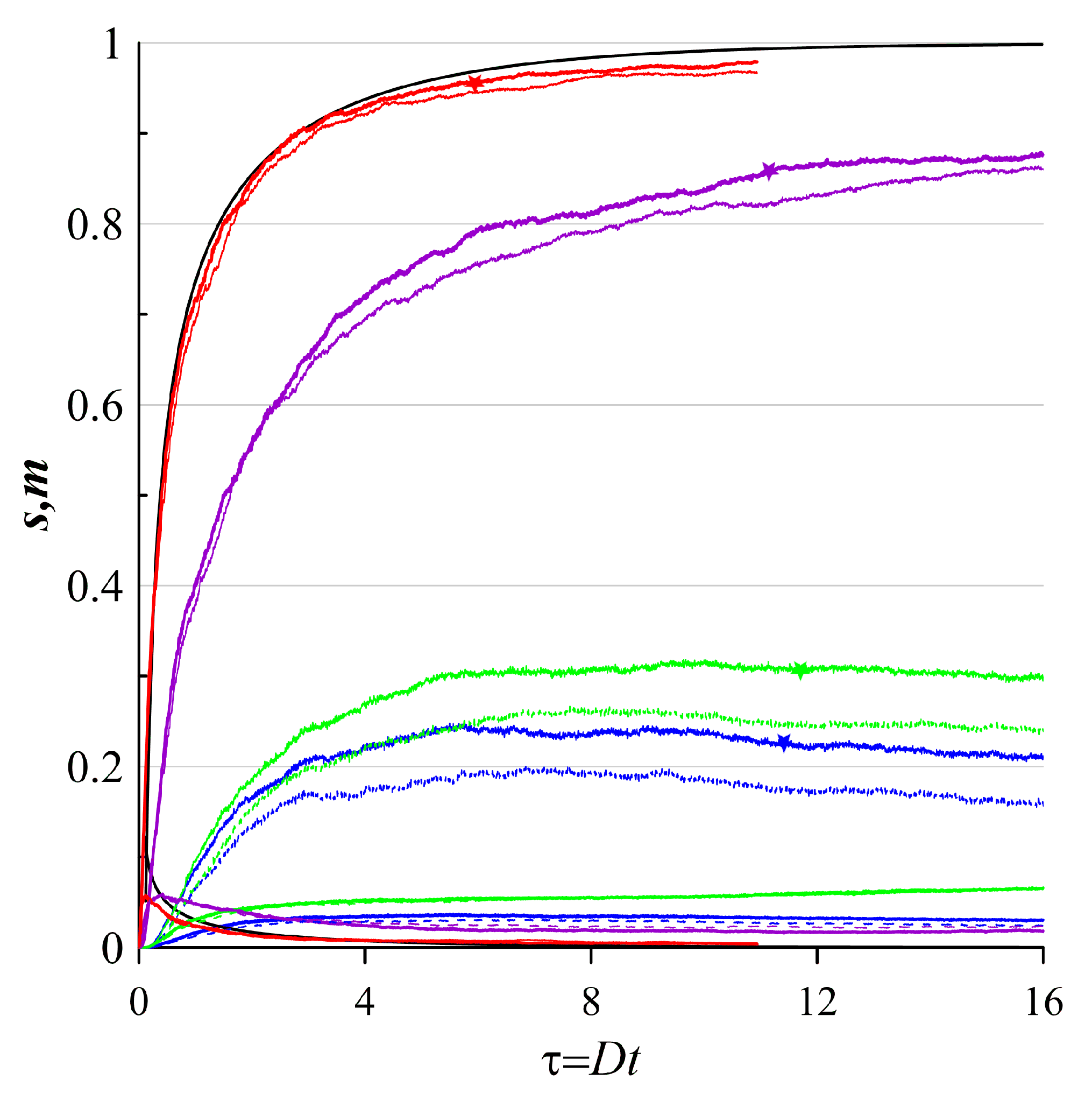
Figure 6.
The same as in Figure 5, but the initial tracer patch is placed near the boundary of the oscillating ellipsoidal vortex.
Figure 6.
The same as in Figure 5, but the initial tracer patch is placed near the boundary of the oscillating ellipsoidal vortex.
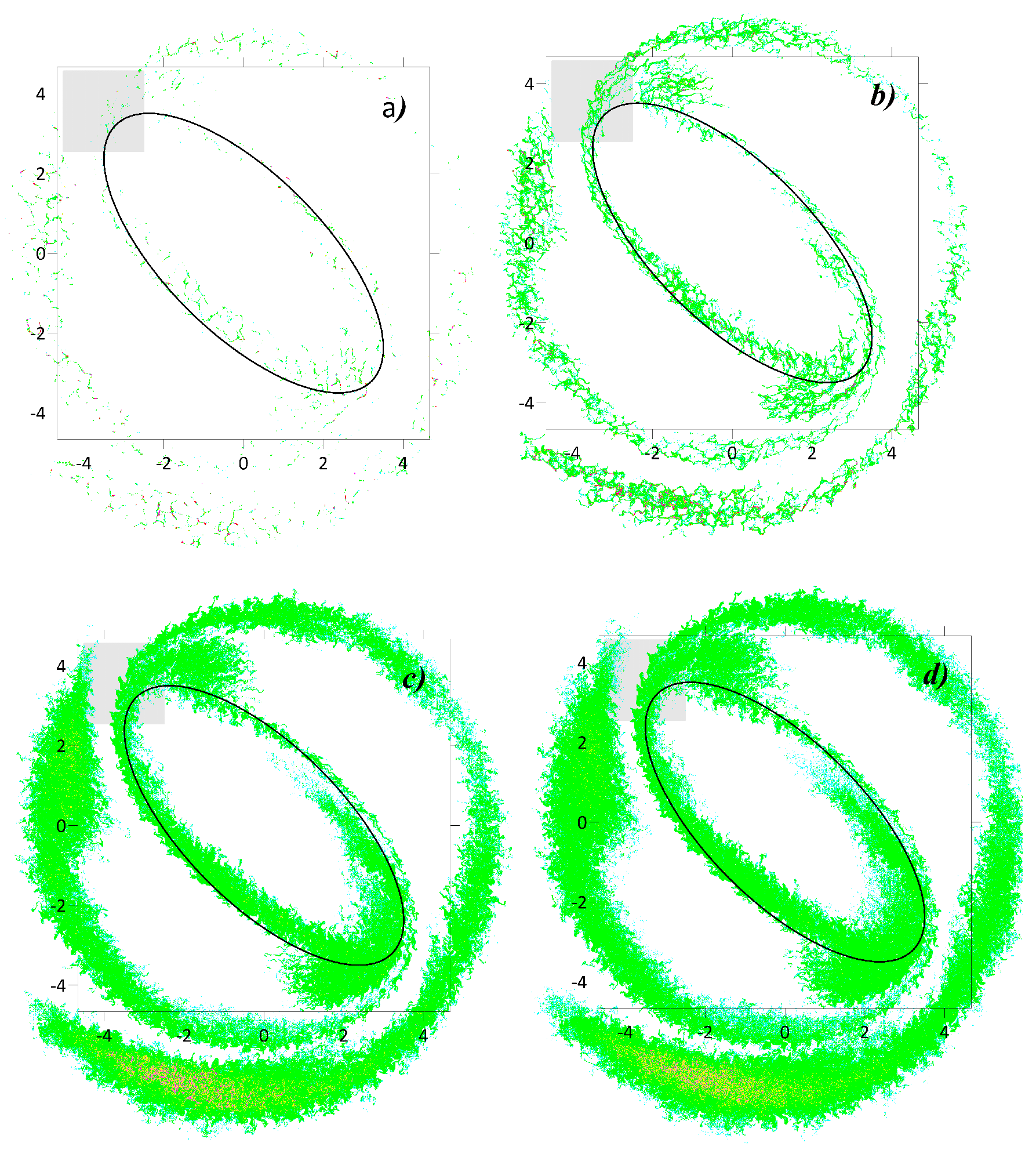
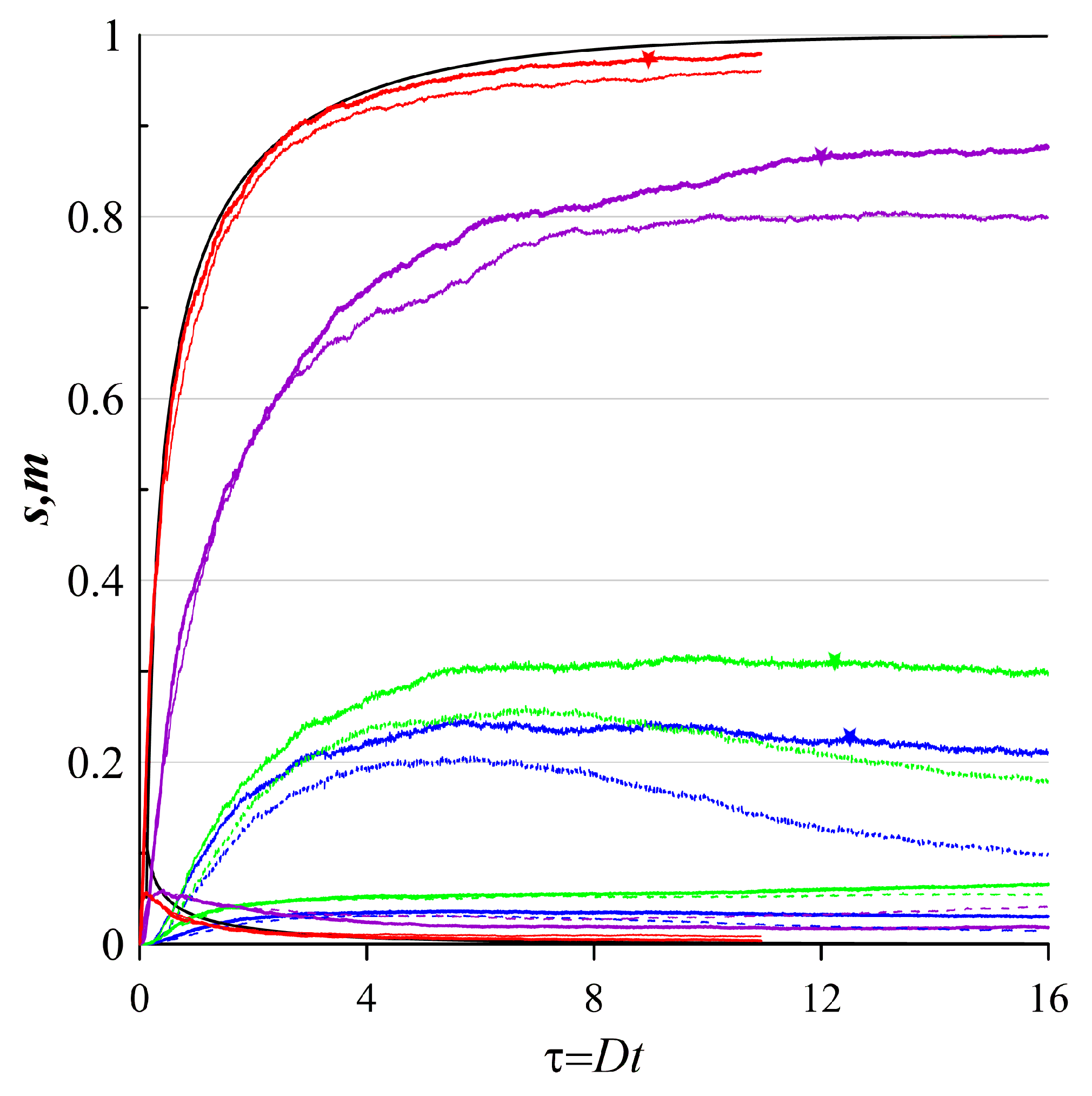
Figure 7.
The same as in Figure 3, but for the rotating ellipsoidal vortex.
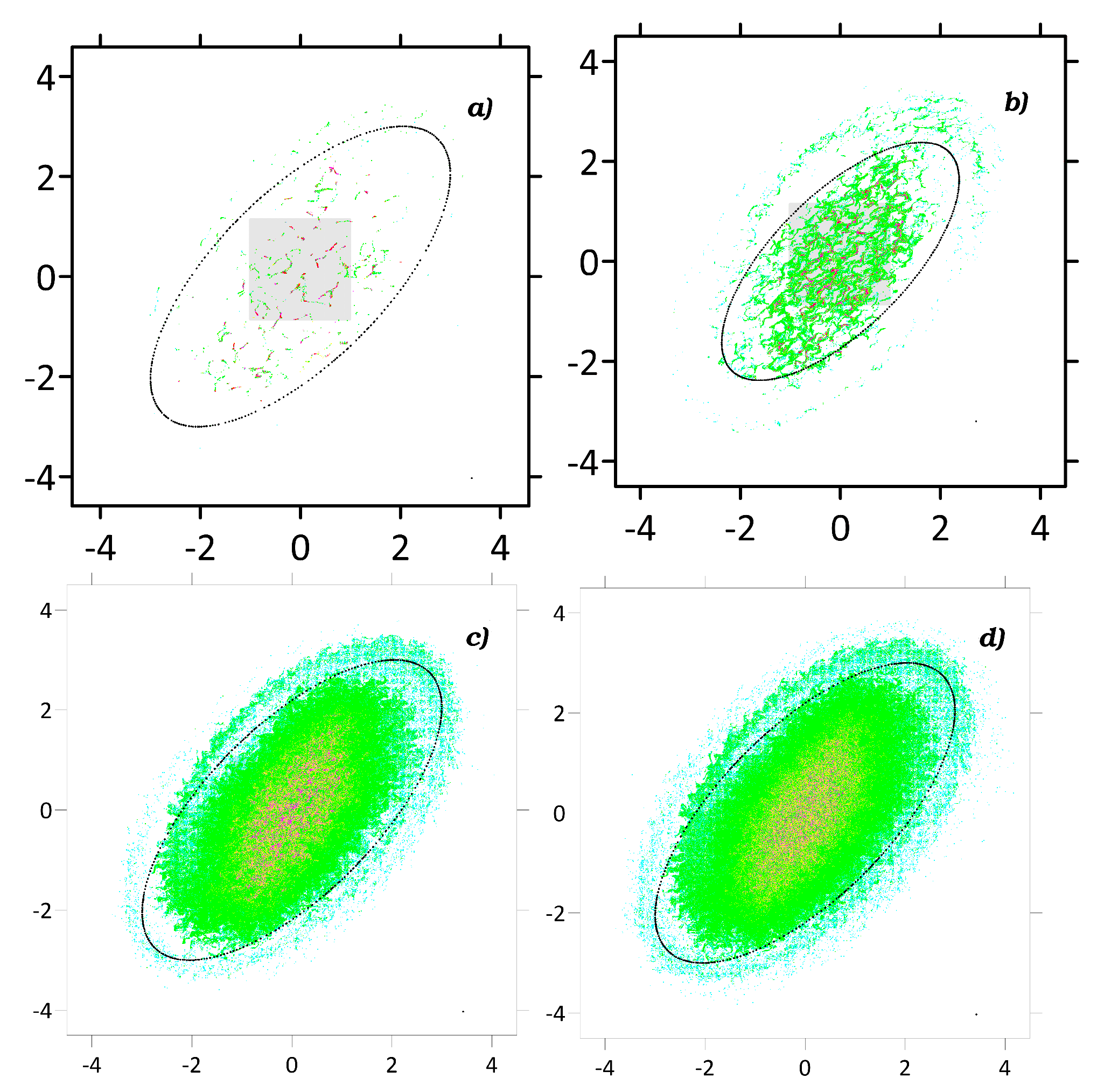
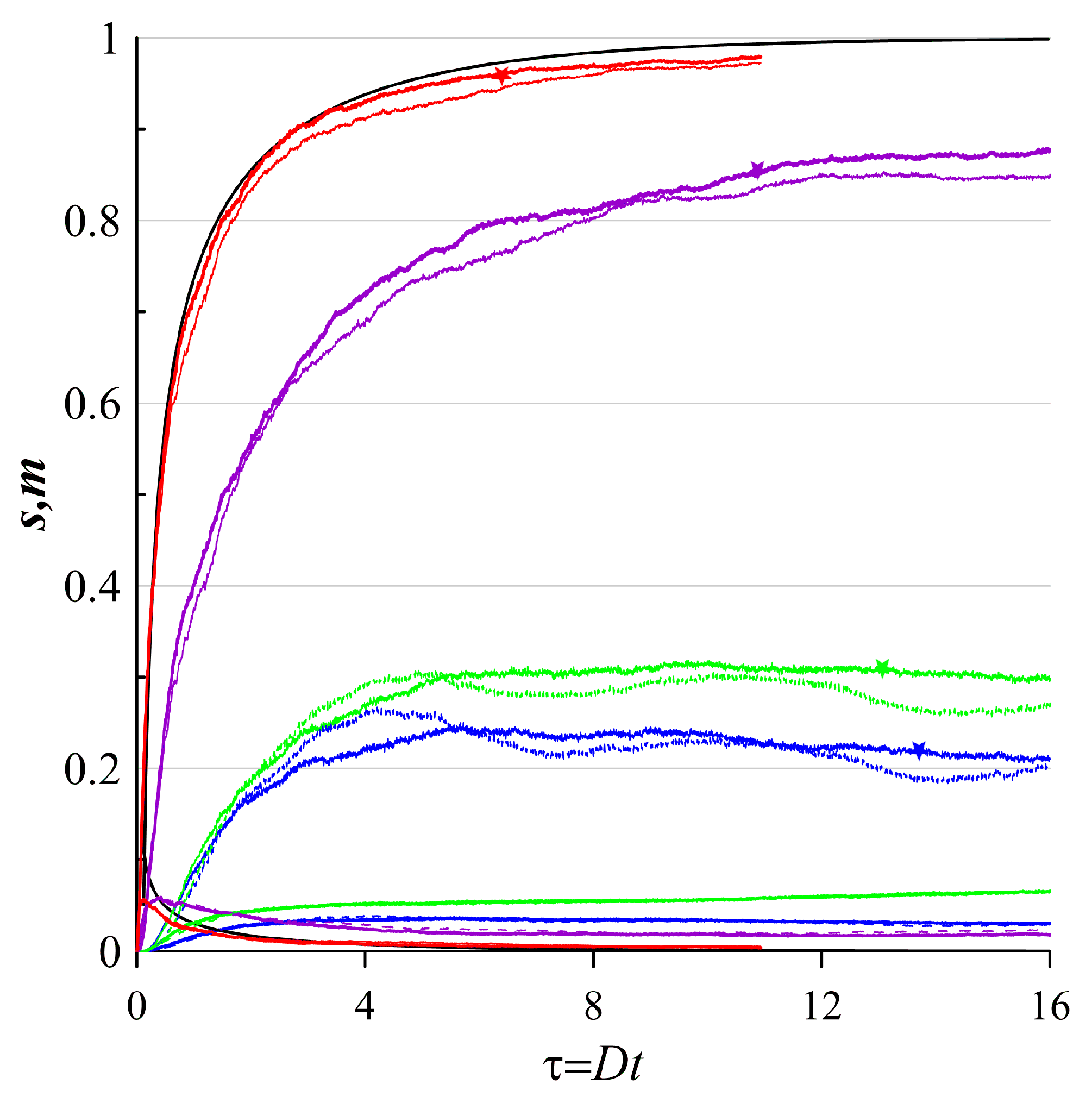
Figure 8.
The same as in Figure 7, but the initial tracer patch is placed near the boundary of the rotating ellipsoidal vortex.
Figure 8.
The same as in Figure 7, but the initial tracer patch is placed near the boundary of the rotating ellipsoidal vortex.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





