Prerpints.org logo
Preprint
Article

Analytical Solution of the SIR-Model for the Not Too Late Temporal Evolution of Epidemics for General Time-Dependent Recovery and Infection Rates

Altmetrics

Downloads

126

Views

56

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Mathematical Modeling

Preprints on COVID-19 and SARS-CoV-2

Submitted:

22 November 2023

Posted:

24 November 2023

You are already at the latest version

Alerts
Abstract
The dynamical equations of the susceptible-infected-recovered/removed (SIR) epidemics model play an important role to predict and/or analyze the temporal evolution of epidemics outbreaks. Crucial input quantities are the time-dependent infection ($a(t)$) and recovery ($\mu (t)$) rates regulating the transitions between the compartments $S\to I$ and $I\to R$, respectively. Accurate analytical approximations for the temporal dependence of the rate of new infections $\dot{J}(t)=a(t)S(t)I(t)$ and the corresponding cumulative fraction of new infections $J(t)=J(t_0)+\int_{t_0}^tdx\dot{J}(x)$ are available in the literature for either stationary infection and recovery rates and for a stationary value of the ratio $k(t)=\mu (t)/a(t)$. Here a new and original accurate analytical approximation is derived for general, arbitrary and different temporal dependencies of the infection and recovery rates which is valid for not too late times after the start of the infection when the cumulative fraction $J(t)\ll 1$ is much less than unity. The comparison of the analytical approximation with the exact numerical solution of the SIR-equations for different illustrative examples proves the accuracy of the analytical approach.
Keywords: 
Subject: Computer Science and Mathematics  -   Applied Mathematics

1. Introduction

The susceptible-infected-recovered/removed (SIR) epidemics model, developed originally by Kermack and McKendrick [1] and refined by Kendall [2], is the simplest realistic and therefore often applied description of the temporal evolution of epidemics [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47]. Here persons from the considered population are assigned to the three compartment fractions S (susceptible), I (infectious) and R (recovered/removed), respectively. The time-dependent infection ( a ( t ) ) and recovery ( μ ( t ) ) rates regulate the transitions between the compartments S → I and I → R , respectively. For a review see [48].
In general the time-dependencies of these two rates will be different and determined by different factors: dedicated medication of infected persons will increase the recovery rate from its initial value at the start of an epidemic outbreak, while non-pharmaceutical interventions, such as social distancing, quarantining and mask obligations, effectively reduce the infection rate from its initial value. As a consequence, the ratio k ( t ) = μ ( t ) / a ( t ) of the two rates also is a time-dependent function, probably increasing at early times from its initial value and decreasing at later times when some of the non-pharmaceutical interventions are lifted. Such a behavior of the ratio k ( t ) indeed has been established recently from the analyis of past Covid-19 mutants [49] as the ratio k ( t ) can be expressed in terms of the well monitored rate of new infections J ˙ ( t ) and its corresponding cumulative fraction J ( t ) . In order to improve the forecast of future epidemic outbreaks with non-stationary ratios k ( t ) it is therefore highly desirable to derive analytical solutions or accurate approximations of these solutions of the SIR-model equations for arbitrary but given time dependencies of the infection and recovery rates and their ratios k ( t ) . This is the purpose of the present manuscript.
In the literature very often the SIR-model equations have been solved numerically with adopted stationary infection ( a 0 ) and recovery ( μ 0 ) rates so that their ratio k 0 = μ 0 / a 0 is also stationary, although an analytical solution in terms of an inverse integral in this case is available [3]. Additionally analytical solutions for arbitrary but given time dependencies of the infection rate a ( t ) have been derived for the infinite [4] and semi-time [5] time domains for the case of a stationary ratio k = μ ( t ) / a ( t ) , implying that the recovery rate has exactly the same time dependence as the infection rate. Analytical approximations have been developed [50] for slowly varying ratios k ( t ) in comparison with the typical time characteristics of the epidemic wave. Below we will derive approximate analytical solutions of the SIR-model equations for the limit of not too late times, where the cumulative number of new infections J ≪ 1 is much smaller than unity. For completeness we investigate the alternative, but less interesting case at late times, when the fraction of susceptible persons S ≪ 1 is much smaller than unity, in an Appendix.

2. SIR Model

The original SIR-equations for the three compartment fractions S ( t ) , I ( t ) , and R ( t ) , at given time-dependent infection and recovery rates read [1,3,48]
d S d t = − a ( t ) S I ,
d I d t = a ( t ) S I − μ ( t ) I ,
d R d t = μ ( t ) I ,
obeying the sum constraint
S ( t ) + I ( t ) + R ( t ) = 1
at all times t ≥ t 0 after the start of the wave at time t 0 , subject to the semi-time initial conditions [5]
I ( t 0 ) = η , S ( t 0 ) = 1 − η , R ( t 0 ) = 0 ,
where η is positive and usually very small, η ≪ 1 . In terms of the reduced time
τ ≡ ∫ t 0 t d x a ( x )
and the ratio
k ( τ ) ≡ μ ( τ ( t ) ) a ( τ ( t ) )
the SIR equations (1) for S ( τ ) , I ( τ ) , and R ( τ ) read [4]
d S d τ = − S I ,
d I d τ = S I − k ( τ ) I ,
d R d τ = k ( τ ) I .
Recently, it has been demonstrated [49] that the reduced SIR equations (2) are equivalent to
k ( τ ) = 1 − J ( τ ) − d d τ ln d d τ ln ( 1 − J ( τ ) ) − 1 ,
where
J ( τ ) = J ( 0 ) + ∫ 0 τ d ξ j ( ξ ) = 1 − S ( τ )
denotes the cumulative number of new infections and
j ( τ ) = S ( τ ) I ( τ ) = − d S ( τ ) d τ
the rate of new infections. With Eq. (8) we can also write Eq. (7) as
k ( τ ) = S ( τ ) − d d τ ln d d τ ln S − 1 ( τ ) = S ( τ ) − d d τ ln I ( τ ) ,
where we used Eq. (9). In the following we will derive approximate analytical solutions of the two nonlinear differential equations (7) and (10) in the two limits of small J ( τ ) ≪ 1 and large J ( τ ) ≃ J ∞ , respectively.
The first limit J ≪ 1 holds at early reduced times τ ≤ τ c of the epidemic outbreak and corresponds to values of S smaller but very close to S ( t 0 ) . Provided it is reached, which depends on the reduced time dependence of the ratio k ( τ ) , the second limit J ≃ J ∞ holds at late reduced time τ > τ c . As a rule of thumb [51] any pandemic wave ends when 70% of the total population are infected, i.e., J ∞ = 0.7 , if nothing is done to reduce the number of infections. We investigate the early time limit next. For completeness we study the less interesting late time limit in Appendix B.

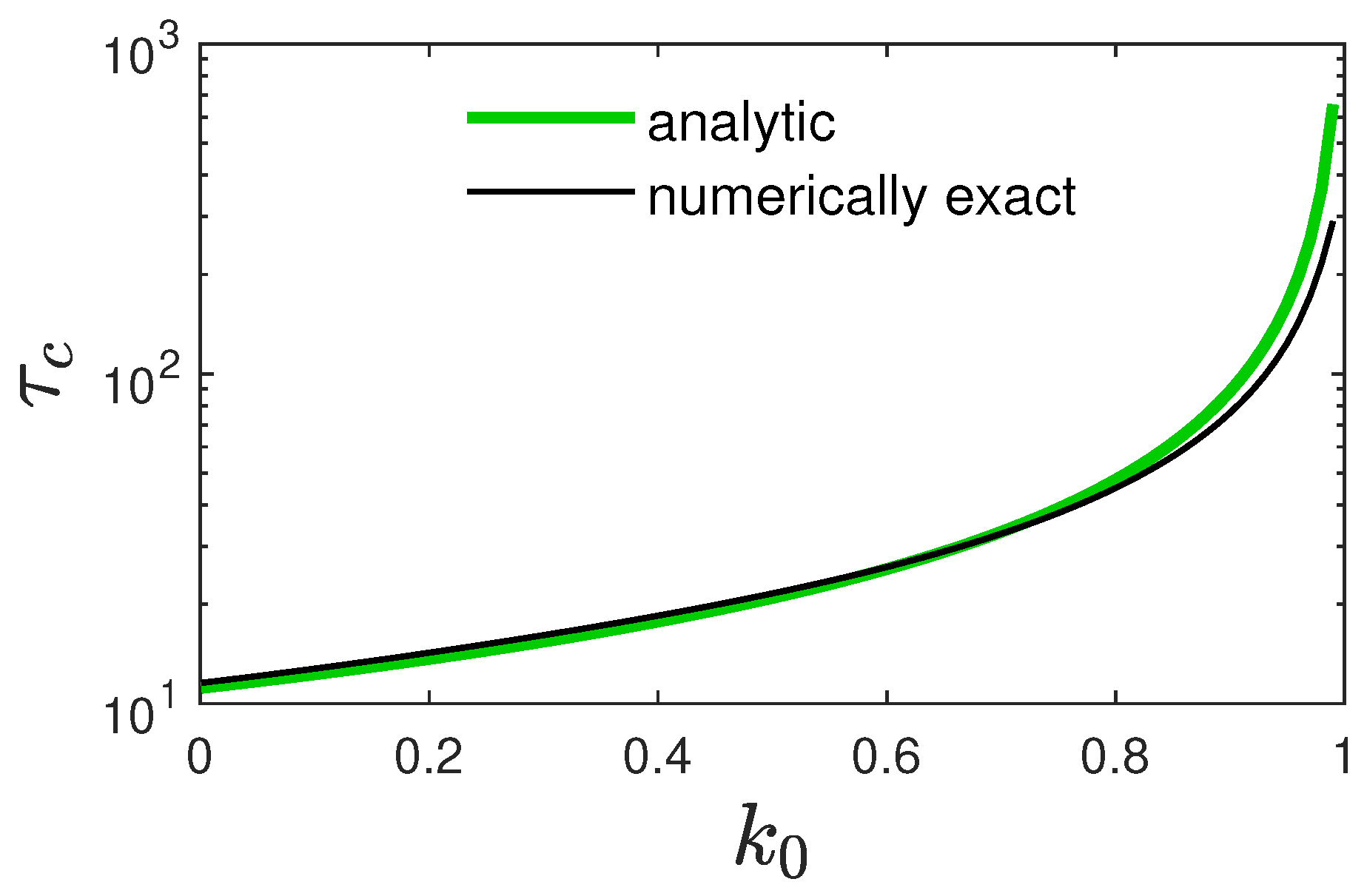
3. Approximate Analytical Solutions

3.1. Solution in the Limit of Small J ≪ 1

Initially at reduced time τ = 0 the cumulative number of new infections is extremely small, J ( 0 ) = η . In the limit J ( τ ) ≪ 1 also at later times between 0 ≤ τ ≤ τ c we use the approximations 1 − J ( τ ) ≃ 1 and ln ( 1 − J ( τ ) ) − 1 ≃ J ( τ ) to obtain for (7)
k ( τ ) ≃ 1 − d d τ ln d J ( τ ) d τ = 1 − d d τ ln j ( τ ) ,
which immediately integrates to
j ( τ ≤ τ c ) = η ( 1 − η ) e τ − ∫ 0 τ d ξ k ( ξ ) = η ( 1 − η ) e ∫ 0 τ d ξ [ 1 − k ( ξ ) ] ,
where we made use of the initial condition j ( 0 ) = η ( 1 − η ) . A further integration of (12) provides
J ( τ ≤ τ c ) = η + η ( 1 − η ) ∫ 0 τ d τ ′ e τ ′ − ∫ 0 τ ′ d ξ k ( ξ ) .
In Appendix A the integral (13) in the case of general variations k ( τ ) is evaluated with the method of steepest descent in terms of error functions as
J ( τ ≤ τ c ) ≃ η + η ( 1 − η ) ∑ m π 2 k ′ ( τ m ) exp τ m − ∫ 0 τ m d ξ k ( ξ ) × erf k ′ ( τ m ) 2 ( τ − τ m ) + erf k ′ ( τ m ) 2 τ m ,
where k ′ ( τ ) denotes d k ( τ ) / d τ . In terms of the real time in this early time limit one has
J ˙ ( t ≤ t c ) = a ( t ) η ( 1 − η ) e ∫ 0 t d x [ a ( x ) − μ ( x ) ] .

3.2. Properties of the Approximate Solution (12)

The approximate solution (12) is predominantly determined by the reduced time variation of the ratio k ( τ ) . For the first and second time derivatives of the solution (12) we obtain
d j d τ = η ( 1 − η ) [ 1 − k ( τ ) ] e τ − ∫ 0 τ d ξ k ( ξ ) ,
d 2 j d τ 2 = η ( 1 − η ) ( 1 − k ( τ ) ) 2 − k ′ ( τ ) e τ − ∫ 0 τ d ξ k ( ξ ) .
Consequently, extrema of the rate of new infections occur at reduced times τ E determined by
k ( τ E ) = 1 .
Then
d 2 j d τ 2 τ = τ E = − η ( 1 − η ) k ′ ( τ E ) e τ E − ∫ 0 τ E d ξ k ( ξ ) ,
so that the extrema are maxima for an increasing reduced time variation with k ′ ( τ E ) > 0 and minima for a decreasing reduced time variation with k ′ ( τ E ) < 0 , respectively. The extreme values of the rate of new infections are given by
j E ( τ E ) = η ( 1 − η ) e ∫ 0 τ E d ξ [ 1 − k ( ξ ) ] .

4. Special Cases

4.1. Constant Ratio k ( t )

We first consider the special case of a stationary ratio k ( t ) = k 0 = const. for which very accurate analytical approximations have been derived [5,52]. In this case the approximations (12) - (15) reduce to
j ( τ ≤ τ c ) = η ( 1 − η ) e ( 1 − k 0 ) τ ,
J ( τ ≤ τ c ) = η + η ( 1 − η ) 1 − k 0 e ( 1 − k 0 ) τ − 1 ,
J ˙ ( t ≤ t c ) = a ( t ) η ( 1 − η ) 1 − k 0 e ( 1 − k 0 ) ∫ 0 t d x a ( x ) ,
and the determining Eq. (B10) becomes
e ( 1 − k 0 ) τ c − 1 = J ∞ ( 1 − k 0 ) η ( 1 − η ) = 0.7 ( 1 − k 0 ) η ( 1 − η ) ,
or equivalently
τ c = 1 1 − k 0 ln 1 + 0.7 ( 1 − k 0 ) η ( 1 − η ) ≃ ln 0.7 ( 1 − k 0 ) η 1 − k 0 ,
which agrees favorably well with the exact numerical result (Figure 1).

4.2. Linearly Increasing Ratio k ( τ ) = k 0 + k 1 τ

We note that for a linearly increasing ratio k ( τ ) = k 0 + k 1 τ the analytical approximation (12) is given by the Gaussian distribution
j ( τ ≤ τ c ) = η ( 1 − η ) e − 1 2 k 1 τ 2 − ( 1 − k 0 ) τ ,
which for a constant infection rate a 0 , so that τ = a 0 ( t − t 0 ) leads to a Gaussian distribution in real time. Such Gaussian distributions have been successfully used to predict the temporal evolution of earlier Covid-19 waves [51,53,54,55,56].

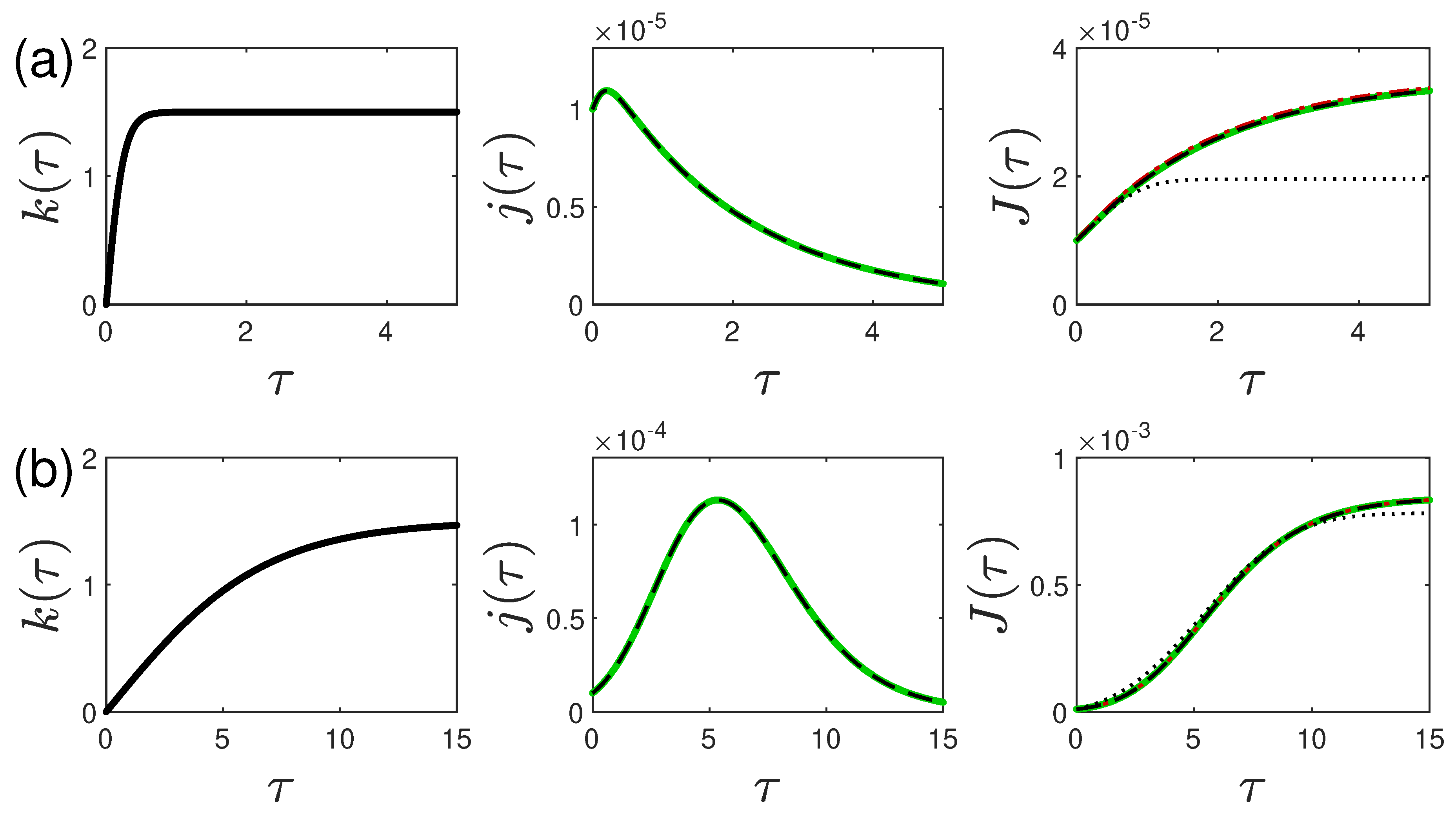
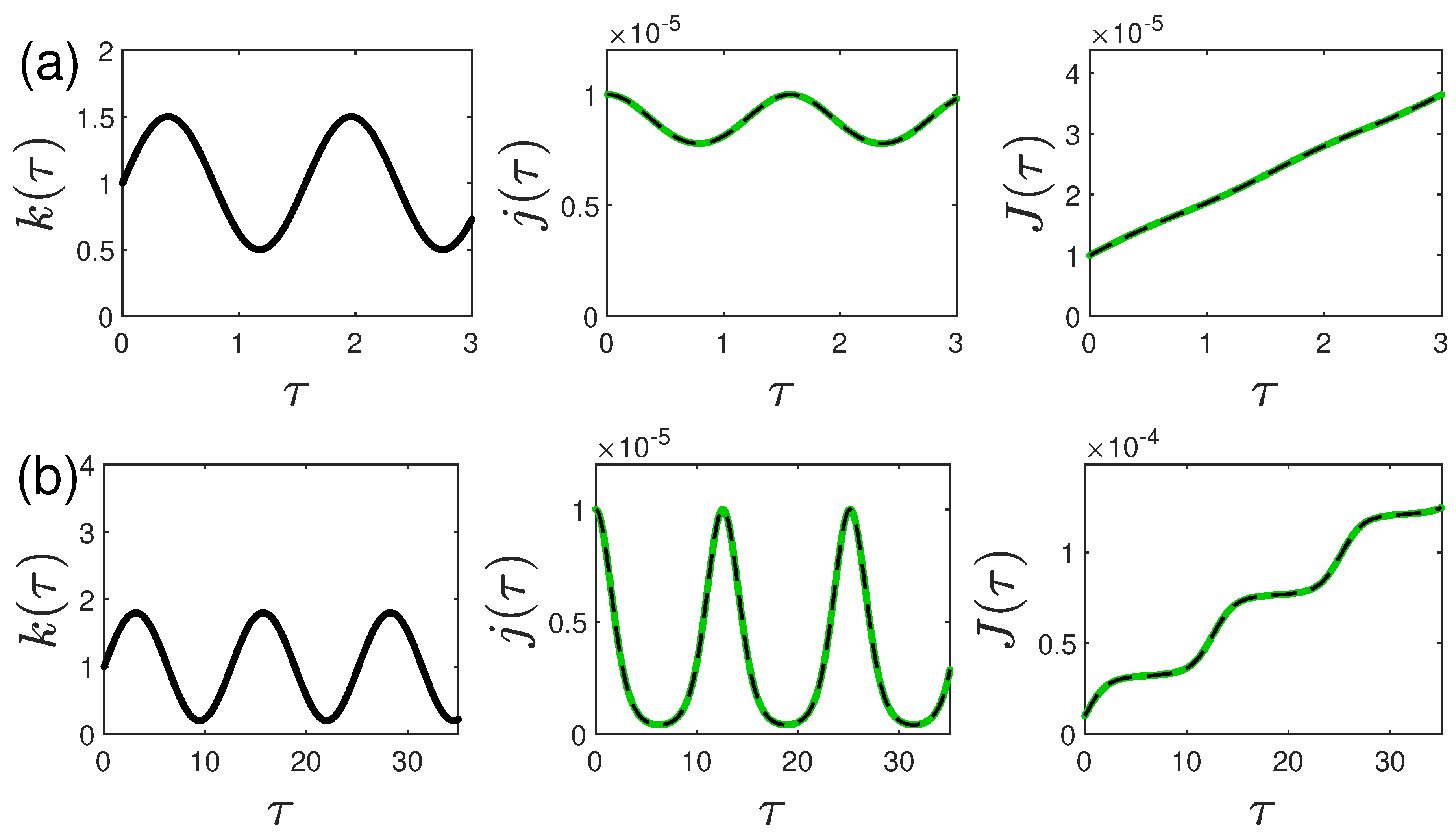
5. Illustrative Examples

In order to illustrate the usefulness of our approximate solution (12) we consider two illustrative examples for the reduced time variation of the ratio k ( τ ) . The first one is monotonically rising, and therefore well suited to represent a single wave of a pandemic outburst. The second one varies periodically in reduced time, and therefore well suited to represent a series of repeating pandemic outbursts. In both cases we compare the exact numerical solution of the SIR-equations (6) with the approximative solution (12). We consider both examples in turn.

5.1. Monotonically Rising Ratio

Here we choose
k ( τ ) = B tanh ( C τ ) ,
with the two positive constants B and C. The ratio (25) increases monotonically from zero at τ = 0 to its maximum value B at large reduced times τ ≫ B − 1 . According to Eq. (18) a single extremum of the rate of new infections occurs at the time τ E given by
B tanh ( C τ E ) = 1 ,
which can be solved only for values of B ≥ 1 with
τ E = C − 1 artanh ( B − 1 ) = 1 C ln B + 1 B 2 − 1 .
Because the first derivative of the ratio (25) is given by
d k d τ = B C cosh 2 ( C τ ) = 1 − tanh 2 ( C τ ) B C ,
one finds
k ′ ( τ E ) = C ( B 2 − 1 ) B > 0 ,
so that the extremum is a maximum. For values of B < 1 the rate of new infections monotonically increases with reduced time. With the choice (25) the rate of new infections (12) can be reduced to
j ( τ ≤ τ c ) = η ( 1 − η ) e τ [ cosh ( C τ ) ] − B / C η ( 1 − η ) e τ [ 1 − tanh 2 ( C τ ) ] B / 2 C .
We note the two asymptotic exponential behaviors j ( τ ≤ C − 1 ≤ τ c ) ≃ η ( 1 − η ) e τ and j ( C − 1 ≤ τ ≤ τ c ) ≃ η ( 1 − η ) 2 B / C e ( 1 − B ) τ .
Only for values of B > 1 a single maximum rate
j max = j ( τ E ) = η ( 1 − η ) B 2 − 1 B 2 B 2 C e C − 1 artanh ( 1 / B ) = η ( 1 − η ) ( B 2 − 1 ) B − 1 2 C ( B + 1 ) 1 C B B C
occurs at τ E provided τ E ≤ τ c , or at τ c in the case τ E > τ c with
j max = j ( τ c ) = η ( 1 − η ) e τ c [ cosh ( C τ c ) ] − B C .
In Figure 2 (center panels) we compare the approximative analytical rate of new infections (30) as a function of the reduced time for this choice of the ratio k ( τ ) with the exact numerical solution of the SIR-equations (6). The agreement ist almost perfect proving the accuracy of our analytical approximation.
The corresponding cumulative number of infections is given by
J ( τ ) = J ( 0 ) + ∫ 0 τ d x j ( x ) = η + η ( 1 − η ) H ( τ ) ,
H ( τ ) = ∫ 0 τ d x e x [ cosh ( C x ) ] − B / C .
Substituting y = e 2 C x , corresponding to x = ln ( y ) / 2 C , the integral (34) becomes
H ( τ ) = 2 B / C 2 C ∫ 0 e 2 C τ d x x B + 1 2 C − 1 ( 1 + x ) − B / C ,
which can be expressed as the difference of two hypergeometric   2 F 1 functions using integral 3.194 of [57]. One obtains
H ( τ ) = 2 B / C B + 1 e ( B + 1 ) τ   2 F 1 B C , B + 1 2 C ; 1 + B + 1 2 C ; − e 2 C τ −   2 F 1 B C , B + 1 2 C ; 1 + B + 1 2 C ; − 1 .
For τ ≪ 1 , the first terms of the series expansion are H ( τ ) = τ + τ 2 / 2 + ( 1 − B C ) τ 3 / 6 , as derived in Appendix C.
For C > 1 , an approximant can be derived upon instead substituting x = ln y in Eq. (B10). This yields
H ( τ ) = 2 B / C ∫ 1 e τ d y [ y C + y − C ] − B / C = 2 B / C ∫ 1 e τ d y y B [ 1 + y 2 C ] − B / C .
As y is greater than unity we approximate 1 + y 2 C ≃ y 2 C providing
H ( τ ) ≃ 2 B / C ∫ 1 e τ d y y − B = e ( 1 − B ) τ − 1 1 − B .
Consequently, the cumulative fraction of infections (33) reads
J ( τ ) ≃ η + η ( 1 − η ) 2 B / C e ( 1 − B ) τ − 1 1 − B = η + η ( 1 − η ) 2 B / C e ( 1 − B ) τ − 1 1 − B for B < 1 2 1 / C τ for B = 1 2 B / C 1 − e − ( B − 1 ) τ B − 1 for B > 1
We first note that the absolute level of the cumulative fraction is proportional to 2 B / C . If the parameter C is small one obtains a much higher amplification of the cumulative fraction at later times compared to its initial value than in cases where C is large. This is clearly evident from the last panels of Figure 2.
Moreover, we notice that for values of B > 1 the cumulative fraction (39) approaches the finite value J ( τ = ∞ , B > 1 ) = η ( 1 − η ) 2 B / C / ( B − 1 ) which is much smaller than J ∞ = 0.7 as η ≪ 1 . In this case the early time solutions (30) and (39) are valid for all times. This is easy to understand because for values of B > 1 the ratio (25) becomes greater than unity after finite times so that then the recovery rate μ ( τ ) > a ( τ ) is greater than the infection rate, so that the rate of new infections is decreasing with time in agreement with the right side of Figure 2. In this case not many new infections add to the cumulative fraction.
The opposite behavior holds for values of B ≤ 1 . In this case at all times the ratio (25) is less or equal unity so that the infection rate is never smaller than the recovery rate. Consequently, the cumulative fraction (39) increases exponentially with time for B < 1 and linearly with time for B = 1 . In this case the early time solutions (30) and (39) can only be used for times less than τ c providing according to Eq. (B10)
∫ 0 τ c d τ e τ [ cosh ( C τ ) ] − B / C = H ( τ c ) = J ∞ η ( 1 − η ) .
With Eq. (39) we obtain
τ c = 1 1 − B ln 1 + ( 1 − B ) J ∞ 2 B / C η ( 1 − η ) .
For B ≤ 1 the rate of new infections (B1) at late times becomes
j ( τ ≥ τ c ) ≃ ( 1 − J ∞ ) A 1 cosh − B / C ( C τ ) = η ( 1 − η ) e τ c cosh − B / C ( C τ ) ,
where we determined A 1 = η ( 1 − η ) e τ c / ( 1 − J ∞ ) from equating the two rates (30) and (37) at τ c whose value is given explicitly by Eq. (41).
For the interesting case of values B > 1 we calculate the cumulative fraction (33) with the integral H ( τ ) by the method of steepest descent according to Eq. (14). Here a single maximum in j ( τ ) occurs at
τ m = τ E = 1 C ln B + 1 B 2 − 1 ,
given by Eq. (27) and k ′ ( τ m ) = ( B 2 − 1 ) C / B , inferred from Eq. (29). Moreover
τ m − ∫ 0 τ m d ξ k ( ξ ) = τ m − B C ln cosh ( C τ m ) = 1 C ln B + 1 B 2 − 1 − B ln B B 2 − 1 .
Consequently, the cumulative number of infections (14) in this case becomes
J ( τ ) ≃ η + η ( 1 − η ) π B 2 C ( B + 1 ) 1 C B − B C ( B 2 − 1 ) B − C − 1 2 C × erf C B 2 − 1 2 B ( τ − τ m ) + erf C B 2 − 1 2 B τ m .
In Figure 2-right we compare the approximation (45) with the exactly integrated cumulative fraction (33)–(39) in this case. The good agreement indicates that the method of steepest descent indeed is appropriate to calculate cumulative fractions for B > 1 and C < 1 . For values C > 1 this method is correct within a factor 1.8 as indicated by Figure 2-a (right). The reason that the method of steepest descent works better for small values of C is the inverse dependence of the exponents in Eq. (31) for the maximum rate and in Eq. (27) for the time of maximum. Consequently, the smaller the value of C the maximum appears at a later time with a larger amplitude as compared to the case of large values of C. In the case of a large amplitude maximum the dominating contribution to the cumulative fraction stems from the maximum.

5.2. Oscillating ratio

Here we choose
k ( τ ) = 1 + α sin ( β τ ) ,
with the two positive constants α and β . The ratio (46) oscillates periodically around its intial value 1 (see Figure 3-a). It is therefore suited well to represent a series of repeating pandemic outbursts. For values of k greater unity the recovery rate is greater than the infection rate, so that the rate of infections decreases. When the ratio k is smaller than unity, the infection rate is greater than the recovery rate and the rate of infectins decreases with time.
With the choice (46) the rate of new infections (12) at early times becomes
j ( τ ≤ τ c ) = η ( 1 − η ) e α β [ cos ( β τ ) − 1 ] .
The approximative analytical rate of new infections (47) as a function of the reduced time for the oscillating ratio (46) is compared with the exact numerical solution of the SIR-equations (6) in Figure 3. The agreement is almost perfect proving the accuracy of our analytical approximation (B11).
Integrating the rate (47) over reduced time provides us with the corresponding cumulative fraction
J ( τ ≤ τ c ) = η + η ( 1 − η ) β e − α β ∫ 0 β τ d y e α β y = η + η ( 1 − η ) e − α β τ I 0 α β + 2 ∑ n = 1 ∞ I k ( α β ) n β sin ( n β τ ) ,
where we have used J ( 0 ) = η and the series expansion (Eq. 9.6.34 of ref. [58])
e z cos θ = I 0 ( z ) + 2 ∑ n = 1 ∞ I n ( z ) cos ( n θ )
in terms of the modified Bessel function of the first kind I n ( z ) . In order to obtain deviations of less than 1 percent from the series (49) at finite summation index n one has to choose N according to Figure 4. For the example provided in Figure 3-a, z = α / β = 0.5 / 4 ≪ 1 , so that just the first term of the expansion, N = 1 , is sufficient to capture the behavior of J ( τ ) for this case. Instead, N = 3 is used to calculate J ( τ ) in Figure 3-b, in accord with z = 0.8 / 0.5 = 1.6 in Figure 4.
The third panel of Figure 3 and Eq. (48) show that the cumulative fractions predominantly increases linearly with reduced time so that at some finite time τ c the cumulative fractions approach J ∞ . There the validity of the early time approximation ends and J ( τ ≥ τ c ) ≃ J ∞ as discussed in Appendix B. The value of τ c and the variation of the corresponding late time spontaneous rate j ( τ ≥ τ c ) can be calculated according to Eqs. (B10) and (B15).
From the part of Eq. (48) that is proportional to τ one can read off the characteristic time τ c using J ( τ c ) ≃ J ∞ , which translates to
τ c ≃ e α / β I 0 α β J ∞ η ( 1 − η ) .

6. Summary and Conclusions

The dynamical equations of the susceptible-infected-recovered/removed (SIR) epidemics model play an important role to predict and/or analyze the temporal evolution of epidemics outbreaks. Crucial input quantities are the time-dependent infection ( a ( t ) ) and recovery ( μ ( t ) ) rates regulating the transitions between the compartments S → I and I → R , respectively. Accurate analytical approximations for the temporal dependence of the rate of new infections J ˙ ( t ) = a ( t ) S ( t ) I ( t ) and the corresponding cumulative fraction of infections J ( t ) = J ( t 0 ) + ∫ t 0 t d x J ˙ ( x ) are available in the literature for either stationary infection and recovery rates and for a stationary value of the ratio k ( t ) = μ ( t ) / a ( t ) . Here apparently for the first time a new accurate analytical approximation is derived for arbitrary and different temporal dependencies of the infection and recovery rates which is valid for not too late times after the start of the infection when the cumulative fraction J ( t ) ≪ 1 is much less than unity. Eqs. (12) and (15) provide analytical expressions for the rate of new infections as a function of real time j ( t ) and reduced time j ( τ ) with the reduced time τ = ∫ t 0 t d x a ( x ) . Likewise, Eq. (14) gives the corresponding cumulative fraction J ( t ) = J ( τ ) .
The comparison of the analytical approximation with the exact numerical solution of the SIR-equations for different illustrative examples proves the accuray of the analytical approach. These examples include the cases of a monotonically rising ratio as well as an oscillating ratio as a function of reduced time. The former one is well suited to represent a single wave of a pandemic outburst, where during the outburst the recovery rate becomes greater than the infection rate due to the combined effects of non-pharmaceutical interventions and/or dedicated medication or vaccination of infected people or non-infected persons, respectively. The case of an oscillating ratio is well suited to represent a series of repeating epidemic outburst over a longer time span. The future predictions or analyses of epidemics on the basis pf the SIR-model equations will certainly benefit from the newly derived analytical solutions.

Author Contributions

All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

No new data were created or analyzed in this study. Data sharing is not applicable to this article.

Conflicts of Interest

The authors declare no conflict of interest.

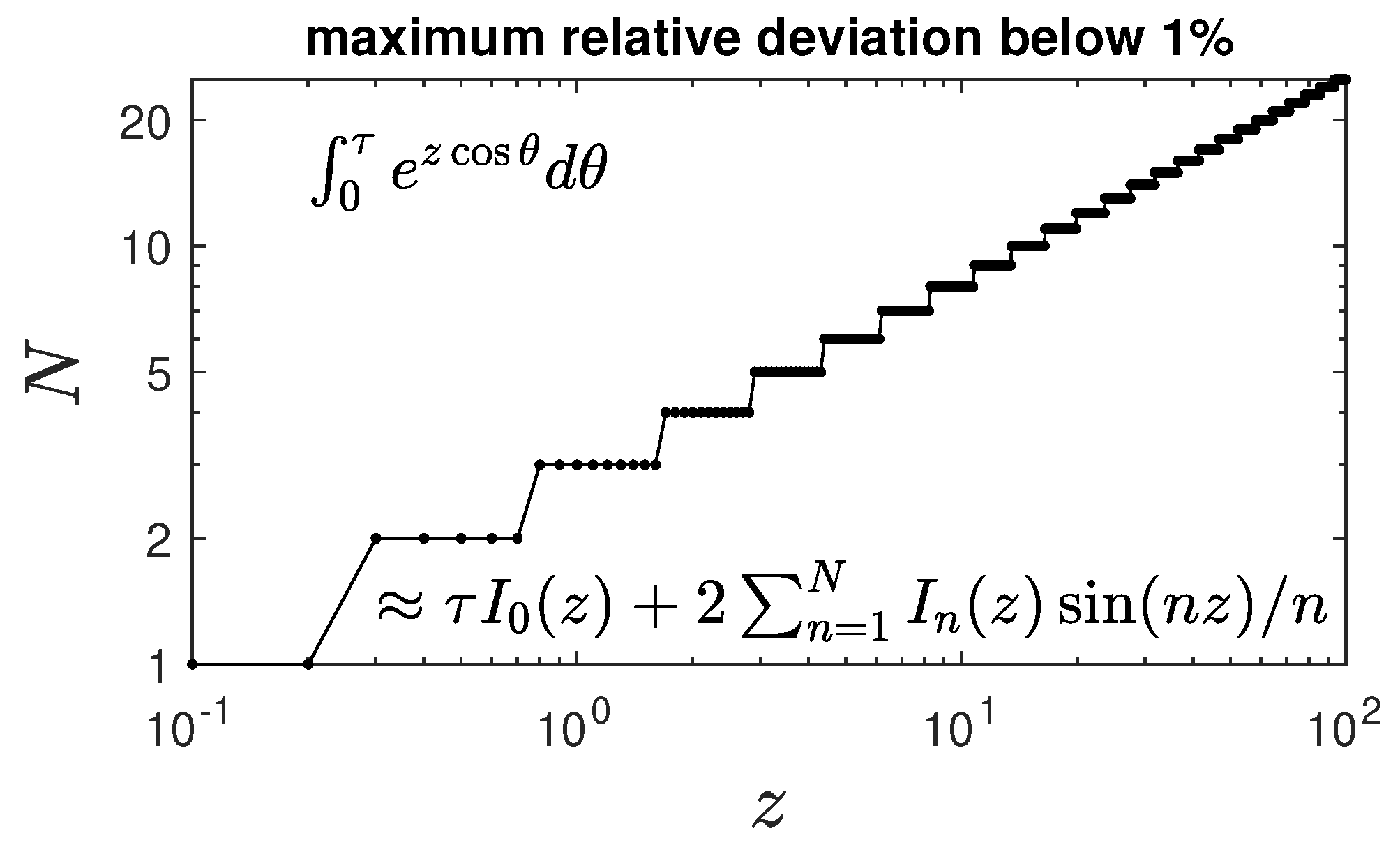
Appendix A. Cumulative Fraction for General Reduced Time Dependencies k(τ)

In the examples discussed in Sect. IV and V the cumulative fractions have been calculated by integrating the respective rates of new infections. If such exact integrations are not possible for general reduced time dependencies of the ratio k ( τ ) we suggest to use the method of steepest descent [59,60]. Here we write the cumulative fraction (13) as
J ( τ ≤ τ c ) = η + η ( 1 − η ) F ( τ ) ,
with
F ( τ ) = ∫ 0 τ d x e − f ( x ) , f ( x ) = ∫ 0 x d ξ k ( ξ ) − x .
We expand the function f ( x ) to second order near its minima values at x = τ m given by
k ( τ m ) = 1 .
We emphasize that, depending on the choosen variation of the ratio k ( τ ) , there may be several minima, as in the case of the oscillating ratio discussed above in Sect. Section 5.2. Then so that
f ( x ) ≃ f ( τ m ) + 1 2 k ′ ( τ m ) ( x − τ m ) 2 .
For a minimum to occur the ratio has to have an increasing reduced time variation with k ′ ( τ E ) > 0 . With the approximation (A4) the integral (A2) can be evaluated in terms of error functions providing
F ( τ ) ≃ ∑ m π 2 k ′ ( τ m ) exp τ m − ∫ 0 τ m d ξ k ( ξ ) × erf k ′ ( τ m ) 2 ( τ − τ m ) + erf k ′ ( τ m ) 2 τ m .
Consequently, the cumulative number of infections (A1) becomes Eq. (14). In principle, calculating the cumulative fraction by the method of steepest descent is essentially identical in approximating the corresponding rate of new infections by a sum of Gaussian distributions centered at their maxima. If there is only one maximum, as in the case discussed in Sect. Section 5.1, the method of steepest descent provides a lower limit to the cumulative fraction because all other contributions far from the maximum are not adequately accounted for.

Appendix B. Solution at Late Times

Appendix B.1. Limit J≃J ∞ =0.7

In this limit R ∞ = J ∞ , S ∞ = 1 − J ∞ = 0.3 , I ∞ = 0 and j ( τ = ∞ ) = 0 . For values of k ≫ S ∞ = 0.3 we approximate (10) as
k ( τ ) ≃ − d ln I ( τ ) d τ .
Equation (B1) integrates to
I ( τ ≥ τ c ) ≃ A 1 e − ∫ 0 τ d ξ k ( ξ ) ,
with the integration constant A 1 . The approximation (B2) is in agreement with the final value I ∞ = 0 . Integrating Eq. (6c) with Eq. (B3) inserted then readily provides
R ( τ ≥ τ c ) ≃ A 2 − A 1 e − ∫ 0 τ d ξ k ( ξ ) = A 2 − I ( τ > τ c )
with the further integration constant A 2 which has to be set to A 2 = J ∞ so that
R ( τ ≥ τ c ) ≃ J ∞ − A 1 e − ∫ 0 τ d ξ k ( ξ ) ,
implying
J ( τ ≥ τ c ) = 1 − S ( τ ≥ τ c ) = I ( τ ≥ τ c ) + R ( τ ≥ τ c ) = J ∞ ,
S ( τ ≥ τ c ) = 1 − J ∞ ,
j ( τ ≥ τ c ) = S ( τ ≥ τ c ) I ( τ ≥ τ c ) = ( 1 − J ∞ ) A 1 e − ∫ 0 τ d ξ k ( ξ ) .
In terms of the real time in this late time limit
J ( t ≥ t c ) = J ∞ = 0.7 ,
J ˙ ( t ≥ t c ) = a ( t ) ( 1 − J ∞ ) A 1 e − ∫ t 0 t d x μ ( x ) .
Caused by our approximation to the exact SIR equations the solutions (B5) and (B7) as well as (B8) and (B9) no longer fulfil the properties j ( τ ) = d J ( τ ) / d τ and J ˙ ( t ) = d J ( t ) / d t . We regard this inconsistency as minor and therefore tolerable because the exponentially decaying rates (B7) and (B9) of new infections contribute little to the corresponding cumulative fractions. The constant A 1 appearing in the approximate solutions (B2), (B4), (B7) and (B9) is determined by the continuity conditions of the rate of new infections and the cumulative fraction at τ c with the approximate solutions (12) - (13) at small values of J ≪ 1 .

Appendix B.2. Continuity Conditions

The reduced time τ c is determined by equating the early (13) and late (B5) cumulative number approximations at τ c providing
∫ 0 τ c d x e x − ∫ 0 x d ξ k ( ξ ) = J ∞ η ( 1 − η ) = 0.7 η ( 1 − η ) .
For predescribed reduced time variations k ( τ ) Eq. (B10) can be reduced further.
Likewise, with the so determined value of τ c the constant A 1 is determined by equating the early (12) and late (B7) rate of new infections at τ c yielding
A 1 = η ( 1 − η ) 1 − J ∞ e τ c .
Consequently, with (B11) the late time approximations (B2), (B4), (B6) and (B7) read
I ( τ ≥ τ c ) = η ( 1 − η ) 1 − J ∞ e τ c − ∫ 0 τ d ξ k ( ξ ) ,
R ( τ ≥ τ c ) = J ∞ − η ( 1 − η ) 1 − J ∞ e τ c − ∫ 0 τ d ξ k ( ξ ) ,
S ( τ ≥ τ c ) = 1 − J ∞ ,
j ( τ ≥ τ c ) = η ( 1 − η ) e τ c − ∫ 0 τ d ξ k ( ξ ) .

Appendix C. Expansion of H(τ) at Small Times

Substituting x = 1 + z in Eq. (35) provides for the integral (B10)
H ( τ ) = 2 B / C 2 C ∫ 0 e 2 C τ − 1 d z ( 1 + z ) B + 1 2 C − 1 ( 2 + z ) − B / C = 1 2 C ∫ 0 e 2 C τ − 1 d z ( 1 + z ) B + 1 2 C − 1 ( 1 + z 2 ) − B / C .
For times much smaller than τ ≪ ln 2 / ( 2 C ) one notices that e 2 C τ − 1 ≪ 1 , i.e., e 2 C τ − 1 ≈ 2 C τ + ( 2 C τ ) 2 / 2 + ( 2 C τ ) 3 / 6 ≡ Z . Expanding the integrand for small values of z ≤ e 2 C τ − 1 ≪ 1 to second order in z provides the approximation
H τ ≪ ln 2 2 C ≃ 1 2 C ∫ 0 Z d z 1 + 1 − 2 C 2 C z + 1 − 6 + B 8 C + 1 8 C 2 z 2 ≃ τ + τ 2 2 + ( 1 − B C ) 6 τ 3 + O ( C τ ) 4 ,
which is the expression mentioned after Eq. (36).

References

  1. Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. A 1927, 115, 700. [Google Scholar] [CrossRef]
  2. Kendall, D.G. Deterministic and stochastic epidemics in closed populations. Proc. Third Berkeley Symp. on Math. Statist. and Prob. 1956, 4, 149. [Google Scholar] [CrossRef]
  3. Harko, T.; Lobo, F.S.N.; Mak, M.K. Exact analytical solutions of the susceptible-infected-recovered (SIR) epidemic model and of the SIR model with equal death and birth rates. Appl. Math. Comput. 2014, 236, 184–194. [Google Scholar] [CrossRef]
  4. Kröger, M.; Schlickeiser, R. Analytical solution of the SIR-model for the temporal evolution of epidemics. Part A: Time-independent reproduction factor. J. Phys. A 2020, 53, 505601. [Google Scholar] [CrossRef]
  5. Schlickeiser, R.; Kröger, M. Analytical solution of the SIR-model for the temporal evolution of epidemics: Part B. Semi-time case. J. Phys. A 2021, 54, 175601. [Google Scholar] [CrossRef]
  6. Cooper, I.; Mondal, A.; Antonopoulos, C.G. A SIR model assumption for the spread of COVID-19 in different communities. Chaos Solitons Fract. 2020, 139, 110057. [Google Scholar] [CrossRef] [PubMed]
  7. Katul, G.G.; Mrad, A.; Bonetti, S.; Manoli, G.; Parolari, A.J. Global convergence of COVID-19 basic reproduction number and estimation from early-time SIR dynamics. PLoS One 2020, 15, e0239800. [Google Scholar] [CrossRef] [PubMed]
  8. Liu, M.; Thomadsen, R.; Yao, S. Forecasting the spread of COVID-19 under different reopening strategies. Sci. Rep. 2020, 10, 20367. [Google Scholar] [CrossRef] [PubMed]
  9. Bagal, D.K.; Rath, A.; Barua, A.; Patnaik, D. Estimating the parameters of susceptible-infected-recovered model of COVID-19 cases in India during lockdown periods. Chaos Solitons Fract. 2020, 140, 110154. [Google Scholar] [CrossRef]
  10. Munoz-Fernandez, G.A.; Seoane, J.M.; Seoane-Sepulveda, J.B. A SIR-type model describing the successive waves of COVID-19*. Chaos Solitons Fract. 2021, 144, 110682. [Google Scholar] [CrossRef]
  11. Liao, Z.; Lan, P.; Liao, Z.; Zhang, Y.; Liu, S. TW-SIR: time-window based SIR for COVID-19 forecasts. Sci. Rep. 2020, 10, 22454. [Google Scholar] [CrossRef] [PubMed]
  12. Law, K.B.; Peariasamy, K.M.; Gill, B.S.; Singh, S.; Sundram, B.M.; Rajendran, K.; Dass, S.C.; Lee, Y.L.; Goh, P.P.; Ibrahim, H.; et al. Tracking the early depleting transmission dynamics of COVID-19 with a time-varying SIR model. Sci. Rep. 2020, 10, 21721. [Google Scholar] [CrossRef] [PubMed]
  13. Sharov, K.S. Creating and applying SIR modified compartmental model for calculation of COVID-19 lockdown efficiency. Chaos Solitons Fract. 2020, 141, 110295. [Google Scholar] [CrossRef] [PubMed]
  14. Dell’Anna, L. Solvable delay model for epidemic spreading: the case of Covid-19 in Italy. Sci. Rep. 2020, 10, 15763. [Google Scholar] [CrossRef] [PubMed]
  15. Quaranta, G.; Formica, G.; Machado, J.T.; Lacarbonara, W.; Masri, S.F. Understanding COVID-19 nonlinear multi-scale dynamic spreading in Italy. Nonlin. Dyn. 2020, 101, 1583–1619. [Google Scholar] [CrossRef] [PubMed]
  16. Nguemdjo, U.; Meno, F.; Dongfack, A.; Ventelou, B. Simulating the progression of the COVID-19 disease in Cameroon using SIR models. PLoS One 2020, 15, e0237832. [Google Scholar] [CrossRef]
  17. Cadoni, M. How to reduce epidemic peaks keeping under control the time-span of the epidemic. Chaos Solitons Fract. 2020, 138, 109940. [Google Scholar] [CrossRef] [PubMed]
  18. Ko, G.S.; Yoon, T. Short-Term Prediction Methodology of COVID-19 Infection in South Korea. COVID 2021, 1, 416–422. [Google Scholar] [CrossRef]
  19. Kaxiras, E.; Neofotistos, G.; Angelaki, E. The first 100 days: Modeling the evolution of the COVID-19 pandemic. Chaos Solitons Fract. 2020, 138, 110114. [Google Scholar] [CrossRef]
  20. Rao, I.J.; Brandeau, M.L. Optimal allocation of limited vaccine to control an infectious disease: Simple analytical conditions. Math. Biosci. 2021, 337, 108621. [Google Scholar] [CrossRef]
  21. Gatto, N.M.; Schellhorn, H. Optimal control of the SIR model in the presence of transmission and treatment uncertainty. Math. Biosci. 2021, 333, 108539. [Google Scholar] [CrossRef] [PubMed]
  22. Peng, T.; Liu, X.; Ni, H.; Cui, Z.; Du, L. City lockdown and nationwide intensive community screening are effective in controlling the COVID-19 epidemic: Analysis based on a modified SIR model. PLoS One 2020, 15, e0238411. [Google Scholar] [CrossRef] [PubMed]
  23. Shimul, S.N.; Alradie-Mohamed, A.; Kabir, R.; Al-Mohaimeed, A.; Mahmud, I. Effect of easing lockdown and restriction measures on COVID-19 epidemic projection: A case study of Saudi Arabia. PLoS One 2021, 16, e0256958. [Google Scholar] [CrossRef]
  24. Cabrera, M.; Cordova-Lepe, F.; Pablo Gutierrez-Jara, J.; Vogt-Geisse, K. An SIR-type epidemiological model that integrates social distancing as a dynamic law based on point prevalence and socio-behavioral factors. Sci. Rep. 2021, 11, 10170. [Google Scholar] [CrossRef] [PubMed]
  25. Yang, Q.; Zhang, X.; Jiang, D. Asymptotic behavior of a stochastic SIR model with general incidence rate and nonlinear Levy jumps. Nonlin. Dyn. 2022, 107, 2975–2993. [Google Scholar] [CrossRef]
  26. Srivastava, H.M.; Area, I.; Nieto, J.J. Power-series solution of compartmental epidemiological models. Math. Biosci. Eng. 2021, 18, 3274–3290. [Google Scholar] [CrossRef] [PubMed]
  27. Djenina, N.; Ouannas, A.; Batiha, I.M.; Grassi, G.; Oussaeif, T.E.; Momani, S. A Novel Fractional-Order Discrete SIR Model for Predicting COVID-19 Behavior. Math. 2022, 10, 2224. [Google Scholar] [CrossRef]
  28. Ghosh, K.; Ghosh, A.K. Study of COVID-19 epidemiological evolution in India with a multi-wave SIR model. Nonlin. Dyn. 2022, 109, 47–55. [Google Scholar] [CrossRef]
  29. Marinov, T.T.; Marinova, R.S. Adaptive SIR model with vaccination: simultaneous identification of rates and functions illustrated with COVID-19. Sci. Rep. 2022, 12, 15688. [Google Scholar] [CrossRef]
  30. Kuhn, M.J.; Abele, D.; Mitra, T.; Koslow, W.; Abedi, M.; Rack, K.; Siggel, M.; Khailaie, S.; Klitz, M.; Binder, S.; et al. Assessment of effective mitigation and prediction of the spread of SARS-CoV-2 in Germany using demographic information and spatial resolution. Math. Biosci. 2021, 339, 108648. [Google Scholar] [CrossRef]
  31. Avram, F.; Adenane, R.; Ketcheson, D.I. A Review of Matrix SIR Arino Epidemic Models. Math. 2021, 9, 1513. [Google Scholar] [CrossRef]
  32. Zanella, M.; Bardelli, C.; Azzi, M.; Deandrea, S.; Perotti, P.; Silva, S.; Cadum, E.; Figini, S.; Toscani, G. Social contacts, epidemic spreading and health system. Mathematical modeling and applications to COVID-19 infection. Math. Biosci. Eng. 2021, 18, 3384–3403. [Google Scholar] [CrossRef] [PubMed]
  33. Chang, Y.C.; Liu, C.T. A Stochastic Multi-Strain SIR Model with Two-Dose Vaccination Rate. Math. 2022, 10, 1804. [Google Scholar] [CrossRef]
  34. Paoluzzi, M.; Gnan, N.; Grassi, F.; Salvetti, M.; Vanacore, N.; Crisanti, A. A single-agent extension of the SIR model describes the impact of mobility restrictions on the COVID-19 epidemic. Sci. Rep. 2021, 11, 24467. [Google Scholar] [CrossRef]
  35. Sadurni, E.; Luna-Acosta, G. Exactly solvable SIR models, their extensions and their application to sensitive pandemic forecasting. Nonlin. Dyn. 2021, 103, 2955–2971. [Google Scholar] [CrossRef] [PubMed]
  36. Osborn, J.; Berman, S.; Bender-Bier, S.; D’Souza, G.; Myers, M. Retrospective analysis of interventions to epidemics using dynamic simulation of population behavior. Math. Biosci. 2021, 341, 108712. [Google Scholar] [CrossRef]
  37. Beneduci, R.; Bilotta, E.; Pantano, P. A unifying nonlinear probabilistic epidemic model in space and time. Sci. Rep. 2021, 11, 13860. [Google Scholar] [CrossRef]
  38. Nakamura, G.; Grammaticos, B.; Deroulers, C.; Badoual, M. Effective epidemic model for COVID-19 using accumulated deaths. Chaos Solitons Fract. 2021, 144, 110667. [Google Scholar] [CrossRef]
  39. Martinez-Fernandez, P.; Fernandez-Muniz, Z.; Cernea, A.; Fernandez-Martinez, J.L.; Kloczkowski, A. Three Mathematical Models for COVID-19 Prediction. Math. 2023, 11, 506. [Google Scholar] [CrossRef]
  40. Ahumada, M.; Ledesma-Araujo, A.; Gordillo, L.; Marin, J.F. Mutation and SARS-CoV-2 strain competition under vaccination in a modified SIR model. Chaos Solitons Fract. 2023, 166, 112964. [Google Scholar] [CrossRef]
  41. Gunaratne, C.; Reyes, R.; Hemberg, E.; O’reilly, U.M. Evaluating efficacy of indoor non-pharmaceutical interventions against COVID-19 outbreaks with a coupled spatial-SIR agent-based simulation framework. Sci. Rep. 2022, 12, 6202. [Google Scholar] [CrossRef]
  42. Cooper, I.; Mondal, A.; Antonopoulos, C.G.; Mishra, A. Dynamical analysis of the infection status in diverse communities due to COVID-19 using a modified SIR model. Nonlin. Dyn. 2022, 109, 19–32. [Google Scholar] [CrossRef]
  43. Yuzbasi, S.; Yildirim, G. A Pell-Lucas Collocation Approach for an SIR Model on the Spread of the Novel Coronavirus (SARS CoV-2) Pandemic: The Case of Turkey. Math. 2023, 11, 697. [Google Scholar] [CrossRef]
  44. Prodanov, D. Computational aspects of the approximate analytic solutions of the SIR model: applications to modelling of COVID-19 outbreaks. Nonlin. Dyn. 2023, 111, 15613–15631. [Google Scholar] [CrossRef]
  45. Liu, T.; Huang, J.; He, Z.; Zhang, Y.; Yan, N.; Zhang, C.J.P.; Ming, W.K. A real-world data validation of the value of early-stage SIR modelling to public health. Sci. Rep. 2023, 13, 9164. [Google Scholar] [CrossRef]
  46. Odagaki, T. New compartment model for COVID-19. Sci. Rep. 2023, 13, 5409. [Google Scholar] [CrossRef] [PubMed]
  47. Calafiore, G.C.; Novara, C.; Possieri, C. A time-varying SIRD model for the COVID-19 contagion in Italy. ANNUAL REVIEWS IN CONTROL 2020, 50, 361–372. [Google Scholar] [CrossRef] [PubMed]
  48. Rahimi, I.; Chen, F.; Gandomi, A.H. A review on COVID-19 forecasting models. Neural Comput. Appl. 2023, 35, 23671–23681. [Google Scholar] [CrossRef] [PubMed]
  49. Schlickeiser, R.; Kröger, M. Determination of a key pandemic parameter of the SIR-epidemic model from past Covid-19 mutant waves and its variation for the validity of the Gaussian evolution. Physics 2023, 5, 205–214. [Google Scholar] [CrossRef]
  50. Kröger, M.; Schlickeiser, R. SIR-solution for slowly time-dependent ratio between recovery and infection rates. Physics 2022, 4, 504. [Google Scholar] [CrossRef]
  51. Schlickeiser, R.; Schlickeiser, F. A gaussian model for the time development of the Sars-Cov-2 corona pandemic disease. Predictions for Germany made on March 30. Physics 2020, 2, 164. [Google Scholar] [CrossRef]
  52. Kröger, M.; Schlickeiser, R. Verification of the accuracy of the SIR model in forecasting based on the improved SIR model with a constant ratio of recovery to infection rate by comparing with monitored second wave data. R. Soc. Open Sci. 2021, 8, 211379. [Google Scholar] [CrossRef]
  53. Lixiang, L.; Yang, Z.; Deng, Z.; Meng, C.; Huang, J.; Meng, H.; Wang, D.; Chen, G.; Zhang, J.; Peng, J. Propagation analysis and prediction of the Covid-19. Infect. Disease Model. 2020, 5, 282. [Google Scholar] [CrossRef] [PubMed]
  54. Ciufolini, I.; Paolozzi, A. Mathematical prediction of the time evolution of the Covid-19 pandemic in Italy by a Gauss error function and Monte Carlo simulations. Eur. Phys. J. Plus 2020, 135, 355. [Google Scholar] [CrossRef] [PubMed]
  55. Schüttler, J.; Schlickeiser, R.; Schlickeiser, F.; Kröger, M. Covid-19 predictions using a Gauss model, based on data from April 2. Physics 2020, 2, 197. [Google Scholar] [CrossRef]
  56. Singhal, A.; Singh, P.; Lall, B.; Joshi, S.D. Modeling and prediction of COVID-19 pandemic using Gaussian mixture model. Chaos Solitons Fract. 2020, 138, 110023. [Google Scholar] [CrossRef]
  57. Gradshteyn, I.S.; Ryzhik, I.M. Tables of Integrals, Series, and Products; Academic Press, New York, 1980. [CrossRef]
  58. Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions; Dover Publ., New York, 1970.
  59. Morse, P.M.; Feshbach, H. Methods of Theoretical Physics, Part I; McGraw-Hill, New York, 1953.
  60. Mathews, J.; Walker, R.L. Mathematical Methods in Physics, 2nd ed.; Benjamin, Menlo Park, California, 1970.
Preprints 91230 g001
Figure 1. Performance of the analytic approximation (23) for the crossover τ c versus k 0 at η = 10 − 5 .
Figure 1. Performance of the analytic approximation (23) for the crossover τ c versus k 0 at η = 10 − 5 .
Preprints 91230 g001
Preprints 91230 g002
Figure 2. Left: Plot of the monotonically rising ratio (25) for (a) C = 4 and (b) C = 0.15 with B = 1.5 and η = 10 − 5 . Middle: Corresponding rate of new infections j ( τ ) as a function of the reduced time for these choices of the ratio k ( τ ) . Right: Corresponding cumulative rate of new infections J ( τ ) . Shown are the numerical (black dashed curve) solution of the SIR-equations (6) in comparison with the analytical approximation (green curve) according to Eqs. (12) and (30). The agreement ist almost perfect. The maximum relative deviations are smaller than (a) 0.5% and (b) 2.5%. In addition, we show (hardly visible red dot-dashed curve) the approximant (39) in panel (a) for C > 1 , and Eq. (36) in panel (b) for C < 1 . The agreement ist against almost perfect. The black dotted lines are obtained for comparison using the method of steepest descent, Eq. (45), which provides a lower limit to the cumulative fraction because all other contributions far from the maximum are not adequately accounted for (Appendix A).
Figure 2. Left: Plot of the monotonically rising ratio (25) for (a) C = 4 and (b) C = 0.15 with B = 1.5 and η = 10 − 5 . Middle: Corresponding rate of new infections j ( τ ) as a function of the reduced time for these choices of the ratio k ( τ ) . Right: Corresponding cumulative rate of new infections J ( τ ) . Shown are the numerical (black dashed curve) solution of the SIR-equations (6) in comparison with the analytical approximation (green curve) according to Eqs. (12) and (30). The agreement ist almost perfect. The maximum relative deviations are smaller than (a) 0.5% and (b) 2.5%. In addition, we show (hardly visible red dot-dashed curve) the approximant (39) in panel (a) for C > 1 , and Eq. (36) in panel (b) for C < 1 . The agreement ist against almost perfect. The black dotted lines are obtained for comparison using the method of steepest descent, Eq. (45), which provides a lower limit to the cumulative fraction because all other contributions far from the maximum are not adequately accounted for (Appendix A).
Preprints 91230 g002
Preprints 91230 g003
Figure 3. Left panels: Plot of the oscillating ratio k ( τ ) according to Eq. (46) for (a) α = 0.5 , β = 4 , and (b) α = 0.8 , β = 0.5 . Centered panels: The corresponding rates of new infections j ( τ ) as a function of reduced time, using η = 10 − 5 . Right panels: Cumulative fraction J ( τ ) . Shown are the numerical (black dashed curve) solution of the SIR-equations (6) in comparison with the analytical approximation (green curve) according to Eqs. (47) and Eq. (48). Because α / β ≪ 1 for case (a), just the first term of the expansion (48) had to be used, while the first three terms of Eq. (48) are used in (b), in accord with Figure 4. The agreement ist almost perfect. The maximum relative deviations are smaller than 0.2% for all cases.
Figure 3. Left panels: Plot of the oscillating ratio k ( τ ) according to Eq. (46) for (a) α = 0.5 , β = 4 , and (b) α = 0.8 , β = 0.5 . Centered panels: The corresponding rates of new infections j ( τ ) as a function of reduced time, using η = 10 − 5 . Right panels: Cumulative fraction J ( τ ) . Shown are the numerical (black dashed curve) solution of the SIR-equations (6) in comparison with the analytical approximation (green curve) according to Eqs. (47) and Eq. (48). Because α / β ≪ 1 for case (a), just the first term of the expansion (48) had to be used, while the first three terms of Eq. (48) are used in (b), in accord with Figure 4. The agreement ist almost perfect. The maximum relative deviations are smaller than 0.2% for all cases.
Preprints 91230 g003
Preprints 91230 g004
Figure 4. The integral ∫ 0 τ e z cos θ is approximated for all τ within 1 % precision by the integrated Eq. (49), resulting in the expression shown inside the figure, if the z-dependent order of the summation, N, is chosen as depicted. The required order grows as N ∝ a .
Figure 4. The integral ∫ 0 τ e z cos θ is approximated for all τ within 1 % precision by the integrated Eq. (49), resulting in the expression shown inside the figure, if the z-dependent order of the summation, N, is chosen as depicted. The required order grows as N ∝ a .
Preprints 91230 g004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated