Prerpints.org logo
Preprint
Article

Experimental and Numerical Study of the Effect of Carbonate Rock Dissolution on Absolute Permeability of 408 Heterogeneous and Naturally Fractured Samples

Altmetrics

Downloads

90

Views

35

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

24 November 2023

Posted:

24 November 2023

You are already at the latest version

Alerts
Abstract
Permeability is an important transport property of porous materials, and its accurate evaluation is relevant in studying applied tasks such as CO2 injection into reservoirs and investigating groundwater quality issues. This study examines the dependence of permeability on total and connected porosity, hydraulic tortuosity, specific surface area, and mean pore radius based on the data of 408 cubic sub-volumes extracted from heterogeneous and naturally fractured cylindrical carbonate samples before and after injection of HCl solutions into them. These parameters were computed using pore-scale modeling of fluid flow. It has been shown that permeability correlates well with porosity and mean pore radius with correlation coefficients of R2≈0.65-0.79 for heterogeneous samples. It was found that the presence of natural fractures significantly influenced the relationship between permeability and other parameters. The relationship between permeability k, tortuosity τ, and specific surface area S is described by power laws k~τ-α and k~S-β, with coefficients α and β substantially exceeding those in the Kozeny-Carman equation. It was also found that there is a parabolic relationship between connected and total porosities both before and after rock dissolution with R2≈0.96-0.99. This allowed for estimation of percolation threshold porosity that are in good agreement with the literature data.
Keywords: 
Subject: Environmental and Earth Sciences  -   Geophysics and Geology

1. Introduction

Absolute permeability k plays an important role when studying fluid flow in the porous medium during the development of oil and gas reservoirs, the injection of СО2 into reservoirs for its further storage, the migration of contaminants in underground aquifers, and the flow of gases in catalytic systems. It presents macroscopic characteristic of porous medium, which depends on its microscopic and macroscopic properties. Absolute permeability usually measured under laboratory conditions on a limited number of rock samples. In practical applications, there is a need for specific relationships between k and other properties of the porous medium. And widely used relationship is the Kozeny-Carman (K-C) equation, which relates k to porosity ϕ , specific surface area, and tortuosity of porous medium [1,2,3,4]. However, the K-C equation predicts incorrect k values for many porous materials [2,5,6], and consequently, its various modifications have been developed [3,4,6,7,8,9,10].
The most widely used equations describe the relationship between k and ϕ ( k ~ ϕ n ) [11,12,13,14,15], connected porosity ϕ c o n . ( k ~ ϕ c o n . n ) and percolation threshold of porosity ϕ c ( k ~ ( ϕ − ϕ c ) n ) [4,6,8,16,17,18,19,20,21]. In the abovementioned equations, n is the power exponent. In addition, an equation is used to describe the relationship between k and ϕ l 2 , where l is the characteristic length of the porous medium [22,23,24,25,26].
The equation k ~ ϕ n is often used to describe the evolution of the relationship between permeability and porosity during rock dissolution [11,12,13,14,15,27,28] to predict the increase in k as ϕ changes during the rock dissolution. Several experimental studies on carbonate dissolution indicated that the fitting of experimental data using the equation k ~ ϕ n led to significantly higher values of n compared to n = 3 that is in K-C equation [12,13,15,27]. High values of n are explained with the formation of wormholes in rock samples as acid solutions interacted with carbonate rocks. Moreover, many authors noted that the values of n change as the rock dissolves [13,14,15,28,29]. Nogues et al. presented the dependence of the exponent n on the porosity during the rock dissolution [29].
Bernabe et al. first mentioned the idea of using the percolation threshold porosity ϕ c to describe the dependence of permeability on porosity while studying the hot pressing of calcite [7]. Later, this idea was implemented to describe the relationship between permeability and porosity using the equation k ~ ( ϕ − ϕ c ) n to study of fluid flow in spherical packing [4] and hot pressing of calcite aggregates [6]. This equation describes better the dependence of permeability on porosity at ϕ → ϕ c .
The percolation threshold of porosity ϕ c – is the value of porosity below which the pore network becomes disconnected, and therefore its permeability vanishes. It can be determined from the dependencies ϕ c o n ~ ( ϕ − ϕ c ) n and k ~ ( ϕ − ϕ c ) n . Zhang et al. found values of ϕ c and n , correspondingly, equal to 4% and n ≈ 2.2 for calcite aggregates [6], while N. S. Martys et al. amounted these values to be 3-9% and n ≈ 4 , respectively, for spherical packing [4]. Different authors have obtained values of ϕ c for limestone samples ϕ c = 5.9 % [17], young sea ice ϕ c = 2.4 % [18], natural microgranite ϕ c = 0.85 % [19], Fontainebleau sandstone ϕ c = 1.9 % [20], Fontainebleau sandstone, fused glass packing, hot-pressed calcite ϕ c = 2.5 ,   3.5 , and 4.5 % , respectively [8] and porous media with randomly placed identical squares ϕ c = 33 % [16].
There are in the literature a study of the relationship between k and the characteristic length of a porous medium l [18,24,25,26,30]. As l the critical pore radius r c r is often used, which is determined during the injection of a nonwetting liquid into rock samples under laboratory conditions [24,25,26]. Katz & Thompson considered l as the size corresponding to the percolation threshold of the electrical conductivity of porous media [30]. Nishiyama & Yokoyama studied 17 sandstone samples and 1 limestone sample, subjected to air displacement of water from these samples so that to determine r c r [25]. As a result of which, relationships were built between k , ϕ , transport porosity ϕ t r a and factor   ϕ r c r 2 . Their results indicated that the permeability of studied samples correlated better with ϕ r c r 2 , than with porosity ϕ , and this relationship was expressed as k = 0.012 ϕ t r a r c r 2 , where ϕ t r a means transport porosity, defined as total porosity without dead-end pores [25]. They examined the applicability of this relationship to describe the permeability of other porous media, and found that this relationship works well for these porous medium as well. They also found that by fitting the hydraulic tortuosity from the K-C equation, a better correlation can be achieved, which is described with the equation k = 8.5 ϕ r c r 2 1.3 .
Review of the previous studies on the subject of this article proved the following: 1) the relationship between k and l has to be studied comprehensively; 2) most studies available have been conducted using either sandstones, volcanic rocks and artificial porous materials or ideal porous media; 3) each study was conducted on a small number of samples; 4) the effect of rock dissolution on the relationships between permeability, porosity, tortuosity and specific surface area has also been studied little.
This paper studies the relationship between permeability, total and connected porosity, hydraulic tortuosity, specific surface area and mean pore radius based on data of 408 cubic sub-volumes selected from heterogeneous and naturally fractured cylindrical carbonate samples before and after injection of hydrochloric acid (HCl) solutions. In addition, the percolation threshold porosity for all samples were determined from the relationship between the connected and total porosity. The microscopic and macroscopic characteristics of the sub-volumes have been obtained through pore-scale modelling.

2. Materials and Methods

2.1. Sample characterization

Four cylindrical samples (#1-#4) were extracted from the core of one of the carbonate oil field of the Republic of Tatarstan. The diameter and length of the samples are about 3 and 5 cm, respectively. The study of the mineral composition using a Bruker D2 Phaser X-Ray diffractometer [31] showed that all samples are almost completely composed of calcite, and the quartz content does not exceed 1% (see Table 1). This allows to exclude the influence of mineral heterogeneity of samples on rock dissolution.
The samples were cleaned from oil and bitumen contained in them on Soxhlet apparatus using an alcohol-benzene mixture, after which they were kept in distilled water to remove water-soluble salts. Next, the samples were dried at a temperature of 104 °C until the change in their mass did not exceed 0.01 g.
Table 1 shows the porosity and permeability of the samples. The porosity was determined by the liquid saturation method, and the permeability was calculated according to Darcy's law.

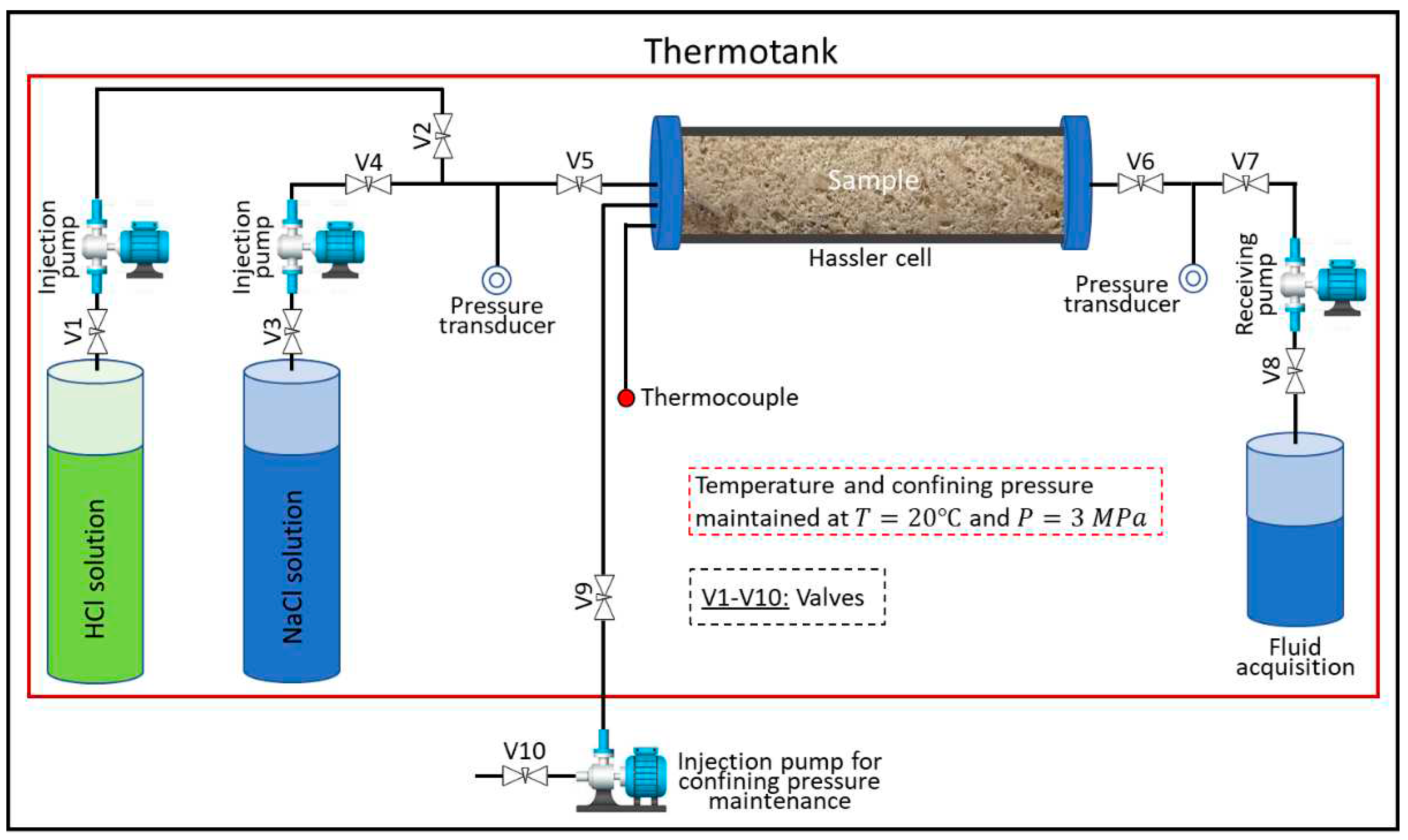
2.2. Experimental methods

Flow-through experiments on the injection of 2% sodium chloride (NaCl) solution and hydrochloric acid (HCl) solutions were carried out using Wille Geotechnik Y1000 electronic rock testing unit. The unit allows measuring the permeability of samples before and after injection of HCl solutions in reservoir conditions. The experimental setup is schematically shown in Figure 1. The experimental procedure is as follows. After cleaning from oil, bitumen and water-soluble salts, the sample is saturated with 2% NaCl solution and kept for 12 hours at a temperature of 20°С and a pressure of 3 MPa (reservoir conditions) [31]. It should be noted that immediately before and after injection of the HCl solution, each sample was scanned using a General Electric V|tome|X S240 X-ray microcomputed tomography at a resolution of about 18 µm. After that, a 2% NaCl solution is injected through the sample and at least at three constant injection rates, the pressure drop at the ends of the sample is measured after their stabilization. Next, valves V3 and V4 are closed, and valves V1 and V2 are opened, then the HCl solution is injected into the sample until breakthrough. After completion of the injection of the HCl solutions, a 2% NaCl solution is injected again into the sample, and at least at three constant injection rates, the pressure drop at the ends of the sample is measured after their stabilization. All experimental data are recorded on a computer. After each experiment, the pressure is released, the sample is unloaded from the core holder unit, the lines for the injection of liquids are flushed.
The water permeability of the samples was calculated according to the Darcy’s law. During all experiments, a constant temperature and confining pressure of 20°C and 3 MPa, respectively, were maintained. The injection rate and mass concentration of HCl in the solution, as well as the permeability of the samples before and after injection of HCl solutions are shown in Table 3.

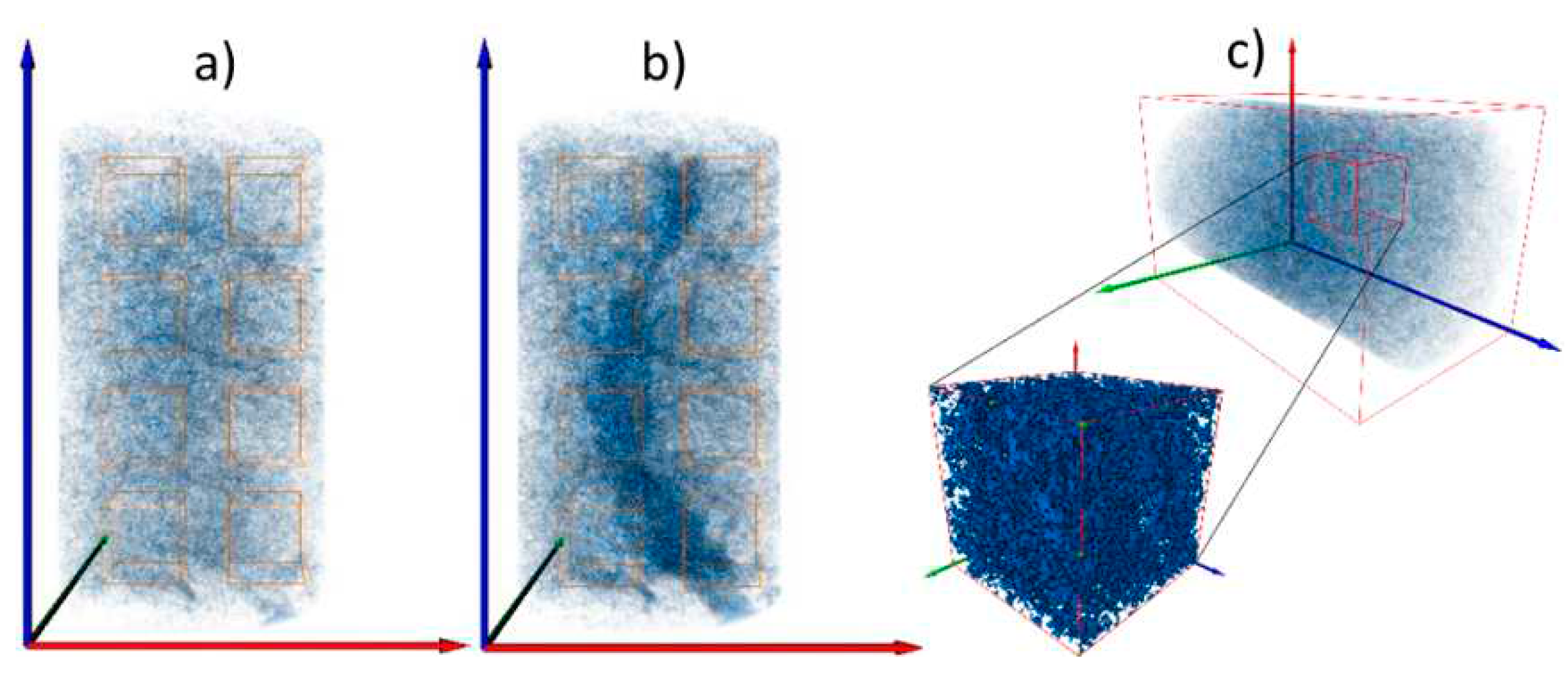
2.3. Pore-network modeling

With the aim to increase the number of samples, we extracted sub-volumes (red cubes) from each sample before (Figure 2a) and after (Figure 2b) their dissolution as it illustrated in Figure 2. Extraction of sub-volumes was carried out using the Avizo Software. The physical volume of each sub-volumes equals ~83 mm3, and this exceeds the representative elementary volume (REV) for each sample (Figure 3). Most importantly, the identity of each sub-volumes and location of extraction from 3D digital sample models was ensured, corresponding to its state before and after injection of HCl solutions, so that it was possible to compare the characteristics of sub-volumes before and after rock dissolution. Those sub-volumes were ejected that were either impermeable or coincident/intersect with wormholes. Thus, 408 sub-volumes were extracted totally from all considered samples (see Table 2).
As the sub-volumes from all cylindrical samples has been extracted, pore-network modelling (PNM) was carried out on them using the Avizo [32]. Avizo is a powerful software that allows to process images obtained using X-ray micro computed tomography and build 3D digital models of samples, as well as performs PNM of the fluid flow in order to determine the microscopic and macroscopic properties of samples [33,34]. As the consequence of PNM, the total and connected porosity, specific surface area, radius of all and only connected pores, hydraulic tortuosity and absolute permeability were computed. Avizo automatically computes the absolute permeability according to Darcy's law, the applicability of which is confirmed by calculations on several randomly chosen sub-volumes (Figure 4). All computations have been conducted on the following boundary conditions: the pressures at the inlet and outlet were 1.3 and 1.0 atm., respectively, and at the other boundaries of the sub-volume, no-flow condition was set. As a working fluid, water has been used, the viscosity of which is 1 mPa*s at room temperature.

3. Results and discussion

3.1. Change in pore space due to rock dissolution

Before building a 3D model of the samples, images of their slices were analyzed for the presence of any features (Figure 5 and Figure 6). Figure 5 shows the original and segmented images of the inlet, middle and outlet slices of Sample #2 before (Figure 5 a) and after (Figure 5 b) injection of HCl solutions. As shown in Figure 5, sample #2 has three natural vertical fractures, which are indicated by red lines. As can be seen from Figure 5a), there is only one fracture on different slices of the sample, which indicates their small length along the sample length.
It has been noted that to remove noises from the original images obtained using X-ray microcomputed tomography, a median filter was used [35]. It can be seen from Figure 5 and Figure 6 that there is a good visual match of the processed images with the original images of sample slices.
Figure 5 also indicates that, unlike the other samples (Figure 6), sample #2 also has vugs of different sizes (Figure 5a), which are marked with orange lines. Note that the pore space on the original and segmented images is marked in black and blue, respectively. The presence of fractures and vugs in the inlet slice of sample #2 caused the formation of secondary wormholes (yellow lines, Figure 5b) along with the main wormhole (green line, Figure 5b) that broke through in the outlet slice of the sample (Figure 7). Due to the presence of natural fractures in the sample #2, further we will consider it separately from the other samples. Thus, samples #1, #3 and #4 will be considered as heterogeneous samples, as well as sample #2 considered as naturally fractured.
The built 3D models of the samples before and after the injection of HCl solutions are shown in Figure 7. The injection of solutions was carried out from the bottom up. As shown in Figure 7, as a result of the dissolution of the carbonate rock, conical wormholes were formed, which led to an increase in the permeability of the samples over its initial value by several times (see Table 3). Sample #1 and #4 show face dissolution near the inlet slice at low injection rates. 2.4 to 4.4 pore volumes of HCl solutions required for breakthrough (see Table 3). The largest increases in permeability (3.79 and 4.1 times) were observed in samples #2 and #4 at injection rate of solutions of 8 and 4 ml/min, respectively.
Table 3. Flow conditions of HCl through the samples and permeability of samples after the injection.
Table 3. Flow conditions of HCl through the samples and permeability of samples after the injection.
Sample name Mass concentration of HCl, % Flow rate, ml/min Permeability after HCl injection, µm2 Permeability ratio Breakthrough pore volumes, PV
#1 18 2 0.98 3.38 2.9
#2 18 8 3.79 8.81 2.4
#3 12 8 3.85 5.42 4.2
#4 12 4 4.10 9.11 4.4
As shown above, a total of 408 sub-volumes were extracted from all the considered cylindrical samples. For visual evaluation the effect of rock dissolution on the pore structure in more detail, Figure 8 illustrates the pore space of three randomly selected sub-volumes extracted from each cylindrical sample before and after injection of HCl solutions. Note that Figure 8 shows only interconnected pores, which play an important role in the fluid flow through them and the formation of their permeability. As shown in Figure 8, noticeable changes in the pore space due to the rock dissolution occurred in samples #2-#4, which led to relatively large increases in their permeability (see Table 3). From Figure 8, we also note that in the sub-volumes extracted from samples #2 and #3, a significant increase in the number of interconnected pores is observed as a result of injection of HCl solutions. In addition, if before the injection of solutions, the connected pore space occupied only a certain part of the sub-volumes, then after the rock dissolution, it already occupies almost the entire part. This contributes to a significant increase in the conductance of sub-volumes and a decrease in the tortuosity of the flow path.

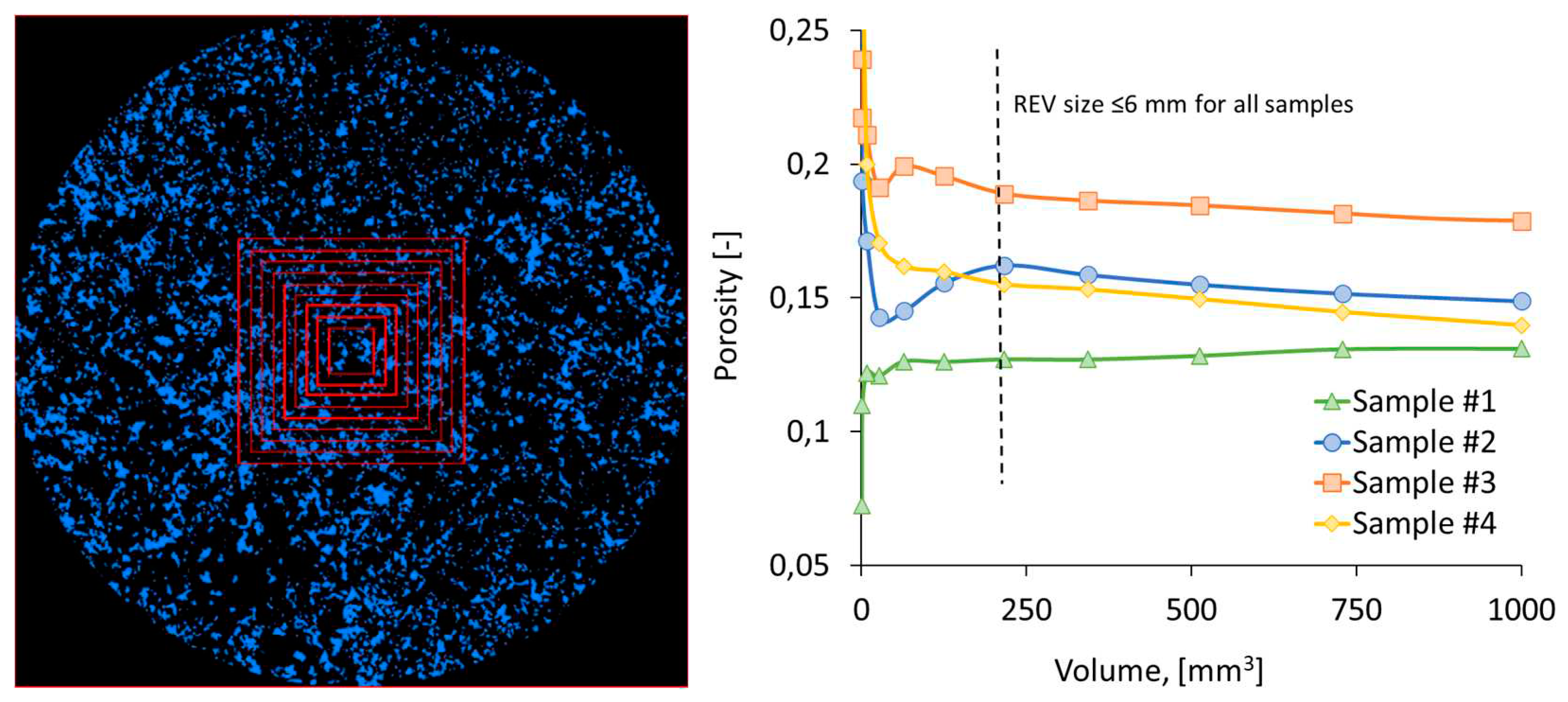
3.2. Connected vs. total porosity

Porosity ϕ is one of the important properties of a porous medium, and is defined as the ratio of pore volume to the total sample volume. Connected porosity ϕ c o n also often used, which is defined by the ratio of the volume of interconnected pores to the total sample volume, and as a rule ϕ ≥ ϕ c o n . Some studies have shown that there is a relationship between ϕ c o n and ϕ [16,18,36]. The study of the pore structure of a young sea ice [18] and basaltic clasts [36] using microcomputed tomography showed that the dependence of the connected porosity on the total porosity obeys a power law according to the percolation theory ϕ c o n ~ ϕ − ϕ c p , where p – power exponent. Koponen et al. approximated the relationship between the connected and total porosities by a cubic polynomial ϕ c o n = a x 3 − 2 a + ϕ c x 2 + a + 1 + ϕ c x , where x = ϕ − ϕ c / 1 − ϕ c [16]. Figure 9 shows the dependence of connected porosity on total porosity for sub-volumes from heterogeneous and naturally fractured samples. Blue circles and orange squares correspond to sub-volumes before and after their dissolution. The colored solid lines indicate the best fitting curves of the relationship between the connected and total porosity with a correlation coefficient R 2 = 0.96 − 0.99 . The fitting equation has the following form ϕ c o n = a ϕ 2 + b ϕ + c , where a ,   b and c – fitting coefficients, the values of which are given in Figure 9.
Relationships between connected and total porosity allows to find ϕ c [36]. The percolation threshold porosity ϕ c is the porosity at which the fluid begins to flow [21]. The porous medium becomes impermeable below ϕ c . Percolation threshold porosity is usually determined based on the relationship k ~ ϕ − ϕ c q , where, q – power exponent [4,6,8,19,20,21]. This relationship is often used as the fact that data on total porosity and absolute permeability are sufficiently collected during the numerous laboratory studies on cores. The percolation threshold porosity can also be determined if the relationship between connected and total porosity are available [16,18,36]. This approach requires additional studies to determine the connected porosity. In this study ϕ c is defined as the positive root of equation a ϕ 2 + b ϕ + c − ϕ c o n = 0 , the value of which is given in Table 4.
As it can be seen from Table 4, ϕ c for heterogeneous and fractured carbonate samples before and after their dissolution are close to the value of 5.9% which is determined during an experimental study of the dissolution of carbonate samples [17]. There is a decrease of ϕ c after dissolution, with the exception of a slight increase for the fractured sample, indicating that pore connectivity is increased due to the formation of new channels during the rock dissolution. The largest change ~ 60%, was observed for an heterogeneous sample. It turned out, ϕ c for Fontainebleau sandstone is 2-3 times lower than that of carbonate samples.

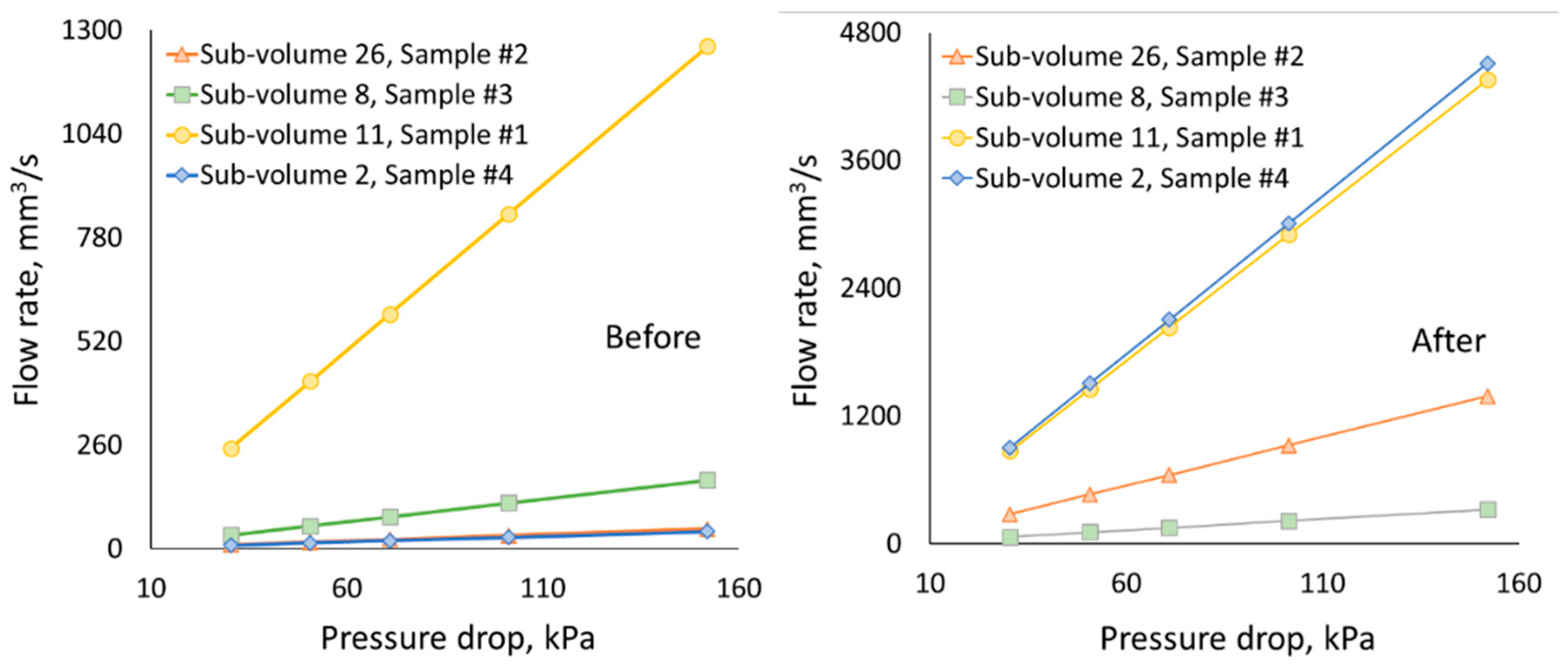
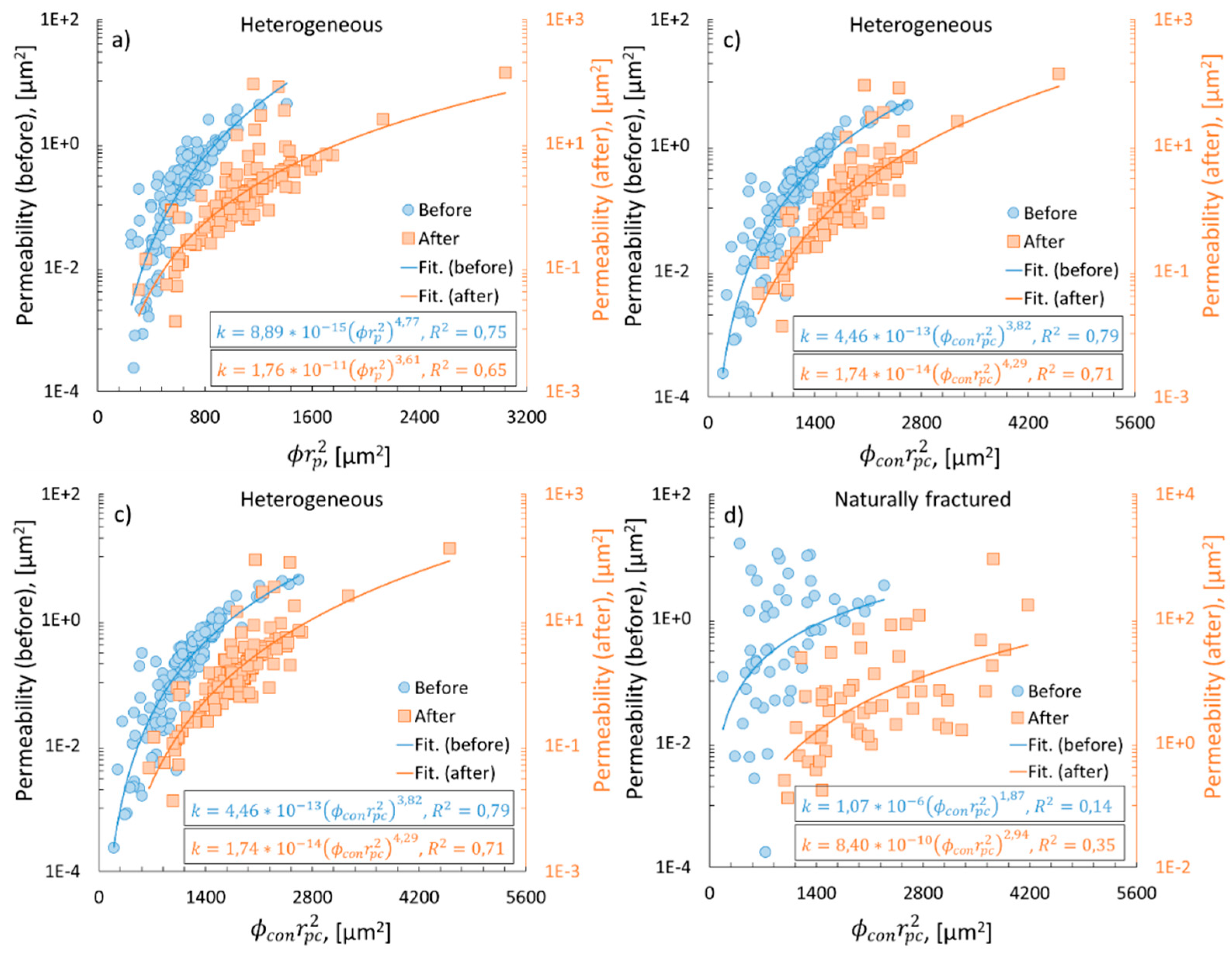
3.3. Permeability vs. porosities

Figure 10 demonstrates the distribution of absolute permeability of sub-volumes on total and connected porosities. In this figure, round and square symbols indicate the permeability of sub-volumes before and after their dissolution, respectively, for heterogeneous (Figure 10 a-c) and naturally fractured (Figure 10 d-f) samples. In order to establish relationships between permeability and porosities, our data were fitted using the equation k = a ϕ n , k = a ( ϕ − ϕ c ) n and k = a ϕ c o n n (Figure 10, solid lines). The values of ϕ c for heterogeneous and naturally fractured samples have been taken from Table 4.
Figure 10 indicates that, due to rock dissolution, not only porosity and permeability increase, but also the coefficients a and n changed. For example, for a heterogeneous sample, before its dissolution, if the relationship between permeability and total porosity (Figure 10a) is described by the equation k = 1,02 * 10 7 ϕ 8,85 , then after dissolution, this equation takes the form of k = 1,10 * 10 5 ϕ 6,27 . A similar trend is observed for fractured sample and equations k = a ( ϕ − ϕ c ) n and k = a ϕ c o n n (Figure 10 b-f). Therefore, this means that due to the rock dissolution the properties of samples changed and samples become different than before dissolution. In other words, the change due to rock dissolution must be considered when modelling fluid flow at larger scales. We also note that the values of power exponent n obtained in this study are significantly larger than the exponent in the K-C equation, in which n = 3 . High values of n for a considered carbonate samples may be due to that the natural rock samples have a more complex pore structure compared to the ideal porous materials, for which the K-C equation works well. Other studies have also shown higher values of n [11,13,15]. For example, Noiriel obtained n = 13 for the dissolution of a cylindrical limestone sample during the injection of СО2 [13]. Voltolini & Ajo-Franklin fitted permeability and porosity data during the dissolution of a limestone sample by СО2 with the equation k ~ ϕ n for which n ≈ 4.9 [15].
Figure 10 clearly demonstrates that there is a large scattering in the permeability distribution of sub-volumes extracted from the naturally fractured sample (Figure 10 d-f) compared to the distributions for heterogeneous samples (Figure 10 a-c), indicating that the relationship between permeability and porosity is weak in the case of naturally fractured samples. Consequently, for such samples, the permeability should be evaluated considering other properties of the rock. However, the scatter of data in the permeability distribution for naturally fractured sample decreased after rock dissolution, which can be seen from the improvement of the correlation coefficient R 2 (Figure 10 d-f). This means that as the rock dissolves, the relationship between permeability and porosity becomes stronger. The correlation coefficients of all types of equations used for heterogeneous samples ranges from 0.64 to 0.78 (Figure 10 a-c), while for a fractured sample this coefficient has significantly low values 0.14-0.36 (Figure 10 d-f).
Sub-volumes extracted from naturally fractured sample have higher permeabilities (Figure 10 d-f) compared to heterogeneous samples (Figure 10 a-c) at relatively low porosities. Figure 10 also demonstrates that, for heterogeneous samples, the equations k = a ( ϕ − ϕ c ) n and k = a ϕ c o n n describe better the sharp decrease in absolute permeability at low porosities (Figure 10 a, c, e, solid lines) compared to the equation k = a ϕ n .

3.4. Permeability vs. tortuosity and specific surface area

According to K-C equation, permeability is a function not only of porosity, but also of hydraulic tortuosity τ and specific surface area S [1,3,5,37]. Permeability is inversely proportional to the square of τ and S . The K-C equation obtained for an ideal porous media, and many studies have shown that the permeability calculated using it do not agree with the measured permeability of various rocks. Therefore, there are some its modifications in the literature [3,5,9,38,39].
Figure 11 demonstrates the dependence of permeability of sub-volumes on τ (Figure 11 a, b) and S (Figure 11 c, d) for heterogeneous and naturally fractured samples before and after their dissolution. As shown in Figure 11, there is a clear relationship between permeability and τ and S . These relationships can be best described by the following power laws of k ~ τ − α and k ~ S − β , where α and β power exponents for τ and S , respectively.
The values of α and β are much higher than those in K-C equation, and α varies from 8.5 to 40.1 (Figure 11 a, b), and β from 5.1 to 17.1 (Figure 11 c, d). LI et al. also have shown that there is a good power-law relationship between k and τ , with the power exponent varying between 3.46 and 8.24 for sub-samples of anisotropic and heterogeneous tight sandstone [40]. Nishiyama & Yokoyama have also obtained a power-law relationship between permeability and tortuosity k = 0.15 / τ 9.09 [25] for various granular porous materials. Values of α and β , much greater than 2 indicate that K-C equation is not an effective tool for predicting the absolute permeability of natural rock samples. Figure 11 also indicates the larger scattering in the distribution of k for naturally fractured sample.

3.5. Permeability vs. mean pore radius

We also computed the mean pore radius r p for each sub-volume extracted from heterogeneous and fractured samples in order to study its relationship with absolute permeability. The pore radius along with the other properties also plays an important role in the evaluation of permeability of porous media. For example, if we assume that a porous medium consists of many capillary tubes (pores) with a radius r , then the permeability of this porous medium can be calculated by following relationship k = ϕ r 2 / 8 . Obviously, the permeability is sensitive to the pore radius. There is in the literature the equation k = c ϕ γ l δ is used to describe the relationship between k and r p for various porous media, where l is the characteristic length of a porous medium [22,23,24,25,26]. Nishiyama & Yokoyama obtained an equation k = 8.5 ϕ r c r 2 1.3 to describe the relationship between permeability, porosity and critical pore radius of various artificial and natural porous materials [25]. It should be stated that below we use the mean radius of interconnected r p c and all pores r p (interconnected + unconnected).
Figure 12 illustrates the permeability of sub-volumes from all samples before and after their dissolution versus ϕ r p 2 (Figure 12 a, b) and ϕ c o n r p c 2 (Figure 12 c, d). Figure 12 a)-b) show that the relationship between permeability and ϕ r p 2 will be well described using the power law   k = c ϕ r p 2 ε , especially for heterogeneous samples, where ε and c are the power exponent and coefficient of proportionality, respectively. As it can be seen from the Figure 12, ε varies from 1.87 to 4.77 before and from 2.94 to 4.29 after rock dissolution, respectively. As it turned out, the relationship k ~ ϕ c o n r p c 2 is stronger compared to the relationship k ~ ϕ r p 2 (Figure 12 a) for heterogeneous samples, which can be seen from the higher coefficients of correlation R 2 of the equation k ~ ϕ c o n r p c 2 (Figure 12 c). Figure 6 demonstrates that the mean pore radius is also one of the important factors that significantly affects the permeability of the porous medium.

4. Conclusions

The present paper analyzed the main characteristics of the 408 cubic sub-volumes extracted from heterogeneous and naturally fractured carbonate samples before and after injecting HCl solutions.
Analysis of X-ray images of the sample slices showed the presence of natural fractures and vugs in sample #2, which contributed to the formation of secondary wormholes. The results also showed that the largest increases in permeability occurred in sub-volumes with poor pore connections before the injection of HCl solutions.
It has been shown that the absolute permeability k of sub-volumes from heterogeneous samples correlates well with porosities both before and after the injection of HCl solutions. However, the best correlation was observed between k and the factors ϕ r p 2 and ϕ c o n r p c 2 , with correlation coefficients R 2 ≈ 0.65 − 0.79 . This indicates that the mean pore radius, in combination with porosity, significantly influences the permeability of the porous medium. This is advantageous as the mean pore radius and porosity can be relatively easily determined.
As the results indicate, the presence of natural fractures noticeably affected the relationship between k and other parameters of the porous medium, resulting in a low R 2 value of approximately 0.15. However, an improvement in the correlation can be observed after rock dissolution, with an R 2 value of approximately 0.35. The results also highlight that for considered samples, the relationship between k and the other parameters changes shape after rock dissolution, i.e., the coefficient a and the power exponent n have different values before and after rock dissolution.
The relationship between k , τ , and specific surface area S is described by power laws k ~ τ − α and k ~ S − β , where α ranges from 8.5 to 40.1 and β ranges from 5.1 to 17.1, significantly exceeding the values in the Kozeny-Carman equation ( α = β = 2 ).
The results demonstrate that the relationship between connected and total porosity is well described by a parabolic equation ϕ c o n = a ϕ 2 + b ϕ + c both before and after rock dissolution giving high correlation coefficients R 2 ≈ 0.96 − 0.99 . The percolation threshold porosity values found in this article align well with those reported in [31] and are approximately three times higher than the values for sandstones. It has been shown that, as a result of rock dissolution, the connectivity between pores increases for heterogeneous samples, as evident from the decrease in the percolation threshold porosity after rock dissolution.

Supplementary Materials

Not applicable.

Author Contributions

The following statements should be used “Conceptualization, B.A. and B.I.; methodology, B.A.; software, D.B. and K.U.; validation, Zh.A., G.I. and K.U.; formal analysis, D.B.; investigation, Zh.A.; resources, D.B.; data curation, B.A.; writing—original draft preparation, Zh.A. and B.I.; writing—review and editing, B.A.; visualization, K.U.; supervision, B.A.; project administration, G.I.; funding acquisition, B.A. All authors have read and agreed to the published version of the manuscript.”

Funding

This research was funded by the Science Committee of the Ministry of Science and Higher Education of the Republic of Kazakhstan (Grant No. AP09058419). Authors also thank Satbayev University for support of Zh. K. Akasheva’s dissertation under Ph.D. program.

Data Availability Statement

All data used in this study can be downloaded at: https://github.com/BakhytzhanAssilbekov/Pore-network-modeling.git.

Conflicts of Interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.

References

  1. Carman PC (1997) Fluid flow through granular beds. Chem Eng Res Des 75:S32–S48. [CrossRef]
  2. Eichheimer P, Thielmann M, Fujita W, Golabek GJ, Nakamura M, Okumura S, Nakatani T, Kottwitz MO (2020) Combined numerical and experimental study of microstructure and permeability in porous granular media. Solid Earth 11:1079–1095. [CrossRef]
  3. Latief FDE, Fauzi U (2012) Kozeny–Carman and empirical formula for the permeability of computer rock models. Int J Rock Mech Min Sci 50:117–123. [CrossRef]
  4. Martys NS, Torquato S, Bentz DP (1994) Universal scaling of fluid permeability for sphere packings. Phys Rev E 50:403–408. [CrossRef]
  5. Blunt MJ, Bijeljic B, Dong H, Gharbi O, Iglauer S, Mostaghimi P, Paluszny A, Pentland C (2013) Pore-scale imaging and modelling. Adv Water Resour 51:197–216. [CrossRef]
  6. Zhang S, Paterson MS, Cox SF (1994) Porosity and permeability evolution during hot isostatic pressing of calcite aggregates. J Geophys Res 99:15741. [CrossRef]
  7. Bernabe Y, Brace WF, Evans B (1982) Permeability, porosity and pore geometry of hot-pressed calcite. Mech Mater 1:173–183. [CrossRef]
  8. Mavko G, Nur A (1997) The effect of a percolation threshold in the Kozeny-Carman relation. GEOPHYSICS 62:1480–1482. [CrossRef]
  9. Rodriguez E, Giacomelli F, Vazquez A (2004) Permeability-Porosity Relationship in RTM for Different Fiberglass and Natural Reinforcements. J Compos Mater 38:259–268. [CrossRef]
  10. Xu P, Yu B (2008) Developing a new form of permeability and Kozeny–Carman constant for homogeneous porous media by means of fractal geometry. Adv Water Resour 31:74–81. [CrossRef]
  11. Luquot L, Rodriguez O, Gouze P (2014) Experimental Characterization of Porosity Structure and Transport Property Changes in Limestone Undergoing Different Dissolution Regimes. Transp Porous Media 101:507–532. [CrossRef]
  12. Menke HP, Bijeljic B, Blunt MJ (2017) Dynamic reservoir-condition microtomography of reactive transport in complex carbonates: Effect of initial pore structure and initial brine pH. Geochim Cosmochim Acta 204:267–285. [CrossRef]
  13. Noiriel C (2004) Investigation of porosity and permeability effects from microstructure changes during limestone dissolution. Geophys Res Lett 31:L24603. [CrossRef]
  14. Smith MM, Sholokhova Y, Hao Y, Carroll SA (2013) CO2-induced dissolution of low permeability carbonates. Part I: Characterization and experiments. Adv Water Resour 62:370–387. [CrossRef]
  15. Voltolini M, Ajo-Franklin J (2019) The effect of CO2-induced dissolution on flow properties in Indiana Limestone: An in situ synchrotron X-ray micro-tomography study. Int J Greenh Gas Control 82:38–47. [CrossRef]
  16. Koponen A, Kataja M, Timonen J (1997) Permeability and effective porosity of porous media. Phys Rev E 56:3319–3325. [CrossRef]
  17. Luquot L, Gouze P (2009) Experimental determination of porosity and permeability changes induced by injection of CO2 into carbonate rocks. Chem Geol 265:148–159. [CrossRef]
  18. Maus S, Schneebeli M, Wiegmann A (2021) An X-ray micro-tomographic study of the pore space, permeability and percolation threshold of young sea ice. Cryosph 15:4047–4072. [CrossRef]
  19. Meredith PG, Main IG, Clint OC, Li L (2012) On the threshold of flow in a tight natural rock. Geophys Res Lett 39:n/a-n/a. [CrossRef]
  20. Revil A, Kessouri P, Torres-Verdín C (2014) Electrical conductivity, induced polarization, and permeability of the Fontainebleau sandstone. GEOPHYSICS 79:D301–D318. [CrossRef]
  21. Sueyoshi K, Yokoyama T, Katayama I (2020) Experimental Measurement of the Transport Flow Path Aperture in Thermally Cracked Granite and the Relationship between Pore Structure and Permeability. Geofluids 2020:1–10. [CrossRef]
  22. Arns C, Knackstedt M, Martys N (2005) Cross-property correlations and permeability estimation in sandstone. Phys Rev E 72:046304. [CrossRef]
  23. Bernabé Y (1995) The transport properties of networks of cracks and pores. J Geophys Res Solid Earth 100:4231–4241. [CrossRef]
  24. Martys N, Garboczi EJ (1992) Length scales relating the fluid permeability and electrical conductivity in random two-dimensional model porous media. Phys Rev B 46:6080–6090. [CrossRef]
  25. Nishiyama N, Yokoyama T (2017) Permeability of porous media: Role of the critical pore size. J Geophys Res Solid Earth 122:6955–6971. [CrossRef]
  26. Schwartz LM, Martys N, Bentz DP, Garboczi EJ, Torquato S (1993) Cross-property relations and permeability estimation in model porous media. Phys Rev E 48:4584–4591. [CrossRef]
  27. Lamy-Chappuis B, Angus D, Fisher Q, Grattoni C, Yardley BWD (2014) Rapid porosity and permeability changes of calcareous sandstone due to CO 2 -enriched brine injection. Geophys Res Lett 41:399–406. [CrossRef]
  28. Rötting TS, Luquot L, Carrera J, Casalinuovo DJ (2015) Changes in porosity, permeability, water retention curve and reactive surface area during carbonate rock dissolution. Chem Geol 403:86–98. [CrossRef]
  29. Nogues JP, Fitts JP, Celia MA, Peters CA (2013) Permeability evolution due to dissolution and precipitation of carbonates using reactive transport modeling in pore networks. Water Resour Res 49:6006–6021. [CrossRef]
  30. Katz AJ, Thompson AH (1986) Quantitative prediction of permeability in porous rock. Phys Rev B 34:8179–8181. [CrossRef]
  31. Bolysbek DA, Kuljabekov AB, Uzbekaliyev KS, Assilbekov BK (2023) Effect of Rock Dissolution on Two-Phase Relative Permeabilities: Pore-Scale Simulations Based on Experimental Data. Appl Sci 13:11385. [CrossRef]
  32. Thermo Fisher Scientific (2019) User’s Guide Avizo Software. 2019.
  33. Li Y, Chi Y, Han S, Zhao C, Miao Y (2021) Pore-throat structure characterization of carbon fiber reinforced resin matrix composites: Employing Micro-CT and Avizo technique. PLoS One 16:e0257640. [CrossRef]
  34. Zhao Y, Zhu G, Zhang C, Liu S, Elsworth D, Zhang T (2018) Pore-Scale Reconstruction and Simulation of Non-Darcy Flow in Synthetic Porous Rocks. J Geophys Res Solid Earth 123:2770–2786. [CrossRef]
  35. Akasheva Z, Bolysbek D, Assilbekov B (2023) STUDY OF CARBONATE ROCK DISSOLUTION USING X-RAY MICROCOMPUTED TOMOGRAPHY: IMPACT OF ACID FLOW RATE. NEWS Natl Acad Sci Repub Kazakhstan Ser Geol Tech Sci 1:20–32.
  36. Navarre-Sitchler A, Steefel CI, Yang L, Tomutsa L, Brantley SL (2009) Evolution of porosity and diffusivity associated with chemical weathering of a basalt clast. J Geophys Res 114:F02016. [CrossRef]
  37. Hommel J, Coltman E, Class H (2018) Porosity–Permeability Relations for Evolving Pore Space: A Review with a Focus on (Bio-)geochemically Altered Porous Media. Transp Porous Media 124:589–629. [CrossRef]
  38. Manmath, N. Panda LWL (2) (1994) Estimation of Single-Phase Permeability from Parameters of Particle-Size Distribution. Am Assoc Pet Geol Bull 78:. [CrossRef]
  39. Yin P, Song H, Ma H, Yang W, He Z, Zhu X (2022) The modification of the Kozeny-Carman equation through the lattice Boltzmann simulation and experimental verification. J Hydrol 609:127738. [CrossRef]
  40. LI T, LI M, JING X, XIAO W, CUI Q (2019) Influence mechanism of pore-scale anisotropy and pore distribution heterogeneity on permeability of porous media. Pet Explor Dev 46:594–604. [CrossRef]
Preprints 91349 g001
Figure 1. Schematic of the experimental setup.
Figure 1. Schematic of the experimental setup.
Preprints 91349 g001
Preprints 91349 g002
Figure 2. Schematic illustration of the extraction process of sub-volumes from a cylindrical sample: a) before injection; b) after injection; c) enlarged sub-volume.
Figure 2. Schematic illustration of the extraction process of sub-volumes from a cylindrical sample: a) before injection; b) after injection; c) enlarged sub-volume.
Preprints 91349 g002
Preprints 91349 g003
Figure 3. Selection of volumes (left) and porosity of the volumes (right) for samples #1-#4 before injection of HCl solutions.
Figure 3. Selection of volumes (left) and porosity of the volumes (right) for samples #1-#4 before injection of HCl solutions.
Preprints 91349 g003
Preprints 91349 g004
Figure 4. Flow rate vs. pressure drop for randomly selected sub-volumes from each sample before (left) and after (right) the injection of HCl solutions.
Figure 4. Flow rate vs. pressure drop for randomly selected sub-volumes from each sample before (left) and after (right) the injection of HCl solutions.
Preprints 91349 g004
Preprints 91349 g005
Figure 5. Original and segmented images of inlet (upper), middle (middle), and outlet (lower) slices of sample #2 before (a) and after (b) injection of HCl solution. Red and orange lines indicate natural fractures and vugs, respectively.
Figure 5. Original and segmented images of inlet (upper), middle (middle), and outlet (lower) slices of sample #2 before (a) and after (b) injection of HCl solution. Red and orange lines indicate natural fractures and vugs, respectively.
Preprints 91349 g005
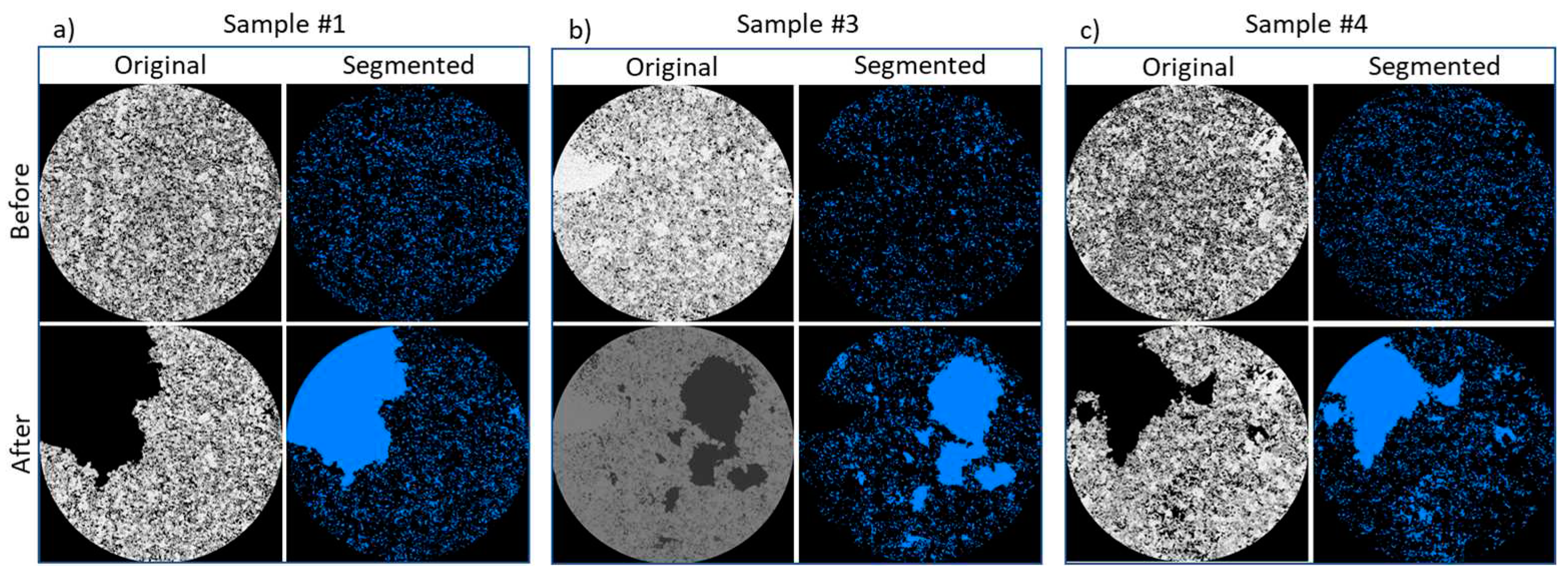
Preprints 91349 g006
Figure 6. Original and segmented images of inlet slices of sample #1 (a), #3 (b), and #4 (c) before (upper) and after (lower) injection of HCl solution.
Figure 6. Original and segmented images of inlet slices of sample #1 (a), #3 (b), and #4 (c) before (upper) and after (lower) injection of HCl solution.
Preprints 91349 g006
Preprints 91349 g007
Figure 7. 3D digital models of sample #1-#4 before and after injection of HCl solutions.
Figure 7. 3D digital models of sample #1-#4 before and after injection of HCl solutions.
Preprints 91349 g007
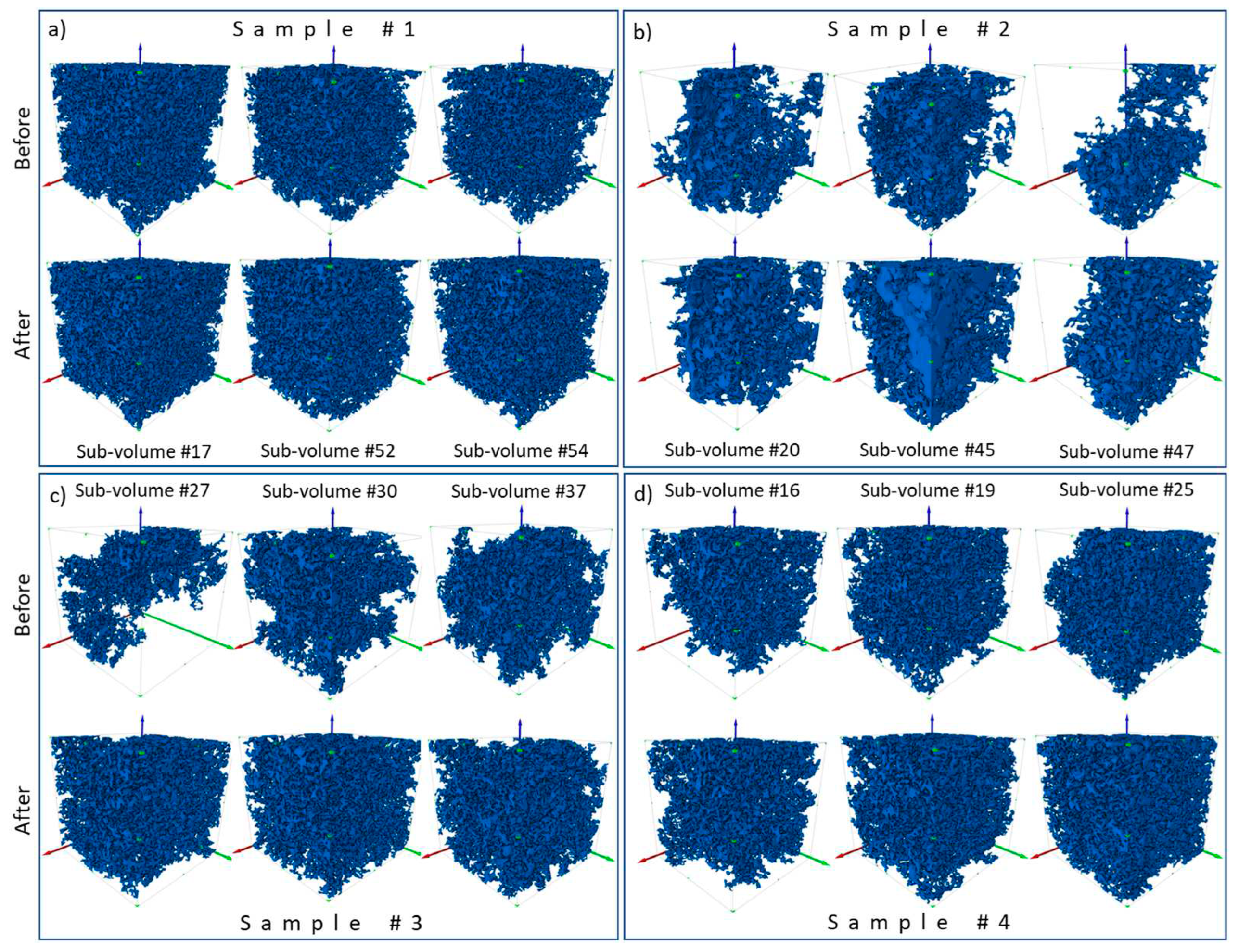
Preprints 91349 g008
Figure 8. Connected pore space of randomly selected sub-volumes extracted from samples #1-#4 before and after injection of HCl solutions.
Figure 8. Connected pore space of randomly selected sub-volumes extracted from samples #1-#4 before and after injection of HCl solutions.
Preprints 91349 g008
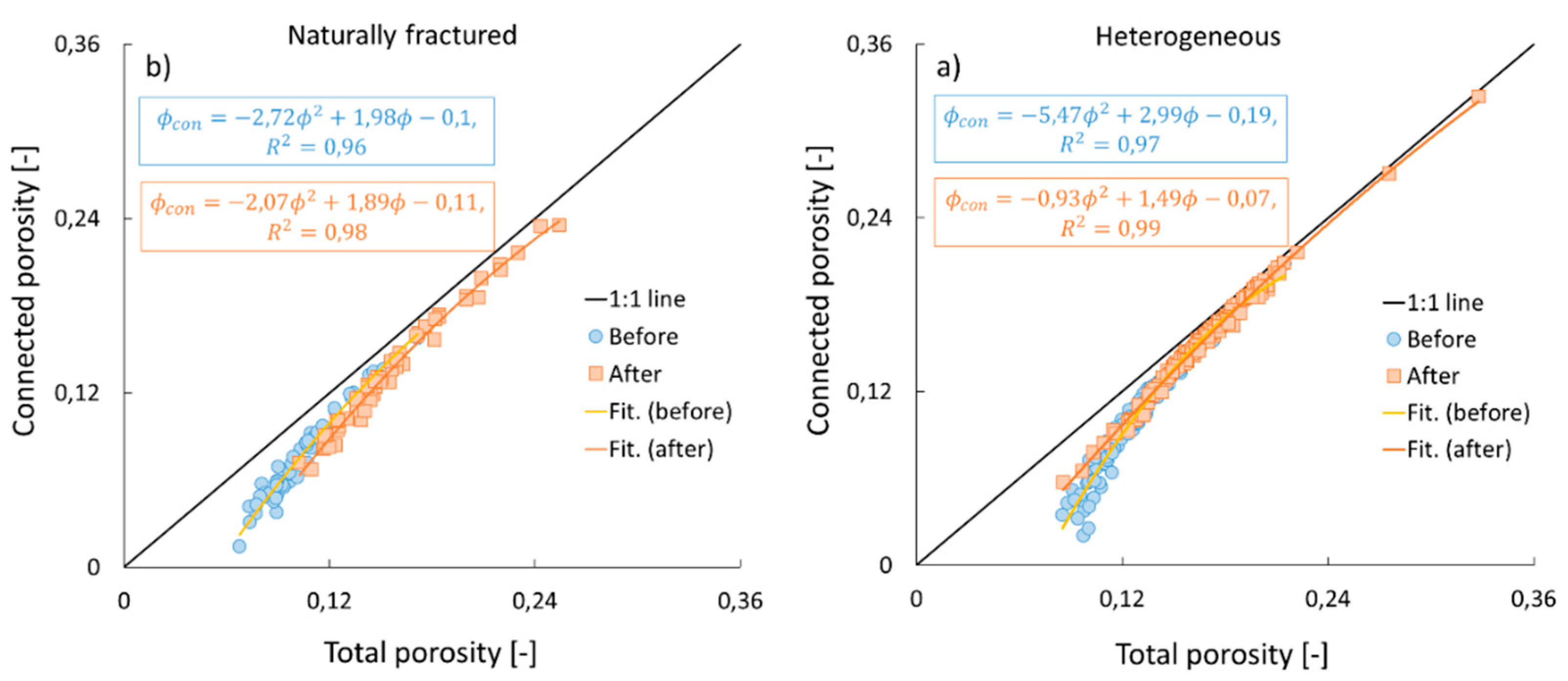
Preprints 91349 g009
Figure 9. Connected and total porosities of sub-volumes extracted from heterogeneous (a) and naturally fractured (b) samples before and after rock dissolution.
Figure 9. Connected and total porosities of sub-volumes extracted from heterogeneous (a) and naturally fractured (b) samples before and after rock dissolution.
Preprints 91349 g009
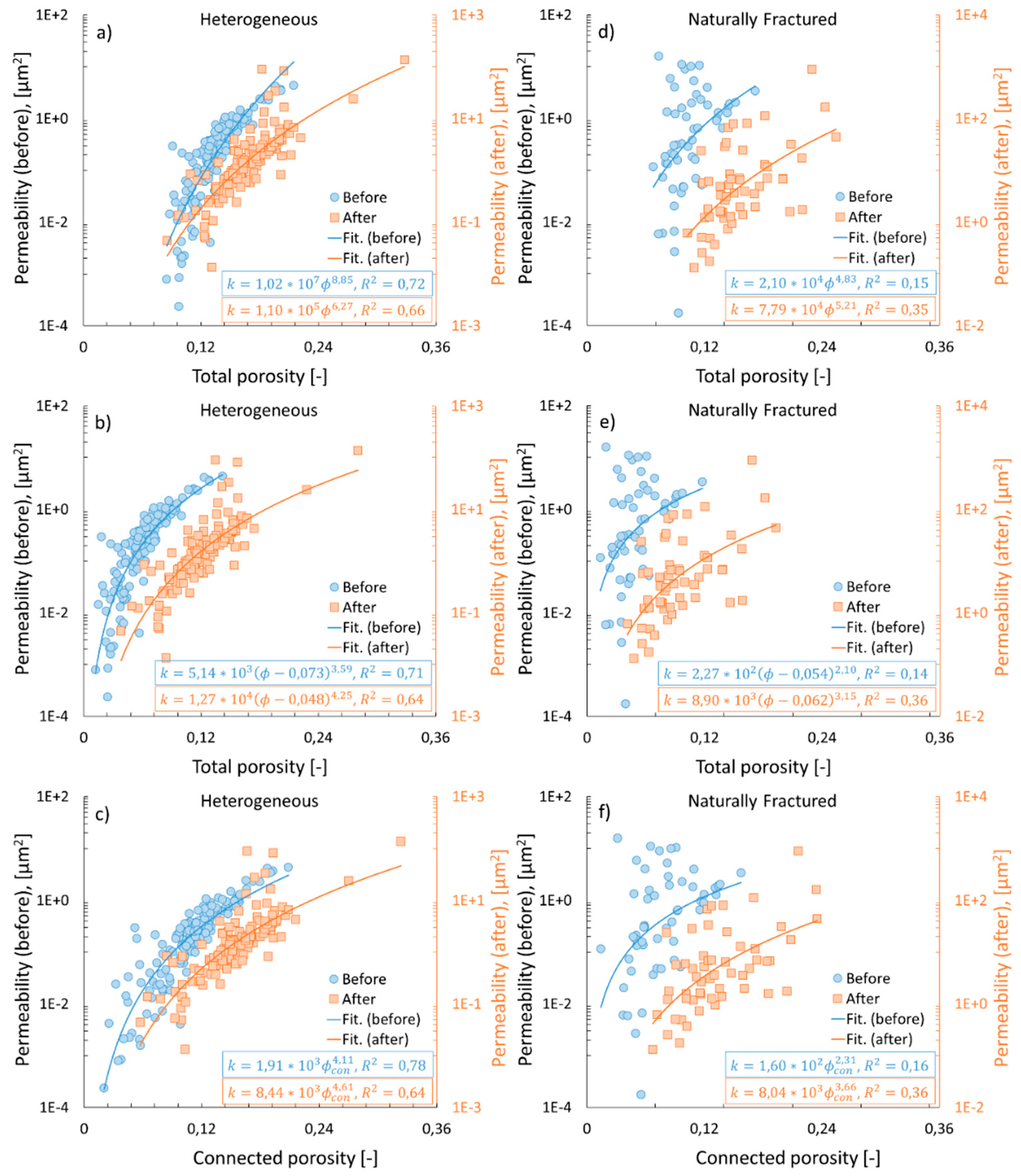
Preprints 91349 g010
Figure 10. Permeability vs. total (a, d), percolation threshold (b, e) and connected (c, f) porosities.
Figure 10. Permeability vs. total (a, d), percolation threshold (b, e) and connected (c, f) porosities.
Preprints 91349 g010
Preprints 91349 g011
Figure 11. Permeability vs. τ (a, b) and S (c, d).
Figure 11. Permeability vs. τ (a, b) and S (c, d).
Preprints 91349 g011
Preprints 91349 g012
Figure 12. Permeability vs. ϕ r 2 .
Figure 12. Permeability vs. ϕ r 2 .
Preprints 91349 g012
Table 1. The main characteristics of the studied samples.
Table 1. The main characteristics of the studied samples.
Sample name Porosity,% Permeability, µm2 Composition, %
Calcite Dolomite Quartz
#1 19.0 0.29 99 - 1
#2 20.6 0.43 100 - -
#3 20.9 0.71 99 - 1
#4 20.0 0.45 100 - -
Table 2. Number of sub-volumes extracted from cylindrical samples.
Table 2. Number of sub-volumes extracted from cylindrical samples.
Name of cylindrical sample #1 #2 #3 #4
Number of sub-volumes extracted Before injection 59 56 52 37
After injection 59 56 52 37
Table 4. Percolation threshold porosity of different porous materials.
Table 4. Percolation threshold porosity of different porous materials.
Reference ϕ c , % Porous material Relationship   type   for   ϕ c determination
[4] 3, 9 Sphere packing, sintered porous media k ~ ϕ − ϕ c q
[6] 4 Hot-pressed calcite k ~ ϕ − ϕ c q
[8] 2.5, 3.5, 4.5 Fontainebleau sandstone, fused glass beads, hot-pressed calcite k ~ ϕ − ϕ c q
[16] 33 Randomly placed squares ϕ c o n = a 1 x 3 − a 2 x 2 + a 3 x
[36] 9-14 Basalt clasts ϕ c o n ~ ϕ − ϕ c p
[17] 5.9 Carbonate rocks k ~ ϕ − ϕ c q
[19] 0.85 Microgranite k ~ ϕ − ϕ c q
[20] 1.9 Fontainebleau sandstone k ~ ϕ − ϕ c q
[21] 0.855 Granite k ~ ϕ − ϕ c q
[18] 2.4 Young sea ice ϕ c o n ~ ϕ − ϕ c p
This study (before)
Heterogeneous
Naturally fractured
7.3
5.4
Carbonate rocks

 ϕ c o n = a ϕ 2 + b ϕ + c
This study (after)
Heterogeneous
Naturally fractured
4.8
6.2		 Carbonate rocks ϕ c o n = a ϕ 2 + b ϕ + c
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated