Enhancing Outlier Detection in Healthcare Data through Mahalanobis Distance Metric Analysis

1. Introduction

The Mahalanobis distance, introduced by Prasanta Chandra Mahalanobis in the year 1936, serves as a measure of the distance between a point and a distribution. The Mahalanobis distance is a measure of how far a point is from the mean of the distribution, considering the relationships between the variables. A point with a large Mahalanobis distance is an outlier, as it is far from the typical values of the distribution. It finds applications in various fields, including data analysis, process control, and outlier detection [1].

The Mahalanobis distance is calculated using the covariance matrix of the data set. The covariance matrix is a measure of how much two variables change together. It is used to calculate the correlation between variables and is an important tool in multivariate analysis. The Mahalanobis distance is calculated by taking the difference between the mean of the data set and the data point, and then multiplying this difference by the inverse of the covariance matrix. The result is a measure of how far the data point is from the mean of the data set, considering the correlation between variables. In practice, you might obtain a covariance matrix from real-world data using methods like sample covariance estimation or other statistical techniques. The choice of the covariance matrix is crucial as it influences the shape and orientation of the generated data distribution.

The Mahalanobis distance can also be used to classify data points. This is done by assigning each data point to the class that has the smallest Mahalanobis distance to the point. This method is known as Mahalanobis distance-based classification. The Mahalanobis distance is a useful tool for identifying outliers in multivariate data. Outliers can have a significant impact on statistical analyses, so it is important to be able to identify and remove them from the data. The Mahalanobis distance can also be used to classify points into different groups or clusters. This is because points that are close to each other in terms of their Mahalanobis distance are likely to belong to the same group or cluster. For example, if two variables are highly correlated, then a point that is far away from the mean in the direction of one variable will also be far away from the mean in the direction of the other variable. The Mahalanobis distance will take this correlation into account and will assign a large distance to the point [2].

In statistics, the Mahalanobis distance is a measure of the distance between a point and a distribution. It is a generalization of the Euclidean distance to higher dimensions and is also known as the "multivariate normal distance". The Mahalanobis distance is used in a variety of applications, including cluster analysis, outlier detection, and pattern recognition. It is a generalization of the Euclidean distance to higher dimensions, and it considers the correlations between the different dimensions of the data. Robust estimation of the parameters in the Mahalanobis' distance and comparison with a critical value of the two distributions constitute the industry standard for multivariate outlier detection [3].

The Mahalanobis distance is also a useful tool for pattern recognition because it can be used to measure the similarity between two points. For example, the Mahalanobis distance can be used to measure the similarity between two images or two fingerprints. The smaller the Mahalanobis distance between two points, the more similar the points are. The Mahalanobis distance is determined by multiplying the inverse of the data's covariance matrix by the square root of the difference between the vectors representing the data point and the mean. As a result of their greater distance from the dataset's mean than would be anticipated given the covariance of the variables, points with large Mahalanobis distances are regarded as outliers [4].

The Mahalanobis distance is a powerful tool that can be used for a variety of tasks in statistics and machine learning. It is a versatile metric that can be used to detect outliers, classify data points, and identify patterns in data.

1.1. A brief biography of Prasanta Chandra

2. Materials and Methods

2.1. Introduction

The Mahalanobis distance is a widely utilised statistic for detecting anomalous observations within clinical datasets, specifically those pertaining to blood glucose levels and audiometric thresholds. Within the domain of blood glucose monitoring, the utilization of Mahalanobis distance facilitates a thorough evaluation of multivariate associations, considering the interconnectedness of diverse clinical factors. This approach has significant utility in identifying aberrant patterns that could indicate suboptimal diabetes management, acute complications, or underlying medical issues. Likewise, within the realm of audiometric data analysis, the Mahalanobis distance metric considers the interdependence of hearing thresholds across various frequency ranges [7].

This metric serves to facilitate the identification of exceptional observations that may suggest the presence of distinct hearing diseases or unanticipated deviations from the established norm. The utilization of the Mahalanobis distance metric on clinical data enables healthcare workers to obtain a quantitative assessment of dissimilarity, hence facilitating the timely detection of atypical situations. This methodology not only enhances the accuracy of diagnosis but also provides guidance for tailored interventions, optimizing the provision of healthcare to patients and perhaps preventing severe complications in diseases such as diabetes or addressing urgent auditory concerns promptly [8].

2.2.1. Calculation of Mahalanobis distance metric

Mahalanobis distance metric can be applied for outlier detection and clustering in patient data. It helps identify individuals with unusual health profiles by considering correlations between different health variables, aiding in personalized medicine and anomaly detection.

The Mahalanobis distance is defined as the square root of the quadratic form. This is the formula for the Mahalanobis distance between a point x and a distribution with mean μ and covariance matrix Σ:

$$\mathrm{MD}(\mathrm{x},\mathsf{\mu },\mathsf{\Sigma })=\sqrt[2]{\left(\right(\mathrm{x}-\mathsf{\mu })\mathrm{ᵀ}\mathsf{\Sigma }⁻¹(\mathrm{x}-\mathsf{\mu }\left)\right)}$$

ᵀ denotes the transpose operation of the matrix

Σ⁻¹ is the inverse of the covariance matrix Σ

The Mahalanobis distance is a measure of how many standard deviations away a point is from the mean of the distribution. A point with a Mahalanobis distance of 0 is located at the mean of the distribution, while a point with a Mahalanobis distance of 1 is located 1 standard deviation away from the mean. The covariance matrix Σ describes the relationships between the variables in the distribution. The diagonal elements of Σ represent the variances of the variables, and the off-diagonal elements represent the covariances between the variables [9].

The Mahalanobis distance is a useful tool for detecting outliers. An outlier is a data point that is far away from the rest of the data. Outliers can be caused by measurement error, data entry errors, or fraud. The Mahalanobis distance can be used to identify outliers by flagging points that have a Mahalanobis distance that is greater than a certain threshold [10].

2.2.2. Using the `scipy.spatial.distance` module

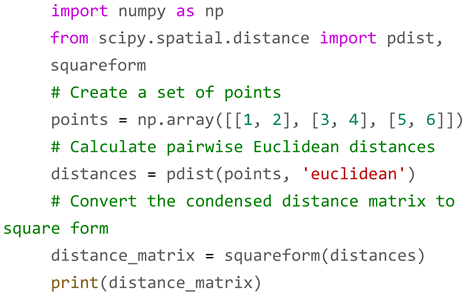
The `scipy.spatial.distance` module in the SciPy library provides various distance metrics for measuring the dissimilarity between arrays or vectors. Here are some key aspects of this module:

Distance Metrics: The module includes a variety of distance metrics such as Euclidean distance, Manhattan distance, Chebyshev distance, Minkowski distance, and others. These metrics are used to quantify the dissimilarity or similarity between two sets of observations.

Functionality: The primary function for calculating distances is `scipy.spatial.distance.pdist`, which computes pairwise distances between observations in a condensed distance matrix format. Other functions like `scipy.spatial.distance.cdist` can calculate distances between two sets of observations.

Usage Example: Here's a simple example using Euclidean distance:

Metric Parameter: When using functions like pdist or cdist, you specify the distance metric through the 'metric' parameter. For example, euclidean, cityblock, chebyshev, mahalanobis etc. You can also define custom distance functions and use them with these modules.

Use Cases: Common use cases include clustering, classification, and data analysis, where understanding the dissimilarity or distance between data points is crucial.

The `scipy.spatial.distance` module is a powerful tool for performing various distance computations and is often used in conjunction with other scientific computing libraries like NumPy and scikit-learn [11].

2.2. Visualization of Mahalanobis distance using Python, Scientific python and Matplotlib modules

You can visualize Mahalanobis distance by drawing ellipses centered at the mean, with the shape of the ellipses determined by the covariance matrix. Scientific python Scipy has module Spatial distance, from which mahalanobis method can be implemented.

from scipy.spatial.distance import mahalanobis

This script generates random data from a bivariate normal distribution, calculates Mahalanobis distance for each data point, and plots the points with colors indicating their Mahalanobis distances. Outliers, having higher Mahalanobis distances, are visually distinct on the plot.

In the example I provided, I manually specified a covariance matrix to generate random data. The covariance matrix determines the relationships between different variables in a multivariate distribution. For simplicity, I chose a 2x2 covariance matrix, and a 0.7 threshold:

$$\mathrm{covariance}\mathrm{matrix}=\left[\begin{array}{cc}1& 0.7\\ 0.7& 1\end{array}\right]$$

In this matrix, the diagonal elements (1 in this case) represent the variances of the individual variables, and the off-diagonal elements (0.7 in this case) represent the covariances between the variables. Adjusting these values will change the spread and correlation of the generated data. In practice, you might obtain a covariance matrix from real-world data using methods like sample covariance estimation or other statistical techniques. The choice of the covariance matrix is crucial as it influences the shape and orientation of the generated data distribution [12].

Here's a simple example of implementing Mahalanobis distance in Python using random data and plotting the results with matplotlib:

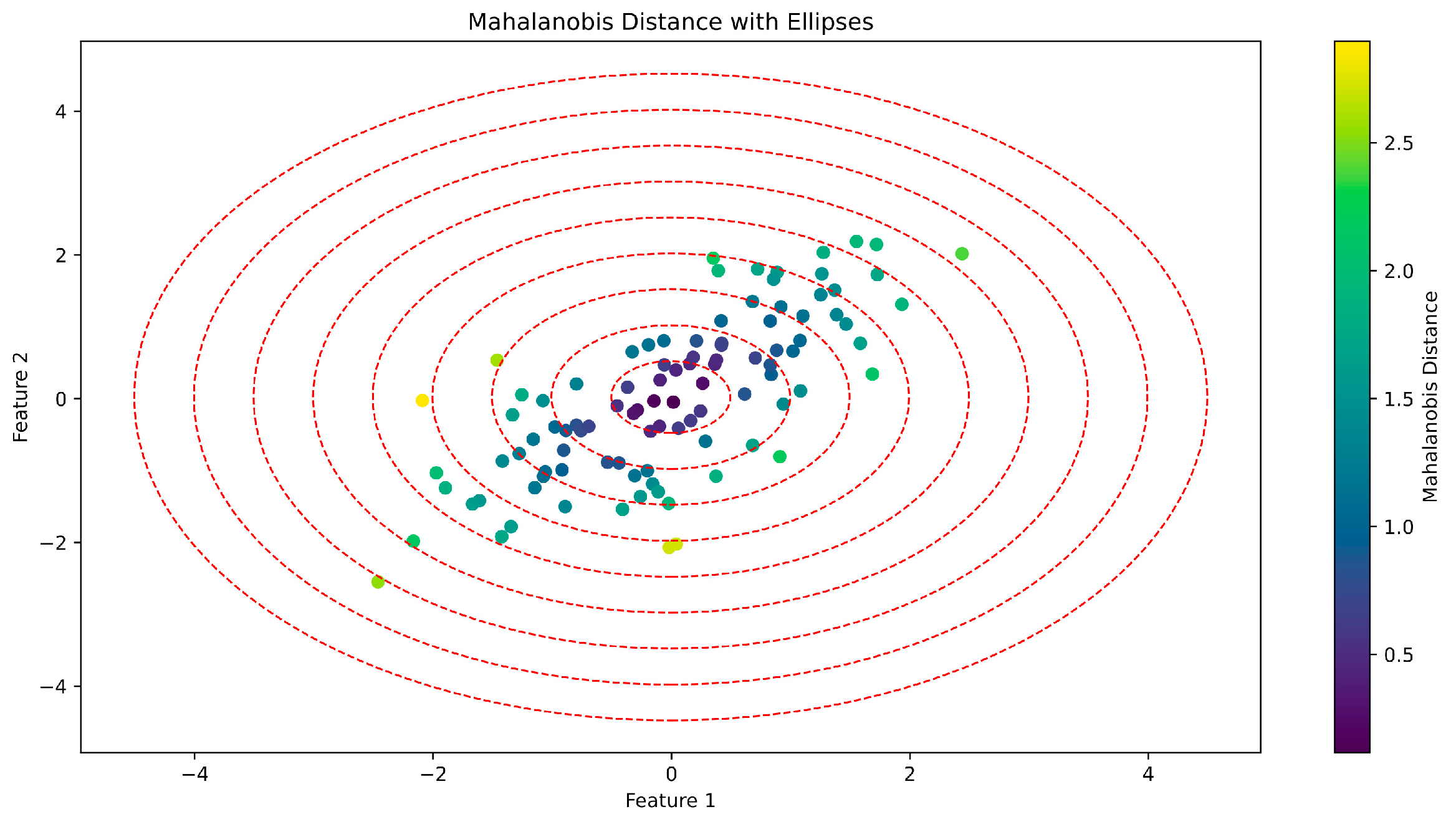
Figure 1. Visualization of Mahalanobis distances by drawing ellipses that are centered at the mean, this figure uses random data, and 10 elliptic fronts to depict the thresholds set by the covariance matrix. Original illustration of authors available on GitHub.

Figure 1. Visualization of Mahalanobis distances by drawing ellipses that are centered at the mean, this figure uses random data, and 10 elliptic fronts to depict the thresholds set by the covariance matrix. Original illustration of authors available on GitHub.

2.4. Methodology for hearing thresholds

This methodology utilises Mahalanobis distance to effectively identify probable outliers in Pure Tone Audiometry data. It considers the multivariate nature of hearing threshold measurements in both ears, hence offering a robust approach.

Data Collection: - The collection of Pure Tone Audiometry (PTA) data was conducted by selecting a sample of 50 patients in a random manner. Documentation of the auditory thresholds at various frequencies for both the right and left auditory organs was done.

Feature Selection: -The auditory thresholds of the right ear and left ear was utilized as features for each individual patient. The data of each patient was denoted by a pair of numbers that correspond to the hearing thresholds in the right and left ears.

Data Preprocessing: - A thorough examination of the dataset was undertaken to identify any instances of missing values or abnormalities, and subsequently take appropriate measures to remedy them. To assure equal contribution from both ears, it was necessary to standardize the data, considering potential variations in measurement scales [13].

Calculation of Mahalanobis Distance: - The Mahalanobis distance was computed for each patient based on the attributes of their right and left ears. The mean vector and covariance matrix were computed using the complete dataset. The mean of the right and left ear features for each patient was calculated assuming that 'data' is a 2D array. The vector was computed as the mean of the data along the axis 0 using the NumPy library. The covariance matrix was computed using the np.cov function in NumPy module, with the data as the input and the rowvar parameter set to False. The inverse of the covariance matrix, denoted as covariance matrix, was computed by taking the inverse of the covariance matrix. The Mahalanobis distances were computed for each point in the data using the formula Mahalanobis (point, mean vector, inverted covariance matrix).

Outlier Identification: - A threshold for Mahalanobis distance to identify probable outliers was determined to be 2.1. Patients whose Mahalanobis distance exceeds the predetermined threshold would be classified as outliers.

The value of the Mahalanobis threshold should be determined depending on the specific properties of the data. Once the threshold was determined, the indices of the outliers may be obtained by comparing the Mahalanobis distances to the threshold using the NumPy function `np.where()`.

Interpretation and Validation: - A an examination of the outliers that were detected, with a focus on determining their clinical significance or the possibility of measurement errors. To ensure the credibility and reliability of the findings, it was essential to engage in a process of validation. This could be achieved by seeking input and insights from domain experts or by conducting a comparative analysis with established examples that are known and recognized within the field.

Sensitivity Analysis: - We also performed sensitivity analysis by manipulating the Mahalanobis distance threshold to examine the influence on outlier detection [14].

3. Results

3.1. General Observation of the output of distance metric calculations

The output indicates data points were as outliers based on the Mahalanobis distance metric. The Mahalanobis distance considers both the mean and the covariance of the dataset. In the context of Mahalanobis distance:

• A smaller Mahalanobis distance indicates that a point is closer to the center of the distribution.
• A larger Mahalanobis distance suggests that a point is farther away from the center and, therefore, may be considered as an outlier.

The identified outliers in the output have higher Mahalanobis distances compared to the specified threshold. However, it's essential to note that "outlier" in this context doesn't necessarily mean the point is an extreme value in one dimension; rather, it is about being an unusual combination of values in the multivariate space defined by the dataset.

Regarding the specific point, it has attributes that, when considered together with the rest of the dataset, contribute to a higher Mahalanobis distance. It might be an outlier due to its combination of values in both dimensions, considering the overall distribution and covariance of the dataset. In practical terms, the concept of an "outlier" can vary based on the characteristics and context of your data. Domain knowledge to interpret as to why certain points are flagged as outliers by the Mahalanobis distance metric [15].

3.2. Application of Mahalanobis Distance Metric Analysis to Hearing Thresholds – Bivariate analysis

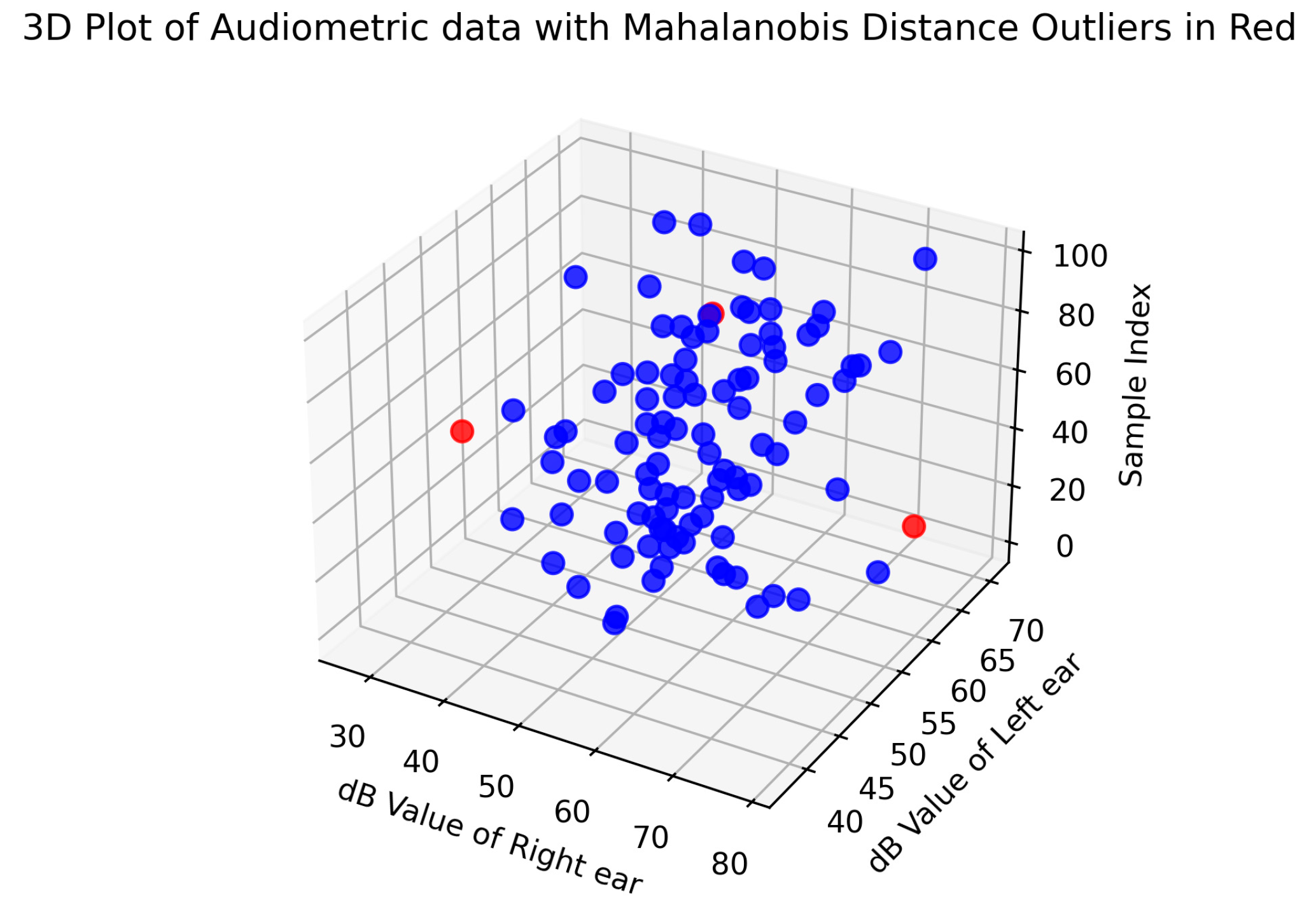
As a case study in actual clinical data, Hearing Thresholds of 100 patients were subjected to Mahalanobis Distance Metric Analysis to search for outliers. Each ear hearing was retained as a variable; hence the analysis was bivariate.

Figure 2. Visualization of dataset of actual hearing threshold of 50 cases who underwent Pure Tone Audiogram. Outliers detected by Mahalanobis distance metric analysis colored in red. original model and illustration of authors available on GitHub, Mahalanobis_Distance_Metric_Analysis repository.

Figure 2. Visualization of dataset of actual hearing threshold of 50 cases who underwent Pure Tone Audiogram. Outliers detected by Mahalanobis distance metric analysis colored in red. original model and illustration of authors available on GitHub, Mahalanobis_Distance_Metric_Analysis repository.

The application of Mahalanobis distance metric analysis to Pure tone audiometry threshold data yielded insightful observations. The method demonstrated a nuanced ability to discern subtle deviations in audiometric measurements, enabling the identification of outliers that might indicate potential hearing abnormalities. Notably, the Mahalanobis distance metric facilitated a more robust characterization of outliers, distinguishing between expected variations and anomalous data points.

Furthermore, the analysis revealed instances where traditional outlier detection methods might overlook certain patterns present in the audiometric data. The Mahalanobis distance metric, with its consideration of data covariance, proved particularly effective in capturing the multidimensional nature of Pure Tone Audiometry readings.

These observations underscore the method's adaptability and sensitivity, showcasing its potential as a valuable tool for improving the precision of outlier detection in healthcare datasets. The findings contribute to a deeper understanding of the nuances within audiometric data and demonstrate the broader applicability of Mahalanobis distance metric in healthcare analytics.

3.3. Application of Mahalanobis Distance Metric Analysis to Model of Blood sugar levels – Univariate analysis

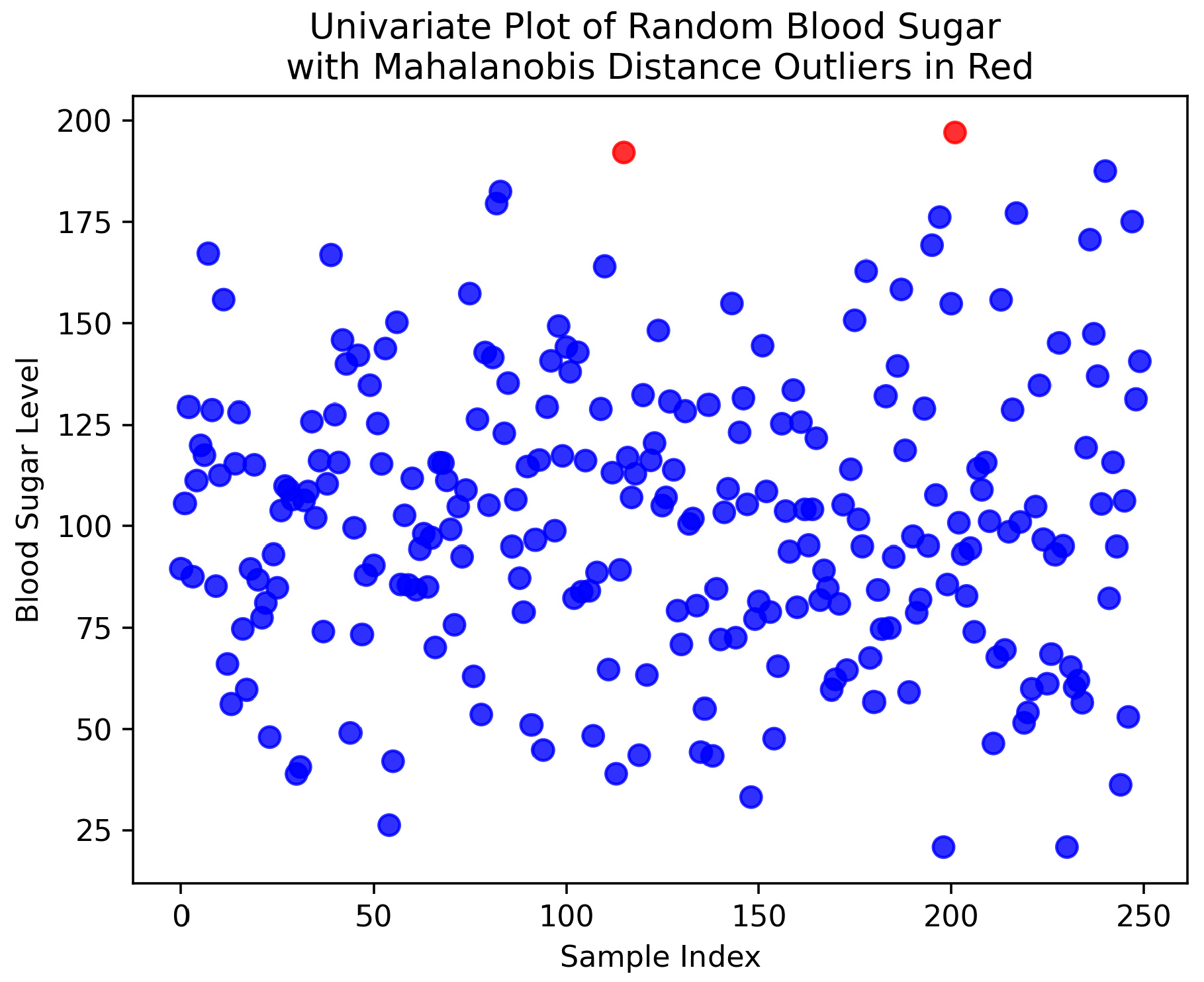
Blood glucose concentration was modeled using SciPy module. A sample of size of about N=250 was used in running the stimulated for a mean of 100 mg%.

Figure 3. Visualization of dataset of stimulated blood sugar levels in mg% of N=250 with mean of 100. Outliers colored in red with hyperglycemia, suspected Diabetes mellitus detected by Mahalanobis distance metric analysis. Original model and illustration of authors available on GitHub, Mahalanobis_Distance_Metric_Analysis repository.

Figure 3. Visualization of dataset of stimulated blood sugar levels in mg% of N=250 with mean of 100. Outliers colored in red with hyperglycemia, suspected Diabetes mellitus detected by Mahalanobis distance metric analysis. Original model and illustration of authors available on GitHub, Mahalanobis_Distance_Metric_Analysis repository.

In the context of blood glucose data, each observation typically represents a univariate measurement, signifying a single feature—specifically, the blood glucose level. When applying Mahalanobis distance, each individual blood glucose measurement is treated as a distinct feature. For instance, measurements taken at different times or under various conditions would constitute separate features. Therefore, the Mahalanobis distance is calculated based on these univariate measurements, providing a means to assess the multivariate distance of each data point within the dataset.

4. Discussion

4.1. Applications of Mahalanobis Distance Metric in clinical data

In the context of patient data, Mahalanobis distance serves as a powerful tool for identifying unusual cases or outliers, especially when dealing with multivariate data. The following is elaborate information about the process and its potential implications for medical diagnosis and treatment:

4.1.1. Multivariate Analysis

Patient data in healthcare often involves multiple variables such as symptoms, lab results, and demographic information. Mahalanobis distance considers the relationships and correlations among these variables. It goes beyond univariate methods by capturing the complex interactions between different aspects of a patient's health profile [16].

4.1.2. Identification of Unusual Cases

When a patient presents with a combination of symptoms that is not commonly observed in the general population or doesn't align with typical disease patterns, Mahalanobis distance can flag this case as an outlier. This is because Mahalanobis distance considers the variability and interdependence of variables, making it sensitive to deviations from the norm.

4.1.3. Enhanced Diagnostic Capability

The identification of unusual cases through Mahalanobis distance can significantly enhance the diagnostic capabilities of healthcare professionals. It provides a quantitative measure of dissimilarity, allowing doctors to prioritize and investigate cases that exhibit unique or unexpected combinations of symptoms.

4.1.4. Personalized Medicine Approach

By pinpointing outliers, Mahalanobis distance contributes to a personalized medicine approach. It acknowledges that patients can manifest illnesses in diverse ways, and tailoring medical interventions based on the specific characteristics of each patient becomes crucial for effective treatment.

4.1.5. Early Detection of Rare Conditions

Rare medical conditions or diseases that present with atypical symptoms can be challenging to diagnose. Mahalanobis distance aids in the early detection of such conditions by highlighting cases that deviate significantly from the norm. This early identification is crucial for initiating timely and appropriate treatment.

4.1.6. Data-Driven Decision Support

Mahalanobis distance provides a data-driven approach to decision-making in healthcare. By utilizing statistical measures to identify outliers, healthcare professionals can augment their clinical judgment with quantitative insights, leading to more informed and objective decision support.

4.1.7. Reducing Diagnostic Errors

In healthcare, diagnostic errors can have serious consequences. Mahalanobis distance acts as a safeguard against overlooking rare or unusual cases, reducing the likelihood of diagnostic errors, and ensuring a more comprehensive assessment of patient data.

4.2. Applications of Mahalanobis distance metric in analysis of patients’ data

In the setting of healthcare, Mahalanobis distance is a valuable statistical metric used for various applications, particularly in the analysis of patient data. Here are some expanded points on its applications:

4.2.1. Outlier Detection

Mahalanobis distance is employed to identify outliers or unusual cases in patient data. By considering correlations between different health variables, Mahalanobis distance provides a more accurate measure of dissimilarity compared to traditional Euclidean distance.

4.2.2. Personalized Medicine

In the context of personalized medicine, Mahalanobis distance helps in assessing how far an individual patient's health profile deviates from the general population. This can aid in tailoring medical interventions and treatments based on the specific characteristics of each patient.

4.2.3. Multivariate Analysis

Healthcare datasets often involve multiple variables such as blood pressure, cholesterol levels, and age. Mahalanobis distance is well-suited for multivariate analysis as it considers the relationships and correlations among these variables, providing a more comprehensive understanding of patient health [17].

4.2.4. Clustering and Classification

Mahalanobis distance can be utilized for clustering patients with similar health profiles. This clustering can assist healthcare professionals in identifying groups of patients who may respond similarly to certain treatments or interventions. It can also be employed in classification tasks to categorize patients into different risk groups.

4.2.5. Anomaly Detection in Medical Imaging

In medical imaging, Mahalanobis distance is applied to identify anomalous patterns or abnormalities in images. This can be crucial in fields such as radiology, where detecting unusual structures or anomalies in medical scans is essential for accurate diagnosis.

4.2.6. Quality Control in Healthcare Processes

Mahalanobis distance is useful for monitoring and maintaining the quality of healthcare processes. By analyzing patterns and deviations in various parameters, it can help identify potential issues in healthcare delivery, such as deviations in treatment effectiveness or unexpected variations in patient outcomes [18].

4.2.7. Handling Multicollinearity

In situations where healthcare variables exhibit multicollinearity (high intercorrelations), Mahalanobis distance provides a robust measure by considering the inverse covariance matrix. This is particularly relevant when dealing with correlated clinical variables.

4.2.8. Fraud Detection in Healthcare Billing

Mahalanobis distance can be applied in healthcare finance to identify unusual patterns in billing data, helping to detect potential fraud or errors in claims.

4.2.9. Outliers in the healthcare data

In the context of patient data, Mahalanobis distance can be used to identify unusual cases or outliers that may indicate a medical condition. For example, if a patient has a set of symptoms that are not commonly seen together, the Mahalanobis distance can be used to identify this case as an outlier. This can help doctors to diagnose and treat the patient more effectively [19].

Mahalanobis distance plays a crucial role in enhancing the analysis of healthcare data by considering the complex relationships and correlations among variables. Its applications range from personalized medicine to anomaly detection, contributing to more informed decision-making in healthcare settings [21].

4.3. Case study Outliers in the healthcare data- Outliers Blood sugar levels

The identification of an outlier within blood glucose values holds significant importance within the healthcare field due to the potential ramifications of abnormal glucose levels on a patient's well-being, which may include the development of life-threatening illnesses. The regulation of blood glucose levels in the human body is highly controlled, and deviations from the established range might indicate a range of health concerns, particularly in relation to illnesses such as diabetes. The identification of outliers in blood glucose readings can have critical implications for an individual's survival [22].

Management of Diabetes: - Blood glucose readings that deviate significantly from the norm are frequently suggestive of suboptimal diabetes management. In individuals with diabetes, the presence of consistently elevated or reduced blood glucose levels can give rise to acute problems such as diabetic ketoacidosis (DKA) or hypoglycemia.

Diabetic ketoacidosis (DKA) is a medical condition characterized by significantly elevated levels of blood glucose, which can lead to dehydration, imbalances in electrolyte levels, and organ dysfunction. These complications present an imminent danger to an individual's life.

Hypoglycemia is a medical condition characterized by abnormally low blood sugar levels. Conversely, significantly diminished levels of blood glucose (hypoglycemia) can result in seizures, unconsciousness, and, in more severe instances, coma. The prompt and timely identification and response are of utmost importance to mitigate the risk of permanent injury or mortality.

Cardiovascular Risks: - The danger of developing cardiovascular disorders, such as heart attacks and strokes, is heightened by prolonged exposure to elevated blood glucose levels. The early detection of anomalies in glucose readings enables timely measures to effectively manage and mitigate associated hazards.

Organ Damage: - Prolonged elevation of blood glucose levels can result in the deterioration of various organs, including the kidneys, eyes, nerves, and blood vessels. The identification of outliers facilitates the intervention of healthcare personnel to mitigate or impede the advancement of such issues.

Emergency Situations: - In instances of emergency, such as diabetic emergencies or critical sickness, the monitoring of blood glucose levels assumes paramount importance. Outliers possess the capacity to indicate the necessity for expeditious medical intervention and serve as a guiding force for healthcare practitioners in formulating prompt and critical life-preserving judgements [23].

Modifications to pharmaceutical Regimens: - The presence of outliers may suggest the necessity of adjusting pharmaceutical regimens. For example, the adjustment of insulin doses in diabetic patients may be necessary to achieve and sustain optimal control of blood glucose levels.

Tailored Patient Care: - The identification of outliers facilitates the provision of personalized patient care. Healthcare practitioners possess the ability to customize therapies, drugs, and lifestyle recommendations according to an individual's unique blood glucose patterns. This approach aims to enhance treatment success and mitigate potential dangers.

In brief, the presence of outliers in blood glucose measurements can function as an initial indicator of potentially critical medical issues, particularly within the framework of diabetes. The prompt emphasizes the need of promptly identifying and effectively managing outliers to avert acute problems, mitigate the likelihood of chronic consequences, and ultimately ensure the welfare and survival of patients. The implementation of regular monitoring and proactive healthcare measures plays a crucial role in effectively regulating blood glucose levels [24].

4.4. Case study Outliers in the healthcare data- Outliers Hearing Threshold

The identification of outliers in hearing threshold values plays a critical role in the diagnosis and rehabilitation of persons who experience hearing impairment. Hearing thresholds are indicative of the minimum sound levels that an individual may perceive across various frequencies. Deviations from these thresholds can have substantial ramifications for clinical decision-making. The identification of outliers in hearing thresholds plays a crucial role within the framework of diagnosing and treating individuals with hearing impairments.

The Importance of Early Detection in Hearing Loss: - The presence of outliers in hearing thresholds can potentially serve as an early indicator of hearing loss, particularly within certain frequency ranges. The timely identification of hearing loss enables timely intervention, which plays a critical role in mitigating the progression of auditory impairment.

Enhancing Diagnostic Precision: - The identification of outliers plays a crucial role in enabling audiologists to accurately diagnose the specific type and severity of hearing impairment. Diverse patterns of outliers may indicate different diseases, including sensorineural, conductive, or mixed hearing loss, which might impact the choice of treatment strategies.

Customizing Rehabilitation procedures: - The identification of outliers in hearing thresholds informs the decision-making process for selecting suitable rehabilitation procedures. For example, individuals who exhibit exceptional frequency outliers may experience advantages from focused therapies, such as the implementation of frequency-specific amplification or cochlear implantation [25].

Counselling and Communication Strategies: - The study of outliers can provide valuable insights to audiologists regarding the unique communication difficulties that individuals may encounter. The data holds significant value in the context of counselling individuals who have hearing impairment, as it enables the provision of recommendations pertaining to communication tactics, adaptive technology, and assistive devices.

Monitoring Progress:-Monitoring Progress in Rehabilitation is a crucial aspect of the rehabilitation process. The monitoring of changes in hearing thresholds is crucial during the rehabilitation process. Outliers within a dataset have the potential to signify unforeseen occurrences, such as abrupt fluctuations in auditory capacity or complications arising from the utilization of a rehabilitation apparatus. The prompt identification of issues permits the implementation of necessary modifications to the rehabilitation strategy.

Customized Treatment Plans: - The existence of outliers plays a role in the development of personalized treatment plans. The personalization of interventions to address the needs of each patient is guided by factors such as the number of outliers, the specificity of their frequency, and their impact on speech perception [26].

Impact on Quality of Life: - Deviations in hearing thresholds are linked to the influence of hearing loss on an individual's quality of life. This information provides audiologists with insights into the possible social, emotional, and cognitive difficulties encountered by patients, hence impacting the comprehensive approach to rehabilitation.

Mitigating Subsequent Auditory Impairment: - Anomalies within data sets may suggest instances of prolonged exposure to elevated noise levels or other external elements that may contribute to auditory impairment. It is imperative to consider these parameters to avert any more decline in auditory thresholds and safeguard the remaining auditory capacity [27].

In essence, the detection of outliers in auditory threshold measurements plays a crucial role in the assessment and treatment of persons suffering from hearing loss. This technology facilitates accurate diagnosis, customized therapies, and continuous monitoring to enhance therapy results. Through the identification and consideration of outliers, audiologists have the capacity to administer tailored care that effectively tackles the distinct obstacles encountered by each person, hence resulting in the enhancement of their communication skills and general quality of life [28].

5. Conclusions

In summary, Mahalanobis distance serves as a valuable tool in the realm of patient data analysis. Its ability to detect unusual cases contributes to more accurate and personalized medical diagnoses, ultimately leading to improved patient care and outcomes.