A Comparison of Two Connectivity Reduction Methods for Spiking Neural Networks with Memristive Plasticity

Memristive spiking neural networks are a promising emerging technology in the field of deep learning. These models can be implemented using neuromorphic hardware and therefore offer low power consumption and low latency, crucial to edge-computing applications. These systems, however, pose several challenges, including on-chip training and connectivity reduction. The latter is essential to ease the manufacturing complexity of the system. On-chip training can be realized using synaptic plasticity enabled by memristors. In this work, we compare two methods of connectivity reduction applicable to memristive spiking networks: an ensemble-based approach and a probabilistic sparse connectivity approach. We evaluate both of these methods in conjunction with a three-layer spiking neural network on the handwritten and spoken digits classification tasks using two memristive plasticity models and a classical time-dependent plasticity rule. On the handwritten digits recognition task, both methods achieve the F1-score of 0.89–0.93, and yield the 0.80–0.96 F1-score on the spoken digits recognition task.

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

1. Introduction

Neural network-based intelligent systems are widely employed in a wide range of tasks, from natural language processing to computer vision and signal processing. In edge computing, however, the use of deep learning methods still poses a variety of challenges, including latency and power consumption constraints, both during training and inference.

Neuromorphic computing devices, in which the information is encoded and processed in the form of binary events called spikes, offer a prospective solution to these problems. Modern neuroprocessors, e.g. TrueNorth [1], Loihi [2], or Altai 1, were shown to achieve power consumption on the order of milliwatts [3]. Thus, these devices offer a powerful inference interface, which can be used to deploy spiking neural networks (SNNs) for inference.

In turn, memristor-based training poses its own unique set of challenges and limitations. The most prominent one arises from the hardware implementation of synapses, where each memristor can have only a limited amount of synapses [4,5,6], imposing limitations on the number of weights that a given network may have. In this regard, sparsely connected spiking networks, where the connectivity can be reduced depending on the hardware specifications, are a plausible solution.

In this study, we compare two methods of reducing connectivity in memristive spiking neural networks: a bagging ensemble of spiking neural networks and a probabilistic sparse SNN. Using a three-layer SNN with inhibitory and excitatory synapses, we solve the handwritten and spoken digits classification tasks and compare the outcomes for the proposed connectivity reduction types and three plasticity models. The main contributions of this work are:

–: We design a probabilistic sparse connectivity approach to creating a two-layer spiking neural network, implement a bagging ensemble of two-layer SNNs, and compare these two methods;
–: We propose an efficiency index that facilitates the comparison among different methods of connectivity reduction, and apply it to the SNNs used in the study;
–: We demonstrate that both connectivity reduction methods achieve competitive results on handwritten and spoken digits classification tasks and can be used with the memristive plasticity models.

The rest of the study is structured as follows: In Section 2 we provide a brief overview of the existing connectivity reduction methods for SNNs. In Section 3 we describe the datasets we use, the plasticity models and the base spiking neural structure, and the sparsity methods we utilize for comparison. In Section 4 we provide the accuracy estimations for the proposed approaches and discuss the obtained results in Section 5. Finally, we draw the conclusions in Section 6.

2. Literature Review

Connectivity reduction concerning spiking and artificial neural networks has been studied in several existing works. For example, the study [7] proposes a probabilistic approach to connectivity reduction in SNNs based on the spatial structure of the network’s layers. It is shown that a spiking neural network pruned according to this method achieves 98% accuracy on the EMNIST [8] dataset. The authors of [9] propose a joined connectivity and weight learning approach inspired by synapse elimination and synaptogenesis in biological neurons. The gradient in this work is redefined as an additional synaptic parameter, facilitating better adaptation of the network topology. A multilayer convolutional SNN trained with error backpropagation and pruned according to the designed method demonstrates an accuracy loss of 3.5% on MNIST [10] and 0.73% on CIFAR-10 [11] datasets. In [12] a two-stage pruning method for on-chip SNNs is developed. The pruning is first performed during training based on the weight update history and spike timing, and then after training via weight thresholding. By training a deep SNN with time-to-first-spike coding using the proposed approach the authors decrease latency by a factor of 2 and reduce the network connectivity by 92% without accuracy loss. Another example can be found in [13], the authors use a method of zeroing weights above a given threshold and achieve a 70% reduction in connectivity. In this paper the network consists of a mixture of formal and spiking convolutional layers, and the resulting sparse hybrid network achieves more than 71% accuracy on the IVS 3cls [14] dataset. Finally, in [15] a sparse SNN topology is proposed, where the connectivity reduction is performed via a combination of pruning and quantization based on the power law weight-dependent plasticity model. After training, the three-layer fully connected SNN designed in the study achieves a classification accuracy of 92% on the MNIST dataset. Another approach to connectivity reduction present in the literature is based on designing locally-connected SNNs, the weights in which are created in a sparse fashion according to a certain rule. In [16], for example, a routing scheme using a hybrid of short-range direct connectivity and address event representation network is developed. Without providing any benchmark results, the authors focus on the details of mapping a given SNN to the proposed architecture and show that it yields up to a 90% reduction in connectivity. In [17], sparsity in a formal multilayer convolutional network is achieved by limiting the number of connections associated with each neuron by a factor of 2. The proposed approach is shown to achieve high accuracy on such classical datasets as DVS-Gesture [18] (98%) MNIST (99%), CIFAR-10 (94%), and N-MNIST [19] (99%). The authors of [20] propose locally connected SNN layers, in which subsets of neurons compete via inhibitory interactions to learn features from different parts of the input space. A three-layer locally connected spiking neural network is used in the study to solve the MNIST and EMNIST classification challenges, on which it achieves 95% and 70% accuracy scores, respectively. Thus, currently employed methods of reducing the connectivity in spiking neural networks are mostly encompassed by pruning, quantization, and local connectivity. However, ensemble learning, where multiple smaller networks are used together to form a stronger classifier can be also viewed as a single sparse network. In this work, we explore this path to connectivity reduction and compare it to a probabilistic locally connected SNN topology proposed in the work [21] and investigated in our previous research with different types of plasticity models[22,23,24].

3. Materials and Methods

3.1. Datasets and Preprocessing

For training and evaluation of the proposed methods, we use two benchmark datasets: scikit-learn Digits [25] and the Free Spoken Digits Dataset [26]. The former consists of 1797

8 \times 8

images of handwritten digits, while the latter contains 3000 audio recordings of the spoken numbers from 0 to 9 in English.

Thus, both datasets have 10 classes, resulting in 180 samples per class for Digits and 300 samples per class for FSDD; additionally, the samples in FSDD vary by speaker: 6 speakers in total, 50 recordings of each digits per speaker with different intonnations.

The raw data was preprocessed as follows:

(1): Feature engineering: for Digits, the original features in the form of pixel intensity were used without changes; for FSDD, features were extracted by splitting the signal into frames, extracting 30 Mel Frequency Cepstral Coefficients [27] (MFCC) and then averaging across frames.
(2): Normalization: Depending on the type of plasticity, the input vectors were normalized either by reducing to zero mean and one standard deviation (Standard Scaling) or by L2 normalization.
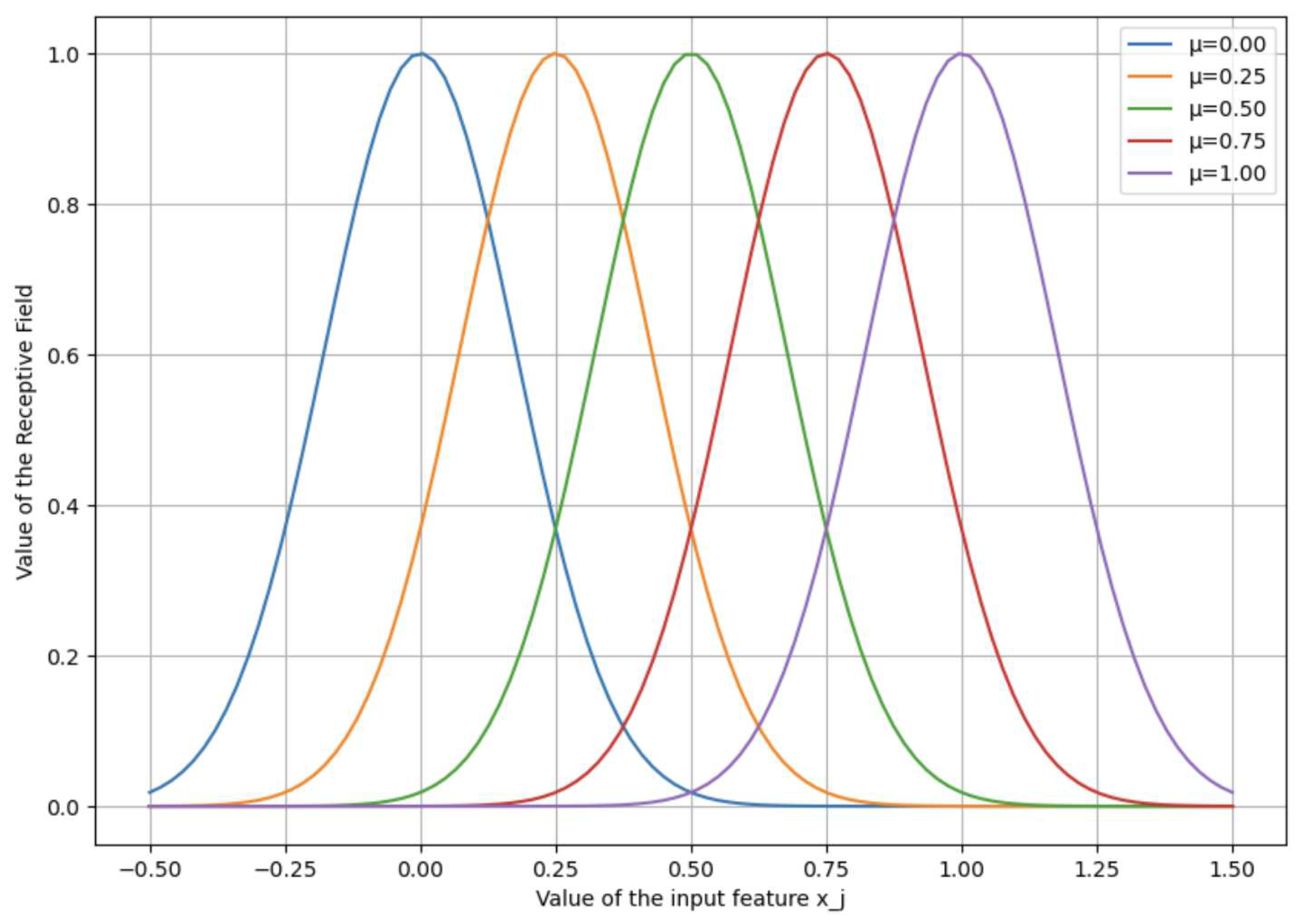
(3): Gaussian Receptive Fields (GRF): This step is necessary to significantly increase the selectivity of the network, as a consequence, increase the number of weights between the input and output layers of the spike network. At this stage, the normalized feature vectors were divided into M equal intervals for each feature. At each interval $j = 1, . . ., M$ , a Gaussian peak was constructed with center $μ_{j}$ and standard deviation $σ$ (see Eq. 1, Figure 1). The value of each component $x_{i}$ of the input vector was replaced by a set of values $G_{j} (x)$ characterizing the proximity of $x_{i}$ to the center of the j-th receptive field. Thus, the dimension of the input vector increased M times.
(4): Spike encoding: To convert the normalized and GRF-processed input vectors into spike sequences, we used a frequency-based approach. With this encoding method, each input neuron (spike generator) emits spikes at frequency $ν$ during the entire sample time $t_{e}$ , where $ν = ν_{m a x} \cdot k$ . Here $ν_{m a x}$ is the maximum frequency of spike emission, and k is the value of the input vector component. After time $t_{e}$ has passed, the generators do not emit spikes for $t_{p} = 50$ ms to allow the neuron potentials to return to their original values.

G_{j} (x_{i}) = e x p (\frac{{(x_{i} - μ_{j})}^{2}}{σ^{2}})

(1)

Figure 1. An example of Gaussian receptive fields with number of fields equal to 5. The input feature

x_{i}

is intersected with overlapping Gaussians to produce a vectorized feature representation

G_{j} (x_{i}), j \in [0, 5) \cap N

Figure 1. An example of Gaussian receptive fields with number of fields equal to 5. The input feature

x_{i}

is intersected with overlapping Gaussians to produce a vectorized feature representation

G_{j} (x_{i}), j \in [0, 5) \cap N

3.2. Synaptic Plasticity Models

In this work, we consider two memristive plasticity models: nanocomposite (NC) [28] and poly-p-xylylene (PPX) [29]. These models were proposed to approximate the real-world dependence of synaptic conductance change

Δ w

on the value of the conductance w and on the time difference

Δ t

between presynaptic and postsynaptic spikes and are defined in Eq. 2 and Eq. 3.

Δ w (Δ t) = \{\begin{matrix} A^{+} \cdot w \cdot [1 + tanh (- \frac{Δ t - μ_{+}}{τ_{+}})] if Δ t > 0; \\ A^{-} \cdot w \cdot [1 + tanh (\frac{Δ t - μ_{-}}{τ_{-}})] if Δ t < 0; \end{matrix}

(2)

In 2,

A^{+} = 0.074

A^{-} = - 0.047

μ^{+} = 26.7

ms,

μ^{-} = - 22.3

ms,

τ^{+} = 9.3

ms,

τ^{-} = 10.8

ms.

Δ w (Δ t) = \{\begin{matrix} \frac{| Δ t |}{τ} α^{+} e^{- β^{+} (\frac{w_{max} - w}{w_{max} - w_{min}})} e^{- γ^{+} {(\frac{Δ t}{τ})}^{2}} if Δ t > 0; \\ \frac{| Δ t |}{τ} α^{-} e^{- β^{-} (\frac{w - w_{min}}{w_{max} - w_{min}})} e^{- γ^{-} {(\frac{Δ t}{τ})}^{2}} if Δ t < 0 . \end{matrix}

(3)

Here

τ = 10

ms,

α^{+} = 0.316

α^{-} = 0.011

β^{+} = 2.213

β^{-} = - 5.969

γ^{+} = 0.032

γ^{-} = 0.146

w_{max} = 1

w_{min} = 0

Additionally, we consider a classical additive Spike Timing-Dependent Plasticity (STDP) [30] model to study the impact of sparcity on the memristor-based network relative to the simpler synapse models.

3.3. Spiking Classification Models

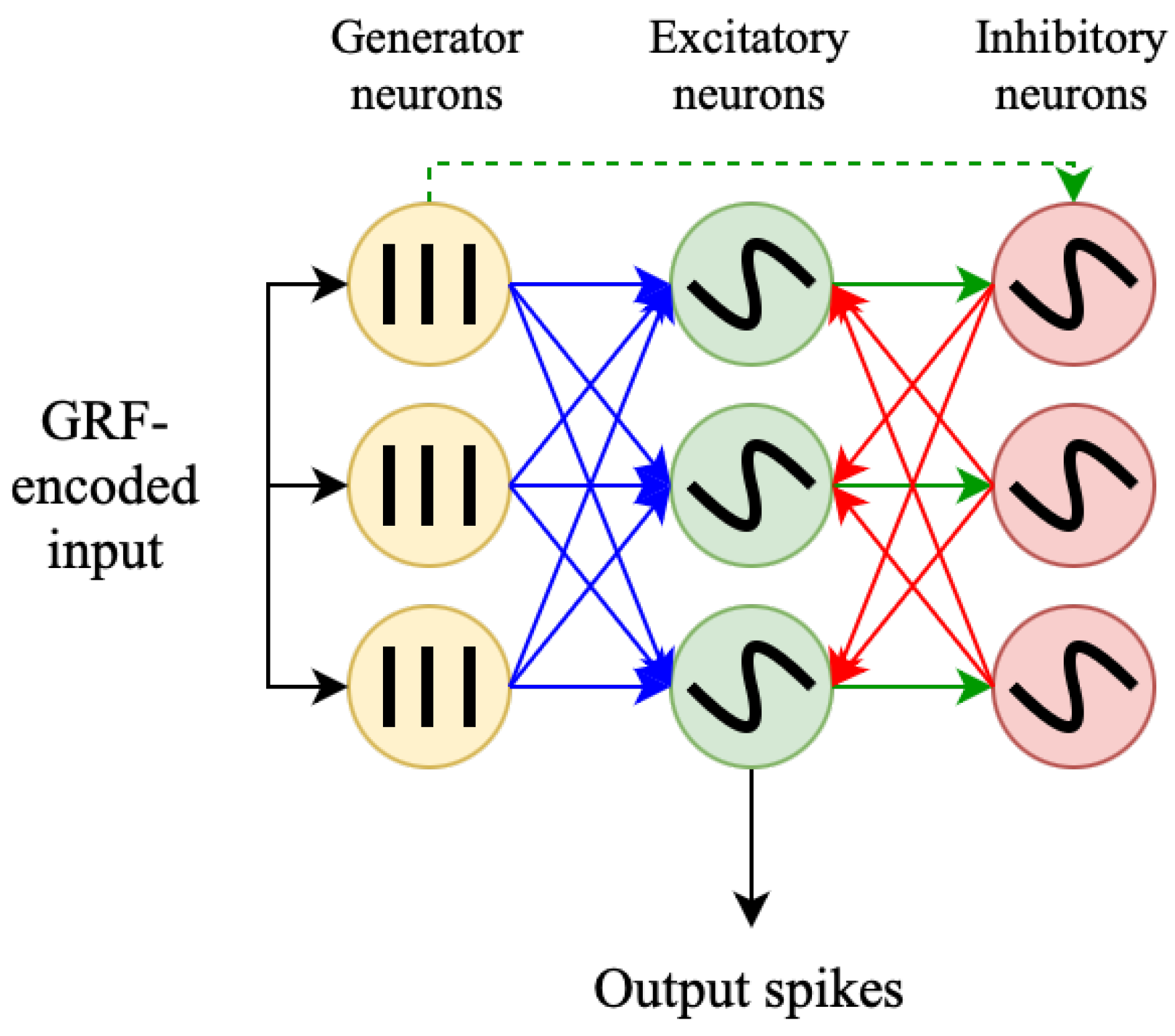
Within the framework of the frequency approach to encoding input data, we considered a hybrid architecture consisting of a three-layer Winner-Takes-All (WTA) network [21] serving as a feature extraction module in combination with a formal classifier.

The WTA network is based on three layers (see Figure 2). The input layer consists of spike generators that convert input vectors into spike sequences according to the algorithm described above. The size of the input layer corresponds to the size of the input vector after preprocessing steps. The generated spike sequences are transmitted to the layer of Leaky Integrate-and-Fire (LIF) neurons with an adaptive threshold (excitatory layer). This layer is connected to the input via trainable weights with one of the previously described plasticities according to the “all-to-all” rule. The number of neurons in the excitatory layer can be optimized depending on the complexity of the problem being solved. In turn, the excitatory layer is connected to the third layer of non-adaptive LIF neurons of the same size, which is called the inhibitory layer. Connections from the excitatory to the inhibitory layer are not trainable and have a fixed positive weight

w_{s y n, e x c} > 0

. In this case, each neuron in the excitatory layer is connected to a single neuron (partner) in the inhibitory layer. The connections directed from the inhibitory layer to the excitatory layer are called inhibitory connections. These connections are static and have weight

w_{s y n, i n h} < 0

. Each neuron in the inhibitory layer is connected to all neurons in the excitatory layer except its partner. Finally, generators in the input layer are also connected to inhibitory neurons by randomly distributed static links with weight

w_{s y n, g e n} > 0

. In all our experiments, the number of such connections is equal to 10% of the number of connections between the input and excitatory layers.

The spiking neural network was implemented using the NEST simulator[31].

We chose logistic regression (LGR) optimized for multi-class problems using the one-versus-all (OVR) scheme as the formal classifier [32].

In this work, we considered two methods for reducing connectivity in the WTA network: an ensemble of several classifiers trained using the bagging technique and sparse connectivity between layers.

3.3.1. Classification Ensemble

The Bagging method was chosen as an ensemble creation technique, in which several identical classifiers are trained on subsets of input data, after which their predictions are aggregated by voting. This method has several advantages compared to using a single larger network, in particular, it reduces the total number of connections within the network and increases the classification speed due to parallelization. In addition, it allows you to break unwanted correlations in the training data set, resulting in improved architecture stability.

Connectivity within an ensemble is controlled using the following parameters:

–: n_estimators: defines the number of models within the ensemble.
–: max_features: determines the proportion of input features that are passed to the input of each of the models in the ensemble.

In addition, the bagging architecture allows you to regulate the number of examples on which each network is trained using the max_samples parameter.

The ensemble was implemented using the BaggingClassifier method of the Scikit-Learn [25] library. In all experiments, based on the preliminary empirical observations the parameters

m a x_f e a t u r e s = 1.0

and

m a x_s a m p l e s = 0.7

were fixed.

3.3.2. Sparse Connectivity

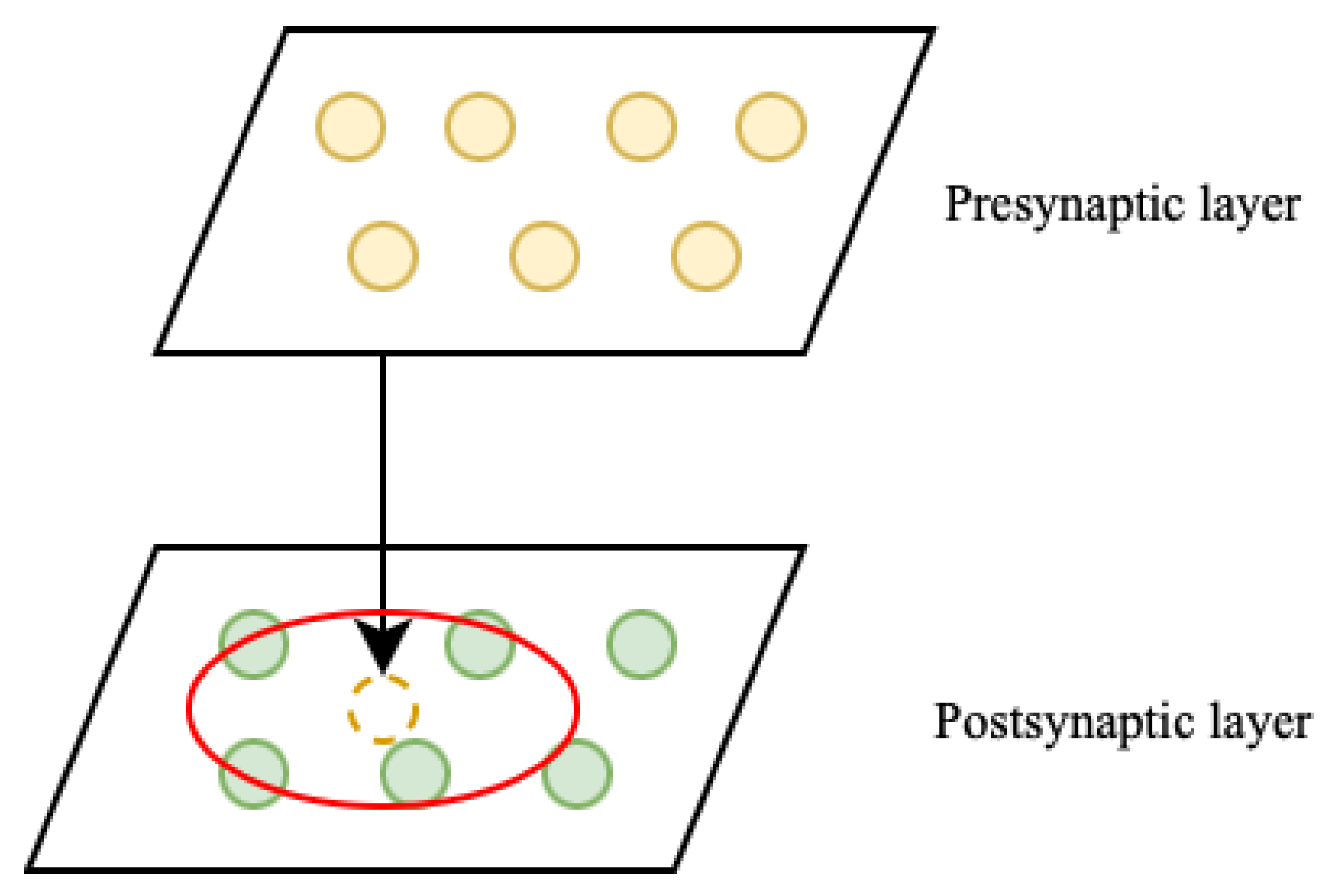
Another way to reduce the connectivity of a spike network is to set a rule that allows you to regulate the number of connections and their organization. To this end, we formally place the neurons of the excitatory and inhibitory layers on two-dimensional square grids of size 1 mm × 1 mm (the dimension was chosen for the convenience of further presentation), oriented mirror-image relative to each other. Neurons on the grids may be arranged irregularly. Initialization of sparse connections occurs according to the following algorithm:

(1): The presynaptic neuron projects onto the plane of the postsynaptic neurons.
(2): The projection of the presynaptic neuron becomes the center of a circular neighborhood, all postsynaptic neurons within which will be connected to this presynaptic neuron with some probability.

This process is shown schematically in Figure 3.

Thus, connectivity within the network is regulated using two parameters:

–: Probability P of connection formation between pre- and postsynaptic neurons.
–: The radius of the circular neighborhood is R. This parameter is defined only for connections between the inhibitory and excitatory layers since neurons in the input layer do not have a spatial structure.

In this work, we regulate the connectivity between the input and excitatory layers using the parameter

P_{g e n_e x c} = 0.4

, as well as between the inhibitory and excitatory layers using the parameters

_{P i n h_e x c} = 0.4

and

R_{i n h_e x c} = 0.9

. The connections between the excitatory and inhibitory, as well as the input and inhibitory layers remain unchanged.

4. Experiments and Results

Experiments on the Digits dataset were conducted using hold-out cross-validation; 20% of training examples were used for testing. On FSDD, a fixed testing data set was used. For all experiments, such parameters as the number of neurons in the networks, the number of receptive fields, and the number of networks in the ensemble were optimized for each plasticity and for each data set by maximizing the training classification accuracy.

In all experiments, the time for submitting one example to the WTA network was 350 ms, followed by a relaxation period of 50 ms; learning took place over one epoch.

As a baseline, we conducted an experiment using the classical WTA network. The parameters for the base WTA network are presented in Table A1.

Additionally, for this and subsequent experiments, we present the number of connections within the network with a breakdown by type of pre- and postsynaptic neurons (see Table 1).

After applying the selected methods for reducing the number of connections in the WTA network, the parameters of the resulting models, which demonstrate the best accuracy, are presented in the Table 2.

The results of experiments of applying different types of reduction methods on the F1-score metric are presented in Table 3.

5. Discussion

Since the number of neurons and connections differs for each plasticity and for each dataset, to evaluate the effectiveness of the connectivity reduction methods, we introduce the connectivity index

κ

defined in Eq. 4:

κ = \frac{N_{s p a r s e}}{N_{b a s e}}

(4)

Here

N_{s p a r s e}

and

N_{b a s e}

are the total number of connections in the sparse network and the equivalent fully connected WTA network, respectively. Based on this definition, the efficiency of the connectivity reduction method can be assessed by calculating the ratio of the classification accuracy to the connectivity index (see Eq. 5, where the efficiency is represented by the index

η

η = \frac{F1_score}{κ}

(5)

The values of connectivity and efficiency indices for different data sets, plasticities and network types are presented in Table 4.

From the table above it follows that in our experiments, the relative efficiency of ensembles of spike networks in comparison with spike networks with sparse connectivity is higher: on average across plasticities and datasets, the efficiency of bagging is 3.0, while the efficiency of the sparse WTA network is on average equal to 1.58. In addition, the average connectivity index

κ

is lower for the Bagging method - 0.34 versus 0.6 for the sparse WTA network.

Despite that, both methods can be effectively used to reduce connectivity depending on the specifics of the problem and the hardware requirements. In the context of on-chip memristive spiking neural networks, the bagging ensemble technique is preferable if there is a strong limitation on the overall network connectivity, especially with regard to plastic synapses. On the other hand, the necessity of orchestrating multiple networks may become a concern. The probabilistic sparse WTA network is simpler in design and can be applied in situations where the connectivity limitations mainly affect inhibitory static synapses.

6. Conclusions

In this work, we have compared two approaches to connectivity reduction in memristive spiking neural networks: the bagging ensemble technique and probabilistic sparse connectivity. Using a three-layer WTA network, we have demonstrated that both methods achieve competitive performance on the handwritten digits and spoken digits classification tasks. On the Digits dataset, the bagging ensemble yields the F1-score of 0.88, 0.92, and 0.91 for the STDP, NC, and PPX plasticity rules, respectively, while the sparse WTA network achieves 0.90, 0.89 and 0.89.

On FSDD the F1-score values lie within the 0.94 – 0.96 range for the ensemble of WTA networks, and within 0.80 – 0.83 interval for the sparse WTA network.

Additionally, by studying the ratio between the proposed connectivity index and the F1-score we show that the bagging ensemble achieves higher efficiency relative to the overall number of connections, while the sparse WTA network effectively reduces the number of inhibitory connections while being significantly simpler in design.

In our future research, we plan to expand the scope of the classification problems that can be solved using the proposed methods, as well as work on hardware implementations of the designed networks.

Author Contributions

Conceptualization, R.R., Y.D., D.V.; methodology, R.R., Y.D. and D.V.; software, Y.D., D.V., A.S.; validation, Y.D., D.V.; formal analysis, A.Sb., V.I.; investigation, R.R., A.Sb., V.I.; resources, R.R.; data curation, A.S.; writing—original draft preparation, Y.D.; writing—review and editing, R.R., A.S.; visualization, Y.D.; supervision, R.R.; project administration, R.R.; funding acquisition, R.R. All authors have read and agreed to the published version of the manuscript.

Funding

The study was supported by a grant from the Russian Science Foundation №21-11-00328, https://rscf.ru/project/21-11-00328/ (accessed 23 November 2023). The bagging ensemble and sparse connectivity model preparation code is available at https://github.com/sag111/Sparse-WTA-SNN (accessed 23 November 2023)

Data Availability Statement

The Digits dataset is publicly available through the Scikit-Learn Python library: https://scikit-learn.org/stable/ (accessed 23 November 2023). The FSDD dataset can be freely obtained from https://github.com/Jakobovski/free-spoken-digit-dataset (accessed 23 November 2023).

Acknowledgments

Computational experiments were carried out using the equipment of the Center for Collective Use "Complex for Modeling and Processing Data of Mega-Class Research Installations" of the National Research Center "Kurchatov Institute", http://ckp.nrcki.ru/ (accessed 23 November 2023).

Conflicts of Interest

The authors declare no conflict of interest. The funding agencies had no role in the design of the study; in the collection, analyses, or interpretation of data; or in the writing of the manuscript.

Abbreviations

The following abbreviations are used in this manuscript:

SNN	Spiking Neural Network
ANN	Artificial Neural Network
STDP	Spike Timing-Dependent Plasticity
NC	Nanocomposite
PPX	Poly-p-xylylene
WTA	Winner-Takes-All
FSDD	Free Spoken Digits Dataset

Appendix A. Experimental Hyperparameters

Here we present the hyperparameters that were used for each of the considered datasets and plasticity models. Only the parameters that differ for spike networks in each experiment are given:

–: norm – input normalization method: L2 or standard scaling (STD);
–: n_fields – number of Gaussian receptive fields (GRF);
–: n_neurons – number of excitatory neurons in the network;
–: n_estimators – number of networks in the bagging ensemble (for the ensemble approach, everywhere else it is equal to 1);
–: $τ_{m, e x c}$ and $τ_{m, i n h}$ – characteristic time of the membrane potential decay for the excitatory and inhibitory neurons in milliseconds;
–: frequency – maximal spiking frequency of the poisson generators;
–: $t_{r e f, e x c}$ and $t_{r e f, i n h}$ – refractory time for the excitatory and inhibitory neurons in milliseconds;
–: $w_{s y n, e x c}$ and $w_{s y n, i n h}$ – synaptic weights of the excitatory-to-inhibitory and inhibitory-to-excitatory connections, respectively.

Table A1. Experimental settings for the base WTA Network.

Dataset	Parameter	STDP	NC	PPX
Digits	norm	L2	STD	STD
Digits	n_fields	5	5	5
Digits	n_neurons	400	400	400
Digits	$τ_{m, e x c}$	130	130	130
Digits	$τ_{m, i n h}$	30	30	30
Digits	frequency	600	350	450
Digits	t $_{r e f, e x c}$	5	4	6
Digits	t $_{r e f, i n h}$	3	3	3
Digits	w $_{s y n, e x c}$	18	20	20
Digits	w $_{s y n, i n h}$	-13	-15	-15
FSDD	norm	L2	STD	L2
FSDD	n_fields	10	10	10
FSDD	n_neurons	400	400	400
FSDD	$τ_{m, e x c}$	130	130	130
FSDD	$τ_{m, i n h}$	30	30	30
FSDD	frequency	800	800	800
FSDD	t $_{r e f, e x c}$	5	4	4
FSDD	t $_{r e f, i n h}$	3	3	3
FSDD	w $_{s y n, e x c}$	20	20	20
FSDD	w $_{s y n, i n h}$	-13	-15	-13

Table A2. Experimental settings for the bagging ensemble of WTA Network.

Dataset	Parameter	STDP	NC	PPX
Digits	norm	STD	STD	STD
Digits	n_fields	7	7	7
Digits	n_neurons	50	50	100
Digits	n_estimators	21	21	5
Digits	$τ_{m, e x c}$	50	50	50
Digits	$τ_{m, i n h}$	60	60	60
Digits	frequency	500	500	500
Digits	t $_{r e f, e x c}$	4	4	4
Digits	t $_{r e f, i n h}$	9	9	9
Digits	w $_{s y n, e x c}$	20	20	20
Digits	w $_{s y n, i n h}$	-15	-15	-15
FSDD	norm	STD	STD	STD
FSDD	n_fields	7	7	7
FSDD	n_neurons	100	100	100
FSDD	n_estimators	11	11	11
FSDD	$τ_{m, e x c}$	130	130	130
FSDD	$τ_{m, i n h}$	30	30	30
FSDD	frequency	550	550	550
FSDD	t $_{r e f, e x c}$	4	4	4
FSDD	t $_{r e f, i n h}$	3	3	3
FSDD	w $_{s y n, e x c}$	13	13	13
FSDD	w $_{s y n, i n h}$	-12	-12	-12

Table A3. Experimental settings for the sparse WTA Network.

Dataset	Parameter	STDP	NC	PPX
Digits	norm	L2	STD	STD
Digits	n_fields	5	5	5
Digits	n_neurons	400	400	400
Digits	$τ_{m, e x c}$	130	130	130
Digits	$τ_{m, i n h}$	30	30	30
Digits	frequency	600	350	450
Digits	t $_{r e f, e x c}$	5	4	6
Digits	t $_{r e f, i n h}$	3	3	3
Digits	w $_{s y n, e x c}$	18	20	20
Digits	w $_{s y n, i n h}$	-13	-15	-15
FSDD	norm	L2	STD	L2
FSDD	n_fields	10	10	10
FSDD	n_neurons	400	400	400
FSDD	$τ_{m, e x c}$	130	130	130
FSDD	$τ_{m, i n h}$	30	30	30
FSDD	frequency	800	800	800
FSDD	t $_{r e f, e x c}$	5	4	4
FSDD	t $_{r e f, i n h}$	3	3	3
FSDD	w $_{s y n, e x c}$	20	20	20
FSDD	w $_{s y n, i n h}$	-13	-15	-13

References

Merolla, P.A.; Arthur, J.V.; Alvarez-Icaza, R.; Cassidy, A.S.; Sawada, J.; Akopyan, F.; Jackson, B.L.; Imam, N.; Guo, C.; Nakamura, Y.; et al. A million spiking-neuron integrated circuit with a scalable communication network and interface. Science 2014, 345, 668–673. [Google Scholar] [CrossRef] [PubMed]
Davies, M.; Srinivasa, N.; Lin, T.H.; Chinya, G.; Cao, Y.; Choday, S.H.; Dimou, G.; Joshi, P.; Imam, N.; Jain, S.; et al. Loihi: A neuromorphic manycore processor with on-chip learning. IEEE Micro 2018, 38, 82–99. [Google Scholar] [CrossRef]
Rajendran, B.; Sebastian, A.; Schmuker, M.; Srinivasa, N.; Eleftheriou, E. Low-Power Neuromorphic Hardware for Signal Processing Applications: A review of architectural and system-level design approaches. IEEE Signal Processing Magazine 2019, 36, 97–110. [Google Scholar] [CrossRef]
Ambrogio, S.; Narayanan, P.; Okazaki, A.; Fasoli, A.; Mackin, C.; Hosokawa, K.; Nomura, A.; Yasuda, T.; Chen, A.; Friz, A.; et al. An analog-AI chip for energy-efficient speech recognition and transcription. Nature 2023, 620, 768–775. [Google Scholar] [CrossRef] [PubMed]
Shvetsov, B.S.; Minnekhanov, A.A.; Emelyanov, A.V.; Ilyasov, A.I.; Grishchenko, Y.V.; Zanaveskin, M.L.; Nesmelov, A.A.; Streltsov, D.R.; Patsaev, T.D.; Vasiliev, A.L.; et al. Parylene-based memristive crossbar structures with multilevel resistive switching for neuromorphic computing. Nanotechnology 2022, 33, 255201. [Google Scholar] [CrossRef] [PubMed]
Matsukatova, A.N.; Iliasov, A.I.; Nikiruy, K.E.; Kukueva, E.V.; Vasiliev, A.L.; Goncharov, B.V.; Sitnikov, A.V.; Zanaveskin, M.L.; Bugaev, A.S.; Demin, V.A.; et al. Convolutional Neural Network Based on Crossbar Arrays of (Co-Fe-B) x (LiNbO3) 100- x Nanocomposite Memristors. Nanomaterials 2022, 12, 3455. [Google Scholar] [CrossRef] [PubMed]
Amiri, M.; Jafari, A.H.; Makkiabadi, B.; Nazari, S. Recognizing intertwined patterns using a network of spiking pattern recognition platforms. Scientific Reports 2022, 12, 19436. [Google Scholar] [CrossRef] [PubMed]
Cohen, G.; Afshar, S.; Tapson, J.; Van Schaik, A. EMNIST: Extending MNIST to handwritten letters. In Proceedings of the 2017 international joint conference on neural networks (IJCNN). IEEE; 2017; pp. 2921–2926. [Google Scholar]
Chen, Y.; Yu, Z.; Fang, W.; Huang, T.; Tian, Y. Pruning of deep spiking neural networks through gradient rewiring. arXiv preprint, arXiv:2105.04916.2021.
LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proceedings of the IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
Krizhevsky, A.; Hinton, G.; et al. Learning multiple layers of features from tiny images 2009.
Nguyen, T.N.; Veeravalli, B.; Fong, X. Connection pruning for deep spiking neural networks with on-chip learning. In Proceedings of the International Conference on Neuromorphic Systems 2021, 2021, 1–8. [Google Scholar]
Lien, H.H.; Chang, T.S. Sparse compressed spiking neural network accelerator for object detection. IEEE Transactions on Circuits and Systems I: Regular Papers 2022, 69, 2060–2069. [Google Scholar] [CrossRef]
Tsai, C.C.; Yang, Y.H.; Lin, H.W.; Wu, B.X.; Chang, E.C.; Liu, H.Y.; Lai, J.S.; Chen, P.Y.; Lin, J.J.; Chang, J.S.; et al. The 2020 embedded deep learning object detection model compression competition for traffic in Asian countries. In Proceedings of the 2020 IEEE International Conference on Multimedia & Expo Workshops (ICMEW). IEEE, 2020, pp. 1–6.
Rathi, N.; Panda, P.; Roy, K. STDP-based pruning of connections and weight quantization in spiking neural networks for energy-efficient recognition. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems 2018, 38, 668–677. [Google Scholar] [CrossRef]
Emery, R.; Yakovlev, A.; Chester, G. Connection-centric network for spiking neural networks. In Proceedings of the 2009 3rd ACM/IEEE International Symposium on Networks-on-Chip. IEEE; 2009; pp. 144–152. [Google Scholar]
Han, B.; Zhao, F.; Zeng, Y.; Pan, W. Adaptive sparse structure development with pruning and regeneration for spiking neural networks. arXiv preprint, arXiv:2211.12219.2022.
Amir, A.; Taba, B.; Berg, D.; Melano, T.; McKinstry, J.; Di Nolfo, C.; Nayak, T.; Andreopoulos, A.; Garreau, G.; Mendoza, M.; et al. A low power, fully event-based gesture recognition system. In Proceedings of the Proceedings of the IEEE conference on computer vision and pattern recognition, 2017, pp. 7243–7252.
Orchard, G.; Jayawant, A.; Cohen, G.K.; Thakor, N. Converting static image datasets to spiking neuromorphic datasets using saccades. Frontiers in neuroscience 2015, 9, 437. [Google Scholar] [CrossRef] [PubMed]
Saunders, D.J.; Patel, D.; Hazan, H.; Siegelmann, H.T.; Kozma, R. Locally connected spiking neural networks for unsupervised feature learning. Neural Networks 2019, 119, 332–340. [Google Scholar] [CrossRef] [PubMed]
Diehl, P.U.; Cook, M. Unsupervised learning of digit recognition using Spike-Timing-Dependent Plasticity. Frontiers in Computational Neuroscience 2015. [Google Scholar] [CrossRef]
Sboev, A.; Vlasov, D.; Rybka, R.; Davydov, Y.; Serenko, A.; Demin, V. Modeling the Dynamics of Spiking Networks with Memristor-Based STDP to Solve Classification Tasks. Mathematics 2021, 9, 3237, 2021. [Google Scholar] [CrossRef]
Sboev, A.; Davydov, Y.; Rybka, R.; Vlasov, D.; Serenko, A. A Comparison of Two Variants of Memristive Plasticity for Solving the Classification Problem of Handwritten Digits Recognition. In Proceedings of the Biologically Inspired Cognitive Architectures Meeting. Springer, 2021, pp. 438–446.
Sboev, A.; Rybka, R.; Vlasov, D.; Serenko, A. Solving a classification task with temporal input encoding by a spiking neural network with memristor-type plasticity in the form of hyperbolic tangent. In Proceedings of the AIP Conference Proceedings. AIP Publishing, 2023, Vol. 2849.
Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. Journal of Machine Learning Research 2011, 12, 2825–2830. [Google Scholar]
Jackson, Z.; Souza, C.; Flaks, J.; Pan, Y.; Nicolas, H.; Thite, A. Jakobovski/free-spoken-digit-dataset: v1.0.8, 2018. [CrossRef]
Aizawa, K.; Nakamura, Y.; Satoh, S. Advances in Multimedia Information Processing-PCM 2004: 5th Pacific Rim Conference on Multimedia, Tokyo, Japan, November 30-December 3, 2004, Proceedings, Part II; Vol. 3332, Springer, 2004.
Demin, V.; Nekhaev, D.; Surazhevsky, I.; Nikiruy, K.; Emelyanov, A.; Nikolaev, S.; Rylkov, V.; Kovalchuk, M. Necessary conditions for STDP-based pattern recognition learning in a memristive spiking neural network. Neural Networks 2021, 134, 64–75. [Google Scholar] [CrossRef] [PubMed]
Minnekhanov, A.A.; Shvetsov, B.S.; Martyshov, M.M.; Nikiruy, K.E.; Kukueva, E.V.; Presnyakov, M.Y.; Forsh, P.A.; Rylkov, V.V.; Erokhin, V.V.; Demin, V.A.; et al. On the resistive switching mechanism of parylene-based memristive devices. Organic Electronics 2019, 74, 89–95. [Google Scholar] [CrossRef]
Song, S.; Miller, K.D.; Abbott, L.F. Competitive Hebbian learning through spike-timing-dependent synaptic plasticity. Nature Neuroscience 2000, 3, 919–926. [Google Scholar] [CrossRef] [PubMed]
Gewaltig, M.O.; Diesmann, M. NEST (Neural Simulation Tool). Scholarpedia 2007, 2, 1430. [Google Scholar] [CrossRef]
Buitinck, L.; Louppe, G.; Blondel, M.; Pedregosa, F.; Mueller, A.; Grisel, O.; Niculae, V.; Prettenhofer, P.; Gramfort, A.; Grobler, J.; et al. API design for machine learning software: experiences from the scikit-learn project. In Proceedings of the ECML PKDD Workshop: Languages for Data Mining and Machine Learning, 2013, pp. 108–122.

1	https://motivnt.ru/neurochip-altai (accessed 23 November 2023)

Figure 2. WTA spiking neural network topology. Poisson generators, adaptive excitatory LIF neurons and inhibitory LIF neurons are shown in yellow, green and red, respectively. Trainable synapses are depicted in blue, excitatory-to-inhibitory connections are shown in green, and inhibitory-to-excitatory connections are denoted in red. Finally, generator-to-inhibitory connections are expressed using a dashed green arrow.

Figure 3. Sparse connectivity: neuron projection. The projection neighborhood is shown in red; all postsynaptic neurons inside it will be connected to the projected presynaptic neuron.

Table 1. Connectivity within the base WTA network.

Connection type	WTA model for Digits	WTA model for FSDD
Gen-to-Exc	128000	120000
Exc-to-Inh	400	400
Inh-to-Exc	159600	159600
Gen-to-Inh	12800	12000

Table 2. Experimental results for the WTA Network.

Reduction type	Connection type	Digits			FSDD
		STDP	NC	PPX	STDP	NC	PPX
Bagging	Gen-to-Exc	470400	470400	224000	231000	231000	231000
	Exc-to-Inh	1050	1050	500	1100	1100	1100
	Inh-to-Exc	51450	51450	49500	108900	108900	108900
	Gen-to-Inh	47040	47040	22400	23100	23100	23100
Sparse Conn.	Gen-to-Exc	51376	51379	51440	231000	231000	231000
	Exc-to-Inh	400	400	400	400	400	400
	Inh-to-Exc	59184	59548	59215	59505	59919	58941
	Gen-to-Inh	12800	12800	12800	12000	12000	12000

Table 3. Experimental results WTA Network.

Reduction type	Digits			FSDD
	STDP	NC	PPX	STDP	NC	PPX
Base (no reduction)	0.84	0.96	0.95	0.90	0.91	0.82
Bagging	0.88	0.92	0.91	0.96	0.93	0.94
Sparse Conn.	0.90	0.89	0.89	0.83	0.83	0.80

Table 4. Efficiency estimation of different sparsity types.

Sparsity	Plasticity	Dataset	$κ$	$η$
Bagging	STDP	Digits	0.35	2.50
Bagging	NC	Digits	0.35	2.61
Bagging	PPX	Digits	0.60	1.52
Bagging	STDP	FSDD	0.25	3.86
Bagging	NC	FSDD	0.25	3.74
Bagging	PPX	FSDD	0.25	3.78
Sparse Conn.	STDP	Digits	0.79	1.14
Sparse Conn.	NC	Digits	0.79	1.13
Sparse Conn.	PPX	Digits	0.79	1.13
Sparse Conn.	STDP	FSDD	0.41	2.02
Sparse Conn.	NC	FSDD	0.41	2.02
Sparse Conn.	PPX	FSDD	0.41	1.96

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer