Preprint
Article
A Distance Based Two-Sample Test of Means Difference for Multivariate Datasets
Altmetrics
Downloads
174
Views
255
Comments
1
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
13 December 2023
Posted:
14 December 2023
You are already at the latest version
Alerts
Abstract
In the paper we present a new test for comparison of the means of multivariate samples with unknown distributions. The test is based on the comparison of the distributions of the distances between the samples’ elements and their means using univariate two-sample Kolmogorov-Smirnov test. The activity of the suggested method is illustrated by numerical analysis of the real-world and simulated data.
Keywords:
Subject: Computer Science and Mathematics - Probability and Statistics
1. Introduction
The problem of comparison of two samples obtained in different measurements appears in a wide range of tasks starting from physical research and ending with social and political studies. The comparison includes the tests of the samples’ distributions and their parameters, and the result of the comparison specifies whether the samples were drawn from the same population or not.
For univariate samples, the problem is solved by different methods: the two-sample Student -test and the Welch -test (both for comparison of the means for normal distributions), the Fisher -test (for comparison of variances for normal distributions), the Wilcoxon rank sum test and the paired permutation test (for comparison of the locations which differ from the means), the Kolmogorov-Smirnov test (comparison of the continuous distributions), the Tukey-Duckworth test (comparison of the samples’ shift), and so on [1].
For multivariate samples, the problem is less studied and was solved for several specific cases. If the samples are drawn from populations with multivariate normal distributions with equivalent variances, then the comparison of the multivariate means is provided by the extension of the Student -test that is the two-sample Hotelling -test [2]. If the variances of the populations are different, then comparison of the multivariate means of the samples can be conducted by the family of the tests, which implement the same extension of the Hotelling statistics [3], or its different versions including the test with missing data [4].
Finally, there exists a small number of methods that address the multivariate two-sample problem in which the samples are drawn from the populations with the unknown or differ from normal distributions. The review of the methods based on the interpoint distances appears in the thesis [5], and of the non-parametric methods – in the thesis [6].
In particular, the mostly applicable Baringhaus-Franz test [7] implements the Euclidean distances between the elements of the samples (inter-sample distances) and the distances between the elements in each sample (intra-sample distances). The resulting statistic is a normalized difference between the sum of the inter-sample distances and the average of the intra-sample distances. Since this statistic is not distribution free, critical values are defined by the bootstrapping techniques [8].
In the paper, we follow the line of using the inter- and intra-sample distances and propose a distribution free test for comparison of the means of multivariate samples with unknown distributions. The proposed test implements the distances between the elements of the samples and the centroid of both samples and the distances between the elements of the samples and their centroids. These distances are considered as random variables, and the test compares distributions of these variables. Acceptance of null hypothesis about the equivalence of the distributions indicates that the populations from which the samples were drawn are equivalent (by equivalence of the means and forms of the distributions) and rejection of the null hypotheses indicates that the samples are drawn from the populations with different means.
Thus, in the proposed test the multivariate data samples are reduced to univariate samples of distances and then the distributions of the univariate samples are compared. If, similar to the Baringhaus-Franz test, the proposed test uses the Euclidian metrics, then the distances are interpreted as deviations of the samples’ elements; however, the choice of the metric function is not crucial and can depend on the nature of the data. Comparison between the distances’ samples is conducted using the standard two-sample Kolmogorov-Smirnov test.
2. Problem Formulation
Let and be two -dimensional samples such that each observation is a random vector , , and each observation , is a random vector , . In the other words, the samples are represented by random matrices
We assume that the numbers and of observations appearing in the considered samples and are equal or at least are rather close. In addition, we assume that for each , the vectors and have equal or at least close spreading parameters.
Denote and the multivariate distributions on the populations and , respectively.
The question is: whether the samples and were drawn from the same population or populations and , from which the samples and were, respectively, drawn, are statistically different.
If populations and are univariate, the samples and are random vectors, and the problem is solved by the standard two-sample tests for different known or arbitrary unknown distributions and . However, for multivariate populations complete analytical solution – the two-sample Hotelling -test [2] – was suggested only for normal and . Together with that, in the last decade were suggested several multivariate two-sample tests [11, 12] based on the multivariate version of the Kolmogorov-Smirnov test [13], but these and similar solutions either implement bootstrapping techniques or have certain limitations. For other directions in considering the problem see, e.g., the work [14] and references herein.
In the paper, we assume that the distributions and are continuous with finite expectations and , respectively, and consider the null hypothesis and alternative hypotheses
From the construction of the test it follows that acceptance of null hypothesis indicates that the populations and have equivalent expectations and rejection of the null hypotheses indicates that these populations are statistically different by the difference of their means.
The test of statistical equivalence of the populations and requires additional test which is conducted after acceptance of the null hypothesis and considers the hypotheses
given . Acceptance of the null hypothesis indicates that the populations and are equivalent, and rejection of this hypothesis indicates that the populations and are different with equivalent expectations.
3. Suggested Solution
The proposed test includes two stages: first, the test reduces the multivariate data to the univariate arrays, and second, it studies these arrays as realizations of certain random variables. For the univariate data the first stage is avoided, and the analysis includes the second stage only.
Let and be independent -dimensional random samples respectively drawn from the populations and with distributions and and finite expectations and . Denote by concatenation of the samples such that if and , then
Expectation of the concatenated sample is
Now we introduce four univariate random vectors which represent the distances between the observations and and the corresponding expectations. The first two vectors
are the vectors of distances between the observations and the expected values of these observations. The third vector is the concatenation of these two vectors and
in which , , and , . Finally, the fourth vector is the vector of distances between the observations and the expectation of the concatenation of the vectors of observations
where , , and , .
It is clear that from the equivalence of the expectations and follows the equivalence of the vectors and and vice versa. Hence, to check the hypothesis that it is enough to check whether the vectors and are statistically equivalent.
Similar to the Baringhaus-Franz test [7], assume that the indicated distances are the Euclidian distances. Then the estimated distances are
where , and are the elements of the multivariate estimated centers of distributions , and , respectively.
For comparison of the vectors and we apply the two-sample Kolmogorov-Smirnov test. Then for the considered vectors and and their empirical distributions and the Kolmogorov-Smirnov statistic
is defined by the difference between the estimated centers of distributions , and .
Note that acceptance of the hypothesis does not indicate the equivalence of the distributions and . To finalize the test and to check the hypothesis (after acceptance of ) we propose to apply the Kolmogorov-Smirnov test and compare the distances vectors and . Here the Kolmogorov-Smirnov statistic
is defined by the difference between the distributions of the vectors and . Acceptance of the hypothesis , together with the accepted hypothesis , indicates that distributions and are statistically equivalent and the samples and were drawn from the same population or two statistically equivalent populations.
4. Examples of Univariate and Bivariate Samples
To clarify the suggested method let us consider two simple examples. We start with the univariate two-sample problem.
Let the samples
of the lengths and be drawn from the population with normal distribution with the expected value (and standard deviation ) and exponential distribution with , respectively. For simplicity, we rounded the values in the samples.
Then the distances vectors are
,
,
,
,
.
The Kolmogorov-Smirnov test with significance level rejects the hypothesis . Thus, it can be concluded that the expectations and are different and the samples and were drawn from different populations or, at least, are significantly shifted.
The same result is obtained by direct comparison of the samples and . The Kolmogorov-Smirnov test with significance level rejects the hypothesis .
Now let both samples
of the lengths and be drawn from the population with normal distribution with the expected value (and standard deviation ).
As expected, the Kolmogorov-Smirnov test with significance level accepts the hypothesis , and then accepts the hypothesis . Thus, it can be concluded that samples and were drawn from the same population, and direct comparison of the samples and confirms this conclusion.
Now let us consider an example of the bivariate two-sample problem. Assume that the samples are represented by the matrices
The first matrix was drawn from normally distributed population with (and standard deviation ) and the second matrix was drawn from exponential distribution with . The mean vectors for these samples are
The values of the samples and their centers are shown in Figure 1.
Then the distances vectors are
,
,
,
.
The Kolmogorov-Smirnov test with significance level rejects the hypothesis . Thus, it can be concluded that the expectations and are different and the samples and were drawn from different populations or, at least, are significantly shifted.
Note that direct comparison of the vectors and results in acceptance of the hypothesis , which, however, does not lead to additional conclusions about the expectations and and about the distributions and .
5. The Algorithm of Two-Sample Test
For convenience, let us formulate the proposed test in the algorithmic form.

Note again that the numbers and of observations in the samples and should be equal or at least rather close, as well as should be equal or at least rather close spreading parameters the vectors and for each .
Application of the squared differences between the samples’ elements and the means leads to certain similarity between the suggested method and the one-way analysis of variance [15] but without crucial requirement of the normal distribution of the samples.
6. Verification of the Method
The suggested method was verified using real-world and simulated data. For verifications, we implemented the algorithm in MATLAB® and used the appropriate functions from its statistical toolbox. The significance level in the two-sample Kolmogorov-Smirnov tests is .
6.1. Trials on the Simulated Data
For the first trials we generated two multivariate samples with different distributions and parameters and then applied the suggested algorithm to these samples. Each sample includes elements. Examples of the simulated bivariate normally distributed samples are shown in Figure 2. In the figure, the samples have different predefined means and different standard deviations. For simplicity here we show the samples with difference in their means only in one dimension; in the other dimension the means are equal to zero.
The results of the tests of these samples by the suggested algorithm are summarized in Table 1.
As it was expected, for the first two samples the test accepted the hypothesis for equivalent expectations and rejected the hypothesis because of different standard deviations. In the next three cases, the test rejected the hypothesis since the expectations were indeed different and because of this difference the hypothesis was also rejected.
In the next trials we compared the activity of the Hotelling -test [2] with the activity of the proposed test. The implementation of the Hotelling -test was downloaded from the MATLAB Central File Exchange [16].
Following the requirement of the Hotelling -test, in the trials, we compared two samples drawn from normally distributed populations with varying standard deviations and the expectations and such that the difference between them changes from zero (equivalent expectations) to the values for which the samples are separated with certainty. Results of the trials are summarized in Table 2.
The obtained results demonstrate that for normally distributed samples the suggested test recognizes the differences between the samples as correct as the Hotelling -test, but as expected, it is less sensitive than the Hotelling -test. Thus, if it is known that the samples were drawn from the populations with normal distributions, then the Hotelling -test is preferable, and if the distributions of the populations are not normal or unknown, then the suggested test can be applied.
For validation of the suggested test on the samples drawn from the populations with not normal distributions it was trialed on several pair of samples with different distributions. For example, in Table 3 we summarized the results of the test on the samples with uniform distributions.
6.2. Trials on the Real-World Data
For additional verification, we applied the suggested algorithm on two widely known datasets. The first is the Iris flower dataset [9], which contains three samples of Iris plant: Iris setosa, Iris versicolour and Iris virginica. The plants are described by numerical parameters: sepal length, sepal width, petal length and petal width. Each sample includes elements.
The sample representing the Iris setosa is linearly separable from the other two samples, the Iris versicolour and the Iris virginica, but these two samples are not linearly separable.
The trial includes six independent two-sample tests. The first three tests consider the samples and compare each of them with each of two others. In these tests it was expected that the suggested method will identify that the samples represent different populations.
The second three tests compared each of the samples with itself. We compared the subsample of the first elements with the subsample of the last elements. In these tests, we certainly expected that the method will identify that the compared parts of the same sample are statistically equivalent.
Results of the tests are summarized in Table 4.
.
As expected, the method correctly identified that the samples representing different types of Iris plants are statistically different. In all comparisons the hypotheses was rejected. Note that the method correctly identified the difference between two linearly non separable samples.
Also, the method correctly identified statistical equivalence of the subsamples taken from the same samples. In these comparisons the methods correctly accepted both the hypothesis and the hypothesis .
The second dataset is the dataset of Swiss banknotes [10], which includes records about genuine and counterfeit banknotes included in the samples and , respectively. Each banknote is characterized by numerical parameters specifying their geometrical sizes.
The suggested test correctly rejected the null hypothesis and separated the records about genuine and counterfeit banknotes with significance level and -value close to zero.
Note that the same result was reported for the two-sample Hoteling test which also rejected the null hypothesis about the equivalence of the samples and separated the records with -value close to zero.
7. Conclusion
The proposed test for comparison of the means of multivariate samples with unknown distributions correctly identifies statistical equivalence and difference between the samples.
Since the test implements the Kolmogorov-Smirnov statistic, it does not require specific distributions of the samples and can be applied to any reasonable data.
In addition, the proposed method, in contrast to the existing tests, does not consider the pairwise relations between all elements of the samples and so it requires less computation power.
The method was verified on simulated and real-world data and in all trials it demonstrated correct results.
Funding
This research has not received any grant from funding agencies in the public, commercial, or non-profit sectors.
Data Availability Statement
The data obtained from open access repositories; the links appear in the references.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Moore D.S., McCabe G.P., Craig B. Introduction to the Practice of Statistics. W. H. Freeman: New York, 2014.
- Hotelling H. The generalization of Student's ratio. Annals of Mathematical Statistics, 1931, 2(3), 360-378. [CrossRef]
- Coombs W.T., Algina J., Oltman D.O. Univariate and multivariate omnibus hypothesis tests selected to control type I error rates when population variances are not necessarily equal. Review of Educational Research, 1996, 66(2), 137-179. [CrossRef]
- Wu Y., Genton M.G., Stefanski L.A. A multivariate two-sample mean test for small sample size and missing data. Biometrics, 2006, 62(3), 877-885. [CrossRef]
- Siluyele I.J. Power Studies of Multivariate Two-Sample Tests of Comparison. MSc Thesis. University of the Western Cape, Cape Town, SA, 2007 .
- Lhéritier, A. Nonparametric Methods for Learning and Detecting Multivariate Statistical Dissimilarity. PhD Thesis. Université Nice Sophia Antipolis, Nice, France, 2015 .
- Baringhaus, L. , Franz C. On a new multivariate two-sample test. J. Multivariate Analysis, 2004, 88, 190–206. [Google Scholar] [CrossRef]
- Efron B. Bootstrap methods: another look at the jackknife. Annals of Statistics, 1979, 7(1), 1-26. [CrossRef]
- Fisher, R.A. The use of multiple measurements in taxonomic problems. Annals of Eugenics, 1936, 7(2), 179-188. The Iris flower dataset was downloaded from the UCI Machine Learning Repository, https://archive.ics.uci.edu/dataset/53/iris (accessed 25 Nov 2023).
- The Two-Sample Hotelling's T-Square Test Statistic. In the course notes Applied Multivariate Statistical Analysis. Eberly College of Science, Pennsylvania State University. The Swiss banknotes dataset was downloaded from the page https://online.stat.psu.edu/stat505/lesson/7/7.1/7.1.15 (accessed 25 Nov 2023).
- Sadhanala, V. , Wang Y.-X., Ramdas A., Tibshirani R.J. A Higher-order Kolmogorov-Smirnov test. In Proc. 22nd Int. Conf. Artificial Intelligence and Statistics (AISTATS), 2019, Naha, Okinawa, Japan, 89, 2621-2630.
- Kesemen O., Tiryaki B.K., Tezel O., Özku E. A new goodness of fit test for multivariate normality. Hacet. J. Math. Stat., 2021, 50(3), 872 – 894. [CrossRef]
- Justel, A. , Peña D., Zamar R. A multivariate Kolmogorov-Smirnov test of goodness of fit. Statistics & Probability Letters, 1997, 35, 251–259. [Google Scholar] [CrossRef]
- Qiu, Z. , Chen J., Zhang J.-T. Two-sample tests for multivariate functional data with applications. Computational Statistics and Data Analysis, 2021, 157, 107160, 1–14. [Google Scholar] [CrossRef]
- Tabachnick B.G., Fidell L.S., Ullman J.D. Using Multivariate Statistics. Pearson Education: London, UK, 20.
- Trujillo-Ortiz, A. Hotelling T2. MATLAB Central File Exchange, https://www.mathworks.com/matlabcentral/fileexchange/2844-hotellingt2 (accessed 25 Nov 2023).
Figure 1.
The bivariate samples and and their centers and .
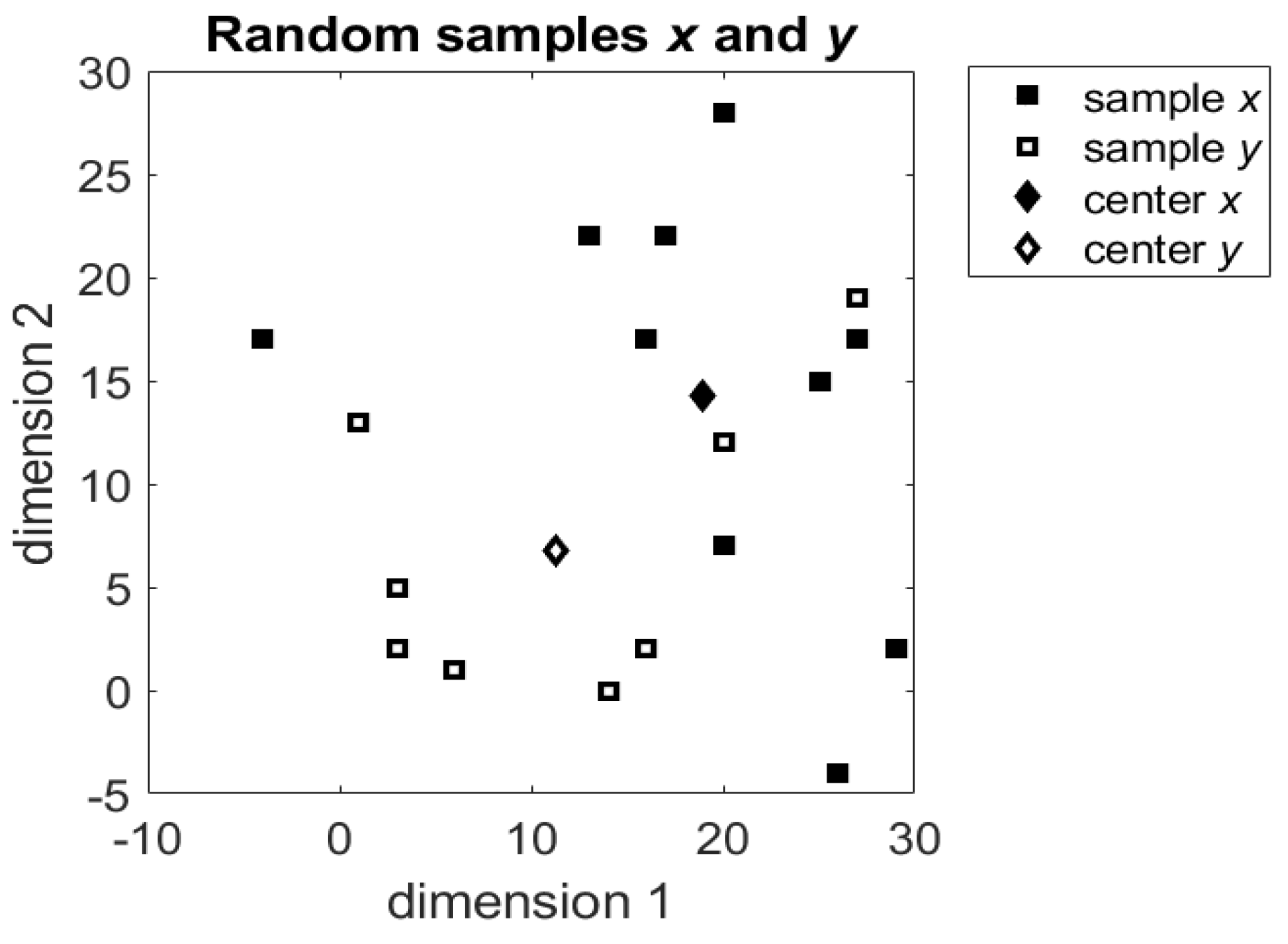
Figure 2.
Randomly generated bivariate normally distributed samples with standard deviations and : (a) expectations ; (b) expectations , ; (c) expectations , ; (d) expectations , and .
Figure 2.
Randomly generated bivariate normally distributed samples with standard deviations and : (a) expectations ; (b) expectations , ; (c) expectations , ; (d) expectations , and .
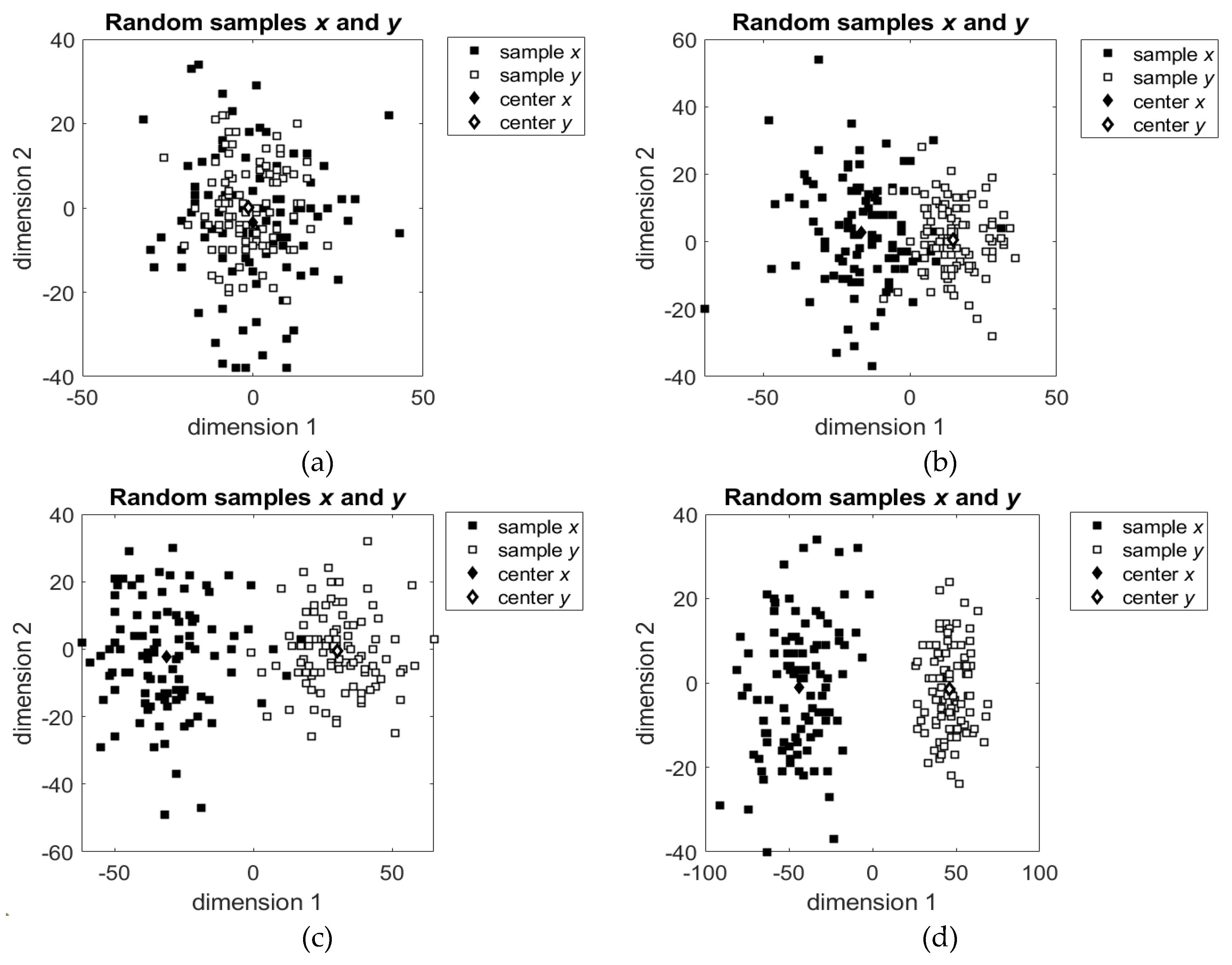
Table 1.
Results of the tests of the illustrative bivariate normally distributed samples with standard deviations and .
Table 1.
Results of the tests of the illustrative bivariate normally distributed samples with standard deviations and .
| Accepted | Rejected | ||
| Rejected | Rejected* | ||
| Rejected | Rejected* | ||
| Rejected | Rejected* |
*Hypothesis was rejected by the rejection of the hypothesis
Table 2.
Results of the Hotelling -test and the suggested test for bivariate normally distributed samples with different expected values and standard deviations.
Table 2.
Results of the Hotelling -test and the suggested test for bivariate normally distributed samples with different expected values and standard deviations.
| test | Suggested test | ||||||
|---|---|---|---|---|---|---|---|
Table 3.
Results of the suggested test for bivariate uniformly distributed samples with different expected values and interval widths.
Table 3.
Results of the suggested test for bivariate uniformly distributed samples with different expected values and interval widths.
Table 4.
Results of the tests of the Iris plant samples.
| Sample | Sample | ||
| Iris setosa | Iris versicolor | Rejected | Rejected* |
| Iris setosa | Iris virginica | Rejected | Rejected* |
| Iris versicolor | Iris virginica | Rejected | Rejected* |
| Iris setosa | Iris setosa | Accepted | Accepted |
| Iris versicolor | Iris versicolor | Accepted | Accepted |
| Iris virginica | Iris virginica | Accepted | Accepted |
*Hypothesis was rejected by the rejection of the hypothesis
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





