Prerpints.org logo
Preprint
Article

Power Transformers Fault Detection with Machine Learning: A Comparison of Classic and autoML Approaches

Altmetrics

Downloads

189

Views

63

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

28 November 2023

Posted:

28 November 2023

You are already at the latest version

Alerts
Abstract
A key component for the proper functioning, availability, and reliability of power grids is the power trans- former. Although these are very reliable assets, the early detection of incipient degradation mechanisms are very important to prevent failures that may shorten their lifetime. In this work a review and comparative analysis, of classical Machine Learning algorithms (such as single and ensemble classification algorithms) and two automatic machine learning classifiers, are presented for the fault diagnosis of power transformers. The goal is to determine whether fully automated ML approaches are worse or better than traditional ML frameworks that require a human in the loop (such as a data scientist) to identify transformer faults from oil-dissolved gases data. The methodology uses a DB compiled from published and proprietary transformer fault samples. Faults data is obtained from the literature, the Duval pentagon method, and user-expert knowledge. The parameters from, either single or ensemble classifiers, were optimized through standard machine learning procedures. The results showed that the best performing algorithm is a robust automatic machine learning classifiers model followed by classical algorithms such as neural networks and stacking ensembles. These results highlight the ability of a robust automatic machine learning model for, handling imbalanced power transformers faults datasets with high accuracy, using the minimum tuning effort by the electrical experts. By providing the most probable transformer fault condition will reduce the time required to find and solve the fault.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Power transformers are key components for the proper functioning of transmission and distribution grids. Although transformers are very reliable assets, the early detection of incipient degradation mechanisms is very important to prevent failures that may shorten their life spawn [1,2]. The life-cycle management of the power transformers is composed of several stages such as transformer specification, erection, commissioning, operation, maintenance, and end of life operations. In particular, for the last two stages, it is of paramount importance to have suitable tools for the assessment of power transformers condition. The economical con- sequences of a power transformer catastrophic failure causes: i. costs for the lost transmission of electricity and ii. direct costs of the power transformer that can vary according to the electrical system, substation topology and technical characteristic of the transformer. For example, consider the case for loss transmission capability due to a transformer failure of a single-phase unit of 230 kV, 33 MVA, located somewhere in Mexico. Then, the economic impact is composed by i. the costs for the loss of transmission which arises up to 6, 177.600 USD (since the cost for loss of transmission is around 2.6 USD/kWh in Mexico), and ii. the direct costs including a 72 hours affectation window (extinguish fires, damaged facilities repairment, soil remediation operations and reserve transformer testing and commissioning, and fitting all the substation and system conditions) with a direct cost around 1, 280, 000 USD. Therefore, grid operators and utilities are in heavy need for tools that allow them to optimize their decision-making processes regarding transformers repairmen, refurbishment, or replacement, under the umbrella of costing, reliability, and safety optimization [3,4].
Condition Assessment (CA) is the process of identifying markers and indexes to, determine and quantify, the degradation level of transformers components [1,5,6]. Power transformers CA strategies includes exhaustive electrical and physicochemical testing, the usage of online and/or offline techniques, the analysis of operation and maintenance parameters, and the use of condition based strategies supported by current standards and expert knowledge. In fact, expert assessment is the most effective, costly, and time consuming CA strategy. It requires taking transformers offline and hiring experts for carrying out the analysis. Thus, utilities are looking forward for more cost-effective CA strategies where few or zero expert intervention is required.
One of the main steps of transformers CA is the identification of faults by a Transformers Fault Diagnosis (TFD) procedure. The TFD focus on the insulation system whose integrity is fully related with transformer reliability [7]. The insulating system is exposed to electrical, mechanical, and thermal stresses. These phenomena are considered to be normal if they were considered by the transformer design characteristics, otherwise they are considered abnormal. Among the abnormal behaviors stand emergency overloading, arc flashes, transient events, thermal faults, to mention a few [8,9]. The transformer insulation system is divided into the insulating fluid (commonly mineral oil) and the solid insulation (kraft paper, pressboard, and other materials). Oil plays a very important role providing a highly reliable insulation, insulation and working as an efficient coolant, removing the heat generated at the core and windings during transformer operation [10]. Further, the insulating oil can provide important information regarding transformer degradation and behavior at a very low cost, eliminating the necessity of carrying out expensive offline testing.
Transformer Insulating oil is a petroleum-derived liquid that can be based on isoparaffinic, naphthenic, naphthenic-aromatic, and aromatic hydrocarbons. No matter its structure, insulating oil can be decomposed by abnormal stresses, producing dissolved byproduct gasses correlated to specific faults. Hence, Dissolved Gas Analysis (DGA) is a widely studied diagnostic technique for which many tools are already available. These are based in the analysis of each byproduct gas, its concentration, and the interrelationship between them. Among the most classical methods to diagnose oil samples stands Rogers ratio, IEC ratio, Dornenburg ratios, Key gas method, Duval Triangles [2,10,11,12,13,14], and Duval Pentagons [3,15], to mention a few. Most of these methods are based on dissolved gas ratio intervals that classify transformers into different faults. However, these are prone to misinterpretations near the fault boundaries [13,14]. Furthermore, classical DGA methods always identify a fault even when there is not, thus, expert assessment is still required to accurately determine if there is a fault or not. On the other side, coarse DGA-based fault classification methods have high accuracy rate but have poor usability, whereas fine TFD can be used for decision-making but its accuracy rate is lower [13]. In general, to decide whether to remove, repair, or replace a transformer in the presence of thermal faults, it is required to determine the fault severity [15], thus, finer TFD is preferred. An important venue for TFD methods is Machine Learning (ML). These data-based algorithms have been proposed to improve TFD performance while avoiding the drawbacks earlier mentioned. ML methods provide high flexibility: are able to handle linear and non-linear relations, are robust to noise, do not necessarily require to take into account the thermodynamics phenomena, and provide high fault diagnosis performance [16]. The ML algorithms that have been used for the TFD endeavor can be divided into supervised and unsupervised approaches. Supervised ML employs different gas-in-oil ratios already diagnosed by experts or chromatography, to build a function that relates these gas ratios with transformers faults or normal/faulty status. Unsupervised employs dissolved gases data to cluster into groups of transformers whose gases ratios are similar to each other. Nevertheless, expert’s diagnosis is always required to assess the performance of the models, thus, this study highlights the supervised approach. Most of the ML works applied to the TFD problem covers one or more of the following steps:
  • ML algorithms: several classifiers have been used such as as Artificial Neural Network (ANN) [1,10,11,13,17], expert-guided ANN [13,18], Bayes Networks [1], Decision Trees (DT) [1,11], Extremme Learning Machine (ELM) [13], K-Nearest Neighbors (KNN) [1,10,11,17], Logical Analysis of Data (LDA) [19], Logistic (LR) and regularized (LASSO) regression [11], Probabilistic Neural Networks (PNN) [10,20], Softmax Regression (SR) [13], Support Vector Machines (SVM) [11,17]; ensembles such as Boosting and Bagging [1], eXtremme Gradient Boosting (XGBoost) [21], Stacked ANN[2]; even state-of-the-art algorithms such as few-shot learning with belief functions [4].
  • Data pre-processing methods: several data transformations have been used such as data binarization [19], key [1,2,4,11,13,20,21] and custom gas ratios [2], logarithmic transformation [1,2,11], mean subtraction, normalization [2], standardization [1,2,11]; imputation of missing values using simple approaches [22]; dimensionality reduction such as Linear Discriminant and Principal Components Analyses [10], and belief functions [4]; feature extraction such as Genetic Programming [17]; knowledge- based transformations such as expert knowledge rules [13] and oil-gas thermodynamics [2].
  • TFD approach: the TFD problem has been posed as a binary classification (normal or faulty trans- former) [1,2,11,21]; as a multi-class classification with coarse [17,19] and fine fault types [2,10,13,20,21], and even diagnosing faults severity [4,10].
  • Classes Imbalance: several strategies have been used for balancing such as bootstrap [17], re-sampling the minority classes [11,13], classes subsetting [11,13], and assigning weight coefficients to the minority class [21].
  • Parameters optimization: algorithm parameters have been optimized by hand [2] and trial-and-error [10]; exact methods such as Grid Search (GS) [11,17] and Mixed Integer Linear Programming [19]; bayesian methods [21]; and metaheuristics such as the Bat algorithm [20], Genetic and Mind Evolutionary algorithms [13].
  • Model overfitting assessment: the problem of overfitting the TFD classifiers has been handled through the usage of classical [1,11,17] and stratified Cross-Validation (s-CV) [21].
  • TFD Performance: algorithms performance has been determined using Accuracy percentage [1,2,4,10,11,13,17,19,20], confusion matrix [2,10,17], the Area Under Receiver Operating Characteristic (ROC) [1,2,11] and Precision-Recall (PR) [21] Curves, and the micro and macro F1-measure [21].
Even while many works have been delved regarding the usage of ML algorithms for the TFD problem, these present one or more shortfalls such as i) training and testing their methods using small datasets, ii) carrying out comparisons using only classical ML supervised algorithms, iii) considering only coarse faults types by setting aside fault severity (not to mention none of the reviewed works considered fault severity as defined by Duval pentagon method), and iv) lack of publicly available data. These issues affect obtaining a clear idea of which sequence of methods and algorithms provides the best performance for the TFD problem, the reproducibility of the research results, and hampering the deployment of ML solutions to solve the TFD problem of real-world utilities.
The construction of high performance ML pipelines, regardless of its application, requires the involvement of data scientists and domain experts. This synergy allows to incorporate domain knowledge into the design of specialized ML pipelines (i.e., the sequence of data pre-processing, domain-driven feature selection and engineering, and optimized ML models for a given problem [23]). However, the construction of specialized ML pipelines using this approach results in a long, expensive, complex, iterative, based on trial and error task. Derived from this analysis (and the related works), it is shown the difficulty of building intelligent models by operational process experts. These power systems experts can be easily overrun by the selection and combination of an ever-growing alternatives of pre-processing methods, ML algorithms, and their parameter optimization, for the solution of the TFD problem. Under these circumstances, the probability of obtaining a final ML pipeline that behaves sub-optimally is higher [23,24]. Hence, there is a growing necessity of providing power systems technicians with ML tools that can be used straightforward into power systems problems (e.g., TFD). In fact, the approaches used for automatically (without human intervention) and simultaneously, obtaining a high performing combination of data pre-processing, learning algorithm(s), and set of hyperparameters, are branded as Automatic Machine Learning (autoML) [24,25]. The autoML is a promising approach that may be used out-of-the-shelf for the TFD problem of real-world industries.
Therefore, in this work a deep comparative analysis of a large supervised ML algorithms pool composed of single, ensemble, and autoML classifiers applied to the TFD problem is presented. The purpose of this deep review is to compare algorithms performance for the TFD problem under the same experimental settings: i) compiling and sharing a Transformers Database (TDb) of the main dissolved gases data of 821 transformers, and their corresponding diagnostic; ii) using single and ensemble ML algorithms, as well as state-of-the-art autoML frameworks, for solving the TFD problem; iii) solving a real-world TFD multi-classification problem using, for the first time (to the best of authors knowledge), Duval Pentagons fault and severity classes [26]. In doing so, this review provides a deeper comprehension of the ML approaches available for the TFD problem, and a view on how much automation can we expect for the TFD problem, particularly when fault severity is taken into consideration.

2. Materials and Methods

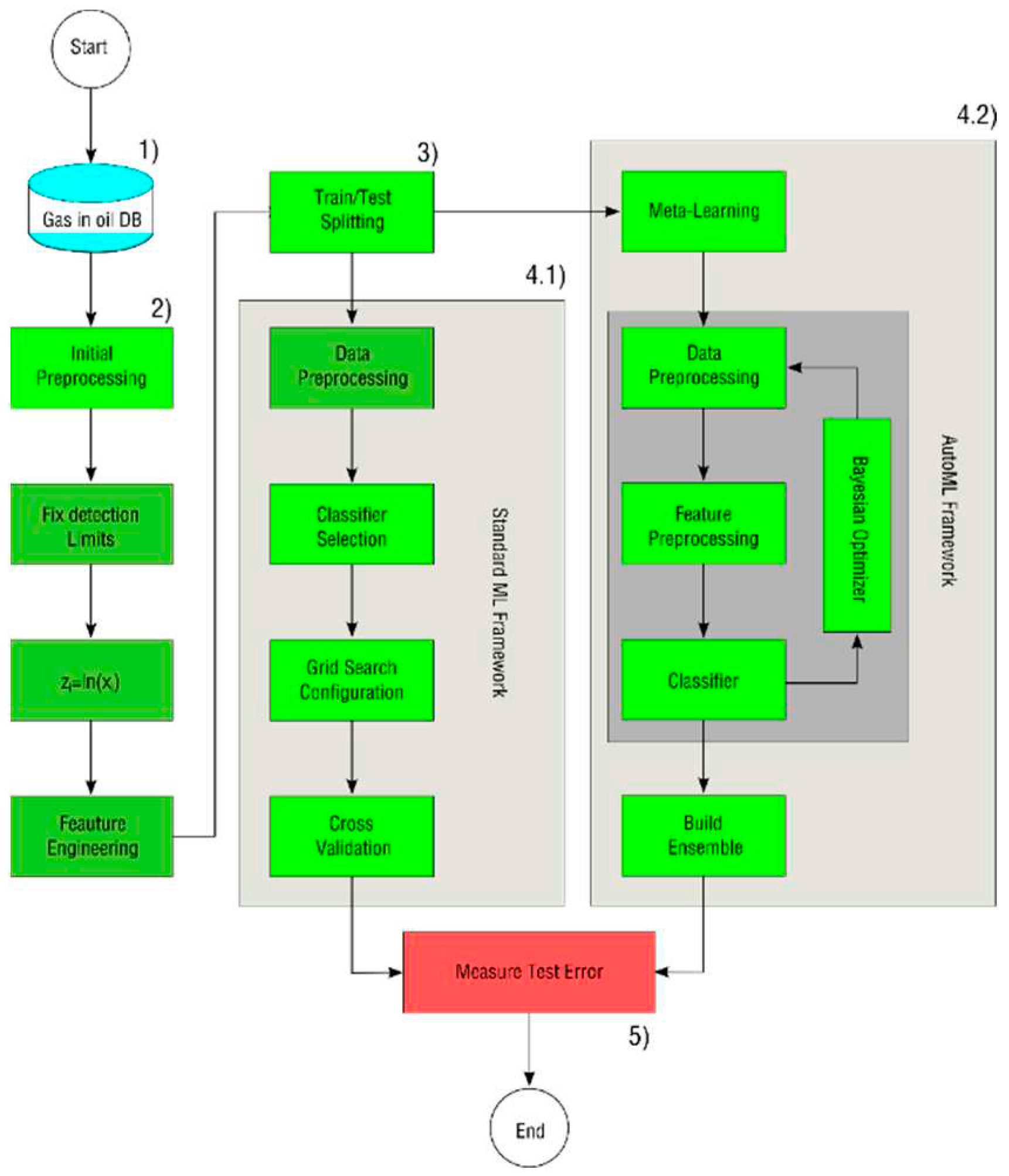
The overall ML system followed by the present work for the multi-class TFD problem is presented in Figure 1. For the purpose of comparison, the pipelines used for single and ensemble classifiers were branded as Standard ML Framework, whereas the pipeline used for autoML was branded as AutoML Framework. In either way, a shared pipeline is specified for both ML approaches. The overall ML system consists of five major sections:
  • Data recollection and labeling, where transformers dissolved gas-in-oil and their corresponding diagnostic were recollected. Diagnostics are double checked, first by the Duval Pentagons method to obtain the fault severity (if not available), then, the IEEE C57.104-2019 standard and expert validation were used for identifying normal operating transformers.
  • Initial pre-processing, where gas-in-oil information were initially pre-processed following several methods studied in the literature, namely the replacement of zero measurements, natural logarithm escalation, and derivation of key gas ratios.
  • Split data into Training (i.e. Xtrain and Ytrain) and Testing (i.e. Xtest and Ytest) datasets. This splitting took into consideration each class proportion for avoiding leaving classes unrepresented in any of the datasets.
  • Train ML system
    • Standard ML framework, where a second data pre-processing stage, training, and parameter optimization was carried out. Parameters from, either single or ensemble classifiers, were optimized through the usage of a Grid Search (GS) and Cross-Validation (CV) procedures.
    • AutoML framework, where a warm-start procedure, additional data and feature pre-processing methods, and classifiers optimization and ensemble construction was carried out automatically.
  • Measuring test error using several multi-class performance measures, where the algorithms are comprehensively evaluated using several multi-class performance measures such as the κ score, balanced accuracy, and the micro and macro F1 − measure.

2.1. DGA Data

A Transformers Database (TDb) comprised by 821 transformers was gathered from different bibliographic sources. These samples were obtained from the specialized literature: a Db from the International Council on Large Electric Systems (CIGRE) Db, a Db from the IEEE [27], technical papers [15,28,29,30,31,32], a CIGRE technical brochure [33], and expert curation. For each transformer were collected the five so-called thermal hydrocarbon gases and, when reported, their corresponding diagnostic. The collected gases are hydrogen (H2), methane (CH4), ethane (C2H6), ethylene (C2H4) and acetylene (C2H2). When available, the associated diagnostic was also recovered from the bibliographic sources. Otherwise, it was obtained by means of an analysis method. In this paper, Duval Pentagons method [15,26] is selected due to the fact that it offers, not only fault types but also the severity for thermal faults. It is important to notice, that in some cases, this analysis method was also used to confirm the literature provided diagnostic.
Duval Pentagons Method [26] first calculates the relative percentage ratios by dividing the concentration of each gas by the Total Gas Content (TGC). Then, the five relative percentage gas ratios are plotted in their corresponding axis in the Duval Pentagon, yielding to a non-regular five-sided polygon. The centroid of the irregular polygon provides the first part of the diagnostic, depending on the pentagon region where this is located. The diagnostic faults available in the first Duval Pentagon are Partial Discharges (PD), low and high energy discharges (D1 and D2 respectively), thermal faults involving temperatures less than 300°C (T1), thermal faults with temperatures ranging from 300 to 700°C (T2), and thermal faults involving temperatures higher than 700°C. There is an additional region in the first Pentagon called Stray Gassing Region (S), which reveals another type of gas generation mechanism. Stray gassing is associated to relative low temperatures, oxygen presence, and the chemical instability of oil molecules caused by a previous hydrogen treatment whose scope is the removal of impurities and undesirable chemical structures in mineral oils. The second part of the Duval Pentagons method allows the user to refine the diagnostic of each gas vector, providing advanced thermal diagnostic options: high temperature thermal faults that occurs in oil only (T3-H), different temperature thermal faults involving paper carbonization (T1-C, T2-C and T3-C), and overheating (T1-O).
However, all the available classical TFD methods (including the Duval Pentagon method) always provide a diagnostic, despite gas concentrations may been too low. In order to avoid those false positives, IEEE C57.104-2019 standard [34] along with expert’s experience were used to tag the corresponding transformers with a normal condition diagnostic. The resulting classes distribution for the available dataset is shown in Table 1.

2.2. Initial Pre-processing of DGA Data

Before any TFD can be carried out, either by the standard ML or the autoML frameworks, the TDb requires to be initially pre-processed. This pre-processing stage consisted of three steps: (i) the replacement of zero measurements; (ii) the scaling of measurement values using the natural logarithm function; and (iii) the derivation of features from dissolved gases ratios. The main reasons for carrying out an initial data pre-processing stage are two-fold. On one hand, data-preprocessing methods does improve the performance of standard ML frameworks for the TFD problem [1,2,4,11,13,20,21]. On the other hand, autoML frameworks have put more attention in the selection of ML models and their HPO, than in the feature engineering (i.e., creation) and data-preprocessing methods [23,35]. Furthermore, the selected autoML algorithm used in this review, does not consider the pre-processing methods used in the proposed pipeline, nor a feature engineering method that can derive dissolved gases ratios from TDb sample measurements.
The initial pre-processing of DGA data is as follows. First, gases measurements whose reported values were zero were considered to be below the limits of detection of the chemical procedure analysis. Thus, for the zero measurements a small constant value was assumed for mathematical convenience (i.e., 1); particularly, for the C2H2 a smaller constant was considered (i.e. 0.1). Second, gases values were scaled using the ln function. This process is generally suggested for scaling features with positively skewed distributions (i.e., heavy-tails), which enable both to improve their normality and for reducing their variances [36]. Third, feature engineering consisting in the estimation of different ratios from transformed gases values were obtained. The relationship between fault types and proportions of dissolved gases in the insulating system have been exploited by traditional DGA methods [7,21,28]. Therefore, several relative ratios based on CH4, C2H6, C2H4, C2H2, and H2 were derived. This are shown in Table 2. In this Table, THC (Total Hydrocarbon Content) stands for the sum of hydrocarbon gas contents, whereas TGC (Total Gas Content) stands for the total amount of dissolved gas contents in the transformer oil.

2.3. Splitting data and Training the ML system

Once data is initially prepared, it is splitted into training and testing datasets. This splitting was carried out taking into consideration classes proportions. Thus, each fault type is represented in both datasets, training (Xtrain, Ytrain) and testing (Xtest, Ytest). The proportions used for splitting the TDb were 70% for training and 30% for testing. Both subsets kept the same classes distribution ratios, as in the full TDb, to assess classifiers performance with imbalanced datasets. Afterwards, the ML systems were trained. Before delving into the details of both ML frameworks i.e., standard and autoML, it is worth to highlight that a second stage of data pre-processing was considered for convenience. This is, to avoid carrying out the same data pre-processing method (i.e., standardization) twice by the autoML approaches.

2.3.1. Standard ML framework

The standard ML framework follows a classical pipeline: i) data pre-processing, ii) selection of the classifier (either single or ensemble), iii) optimize classifiers parameters (using a GS-CV procedure). To complete the data pre-processing treatment, TDb gases measures are standardized by subtracting its mean and scaling values by their variance. Next, a classification algorithm is selected, either a single (ANN, DT, Gaussian Processes (GP), Na¨ıve Bayes (NB), KNN, LR, and SVM) or an ensemble algorithm. The main difference between single and ensemble classifiers is that, the first looks forward to obtain a robust model which attains a good generalization, whereas the second employs several instances of the same classifier. Usually, the classifiers composing the ensemble perform slightly better than a random classifier (e.g., by overfitting), and by using different combining strategies a good generalization is attained. Among the ensemble strategies stand Boosting (Bagging Classifier (BC), Histogram (HGB) and Extreme (XGBoost) Gradient Boosting), Bagging (Random Forest (RF)), and Stacking (SE). The stacked ensemble is a particular case, where two or more strong classifiers are sequentially chained. For this study, a ANN followed by SVM is employed.
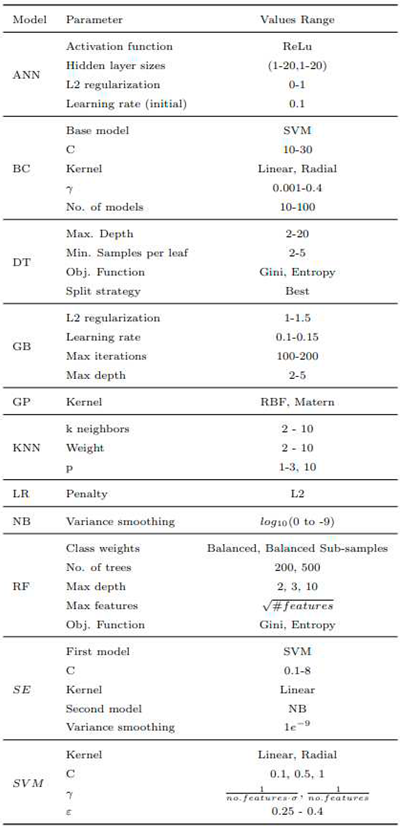
Single and ensemble classifiers have been neatly discussed elsewhere, however, for the sake of completeness, they are briefly detailed in Appendix A.1 and Appendix A.2, respectively. On the other hand, in Table 3 the parameters employed by single and ensemble classifiers are presented. The optimal values are estimated using a grid search cross validation procedure with k = 5 folds.

2.3.2. AutoML Problem and Frameworks

In accordance to [23], an ML pipeline h : X → Y involves the, computational-intensive and repetitive, sequential combination of algorithms that maps any given observation, i.e., x ∈ X, into a discrete (e.g., class) or continuous value, i.e., y ∈ Y.
To define an ML pipeline, i.e., h, lets first define its components. The set of specific algorithms, e.g., data pre-processing, feature selection, and classification, is defined as A = {A1, A2, . . . , An}. For each algorithm Ai, a configuration vector of hyperparameters is defined as λ(i) ∈ ΛA(i). Algorithms of A are connected with each other in accordance to a structure g. Such structure is defined as a Directed Acyclic Graph (DAG) where nodes represent algorithms and edges represent the data flow. The structure has implicit constrains (e.g., an imputation algorithm must precede a classification one), thus, it belongs to a set of valid pipeline structures G; its cardinality (i.e., number of consecutive sequential algorithms) is given by |g|. Therefore, an ML pipeline is formally given by P(g, A, λ) where, g ∈ G stands for the structure of the valid pipeline, the vector A ∈ A|g| stands for the algorithms selected for each node, and the vector λ ∈ ΛA stands for the hyperparameters for each of the selected algorithm in the pipeline.
Therefore, given a problem defined by the i.i.d. samples D = {(x1, y1), . . . , (xm, ym)} drawn from the joint probability distribution P (X, Y), an ML pipeline is created by finding the structure, algorithms, and their corresponding hyperparameters which minimizes the Empirical Pipeline Performance (EPP) R ^ such as:
R ^ P g , A , λ , D = 1 m ∑ i m L ( h ( X i ) , Y i ) ,
where h(xi) is the predicted output of the pipeline P, and L is a loss function. Further, to avoid overfitting P cross-validation is considered. Hence, D is splitted into k disjoint folds, this is {Dvalid(1) , …, Dvalid(k)} and { Dtrain(1) , . . . , Dtrain(k)}. By rewriting Eq. 1 to include these, the final objective function is obtained:
P g , A , λ , €     arg ⁡ m i n g ϵ G , A ∈ A g , λ ∈ ʌ     1 k ∑ i k R ^   P g , A , λ , D t r a i n t   ,   D v a l i d t              
To minimize the cost function presented in Eq. 2, three sub-problems must be addressed altogether: the i) Structure Search, the ii) Algorithms selection, and iii) algorithms HyperParameter Optimization (HPO). On one hand, in a recent survey [23] it was stated that most of the autoML frameworks avoid solving the structure search by following a best practice fixed pipeline structure. This approach removes the burden of determining the graph structure g in Eq. 2. On the other hand, the algorithms selection and its HPO are simultaneously determined by solving the Combined Algorithm Selection and Hyperparameter optimization (CASH) problem [23,24,25]. Solving the CASH problem is similar to solving Eq. 2. If the pipeline structure g is fixed i.e., |g|= 1, the CASH problem is defined as
A , λ * a r g   m i n A ∈ A , ʎ ∈ A R P g , A , λ , D , D            
To simultaneously consider which sequence of algorithms use and their corresponding hyperparameters, λr vector is defined. This allows to map the sequence of algorithms into the Λ configuration space such that
ʌ = ʌ A 1 x   .     .     . ʌ A n x   λ r .                              
In consequence, the CASH minimization problem is stated as
λ * ∈   arg ⁡ m i n R ( p g , λ , D , D ) . λ ∈ ʌ                            
Eq. 4 is a mixed-integer nonlinear optimization problem. Its solution involves finding algorithms numerical or categorical hyperparameters, which are mandatory or conditional (whose value depends on the selection of other hyperparameters) [23].
To solve all of these numerical cruxes, several autoML frameworks based on classical ML and ensembles [23,37], as well as neural networks deep learning frameworks [38], have been proposed. Due to the infancy of the autoML area, recent reviews reveal that most of the available autoML tools obtain competitive, but similar, results across several ml tasks [23,35]. Therefore, we selected the auto-Sklearn algorithm, which is one of the first autoML frameworks, and provides robust and expert-competitive results in several ml tasks [23,25,37]. The auto-Sklearn is an algorithm based upon Python scikit-learn (sklearn) library [39]. It is employed for building classification and regression pipelines searching over classical ML and ensemble models. This algorithm explores semi-fixed structured pipelines by setting an initial fixed set of data cleaning steps. Then, a Sequential Model-based Algorithm Configuration (SMAC) using a Bayesian Optimization in combination with a Random Forest regression, allows the selection and tuning of optional pre-processing and mandatory modeling algorithms. Also, Auto-sklearn provides parallelization features, meta-learning to initialize the optimization procedure, and ensemble learning through the combination of the best pipelines [23,25,37].
To improve the analysis between standard and autoML frameworks, two autoML versions are considered, namely, vanilla auto-Sklearn and robust auto-Sklearn models. The main differences between these two are: i) the vanilla model only considers a single regression model whereas the robust model employs an ensemble, and ii) the vanilla model does not employ the meta-learning warm-start stage to initialize the optimization procedure, whereas the robust model does employ it. In this sense, the vanilla model serves as a baseline for the autoML framework.

2.4. Classification Performance Metrics

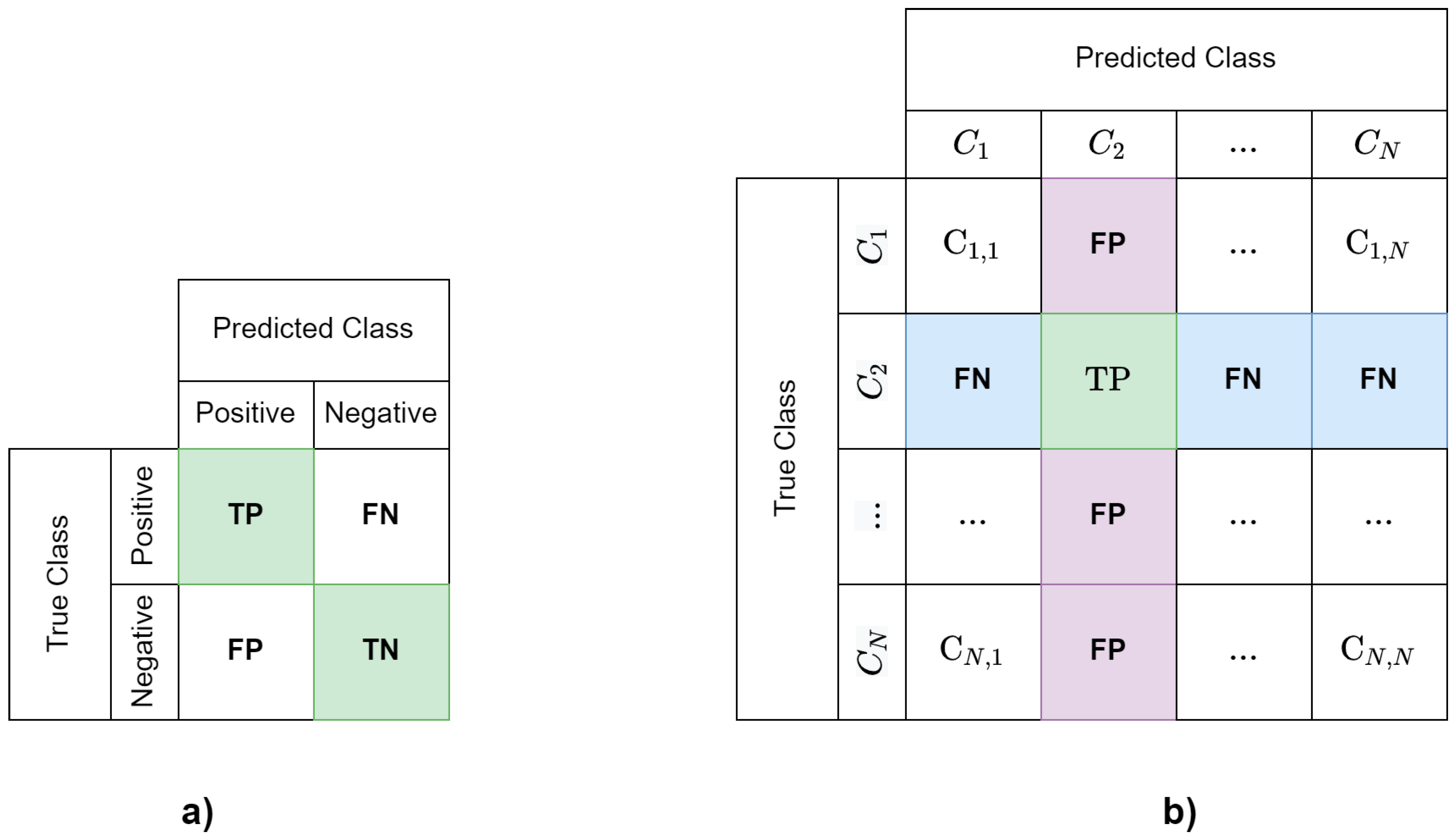
In order to compare the performance of the Standard and the AutoML algorithms, several multi- classification metrics are employed. As mentioned before, several classification metrics have been employed for the analysis of algorithms performance for the TFD problem (i.e., the accuracy percentage, confusion matrix, the Area Under the Receiver Operating Characteristic (AUCROC) and Precision-Recall (AUCPR) Curves, and the micro and macro F1-measure. However, neither the accuracy percentage nor the AUCROC, are sensitive to classes imbalance. Further, neither the AUCROC nor the AUCPR are suitable for analyzing a multi-classification problem. Therefore, in this work the Confusion Matrix (CM), the Balanced Accuracy (BA), the F1-measure (F1) using micro and macro averages, the Cohen’s Kappa (κ) metric, and Matthews Correlation Coefficient (MCC) are employed.
On one hand, the CM is a tool to a understand the errors of classifiers in binary, multi-class, and even multi-label scenarios. On the other, the remaining performance metrics used in this work are obtained from it. The selected metrics are usefulness for assessing the overall performance of a classifier in a multi-class problem. From these, MCC and κ (and in a lower sense, F1-macro) are more robust than the remaining for assessing the expected performance of classifiers in the presence of classes imbalance.

2.5. Software

All the experimentation required for TFD ML algorithms comparison, i.e., pre-processing, training, and testing were conducted using the programming language Python in a Jupyter notebook. Standard Python packages such as numpy [40] and pandas [41] were used for the initial pre-processing stages. For training classical and most of the ensemble ML algorithms, the sklearn [39] package is employed (in the case of xGB the xgboost [42] package is used). For the AutoML case, the autosklearn package is used [25]. The computer notebook is available at a Github repository.
It is worth to note that, while it would be a good idea to use the MCC and κ as a cost function for training the algorithms, due to sklearn package limitations1, algorithms training cost function is restrained to F1-macro.

3. Results

This section presents the TFD classification results obtained for algorithms of both, the standard and the autoML frameworks. For each classifier, five (5) performance metrics are calculated (as described in the above section). Using these metrics, a quantitative comparative analysis is carried out to determine the best algorithm(s). To have a deeper analysis of the performance for the rest of the algorithms, a Multi-Objective Decision Making (MODM) comparison is carried out. Afterwards, classes imbalance, false positives, and false negatives of the best performing algorithm are analyzed through the CM.

3.1. Overall classifiers performance for the TFD problem

In Table 4, the performance of standard and the autoML frameworks results for the five quality metrics are presented. Best performing solutions are highlighted in bold. Observe that, in general, the best performing algorithm is the robust auto-Sklearn model for the five quality metrics. This model outperformed the rest of the algorithms, particularly, for the F1-macro measure where the closest competitors (ANN and SE models) attained approximately 10% lower F1-macro scores. These results show the ability of the robust auto- Sklearn model for handling the imbalanced TDb, providing the highest classification performance among all the tested algorithms, using the minimum tuning effort by the human-in-loop (i.e., electrical experts carrying out a TFD). Therefore, the robust auto-Sklearn model should be preferred for an out-of-the-shelf solution for the TFD problem.
MCC. Therefore, to improve the performance comparison, metric results for each algorithm are transformed using vanilla auto-Sklearn result as a baseline as follows:
N i A = 1 − M i A M i a u t o   S k l e a r n   v a i n i l l a                            
where Mi(A) corresponds to the i metric result for algorithm A, Mi(auto − Sklearn vanilla) corresponds to the i metric result for the vanilla auto-Sklearn model, and Ni(A) corresponds to the baseline transformed value for the i metric and algorithm A. For instance, for BA and ANN the baseline transformed value B˜A(ANN) is obtained such as 1 − B A ( a u t o − S k l e a r n v a n i l l a ) B A ( A N N ) . The transformed values can be interpreted as follows, an Ni(A) > 0 value implies that the performance of A algorithm is better than the vanilla auto- Sklearn algorithm. In contrast, if Ni(A) < 0, then, the A algorithm performance is worse than the vanilla auto-Sklearn algorithm.
Once metric values are transformed, a MODM comparison is carried out. MODM deal with problems where two or more performance criteria are used altogether for taking a decision: in our case, looking forward for the algorithm which is able to identify specific electric transformer faults, as accurate as possible, in terms of five performance metrics. In a MODM, models quality is defined by a n-dimensional vector where n corresponds to the number of metrics used. Hence, an algorithm solving a MODM must consider either, a way to simplify a vector of quality metrics into a single scalar, or a way to handle multiple objective functions all at once.
Regarding the methods that solve a multiple objective functions all stand the Pareto Approach (PA) [43]. In the PA, instead of handling the burden of collapsing multiple metrics into a single value, PA looks forward finding a set of solutions (e.g., TFD classification algorithms) that are non-dominated. To define this concept, is easier first to define the opposite, dominance. A solution si is said to dominate sj iff, si is strictly better than sj in at least one of the quality metrics ci, i = 1, . . . , n, and equal or better in the remaining metrics. Formally, this is i) ∃ci | ci(si) > cj(si) and ii) ∀ci | ci(si) ≥ cj(si) (where ci(si) stands for the quality metric value for solution si) [43]. On the other hand, two solutions si and sj are said to be non-dominating with respect to each other iff: i) quality metric values for solution si are strictly better than sj in at least one of the ci, i = 1, . . . , n, and ii) quality metric values for solution si are strictly worse than sj in at least one of the quality metrics ci, i = 1, . . . , n. 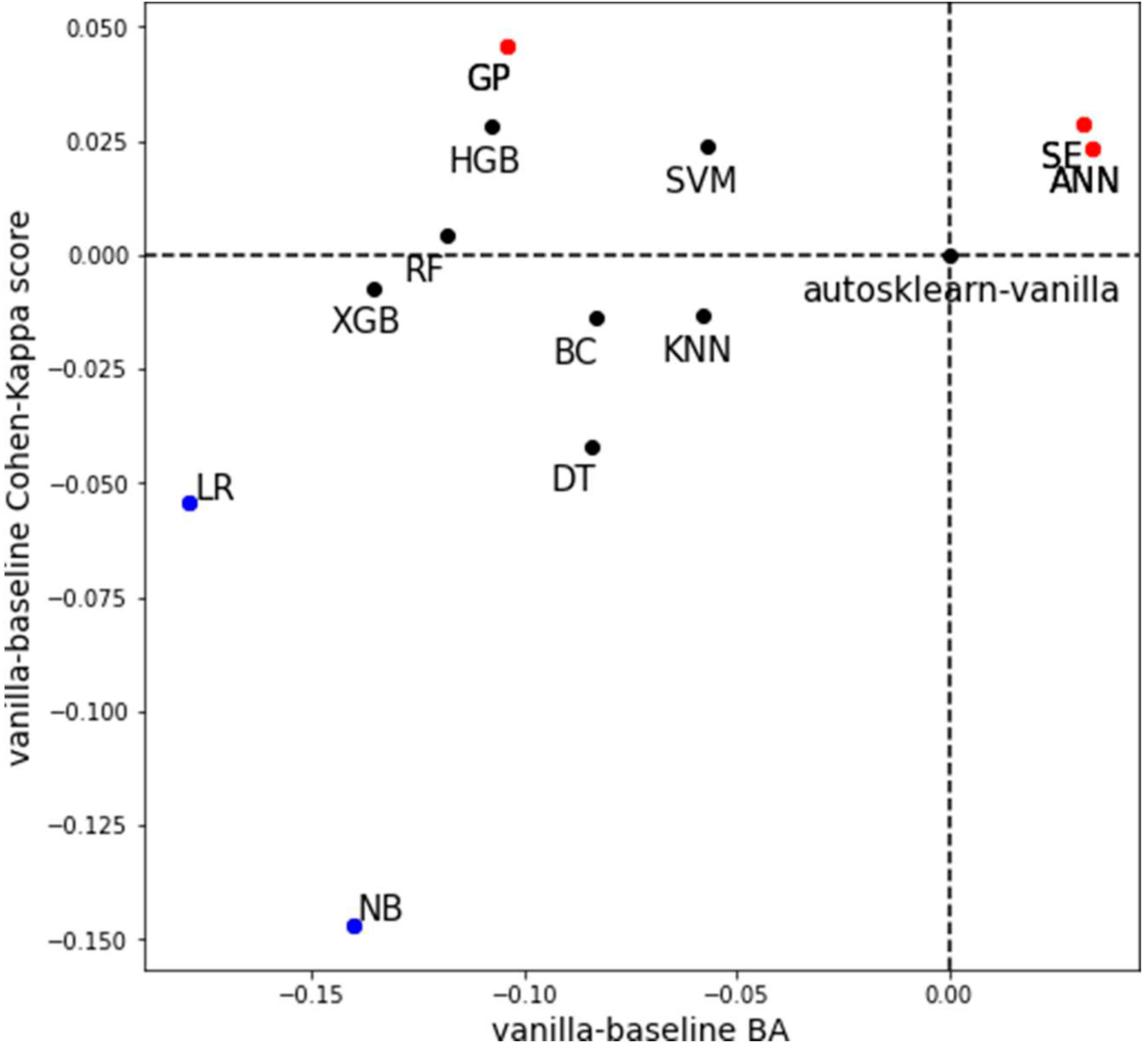The set of non-dominated solutions is also known as the Pareto frontier. In Figure 2 the Pareto analysis carried out on the vanilla transformed quality metrics, excluding the robust auto-Sklearn model, is shown.
Preprints 91627 g002
Figure 2. Models fault classification performance.
Figure 2. Models fault classification performance.
Preprints 91627 g002
Observe that the vanilla auto-Sklearn model is shown at the origin (0,0); algorithms in the pareto frontier are depicted in red, whereas the worst performing algorithms are displayed in blue. From this figure note that the SE, ANN, and GP algorithms performed better than the vanilla auto-Sklearn (for BA the improvements were 3%, 3%, and -10%, respectively, whereas for κ the improvements were 3%, 2%, and 4.5%, respectively). Hence, and without considering the robust auto-Sklearn algorithm, either of these can be selected for the TFD problem. On the other side, HGB and SVM, while performed better for the κ metric than the vanilla auto-Sklearn (3% and 2% respectively), could be considered as good as the vanilla auto-Sklearn model, in a Pareto front sense (and in a lesser sense, the RF case). The remaining algorithms should be considered to perform worse than the vanilla auto-Sklearn model. Specifically, LR and NB algorithms performed considerably worse than the vanilla model: for the BA metric 17% and 14% worse, and for the κ metric 5% and 14%, respectively. In summary, single autoML frameworks provide a good identification of transformers faults with minimal human intervention, still, classical ML approaches such as ANN, SE, or GP classifiers would provide better results for the TFD problem.

3.2. Transformers fault diagnosis in detail

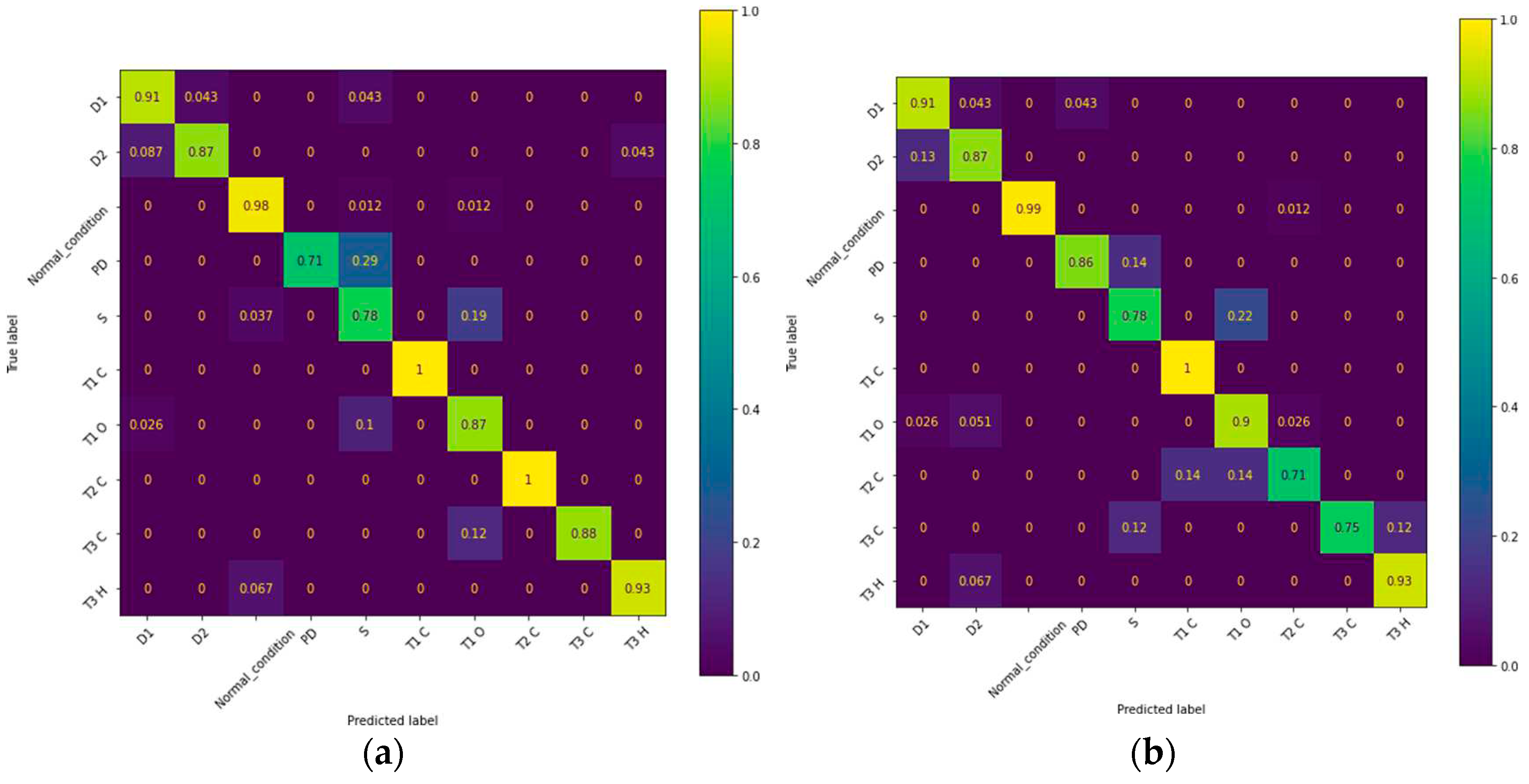
In accordance to the above results, the overall best performing algorithm for the TFD problem is the robust auto-Sklearn algorithm. However, how was its performance for each transformer fault type? and how its performance is compared against one of the algorithms belonging to the Pareto frontier such as the SE algorithm? In Figure 3 confusion matrix for both algorithms are presented: in Figure 3a the robust auto-Sklearn is shown, whereas in Figure 3b the SE is displayed. Observe that, in general, for both algorithms most fault types were identified with a good (≥ 80%) to very good (≥ 90%) accuracy, excepting: in (a) for PD and S with an accuracy of 71% and 78%, respectively; in b) for S, T2-C, and T3-C, with an accuracy of 78%, 71%, and 75%, respectively. To examine the regular performance on these fault types it is useful to recall that when analyzing the performance of an algorithm using the multi-class CM (see section Appendix B.1), rows indicate FN and columns indicate FP, respectively. Thus, for the case of the robust auto-Sklearn algorithm, PD faults were misclassified 29% of the times as S fault types; S faults were misclassified 19% of the times as T1-O fault and 3.7% as Normal condition. For the case of the SE algorithm, S faults are misclassified 22% times as a T1-O faults; T2-C faults are misclassified 14% of the times as T1-O and T1-C each; T3-C faults are misclassified 12% of the times as T3-H and S each. From all of these errors, the robust auto-Sklearn algorithm incurs in the most expensive ones (i.e., classifying a fault as a normal condition). Further, the misclassification from both algorithms can be attributed to the fault regions described by these for each fault type. These do not necessarily match the Duval pentagon fault regions, which are geometrically contiguous and do not overlap [15]. In addition, recall that all of these classes, i.e., PD, S, T2-C, and T3-C, are under represented in the DB (see Table 1). In the light of these, we can conclude that samples misclassified may lay at the classes limits, and/or class boundaries found by the algorithms have a different geometric shape that the one defined by the Duval pentagon. Therefore, increasing the sample size of imbalanced classes (either real or synthetic samples) should be useful for improving the boundaries defined in the feature space for each class by both algorithms. Finally, it is worth to note that both algorithms classified with 100% of accuracy the low thermal faults involving paper carbonization (i.e., T1-C), which is the most under represented class in the DB.

3. Conclusions

This paper presents a review and comparative analysis, of classical Machine Learning algorithms (such as single and ensemble classification algorithms) and two automatic machine learning classifiers for the fault diagnosis of power transformers. The purpose of this work is to compare under the same experimental settings the performance of classical ML classification algorithms, that requires a human-in-the-loop expert for tuning these, and two autoML approaches which requires almost zero human operation. For such purposes, transformers faults data was gathered from literature and Mexican and foreign utilities and test laboratories databases. Then, raw data was curated, specifically faults were validated and assigned using both the Duval pentagon method and expert knowledge. The methodology used for comparison included: i) several pre-processing steps for feature engineering and data normalization; ii) different ML approaches (single ML and ensemble algorithms were trained and tuned using a GS-CV by a data scientist, whereas, the autoML models were trained and tuned using a bayesian optimization in combination with a Random Forest regression with zero human intervention); iii) several algorithms performance approaches using global metrics, a pareto front analysis, and a CM to have a detailed looked into the type of biases algorithms suffer. A key contribution of this work is that it defines for the first time (to the best of authors knowledge), fault classes using Duval Pentagons and severity classes.
Preprints 91627 g003
Figure 2. Confusion matrix for the (a) robust auto-Sklearn model and (b) for the stacking ensemble algorithms.
Figure 2. Confusion matrix for the (a) robust auto-Sklearn model and (b) for the stacking ensemble algorithms.
Preprints 91627 g003
Results showed that the robust auto-Sklearn achieved the best global performance metrics over either single or ensemble ML algorithms. On the other side, the PA showed that the vanilla autoML approach performed worse than some single (ANN, SVM) and ensemble (SE, HGB, GP, and RF) ML algorithms. Even the CM revealed that, while the robust auto- Sklearn algorithm obtained the highest global performance metric values, it misclassifies some TF as a normal condition. This type of error can have a very negative impact in power grid performance (blackouts) with high economical costs. Nevertheless, the misclassification can be attributed to the imbalanced BD. Increasing the sample size of the imbalanced classes (either real or synthetic samples) should be useful for improving the boundaries defined in the feature space for each class. In conclusion, the robust auto-Sklearn model is not only a good out-of-the-shelf solution for the TFD while handling imbalanced datasets, but also achieved the highest global classification performance scores using the minimum tuning effort by a human (i.e., electrical experts carrying out a fault diagnosis). As future work, this model will be incorporated into a power transformer condition assessment of a maintenance management system. It is expected that, failure classification indicating the most probable defect will be used to help engineers to reduce the time needed to find and repair incipient faults, avoiding catastrophic failures and fires.

Funding

This research received no external funding.

Acknowledgments

The authors would like to thank Dr. Liñan from Instituto Nacional de Electricidad y Energías Limpias for his comments and reviews.

Conflicts of Interest

The author G.S.B. wants to clarify that the presented work is all his own opinion and research lines, and not necessarily the opinion of BBVA Mexico.

Appendix A. Machine Learning algorithms.

Appendix A.1. Single classifiers

Appendix A.1.1. Artificial neural networks

Artificial Neural Networks (ANN) are models inspired by the central nervous system, which are made of interconnected neurons [44]. The calculation of a single layer perceptron is performed by the following equation:
y ˆ X = g ∑ i = 1 n ( w i x i ) + b i a s
Where g is the activation function. Most artificial neural networks are composed of three types of layers of neurons: an input layer, one or more hidden layers and an output layer. These are called Multilayer Perceptrons (MLPs). The input layer is responsible for receiving a given input vector and transform into an output that becomes the input for another layer. Hidden layers transforms the output from a previous layer by means of an activation function. Output layer makes the final weighted sum.
y ˆ X = g ∑ i = 1 n w i x i + b i a s

Appendix A.1.2. Decision trees

A decision tree is a classification method which creates a recursive partition of the data set [45]. It consists of nodes that builds a tree, which has a node called ”root” that has no incoming connections, and a set of nodes that have exactly one incoming connection. Nodes with outgoing connections are called internal nodes and all other nodes (except the root node) are called leaves or decision nodes. Each internal node splits the dataset into two or more sub-datasets using certain a condition or criteria of the input variables.
The objective is to construct the following classifier:
Y X = ∑ i = 1 n Y i x l i X

Appendix A.1.3. Gaussian processes

The Gaussian process classifier is a classification method that assumes the class densities follows a normal distribution [46]. A Gaussian process, is a generalization of multivariate Gaussian distribution of infinite random variables.
A multivariate Gaussian distribution is defined by the following equation:
N x ; µ , ∑ = 1 2 π d 2 ∑ − 1 2 e x p − 1 2 x − µ ∑ − 1   x − µ T
Where x is the vector of random variables, µ is the vector of means, and Σ is the covariance matrix of all random variables.
A Gaussian process is a random process in which any point t ∈ Rd is assigned to a random variable Zt such that every (Zt1 , Zt2 ,...,Ztd) is a multivariate Gaussian.

Appendix A.1.4. K-nearest neighbor

K Nearest Neighbors (KNN) is one of the most basic and essential classification algorithms in Machine Learning [47]. It belongs to the domain of supervised learning and finds intense application in pattern recognition, data mining, and intrusion detection. The KNN classifier is also an instance-based, non- parametric learning algorithm. Instance-based learning means that our algorithm does not explicitly learn a model. Instead, he chooses to memorize the training instances that are later used as ”knowledge” for the prediction phase. Specifically, this means that only when a query is made to our database, that is, when we ask it to predict a label with an input, the algorithm will use the training instances to give an answer.
The KNN algorithm assumes that pairs (X1, Y1), (X2, Y2) . . . (Xn, Yn) takes values in the coordinate space Rd, where Xn ∈ Rd and Yn is the label of the element Xn. Then, to perform a classification y of a new point x ∈ Rd, the KNN uses some distance measure ∥·∥ in Rd such that the dataset of pairs (X(1), Y(1)), (X(2), Y(2)) . . . (X(n), Y(n)) is reordered given that ∥X(1) − x∥ ≤ ∥X(2) − x∥ . . . ∥X(n) − x∥. The class y is assigned given the maximum probability of the Y(1) . . . Y(K) estimated, where K is the number of neighbors selected to make the classification.

Appendix A.1.5. Naıve Bayes

In simple terms, it assumes that the presence or absence of a particular characteristic is not related to the presence or absence of any other characteristic, given the variable class [48]. For example, a fruit can be considered an apple if it is red, round, and about 7 cm in diameter. A Naive Bayes classifier considers that each of these characteristics contributes independently to the probability that this fruit is an apple, regardless of the presence or absence of the other characteristics. This method is based on the Bayes theorem, which is described as follows:
P A R = P R A P ( A ) P ( R )
Naive Bayes method assumes that the probability of all variables is constant, so the Bayes theorem can be rewritten as follows:
P A R = P R . ∏ i = 1 n P R A

Appendix A.1.6. Logistic regression

Regression analysis determines how a variable y is related to one or more, other variables X = x1, x2, ..., xk. In logistic regression [49], the yis are considered binary variables and the distribution of yi given X is assumed to follow a Bernoulli distribution (which is a special case of a binomial distribution) such that:
l o g p y i = 1 X 1 − p y i = 1 X = β 0 + ∑ j = 1 k β j X j i
Of the several methods to estimates the βs, the method of maximum likelihood is one most commonly used for logistic regression.

Appendix A.1.7. Support vector machines

Support Vector Machines (SVM) are supervised learning models used for data prediction and classification [50]. This method was first presented by [51] in 1998. Even though SVM are commonly used for classification problems where training data is linearly separable, nonlinear data can be mapped into a high dimensional feature space, with help of a kernel function where linear regression can be applied (The hyperplane). The method builds two bounds with radius epsilon (ϵ) parallel to the hyperplane that covers the most quantity of data, where ϵ defines a margin of tolerance where no penalty is given to errors and ϵ is the distance between data not covered by support vectors and bounds [52]. By minimizing the following expression:
y = m a x 2 w
Subject to:
w . x + b   ≥ 1 , ⩝ x = C 1
w . x + b   ≥ − 1 , ⩝ x = C 2

Appendix A.2. Ensembles

Ensemble methods are algorithms that improves accuracy by joining/merging 2 or more simpler algorithms. Basically, there are two kinds of Ensemble algorithms: sequential and parallel. Sequential ensemble algorithms have the characteristic to maintain dependence across the different models generated. On the other hand, parallel ensemble algorithms look for independence among the different models.

Appendix A.2.1. Random forest

Random forest is a parallel type ensemble algorithm [53]. A random forest, is a combination of decision trees so that each tree analyzes on a random segment of the data with the same distribution for each of them. The essential idea is to average many noisy but approximately unbiased models, and thereby reduce variance.

Appendix A.2.2. Bagging classifier

Bagging classifier is a parallel ensemble algorithm. This algorithm is very similar to the random forest [54]. It takes several samples of the data with the same distribution to train different models using a variety of methods. The final classifier makes a prediction by combining the predictions of all other models.

Appendix A.2.3. Gradient boosting

Gradient boosting is a sequential ensemble algorithm [55]. Gradient boosting has two important characteristics: weak models and a differentiable loss function. This algorithm uses weak models as an optimization parameter and it decides to add or remove models depending on the gradient value of the loss function.

Appendix A.2.4. Stacking ensemble

Stacking ensemble is a sequential algorithm [56]. It uses a meta learning algorithm to learn how to best combine the predictions of two or more basic machine learning algorithms. The predictions of the basic machine learning algorithms are used to create a second training set. This second training set is used to train the meta learning algorithm.

Appendix B. Performance Measures

Appendix B.1. Confusion matrix

A Confusion Matrix (CM) is employed to assess a classifiers performance by comparing predictions against true class labels. From it, several performance measurements can be obtained [57,58,59]. Most of CM derived performance metrics were devised for binary classification problems, and only a few are available for a multi-class problem [59].
The confusion matrix for the binary and the multi-class problems are presented in Figure B.1. The TP stands for True Positive, FP stands for False Positive, TN stands for True Negative, and FN stands for False Negative. Thus, columns represent classifiers predictions whereas rows represent the true class. Thus, the CM element at row i and column j (i.e., Ci,j) provides the frequency of the predicted class j for the actual class i.
In the case of a binary classification problem, the CM is given by a 2 × 2 matrix. In the case of multi-class problem, the matrix is given by the N different class labels ci|i = 1, 2, . . . , N , thus, the CM is of size N × N.
Preprints 91627 g0a1
Figure B.1. On (a) the CM for a binary classification problem, on (b) the CM for a multi-classification problem. TP stands for True Positive, TN stands for True Negative, FP stands for False Positive, and FN stands for False Negative. Observe that in the multi-class case, only C2 is being shown.
Figure B.1. On (a) the CM for a binary classification problem, on (b) the CM for a multi-classification problem. TP stands for True Positive, TN stands for True Negative, FP stands for False Positive, and FN stands for False Negative. Observe that in the multi-class case, only C2 is being shown.
Preprints 91627 g0a1

Appendix B.2. Precision and Recall

Two performance measures obtained from the confusion matrix of a binary classification problem, namely Precision (Prec) and Recall (Rec):
P r e c = T P T P + F P
R e c = T P T P + F N
Loosely speaking, Precision quantifies a classifier discrimination ability for separating between the classes, whereas Recall quantifies a classifier ability of identifying the samples of a given class in the data set.

Appendix B.2.1. Micro and Macro averages for Multi-class

To use these metrics in a multi-classification problem, one must choses from macro or micro averaging. In the case of the former, the metric is calculated for each class and then averaged (i.e., treating all classes equally). In the case of the latter, the contribution of each class is aggregated before computing the average metric, putting more weight on the most populous classes. Formally, if we define Preci and Reci as the precision and recall obtained for class i ∈ N , respectively. Then, the macro and micro Prec and Rec are defined as follows
    P r e c m a c r o = 1 N ∑ i = 1 N P r e c i  
R e c m a c r o = 1 N ∑ i = 1 N R e c i
    P r e c m i c r o = ∑ i = 1 N   T P i   ∑ i = 1 N     T P i + F P i
    R e c m i c r o = ∑ i = 1 N   T P i   ∑ i = 1 N     T P i + F N i
where N is the number of available classes.

Appendix B.3. Balanced Accuracy

BA is one of the most common multi-class performance measure used when classes imbalance is present. It is obtained as follows:
B A = 1 N ∑ i = 1 N R e c i ,      
where Reci stands for the recall obtained for class i ∈ N . Hence, the BA is the same as the Recmacro [58]. This function takes values between BA ∈ [0, 1] where a perfect classifier attains an BA = 1 while a BA = 0 is obtained by a classifier always predicting the wrong class.

Appendix B.4. F-1 Measure

Other metric obtained from the Eqs. B.1 and B.2 is the F1 score. It assesses a model performance using the harmonic mean of the Precision and Recall measures. As in the case of Prec and Rec, in the multi-class setting is obtained by macro or micro averaging. Thus, the F1 score for both averaging approaches is defined as follows:
F 1 m a c r o = 2 . R e c m a c r o . P r e c m a c r o R e c m a c r o . P r e c m a c r o
F 1 m i c r o = 2 . R e c m i c r o . P r e c m i c r o R e c m i c r o . P r e c m i c r o
In both cases, the F1 function takes values between F1 ∈ [0, 1]. More specifically, in the case of Eq. B.8, high values indicate that the algorithm has good performance on all the classes, whereas low values indicate that all classes were predicted poorly. In contrast, the Eq. B.9 gives more importance to populous classes, neglecting errors in classes with few samples [58]. Consequently, F1macro is a better metric than F1micro for assessing the performance of classifiers in the presence of classes imbalance.

Appendix B.5. Matthews Correlation Coefficient

A more recent metric, which is robuster to classes imbalance is MCC. This can be formally defined as
M C C = c x s − ∑ i = 1 N p i x t i s 2 − ∑ i = 1 N p i 2 s 2 − ∑ i = 1 N t i 2
where c = ΣN i=1 TPi corresponds to the TP for class i, s is the total number of samples, pi = TPi +FPi is the sum of times the classifier predicted class i (either correctly or incorrectly classified), and ti = TPi +FNi is the total number of samples class i appears in the dataset.
MCC values ranged from MCC ∈ [−1, 1]. For higher positive values (MCC ≈ 1), the MCC indicates a strong positive correlation between predictions and the true Labels. On the contrary, large negative values (MCC < 0) indicate that the classifier does identify the classes but systematically predict them wrong (rather as consequence of an implementation problem). If the classifier is randomly guessing there will be no correlation between predictions and true labels, hence, the MCC is (≈ 0). Another virtue of MCC is that is sensitive to classes imbalance, hence, good for measuring a classifier performance when such feature is present in the dataset [58].

Appendix B.6. Cohen’s Kappa

The last performance measure is κ. This metric was initially devised as statistical hypothesis test for quantifying the level of agreement between two raters on a nominal scale [58,60]. This metric has been extended for binary and multi classification problems. In the case of the latter, the κ function is defined as follows
K = c x s − ∑ i = 1 N p i x t i s 2 − ∑ i = 1 N p i x t i
where, similar to the MCC metric, c = ∑ i = 1 N T P i corresponds to the TP for class i, s is the total number of samples, pi = TPi + FPi is the sum of times the classifier predicted class i (either correctly or incorrectly classified), and ti = TPi + FNi is the total number of samples class i appears in the dataset. Thus, both the MCC and the κ are highly related, providing slightly larger values for κ in comparison to the MCC. Cohen’s Kappa values ranges from κ ∈ [−1, 1], where a κ = 1 points out a perfect agreement between classifier predictions and true labels, a κ = 0 points out a random agreement attained due to the independence between predictions and the actual labels, and κ < 0 points out that the classifier is performing worse than a random classifier. Some key advantages of κ are, i) it measures the dependency between a model predictions and the true classes distribution, ii) is useful for assessing classifiers performance when classes imbalance is present, and iii) it can be used to compare classifiers performance on two different datasets (e.g., two TFD datasets with different faults and/or severity details)

References

  1. Senoussaoui, M.E.A.; Brahami, M.; Fofana, I. Combining and comparing various machine learning algorithms to improve dissolved gas analysis interpretation. IET Gener. Transm. Distrib. 2018, 12, 3673–3679. [Google Scholar] [CrossRef]
  2. Taha, I.B.; Dessouky, S.S.; Ghoneim, S.S. Transformer fault types and severity class prediction based on neural pattern-recognition techniques. Electr. Power Syst. Res. 2020, 191, 106899. [Google Scholar] [CrossRef]
  3. Velásquez, R.M.A.; Lara, J.V.M. Root cause analysis improved with machine learning for failure analysis in power transformers. Eng. Fail. Anal. 2020, 115, 104684. [Google Scholar] [CrossRef]
  4. Xu, Y.; Li, Y.; Wang, Y.; Zhong, D.; Zhang, G. Improved few-shot learning method for transformer fault diagnosis based on approximation space and belief functions. Expert Syst. Appl. 2021, 167, 114105. [Google Scholar] [CrossRef]
  5. Arias, R.; Mejia, J. Health index for transformer condition assessment. IEEE Lat. Am. Trans. 2018, 16, 2843–2849. [Google Scholar] [CrossRef]
  6. Ghoneim, S.S.M.; Taha, I.B.M. Comparative study of full and reduced feature scenarios for health index computation of power transformers. IEEE Access 2020, 8, 181326–181339. [Google Scholar] [CrossRef]
  7. Rogers, R.R. IEEE and IEC Codes to Interpret Incipient Faults in Transformers, Using Gas in Oil Analysis. IEEE Trans. Electr. Insul. 1978, 13, 349–354. [Google Scholar] [CrossRef]
  8. W.G. A2. 37, Transformer reliability surveys, CIGRE Technical Brochure 642. 2015.
  9. Bartley, W. Analysis of transformer failures. Proceedings of International Association OF Engineering Insurers, 36th Annual Conference; 2013; pp. 1–12. [Google Scholar]
  10. Nagpal, T.; Brar, Y.S. Artificial neural network approaches for fault classification: comparison and performance. Neural Comput. Appl. 2014, 25, 1863–1870. [Google Scholar] [CrossRef]
  11. Mirowski, P.; LeCun, Y. Statistical Machine Learning and Dissolved Gas Analysis: A Review. IEEE Trans. Power Deliv. 2012, 27, 1791–1799. [Google Scholar] [CrossRef]
  12. Golarz, J. Understanding Dissolved Gas Analysis (DGA) techniques and interpretations, In Proceedings of the IEEE Power Engineering Society Transmission and Distribution Conference, July 2016.
  13. Wu, Q.; Zhang, H. A novel expertise-guided machine learning model for internal fault state diagnosis of power transformers. Sustainability 2019, 11, 1562. [Google Scholar] [CrossRef]
  14. ELi, E.; Wang, L.; Song, B. Fault diagnosis of power transformers with membership degree. IEEE Access 2019, 7, 28791–28798. [Google Scholar]
  15. Cheim, L.; Duval, M.; Haider, S. Combined Duval Pentagons: A Simplified Approach. Energies 2020, 13, 2859. [Google Scholar] [CrossRef]
  16. Wang, J.; Zhang, X.; Zhang, F.; Wan, J.; Kou, L.; Ke, W. Review on evolution of intelligent algorithms for transformer condition assessment. Front. Energy Res. 2022, 10. [Google Scholar] [CrossRef]
  17. Shintemirov, A.; Tang, W.; Wu, Q.H. Power transformer fault classification based on dissolved gas analysis by implementing bootstrap and genetic programming, IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2009, 39, 69–79. [Google Scholar] [CrossRef]
  18. Wu, X.; Wang, P.; Wang, L.; Xu, Y.; Zhao, Z. Transformer combination weighting evaluation model based on bp neural network, In Proceedings Genetic and Evolutionary Computing. ICGEC 2021. Lecture Notes in Electrical Engineering, 833. 2022. [Google Scholar]
  19. Mortada, M.-A.; Yacout, S.; Lakis, A. Fault diagnosis in power transformers using multi-class logical analysis of data. J. Intell. Manuf. 2014, 25, 1429–1439. [Google Scholar] [CrossRef]
  20. Yang, X.; Chen, W.; Li, A.; Yang, C.; Xie, Z.; Dong, H. BA-PNN-based methods for power transformer fault diagnosis. Adv. Eng. Inform. 2019, 39, 178–185. [Google Scholar] [CrossRef]
  21. Zhang, D.; Li, C.; Shahidehpour, M.; Wu, Q.; Zhou, B.; Zhang, C.; Huang, W. A bi-level machine learning method for fault diagnosis of oil-immersed transformers with feature explainability. Int. J. Electr. Power Energy Syst. 2022, 134, 107356. [Google Scholar] [CrossRef]
  22. Cheim, L. Machine Learning Tools in Support of Transformer Diagnostics. Proceedings CIGRE Paris Session 2018, CIGRE; 2018; pp. A2–206. [Google Scholar]
  23. Zöller, M.-A.; Huber, M.F. Benchmark and Survey of Automated Machine Learning Frameworks. J. Artif. Intell. Res. 2021, 70, 409–472. [Google Scholar] [CrossRef]
  24. Thornton, C.; Hutter, F.; Hoos, H.H.; Leyton-Brown, K. Auto-WEKA: Combined selection and hyperparameter optimization of classification algorithms. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining Part F128815; 2013; pp. 847–855. [Google Scholar]
  25. Feurer, M.; Klein, A.; Eggensperger, K.; Springenberg, J.T.; Blum, M.; Hutter, F. Efficient and Robust Automated Machine Learning. Adv. Neural Inf. Process. Syst. 2015, 2962–2970. [Google Scholar]
  26. Duval, M.; Lamarre, L. The Duval pentagon-a new complementary tool for the interpretation of dissolved gas analysis in transformers. IEEE Electr. Insul. Mag. 2014, 30, 9–12. [Google Scholar]
  27. Li, E. Dissolved gas data in transformer oil—fault diagnosis of power transformers with membership degree (2019).
  28. Jakob, F.; Dukarm, J.J. Thermodynamic estimation of transformer fault severity. IEEE Trans. Power Deliv. 2015, 30, 1941–1948. [Google Scholar] [CrossRef]
  29. J. Dukarm, F. J. Dukarm, F. Jakob, Thermodynamic estimation of transformer fault severity. Proceedings IEEE/PES Transmission and Distribution Conference and Exposition (T&D 2016), 2016; 1. [Google Scholar]
  30. S. M. P. Londono, J. A. Cadena, J. M. Cadena, Aplicacion de redes neuronales probabilısticas en la deteccion de fallas incipientes en transformadores. Sci. Tech. 2008, 2, 48–53.
  31. Ranga, C.; Chandel, A.K.; Chandel, R. Condition assessment of power transformers based on multi-attributes using fuzzy logic. IET Sci. Meas. Technol. 2017, 11, 983–990. [Google Scholar] [CrossRef]
  32. Mharakurwa, E.T.; Goboza, R. Multiparameter-based fuzzy logic health index assessment for oil-immersed power transformers Adv. Fuzzy Syst. 2019, 2019, 1–12. [Google Scholar] [CrossRef]
  33. CIGRE TB 761 Condition assessment of power transformers, 2019.
  34. IEEE Guide for the Interpretation of Gases Generated in Mineral Oil-Immersed Transformers, 2019.
  35. Truong, A.; Walters, J.; Goodsitt, K.; Hines, C.B.; Bruss, R. Truong, A. Walters, J. Goodsitt, K. Hines, C. B. Bruss, R. Farivar, Towards automated machine learning: Evaluation and comparison of AutoML approaches and tools. Proceedings IEEE 31st international conference on tools with artificial intelligence (ICTAI); 2019; pp. 1471–1479. [Google Scholar]
  36. Osborne, Notes on the use of data transformations, Practical assessment. research, and evaluation 2002, 9, 6.
  37. M. Feurer, K. Eggensperger, S. Falkner, M. Lindauer, F. Hutter, Auto-Sklearn 2.0: Hands-free AutoML via Meta-Learning. arXiv 2020, arXiv:2007.04074.
  38. X. He, K. Zhao, X. Chu, AutoML: A survey of the state-of-the-art, Knowledge-Based Systems 212 (Dl). arXiv 2021, arXiv:1908.00709.
  39. F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot, E. Duchesnay, Scikit-learn: Machine learning in Python. Journal of Machine Learning Research 2011, 12, 2825–2830.
  40. T. E. Oliphant, A guide to NumPy, Vol. 1, Trelgol Publishing USA. 2006.
  41. W. McKinney, pandas: a foundational python library for data analysis and statistics. In Workshop Python for High Performance and Scientific Computing; 2011; pp. 1–9.
  42. T. Chen, C. Guestrin, XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD ’16; ACM: New York, NY, USA, 2016; pp. 785–794.
  43. Freitas, A.A. A critical review of multi-objective optimization in data mining. ACM SIGKDD Explor. Newsl. 2004, 6, 77–86. [Google Scholar] [CrossRef]
  44. T. Hastie, R. Tibshirani, J. Friedman. In The Elements of Statistical Learning; Springer Series in Statistics; Springer: New York, NY, USA, 2001.
  45. Rokach, L.; Maimon, O. Data mining with decision trees: theory and applications. World scientific 2007, 69. [Google Scholar]
  46. G. d. G. Alexander, Matthews, jiri hron, mark rowland, richard e. turner, and zoubin ghahramani. gaussian process behaviour in wide deep neural networks, In Proceedings of International Conference on Learning Representations, 4, 77–86, 2018.
  47. T. M. Mitchell, T. M. Mitchell. In Machine learning; McGraw-hill: New York, NY, USA, 1997; Volume 1.
  48. G. Shobha, S. Rangaswamy, Chapter 8 - machine learning, in: V. N. Gudivada, C. Rao (Eds.), Computational Analysis and Understanding of Natural Languages: Principles, Methods and Applications, Vol. 38 of Handbook of Statistics, Elsevier, 197–228. 2018.
  49. Y. Benjamini, M. Leshno, Statistical methods for data mining, in: Data mining and knowledge discovery handbook, Springer. 2005.
  50. B. Scholkopf, A. J. Smola, F. Bach, et al., Learning with kernels: support vector machines, regularization, optimization, and beyond, MIT press. 2002.
  51. V. N. Vapnik, Statistical Learning Theory, Wiley-Interscience. 1998.
  52. S. R. Gunn, Support vector machines for classification and regression. 1998.
  53. G. Biau, E. Scornet, A random forest guided tour, Test 25, 197–227. 2016.
  54. C. D. Sutton, Classification and regression trees, bagging, and boosting, Handbook of statistics 24, 303–329. 2005.
  55. J. H. Friedman, Stochastic gradient boosting, Computational statistics & data analysis 38 (4), 367–378. 2002.
  56. Moon, J.; Jung, S.; Rew, J.; Rho, S.; Hwang, E. Combination of short-term load forecasting models based on a stacking ensemble approach. Energy Build. 2020, 216, 109921. [Google Scholar] [CrossRef]
  57. Kautz, T.; Eskofier, B.M.; Pasluosta, C.F. Generic performance measure for multiclass-classifiers. Pattern Recognit. 2017, 68, 111–125. [Google Scholar] [CrossRef]
  58. M. Grandini, E. Bagli, G. Visani, Metrics for multi-class classification: an overview. arXiv 2020, arXiv:2008.05756.
  59. Markoulidakis, I.; Rallis, I.; Georgoulas, I.; Kopsiaftis, G.; Doulamis, A.; Doulamis, N. Multiclass Confusion Matrix Reduction Method and Its Application on Net Promoter Score Classification Problem. Technologies 2021, 9, 81. [Google Scholar] [CrossRef]
  60. M. J. Warrens, Five ways to look at cohen’s kappa. Journal of Psychology & Psychotherapy 2015, 5, 1.
Preprints 91627 g001
Figure 1. ML methodology developed for the comparison of single, ensemble, and autoML classifiers for the transformers fault classification problem.
Figure 1. ML methodology developed for the comparison of single, ensemble, and autoML classifiers for the transformers fault classification problem.
Preprints 91627 g001
Table 1. Transformers Faults classes distribution.
Table 1. Transformers Faults classes distribution.
Fault Type Freq. %
Normal condition 270 33
D1 78 10
D2 77 9
PD 23 3
S 83 11
T1-C 4 > 1
T1-O 97 16
T2-C 23 3
T3-C 25 3
T3-H 97 12
Table 2. Derived features from dissolved gases.
Table 2. Derived features from dissolved gases.
Feature Name Definition Feature Name Definition
F1 H2 F13 CH4/THC
F2 CH4 F14 C2H2/THC
F3 C2H2 F15 C2H4/THC
F4 C2H4 F16 C2H6/THC
F5 C2H6 F17 CH4/H2
F6 THC = CH4 + C2H2 + C2H4 + C2H6 F18 C2H6/CH4
F7 TGC = H2 + THC F19 C2H4/CH4
F8 H2/TGC F20 C2H2/CH4
F9 CH4/TGC F21 C2H4/C2H6
F10 C2H2/TGC F22 C2H2/C2H6
F11 C2H4/TGC F23 C2H2/C2H4
F12 C2H6/TGC - -
Table 3. Fault classification models parameters.
Table 3. Fault classification models parameters.
Preprints 91627 i001
Table 4. Classifiers performance attained on the transformers fault detection problem.
Table 4. Classifiers performance attained on the transformers fault detection problem.
Model BA F1-micro F1-macro κ MCC
vanilla auto-Sklearn 0.812 0.866 0.769 0.837 0.837
robust auto-Sklearn 0.893 0.906 0.909 0.885 0.885
ANN 0.840 0.882 0.785 0.856 0.857
BC 0.745 0.858 0.742 0.825 0.826
DT 0.744 0.837 0.695 0.802 0.802
GP 0.728 0.900 0.746 0.875 0.876
HGB 0.723 0.886 0.706 0.860 0.862
KNN 0.765 0.858 0.756 0.823 0.823
LR 0.666 0.823 0.673 0.791 0.792
NB 0.700 0.764 0.650 0.714 0.715
RF 0.717 0.870 0.721 0.840 0.841
SE 0.838 0.886 0.809 0.860 0.861
SVM 0.766 0.882 0.767 0.856 0.857
XGB 0.702 0.861 0.683 0.831 0.833
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated