Prerpints.org logo
Preprint
Article

Research on Multi-Objective Optimization of High-Speed Solenoid Valve Drive Strategies under the Synergistic Effect of Dynamic Response and Energy Loss

Altmetrics

Downloads

80

Views

44

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

28 November 2023

Posted:

29 November 2023

You are already at the latest version

Alerts
Abstract
Under high-frequency operating conditions, the high-speed solenoid valve (HSV) experiences energy loss and heat generation, which significantly impact its operational lifetime. Reducing the energy loss of HSV without compromising its opening response characteristics poses a significant challenge. To address this issue, a finite element simulation model of HSV coupled with a current feedback model is constructed to investigate the synergistic effects of dynamic response and energy loss. Predictive models for the opening response time, HSV driving energy, and Joule energy using Back Propagation neural network (BPNN) are established. Furthermore, a multi-objective optimization study on the current driving strategy using Non-dominated Sorting Genetic Algorithm II (NSGA-II) is conducted. After optimization, although there was a 6.24% increase in the opening response time, both HSV drive energy and Joule energy were significantly reduced by 15.67% and 22.49%, respectively. The proposed multi-objective optimization method for HSV driving strategy holds great significance in improving its working durability.
Keywords: 
Subject: Engineering  -   Energy and Fuel Technology

1. Introduction

Faced with increasingly stringent emission regulations and a variety of combustion modes, the fuel injection system of diesel engines and other power machinery is required to flexibly control fuel injection strategies such as fuel injection volume, fuel injection pressure, and fuel injection interval [1]. As the core component of the injector, the dynamic response characteristics of high-speed solenoid valves (HSV) directly determine the fuel injection accuracy of electronically controlled injectors. Moreover, energy loss during its operation generates heat that affects the service life of the fuel injector [2]. Therefore, the optimization of the dynamic response characteristics and energy loss of HSV is significantly important for improving the efficiency of the fuel injection system.
Optimization studies of the HSV as the actuator of the fuel injector have been conducted from various aspects. Regarding electromagnetic materials used in HSVs, Wang et al. [3] designed a novel magnetic circuit structure based on Al-Fe soft magnetic alloy which effectively reduces magnetic resistance and increases magnetic conductivity resulting in shorter dynamic response time for HSVs. Tao et al. [4], using finite element methods, discussed the influence of soft magnetic materials and structural parameters on the magnetic circuit of the HSV while proposing an optimization design method that can achieve greater electromagnetic force and lower power consumption. In terms of the structure of the HSV, Liu et al. [5] proposed a novel HSV with permanent magnet based on the parallel magnetic circuit principle, which can reduce the peak current, peak voltage, and holding current of the new HSV by 20.5%, 7.8%, and 43.9% respectively, while increasing the response speed by 11.9% compared to the original HSV. Ebrahimi et al. [6] optimized the design of an HSV, which is composed of two opposing helical coils with a shared permanent magnet core. They considered factors such as wire length, inner diameter, average diameter, number of turns, and fill density of the coil in their optimization process. Additionally, they studied the effect of coil cross-sections with the same area but different perimeters and eccentricities on the magnetic field. The results showed that increasing eccentricity significantly enhances both the magnetic field and force at the center of the coil. In terms of driving strategy for HSVs, Zhao et al. [7,8] found that increasing boost voltage improves opening response speed, however, this improvement diminishes as boost voltage continues to increase. They concluded that there exists an optimal boost voltage that achieves a balance between dynamic response time and effective electromagnetic energy conversion rate. Farid et al. [9] achieved significant reduction in dynamic response time by optimizing driving parameters such as peak current, holding current, and reverse current. Lu et al. [10] proposed a dual-power-source driving method to improve opening response time for HSVs. Their research indicated that this driving strategy can also significantly reduce the time interval between two injections.
The aforementioned researchers have focused on optimizing the dynamic response characteristics of HSV. According to Faraday's law of electromagnetic induction, induced currents are generated inside a conductor when the magnetic field changes, forming closed loops that cause eddy currents. Therefore, during high-frequency operation, HSV inevitably generates eddy current energy. Eddy currents can reduce the delay time between the start of the driving current decrease and the start of armature downward movement [11], but excessive eddy currents can affect the effective conversion of kinetic energy and prolong the open response time of HSV. According to Ampere's circuital law and Ohm's law, passing current through a coil generates Joule heating losses. Xie et al. [12] found that driving strategy is one of the most important factors affecting power loss and thermodynamic characteristics of HSV, with power loss being the main heat source that raises coil temperature. At the same time, temperature rise reduces magnetic flux density and weakens magnetic induction intensity of HSV, increasing total energy loss significantly and affecting durability of HSV [13]. Therefore, considering service life, energy loss characteristics need to be taken into account when optimizing HSV.
Currently, most research focuses more on the influence of structural and driving parameters on the dynamic response of the HSV or explores factors that affect the durability of the HSV. However, collaborative optimization for both dynamic response and energy loss is rarely carried out when optimizing the operating characteristics of HSV. In this paper, the HSV in high-pressure common rail injectors as research object, the prediction models for opening response time, HSV driving energy, and Joule energy based on BPNN were constructed. Considering the synergistic effect of dynamic response and energy loss, the current drive strategy of HSV is optimized by multi-objective genetic algorithm.
The rest of this paper is organized as follows: Section 2 describes the construction and validation process of the finite element model for the HSV coupled with a current feedback model. Section 3 discusses the impact of different driving strategies on the dynamic response and energy loss characteristics of the HSV. Section 4 describes the training and validation process for neural network prediction models for the opening response time, HSV driving energy, and Joule energy. Additionally, multi-objective collaborative optimization involving response time and energy loss is performed using genetic algorithm. Finally, Section 5 summarizes the work described in this paper.

2. Establishment and verification of HSV simulation model

2.1. Mathematical model

The HSV consists mainly of an armature, iron core, coil, and reset spring. When driven by a periodically varying current, the HSV generates a periodically varying electromagnetic force at the core. The interaction between this electromagnetic force and the elastic force of the reset spring causes the armature to produce reciprocating lifting motion. The HSV is a complex electromagnetic-mechanical coupling system, and the periodic current drive strategy directly affects its operating characteristics. When modeling the system, it is necessary to consider the interaction among the circuit, magnetic circuit, mechanical system, and various forms of energy generated within these systems.
In a circuit system, the coil current, voltage, resistance and inductance of the relationship as follows:
U = R I + N d Φ d t
where U is the coil driving voltage, R is the coil resistance, I is the current through the coil, N is the number of turns of the coil, Φ is the magnetic flux, and t is the time.
In the magnetic circuit system, the relationship between the electromagnetic force and the magnetic flux and the absorption area is as follows:
F mag = Φ 2 μ · S
where Fmag is the electromagnetic force, μ is the magnetic conductivity of air, and S is the suction area.
When fuel resistance is considered, the mechanical motion system of the HSV is:
F m a g - λ d x d t - k x - F 0 = m d 2 x d t 2
where λ is the damping coefficient, k is the spring stiffness, x is the armature displacement, F0 is the spring preload force and m is the armature mass.
In the HSV operation process, the total energy input to the circuit is the HSV drive energy Eele. is defined as:
E ele . = ∫ 0 t U I d t
Various energies are also generated during HSV operation, including eddy energy, Joule energy, elastic energy, damping energy, kinetic energy and so on. When the driving current changes, the magnetic field changes, resulting in induced eddy currents in the iron core, forming eddy energy Eedd. is defined as:
E edd . = ∫ 0 t C e d d . f 2 B m d 2 ρ d t
where Cedd. is the eddy current coefficient, f is the frequency of magnetic field, Bm is the magnetic induction intensity, d is the wall thickness of the iron core, and ρ is the resistivity.
When the current passes through the coil, a certain amount of heat is generated, which is defined as joule energy EJou.:
E Jou . = ∫ 0 t I 2 R d t
The spring will be compressed when the armature moves and the elastic energy Eela. generated, is:
E ela . = 1 2 k x 2
The force of friction between the components will affect the armature movement, and then generate damping energy Edam.. At the same time, due to movement the armature will have kinetic energy Ekin..
E dam . = ∫ 0 x λ V d d x
E kin . = 1 2 m V d 2
where Vd is the moving speed of armature.

2.2. HSV finite element model coupled with current feedback model

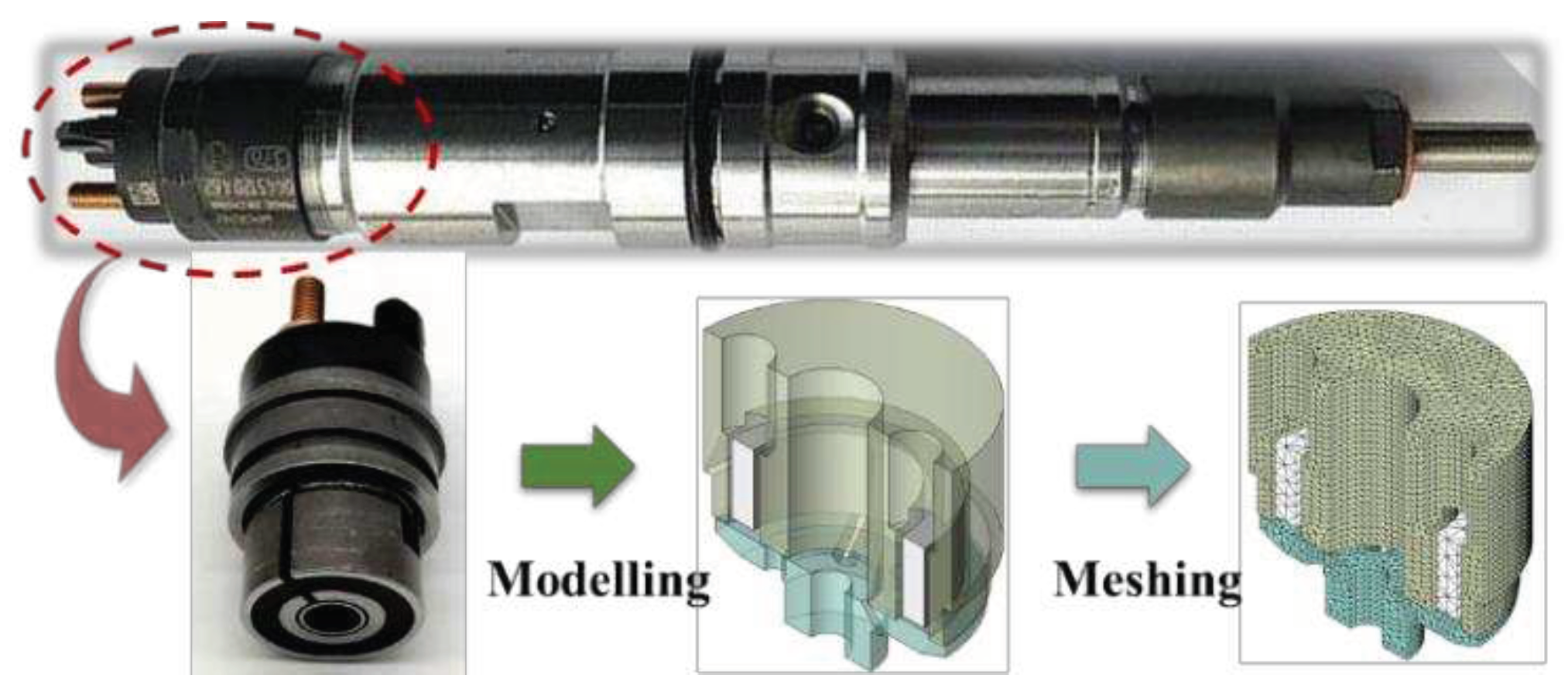
When constructing the finite element model (FEM), simplifications and assumptions regarding the geometric structure and simulation conditions of the simulated object can help improve grid quality and computational efficiency. In this study, non-magnetic components such as gaskets and reset springs were ignored when constructing the FEM of the HSV. Only the armature, core, and coil were modeled. Due to the symmetric structure of the HSV, only half of the model was developed. The gaps between coils were ignored and treated as an annular structure when modeling the multi-turn coil. In the simulation, elastic collisions between the armature and electromagnetic iron, as well as between the armature and valve seat, were disregarded along with any resulting deformation caused by these collisions. Based on the structure of the HSV, the maximum gap was 0.12 mm, the air gap was 0.07 mm, the number of coil turns was 52, and the preload force of the spring was 60 N. The FEM of HSV established on the Ansoft Maxwell software platform is shown in Figure 1.
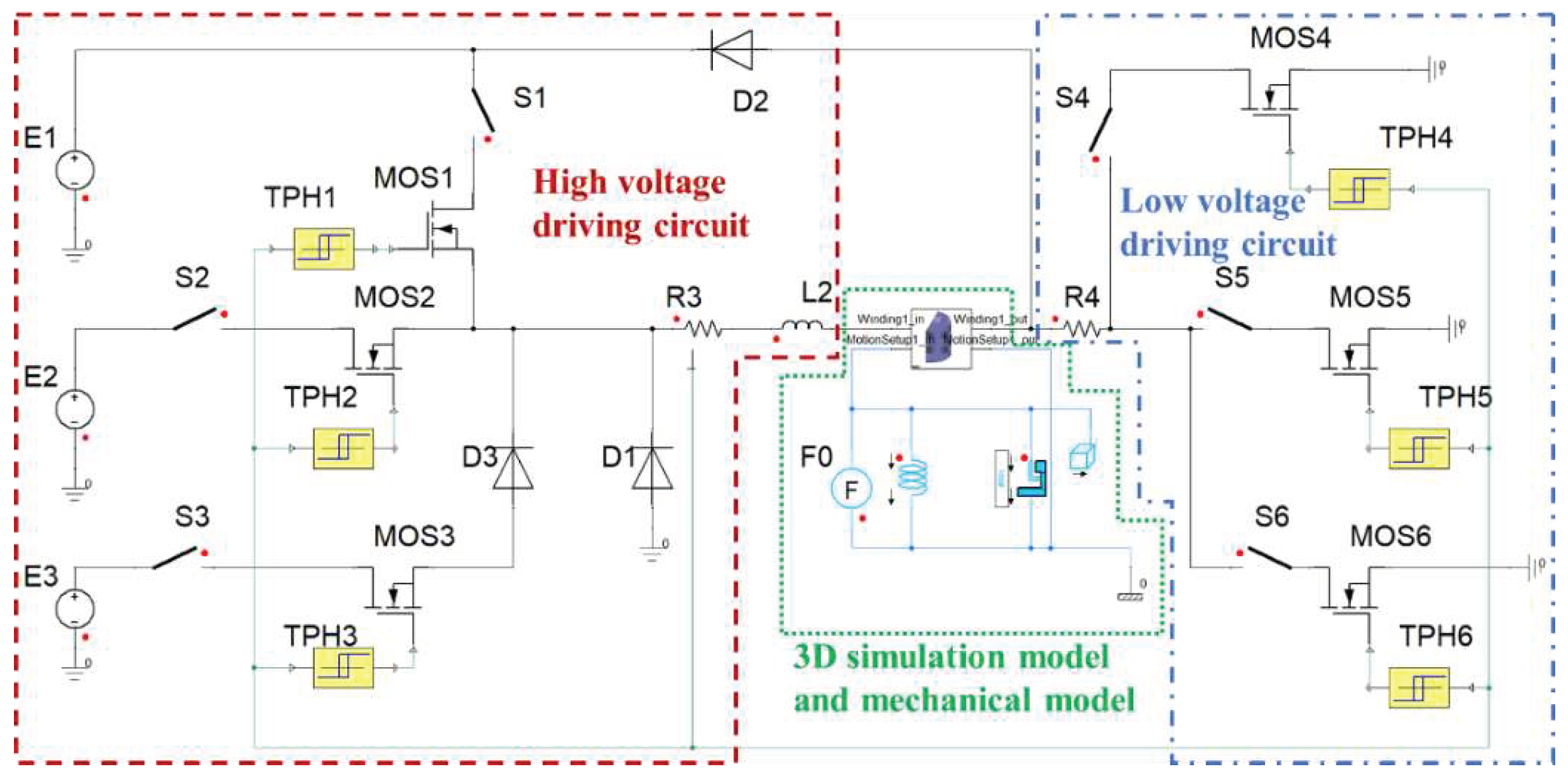
Although the Ansoft Maxwell electromagnetic simulation software contains a circuit simulation module for driving the electromagnetic actuator, it cannot realize the construction of the "peak-hold-hold" current feedback driving strategy of the HSV. Therefore, this study used the Ansoft Maxwell software to establish a detailed 3D FEM model of the HSV and utilized Simplorer software to create an actual current feedback driving strategy. The FEM was coupled with coupled with current feedback model using Simplorer platform to simulate the dynamic process of the HSV [14]. The calculation model for dynamic response of high-speed solenoid valve with current feedback is shown in Figure 2, where E1-E3 represent power supplies, S1-S6 are switches, MOS1-MOS6 are power switches, TPH1-TPH6 are hysteresis comparators, D1-D3 are diodes, L2 represents coil inductance, R3 is coil resistance, R4 is sampling resistor and F0 denotes preload force of spring.

2.3. Verification of HSV simulation model

The accuracy of the FEM of the HSV constructed in the previous section needs to be ensured through experimental data validation. Experimental data for the HSV is obtained from a dynamic response characteristic test bench. Information regarding the setup and measurement equipment of this test bench can be found in previous studies [7,8,14]. The HSV dynamic response test bench accurately measures armature displacement within the range of 0-1 mm, while maintaining a peak voltage between 42-80 V and ensuring that both peak current and holding current are within limits of 25 A and 12 A, respectively.
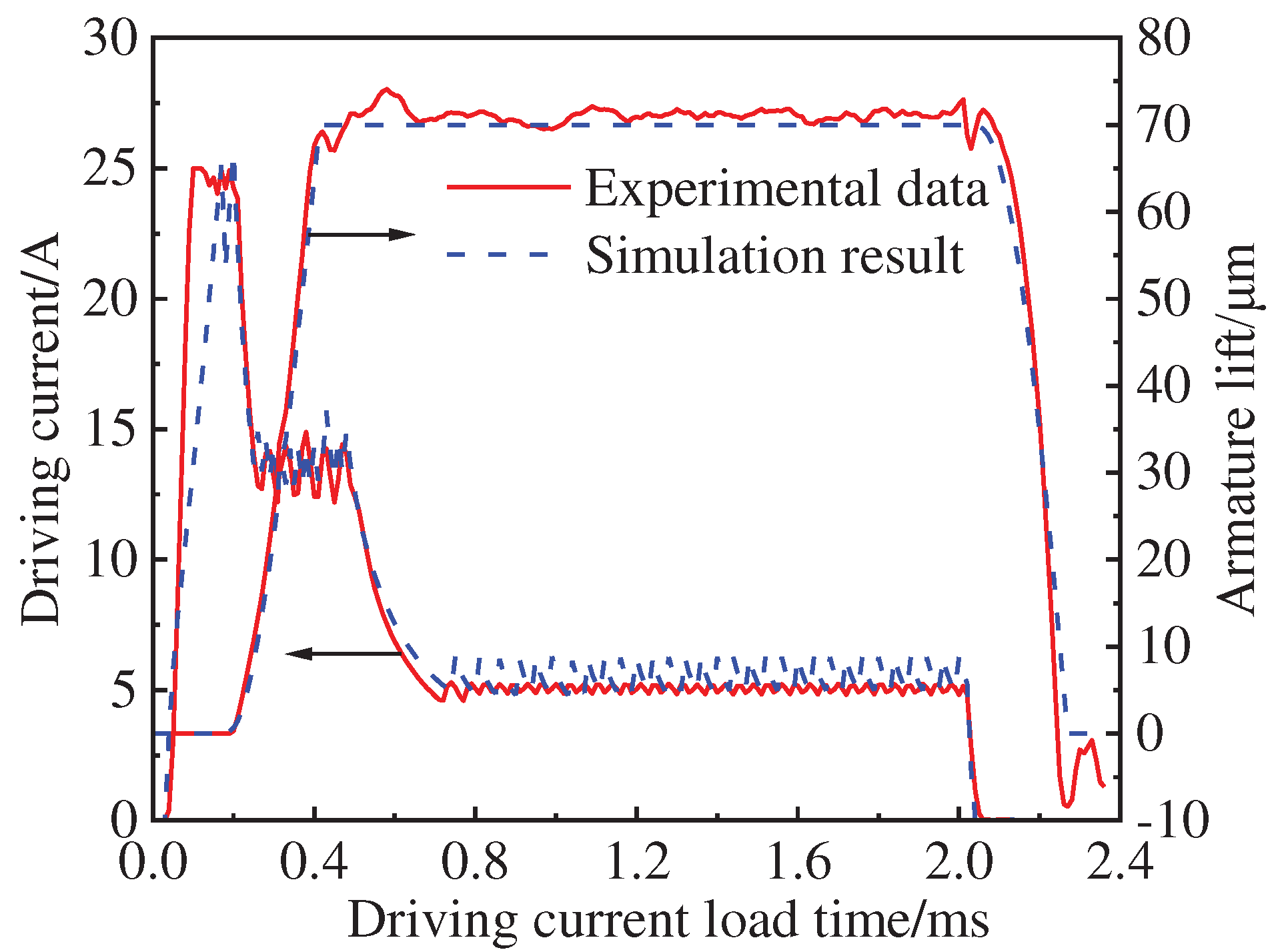
The comparison results of the experimental data and simulated values for the armature lift and driving current curve are shown in Figure 3. In this study, the time from the start of drive current loading to when the armature reaches maximum displacement is defined as the opening stage, with its corresponding time being referred to as the opening response time. Similarly, the time from when drive current is cut off to when the armature returns to its initial position is defined as the closing stage, with its corresponding time known as the closing response time. The interval between these two stages is referred to as the holding stage. During both opening and closing stages of HSV, FEM accurately predicts and captures moments of armature pull-in and reset motion process. However, due to collisions between armature and iron core and valve seat during actual operation along with fluctuations in drive circuit current, there may be some variation in armature lift during holding stage. Nevertheless, the error between experimental and simulated values remains within an acceptable range during this stage. Through analysis, it can be concluded that FEM model established in this study achieves accurate prediction of actual working process of HSV while providing a solid foundation for future research.

3. Influence of driving strategies on HSV working characteristics

3.1. Dynamic response characteristics

The driving current loading strategy during the opening stage not only affects the response time of the HSV but also significantly impacts energy loss. This study analyzes the driving strategy at the moment of HSV opening, investigating the effects of different strategies on dynamic response and energy consumption characteristics during this stage. The original driving strategy for the HSV is a "peak-hold-hold" type. To optimize it, this study proposes two modified strategies based on the original. Figure 4 illustrates the timing of current loading for both the original "peak-hold-hold" strategy and two "peak-hold" strategies. Driving Strategy 1 represents the original approach, while in Driving Strategy 2, peak current loading time is equal to that of Driving Strategy 1 plus first-order hold current loading time. In Driving Strategy 3, peak current falls between Strategies 1 and 2 with a consistent peak current loading time as in Strategy 2. Specific parameters for each driving strategy are shown in Table 1.
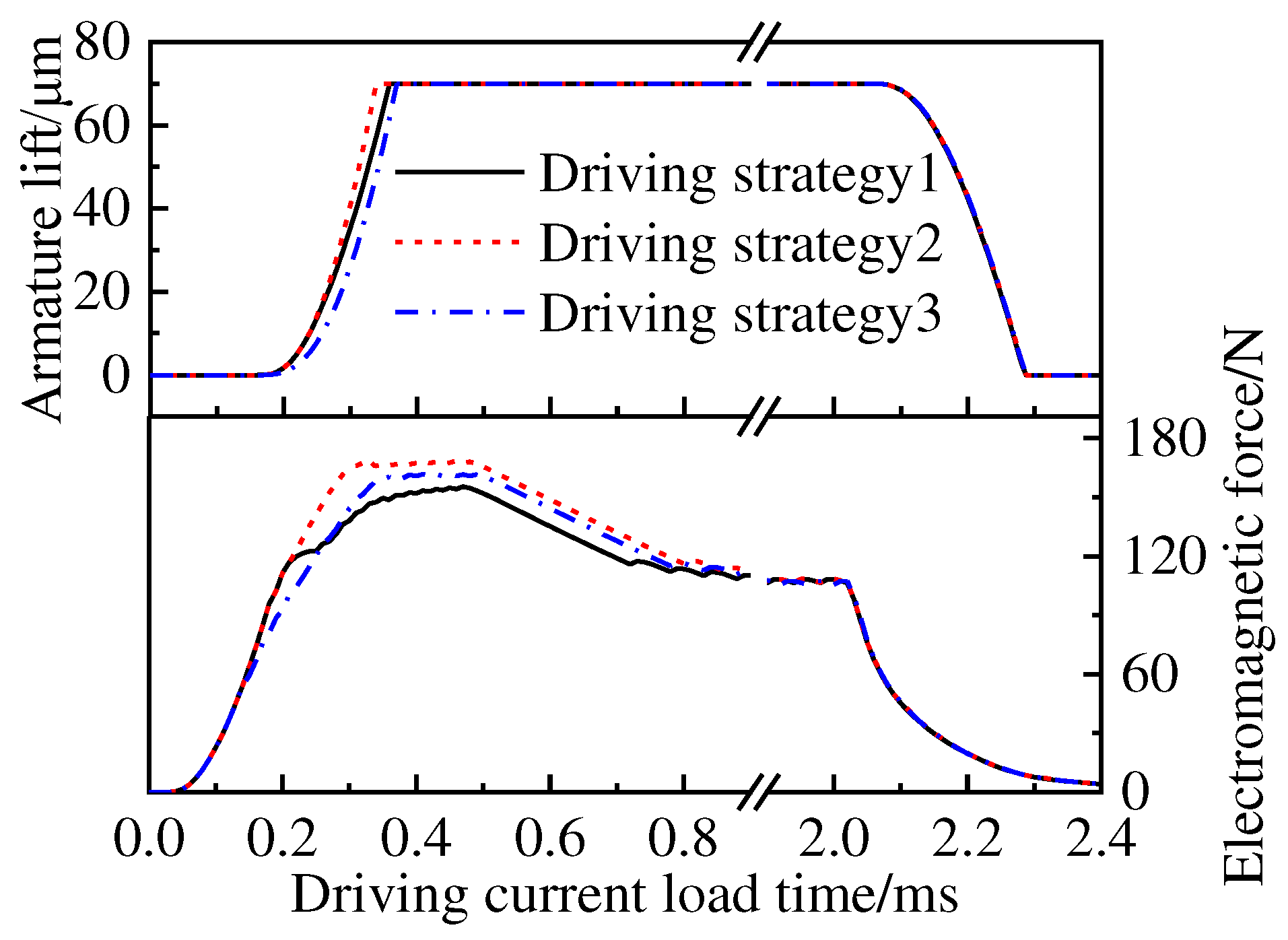
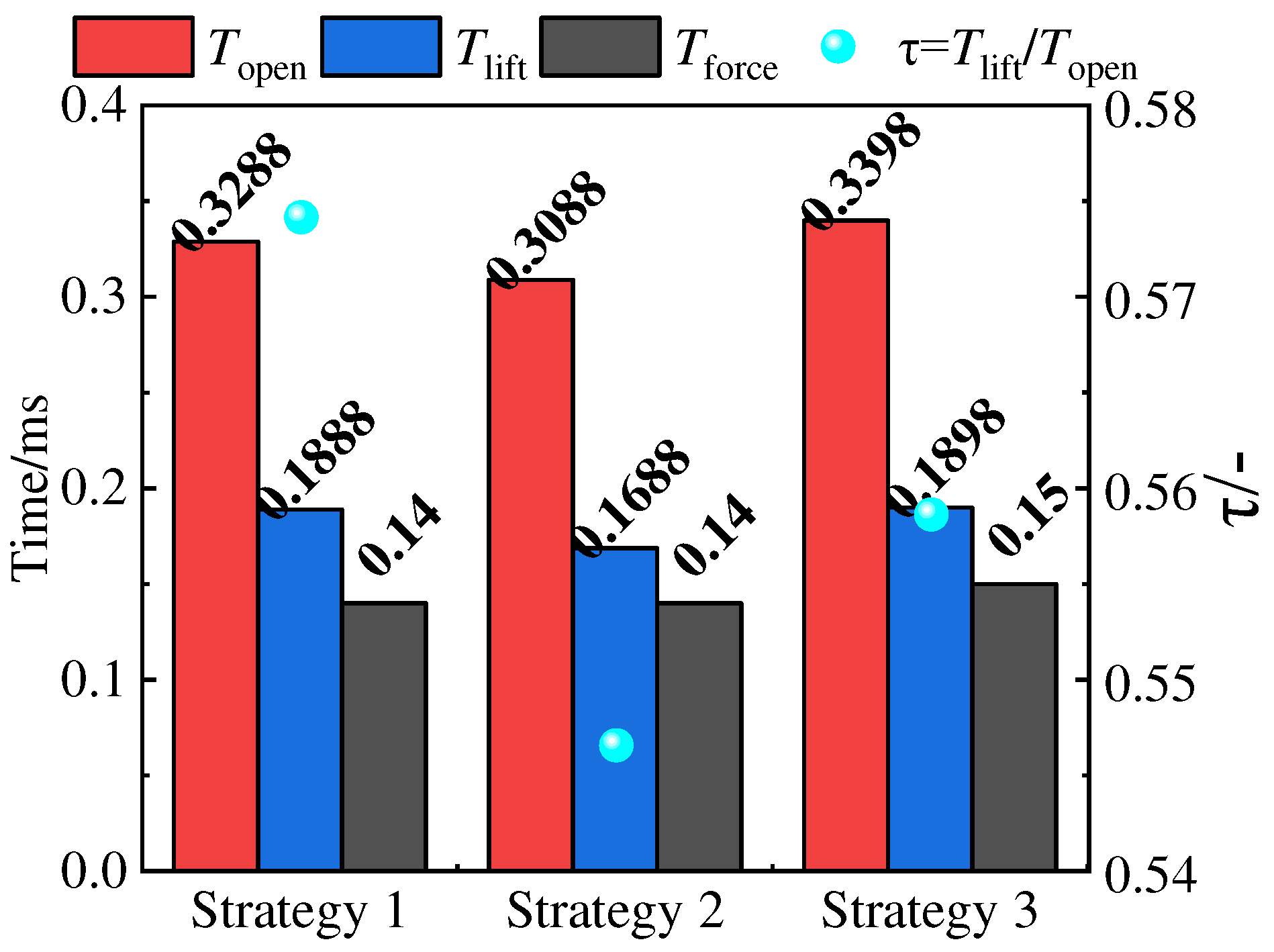
The comparison of the armature lift and electromagnetic force curves of the HSV under different driving strategies is shown in Figure 5. During the opening stage, the armature rising time of the HSV is the same for all three driving strategies, while driving strategy 2 has the shortest time for the armature to reach maximum displacement, and driving strategy 3 has the longest time. Additionally, in the early stage of motion, there is an overlap between lift curves for driving strategies 1 and 2. This occurs because in driving strategy 1, the armature has not yet reached maximum displacement when the driving current begins to decrease to 14 A, entering into a first-order holding stage. Within a certain range, a larger peak current and first-order holding current result in a shorter opening response time for the HSV. From observing changes in trend within electromagnetic force curves, it can be seen that electromagnetic force starts generating from when current begins loading and reaches its peak when armature moves near maximum displacement before starting to decrease. At 0.49 ms, current enters final holding stage where electromagnetic force decreases to 110 N. The magnitude of electromagnetic force strongly correlates positively with current within circuit. Therefore, increasing current during opening stage can be considered to minimize opening time. Considering pre-loading force of spring at 60 N allows room for current decrease during holding stage. However, any changes made to driving strategy need to consider variation in energy consumption.
From the figure above, it can be observed that the moment when the displacement of the armature begins to change during the opening stage is inconsistent with the time when the electromagnetic force increases. The armature only starts to move when the electromagnetic force reaches around 110 N. Therefore, to thoroughly evaluate the impact of different driving strategies on the opening stage of the HSV, the ratio of the armature motion time (Tlift) to the solenoid valve opening response time (Topen) is defined as the effective time ratio (τ). The overcoming resistance time (Tforce) of the HSV is then calculated as the difference between the HSV opening response time and the armature motion time, Tforce=Topen-Tlift. Figure 6 illustrates the effects of different driving strategies on Topen, Tlift, Tforce, and τ. A comparison between driving strategies 1 and 2 reveals that their Tforce values are consistent, both at 0.14 ms, while the Tlift of driving strategy 2 is shorter than that of driving strategy 1, indicating that increasing the first-order holding current can reduce Tlift in the peak-hold-hold driving strategy. Contrasting driving strategies 1 and 3, it is found that the deviation of Tlift is only 0.53%, while the deviation of Topen is 3.35%. Consequently, the peak current significantly affects Tforce in the peak-hold-hold driving strategy. In terms of τ, driving strategy 1 is the largest, followed by driving strategy 3, and driving strategy 2 is the smallest, indicating that driving strategy 1 can effectively convert kinetic energy for armature motion.

3.2. Energy loss characteristics

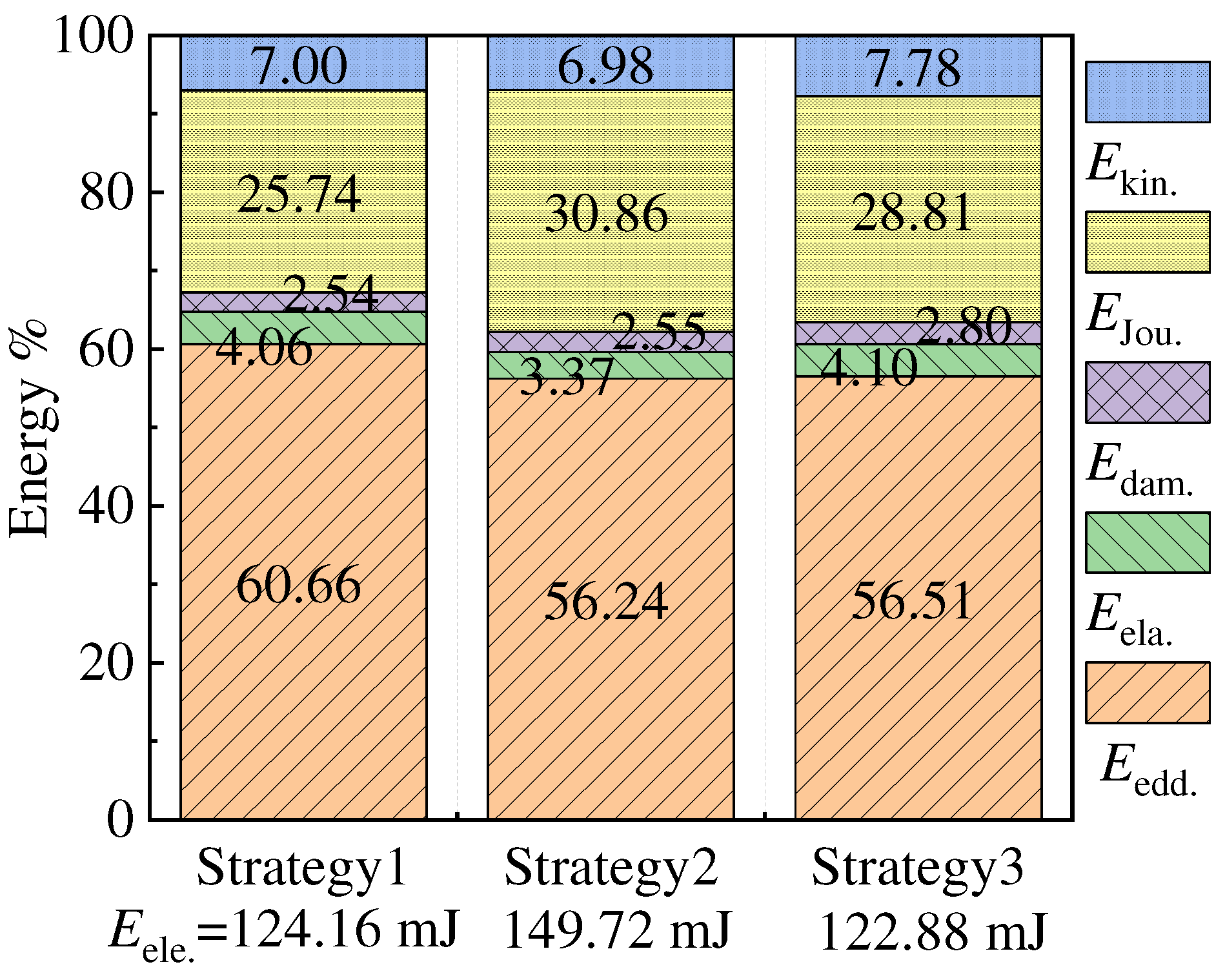
The larger the driving current during the opening stage, the shorter the response time of HSV. However, a larger driving current also leads to greater energy loss. Therefore, when optimizing driving strategies, it is necessary to consider the synergistic effect of dynamic response and energy loss. Figure 7 illustrates the energy loss during the opening stage under different driving strategies. Across various driving strategies, eddy current energy and Joule energy during opening stage account for more than 85% of the total energy, with eddy current energy representing over 55% of the total energy. Due to longest peak current loading time in strategy 2, HSV has a highest total energy consumption at 149.72 mJ compared to strategies 1 and 3 which have relatively similar total energies. Since the rate of change of the current increases, so does the eddy current energy. Similarly, as the current increases, so does the Joule energy. Consequently, during the opening stage, driving strategy 1 has a higher proportion of eddy current energy and a lower proportion of Joule energy compared to driving strategies 2 and 3 which have similar proportions of eddy current energy but with driving strategy 2 having a higher proportion of Joule energy. However, in terms of specific energy loss, the eddy current energy and Joule energy of drive strategy 2 are the largest, 84.20 mJ and 46.20 mJ, respectively. The eddy current energy of drive strategy 3 and the Joule energy of drive strategy 1 are the smallest, 69.07 mJ and 31.96 mJ, respectively.
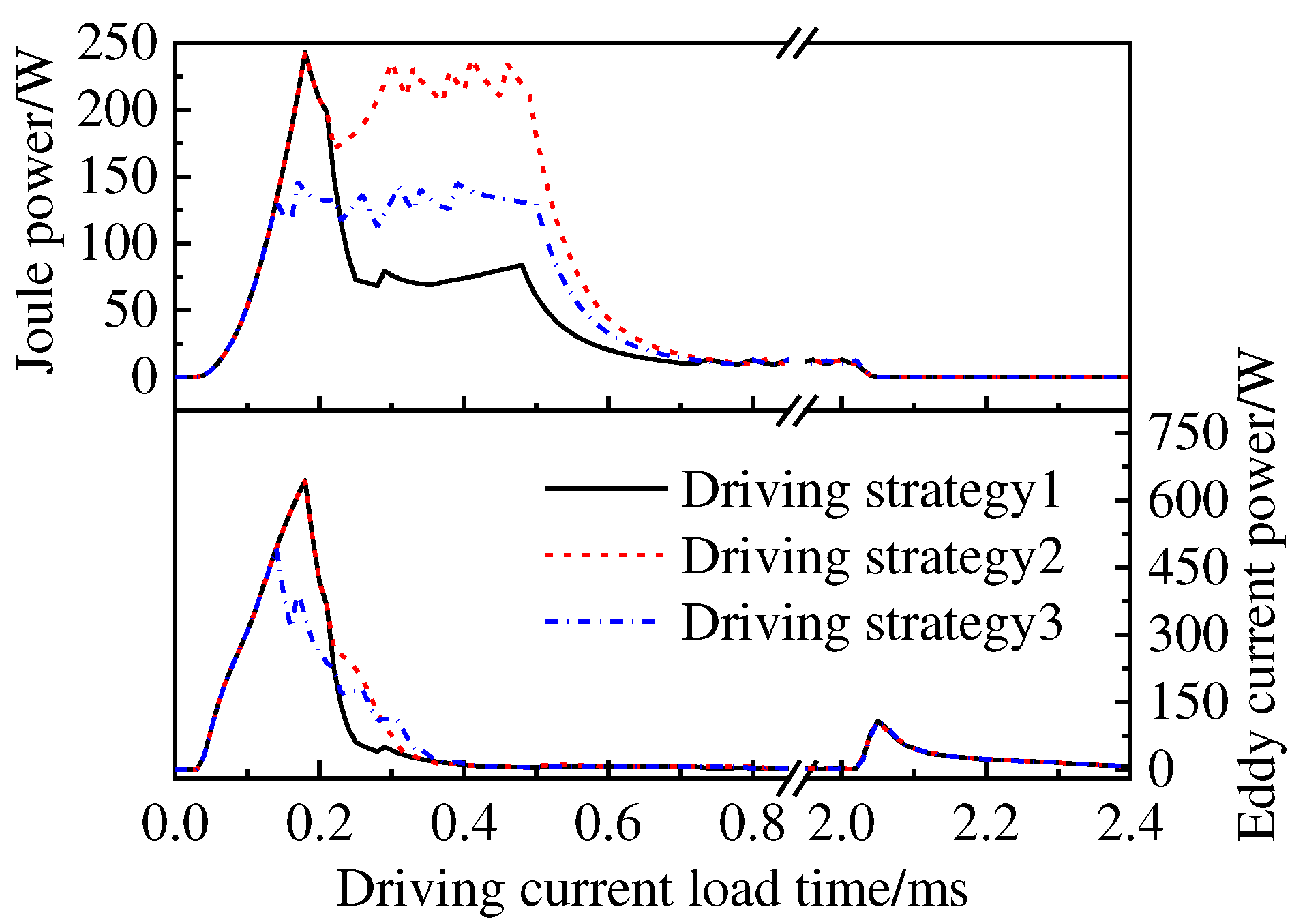
The trend of eddy current energy and Joule energy, which account for the largest proportion of energy loss, over the entire HSV working cycle is illustrated in Figure 8. Regarding Joule energy, its trend follows that of the drive current. When the driving current fluctuates around 24.5 A, 230 W of Joule energy will be generated. When the drive current fluctuates around 19 A, 138 W of Joule energy will be generated, and when the drive current is at 14 A, the Joule energy is 75 W. Combined with Equation (6), it can be observed that Joule energy is proportional to the square of the current, thus a larger peak current lead to greater Joule energy loss. As for eddy current energy, its value increases with a higher rate of change in current. Therefore, during stages of peak current loading, there is a significant instantaneous change in current resulting in a large amount of eddy current energy loss inside both armature and core components of HSV. Under different driving strategies, as the currents enter into holding stage, there will be a significant reduction in eddy current energy inside HSV.
Combined with the previous analysis of the dynamic response characteristics of the HSV, it can be concluded that in the peak-hold-hold driving strategy, increasing the peak current can shorten the time required to overcome resistance for the HSV. However, this will significantly increase Joule energy loss. On the other hand, increasing the first-order holding current can reduce armature motion time and rapidly changing current can increase eddy current energy.

4. Optimization of HSV driving strategy based on BPNN-NSGA-Ⅱ

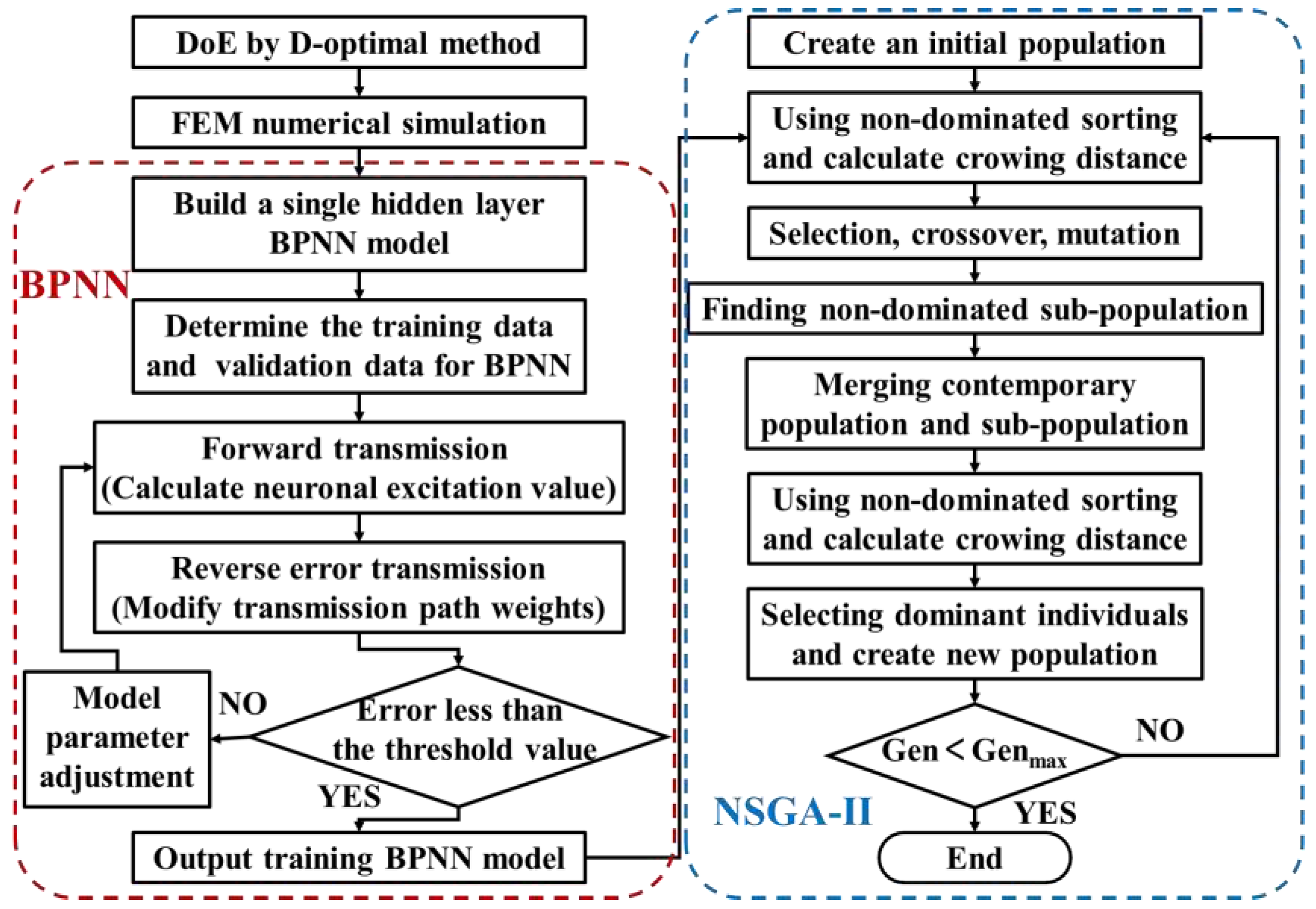
The trade-off relationship between energy loss and opening response time requires decision-making based on specific requirements when optimizing driving strategies. This study utilized multiple parameters within the peak-hold-hold driving strategy of an HSV on a diesel engine as variables, with Joule energy, HSV driving energy, and opening response time as targets for optimization. The BPNN was employed to construct predictive models for optimizing objectives while NSGA-II was used for multi-objective optimization analysis. Figure 9 illustrates the multi-objective optimization process coupled with BPNN and NSGA-II.

4.1. Prediction model of BPNN

4.1.1. Sample Data

In this study, six parameters in driving strategy were selected for a high-pressure common rail injector HSV, including peak voltage, peak current, peak current loading time, first-order holding current, first-order holding current loading time and second-order holding current. The geometric structure parameters remained unchanged. Table 2 presents the variation of the six-factor five-level parameter for HSV driving parameters. In the table, the baseline values represent the original driving parameters of the HSV sample. The selection range for each parameter is based on the standard value with an equal increase or decrease as upper and lower limits of parameter change. When selecting these limits, it was essential to ensure that all combinations of parameter changes can work normally for HSV. The experimental design method chosen was D-optimal design method which statistically studies different experimental designs and establishes an optimal approach. Therefore, regression values obtained based on this method exhibit a high degree of fit with observed values and hold statistical significance [15,16,17].
Using the D-optimal design method resulted in obtaining 94 sets of sample data for developing predictive model while randomly selecting 19 sets as testing set for BPNN; remaining 75 sets were utilized as training set. All sample points in both training and testing sets were obtained through FEM simulation calculations constructed in previous section.

4.1.2. Model Training

A typical n-dimensional input neuron model consists of inputs, network weights and thresholds, summation units, transfer functions, and outputs [18,19]. The n input variables of the neuron can be represented as a column vector X:
X = [ x 1 , x 2 , ⋅ ⋅ ⋅ , x n ] T
The weight of network connects the input variables with the neuron and can be represented as a vector W:
W = [ w 11 , w 12 , ⋅ ⋅ ⋅ , w 1 n ]
The threshold of the network is a scalar, denoted as b. The performance of network can be adjusted through the weights and thresholds.
The summation unit is the first process for processing the input signals in the neural network, used to weight the input signals:
n e t = ∑ k = 1 n x k w 1 k + b
The function operation on the weighted signal is the second process for processing the input signal in the neural network, and the most commonly used function is the Sigmoid function:
f ( x ) = 1 1 + e − x
After weighted summation and function operation of the input signal, the final output is:
y = f ( w x + b )
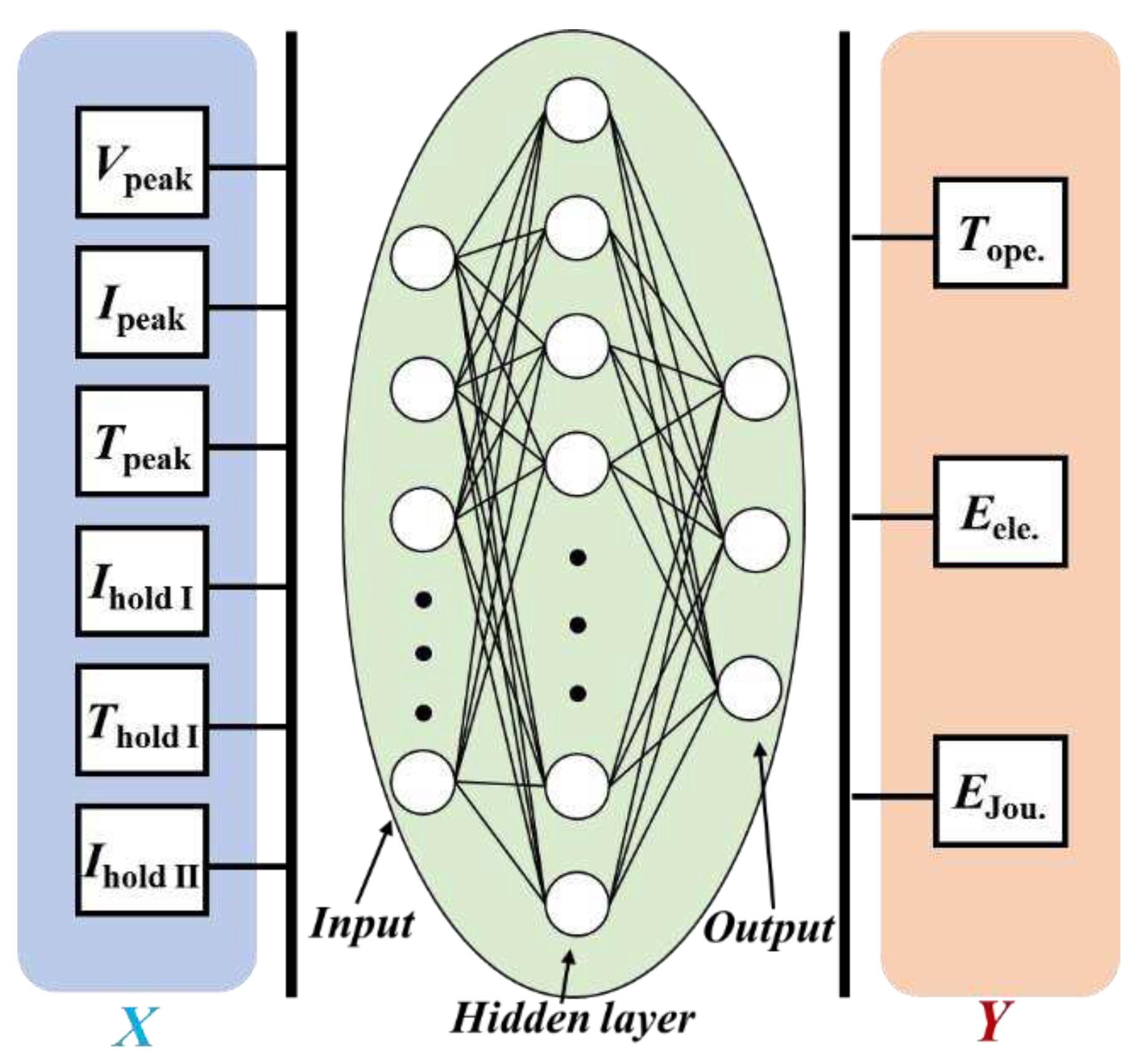
A typical BPNN model consists of an input layer, a hidden layer, and an output layer. During the training process of the predictive model, the neurons in each layer are only influenced by the neurons in the previous layer. When the signal propagates from the input layer to the hidden layer and then to the output layer without reaching the expected threshold, it will be propagated back from the output layer to the input layer. After adjusting the network weights of each layer, this signal propagation is repeated. After multiple forward and backward signal transmissions, finally, the expected signal can be obtained. The structure of BPNN is uncertain, and selecting a reasonable number of network layers and neurons is a prerequisite for achieving optimal performance.
For this study, the number of neurons in the input layer corresponds to the number of driving parameters, while the number of neurons in the output layer corresponds to the number of optimization objectives. In other words, there are 6 neurons in the input layer and 3 neurons in the output layer. The accuracy of predictive model is affected by both the number and size of hidden layers. Generally speaking, a single hidden layer is preferred for constructing BPNNs. If a single hidden layer fails to produce accurate results, double or multiple hidden layers can be used instead [20,21]. Based on preliminary research findings that indicate satisfactory accuracy levels with a single hidden layer structure network, this study has chosen to use such a structure for BPNN as shown in Figure 10.
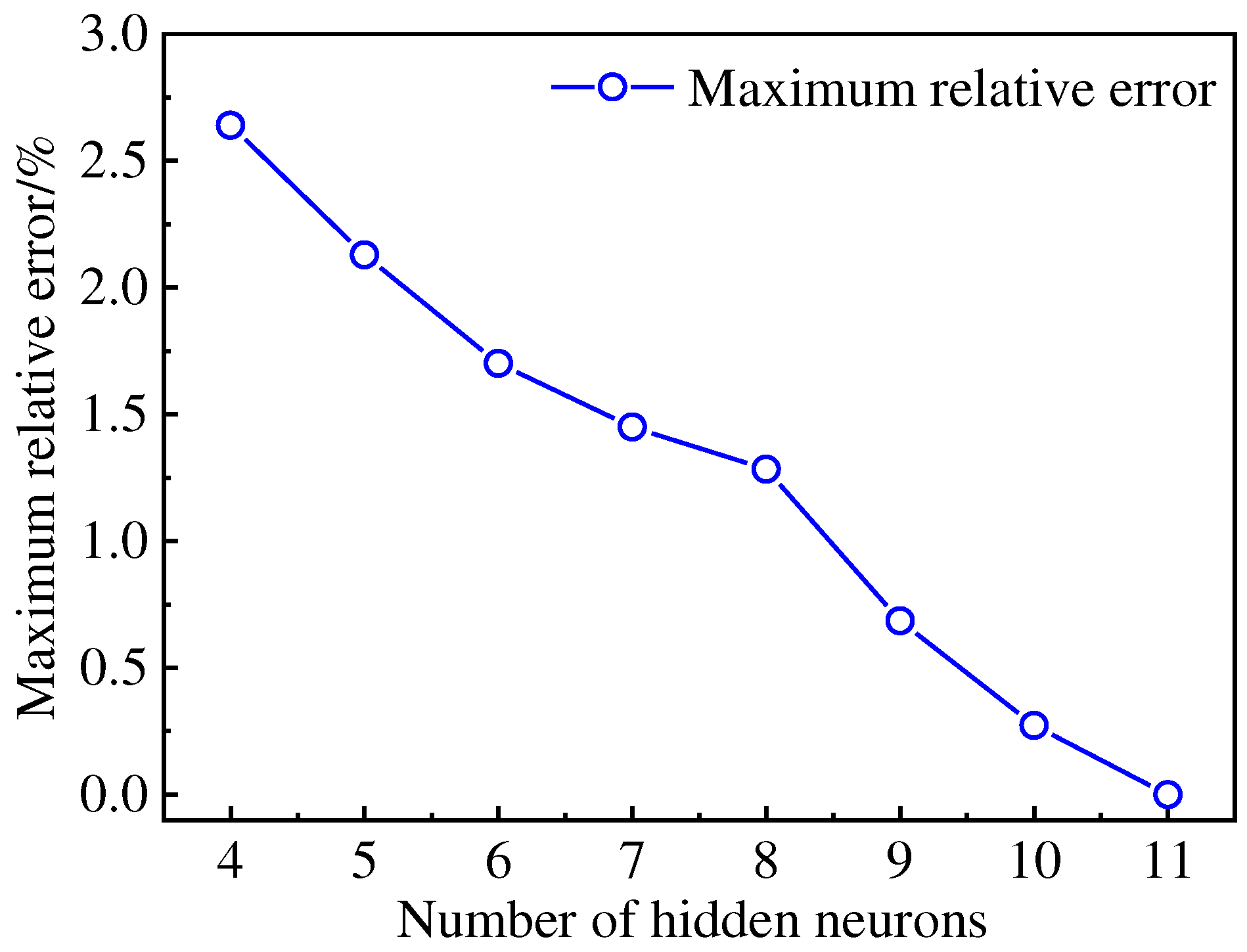
The number of the hidden layer has been determined, and it is necessary to further determine the number of neurons in the hidden layer. In this study, the method of repeated experiments was used to compare the relative errors of models with different numbers of neurons, as shown in Figure 11. As the number of neurons within the hidden layer increases, the relative error of the predictive model for Joule energy gradually decreases. When there are more than 8 neurons, the relative error is less than 1%. However, when there are 11 neurons, overfitting occurs with a relative error of 1.57 × 10-10 %. Therefore, through comparison, it is concluded that there should be 10 neurons in the hidden layer of BPNN in this study where the relative error for predicting Joule energy is 0.27%.

4.1.3. Model Verification

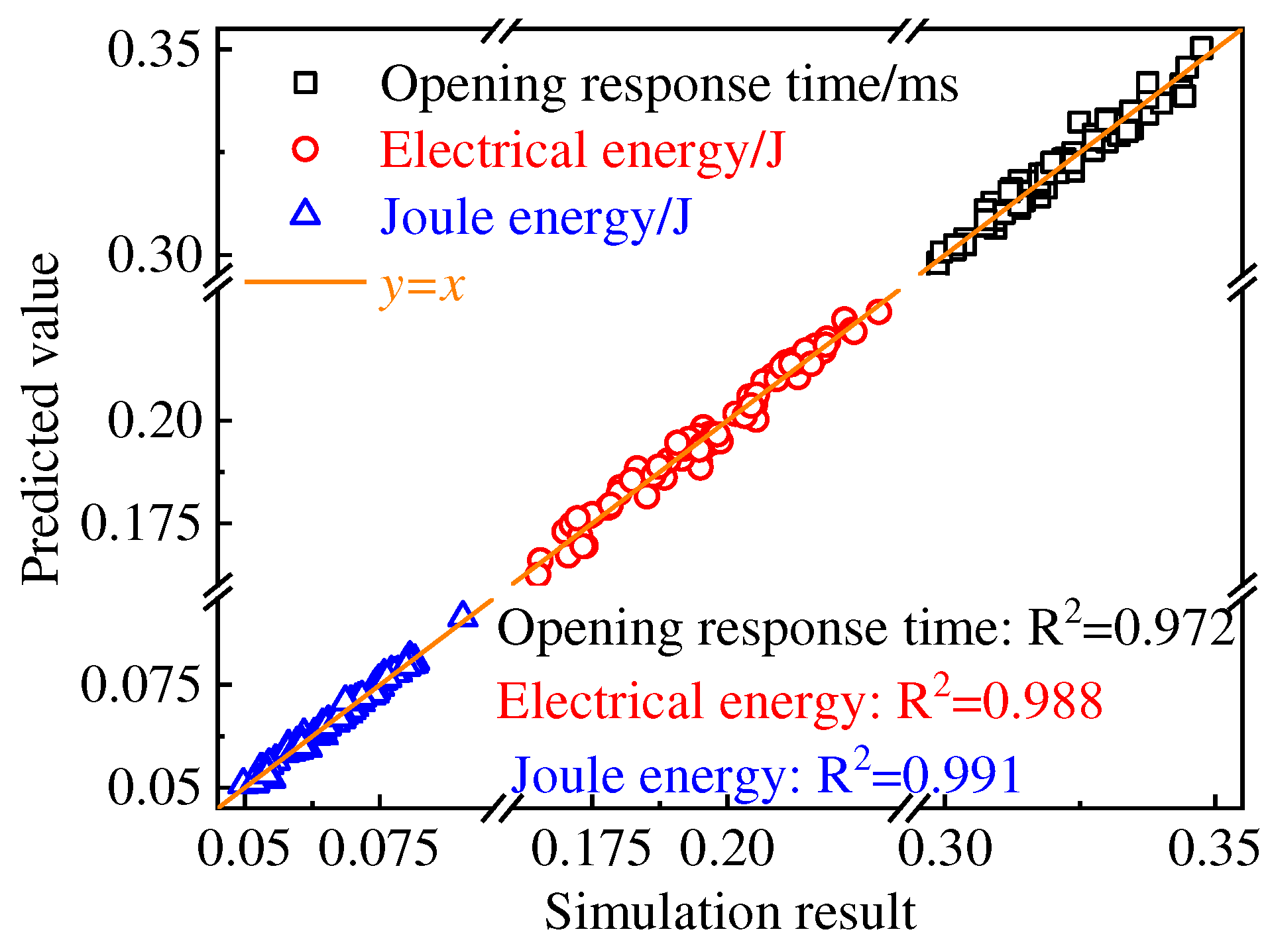
The predictive models for the opening response time, HSV driving energy, and Joule energy have been obtained through repeated training and validation. Figure 12 shows the comparison between the predictive values obtained from the BPNN-trained model and the simulation results obtained from FEM, where Equation (15) is used to calculate the R2 values of each model. The R2 values of the predictive models for the opening response time, HSV driving energy, and Joule energy are 0.972, 0.988, and 0.991 respectively. Therefore, the BPNN-trained predictive model demonstrates good prediction accuracy and generalization ability, making it suitable for subsequent multi-objective optimization analysis.
R 2 = 1 − ∑ i = 1 n ( y i − f ( x i ) ) 2 ∑ i = 1 n ( y i − y ¯ ) 2

4.2. Multi-objective Optimization Model of NSGA-Ⅱ

The genetic algorithm simulates the process of natural selection to solve problems and select results. It has great potential in solving complex optimization problems and is widely used in automatic control, transportation, and other fields [22,23]. For multi-objective optimization problems, Srinivas et al. [24] proposed the NSGA algorithm based on the non-dominated sorting principle. Deb et al. [25] further introduced the elite strategy, crowding distance, and crowding comparison operators, and proposed the NSGA-II algorithm. In this study, a multi-objective optimization mathematical model was constructed based on the predictive model trained by BPNN, and the NSGA-II algorithm was used for optimization research.
The multi-objective optimization mathematical model comprises variables, objectives, and constraints. The following definitions and constraints are formulated for the three-objective optimization problem in this study:
X = [ x 1 , x 2 , ⋅ ⋅ ⋅ x 6 ] T = [ V p e a k , I p e a k , T p e a k , I h o l d   I , T h o l d   I , I h o l d   II ] T
M i n F X = [ f 1 x ′ , f 2 x ′ , f 3 x ′ ] T = [ T ope . , E ele . , E Jou . ] T
s . t . M i n i m u m ≤ X ≤ M a x i m u m ; f x ′ ≤ f x ;
where xi (i=1, 2, ···, 6) is the initial value of the variable, x ′ i (i=1, 2, ···, 6) is the optimized value of the variable, and f (x) is the BPNN predictive model.

4.3. Optimization Results

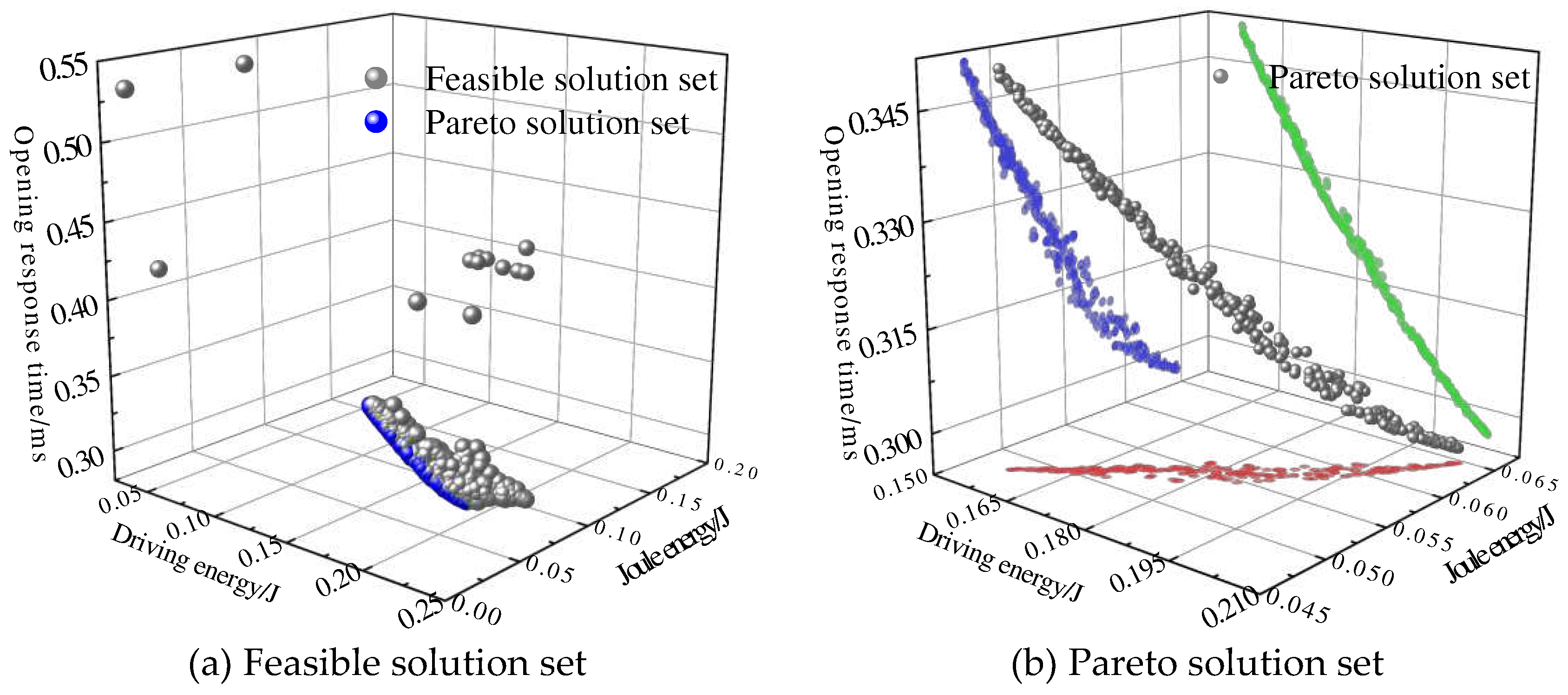
The termination iteration in the genetic algorithm was set to 2000, with a crossover rate of 0.9 and a mutation rate of 0.5. After iterative calculations based on the multi-objective optimization model, Figure 13 (a) shows the distribution of all feasible solutions that satisfy the constraints, while Figure 13 (b) shows the distribution of the Pareto solution set. The Pareto solution set refers to a group of solutions where no solution can be improved in terms of one objective function without sacrificing the values of other objective functions. For a two-objective optimization problem, the Pareto solution set forms a curve, while for three or more objectives, it forms a surface or hypersurface. From Figure 13 (a), it can be observed that the majority of feasible solutions are concentrated together, with only a few distributed on the periphery, indicating that the genetic algorithm iterated near the optimal solution within a limited number of iterations. As for the Pareto solution set shown in Figure 13 (b), they are distributed outside the feasible solutions and formed an irregular surface. This indicates an inverse relationship between Tope. and Eele., meaning that as HSV driving energy decreases, opening response time increases. Additionally, there is a positive correlation between Eele. and EJou., where an increase in driving energy leads to a larger Joule energy. There exists a trade-off relationship between the Tope., Eele., and EJou., and there is no optimal solution that simultaneously minimizes Tope., Eele., and EJou..
In this study, the minimum distance method [26] was used to filter the Pareto solution set in order to obtain the optimal solution that achieves the best overall performance of HSV. Considering the different units of Tope., Eele., and EJou., implementing the minimum distance method requires defining dimensionless objective functions, calculating the minimum distance, and selecting the point with the minimum distance. The dimensionless definition of objective function is given by Equations (19) - (22). By comparing the Pareto solutions with their corresponding objective values before optimization, the influence of different units on decision-making is eliminated.
T ope . * = T ope . ′ T ope .
E ele . * = E ele . ′ E ele .
E Jou . * = E Jou . ′ E Jou .
min D = T ope . * 2 + E ele . * 2 + E Jou . * 2
where Tope. And T ope . ′ represent the pre-optimized and post-optimized opening response time, and T ope . * represents the dimensionless opening response time. The same applies to the Eele., and EJou..
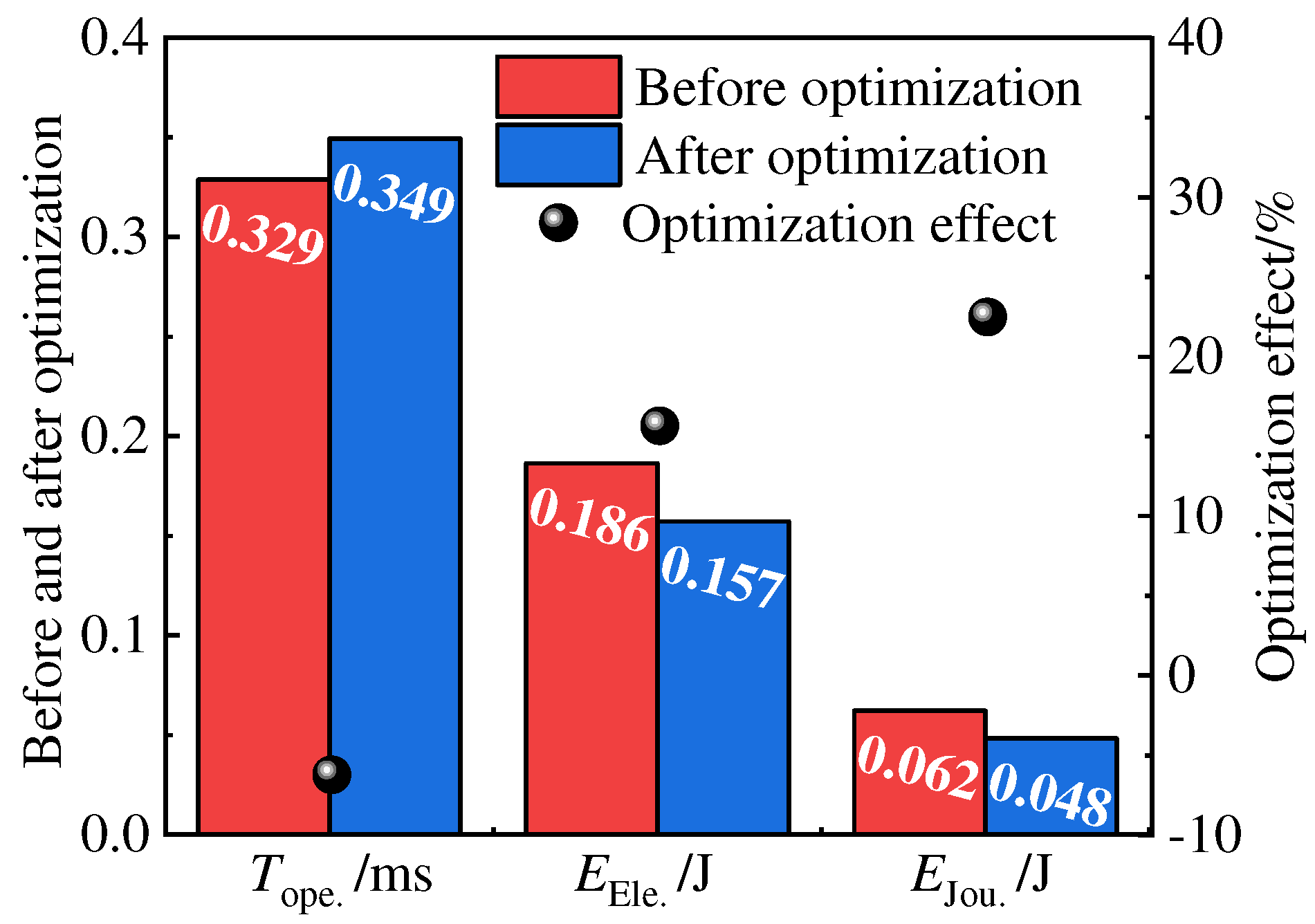
Figure 14 shows the comparison of the opening response time, HSV driving energy, and Joule energy of the HSV before and after optimization. After optimization, the opening response time increased by 6.24% from 0.329 ms to 0.349 ms. However, both the HSV driving energy and Joule energy decreased to different extents. The HSV driving energy reduced by 15.67% from 0.186 J to 0.157 J, while the Joule energy decreased by 22.49% from 0.062 J to 0.048 J. The optimization results indicate that using the minimum distance method for filtering the Pareto solution set resulted in a little bit longer opening response time for the HSV, reduced energy consumption, and decreased Joule heat generation. Since Joule heat directly affects the working life of the HSV, the optimized HSV can reduce energy by 38 %, thus significantly enhancing the working life of the HSV.

5. Conclusions

This study focuses on the HSV of a diesel injector, considering the synergistic effects of dynamic response and energy loss. It conducts a multi-objective optimization study on the driving strategy of the HSV and draws the following conclusions:
(1) A FEM of the HSV coupled with a current feedback model was constructed. The analysis, based on the validated model, investigated the impact of different driving strategies on the dynamic response characteristics and energy loss of the HSV. The peak current significantly affects the time for the HSV to overcome resistance, while increasing the first-order holding current can shorten armature movement time. Eddy current energy and Joule energy account for over 85% of the total energy. Lower energy loss can reduce Joule heat generation, thus improving the working life of the HSV.
(2) A set of 94 sample points was generated based on the D-optimal design method, and a study was conducted in order to develop prediction models for the opening response time, HSV driving energy, and Joule energy by utilizing BPNN. The R2 values of the prediction models were 0.972, 0.988, and 0.991, respectively. A multi-objective optimization model was established based on these prediction models, and NSGA-II was used for optimization analysis resulting in a Pareto solution set for the three optimization objectives. There is a trade-off relationship between the opening response time, HSV driving energy, and Joule energy.
(3) The Pareto solution set was filtered using the minimum distance method to obtain the final optimization results. After optimization, the opening response time extended from 0.329 ms to 0.349 ms, HSV driving energy decreased from 0.186 J to 0.157 J, and Joule energy decreased from 0.062 J to 0.048 J. The optimization effects were -6.24%, 15.67%, and 22.49%, respectively. The optimized HSV significantly reduced energy consumption and generation of Joule energy while only slightly extending the dynamic response time.
The multi-objective optimization method based on BPNN-NSGA-II proposed in this paper demonstrates good capability for optimizing HSV and addressing energy loss issues, thereby enhancing its working lifetime. In the next stage, design and testing of HSV samples will be carried out based on the multi-objective optimization results to further evaluate the effectiveness of the optimizations.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grant number: 52061135203).

References

  1. Duan X, Lai M C, Jansons M, et al. A review of controlling strategies of the ignition timing and combustion phase in homogeneous charge compression ignition (HCCI) engine[J]. Fuel, 2021, 285: 119142. [CrossRef]
  2. Ishii E, Yoshimura K, Yasukawa Y, et al. Effects of Opening and Closing Fuel-Injector Valve on Air/Fuel Mixture[J]. Journal of Engineering for Gas Turbines and Power, 2017, 139(9): 139(9): 092804. [CrossRef]
  3. Wang Q, Yang F, Yang Q, et al. Experimental analysis of new high-speed powerful digital solenoid valves[J]. Energy Conversion and Management, 2011, 52(5): 2309-2313. [CrossRef]
  4. Tao G, Chen H Y, J Y. Y, et al. Optimal design of the magnetic field of a high-speed response solenoid valve [J]. Journal of Materials Processing Technology, 2002, 129(1-3): 555-558. [CrossRef]
  5. Liu P, Fan L, Zhou W, et al. Dynamic performances analysis and optimization of novel high-speed electromagnetic actuator for electronic fuel injection system of diesel engine[J]. Journal of Mechanical Science and Technology, 2017, 31(8): 4019-4028. [CrossRef]
  6. Ebrahimi N, Schimpf P, Jafari A. Design optimization of a solenoid-based electromagnetic soft actuator with permanent magnet core[J]. Sensors and Actuators A: Physical, 2018, 284: 276-285. [CrossRef]
  7. Zhao J, Wang M, Wang Z, et al. Different boost voltage effects on the dynamic response and energy losses of high-speed solenoid valves[J]. Applied Thermal Engineering, 2017, 123: 1494-1503. [CrossRef]
  8. Zhao J, Yue P, Grekhov L, et al. Hold current effects on the power losses of high-speed solenoid valve for common-rail injector[J]. Applied Thermal Engineering, 2018, 128: 1579-1587. [CrossRef]
  9. Lu H, Deng J, Hu Z, et al. Impact of Control Methods on Dynamic Characteristic of High Speed Solenoid Injectors[J]. SAE International Journal of Engines, 2014 7(3):1155-1164. [CrossRef]
  10. Farid B, Tyler H, John L, et al. The impact of peak-and-hold and reverse current solenoid driving strategies on the dynamic performance of commercial cartridge valves in a digital pump/motor[J]. International Journal of Fluid Power, 2016, 17(1): 37-47. [CrossRef]
  11. Li M, Zhang Y. Influence of eddy current on transient characteristics of common rail injector solenoid valve[J]. Journal of Beijing Institute of Technology, 2015, 24(01): 26-34. [CrossRef]
  12. Xie N, Zhang Z, Yin C. Power losses and thermodynamic analysis of the solenoid fuel injector[J]. International Journal of Applied Electromagnetics and Mechanics, 2017, 54(3): 405-419. [CrossRef]
  13. Cheng Q, Xu M, Zhang Z, et al. FEM simulation and performance analysis of a novel heated tip SIDI injector[J]. International Journal of Heat and Fluid Flow, 2016, 59: 87-99. [CrossRef]
  14. Zhao J, Zirka S E, Moroz Y I. Duality-Derived Models of High-Speed Electromagnetic Valves[J]. IEEE Transactions on Industrial Electronics, 2021, 68(10): 9876. [CrossRef]
  15. Eriksson, L., Johansson, E., Kettaneh-Wold, N., Wikström, C., Wold, S., 2008. Design of experiments. In: Principles and Applications, Third Revised and Enlarged. Umetrics Academy, Umea, Sweden.
  16. Myers, R.H., Montgomery, D.C., Anderson-Cook, C.M., 2009. Response Surface Methodology: Process and Product Optimization Using Designed Experiments, thirded. John Wiley and Sons, New Jersey, USA.
  17. Kuram E, Ozcelik B, Bayramoglu M, et al. Optimization of cutting fluids and cutting parameters during end milling by using D-optimal design of experiments[J]. Journal of Cleaner Production, 2013, 42(3):159-166. [CrossRef]
  18. Lecun Y ,Bengio Y，Hinton G .Deep Learning[J]. Nature, 2015, 521(7553): 436-444. [CrossRef]
  19. Wang G, Awad O I, Liu S, et al. NOx emissions prediction based on mutual information and back propagation neural network using correlation quantitative analysis[J]. Energy, 2020, 198: 117286. [CrossRef]
  20. Ma X, Liu D. Comparative Study of Hybrid Models Based on a Series of Optimization Algorithms and Their Application in Energy System Forecasting[J]. Energies, 2016, 9(8):640. [CrossRef]
  21. Dong Y, Ma X, Ma C, et al. Research and Application of a Hybrid Forecasting Model Based on Data Decomposition for Electrical Load Forecasting[J]. Energies, 2016, 9(12):1050. [CrossRef]
  22. Yu Z, Wei S, Wu C, et al. Development and verification of RP-3 aviation kerosene surrogate fuel models using a genetic algorithm[J]. Fuel, 2022, 312:122853. [CrossRef]
  23. Marler R T, Arora J S. Survey of multi-objective optimization methods for engineering[J]. Structural and Multidisciplinary Optimization, 2004, 26(6): 369-395. [CrossRef]
  24. Srinivas N, Deb K. Multiobjective function optimization using nondominated sorting genetic algorithms[J]. Evolutionary Computation, 1995, 2(3):221-248. [CrossRef]
  25. Deb K, Agrawal S, Pratap A, et al. A fast elitist nondominated sorting genetic algorithm for multi-objective optimization: NSGA-II [C]. International Conference on Parallel Problem Solving from Nature, Paris, 2000, 849-858.
  26. Gu Y, Fan L, Lan Q, et al. Multi-objective optimization of fuel injection performance of a common rail injector[J]. International Journal of Engine Research, 2023, 24: 3282-3296. [CrossRef]
Preprints 91637 g001
Figure 1. The simplified 3D simulation model of HSV.
Figure 1. The simplified 3D simulation model of HSV.
Preprints 91637 g001
Preprints 91637 g002
Figure 2. Dynamic response simulation model of HSV with current feedback.
Figure 2. Dynamic response simulation model of HSV with current feedback.
Preprints 91637 g002
Preprints 91637 g003
Figure 3. Comparison of simulation results and experimental data of HSV FEM.
Figure 3. Comparison of simulation results and experimental data of HSV FEM.
Preprints 91637 g003
Preprints 91637 g004
Figure 4. Schematic diagram of current loading timing for different driving strategies.
Figure 4. Schematic diagram of current loading timing for different driving strategies.
Preprints 91637 g004
Preprints 91637 g005
Figure 5. Comparison of armature lift and electromagnetic force curves under different driving strategies.
Figure 5. Comparison of armature lift and electromagnetic force curves under different driving strategies.
Preprints 91637 g005
Preprints 91637 g006
Figure 6. Comparison of dynamic response parameters in the opening stage under different strategies.
Figure 6. Comparison of dynamic response parameters in the opening stage under different strategies.
Preprints 91637 g006
Preprints 91637 g007
Figure 7. Comparison of different energy proportion in opening stage under different driving strategies.
Figure 7. Comparison of different energy proportion in opening stage under different driving strategies.
Preprints 91637 g007
Preprints 91637 g008
Figure 8. Comparison of eddy current energy loss and Joule energy loss curves under different driving strategies.
Figure 8. Comparison of eddy current energy loss and Joule energy loss curves under different driving strategies.
Preprints 91637 g008
Preprints 91637 g009
Figure 9. Multi-objective optimization flow chart of BPNN-NSGA-Ⅱ.
Figure 9. Multi-objective optimization flow chart of BPNN-NSGA-Ⅱ.
Preprints 91637 g009
Preprints 91637 g010
Figure 10. Structure diagram of a single hidden layer BPNN.
Figure 10. Structure diagram of a single hidden layer BPNN.
Preprints 91637 g010
Preprints 91637 g011
Figure 11. Influence of the hidden layer neurons number on the relative error (Joule energy model as an example).
Figure 11. Influence of the hidden layer neurons number on the relative error (Joule energy model as an example).
Preprints 91637 g011
Preprints 91637 g012
Figure 12. Comparison of the predicted value and the simulation result of the model constructed by BPNN.
Figure 12. Comparison of the predicted value and the simulation result of the model constructed by BPNN.
Preprints 91637 g012
Preprints 91637 g013
Figure 13. Feasible solution set and Pareto solution set: (a) feasible solution set and (b) Pareto solution set.
Figure 13. Feasible solution set and Pareto solution set: (a) feasible solution set and (b) Pareto solution set.
Preprints 91637 g013
Preprints 91637 g014
Figure 14. Comparison of optimization objectives before and after optimization.
Figure 14. Comparison of optimization objectives before and after optimization.
Preprints 91637 g014
Table 1. Parameter comparison of different driving strategies.
Table 1. Parameter comparison of different driving strategies.
Design variable Symbol
/Unit		 Driving
strategy 1		 Driving
strategy 2		 Driving
strategy 3
Peak voltage Vpeak/V 70 70 70
Peak current Ipeak/A 24.5 24.5 19
Peak current loading time Tpeak/s 0.00023 0.00049 0.00049
First-order holding current Ihold Ⅰ/A 14 - -
First-order holding current loading time Thold Ⅰ/s 0.00049 - -
Second-order holding current Ihold Ⅱ/A 5 5 5
Table 2. The parameter variation ranges.
Table 2. The parameter variation ranges.
Design variable Level
Upper Standard Lower
Vpeak/V 65 67.5 70 72.5 75
Ipeak/A 23 23.75 24.5 25.25 26
Tpeak/s 0.00021 0.00022 0.00023 0.00024 0.00025
Ihold Ⅰ/A 12 13 14 15 16
Thold Ⅰ/s 0.00045 0.00047 0.00049 0.00051 0.00053
Ihold Ⅱ/A 4 4.5 5 5.5 6
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated