Prerpints.org logo
Preprint
Article

Efficiency of Micro and Small Wood-Processing Enterprises in the EU – Evidence From DEA and Fractional Regression Analysis

Altmetrics

Downloads

90

Views

30

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

27 November 2023

Posted:

28 November 2023

You are already at the latest version

Alerts
Abstract
Micro and small wood-processing enterprises represent the heart of the European forest-based industries, being among the key drivers of economic growth in rural, mountainous, and poor regions. Their economic efficiency is of fundamental importance for their existence and the pro-vision of income for the local population in rural areas. Data Envelopment Analysis (DEA) is nonparametric, linear-programming-based approach, commonly used to analyse the efficiency of organizational units. This method allows estimating the economic efficiency of a certain eco-nomic system without assumptions about the functional form between resources and products. Furthermore, DEA determines the efficiency frontier and gives results of whether an enterprise, i.e., a Decision Making Unit (DMU) is efficient or not. The main objective of this study was to investigate and evaluate the economic efficiency of micro and small wood-processing enterpris-es in the EU countries and reveal the hidden inputs that facilitate efficiency generation. The eco-nomic efficiency evaluation was carried out on the basis of the official statistical data for the mi-cro and small wood-processing companies in the EU member states for the period 2015-2020 by performing a two-stage DEA analysis. The data used were standardized by value per employee. In addition to the first stage of DEA, fractional regression probit and logit models with four contextual variables were used to reveal the influence of the hidden inputs in the model. The results showed that the micro and small wood-processing enterprises can be regarded as more scale-efficient than technically-efficient entities. The only contextual variable affecting the eco-nomic efficiency was Investments per Person Employed, improving the efficiency by 2% per 1% increase of the investments.
Keywords: 
Subject: Business, Economics and Management  -   Economics

1. Introduction

The economic efficiency of wood processing enterprises is a key factor for their development in the current conditions of increased global competition and developed supply chains. Micro and small enterprises (MSE) play an important role in the local economies [1]. They are considered the main driver of economic growth, especially in rural areas [2]. These reasons make research on growth, performance, and the factors behind them to be so topical in recent years. Many researchers have investigated the efficiency of wood-processing enterprises. Medvedev et al. [3] analyzed wood-processing enterprises and revealed the role of the optimal use of wood resources for enhancing their efficiency. In similar research, Lähtinen [4] outlined that diversified tangible and intangible resources are the key tool for the improvement of the economic performance of wood-processing enterprises. Kocianová et al. [5] surveyed 3,500 wood-processing family enterprises. The authors revealed that the implementation of complex strategies is vital for the performance and development of micro and small enterprises. The reuse, recycling and upcycling of wood waste and by-products play an important part in these strategies. This is the reason many other authors [6-11] analyzed the efficiency of the whole forest-wood value chain. Korkmaz [6] and Sporcic et al. [7] estimated the efficiency of forest enterprises. Korkmaz [6] assessed selected efficiency determinants of 37 forest enterprises, such as capital, production in value and quantity, number of employees, value-added, and others. Sporcic et al. [7] investigated determinants like revenues, labour, and expenditures. Kovalcik [8] compared the Slovak forestry efficiency to other European countries using determinants such as taxes, subsidiaries, and interests. Zhang et al. [10] and Han et al [11] included as determinants (in the context of inputs in the methodology implemented) the trivial factors of production such as land, capital invested, etc. The approach regarding the determinants for wood-processing and furniture enterprises [12, 13] is similar. In many studies [14-19], the so-called parametric approaches [18-25] have been used. This means that the exact functional form of the relation between determinants (factors) and efficiency is implemented. Sedivka [12] calculated the technical efficiency of 203 Czech sawmills using the Cobb-Douglass production function. Prasetiyo et al. [7] used Pareto analysis, an X-Y matrix, and process capability analysis. Sujova et al. [17] used ratios to estimate the efficiency of the investments in the entire Czech wood-processing industry. Sedliačiková et al. [18] provided a MANOVA analysis to outline the important managerial determinants of wood-processing enterprises’ performance that influence the efficient financial model. The nonparametric methodologies in addition to relaxing the analysis of the exact functional form (technology) between inputs (determinants) and outputs of a certain production, define the stochastic frontier of efficiency. One of the most applied nonparametric linear approaches is Data Envelopment Analysis (DEA) [24]. DEA defines an efficiency frontier that “envelopes” the observed input and output data for each Decision Making Unit (DMU) [26].
DEA is among the widely used methodologies when analyzing the efficiency of wood-processing enterprises. Krišťáková et al. [27] used the DEA and Malmquist Productivity Index to estimate the efficiency scores and the productivity change of Bulgarian and Slovak large wood-processing enterprises. Yang et al. [30] used DEA for efficiency estimation of leading wood-processing enterprises. They revealed that 60% of the enterprises are efficient. This is a typical use of that methodology to assess whether an enterprise is efficient or not, i.e. are they on the efficient frontier or not. Other authors [29, 31- 33] implemented DEA in the entire wood-processing industry. DEA is often combined with supplementary evaluation techniques. In their research, Zhang et al. [34] investigated the wood-processing industry with a combination of DEA and life cycle assessment. Dia and Shahi [35] presented the common use of DEA and the bootstrap procedure for the purposes of wood-processing. This is the next step in DEA analysis when it is improved further with additional methodology to reveal deeply the factors that caused the DEA levels of efficiency. The main objective of this research work was to evaluate the economic efficiency of micro and small wood-processing enterprises in the EU member states using the DEA approach supplemented by a fractional regression analysis and reveal the hidden inputs that facilitate efficiency generation..

2. Materials and Methods

2.1. Data Envelopment Analysis (DEA)

Data Envelopment Analysis (DEA) was developed by Charnes, Cooper, and Rhodes [49] with the so-called (CCR)model (CCR). Charnes et al. [50], stated that the efficiency of DMUs can be obtained from the maximum of ratio of weighted outputs to weighted inputs. Banker, Charnes, and Cooper [51] further developed DEA with a model (BCC) that is applicable in so-called variable returns to scale and estimates the pure technical efficiency of the enterprises. Coelli et al. [26] described DEA as a linear programming technique, which gives a linear frontier that “envelopes” the observed input and output data for different units under research, which are called Decision Making Units (DMUs). DEA approach includes various models from the classic ones to more complicated ones like Slack Based Measurement [52,53]. The key principle of applying DEA is to maximize the efficiency rate. DEA estimates the efficiency scores of all DMUs by comparing the efficiency rate of each unit with that of the best performer. Cook et al. [54-55] and Zhu [56] pointed out that the main issue when using DEA is to preliminary define the purpose of the estimation. In the current research, for the purpose of the first stage of DEA analysis, the input-oriented CCR (also called CRS – constant returns to scale) model was used, following the requirements set by Fernandes et al. [40] that this model does not overestimate the efficiencies of the larger DMUs. The model for CCR is the following:
where λj are the individual scalars of each DMUj jϵ[1, n], xij are the amounts of inputs of type i in DMU j, xi0 is the amount of i-th input of DMU0 being under efficiency estimation. The yrj are the outputs of type r in DMU j, and the consequent yr0 for the DMU, which is being assessed. If the sum of lambdas (λ) equals unity (Σλ=1), then the model becomes BCC with variable returns to scale. The BCC efficiency is so-called pure technical efficiency (PTE) and is usually denoted by BCC or VRS (θVRS). This model calculates the pure ability of the DEA inputs to transform into DEA outputs taking into account the different scales of each DMU.
min ⁡ θ C R S ∑ j = 1 n λ j x i j ≤ θ x i 0 ∑ j = 1 n λ j y r j ≥ y r 0
where λj are the individual scalars of each DMUj jϵ[1, n], xij are the amounts of inputs of type i in DMU j, xi0 is the amount of i-th input of DMU0 being under efficiency estimation. The yrj are the outputs of type r in DMU j, and the consequent yr0 for the DMU, which is being assessed. If the sum of lambdas (λ) equals unity (Σλ=1), then the model becomes BCC with variable returns to scale. The BCC efficiency is so-called pure technical efficiency (PTE) and is usually denoted by BCC or VRS (θVRS). This model calculates the pure ability of the DEA inputs to transform into DEA outputs taking into account the different scales of each DMU.
The scale efficiency (SE) is a very important indicator that combines the CCR and BCC efficiencies. It is a proportion of CCR efficiency in the BCC efficiency. The model is as follows:
S E = θ C C R θ B C C

2.2. Fractional Regression Model (FRM)

The fractional regression model was developed by Papke and Wooldridge [57]. According to Ramalho et al. [48] the FRM only requires specification of the regression equation and type of the probability distribution, i.e., functional form. As Ana Isabel Martins [58] states in her research on FRM, it does not require transformations to the original data, as it is in the traditionalists’ models like OLS or Tobit regression models, and allows direct estimation of the dependent variable. For these preliminary actions, Papke and Wooldridge also made a special note that their model did not need any ad-hoc transformations. All described features of FRM make it very easily applicable and interpretable. The FRM is widely implemented with logit, probit, and the heteroskedastic probit function. The estimation procedure is based on the Bernoulli log-likelihood function [57]:
l n L = y i l n G ( x i b ) + ( 1 − y i ) l n [ 1 − G x i b ]
where yi is the dependent variable. The G(xib) is a known nonlinear function [59], 0< G(xib) <1. The b is the vector of coefficients of the covariates., xi are explanatory variables.
The functional forms for the G(xib) used in the current research are:
Logit: G(xib)=exp(xib)/{1+exp(xib)},
Probit: G(xib)= Φ(xib),

2.3. Inputs and outputs for DEA

Ana Isabel Martins [58] stated that the independent variables in the regression model for the second stage might correspond to input variables used in the DEA model or include other variables. This can be quite questionable in the context of other research works. Simar and Wilson [36,37,41] write about the incontrollable variables, or environmental, until in their DEA model the variables are actually controllable. The meaning of the term “controllable” should also be considered. In the context of the DEA analysis DMUs can control their inputs and outputs.
The selection of the inputs and outputs for the first stage (DEA analysis) is vital for further analysis with the regression model. Some of the most commonly used variables for inputs/outputs in research related to forestry and forest-based industries are given in Table 1.
As it can be seen, the authors used the very typical for every economic unit variables like revenues and expenditures. Some of the authors [13,34] used relative variables per unit of measure as capital or output value. It is a good approach for reducing the differences between each DMU and in this way making the comparison better and easier to interpret. Usage of the total amount of input/outputs is a trivial alternative that does not reduce the applicability of DEA, but the later analysis with the recommendations of DEA proposed slacks is sometimes not quite applicable in the way the model proposes the reduction of inputs or increase in outputs.
Fernandes et al. [40] stated that consistent results can be reached by reducing the number of inputs and outputs compared to that of DMUs. They followed the ‘rule of thumb’ [60] which means that the number of DMUs under evaluation by DEA must be three times higher than the number of inputs and outputs. The same approach was selected in the current study, as it is widely used by many authors. The following variables (xi) were incorporated as inputs for DEA analysis:
Total purchases per employee (TPRCH). Costs of goods and services form a significant share of the costs of woodworking companies. Companies in each of the countries can be compared in terms of the amount of these costs per employee. In this way, the differences arising from the different numbers of personnel within the intervals defined by Eurostat for the size of small and medium-sized enterprises are removed. This indicator reveals the ability of companies to optimally plan their procurement.
Personnel cost per employee (PCOST). This input reveals the ability of companies in the countries being compared to provide the necessary remuneration for the pooled labour resources. At the same time, it also shows the securities burden, which can affect economic efficiency.
Outputs for DEA were also estimated per employee. They were as follows:
  • Revenues per employee (REV). Revenue is a key indicator that characterizes the ability of companies to carry out market transactions.
  • Value added per employee (VADDED). The main source of efficiency for wood-processing companies is their ability to add value. The higher added value per employee indicates the quality of the human resources used and the entrepreneurial skills of the managers. By means of added value, the prerequisites for some companies to be less efficient than others are revealed.

2.4. Variables for the second-stage fractional regression analysis

As previously mentioned, many authors stated in their research that the second stage’s variables in the regression model are contextual variables.
The variables used in the time series analysis like covariates are the following:
Gross domestic product (GDP). The GDP reveals the overall conditions of the economy in each studied country.
  • Harmonized index of consumer prices (HICP). Inflation influences the share of expenditures for furniture, homes, etc. in the household’s budget. Inflation, if higher can be very dangerous from one side because consumers spend more on other goods and services with higher priority. On the other side, inflation can be a trigger for people to invest their money. In this study, we examine the influence of this variable.
  • Investment per person employed for all sectors of interest (IVP) – wood processing. This indicator reveals the overall investment dynamics in the sector regardless of the size of the enterprises. It reveals the innovativeness of the enterprises.
  • Index of Number of enterprises for all C16 sectors (ENTNUM). This variable gives information about the expectations and the competition. The number of enterprises indirectly reveals the expansion. It is not in the meaning of the business cycle but of the understanding of economic conditions by the entrepreneurs after the annual improvement of the economy.

2.5. Data for the analysis

In the current study we used data from the Eurostat Structural Business Statistics Historical Data by Enterprise Size Class [61] for DEA inputs and outputs in the sector C16 “Manufacture of wood and of products of wood and cork, except furniture; manufacture of articles of straw and plaiting materials”, Eurostat Structural Business Statistics Historical Data [62] for the “Investment per person employed” in C16 variable. For the “Harmonised index or consumer prices” [63] and GDP we used the National Accounts folder of the Eurostat database. The period of research was 2015-2020, which is appropriate to reveal the recent and at the same time structural features of the efficiency of micro and small wood-processing enterprises. At the same time, the defined time period is relevant in terms of availability of comparable data within the Eurostat database.
To achieve the objective of the current study, the following hypotheses were tested:
H1: The GDP influences positively the efficiency of enterprises. The increase in the GDP reveals the overall economic growth. These factors can influence enterprises in both directions, i.e. positive or negative [47]. It is hypothesized that GDP will influence positively the micro and small wood-processing enterprises through the generation of more income. This is in line with the findings reported by Silva et al. [45].
H2: The inflation has a negative effect on enterprises’ efficiency. The inflation rate influences the ability of the economic agents to purchase commodities like wooden materials, furniture or housing. Some authors [45] used the purchasing power standards to reveal the ability of households and enterprises to purchase. They revealed the negative influence of purchasing power on disposable income.
H3: Investments made by enterprises raise their efficiency. Investments improve the ability of the enterprises to improve their scale and pure technical efficiency. According to Diaz-Balteiro et al. [31], Silva et al. [45] and other, investments in R&D or any innovative activities have positive influence on efficiency.
H4: The number of enterprises has a negative impact on efficiency levels. This proposition comes from the research of Silva et al. [45]. They estimated negative influence of the trade freedom, and despite being insignificant in their model, it gives a clue that the competition can have an effect on the efficiency.

3. Results

3.1. Descriptive statistics

The analysis of the DEA efficiency requires a profound study of the inputs and outputs’ statistical features. They reveal the comparative position of each country before the efficiency scores estimation. The results for the descriptive statistics of inputs and outputs for the EU member states in the period 2015-2020 are presented in Table 2.
The data included in Table 2 shows that revenues (REV) and expenditure on goods and services (TPRCH) were closely related to each other. The average variation of purchased goods and services for the studied population was 8.86%, and the variation of income was 8.68%. The correlation coefficient between the two variables is 0.99. This reveals that efficiency is hardly supported by the adaptability of inventory management to market fluctuations. This is something usual for micro and small enterprises which do not manufacture production series in large quantities. The variation of personnel costs (PCOST) was higher than that of revenues and purchases (9.91%). If such an input is not so strongly related to the output it can endanger the efficiency. The correlation coefficient is 0.92, which means that the micro and small enterprises adapt their personnel annually. The output with the higher variation was value added (VADDED). The reason for that is not quite clear, but this result reveals the danger that can affect micro and small enterprises. For them is vital to have stability in adding value to be facilitated in their efforts for improvement. The correlation coefficient between REV and VADDED is 0.95.

3.2. DEA Analysis

The results obtained for the DEA efficiency are presented in Table 3. The efficiency scores are given for each country being estimated with the respective descriptive statistics.
The table shows that in general, the wood-processing enterprises in the studied countries were quite efficient. The efficiency scores of some countries were much higher than that in previous research by Krišťáková et al. [27]. In the table there are countries with very stable efficiency like the Czech Republic, Slovakia, Cyprus, Lithuania, and Spain, which are below the level of average EU variation. Enterprises in the Czech Republic, Slovakia and Cyprus are leaders in CCR efficiency. These are results based on the historical improvement of efficiency during the period of research. On the other side of efficiency are the wood-processing enterprises in Bulgaria, Romania, Greece, and Spain. They have lower average efficiency and above-average variation. Here it is interesting the appearance of Finland. Enterprises in industrial giants like Germany and Italy are characterised by a lower efficiency than the leaders with above-average variation. Due to the narrower focus of the current research, particularly on micro and small enterprises, some of the results can differ from other research. The results in Table 2 differ from those reported by Schmidt-Ehmcke [65] which placed Germany and Denmark on the top of the efficiency ranking. At the same time, the results obtained are in line with previous studies like Krišťáková et al. [27] that the Slovak wood-processing enterprises performed better than the Bulgarian ones in terms of CCR efficiency. 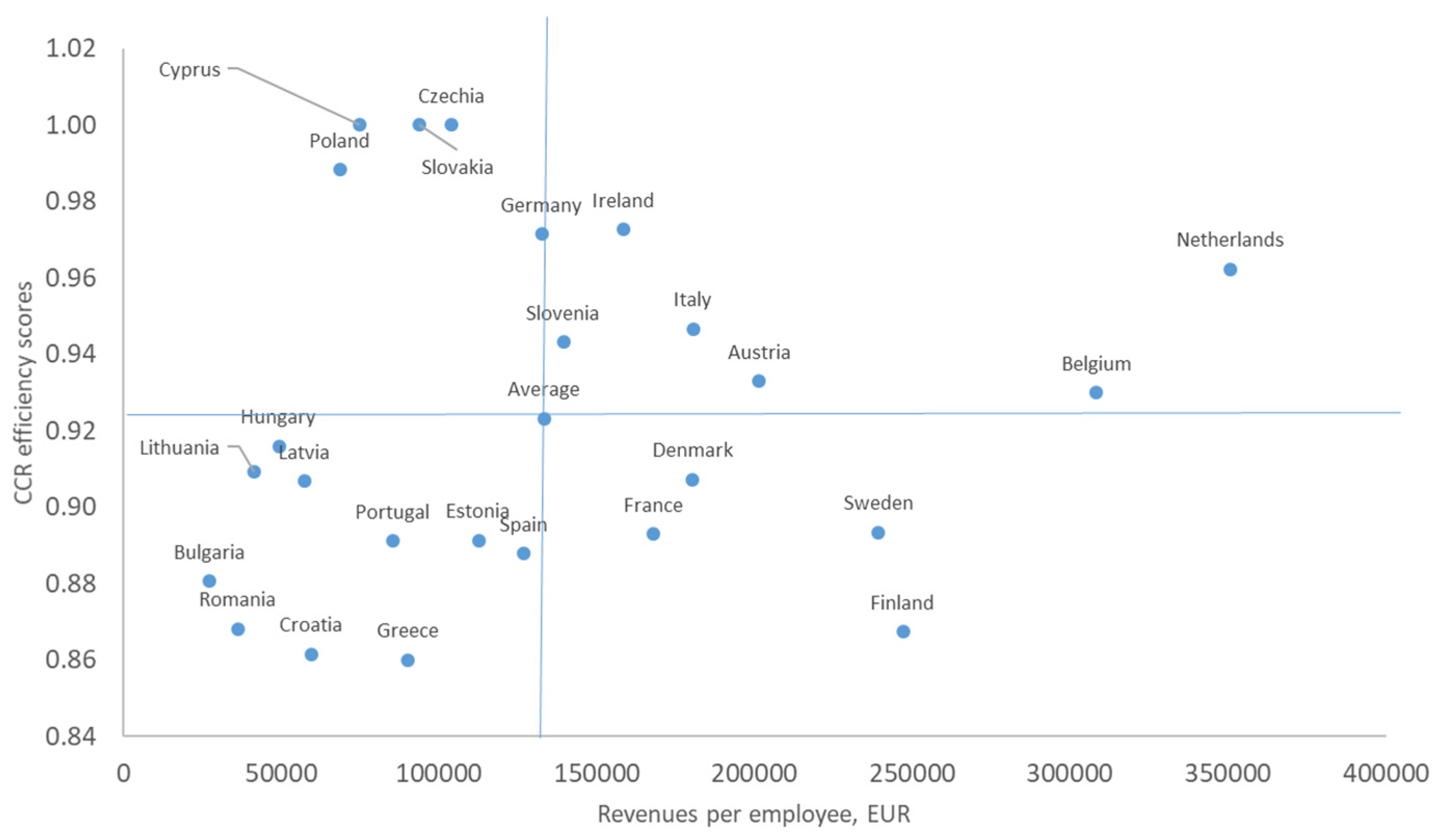The relations of the CCR efficiency can be revealed in Figure 1, with a comparison between efficiency scores and the revenues. The costs are in high correlation with the revenues, which determines revenues like a sufficient variable for the comparison. They are inputs in DEA model from one side and elements of the cost efficiency from another.
The figure shows that there were low-efficient wood-processing enterprises with low levels of revenue in Bulgaria, Romania, Greece, Croatia, Greece, Portugal, Spain, Estonia, Lithuania, Latvia, and Hungary. The average efficiency in these countries was 0.89 and the variation was 2.31%, which is higher than the average EU level. Enterprises with higher revenues than the average and lower efficiency are located in France, Denmark, Finland, and Sweden. Their efficiency was lower than the average for small and micro wood processing enterprises in the EU. The usual relationship with higher revenues and high efficiency scores was determined for the wood-processing enterprises in Ireland, Italy, Austria Belgium, Slovenia, and the Netherlands. The excellent enterprises are in the quadrant with lower revenues and higher efficiency. The Germany has the worst position there, until the Czech Republic, Slovakia, and Cyprus are the best performers. The results can be additionally supported by the calculation of scale efficiency (SE). Table 4 presents the results for the scale efficiency scores obtained from model (2).
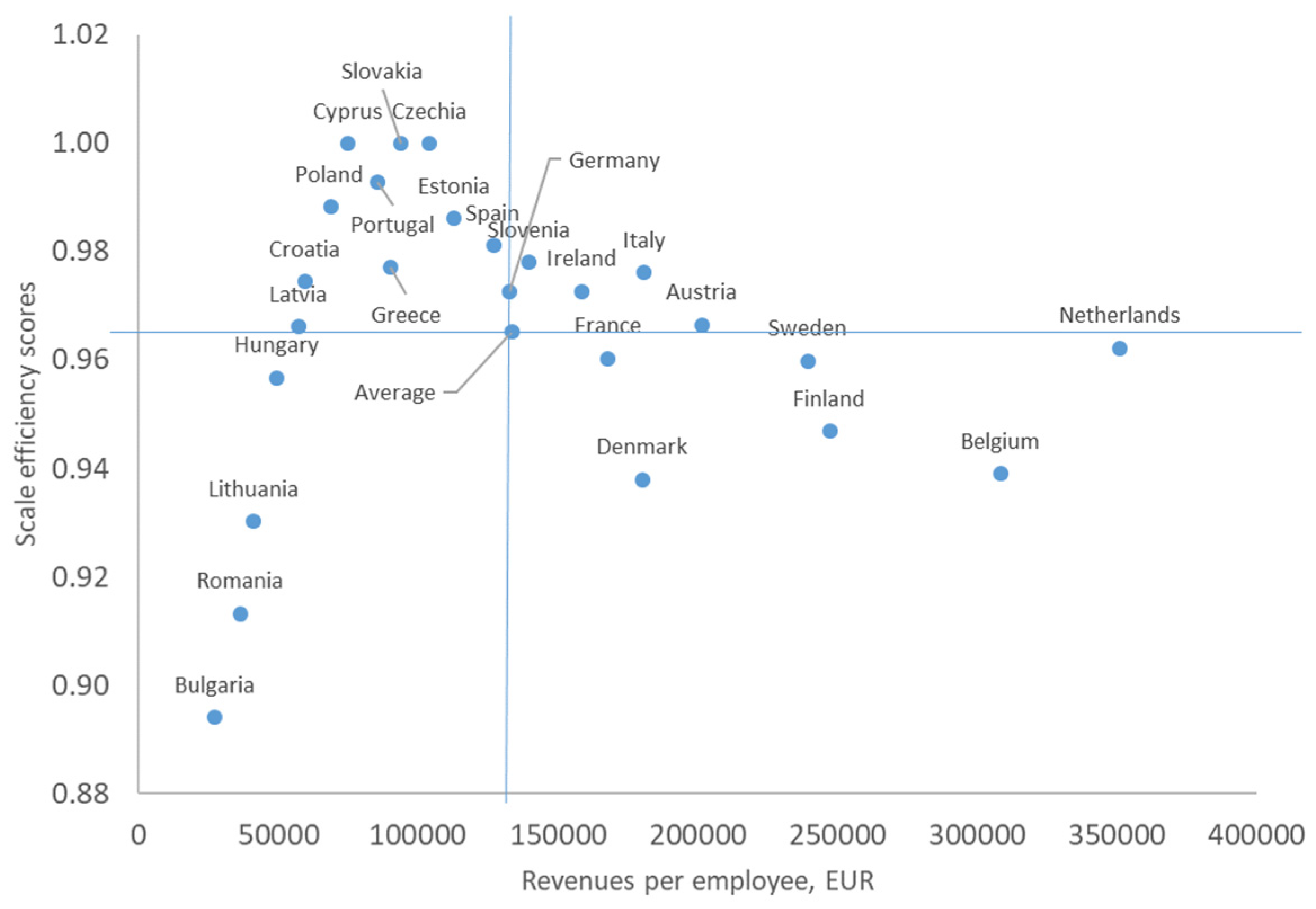
The results present the higher scale efficiency of the micro and small wood-processing enterprises in the EU member states in comparison with the determined CCR efficiency. This means that the scale is the main strength of these enterprises. When using DEA, it is common to obtain higher results for the scale efficiency, but in this case, the scale of the enterprises in the studied countries is a factor for their overall efficiency. In general, the returns to scale of the EU micro and small wood-processing enterprises are increasing. This means that an increase in productivity surpasses the increase in costs. The role of the scale for wood-processing enterprises is better revealed in Figure 2.
The figure reveals that many enterprises in the low revenues quadrant with lower efficiency moved to the higher efficiency quadrant. This is a usual result according to other research [66]. The Bulgarian, Romanian, and Hungarian enterprises remained in the lower efficiency zone. The reason for that is the high pure technical efficiency. Otherwise, the scale efficiency becomes leading as in [7, 8]. When the denominator of the model (2) was higher, i.e., BCC efficiency was better, the scale efficiency was not high. In the interval of the revenues per employee up to 70,000-80,000 EUR per employee revenues, the tendency was for a constant increase in the scale efficiency. These enterprises rely on the scale to improve economic efficiency. All these enterprises work in increasing returns to scale (IRS). Probably this is the reason they focus mainly on scale efficiency but not to the same degree on pure technical efficiency (BCC). After the peak, composed of enterprises from Slovakia, the Czech Republic, and Cyprus, the trend is downward. This reveals. that after the peak companies rely more on pure technical efficiency. This means that they have better capabilities to invest in newer and more productive technologies. Companies after the peak allocate better the inputs to outputs.

3.3. Fractional regression

All the results are derived by separate calculations for CCR scores and BCC scores as dependent variables. Values of the CCR and BCC efficiency are calculated on an average basis for the entire period. The fractional regression analysis was made for probit (model (5)) and for logit (model (4)) models. Firstly, the analysis was made for the micro and small wood processing enterprises and aft for the whole sector. The results of the fractional regression for the micro and small wood-processing enterprises are presented in Table 4.
Table 4. Results of cross sectional analysis with two types of fractional regression by models (4) and (5).
Table 4. Results of cross sectional analysis with two types of fractional regression by models (4) and (5).
CCR- dependent BCC- dependent
Coefficients in each model Coefficients in each model
Covariate Probit Logit Probit Logit
GDP -0.00000010 -0.000000206 0.0000000 7.93E-08
HICP 0.0112011 0.0136995 0.1199848 0.260742
IVP 0.0022762 0.0035975 -0.0070483 -0.01579
ENTNUM 0.0000371* 0.0000768* 0.0000905 0.000192
*Statistically significant at α=0.05.
The results in the table reveal that the only significant factor for the micro and small wood processing enterprises in the EU is the number of these enterprises. The first three hypotheses failed in this regression analysis. Neither the GDP, HICP, nor IVP influences the efficiency. Only the competition, but in the opposite way of the H4. The number of the enterprise did not affect the efficiency. It drives enterprises toward efficiency and economies. The intense competition determines the wood-processing enterprises’ production to be eco-friendlier and more sustainable, supporting the ongoing twin, e.g., digital and green transition of the industry in line with the circular economy principles [67]. The investments are not significant and this reveals that the enterprises tried to adapt their organizational and managerial capabilities to the external environment changes. This can be achieved by optimization inside the micro and small enterprises. This optimization did not include investments in technologies. This is why the IVP variable is not significant. The owners or entrepreneurs in wood processing enterprises in the EU made decisions that mainly influenced the capacity. This is the reason models with CCR as dependent variables are significant and those with BCC are not. The results show that usual factors like R&D and FDI [31, 45] do not influence small and micro enterprises in C16. This result is quite annoying because it clarifies the strategy of entrepreneurs in this sector. It also reveals a problem with funding for these investments and the way the entrepreneurs get information about the available funding sources. The model in the Table 4 was tested with a link test [67] which is called the Pregibon test [69] for model specification. According to this test, the dependent variable is regressed to fitted values of the initial fractional regression and to the squared fitted values. If the squared values are significant the test failed. The test revealed that the model is misspecified p-value of the squared fitted variable is 0.006. After the test, only the ENTNUM variable remained in the model. The results are presented in Table 5.
The results reveal that the number of enterprises influences positively the CCR efficiency. It does not influence the pure technical efficiency. The marginal effect of the number of enterprises is 0.01, which means that one more micro or small wood processing enterprise will probably improve the efficiency of the existing ones by 10%.
Fractional regression analysis of the whole C16 economic sector in the EU was performed in order to better understand and improve the analysis, and to highlight the specifics of the micro and small wood-processing enterprises. The results are presented in the Table 6.
The results given in Table 6 reveal that the regressions with BCC as a dependent variable were correctly specified. According to the results obtained for the CCR efficiency none of the selected variables was significant. This means that the scale of the enterprises in the whole C16 does not depend on the level of the economy, inflation, and competition in a particular moment. These are interesting results, that reveal that the scale of the enterprises depends mostly on decisions that are not related to the macroeconomic conditions in each of the countries. The quality part of the efficiency is related to the pure technical one or BCC. The results for that efficiency reveal that the investments per person IVP are statistically significant variables. Nothing influences the optimality of resource allocation better than investments. They are vital for micro and small wood-processing enterprises, but they do not influence them. IVP are factor for all the sector despite the micro and small enterprises. The enterprises should develop internal determinants like management quality and human resources [70] from one side that can be a result of appropriate behavioural aspects [71]. From another the right alternatives for the production process [72]. The marginal effects of the IVP variable in the two models are calculated according to Ramalho et al. [68]. The estimated marginal effect of IVP in the probit model is 0.021 and in the logit model is 0.02. These values mean that with one percent higher investments per person employed in the sector, the efficiency of the micro and small wood-processing enterprises rises by about 2%. This result reveals the importance of the investments. The results in Table 6 provide information for the main direction of development set up by the medium-sized and big enterprises. This means that the technologies are not in the focus of the entrepreneurs of small businesses in C16. As other authors [31,47] revealed that investments in the form of direct foreign investments can improve efficiency, but these investments can be made in mid-sized and big enterprises. The results given in Table 4 and Table 6 show that the small and micro wood-processing enterprises are vulnerable. The results are interesting in the fact that the macroeconomic conditions do not have any effect on the C16 efficiency. This can place a hypothesis that the European woodworking sector is quite closed in its efficiency factors. Most of the hypotheses in the current research failed with the exception of H3 for the IVP influence. Proving this hypothesis reveals that the overall improvement and the strategic orientation of the wood-based sector is technologically determined. The micro and small enterprises with their capacity adaptation will probably cumulate capital for investments.

5. Conclusions

In this study, the total and pure technical efficiency of the micro and small wood-processing enterprises in the EU was determined using DEA and fractional regression analysis. The results showed that the enterprises are efficient mainly due to their scale. Pure technical efficiency, which is the result of optimality in the distribution of resources, is a problem for a large number of enterprises. Four hypotheses were put forward, of which only one was proven. Hypotheses H1, H2, and H3 were not confirmed by the empirical study for the micro and small enterprises. Businesses with a small volume of sales can be very efficient, with Cypriot businesses being a typical example of this. At the same time, the research found that there are micro and small wood-processing enterprises in the EU that are sustainably efficient in terms of both pure technical and scale efficiency. Hypothesis H4 was proven for the micro and small enterprises. The H3 was proven for the whole C16. The investments are vital for micro and small wood-processing enterprises, but they do not rely on them. They use process improvements regarding the scale, but not the cutting-edge technologies that can improve pure technical efficiency. The investments in the sector push forward the technological improvement of the production processes and from there economic efficiency. The results from the fractional regression analysis revealed that technologies in C16 were influenced by the investments but the scale was not. This is a very significant contribution as a result of the empirical analysis in this study. Regression with BCC as a variable revealed that for the period from 2015 to 2020, the enterprises in C16 tried to improve the technology and optimal resource allocation. The current study also revealed that there is an interval of the revenues per employee that the efficiency is maximized. For the EU this interval should be between 70,000 EUR and 100,000 EUR. This is quite beneficial for the industrial practice because it can be accepted as a threshold to switch between managerial measures for efficiency improvement and investment based. The current study is limited to the implementation of CCR and BCC DEA models. Numerical results are based on data for the C16 economic sector under the investigated period. Fractional regression included four contextual variables. Further research is needed to clarify the influence of other external factors. Directions for future research can be complemented with the comparison between micro/small, and large enterprises. There will be clarified the substantial difference, if it exists, between factors for efficiency in small and bigger companies. The main limitation of the survey is that the achieved results are presented in a sample of woodworking enterprises operating only in the selected countries. The results are valid for the selected variables. Further research should include efficiency analysis of different variables and scale of enterprises. Future directions of research can also include regression analyses to further outline the differences between small and large enterprises within the wood-based sector in the EU.

Acknowledgments

This research was supported by Slovak Research and Development Agency, projects number APVV-20-0004, APVV-21-0051, APVV-22-0238, and also project VEGA no. 1/0011/24.

References

  1. Pangarso A, Sisilia K, Setyorini R, Peranginangin Y, Awirya AA. The long path to achieving green economy performance for micro small medium enterprise. Journal of Innovation and Entrepreneurship. 2022 , 1-9.
  2. Tefera H, Gebremichael A, Abera N. Growth determinants of micro and small enterprises: evidence from Northern Ethiopia. Journal of Economics and Sustainable Development. 2013; 127-135.
  3. Medvedev S, Mokhirev A, Rjabova T. Methodical approach to increase efficiency of use of wood resource potential of the region. InIOP Conference Series: Earth and Environmental Science. 2019, 012036.
  4. Lähtinen, K. Linking resource-based view with business economics of woodworking industry: earlier findings and future insights. Silva Fennica. 2007. 149–165.
  5. Kocianová A, Sedliačiková M, Schmidtová J, Melichová M, Hoghová L. Prerequisites for the development of the woodprocessing family enterprises. Acta Facultatis Xylologiae Zvolen. 2022, 133-146.
  6. Korkmaz, E. Measuring the productive efficiency of forest enterprises in Mediterranean Region of Turkey using data envelopment analysis. Afr. J. Agric. Res. 2011, 4522–4532. [Google Scholar]
  7. Sporcic, M.; Martinic, I.; Landekic, M.; Lovric, M. Measuring Efficiency of Organizational Units in Forestry by Nonparametric Model. Croat. J. For. Eng. 2009, 1–13. [Google Scholar]
  8. Kovalčík, M. Efficiency of the Slovak forestry in comparison to other European countries: An application of Data Envelopment Analysis. Cent. Eur. For. J. 2018, 46–54. [Google Scholar] [CrossRef]
  9. Neykov, N.; Krišťáková, S.; Hajdúchová, I.; Sedliačiková, M.; Antov, P.; Giertliová, B. Economic Efficiency of Forest Enterprises—Empirical Study Based on Data Envelopment Analysis. Forests. 2021, 462. [Google Scholar] [CrossRef]
  10. Zhang X, Xu D. Assessing the eco-efficiency of complex forestry enterprises using LCA/time-series DEA methodology. Ecological Indicators. 2022, :109166.
  11. Han X, Frey GE, Geng Y, Cubbage FW, Zhang Z. Reform and efficiency of state-owned forest enterprises in Northeast China as “social firms. Journal of Forest Economics. 2018, 18-33.
  12. Sari, D.; Handayani, N.; Ulkhaq, M.; Budiawan, W.; Maharani, D.; Ardi, F. A data envelopment analysis approach for assessing the efficiency of small and medium sized wood-furniture enterprises: a case study, MATEC Web of Conferences 204, 2019. [CrossRef]
  13. Ma, Y. An Analysis on the Relative Efficiency of Furniture Enterprises in Guangdong Province Based on DEA-BCC and Clustering Method. Open J. Bus. Manag. 2016, 349–354. [Google Scholar] [CrossRef]
  14. Sedivka, P. Estimation of Technical Efficiency in Production Technologies of Czech Sawmills. Drv. Ind. 2009, 197–207. [Google Scholar]
  15. Prasetyo, V.; Belleville, B.; Ozarska, B. Furniture Production Efficiency in the Indonesian Context. 29th International Conference on Wood Modification and Technology “Implementation of Wood Science in Woodworking Sector”, December 6-7, 2018, Zagreb, Croatia.
  16. Analysis of investment effectiveness in the wood processing industry of the Czech Republic. Procedia Economics and Finance. 2015,382-388.
  17. Šulyová, D.; Koman, G. The Significance of IoT Technology in Improving Logistical Processes and Enhancing Competitiveness: A Case Study on the World’s and Slovakia’s Wood-Processing Enterprises. Sustainability. 2020, 7804. [Google Scholar] [CrossRef]
  18. Sedliačiková M, Hajdúchová I, Krištofík P, Viszlai I, Gaff M. Improving the performance of small and medium wood-processing enterprises. BioResources. 2016, 439-450.
  19. Michal, J.; Březina, D.; Šafařík, D.; Babuka, R. Sustainable Development Model of Performance of Woodworking Enterprises in the Czech Republic. Forests, 2021, 12, 672. [CrossRef]
  20. Tofallis, C. Combining two approaches to efficiency assessment. J. Oper. Res. Soc. 2001, 1225–1231. [Google Scholar] [CrossRef]
  21. Hollingsworth, B. Non-Parametric and Parametric Applications Measuring Efficiency in Health Care. Health Care Manag. Sci. 2003, 6, 203–218. [Google Scholar] [CrossRef] [PubMed]
  22. Murillo-Zamorano, LR. Economic efficiency and frontier techniques. Journal of Economic surveys. 2004, 33–77. [Google Scholar] [CrossRef]
  23. Huang TH, Wang MH. Comparison of economic efficiency estimation methods: Parametric and non–parametric techniques. The Manchester School. 2002, 682-709.
  24. Sharma KR, Leung P, Zaleski HM. Technical, allocative and economic efficiencies in swine production in Hawaii: a comparison of parametric and nonparametric approaches. Agricultural economics. 1999, 23-35.
  25. Ajibefun, Igbekele A. An evaluation of parametric and non-parametric methods of technical efficiency measurement: application to small scale food crop production in Nigeria. Journal of agriculture and social sciences 4.3. 2008, 95-100.
  26. Coelli, T.; Rahman, S.; Thirtle. C. Technical, Allocative, Cost and Scale Efficiencies in Bangladesh Rice Cultivation: A Non-Parametric Approach. J. Agric. Econ. 2005, 607-626.
  27. Krišťáková, S.; Neykov, N.; Antov, P.; Sedliačiková, M.; Reh, R.; Halalisan, A.-F.; Hajdúchová, I. Efficiency of Wood-Processing Enterprises—Evaluation Based on DEA and MPI: A Comparison between Slovakia and Bulgaria for the Period 2014–2018. Forests, 2021, 12, 1026. [CrossRef]
  28. Malmquist, S. Index numbers and indifference surfaces. Trabajos de Estatistica. 1953, 209– 242.
  29. Zhang K, Yuan B, Li Y. Efficiency analysis of wood processing industry in China during 2006-2015. InIOP Conference Series: Materials Science and Engineering 2018 Mar 1 (Vol. 322, No. 5, p. 052062). IOP Publishing.
  30. Yang JM, Shi W, She GH, Zhang ZG. Efficiency evaluation of wood processing leading enterprises in Jiangsu based on DEA model. Journal of Nanjing Forestry University. 2008, 127–130. [Google Scholar]
  31. Diaz-Balteiro L, Herruzo AC, Martinez M, González-Pachón J. An analysis of productive efficiency and innovation activity using DEA: An application to Spain’s wood-based industry. Forest Policy and Economics. 2006, 762-73.
  32. Kropivšek J, Grošelj P. Long-term Financial Analysis of the Slovenian Wood Industry Using DEA. Wood Industry/Drvna Industrija. 2019, 61-70.
  33. Kropivšek J, Perić I, Pirc Barčić A, Grošelj P, Motik D, Jošt M. A comparative evaluation of operational efficiency of wood industry using data envelopment analysis and Malmquist productivity index: the cases of Slovenia and Croatia. Drvna industrija. 2019, 287-98.
  34. Zhang, M.; Ma, N.; Yang, Y. Carbon Footprint Assessment and Efficiency Measurement of Wood Processing Industry Based on Life Cycle Assessment. Sustainability. 2023, 15, 6558. [Google Scholar] [CrossRef]
  35. Dia M, Shahi SK. Relative Performance Evaluation of Ontario’s Sawmills with Bootstrap DEA. 2019 8th International Conference on Modelling Simulation and Applied Optimization (ICMSAO) 2019 Apr 15 IEEE., 1-6.
  36. Simar L, Wilson PW. Estimation and inference in two-stage, semi-parametric models of production processes. Journal of econometrics. 2007, 31-64.
  37. Simar L, Wilson PW. Two-stage DEA: caveat emptor. Journal of Productivity Analysis. 2011, 205-218.
  38. Coelli TJ, Rao DS, O’Donnell CJ, Battese GE. An introduction to efficiency and productivity analysis. Springer science & business media; 2005.
  39. Yang H, Pollitt M. Incorporating both undesirable outputs and uncontrollable variables into DEA: The performance of Chinese coal-fired power plants. European journal of operational research. 2009, 1095-1105.
  40. Fernandes FD, Stasinakis C, Bardarova V. Two-stage DEA-Truncated Regression: Application in banking efficiency and financial development. Expert Systems with Applications. 2018, 284-301.
  41. Simar L, Wilson PW. Estimating and bootstrapping Malmquist indices. European journal of operational research. 1999, 459–471.
  42. A’Hearn B. A restricted maximum likelihood estimator for truncated height samples. Economics & Human Biology. 2004, 5-19.
  43. Hoff, A. Second stage DEA: Comparison of approaches for modeling the DEA score. European journal of operational research. 2007, 425–435. [Google Scholar] [CrossRef]
  44. Kaya Samut P, Cafrı R. Analysis of the efficiency determinants of health systems in OECD countries by DEA and panel Tobit. Social Indicators Research. 2016, 113–132. [Google Scholar]
  45. Da Silva AV, Costa MA, Lopes AL, do Carmo GM. A close look at second stage data envelopment analysis using compound error models and the Tobit model. Socio-Economic Planning Sciences. 2019. 111-126.
  46. Kounetas K, Anastasiou A, Mitropoulos P, Mitropoulos I. Departmental efficiency differences within a Greek university: An application of a DEA and Tobit analysis. International Transactions in Operational Research. 2011, 545-59.
  47. Tan, J.; Su, X.; Wang, R. Exploring the Measurement of Regional Forestry Eco-Efficiency and Influencing Factors in China Based on the Super-Efficient DEA-Tobit Two Stage Model. Forests. 2023, 14, 300. [Google Scholar] [CrossRef]
  48. Ramalho EA, Ramalho JJ, Henriques PD. Fractional regression models for second stage DEA efficiency analyses. Journal of Productivity Analysis. 2010, 239–255. [Google Scholar]
  49. Charnes, A.; Cooper, W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 429–444. [Google Scholar] [CrossRef]
  50. Charnes, A.; Cooper, W.; Golany, B.; Seiford, L.; Stutz, J. Foundations of data envelopment analysis for Pareto-Koopmans efficient empirical production functions. J. Econ. 1985, 91–107. [Google Scholar] [CrossRef]
  51. Banker, R.D.; Charnes, A.; Cooper, W.W. Some Models for Estimating Technical and Scale Inefficiencies in Data Envelopment Analysis. Manag. Sci. 1984, 1078–1092. [Google Scholar] [CrossRef]
  52. Tone K, Toloo M, Izadikhah M. A modified slacks-based measure of efficiency in data envelopment analysis. European Journal of Operational Research. 2020, 560-71.
  53. Morita H, Hirokawa K, Zhu J. A slack-based measure of efficiency in context-dependent data envelopment analysis. Omega. 2005, 357-62.
  54. Cook, W.D.; Tone, K.; Zhu, J. Data envelopment analysis: Prior to choosing a model. Omega. 2014, 1–4. [Google Scholar] [CrossRef]
  55. Cook, W.D.; Zhu, J. Data envelopment analysis: A handbook of modeling internal structure and network. Springer, New York, 2014.
  56. Zhu, J. Data Envelopment Analysis. A Handbook of Models and Methods. Springer, New York 2015.
  57. Papke LE, Wooldridge JM. Econometric methods for fractional response variables with an application to 401 (k) plan participation rates. Journal of applied econometrics. 1996, 619-32.
  58. Martins, A. I. Efficiency determinants in Portuguese banking industry: an application through fractional regression models. Tourism & Management Studies. 2018, 63-71. [CrossRef]
  59. Gutiérrez E, Lozano S. Efficiency assessment and output maximization possibilities of European small and medium sized airports. Research in Transportation Economics. 2016, 3-14.
  60. Cooper, William W., Lawrence M. Seiford, and Kaoru Tone. Data envelopment analysis: a comprehensive text with models, applications, references and DEA-solver software. New York: Springer, 2007. Vol. 2.
  61. EUSTAT-SBS-EMP-SIZE-CLASS. https://ec.europa.eu/eurostat/databrowser/view/sbs_sc_ind_r2__custom_8080729/default/table (accessed on 25 October 2023).
  62. EUSTAT-SBS, https://ec.europa.eu/eurostat/databrowser/view/sbs_na_ind_r2__custom_8088821/default/table (accessed on 27 October 2023).
  63. HICP. https://ec.europa.eu/eurostat/databrowser/view/prc_hicp_aind__custom_8089386/default/table (accessed on 27 October 2023).
  64. GDP, https://ec.europa.eu/eurostat/databrowser/view/nama_10_gdp__custom_8089939/default/table (accessed on 27 October 2023).
  65. Schmidt-Ehmcke, Jens and Zloczysti, Petra, Research Efficiency in Manufacturing: An Application of DEA at the Industry Level (May 1, 2009). DIW Berlin Discussion Paper No. 884, Available at SSRN: https://ssrn.com/abstract=1460765 or http://dx.doi.org/10.2139/ssrn.1460765.
  66. Lin, C.-S.; Chiu, C.-M.; Huang, Y.-C.; Lang, H.-C.; Chen, M.-S. Evaluating the Operational Efficiency and Quality of Tertiary Hospitals in Taiwan: The Application of the EBITDA Indicator to the DEA Method and TOBIT Regression. Healthcare. 2022, 10, 58. [Google Scholar] [CrossRef]
  67. Li N, Toppinen A, Lantta M. Managerial perceptions of SMEs in the wood industry supply chain on corporate responsibility and competitive advantage: evidence from China and Finland. Journal of Small Business Management. 2016, 162-86.
  68. Lee, CC. Analysis of overall technical efficiency, pure technical efficiency and scale efficiency in the medium-sized audit firms. Expert Systems with Applications. 2009, 11156–11171. [Google Scholar] [CrossRef]
  69. Ramalho, E. , Ramalho & Murteira Alternative estimating and testing empirical strategies for fractional regression models. Journal of Economic Surveys. 2011, 19–68. [Google Scholar]
  70. Pregibon D. Score tests in GLIM with applications. InGLIM 82: Proceedings of the International Conference on Generalised Linear Models. 1982, 87-97.
  71. Moresová M, Sedliačiková M, Drábek J, Šuleř P, Vetráková M. The impact of internal determinants on management of family business in Slovakia. Polish journal of management studies. 2021, 307–20. [Google Scholar]
  72. Sedliacikova M, Moresova M, Alac P, Drabek J. How Do Behavioral Aspects Affect the Financial Decisions of Managers and the Competitiveness of Enterprises? Journal of Competitiveness. 2021, 99–116. [Google Scholar]
  73. Malkovska, P., E. Dragozova. 2018. Alternatives for development in green infrastructure projects. International Scientific Publications, Ecology & Safety. 2018, 341-349. https://www.scientific-publications.net/en/article/1001758/.
Preprints 91544 g001
Figure 1. Scatterplot between CCR and the revenues per employee of the wood-processing micro and small companies in the EU member states for the period 2015-2020. The vertical line depicts the border of the revenues, and the horizontal one depicts average efficiency.
Figure 1. Scatterplot between CCR and the revenues per employee of the wood-processing micro and small companies in the EU member states for the period 2015-2020. The vertical line depicts the border of the revenues, and the horizontal one depicts average efficiency.
Preprints 91544 g001
Preprints 91544 g002
Figure 2. Scatterplot between scale efficiency and the revenues per employee of the wood-processing micro and small companies in the EU member states for the period 2015-2020.
Figure 2. Scatterplot between scale efficiency and the revenues per employee of the wood-processing micro and small companies in the EU member states for the period 2015-2020.
Preprints 91544 g002
Table 1. Selected research on DEA with some of their inputs/outputs.
Table 1. Selected research on DEA with some of their inputs/outputs.
Inputs Outputs Publication
Capital, Production costs, Employee costs, Total amount of employee Amount of production, amount of sales, Value added Korkmaz [6]
Expenditures Revenues Sporcic et al. [7]
Compensation of
employees fixed capital consumption, other taxes on
production, interests, and rents paid		 Total output of the forestry, other subsidies on production and interest receivable Kovalčík [8]
Labour, material and overhead costs Amount of
wood-furniture produced in units		 Sari et al. [12]
Fixed assets, factory area, staff numbers, employee salary Per capital output value, annual gross output value and annual operating income Ma [13]
Labour, material costs, other costs Revenues Krišťáková et al. [27]
Employees, energy use per unit of output value, fixed asset inputs per unit of output value Wood processing output value and man-made board output value Zhang et al. [34]
Table 2. Average amount in euro per employee and variation of DEA inputs and outputs for the period 2015-2020.
Table 2. Average amount in euro per employee and variation of DEA inputs and outputs for the period 2015-2020.
TPRCH PCOST REV VADDED
Country Average amount Variation, % Average amount Variation, % Average amount Variation, % Average amount Variation, %
Belgium 231645.5 7.60% 42550.58 2.74% 308 226.28 7.55% 77109.16 13.15%
Bulgaria 22024.36 5.12% 3808.019 14.78% 27 361.51 7.94% 7188.434 15.89%
Czechia 75141.35 11.14% 11924.06 15.40% 104 138.15 12.01% 31287.16 12.59%
Denmark 120904.3 10.79% 46195.97 9.43% 180 376.28 11.10% 62947.75 11.01%
Germany 84170.28 6.84% 30077.29 6.27% 132 561.80 3.64% 47262.78 3.63%
Estonia 90413.42 11.10% 15053.14 12.30% 112 673.98 9.52% 24223.99 11.97%
Ireland 100088.9 12.82% 40530.96 4.65% 158 446.84 9.69% 60592.93 7.31%
Greece 77306.84 13.95% 11715.92 12.10% 90 243.05 14.81% 14446.85 14.80%
Spain 92430.95 5.11% 26159.6 5.30% 126 925.96 5.00% 36278.86 6.06%
France 117996.4 18.85% 39385.57 14.30% 167 944.21 16.80% 49206.02 13.51%
Croatia 47993.15 8.91% 9436.786 11.84% 59 581.79 7.54% 15608.56 8.85%
Italy 128534.4 3.95% 29788.09 3.82% 180 587.31 3.77% 52348.79 4.96%
Cyprus 45620.9 6.90% 16803.78 4.90% 75 087.36 6.85% 29226.04 9.42%
Latvia 44996.85 12.98% 7386.606 17.15% 57 383.50 14.30% 13232.22 18.89%
Lithuania 29951.19 16.17% 7723.088 18.14% 41 341.14 16.48% 12194.75 19.50%
Hungary 37445.33 9.83% 7155.067 11.60% 49 455.53 11.72% 12525.39 18.99%
Netherlands 244957.5 5.13% 57875.63 10.74% 350 841.10 5.47% 108709.6 8.04%
Austria 141691.8 2.37% 37213.83 4.91% 201 411.15 3.12% 61228.8 5.94%
Poland 50712.18 12.46% 7618.106 11.06% 68 673.89 8.76% 14315.15 18.69%
Portugal 64570.62 4.15% 14582.28 5.41% 85 303.53 4.21% 22119.7 7.24%
Romania 29597.36 6.38% 5120.616 16.67% 36 326.12 8.55% 8425.515 31.17%
Slovenia 102777.2 12.77% 19909.61 16.70% 139 455.35 12.74% 37941.55 12.27%
Slovakia 75815.82 4.08% 8884.362 11.51% 93 868.74 4.21% 18505.81 6.22%
Finland 197969.5 7.08% 37486.78 3.16% 247 110.58 6.97% 54868.86 5.38%
Sweden 176350.3 4.95% 45461.04 2.83% 239 331.85 4.26% 66221.07 4.93%
Average 97244.26 8.86% 23193.87 9.91% 133386.28 8.68% 37520.63 11.62%
Table 3. DEA-CCR scores for combined efficiency (CCR) estimated by the model (1).
Table 3. DEA-CCR scores for combined efficiency (CCR) estimated by the model (1).
DMU 2015 2016 2017 2018 2019 2020 Average Variation
Belgium 0.92 0.92 0.87 0.93 0.94 1.00 0.93 3.56%
Bulgaria 0.85 0.87 0.90 0.88 0.88 0.90 0.88 1.76%
Czechia 1.00 1.00 1.00 1.00 1.00 1.00 1.00 0.00%
Denmark 0.89 0.91 0.96 0.90 0.88 0.91 0.91 2.50%
Germany 0.96 0.97 0.98 0.97 0.95 1.00 0.97 1.59%
Estonia 0.92 0.90 0.89 0.86 0.86 0.91 0.89 2.33%
Ireland 0.96 1.00 0.94 0.98 0.96 1.00 0.97 2.10%
Greece 0.89 0.82 0.86 0.87 0.85 0.87 0.86 2.43%
Spain 0.88 0.89 0.90 0.89 0.88 0.89 0.89 0.73%
France 0.87 0.90 0.94 0.89 0.86 0.90 0.89 2.71%
Croatia 0.89 0.88 0.84 0.85 0.85 0.86 0.86 2.07%
Italy 0.95 0.96 0.94 0.93 0.94 0.96 0.95 0.83%
Cyprus 1.00 1.00 1.00 1.00 1.00 1.00 1.00 0.00%
Latvia 0.90 0.90 0.88 0.91 0.90 0.94 0.91 1.87%
Lithuania 0.91 0.91 0.91 0.91 0.89 0.92 0.91 0.78%
Hungary 0.90 0.89 0.86 0.95 0.96 0.94 0.92 3.61%
Netherlands 0.92 0.97 0.97 0.96 0.98 0.96 0.96 1.80%
Austria 0.93 0.94 0.92 0.93 0.94 0.95 0.93 1.06%
Poland 1.00 1.00 1.00 0.97 0.98 0.99 0.99 1.03%
Portugal 0.87 0.89 0.88 0.89 0.92 0.90 0.89 1.58%
Romania 0.88 0.85 0.78 0.88 0.90 0.92 0.87 4.93%
Slovenia 0.96 0.95 0.93 0.96 0.92 0.94 0.94 1.22%
Slovakia 1.00 1.00 1.00 1.00 1.00 1.00 1.00 0.00%
Finland 0.86 0.87 0.84 0.87 0.87 0.89 0.87 1.61%
Sweden 0.89 0.89 0.88 0.90 0.89 0.92 0.89 1.22%
Average 0.92 0.92 0.91 0.92 0.92 0.94 0.92 1.73%
Table 4. Scale Efficiency scores from the model (2).
Table 4. Scale Efficiency scores from the model (2).
DMU 2015 2016 2017 2018 2019 2020 Average Variation RTS
Belgium 0.92 0.96 0.87 0.94 0.94 1.00 0.94 3.70% DRS
Bulgaria 0.85 0.87 0.90 0.88 0.97 0.90 0.89 3.73% IRS
Czechia 1.00 1.00 1.00 1.00 1.00 1.00 1.00 0.00% IRS
Denmark 0.93 0.95 0.96 0.94 0.91 0.94 0.94 1.46% CRS
Germany 0.96 0.97 0.98 0.97 0.95 1.00 0.97 1.54% IRS
Estonia 0.95 1.00 0.98 1.00 1.00 1.00 0.99 1.66% DRS
Ireland 0.96 1.00 0.94 0.98 0.96 1.00 0.97 2.10% IRS
Greece 0.95 1.00 0.97 0.98 0.98 0.99 0.98 1.56% CRS
Spain 0.96 0.99 0.98 0.98 0.99 0.99 0.98 0.98% IRS
France 0.95 0.97 0.99 0.95 0.94 0.97 0.96 1.61% CRS
Croatia 0.97 0.99 0.98 0.97 0.97 0.97 0.97 0.66% IRS
Italy 0.95 0.98 0.97 0.97 0.99 1.00 0.98 1.36% DRS
Cyprus 1.00 1.00 1.00 1.00 1.00 1.00 1.00 0.00% IRS
Latvia 0.96 0.97 0.97 0.96 0.96 0.97 0.97 0.49% IRS
Lithuania 0.91 0.91 0.91 0.94 0.95 0.96 0.93 2.13% IRS
Hungary 0.94 0.96 0.97 0.95 0.96 0.96 0.96 0.76% IRS
Netherlands 0.92 0.97 0.97 0.96 0.98 0.96 0.96 1.80% DRS
Austria 0.94 0.97 0.96 0.97 0.97 0.98 0.97 1.13% DRS
Poland 1.00 1.00 1.00 0.97 0.98 0.99 0.99 1.03% IRS
Portugal 0.98 1.00 0.99 0.99 0.99 0.99 0.99 0.50% IRS
Romania 0.90 0.92 0.88 0.92 0.92 0.93 0.91 1.78% IRS
Slovenia 0.96 0.96 0.97 0.99 0.99 1.00 0.98 1.57% DRS
Slovakia 1.00 1.00 1.00 1.00 1.00 1.00 1.00 0.00% IRS
Finland 0.93 0.98 0.91 0.92 0.96 1.00 0.95 3.12% DRS
Sweden 0.93 0.97 0.95 0.96 0.97 0.98 0.96 1.62% DRS
Average 0.95 0.97 0.96 0.97 0.97 0.98 0.97 1.45% IRS
Table 5. Results of the cross-sectional analysis with two types of fractional regression by models (4) and (5) for single variable ENTNUM – number of enterprises in the interval 1-49 persons employed.
Table 5. Results of the cross-sectional analysis with two types of fractional regression by models (4) and (5) for single variable ENTNUM – number of enterprises in the interval 1-49 persons employed.
CCR- dependent BCC- dependent
Coefficients in each model Coefficients in each model
Covariate Probit Logit Probit Logit
ENTNUM 0.00003* 0.0000634* 0.0000267 0.0000594
*Statistically significant at α=0.05.
Table 6. Results of the cross sectional analysis with two types of fractional regression by models (4) and (5) for the whole C16 sector in the EU.
Table 6. Results of the cross sectional analysis with two types of fractional regression by models (4) and (5) for the whole C16 sector in the EU.
CCR- dependent BCC- dependent
Coefficients in each model Coefficients in each model
Covariate Probit Logit Probit Logit
GDP -0.000 -0.000 -0.000 -0.000
HICP -0.023 -0.050 -0.077 -0.200
IVP 0.013 0.028* 0.053 0.121*
ENTNUM -0.000 -0.000 -0.000 -0.000
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated