Preprint
Article
Exploratory Dividend Optimization with Entropy Regularization
Altmetrics
Downloads
76
Views
34
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
28 November 2023
Posted:
28 November 2023
You are already at the latest version
Alerts
Abstract
This paper studies the dividend optimization problem in the entropy regularization framework by following the same continuous-time reinforcement learning setting as in Wang et al. (2020). The exploratory HJB is established and the optimal exploratory dividend policy is a truncated exponential distribution. We show that, for suitable choices of the maximal dividend paying rate and the temperature parameter, the value function of the exploratory dividend optimization problem could be significantly different from the value function in the classical dividend optimization problem. In particular, the value function of the exploratory dividend optimization problem could be classified into three cases based on its monotonicity. Numerical examples are also presented to show the impact of temperature parameter on the solution.
Keywords:
Subject: Business, Economics and Management - Finance
1. Introduction
The risk management problem of an insurance company has been studied extensively in the literature. It dates back to the Cramér-Lundberg (C-L) model of Lundberg (1903) which described the surplus process of the insurance company in terms of two cash flows: premiums received and claims paid. Consider an insurance company with claims arriving at Poisson rate , i.e., the total number of claims up to time t is Poisson distributed with parameter . Denote by the size of the i-th claim, where ’s are independently and identically distributed with and for some constants . Let denote the surplus process of the insurance company. Then
where is the initial surplus level, and is the premium rate which is the amount of premium received by the insurance company per unit of time.
De Finetti (1957) first proposed the dividend optimization problem: An insurance company maximizes the expectation of cumulative discounted dividends until the ruin time by choosing dividend strategies, that is, when and how much of the surplus should be distributed as dividends to the shareholders. De Finetti (1957) derived that the optimal dividend policy under a simple discrete random walk model should be a barrier strategy. Gerber (1969) then generalized the dividend problem from a discrete-time model to the classical C-L model and showed that the optimal dividend strategy should be band strategy, which degenerates to a barrier strategy for exponentially distributed claim size.
With the development of technical tools such as dynamic programming, the dividend optimization problem has been analyzed under the stochastic control framework. In particular, in C-L model can be approximated by a diffusion process that evolves according to
where , , and is a standard Brownian motion; see, e.g., Schmidli (2007). It is worth noting that the diffusion approximation for the surplus process works well for large insurance portfolios, where an individual claim is relatively small compared to the size of the surplus. Under the drifted Brownian motion model the optimal dividend strategy is a barrier strategy, and if the dividend rate is further upper bounded, the optimal dividend strategy is threshold-type; see, e.g., Jeanblanc-Picqué and Shiryaev (1995) and Asmussen and Taksar (1997). Other extensions on the dividend optimization problem include Jgaard and Taksar (1999), Asmussen et al. (2000), Azcue and Muler (2005), Azcue and Muler (2010), Gaier et al. (2003), Kulenko and Schmidli (2008), Yang and Zhang (2005), Choulli et al. (2003), Gerber and Shiu (2006), Avram et al. (2007) and Yin and Wen (2013), etc.
Previous literature studied the dividend optimization problem based on the complete information of the environment, i.e., all the model parameter values are known. This assumption is no longer valid if the environment is a black-box or the model parameter values are unknown. One way to handle this issue is to use the past information to estimate the model parameters and then solve the problem with the estimated parameters. However, the optimal strategy in the classical dividend optimization problem is a barrier-type or threshold-type, which is extremely sensitive to the model parameter values; a slight change in the model parameters would lead to a totally different strategy.1
In contrast to the traditional approach that separates the estimation and optimization, reinforcement learning aims to learn the optimal strategy through trial-and-error interactions with the unknown environment without estimating the model parameters. In particular, one takes different actions in the unknown territory and receives feedbacks to learn the optimal action and use it to further interact with the environment. In recent years, reinforcement learning had successful applications in many fields such as health-care, autonomous control, natural language processing, and video games; see, e.g., Zhao et al. (2009), Komorowski et al. (2018), Mirowski et al. (2016), Zhu et al. (2017), Radford et al. (2017), Paulus et al. (2017), Mnih et al. (2015), Jaderberg et al. (2019), Silver et al. (2016), Silver et al. (2017). There is no doubt that reinforcement learning has become one of the most popular and fastest-growing fields today.
Exploration and exploitation are the key concepts in reinforcement learning, and they proceed simultaneously. On one hand, exploitation is to utilize the so-far-known information to derive the current optimal strategy which might not be optimal from the long-term view. On the other hand, exploration emphasizes learning from trial-and-error interactions with the environment to improve its knowledge for the sake of long-term benefit. While the optimal strategy of the classical dividend optimization problem is deterministic when the model parameter values are fully known, randomized strategies are considered to encourage exploration of other actions in the unknown environment. Although the exploration causes a cost in the short term, it helps to learn the optimal (or near-optimal) strategy and bring benefit from the long-term point of view.
Obviously, how to balance the trade-off between exploitation and exploration is an important issue. The -greedy strategy is a frequently used randomized strategy in reinforcement learning. It balances the exploration and exploitation by illustrating that the agent should stick to the current optimal policy most of the time, while the agent could sometimes randomly take other non-optimal actions to explore the environment; see, e.g., Auer et al. (2002). Boltzmann exploration is another randomized strategy extensively studied in RL literature. Instead of assigning constant probabilities to different actions based on current information, Boltzmann exploration uses the Boltzmann distribution to allocate the probability to different actions, where the probability of each action is positively related to its reward. In other words, agent should choose action with higher expected rewards with higher probability; see, e.g., Cesa-Bianchi et al. (2017).
Another way to introduce a randomized strategy is to intentionally include a regularization term to encourage exploration. Entropy is a frequently used criterion in the RL family that measures the level of exploration. The entropy regularization framework directly incorporates entropy as a regularization term into the original objective function to encourage exploration; see, e.g., Todorov (2006), Ziebart et al. (2008), Nachum et al. (2017). In the entropy regularization framework, the weight of exploration is determined by the coefficient imposed on the entropy, which is called the temperature parameter. The larger the temperature parameter, the greater the weight of exploration. A temperature parameter that is too large may result in too much focus on exploring the environment and little effort in exploiting the current information; otherwise, if the temperature parameter is too small, one may stick to the current optimal strategy without the opportunity to explore better solutions. Therefore, careful selections of the temperature parameter is important for designing reinforcement learning algorithms.
While most existing literature in reinforcement learning focus on the Markov decision process, recently Wang et al. (2020) extended the entropy regularization framework to the continuous-time setting. The authors showed that the optimal distributional control is Gaussian distribution in the linear-quadratic stochastic control problem. In the series work, Wang and Zhou (2020) studied continuous-time mean-variance portfolio selection problem under the entropy-regularized RL framework and showed that the precommitted strategies are Gaussian distributions with time-decaying variance. Dai et al. (2023) considered the equilibrium mean-variance problem with log return target and showed that the optimal control is Gaussian distribution with the variance term not necessarily decaying in time.
This paper studies the dividend optimization problem in the entropy regularization framework to encourage the exploration in the unknown environment. We follow the same setting as in Wang et al. (2020) which use Shannon’s differential entropy. The key idea is to use distribution as the control to solve the entropy-regularized dividend optimization problem. Consequently, the optimal dividend policy is a randomization over the possible dividend paying rates. We derive the so-called exploratory HJB and establish the theoretical results to guarantee the existence of the solution. We obtain that the optimal exploratory dividend policy is a truncated exponential distribution whose parameter depends on the surplus level and the temperature parameter. We show that, for suitable choices of the maximal dividend paying rate and the temperature parameter, the value function of the exploratory dividend optimization problem could be significantly different from the value function in the traditional problem. In particular, we classify the value function of the exploratory dividend optimization problem into three cases based on its monotonicity.
Recently, Bai et al. (2023) also study the optimal dividend problem under the continuous time diffusion model. The authors then use a policy improvement argument along with policy evaluation devices to construct approximating sequences of the optimal strategy. The difference is that in their paper the feasible controls are open-loop, while we consider feedback controls only. We show that the value function is decreasing when the maximal dividend paying rate is relatively small compared to the temperature parameter, where in their paper the maximal dividend paying rate is assumed to be larger than one and thus the value function is always increasing.
The rest of the paper is organized as follows. In Section 2, we introduce the formulation of the entropy-regularized dividend optimization problem. In Section 3, we present the exploratory HJB and the theoretical results to solve the exploratory dividend problem. We then discuss the three cases of the value function for the exploratory dividend problem in Section 4. Some numerical examples to show the impact of parameters on the optimal dividend policy and the value function are presented in Section 5. Section 6 concludes.
2. Problem
2.1. The Model
Suppose an insurance company has surplus at time t, with
where , , and is a standard Brownian motion defined on the filtered probability space . As remarked by Asmussen and Taksar (1997), such a surplus process (1) can be viewed either as a direct modelling with drifted Brownian motion or as an approximation to the classical compound Poisson model.
A dividend strategy or policy is defined as , where is the dividend paying rate at time t, i.e., the cumulative amount of dividends paid from time to time is given by . We consider herein the Markov feedback controls, i.e., , where is a function of the surplus level . Note that is nonnegative for any t. Further, we assume that is upper bounded by a positive constant M, which is consistent with the assumption made in the literature. We give the formal definition of the admissible dividend policy below.
Definition 1.
A dividend policy is said to be admissible if is -adapted and for all .
Denote by the set of admissible dividend policies. For an insurance company whose surplus process evolves according to (1) and pays the dividend according to policy , the controlled surplus process for this insurance company is
Define the ruin time to be the first time that the surplus level hits zero, i.e.,
For an insurance company starting with initial surplus , the problem is to find the optimal dividend policy that maximizes the expected value of exponentially discounted dividends to be accumulated until the ruin time, that is,
where is the discounting rate. Then the optimal dividend problem is
2.2. Classical Optimal Dividend Problem
First, we briefly review the results of solving the dividend optimization problem (3) classically. Let be the value function of the dividend optimization problem:
Assume that the value function is twice-continuously differentiable. The standard dynamic programming approach leads to the following Hamilton-Jacobi-Bellman equation,
with boundary condition . It can be easily seen that the optimal dividend paying rate at surplus level x is
Assume that is a concave function. Then there exists a nonnegative constant such that when and when . Substitute (5) into (4), then it turns into the following ODEs:
Combining with the boundary condition, one can derive that
where
, and are determined by the smooth pasting conditions, i.e.,
If , there exists unique solution to (8). In this case, is given by (7), where are determined uniquely through (8). Consequently, the optimal dividend policy is to pay the maximal rate M when surplus level x exceeds threshold and to pay nothing if else. If , then . In this case, the optimal dividend policy is always to pay the maximal rate M. Detailed proofs can be found in Asmussen and Taksar (1997). It is also straightforward to check that the optimal value function is concave on x and always smaller than which is the limit of as x going to infinity. Figure 1 below illustrates the value function and the corresponding optimal dividend policy under the following parameter values: , , , (left panels), (middle panels), and (right panels), respectively.
2.3. Exploratory Formulation
The above optimal dividend policy (5) is implemented based on the complete information, i.e., the model parameters and are known. In reality, however, it is difficult to know exactly the values of and , due to the uncertainty in premium rate, claim arrival process and claim size. Therefore, we consider a technique named reinforcement learning to learn the optimal (or near-optimal) dividend paying strategy through trial-and-error interactions with the unknown territory.
Whereas the majority of the work in reinforcement learning consider Markov decision process in discrete time, we follow the pioneering work of Wang et al. (2020) who model the reinforcement learning in continuous time as a relaxed stochastic control problem. At time t with surplus level the dividend paying rate a is randomly sampled according to a distribution , where , satisfying for any . We call the distributional dividend policy. Following the same procedure as in Wang et al. (2020), we derive the exploratory dynamic of the surplus process under to be
and the expected value of total discounted dividends under exploration to be
where the ruin time is
In addition to the expected value of total discounted dividends under exploration, Shannon’s differential entropy is introduced into the objective to encourage exploration. For a given distribution , the entropy is defined as
Thus, the objective of entropy-regularized exploratory dividend problem is
where is the so-called temperature parameter. Note that controls the weight to be put on the exploration and is exogenously given. If , the distribution degenerates to the Dirac measure, which is the solution to classical optimal dividend problem without exploration. The entropy-regularized exploratory dividend problem is
where is the set of admissible exploratory dividend policies. We give the formal definition of admissible exploratory dividend policy below.
Definition 2.
An exploratory dividend policy π is admissible if the following conditions are satisfied:
- (i)
- for any , where is a set of probability density functions with support ;
- (ii)
- the stochastic differential equation (9) has a unique solution under π;
- (iii)
- .
The following proposition will be used later.
Proposition 1.
For any distribution π on support , the entropy .
3. Exploratory HJB Equation
To solve exploratory optimal dividend problem (12), we first derive the corresponding HJB equation, the so-called exploratory HJB; see Wang et al. (2020), Tang et al. (2022), etc.
Let be the value function of entropy-regularized exploratory dividend problem, that is,
Assume that the value function is twice-continuously differentiable. Following the standard arguments in dynamic programming, we derive the exploratory HJB equation below:
with boundary condition
3.1. Exploratory Dividend Policy
To solve the supremum in (13) together with the constraint that , we introduce the Lagrange multiplier :
Maximizing the integrand above pointwisely and using the first-order condition leads to the solution
Because , we solve that
where
Recall that the classical optimal dividend policy given in (5) is two-threshold strategy, i.e., it pays nothing, , if or pays the maximal rate, , if . In contrast, the exploratory dividend policy is not restricted to two extreme actions only but gives the probability to take certain actions. This result is very similar to [38] in which the authors study the temperature control problem for Langevin diffusions by incorporating randomization of the temperature control and regularizing its entropy. The classical optimal control of such a problem is of the bang-bang type, whereas the exploratory control is a state-dependent, truncated exponential distribution. Likewise, the optimal distribution given in (15) is also a continuous version of Boltzmann distribution or Gibbs measure which is widely used in discrete reinforcement learning.
When , is decreasing in a so it has large probability to take small dividend pay-out rate close to 0; when , is increasing in a so it has large probability to take large dividend pay-out rate close to M ; when , it degenerates to a uniform distribution on . In other words, the optimal exploratory dividend policy is an “exploration” of the classical dividend pay-out policy: it searches around the current optimal dividend rate given by the classical solution, 0 or M, with the probability to take a certain rate decreasing as it moving away from the classical solution.
The exploratory surplus process under the optimal policy is well-posed. Note that the optimal distributional policy is , where
Applying the optimal distributional policy (17) into the exploratory surplus process (9), we obtain that
Since , the SDE (18) has bounded drift and constant volatility. As a result, there exists unique solution to (18).
3.2. Verification Theorem
Substituting the optimal distribution as shown in (15) into the HJB equation (13), we have the following equation for :
or equivalently,
The following verification theorem shows that that solves (19) is indeed the value function of the exploratory dividend problem (12).
Theorem 1.
Theorem 1 shows that solution to the exploratory HJB equation (19) could be the value function of exploratory dividend problem (12). On the other hand, a similar argument could show that the value function shall also satisfy (19), while the optimal exploratory dividend strategy is given by (17). To establish a rigorous statement, we need the following result. The next proposition shows that the value function converges as x going to infinity.
3.3. Solution to Exploratory HJB
Compared with the differential equation (6) which solves the classical value function, the exploratory HJB equation (19) has a nonlinear term , which makes it difficult to be solved explicitly. The theorem below guarantees the existence and uniqueness of solution .
Theorem 2.
Theorem 2 follows from the results in Tang et al. (2022, Theorem 3.9, 3.10) and in Strulovici and Szydlowski (2015, Proposition 1). It is straightforward to check that the conditions to guarantee the existence and uniqueness of the solution to (19) and its twice-continuous differentiability are satisfied.
Theorem 2 also states that when becomes smaller, the exploratory value function converges to the classical value function. Indeed, a stronger convergence is established by Tang et al. (2022) that V converges to locally uniformly as going to 0. Note that the parameter is the weight to be put on the exploration in contrast to the exploitation. If it is more close to 0, the entropy term has smaller effect on the total objective value and the optimal exploratory distribution in (15) are more concentrated and close to the Dirac distribution – the optimal solution to the classical dividend optimization problem. Then not surprisingly, the exploratory value function also converges to the classical value function as going to 0.
Now, thanks to Theorem 2, we have that solves the exploratory HJB equation (19). On the other hand, it is straightforward to show that according to (20), if , the limit of is negative; if , the limit of is positive; if , the limit of is zero. The next theorem shows that indeed, we classify into three cases based on its monotonicity.
Theorem 3.
Let be the solution to (19) with boundary condition (14) and (20). Then is monotone. To be more specific,
- (i)
- if , is non-increasing.
- (ii)
- if , is non-decreasing.
- (iii)
- if , .
The following corollary is a direct result from above theorem.
Corollary 1.
Note that in Theorem 1 we need and to be bounded so that V – solution to (19) – is indeed the value function of exploratory optimal dividend problem. Corollary 1 verifies the boundedness conditions are satisfied. In other words, the solution to the exploratory HJB equation (19) is the value function of the exploratory dividend problem.
4. Discussion
In view of Theorem 3, value functions can be classified into three cases according to the monotonicity: (1) ; (2) ; (3) . The following proposition will be useful in analyzing the properties of value functions.
Proposition 3.
(a) Define
Then is increasing. Therefore, and ;
-
(b) DefineThen , and is decreasing on . Therefore, and .
Case 1: .
The value function in this case is non-increasing and thus non-positive, as a sharp contrast to the results of classical dividend problem. To see the reason, on one hand, note that for ,
Then due to Proposition 1, the entropy term is negative, that is, . On the other hand, when is large, it implies that the exploration parameter is relatively large compared with the maximal dividend paying rate M. Then the negative entropy has a large weight in the total objective value, dominating the total expected dividends and leading to a negative value function.
Case 2: .
When , the value function is non-decreasing, which is closer to the increasing value function in classical dividend optimization problem than it does in Case 1. This is because a relatively small compared with M decreases the weight of entropy term in the total objective value. Note that in classical dividend optimization the limit of value function is , while in the current exploratory dividend optimization the limit of value function is given in (20). Therefore, if (i) , the limit of is no larger than that of ; if (ii) , then asymptotically achieves a higher value than that of the classical dividend optimization. Then if and , the limit of is larger than that of .
As shown in Proposition 3, for any , . Therefore, when , it always belongs to Case 2 for any . On the other hand, for any , . Therefore, when or , since , it cannot be Case 2 (ii); when and , it is always Case 2 (i). Note that corresponds to the classical dividend optimization and , by definition. Since for any positive constant M, classical dividend optimization can be viewed as a special Case 2 (i). It implies that exploratory dividend optimization is a generalization of the classical dividend optimization.
Case 3: .
As shown in Theorem 3, the value function in this case should be constantly zero. This is because compared with M happens to strike a balance between exploitation and exploration such that the total expected dividends is offset by the entropy.
Figure 2 depicts the different cases of value functions given different combinations of M and . When , the value function falls into Case 1 area. When , the value function corresponds to Case 2, which can be further classified into two cases based on the comparison of M and , i.e., whether the value function asymptotically achieves a higher value than that of the classical problem. When , the value function should be Case 3 type.
5. Numerical Examples
In this section, we present numerical examples of optimal exploratory policy and corresponding value function which solves exploratory HJB equation (19) based on the theoretical results obtained in the previous sections.2 To have a clear vision on the weight of cumulative dividends and that of entropy in the total objective value, we further decompose into two parts: the expected total discounted dividends under the optimal exploratory dividend policy
and the expected total weighted discounted entropy under the optimal exploratory dividend policy
where the entropy of is derived via substituting the optimal distribution (15) into the definition of entropy (10), i.e.,
Hence, . We show examples of three cases, respectively, with commonly used parameters: , , .
First, let , . Then and it belongs to Case 1. Note that in this case is decreasing and non-positive, as a sharp contrast to the results of classical dividend problem. The figure on the top row, left column of Figure 3 plots the corresponding value function and its two components and .3 The figure on the middle row, left column of Figure 3 plots the mean of the optimal distribution , which is decreasing on x. The figure on the bottom row, left column of Figure 3 shows the density function of the optimal distribution with respect to different surplus level x. Because , the optimal distribution is a truncated exponential distribution with rate for any . Therefore, it is more likely to pay high dividend rate. Furthermore, as surplus x increases, the density function becomes more flat because is increasing to 0 and the rate is decreasing on x.
Second, let , . Then and it belongs to Case 2 (i). The figure on the top row, middle column of Figure 3 shows the corresponding value function, and . In contrast to Case 1, in this case becomes positive since M is sufficiently large, making the value function positive. The figure on the middle row, middle column of Figure 3 plots the mean of the optimal distribution , which is increasing on x. The figure on the bottom row, middle column of Figure 3 shows the density function of optimal distribution with respect to different surplus level x. When x is small, it is more likely to choose a low dividend paying rate, because paying too high dividend rate would probably cause the insurance company to go bankruptcy and harms the shareholder’s benefit in the long run. When x becomes larger, it is more likely to pay high dividend rate.
Third, let , . Then and it belongs to Case 2 (ii). The figure on the top row, right column of Figure 3 shows the corresponding value function, and . In this case, the limit of is higher than that of the classical value function , which is . Note that the expected total discounted dividends under exploratory policy does not exceed that of the classical policy , because the classical optimal dividend policy fully exploits the known environment. For sufficiently large M and , is large enough to make larger than . The figure on the middle row, right column of Figure 3 plots the mean of the optimal distribution and the figure on the bottom row, right column of Figure 3 plots the density function of the optimal distribution, which are similar to that of Case 2 (i).
When , , it belongs to Case 3 and the value function in this case should be constantly zero.
We also vary the value of while keeping the other parameter values unchanged. Figure 4 shows the value function under different values of with and respectively. Note that when , degenerates to the classical value function . For , it is Case 2 (ii) when is small and then becomes Case 3 and Case 1 as getting larger. As aforementioned, it cannot be Case 2 (ii) since . Indeed, the left panel of Figure 4 shows the value function could not exceed the classical one as getting smaller. On the other hand, for , it can only be Case 2 and even Case 2 (ii) if is large enough. The right panel of Figure 4 shows the value function is always increasing on x for different values of and it can exceed the classical value function for a sufficiently large .
6. Conclusion
This paper studies the dividend optimization problem in the entropy regularization framework. In an unknown environment, the entropy is incoprated into the objective function to encourage the exploration and an exploratory dividend policy is introduced. We establish the exploratory HJB equation, we find that the optimal distributional control is a truncated exponential distribution. Compared to the classical value function, the value function in the exploratory dividend problem is classified into three cases. The monotonicity of the value function is determined by the maximal dividend paying rate and the temperature parameter which controls the weight of exploration.
One future research direction is to consider the exploratory dividend policy under the non-exponential discounting which makes the problem time-inconsistent. Furthermore, reinsurance could also be considered as part of the insurance company’s strategy in addition to the dividend policy, which is more technically challenging under the entropy regularization framework. Finally, one could take other definitions of the entropy, instead of the Shannon’s differential, as a measure of the level of exploration in reinforcement learning.
Appendix A. Proof
Proof of Proposition 1
By definition (10),
where the inequality is due to Jensen’s inequality. Q.E.D.
Proof of Theorem 1
Let be an exploratory dividend policy. Because V solves (13), for any ,
which shows that
Applying Itô’s Lemma on ,
where the inequality is due to (A1). Then taking expectation on both sides,
For the first term on the right hand side of (A2), noting that is bounded, then by bounded convergence theorem,
For the second term on the right hand side of (A2), since is admissible and satisfies Definition 2 (iii),
Because is non-negative, by monotone convergence theorem,
Noting that for any , by monotone convergence theorem,
and .
On the other hand, the above inequality becomes an equality if the supremum in (13) is achieved, that is, , where is given by (15). Thus, is the value function. Q.E.D.
Define function to be
where function is given in (16).
Lemma A1.
The function defined in (A3) is maximized when , and
Moreover, when , when , and when .
Proof.
Take the first-order derivative of function :
where , . Take the first-order derivative of :
where , . Take the first-order derivative of :
where , . Take the first-order derivative of :
Note that for and for . Hence, is increasing on and decreasing on , and . Then , which means that is increasing. As a result, for and for . Hence, for and for , which means that is increasing on and decreasing on . As a result, for .
The above analysis shows that is positive when , i.e., , and negative when , i.e., . Thus the maximum is obtained at :
Moreover, when , ; when , ; when , . □
Proof of Proposition 2
On one hand,
where the inequality follows from Lemma A1. Letting and by dominated convergence theorem,
On the other hand, consider an exploratory policy , where
Then
Letting and by dominated convergence theorem,
which then together with the previous inequality leads to (20). Q.E.D.
Define a function h as
where is given.
Lemma A2.
The function h defined in (A4) satisfies following properties:
- (i)
- is continuous and decreasing in x;
- (ii)
- there exists a unique such that ;
- (iii)
- , for some constant which depends on k only;
- (iv)
- , .
Proof.
We first show that function is continuous at . By L’Hôpital rule, . Hence, .
Taking the first-order derivative of h, for ,
where . Then
which is positive when and negative when . Therefore, is increasing on then decreasing on and . Combining with the fact that for , we show that for . It then completes the proof of that is decreasing in x.
To show , note that and . By the continuity and monotonicity of , there must exist a unique such that . In particular, when , .
Note that for , . which implies
Combining with the fact that for ,
Based on the previous results, for ,
similarly, for ,
To show ,
It remains to prove . Without loss of generality, we assume . Then
□
Proof of Theorem 2
It is straightforward to show that Assumption 3.8 in Tang et al. (2022) hold for our exploratory dividend problem. The well-posedness of SDE (18) for the optimal exploratory surplus process is also established. Then, by applying the results of Tang et al. (2022, Theorem 3.9, 3.10), the existence and uniqueness of solution to (19) and convergence of V to are established.
To show the twice-continuously differentiability of , we apply the results in Strulovici and Szydlowski (2015, Proposition 1) (with the infinite domain). We rewrite the HJB equation (19) into the following form:
where
and h is defined in (A4) with . According to Proposition 1 in Strulovici and Szydlowski (2015), if H satisfies Condition 1-3, then there exists a twice-continuously differentiable solution to the HJB equation.
To check Condition 1 in Strulovici and Szydlowski (2015, Proposition 1), note that for ,
where the second inequality comes from Lemma A2 , and is a constant. Taking , we have
Secondly, for ,
where the second inequality comes from Lemma A2 . Taking , we have
To check Condition 2, note that for all , is nonincreasing in p.
It remains to check Condition 3. For each , choose such that
where c is a constant satisfying Lemma A2. Then for all , ,
where the third inequality is due to Lemma A2 and last inequality due to (A5). Secondly,
where the third inequality is due to Lemma A2 (iii) and last inequality due to (A5). Q.E.D.
First, suppose . Then . According to (20), . Define . Note that is not a constant in this case and hence, does not always equal to 0, which implies that .
Assume that . Since , there must exist some interval such that is decreasing in order to reach its negative limit, which means that there exists some point such that changes its sign from positive to negative. Define this point as
Hence, . Then according to (A6),
which implies that . But a contradiction happens because is non-negative on , which leads to .
Then, assume that and there exists some point such that . Define as
Hence, . According to (A6),
Therefore,
Since , is strictly increasing in a local neighborhood after . Then, after point there should exists some interval such that is strictly decreasing in order to achieve the limit. Define as
Hence, . Note that is strictly positive in a local neighborhood after and non-negative on , thus . Then according to (A6),
which is a contradiction. Therefore, and is decreasing.
For the other two cases, the proof is similar. Q.E.D.
Proof of Corollary 1
Because according to Theorem 3 is monotone and its limit as shown in (20) is finite, it is straightforward that and are bounded. Q.E.D.
Proof of Proposition 3
(a) Taking the first-order derivative of , for ,
where , . Since for , is decreasing on . Therefore, for , which shows that is increasing. By L’Hôpital rule,
- (b) Note that for , . Therefore, .
Taking the first-order derivative of , for ,
Since for , is increasing on . Therefore, for , which shows that is decreasing. By L’Hôpital rule,
Q.E.D.
References
- Wang, H.; Zariphopoulou, T.; Zhou, X.Y. Reinforcement Learning in Continuous Time and Space: A Stochastic Control Approach. Journal of Machine Learning Research 2020, 21, 1–34. [Google Scholar]
- Lundberg, F. Approximerad framställning af sannolikhetsfunktionen. Återförsäkring af kollektivrisker. Akademisk afhandling; Almqvist &Wiksells, 1903.
- De Finetti, B. Su un’impostazione alternativa della teoria collettiva del rischio. Transactions of the XVth international congress of Actuaries. New York, 1957, Vol. 2, pp. 433–443.
- Gerber, H.U. Entscheidungskriterien für den zusammengesetzten Poisson-Prozess. PhD thesis, ETH Zurich, 1969.
- Schmidli, H. Stochastic control in insurance; Springer Science & Business Media, 2007.
- Jeanblanc-Picqué, M.; Shiryaev, A.N. Optimization of the flow of dividends. Uspekhi Matematicheskikh Nauk 1995, 50, 25–46. [Google Scholar] [CrossRef]
- Asmussen, S.; Taksar, M. Controlled diffusion models for optimal dividend pay-out. Insurance: Mathematics and Economics 1997, 20, 1–15. [Google Scholar] [CrossRef]
- Jgaard, B.H.; Taksar, M. Controlling risk exposure and dividends payout schemes: insurance company example. Mathematical Finance 1999, 9, 153–182. [Google Scholar] [CrossRef]
- Asmussen, S.; Højgaard, B.; Taksar, M. Optimal risk control and dividend distribution policies. Example of excess-of loss reinsurance for an insurance corporation. Finance and Stochastics 2000, 4, 299–324. [Google Scholar] [CrossRef]
- Azcue, P.; Muler, N. Optimal reinsurance and dividend distribution policies in the Cramér-Lundberg model. Mathematical Finance: An International Journal of Mathematics, Statistics and Financial Economics 2005, 15, 261–308. [Google Scholar] [CrossRef]
- Azcue, P.; Muler, N. Optimal investment policy and dividend payment strategy in an insurance company. The Annals of Applied Probability 2010, 20, 1253–1302. [Google Scholar] [CrossRef]
- Gaier, J.; Grandits, P.; Schachermayer, W. Asymptotic ruin probabilities and optimal investment. The Annals of Applied Probability 2003, 13, 1054–1076. [Google Scholar] [CrossRef]
- Kulenko, N.; Schmidli, H. Optimal dividend strategies in a Cramér–Lundberg model with capital injections. Insurance: Mathematics and Economics 2008, 43, 270–278. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, L. Optimal investment for insurer with jump-diffusion risk process. Insurance: Mathematics and Economics 2005, 37, 615–634. [Google Scholar] [CrossRef]
- Choulli, T.; Taksar, M.; Zhou, X.Y. A diffusion model for optimal dividend distribution for a company with constraints on risk control. SIAM Journal on Control and Optimization 2003, 41, 1946–1979. [Google Scholar] [CrossRef]
- Gerber, H.U.; Shiu, E.S. On optimal dividend strategies in the compound Poisson model. North American Actuarial Journal 2006, 10, 76–93. [Google Scholar] [CrossRef]
- Avram, F.; Palmowski, Z.; Pistorius, M.R. On the optimal dividend problem for a spectrally negative Lévy process. The Annals of Applied Probability 2007, 17, 156–180. [Google Scholar] [CrossRef]
- Yin, C.; Wen, Y. Optimal dividend problem with a terminal value for spectrally positive Levy processes. Insurance: Mathematics and Economics 2013, 53, 769–773. [Google Scholar] [CrossRef]
- Zhao, Y.; Kosorok, M.R.; Zeng, D. Reinforcement learning design for cancer clinical trials. Statistics in medicine 2009, 28, 3294–3315. [Google Scholar] [CrossRef] [PubMed]
- Komorowski, M.; Celi, L.A.; Badawi, O.; Gordon, A.C.; Faisal, A.A. The artificial intelligence clinician learns optimal treatment strategies for sepsis in intensive care. Nature medicine 2018, 24, 1716–1720. [Google Scholar] [CrossRef]
- Mirowski, P.; Pascanu, R.; Viola, F.; Soyer, H.; Ballard, A.J.; Banino, A.; Denil, M.; Goroshin, R.; Sifre, L.; Kavukcuoglu, K. ; others. Learning to navigate in complex environments. arXiv:1611.03673. [CrossRef]
- Zhu, Y.; Mottaghi, R.; Kolve, E.; Lim, J.J.; Gupta, A.; Fei-Fei, L.; Farhadi, A. Target-driven visual navigation in indoor scenes using deep reinforcement learning. 2017 IEEE international conference on robotics and automation (ICRA). IEEE, 2017, pp. 3357–3364. [CrossRef]
- Radford, A.; Jozefowicz, R.; Sutskever, I. Learning to generate reviews and discovering sentiment. arXiv:1704.01444. [CrossRef]
- Paulus, R.; Xiong, C.; Socher, R. A deep reinforced model for abstractive summarization. arXiv:1705.04304. [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; others. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Jaderberg, M.; Czarnecki, W.M.; Dunning, I.; Marris, L.; Lever, G.; Castaneda, A.G.; Beattie, C.; Rabinowitz, N.C.; Morcos, A.S.; Ruderman, A.; others. Human-level performance in 3D multiplayer games with population-based reinforcement learning. Science 2019, 364, 859–865. [Google Scholar] [CrossRef] [PubMed]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; Van Den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; others. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef]
- Silver, D.; Schrittwieser, J.; Simonyan, K.; Antonoglou, I.; Huang, A.; Guez, A.; Hubert, T.; Baker, L.; Lai, M.; Bolton, A.; others. Mastering the game of go without human knowledge. Nature 2017, 550, 354–359. [Google Scholar] [CrossRef]
- Auer, P.; Cesa-Bianchi, N.; Fischer, P. Finite-time analysis of the multiarmed bandit problem. Machine learning 2002, 47, 235–256. [Google Scholar] [CrossRef]
- Cesa-Bianchi, N.; Gentile, C.; Lugosi, G.; Neu, G. Boltzmann exploration done right. Advances in neural information processing systems 2017, 30. [Google Scholar]
- Todorov, E. Linearly-solvable Markov decision problems. Advances in neural information processing systems 2006, 19. [Google Scholar]
- Ziebart, B.D.; Maas, A.L.; Bagnell, J.A.; Dey, A.K. ; others. Maximum entropy inverse reinforcement learning. Aaai. Chicago, IL, USA, 2008, Vol. 8, pp. 1433–1438.
- Nachum, O.; Norouzi, M.; Xu, K.; Schuurmans, D. Bridging the gap between value and policy based reinforcement learning. Advances in neural information processing systems 2017, 30. [Google Scholar]
- Wang, H.; Zhou, X.Y. Continuous-time mean–variance portfolio selection: A reinforcement learning framework. Mathematical Finance 2020, 30, 1273–1308. [Google Scholar] [CrossRef]
- Dai, M.; Dong, Y.; Jia, Y. Learning equilibrium mean-variance strategy. Mathematical Finance 2023, 33, 1166–1212. [Google Scholar] [CrossRef]
- Bai, L.; Gamage, T.; Ma, J.; Xie, P. Reinforcement Learning for optimal dividend problem under diffusion model. arXiv:math/2309.10242. [CrossRef]
- Tang, W.; Zhang, Y.P.; Zhou, X.Y. Exploratory HJB equations and their convergence. SIAM Journal on Control and Optimization 2022, 60, 3191–3216. [Google Scholar] [CrossRef]
- Gao, X.; Xu, Z.Q.; Zhou, X.Y. State-dependent temperature control for Langevin diffusions. SIAM Journal on Control and Optimization 2022, 60, 1250–1268. [Google Scholar] [CrossRef]
- Strulovici, B.; Szydlowski, M. On the smoothness of value functions and the existence of optimal strategies in diffusion models. Journal of Economic Theory 2015, 159, 1016–1055. [Google Scholar] [CrossRef]
| 1 | For example, the dividend paying rate under the threshold strategy is the maximal rate if the surplus exceeds the threshold; otherwise, it pays nothing. Since the threshold is determined by the model parameters, the change in the estimated parameters may dramatically change the dividend paying rate from zero to the maximal rate, or conversely. |
| 2 | |
| 3 | For each initial surplus x, we discretize the continuous time into small pieces () and sample 2000 independent surplus processes to simulate and . |
Figure 1.
The classical value functions (top) and the optimal dividend-paying rate (bottom) for , , , (left panels), (middle panels), and (right panels), respectively.
Figure 1.
The classical value functions (top) and the optimal dividend-paying rate (bottom) for , , , (left panels), (middle panels), and (right panels), respectively.
Figure 2.
Cases of value functions given M and .
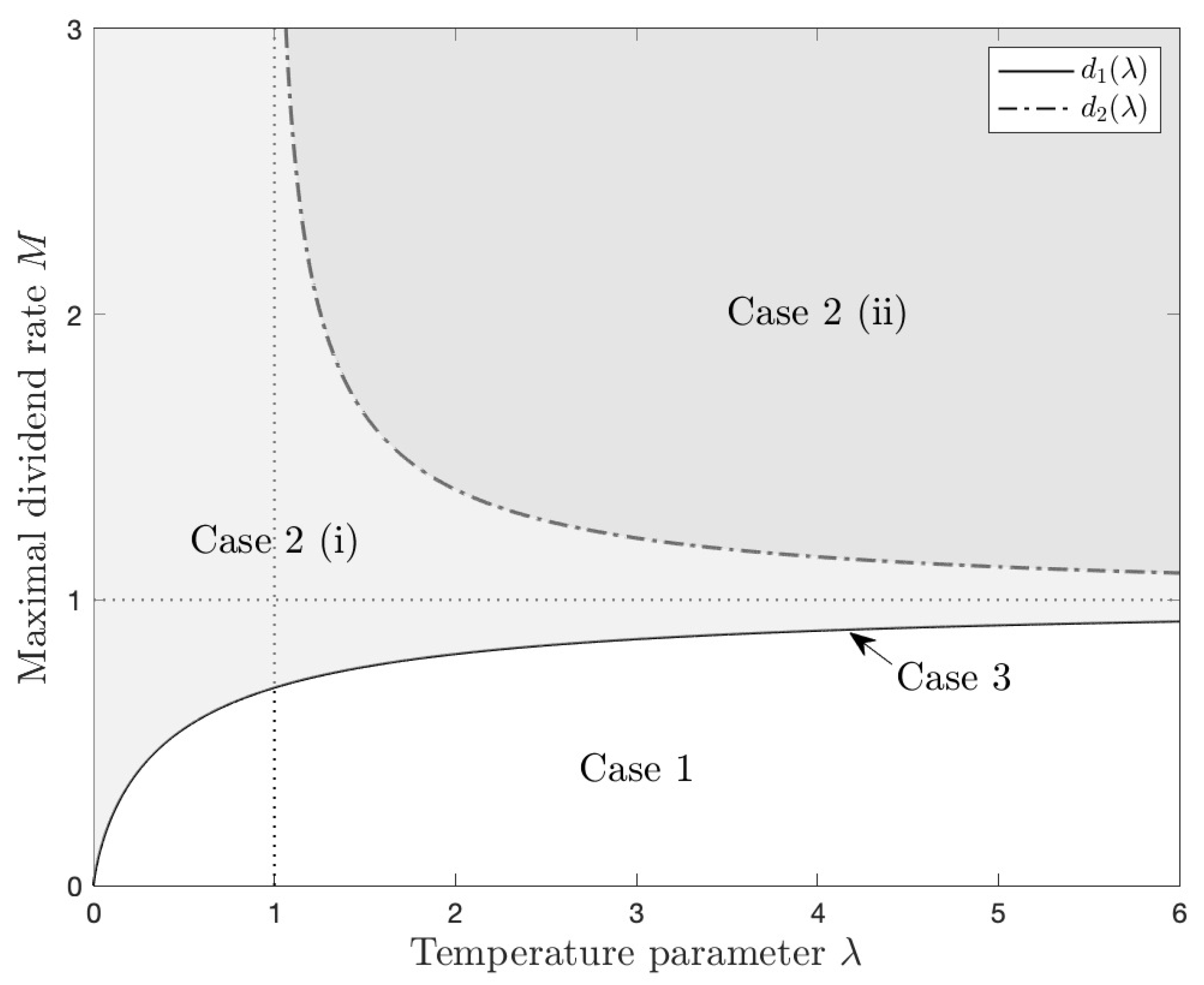
Figure 3.
Let , , , . Let (left column); (middle column); (right column), respectively. The figures on the top row show the value function , the expected total discounted dividends and the expected total weighted discounted entropy . The figures on the middle row show the mean of the optimal distribution . The figures on the bottom row show the density function of the optimal distribution with respect to different surplus level x.
Figure 3.
Let , , , . Let (left column); (middle column); (right column), respectively. The figures on the top row show the value function , the expected total discounted dividends and the expected total weighted discounted entropy . The figures on the middle row show the mean of the optimal distribution . The figures on the bottom row show the density function of the optimal distribution with respect to different surplus level x.
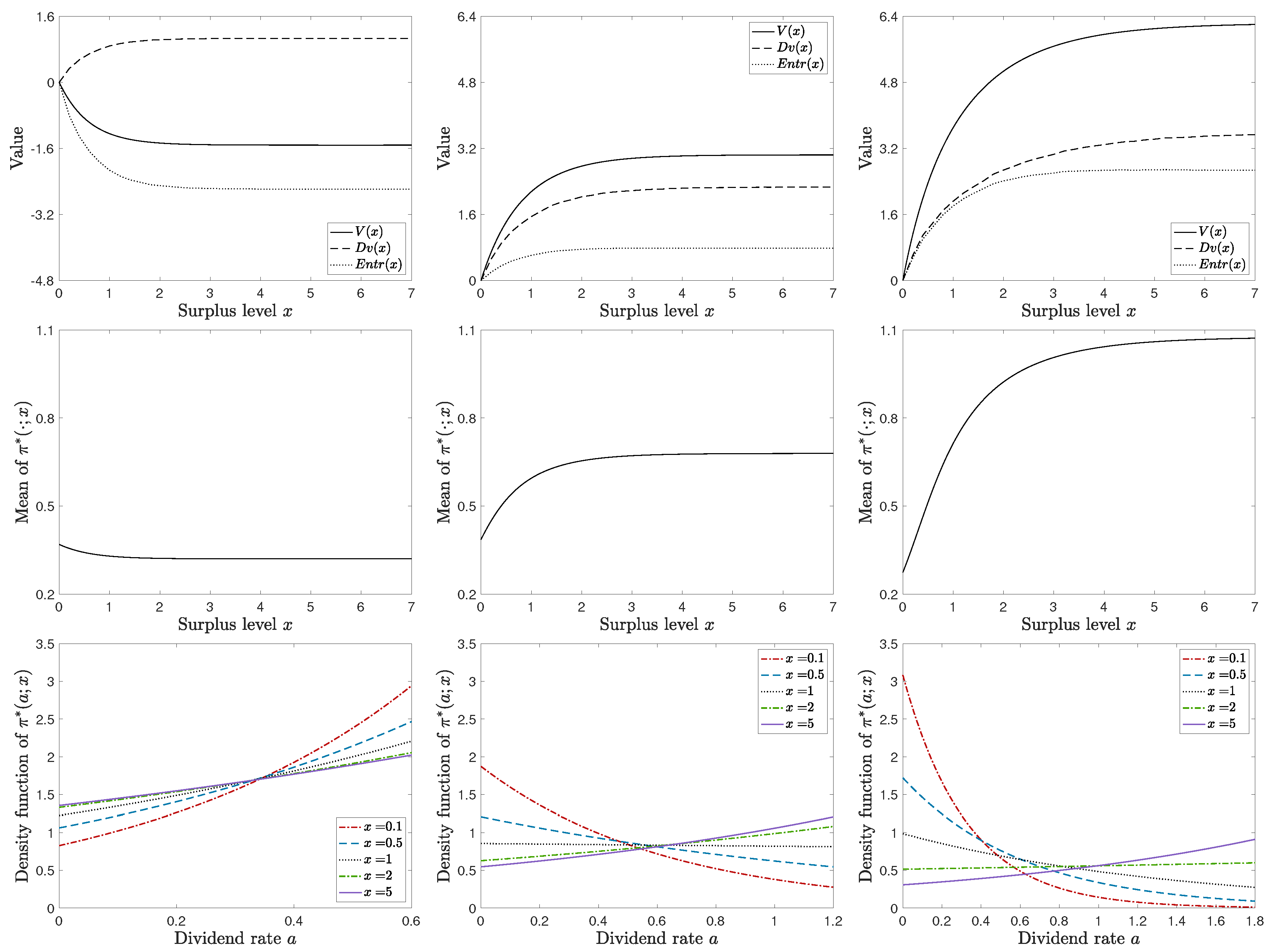
Figure 4.
The value function given different values of with (left) and (right)
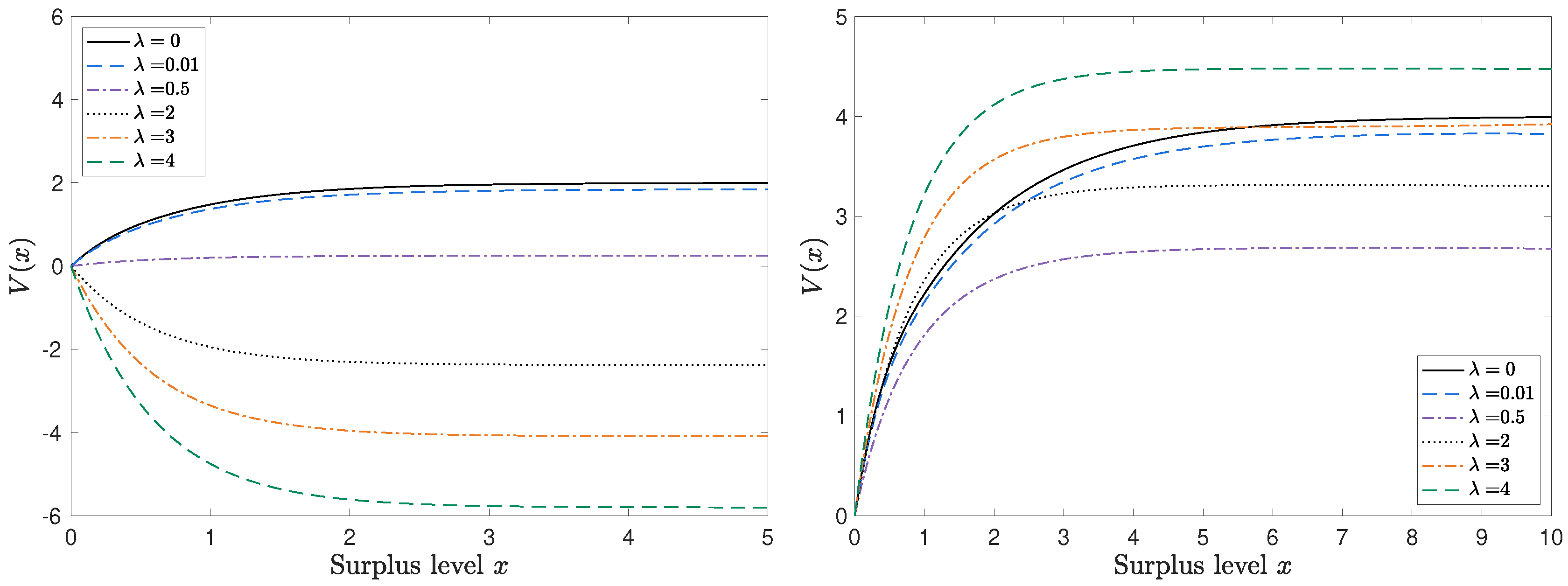
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





