Prerpints.org logo
Preprint
Article

Network Approach Identifies the Control Cities of O3 Pollution

Altmetrics

Downloads

76

Views

20

Comments

0

Submitted:

28 November 2023

Posted:

28 November 2023

You are already at the latest version

Alerts
Abstract
In recent years, ozone (O3) pollution has been rapidly spreading, restricting further improvement of air quality in China. Investigating the interaction of O3 concentration and identifying their driven cities are important for the prevention and control of O3 pollution in China. However, the complex interaction between O3 pollution between the cities and their driven cities has not yet been revealed. In this study, we address this gap based on complex network methods. Specifically, an ozone relational network is constructed using an association calculation method. The driven nodes and spatial clusters were analyzed based on the maximum matching algorithm and the Louvain algorithm. The findings of the study reveal an aggregation phenomenon in the ozone network concerning distance. Furthermore, as the threshold Tc varies, the proportion of driven nodes exhibits a positive correlation. Moreover, a closer threshold value corresponds to a higher coincidence ratio of the driven nodes. The results provide scientific guidance for national O3 pollution prevention and regional synergy formatting. Furthermore, the introduced network-based approaches offer a mythological framework for the study of air pollution in key cities and clusters.
Keywords: 
Subject: Environmental and Earth Sciences  -   Atmospheric Science and Meteorology

1. Introduction

With the rapid development of human society, environmental issues are receiving increasing attention [1,2]. Among these, air pollution is one of the world's most significant environmental problems, with a direct impact on the physical and mental health of its inhabitants [3]. A large number of actions have been taken to improve air quality. To improve air quality, the government released a series of policies, such as the State Council issued Air Pollution Prevention and Control Action Plan and the Blue Sky Defense War [4,5]. It’s glad to see the PM2.5 concentrations in China have significantly decreased, however, the concentration of ozone (O3) is showing an upward and spreading trend, becoming a limiting factor for further improvement of our air quality [6,7]. controlling O3 pollution become urgent issues that need to be addressed in each city.
O3 pollution is a secondary pollutant generated by photochemical reactions that have adverse effects on human health and ecosystems [8]. Nitrogen oxides and VOCs are one of the main precursor pollutants for the formation of O3 [9,10,11,12]. The relationship between O3, NOx, and VOCs is not a simple linear dependence, but rather a non-linear variation [13]. The photochemical reaction of O3 is very complex and is influenced by both meteorological conditions and the control of precursor pollutants [14,15]. Seasonal characteristics are observed in ozone pollution, as it is notably affected by the summer monsoon [16]. Moreover, in China, there has been a positive correlation between surface O3 concentration and the ENSO index during summers from 1990 to 2019 [17]. A comprehensive study on meteorological variables, including surface ozone, relative humidity, and temperature, was conducted in 74 major Chinese cities from 2017 to 2018. The findings revealed that ozone levels in each city decreased with increasing relative humidity, showing a negative overall correlation [18]. This suggests that net ozone production decreases as relative humidity increases [19].
In addition to industrial emissions and meteorological conditions, inter-regional atmospheric transport is an important factor in the formation of O3 pollution [20,21,22,23]. Identifying driving cities is beneficial for managing atmospheric environmental quality. A large number of studies have applied numerical models, such as WRF-Chem, CMAQ, and CAMx, to analyze the transport characteristics of O3 [24,25,26]. However, these studies mainly focus on limited cities and limited time. Research has pointed out that longer time scale analysis is of greater significance for studying the causes of O3 and managing joint prevention and control. In addition, research on identifying O3 driven cities is even rarer.
In recent years, complex network methods have gradually been introduced into the field of atmospheric environment [27]. A notable study conducted by Tian et al. delved into the ozone transport network in California, examining the phenomenon of networked communities. Similarly, Wang et al. applied an optimized complex network approach and source resolution model to analyze the transport patterns of O3 in the Yangtze River Delta region [28,29]. Despite the abundance of valuable findings in ozone research, the application of complex network methods, especially control network theory, to comprehend certain ozone phenomena remains relatively rare.
In this study, the O3 network is based on the cross-correlation function [30,31,32]. Subsequently, we employ the Louvain community partitioning algorithm to delineate communities within the ozone network [33]. We then employ the maximum matching control network theory to explore the driven nodes of the ozone network, among other aspects. The research findings reveal significant associations within the ozone network, primarily concentrated in regions such as Northeast China, North China, Sichuan-Chongqing, and Southeast coastal areas. Furthermore, network control theory demonstrates that the driven nodes within the ozone network are distinct from hub nodes. Additionally, we investigate the impact of the edge weight threshold on the maximum number of connected community nodes, the number of driven nodes, and the co-occurrence of driven nodes. Finally, we carefully examine the correlation between the predicted sequences and node distances for two distinct types of nodes. This comprehensive analysis uncovers a noteworthy and intricate relationship among these variables. Our research results provide reference for the development of strategies and countermeasures for O3 pollution.

2. Materials and Methods

2.1. Data

The maximum daily average 8-hour (MDA8) O3 concentration used in this study are acquired from the China National Environmental Monitoring Centre (CNEMC). The The temporal span of the dataset encompasses the period from January 1, 2015, to December 31, 2019, encompassing a duration of 1,800 days. Our dataset comprises a grand total of 604,800 individual records.

2.2. Methods

In order to verify and understand the applicability of the complex network theory in the O3 network, we introduce the obtained O3 data in this section, as well as the cross-correlation O3 network construction method, the O3 network community partition algorithm Louvain Community Classification and the driven node discovery method maximum matching algorithm [33,34].

2.2.1. Network construction

In recent years, more and more studies have focused on the use of complex network theories and methods to study climate phenomena. Among them, the cross-correlation function has achieved many meaningful results in the study of atmospheric gases, such as the influence of distance and so on. In this work, we employ the cross-correlation function to calculate the correlation between O3 observation sites and use it as the link weight for constructing the O3 network [35,36,37,38,39]. The specific calculation process of the cross-correlation function algorithm is shown in the equation (1) and (2):
X C i , C j τ = ∑ t = 1 L − τ C i t − C i ¯ C j t + τ − C j ¯ ∑ t = 1 L − τ C i t − C i ¯ 2 ⋅ ∑ t = 1 L − τ C j t + τ − C j ¯ 2
X C i , C j − τ = ∑ t = 1 L − τ C i t + τ − C i ¯ C j t − C j ¯ ∑ t = 1 L − τ C i t + τ − C i ¯ 2 ⋅ ∑ t = 1 L − τ C j t − C j ¯ 2
where  τ represents the delay time and τ ≥ 0 , vectors C i and C j represent the values of O3 data for two cities i and j , C i ¯ and C j ¯ are the averages of O3 for these two cities. Time delay τ ∈ − 30 , 30 , X C i , C j τ take the O 3 data of city i as C 0 : L m a x − τ , the O 3 data of city j as T τ : L m a x , while L m a x is the total number of records of O3 data for a city. X C i , C j − τ take the O3 data of city i as C τ : L m a x , and the O3 data of city j as C 0 : L m a x − τ .
Equations (3) and (4) are used to calculate the positive and negative link weights of the O3 network.
W C i , C j p o s = m a x X C i , C j − m e a n X C i , C j s t d X C i , C j
W C i , C j n e g = m i n X C i , C j − m e a n X C i , C j s t d X C i , C j
W C i , C j p o s and W C i , C j n e g are the positive and negative link weights respectively. In the process of building a city O3 network, the city is used as a node of the network, and the link weight threshold between nodes is set to T C , when τ C i , C j p o s > 0 and W C i , C j p o s ≥ T C , there exists a link between city i and city j , with direction from city i to city j . The link weight is W C i , C j p o s , and all eligible links are connected to form a positive O3 network (PoN). When τ C i , C j n e g < 0 and W C i , C j n e g ≤ − T C , there exist a link between city i and city j , and direction from city i to city j with the weight W C i , C j n e g , which forms a negative O3 network (NoN).Interventionary studies involving animals or humans, and other studies that require ethical approval, must list the authority that provided approval and the corresponding ethical approval code.

2.2.2. Louvain Community Classification Algorithm

In this section, we introduce an algorithm to quickly divide the network community, which is Louvain algorithm. The algorithm is a method for extracting the structure of large-scale network communities with modularity as the optimization goal. It uses module gain to divide the community, which can quickly and effectively divide the community of the directed weighted network.
Louvain algorithm is a method of extracting large network community structure based on modular optimization, which uses module gain to divide the community, which can effectively divide the community and calculate fast. Applying the Louvain algorithm to the community division of the directed weighted O3 network can quickly obtain the community division results. Modularity is used to measure the quality of community division, the value range is [-1,1], which is a measure of the density of links within the community and links between different communities. In highly modular communities, there are dense links between internal nodes, while sparse links between different communities nodes. Modularity calculation formula is defined as equation (5):
Q = 1 2 m ∑ i , j A i j − k i k j 2 m δ c i , c j
The Louvain algorithm steps in dividing the community are as follows,
Step 1: Initialize each node in the network to a different community, the network with n nodes has n initial communities.
Step 2: Suppose the current node a has 0 . . . k neighbor nodes, calculate the modular gain after putting node a into the community of any neighboring node Δ Q , which is shown as equation (6). Then select the community with the largest gain value to place node a . If the modular gain is not positive, node a remains in the original community.
Step 3: Repeat step 2 until all nodes are in communities where they cannot get modular gain through movement.
Δ Q = ∑ i n + k i , i n 2 m − ∑ t o t + k i 2 m 2 − ∑ i n 2 m − ∑ t o t 2 m 2 − k i 2 m 2

2.2.3. Maximum matching algorithm

With the introduction of the controllability of complex networks, more and more researchers focus on this field, and many interesting results have been achieved [34]. Here, we use the maximum matching control algorithm to study the O3 network. The maximum matching algorithm is a structural controllability framework that can effectively identify the minimum set of driven nodes for a control network. The maximum matching in the network marks the maximum link set that does not share the starting node or the ending node, and the remaining nodes that are not matched are the minimum driven node set. These drive nodes enable control of the network. Generally, the maximum matching algorithm of a bipartite graph is used to find the minimum set of driven nodes of the network.
First, we need to convert the ordinary network into a bipartite graph network. The detailed conversion process can be found in reference [34]. Here we briefly describe the conversion steps. At the beginning, let G = V , E , V = c 1 , c 2 , . . . , c n , E = c 1 , c 2 , c 1 , c 2 , c 1 , c 4 , c 5 , c 3 . . . , c 1 , c 2 indicates there exist a link from c 1 to c 2 . Constructing two disjoint subsets, denoted by + as the source node, and denoted by − as the target node, V + = c 1 + , c 2 + , . . . , c n + , V − = c 1 − , c 2 − , . . . , c n − . In a bipartite graph, any two edges in the V + and V − node sets are not attached to the same vertex, and finding the subset with the largest number of edges is the maximum matching of the graph.

2.2.4. LSTM time series forecasting

Long Short-Term Memory (LSTM) is a type of recurrent neural network, which is widely used in time series forecasting [40]. The LSTM model learns the data that can be observed at the t moment and predicts the data at the t + 1 moment. We used LSTM to perform univariate prediction of O3 data, selected O3 data for a total of 3 years from 2015 to 2017, and entered the O3 data of the previous two and a half years to predict the O3 data of the last half year. The steps are as follows,
Step 1: Pretreatment data, including loading O3 data sorted by date, differential conversion of data, conversion of data into supervised learning data, and data normalization.
Step 2: Construct LSTM model for predictive training. After the inverse scaling and inverse differential transformation of the predicted values, the MSELoss between the real values and predicted values is calculated to obtain the prediction accuracy of the model, and the model parameters are adjusted through reverse gradient propagation to improve the prediction accuracy of the model.
Step 3: Predict O3 data of the city with the above-trained model.

3. Results and discussion

We present the main results of the correlated multi-layered networks composed of the TI and AQI as described above.

3.1. The characteristics of O3 network

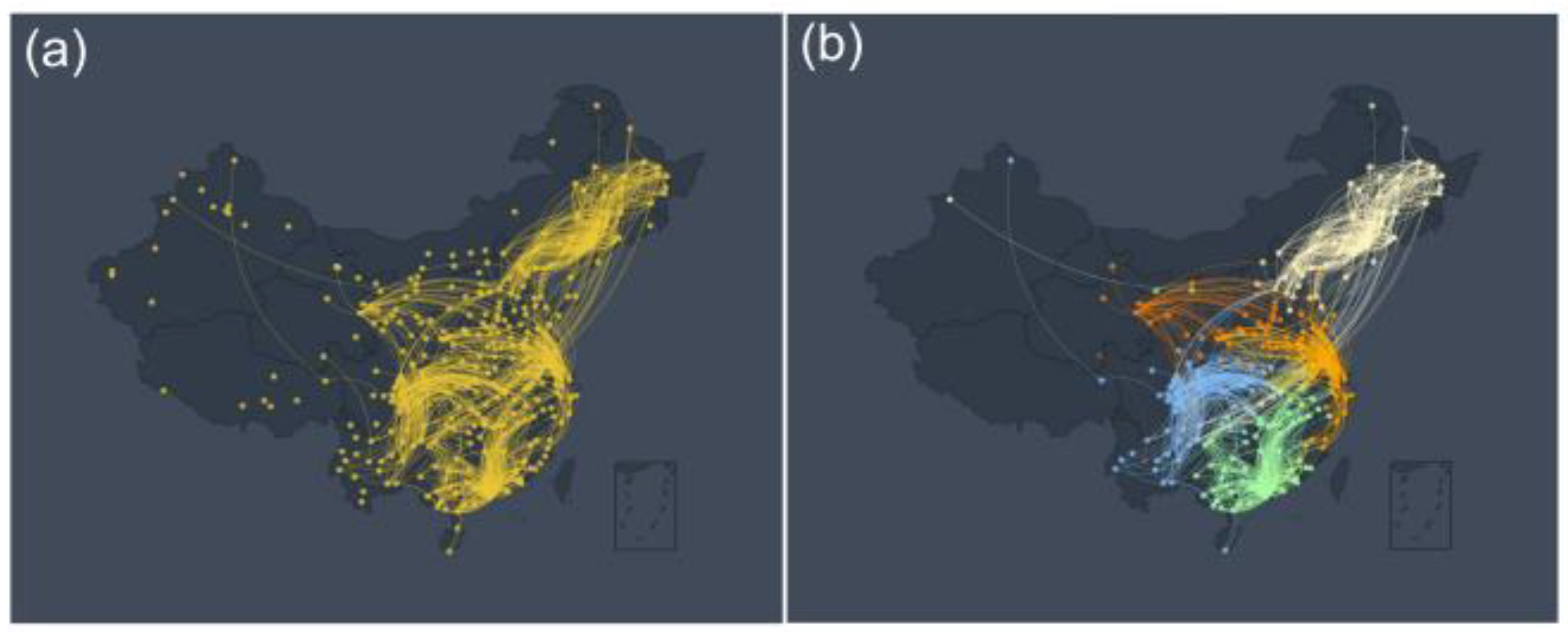
In order to visually display the network connection between various monitoring sites in China. First, we constructed the O3 link network according to the above link weight calculation method [30,31,32,35,36,37,38,39]. According to the method in Section Ⅱ B we get the connection weights of 336 cities in China and build an O3 network, which consists of 336×335=112560 edges. To better describe the network structure, we extract the edge whose weight W C i , C j p o s ≥ T C with T C =3.8 and obtain 1942 edges, which satisfies the sparse network requirement e < n l o g n [41]. Additionally, we discuss the effect of edge weights in Section Ⅲ C. The extracted network in Figure 1 (a) indicates more reasonable and understandable relationships. As can be seen from it, the network community structure can be observed through the above network construction method. For example, there are obvious community effects in Northeast China, North China, Sichuan-Chongqing, and Southeast coastal areas. These results are similar to the regional community effects seen in other previous meteorological studies [28,40]. Of course, we observe a sporadic and isolated distribution of nodes in the southwest and most of the northwest. One reason is that due to the limitation of data acquisition, currently there are only a small number of data collection sites in the southwest and northwest, resulting in a long distance between the sites and little mutual influence between the sites. As an illustration, consider the scenario where the distance between stations within a given community spans 500 kilometers, while the separation between stations in distinct communities extends to 1,500 kilometers. An additional factor contributing to this phenomenon could be attributed to the topographical features of the southwest and northwest regions. These areas are characterized by a multitude of mountains and basins, thereby impeding the free movement of air to a notable extent. It is therefore speculated that our O3 network construction method is effective and has practical value to a certain extent and can provide a new idea for the research and analysis of O3 to a certain extent.
To further verify the community structure presented by the O3 network, we use the network community partition algorithm to divide the community of the O3 network. Network community division is a commonly used network analysis technique, which has a large number of applications in social, biological, and other networks [41,42]. In this work, we employ the Louvain community partitioning algorithm, which is especially suitable for the current O3 network due to that it can quickly and effectively divide the community of directed weighted networks. Figure 1(b) shows several obvious community structures after segmentation according to the Louvain community partitioning algorithm with T C = 3.8 . These community structures corroborate our intuitive observations in Figure 1(a). For similar reasons as in Figure 1(a), community network structures rarely appear in northwest and southwest China. Nevertheless, the structure of the community partitioning algorithm can still confirm our intuitive conjecture that the community structure exists in the O3 network. This result implies that there are spatial and temporal characteristics of regional aggregation among the O3 networks, e.g., the Yangtze River Delta [43,44,45,46]. In general, the O3 detection data can be correlated according to network analysis techniques, and obvious community structure can be observed, suggesting the spatiotemporal characteristics of O3 distribution.
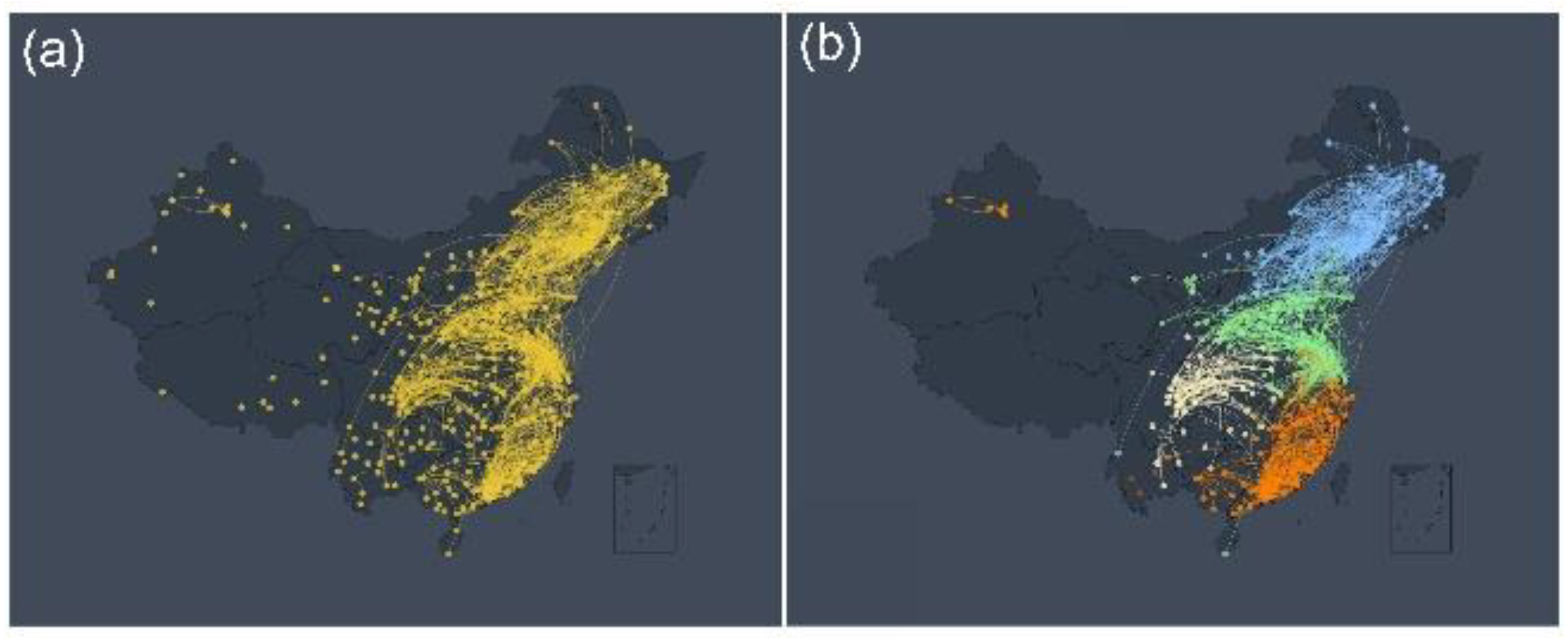
Preprints 91708 g001
Figure 1. The O3 Network and Community Structure. (a) A network of O3 monitoring stations in China constructed according to the link weight calculation method. Yellow nodes represent O3 observation stations, and links between stations indicate links between stations that meet the connectivity threshold TC = 3.8. (b) This figure is a network structure diagram after the community division of Figure 1(a) according to the Louvain community partitioning algorithm. The nodes and edges of different colors represent different network communities. For example, blue nodes represent the Northeast China community, green nodes represent the North China community, orange nodes represent the Southeast coastal community, and yellow nodes represent the Sichuan-Chongqing community.
Figure 1. The O3 Network and Community Structure. (a) A network of O3 monitoring stations in China constructed according to the link weight calculation method. Yellow nodes represent O3 observation stations, and links between stations indicate links between stations that meet the connectivity threshold TC = 3.8. (b) This figure is a network structure diagram after the community division of Figure 1(a) according to the Louvain community partitioning algorithm. The nodes and edges of different colors represent different network communities. For example, blue nodes represent the Northeast China community, green nodes represent the North China community, orange nodes represent the Southeast coastal community, and yellow nodes represent the Sichuan-Chongqing community.
Preprints 91708 g001
The aim of this study is to observe the network connectivity between various monitoring points in China during different periods. Initially, we constructed the O3 link network according to the above link weight calculation method. As can be seen from Figure 2(a) and Figure 3(a), the network community structure can be clearly observed, and these results are similar to Figure 1(a). To ensure comparability between different networks, we take the same number of edges in different networks. The edge thresholds of the corresponding networks for these two time periods are TC =3.3 and TC =3.1, respectively. However, an interesting phenomenon is that although there are obvious community structures in the network at different periods, there are significant differences in the size of these community structures. These results suggest that different times have important effects on the construction of the O3 link network. Future research should focus more on the explainable practical role of these network structures.
To further verify the community structure presented by the O3 network in different periods, we employ the Louvain community partitioning algorithm to divide the community of the O3 network. Obviously, Figure 2(b) and Figure 3(b) show several obvious community structures divided according to the Louvain community division algorithm into two different periods respectively. Their thresholds are TC=3.3 and TC=3.1, respectively. These community structures corroborate our intuitive observations in Figure 2(a) and Figure 3(a). At the same time, these results indicate that the community structure formed has changed slightly over time. For example, there are certain differences in the community structure between North China and the Yangtze River Delta. In general, these results verify the existence of a distinct community structure in the O3 network and also confirm the spatiotemporal characteristics of O3 distribution.
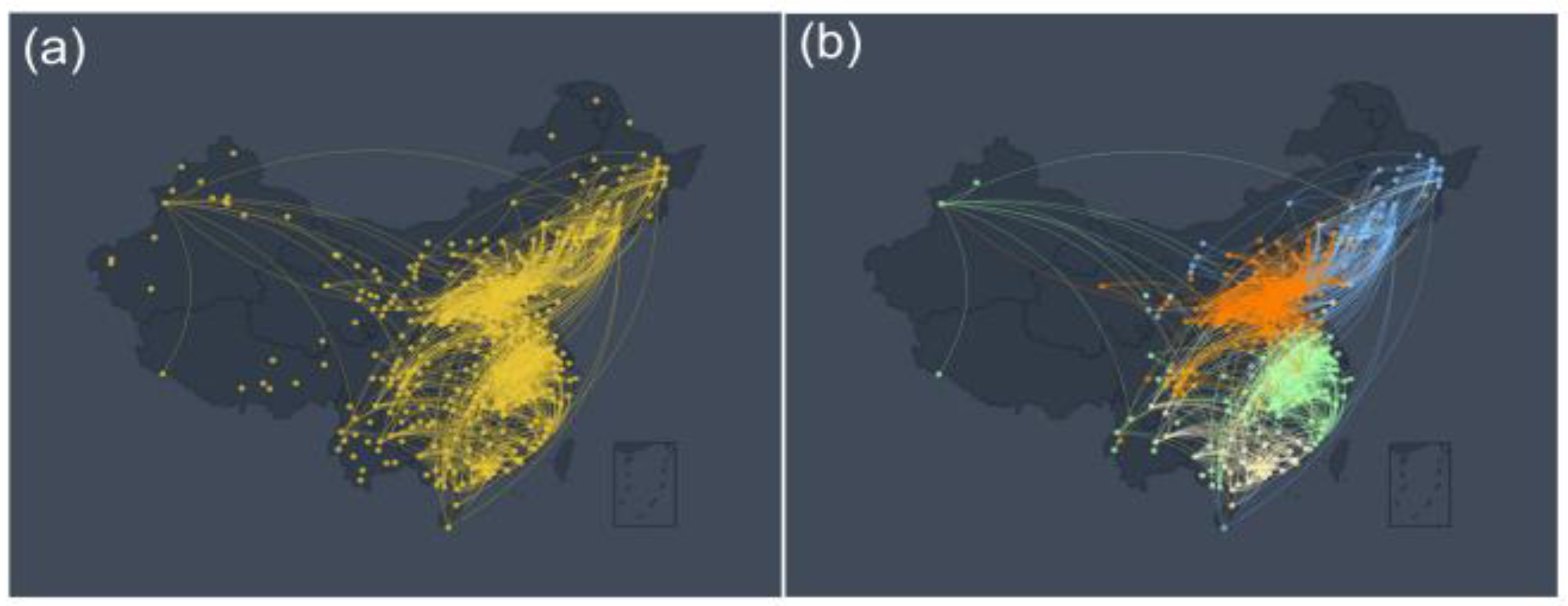
Preprints 91708 g003
Figure 3. The O3 Network and Community Structure from October to February. (a) A network of O3 monitoring stations in China constructed according to the link weight calculation method. Yellow nodes represent O3 observation stations, and links between stations indicate links between stations that meet the connectivity threshold TC = 3.1. (b) This figure is a network structure diagram after the community division of Figure 3 (a) according to the Louvain community partitioning algorithm. The nodes and edges of different colors represent different network communities. For example, blue represents the Northeast China community, green represents the Yangtze River Delta community, orange represents the North China community, and yellow represents the Southeast coastal community.
Figure 3. The O3 Network and Community Structure from October to February. (a) A network of O3 monitoring stations in China constructed according to the link weight calculation method. Yellow nodes represent O3 observation stations, and links between stations indicate links between stations that meet the connectivity threshold TC = 3.1. (b) This figure is a network structure diagram after the community division of Figure 3 (a) according to the Louvain community partitioning algorithm. The nodes and edges of different colors represent different network communities. For example, blue represents the Northeast China community, green represents the Yangtze River Delta community, orange represents the North China community, and yellow represents the Southeast coastal community.
Preprints 91708 g003

3.2. Control Algorithms and Drivens Nodes

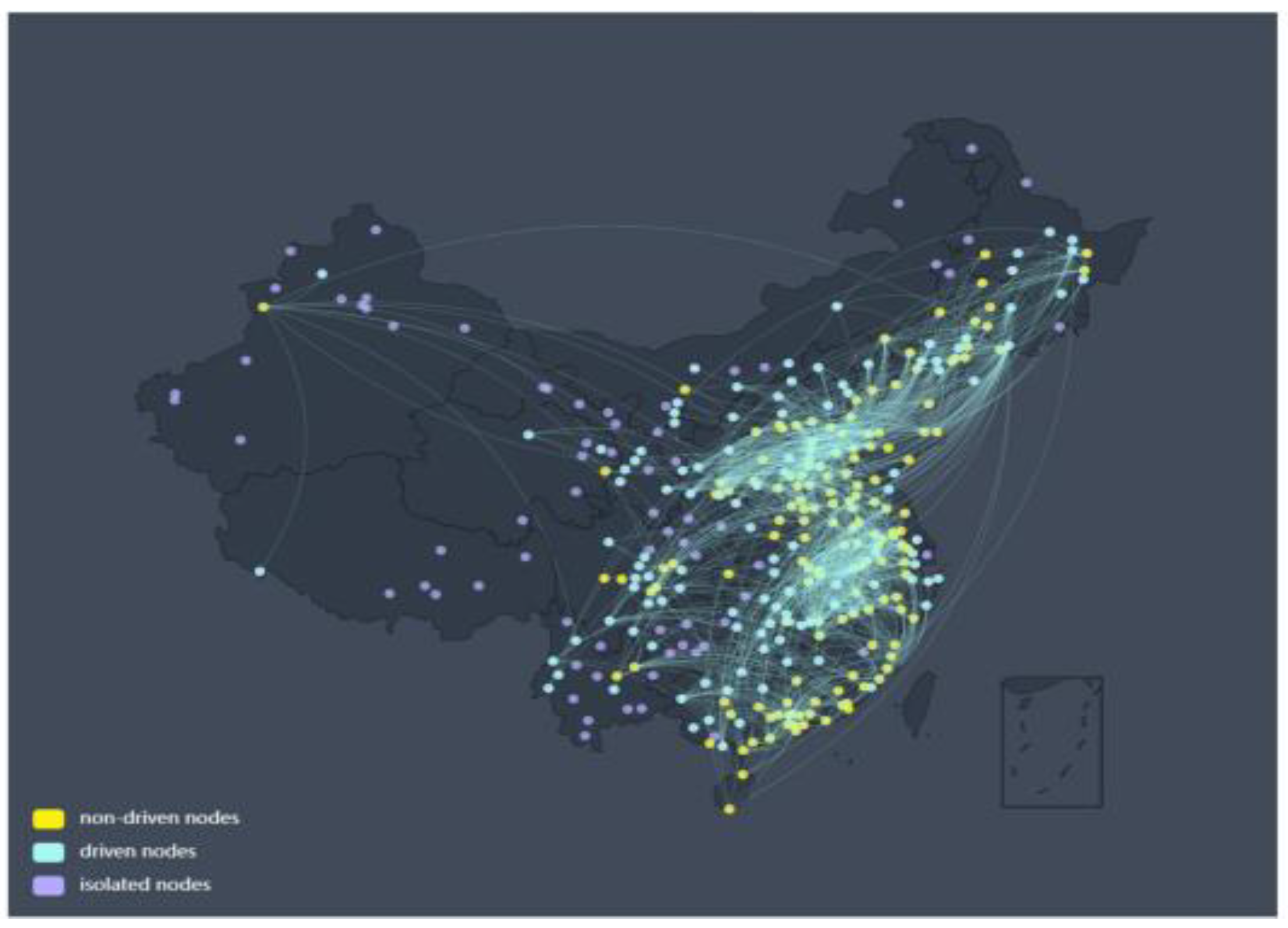
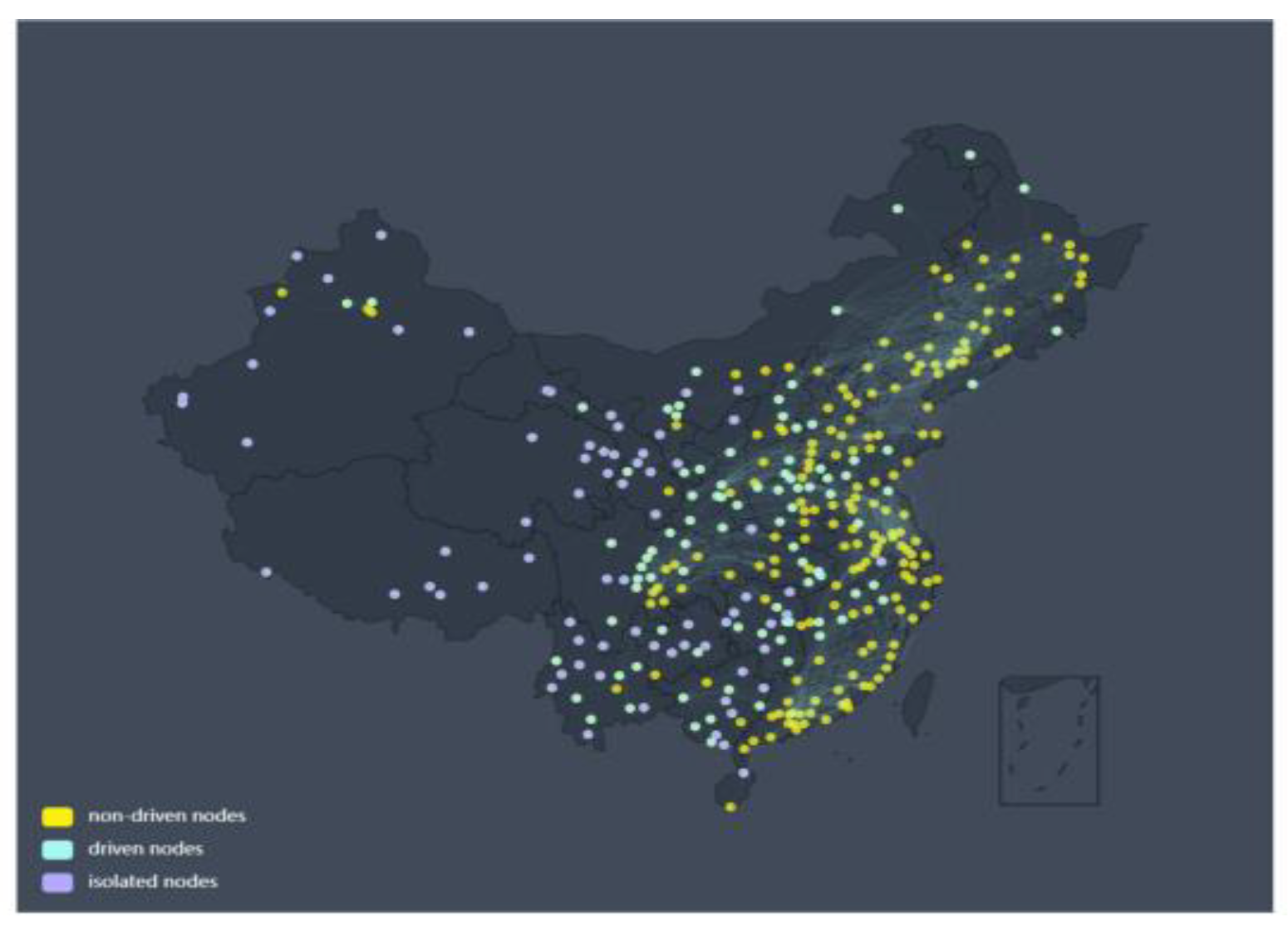
This study aims to explore the controllability of the O3 network, we select the maximum matching algorithm to distinguish the driven and non-driven nodes of the network [47]. This is due to the steps of the maximum matching algorithm and the results are easy to understand. Figure 4 shows the schematic diagram of the control network obtained by the maximum matching method. The edge threshold in this network is the same as the previous one and still takes Tc =3.8. Here, the yellow nodes represent the non-driven nodes, and the cyan nodes indicate driven nodes. The outcomes depicted in Figure 4 incontrovertibly establish the presence of driven nodes within the network. For instance, driven nodes predominantly inhabit the central region, while non-driven nodes are primarily situated in coastal areas. The distribution of these driving nodes in space concurs with the region-dependent phenomena observed in conventional O3 studies. These results fill the gap in our understanding of the O3 network-driven nodes and have certain enlightening significance. This method of using control theory to understand the O3 network, especially its drivers, is novel and interesting. Future work should therefore focus on understanding the practical significance and use of driven nodes in O3 networks. This suggests that the network control theory and technology can be tried to be applied to studying O3 networks.
To gain a deeper understanding of the relationship between the O3 control network and different periods, we compare the O3 control network in two different periods from May to September and from October to February. The O3 control networks for two different periods are shown in Figure 5 and Figure 6, respectively. Similar to the previous results in Figure 2 and Figure 3, the edge thresholds of the corresponding networks in these two time periods are T C = 3.3 and T C = 3.1 , respectively. From these figures, it can be seen that there are significant differences in the O3 control network during the two different periods. Although the methods and processing procedures used in these two networks are the same as before, their results are significantly different.
Figure 5 is a schematic diagram of the control network for O3 data from May to September obtained by the maximum matching method. To ensure comparability between different networks, we take the same number of edges in different networks. The edge threshold in this network is T C = 3.3 . Similar to Figure 4, yellow nodes represent the non-driven nodes, and cyan nodes indicate driven nodes. Comparing Figure 4, Figure 5 and Figure 6, it can be seen that in different periods, the control network presents significant differences, and the nodes change from driven nodes to non-driven nodes in different periods, and vice versa. For example, some nodes in the Yangtze River Delta are non-driven nodes from May to September and change into driven nodes from October to February. These results are similar to the seasonal variation of climate characteristics in the Yangtze River Delta region in previous studies [45,46]. These results indicate that it is meaningful to use control theory to understand the O3 network. Future research should focus more on understanding the practical implications of seasonal changes in O3 network nodes over time.
Preprints 91708 g006
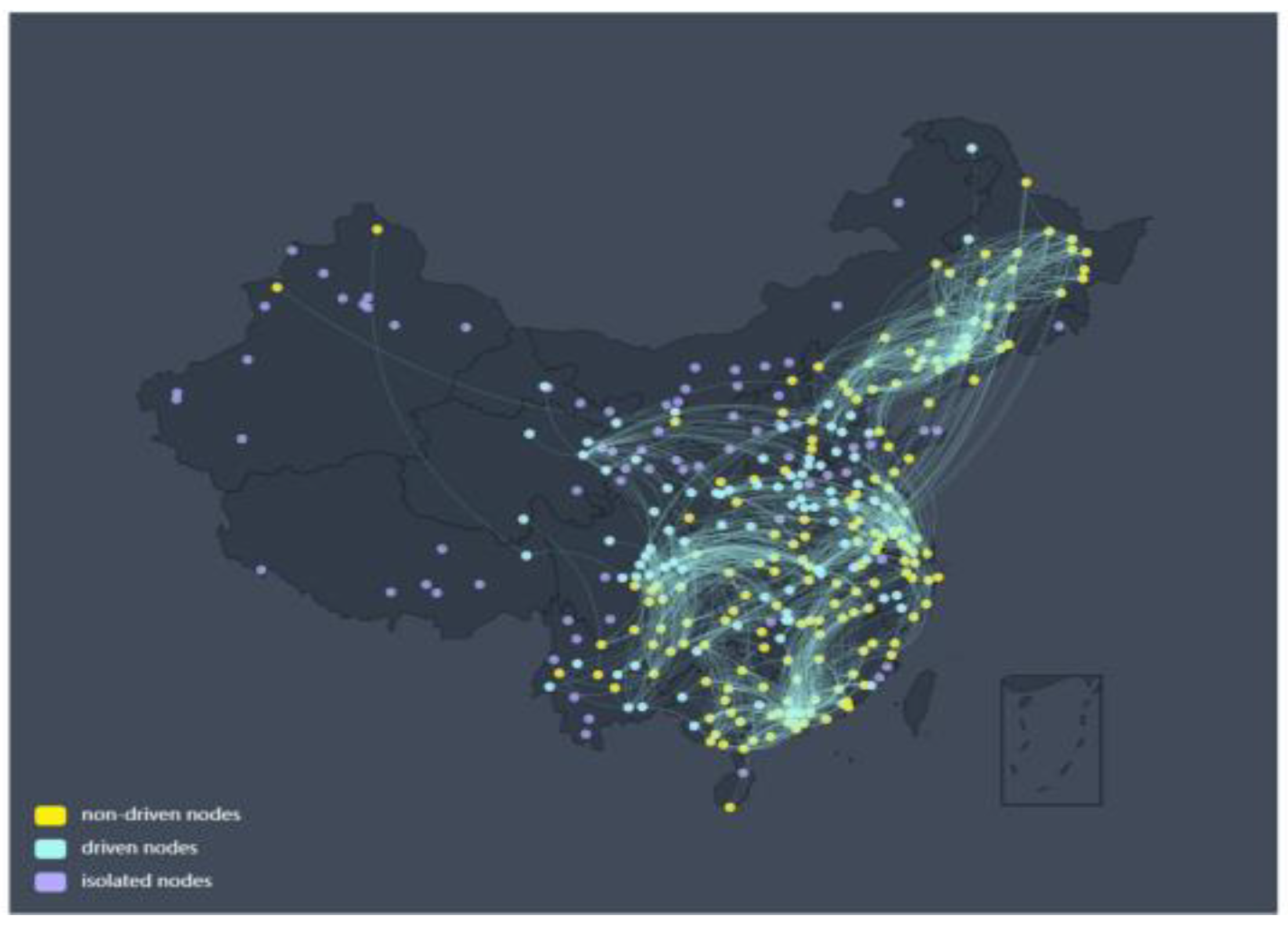
Figure 6. O3 Network from October to February from the Perspective of Network Control Theory. The figure shows the isolated, driven, and non-driven nodes of the O3 network with a threshold of TC = 3.1. Yellow represents non-driven nodes, cyan for driven nodes, and purple for isolated nodes.
Figure 6. O3 Network from October to February from the Perspective of Network Control Theory. The figure shows the isolated, driven, and non-driven nodes of the O3 network with a threshold of TC = 3.1. Yellow represents non-driven nodes, cyan for driven nodes, and purple for isolated nodes.
Preprints 91708 g006

3.3. Weights effect

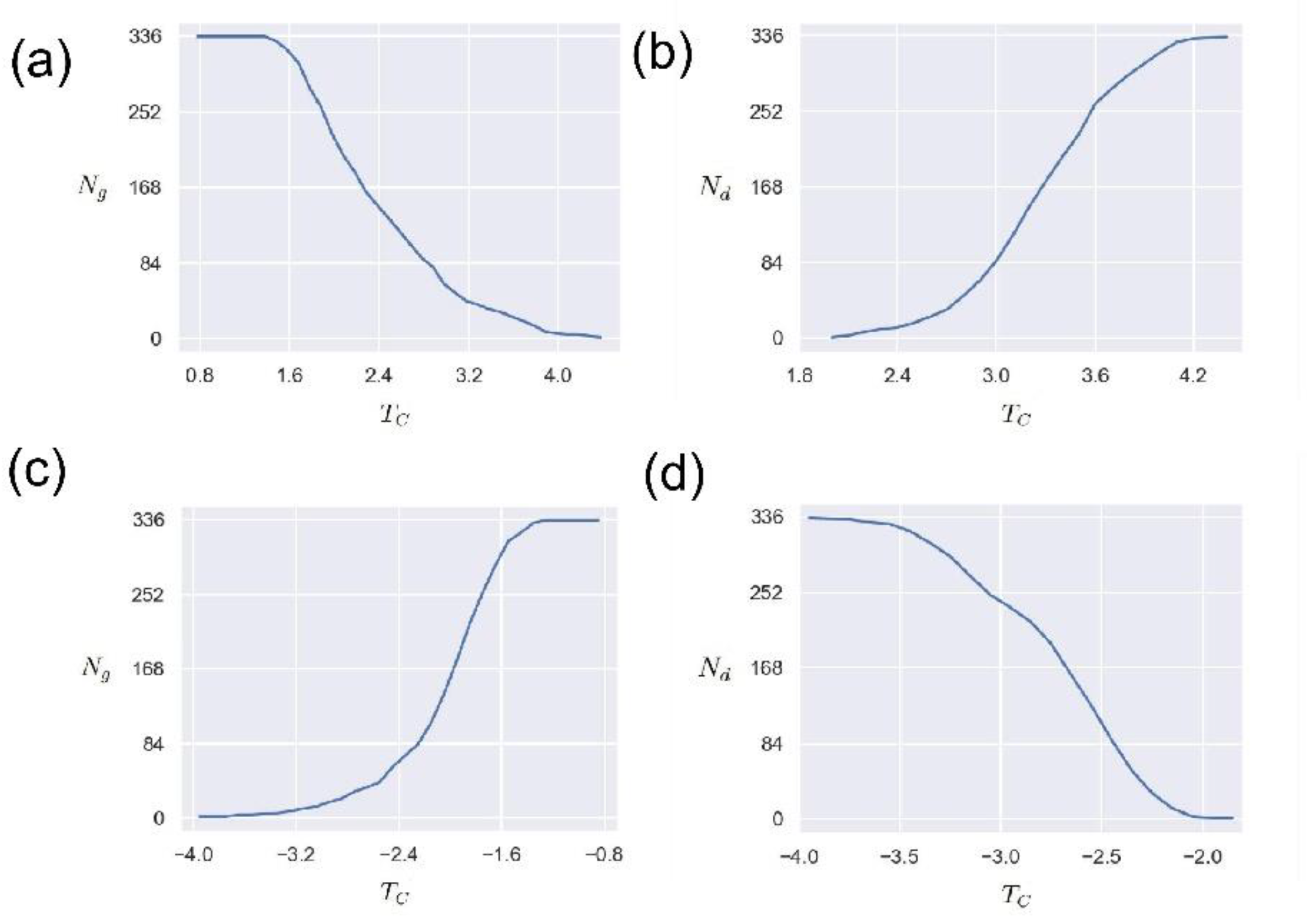
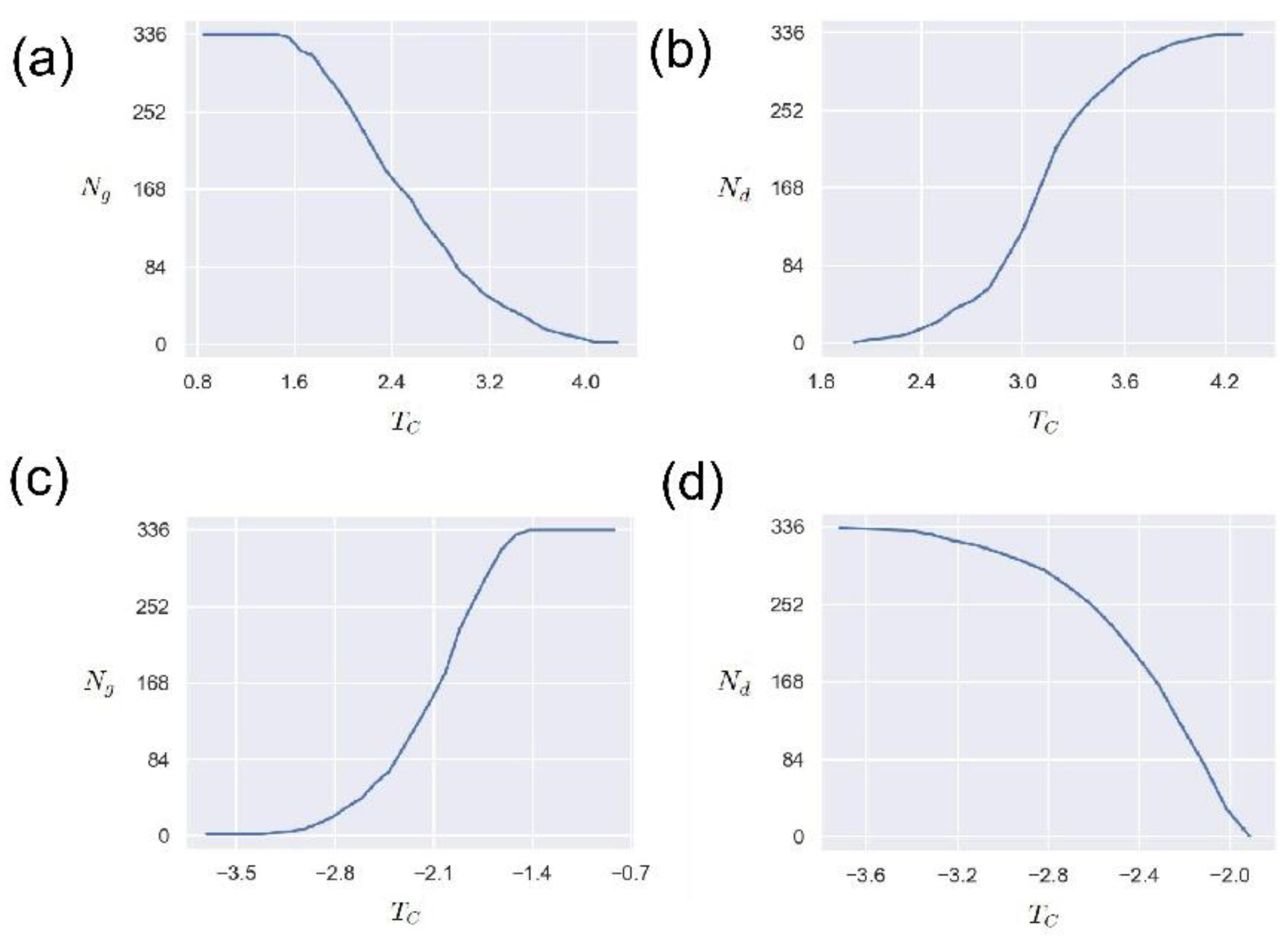
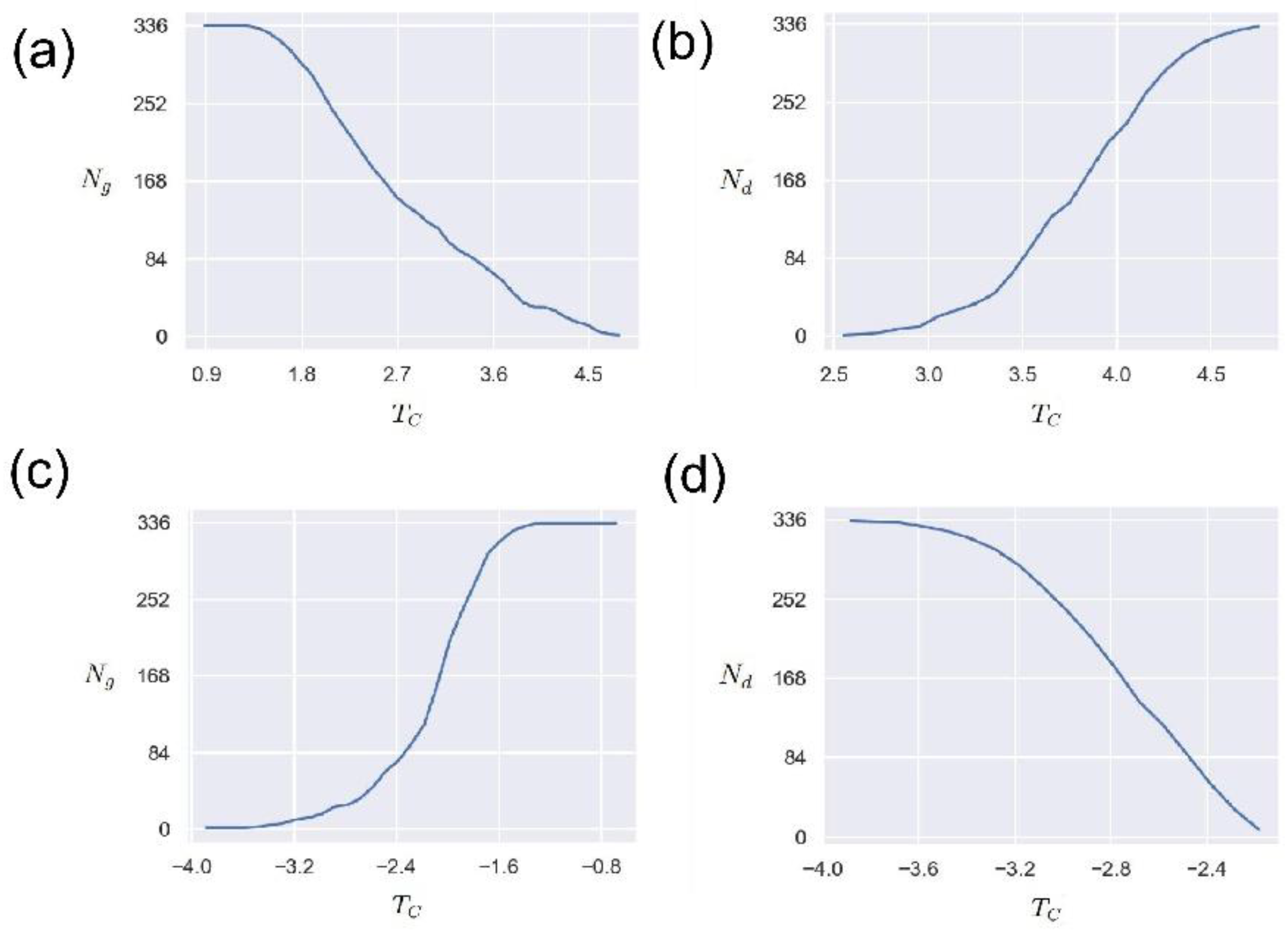
In order to study the influence of the network edge weight threshold T C , we study the changes in the number of nodes ( N g ) in the network’s giant connected community (GCC) and the number of driven nodes ( N d ) when the threshold T C changes in this section. The maximum connected community of the network is one of the important indicators reflecting the connectivity of the network, that is, the number of nodes contained in a connected maximum sub-network.
Figure 7 (a) shows the variation of the number of nodes N g in the giant connected community with the threshold T C . It can be seen that for the positive edge network, the threshold T C has an obvious anti-correlation with the number of nodes in the giant connected community. This means that the larger the threshold, the smaller the number of giant connected community nodes. This is because the larger the threshold T C is, the less the number of eligible edges is, and the corresponding network connectivity is reduced. Such results imply that the threshold T C can be used as an indicator to measure and control the connectivity of the O3 network.
Figure 7 (b) presents the relationship between the number of driven nodes N d and the threshold T C . As can be seen from Figure 7 (b), as the threshold increases, the number of driven nodes also increases, demonstrating a positive correlation. This phenomenon is understandable. As the threshold increases, the connectivity of the O3 network decreases, and the number of isolated nodes increases, thereby driving the increase in the number of nodes. It should be noted that this positive correlation is not linear, but a nonlinear relationship. Future research should pay more attention to the significance of these nonlinear relationships in practical O3 application scenarios. In conclusion, these results provide an attempt to understand the O3 network through network control theory, and the network weight threshold T C has an important influence.According to the cross-correlation function network construction method, the case where the edge weight takes a negative value is also a direction that needs to be explored. Therefore, here we explore the effect of the threshold T C on the maximum number of connected community nodes N g and the number of driven nodes N d when the edge weight is negative. Figure 7(c) and Figure 7(d) display the changing trends of N g and N d when the edge connection weight threshold is negative, respectively. It is worth noting that these trends are the opposite of those in Figure 7(c) and Figure 7(d). That is, with the increase of the threshold T C , N g increases with the increase, but N d shows a downward trend. These results are reasonable. One reasonable explanation is that as the threshold T C increases, more and more qualified edges are connected, so N g increases accordingly. For N d , the stronger the network connectivity is, the stronger its controllability is, and the fewer driven nodes to be controlled. It is difficult to find a meaningful threshold, or what are the criteria and operating steps for taking a suitable threshold. These issues are worthy of in-depth research and analysis. Overall, these curves indicate that the complex network method can be applied to the analysis of O3 networks, and how selecting the threshold is a key point.
Figure 8(a) and Figure 9(a) show the change in the number of nodes N g in the giant connected community of the O3 network for two different periods when the thresholds are T C = 3.3 and T C = 3.1 . It can be seen that for the positive edge network, the threshold T C has an obvious inverse correlation with the number of nodes in the giant connected community. Such results are similar to those of Figure 7(a). This means that the larger the threshold, the smaller the number of connected mega-community nodes. This is because the larger the threshold T C is, the less the number of eligible edges is, and the corresponding network connectivity is reduced.
Figures 8(b) and Figure 9(b) show the relationship between the number of driving nodes N d and the threshold T C in the O3 network in two different periods, respectively. A similar trend can be observed from these two figures, that is, as the threshold T C increases, the number of driving nodes N d increases too, showing a positive correlation. This is due to the fact that as the threshold increases, the connectivity of the O3 network decreases and the number of isolated nodes increases, thereby driving the increase in the number of nodes. It should be noted that this positive correlation is not linear, but a nonlinear relationship. The above results are similar to those of Figure7(b), however, it can be observed that their thresholds T C have different ranges. These results further verify that the network weight threshold T C has a consistent and stable important influence on the O3 network.
Preprints 91708 g008
Figure 8. The effect of threshold TC versus the number of GCC Ng and the number of driven nodes Nd from May to September. (a) The relationship between the threshold TC and the giant connected community nodes Ng. The horizontal axis is the value of threshold TC, and the vertical axis is the value of Ng. The network edge weights are positive. (b) The relationship between the threshold TC and the number of driven nodes Nd. The horizontal axis is the value of threshold TC, and the vertical axis is the value of Nd. The network edge weights are positive. (c) The relationship between the threshold TC and the giant connected community nodes Ng. The horizontal axis is the value of threshold TC, and the vertical axis is the value of Ng. The network edge weights are negative. (d) The relationship between the threshold TC and the number of driven nodes Nd. The horizontal axis is the value of threshold TC, and the vertical axis is the value of Nd. The network edge weights are negative.
Figure 8. The effect of threshold TC versus the number of GCC Ng and the number of driven nodes Nd from May to September. (a) The relationship between the threshold TC and the giant connected community nodes Ng. The horizontal axis is the value of threshold TC, and the vertical axis is the value of Ng. The network edge weights are positive. (b) The relationship between the threshold TC and the number of driven nodes Nd. The horizontal axis is the value of threshold TC, and the vertical axis is the value of Nd. The network edge weights are positive. (c) The relationship between the threshold TC and the giant connected community nodes Ng. The horizontal axis is the value of threshold TC, and the vertical axis is the value of Ng. The network edge weights are negative. (d) The relationship between the threshold TC and the number of driven nodes Nd. The horizontal axis is the value of threshold TC, and the vertical axis is the value of Nd. The network edge weights are negative.
Preprints 91708 g008
Similar to Figure 7(c) and Figure 7(d), Figure 8(c), Figure 9(c), Figure 8(d) and Figure 9(d) present the relationship between the threshold T C on the maximum number of connected community nodes N g and the number of driven nodes N d when the edge weights are negative at two different periods. It can be seen from the above figures that the trend of the negative edge weights in the two different periods is basically similar. That is, as the threshold T C increases, N g increases with the increase, but N d tends to decrease. These results demonstrate that although the range of the threshold T C varies in different periods, the impact of the threshold value on the maximum number of connected community nodes N g and the number of driven nodes N d in the network is consistent. These results indicate that it is a feasible scheme to study the O3 networks using T C , N g , and N d . Future research should focus more on exploring the practical implications of these results.
Preprints 91708 g009
Figure 9. The effect of threshold TC versus the number of GCC Ng and the number of driven nodes Nd from October to February. (a) The relationship between the threshold TC and the giant connected community nodes Ng. The horizontal axis is the value of threshold TC, and the vertical axis is the value of Ng. The network edge weights are positive. (b) The relationship between the threshold TC and the number of driven nodes Nd. The horizontal axis is the value of threshold TC, and the vertical axis is the value of Nd. The network edge weights are positive. (c) The relationship between the threshold TC and the giant connected community nodes Ng. The horizontal axis is the value of threshold TC, and the vertical axis is the value of Ng. The network edge weights are negative. (d) The relationship between the threshold TC and the number of driven nodes Nd. The horizontal axis is the value of threshold TC, and the vertical axis is the value of Nd. The network edge weights are negative.
Figure 9. The effect of threshold TC versus the number of GCC Ng and the number of driven nodes Nd from October to February. (a) The relationship between the threshold TC and the giant connected community nodes Ng. The horizontal axis is the value of threshold TC, and the vertical axis is the value of Ng. The network edge weights are positive. (b) The relationship between the threshold TC and the number of driven nodes Nd. The horizontal axis is the value of threshold TC, and the vertical axis is the value of Nd. The network edge weights are positive. (c) The relationship between the threshold TC and the giant connected community nodes Ng. The horizontal axis is the value of threshold TC, and the vertical axis is the value of Ng. The network edge weights are negative. (d) The relationship between the threshold TC and the number of driven nodes Nd. The horizontal axis is the value of threshold TC, and the vertical axis is the value of Nd. The network edge weights are negative.
Preprints 91708 g009
The coincidence degree of the driven node is a problem that needs attention, which can reflect the reliability of the driven node to a certain extent. Here, we propose to use the Jaccard coefficient to represent the coincidence of the driven nodes at two different thresholds [48]. That is the ratio of intersection over union ρ = N d T C m ∩ N d T C n N d T C m ∪ N d T C n , where N d T C m and N d T C m represent the set of driven nodes when the thresholds are T C m and T C n , respectively.
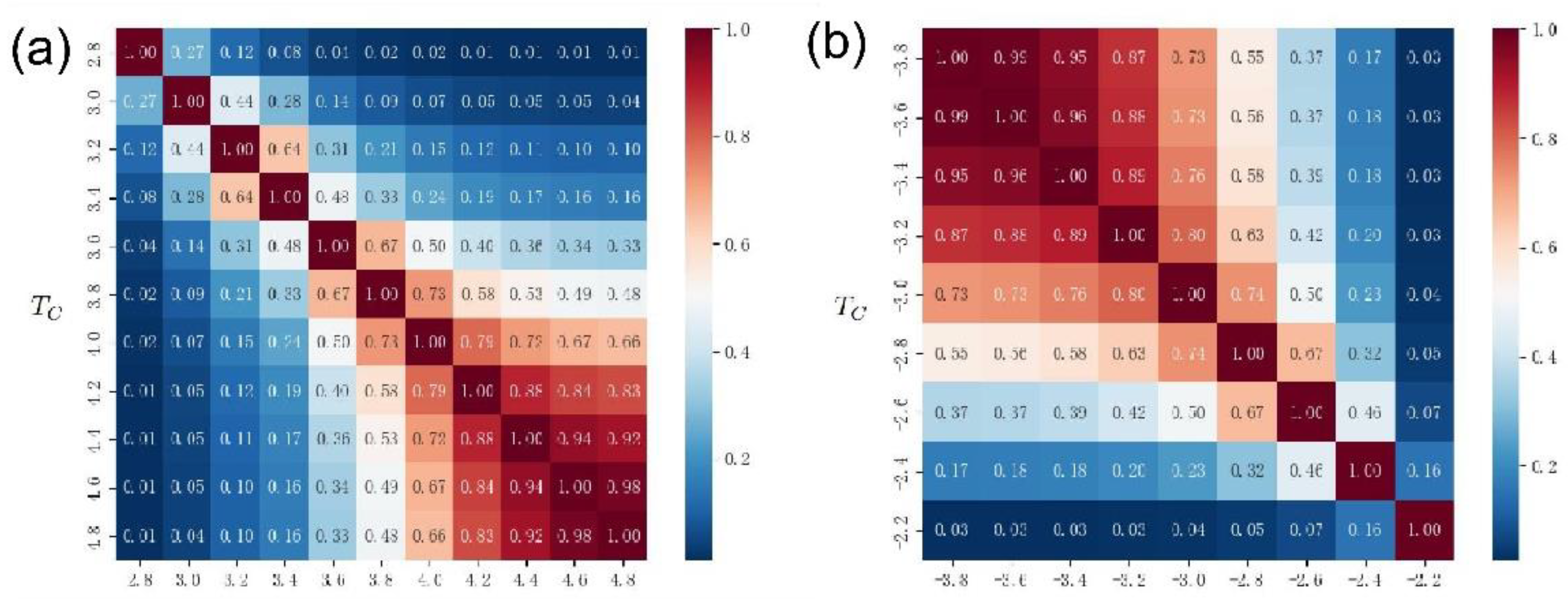
Figure 10(a) presents the Jaccard coefficients of the driven nodes for different thresholds T C . In general, the closer the threshold, the higher the Jaccard coefficient. This result indicates that the closer the two thresholds are, the more identical nodes are obtained for the two sets of driven nodes. Meanwhile, an interesting phenomenon is that when both thresholds are large, the Jaccard coefficient is large, and vice versa. Such results on the one hand confirm that the size of the edge connection threshold T C controls the number of driven nodes by controlling the network connectivity. On the other hand, it demonstrates that there are some deep mechanisms in the O3 network, that is, some nodes could be selected repeatedly instead of just randomly selected. Future research should pay more attention to the mechanism behind the above phenomenon. The above results indicate that the O3 network can be understood and analyzed using controllability methods, and is a research area worthy of further understanding.
Figure 10(b) presents the Jaccard coefficients of the co-occurrence of drive nodes with different thresholds T C when the edge weights take negative values. In general, the closer the threshold, the higher the Jaccard coefficient. This result is similar to that in Figure 10(a) when the edge weights are taken as positive values. However, an interesting phenomenon is that when both thresholds are small, the Jaccard coefficient of the co-occurrence of the driven node is large, and vice versa. This result is opposite to the result when Figure 10(a) is connected with a positive value. A possible explanation is that in the case of negative edge weights, the smaller the threshold T C , the more isolated nodes in the network, so the higher the co-occurrence ratio of driven nodes. This result is basically consistent with the previous findings in Figures 7(c) and (d).
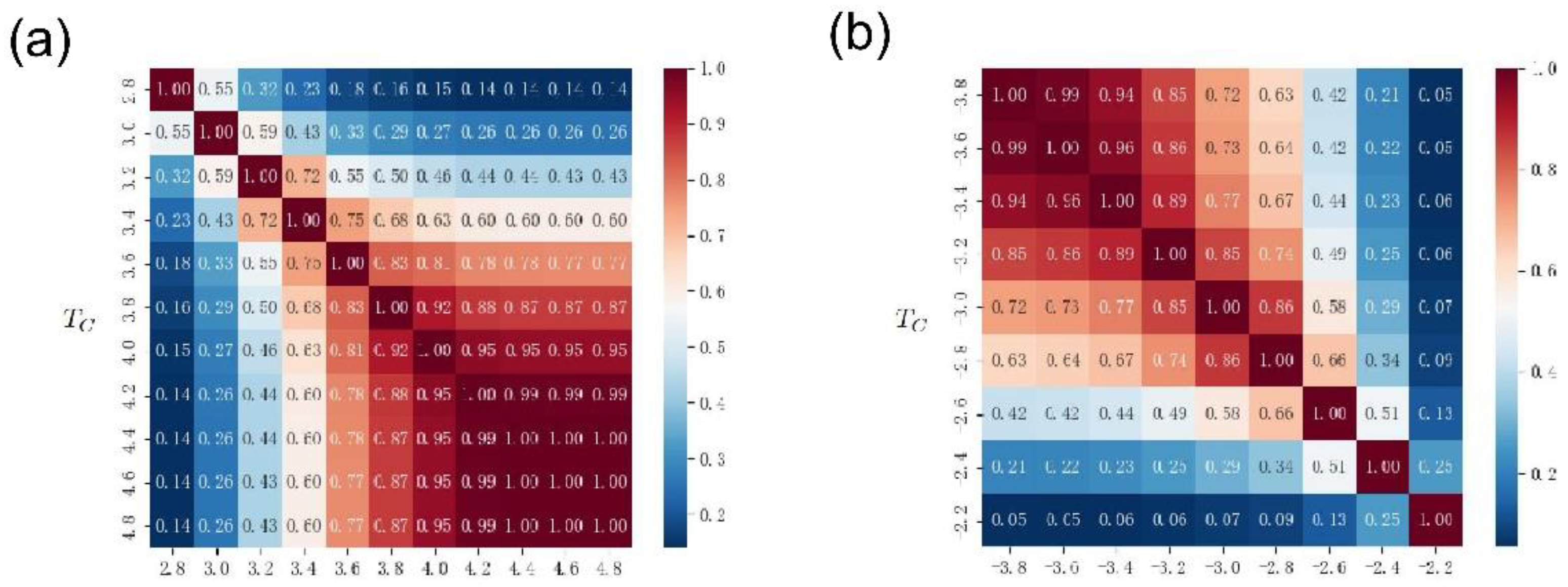
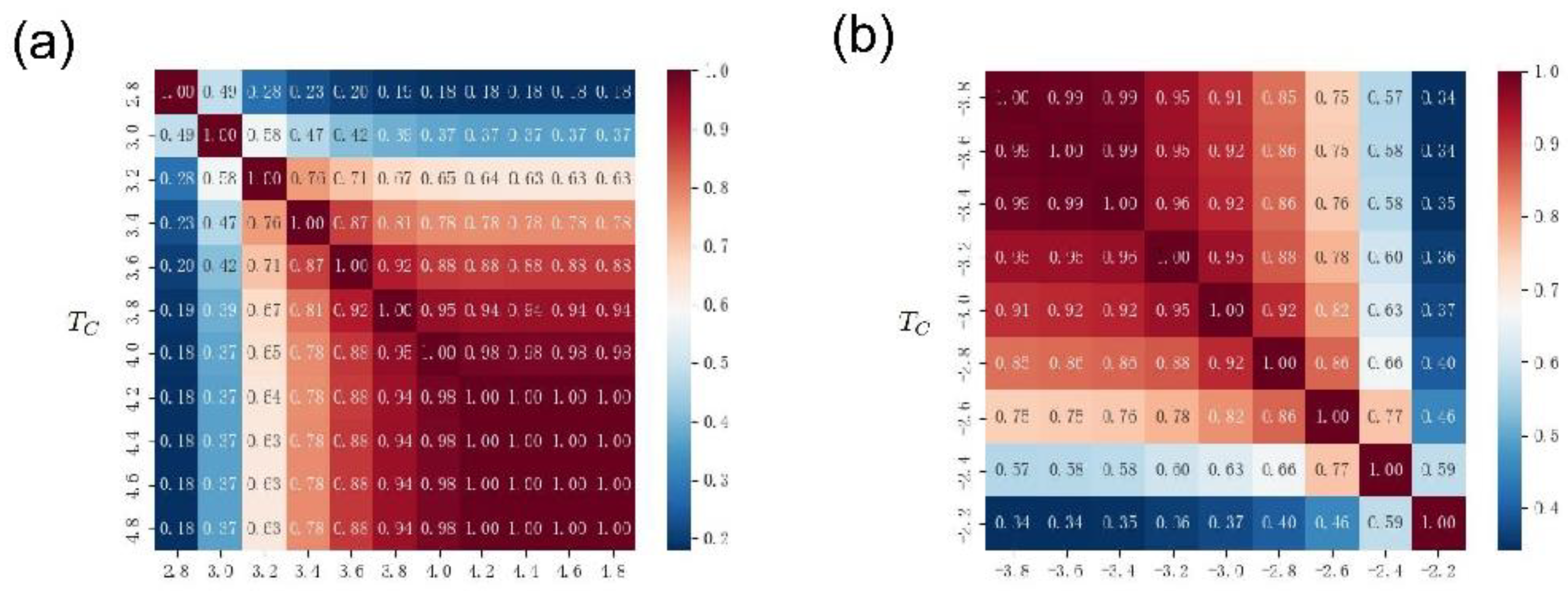
Figure 11(a) and Figure 12(a) show the Jaccard coefficients of the driving nodes with different thresholds T C in two time periods, respectively. Similar to the results in Figure 10(a), the closer the threshold, the higher the Jaccard coefficient. That is, the closer the two thresholds are, the more identical nodes are obtained by the two groups of driven nodes. Meanwhile, an interesting phenomenon is that when both thresholds are large, the Jaccard coefficient is large, and vice versa. Moreover, when the threshold is large, the coincidence degree of the Jaccard coefficients of the two different periods is 1. On the one hand, this result is similar to the phenomenon in Figure 10(a), that is, the size of the edge connection threshold T C is controlled by Network connectivity to control the number of driven nodes. On the other hand, if divided by different periods, a stronger repeated selection mechanism can be observed. That is to say, there is a stable strong link relationship between some nodes. Future research should focus on the underlying mechanisms leading to these phenomena.
Figure 11(b) and Figure 12(b) display the Jaccard coefficients for the co-occurrence of driving nodes with different thresholds T C when edge weights take negative values. These results are similar to those in Figure 10(b), the closer the two thresholds are, the higher the Jaccard coefficient. When both thresholds are small, the co-occurrence Jaccard coefficient of the driving node is large, and vice versa. This result is in contrast to the positive-valued edge results shown in Figure 11(a) and Figure 12(a). The possible reason for this phenomenon is that in the case of negative edge weights, the smaller the threshold T C , the more isolated nodes in the network, and therefore the higher the co-occurrence rate of driving nodes.

3.4. Geographic distance and Spearman coefficient

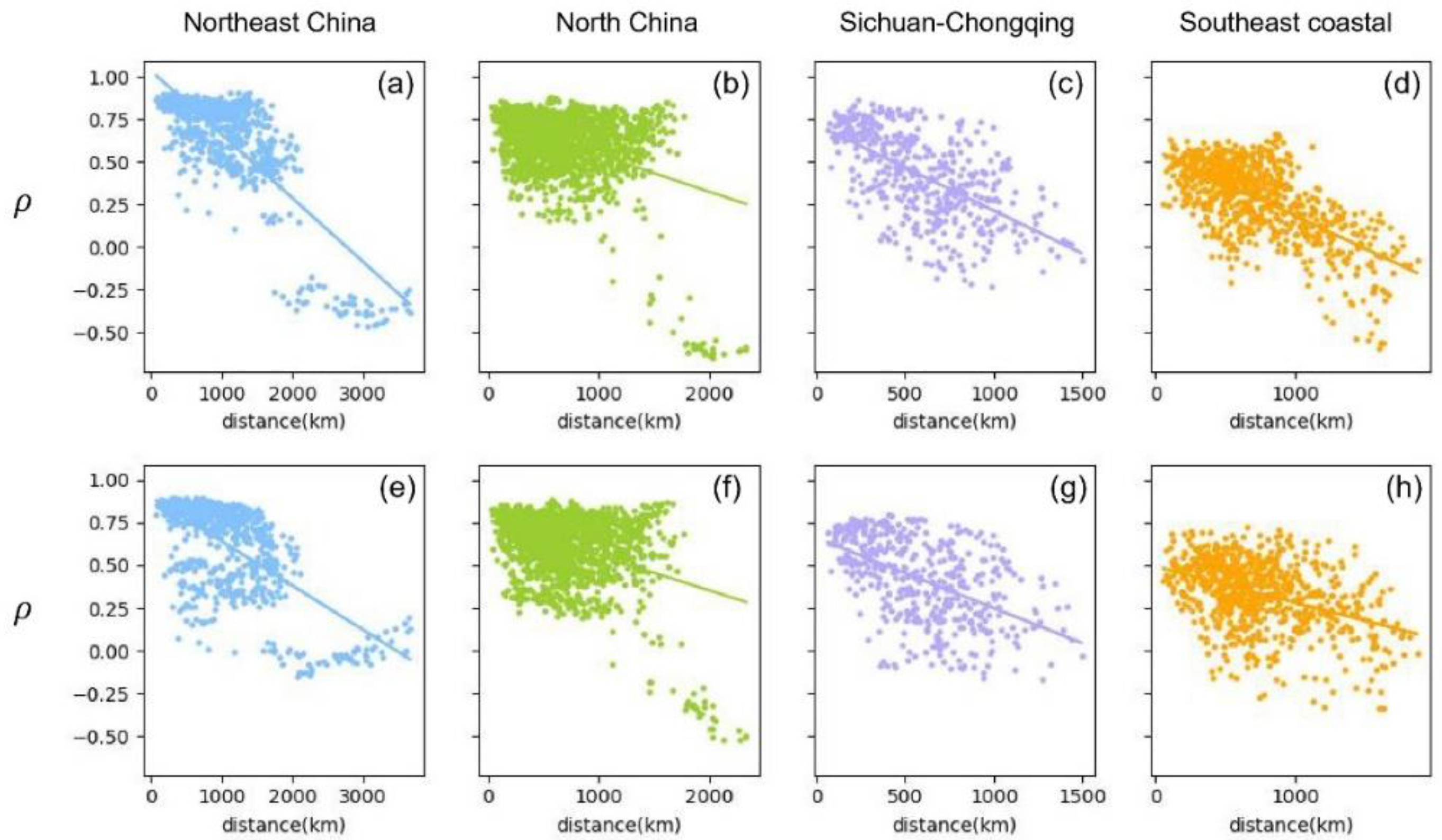
In order to further distinguish driven nodes from non-driven nodes, we use prediction methods to measure the difference between the two types of nodes. An increasing number of studies use predictive methods to understand the correlation between different quantities [49], for example, defining the influence of different variables by the predictability of one variable on another variable [50]. Figure 13 shows the degree of correlation between the predicted results and the true sequence for the driven and non-driven nodes. On the one hand, we employ the LSTM algorithm and use the O3 data sequence C d of the driven node to predict the O3 data sequence C ~ n d of the non-driven node; then calculate the Spearman correlation ρ between the predicted non-driven O3 data sequence C ~ n d and the original non-driven sequence C n d ; finally, Figures 13(a-d) displays the relationship of Spearman correlation ρ and distance from driven nodes to non-driven nodes in four different regions. Here we use the Spearman correlation coefficient calculation because the method has a better correlation calculation effect on nonlinear data. It can be seen from these figures that there is a significant negative correlation between the Spearman coefficient and the distance. These results are consistent with the trends of other pollutants changing with distance obtained in the past. It should be noted that in the Northeast and North China regions, there are different node clusters, which may be due to the relatively wide and uneven geographical distribution of cities in these regions.
On the other hand, we apply the same method and obtain the Spearman correlation of non-driven nodes predicting driven node sequences, and the relationship between ρ and distance is shown in Figures 13(e-h). A similar trend was observed in all cases, with no sudden changes. This trend further validates the role of distance in O3 variation between different sites. Comparing Figures 13(a-d) with Figures 13(e-h), it can be seen that the negative correlation of driven nodes predicting non-driven nodes is stronger than that of non-driven nodes predicting driven nodes. These results suggest that driven nodes have more influence in the O3 network than non-driven nodes.
Preprints 91708 g013
Figure 13. Scatter diagram of the relationship between the distance of city Ci and city Cj and the Spearman coefficient of their O3 data in the Northeast China, North China, Sichuan-Chongqing and Southeast coastal areas. Figures (a-d) are the data of the direction of the driven to non-driven nodes, the vertical axis represents the Spearman coefficient between the O3 data of the city Ci (Ci ∈ driven nodes) and the city Cj (Cj ∈ non-driven nodes), the horizontal axis represents the geographical distance between the city Ci and the city Cj. Figures (e-h) are the data of the direction of the non-driven to driven nodes, and the vertical axis represents the Spearman coefficient between the O3 data of city Ci (Ci ∈ non-driven nodes) and city Cj (Cj ∈ driven nodes). The fitted slopes of scattered data are as follows, −3.74×10−4, −2.17×10−4, −5.04×10−4, −3.82×10−4, −2.60×10−4, −2.06×10−4, −4.12×10−4, −2.11×10−4. Overall, we observe the distance between nodes is negatively correlated with their Spearman coefficient.
Figure 13. Scatter diagram of the relationship between the distance of city Ci and city Cj and the Spearman coefficient of their O3 data in the Northeast China, North China, Sichuan-Chongqing and Southeast coastal areas. Figures (a-d) are the data of the direction of the driven to non-driven nodes, the vertical axis represents the Spearman coefficient between the O3 data of the city Ci (Ci ∈ driven nodes) and the city Cj (Cj ∈ non-driven nodes), the horizontal axis represents the geographical distance between the city Ci and the city Cj. Figures (e-h) are the data of the direction of the non-driven to driven nodes, and the vertical axis represents the Spearman coefficient between the O3 data of city Ci (Ci ∈ non-driven nodes) and city Cj (Cj ∈ driven nodes). The fitted slopes of scattered data are as follows, −3.74×10−4, −2.17×10−4, −5.04×10−4, −3.82×10−4, −2.60×10−4, −2.06×10−4, −4.12×10−4, −2.11×10−4. Overall, we observe the distance between nodes is negatively correlated with their Spearman coefficient.
Preprints 91708 g013
This section may be divided by subheadings. It should provide a concise and precise description of the experimental results, their interpretation, as well as the experimental conclusions that can be drawn.

4. Conclusions

The rapid development of human society has made life more and more convenient, but it has also caused more and more environmental problems. In particular, with the destruction of the O3 layer by modern human pollution, the study of O3 has attracted more and more attention. Traditional research on O3 generally focuses on the influence of different factors, etc. These results have greatly enriched our understanding and cognition of O3. However, the problem of O3 is a multifaceted and complex system problem. Therefore, using the theory and method of the complex network to analyze and study such a complex system as O3 has great theoretical and practical application value. In this research, we integrated the complex network theories and technologies from the network construction method cross-correlation function, the Louvain community partitioning algorithm and the maximum matching network control theory, and systematically studied the characteristics of O3 in China.
Our findings illustrate that the O3 network prominently exhibits a structured community framework, delineating regions such as Northeast China, North China, Sichuan-Chongqing, and the Southeast coastal areas. Notably, driving nodes are predominantly concentrated within central regions, in contrast to non-driven nodes, which are primarily situated along coastal perimeters. Furthermore, the threshold denoted as T C exhibits a conspicuous inverse relationship with the number of nodes constituting the giant connected community. Moreover, as the threshold value increases, there is a corresponding augmentation in the count of driving nodes, indicating a positive correlation. It is noteworthy that these trends manifest in an opposing manner within the Negative O3 network.
Additionally, an intriguing observation emerges wherein significant interplay occurs between the Jaccard coefficient and both thresholds, whereby a larger value is observed when thresholds are substantial, and vice versa. In the context of the negative O3 network, a parallel trend emerges, where a diminutive Jaccard coefficient aligns with diminutive thresholds, and vice versa. Furthermore, a discernible pattern of substantial negative correlation surfaces between the Spearman coefficient and the distance, as evident from the depicted figures.
Our study presents a valuable endeavor to probe the O3 network through the lens of complex network theory and methodologies, yielding substantive and insightful outcomes. These encouraging results warrant broader validation across larger geographical expanses. Subsequent research should underscore considerations concerning threshold selection and its subsequent interpretation, among other pertinent aspects.

Author Contributions

Z.Z. and D.X. conducted the experiments; H.S. and W.W. guided the experiments; Z.Z. processed the data results and wrote the manuscript; D.X. and H.S. modified the grammar and format of the whole article; W.W. and N.Y. guided the writing of manuscripts. All authors have read and agreed to the published version of the manuscript.

Funding

This work is supported by the National Natural Science Foundation of China (Grant No. 62176148; No. 42205062); the Basic and Applied Basic Research of Colleges and Universities in Guangdong Province (Special Projects in Digital Economic: 2021ZDZX3025); the Scientific Research Foundation of Shantou University (Grant No. NTF19015); the 2020 Li Ka Shing Foundation Cross-Disciplinary Research (Grant No. 2020LKSFG09D).

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Acknowledgments

The authors would like to thank the science teams of CNEMC for providingdata used in this study.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Hao, J.; He, K.; Duan, L.; Li, J.; Wang, L. Air pollution and its control in China. Front. Environ. Sci. Eng. China 2007, 1, 129–142. [Google Scholar] [CrossRef]
  2. Wang, S.; Hao, J. Air quality management in China: Issues, challenges, and options. J. Environ. Sci. 2012, 24, 2–13. [Google Scholar] [CrossRef] [PubMed]
  3. Wang, S.X.; Zhao, B.; Cai, S.Y.; Klimont, Z.; Nielsen, C.P.; Morikawa, T.; Woo, J.H.; Kim, Y.; Fu, X.; Xu, J.Y.; et al. Emission trends and mitigation options for air pollutants in East Asia. Atmospheric Chem. Phys. 2014, 14, 6571–6603. [Google Scholar] [CrossRef]
  4. The State Council of the People's Republic of China. Air Pollution Prevention and Control Action Plan. Available online: http://www.gov.cn/zwgk/2013-09/12/content_2486773.html (accessed on 10 September 2013).
  5. Three-year Action Plan to Win the Blue Sky Defense War. Available online: http://www.gov.cn/zhengce/content/2018/7/03/content_5303158.html.
  6. Wang, Y., Gao, W., Wang, S., Song, T., Gong, Z., Ji, D., Wang, L., Liu, Z., Tang, G., Huo, Y., Tian, S., Li, J., Li, M., Yang, Y., Chu, B., Petaja, T., Kerminen, V., He, H.,Hao, J., Kulmala, M., Wang, Y., Zhang, Y. Contrasting trends of PM2.5 and surface-O3 concentrations in China from 2013 to 2017. Natl. Sci. Rev. 2020, 7, 1331–1339.
  7. Guo, Y.; Li, K.; Zhao, B.; Shen, J.; Bloss, W.J.; Azzi, M.; Zhang, Y. Evaluating the real changes of air quality due to clean air actions using a machine learning technique: Results from 12 Chinese mega-cities during 2013–2020. Chemosphere 2022, 300, 134608. [Google Scholar] [CrossRef] [PubMed]
  8. Wei, J.; Li, Z.; Li, K.; Dickerson, R.R.; Pinker, R.T.; Wang, J.; Liu, X.; Sun, L.; Xue, W.; Cribb, M. Full-coverage mapping and spatiotemporal variations of ground-level ozone (O3) pollution from 2013 to 2020 across China. Remote Sens. Environ. 2021, 270, 112775. [Google Scholar] [CrossRef]
  9. X. Lu, X. P. Ye, M. Zhou, Y. Zhao, H. Weng, H. Kong, K. Li, M. Gao, B. Zheng, J. Lin, F. Zhou, Q. Zhang, D. Wu, L. Zhang & Y. Zhang. The underappreciated role of agricultural soil nitrogen oxide emissions in O3 pollution regulation in North China. Nat. Commun. 2021, 12, 5021–5029.
  10. T. Wang, L.K. Xue, P. Brimblecombe, Y. F. Lam,, L. Li, & L. Zhang. O3 pollution in China: a review of concentrations, meteorological influences, chemical precursors, and effects. Sci. Total Environ. 2017, 575, 1582–1596.
  11. M. Shao, Y. Zhang, L. Zeng, X. Tang, J. Zhang, L. Zhong, B. Wang. Ground-level O3 in the Pearl River Delta and the roles of VOC and NOx in its production. J. Environ. Manag. 2009, 90, 512–518. [CrossRef]
  12. McDonald, B.C.; de Gouw, J.A.; Gilman, J.B.; Jathar, S.H.; Akherati, A.; Cappa, C.D.; Jimenez, J.L.; Lee-Taylor, J.; Hayes, P.L.; McKeen, S.A.; et al. Volatile chemical products emerging as largest petrochemical source of urban organic emissions. Science 2018, 359, 760–764. [Google Scholar] [CrossRef]
  13. He, L.; Duan, Y.; Zhang, Y.; Yu, Q.; Huo, J.; Chen, J.; Cui, H.; Li, Y.; Ma, W. Effects of VOC emissions from chemical industrial parks on regional O3-PM2.5 compound pollution in the Yangtze River Delta. Sci. Total. Environ. 2023, 906, 167503. [Google Scholar] [CrossRef] [PubMed]
  14. Guan, Y.; Liu, X.; Zheng, Z.; Dai, Y.; Du, G.; Han, J.; Hou, L.; Duan, E. Summer O3 pollution cycle characteristics and VOCs sources in a central city of Beijing-Tianjin-Hebei area, China. Environ. Pollut. 2023, 323, 121293. [Google Scholar] [CrossRef] [PubMed]
  15. Wang, R.; Duan, W.; Cheng, S.; Wang, X. Nonlinear and lagged effects of VOCs on SOA and O3 and multi-model validated control strategy for VOC sources. Sci. Total Environ. 2023, 887, 164113. [Google Scholar] [CrossRef] [PubMed]
  16. Liu, C.; Geng, H.; Shen, P.; Wang, Q.; Shi, K. Coupling detrended fluctuation analysis of the relationship between O3 and its precursors –a case study in Taiwan. Atmospheric Environ. 2018, 188, 18–24. [Google Scholar] [CrossRef]
  17. Y. Yang, M. Li, H. Wang, H. Li, P. Wang, K. Li, M. Gao, and H. Liao. Enso modulation of summertime tropospheric O3 over china. Environ. Res. Lett. 2022, 17, 034020. [CrossRef]
  18. M. Li, S. Yu, X. Chen, Z. Li, Y. Zhang, L. Wang, W. Liu, P. Li, E. Lichtfouse, D. Rosenfeld, and J. H. Seinfeld. Large scale control of surface. O3 by relative humidity observed during warm seasons in china. Atmos. Environ. 2021, 19, 3981–3989.
  19. S. C. Kavassalis and J. G. Murphy. Understanding O3-meteorology correlations: A role for dry deposition. Geophys. Res. Lett. 2017, 44, 2922–2931. [CrossRef]
  20. Qi, H.; Duan, W.; Cheng, S.; Huang, Z.; Hou, X. Spatial clustering and spillover pathways analysis of O3, NO2, and CO in eastern China during 2017–2021. Sci. Total. Environ. 2023, 904, 166814. [Google Scholar] [CrossRef]
  21. M. Y. Qi, L. T. Wang, S. M. Ma, L. Zhao, X. H. Lu, Y. Y. Liu, Y. Zhang, J. Y. Tan, Z. T. Liu, S. T. Zhao, Q. Wang, R. G. Xu. Evaluation of PM2.5 fluxes in the "2+26" cities: transport pathways and intercity contributions. Atmos. Pollut. Res. 2021, 12, 101048.
  22. Yang, W.; Du, H.; Wang, Z.; Zhu, L.; Wang, Z.; Chen, X.; Chen, H.; Wang, W.; Zhang, R.; Li, J.; et al. Characteristics of regional transport during two-year wintertime haze episodes in North China megacities. Atmospheric Res. 2021, 257, 105582. [Google Scholar] [CrossRef]
  23. L. Shen, J. Liu, T. Zhao, X. Xu, H. Han, H. Wang, Z. Shu. Atmospheric transport drives regional interactions of O3 pollution in China. Sci. Total Environ. 2022, 830, 154634. [CrossRef] [PubMed]
  24. T. T. Fang,Y. Zhu, S. X. Wang, J. Xing,, B. Zhao, S. J. Fan, M. H. Li, W. W. Yang, Y. Chen, R. L. Huang. Source impact and contribution analysis of ambient O3 using multi-modeling approaches over the Pearl River Delta region, China. Environ. Pollut. 2021, 289, 117860. [CrossRef] [PubMed]
  25. U. Kalsoom, T. Wang, C. Ma, L. Shu, C. Huang, L. Gao. Quadrennial variability and trends of surface O3 across China during 2015–2018: a regional approach. Atmos. Environ. 2021, 245, 117989. [CrossRef]
  26. Mao, J., Yan, F., Zheng, L., You, Y., Wang, W., Jia, S., Liao, W., Wang, X., Chen, W. O3 control strategies for local formation and regional transport dominant scenarios in a manufacturing city in southern China. Sci. Total Environ. 2022, 813, 151883. [CrossRef] [PubMed]
  27. Y. Zhang, D. Chen, J. Fan, S. Havlin, and X. Chen. Correlation and scaling behaviors of fine particulate matter (PM2.5) concentration in China. EPL 2018, 122, 58003. [CrossRef]
  28. G. Tian, M. H. Gunes. Complex network analysis of O3 transport in Complex Networks V (Springer). 2014, 87–96. [Google Scholar]
  29. Q. Wang, X. Wang, R. Huang, J. Wu, Y. Xiao, M. Hu, Q. Fu, Y. Duan, and J. Chen. Regional transport of PM2.5 and O3 based on complex network method and chemical transport model in the yangtze river delta, Chin. J. Geophys. Res-Atmos. 2022, 127, e2021JD034807. [CrossRef]
  30. Fan, J.; Meng, J.; Ashkenazy, Y.; Havlin, S.; Schellnhuber, H.J. Network analysis reveals strongly localized impacts of El Niño. Proc. Natl. Acad. Sci. USA 2017, 114, 7543–7548. [Google Scholar] [CrossRef]
  31. Ying, N.; Zhou, D.; Chen, Q.; Ye, Q.; Han, Z. Long-term link detection in the CO2 concentration climate network. J. Clean. Prod. 2018, 208, 1403–1408. [Google Scholar] [CrossRef]
  32. Zhang, Y.; Fan, J.; Chen, X.; Ashkenazy, Y.; Havlin, S. Significant Impact of Rossby Waves on Air Pollution Detected by Network Analysis. Geophys. Res. Lett. 2019, 46, 12476–12485. [Google Scholar] [CrossRef]
  33. Blondel, V.D.; Guillaume, J.-L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech. Theory Exp. 2008, 2008, P10008. [Google Scholar] [CrossRef]
  34. Y. Y. Liu, J. J. Slotine, and A. L. Barabási. Controllability of complex networks. Nature 2011, 473, 167–173. [CrossRef] [PubMed]
  35. Zhao, Z.-D.; Zhao, N.; Ying, N. Association, Correlation, and Causation Among Transport Variables of PM2.5. Front. Phys. 2021, 9. [Google Scholar] [CrossRef]
  36. Ying, N.; Zhou, D.; Han, Z.G.; Chen, Q.H.; Ye, Q.; Xue, Z.G. Rossby Waves Detection in the CO2 and Temperature Multilayer Climate Network. Geophys. Res. Lett. 2020, 47, e2019GL086507. [Google Scholar] [CrossRef]
  37. N. Ying, D. Zhou, Z. Han, Q. Chen, Q. Ye, Z. Xue, and W. Wang. Climate networks suggest rossby-waves–related CO2 concentrations to surface air temperature. EPL 2020, 132, 19001. [CrossRef]
  38. Wang, W.; Yang, S.; Yin, K.; Zhao, Z.; Ying, N.; Fan, J. Network approach reveals the spatiotemporal influence of traffic on air pollution under COVID-19. Chaos: Interdiscip. J. Nonlinear Sci. 2022, 32, 041106. [Google Scholar] [CrossRef] [PubMed]
  39. N. Ying, W. Duan, Z. Zhao, and J. Fan. Complex networks analysis of PM2.5: transport and clustering. Earth Syst. Dynam. Discuss. 2022, 1–18.
  40. J. Liu, L. Wang, M. Li, Z. Liao, Y. Sun, T. Song, W. Gao, Y. Wang, Y. Li, D. Ji, B. Hu, V. M. Kerminen, Y. Wang, and M. Kulmala. Quantifying the impact of synoptic circulation patterns on O3 variability in northern china from april to october 2013–2017. Atmos. Chem. Phys. 2019, 19, 14477–14492. [CrossRef]
  41. Girvan, M.; Newman, M.E.J. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef]
  42. Newman, M.E.J. The Structure and Function of Complex Networks. SIAM Rev. 2003, 45, 167–256. [Google Scholar] [CrossRef]
  43. J. Ding, C. B. Fu, X. Q. Yang, J. N. Sun, L. F. Zheng, Y. N. Xie, E. Herrmann, W. Nie, T. Petäjä, V. M. Kerminen, and M. Kulmala. O3 and fine particle in the western yangtze river delta: an overview of 1 yr data at the sorpes station. Atmos. Chem. Phys. 2013, 13, 581–5830.
  44. J. Gao, B. Zhu, H. Xiao, H. Kang, X. Hou, and P. Shao. A case study of surface O3 source apportionment during a high concentration episode, under frequent shifting wind conditions over the yangtze river delta, China. Sci. Total Environ. 2016, 544, 853–863. [CrossRef]
  45. L. Shu, T. Wang, M. Xie, M. Li, M. Zhao, M. Zhang, and X. Zhao. Episode study of fine particle and O3 during the capum-yrd over yangtze river delta of china: Characteristics and source attribution. Atmos. Environ. 2019, 203, 87–101. [CrossRef]
  46. L. Shu, T. Wang, H. Han, M. Xie, P. Chen, M. Li, and H. Wu. Summertime O3 pollution in the yangtze river delta of eastern china during 2013-2017: Synoptic impacts and source apportionment. Environ. Pollut. 2020, 257, 113631. [CrossRef]
  47. Y.-Y. Liu, J.-J. E. Slotine, and A. L. Barabasi. Controllability of complex networks. Nature 2011, 473, 167–173. [CrossRef] [PubMed]
  48. P. Jaccard. Distribution de la flore alpine dans le bassin des dranses et dans quelques régions voisines. Bull Soc Vaudoise Sci Nat 1901, 37, 241–272.
  49. Ludescher, J.; Martin, M.; Boers, N.; Bunde, A.; Ciemer, C.; Fan, J.; Havlin, S.; Kretschmer, M.; Kurths, J.; Runge, J.; et al. Network-based forecasting of climate phenomena. Proc. Natl. Acad. Sci. 2021, 118. [Google Scholar] [CrossRef]
  50. Sugihara, G.; May, R.; Ye, H.; Hsieh, C.-H.; Deyle, E.; Fogarty, M.; Munch, S. Detecting Causality in Complex Ecosystems. Science 2012, 338, 496–500. [Google Scholar] [CrossRef]
Preprints 91708 g002
Figure 2. The O3 Network and Community Structure from May to September. (a) A network of O3 monitoring stations in China constructed according to the link weight calculation method. Yellow nodes represent O3 observation stations, and links between stations indicate links between stations that meet the connectivity threshold TC = 3.3. (b) This figure is a network structure diagram after the community division of Figure 2 (a) according to the Louvain community partitioning algorithm. The nodes and edges of different colors represent different network communities. For example, yellow nodes represent the Northeast China community, orange nodes represent the North China community, green nodes represent the Southeast coastal community, and blue nodes represent the Sichuan-Chongqing community.
Figure 2. The O3 Network and Community Structure from May to September. (a) A network of O3 monitoring stations in China constructed according to the link weight calculation method. Yellow nodes represent O3 observation stations, and links between stations indicate links between stations that meet the connectivity threshold TC = 3.3. (b) This figure is a network structure diagram after the community division of Figure 2 (a) according to the Louvain community partitioning algorithm. The nodes and edges of different colors represent different network communities. For example, yellow nodes represent the Northeast China community, orange nodes represent the North China community, green nodes represent the Southeast coastal community, and blue nodes represent the Sichuan-Chongqing community.
Preprints 91708 g002
Preprints 91708 g004
Figure 4. O3 Network from the Perspective of Network Control Theory. The figure shows the isolated, driven, and non-driven nodes of the O3 network with a threshold of TC = 3.8. Yellow represents non-driven nodes, cyan for driven nodes, and purple for isolated nodes.
Figure 4. O3 Network from the Perspective of Network Control Theory. The figure shows the isolated, driven, and non-driven nodes of the O3 network with a threshold of TC = 3.8. Yellow represents non-driven nodes, cyan for driven nodes, and purple for isolated nodes.
Preprints 91708 g004
Preprints 91708 g005
Figure 5. O3 Network from May to September from the Perspective of Network Control Theory. The figure shows the isolated, driven, and non-driven nodes of the O3 network with a threshold of TC = 3.3. Yellow represents non-driven nodes, cyan for driven nodes, and purple for isolated nodes.
Figure 5. O3 Network from May to September from the Perspective of Network Control Theory. The figure shows the isolated, driven, and non-driven nodes of the O3 network with a threshold of TC = 3.3. Yellow represents non-driven nodes, cyan for driven nodes, and purple for isolated nodes.
Preprints 91708 g005
Preprints 91708 g007
Figure 7. The effect of threshold TC versus the number of GCC Ng and the number of driven nodes Nd. (a) The relationship between the threshold TC and the giant connected community nodes Ng. The horizontal axis is the value of threshold TC, and the vertical axis is the value of Ng. The network edge weights are positive. (b) The relationship between the threshold TC and the number of driven nodes Nd. The horizontal axis is the value of threshold TC, and the vertical axis is the value of Nd. The network edge weights are positive. (c) The relationship between the threshold TC and the giant connected community nodes Ng. The horizontal axis is the value of threshold TC, and the vertical axis is the value of Ng. The network edge weights are negative. (d) The relationship between the threshold TC and the number of driven nodes Nd. The horizontal axis is the value of threshold TC, and the vertical axis is the value of Nd. The network edge weights are negative.
Figure 7. The effect of threshold TC versus the number of GCC Ng and the number of driven nodes Nd. (a) The relationship between the threshold TC and the giant connected community nodes Ng. The horizontal axis is the value of threshold TC, and the vertical axis is the value of Ng. The network edge weights are positive. (b) The relationship between the threshold TC and the number of driven nodes Nd. The horizontal axis is the value of threshold TC, and the vertical axis is the value of Nd. The network edge weights are positive. (c) The relationship between the threshold TC and the giant connected community nodes Ng. The horizontal axis is the value of threshold TC, and the vertical axis is the value of Ng. The network edge weights are negative. (d) The relationship between the threshold TC and the number of driven nodes Nd. The horizontal axis is the value of threshold TC, and the vertical axis is the value of Nd. The network edge weights are negative.
Preprints 91708 g007
Preprints 91708 g010
Figure 10. Heat map of co-occurrence rate of driven nodes under different thresholds TC. (a) The horizontal and vertical axes represent different thresholds TC. The higher the Jaccard coefficient of the co-occurrence of the driven nodes, the darker red the pattern color is, and vice versa, the darker blue. This figure displays the case where the edge weights take a positive value. (b) The horizontal and vertical axes represent different thresholds TC. The higher the Jaccard coefficient of the co-occurrence of the driven nodes, the darker red the pattern color is, and vice versa, the darker blue. This figure displays the case where the edge weights take a negative value.
Figure 10. Heat map of co-occurrence rate of driven nodes under different thresholds TC. (a) The horizontal and vertical axes represent different thresholds TC. The higher the Jaccard coefficient of the co-occurrence of the driven nodes, the darker red the pattern color is, and vice versa, the darker blue. This figure displays the case where the edge weights take a positive value. (b) The horizontal and vertical axes represent different thresholds TC. The higher the Jaccard coefficient of the co-occurrence of the driven nodes, the darker red the pattern color is, and vice versa, the darker blue. This figure displays the case where the edge weights take a negative value.
Preprints 91708 g010
Preprints 91708 g011
Figure 11. Heat map of co-occurrence rate of driven nodes under different thresholds TC from May to September. (a) The horizontal and vertical axes represent different thresholds TC. The higher the Jaccard coefficient of the co-occurrence of the driven nodes, the darker red the pattern color is, and vice versa, the darker blue. This figure displays the case where the edge weights take a positive value. (b) The horizontal and vertical axes represent different thresholds TC. The higher the Jaccard coefficient of the co-occurrence of the driven nodes, the darker red the pattern color is, and vice versa, the darker blue. This figure displays the case where the edge weights take a negative value.
Figure 11. Heat map of co-occurrence rate of driven nodes under different thresholds TC from May to September. (a) The horizontal and vertical axes represent different thresholds TC. The higher the Jaccard coefficient of the co-occurrence of the driven nodes, the darker red the pattern color is, and vice versa, the darker blue. This figure displays the case where the edge weights take a positive value. (b) The horizontal and vertical axes represent different thresholds TC. The higher the Jaccard coefficient of the co-occurrence of the driven nodes, the darker red the pattern color is, and vice versa, the darker blue. This figure displays the case where the edge weights take a negative value.
Preprints 91708 g011
Preprints 91708 g012
Figure 12. Heat map of co-occurrence rate of driven nodes under different thresholds TC from October to February. (a) The horizontal and vertical axes represent different thresholds TC. The higher the Jaccard coefficient of the co-occurrence of the driven nodes, the darker red the pattern color is, and vice versa, the darker blue. This figure displays the case where the edge weights take a positive value. (b) The horizontal and vertical axes represent different thresholds TC. The higher the Jaccard coefficient of the co-occurrence of the driven nodes, the darker red the pattern color is, and vice versa, the darker blue. This figure displays the case where the edge weights take a negative value.
Figure 12. Heat map of co-occurrence rate of driven nodes under different thresholds TC from October to February. (a) The horizontal and vertical axes represent different thresholds TC. The higher the Jaccard coefficient of the co-occurrence of the driven nodes, the darker red the pattern color is, and vice versa, the darker blue. This figure displays the case where the edge weights take a positive value. (b) The horizontal and vertical axes represent different thresholds TC. The higher the Jaccard coefficient of the co-occurrence of the driven nodes, the darker red the pattern color is, and vice versa, the darker blue. This figure displays the case where the edge weights take a negative value.
Preprints 91708 g012
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated