Preprint
Article
Spectral Decomposition of Gramians of Continuous Linear Systems in the Form of Hadamard Products
Altmetrics
Downloads
66
Views
28
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
28 November 2023
Posted:
29 November 2023
You are already at the latest version
Alerts
Abstract
New possibilities of Gramian computation by using canonical transformations into diagonal, controllable and observable canonical forms are shown. With the help of such a technique the Gramian matrices can be represented in the form of products of Hadamard matrices of multipliers and matrices of the transformed right-hand side of Lyapunov equations. It is shown that the multiplier matrices are invariant under various canonical transformations of linear continuous systems. The modal Lyapunov equations for continuous SISO LTI systems in diagonal form are obtained and their new solutions based on Hadamard decomposition are proposed. New algorithms for element-by-element computation of Gramian matrices for stable continuous MIMO LTI systems are developed. For continuous SISO LTI systems given by equations of state in controllable and observable canonical forms, new algorithms for the computation of controllability Gramians and their traces in the form of Hadamard products in the form of Xiao matrices are developed. The application of transformations to the canonical forms of controllability and observability allowed to simplify the formulas of spectral decompositions in the form of Xiao matrices. In the paper new spectral decompositions in the form of Hadamard’s products for solutions of Sylvester algebraic and differential equations of MIMO LTI systems, including spectral decompositions of finite and infinite cross-Gramians of continuous MIMO LTI systems. Recommendations on the use of the obtained results are given.
Keywords:
Subject: Computer Science and Mathematics - Applied Mathematics
MSC: 11C08; 11C20; 11E39; 11F22; 44A10; 45D05
1. Introduction
The first spectral expansions of Gramians for linear continuous and discrete systems with simple spectra were obtained in [1] by the spectral expansion of the integral representation of the solution of the Lyapunov or Sylvester equations. It is well known that the Gramians are solutions of the Sylvester and Lyapunov equations, to which a huge number of scientific papers have been devoted, among which we note [2,3,4,5,6,7,8,9,10,11,12,13]. These equations also play a fundamental role in a control theory. Researches in the field of linear control systems are closely related to the problem of reduction the order of the model by constructing an approximating model of lower dimension. Even in the case of linear systems of high dimensionality, the use of projection methods allows us to reduce the significantly dimensionality of the approximating model [6,10]. Among these methods, we note balanced truncation , singular decomposition, Krylov subspace method; methods for drsign a simplified model, based Gramian H2 -norm optimal methods, and hybrid methods. Iterative algorithms for their implementation have been developed for most of the methods. The Sylvester and Lyapunov matrix equations in applied problems of control theory were studied in [12,13] In recent years, there has been an interest in developing of the methods for computing various energy metrics to analyse the stability and degree of controllability, reachability and observability of these systems. Such metrics for linear stable systems and unstable linear systems have been proposed in a number of papers[14,15,16,17,18,19,20,21].Simplified models for large networks based on output controllability Gramians, allowing the computation of energy indices, were proposed in [16]. The important problem of optimal placement of sensors and actuators based on various energy functionals, including invariant ellipsoids, was considered in [15,17,18,20]. Paper [17] formulates a general approach to solving the problem of optimal placement of sensors and actuators for multivariable control systems, which is based on the decomposition of the system into stable and unstable subsystems. It is shown that the degree of controllability of the system is determined on the basis of energy metrics based on the use of finite and infinite controllability Gramians.A general method for computing the inverse controllability Gramian for equations of state given in canonical forms of controllability is proposed. In [18], a method for optimal placement of virtual inertia on the graph of an energy system is proposed. This method is based on the use of energy metrics of coherennce of generators and the square of the H2 and the square of the H2 -norm of the system transfer function, which is given by a standard dynamic model in the state space. The problem is formalised as a nonconvex optimization problem with constraints in the form of observability Gramian values. It is well known that energy-efficient control problems are also solved using Gramians. In recent years, these approaches have been developed for complex energy, social, transport and biological networks in [17,18,19]. In [16,17], it is shown that the closer the eigenvalues of the dynamics matrix are to the imaginary axis, the less energy is required to make the network fully controllable. In [19,20,21] These ideas have been developed for digital ecosystems, vibroacoustics control systems and thermal plants control systems. Thus, the degree of controllability (reachability) of the network is related to the minimum energy, which allows us to introduce new metrics in the form of the minimum eigenvalue of the controllability Gramian and the maximum eigenvalue of its inverse Gramian, as well as the traces of these Gramians. Note that in most of the above mentioned works the spectrum of the dynamics matrix of the system is used, which makes it completely natural to use spectral analysis methods to solve the problems listed above.
Main contribution
In Section 2, the formulations of the problems of computing controllability and observability Gramians are considered in the framework of a unified concept. An important feature of the concept of the paper is the consideration of Hadamard products for the spectral decomposition of Gramians, which allows us to reduce the computation of sub-Gramian and Gramian matrices to the computation of numerical sequences of their elements. The use of canonical forms of controllability has previously set the stage for a new approach to the computation of Gramians based on the use of Routh-Gurwitz tables and Xiao matrices [22,23,24,25,26]. In this paper, we propose to improve this approach by using spectral decompositions of Gramians by extending its scope of application to multivariable linear control systems given by a standard (A,B,C) state-space representation. In Section 3, we introduce modal Lyapunov equations of the second type for the state equations of MIMO LTI systems in a diagonal canonical form. These equations allow the computation of various sub-Gramians in a closed form. Their spectral decompositions in the form of Hadamard products are obtained and formulas for the multiplier matrices are derived. For the SISO LTI system in the canonical forms of controllability and observability, spectral decompositions in the form of Hadamard products are obtained, whose multiplier matrices are Xiao matrices to play an important role in the following exposition. These equations allow us to compute various sub-Gramians in closed form. Their spectral decompositions in the form of Hadamar products are obtained and formulas for the multiplier matrices are derived. It is proved that for stable systems the Xiao matrices are positively defined and are invariants under similarity transformations. In the rest of the section, the general case of linear continuous MIMO LTI systems represented by (A,B,C) equations of state is considered. New spectral decompositions of the controllability and observability Gramians in the form of Hadamard products are obtained. It is shown that the multiplier matrices are the same in both MIMO LTI and SISO LTI cases provided that the system is stable, fully controllable and observable for both the simple and pairwise spectra of the dynamics matrix. The new analysis of the properties of multiplier matrices is given. An important property of multiplier matrices is their positive definiteness, which manifests itself in the positivity of the energy metrics associated with this property [15,16]. In Section 4, the obtained results are developed for the construction of spectral expansions of solutions of a wide class of Sylvester matrix differential equations. In particular, we obtain closed formulas for the Hadamard products of the matrices of spectral expansions of cross-Gramian MIMO LTI systems, as well as their traces and diagonal elements.
2. Discussion of the results and problem statement
We consider the Lyapunov equations for continuous stationary MIMO LTI in diagonal canonical form
или
where the matrix T is composed of the right eigenvectors , and the matrix is composed of the left eigenvectors corresponding to the eigenvalue . Let us introduce the notations
The following relations are valid [15]
where the matrix is a solution of the corresponding Lyapunov equation. With respect to systems (1) and (2), we will assume that various structural conditions for stability, controllability, observability and spectrum properties of the dynamic matrix are fulfilled. In [26] the following spectral decomposition of the controllability Gramian was obtained
Let us consider further SISO LTI (linear time invariant system with one input and one outputs) of a linear system in the canonical form of observability [9]. In this case the following formulas are valid
According to the principle of duality we obtain the expressions [26]
In addition,
Let us call Xiao matrix (Zero plaid structure) a matrix of the form [23]
The corresponding matrix elements are calculated by the formulas
The aim of the paper is to develop a general approach and study the properties of spectral decompositions of solutions of differential and algebraic Sylvester and Lyapunov equations in the form of Hadamard products, including modal equations.
3. Main results
Spectral Gramian decompositions allow us to represent the Gramian matrix as a sum of summands containing multiples of summations over different indices. In this case the role of the indices can be different. Some indices play the role of leading indices, while others are slave indices. The distribution of indexes' roles is determined by specificity of the applied tasks of condition monitoring and management. In addition, computations in the real or complex domain require a different approach to the choice of method and algorithm for computing or analysing Gramian properties. The main idea of the derivation of modal Lyapunov equations is to decompose the matrix of the right-hand side of the Lyapunov equation into the sum of matrices corresponding to the individual eigenvalues of the dynamics matrix or their combinations and the corresponding transformation of the matrices of the left-hand side.The main types of spectral decompositions are decompositions by simple, multiple or Raman (pairwise) spectra. The Gramian matrix is in general an Hermite complex matrix, which can be represented as the sum of the symmetric and the cosymmetric matrix. Many applications of the Lyapunov equations are based on the use of matrix of dynamics, input-output and Faddeev matrices, and in this case the Gramian matrices are valid [30]
or
where Q is the matrix of the right-hand side of the Lyapunov equations, R_i,R_j are deductions of the resolvent of the dynamics matrix in its corresponding eigenvalue.
Let us call equations (5) - (8) modal Lyapunov equations of the first type. On the other hand, there are applications in which it is possible to use complex matrices of solutions of Lyapunov equations
Or
Let us call equations (9) – (12) modal Lyapunov equations of the second type.
Theorem 1.
[27]. Consider the modal Lyapunov equations of the second type for a continuous stationary MIMO LTI system in a diagonal canonical form
Above, the corresponding unit vectors are denoted by Suppose that the system is stable and has a simple spectrum. Then the controllability and observability Gramians exist, are singular and can be represented in the form of Hadamard products
If, in addition, the pair (A,B) is controllable and the pair (A,C) is observable, then the matrices of multipliers Ω_c and Ω_o are definitely positive, their diagonal elements and traces are positive numbers.The Hermite components of the Gramians have the form [2]
For Gramians and sub-Gramians of controllability and observability in the form of Hadamard's products the formulas are valid
Proof.
The proof of the general formulas is based on the results of [27] and taking into account the separability properties of spectral expansions of Gramians. The validity of the formulas of the modal Lyapunov equations (16) - (19) is established by substituting the formulas into the original Lyapunov equations and taking into account the equalities
In [26], the general formulas for computing spectral expansion of Gramians are derived, which are also applicable to the modal equations of MIMO LTI systems
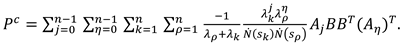
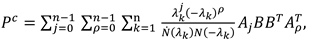
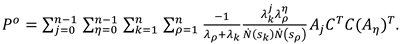
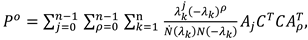
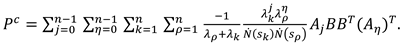
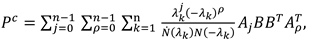
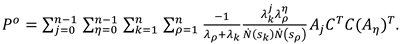
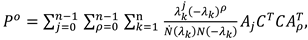
Above, Aj denotes the Faddeev matrices, which are expressed through linear combinations of the products of the coefficients of the characteristic equations and the degree of the dynamics matrix of the system [28,29]. When performing the transformations, it should be taken into account that the deductions of the resolvent of the dynamics matrix in its eigenvalues for the diagonal canonical form are strongly simplified
Res
Therefore formulas ( 20) - ( 23) pass to formulas
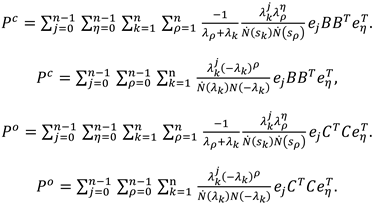
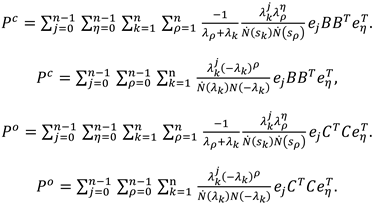
Theorem 2.
Consider the modal Lyapunov equations for a continuous stationary SISO LTI system in the canonical forms of controllability and observability of the form
Suppose that the system is stable, has a simple spectrum, pair (A,B) is controllable, pair (A,C) is observable.
Then the modal Gramians of controllability and observability exist and are singular. The modal Gramians of controllability for equations of state in the canonical form of controllability coincide with the Gramians of observability for equations of state in the canonical form of observability. The following decompositions of the Gramian matrices in the form of Hadamard products are valid
Hadamard decomposition on the pair spectrum have the form
Hadamard decomposition of the controllability and observability sub-Gramians over a simple spectrum has the form
Hadamard products are invariant under the similarity transformations.
Proof.
The singularity of solutions of modal equations follows from the stability of these equations. The coincidence of the solution matrices of the modal equations follows from the coincidence of the solution matrices of the original equations and [26].In this paper, analytical expressions of the solution matrices in the form of spectral expansions for a simple spectrum were derived
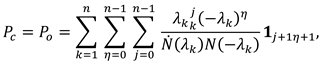
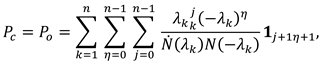
and for the pair spectrum in the form
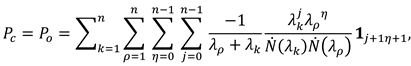
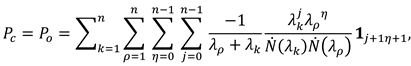
Let represent the matrix factors of the Hadamard decomposition in the form
We have scalar matrices of multipliers in the form
Let represent the matrix factors of the Hadamard decomposition in the form
We have scalar matrices of multipliers in the form
Hence formulas (24) to (29) follow. Since multiplier matrices are the known functions of eigenvalues that serve as invariants under similarity transformations, multiplier matrices and Hadamard products are invariants under these transformations.
Corollary 1.
The controllability and observability Gramians for the equations of state in the canonical forms of controllability and observability are Xiao matrices that are invariants under similarity transformations. The Xiao matrix is positively defined.
Proof.
The following formulas are valid
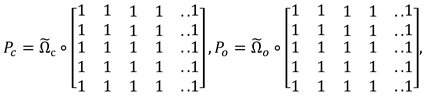
Let us prove the fulfilment of the first property of Xiao matrices (3). Its fulfilment for zero elements of matrices is proved in [26]. The alternation of signs of the side diagonal elements passing through the diagonal element follows from the sequence of these elements in the form
The fulfilment of property (4) is similarly checked. Since the multiplier matrices are known functions of the eigenvalues, the Xiao matrices are invariant under the similarity transformation. We will show the validity of this statement for its controllability Gramians. The transformation matrixcan be represented as the product of the Kalman controllability matrix by the Hankel matrix [24]
A substitution when calculating the controllability matrix leads to the equality
It follows that the controllability matrix is nondegenerate when transforming the state equations into the canonical form of controllability or observability. So the multiplier matrix, which is the Xiao matrix, is positively defined.
Theorem 3.
Let us consider the spectral decompositions of the solutions of the equations of linear continuoues stationary MIMO LTI systems. Suppose that the system is stable, the matrices A, B , C are real, the matrix A has a simple spectrum, the pair (A,B) is controllable, and the pair (A,C) is observable. Then the following statements are true.
1.Spectral decompositions of its controllability and observability Gramians and controllability or observability sub-Gramians in the form of Hadamard products for the case of pair spectrum of the dynamics matrix have the following form
2. For the case of decomposition of the controllability Gramian by a simple spectrum of the dynamics matrix in the form of Hadamard products, we obtain the same formulas (1) - (4),except for the formulas of the multiplier matrix, which takes the form
3. Exactly the same formulas as (45) - ( 49) will be valid for the observability Gramians in the form of Hadamard products. Only the formulas for the matrices Ψ_o are changing
4. The Hermite component of the controllability and observability Gramians has the form [2]
The spectral decompositions of the Hermite components of the controllability
and observability Gramians have the form of Hadamard matrices
The multiplier matrices in all Gramian decompositions are Xiao matrices.
Proof.
Let us return to the general formulas for spectral expansions of Gramians (20)-(23). Consider first the pairwise spectrum decompositions of Gramians. We divide the summation indices into two groups: the first group covers the summation over the indices "j,η" of the decompositions of the resolvent into Faddeev series, the second group covers the summation over the pair spectrum. Let us distinguish the controllability subgramian and represent its spectral decomposition as
Taking into account the designation
we have
Taking into account the previous calculations, we obtain the spectral decomposition of the controllability Gramian of the system in the form
Repeating similar reasoning for the case of the decomposition of the controllability Gramian over the simple spectrum of the dynamics matrix, we obtain the same formulas (47) - (51) as in the previous case, except for the formulas for the matrix
In [26] it is proved that the multiplier matrices are Xiao matrices. They coincide with formulas (27) - (28) of Theorem 2. It is easy to find that exactly the same formulas will be true for the observability Gramian’s multipliers if the conditions of the theorem are preserved. Only the formulas for the matrices are changing
Note that the developed method and algorithms for computing Gramians in the form of Hadamard products provide a convenient way to compute and subsequently analyse the elements of Gramian matrices, which is an advantage when computing diagonal elements and traces of Gramians and sub-Gramians, as well as spectral decompositions of energy functionals [31].
In all the cases discussed above we are talking about the complex Gramians and sub-Gramians of controllability and observability. Under the conditions of the theorem, the controllability and observability Gramians are always real matrices, but the sub-Gramians can be complex. As can be seen from the last expressions, when calculating the Hermite components of the Hadamard products of sub-Gramians, we obtain the formulae
Therefore, the matrix part of the subgramians in the form of the Hadamard product becomes a symmetric matrix, and its multiplier matrix becomes a real matrix. As a result of these transformations we obtain formulas (41) - (46).
4. Spectral expansions of solutions of Sylvester differential equations on a finite interval
Let us consider two linear stationary continuous MIMO LTI dynamic systems of the form
where x. We will consider real matrices of corresponding sizes A,B,C. Let us assume that system (53) is stable, unless otherwise stated, completely controllable and observable, all eigenvalues of matrix A are different.
where We will consider real matrices of corresponding sizes A, B, C, , ,. Let us assume that system (54) is stable, unless otherwise stated, completely controllable and observable, all eigenvalues of the matrix are different and do not coincide with the eigenvalues of matrix A. Following [27], consider the following continuous differential equations associated with these systems of the form
где R – вещественная матрица размера (nxn).
where is a real matrix of size(nx). This section will focus on the Sylvester differential equation (70). The main method for constructing a solution and its spectral expansions is operational calculus and expansion of the resolvents of the dynamics matrices and into the Faddeev-Leverrier series. The latter have the form [28,29]
where , are Faddeev matrices constructed for resolvent matrices using the Faddeev-Leverrier algorithm; - characteristic polynomials of matrices are the coefficients of these polynomials. The first method of spectral expansions of solutions to Sylvester differential equations is based on the lemma
Lemma
[27]. Let us consider solving equations on a finite interval [0,t)∈[0,T]. Let us assume that systems (67), (68). are stable, matrices Am, Bm, R, R1 are real, matrices Am, Bm have a simple spectrum, their eigenvalues are different, do not belong to the imaginary axis of the eigenvalue plane, as well as conditions are valid
Let's transform the dynamics matrices to diagonal form
where –matrices of dimentions [nn] и [
Then the Sylvester differensial equation solution on finite interval [0,t)∈[0,T] have the form
The second method of spectral decompositions of solutions of the Sylvester differential equations is based on using the Laplace transform to compute the Lyapunov integral and decomposing the resolvents of the dynamics matrices and.into a Faddeev-Leverier series.
Theorem 4.
Let us consider spectral expansions of solutions to Sylvester differential equations for MIMO LTI systems (67), (68). Let us assume that these systems are stable, the matrices A, B and R are real, the matrices A, B have a simple spectrum, their eigenvalues are different, do not belong to the imaginary axis of the eigenvalue plane, and the conditions are met
Then the following statements are true.
1. Spectral expansions of solutions to Sylvester differential equations (53), (54) in the form of Hadamard products for the case of the combination spectrum of dynamics matrices have the form
2. For the case of expansion of solutions of Sylvester’s differential equations over the simple spectrum of the dynamics matrix, the same formulas (57) – (58) are valid, but with new multiplier matrices
The Hermitian component of spectral expansions of solutions to the Sylvester equations has the form
where the spectral decompositions of the matrices are determined by formulas (59) – (62).
Let us apply the Laplace transform to both sides of the equation, considering the initial conditions to be zero and using the theorem on the Laplace transform of the product of real functions of time, the image of which is a fractional-rational algebraic fraction [27]. In our case, this fraction contains one zero pole, and all other poles are simple. In this case, the direct transformation has the form
где функции принимают вид
Substituting these expressions into (77), we obtain an image of the expansion of the solution to Sylvester’s differential equations (70) in terms of the combination spectrum of the dynamics matrices in the form
Having performed the inverse transformation, we obtain the spectral expansion of the solution to the Sylvester differential equations (56) in the combination spectrum of the dynamics matrices in the time domain
Equality (648) expresses the spectral expansion of solutions to Sylvester differential equations in the combination spectrum of matrices A_m and B_m. This proves the first statement of the theorem.
Using the identity
Let us obtain similar expansions for the simple spectrum of the matrix
The resulting expansions prove the second statement of the theorem. The third statement follows from statements 1 and 2.Equality (66) expresses the spectral expansion of solutions to the Sylvester equations in the simple spectrum of the matrix.
Let us apply the results of the theorem to the calculation of spectral decompositions finite cross-Gramian of a continuous stable MIMO LTI system,
which is a solution to the simple Sylvester differential equation
Corollorary 2.
Let us consider the spectral expansions of solutions of Sylvester differential equations for the MIMO LTI system (83). Let us assume that the system is stable, matrix A, B and C, are real, their dimensions have been harmonised , matrix A has a simple spectrum, and the conditions are met
Then the following statements are true.
1.The spectral decomposition of the cross-Gramian image has the form
2.The spectral decomposition of the cross-Gramian over the pair spectrum of matrix A in the time domain has the form
The Hadamard decomposition for a finite cross-Gramian has the form
3.The diagonal terms and trace of the cross-Gramian have the form
5. Conclusion
The paper shows that the Gramians Hadamard decomposition and its multiplier matrices play an important role in the problems of analysing structural properties for a wide class of continuous linear dynamical systems given by their different equations of state.
The following main results are obtained in the paper:
- a new method is proposed and new algorithms are developed for the element-by-element computation of finite and infinite controllability, observability Gramians and cross-Gramian within a unified Hadamar decomposition,
- a method and algorithms for computing Gramians and sub-Gramians on the basis of Hadamar decomposition of the solutions of modal Lyapunov equations of the second type are developed,
- properties of multiplier matrices, including Xiao matrices, for continuous linear systems given by the standard (A,B,C) representation in the state space, are investigated.
New possibilities of Gramian computation by using canonical transformations into diagonal, controllable and observable canonical forms are shown. In this case, the Gramian matrices can be represented as Hadamard product matrices of the multiplier matrices and matrices of the transformed right-hand side of the Lyapunov equations. It is shown that the multiplier matrices are invariant under various canonical transformations of linear continuous systems. Modal Lyapunov equations for continuous SISO LTI systems in diagonal form are obtained, new algorithms for the elementwise computation of Gramian matrices for stable continuous MIMO LTI systems are obtained. For continuous SISO LTI systems in controllable and observable canonical forms new algorithms for the computation of controllability Gramians and their traces in the form of Hadamar products in the form of Xiao matrices are developed. The use of transformations into canonical forms of controllability and observability made it possible to simplify the formulas of spectral decompositions in the form of Xiao matrices and simplify the calculations of Gramians. The article obtains new spectral expansions in Hadamard form for solutions of algebraic and differential Sylvester equations and spectral expansions of finite and infinite cross-Gramians of continuous MIMO LTI systems. The results obtained can be used for the optimal selection of locations for sensors and actuators in multivariable control systems and dynamic networks, for calculations and analysis of empirical Gramians, for assessing the risk of loss of stability in electric power systems, in problems of analysis and synthesis of modal control systems.
Funding
The APC research was funded by the Russian Science Foundation. This work was supported by the Russian Science Foundation project number 19-19-00673.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- Antoulas, A.C. Approximation of Large-Scale Dynamical Systems; SIAM Press: Philadephia, 2005. [Google Scholar]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press, 1984. [Google Scholar]
- Polyak, B.T.; Khlebnikov, M.V.; Rapoport, L.B. Theory of Automatic Control; Textbook. M.: LENAND, 2019; 504p, [in Russian]. [Google Scholar]
- Zubov, N.E.; Zybin, E.Yu.; Mikrin, E.A.; Misrikhanov, M.S.; Ryabchenko, V.N. General analytical forms of the solution of the Sylvester and Lyapunov equations for continuous and discrete dynamic systems. J. Comput. Syst. Sci. Int. 2017, 56, 1–18. [Google Scholar] [CrossRef]
- Ikramov, K.D. Numerical Solution of Matrix Equations. Faddeev, D.K., Ed.; Nauka: Moscow, 1984; [in Russian]. [Google Scholar]
- Benner, P.; Damm, T. Lyapununov equations, Energy Functionals and Model Order Reduction of Bilinear and Stochastic Systems. SIAM J. Control Optim. 2011, 49, 686–711. [Google Scholar] [CrossRef]
- Andreev, Y.N. Control of finite-dimensional linear objects; Nauka: Moscow, 1976; Volume 424, [in Russian]. [Google Scholar]
- Gantmacher, F.R. The theory of matrices; Chelsea Publishing Company: New York, 1959. [Google Scholar]
- Kailath, T. Linear Systems, Prentice-Hall Information and System Sciences Series, N.Y. 1980.
- Simoncini, V. Computational methods for linear matrix equations. SIAM Rev. 2014, 58, 377–441. [Google Scholar] [CrossRef]
- Tynda, A. N.; Sidorov, D.N.Inverse Problem for the Integral Dynamic Models with Discontinuous Kernels. mathematics 2021, 10, 2022. [Google Scholar] [CrossRef]
- Himpe, C. The Empirical Gramian Framework. Algorithms 2018, 11. [Google Scholar] [CrossRef]
- Krasnova, S.A.; Utkin, V.A. Cascade synthesis of state observers of dynamic systems; Moscow: Nauka Publishing House, 2006; 272p, [in Russian]. [Google Scholar]
- Lindmark, G.; Altafini, C. A driver mode selection strategy for minimizing the control energy for complex networks. IFAC- PapersOnLine 2018, 50. [Google Scholar] [CrossRef]
- Dilip, A.S.A. The controllability Gramian, the Hadamard product and the optimal actuator/ leader and sensor selection problem. Nature Physics 2015, 11, 779–786. [Google Scholar] [CrossRef]
- Сasadei, G.; Wit, C.C.D.; Zampieri, S. Model Reduction Based Approximation of the Output Controllability Gramians in Large-Scale Networks. IEEE Transactions on Control of Network Systems 2020, 7, 1778–1788. [Google Scholar] [CrossRef]
- Pasqualetti, F.; Zampieri, S.; and, F. Bullo, Controllability metrics, limitations and algorithms for complex networks. American Control Conference 2014, 3287–3292. [Google Scholar] [CrossRef]
- Poolla, B.K.; Bolognani, S.; Dörfler, F. Optimal Placement of Virtual Inertia in Power Grids. arXiv 2021, arXiv:arXiv:1510.01497v5. [Google Scholar] [CrossRef]
- Bakhtadze, N.N.; Novikov, D.A.; Elpashev, D.V. Integrated Resource Management in the Digital Ecosystem of the Enterprise Based on Intelligent Consorts IFAC-PapersOnLine; Elsevier: Nantes, France, 2022; Volume 55, pp. 2330–2335. [Google Scholar]
- Kumar, R.; Khan, M. Pole placement techniques for active vibration control of smart structures: A feasibility study. Journal of Vibration and Acoustics. 2007, 125, 601–615. [Google Scholar] [CrossRef]
- Solodusha, S.; Bulatov, M. Integral equations related to volterra series and inverse problems: Elements of theory and applications in heat power engineering. mathematics 2021, 9, 1905. [Google Scholar] [CrossRef]
- Sreeram, V.; Agathoklis, P. Solution of Lyapunov equation with system matrix in companion form. IEE Proc. D Control. Theory Appl. 1991, 138, 529–534. [Google Scholar] [CrossRef]
- Xiao, C.S.; Feng, Z.M.; Shan, X.M. On the Solution of the Continuous-Time Lyapunov Matrix Equation in Two Canonical Forms IEE Proceedings-D. 1992, 139, 286–290. [Google Scholar] [CrossRef]
- Hauksdottir, A.S.; Sigurdsson, S.P. The continuous closed form controllability Gramian and its inverse. In Proceedings of the 2009 American Control Conference Hyatt Regency Riverfront, St. Louis, MO, USA, 10-12 June 2009; pp. 5345–5351. [Google Scholar] [CrossRef]
- Mehr, F. Determination of Design of Optimal Actuator Location Based on Control Energy; University of London: London, 20018. [Google Scholar]
- Yadykin, I.B. Spectral Decompositions of Gramians of Continuous Stationary Systems Given by Equations of State in Canonical Forms mathematics. 2022, 10, 2339. [Google Scholar] [CrossRef]
- Yadykin, I.B.; Galyaev, A.A. On the methods for calculation of grammians and their use in analysis of linear dynamic systems Automation and Remote Control; Pleiades Publishing, Ltd., 2013; Volume 74, pp. 207–224. [Google Scholar]
- Hanzon, B.; Peeters, R.L.M. A Faddeev Sequence Method for solving Lyapunov and Sylvester Equations, Linear Algebra and its Applications. 1996; 241-243, 401–430. [Google Scholar] [CrossRef]
- Faddeev, D.K.; Faddeeva, V.N. Computational Methods of Linear Algebra; Freeman: San-Francisko, CA, USA, 2016. [Google Scholar]
- Iskakov, A.B.; Yadykin, I.B. Lyapunov modal analysis and participation factors applied to small-signal stability of power systems. Automatica 2021, 132, 109814. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated




