Prerpints.org logo
Preprint
Article

Symmetry and Asymmetry of One-Way Einstein-Rosen Bridge Inside Black Hole

Altmetrics

Downloads

81

Views

24

Comments

0

Submitted:

28 November 2023

Posted:

29 November 2023

You are already at the latest version

Alerts
Abstract
We elucidate the versatility of intriguing symmetry and asymmetry phenomena outside and inside black holes. For description of the test particle (planet and photon) motion it is used the Kerr-Newman metric of the rotating and electrically charged black hole. In particular, it is demonstrated the symmetry and asymmetry of the one-way Einstein-Rosen bridge inside black hole toward and through the plethora of endless and infinite universes.
Keywords: 
Subject: Physical Sciences  -   Theoretical Physics

1. Introduction

We elucidate the versatility of intriguing symmetry and asymmetry phenomena outside and inside black holes. For description of the test particle (planet and photon) motion it is used the Kerr-Newman metric of the rotating and electrically charged black hole. In particular, it is demonstrated the symmetry and asymmetry of the one-way Einstein-Rosen bridge inside black hole toward and through the plethora of endless and infinite universes.

2. Kerr-Newman Metric for Rotating and Electrically Charged Black Hole

The famous Kerr–Newman metric or geometry (see e. g., [1,2,3,4,5]), which is the exact solution of Einstein’s equations [6,7,8,9,10] for a rotating and electrically black hole, is:
d s 2 = − Δ Σ [ d t − a sin 2 θ d φ ] 2 + sin 2 θ Σ [ ( r 2 + a 2 ) d φ − a d t 2 ] 2 + Σ Δ d r 2 + Σ d θ 2 ,
where ( r , θ , ϕ ) are spherical coordinates and t is the time of static distant observer at the asymptotically radial infinity. In this metric
Δ = r 2 − 2 M r + a 2 + q 2 , Σ = r 2 + a 2 cos 2 θ ,
M — black hole mass, q — black hole electric charge, a = J / M — specific black hole angular momentum (spin). The two roots of equation Δ = 0 are r + = 1 + M 2 − a 2 − q 2 — the event horizon of the black hole and r − = 1 − M 2 − a 2 − q 2 — the Cauchy horizon of the black hole.
For simplification of equation and presentation of Figures we will use often units G = 1 , c = 1 , M = 1 and dimensionless radius r ⇒ r / M and dimensionless time t ⇒ t / M .
In the Kerr-Newman metric there the following integrals of motion for test particles [2]: μ — particle mass, E — particle total energy, L — particle azimuthal angular moment and Q — the Carter constant, related with the non-equatorial particle motion. The corresponding equations of test particle motion in the Kerr-Newman metric in the differential form are:
Σ d r d t a u = R ,
Σ d θ d τ = Θ ,
Σ d φ d τ = − a ( a E − L sin 2 θ ) + sin 2 a Δ ,
Σ d t d τ = − a ( a E sin 2 − L ) + ( r 2 + a 2 ) P Δ .
Here P = E ( r 2 + a 2 ) − a L , τ — the proper time of a test massive particle or an affine parameter along the trajectory of a massless particle ( μ = 0 ) like photon. Respectively, the effective radial potential R ( r ) is
R ( r ) = P 2 − Δ [ μ 2 r 2 + ( L − a E ) 2 + Q ] ,
and the effective polar potential Θ ( θ ) is
Θ ( θ ) = Q − cos 2 θ [ a 2 ( μ 2 − E 2 ) + L 2 sin − 2 θ ] .
Trajectories of massive particles ( μ ≠ 0 ) depend on three parameters: γ = E / μ , λ = L / μ and Q / μ 2 . Meantime, trajectories of massless particles like photons (null geodesics) depend on two parameters: λ and Q.
The nontrivial specific feature of the rotating Kerr black hole ( a ≠ 0 ) is the existence of so-called ergosphere [4,5,9,11,12] with the outer boundary
r ES ( θ ) = 1 + 1 − q 2 − a 2 cos 2 θ .
Inside the ergosphere any test object is dragged into insuperable rotation around black hole with infinite azimuthal winding by approaching the black hole event horizon.
In the following Sections we will describe the symmetry and asymmetry of test object motion in the gravitational filed of the Kerr-Newman black hole. We use equations of motion in the Kerr–Newman metric (3)–(6) in our analytic and numerical calculations of test particle geodesic trajectories [13,14,15,16,17,18,19,20,21,22,23].

3. One-Way Einstein-Rosen Bridge Inside Black Hole

We start to elucidate the versatility of intriguing symmetry and asymmetry phenomena outside and inside black holes by using the Carter-Penrose diagrams (for details see, i. e., [4,5,9,10]), describing in particular, the global space-time structure of black holes. The evident manifestation of symmetry of this global structure is infinite space volumes as outside and inside the black hole event horizon. See at Figure 1 the corresponding Carter-Penrose diagram for the Reissner–Nordstöm black hole, which is a special spherically symmetric case of Kerr-Newman black hole without rotation i. e., a = 0 but q ≠ 0 . From the pure geometric point of view this diagram is both left-right and up-down symmetric. On the contrary, from the physical or space-time point view this diagram is absolutely asymmetric due to the inexorable upward flow of time not only at this diagram but throughout the whole universe. More precisely it means that in the General Relativity all objects are allowed to move only inside the the upward directed light cones (at ± 45 ∘ with respect to the upward direction. The upward directed light cone is the inexorable asymmetry of the world.
2 D presentation of the voyage through the interiors of Reissner–Nordstöm black hole with interiors by using the Einstein-Rosen bridge is shown at Figure 2. The electric charge of the black hole is e = 0 . 99 . A test planet (or spaceship) with the electric charge ε = − 1 . 5 is periodically orbiting around black holes with orbital parameters parameters γ = 0 . 5 , λ = 0 . 5 , corresponding to the maximal radius (apogee) r max = 1 . 65 and minimal radius (perigee) r man = 0 . 29 , respectively, in dimensional units. The periodic planet geodesic trajectories (magenta curves, both at Figure 2 and Figure 3), were calculated numerically with using equations of motion (3)–(6) for massive test particles ( μ ≠ 0 ). Note, that the periodical motion of the test planet are limited in time due to energy losses in inevitable emission of the gravitational waves.
The picture at Figure 2 is geometrically absolutely symmetric or, in other words, it is completely or nicely symmetric. The geodesic trajectories of test planet ( μ ≠ 0 ) at this Figure 2 and at Figure 4 (the red-colored curves), are numerically calculated [13,14,15,16,17,18,19,20,21,22,23], by using the corresponding equations of motion in the Kerr-Newman metric (3)–(6).
At the same time, this picture is misleading and physically controversial: Indeed the voyage is starting at apogee r a from the position at point A, then reach the perigee r p and return back the apogee r a at the point B for a finite proper time, demonstrating the absolute geometric symmetry. Meanwhile, there is a crucial hitch: this apogee r a at the point B is not in the native universe, but in the other quite distant universe, as it is clearly viewed at the Carter-Penrouse diagram at Figure 1. This hitch again destroys the Einstein-Rosen bridge symmetry.
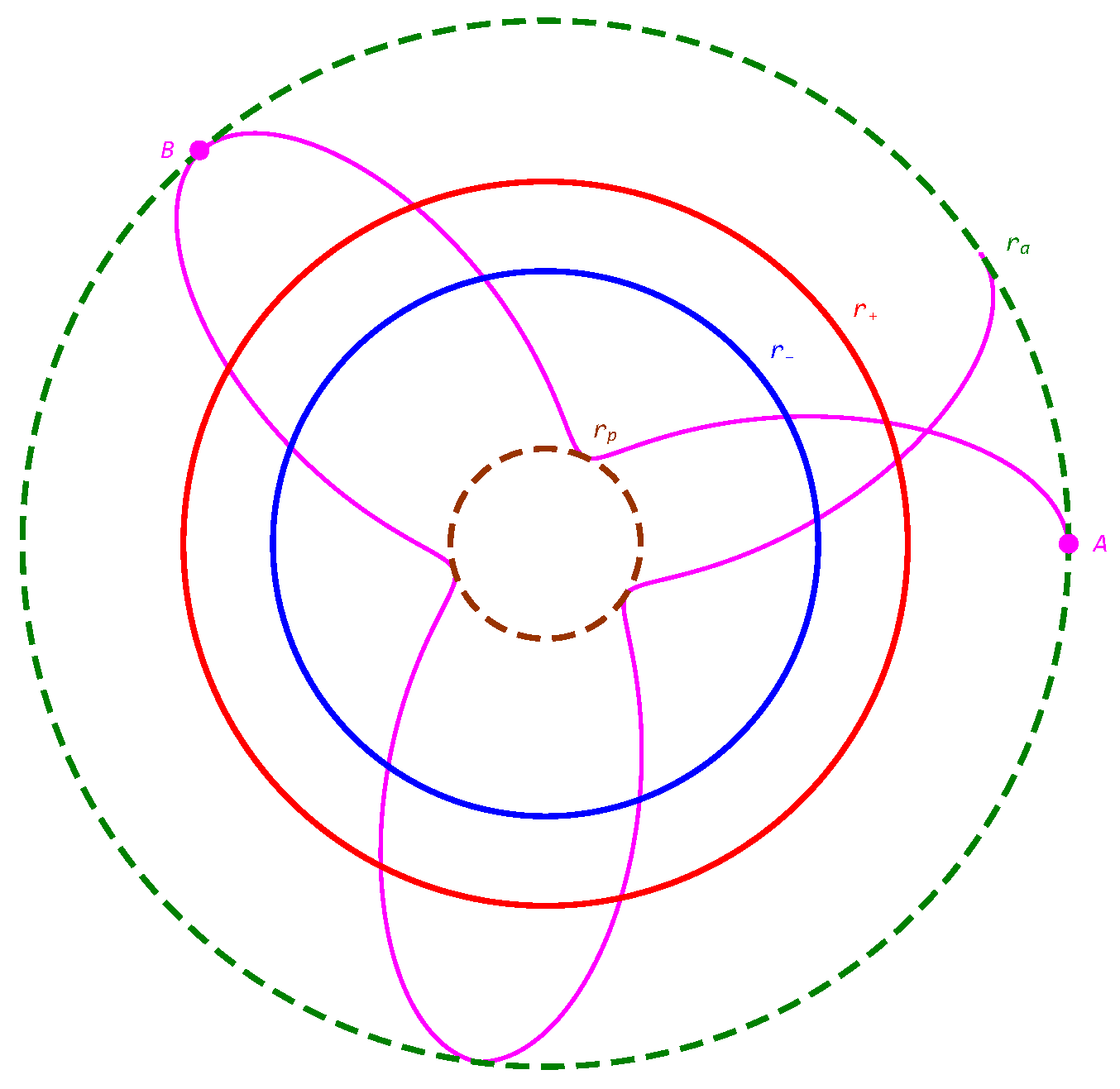
Preprints 91721 g002
Figure 2. 2 D presentation of the voyage through the Reissner–Nordstöm black hole interiors by using the Einstein-Rosen bridge. This picture is geometrically absolutely symmetric or, in other words, it is nicely symmetric. At the same time, this picture is misleading and physically controversial: Indeed the voyage is starting at apogee r a from the position at point A, then reach the perigee r p and return back the apogee r a at the point B for a finite proper time, demonstrating the absolute geometric symmetry. Meanwhile, there is a crucial hitch: this apogee r a at the point B is not in the native universe, but in the other quite distant universe, as it is clearly viewed at the Carter-Penrouse diagram at Figure 1. The apogee r a and perigee r p radii are shown by dashed circles. Respectively, the event radii of event horizon r + and Cauchy horizon r − are shown by solid circles. The magenta curve here and at the Figure 3 is numerically calculated geodesic trajectory with using equations of motion (3)–(6) for massive test particles ( μ ≠ 0 ).
Figure 2. 2 D presentation of the voyage through the Reissner–Nordstöm black hole interiors by using the Einstein-Rosen bridge. This picture is geometrically absolutely symmetric or, in other words, it is nicely symmetric. At the same time, this picture is misleading and physically controversial: Indeed the voyage is starting at apogee r a from the position at point A, then reach the perigee r p and return back the apogee r a at the point B for a finite proper time, demonstrating the absolute geometric symmetry. Meanwhile, there is a crucial hitch: this apogee r a at the point B is not in the native universe, but in the other quite distant universe, as it is clearly viewed at the Carter-Penrouse diagram at Figure 1. The apogee r a and perigee r p radii are shown by dashed circles. Respectively, the event radii of event horizon r + and Cauchy horizon r − are shown by solid circles. The magenta curve here and at the Figure 3 is numerically calculated geodesic trajectory with using equations of motion (3)–(6) for massive test particles ( μ ≠ 0 ).
Preprints 91721 g002
Figure 4 shows the embedding diagram for the voyage through black hole interiors by using the Einstein-Rosen bridge. The embedding diagram is very useful for the training of intuitive understanding of the peculiarities of the enigmatic black holes. In this embedding diagram the Einstein-Rosen bridge connects two asymptotically flat universes like wormhole tunnel [24,25], but with the only one-way motion from the initial point A to the final point B. The geometrical symmetry of this embedding diagram is deceptive. In fact, this embedding diagram demonstrate the asymmetric space-time origin of the one-way Einstein-Rosen bridge (remember about loss-cone).
The completely symmetric picture of the periodic orbital motion of the test planet or spaceship around the central singularity of the Reissner–Nordstöm black hole inside the Cauchy horizon r − is shown at Figure 3. The electric charge of the black hole is e = 0 . 99 and test planet (or spaceship) with the electric charge ε = − 1 . 5 is periodically orbiting around black holes with orbital parameters parameters γ = 1 . 7 , λ = 0 . 1 , corresponding to the maximal radius (apogee) r max = 0 . 75 and minimal radius (perigee) r man = 0 . 09 , respectively. The asymmetric Reissner–Nordstöm bridge is only needed for penetration into this very exotic region at 0 < r < r − , where exist the nearly stable periodic orbits for test particles [26,27,28,29,30,31,32], which are very similar to the periodic orbits outside the black hole event horizon r + .
Preprints 91721 g003
Figure 3. Both the geometrical and physical completely symmetric picture of the periodic orbital motion of the test planet or spaceship around the central singularity of the Reissner–Nordstöm black hole inside the Cauchy horizon r − . The asymmetric Reissner–Nordstöm bridge is only needed for penetration into this very exotic region at 0 < r < r − , where exist the nearly stable periodic orbits for test particles, which are very similar to the periodic orbits outside the black hole event horizon r + . The apogee r a and perigee r p radii are shown by dashed circles. Respectively, the event radii of event horizon r + and Cauchy horizon r − are shown by solid circles.
Figure 3. Both the geometrical and physical completely symmetric picture of the periodic orbital motion of the test planet or spaceship around the central singularity of the Reissner–Nordstöm black hole inside the Cauchy horizon r − . The asymmetric Reissner–Nordstöm bridge is only needed for penetration into this very exotic region at 0 < r < r − , where exist the nearly stable periodic orbits for test particles, which are very similar to the periodic orbits outside the black hole event horizon r + . The apogee r a and perigee r p radii are shown by dashed circles. Respectively, the event radii of event horizon r + and Cauchy horizon r − are shown by solid circles.
Preprints 91721 g003
Preprints 91721 g004
Figure 4. Embedding diagram for the voyage through black hole interiors by using the Einstein-Rosen bridge. This bridge connects two asymptotically flat universes like wormhole tunnel, but with the only one-way motion from the initial point A to the final point B. The geometrical symmetry of this embedding diagram is deceptive. In fact, this embedding diagram demonstrate the asymmetric space-time origin of the one-way Einstein-Rosen bridge (remember about loss-cone).
Figure 4. Embedding diagram for the voyage through black hole interiors by using the Einstein-Rosen bridge. This bridge connects two asymptotically flat universes like wormhole tunnel, but with the only one-way motion from the initial point A to the final point B. The geometrical symmetry of this embedding diagram is deceptive. In fact, this embedding diagram demonstrate the asymmetric space-time origin of the one-way Einstein-Rosen bridge (remember about loss-cone).
Preprints 91721 g004

4. Symmetry and Asymmetry of Test Particle Trajectories Near Rotating Black Hole

Figure 5, Figure 6 and Figure 7 demonstrate both symmetry and asymmetry features of massive and massless particle trajectories plunging into rotating Kerr black hole with spin a = 0 . 9982 ). Magenta arrows shows the direction of the black hole rotation in accordance with the gimlet rule. The multi–colored curves at Figure 7 and Figure 8 are the geodesic trajectories for massless test particles like photons ( μ = 0 ) numerically calculated with using equations of motion (3)–(6). By approaching the black hole the trajectories of all particles, both massive and massless ones, are infinitely winding up on the black hole event horizon in the direction of the black hole rotation and at the fixed latitudes. This winding up is a manifestation of symmetry of behaviour of all trajectories, plunging into rotating black hole. At the same the direction of the black hole rotation is a corresponding manifestation of asymmetry of the gravitational field of the Kerr metric.
At last, for completeness of black hole symmetric and asymmetric properties, at Figure 8 is shown the trajectory of the test planet ( μ ≠ 0 ) with parameters γ = 1 , λ = 1 and Q = 0 . 5 . This test planet is plunging into the spherically symmetric and nonrotating Schwarcshild black hole (with both the spin a = 0 and electic charge q = 0 ), starting from the radial distance r = 6 . It must be especially checked that the traversable (though only one-way in time and direction) Einstein-Rosen bridge is absent at all inside the Schwarcshild black hole (see for details, e. g., [4,6]).
Preprints 91721 g005
Figure 5. Trajectory of the test planet with parameters γ = 0 . 85 , λ = 1 . 7 and Q = 1 , which is plunging into the fast rotating Kerr black hole with spin a = 0 . 9982 . This planet is winding up on the black hole event horizon higher the equatorial plane. The blue curve here and in the Figure 6 is the numerically calculated geodesic trajectory with using equations of motion (3)–(6) for massless test particles like photons ( μ = 0 ).
Figure 5. Trajectory of the test planet with parameters γ = 0 . 85 , λ = 1 . 7 and Q = 1 , which is plunging into the fast rotating Kerr black hole with spin a = 0 . 9982 . This planet is winding up on the black hole event horizon higher the equatorial plane. The blue curve here and in the Figure 6 is the numerically calculated geodesic trajectory with using equations of motion (3)–(6) for massless test particles like photons ( μ = 0 ).
Preprints 91721 g005
Preprints 91721 g006
Figure 6. Trajectory of the test planet with parameters γ = 0 . 85 , λ = 1 . 7 and Q = 1 , which is plunging into the fast rotating Kerr black hole with spin a = 0 . 9982 . This planet is winding up on the black hole event horizon higher the equatorial plane. The blue curve here and in the Figure 7 is the numerically calculated geodesic trajectory with using equations of motion (3)–(6) for massless test particles like photons ( μ = 0 ).
Figure 6. Trajectory of the test planet with parameters γ = 0 . 85 , λ = 1 . 7 and Q = 1 , which is plunging into the fast rotating Kerr black hole with spin a = 0 . 9982 . This planet is winding up on the black hole event horizon higher the equatorial plane. The blue curve here and in the Figure 7 is the numerically calculated geodesic trajectory with using equations of motion (3)–(6) for massless test particles like photons ( μ = 0 ).
Preprints 91721 g006
Preprints 91721 g007
Figure 7. Trajectory of the photon with parameters λ = 2 and Q = 1 , which is plunging into the fast rotating Kerr black hole with a = 0 . 9982 and is winding up on the black hole event horizon below the equatorial plane. The multi–colored curve is the numerically calculated geodesic trajectory with using equations of motion (3)–(6) for massless test particles like photons ( μ = 0 ).
Figure 7. Trajectory of the photon with parameters λ = 2 and Q = 1 , which is plunging into the fast rotating Kerr black hole with a = 0 . 9982 and is winding up on the black hole event horizon below the equatorial plane. The multi–colored curve is the numerically calculated geodesic trajectory with using equations of motion (3)–(6) for massless test particles like photons ( μ = 0 ).
Preprints 91721 g007
Preprints 91721 g008
Figure 8. Trajectory of the photon with parameters λ = − 6 . 5 and Q = 4 , which is plunging into the fast rotating Kerr black hole with a = 0 . 9982 and is winding up on the black hole event horizon below the equatorial plane.
Figure 8. Trajectory of the photon with parameters λ = − 6 . 5 and Q = 4 , which is plunging into the fast rotating Kerr black hole with a = 0 . 9982 and is winding up on the black hole event horizon below the equatorial plane.
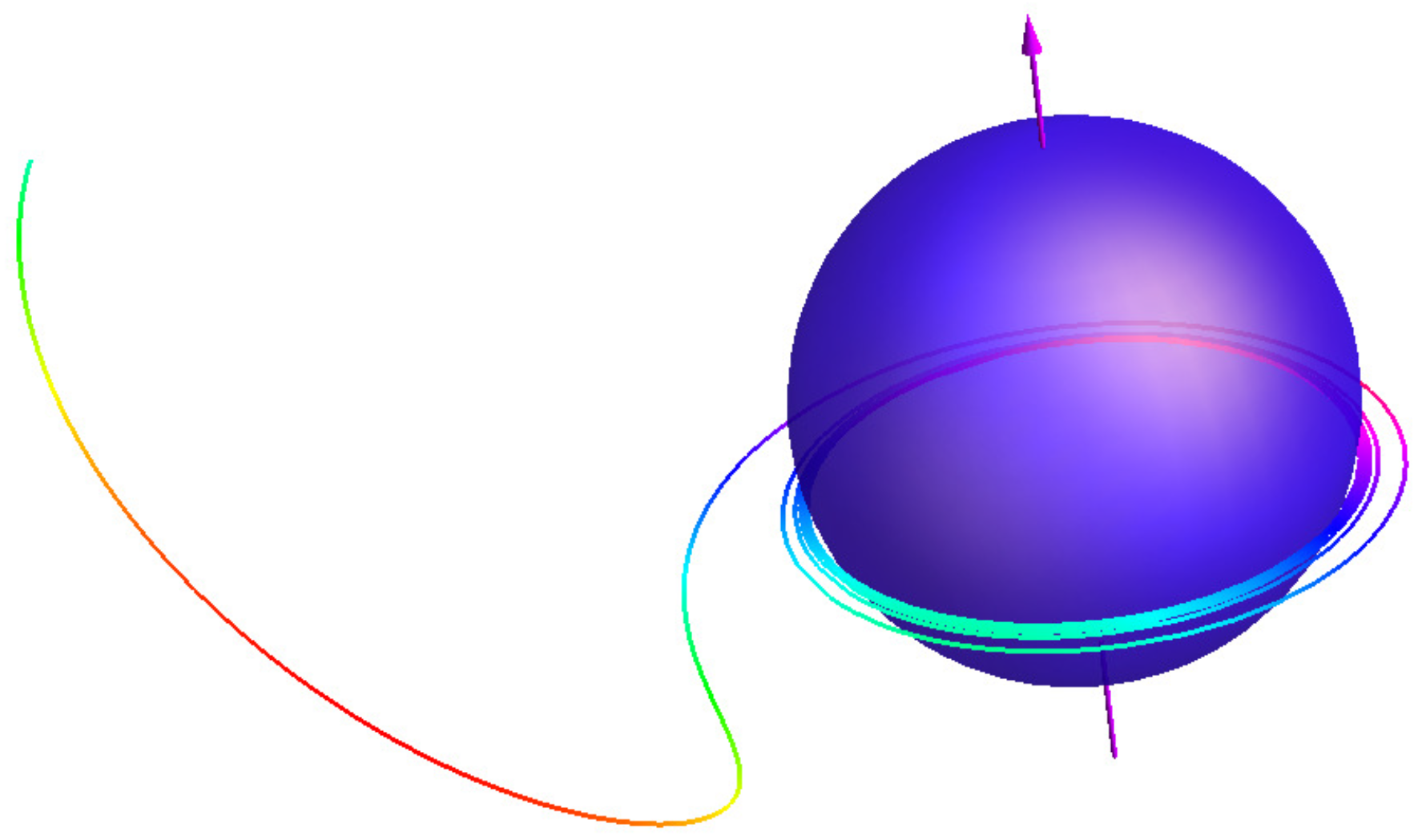
Preprints 91721 g008
Preprints 91721 g009
Figure 9. A trivial but though very expressive trajectory of a test planet ( μ ≠ 0 ) with parameters γ = 1 , λ = 1 and Q = 0 . 5 , which is plunging into the the spherically symmetric and nonrotating Schwarcshild black hole (with both the spin a = 0 and electric charge q = 0 ). The starting point for this crazy voyage is at the radial distance r = 6 .
Figure 9. A trivial but though very expressive trajectory of a test planet ( μ ≠ 0 ) with parameters γ = 1 , λ = 1 and Q = 0 . 5 , which is plunging into the the spherically symmetric and nonrotating Schwarcshild black hole (with both the spin a = 0 and electric charge q = 0 ). The starting point for this crazy voyage is at the radial distance r = 6 .
Preprints 91721 g009

5. Conclusions and Discussion

It is demonstrated the symmetry and asymmetry of the voyage on one-way Einstein-Rosen bridge inside black hole toward the endless multiplanetary future. The apparent symmetry of both the Carter-Penrose and embedding diagrams is mainly related with a pure geometrical vision of this phenomenon. Quite the contrary, the physical (space-time) vision elucidates the absolute asymmetry of the Einstein-Rosen bridge due to existence of the light-cone limitation for possible motions.
Note, that the traversable (though only one-way in time and direction) Einstein-Rosen bridge exist only in the case of both rotating Kerr a ≠ 0 and electrically charged Reissner–Nordström q ≠ 0 black holes. It is absent at all inside the Schwarcshild black hole (see for details, e. g., [4,6])
The infinite winding up of trajectories of all particles on the black hole event horizon is a manifestation of symmetry of behaviour of all trajectories, plunging into rotating black hole. At the same the direction of the black hole rotation is a corresponding manifestation of asymmetry of the gravitational field of the Kerr metric.

Author Contributions

Investigation, V.I. Dokuchaev and K.E. Prokopiev. The authors contributed to the paper equally.

Acknowledgments

We are grateful to E. O. Babichev, V. A. Berezin, Yu. N. Eroshenko and A. L. Smirnov for stimulating discussions.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Kerr, R. P. Gravitational field of a spinning mass as an example of algebraically special metrics Phys. Rev. Lett. 1963, 11, 237–238.
  2. Carter, B. Global Structure of the Kerr Family of Gravitational Fields. Phys. Rev. 1968, 174, 1559–1570. [CrossRef]
  3. Novikov I.D, Thorne K.S. in Black Holes (Eds C DeWitt, B S DeWitt) (New York: Gordon and Breach, 1973) p. 343–350.
  4. Misner, C.W.; Thorne, K.S.; Wheeler J.A. Gravitation; W. H. Freeman: San Francisco, CA, USA, 1973.
  5. Chandrasekhar, S. The Mathematical Theory of Black Holes. In The International Series of Monograph on Physics; Clarendon Press: Oxford, UK, 1983; Chapter 7, Volume 69.
  6. R. Penrose Structure of space-time/ Battelle Rencontres 1967. Lectures in Mathematical Physics Chapter VII. Editted by Cecille M. Dewitt and John A, Wheeler.(W. A.Benjamin Inc. New York-Amsterdam 1968) Chapter 2.
  7. Bardeen, J.M. Black Holes; DeWitt, C., DeWitt, B. S., Eds.; Gordon and Breach Science Publishers: New York, NY, USA, 1973; pp. 215–239.
  8. Yvonne Choquet-Bruhat, Cecile DeWitt-Morette, Margarete Dillard-Bleick, Analysis, Manifolds and Physics, Part 1: Basics (Elsevier Science B. V. Amsterdam, The netherland, 1977), Chapter V.
  9. Wald R M General Relativity (Chicago, IL: The Univ. of Chicago Press, 1984).
  10. Hawking S.W.; Ellis, G.F.R. The Large Scale Structure of Space–Time (Cambridge Monographs on Mathematical Physics Cambridge: University Press, 2011).
  11. Bardeen, J.M.; Press, W.H.; Teukolsky, S.A. Rotating Black Holes: Locally Nonrotating Frames, Energy Extraction, and Scalar Synchrotron Radiation. Astrophys. J. 1972, 178, 347–370. [CrossRef]
  12. Bardeen, J.M.; Carter, B.; Hawking S.W. The four laws of black hole mechanics. Commun. Math. Phys. 1973, 31 161–170.
  13. Babichev, E.O.; Dokuchaev, V.I.; Eroshenko, Y.N. Black holes in the presence of dark energy. Phys. Usp. 2013, 56, 1155–1175. [CrossRef]
  14. Dokuchaev, V.I. Spin and mass of the nearest supermassive black hole. Gen. Relat. Gravit. 2014, 46, 1832–1845. [CrossRef]
  15. Dokuchaev, V.I.; Eroshenko, Yu. N. Physical laboratory at the center of the Galaxy. Phys. Usp. 2015, 58, 772–784. [CrossRef]
  16. Dokuchaev, V.I.; Eroshenko, Yu. N. Weighing of the dark matter at the center of the Galaxy. JETP Lett. 2015, 101, 777–782. [CrossRef]
  17. Dokuchaev, V.I.; Nazarova, N.O. Gravitational lensing of a star by a rotating black hole. J. High Energy Phys. Lett. 2017, 106, 637–642. [CrossRef]
  18. Dokuchaev, V.I.; Nazarova, N.O. Star Motion Around Rotating Black Hole. 2017, Available online: https://youtu.be/P6DneV0vk7U. [CrossRef]
  19. Dokuchaev, V.I.; Nazarova, N.O. Event horizon image within black hole shadow. J. Exp. Theor. Phys. 2019, 128, 578–585. [CrossRef]
  20. Dokuchaev, V.I.; Nazarova, N.O.; Smirnov, V.P. Event horizon silhouette: Implications to supermassive black holes in the galaxies M87 and Milky Way. Gen. Relat. Gravit. 2019, 51, 81. [CrossRef]
  21. Dokuchaev, V.I.; Nazarova, N.O. The Brightest Point in Accretion Disk and Black Hole Spin: Implication to the Image of Black Hole M87*. Universe 2019, 5, 183. [CrossRef]
  22. Dokuchaev, V.I. To see the invisible: Image of the event horizon within the black hole shadow. Int. J. Mod. Phys. D 2019, 28, 1941005. [CrossRef]
  23. Dokuchaev, V.I.; Nazarova, N.O.Infall of the star into rotating black hole viewed by a distant observer. 2019. Available online: https://youtu.be/fps-3frL0AM.
  24. Wheeler, J.A. Geometrodynamics, Academic Press: New York, NY, USA, 1962; 334p.
  25. Morris, M.S.; Thorne, K.S. Wormholes in spacetime and their use for interstellar travel: A tool for teaching general relativity. Am. J. Phys. 1988, 56, 395-412. [CrossRef]
  26. Bičák, J.; Stuchlík, Z.; Balek V. The motion of the charged particles in the field of rotating charged black holes and naked singularities I. The general features of the radial motion and the motion along the axis of symmetry. Bull. Astron. Inst. Czech. 1989, 40, 65–92.
  27. Balek, V.; Bčák, J.; Stuchl/’ik, Z. The motion of the charged particles in the field of rotating charged black holes and naked singularities II. The motion in the equatorial plane. Bull. Astron. Inst. Czech. 1989, 40, 133-165.
  28. Grunau, S.; Kagramanova, V. Geodesics of electrically and magnetically charged test particles in the Reissner–Nordström spacetime: Analytical solutions. Phys. Rev. D 2011, 83, 044009. [CrossRef]
  29. Olivares. M.; Saavedra, J.; Leiva, C.; Villanueva, J.R. Motion of charged particles on the Reissner–Nordström (anti)-de Sitter black holes. Mod. Phys. Lett. A 2011, 26, 2923–2950.
  30. Hackmann, E.; Kagramanova, V.; Kunz, J.; Lämmerzahl, C. Analytical solution of the geodesic equation in Kerr-(anti-) de Sitter space-times. Phys. Rev. D 2010, 81, 044020.
  31. Pugliese, D.; Quevedo, H.; Ruffini, R. Circular motion of neutral test particles in Reissner–Nordström spacetime. Phys. Rev. D 2011, 83, 024021, 23pp. [CrossRef]
  32. Dokuchaev, V.I. Is there life inside black holes? Class. Quantum Grav. 2008, 28, 235015.
Preprints 91721 g001
Figure 1. Carter-Penrose diagram for the spherically symmetric Reissner–Nordstöm black hole with electric charge q = 0 . 99 . The spaceship starts from the point A at R + -region toward its multi-planetary future inside the black hole. The astronauts are planning to use the Einstein-Rosen bridge magenta curve) and intersect both the black hole event horizon r + and Cauchy horizon r + at finite their proper time. After appearing near the black hole singularity at r = 0 , the space ship uses its powerful engines to change the direction of motion and escape the tidal destruction at small radii. In result, the voyage is happily finishing at point B (may be at the Earth-like planet) in other infinite universe. The symmetry is in possibility to repeat the complete route of this voyage staring from the point B but only in the forward direction in time toward the another multi-planetary future. It is impossible to return back to the native Earth due to impossibility of any motion beyond the light cone. This is asymmetry of motion on the Einstein-Rosen bridge inside black hole.
Figure 1. Carter-Penrose diagram for the spherically symmetric Reissner–Nordstöm black hole with electric charge q = 0 . 99 . The spaceship starts from the point A at R + -region toward its multi-planetary future inside the black hole. The astronauts are planning to use the Einstein-Rosen bridge magenta curve) and intersect both the black hole event horizon r + and Cauchy horizon r + at finite their proper time. After appearing near the black hole singularity at r = 0 , the space ship uses its powerful engines to change the direction of motion and escape the tidal destruction at small radii. In result, the voyage is happily finishing at point B (may be at the Earth-like planet) in other infinite universe. The symmetry is in possibility to repeat the complete route of this voyage staring from the point B but only in the forward direction in time toward the another multi-planetary future. It is impossible to return back to the native Earth due to impossibility of any motion beyond the light cone. This is asymmetry of motion on the Einstein-Rosen bridge inside black hole.
Preprints 91721 g001
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated