Prerpints.org logo
Preprint
Article

Coherent Off-Axis Terahertz Tomography with a Multi-Channel 2 Array and F-theta Optics

Altmetrics

Downloads

154

Views

51

Comments

1

A peer-reviewed article of this preprint also exists.

Submitted:

12 December 2023

Posted:

13 December 2023

You are already at the latest version

Alerts
Abstract
Terahertz tomography is a promising method among non-destructive inspection techniques to detect faults and defects in dielectric samples. Image quality recently significantly improved through the incorporation of a priori information and off-axis data. However, this improvement has come at the cost of increased measurement time. To aim toward industrial applications, it is therefore necessary to speed up the measurement by parallelizing the data acquisition employing multi-channel setups. In this work, we present two tomographic frequency-modulated continuous wave (FMCW) systems working at a bandwidth of 230-320 GHz, equipped with an eight-channel detector array, and compare their imaging results with a single-pixel setup. While in the first system, the additional channels are used exclusively to detect radiation refracted by the sample, the second system features an f-θ lens, focusing the beam at different positions on its flat focal plane, and thus utilizing the whole detector array directly. The usage of the f-θ lens in combination with a scanning mirror eliminates the necessity of the formerly used slow translation of a single-pixel transmitter. This opens up the potential for a significant increase in acquisition speed, in our case by a factor of four to five, respectively.
Keywords: 
Subject: Physical Sciences  -   Applied Physics

1. Introduction

Terahertz imaging is a versatile technique in the field of non-destructive testing and imaging [1,2,3]. Possible measurement scenarios include material characterization [4], layer thickness determination [5], as well as moisture and liquid detection [6], spanning various industry fields, such as automotive, aviation, polymers, petrochemicals, pharmaceutical industry, and many more [1,7,8]. Most imaging setups employ raster-like scanning from one side, either in transmission or reflection geometry, to create volumetric sample representations. If the sample under investigation features complex structures, optical effects can lead to image distortion, artifacts, and ambiguity of feature size. Additional challenges arise when attempting to image concealed areas obscured by these sample features. To inspect additively manufactured [9] or extruded plastic objects [10], such as pipes and window profiles, the application of terahertz transmission tomography [11,12,13] can help overcome these limitations of one-sided imaging approaches. The application of terahertz radiation in a tomographic configuration promises visual 3D scans of samples similar to what we know from X-ray tomographs but without the requirement of radiation protection measures. Additionally, unlike classic X-ray-based imaging methods, phase-sensitive coherent terahertz tomography detects the time-of-flight of the radiation, allowing a reconstruction of the complex refractive index. This can be beneficial, especially for low-absorbing materials, which do not lower the intensity of a passing signal significantly [14].
In a classical tomographic system using X-ray radiation, projections of an object are acquired by transmitting narrow collimated X-ray beams from various angles through the sample. The radiation travels in usually straight beam paths, allowing for convenient and fast reconstruction using the filtered back-projection algorithm (FBP). Terahertz radiation on the other hand has a significantly longer wavelength than X-ray radiation. Consequently, beam collimation leads to comparatively large beam diameters. To detect small features in the sample, one has to use quasi-optical approaches to focus the beam in the center of the imaging scene. Furthermore, the significantly lower photon energy of terahertz radiation in comparison to X-rays, leads to strong interactions between the radiation and the sample material. These interactions include reflection, refraction, and scattering as well as absorption and a change in the time-of-flight of the radiation. While the latter two are essential for the tomographic imaging principle, the former lead to a deviation of the terahertz beams from their originally straight beam paths. These optical effects, if not accounted for in the reconstruction scheme, result in image distortion and artifacts. To accomplish this, we designed a tomographic single-pixel setup featuring one transmitter and one independently moveable detector, allowing the detection of off-axis radiation deflected by the sample [15]. To be able to include the data from the off-axis measurements and additional a priori information about the sample in the reconstruction process, we implemented a flexible, iterative, and fast algorithm, the Conjugate Gradient Least Square reconstruction algorithm [14]. The imaging results can be observed in Figure 1 and [15].
These good reconstruction results from the off-axis data come at the cost of very long acquisition times since the entire detection plane must be raster-scanned for deflected radiation for each transmitter position. The acquisition time for the B-scan presented in Figure 1 is over 8 hours. Since acquisition times of this magnitude are not suitable for potential industrial applications, we propose the use of a multi-channel array to acquire multiple data points simultaneously and thus speed up the scanning process. In this work, we demonstrate the first terahertz tomography setup featuring an eight-channel detector array. To ensure that enough power enters the small detector aperture, creating high-contrast images with a good resolution, it is necessary to ensure a high-quality focused beam from the transmitter. Previous work has shown the influence of the beam shape on terahertz tomography, and the improvement of the depth-of-field using Bessel beams [16,17].
In our case, we equip the system with a telecentric f-θ lens, serving two purposes: Firstly, it creates a Gaussian beam focused in the center of the imaging scene, which delivers a trade-off between high image resolution and depth-of-field. Secondly, in combination with a rotary scanning mirror, the quasi-optical lens allows for a fast scan of the detector plane, addressing the full detector array only by rotating the mirror. All in all, this yields a significant increase in the scanning velocity.

2. Materials and Methods

The three setups covered in this work are depicted in Figure 3. The single-pixel setup (Setup 1, Figure 3(a)) features one transmitter and one receiver applying the frequency-modulated continuous wave (FMCW) principle to emit and detect terahertz radiation sweeping in a range from 230 to 320 GHz. They are equipped with Pickett-Potter horn antennas emitting a beam, which is collimated by a PTFE lens ( f = 50 m m ) and focused to the center of rotation by a second f = 200 m m lens. The lens configuration shapes the beam approximately into a Gaussian beam with a beam waist of w 0 = 5.2   m m . The receiver unit, which features the same lens setup, mixes the detected radiation with a local oscillator signal, coherently acquiring the signal amplitude and phase. This allows a determination of a sample’s full refractive index from the measured amplitude reduction and time delay of the signal. The single-pixel setup is described in more detail in [14,15]. In [15] we presented an algorithm to include a priori information and off-axis measurements in the tomographic reconstruction process. The latter requires time-costly scans of the whole detector plane, which have to be acquired by moving the single-pixel detector along the whole range of motion for every transmitter position and angle. To reduce this acquisition time, we developed Setups 2 and 3.
In Setup 2, displayed in Figure 3(b), the receiver unit is replaced with an eight-channel detector array, operating at the same frequency range as System 1 (230 to 230 GHz) [18]. A photograph of the eight-channel array is presented in Figure 2. Analogous to the single-pixel receiver in System 1, each channel features a Picket-Potter horn antenna, which channels the received terahertz signal to a subharmonic mixer fed secondly with a local oscillator signal stemming from the voltage-controlled oscillator in the transmitter. One local oscillator signal is sufficient to allow the simultaneous homodyne signal acquisition of eight detection channels. With this setup, we can potentially achieve an increase in measurement velocity by a factor of eight when acquiring scans of the whole detector plane. However, it still requires a stepped movement of the transmitter. To render this movement of the transmitter unnecessary and increase the imaging speed even further, we introduce a telecentric f- θ lens combined with a rotating scanning mirror, building up Setup 3.
Preprints 93147 g002
Figure 2. The detector array employed in Setup 2 and 3 features eight independent channels with one antenna and one homodyne mixer each. It is fed with a local oscillator signal and performs coherent detection of eight pixels simultaneously. The width of each antenna is 8 mm, so that the whole array spans 64 mm in total.
Figure 2. The detector array employed in Setup 2 and 3 features eight independent channels with one antenna and one homodyne mixer each. It is fed with a local oscillator signal and performs coherent detection of eight pixels simultaneously. The width of each antenna is 8 mm, so that the whole array spans 64 mm in total.
Preprints 93147 g002
Preprints 93147 g003
Figure 3. Tomographic setups compared in this work: (a) shows the single-pixel setup with single transmitter and receiver unit moveable independently from each other. Two lenses in front of the transmitter collimate and focus the beam in the center of the sample. The receiver features the same lens setup to improve detection. (b) The single receiver pixel is replaced by an 8-channel array increasing the number of acquired pixels at a time.To increase the resolution in the detection plane the array is moved in a step-wise fashion, and so is the transmitter as well. In (c) the necessity of moving the transmitter is circumvent with a combination of a scanning mirror and an f- θ lens replacing the focussing lens of the transmitter optics. The collimated beam is guided by the mirror onto the f- θ lens from different angles, leading to a parallel shift of the focused beam.
Figure 3. Tomographic setups compared in this work: (a) shows the single-pixel setup with single transmitter and receiver unit moveable independently from each other. Two lenses in front of the transmitter collimate and focus the beam in the center of the sample. The receiver features the same lens setup to improve detection. (b) The single receiver pixel is replaced by an 8-channel array increasing the number of acquired pixels at a time.To increase the resolution in the detection plane the array is moved in a step-wise fashion, and so is the transmitter as well. In (c) the necessity of moving the transmitter is circumvent with a combination of a scanning mirror and an f- θ lens replacing the focussing lens of the transmitter optics. The collimated beam is guided by the mirror onto the f- θ lens from different angles, leading to a parallel shift of the focused beam.
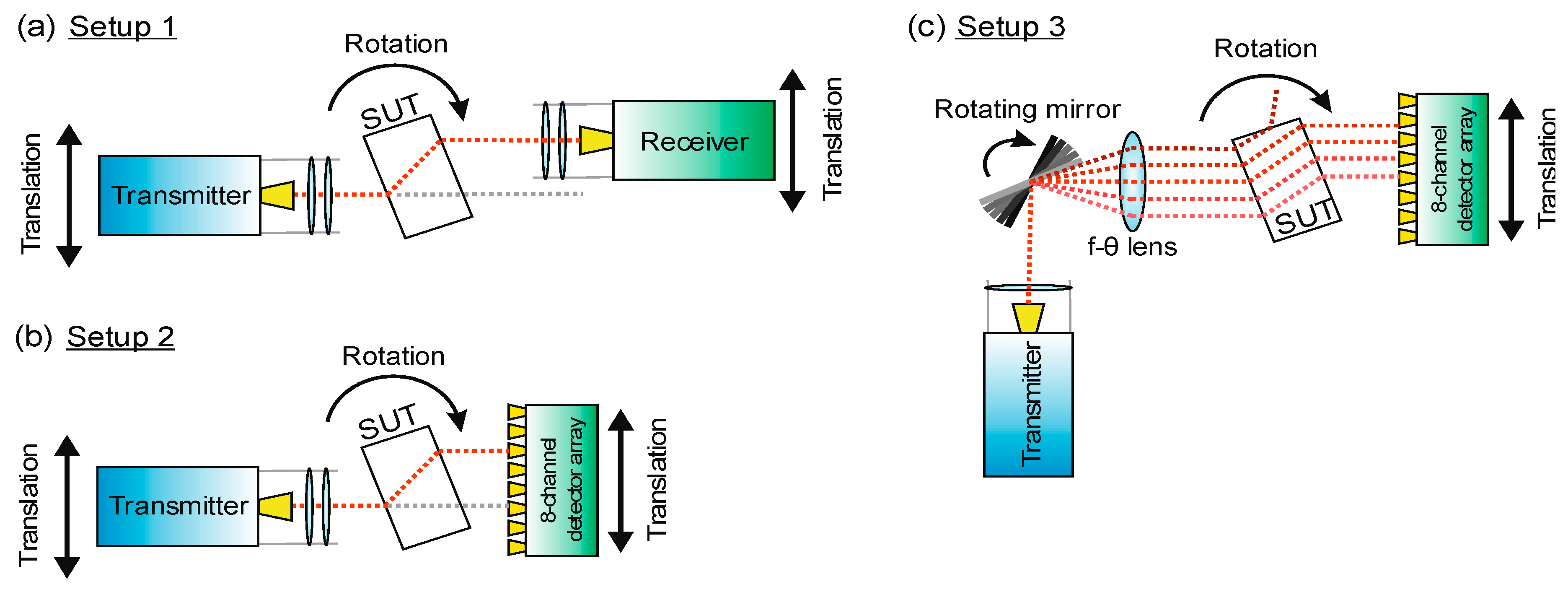
Preprints 93147 g003
Setup 3, shown in Figure 3(c), is designed to keep the transmitter at a fixed position, while still being able to scan the detector plane and address the eight channels of the receiver array quickly. Therefore, after leaving the transmitter, the terahertz beam is collimated and guided by the scanning mirror onto the f-θ lens. The lens design, which is covered in detail in section 2.1, is optimized to focus the beams in the rotational center of the setup. Thereby the incident angle θ , in which the beam enters the lens determines the distance of the focus point from the optical axis. This way, a translation of the focused beam along the detector plane can be achieved simply by turning the mirror, allowing the fast acquisition of a projection of the sample.
An important difference between Setup 1 and the following two setups is the lack of focusing optics in front of the detector array, which is difficult to implement due to limited physical space between the densely positioned array antennas. As a result, we expect less directivity of the detector pixels and ultimately a lowered resolution in the reconstructed images as a price to pay for the increased measurement speed.

2.1. Design of the f-θ optics

f-θ lenses are commonly used in many applications involving the displacement of a laser beam for scanning, engraving [20], optical coherence tomography (OCT) [21], or material processing applications. Unlike the common spherical lens, which has a curved focal plane, an f-θ lens provides a flat focal plane with low field curvature, a large field of view, and homogenous beam characteristics in the image plane throughout the entire scan field.
These objective lenses are increasingly applied in microwave and terahertz applications for 3D imaging [22], food safety inspection [23], non-destructive testing [24], etc. Thanks to the non-dispersive characteristics of the available lens fabrication material in terahertz and sub-terahertz, f-θ lenses are incorporated with various transmitters and receivers operating in this frequency region, such as FMCW radars with varying bandwidths [22,24,25] and TDS systems up to 1.25 THz [26].
In this work, the f-θ lens is designed and optimized for an effective focal length of f = 223   m m , a diameter of d = 102   m m , and a scan line of L m a x = 71   m m , as shown in Figure 4. It is fabricated out of high-density polyethylene (HDPE) using computer numerical control (CNC) milling. The scanning mirror moves θ = ± 4.5 ° , deflecting the beam onto the f-θ lens with 2 θ = ± 9 ° . The displacement of the probing beam from the optical axis is proportional to the incident angle θ :
L = 2 θ ⋅ f
Two objectives were the main criteria for the design of the lens:
  • Creating a flat focal plane with telecentricity in the image plane, which guarantees a normal incidence of the focused beam onto the sample.
  • Ensuring that the focus at each measurement point is as small as possible, ideally only limited by diffraction, and for the beam shape to be consistent throughout the mirror angles θ.
The lens design includes aspherical surfaces to eliminate geometrical aberrations. Before entering the f-θ lens, the beam is collimated using a f = 10   c m lens. The beam size after collimation has been measured to be approximately 32   m m . We assess the quasi-optical performance of the objective lens by validating the Gaussian beam propagation. To do so, we simulate the optical behavior of the f-θ lens with the optical design software Zemax, modeling the horn antenna and the collimating lens as ideal components.
In Figure 5, we compare raster scans of Gaussian beams created by the f-θ lens under incidence from different angles θ with a scan of the reference beam prduced by the standard PTFE focusing lens employed in Setup 1 and 2. The raster scan images in Figure 5 are acquired by moving the detector array stepwise along the beam axis and perpendicular to it. As expected, the beam focus lies in the origin of the diagram, the abscissa represents the direction of the beam propagation. The beam waist is defined by a decay of intensity to 1 / e 2 (indicated by the green lines in the figure) is consistent throughout the range of θ . With a values of around w 0 3 = 5.5   mm , the measured focus beam widths of the Gaussian beams leaving the f-θ lens are slightly wider than the beam width of the reference beam of w 0 1 , 2 = 5.2   mm (Figure 5(a)). As an example, we show three images of the beams for mirror angles between θ ( a ) = 3.5 ° and θ ( c ) = − 2.5 ° in Figure 5(b)-(d). The difference in beam width between the systems will presumably result in a lowered resolution in the reconstructed images. Especially for very excentric mirror positions, the beams tend to widen slightly before the focus ( X ≤ 0   m m ) in Figure 5(b) and (d). Nevertheless, for X ≥ 0   m m all beams show an intensity distribution, that is consistent with the Gaussian beam approximation with w 0 3 = 5.5   mm . This indicates, that the f-θ lens enables a scan of the imaging scene with beams focused in the imaging plane, that can be successfully described by the Gaussian beam model.
2.2 Image reconstruction process
The image reconstruction employed in this work has been discussed at length in [14], and the incorporation procedure of a priori information is covered comprehensively in [15]. Here, we will therefore only give a brief introduction to the aforementioned concepts. The reconstruction algorithm is based on the Conjugate Gradient Least Square algorithm (CGLS) [19]. It is a fast, versatile technique to approximate iteratively the solution to the inverse problem
A ⋅ x → = b →
In this case x → represents the unknown image vector and b → stands for the measured data acquired in the measurement process, also referred to as a sinogram. The matrix A models the path on which the probing beam of terahertz radiation travels through the imaging scene. When on this path r → , the beam interacts with an object, which has a refractive index of
n ~ = n + i n ″ ,
differing from the refractive index of air n ~ a i r ≈ 1 + 0 i . The time of flight (TOF) is directly proportional to the real refractive index
T = 1 c 0 ∫ n − n a i r d r → ,
whereas the relative intensity loss τ = I ( r → ) I 0 is according to Lambert-Beer’s law:
τ = exp ⁡ − ∫ 4 π n ″ f c 0 d r → .
Inserting the definition of the absorption coefficient α = 4 π n ″ f / c 0 , we can express the intensity loss in its logarithmic representation as:
τ l n = ln ⁡ τ = − ∫ α d r → .
Discretizing the imaging scene I → as a square area of p 2 pixels, (4) and (6) become
T B = 1 c 0 ∑ i ∈ B n ′ x i − n a i r x i = ∑ i ∈ I A → i ⋅ I → T ,
τ B = − ∑ i ∈ B α x i x i = ∑ i ∈ I A → i ⋅ I → τ .
Here x i represent the length of the path on which the beam B crosses pixel i . n and α are assumed to be constant within one pixel. The column vectors A → i of the matrix A are populated with the x i values, determining which pixels contribute to which beam to which extent. This way, by inserting the measured TOF values T B into the sinogram vector b → in (2), we can solve b → T = A ⋅ I → T for the real refractive index distribution I → T of the imaging scene, and b → τ = A ⋅ I → τ for the image showing the absorption coefficient, respectively.
The flexibility of the CGLS algorithm comes with the possibility to freely design the Matrix A . As it is explained thoroughly in [15], this opens up the opportunity to incorporate a priori information into the tomographic reconstruction process, allowing more precise modeling of the measurement process. While the above model of the interaction between the beam and the sample is based on the assumption that the probing beams had a vanishing diameter, it is in fact a Gaussian beam with a diameter relevant to the feature size of the objects (see Section 2.1). Ignoring this leads to significant distortions and reconstruction errors in the image [15]. We were able to incorporate the non-vanishing beam size into the matrix A by considering one beam as a combination of one-dimensional infinetly thin rays with different starting positions and directions (see Figure 6). This model describes the probing beam more accurately but preserves the linear relation between the sinogram values and the image pixels in (7) and (8).
The second set of a priori information we consider in the reconstruction process is the shape of the sample and its refractive index. In the field of NDT, this is a relevant scenario, since the desired shape and material of a sample are often known a priori. Since the wavelength of the terahertz radiation in use is in the same order of magnitude as the features to be observed, optical effects occurring at the interfaces between the sample and the surrounding air can influence the beam propagation severely. These optical effects include refraction and reflection, which alter the beam propagation directions according to Snell’s law. Considering the outer boundaries of a sample as well as its refractive index, one can apply ray tracing to predict the ray paths on which the radiation travels through the imaging scene (see Figure 6).
Figure 6 displays, that for certain sample geometries and angles, the probing radiation can be deviated far from its originally straight paths. To be able, nevertheless, to consider the deviated radiation in the reconstruction process, we conduct off-axis measurements, i.e., a scan of the whole detector plane for deviated radiation. From the ray-tracing simulations, we determine the position of the highest intensity and include the values measured at this position in the reconstruction as described in [15]. While this procedure increases the quality of the reconstructed images, it renders the acquisition very time-consuming, when working with Setup 1, because one has to scan the whole detector plane stepwise or in a continuous movement for every transmitter position (and rotation angle). Hence, we developed Setup 2 and finally Setup 3 to reduce the acquisition time. The former facilitates the simultaneous acquisition of data at eight different positions in the detection plane. The latter allows a continuous acquisition at eight different positions in the detector plane, while the rotation of the mirror leads to scanning beams moving through the emitter plane.

3. Results

To test and compare the imaging capabilities of the three setups presented in Figure 3, we designed four samples, shown in Figure 7. The first three samples are made of Polyethylene (PE), which has a real refractive index of n P E = 1,52 and a very low absorption coefficent of α P E < 0.005   m m − 1 . While Sample 1 is a stepped wedge, Samples 2 and 3 have a rectangular base shape. Into Sample 3 we milled an obround hole. Sample 4 is a piece of a district heating pipe, consisting of four inner tubes made from plastic and a filling of porous foam. An outer layer of plastic protects the foam filling of the pipe. The outer layer has an undulating structure, so that its diameter ( c 1 in Figure 7 (c)) varies in a range between 137 mm and 143 mm. The specific materials used for production are protected intellectual property. We were able to determine the real refractive index of the tubes and outer layer as n 4 ≈ 1,6 . The absorption coefficent is approximately   α 4 ≈ 0.5   m m − 1 . The foam filling has an almost vanishing absorption coefficient and a real refractive index close to 1. Since it does not interact strongly with radiation in the terahertz range than air, its influence can be neglected. The dimensions of the samples are given in Table 1.
Figure 8 displays the images of the first sample, created with the three systems. Figure 8(a)-(c) shows the reconstructions of the absorption coefficient α from the intensity sinograms. Due to the low absorption coefficient of PE, the absorption occurring inside the sample is very limited. The changes in the measured intensity are dominated by optical effects occurring at the sample edges [15]. Consequently, even though the consideration of said effects a priori reduces their influence on the reconstruction images, the edges of the sample appear much too prominently in the reconstruction. This hinders a quantitative analysis of the object's absorption coefficient consistently throughout all three measurement setups. For Samples 2 and 3 we therefore refrain from presenting the reconstructions resulting from the intensity data. The images displayed in Figure 8(d)-(f) on the other hand clearly show the shape of Sample 1 and correctly determine the quantitive value of the real refractive index n of the sample. Between the images created with the different systems there are only subtle differences in reconstruction quality or resolution. The reconstruction acquired with System 2 (Figure 8(e)) shows stronger contrast than the other two. Especially in comparison with Figure 8(f) (System 3), it exhibits a slightly better resolution, due to the smaller focus of the probing beam.
The images of Samples 2 and 3 can be observed in Figure 9. All six images display the real refractive index n , reconstructed from the TOF of the radiation passing through the samples. Figure 9(a)-(c) correspond to Sample 2. All three systems reconstruct the shape of the sample correctly. The reconstructions created with Systems 2 and 3 (Figure 9(b) and (c)) appear sharper and the inner part is more uniform than in Figure 9(a). Quantitatively all three systems reconstruct the refractive index correctly. For Sample 3 (Figure 9(d)-(f)), System 1 produces the most accurate reconstruction. The image is sharper and the shape of the sample, especially the drilled-out hole is better visible than in the other reconstructions. Nevertheless, in all three images the shape of the sample and especially the difference in comparison to Sample 2 is distinguishable and so is the quantitative value of the real refractive index n of Sample 3.
Figure 10 shows the reconstructions of the district heating pipe (Sample 4). Figure 10 (a)-(c) display the absorption coefficient α of Sample 4 based on intensity projections, while Figure 10 (d)-(f) show the real refractive index n . In Figure 10(a) the shape of the pipe as well as the foam filling are clearly noticeable. Assumably, this is rather a result of the scattering properties of the foam, than its absorption. The four inner tubes are visible. In the case of the two larger tubes, one can also distinguish the air core from the wall. For the smaller tubes on the other hand the inner wall is reconstructed as one dark spot, appearing as highly absorbing. Again, this is the result of scattering and strong refraction of the beams in the small tube core. The artifacts resembling an interference pattern are the cause of multiple reflections between the tubes.
The same effect can be observed between the inner tubes in Figure 10(b). However, here all four air cores of the inner tubes are distinguishable from the tube walls. Also, the contrast of the image seems to be higher than in Figure 10(a). In the reconstruction acquired with System 3 (Figure 10(c)), four tubes are detectable as well, the air cores of the two biggest tubes being distinguishable. The artifacts between the tubes are reduced, and the outer tube and the foam are visible. Overall, the resolution is lower in Figure 10(b) and (c) due to the aforementioned lack of focusing optics for the detector array. The same holds for the reconstructions of the real refractive index n . Even though Figure 10(d)-(f) are less detailed than their counterparts based on the intensity projections, all four tubes are identifiable in the images. In Figure 10(d), the reconstruction acquired with System 1, the inner and outer walls of the tubes are visible, as well as the general shape of the pipe. In Figure 10(e) and (f) strong artifacts of the inner tubes govern the reconstructions. Nevertheless, in Figure 10(e) the air cores are again visible for all four tubes, and their shape is reconstructed more accurately than in Figure 10(b). In Figure 10(f) there are strong artifacts between the tubes, whose cores are barely visible.
The benefits of Setups 2 and 3 become evident when considering the acquisition times of the sinograms the shown images are reconstructed from. Using the detector array we reduce the measurement time by a factor of four, combining it with the scanning mirror and the f-θ optics, we can measure even five times as fast in comparison with Setup 1.

4. Discussion and Outlook

Overall, System 1 delivers the best reconstruction images. This can be observed mainly in Figure 9(d)-(f) and Figure 10 (Samples 3 and 4). Its main advantage is the focus optics in front of the detector, which yield a decrease in the effective detection aperture below the antenna’s physical aperture and a displacement into the center of the setup. In Setup 2 and 3, limited physical space resulting from the high receiver density, the small aperture of the detecting antennas, and the comparably large wavelength render the implementation of focusing optics very challenging. The design of quasi-optical elements reducing the effective aperture of the detector array is currently subject to further investigation and could pave the way to eliminating the shortcomings of the newly designed setups.
Another reason for the lower image quality of Samples 3 and 4 is the fact, that for these two samples, the amount of a priori information incorporated in the reconstruction, is lower than for Samples 1 and 2. The inner structure of the samples is not part of the ray tracing simulations. This excludes the drilled-out defects or inner pipes in Samples 3 and 4. The resulting deviations of the beam paths from simulated ones, lead to the blurring of the reconstructed image when acquired with the low aperture detector array.
Comparing Systems 2 and 3, we generally observe a decrease in contrast and resolution when employing the f-θ lens, again, especially for Samples 3 and 4. The reason for this must be the focusing capability of the f-θ lens, which marks the only difference between the two systems. Figure 5 displays the increased focus beam width, and that for large angles θ , i.e. configurations for which the probe beam is displaced fairly far from the optical axis, the beam quality decreases before the focus. Since this part of the beam is where the first interaction with the sample occurs, optical effects like refraction can alter the beam paths strongly from the trajectories predicted in the ray tracing simulations. This, in turn, lowers the resolution of the reconstructed image.
Currently, we are aiming towards building a setup, which applies a SiGe-MMIC multi-channel array not only in the detector plane but also as a transmitter unit. We already performed promising preliminary measurements with a system featuring two multi-channel arrays [27,28,29]. The system could potentially allow the elimination of any mechanical movement (other than rotating the sample), but the high density and the resulting small aperture of the transmitting antennas lead to strongly diverging emitter characteristics and suboptimal resolution. One solution might be digital beamforming [30] to re-establish the directivity of the beams. This could even pave the way to shaping the beam to a Bessel or Airy shape if desired [16,31,32].

5. Conclusions

In this work, we present two novel terahertz tomography setups featuring an eight-channel detector array. To the authors’ knowledge, they are the first tomography setups, which allow the simultaneous acquisition of eight sinogram or off-axis measurement pixels in the terahertz range. This allows for an increase in acquisition speed by a factor of four or even five if combined with an f-θ lens, and therefore marks a large step towards the applicability of terahertz tomography in an industrial context. Especially if 3D representations of the sample, such as the one of Sample 4 in Figure 11 are desired, an increase of measurement speed is crucial. In the current configuration of the systems, this increase comes at the cost of a minor loss in resolution and detail in the reconstructed image.
All in all, each evolution of the systems presented in this work accounts for a slight decrease in imaging quality as the trade-off for an increase in measurement speed. On the other hand, the designs of Setup 2 and 3 mark important steps towards the conceptualization of a stationary setup, based on two chip-based multi-channel arrays, which render mechanical movements of transmitter and receiver unnecessary. With this work, we lay the ground for much simpler, faster, and more robust system designs. With the systems presented here and the vision of relying more and more on fully integrated electronic arrays, we are confident to make terahertz tomography ready for the industrial market in the near future.

Author Contributions

Conceptualization, K.H.M. and F.F.; methodology, K.H.M., S.M. and F.F.; software, K.H.M., validation, K.H.M. formal analysis, A.K. and K.H.M..; investigation, K.H.M.; resources, S.M. and F.F.; data curation, S.M. and K.H.M.; writing—original draft preparation, K.H.M.; writing—review and editing, K.H.M., S.M., A.K., G.F. and F.F.; visualization, K.H.M.; supervision, A.K., G.F. and F.F.; project administration, K.H.M. and F.F. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are contained within the article.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Nüßler, D.; Jonuscheit, J. Terahertz Based Non-Destructive Testing (NDT): Making the Invisible Visible. tm - Technisches Messen 2021, 88, 199–210. [Google Scholar] [CrossRef]
  2. Amenabar, I.; Lopez, F.; Mendikute, A. In Introductory Review to THz Non-Destructive Testing of Composite Mater. J Infrared Milli Terahz Waves 2013, 34, 152–169. [Google Scholar] [CrossRef]
  3. Wang, Q.; Xie, L.; Ying, Y. Overview of Imaging Methods Based on Terahertz Time-Domain Spectroscopy. Applied Spectroscopy Reviews 2021, 1–16. [Google Scholar] [CrossRef]
  4. Barowski, J.; Zimmermanns, M.; Rolfes, I. Millimeter-Wave Characterization of Dielectric Materials Using Calibrated FMCW Transceivers. IEEE Trans. Microwave Theory Techn. 2018, 66, 3683–3689. [Google Scholar] [CrossRef]
  5. O’Hara, J. F.; Withayachumnankul, W.; Al-Naib, I. A Review on Thin-Film Sensing with Terahertz Waves. J Infrared Milli Terahz Waves 2012, 33, 245–291. [Google Scholar] [CrossRef]
  6. Federici, J. F. Review of Moisture and Liquid Detection and Mapping Using Terahertz Imaging. J Infrared Milli Terahz Waves 2012, 33, 97–126. [Google Scholar] [CrossRef]
  7. Naftaly; Vieweg; Deninger. Industrial Applications of Terahertz Sensing: State of Play. Sensors 2019, 19, 4203. [Google Scholar] [CrossRef] [PubMed]
  8. Ellrich, F.; Bauer, M.; Schreiner, N.; Keil, A.; Pfeiffer, T.; Klier, J.; Weber, S.; Jonuscheit, J.; Friederich, F.; Molter, D. Terahertz Quality Inspection for Automotive and Aviation Industries. J Infrared Milli Terahz Waves 2020, 41, 470–489. [Google Scholar] [CrossRef]
  9. Perraud, J. B.; Obaton, A. F.; Bou-Sleiman, J.; Recur, B.; Balacey, H.; Darracq, F.; Guillet, J. P.; Mounaix, P. Terahertz Imaging and Tomography as Efficient Instruments for Testing Polymer Additive Manufacturing Objects. Appl. Opt. 2016, 55, 3462. [Google Scholar] [CrossRef]
  10. Fosodeder, P.; Hubmer, S.; Ploier, A.; Ramlau, R.; van Frank, S.; Rankl, C. Phase-Contrast THz-CT for Non-Destructive Testing. Opt. Express 2021, 29, 15711. [Google Scholar] [CrossRef]
  11. Wang, S.; Zhang, X.-C. Pulsed Terahertz Tomography. J. Phys. D: Appl. Phys. 2004, 37, R1–R36. [Google Scholar] [CrossRef]
  12. Guillet, J. P.; Recur, B.; Frederique, L.; Bousquet, B.; Canioni, L.; Manek-Hönninger, I.; Desbarats, P.; Mounaix, P. Review of Terahertz Tomography Techniques. J Infrared Milli Terahz Waves 2014, 35, 382–411. [Google Scholar] [CrossRef]
  13. Brahm, A.; Bauer, M.; Hoyer, T.; Quast, H.; Loeffler, T.; Riehemann, S.; Notni, G.; Tunnermann, A. All-Electronic 3D Computed THz Tomography. In 2011 International Conference on Infrared, Millimeter, and Terahertz Waves; IEEE: Houston, TX, USA, 2011; pp. 1–2. [Google Scholar] [CrossRef]
  14. May, K. H.; Keil, A.; Von Freymann, G.; Friederich, F. The Conjugate Gradient Least Square Algorithm in Terahertz Tomography. IEEE Access 2021, 9, 142168–142178. [Google Scholar] [CrossRef]
  15. May, K. H.; Keil, A.; Von Freymann, G.; Friederich, F. A Priori Information and Off-Axis Measurements in Terahertz Tomography. IEEE Access 2023, 11, 18311–18325. [Google Scholar] [CrossRef]
  16. Wang, D.; Li, B.; Rong, L.; Xu, Z.; Zhao, Y.; Zhao, J.; Wang, Y.; Zhai, C. Extended Depth of Field in Continuous-Wave Terahertz Computed Tomography Based on Bessel Beam. Optics Communications 2019, 432, 20–26. [Google Scholar] [CrossRef]
  17. Busch, S. F.; Town, G. E.; Scheller, M.; Koch, M. Focus Free Terahertz Reflection Imaging and Tomography with Bessel Beams. J Infrared Milli Terahz Waves 2015, 36, 318–326. [Google Scholar] [CrossRef]
  18. May, K. H.; Keil, A.; Freymann, G. V.; Friederich, F. A.; Freymann, G. V.; Friederich, F. A Multi-Channel Terahertz Tomography Setup. In 2023 48th International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz); IEEE: Montreal, QC, Canada, 2023; pp. 1–2. [Google Scholar] [CrossRef]
  19. Björck, Å. Numerical Methods for Least Squares Problems; SIAM Soc. for Industrial and Applied Mathematics: Philadelphia, Pa, 1996. [Google Scholar]
  20. Araki, T.; Hirai, T.; Kyotani, T. Development of F-Theta Lens for UV Lasers. SEI Tech. Rev. 2009, 69, 59–65. [Google Scholar]
  21. McKenna, J. Notable Advances in Photonics: The JOPT Highlights of 2016. J. Opt. 2017, 19, 040401. [Google Scholar] [CrossRef]
  22. Mohammadzadeh, S.; Keil, A.; Leuchs, S.; Krebs, C.; NuBler, D.; Seewig, J.; Friederich, F. Hand-Guided Mobile Terahertz 3D Imaging Platform with Aspherical Telecentric f-θ Optics. In 2021 18th European Radar Conference (EuRAD); IEEE: London, United Kingdom, 2022; pp. 377–380. [Google Scholar] [CrossRef]
  23. Jansen, C.; Wietzke, S.; Peters, O.; Scheller, M.; Vieweg, N.; Salhi, M.; Krumbholz, N.; Jördens, C.; Hochrein, T.; Koch, M. Terahertz Imaging: Applications and Perspectives. Appl. Opt. 2010, 49, E48. [Google Scholar] [CrossRef]
  24. Mohammadzadeh, S.; Friederich, F. Design of a Quasioptical Scanning System for a Fast Mobile FMCW Terahertz Imaging System. J. Phys.: Conf. Ser. 2020, 1537, 012017. [Google Scholar] [CrossRef]
  25. Mohammadzadeh, S.; Klier, J.; Seewig, J.; Freymann, G. V.; Friederich, F. Ultra-Wideband Terahertz 3D Imaging with Aspherical Telecentric f-θ Optics. In 2023 48th International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz); IEEE: Montreal, QC, Canada, 2023; pp. 1–2. [Google Scholar] [CrossRef]
  26. Harris, Z. B.; Khani, M. E.; Arbab, M. H. Terahertz Portable Handheld Spectral Reflection (PHASR) Scanner. IEEE Access 2020, 8, 228024–228031. [Google Scholar] [CrossRef] [PubMed]
  27. Nüßler, D.; Friederich, F. Terahertz Imaging Arrays for Industrial Inline Measurements. In 2022 52nd European Microwave Conference (EuMC); IEEE: Milan, Italy, 2022; pp. 36–39. [Google Scholar] [CrossRef]
  28. Hussung, R.; Keil, A.; Friederich, F. Handheld Millimeter Wave Imaging System Based on a Two-Dimensional Multistatic Sparse Array. In 2020 45th International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz); IEEE: Buffalo, NY, USA, 2020; pp. 1–2. [Google Scholar] [CrossRef]
  29. Hussung, R.; Mohammadzadeh, S.; Cibiraite-Lukenskiene, D.; Keil, A.; Friederich, F. Handheld Millimeter-Wave Imaging at Video Rates and Its Applications. In 2022 International Workshop on Antenna Technology (iWAT); IEEE: Dublin, Ireland, 2022; pp. 79–81. [Google Scholar] [CrossRef]
  30. Ntouni, G. D.; Merkle, T.; Loghis, E. K.; Tzeranis, G.; Koratzinos, V.; Skentos, N. D.; Kritharidis, D. Real-Time Experimental Wireless Testbed with Digital Beamforming at 300 GHz. In 2020 European Conference on Networks and Communications (EuCNC); IEEE: Dubrovnik, Croatia, 2020; pp. 271–275. [Google Scholar] [CrossRef]
  31. Lu, Y.; Jiang, B.; Lü, S.; Liu, Y.; Li, S.; Cao, Z.; Qi, X. Arrays of Gaussian Vortex, Bessel and Airy Beams by Computer-Generated Hologram. Optics Communications 2016, 363, 85–90. [Google Scholar] [CrossRef]
  32. Ntouni, G. D.; Merkle, T.; Loghis, E. K.; Tzeranis, G.; Koratzinos, V.; Skentos, N. D.; Kritharidis, D. Real-Time Experimental Wireless Testbed with Digital Beamforming at 300 GHz. In 2020 European Conference on Networks and Communications (EuCNC); IEEE: Dubrovnik, Croatia, 2020; pp. 271–275. [Google Scholar] [CrossRef]
Preprints 93147 g001
Figure 1. A priori information about the sample (a) outer outline and off-axis measurements of the time-of-flight including deflected radiation facilitates the (b) tomographic reconstruction of the refractive index.
Figure 1. A priori information about the sample (a) outer outline and off-axis measurements of the time-of-flight including deflected radiation facilitates the (b) tomographic reconstruction of the refractive index.
Preprints 93147 g001
Preprints 93147 g004
Figure 4. 3-dimensional representation of the Zemax ray tracing simulation of the telecentric f-θ lens and the rotating scanning mirror. The inlet shows the angle definitions at the mirror.
Figure 4. 3-dimensional representation of the Zemax ray tracing simulation of the telecentric f-θ lens and the rotating scanning mirror. The inlet shows the angle definitions at the mirror.
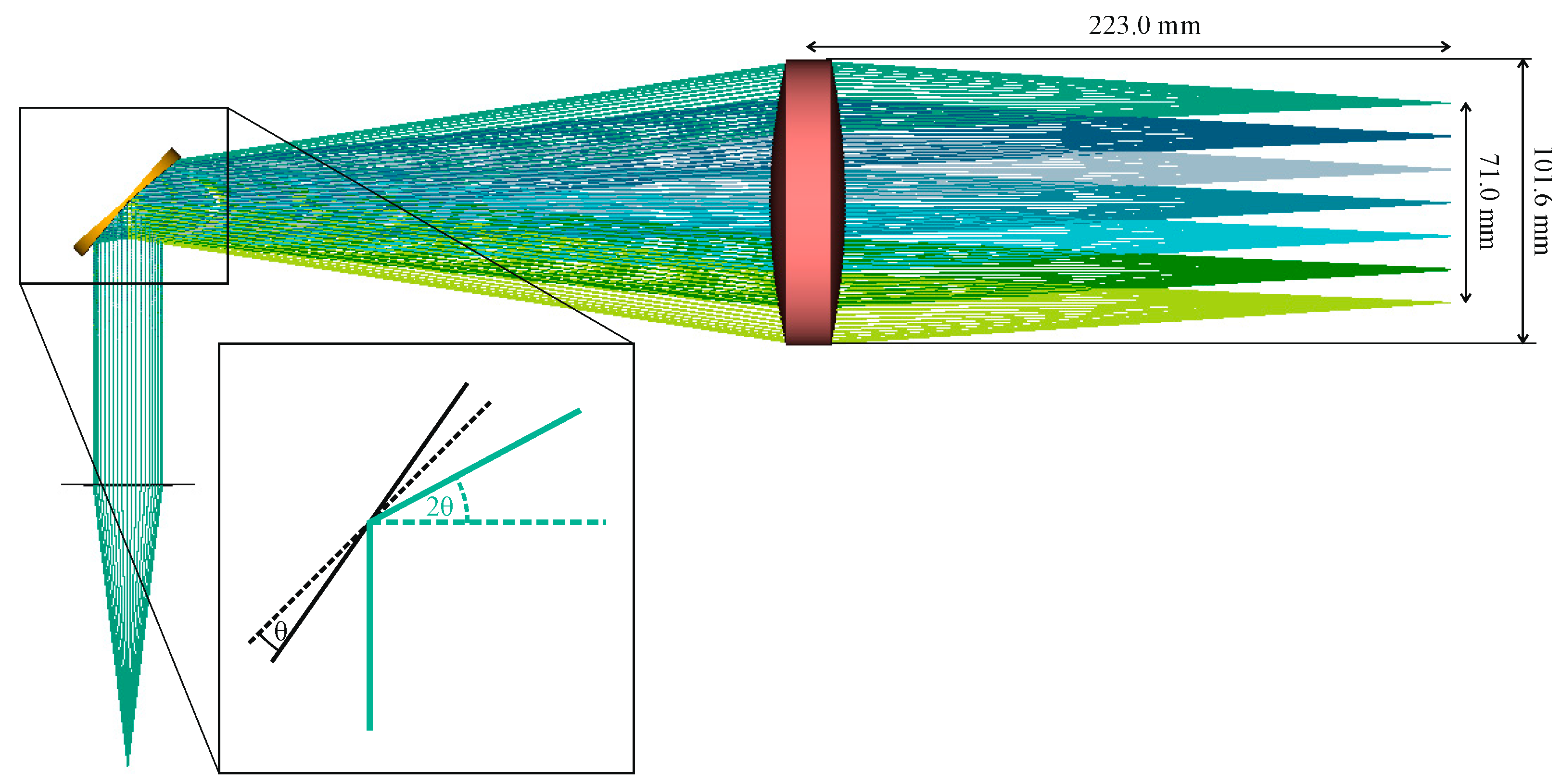
Preprints 93147 g004
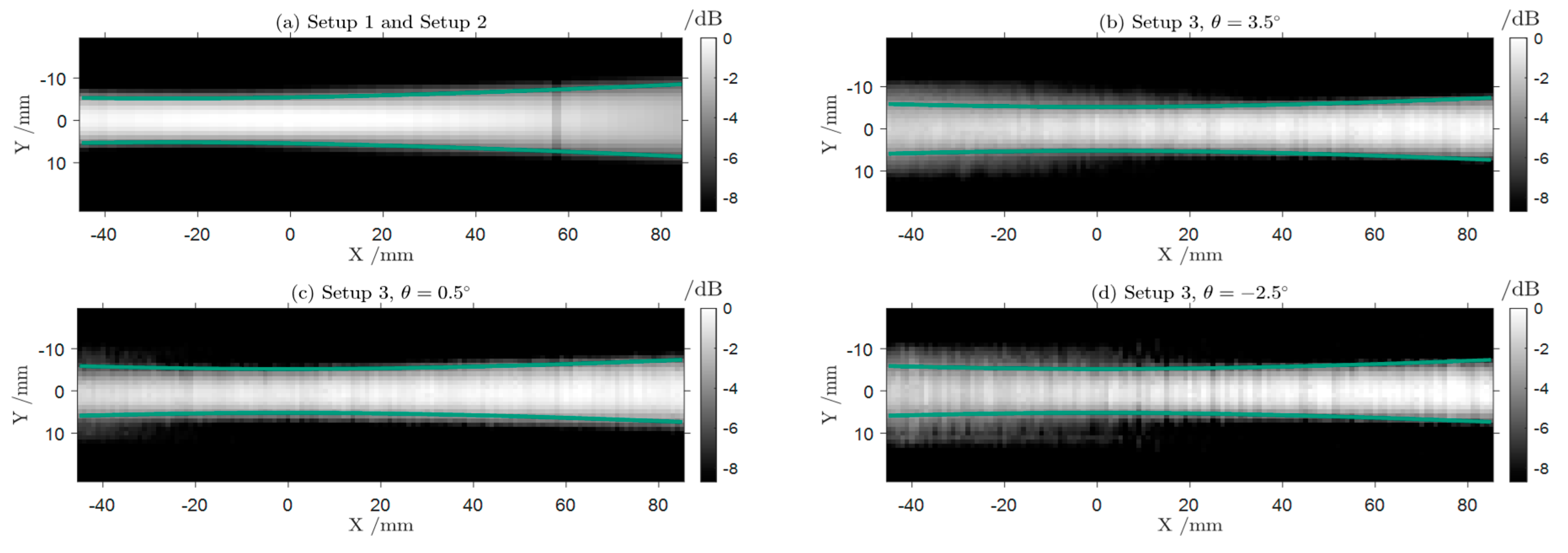
Preprints 93147 g005
Figure 5. X-Y scans of the beam intensities of the different systems. The green lines indicate the boundaries of a Gaussian beam (defined by an intensity decay to 1 / e 2 of the intensity on the beam axis) for a wavelength of λ = 1   m m fitted to the data. (a) represents the beam created with the standard biconvex lens employed in Setup 1 and 2. The beamwidth at the focus of the fitted Gaussian beam is w 0 1 , 2 = 5.2   mm . (b)-(d) Beam shaped by the f - θ lens at different mirror positions. In general the Gaussian beam is achieved, especially for positive X-values where the detector is positioned. The results of the fitted Gaussian beams indicate a consistent but slightly wider beam width of w 0 3 = 5.5   mm .
Figure 5. X-Y scans of the beam intensities of the different systems. The green lines indicate the boundaries of a Gaussian beam (defined by an intensity decay to 1 / e 2 of the intensity on the beam axis) for a wavelength of λ = 1   m m fitted to the data. (a) represents the beam created with the standard biconvex lens employed in Setup 1 and 2. The beamwidth at the focus of the fitted Gaussian beam is w 0 1 , 2 = 5.2   mm . (b)-(d) Beam shaped by the f - θ lens at different mirror positions. In general the Gaussian beam is achieved, especially for positive X-values where the detector is positioned. The results of the fitted Gaussian beams indicate a consistent but slightly wider beam width of w 0 3 = 5.5   mm .
Preprints 93147 g005
Preprints 93147 g006
Figure 6. Ray tracing simulation of a probing beam passing through a rectangular object. Including a priori information about the sample in the reconstruction process significantly improves the reconstruction.
Figure 6. Ray tracing simulation of a probing beam passing through a rectangular object. Including a priori information about the sample in the reconstruction process significantly improves the reconstruction.
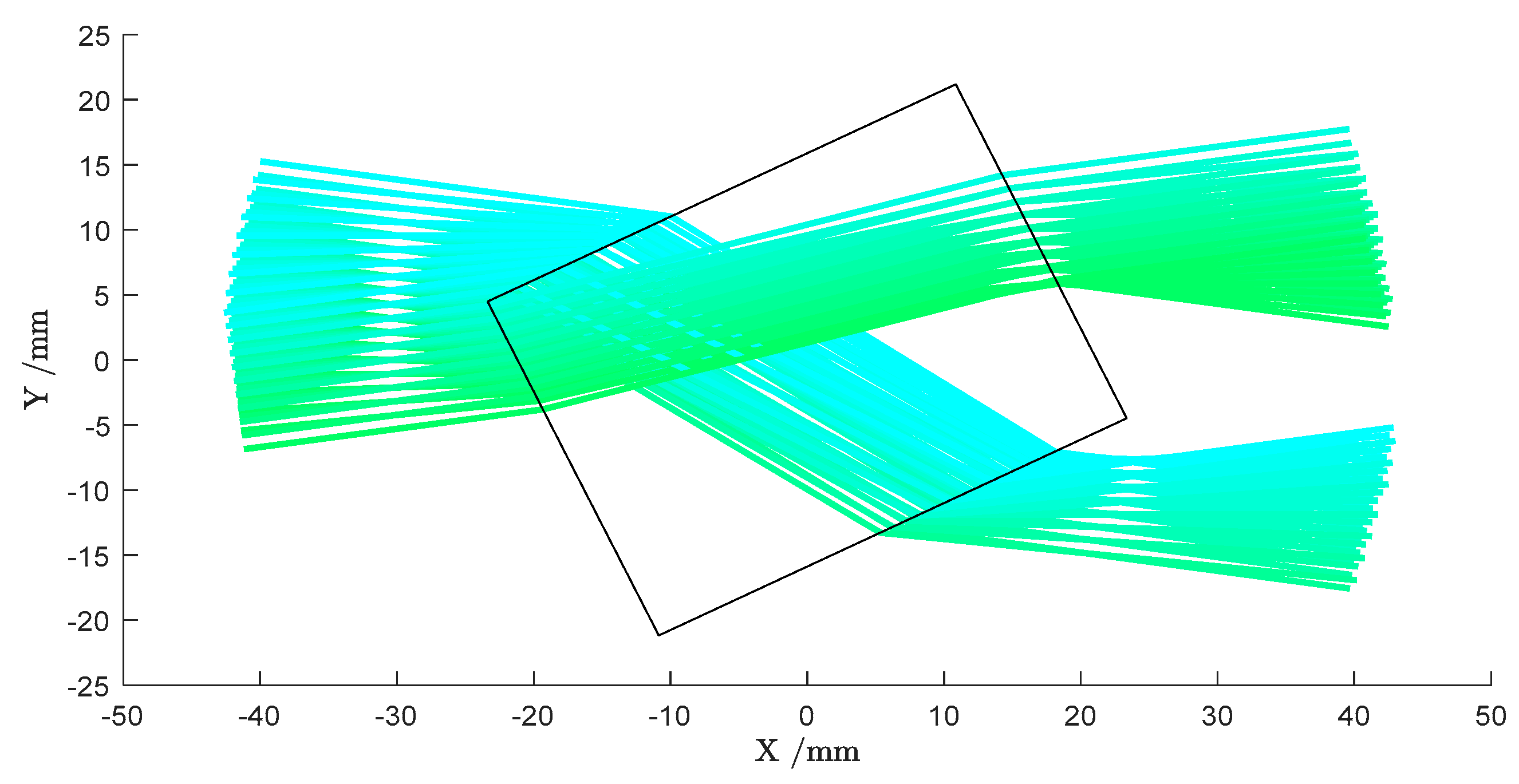
Preprints 93147 g006
Preprints 93147 g007
Figure 7. Samples 1-4 imaged in this work: (a) Sample 1: Stepwedge made from Polyethylen (PE), (b) Samples 2 and 3: PE cuboids, Sample 3 has a stadium-shaped drilled-out hole, (c) Sample 4: district heating pipe with four inner pipes. The indicated dimensions can be found in the table below.
Figure 7. Samples 1-4 imaged in this work: (a) Sample 1: Stepwedge made from Polyethylen (PE), (b) Samples 2 and 3: PE cuboids, Sample 3 has a stadium-shaped drilled-out hole, (c) Sample 4: district heating pipe with four inner pipes. The indicated dimensions can be found in the table below.
Preprints 93147 g007
Preprints 93147 g008
Figure 8. Reconstructions of Sample 1, (a)-(c) representing the absorption coefficent α and (d)-(f) the real refractive index n created with Systems 1, 2 and 3.
Figure 8. Reconstructions of Sample 1, (a)-(c) representing the absorption coefficent α and (d)-(f) the real refractive index n created with Systems 1, 2 and 3.
Preprints 93147 g008
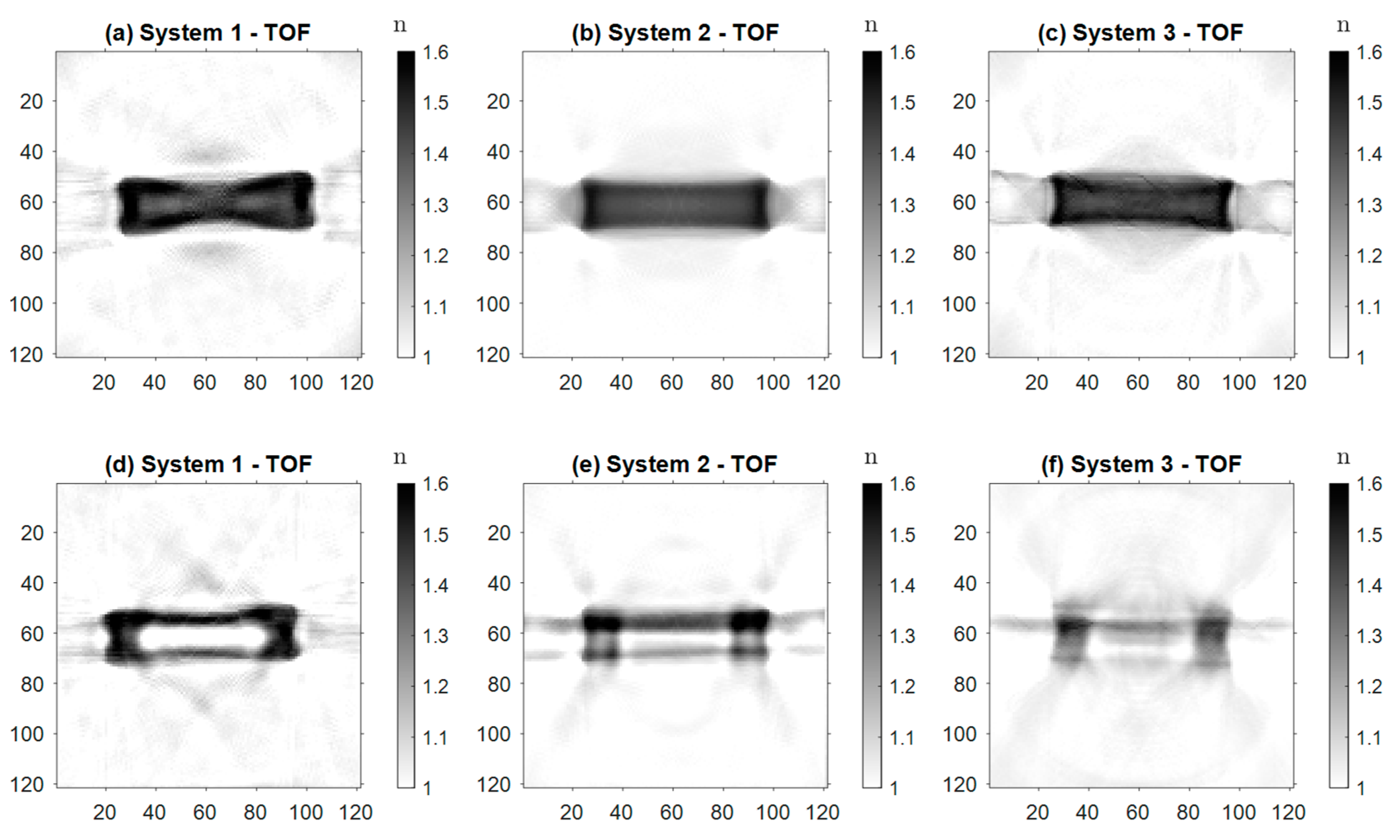
Preprints 93147 g009
Figure 9. Reconstructions of the real refractive index n (a)-(c) of Sample 2 and (d)-(f) of Sample 3, created with System 1, 2 and 3.
Figure 9. Reconstructions of the real refractive index n (a)-(c) of Sample 2 and (d)-(f) of Sample 3, created with System 1, 2 and 3.
Preprints 93147 g009
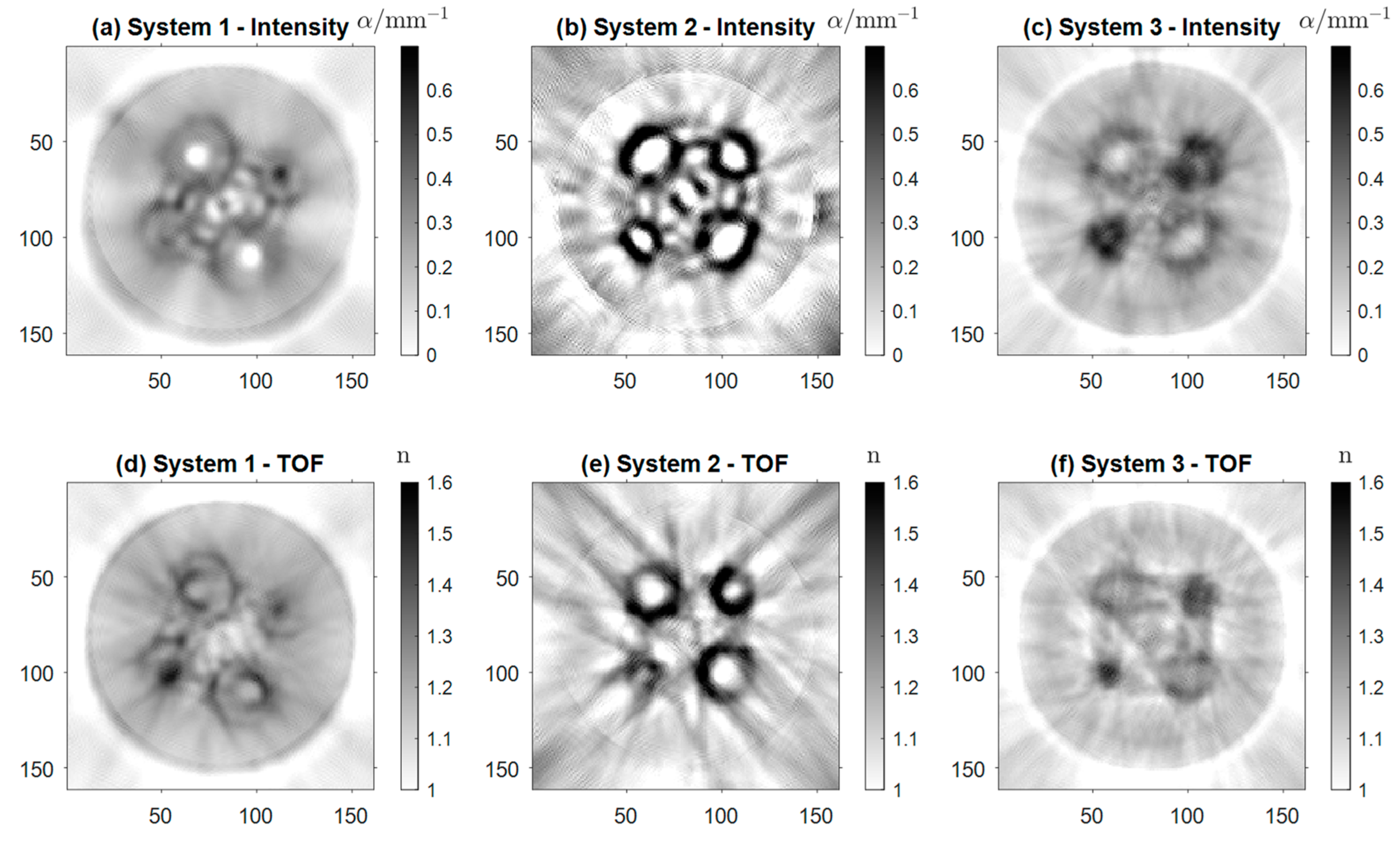
Preprints 93147 g010
Figure 10. Reconstructions of Sample 4, (a)-(c) representing the absorption coefficent α and (d)-(f) the real refractive index n created with Systems 1, 2 and 3.
Figure 10. Reconstructions of Sample 4, (a)-(c) representing the absorption coefficent α and (d)-(f) the real refractive index n created with Systems 1, 2 and 3.
Preprints 93147 g010
Preprints 93147 g011
Figure 11. 3D image created by vertically stacking multiple cross-sectional scans of Sample 4. Acquired with Setup 1.
Figure 11. 3D image created by vertically stacking multiple cross-sectional scans of Sample 4. Acquired with Setup 1.
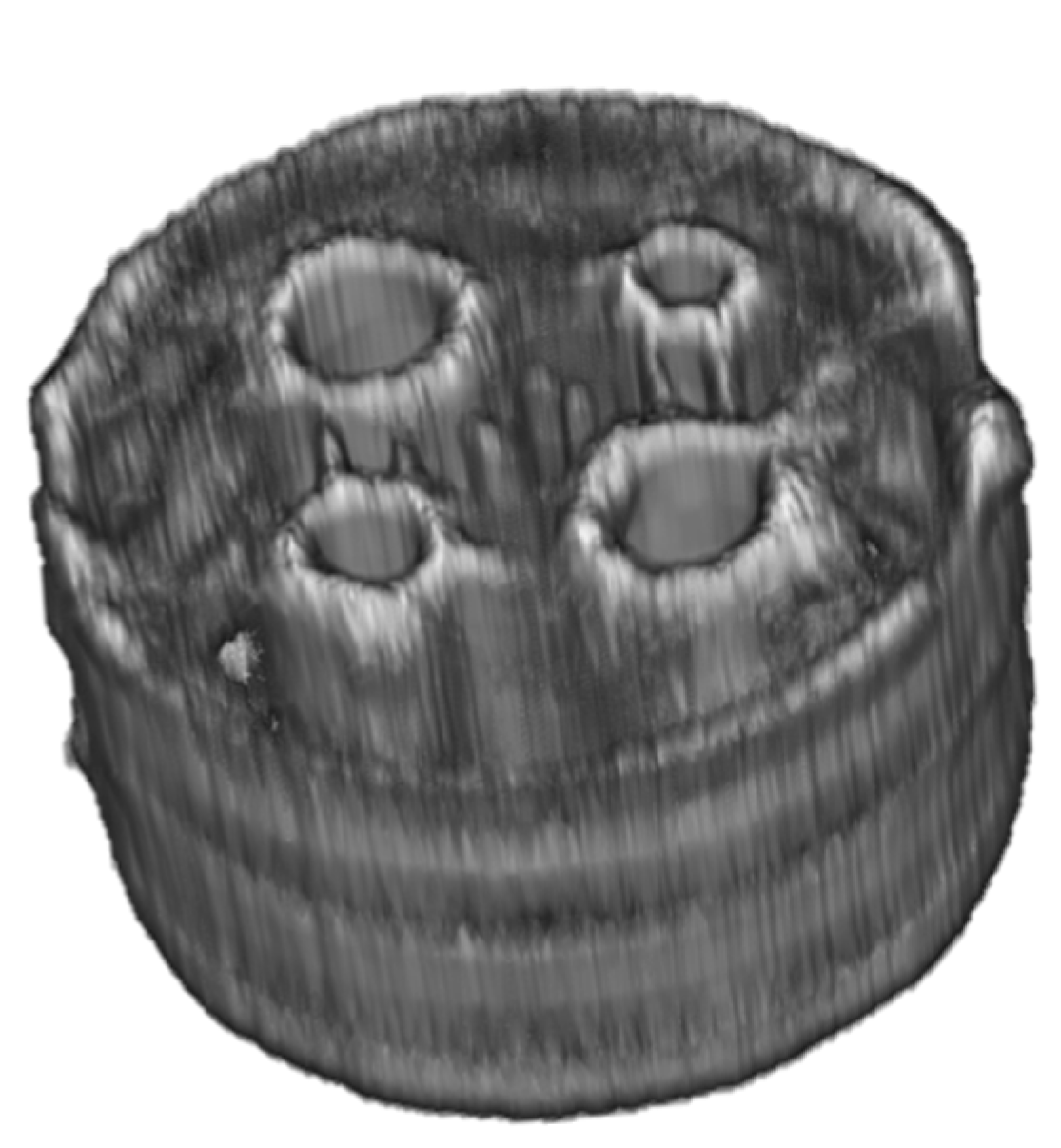
Preprints 93147 g011
Table 1. Sample dimensions as indicated in Figure 7.
Table 1. Sample dimensions as indicated in Figure 7.
Sample Dimension 1 Dimension 2 Dimension 3 Dimension 4
1 a 1 = 120   m m a 2 = 8   m m a 3 = 40   m m a 4 = 40   m m
2 & 3 b 1 = 75   m m b 2 = 20   m m b 3 = 50   m m b 4 = 10   m m
4 c 1 = 137 − 143   m m c 2 = 35   m m c 3 = 25   m m c 4 = 20   m m
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated