Prerpints.org logo
Preprint
Article

Vision-Based Concrete-Crack Detection on Railway Sleepers Using Dense U-net Model

Altmetrics

Downloads

123

Views

35

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

30 November 2023

Posted:

30 November 2023

You are already at the latest version

Alerts
Abstract
Crack inspection in railway sleepers is crucial for ensuring rail safety and avoiding deadly accidents. Traditional methods for detecting cracks on railway sleepers are very time-consuming and lack efficiency. Therefore nowadays, researchers are paying attention to the vision-based algorithm, especially Deep Learning algorithms. In this work, we adopted the U-net for the first time for detecting cracks on a railway sleeper and proposed a modified U-net architecture named Dense U-net for segmenting the cracks. In the Dense U-net structure, we established several short connections between the encoder and decoder blocks, which enabled the architecture to obtain better pixel information flow. Thus, the model extracted the necessary information in more detail to predict the cracks. We collected images from railway sleepers, processed them in a dataset, and finally trained the model with the images. The model achieved an overall F1-score, precision, Recall, and IoU of 86.5% 88.53%, 84.63%, and 76.31% respectively. We compared our suggested model with the original U-net, and the results demonstrate that our model outperformed the U-net in both quantitative and qualitative results. Moreover, we considered the necessity of crack severity analysis and measured a few parameters of the cracks (e.g., length, maximum width, area, density). The engineers must know the severity of the cracks to have an idea about the most severe locations and take the necessary steps to repair the badly affected sleepers.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

In South Korea traveling by train is one of the most convenient modes of transportation. A study shows that the railroads in South Korea cover a length of 3688 Km. A railroad commonly consists of steel rail, ballast bed, railway sleeper, railway fastener, and other parts of a railway track. Among all the components, the sleeper is a crucial component of a railway track. The principal roles of a railway sleeper include distributing loads of the trains from the steel rails to the ballast bed, reducing track movement, and stabilizing the track gauge during train travel, all of which assure safe travel for the train passengers. Timber sleepers, concrete sleepers, and to a lesser extent, steel sleepers reinforce polymeric sleepers that are commonly used on railway tracks. However, literature shows that concrete sleepers are mostly used (60%-80%) for several advantages in a railway network [1]. These concrete sleepers can be damaged in the form of cracks due to rain erosion, exposure to the sun, the reaction of salts in the earth with concrete sleepers, long-term navigation, an overload of trains, and so on. These cracks can introduce dangerous situations and can cause deadly accidents based on the daily loads of traffic and the severity of the cracks. So, crack detection at an early stage is essential to inspect and evaluate the structural health and serviceability of the concrete sleepers. over the years, manual inspection has been a common and traditional method for detecting cracks in concrete sleepers. However, manual inspection has blind spots, and it lacks both efficiency and accuracy. Moreover, this method is so time-consuming, more arduous, and expensive because, in this technique, the inspectors detect the cracks with only their human vision by roaming along the railway tracks. Besides these, the inspection performance can be varied from time to time based on the experience level of the inspector. Replacing the manual inspection with vision-based technologies can overcome these problems, and the sleeper cracks can be detected effectively. Recently, many advances have been made in the computer vision field. And the image-based techniques have already shown mesmerizing performance in other concrete structures like concrete pavement [2], buildings [3], tunnels [4], concrete bridges [5], etc. The image processing techniques make the concrete crack detection task fast and accurate. Therefore, utilizing the image processing methods will ensure automated sleeper crack detection and alleviate the personnel’s tedious and repetitive tasks. There are primarily two types of processing methods. The first method is to extract the features, remove the noises, and then implement classification. The image features are extracted by different types of feature extraction methods like wavelet transformation [6], Percolation methods [7], Otsu’s method [8], Morphological approach [9], etc. After extracting the features classification algorithms including support vector machine (SVM) [10], edge detector [11], decision tree [12] and others are employed to classify the cracks on the images. Traditional image processing methods must need to select the most relevant feature extraction approach. Even though numerous image feature extraction methods exist, there is no global feature extraction strategy to cope with images in various situations. As a result, a significant series of experiments or even novel feature extraction feature techniques must be devised to identify a suitable feature extraction approach for a specific situation. However, these methods fail to deal with images having complex patterns, extreme noises, and intensity inhomogeneity.
The other approach to image processing is utilizing the Deep Learning (DL) technology, especially the Convolutional Neural Network (CNN). CNN utilizes many hidden Neural Network (NN) layers to extract the underlying features automatically and classify the images. With the development of the AlexNet [13] using CNN in 2012, the advancement curve observed a huge surge in the field of computer vision. Following this, other CNN models with various depths have been designed. The classification was furthermore increased in 2014 by using the newly developed VGG [14], and GoogleNet [15] model. Understanding the advancement of the CNN model and considering the necessity of monitoring the cracks in concrete structures, including railway sleepers, researchers nowadays are more willing to use CNN models for detecting cracks. Zhang et al. introduced a Convolutional Neural Network (CNN) classifier in 2016 for detecting cracks in concrete structures [16]. The primary objective of this study was to develop a patch-based classifier for detecting cracks in concrete structures. After that, many other CNN models have been designed for solving crack image classification, detection, and segmentation tasks. Among the three types of solutions, crack segmentation has become the most popular research. Crack segmentation provides pixel-wise classification, where each of the pixels is classified as cracks or non-cracks. The predicted image from the CNN-based segmentation model highlights the cracks on the image and provides an idea about the cracks’ location and geometric shape. Furthermore, the segmented pictures can be utilized to extract a few key pieces of information (such as crack length, width, and area) that can estimate the severity of cracks in concrete sleepers. Though there are already many developed DL models and past research on utilizing CNNS to detect concrete cracks has generated significant results, only a few research studies have been conducted for segmenting cracks on railway sleepers using the CNNS. Despite a little research, there is still room to develop new methods to achieve higher accuracy and contribute to railway sleeper crack detection. So, in this paper, we utilize CNN to develop a Dense U-net model by modifying the original U-net architecture to detect cracks on the railway sleeper images. Moreover, we design an algorithm for quantifying the cracks. The following are the primary contributions of this research study.
  • Collecting railway sleeper images and processing them in the form of a dataset.
  • Proposing a modified U-net model for the first time to detect cracks on railway sleepers.
  • Quantifying the cracks of railway sleepers for knowing the severity of the cracks.
The remainder of this study is structured as follows: The existing crack detection techniques are briefly discussed in Section 2. Section 3 provides a concise overview of the methodology of this work. Section 4 shows as well as discusses the experimental procedure and evaluation result of crack detection on railway sleepers. Finally, Section 5 brings the paper to a conclusion.

2. Related Work

2.1. Vision Based Crack Detection Methods

Many vision-based crack identification methods have already been suggested for solving the problem of manual inspection in the case of detecting cracks on concrete structures. Early use of Computer Vision (CV) based techniques was limited to some traditional approaches. For example, Yamaguchi et al. utilized a percolation-based image processing approach to identify cracks in concrete. The authors focused not only on crack detection but also reduced the computation time by proposing termination and skip-added procedures [19]. Hoang et al. proposed a Min-Max Gray Level Discrimination (M2GLD) method to integrate with the Otsu method for detecting cracks in building structures. Their model also could find out a few crack characteristics, e.g., width, area, parameter[20]. Abdul Qader et al. investigated the effectiveness of four edge detection algorithms in finding cracks on concrete bridges. The authors claimed that the fast haar transform was the best among the four methods for detecting cracks [21]. Fujita et al. considered crack detection on noisy concrete structures. The authors used the subtraction pre-processing method for removing noise like shades and bad illumination conditions and introduced the Hessian matrix for differentiating the concrete cracks from the background [22]. Hutchison et al. presented a hybrid method based on the FHT algorithm and Canny edge detector for detecting cracks in concrete structures. The authors also calculated the parameters of the predicted cracks [23].
However, the primary limitation of these classical IPTs is that the techniques pay more attention to extracting local features rather than global properties like cracks of an image which may downgrade the detection task. So, to improve the crack detection task, researchers started combining classification methods with the classical IPTs. As a consequence, Jahanshahi et al. developed a unique approach based on morphological operations and classifier techniques. The morphological operator was used to extract the necessary features and the classifier algorithms classified real cracks [24]. Shi et al. presented a new framework name Crack-Forest based on Random Structured Forest for detecting cracks as well as characterizing the cracks on concrete roads [25]. Chun et al. presented a hybrid crack detection framework by combining a canny edge detector for extracting geometric features of the cracks and a supervised ML algorithm named Light Gradient Boosting Machine (LightGBM). The authors evaluated their framework by using photos containing cracks with adverse conditions [26].
In recent years Deep Learning (DL) models have outperformed classical CV-based techniques for detecting objects. Furthermore, DL models don’t need external feature learning; they can perceive features from a significant quantity of input data. Therefore, researchers are paying attention to detecting concrete cracks with more precision using DL algorithms. Cha et al. introduced a Convolutional Neural Network (CNN) classifier for the first time and a sliding window technique for detecting cracks in concrete structures. The authors tested the robustness of their model by predicting external images and showed that their model outperformed Sobel and Canny edge detection method [27]. Xu et al. presented a DL model by using a Restricted Boltzmann Machine (RBM) algorithm to detect cracks on bridge structures. The authors trained their model by the consumer-grade camera images and used a divergence learning algorithm for getting optimal parameters [28]. Chen et al. introduced a novel DL framework named NB-CNN by fusing Naive Bayes data with a CNN classifier for extracting cracks on a nuclear power plant from video frames. Their method could maintain the spatiotemporal video coherence and produce better results than LBP-SVM [29]. Maeda et al. presented a benchmark road crack dataset for the first time using smartphone images and used a CNN to classify eight types of cracks on road surfaces [30]. Deng et al. proposed the You Only Look Once (YOLO) version 2 model for locating cracks with bounding boxes on concrete structures. The model was able to distinguish cracks from handwritten scripts present in the concrete structure [31]. Hyuan et al. presented a method called Crack Deep Network (CrackDN) based on Faster Region CNN (Fast RCNN) to identify sealed and unsealed cracks having diverse backgrounds in pavement images. The authors extracted features by a Zeiler-Fragus Network (ZF-Net) based CNN embedded with a sensitivity network in parallel. Finally, they utilized a Region proposal Refinement Network (RPRN) for classifying the cracks [32]. However, these models can only classify and localize the cracks in a concrete structure instead of detecting cracks at pixel level.
Therefore among the DL models nowadays, encoder-decoder-based pixel-level crack detection models (i.e., FCN [33], U-net [34]) are becoming more popular for improving the detection accuracy as these models can extract the geometrical shape of the cracks along with localizing them. Li et al. proposed a novel encoder-decoder-based model called FCN for detecting cracks where the VGG19 model was used as the downsampler of the proposed FCN. After predicting the crack images, the authors also generated crack skeletons to measure morphological features [35]. Bang et al. proposed an FCN model based on the ResNet-152 encoder network for detecting pavement cracks from black-box camera images. The authors examined their model with transfer learning and without the transfer learning processes. However, Resnet-152 with transfer learning performed better [36]. Manjurul et al. proposed an FCN model using the VGG16 as an encoder network to detect cracks on concrete surfaces. The authors tested their model on a benchmark dataset and showed that their model obtained 10.93%, 20.93% improvement then the CNN and SVM model, respectively, in respect of the SA [37]. Liu et al. adopted U-net, which is another encoder-decoder-based network (the improved version of FCN) for the first time to detect cracks in concrete structures. The authors introduced the focal loss function for handling the class imbalance problem in their work [38]. Ji et al. also utilized the U-net model with zero paddings in their work for automatically detecting cracks in concrete structures. They trained the model using 200 images collected by an unmanned aerial vehicle and obtained better results than the Canny and Sobel method [39].
However, U-net models can also fall behind in predicting extremely narrow cracks and detecting cracks in adverse conditions. So, nowadays, researchers are continuously integrating different approaches with U-net to address these challenges. Yan et al. proposed a model called Res-Unet by incorporating residual connections to the original U-net for detecting cracks on the concrete bridge structures [40]. Chen et al. integrated a switch module named SWM with the U-net architecture to boost the running speed and reduce the computational complexity of U-net. The SWM model allows the pixel classification result obtained by the VGG13 encoder to be passed into the decode module if there is a crack; otherwise, it just discards the result to save the computation time [41]. Sun et al. considered the problem of detecting thin cracks with adverse environmental conditions in concrete structures. For this, the authors modified the U-net architecture by adding a Pyramid Pooling Module (PPM) into it, and the model successfully predicted the thin cracks [42]. Lin et al. proposed a U-net model with an attention mechanism to detect cracks on concrete structures. The authors utilized the attention gate module in three different fashions (i.e., Attention U-net, Advanced Attention U-net, and Full Attention U-net). They remarked that the full attention strategy was the best for detecting cracks with less computation complexity [43]. Augustauskas et al. improved the U-net model by adding residual blocks, an atrous spatial pyramid pooling module, attention gate module for detecting concrete cracks. The authors tested their model with a few datasets and showed by ablation study that the improved model outperformed U-net with no notable computational complexity [44].

2.2. Crack Detection on Railway Sleepers

Though there are many research works for detecting cracks on various concrete structures, there are not many equivalent works to detect cracks on railway sleepers. Rather vision-based techniques are employed to a lower extent for solving some other similar types of problems in railway industries. For example, Babenko et al. measured the rail gauge using a vision-based technique by including MACH filter [45]. Gilbert et al. presented a method by combining HoG features and SVM for detecting defective fasteners in railway tracks [46]. Mazeeo et al. employed a neural network classifier for detecting the presence of rail bolts (used for fastening the rail steel with sleeper) by using camera images [47].
Crack monitoring in rail tracks can be viewed from various perspectives, each with its own set of objectives. Gilbert et al. presented a machine vision system by adopting SVM for detecting cracks on railway joint bars. The authors developed such a system where they can detect cracks when the rail is moving at a speed of 70 mph as well as pass the detected image with GPS information to a host computer [48]. In a later work, the authors detect cracks on concrete sleepers by using iterative shrinkage and wavelet transformation [49]. Sajjad et al. detected cracks on not only wooden sleepers but also on concrete sleepers by utilizing a vision-based technique. However, as the authors developed the system based on a binary thresholding technique, it may lose robustness during environmental & illumination changes [50]. Delfourazi et al. proposed a crack detection method for railway sleepers using the template matching technique first to detect the concrete sleepers. Then, they use linear SVM and Radial-basis Function SVM (RBF-SVM) to classify the crack types on the sleepers. Numerical results showed that RBF-SV performed better [51]. Kim et al. proposed an advanced method using the Adaboost algorithm for detecting cracks on railway sleepers. Their algorithm identified the cracks with an identification rate of more than 90% [52]. Wang et al. proposed a two-stage algorithm for detecting cracks on concrete railway sleepers with less computation time. First, they used an edge detection technique called neighborhood range algorithm for selecting crack areas and then utilized CNN on top of it to successfully classify the crack types [53]. Xia et al. presented a novel framework named CF-NET based on the RetinaNet object detection framework to detect cracks with bounding boxes on railway sleepers [54].
The literature shows that already there are some remarkable DL-based research works for detecting cracks in different concrete structures. However, most crack detection systems for railway sleepers rely on traditional image processing techniques. Though there are a few CNN-based works, they can not detect cracks at a pixel level. To the best of the authors’ knowledge, no prior research work has utilized a DL model based on encoders and decoders to identify pixel-level cracks on railway sleepers. So, for the first time, in this work, we adopt U-net and propose a modified U-net architecture named Dense U-net for detecting railway sleeper cracks at a pixel level. Moreover, we also calculate a few parameters of the cracks (e.g., length, maximum width, area, density).

3. Methodology

The method we proposed in this study includes a supervised learning technique and a few morphological operations for detecting cracks at a pixel level on railway sleepers and analyzing the geometric patterns of the cracks from RGB images. The overall methodology of this work is divided into several steps, which are illustrated in Figure 1. The description of each phase is presented in the following subsections.

3.1. Dataset Description

The dataset we used in this study is images from a few railway sleepers collected from Busan station, South Korea. We captured 113 images with a resolution of 3500×2500 pixels by using a Sony a7r III mirrorless camera. As the resolution of the images is so high, it may increase the computational complexity, so we can not use the high-resolution images directly in the Deep Learning model. Furthermore, it is also not convenient to resize the images in some smaller resolutions because of maintaining the image quality. To overcome this issue, we split each image into nine different parts and got 1017 images. However, some images among these 1017 images do not contain sleepers. Instead, they contain the lab floor, bucket, and other noises. So we eliminated those images, and finally, our dataset included 660 images. Later we manually annotated our dataset for the segmentation task. Examples of a few images (original and the mask) of our utilized dataset are displayed in Figure 2.

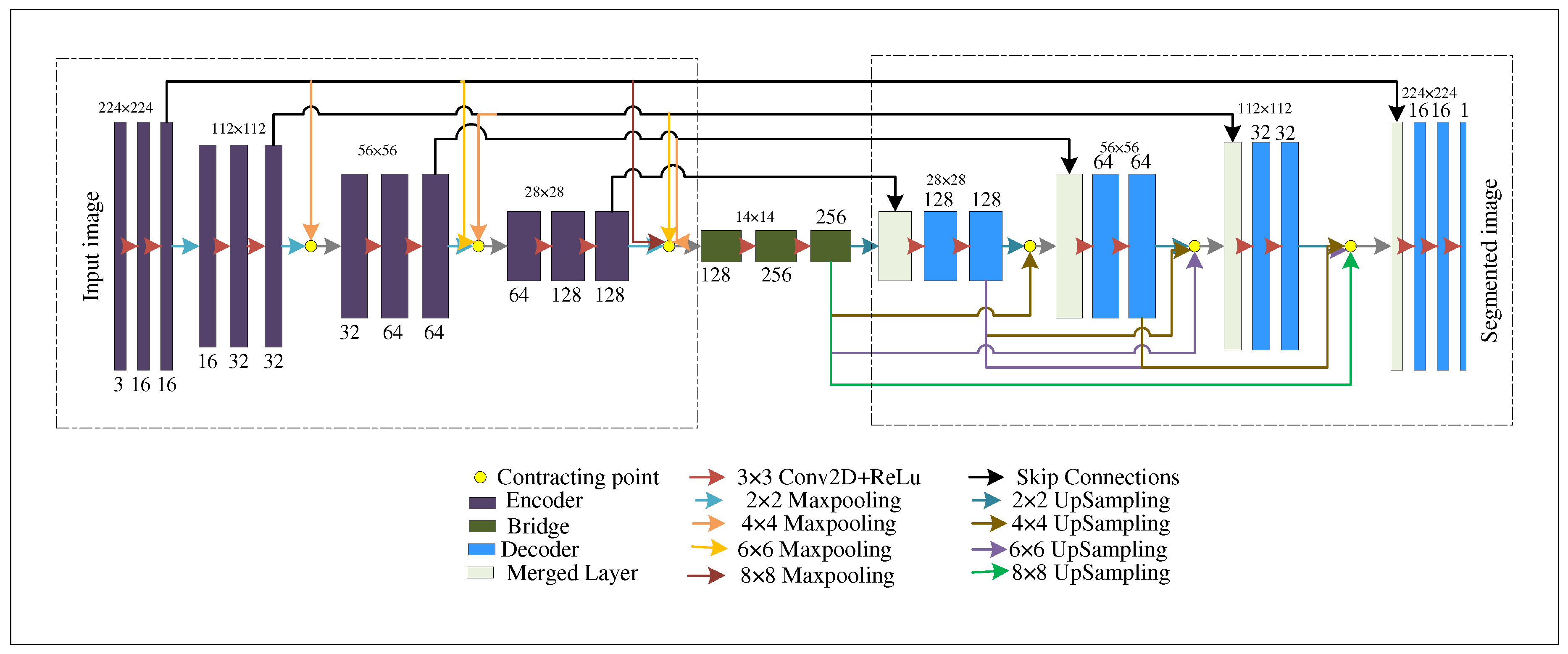
3.2. Model Architecture

This paper designed a railway sleeper crack detection system based on Ronneberger’s U-net architecture. U-net is a classic Encoder-Decoder [56] model where the Encoder part extracts necessary features of the images, and the decoder part of the model generates predicted images (exact resolution with input image) by combining the features extracted from the Encoder module. Unlike the FCN model, U-net architecture uses skip connections for maximum information flow from the Encoder to the Decoder module. To improve the result of the original U-net model, in this study, we proposed a Dense U-net model by combining the concept of both U-net and DenseNet [57] architectures. The architecture of the proposed Dense U-Net method is illustrated in Figure 3.
The Encoder module’s structure is shown in the left dotted box. The Encoder module consists of a total of 4 encoder blocks. Each of the Encoder blocks consists of two repeated convolution layers for extracting the features, followed by an activation function layer. We used a kernel size of 3×3 and the Rectified Linear Unit (ReLu) activation function throughout the architecture.
The convolution kernels traverse through the images and perform element-wise multiplication with the corresponding elements of the receptive fields. The mathematical equation of the convolution operation is as follows:
F ( p , q ) = ( A ∗ B ) ( p , q ) = ∑ c ∑ d A ( c , d ) B ( p − c , q − d )
where A is the input image, B is the filter, p, q denotes the rows, and the columns of the image, c, and d are loop controllers. After stacking the outputs from all of the kernels, the feature map function from a particular layer l can be achieved; which can be stated as follows:
v l = f ( b l + W l . z l − 1 )
f ( z ) = ReLu ( z ) = z , if z > 0 0 , otherwise
where v is the extracted feature, b denotes the bias vector, W denotes the weight matrix, z is the input from the previous layer. The utilized ReLu activation function converts the output values to z if z is a positive number, otherwise, the output is 0. The dimension of the extracted features can be calculated by utilizing the equation below:
( M , N , N c ) × ( f , f , f c ) = ( [ ( A + 2 p − f ) / S + 1 ] )
where, S=number of stride, p=number of padding, N c =number of channels, f c =number of filters, A is input image, f= size of the kernel. Finally, at the end of each Encoder block, we used a 2×2 Maxpooling layer to reduce the spatial dimensions of the feature maps to one-quarter in size. If a feature map has a dimension of N×1, then the Maxpooling will be
o j = m a x N × 1 { o i n × 1 d ( n , 1 ) }
where, d(n,1) is a window patch from the N×1 dimensional feature map and o j is the maximum value among the considered patch.
As the DenseNet model argued that short connections among the layers of a DL network improve the feature propagation, we established a few short linkages among the Encoder layers and the original contracting path. We designed the short connections in such a way so that an encoder block, as well as the bridge between the encoder and decoder module, can get the features produced by all of the previous encoder layers directly through the short connections. Mathematically, the e t h encoder layer E e is receiving the features of all the previous encoder layers, v E 0 , v E 1 ,...... v E e − 1 , as input:
v E e = C ( [ v E 0 , v E 1 , . . . . v E e − 1 ] )
where C denotes the concatenation of all the features from E 0 , E 1 , .... E e − 1 encoder layers. Before concatenation, we are reshaping the features from different encoder blocks in a particular spatial size using max pooling of different levels (see Figure 3). We are reshaping the features of different encoder blocks using multi-kernel max pooling (e.g., 2×2, 4×4, 6×6, 8×8 ), i.e., using multiple receptive fields. We are getting several sub-feature maps from the encoder blocks and capturing pixel information from multi-scale local ranges. As a result, while passing fine-grained low-level information to the proceeding encoder layers, a scale-invariant model is also being developed to share more pixel information. Moreover, the model can share information from multiple scales and increase the architecture’s robustness to extract essential redundant features for detecting cracks of different sizes.
The decoder module’s structure is shown in the right dotted box. The decoder module also consists of 4 decoder blocks. Each block in the decoder consists of a merged layer (see paste colored block in Figure 3), and then the structure contains two repeated 3×3 convolution blocks like the encoder. The merged layer includes two inputs: one is the feature map from the corresponding encoder layer (black arrow in Figure 3 ), and the other one is the concatenation (yellow circle in Figure 3 ) of the outputs of the previous encoder blocks. The merged layer also includes a bridge as we also construct the short linkages in the decoder module. Before concatenating, we upsampled the features from different blocks in the same spatial size. For example, the merged layer of the last block of the decoder module receives the feature map from the first encoder block, whose shape is 224×224×16. So the other input must be in the same shape. We upsampled the feature maps from all of the previous decoder blocks whose initial shapes were 14×14×256, 28×28×128, 56×56×64, 112×112×32 and converted them in the shape of 224×224×16 by using different upsampling levels. After getting the same size, we concatenate them and provide them as the second input of the merged layer. In this strategy, the decoder blocks are not only considering the feature maps of the corresponding encoder blocks but also use the feature maps of all the previous decoder blocks and the bridge. As a result, a better flow of pixel reconstruction has been established, and the U-net model has become more efficient. Finally, a 1×1 convolution has been utilized to categorize the "Crack" and the "Non-crack" pixels at the last layer.

3.3. Loss Function and Hyperparameters

The crack segmentation problem can be considered a class imbalance problem since the number of pixels containing cracks can be very low. Therefore, for handling the class imbalance problem during crack prediction, we have used the dice loss function [58] in this work. The dice loss function can be calculated using the following formula:
D i c e L o s s = 1 − 2 ∑ i m i n i + γ m i 2 + n i 2 + γ
where m represents the predicted probabilities of the classes, n denotes the ground truth data, and γ denotes the smoothing factor. In this paper, we divided the dataset into 7:3 for training and testing the model and resized input images and ground truths in the size of (224×224×3) and (224×224×1), respectively. We chose the Adam optimizer [59] for optimizing our model. We set the batch size at 8, the learning rate at 0.0001, and trained the model till 100th epochs.

3.4. Crack Severity Analysis

The Dense U-net model provides us with the segmented cracks from the images. However, it is also needed to determine the number of cracks and other morphological features (e.g., length, maximum width, area, density) to analyze the severity of cracks in any particular sample picture. And for that, we utilized the conventional image processing technique described below.

3.4.1. Counting the Cracks

In the first step of our crack severity analysis section, we have calculated the number of individual cracks in railway sleeper images. For counting the cracks, we have utilized the concept of contour detection in the images. Contour detection is a process that can be explained as a closed curve with an orientation that joins all the continuous points (along with the boundaries) having similar pixel intensities. Let an image as 2D function f(x,y) then,
f ( x , y ) = c
where c is the constant pixel value. So, using the contour detection process, we are getting the connected regions of the crack denoting pixels predicted by the Dense U-net model and crack boundaries. Thus we can calculate the number of detected contours, i.e., the number of individual crack objects.

3.4.2. Extracting Morphological features

After extracting the individual crack objects from the previous step, we calculated the cracks’ morphological features (length, width, area, density). To calculate the length and the maximum width of the cracks, we have applied the Algorithm 1. From the previous section, we have got the boundaries of the contours, i.e., cracks. Let a contour C=[X,Y] which is an array of two columns and N rows (i.e length of the contour) and where, x 0 , x 1 ,...... x n ∈X denotes the rows of the image and y 0 , y 1 ,...... y n ∈Y denotes the columns of the image. Let ( x 0 , y 0 ) and ( x n , y n ) are the starting point and the ending point of the contour i.e. crack respectively. To find out the length of the crack, we have calculated the distance between the starting point and the ending point of the crack boundary using the distance formula. After then for calculating the maximum width of a crack, we have traversed from the starting column y 0 to the ending column y n of the crack boundary. During this crossing, we have found out and stored the rows where any particular column y j has traveled in a list named occurs. We estimated the number of rows traveled by any column y j when this searching loop was completed, and we appended the results for each column to a list entitled widths. Finally, we have searched for the maximum value in the list, and thus we have calculated the maximum width of a crack.
Algorithm 1: Algorithm for length and width calculation
Preprints 91868 i001
We calculated the area of the contours as the area of the individual cracks. After that, we added the area of the individual cracks and got the total area covered by the cracks in an image. Finally, we divided the total area of the cracks by the number of pixels to get the density of the cracks in an image.

4. Results & Discussions

In this study, we implemented our proposed neural network model in a Python programming language using the Deep learning framework of Keras. We trained the model and conducted our experiments in a computer configured with a Windows 10 operating system, 32 GB RAM, Intel core i9-11900k @ 3.50 GHz CPU processor, and NVIDIA Geforce RTX 3080Ti graphics card.
To evaluate the performance of our proposed model, the segmentation effect of the railway sleeper images was tested. Both the original U-net model and the improved Dense U-net model were examined on the same test set to compare their effectiveness. The quantitative and qualitative results are discussed in the following sections.

4.1. Quantitative Results

In this section, we are presenting the quantitative results achieved by our proposed Dense U-net model. For verifying the performance of our proposed model we calculated Accuracy, Recall, Precision, F1-score, IoU as the assessment metrics by using the following equations.
A c c u r a c y = T P + T N T P + T N + F P + F N
P r e c i s i o n = T P T P + F P
R e c a l l = T P T P + F N
F 1 − s c o r e = 2 × P r e c i s i o n × R e c a l l P r e c i s i o n + R e c a l l
I o U = A r e a o f o v e r l a p A r e a o f U n i o n
Table 1 presents the test results of both the U-net and the Dense U-net model. We can see from Table 1 that the segmentation result of the Dense U-net model is better than the result of the original U-net model. Though the Precision value of the Dense U-net model is 0.9% lower than the U-net model, the Recall value is increased by 4.7%, hence the overall F1-score (an important evaluation metric for segmentation task) is also increased by 2.15%. In this work, we considered one more important metric, IoU, which increased by 3.28% in the Dense U-net model. Thus the experimental results show that our proposed Dense U-net model is more effective than the original U-net model in the case of segmenting the railway sleeper images.

4.2. Qualitative Results

In this subsection, we are presenting the qualitative analysis of some representative images from the test set, as demonstrated in Figure 4. The first column of Figure 4 displays the actual railway sleeper images; the second column displays the corresponding ground truth images, and the last two columns display the segmented results by the U-net model and the Dense U-net model, respectively.
To understand the detailed segmentation performance of the model more clearly, some portions of the images are highlighted by a green circle. We can see that both the original U-net model and the Dense U-net model predict the cracks on the railway sleeper images quite well. However, if we go for a detailed inspection, in the first, second, third, and eighth images, some tiny cracks are detected by a lesser intensity of the pixels. In contrast, the Dense U-net model predicted higher pixel intensity in more detail. In the case of the fourth image, the U-net model couldn’t predict a more significant portion of the tiny cracks when the railway sleeper is black-colored; in contrast, the Dense U-net model predicted better even in a noisy environment. From the fifth picture, it can be viewed that the original U-net model missed multiple narrow portions of the cracks, but the modified U-net model predicted them well. Both of the models segmented them accurately from the sixth, seventh, and tenth images. In the case of the ninth image, the original U-net model mistakenly predicted a non-crack portion as a crack, but the Dense U-net model avoided that portion efficiently. These experimental results show that our proposed Dense U-net model is more accurate than the conventional U-net model for predicting the cracks on the railway sleeper images.
Preprints 91868 g004a
Figure 4. Comparison of original U-net and Dense U-net crack segmentation result
Figure 4. Comparison of original U-net and Dense U-net crack segmentation result
Preprints 91868 g004a
Preprints 91868 g004b
Figure 4. Comparison of original U-net and Dense U-net crack segmentation result. (a) Original Image (b) Ground Truth (c) U-net (d) Dense U-net
Figure 4. Comparison of original U-net and Dense U-net crack segmentation result. (a) Original Image (b) Ground Truth (c) U-net (d) Dense U-net
Preprints 91868 g004b

4.3. Crack Measurement Results

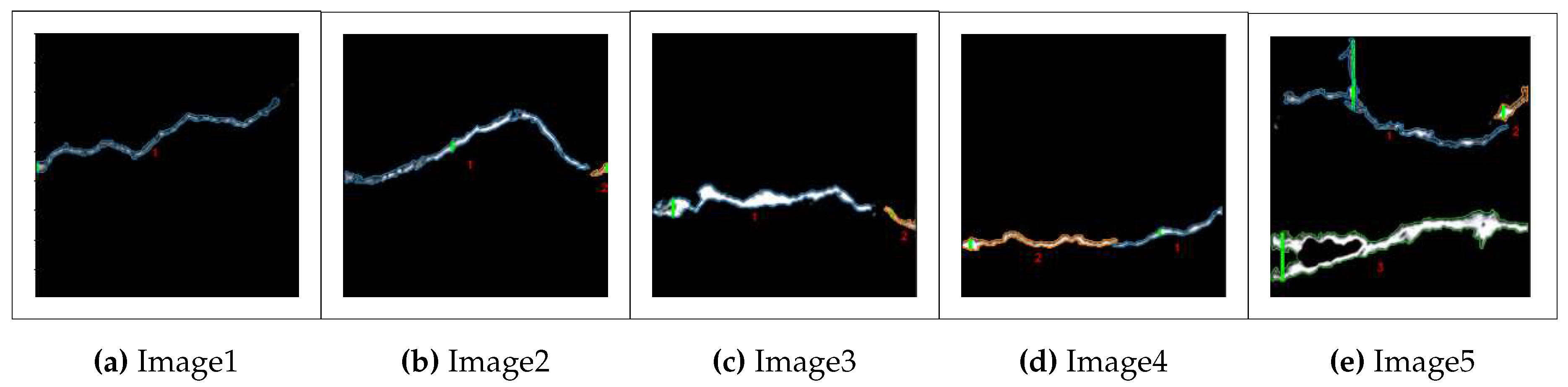
In the previous section, we provided the visualization of the segmented cracks by both of the models. We found that the Dense U-net model can detect cracks in more detail. So, we are considering the output of the Dense U-net model for finding the number of cracks and the morphological features of the individual cracks in an image. Figure 5 shows a few images in which the individual crack boundaries are designated with different colors; the locations of the cracks that contain the maximum widths are highlighted by a green line, as well as the cracks are labeled by one specific number.
Figure 5 displays the first image contains only one crack, each of the second, third, and fourth images contains two different cracks, and finally, the fifth picture contains three different cracks. After finding the number of cracks, we have also calculated the length, maximum width, and area of the individual cracks by following the approach presented in Section 3.4.2. We have also determined the entire area of the cracks and the crack density so that we can have a better idea about the severity of cracks in a particular image. Furthermore, we have counted the number of white image pixels to justify the determined area by the method. Table 2 Summarizes the measurement results for all the pictures in Figure 5.
From Table 2, it is evident that in the first image, the crack is the least severe. Only 1.77% of the image contains the cracks. In the second image, there are two separate cracks. One of the cracks is more prominent (208.24 pixels in length), and the other is smaller (17.20 pixels). The maximum width of the two cracks is 9 and 6 pixels, respectively, in this image. We can see that the crack area in the second image is 1288.82 pixels, and it has about 2.56% of crack density. The second, third, and fourth images also contain two separate cracks. Still, the crack density of the third image is higher (3.33%) than the other images, which contain one and two individual cracks. The maximum width of the major crack is also relatively thicker (15 pixels) in this image. In the case of the fifth image, we can see that there is a total of three individual cracks. If we notice carefully, it can be seen that there is a vast difference between the estimated total area and the sum of white pixels for this picture. The main reason behind this is the third crack of this image has a non-crack portion inside the crack boundary. As the other crack portions are continuous, our model counted it as a single crack. Still, for having a non-crack portion, the area calculated by our method has become much greater than the total number of pixels. Furthermore, the maximum width of the first and third cracks is overestimated and not also estimated in the correct location. We have used the boundary positions of the cracks to calculate the maximum width. So, if a crack object has multiple horizontally parallel branches, in that case, there are multiple branches of a crack in the same column of the image, our model estimates the distance from the starting point of the first crack to the ending point of the last crack as the width of that location. However, for this image, if we consider the sum of white pixels as area, the density of the cracks becomes 10.21% which is the highest among all the sample pictures in Figure 5.

5. Conclusions

In this research work, we presented a modified U-net network named Dense-Unet for detecting cracks on the concrete sleepers of a railroad. To modify the original U-net structure, several short connections were established between each of the encoder and decoder blocks, which extract denser and multi-scale necessary features and obtain and pass denser pixel information. Both the quantitative and qualitative results showed the proposed algorithm performed better than the conventional U-net model when predicting cracks on the concrete sleepers. The overall F1-score reached 86.56%, which was 2.15% greater than the original U-net model. Furthermore, we analyzed the severity of cracks in the predicted images by calculating the length, Maximum width, area, and ratio of the cracks. The limitation of our method for severity analysis is that if a crack object has multiple horizontally parallel branches, our model overestimates the maximum width and overlooks the maximum width location. In our future work, we plan to develop an algorithm for detecting crack severity by removing these errors.

Author Contributions

Conceptualization, M.K. and S.K.; methodology, M.K., A.N. and S.K.; software, M.K. and S.K.; validation, S.K., A.N. and M.K.; writing—original draft preparation, M.K., S.K. and A.N.; writing—review and editing, S.K., A.N. and M.K. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the Korea Institute of Marine Science and Technology Promotion (KIMST) grant funded by the Ministry of Oceans and Fisheries for the project titled ‘Development of smart maintenance monitoring techniques to prepare for disaster and deterioration of port infrastructures’.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The works in the paper were performed at the department of ICT integrated Ocean Smart Cities Engineering at Dong-A University, Busan, South Korea when Md. Al-Masrur Khan was a master’s degree student at Dong-A University.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. “International Union of Railways (UIC),” International Year Book and Statesmen’s Who’s Who.
  2. Y. Tang, A. A. Zhang, L. Luo, G. Wang, and E. Yang, “Pixel-level pavement crack segmentation with encoder-decoder network,” Measurement, vol. 184, p. 109914, 2021. [CrossRef]
  3. M. Zheng, Z. Lei, and K. Zhang, “Intelligent detection of building cracks based on Deep Learning,” Image and Vision Computing, vol. 103, p. 103987, 2020. [CrossRef]
  4. Y. Ren, J. Huang, Z. Hong, W. Lu, J. Yin, L. Zou, and X. Shen, “Image-based concrete crack detection in tunnels using deep fully convolutional networks,” Construction and Building Materials, vol. 234, p. 117367, 2020. [CrossRef]
  5. H. Fu, D. Meng, W. Li, and Y. Wang, “Bridge Crack Semantic segmentation based on improved deeplabv3+,” Journal of Marine Science and Engineering, vol. 9, no. 6, p. 671, 2021. [CrossRef]
  6. R. Nigam and S. K. Singh, “Crack detection in a beam using wavelet transform and photographic measurements,” Structures, vol.25, pp. 436–447, 2020. [CrossRef]
  7. Tomoyuki Yamaguchi, Shingo Nakamura, and Shuji Hashimoto, “An efficient crack detection method using percolation-basedimage processing,” 2008 3rd IEEE Conference on Industrial Electronics and Applications, 2008. [CrossRef]
  8. A. M. Talab, Z. Huang, F. Xi, and L. HaiMing, “Detection crack in image using Otsu method and multiple filtering in imageprocessing techniques,” Optik, vol. 127, no. 3, pp. 1030–1033, 2016. [CrossRef]
  9. H.-B. Yun, S. Mokhtari, and L. Wu, “Crack Recognition and Segmentation Using Morphological Image-Processing Techniquesfor Flexible Pavements,” Transportation Research Record: Journal of the Transportation Research Board, vol. 2523, no. 1, pp.115–124, 2015. [CrossRef]
  10. J. Suykens, J. Vandewalle, “Least squares support vector machine classifiers,” Neural Processing Letters. vol. 9(3), pp. 293-300, June 1999. [CrossRef]
  11. Z. Q. Chen and T. C. Hutchinson, “Image-Based Framework for Concrete Surface Crack Monitoring and Quantification,”Advances in Civil Engineering, vol. 2010, pp. 1–18, 2010. [CrossRef]
  12. M. A. Friedl, C. E. Brodley, “Decision tree classification of land cover from remotely sensed data,” Remote Sensing of Environment. vol. 61, pp. 399-409, September 1997. [CrossRef]
  13. A. Krizhevsky, I. Sutskever, and G. E. Hinton, “ImageNet classification with deep convolutional Neural Networks,” Communications of the ACM, vol. 60, no. 6, pp. 84–90, 2017. [CrossRef]
  14. K. Simonyan, A. Zisserman, “Very deep convolutional networks for large-scale image recognition,” Computer Science. September 2014. [CrossRef]
  15. C. Szegedy, W. Liu, Y. Jia, P. Sermanet, S. Reed, D. Anguelov, et al., “Going deeper with convolutions,” 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). pp. 1-9, September 2014. [CrossRef]
  16. L. Zhang, F. Yang, Y. Daniel Zhang and Y. J. Zhu, "Road crack detection using deep convolutional neural network," 2016 IEEE International Conference on Image Processing (ICIP), 2016, pp. 3708-3712. [CrossRef]
  17. Xuhang Tong, Jie Guo, Yun Ling, and Zhouping Yin, “A new image-based method for concrete bridge bottom crack detection,”2011 International Conference on Image Analysis and Signal Processing, 2011. [CrossRef]
  18. S. Mathavan, K. Vaheesan, A. Kumar, C. Chandrakumar, K. Kamal, M. Rahman, and M. Stonecliffe-Jones, “Detection of pavementcracks using tiled fuzzy Hough transform,” Journal of Electronic Imaging, vol. 26, no. 05, p. 1, 2017. [CrossRef]
  19. Tomoyuki Yamaguchi, Shingo Nakamura, and Shuji Hashimoto, “An efficient crack detection method using percolation-based image processing,” 2008 3rd IEEE Conference on Industrial Electronics and Applications, 2008. [CrossRef]
  20. N.-D. Hoang, “Detection of surface crack in building structures using image processing technique with an improved Otsu method for image thresholding,” Advances in Civil Engineering, vol. 2018, pp. 1–10, 2018. [CrossRef]
  21. I. Abdel-Qader, O. Abudayyeh, and M. E. Kelly, “Analysis of edge-detection techniques for crack identification in Bridges,” Journal of Computing in Civil Engineering, vol. 17, no. 4, pp. 255–263, 2003. [CrossRef]
  22. Y. Fujita and Y. Hamamoto, “A robust automatic crack detection method from noisy concrete surfaces,” Machine Vision and Applications, vol. 22, no. 2, pp. 245–254, 2010. [CrossRef]
  23. T. C. Hutchinson and Z. Q. Chen, “Improved image analysis for evaluating concrete damage,” Journal of Computing in Civil Engineering, vol. 20, no. 3, pp. 210–216, 2006. [CrossRef]
  24. M. R. Jahanshahi, S. F. Masri, C. W. Padgett, and G. S. Sukhatme, “An innovative methodology for detection and quantification of cracks through incorporation of depth perception,” Machine Vision and Applications, vol. 24, no. 2, pp. 227–241, 2011. [CrossRef]
  25. Y. Shi, L. Cui, Z. Qi, F. Meng and Z. Chen, "Automatic Road Crack Detection Using Random Structured Forests," in IEEE Transactions on Intelligent Transportation Systems, vol. 17, no. 12, pp. 3434-3445, Dec. 2016. [CrossRef]
  26. P. Chun, S. Izumi, and T. Yamane, “Automatic detection method of cracks from concrete surface imagery using two-step light gradient boosting machine,” Computer-Aided Civil and Infrastructure Engineering, vol. 36, no. 1, pp. 61–72, 2020. [CrossRef]
  27. Y.-J. Cha, W. Choi, and O. Büyüköztürk, “Deep learning-based crack damage detection using convolutional neural networks,” Computer-Aided Civil and Infrastructure Engineering, vol. 32, no. 5, pp. 361–378, 2017. [CrossRef]
  28. Y. Xu, S. Li, D. Zhang, Y. Jin, F. Zhang, N. Li, and H. Li, “Identification framework for cracks on a steel structure surface by a restricted boltzmann machines algorithm based on consumer-grade camera images,” Structural Control and Health Monitoring, vol. 25, no. 2, 2017. [CrossRef]
  29. F.-C. Chen and M. R. Jahanshahi, “NB-CNN: Deep Learning-Based Crack Detection Using Convolutional Neural Network and Naïve Bayes Data Fusion,” IEEE Transactions on Industrial Electronics, vol. 65, no. 5, pp. 4392–4400, 2018. [CrossRef]
  30. H. Maeda, Y. Sekimoto, T. Seto, T. Kashiyama, and H. Omata, “Road Damage Detection and Classification Using Deep Neural Networks with Smartphone Images,” Computer-Aided Civil and Infrastructure Engineering, vol. 33, no. 12, pp. 1127–1141, 2018. [CrossRef]
  31. J. Deng, Y. Lu, and V. C.-S. Lee, “Imaging-based crack detection on concrete surfaces using You Only Look Once network,” Structural Health Monitoring, p. 147592172093848, 2020. 14759217209 3848, 2020. [CrossRef]
  32. J. Huyan, W. Li, S. Tighe, J. Zhai, Z. Xu, and Y. Chen, “Detection of sealed and unsealed cracks with complex backgrounds using deep convolutional neural network,” Automation in Construction, vol. 107, p. 102946, 2019. [CrossRef]
  33. J. Long, E. Shelhamer, and T. Darrell, “Fully convolutional networks for semantic segmentation,” 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2015. [CrossRef]
  34. O. Ronneberger, P. Fischer, and T. Brox, “U-Net: Convolutional Networks for Biomedical Image Segmentation,” Lecture Notes in Computer Science, pp. 234–241, 2015. [CrossRef]
  35. X. Yang, H. Li, Y. Yu, X. Luo, T. Huang, and X. Yang, “Automatic pixel-level crack detection and measurement using fully convolutional network,” Computer-Aided Civil and Infrastructure Engineering, vol. 33, no. 12, pp. 1090–1109, 2018. [CrossRef]
  36. S. Bang, S. Park, H. Kim, and H. Kim, “Encoder–decoder network for pixel-level road crack detection in black-box images,”Computer-Aided Civil and Infrastructure Engineering, vol. 34, no. 8, pp. 713–727, 2019. [CrossRef]
  37. M. M. Islam and J.-M. Kim, “Vision-Based Autonomous Crack Detection of Concrete Structures Using a Fully Convolutional Encoder–Decoder Network,” Sensors, vol. 19, no. 19, p. 4251, 2019. [CrossRef]
  38. Z. Liu, Y. Cao, Y. Wang, and W. Wang, “Computer vision-based concrete crack detection using U-net fully convolutional networks,” Automation in Construction, vol. 104, pp. 129–139, 2019. [CrossRef]
  39. J. Ji, L. Wu, Z. Chen, J. Yu, P. Lin, and S. Cheng, “Automated pixel-level surface crack detection using U-Net,” Lecture Notes in Computer Science, pp. 69–78, 2018. [CrossRef]
  40. W. Yan, Y. Junjie, M. Junteng, C. Yong, and W. Kai, “Automatic detection method of bridge cracks based on residual network,” IOP Conference Series: Earth and Environmental Science, vol. 643, p. 012045, 2021. [CrossRef]
  41. H. Chen, H. Lin, and M. Yao, “Improving the Efficiency of Encoder-Decoder Architecture for Pixel-Level Crack Detection,” IEEE Access, vol. 7, pp. 186657–186670, 2019. [CrossRef]
  42. M. Sun, “Semantic segmentation using modified U-Net architecture for crack detection,” dissertation.
  43. F. Lin et al. "Crack Semantic Segmentation using the U-Net with Full Attention Strategy." arXiv preprint. arXiv:2104.14586v1. [CrossRef]
  44. R. Augustauskas and A. Lipnickas, “Improved pixel-level pavement-defect segmentation using a Deep Autoencoder,” Sensors, vol. 20, no. 9, p. 2557, 2020. [CrossRef]
  45. P. Babenko, “Visual inspection of railroad tracks,” thesis, University of Central Florida, Orlando, FL, 2009.
  46. X. Gibert, V. M. Patel, and R. Chellappa, “Robust fastener detection for Autonomous Visual Railway Track Inspection,” 2015 IEEE Winter Conference on Applications of Computer Vision, 2015. [CrossRef]
  47. P. L. Mazzeo, M. Nitti, E. Stella, and A. Distante, “Visual recognition of fastening bolts for railroad maintenance,” Pattern Recognition Letters, vol. 25, no. 6, pp. 669–677, 2004. [CrossRef]
  48. X. Gibert-Serra, A. Berry, C. Diaz, W. Jordan, B. Nejikovsky, and A. Tajaddini, “A machine vision system for Automated Joint Bar inspection from A moving rail vehicle,” ASME/IEEE 2007 Joint Rail Conference and Internal Combustion Engine Division Spring Technical Conference, 2007. [CrossRef]
  49. X. Gibert, V. M. Patel, D. Labate, and R. Chellappa, “Discrete shearlet transform on GPU with applications in anomaly detection and denoising,” EURASIP Journal on Advances in Signal Processing, vol. 2014, no. 1, 2014. [CrossRef]
  50. S. P. Mohammad, “Machine Vision for Automating Visual Inspection of Wooden Sleepers,” thesis, 2008.
  51. S. A. Tabatabaei, A. Delforouzi, M. H. Khan, T. Wesener, and M. Grzegorzek, “Automatic detection of the cracks on the concrete railway sleepers,” International Journal of Pattern Recognition and Artificial Intelligence, vol. 33, no. 09, p. 1955010, 2019. [CrossRef]
  52. M. Kim, K. Kim, and S. Choi, “Development of automatic crack identification algorithm for a concrete sleeper using pattern recognition,” Journal of the Korean Society for Railway, vol. 20, no. 3, pp. 374–381, 2017. [CrossRef]
  53. G. Wang, Y. Liu, and J. Xiang, “A two-stage algorithm of railway sleeper crack detection based on edge detection and CNN,” 2020 Asia-Pacific International Symposium on Advanced Reliability and Maintenance Modeling (APARM), 2020. [CrossRef]
  54. B. Xia, J. Cao, X. Zhang, and Y. Peng, “Automatic Concrete Sleeper Crack Detection using a one-stage detector,” International Journal of Intelligent Robotics and Applications, vol. 4, no. 3, pp. 319–327, 2020. [CrossRef]
  55. “Free vector icons and stickers - thousands of resources to download,” Flaticon. [Online]. Available: https://www.flaticon.com/ [Accessed: 17-Nov-2021].
  56. V. Badrinarayanan, A. Kendall, and R. Cipolla, “SegNet: A deep convolutional encoder-decoder architecture for image segmentation,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 39, no. 12, pp. 2481–2495, 2017. [CrossRef]
  57. G. Huang, Z. Liu, L. Van Der Maaten, and K. Q. Weinberger, “Densely connected Convolutional Networks,” 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2017. [CrossRef]
  58. C. H. Sudre, W. Li, T. Vercauteren, S. Ourselin, and M. Jorge Cardoso, “Generalised dice overlap as a deep learning loss function for highly unbalanced segmentations,” Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support, pp. 240–248, 2017. [CrossRef]
  59. P. KIngma et al. "Adam: A Method for Stochastic Optimization." arXiv preprint. arXiv:1412.6980v9. [CrossRef]
Preprints 91868 g001
Figure 1. Methodology of the proposed work.(The vector images in this diagram are completely random and do not reflect the original data. The photos were collected from [55])
Figure 1. Methodology of the proposed work.(The vector images in this diagram are completely random and do not reflect the original data. The photos were collected from [55])
Preprints 91868 g001
Preprints 91868 g002
Figure 2. Example images and their corresponding ground truth from our dataset. The first row presents the original images and the second row presents the ground truth images
Figure 2. Example images and their corresponding ground truth from our dataset. The first row presents the original images and the second row presents the ground truth images
Preprints 91868 g002
Preprints 91868 g003
Figure 3. Structure of the Dense U-net model.
Figure 3. Structure of the Dense U-net model.
Preprints 91868 g003
Preprints 91868 g005
Figure 5. Counting and denoting the individual cracks.
Figure 5. Counting and denoting the individual cracks.
Preprints 91868 g005
Table 1. Comparison between original and Dense U-net results.
Table 1. Comparison between original and Dense U-net results.
Model Accuracy(%) Precision(%) Recall(%) F1-score(%) IoU(%) Dice Loss(%)
U-net 99.10 89.43 79.93 84.41 73.03 2.96
Dense U-net 99.17 88.53 84.63 86.56 76.31 2.93
Table 2. Morphological features of the cracks (unit: pixels).
Table 2. Morphological features of the cracks (unit: pixels).
Image Cracks Length Maximum Width Area Total Area Sum of White Pixels Density (%)
1 1 213.47 7 892.82 892.82 873 1.77
2 1 208.24 9 1227.40
2 17.20 6 61.41 1288.82 1247 2.56
3 1 185.04 15 1560.91
2 27.51 5 113.36 1674.28 1645 3.33
4 1 96.84 5 406.74
2 132.00 9 637.97 1044.72 1000 2.08
5 1 194.25 60 1292.92
2 32.20 12 254.74 5960.44 5123 11.87
3 224.96 40 4413.46
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated