Preprint
Article
A Novel CNN Model for Classification of Chinese Historical Calligraphers’ Styles in Regular Script Font
Altmetrics
Downloads
74
Views
28
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
30 November 2023
Posted:
30 November 2023
You are already at the latest version
Alerts
Abstract
Chinese calligraphy, revered globally for its therapeutic and mindfulness benefits, encompasses styles such as Regular (Kai Shu), Running (Xing Shu), Official (Li Shu), and Cursive (Cao Shu) scripts. Beginners often start with Regular script, advancing to more intricate styles like Cursive. Each style, marked by unique historical calligraphers' contributions, requires learners to discern distinct nuances. The integration of AI in calligraphy analysis, collection, recognition, and classification are pivotal. This study introduces an innovative Convolutional Neural Network (CNN) architecture, pioneering the application of CNN in the classification of Chinese calligraphy. Focusing on the four principal calligraphers' styles from the Tang dynasty (690-907 A.D), this research spotlights the era when the traditional regular script font (Kai Shu) was refined. A comprehensive dataset of 8282 samples from these calligraphers, representing the zenith of regular style, was compiled for CNN training and testing. The model distinguishes personal styles for classification, showing superior performance over existing networks. Achieving 89.5-96.2% accuracy in calligraphy classification, our approach underscores the significance of CNN in both font and artistic style categorization. This research paves the way for advanced studies in Chinese calligraphy and its cultural implications.
Keywords:
Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning
1. Introduction
Chinese calligraphy is a revered art form with a rich history dating back thousands of years, and it is considered a valuable cultural heritage of the world. Even today, tens of millions of people around the globe collect or practice this art form. Moreover, there are numerous historical calligraphies works that require authentication for commercial purposes in the art collection and auction market, as well as in the field of culture study and research. Additionally, practitioners of calligraphy require evaluation methods to aid in their study and practice of calligraphy styles and aesthetics. Consequently, automatic recognition of calligraphy styles through image processing techniques holds great significance in art collections, auctions, and academic pursuits.
Our previous research works have inspired us to explore the use of the notion of fractal dimension from modern Chaos theory to measure Chinese artworks [2], providing a quantifiable measurement in explaining Chinese unique aesthetic principles. Our research has revealed that, by tradition, Chinese calligraphy employs a unique ancient way of measurement to maintain visual balance in each Chinese character (Figure 1). This so-called Nine-palaces grid (Figure 2) is frequently used to evaluate the beauty of calligraphy works in Chinese. The grid system is also utilized in practicing Chinese calligraphy to help practitioners develop their sense of balance and beauty in writing. We contend that such a grid system approach is akin to the 3x3 convolution filter, or kernel, employed in Convolutional Neural Networks (CNNs) to detect the underlying traits and features of any visual pattern.
Encouraged by the discovery, we decide to use Convolutional Neural Networks (CNN) methods to further analyse Chinese calligraphy works. Since classic CNN methods [5] have already done quite high accurate job in recognizing human handwriting of digits such as trained by the MNIST dataset. We used CNN methods to further analyse Chinese calligraphy works. The recent development of computer imageries, data science, and deep learning shows a surge of interest in image digitizing and character recognition in the field of Machine Learning and Convoluted Neural Network research and application. Utilising CNN for the recognition of the Chinese handwriting calligraphy characters becomes a novel one. Chinese calligraphy has a rich history of historical works and calligraphers. Numerous scholars and followers have studied, admired, and copied the Chinese calligraphy styles. As we research through all the current literature on the field, many works have already been done in applying CNN in Chinese calligraphy studies. However, most of the studies focus on the classification of five basic fonts namely are known as seal clerical, cursive, semi-cursive, and regular (Table 1). These fonts visually look distinctive from each other and were appropriated and developed through various Chinese historical periods. They are rather a broader categorization. In fact, even within each of these font categories, numerous historical calligraphers have their unique personal styles and flavours that differentiate them from each other and reflect their distinctive individual personalities, feelings, spiritual and intellectual levels.
Our main research question is “does the CNN can recognize unique personal calligraphy styles even from within the same font type such as a standard regular script (kai shu) of Chinese calligraphy?”. To investigate this research question, we collect and developed a dataset of four famous historical calligraphers, spanning the Chinese Tang dynasty (690-907 A.D) period, who are considered to have appropriated the regular script style within the period [1]. Tang dynasty calligraphy styles share some of the common features as regular script style while each had achieved a unique characteristic of its own and have been considered to have reached the highest aesthetic level of their calligraphy styles. [1] And set as exemplars for the generations to come down history. It is from these calligraphers of the period that the regular script has been established and has been used for empirical official documents ever since. After developing the dataset, we then trained and developed a calligraphy recognition system based on a convolutional neural network model. The system can recognize and differentiate the four historical personal calligraphy styles with a great accuracy rate. We implement a calligraphy-style data set to train the network and then use the trained system to evaluate any given amateur works to test the system’s feasibility. Our experimental results show that the system is reliable assistance in evaluating the personal progress of the learning styles of calligraphy. The major goal of this study was to investigate practical approaches to increase image categorisation accuracy while keeping the application programme's execution time under control.
Table 1.
| Seal (zhuan): |  |
| Clerical (li): |  |
| Cursive (cao): | 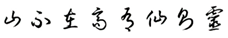 |
| Semi-cursive (xing): | 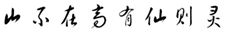 |
| Regular (kai): |  |
2. Related works
A lot of research has been done in the field of calligraphy recognition and classification. Li [6] proposed present a Support Vector Machine-based method in 2013 with a recognition rate of 96% for the official and regular scripts; Lin [7] presented a location-based hashing-based method in 2014 with a recognition rate of 81%, 90%, 100%, 81%, 63% for seal, official, regular, running, and cursive scripts, respectively. In 2014, Mao [8] developed a method based on using Gabor filters as a texture discriminator with a recognition rate of 99%, 98%, 100%, 51%, 71% for seal, official, regular, running, and italic fonts; Wang et al. [9] carried out a principal component analysis based method in 2016 with a recognition rate of 99%, 96%, 91%, 73%, 24% of seal, official, regular, running and italic fonts, Yan [10] developed a local pixel probability pooling based method in 2018 with a recognition rate of 92.4% of official, regular and running fonts. Cui [11] designed a system for recognizing Chinese calligraphy and its font using context images based on a multi-level convolutional neural network.
In using a CNN as means of recognizing and classifying calligraphy works, Chen [12] combined the CNN approach with traditional recognition algorithms to identify the calligraphy image and the corresponding Chinese characters. Liu [13] also proposed a CNN approach to identify a specific historical calligrapher in Chinese history for authentication purposes. Zhai [14] used a deep neural network model to extract the inscription from paintings and focused on identifying calligraphy and painting regions. Li [15] used CNN to recognize different traditional Chinese calligraphy styles and achieved a test accuracy of 88.6%. Zou et al. [16] improved the performance of CNN on handwritten Chinese character recognition by combining cross-entropy with the similarity ranking function and using it as a loss function. Wen and Sig¨uenza [17] proposed a CNN-based method for Chinese calligraphy style recognition based on a full-page document. Wang et al. [18] proposed an automatic evaluation approach for Chinese calligraphy based on disk B-spline curve (DBSC) vectorization of characters, iterative closest point (ICP) registration between handwritten and standard character skeletons, and comprehensive shape similarity metrics calculated on both the global character and individual strokes. Gao et al. [19] proposed using deep convolutional neural network features with modified quadratic discriminant function classification for automatic Chinese calligraphic style recognition, showing significantly improved performance over global GIST and local SIFT descriptors, achieving 99.8% on SCL and 94.2% on CCD with MQDF. Wang et al. [20] propose combining the softmax cross-entropy loss with an average variance similarity ranking loss boosts convolutional neural network accuracy on handwritten Chinese character recognition from 93.79% with softmax alone to 95.58%, a 1.79% absolute improvement.
3. A CNN model for the classification of Chinese calligraphy images
In this section, we provide a concise introduction to the functioning of Convolutional Neural Networks (CNNs) in the context of image analysis, a topic central to our study. The CNN concept is inspired by Hubel and Wiesel's discovery [21] of the visual perception structure in animals' visual cortex, in which cells detect light in receptive fields. Neocognition [22], a computational model based on local neuron connectivity and hierarchically organized image transformations, was proposed as a primitive CNN. LeCun and collaborators established the modern CNN framework in a 1998 paper [5]. Since 2006, research has focused on training challenges, shifting to deeper structures. Notable works include AlexNet[], VGGNet[], GoogLeNet[], and ResNet[], reflecting a trend towards deeper architectures for enhanced performance.
A typical Convolutional Neural Network (CNN) consists of three types of fundamental layers: convolutional layers, pooling layers, and fully connected layers. The convolutional layer plays a pivotal role in feature extraction by utilizing multiple filter kernels to compute diverse feature maps from the input image or the previous layer's feature map. These filters traverse the input image, engaging in a mathematical operation known as convolution. During this process, each filter element-wise multiplies its values with the corresponding pixels in the input image and subsequently aggregates the results to yield a singular output. By applying a range of filters to the input image, the convolutional layer can discern various patterns and features. When multiple convolutional layers are employed, the network can progressively learn and represent multi-level abstractions of the original image. Mathematically, the k- th feature map at the l-th layer can be computed using the following convolutional operations [28]:
where w and b are the weight matrix and bias term at the l-th layer respectively, and x is the input image patch (or previous layer feature map) centered at location (i,j). After the convolutional operations, an activation function is applied to introduce nonlinearity to the CNN to produce an activation map. This can be expressed as follows:
where ϕ (·) is the activation function. The most common activation function is the Rectified Linear Unit (ReLU) function [29].
As the dimension of the activation maps is typically very large, down-sampling is necessary to reduce the size of the activation map. This process is crucial not only for managing the computational load during network training but also for diminishing the count of training samples associated with the majority class. The mechanism of down-sampling is realized through the pooling operation, strategically implemented within the pooling layers of the Convolutional Neural Network (CNN). Mathematically, the pooling operation can be succinctly expressed as follows:
where y is the output of the pooling operation associated with the k-th feature map, fpool(·) denotes the pooling function and Rij is a local neighboring around the location (i,j). The popular pooling operations in applications are max pooling or average pooling [30].
After traversing multiple convolutional and pooling layers, the resultant feature map undergoes flattening, serving as input for one or more fully connected layers within the CNN. It is within these fully connected layers that the CNN engages in high-level reasoning. These layers transform the 2D feature map into a one-dimensional feature vector. In the context of a classification task, this derived vector is then passed through a softmax function, assigning it to a specific category.
Figure 3 illustrates the proposed style-oriented CNN architecture designed for Chinese calligraphy classification. In this framework, the input image comprises a Chinese character extracted from a curated collection of stylized fonts. The network's output corresponds to the categories representing the distinctive styles of calligraphers. The labels O, C, Y, and L denote Ouyang Xun, Chu Cunliang, Yan Zhengqin, and Liu Gongquan, respectively.
To train a CNN network, it is necessary to define an objective function, which is also known as a loss function that evaluates how well the network will perform during training and testing. For the image classification task, the cross-entropy loss is the most commonly used loss function. This function calculates the difference between the predicted class probabilities and the true class labels. Mathematically, the cross-entropy loss function can be expressed as follows [30]:
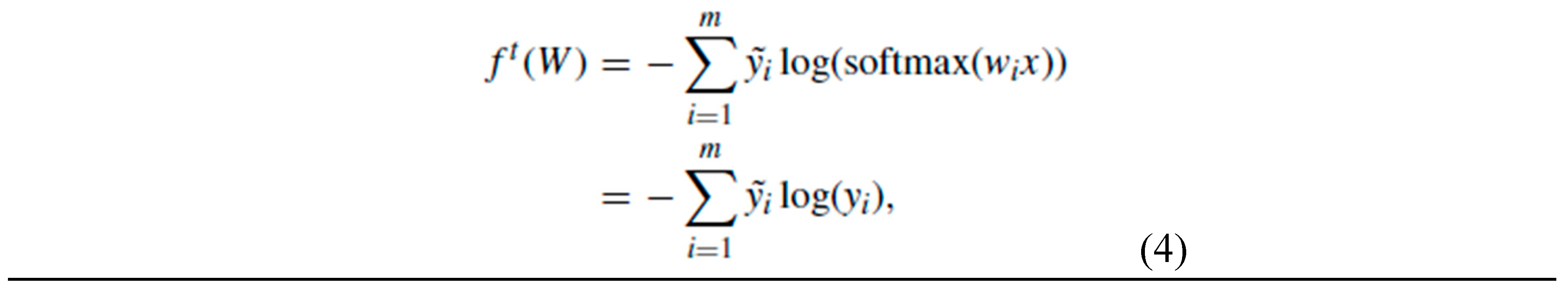 where m represents the total number of classes, yi denotes the i-th prediction class, ŷi is the i-th true class of training samples, and wi is the weight vector.
where m represents the total number of classes, yi denotes the i-th prediction class, ŷi is the i-th true class of training samples, and wi is the weight vector.A dataset consisting of images and labels is required to train the CNN network in order to resolve the image classification problem. The network employs a learning algorithm to adjust its free parameters and to achieve the desired output. During training, the loss function acts as a guide for CNN, helping it learn to make more accurate predictions by minimizing the error between predicted and the true outputs. The dataset we used for this specific problem includes images of calligraphy work, similar to handwritten digits or handwritten English characters but featuring Chinese words converted into images, with four distinct categories namely: Ouyang Xun, Chu Suiliang, Yan Zhenqing and Liu Gongquan. The Chinese characters vary in complexity based on their texture, shape, and other factors such as stroke angles, amount and thickness, etc. In the next section, we offer a detailed description of the numerical experiments that we have carried out using the CNN model with suitable architecture parameters on our specific dataset.
4. Experiments and Analysis
4.1. Dataset construction
Acquiring a large and comprehensive dataset is critical to model complexity for accurately classifying calligraphy styles. The training accuracy of the model related to epistemic uncertainty can be enhanced using more data. Epistemic uncertainty refers to the uncertainty of the model and is often due to a lack of training data. Unfortunately, in our previous experiments, we were unable to find appropriate data for our research. As a result, we recognized the importance of constructing our own dataset so that epistemic uncertainty can be focussed. We constructed new dataset named Chinese Calligraphy Dataset CQU (CCD-CQU).
The preparation of the dataset was a time-consuming process as we had specific target calligraphers from a particular period: Tan dynasty (690-970 A.D). Chinese calligraphy works we used for our study is sourced from a public website that has encyclopaedic collection of scanned and digitized picture of Chinese calligraphy works from different authors and periods (http://www.yac8.com). The Chinese calligraphy works were identified according to the targeted authors’ works and were sorted chronologically.
For Ou Yangxun (557-641 A.D.), we focused on his famous inscription work "Jiu Cheng Gong Li Quan Ming " stele (《九成宫醴泉铭》), which is considered one of the finest representatives of his calligraphy art. It was originally an essay documenting the trip of emperor Tang Taizong (599-649 A.D.). His calligraphy style is often regarded as strict, neat, and well-organized, making it a popular choice for calligraphy teachers to assign to their students to copy from as their first example.
For Chu Suiliang (596 – 658 A.D.), we collected works not only from famous inscription stele sources such as "Yan Ta Sheng Jiao Xu" (《雁塔圣教序》), "Meng Fa Shi Bei Ming" (《孟法师碑铭》), and "Qian Zi Wen Bei" (《千字文碑》), but also some rare collections of his actual writing on paper, such as "Ying Fu Jing" (《阴符经》). These works spanned his lifetime and are representative of his calligraphy style.
For Yan Zhenqing (709 -785 A.D.), we selected the main body of characters from his famous inscription stele "Duo Bao Ta Bei" (《多宝塔碑》) and also included his alleged actual writing on paper, such as "Zhu Shan Lian Ju" (《竹山连句》). Yan has over 138 legacy works, and "Duo Bao Ta Bei" was written when he was at the peak of his career and writing style.
For Liu Gongquan (778-865 A.D.), we chose the main body of calligraphy characters from the famous "Mysterious Tower Stele" (《玄秘塔碑》), which is considered the masterpiece of his calligraphy art and often the first choice for followers to copy and practice the regular script style as well.
We also include miscellaneous examples from other copybooks that extract individual characters from various historical documents or rubbed from inscriptions for followers to study. We collected over 2000 images of the calligraphy characters for each author. We processed them in Photoshop by cropping, resizing, and reducing them into 64 x 64 pixels in dimension and in black and white images (Figure 4 (a)-(d)) so that it would be faster for CNN to train and test. There are characters which are repeated and have differences in value, contrast, and variations and noises in the background. The assumption we worked on was that these nuances were not significant for the learning algorithm and probably would be even more beneficially challenging for deep learning to train with.
4.2. Numerical experiments, results, and discussion
To improve the performance of the neural network model, it is a common practice to train the model with more data so that uncertainty can be captured. Data augmentation has been typically used to obtain additional training samples by applying transformations such as flipping, cropping, rotating, scaling, and elastic deformations to the dataset samples. Therefore, we have added an equal amount of image data through data augmentation procedures. These procedures involve generating 50% of augmented images through rotation with angles ranging from 10 to 180 degrees, with uniform distribution intervals of 10 degrees. The remaining 50% of image data were generated by adding a random background. Figure 5a and Figure 5b illustrate some samples of augmented data images. Overall, there were 16564 images processed in the experiment.
Figure 5a.
Rotated image data samples

Figure 5b.
Image data samples with adding random background noise

The behaviour of CNNs is highly complex. In the studied classification problem using the CNN method, the dataset is the base where the built network requires learning. On the other hand, the performance accuracy of a CNN model for a specific learning task is significantly influenced by its architecture and algorithmic parameters [31]. To ensure the best possible accuracy, we carefully studied and tuned the hyperparameters of our CNN model, resulting in the design of five different architectures for our application. The key parameters of our architecture are summarized in Table 2, whereas Tables 3(1)-(5) outline the detailed configuration manners for filters of varying sizes, which are referred to as configuration types 1 to 5 in the following discussions.
As a CNN model is composed of iterative blocks of convolutional layers and pooling layers, the combination way of convolution and pooling operations can vary significantly. Each specific combination of convolution and pooling operation can be treated as a configuration of a distinct architecture for the network in the numerical experiments for. For instance, AlexNet [24], a well-known CNN model, employs a 11x11 convolution filter with a stride of 4 as the initial layer, followed by a 5x5 filter, and subsequently uses a 3x3 filter for all other convolutional layers. The VGG model [25], on the other hand, employs two continuous convolutional layers followed by a pooling layer, repeated twice, and then follows this up with three continuous layers plus a pooling layer, with each convolution operation using a 3x3 filter.
In our design, configuration types 1, 2, and 4 use convolution filter sizes of 3x3, 5x5, and 7x7, respectively. Configuration type 3 uses a 5x5 filter size for the first convolution, followed by all others using a 3x3 filter size. Configuration type 5 follows a VGG-like style with a total of 7 convolutional layers. Each configuration starts with a certain number of filters (K), with the number of filters doubling at the subsequent convolution layer. The five configurations have a total number of layers of 11, 9, 11, 9, and 15 layers, respectively. In addition to the architecture parameters, we have also included the algorithm-related parameters in Table 4.
Table 2.
Critical architecture parameters of our CNN design.
| Parameters | Values |
| Input image size | 64×64×1 |
| Filter size (F×F) | 3×3, 5×5, 7×7 |
| Number of filters (K) | 16, 24, 32, 48 |
| Pooling size (Max Pooling) | 2×2 stride=2 |
| Configuration type (Cn) | C1, C2, C3, C4, C5 |
| Neuron numbers of FC Layer (N) |
512, 256, 128 |
Table 3.
CNN configuration type (1)-(5).
| (1) Filter size 3×3 (K=32) | |||
| Block | Layer | Layer type |
Description (feature map size) |
| Block 1 | L1 | Conv+ReLU | 32@62×62 |
| L2 | Max Pooling | 32@31×31 | |
| Block 2 | L3 | Conv+ReLU | 64@29×29 |
| L4 | Max Pooling | 64@14×14 | |
| Block 3 | L5 | Conv+ReLU | 128@12×12 |
| L6 | Max Pooling | 128@6×6 | |
| Block 4 | L7 | Conv+ReLU | 256@4×4 |
| L8 | Max Pooling | 256@2×2 | |
| Block 5 (FC layers) |
L9 | FC1 | 512 neurons |
| L10 | FC2 | 256 neurons | |
| L11 | FC3 (softmax) | 4 neurons | |
| (2) Filter size 5×5 (K=32) | |||
| Block | Layer | Layer type |
Description (feature map size) |
| Block 1 | L1 | Conv+ReLU | 32@60×60 |
| L2 | Max Pooling | 32@30×30 | |
| Block 2 | L3 | Conv+ReLU | 64@26×26 |
| L4 | Max Pooling | 64@13×13 | |
| Block 3 | L5 | Conv+ReLU | 128@9×9 |
| L6 | Max Pooling | 128@4×4 | |
| Block 4 (FC layers) |
L7 | FC1 | 512 neurons |
| L8 | FC2 | 256 neurons | |
| L9 | FC3 (softmax) | 4 neurons | |
| (3) Filter sizes 5×5, 3×3 (K=32) | |||
| Block | Layer | Layer type |
Description (feature map size) |
| Block 1 | L1 | Conv+ReLU | 32@60×60 |
| L2 | Max Pooling | 32@30×30 | |
| Block 2 | L3 | Conv+ReLU | 64@28×28 |
| L4 | Max Pooling | 64@14×14 | |
| Block 3 | L5 | Conv+ReLU | 128@12×12 |
| L6 | Max Pooling | 128@6×6 | |
| Block 4 | L7 | Conv+ReLU | 256@4×4 |
| L8 | Max Pooling | 256@2×2 | |
| Block 5 (FC layers) |
L9 | FC1 | 512 neurons |
| L10 | FC2 | 256 neurons | |
| L11 | FC3 (softmax) | 4 neurons | |
| (4) Filter size 7×7 (K=32) | |||
| Block | Layer | Layer type |
Description (feature map size) |
| Block 1 | L1 | Conv+ReLU | 32@58×58 |
| L2 | Max Pooling | 32@29×29 | |
| Block 2 | L3 | Conv+ReLU | 64@23×23 |
| L4 | Max Pooling | 64@11×11 | |
| Block 3 | L5 | Conv+ReLU | 128@5×5 |
| L6 | Max Pooling | 128@2×2 | |
| Block 5 (FC layers) |
L7 | FC1 | 512 neurons |
| L8 | FC2 | 256 neurons | |
| L9 | FC3 (softmax) | 4 neurons | |
| (5) VGG-like style (filter size 3×3, K=32) | |||
| Block | Layer | Layer type |
Description (feature map size) |
| Block1 | L1 | Conv+ReLU | 32@62×62 |
| L2 | Conv+ReLU | 32@60×60 | |
| L3 | Max Pooling | 32@30×30 | |
| Block2 | L4 | Conv+ReLU | 64@28×28 |
| L5 | Conv+ReLU | 64@26×26 | |
| L6 | Conv+ReLU | 64@24×24 | |
| L7 | Max Pooling | 64@12×12 | |
| Block3 | L8 | Conv+ReLU | 128@10×10 |
| L9 | Conv+ReLU | 128@8×8 | |
| L10 | Conv+ReLU | 128@6×6 | |
| L11 | Max Pooling | 128@3×3 | |
| Block4 | L12 | Conv+ReLU | 256@1×1 |
| Block5 (FC layers) |
L13 | FC1 | 256 neurons |
| L14 | FC2 | 128 neurons | |
| L15 | FC3 (softmax) | 4 neurons | |
Table 4.
Algorithm-related parameters.
| Optimizer adam |
| Learning rate 1.0e-4 |
| Batch size 32, 64 |
| Dropout rate 0.25, 0.5 |
In this study, the main objective was to explore feasible ways to maximize image classification accuracy, while ensuring that the application program’s running time remains manageable. Given a set of fixed algorithm-related parameters, the performance accuracy of a CNN model can be defined approximately as a function of the architecture parameters (F, K, C, N) as below,
where F is the filter size, K is the number of filters, C represents the configuration manner, and N represents the number of neurons at the fully connected layers (which may consist of two or more components).
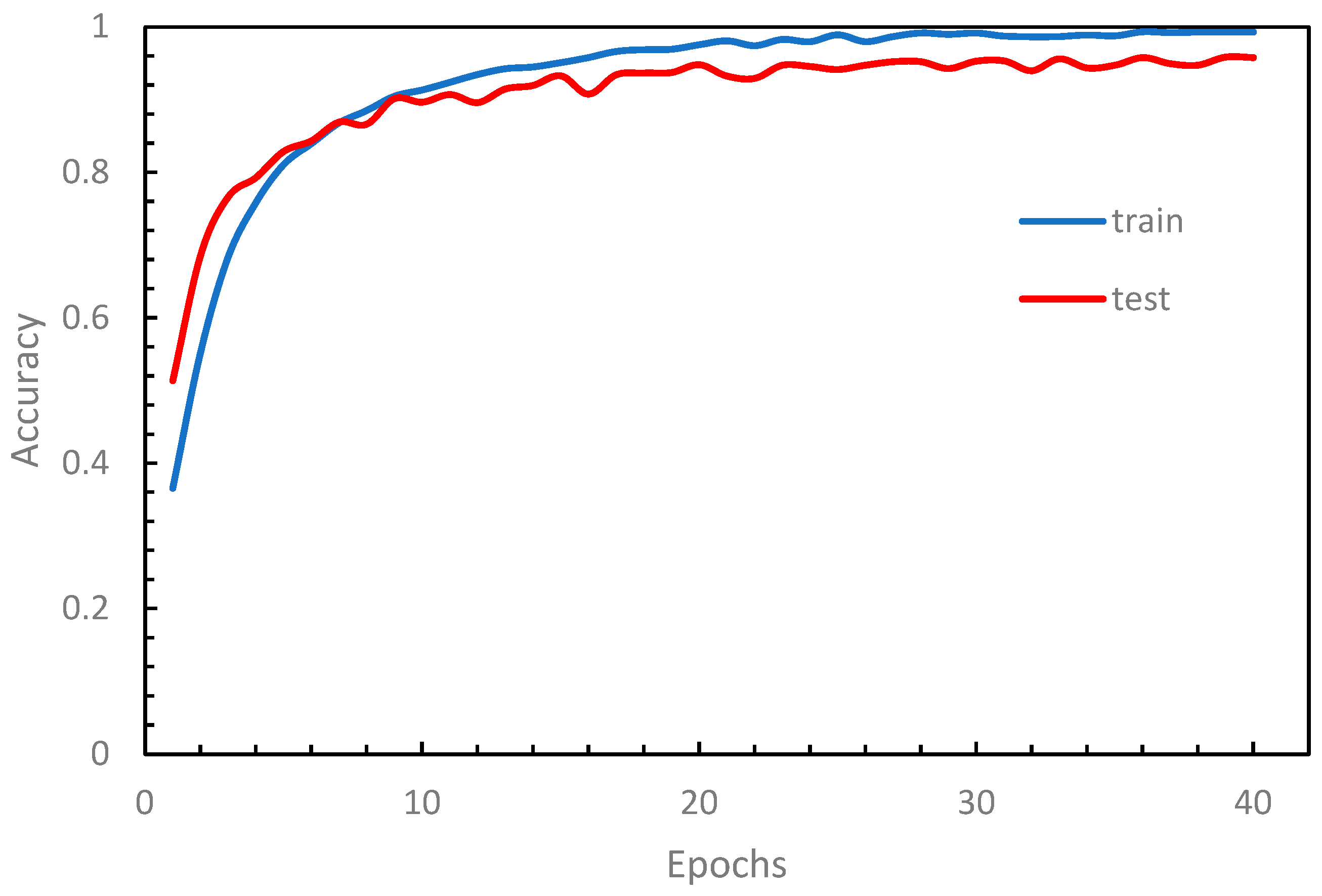
We implemented a Python application program using the TensorFlow library [32] based on the design described above. To evaluate the performance of our model, we conducted numerical experiments on our dataset, which was divided into 80% for training and 20% for testing. The results of a typical training example are shown in Figure 6, where the loss function tends to stabilize after 25 epochs, indicating a convergence in the training process. Figure 7 illustrates the performance curves against the epoch, where both the training and testing accuracy curves approach stability after 25 epochs. The running time for each modification on an ordinary PC with a single GPU ranges between approximately 12 minutes and 45 minutes, depending on the configuration type and the number of filters (K). The VGG-like architecture takes a longer running time due to its deeper structure.
The recorded accuracies for each modification are presented in Table 5. The accuracy on the training dataset varied from 93.7% to 99.5%, which indicates that the designed networks are well-trained. On the other hand, the accuracies on the testing dataset ranged between 89.5% and 96.2%. Fig.8 depicts the test error graph for different configuration types and starting numbers of filters (K). Configuration type 1 with K=32 yielded the lowest error rate of 3.8%, which is more in line with human recognition abilities for this type of image. The graph reveals that for configuration type 1 which has a small filter size (3x3), the test error decreases as the number of filters increases, but it reaches a saturation point at K=32. Configuration types 1 and 3 have lower error rates, while configuration types 2 and 4 have relatively high error values. For a small-size image input, a smaller filter size achieves better accuracy, while a larger filter size may result in some information loss in the extracted feature maps. Furthermore, configuration type 5 is a VGG-like style configuration with a deeper structure, but it did not produce as impressive accuracy as expected. This could be attributed to the fact that the additional convolutional operations may not necessarily extract more meaningful features for this particular image dataset. Moreover, as illustrated in Figure 10, the optimal number of filters for most configurations should be 24 or 32. The experimental results have clearly demonstrated that the built network with the carefully-tuned architecture parameters can correctly recognize the different font styles i.e. categories in our dataset. The outstanding performance accuracy is attributed to the correct extraction of font style features. A Chinese character is typically composed of eight basic components such as dots, horizontals, verticals, hooks, lifts (or raises), curves, throws, and presses, each of which has a dynamic corresponding form known as sideways, tighten, bow or strive, leap, whip, sweep, peck, and hack. Different calligraphers apply these basic writing forms in unique ways, including variations in motion direction, graphic manner, stroke way, and the force applied to create their works. For example, Ou preferred using sharp and bold strokes, whereas Chu often intentionally handled the strokes, lines, and dots, with turning points to reflect an aesthetic and abstract value that transcends the characters’ physical appearance. These special writing manners result in individual font styles and their features in the image are reflected in texture, shape, angle, and pattern. These features are effectively extracted by convolutional operations using various filters in a series of feature maps, which leads to accurate classification. Increasing the size of the training dataset in future work is likely to further improve prediction accuracy.
Table 6 presents the selected test accuracies of individual classes for configuration types 1 and 2 with K=32. The results indicate that the different category characters exhibit varying performance accuracy, with class O having the lowest accuracy. This could be attributed to the imbalanced sample data, as the O class has the fewest number of images. Imbalanced training data can lead to several problems that affect classification accuracy [33,34]. If one class has significantly fewer samples than the others, the network may exhibit biased behaviours towards that class and may classify even the least number of sample images as belonging to that corresponding class. The underlying cause is that CNN attempts to minimize overall errors, which may cause it to focus more on the dominant classes and less on the minority classes. Consequently, for the fewer samples in the minority classes, the network may not have sufficient information to learn the features belonging to that class, thus reducing the classification accuracy.
Figure 8.
Performance errors for various configurations.
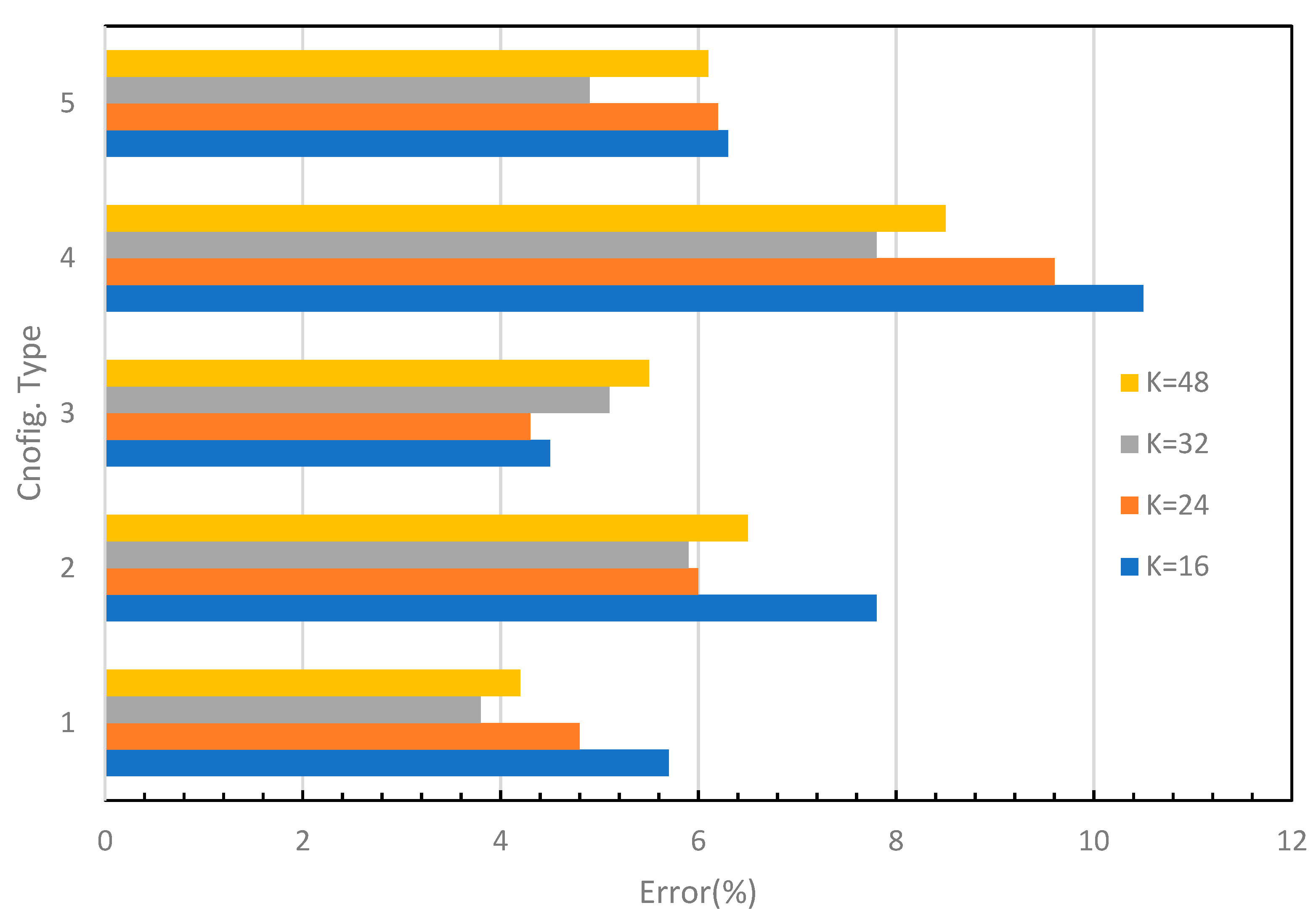
Table 5.
The accuracy obtained on our dataset with different architecture parameters.
| Architecture | Accuracy | ||
| K | Configuration | training | testing |
| 16 | C1 | 98.6% | 94.3% |
| C2 | 96.3% | 92.2% | |
| C3 | 98.7% | 95.5% | |
| C4 | 93.7% | 89.5% | |
| C5 | 96.6% | 93.7% | |
| 24 | C1 | 99.2% | 95.2% |
| C2 | 98.9% | 94.0% | |
| C3 | 99.0% | 95.7% | |
| C4 | 95.7% | 90.4% | |
| C5 | 98.1% | 93.8% | |
| 32 | C1 | 99.5% | 96.2% |
| C2 | 98.2% | 94.1% | |
| C3 | 98.9% | 94.9% | |
| C4 | 95.2% | 92.2% | |
| C5 | 98.7% | 95.1% | |
| 48 | C1 | 99.1% | 95.8% |
| C2 | 97.7% | 93.5% | |
| C3 | 98.3% | 94.5% | |
| C4 | 96.8% | 91.5% | |
| C5 | 98.2% | 93.9% | |
Figure 9.
Performance errors vs the number of filter (K).
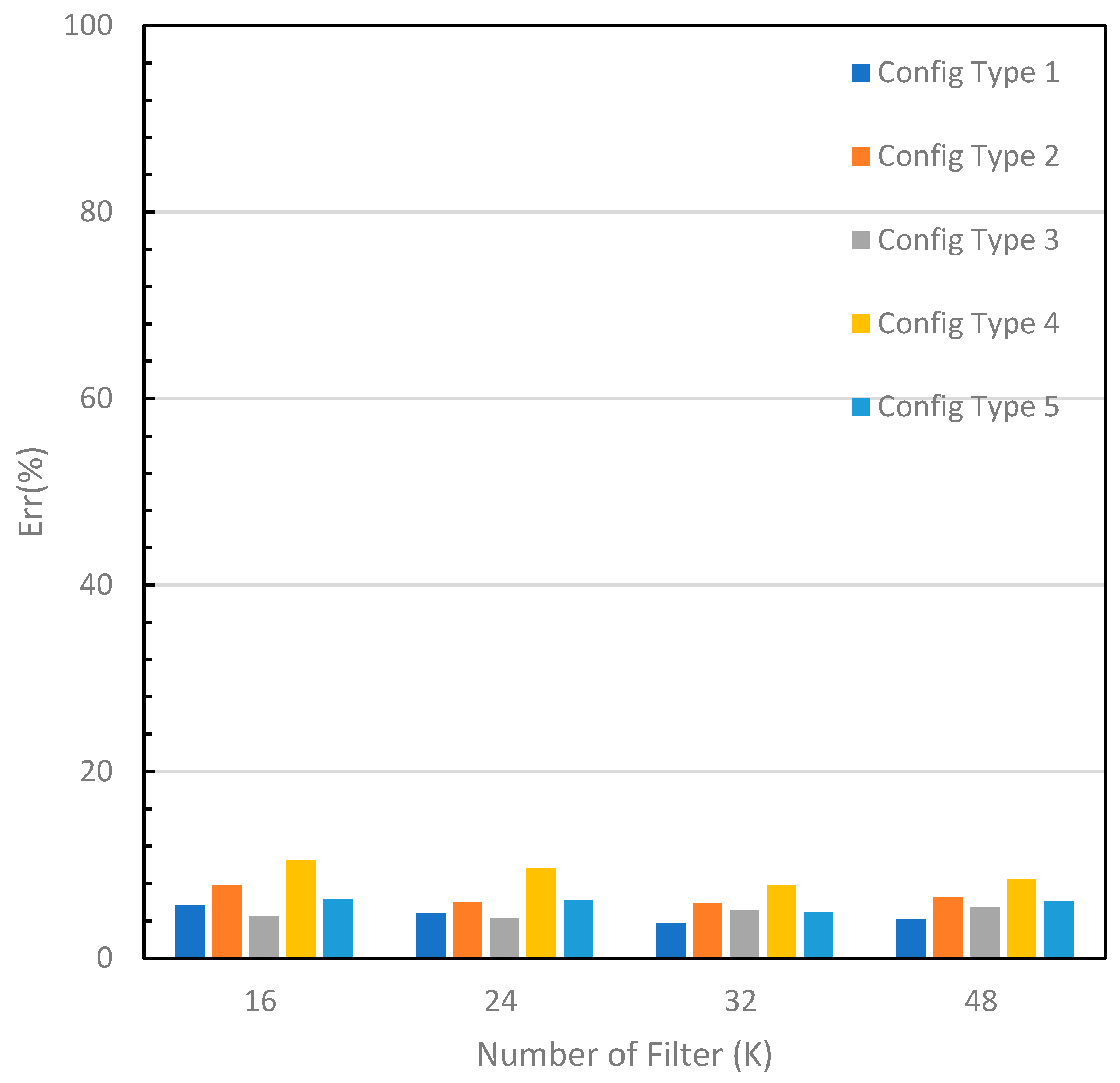
Table 6.
Individual class accuracy for configuration type 1 & 2 and K=32 .
| class | Type 1 (C1) | Type 2 (C2) |
| O | 93.82% | 92.08% |
| C | 98.32% | 96.16% |
| L | 96.96% | 95.22% |
| Y | 95.71% | 93.03% |
In any classification problem, misclassification is a common issue. In this study, we analyzed a few typical misclassification examples. Figs.10-13 depict the five test patterns that our CNN misclassified. Below each image, the correct answer (left) and the network prediction (right) are displayed. The errors were mostly caused by the following reasons:
Figure 10.
mis-classified example 1.

Firstly, the issue of symmetry can make it difficult for calligraphers to write characters in a distinct order of strokes. For instance, the character "會" (Figure. 10) is symmetrical and can easily be written similarly in terms of strokes and order.
Secondly, the stroke width is another factor that can contribute to the difficulty of character recognition. In the examples provided (Figure. 12), challigrapher 1, 3 have stroke widths that are similar in thickness, while 0 and 2 being thinner and elegant, calligrapher 1 and 3 are thicker and bolder. This similarity in stroke width can confuse the CNN when trying to differentiate between certain characters.
Figure 11.
mis-classified example 2.

Lastly, the simplicity of some characters, such as character "三," (Figure 12 right) which only has 2-3 strokes, can make them challenging to differentiate. Additionally, big stains or noise signals in the examples (Figure 12 left) can further hinder the accuracy of CNN detection, compounding with the aforementioned problems.
Figure 12.
mis-classified example 2.

Overall, these examples provide valuable insights into the challenges faced by CNNs in character recognition and highlight the need for continued improvement in this field.
5. Conclusions and future works
This study elucidates the utilization of a novel Convolutional Neural Network (CNN) architecture to distinguish among the four primary styles of historical calligraphers from the Tang dynasty (690-907 A.D.). The proposed model exhibits superior performance, achieving accuracy rates between 92% and 98% in Chinese calligraphy classification. This achievement is attributed to the optimal architecture parameters identified during our research. Furthermore, the training dataset curated for this purpose has proven effective and accessible, with potential for expansion through the inclusion of additional examples.
Key contributions of this research include:
- Development of a comprehensive image dataset for Chinese calligraphy (regular script) classification, comprising over 8,000 images, serving as a valuable resource for future scholarly endeavors.
- Pioneering the application of CNN in the classification of personal styles in Chinese calligraphy.
- Achieving elevated performance metrics with the CNN model, evidenced by accuracy rates ranging from 89.5% to 96.2%.
Enhancements such as data augmentation techniques, including image shifting, rotation, and the introduction of random background noise, have the potential to further refine accuracy. Future experiments will leverage multiple high-performance GPUs to evaluate training durations, currently ranging from 10 to 40 minutes. A proficiently trained network can swiftly predict classifications for new image data, presenting commercial opportunities such as the development of personal trainer applications for the study, evaluation, and improvement of Chinese calligraphy.
Prospective research avenues might explore applying this methodology to various script styles and artists' personal styles or creating new datasets for these purposes. Given the complexity of the cursive style, often challenging for untrained observers, a CNN-based tool could provide significant support to scholars and practitioners in this artistic domain.
Author Contributions
Study conception and design: Q.H. Methodology: Q.H., M.L. and L.L. Measurement: Q.H. M.L. and D.A. Data analysis: M.L. and D.A. Validation: Q.H., M.L. D.A.Writing—original draft preparation: Q.H., M.L. Writing—review and editing: Q.H., M.L, L.L and M.J. Acquisition of research funds: Q.H. M.L. and L.L All authors have read and agreed to the published version of the manuscript.
Data Availability Statement
The datasets supporting the conclusions of this study are available. upon request from the principal author (q.huang@cqu.edu.au). The authors commit to providing. access to the data and materials promptly to researchers with a qualified purpose in accordance with. the ethical approval vetting the collection of the data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liu, S. (Ed.). (2003). Full Colour Art History of Chinese Calligraphy (1st ed.). Ningxia People's Publishing House. pp. 114-115.
- Huang, Q., & Balsys, R.J. (2009). Applying Fractal and Chaos Theory to Animation in the Chinese Literati Tradition. In Proceedings of the Sixth International Conference on Computer Graphics, Imaging and Visualization, CGIV '09. [CrossRef]
- Fitzgerald, C. P. (1969). The horizon history of China. American Heritage Publishing Co., Inc.
- Wong, E. (1997). The Shambhala Guide to Taoism. Shambhala Publications, Inc.
- Y. LeCun, L. Bottou, Y. Bengio, P. Haffner, Gradient-based learning applied to document recognition, Proc. IEEE 86 (11) (1998) 2278–2324. [CrossRef]
- W. Li, Research on Key Technologies of Chinese Calligraphy Synthesis and Recognition for Chinese Character of Video, Ph.D. Thesis, School of Information Science and Engineering, Xiamen University, Xiamen, China, 2013.
- Y. Lin, Research and Application of Chinese Calligraphic Character Recognition, Ph.D. Thesis, College of Computer Science, Zhejiang University, Hangzhou, China, 2014.
- T. J. Mao, Calligraphy Writing Style Recognition, Ph.D. Thesis, College of Computer Science, Zhejiang University, Hangzhou, China, 2014.
- X. Wang, X. F. Zhang and D. Z. Han, Calligraphy style identification based on visual features, Modern Computer, vol.21, pp.39-46, 2016.
- Y. F. Yan, Calligraphy Style Recognition Based on CNN, Ph.D. Thesis, College of Information and Computer, Taiyuan University of Technology, Taiyuan, China, 2018.
- Cui, W., & Inoue, K. (2021). Chinese calligraphy recognition system based on convolutional neural network. ICIC Express Letters, 15(11), 1187-1195. [CrossRef]
- L. Chen, "Research and Application of Chinese Calligraphy Character Recognition Algorithm Based on Image Analysis," 2021 IEEE International Conference on Advances in Electrical Engineering and Computer Applications (AEECA), Dalian, China, 2021, pp. 405-410. [CrossRef]
- Liu, J., Liu, Y., Wang, P., Xu, R., Ma, W., Zhu, Y., Zhang, B. (2021) Fake Calligraphy Recognition Based on Deep Learning, Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 12736 LNCS, pp. 585-596.
- C. Zhai , Z. Chen , J. Li , B. Xu , Chinese image text recognition with BLSTM-CTC: a segmentation-free method, in: 7th Chinese Conference on Pattern Recognition - (CCPR), 2016, pp. 525–536 .
- [15]B. Li, Convolution Neural Network for Traditional Chinese Calligraphy Recognition, CS231N Final Project, http://cs231n.stanford.edu/reports/2016/pdfs/257 Report.pdf, 2016.
- J. Zou, J. Zhang and L. Wang, Handwritten Chinese character recognition by convolutional neural network and similarity ranking, arXiv.org, arXiv: 1908.11550, 2019.
- Y. Wen and J. S. Sig¨uenza, Chinese calligraphy: Character style recognition based on full-page document, Proc. of the 2019 8th International Conference on Computing and Pattern Recognition (ICCPR'19), pp.390-394, 2019. [CrossRef]
- Wang, M., Fu, Q., Wang, X., Wu, Z., & Zhou, M. (2016). Evaluation of Chinese calligraphy by using DBSC vectorization and ICP algorithm. Mathematical Problems in Engineering, 2016, 4845092. [CrossRef]
- Gao, P., Gu, G., Wu, J., & Wei, B. (2017). Chinese calligraphic style representation for recognition. International Journal on Document Analysis and Recognition (IJDAR), 20(1), 59-68. [CrossRef]
- Wang, L., Zhang, J., & Zou, J. (2023). Handwritten Chinese character recognition by convolutional neural network and similarity ranking. In Proceedings of the Conference on Handwritten Chinese Character Recognition (HCCR 2023) (pp. 105-110). Department of Electrical and Computer Engineering, University of Western Ontario.
- D.H. Hubel, T.N. Wiesel, Receptive fields and functional architecture of monkey striate cortex, J. Physiol. (1968) 215–243. [CrossRef]
- K. Fukushima, S. Miyake, Neocognitron: a self-organizing neural network model for a mechanism of visual pattern recognition, in: Competition and Cooperation in Neural Nets, 1982, pp. 267–285.
- Goodfellow, I., Bengio,Y., and Courvile, A. (2016). Deep learning (Vol.). Cambridge, Massachusetts.
- A. Krizhevsky, I. Sutskever, and G. Hinton. Imagenet classification.
- with deep convolutional neural networks. NIPS Conference, pp. 1097–1105. 2012.
- K. Simonyan and A. Zisserman. Very deep convolutional networks for large-scale image recognition.arXiv:1409.1556, 2014. https://arxiv.org/abs/1409.1556.
- Zhou, Bolei, Aditya Khosla, Agata Lapedriza, Antonio Torralba, and Aude Oliva. "Places: An image database for deep scene understanding." arXiv preprint arXiv:1610.02055 (2016).
- K. He, X. Zhang, S. Ren, and J. Sun. Deep residual learning for image recognition. IEEE Conference on Computer Vision and Pattern Recognition, pp. 770–778, 2016.
- Jiuxiang Gu etc. (2018) Pattern Recognition 77, 354-377. Recent advances in convolutional neural networks. [CrossRef]
- LeCun Y., Bengio Y., Hinton G. 2015 Deep Learning. Nature, 521 (7553),436-444. [CrossRef]
- Yangfan Zhou, Xin Wang, Mingchuan Zhang, Junlong Zhu, Ruijuan Zhen, and Qingtao Wu (2015) MPCE: A maximum probability based cross-entropy loss function for neural network classification. IEEE Access, Volume 7, 146331-146341. [CrossRef]
- Toshi Sinha, Ali Haidar, Brijesh Verma, Particle swarm optimization based approach for finding optimal values of convolutional neural network parameters, 2018 IEEE Congress on Evolutionary Computation (CEC), pp.1-6. [CrossRef]
- https://www.tensorflow.org/tutorials/images/classification.
- Justin M. Johnson, and Taghi M. Khoshgoftaar. 2019. Volume 6, 1-54, Journal of Big Data. Survey on deep learning with class imbalance.
- Szilvia Szeghalmy, and Attila Fazekas. Sensors, MDPI (in press).A Comparative Study of the Use of Stratified Cross-Validation and Distribution-balanced Stratified Cross-Validation Imbalanced Learning. [CrossRef]
Figure 1.
Left: middle split yields a sense of unbalance. Right: The well-developed character measured by Nine-Palaces grid from Fitzgerald [3].
Figure 1.
Left: middle split yields a sense of unbalance. Right: The well-developed character measured by Nine-Palaces grid from Fitzgerald [3].

Figure 2.
The root structure of the Nine Palaces (Wong [4]).
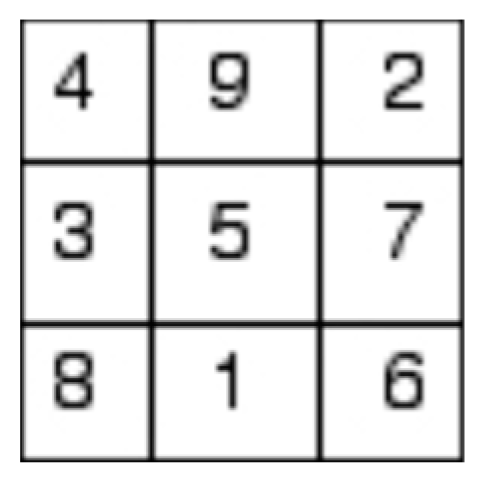
Figure 3.
The proposed style-oriented CNN architecture for Chinese calligraphy classification.
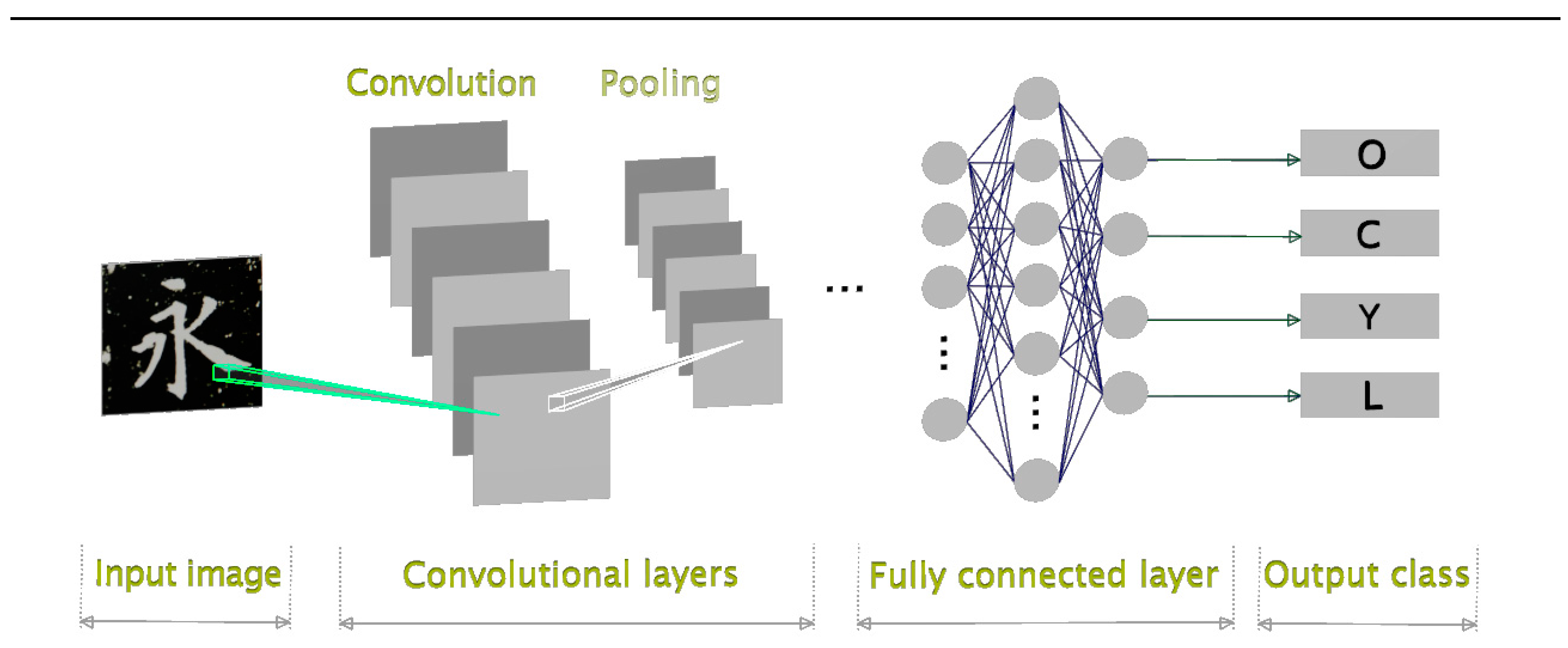
Figure 4.
a: Chu Suiliang calligraphy examples. Figure 4b: Ou Yangxun calligraphy examples. Figure 4c: Liu Gongquan calligraphy examples. Figure 4d: Yan Zhengqing calligraphy examples.

Figure 6.
cross-entropy loss curves.
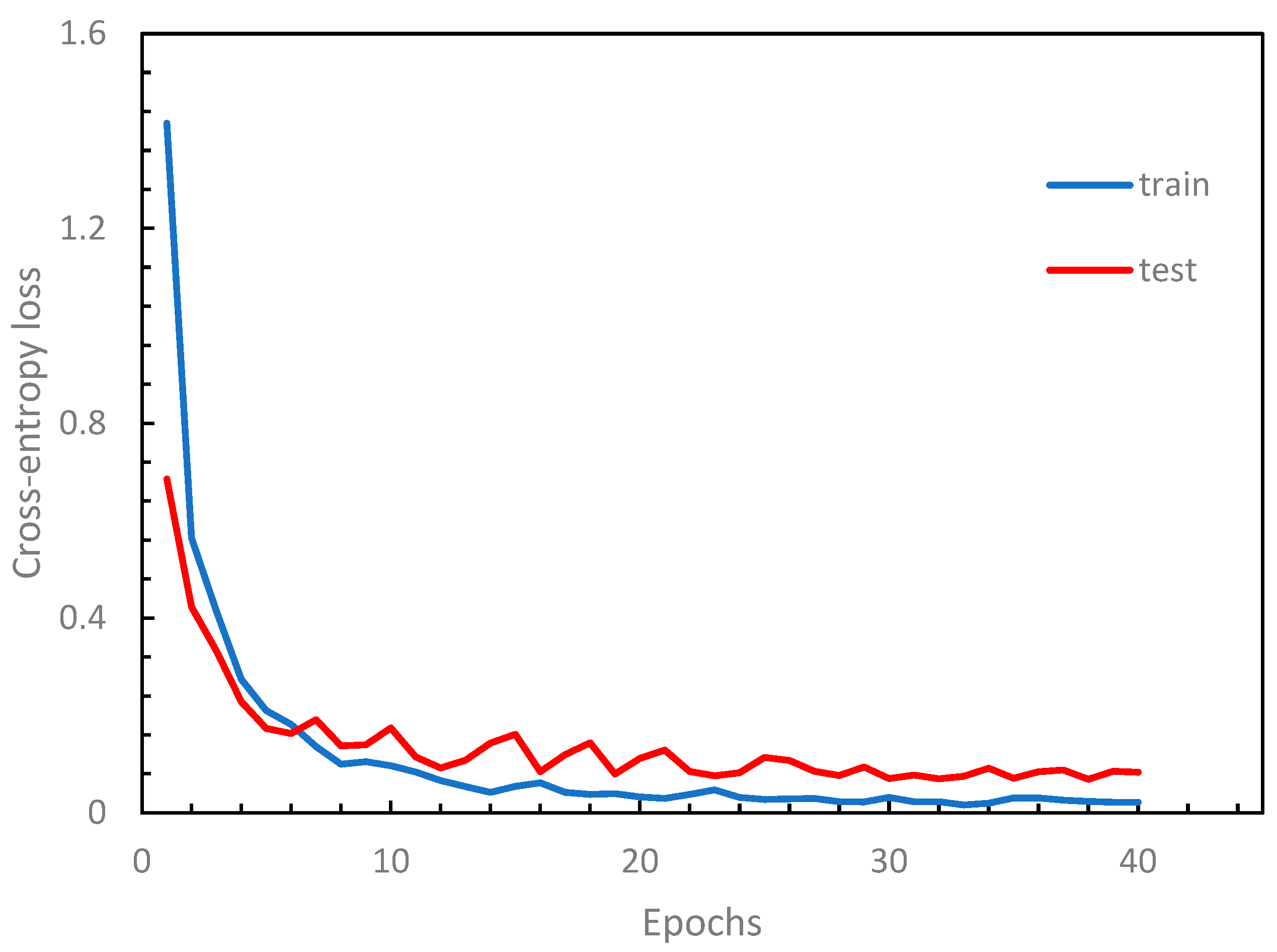
Figure 7.
Accuracy curves.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated









