Prerpints.org logo
Preprint
Article

The Multiple Roles of Temporal Collinearity in Hox Gene Clustering for Vertebrates, Invertebrates, Complete and Split Hox Clusters

Altmetrics

Downloads

114

Views

50

Comments

0

This version is not peer-reviewed

Submitted:

30 November 2023

Posted:

01 December 2023

You are already at the latest version

Alerts
Abstract
Hox gene clusters are crucial in Embryogenesis. It was observed that some Hox genes are located in order along the telomeric to centromeric direction of the DNA sequence: Hox1, Hox2, Hox3…. These genes are expressed in the same order in the ontogenetic units of the Drosophila embryo along the Anterior-Posterior axis. The two entities (genome and embryo) differ significantly in linear size and in-between distance. This strange phenomenon was named Spatial Collinearity (SP). Later, it was observed that, particularly in the Vertebrates, a Temporal Collinearity (TC) coexists: first is Hox1 expressed, later Hox2 and even later Hox3,…,. According to a Biophysical Model (BM), pulling forces act at the anterior end of the cluster while a cluster fastening applies at the posterior end. Hox clusters are irreversibly elongated along the force direction. During Evolution, the elongated Hox clusters are broken at variable lengths thus split clusters may be created. An Empirical Rule was formulated distinguishing development due to a complete Hox cluster from development due to split Hox clusters. BM can ‘explain’ this Empirical Rule. In a spontaneous mutation where the cluster fastening is dismantled, a minimal pulling force can automatically shift the cluster inside the Hox activation domain. This cluster translocation can probably explain the absence of Temporal Collinearity in Drosophila.
Keywords: 
Subject: Biology and Life Sciences  -   Cell and Developmental Biology

1. Introduction

Hox genes play an important role in the development of most animals and plants.Some Hox genes form clusters which are crucial for the Embryogenesis of Metazoa. The importance of this clustering was first noticed by E.B. Lewis who studied the genetics of Drosophila [1]. In 1978, Lewis observed that some genes of the genome (later coined Hox genes) were located in order along the telomeric to centromeric direction as (Hox1, Hox2, Hox3…). Lewis noticed that in the Hox gene clusters the genes are sequentially ordered and they are expressed in the same order along the antero-posterior axis of the Drosophila embryo [1]. This is an astonishing event since this correlation occurs between extremely distant locations - the genetic sequence in the cell nucleus in one hand and the Drosophila embryo in the other. These two local domains are about 4 orders of magnitude apart from each other. Biomolecular interaction alone cannot create such correlations [2]. This surprising phenomenon was named Spatial Collinearity (SC). Some years later, another collinearity was observed particularly in the Vertebrates: Temporal Collinearity (TC). According to TC, the first Hox gene (Hox1) of the Hox cluster starts being expressed. Later, Hox2 is expressed and even later Hox3 followed until all Hox genes are expressed following the sequence Hox1, Hox2, Hox3,… [3].
In order to explain these phenomena, a biophysical model (BM) was proposed in 2001 according to which, pulling physical forces can justify the data [2], [4]. Several experimental findings were successfully compared to the BM predictions [5,6].
A simple heuristic expression for these pulling forces F was proposed [7].
F = N * P
In the above equation, the pulling physical forces F are located opposite the telomeric end of the Hox cluster(Figure 1). In Eq. (1)F stands for a quasi - Coulomb force where, for simplicity, the relative distance between the electric charges is omitted [8]. It turns out that this omission reflects a deep connection to the fundamental phenomenon of Symmetry (see the Appendices). Ν and P are standing for the negative and positive charges acting on a Hox cluster.In the above heuristic formulation, the Hox cluster consists of a deployed finite sequence of Hox genes along the telomeric to centromeric ends of the cluster (Hox1, Hox2, Hox3,…). The numbers assign the gene order in the cluster. Thesenumbers determine the order membership to the evolutionary Paralogy Group (PG).(Here is followed Duboule’s definitions of PG [9]).
The contemporary cephalochordate Amphioxus is a descendant of the ancestor Amphioxus which coexisted with both Drosophila and vertebrates [9]. Amphioxus lived after the Cambrian period of evolutionary explosion 500 million years ago (Mya). Vertebrates and Drosophila appeared a few Mya later. Amphioxus has 14 Hox genes whereas vertebrates and Drosophila have 13 (Hox14 is missing).
As mentioned above, N represents the microscopic contribution to F and it is a real entity – the negative electric charge of the DNA sequence. P represents a positively charged molecular structure located opposite the telomeric end of the Hox cluster (Figure 1). Contrary to N, P is a fictitious entity as yet, standing for the embryonic-macroscopic contribution to F. The known morphogens of the present time like Sonic Hedgehog, Fibroblast Growth Factors, Retinoic Acid and the plethora of other morphogenetic factors were fictitious fifty years ago. The existence of P does not contradict any First Principle so it is legitimate to anticipate its existence as advocated in [4]. F pulls the Hox genes sequentially out of the cluster (Figure 1). Eq.(1) is a heuristic expression that was successfully tested in several experiments [5,6,7,8].
Hox genes control the normal development of animals (wild type). Spontaneous mutation of these genes cause severe malformations (Homeosis), consisting of parts of the animal growing in the wrong location of the body. In Homeosis PG ordering is violated.
About twenty years ago, an important advancement was achieved concerning the transfer of specific molecules from outside the cell into the inner domain of the cell nucleus [10,11,12,13].For example, it was noticed that significant amounts of Activin are gathered outside the cell nucleus. Controlled amounts of this activin were transduced inside the nucleus causing specific modifications on the genome. It is assumed that BM combined with the action of transduction technology can affect Hox gene expression. This possibility is incorporated in the present hypothesis.
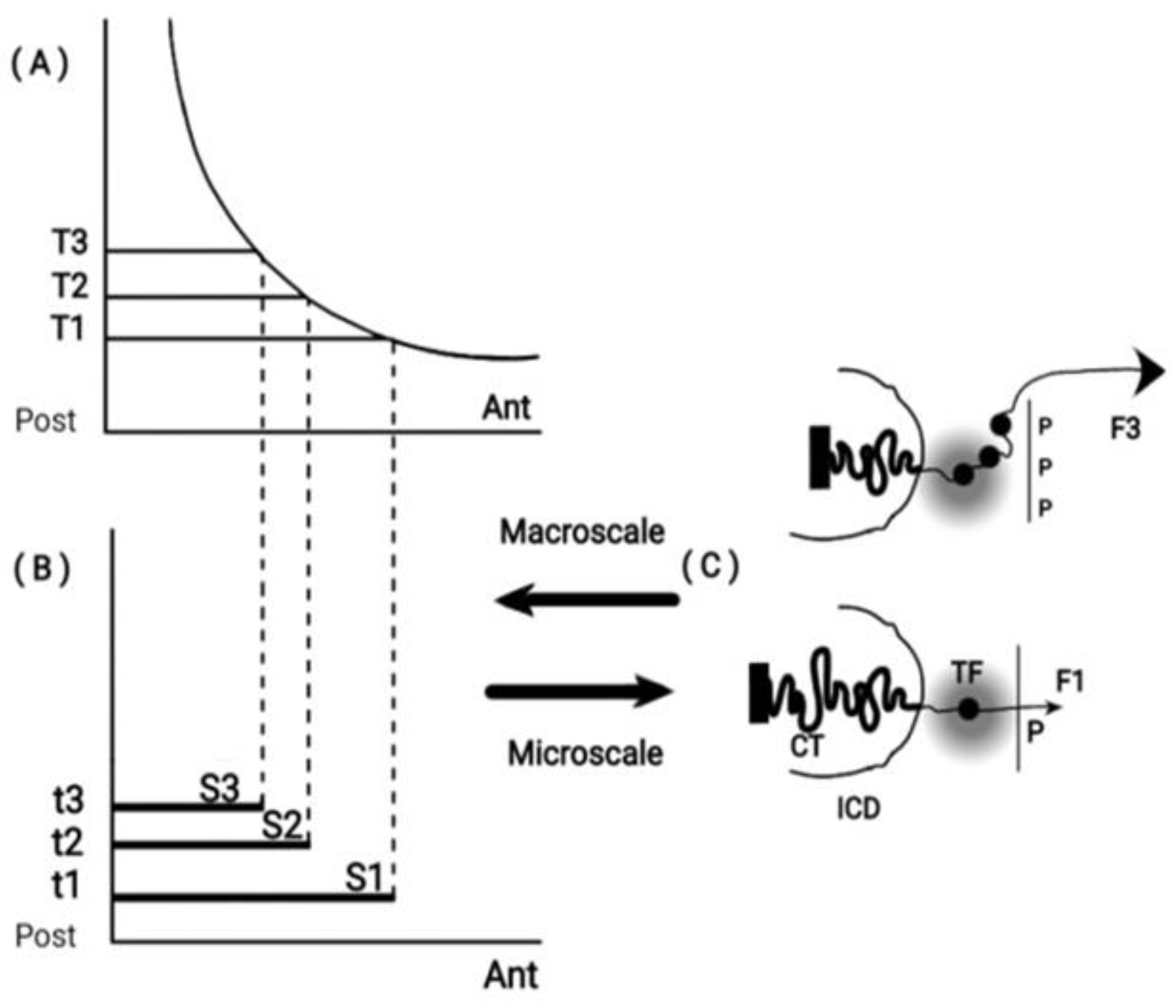
BM is based on the hypothesis that pulling forces are applied at the telomeric end of the Hox cluster. This hypothesis was elaborated in detail and it was concluded that the cluster is elongated along the direction of the force [14]. This BM prediction was later confirmed [15,16,17]. In some cases the measured elongation of the activated Hox cluster was five times longer than the length of the inactive Hox cluster [16]. When Hox cluster activation is initiated, a weak force (F1) pulls the first gene of the cluster (Hox1) out of its niche toward the interchromosome domain (ICD) (Figure 2).
Particularly Hox1 is directed towards the transcription factory domain (TFD) where Hox gene activation (expression) is possible [18,19]. The pulling forces increase irreversibly so under force F2, Hox2 is extruded from its niche. This process continues until all Hox genes are transferred in the TF. For the efficient function of an elongated elastic spring, besides the pulling force at one of its ends, a proper fastening should be applied at its other end. Accordingly, the Hox cluster should be fastened at the centromeric end (Figure 2).
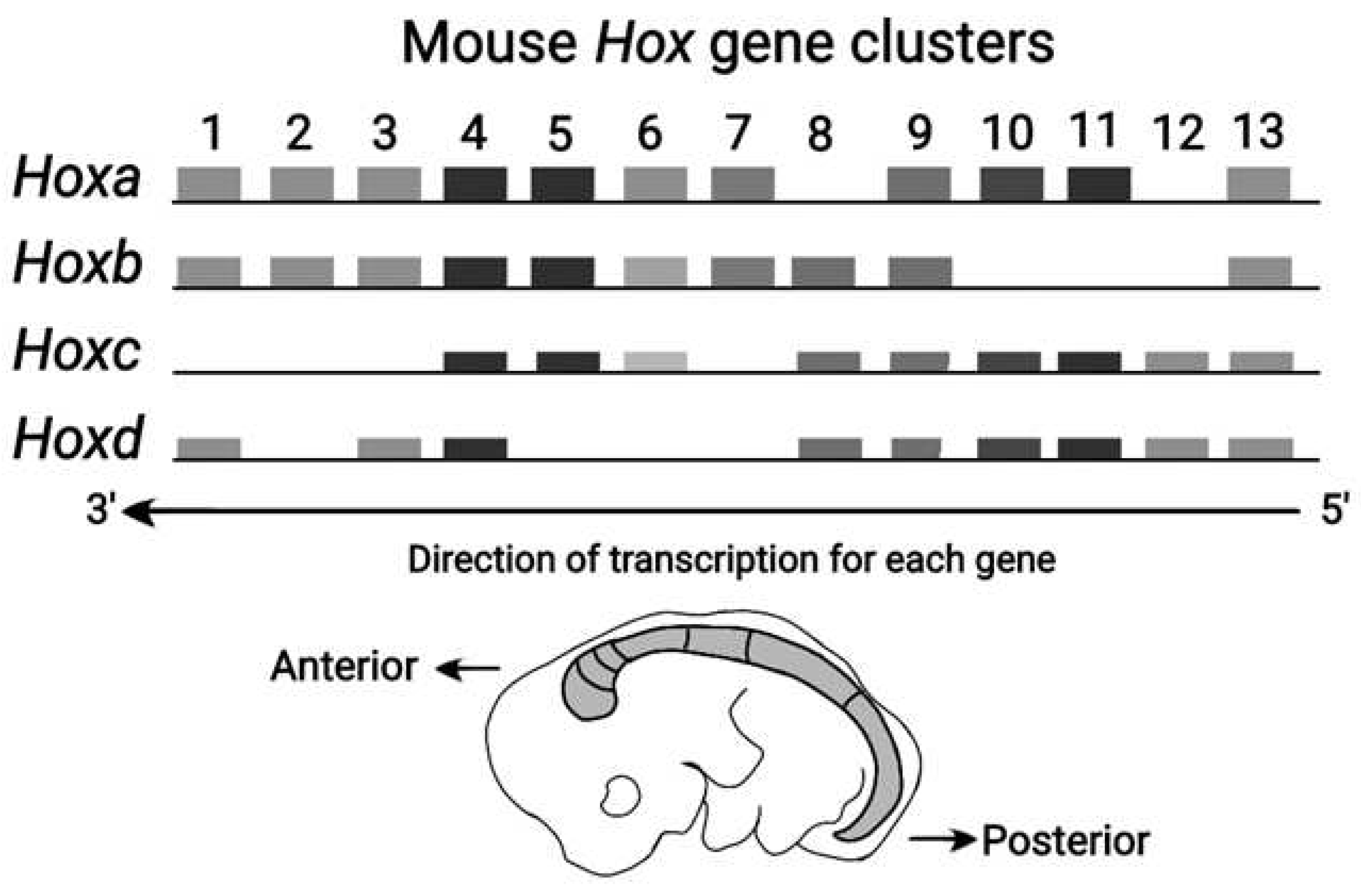
The Vertebrate Hox clusters comprise four homologue clusters (HoxA, HoxB, HoxC, HoxD) as shown in Figure 3 [11]. Each homologue cluster is included in a separate chromosome. In these homologue clusters the PG identity is conserved. However, in the course of Evolution, modifications of the mouse genes are possible up to the point of gene deletion. This ordered mouse Hox clusters remind of a ratchet allowing motion in one irreversible direction only [8]. Note that some ‘teeths’ of the ratchet may be missing (e.g. Hox genes are deleted).

2. Symmetries entangled with gene ordering in Hox gene clusters

Symmetry is an important concept in Science as stressed in [20,21] (see also the Appentices below). Self-similarity is the particular symmetry of objects which, although different, they look the same if depicted under suitable scale units. Such objects are the fractals where the part looks like the whole with a typical example being the Barnsley fern that can be easily drawn with a computer program.B. Mandelbrot invented this branch of Applied Mathematics and introduced the term of fractals [22].
Theoretically self-similarity is a continuous symmetry extending to all geometric scales. In contrast, the genetic linear ordering (Hox1, Hox2,…Hox13) of a Hox cluster and the corresponding ontogenetic units of the embryo along the AP-axis refer to only two geometric scales (genetic and embryonic). In this spirit, these two entities can be considered as defectively self similar [8,21].In this remnant self-similarity, the PG ordering is conserved where some Hox genes of the cluster may fade out up to extinction during the Whole Genome Duplication of the evolutionary process [20,21].
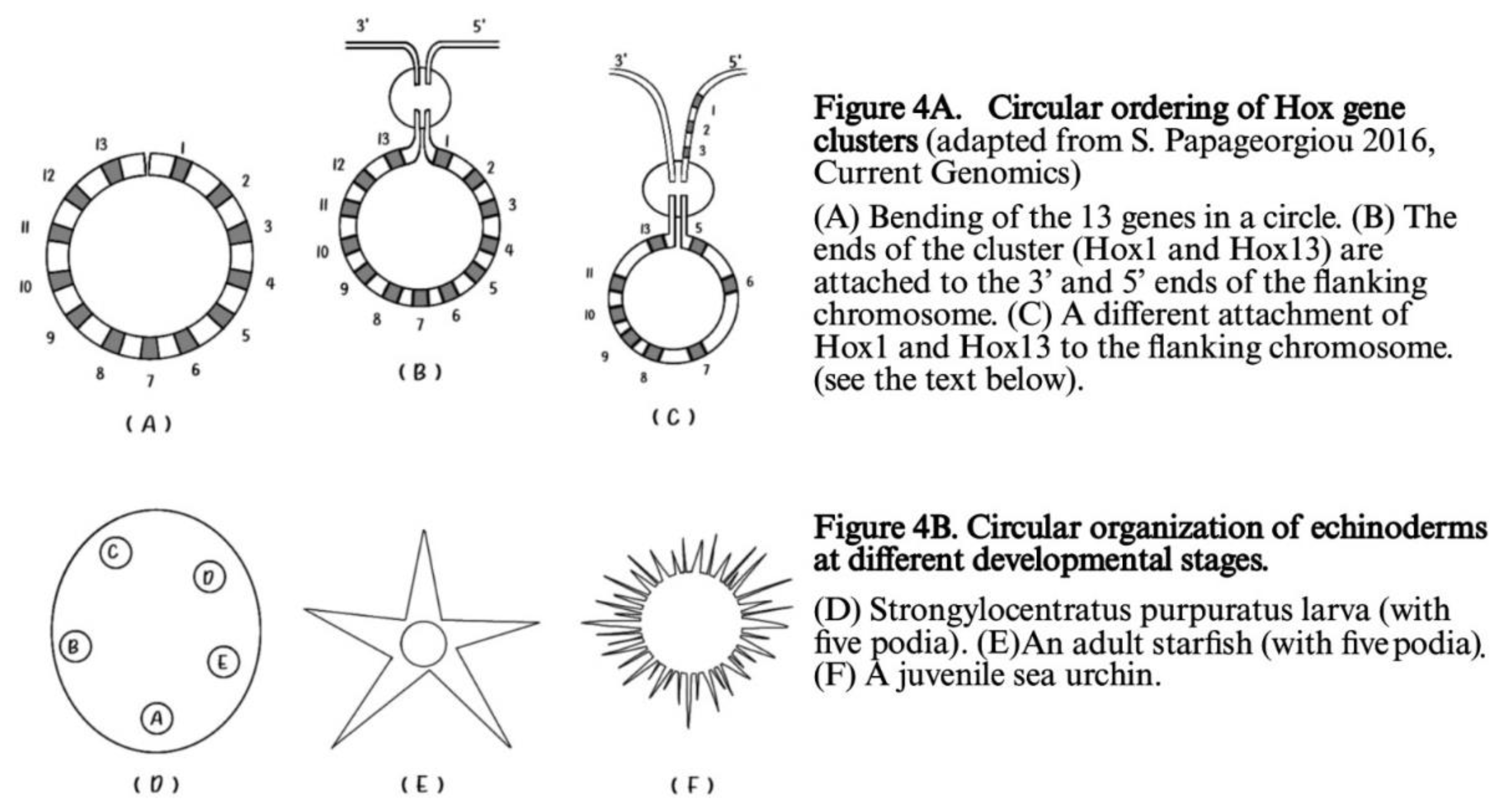
Besides the ordering of Hox genes on a finite straight line, in many early larva embryos (e.g. the echinoderms) a circular ordering is superimposed on this finite line as shown in Figure 4 [23].
In Figure 4A the two ends of the circular cluster are attached to the 3’ and 5’ ends of the flanking chromosome. If the 3’ end of the flanking chromosome is attached to Hox1(and 5’ to Hox13) no novelty is created and A.planci normal Hox gene order gene is reproduced. In contrast, if the 5’ end of the flanking chromosome is attached to Hox1, Hox2. Hox3 (shown in Figure 4A) a novelty is created. A second breaking follows leading to a new Hox gene order which corresponds to the Hox gene order of the sea urchin [23].
The circular Hox gene clusters can be incorporated in the flanking DNA sequence of the genome. A recent review by T. Hanscom refers to the well known technique of double strand break (DSB) [24]. In the above review, besides the usual medical applications of the DSB methodology, it is extensively emphasized the novel trends of research to explore how DSB can leverage genome evolution. It is here schematically depicted the incorporation of a Hox cluster in the flanking genome (Figure 5).
Preprints 91908 g005
Figure 5. (A) LDouble Strand Break Left (T) and Right (C) in the middle ( INS) follows orientation (T→C) R. (B) L Double Strand Break Left (T) and Right (C)in the middle (INS) follows orientation (T←C) R.
Figure 5. (A) LDouble Strand Break Left (T) and Right (C) in the middle ( INS) follows orientation (T→C) R. (B) L Double Strand Break Left (T) and Right (C)in the middle (INS) follows orientation (T←C) R.
Preprints 91908 g005
In (A) the inserted graft in the middle follows the orientation T→ C In(B) the inserted graft in the middle followsthe reverse orientation (T ← C)

3. Complete vs split Hox clusters

Hox Gene Collinearity both Spatial and Temporal has been unequivocally confirmed in the Vertebrates. However, in recent years it was found that this is not true in many other animal species, particularly in invertebrates. For instance, it was observed that Hox colinearity is violated in the lophotrochozoa and this violation was associated with the brachiopods whose Hox cluster is broken [25]. In brachiopods both spatial and temporal collinearities are violated, while lophotrochozoan morphological novelties result from Hox Collinearity violation [25]. It was argued above that for the insertion of a circularly organized Hox cluster in the flanking genome, a break (split) of the cluster is necessary. It is clear that Hox cluster splitting is a necessary step for evolutionary novelties.
It has been emphasized that tight Hox clustering is lost during Evolution [26,27,28,29]. More specifically D. Ferrier and P. Holland assumed that Hox clusters are necessarily constrained by TC in their gene order. Moreover, when TC is no more needed, ‘Hox gene clusters may fall apart’ [26,27]. Similar arguments were put forward before and after the above assumption [28,29].
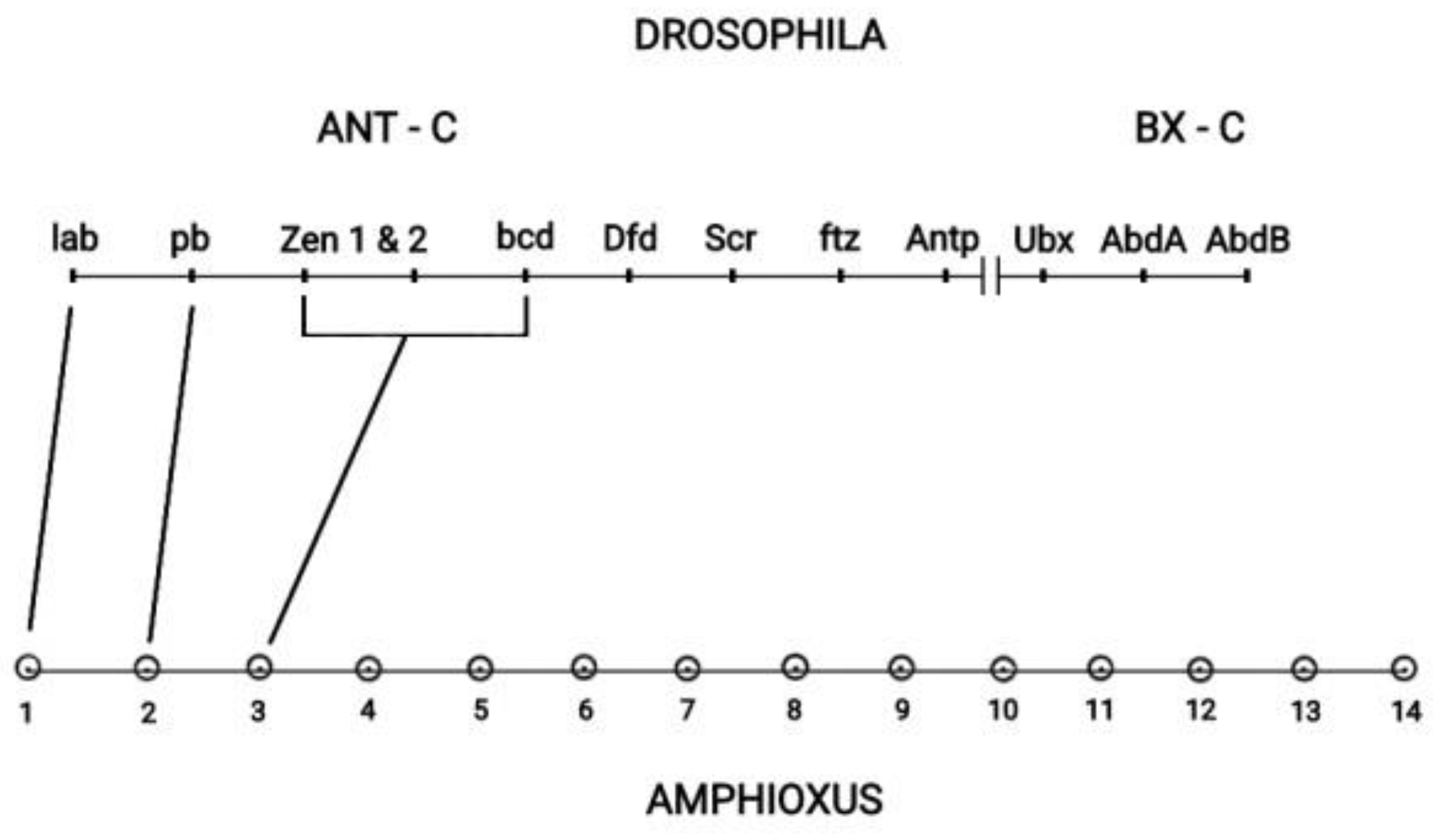
The Drosophila Hox cluster has 13 genes contained in the two subclusters ANT-C and BX-C depicted in Figure 6 [27]. Drosophila has a typically split Hox cluster. It was shown that this cluster consists of two subclusters Ant-C and BX-C [27]. Drosophila together with the vertebrate Hox cluster originate from a large ancestral Hox cluster [27]. Cloning had later identified Amphioxus as the common ancestor of insects and vertebrates [28], and a one-to-one correspondence between the Amphioxus Hox genes and the Drosophila Hox genes was confirmed [27]. However in this correspondence some Drosophila Hox genes of the ANT-C subcluster developed novel evolutionary non-Hox functions. For instance, the Drosophila complex of Hox genes (zen1, zen2, bcd) corresponds to the ancestral Amphioxus Hox3 gene. Some Central genes have evolved from tandem evolutionary duplications [27]. (see Figure 1 in [27]). The BX-C subcluster consists of the 3 last genes (Ubx, Abd-A, Abd-B) of the Drosophila Hox cluster. The summarizing conclusion from the above analysis is that TC is responsible for a complete Hox cluster. If this is not possible (or not needed) the Hox cluster is split. In any case SC is a necessity for a Hox cluster [26].
Preprints 91908 g006
Figure 6. The ANT-C and BX-C subclusters of Drosophila - Amphioxus (adapted from D.E.K. Ferrier in Hox Gene Expression editor S. Papageorgiou. Editions Springer and Landes Bioscience 2007).
Figure 6. The ANT-C and BX-C subclusters of Drosophila - Amphioxus (adapted from D.E.K. Ferrier in Hox Gene Expression editor S. Papageorgiou. Editions Springer and Landes Bioscience 2007).
Preprints 91908 g006

4. Predictions and Discussion

4.1. Empirical Rule on complete and split Hox clusters

With the above established knowledge, D. Duboule formulated recently a useful Empirical Rule (ER) for the Hox Gene clusters [28]:‘A complete Hox cluster controlling development in time along the Anterior-Posterior axis is non-split, whereas animals developing according to a time-independent mechanism to produce their main body axis are licensed to split their clusters…
In a significant experiment of extended posterior upstream excisions, T. Kondo and D. Duboule had noticed that several Hox gene expressions (and in particular Hoxd4 and Hoxd10) were unexpectedly absent as if Temporal Collinearity (TC) had disappeared [30]. In this case, TC disappearance is not real - it is only fictitious. However, in a different interpretation of this Kondo and Duboule experiment a ‘prediction in retrospect’ of BM was formulated according to which TC really (and not fictitiously) disappears indeed [31]. (See also section 4.3).

4.2. Development in the secondary developmental axis

In chick limbs, the apical ectodermal ridge (AER) controls development responding to morphogen Fibroblast Growth Factor (FGF). If the ectodermal ridge is excised, Hox13 (the last gene of the cluster) switches off. The results from this experiment are illuminating [32]: Hox13 expression can be initiated again (in the absence of the ridge) if beads soaked in FGF are implanted distally. This occurs after a fixed time interval. If the FGF dose is increased the Hox13 rescue occurs earlier. Furthermore, the rate of Hox13 spreading is faster initially and slower at later stages - a sign that passive diffusion is the main mechanism of signal propagation [32]. In the above chick limb bud experiment in the secondary developmental axis, Hox13 expression is most sensitive to AER excision [32]. However, Hox10 and Hox11 are less sensitive to this excision indicating that TC is not uniform along the developmental axis.

4.3. Development in the mouse primary A-P axis

It is interesting to compare the above limb findings [32] to a similar experiment of upstream DNA excision in mouse embryos as described in [30]. In this excision experiment, TC disappearance was in agreement with the BM pulling forces model [31]. According to BM it is eventually expected TC to reappear. This expectation remains to be tested [31]. To this end it was proposed the reverse experimental path - the insertion of TGF-beta signals. (A detailed description is included in [31]). The proposed disappearance experiment and the eventual reappearance of TC is not completed. The direct course of disappearance is confirmed but the palindromic cource of reappearance remains to be tested and the eventual experimental confirmation will be decisive [31].

4.4. A spontaneous mutation in the Drosophila case

In the Introduction it was stressed that spontaneous genetic mutations can lead to evolutionary novelties as in the case of Homeosis. If, in a spontaneous Drosophila mutation, the Hox cluster fastening is dismantled (Figure 2D), the slightest pulling force will automatically slide the cluster in the transcription factory domain. The repercussion on both genetic structure and function of the cluster will be dramatic: TC will automatically disappear. According to a generally accepted argument, TC is constrained to inexistence if TC is no more needed [26,27,28,29]. This occurs when the complete Hox cluster is shifted inside the transcription factory domain (Figure 2D). Therefore, the loss of TC in Drosophila could be ascribed to a spontaneous genetic mutation that suppresses the Hox cluster fastening.

4.5. Quantitative Collinearity

Relying on Lewis observation in [1], A. Durston proposed a Hox cluster property (Posterior Prevalence) (PP) to guarantee the dominance of posterior Hox gene expressions over simultaneously expressed anterior Hox expressions [33,34].
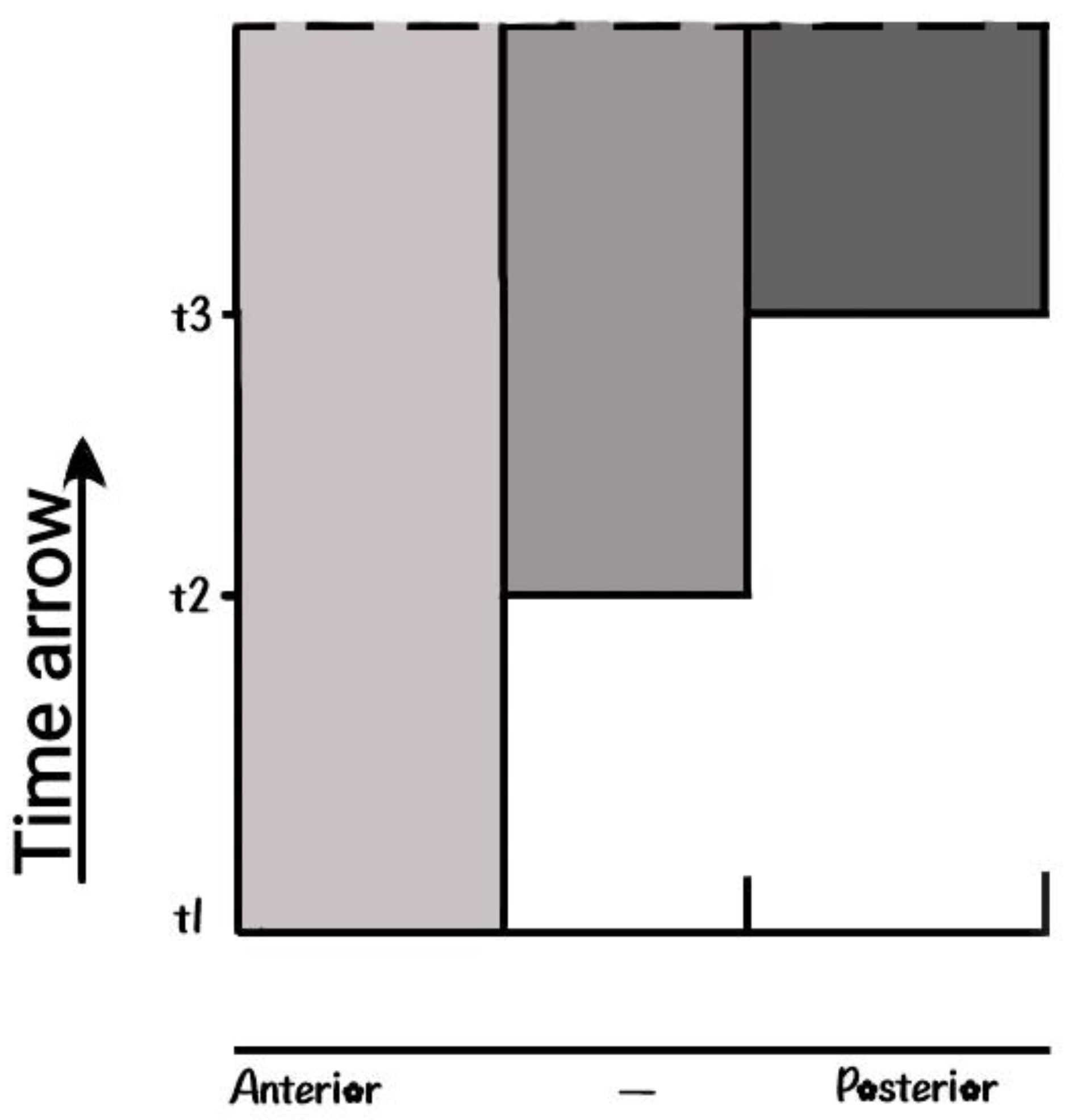
Besides Spatial and Temporal collinearities, a third collinearity has also been traced: Quantitative Collinearity (QC). This was a puzzling issue and for a long time it was examined following a parallel path with the PP hypothesis. QC is determined following two directions in the two-dimensional plane. First is the direction along the down-up time direction (Figure 7) and second is the expression intensity along the anterior- posterior axis. For the HoxD expression of a sequence of cells along the horizontal dashed line, the intensity is stronger at the posterior side [4], [14]. The intensity at any point depends on its distance from the morphogen source. It turns out that in the limb, passive Diffusion is the main signal propagating mechanism whose size of spreading depends on the vicinity to the morphogen source [4], [14]. It was measured that this size is higher near the morphogen source compared to the size of spreading at a distant location [32]. For the HoxD cluster, the expression intensity increases following the order HoxD10….HoxD13 (Figure 7) [4], [14]. Note that the same mechanism applies to the Morphogen Fibroblast Growth Factor in the chicken limb bud [32], where the morphogen source is at the tip of the bud in the AER. A similar mechanism applies for the expression of split clusters as mentioned in Section 3.
Preprints 91908 g007
Figure 7. Quantitative Collinearity The split clusters of section 3 and Quatitative collinearity of section 4.3 are described by identical mechanisms.
Figure 7. Quantitative Collinearity The split clusters of section 3 and Quatitative collinearity of section 4.3 are described by identical mechanisms.
Preprints 91908 g007
Besides Hox gene quantitative collinearity, Figure 7 can also describe the split Hox cluster activation. It is strange that so divergent phenomena can be described by the same mechanism. This hints at a scarcity or universal parsimony of the developmental mechanisms. Is this an evolutionary advantage or disadvantage? We believe this is surely an evolutionary advantage since it is used in several divergent developmental pathways, as for instance in the case of primary and secondary developmental axes. Note that the morphogen source in the limb is located at a quite different position - namely the AER in the distal tip of the bud [32].

5. Conclusion

5.1. Physical forces may cause a tension in the Hox clusters

New technological advances (e.g. STORM- the stochastic optical reconstruction microscopy) made possible the measurement of quantities and properties that were inaccessible before. Physical tension in Hox clusters is such a case and more specifically the tension of DNA topological domains which are important for Hox gene activation. Amândio et al. have recently measured mouse HoxD clusters under physical tension [35]. The origin of this tension is elusive. This team has even considered the possibility of the BM physical forces to be responsible for this phenomenon. In this case they argue that ‘the forces would be generated by the local chromatin interactions themselves, rather than through an asymmetrically localized point of attachment to the nuclear environment’ [35]. Indeed this is most probable worth further examining.

5.2. Complex Expression patterns

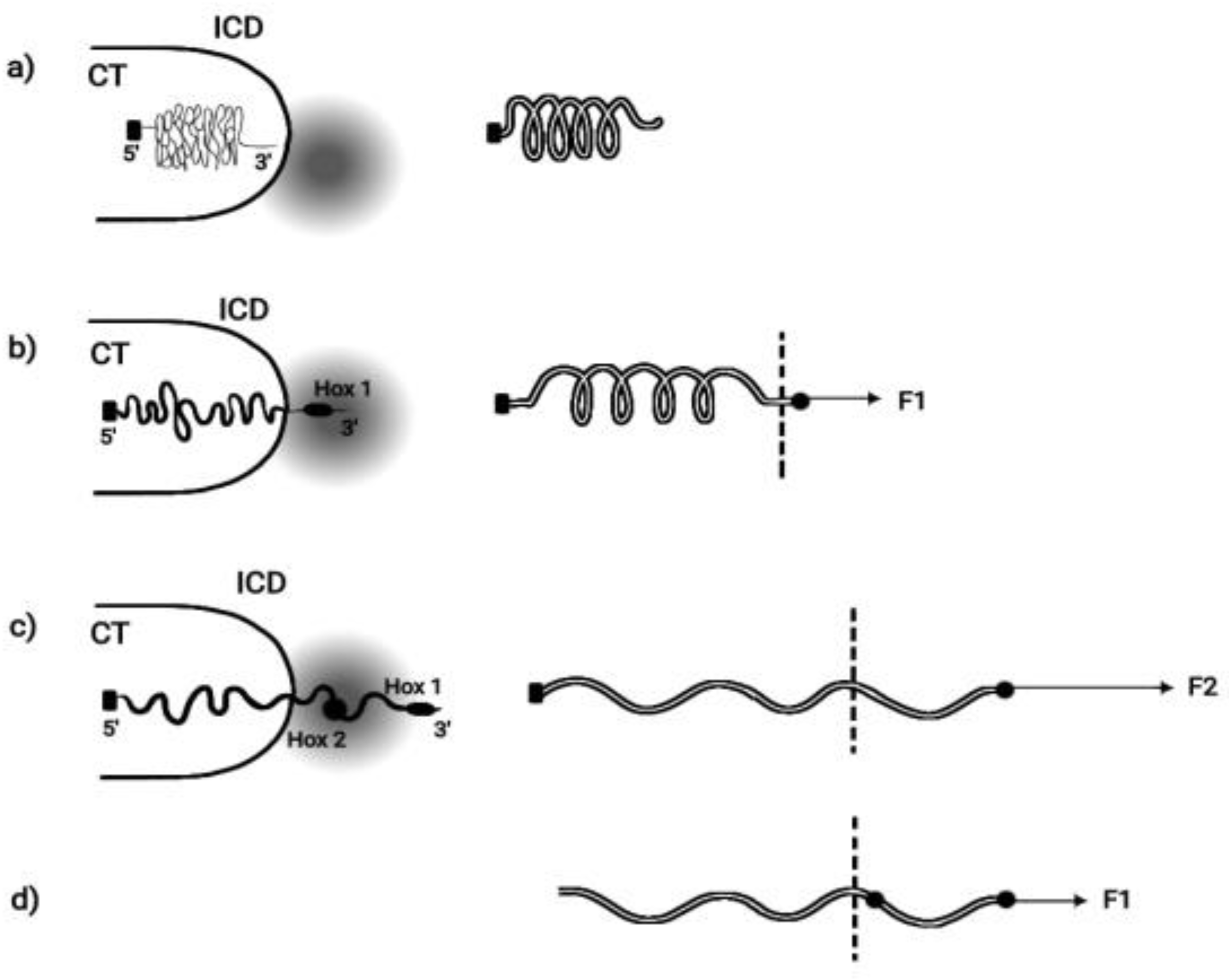
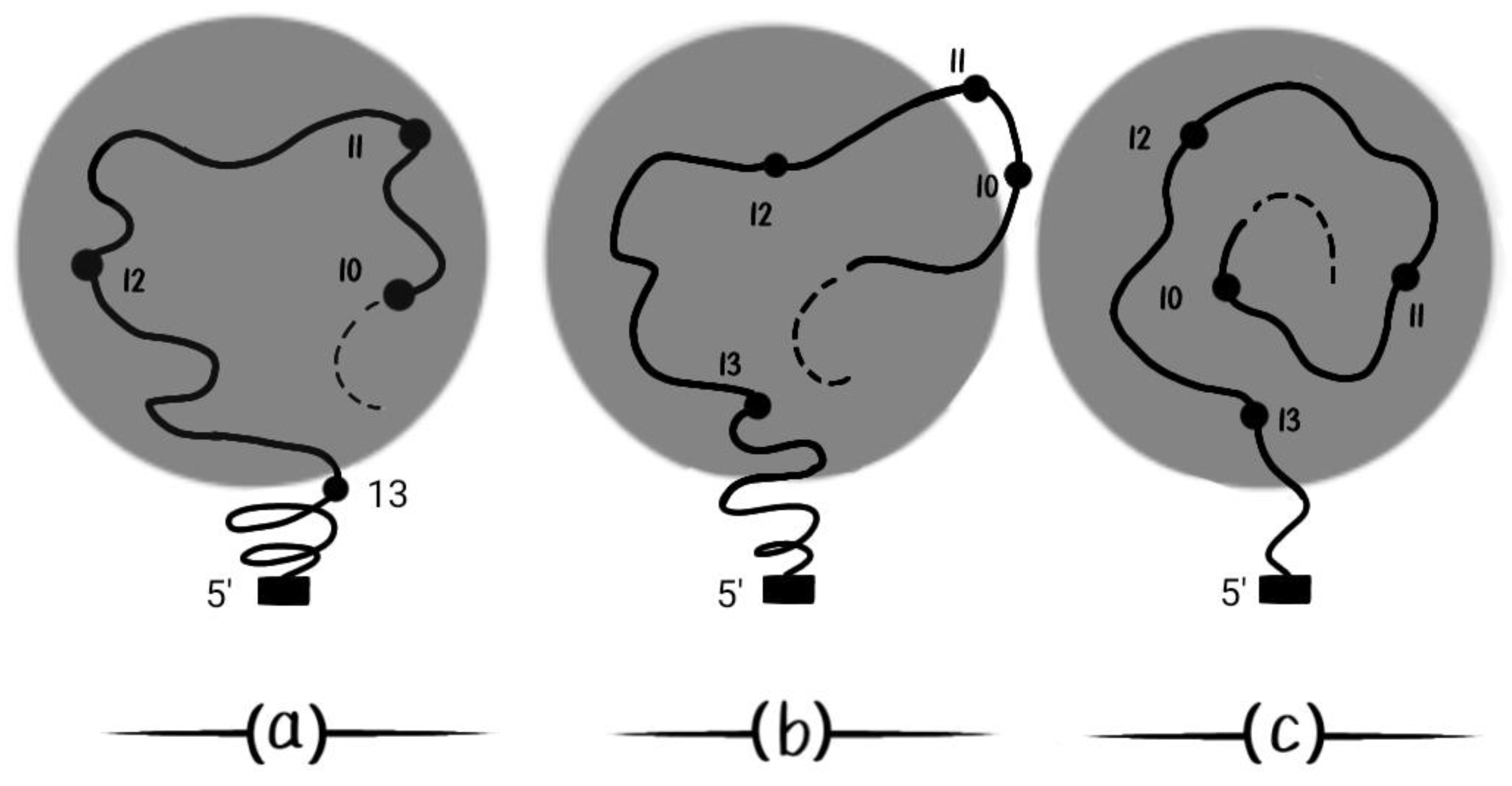
According to BM, it is expected that complex patterns can be created by splitting the early (simply connected) Hox gene expression into expression domains separated by a ‘ditch’ zone [36]. This splitting was already confirmed in 2013 [37]. Following this line of thought [36,37], BM further predicts that a small DNA strip containing (Hox10 and Hox11) has a strange expression behavior in time (Figure 8). These genes can be pushed in and out of the Hox cluster activation domain which is depicted in the dark circle ( Figure 8). In Figure 8(a) Hox10, Hox11, Hox12 are activated. In Figure 8(b) (Hox10, Hox11) are pushed out of the activation domain. In Figure 8(c) (Hox10, Hox11) reenter later in the activation domain following the increased force of BM in the time course [36,37].
It is interesting that the theoretical prediction ‘Biophysics precedes Biochemistry’ [36] was experimentally confirmed soon after ‘…structural organization of HoxD cluster may predate transcriptional activation’ [16].

5.3. Comments on TC disappearance and reappearance

According to chick limb bud experiments, morphogen signaling for Hox gene expression is necessary but not sufficient [32]. Therefore complementary cues must come into play for a proper gene expression. For instance such cues can distinguish gene expression in the liver from the heart or even when this should occur.
The BM forces vary along the developmental axes following the distances from their origin. Passive diffusion is the main signaling mechanism and the closer to the source origin the stronger the force as noticed in [32]. Besides the source localization of [32], recent more accurate techniques have been exploited (CRISP technology).
In the chick limb experiments mentioned above, the excision of the morphogen source causes the disappearance of HoxA13 at the distant tip. However, this expression reappears by exposure of the bud to an FGF soaked bead. It would be interesting to perform an analogous experiment in the primary mouse axis and compare the results as proposed in [31].

6. Appendices on Symmetries

6.1. Appendix1 Symmetry in Science

Symmetry is the cornerstone of Science and several other human intellectual activities. Many distinguished scientists have proposed their definitions of the term [38]. When an action is applied on any material object (or physical system) it causes a change. If this change leaves the system invariant, the system is symmetric. This means that any point of the system moves to another point contained in the system. I consider the compact definition of Frank Wilczek (in the form of an aphorism) is appropriate in the following context: Symmetry is a change without change [39]. The human intellect incorporates a wider realm than pure scientific thinking. Therefore, Wilczek’s definition of Symmetry could be complemented with unusual thoughts e.g. ‘Symmetry is complicated, ‘Symmetry is beautiful’ or even ‘lack of symmetry is ugly’.
Besides the obvious external symmetries in Space and Time there appeared in the last century the need to introduce several internal symmetries and particularly in the field of elementary particles with exotic names like bosons, quarks, charmed particles, mesons etc. Historically, in 1932 W. Heisenberg was the first who introduced such an esoteric term (the isotopic spin or isospin) to described the symmetry of protons and neutrons under the strong nuclear interactions [39,40,41].

6.2. Appendix2 Noether’s Theory in Hox Gene Collinearity

In 1918 Emmy Noether formulated and proved in Classical Mechanics a fundamental theorem on Symmetry. In simple terms, Noether proved that a physical system obeying a symmetry law is followed by a conserved physical quantity. For example, if the physical system is invariant under time translations (that means it is independent of when is put the origin of measuring the time) the energy of the system is conserved. The significance of Noether’s theory is evident. Its application extends from the symmetry in Classical Mechanics to the complicated symmetries of elementary particle - constituents of the universe [40,41].
Among its numerous applications, Noether theory was used in the study of symmetry in the important biological issue of Hox Gene Collinearity (HGC) [21]. In this case, self-similarity is the symmetry involved which is a continuous symmetry applying to all spatial lengths. The finite sequence of ordered Hox genes is the associated conserved quantity [21]. In this case, the symmetry is a ‘primitive’ self similarity since it applies to only two discrete spatial dimensions - the genome and the embryonic dimensions [20]. Consequently, PG is preserved like an irreversibly advancing ‘ratchet’ where some Hox genes are probably missing ([21], Figure 2 and Figure 3). In another biological application, Noether’s theory was recently used in a comparison of DNA sequences of different animal phyla [42].

6.3. Appendix 3 The quasi-Coulomb force

As mentioned in the Introduction, a heuristic pulling force F of BM is represented by Eq.(1):
F = N * P
Eq.(1) has the form of a quasi-Coulomb force. The proper Coulomb force (CF) is defined by the following equation
CF = (Q1 * Q2)/ R2
where Q1 and Q2 are the electric charges (positive or negative) and R the distance between Q1 and Q2. CF may be attractive (if one charge is positive and the other negative) or repulsive (if both charges are either positive or negative).
The quasi-Coulomb force F has the form
F = Q1 * Q2
where the dependence on R is missing. The arbitrary absence of Geometry is motivated here by sheer simplicity as mentioned in the Introduction. However, it turns out that this simplicity is crucial because it is related to the internal Symmetry. For example, the equations of a dynamic system are invariant under space translations.Noether proved that such a symmetric system is necessarily followed by a conserved quantity - in this case the momentum (see Appendix 2).
In any measurement, Symmetry in a variable quantity appears when this variable is absent in its constituent equations. In the example below, the reasoning of Iliopoulos is followed [40].
Consider a completely symmetric body (the sphere) in 3D space as described in a Cartesian system of axes (x, y, z) or a Polar coordinates system ( z, φ, θ). Any measurement in the sphere contains the angles θ and φ. It turns out that the equation of the sphere is:
x2+ y2 + z2 = R2
where R is the radius of the sphere. In this equation, the variables (θ, φ) are indeed missing in agreement with the above symmetry requirement: no angular dependence is observable [40,41].
In Eq.(1’) for the quasi-Coulomb force F, the term R-2 is missing, so F is an even simpler equation than the proper Coulomb force. The meaning of this omission is that the heuristic pulling force of the BM is a quantity independent of the 3D geometric space:
F = Q1 * Q2.
Note that in this space, the symmetry of F becomes internal, reminiscent of Heisenberg’s internal variable- the isotopic spin (see Appendix 1)].

Epilogue

All Natural Sciences are interconnected with the other branches of human intellectual activity. A short epistemological overview is included in [43].

List of Abreviation

AER Apical Ectodermal Ridge
BM Biophysical Model
CF Coulomb Force
DSB Double Strand Break
ER Empirical Rule
FGF Fibroblast Growth Factor
HGC Hox Gene Collinearity
ICD Interchromosome domain
Mya Million years ago
PG Paralogy Group
PP Posterior Prevalence
QC Quantitative Collinearity
SC SpatialCollinearity
TC TemporalCollinearity
TFD Transcription Factory Domain
wt wild type

References

  1. Lewis E.B. A gene complex controlling segmentation in Drosophila. Nature1978, 276, 565. [CrossRef]
  2. Papageorgiou S. A physical force may expose Hox genes to express in a morphogenetic density gradient. Bull. Math.Biol. 2001, 63,185-200. [CrossRef]
  3. DolléP et al., HOX-4 and the morphogenesis of mammalian genitalia. Genes and Development 1991. [CrossRef]
  4. Papageorgiou S. Pulling forces acting on Hox gene clusters cause expression collinearity. Int. J. Dev.Biol.2006, 50, 301-308. [CrossRef]
  5. Tarchini B, DubouleD ControlHoxd genes collinearity during animal development. Dev Cell 2006, 10, 93-103. [CrossRef]
  6. Tschopp P et al. Uncoupling time and space in the collinear regulation of hox genes. PLOS Genetics 2009, 5(3).
  7. PapageorgiouS A biophysical mechanism may control the collinearity of hoxd genes duting the early phase of limb development. Human Genomics2009, 3, 275-280.
  8. PapageorgiouS Physical laws shape up Hox gene collinearity. J. Dev. Biol2021, 9, 17.
  9. DubouleD The rise and fall of Hox gene clusters. Development 2007, 134, 2549-2560.
  10. Shimizu K, Gurdon J.B. A quantitative analysis of signal transduction from activin receptor to nucleus. Proc. Nat. Academy of Sci.1999, 8;96(12): 6791-96. [CrossRef]
  11. AfzalZ, Krumlauf R. Transacriptional regulation and implications for controlling Hox gene expression J. Dev. Biol.2022, 10; 10(1):4.
  12. SimeoniI, Gurdon J.B. Interpretation of BMP signaling in earlyXenopus development Dev.Biol. 2007, 308 (1): 82-92.
  13. Bourillot Y-P et al. A changing morphogen gradient is interpreted by continuous transduction flow. Development2002, 129(9): 2167-80. [CrossRef]
  14. Papageorgiou S Comparison of models for the collinearity of Hox genes in the developmental axes of vertebrates. Curr. Genomics2012, 13(3): 245-51.
  15. NoordermeerD et al. Temporal dynamics and development memory of 3D chromatin architecture at hox gene loci., eLIFE2014, 3, e02557.
  16. Fabre P et al.Nanoscale spatial organization of the HoxD gene cluster organization in distinct transcriptional states Proc. Nat. Acad. Sci.2015, 112, 13964- 13969.
  17. Fabre P et al. Visualizing HoxD gene cluster at the nanoscale level. Cold Spring Harb. Symp. Quant. Biol. 2015, 80, 9-16.
  18. Papantonis A, Cook P.R. Fixing the model for transcription: the DNA moves, not the polymerase. Transcription 2011, 2(1):41-44.
  19. Brackley C.A. et al. Complex small-world regulatory networks emerge from the 3D organization of the human genome. Nat. Commun2021, 12(1): 5756.
  20. Papageorgiou S Disappearance of temporal collinearity in vertebrates and its eventual reappearance. Biology 2021, 10(10):1018.
  21. Papageorgiou S Hox gene collinearity may be related to Noether Theory on Symmetry and its linked conserved quantity. J. Multidiscipl. Sci.J 2020, 3, 13.
  22. Mandebrot B.B. ‘The Fractal Geometry of Nature’, Editions Freeman, New York, 1982.
  23. Papageorgiou S Hox gene collinearity: From A-P patterning to radially symmetric animals. Curr.Genom.2016, 17, 444-449.
  24. Hanscom T et al. Regulation of Error-Prone DNA Double-Strand Break Repair and its impact on genome evolution Cells2020, 9, 1657.
  25. Schiemann S.M., Heznol A. et al. Clustered brachiopod Hox genes are not expressed collinearly and are associated with lophotrochozoan novelties. PNAS USA2017, 114(10) E1913-E1922.
  26. Ferrier D, Holland P. CionaintestinalisParaHox genes: Evolution of Hox/ParaHox cluster integrity, developmental mode, and temporal collinearity. Mol. Phyl. Evol.2002, 24:412-417.
  27. Ferrier D in ‘HOX GENE EXPRESSION’ Editor S. Papageorgiou, Landes Bioscience and Springer Science, USA 2007.
  28. Duboule D The (unusual) heuristic value of Hox gene clusters: a mater of time? Dev. Biol. 2022, 484:75-87.
  29. 29. Akam M A common segment in genes for segments of Drosophila, Nature1984, 308, 402-403.
  30. Kondo T, DubouleD Breakingcollinearity in the mouse HoxD complex. Cell1999, 97, 407-417.
  31. Papageorgiou S Disappearance of Temporal collinearity in Vertebrates and its eventual reappearance. Biology2021, 10(10): 1018.
  32. Vargesson N et al. Characterisation of Hoxageneexpressionin the chick limb bud in response to FGF. Dev. Dynamics2001. [CrossRef]
  33. Durston A.J. Global Posterior Prevalence is unique to Vertebrates: a dance to the music of Time?Dev. Dynamics 2012, 241: 1799-1807.
  34. Papageorgiou S. A model that reproduces an Empirical Rule distinguishing the developmental path of complete Hox gene cluster from split clusters. Preprints. 202305.0607.v1.
  35. Amândio A.R. et al. Sequential in cismutagenesis in vivo reveals various functions for CTCF sites at the mouse HoxD cluster. Genes & Development2021, 35(21-22):1490-1509.
  36. Papageorgiou S Biophysics precedes Biochemistry in Hox gene collinearity WebMedCentral+, 2014.
  37. Andrey G. et al. A switch between topological domains underlies HoxD genes collinearity in mouse limbs. Science 2013, 340; DOI: 1234167.
  38. Weyl H. Symmetry, Princeton University Press 1952.
  39. Wilczek F. A Beautiful Question,Penguin Books, 2016.
  40. Iliopoulos J. Aux origines de la masse: particulesélémantairesetsymmétries fondamentales, Editions EDP Sciences, Paris, France, 2014.
  41. Marinho R.M. Noether’s theorem in classical mechanics revisited. Eur. J Phys. 2006, 28.
  42. Almirantis Y, Provata A, Li W Noether’s Theory as a metaphor for Chargaff’s 2nd parity rule in Genomics. J. Mol. Evol.,2022. [CrossRef]
  43. Papageorgiou S. In ‘Chaos, Information processing and Paradoxical Games’ Editors Nicolis G - Basios V, World Scientific, 2015.
Preprints 91908 g001
Figure 1. Macro-scale and Micro-scale Hox gene clustering (adapted from S. Papageorgiou, Biology 2017: 6,32). (A)Morphogen Gradient Concentration (T1, T2. T3). (B) Time sequence (t1, t2, t3) combine with (T1, T2,T3) for expression domains S1, S2, S3 of Hox1, Hox2, Hox3. (C) (bottom) a small force F1 pulls Hox1 out of the chromatin territory CT toward the Interchromosome Domain (ICD) and the Transcription Factory (TF) regime (grey domain). Polar Molecule P is opposite the telomeric end. At a later stage (top), a stronger force F3 (3P) pulls Hox1, Hox2, Hox3 out of CT in TF.
Figure 1. Macro-scale and Micro-scale Hox gene clustering (adapted from S. Papageorgiou, Biology 2017: 6,32). (A)Morphogen Gradient Concentration (T1, T2. T3). (B) Time sequence (t1, t2, t3) combine with (T1, T2,T3) for expression domains S1, S2, S3 of Hox1, Hox2, Hox3. (C) (bottom) a small force F1 pulls Hox1 out of the chromatin territory CT toward the Interchromosome Domain (ICD) and the Transcription Factory (TF) regime (grey domain). Polar Molecule P is opposite the telomeric end. At a later stage (top), a stronger force F3 (3P) pulls Hox1, Hox2, Hox3 out of CT in TF.
Preprints 91908 g001
Preprints 91908 g002
Figure 2. Mechanical analogue of Hox cluster decondensation(adapted from S. Papageorgiou, Current Genomics 2012, 13:3). a) (left) Before activation Hox cluster is condensed inside (CT). (right) Mechanical analogue: uncharged elastic spring fixed at its left end. b) (left) BM pulling force decondenses the cluster and Hox1 is extruded in (ICD) in the transcription factory (TF) domain (shadow disc) The cluster is fastened posteriorily. (right) A small force F1slightly expands the spring and black spot moves beyond the dashed line. Spring fixed posteriorily. c) (left) Hox cluster is further decondensed and Hox1, Hox2, Hox3 move in (ICD). (right) F2> F1 and the spring is further expanded. d) (left) The fastening of the cluster is removed and, with a smaller force F1, the cluster can slide beyond the dashed line. (right) the loose spring slides freely beyond the dashed line.
Figure 2. Mechanical analogue of Hox cluster decondensation(adapted from S. Papageorgiou, Current Genomics 2012, 13:3). a) (left) Before activation Hox cluster is condensed inside (CT). (right) Mechanical analogue: uncharged elastic spring fixed at its left end. b) (left) BM pulling force decondenses the cluster and Hox1 is extruded in (ICD) in the transcription factory (TF) domain (shadow disc) The cluster is fastened posteriorily. (right) A small force F1slightly expands the spring and black spot moves beyond the dashed line. Spring fixed posteriorily. c) (left) Hox cluster is further decondensed and Hox1, Hox2, Hox3 move in (ICD). (right) F2> F1 and the spring is further expanded. d) (left) The fastening of the cluster is removed and, with a smaller force F1, the cluster can slide beyond the dashed line. (right) the loose spring slides freely beyond the dashed line.
Preprints 91908 g002
Preprints 91908 g003
Figure 3. Mouse Hox Gene Clusters (adapted from Z. Afzal and R. Krumlauf, J DevBiol 2022) HoxA, HoxB, HoxC and HoxD are depicted in the direction of transcription for each gene. The mouse embryo is also shown in the Anterior – Posterior direction.
Figure 3. Mouse Hox Gene Clusters (adapted from Z. Afzal and R. Krumlauf, J DevBiol 2022) HoxA, HoxB, HoxC and HoxD are depicted in the direction of transcription for each gene. The mouse embryo is also shown in the Anterior – Posterior direction.
Preprints 91908 g003
Preprints 91908 g004
Figure 4.
Figure 4.
Preprints 91908 g004
Preprints 91908 g008
Figure 8. According to BM, a small fragmental strip of the HoxD cluster is pushed in and out of the cluster expression domain.
Figure 8. According to BM, a small fragmental strip of the HoxD cluster is pushed in and out of the cluster expression domain.
Preprints 91908 g008
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated