Prerpints.org logo
Preprint
Article

Utilizing Dynamic Strategies for Making Informed Investment Decisions in the Stock Market

Altmetrics

Downloads

114

Views

65

Comments

0

This version is not peer-reviewed

Submitted:

29 November 2023

Posted:

30 November 2023

You are already at the latest version

Alerts
Abstract
Among the plethora of financial management tools available, stock investments stand out as the most recognizable and widely accepted option. However, investors often make buying and selling decisions based on unverified information provided by stock analysts. Since the credibility of this information remains uncertain, it frequently results in investment losses. Ordinary investors relying solely on rumors often miss out on prime opportunities for buying and selling stocks. In the current volatile investment landscape, various investment strategies cater to different situations. If individuals can effectively identify opportunities within this complex environment and dynamically adapt suitable investment strategies at any given time, substantial returns can be achieved. The ability of investors to promptly detect shifts in the current stock market environment and make accurate decisions regarding stock selection, timing, and capital allocation strategies is of utmost importance. This study presents a dynamic framework for investment decision support, which utilizes evolutionary strategies to determine the optimal timing for key strategic tools such as stock selection, timing, and capital allocation. By leveraging historical data for training and testing, this approach aims to assist investors in adapting to the ever-changing stock market environment. If investors can successfully identify and implement an appropriate investment strategy to aid in making accurate decisions, it is possible to achieve significant excess returns.
Keywords: 
Subject: Business, Economics and Management  -   Finance

1. Introduction

In recent years, fixed deposit interest rates have been steadily declining, while individuals earn low wages and face inflation. Consequently, the personal pursuit of increased wealth has gained significant importance. Investing in stocks presents a potential solution as it offers investors the opportunity to not only gain profits from stock price fluctuations, but also participate in the annual distribution of company dividends. However, it is essential to acknowledge the inherent risks associated with stock investments. Oftentimes, investors make decisions based on rumors and hearsay, resulting in repeated losses.
Common stock investment analysis typically involves fundamental and technical analyses. Fundamental analysis helps investors gain insights into a company's financial health and evaluate its profit stability. The simplest approach to devising a stock selection strategy involves utilizing financial analysis to assess a company's historical performance and estimate its true value. However, comprehending financial indicators can be challenging for ordinary investors. Furthermore, to determine whether an industry is declining or if a specific company's competitiveness is diminishing, individuals often rely on newspapers, magazines, or other media outlets. This reliance on traditional sources can potentially result in missed investment opportunities.
Technical analysis relies on analyzing historical stock market data to predict the future price movements, aiding in determining optimal investment timing. It involves the use of various indicators to assess the buying and selling points for stocks. However, despite its popularity, technical analysis does come with its challenges. One common issue is that investors often simultaneously employ multiple technical indicators, leading to conflicting signals and perplexing investors. This complexity can make it challenging to make informed decisions with confidence.
It is true that many existing studies often focus on the individual aspects of investment analysis, such as stock selection, timing, or capital allocation, rather than considering all three components together. This paper aims to address this gap by compiling various common investment analysis tools, which can be utilized by investors to adapt their strategies based on changes in the investment environment. The stock selection strategy incorporates fundamental analysis indicators used by Warren Buffett and stock selection indicators employed by Peter Woods. These indicators can help investors assess the financial health and value of a company before making investment decisions.
For timing strategy, this paper suggests using the Ohlson model, Intertemporal Capital Asset Pricing Model (ICAPM), and arbitrage pricing theory (APT) as reference tools. These models can aid in understanding the optimal timing of buying or selling stocks. In terms of capital allocation strategy, the paper proposes the use of the Kelly formula and the optimal F. By integrating these evolutionary strategies, investors can create a comprehensive investment strategy that accounts for risk management and potential returns. By considering all three aspects—stock selection, timing, and capital allocation—in a holistic manner, investors can enhance their decision-making process and potentially achieve better investment outcomes.
In a highly unpredictable investment environment, where different situations require different investment analysis tools, the ability to adapt and dynamically generate new investment strategies becomes crucial in obtaining a high-risk premium. If investors can effectively utilize various tools to assess the dynamic investment environment and accurately judge the appropriate stock selection, timing, and capital allocation strategies, they have the potential to achieve desirable excess returns. The key lies in promptly integrating diverse investment environment detection tools and making informed decisions based on the specific circumstances at hand. By doing so, investors can capitalize on market opportunities and optimize their investment outcomes.
The aim of this study is to propose a framework for recommending a dynamic investment strategy. Initially, evolutionary strategies are employed to determine the optimal utilization of different investment strategies using historical data. Subsequently, when the investors intend to invest in the stock market, they can assess the current investment environment and identify suitable strategies for stock selection, timing, and capital allocation based on specific market conditions. By doing so, this framework assists investors in making accurate investment decisions, thus facilitating the attainment of a favorable risk premium.

2. Literature Review

A successful investment necessitates a well-crafted strategy to achieve desirable returns. In stock investment, the strategies encompass stock selection, timing, and capital allocation. The following discussion will delve into the current and recent research trends of these strategies based on the existing literature.
In the field of stock selection strategy, researchers have explored various approaches to identify high-quality stocks with promising prospects. Chiu et al. (2010) introduced a stock selection model that utilized a genetic algorithm to optimize vector regression. They incorporated technical indicators into the regression and employed a grouping method to identify the stocks with high returns. Their experimental results showcased the superiority of medium- and long-term technical indicators over short-term ones.
Similarly, James et al. (2014) tested seven different stock selection models through trading experiments. Each model employed an index for screening stocks and selected 15 companies with the highest investment potential and profitability. This allowed them to create a portfolio of stocks with good prospects for investors.
Yodmun (2016) proposed a stock selection method that involved grouping and screening stocks. Through fuzzy quantitative analysis, they sorted the obtained investment weights and utilized a fuzzy hierarchical analysis method to further rank them based on these weights. The final investment weight facilitated the selection of appropriate stocks and the formation of a well-suited investment portfolio.
These studies highlight the diverse approaches employed in stock selection strategies, ranging from genetic algorithms and technical indicators to fuzzy quantitative analysis. By incorporating these methods, investors can make informed decisions to maximize returns and construct a portfolio aligned with their investment objectives.
Most of the literature on stock investment timing strategies relies on using technical indicators to evaluate the stock's trend. The presence of a golden cross signifies a stock's low point, indicating an optimal time to buy. Conversely, a death cross indicates a high point in the stock's price, suggesting that it should be sold for a profit. Chien et al. (2010) introduced a genetic algorithm that grouped related technical indicators and identified trading signals for buying and selling in the stock market. Yilan (2011) employed a genetic algorithm and support vector regression model to predict stocks, yielding favorable results when compared to the backpropagation neural network predictions. Zakamulin (2014) conducted experiments to assess the real-world performance of simple moving average and time series momentum rules. The results indicated that the previous studies overestimated the performance of these timing strategies, highlighting their limited applicability to all the financial markets. Sahin et al. (2014) optimized the Relative Strength Index (RSI) parameters using a genetic algorithm, revealing its effective performance in stable market trends. Ma et al. (2015) proposed a timing strategy based on nine technical analyses related to the capacity utilization and unemployment rates, which demonstrated a good performance when applied to S&P500. Ahmad (2017) evaluated the performance of moving averages in the stock market and compared it to those of the buy and hold strategies. The research revealed that the moving average strategy yielded significantly better average rates of return than the buy and hold approach did.
The capital allocation strategy involves allocating funds based on investment targets and risk ratios. This approach aims to enhance portfolio returns, while simultaneously reducing the risks. Chen et al. (2011) introduced an approach utilizing an associative genetic algorithm and guided mutation to efficiently optimize portfolio allocation. Kocak (2014) applied cooperative game theory to determine the weight of each stock in the portfolio. Through the group analysis of the transaction risk, the five best stocks were selected, and the optimal investment portfolio was constructed based on the investment ratio of each group. Madhogarhia (2015) explored dynamic asset allocation across different periods and asset classes. They employed mean reversion and relative valuation methods to allocate funds to each asset class, aiming to achieve high returns.
There are many related studies that continuously propose effective strategies for stock selection, timing, and capital allocation. Each strategy can only be used at suitable times. This study aims to determine the appropriate timing for common investment strategies and assist investors in understanding which strategies to employ in the current investment environment to achieve excess returns. The stock selection strategy in this thesis utilizes the stock selection indicators of Warren Buffett and Peter Lynch as the foundation for screening the investment targets. The timing strategy does not rely on the technical indicators that most people use to predict stock movements, but instead, it utilizes the Ohlson model, Intertemporal Capital Asset Pricing Model (ICAPM), and arbitrage pricing theory (APT) as the basis for buying and selling decisions. Capital allocation takes into consideration the Kelly formula and the optimal F. Furthermore, evolutionary strategies are employed to determine the optimal capital allocation ratio.

Stock Selection Strategy

Choosing good investment targets can result in good returns. Buffett's stock selection rules provide a way to find companies with stable operations that people can invest in. Buffett does not care about the rise and fall of stock prices, but pays attention to the company's financial performance. Investors can determine the true value of a company by observing all the factors that affect finance and profitability, such as financial statements, profitability, and the corporate organizational structure. Buffett also believes that as long as the company's earnings continue to grow, it is only a matter of time before the stock price rises sharply.
Buffett believes that investors should adopt a long-term approach to investment. They should carefully observe and analyze and concentrate their funds on high-quality stocks. Once the business operation becomes profitable, the company can retain the surplus and reinvest it. This approach aims to achieve a higher-than-average return on shareholders' equity. Weigand et al. (2007) used the P/E ratio proposed by Buffett to predict future stock price returns. The results showed that the P/E ratio is a good predictor of long-term stock price returns.
In the fund management process, Peter Lynch achieved an average annual rate of return of 29%. Ye (2013) utilized seven stock selection rules to screen stocks, establishing a portfolio of the selected stocks. The results showed that using Peter Woods' stock picking method yielded returns five times higher than the market returns during the study period. Kartikasari (2016) employed two stock selection criteria to screen individual stocks. The research results indicated that the rate of return using Peter Woods' stock selection criteria was positive throughout the study period. As a result, investors are advised to employ the Peter Woods criteria for selecting good stocks.

Timing Strategy

Investors often seek to buy stocks at low prices and sell them at high prices, timing the market to maximize their returns. This research utilizes the Ohlson model, Intertemporal Capital Asset Pricing Model (ICAPM), and arbitrage pricing theory (APT) in order to predict whether the stock prices will rise or fall, which represents a timing strategy.
The Ohlson stock price evaluation model proposed by Ohlson in 1995 is based on three fundamental assumptions: the present value of expected dividends (PVED), the clean surplus relation (CSR), and the linear information dynamic (LID). From these assumptions, the Ohlson model derives a formula for stock price evaluation. The Ohlson model provides a framework for evaluating stock prices. It takes into account the expected dividends, book value changes, and the relationship between the book and market values to estimate the intrinsic value of a stock.
P t = b v t + α 1 x t a + α 2 v t
In which α 1 = ω / ( R f − ω ) ≥ 0 ； α 2 = R f / ( R f − ω ) ( R f − γ ) > 0 The company's stock price can be calculated based on the current book value, abnormal earnings, and other information, as evident from the formula.
Bernard (1995) believed that the Ohlson Model can establish a relationship between the accounting information and company value. Additionally, this paper emphasizes the importance of companies not only focusing on stock price behavior, but also paying attention to fundamental analysis. In a study conducted by Lee et al. (2011), the impact of corporate governance variables on the value of Taiwan companies in the Ohlson model was tested. The results confirmed that apart from book value and residual income, variables such as the directors and supervisors' shareholdings, major shareholders' shareholdings, and critical control level also contribute to explaining the market value. This suggests a significant relationship between corporate governance and the value. Chang et al. (2013) incorporated corporate governance variables into the Ohlson evaluation model to predict stock prices. The study combined neural networks and evolutionary strategies to predict stock prices, leveraging the prediction ability of neural networks and the optimization ability of evolutionary strategies. The results demonstrated that this approach yielded favorable stock price prediction capabilities. Furthermore, Kuo (2017) enhanced the residual income valuation model in the Ohlson model by adding industry- and company-specific factors. The study utilized data from Taiwan's stock market and concluded that this approach improved the predictive power of the residual income valuation models.
The Intertemporal Capital Asset Pricing Model (ICAPM) was proposed by Merton in 1973 as an extension of the Capital Asset Pricing Model (CAPM). While the CAPM considers only a single variable, which may be insufficient to fully explain expected excess returns, the ICAPM incorporates intertemporal and relevant state variables with the model. By adding intertemporal and state variables, the ICAPM aims to capture the investors' considerations of the future market returns when making investment decisions. This extended framework allows for a more comprehensive understanding of the factors that influence asset pricing and the expected returns.
Docherty et al. (2013) conducted a study where they classified several economic variables as state variables in the Intertemporal Capital Asset Pricing Model (ICAPM). These variables included expected inflation, unexpected inflation, the industrial production indices, changes in the term structure, the dividend yields, the risk-free interest rates, market volatility, and the term spreads. Their findings suggest that these variables can contribute to explaining the expected returns of assets within the ICAPM framework. In another study by Huang et al. (2014), the variables in the ICAPM were expanded to include seven factors. These factors consisted of the dividend rate, risk-free rate, default spread, period spread, market liquidity index, average volatility, and wealth ratio. Through experimentation, they observed that the expected returns of stocks could be influenced by variables such as the dividend yield, default spread, and period spread. Campbell (2018) proposed an ICAPM variant that incorporated stochastic volatility. The variables in this model included the logarithm of the actual return rate, the expected market difference, the logarithm of the S&P500 price return, the three-month treasury bill yield, and the default spread. The test results indicated a high correlation between the default spread and future volatility. These studies highlight the potential significance of different variables within the ICAPM framework and demonstrate the importance of considering a range of factors beyond a single variable in the asset pricing models.
The arbitrage pricing model (APT) was introduced in 1976 as a framework that extends the traditional Capital Asset Pricing Model (CAPM) by considering multiple risk factors. The APT suggests that asset returns can be explained by a linear combination of various risk factors, not just market risk. Ouysse et al. (2010) examined the role of 21 economic variables in securities pricing. They observed that four economic risk variables, namely non-economic inflation, expected inflation, unemployment, and changes in the industrial index, had an impact on market pricing. This highlights the significance of considering a range of risk factors beyond market risk in asset pricing. Verma (2015) investigated the application of the APT to the stock market, specifically testing the effects of variables, such as the gold price, oil price, exchange rate, and money supply, on the stock price index. Through regression analysis, they found that all the factors, except for the interest rate variables, influenced the stock price index. This suggests that these variables play a role in explaining stock market movements according to the APT framework. Baek et al. (2015) explored the three-factor model within the APT framework and identified the existence value and risk premium of the financial industry as important variables through asset pricing tests. This indicates that industry-specific factors can significantly impact asset pricing, highlighting the need for considering industry-related variables in asset pricing models. Menacer et al. (2018) examined the relationship between the stocks and overall economic variables, including the money supply, interest rates, inflation rates, and foreign exchange rates. Their empirical results demonstrated that these overall economic variables had a significant impact on stock returns. This underscores the importance of monitoring macroeconomic factors when analyzing stock market performance. Mahapatra (2018) and colleagues conducted research on the impact of exchange rate fluctuations on the stock market. They found that exchange rate risk factors had a notable influence on stock market prices, particularly after 2008. This study highlights the connection between exchange rate movements and stock market returns. Overall, these studies contribute to our understanding of the APT framework by exploring the role of various risk factors and economic variables in asset pricing.

Capital Allocation Strategy

The Kelly formula, also known as the Kelly Criterion, was proposed in 1956. The Kelly Criterion suggests that when a gambler participates in a game over an extended period, they should strive to maximize the geometric average rate of return. The Kelly formula was initially employed in gambling, as it allows the maximization of the expected growth rate of funds in many scenarios.
The optimal F was proposed by Vince (2009, 2011), which utilizes the concept of the Kelly formula. However, it does not impose limitations on fixed probabilities and odds. Hermes (2017) examined the influence of optimizing the F value on money management in trading problems, considering multiple investment strategies. The research conducted by Hermes confirms that the F value can discover the optimal value for the optimization problem, while also highlighting the validity and uniqueness of the F value.

Artificial Neural Network and Evolution Strategies

Artificial neural networks (ANN) are learning systems inspired by human brain neural networks. Among these networks, the most representative and widely used one is the Backpropagation Network (BPN), which belongs to the supervised network learning mode. Niaki et al. (2013) employed an ANN to predict the daily index trend of the S&P500 index. The experimental results demonstrated a significant enhancement in predictive ability when using the ANN, surpassing that of the statistical logit model. Charumathi et al. (2014) utilized the predictive power of neural networks to enhance the Ohlson model. Their research findings exhibited the high level of accuracy of the Ohlson model. Moghaddam et al. (2016) investigated the predictive power of neural networks in forecasting the Nasdaq daily stock index. The results showed that neural networks performed exceptionally well in predicting stock indexes. In a study conducted by Qiu et al. (2016), a genetic algorithm was utilized to adjust the weights and biases of the neural network model, with the aim to improve the prediction accuracy. The experiments focused on predicting the daily stock market index's change in direction, and the results indicated that the neural model enhanced by the genetic algorithm achieved more accurate predictions.
Evolutionary strategies (ES) were proposed by Ingo Rechenberg and Hans-Paul Schwefel in the 1960s to optimize the parameters of fluid dynamics models. Let 𝜇 represent the population size of the parent generation and λ represent the population size of the offspring. There are two ways to select the chromosomes: (𝜇, λ) and (𝜇+λ). In the (𝜇, λ) strategy, the 𝜇 best chromosomes are selected from λ offspring as the parents of the next generation. In (𝜇+λ) strategy, the best 𝜇 individuals are selected from the 𝜇 parents and the λ offspring to be the parents of the next generation. Repoussis et al. (2010) proposed evolutionary strategies to solve the open vehicle routing problem. Previous experiments show that this research is more efficient and accurate than the other methods are in finding the best solution when dealing with large amounts of data using evolutionary strategies. Bonde (2012) used genetic algorithms and evolutionary strategies to predict whether the stock prices of eight companies would rise or fall the next day. In the experiment, the (𝜇, λ) strategy was employed. The conclusion was that both the genetic algorithm and the evolutionary strategies showed good accuracy. Beyer et al. (2014) proposed an evolutionary strategy scenario tree with multiple objectives to solve the non-linear problem resulting from non-linear risk value transactions. The study found that incorporating risk in the evolutionary tree node can lead to the best investment strategy in terms of investment weight.

3. Research Structure

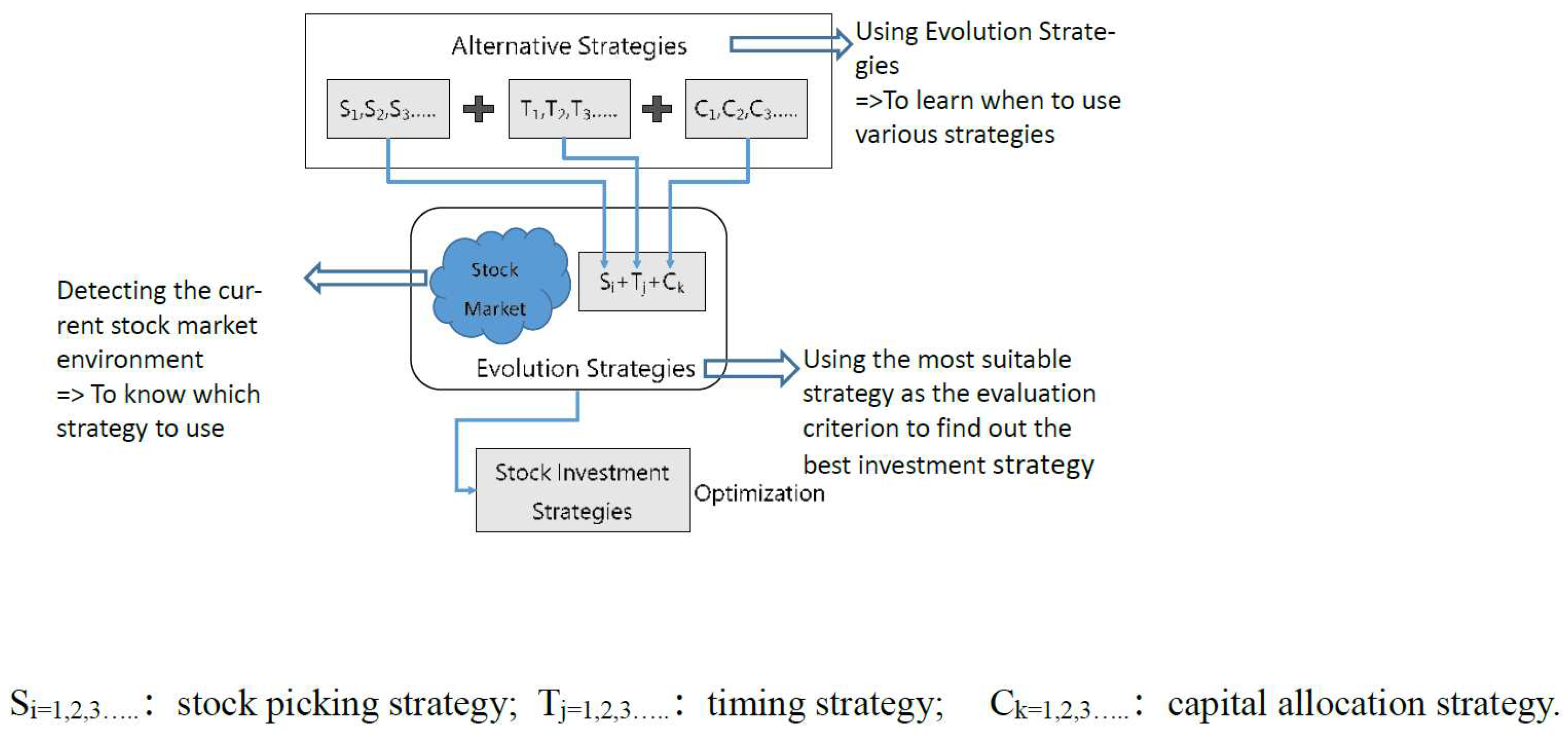
This study proposes a framework for a dynamic investment strategy. It utilizes historical data from the stock market to determine the optimal time to employ different strategic tools, with the assistance of evolutionary strategies. This framework aims to address the scope of applying the variables associated with various tools. Additionally, it detects the current environment of the stock market to determine the appropriate tools for stock selection, timing, and capital allocation, thereby forming a comprehensive investment strategy. The research architecture is illustrated in Figure 3-1.
Preprints 91811 g001
Figure 3-1. Research framework.
Figure 3-1. Research framework.
Preprints 91811 g001
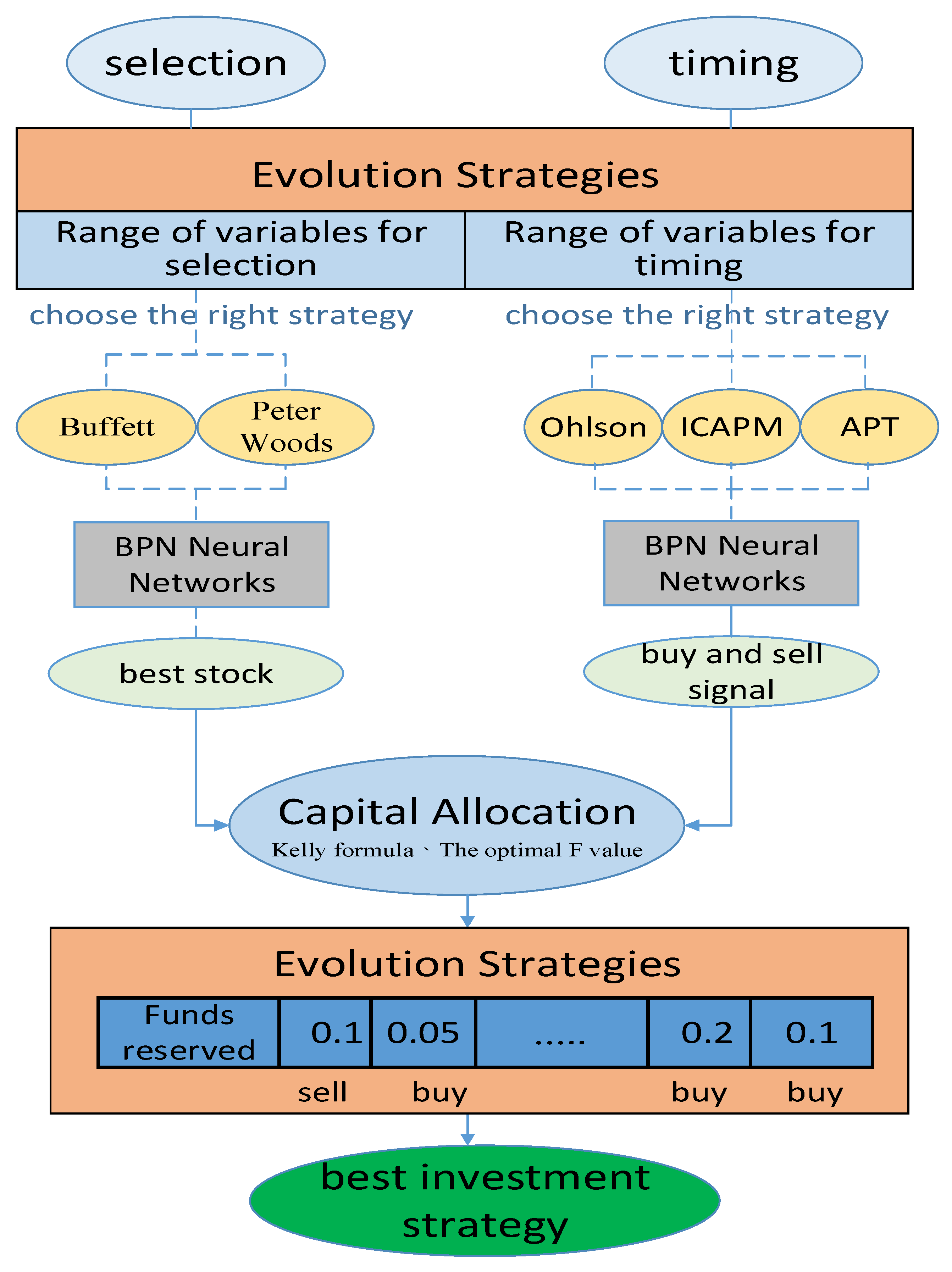
Firstly, the system identifies the current stock market environment in order to determine whether to use either Buffett or Peter Woods' stock selection indicators for screening potential investment targets. It then selects the most suitable strategy using three timing tools: the Ohlson model, ICAPM, and APT, to determine the optimal timing for buying and selling stocks. Regarding fund allocation, it chooses the strategy that best aligns with the current investment environment, selecting either the Kelly formula or the optimal F. Finally, based on the chosen stock selection, timing, and capital allocation strategies, evolutionary strategies are employed to determine the optimal investment ratio for achieving high returns. The goal is to discover the stock selection, timing, and capital allocation strategies that are most compatible with the current investment environment among the alternative strategies, thus creating a comprehensive dynamic investment model. To validate the model's effectiveness, real investments are made in the stock market, and the experiments are conducted.
In this research experiment, the investment target is to select one of the major stocks that each represent a class. The selection criterion is based on the stock with the highest trading price multiplied by its trading volume. Therefore, the experiment focuses on identifying the top-ranking stock from each class as the investment target.
Preprints 91811 g002
Figure 3-2. Learning, detection, and decision processes.
Figure 3-2. Learning, detection, and decision processes.
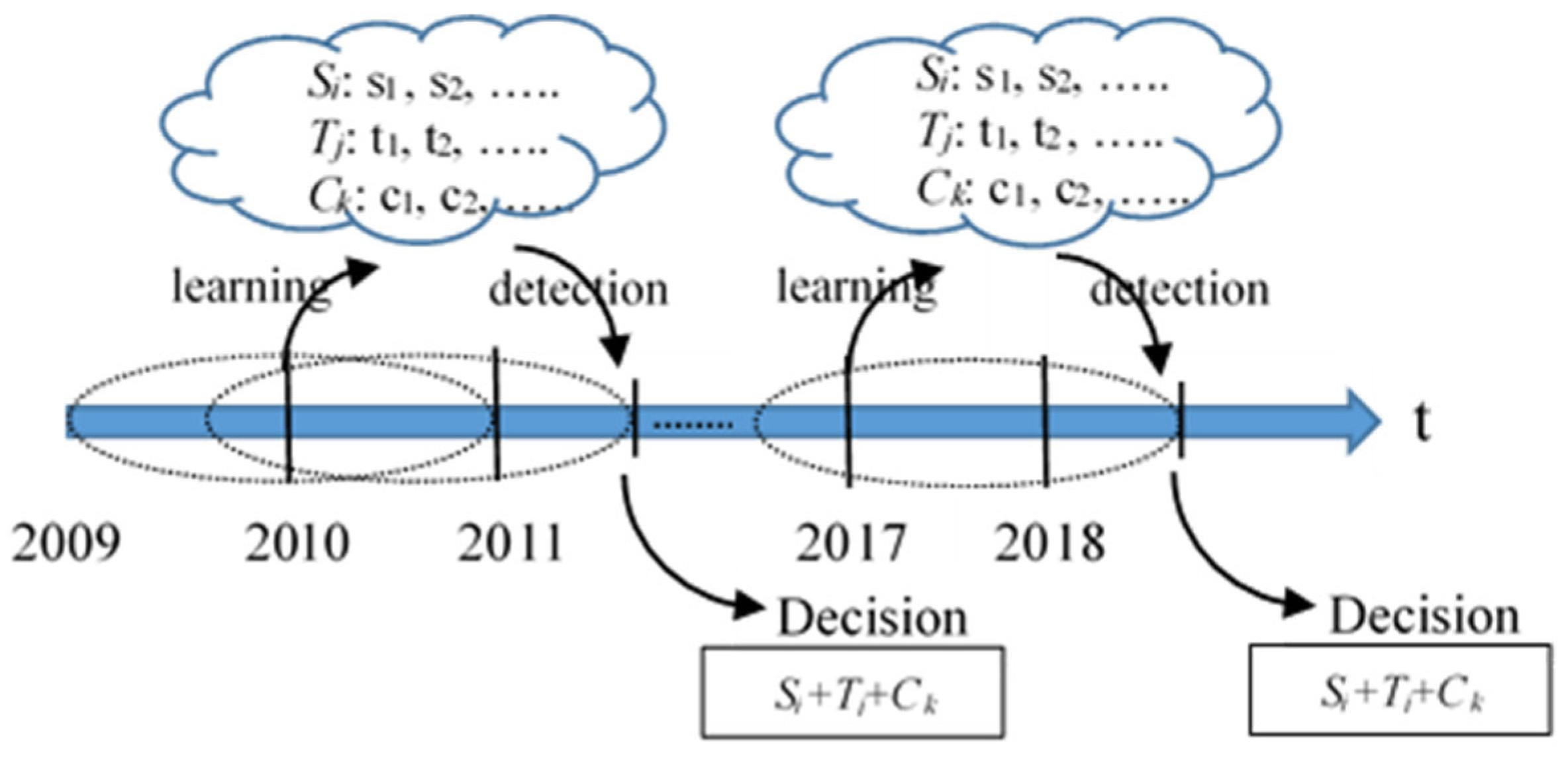
Preprints 91811 g002
Figure 3-2 illustrates the process of learning, detecting, and deciding. The first step involves training, testing, and verifying the historical data of the stock market from the last few years. Evolutionary strategies are utilized to determine the optimal timing for various stock selection, timing, and capital allocation strategies by employing continuous reorganization, sorting, and selection operations. Subsequently, the detection of the environmental conditions takes place in order to identify the suitable strategy for investment in the current environment. The experimentation process utilizes the sliding window method, wherein the optimal range of variables is trained using historical data for each investment date. Consequently, the range of variables on the investment day is detected to identify the appropriate investment tools.

3.1. Stock selection strategy

In this study, the stock screening process involves the utilization of Buffett and Peter Lynch’s indicators. These indicators draw upon significant information, such as the company's stock price and financial reports. Buffett's stock selection criteria encompass multiple variables, including the return on net worth (ROE), price-to-earnings ratio, shareholding ratio of the directors and supervisors, share-price-to-book-value ratio, earnings per share, share-price-to-revenue ratio, and cash dividend rate. On the other hand, Peter Lynch’s stock selection criteria rely on variables, like the price-to-earnings ratio, revenue growth rate, pre-tax net profit growth rate, and debt ratio. To find the optimal ranges for these strategy variables, evolutionary strategies are employed, leveraging the historical data.
To encode the variables of the stock selection strategy using the chromosome, the approach shown in Figure 3-3 is followed. Real number encoding is employed, which includes the central value a i and the range value δj of each variable. Initially, the chromosome is randomly generated to form the initial population. Once the initial chromosomes are created, the population undergoes continuous recombination, replication, and screening based on fitness evaluation. Through this iterative process, the population evolves over time, striving to achieve the best solution.
Preprints 91811 g003
Figure 3-3. Chromosome coding stock selection.
Figure 3-3. Chromosome coding stock selection.
Preprints 91811 g003
The range of variation for each chromosome is determined by subtracting the range value from the center value and adding the range value to the center value. For instance, taking ROE as an example, the variable range can be expressed as a 1 − δ 1 ≤ ROE ≤ a 1 + δ 1 . Similarly, each variable's range is determined in a similar manner. In the case of evolutionary strategies, it is necessary to set the parameters. With a total of 11 dependent variables, the overall length of the chromosomes is 22 (calculated as 11 multiplied by 2). The population size is set as 50, while the evolutionary strategy adopted is (1, 7), resulting in a total of 350 offspring. The termination condition for the evolution process is met when there is no improvement in fitness value after 1000 consecutive generations.

3.2. Timing Strategy

This research incorporates three models, namely the Ohlson model, ICAPM, and APT, as timing strategies to determine buying and selling decisions. The Ohlson model is examined with respect to experimental variables that can be further categorized into three main parts, totaling seven variables. The first part pertains to the Ohlson equity evaluation model, the second part relates to the equity structure of corporate governance, and the final part concerns the composition of the board of directors within the corporate governance framework. These variables include the book value, abnormal earnings, shareholding ratio of the directors and supervisors, shareholding ratio of the major shareholders, shareholding of the necessary companies, board size, and the proportion of outside directors.
In the context of the ICAPM, the experimental variables considered encompass the Taiwan option volatility index, period spread, funding liquidity risk spread, and dividend yield. These variables play a role in assessing the relationship between the risk and expected returns. On the other hand, for the APT analysis, this research employs a multi-factor model to investigate how various variables affect the stock prices. The experimental variables utilized in this study include the money supply, interest rate, inflation rate, foreign exchange rate, unemployment rate, and the industrial index. These variables are utilized to identify and analyze the different factors that can impact the stock prices.
In the Ohlson model strategy, evolutionary strategies are employed to determine the optimal range of strategy variables using the historical stock market data. This involves encoding the timing strategy variables into chromosomes using real number encoding. Each chromosome consists of the central value a i and the range value δj of the variable. The initial population is generated by randomly creating chromosomes. To evolve towards the optimal solution, a series of steps, including recombination, replication, and selection based on fitness value evaluation, are carried out. The range of each chromosome is determined as the central value minus the range value and the central value plus the range value. This range represents the allowable variation in each variable within the chromosome. For example, considering the VIX (Volatility Index) as shown in Figure 3-4, the variable range is defined as a 8 − δ 8 ≤ VIX ≤ a 8 + δ 8 . Similarly, the range for each variable is determined in a similar manner.
Preprints 91811 g004
Figure 3-4. Chromosome encoding timing.
Figure 3-4. Chromosome encoding timing.
Preprints 91811 g004
In this approach, the predictive ability of the BPN is utilized. The historical data of the three timing strategies are divided into training, verification, and testing sets. The daily variables of the investment day serve as inputs to the trained neural network, which then predicts the stock price for that day. By comparing this predicted price with the stock price of the previous day, a trading signal is determined. Since the total number of dependent variables is 17, each chromosome has a length of 34 (=17*2). The population size is set to 50 individuals. The evolution strategy used is (1, 7), meaning that for each parent, seven offspring are generated. Thus, a total of 350 offspring are created in each generation. The termination condition for the evolutionary process is set, as the fitness value remains unchanged for 1000 consecutive generations.

Capital Allocation Strategy

In this study, the historical data of each variable in the capital allocation strategy are used to calculate the investment ratio using two different formulas. These formulas take into account the historical rate of return and other relevant factors to determine the allocation of capital. The next step involves calculating the expected rate of return using the investment ratios obtained from the two strategies. This allows a comparison of the potential returns provided by each strategy. To further analyze and test the strategies, a capital allocation strategy with a higher expected rate of return is selected. However, it is important to note that the Kelly formula has a characteristic that suggests that one should not bet when the calculated expected value is less than zero. Therefore, if the investment ratio calculated by the Kelly formula is less than zero, the experiment utilizes the ratio of the optimal F for testing purposes instead. By taking these steps and comparing the expected returns, the study aims to identify the capital allocation strategy with the highest potential for favorable outcomes.
  • Kelly formula
f * = b p − q b
  • f * ：the proportion of funds that should be invested next time.
  • b ：betting odds; p ：win rate; q ：loss rate.
  • Optimized F value
H P R n = 1 − f * P n W C S
T W R = H P R 1 * H P R 2 * … * H P R n
Pn = Profit from the N-th transaction
HPRn = The income appreciation rate of the N-th transaction capital
WCS = maximum loss
TWR = The rate of appreciation of final capital compared to initial capital after all trades
f = proportional risk per trade

The Best Investment Strategy

After determining the investment targets selected using the stock selection strategy and evaluating the buying and selling signals of the timing strategy, this study utilizes the evolutionary strategy to optimize the allocation of the capital ratio for the cash reserve and eight stocks.
Preprints 91811 g005
Figure 3-5. Optimal investment strategies chromosomal coding.
Figure 3-5. Optimal investment strategies chromosomal coding.
Preprints 91811 g005
As depicted in Figure 3-5, X0 represents the allocation of funds to the cash reserve, while X1 represents the proportion of funds invested in the first class of shares. Similarly, X2 denotes the proportion of funds invested in the second class of shares, and so forth, for the remaining classes of shares. To encode the chromosomes, real numbers are utilized, dividing the funds into 100 equal parts, with each part representing 1%. For instance, if X5 accounts for six equal parts, it indicates that the fifth class of shares will receive an investment of 6% of the total funds.
The evaluation process in this study encompasses strategies, such as stock selection, timing, and capital allocation for evolution. In each generation, excellent chromosomes are chosen using this evaluation method to ultimately find the optimal solution. Stock selection involves identifying investment targets through the most suitable stock selection strategy. It aims to increase the capital allocation ratio for the selected stocks, while reducing the capital investment ratio for stocks not selected using the stock selection strategy. Timing is determined by identifying the most suitable timing strategy. After the BPN learning process, a buying and selling signal is generated. This signal assists in making decisions regarding when to buy or sell stocks. Capital allocation involves selecting the appropriate allocation strategy. For instance, if the Kelly strategy is determined to be the best approach, the calculated Kelly value ratio is used to determine the fitness value of each chromosome in the evolution process.
Once the total return on investment has been evaluated, the fitness value of each chromosome is calculated after normalization. This fitness value represents the chromosome's performance in terms of investment returns. The chromosomes evolve from generation to generation based on survival of the fittest, where those with higher fitness values have a higher chance of being selected for the next generation. In the evolution process, the parameter settings include a chromosome length of nine and a total of 50 chromosomes. Since the (1, 7) evolution strategy is adopted, the number of offspring generated in each generation is 350. This strategy ensures a diverse population for better exploration and exploitation of the solution space. The evolution termination condition is determined based on the stability of the fitness values. If the fitness values remain unchanged for 1000 consecutive generations, it is considered that evolution has converged. This condition implies that the algorithm has reached a point where there is no significant improvement in the fitness values, indicating that a stable and optimized solution has been found.

4. Experiment Analysis

The data for this research are sourced from the Taiwan Economic Journal (TEJ). The training and testing period spans 10 years, from January 1, 2008, to December 31, 2017. The data are collected on a weekly basis and include information about the listed stocks in Taiwan. In order to evaluate the performance of the evolutionary algorithm, a sliding window method is employed as the testing method. This method involves dividing the entire dataset into overlapping windows of a specific size. In this case, the window size is set to 3 months. The sliding window method allows the evaluation of the algorithm's performance across different time periods within the overall testing period. By sliding the window across the data, multiple sub-periods can be evaluated, which helps to assess the algorithm's robustness and generalization capabilities.
Figure 4-1 represents the experimental design architecture used in the research. It outlines the sequential steps involved in the strategy development process. In the first step, evolution strategies are employed to identify the optimal timing for both the stock selection and timing strategies for each specific period. These strategies are evolved using the principles of natural selection and survival of the fittest, allowing the exploration and exploitation of the solution space. The second step involves utilizing the prediction capabilities of the Backpropagation Neural Network (BPN) to train the timing strategy. The BPN network is trained using the available data to predict the rise and fall of stock prices in the current week. This prediction helps generate trading signals that can guide investment decisions. Finally, based on the current market conditions, the best capital allocation strategy for the week is determined. This step involves considering various factors and indicators to determine the most appropriate allocation of capital in order to achieve optimal returns given the prevailing stock market conditions. Overall, this experimental design architecture integrates evolutionary strategies, predictive modeling, and capital allocation to develop a comprehensive approach to stock trading and timing strategies.
In the research, three investment strategies for stock selection, timing, and capital allocation have been identified as suitable for the current week. These specific strategies serve as evaluation criteria for the evolution strategies. Using these as evaluation criteria, the evolution strategies aim to evolve the optimal capital allocation ratio for the current week. The evolution strategies employ a rule-based approach to determine the best investment strategy for each week. By applying this rule-based approach, the system evaluates and compares various capital allocation ratios using the three identified investment strategies. The goal is to find the capital allocation ratio that maximizes investment performance and aligns with the specific investment strategies employed. This iterative process allows the system to continually adapt and evolve the capital allocation ratio based on the performance of the selected investment strategies. By identifying the best investment strategy through evaluation and optimization, the system aims to enhance the overall profitability and effectiveness of the investment approach for each week.
Preprints 91811 g006
Figure 4-1. Experimental design architecture.
Figure 4-1. Experimental design architecture.
Preprints 91811 g006
The investment target of the experiment is to select representative stocks from eight major industries. The experiment focuses on a total of eight specific stocks that act as research objects. Each of these stocks represents a different industry:
Cement industry stock: Taiwan Cement Corp. (stock symbol: 1101).
Food industry stock: Uni-President (stock symbol: 1216).
Plastic industry stock: China Petroleum & Chemical Corporation (SINOPEC) (stock symbol: 1314).
Textile industry stock: ECLAT TEXTILE CO. (stock symbol: 1476).
Mechanical and electrical industry stock: Tatung Corporation (stock symbol: 2371).
Paper industry stock: TAIWAN PULP & PAPER CORPORATION (stock symbol: 1902).
Construction industry stock: Kindom Development Co. (stock symbol: 2520).
Financial industry stock: Cathay Financial Holdings Co. (stock symbol: 2882).
These stocks have been selected based on their representation of the respective industries, making them suitable for the research objectives of the experiment. By analyzing and evaluating the performance of these stocks, the experiment aims to formulate effective investment strategies tailored to the portfolio.
The paper utilizes the reverse transfer neural network model to learn the Ohlson model, ICAPM, and APT strategies for predicting the stock prices. Table 4-1 presents the annual average accuracy rates of the trading signals for each stock from 2009 to 2018. Notably, the highest accuracy rate achieved is 83.56%. The highest annual average accuracy rate recorded is 75.71%, while the lowest one is 64.18%. The ten year average total accuracy rate stands at 69.65%, which is approximately 70%.
Table 4-1. Accuracy rate of buying and selling signals from 2009 to 2018.
Table 4-1. Accuracy rate of buying and selling signals from 2009 to 2018.
Year 2009 2010 2011 2012 2013 2014 2015 2016 2017 2018
Stock symbol
1101 78.38 72.55 74.51 72.55 78.85 77.36 66.67 78.43 71.15 79.36
1216 67.57 68.63 74.51 70.59 65.38 64.15 68.63 68.63 63.46 72.51
1314 67.57 62.75 70.59 72.55 71.15 60.38 72.55 64.71 55.77 69.83
1476 64.86 72.55 72.55 62.75 65.38 62.26 82.35 66.67 59.62 73.35
1902 72.97 64.71 80.39 70.59 61.54 73.58 52.94 64.71 65.38 80.64
2371 78.38 72.55 72.55 64.71 63.46 58.49 64.71 58.82 69.23 83.56
2520 64.86 74.51 78.43 66.67 78.85 71.70 62.75 66.67 53.85 69.82
2882 78.38 74.51 70.59 68.63 76.92 75.47 66.67 62.75 75.00 76.62
Average 71.62 70.35 74.27 68.63 70.19 67.92 67.16 66.42 64.18 75.71
Unit: %.
Table 4-2 shows the number of times the most suitable investment strategies were chosen each year between 2009 and 2018. For example, in 2009, the stock selection strategy included eleven instances of Buffett's stock selection strategy and one instance of Peter Woods' stock selection strategy. As for market timing strategies, the Ohlson model was used five times, the APT was used five times, and the ICAPM was used twice. In terms of capital allocation, the optimal F was used eight times, the Kelly formula was used four times, and the rest were inferred.
From 2009 to 2018, in terms of the stock selection strategies, both Buffett's stock selection strategy and Peter Woods' stock selection strategy were used almost the same amount. Buffett adopts a long-term perspective in investing, emphasizing holding stocks from fundamentally strong companies. This strategy helps mitigate market volatility and achieve sustainable and stable investment returns. Peter Woods, on the other hand, focuses on uncovering stocks with growth potential, particularly in small- or medium-sized companies. Peter Woods pursues a strong growth performance and believes that these companies have the potential to deliver good long-term results. Therefore, regardless of the stock market environment from 2009 to 2018, both Buffett's and Peter Woods' stock selection strategies have the potential to provide the investors with favorable investment returns.
In terms of the market timing strategies used between 2009 and 2012, the Ohlson model, APT theory, and ICAPM theory were profitable as market timing strategies regardless of the stock market environment. However, from 2013 to 2018, the ICAPM theory proved to be more suitable as a market timing strategy, with less frequent usage of the Ohlson model and APT theory, averaging only 1.5 times and 2.4 uses, respectively. The main reason for this could be the difficulty in finding suitable variables for the Ohlson model and APT theory. The ICAPM theory was used an average of 8.1 times, as it incorporates cross-period factors, considering the impact of investor time preferences and the interaction of risk and return over multiple periods. Therefore, the ICAPM provides a more accurate pricing model for complex stock financial instruments, enabling precise market timing decisions.
In terms of capital allocation strategies, the optimal F was found to be the most suitable strategy between 2009 and 2018, being used 10.7 times. The Kelly Criterion tends to overly avoid small bankruptcy risks and, on the other hand, excessively pursue excess profits after becoming wealthy. The optimal F-value tackles the issue of Kelly formula being applicable only to gambling and not to trading. Its purpose is to calculate the risk capital proportion that maximizes profits, making the optimization process of gambling outcomes more similar to the profit and loss process in investment trading.
Table 4-2. Adoption status of stock selection, market timing, and capital allocation strategies from 2009 to 2018.
Table 4-2. Adoption status of stock selection, market timing, and capital allocation strategies from 2009 to 2018.
Strategy Selection Strategy Timing Strategy Capital Allocation Strategy
year Buffett Peter Woods Ohlson APT ICAPM Optimal F Kelly Formula
2009 11 1 5 5 2 8 4
2010 5 7 2 5 5 10 2
2011 4 8 6 3 3 12 0
2012 5 7 1 4 7 10 2
2013 1 11 0 1 11 10 2
2014 4 8 0 1 11 12 0
2015 5 7 0 2 10 12 0
2016 5 7 0 1 11 12 0
2017 6 6 0 1 11 11 1
2018 7 5 1 1 10 10 2
Average 5.3 6.7 1.5 2.4 8.1 10.7 1.3
This study incorporates stock selection, timing, and capital allocation strategies to execute portfolio transactions. The experimental data used in the study are sourced from the Taiwan stock market from 2009 to 2018. The monthly portfolio returns obtained from the experiments are summarized in Table 4-3. Additionally, Table 4-3 presents a performance comparison between the Taiwan stock market and the Taiwan 50 Index (TWN50) for the corresponding years. The TWN50 consists of the 50 stocks with the highest total market capitalization among all the stocks listed on the Taiwan Stock Exchange. It serves as a benchmark for evaluating the performance of large-cap stocks in Taiwan.
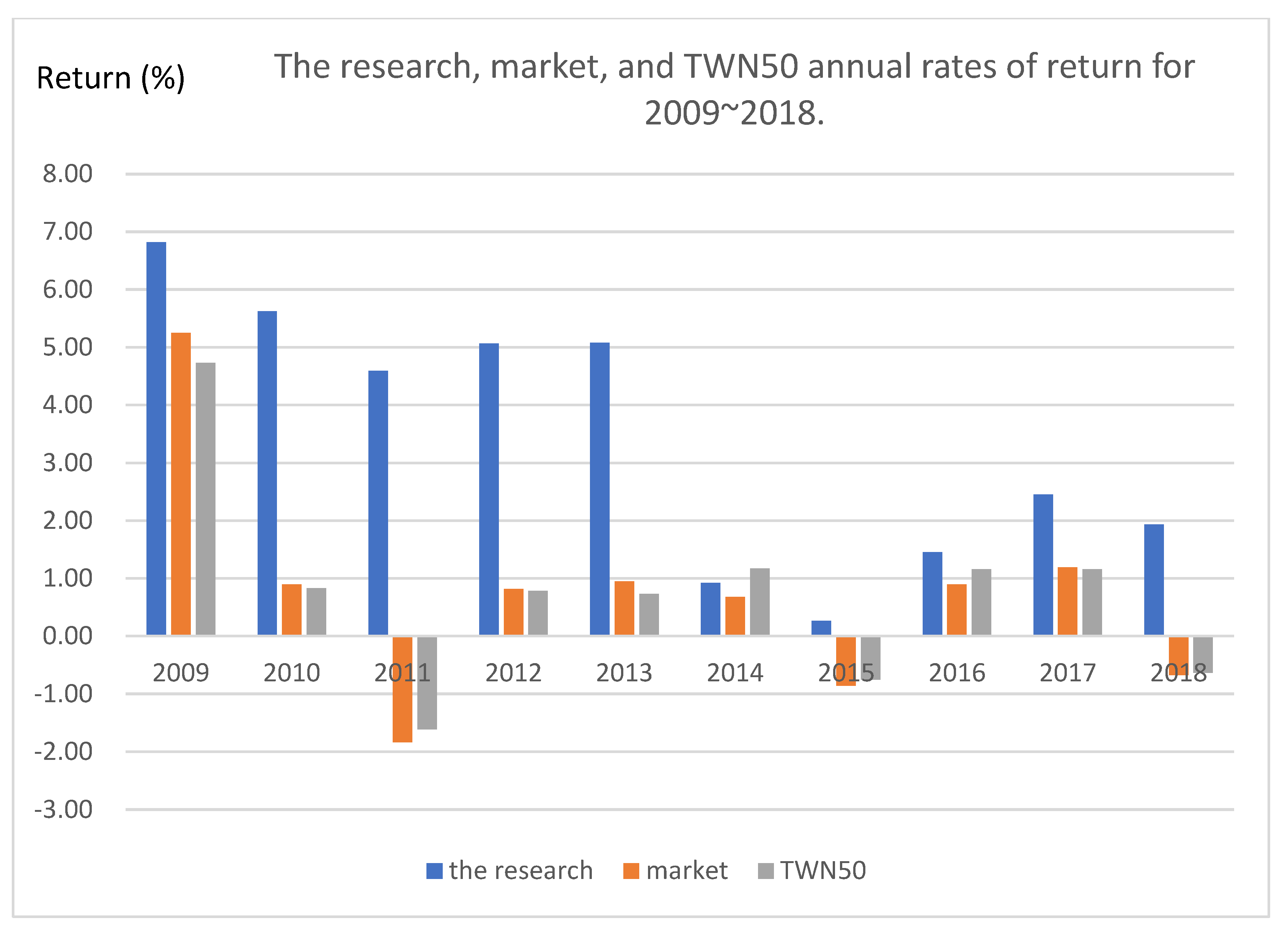
Figure 4-2 illustrates the performance of the dynamic investment decision-making framework proposed in the paper over the ten-year experimental period. The framework allows the identification of different stock market environments at specific time points and enables the application of appropriate stock selection, timing, and capital allocation strategies to aid investors in making buy or sell decisions. The highest average annual rate of return achieved during the experiment was 6.82% in 2009. Notably, the Taiwan stock market encountered downturns in 2011, 2015, and 2018, with average annual market returns of -1.84%, -0.86%, and -0.68% respectively. However, the research model generated positive returns during these years, with rates of 4.59% in 2011, 0.26% in 2015, and 1.93% in 2018. Even though the rate of return was relatively low in 2015 (0.26%), it remained positive, ensuring that the investment did not result in losses. Furthermore, the investment decision-making model proposed by the research institute outperformed the Taiwan stock market and TWN50 by a margin greater than 4% in 2010, 2011, 2012, and 2013. Particularly in 2011, the rate of return surpassed 6.43% (=4.59% - (-1.84%)). Throughout the experimental period, with the exception of 2014, the average annual return performance of the model surpassed those of both the stock market and the TWN50. Even in 2014, the research model yielded results slightly lower than the TWN50 index, but still outperformed the Taiwan stock market.
Based on the experimental results, it is evident that Taiwan's stock market exhibits unpredictability and volatility. Merely relying on fundamental analysis and technical divisions proves insufficient in navigating this intricate landscape. Hence, this study introduces a novel model for making dynamic investment decisions. Initially, the system identifies investment strategies that align with the prevailing conditions of the stock market. Subsequently, it utilizes these strategies as fitness evaluation functions for evolutionary computations. By employing the evolutionary principle of survival of the fittest, the model employs three investment evaluation rules to identify the optimal investment strategy. Consequently, investors can accurately seize opportunities, make informed decisions, attain favorable risk premiums, and streamline their investment and financial management endeavors.
Table 4-3. Comparison table of monthly return rates of the research, market, and TWN50 investment portfolios in 2009~2018.
Table 4-3. Comparison table of monthly return rates of the research, market, and TWN50 investment portfolios in 2009~2018.
2009 2010 2011 2012 2013
Unit:% Research Market TWN50 Research Market TWN50 Research Market TWN50 Research Market TWN50 Research Market TWN50
Jan. 0.93 -7.48 -7.86 -3.17 -6.69 -5.78 -3.40 1.93 2.96 -4.51 6.29 5.66 18.04 1.95 1.78
Feb. 4.38 7.28 7.96 7.41 -2.67 -3.00 -2.98 -5.97 -6.23 8.55 8.04 6.93 -1.07 0.61 0.68
Mar. 17.86 14.34 11.76 20.63 6.51 4.77 5.79 0.97 1.27 0.68 -2.32 -1.82 9.31 0.26 -0.46
Apr. 22.46 15.00 14.28 -5.01 1.06 1.49 5.28 3.74 4.11 -5.70 -5.44 -5.31 1.11 2.21 2.62
May. -0.50 14.98 12.85 -16.17 -7.87 -8.22 33.58 -0.21 -1.05 0.06 -2.67 -3.24 -4.92 1.99 1.18
Jun. 0.78 -6.65 -6.29 21.94 -0.61 -1.69 -17.36 -3.74 -4.80 4.87 -0.07 -0.42 2.36 -2.33 -1.68
Jul. 27.45 10.04 9.10 5.21 5.88 6.10 0.11 -0.10 -0.88 15.18 -0.35 -0.70 14.19 0.57 -0.82
Aug. -3.61 -3.56 -2.37 23.97 -1.86 -1.98 -10.27 -10.44 -9.05 3.29 1.74 1.98 -7.60 -1.06 -1.29
Sep. 8.38 10.01 10.01 -8.43 8.16 7.96 52.46 -6.67 -5.87 32.23 4.30 4.89 -7.51 1.89 1.09
Oct. 5.40 -2.25 -2.44 4.72 0.60 0.80 -2.86 5.01 5.04 -9.51 -7.12 -5.69 11.62 3.38 4.10
Nov. -22.73 3.30 2.66 8.19 1.03 1.31 -2.28 -9.01 -7.94 -14.01 5.78 6.46 20.85 -0.51 -0.64
Dec. 20.98 7.99 7.11 8.19 7.17 8.18 -2.97 2.43 3.09 29.65 1.57 0.67 4.54 2.43 2.22
Average 6.82 5.25 4.73 5.62 0.89 0.83 4.59 -1.84 -1.61 5.06 0.81 0.78 5.08 0.95 0.73
2014 2015 2016 2017 2018
Unit:% Research Market TWN50 Research Market TWN50 Research Market TWN50 Research Market TWN50 Research Market TWN50
Jan. -0.90 -1.73 -1.97 -22.57 0.59 0.96 -6.18 -2.31 -2.64 9.29 2.10 1.99 -6.87 4.33 5.50
Feb. 12.33 2.09 1.46 85.02 2.78 3.42 25.74 3.27 3.23 26.48 3.20 2.43 -3.37 -2.60 -2.76
Mar. 4.84 2.43 3.63 -21.20 -0.37 -1.16 -8.80 3.97 5.59 -1.36 0.63 0.53 -3.05 0.96 0.48
Apr. 12.17 -0.65 0.72 4.81 2.44 2.68 4.12 -4.20 -4.95 5.01 0.62 1.63 -0.94 -2.40 -3.29
May. 9.15 3.24 3.32 2.92 -1.21 0.18 9.12 1.88 2.73 -10.84 1.71 2.08 -0.64 2.04 1.09
Jun. -4.90 3.49 4.54 -3.15 -3.90 -3.09 -15.11 1.53 2.02 21.29 3.53 4.42 20.26 -0.35 -0.33
Jul. -11.85 -0.82 -0.75 -2.02 -7.05 -5.80 17.37 3.67 4.33 -6.66 0.31 0.48 23.61 2.04 4.28
Aug. 17.18 1.29 2.93 2.96 -5.66 -5.13 2.49 0.94 0.97 -8.26 1.52 0.94 -4.44 0.06 1.09
Sep. -8.17 -4.97 -5.24 -2.14 0.08 -2.23 1.13 1.08 1.31 23.17 -1.91 -2.46 -8.83 -0.52 0.04
Oct. 6.73 0.09 2.67 -6.41 4.56 3.79 6.93 1.34 2.49 -3.94 3.95 5.32 -4.27 -10.94 -10.39
Nov. -19.25 2.37 3.35 -8.48 -2.73 -2.58 -4.11 -0.53 -1.09 -17.34 -2.16 -4.13 -3.16 0.88 -2.07
Dec. -6.23 1.31 -0.61 -26.60 0.21 -0.11 -15.27 0.14 -0.05 -7.44 0.78 0.63 14.90 -1.62 -1.26
Average 0.92 0.68 1.17 0.26 -0.86 -0.76 1.45 0.90 1.16 2.45 1.19 1.16 1.93 -0.68 -0.63
Preprints 91811 g007
Figure 4-2. The research, market, and TWN50 annual rates of return for 2009~2018.
Figure 4-2. The research, market, and TWN50 annual rates of return for 2009~2018.
Preprints 91811 g007

5. Conclusions and Future Research

In the study, evolutionary strategies were employed to determine the optimal time to implement various investment strategies based on the historical data. When someone engages in stock market investment, the system initially identifies the prevailing market environment and determines which investment strategies, such as stock selection, timing, and capital allocation, are most appropriate for different periods. Subsequently, evolution strategies are employed to identify the best investment strategy, thus assisting with investment decision making. This approach harnesses evolutionary strategies to adapt to changing market conditions and optimize the investment strategies accordingly. By dynamically adjusting the investment approach based on the detected stock market environment, the system aims to enhance the potential for successful investment outcomes.
Each strategy tool possesses its own benefits and limitations. Consequently, this study employs multiple tools in order to ascertain a collaborative decision-making process. The tools employed include Warren Buffett's fundamental analysis indicators and Peter Woods' stock selection indicators as stock selection strategies. The Ohlson model, ICAPM, and APT are employed as reference tools for timing. The capital allocation strategy entails an initial evaluation to determine the most appropriate utilization of either the Kelly value or the optimal F. Subsequently, an evolutionary strategy is applied to optimize and acquire a comprehensive investment strategy.
The experimental results reveal that different economic conditions in various periods can impact the outcomes. Based on the strategies utilized in this study, the optimal timing for each strategy variable can be identified, enabling the determination of the most suitable investment strategy for the current stock market environment. The most suitable strategy is then employed as the evaluation function for fitness value in evolutionary strategies, leading to the development of the best one. Subsequently, the same methodology is applied to each transaction to adapt to the dynamic changes in the stock market environment.
From 2009 to 2018, extensive experimental analysis demonstrated that the dynamic decision-making model proposed in this paper consistently achieved a good rate of return, regardless of whether the stock was in a bull or bear market. Even during market downturns, the system still generated a positive profit. Moving forward, future research should focus on incorporating additional criteria for stock selection, timing, and capital allocation to enhance its ability to respond to the unpredictable and ever-changing stock market environment. Particularly, when it comes to timing accuracy, it is beneficial to explore various timing strategies and leverage other artificial intelligence techniques to further improve the precision. By correctly grasping the timing of buying and selling, significant risk premiums can be obtained regardless of whether the market is experiencing an upward or downward trend. This empowers the investors to make tailored investment decisions based on the current conditions and easily reap benefits.

References

  1. Ahmad, M. I., Guohui, W., Rafiq, M. Y., Hasan, M., &Sattar, A. Assesing Performance of Moving Average Investment Timing Strategy Over the UK Stock Market. The Journal of Developing Areas 2017, 51(3), 349-362.
  2. Baek, S., & Bilson, J. F. Size and value risk in financial firms. Journal of Banking & Finance 2015, 55, 295-326.
  3. Bernard, V. L. The Feltham-Ohlson framework: implications for empiricists. Contemporary Accounting Research 1995, 11(2), 733-747.
  4. Beyer, H. G., Finck, S., & Breuer, T. Evolution on trees: On the design of an evolution strategy for scenario-based multi-period portfolio optimization under transaction costs. Swarm and Evolutionary Computation 2014, 17, 74-87.
  5. Bonde, G., & Khaled, R. Stock price prediction using genetic algorithms and evolution strategies. In Proceedings of the International Conference on Genetic and Evolutionary Methods (GEM) (p. 1). The Steering Committee of the World Congress in Computer Science, Computer Engineering and Applied Computing (WorldComp) 2012.
  6. Campbell, J. Y., Giglio, S., Polk, C., & Turley, R. An intertemporal CAPM with stochastic volatility. Journal of Financial Economics 2018, 128(2), 207-233.
  7. Chang, Y. H., & Wang, S. C. Integration of Evolutionary Computing and Equity Valuation Models to Forecast Stock Values Based on Data Mining. Asia Pacific Management Review 2013, 18(1), 63-78.
  8. Charumathi, B., &Suraj, E. S. Refining Ohlson Model for Valuing Bank Stocks-An Artificial neural network Approach. Independent Business Review 2014, 7(2), 32.
  9. Chen, Y., Mabu, S., &Hirasawa, K. Genetic relation algorithm with guided mutation for the large-scale portfolio optimization. Expert Systems with Applications 2011, 38(4), 3353-3363.
  10. Chien, Y. W. C., & Chen, Y. L. Mining associative classification rules with stock trading data–A GA-based method. Knowledge-Based Systems 2010, 23(6), 605-614.
  11. Chiu, D. Y., &Chian, S. Y. Exploring stock market dynamism in multi-nations with genetic algorithm, support vector regression, and optimal technical analysis. In Networked Computing and Advanced Information Management (NCM), 2010 Sixth International Conference on (pp. 694-699). IEEE.
  12. Deb, K. Multi-objective optimization using evolutionary algorithms (Vol. 16). John Wiley & Sons 2001.
  13. Hermes, A., & Maier-Paape, S. Existence and Uniqueness for the Multivariate Discrete Terminal Wealth Relative. Risks 2017, 5(3), 44.
  14. James, P., Cheh, J. J., & Kim, I. W. A comparative analysis on performance of seven all star investment models. Pan-Pacific Journal of Business Research 2014, 5(2), 23.
  15. Kartikasari, D. A Test of Graham's and Lynch's Stock Screening Criteria on Shares Traded on the Indonesian Stock Exchange (Idx) 2016.
  16. Kocak, H. Canonical Coalition Game Theory for Optimal Portfolio Selection. Asian Economic and Financial Review 2014, 4(9), 1254.
  17. Kuo, C. Y. Is the accuracy of stock value forecasting relevant to industry factors or firm-specific factors? An empirical study of the Ohlson model. Review of Quantitative Finance and Accounting 2017, 49(1), 195-225.
  18. Lee, S. C., Lin, C. T., & Chang, P. T. An Ohlson valuation framework for valuing corporate governance: The case of Taiwan. Pacific-Basin Finance Journal 2011, 19(4), 420-434.
  19. Ma, J., & Wang, Y. Technical Analysis, Business Cycle, and Stock Market Returns. Advances in Management and Applied Economics 2015, 5(2), 43.
  20. Madhogarhia, P. K., & Lam, M. Dynamic asset allocation. Journal of Asset Management 2015, 16(5), 293-302.
  21. Mahapatra, S., &Bhaduri, S. N. Dynamics of the impact of currency fluctuations on stock markets in India: Assessing the pricing of exchange rate risks. Borsa Istanbul Review 2018.
  22. Menacer, A., &Nurein, S. A. MACROECONOMIC VARIABLES AND ISLAMIC BANK STOCK RETURNS: PANEL DATA EVIDENCE FROM GCC COUNTRIES. International Journal of Information, Business and Management 2018, 10(1), 214-229.
  23. Moghaddam, A. H., Moghaddam, M. H., &Esfandyari, M. Stock market index prediction using artificial neural network. Journal of Economics, Finance and Administrative Science 2016, 21(41), 89-93.
  24. Niaki, S. T. A., &Hoseinzade, S. Forecasting S&P 500 index using artificial neural networks and design of experiments. Journal of Industrial Engineering International 2013, 9(1), 1.
  25. Ohlson, J. A. Earnings, book values, and dividends in equity valuation. Contemporary accounting research 1995, 11(2), 661-687.
  26. Ouysse, R., & Kohn, R. Bayesian variable selection and model averaging in the arbitrage pricing theory model. Computational Statistics & Data Analysis 2010, 54(12), 3249-3268.
  27. Qiu, M., & Song, Y. Predicting the direction of stock market index movement using an optimized artificial neural network model. PloS one 2016, 11(5), e0155133.
  28. Repoussis, P. P., Tarantilis, C. D., Bräysy, O., &Ioannou, G. A hybrid evolution strategy for the open vehicle routing problem. Computers & Operations Research 2010, 37(3), 443-455.
  29. Sahin, U., &Ozbayoglu, A. M. TN-RSI: Trend-normalized RSI indicator for stock trading systems with evolutionary computation. Procedia Computer Science 2014, 36, 240-245.
  30. Verma, A., & Kumar, C. V. R. S. A Test of the Arbitrage Pricing Theory in the Bombay Stock Market. FIIB Business Review 2015, 4(2), 45-52.
  31. Weigand, R. A., & Irons, R. The market p/e ratio, earnings trends, and stock return forecasts. The Journal of Portfolio Management 2007, 33(4), 87-101.
  32. Ye, Y., "Application of the stock selection criteria of three value investors, Benjamin Graham, Peter Lynch, and Joel Greenblatt: a case of Shanghai stock Exchange from 2006-2011", Internal Journal of Scientific and Research Publications 2013, Vol. 3 No.8, pp. 2250-3153.
  33. Yilan, B. Stock Market Prediction Model Based on Genetic Algorithm and Support Vector Regression. Energy Procedia 2011, (11), 4025-4029.
  34. Yodmun, S., &Witayakiattilerd, W. Stock Selection into Portfolio by Fuzzy Quantitative Analysis and Fuzzy Multicriteria Decision Making. Advances in Operations Research 2016.
  35. Zakamulin, V. The real-life performance of market timing with moving average and time-series momentum rules. Journal of Asset Management 2014, 15(4), 261-278.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated